Prerpints.org logo
Preprint
Article

Approximate and Sample Entropy of the Center of Pressure during Unperturbed Tandem Standing: Effect of Altering the Tolerance Window

Altmetrics

Downloads

105

Views

43

Comments

0

Submitted:

22 July 2024

Posted:

24 July 2024

You are already at the latest version

Alerts
Abstract
Approximate entropy (ApEn) and sample entropy (SampEn) are statistical indices designed to quantify the regularity or predictability of time series data. Although ApEn has been a prominent choice for use in the analysis of non-linear data, it is currently unclear as to which method and parameter selection combination is optimal for its application in biomechanics. The goal of this research was to examine the differences between ApEn and SampEn related to center of pressure (COP) data during tandem standing balance tasks, while also changing the tolerance window, r. Six participants completed five, 30-second trials, feet-together and tandem standing with eyes-open and eyes-closed. COP data (fs = 60 Hz, downsampled from 1200 Hz) from ground reaction force platforms were collected. ApEn and SampEn were calculated using a constant vector length, i.e., m = 2, but differing values of r (tolerance window). For each of the participants, four separate one-way analysis of variance analyses (ANOVA) were conducted for ApEn and SampEn in the anterior-posterior (AP) and medial-lateral (ML) directions. Dunnett's intervals were applied to the one-way ANOVA analyses to determine which tandem conditions differed significantly from the baseline condition. ApEn and SampEn provided comparable results in the predictability of patterns for different stability conditions, with increasing instability, i.e., tandem eyes closed postures, being associated with greater unpredictability. The selection of r had a relatively consistent effect on mean ApEn and SampEn values across r = 0.15 * SD to r = 0.25 * SD, where both entropy methods tended to decrease as r increased. Mean SampEn values were generally lower than ApEn values. The results suggest that both ApEn and SampEn indices demonstrated relative consistency and were equally effective in quantifying the level of the center of pressure signal regularity during quiet tandem standing postural balance tests.
Keywords: 
Subject: Engineering  -   Bioengineering

1. Introduction

Entropy is defined as the loss of information in a time series or signal, which quantifies the amount of uncertainty regarding the order of an output signal [1]. Within the past twenty years, the use of entropy methods to define periodicity or regularity in human physiological and biomechanical data has become prevalent [2]. Two commonly used methods for evaluating biological time-series data are approximate entropy (ApEn) and sample entropy (SampEn). Because entropy quantifies the likelihood of the next state of a system, based on what is known about the present state of a time series, it has been used to identify physiological changes with aging [3,4], cardiovascular status [5,6,7], and respiratory pathology [1,8,9]. Entropy calculations can take more forms, but ApEn and SampEn have been particularly useful for understanding more about the changes in postural control systems [10,11,12,13,14,15], human gait mechanics [16,17], and standing balance [2,10,13,18,19,20,21].
In 1991, Pincus used ApEn to measure signal regularity and quantify levels of complexity within a time series; low values of ApEn tended to indicate a more regular and predictable signal and larger values suggested greater unpredictability [22]. With biological data sets, in general, but human movement in particular, quantifying levels of complexity has become important. For example, newer motor control theories, e.g., dynamical systems theory, do not consider variability in movement as an error [17]. Dynamical systems theory considers the complexity of movement patterns, i.e., variability, to be associated with system stability.
ApEn and SampEn have been shown to demonstrate the state and changes in the complexity of various physiological signals related to seated postural control in individuals with chronic stroke [23], electrocardiograms [24], electroencephalograms (EEG) [25], heart rate variability [26,27], and neural respiratory time series [8]. In complex systems, e.g., cardiac, respiratory, somatosensory, etc., lower ApEn values reflect systems that are persistent, repetitive, and predictive, with apparent patterns that repeat themselves throughout the series [6,28]. So, it is more appropriate to use terms like probability, predictability, and regularity, when describing the nature of a measurable complex system. In summary, the use of ApEn and SampEn was not meant to comprehensively analyze complex systems but to statistically quantify the dynamics of time series related to complex systems [29].
Based on the work by Pincus [26,28] and Cavanaugh et al. [18,19], we can assume that the diverse and interconnected components, i.e., visual, vestibular, and somatosensory, of the complex healthy human postural control system are capable of adapting to a wide variety of task demands, i.e., internal and external perturbations. Thus, this postural control system, when allowed to operate with minimal constraints, i.e., at rest during quiet standing, demonstrates an output, e.g., the center of pressure excursion, that appears to fluctuate in a relatively random (nonlinear) fashion that reflects its readiness to respond to internal and external perturbations. However, it has been shown that the anterior-posterior (AP) and medial-lateral (ML) oscillations are relatively small and random and are not sensitive enough to detect subtle alterations in postural control related to cerebral concussion [10]. Based on Pincus’ groundbreaking work, the use of ApEn in the assessment of postural sway in healthy [10] and concussed young adults has provided insight into the control of static and dynamic balance [18,19]. Cavanaugh et al. [18] reported that ApEn values for the AP and ML COP time series generally declined immediately after injury (i.e., concussion) in both steady and unsteady injured athletes suggesting a postural control system that was more constrained after injury. Interestingly, depressed ApEn values were still evident 48 to 96 hours after injury although postural instability had resolved.
Both ApEn and SampEn methods utilize three input parameters: N is the data length, m is the length of the window of the different vector comparisons (often referred to as the embedding dimension, vector length, pattern length, segment length, or pattern window), and r is the tolerance (sometimes referred to as radius or tolerance window), i.e., function criterion of similarity or type of signal filter. Both indices quantify complexity in the data by looking at the difference in m point vs. m+1 point patterns, over the N point data length.
ApEn measures the logarithmic probability that nearby pattern runs remain close in the next incremental comparison [19]. Given the input parameters, ApEn (m, r, and N) [26] is denoted by the expression:
A p E n ( m , r , N ) = − 1 N − m ∑ i = 1 N − m l o g A i B i
B i (r) is the probability that two sequences are similar for m points with self-counting and A i (r) is the probability that two sequences are similar for m + 1 matches with self-counting. Self-counting suggests that given one template the segment in the sequence is compared to all the blocks in the sequence, including itself. For ApEn, self-counting is needed in the calculation of conditional probabilities to ensure the logarithms remain finite. Statistically, selecting m and r as input parameters would be the equivalent of dividing the space of states into cells of width r, to estimate the conditional probabilities of the m-th order [19]. Greater values of m and smaller values of r describe details of sharper, more probabilistic parameters [19]. However, when dealing with stochastic processes, the analysis of conditional probabilities causes large values of m or minimal values of r to produce statistically low estimates. Ultimately, the value of the estimate depends on m and r. Pincus [28] suggested taking m as 2 and r as 0.2 * SDx, where SDx is the standard deviation of the original data <x(n)>, i.e.,
S D x = 1 N − 1 ∑ n − 1 N x n − 1 N ∑ n − 1 N x n 2
Pincus [28] has offered that one of the advantages of ApEn is that the algorithm was finite for stochastic, noisy deterministic, and composite processes, i.e., models for complex biological systems. ApEn can differentiate between different mixed methods of deterministic and random components occurring with a different probability and is robust to outliers because the pattern formed by wild points will rarely be repeated in the waveform [7]. It has been demonstrated that an increasing ApEn corresponds to intuitively increasing process complexity in a biological modeling platform. However, the limitations of ApEn include that relative consistency is not guaranteed, and depending on the value of r, the ApEn values will change [1]. Additionally, the value of ApEn depends on the length of the data series. Lastly, the self-counting aspect of the algorithm creates a statistical bias that particularly impacts situations with small data sets, that is when only a few or even no matches are present, the entropic result is biased toward zero [1].
Richman and Moorman [6] introduced SampEn as an alternative to counteract the limitations of ApEn, claiming that SampEn, as a statistical alternative, solved the self-counting problem eliminating the bias associated with ApEn. Eliminating self-counting is justified given that entropy is conceived as a measure of the rate of information production. ApEn uses the whole series to determine its value, needing only a template vector to find a match of length m + 1 to be defined [19]. SampEn contrasts with ApEn, where each template vector must find a match to be determined [2]. SampEn (m, r, and N) is defined as the negative value of the logarithm of the conditional probability that two similar sequences of m points remain identical at the next point m + 1, counting each vector over all the other vectors except on itself [19].
S a m p E n m , r , N = − l o g A m ( r ) B m r
B m r is the probability that two sequences are similar for m points, A m ( r ) is the probability that two sequences are similar for m + 1 matches, where the ratio is a conditional probability. The use of SampEn appears to quantify regularity more effectively and eliminates many of the problems associated with ApEn [6]. SampEn maintains the relative consistency and is also mostly independent of the length of the time series [6]. SampEn was created to address the bias and inconsistencies of ApEn, yet both methods retain similarities [6]. There is no consensus on which method is preferable, but one’s choice should be dependent on the research question and time series being evaluated.
When using ApEn and SampEn important consideration must be given to parameter selection, as these choices may have the greatest impact on the final entropy value even in the presence of noise [30]. Given a time series with N data points, the calculation of entropy requires a priori determination of two unknown parameters, embedding dimension, m, and threshold, r [31]. Multiple pairings of parameter selections allow one to examine relative consistency where a better discrimination capacity can be accomplished. Incorrect parameter choice, and lack of due diligence in selecting m, r, and N can undermine the interpretation and application of entropy results.
According to Yentes et al. [17] when the sampling rate is too high, i.e., frequency collection rates greater than 1000 Hz, redundancy likely exists within the data, which tends to artificially reduce entropy values [21]. Redundancy, i.e., repetitiveness of, or repeating, values, results in smaller entropy values and more signal regularity secondary to the counting of repeated matches. The redundant data problem can be solved by downsampling overly redundant time series data sets. Although downsampling removes real data, sensitivity analyses have demonstrated that the loss of data does not impact the subsequent application of the revised data set [12,16]. Previous studies have demonstrated the link between entropy and sampling rate. Powell et al [32] simulated different sampling rates by resampling ankle joint angle time series and found that higher sampling rates significantly reduced ApEn values. Conversely, results from Rhea et al. [33] suggest that excessive downsampling, e.g., to 25 Hz, artificially altered the standing center of pressure displacement and velocity SampEn values.
Based on the literature, it is clear that the appropriate selections of N, m, and r are critical for computing ApEn and SampEn values that can enhance the interpretation of inherently non-linear biological time series. Further, there is a lack of agreement on best practices. Therefore, the purposes of this research were to: 1) examine and evaluate the effect of altering input tolerance, r, on ApEn and SampEn values related to the center of pressure time series during quiet standing postures, i.e., feet together and tandem standing, and under eyes-open and eyes-closed conditions, and 2) assess which entropy measure was less biased and most consistent. Specific center of pressure metrics were chosen because they represent a single measurement of the complex postural control mechanism used to maintain balance and incorporate essential somatosensory and neuromotor inputs that influence stability [21].

2. Materials and Methods

2.1. Participants

Eight individuals (age: 24.8 ± 3.3 years; height: 171 ± 10.5 cm; body mass: 71.0 ± 13.5 kg) participated after voluntarily providing their signed informed consent. Center of pressure force plate data were collected from eight participants but those whose COP data contained signal dropout were omitted. Therefore, six participants’ data from the original cohort were included in the analysis. All participants were in good health and with no history of neurological or muscular disorders or injuries [35]. Before data collection commenced, foot dominance for each subject was determined based on the leg with which they preferred to kick a ball. This study was approved by the Grand Valley State University Institutional Review Board (18-246-H), and data from a previous data collection were used in this study to extend a prior analysis.

2.2. Instrumentation

Vicon Nexus v2.8 motion capture software (Vicon Motion System Ltd., Oxford Metrics, UK) and Vicon 16 MX T40 cameras (120 Hz) were used to track the movement trajectories of a modified Full-Body Plug-in-Gait model. Capturing motion was synchronized with the collection of ground reaction forces from floor-embedded AMTI (Advanced Mechanical Technology Inc., Watertown, MA) force plates (1200 Hz). Surface electrodes were used to collect the electromyographical (EMG) signals (1200 Hz) from bilateral gastrocnemius, soleus, and tibialis anterior muscles using a 16-channel MA300-XVI patient unit acquisition system (Motion Lab Systems Inc., Baton Rouge, LA). Only ground reaction force plate data were used for this study. The force plates were oriented with one directly in front of the other (Figure 1). Center of pressure data were extracted using Vicon NEXUS motion capture software v2.8 (Oxford Metrics, Oxford, UK) and exported to Excel for later analysis.

2.3. Experimental Procedure

Ground reaction force data were collected for 30 seconds until five successful trials were completed per stability condition (Table 1). Unsuccessful trials were defined by a major loss of balance, i.e., having to make significant changes in foot position, and/or if participants demonstrated large movements of their torso and changed their arm positions. Successful trials consisted of time series totaling 36,000 data points. The standing postural condition of eyes open feet together (EOFT) was defined as the most stable and hence was used as a baseline for all entropy comparisons. Participants were asked to hold a quiet standing position for thirty seconds without moving their bodies or stepping out of position. Balance tasks were performed barefoot with the arms positioned with the shoulders and elbows flexed, forearms supinated, and the fingers touching the anterior aspect of the shoulder; the hips and knees were extended with the ankles maintained in neutral (i.e., neither dorsiflexed nor plantarflexed). Participants progressed through increasingly unstable balance conditions by changing visual status, with 2-minute breaks between each trial. Conditions included eyes open or closed, and changing foot position, i.e., feet together on force plate 5 or tandem stance using force plates 3 and 5 shown (Figure 1). The order of testing conditions was not randomized.

2.4. Data Reduction

2.4.1. Determining Total Body Center of Pressure from Two Force Plates

The extracted COP data files were analyzed using nonlinear analysis in the time and frequency domains. The tandem trial output data sets differed from the feet-together trials in that two separate COP signals for tandem balance conditions were produced (one for data from each of the force plates), while feet-together resulted in data from a single force plate. The two-column tandem trials were combined into one resultant COP using Equation 4 [36,37]:
C O P n e t = C O P L F z L F z L + F z R + C O P R F z R F z L + F z R    
where COPL and COPR are the values of the COP signal from the left and right foot, respectively, and FzL and FzR are the vertical forces exerted on the force plates under the left and right foot, respectively. Approximate entropy (ApEn) and sample Entropy (SampEn) were determined using the C O P n e t data in the anterior-posterior and medial-lateral directions.

2.4.2. Downsampling and Sensitivity Analysis

The total number of data points to be used for this project needed to be examined based on previous work by Tipton [21]. The original COP datasets, recorded at 1200 Hz for 30 seconds, however, were likely too large since it has been demonstrated that sampling data beyond 1000 Hz leads to redundant information [21]. MATLAB’s built-in downsample function was used to decrease the 1200 Hz sample rate by a factor of 20 to 60 Hz. Simple sensitivity analyses as illustrated in Figure 2, Figure 3, Figure 4 and Figure 5 demonstrate the change in the time series before (Figure 2 and Figure 4) and after (Figure 3 and Figure 5) downsampling from a representative participant tested with eyes open feet together and eyes closed tandem standing postures, respectively. Observation evaluation of the figures suggested that the elimination of data points by downsampling did not impact the revised data set.

2.4.3. Determination of Approximate and Sample Entropy

Approximate and sample entropy were determined over a 30-second interval for all five trials under each condition using custom MATLAB® (The MathWorks, Natick, MA) code. Given each COP time series, where N = 60 datapoints, a sequence of m = 2 length vectors was formed. Comparisons were then made against each data segment that was two numbers long. Vectors were considered alike if vector components fell within a tolerance level (or window), ±   r * S D [28]. The tolerance levels were evaluated over a range of r = 0.05 * SD to r = 0.3 * SD; i.e., with 0.05 step sizes. The total number of like vectors' logarithm sum was divided by N − m + 1 to get the total number of like vectors, including a template comparison to itself [17]. Looking one vector higher, m was raised by 1, i.e., ( m + 1 ), the procedure was repeated. By deducting the conditional probabilities of m + 1 from m, ApEn was calculated.
A p E n ( m , r , N ) = − 1 N − m ∑ i = 1 N − m l o g A i B i
SampEn uses the whole series together, requiring only that a template vector find a match of length m + 1 to be defined [6]. This contrasts with ApEn where each template vector (including itself) must find a match to be defined. So, the use of SampEn eliminates many of the problems associated with ApEn, in that it is useful to quantify regularity in a system more effectively [6]. The same input parameters as ApEn were used and vectors were deemed similar if both their tail and head fell under the predetermined tolerance level. The sum of the total number of like vectors for m points was divided by N − m + 1 and defined as B m r . Further, SampEn defined A m r as the subset of B m r that two sequences are similar for m + 1 [17]. SampEn was calculated as the conditional probability:
S a m p E n m , r , N = − l o g A m ( r ) B m r

2.5. Statistical Analysis

Statistical analysis and graphics were performed with R Statistical Software (v4.4.0; R Core Team 2024) [38] running in RStudio: Integrated Development Environment for R [39]. Descriptive graphics were generated to present an overall picture of entropy for the center of pressure excursions along the anterior-posterior (AP) and medial-lateral (ML) axes, overlaying the approximate and sample entropy values. The r values and Method, i.e., ApEn and SampEn, quantities were derived from a single set of raw data. The raw data that were collected consisted of five trials for each of the six participants at each of the five standing posture conditions, e.g., EOFT, etc, for a total of 5 × 6 × 5 (or 150) data points. There are 30 cells in the graphics of condition by participant with each cell derived from five data points, i.e., 5 trials. There are 60 points in each cell from the 12 different calculations performed on each of the five data points. Lines are Loess curves that were used to provide a visual pattern for each Method within each cell.
There were 144 one-way ANOVAs with Dunnett’s post-hoc tests, one for each data set collected. Tables and graphics were generated for Shapiro and Levene’s test p-values that were below 0.05, indicating potential normality and heteroscadicity issues.
Nonparametric tests were considered but few of the 144 tests indicated a possible need for them. It is known that ANOVA is robust to failures of normality, especially for symmetric errors. All Shapiro test issues showed roughly symmetric errors in the Q-Q plots. ANOVA is also known to be robust to failures of equal variance in the case of equal group sizes. All group sizes were equal except for participant #5, for condition ECTDB, which did not fail either Shapiro or Levene’s tests.
All of the ANOVA F-tests except six had p-values < 0.05. Given the exploratory nature of this study and for the completeness of the graphics, Dunnett’s intervals were included in the confidence interval graphics even though the F-test was not statistically significant. We graphed 95% confidence intervals in a format similar to the raw data graphics but plotted only the confidence intervals, not the raw data. Significant intervals do not contain zero (horizontal black line). The two entropy methods, i.e. ApEn and SampEn, are shown in separate rows.
For a comparison of ApEn and SampEn methods for each value of r, we constructed histograms of their difference at each value of r. Values to the left of the vertical black line (zero) indicated that ApEn was larger, whereas values to the right of the vertical black line indicated that SampEn was larger.

3. Results

3.1. General Observations of Approximate and Sample Entropy

Approximate and sample entropy were determined for all trials and conditions, so it was important to examine the ApEn and SampEn values over the 30-second time series for m = 2, r = 0.2 * SD to establish the fidelity of the data. Note we chose the values of m and r because they reflect the most commonly chosen parameters in previously published studies. Each second of COP data consisted of 60 points. Figure 6 and Figure 7 illustrate these data for one trial of an eyes open, feet together (EOFT) condition and one trial of an eyes closed feet tandem condition (ECTDB) for one representative participant. Visual inspection of each plot suggests that the ApEn and SampEn magnitudes were comparable and the spikes over the 30-second time series appeared similar. Having established this for a representative participant and trial it seemed appropriate to determine the mean ApEn and SampEn values for further statistical analysis.
Figure 8 and Figure 9 provide a perspective of ApEn and SampEn values for each tolerance window and all participants under each standing postural test condition, except with feet together and eyes closed. See the Appendix A for means and standard deviations of the approximate and sample entropy values for the anterior-posterior and medial-lateral COP excursion time series for each participant and three representative conditions, i.e., EOFT, EOTDB, and ECTDB. For the COP excursion in the anterior-posterior direction, (Figure 8) entropy values suggested that:
  • magnitudes were larger in the most stable standing condition, i.e., eyes open feet together, for r = .05 * SD and 0.1 * SD
  • ApEn (red) and SampEn (blue) Loess curves were similar
  • entropy values generally decreased as r increased, leveling off after; r = 0.2 * SD
  • entropy values were larger in magnitude with tandem standing postures compared to eyes open feet together, but there do not appear to be differences in entropy values between eyes open and eyes closed for the tandem standing postures, and
  • participant #4 demonstrated different entropy value patterns for the eyes open feet together and eyes open tandem dominant back conditions, compared to the other five participants.
For the medial-lateral excursion of the COP (Figure 9) first note that the entropy scale (vertical axis) is different than in Figure 8, yet patterns of entropy values were similar in Figure 9. On the whole, we observed that:
  • entropy magnitudes were generally smaller in eyes open feet together condition but there do not appear to be differences in entropy values between eyes open and eyes closed for the tandem standing postures
  • ApEn (red) and SampEn (blue) Loess curves were similar
  • entropy values generally decreased as r increased, but the decreasing slope of the Loess curves as r increased appeared to be reduced for medial-lateral excursions, and
  • both participants #4 and #5 exhibited different entropy patterns, with more variability.
Because of the variability noted among participants #4 and #5 in Figure 8 and Figure 9, we take a closer look at the variability across participants and trials for both ApEn and SampEn for the COP excursion in the medial-lateral direction (Figure 10 and Figure 11, respectively). What we observed was that, overall, ApEn and SampEn values were quite similar. In particular, we noted that the lowest entropy values were generally less variable and associated with the eyes open feet together standing posture, and the largest values were associated with the eyes closed tandem conditions. As noted previously but more apparent in Figure 10 and Figure 11, participants #4 and #5 were quite different, i.e., larger entropy values, than the other participants. Additionally, a greater variability of the entropy values was demonstrated across all participants and trials for the tandem standing postures (both eyes open and closed conditions).

3.2. ApEn and SampEn: Comparing Entropy across Conditions

We chose the eyes open feet together as the baseline assuming that this postural stance would result in less postural instability (i.e., more postural or balance control) than tandem standing tasks, especially the tandem tasks with eyes closed. We compared the ApEn (Figure 12) and SampEn (Figure 13) values for each of the tandem stances with the baseline postural stance across all trials by running 144 one-way ANOVAs with Dunnett’s post-hoc tests. Despite some outliers, both ApEn and SampEn significantly distinguished differences in standing postural control between the baseline posture, i.e., EOFT, and the eyes open and eyes closed tandem stances.

3.3. Comparing ApEn and SampEn Values Across Different Tolerance Windows

To make direct comparisons between ApEn and SampEn values across different tolerance windows, i.e., r values, we created histograms of their difference at each r (Figure 14). It is notable that, although in Figure 8 and Figure 9 similarities between ApEn and SampEn were observed, the significant differences between the alternative approach to calculating entropy show that ApEn values for COP excursion in the anterior-posterior and medial-lateral directions were larger than SampEn values.

4. Discussion

Understanding how individuals respond to different postural, both static and dynamic, conditions and utilizing the best method to measure those conditions is important when comparing how a healthy nervous system responds versus how a brain-injured individual responds to the same conditions. Previous research that has examined children and adults with mild traumatic brain injury, e.g., concussion, has suggested that the use of the center of pressure (COP) data can be useful in delineating a normal from an abnormal response to the perturbations of static and dynamic balance [10,13,14,18,40,41]. Since it has been shown that the COP time series is non-linear, traditional methods of assessing various COP parameters, e.g., statistical use of means and standard deviation, have not been effective [41]. Previous work using non-linear metrics, such as approximate and sample entropy, to study normal and pathological balance has been useful [3,18,19,44,45,46]. However, a consensus on the optimal input parameter, i.e., N, m, and r, selection for the calculation of ApEn and SampEn has not yet been established. Previous work by Yentes et al. [16,17,30] has examined this challenge and made recommendations relative to gait data [16,30] and short data sets [17], but there is a paucity of research on this matter in investigations involving standing postural control. In our laboratory, Tipton et al. [21] measured the center of pressure of healthy college-aged participants under various quiet standing postures and used ApEn to characterize the time series, but their method was limited by an overly redundant data set and included the determination of the tolerance window, r, that was atypical. Based on the need described in the literature for more work investigating the diverse application of ApEn and SampEn analyses, and the methodological limitations of the previous research in our laboratory, the primary purpose of this study was to compare ApEn and SampEn under various stability conditions and examine the effects of different tolerance window values. The results revealed: 1) that even though SampEn tended to yield lower mean values than ApEn, both indices equally quantified the regularity of a COP time series in both the anterior-posterior and medial-lateral directions; 2) both ApEn and SampEn effectively differentiated a more stable quiet standing posture, i.e., eyes open feet together, from less stable standing postures, i.e., eyes open and eyes closed tandem standing postures; and 3), the selection of r had a relatively consistent effect with both entropic statistical analyses.
It has been demonstrated that high sampling rates reduce entropy values, likely since higher rates are well above the frequency of the tested behavior creating an artificial increase in the number of matches [12,30]. We used Tipton et al.’s [21] raw COP time series but modified it because their decision not to reduce data redundancy may have resulted in ApEn values that were biased, i.e. greater predictability. Therefore, we chose to downsample the COP time series data which allowed us to use a more accepted method for determining tolerance windows. Others have demonstrated the importance of how data management is handled and interpreted. For example, Rhea et al. [33] noted that downsampling from 100 Hz to 50 Hz and 25 Hz produced a dataset that appeared to be linearly less regular, i.e., increasing SampEn. They cautioned that researchers must identify how much change is driven by the neuromotor system and how much is a function of the data processing technique. Lubetsky et al. [12] noted that since postural sway typically lies between 0.15 and 0.4 Hz (and as high as 3 Hz) a sampling rate of 25 Hz should be sufficient to detect time series patterns and better reflect the underlying postural sway pattern. Thus, they were interested in evaluating how sample entropy of COP time series data sampled at 100 Hz (N = 2000) from prolonged standing tasks on normal and compliant surfaces would be affected by downsampling by 2, 3, and 4. They found that although downsampling increased SampEn values, it had an insignificant effect on the comparisons to the original datasets. However, they concluded that if such procedures are performed by other researchers, they should be well justified. Yentes et al. [17] recommended, as best practice, that practitioners not exceed sampling data beyond 1000 Hz, but that a prior power spectral density analysis might be considered to assist in selecting an appropriate sampling rate. In the present study, our initial entropy estimates based on a 1200 Hz data collection rate yielded very low entropy values between 0.005 and 0.030. Therefore, we concluded that downsampling was necessary for the processing of our entropy results. We found that, when using 1,800-point arrays, the raw COP waveforms were observationally nearly identical when comparing unfiltered data to the downsampled data and that the entropy values that resulted, i.e., average ApEn and SampEn, ranged from 0.08 to 0.90; values consistent with other published works.
Incorrect parameter selection, i.e., vector length, m, tolerance or threshold window, r, and data length, N), regardless of the biological time series being considered, can undermine the ApEn and SampEn discrimination capacity [47]. For this study, the embedding dimension, m = 2, and dataset length, N, were fixed input parameters. We wanted to focus our attention on assessing entropy outcomes relative to changes in the tolerance window since this parameter may have the greatest influence on the calculation of entropy [30] and is considered one of the most difficult to select [16]. Selecting a tolerance window too small limits the number of matches found and selecting too large a window could lead to too many matches found and increase the probability [30]. Many approaches to calculating r have been suggested, including utilizing the standard deviation (SD) of the whole time series [26,45], the standard error of the entropy values [48], predefined tolerance levels [49,50], and using a heuristic stochastic model [47]. Typically, the tolerance window is calculated as r times the standard deviation of the time series [26]. However, many researchers have reported determining, and using, r as 0.2 * SD, with the rationale that it was commonly used in previous research. Yentes et al. [30] recommended that researchers try multiple r values, and if using the default method, i.e., r * SD, test the relative consistency of r = 0.15, 0.25, and 0.30 * SD. For this study, we calculated ApEn and SampEn related to the anterior-posterior and medial-lateral COP excursions during a variety of quiet standing postures and used r = 0.05, 0.10, 0.15, 0.20, 0.25, and 0.30 * SD (Figure 8 and Figure 9). For COP anterior-posterior excursion we found that entropy magnitudes (ApEn and SampEn) in the EOFT condition were larger for r = 0.05 *SD and 0.10 * SD, and values decreased as r increased, leveling off after r = 0.20 * SD. Entropy magnitudes for COP medial-lateral excursion were generally reduced in the EOFT condition compared to the AP excursion data, but decreasing entropy with increasing r mirrored the pattern seen for the AP data. There are no comparable publications related to quiet standing, although Yentes et al. [16] reported a similar relationship between SampEn and changing r, but a more variable relationship between ApEn and changing r. On the other hand, our data demonstrated relative consistency for both ApEn and SampEn with changes in the tolerance window, particularly for r = 0.20, r = 0.25, and r = 0.30 * SD. Based on the good consistency of both ApEn and SampEn using a range of r’s equal to 0.20, 0.25, and 0.30 * SD we suggest that future research investigating postural sway based on COP time series consider the method we used. Despite the consistency of the ApEn and SampEn values we found, we caution the reader that our choice for determining the tolerance window is limited by any factor, such as data length, nonstationarity of the data, spikes, and outliers, that affect data variance.
Outliers and spikes were identified in some of our data, particularly for participants #4 and #5 (see Figure 8, Figure 9, Figure 10 and Figure 11), in the ApEn and SampEn values for r = 0.05 and r = 0.1 * SD, likely due to the overly stringent conditions. Molina-Picó et al. [34] evaluated the impact of abnormal spikes on the interpretation of entropy results in the context of biosignal analysis and suggested removing these results, as they can misrepresent the signal regularity. We believe additional research is needed related to reproducing our findings relative to the entropy values using smaller r values. For this project, we presented the data using smaller r values, but are skeptical about their clinical interpretation and meaningfulness.
Although we determined ApEn and SampEn for both EOFT and ECFT postures, we chose to use the EOFT posture as a relative baseline for postural stability. An additional purpose of this study was to ascertain whether these two entropies could differentiate signal predictability similarly when comparing a relatively stable quiet standing posture from postures that were more difficult to maintain over a 30-second time frame. Our data showed that ApEn and SampEn values were larger for tandem standing positions whether the eyes were open or closed, and whether the dominant foot (leg) was placed back or forward (Figure 12 and Figure 13). Thus, we concluded that the tandem standing positions produced anterior-posterior and medial-lateral COP excursions associated with a system that produced a time series that was more random, less probable and predictable, and one with a greater amount of new information gained from the next data points in the time series [30]. In another study that assessed quiet standing balance and altering visual conditions, Ramdani et al. [13] used SampEn to analyze human postural sway. They reported that SampEn distinguished between the eyes open and eyes closed conditions of participants standing on a single force plate. Specifically, in the eyes closed condition, SampEn was lower. Other research results concur with Ramdani’s findings [49], whereas some reported contradictory results [52]. One limitation of the present study was that we did not examine whether ApEn and SampEn could distinguish the eyes open from the eyes closed tandem standing postures. Future research should address this.
Since both ApEn and SampEn values were significantly larger with tandem standing postures, compared to the eyes open feet together posture, we wondered which entropic measure was “better”? We are not aware of any previous research that compared ApEn and SampEn from the COP time series for standing balance by altering only the tolerance window. Yentes et al. [16] investigated the step time series of walking trials and evaluated various combinations of N, m, and r. They concluded that SampEn demonstrated excellent relative consistency for long gait data sets when using two different modes of walking, i.e., overground versus treadmill. On the other hand, our results suggest that both ApEn and SampEn demonstrated similar relative consistency.
In addition to reported differences in relative consistency for ApEn and SampEn between Yentes et al. [16] and our findings, there were also differences when comparing the two entropy value magnitudes. We found that, overall, ApEn magnitudes were larger than SampEn values, whereas Yentes et al. reported that generally mean ApEn values were lower than mean SampEn values in the analysis of step time gait data.
The results of this project may be limited by several methodological decisions. Our sample was limited by convenience and its small size. Additional research is suggested using a larger cross-sectional sample. In addition, will be important to test our methods against different neuropathologies, like post-concussion individuals. As noted in the discussion, there are several suggested methods for determining the tolerance window. It may be useful to compare ApEn and SampEn values using the standard method we used and the other accepted methods, e.g., a fixed tolerance window [49,50] and the method suggested by Chon et al. [47]. Our results may have been influenced by the data resolution of the downsampling technique employed.

5. Conclusions

The primary purpose of this study was to investigate the impact of varying one of the input parameters, i.e., tolerance window, r, used to calculate ApEn and SampEn. Based on our results we cannot recommend an optimal r value. However, we can suggest that the algorithms r = 0.20, r = 2.5, or r = 0.30 * SD may be equally suitable for determining ApEn and SampEn values that provide insight into the anterior-posterior and medial-lateral excursions of COP time series for selected quiet standing postures. This recommendation is based on the good relative consistency of entropy values with changing tolerance windows, as well as the ability of both ApEn and SampEn to distinguish more from less stable quiet standing postures. Our results demonstrated that although, on average, ApEn values were larger than SampEn values, one estimation technique was not particularly “better” than the other; that is, if used in longitudinal measures of COP time series either entropy algorithm would be acceptable. One possible factor influencing the choice between ApEn and SampEn is algorithm complexity. Since SampEn includes an additional step removing “self-counting”, if computational speed becomes a consideration then ApEn may have a slight edge.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org.

Author Contributions

Conceptualization, JW, SR, GA; Methodology, JW, SR, GA; Software, JW; Validation, JW; Formal Analysis, JW; SR, GA, DWZ; Resources, GA; Data curation, JW, SR; Writing (original draft) – JW; Writing (review and editing), JW, SR, GA, DWZ; Visualization – JW, SR, DWZ; Supervision, SR, GA, DWZ; Project administration, SR, GA; All authors have read and agreed to the published version of the Manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

The study was conducted following the Declaration of Helsinki, and approved by the Institutional Review Board of Grand Valley State University (18-246-H and date of approval) for studies involving humans.

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Data Availability Statement

The data presented in this study are available on request from the corresponding author due to restrictions imposed by our institution on retired faculty.

Acknowledgments

We acknowledge University administrative support for the use of equipment and materials needed for motion capture in the Biomechanics and Motor Performance Laboratory and all study participants.

Conflicts of Interest

The authors declare no conflicts of interest.

Appendix A

Table A1. Approximate and sample entropy values for each participant for the anterior-posterior center of pressure time series for eyes open feet together.
Table A1. Approximate and sample entropy values for each participant for the anterior-posterior center of pressure time series for eyes open feet together.
Participants Method 0.05 0.1 0.15 0.2 0.25 0.3
1 Approximate 0.49(0.053) 0.3(0.054) 0.18(0.037) 0.13(0.025) 0.094(0.019) 0.075(0.015)
Sample 0.43(0.058) 0.25(0.052) 0.16(0.037) 0.11(0.027) 0.087(0.021) 0.07(0.017)
2 Approximate 0.53(0.026) 0.39(0.059) 0.25(0.052) 0.18(0.036) 0.13(0.026) 0.1(0.02)
Sample 0.48(0.039) 0.32(0.055) 0.21(0.045) 0.15(0.033) 0.12(0.025) 0.096(0.02)
4 Approximate 0.98(0.059) 0.59(0.064) 0.37(0.047) 0.26(0.036) 0.19(0.028) 0.15(0.021)
Sample 1(0.09) 0.51(0.071) 0.32(0.052) 0.22(0.039) 0.17(0.03) 0.13(0.023)
5 Approximate 0.55(0.11) 0.37(0.076) 0.24(0.06) 0.16(0.041) 0.12(0.03) 0.097(0.023)
Sample 0.49(0.13) 0.29(0.068) 0.19(0.048) 0.14(0.034) 0.11(0.026) 0.087(0.02)
6 Approximate 0.46(0.053) 0.28(0.064) 0.17(0.042) 0.12(0.028) 0.088(0.02) 0.071(0.017)
Sample 0.37(0.049) 0.22(0.052) 0.14(0.036) 0.1(0.026) 0.08(0.02) 0.066(0.017)
8 Approximate 0.51(0.039) 0.33(0.084) 0.22(0.074) 0.15(0.053) 0.11(0.039) 0.09(0.029)
Sample 0.44(0.062) 0.27(0.066) 0.18(0.056) 0.13(0.043) 0.1(0.034) 0.082(0.027)
Note: Mean (standard deviation) entropy values for each participant across six different threshold windows (r).
Table A2. Approximate and sample entropy values for each participant for the anterior-posterior center of pressure time series for eyes open tandem dominant back.
Table A2. Approximate and sample entropy values for each participant for the anterior-posterior center of pressure time series for eyes open tandem dominant back.
Participants Method 0.05 0.1 0.15 0.2 0.25 0.3
1 Approximate 0.55(0.0092) 0.45(0.019) 0.33(0.013) 0.24(0.011) 0.18(0.0075) 0.14(0.0049)
Sample 0.49(0.03) 0.37(0.035) 0.27(0.026) 0.2(0.019) 0.16(0.014) 0.13(0.01)
2 Approximate 0.6(0.017) 0.53(0.031) 0.42(0.047) 0.32(0.05) 0.25(0.046) 0.2(0.039)
Sample 0.6(0.028) 0.46(0.031) 0.35(0.037) 0.27(0.036) 0.21(0.034) 0.17(0.03)
4 Approximate 0.88(0.097) 0.6(0.094) 0.45(0.091) 0.34(0.08) 0.26(0.064) 0.2(0.052)
Sample 0.92(0.15) 0.55(0.11) 0.4(0.096) 0.3(0.081) 0.24(0.066) 0.19(0.054)
5 Approximate 0.59(0.048) 0.49(0.039) 0.37(0.039) 0.27(0.031) 0.21(0.024) 0.16(0.019)
Sample 0.57(0.048) 0.41(0.057) 0.3(0.051) 0.23(0.04) 0.18(0.031) 0.14(0.024)
6 Approximate 0.56(0.02) 0.48(0.031) 0.34(0.036) 0.25(0.03) 0.18(0.024) 0.15(0.018)
Sample 0.53(0.027) 0.41(0.031) 0.29(0.029) 0.22(0.025) 0.17(0.021) 0.13(0.016)
8 Approximate 0.59(0.0059) 0.52(0.02) 0.4(0.029) 0.3(0.026) 0.22(0.021) 0.18(0.017)
Sample 0.57(0.011) 0.45(0.016) 0.34(0.022) 0.25(0.02) 0.2(0.016) 0.16(0.013)
Note: Mean (standard deviation) entropy values for each participant across six different threshold windows (r).
Table A3. Approximate and sample entropy values for each participant for the anterior-posterior center of pressure time series for eyes closed tandem dominant back.
Table A3. Approximate and sample entropy values for each participant for the anterior-posterior center of pressure time series for eyes closed tandem dominant back.
Participants Method 0.05 0.1 0.15 0.2 0.25 0.3
1 Approximate 0.58(0.0071) 0.53(0.015) 0.41(0.02) 0.31(0.025) 0.24(0.022) 0.19(0.02)
Sample 0.57(0.021) 0.46(0.018) 0.35(0.019) 0.27(0.019) 0.21(0.017) 0.17(0.015)
2 Approximate 0.58(0.023) 0.49(0.039) 0.37(0.037) 0.27(0.031) 0.2(0.025) 0.16(0.02)
Sample 0.55(0.04) 0.42(0.045) 0.31(0.039) 0.23(0.03) 0.18(0.023) 0.14(0.018)
4 Approximate 0.58(0.012) 0.5(0.033) 0.39(0.042) 0.29(0.041) 0.22(0.035) 0.17(0.029)
Sample 0.57(0.023) 0.44(0.031) 0.34(0.041) 0.26(0.039) 0.2(0.033) 0.16(0.028)
5 Approximate 0.58(0.023) 0.54(0.025) 0.44(0.025) 0.35(0.021) 0.27(0.018) 0.22(0.016)
Sample 0.58(0.053) 0.48(0.048) 0.37(0.042) 0.29(0.033) 0.23(0.025) 0.19(0.019)
6 Approximate 0.59(0.0099) 0.54(0.026) 0.42(0.033) 0.31(0.032) 0.24(0.026) 0.19(0.021)
Sample 0.59(0.014) 0.47(0.018) 0.36(0.021) 0.27(0.021) 0.21(0.018) 0.17(0.016)
8 Approximate 0.6(0.0069) 0.56(0.02) 0.45(0.037) 0.34(0.039) 0.26(0.034) 0.21(0.027)
Sample 0.61(0.017) 0.49(0.025) 0.38(0.034) 0.3(0.033) 0.23(0.029) 0.19(0.023)
Note: Mean (standard deviation) entropy values for each participant across six different threshold windows (r).
Table A4. Approximate and sample entropy values for each participant for the medial-lateral center of pressure time series for eyes open feet together.
Table A4. Approximate and sample entropy values for each participant for the medial-lateral center of pressure time series for eyes open feet together.
Participants Method 0.05 0.1 0.15 0.2 0.25 0.3
1 Approximate 0.27(0.054) 0.11(0.025) 0.07(0.014) 0.05(0.0093) 0.039(0.0071) 0.032(0.0059)
Sample 0.22(0.05) 0.1(0.022) 0.063(0.012) 0.046(0.0082) 0.036(0.0063) 0.029(0.0052)
2 Approximate 0.46(0.054) 0.25(0.059) 0.15(0.037) 0.11(0.024) 0.082(0.018) 0.066(0.015)
Sample 0.38(0.064) 0.21(0.05) 0.13(0.03) 0.093(0.02) 0.073(0.015) 0.059(0.012)
4 Approximate 1(0.12) 0.63(0.13) 0.41(0.1) 0.28(0.077) 0.21(0.06) 0.17(0.048)
Sample 1.1(0.16) 0.57(0.11) 0.36(0.073) 0.25(0.054) 0.19(0.041) 0.15(0.033)
5 Approximate 0.57(0.031) 0.39(0.055) 0.25(0.051) 0.17(0.037) 0.13(0.028) 0.1(0.021)
Sample 0.52(0.034) 0.33(0.048) 0.21(0.04) 0.15(0.029) 0.12(0.022) 0.094(0.017)
6 Approximate 0.49(0.064) 0.32(0.12) 0.21(0.095) 0.15(0.068) 0.11(0.05) 0.088(0.038)
Sample 0.42(0.075) 0.27(0.093) 0.18(0.075) 0.13(0.056) 0.1(0.043) 0.081(0.034)
8 Approximate 0.51(0.042) 0.32(0.067) 0.2(0.047) 0.14(0.031) 0.11(0.022) 0.084(0.017)
Sample 0.45(0.045) 0.27(0.052) 0.17(0.037) 0.12(0.026) 0.096(0.02) 0.077(0.016)
Note: Mean (standard deviation) entropy values for each participant across six different threshold windows (r).
Table A5. Approximate and sample entropy values for each participant for the medial-lateral center of pressure time series for eyes open tandem dominant back.
Table A5. Approximate and sample entropy values for each participant for the medial-lateral center of pressure time series for eyes open tandem dominant back.
Participants Method 0.05 0.1 0.15 0.2 0.25 0.3
1 Approximate 0.52(0.042) 0.37(0.057) 0.26(0.051) 0.19(0.045) 0.14(0.036) 0.11(0.028)
Sample 0.45(0.068) 0.29(0.065) 0.2(0.049) 0.14(0.036) 0.11(0.028) 0.091(0.022)
2 Approximate 0.66(0.058) 0.61(0.047) 0.54(0.071) 0.45(0.087) 0.37(0.092) 0.31(0.086)
Sample 0.71(0.11) 0.55(0.078) 0.46(0.081) 0.38(0.08) 0.31(0.074) 0.26(0.067)
4 Approximate 1.3(0.046) 1.1(0.11) 0.86(0.097) 0.68(0.079) 0.55(0.068) 0.46(0.06)
Sample 1.7(0.17) 1.1(0.14) 0.79(0.11) 0.61(0.086) 0.49(0.072) 0.4(0.06)
5 Approximate 0.81(0.22) 0.69(0.14) 0.57(0.13) 0.48(0.13) 0.4(0.13) 0.34(0.12)
Sample 0.91(0.32) 0.64(0.17) 0.5(0.14) 0.4(0.13) 0.33(0.11) 0.28(0.1)
6 Approximate 0.58(0.032) 0.46(0.058) 0.33(0.072) 0.24(0.063) 0.18(0.051) 0.14(0.04)
Sample 0.56(0.052) 0.4(0.062) 0.28(0.059) 0.21(0.05) 0.16(0.04) 0.13(0.033)
8 Approximate 0.66(0.058) 0.55(0.084) 0.44(0.11) 0.35(0.11) 0.27(0.091) 0.22(0.075)
Sample 0.67(0.1) 0.48(0.094) 0.37(0.097) 0.28(0.087) 0.22(0.074) 0.18(0.063)
Note: Mean (standard deviation) entropy values for each participant across six different threshold windows (r).
Table A6. Approximate and sample entropy values for each participant for the medial-lateral center of pressure time series for eyes closed tandem dominant back.
Table A6. Approximate and sample entropy values for each participant for the medial-lateral center of pressure time series for eyes closed tandem dominant back.
Participants Method 0.05 0.1 0.15 0.2 0.25 0.3
1 Approximate 0.65(0.033) 0.57(0.056) 0.47(0.085) 0.37(0.09) 0.29(0.083) 0.23(0.07)
Sample 0.67(0.061) 0.51(0.068) 0.4(0.083) 0.31(0.081) 0.25(0.073) 0.2(0.063)
2 Approximate 0.65(0.046) 0.59(0.068) 0.52(0.088) 0.44(0.089) 0.37(0.082) 0.31(0.071)
Sample 0.69(0.085) 0.54(0.092) 0.44(0.099) 0.36(0.094) 0.29(0.083) 0.25(0.071)
4 Approximate 0.73(0.058) 0.65(0.035) 0.59(0.043) 0.52(0.059) 0.44(0.068) 0.38(0.071)
Sample 0.82(0.092) 0.63(0.05) 0.52(0.052) 0.44(0.059) 0.37(0.062) 0.31(0.062)
5 Approximate 0.63(0.028) 0.59(0.056) 0.51(0.094) 0.43(0.11) 0.36(0.11) 0.3(0.1)
Sample 0.68(0.064) 0.53(0.076) 0.42(0.1) 0.34(0.11) 0.28(0.1) 0.24(0.094)
6 Approximate 0.63(0.038) 0.56(0.051) 0.45(0.064) 0.35(0.063) 0.27(0.056) 0.21(0.047)
Sample 0.63(0.07) 0.48(0.071) 0.37(0.069) 0.29(0.058) 0.23(0.049) 0.18(0.041)
8 Approximate 0.66(0.076) 0.56(0.13) 0.46(0.15) 0.38(0.14) 0.31(0.13) 0.25(0.11)
Sample 0.7(0.13) 0.5(0.14) 0.39(0.14) 0.31(0.12) 0.25(0.11) 0.21(0.093)
Note: Mean (standard deviation) entropy values for each participant across six different threshold windows (r).

References

  1. Delgado-Banal, A.; Marshak, A. Approximate entropy and sample entropy: a comprehensive tutorial. Entropy 2019, 10, 541. [Google Scholar] [CrossRef] [PubMed]
  2. St-Amant, G.; Rahman, T.; Polskaia, N.; Fraser, S.; Lojoie, Y. Unveiling the cerebral and sensory contributions to automatic postural control during dual-task standing. Hum Mov Sci. 2020, 70, 102587. [Google Scholar] [CrossRef] [PubMed]
  3. Borg, F.G.; Laxåback, G. Entropy of balance—some recent results. J Neuroeng Rehabil. 2010, 7, 38. [Google Scholar] [CrossRef] [PubMed]
  4. Richer, N.; Lojoie, Y. Automaticity of postural control while dual-tasking revealed in young and older adults. Exp Aging Res. 2020, 46, 1–21. [Google Scholar] [CrossRef] [PubMed]
  5. Ferrario, M.; Signorini, M.G.; Magenes, G.; Cerutti, A. Comparison of entropy-based regularity estimators: application of the fetal heart rate signal for the identification of fetal distress. IEEE Trans Biomed Eng. 2006, 53, 119–125. [Google Scholar] [CrossRef] [PubMed]
  6. Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am J Physiol Heart Circ Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [PubMed]
  7. Pincus, S.M.; Viscarello, R.R. Approximate entropy: a regularity measure for fetal heart rate analysis. Obstet Gynecol. 1992, 79, 249–255. [Google Scholar] [PubMed]
  8. Chen, X.; Solomon, I.; Chon, K. Comparison of the use of approximate entropy and sample entropy: applications to neural respiratory signal. Proceedings of 27th Annual International Conference of the IEEE Eng Med Biol Soc., Shanghai, China, 17-18 January 2006). [Google Scholar] [CrossRef]
  9. Estrada, L.; Torres, A.; Sarlabous, L.; Jané, R. Influence of parameter selection in fixed sample entropy of surface diaphragm electromyography for estimating respiratory activity. Entropy 2017, 19, 460. [Google Scholar] [CrossRef]
  10. Cavanaugh, J.T.; Guskiewicz, K.M.; Stergiou, N. A nonlinear dynamic approach for evaluating postural control: new directions for the management of sport-related cerebral concussion. Sports Med. 2005, 35, 935–950. [Google Scholar] [CrossRef] [PubMed]
  11. Hansen, C.; Wei, Q.; Shieh, J.S.; Fourcade, P.; Isableu, B.; Majed, L. Sample entropy, univariate, and multivariate multi-scale entropy in comparison with classical postural sway parameters in young healthy adults. Front Hum Neurosci. 2017, 11, 206. [Google Scholar] [CrossRef] [PubMed]
  12. Lubetzky, A.V.; Harel, D.; Lubetzky, E. On the effects of signal processing on sample entropy for postural control PLoS One. 2018, 13, e0193460. [CrossRef]
  13. Ramdani, S.; Seigle, B.; Lagarde, J.; Bouchara, F.; Bernard, P.L. On the use of sample entropy to analyze human postural sway data. Med Eng Phys. 2009, 31, 1023–1031. [Google Scholar] [CrossRef]
  14. Reilly, N.; Prebor, J.; Moxey, J.; Schusler, E. Chronic impairments of static postural stability associated with history of concussion. Exp Brain Res. 2020, 238, 2783–2793. [Google Scholar] [CrossRef] [PubMed]
  15. Rhea, C.K.; Silver, T.A.; Hong, S.L.; Ryu, J.H.; Studenka, B.E.; Hughes, C.M.L.; Haddad, J.M. Noise and complexity in human postural control: interpreting the different estimations of entropy. PLoS One 2011, 6, e17696. [Google Scholar] [CrossRef] [PubMed]
  16. Yentes, J.M.; Denton, W.; McCamley, J.; Raffalt, P.C.; Schmid, K.K. Effect of parameter selection on entropy calculations for long walking trials. Gait Posture 2018, 60, 128–134. [Google Scholar] [CrossRef] [PubMed]
  17. Yentes, J.M.; Hunt, N.; Schmid, K.K.; Kaipust, J.P.; McGrath, D.; Stergiou, N. The appropriate use of approximate entropy and sample entropy with short data sets. Ann Biomed Eng. 2013, 41, 349–365. [Google Scholar] [CrossRef] [PubMed]
  18. Cavanaugh, J.T.; Guskiewicz, K.M.; Giuliani, C.; Marshall, S.; Mercer, V.S.; Stergiou, N. Recovery of postural control after cerebral concussion: new insights using approximate entropy. J Athl Train. 2006, 41, 305–313. [Google Scholar] [PubMed] [PubMed Central]
  19. Cavanaugh, J.T.; Mercer, V.S.; Stergiou, N. Approximate entropy detects the effect of a secondary cognitive task on postural control in healthy young adults: a methodological report. J Neuroeng Rehabil. 2007, 4, 42. [Google Scholar] [CrossRef] [PubMed]
  20. Saraiva, M.; Vilas-Boas, J.P.; Fernandes, O.J.; Castro, M.A. Effects of motor task difficulty on postural control complexity during dual tasks in young adults: a nonlinear approach. Sensors 2023, 23, 628. [Google Scholar] [CrossRef] [PubMed]
  21. Tipton, N.; Alderink, G.; Rhodes, S. Approximate entropy and velocity of center of pressure to determine postural stability: a pilot study. Appl Sci. 2023, 13, 9259. [Google Scholar] [CrossRef]
  22. Pincus, S.M. Quantifying complexity and regularity of neurological systems. Methods Neurosci. 1995, 28, 336–363. [Google Scholar] [CrossRef]
  23. Perlmutter, S.; Lin, F.; Makhsous, M. Quantitative analysis of static sitting posture in chronic stroke. Gait Posture 2010, 32, 53–56. [Google Scholar] [CrossRef] [PubMed]
  24. Castiglioni, P.; Di Rienzo, M. How the threshold “r” influences approximate entropy analysis of heart-rate variability. IEEE Explore 2008 Computers in Cardiology, Bologna, Italy 2008, 35, 561–564. [CrossRef]
  25. Tononi, G.; Edelman, G.M.; Sporns, O. Complexity and coherency: integrating information in the brain. Trends Cogn Sci. 1998, 2, 474–484. [Google Scholar] [CrossRef] [PubMed]
  26. Pincus, S.M. Approximate entropy as a measure of system complexity. Pro Natl Acad Sci. U S A 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [PubMed]
  27. Liu, C.; Liu, C.; Shao, P.; Li, L.; Sun, X.; Wang, X.; Liu, F. Comparison of different threshold values r for approximate entropy: application to investigate the heart rate variability between heart failure and healthy control groups. Physiol Meas. 2011, 32, 167–180. [Google Scholar] [CrossRef] [PubMed]
  28. Pincus, S. Approximate entropy (ApEn) as a complexity measure. Chaos 1995, 5, 110–117. [Google Scholar] [CrossRef]
  29. Duarte, M.; Sternad, D. Complexity of human postural control in young and older adults during prolonged standing. Exp Brain Res. 2008, 191, 265–276. [Google Scholar] [CrossRef] [PubMed]
  30. Yentes, J.M.; Raffalt, P.C. Entropy analysis in gait research: methodological considerations and recommendations. Ann Biomed Eng. 2021, 49, 979–990. [Google Scholar] [CrossRef]
  31. Lu, S.; Chen, X.; Kanters, J.; Solomon, I.C.; Chon, K.H. Automatic selection of the threshold value r for approximate entropy. IEEE Trans Biomed Eng. 2008, 55, 1966–1972. [Google Scholar] [CrossRef] [PubMed]
  32. Powell, D.W.; Szekely, B.; Blackmore, S.E.; Nelson, A.; Schallert, A.; Lester, D.B.; Murray, N.G.; Puppa, M. Effects of sampling rate and movement frequency on entropic measures of regularity. J Nat Sci. 2018, 4, e504. [Google Scholar]
  33. Rhea, C.K.; Kiefer, A.W.; Wright, W.G.; Raisbeck, L.D.; Haran, F.J. Interpretation of postural control may change due to data processing techniques. Gait Posture 2015, 41, 731–735. [Google Scholar] [CrossRef] [PubMed]
  34. Molina-Picó, A.; Cuesta-Frau, D.; Aboy, M.; Crespo, C.; Miró-Martinez, P.; Oltra-Crespo, S. Comparative study of approximate entropy and sample entropy robustness to spikes. Artif Intell Med. 2011, 53, 97–106. [Google Scholar] [CrossRef] [PubMed]
  35. McCrumb, D.D. Analysis of connectivity in EMG signals to examine neural correlations in muscular activation of lower leg muscles for postural stability. Master’s thesis. Grand Valley State University, Grand Rapids, MI 49503 USA, 2019.
  36. Combined Output from Multiple Force Plates—Nexus 2.6 Documentation—Vicon Documentation. Available online: https://docs.vicon.com/display/Nexus26/Combined+output+from+multiple+force+plates (accessed on 17 May 2021).
  37. Exell, T.; Kerwin, D.; Irwin, G.; Gittoes, M. Calculating Centre of Pressure from Multiple Force Plates for Kinetic Analyses of Sprint Running. Port. J. Sport Sci. 2011, 11, 4. [Google Scholar]
  38. R Core Team (2024). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing. Vienna, Austria. https://www.R-project.org. (accessed 10 June 2024).
  39. Posit Team (2024). RStudio: Integrated Development Environment for R.Posit Software, PBC, Boston, MA. https://www.posit.co/. (accessed 10 June 2024).
  40. Potvin-Desrochers, A.; Richer, N.; Lajoie, Y. Cognitive tasks promote automatization of postural control in young and older adults. Gait Posture 2017, 57, 40–45. [Google Scholar] [CrossRef] [PubMed]
  41. Quatman-Yates, C.C.; Bonnette, S.; Hugentobler, J.A.; Médé, B.; Kiefer, A.W.; Kurowski, B.G.; Riley, M.A. Postconcussion postural sway variability changes in youth: the benefit of structural variability analyses. Pediatr Phys Ther. 2015, 27, 316–327. [Google Scholar] [CrossRef] [PubMed]
  42. Senthinathan, A.; Mainwaring, L.M.; Hutchinson, M. Heart rate variability of athletes across concussion recovery milestones: a preliminary study. Clin J Sport Med. 2017, 27, 288–295. [Google Scholar] [CrossRef] [PubMed]
  43. Brink, K.J.; McKenzie, K.L.; Likens, A.D. Nonlinear analyses distinguish load carriage dynamics in walking and standing: a systematic review. J Appl Biomech. 2022, 38, 434–447. [Google Scholar] [CrossRef] [PubMed]
  44. Barbado Murillo, D.; Sabido Solana, R.; Vera-Garcia, F.J.; Gusi Fuertes, N.; Moreno, F.J. Effect of increasing difficulty in standing balance tasks with visual feedback on postural sway and EMG: complexity and performance. Hum Mov Sci. 2012, 31, 1224–1237. [Google Scholar] [CrossRef] [PubMed]
  45. Montesinos, L.; Castaldo, R.; Pecchia, L. On the use of approximate entropy and sample entropy with center of pressure time-series. J Neuroeng Rehabil. 2018, 15, 116. [Google Scholar] [CrossRef] [PubMed]
  46. Rose, M.H.; Bandholm, T.; Jensen, B.R. Approximate entropy based on attempted steady isometric contractions with the ankle dorsal- and plantarflexors: reliability and optimal sampling frequency. J Neurosci Methods 2009, 177, 212–216. [Google Scholar] [CrossRef] [PubMed]
  47. Chon, K.; Scully, C.G.; Lu, S. Approximate entropy for all signals. IEEE Open J Eng Med Biol. 2009, 28, 18–23. [Google Scholar] [CrossRef] [PubMed]
  48. Lake, D.E.; Richman, J.S.; Griffin, M.P.; Moorman, J.R. Sample entropy analysis of neonatal heart rate variability. Am J Physiol Regul Integr Comp Physiol. 2002, 283, R789–R97. [Google Scholar] [CrossRef] [PubMed]
  49. Forrest, S.M.; Challis, J.H.; Winter, S.L. The effect of signal acquisition and processing choices on ApEn values: towards a “gold standard” for distinguishing effort levels from isometric force records. Med Eng Phys. 2014, 36, 676–683. [Google Scholar] [CrossRef] [PubMed]
  50. Sarlabous, L.; Torres, A.; Fiz, J.A.; Gea, J.; Martinez-Llorens, J.M.; Morera, J.; Jane, R. Interpretation of the approximate entropy using fixed tolerance values as a measure of amplitude variations in biomedical signals. Proceedings of 2010 Annual International Conference of the IEEE Engineering in Medicine and Biology, Buenos Aires, Argentina; 2010; pp. 5967–5970. [Google Scholar] [CrossRef]
  51. Donker, S.F.; Roerdink, M.; Greven, A.J.; Beek, P.J. Regularity of center-of-pressure trajectories depends on the amount of attention invested in postural control. Exp Brain Res. 2007, 181, 1–11. [Google Scholar] [CrossRef] [PubMed]
  52. Sabatini, A.M. Analysis of postural sway using entropy measures of signal complexity. Med Biol Eng Comput. 2000, 38, 617–624. [Google Scholar] [CrossRef] [PubMed]
Preprints 112881 g001
Figure 1. Force plate foot placement for feet together and feet tandem standing balance conditions, where the x-axis (anterior-posterior (AP) direction) and y-axis (medial-lateral (ML) direction define the center of pressure orientation. Note: D = dominant foot; ND = nondominant foot; DF = dominant foot forward; and DB = dominant foot back [21,35].
Figure 1. Force plate foot placement for feet together and feet tandem standing balance conditions, where the x-axis (anterior-posterior (AP) direction) and y-axis (medial-lateral (ML) direction define the center of pressure orientation. Note: D = dominant foot; ND = nondominant foot; DF = dominant foot forward; and DB = dominant foot back [21,35].
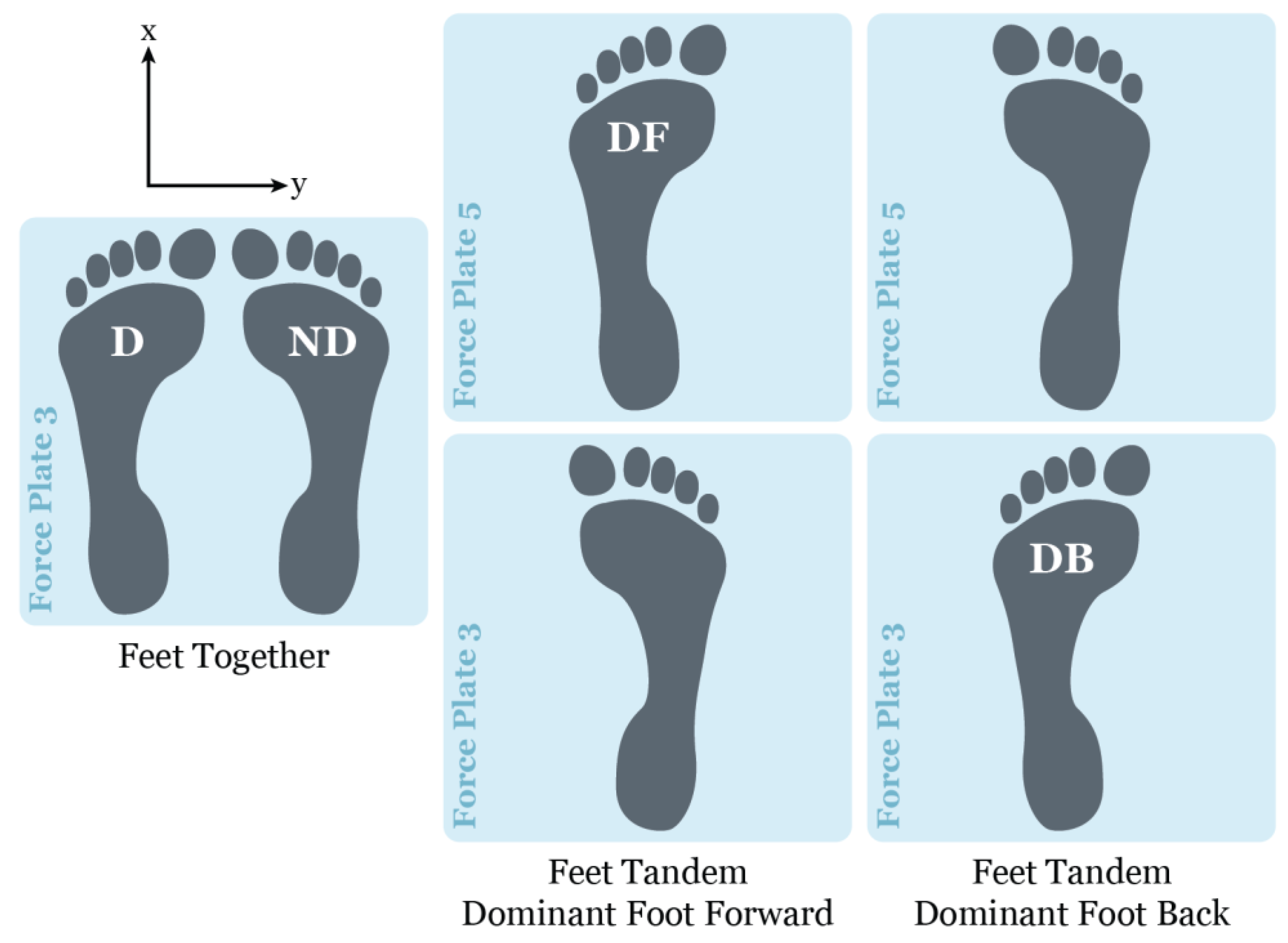
Preprints 112881 g001
Preprints 112881 g002
Figure 2. Representative time series for raw center of pressure (COP) data of participant 1 eyes open, feet together (EOFT) Trial 4, where fs = 1200 Hz, in the anterior-posterior (AP) and medial-lateral (ML) directions, respectively.
Figure 2. Representative time series for raw center of pressure (COP) data of participant 1 eyes open, feet together (EOFT) Trial 4, where fs = 1200 Hz, in the anterior-posterior (AP) and medial-lateral (ML) directions, respectively.
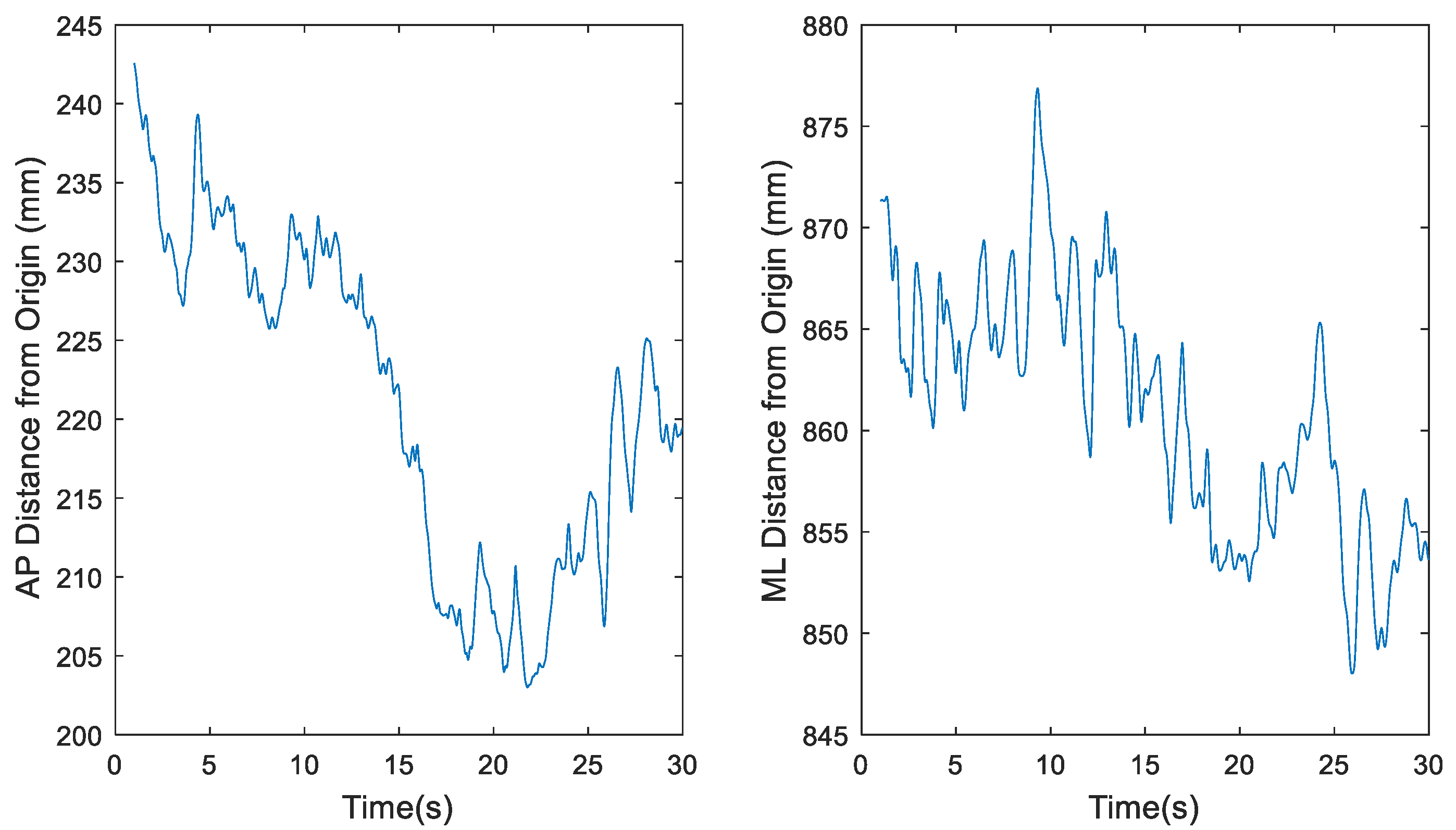
Preprints 112881 g002
Preprints 112881 g003
Figure 3. Representative time series for downsampled center of pressure (COP) data of participant 1 eyes open, feet together (EOFT) Trial 4, where fs = 60 Hz, in the anterior-posterior (AP) and medial-lateral (ML) directions, respectively.
Figure 3. Representative time series for downsampled center of pressure (COP) data of participant 1 eyes open, feet together (EOFT) Trial 4, where fs = 60 Hz, in the anterior-posterior (AP) and medial-lateral (ML) directions, respectively.
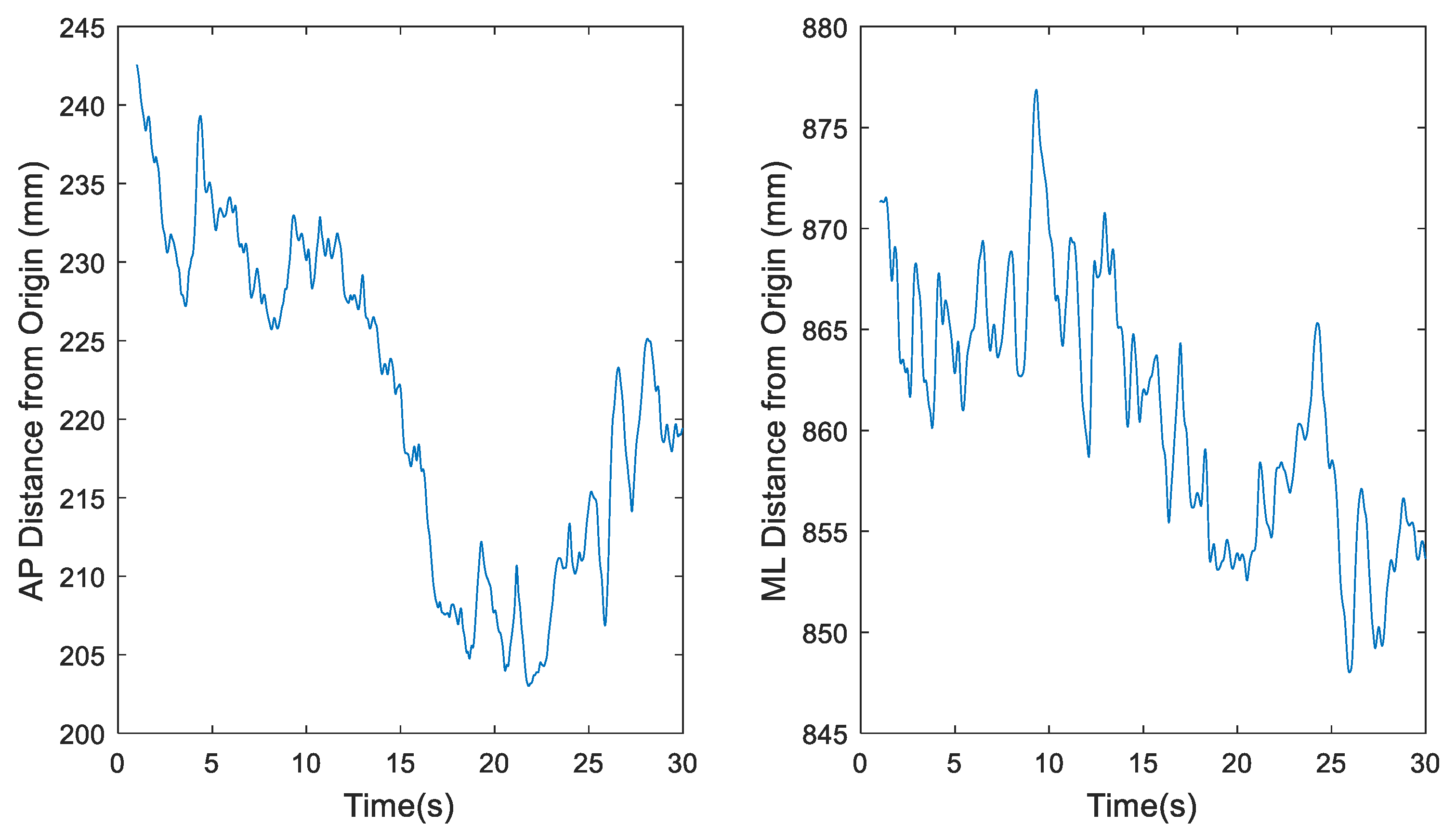
Preprints 112881 g003
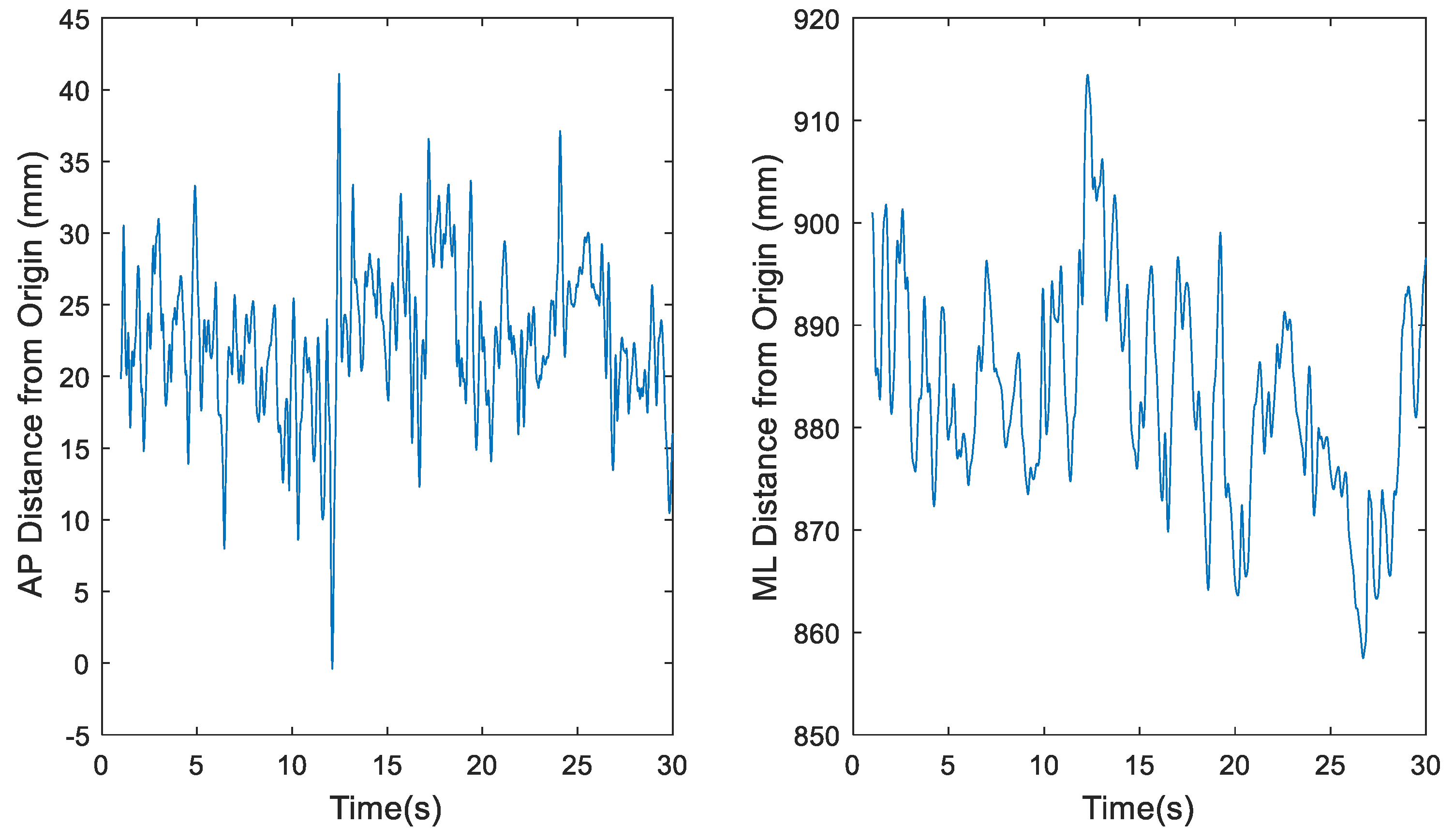
Preprints 112881 g004
Figure 4. Representative time series for raw center of pressure (COP) data of participant 1 eyes closed, feet tandem, dominant foot forward (ECTDF) Trial 29, where fs = 1200 Hz, in the anterior-posterior (AP) and medial-lateral (ML) directions, respectively.
Figure 4. Representative time series for raw center of pressure (COP) data of participant 1 eyes closed, feet tandem, dominant foot forward (ECTDF) Trial 29, where fs = 1200 Hz, in the anterior-posterior (AP) and medial-lateral (ML) directions, respectively.
Preprints 112881 g004
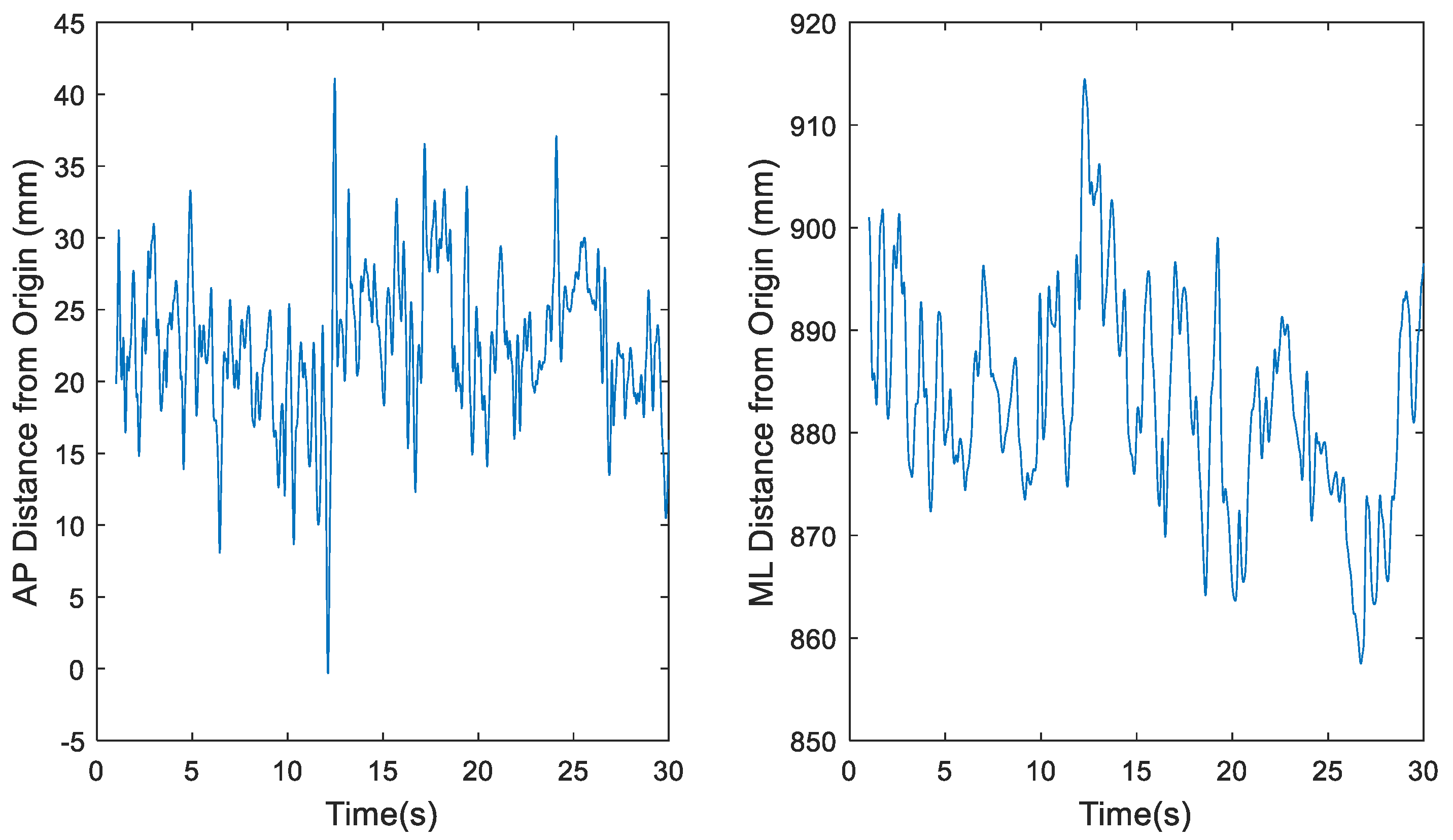
Preprints 112881 g005
Figure 5. Representative time series for the downsampled center of pressure (COP) data of participant 1 eyes closed, feet tandem, dominant foot forward (ECTDF) Trial 29, where fs = 60 Hz, in the anterior-posterior (AP) and medial-lateral (ML) directions, respectively.
Figure 5. Representative time series for the downsampled center of pressure (COP) data of participant 1 eyes closed, feet tandem, dominant foot forward (ECTDF) Trial 29, where fs = 60 Hz, in the anterior-posterior (AP) and medial-lateral (ML) directions, respectively.
Preprints 112881 g005
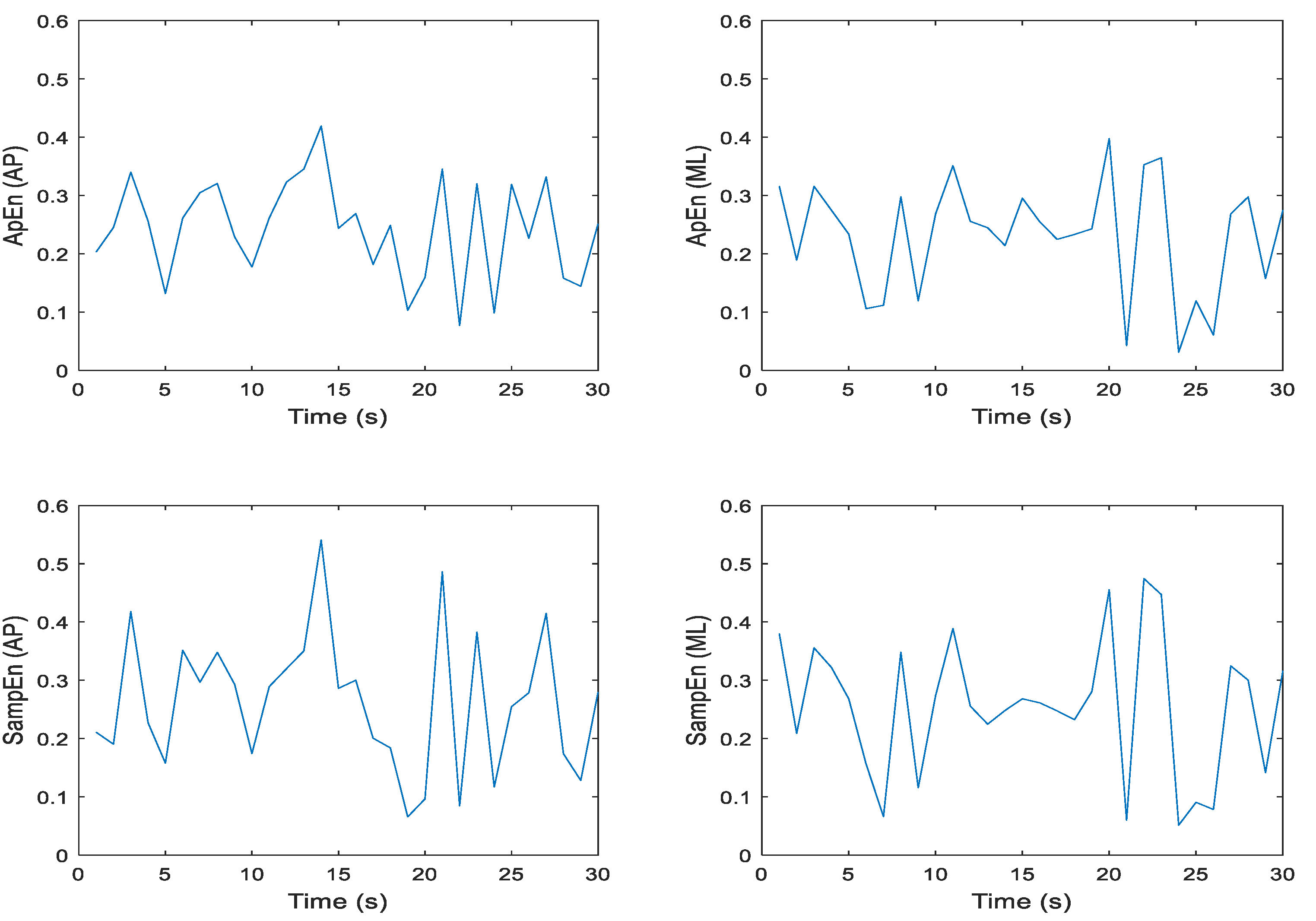
Preprints 112881 g006
Figure 6. Representative time series for ApEn and SampEn calculated every second for 30 seconds for participant 1 eyes open, feet together (EOFT), Trial 03 COP data; where N = 60 datapoints, m = 2, and r = 0.2 * SD; in the anterior-posterior (AP) and medial-lateral (ML) directions, respectively.
Figure 6. Representative time series for ApEn and SampEn calculated every second for 30 seconds for participant 1 eyes open, feet together (EOFT), Trial 03 COP data; where N = 60 datapoints, m = 2, and r = 0.2 * SD; in the anterior-posterior (AP) and medial-lateral (ML) directions, respectively.
Preprints 112881 g006
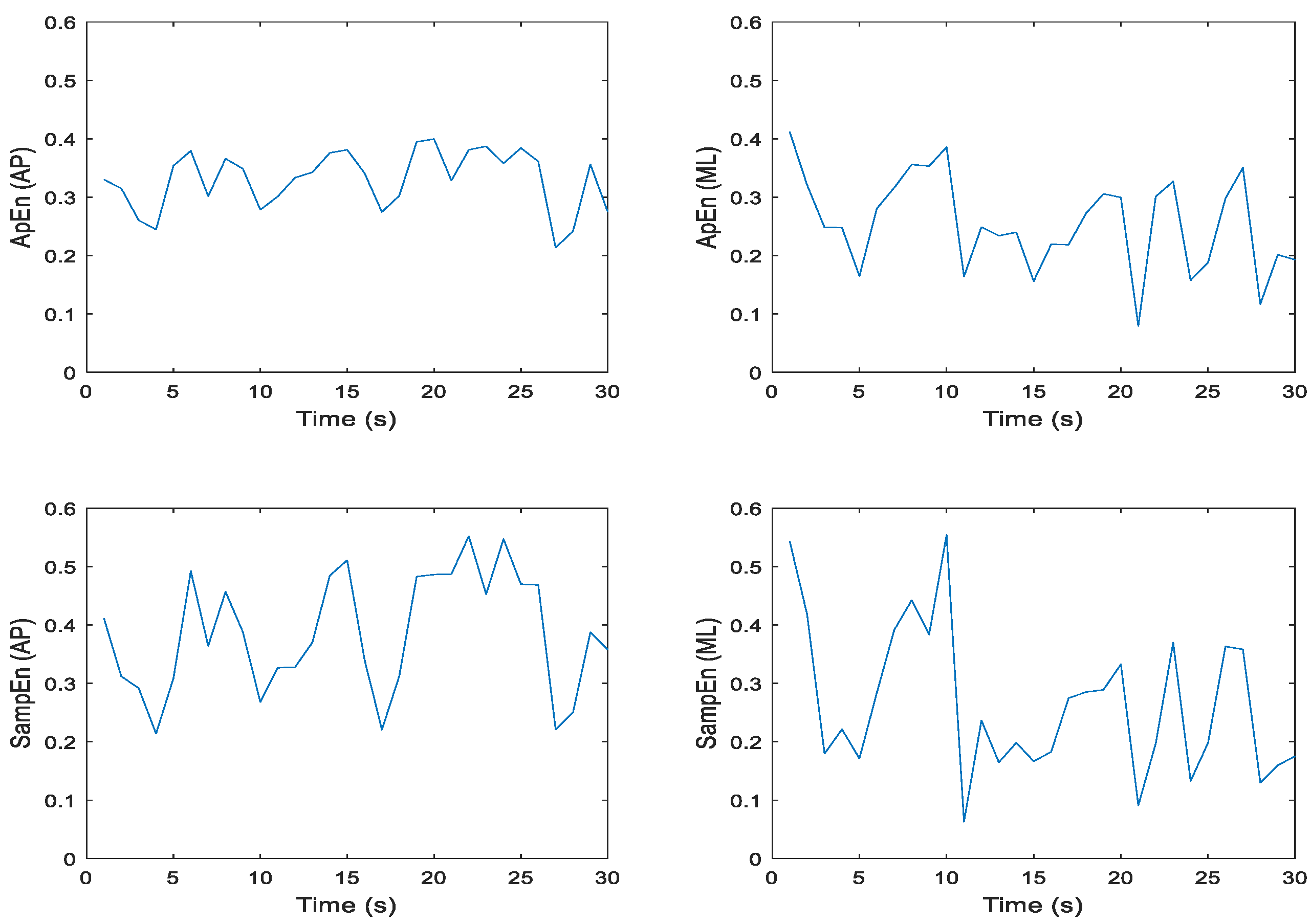
Preprints 112881 g007
Figure 7. Representative time series for ApEn and SampEn calculated every second for 30 seconds of participant 1 eyes closed, feet tandem, dominant foot back (ECTDB), Trial 19 COP data; where N = 60 datapoints, m = 2, and r = 0.2 * SD; in the anterior-posterior (AP) and medial-lateral (ML) directions, respectively.
Figure 7. Representative time series for ApEn and SampEn calculated every second for 30 seconds of participant 1 eyes closed, feet tandem, dominant foot back (ECTDB), Trial 19 COP data; where N = 60 datapoints, m = 2, and r = 0.2 * SD; in the anterior-posterior (AP) and medial-lateral (ML) directions, respectively.
Preprints 112881 g007
Preprints 112881 g008
Figure 8. Anterior-posterior (AP) direction approximate (red) and sample (blue) entropy values (vertical axis) versus six different tolerance windows (horizontal axis), i.e., r, while standing in five different postures, i.e., eyes open feet together (EOFT), etc., for each participant. Note that 12 r and Method, i.e., ApEn or SampEn, quantities were derived from each COP time series. There were five time series for each cell giving 60 graphed points in each cell. Loess curves are provided to help visualize the relationship between r and entropy values for each method in each cell.
Figure 8. Anterior-posterior (AP) direction approximate (red) and sample (blue) entropy values (vertical axis) versus six different tolerance windows (horizontal axis), i.e., r, while standing in five different postures, i.e., eyes open feet together (EOFT), etc., for each participant. Note that 12 r and Method, i.e., ApEn or SampEn, quantities were derived from each COP time series. There were five time series for each cell giving 60 graphed points in each cell. Loess curves are provided to help visualize the relationship between r and entropy values for each method in each cell.
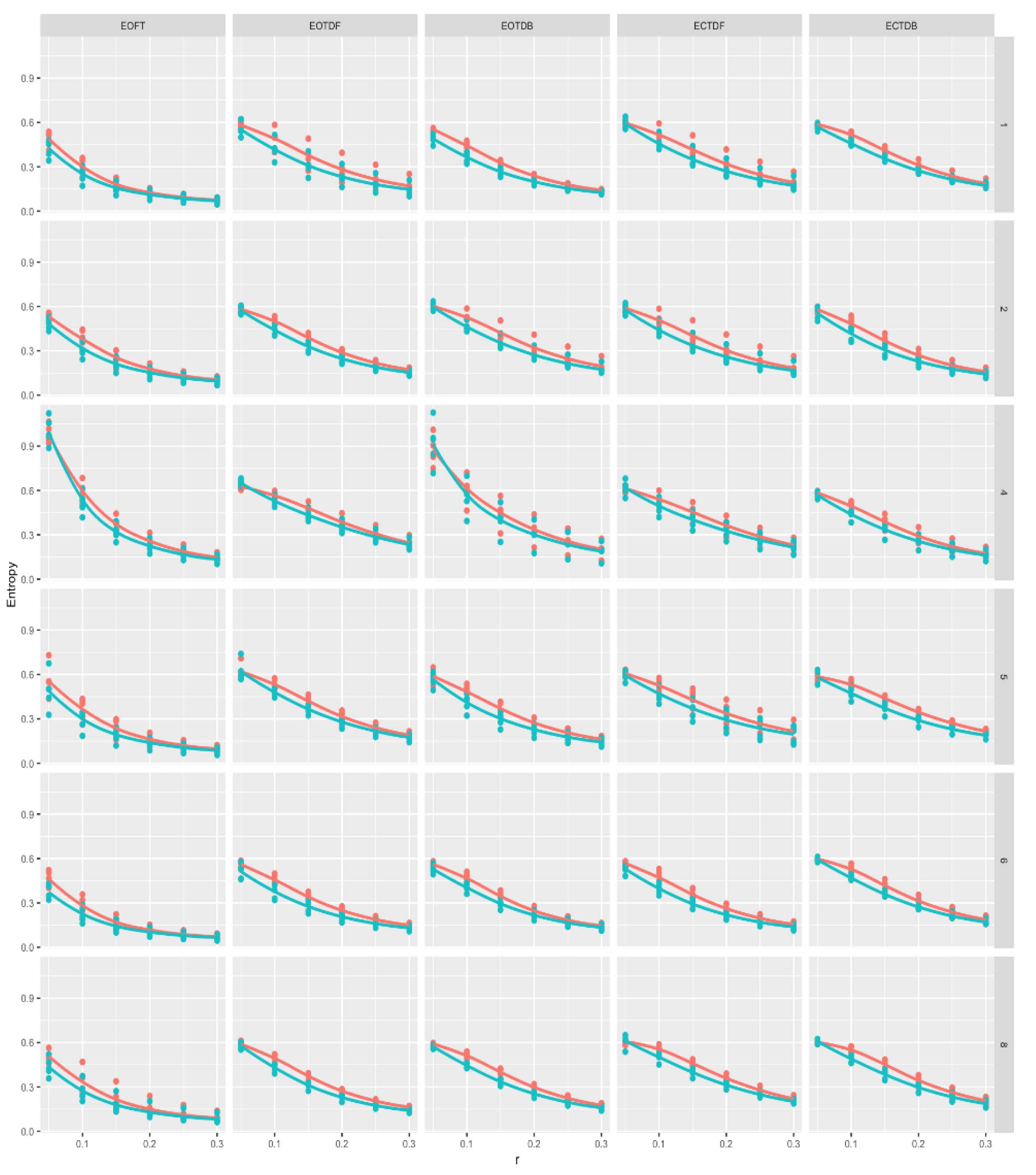
Preprints 112881 g008
Preprints 112881 g009
Figure 9. Medial-lateral (ML) direction approximate (red) and sample (blue) entropy values (vertical axis) versus six different tolerance windows (horizontal axis), i.e., r, while standing in five different postures, i.e., eyes open feet together (EOFT), etc., for each participant. Note that 12 r and Method, i.e., ApEn or SampEn, quantities were derived from each COP time series. There were five time series for each cell giving 60 graphed points in each cell. Loess curves are provided to help visualize the relationship between r and entropy values for each method in each cell.
Figure 9. Medial-lateral (ML) direction approximate (red) and sample (blue) entropy values (vertical axis) versus six different tolerance windows (horizontal axis), i.e., r, while standing in five different postures, i.e., eyes open feet together (EOFT), etc., for each participant. Note that 12 r and Method, i.e., ApEn or SampEn, quantities were derived from each COP time series. There were five time series for each cell giving 60 graphed points in each cell. Loess curves are provided to help visualize the relationship between r and entropy values for each method in each cell.
Preprints 112881 g009
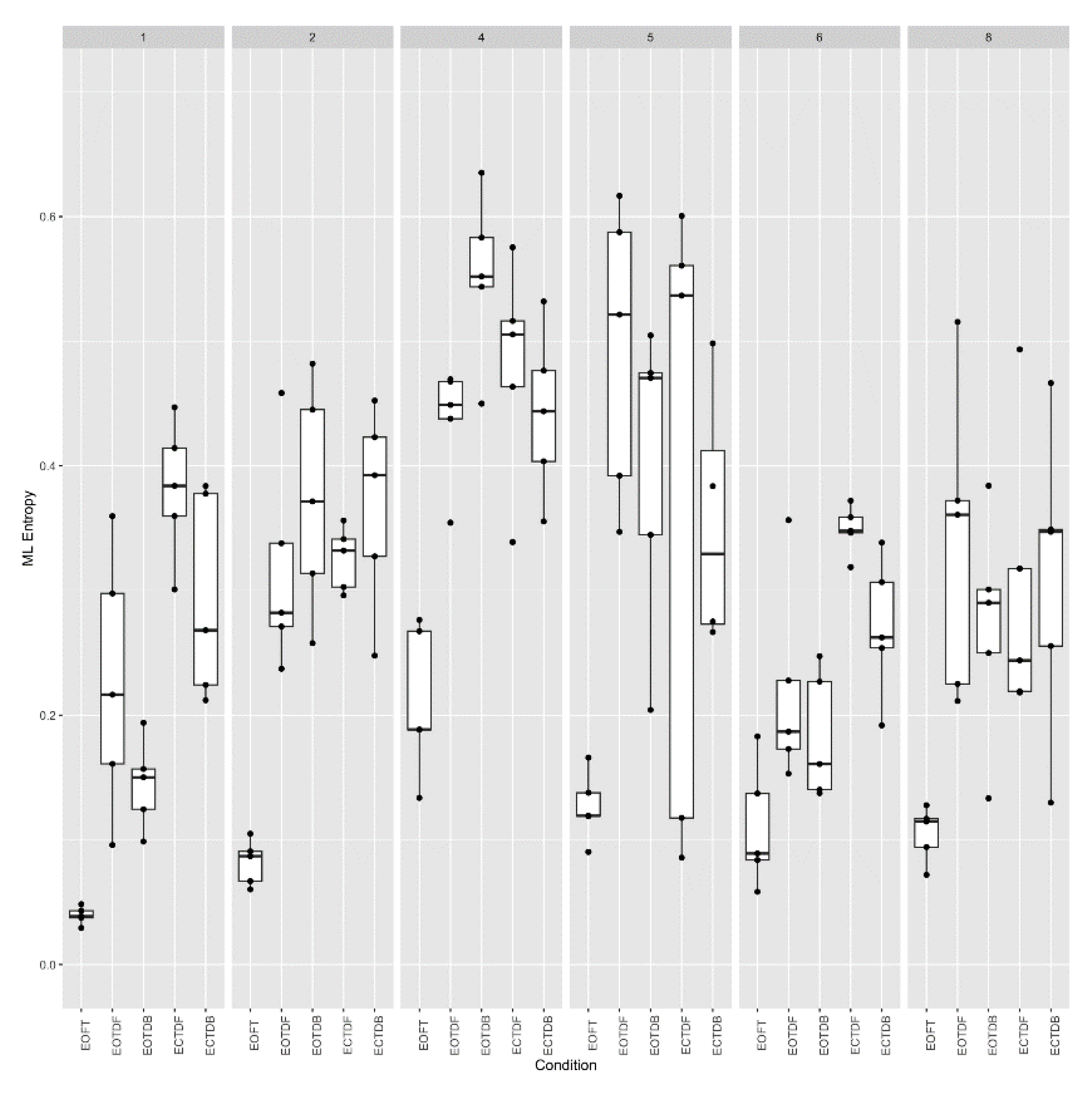
Preprints 112881 g010
Figure 10. Approximate entropy (vertical axis) (m = 2, r = 0.25 * SD) across six participants for all standing postural test conditions (horizontal axis). Data collected consisted of five trials for each participant at each stance condition. Each boxplot is derived from the five calculated entropy values for each condition for each participant (30 boxplots).
Figure 10. Approximate entropy (vertical axis) (m = 2, r = 0.25 * SD) across six participants for all standing postural test conditions (horizontal axis). Data collected consisted of five trials for each participant at each stance condition. Each boxplot is derived from the five calculated entropy values for each condition for each participant (30 boxplots).
Preprints 112881 g010
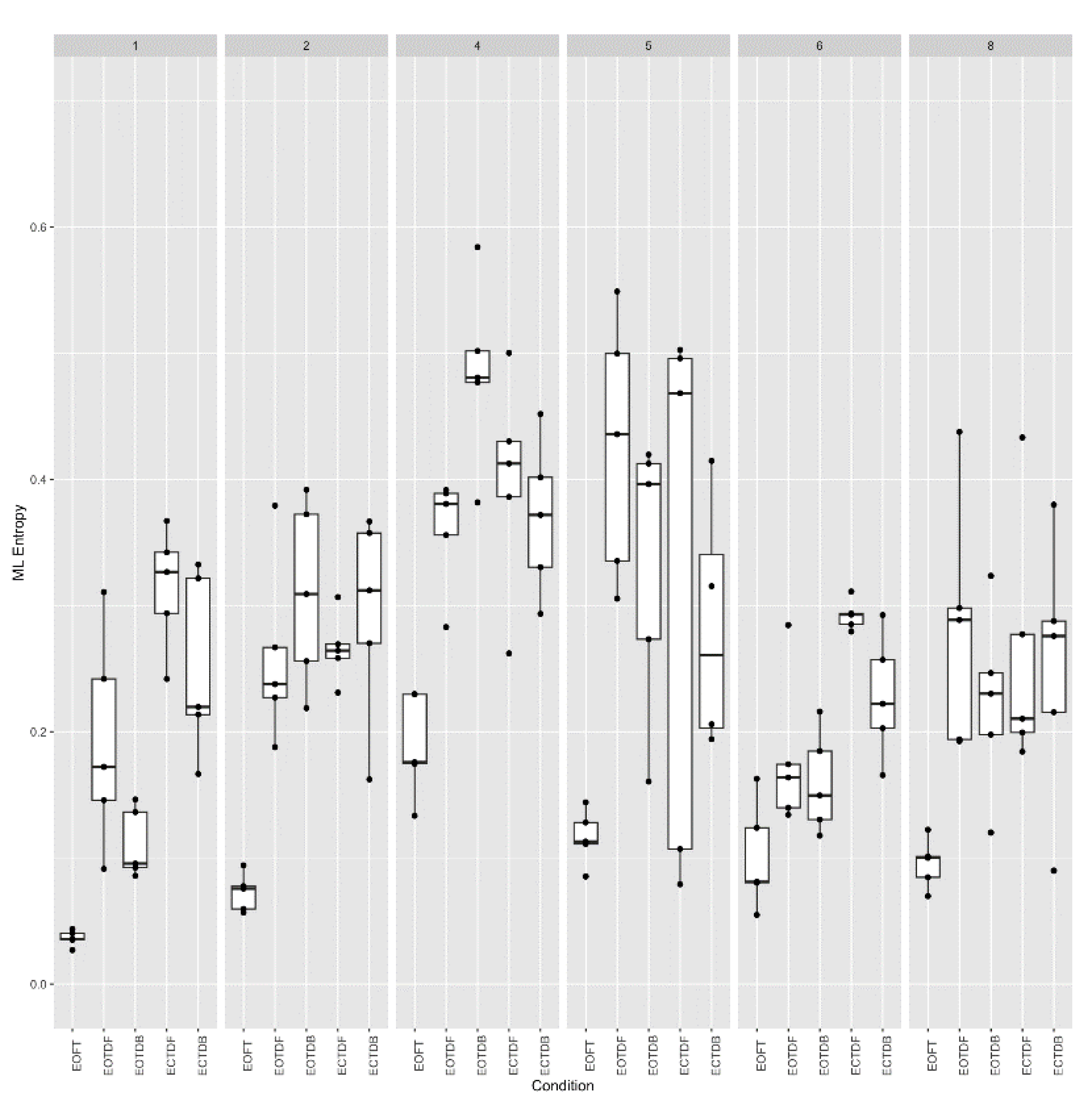
Preprints 112881 g011
Figure 11. Sample entropy (vertical axis) (m =2, r = 0.25 * SD) across six participants for all standing postural test conditions (horizontal axis). Data collected consisted of five trials for each participant at each stance condition. Each boxplot is derived from the five calculated entropy values for each condition for each participant (30 boxplots).
Figure 11. Sample entropy (vertical axis) (m =2, r = 0.25 * SD) across six participants for all standing postural test conditions (horizontal axis). Data collected consisted of five trials for each participant at each stance condition. Each boxplot is derived from the five calculated entropy values for each condition for each participant (30 boxplots).
Preprints 112881 g011
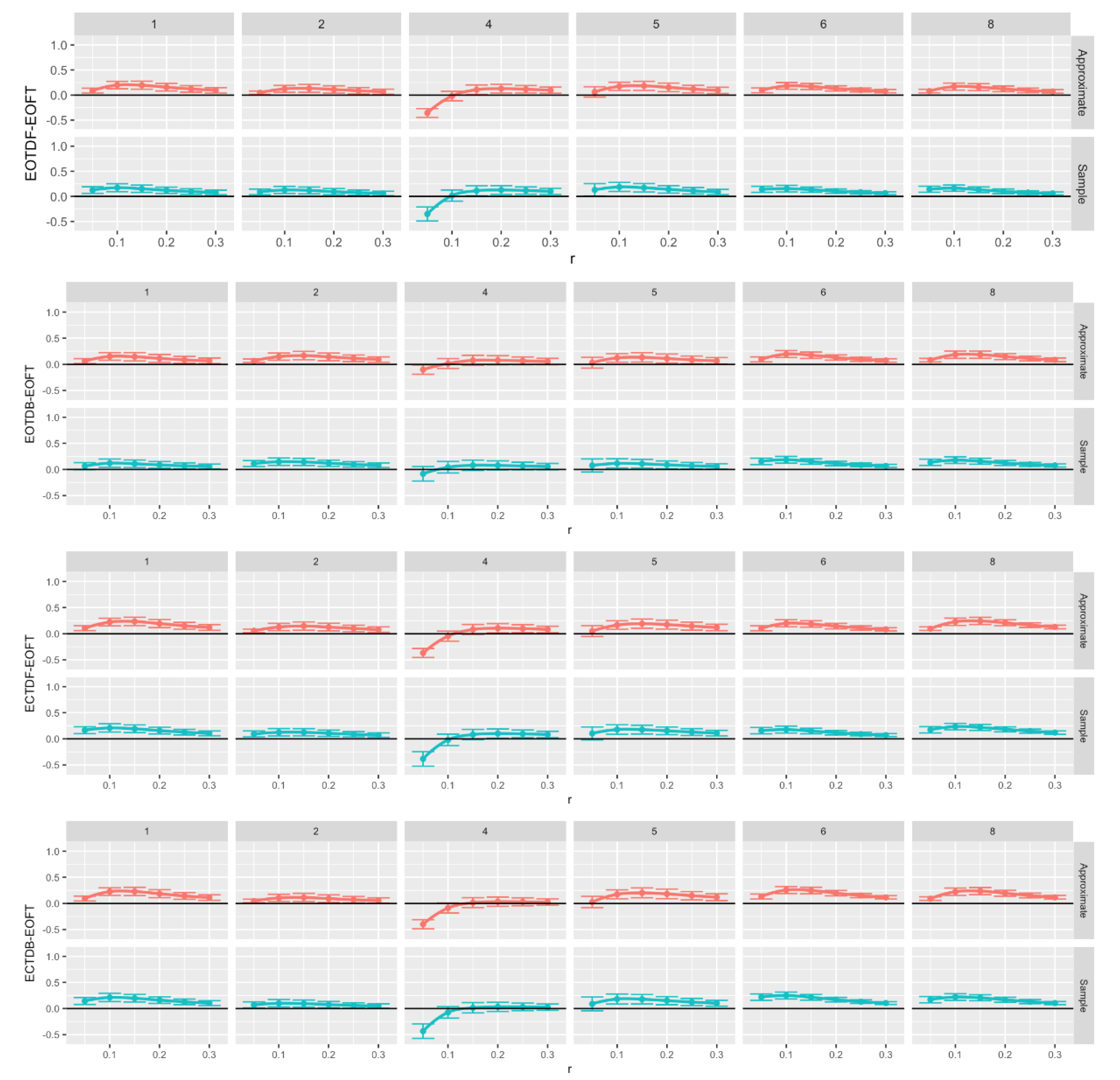
Preprints 112881 g012
Figure 12. Comparison of Approximate (red) and sample (blue) entropy values across standing postural conditions for the center of pressure data in the anterior-posterior (AP) direction for each participant. Note that all F-tests, except six, had p < 0.05. What is graphed are Dunnet’s 95% confidence intervals. Loess curves through the confidence interval centers are included to aid visualization. Significant intervals can be found above the black (zero) horizontal line. Comparison pairs along the vertical axis, with r values along the horizontal axis.
Figure 12. Comparison of Approximate (red) and sample (blue) entropy values across standing postural conditions for the center of pressure data in the anterior-posterior (AP) direction for each participant. Note that all F-tests, except six, had p < 0.05. What is graphed are Dunnet’s 95% confidence intervals. Loess curves through the confidence interval centers are included to aid visualization. Significant intervals can be found above the black (zero) horizontal line. Comparison pairs along the vertical axis, with r values along the horizontal axis.
Preprints 112881 g012
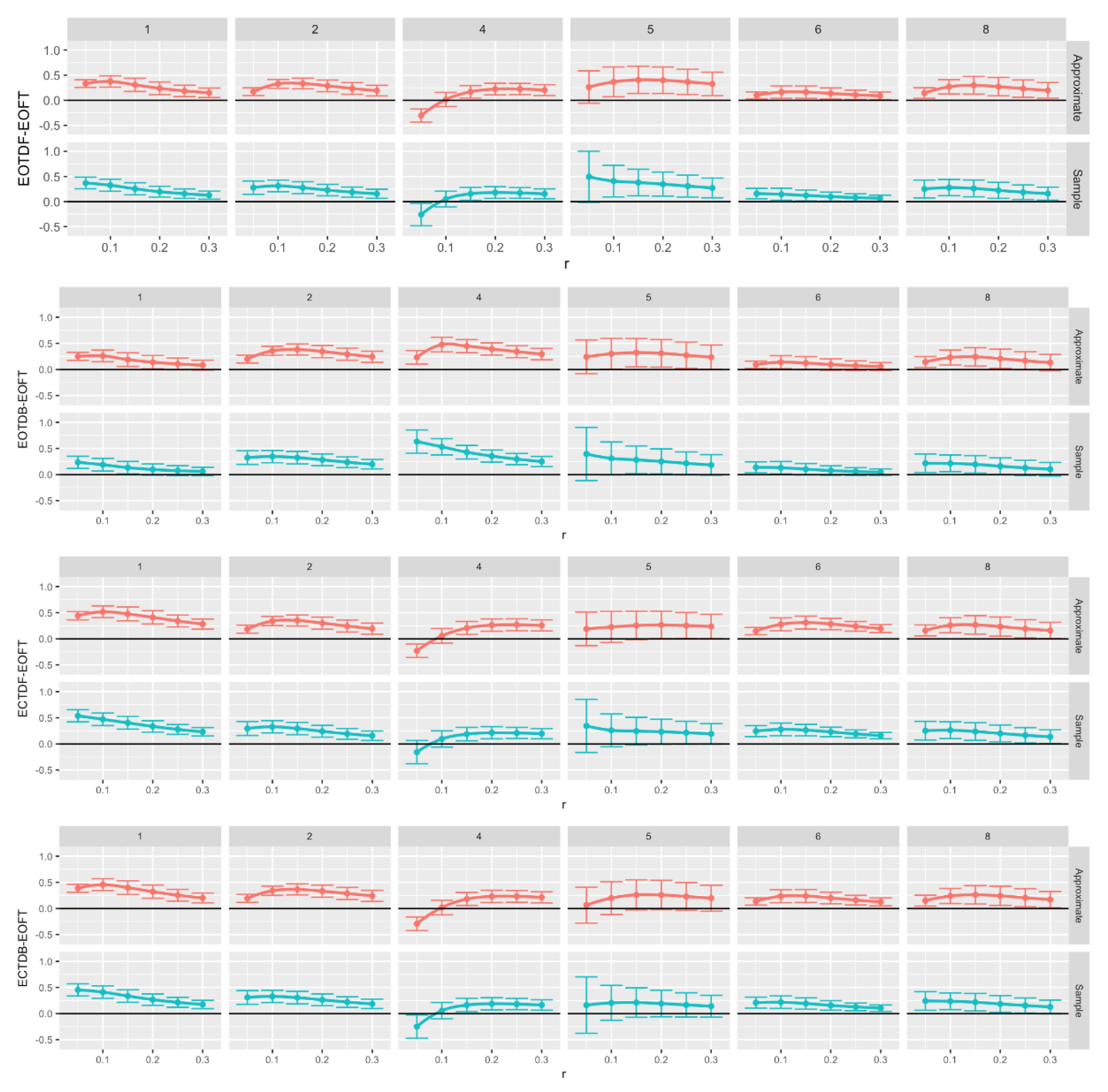
Preprints 112881 g013
Figure 13. Comparison of Approximate (red) and sample (blue) entropy values across standing postural conditions for the center of pressure data in the medial-lateral (ML) direction for each participant. Note that all F-tests, except six, had p < 0.05. What is graphed are Dunnet’s 95% confidence intervals. Loess curves through the confidence interval centers are included to aid visualization Significant intervals can be found above the black (zero) horizontal line. Comparison pairs along the vertical axis, with r values along the horizontal axis.
Figure 13. Comparison of Approximate (red) and sample (blue) entropy values across standing postural conditions for the center of pressure data in the medial-lateral (ML) direction for each participant. Note that all F-tests, except six, had p < 0.05. What is graphed are Dunnet’s 95% confidence intervals. Loess curves through the confidence interval centers are included to aid visualization Significant intervals can be found above the black (zero) horizontal line. Comparison pairs along the vertical axis, with r values along the horizontal axis.
Preprints 112881 g013
Preprints 112881 g014
Figure 14. Histograms, i.e., count (vertical axis) of the difference between SampEn and ApEn, i.e., Sample-Approximate (horizontal axis). Values to the left of the vertical black line indicate that ApEn was larger and values to the right of the vertical black line indicate that SampEn was larger.
Figure 14. Histograms, i.e., count (vertical axis) of the difference between SampEn and ApEn, i.e., Sample-Approximate (horizontal axis). Values to the left of the vertical black line indicate that ApEn was larger and values to the right of the vertical black line indicate that SampEn was larger.
Preprints 112881 g014
Table 1. Quiet Standing Balance Test Conditions.
Table 1. Quiet Standing Balance Test Conditions.
Balance Condition Description
EOFT Eyes Open, Feet Together
ECFT Eyes Closed, Feet Together
EOTanDF Eyes Open, Feet Tandem, Dominant Foot Forward
ECTanDF Eyes Closed, Feet Tandem, Dominant Foot Forward
EOTanDB Eyes Open, Feet Tandem, Dominant Foot Back
ECTanDB Eyes Closed, Feet Tandem, Dominant Foot Forward
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated