E-GTN: Advanced Terrain Sensing Framework for Enhancing Intelligent Decision Making of Excavators

The shift towards autonomous excavators in construction and mining is a significant leap towards enhancing operational efficiency and ensuring worker safety. However, it presents challenges such as the need for sophisticated decision-making and environmental perception due to complex terrains and diverse conditions. Our study introduces the E-GTN framework, a novel approach tailored for autonomous excavation that leverages advanced multisensor fusion and a custom-designed convolutional neural network to address these challenges. Results demonstrate that GridNet effectively processes grid data, enabling the reinforcement learning algorithm to make informed decisions, thereby ensuring efficient and intelligent autonomous excavator performance. The study concludes that the E-GTN framework offers a robust solution for the challenges in unmanned excavator operations, providing a valuable platform for future advancements in the field.

Keywords:

Subject: Engineering - Mechanical Engineering

1. Introduction

Excavators, the backbone of construction, mining, and infrastructure projects, are transitioning from being manually operated to becoming autonomous as part of digitization and intelligentization in the construction machinery industry[1]. This shift towards unmanned excavation is not just a leap in operational efficiency and production capacity, especially in the mining sector, but also a step forward in worker safety by reducing exposure to hazardous conditions. However, the transition to unmanned systems introduces considerable challenges, as the current reliance on expert experience and dynamic programming for trajectory planning is limited by its inability to match the efficiency of manual excavation and its poor adaptability to diverse environmental conditions and soil types [2].

The challenges of unmanned excavation are multifaceted, involving the intricacies of data complexity and the need for robust and reliable operations[3]. Excavators must navigate complex terrains, adapt to varying excavation areas, and integrate a wealth of mechanical and sensor data to accurately perceive and respond to their environment[4]. Discrepancies between virtual simulations and real-world scenarios necessitate careful data sampling and raise issues of integration among simulation platforms, control systems, and reinforcement learning algorithms. These complexities can lead to overfitting and a degradation in performance, underscoring the need for advanced solutions that can handle the sophisticated decision-making and environmental perception required for effective unmanned excavator operations[5].

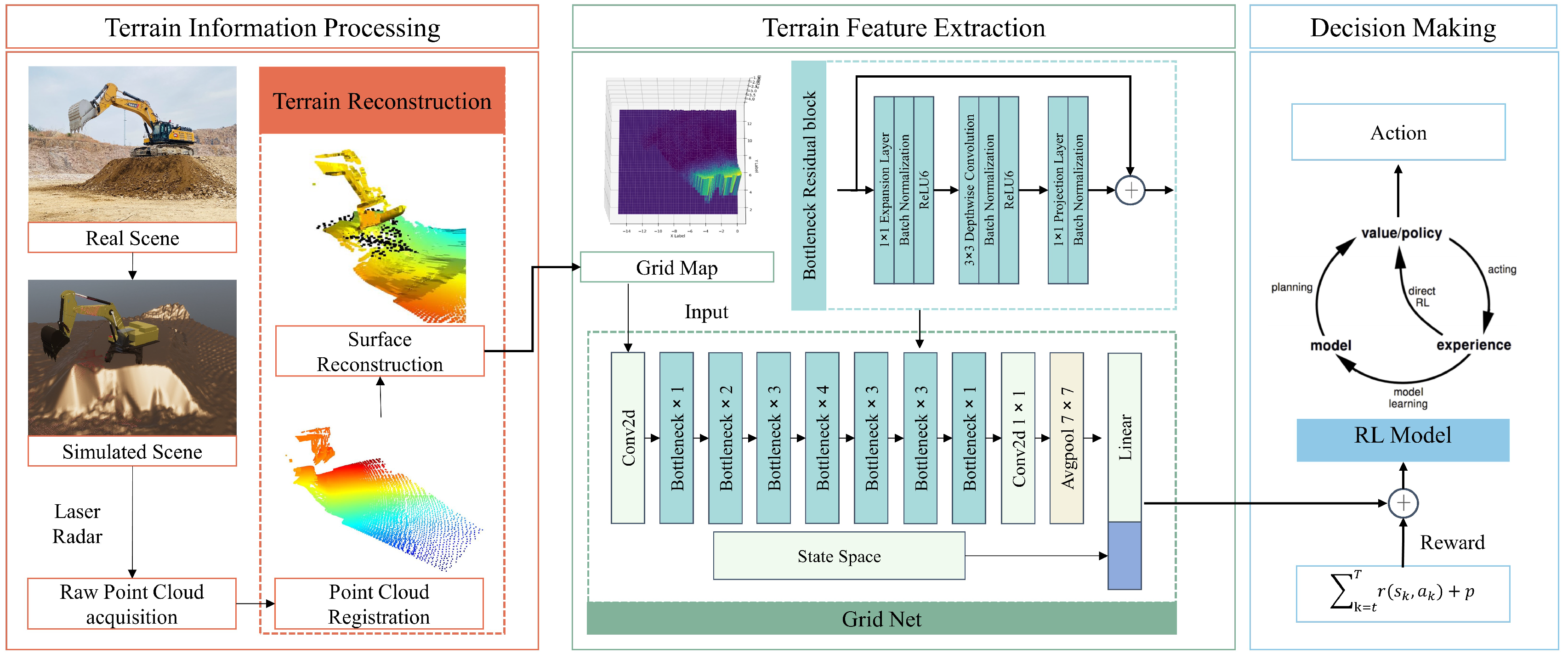
To address these challenges, we designed the E-GTN framework. It is a specialized pipeline designed for the autonomous mining domain, focusing on terrain information extraction related to reinforcement learning tasks in unmanned mining operations.The E-GTN framework first uses LiDAR to capture raw point cloud data to reconstruct terrain features in multiple ways. The terrain feature extraction module is the core of the E-GTN framework and utilizes a convolutional neural network for advanced feature extraction. Our customized GridNet proficiently processes grid data to extract key terrain features that contribute to reinforcement learning tasks in autonomous mining. Finally, the decision module utilizes the features extracted by the GridNet to inform the reinforcement learning algorithm, ensuring efficient and intelligent autonomous excavator operation.E-GTN ensures a smooth transition from data collection to extraction for terrain features, simplifying the entire process. The operational environment awareness technology provides the necessary technical support for the next path generation worker, which is the precursor of the excavation trajectory generation technology.

Our main contributions are as follows:

1.: We introduce advanced multisensor fusion for terrain environment reconstruction within the E-GTN framework, significantly enhancing the terrain’s geometric representation and laying the groundwork for high-fidelity environmental reconstruction.
2.: We present a convolutional network-based perception for grid-based excavation environments through the Terrain Feature Extraction module, enabling the application of our custom-designed model, GridNet, to extract salient terrain features crucial for the reinforcement learning algorithm.
3.: We model the decision-making process as a Markov Decision Process (MDP), and develop an advanced Deep Reinforcement Learning (DRL) algorithm for excavation tasks, which provides a comprehensive platform benefiting scholars and practitioners in related fields.

2. Related Work

In the field of autonomous machinery, unmanned excavators, while not as complex as self-driving cars, face a unique set of challenges. The static character of the typical excavator working environment and the reduction in the variety of objects compared to an autonomous driving scenario. However, the terrain features of excavator scenarios are highly variable and detailed in form.

Significant research, both domestic and international, has been conducted on environmental perception technologies for unmanned excavators. Pioneering systems developed by scholars like Anthony et al.[6] utilized LiDAR on excavators for environmental perception, laying the groundwork for subsequent systems. Despite their limitations in integrating driving and positioning, these early systems demonstrated the potential for stationary data collection. Yamamoto et al.[7], tailoring to specific excavation projects, developed an automated hydraulic excavator prototype based on 3D information, focusing on environmental perception through a combination of LiDAR and cameras, supplemented with gyroscopes and GPS for comprehensive data collection.

Further advancements by Chae et al.[8] introduced a mobile 3D environment recognition system for civil engineering, utilizing movable 3D laser scanners to scan and input site terrain for processing. Shariati et al.[9] proposed a multi-frame convolutional approach, providing a complete solution for unmanned excavators by exploiting temporal information between continuous frames and extracting richer features through CNNs. This mature technology has been tested globally, achieving recognition accuracy above 90% at 10fps, serving as a foundational step in various implementations. Forkel’s work[10] on large-scale grid mapping with LiDAR for autonomous driving was notable but lacked focus on under-vehicle information crucial for unmanned excavator perception. Collaborative research by Baidu and the University of Maryland[3] developed an Autonomous Excavator System (AES) that combined cameras, positioning systems, and LiDAR for extended autonomous excavation.

Our proposed technical solution preprocesses the excavation scene’s point cloud, reduces the dimensionality of the 3D point cloud to a 2D grid through pseudo-imaging, and employs CNNs to extract and analyze terrain features from the grid. This approach yields features suitable for reinforcement learning models in intelligent unmanned excavator trajectory generation without excessive computational resource demands.

3. Methods

We introduce the E-GTN framework, a specialized pipeline designed for the autonomous excavation domain, focusing primarily on the extraction of terrain information pertinent to reinforcement learning tasks in unmanned excavation operations.The overall structure of E-GTN is shown in Figure 1.

In the Terrain Information Processing stage of our E-GTN framework, we commence with the capture of raw point cloud data using laser radar. This data is then processed using voxel grid downsampling and normal estimation to reduce complexity and enhance feature representation. The resulting downsampled point cloud is essential for creating a detailed and computationally manageable model of the terrain, which is critical for accurate environmental reconstruction and subsequent analysis.

The Terrain Feature Extraction module is the centerpiece of the E-GTN framework, where the downsampled point cloud is meticulously transformed into a structured grid map. This grid map undergoes normalization and is treated as a pseudo-image, allowing us to leverage Convolutional Neural Networks (CNN) for advanced feature extraction. Our tailored model GridNet adeptly processes the grid data to distill critical terrain features that are instrumental for the reinforcement learning tasks in autonomous excavation.

Finally, the Decision Making module utilizes the features extracted by GridNet to inform the reinforcement learning algorithm. While this section is less emphasized, it is still pivotal as it enables the autonomous system to make strategic decisions based on the terrain information provided. The integration of these modules within the E-GTN framework ensures a seamless flow from data acquisition to decision execution, facilitating efficient and intelligent autonomous excavator operations.

3.1. Terrain Information Processing

3.1.1. Raw Point Cloud Acquisition

Given the raw point cloud data P, we apply a voxel grid downsampling method. For each voxel V with edge length l, the subset of points

P_{V} \subseteq P

is replaced with their centroid

c_{V}

to obtain the downsampled point cloud

P^{'}

c_{V} = \frac{1}{| P_{V} |} \sum_{p \in P_{V}} p, P^{'} = ⋃_{V} c_{V}

(1)

where

| P_{V} |

denotes the number of points in voxel V. The next step involves estimating the normal at each point in

P^{'}

. Using a neighborhood defined by a radius search in a KD-tree structure [11] , the normal vector

{\vec{n}}_{p}

at point p is computed as the eigenvector corresponding to the smallest eigenvalue of the covariance matrix constructed from the neighbors of p.

For feature description, we compute the Fast Point Feature Histograms (FPFH) [12]for each point p in

P^{'}

based on the normal vectors and the relative positions within a neighborhood

N (p)

F P F H (p) = S P F H (p) + \frac{1}{k} \sum_{p_{k} \in N (p)} \frac{1}{ω_{p k}} S P F H (p_{k})

(2)

where

S P F H (p)

is the Simplified Point Feature Histogram for point p,

ω_{p k}

is the inverse Euclidean distance between p and

p_{k}

, and k is the number of neighbors.

To align the point clouds into a common coordinate frame, we first apply an initial rough alignment using feature matching. A RANSAC-based approach with FPFH features estimates the transformation

(R_{i}, t_{i})

by maximizing the consensus set of matched features:

(R_{i}, t_{i}) = arg max_{R, t} | {(p, q) \in P^{'} \times Q^{'} : ∥ (R p + t) - q ∥ < ϵ} |

(3)

where

Q^{'}

is the downsampled point cloud from the other laser scanner and

ϵ

is a threshold for matching.

Subsequently, the Iterative Closest Point (ICP) algorithm [13] refines the transformation

(R, t)

by minimizing the mean squared error between the corresponding points:

(R^{*}, t^{*}) = arg min_{R, t} \sum_{(p, q) \in C} {∥ (R p + t) - q ∥}^{2}

(4)

where

C

is the set of corresponding point pairs between the registered point cloud

P^{'}

and the target cloud

Q^{'}

, and

(R^{*}, t^{*})

is the optimized transformation. Through these steps, we ensure the integrity and computational efficiency of the data, leading to a high-fidelity reconstruction of the excavation site suitable for further simulation and analysis.

3.1.2. Environment reconstruction

In our study, the Region of Interest (ROI) is delineated by an axis-aligned bounding box to focus on terrain changes in front of the excavator bucket. The ROI is defined by coordinates

\min_{ROI}

and

\max_{ROI}

, significantly reducing data processing volume and increasing efficiency.

The Poisson surface reconstruction algorithm[14] seeks a smooth surface that approximates the normals of the point cloud. The mathematical formulation involves solving the Poisson equation:

Δ f = div (N)

(5)

where f is the scalar field whose gradient approximates the point cloud normals

N

Δ

is the Laplacian, and div is the divergence operator. The normals

N

are estimated from the input point cloud, and the divergence of

N

forms the right-hand side of the equation, representing the flux of the normal vectors.

The boundary conditions for the domain

Ω

are typically set to Neumann conditions:

\frac{\partial f}{\partial n} |_{\partial Ω} = N \cdot n

(6)

where

\frac{\partial f}{\partial n}

is the derivative of f in the direction of the outward normal

n

on the boundary

\partial Ω

After solving the Poisson equation, the surface S is extracted as the isosurface where the scalar field f equals a chosen iso-value

τ

, typically zero:

S = {x \in Ω ∣ f (x) = τ}

(7)

resulting in a triangular mesh that represents the continuous surface of the point cloud data. This reconstruction fills gaps and creates a model with uniform density, facilitating further processing and analysis.

3.2. Terrain Feature Extraction

3.2.1. Point Cloud to Grid Dimensionality Reduction Mapping

In the preprocessing phase, the original point cloud data, which includes a set of points each with coordinates, intensity, and environmental label, is denoted as

P = \{p_{i}\}

, where

p_{i} = [x_{i}, y_{i}, z_{i}, I_{i}, l_{i}]

and

i = 1, \dots, N

. Here, N is the total number of points in the point cloud,

I_{i}

represents the intensity, and

l_{i}

is the label of the i-th point.

Filtering based on the label l retains only the points associated with the target environment, resulting in a reduced point cloud

P^{'} = \{p_{i}^{'}\}

, where

p_{i}^{'} = [x_{i}^{'}, y_{i}^{'}, z_{i}^{'}]

and

i^{'} = 1, \dots, N^{'}

. Here,

N^{'}

is the count of points in the filtered point cloud.

The grid map parameters are computed as follows:

bad hbox = ⌊\frac{W}{Δ x}⌋, bad hbox = ⌊\frac{H}{Δ y}⌋

(8)

where W and H are the width and height of the scene, respectively, and

Δ x

and

Δ y

are the grid resolutions in the respective dimensions. An empty grid map

G

is initialized with zero values:

G = 0_{bad hbox \times bad hbox}

(9)

For each point

p_{i}^{'}

within the specified range, the corresponding grid indices

(i_{x}, i_{y})

are calculated by:

i_{x} = ⌊\frac{x_{i}^{'} - x_{\min}}{Δ x}⌋, i_{y} = ⌊\frac{y_{i}^{'} - y_{\min}}{Δ y}⌋

(10)

where

x_{\min}

and

y_{\min}

are the minimum coordinates of the grid. The z-coordinate is mapped to the grid if it falls within the specified range

[z_{\min}, z_{\max}]

G (i_{y}, i_{x}) = \{\begin{matrix} z_{i}^{'} & if z_{\min} \leq z_{i}^{'} \leq z_{\max} \\ 0 & otherwise \end{matrix}

(11)

The grid

G

is then reshaped into a vector for efficient storage and processing:

g = reshape (G, bad hbox \cdot bad hbox)

(12)

For visualization and further analysis, the grid map is normalized and converted into a pseudo-image

I_{grid}

I_{grid} = \frac{G - min (G)}{max (G) - min (G)}

(13)

This pseudo-image is then scaled to the range [0, 1] to standardize the data for subsequent processing steps:

I_{grid} = \frac{I_{grid}}{255}

(14)

The normalized grid map

I_{grid}

is now ready for feature extraction and environmental perception tasks, providing a consistent input for machine learning algorithms.

3.2.2. Terrain Feature Extraction Network

To facilitate the processing of grid data by Convolutional Neural Networks (CNNs), which are typically designed for RGB images, the channel dimension of the grid data must be expanded to simulate a three-channel image. This expansion is denoted by the operation

bad hbox

, which replicates the single-channel grid pseudo-image

G

across three channels, yielding a tensor

{Grid}_{RGB}

with dimensions

[3, H_{g}, W_{g}]

, where

H_{g}

and

W_{g}

represent the height and width of the grid, respectively:

{Grid}_{RGB} = bad hbox (G) \in R^{3 \times H_{g} \times W_{g}}

(15)

For batch processing, the tensor is further extended to accommodate a batch size of

b s

, resulting in a four-dimensional tensor

{Grid}_{batch}

{Grid}_{batch} \in R^{b s \times 3 \times H_{g} \times W_{g}}

(16)

The environmental state vector

State

is defined to encapsulate additional necessary inputs from the environment, excluding the target point cloud. It is represented as

State \in R^{b s \times S_{d}}

, where

S_{d}

is the dimensionality of the state information.

The feature extraction network, denoted as GridNet, is composed of a CNN model

{CNN}_{GridNet}

for processing grid data and a fully connected network

{FCN}_{GridNet}

for processing state data. The CNN model, incorporating depthwise separable convolutions and an inverted residual structure, transforms the input dimensions as follows:

{CNN}_{GridNet} : R^{3 \times H_{g} \times W_{g}} \to R^{C_{g}}

(17)

where

C_{g}

represents the number of feature channels produced by the CNN. The fully connected network processes the state vector:

{FCN}_{GridNet} : R^{S_{d}} \to R^{C_{s}}

(18)

where

C_{s}

is the size of the feature vector for the state data.

The environmental feature vector

Feat

is obtained by concatenating the output of the CNN and FCN models:

Feat = concat ({CNN}_{GridNet} ({Grid}_{RGB}), {FCN}_{GridNet} (State)) \in R^{C_{g} + C_{s}}

(19)

MobileNetV2[15] is selected for its efficiency and is specifically adapted for this application. This structure initially expands the channel count of the input feature map through a lightweight expansion layer. It elevates the dimensions before applying depthwise separable convolutions for feature extraction. Finally, a linear projection layer reduces the dimensions back to the original size.

3.3. Decision Making

Within the scope of excavator operations, we confront the dynamic optimization challenge by conceptualizing the joint optimization of excavation strategies as a MDP [16]. To effectively address this MDP, we have engineered an adept DRL [17] algorithm. This algorithm is specifically tailored to navigate the intricacies of continuous excavation tasks, thereby refining the decision-making process in a real-time setting.

The MDP framework of our DRL model is succinctly encapsulated by the tuple

〈 S, A, P, r 〉

, where S delineates the state space, A signifies the action space, P represents the set of state transition probabilities, and r constitutes the reward function.

3.3.1. State Space

At any decision epoch t, the state space

S (t)

is formulated to provide a detailed depiction of the excavator’s operational status and its environmental engagement. The state space is concisely defined as:

S (t) ≜ {J (t), S (t), V_{s o i l} (t)}

(20)

where

J (t)

encompasses the joint angles of the excavator,

S (t)

entails the angular velocities of the joints,

V_{s o i l} (t)

quantifies the volume of soil excavated at time t.

Given the continuum of the state space, we model the state transition probability as a probability density function f, which quantifies the probability of migrating to the subsequent state

s (t + 1)

consequent to executing an action

a (t)

P r (s (t + 1) | s (t), a (t)) = \int_{S^{t + 1}} f (s (t), a (t), s^{'}) d s^{'}

(21)

3.3.2. Action Space

The action space

A (t)

, at time t, is comprised of a series of potential excavator movements, each represented by the discrete adjustments in the joint angles:

A (t) ≜ {Δ J_{s w i n g} (t), Δ J_{b o o m} (t), Δ J_{a r m} (t), Δ J_{b u c k e t} (t)}

(22)

Each component of

A (t)

specifies an incremental modification to a corresponding joint angle, thereby facilitating precise control over the excavator’s movements and excavation activities.

4. Experiments

4.1. Data Acquisition

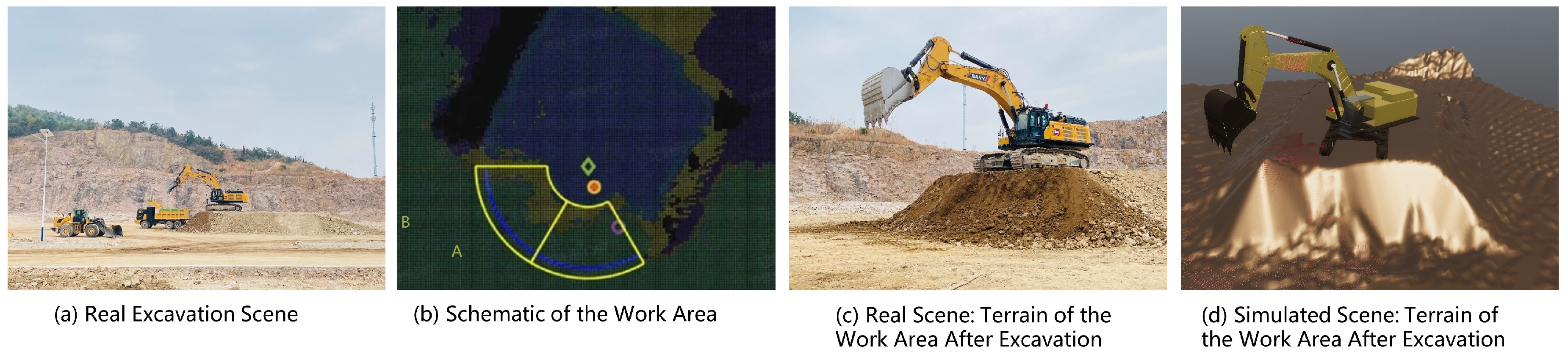
Data for our study was sourced from actual excavation sites, as depicted in Figure 2 (a). The data collection involved an SY870 excavator[18] performing earthmoving tasks, with the operator ensuring consistent excavation criteria and ground leveling post-operation. The excavator’s position remained fixed during the tasks, and the terrain was restored after each session to maintain consistent conditions for every new excavation. The SY870 is a hefty machine with a 4.5 cubic meter bucket capacity. In the unloading phase, excavated soil was loaded into mining trucks.

Throughout the excavation processes, the excavator’s location was kept constant. The operator used a uniform standard to determine the end of the excavation process. The goal was to keep the post-excavation ground as level as possible and to ensure a constant excavation speed. To avoid operational anomalies, the operator restored the terrain after each excavation to ensure the initial conditions for subsequent operations were as consistent as possible. Figure 2 (b) shows the work area of the excavation operation, with Area A being the excavation zone and Area B being the unloading zone. The width of the spoil platform at the excavation site was 13 meters, and the work area was 6.5 meters by 1.4 meters by 4 meters.

To simulate actual operations, radar devices were installed on both sides of the excavator’s cabin and boom to collect real-time data about the surrounding environment and terrain. During operations, this data was stored at a frequency of 50 Hz in Rosbag packages. The dataset includes the angular velocity of each joint of the excavator, joint force, piston rod speed, volume of soil excavated, ground support force, and LIDAR point clouds. The operator’s excavation trajectory, followed during the operation, was transmitted to a simulation platform (Unity) via the UDP protocol in Matlab to acquire data on the excavation process in a simulated environment. Figure 2 (c) illustrates the terrain of the work area after the completion of the excavation in the real scenario. Figure 2 (d) displays the terrain of the work area after the excavation in the simulated scenario, which is essentially consistent with the terrain in the real scenario.

4.2. Environment Reconstruction

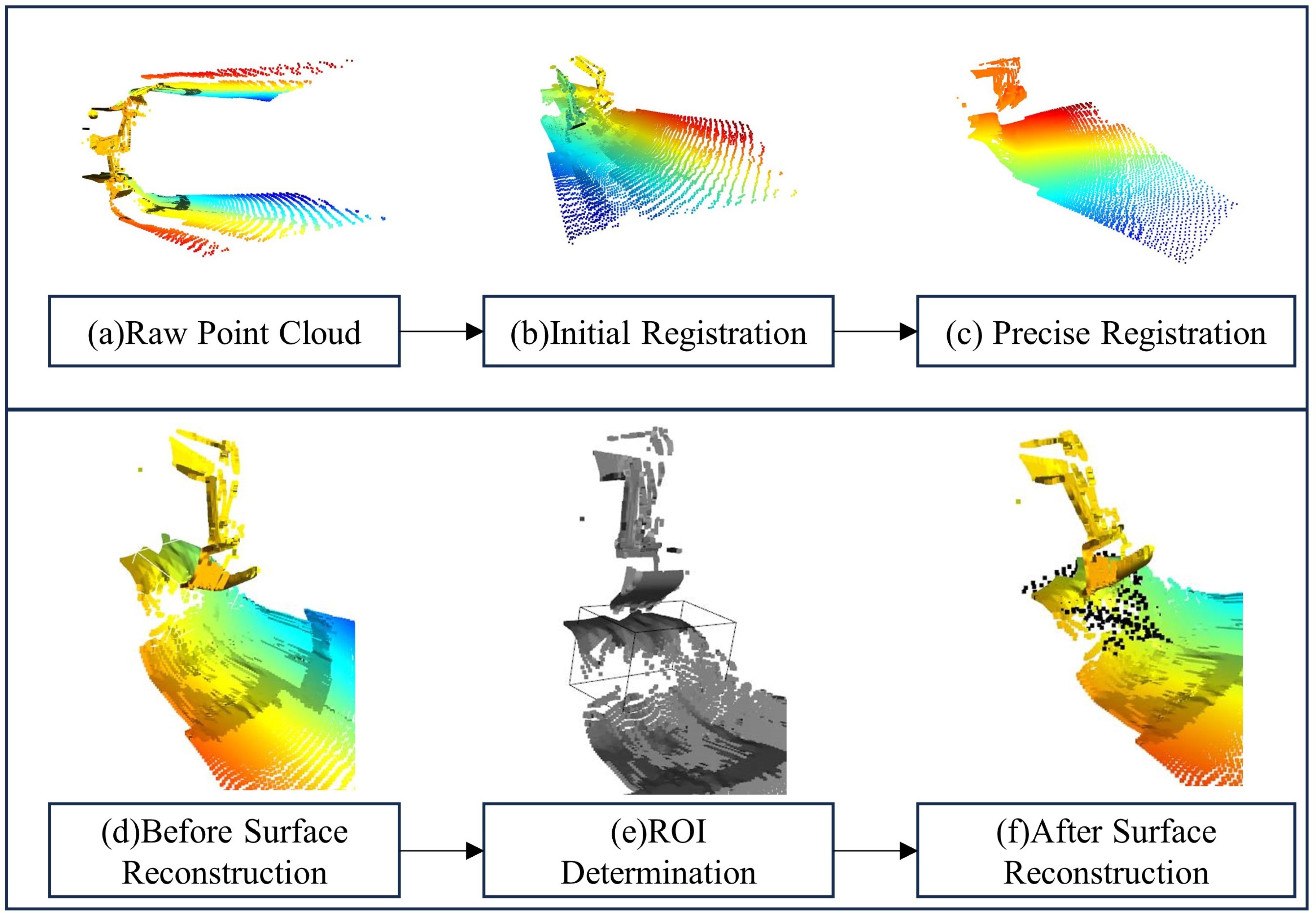
After capturing the original point cloud data, we processed the terrain information based on the point cloud. The process began with preliminary steps such as downsampling, normal estimation, and FPFH feature extraction. This was followed by initial registration and then precise alignment using the ICP method for the point clouds collected by the left and right radars of the bucket. Next, we reconstructed the point cloud by first removing outliers and any unreasonable points. We then defined the ROI for the actual excavation process. After selecting the ROI, we used Poisson surface reconstruction techniques to rebuild the point cloud, filling in gaps and preparing for the conversion of the point cloud to a grid and feature extraction.

In our study, we used the Open3D library’s estimate_normals method to estimate the direction of normals, utilizing a KD-tree for rapid neighborhood searches. Considering both accuracy and computational efficiency, we set the KDTreeSearchParamHybrid parameter with a search radius of 0.1 meters and a maximum of 30 nearest neighbors.

The primary aim of preliminary registration was to achieve a rough alignment, providing a good starting point for precise registration. We used the Open3D library’s registration_fast_based_on_feature_ matching method for this step. This method inputs the left and right point clouds and their corresponding FPFH features to quickly estimate an initial transformation matrix.

For precise registration, we implemented the ICP algorithm to optimize the alignment accuracy of the point clouds. Using the Open3D library’s registration_icp method, we input the processed point clouds from both radars, an initial transformation matrix obtained from the preliminary registration, a maximum distance for corresponding points set at 0.2 meters, and a point-to-point transformation estimation method. With a good initial alignment, we refined the alignment by optimizing the direct Euclidean distance between points.

Figure 3 (a) shows the unregistered point clouds from the left and right radars, where the misalignment is evident. Figure 3 (b) illustrates the point clouds after preliminary registration, showing basic alignment. After ICP registration, as shown in Figure 3 (c), the left and right point clouds are well-aligned, resulting in a fused point cloud.

In our research, we focused on the terrain changes in front of the excavator bucket before and after each scoop. In Open3D, we created an axis-aligned bounding box as the ROI to study the terrain changes in detail. As shown in Figure 3 (e), we defined the ROI boundaries as (3, 2, -4) and (6, 5, 1), with ’x+’ pointing down and ’z-’ to the right.

Surface reconstruction organized the points in the point cloud into a smooth surface, effectively representing the continuity and smoothness of the surface. The reconstructed model usually has uniform data density, making the surface features more consistent and continuous. The pre-reconstruction point cloud, as seen in Figure 3 (d), shows an uneven distribution of points within the ROI and some gaps. After reconstruction, as shown in Figure 3 (f), the holes and missing parts in the point cloud were filled in, adding points to the area (marked in black), transforming the sparse and incomplete point cloud into a continuous surface model, ready for further modeling operations.

4.3. Terrain Feature Extraction

Firstly, we convert the point cloud into a grid format. The grid map’s width and height are calculated by dividing the real-world scene’s width and height by the resolution. We initialize an empty grid map with the shape (grid_height, grid_width), which corresponds to the size of the grid map. In our study, we focused on a region of interest, selecting a local grid map of (150,120) with 18,000 grids, representing a 15m x 12m real-world scene at a resolution of 0.1m. We then create an array matching the grid map size, representing the empty grid map as an all-zero array, initializing each grid value to zero. The point cloud `lidar` is then iterated over, mapping the points onto the grid map, uniformly stretching them to fit the grid map. The grid map values are the z-coordinates sampled within each grid’s range, thus reducing the three-dimensional point cloud to a two-dimensional grid map. This pseudo-image, equivalent to a single-channel grayscale image, is then dimensionally expanded by duplication to meet the model’s input requirements, unlike RGB images which have three channels.

Next, we use the MobileNetV2 network as the backbone for GridNet to perform deep learning feature extraction. We select the network’s last layer, extracting image features as a (512,1) vector, which is then passed through a Linear layer to generate a (256,1) feature vector. This vector encapsulates the basic features of the terrain state, providing a compact yet information-rich representation. These vectors are particularly suitable as input states for the RL algorithm in the next step of the unmanned excavator’s path generation. Compared to other networks mentioned, MobileNetV2 requires fewer computational resources, has a lower parameter count, and operates efficiently, making it suitable for use on mobile devices. In the final grid information extraction, MobileNetV2 processes a total of 300 scoops, including the first and middle scoops. The extracted grid feature information and state feature information are then input into the reinforcement learning model.

This section details training and testing the Decision Transformer (DT) [19], an offline RL algorithm, for generating excavator trajectories. The DT model handles sequence lengths up to 40 and segments up to 200, accommodating the unpredictable data lengths in real-world applications. Its linear embedding layer, operating in a 512-dimensional space, and a decoder with three layers and eight attention heads each, allow for detailed input representation. The model uses a tanh function for action outputs within a continuous range and employs a 0.1 dropout rate for robustness against overfitting. ReLU activations facilitate learning complex patterns. Training datasets with varied segment lengths are batch-sampled and preprocessed. Actions are scaled between -1 and 1, with states and features standardized. The AdamW optimizer, with a learning rate and weight decay of 1e-3, progressively increases the rate over 100 iterations. A custom loop minimizes the error between predicted and actual actions across 500 iterations of 100 steps each.

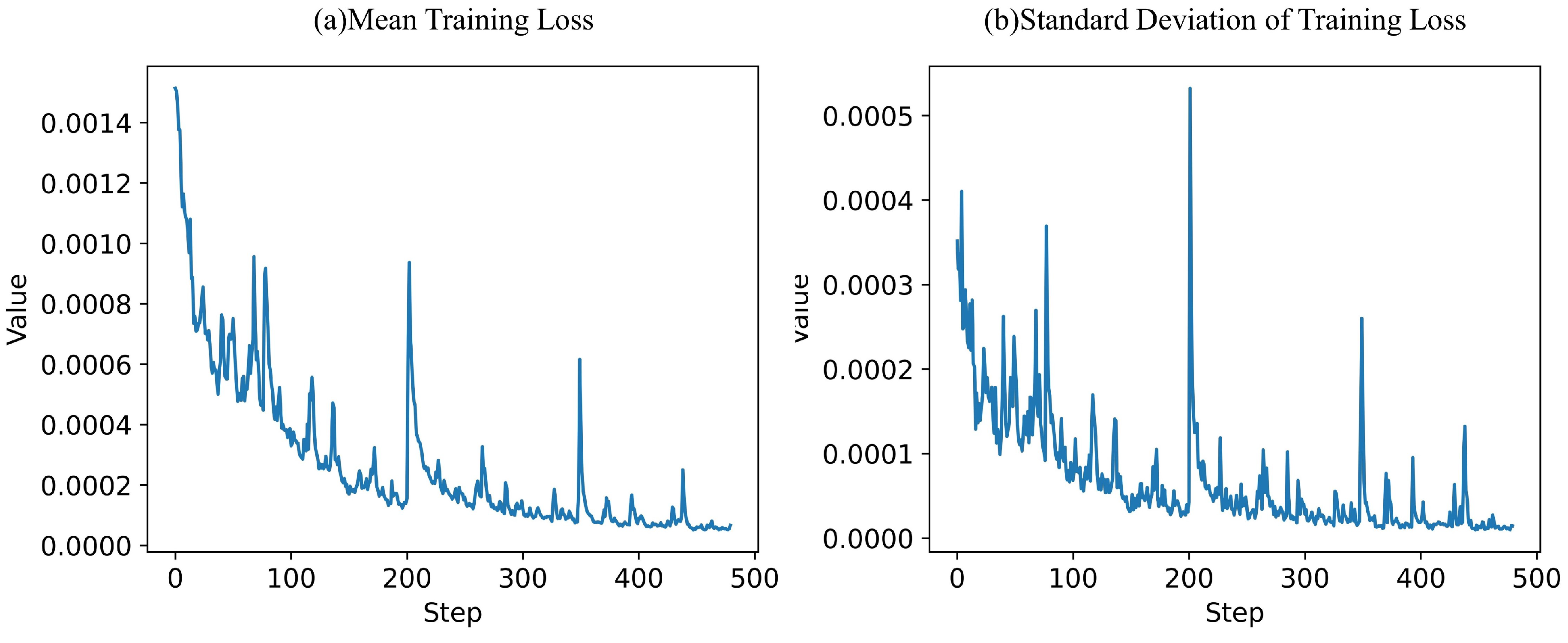
The trend in the training loss statistics for the algorithm is indicative of its learning performance. As shown in Figure 4, the mean training loss (a) decreases significantly in the initial steps, suggesting rapid learning and model improvement. The loss continues to gradually decrease, stabilizing towards the end of the training process, which is a sign of the model converging to a solution. The standard deviation of the training loss (b) exhibits a few peaks, which indicates variability in the loss across different training batches. However, similar to the mean, the standard deviation generally decreases over time, implying that the model’s predictions are becoming more consistent as training progresses.

5. Results

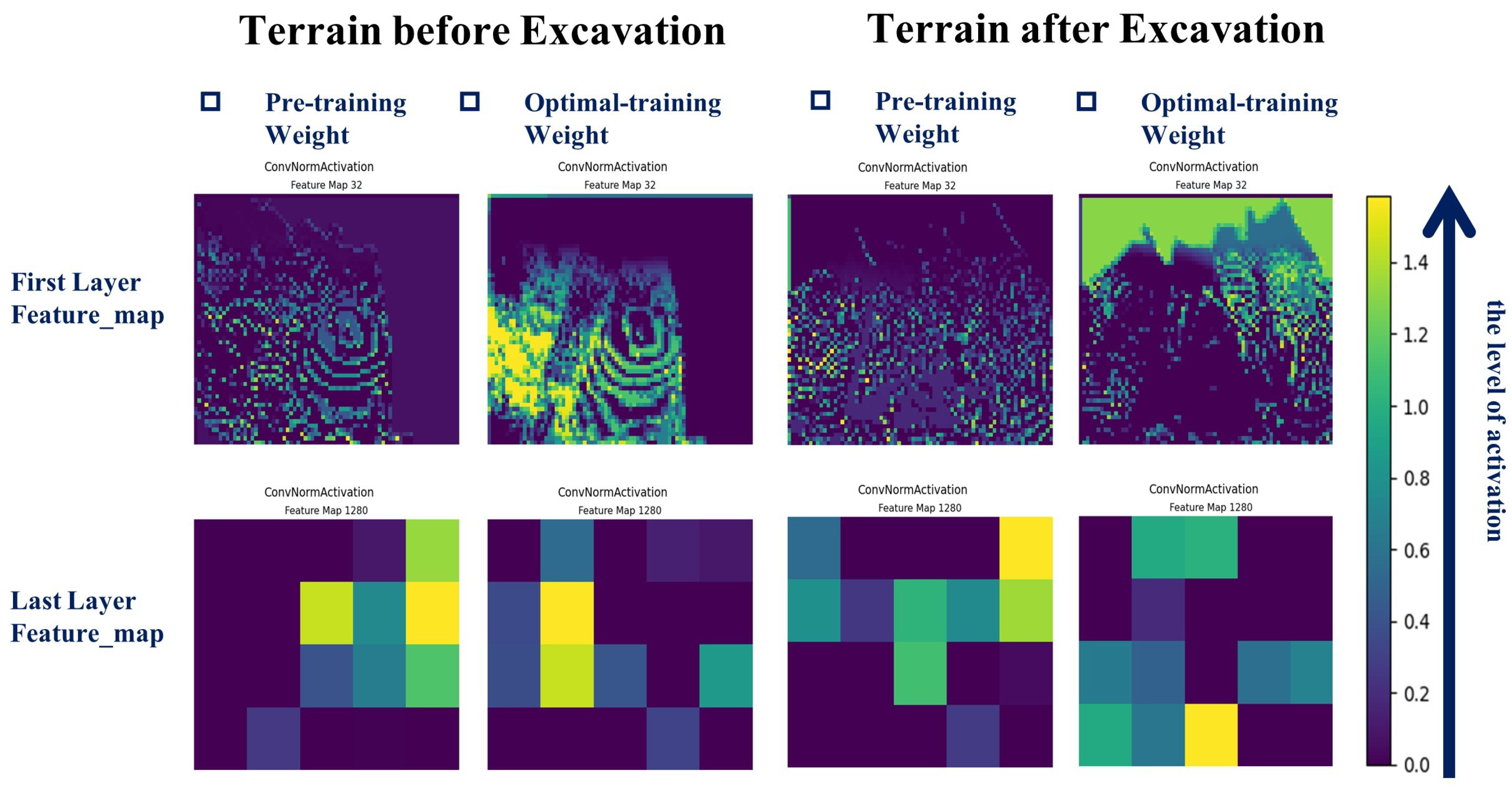
Upon completing the training, we extracted the terrain features before and after excavation and input them into our Grid Net. The visualized results are shown in Figure 5. A comparison between the feature maps before and after training reveals a noticeable difference: post-training, there is an increased level of feature activation, indicating that the network’s ability to extract features has improved.

The images on the left represent the terrain before excavation, while the images on the right depict the terrain after excavation. In both cases, the feature maps are shown for pre-training and optimal-training weights. For the first layer feature maps, the pre-training images are more chaotic and less defined, while the optimal-training images show more distinct patterns and clearer feature representations. This suggests that the network has learned to emphasize relevant features for the task at hand.

Similarly, the last layer feature maps exhibit a stark contrast. The pre-training images are almost uniform with little to no distinctive features, whereas the optimal-training images display well-defined, high-activation regions. This signifies that the network, after training, can better identify and highlight the most critical features of the terrain.

The scale on the right indicates the level of activation, with higher values corresponding to stronger activations. The optimal-training feature maps generally show higher activation levels compared to the pre-training ones, which is a strong indicator of the network’s enhanced feature extraction capability after training.

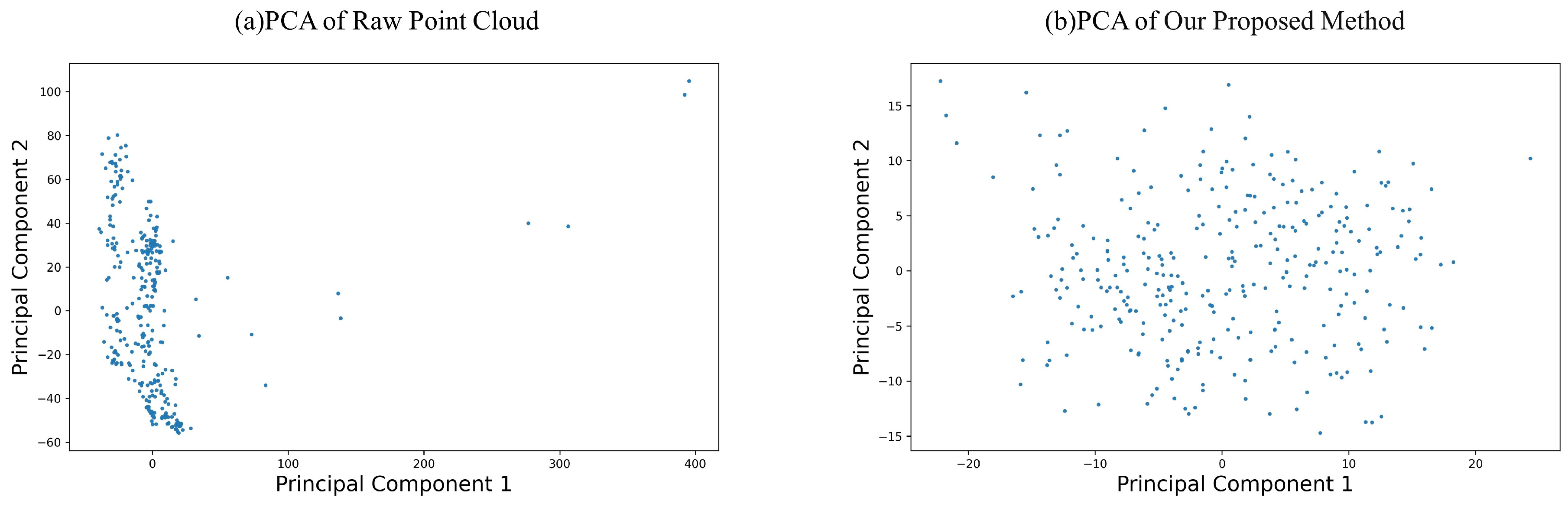
In our study, we employed Principal Component Analysis (PCA) as a preliminary method to assess the effectiveness of feature extraction by GridNet. Figure 6 (b) presents the PCA results of the feature vectors extracted by GridNet. The first two principal components account for an Explained variance ratio of 0.39 and 0.16, respectively, cumulatively explaining over 50% of the variance. The scatter plot associated with these components shows a relative dispersion of data points, lacking a clear clustering trend. This dispersion suggests that the extracted features have a high level of complexity and may capture more nuanced variations within the data.

Conversely, Figure 6 (a) illustrates the PCA results of the raw grid data. Here, the first two principal components have an Explained variance ratio of 0.25 and 0.19, which together explain less than 50% of the total variance. The scatter plot reveals a concentrated distribution of data points, indicating a strong clustering tendency. This concentration implies that the raw data may inherently contain less complexity or fewer distinct patterns before the application of feature extraction techniques.

The comparative analysis of the PCA results before and after the application of GridNet allows us to infer that the feature extraction process not only accounts for a greater proportion of the variance but also increases the complexity of the feature representation. This is indicated by the spread of data points in the scatter plot post-extraction, which contrasts with the more clustered distribution seen in the raw data. The ability of GridNet to elucidate a higher amount of variance and to disperse the data points suggests that it is capturing more significant variables within the dataset.

The feature extraction process through GridNet, as evidenced by the PCA, appears to be effective in distilling important variables from the data. This is an encouraging sign that the network can isolate and amplify aspects of the data that are most informative for subsequent analysis. The increased complexity and variance explained by the extracted features are indicative of GridNet’s robustness in representing terrain data in a way that is conducive to advanced terrain analysis and decision-making processes in automated systems.

6. Conclusions

In conclusion, our E-GTN framework has proven to be a robust solution to the challenges posed by unmanned excavator operations. By integrating advanced multisensor fusion, we have significantly enhanced the geometric representation of the terrain, which is foundational for high-fidelity environmental reconstruction. Our GridNet has successfully processed grid data to extract salient terrain features, demonstrating its critical role in the reinforcement learning tasks for autonomous excavation. The decision-making module, informed by these extracted features, has facilitated efficient and intelligent operation, showcasing the potential of our framework to revolutionize the construction machinery industry. The successful application of our E-GTN framework underscores its value as a comprehensive platform for scholars and practitioners in related fields, paving the way for future advancements in autonomous excavation technologies.

Author Contributions

Conceptualization: Qianyou Zhao; Methodology: Qianyou Zhao, Duidi Wu and Yixuan Meng; Formal analysis and investigation: Qianyou Zhao, Duidi Wu; Writing - original draft preparation: Qianyou Zhao; Writing - review and editing: Jin Qi and Jie Hu; Funding acquisition: Le Gao and Jie Hu; Resources: Le Gao; Supervision: Jie Hu.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data are available on request to the authors.

Acknowledgments

This research is supported by National Natural Science Foundation of China (52035007, U23B20102), Ministry of Education "Human Factors and Ergonomics" University Industry Collaborative Education Project (No.202209LH16).We would also like to extend our sincere thanks to Sany Company for their support and contribution to this research.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Hemami, A.; Hassani, F. An overview of autonomous loading of bulk material. 26th International Symposium on Automation and Robotics in Construction. International Association for Automation and Robotics in Construction (IAARC …, 2009, pp. 405–411.
Dadhich, S.; Bodin, U.; Andersson, U. Key challenges in automation of earth-moving machines. Automation in construction 2016, 68, 212–222. [Google Scholar] [CrossRef]
Zhang, L.; Zhao, J.; Long, P.; Wang, L.; Qian, L.; Lu, F.; Song, X.; Manocha, D. An autonomous excavator system for material loading tasks. Science Robotics 2021, 6, eabc3164. [Google Scholar] [CrossRef] [PubMed]
IndustryResearch. Global Excavator Market Report, 2020. https://www.industryresearch.co/global-excavator-market-18836753, Last accessed on 2024-3-30.
Afshar, R.R.; Zhang, Y.; Vanschoren, J.; Kaymak, U. Automated reinforcement learning: An overview. arXiv preprint arXiv:2201.05000, arXiv:2201.05000 2022.
Stentz, A.; Bares, J.; Singh, S.; Rowe, P. A robotic excavator for autonomous truck loading. Autonomous Robots 1999, 7, 175–186. [Google Scholar] [CrossRef]
Yamamoto, H.; Moteki, M.; Ootuki, T.; Yanagisawa, Y.; Nozue, A.; Yamaguchi, T.; others. Development of the autonomous hydraulic excavator prototype using 3-D information for motion planning and control. Transactions of the Society of Instrument and Control Engineers 2012, 48, 488–497. [Google Scholar] [CrossRef]
Chae, M.J.; Lee, G.W.; Kim, J.Y.; Park, J.W.; Cho, M.Y. A 3D surface modeling system for intelligent excavation system. Automation in construction 2011, 20, 808–817. [Google Scholar] [CrossRef]
Shariati, H.; Yeraliyev, A.; Terai, B.; Tafazoli, S.; Ramezani, M. Towards autonomous mining via intelligent excavators. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, 2019, pp. 26–32.
Forkel, B.; Kallwies, J.; Wuensche, H.J. Probabilistic terrain estimation for autonomous off-road driving. 2021 IEEE International Conference on Robotics and Automation (ICRA). IEEE, 2021, pp. 13864–13870.
Foley, T.; Sugerman, J. KD-tree acceleration structures for a GPU raytracer. Proceedings of the ACM SIGGRAPH/EUROGRAPHICS conference on Graphics hardware, 2005, pp. 15–22.
Rusu, R.B.; Blodow, N.; Beetz, M. Fast point feature histograms (FPFH) for 3D registration. 2009 IEEE international conference on robotics and automation. IEEE, 2009, pp. 3212–3217.
Chetverikov, D.; Svirko, D.; Stepanov, D.; Krsek, P. The trimmed iterative closest point algorithm. 2002 International Conference on Pattern Recognition. IEEE, 2002, Vol. 3, pp. 545–548.
Kazhdan, M.; Bolitho, M.; Hoppe, H. Poisson surface reconstruction. Proceedings of the fourth Eurographics symposium on Geometry processing, 2006, Vol. 7.
Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. Mobilenetv2: Inverted residuals and linear bottlenecks. Proceedings of the IEEE conference on computer vision and pattern recognition, 2018, pp. 4510–4520.
Parkes, D.C.; Singh, S. An MDP-based approach to online mechanism design. Advances in neural information processing systems 2003, 16. [Google Scholar]
François-Lavet, V.; Henderson, P.; Islam, R.; Bellemare, M.G.; Pineau, J.; others. An introduction to deep reinforcement learning. Foundations and Trends® in Machine Learning 2018, 11, 219–354. [Google Scholar] [CrossRef]
SY750H | Large Excavator, 2024. https://www.sanyglobal.com/product/excavator/large_excavator/115/847/, Last accessed on 2024-3-30.
Chen, L.; Lu, K.; Rajeswaran, A.; Lee, K.; Grover, A.; Laskin, M.; Abbeel, P.; Srinivas, A.; Mordatch, I. Decision transformer: Reinforcement learning via sequence modeling. Advances in neural information processing systems 2021, 34, 15084–15097. [Google Scholar]

Figure 1. Overall Architecture of E-GTN.

Figure 2. Excavation Operation: Real to Simulated.

Figure 3. Terrain reconstruction based on point cloud.

Figure 4. Model Training Loss.

Figure 5. Comparation of Feature Map Activations.

Figure 6. Comparation of Feature Map Activations.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

E-GTN: Advanced Terrain Sensing Framework for Enhancing Intelligent Decision Making of Excavators

Abstract

1. Introduction

2. Related Work

3. Methods

3.1. Terrain Information Processing

3.1.1. Raw Point Cloud Acquisition

3.1.2. Environment reconstruction

3.2. Terrain Feature Extraction

3.2.1. Point Cloud to Grid Dimensionality Reduction Mapping

3.2.2. Terrain Feature Extraction Network

3.3. Decision Making

3.3.1. State Space

3.3.2. Action Space

4. Experiments

4.1. Data Acquisition

4.2. Environment Reconstruction

4.3. Terrain Feature Extraction

5. Results

6. Conclusions

Author Contributions

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe