Prerpints.org logo
Preprint
Article

Radiofrequency Enhancer to Recover Signal Dropouts in 7 Tesla Diffusion MRI

Altmetrics

Downloads

147

Views

67

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

22 July 2024

Posted:

24 July 2024

You are already at the latest version

Alerts
Abstract
Diffusion magnetic resonance imaging (dMRI) is an imaging technique that provides information on the microstructural organization of biological tissue. dMRI allows for non-invasive visualization and quantitative assessment of white matter architecture in the brain by characterizing restrictions on the random motion of water molecules. Ultra-high field MRI scanners, such as those operating at 7 Tesla (7T) or higher, can boost signal-to-noise ratio (SNR) to improve dMRI compared with what is attainable at conventional field strengths such as 3T or 1.5T. However, at 7T wavelength effects cause lower transmit magnetic field efficiency in the human brain, mainly in the posterior fossa region, manifesting as signal dropouts in this region. Recently, we reported a simple approach of using a wireless radiofrequency (RF) surface array to improve transmit efficiency and signal sensitivity at 7T. Here we demonstrate the feasibility and effectiveness of using this RF enhancer for in-vivo dMRI at 7T. The use of the RF enhancer can effectively recover signal dropouts in the regions with intrinsically lower SNR such as cerebellum, leading to a better depiction of principal fiber orientations and enhanced visualization of extended tracts to the brainstem and pons enabling more comprehensive delineation of the full white matter architecture.
Keywords: 
Subject: Engineering  -   Bioengineering

1. Introduction

Diffusion magnetic resonance imaging (dMRI) is an MRI technique that assesses water molecular diffusion in biological tissues. dMRI provides insight into the microscopic details of the tissue microstructure as molecules diffuse variably throughout tissues based on local microstructure [1,2]. Water molecules preferentially diffuse parallel to the longitudinal axis of white matter axons and are restricted perpendicular to these axons, resulting in diffusion directionality called anisotropy [3,4]. The information obtained from dMRI can be utilized to assess additional tissue characteristics, such as fractional anisotropy (FA), mean diffusivity, and connectivity. dMRI has been widely used in investigating various brain pathologies, including epilepsy, stroke, and other neurological disorders [5,6,7,8].
Ultra-high-field (UHF) MRI at 7 Tesla (7T) or higher field strengths improves signal-to-noise ratio (SNR) compared to lower field strengths such as 3T and 1.5T [9,10,11,12]. The increased SNR translates to improved visualization of anatomical structures, thus enhancing its diagnostic utility. For example, dMRI at 7T provides almost two times higher spatial resolution in comparison with the 3T dMRI acquisition [13]. Despite these benefits, the shorter wavelength associated with the increased frequency at 7T causes inhomogeneity in the transmit field ( B 1 + ) when using the conventional single-channel transmit (1Tx) head coils. This leads to flip angle nonuniformity over the brain [14,15]. Typically, a 1Tx head coil is driven in quadrature mode generating circularly polarized (CP) excitation with highly homogenous B 1 + at lower field strengths (1.5T and 3T). However, at 7T CP excitation confers inhomogeneous B 1 + in the human brain, with lower transmit efficiency especially in the posterior fossa, which results in signal dropouts in this challenging region. In addition, the higher RF energy required to achieve uniform flip angle distribution causes restrictions due to specific absorption rate (SAR) limits particularly in diffusion sequences, where uniformly high-energy refocusing pulse is strongly preferred. Therefore, with B 1 + inhomogeneity increasing with field strength, developing techniques to mitigate such inhomogeneity become important.
This inhomogeneity can be reduced using active RF shimming, RF pulse design, and passive RF shimming techniques. For example, parallel transmit (pTx) is an active RF shimming method that uses multiple independently driven RF transmission channels to improve B 1 + homogeneity by controlling the magnitude and phase of each channel [16,17]. Demonstrated pTx for human connectome project-style whole-brain dMRI at 7T showed major advantages in rapid acquisition of high-quality data [13]. However, the requirement of multiple channels and RF amplifiers make this technique particularly complex. Another approach to reduce B 1 + inhomogeneity is to use adiabatic pulses that generate a quadratic phase distribution to allow the phase to be fully refocused [18]. Although adiabatic RF pulses can deal with B 1 + inhomogeneity issue they are typically associated with a high RF power deposition, meaning that SAR restrictions at UHF become an even bigger problem. Passive RF shimming techniques such as placement of dielectric pads represent simple hardware solutions to alter the B 1 + field distribution and increase the B 1 + homogeneity in the most affected brain regions [19,20,21,22]. Such dielectric pads have improved the 7T dMRI in the regions with lower B 1 + , such as the cerebellum and temporal lobe. Dielectric pads are small bags filled with a suspension of high-permittivity material that can be placed inside the head coil to be close to brain, but dielectric pads may lose their electrical and physical properties over time. Various other passive RF shimming approaches, such as metamaterials, metasurfaces, and meta-arrays, have been documented in various studies to mitigate the wavelength effect in UHF systems [23,24,25,26,27,28].
In our recent study, we reported a reliable wireless RF enhancer that was based on an inductive-coupling between the RF enhancer and the CP 1Tx head coil, to improve the transmit efficiency while avoiding the hardware complexity and other disadvantages of these prior methods [29,30]. Here, we demonstrate the advantages of using the RF enhancer in improving in-vivo whole brain dMRI at 7T.

2. Materials and Methods

2.1. Theoretical Background

Considering a single wireless RLC resonator inside an MRI coil, interaction of the electromagnetic (EM) field generated by the MRI coil with the wireless resonator through inductive coupling results in enhancing the magnetic (H) and electric (E) fields in the vicinity of the resonator [31,32,33]. The H-field enhancement can be used to improve MRI coil B 1 + efficiency in the regions with intrinsically lower efficiency. Nevertheless, the enhancement of the E-field, particularly near the capacitor, may result in elevated SAR, raising safety concerns related to tissue heating. This issue might be addressed by replacing the conventional RLC resonators with multilayer printed circuit resonators with the distributed capacitor technology to confine E-field generated by the resonator without allowing to distribute [32]. In our previous works we have studied various multilayer resonator architectures to use in RF sensing [28,29,30,31,32,34,35]. One design that is well-known from the microwave/metamaterial community is the broadside-coupled split-ring resonator (BC-SRR). The BC-SRR composed of two conductive resonators and a dielectric substrate (interlayer) sandwiched between the top and bottom rings [36,37]. Each ring has one gap, and the rings are placed across the interlayer such that the gaps are aligned counter-oriented (Figure 1a). The EM field applied externally by the MRI coil excites the BC-SRR inducing a current on the resonator (Figure 1b) and consequently results in a secondary H-field (Figure 1c). The associated E-field is built along the capacitive region and across the gap due to the charge stored across the gaps and the interlayer (Figure 1d). These stored H-field and E-field leads to a resonant spectral response and form a RF resonator.
The BC-SRR structure can be modeled by a simple series RLC resonator circuit with a single lumped capacitance and lumped inductance, where the per unit capacitance ( C u ) and inductance ( L u ) are given by equations 1 and 2, respectively. The resonance frequency ( f 0 ) of the resonator can be calculated using equation 3 [38].
C u = 1 2 ε 0 ε e f f 2 w d h + 1.393 + 1.667 + 0.667 ln ⁡ 2 ω d h + 1.444
  L u = 0.00508 l 2.303 l o g 10 4 l d − 2.451 ,   i n   t h e   u n i t   o f   μ H ,
  f 0 = 1 2 π C u L u
where ε 0   is the permittivity of free space, ε e f f   is the effective permittivity of the capacitive region between two conductive layers, w d   is the metallization width, h is the thickness of the capacitive region, l is the conductor length, and d is the conductor thickness.
In the case of placing BC-SRR inside the MRI coil, interaction of the resonator with the CP magnetic field, B r f generated by the MRI coil leads to circulating current in the resonator, which results in a secondary magnetic field, B r e in the resonator vicinity.
Assume the CP magnetic field generated by the MRI coil (quadrature birdcage) expressed as Equation 4 [39,40].
B r f t = B 1 + c o s ω L t   i − s i n ω L t   j  
B 1 + is an amplitude modulation function and ω L = 2 π f L is the carrier frequency of the transmission operating in Larmor frequency.
The inductive coupling between the resonator and B r f t results in a linearly polarized magnetic field ( B r e ) generated by a resonator, which can be expressed as Equation 5.
B r e t = 2 B r e + cos ⁡ ω L t i
Assume the angle between CP magnetic field lines and normal vector of the resonator is zero, therefore, from Faraday’s law of induction, the electromotive force ( ε ) generated by B r f t is given:
ϵ = − d ϕ d t = π r 2 ω L B 1 +
where r is the radius of the resonator.
If the resonator is considered as a series RLC circuit, the input impedance can be written as:
  Z r e = R 1 + i ω L L R f L 2 − f 0 2 f L 2
where R represents the ohmic losses, L is the resonator inductance, f 0 = 1 / 2 π L C is the resonance frequency of the resonator. Assume f = f L − f 0 and consider f is relatively small compared to f 0 . The impedance can be simplified to:
Z r e = R 1 + i 2 ω L L R f f 0
The associated ohmic loss, R, is typically small, therefore the induced current on the resonator can be written as:
I r e = ϵ Z r e ≃ π r 2 B 1 + L f 0 f
The modulation magnetic field generated by the induced current at distance z away from the resonator center is given by:
B r e t ≃   μ π r B 1 + L 1 + z r 2 3 2 f 0 f c o s ω L t i
This linearly polarized field decomposes into two CP magnetic fields [30,41]. One a circularly forward-polarized field and the other a circularly reverse-polarized field, which mathematically can be expressed as Equation (11):
B r e t ≃   μ π r B 1 + 2 L 1 + z r 2 3 2 f 0 f c o s ω L t i − s i n ω L t j + μ π r B 1 +   2 L 1 + z r 2 3 2 f 0 f c o s ω L t i + s i n ω L t j  
The first term represents the circularly forward-polarized field and the second one represents the circularly reverse-polarized field. We will neglect the second term, which has a negligible effect on the spin excitation, and consider only the forward-polarized field, which is more resonant with the spins and rotates in the same direction as the recessing spins.
Therefore, the total magnetic field at the distance z from the resonator center is explained by Equation (12):
B t + t ≃   B r f t + μ π B 1 + 2 L 1 + z r 2 3 2 f 0 f c o s ω L t i − s i n ω L t j = 1 + μ π 2 L 1 + z r 2 3 2 f 0 f   B 1 + c o s ω L t i − s i n ω L t j  
w h e r e B 1 + is the original magnitude of B t + t , when there is no resonator in place. Considering a resonator in this study tuned below the Larmor frequency ( f L > f 0 ) , then the total magnetic field, B t + can be cancelled in the region effected by the resonator. Therefore, the desired off-resonance frequency, f 0 should be above the Larmor frequency to enhance the transmit field. In general, transmit field efficiency is lower at the inferior region of the coil and higher compensation may be required. We adjust off-resonance frequency 5% above the Larmor frequency to obtain optimized transmit efficiency in the presence of the resonator [30,41]. The coupling between the resonator and the birdcage coil depends on the resonator orientation relative to the coil. Therefore, the transmit field profile of the resonator, B r e depends on its relative orientation to the coil.
Inductive coupling of a matrix of resonators with the birdcage coil is more complicated than a coupling of a single resonator. All of the resonators in the matrix are inductively coupled to the MRI coil, therefore their interaction is considered well in global homogenization. To this end, we performed full-wave electromagnetic simulations for more complementary results.

2.2. RF Enhancer

The electrical characteristics of a single BC-SRR were analyzed with finite element simulations conducted in Sim4Life (Zurich Med Tech) to optimize the design parameters including diameter, metallization width, and dielectric (interlayer) thickness. For the target operating frequency at 7T MRI (312 MHz, 5% above the Larmor frequency) a circular BC-SRR with a diameter of 60 mm, metallization width of 4 mm and interlayer thickness of 250 μm was designed. An RF enhancer matrix consists of 12 BC-SSRs (a 3×4 matrix) was created, with adjusting the distance between neighboring elements based on geometrical decoupling technique (0.76d mm, center-to-center) to minimize the coupling between the elements (Figure 2). We evaluated the effect of the RF enhancer on the EM field and SAR distributions of the head coil within the head model (relative permittivity of 60 and conductivity of 0.5 S/m) while the enhancer was placed between the head and the coil (Figure 2).
The birdcage head coil was designed similar to the transmit head coil (Nova Medical, Wilmington, MA, USA) used in the MRI experiments. The coil had 12 rungs connected at each end to two end rings and shielded by an open cylinder (23 cm in diameter and 27 cm in length). Any EM interfering may impact the coil electrical characteristics, therefore the effect of inserting the wireless RF enhancer inside the coil was assessed by analyzing the S-parameters through EM simulations. A single BC-SRR was prototyped using the optimized design parameters obtained from EM modeling (mentioned above). For BC-SRR fabrication, a copper layer of a circular resonator ring was patterned on one side of a flexible interlayer substrate (Kapton, polyimide films, DuPont™). Subsequently, another copper layer of a circular resonator ring was patterned on the opposite side of the substrate with a counter orientation but aligned along the same axis as the first layer. The distributed capacitance between two conductor layers was employed to finely tune the frequency. Adjusting the gap size can affect both capacitance and inductance values, thereby impacting the overall operating frequency.
The benchtop resonance behavior was studied by measuring the reflection coefficient (S11) using a calibrated vector network analyzer (VNA, E5071C, Agilent Technologies, Santa Clara, CA, USA) that was directly connected to a single sniffer probe (a simple small loop coil). The decoupling level between the elements was evaluated by measuring transmission coefficient (S21) using coupled double pick-up probe technique. The double pick-up probe technique uses two overlapped small (1.5 cm in diameter) sniffer coils made from semi-rigid coaxial cable. During the benchtop experiment the sniffer loop 1 that is connected to port 1 of the VNA transmits RF energy to the resonant element under test and sniffer loop 2 that is connected to port 2 of the VNA as a pick-up coil to detect currents circulated in the resonator under test. The quality factor (Q-factor) of each BC-SRR was calculated as f 0 /Δ f , where Δ f is the FWHM bandwidth of the measured S21 using the double pick-up probe. Bench top experiments were conducted under loaded and unloaded (free space) conditions. For loaded condition we used a cylindrical phantom (15 cm in diameter and 30 cm in height; relative permittivity: 75; conductivity: 0.60 S/m).
The distributed capacitance between two metal layers is one of the key factors that controls the operating frequency and governed by the interlayer thickness. The distributed capacitance is inversely proportional to the interlayer thickness. A thinner interlayer confines higher electric field intensities in the interlayer region to achieve higher distributed capacitance, resulting in lowered f 0 . The effect of the interlayer thickness was evaluated by measuring S-parameters of BC-SRRs with different interlayer thicknesses. We also assessed the bending effect on the f 0 under various bending conditions.

2.3. MRI Experiments

We conducted the phantom experiments to examine the voxel-wise behavior of the RF enhancer on B 1 + efficiency and signal sensitivity ( B 1 − ). Measurements of B 1 + and B 1 − values at varying distances from the enhancer were taken under different applied RF voltages. In-vivo MRI experiments were conducted on three healthy subjects on a 7T scanner (Magnetom, Siemens Healthineers, Erlangen, Germany) using single-channel transmit and 32-channel receive (1Tx/32Rx) Nova head coil. The human experimental procedures were approved by the local institutional review board. During the in-vivo experiment the enhancer was seated within the inferior position of the coil behind the upper (suboccipital) neck and covering the posterior fossa to recover the signal dropout due to a lower B 1 + efficiency in this region.
In-vivo dMRI were obtained with and without the enhancer with 1.05 mm isotropic resolutions, GRAPPA acceleration factor=3, repetition time/echo time (TE/TR)=67.6/7200 ms, b-value=1500 s/mm2, field-of-view (FOV)=210 × 210 mm2, multiband acceleration factor=2, total scan time=18.5 minutes), 64 diffusion directions and four b0 acquisitions, each acquired twice with anterior-posterior (AP) and PA phase encode directions to allow gradient nonlinearity correction in post-processing.
In-vivo dMRI data were first evaluated by calculating the SNR on a voxel-wise basis in the cerebellum from b0 images acquired with and without the enhancer in place. The diffusion weighted imaging (DWI) series from both AP and PA directions were then compiled into a single volume, and the combined diffusion image was denoised and corrected for eddy-current distortions, subject motion, and B 1 + inhomogeneity using MRtrix [42]. The post-processed diffusion data was subsequently used to generate whole-brain tractography using TractSeg [43], of which tracts of the posterior fossa were selected for study. These tracts are the Corticospinal tract (CST), Superior Cerebellar Peduncle (SCP), and Inferior Cerebellar Peduncle (ICP).

3. Results

As we mentioned earlier, and displayed in Figure 1, the coupling between the applied magnetic field and BC-SRR induces a surface current on the metallization layers, consequently, it results in additional H-field near the resonator. The E-field at the dielectric layer between conductive metallization layers indicates that the E-field is mainly confined in the interlayer region does not spill over to the surrounding tissue.
Similar to a single resonator, interaction of the RF enhancer (matrix of BC-SRRs) with the EM field generated by the MRI coil caused a secondary magnetic field near the enhancer, leading to an improvement in the total magnetic field near the enhancer. Numerical simulations show that the presence of the enhancer resulted in 2.1-fold enhancement in B 1 + efficiency in the region of interest (ROI) encircled with dashed yellow (Figure 3a). We also studied the SAR distribution in the head model that shows SAR maps in the region with the highest SAR with 10 gr averaging without and in the presence of the RF enhancer. These results show that by placing the enhancer the SAR level is increased 38% 10 gr of averaging in the ROI encircled with dashed yellow (Figure 3b). These numbers should be considered to determine the upper limit of the applied RF power for the imaging sequences to stay within the safe levels.
The simulation results also show that inserting the RF enhancer inside the coil causes a slight shift (< 1MHz) in the resonance behavior of the coil.
The BC-SRR electrical characteristics are studied in terms of measured S-parameters and Q-factor using a VNA under unloaded and loaded conditions (Figure 5a). S-parameter measurements of a single BC-SRR are shown in Figure 5b. An average loaded Q-factor of 14 and an average unloaded Q-factor of 31 were calculated. We evaluated the interlayer thickness effect on the f 0 under various thicknesses of 70 μm, 125 μm, 175 μm, and 250 μm (Figure 6a). Thinner interlayers led to the higher distributed capacitance, and consequently resulting in lowered f 0 . We also assessed the bending effect on the f 0 under various bending conditions of 15°, 30°, 45° and 90° which caused 0.5 MHz, 1.1 MHz, and 1.8 MHz up shift in the frequency, respectively (Figure 6b).
BC-SRRs with optimized design parameters, tuned to 312 MHz (Figure 2b, 5% above the Larmor frequency at 7T) were used to build a matrix of resonators. The resonator elements are decoupled from each other using critically overlapping technique. From the perspective of S-parameter measurement, to minimize the inductive decoupling between resonators, the distance between neighboring resonators should be adjusted such that the frequency with minimum S21 is equal to the tuned frequency, 312 MHz. Decoupling between two resonators was assessed by measuring S21 while all other neighboring resonators were detuned. The coupling measurements of a single resonator relative to the adjacent resonators show an acceptable decoupling level between the neighboring resonators (< − 17 dB).
Specific safety considerations are necessary to assess the interaction of the applied EM field with the surface array so that SAR level and tissue heating are not significantly elevated. Following a suitable modification of ASTM standards (Supplementary A), safety heating test was performed to ensure that tissue heating remained below established safety limits [44,45].
For the phantom MRI experiment, the RF enhancer was positioned inside the head coil, particularly in regions with lower transmit efficiency, with the phantom placed on top of the enhancer (Figure 7a). The experiment was conducted both with and without the enhancer in place under different applied voltages. When the enhancer was absent, the B 1 + value exhibited a linear increase with the applied RF voltage at different distances from the enhancer (Figure 7a). With the enhancer in place, the B 1 + value increased linearly with the applied RF voltage up to approximately 200 V (Figure 7c), beyond which the rate of increase in B 1 +   value decreased due to the RF over-flipping. On average, the addition of the enhancer resulted in a B 1 +   enhancement of 2.3-fold across all applied voltages and distances. Assessing B 1 − sensitivity without the enhancer revealed that increasing the applied voltage led to an increase in the B 1 − value (Figure 7d). However, at greater distances from the enhancer, the rate of increase in B 1 − decreased at higher voltage levels due to approaching the Ernst angle. In the presence of the enhancer, increasing the applied voltage resulted in an increase in B 1 − values, but at higher voltages, the rate of increase decreased (Figure 7e). Comparing B 1 − values, the presence of the enhancer yielded an average enhancement of 1.7-fold.
intensity from different distances under varying applied RF voltage without using the enhancer. c) Pixel-wise B 1 + intensity from different distances under varying applied RF voltage using the enhancer. d) B 1 − changes by varying the applied RF voltage at different distances without the enhancer. e) B 1 − changes by varying the applied RF voltage at different distances in the presence of the enhancer.
The spatial distribution of the B 1 + maps in the in-vivo MRI experiments showed that present of the enhancer improved performance in the posterior fossa. The average transmit efficiency across the ROI showed a mean 1.9-fold improvement in the presence of the enhancer. This improvement may transfer to the SNR enhancement in the MR images. Quantitatively comparing B 1 − maps obtained without the enhancer and using the enhancer showed an average of 1.4-fold enhancement in the ROI in the presence of the enhancer. Qualitative assessment exhibited that presence of the enhancer effectively improved MR signal in this region and recovered the signal dropouts within the region (See supplementary B for detailed explanations).
Analysis of dMRI with and without the enhancer indicated improved SNR and contrast in the posterior fossa in the b0 images in three different planes (Figure 8a). SNR was calculated by dividing the signal intensity in the ROI by the standard deviation of the noise. SNR enhancement of 2.9-fold, 2.7-fold, and 2.4-fold was calculated in the coronal, axial, and sagittal planes, respectively. To isolate the effect of the enhancer, FA maps were obtained in three different planes to compare fibers conspicuity in the presence of the RF enhancer. The use of the standard 1Tx head coil without the enhancer yielded lower signal intensity in the cerebellum. This translated into noisy depictions of principle fiber orientations within these regions. In contrast, the use of the enhancer significantly improved local signal sensitivity, and thereby the SNR. The use of the enhancer recovered tissue in the cerebellum and improved fiber orientation estimation performances in this region (Figure 8b).
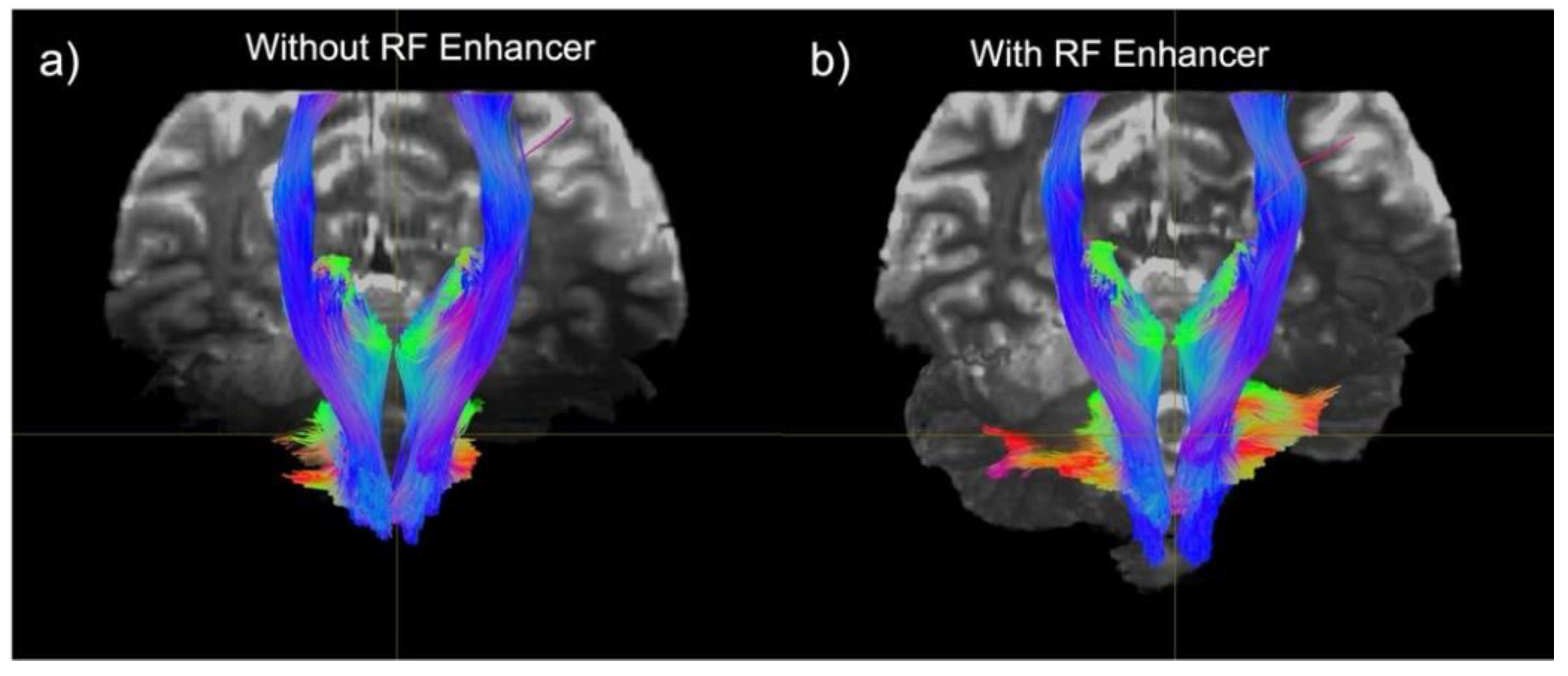
We subsequently generated tractography maps to analyze the effect of the RF enhancer on white-matter pathway visualization. We found improvement in SNR resulting in enhanced visualization of tracts in the cerebellum and brainstem. Improvement in SNR can be seen as increased conspicuity in cerebellar and corticospinal tracts, and in increased coverage of the cerebellum in the background b0 image (Figure 9).

4. Discussion

In this study, we demonstrated how a novel inductively coupled RF enhancer improves dMRI at 7T. The wireless RF enhancer is a thin and flexible structure consisting of multiple BC-SRRs tuned to operate at 7T MRI. The proposed device works based on the inductive coupling between the MRI coil and the enhancer during both the RF transmission and signal reception. In-vivo placement of the enhancer inside the head coil over the posterior fossa (Figure 2), a region with intrinsically-reduced transmit efficiency, enhances B 1 + efficiency to improve signal sensitivity in a region known to have poorer SNR. With this position, it will be possible to closely examine the effectiveness of the surface enhancer on the human brain dMRI at 7T. We started by using EM simulation to optimize the design parameters for tuning the resonator’s operating frequency. Our prior publications have shown that optimization of transmit efficiency enhancement with the RF enhancer requires the resonance frequency to be adjusted 5% above the Larmor frequency [30,41].
Placing of the RF enhancer in the caudal part of the head may cause bending on the device that may affect the electrical characteristics and EM distribution. Through benchtop experiments, we demonstrated that the resonance frequency shift associated with varying bending angles was negligible. Research by other groups indicated that bending the resonator up to 45° did not significantly affect the field distributions [23,46].
The mechanism through which the enhancer increases SNR lies in B 1 + efficiency and B 1 − sensitivity within the area effected by the enhancer. The enhancer yields more uniform magnetic field distribution across the anatomy of interest. However, enhancement of the electric field may result in elevated SAR raising safety concerns related to tissue heating. Heating test based on ASTM guideline reported a 34% increase in SAR. Therefore, to safely conduct the scan in the presence of the enhancer the SAR limits applied by the sequence should not exceed 66%.
The in-vivo performance of the enhancer was assessed in three human subjects. Integration of the enhancer with the head coil led to 2.1-fold B 1 + efficiency and 1.4-fold normalized B 1 − sensitivity enhancement within the ROI. These enhancements resulted in clear structural visualization and better depiction of white matter bundles and fiber orientation.
We have designed this device to recover the signal dropouts and in the regions with intrinsically lower transmit efficiency without material degradation or complex hardware requirements. This proposed technique to improve dMRI at 7T can be used in conjunction with other B 1 + shimming methods such as dielectric pads and pTx systems. Studies by our team and others showed that a hybrid configuration through combining a resonators structure with a high permittivity material might improve the MRI at 7T [23,28]. Combining the RF enhancer with pTx systems may require additional SAR safety evaluations due to the interaction of the varying profile of the EM filed with the device which may cause high SAR hot spots.

5. Conclusions

We have evaluated the advantages of using the RF enhancer in conjunction with 1Tx head coil configurations for improving cerebellar dMRI at 7T. Our results show that using the device can significantly improve B 1 + efficiency and signal sensitivity in dMRI of the posterior fossa compared with a standard 1Tx configuration. Most notably, our data suggest that the use of the enhancer allowed for better depiction of principal fiber orientations and enhanced visualization of extended tracts to the brainstem and pons enabling more comprehensive delineation of the full white matter architecture. In conclusion, we believe that the enhancer will have great utility for rapid acquisition of high-quality, high-resolution whole brain dMRI, desirable for many neurological and clinical applications. The clinical importance of accurately mapping white matter tracts is salient when considering individualized treatment approaches for conditions such as epilepsy and movement disorders, where neurosurgical interventions with stimulation are increasingly common. The conceptualization of epilepsy as a network disorder emphasizes the importance of delineating structural connectivity, particularly involving the brainstem, to inform surgical planning and diagnostics.

Author Contributions

Conceptualization, A.A. and P.B.; methodology, V.S., M.L, A.A.G., G.V., and A.A; validation, V.S. and A.F.; formal analysis, V.S., and A.A.; investigation, A.A. and B.D.; resources, A.A. and P.B.; data curation, V.S., A.A.G., and A.F.; writing—original draft preparation, V.S. and A.F.; writing—review and editing, A.A., B.D., and P.B.; visualization, A.A, and B.D.; supervision, A.A, and P.B.; funding acquisition, A.A. and P.B.

Funding

This present study was supported by a NIH grants R01CA202911 and K01AG075178-01.

Institutional Review Board Statement

The study was conducted in accordance with the Declaration of Helsinki, and approved by the Institutional Review Board (or Ethics Committee) of the Icahn School of Medicine at Mount Sinai (study number:15-01168; approval date: 2/28/2022).

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Conflicts of Interest

“The authors declare no conflict of interest.”

References

  1. Callaghan, P.T., 45Physics of Diffusion, in Diffusion MRI: Theory, Methods, and Applications, P.D.K. Jones, Editor. 2010, Oxford University Press. p. 0.
  2. Mueller, B.A.; Lim, K.O.; Hemmy, L.; Camchong, J. Diffusion MRI and its Role in Neuropsychology. Neuropsychol. Rev. 2015, 25, 250–271. [CrossRef]
  3. Aboitiz, F.; Scheibel, A.B.; Fisher, R.S.; Zaidel, E. Fiber composition of the human corpus callosum. Brain Res. 1992, 598, 143–153. [CrossRef]
  4. Coelho, S.; Pozo, J.M.; Jespersen, S.N.; Jones, D.K.; Frangi, A.F. Resolving degeneracy in diffusion MRI biophysical model parameter estimation using double diffusion encoding. Magn. Reson. Med. 2019, 82, 395–410. [CrossRef]
  5. Lehéricy, S.; Ducros, M.; Van De Moortele, P.; Francois, C.; Thivard, L.; Poupon, C.; Swindale, N.; Ugurbil, K.; Kim, D. Diffusion tensor fiber tracking shows distinct corticostriatal circuits in humans. Ann. Neurol. 2004, 55, 522–529. [CrossRef]
  6. Shao, X.; Ma, S.J.; Casey, M.; D’orazio, L.; Ringman, J.M.; Wang, D.J. Mapping water exchange across the blood–brain barrier using 3D diffusion-prepared arterial spin labeled perfusion MRI. Magn. Reson. Med. 2019, 81, 3065–3079. [CrossRef]
  7. Uğurbil, K.; Xu, J.; Auerbach, E.J.; Moeller, S.; Vu, A.T.; Duarte-Carvajalino, J.M.; Lenglet, C.; Wu, X.; Schmitter, S.; Van de Moortele, P.F.; et al. Pushing spatial and temporal resolution for functional and diffusion MRI in the Human Connectome Project. NeuroImage 2013, 80, 80–104. [CrossRef]
  8. Gallichan, D. Diffusion MRI of the human brain at ultra-high field (UHF): A review. NeuroImage 2018, 168, 172–180. [CrossRef]
  9. Maruyama, S.; Fukunaga, M.; Fautz, H.-P.; Heidemann, R.; Sadato, N. Comparison of 3T and 7T MRI for the visualization of globus pallidus sub-segments. Sci. Rep. 2019, 9, 1–8. [CrossRef]
  10. Sadeghi-Tarakameh, A.; DelaBarre, L.; Lagore, R.L.; Torrado-Carvajal, A.; Wu, X.; Grant, A.; Adriany, G.; Metzger, G.J.; Van de Moortele, P.; Ugurbil, K.; et al. In vivo human head MRI at 10.5T: A radiofrequency safety study and preliminary imaging results. Magn. Reson. Med. 2020, 84, 484–496. [CrossRef]
  11. Verma, G.; Balchandani, P. Ultrahigh field MR Neuroimaging. Top. Magn. Reson. Imaging 2019, 28, 137–144. [CrossRef]
  12. Vu, A.; Auerbach, E.; Lenglet, C.; Moeller, S.; Sotiropoulos, S.; Jbabdi, S.; Andersson, J.; Yacoub, E.; Ugurbil, K. High resolution whole brain diffusion imaging at 7 T for the Human Connectome Project. NeuroImage 2015, 122, 318–331. [CrossRef]
  13. Wu, X.; Auerbach, E.J.; Vu, A.T.; Moeller, S.; Lenglet, C.; Schmitter, S.; Van de Moortele, P.; Yacoub, E.; Uğurbil, K. High-resolution whole-brain diffusion MRI at 7T using radiofrequency parallel transmission. Magn. Reson. Med. 2018, 80, 1857–1870. [CrossRef]
  14. Vaughan JT, G.M., Collins CM, et al, 7T vs. 4T: RF power, homogeneity, and signal-to-noise comparison in head images. Magn Reson Med, 2001. 46(1): p. 24-30.
  15. Ladd, M.E.; Bachert, P.; Meyerspeer, M.; Moser, E.; Nagel, A.M.; Norris, D.G.; Schmitter, S.; Speck, O.; Straub, S.; Zaiss, M. Pros and cons of ultra-high-field MRI/MRS for human application. Prog. Nucl. Magn. Reson. Spectrosc. 2018, 109, 1–50. [CrossRef]
  16. Van de Moortele PF, A.C., Adriany G, et al, B1 destructive interferences and spatial phase patterns at 7 T with a head trans- ceiver array coil. Magn Reson Med, 2005. 54: p. 1503-1518.
  17. Katscher, U.; Börnert, P. Parallel RF transmission in MRI. NMR Biomed. 2006, 19, 393–400. [CrossRef]
  18. Balchandani, P.; Khalighi, M.M.; Glover, G.; Pauly, J.; Spielman, D. Self-refocused adiabatic pulse for spin echo imaging at 7 T. Magn. Reson. Med. 2012, 67, 1077–1085. [CrossRef]
  19. Vorobyev, V.; Shchelokova, A.; Zivkovic, I.; Slobozhanyuk, A.; Baena, J.D.; del Risco, J.P.; Abdeddaim, R.; Webb, A.; Glybovski, S. An artificial dielectric slab for ultra high-field MRI: Proof of concept. J. Magn. Reson. 2020, 320, 106835. [CrossRef]
  20. Webb, A. Dielectric materials in magnetic resonance. Concepts Magn. Reson. Part A 2011, 38A, 148–184. [CrossRef]
  21. Yang QX, M.W., Wang J, et al, Manipulation of image intensity distribution at 7.0 T: passive RF shimming and focusing with dielectric materials. J Magn Reson Imaging, 2006. 24(1): p. 197-202.
  22. Haines, K., N.B. Smith, and A.G. Webb, New high dielectric constant materials for tailoring the B1+ distribution at high magnetic fields. J Magn Reson, 2010. 203(2): p. 323-7.
  23. Schmidt, R.; Slobozhanyuk, A.; Belov, P.; Webb, A. Flexible and compact hybrid metasurfaces for enhanced ultra high field in vivo magnetic resonance imaging. Sci. Rep. 2017, 7, 1–7. [CrossRef]
  24. Koloskov, V.; Brink, W.M.; Webb, A.G.; Shchelokova, A. Flexible metasurface for improving brain imaging at 7T. Magn. Reson. Med. 2024, 92, 869–880. [CrossRef]
  25. Motovilova, E.; Huang, S.Y. Hilbert Curve-Based Metasurface to Enhance Sensitivity of Radio Frequency Coils for 7-T MRI. IEEE Trans. Microw. Theory Tech. 2019, 67, 615–625. [CrossRef]
  26. Gomez, T.S.V.; Dubois, M.; Rustomji, K.; Georget, E.; Antonakakis, T.; Vignaud, A.; Rapacchi, S.; Girard, O.M.; Kober, F.; Enoch, S.; et al. Hilbert fractal inspired dipoles for passive RF shimming in ultra-high field MRI. Photon- Nanostructures - Fundam. Appl. 2022, 48, 100988. [CrossRef]
  27. Stoja, E.; Konstandin, S.; Philipp, D.; Wilke, R.N.; Betancourt, D.; Bertuch, T.; Jenne, J.; Umathum, R.; Günther, M. Improving magnetic resonance imaging with smart and thin metasurfaces. Sci. Rep. 2021, 11, 1–12. [CrossRef]
  28. Alipour, A.; Seifert, A.C.; Delman, B.N.; Hof, P.R.; Fayad, Z.A.; Balchandani, P. Enhancing the brain MRI at ultra-high field systems using a meta-array structure. Med Phys. 2023, 50, 7606–7618. [CrossRef]
  29. Alipour, A., et al., Enhanced Ultra-High Field Brain MRI Using a Wireless Radiofrequency Sheet. International Society for Magnetic Resonance in Medicine, 2021.
  30. Alipour, A.; Seifert, A.C.; Delman, B.N.; Robson, P.M.; Shrivastava, R.; Hof, P.R.; Adriany, G.; Fayad, Z.A.; Balchandani, P. Improvement of magnetic resonance imaging using a wireless radiofrequency resonator array. Sci. Rep. 2021, 11, 1–12. [CrossRef]
  31. Alipour, A.; Gokyar, S.; Algin, O.; Atalar, E.; Demir, H.V. An inductively coupled ultra-thin, flexible, and passive RF resonator for MRI marking and guiding purposes: Clinical feasibility. Magn. Reson. Med. 2018, 80, 361–370. [CrossRef]
  32. Gokyar, S.; Alipour, A.; Unal, E.; Atalar, E.; Demir, H.V. Magnetic Resonance Imaging Assisted by Wireless Passive Implantable Fiducial e-Markers. IEEE Access 2017, 5, 19693–19702. [CrossRef]
  33. Syms, R.R.A.; Young, I.R.; Ahmad, M.M.; Rea, M. Magnetic resonance imaging using linear magneto-inductive waveguides. J. Appl. Phys. 2012, 112. [CrossRef]
  34. Alipour, A.; Unal, E.; Gokyar, S.; Demir, H.V. Development of a distance-independent wireless passive RF resonator sensor and a new telemetric measurement technique for wireless strain monitoring. Sensors Actuators A: Phys. 2017, 255, 87–93. [CrossRef]
  35. Gokyar, S.; Alipour, A.; Unal, E.; Atalar, E.; Demir, H.V. Wireless deep-subwavelength metamaterial enabling sub-mm resolution magnetic resonance imaging. Sensors Actuators A: Phys. 2018, 274, 211–219. [CrossRef]
  36. Freire, M.J.; Lopez, M.A.; Meise, F.; Algarin, J.M.; Jakob, P.M.; Bock, M.; Marques, R. A Broadside-Split-Ring Resonator-Based Coil for MRI at 7 T. IEEE Trans. Med Imaging 2013, 32, 1081–1084. [CrossRef]
  37. Marques, R.; Mesa, F.; Martel, J.; Medina, F. Comparative analysis of edge- and broadside-coupled split ring resonators for metamaterial design - Theory and experiments. IEEE Trans. Antennas Propag. 2003, 51, 2572–2581. [CrossRef]
  38. Dia, K.K.H.; Hajiaghajani, A.; Escobar, A.R.; Dautta, M.; Tseng, P. Broadside-Coupled Split Ring Resonators as a Model Construct for Passive Wireless Sensing. Adv. Sens. Res. 2023, 2. [CrossRef]
  39. Eryaman, Y.; Akin, B.; Atalar, E. Reduction of implant RF heating through modification of transmit coil electric field. Magn. Reson. Med. 2010, 65, 1305–1313. [CrossRef]
  40. Celik, H.; Atalar, E. Reverse polarized inductive coupling to transmit and receive radiofrequency coil arrays. Magn. Reson. Med. 2012, 67, 446–456. [CrossRef]
  41. Wang, S.; Murphy-Boesch, J.; Merkle, H.; Koretsky, A.P.; Duyn, J.H. $B_1$ Homogenization in MRI by Multilayer Coupled Coils. IEEE Trans. Med Imaging 2009, 28, 551–554. [CrossRef]
  42. Tournier, J.-D.; Smith, R.; Raffelt, D.; Tabbara, R.; Dhollander, T.; Pietsch, M.; Christiaens, D.; Jeurissen, B.; Yeh, C.-H.; Connelly, A. MRtrix3: A fast, flexible and open software framework for medical image processing and visualisation. NeuroImage 2019, 202, 116137. [CrossRef]
  43. Wasserthal, J.; Neher, P.; Maier-Hein, K.H. TractSeg - Fast and accurate white matter tract segmentation. NeuroImage 2018, 183, 239–253. [CrossRef]
  44. ASTM, Measurement of radio frequency induced heating on or near passive implants during magnetic resonance imaging. F2482-11a, 2011. ASTM F2482-11a.
  45. FDA, Safety Guidelines for Magnetic Resonance Imaging Equipment in Clinical Use. 2014.
  46. Moniruzzaman; Islam, M.T.; Islam, R.; Misran, N.; Samsuzzaman Coupled ring split ring resonator (CR-SRR) based epsilon negative metamaterial for multiband wireless communications with high effective medium ratio. Results Phys. 2020, 18, 103248. [CrossRef]
Preprints 112945 g001
Figure 1. a) 3D schematic of a BC-SRR. b) Surface current distribution along the rings. c) Cross-section view of the magnetic (H) field distribution generated by the BC-SRR. d) Cross-section view of the electric (E) field distribution generated by the BC-SRR.
Figure 1. a) 3D schematic of a BC-SRR. b) Surface current distribution along the rings. c) Cross-section view of the magnetic (H) field distribution generated by the BC-SRR. d) Cross-section view of the electric (E) field distribution generated by the BC-SRR.
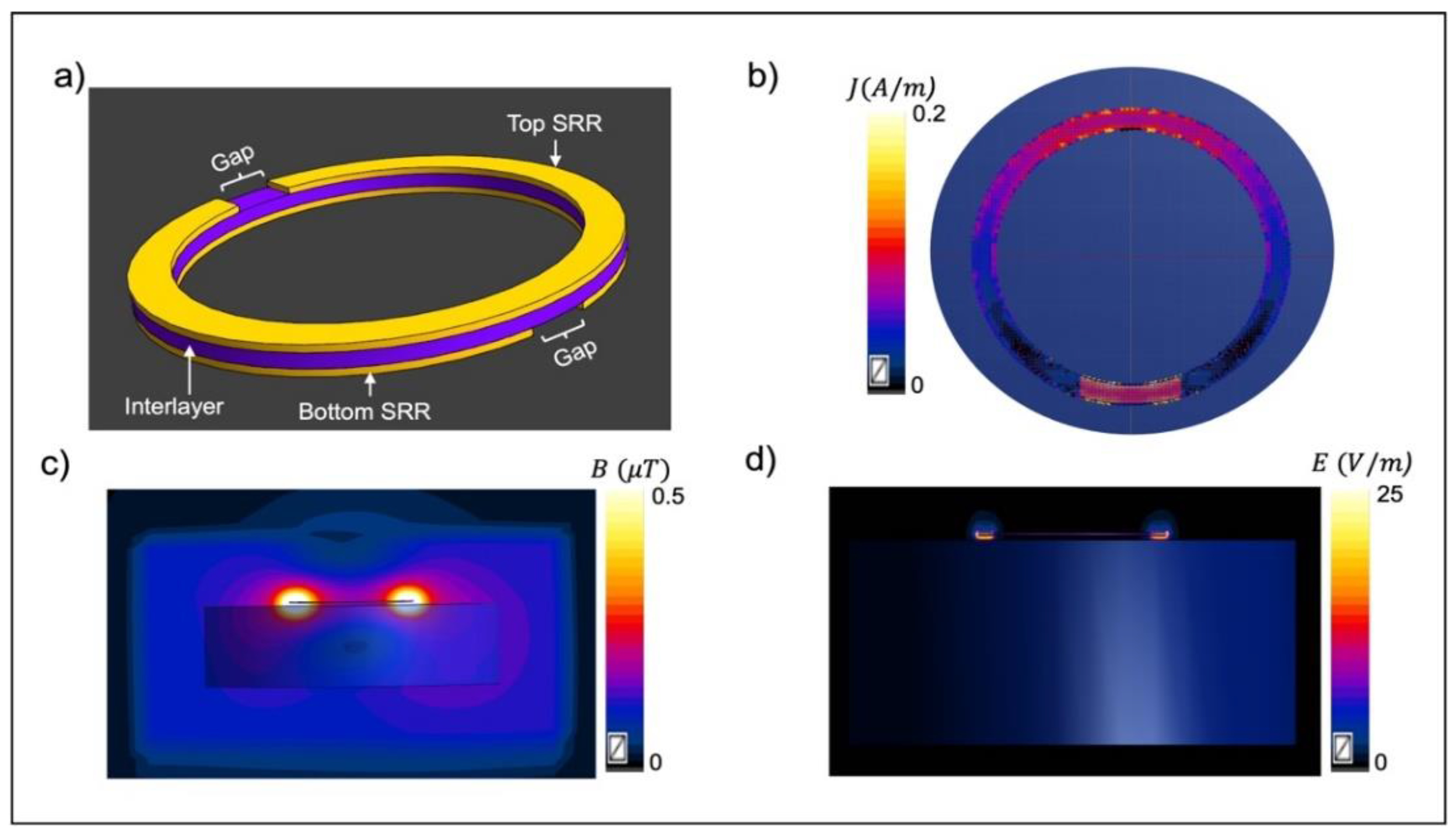
Preprints 112945 g001
Preprints 112945 g002
Figure 2. Schematic of the MRI birdcage head coil, RF enhancer, and head model. The enhancer is positioned at the base of the skull covering the posterior fossa (right). The head together with the enhancer goes inside the head coil (left).
Figure 2. Schematic of the MRI birdcage head coil, RF enhancer, and head model. The enhancer is positioned at the base of the skull covering the posterior fossa (right). The head together with the enhancer goes inside the head coil (left).
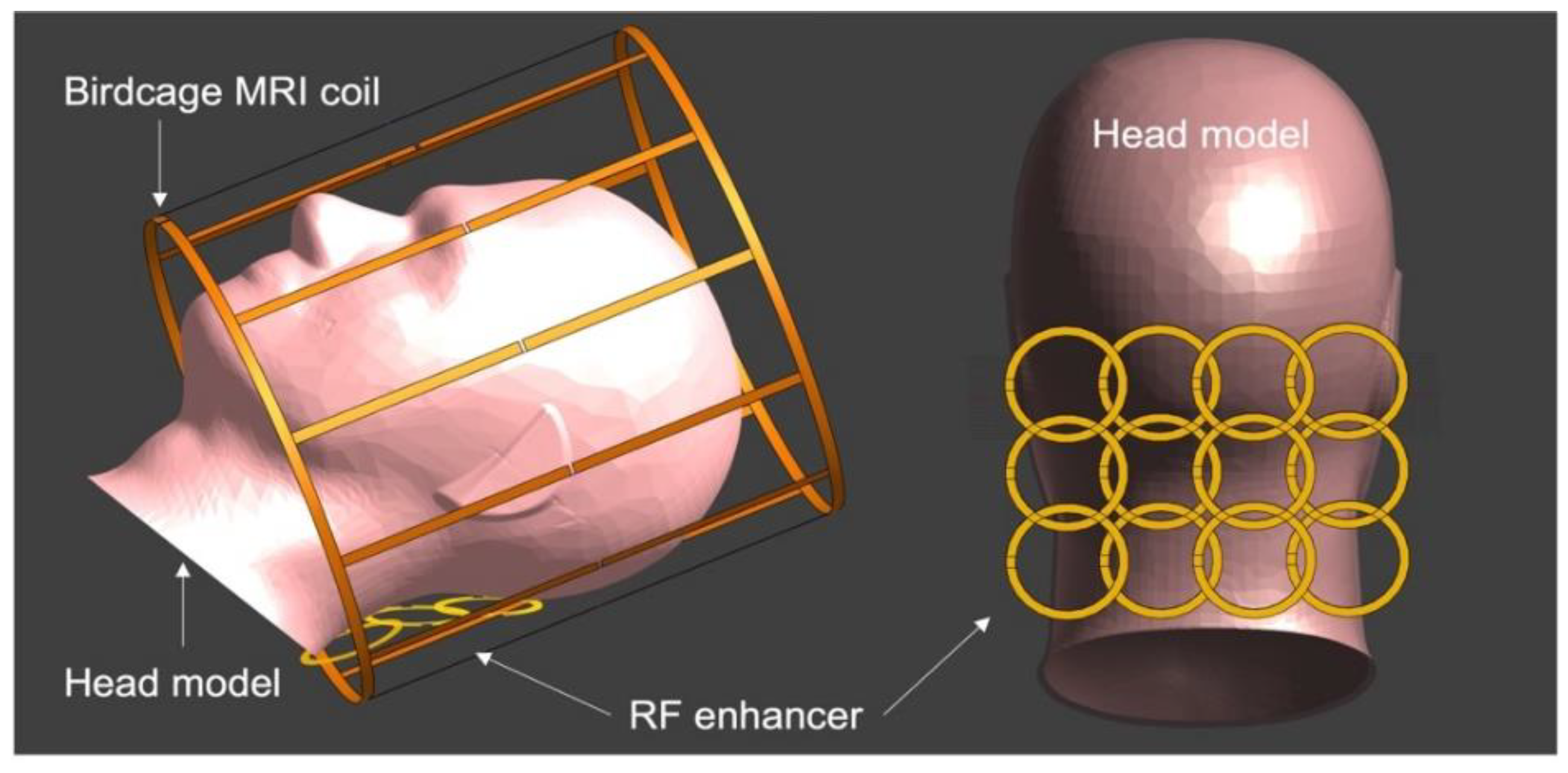
Preprints 112945 g002
Preprints 112945 g003
Figure 3. a) The use of the enhancer resulted in a 2.1-fold improvement in transmit efficiency in the ROI (encircled with dashed yellow) in the presence of the RF enhancer (left) compared to the cases without the enhancer (right). b) In the presence of the RF enhancer, the local SAR increased by 38% in the area covered by the enhancer, as indicated by a circle.
Figure 3. a) The use of the enhancer resulted in a 2.1-fold improvement in transmit efficiency in the ROI (encircled with dashed yellow) in the presence of the RF enhancer (left) compared to the cases without the enhancer (right). b) In the presence of the RF enhancer, the local SAR increased by 38% in the area covered by the enhancer, as indicated by a circle.
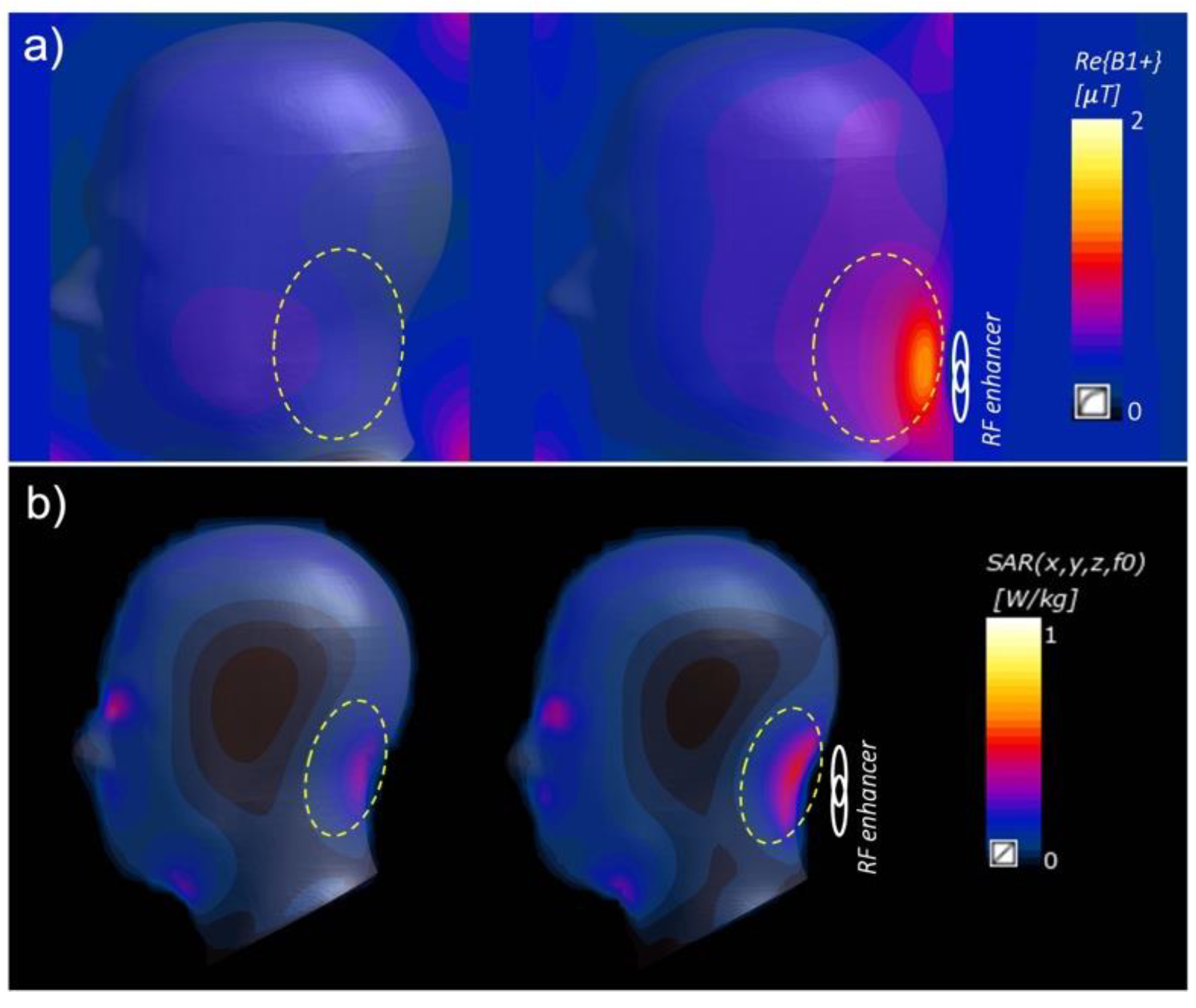
Preprints 112945 g003
Preprints 112945 g004
Figure 4. Effect of the RF enhancer on the resonance behavior of the birdcage coil. Comparing the S11 results from the coil without the enhancer (a) and the coil with the enhancer (b) shows that adding the enhancer results in a slight up-shift (> 1MHz) in the resonance frequency of the birdcage coil.
Figure 4. Effect of the RF enhancer on the resonance behavior of the birdcage coil. Comparing the S11 results from the coil without the enhancer (a) and the coil with the enhancer (b) shows that adding the enhancer results in a slight up-shift (> 1MHz) in the resonance frequency of the birdcage coil.
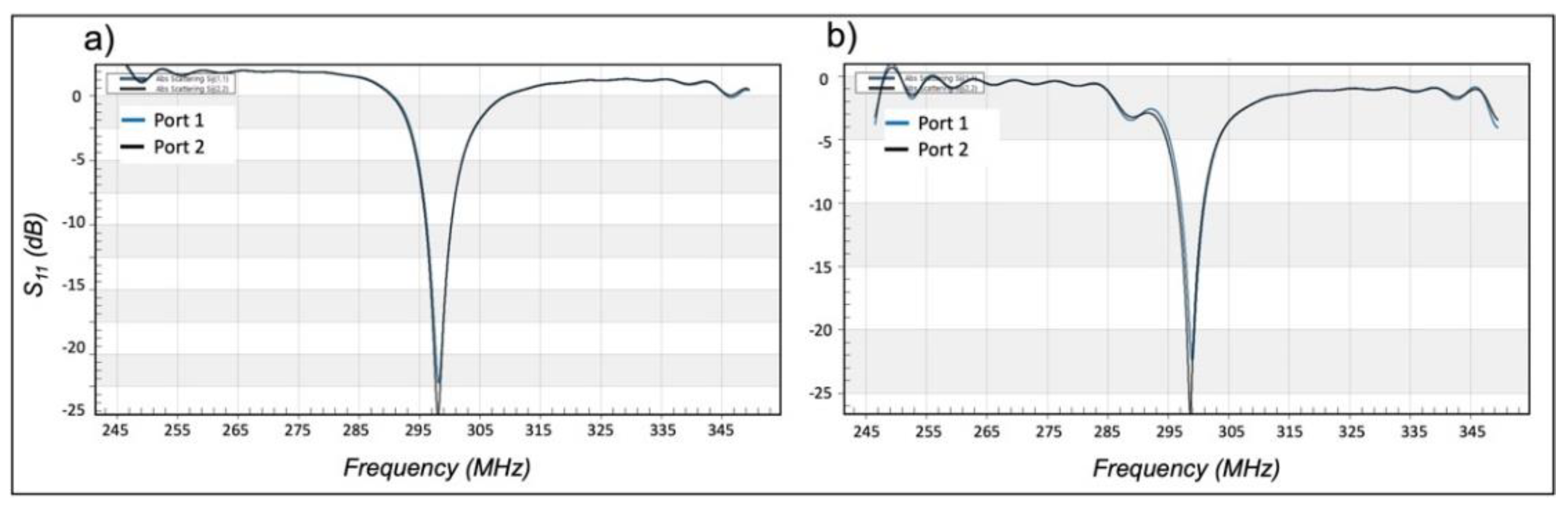
Preprints 112945 g004
Preprints 112945 g005
Figure 5. a) Benchtop test setup for measuring the resonance behavior of a single BC-SRR. b) S-Parameter measurement results for a BC-SRR under test in both unloaded (dashed line) and loaded (solid line) conditions.
Figure 5. a) Benchtop test setup for measuring the resonance behavior of a single BC-SRR. b) S-Parameter measurement results for a BC-SRR under test in both unloaded (dashed line) and loaded (solid line) conditions.
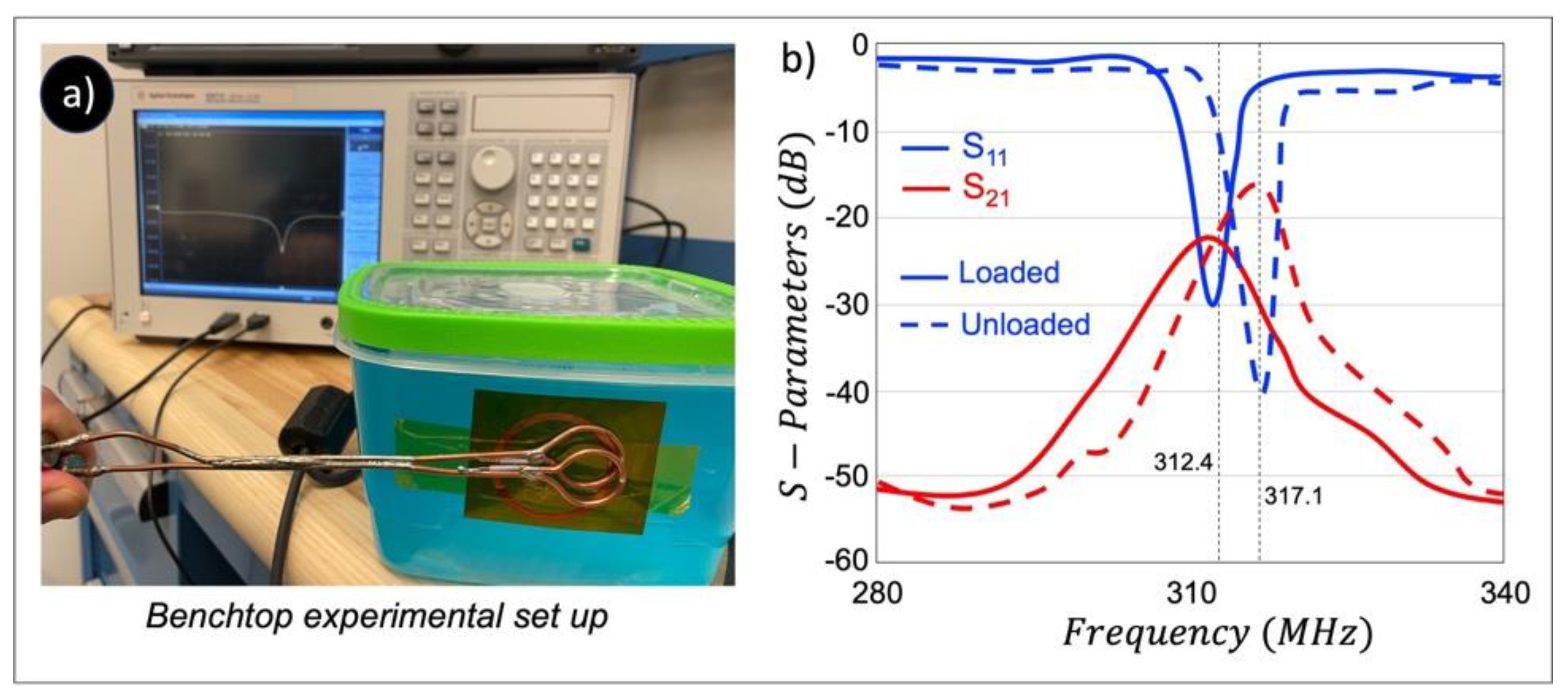
Preprints 112945 g005
Preprints 112945 g006
Figure 6. Evaluation of the effect of the interlayer thickness (a) and bending effect (b) on the resonance behavior of a single BC-SRR.
Figure 6. Evaluation of the effect of the interlayer thickness (a) and bending effect (b) on the resonance behavior of a single BC-SRR.
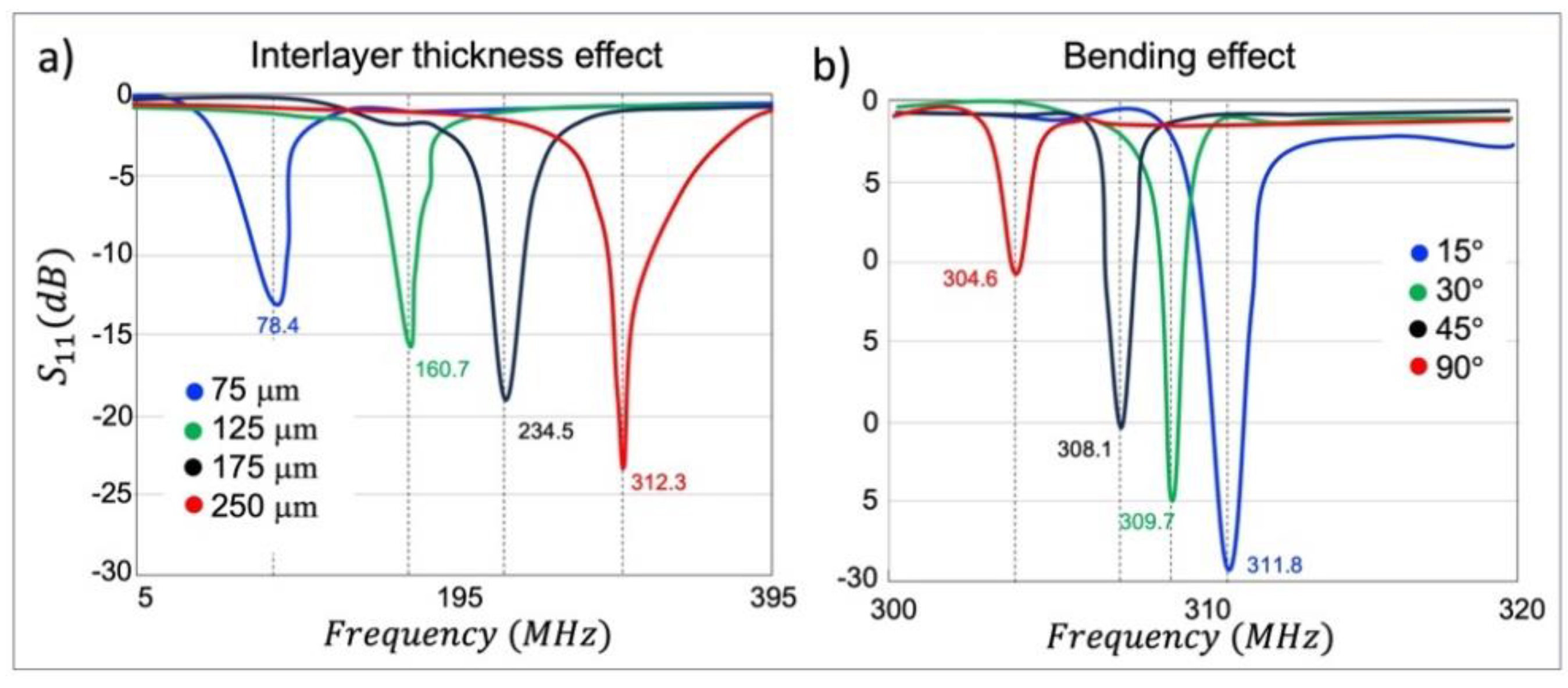
Preprints 112945 g006
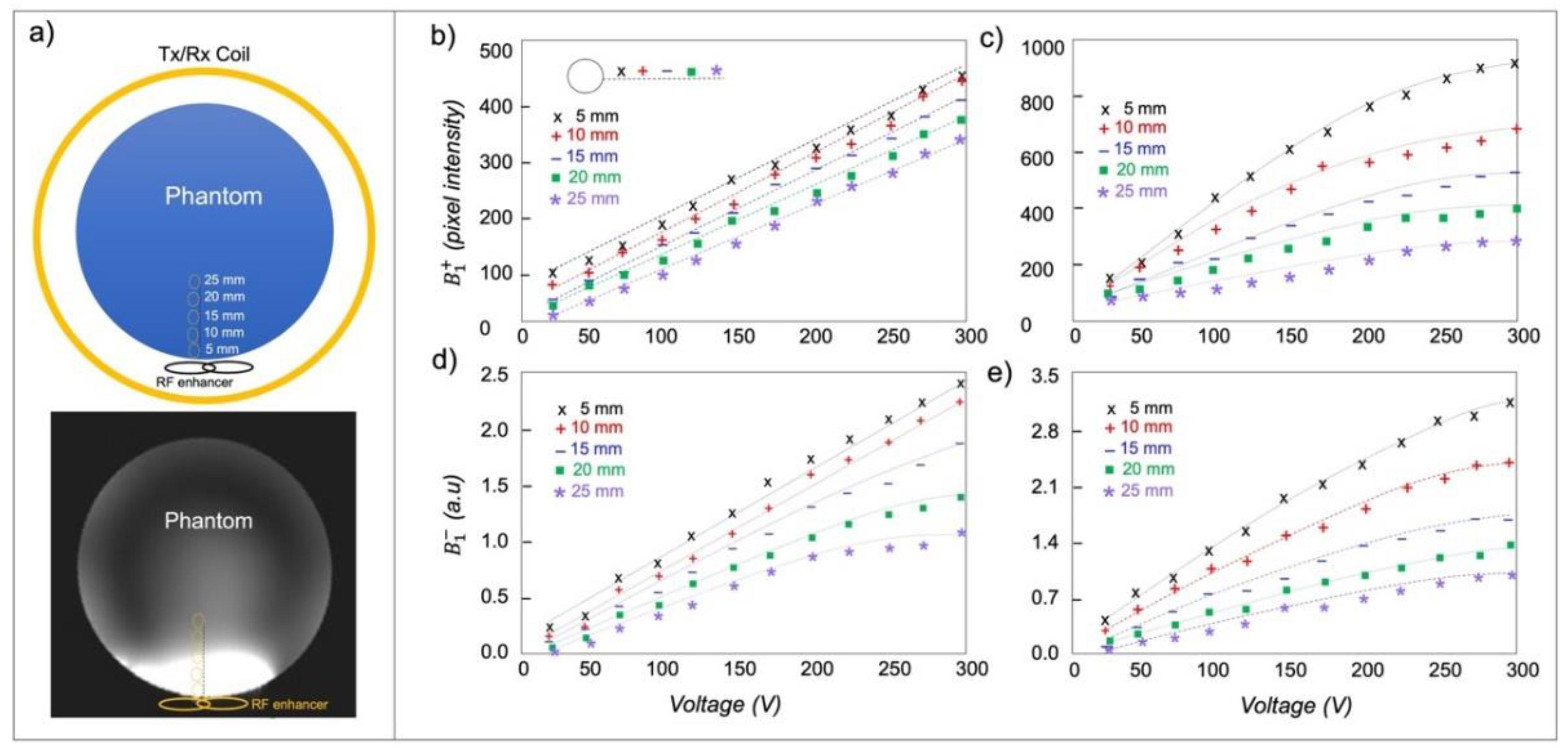
Preprints 112945 g007
Figure 7. a) schematic of the MRI phantom experiment with the corresponding MRI images in the coronal plane with the enhancer. b) Pixel-wise B 1 +
Figure 7. a) schematic of the MRI phantom experiment with the corresponding MRI images in the coronal plane with the enhancer. b) Pixel-wise B 1 +
Preprints 112945 g007
Preprints 112945 g008
Figure 8. a) Comparison of b0 images of dMRI data acquisition using the single-channel transmit coil without the enhancer (left column) and with the enhancer (right column). Note that the use of the RF enhancer increased the SNR across the cerebellum and brain stem (encircled by dashed yellow) by an average factor of 2.6. Numbers indicate the SNR in the ROI. b) Comparing color fractional anisotropy (FA) maps (in the range of [0 1]) obtained using a single channel transmit head coil without the enhancer (left column) and with the enhancer (right column). The color representing the orientation of the principal fiber (red: left-right; green: A-P; blue: inferior-superior). The result was a clearer depiction of fibers and better estimation of multiple fiber orientations.
Figure 8. a) Comparison of b0 images of dMRI data acquisition using the single-channel transmit coil without the enhancer (left column) and with the enhancer (right column). Note that the use of the RF enhancer increased the SNR across the cerebellum and brain stem (encircled by dashed yellow) by an average factor of 2.6. Numbers indicate the SNR in the ROI. b) Comparing color fractional anisotropy (FA) maps (in the range of [0 1]) obtained using a single channel transmit head coil without the enhancer (left column) and with the enhancer (right column). The color representing the orientation of the principal fiber (red: left-right; green: A-P; blue: inferior-superior). The result was a clearer depiction of fibers and better estimation of multiple fiber orientations.
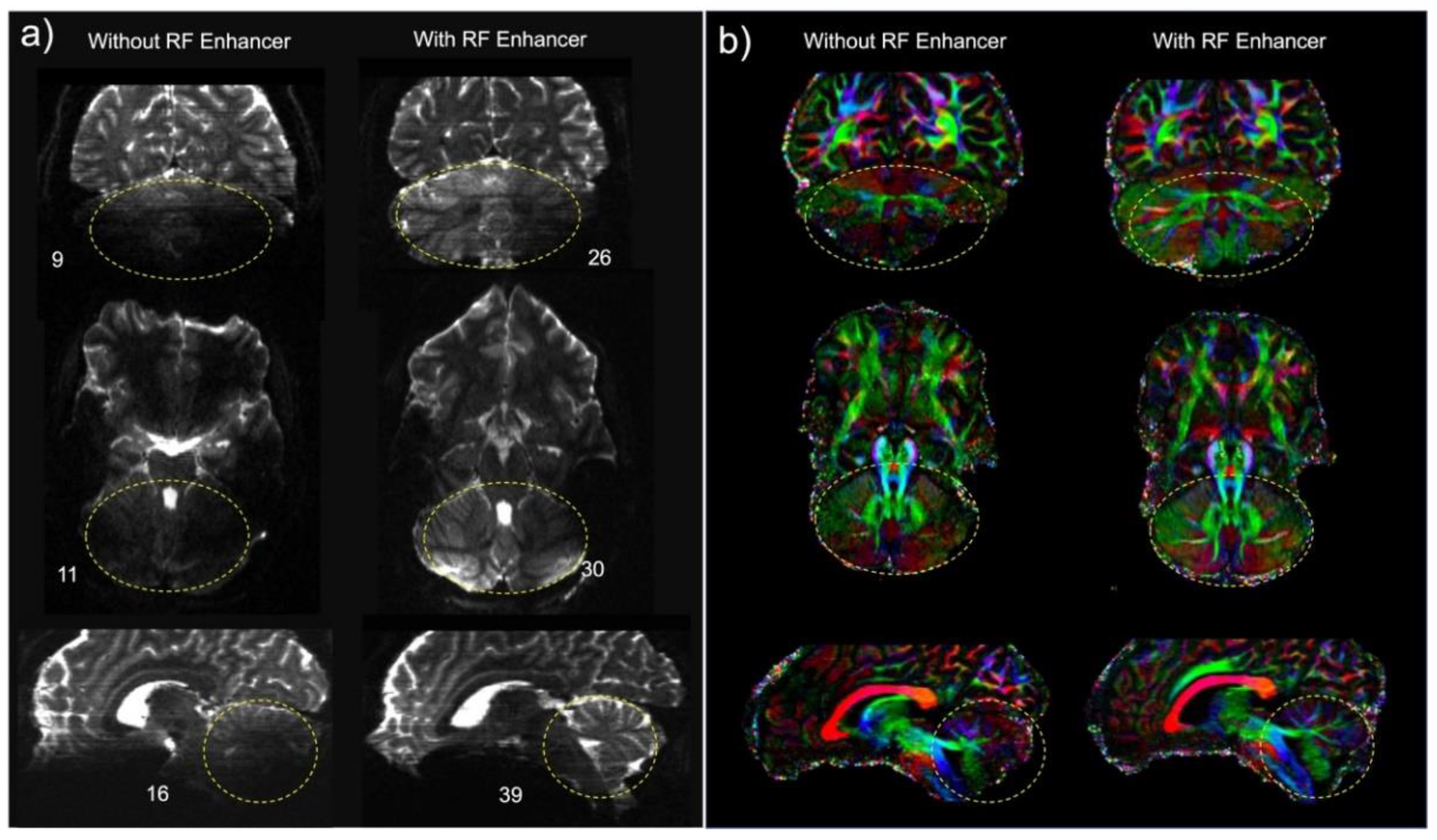
Preprints 112945 g008
Preprints 112945 g009
Figure 9. Comparison of tractography generated using a 1Tx head coil without the enhancer (a) and with the enhancer (b). The fibers shown make up the primary white-matter pathways of the brainstem and cerebellum: the Corticospinal tract, and the Superior and Inferior Cerebellar Peduncles. Tracts are overlaid onto their respective b0 images.
Figure 9. Comparison of tractography generated using a 1Tx head coil without the enhancer (a) and with the enhancer (b). The fibers shown make up the primary white-matter pathways of the brainstem and cerebellum: the Corticospinal tract, and the Superior and Inferior Cerebellar Peduncles. Tracts are overlaid onto their respective b0 images.
Preprints 112945 g009
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated