Prerpints.org logo
Preprint
Article

Human-Inspired Decision-Making in AI: Leveraging Insights from Visual Perception for Real-Time Sensor Data Processing

Altmetrics

Downloads

122

Views

62

Comments

0

Submitted:

24 July 2024

Posted:

25 July 2024

You are already at the latest version

Alerts
Abstract
This paper introduces a novel decision-making approach grounded in insights into human visual perception of change. Modern technologies such as internet of things (IoT) provide us with large amounts of sensor data that need to be processed in real time and decisions made with a high degree of accuracy and reliability. Artificial intelligence (AI) methods are welcome in this context and need to be upgraded to meet actual challenges. While modern computing capabilities facilitate rapid data processing, the real-time demands of vast sensor data necessitate swift responses across the cyber chain, often leading to compromises in solution quality to circumvent combinatorial search complexities. Determining the adequacy of a solution entails varied approaches, often relying on heuristic methodologies. We illustrate our original approach with an example of a selected detail of a differential evolution algorithm, where we have to make a decision to adopt the best solution so far. We propose an approach inspired by human perceptual features that exploits the Weber-Fechner law to emulate human judgements, and offers a promising way to improve decision making in AI applications and real-time requirements fulfillment. Our proposed methodology demonstrates applicability across diverse AI scenarios involving numerical data, effectively mirroring human perception abilities.
Keywords: 
Subject: Engineering  -   Other

1. Introduction

Modern technologies such as the Internet of Things (IoT) bring the availability of large amounts of sensor data. This data needs to be processed appropriately. Often, we need to ensure real-time processing in order to establish a cyber-loop of control. Huge amounts of data can be processed efficiently by using artificial intelligence (AI) methods. However, the use of AI approaches typically requires a lot of computational resources: both hardware and computational time. This is in correlation with the requirement to operate in real-time, despite the increasing computing power available in modern computing devices. In addition, it makes sense to place the signal processing as close as possible to the sensors, which again results in rather limited computational possibilities due to the limitations of computers. The authors of this paper are of the opinion that methods close to human cognitive processes can be used to compensate for the limited computational resources. With our paper, we want to highlight the possibility of using human-inspired decision-making in AI for real-time processing of sensor data. We have used insights about human properties of visual perception and applied them to the case of a selected detail of a Differential Evolution (DE) algorithm, when we have to make a judgment about adopting the best solution so far. With the proposed original approach, we have ensured the completion of the DE process within the set constraints of the work in real-time and in the way a human would do it.
The first known theories of the eye and visual perception are owed to Greek philosophers (Hippocrates, Aristotle, Plato) [1], but Aristotle linked the eye and the center of sensation, which was the heart; this theory was valid until the experiments carried out by Galen of Pergamon in the second century AD. The science linking physical stimuli and psychological processes in humans was founded by Gustav Fechner and called psychophysics. Psychophysics define [2] as “study of quantitative relations between psychological events and physical events or, more specifically, between sensations and the stimuli that produce them”. For our solution, we have resisted the Weber - Fechner law of [3], which is based on Weber’s insight that the smallest increase in stimulus that will cause a perceptible increase in sensation is coextensive with the pre-existing stimulus, and builds on this insight with the formulation that the intensity of our sensation increases with the logarithm of the increase in energy, and not as intensely as the actual increase in energy. Interestingly, Gustav Fechner confirms [4] that his law [3] has a predecessor in [5,6]. In [5] Bernoulli establishes a principle from the field of economic science, that utility increased only logarithmically with return. Therefore Fechner’s law has much in common with the economist’s law of diminishing returns.
Psychophysics as the measurement of sensation in relation to its stimulus provides the researcher with insight into the determining relationship between a sensation and the physical stimulus that triggered it [7,8,9]. Increasingly, elements of psychophysics are also being applied to machine learning as a result of the growing overlap between biological and artificial perception [10], and machine perception that is guided by behavioural measurements [11] has significant potential to fuel further progress in AI [12].
“Can machines think?” is a question that has intrigued us since the 1950s, when Turing’s seminal paper in Mind [13] was published. But, it has long been accepted that the human brain is superior to machines, despite the enormous advances in computing power, in the case of perceptual tasks that appear intuitive to humans [14], while on the other hand machines prove to be efficient at cognitive tasks that require extensive mental effort for humans [15] as well as in learning processes [16], repetitive tasks [17] or managing large databases [18]. We should note that AI was still in its beginnings linked to human cognition processes, especially in the field of expert systems started with the work of Edward Albert Feigenbaum. AI systems emulate human decision-making. Machines perform tasks that normally require human intelligence: reasoning, learning, perception, decision-making and problem-solving. The pioneering field of AI are expert systems. Expert systems are computer programs that emulate the knowledge and reasoning of human experts in a specific domain [19,20,21], for example medicine [22], environmental monitoring [23] or computer vision [24].
The contribution of fuzzy set theory by mathematician Lotfi Aliasker Zadeh [25] establishes the field of fuzzy logic, which also seeks to go beyond the binary world of Boolean logic by taking into account that truth values are in the range between completely false and completely true, and is inspired by the human properties of perception. The fuzzy systems approach can be effectively applied to technical, engineering and social science applications [26,27,28].
Similarly, the field of artificial neural networks (NN) is conceptually closely linked to the human nervous system in its early days. The theoretical basis for the development of artificial NN can be found in the work of psychologist William James (1842-1910). The invention of the perceptron algorithm [29] and its hardware implementation [30] caused artificial NN to diverge significantly from their roots - biological neural systems. Artificial NN are used to solve AI learning tasks in particular. We are now talking about third-generation NN, called spiking NN, which are again closer to biological NN in terms of constructing large-scale brain models and describing key aspects of neural function. The brain can be considered the ultimate inspiration for the development of NN and new machine learning techniques [31,32], as well as for the development of new hardware [33] or software solutions [34,35]. Visual recognition NN models with a high correlation to human perceptual behavior also have a high correlation with the corresponding neural activity [11]. Psychologically faithful deep neural networks could be constructed by training with psychophysics data [36].
More recently, the growing influence of psychophysics on specific segments of AI is again becoming apparent. We are witnessing the development of biologically inspired models that have attempted to mimic the human visual system [37]. With the rise of black-box AI, the need to formulate explanations for AI results is increasing sharply, the potential of the field of psychology to provide solutions is becoming apparent [38] and the notion of Artificial Cognition is gaining ground. Researchers are finding that black-box models and modern machine-learning and NN algorithms are failing to negate the insights of psychophysics and that insights from both fields need to be integrated for successful, explainable AI [39,40,41,42]. Applying the insights of psychophysics appears to be the way forward for successful human interpretation of data through AI. Human visual and mental abilities have evolved over millions of years, and understanding and using them can help improve AI in new ways [43].
The differential evolution algorithm is a fairly simple and enviably powerful in minimization procedures can also be nonlinear and non-differentiable continuous space functions, proposed by Rainer Storn and Kenneth Price [44,45]. It is also very useful in solving specific engineering problems [46]. The DE algorithm has been an attractive optimization algorithm for more than two decades [47,48]. Setting the DE parameters depends on the characteristics of the problem to be solved, and is a challenging task. Various DE parameter tuning methods have been proposed [49,50,51,52,53]. In [54] we find a proposal for an efficient self-adaptation solution to tune the parameters F, CR and NP to directly influence the mutation, crossover and selection processes in DE algorithm. They have an impact on exploration and exploitation of the search space. We estimate that the black-magic tuning of the key parameters of the DE algorithm, which is sensitive to the choice of the mutation strategy and associated control parameters, is already well researched, although improvements would still be welcome. Here we are referring in particular to the need to involve a human expert in the time-consuming process of parameter tuning, who usually has to perform the parameter tuning according to the task to be solved. The authors of this paper note that the termination of a solution search in DE algorithm is also temporally unpredictable and highly dependent on the properties of the search space, i.e., the nature of the problem to be solved [55,56], and hence it is found that, as a general rule, human judgement of the termination of the search is more efficient than solutions that are embedded in a computational algorithm. Uncertainty in the estimation of the time needed to complete the DE process, and often the need for human intervention to assess the acceptability of the result, is a problem when using DE in real-time. This fact motivated our work described in the following sections, as the DE method was useful for off-line procedures, but not for real-time work, for example when processing instantaneous data from a set of sensors.

2. Materials and Methods

In this section, we will present the solution for determining the termination of a DE procedure using insights from human visual perception. By not interfering with the DE algorithm, we retain the possibility of using all previous developed DE parameter tuning methods. However, we increase the usefulness of the DE method for real-time systems by determining the execution time, because we make the decision to terminate the DE execution dynamically, as a human would, and the DE execution is terminated in fewer or the same number of steps as it would have been with a statically set termination criterion for the DE algorithm.
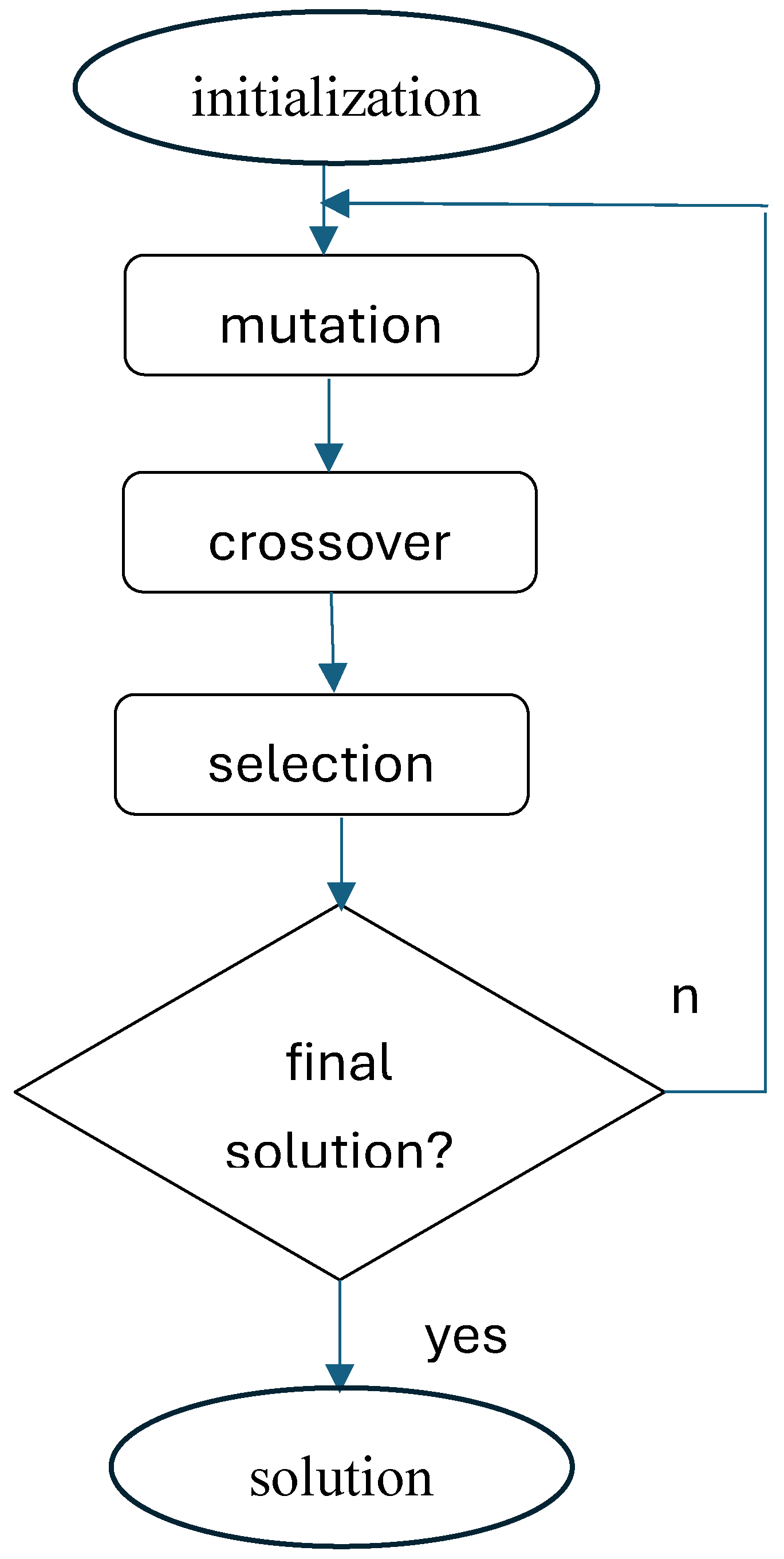
The method we will consider is the DE method [44,45]. In Figure 1 we see a flowchart of the DE algorithm. We will not interfere with the DE algorithm except at the branching point.
At the branch point of the algorithm in Figure 1, we will introduce a condition that takes into account the insights of psychophysics regarding human visual perception of change. We will use the Weber-Fechner law [57], which states that a person’s subjective sensation is proportional to the logarithm of the (objectively measured) intensity of the stimulus. The law, written in equation form, reads:
p = k   l n S S 0
where:
-
p denotes human perception,
-
S denotes stimulus,
-
S0 denotes a sensory threshold,
-
and k is a sense-dependent constant to be determined.
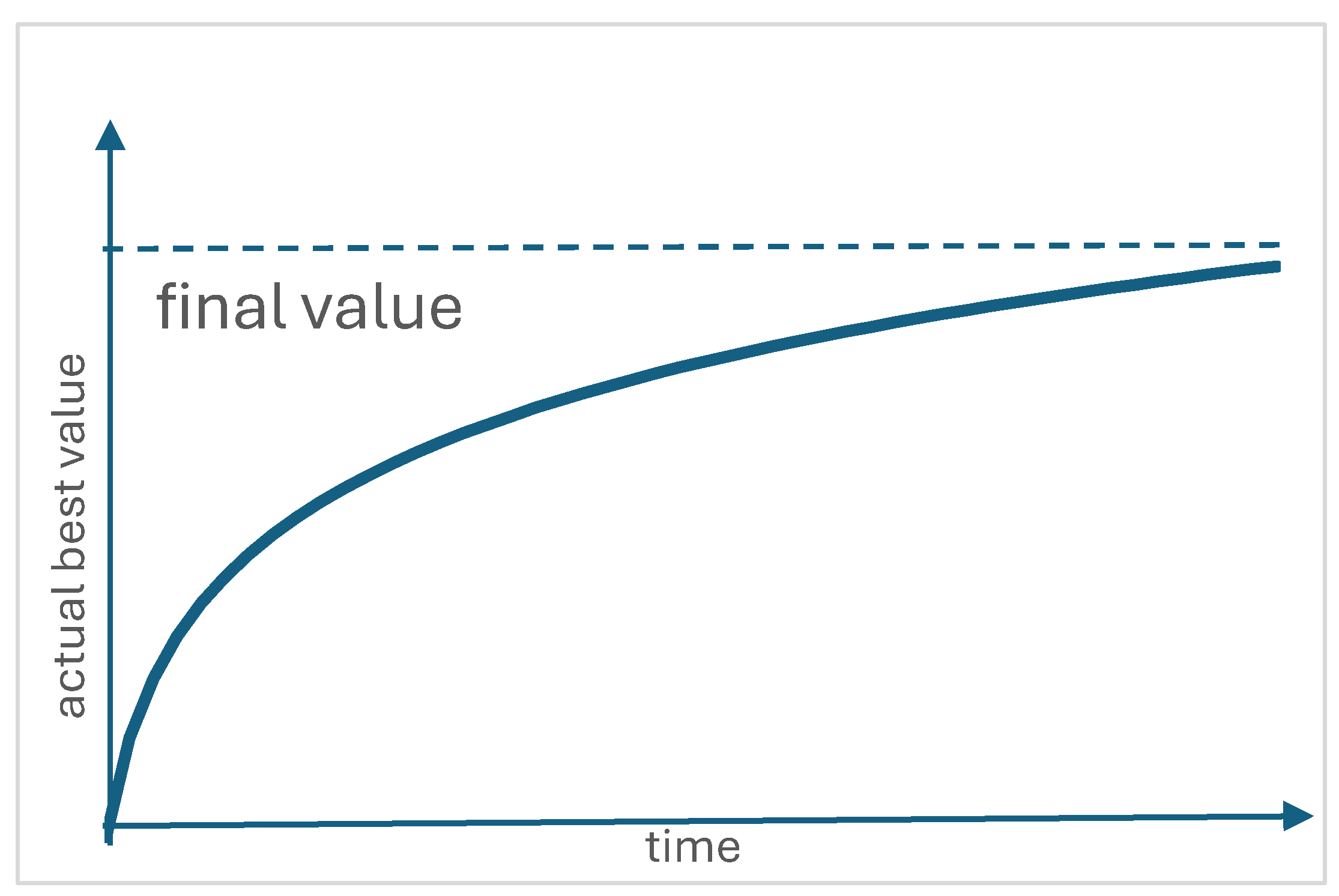
Let us return to solving the problem with DE. The algorithm stores the best solution so far [45], and the mutation and crossover mechanisms ensure that it searches over the whole definition range. We know from experience [55,56], that we approach the true solution along the curve shown in Figure 2.
Figure 2 shows the current best solution. We are particularly interested in the final part of the search results curve. As the number of iterations increases over time, we are getting closer and closer to the final solution, or asymptotically closer to it. The closer we are to the final solution, the closer in value the current best solutions are. We usually form a predefined interval around the value of the current best solution and count how many new solutions are within this interval. The width of the interval is determined experimentally. It is clear that convergence in the DE method is a matter of the shape of the search space and cannot be guaranteed, otherwise the whole search space would have to be scanned, which would be too time-consuming. In order to stay on the “safe side” we set static parameters with a large reserve, which means a large or too large number of iterations. When a chosen number of hits within the chosen interval is reached, we conclude that the best solution will not change anymore and that we have reached the final solution. We stop the DE process. The number of DE iterations required sometimes increases beyond a reasonable limit, so we often intervene and expertly assess whether the best solution has already been reached; sometimes we also change the relevant parameters of the algorithm. Our approach aims to avoid static parameters that determine the termination of the DE process.
Let us ask ourselves, how did we decide that the current solution is already the final solution? We need a visual representation of the solution process, which is similar to the one shown in Figure 2. The number of iterations mirrored in the runtime and the number of last successful hits around the best value are decisive. Let us denote the number of all executions by Sa and the last number of successful hits by Ss. In equation (1) we can set sensory threshold values to 1, as well as the value of sense-dependent constant to 1. By considering the logarithmic relation from the Weber-Fechner law, we can write the heuristic with the formula (2):
ln S a + ln S s = ln S a * S s = K d
This equation describes the static characteristic, or the limit at which we decide and accept the solution as final, whether to proceed with new iterations of DE. The decision constant Kd is chosen experientially according to the nature of the task, or it is determined according to the time we have available to perform a DE iterations. The number of iterations required, and hence the required DE execution time, can also be reduced, depending on the fulfilment of the criterion we have defined. The sum of the logarithms of the product of Sa and Ss must be greater than Kd for the solution to be declared final. In psychophysics terms, the logarithm of the stimulus product in equation (2) must be large enough to induce a perception or initiate a decision to complete the DE procedure! This is the condition that appears in the branch in Figure 1.
With the proposed approach, we implemented the DE termination decision by following the human perception mode - as described by equation (2). In the dynamic criterion, we included both the number of iterations performed and the number of hits in the neighborhood of the best value. If the number of iterations is high, and the search space is better searched, then the number of consecutive hits can be smaller. This is how a human would make the decision to terminate the process.

3. Results

Let’s look at an example of using the approach we have described. Let’s generate a Table1 using the written equation (2) of the static characteristic of the DE algorithm result evaluation. Let us assume that we have enough time to run 10000 iterations of DE. Due to the requirement to work in real-time, we should not exceed this limit. So:
S a m a x = 10000
From this we determine Kd:
K d = ln S a m a x = 9 , 21
From the static characteristic equation, we can tabulate the values, given in Table 1, using equation (3).
S a = e ( K d − ln S s
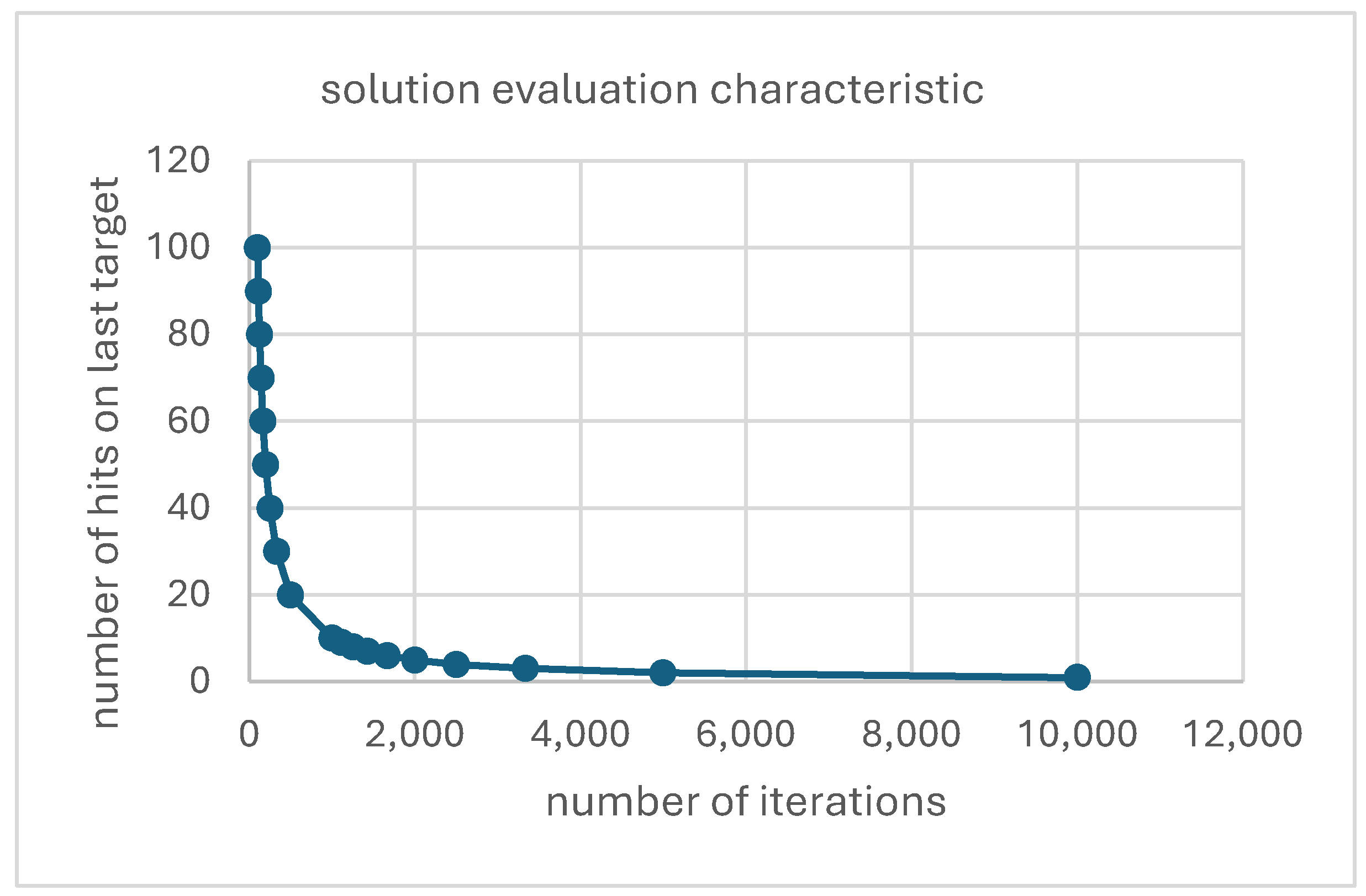
For ease of reference, let’s look at the results in Figure 3.
Figure 3 clearly shows the demarcation between the area where the current best solution of the DE process is adopted in the DE branch and the area where the DE process is continued. This is done in the same way as a human would use to make a decision. The decision depends on the number of DE iterations performed and the number of hits in the interval around the last best solution. The number of hits required decreases as the total number of iterations performed increases. When the allowed real-time processing time has elapsed, the final solution is the last best solution from the DE procedure.
With the proposed innovative solution equation (2), using the insights of the Weber-Fechner law equation (1), that describe human visual perception, we have defined a criterion function to evaluate the DE result in a way that a human would intuitively use in judgment.
The time to find a solution, or the number of iterations of the DE algorithm, can be reduced compared to using a static criterion, as our dynamic estimation also contains a search space searchability component, and this estimation is similar to the estimation that would be perceived - made - by a human. Moreover, a solution is guaranteed within a chosen number of iterations of the algorithm, as can be seen in Figure 3. This has extended the applicability of the DE algorithm to real-time processes requirements.

4. Discussion

In this paper, we present an approach that allows to define the criterion function used in the DE algorithm in a way that is similar to human perception.
The advantages of this approach are
- a maximum number of iterations of the algorithm is defined, so that we stay within the time requirements for real-time work,
- there is no fixed parameter for the termination of the process, it is dynamic,
- the number of iterations required can be reduced compared to a statically defined limit, and this happens in the way a human would use it,
- after the allowed time has elapsed, a solution is obtained (which is better than no solution).
The disadvantages are:
- the need to determine a new coefficient K,
- increased need for computational power due to the dynamic criterion,
- we cannot guarantee that the global minimum has been reached, since we have not interfered with the original DE algorithm, and we do not check the transparency of the par-parameter space.
We have described how we can improve the usability of a well-known DE procedure and extend its applicability to the processing of sensor datasets when we need a real-time result. The proposed approach is based on Weber-Fechner law and could be applied to various cases in the AI domain when we have numerical data and need to make a judgement that could be well performed by a human.

Supplementary Materials

Not applicable.

Author Contributions

Conceptualization, O.T. and T.Ž.; methodology, O.T., D.H. and M.T; software, O.T. and D.H.; validation, O.T. and M.T.; writing—original draft preparation, O.T. and T.Ž.; writing—review and editing, O.T., D.H., T.Ž. and M.T.; supervision, M.T.; funding acquisition, M.T. All authors have read and agreed to the published version of the manuscript.

Funding

The Slovenian Research and Innovation Agency (ARIS) supported the research work with program grant P2-0028 (Mechatronic systems).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

Authors thank Prof. Miro Milanovič for fruitful academic discussions and given support.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Kalloniatis, M.; Luu, C. Psychophysics of vision. Available from webvision.med.utah.edu 2011.
  2. Encyclopedia Britannica. Psychophysics. https://www.britannica.com/science/psychophysics (5.7.2024).
  3. Fechner, G. Elemente der psychophysik. Breitkopf and hrtel. English edition, 1966: Elements of psychophysics, vol. 1, trans. He adler. Holt, Rinehart and Winston.[DL]: 1860.
  4. Carterette, E.C.; Friedman, M.P. Historical and philosophical roots of perception edited by edward c. Carterette and morton p. Friedman. Academic Press: New York, 1974.
  5. Bernoulli, D. Specimen theoriae novae de mensura sortis. 1738.
  6. Bernoulli, D. Exposition of a new theory on the measurement of risk. Econometrica 1954, 22, 23-36.
  7. Prins, N. Psychophysics: A practical introduction. Academic Press: 2016.
  8. Grieggs, S.; Shen, B.; Rauch, G.; Li, P.; Ma, J.; Chiang, D.; Price, B.; Scheirer, W.J. Measuring human perception to improve handwritten document transcription. IEEE Transactions on Pattern Analysis and Machine Intelligence 2021, 44, 6594-6601.
  9. Read, J.C. The place of human psychophysics in modern neuroscience. Neuroscience 2015, 296, 116-129.
  10. Dulay, J.; Poltoratski, S.; Hartmann, T.S.; Anthony, S.E.; Scheirer, W.J. Guiding machine perception with psychophysics. arXiv preprint arXiv:2207.02241 2022.
  11. RichardWebster, B.; Dulay, J.; DiFalco, A.; Caldesi, E.; Scheirer, W.J. Psychophysical-score: A behavioral measure for assessing the biological plausibility of visual recognition models. arXiv preprint arXiv:2210.08632 2022.
  12. Huang, J.; Prijatelj, D.; Dulay, J.; Scheirer, W. Measuring human perception to improve open set recognition. IEEE Transactions on Pattern Analysis and Machine Intelligence 2023, 45, 11382-11389.
  13. Turing, A.M. Computing machinery and intelligence. Springer: 2009.
  14. Moravec, H. Mind children: The future of robot and human intelligence. Harvard University Press: 1988.
  15. Vinyals, O.; Babuschkin, I.; Czarnecki, W.M.; Mathieu, M.; Dudzik, A.; Chung, J.; Choi, D.H.; Powell, R.; Ewalds, T.; Georgiev, P. Grandmaster level in starcraft ii using multi-agent reinforcement learning. Nature 2019, 575, 350-354.
  16. Elshaer, I.A.; Hasanein, A.M.; Sobaih, A.E.E. The moderating effects of gender and study discipline in the relationship between university students’ acceptance and use of chatgpt. European Journal of Investigation in Health, Psychology and Education 2024, 14, 1981-1995.
  17. Schoenherr, J.R.; Abbas, R.; Michael, K.; Rivas, P.; Anderson, T.D. Designing ai using a human-centered approach: Explainability and accuracy toward trustworthiness. IEEE Transactions on Technology and Society 2023, 4, 9-23.
  18. Chang, Y.-H.; Huang, C.-W. Utilizing genetic algorithms in conjunction with ann-based stock valuation models to enhance the optimization of stock investment decisions. AI 2024, 5, 1011-1029.
  19. Feigenbaum, E.; McCorduck, P. The fifth generation: Artificial intelligence and japan’s computer challenge to the world. Reading, Mass.: Addison-Wesley: 1983.
  20. Feigenbaum, E.A. Some challenges and grand challenges for computational intelligence. Journal of the ACM (JACM) 2003, 50, 32-40.
  21. Jackson, P. Introduction to expert systems (3rd edition). Addison-Wesley: 1998.
  22. Shortliffe, E.H.; Davis, R.; Axline, S.G.; Buchanan, B.G.; Green, C.C.; Cohen, S.N. Computer-based consultations in clinical therapeutics: Explanation and rule acquisition capabilities of the mycin system. Computers and biomedical research 1975, 8, 303-320.
  23. Akanbi, A.K.; Masinde, M. In Towards the development of a rule-based drought early warning expert systems using indigenous knowledge, 2018 International Conference on Advances in Big Data, Computing and Data Communication Systems (icABCD), 2018; IEEE: pp 1-8.
  24. Matsuzaka, Y.; Yashiro, R. Ai-based computer vision techniques and expert systems. AI 2023, 4, 289-302.
  25. Zadeh, L.A. Fuzzy sets. Information and control 1965, 8, 338-353.
  26. Bayhun, S.; Demirel, N.Ç. Hazard identification and risk assessment for sustainable shipyard floating dock operations: An integrated spherical fuzzy analytical hierarchy process and fuzzy cocoso approach. Sustainability 2024, 16, 5790.
  27. Majid, S.Z.; Saeed, M.; Ishtiaq, U.; Argyros, I.K. The development of a hybrid model for dam site selection using a fuzzy hypersoft set and a plithogenic multipolar fuzzy hypersoft set. Foundations 2024, 4, 32-46.
  28. Flores, T.K.S.; Villanueva, J.M.M.; Gomes, H.P. Fuzzy pressure control: A novel approach to optimizing energy efficiency in series-parallel pumping systems. Automation 2023, 4, 11-28.
  29. McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. The bulletin of mathematical biophysics 1943, 5, 115-133.
  30. Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychological review 1958, 65, 386.
  31. Schliebs, S.; Kasabov, N. Evolving spiking neural network—a survey. Evolving Systems 2013, 4, 87-98.
  32. Kasabov, N.K. Neucube: A spiking neural network architecture for mapping, learning and understanding of spatio-temporal brain data. Neural Networks 2014, 52, 62-76.
  33. Babacan, Y.; Kaçar, F.; Gürkan, K. A spiking and bursting neuron circuit based on memristor. Neurocomputing 2016, 203, 86-91.
  34. Beyeler, M.; Carlson, K.D.; Ting-Shuo, C.; Dutt, N.; Krichmar, J.L. In Carlsim 3: A user-friendly and highly optimized library for the creation of neurobiologically detailed spiking neural networks, 2015 International Joint Conference on Neural Networks (IJCNN), 12-17 July 2015, 2015; pp 1-8.
  35. Hazan, H.; Saunders, D.J.; Khan, H.; Patel, D.; Sanghavi, D.T.; Siegelmann, H.T.; Kozma, R. Bindsnet: A machine learning-oriented spiking neural networks library in python. Frontiers in neuroinformatics 2018, 12, 89.
  36. Chandran, K.S.; Paul, A.M.; Paul, A.; Ghosh, K. Psychophysics may be the game-changer for deep neural networks (dnns) to imitate the human vision. Behavioral and Brain Sciences 2023, 46, e388.
  37. Dapello, J.; Marques, T.; Schrimpf, M.; Geiger, F.; Cox, D.; DiCarlo, J.J. Simulating a primary visual cortex at the front of cnns improves robustness to image perturbations. Advances in Neural Information Processing Systems 2020, 33, 13073-13087.
  38. aylor, J.E.T.; Taylor, G.W. Artificial cognition: How experimental psychology can help generate explainable artificial intelligence. Psychonomic Bulletin & Review 2021, 28, 454-475.
  39. Schoenherr, J.R. Black boxes of the mind: From psychophysics to explainable artificial intelligence. Proc. Fechner Day 2020, 2020, 46-51.
  40. Rudin, C. Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead. Nature machine intelligence 2019, 1, 206-215.
  41. Carmichael, Z.; Scheirer, W.J. In Unfooling perturbation-based post hoc explainers, Proceedings of the AAAI Conference on Artificial Intelligence, 2023; pp 6925-6934.
  42. Liang, L.; Acuna, D.E. In Artificial mental phenomena: Psychophysics as a framework to detect perception biases in ai models, Proceedings of the 2020 Conference on Fairness, Accountability, and Transparency, 2020; pp 403-412.
  43. Dulay, J.; Poltoratski, S.; Hartmann, T.S.; Anthony, S.E.; Scheirer, W.J. Informing machine perception with psychophysics. Proceedings of the IEEE 2024, 112, 88-96.
  44. Price, K.V. In Differential evolution: A fast and simple numerical optimizer, Proceedings of North American fuzzy information processing, 1996; IEEE: pp 524-527.
  45. Storn, R.; Price, K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. Journal of global optimization 1997, 11, 341-359.
  46. Qing, A. Differential evolution: Fundamentals and applications in electrical engineering. John Wiley & Sons: 2009.
  47. Bilal; Pant, M.; Zaheer, H.; Garcia-Hernandez, L.; Abraham, A. Differential evolution: A review of more than two decades of research. Engineering Applications of Artificial Intelligence 2020, 90, 103479.
  48. Joshi, R.; Sanderson, A.C. Minimal representation multisensor fusion using differential evolution. IEEE Transactions on Systems, Man, and Cybernetics-Part A: Systems and Humans 1999, 29, 63-76.
  49. Mallipeddi, R.; Suganthan, P.N.; Pan, Q.-K.; Tasgetiren, M.F. Differential evolution algorithm with ensemble of parameters and mutation strategies. Applied soft computing 2011, 11, 1679-1696.
  50. Yang, Q.; Ji, J.-W.; Lin, X.; Hu, X.-M.; Gao, X.-D.; Xu, P.-L.; Zhao, H.; Lu, Z.-Y.; Jeon, S.-W.; Zhang, J. Bi-directional ensemble differential evolution for global optimization. Expert Systems with Applications 2024, 252, 124245.
  51. Zamuda, A.; Brest, J. Self-adaptive control parameters׳ randomization frequency and propagations in differential evolution. Swarm and Evolutionary Computation 2015, 25, 72-99.
  52. Li, J.; Meng, Z. Differential evolution with exponential crossover: An experimental analysis on numerical optimization. IEEE Access 2023, 11, 131677-131707.
  53. Azzam, S.M.; Emam, O.; Abolaban, A.S. An improved differential evolution with sailfish optimizer (desfo) for handling feature selection problem. Scientific Reports 2024, 14, 13517.
  54. Wang, Y.; Li, H.-X.; Huang, T.; Li, L. Differential evolution based on covariance matrix learning and bimodal distribution parameter setting. Applied Soft Computing 2014, 18, 232-247.
  55. Polajzer, B.; Stumberger, G.; Ritonja, J.; Tezak, O.; Dolinar, D.; Hameyer, K. Impact of magnetic nonlinearities and cross-coupling effects on properties of radial active magnetic bearings. IEEE Transactions on Magnetics 2004, 40, 798-801.
  56. Tezak, O.; Dolinar, D.; Milanovic, M. In Snubber design approach for dc-dc converter based on differential evolution method, The 8th IEEE International Workshop on Advanced Motion Control, 2004. AMC’04., 2004; IEEE: pp 87-91.
  57. Fechner, G.T. Elemente der psychophysik. Breitkopf u. Härtel: 1860; Vol. 2.
Preprints 113178 g001
Figure 1. Flow diagram of the DE algorithm.
Figure 1. Flow diagram of the DE algorithm.
Preprints 113178 g001
Preprints 113178 g002
Figure 2. Idealized solution search curve.
Figure 2. Idealized solution search curve.
Preprints 113178 g002
Preprints 113178 g003
Figure 3. Example of the solution evaluation characteristic.
Figure 3. Example of the solution evaluation characteristic.
Preprints 113178 g003
Table 1. Table of the evaluation characteristics.
Table 1. Table of the evaluation characteristics.
Sa=number of iterations Ss=number of hits on last target
10.000 1
5.000 2
3.333 3
2.500 4
2.000 5
1.667 6
1.429 7
1.250 8
1.111 9
1.000 10
500 20
333 30
250 40
200 50
167 60
143 70
125 80
111 90
100 100
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated