Prerpints.org logo
Preprint
Article

Application of a Novel Groundwater Storage Analysis Tool to Assess Drought Impacts in a Groundwater-Driven Basin in the Klamath Watershed, Oregon, USA

Altmetrics

Downloads

132

Views

63

Comments

0

Submitted:

24 July 2024

Posted:

25 July 2024

You are already at the latest version

Alerts
Abstract
Groundwater is becoming increasingly important in the Pacific Northwest of the USA due to declining snowpack volumes and shifts in precipitation type and timing, all connected with climate change. The Upper Williamson Basin of the Klamath Watershed is a groundwater dominated watershed with massive fluctuations in year-to-year streamflow volumes over the past four decades, including the complete absence of any live flow for several years. The precise relationship between groundwater and streamflow in the basin has been difficult to assess due to a limited number of monitoring wells and significant gaps in the water level time history. To address this challenge, we use a novel imputation technique that leverages Earth observations and machine learning to impute gaps in water level records. We use these more complete datasets to compute a groundwater storage change time series for the basin. We show that groundwater storage is highly correlated to streamflow and that groundwater storage is correlated to rainfall with a three- to four-year delay that appears variable depending on groundwater storage volumes. The tools and relationships we present make it possible for water managers to estimate when streamflows will return to the basin and be more informed to support better management.
Keywords: 
Subject: Engineering  -   Civil Engineering

Introduction

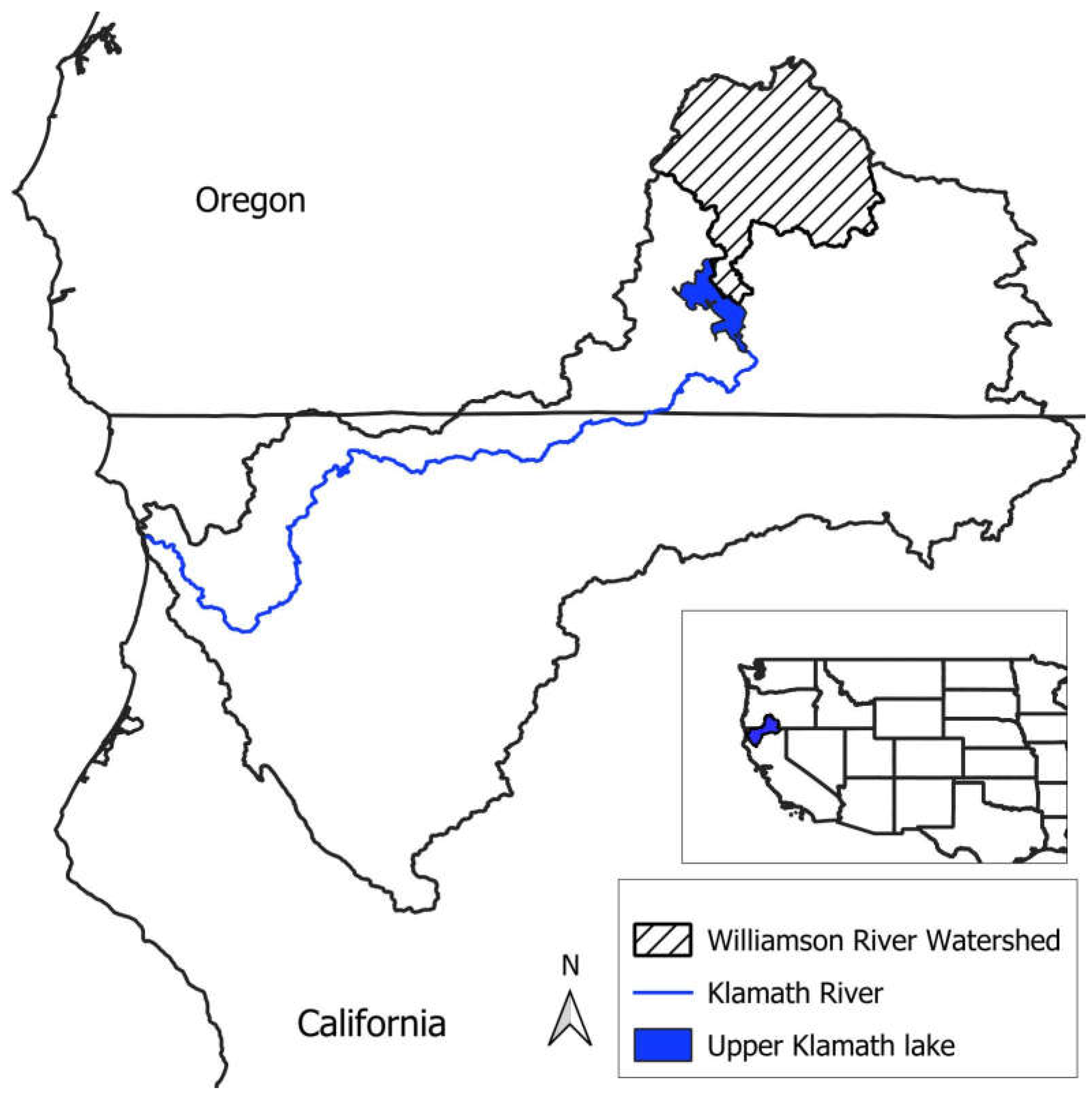
The Williamson River watershed is the northernmost sub-basin of the Klamath River watershed (Figure 1). The river is one of three main tributaries to Upper Klamath Lake. Situated in a high desert environment on the eastern slope of the Cascade Range, the watershed falls under the rain shadow of Mount Mazama (Crater Lake National Park), with nearly all precipitation occurring as snowfall. Because of the extensive volcanic geology that underlies this watershed, this portion of the Klamath River Basin exhibits hydrology typical of a groundwater-controlled basin. At the center is the Klamath marsh, a 124+ sq. mile (200+ km2) farmed wetland complex and National Wildlife Refuge that is the terminus for surficial flows due to the high levels of evapotranspiration. The Williamson River is then regenerated by groundwater emerging from various springs and seeps near the southern portion of the marsh where it re-forms into a channel and flows south into Upper Klamath Lake.
Beginning in 2001, there has been an overall trend in the decreasing volume of water leaving the basin as surface flow. Prior to 2000, stream flow leaving this basin as measured at a United States Geological Survey (USGS) gage could be roughly correlated with the mountain snowpack from the previous 2 to 3 years [1,2,3]. Since the turn of the millennia, climate change, drought, and supplemental groundwater use have as-yet unquantified impacts to the aquifer [4] potentially disrupting a previously balanced hydrologic system. Notably, in water years (WYs) 2015 and 2021 to the present, no live flow has been measured leaving the basin. The downward trend to complete absence of headwaters from this basin is concerning and has impacts to irrigators, federal agencies, NGOs, and water managers.

1.1. Watershed Overview

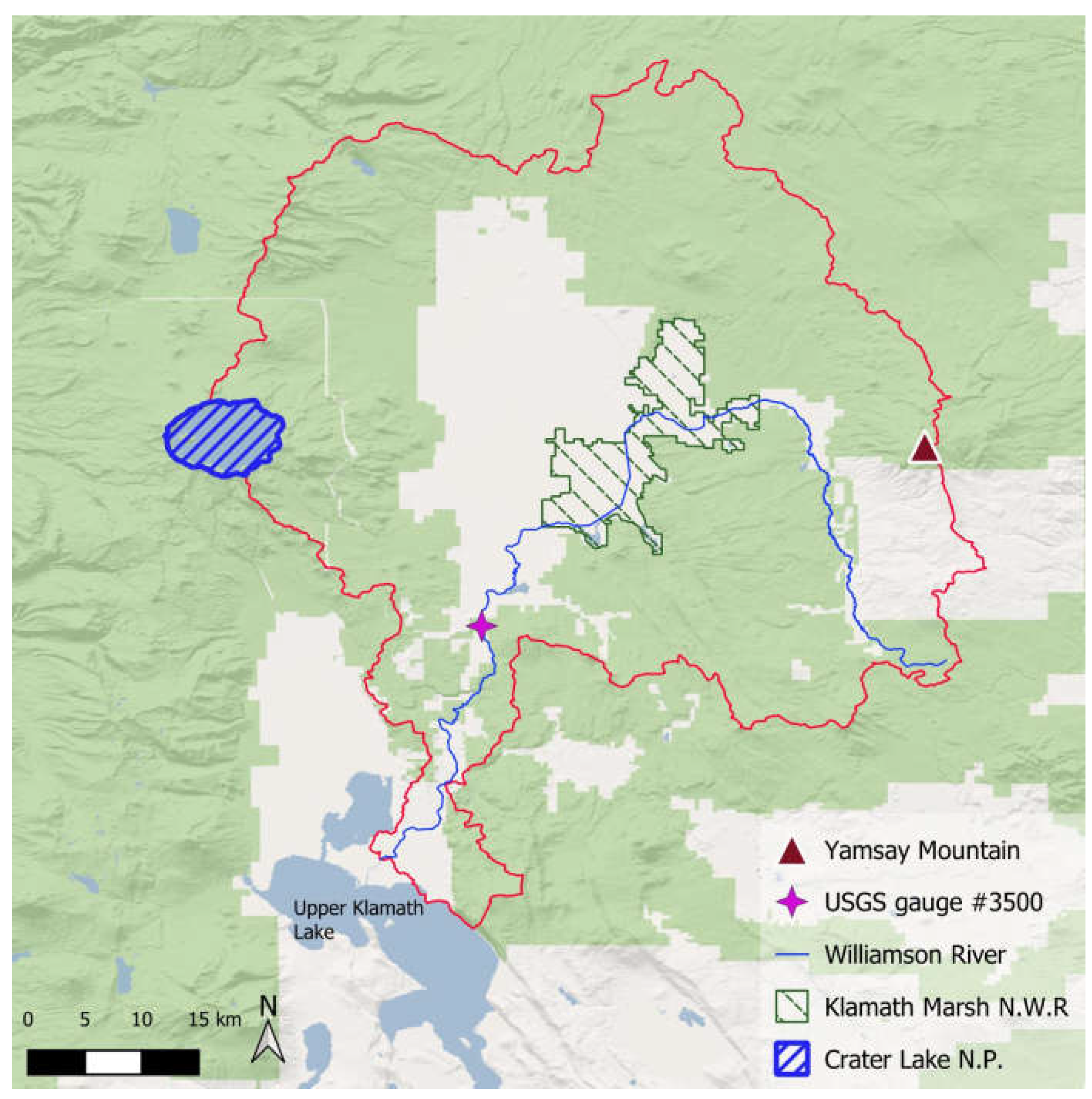
The Williamson River originates in the southeastern corner of the basin and flows north for approximately 20 Miles (32 Km) along the eastern edge, where it is fed by ground and surface water inputs from the Yamsay volcanic mountain complex. The river then turns south flowing into the Klamath Marsh in the center of the basin (Figure 2). In the marsh it flows through various irrigation canals, restored streambeds, and culverts before it sheet flows across the marsh is dissipated by high levels of evapotranspiration and groundwater infiltration [1,2,5,6,7]. Exiting the marsh, the water is replenished/replaced by seeps and springs fed by groundwater with origins in the Cascades to the west of the basin. There is no defined channel as water flows from the Marsh, but the flow gradually coalesces into single stream as it flows over a topographic high created by a basaltic intrusion (locally named ‘Kirk Reef’). Kirk Reef acts as a retention feature dam that restrains small amounts of water from local snowmelt and rainfall. Immediately downstream of Kirk Reef is the first Williamson River gage, the US Geological Survey (USGS) streamflow gage number 11493500 (gage #3500). The river then travels southward through the Williamson Canyon, converges with the Sprague River and enters Upper Klamath Lake.
The Williamson basin is approximately 1436 Mi2 (3720 km2) in size and is located on the eastern edge of the Cascade volcanic range. The northern, eastern and southern boundaries are enclosed by tertiary volcanics and the fault-block geology of the basin and range province. Mount Mazama is the high point of the basin at 8,157 ft (2,486 m), which then slopes downward to 4090 ft (1245 m) in elevation at the Klamath Marsh. A simplified geology of the basin subdivides the lithology into three major geological units: 1) the surficial pumice blanket; 2) intertwined beds of sand, clay, gravel, pyroclastics and basalt (Yonna formation); and 3) the underlying andesitic/basaltic bedrock which is the main water bearing unit [1,3,5,6,7,8]. On the surface, pyroclastic-fall pumice, ash and other volcaniclastics from Mt. Mazama blanket the basin from the Crater Lake down to the Klamath Marsh. Newcomb and Hart [8] labeled this the “Mazama Pumice Plain” and documented the highly porous nature with infiltration rates on the order of 3.28x10-4 ft/s (10-4 m/s) [6]. Internally, the bedrock aquifer has interbedded vesicular scoriaceous tuff, is highly fractured, and displays columnal jointing. Aquifer pumping tests have a high average transmissivity of approximately 170,000 ft2/day (15,800 m2/day) [4].
Historically, the groundwater levels have fluctuated in response to climatic cycles, ranging from years to decades, with the groundwater levels and springs responding to wet and dry periods. Areas with groundwater level changes of 5 ft (1.5 m) have been noted by researchers as common, with fluctuations up to 12 ft (3.6 m) observed in regions closer to the cascades, [9].

1.2. Precipitation

The Cascade mountains (including Mount Mazama) receive upward of 60 in (150 cm) of precipitation per year, mostly as snow. The central and eastern portions, in the rain shadow, receive as little as 18 in (45 cm) of precipitation per year [1,5]. Temps range from highs of 40 °C to lows of -31 °C. The revised Köppen-Geiger classification identifies the Williamson Basin as warm, dry-summer continental with the high elevation rim classified as being dry, sub-arctic [10].
Snowfall and snowmelt recharge the groundwater system through the highly porous desert soils and alluvium along the high elevations of the Cascade Range. Previous research estimates that this spongelike geology can absorb and move upwards of 30,000 acre-feet (3.7x107 m3) of water into the aquifer [3,8]. Because of this, many named and unnamed tributaries disappear into the subsurface, leaving the area absent of typical drainage morphology. Maps show the Sand, Scott, Miller, and Cottonwood Creek all disappear into the alluvium before reaching confluence with the Williamson River.
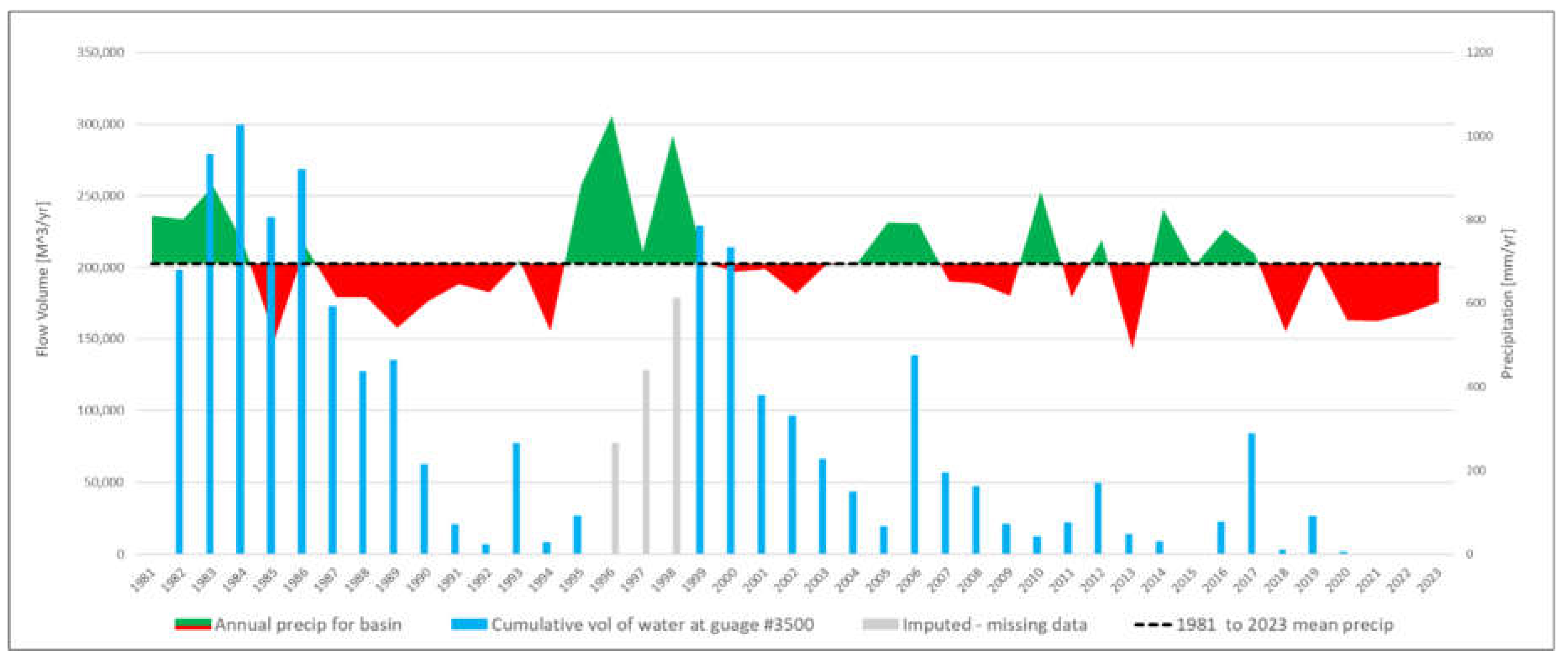
Because the marsh acts as both a terminus for surface flow and the groundwater driven headwaters of the Williamson River, rainfall/runoff models of this watershed are typically inaccurate. An analysis of 12-month cumulative precipitation volume to gauged flows confirms that a weak correlation exists between precipitation and flow on a year-to-year basis (Figure 3). Nevertheless, streamflow generally declines following dry periods and increases during wet periods, although the full impact of the precipitation on the streamflow is delayed by several years. This delay between precipitation and streamflow can be explained by groundwater as will be illustrated later in this paper.
Uncoupled from a conventional rain-runoff relationship, the actual headwaters of the Williamson River are at the Klamath Marsh. Isotropic analysis performed my Melady (2002), and Cummings (2007) confirmed distinct differences in thein deuterium and oxygen isotope ratios in the surface and groundwater, along with distinguishable concentrations of magnesium, calcium, potassium, and sodium. [1,6].

1.3. Drought Impacts

Annual precipitation and streamflow data for the basin shows two multi-year drought periods since 1981 (Figure 3). The first drought was from WY 1990 to WY 1994, culminating in extremely low streamflow. The second drought was longer, beginning in WY 2020 and continuing to the present.
While the first drought was shorter, there were three drier than normal years prior to the WY 1990-1994 drought which can be included. This first drought period culminated in extremely low flows that were temporarily relieved by a wetter than normal winter in WY 1993. On average, observed flow volumes during this first drought period ranged from between 75 to 29 percent lower than flows in the previous decade. Unfortunately, the gage was deactivated in October 1995 and reactivated September 1998. After the gage was re-activated, the water volumes in WY 2000 and WY 2001 indicate that aquifer is capable of being recharged and that the storage compacity of this system is not impaired by such impacts.
By comparison, The current drought that began in WY 2000 was the result of similar low snowpack volumes. However, unlike the first drought period, four of the previous five years have normal to above normal precipitation. While some immediate periods have normal to slightly above normal precipitation, Figure 3 shows that precipitation had been declining since about 1998, with 2006, 2007, 2011, 2013, 2015 and 2017 having above average events and a few years with precipitation about average. The remaining years since 1998 are below average, with 2014 and post-2018 extremely low. This long-term decline in precipitation, starting in about 2008, resulted in the annual flow volume observed in WY 2021 as one of the lowest on record with April 8, 2021, as the last date any water was measured leaving this watershed.
The 1990 to 1994 drought was buffered by below average snowpack from the preceding years, whereas the second period of drought has more than adequate SWE to act as buffer, but there was not enough carryover from the prior years for the springs and seeps to be productive.

1.4. Prior Research

Prior research on the Williamson basin has shown that the river receives as much as 99% of its flow from groundwater discharge during periods of low precipitation [5]. The USGS has found a substantial groundwater flow system consisting of eight aquifers in the upper Klamath basin, mainly composed of late Tertiary to Quaternary volcanic rocks with high transmissivity [9]. The USGS and United State Bureau of Reclamation developed a model using the Precipitation-Runoff Modeling System (PRMS) to forecast streamflow in the Upper Klamath Basin [11]. PRMS is a physics-based deterministic model that simulates processes such as streamflow, evapotranspiration, snow, and groundwater processes [12]. While the model has been calibrated to historical data and gives reasonably good results, it may become less reliable as the region experiences unprecedented droughts [11]. Chang and Jones [13] predict that climate change is expected to have a dramatic impact on water resources in the 21st century in Oregon, particularly in basins that are highly dependent on groundwater. Mayer and Naman [14] examined 25 basins in the region and showed that warming temperatures and snowpack reductions have altered seasonal streamflow characteristics and have resulted in sometimes dramatic reductions in baseflow, especially in groundwater-dependent basins like the Williamson basin where long-term groundwater depletion could result in periods where even higher than normal precipitation does not result in flow. Hess and Stonewall [15] examined the drought of 2013 that caused a near complete cessation of streamflow in the basin and found that changes in regulated diversions mitigated the impact of the drought. Tague, et al. [16] examined streamflow responses to climate change in the Oregon Cascades and found reductions in summer streamflow with increasing temperatures.
The interplay between groundwater storage and baseflow in streams has long been a focus of research [17,18,19,20,21]. Most streamflow forecasting is focused on short-term (7-28 day) forecasts where the emphasis is typically on predicting peak flows in response to precipitation events [22,23,24,25,26,27]. Groundwater models can simulate groundwater-surface water interaction in aquifers where both groundwater and surface water are well characterized [28,29,30]. Relationships between streamflow at specific gages and groundwater levels at nearby monitoring wells can be insightful, but a more holistic approach is generally required for basin-scale analysis looking at total aquifer storage changes. Some researchers have examined the correlation between long-term streamflow and overall groundwater storage in a basin [31,32,33]. This process is promising but can be hindered by scarcity of groundwater data over long periods of time.
In recent years, researchers in the Hydroinformatics Laboratory at Brigham Young University have developed a suite of tools for assessing groundwater storage change using a combination of Earth observations and in situ data. For large basins, they developed the GRACE Groundwater Subsetting Tool (GGST) that uses data from the NASA Gravity Recovery and Climate Experiment (GRACE) mission combined with simulated terrestrial water datasets from the Global Land Data Assimilation System (GLDAS) to derive groundwater storage change estimates [34,35]. This system has been used to assess groundwater storage changes resulting from climate change in West Africa and other locations [36,37,38]. While this method works well for large aquifers, the resulting groundwater storage anomaly grid resolution is at a scale of 1o x 1o making it too coarse for use with smaller basins such as the Williamson basin. For smaller basins, they have developed a second suite of tools called the Groundwater Data Mapper (GWDM), consisting of a web application and a suite of Python scripts [39,40]. The GWDM uses a multi-step process that combines in situ water level data with Earth observations using a machine learning algorithm combined with spatio-temporal interpolation to generate a time series of estimated groundwater storage change for a basin or aquifer [41,42].

1.5. Research Objectives

The Williamson basin is a groundwater driven watershed. While there is a correlation between precipitation flow there is a significant lag because of the intermediate groundwater storage step. The underlying geology stores and releases snowmelt from the cascades into the center of the basin, where it regenerates depleted surficial flows. As the volume of water that flows out of the basin is directly linked to the water in the aquifer, we hypothesize that impacts from climate change, drought, and possibly pumping are preventing the aquifer from fully recharging. Our study characterizes this relationship between precipitation, groundwater storage, and stream flow in the Williamson Basin. The goal of this study is to provide resource managers in the area with a better understanding of the hydrology in the basin and new insights and tools to support decision making. The larger objective of this study is to provide resource managers and researchers with a case study to highlight processes and issues in areas where streamflow is governed by groundwater interactions.
To better understand this system, we use the GWDM tools to find the groundwater storage history for the basin and then determine the correlation between storage levels and streamflow leaving the basin. These tools allow us to maximize the sparse groundwater data in the basin by imputing gaps in the groundwater level history using Earth observations and machine learning. Using this history, we analyze the relationship between groundwater storage, rainfall, and soil moisture for the basin. This information could give water managers in the basin a tool for predicting when the streams will start flowing again.

2. Data

2.1. Monitoring Wells

Both the USGS and the Oregon Water Resource Department (OWRD) have monitoring wells set up in the basin study area. We used 12 active monitoring wells (4 USGS, 8 OWRD) and 11 inactive wells (all OWRD), with various periods of activity since the 1960s. When active, more recent measurements have a resolution of 0.01 ft (0.3 cm), but older measurements are sometimes recorded with a coarser resolution of 0.1 - 1.0 ft (3 – 30 cm). Figure 4 shows the monitoring well locations used in this study. Well records prior to 1968 did not include enough data for the GWDM tools due to both the low number of data points and a low data resolution. After removing wells with insufficient data, the data set includes 12 wells with 1312 water level records. We examined water level data to remove outliers resulting from recording errors or faulty depth measurements and eliminated 4 records that appeared to be outliers. This resulted in a total of 1308 measurements that we used in the analysis. A full list of well locations and water level records is available on the HydroShare.org data repository [43].

2.1.1. Streamflow Data

The section of the Williamson River under study does not have continuous, year-round flow. Recorded dry periods have ranged from days to years. For example, an extended period of no measurable flow lasted from June 3, 2014 to February 25, 2016 with no flow occurring during the entire 2015 WY. Flow in the Williamson River is measured at USGS stream gage #3500 located at approximately 42.740°N, -121.834°W, it is 0.31 miles (0.5 KM) south of the topographic high known as Kirk Reef (Figure 2). Installed 1954, it measures discharge on a daily timestep gage in cubic-feet per second (CFS). We computed cumulative annual flow volumes as thousands-of-acre-feet-per-year (TAF), which is the measurement commonly used by irrigators and western water managers. One acre-ft is approximately 1233.5 cubic meters and one acre-ft per day is approximately 0.504 CFS (0.0143 m3/second).
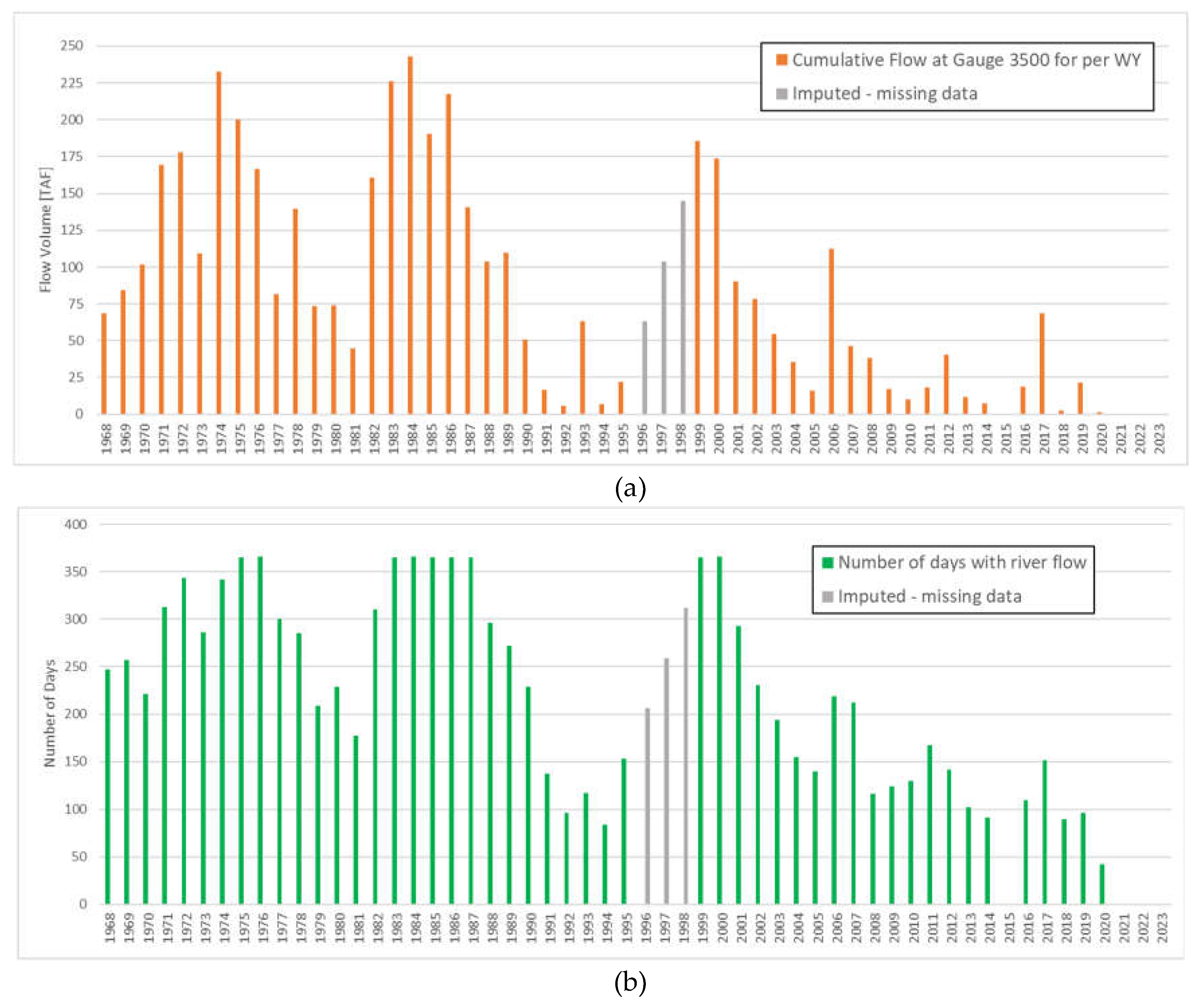
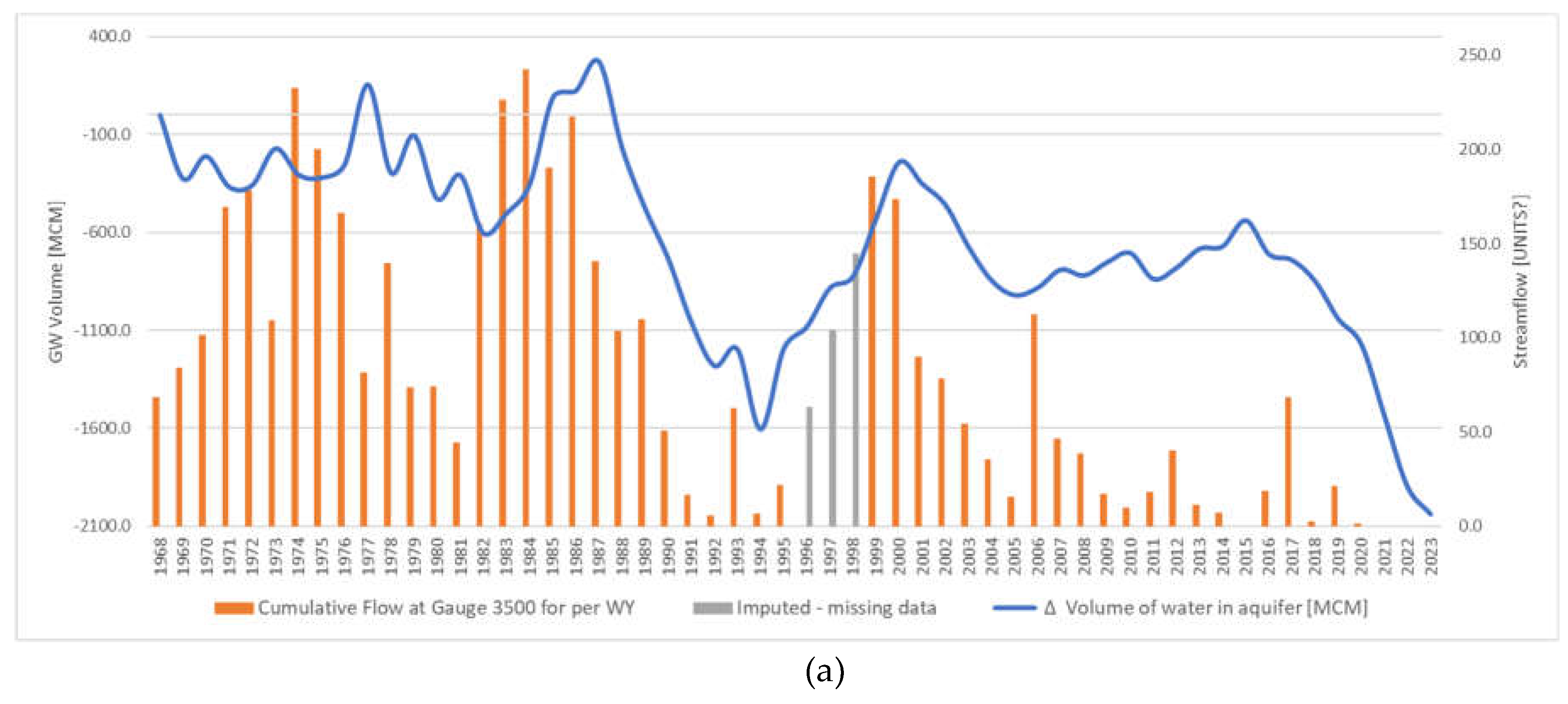
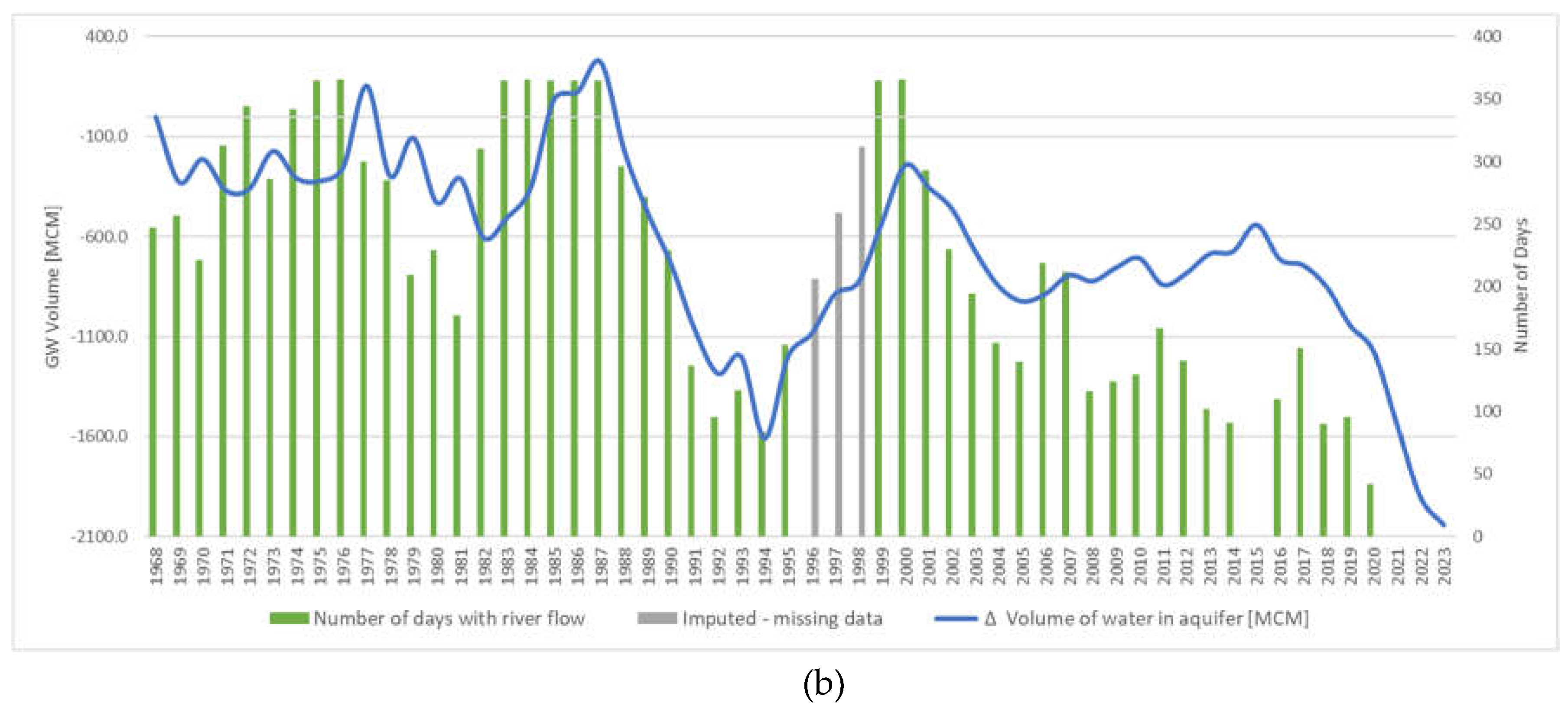
Figure 5 shows the cumulative annual flow per WY in TAF (Figure 5a), and the number of days per year of non-zero flow (Figure 5b) at gage #3500. The gage was deactivated in October 1995 and reactivated September 1998, creating a 3-year gap in the data. For our analysis, we imputed streamflow values for this 3-year gap using linear interpolation to ensure that the missing values are not interpreted as zero flow, since zero flow values do occur in the record.

2.1.2. GLDAS Soil Moisture Data

Our groundwater imputation uses the soil moisture dataset from the NASA Global Land Data Assimilation System (GLDAS) [44]. GLDAS consists of three separate land surface models: LSM, Noah, and VIC. We use the monthly-averaged results from the Noah model which are at a resolution of 0.25x0.25 degrees. These data were downloaded from the Goddard Earth Sciences Data and Information Services Center (GES DISC) website [45].

2.1.3. Precipitation Data

Our precipitation data come from the CHIRPS gridded data product developed by the Climate Hazards Center at UC Santa Barbara in collaboration with the USGS Earth Resources Observation and Science (EROS) Center [46]. The CHIRPS data set is derived from a variety of NASA and NOAA Earth observation sources and aggregated to a high-resolution global grid (0.05 degree) covering a period from 1981 to the present. To obtain CHIRPS data for the Williamson basin, we used the NASA SERVER ClimateSERV website [47] where we uploaded a GEOJSON file of the boundaries basin and downloaded a time series of daily rainfall data in a CSV file that contained the daily average of the CHIRPS grid cells in the interior of the basin.

3. Methods

To generate an estimate of the historical groundwater storage changes in the Williamson basin, we used the Groundwater Data Mapper (GWDM) tools [40]. The GWDM uses a combination of in situ water level data and Earth observations to estimate aquifer storage changes using a multi-step process [39,41,42]. In the first step, the user imports well locations and historical water levels to generate a water level time series for each well. However, it is common to have significant gaps in historical water level records at a well, ranging from several months to several years. Furthermore, aquifer storage change assessment requires a relatively complete water level record at each well. Thus, GWDM uses a machine learning algorithm to impute missing data for each well over the study period. 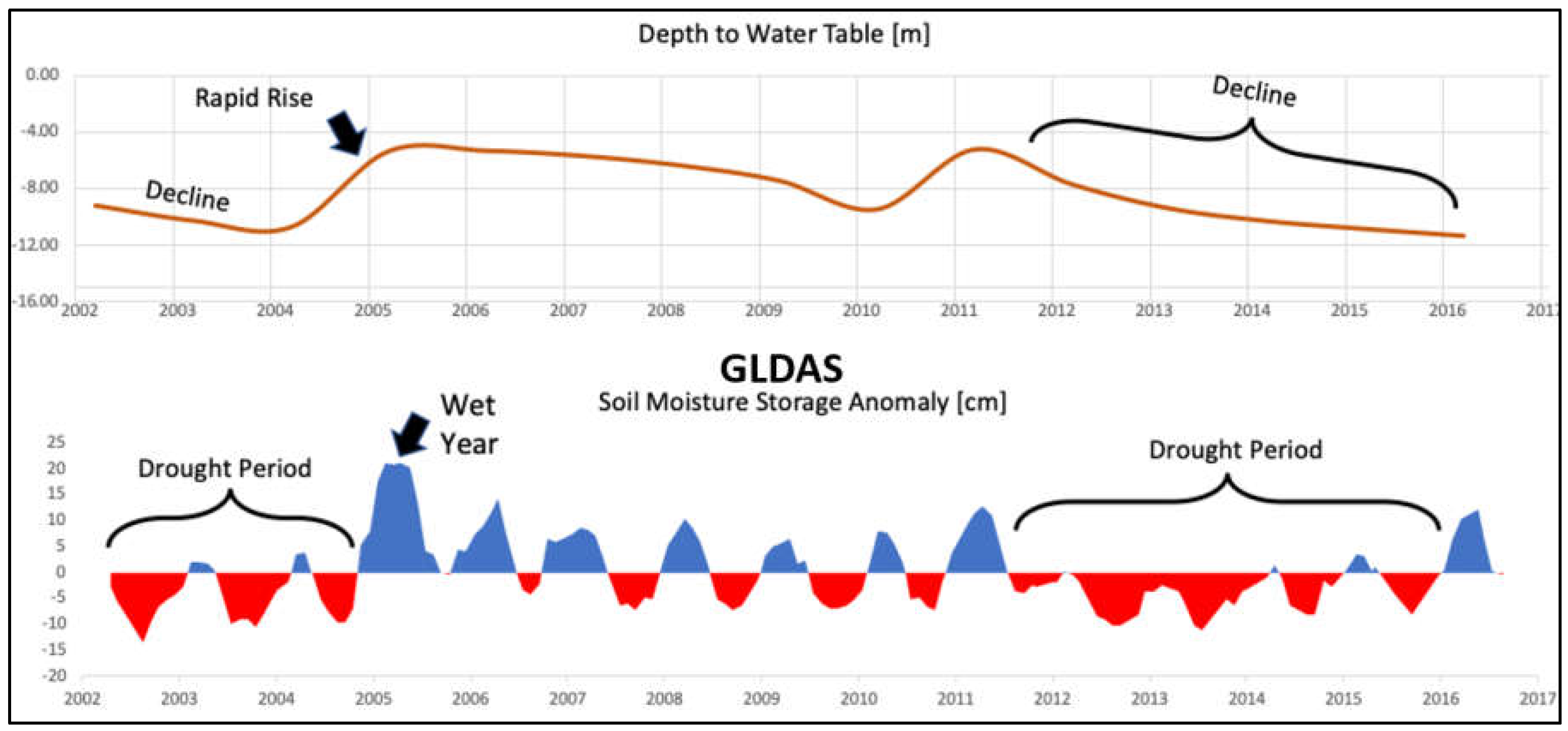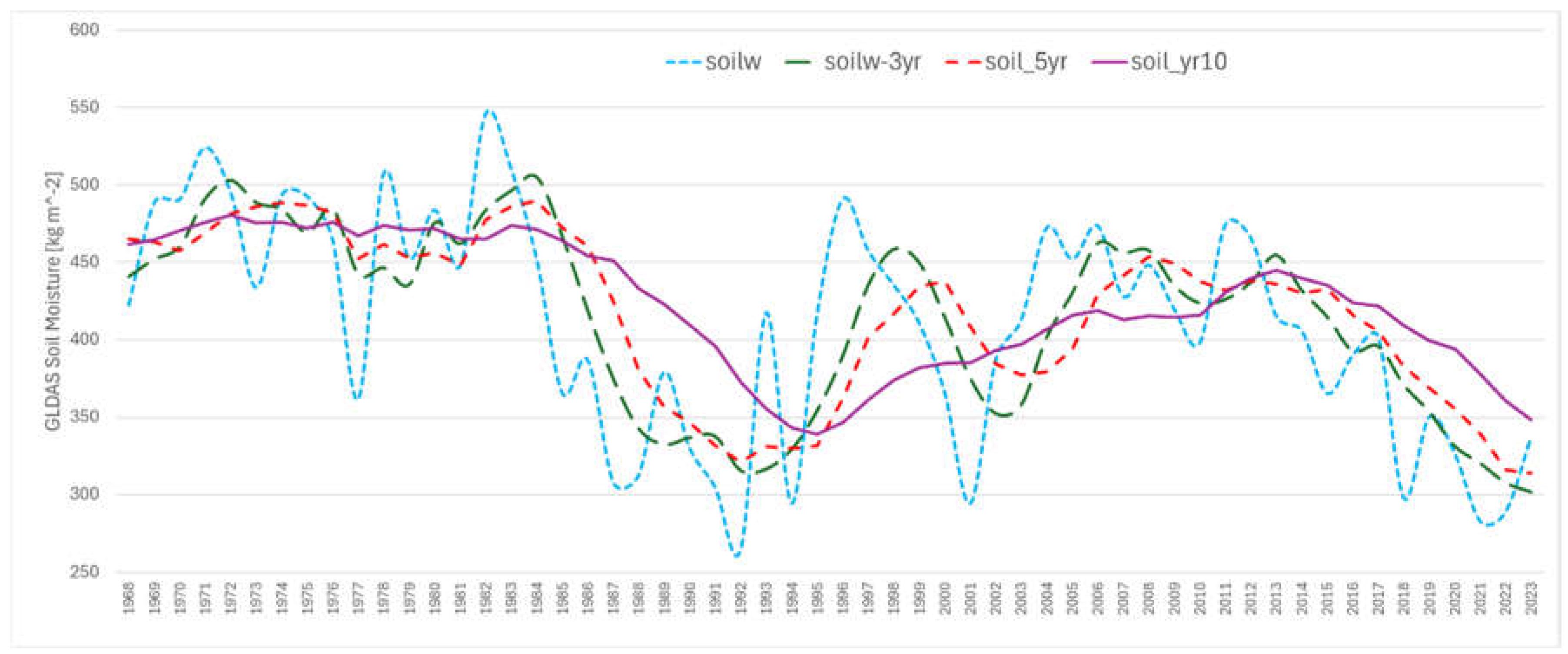The theoretical basis for this algorithm is that groundwater levels are highly correlated with drought indicators such as soil moisture (Figure 6). During a drought there is less groundwater recharge and groundwater is pumped at a higher rate to meet agricultural, municipal, and industrial needs. During wet periods, there is a higher rate of recharge and less pumping. As a result, groundwater levels drop during drought periods and rise during wet periods.
The GWDM uses this correlation to build a machine learning model for each well using the Extreme Learning Machine algorithm [39]. The features used to train the model are monthly GLDAS soil moisture anomalies and the three-, five- and ten-year moving average of the soil moisture anomaly. The moving averages help capture longer term trends in the data. The model features include the year, and one-hot encoded month indices. We train a regression model on these features with the observed water levels as labels.
Once trained, we impute missing measurements at each well, resulting in a water level value for each month. The GWDM samples these imputed water level time series at periodic intervals such as one year, and spatially interpolates these water levels to generate a two-dimensional raster of the water levels in the aquifer at each time interval.
In the final step, GWDM uses raster algebra to calculate the volume between each subsequent pair of rasters. This volume is multiplied by an average storage coefficient for the aquifer to generate a groundwater storage change estimate for that time interval. GWDM then integrates these changes to generate a groundwater storage curve for the aquifer that shows storage change over time. The entire process is described in more detail in [40,41,42,48].
The GWDM tools include a suite of Python scripts for cleaning and formatting data, and for performing the imputation and volumetric analysis [40]. The wells, water levels time series, interpolated water level rasters, and groundwater storage time series can be uploaded and visualized to a GWDM web application developed using the Tethys Platform software [39,49,50]

4. Results

4.1. Precipitation and Flow Data

Before exploring the relationship between groundwater and streamflow in the basin, we first examined the relationship between precipitation and streamflow. An analysis of 12-month cumulative precipitation volume to gaged flows confirm that a weak correlation exists between precipitation and flow on a year-to-year basis (Figure 7). The Pearson correlation coefficient r of annual cumulative rainfall to annual cumulative flow by water year is r(n=41)=0.29 with p=0.06, only slightly correlated. Nevertheless, streamflow generally declines following dry periods and increases during wet periods, but the full impact of the precipitation on the streamflow is delayed by several years.
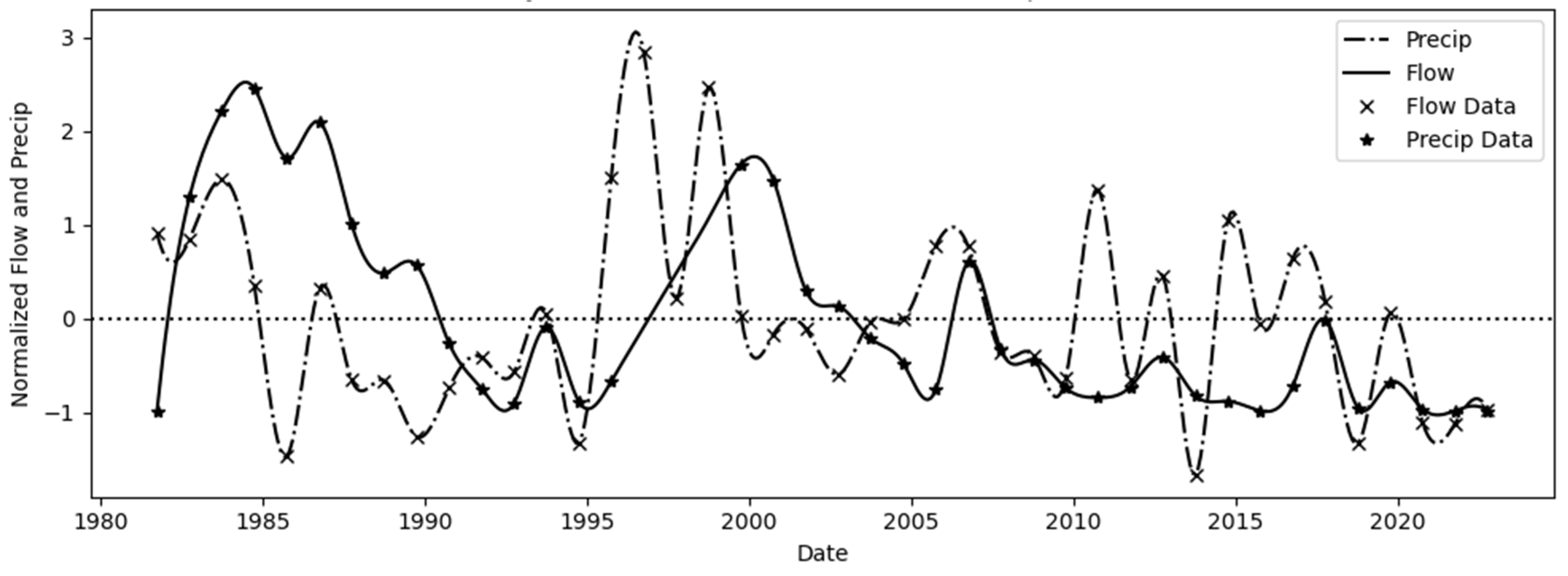
To better characterize the correlation between cumulative annual precipitation and cumulative annual stream flow we interpolated the annual data to estimate values at the start of each month (Figure 7). Cumulative annual flow data for three water years, 1996-1998, were not available because the gage was deactivated during this period, so data in this time period are all interpolated. Before interpolation, we normalized both data sets using standard score (z-score) normalization:
z = x − μ σ
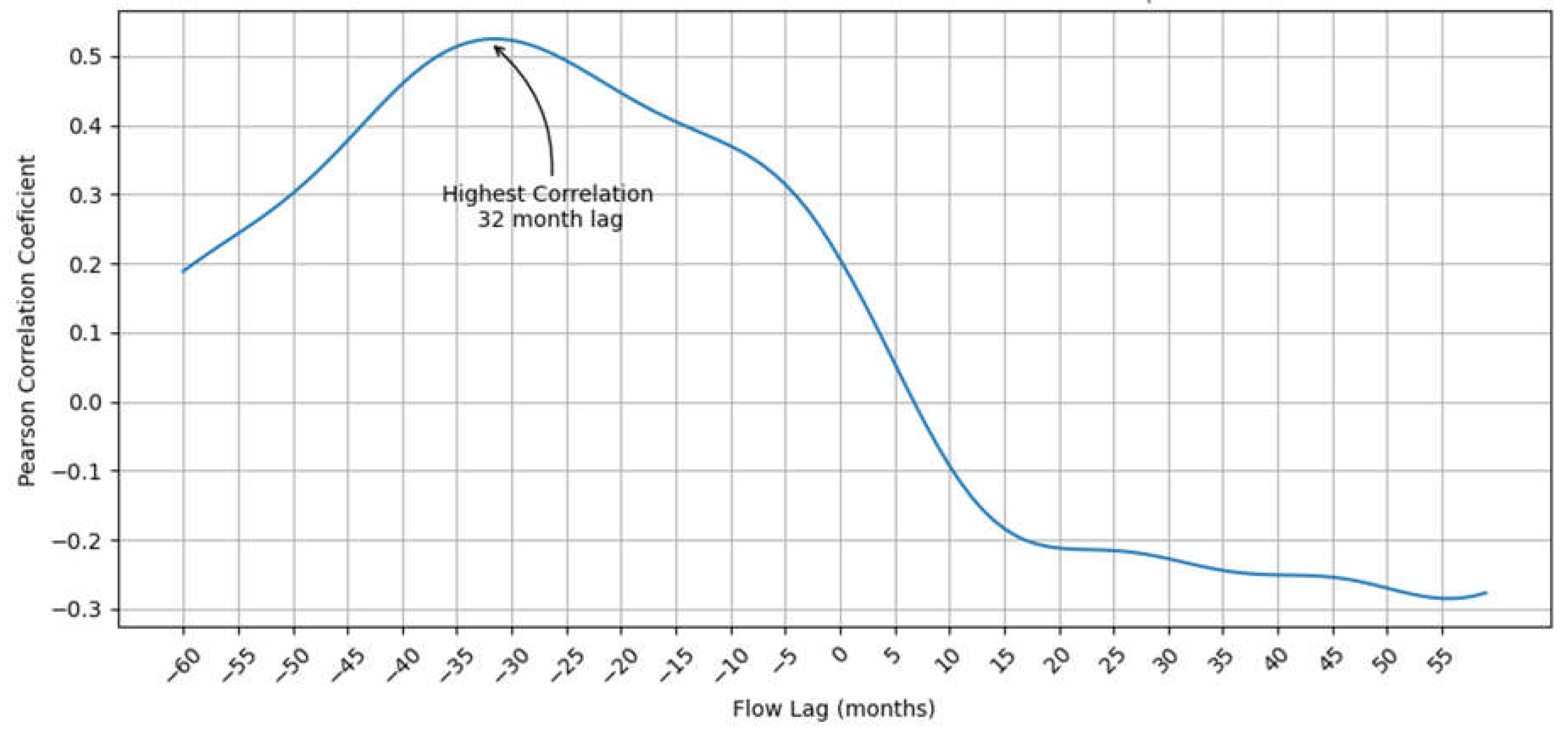
Where x is the measured values, µ and σ are the mean and standard deviation of the dataset being normalized, and z is the normalized value which is unitless. The z-value represents the number of standard deviations any value is from the mean. We interpolated these normalized annual values to values at the start of each month using cubic interpolation implemented by the numpy Python package [51]. We then computed the Pearson correlation coefficient using monthly lags from -60 to +60 lags (±5 years) (Figure 8).
Using interpolated monthly data, we found that the highest correlation occurs at a lag of -32 months, with r = 0.525, p<0.001. The computed p-value is essentially zero but is based on the interpolated monthly values, so it is not representative of the data. Figure 8 shows that there is not a sharp peak in the correlation values, but a relatively smooth transition. This indicates that the lag which produces the highest correlation probably changes over the 43-year study period. We would expect a longer lag at low groundwater levels and a shorter lag at high groundwater levels.
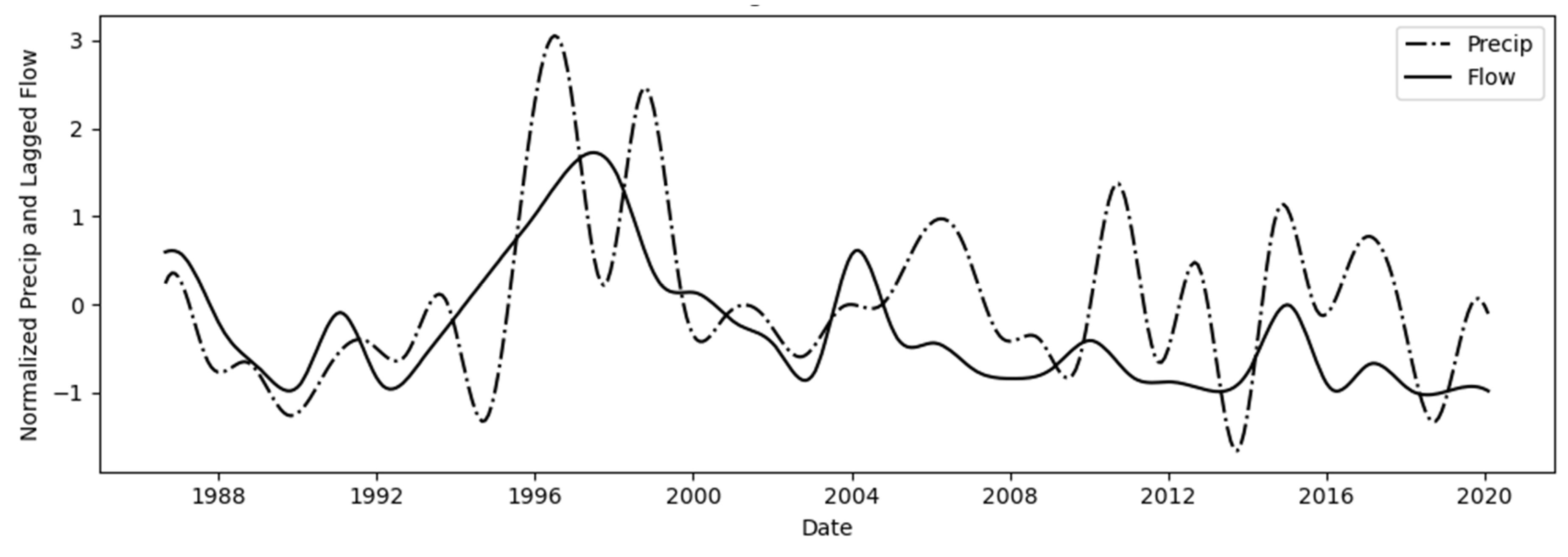
Figure 9 shows cumulative annual precipitation data plotted with cumulative annual flow data lagged by 32 months. In general, these two data sets are visually correlated with the flow lagged. The no-data period from 1996 to 1998, is not as visually correlated as the interpolated data do not follow precipitation. The 32-month lag we found is similar to the lag we found using only annual data which resulted in a 3-year lag, i.e., 36 months. The correlation coefficient, r, improved from r=0.51 to r=0.525 for the annual 3-year lag to the monthly 32-month lag, respectively.
The flow in the Willianson River is uncoupled from a conventional rain-runoff relationship with no short-term relationship between precipitation and flow. Studies have shown that the actual headwaters of the Williamson River are at the Klamath Marsh and related groundwater. Isotropic analyses have shown distinct differences in deuterium and oxygen isotope ratios in the surface and groundwater, along with distinguishable concentrations of magnesium, calcium, potassium, and sodium. [1,6]. These studies, combined with the demonstrated lag between precipitation and stream flow, indicate that flow in the Williamson River is governed by groundwater. The lagged correlation indicates that precipitation in this basin recharges groundwater on about a 3-year time period. However, while precipitation and recharge are coupled and demonstrate correlation in time. The correlation between groundwater and streamflow may be more complex as groundwater needs to reach a certain level before it can discharge to the surface. Levels below this can result in no-flow conditions, as have been experienced in the Klamath Basin.

4.2. Groundwater Storage Change

To better understand the correlation between groundwater and streamflow, we computed the groundwater storage change using the GWDM tools described in the Methods section above. We first obtained the monthly GLDAS soil moisture data set using the GLDAS grid cell containing the centroid of the Williamson basin. We then computed the 3-, 5-, and 10-yr moving averages of the soil moisture to produce the data shown in Figure 10 for the period from 1968 to 2023.
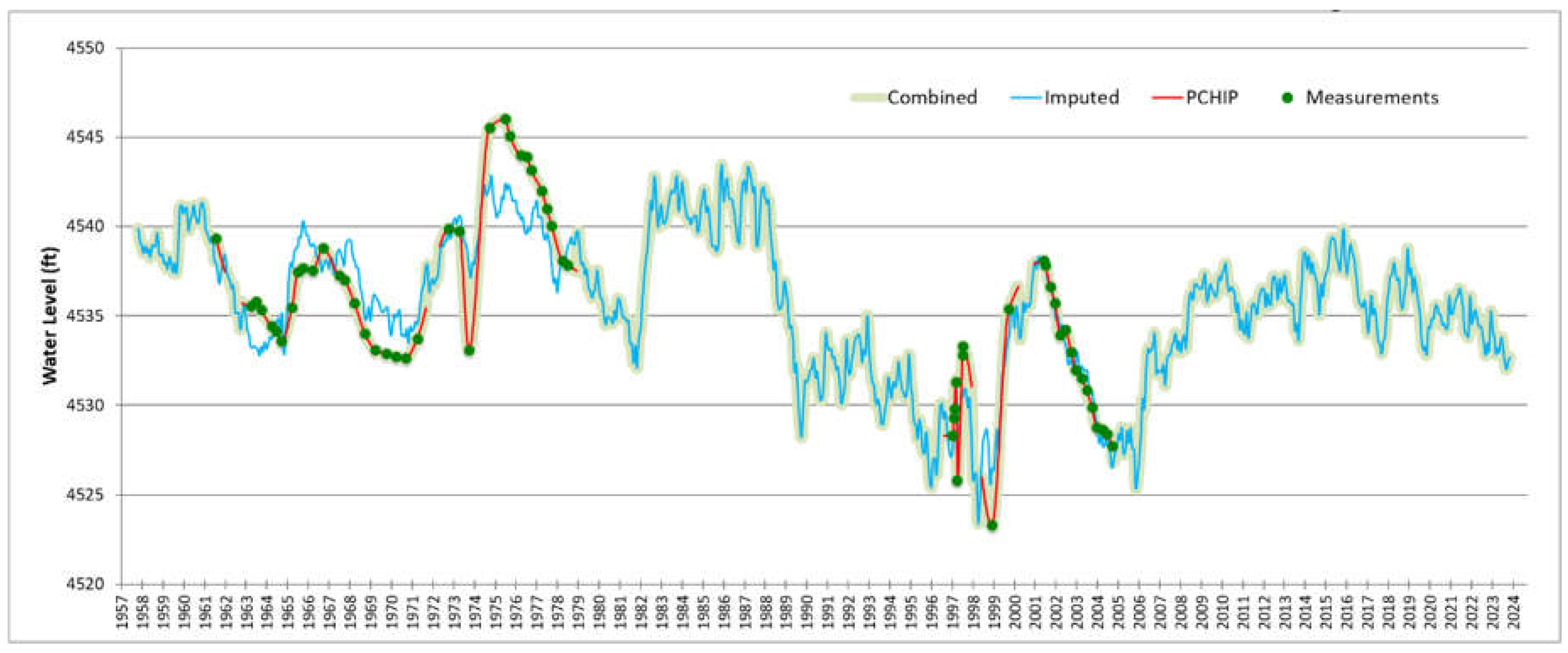
Next, we used PCHIP interpolation to impute data for all gaps in the monthly water level records for each well. We retained these imputed values for gaps less than two years. We then deleted the PCHIP interpolated values for gaps greater than or equal to two years. At the beginning and end of each of these gaps, we retained 180 days of data imputed using PCHIP. We combined the soil moisture datasets with data indicating the year and one-hot encoded month of the measurement and used these features to train an Extreme Learning Machine (EML) model for each well. We imputed missing data to generate a complete water level record for each well from 1968 to 2023. Finally, we combine the measured, PCHIP, and EML datasets into a single water level dataset. For all months where there is either a measurement or PCHIP interpolated value, we use that value. If no measurement or PCHIP value is available, we use the EML-imputed data value. An example set of water level time series for well KLAM0000496 in the Williamson basin is shown in Figure 11.
We sampled the time series at each well on yearly intervals from 1968 to 2023. We then spatially interpolated to a 150x150 grid that is clipped to the basin boundaries for each year, resulting in a groundwater elevation map for each year in the study period. 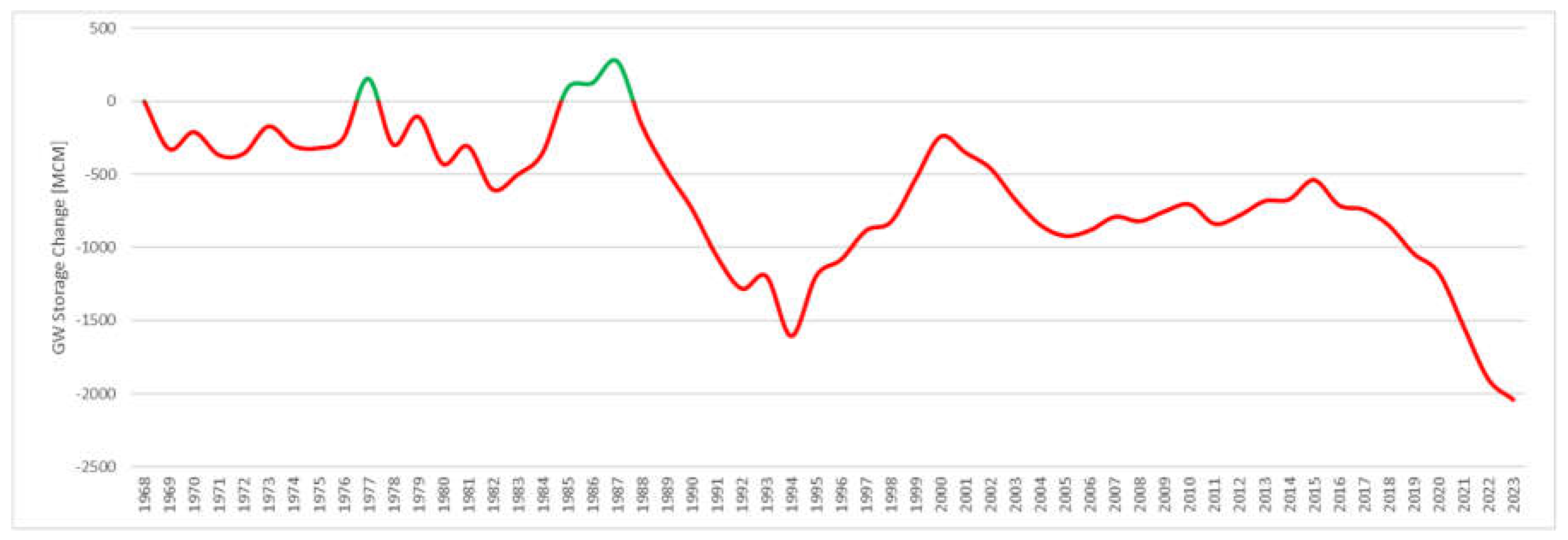We calculated the volume between each subsequent pair of groundwater elevation rasters then multiplied the value, which represents the water level change, by a representative unconfined storage coefficient for the basin (0.1) to generate annual groundwater volume changes in the basin as shown in Figure 12. The volumetric storage change values are relative to the starting value of zero in 1968.
Figure 12 shows that groundwater storage was relatively constant from 1968 through 1987 and then dropped significantly for 7 years before partially rebounding from 1994 to 2000. This rebound was followed by a decline from 2000 to 2005 and then a steeper decline starting in 2015 that continued through the end of 2023. These data show that the basin has lost approximately 2,000 million cubic meters (1,600 TAF) over the 55-year study period. Soil moisture shows a similar decline (Figure 10) indicating both processes are driven by the climatic conditions.

4.3. Groundwater - Streamflow Correlation

Figure 13a compares the groundwater storage curve to the streamflow data from Gage 3500. Visually, there is a strong correlation between the decline in groundwater storage and declining streamflow from 1985 to 1995 followed by a rebound in both from 1985 to 2000. After the rebound, both decline through 2005 which is followed by a steeper decline in groundwater storage starting in 2015 which results in a complete cessation of streamflow in 2021. The Pearson correlation coefficient between the groundwater storage and streamflow is r(54)=.64, p<0.01, indicating a high degree of correlation.
Figure 13b shows the groundwater storage and the days per year with non-zero streamflow. The same overall behavior is observed, but groundwater storage is even more strongly correlated with flow-days, resulting in a Pearson correlation coefficient of r(54)=.79, p<0.01.

4.4. Groundwater – Rainfall Correlation

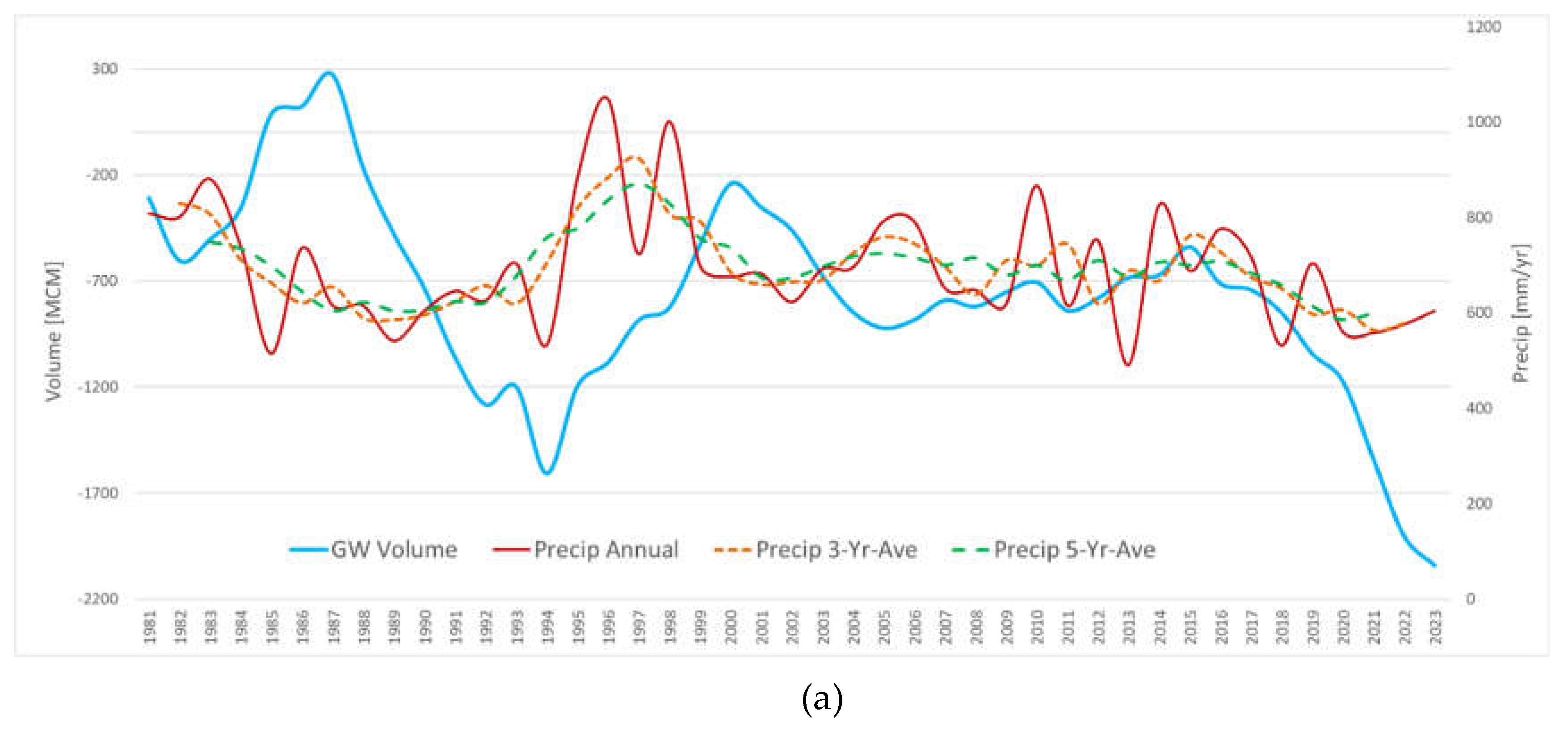
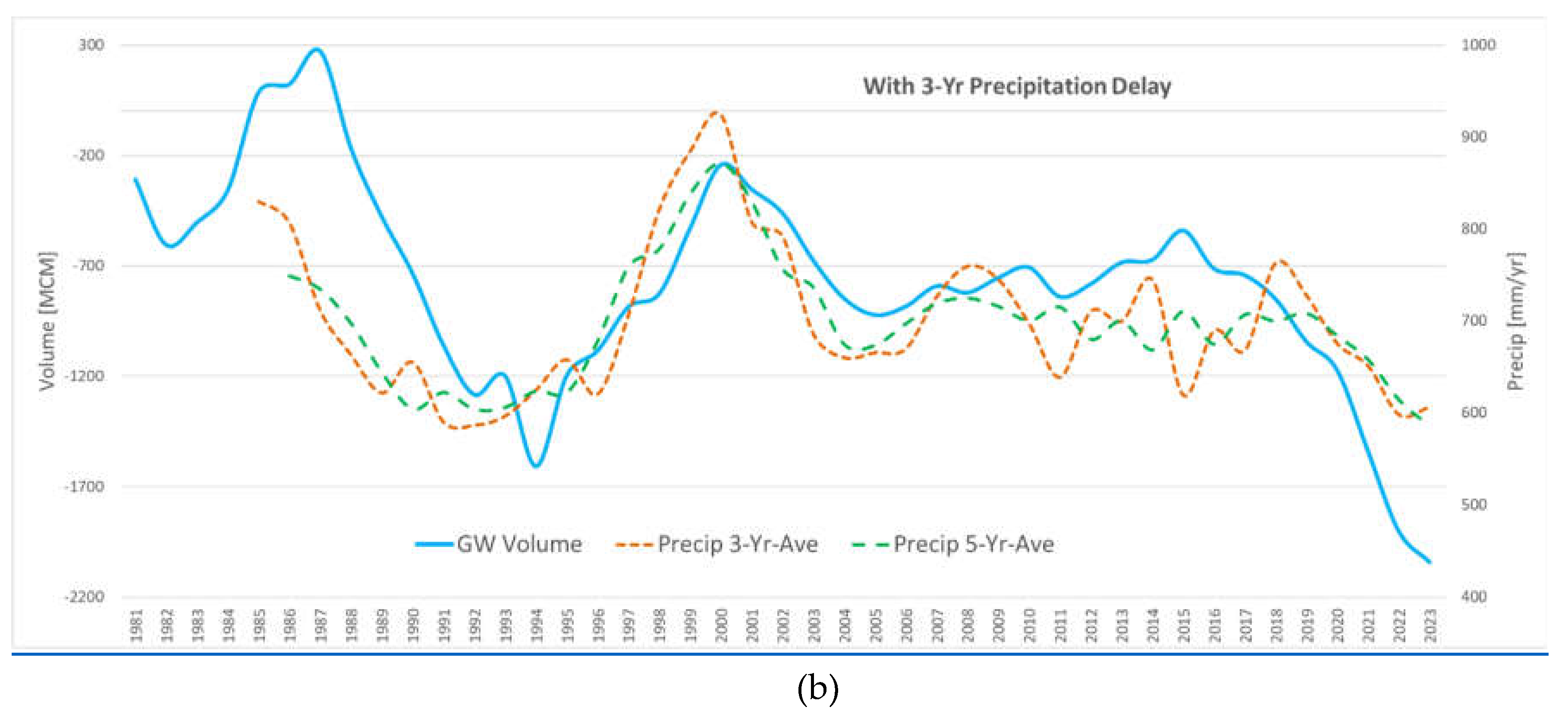
We next examined the relationship between groundwater storage change and precipitation. We started the comparison in 1981 as opposed to 1968, as CHIRPS data are not available prior to 1981. Figure 14(a) shows groundwater storage change versus cumulative annual precipitation, and the 3- and 5-year moving average of the cumulative precipitation. The figure shows that long-term changes in groundwater storage mirror fluctuations in precipitation, particularly the 3- and 5-yr moving averages, but the peaks and valleys are offset. We evaluated different lags and found that if we lag groundwater storage by 3 years, we get excellent correlation with both the 3- and 5-yr precipitation curves as shown in Figure 14(a). This matches the lag we found between precipitation and streamflow in Section 4.1.
The Pearson correlation coefficient for lagged groundwater storage and 3-yr and 5-yr moving average precipitation are r(37)=.60, p<0.01, and r(36)=.64, p<0.01, respectively. This indicates that it takes 3 years for precipitation to fully percolate through the vadose zones in the basin to effectively recharge the groundwater in the aquifers. Even though the precipitation in the basin started to rebound in 2021 as shown by the solid red line in Figure 14(a), the groundwater still has not started to rebound as it is most closely correlated with the 3- and 5-yr moving average of precipitation with a 3-yr delay. Once groundwater has rebounded to a high enough level to feed the seeps and springs at the head of the Williamson River, we expect flow to resume.

5. Discussion

The relationship between the groundwater storage volume and Williamson River flow has traditionally been known to hydrogeologists and those with local knowledge, but these basin processes are less familiar and opaque to the various federal agencies, water managers and the general public. It is general knowledge that streamflow in the basin is highly dependent on groundwater, but the precise relationship of groundwater vs streamflow has not been well understood. Examining water levels at individual groundwater monitoring well locations does not capture the full behavior of the groundwater-surface water interaction as individual wells may not provide insight into aquifer storage due to incomplete records and local behavior at a well.
The tools we used and demonstrated in this study provide methods to address these issues. The groundwater level imputation at each well addresses sparse data using correlations between well data and Earth observations. The interpolation and mapping algorithm is a way to take records from individual wells and generate a time series of aquifer level maps that can be used to compute aquifer volume changes. Computing these storage changes and integrating over time provides the basis for the analysis we presented in this paper. These tools provide insights that allow us to better characterize the relationship between precipitation, groundwater, and streamflow in the Klamath basin and the effects of climate change on this area.
Our analysis confirms that the overall volume of water within the aquifer is strongly correlated with measurable flow leaving the watershed. As illustrated by the drought in the 1990’s and the current drought, once the groundwater storage relative to the 1968 baseline drops below approximately -1800 MCM (1,500 TAF), streamflow in the basin ceases completely. Unfortunately, due to the multi-year delay between precipitation and groundwater storage, the groundwater has not yet responded to recent increases in precipitation, although the pattern suggests that it should rebound soon and if precipitation continues at recent rates, we should expect streamflow to return in the next 3-5 years. The groundwater storage increase from 1994 to 2000 illustrates that with sufficient precipitation, the aquifer is capable of rebounding substantially. This understanding can and will assist in management decisions. A high water supply forecasted from an above-normal snowpack can be properly managed, and the forecast adjusted with awareness about how much water the aquifer will absorb. Biologists and natural resource managers, aware of the timeframe and water availability, can adjust management and conservation plans for aquatic species.
More concerning is the trend seen in aquifer volume since 2001 with the continuous decline in streamflow seen in Figure 13a. The groundwater storage held relatively steady from 2005 to 2015, but the streamflow gradually declined over the same period. The trend is likely anthropogenic. It coincides with actions taken by various federal agencies as part of a biological consultation. As a result of the National Marine Fisheries Service (NMFS) 2002 biological opinion on the endangered Chinook Salomon (Oncorhynchus tshawytscha), the Bureau of Reclamation reduced demand and stored extra water for the endangered species. The goal was to create a “water bank and water supply to provide flows to the Klamath River below Iron Gate Dam to improve coho salmon habitat” [52]. Designed to save water for habitat flows, up to 100 TAF of water was to be conserved in Upper Klamath Lake. Conservation was achieved through land idling, increased storage of surface water and the encouragement of groundwater usage to supplement/replace diverted live flow or deliveries of project water [4,52].

6. Conclusions

Our analysis demonstrates that the groundwater level imputation method in the GWDM tools that leverages Earth observations and machine learning can successfully be used to develop a groundwater storage history for a small basin with a limited number of monitoring wells, including sparse water level measurements over time. The resulting storage time history provides a holistic understanding of groundwater changes in the basin and how those changes impact streamflow. Using the data from this analysis we have demonstrated that both streamflow quantities and number of days per year with streamflow are highly correlated with the groundwater storage levels and once the groundwater storage drops below -1800 MCM (1,500 TAF) relative to the 1968 baseline, the streamflow in the basin completely ceases. Furthermore, we have shown that there is a 3-yr lag between the 3- and 5-yr moving average precipitation in the basin and groundwater storage and as a result, even though precipitation is starting to rebound in the basin, it will take several more years of elevated precipitation before the streams begin to flow again. This time includes both the 3-year lag and the time required to recharge the aquifer to the critical level. This approach is a new tool that water managers can use in groundwater-dependent basins to better understand and more effectively manage precious water resources.

Supplementary Materials

The groundwater data used in this study, including well locations and water level time series can be downloaded at http://www.hydroshare.org/resource/1d9791b2ef74454d8b335aab72d9bc97.

Author Contributions

Conceptualization, D.S., N.L.J and G.P.W.; methodology, D.S., N.L.J and G.P.W.; software, N.L.J and G.P.W.; data curation, D.S. and N.L.J.; writing—original draft preparation, D.S. and N.L.J.; writing—review and editing, G.W.P.; visualization, D.S., N.L.J and G.P.W.; All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding

Data Availability Statement

All datasets used in this the creation of the research paper are freely available on the internet through Federal and State environmental and research agencies. Federally run monitoring well have logs can be found through the US Geological Survey groundwater mapper website (https://waterdata.usgs.gov/nwis/gw) and entering the associated well number. Other monitoring wells’ data can be accessed at Oregon’s Water Resource Department (https://www.oregon.gov/owrd/pages/index.aspx) by locating the well by county (Klamath) and well ID number. All flow data is available through the US Geological Survey (https://waterdata.usgs.gov/nwis/sw) by entering the identification number of the gage utilized.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Melady, J. Hydrogeologic Investigation of the Klamath Marsh, Klamath County, Oregon. Master, Portland State University, 2002. [Google Scholar]
  2. Mayer, T.; Wurster, F.; Craver, D. Klamath Marsh Hydrology and Water Rights; USFWS, 2007; p. 22. [Google Scholar]
  3. Leonard, A.R.; Harris, A.B. Ground Water in Selected Areas in the Klamath Basin, Oregon; State of Oregon, 1974; p. 104. [Google Scholar]
  4. Gannet, M.W.; Lite, K.E., Jr.; la Marche, J.L.; Polette, D.J. Ground-Water Hydrology of the Upper Klamath Basin, Oregon and California: U.S. Geological Survey Scientific Investigations Reportentific Investigations Report; Scientific Investigations Report; 2007; p. 84. [Google Scholar]
  5. Conaway, J.S. Hydrogeology and Paleohydrology in the Williamson River Basin, Klamath County Oregon. Masters of Science, Portland State University, 2000. [Google Scholar]
  6. Cummings, M.L. Hydrogeology of the Williamson River Basin, Upper Klamath Basin, Klamath County, Oregon. Portland State University, 2007; p. 70. [Google Scholar]
  7. Stannard, D.I.; Gannett, M.W.; Polette, D.J.; Cameron, J.M.; Waibel, M.S.; Spears, J.M. Evapotranspiration from Wetland and Open-Water Sites at Upper Klamath Lake, Oregon, 2008–2010; USGS, 2013; p. 66. [Google Scholar]
  8. Newcomb, R.C.; Hart, D.H. Preliminary Report on the Ground-Water Resources of the Klamath River Basin, Oregon; U.S. Geological Survey], 1958. [Google Scholar]
  9. Gannett, M.W.; Wagner, B.J.; Lite, K.E., Jr. Groundwater Simulation and Management Models for the Upper Klamath Basin, Oregon and California: U.S. Geological Survey Scientific Investigations Report; Scientific Investigations Report; USGS, 2012; p. 92. [Google Scholar]
  10. Beck, H.E.; Zimmermann, N.E.; McVicar, T.R.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and Future Köppen-Geiger Climate Classification Maps at 1-Km Resolution (With Publisher Correction). Sci. Data 2020, 7, 274. [Google Scholar] [CrossRef] [PubMed]
  11. Risley, J.C. Using the Precipitation-Runoff Modeling System to Predict Seasonal Water Availability in the Upper Klamath River Basin, Oregon and California; U.S. Geological Survey, 2019. [Google Scholar]
  12. Markstrom, S.L.; Regan, R.S.; Hay, L.E.; Viger, R.J.; Webb, R.M.; Payn, R.A.; LaFontaine, J.H. PRMS-IV, the Precipitation-Runoff Modeling System, Version 4; U.S. Geological Survey, 2015. [Google Scholar]
  13. Chang, H.; Jones, J. Climate Change and Freshwater Resources in Oregon. Or. Clim. Assess. Rep. 2010. [Google Scholar]
  14. Mayer, T.D.; Naman, S.W. Streamflow Response to Climate as Influenced by Geology and Elevation1. JAWRA J. Am. Water Resour. Assoc. 2011, 47, 724–738. [Google Scholar] [CrossRef]
  15. Hess, G.W.; Stonewall, A.J. Comparison of Historical Streamflows to 2013 Streamflows in the Williamson, Sprague, and Wood Rivers, Upper Klamath Lake Basin, Oregon; U.S. Geological Survey, 2014. [Google Scholar]
  16. Tague, C.; Grant, G.; Farrell, M.; Choate, J.; Jefferson, A. Deep Groundwater Mediates Streamflow Response to Climate Warming in the Oregon Cascades. Clim. Change 2008, 86, 189–210. [Google Scholar] [CrossRef]
  17. Brutsaert, W. Long-Term Groundwater Storage Trends Estimated from Streamflow Records: Climatic Perspective. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
  18. Dudley, R.W.; Hodgkins, G.A. Historical Groundwater Trends in Northern New England and Relations with Streamflow and Climatic Variables. JAWRA J. Am. Water Resour. Assoc. 2013, 49, 1198–1212. [Google Scholar] [CrossRef]
  19. Huntington, J.L.; Niswonger, R.G. Role of Surface-Water and Groundwater Interactions on Projected Summertime Streamflow in Snow Dominated Regions: An Integrated Modeling Approach. Water Resour Res 2012, 48, W11524. [Google Scholar] [CrossRef]
  20. Ayers, J.R.; Villarini, G.; Schilling, K.; Jones, C.; Brookfield, A.; Zipper, S.C.; Farmer, W.H. The Role of Climate in Monthly Baseflow Changes across the Continental United States. J. Hydrol. Eng. 2022, 27, 04022006. [Google Scholar] [CrossRef]
  21. Arnold, J.G.; Allen, P.M. Automated Methods for Estimating Baseflow and Ground Water Recharge from Streamflow Records1. JAWRA J. Am. Water Resour. Assoc. 1999, 35, 411–424. [Google Scholar] [CrossRef]
  22. Hales, R.C.; Nelson, E.J.; Souffront, M.; Gutierrez, A.L.; Prudhomme, C.; Kopp, S.; Ames, D.P.; Williams, G.P.; Jones, N.L. Advancing Global Hydrologic Modeling with the GEOGloWS ECMWF Streamflow Service. J. Flood Risk Manag. n/a. [CrossRef]
  23. Sanchez Lozano, J.; Romero Bustamante, G.; Hales, R.; Nelson, E.J.; Williams, G.P.; Ames, D.P.; Jones, N.L. A Streamflow Bias Correction and Performance Evaluation Web Application for GEOGloWS ECMWF Streamflow Services. Hydrology 2021, 8, 71. [Google Scholar] [CrossRef]
  24. Nelson, E.J.; Pulla, S.T.; Matin, M.A.; Shakya, K.; Jones, N.; Ames, D.P.; Ellenburg, W.L.; Markert, K.N.; David, C.H.; Zaitchik, B.F.; et al. Enabling Stakeholder Decision-Making With Earth Observation and Modeling Data Using Tethys Platform. Front. Environ. Sci. Lausanne 2019. [Google Scholar] [CrossRef]
  25. Snow, A.D.; Christensen, S.D.; Swain, N.R.; Nelson, E.J.; Ames, D.P.; Jones, N.L.; Ding, D.; Noman, N.S.; David, C.H.; Pappenberger, F.; et al. A High-Resolution National-Scale Hydrologic Forecast System from a Global Ensemble Land Surface Model. JAWRA J. Am. Water Resour. Assoc. 2016, 52, 950–964. [Google Scholar] [CrossRef] [PubMed]
  26. Gochis, D.J.; Barlage, M.; Dugger, A.; FitzGerald, K.; Karsten, L.; McAllister, M.; McCreight, J.; Mills, J.; RafieeiNasab, A.; Read, L. The WRF-Hydro Modeling System Technical Description. Version 51 1 2018. [Google Scholar]
  27. NOAA The National Water Model. Available online: https://water.noaa.gov/about/nwm (accessed on 8 July 2024).
  28. Markstrom, S.L.; Niswonger, R.G.; Regan, R.S.; Prudic, D.E.; Barlow, P.M. GSFLOW—Coupled Ground-Water and Surface-Water Flow Model Based on the Integration of the Precipitation-Runoff Modeling System (PRMS) and the Modular Ground-Water Flow Model (MODFLOW-2005). Available online: https://pubs.usgs.gov/tm/tm6d1/ (accessed on 8 July 2024).
  29. Hunt, R.J.; Walker, J.F.; Selbig, W.R.; Westenbroek, S.M.; Regan, R.S. Simulation of Climate-Change Effects on Streamflow, Lake Water Budgets, and Stream Temperature Using GSFLOW and SNTEMP, Trout Lake Watershed, Wisconsin; U.S. Geological Survey, 2013. [Google Scholar]
  30. Ntona, M.M.; Busico, G.; Mastrocicco, M.; Kazakis, N. Modeling Groundwater and Surface Water Interaction: An Overview of Current Status and Future Challenges. Sci. Total Environ. 2022, 846, 157355. [Google Scholar] [CrossRef] [PubMed]
  31. Hughes, J.D.; Petrone, K.C.; Silberstein, R.P. Drought, Groundwater Storage and Stream Flow Decline in Southwestern Australia. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
  32. Carroll, R.W.H.; Niswonger, R.G.; Ulrich, C.; Varadharajan, C.; Siirila-Woodburn, E.R.; Williams, K.H. Declining Groundwater Storage Expected to Amplify Mountain Streamflow Reductions in a Warmer World. Nat. Water 2024, 2, 419–433. [Google Scholar] [CrossRef]
  33. Zipper, S.; Brookfield, A.; Ajami, H.; Ayers, J.R.; Beightel, C.; Fienen, M.N.; Gleeson, T.; Hammond, J.; Hill, M.; Kendall, A.D.; et al. Streamflow Depletion Caused by Groundwater Pumping: Fundamental Research Priorities for Management-Relevant Science. Water Resour. Res. 2024, 60, e2023WR035727. [Google Scholar] [CrossRef]
  34. Jones, N.L. GGST — GRACE Groundwater Subsetting Tool 2.0 Documentation. Available online: https://ggst.readthedocs.io/en/latest/ (accessed on 22 March 2024).
  35. McStraw, T.C.; Pulla, S.T.; Jones, N.L.; Williams, G.P.; David, C.H.; Nelson, J.E.; Ames, D.P. An Open-Source Web Application for Regional Analysis of GRACE Groundwater Data and Engaging Stakeholders in Groundwater Management. JAWRA J. Am. Water Resour. Assoc. n/a. [CrossRef]
  36. Barbosa, S.A.; Pulla, S.T.; Williams, G.P.; Jones, N.L.; Mamane, B.; Sanchez, J.L. Evaluating Groundwater Storage Change and Recharge Using GRACE Data: A Case Study of Aquifers in Niger, West Africa. Remote Sens. 2022, 14, 1532. [Google Scholar] [CrossRef]
  37. Obuobie, E.; Diekkrueger, B.; Agyekum, W.; Agodzo, S. Groundwater Level Monitoring and Recharge Estimation in the White Volta River Basin of Ghana. J. Afr. Earth Sci. 2012, 71–72, 80–86. [Google Scholar] [CrossRef]
  38. Yidana, S.M.; Dzikunoo, E.A.; Mejida, R.A.; Ackom, E.K.; Chegbeleh, L.P.; Loh, Y.S.A.; Banoeng-Yakubo, B.K.; Akabzaa, T.M. Evaluating Groundwater Resources Trends through Multiple Conceptual Models and GRACE Satellite Data. Environ. Monit. Assess. 2024, 196, 290. [Google Scholar] [CrossRef] [PubMed]
  39. Evans, S.W.; Jones, N.L.; Williams, G.P.; Ames, D.P.; Nelson, E.J. Groundwater Level Mapping Tool: An Open Source Web Application for Assessing Groundwater Sustainability. Environ. Model. Softw. 2020, 131, 104782. [Google Scholar] [CrossRef]
  40. Jones, N.L. GWDM — Ground Water Data Mapper 2.0 Documentation. Available online: https://gwdm.readthedocs.io/en/latest/ (accessed on 22 March 2024).
  41. Evans, S.; Williams, G.P.; Jones, N.L.; Ames, D.P.; Nelson, E.J. Exploiting Earth Observation Data to Impute Groundwater Level Measurements with an Extreme Learning Machine. Remote Sens. 2020, 12, 2044. [Google Scholar] [CrossRef]
  42. Ramirez, S.G.; Williams, G.P.; Jones, N.L. Groundwater Level Data Imputation Using Machine Learning and Remote Earth Observations Using Inductive Bias. Remote Sens. 2022, 14, 5509. [Google Scholar] [CrossRef]
  43. Jones, N.L.; Williams, G.P.; Shepherd, D. 2024 Oregon Williamson Basin Groundwater Study Data 2024.
  44. NASA Global Land Data Assimilation System (GLSDAS). Available online: https://ldas.gsfc.nasa.gov/gldas (accessed on 10 July 2024).
  45. NASA Goddard Earth Sciences Data and Information Services Center (GES DISC). Available online: https://disc.gsfc.nasa.gov/ (accessed on 10 July 2024).
  46. UCSB CHIRPS: Rainfall Estimates from Rain Gauge and Satellite Observations | Climate Hazards Center - UC Santa Barbara. Available online: https://www.chc.ucsb.edu/data/chirps (accessed on 10 July 2024).
  47. NASA SERVIR ClimateSERV 2.0 - Data and Tools for Sustainable Development. Available online: https://climateserv.servirglobal.net/ (accessed on 10 July 2024).
  48. Ramirez, S.G.; Williams, G.P.; Jones, N.L.; Ames, D.P.; Radebaugh, J. Improving Groundwater Imputation through Iterative Refinement Using Spatial and Temporal Correlations from In Situ Data with Machine Learning. Water 2023, 15, 1236. [Google Scholar] [CrossRef]
  49. Tethys Tethys Platform. Available online: http://www.tethysplatform.org/ (accessed on 5 March 2024).
  50. Nelson, E.J.; Pulla, S.T.; Matin, M.A.; Shakya, K.; Jones, N.; Ames, D.P.; Ellenburg, W.L.; Markert, K.N.; David, C.H.; Zaitchik, B.F. Enabling Stakeholder Decision-Making with Earth Observation and Modeling Data Using Tethys Platform. Front Environ Sci 2019, 7, 148. [Google Scholar] [CrossRef]
  51. Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array Programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
  52. U.S. National Marine Fisheries Service 2002 Klamath Project Biological Opinion 2002.
Preprints 113218 g001
Figure 1. Location of the Williamson Basin as it relates to Upper Klamath Lake and the Klamath river. Klamath River Watershed in Northern California and Southern Oregon.
Figure 1. Location of the Williamson Basin as it relates to Upper Klamath Lake and the Klamath river. Klamath River Watershed in Northern California and Southern Oregon.
Preprints 113218 g001
Preprints 113218 g002
Figure 2. Flow path of the Williamson River (in blue) as it flows northward, then turning south through the Klamath National Wildlife Refuge and entering Upper Klamath Lake.
Figure 2. Flow path of the Williamson River (in blue) as it flows northward, then turning south through the Klamath National Wildlife Refuge and entering Upper Klamath Lake.
Preprints 113218 g002
Preprints 113218 g003
Figure 3. Cumulative flow at gage #3500 vs cumulative precipitation by water year, 1981-2023. Flow data for water years 1996-1998 are absent from the record due to de-activation of the gauge, therefore linearly imputed values are shown.
Figure 3. Cumulative flow at gage #3500 vs cumulative precipitation by water year, 1981-2023. Flow data for water years 1996-1998 are absent from the record due to de-activation of the gauge, therefore linearly imputed values are shown.
Preprints 113218 g003
Preprints 113218 g004
Figure 4. Locations of the various monitoring wells (both USGS Oregon Department of Water Resources) used in this study.
Figure 4. Locations of the various monitoring wells (both USGS Oregon Department of Water Resources) used in this study.
Preprints 113218 g004
Preprints 113218 g005
Figure 5. (a) Cumulative annual flow volume and (b) number of days with measurable flow at Gage #3500 per WY from 1968 to 2023.
Figure 5. (a) Cumulative annual flow volume and (b) number of days with measurable flow at Gage #3500 per WY from 1968 to 2023.
Preprints 113218 g005
Preprints 113218 g006
Figure 6. Correlation between groundwater levels and GLDAS soil moisture for a monitoring well in Utah, USA.
Figure 6. Correlation between groundwater levels and GLDAS soil moisture for a monitoring well in Utah, USA.
Preprints 113218 g006
Preprints 113218 g007
Figure 7. Cumulative annual precipitation and flow data interpolated normalized and interpolated to monthly values using standard score or z-score normalization to plot both datasets on the same scale. Data were normalized to the study period, not long-term average and variance.
Figure 7. Cumulative annual precipitation and flow data interpolated normalized and interpolated to monthly values using standard score or z-score normalization to plot both datasets on the same scale. Data were normalized to the study period, not long-term average and variance.
Preprints 113218 g007
Preprints 113218 g008
Figure 8. Lagged correlation of cumulative annual precipitation and cumulative annual stream from with lags from -60 to +60 months. The highest correlation r = 0.525 occurred at lag = -32 months.
Figure 8. Lagged correlation of cumulative annual precipitation and cumulative annual stream from with lags from -60 to +60 months. The highest correlation r = 0.525 occurred at lag = -32 months.
Preprints 113218 g008
Preprints 113218 g009
Figure 9. Cumulative annual precipitation compared to cumulative annual flow with a lag of 32 months. The period from 1996 – 1998 has no annual flow data, data in this period were interpolated.
Figure 9. Cumulative annual precipitation compared to cumulative annual flow with a lag of 32 months. The period from 1996 – 1998 has no annual flow data, data in this period were interpolated.
Preprints 113218 g009
Preprints 113218 g010
Figure 10. GLDAS soil moisture datasets for the Williamson basin.
Figure 10. GLDAS soil moisture datasets for the Williamson basin.
Preprints 113218 g010
Preprints 113218 g011
Figure 11. Water level measurements, short-term PCHIP interpolated values, ELM-imputed values, and combined dataset for the KLAM0000496 well in the Williamson Basin.
Figure 11. Water level measurements, short-term PCHIP interpolated values, ELM-imputed values, and combined dataset for the KLAM0000496 well in the Williamson Basin.
Preprints 113218 g011
Preprints 113218 g012
Figure 12. Net groundwater storage change for the Williamson Basin from 1968 to 2023.
Figure 12. Net groundwater storage change for the Williamson Basin from 1968 to 2023.
Preprints 113218 g012
Preprints 113218 g013aPreprints 113218 g013b
Figure 13. Groundwater storage change in the Williamson Basin vs (a) cumulative volume of water measured and (b) number of days with measurable flow at Gage #3500 per WY from 1968 to 2023.
Figure 13. Groundwater storage change in the Williamson Basin vs (a) cumulative volume of water measured and (b) number of days with measurable flow at Gage #3500 per WY from 1968 to 2023.
Preprints 113218 g013aPreprints 113218 g013b
Preprints 113218 g014aPreprints 113218 g014b
Figure 14. Groundwater storage change in the Williamson Basin from 1981 to 2023 vs (a) cumulative annual precipitation and 3- and 5-yr moving average cumulative annual precipitation and (b) 3- and 5-yr moving average cumulative annual precipitation with a 3-yr lagged groundwater storage.
Figure 14. Groundwater storage change in the Williamson Basin from 1981 to 2023 vs (a) cumulative annual precipitation and 3- and 5-yr moving average cumulative annual precipitation and (b) 3- and 5-yr moving average cumulative annual precipitation with a 3-yr lagged groundwater storage.
Preprints 113218 g014aPreprints 113218 g014b
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated