Prerpints.org logo
Preprint
Article

Enhancing Spreading Factor Assignment in LoRaWAN with a Geometric Distribution Approach for Practical Node Distributions

Altmetrics

Downloads

96

Views

21

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

24 July 2024

Posted:

25 July 2024

You are already at the latest version

Alerts
Abstract
This paper proposes the GD (Geometric Distribution) algorithm, a novel approach to enhance the default Adaptive Data Rate (ADR) mechanism in the Long Range Wide Area Network (LoRaWAN). By leveraging the Probability Mass Function (PMF) of the GD model, the GD algorithm effectively addresses massive device distribution challenges in real-life scenarios. To evaluate the algorithm's performance, the LoRaWAN simulations were conducted using the fixed node pattern derived from actual locations of dairy farms in Ratchaburi province, Thailand. The research established scenarios for assessing the network's performance namely, DER (Data Extraction Rate) and SF (Spreading Factor) assignment. Comparative analyses were performed against the uniform random node pattern and established algorithms, including the default ADR scheme, EXPLoRa, Quantile Classification of Variance from the Mean (QCVM), and Standard Deviation (SD). The GD algorithm demonstrated significant improvements over existing methodologies for both fixed and uniform random patterns. The fixed pattern exhibited an enhancement of 14.3%, while the uniform random pattern showed 4.8% enhancement over the default ADR scheme. Further assessments covered the coverage area, payload size, and energy consumption. The GD algorithm consistently achieved the optimal DER values with a coverage area and payload size, albeit often at the expense of increased energy consumption.
Keywords: 
Subject: Engineering  -   Telecommunications

1. Introduction

Low Power Wide Area Network (LPWAN) [1] has now emerged as one of the most popular wireless networks for the Internet of Things (IoT). LPWAN has found various applications such as smart city, smart logistics, and smart farming. Long Range Wide Area Network (LoRaWAN) [2] is one of the LPWAN technologies that has received much attention for the past several years due to its low power consumption, large coverage area, high security, long battery life, and low cost. Compared with proprietary LPWAN technologies such as NB-IoT [3] and Sigfox [4], the non-proprietary LoRaWAN opens for individual users to adopt, build, learn, and research on the technology freely.
LoRaWAN uses the chirp spread spectrum (CSS) as a signal modulation technique in the physical layer. The packet and propagation characteristics are classified into groups of spreading factors (SFs) that are determined based on the received signal strength indicator (RSSI) and propagation distance of each packet. The typical values of SF are 7-12. The smaller SF offers higher data rate and shorter time-on-air (ToA) while the larger SF offers lower data rate and longer ToA. Since LoRaWAN adopts the pure ALOHA protocol, which allows simultaneous packet transmission by multiple end devices or nodes over a common radio channel; therefore, it inevitably suffers from packet loss due to collision. Note that, a packet collision is confirmed when two or more colliding packets have the same SF value and frequency, or same chirp rate. To alleviate the problem, altering data rate and thus ToA of end devices or SF allocation, is a widely used approach.
Various pieces of research focused on the applications of LoRaWAN. Examples include deploying gas sensors to remotely collect data for air pollution control [5] and the integration of LoRaWaN to the smart water resource management equipped with measurement systems of water availability, soil moisture, topography, and plant identification [6,7]. They found that LoRaWAN could improve the data transmission and thus the data extraction rate (DER), which is the ratio between the success sending data packet and all data packets in a defined period.
Other previous research explored and improved LoRaWAN performance in different environments. The LoRaWAN network infrastructure was implemented for a universal sensor, and proved to consume lower energy and operated well under real-life conditions [8]. The LoRaWAN performance with mobile nodes was evaluated in an urban environment and was found to provide shorter data transmission range than the open environments [9]. The path-loss propagation model for LoRaWAN was then optimized in some certain environment to ensure the positive results [10].
A default mechanism used for optimizing data rate, ToA, and energy consumption of an end device in LoRaWAN is the adaptive data rate (ADR) [11]. The ADR optimizes these parameters by considering RSSI and link budget. When multiple nodes are placed in a confined area, their RSSI values are nearly the same, so do their SF values. Although the ADR is activated, the SF vallues are not sufficiently distributed, thus the packet collisions still occur. Therefore, several previous works aimed on improving the network performance, reducing packet collision by better SF allocation or assignment.
Basically, there are six techniques for improving SF assignments, which were summarized in [2]. The techniques include SNR-based, mathematical model, RSSI-based, ToA, distance-based, and AI and machine learning techniques.
The SNR-based SF technique focuses on optimizing the gain and transmit power to reduce the transmission failure associated by noise and interference. In [12] equal-interval-based (EIB) and equal-area-based (EAB) SF allocation methods were proposed. Both methods compared SNR values with SNR thresholds based on the gateway specification. In [13], the SNR optimization algorithm was proposed to improve the packet delivery ratio (PDR) and energy efficiency over the original ADR.
The RSSI-based and ToA techniques were designed to mitigate SF collisions during message transmission. Specifically, they aimed to prevent multiple devices from transmitting messages using the same SF values and radio channels simultaneously, thereby enhancing overall network efficiency and reliability. For instance, the EXPLoRa-SF algorithm compared the RSSI values with the sensitivity levels and divided them into six groups with equal number of nodes [14]. Then, the EXPLoRa-AT algorithm proposed to use the “sequential waterfilling” to select the optimal SF values for certain ToAs for proper selection of radio channel for message transmission [15].
The distance-based technique involves calculating the optimal transmit power allocation by considering both distance and assigned SF value [16]. The concept of this technique in fact, aligns closely with SNR-based SF allocation, which focuses on adjusting the transmit power to resist noise and interference.
In [17] and [18], mathematical models combined with machine learning approaches were reported. In [18], the reinforcement learning (RL)-based method for SF channel allocation in one-hop and in the LoRa mesh network was proposed. The equation for properly selecting the new SF value based on environmental conditions was then developed. The RL method optimized the SF value by providing positive rewards if the SF effectively reduces collision rates and negative rewards otherwise. Consequently, the optimal SF value that minimizes data collision rates was determined. In addition, [18] proposed an algorithm that incorporates node distance information, then utilized the supervised machine learning for transmit power allocation and employed the RL method for SF allocation.
Apart from the abovementioned techniques, the statistical approach has become another promising approach to improve SF assignment. In [19], the researchers proposed the Quantile Classification of Variance from the Mean (QCVM) method that uses the statistical method namely, the quantile classification to group RSSI data considering their average and probability density function (PDF). Then, they proposed the Standard Deviation (SD) classification method that analyzed RSSI data of nodes before separating them by the standard deviation (SD) and re-assigning the SF values [20].
It was known that most SF allocation algorithm developments began with simulations prior to the actual implementations. The node locations were commonly generated in the uniform random distribution, which is the default setting in most LoRaWAN simulators. However, the real-life node patterns often exhibit non-uniform or biased node distributions; thus, the uniform random distribution does not always give accurate insights in real-world scenarios, and potentially compromising the efficacy of prior algorithms in such contexts.
This research introduces the Geometric Distribution (GD) algorithm, a novel approach that leverages the Probability Mass Function (PMF) of the geometric distribution mathematical model [21] to address the challenge of non-uniform or biased SF node distribution. By incorporating this framework, the GD algorithm aims to enhance the default Adaptive Data Rate (ADR) mechanism in the LoRaWAN. The key of the GD algorithm is to identify the optimal distribution format for the intensive SF values by assigning weights to each SF category. The algorithm seeks to determine the weight factors (w) that best capture the number of occurrences for each SF. These weight factors (w) are intricately linked to the geometric distribution factor (p-value) for which we aimed to identify the optimal value and corresponding weight factors (w) that yield the highest DER.
Our research applied the proposed GD algorithm to the LoRaWAN simulations conducted using the LoRaSIM simulator. To assess the impact of node distribution on network performance, a comparative analysis was undertaken. This analysis compared results obtained from the uniform random node distribution scenario to those obtained from the fixed node distribution assumed based on locations of dairy farms around the Photharam district, Ratchaburi province, Thailand [22]. This particular site was selected because it plans to implement Internet of Things (IoT) sensors to collect behavior data from dairy cows. The novelty of our algorithm lies in its ability to work effectively with biased node distributions and still achieve high DER values. This adaptability ensures the algorithm’s efficacy across various scenarios, providing valuable insights for improving network performance under diverse conditions.
The paper is divided into subsections as follows. Section 2 provides a brief overview of LoRaWAN. Section 3 delves into the comparison of fixed and random node simulation, while Section 4 and Section 5 expound on the geometric distribution mathematical model and the proposed algorithm, respectively. Section 6 covers the details of the experiment simulation, and the discussion and analysis of results are presented in Section 7. The research concludes with a summarizing section outlining the key findings and implications of the study.

2. LoRaWAN Overview

LoRa is a protocol in the physical layer of an IoT network. This protocol operates in the industrial, scientific, and medical radio band (ISM band) or 902 – 928 MHz in Thailand. LoRa protocol can endure the noise floor and interference by Chirp Spread Spectrum (CSS) techniques. The highlighted advantages are low power consumption and long-range coverage area. The characteristics of the CSS modulation depend on the LoRa’s parameters such as bandwidth (BW), SF, Coding Rate (CR), and the airtime defined in terms of the Symbol time (TS) shown in equation (1). The bit rate (Rb) is related to BW, SF, and CR as shown in equation (2).
T s = 2 S F B W ,
R b = S F × B W 2 S F × C R ,
LoRaWAN is a network architecture consisting of end devices or nodes that employ the LoRa protocol for transmitting and receiving packets, LoRa gateway, network server, and application server. In LoRaWAN, we can define the data rate, airtime, and signal range by assigning the SF values, which is the unique parameter in the LoRa modulation, as shown in Figure 1.
LoRaWAN utilizes the Adaptive Data Rate (ADR), which is a default mechanism for optimizing the data rate, airtime, distance, and energy consumption, when the signal strength varies dynamically such as in the case of dense and moving nodes. The link budget is the RSSI sensitivity level, which depends on the Signal-to-Noise Ratio (SNR), Noise Figure of receiver (NF), and BW. The link budget is presented in terms of the sensitivity value (S) shown in equation (3). The SNR limit is dependent on the end device, and the NF of a typical LoRa gateway chipset is 7 dB [11]. The sensitivity level is also displayed in Figure 1.
S = − 174 + 10 log ⁡ B W + N F + S N R l i m ,

3. Network Simulations for Fixed and Uniform Uniform Random Patterns of Nodes

The network simulation is the important approach to better anticipate the results of the actual network performance. It also shed some lights on what the network performance would be like in case the actual implementation cannot take place. However, most previous simulation works relied on generating a uniform random node pattern that could significantly deviate from the real-world scenario. This section aims on understanding the effect of node patterns on SF assignment and network performance by comparing fixed and random node patterns using the default ADR scheme.
Before constructing the node pattern, the propagation path loss model suitable for the study area was selected for the simulation. In our investigation, we conducted a survey at a considerable number of dairy farms in the Photharam district of Ratchaburi, Thailand. This area has a potential to adopt smart livestock technologies, and some farms had already pursued that. We installed the LoRa gateway at Centermilk Farm and then conducted several drive tests in 5 km radius as shown in Figure 2 to measure the LoRa signal strength before creating a map to locate dairy farms within the test area. Photharam district is situated outside urban areas, characterized by small buildings and villages. While present, these structures are not as numerous or densely populated as in urban. This environment thus aligns better with the suburban Hata-Okumura path loss model [23] as indicated by equations (4)-(8).
A = 69.55 + 26.16 log ⁡ ( f ) − 13.82 log ⁡ ( h b ) ,
B = 44.9 − 6.55 log ⁡ ( h b ) ,
a ( h m ) = ( 1.1 log ⁡ ( f ) − 0.7 ) h m − ( 1.56 log ⁡ ( f ) − 0.8 ) ,
C = − 2 ( log ⁡ ( f 28 ) ) 2 − 5.4 ,
L c = A + B log ⁡ ( d ) − a ( h m ) + C ,
where Lc is the power of path loss,
d is the distance of end devices in meter,
hm is the height of end devices in meter,
f is the frequency in Kilohertz
hb is the height of the gateway in meter.
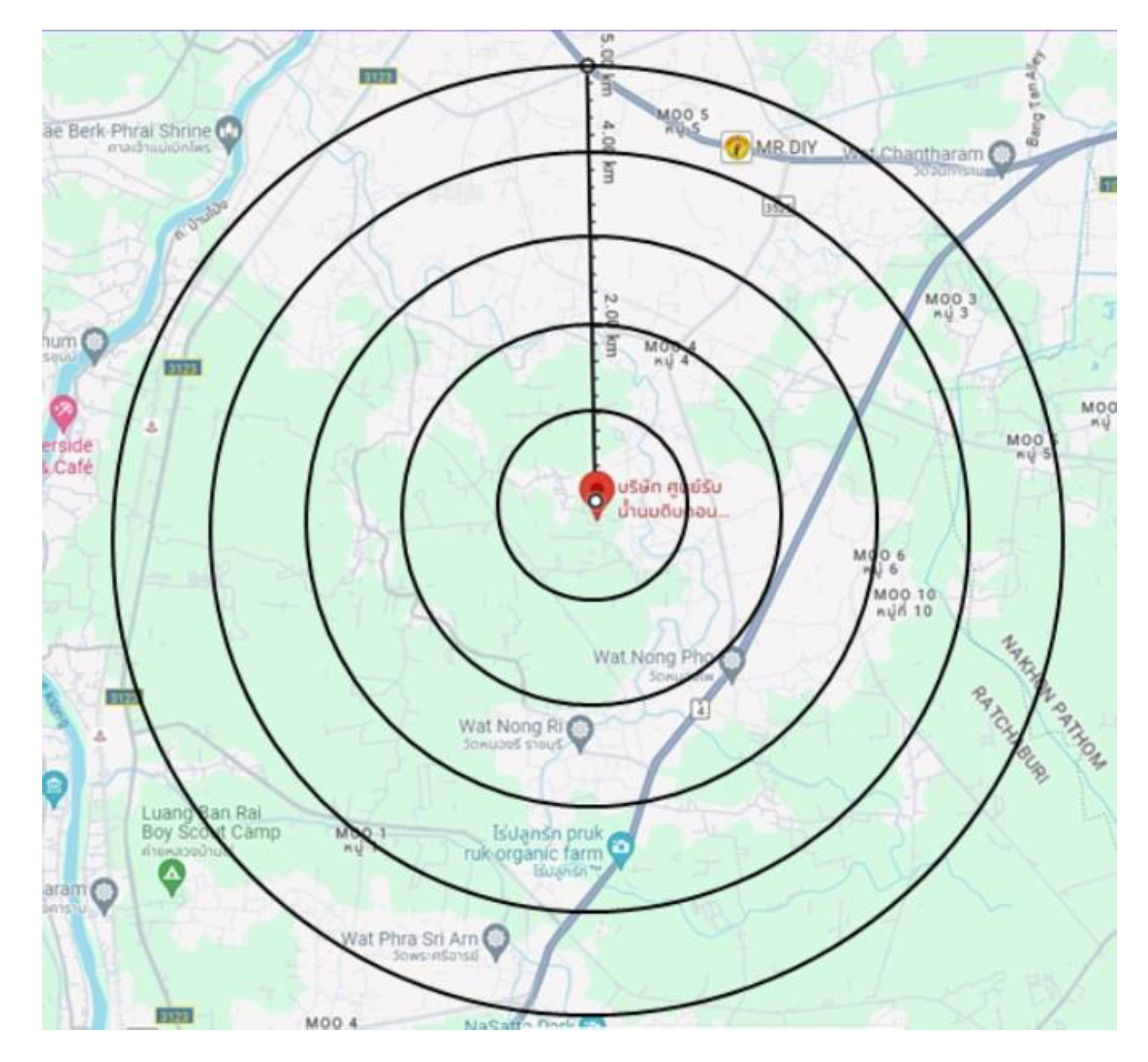
Preprints 113197 g002
Figure 2. Location of dairy farms at Photharam district, Ratchaburi, Thailand.
Figure 2. Location of dairy farms at Photharam district, Ratchaburi, Thailand.
Preprints 113197 g002
In our research, we assigned 1,500 nodes to represent 1,500 connected dairy cows raised on the dairy farms in Photharam district, Ratchaburi. Note that, the connected dairy cows are those tagged with the IoT sensors. We introduced node positions in the 2D plane with x and y coordinates, as expressed in equations (9) and (10). Subsequently, we calculated the distance D from the node to a gateway using the Pythagorean formula as shown in equation (11).
x = C × D m a x cos ⁡ A B ,
y = C × D m a x   s i n ( A B ) ,
D = x 2 + y 2 ,
where Dmax is the coverage area in meter,
x and y are the positions in the 2-dimensional plane,
D is the distance between the node and the gateway in meter,
A, B, and C are the values between 0 to 1.
First, we utilized the LoRaSim simulator to randomize A, B, and C constants to generate the uniform random node pattern as shown in Figure 3. Then, we assigned certain values of A, B, and C constants using Equations (9)-(11) to reflect the actual locations of dairy farms, and consequently, the connected cows raised on those farms. The actual or fixed pattern shown in Figure 4 clearly exhibits a biased node distribution where most nodes are confined within 2 km radius from the center.
After the node pattern was constructed, the node’s SF values of both patterns were assigned using the default ADR mechanism in LoRaSim. The proportion of SF assignment was observed and measured and the DER values were computed. The results are shown in the Table 1. At distances 2 and 3 km for both uniform random and fixed patterns, every node is assigned as SF7. The DER values are nearly identical at around 51%. At 4 and 5 km, more nodes are distributed to SF8 and SF9 respectively, but the majority is still SF7. For the fixed node pattern, above 89% of nodes are SF7, while the number is clearly lower for the uniform random pattern. This disparity in SF assignment directly affects DER values, with the uniform random pattern exhibiting 6.2% and 8.7% higher than those of the fixed pattern at 4 and 5 km, respectively. The results somewhat indicate insufficiency of the default ADR scheme in handling actual node distributions.

4. Geometric Distribution Approach

To tackle challenges arising from the biased node distribution, a novel algorithm designed to optimize the SF assignment for each node called the geometric distribution (GD) algorithm is proposed here. The geometric distribution is basically known as a discrete probability distribution used to model events with two outcomes in repeated trials until success is achieved. The Probability Mass Function (PMF) is a measure providing probabilities for possible values of a random variable. In an attempt to distribute the biased number of SF nodes, the probability of success rate (p-value) of the PMF is the key feature.
The PMF is presented in equation (12). Notably, the PMF exhibits a distinct characteristic— the probability of success is highest on the first trial (x = 1) and decreases in subsequent trials. The p-value is a crucial parameter, influencing the likelihood of success and the overall distribution of success rates. Figure 5 presents a visual representation of the probability of success derived from the GD PMF.
P ( x ) = ( 1 − p ) x − 1 p ,   x = 1 ,   2 ,   3 ,   …

5. The Geometric Distribution Algorithm for SF Assignment

Reverting to the DER results run by the default ADR scheme, a significant challenge arose since more than 70% of all nodes from the uniform random and fixed patterns were assigned SF7 at 4 and 5 km. To significantly improve the DER, we needed to find the optimal SF distribution by redistributing the number of SF7 nodes using the PMF and determined the weight factor for each SF. Initially, we employed a weight factor (w), as defined in equations (13)
N S F max = w 1 * N S F max + w 2 * N S F max + , … , + w 6 * N S F max ,
where NSF max is the total number of majority SF nodes
wn is the weight factor of new SF7 (n = 1) to new SF12 (n = 6) and is defined as
w n = p ( 1 − p ) n − 1 ,
where n = 1-6
From (12), the summation of w1 to w6 must be 1, that is
∑ n = 1 6 p ( 1 − p ) n − 1 = 1 ,
By using this approach, the weight factor always decreases when p in equation (14) increases. The summation of the new weight factors must be 1, as shown in (15). The numbers of new SF7-SF12 respectively, are obtained by multiplying w1 – w6 by NSF max, respectively.
The GD algorithm was then developed and is shown in Algorithm I. First, we input the highest number of nodes with similar SF, which in our case is the SF7, to the proposed GD algorithm. Then, SF7 nodes were separated using the GD approach. The process entered a loop starting at p = 1 and the corresponding weight factors w[x] were multiplied by the SF7 count (NSF max) to obtain the number of new SFs. The loop iterated as the p-value decreased by 0.1 decrement. The weight factors were recalculated at each p-value and thus, the number of new SFs was obtained. The loop continued until the p-value reached 0.1, marking the end of the algorithm. The resulting set of weight factors at the p-value equal 1 to 0.1 is presented in Table 2.
Algorithm I: Geometric distribution
1:
2:
3:
4:
5:
6:
7:
8:
9:
10:
11:
12:
13:
 Input: Number of highest SF (NSF max)
Define: Weight factor (w)
        Geometric distribution factor (p)
Initialize: p = 1
Do
 // Calculate the weight factor of each SF
 w[x] ← p * (1 - p) ^ (x - 1) let x = 1, 2, 3, 4, 5, 6
// Calculate the number of each SF
SF[y] ← NSF max* w[x] let x = 1, 2, 3, 4, 5, 6 and y = 7, 8, 9, 10, 11, 12
// Return the new number of each SF
Return SF[7], SF[8], SF[9], SF[10], SF[11], SF[12]
p ← p – 0.1
While p > 0.1 // p starts at 1 to 0.1, with 0.1 decrement
The complete implementation workflow is shown in Figure 6. Initially, nodes were classified according to sensitivity levels outlined in Figure 1. After applying the GD algorithm, the sets of weight-classified SF nodes were input to the simulation to determine Data Extraction Rate (DER) values for probabilities ranging from p = 1 to 0.1. The p-value that produced the optimal SF and DER values was selected, and finally, the optimized SF values were applied to the nodes.

6. Geometric Distribution Algorithm Performance Assessment

To assess the performance of the GD algorithm, we designed three experiments for network simulation with two node patterns: uniform random and fixed as depicted in Figure 3 and Figure 4, respectively. Following this, we employed the LoRaSim simulator to generate the uniform random node pattern and to compute DER values for all experiments. Experiment 1 was the evaluation of the GD algorithm for both uniform random and fixed patterns. Experiment 2 was the comparison of the optimal SF assignment and corresponding DER values obtained from the GD algorithm and other previous works for both uniform random and fixed patterns. The parameters for experiments 1 and 2 were configured according to the specifications outlined in Table 3. The third experiment was the comparison of the GD algorithm-based network performance of the fixed pattern with other previous works by considering key parameters namely, coverage area (2 to 5 km.), payload size (10 to 255 bytes), and energy consumption with the simulation time from 1 to 12 hours.

7. Results and Discussion

A. Experiment 1: Evaluation of the GD Algorithm for Uniform Random and Fixed Patterns

By using the GD algorithm, the new SF assignment for both uniform random and fixed patterns are presented in Figure 7 and Figure 8, respectively. For both patterns, the SF values are assigned across different probability values (p-value) ranging from 1 to 0.1. At p = 1, the SF distribution aligns with the default ADR scheme. As the p-value decreases, the number of SF7 nodes gradually separates into SF8-SF12, due to the weight factor (w).
By decreasing the p-value, the DER values of both patterns increase until reaching the optimal DER value at p = 0.5 and then decrease monotonically as shown in Figure 9. The optimal DER value of the fixed pattern is approximately 73.5%, slightly better than that of the uniform random pattern (71.8%), and both DER values are clearly higher than the default ADR scheme. The numbers of new SFs for the uniform random and fixed patterns at p = 0.5 are shown as the bar graphs in Figure 7 and Figure 8, respectively. Note that, the optimal p-values and corresponding DER values might be different for different node distributions.

B. Experiment 2: Comparison of the GD Algorithm with Previous Reported Algorithms

In this experiment, the simulation was conducted to compare DER values between the GD algorithm at the optimal p = 0.5, the default ADR scheme [11], and previously reported algorithms namely, EXPLoRa [14], QCVM [19], and SD [20]. Table 4 and Table 5 display the SF assignment for uniform random and fixed patterns, respectively. The result in Figure 10 clearly addresses a substantial impact of SF distribution on the DER value. Optimizing the SF distribution with the GD algorithm results in the overall highest DER at 4.8% and 14.3% improvement over the default ADR scheme for uniform random and fixed patterns, respectively.

C. Experiment 3: Network Performance Evaluation of the GD Algorithm Based on Coverage Area, Payload Size, and Energy Consumption

We aimed on assessing the GD algorithm on the expansion of the coverage area as it is a crucial factor influencing SF assignment [20,21]. By expanding the coverage area from 2 to 5 km (to reflect the actual farm area), the proposed GD algorithm achieved the DER of 74%, higher than other algorithms, as shown in Figure 11. The DER of the default ADR scheme also improved at 4-5 km due to more node allocation to SF8 and SF9.
We also assessed the GD algorithm on the payload size, which plays an important role in defining the range of transmitted data. From Figure 12, a decline in DER as the payload size increases is observed for all algorithms. Remarkably, the proposed algorithm demonstrates notable improvement, surpassing the default ADR scheme by more than 13% at a payload size of 255 bytes. This finding indicates the potential of the GD algorithm to successfully carry the larger load over the air.
The time-on-Air (ToA) and node power are also one of the important factors determining the energy consumption of the node, which after combining all nodes, amounts to the total energy consumption of the network. Note that, the energy consumption of gateway and servers are omitted here. The relationship between ToA and energy consumption (E), measured in joules, is represented by equation (16). Figure 13 displays the energy consumption when increasing the simulation time from 1 hour to 12 hours. Since ToA increases with the SF value, the SF assignments can then be used to justify the results. For EXPloRa where there are a greater number of large SF nodes, the energy consumption is clearly higher than other algorithms. On the other hand, the default ADR scheme offers the lowest energy consumption as almost 90% of the nodes are SF7. The proposed GD algorithm offers relatively the same energy consumption as the SD, but slightly higher than that of the QCVM due to neither SF10, SF11 nor SF12 were assigned for QCVM.
E = ∑ n = 1 S ( T a i r t i m e × ( T X n o d e + 2 ) × V ) 1 0 6 ,
where Tairtime is the time on air of the successfully sent node in seconds.
TXnode is the transmission power (dBm) of the successfully sent node.
V is the supplied voltage to the node (3 V) [2]

8. Conclusions

This research endeavored to enhance the performance of the LoRaWAN by addressing collision probability issues, specifically aiming to reduce instances of the same SF. Various algorithms employed in the past often incorporated RSSI optimization on random and normally distributed node patterns. Our contribution to this domain introduced a novel algorithm based on the geometric distribution (GD), where we applied this algorithm to real-world scenarios that possessed certain node patterns. Results from our study indicated that the proposed algorithm achieved significant improvements in both optimal SF assignment and DER values compared to previous algorithms. Specifically, the fixed pattern exhibited an impressive enhancement of 14.3%, while the uniform random pattern exhibited 4.8% enhancement over the default ADR scheme.
Expanding the coverage area and increasing the package size further underscored the efficacy of the proposed algorithm, consistently yielding the highest DER values. However, it was important to note that achieving these improvements required allowing higher energy consumption since larger SF values were also assigned.
Looking ahead, the GD algorithm emerges as a valuable tool for resource allocation, especially in scenarios, where there are mostly the same SF nodes in one area. This algorithm holds promise for optimizing resource distribution and finding the most efficient pathways. Furthermore, the application of this algorithm extends beyond LoRaWAN to other wireless communication technologies, including Sigfox, Wi-Fi, and 5G. The adaptability and effectiveness of the geometric distribution algorithm position it as a potential solution for future advancements in long range wireless communication optimization.

Acknowledgments

The author was supported by the “Petchra Pra Jom Klao Master’s Degree Research Scholarship from King Mongkut’s University of Technology Thonburi” Contract No 29/2561.

References

  1. Augustin, A.; Yi, J.; Clausen, T.; Townsley, W.M. A Study of LoRa: Long Range & Low Power Networks for the Internet of Things. Sensors 2016, 16, 1466. [Google Scholar] [CrossRef] [PubMed]
  2. Haxhibeqiri, J.; De Poorter, E.; Moerman, I.; Hoebeke, J. A Survey of LoRaWAN for IoT: From Technology to Application. Sensors 2018, 18, 3995. [Google Scholar] [CrossRef] [PubMed]
  3. Mwakwata, C.B.; Malik, H.; Mahtab Alam, M.; Le Moullec, Y.; Parand, S.; Mumtaz, S. Narrowband Internet of Things (NB-IoT): From Physical (PHY) and Media Access Control (MAC) Layers Perspectives. Sensors 2019, 19, 2613. [Google Scholar] [CrossRef] [PubMed]
  4. Sigfox. Available online: https://www.sigfox.com.
  5. Mohamad, M. Performance Analysis of Air Monitoring System Using 433 MHz LoRa Module. Przegląd Elektrotechniczny 2024, 1, 225–229. [Google Scholar] [CrossRef]
  6. Sujono, H. Drip Irrigation Control System Based on Mamdani Fuzzy Logic and Internet of Things (IoT). Przegląd Elektrotechniczny 2024, 1, 65–69. [Google Scholar] [CrossRef]
  7. Boonsong, W. Proposed Precision Analysis of Water Quality Monitoring Embedded IoT Network. Przegląd Elektrotechniczny 2023, 1, 177–180. [Google Scholar] [CrossRef]
  8. Sambor, S. Przykład Zastosowania Sieci LoRaWAN Do Monitorowania Parametrów Środowiskowych W Budynku Wielkopowierzchniowym. PRZEGLĄD ELEKTROTECHNICZNY 2022, 1, 29–34. [Google Scholar] [CrossRef]
  9. Zankiewicz, A. Eksperymentalna Analiza Efektywności Transmisji Danych W Sieci LoRaWAN W Eksploatacji Na Terenie Miejskim. Przegląd Elektrotechniczny 2023, 1 (5), 43–50. [CrossRef]
  10. El Chall, R.; Lahoud, S.; El Helou, M. LoRaWAN Network: Radio Propagation Models and Performance Evaluation in Various Environments in Lebanon. IEEE Internet of Things Journal 2019, 6, 2366–2378. [Google Scholar] [CrossRef]
  11. Semtech Corporation. Understanding the LoRa Adaptive Data Rate. Available online: https://lora-developers.semtech.com/uploads/documents/files/Understanding_LoRa_Adaptive_Data_Rate_Downloadable.pdf (December 2019).
  12. Saluja, D.; Singh, R.; Baghel, L. K.; Kumar, S. Scalability Analysis of LoRa Network for SNR-Based SF Allocation Scheme. IEEE Transactions on Industrial Informatics 2021, 17, 6709–6719. [Google Scholar] [CrossRef]
  13. Al-Gumaei, Y. A.; Aslam, N.; Chen, X.; Raza, M.; Ansari, R. I. Optimizing Power Allocation in LoRaWAN IoT Applications. IEEE Internet of Things Journal 2022, 9, 3429–3442. [Google Scholar] [CrossRef]
  14. Cuomo, F.; Campo, M.; Caponi, A.; Bianchi, G.; Rossini, G.; Pisani, P. EXPLoRa: Extending the Performance of LoRa by Suitable Spreading Factor Allocations. 2017 IEEE 13th International Conference on Wireless and Mobile Computing, Networking and Communications (WiMob) 2017. [CrossRef]
  15. Garlisi, D.; Tinnirello, I.; Bianchi, G.; Cuomo, F. Capture Aware Sequential Waterfilling for LoRaWAN Adaptive Data Rate. IEEE Transactions on Wireless Communications 2021, 20, 2019–2033. [Google Scholar] [CrossRef]
  16. Hoeller, A.; Demo Souza, R.; Montejo-Sanchez, S.; Alves, H. Performance Analysis of Single-Cell Adaptive Data Rate-Enabled LoRaWAN. IEEE wireless communications letters 2020, 9, 911–914. [Google Scholar] [CrossRef]
  17. Hong, S.; Yao, F.; Zhang, F.; Ding, Y.; Yang, S.-H. Reinforcement Learning Approach for SF Allocation in LoRa Network. IEEE internet of things journal 2023, 10, 18259–18272. [Google Scholar] [CrossRef]
  18. Usama Minhaj, S.; Mahmood, A.; Fakhrul Abedin, S.; Ali Hassan, S.; Talha Bhatti, M.; Ali, S.; Gidlund, M. Intelligent Resource Allocation in LoRaWAN Using Machine Learning Techniques. IEEE Access 2023, 11, 10092–10106. [Google Scholar] [CrossRef]
  19. Tempiem, P.; Silapunt, R. Quantile Classification of Variance from the Mean for Spreading Factor Allocation in LoRaWAN. 2020. [CrossRef]
  20. Tempiem, P.; Silapunt, R. Spreading Factor Allocation Using the Standard Deviation Classification Method. 2021. [CrossRef]
  21. Britannica. Geometric Distribution Probability. Available online: https://www.britannica.com/topic/geometric-distribution (Febuary 2024).
  22. Kamonkusonman, K.; Phunthawornwong, M.; Tempiem, P.; Silapunt, R. Utilization-Weighted Algorithm for LoRaWAN Capacity Improvement for Local Smart Dairy Farms in Ratchaburi Province of Thailand. IEEE Access 2021, 9, 141738–141746. [Google Scholar] [CrossRef]
  23. F. Molisch, Wireless Communications Handbook. John Wiley & Sons, CA: University of Southern California, 2011.
Preprints 113197 g001
Figure 1. Relationship of SF, data rate, airtime, energy, and sensitivity level.
Figure 1. Relationship of SF, data rate, airtime, energy, and sensitivity level.
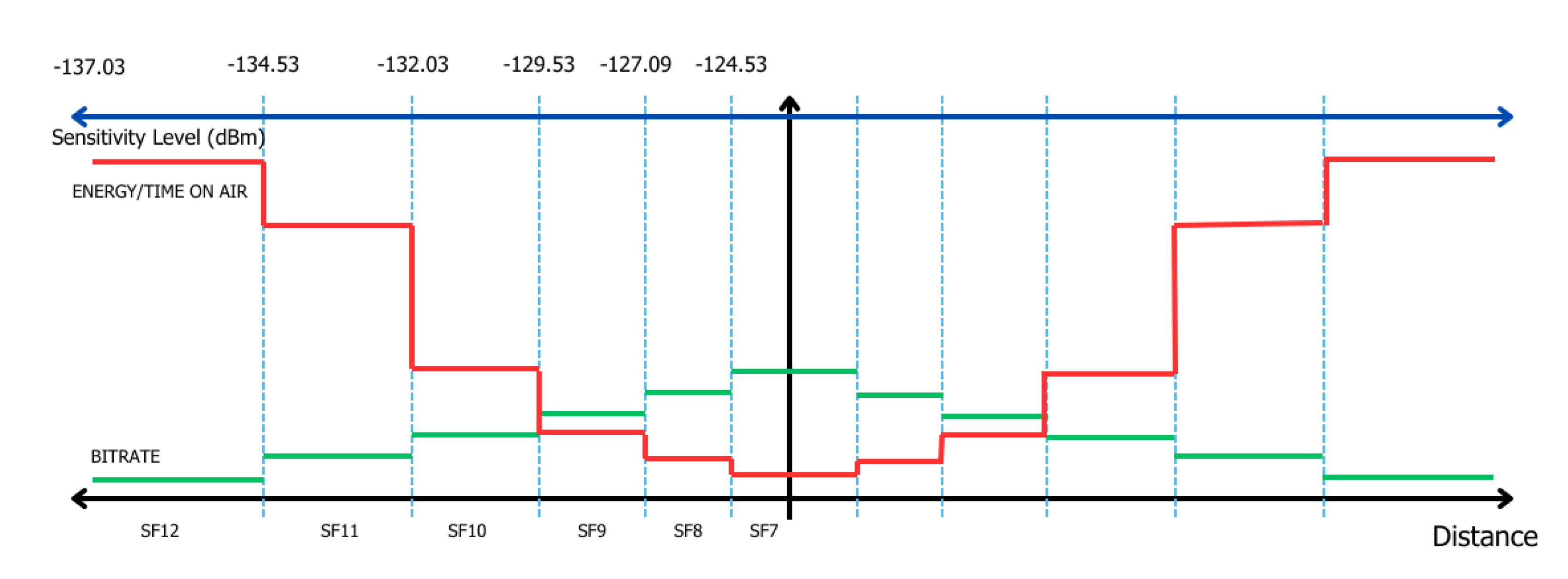
Preprints 113197 g001
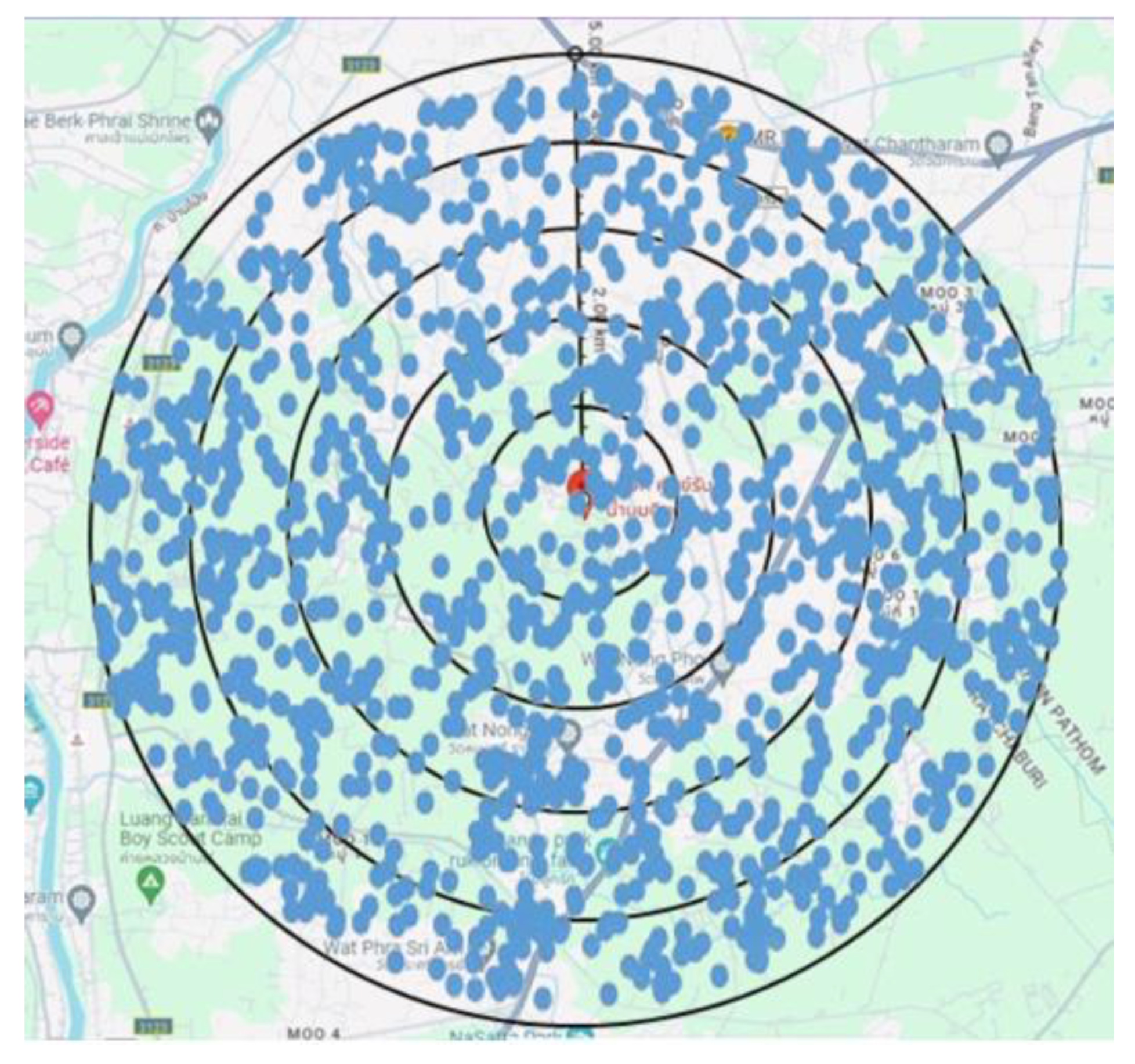
Preprints 113197 g003
Figure 3. Uniform random node pattern.
Figure 3. Uniform random node pattern.
Preprints 113197 g003
Preprints 113197 g004
Figure 4. Fixed node pattern.
Figure 4. Fixed node pattern.
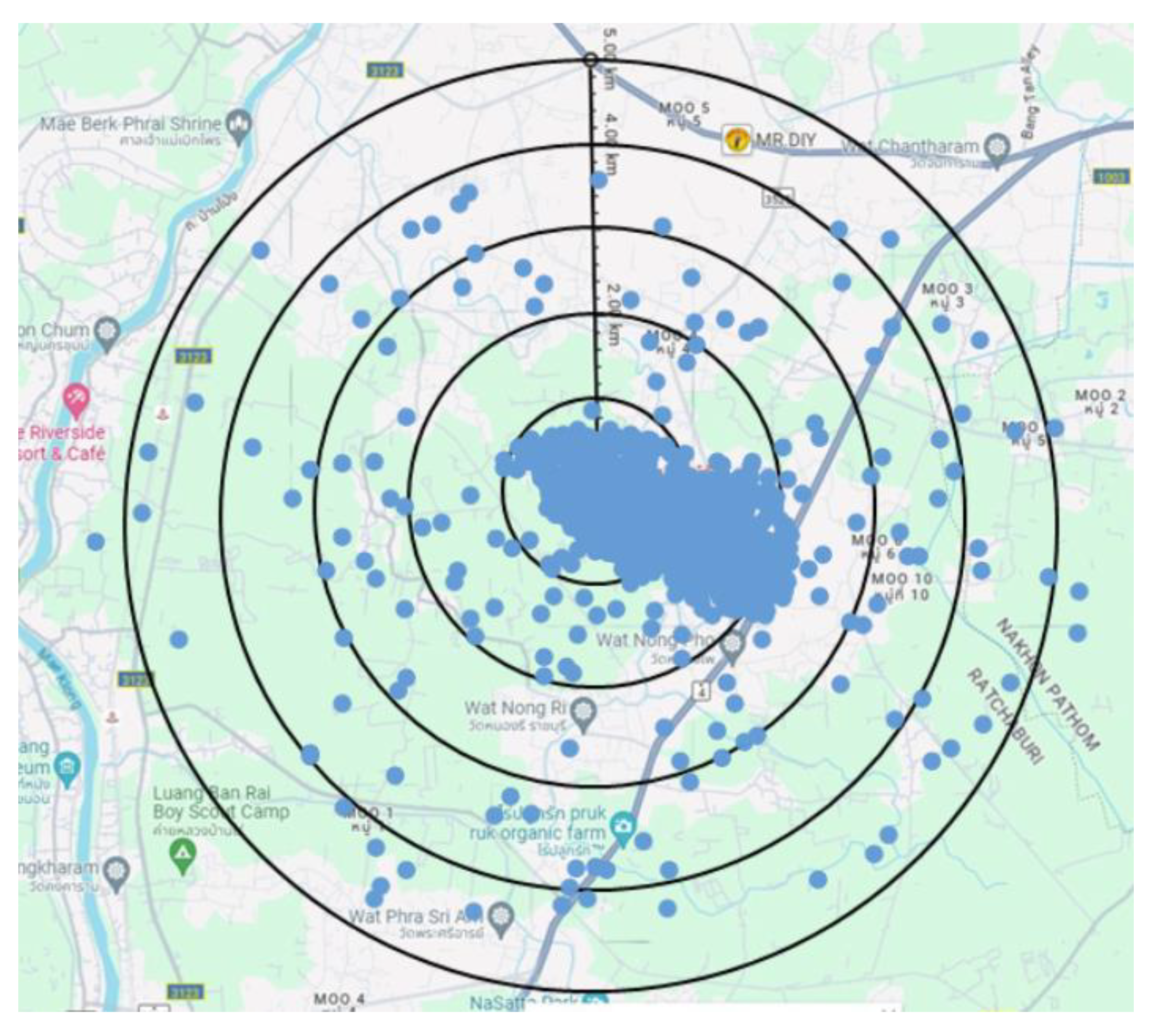
Preprints 113197 g004
Preprints 113197 g005
Figure 5. The probability of success from the GD PMF at (a) p = 0.8, (b) p = 0.6, and (c) p = 0.2.
Figure 5. The probability of success from the GD PMF at (a) p = 0.8, (b) p = 0.6, and (c) p = 0.2.
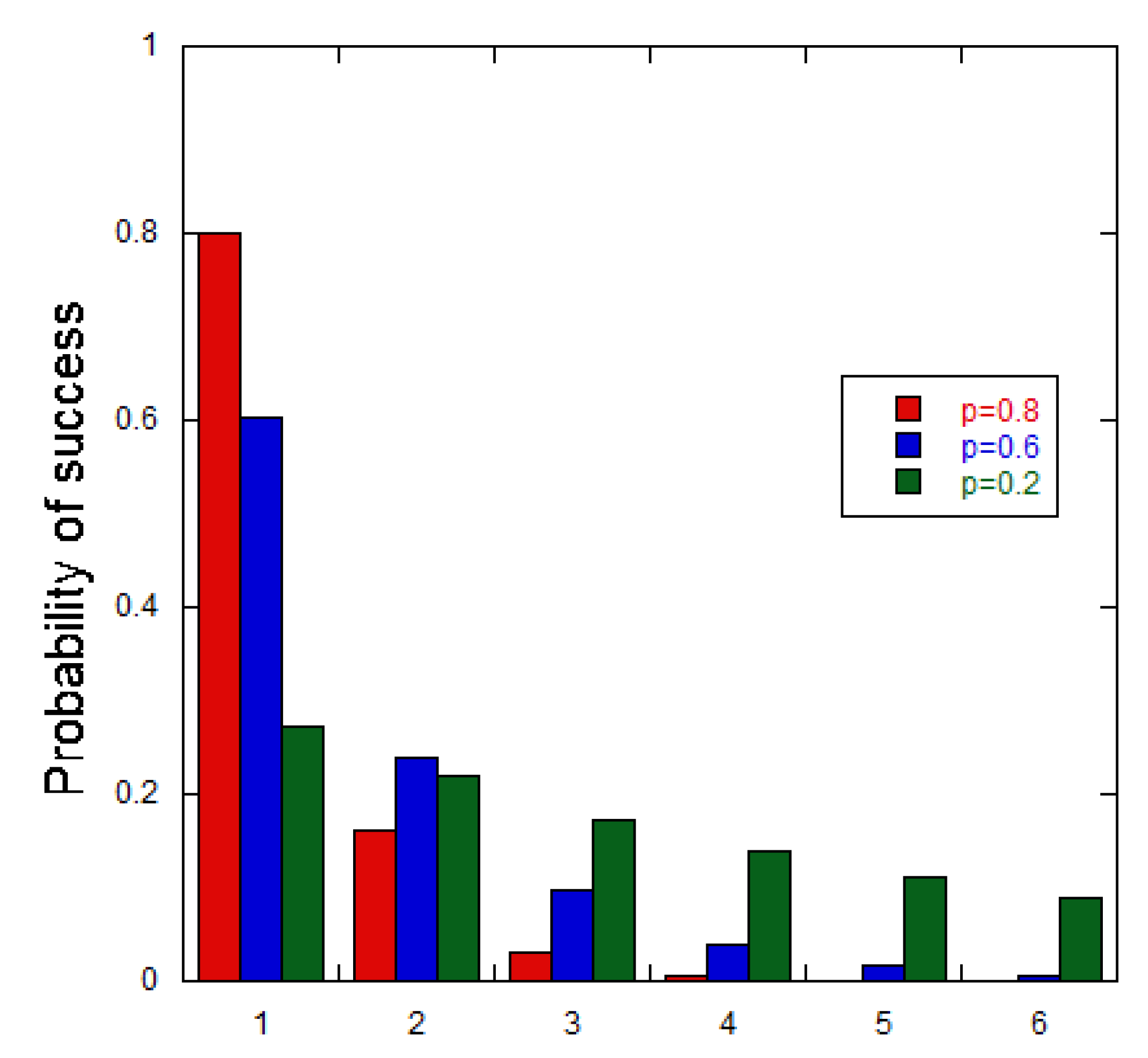
Preprints 113197 g005
Preprints 113197 g006
Figure 6. GD algorithm-based SF assignment workflow.
Figure 6. GD algorithm-based SF assignment workflow.
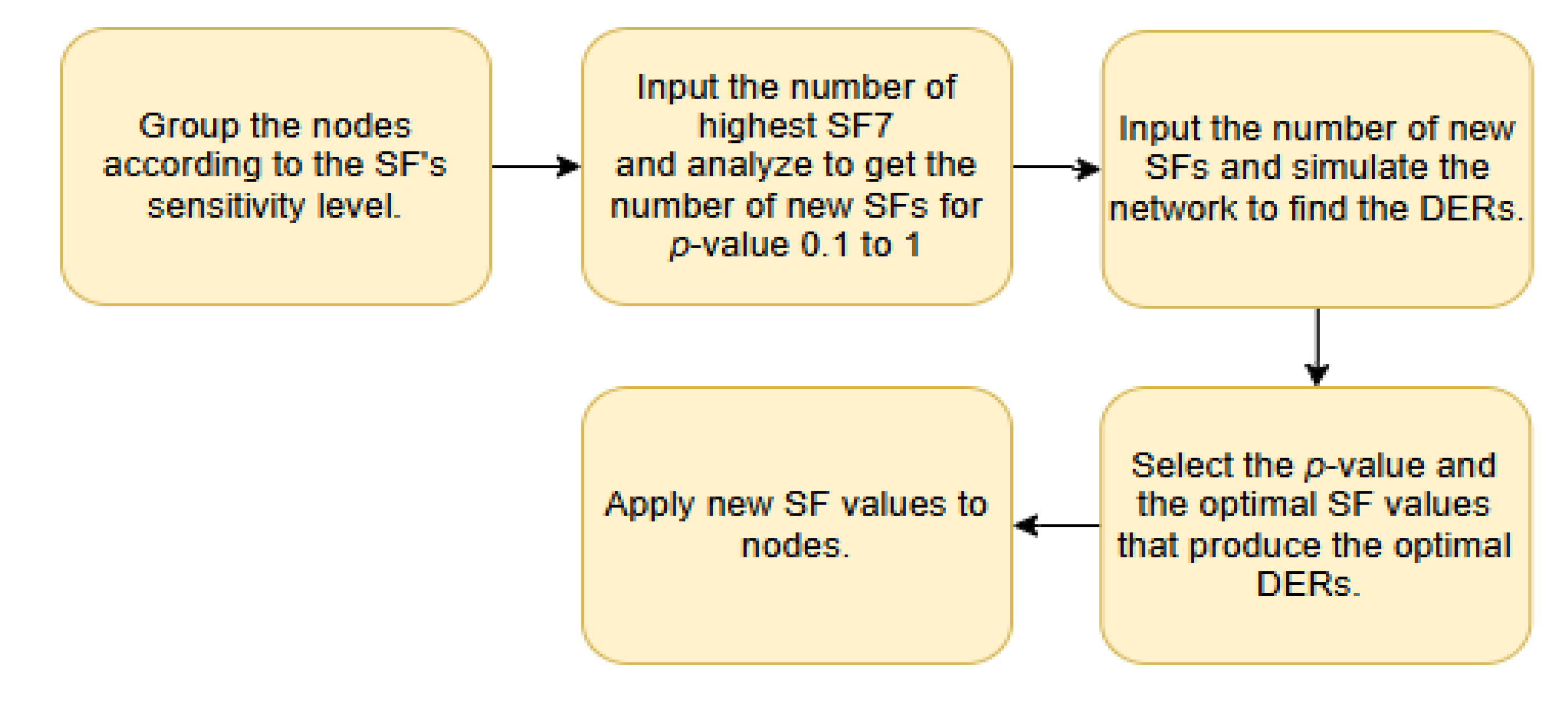
Preprints 113197 g006
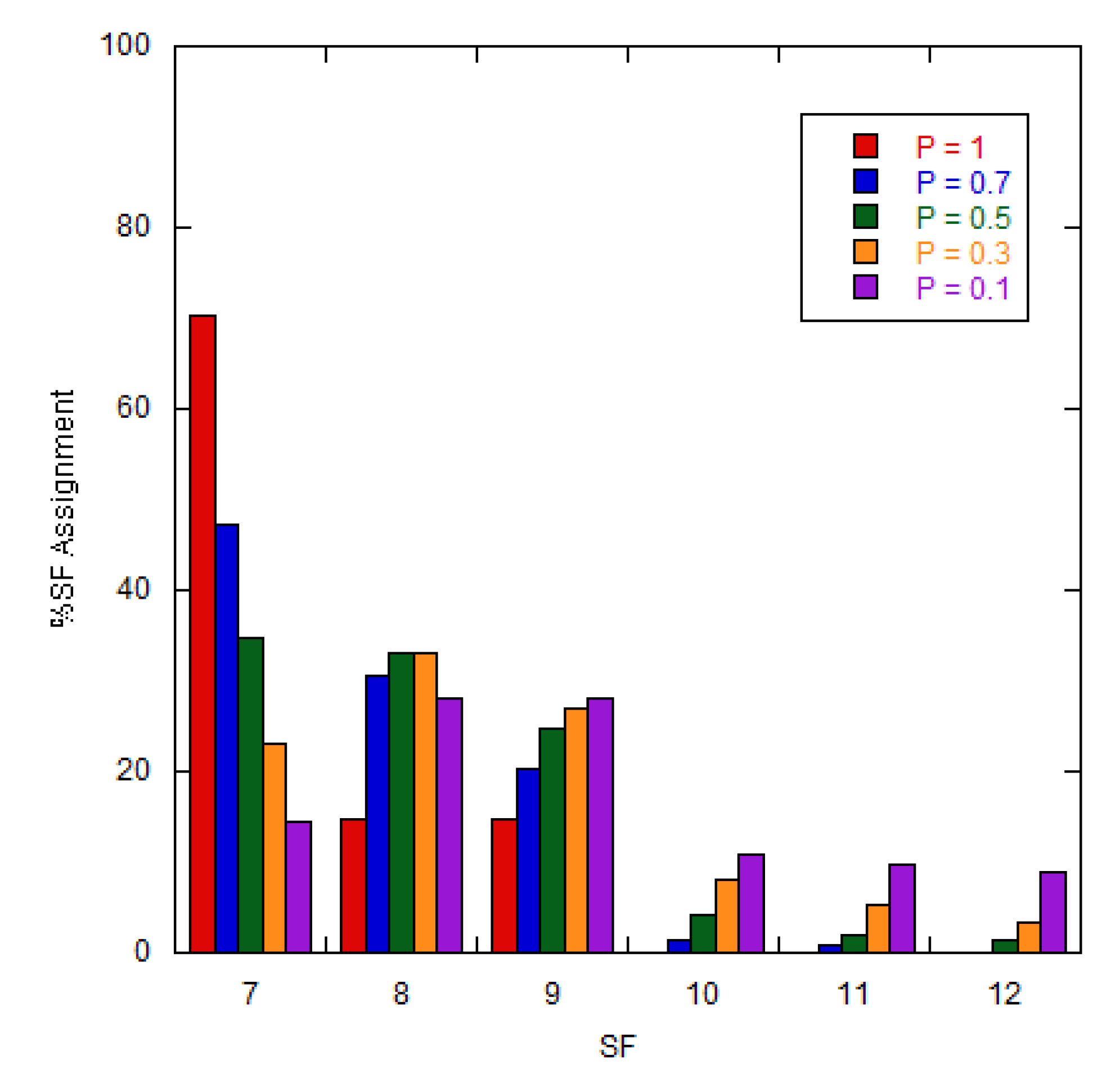
Preprints 113197 g007
Figure 7. SF assignment for the uniform random pattern using the GD algorithm.
Figure 7. SF assignment for the uniform random pattern using the GD algorithm.
Preprints 113197 g007
Preprints 113197 g008
Figure 8. SF assignment for the fixed pattern using the GD algorithm.
Figure 8. SF assignment for the fixed pattern using the GD algorithm.
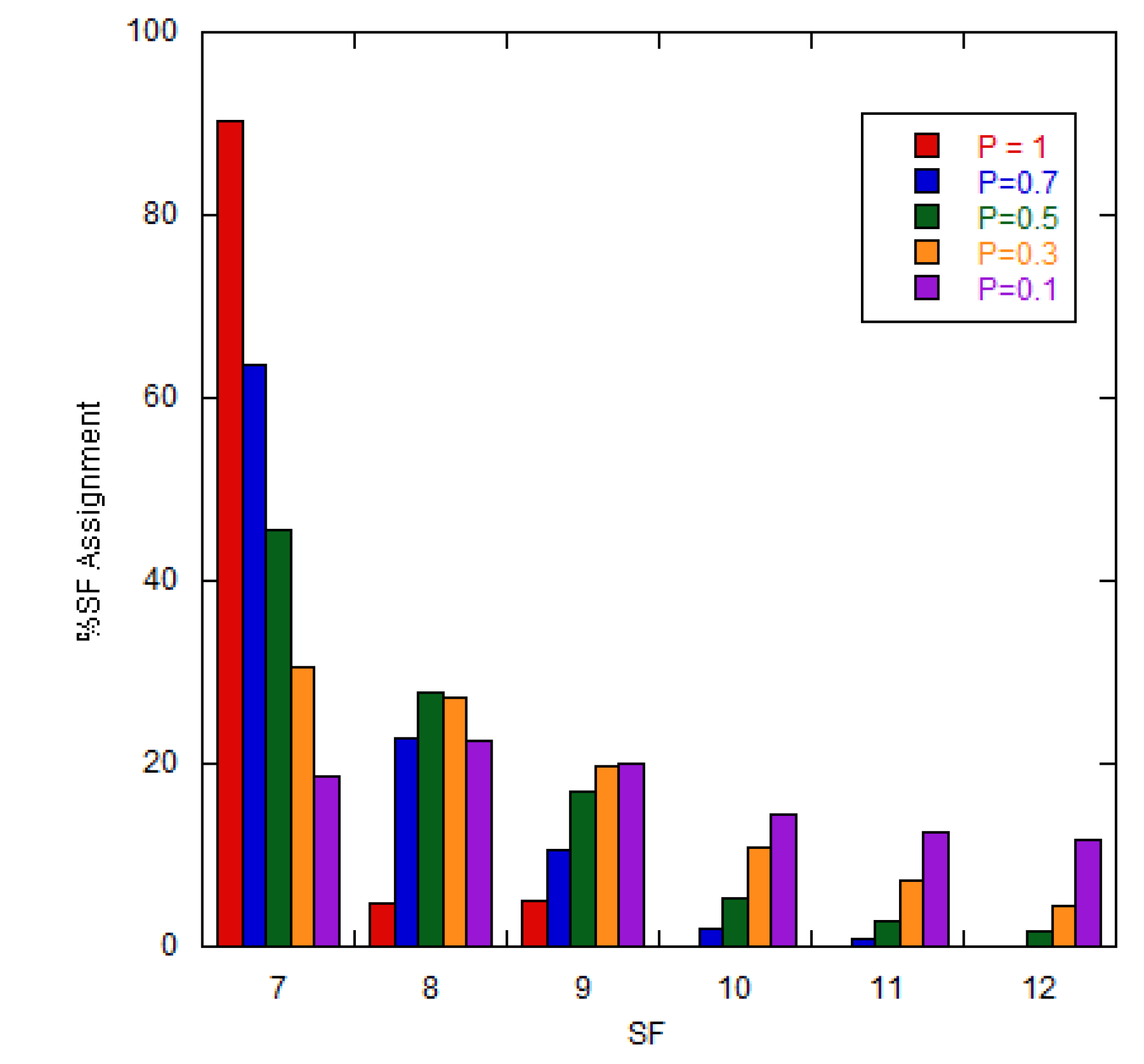
Preprints 113197 g008
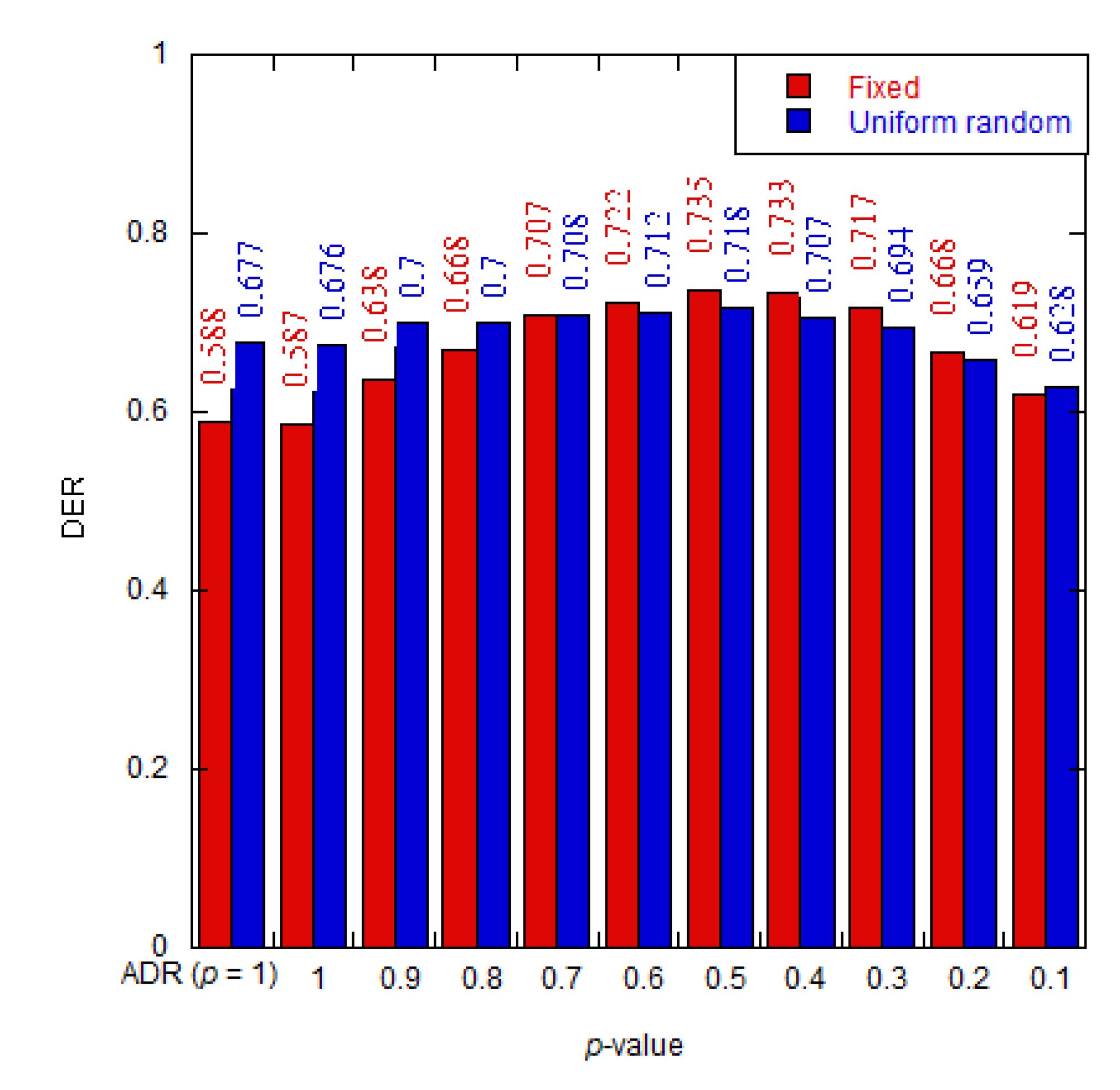
Preprints 113197 g009
Figure 9. DER values after applying the GD algorithm to the fixed and uniform random patterns.
Figure 9. DER values after applying the GD algorithm to the fixed and uniform random patterns.
Preprints 113197 g009
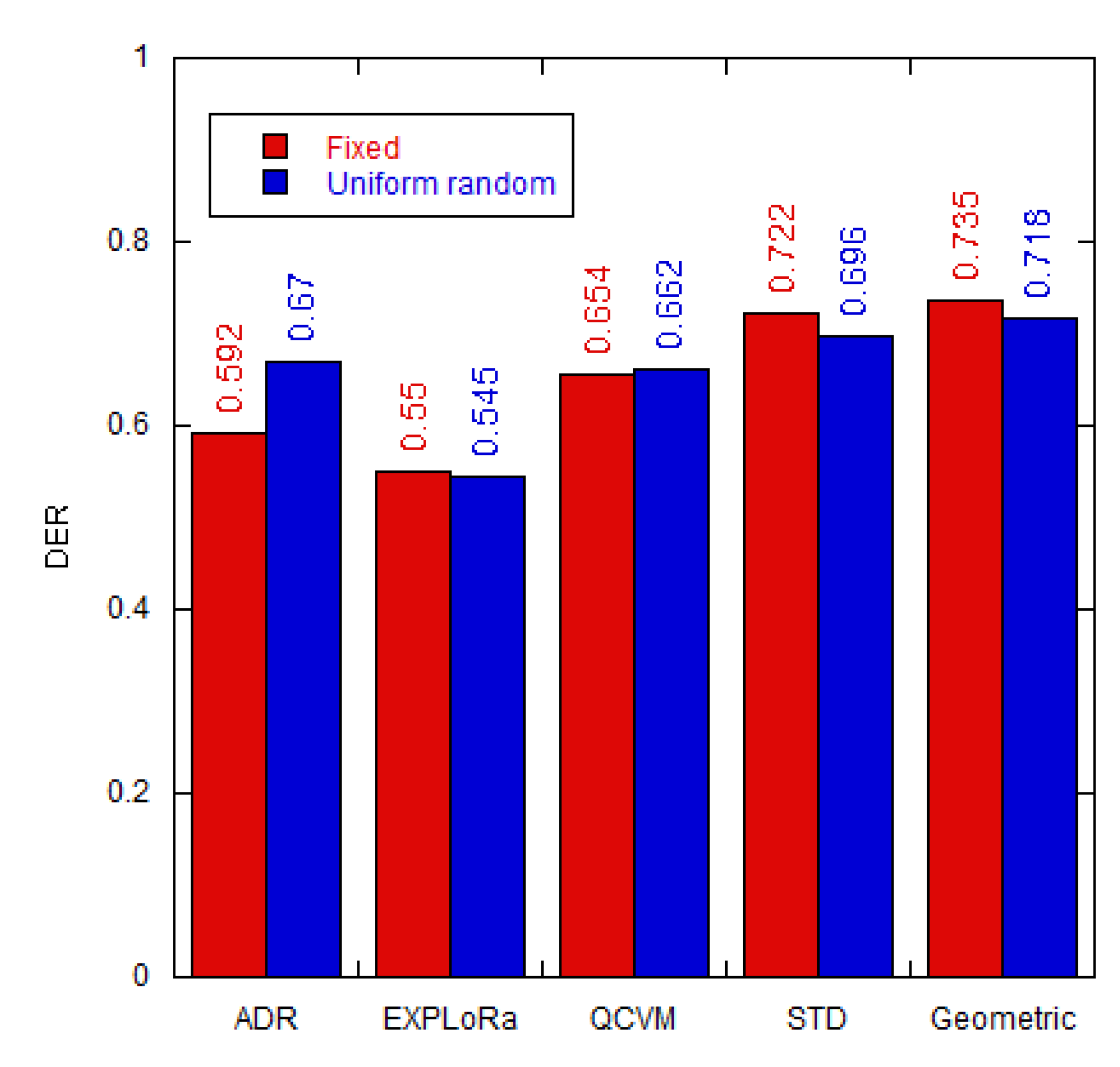
Preprints 113197 g010
Figure 10. DER comparison between different algorithms for fixed and uniform random patterns.
Figure 10. DER comparison between different algorithms for fixed and uniform random patterns.
Preprints 113197 g010
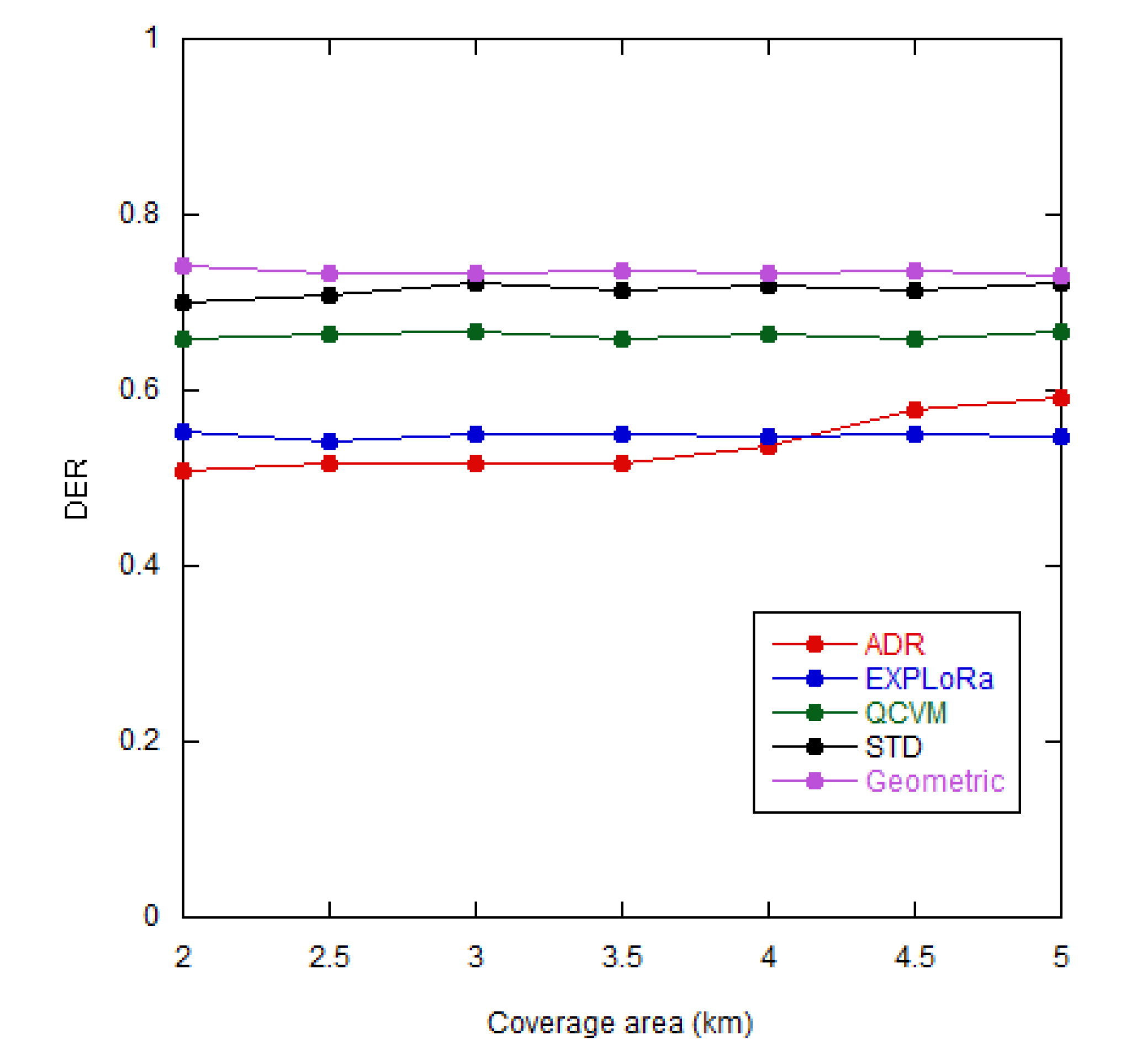
Preprints 113197 g011
Figure 11. The DER values vs the coverage area for different algorithms.
Figure 11. The DER values vs the coverage area for different algorithms.
Preprints 113197 g011
Preprints 113197 g012
Figure 12. The DER values vs the payload size (Bytes) for different algorithms.
Figure 12. The DER values vs the payload size (Bytes) for different algorithms.
Preprints 113197 g012
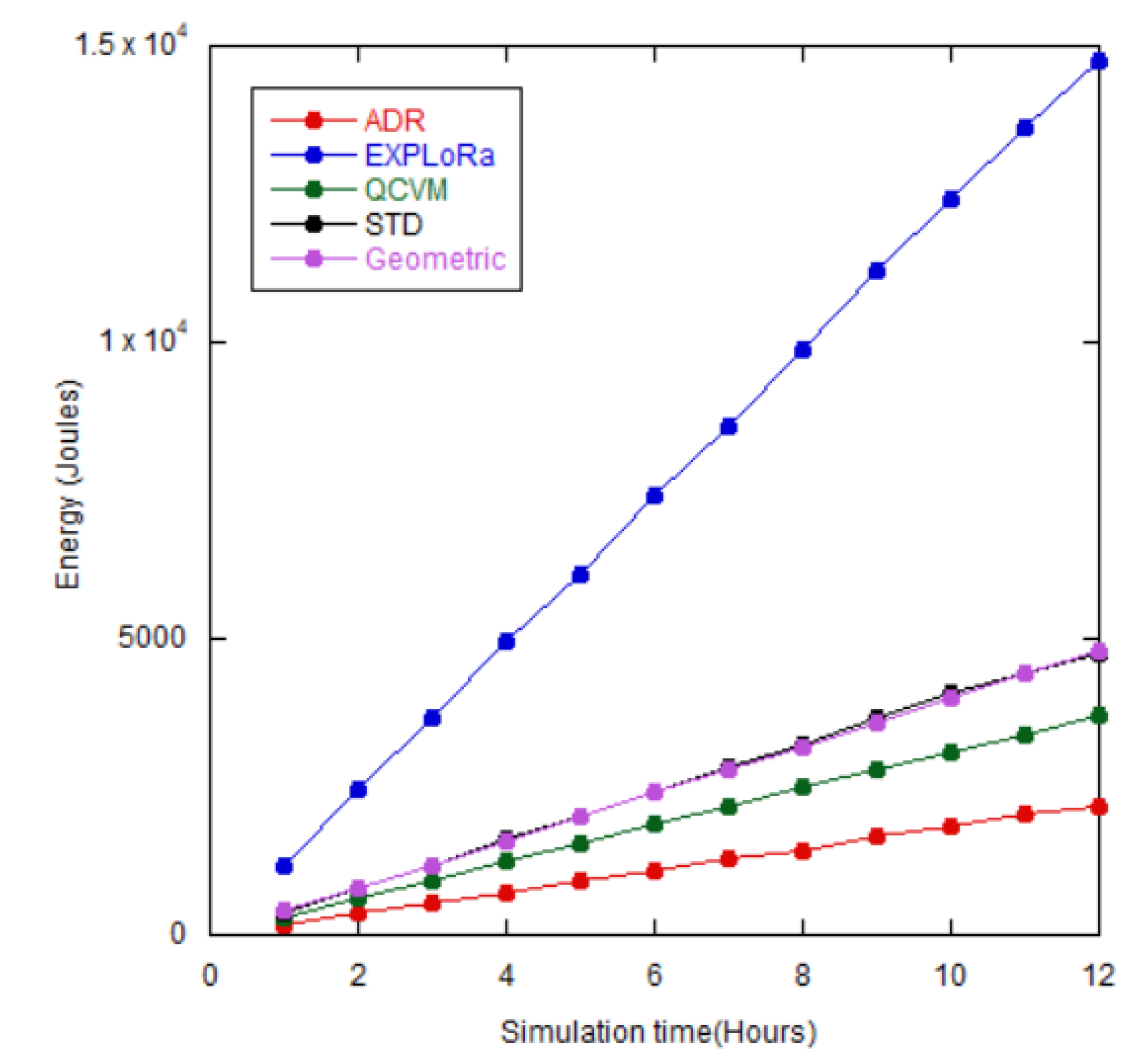
Preprints 113197 g013
Figure 13. Energy consumptions from 1 hour to 12 hours of simulation time for different algorithms.
Figure 13. Energy consumptions from 1 hour to 12 hours of simulation time for different algorithms.
Preprints 113197 g013
Table 1. The DER of the original ADR for the uniform random and fixed node patterns.
Table 1. The DER of the original ADR for the uniform random and fixed node patterns.
Coverage area Pattern %SF7 %SF8 %SF9 %SF10 %SF11 %SF12 DER Value
2 km Uniform
random		 100.00 0.00 0.00 0.00 0.00 0.00 0.514
Fixed 100.00 0.00 0.00 0.00 0.00 0.00 0.510
3 km Uniform
random		 100.00 0.00 0.00 0.00 0.00 0.00 0.512
Fixed 100.00 0.00 0.00 0.00 0.00 0.00 0.514
4 km Uniform
random		 87.60 12.40 0.00 0.00 0.00 0.00 0.600
Fixed 96.53 3.47 0.00 0.00 0.00 0.00 0.538
5 km Uniform
random		 70.33 15.40 14.27 0.00 0.00 0.00 0.676
Fixed 89.53 4.93 5.53 0.00 0.00 0.00 0.589
Table 2. The resulting set of weight factor (w) with p-value = 1 to 0.1.
Table 2. The resulting set of weight factor (w) with p-value = 1 to 0.1.
p-value w1 w2 w3 w4 w5 w6
1 1 0 0 0 0 0
0.9 0.90 0.09 0.01 0.00 0.00 0.00
0.8 0.80 0.16 0.03 0.01 0.00 0.00
0.7 0.70 0.21 0.06 0.02 0.01 0.00
0.6 0.60 0.24 0.10 0.04 0.02 0.01
0.5 0.51 0.25 0.13 0.06 0.03 0.02
0.4 0.42 0.25 0.15 0.09 0.05 0.03
0.3 0.34 0.24 0.17 0.12 0.08 0.06
0.2 0.27 0.22 0.17 0.14 0.11 0.09
0.1 0.21 0.19 0.17 0.16 0.14 0.13
Table 3. Simulation parameters.
Table 3. Simulation parameters.
Parameter Value
Number of nodes 1,500
Number of gateway 1
Node transmitted power 14 dBm
Simulation time 43,200 sec (12 Hours)
Average sending message time 1,800 sec (30 minutes)
Bandwidth 125 kHz
Frequency (AS923) 923 MHz
Path-loss model Suburban Hata-Okumura
Payload size 255 bytes
Coverage area 5 km
Table 4. SF allocation from the GD algorithm at p = 0.5, default ADR scheme, and previous algorithms for the uniform random pattern.
Table 4. SF allocation from the GD algorithm at p = 0.5, default ADR scheme, and previous algorithms for the uniform random pattern.
Algorithm %SF7 %SF8 %SF9 %SF10 %SF11 %SF12
Default ADR 70.00 16.53 13.47 0.00 0.00 0.00
EXPLoRa 16.67 16.67 16.67 16.67 16.67 16.67
QCVM 33.40 33.40 33.20 0.00 0.00 0.00
SD 25.60 37.47 14.27 14.47 6.33 1.87
GD
(p = 0.5)		 34.73 33.13 24.60 4.07 2.07 1.40
Table 5. SF allocation from the GD algorithm at p = 0.5, default ADR scheme, and previous algorithms for the fixed pattern.
Table 5. SF allocation from the GD algorithm at p = 0.5, default ADR scheme, and previous algorithms for the fixed pattern.
Algorithm %SF7 %SF8 %SF9 %SF10 %SF11 %SF12
Default ADR 89.67 5.40 4.93 0.00 0.00 0.00
EXPLoRa 16.67 16.67 16.67 16.67 16.67 16.67
QCVM 33.40 33.40 33.20 0.00 0.00 0.00
SD 35.20 32.73 17.33 12.67 1.33 0.73
GD
(p = 0.5)		 45.53 27.67 16.93 5.40 2.67 1.80
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated