Prerpints.org logo
Preprint
Article

A Tool for a Fast and Accurate Evaluation of the Energy Production of Bifacial PV Modules

Altmetrics

Downloads

134

Views

46

Comments

0

Submitted:

25 July 2024

Posted:

26 July 2024

You are already at the latest version

Alerts
Abstract
In this work, we propose an in-house simulation tool designed for the analysis and optimization of bifacial photovoltaic (PV) modules, which are currently under the spotlight in the renewable energy scenario. The tool is conceived to support researchers and engineers by providing fast and accurate predictions of the PV module yield under various operating and environmental conditions. For a chosen geographical site, the impact of module orientation, tilt, albedo, sky conditions, ambient temperature, and so on, can be effortlessly determined. In case of nonuniformity across the cells dictated by localized architectural shading, dirt, bird drops, defects, a circuit-based cell-level approach can be activated to compute the module production. An extensive simulation campaign is performed by assuming that the panels are installed in Naples without loss of generality. Results are shown to give detailed insights into the performance of bifacial modules, thus providing unambiguous guidelines for their correct installation. Further analyses are conducted to demonstrate the tool capability to quantify the detrimental influence of a poorly-irradiated cell on the backside, as well as of cracked cells.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

The global energy landscape is rapidly shifting towards renewable energy sources to alleviate the climate change and reduce the dependence on fossil fuels. Among the renewable sources, photovoltaic (PV) technology stands out for its scalability, decreasing costs, and widespread adoption.
Traditionally, the market has been dominated by monofacial PV modules (hereinafter also referred to as panels), which capture sunlight only on one side (front). However, in recent times bifacial PV modules, engineered to capture sunlight also on the backside (henceforth denoted as rear) have emerged as a valuable alternative, as they are supposed to offer higher energy yields at a price of a minor and affordable upgrade of the fabrication equipment; promising results have been obtained in many applications like agrivoltaics, aquavoltaics, or in high-reflection environments such as deserts, snow-covered areas, and urban architectures with reflective surfaces (e.g., [1,2,3,4,5,6,7,8,9,10,11] and references therein).
The literature is populated by papers dealing with the comparison between monofacial and bifacial panels in terms of cost, efficiency, and production under various operating conditions [12,13,14,15,16,17,18]. However, there is still a lack of unambiguous guidelines defining in which circumstances (in terms of orientation, inclination, reflection from ground, partial shading on the front or rear, and so on) bifacial modules offer clear and distinct advantages with respect to the monofacial counterparts. This challenge can only be addressed resorting to advanced simulation tools suited to predict the performance of bifacial and monofacial modules in any environment, thereby supporting engineers and researchers to make choices oriented to energy yield and return-on-investment maximization.
In this paper, we present a comprehensive simulation tool conceived and designed for bifacial PV modules, a simplified variant of which is dedicated to the monofacial ones. The tool allows for a fast, yet accurate enough, evaluation of the energy performance of the modules, it is user-friendly and totally immune to convergence problems. The information to be provided are the day of the year, the coordinates of the geographical site where the module is installed, the evolution along the day of total and diffuse irradiance on the horizontal plane, as well as of ambient temperature, in that site (available on online databases), orientation, tilt, albedo, and some datasheet parameters. The tool determines the I–V characteristic of the module, and thus the maximum produced power, at each clock time in the day. The computation is automated and very fast, taking only tens of seconds to cover a whole day with a 15-minute discretization.
The tool is entirely developed as a Matlab code, except when there are discrepancies among the cells in terms of irradiances (on the front and/or on the rear), temperature, or other parameters. In such a nonuniform case, Matlab is still used to determine front/rear irradiances and temperature on the cells behaving uniformly, but the circuit simulation program OrCAD PSPICE [19] is invoked to compute the I–V characteristics along the day with a high-granularity cell-level approach. By virtue of this feature, it is possible to predict the impact of partial architectural shading, bird drops, snow, and defects (e.g., cracks).
The reminder of this work is articulated as follows. In Section 2, the details of the tool are given. A clear and extensive overview of the adopted models is provided using a tutorial style, with the aim to inspire and ease the reader’s own implementation. In Section 3, the tool is adopted to explore the daily, monthly, and yearly energy production of bifacial PV modules located in Naples by varying orientation and tilt. The bifacial performance is compared to that of a south-oriented monofacial module tilted by 30°, which is the well-established optimum condition in Naples and is therefore taken as a reference. It is found that west- or east-oriented vertical bifacial modules allow matching or even exceeding (depending on the albedo) the yearly-produced energy of the reference monofacial one; this suggests their adoption for e.g., agrivoltaics or noise barriers along highways. Moreover, a counter-intuitive result is also achieved: it is shown that the reduction of the current photogenerated of one cell on the rear (e.g., due to a mud spot) can lead to bypass activation even if the Sun rays are only hitting the front. Lastly, the detrimental impact of cracked cells is quantified. Conclusions are finally drawn in Section 4.

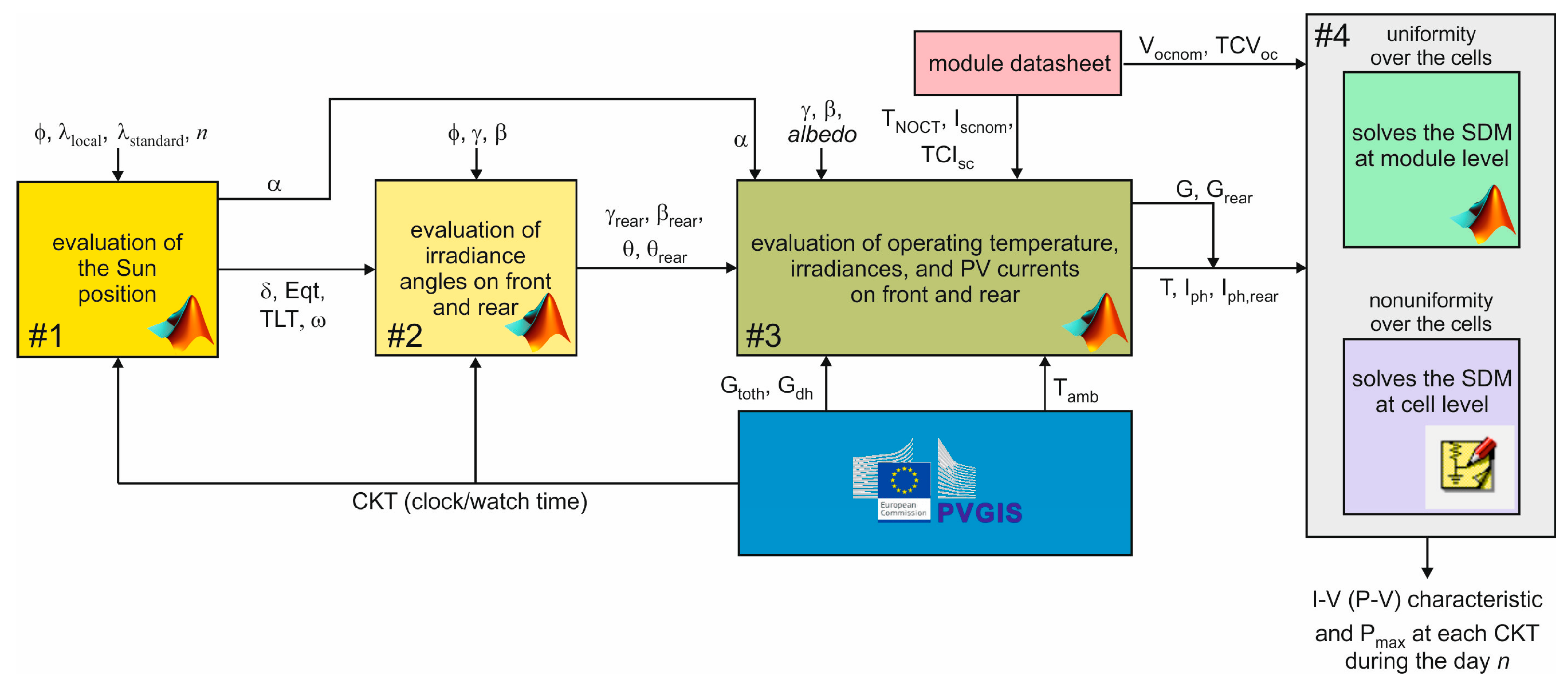
2. The Tool

The block diagram of the tool is represented in Figure 1. As can be seen, the tool is articulated into four blocks. Blocks #1, #2, and #3 are Matlab codes, while for #4 two options are possible: (1) if all the cells in the module share the same irradiance on the front, the same irradiance on the rear, the same operating temperature, and thus the same photogenerated current on the front and the same on the rear, as well as the same parameters, a Matlab block is used to solve the single-diode model (SDM) described in Section 2.4 at a module level, that is, the voltage drop across the module is obtained by multiplying the voltage drop across the cell Vcell by the number of cells embedded in the panel; (2) if there is a nonuniformity over the cells in the module (either on the front or on the rear), in terms of e.g. irradiances, electrical parameters (dictated by e.g., architectural shading, defects) then the solution is demanded to the circuit simulator PSPICE, in which each cell is individually described by its own subcircuit. PSPICE was chosen since it is equipped with a robust engine suited for the solution of systems of nonlinear algebraic equations, which ensures short CPU times and unlikely occurrence of convergence problems.
The detailed description of each block is provided in the following.

2.1. Block #1

Block #1 is fed with
  • The latitude ϕ and the local longitude λ, denoted as λlocal, of the geographical site where the PV module is installed (ϕ is equal to 0° at the equator, and ranges from 0° to 90° to the north, from 0° to -90° to the south; λlocal is equal to 0° at the Prime, or Greenwich, meridian, and ranges from 0° to 180° to east, from 0° to -180° to west).
  • The longitude λstandard of the standard meridian on which the clock time (CKT, also referred to as watch time or standard local time) is based.
  • The day of the year n.
  • The CKT values during the day, i.e., the daytime discretization.
and calculates
  • The solar declination δ, i.e., the angle between the Sun rays (the beam radiation) and the equatorial plane, which is positively defined in the northern hemisphere. Angle δ can be reasonably assumed constant during a day (it varies by at most 0.5°), and dependent on the day of the year n through the empirical Cooper’s relation
δ = 23.45 ⋅ sin 360 365 ⋅ 284 + n
On the summer solstice, δ assumes the maximum value 23.45° (23°27’); on the winter solstice it is equal to the minimum value -23.45° (-23°-27’); δ=0° on the spring and autumn equinoxes.
  • The so-called True Local Time (TLT), which can be obtained from the CKT by applying two corrections. The first correction is dictated by the difference between the local longitude λlocal and the longitude of the standard meridian λstandard; more specifically, the displacement of 1° between these longitudes corresponds to 4 minutes. The second correction is made to account for the non-constancy of the rotation rate of the Earth around the Sun during the year. This effect can be described by introducing a characteristic time referred to as Equation of Time (Eqt) expressed in minutes, which depends on n through the following relation [20,21,22]:
E q t = K 1 ⋅ K 2 + K 3 cos B − K 4 sin B − K 5 cos 2 B − K 6 sin 2 B                 B = n − 1 ⋅ 360 365
with K1=229.2 minutes, K2=0.000075, K3=0.001868, K4=0.032077, K5=0.014615, K6=0.04089 [21,22] (or 0.040849 [20] without appreciable Eqt variation). By applying both corrections, under standard time/conditions the relation between TLT (in hours) and CKT is given by
T L T = C K T − 4 60 ⋅ λ s t a n d a r d − λ l o c a l + E q t 60
which, under daylight-saving time/conditions, is modified into
T L T = C K T − 1 − 4 60 ⋅ λ s t a n d a r d − λ l o c a l + E q t 60
that is, a further hour must be deducted.
  • The hour angle ω, i.e., the angular displacement of the Sun with respect to the local meridian compared to the case in which TLT=12 due to the rotation from west to east of the Earth around its axis (also denoted as angle subtended by the Sun [23]). Angle ω is negative in the morning, positive in the afternoon, and given by [20,22,24,25,26,27]
ω = 15 ⋅ T L T − 12
As can be seen, a one-hour deviation corresponds to a displacement of 15°.
  • The solar altitude, or elevation, α, i.e., the angle between the horizontal plane (also denoted as plane of horizon) and the Sun rays; α is a function of latitude ϕ, solar declination δ, and hour angle ω according to [20,21,23,24,25,26]
sin α = sin ϕ ⋅ sin δ + cos ϕ ⋅ cos δ ⋅ cos ω
The outcomes of block #1 for some application examples are reported in Table 1.

2.2. Block #2

Block #2 is fed with
  • The latitude ϕ of the site.
  • The CKT values.
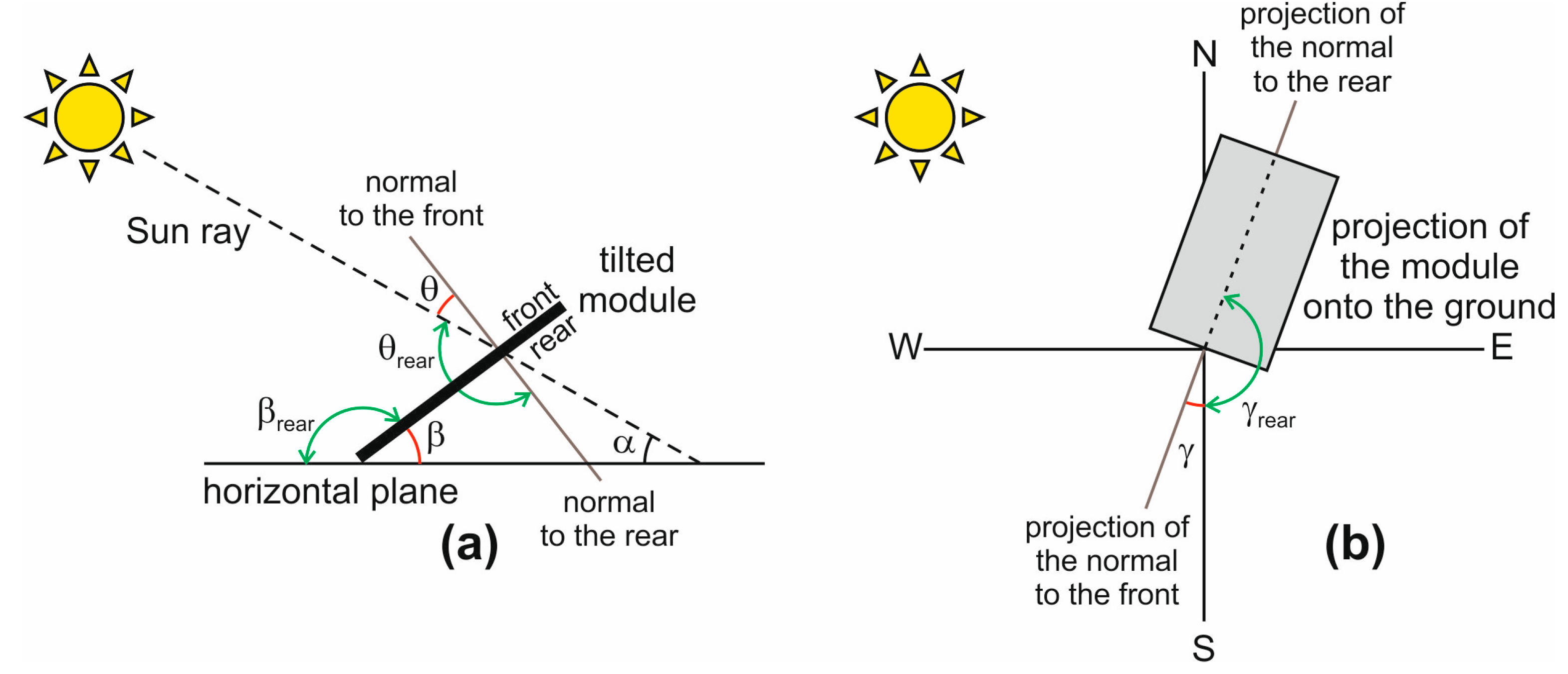
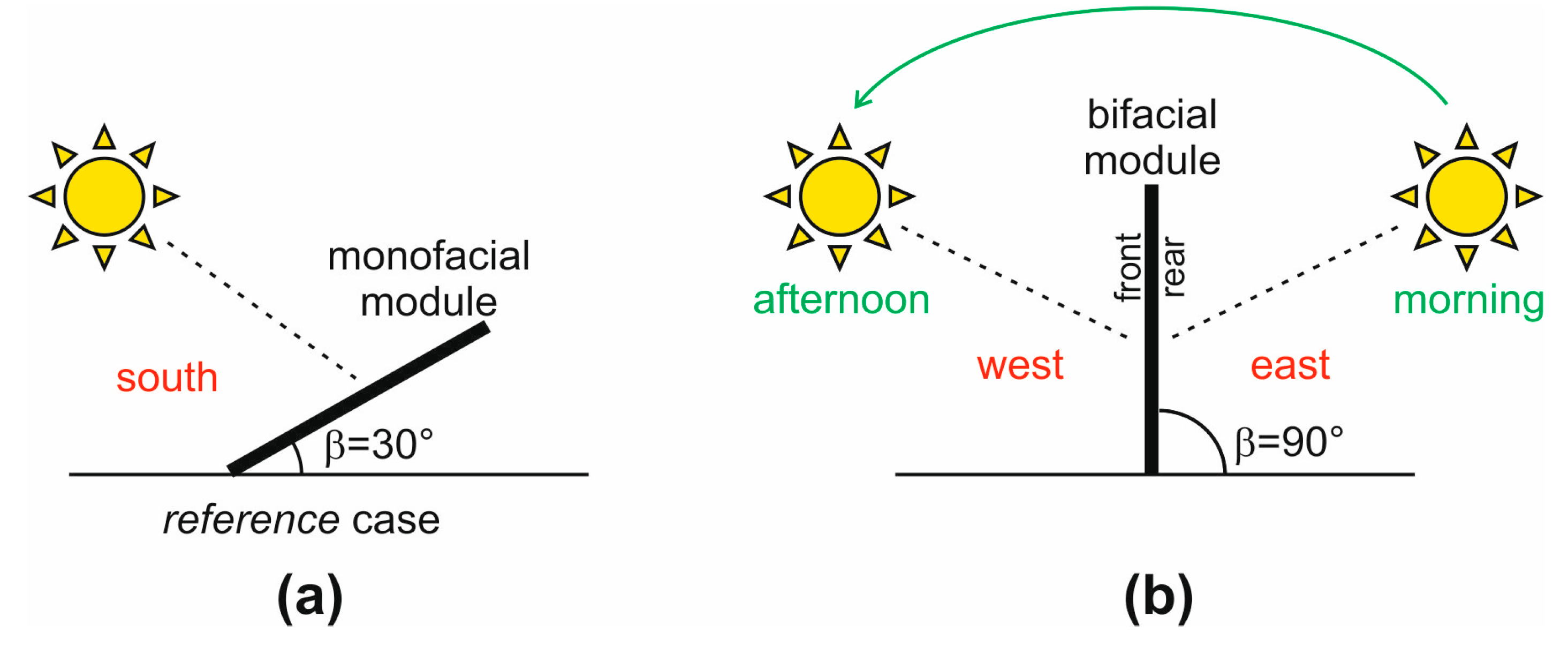
  • The azimuth angle of the module front γ, which defines the module orientation, as it is the angular displacement from south of the projection of the normal to the module front onto the horizontal plane. An azimuth γ=0° means that the front is south-oriented; γ is positive clockwise (to west), reaching 180° next to north, and is negative counter-clockwise (to east), reaching -180° next to north [21]. Hence, γ=90° corresponds to a module with west-oriented front, while γ=-90° identifies an east-oriented front.
  • The tilt angle of the module front β, which is the inclination with respect to the horizontal plane.
  • The solar declination δ and the hour angle ω computed by block #1.
and calculates
  • The azimuth angle of the module rear γrear=γ-180°.
  • The tilt angle of the module rear as the complement of β, that is, βrear=180°-β.
  • The incidence angles of the Sun rays on the module front θ and rear θrear (both being ≥0). θ is the angle between the Sun rays and the normal to the module front, and is evaluated from [21,22,23,27]
cos θ = cos δ ⋅ cos ω ⋅ sin ϕ ⋅ cos γ ⋅ sin β + cos ϕ ⋅ cos β + + sin δ ⋅ sin ϕ ⋅ cos β − cos ϕ ⋅ cos γ ⋅ sin β + + cos δ ⋅ sin ω ⋅ sin γ ⋅ sin β
It can be inferred that θ=0° for a horizontal module (β=0°) at the equator (ϕ=0°) at TLT=12 (noon, ω=0°) of the equinoxes (δ=0°); angle θ may exceed 90°, which means that the Sun is behind the surface.
As an example, if it is required to determine the angle of incidence of the Sun rays on the front of a module installed at Madison, WI, USA, with orientation γ=15° and tilt β=45° at CKT=10.7 (10:42 AM) on February 13 (n=44), then block #1 evaluates that δ=-13.95°, Eqt=-14.26 minutes, TLT=10.50 (10:30 AM), ω=-22.50°, α=29.38°, and block #2 calculates θ=35° [21].
It is noteworthy that the θ formulation provided in [20] turned out to be wrong.
θrear is the angle between the Sun rays and the normal to the module back, and is computed as 180°-θ or equivalently from
cos θ r e a r = cos δ ⋅ cos ω ⋅ sin ϕ ⋅ cos γ r e a r ⋅ sin β r e a r + cos ϕ ⋅ cos β r e a r + + sin δ ⋅ sin ϕ ⋅ cos β r e a r − cos ϕ ⋅ cos γ r e a r ⋅ sin β r e a r + + cos δ ⋅ sin ω ⋅ sin γ r e a r ⋅ sin β r e a r
Figure 2 is intended to provide a clear understanding some key angles introduced so far.

2.3. Block #3

The inputs of block #3 are
  • The solar altitude α evaluated by block #1.
  • The azimuth angles γ, γrear, the tilt angles β, βrear, and the incidence angles θ, θrear.
  • The total irradiance Gtoth, the diffuse irradiance Gdh hitting the horizontal plane (the beam, or direct, irradiance Gbh is determined as Gtoth-Gdh), and the ambient temperature Tamb vs. CKT at the selected geographical site. For the analysis performed in Section 3, these data were taken from the PhotoVoltaic Geographical Information System (PVGIS) website [28]. Here it is stated that they were evaluated for the mean day of the chosen month from satellite data through a sophisticate algorithm accounting for sky obstruction (shading) by local terrain features (hills or mountains) calculated from a digital elevation model.
  • The albedo value, namely, the ratio of reflected upward radiation from the ground to the incident downward radiation upon it (typical albedo values are 0.04 for fresh asphalt, 0.1-0.15 for soil ground, 0.25-0.3 for green grass, 0.4 for desert sand, 0.55 for fresh concrete, and 0.8 for freshly fallen snow).
  • Some key parameters available in the datasheet, i.e., the temperature TNOCT, the short circuit current Iscnom, and the percentage temperature coefficient TCIsc of the short-circuit current Isc, the definitions of which will be provided in the following.
  • The block calculates
  • The beam irradiance impinging on the module front as [21,23,29,30,31]
G b = G b h ⋅ cos θ sin α
and on the rear
G b , r e a r = G b h ⋅ cos θ r e a r sin α = − G b h ⋅ cos θ sin α
  • The diffuse irradiance on the front coming from the sky, for which there are two options.
If the sky is completely and densely overcast, the same irradiance is coming from any point of the sky, which is thus called isotropic. In this case, the diffuse irradiance is expressed as
G d i = G d h ⋅ F i
where the dimensionless front-sky view factor Fi (<1) accounts for the reduction of the sky dome due to the tilt angle β; using the cross-string approach [32], it can be determined that
F i = 1 + cos β 2 = cos 2 β 2
Formulation (12), sometimes referred to as Kondrat’yev’s view factor [33], is widely accepted [2,9,12,20,21,23,24,25,29,34,35,36,37,38,39,40,41,42], and coincides with the ratio between the projection on the horizontal plane of the portion of hemisphere seen from the titled panel and the projection of the whole sky dome [43].
Analogously, for the module rear
G d i , r e a r = G d h ⋅ F i , r e a r
with the rear-sky view factor [2,40,42]
F i , r e a r = 1 + cos β r e a r 2 = cos 2 β r e a r 2 = 1 − cos β 2 = sin 2 β 2
If the sky is clear or at least partially cloudy, the diffuse irradiance depends on the position of the Sun in the sky due to effects like the horizon brightening and circumsolar radiation, and the sky is thus referred to as anisotropic. In this case, the diffuse irradiance can be expressed as
G d a = G d h ⋅ F a
where the front-sky view factor Fa is given by the sum of two terms Fa1 and Fa2 accounting for the horizon brightening and circumsolar radiation, respectively [21,29,31]
F a = F a 1 + F a 2 = F i ⋅ 1 − A i ⋅ 1 + f ⋅ sin 3 β 2 + A i ⋅ cos θ sin α
In (16),
f = G b h G b h + G d h
and Ai is the anisotropic index, given by
A i = G b h G 0
where G0 is the solar irradiance incident on a horizontal plane outside the atmosphere, also referred to as extraterrestrial irradiance on a horizontal surface, whose expression is
G 0 = G s c ⋅ 1 + 0.033 ⋅ cos 360 365 ⋅ n ⋅ cos ϕ ⋅ cos δ ⋅ cos ω + sin ϕ ⋅ sin δ
Gsc being the solar constant, equal to 1353 W/m2.
Differently from the isotropic view factor Fi, the anisotropic one Fa can be >1 if the panel is oriented to the portion of the sky dome where the Sun is located. It is worth noting that Fa reduces to Fi if Gbh=0 W/m2 (uniformly cloudy, or isotropic, sky), which implies that f=0 and Ai=0.
For the rear of the module,
G d a , r e a r = G d h ⋅ F a , r e a r
where
F a , r e a r = F a 1 , r e a r + F a 2 , r e a r = F i , r e a r ⋅ 1 − A i ⋅ 1 + f ⋅ sin 3 β r e a r 2 + A i ⋅ cos θ r e a r sin α
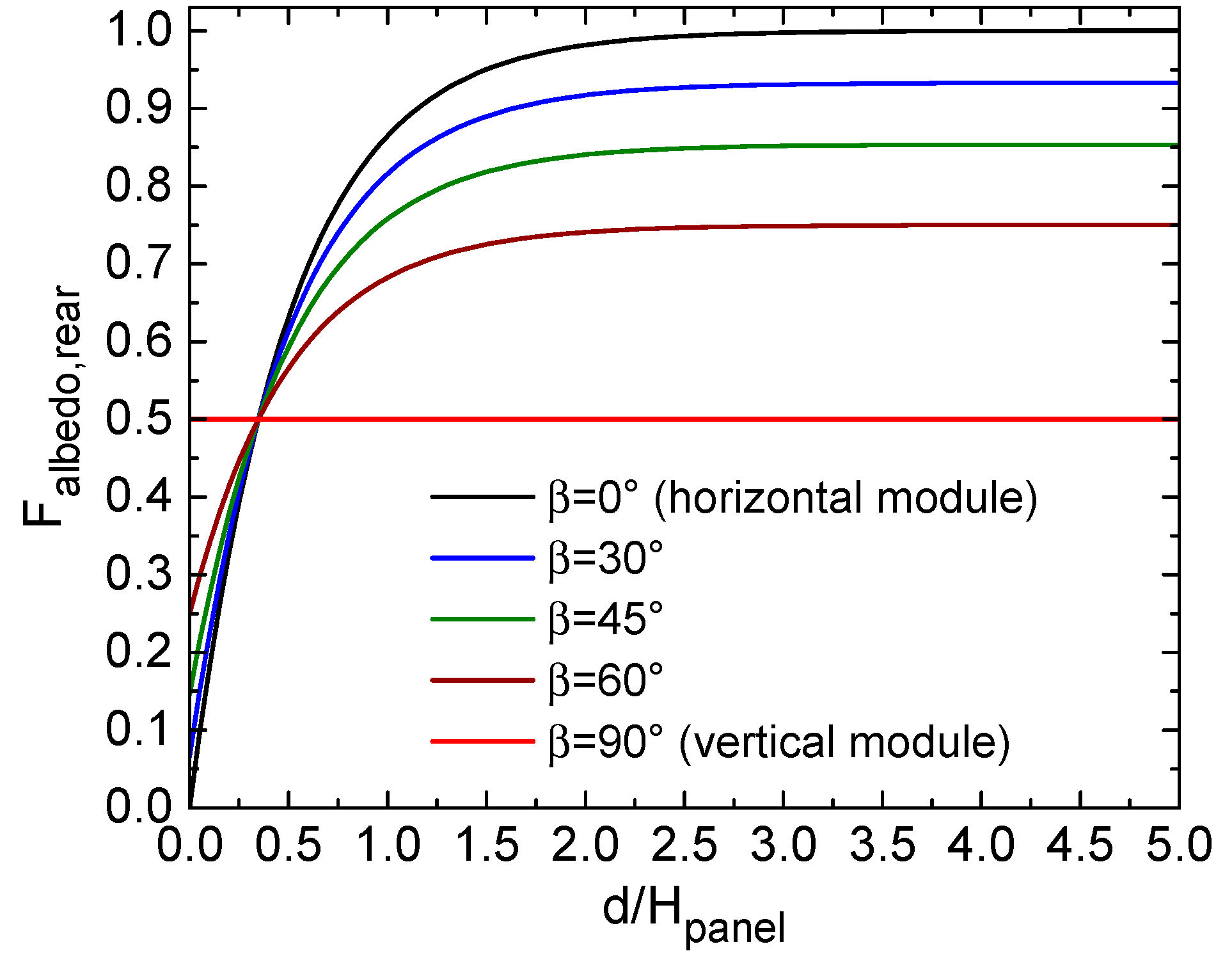
  • The diffuse irradiance on the front due to the reflection from the ground, typically considered as a Lambertian (isotropic) process, calculated as
G d , a l b e d o = G t o t h ⋅ a l b e d o ⋅ F a l b e d o
where the front-ground view factor Falbedo is expressed as [2,9,10,12,13,20,21,29,30,31,34,35,36,37,38,40,42,44,45]
F a l b e d o = 1 − cos β 2 = sin 2 β 2
Model (23). correctly works in the entire range of practical β values, namely, from β=0° (horizontal panel) to β=90° (vertically deployed panel); Falbedo=0 if β=0° since the front does not see the ground; Falbedo=0.5 if β=90° since the front sees half ground.
By referring to the module rear,
G d , a l b e d o , r e a r = G t o t h ⋅ a l b e d o ⋅ F a l b e d o , r e a r
For the rear-ground factor Falbedo,rear we examined the feasibility of the analogous of (23), namely [39,40,41,42]
F a l b e d o , r e a r = 1 − cos β r e a r 2 = sin 2 β r e a r 2 = 1 + cos β 2 = cos 2 β 2
Unfortunately, different from (23), model (25) does not provide meaningful results under all the possible configurations. Let us define as d the vertical distance between the lowest point of the module and the ground. If d=0 and β=0° the panel backside lies on the ground, which would imply Gd,albedo,rear=0, but (25) predicts Falbedo,rear=1, which is the consequence of its view factor nature. To tackle this issue, we propose an alternative, still simple enough, model for factor Falbedo,rear to also account for the dependence on d, which is given by
F a l b e d o , r e a r = 1 − g r e a r d ⋅ cos β r e a r 2 = 1 + g r e a r d ⋅ cos β 2
where
g r e a r d = 1 − 2 ⋅ exp − 2 d H p a n e l
Hpanel being the module height. The behavior of Falbedo,rear expressed by (26), (27) as a function of the ratio d/Hpanel for various tilt angles β is reported in Figure 3.
If d=0, then grear=-1 and (26) reduces to
F a l b e d o , r e a r = 1 + cos β r e a r 2 = 1 − cos β 2
Which shows that if β=0°, then Falbedo,rear=0, i.e., there is no reflection contribution since the panel lies on the ground, while if β=90°, then Falbedo,rear=0.5 as the module backside sees half ground.
For β<90°, Falbedo,rear increases with d, as the module rear sees more and more ground. If d is significantly higher than Hpanel, then then grear=1 and (26) saturates to (25), from which, if β=0°, then Falbedo,rear=1 as in this case the rear of the horizontal suspended panel sees all the ground.
If β=90°, then Falbedo,rear=0.5 independently of d, since it can be assumed that the rear sees half ground regardless of the distance from panel to ground.
This simple model given by (24) with (26), (27) inherently assumes that the ground is completely unshaded. If a large portion of the ground is shaded (e.g., in the case of a large PV field composed of horizontal bifacial modules suspended on a framework), (24) can be replaced by
G d , a l b e d o , r e a r = G d h ⋅ a l b e d o ⋅ F a l b e d o , r e a r
Accounting for a limited shadow on an irradiated ground, as the one produced by the panel itself, would markedly increase the complexity of the model; examples are the approaches in [12,13,40] under the assumption of infinite-length modules, and the complex procedure in [46].
  • The total irradiances on the front (G) and rear (Grear). The total irradiance on the front is calculated as
G = G b + G d i + G d , a l b e d o
for an isotropic sky, or
G = G b + G d a + G d , a l b e d o
for an anisotropic one.
The total irradiance on the rear is evaluated as
G r e a r = G b , r e a r + G d i , r e a r + G d , a l b e d o , r e a r
for an isotropic sky, and
G r e a r = G b , r e a r + G d a , r e a r + G d , a l b e d o , r e a r
for an anisotropic one.
  • The operating temperature T of the cells as a function of CKT. By disregarding the self-heating, which is a reasonable approximation when the cells are producing power, T [°C] is a function of Tamb and G according to the following linear law [6,12,26,47,48]:
T = T a m b + T N O C T − 20 ° ⋅ G G n o m T
TNOCT being the normal (nominal) operating cell temperature (NOCT) measured under open-circuit conditions at Tamb=20°C, nominal irradiance GnomT=800 W/m2 impinging on the front, AM 1.5, and wind speed lower than 1 m/s. As mentioned earlier, Tamb vs. CKT is available from PVGIS, and the total irradiance on the panel front G was previously determined by the tool. Formulation (34) is also referred to as NOCT model.
  • One the irradiance G and the temperature T vs. CKT are known, the current photogenerated by the module front is evaluated for each CKT as [23,49]
I p h = I s c n o m ⋅ G G n o m + κ ⋅ T − 25 °
where the datasheet parameter Iscnom is the short-circuit current measured by keeping the frontside under standard test conditions (STCs), i.e., nominal irradiance Gnom=1000 W/m2, 1.5 Air Mass, and cell temperature equal to 25°C, and covering the backside or at least markedly limiting its irradiance. It is worth noting that the first term on the RHS is the photogenerated current that would be obtained for an irradiance G at T=25°C. The temperature coefficient κ [A/°C] can be easily determined from the datasheet parameter TCIsc [%/°C], namely, the percentage temperature coefficient of Isc measured by the module manufacturer under the same conditions mentioned above; TCIsc is given by
T C I s c = 100 I s c n o m ⋅ ∂ I s c ∂ T = 100 I s c n o m ⋅ κ
Equation (35) allows accounting for the positive temperature coefficient of Iph due to the bandgap shrinking and the resulting increase in the number of photons with enough energy to generate electron-hole pairs, and can be recast as
I p h = I s c n o m ⋅ G G n o m + κ ⋅ T − T 0 + T 0 − 25 ° = I s c n o m ⋅ G G n o m + κ ⋅ Δ T + T 0 − 25 °
where T0 is a reference temperature and ΔT=T-T0; by assuming T0=27°C [39,50]
I p h = I s c n o m ⋅ G G n o m + κ ⋅ Δ T + 2 °
The current photogenerated by the module rear vs. CKT is calculated as
I p h , r e a r = E R F ⋅ I s c n o m ⋅ G r e a r G n o m + κ ⋅ T − 25 ° = E R F ⋅ I s c n o m ⋅ G r e a r G n o m + κ ⋅ Δ T + 2 °
where ERF (<1) is an efficiency reduction factor needed to account for the fact that the PV cell is asymmetric, being technologically designed to maximize light absorption on the front (The parameter usually provided in the datasheet of the module is the so-called bifaciality factor, namely, the ratio between the power produced by the rear illuminated under STCs while the front is covered, and the power produced by the front illuminated under STCs while the rear is covered), and T is given by (34), that is, it assumed to coincide with the temperature due to the irradiance G impinging on the panel front.

2.4. Block #4

Block #4 is intended to evaluate the I–V characteristic of the module (and consequently the maximum produced power Pmax) at each CKT during the day.
The individual cell is described through an extended version of the SDM presented in [39,41,48,50] and inspired by [51]. In particular, the cell current Icell is expressed as
I c e l l = I p h + I p h , r e a r − I D − I s h + I a v
Iph and Iph,rear being given by (38) and (39). In (40), ID is the current flowing through the intrinsic resistance-free diode. The expression of ID is derived from the well-known Shockley’s equation
I D T = I 0 T ⋅ exp V D η ⋅ V T − 1
where VD is the voltage drop across the diode, given by
V D = V c e l l + R s ⋅ I c e l l
Vcell and Rs being the voltage drop over the cell and the series resistance, the dimensionless parameter η is the ideality coefficient, and V T = k q ⋅ T + 273 is the thermal voltage, k and q being the Boltzmann’s constant and the elementary charge. As described in detail in [41,50,52], (41) can be conveniently modified into
I D Δ T = I 0 T 0 ⋅ exp V D + ϕ 0 ⋅ Δ T η V T 0 + η k q ⋅ Δ T − 1
which better evidences the diode current dependence on the temperature rise ΔT=T-T0. The value of the key coefficient ϕ0 is extracted through the following procedure. As illustrated in Figure 1, block #4 also receives the open-circuit voltage Vocnom of the module front and the temperature coefficient TCVoc of the open-circuit voltage Voc, both measured by keeping the frontside under STCs and the backside covered; TCVoc is given by
T C V o c = 100 V o c n o m ⋅ ∂ V o c ∂ T
from which ∂ V o c ∂ T is determined. Then block #4 executes Matlab simulations of the module with covered backside (setting Iph,rear=0 A) with G=Gnom=1000 W/m2 and T=25°C and 30°C and automatically calculates ∂ V o c ∂ T ; parameter ϕ0 is calibrated to obtain a good agreement between the ∂ V o c ∂ T value resulting from simulations and the one calculated from (44).
Ish is the current traversing the shunt resistance Rsh, given by
I s h = V D R s h
Resistance Rsh is assumed to be temperature-insensitive; nevertheless, Rsh might exhibit a negative temperature coefficient induced by the thermal trapping-detrapping of carriers through the defect states in the space-charge region [53].
Iav is the (positive) avalanche current induced by a reiterate impact-ionization mechanism (avalanche multiplication) in the space-charge region of the cell when subject to high reverse voltages, e.g., in the presence of localized shading; Iav is expressed as
I a v = − V D R s h ⋅ a I I 1 − V D B V m I I
where BV (<0 V) is the breakdown voltage of the junction, while aII and mII are dimensionless fitting parameters. From (46) it can be inferred that, if VD is positive, then the denominator of (46) is high and Iav is negligible; instead, if VD is negative and approaches the negative BV, then the positive Iav increases and tends to infinity. The temperature-related mitigation of avalanche multiplication can be enabled through the relation
B V T = B V T 0 ⋅ exp b I I ⋅ Δ T
bII [°C-1] (>0) being another fitting parameter.
For the series resistance Rs, a positive temperature coefficient is accounted for according to the following power relation:
R s T = R s T 0 ⋅ T + 273 T 0 + 273 m R = R s T 0 ⋅ T 0 + 273 + Δ T T 0 + 273 m R
with mR>0, although in principle any other law (e.g., exponential [54] or linear) can be implemented.
It was mentioned that if all the cells in the module share the same G, Grear, T, and thus the same Iph, Iph,rear, as well as the same parameters, the tool resorts to Matlab to solve the SDM given by (40) with (42), (43), (45), (46), (48) at a module level: once the Icell–Vcell characteristic is evaluated at a selected CKT, the I–V curve of the module is obtained by considering I=Icell and V=N∙Icell, N being the number of cells in the module.
Instead, if any nonuniformity is present, the commercial circuit simulator OrCAD PSPICE is enabled to compute the I–V characteristic by extending the approach proposed in [39,41,48,50,55] for monofacial panels to the bifacial counterparts. Such an approach can be described as follows.
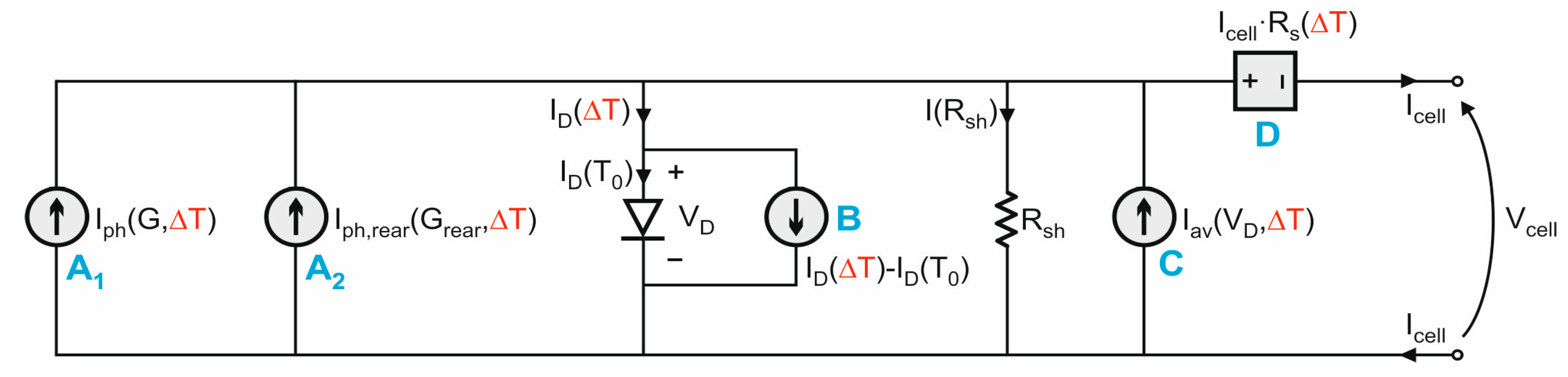
  • The module is composed by N series-connected cells, each modeled with a subcircuit implementing the SDM described above, which is fed with G, Grear, ΔT.
  • The module can be partitioned into a chosen number of subpanels, each equipped with a bypass diode.
  • The PSPICE temperature of all components embedded in the circuit is forced to the reference value T0=27°C; the temperature rise ΔT, represented as a voltage, is provided to analog behavioral modeling, or ABM, components (nonlinear current/voltage sources) to modify the temperature-sensitive parameters.
An illustrative sketch of the subcircuit modeling the individual cell is shown in Figure 4.
The ABM components A1 and A2 calculate the current photogenerated on the module front using (38) and (39), respectively. The standard diode, being at the reference temperature T0, conducts the current
I D T 0 = I 0 T 0 ⋅ exp V D η V T 0 − 1
VT0 being equal to k q ⋅ T 0 + 273 . In order to allow the flow of the temperature-dependent current ID(ΔT) given by (43) in the diode branch, the ABM B is used, which computes and forces the current ID(ΔT)-ID(T0), where ID(ΔT) is given by (43).
To account for the avalanche multiplication, the cell current Icell is computed as the sum of an avalanche-free current (i.e., the current that would flow in the absence of avalanche), and an avalanche-dictated current Iav forced by the ABM C and given by (46).
The power dependence on temperature of the series resistance Rs is implemented by forcing on the branch traversed by Icell a voltage drop given by the product by Icell and Rs, where Rs is expressed by (48). This is put into practice by making use of the ABM designated as D in Figure 4, which accepts as inputs the temperature rise ΔT and the current Icell (transformed into a voltage) and imposes the drop Icell∙Rs(ΔT).

2.5. Simplified variant of the tool for monofacial modules

A simplified tool variant is also available, which allows simulating monofacial modules. In this variant, block #1 coincides with the one of the tool for bifacial panels, block #2 only determines the incidence angle θ, block #3 evaluates G, T, Iph, and block #4 solves the SDM only with the source for the current Iph photogenerated by the front.

3. Results and Discussion

3.1. Optimization of Orientation and Tilt for a Bifacial Module

This Section demonstrates the effectiveness of the proposed tool in optimizing the orientation and tilt of a bifacial module at a chosen geographical site.
The site selected as a case-study is Naples (ϕ=40°50’, λlocal=14°15’). It is widely accepted that for the northern hemisphere the yearly energy production for a monofacial panel is maximized if the panel is oriented to south (γ=0°) and the tilt angle is determined by the empirical rule of thumb β=ϕ-15° to ϕ-10°, which allows the best performance (the minimum average θ value) from the spring equinox to the autumn one, i.e., when there is the maximum energy availability [21,22,26,56,57] (A few papers report different findings, an example being [36], where it is stated that the best choice (in terms of daily global solar radiation) for ϕ falling in the range from 36° to 46° is β=ϕ-26° to ϕ-28° from April to September, while along the whole year is β=ϕ-6° to ϕ-12°.). Hence, for the specific case of Naples, γ and β were chosen equal to 0° and 30° (≈ϕ-10°), respectively. Such a condition, schematically shown in Figure 5a, will be henceforth considered as a reference to assess the performance of bifacial modules in the same technology.
The analysis was performed by considering the monofacial ET Solar silicon module ET-M54050 embedding N=40 cells and subdivided in two 20-cell subpanels, each equipped with a bypass diode [39,41,48,50]. The key datasheet parameters are peak power of 50 Wp, Iscnom=2.81 A, TNOCT=44.4°C, TCIsc=0.06%/°C, TCVoc=-0.397%/°C, while the other (either calculated or optimized) model parameters are κ=1.69 mV/°C, I0(T0)=8 nA, η=1.2, ϕ0=4.4 mV/°C, BV=-15 V, Rsh=100 Ω, Rs(T0)=12 mΩ, mR=1.5, aII=0.1, mII=1.1. The extension of the cell model to the bifacial case was made by adding in parallel to the current source Iph another current source forcing a photogenerated current Iph,rear given by (39), where ERF was chosen equal to 0.9, that is, the efficiency on the rear was assumed to be 90% of that on the front side.
The investigation was carried out for d=0 (i) by initially assuming that the cells share the same irradiance and electrical parameters, (ii) by considering clear-sky anisotropic conditions; (iii) by neglecting the reflection from the ground (albedo=0) for both the monofacial panel and for the front of the bifacial panel. Instead, the reflection from the ground was taken into account for the rear of the bifacial panel, according to (33), Gd,albedo,rear being given by (26), (27).
Under the above assumptions, the tool was used to evaluate the I–V characteristic of both the monofacial and the corresponding bifacial panel as a function of CKT for a given day of the year n; consequently, the maximum power produced Pmax was determined for each CKT, and the daily produced energy was calculated by integrating Pmax over the whole day. The monthly energy was obtained by multiplying the energy produced in a representative day of the selected month (the 15th in our analysis) by the number of days in that month; for instance, the energy produced in April was determined multiplying by 30 the energy produced on April 15. This simplified approach allowed speeding up the analysis without significantly sacrificing the accuracy of the results.
Figure 6 shows the energy production along one year normalized to the peak power (50 Wp) for the reference monofacial module (south oriented, i.e., with γ=0° and tilted by β=30°) and for the corresponding (γ=0°, β=30°) bifacial module, the latter for various albedo values. It can be inferred that the energy increment obtained with a bifacial module under this condition is marginal due to the poor irradiance contribution of the rear.
In Figure 7, both the monofacial and bifacial panels are south-oriented (γ=0°) and vertically deployed (β=90°); the vertical arrangement draws interest as more bifacial modules can be installed in the same field. In this case, using a monofacial module is not convenient since from April to September the angle of incidence is on average rather high, and therefore the energy production is low. Differently from the β=30° condition, here using a bifacial panel allows obtaining a significant gain, as the backside is also hit by beam irradiance.
Figure 8 and Figure 9 report the case of west- (γ=90°) and east-oriented (γ=-90°) vertical (β=90°) modules, respectively. Again, the monofacial module is compared to the corresponding bifacial one for different albedo values. The following considerations are in order:
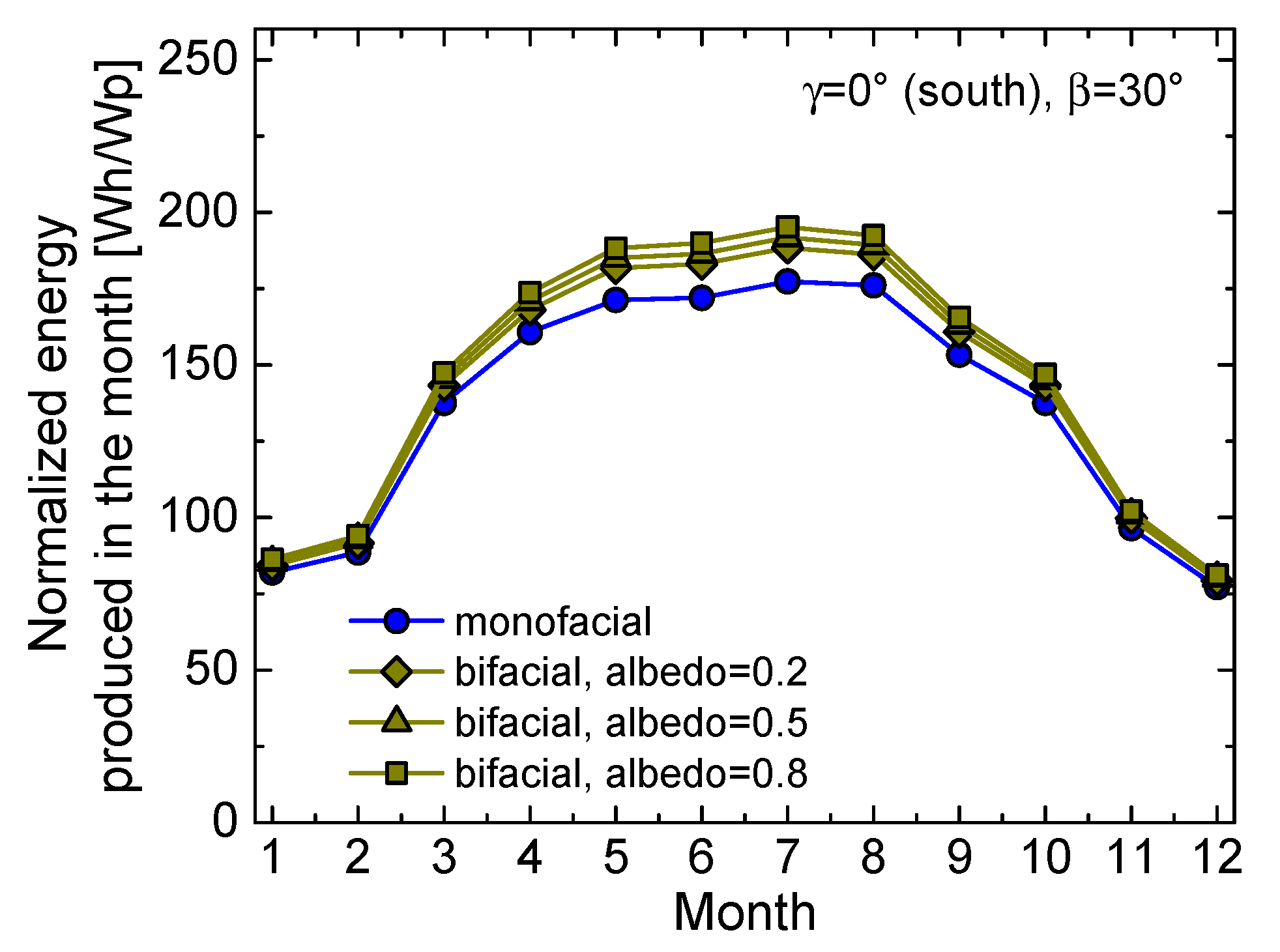
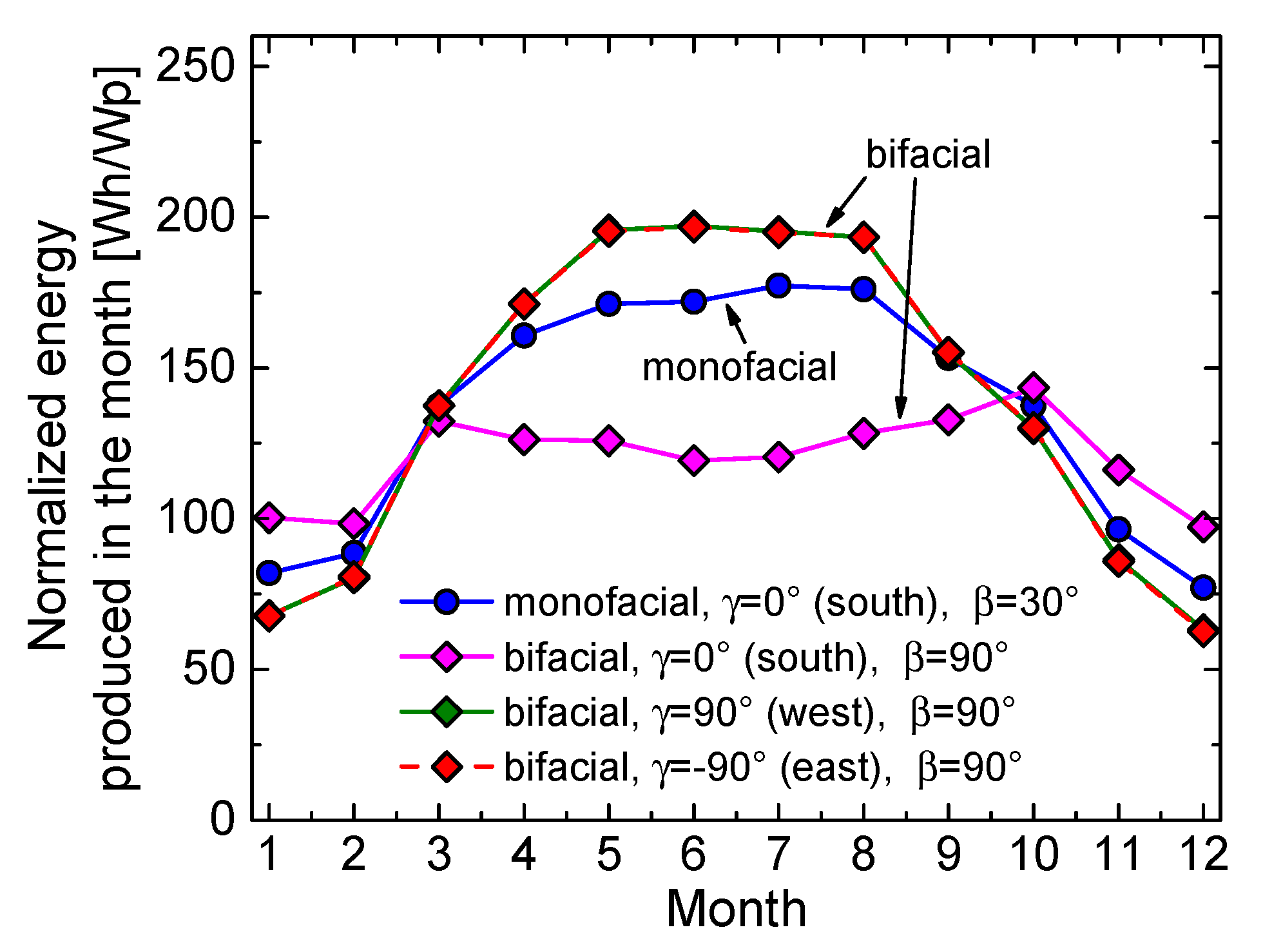
  • By specifically referring to the monofacial module, the energy produced by orienting the frontside to west is slightly better than the one obtained by orienting it to east; this result is reasonable since Naples faces the sea to the west while mountains lie to the east.
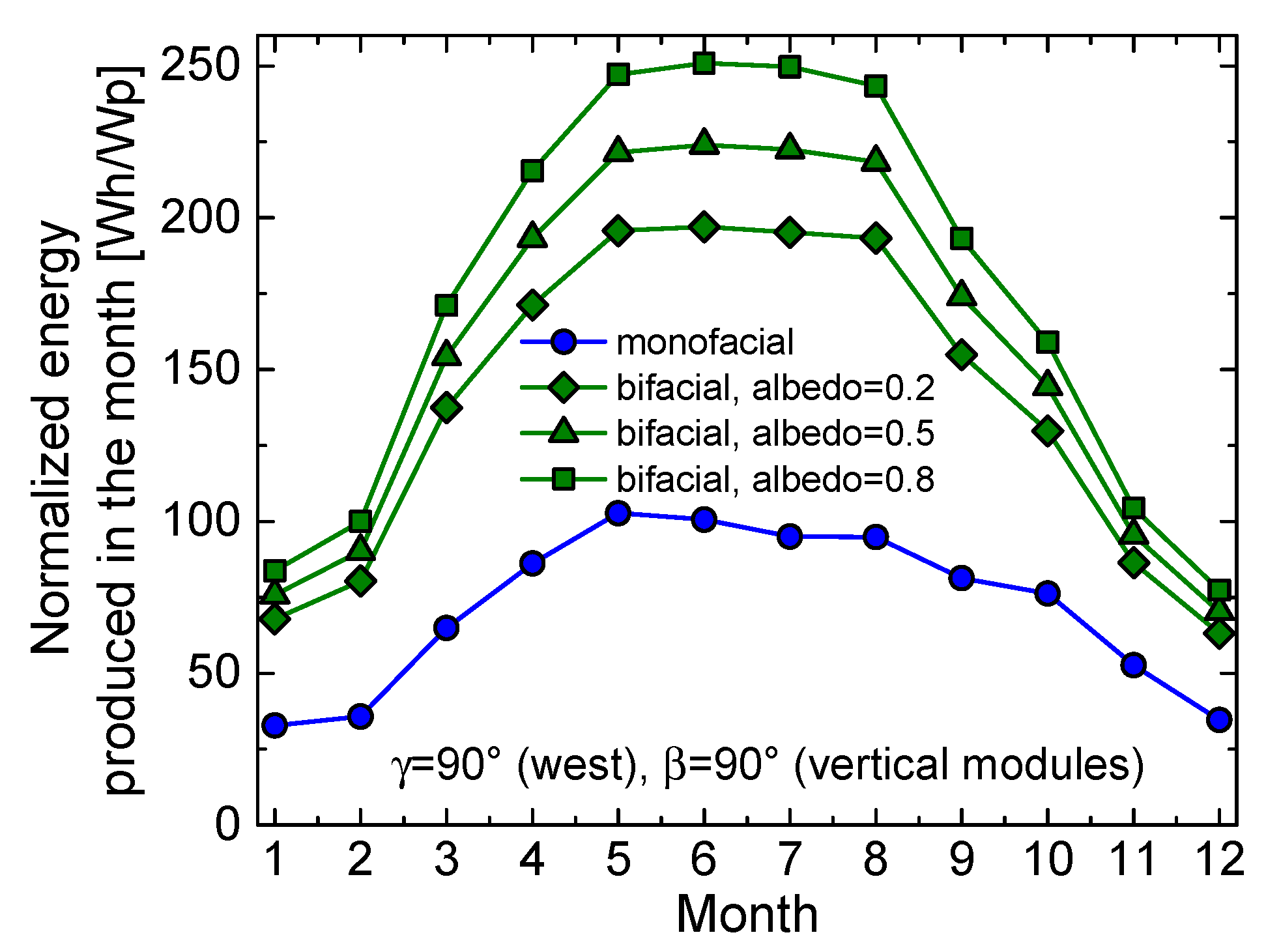
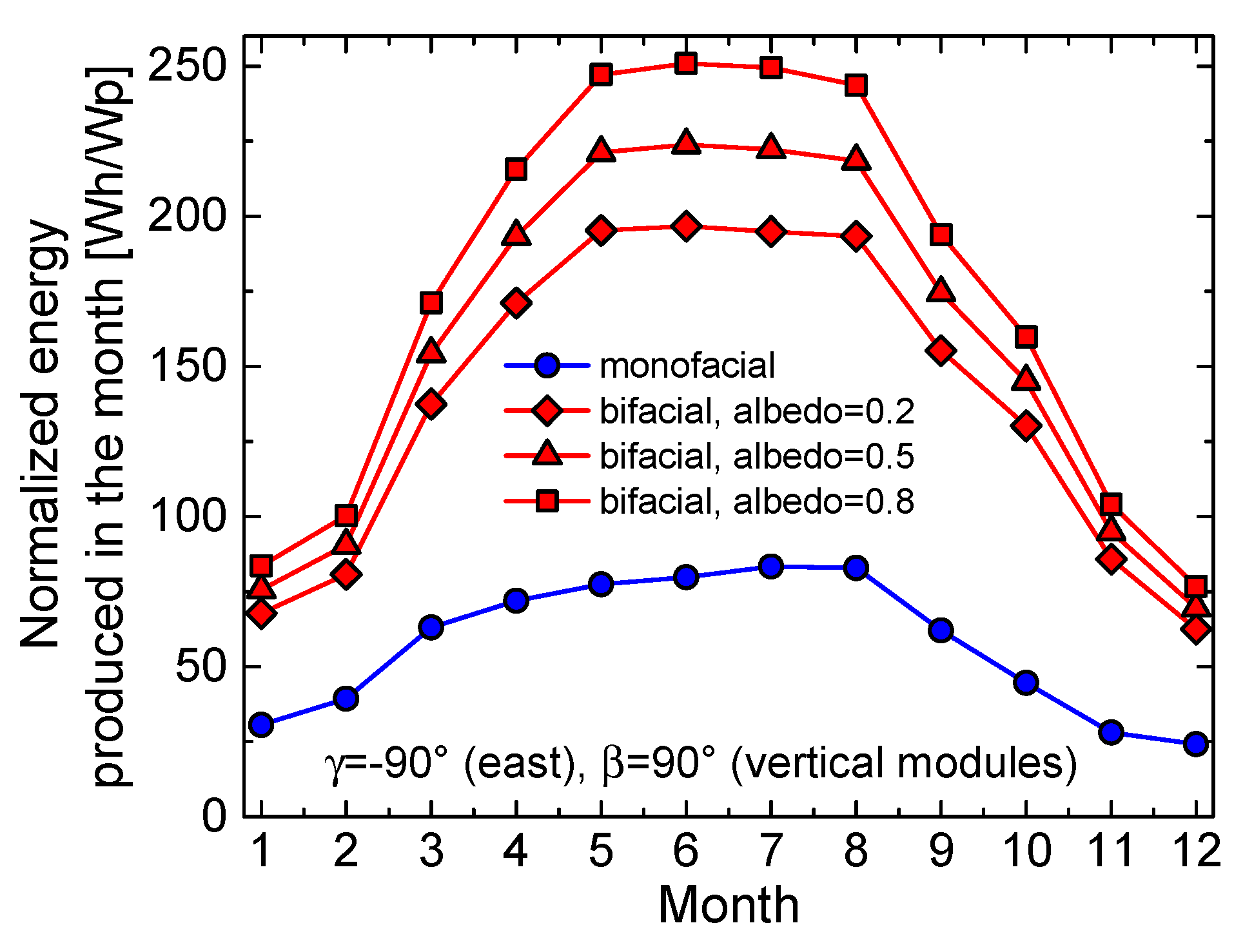
  • As a main finding, it is observed that in these cases the bifacial module allows achieving a significant improvement. While the monofacial panel receives beam irradiance for only half of the day, bifacial panels benefit from effective beam irradiance (hitting the module sides with low incidence angles) both in the morning (rear for a west-oriented panel, as sketched in Figure 5b, and front for an east-oriented one) and afternoon (the other way around).
  • West- and east-oriented vertical bifacial panels produce the same amount of energy.
In Figure 10, the normalized energies produced by the vertical bifacial panels for a south-, west-, and east-oriented front (the albedo being 0.2) are compared to the reference monofacial case. By inspecting the curves, it can be inferred that:
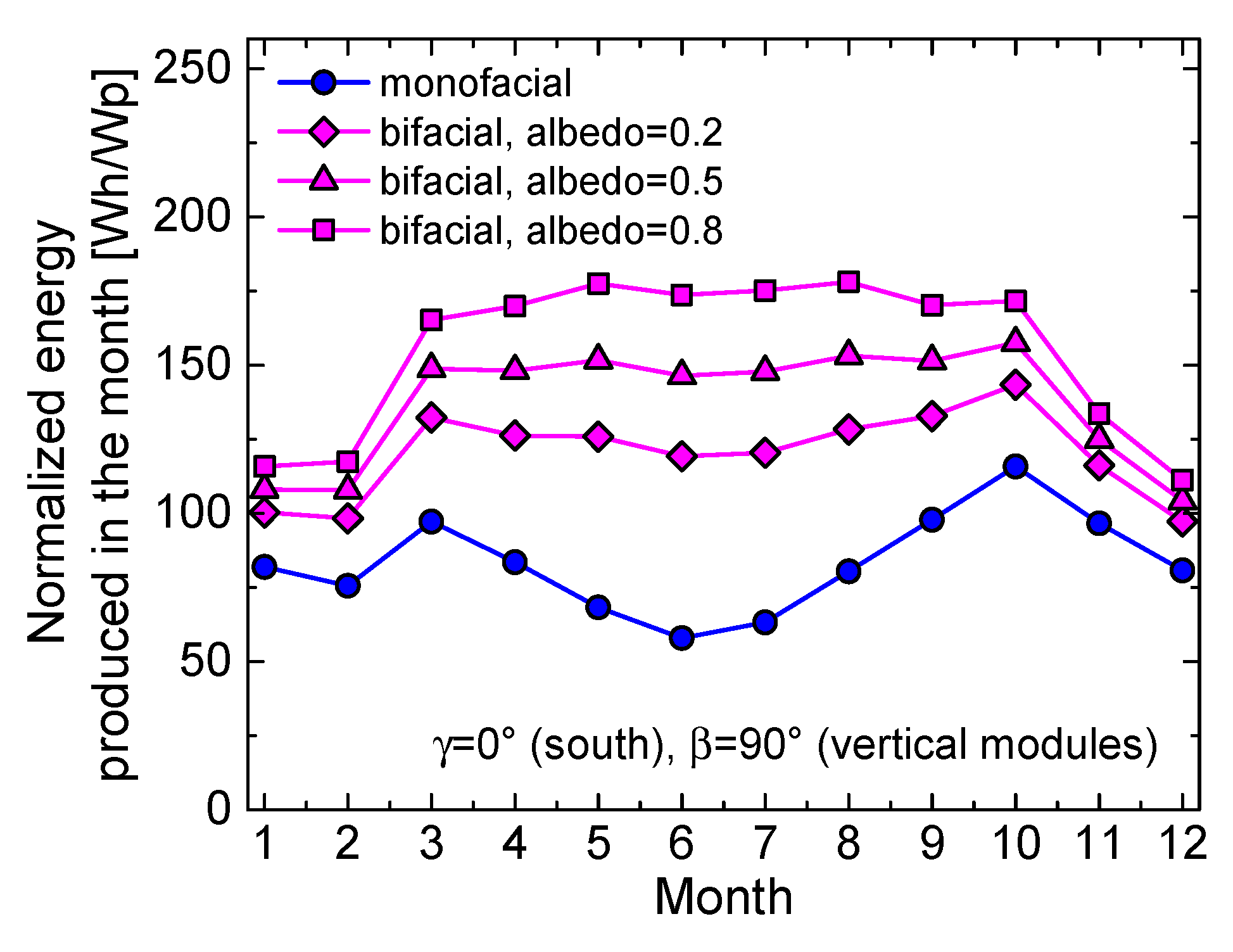
  • West- and east-oriented vertical bifacial modules (which produce the same energy) offer equal or even improved performance with respect to the reference monofacial counterpart during the time span from April to September, in which they benefit from a low incidence angle of the Sun rays hitting the front and rear of the panel in the mid-morning and the mid-afternoon [1,10]. In terms of yearly energies (all reported in Table 2), the gain compared to the reference monofacial case amounts to 2.5% and 15% for albedo values equal to 0.2 and 0.5, respectively.
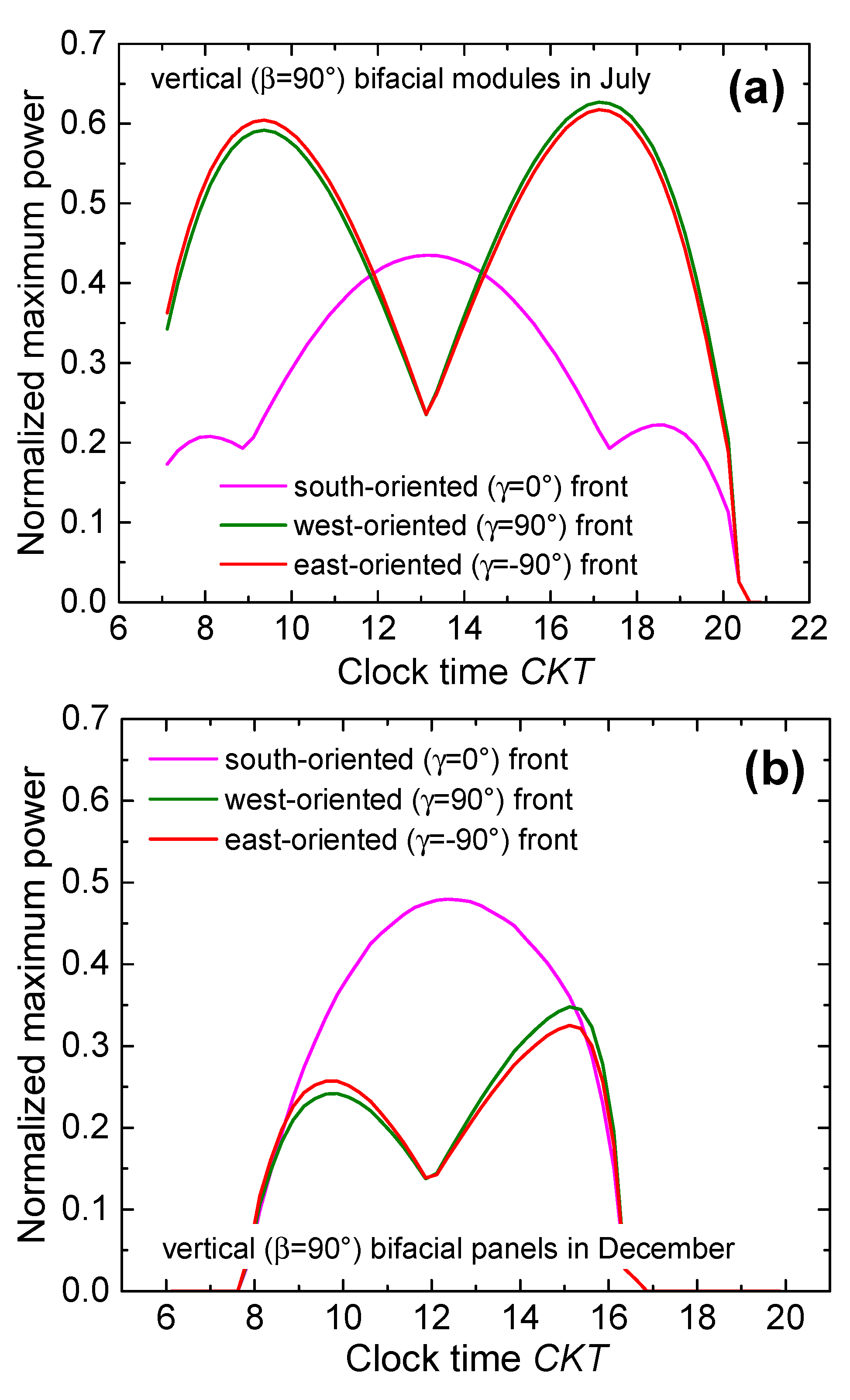
  • West- and east-oriented vertical bifacial modules also provide a considerable production improvement with respect to the south-oriented vertical bifacial counterpart, which is estimated to be 13-15%, regardless of the albedo. This is again due to the much better performance of west- and east-oriented panels from April to September, while during wintertime the south-oriented module performs better. An in-depth insight into this behavior can be achieved by showing the normalized maximum power over CKT on July 15 (Figure 11a) and December 15 (Figure 11b) for such cases. In July (and more in general during the whole period from late spring to early autumn), it is confirmed that the orientations of the module front to west and east allow for a very effective exploitation of the beam light impinging on one of the two sides in the mid-morning and on the other in the mid-afternoon, whereas in December (and more in general during wintertime) the orientation to south is better over the mid-day. Along the whole year, the first effect markedly prevails over the second.
Lastly, west- and east-oriented vertical bifacial modules are compared to the south-oriented bifacial one tilted by the optimum β=30°. From Table 2, it can be inferred that for albedo=0.2 the latter performs slightly better, while the vertical ones ensure a superior production for higher albedo values (Such findings align fairly well with those derived in [2], where a simplified analysis only based on the evaluation of annual irradiance [kWh/m2] incident on single (i.e., not included in rows) bifacial PV modules was performed by considering Tel Aviv (ϕ=32°04’, λlocal=34°46’) as a geographical site. West- (γ=90°) and east-oriented (γ=-90°) vertical (β=90°) bifacial modules are compared with a south-oriented (γ=0°) bifacial one tilted by β=20°, optimum angle given by the empirical rule ϕ-15° to ϕ-10°. It was found that (i) the annual incident irradiance is significantly higher for the latter panel, although its rear side suffers from a negligible irradiance contribution; (ii) vertical bifacial PV modules can produce more annual energy than a bifacial one with an optimum tilt angle if the ground albedo is very high.).
As key conclusion of this analysis is that west- and east-oriented vertical bifacial panels can be recommended for some applications in Naples (and more in general in Italy), e.g., for agrivoltaics, as the vertical installation does not significantly reduce the land available for cultivation, or for building noise barriers along highways.

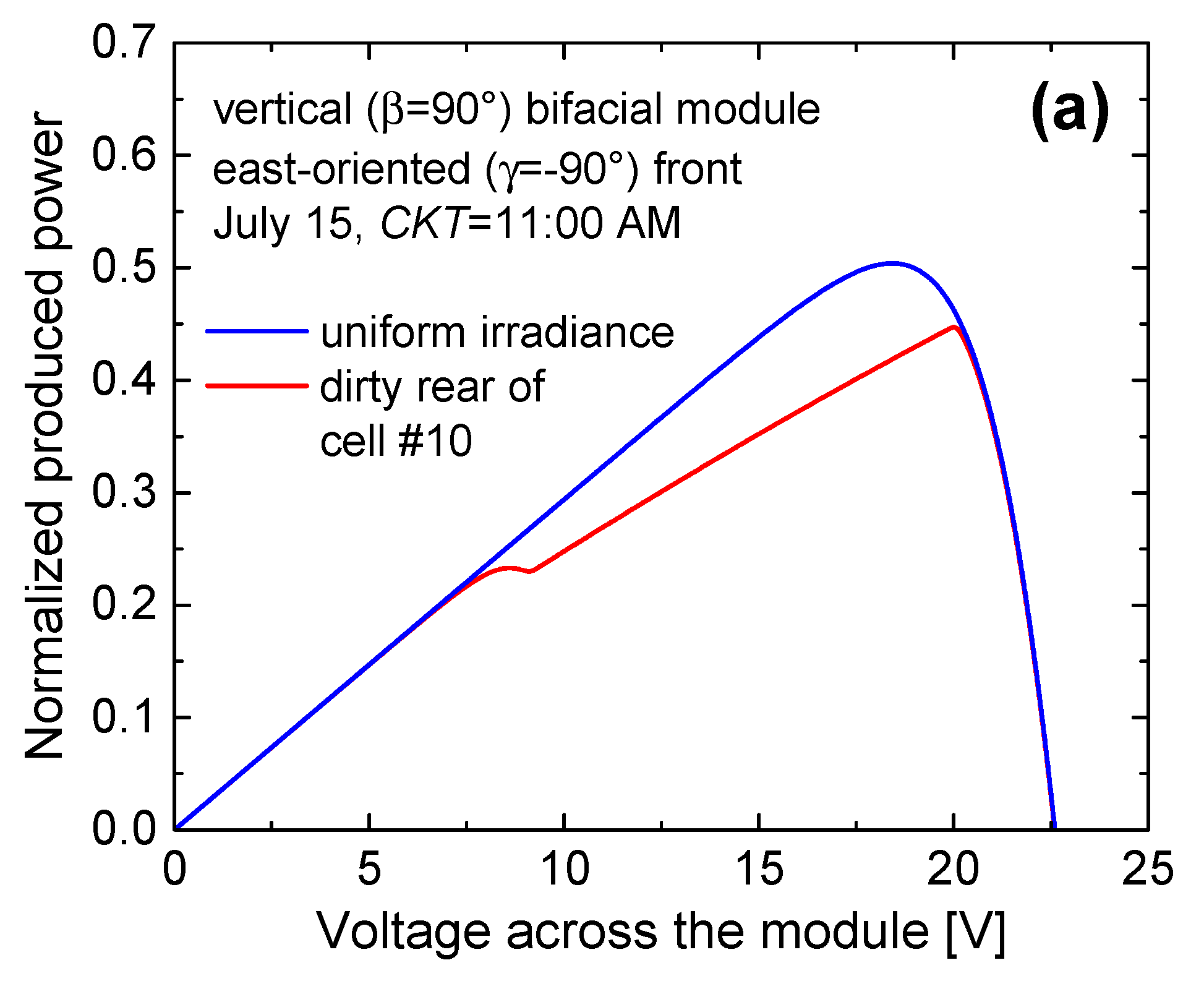
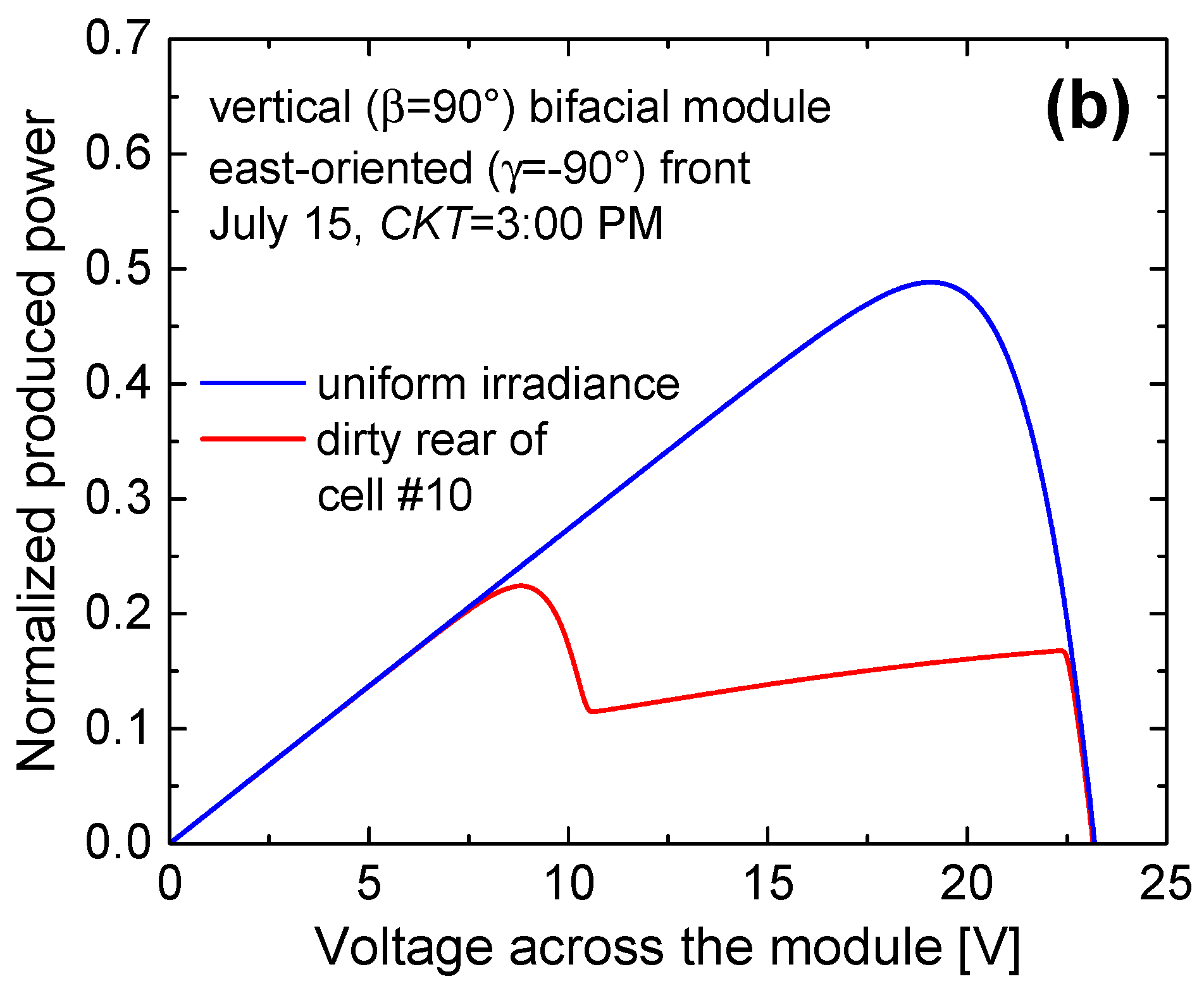
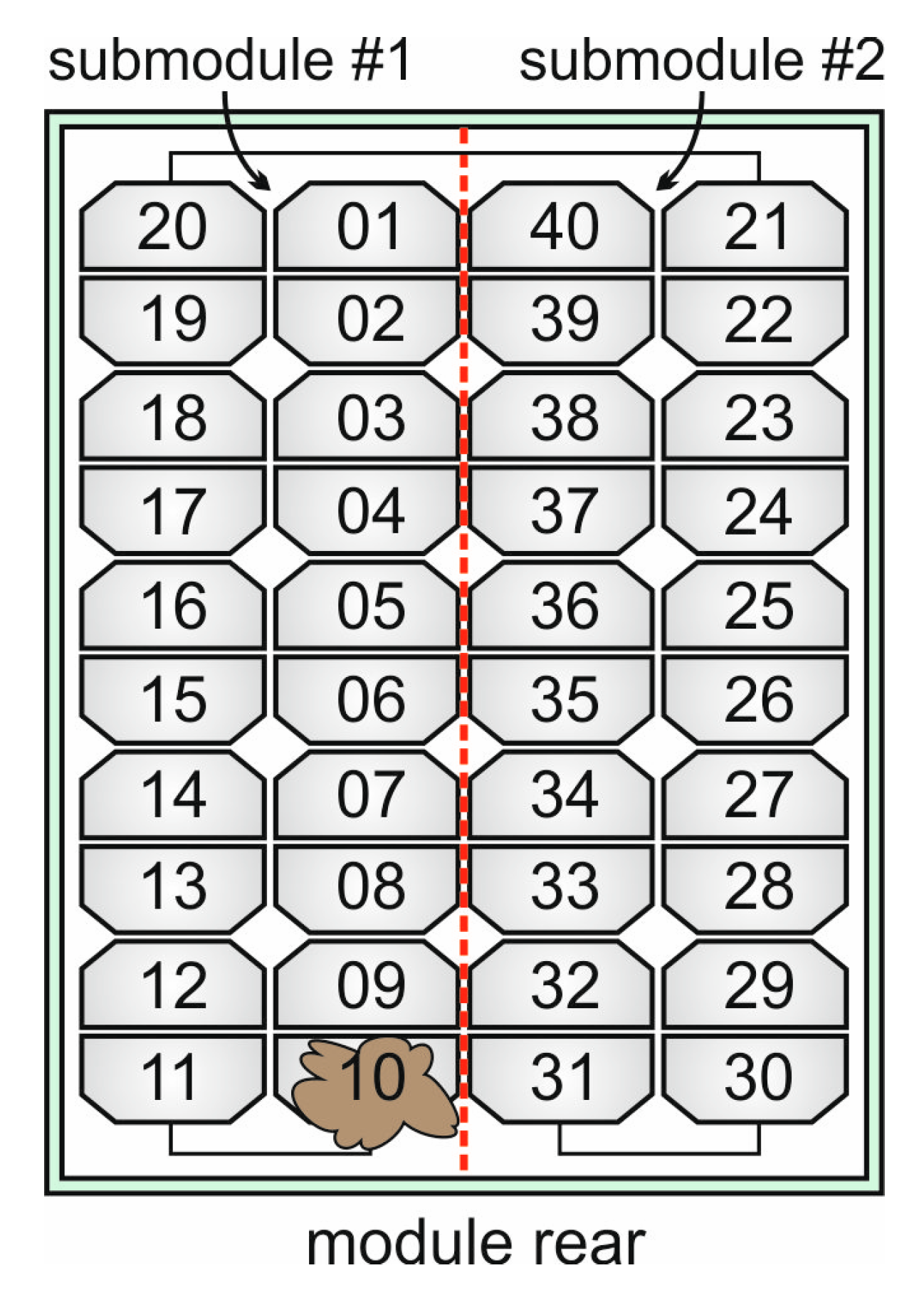
3.2. Nonuniform Irradiance Distribution over the Panel Rear

Let us consider the scenario of a vertical (β=90°) bifacial module with east-oriented front (γ=-90°) located in Naples for agrivoltaics applications (albedo=0.2, d=0, ERF=0.9) on July 15. Under clear-sky conditions, the outcomes of block #3 are:
  • G=370.49 W/m2, T=38.55°C, Iph=1.064 A, Grear=153.33 W/m2, Iph,rear=0.408 A at 11:00 AM;
  • G=88.23 W/m2, T=31.5°C, Iph=0.259 A, Grear=436.45 W/m2, Iph,rear=1.114 A at 3:00 PM.
The normalized power vs. voltage characteristics of the module under uniform irradiance conditions are reported in Figure 12a (CKT=11:00 AM) and 12b (CKT=3:00 PM); the maximum powers normalized to the peak value provided in the datasheet are 0.504 and 0.488, respectively. A likely case of a mud spot partially covering the rear of cell #10, sketched in Figure 13, was then considered, which was assumed to reduce the irradiance down to 10% of that of the clean cells. As can be seen, the PSPICE simulations lead to a counter-intuitive result, that is, although the spot is located on the rear, submodule #1 embedding cell #10 is bypassed also in the morning (CKT=11:00 AM) when the Sun rays hit the module front; such unexpected detrimental behavior should also be considered when comparing west- or east-oriented vertical bifacial panels to the reference monofacial counterpart. On the other hand, as expected, the power production dramatically reduces in the afternoon (CKT=3:00 PM), when the Sun rays impinge on the backside.

3.3. Cracked Cell(s)

The proposed tool is also suited to describe a condition with malfunctioning or defected cells. Let us again consider the scenario of a vertical (β=90°) bifacial module with east-oriented front (γ=-90°) located in Naples for agrivoltaics applications (albedo=0.2, d=0, ERF=0.9) on July 15. Under clear-sky conditions, the outcomes of block #3 at 10:00 AM are: G=463.22 W/m2, T=40.29°C, Iph=1.327 A, Grear=143.19 W/m2, Iph,rear=0.385 A. Figure 14 illustrates the normalized power against voltage for the panel under normal conditions, i.e., with all non-defected cells. Then the PSPICE-based tool version was used to assess the impact of cracked cells [58], which were emulated by setting the shunt resistance Rsh to 1 Ω instead of 100 Ω. More specifically, the cases of one, two, and three cracked cells belonging to submodule #1 were simulated, and the resulting power–voltage curves were reported in Figure 14 as well. 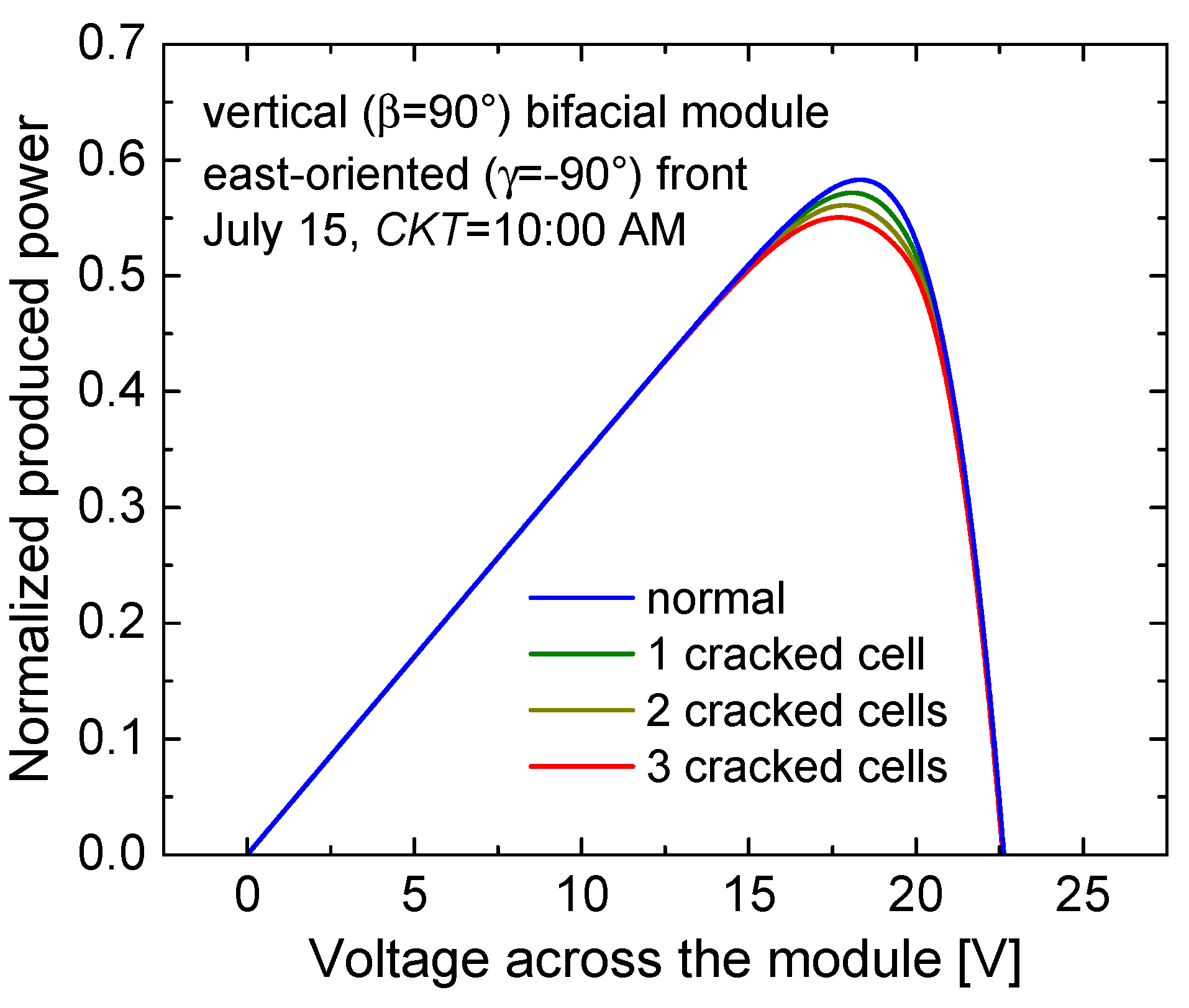It can be observed that the yield degradation is perceptible only for a significant number of damaged cells.

4. Conclusions

Bifacial PV modules are relentlessly drawing attention by virtue of their feature of collecting sunlight on both sides. In this paper, we have proposed an in-house tool specifically conceived to accurately simulate such modules in a short time and without occurrence of convergence problems. Once the day of the year and the geographical site are selected, the tool is suited to account for all the operating and environmental conditions, as well as for a nonuniformity condition across the cells induced by localized shading, dirt, bird drops, or defects. The tool is user-friendly, poorly resource-demanding, and very fast: the calculation of the I–V characteristics along an entire day with a 15-minute discretization takes only tens of seconds. A simulation campaign has been performed with the aim to optimize orientation and tilt of bifacial modules in Naples, chosen as a case-study. The normalized energies produced by such modules under clear-sky conditions have been compared to the reference one obtained with a monofacial panel in the same technology oriented to south and tilted by 30°, which is assumed to be the optimized configuration in Naples. As a main finding, it has been determined that either west- or east-oriented vertical bifacial modules allow equalizing or, for medium/high albedos, even improving the performance with respect to the reference case. This is mainly due to the low incidence angle of the Sun rays impinging on the front and rear of the bifacial module in the mid-morning and mid-afternoon during the time frame from late spring to early autumn. Thanks to the cell-level granularity ensured by the circuital PSPICE-based version of the tool, the impact of dirt obscuring a cell on the rear has been assessed; it has been surprisingly shown that the submodule embedding that cell is driven into bypass even when the Sun rays are hitting the front. Lastly, the influence of cracked cells has been examined. By virtue of such promising results, we believe that our tool is a good candidate to provide trenchant support for researchers and engineers, as it ensures that no critical factors affecting the bifacial module performance are overlooked.

Author Contributions

Conceptualization, V.d., S.D., M.D., and P.G.; methodology, V.d. and S.D.; software, V.d.; validation, V.d., S.D., P.G.; formal analysis, V.d.; investigation, V.d.; writing—original draft preparation, V.d.; writing—review and editing, V.d.; visualization, V.d.; supervision, V.d., S.D., M.D., and P.G. All authors have read and agreed to the published version of the manuscript.

Funding

This work has been supported by the Italian Ministry of Research (MUR) by means of the following grants: (i) PRIN2022-DOGPHOSS (cod. P20229FWZK), and (ii) PRIN2020–HOTSPHOT (cod. 2020LB9TBC).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Guo, S.; Walsh, T.M.; Peters, M. Vertically mounted bifacial photovoltaic modules: A global analysis. Energy 2013, 61, 447–454. [Google Scholar] [CrossRef]
  2. Appelbaum, J. Bifacial photovoltaic panels field. Renew. Energy 2016, 85, 338–343. [Google Scholar] [CrossRef]
  3. Guerrero-Lemus, R.; Vega, R.; Kim, T.; Kimm, A.; Shephard, L.E. Bifacial solar photovoltaics – A technology review. Renew. Sustain. Energy Rev. 2016, 60, 1533–1549. [Google Scholar] [CrossRef]
  4. Sun, X.; Khan, M.R.; Hussain, M.M.; Alam, M.A. The potential of bifacial photovoltaics: A global perspective. In Proceedings of the IEEE Photovoltaic Specialist Conference (PVSC), Washington, NY, USA, 25–30 June 2017; pp. 1055–1057. [Google Scholar]
  5. Deline, C.; MacAlpine, S.; Marion, B.; Toor, F.; Asgharzadeh, A.; Stein, J.S. Assessment of bifacial photovoltaic module power rating methodologies–Inside and out. IEEE J. Photovolt. 2017, 7, 575–580. [Google Scholar] [CrossRef]
  6. Gu, W.; Ma, T.; Ahmed, S.; Zhang, Y.; Peng, J. A comprehensive review and outlook of bifacial photovoltaic (bPV) technology. Energy Convers. Manag. 2020, 223, 113283. [Google Scholar] [CrossRef]
  7. Kopecek, R.; Libal, J. Bifacial photovoltaics 2021: Status, opportunities and challenges. Energies 2021, 14, 2076. [Google Scholar] [CrossRef]
  8. Bouchakour, S.; Valencia-Caballero, D.; Luna, A.; Roman, E.; Boudjelthia, E.A.K.; Rodriguez, P. Modelling and simulation of bifacial PV production using monofacial electrical models. Energies 2021, 14, 4224. [Google Scholar] [CrossRef]
  9. Mouhib, E.; Micheli, L.; Almonacid, F.M.; Fernández, E.F. Overview of the fundamentals and applications of bifacial photovoltaic technology: Agrivoltaics and aquavoltaics. Energies 2022, 15, 8777. [Google Scholar] [CrossRef]
  10. Garrod, A.; Ghosh, A. A review of bifacial solar photovoltaic applications. Front. Energy 2023, 17, 704–726. [Google Scholar] [CrossRef]
  11. Zhong, J.; Zhang, W.; Xie, L.; Zhao, O.; Wu, X.; Zeng, X. Development and challenges of bifacial photovoltaic technology and application in buildings: A review. Renew. Sustain. Energy Rev. 2023, 187, 113706. [Google Scholar] [CrossRef]
  12. Rodríguez-Gallegos, C.D.; Bieri, M.; Gandhi, O.; Singh, J.P.; Reindl, T.; Panda, S.K. Monofacial vs bifacial Si-based PV modules: Which one is more cost effective? Solar Energy 2018, 176, 412–438. [Google Scholar] [CrossRef]
  13. Gu, W.; Ma, T.; Li, M.; Shen, L.; Zhang, Y. A coupled optical-electrical-thermal model of the bifacial photovoltaic module. Applied Energy 2020, 258, 114075. [Google Scholar] [CrossRef]
  14. Ayadi, O.; Jamra, M.; Jaber, A.; Ahmad, L.; Alnaqep, M. An experimental comparison of bifacial and monofacial PV modules. In Proceedings of the IEEE International Renewable Engineering Conference (IREC), Amman, Jordan, 14–15 April 2021. [Google Scholar]
  15. Tina, G.M.; Bontempo Scavo, F.; Merlo, L.; Bizzarri, F. Comparative analysis of monofacial and bifacial photovoltaic modules for floating power plants. Applied Energy 2021, 281, 116084. [Google Scholar] [CrossRef]
  16. Matarneh, G.A.; Al-Rawajfeh, M.A.; Gomaa, M.R. Comparison review between monofacial and bifacial solar modules. Technology Audit and Production Reserves – Alternat. Renew. Energy Sources 2022, 6, 24–29. [Google Scholar] [CrossRef]
  17. Eidiani, M.; Zeynal, H.; Ghavami, A.; Zakaria, Z. Comparative analysis of mono-facial and bifacial photovoltaic modules for practical grid-connected solar power plant using PVsyst. In Proceedings of the IEEE International Conference on Power and Energy (PECon), Langkawi, Kedah, Malaysia, 5–6 December 2022; pp. 499–504. [Google Scholar]
  18. Juaidi, A.; Kobari, M.; Mallak, A.; Titi, A.; Abdallah, R.; Nassar, M.; Albatayneh, A. A comparative simulation between monofacial and bifacial PV modules under Palestine conditions. Solar Compass 2023, 8, 100059. [Google Scholar] [CrossRef]
  19. PSPICE user’s manual, Cadence OrCAD 16.5, 2011.
  20. Eicker, U. Solar Technologies for Buildings; John Wiley & Sons Ltd: Chichester, West Sussex, UK, 2003. [Google Scholar]
  21. Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006. [Google Scholar]
  22. Tiwari, G.N.; Dubey, S. Fundamentals of Photovoltaic Modules and their Applications; The Royal Society of Chemistry (RSC): Cambridge, UK, 2010. [Google Scholar]
  23. Passias, D.; Källbäck, B. Shading effects in rows of solar cell panels. Solar Cells 1984, 11, 281–291. [Google Scholar] [CrossRef]
  24. Appelbaum, J.; Bany, J. Shadow effect of adjacent solar collectors in large scale systems. Solar Energy 1979, 23, 497–507. [Google Scholar] [CrossRef]
  25. Bany, J.; Appelbaum, J. The effect of shading on the design of a field of solar collectors. Solar Cells 1987, 20, 201–228. [Google Scholar] [CrossRef]
  26. Messenger, R.A.; Ventre, J. Photovoltaic System Engineering, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
  27. Sadineni, S.B.; Boehm, R.F.; Hurt, R. Spacing analysis of an inclined solar collector field. In Proceedings of the ASME 2nd International Conference on Energy Sustainability, Jacksonville, FL, USA, 10–14 August 2008. [Google Scholar]
  28. PVGIS – PhotoVoltaic Geographical Information System. Available online: https://pvgis.com/ (accessed on 4 March 2024).
  29. Reindl, D.T.; Beckman, W.A.; Duffie, J.A. Evaluation of hourly tilted surface radiation models. Solar Energy 1990, 45, 9–17. [Google Scholar] [CrossRef]
  30. Quaschning, V.; Hanitsch, R. Shade calculations in photovoltaic systems. In Proceedings of the ISES Solar World Conference, Harare, Zimbabwe, 11–15 September 1995. [Google Scholar]
  31. Yang, H.; Lu, L. The optimum tilt angles and orientations of PV claddings for building-integrated photovoltaic (BIPV) applications. ASME J. Solar Energy Engineering 2007, 129, 253–255. [Google Scholar] [CrossRef]
  32. Hottel, H.C.; Sarofim, A.F. Radiative Transfer; McGraw-Hill: New York, NY, 1967. [Google Scholar]
  33. Kondrat’yev, K.Ya. Radiative Heat Exchange in the Atmosphere; Pergamon Press: Oxford, NY, USA, 1965. [Google Scholar]
  34. Liu, B.Y.H.; Jordan, R.C. A rational procedure for predicting the long-term average performance of flat-plate solar-energy collectors – With design data for the U.S., its outlying possessions and Canada. Solar Energy.
  35. Garnier, B.J.; Ohmura, A. The evaluation of surface variations in solar radiation income. Solar Energy 1970, 13, 21–34. [Google Scholar] [CrossRef]
  36. Calabrò, E. Determining optimum tilt angles of photovoltaic panels at typical north-tropical latitudes. J. Renew. Sustain. Energy 2009, 1, 033104. [Google Scholar] [CrossRef]
  37. Gueymard, C.A. Direct and indirect uncertainties in the prediction of tilted irradiance for solar engineering applications. Solar Energy 2009, 83, 432–444. [Google Scholar] [CrossRef]
  38. Maor, T.; Appelbaum, J. View factors of photovoltaic collector systems. Solar Energy 2012, 86, 1701–1708. [Google Scholar] [CrossRef]
  39. d’Alessandro, V.; Magnani, A.; Codecasa, L.; Di Napoli, F.; Guerriero, P.; Daliento, S. Dynamic electrothermal simulation of photovoltaic plants. In Proceedings of the IEEE 5th International Conference on Clean Electrical Power (ICCEP), Taormina, Italy, 16–18 June 2015; pp. 682–688. [Google Scholar]
  40. Appelbaum, J. The role of view factors in solar photovoltaic fields. Renew. Sustain. Energy Rev. 2018, 81, 161–171. [Google Scholar] [CrossRef]
  41. Guerriero, P.; Codecasa, L.; d’Alessandro, V.; Daliento, S. Dynamic electro-thermal modeling of solar cells and modules. Solar Energy 2019, 179, 326–334. [Google Scholar] [CrossRef]
  42. Durusoy, B.; Ozden, T.; Akinoglu, B.G. Solar irradiation on the rear surface of bifacial solar modules. Scientific Reports 2020, 10, 13300. [Google Scholar] [CrossRef]
  43. Rakovec, J.; Zakšek, K. On the proper analytical expression for the sky-view factor and the diffuse irradiation of a slope for an isotropic sky. Renew. Energy 2012, 37, 440–444. [Google Scholar] [CrossRef]
  44. Yang, D.; Dong, Z.; Nobre, A.; Khoo, Y.S.; Jirutitijaroen, P.; Walsh, W.M. Evaluation of transposition and decomposition models for converting global solar irradiance from tilted surface to horizontal in tropical regions. Solar Energy 2013, 97, 369–387. [Google Scholar] [CrossRef]
  45. Yusufoglu, U.A.; Lee, T.H.; Pletzer, T.M.; Halm, A.; Koduvelikulathu, L.J.; Comparotto, C.; Kopecek, R.; Kurz, H. Simulation of energy production by bifacial modules with revision of ground reflection. Energy Procedia 2014, 55, 389–395. [Google Scholar] [CrossRef]
  46. Alam, M.; Gul, M.S.; Muneer, T. Ground view factor computation model for bifacial photovoltaic collector field: uniform and non-uniform surfaces. Energy Reports 2021, 7, 9133–9149. [Google Scholar] [CrossRef]
  47. Tsai, H.-L. Insolation-oriented model of photovoltaic module using Matlab/Simulink. Solar Energy 2010, 84, 1318–1326. [Google Scholar] [CrossRef]
  48. d’Alessandro, V.; Di Napoli, F.; Guerriero, P.; Daliento, S. An automated high-granularity tool for a fast evaluation of the yield of PV plants accounting for shading effects. Renew. Energy 2015, 83, 294–304. [Google Scholar] [CrossRef]
  49. Rauschenbach, H.S. Solar Cell Array Design Handbook – The Principles and Technology of Photovoltaic Energy Conversion; Van Nostrand Reinhold Company: New York, NY, USA, 1980. [Google Scholar]
  50. d’Alessandro, V.; Di Napoli, F.; Guerriero, P.; Daliento, S. A novel circuit model of PV cell for electrothermal simulations. Proceedings of 3rd Renewable Power Generation (RPG) conference, Naples, Italy, 24–25 September 2014. [Google Scholar]
  51. Bishop, J.W. Computer simulation of the effects of electrical mismatches in photovoltaic cell interconnection circuits. Solar cells 1988, 25, 73–89. [Google Scholar] [CrossRef]
  52. d’Alessandro, V.; Sasso, G.; Rinaldi, N.; Aufinger, K. Thermal behavior of toward-THz SiGe:C HBTs. IEEE Trans. Electron Devices 2014, 61, pp–3386. [Google Scholar]
  53. Banerjee, S.; Andreson, W.A. Temperature dependence of shunt resistance in photovoltaic devices. Appl. Phys. Lett. 1986, 49, 38–40. [Google Scholar] [CrossRef]
  54. Ding, J.; Cheng, X.; Fu, T. Analysis of series resistance and P–T characteristics of the solar cell. Vacuum 2005, 77, 163–167. [Google Scholar] [CrossRef]
  55. Catalano, A.P.; Scognamillo, C.; Guerriero, P.; Daliento, S.; d’Alessandro, V. Using EMPHASIS for the thermography-based fault detection in photovoltaic plants. Energies 2021, 14, 1559. [Google Scholar] [CrossRef]
  56. Heywood, H. Operating experience with solar water heating. J. Inst. Heat. Vent. Eng. 1971, 39, 63–69. [Google Scholar]
  57. Gueymard, C.A.; Myers, D. Solar resource for space and terrestrial application, Chapter 19 in Solar Cells and their Applications, 2nd ed.; Fraas, L, Partain, L., Eds.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2010; pp. 427–461. [Google Scholar]
  58. Dhimish, M.; d’Alessandro, V.; Daliento, S. Investigating the impact of cracks on solar cells performance: Analysis based on nonuniform and uniform crack distributions. IEEE Trans. Ind. Informat. 2022, 18, 1684–1693. [Google Scholar] [CrossRef]
Preprints 113313 g001
Figure 1. Simplified flow-chart of the proposed tool.
Figure 1. Simplified flow-chart of the proposed tool.
Preprints 113313 g001
Preprints 113313 g002
Figure 2. (a) Side view of the tilted PV module illustrating some key angles, namely, the solar altitude α, the tilt angles of the front (β) and rear (βrear) of the module, the incidence angles on the front (θ) and rear (θrear); (b) top view showing the projection of the module and its normal onto the ground, the azimuth angle γ defining the module orientation, and the azimuth of the backside γrear.
Figure 2. (a) Side view of the tilted PV module illustrating some key angles, namely, the solar altitude α, the tilt angles of the front (β) and rear (βrear) of the module, the incidence angles on the front (θ) and rear (θrear); (b) top view showing the projection of the module and its normal onto the ground, the azimuth angle γ defining the module orientation, and the azimuth of the backside γrear.
Preprints 113313 g002
Preprints 113313 g003
Figure 3. Term Falbedo,rear as a function of d/Hpanel for various tilt angles β according to (26), (27).
Figure 3. Term Falbedo,rear as a function of d/Hpanel for various tilt angles β according to (26), (27).
Preprints 113313 g003
Preprints 113313 g004
Figure 4. Simplified schematic of the subcircuit adopted to model a PV cell in a bifacial module evidencing the ABM parts denoted as A1, A2, B, C, D.
Figure 4. Simplified schematic of the subcircuit adopted to model a PV cell in a bifacial module evidencing the ABM parts denoted as A1, A2, B, C, D.
Preprints 113313 g004
Preprints 113313 g005
Figure 5. (a) Side view of the south-oriented (γ=0°) monofacial module tilted by β=30°, taken as a reference; (b) side view of a vertical (β=90°) bifacial module with front facing the west (γ=90°).
Figure 5. (a) Side view of the south-oriented (γ=0°) monofacial module tilted by β=30°, taken as a reference; (b) side view of a vertical (β=90°) bifacial module with front facing the west (γ=90°).
Preprints 113313 g005
Preprints 113313 g006
Figure 6. Normalized energy produced in the months of the year for south-oriented (γ=0°) modules with a tilt angle β=30° installed in Naples. The albedo-less monofacial module (blue line with circles) is compared to the bifacial counterpart for various albedo values (dark yellow lines with rhombi, triangles, and squares).
Figure 6. Normalized energy produced in the months of the year for south-oriented (γ=0°) modules with a tilt angle β=30° installed in Naples. The albedo-less monofacial module (blue line with circles) is compared to the bifacial counterpart for various albedo values (dark yellow lines with rhombi, triangles, and squares).
Preprints 113313 g006
Preprints 113313 g007
Figure 7. Normalized energy produced in the months of the year for south-oriented (γ=0°) vertical (β=90°) modules installed in Naples. The monofacial panel (blue line with circles) is compared to the bifacial counterpart for various albedo values (magenta lines with rhombi, triangles, and squares).
Figure 7. Normalized energy produced in the months of the year for south-oriented (γ=0°) vertical (β=90°) modules installed in Naples. The monofacial panel (blue line with circles) is compared to the bifacial counterpart for various albedo values (magenta lines with rhombi, triangles, and squares).
Preprints 113313 g007
Preprints 113313 g008
Figure 8. Normalized energy produced in the months of the year for west-oriented (γ=90°) vertical (β=90°) modules installed in Naples. The monofacial panel (blue line with circles) is compared to the bifacial counterpart for various albedo values (green lines with rhombi, triangles, and squares).
Figure 8. Normalized energy produced in the months of the year for west-oriented (γ=90°) vertical (β=90°) modules installed in Naples. The monofacial panel (blue line with circles) is compared to the bifacial counterpart for various albedo values (green lines with rhombi, triangles, and squares).
Preprints 113313 g008
Preprints 113313 g009
Figure 9. Normalized energy produced in the months of the year for east-oriented (γ=-90°) vertical (β=90°) modules installed in Naples. The monofacial panel (blue line with circles) is compared to the bifacial counterpart for various albedo values (red lines with rhombi, triangles, and squares).
Figure 9. Normalized energy produced in the months of the year for east-oriented (γ=-90°) vertical (β=90°) modules installed in Naples. The monofacial panel (blue line with circles) is compared to the bifacial counterpart for various albedo values (red lines with rhombi, triangles, and squares).
Preprints 113313 g009
Preprints 113313 g010
Figure 10. Normalized energy produced in the months of the year for the reference south-oriented (γ=0°) monofacial panel tilted by β=30° (blue line with circles), and various vertical (β=90°) bifacial panels, namely, with south-oriented (γ=0°, magenta line with rhombi), west-oriented (γ=90°, green line with rhombi), and east-oriented (γ=-90°, red line with rhombi) front, the latter two being practically coinciding, all installed in Naples. An albedo=0.2 was considered for the rear of the bifacial modules.
Figure 10. Normalized energy produced in the months of the year for the reference south-oriented (γ=0°) monofacial panel tilted by β=30° (blue line with circles), and various vertical (β=90°) bifacial panels, namely, with south-oriented (γ=0°, magenta line with rhombi), west-oriented (γ=90°, green line with rhombi), and east-oriented (γ=-90°, red line with rhombi) front, the latter two being practically coinciding, all installed in Naples. An albedo=0.2 was considered for the rear of the bifacial modules.
Preprints 113313 g010
Preprints 113313 g011
Figure 11. Normalized maximum power vs. CKT on (a) July 15 and (b) December 15 for vertical (β=90°) bifacial modules, with south- (γ=0°, magenta line), west- (γ=90°, green), and east-oriented (γ=-90°, red) front. An albedo=0.2 was considered for the rear of the bifacial modules.
Figure 11. Normalized maximum power vs. CKT on (a) July 15 and (b) December 15 for vertical (β=90°) bifacial modules, with south- (γ=0°, magenta line), west- (γ=90°, green), and east-oriented (γ=-90°, red) front. An albedo=0.2 was considered for the rear of the bifacial modules.
Preprints 113313 g011
Preprints 113313 g012aPreprints 113313 g012b
Figure 12. Normalized power vs. voltage for an east-oriented (γ=-90°) vertical (β=90°) bifacial module installed in Naples on July 15 at (a) CKT=11:00 AM and (b) CKT=3:00 PM. The case of uniform irradiance on front and rear (blue curves) is compared to the case in which a mud spot partially covers cell #10 (Figure 13) on the rear (red curves). The analysis was performed by assuming albedo=0.2 for the reflection on the backside and ERF=0.9.
Figure 12. Normalized power vs. voltage for an east-oriented (γ=-90°) vertical (β=90°) bifacial module installed in Naples on July 15 at (a) CKT=11:00 AM and (b) CKT=3:00 PM. The case of uniform irradiance on front and rear (blue curves) is compared to the case in which a mud spot partially covers cell #10 (Figure 13) on the rear (red curves). The analysis was performed by assuming albedo=0.2 for the reflection on the backside and ERF=0.9.
Preprints 113313 g012aPreprints 113313 g012b
Preprints 113313 g013
Figure 13. Schematic representation of the module rear illustrating the likely case of a mud spot partially covering cell #10.
Figure 13. Schematic representation of the module rear illustrating the likely case of a mud spot partially covering cell #10.
Preprints 113313 g013
Preprints 113313 g014
Figure 14. Normalized power against voltage for a vertical (β=90°) east-oriented (γ=-90°) bifacial module installed in Naples on July 15 at CKT=10:00 AM. The case of all normally-working defect-free cells (blue curve) is compared to the case in which one (green), two (brown), and three (red) cells are cracked, a cracked cell being emulated by considering a very low shunt resistance in the subcircuit depicted in Figure 4. The analysis was executed by setting albedo=0.2 and ERF=0.9.
Figure 14. Normalized power against voltage for a vertical (β=90°) east-oriented (γ=-90°) bifacial module installed in Naples on July 15 at CKT=10:00 AM. The case of all normally-working defect-free cells (blue curve) is compared to the case in which one (green), two (brown), and three (red) cells are cracked, a cracked cell being emulated by considering a very low shunt resistance in the subcircuit depicted in Figure 4. The analysis was executed by setting albedo=0.2 and ERF=0.9.
Preprints 113313 g014
Table 1. Outputs of block #1 for selected geographical sites, days of the year, clock times.
Table 1. Outputs of block #1 for selected geographical sites, days of the year, clock times.
Naples
Italy		 Stuttgart
Germany [20]		 Madison
WI, USA [21]		 Cape Town
South Africa
inputs
ϕ=40°50’
λlocal=14°15’
λstandard=15°
July 15 (n=196),
CKT=16 (4:00 PM)
daylight-saving time		 inputs
ϕ=48°46’
λlocal=9°10’
λstandard=15°
July 1 (n=182),
CKT=12 (12:00 AM)
daylight-saving time		 inputs
ϕ=43°04’
λlocal=-89°-23’
λstandard=-90°
February 3 (n=34),
CKT=10.5 (10:30 AM)
standard time		 inputs
ϕ=-33°-55’
λlocal=18°25’
λstandard=30°
December 10 (n=344),
CKT=9.25 (9:15 AM)
standard time
outputs
δ=21.52°
Eqt=-5.79 minutes
TLT=14.85 (2:51 PM)
ω=42.80°
α=49.13°		 outputs
δ=23.12°
Eqt=-3.46 minutes
TLT=10.55 (10:33 AM)
ω=-21.70°
α=59.15°		 outputs
δ=-16.97°
Eqt=-13.49 minutes
TLT=10.32 (10:19 AM)
ω=-25.26°
α=25.64°		 outputs
δ=-23.05°
Eqt=7.14 minutes
TLT=8.60 (8:36 AM)
ω=-51.05°α=44.31°
Table 2. Normalized yearly energies for all the cases considered in Section 3.1.
Table 2. Normalized yearly energies for all the cases considered in Section 3.1.
Orientation (γ) and tilt (β) Normalized yearly-produced energy [Wh/Wp]
Monofacial Bifacial
γ=0° (south), β=30° 1630 (reference) 1709 (albedo=0.2)
1736 (albedo=0.5)
1763 (albedo=0.8)
γ=0° (south), β=90° 1000 1440 (albedo=0.2)
1650 (albedo=0.5)
1860 (albedo=0.8)
γ=90° (west), β=90° 855 1670 (albedo=0.2)
1880 (albedo=0.5)
2095 (albedo=0.8)
γ=-90° (east), β=90° 685 1670 (albedo=0.2)
1880 (albedo=0.5)
2095 (albedo=0.8)
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated