Prerpints.org logo
Preprint
Article

Infidelity Analysis of Digital Counter-Diabatic Driving in Two Qubit System

Altmetrics

Downloads

106

Views

32

Comments

0

This version is not peer-reviewed

Quantum Information and Quantum Computing, 2nd Volume

Submitted:

25 July 2024

Posted:

26 July 2024

You are already at the latest version

Alerts
Abstract
Digitized counter-diabatic (CD) optimization algorithms have been proposed and extensively studied to enhance performance in quantum computing by accelerating adiabatic processes while minimizing energy transitions. While adding approximate counter-diabatic terms can initially introduce adiabatic errors that decrease over time, Trotter errors from decomposition approximation persist. On the other hand, increasing the high-order nested commutators for CD terms may improve adiabatic errors but could also introduce additional Trotter errors. In this article, we examine the two-qubit model to explore the interplay between approximate CD, adiabatic errors, Trotter errors, coefficients and commutators. Through these analysis, we aim to gain insights into optimizing these factors for better fidelity, shallower circuit depth, and reduced gate number in near-term gate-based quantum computing.
Keywords: 
Subject: Physical Sciences  -   Quantum Science and Technology

1. Introduction

The adiabatic theorem ensures that a quantum system remains in its eigenstate if the time-dependent parameters in the Hamiltonian evolve slowly enough. This principle gives rise to an analog paradigm for quantum computing, which aims to minimize functions encoded in spin problem Hamiltonians[1,2]. In adiabatic quantum computing[3,4], the system is initially prepared in a superposition state as the eigenstate of a transverse field Hamiltonian. Gradually, the transverse field is turned off while the problem Hamiltonian is turned on synchronously. This process ideally leads the system to its ground state, which encodes the classical solution of the problem. However, if the process is non-adiabatic, the final state will deviate from the ground state, resulting in inaccurate solutions that are difficult to verify. The induced diabatic errors are usually inevitable because the coherence time of the quantum system is limited[5], necessitating a shorter operation time to preserve quantum coherence. This insight has inspired the development of quantum annealer that solves QUBO problem by exploiting the principles of adiabatic theorem and quantum tunneling with thousands of noisy flux qubits[6,7]. Although quantum annealers have shown remarkable advantages in scalability, there are still some fundamental limitations. Besides the coherence time, the most critical issues are the feasible interaction types and qubit connectivity[8]. More specifically, one cannot use the SWAP operation to embed the problem without a gate model. Therefore, minor embedding must be addressed as a preliminary step to map the problem to the topology graph of the annealer.
To circumvent this issue, the paradigm of digital adiabatic quantum computing has been proposed[9], offering a more flexible and equivalent approach. It has been demonstrated in superconducting circuit quantum computer with pioneering experimental technology. Using Suzuki-Trotter decomposition[10,11,12,13], it replaces continuous evolution with blocks of quantum gates that approximate the quantum dynamics during discrete timesteps. This allows for the simulation of quantum annealing with longer annealing times while preserving quantum coherence. This paradigm is also related to variational algorithms, such as the quantum approximate optimization algorithm (QAOA)[14,15,16,17,18], which minimizes energy by optimizing the digitized annealing schedule. Additionally, diabatic errors can be suppressed by introducing auxiliary interactions to realize counter-diabatic driving[19,20,21,22,23]. Although such terms are not implementable in state-of-the-art quantum annealers, they can be effectively realized in digital adiabatic quantum computing and variational algorithms[24,25]. However, the decomposition introduces a new source of infidelity known as Trotter errors[26,27]. Specifically, canceling diabatic errors through counter-diabatic driving can increase Trotter errors, suggesting an interplay between diabatic and Trotter errors. It is therefore natural to explore whether counter-diabatic driving can be further optimized to compensate not only for energy excitations but also for the infidelity induced by Trotter decomposition.
In this article, we present an infidelity analysis of digital counter-diabatic quantum computing in a two-qubit system. As a minimal model, it provides an analytical approach to study infidelity induced by both diabatic errors and Trotter errors, allowing for extension to larger models. Using nested commutators[22], we derive explicit time-dependent auxiliary terms that cancel energy excitations induced by a non-adiabatic annealing schedule. We calculate the coefficients of the first- and second-order nested commutators, evaluating the infidelity induced by their Trotterizations. Additionally, we propose optimized coefficients for compensating Trotter errors, allowing scaling up to multiple qubit problems. By examining the interplay between diabatic errors and Trotter errors, we gain insight into optimizing the performance of digital adiabatic quantum computing, achieving better fidelity and shallower circuit depth in near-term gate-based quantum computing.

2. Digitized Counter-Diabatic Driving

Adiabatic quantum computing can be characterized by a time-dependent Hamiltonian:
H 0 ( t ) = [ 1 − λ ( t ) ] H i + λ ( t ) H f ,
where H i and H f are the initial Hamiltonian with a trivial ground state and the final Hamiltonian to be solved, respectively. According to the adiabatic theorem, the quantum system is expected to remain in the instantaneous eigenstate of H 0 ( λ ) if the parameter is tuned slowly enough. This process results in the ground state of H f if λ ( t ) satisfies the boundary conditions λ ( 0 ) = 0 and λ ( T ) = 1 . In practice, the operation time required to maintain adiabatic criteria is longer than the coherence time of the quantum device. Consequently, the actual operation time, known as annealing time in a quantum annealer, is reduced, inducing unwanted energy excitations due to the diabatic effect. One solution is to find an optimal annealing schedule, whose digitized version is equivalent to QAOA. A parallel approach, called counter-diabatic driving, suppresses energy excitations by adding an auxiliary term H c d to the total Hamiltonian while keeping λ ( t ) fixed. For a many-body Hamiltonian, the nested commutator method provides the counter-diabatic (CD) term in a series of l-order as follows:
H c d = λ ˙ A λ ,
A λ ( l ) = i ∑ k = 1 l α k [ H 0 , [ H 0 , … , [ H 0 , ∂ λ H 0 ] … ] ] ,
which is indeed the exact gauge potential for diabatic transitions in the l → ∞ limit. The coefficients α k can be derived by minimizing the effective action:
S = Tr G l 2 G l = ∂ λ H 0 − i [ H 0 , A λ ( l ) ] .
Thus, one has the propagator
U ( t , 0 ) = T exp − i ∫ 0 t H 0 ( t ′ ) d t ′ ,
that provides the wave function | Ψ ( t ) 〉 = U ( t , 0 ) | Ψ ( 0 ) 〉 at any arbitrary time t ∈ [ 0 , T ] . Note that the gauge potential A λ ( l ) is not perfect, i.e., diabatic error still exists, causing the wave function | Ψ ( t ) 〉 to deviate from the instantaneous eigenstate | Ψ ˜ ( t ) 〉 .
As we can see, the gauge potential is a series of commutators, consisting of interaction terms that are not implementable in state-of-the-art quantum annealers. However, this is no longer a problem in digital adiabatic quantum computing, as the propagator U ( T , 0 ) can be realized in gate-model quantum computers using quantum simulation and Suzuki-Trotter decomposition:
U ^ dig ( T , 0 ) = ∏ n = 1 M e − i H 0 ( n δ t ) δ t e − i H c d ( n δ t ) δ t ,
where M is the number of Trotter steps of length δ t . With finite M, the circuit comprises M blocks of the same structure, leading to Trotter errors that scale as O ( δ t 2 ) [27]. It is important to note that the CD terms introduce additional Trotter error due to their non-commutation with both the initial Hamiltonian H i and the final Hamiltonian H f .
We analyze the infidelity, defined as ϵ = 1 − F , where F ( t ) = | 〈 Ψ ˜ ( t ) | Ψ dig ( t ) 〉 | 2 is the probability overlap between the wave function and the instantaneous eigenstate. Infidelity arises from both the diabatic error due to imperfect CD terms and the Trotter error from digitalization. There is a trade-off between these errors, as the diabatic error can be reduced by increasing the order l of the gauge potential A λ ( l ) , which simultaneously introduces extra Trotter error from nested commutators. Meanwhile, a higher order of Suzuki-Trotter decomposition reduces the Trotter error at the cost of more operators, resulting in a deeper circuit and larger gate numbers. By analyzing nested commutators in approximate CD terms and infidelity, it is possible to refine these variables to enhance fidelity without increasing circuit depth.

3. Two-Qubit System

We consider the two-qubit Hamiltonian H 0 ( λ ) that consists of the initial and final Hamiltonians as follows:
H i = − 2 J σ 1 z σ 2 z − h ( σ 1 z + σ 2 z ) , H f = − 2 J σ 1 z σ 2 z − h ( σ 1 z + σ 2 z ) + 2 h ( σ 1 x + σ 2 x ) ,
where the spin-0 state ( | ↑ ↓ 〉 − | ↓ ↑ 〉 ) / 2 is decoupled from the Hilbert space, effectively resembling a three-level system. Accordingly, we have the annealing schedule:
λ ( t ) = sin 2 ( π / 2 ) sin 2 ( π t / 2 T ) ,
satisfying the boundary conditions λ ( 0 ) = 0 and λ ( T ) = 1 . The first and second-order derivatives at t = 0 and t = T are zero, ensuring smooth quantum annealing. Thus, one can calculate the gauge potential of arbitrary order l. For instance, the first-order expansion of the nested commutator leads to:
A λ ( 1 ) = 8 α 1 J h ( σ 1 y σ 2 z + σ 1 z σ 2 y ) + 4 α 1 h 2 ( σ 1 y + σ 2 y ) ,
where the coefficient is given by:
α 1 = − J 2 + h 2 / 4 ( 4 J 2 + h 2 ) 2 + ( 4 J h ) 2 + ( 2 λ h 2 ) 2 + ( 8 J λ h ) 2 .
Therefore, A λ ( 1 ) provides a pool of CD operators as { σ 1 y σ 2 z , σ 1 z σ 2 y , σ 1 y , σ 2 y } . The second-order gauge potential A λ ( 2 ) is also explicitly solvable, introducing two more operators { σ 1 x σ 2 y , σ 1 y σ 2 x } to the pool. It is worthwhile to emphasize that the algebra forbids the existence of other types of CD operators with higher orders of the nested commutator. Meanwhile, A λ ( 2 ) is indeed the exact gauge potential since there are only two excitation frequencies.
For the numerical simulation, we set the annealing time to T = 0.1 , the exchange energy to J = 1 , and the local bias to h = 2 . As shown in Figure 1a, the conventional total Hamiltonian H 0 ( λ ) does not describe an adiabatic process, resulting in a fidelity around F = 0.67 . With the first- and second-order nested commutators for the CD terms, the fidelity increases to F = 0.92 and F = 1 , respectively.
The annealing process can be digitized for implementation in gate-model quantum computers. By varying the time interval δ t , we observe both diabatic and Trotter errors, as shown in Figure 1b. Diabatic errors primarily contribute to the infidelity in the l = 1 CD protocol, while they vanish in the l = 2 CD protocol. Meanwhile, Trotter error-induced infidelity is linearly suppressed on a logarithmic scale as δ t decreases. Thus, we analyze the infidelity using the Fubini-Study angle [28], aiming to enhance fidelity through optimizing the digitized CD terms with insights gained explicitly from Taylor expansion and the Baker-Campbell-Hausdorff (BCH) formula.

3.1. Improving Diabatic Error with l = 1 CD

We first consider improving the performance of digital counter-diabatic computing with l = 1 gauge potential, which corresponds to a shallower quantum circuit. As shown in Figure 1b, diabatic error is dominant when the order of the nested commutator is set to l = 1 . Therefore, it is reasonable to focus solely on reducing the diabatic error without increasing the circuit depth, while postponing efforts to reduce the Trotter error. The operator pool of A λ ( 1 ) can be divided into two sub-Hamiltonians:
H C D ( 1 ) = σ 1 y + σ 2 y ,
H C D ( 2 ) = σ 1 y σ 2 z + σ 1 z σ 2 y ,
resulting in the digitized CD propagator:
U C D [ n δ t , ( n − 1 ) δ t ] = ∏ j = 1 2 e − i c j ( n δ t ) H C D ( j ) δ t ,
where c j ( n δ t ) are the corresponding time-dependent coefficients at t = n δ t . Note that diabatic error can be further canceled by increasing the order of the nested commutator to obtain a more accurate gauge potential. We observe that local and two-body operators in H C D ( j ) also appear in the potential A λ ( 2 ) of higher order. Hence, we incorporate the corresponding coefficients from the l = 2 CD protocol to improve fidelity without increasing the circuit depth by introducing more types of CD operators. Figure 2a serves as an example depicting the variation in the coefficients at M = 20 Trotter steps, where the coefficient c 2 for two-body interaction is slightly adjusted, but the coefficient c 1 for local rotation is significantly changed. The real-time optimized infidelity between the actual wave function and the instantaneous eigenstate is illustrated in Figure 2a. By reducing the final infidelity to ϵ = 3.7 × 10 − 2 ,
We attempt to explain the effectiveness by analyzing the geometrical distance between the final state | Ψ d i g ( T ) 〉 and the target state | Ψ ˜ ( T ) 〉 based on the Fubini-Study metric:
θ F S ( | Ψ ˜ ( T ) 〉 , | Ψ d i g ( T ) 〉 ) = arccos | 〈 Ψ ˜ ( T ) | Ψ d i g ( T ) 〉 | .
By applying the triangle inequality, we obtain an inequality that aggregates an error upper bound over M steps:
θ F S ( | Ψ ˜ ( T ) 〉 , | Ψ d i g ( T ) 〉 ) ≤ ∑ n = 1 M Θ n ,
where
Θ n = arccos | 〈 Ψ ˜ ( n δ t ) | U ^ d i g [ n δ t , ( n − 1 ) δ t ] | Ψ ˜ [ ( n − 1 ) δ t ] 〉 | .
Θ n characterizes the overlap between the deviated state after evolving a single Trotter step on the instantaneous eigenstate | Ψ ˜ [ ( n − 1 ) δ t ] 〉 and the ideal instantaneous eigenstate | Ψ ˜ [ n δ t ] 〉 . Hence, the smaller Θ n is, the more U ^ dig approximates ideal adiabatic quantum computing.
We illustrate the evolution of Θ n at M = 20 Trotter steps with the standard l = 1 CD protocol and its optimization in Figure 3a. The angle Θ n after partially optimizing the coefficients from terms in l = 2 is significantly decreased, demonstrating that the performance is improved by steering the state along the instantaneous eigenstate.
By optimizing the coefficients, we observe a reduction in the upper bound on errors. In Figure 3b, we present the upper bounds for both the conventional l = 1 CD protocol and the optimized protocol, maintaining the same circuit depth. Summing the reduced Fubini-Study angles Θ n results in a looser upper bound due to the nature of the triangle inequality. As the number of Trotter steps M increases, the upper bound will gradually tighten until it aligns with the error scaling.

3.2. Improving Trotter Error with l = 2 CD

By increasing the order of the nested commutator, the diabatic error is significantly reduced. The two-qubit Hamiltonian with the l = 2 CD protocol demonstrates that the evolution closely follows the instantaneous eigenstate of the original Hamiltonian. Therefore, this Hamiltonian serves as an appropriate model for studying Trotter error and its suppression. It introduces an additional sub-Hamiltonian to the operator pool of A λ ( 2 ) as H C D ( 3 ) = σ x σ y + σ y σ x , which subsequently gives the digitized CD propagator
U C D [ n δ t , ( n − 1 ) δ t ] = ∏ j = 1 3 e − i c j ( n δ t ) H C D ( j ) δ t .
As shown in Figure 1b, when the number of Trotter steps is limited, a longer δ t causes a significant difference between the Hamiltonians at consecutive time intervals. This results in a noticeable presence of commutators and nested commutators in the higher-order terms of the Trotter decomposition, which introduces Trotter errors. To explain this further, the higher-order terms are derived by applying a Taylor expansion to the exponents. The product of three exponents in one Trotter step can be expressed as in Eq. (21), which is related to the well-known BCH formula. When δ t → 0 , the first-order Trotter decomposition is enough to achieve high precision. This means that the effects of higher-order expansions are mainly influenced by δ t and the coefficients, while commutators and nested commutators determine the operators that can be classified. Typically, higher-order expansions introduce additional operators beyond the CD operator pool. However, in this system, the commutative relationship between these operators is straightforward: [ H C D ( j ) , H C D ( k ) ] = − 2 i ε j k l H C D ( l ) with j , k , l = 1 , 2 , 3 . Therefore, the commutators revert back to operators already included in the CD operator pool. This means there is a closure of the commutative relationship for the operators in the second-order CD terms.
To replace the commutators in Eq.(21) and collect the terms of the same operators, we have
∏ j = 1 3 e − i c j H c d ( j ) δ t = e − i δ t ∑ j = 1 3 c j H c d ( j ) + 2 i 2 ( − i δ t ) 2 { − c 1 c 2 H c d ( 3 ) + c 1 c 3 H c d ( 2 ) − c 2 c 3 H c d ( 1 ) } + ⋯ = e − i δ t ( c 1 − δ t c 2 c 3 + ⋯ ) H c d ( 1 ) + ( c 2 + δ t c 1 c 3 + ⋯ ) H c d ( 2 ) + ( c 3 − δ t c 1 c 2 + ⋯ ) H c d ( 3 ) = e − i δ t ( c ˜ 1 H c d ( 1 ) + c ˜ 2 H c d ( 2 ) + c ˜ 3 H c d ( 3 ) ) .
In this context, the combination of coefficients is represented by new coefficients c ˜ j , resulting in an expression that resembles an effective evolution operator U ^ c d , d i s c r e t e = e − i δ t c 1 H c d ( 1 ) + c 2 H c d ( 2 ) + c 3 H c d ( 3 ) . Since contributions from higher-order terms are included, this allows for the possibility of offsetting Trotter errors during the decomposition process by comparing with U ^ c d , d i s c r e t e . For instance, the coefficients in digitization can be adjusted accordingly. The specifics are as follows: substitute c j ( n δ t ) with c ˜ j , and the coefficients that require modification in the product (17) are renamed as c j * , which can be obtained by solving a series of transformation equations. Below are the equations for the 2nd-order approximation.
c 1 ( n δ t ) = c 1 * − δ t c 2 * c 3 * c 2 ( n δ t ) = c 2 * + δ t c 1 * c 3 * c 3 ( n δ t ) = c 3 * − δ t c 1 * c 2 * ,
and the 3rd-order approximation
c 1 ( n δ t ) = c 1 * − δ t c 2 * c 3 * − δ t 2 3 ( c 2 * ) 2 + ( c 3 * ) 2 c 1 * c 2 ( n δ t ) = c 2 * + δ t c 3 * c 1 * − δ t 2 3 ( c 1 * ) 2 + ( c 3 * ) 2 c 2 * c 3 ( n δ t ) = c 3 * − δ t c 1 * c 2 * − δ t 2 3 ( c 1 * ) 2 + ( c 2 * ) 2 c 3 * .
Essentially, this procedure aims to approximate U ^ c d , d i s c r e t e as closely as possible, ultimately achieving equality when the Taylor expansion is infinite. To balance computational efficiency with accuracy, we utilize the Taylor expansion up to the third order. The number of equations is determined by the number of coefficients, which can be reduced by merging terms of mutually commutative operators. The process of solving these equations must be repeated M times to minimize Trotter errors at each Trotter step. The final infidelity can be improved by applying the solutions c j * in chronological order during digitization, which rewrites the optimized time-evolution operator as U ^ * ( 0 , T ) = ∏ n = 1 M ∏ j = 1 3 e − i c j * H c d ( j ) δ t .
The results, illustrated in Figure 4a, show notable improvements in Trotter errors within the range of 0.02 ≥ δ t ≥ 0.001 , and quickly approach the same error scaling within a limited number of total steps M. Based on the property of closure in commutators among the CD operator pool, the optimization of digitization for a two-qubit system can be enhanced by modifying the coefficients at all steps. In general, superior digital dynamics can be achieved for any Hamiltonian of CD terms that possess such a feature.
Additionally, the error upper-bounds of different conditions derived by Eq.(14) are also contained in Figure 4b, showing the inclusion of 2nd-order CD terms is sufficient to achieve high-accuracy fidelity.

4. Conclusion

This work analyzes the infidelity of digitized approximate counter-diabatic driving in terms of Trotter errors and diabatic errors for a two-qubit system. In the l = 1 CD driving, the evolution process cannot reach adiabaticity due to the incompleteness of the operator pool, resulting in infidelity mainly attributed to diabatic errors. A suitable selection of the coefficients of the CD operators can help improve the diabatic errors. Here, we choose the corresponding coefficients of the same operators that appear in the l = 2 CD terms as an alternative and find an improvement of about 3.7 % . We use statistical distance to find better performance of the alternative driving in the Fubini-Study angle at each step, leading to a lower error upper bound. The l = 2 CD driving achieves perfect fidelity, so Trotter errors dominate when the number of Trotter steps M is not large. By applying the BCH formula, we find a commutative closure of the operator pool in the l = 2 CD terms, which results in a series of equations to optimize the coefficients to eliminate Trotter errors. This method is also applicable for Hamiltonians whose CD terms have the same property.
c o s ( Θ n ) = | 〈 ψ ˜ n | e − i H 0 δ t ∏ j = 1 2 e − i c j H c d ( j ) δ t | ψ ˜ n − 1 〉 | ≈ | 〈 U ^ 0 , n † ψ ˜ n | I − i δ t c 1 H c d ( 1 ) + c 2 H c d ( 2 ) + 1 2 ( − i δ t ) 2 ( c 1 H c d ( 1 ) ) 2 + ( c 2 H c d ( 2 ) ) 2 + 2 c 1 c 2 H c d ( 1 ) H c d ( 2 ) | ψ ˜ n − 1 〉 | = | e i E 0 δ t 〈 ψ ˜ n | ψ ˜ n − 1 〉 + 〈 ψ ˜ n | O ( δ t ) | ψ ˜ n − 1 〉 + 〈 ψ ˜ n | O ( δ t 2 ) | ψ ˜ n − 1 〉 | = | ( a 0 + i b 0 ) + δ t ( a 1 + i b 1 ) + δ t 2 ( a 2 + i b 2 ) |
∏ j = 1 3 e − i c j H c d ( j ) δ t = I − i δ t ∑ j = 1 3 c j H c d ( j ) + 1 2 ( − i δ t ) 2 ∑ j = 1 3 ( c j H c d ( j ) ) 2 + 2 c 1 c 2 H c d ( 1 ) H c d ( 2 ) + 2 c 1 c 3 H c d ( 1 ) H c d ( 3 ) + 2 c 2 c 3 H c d ( 2 ) H c d ( 3 ) + ⋯ = I − i δ t ∑ j = 1 3 c j H c d ( j ) + 1 2 ( − i δ t ) 2 ∑ j = 1 3 c j H c d ( j ) 2 + c 1 c 2 [ H c d ( 1 ) , H c d ( 2 ) ] + c 1 c 3 [ H c d ( 1 ) , H c d ( 3 ) ] + c 2 c 3 [ H c d ( 2 ) , H c d ( 3 ) ] + ⋯ = e − i δ t ∑ j = 1 3 c j H c d ( j ) + 1 2 ( − i δ t ) 2 c 1 c 2 [ H c d ( 1 ) , H c d ( 2 ) ] + c 1 c 3 [ H c d ( 1 ) , H c d ( 3 ) ] + c 2 c 3 [ H c d ( 2 ) , H c d ( 3 ) ] + ⋯

Appendix

We analyze the improvements in the first-order CD driving by using Taylor expansion at one step. At any given time n δ t , the exponentiation operator e − i c j ( n δ t ) H c d ( j ) δ t is possible to represented into:
e − i c j H c d ( j ) δ t = I − i c j H c d ( j ) δ t + 1 2 ( − i c j H c d ( j ) δ t ) 2 + ⋯ ,
where j = 1 , 2 and ( n δ t ) is omitted for convenience, so as in the following derivation.
So Eq.(15) can be represented as Eq.(20) where U ^ 0 , n = e − i H 0 δ t and E 0 = E 0 ( n δ t ) is the instantaneous ground state energy, here the distance is written in a c o s ( Θ n ) function. On the right side of this equation, the fidelity is divided into many parts based on the expansion order. We keep the expansion to the second order. Since these parts are all inner products, the result of c o s ( Θ n ) can be described as a sum of numbers a k + i b k , k = 0 , 1 , 2 with different orders of δ t . Thereinto, a 0 + i b 0 = 〈 U ^ 0 , n † ψ ˜ n | ψ ˜ n − 1 〉 has no relation with CD terms. But the rest of a k + i b k also have non-neglectable contributions, which are only dependent on the coefficients c 1 and c 2 . Because the corresponding inner products 〈 U ^ 0 , n † ψ ˜ n | H c d j | ψ ˜ n 〉 is fixed in one certain Trotter step. In this model, a k + i b k are all real numbers so b k = 0 , ∀ k . Here we list the values of a k for n = 10 , M = 20 :
Table 1. values of each part in c o s ( L 10 )
Table 1. values of each part in c o s ( L 10 )
a 0 δ t a 1 δ t 2 a 2
original 0.99638 0.00403 -0.00140
alternative 0.99638 0.00571 -0.00260
Note that c 1 ( 10 δ t ) have little change, a 1 and a 2 are mainly effected by c 2 ( 10 δ t ) . The sum of a k in the alternative has about 0.0005 improvement of fidelity at step n = 10 , leading to a smaller L 10 . Generally, the smaller L n at each step, the smaller statistical distance is. Thus the diabatic errors are reduced by changing the coefficients.

References

  1. Farhi, E.; Goldstone, J.; Gutmann, S.; Lapan, J.; Lundgren, A.; Preda, D. A Quantum Adiabatic Evolution Algorithm Applied to Random Instances of an NP-Complete Problem. Science 2001, 292, 472–475. [Google Scholar] [CrossRef]
  2. Pastorello, D.; Blanzieri, E. 2019; arXiv:quant-ph/1909.06870].
  3. Das, A.; Chakrabarti, B.K. Colloquium: Quantum annealing and analog quantum computation. Reviews of Modern Physics 2008, 80, 1061–1081. [Google Scholar] [CrossRef]
  4. Albash, T.; Lidar, D.A. Adiabatic quantum computation. Reviews of Modern Physics 2018, 90, 015002. [Google Scholar] [CrossRef]
  5. Schlosshauer, M. Quantum decoherence. Physics Reports 2019, 831, 1–57. [Google Scholar] [CrossRef]
  6. Pastorello, D.; Blanzieri, E. Quantum annealing learning search for solving QUBO problems. Quantum Information Processing 2019, 18, 303. [Google Scholar] [CrossRef]
  7. Cruz-Santos, W.; Venegas-Andraca, S.E.; Lanzagorta, M. A QUBO formulation of minimum multicut problem instances in trees for D-Wave quantum annealers. Scientific reports 2019, 9, 17216. [Google Scholar] [CrossRef]
  8. Holmes, A.; Johri, S.; Guerreschi, G.G.; Clarke, J.S.; Matsuura, A.Y. Impact of qubit connectivity on quantum algorithm performance. Quantum Science and Technology 2020, 5, 025009. [Google Scholar] [CrossRef]
  9. Barends, R.; Shabani, A.; Lamata, L.; Kelly, J.; Mezzacapo, A.; Heras, U.L.; Babbush, R.; Fowler, A.G.; Campbell, B.; Chen, Y.; others. Digitized adiabatic quantum computing with a superconducting circuit. Nature 2016, 534, 222–226. [Google Scholar] [CrossRef]
  10. Trotter, H.F. On the Product of Semi-Groups of Operators. Proceedings of the American Mathematical Society 1959, 10, 545–551. [Google Scholar] [CrossRef]
  11. Suzuki, M. General theory of fractal path integrals with applications to many-body theories and statistical physics. Journal of Mathematical Physics 1991, 32, 400–407. [Google Scholar] [CrossRef]
  12. Ruth, R.D. A Can0nical Integrati0n Technique. IEEE Transactions on Nuclear Science 1983, 30, 2669–2671. [Google Scholar] [CrossRef]
  13. Childs, A.M.; Su, Y.; Tran, M.C.; Wiebe, N.; Zhu, S. Theory of Trotter Error with Commutator Scaling. Physical Review X 2021, 11. [Google Scholar] [CrossRef]
  14. Farhi, E.; Goldstone, J.; Gutmann, S. 2014; arXiv:quant-ph/1411.4028].
  15. Chandarana, P.; Vieites, P.S.; Hegade, N.N.; Solano, E.; Ban, Y.; Chen, X. Meta-learning digitized-counterdiabatic quantum optimization. Quantum Science and Technology 2023, 8, 045007. [Google Scholar] [CrossRef]
  16. Chandarana, P.; Hegade, N.N.; Paul, K.; Albarrán-Arriagada, F.; Solano, E.; del Campo, A.; Chen, X. Digitized-counterdiabatic quantum approximate optimization algorithm. Physical Review Research 2022, 4, 013141. [Google Scholar] [CrossRef]
  17. Wurtz, J.; Love, P.J. Counterdiabaticity and the quantum approximate optimization algorithm. Quantum 2022, 6, 635. [Google Scholar] [CrossRef]
  18. Chai, Y.; Han, Y.J.; Wu, Y.C.; Li, Y.; Dou, M.; Guo, G.P. Shortcuts to the quantum approximate optimization algorithm. Phys. Rev. A 2022, 105, 042415. [Google Scholar] [CrossRef]
  19. Demirplak, M.; Rice, S.A. Adiabatic population transfer with control fields. The Journal of Physical Chemistry A 2003, 107, 9937–9945. [Google Scholar] [CrossRef]
  20. Demirplak, M.; Rice, S.A. Assisted adiabatic passage revisited. The Journal of Physical Chemistry B 2005, 109, 6838–6844. [Google Scholar] [CrossRef]
  21. Del Campo, A. Shortcuts to adiabaticity by counterdiabatic driving. Physical Review Letters 2013, 111, 100502. [Google Scholar] [CrossRef]
  22. Claeys, P.W.; Pandey, M.; Sels, D.; Polkovnikov, A. Floquet-Engineering Counterdiabatic Protocols in Quantum Many-Body Systems. Physical Review Letters 2019, 123, 090602. [Google Scholar] [CrossRef]
  23. Takahashi, K. Shortcuts to adiabaticity for quantum annealing. Phys. Rev. A 2017, 95, 012309. [Google Scholar] [CrossRef]
  24. Sels, D.; Polkovnikov, A. Minimizing irreversible losses in quantum systems by local counterdiabatic driving. Proceedings of the National Academy of Sciences 2017, 114, E3909–E3916. [Google Scholar] [CrossRef]
  25. Passarelli, G.; Cataudella, V.; Fazio, R.; Lucignano, P. Counterdiabatic driving in the quantum annealing of the p-spin model: A variational approach. Phys. Rev. Res. 2020, 2, 013283. [Google Scholar] [CrossRef]
  26. Suzuki, M. Generalized Trotter’s formula and systematic approximants of exponential operators and inner derivations with applications to many-body problems. Communications in Mathematical Physics 1976, 51, 183–190. [Google Scholar] [CrossRef]
  27. Suzuki, M. Decomposition formulas of exponential operators and Lie exponentials with some applications to quantum mechanics and statistical physics. Journal of Mathematical Physics 1985, 26, 601–612. [Google Scholar] [CrossRef]
  28. Hatomura, T. State-dependent error bound for digital quantum simulation of driven systems. Physical Review A 2022, 105, L050601. [Google Scholar] [CrossRef]
Preprints 113307 g001
Figure 1. (a)Fidelity F ( t ) between the evolving state and the instantaneous ground state in the two-qubit system for the original Hamiltonian and CD driving protocols with the first and second order. (b)Final infidelity of digitized approximate simulations, ϵ ( T ) = 1 − F ( T ) , against the time interval δ t of each step. In the shaded regions, Trotter product formula is non-convergent. The dash lines show error scalings, about 7.7 × 10 − 2 and 1.5 × 10 − 6 separately for the first- and second-order driving.
Figure 1. (a)Fidelity F ( t ) between the evolving state and the instantaneous ground state in the two-qubit system for the original Hamiltonian and CD driving protocols with the first and second order. (b)Final infidelity of digitized approximate simulations, ϵ ( T ) = 1 − F ( T ) , against the time interval δ t of each step. In the shaded regions, Trotter product formula is non-convergent. The dash lines show error scalings, about 7.7 × 10 − 2 and 1.5 × 10 − 6 separately for the first- and second-order driving.
Preprints 113307 g001
Preprints 113307 g002
Figure 2. (a)Original coefficients and the alternative under Trotter steps M = 20 . The alternative coefficients are selected from the ones associated with H c d ( 1 ) and H c d ( 2 ) in the 2nd-order CD terms. (b)Fidelity F ( t ) of the first-order CD driving with the original coefficients and the alternative.
Figure 2. (a)Original coefficients and the alternative under Trotter steps M = 20 . The alternative coefficients are selected from the ones associated with H c d ( 1 ) and H c d ( 2 ) in the 2nd-order CD terms. (b)Fidelity F ( t ) of the first-order CD driving with the original coefficients and the alternative.
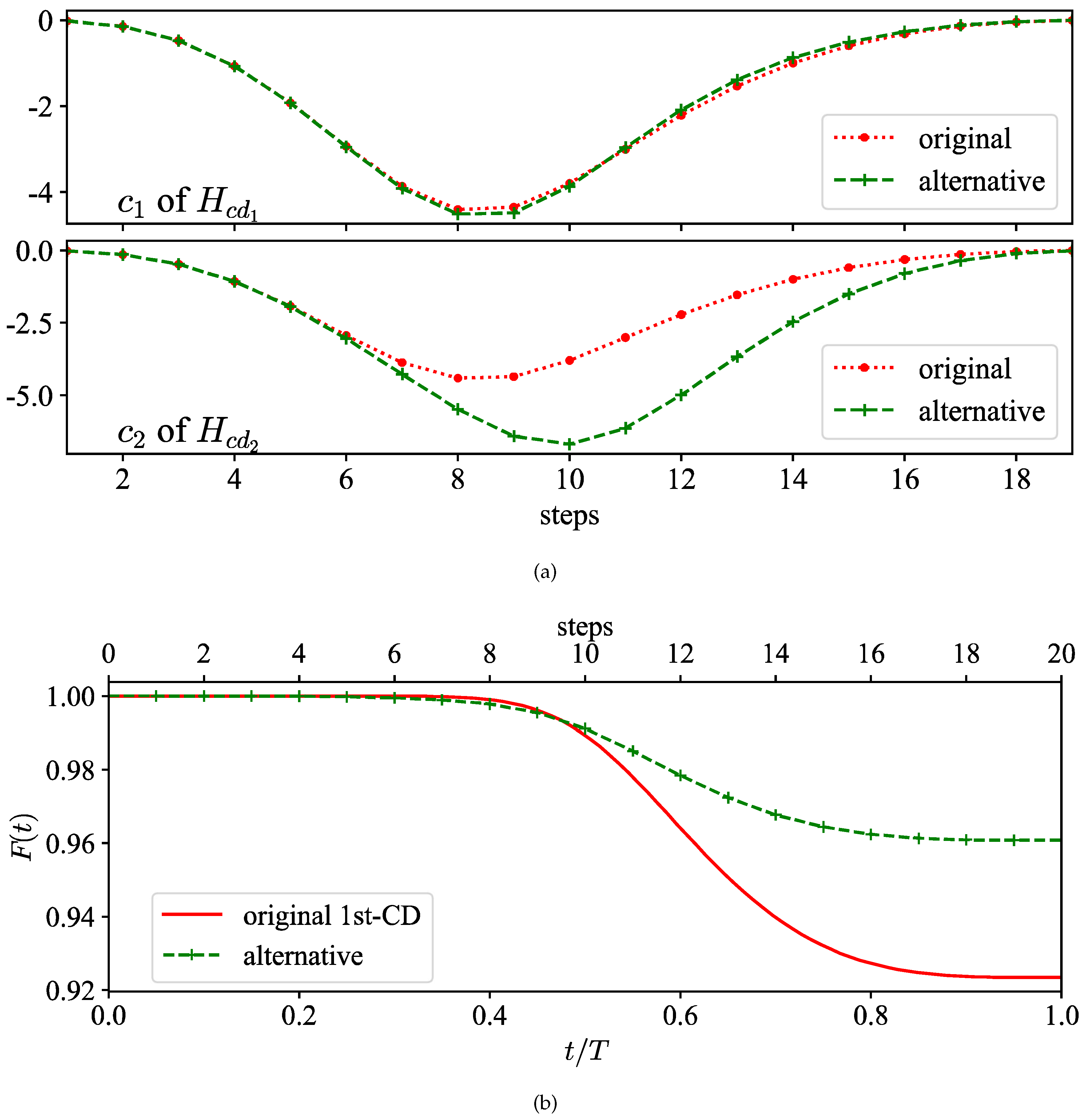
Preprints 113307 g002
Preprints 113307 g003
Figure 3. (a)The distance between digital simulated dynamics and true dynamics at each step for original and alternative drivings. (b)Infidelity of the two drivings, against the time interval δ t . The gray dot lines are the error upper-bound derived from Fubini-Study angles.
Figure 3. (a)The distance between digital simulated dynamics and true dynamics at each step for original and alternative drivings. (b)Infidelity of the two drivings, against the time interval δ t . The gray dot lines are the error upper-bound derived from Fubini-Study angles.
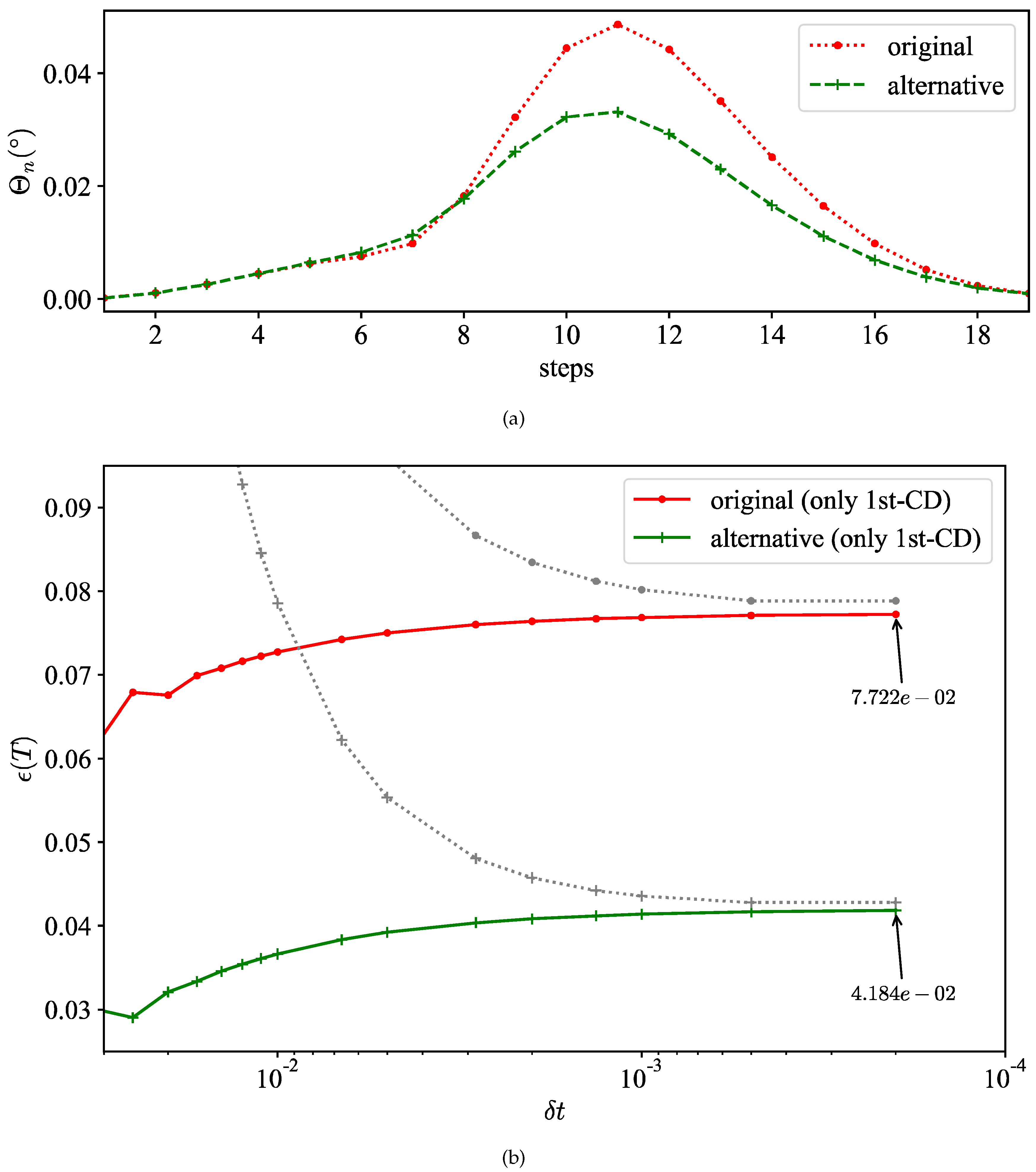
Preprints 113307 g003
Preprints 113307 g004
Figure 4. (a)Infidelity ϵ ( T ) of the second-order CD driving using optimized coefficients in the second- and third-order approximation. The dash line is the result of the discrete effective operators. All these drivings converge to an error scaling of 1.362 × 10 − 6 . (b)The error upper-bound derived from Fubini-Study angles for the second-order CD driving with and without the optimization. It shows the optimizations in coefficients are very delicate. Moreover, the upper-bounds are much bigger than the corresponding infidelity in (a), suggesting l = 2 is sufficient for a high-accuracy fidelity.
Figure 4. (a)Infidelity ϵ ( T ) of the second-order CD driving using optimized coefficients in the second- and third-order approximation. The dash line is the result of the discrete effective operators. All these drivings converge to an error scaling of 1.362 × 10 − 6 . (b)The error upper-bound derived from Fubini-Study angles for the second-order CD driving with and without the optimization. It shows the optimizations in coefficients are very delicate. Moreover, the upper-bounds are much bigger than the corresponding infidelity in (a), suggesting l = 2 is sufficient for a high-accuracy fidelity.
Preprints 113307 g004
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated