Prerpints.org logo
Preprint
Article

Sustainability of Automated Manufacturing Systems with Resources by Means of Their Deadlock Prevention

Altmetrics

Downloads

101

Views

21

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

25 July 2024

Posted:

26 July 2024

You are already at the latest version

Alerts
Abstract
This paper is devoted to Petri net (PN) based models of Automated Manufacturing Systems (AMS) with resources in order to prevent deadlocks in them. The sustainability can be seen as the process of deadlock-freeness leading to correct and fluent production, because AMS with deadlocks work neither correctly nor fluently, need reconstruction and cause downtime in production. A class S3PR (Systems of Simple Sequential Processes with Resources) of such PN models is well known as to the deadlock prevention point of view. Here, Extended S3PR (ES3PR) will be explored as to modelling and deadlock prevention. While in case of S3PR Ordinary Petri Nets (OPN) were used for these aims, here, for ES3PR Generalized Petri Nets (GPN) are used. The reason for such a procedure is a possible presence of multiplex directed arcs in the structure of PN models of AMS. The significant alternation is that while in former case the elementary and dependent siphons were sufficient for the supervisor synthesis, here, in later case, the GPN and their siphons have to satisfy the max-cs property.
Keywords: 
Subject: Engineering  -   Control and Systems Engineering

1. Introduction

It is very important to deal with deadlocks in industrial MAS (Multi Agent Systems). AMS (Automated Manufacturing Systems) where two or more production lines share robots, machine tools, conveyors, automatically controlled vehicles, etc., are a typical example of such systems. These shared entities represent resources. Such production systems are very important in social practice. They should fluently produce expected products without any obstacles. However, deadlocks occurring in them prevent this. In general, deadlock is a status when two (or more) processes are waiting to continue their activity, but are preventing each other from doing so. Namely, they are competing for the same resources. A deadlock is an undesirable state in the global system, because the system itself, or a part of it, stagnates. Sustainability of the manufacturing process continuity is strongly disturbed. Therefore, the original intention of such a system cannot be achieved. In order to sustain processes in AMS fluently work it is necessary to prevent deadlocks.
S3PR, i.e., Systems of Simple Sequential Processes with Resources, modeling the Resource Allocation Systems (RAS) on the base of PN were defined, analyzed and controlled in [1]. S3PR were modeled there by Ordinary PN (OPN) and controlled by siphons. Here, more complicated Extended S3PR (ES3PR) models of RAS are analyzed by Generalized PN (GPN) and controlled by their siphons.

1.1. Basic PN Terminology

A Petri net is a quadruplet N = (P, T, F, W) with P and T being finite nonempty sets, a set of places P = {p1, p2, …, pn} (|P| = n) and a set of transitions T = {t1, t2, …, tm} (|T| = m), where P ∪ T ≠ ∅ and P ∩ T = ∅, and ∅ means an empty set. The set F = (P × T) ∪ (T × P) is a flow relation of N. Such flow consists of directed arcs from places to transitions and vice versa. The mapping W: (P × T) ∪ (T × P) → ℕ assigns a weight to an arc: W(f) > 0 if f ∈ F and W(f) = 0 otherwise. Here ℕ = {0, 1, 2, …} is the set of natural numbers plus zero. The net N is ordinary net if ∀ f ∈ F, W(f) = 1. Such net is denoted as N = (P, T, F). If ∃f ∈ F, W(f) > 1, N = (P, T, F, W) is named as a generalized net GPN.
The set M expressing states of marking of particular PN places, simply said the PN marking M, is an (n × 1) vector named also as the state vector. Its evolution is performed by means of the matrix/vector equation Mk+1 = Mk + [N]. σk, k ∈ ℕ, where M0 is an initial marking. This equation represents the mathematical model of the net N. The matrix [N] = [Post]T − [Pre] is the (n × m) incidence matrix. It represents the matrix notation of the set F. It can also be expressed as [N] (p, t) = W (t, p) − W (p, t). After all, σk is a (m × 1) vector expressing firing of transitions named also as the control vector. Namely, it expresses the state of transitions (a transition may be firable—it is indicated by 1, or not—it is indicated by 0).
For a place p, M(p) is an integer indicating the number of tokens placed inside of this place. We say that the place p is marked by M iff M(p) > 0. The abbreviation iff means if and only if in the whole paper.
A subset D ⊆ P is marked by M iff at least one place p ∈ D is marked by M. Thus, M (D) = Σp∈D M (p) denotes the sum of tokens in all places in D.
●x = {y ∈ P ∪ T | (y, x) ∈ F} is the preset of a node x ∈ P ∪ T, while x● = {y ∈ P ∪ T | (x, y) ∈ F} is the postset of a node x ∈ P ∪ T.
A transition t such that |t●| > 1 is named as a fork. A transition t such that |●t| > 1 is named as a join. A place p such that |p●| > 1 is named as a choice. A place p such that |●p| > 1 is named as an attribution.
SP (x1, xn) means a simple path from x1 to xn. It is a path whose all nodes are different.
We say that a transition t ∈ T is enabled at a marking M iff ∀p ∈ ●t, M(p) ≥ W (p, t). After firing t a new marking M′ is evolved such that ∀p ∈ P, M′ (p) = M(p) − W (p, t) + W (t. p). However, enabled transition t may be fired, but it may not be fired.
A non-empty subset of places S ⊆ P is a siphon iff ●S ⊆ S●. A non-empty subset of places S ⊆ P is a trap iff S● ⊆ ●S. Siphon S is minimal iff it contains no other siphons (as its proper subset). If a minimal siphon S does not contain a marked trap, it is named strict.
A column vector I: P → Z indexed by P, where Z is the set of integers, is named the P-vector. A column vector J: T → Z indexed by T is named the T-vector. For the economy of space, a P-vector I is denoted by Σp∈P I (p)p and T-vector J is denoted by Σt∈ T J(t)t.
Let I is a P-invariant of (N, M0). Then ∀M ∈ R (N, M0), IT.M = IT.M0. Here R (N, M0) is the state space of N. In other words, it is a set of all reachable markings of N.
As we can see, the invariant I is a P-vector. ||I|| = {p ∈ P | I(p) ≠ 0} means a support of P. ||I||+ = {p ∈ P | I(p) > 0} is the positive support of P and ||I||- = {p ∈ P | I(p) < 0} is the negative support of P.
P-invariant of (N, M0) is a natural solution of the equation IT.[N] = 0. If all elements of P-invariant I are nonnegative this invariant is named as P-semiflow.
T-invariant of (N, M0) is a natural solution of the equation [N]. J = 0. It gives information about a possible loop in the net, i.e., about a sequence of transitions which leads back to the marking it starts in. If all elements of T-invariant J are nonnegative this invariant is named as T-semiflow.
When a place p is given, then max t ∈ p● {W (p, t)} is denoted by maxp●.
More details about PN are introduced in [1,2,3,4] and in basic papers about PN [17,18,19,20].

1.2. Structure of the Article

In the next section preliminaries concerning definitions of particular PN models of AMS are introduced.
The third section is devoted to control of ES3PR paradigm od AMS model. It represents one of two substantive parts of this paper. Since ES3PR model belongs to a subclass of S4PR paradigm of models, accordingly such paradigm is defined there. The basic influence of siphons to the control of PN models of AMS is emphasized there too. Finally, definitions concerning the siphon-based control as well as the procedure making possible to find parameters of the supervisor, ensuring the deadlock-freeness of the ES3PR model, are introduced. To illustrate ES3PR model, simple example is presented in Figure 1 and its siphons are computed. Unfortunately, these siphons, satisfying for S3PR models cannot be used for the supervisor synthesis of ES3PR model, Namely, they do not ensure the deadlock-freeness.
In the fourth section, representing the second of two substantive parts of the paper, controllability of siphons in GPN is analyzed and elementary and dependent siphons are checked as to max-cs property. Then the supervisor computed in the sense of such a procedure is set. The Figure 2 illustrates the interconnections between the original uncontrolled model and the supervisor ensuring the deadlock-freeness.
Fifth section represents conclusions, where the topic and contribution of the paper is evaluated and the further work in future is pointed out to.

2. Preliminaries

As to nomenclature of sets in PN used below, PS is a set of operation places, PR is a set of resource places, P0 is a set of idle places.
Definition 1 [6]: An ordinary Petri net N = (PS ∪ {p0}, T, F) is a Simple Sequential Process (S2P) when the following hold true:
1. PS ≠ ∅, p0 ∉ PS.
2. N is a strongly connected state machine (i.e., OPN where each transition has only one input place and only one output place).
3. Every circuit in N contains place p0.
Definition 2 [6]: An extended simple sequential process with resources—ES2PR is a generalized pure Petri net N = (PS ∪ {p0} ∪ PR, T, F, W), such that:
1. The subnet generated by the set X = PS ∪ {p0} × T is an S2P.
2. PR ≠ ∅ and (PS ∪ {p0}) ∩ PR = ∅.
3. ∀t ∈ T, ∀p ∈ ●t, W (p, t) = 1.
4. ∀r ∈ PR, ∃ a minimal P-semiflow Ir such that {r} = ||Ir|| ∩ PR, p0 ∉ ||Ir||, ||Ir|| ∩ PS ≠ ∅ and Ir(r) = 1.
Definition 3 [6]: Let N = (PS ∪ {p0} ∪ PR, T, F, W) be an ES2PR. An initial marking M0 is acceptable for N iff:
1. M0(p0) > 0.
2. ∀p ∈ PS, M0(p) = 0.
3. ∀r ∈ PR, M0(r) > 0

4. Elements in the support of each minimal T-semiflow can be fired sequentially.

Definition 4 [6]: An ES3PR is the composition of a finite set of ES2PR via the fusion of resource places.
Definition 5 [6]: Let Ni = (Pi, Ti, Fi, Wi) (i = 1, 2) be two generalized Petri nets. Then:
1. N1 and N2 are composable (via fusion of places) iff T1 ∩ T2 = ∅, and PC = P1 ∩ P2 ≠ ∅.
2. Net N = (P, T, F, W) is called the composed net of N1 and N2, denoted by N1 ○ N2, where P = P1 ∪ P2, T = T1 ∪ T2, W (p, t) = if t ∈ T1 then W1 (p, t) else W2 (p, t).
Definition 6 [6]: Let Im be a set of indices, Ni = (Pi, Ti, Fi, Wi) (i ∈ Im) be a set of generalized Petri nets. We denote by N = ◯i ∈ Im Ni the net obtained by the following operation: if card (Im) = 1 then N = N1 else N = Nk ○ ◯ i ∈ Im \ {k} Ni.
Definition 7 [6]: An ES3PR is the composition of a finite set of ES2PR via the fusion of resource places.
Definition 8 [6]: (N, M0), ◯i∈Im Ni, Ni= (Pi, Ti, Fi, Wi), and (Ni, M0i) being initially acceptably marked ES2PR, is an acceptably marked ES3PR iff:
1. ∀i ∈ Im, ∀p ∈ PSi ∪ {p0i}, M0(p) = M0i (p).
2. ∀i ∈ Im, ∀r ∈ PR, M0(r) = if card (Im) = 1 then M0i(r) else maxi∈Im M0i(r).
In [10] the following property was proved:
Let N = (PS ∪ P0 ∪ P, T, F, W) be an ES3PR, where P0 = ∪i ∈ Im {p0i}. Then, rank ([N]) = |PS|.
In [11] the following Theorem was proved:
Theorem 1 [11]: Let S be a strict minimal siphon in an ES3PR N = (PS ∪ P0 ∪ P, T, F, W). Then S = SR ∪ SS satisfies S ∩ P0 = ∅, S ∩ PR = SR ≠ ∅, and S ∩ PS = SS ≠ ∅.

3. Control of ES3PR

The paradigm ES3PR models a class of concurrently cyclic sequential processes sharing common resources. An approach to the deadlock prevention by controlling siphons in ES3PR will be presented here. Namely,
1. the control of elementary siphons
2. finding the relevant approach to finding conditions for control of dependent siphons;
3. finding the way of making the ES3PR deadlock-free.
With respect to [6] ES3PR is a subclass of S4R (Systems of Sequential Systems with Shared Resources) defined by the next definition.
Definition 8 [6]: An S4R is a generalized pure net N = ◯i ∈ImNi = (P, T, F, W), where
  • Ni = (PSi ∪ {p0i} ∪ PRi, Ti, Fi, Wi), i ∈ Im
  • P = Ps ∪ P0 ∪ PR is a partition such that
    • PS = ∪ i ∈ Im PSi, PSi ≠ ∅ and PSi ∩ PSj = ∅, ∀i ≠ j (i, j ∈ Im)
    • PR = ∪ i ∈ Im PRi = {r1, r2, …, rn}, n > 0
    • P0 = ∪ i ∈ Im {p0i}
    • The elements in P0, PS, and PR are called idle, operation, and resource places, respectively
    • The output transitions of an idle place are called source transitions.
  • T = ∪ i ∈ Im Ti, Ti ≠ ∅, Ti ∩ Tj = ∅ for all i ≠ j.
  • ∀i ∈ Im the subset Ni generated by PSi ∪ {p0i} ∪ Ti is a strongly connected state machine such that every cycle contains p0i
  • ∀r ∈ PR, there exists a unique minimal P-semiflow Ir ∈ IN|P| (here IN = {0, 1, 2, …}) such that {r} = ||Ir|| ∩ PR, P0 ∩ ||Ir|| = ∅, PS ∩ ||Ir|| ≠ ∅ and Ir(r) = 1
  • PS = ∪ r ∈ PR (||Ir||\{r})
  • N is a strongly connected net.
In [11] the following Theorem was proved:
Theorem 2 [11]: Let (N, M0) be a marked S4R net. N is live under M0 iff it satisfies max-cs property.
Consider that r is a resource place, S is a strict minimal siphon and H(r) = Ir\{r} in a S4R net. We can define Th(S) = Σr∈SR H (r) \ S. It can be seen that |Th(S)| ⊆ PS is true. Use Σp∈|Th(S)| hS(p)p to denote Th(S). hS(p) indicates that if the number of tokens in p increases by one, the siphon S loses hS (p) tokens
In [9] the following Lemma was proved:
Lemma 1 [9]: Let (N, M0) be a marked net and S be a siphon of N. S is max-controlled if there exists a P-invariant I such that ∀p ∈ (||I||- ∩ S), maxp● = 1, ||I||+ ⊆ S, and Σp∈ P I (p)M0(p) > Σp∈ S I(p) (maxp● − 1).
This Lemma will be applied below, within the context of Figure 2.

3.1. Siphons in Petri Nets Control

Siphons and traps were formally defined above at the end of the Section Introduction. Elementary and dependent siphons in OPN were proposed in [12]. Later, the terminology was more specified in [16]. In this section siphons and traps are defined in GPN.
With respect to [7] we have the following knowledge:
Definition 9 [7]: Let S ⊆ P be a subset of places of N = (P, T, F, W). P-vector λS is called the characteristic P-vector of S iff ∀p ∈ S, λS(p) = 1; otherwise λS(p) = 0.
Definition 10 [7]: Let S ⊆ P be a subset of places of N = (P, T, F, W). ηS is called the characteristic T-vector of S iff ηTS = λTS .[N] .
Definition 11 [7]: Let N = (P, T, F, W) be a net with |P| = n, which has k siphons S1, …, Sk, m, k ∈ ℕ +. We define [λ]k×n = [λS1|λS2|… |λSk]T and [η]k×m = [λ]k×n.[N]n×m = [ηS1|ηS2||…|ηSk]T is called the characteristic matrix of the siphons in N.
Definition 12 [7]: Let ηSα, ηSβ, …, and ηSγ ({α, β, …, γ} ⊆ {1, 2, ..., k}) be a linearly independent maximal set of the matrix [η]. Then ΠE = {Sα, Sβ, …, Sγ} is called a set of elementary siphons in N.
Definition 13 [7]: S ∉ ΠE is called a strongly dependent siphon if ηs = ΣS ∈ ΠE ai.ηsi, where ai ≥ 0.
Definition 14 [7]: S ∉ ΠE is called a weakly dependent siphon if ∃ non-empty A, B ⸦ ΠE, such that A ∩ B = ∅ and ηS = Σ Si∈A ai.ηSi − ΣSi∈ B ai.ηSi, where ai > 0.
Lemma 2 [7]: The number of elements in any set of elementary siphons in net N equals to rank ([η]).
Verbally said, this important Lemma shows that the rank ([η]) directly determines the number of elementary siphons, However, it simultaneously determines also the number of dependent siphons because Π = ΠE ∪ ΠD.
Theorem 3 [7]: Let NES be the number of elementary siphons in net N = (P, T, F, W). Then NES ≤ min {|P|, |T|}.
Corollary 1 [7]: Let N = ◯i ∈ Im Ni, Ni= (Pi, Ti, Fi, Wi) be an ES3PR. Then, NES ≤ |PS|.
Verbally said, this important Corollary indicates that the maximal number of elementary siphons in an ES3PR net is not greater than the number of its operation places p ∈ PS.

3.2. Procedure of Setting the Supervisor for ES3PR

In [6,7] it can be found the following definition:
Defnition 15 [6,7]: Let S be a strict minimal siphon in an ES3PR net model of a plant (Nµ0, Mµ0) where Nµ0 = ◯i∈{1, …, n} Ni = (P0 ∪ PS ∪ PR, T, Fµ0, Wµ0). Let {α, β, …, γ} ⊆ {1, 2, …, n} such that i ∈ {α, β, …, γ}, |ThS| ∩ p ∈ PSi ≠ ∅ and ∀j ∈ {1, 2, …, n} \ {α, β, …, γ}, |ThS| ∩ p ∈ PSj ≠ ∅. For S, a nonnegative P-vector kS is constructed as follows:
Step 1: ∀p ∈ P0 ∪ PS ∪ PR, kS(p): = 0;
Step 2: ∀p ∈ |Th(S)|, kS(p): = hS(p), where Th(S) = Σp∈|Th(S)| hS(p)p;
Step 3: ∀i ∈ {α, β, …, γ}, let ps ∈ ||ThS|| ∩ PSi be such a place that ∀pt ∈ SP (pu, p0i), pu ∈ ps••, pt ∉ |T h(S)|. Suppose that there are m such places p1s, p2s, …, pms. Assuredly, we have {pis |i = 1, 2, …, m} ⊆ |Th(S)| ∩ PSi. ∀pis let piν ∈ SP (p0i, pis) be such a place that hS(piν) > hS(pw), ∀pw ∈ SP (p0i, pis). ∀px ∈ SP (p0i, pis), kS(px): = hS(piν).
Step 4: ∀Im’ ⊆ {1, 2, …, m}. ∀py ∈ ∩ i∈Im’ SP (p0i, pis), kS(py): = hS(piz), where piz ∈ |Th(S)| ∩ PSi, and ∄p ∈ Th(S) ∩ PSi, s.t. hS(p) > hS(piz).
In general, such procedure makes possible to finalize the supervisor synthesis, especially to set markings of the supervisor monitors VSi, i = 1, 2, …

3.3. Illustrative Example of ES3PR—Siphons and P-Invariants

Let us apply the theory of siphon-based control, introduced above, on the example of ES3PR. Consider the GPN in Figure 1 modelling an AMS. Here, the set of operation places is PS = {p1, p2, p3, p4, p5, p7, p8, p9}, the set of resource places is PR = {p11, p12, p13, p14, p15, p16}, and the set of idle places is P0 = {p6, p10}.
As we can see in Figure 1, there exists one arc with the weight equal to 2—notice the arc from t6 to p13. Consequently, in Figure 1 is GPN. The state space of the net N expressed by the reachability tree (RT) has 308 nodes (including the initial state). Because of such large amount of nodes, the RT cannot be displayed here. The minimal siphons are introduced in Table 1.
As we can see in Table 1, there exist 11 minimal siphons in this GPN model of AMS. They can be enumerated e.g., by the tool GPenSIM [13,14,15] or by another PN tools. Because the traps corresponding to the crossed siphons are marked, crossed siphons may be omitted from the list of siphons. Hence, only 4 of them are strict minimal siphons—S3, S7, S8 and S10. Other 7 siphons are not relevant because they are equal to corresponding traps.
Let us renumber siphons S3, S7, S8 and S10 to siphons S3, S1, S2 and S4, respectively. Consequently, S1 = {p5, p8, p15, p16}, S2 = {p4, p9, p14, p15}, S3 = {p4, p13} and S4 = {p5, p9, p14, p15, p16}. In the form of row P-vectors they are as follows:
S1 = (0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1)
S2 = (0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0)
S3 = (0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0)
S4 = (0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 1)
Corresponding matrix [λ] = [S1T, S2T, S3T, S4T]T can be utilized (analogically to [1] in the case of S3PR paradigm) for finding potential interconnections with the supervisor eliminating the deadlocks. Namely, when we multiply matrix [λ] by [N], being (16 × 11) dimensional incidence matrix of GPN in Figure 1, we obtain the matrix [η] = [λ]. [N] = [η1T, η2T, η3T, η4T]Tconsisting of the following T-vectors
η1 = (0, 0, 0, 0, −1, 1, 0, −1, 1, 0, 0)
η2 = (0, 0, 0, −1, 1, 0, 0, 0, −1, 1, 0)
η3 = (0, 0, 0, −1, 0, 1, 0, 0, 0, 0, 0)
η4 = (0, 0, 0, −1, 0, 1, 0, −1, 0, 1, 0).
Hence, we have λS1 = p5 + p8 + p15 + p16, λS2 = p4 + p9 + p14 + p15, λS3 = p4 + p13, λS4 = p5 + p9 + p14 + p15 + p16 and ηS1 = − t5 + t6 − t8 + t9, ηS2 = − t4 + t5 − t9 + t10, ηS3 = − t4 + t6, and ηS4 = − t4 + t6 − t8 + t10. It is easy to verify that ηS4 = ηS1 + ηS2. However, this set of vectors ηSi , i = 1, …, 4 is not linearly independent, because η4 = η1 + η2, i.e., rank([η]) = 3, and rank([η]) = NES = 3 < rank([N]) = 8. It means that there are three elementary siphons and one strongly dependent siphon. Thus, ΠE = {S1, S2, S3} and ΠD= {S4}.
In Figure 1 we have p01 = p6, p02 = p10, PS1 = {p1, …, p5}, PS2 = {p7, …, p9}, PR1 = {p11, …, p16}, and PR2 = {p14, …, p16}. Unfortunately, the system is deadlocked.
GPN in Figure 1 has eight minimal P-invariants (see Table 2). They may also be computed e.g., by PN tools [13,14,15]. Namely, I1 = p2 + p11, I2 = p1 + p12, I3 = p3 + 2p4 + p13, I4 = p3 + p9 + p14, I5 = p4 + p8 + p15, I6 = p5 + p7 + p16, I7 = p1 + p2 + p3 + p4 + p5 + p6 and I8 = p7 + p8 + p9 + p10. P-invariants in the form of row vectors we can see in Table 2. Negative elements in the vectors ηi in S3PR paradigm (see [1]) mean that directed arcs are emerging from the GPN model and enter through corresponding transition ti (index i depends on the position of the transition in a vector ηj) to the supervisor, while positive elements represent directed arcs in opposite direction, i.e., from the supervisor to GPN model through corresponding transitions. However in case of ES3PR as well as S4PR paradigms the supervisor synthesis is not so simple like in S3PR paradigm. The structural properties presented here will be applied in the continuation of this Example introduced in the Section 4.3.
If we applied these parameters (which are suitable for S3PR) to ES3PR, we would find that the responding supervisor does not comply for such paradigm of the AMS model, because it does not prevent deadlocks.

4. Controllability of Siphons in Generalized Petri Nets

The deadlock prevention policy for GPN consists in the request that all siphons (elementary as well as dependent) must satisfy maximal cs-property. The elementary siphons in the GPN model are properly supervised by means of explicitly adding monitors for them with appropriate initial markings.
Therefore, the controllability of both the elementary siphons and the dependent ones will be analysed.
For the siphon control the facts from the Section 3.1 will be utilized. In [8,9] the following three important definitions are introduced:
Definition 16 [8,9]: Let the net (N, M0) be a marked net and S be a siphon of N. S is said to be max-marked (min-marked) at a marking M iff ∃p ∈ S such that M(p) ≥ maxp• (M(p) ≥ minp•);
Definition 17 [8,9]: Let the net (N, M0) be a marked net and S be a siphon of N. S is said to be max-controlled iff S is max-marked at any reachable marking;
Definition 18 [8,9]: A net (N, M0) is said to be satisfying the max cs-property (controlled-siphon property) iff each minimal siphon of N is max-controlled.
Thus, in our case (see Example in the Section 4,2), we have four strict minimal siphons. All of them have to be max-controlled. Each siphon satisfying the cs-property can be always sufficiently marked. Consequently, it can allow firing a transition once at least.
Namely, in [8] the following Lemma is proved:
Lemma 3 [8,9]: If a net (N, M0) satisfies the max cs-property, it is deadlock-free.
As it was explained above, strict minimal siphons in an ES3PR consist of both elementary siphons and dependent ones. Monitors are explicitly added only to the elementary siphons. However, so that they satisfy max cs-property. The question arises as to how to ensure max-cs property in case of dependent siphons. This is ensured by means of max cs-property of elementary siphons. Namely, this is performed by properly selection of the control depth variables ξSi of its elementary siphons Si. Below, in the next Section 4.1 and 4.2, results relevant not only to the controllability of elementary siphons but also to the controllability of dependent siphons are presented too.

4.1. Controllability of Elementary Siphons

Here, for elementary siphon control especially the knowledge from the Section 3.1 will be utilized. Moreover, the following definition for settings the markings to monitors VSi creating the supervisor will be applied.
Definition 19 [6]: Let S be a strict minimal siphon in an ES3PR model (Nμ0, Mμ0), where N = ◯i ∈ {1.,…, n} Ni = (P0 ∪ PS ∪ PR, T, Fμ0,Wμ0). Let {α, β, ..., γ} ⊆ {1,2, ..., n} such that ∀i ∈ {α, β, ..., γ}, |Th(S)| ∩ PSi ≠ ∅ and ∀j ∈ {1, 2, ..., n} \ {α, β, ..., γ}, |Th(S)| ∩ PSj ≠ ∅. For S, a nonnegative P-vector kS is constructed by 4 steps introduced above in the Definition 15.
Besides, almost every fact introduced below in the Section 4.2 touch both elementary siphons and dependent ones.

4.2. Controllability of Dependent Siphons

In addition to the control of elementary siphons, the control of dependent siphons is also very important.
Lemma 4 [8]: Let (N, M0) be a marked net and S be a siphon of N. S is max-controlled if there exists a P-invariant I such that ∀p ∈ (||I||− ∩ S), maxp• = 1, ||I||+ ⊆ S, and Σp∈P I(p)M0(p) > Σp∈S I(p) (maxp• − 1).
When in an S4R net r is a resource place, S is a strict minimal siphon and H(r) = Ir\{r}. Let Th(S) = Σr∈ SR H(r)\S. We can see that |Th(S)| ⊆ PS is true. Let us use Σp∈|Th(s)| hS(p)p to denote Th(S). With respect to the Theorem 2 in the beginning of the Section 3, hS(p) shows that siphon S loses just hS(p) tokens if the number of tokens in p increases by one.
In [6] the following Theorem (such Theorem is also introduced in [7]) dealing with strongly dependent siphons is introduced:
Theorem 4 [6,7]: Let (N, M0), N = (P, T, F, W), be a marked net and S be a strongly dependent siphon with ηS = Σi∈{1,n} aiηSi, where S1, …, Sn are elementary siphons of S. S is max-controlled if
1. ∀i ∈ {1, 2, …, n}, Ii is a P-invariant of N, ||Ii||+ = Si, and ∀p ∈ Si, Ii(p) = 1;
2. M0(S) > Σi∈{1,n} Σp∈||Ii||− (ai|Ii(p)|M0(p)) + Σp∈ S (maxp• − 1).
In our Example 3.3 of ES3PR the siphon S4 = {p5, p9, p14, p15, p16} is, due to ηS4 = ηS1 + ηS2, a strongly dependent siphon and S1 and S2 are its elementary siphons. Using previous Theorem 4 we can verify the controllability of S4. As to Figure 2, h1 and h2 are P-invariants satisfying the condition 1 of the Theorem 4. Now, we only have to check the condition 2 of the Theorem 4: Σi∈{1,2} Σp∈||hi||− (ai|hi(p)|Mµ1(p)) + Σp∈S4 (maxp•−1). After computing the supervisor consisting of monitors VSi , i = 1, …, 3, we may denote the controlled net as (Nµ1 , Mµ1).

4.3. Illustrative Example of ES3PR—Control

Let us continue in the illustrative example introduced in the Section 3.3. While there rather the GPN model and its structural properties were presented, here the supervisor synthesis will be performed.
In our Example of ES3PR we have P0 = {p6, p10} where p01 = p6, p02 = p10, PS1 = {p1, …, p5}, PS2 = {p7, …, p9}, PR1 = {p11, …, p16}, PR2 = {p14, …, p16}.
Ip15 = p4 + p8 + p15 and Ip16 = p5 + p7 + p16 are minimal P-semiflows associated with resource places p15, p16, respectively. Hence, Th(S1) = (H(p15) + H(p16)) \S1 = ((p4 + p8) + (p5 + p7)) \ {p5, p8} = p4 + p7. Ip14 = p3 + p9 + p14 and Ip15 = p4 + p8 + p15 are minimal P-semiflows associated with resource places p14, p15, respectively. Hence, Th(S2) Σp ∈ P h2(p)Mµ1 (p) = Mµ1 (p14) + Mµ1 (p15) − Mµ1 (VS2) = 2 + 1 − 2 = 1 > Σp ∈ S2 h2(p)(maxp• − 1) = 0. Thus, we can say that S2 is max-controlled by P-invariant h2.
P-invariants hi, i = 1, 2, 3 indicate how the structure of interconnections of monitors VSi (in Figure 2 right) with the net model representing the original uncontrolled plant will look like. Marking of particular monitors VSi needs to be computed as it can be seen below: h1 and h2 are P-invariants satisfying the condition 1 of the above introduced Theorem 4.
To check the condition 2 of the Theorem 4, Σi ∈ (1,n) Σp ∈ ||hi||− (ai|hi(p)|Mµ1(p)) + Σp ∈ S4 (maxp• −1) = Mµ1(p1) + Mµ1(p3) + Mµ1(p7) + Mµ1(VS1) + Mµ1(VS2) + (1−1) = (0 + 0 + 0 + 2 + 2 + 0) = 4. While Mµ1(S4) = Mµ1(p14) + Mµ1(p15) + Mµ1(p16) = 5. Thus, S4 is max-controlled. When we consider VS1, VS2 we see that based on them we have Σi ∈ (1,2)Σp ∈ ||hi||− (ai|hi(p)|Mµ1 (p)) + Σp ∈ S4 (maxp• −1) = Mµ1(p1) + Mµ1(p3) + Mµ1(p7) + Mµ1(VS1) + Mµ1(VS2) + (1−1) = (0 + 0 + 0 + 2 + 2 + 0) = 4. While Mµ1(S4) = Mµ0(S4) = Mµ1(p14) + Mµ1 (p15) + Mµ1 (p16) = 5. Thus, S4 is max-controlled. Because gS = kS + VS is a P-invariant of the resultant net system (Nµ1, Mµ1), a monitor VS is added to the original net model (Nµ0, Mµ0). Thus, Nµ1 = (P0 ∪ PS ∪ PR ∪ VS, T, Fµ1, Wµ1), ∀p ∈ P0 ∪ PS ∪ PR, Mµ1(p) = Mµ0(p). Let hS = Σr∈SR Ir − gS and Nµ1(VS) = Mµ0(S) − ξS (ξS ∈ ℕ). Then S is max-controlled if ξS > Σp ∈ S hS(p) (maxp• − 1).
As we can see in Figure 2, (Nµ0, Mµ0) is an ES3PR being the model of plant net, (Nµ1, Mµ1) is its liveness-enforcing supervisor. Monitors are added to control elementary siphons S1–S3 only. They enforce liveness for (Nµ0, Mµ0),
The number NES of elementary siphons is bounded—see Theorem 3 in the Section 3.1 (it is smaller than minimum of the pair the place count and the transition count). Therefore, dependent siphons have to be implicitly controlled by fittingly setting the initial number of tokens in monitors. Thus, we can get a structurally simple liveness-enforcing PN supervisor for an ES3PR paradigm of the plant net model.
In Figure 1 we have PS1 = {p1, …, p5}, PS2 = {p7, …, p9}. For S1 = {p5, p8, p15, p16} we have Th(S1) = p4 + p7. With respect to the procedure described in the Section 3.1: For PS1 we have p1s = p4, p1ν = p4, p1z = p4. For PS2 we have p2s = p2ν = p2z = 7. Finally, kS1 (p1) = kS1 (p3) = kS1 (p4) = kS1 (p7) = 1. ∀p ∈ PS \ {p1, p3, p4, p7}, kS1 (p) = 0. Naturally, we obtain kS1 (p6) = kS1(p10) = kS1 (p11) = kS1(p12) = kS1(p13) = kS1(p14) = kS1 (p15) = kS1 (p16) = 0 since p6 and p10 are idle places and p11, …, p16 are resource places. Let KS = {p | kS (p) ≠ 0, p ∉ |Th(S)|}. In Figure 1 we have KS1 = {p1, p3}.
In Figure 2 we have the following results:
1. g1 = p1 + p3 + p4 + p7 + VS1 and l1 = Ip15 + Ip16 = p4 + p8 + p15 + p5 + p7 + p16 are P-semiflows. Let h1 = l1 − g1. h1 = p5 + p8 + p15 + p16 − p1 − p3 − VS1 is a P-invariant. When we notice that ||h1||− ∩ S1 = ∅, ||h1||+ = S1, and Σp ∈ P h1(p)Mµ1 (p) = Mµ1 (p15) + Mµ1 (p16) − Mµ1 (VS1) = 1 + 2 − 2 = 1 > Σp ∈ S1 h1(p)(maxp• − 1) = 0 we can say that S1 is max-controlled by P-invariant h1.
2. g2 = p1 + p3 + p7 + p8 + VS2 and l2 = Ip14 + Ip15 = p3 + p9 + p14 + p4 + p8 + p15 are P-semiflows of the controlled net. Let h2 = l2 − g2. h2 = p4 + p9 + p14 + p15 − p1 − p7 − VS2 is hence a P-invariant. When we notice that ||h2||− ∩ S2 = ∅, ||h2||+ = S2, and Σp ∈ P h2(p) Mµ1(p) == Mµ1 (p14) + Mµ1 (p15) − Mµ1 (VS1) = 2 + 1 − 2 = 1 > Σp ∈ S2 h1(p)(maxp• − 1) = 0, we can say that S2 is max-controlled by P-invariant h2.
3. g3 = p1 + p3 + VS3 and l3 = Ip13 = p3 + p4 + p13 are P-semiflows. Let h3 = l3 − g3. h3 = p4 + p13 − p1 − VS3 is a P-invariant. When we notice that ||h3||− ∩ S3 = ∅, ||h3||+ = S3 and Σp ∈ P h3(p)Mµ1 (p) = Mµ1(p16) − Mµ1 (VS3) = 2 − 1 = 1 > Σp ∈ S3 h3(p)(maxp• − 1) = 0 which implies that S3 is max-controlled by P-invariant h3.
The supervised ES3PR is deadlock free. Left the original GPN model of plant is displayed, while right its supervisor is placed. Both pictures are shown separately to avoid complicated and non-transparent interconnections between both the plant and the supervisor. Namely, their cooperation is brighter when one observes insinuated transitions of the supervisor and corresponding real ones in the plant.
As we can see in Figure 2, 0 < ξS1 < 3, 0 < ξS2 < 3, 0 < ξS3 < 2, and ξS1 + ξS2 > 1. Let ξS1 = ξS2 = ξS3 = 1. Hence, we have Mµ1(VS1) = 2, Mµ1 (VS2) = 2, and Mµ1 (VS3) = 1. It is easy to verify that all strict minimal siphons are max-controlled—see results 1–3 introduced above in this Section 3.5. Consequently, the net system in Figure 2 is live, i.e., deadlock free.

5. Conclusions

Liveness (deadlock-freeness) is a very important property of PN from behavioural point of view. Siphons, traps and invariants are structural objects of PN. Especially siphons are closely related to the PN liveness. There are many deadlock prevention control policies for AMS (alternatively named also flexible manufacturing systems—FMS) based on siphons. Namely, AMS are frequently modelled by PN possessing siphons. There are many paradigms of PN models of AMS like S3PR, ES3PR, S4R, GS3PR and many others.
To prevent deadlocks in AMS liveness-enforcing supervisors are used. Most of existing methods of their design are based on adding monitors (control places) for siphons. Monitors are based on exact controllability conditions for siphons. In such a way a liveness-enforcing supervisor with permissive behaviour is obtained. However, as we have found, conditions of max controllability of siphons, are overly restrictive and in general only sufficient.
The subject of this paper was to deal with the problem of deadlocks in ES3PR paradigm of GPN models of AMS. This paper may be seen as a free continuation of the author’s paper [1], where similar problem was resolved for the S3PR paradigm of ordinary PN (OPN) models of AMS. A difference between OPN and GPN consists in the weights of directed arcs. While in OPN weights of directed arcs are only 1, in GPN may be greater than 1, i.e., there may occur multiplex arcs. Therefore, the approach used in [1] to deal with deadlocks in S3PR is insufficient for dealing with deadlocks in ES3PR and it was necessary to find another one.
An empty siphon in an OPN can cause some transitions to be disabled forever. Therefore, it is necessary to prevent emptying siphons. Such a case in GPN is much more complicated. In consequence of arcs with greater weights, an insufficiently marked siphon can lead to the occurrence of other deadlocks. Therefore, setting the marking of monitors VSi (which create the supervisor), is very important as well as the selection of the control depth variables ξSi of elementary siphons Si.
ES3PN models of APN can be understood to be a subset of S4PR models, which are even much more complicated.
The approach presented here is based on verification of the max cs-property of a net (N, M0). When such net N satisfies this property, we can say that it is deadlock-free. In case of GPN, a marked S4PR net is live if it satisfies the cs-property. This means that the cs-property is a sufficient but not necessary condition (unlike ES3PR) for the liveness of an S4R.
It was presented here, that the deadlock prevention in GPN models of AMS is much more complicated as that in OPN models of AMS. Simultaneously, the deadlock prevention of ES3PR (as a subclass of GPN models of AMS) was performed and illustrated on the example.
More complex analysis of the deadlock prevention problem depends on specific paradigms of GPN. Namely, there are many paradigms of GPN with specific properties and corresponding specific polices how to deal with deadlocks in them. For example, the specific paradigm GS3PR (generalised systems of simple sequential processes with resources) was analysed in [22] as concerns the problem of the deadlock prevention.
In future it will be necessary to concern in more and more complicated structures of AMS modelled by GPN.
A serious review of siphon-based approaches to control GPN are presented in [21]. An application on a specific paradigm GS3PR was presented in [22].
In this paper was shown that prevention of deadlocks in AMS with resources ensures a correct allocation of resources and thereby ensure the continuous and fluent operation of AMS. Thus, by means of controlling siphons of their PN-based models, the fluent and continuous operation of constituents in industrial production can be sustainable what is very important in social practice.

Acknowledgments

This work was partially supported by the Slovak Grant Agency for Science VEGA under Grant No. 2/0020/21.

References

  1. Čapkovič, F. Petri Net Based S3PR Models of Automated Manufacturing Systems with Resources and Their Deadlock Prevention. Acta Polytechnica Hungarica, Vol. 20, No. 6, 2023, pp. 79-96. [CrossRef]
  2. Čapkovič, F. Modeling and Control of Discrete-Event Systems with Partial Non-Deteminism Using Petri Nets. Acta Polytechnica Hungarica, Vol. 17, No. 4, 2020, pp.
  3. Čapkovič, F. Control of Deadlocked Discrete-Event Systems Using Petri Nets. Acta Polytechnica Hungarica, Vol. 19, No. 2, 2022, pp.
  4. Čapkovič, F. Modeling and Control of Resource Allocation Systems within Discrete-Event Systems by Means of Petri Nets—Part 1: Invariants, Siphons and Traps in Deadlock Avoidance. Computing and Informatics, Vol. 40, No. 3, 2021, pp. 648-689.
  5. Li, Z.W.; Zhou, M.C. Deadlock Resolution in Automated Manufacturing Systems. A Novel Petri Net Approach. London, Springer Press, 2009.
  6. Li, Z.W.; Uzam, M.; Zhou, M.C.: Deadlock Control of Concurrent Manufacturing Process Sharing Finite Resources. The International Journal of Advanced Manufacturing Technology, Vol. 38, 2008, pp. 787-800. [CrossRef]
  7. Li, Z.W.; Zhang, J.; Zhao, M. Liveness-Enforcing Supervisor Design for a Class of Generalized Petri Net Models of Flexible Manufacturing Systems. IET Control Theory & Applications, Vol. 1, No. 4, 2007, pp. 955–967. [CrossRef]
  8. Barkaoui, K.; Abdallah, I.B. A Deadlock Prevention Method for a Class of FMS. In Proceedings of IEEE International Conference on Systems, Man, and Cybernetics, Vancouver, Canada, 1995, pp. 4119–4124.
  9. Barkaoui, K.; Pradat-Peyre, J.F. On Liveness and Controlled Siphons in Petri Nets. In: Proceedings of 17th International Conference on Application and Theory of Petri Nets, Osaka, Japan, June 24–28, 1996, LNCS, Vol. 1091. New York, Springer, pp. 57–72.
  10. Tricas, F.; García-Vallès, F.; Colom, J.M.; Ezpeleta, J. A Partial Approach to the Problem of Deadlocks in Processes with Resources, Technical Report, GISI-RR-97–05, University of Zaragoza, Spain, 1997.
  11. Abdallah, I.B. El Maraghy, H.A. Deadlock Prevention and Avoidance in FMS: A Petri Net Based Approach. The International Journal of Advanced Manufacturing Technology, Vol. 14, 1998, pp. 704–715.
  12. Li, Z.W.; Zhou, M.C. Elementary Siphons of Petri Nets and Their Application to Deadlock Prevention in Flexible Manufacturing Systems. IEEE Transactions on Systems, Man and Cybernetics—Part A: Systems and Humans, Vol. 34, No. 1, 2004, pp. 38–51.
  13. Davidrajuh, R. GPenSIM, General Purpose Petri Net Simulator for MATLAB Platform. Available: http://www.davidrajuh.
  14. Davidrajuh, R. General Purpose Petri Net Simulator GPenSIM v. 9.0, 2014, Available: http://www.davidrajuh.net/gpensim/v9/GPenSIM_v9_User_Manual.pdf.
  15. . Davidrajuh, R. Modeling Discrete-Event Systems with GPenSIM. Springer, 2018. ISBN-13: 978-3-319-73101-8. Available: https://link.springer.com/book/10.1007/978-3-319-73102-5.
  16. Li, Z.W.; Zhou, M.C. Clarifications on the Definitions of Elementary Siphons of Petri Nets. IEEE Transactions on Systems, Man and Cybernetics Cybernetics—Part A: Systems and Humans, Vol. 36, No. 6, 2006, pp. 1227–1229.
  17. Petri, C.A. Communication with Automata. Ph.D. Thesis. Technical University of Darmstadt, 1962, 128 pages (in German).
  18. Peterson, J.L. Petri Net Theory and the Modeling of Systems. Englewood Cliffs, NJ: Prentice-Hall, 1981.
  19. Murata, T. Petri Nets: Properties, Analysis and Applications, Proceedings of the IEEE, Vol. 77, No. 4, 1989, pp. 541-580.
  20. Desel, J.; Reisig, W. Place/Transition Petri Nets. In: W. Reisig, G. Rozenberg (Eds.): Advances of Petri Nets, Lecture Notes in Computer Science, Vol. 1491, Springer, Heidelberg, 1998, pp. 122-173.
  21. Hou,Y. F.; Barkaoui, K. Deadlock Analysis and Control Based on Petri Nets: A Siphon Approach Review. Advances in Mechanical Engineering, Vol. 9, No. 5, 2017, pp. 1- 30. [CrossRef]
  22. Liu, G.Y.; Barkaoui, K. Necessary and Sufficient Liveness Condition of GS3PR Petri Nets. International Journal of Systems Science, Vol. 46, No. 7, 2015, pp. 1147-1160.
Preprints 113266 g001
Figure 1. The GPN model of AMS, where W(t6,p13) = 2.
Figure 1. The GPN model of AMS, where W(t6,p13) = 2.
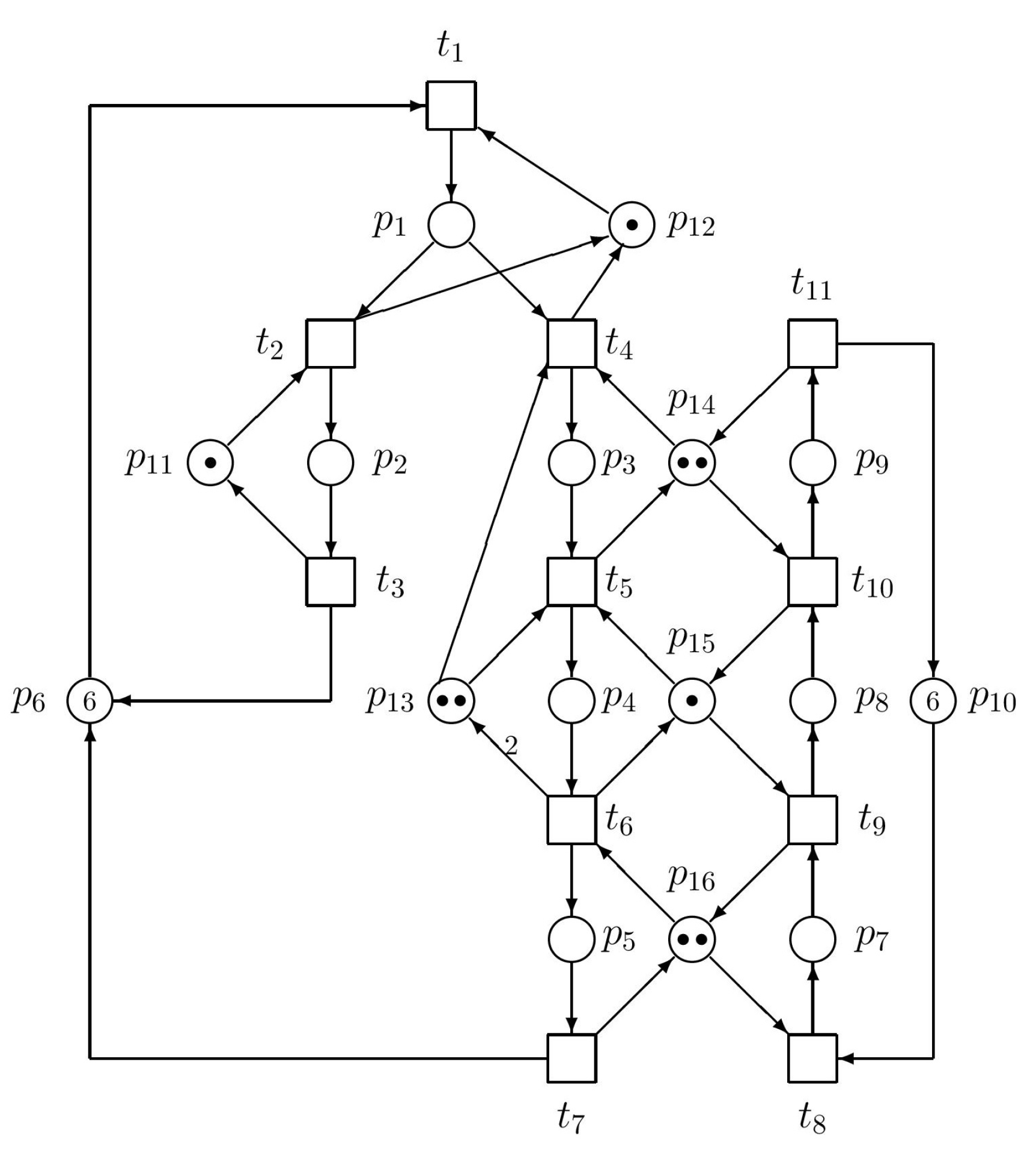
Preprints 113266 g001
Preprints 113266 g002
Figure 2. The ES3PR paradigm of the original GPN model of AMS (left) and the supervisor (right) consisting of three monitors.
Figure 2. The ES3PR paradigm of the original GPN model of AMS (left) and the supervisor (right) consisting of three monitors.
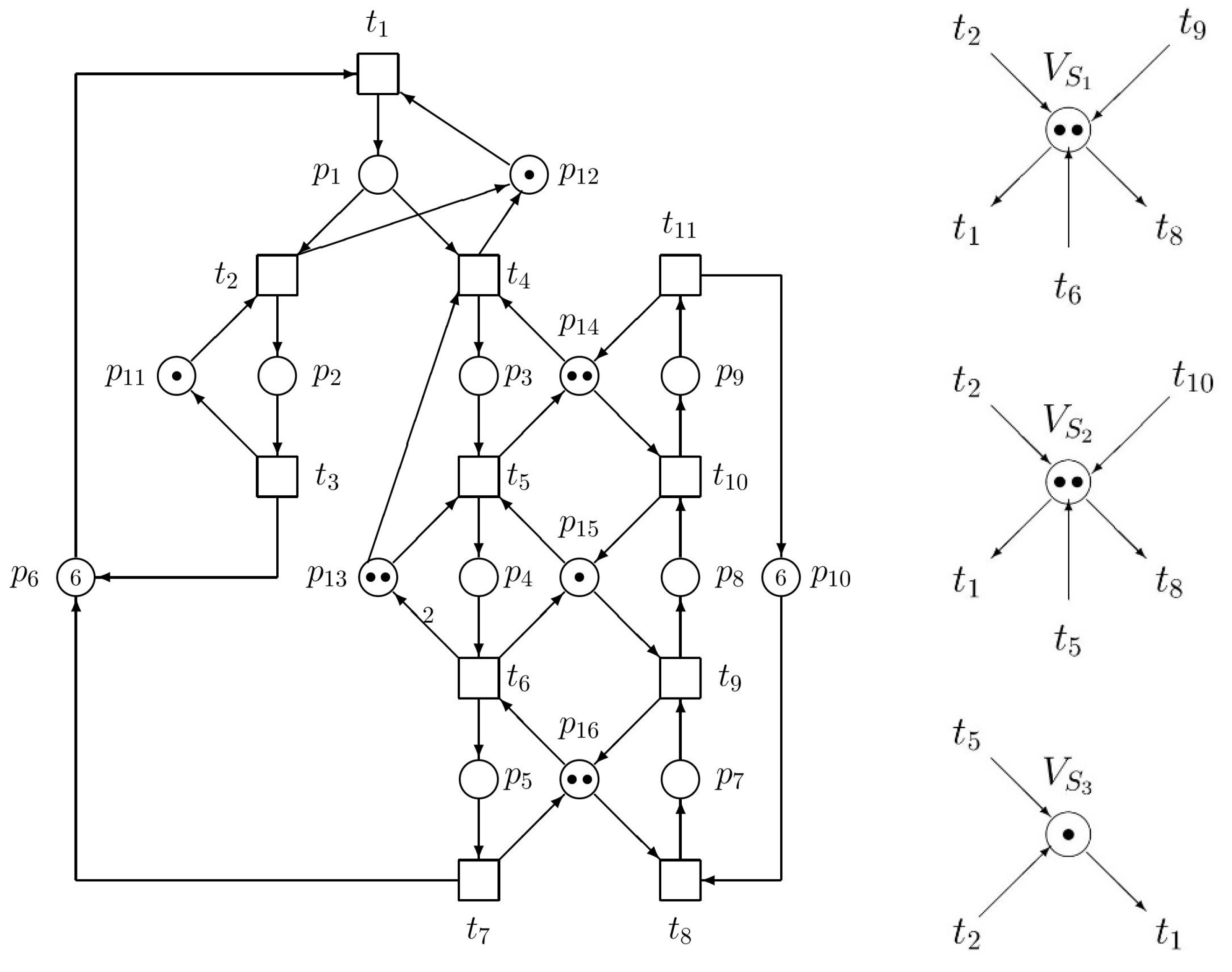
Preprints 113266 g002
Table 1. Siphons and traps of the PN model.
Table 1. Siphons and traps of the PN model.
No. Siphons Traps Notice
1. S1 = {p1, p12}
 Tr1 = {p1, p12} Eliminate S1, because
S1 = Tr1
2. S2 = {p2, p11} Tr2 = {p2, p11} Eliminate S2 because
S2 = Tr2
3. S3 = {p4, p13} Tr3 = {p3, p4, p13}
4. S4 = {p5, p7, p16} Tr4 = {p5, p7, p16} Eliminate S4 because
S4 = Tr4
5. S5 = {p4, p8, p15} Tr5 = {p4, p8, p15} Eliminate S5 because
S5 = Tr5
6. S6 = {p3, p9, p14} Tr6 = {p3, p9, p14} Eliminate S6 because
S6 = Tr6
7. S7 = {p5, p8, p15, p16} Tr7 = {p4, p7, p15, p16}
8. S8 = {p4, p9, p14, p15} Tr8 = {p3, p8, p14, p15}
9. S9 = {p7, p8, p9, p10} Tr9 = {p7, p8, p9, p10} Eliminate S9 because
S9 = Tr9
10. S10 = {p5, p9, p14, p15, p16} Tr10 = {p3, p7, p14, p15, p16}
11. S11 = {p1, p2, p3, p4, p5, p6} Tr11 = {p1, p2, p3, p4, p5, p6} Eliminate S11 because
S11 = Tr11
Table 2. P-invariants in the form of row vectors.
Table 2. P-invariants in the form of row vectors.
p1 p2 p3 p4 p5 p6 p7 p8 p9 p10 p11 p12 p13 p14 p15 p16
I1 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0
I2 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0
I3 0 0 1 2 0 0 0 0 0 0 0 0 1 0 0 0
I4 0 0 1 0 0 0 0 0 1 0 0 0 0 1 0 0
I5 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0
I6 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 1
I7 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0
I8 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated