Preprint
Article
Questioning the Lorentz Factor in Special Relativity: Introducing the Yuyunrui Factor
Altmetrics
Downloads
78
Views
115
Comments
0
Submitted:
26 July 2024
Posted:
26 July 2024
You are already at the latest version
Alerts
Abstract
Newton's kinetic energy equation delineates the laws of motion for objects travelling at speeds much less than the speed of light, an equation extensively validated at these lower velocities. Any new, more complete formulation of kinetic energy must approximate Newton's kinetic energy equation under these conditions. Einstein's special relativity, utilizing the Lorentz factor, introduces a new perspective on spacetime, adhering to the requirement that the Newtonian kinetic energy equation serves as an approximation at low velocities. In this paper, we identify all factor expressions satisfying the condition that their approximate solutions at low velocities align with Newton's kinetic energy equation. We introduce the Yuyunrui factor, incorporating two real number hyperparameters, $\alpha$ and $\beta$, encompassing all potentially correct factors, with the Lorentz factor as a specific instance where $(\alpha=0$, $\beta=1)$. We classify all potentially correct $(\alpha, \beta)$ combinations into six categories based on their distinct scaling effects and present the corresponding scaling effects. The combinations of $(\alpha, \beta)$ values applicable in the real world are necessarily included within these candidates, with the precise values requiring rigorous experimental validation. This work aims to refine our understanding of special relativity beyond the Lorentz factor.
Keywords:
Subject: Physical Sciences - Particle and Field Physics
1. Introduction
Newton’s classical kinetic energy equation[1] describes the laws of motion for objects moving at speeds much less than the speed of light. This discovery is one of the most significant achievements in our quest to understand the natural world’s motion. As our understanding evolves from basic to more complex phenomena, we must continually refine and expand upon established laws to accommodate new physical insights. Newton’s kinetic energy equation, although thoroughly verified for low-velocity conditions, also requires adjustments to address their limitations when approaching higher velocities.
Since Newton’s kinetic energy equation has been validated extensively at speeds much less than the speed of light, they serve as a crucial foundation for analyzing motion in this regime. Consequently, any new, more comprehensive kinetic energy equations must approximate Newton’s kinetic energy equation at low velocities. This prerequisite ensures continuity and accuracy in our theoretical framework.
Einstein’s special relativity[2], underpinned by the Lorentz factor[3], introduces a novel perspective on space and time, encapsulated in the concept of time dilation[4,5]. This theory represents another monumental step in understanding the laws of motion, fulfilling the requirement that Newton’s kinetic energy equation is an approximate solution at low velocities. However, the Lorentz factor has been widely accepted without rigorous empirical verification, which raises questions about its foundational assumptions.
This paper aims to critically examine the Lorentz factor. We contend that its acceptance has been based on assumptions rather than rigorous experimental validation. Specifically, the assumption that dimensions perpendicular to the direction of motion remain unchanged lacks factual support. This premise, not grounded in objective verification, calls into question the accuracy of the time dilation factor derived from the Lorentz factor.
While we challenge the Lorentz factor, we do not dispute the classical mass-energy equation[2,6] or the observable phenomenon of time dilation, which has been confirmed through numerous experiments[7]. Our focus is on the plausibility of the Lorentz factor and exploring alternative factors that could provide a more accurate description of motion.
To address these concerns, we have conducted research independent of the Lorentz factor’s assumptions. We identified all factor expressions satisfying the condition that their approximate solutions at low velocities align with Newton’s kinetic energy equation. Based on this, we propose the Yuyunrui factor, incorporating two hyperparameters, and , which encompass all potential correct factors. The Lorentz factor is a special case of the Yuyunrui factor when , . We classify the combinations of into six broad categories based on their scaling effects and detail these effects. Rigorous experimental validation is required to identify the correct combinations of applicable in the real world.
In summary, while acknowledging the profound impact of Newton’s kinetic energy equation and Einstein’s special relativity on our understanding of the physical world, we must address the unresolved issues surrounding the Lorentz factor. By refining our theoretical models and subjecting new hypotheses to rigorous empirical testing, we can advance our understanding of the true laws governing motion in nature.
2. Method
2.1. Premise of Analysis: The Speed of Light Invariance Hypothesis
The foundation of our analysis rests on a well-verified premise in modern physics: the invariance of the speed of light. This principle, which asserts that the speed of light in a vacuum remains constant and independent of the motion of the light source or observer[3,8,9], has been confirmed by numerous experiments and is a cornerstone of Einstein’s theory of special relativity.
Based on the Pythagorean Theorem, the relationship between t and as shown in Figure 1 can be expressed by the following equation:
According to Equation (1), for , the following relational equation is satisfied:
where the angle is defined as the angle between the direction of light propagation as observed by the observer M within the moving frame and the velocity of the object. This angle ranges from 0 to and is not affected by the scaling effect due to changes in the object’s speed, as the object’s size remains constant to the observer M in the moving frame. When , the direction of light propagation is the same as the direction of the object’s motion. Conversely, when , the direction of light propagation is entirely opposite to the direction of the object’s motion. It is important to note that the angles and represent the same physical situation, both corresponding to the angle .
We define the unidirectional time scaling factor between and t as , where:
The unidirectional time scaling factor characterizes the relative passage of time for different directions within a moving object. Notably, signifies complete stasis of time in the direction characterized by angle . Values of correspond to a slowdown in the passage of time, while indicates no relative change. Conversely, suggests an acceleration of time in that specific direction.
To understand the time dilation effect, it is essential to define a clock as a timekeeping instrument based on periodic reciprocating motion. This principle underlies all clocks, whether mechanical, electronic, or atomic. In a mechanical clock, the periodic motion is provided by a pendulum or balance wheel, which drives the clock’s gears and hands. An electronic clock relies on the oscillation of a quartz crystal, which vibrates at a precise frequency when an electric current is applied, converting these vibrations into electrical impulses for timekeeping. In an atomic clock[10,11], vibrations of atoms like cesium or rubidium, when exposed to an electromagnetic field, oscillate at a highly stable frequency, making atomic clocks the most accurate.
Applying this principle to the analysis of time dilation, we introduce the Einstein Light Clock[2,4], which is a theoretical apparatus for measuring time intervals based on the behavior of light. It consists of two mirrors separated by a fixed distance h, which is the distance light travels from one mirror to the other in a light clock. A beam of light travels from one mirror to the other and back again, completing a round trip. Each round trip constitutes one "tick" of the clock. This setup allows time to be measured based on the number of ticks the light completes between the mirrors. To analyze the relationship between the time dilation effect and the angle, we consider placing the light clock at a angle to the direction of motion, as shown in Figure 2. Here, ranges from 0 to . When light propagates from one mirror to the other at an angle , it returns from the other mirror to the starting mirror at an angle . This placement allows for examining how the effect of time dilation on the light clocks varies with .
When the light clock in the moving frame is positioned at an angle to its direction of velocity, the time interval for each tick of the light clock in the moving frame can be measured in two different frames of reference. The time interval measured in the rest frame is denoted as , and the time interval measured in the moving frame is denoted as . These intervals can be expressed respectively as follows:
The time scaling factor of the light clock , which represents the ratio of the time intervals measured by the clocks in the moving frame and the rest frame, is defined as follows:
The time scaling factor of the light clock is related to both the velocity v of the moving object and the angle . The correlation with the velocity v reflects the time dilation effect on moving objects as described by special relativity. Specifically, the time dilation’s effect on a light clock depends on the angle , demonstrating how the effect of time dilation on the light clock is distributed in three dimensions within a moving frame.
When the time scaling factor of the light clock , the time of the light clock in that direction is completely stationary. When , the time of the light clock in that direction slows down. When , the time of the light clock in that direction is no relative change in time compared to the rest frame.
A noteworthy aspect of the light clock’s operation arises when and . In this scenario, light travelling along direction within the clock can propagate from one mirror to the other. However, the return path along becomes impossible. This effectively traps the light, preventing it from completing a full round trip (tick) within the clock. Consequently, the displayed time freezes, appearing to the rest frame observer as a completely static clock ().
It’s crucial to emphasize that this time stasis on the light clock does not contradict the ability of photons to propagate along when within the moving frame. The halted clock reading signifies a standstill in the timekeeping mechanism, not the cessation of light propagation in all directions. Notably, in directions corresponding to , light propagation can be remains feasible.
According to Equation (6), the time dilation’s effect varies when the light clock is placed at different angles along the direction of motion within the moving frame. To eliminate the variation in time dilation’s effect caused by different angles in three-dimensional space inside the moving frame, and to ensure a comprehensive consideration of the time scaling factor of the light clock , we introduce a consensus time scaling factor of the light clock. This factor is determined by placing a light clock in each direction indicated by the uniformly distributed arrows from the origin to the external three-dimensional space, as illustrated in Figure 3. The mean value of the time scaling factors from all these light clocks is then taken to establish the consensus time scaling factor of the light clock, denoted as . This consensus time scaling factor of the light clock satisfies the following expression:
By substituting formula (6) into formula (7), we obtain the expression for the consensus time scaling factor of the light clock as follows:
where
The consensus time scaling factor of the light clock aligns with the principles of atomic clocks[10,11], which depend on the isotropic absorption and emission of photons during atomic vibrations. These vibrations occur uniformly in three dimensions, ensuring consistent and reliable timekeeping. Thus, applying a similar comprehensive consideration to the time scaling factor of the light clock in the three-dimensional space of a moving frame ensures more accurate and uniform time measurement, as supported by the three-dimensional isotropic properties fundamental to atomic clocks.
2.2. Compatibility of New Kinetic energy Formulae with Newton’s kinetic energy equation at Low Velocities
Given that Newton’s kinetic energy equation[1] has been extensively validated at velocities much less than the speed of light and serves as a crucial foundation for analyzing the motion of objects at such velocities, any accurate and comprehensive kinetic energy equation proposed to replace Newton’s kinetic energy equation must fulfil the condition that their approximate solutions at low velocities align with Newton’s kinetic energy equation[12]. This ensures continuity and consistency in the understanding of motion laws across different velocity regimes.
According to Einstein’s derivation based on the Lorentz factor in special relativity [4], the time scaling factor between the running time of the light clock within the moving frame and that of the light clock within the rest frame, denoted by , satisfies the following expression:
where is the Lorentz factor.
In special relativity, the total energy (E) of an object with mass m moving with velocity v is given by:
The rest energy () of the object (the energy when it is at rest) is:
The relativistic kinetic energy () is the total energy minus the rest energy:
Newton’s classical kinetic energy formula () is:
This formula is derived under the assumption that velocities are much smaller than the speed of light (c), which means:
The formula (15) confirms that the relativistic kinetic energy reduces to the Newtonian form at low velocities, thereby ensuring consistency between the two theories. Consequently, any valid consensus time scaling factor of the light clock must satisfy this precondition to uphold Newton’s kinetic energy equation at low velocities, as stated in the flowing equation (16). The formula (15) must still hold after replacing with :
3. Disscussion
We classify all the combinations of and values that satisfy the constraints shown in Eqs. (17), (18), (19), and (20) into the following six categories based on different scaling effects. The details are shown in Table 1.
3.1. Yuyunrui Factor
The Lorentz factor, commonly used in the theory of relativity, is derived under the assumption that dimensions perpendicular to the direction of velocity remain constant. However, this assumption lacks rigorous experimental verification, thus providing a solid basis for reevaluation. Moreover, the Lorentz factor might obscure the discovery of more accurate factors in real-world applications.
To address these potential shortcomings, we propose replacing the Lorentz factor with the Yuyunrui factor. The Yuyunrui factor does not presuppose invariance in dimensions perpendicular to the direction of velocity and incorporates two hyper-parameters, and , as shown in Table . Table 1. This factor encompasses all possible correct factors, facilitating the identification of the true factors through future exploration.
The Yuyunrui factor, denoted by , is defined as:
Under the new Yuyunrui factor, the expressions for relativistic mass and relativistic kinetic energy () of an object moving at velocity v are reformulated as follows:
The Lorentz factor is a special case of the Yuyunrui factor, specifically when and , and is represented as follows:
3.2. Analysis of the Unidirectional Time Scaling Factor in Three Dimensions at Light Speed
In the framework of special relativity, an object moving at the speed of light experiences time as if it has stopped, from an external observer’s perspective[13]. However, this framework lacks a detailed analysis of the numerical distribution of the time dilation effect in three-dimensional space. Without this analysis, our understanding of time dilation at light speed remains incomplete.
To address this issue, we explore the relationship between and in three-dimensional space. We know that the unidirectional time scaling factor within a moving object in three-dimensional space is crucially related to , the angle between the direction of light propagation and the object’s velocity. Analyzing the distribution of helps us understand the nuances of the time dilation effect.
Consider a spaceship traveling at the speed of light. Objects inside move at an angle to the spaceship’s velocity. An observer in the rest frame will perceive these objects according to the distribution of presented in Table 2. This table demonstrates how objects appear to an observer when moving inside the spaceship at various angles relative to its velocity.
Analyzing this scenario provides a deeper understanding of how the unidirectional time scaling factor affects objects moving at different angles relative to the spaceship’s motion. This analysis elucidates the time dilation effect in three-dimensional space, offering insights into the specific numerical distribution of the time dilation factor at light speed. Understanding this relationship is crucial, as it addresses the lack of detailed analysis of the time dilation factor’s distribution within the framework of special relativity, thereby enhancing our comprehension of relativistic effects on moving objects.
Data from Table 2 show that there exists non-zero time scaling factor for all six categories of combinations when the object’s speed reaches the speed of light (c). This implies that for a light-speed object, any internal energy travelling in a direction with non-zero might detach from the main body, leading to potential energy loss. This observation challenges the traditional notion that photons experience no passage of time. Consequently, the concept of time for objects at light speed may require further investigation. Additionally, the possibility of photon energy weakening over time merits exploration. Specifically, in the absence of external energy input, a photon’s internal energy travelling in a direction with non-zero might exhibit a gradual decrease in the photon’s overall energy.
This analysis underscores the potential need to revisit our understanding of time passage and energy dissipation for objects reaching the speed of light. Further theoretical and experimental investigations are crucial to validate these findings and determine the true nature of time and energy at relativistic speeds.
3.3. visualization of the scaling and time dilation effect for six categories
In order to intuitively visualize the scaling and time dilation effect corresponding to different combinations of and in the six categories, we select one combination of and values from each category for plotting. Specifically, we choose the following combinations:
- Category I:
- Category II: , we select
- Category III: , we choose
- Category IV: , we select
- Category V: , we choose
- Category VI: , we select
The scaling effects corresponding to these selected combinations of and values are illustrated in Figure 4. The key indices reflecting the dilation effect of these combinations, and , are distributed in three-dimensional space at different velocities as shown in Figure 5 and Figure 6, respectively.
A visualisation of six representative combinations of the consensus time scaling factor of the light clock is shown in Figure 7. This figure illustrates that these different combinations follow a similar pattern, all decreasing as the object’s speed of motion increases, and approaching zero when the speed reaches that of light. This demonstrates that, even if the Lorentz factor is not the truly correct factor in nature, it provides a close approximation to the true factor.
Test whether the relativistic kinetic energy derived using the Yuyunrui factor satisfies the key criterion of approximate equivalence to Newton’s classical kinetic energy formulae at velocities much less than the speed of light, denoted as , in six representatives combinations visualised in Figure 8. The value of is approximately equal to 1/2 when the object is moving at a speed much less than the speed of light, and exactly 1/2 when the object’s speed is zero.
4. Conclusions
We have identified factorial expressions that satisfy the condition that Newton’s kinetic energy formulas apply only at velocities much less than the speed of light, under the assumption that the speed of light is constant and considering time dilation and scaling effect in real three-dimensional space in the moving frame. Based on this, we propose the Yuyunrui factor, which includes two hyperparameters, α and β, and encompasses all possible correct factors. The Lorentz factor is a special case of the Yuyunrui factor when α = 0 and β = 1. We classified all numerical combinations of α and β that meet the constraints into six major categories based on different scaling effects, demonstrating the specific scaling effects under each combination. The numerical combinations of α and β that are possibly applicable in the real world are included, but specific values must still be validated through rigorous experimental verification.
References
- Newton, I. Philosophiae naturalis principia mathematica; Vol. 1, G. Brookman, 1833.
- Einstein, A. On the electrodynamics of moving bodies 1905.
- Lorentz, H.A. Electromagnetic phenomena in a system moving with any velocity smaller than that of light. In Collected Papers: Volume V; Springer, 1937; pp. 172–197.
- Pauli, W. Theory of relativity; Courier Corporation, 2013.
- Ives, H.E.; Stilwell, G.R. An experimental study of the rate of a moving atomic clock. JOSA 1938, 28, 215–226. [Google Scholar] [CrossRef]
- Eddington, S.A.S. The nature of the physical world; University of Michigan Press, 1968.
- Bailey, J.; Borer, K.; Combley, F.; Drumm, H.; Krienen, F.; Lange, F.; Picasso, E.; Von Ruden, W.; Farley, F.; Field, J.; et al. Measurements of relativistic time dilatation for positive and negative muons in a circular orbit. Nature 1977, 268, 301–305. [Google Scholar] [CrossRef]
- Shankland, R.S. Michelson-morley experiment. American Journal of Physics 1964, 32, 16–35. [Google Scholar] [CrossRef]
- Michelson, A.A.; Morley, E.W. On the relative motion of the Earth and the luminiferous ether. American journal of science 1887, 3, 333–345. [Google Scholar] [CrossRef]
- Essen, L.; Parry, J.V. An atomic standard of frequency and time interval: a caesium resonator. Nature 1955, 176, 280–282. [Google Scholar] [CrossRef]
- Ramsey, N.F. History of atomic clocks. Journal of research of the National Bureau of Standards 1983, 88, 301. [Google Scholar] [CrossRef] [PubMed]
- Tymms, V. Newtonian mechanics for undergraduates; World Scientific Publishing Company, 2015.
- Weinberg, S. The quantum theory of fields; Vol. 2, Cambridge university press, 1995.
Figure 1.
The red dotted lines depict the dimensions of the object as observed in the moving frame M, where h represents the dimension perpendicular to the direction of motion and w represents the dimension along the direction of motion. The blue solid lines illustrate the shape of the object as observed in the rest frame R under the scaling effects of special relativity. Here, is the dimensional scaling factor in the direction of motion, and is the scaling factor perpendicular to the direction of motion, with and under the Lorentz factor. The angle is between the light ray observed by observer M and the velocity of motion, ranging from , and it is not affected by velocity-induced scaling, as the object’s size remains constant to the observer in the moving frame. Points and D represent the same location on the moving object. Point is where the light ray reaches as observed by observer M in the moving frame along the , and point D is where the light ray reaches as observed by observer R in the rest frame under the scaling effect. The variable t denotes the time for light to travel from O to D as recorded by the clock R in the rest frame, and is the time for light to travel from to as recorded by the clock M in the moving frame.
Figure 1.
The red dotted lines depict the dimensions of the object as observed in the moving frame M, where h represents the dimension perpendicular to the direction of motion and w represents the dimension along the direction of motion. The blue solid lines illustrate the shape of the object as observed in the rest frame R under the scaling effects of special relativity. Here, is the dimensional scaling factor in the direction of motion, and is the scaling factor perpendicular to the direction of motion, with and under the Lorentz factor. The angle is between the light ray observed by observer M and the velocity of motion, ranging from , and it is not affected by velocity-induced scaling, as the object’s size remains constant to the observer in the moving frame. Points and D represent the same location on the moving object. Point is where the light ray reaches as observed by observer M in the moving frame along the , and point D is where the light ray reaches as observed by observer R in the rest frame under the scaling effect. The variable t denotes the time for light to travel from O to D as recorded by the clock R in the rest frame, and is the time for light to travel from to as recorded by the clock M in the moving frame.
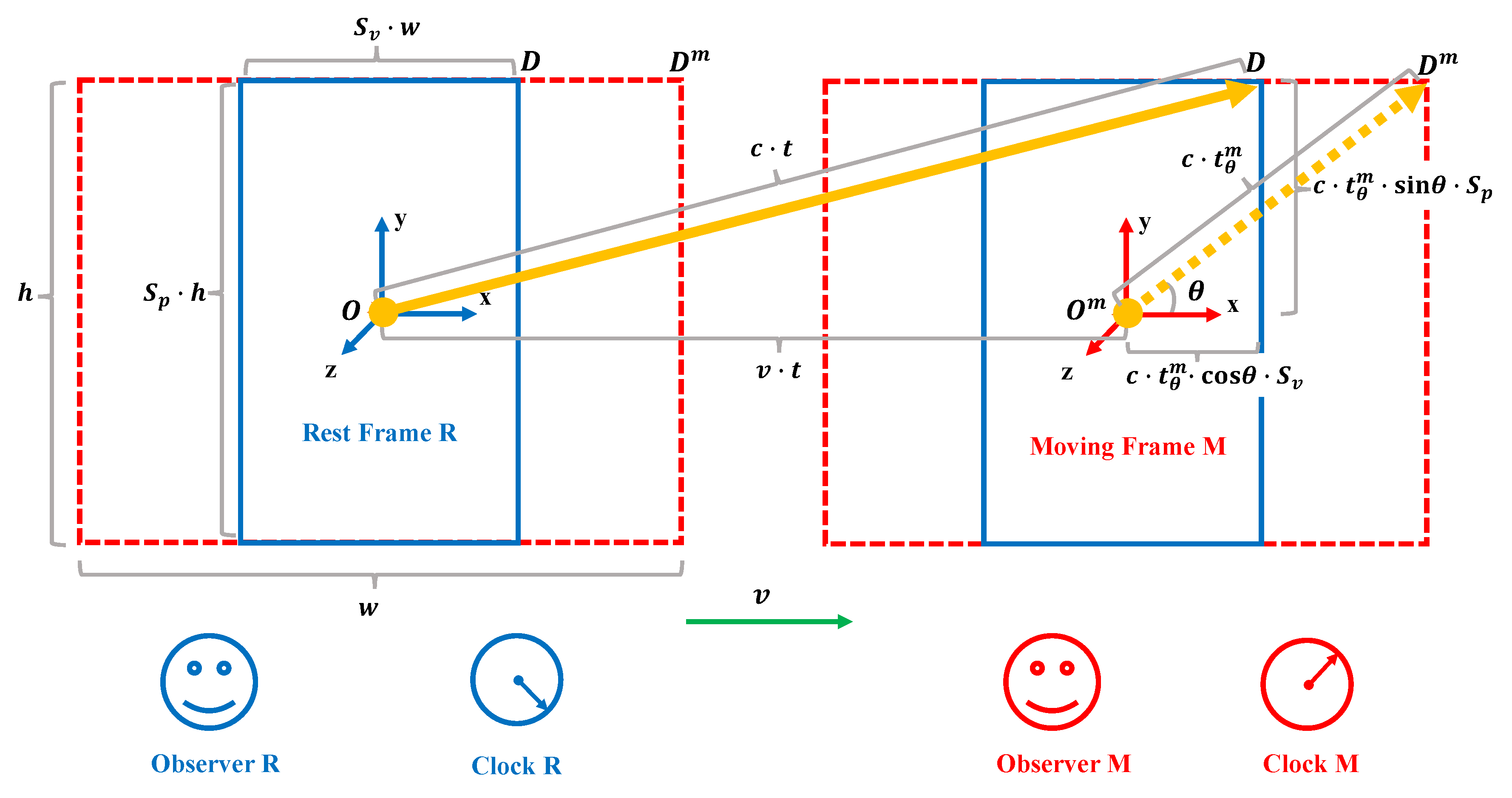
Figure 2.
A light clock consists of two mirrors separated by a fixed distance h, h is the distance that light travels from one mirror to the other in the light clock. A beam of light travels from one mirror to the other and back again, completing a round trip. Each round trip constitutes one "tick" of the clock. The axis of the light clock is positioned at an angle with respect to the direction of motion, where ranges from 0 to . When light propagates from one mirror to the other at an angle , it returns from the second mirror to the first at an angle of .
Figure 2.
A light clock consists of two mirrors separated by a fixed distance h, h is the distance that light travels from one mirror to the other in the light clock. A beam of light travels from one mirror to the other and back again, completing a round trip. Each round trip constitutes one "tick" of the clock. The axis of the light clock is positioned at an angle with respect to the direction of motion, where ranges from 0 to . When light propagates from one mirror to the other at an angle , it returns from the second mirror to the first at an angle of .
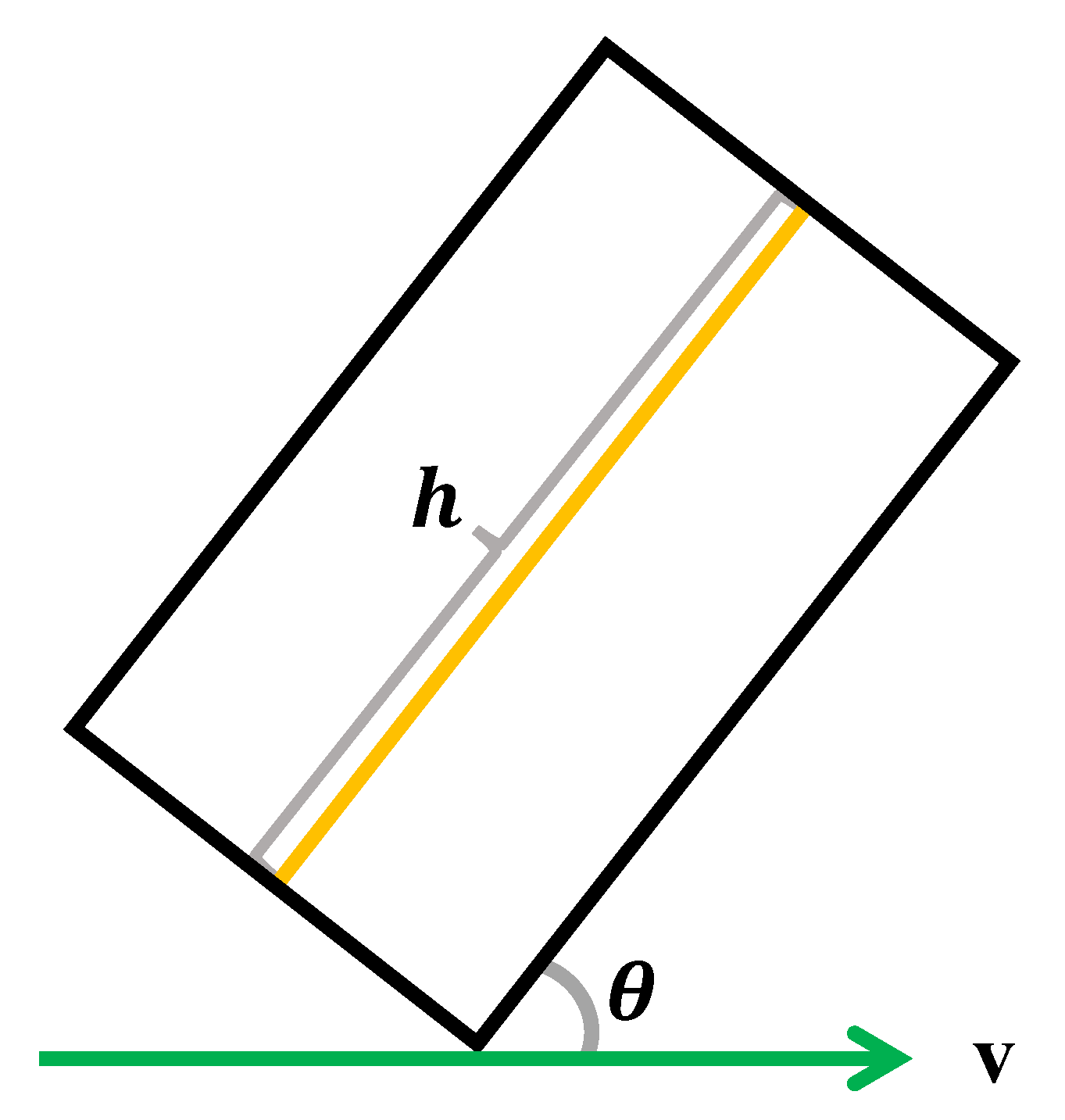
Figure 3.
Illustration of the uniform distribution of vectors originating from the origin and extending outward in three-dimensional space.
Figure 3.
Illustration of the uniform distribution of vectors originating from the origin and extending outward in three-dimensional space.

Figure 4.
Visualisation of the scaling effect for six representative combinations. Each of these diagrams shows the shape of a standard ball of radius 1 at a speed equal to 0, as seen by an observer in a rest frame under the effect of scaling at speeds equal to 0, , , , and , respectively.
Figure 4.
Visualisation of the scaling effect for six representative combinations. Each of these diagrams shows the shape of a standard ball of radius 1 at a speed equal to 0, as seen by an observer in a rest frame under the effect of scaling at speeds equal to 0, , , , and , respectively.
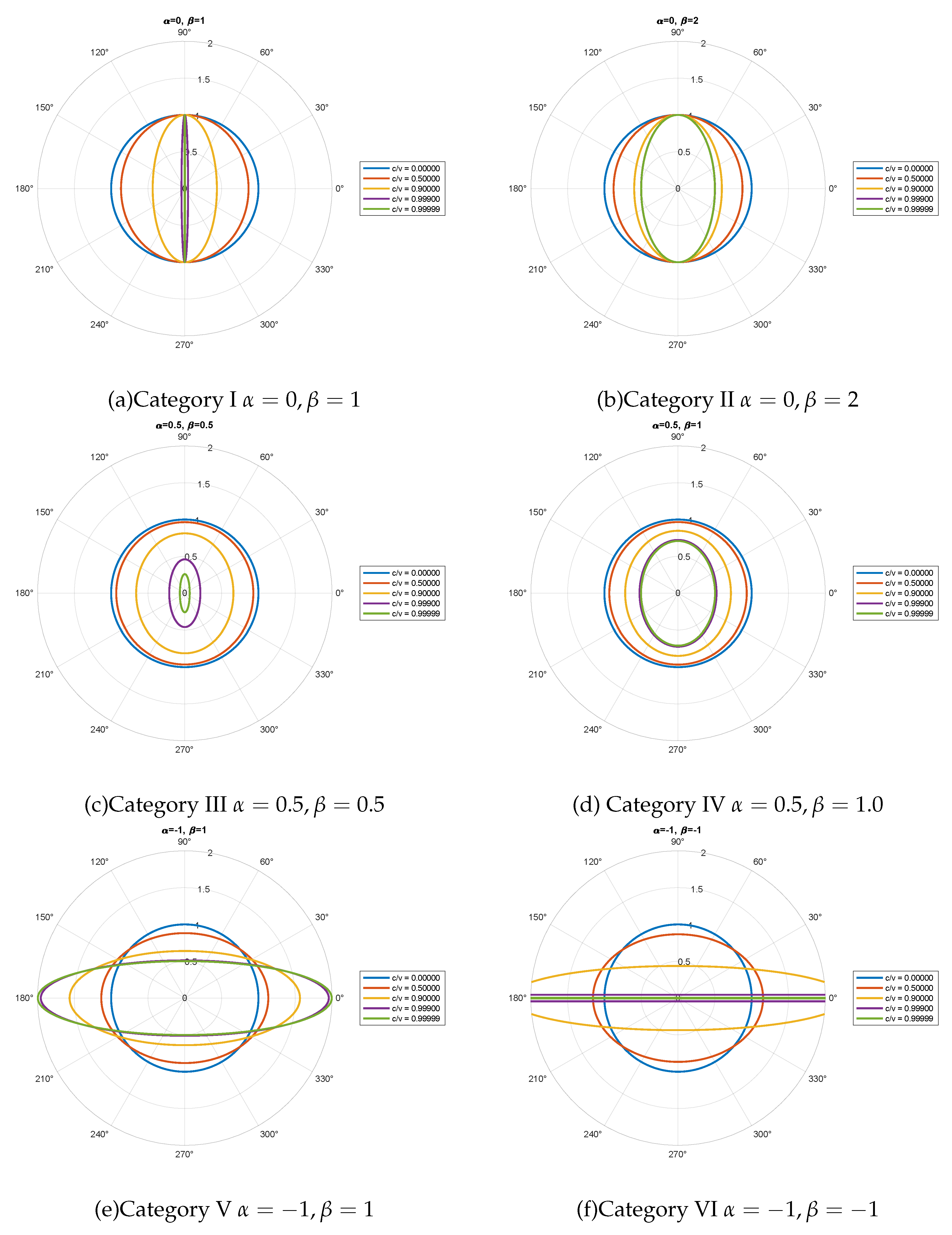
Figure 5.
Visualisation of the unidirectional time scaling factor on six representatives combinations of the light rays in the moving frame travelling along a direction at an angle to the direction of motion. When , it means that the time of the light clock in that direction is completely stationary. When , it means that the time of the light clock in that direction is slowing down. When , it means that the time of the light clock in that direction is neither faster nor slower. When , it means that the time of the light clock in that direction is getting faster. Each plot shows the visualisation of the unidirectional time scaling factor at speeds of motion equal to 0, 0.5c, 0.9c, 0.999c, and 0.99999c, respectively.
Figure 5.
Visualisation of the unidirectional time scaling factor on six representatives combinations of the light rays in the moving frame travelling along a direction at an angle to the direction of motion. When , it means that the time of the light clock in that direction is completely stationary. When , it means that the time of the light clock in that direction is slowing down. When , it means that the time of the light clock in that direction is neither faster nor slower. When , it means that the time of the light clock in that direction is getting faster. Each plot shows the visualisation of the unidirectional time scaling factor at speeds of motion equal to 0, 0.5c, 0.9c, 0.999c, and 0.99999c, respectively.
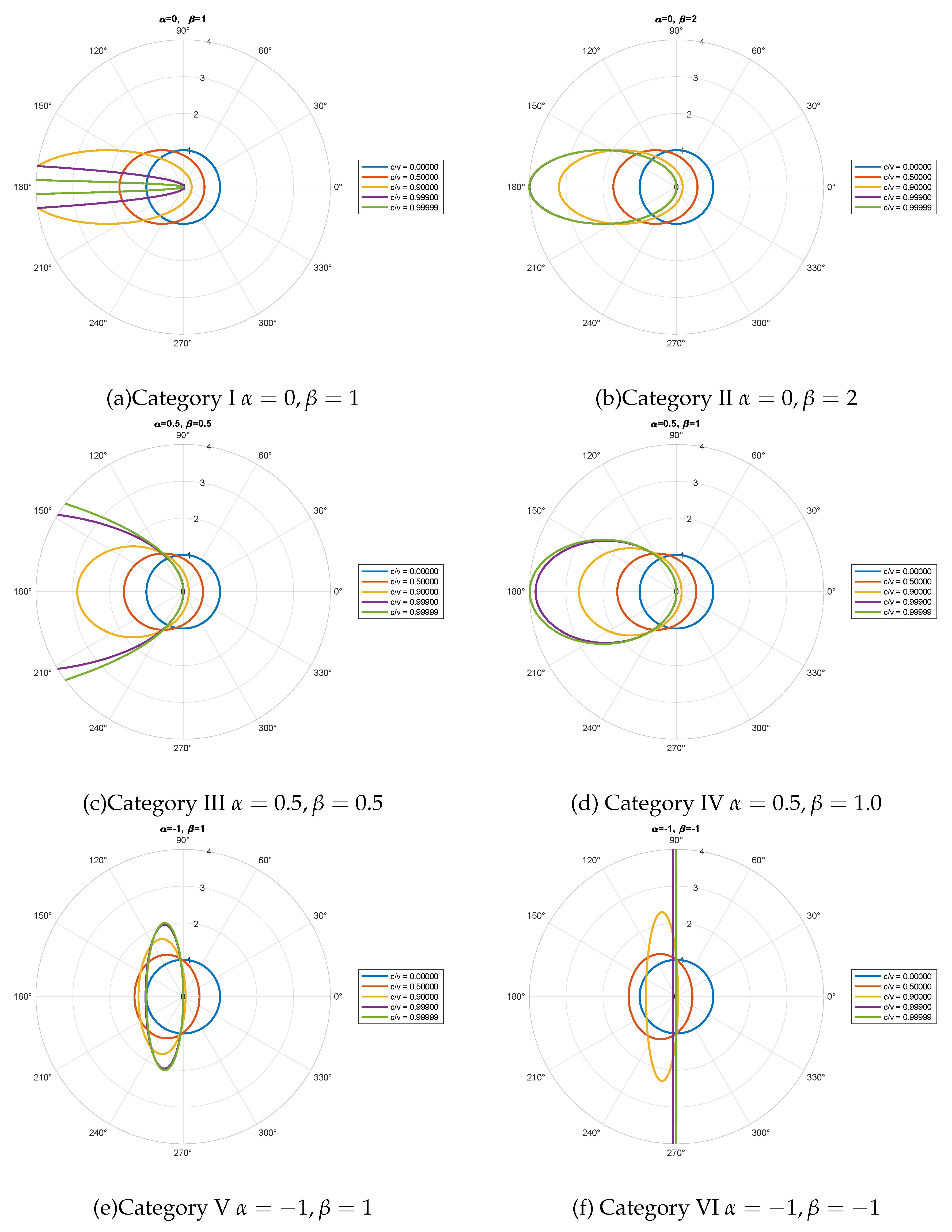
Figure 6.
Visualisation of The time scaling factor of the light clock on six representatives combinations of the light clock in three dimensions within the moving frame, along the direction of motion at an angle . When , the time of the light clock in that direction is completely stationary. When , the time of the light clock in that direction slows down. When , the time of the light clock in that direction is neither faster nor slower. Each plot shows a visualisation of The time scaling factor of the light clock at speeds of motion equal to 0, 0.5c, 0.9c, 0.999c, and 0.99999c, respectively.
Figure 6.
Visualisation of The time scaling factor of the light clock on six representatives combinations of the light clock in three dimensions within the moving frame, along the direction of motion at an angle . When , the time of the light clock in that direction is completely stationary. When , the time of the light clock in that direction slows down. When , the time of the light clock in that direction is neither faster nor slower. Each plot shows a visualisation of The time scaling factor of the light clock at speeds of motion equal to 0, 0.5c, 0.9c, 0.999c, and 0.99999c, respectively.
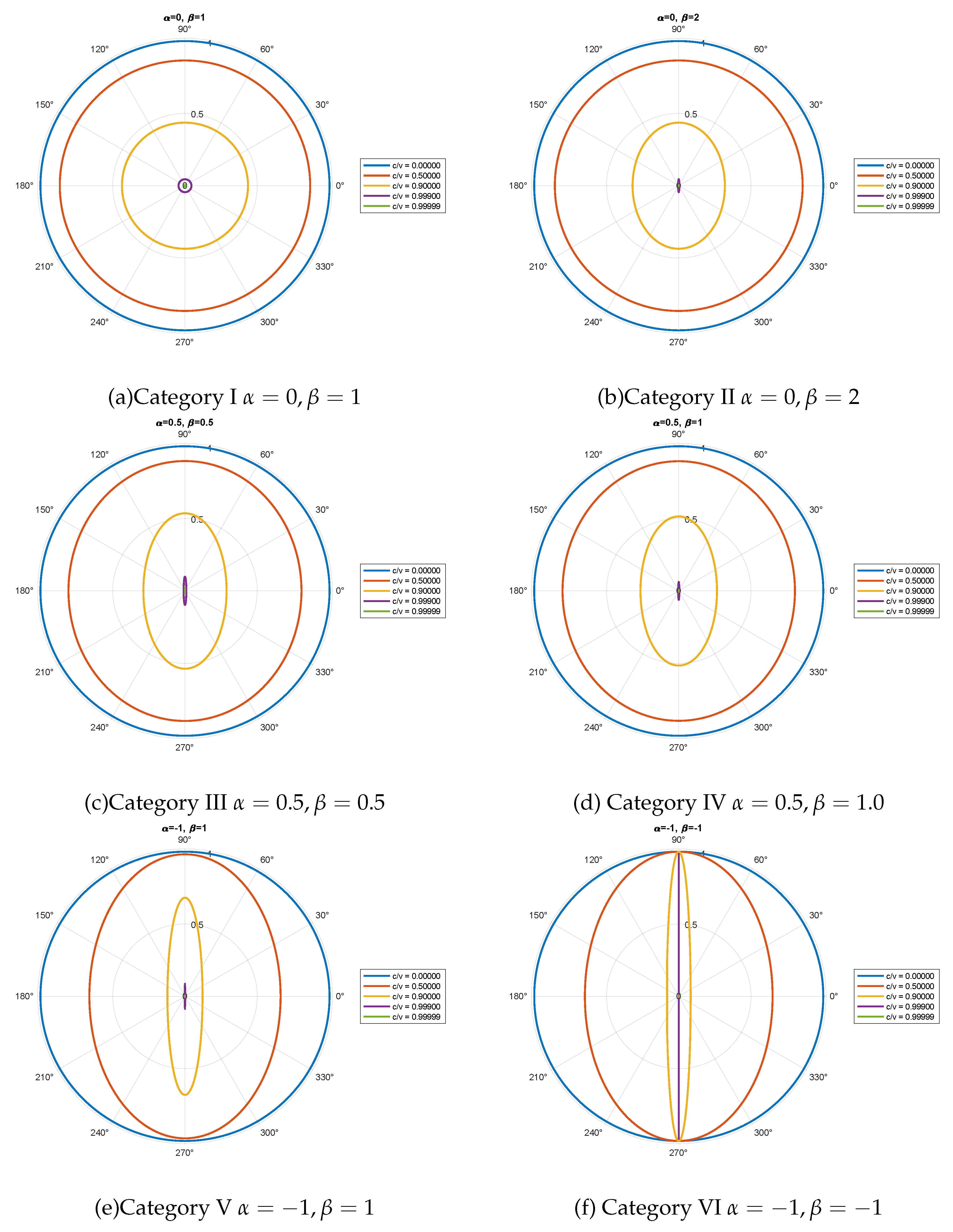
Figure 7.
Visualisation of the consensus time scaling factor of the light clock of the six representatives combinations of numerous light clocks placed in three dimensions in the moving frame along the direction of the arrows pointing uniformly towards the external space. is visualised after being subjected to the time dilation effect. When , it means that the consensus time of the light clock is completely stationary. When , it means that the consensus time of the light clock is neither faster nor slower. When , it means that the consensus time of the light clock is slower. Each of these plots shows a visualisation of the consensus time scaling factor of the light clock at speeds of motion equal to 0, 0.5c, 0.9c, 0.999c, and 0.99999c, respectively.
Figure 7.
Visualisation of the consensus time scaling factor of the light clock of the six representatives combinations of numerous light clocks placed in three dimensions in the moving frame along the direction of the arrows pointing uniformly towards the external space. is visualised after being subjected to the time dilation effect. When , it means that the consensus time of the light clock is completely stationary. When , it means that the consensus time of the light clock is neither faster nor slower. When , it means that the consensus time of the light clock is slower. Each of these plots shows a visualisation of the consensus time scaling factor of the light clock at speeds of motion equal to 0, 0.5c, 0.9c, 0.999c, and 0.99999c, respectively.
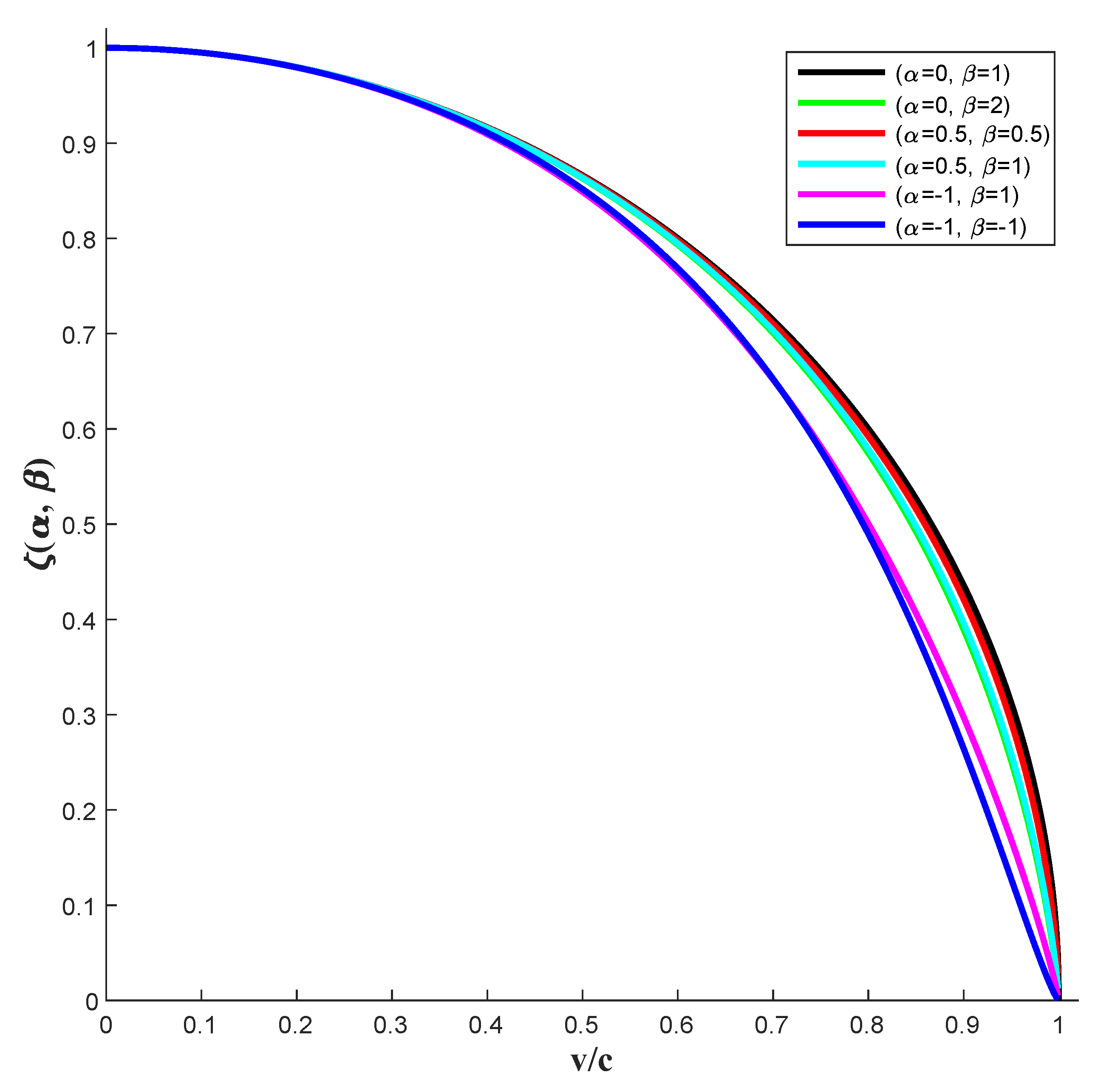
Figure 8.
Test of six combinations for a refined kinetic energy formula to replace Newton’s. Visualization of the key indicator , which should approximate for velocities much less than the speed of light and be exactly when stationary. All combinations satisfy this prerequisite.
Figure 8.
Test of six combinations for a refined kinetic energy formula to replace Newton’s. Visualization of the key indicator , which should approximate for velocities much less than the speed of light and be exactly when stationary. All combinations satisfy this prerequisite.
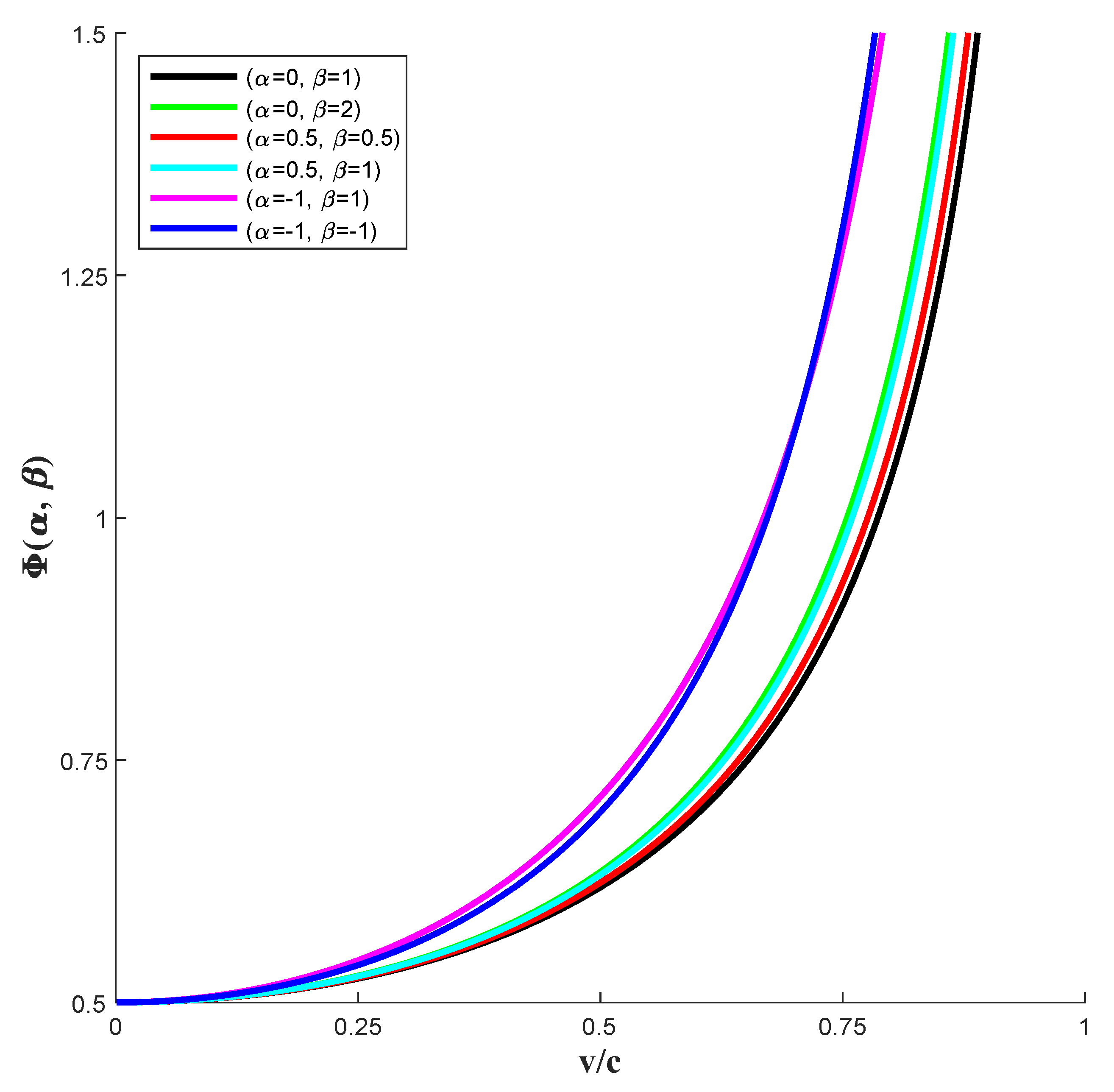
Table 1.
Categories of combinations and their corresponding scaling effects.
| Category | Expression | Description |
|---|---|---|
| I: = 1 | Dimensions in the direction of velocity contract as the object moves, reducing to zero as v approaches c, while dimensions perpendicular to the direction of velocity remain unchanged. | |
| II: > 1 | Dimensions in the direction of velocity contract and reduce to as v approaches c, while dimensions perpendicular to the direction of velocity remain unchanged. | |
| III: = 12+ 1 | Dimensions in both the direction of velocity and perpendicular to it reduce during motion, reaching zero as v approaches c. | |
| IV: > 12+ 1 | given by formula (17), | Dimensions in both the direction of velocity and perpendicular to it reduce, reaching and respectively as v approaches c. |
| V: > 0 | given by formula (17), | Dimensions increase in the direction of velocity and decrease perpendicular to the direction of velocity, reaching and respectively as v approaches c. |
| VI: < 0 | given by formula (17), | Dimensions increase in the direction of velocity, expanding to infinity as v approaches c, while dimensions perpendicular to the direction of velocity decrease to zero. |
Table 2.
The analysis of for six different categories combinations when the object’s speed equals the speed of light. Observed phenomena from a rest frame when part of the internal object travels unidirectionally along , and potential directions for internal object detachment.
Table 2.
The analysis of for six different categories combinations when the object’s speed equals the speed of light. Observed phenomena from a rest frame when part of the internal object travels unidirectionally along , and potential directions for internal object detachment.
| Category | Expression | Description |
|---|---|---|
| I: = 1 | when when | If the angle between the direction of the object’s motion and the spaceship’s motion is in the range , the time spent traveling unidirectionally in this direction appears to the observer in the rest frame as completely stationary. However, at an angle of , the time appears non-stationary. |
| II: > 1 | when when | When the angle is in the range , the time traveling unidirectionally appears completely stationary to the observer in the rest frame. For angles , the time appears non-stationary, increasing with the angle and reaching its fastest at . |
| III: = 12+ 1 | when when | For angles , the unidirectional travel time appears stationary to the rest frame observer. When , the travel time is non-stationary and increases with the angle, reaching its maximum at . |
| IV: > 12+ 1 | when when | For angles , the unidirectional travel time appears stationary to the observer in the rest frame. When , the travel time becomes non-stationary and speeds up with the angle, reaching its peak at . |
| V: > 0 | when when | When the angle is in the range , the unidirectional travel time appears stationary to the rest frame observer. For angles , the passage of time first speeds up and then slows down. |
| VI: < 0 | when when | If the angle is not equal to , the unidirectional travel time appears stationary to the rest frame observer. At an angle of , the travel time appears non-stationary. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





