Prerpints.org logo
Preprint
Article

1D Electronic Noise Filtering Using an Autoencoder

Altmetrics

Downloads

80

Views

26

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

25 July 2024

Posted:

26 July 2024

You are already at the latest version

Alerts
Abstract
Autoencoders are neural networks that have applications in denoising processes. Their use is widely reported in imaging (2D), though 1D series can also benefit from this function. Here, three canonical waveforms are used to train a neural network and achieve a signal-to-noise reduction with curves whose noise energy was above that of the signals. A real-world test is carried out with the same autoencoder subjected to a set of time series corrupted by noise generated by a zener diode, biased on the avalanche region. Results showed that, observed some guidelines, the autoencoder can indeed denoise 1D waveforms usually observed in electronics, particularly square waves found in digital circuits.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

Autoencoders are neural networks operated by means of unsupervised learning. The input data is compressed to a smaller-scale representation, called latent variable, which contains the most relevant characteristics of the raw data. This compression function is carried out by the encoder, and the decoder, which comes in sequence, decompress the data back into is original dimension. The latent variable is a minimal representation of the features contained in the data, and it operates as a kind of bottleneck in the convolutional neural network (CNN) architecture. Their main role can be seen as a creating a rough copy of the input data, which resembles the training data [1]. Layers named MaxPooling1D concentrate the inputs from the preceding layer into single neurons, thereby reducing the data dimensionality [2]. When the input data contains complex values, the real and imaginary parts need to be treated separately, since CNNs deal primarily with real numbers [3].
The goal of a denoising autoencoder is the creation of a model which is more robust against noise energy. Recurrent neural networks, where there is feedback from the output to previous layers, is sometimes used for arbitrarily long sequences [4]. Although usually applied for images, some cases report improvements in the quality of 1D waveforms. Signals from ultrasonic non-destructive testing have been subjected to denoising using an autoencoder and compared with singular value decomposition (SVD), principal component analysis (PCA) and wavelet, with the CNN providing better performance, particularly regarding the robustness [5]. Signals from seismic sensors had activation functions added to the neurons as to introduce non-linearity in the process, improving the overall performance [6]. Another 1D application reported the use of a denoising network followed by a feature extraction on the diagnosis of a mechanical gearbox [7]. Real known defect conditions were used in the training phase. In a similar approach, the denoising followed a 1D CNN, and was used to diagnose fault conditions in rotating machinery [8]. The preliminar denoising procedure is of paramount importance given the fact that real-world acquired signals are contaminated with noise, which otherwise might demand extra effort in the classification network.
When noisy conditions to be used in the training are not easy to achieve using experimental tests, the corrupted data can be created using several different alternatives, such as using a Gaussian noise distribution and back and forth Fourier Transforms for the case of EEG [2]. EKG signals, in turn, had high-frequency artifacts caused by electrode movements cleaned using a Discrete-Cosine and wavelet transforms pre-processing, followed by an autoencoder, which helped improve the signal-to-noise ratio (SNR) by approximately 25 dB [9].
With regard to the field of communications, cognitive radio networks are meant to operate in a crowded electromagnetic environment using the most efficient modulation scheme and frequency range at the moment, therefore they need to continuously learn about the available electromagnetic resource. CNN’s were reported to identify eight kind of communication signals (e.g., Costas and Barker codes, binary phase shift or frequency modulation, etc) in order to be applied in Cognitive Radio networks [10].
A convolutional autoencoder was integrated to an automated optical inspection (AOI) system, which used images from a charged-coupled device (CCD) camera to identify defects in printed-circuit (PCB) boards [11]. Similarly, vibration signals from permanent magnet synchronous motors were processed by an autoencoder in order to decrease the noise levels prior to be classified in terms of types of fault by a support vector machine (SVM) [12]. Taking advantage of the prediction capabilities an autoencoder provides, a supervised-learning network was trained to predict the reliability of digital circuits, whose results were then compared to a Monte-Carlo based analysis [13].
Radars, in particular, operate with very low-amplitude signals, contaminated with noise and clutter which often have more energy than the signals of interest. Hyper-parameters of a CNN network have been analyzed to provide radar waveforms recognition and classification, in real time [14]. Another similar study has focused on low-probability of intercept (LPI) radar waveforms, identified by a dense CNN, with the original signals converted into time-frequency waveforms using Choi-Williams (CWD) distribution [15], achieving a success rate of 93.4 % for an SNR of -8 dB. The Intra-pulse modulation in radar signals have been recognized using a convolutional denoising autoencoder and a deep convolutional neural network, with the raw data converted to images using the Cohen time-frequency distribution [16].
Real-world electronic signals are usually contaminated with noise, which arise from disturbances such as unwanted electromagnetic coupling among the circuit components, shot noise observed in semiconductors and man-made electromagnetic interference (EMI). Band-pass filtering is one alternative to reduce the noise power within the signal bandwidth, at expenses of the tradeoff between the filter time and frequency domains. Steep roll-offs in frequency imply large group delays that eventually distort the time response. More sophisticated alternatives to 1D denoising are wavelets [17], empirical mode decomposition [18] and curvelets [19]. For that matter, this paper presents an autoencoder used for denoising signals commonly found in electronics, i.e., square, triangular and sine waves. In particular, square waves are usually employed in digital electronics, and preserving their original waveform shape is directly correlated with the data throughput [20]. Disturbed digital waveforms imply false readings, since the wave amplitude is used for decision making between the binary logic levels. An ensemble of clean and noisy waveforms are generated by Matlab/Octave and later used for the training and test of a CNN implemented in Python. For the sake of comparison to real-world signals, a noise circuit was built and added to a signal generator, outputting the same three wave shapes, and the denoising process was applied using the previously trained neural networks. Its fast response enables its use as an option after analog signals are acquired and digitized.

2. Materials and Methods

2.1. Waveform Generation

The data to be used in the training was prepared in Matlab. Each time series was set to contain 1000 samples of real numbers, distributed in the square, triangular and sine types, each case with 2000 different waveforms to be inserted into the CNN. The parameter to be evaluated, the signal-to-noise ratio (SNR), in dB, was computed according to:
S N R = 10 log 10 ∑ i = 1 2000 s i 2 ∑ i = 1 2000 s n i 2
where s and s n are the clean and noisy waveforms, respectively. Each waveform has the following characteristics:

2.2. Square Wave

Its duty cycle was set to be 50 %, the on and off parts were set to 20 points. Amplitude is set to vary between 0 and 1, and the different samples had the phase randomly varied. Noise is numerically added using the rand function in Matlab. 2000 waveforms were stored without noise and 2000 contaminated with noise. The complete waveform generation and file storage took 4.1 seconds, using Matlab 2018a.

2.3. Triangular Wave

Similar to the square wave, there were 2000 series, each with 1000 points. The rising and fall times were set to be comprised of 20 points, and their amplitude varying between 0 and 1. Generation and storage took about 4.6 seconds.

2.4. Sine Wave

Sine waves were generated, in contrast to the former two cases, with both frequency and phase allowed to vary within the samples. Generation of data, storage and plotting figures took about 3.9 seconds.
Three different samples of the waveforms, clean and noisy, are shown in Figure 1. The sine waves are shown with the 2 π scale on the x-axis.
The respective SNR histograms of the created input data are shown in Figure 2. They show that the noise energy is larger than that of the signal, across all the 2000 samples.

2.5. CNN

An autoencoder is a neural network that takes an input and reproduces the same input as the output, by means of unsupervised learning [21]. The deployed network representation is shown in Figure 3, based on Python Tensorflow and Keras, the latter an application programming interface (API) that runs on top of the former. The aforementioned vectors of length 1000 (dimension 1000x1) are supplied as input, and sequential convolutional filters are used, followed by MaxPooling and upsampling blocks, which downsample and upsample the incoming data by a factor of 2, respectively. Convolutional filters extract the features from the input data, whereas the MaxPooling performs an averaging operation on the former convolutional filter data and reduce the number of parameters. This first half-part of the CNN is named encoder network. In other words, convolutional layers detect patterns on the incoming data, and MaxPooling reduces their dimensionality. The process is then reversed, in the so-called decoder network, in order to retrieve the same original input length, and instead of MaxPooling the dimensionality is progressively increased by means of Upsampling layers. 20% of the total number of samples was allocated to test, the rest is used for the training. Throughout the CNN, the activation function was the Rectified Linear Unit (RELU).
50 epochs were used for the training. Table 1 shows the elapsed time for the three cases, it can be seen that no relevant difference was observed for the waveshapes. The Loss parameter evolution across the epochs are are shown in Figure 4. The square wave required more efforts to be be trained, in contrast to the other two waveforms.
Samples of the clean and noisy signals are shown in Figure 5, done after the training was finished. The output waveforms are visually clearer, showing the success of the denoising network, cleaning severely contaminated signals, independent of the waveshape type.
A SNR histogram analysis is applied to the input and output signals (Figure 6). It can be seen that the sine case had the worst performance, given the smaller distance between the noisy and denoised samples. This difference can be ascribed to the larger variation of the seed signals, i.e., either the frequency and phase were made to vary in contrast to the other two cases.

3. Real-World Noisy Signal

In order to evaluate the performance of the denoising autoencoder against real-world signals, a test was performed with a circuit subjected to a controlled level of noise. For the noise source, a Zener diode was employed, biased on its avalanche area [22]. The test was carried out using the circuit displayed in Figure 7.
An oscilloscope stored the noisy waveforms, in ascii format, and were afterwards read and processed by the CNN, trained using the Matlab-generated signals, i.e., there was not another training with the Zener-contaminated signals. The instrument maximum time series length is by default 2000 points, so the acquired data vector was later truncated to 1000, in order to be consistent with the trained input signals. Individual circuit components were manually optimized, based on the visual noise amplitude seen on the oscilloscope. For instance, the 6.6 V diode was chosen among others due to its observed higher noise levels. The signal generator couples to the Zener by means of a 1 k Ω resistor, and the capacitor blocks DC levels from entering into the signal generator and oscilloscope inputs. Differently from the computer-generated square waveforms, the generator had finite rise and fall times (set to its minimum default value of 17 ns). The generator was set to output square, triangular and sine waves, displayed in Figure 8, together with the cleaned signals after the autoenconder.
Alongside the time-domain results their power spectra is shown, for either raw and processed waveforms. It is possible to see that the CNN operates as a low-pass filter, attenuating frequencies above the range where the signals concentrate most of their energies. It is interesting to stress that this effect was automatically found by the neural network operation after the training step. In the rectangular signal case, in particular, one notices that harmonics above the third are cut, probably due to CNN training that was performed with a perfect shape (i.e., null rise and fall times). Among the whole ensemble encompassing the three signals, the triangular wave had the worst behavior, with its shape slightly rounded in the time domain, effect visualized on its power spectrum with its second harmonic completely attenuated from the denoised version.
It was found that the acquired signals did not need to be compressed into the original normalized range (0 to 1), but it was very sensitive to the its baseline, i.e., a DC offset had to be added otherwise the lower part of the signals were not correctly denoised. It points out that the training signals should be comprised of a more diverse ensemble, particularly with randomly chosen DC offsets. Figure 9 shows an example, where the offset is not added to the acquired square wave. It is the reason that justifies both initial and final discontinuities observed in the denoised waveforms seen in Figure 8.

4. Discussion

The observed results showed that the autoencoder indeed reduced the noise levels in typical waveforms usually found in electronic circuits. Tests performed using a Zener diode noise generator proved that the training phase has, however, to fulfill a broader set of parameters to become more general. Namely, phase, frequency and DC offsets have to cover the range expected to be found in the noisy signals to be later cleaned by the CNN. Waveform amplitudes were not found to have a relevant impact on the denoising, so the training could be performed with the usual normalized values. Also, though more time consuming and less convenient, a more robust option would have the training performed with real-world instruments, so that the signals better resemble the future noisy waveforms. It is not easy to predict which parameter, found in the real-world case, might impact on the network response.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning, 1st ed.; MIT Press: Cambridge, USA, 2016; pp. 499–500. [Google Scholar]
  2. Leite, N. M. N.; Pereira, E. T.; Gurjão, E. C.; Veloso, L. R. Deep Convolutional Autoencoder for EEG Noise Filtering. In Proceedings of the IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Madrid, Spain, 03-06 December 2018. [Google Scholar]
  3. Fuchs, J.; Dubey, A.; Lübke, M.; Weigel, R.; Lurz F., E. F. In The Automotive Radar Interference Mitigation using a Convolutional Autoencoder. In Proceedings of the IEEE International Radar Conference (RADAR), Washington DC, US, 28-30 April 2020. [Google Scholar]
  4. Yasenko, L.; Klyatchenko, Y.; Tarasenko-Klyatchenko, O. Image noise reduction by denoising autoencoder. Proceedings of 11th IEEE International Conference on Dependable Systems, Services and Technologies, DESSERT’2020, Kyiv, Ukraine, 14-18 May 2020. [Google Scholar]
  5. Gao, F.; Li, B.; Chen, L.; Wei, X.; Shang, Z.; He, C. Ultrasonic signal denoising based on autoencoder. Review of Scientific Instruments 2020, 91, 1–9. [Google Scholar] [CrossRef] [PubMed]
  6. Saad, O. M.; Chen, Y. Deep denoising autoencoder for seismic random noise attenuation. Geophysics 2020, 85, 367–376. [Google Scholar] [CrossRef]
  7. Yu, J.; Zhou, X. One-Dimensional Residual Convolutional Autoencoder Based Feature Learning for Gearbox Fault Diagnosis. IEEE Transactions on Industrial Informatics 2020, 16, 6347–6358. [Google Scholar] [CrossRef]
  8. Liu, X.; Zhou, Q.; Zhao, J.; Shen, H.; Xiong, X. Fault Diagnosis of Rotating Machinery under Noisy Environment Conditions Based on a 1-D Convolutional Autoencoder and 1-D Convolutional Neural Network. Sensors 2019, 19, 1–20. [Google Scholar] [CrossRef] [PubMed]
  9. Sheu, M. H.; Jhang, Y. S.; Chang, Y. C.; Wang, S. T.; Chang, C. Y.; Lai, S. C. Lightweight Denoising Autoencoder Design for Noise Removal in Electrocardiography. IEEE Access 2022, 10, 98104–98116. [Google Scholar] [CrossRef]
  10. Zhang, M.; Diao, M.; Guo, L. Convolutional Neural Networks for Automatic Cognitive Radio Waveform Recognition. IEEE Access 2017, 5, 11074–11082. [Google Scholar] [CrossRef]
  11. Kim, J.; Ko, J.; Choi, H.; Kim, H. Printed Circuit Board Defect Detection Using Deep Learning via a Skip-Connected Convolutional Autoencoder. Sensors 2021, 21, 1–13. [Google Scholar] [CrossRef] [PubMed]
  12. Xu, X.; Feng, J.; Zhan, L.; Li, Z.; Qian, F.; Yan, Y. Fault Diagnosis of Permanent Magnet Synchronous Motor Based on Stacked Denoising Autoencoder. Entropy 2021, 23, 1–13. [Google Scholar] [CrossRef] [PubMed]
  13. Xiao, J.; Ma, W.; Lou, J.; Jiang, J.; Huang, Y.; Shi, Z.; Shen, Q.; Yang, X. Circuit reliability prediction based on deep autoencoder network. Neurocomputing 2019, 370, 140–154. [Google Scholar] [CrossRef]
  14. Kong, S. H.; Kim, M.; Zhan, L; Hoang, Z.M. Automatic LPI Radar Waveform Recognition using CNN. IEEE Access 2018, 6, 4207–4219. [Google Scholar] [CrossRef]
  15. Si, W.; Wan, C.; Zhang, C. Towards an accurate radar waveform recognition algorithm based on dense CNN. Multimedia Tools and Applications 2021, 80, 1179–1192. [Google Scholar] [CrossRef]
  16. Qu, Z.; Wang, W.; Hou; Hou, C. Radar Signal Intra-Pulse Modulation Recognition Based on Convolutional Denoising Autoencoder and Deep Convolutional Neural Network. IEEE Access 2019, 7, 112339–112347. [Google Scholar] [CrossRef]
  17. Taswell, C. The what, how, and why of wavelet shrinkage denoising. Computing in Science and Engineering 2000, 2, 12–19. [Google Scholar] [CrossRef]
  18. Gomez, J. L.; Velis, D. R. A simple method inspired by empirical mode decomposition for denoising seismic data. Geophysics 2016, 81, 403–413. [Google Scholar] [CrossRef]
  19. Moore, R.; Ezekiel, S.; Blasch, E. Denoising one-dimensional signals with curvelets and contourlets. Proceedings of NAECON 2014 - IEEE National Aerospace and Electronics Conference, Dayton, US, 24-27 June 2014. [Google Scholar]
  20. Green, L. Understanding the importance of signal integrity. IEEE Circuits and Devices Magazine 1999, 15, 7–10. [Google Scholar] [CrossRef]
  21. Sewak, M.; Karim, M. R.; Pujari, P. Practical Convolutional Networks, 1st. ed.; Publisher: Packt Birmingham, UK, 2018; pp. 1–211. [Google Scholar]
  22. Abdipour, A.; Moradi, G.; Saboktakin, S. Design and implementation of a noise generator. In Proceedings of the IEEE International RF and Microwave Conference, Kuala Lampur, Malaysia, 02-04 December 2008. [Google Scholar]
Preprints 113300 g001
Figure 1. Signal waveforms, clean and noisy (a) square, (b) triangular, and (c) sine.
Figure 1. Signal waveforms, clean and noisy (a) square, (b) triangular, and (c) sine.
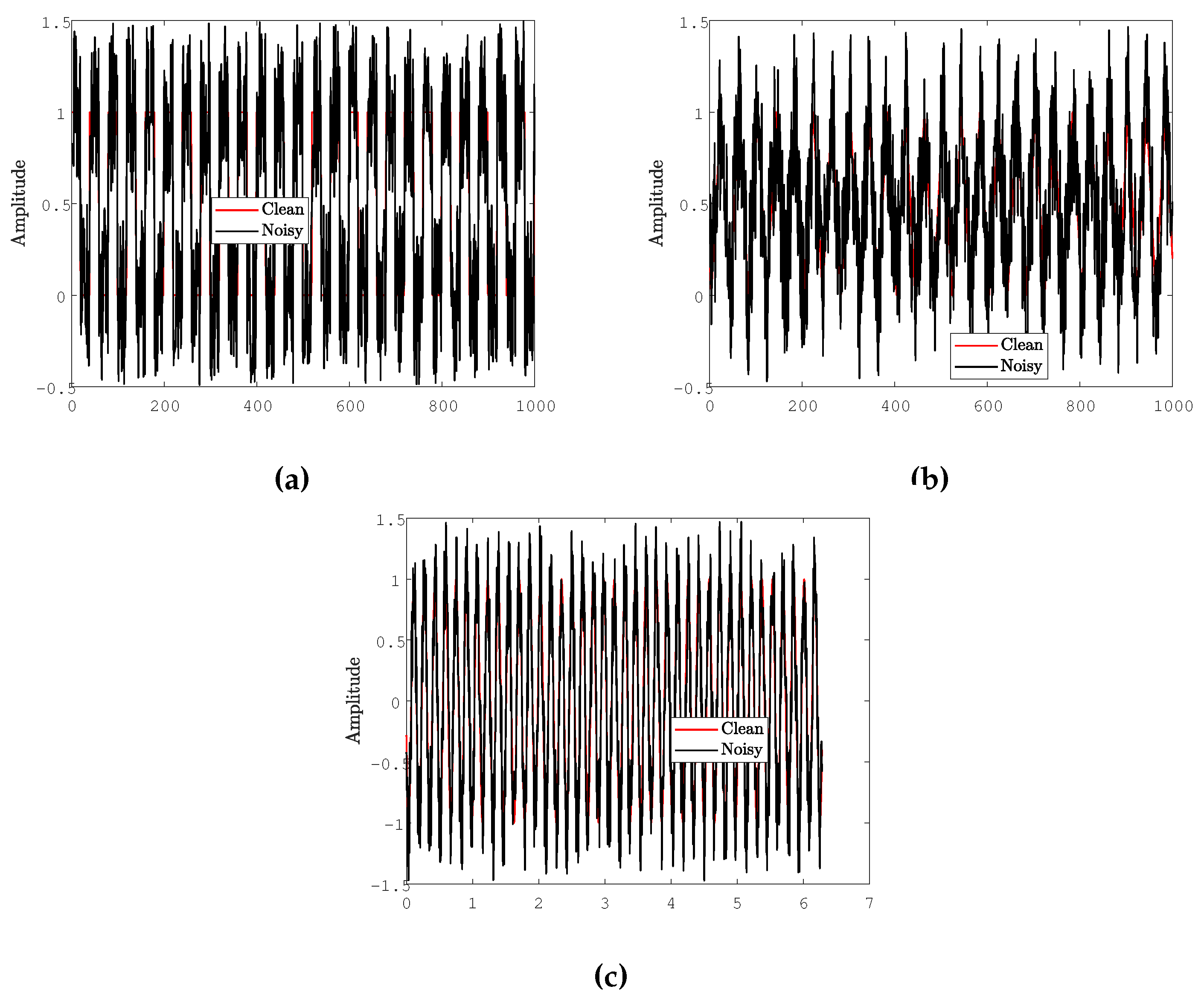
Preprints 113300 g001
Preprints 113300 g002
Figure 2. Histogram of the SNR relative to the waveforms of (a) square, (b) triangular, and (c) sine samples.
Figure 2. Histogram of the SNR relative to the waveforms of (a) square, (b) triangular, and (c) sine samples.
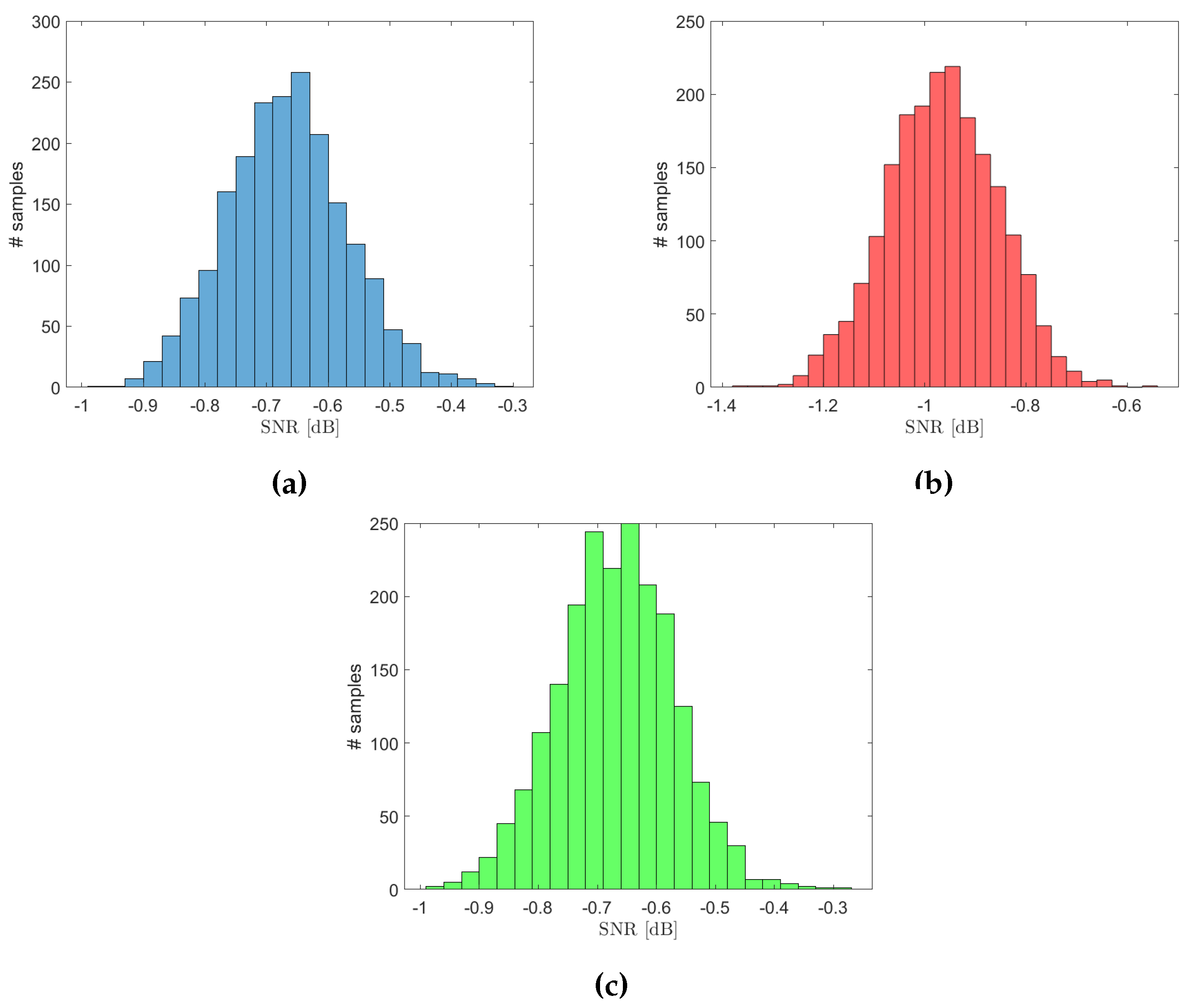
Preprints 113300 g002
Preprints 113300 g003
Figure 3. Block diagram of the used CNN.
Figure 3. Block diagram of the used CNN.
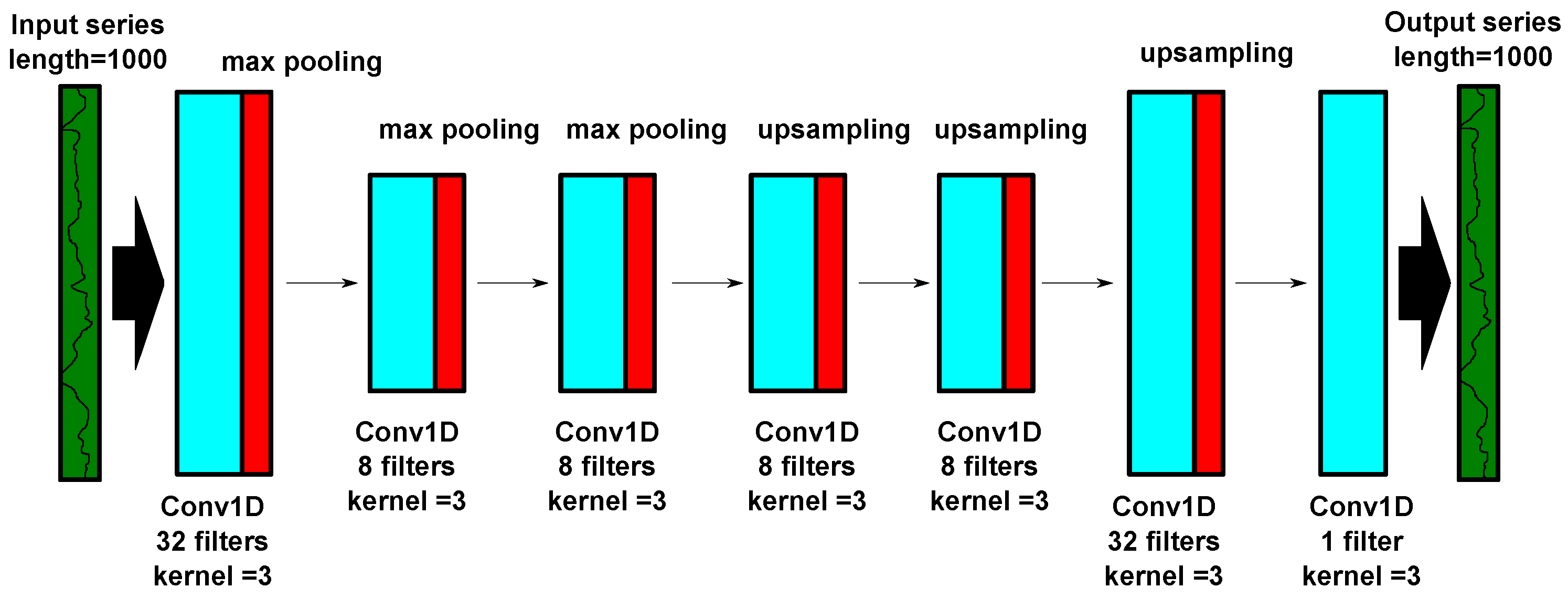
Preprints 113300 g003
Preprints 113300 g004
Figure 4. Loss evolution along the 50 epochs for the cases of (a) square, (b) triangular, and (c) sine signals.
Figure 4. Loss evolution along the 50 epochs for the cases of (a) square, (b) triangular, and (c) sine signals.
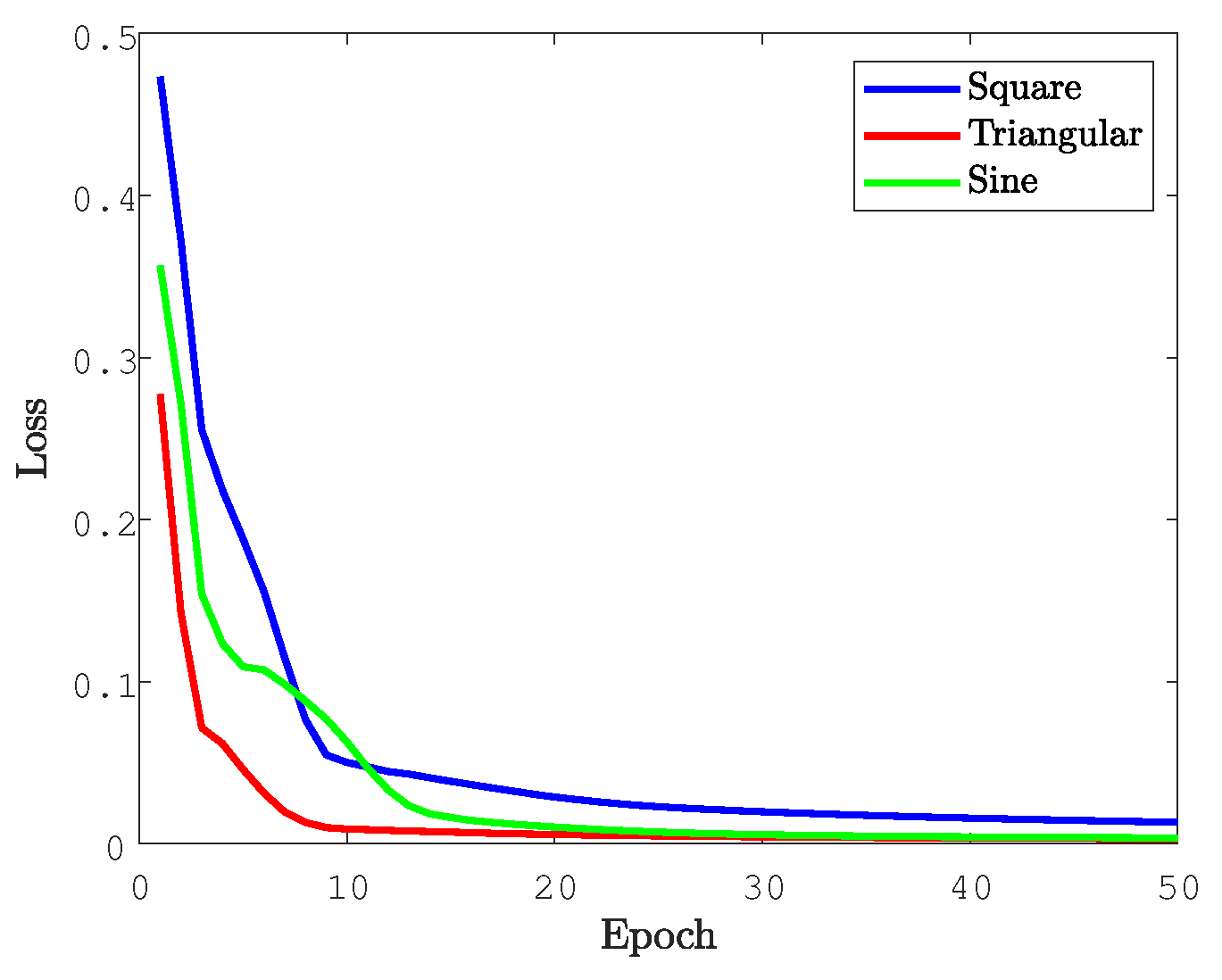
Preprints 113300 g004
Preprints 113300 g005
Figure 5. Noisy (red) and denoised (green) waveforms from the (a) square, (b) triangular, and (c) sine samples.
Figure 5. Noisy (red) and denoised (green) waveforms from the (a) square, (b) triangular, and (c) sine samples.
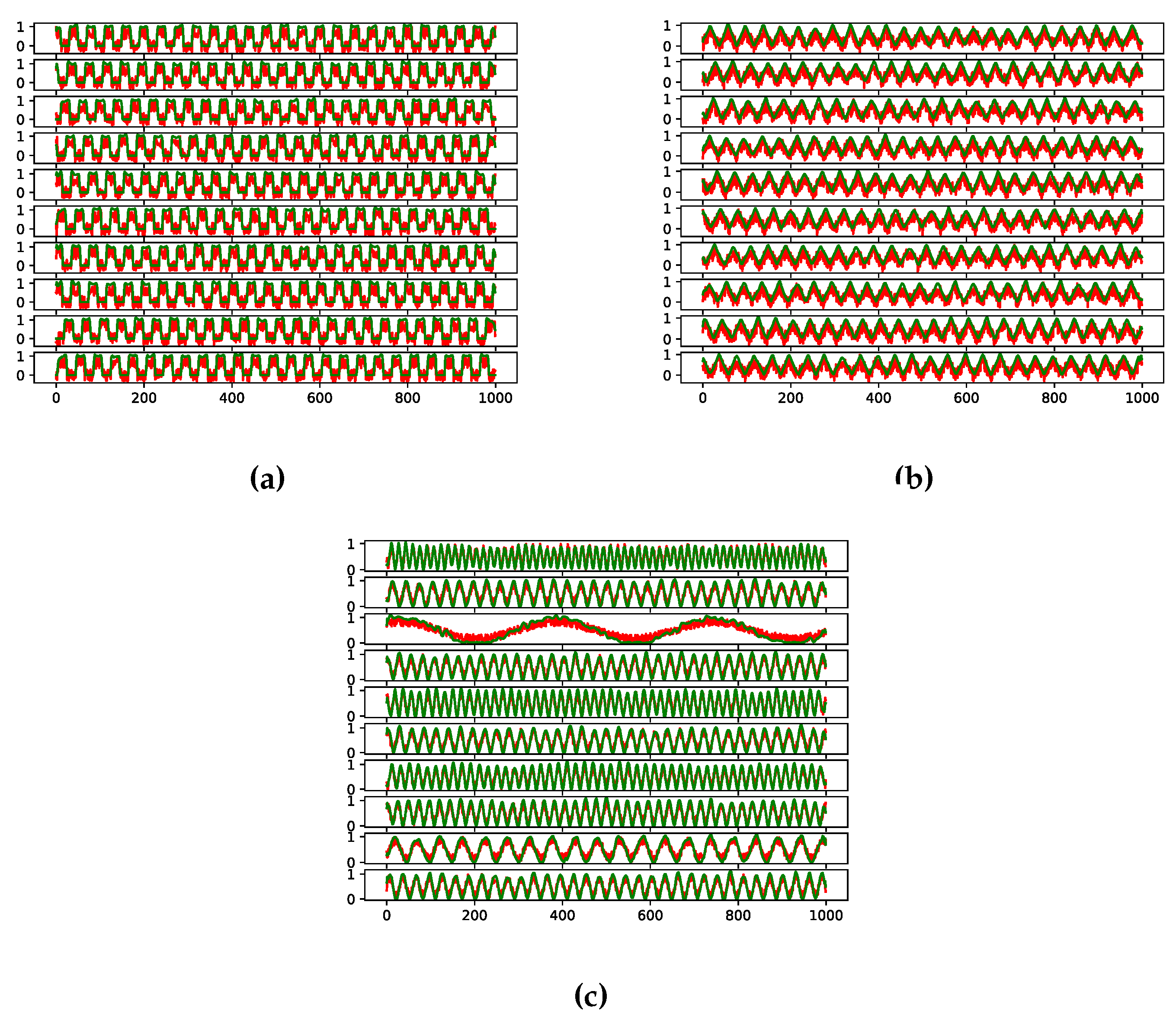
Preprints 113300 g005
Preprints 113300 g006
Figure 6. SNR histograms for the (a) square, (b) triangular, and (c) sine samples, before and after de denoising.
Figure 6. SNR histograms for the (a) square, (b) triangular, and (c) sine samples, before and after de denoising.
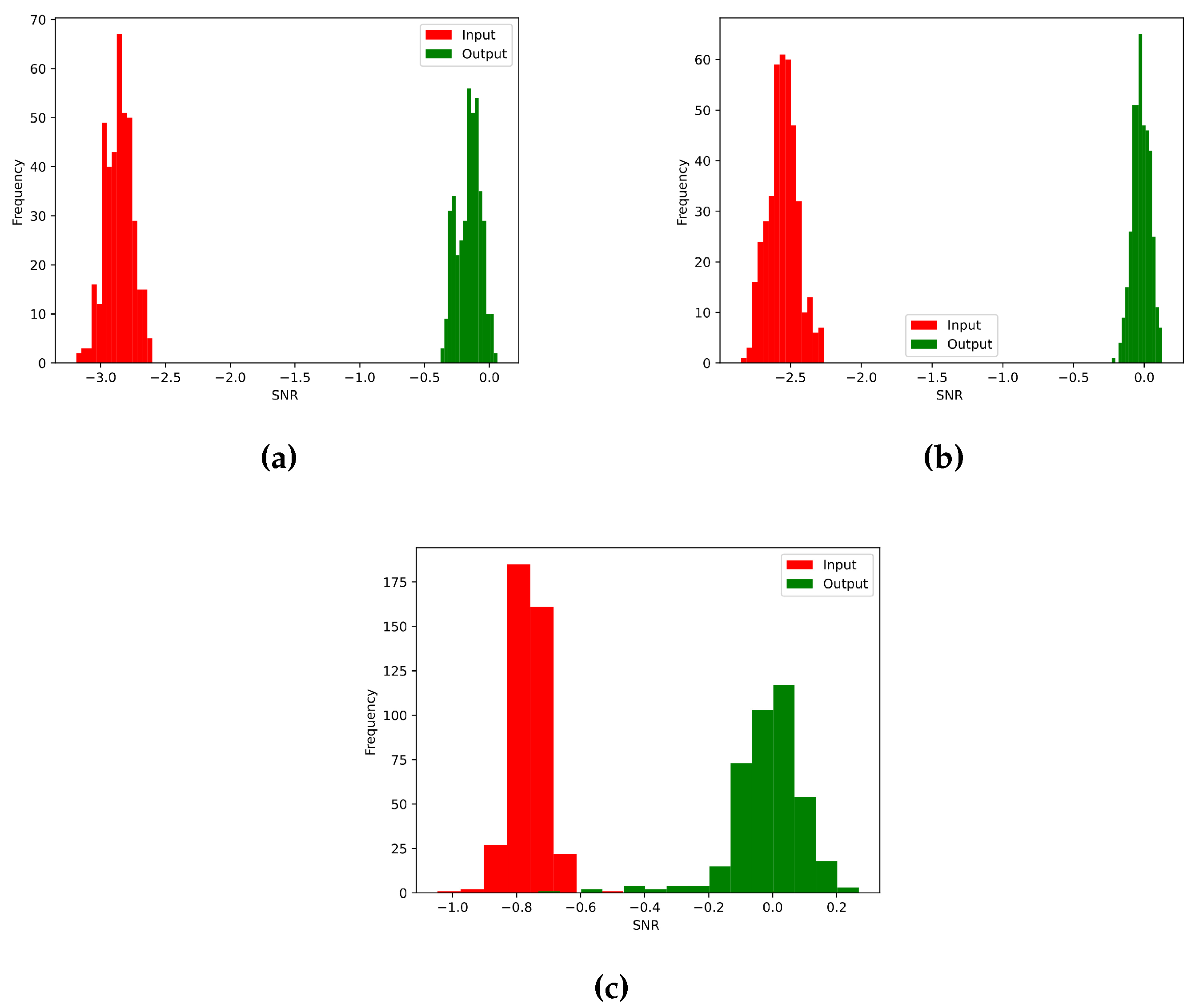
Preprints 113300 g006
Preprints 113300 g007
Figure 7. Zener diode used as a noise generator.
Figure 7. Zener diode used as a noise generator.
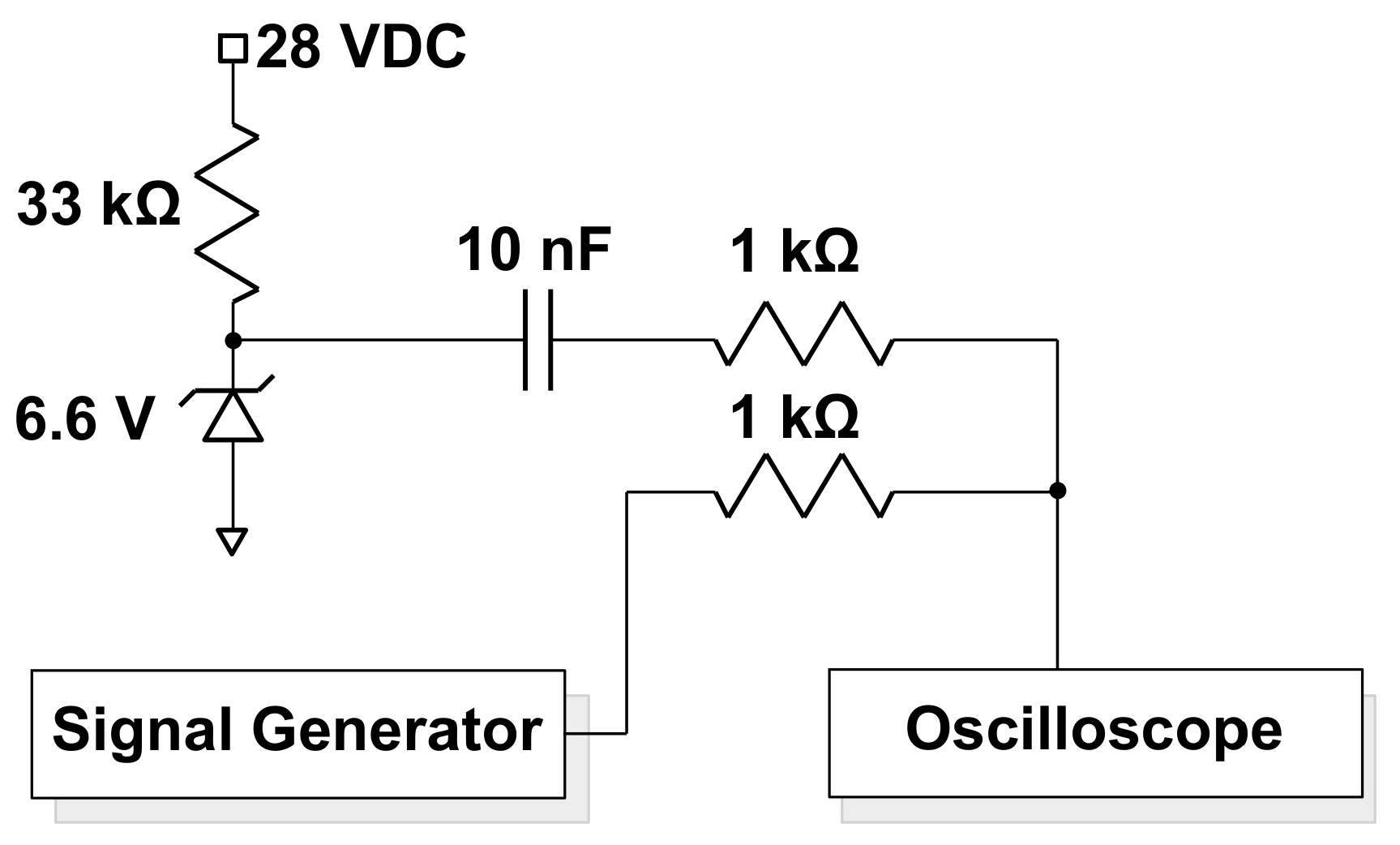
Preprints 113300 g007
Preprints 113300 g008
Figure 8. Time domain and power spectra of the real-world signals, original and denoised.
Figure 8. Time domain and power spectra of the real-world signals, original and denoised.
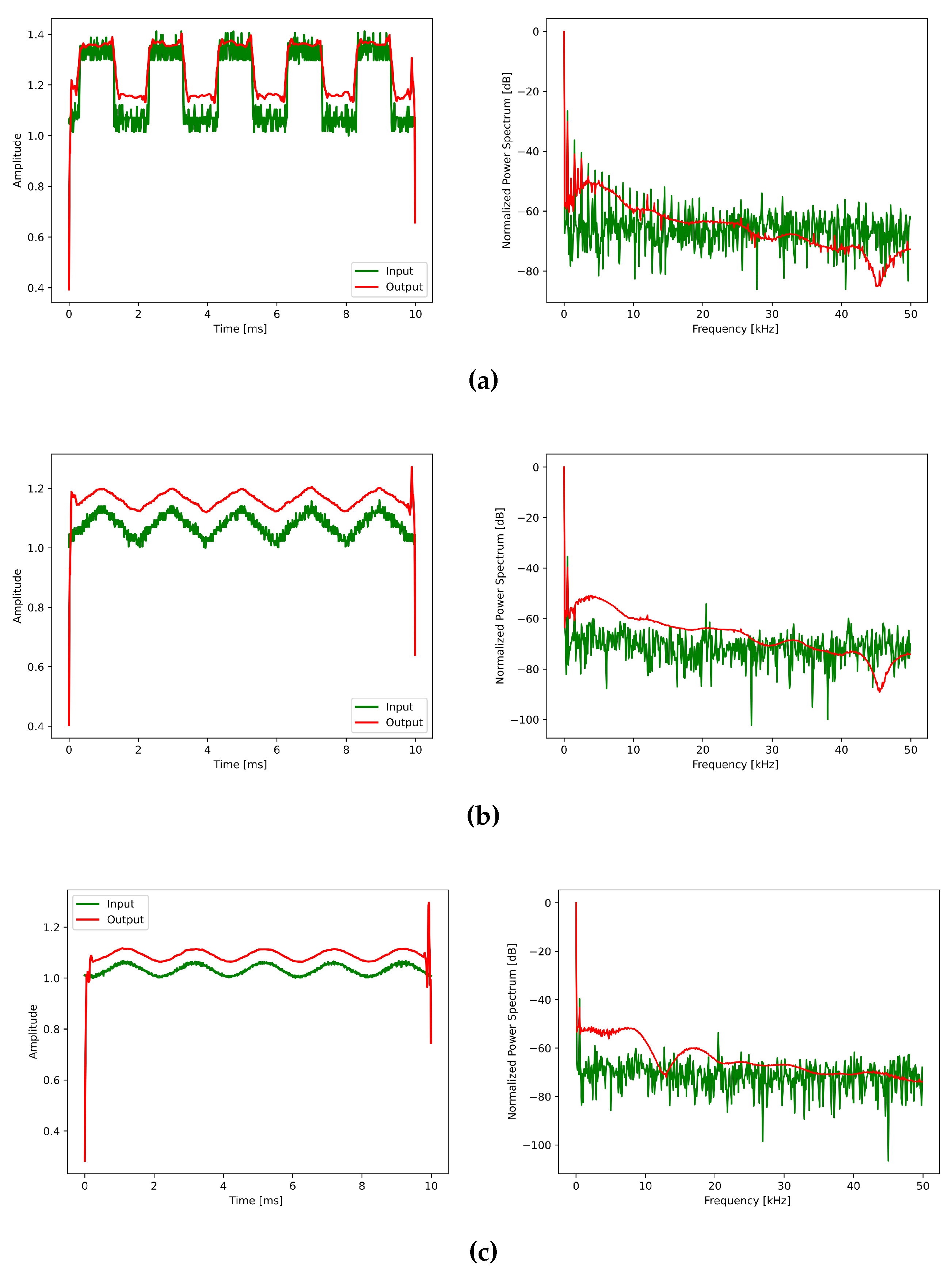
Preprints 113300 g008
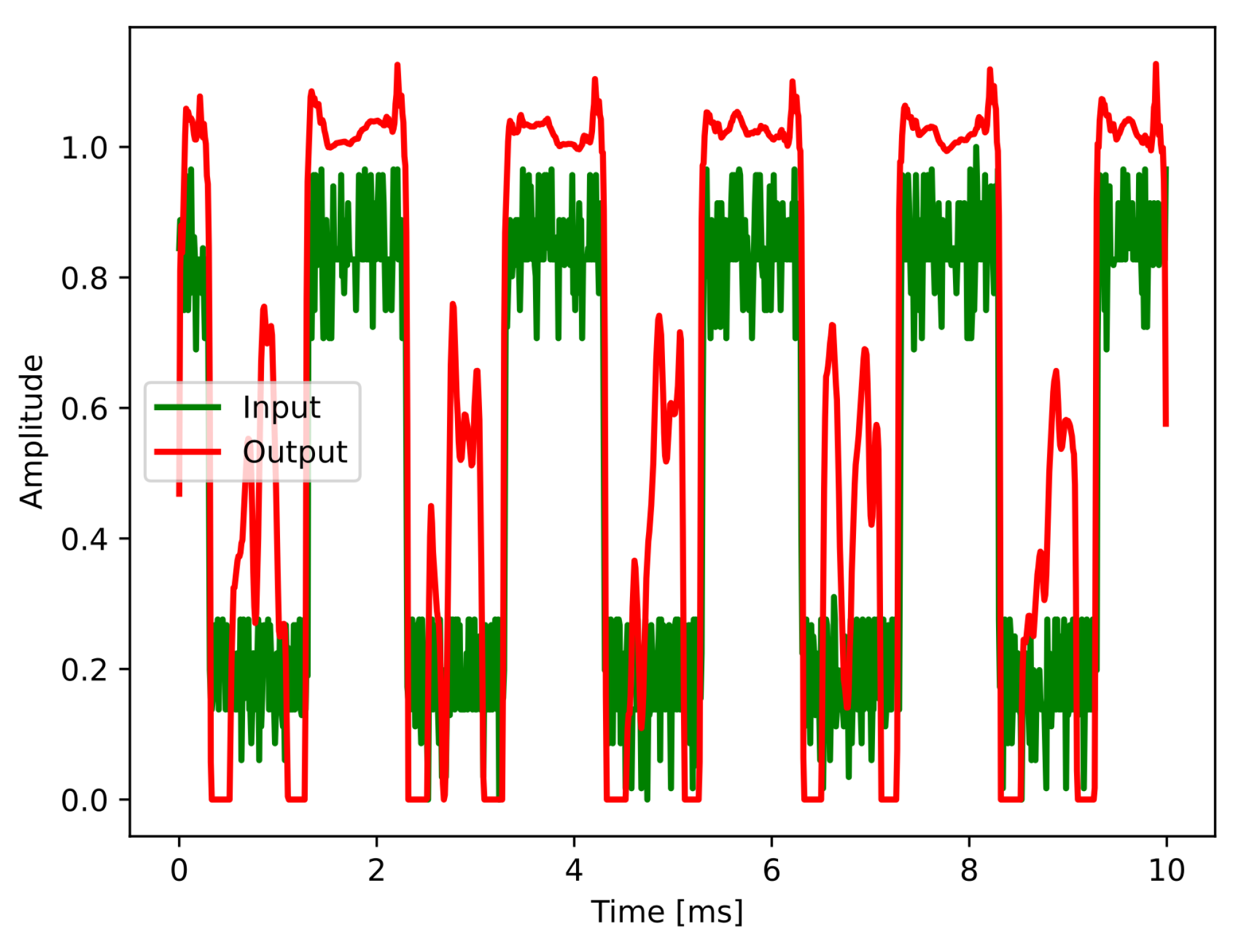
Preprints 113300 g009
Figure 9. Example of error in the denoising process.
Figure 9. Example of error in the denoising process.
Preprints 113300 g009
Table 1. Elapsed Time
Table 1. Elapsed Time
Waveform Time [secs]
Rectangular 82.7
Triangular 82.2
Sine 81.5
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated