Prerpints.org logo
Preprint
Article

Improved Thermal Stability under High Power Conversion Efficiency Condition in Inverted Ternary Organic Solar Cells with Three Different Electron Transport Layers

Altmetrics

Downloads

120

Views

121

Comments

0

Submitted:

25 July 2024

Posted:

26 July 2024

You are already at the latest version

Alerts
Abstract
The efficiency of organic solar cells (OSCs) is influenced by various factors, among which environmental temperature plays a significant role. Previous studies have shown that the thermal stability of these cells can be enhanced by incorporating a third component into their structure. Ternary organic solar cells, in particular, have shown promising results in improving thermal stability. A well-designed electron transport layer (ETL) can significantly bolster thermal stability by facilitating efficient charge transport and reducing charge recombination. In this study, we investigated the effect of temperature on the efficiency of inverted ternary structures, ranging from 300 K to 400 K. The structures examined include FTO/SnO2/PM6:D18:L8-BO/PEDOT: PSS/Ag, FTO/Spiro-OMeTAD/PM6:D18:L8-BO/PEDOT: PSS/Ag, and FTO/PC60BM/PM6:D18:L8-BO/PEDOT: PSS/Ag. Through simulations employing three different electron transport layers—SnO2, Spiro-OMeTAD, and PC60BM—we observed that at 340 K (65°C) these structures maintained 92% of their original high efficiency of ~20% at 300 K, which represents a high level of thermal stability under the high PCE condition.
Keywords: 
Subject: Chemistry and Materials Science  -   Electronic, Optical and Magnetic Materials

1. Introduction

Nowadays, the international community faces a multifaceted global energy challenge, closely intertwined with the issue of global warming primarily induced by greenhouse gases, especially CO2, in the atmosphere [1,2,3,4,5,6]. Fossil fuels, as the principal sources of approximately 90% of CO2 emissions and over 70% of all greenhouse gas emissions worldwide, are significant drivers of climate change [7,8,9,10,11,12]. These gases trap solar heat, contributing to a rise in global temperatures [13,14,15,16].
Addressing global warming necessitates sustainable interventions, including reducing air pollution, which can be achieved through adopting renewable energy sources, minimizing waste, and conserving natural resources [13,17,18,19]. In this context, photovoltaic energy emerges as a sustainable and long-lasting solution that could mitigate the impacts of global warming [20,21,22]. OSCs, in particular, represent a promising alternative to traditional silicon-based panels due to their environmental benefits and cost-efficiency in production [23]. Their widespread adoption could significantly enhance global solar energy utilization and reduce the ecological impacts of human activities [20]. Particularly, the role of OSCs in reducing global warming effects is increasingly recognized [23,24,25]. Although their potential benefits are substantial, further research and development are critical to improve their efficiency and thermal stability [26,27,28,29,30].
Improving the thermal stability of OSCs is vital for advancing their commercial viability and operational reliability. Ongoing research focuses on developing new materials and structures that optimize both power conversion efficiency (PCE) and thermal stability. Recent research by Zhang et al.[29] highlights the efficacy of the ternary blend approach in enhancing the thermal stability of OSCs, and it was found that the PCE of the device at 75°C remained on average 80% of its PCE at 25°C. Key contributors to the charge-transfer state energy in these cells were identified as PBDB-T and IDT-PDOT-C6, with ITC6-2F playing a crucial role in facilitating charge carrier transfers to IDT-PDOT-C6. This mechanism promotes the generation of additional excitons reaching the donor/acceptor interface, thereby achieving high-efficiency photoelectric conversion [29]. Anass et al.[31] studied the temperature influence on the performance of the solar cells with [(Cbz-Mth)-B-T]2–PCBM as an active blend, and they found that their structure kept 89% of its room-temperature PCE at 75°C. Another study done by Muhammad et al.[32] performed a simulation by stepping up the temperature from 300 K to 400 K to study the impact of the raised temperature on the efficiency of their solar cells with PBDB-T: ITIC-OE as a photoactive layer, and they obtained a loss ratio of the efficiency between the temperature range of 300-350 K to approximately 9%, which is a highly stable device. Moreover, the use of charge transport layers is paramount in improving the PCE of OSCs. These layers are essential for the efficient extraction and mobility of charges, while also preventing electron leakage, and are utilized extensively across various materials in the inverted OSCs architecture [33,34,35,36,37]. The previous studies found that the best thermal stability achieved by OSCs at 350 K is 9% in the studies done by Anass et al.[31] and Muhammad et al. [32], but PCEs achieved in these studies are 7.4% and 6.2%, respectively, which are relatively low. It is challenging to achieve high thermal stability and high PCE at the same time.
This study aims to explore how temperature variations affect the efficiency of inverted bulk heterojunction (BHJ) OSCs. Through simulations using three different electron transport layers—SnO2, Spiro-OMeTAD, and PC60BM, we seek to derive insights into the performance and thermal stability of these cells, specifically focusing on analyses of their high thermal stability (quantified by the PCE loss ratio) at 350K under the high PCE of ~ 20%. This could potentially lead to the development of more efficient and stable OSCs in laboratory settings.

2. The Simulation Model

The simulation employs Oghma-Nano software, which utilizes a 1-dimensional drift-diffusion model for its electrical modeling. The model includes the solution of bi-polar drift-diffusion, charge carrier continuity, Poisson equation, and Maxwell-Boltzmann equation for free charge carrier statistics. The mathematical model can be found in the software's documentation for more detailed information [38]. The simulated structure of the device is FTO/SnO2/PM6:D18:L8-BO/ PEDOT: PSS/Ag, and the input parameters and thickness are included in Table 1, Table 2, Table 3 and Table 4.
Bi-polar drift-diffusion equations at the position for both electrons and holes are represented in Equations (1) and (2),
J n = q μ e n f ∂ φ ∂ x + q D n ∂ n ∂ x
and
J p = q μ h p f ∂ φ ∂ x + q D p ∂ p ∂ x
where Jn,p is the electron and hole current density, q is the elementary charge, μe, and μh are the mobilities of electrons and holes, respectively; Dn and Dp are the electron and hole diffusion coefficients, respectively; n is the density of electrons, and p is the density of holes. The charge carrier continuity equations are mentioned in Equations (3) and (4),
∂ J n ∂ x = q (   R n − G + ∂ n ∂ t   )
and
∂ J p ∂ x = − q (   R p − G + ∂ p ∂ t )
where Rn and p are the recombination rate of electrons and holes, respectively; G is the generation rate.
The solution to Poisson's equation is used to determine the distribution of potential within the device, and it is represented as follows in Equation (5),
∂ ℇ 0   ℇ r ∂ x   ∂ φ ∂ x = q ( n − p )
where ɛ0, ɛr the constants of permittivity in free space and the relative permittivity are constant, respectively; φ is the voltage profile. The model applies Maxwell-Boltzmann statistics to solve free carriers statistics as mentioned in Equations (6) and (7),
n = N c e x p ⁡ F n − E c K B T
and
p = N v e x p ⁡ E v − F p K B T
where Nc, Nv are the constants of the effective density of states in the conduction and valence band of a semiconductor, Fn,p are constants of the energy level of the Fermi level in the valence and conduction band of a semiconductor, Ec is the conduction band, Ev is the valence band, KB is Boltzmann constant, T is the temperature.
The boundary conditions between the layer interfaces are represented as tunneling of electrons and holes through layer interfaces provided by Equations (8) and (9),
J n = − q T e n 1 − n 1 e q − n 0 − n 0 e q
and
J p = − q T h p 1 − p 1 e q − p 0 − p 0 e q
where Te and Th is the rate constants of tunneling of electrons and holes, respectively, n1,2 is the number of electrons in the layers before and after the interface; p1,2 is the number of holes before and after the interface; n 1,2 e q is the equilibrium number of electrons in before and after the interface; p 1,2 e q is the equilibrium number of holes in the layers before and after the interface.
More details of the above electrical model of our simulation can be found in Refs. [39,40,41].

3. Results and discussion

The density of current-voltage (J-V) was simulated under AM 1.5 G illumination with an intensity of 100 mW cm-2 and a temperature range between 300 K and 400 K. The 1st structure is represented in Figure 1, and its results are presented in Figure 2 and Figure 3. S1 showed the best PCE of 20.08 % at 300 K with a short circuit current (Jsc) of 27.4 mA cm-2, an open circuit voltage (Voc) of 0.89 V, and a fill factor (FF) of 82.2%, while the performance relatively decreased between the range of 310 and 400 K to reach a PCE of 15.53%, a Jsc of 27.35 mAcm-2, a Voc of 0.73 V, and a FF of 77.7% at 400 K. As the results mentioned, the major parameters that cause a reduction in the efficiency of OSCs during the enhancement of temperature are the Voc and FF (see Figure 3 (b),(c)).
q V o c = E g − Δ E
and
Δ E = 2 E F , h − E H O M O D − K B T l n µ e   µ h
where EF,h is the energy corresponding fermi-level; E H O M O D is the electron donor energy.
The increase in temperature causes an augmentation of the energy loss (ΔE) as demonstrated by eq (11), and then the Voc decreases as a result of that augmentation. The FF showed a negative correlation with temperature which decreased when the temperature increased from 300K to 400K ( from 26.85°C to 126.85 °C). The performance decrease of FF due to the increase of the exponential of the temperature as demonstrated in eq (12). The Jsc showed relative stability under the increase in temperature. The reduction in Jsc can be attributed to the bandgap energy (Eg) effect.
The FF determines the maximum power output by the OSC, it is defined below in eq (12),
F F = P m a x V o c J s c = V m V o c 1 − e q A k T ( V m − V o c )
where Pmax is the maximum power delivered by the OSC, Vm is the maximum voltage, A is the ideality factor of the semiconductor.
As temperature rises, the Jsc experiences a marginal increase due to the reduction in Eg. Consequently, a greater number of photons possess adequate energy to generate electron-hole pairs. Nevertheless, the impact of this phenomenon is quite minor. The exponential relationship between temperature and the reverse saturation current of photovoltaic cells is observed in eq (13). Additionally, this factor can have an impact on the Jsc.
J V = J 0 e x p e V A K T − 1 + J p h
where J0 is the reverse saturation current density, e is the charge of an electron, and Jph is the photo-current density.
The 2nd structure is presented in Figure 4, and its results are presented in Figure 5 and Figure 6. S2 showed the best PCE of 20.11% at 300 K with a Jsc of 27.43 mA cm-2, a Voc of 0.89 V, and an FF of 82.3%, while the efficiency relatively decreased between the range of 310 and 400 K to reach a PCE of 15.55%, a Jsc of 27.38 mA cm-2, a Voc of 0.73, and a FF of 78% at 400 k. The results are slightly the same as S1. As S2 results depicted, the major parameters that cause a decrease in the performance of this device during the enhancement of temperature are fundamentally the same as before Voc and FF (see Figure 6 (b), (c)).
The increase in temperature caused an enhancement of the ΔE as demonstrated by eq (11), and then the Voc decreased as a consequence of that enhancement. The diminution in Jsc can be attributed to the concept of Eg. As temperature rises, the short-circuit current, Jsc, experiences a slight increase due to the reduction in Eg. This decrease in bandgap energy enables a greater number of photons to possess sufficient energy for the generation of excitons. The reverse saturation current of photovoltaic cells exhibits an exponential growth pattern about temperature. Additionally, this factor can have an impact on the magnitude of the Jsc as demonstrated in eq (15).
The 3rd structure is presented in Figure 7, and its outcomes are depicted in Figure 8 and Figure 9. At a temperature of 300 K, S3 exhibited the highest PCE of 18.9%. This was accompanied by a Jsc of 25.8 mA cm-2, a Voc of 0.89 V, and a FF of 82.36%. However, when the temperature increased within the range of 310 to 400 K, the performance of S3 declined.
At 400 K, the PCE reduced to 14.6%, with a Jsc of 25.76 mA cm-2, a Voc of 0.73 V, and an FF of 78%. According to the findings from the S3 results, it can be observed that the primary factors contributing to the decline in device performance as temperature increases remain consistent with the Voc, and FF (refer to Figure 9 (b),(c)).
The rise in temperature leads to an increase in ΔE, as indicated by eqs (10, 11). Consequently, the Voc decreases as a result of this increase. The decrease in Jsc can be ascribed to Eg. The Jsc undergoes a marginal augmentation as the temperature increases, primarily as a result of the decrease in the Eg. The reduction in bandgap energy facilitates an increased likelihood of photons possessing the necessary energy to produce electron-hole pairs. The temperature-dependent behavior of photovoltaic cells' reverse saturation current is characterized by an exponential increase as noted before in S1 and S2. Moreover, this particular element can influence the amount of Jsc, as exemplified in eq (11).
We observe that All the structures S1, S2, and S3 showed good performance under the temperature range between 300 and 340K (from 26.85°C to 66.85 °C) (see Figure 5), which they lost from their initial efficiency of only 8.8%, 8.8%, 8.9%, respectively. The performance parameters Jsc, Voc, and FF showed slightly the same progression, while S3 depicted less PCE of 18.9% in comparison to S1 and S2 depicted 20.08%, and 20.11%, respectively. The inverted structure employing SnO2 and Spiro-OMeTAD achieved the best PCE of 20.08% and 20.11%, respectively, in the other hand, the inverted structure using PC60BM as an electron transport layer (ETL) showed less PCE. But, all devices worked efficiently in terms of performance.
All the studies showed a stable loss ratio of 11 % between 300 k and 350 K according to the results mentioned in Table 5. We investigated our results of the loss ratio of PCE in the function of raising the temperature with some other numerical studies as mentioned in Table 6. The current study demonstrated the thermal stability of a device with a loss ratio of 11% throughout a temperature from 300 K to 350 K, in contrast to the results of Khan et al. and Kim et al., whose studies reported loss ratios of 15% and 17%, respectively. The studies done by Anass et al. and Muhammad et al. have demonstrated an enhancement in thermal stability when compared to previous research. Furthermore, in addition to its thermal stability, our structure has demonstrated a much higher PCE than Anass et al. And Muhammad et al. Our structures can maintain high thermal stability at high PCE conditions, representing a notable advancement in the OSCs. Our structures can maintain high thermal stability at high PCE conditions of ~20%.

4. Conclusions

Our research demonstrated that the efficiency of inverted ternary organic solar cells incorporating SnO2, Spiro-OMeTAD, and PC60BM is robust to temperature increases, sustaining less than 10% efficiency loss at 65°C compared to their baseline efficiency at 25°C. This finding underscores the commendable thermal stability of these structures. In addition, we achieved such thermal stability at the high PCE condition, indicating superb environmental adaptability of investigated structures. However, the configuration using PC60BM as the electron transport layer exhibits relatively lower PCE, highlighting an area for potential improvement. Future studies should expand on these preliminary findings with comprehensive evaluations focusing on the effects of operational temperature on newly synthesized organic semi-conductor materials to discover more stable structures and futher increase the thermal stability of the organic solar cells. This includes investigating charge mobilities, optimizing cooling systems, assessing material quality, and testing endurance under varying ambient temperatures.

Author Contributions

M.E.A.B.: conceptualization, methodology, writing original draft preparation, formal analysis, investigation and data curation; Q.W.: resources, writing review and editing; C.Z.: formal analysis, investigation, project administration, resources, funding acquisition and supervision. All authors have read and agreed to the published version of the manuscript.

Data Availability Statement

The data are available upon reasonable requests from the corresponding author.

Conflicts of Interest

The authors declare no conflict of interest.

Nomenclature

q The electrical charge
n The concentration of free electrons
n0 The equilibrium density of electron
Nc,v The effective density of states in the conduction band
p0 Equilibrium density of holes
P Concentration of free holes
Jn,p The current density of the electrons and holes
vth The thermal emission velocity of the carriers
Ec,v The conduction and valence band
EF,h,e The energy corresponding fermi-level
Fn,p The Fermi level in the conduction and valence band
Dn,p The diffusion coefficient of the electrons and holes
Rn The recombination rate of electrons
Rp The recombination rate of holes
G The carrier generation rate
KB Boltzmann constant
T The Temperature
Greek Symbols
ℇ 0 The permittivity of free space
ℇ r Relative permittivity
φ The voltage profile
µe,h Electron and hole mobility
ΔE The energy offset
ω The angular frequency of the wave
λ The wavelength
Superscripts
D Electron donor
A Electron Acceptor

References

  1. E. D. COYLE and R. A. SIMMONS, Eds., “Introduction,” in Understanding the Global Energy Crisis, Purdue University Press, 2014, pp. 1–8. [Online]. Available: http://www.jstor.org/stable/j.ctt6wq56p.5.
  2. H. Melin, “Towards a solution to the energy crisis,” Nat Astron, vol. 4, no. 9, pp. 837–838, 2020. [CrossRef]
  3. D. Mhlanga and E. Ndhlovu, “The Implications of the Russia–Ukraine War on Sustainable Development Goals in Africa,” Fudan Journal of the Humanities and Social Sciences, vol. 16, no. 4, pp. 435–454, 2023. [CrossRef]
  4. P. F. Borowski, “Mitigating Climate Change and the Development of Green Energy versus a Return to Fossil Fuels Due to the Energy Crisis in 2022,” Energies (Basel), vol. 15, no. 24, 2022. [CrossRef]
  5. J. A. Burney, “The downstream air pollution impacts of the transition from coal to natural gas in the United States,” Nat Sustain, vol. 3, no. 2, pp. 152–160, 2020. [CrossRef]
  6. Y. Guan et al., “Burden of the global energy price crisis on households,” Nat Energy, vol. 8, no. 3, pp. 304–316, 2023. [CrossRef]
  7. F. Creutzig, “Fuel crisis: slash demand in three sectors to protect economies and climate.,” Nature, vol. 606, no. 7914, pp. 460–462, Jun. 2022. [CrossRef]
  8. Y. Parag, T. Fawcett, S. Hampton, and N. Eyre, “Energy saving in a hurry: A research agenda and guidelines to study European responses to the 2022–2023 energy crisis,” Energy Res Soc Sci, vol. 97, p. 102999, 2023. [CrossRef]
  9. “The politics of energy security,” Nat Energy, vol. 8, no. 10, p. 1047, 2023. [CrossRef]
  10. N. Frilingou et al., “Navigating through an energy crisis: Challenges and progress towards electricity decarbonisation, reliability, and affordability in Italy,” Energy Res Soc Sci, vol. 96, p. 102934, 2023. [CrossRef]
  11. T. Ingram, M. Wieczorek-Kosmala, and K. Hlaváček, “Organizational Resilience as a Response to the Energy Crisis: Systematic Literature Review,” Energies (Basel), vol. 16, no. 2, 2023. [CrossRef]
  12. J. D. Hunt., D. Stilpen, and M. A. V. de Freitas, “A review of the causes, impacts and solutions for electricity supply crises in Brazil,” Renewable and Sustainable Energy Reviews, vol. 88, pp. 208–222, 2018. [CrossRef]
  13. D. J. Wuebbles, D. W. Fahey, and K. A. Hibbard, “Climate Science Special Report: Fourth National Climate Assessment, Volume I.” in U.S. National Climate Assessment. United States, 2017. doi: doi: 10.7930/J0J964J6.
  14. D. Klingelhöfer, R. Müller, M. Braun, D. Brüggmann, and D. A. Groneberg, “Climate change: Does international research fulfill global demands and necessities?,” Environ Sci Eur, vol. 32, no. 1, p. 137, 2020. [CrossRef]
  15. D. Welsby, J. Price, S. Pye, and P. Ekins, “Unextractable fossil fuels in a 1.5 °C world,” Nature, vol. 597, no. 7875, pp. 230–234, 2021. [CrossRef]
  16. C. Kroeger, “Heat is associated with short-term increases in household food insecurity in 150 countries and this is mediated by income,” Nat Hum Behav, vol. 7, no. 10, pp. 1777–1786, 2023. [CrossRef]
  17. C. Guivarch et al., “Using large ensembles of climate change mitigation scenarios for robust insights,” Nat Clim Chang, vol. 12, no. 5, pp. 428–435, 2022. [CrossRef]
  18. P. Achakulwisut, P. Erickson, C. Guivarch, R. Schaeffer, E. Brutschin, and S. Pye, “Global fossil fuel reduction pathways under different climate mitigation strategies and ambitions,” Nat Commun, vol. 14, no. 1, p. 5425, 2023. [CrossRef]
  19. C. Kemfert, F. Präger, I. Braunger, F. M. Hoffart, and H. Brauers, “The expansion of natural gas infrastructure puts energy transitions at risk,” Nat Energy, vol. 7, no. 7, pp. 582–587, 2022. [CrossRef]
  20. V. Masson, M. Bonhomme, J.-L. Salagnac, X. Briottet, and A. Lemonsu, “Solar panels reduce both global warming and urban heat island,” Front Environ Sci, vol. 2, 2014. [CrossRef]
  21. N. A. Dunne, P. Liu, A. F. A. Elbarghthi, Y. Yang, V. Dvorak, and C. Wen, “Performance evaluation of a solar photovoltaic-thermal (PV/T) air collector system,” Energy Conversion and Management: X, vol. 20, p. 100466, 2023. [CrossRef]
  22. F. J. M. M. Nijsse et al., “The momentum of the solar energy transition,” Nat Commun, vol. 14, no. 1, p. 6542, 2023. [CrossRef]
  23. N. Thejo Kalyani and S. J. Dhoble, “Chapter 10 - Empowering the Future With Organic Solar Cell Devices,” in Nanomaterials for Green Energy, B. A. Bhanvase, V. B. Pawade, S. J. Dhoble, S. H. Sonawane, and M. Ashokkumar, Eds., in Micro and Nano Technologies. , Elsevier, 2018, pp. 325–350. [CrossRef]
  24. L. X. Chen, “Organic Solar Cells: Recent Progress and Challenges,” ACS Energy Lett, vol. 4, no. 10, pp. 2537–2539, Oct. 2019. [CrossRef]
  25. D. Lee, J. Kim, G. Park, H. W. Bae, M. An, and J. Y. Kim, “Enhanced Operating Temperature Stability of Organic Solar Cells with Metal Oxide Hole Extraction Layer,” Polymers (Basel), vol. 12, no. 4, 2020. [CrossRef]
  26. P. Cheng and X. Zhan, “Stability of organic solar cells: challenges and strategies,” Chem. Soc. Rev., vol. 45, no. 9, pp. 2544–2582, 2016. [CrossRef]
  27. L. Duan and A. Uddin, “Progress in Stability of Organic Solar Cells,” Advanced Science, vol. 7, no. 11, p. 1903259, 2020. [CrossRef]
  28. W. Yang et al., “Balancing the efficiency, stability, and cost potential for organic solar cells via a new figure of merit,” Joule, vol. 5, no. 5, pp. 1209–1230, 2021. [CrossRef]
  29. C. Zhang et al., “High-efficiency ternary nonfullerene organic solar cells with record long-term thermal stability,” J. Mater. Chem. A, vol. 8, no. 43, pp. 22907–22917, 2020. [CrossRef]
  30. X. Xu et al., “Thermally stable, highly efficient, ultraflexible organic photovoltaics,” Proceedings of the National Academy of Sciences, vol. 115, no. 18, pp. 4589–4594, 2018. [CrossRef]
  31. El Karkri, Z. El Malki, M. Bouachrine, F. Serein-Spirau, and J.-M. Sotiropoulos, “Characterization and simulation study of organic solar cells based on donor–acceptor (D–π–A) molecular materials,” RSC Adv., vol. 10, no. 32, pp. 18816–18823, 2020. [CrossRef]
  32. M. R. Khan and B. Jarząbek, “Optimization and Efficiency Enhancement of Modified Polymer Solar Cells,” Aug. 2023. [CrossRef]
  33. C. Anrango-Camacho, K. Pavón-Ipiales, B. A. Frontana-Uribe, and A. Palma-Cando, “Recent Advances in Hole-Transporting Layers for Organic Solar Cells,” Nanomaterials, vol. 12, no. 3, 2022. [CrossRef]
  34. H. Tang et al., “Interface Engineering for Highly Efficient Organic Solar Cells,” Advanced Materials, vol. n/a, no. n/a, p. 2212236. [CrossRef]
  35. J. Niederhausen, K. A. Mazzio, and R. W. MacQueen, “Inorganicorganic interfaces in hybrid solar cells,” Electronic Structure, vol. 3, no. 3, p. 33002, Sep. 2021. [CrossRef]
  36. T. Kong, R. Wang, D. Zheng, and J. Yu, “Modification of the SnO2 Electron Transporting Layer by Using Perylene Diimide Derivative for Efficient Organic Solar Cells,” Front Chem, vol. 9, 2021. [CrossRef]
  37. A. Eliwi et al., “Optimization of SnO2 electron transport layer for efficient planar perovskite solar cells with very low hysteresis,” Mater. Adv., vol. 3, no. 1, pp. 456–466, 2022. [CrossRef]
  38. “Manual: OghmaNano - Organic and hybrid Material Nano Simulation tool.” Accessed: Dec. 06, 2023. [Online]. Available: https://www.oghma-nano.com/docs.html?page=Manual.
  39. R. C. I. MacKenzie et al., “Interpreting the Density of States Extracted from Organic Solar Cells Using Transient Photocurrent Measurements,” The Journal of Physical Chemistry C, vol. 117, no. 24, pp. 12407–12414, Jun. 2013. [CrossRef]
  40. F. Deschler, D. Riedel, B. Ecker, E. von Hauff, E. Da Como, and R. C. I. MacKenzie, “Increasing organic solar cell efficiency with polymer interlayers,” Phys. Chem. Chem. Phys., vol. 15, no. 3, pp. 764–769, 2013. [CrossRef]
  41. R. C. I. MacKenzie, C. G. Shuttle, M. L. Chabinyc, and J. Nelson, “Extracting Microscopic Device Parameters from Transient Photocurrent Measurements of P3HT:PCBM Solar Cells,” Adv Energy Mater, vol. 2, no. 6, pp. 662–669, 2012. [CrossRef]
  42. L. Zhu et al., “Single-junction organic solar cells with over 19% efficiency enabled by a refined double-fibril network morphology,” Nat Mater, vol. 21, no. 6, pp. 656–663, 2022. [CrossRef]
  43. W. Farooq, A. D. Khan, A. D. Khan, and M. Noman, “Enhancing the power conversion efficiency of organic solar cells,” Optik (Stuttg), vol. 208, p. 164093, 2020. [CrossRef]
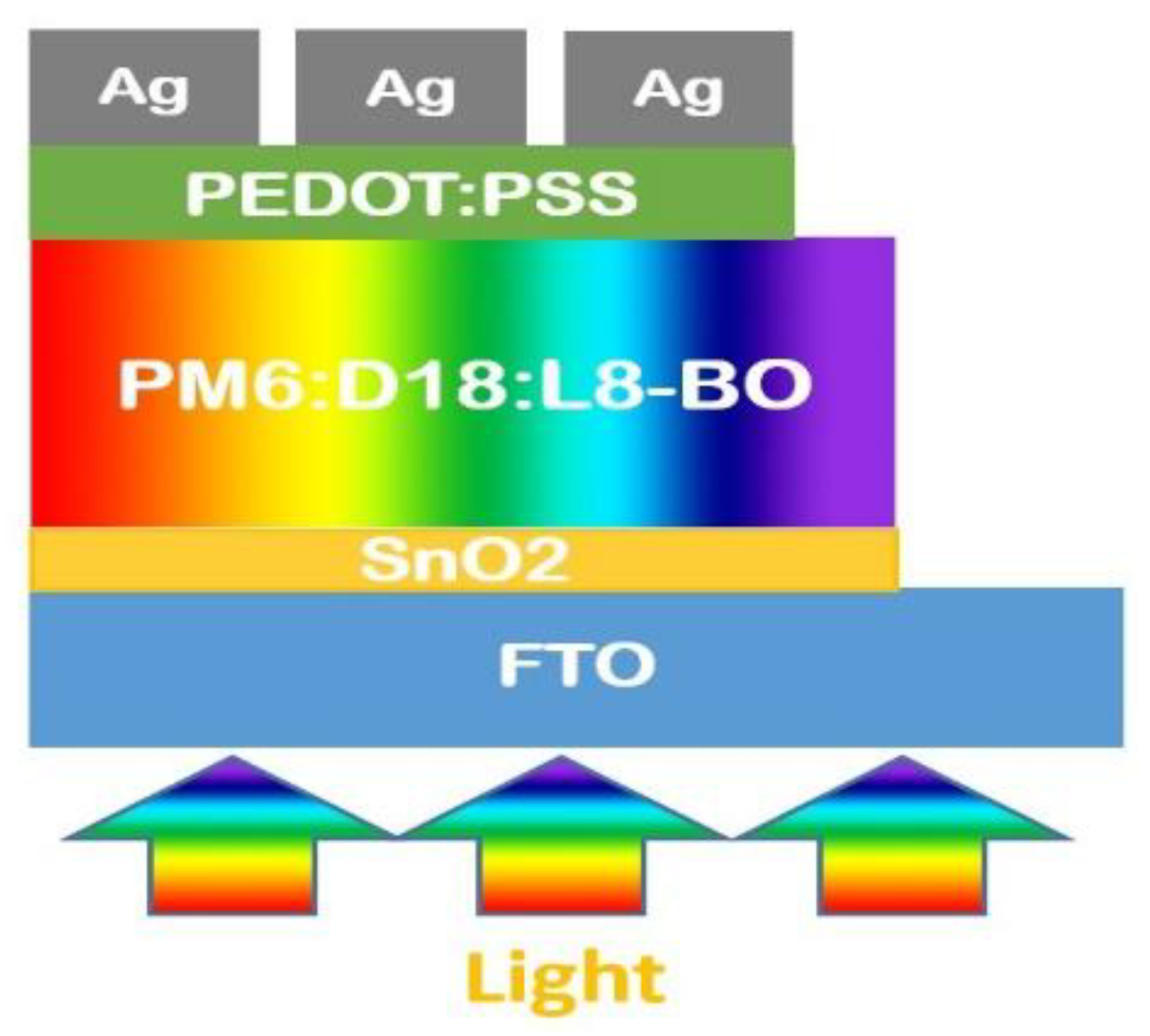
Preprints 113310 g001
Figure 1. Schematic of the structure of an S1 OSC model under light exposure.
Figure 1. Schematic of the structure of an S1 OSC model under light exposure.
Preprints 113310 g001
Preprints 113310 g002
Figure 2. J-V the curves of the S1 device in the temeprature range of 300-400 K for a device area of 4.84 mm2.
Figure 2. J-V the curves of the S1 device in the temeprature range of 300-400 K for a device area of 4.84 mm2.
Preprints 113310 g002
Preprints 113310 g003
Figure 3. The temperature affects the performance of the S1 device: (a) Jsc as a function of temperature; (b) Voc as a function of temperature; (c) FF as a function of temperature; and (d) PCE as a function of temperature.
Figure 3. The temperature affects the performance of the S1 device: (a) Jsc as a function of temperature; (b) Voc as a function of temperature; (c) FF as a function of temperature; and (d) PCE as a function of temperature.
Preprints 113310 g003
Preprints 113310 g004
Figure 4. Schematic of the structure of an S2 OSC model under light exposure.
Figure 4. Schematic of the structure of an S2 OSC model under light exposure.
Preprints 113310 g004
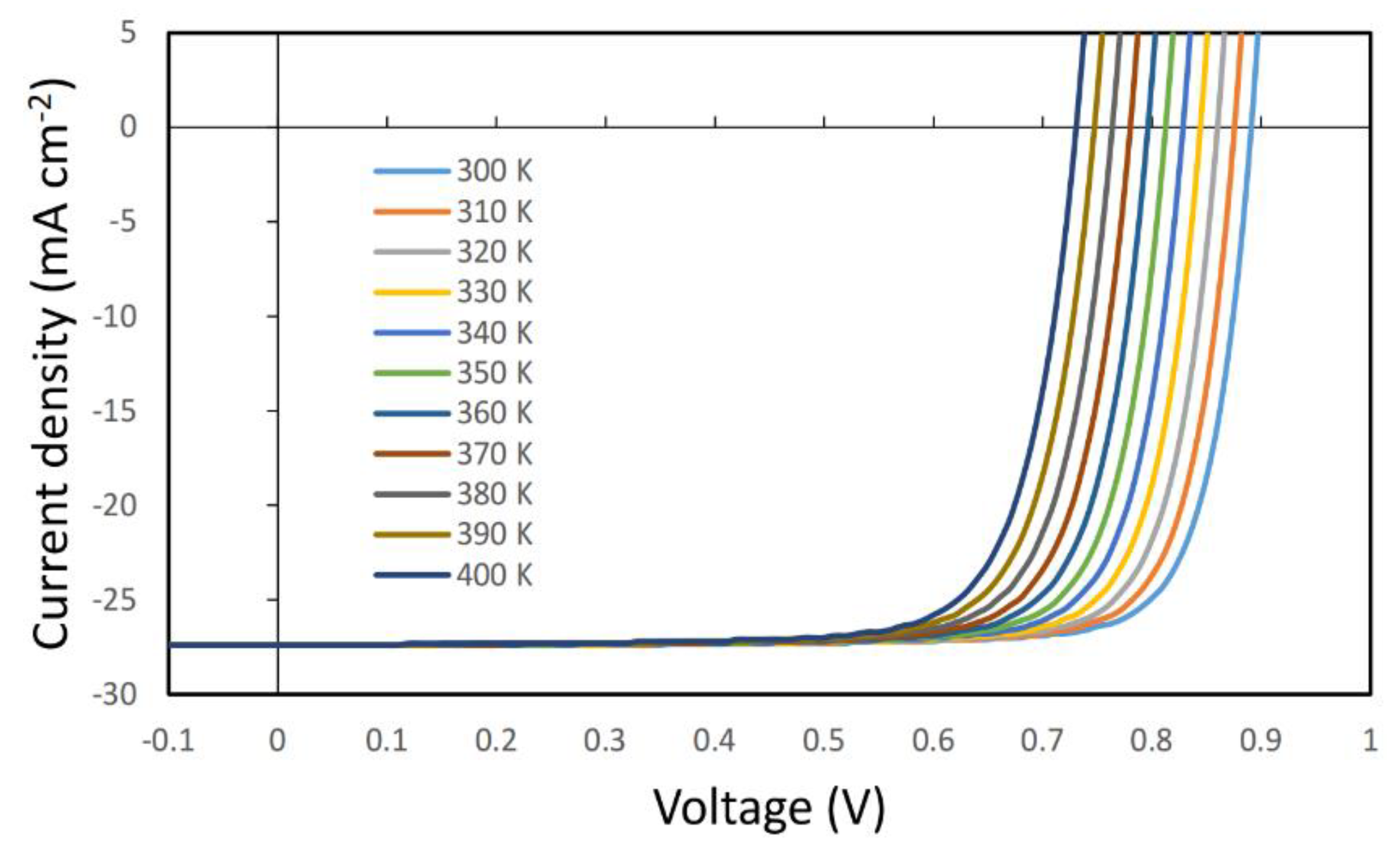
Preprints 113310 g005
Figure 5. J-V curves of the S2 device in the temperature range of 300-400 K for a device area of 4.84 mm2.
Figure 5. J-V curves of the S2 device in the temperature range of 300-400 K for a device area of 4.84 mm2.
Preprints 113310 g005
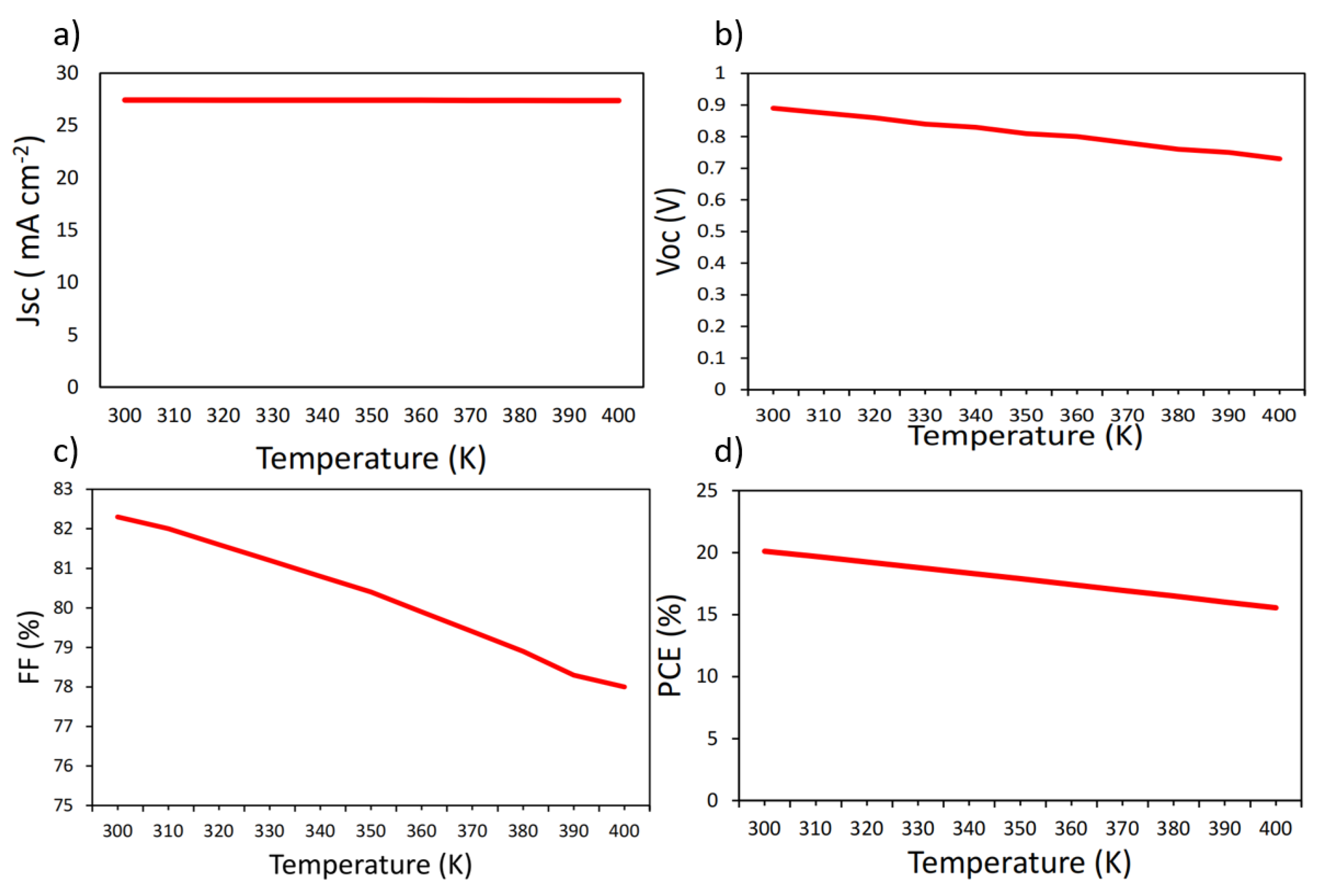
Preprints 113310 g006
Figure 6. The temperature affects the performance of the S2 device: (a) Jsc as a function of temperature; (b) Voc as a function of temperature; (c) FF as a function of the temperature; and (d) PCE as a function of temperature.
Figure 6. The temperature affects the performance of the S2 device: (a) Jsc as a function of temperature; (b) Voc as a function of temperature; (c) FF as a function of the temperature; and (d) PCE as a function of temperature.
Preprints 113310 g006
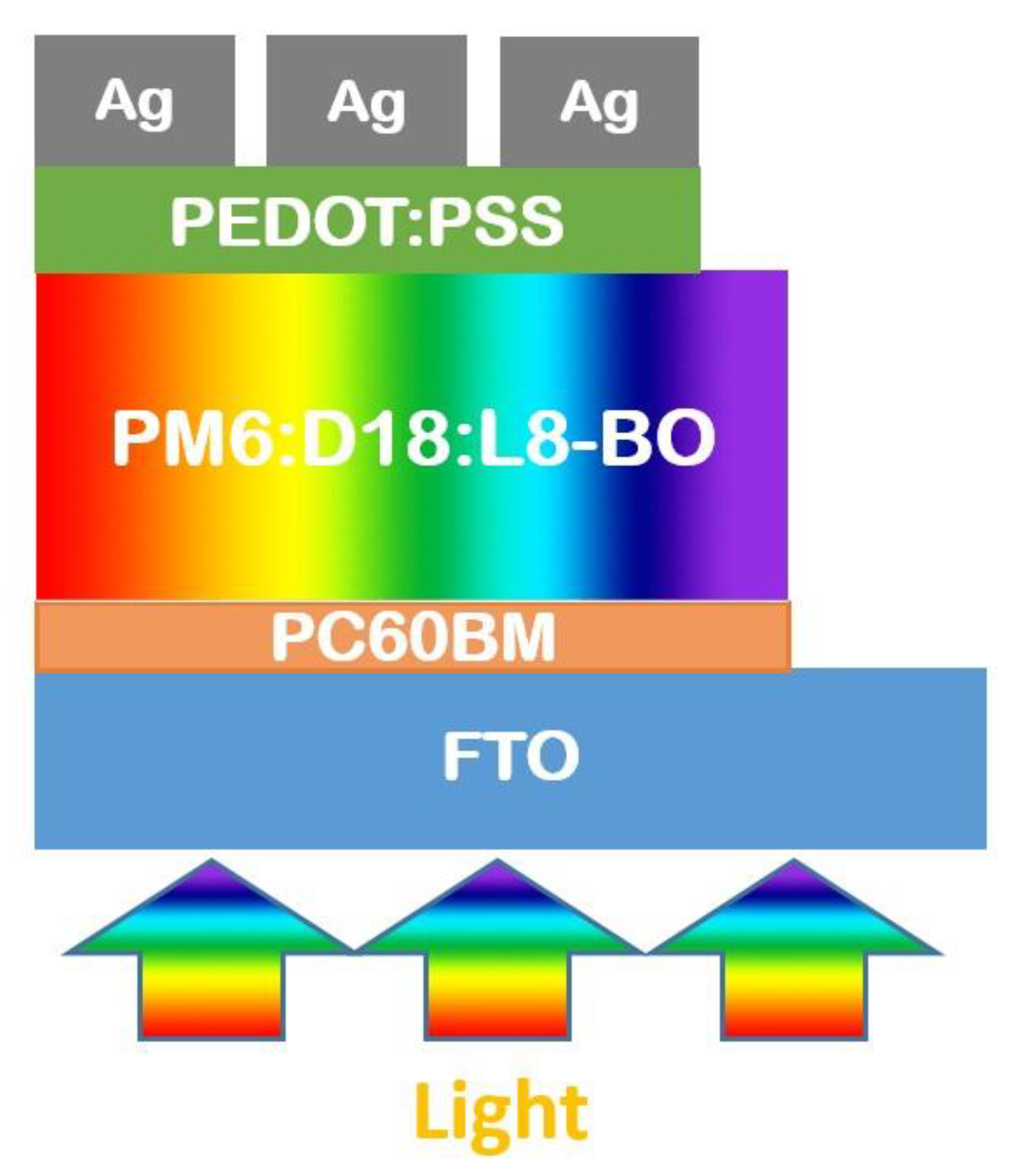
Preprints 113310 g007
Figure 7. Schematic of the structure of an S3 OSC model under light exposure.
Figure 7. Schematic of the structure of an S3 OSC model under light exposure.
Preprints 113310 g007
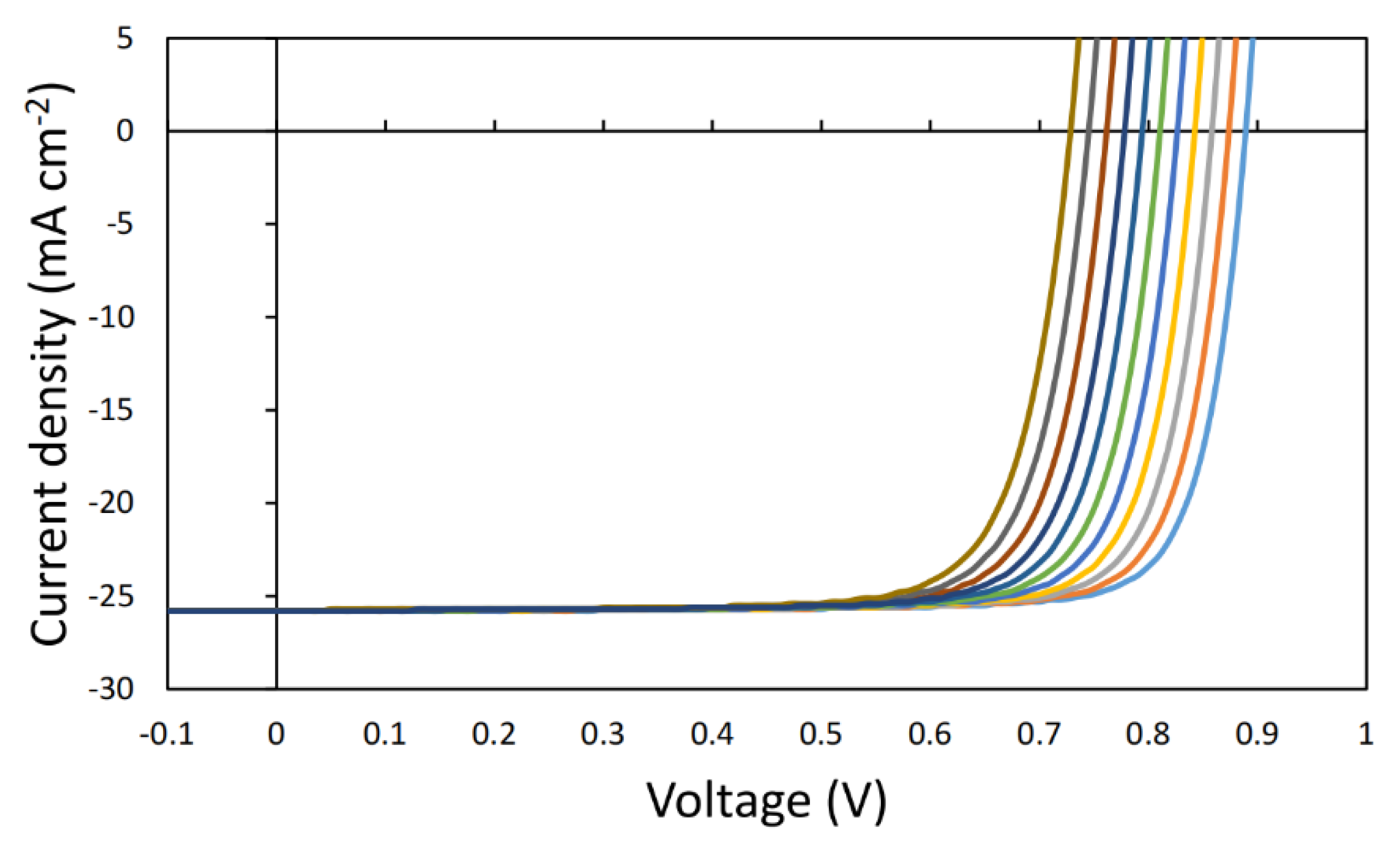
Preprints 113310 g008
Figure 8. J-V curves of S3 device in the temperature range of 300-400 K for a device area of 4.84 mm2.
Figure 8. J-V curves of S3 device in the temperature range of 300-400 K for a device area of 4.84 mm2.
Preprints 113310 g008
Preprints 113310 g009
Figure 9. The temperature affects the performance of the S3 device: (a) Jsc as a function of temperature; (b) Voc as a function of temperature; (c) FF as a function of the temperature; and (d) PCE as a function of temperature.
Figure 9. The temperature affects the performance of the S3 device: (a) Jsc as a function of temperature; (b) Voc as a function of temperature; (c) FF as a function of the temperature; and (d) PCE as a function of temperature.
Preprints 113310 g009
Table 1. Simulation parameters of Oghma-nano software.
Table 1. Simulation parameters of Oghma-nano software.
Parameters Values
Electron mobility (μe)
Hole mobility (μh)
Effective density of free electron (Nc at 300K)
Effective density of free hole (Nv at 300K)
n to P Recombination rate constant
Free carrier statistics
Density of states distribution (DoS)
Free electron (n) to Trapped electron (strap)
Trapped electron (ntrap) to Free hole (P)
Trapped Hole (Ptrap) to Free electron (n)
Free hole (P) to Trapped hole (Ptrap)
Number of traps (Nt)
Energy bandgap (Eg)
Relative permittivity (Ɛr)		 1.49e-07 m-2V-1s-1
1.42e-07 m-2V-1s-1
1e26 m-3
1e26 m-3
1.15e-17 m-3s-1
Maxwell Boltzmann-numerical + analysis
Complex
1e-15 m-2
1e-20 m-2
1e-20 m-2
1e-15 m-2
5 Trap
1.29 eV
3.0 a.u
Table 2. The thickness of the layers the blends S1 devices for optimum efficiency.
Table 2. The thickness of the layers the blends S1 devices for optimum efficiency.
Layer Thickness (nm) Materials Type
ITO 130 Oxides Contact
SnO2 5 Polymers Other
PM6:D18:L8-BO 80 Blends Active
PEDOT: PSS 20 Oxides Other
Ag 100 Metal Contact
Table 3. The thickness of the layers blends S2 devices for optimum efficiency.
Table 3. The thickness of the layers blends S2 devices for optimum efficiency.
Layer Thickness (nm) Materials Type
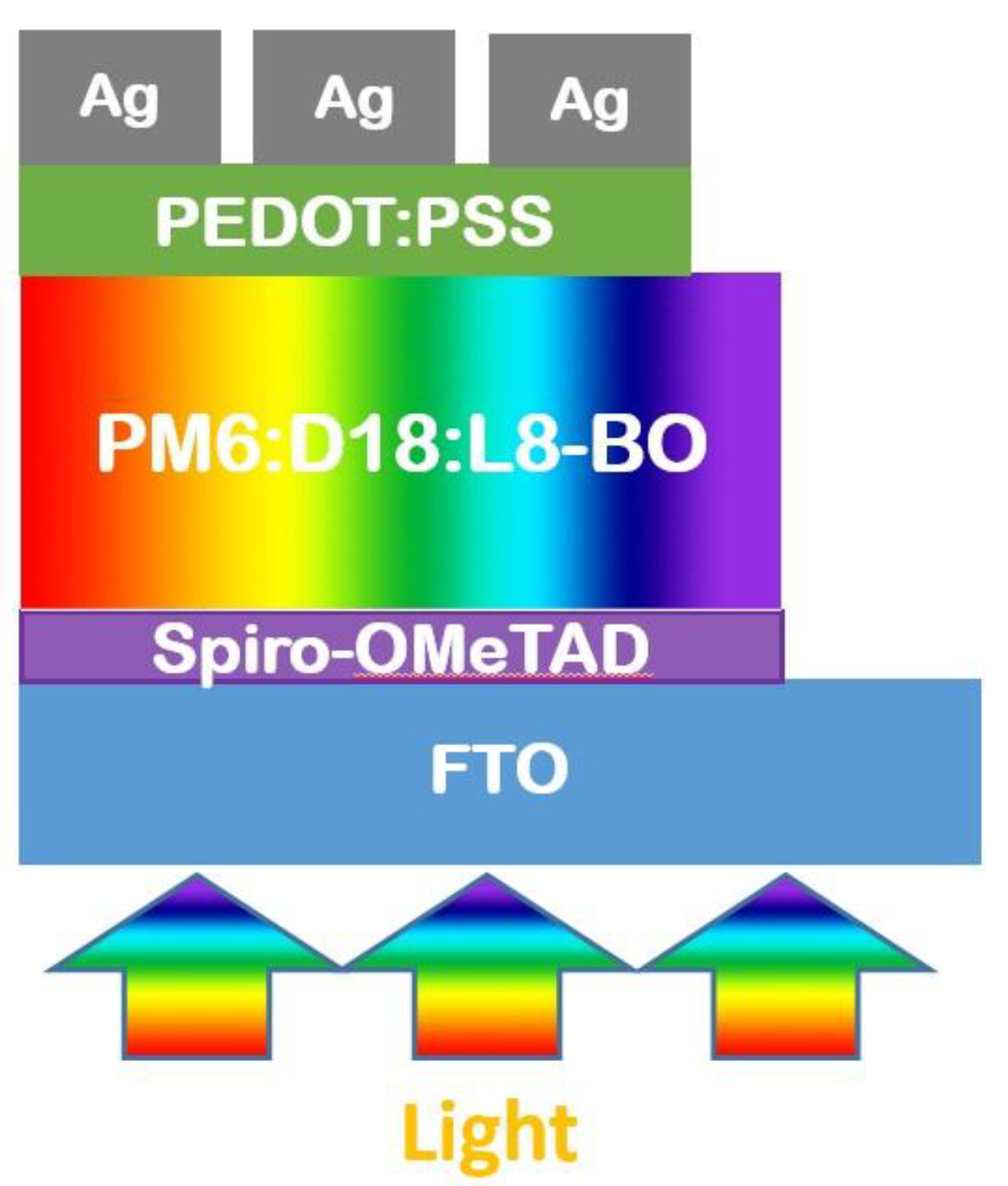
ITO 130 Oxides Contact
Spiro-OMeTAD 5 Polymers Other
PM6:D18:L8-BO 80 Blends Active
PEDOT: PSS 20 Oxides Other
Ag 100 Metal Contact
Table 4. The thickness of the layers of the blend S3 devices for optimum efficiency.
Table 4. The thickness of the layers of the blend S3 devices for optimum efficiency.
Layer Thickness (nm) Materials Type
ITO 130 Oxides Contact
PC60BM 5 Polymers Other
PM6:D18:L8-BO 80 Blends Active
PEDOT: PSS 20 Oxides Other
Ag 100 Metal Contact
Table 5. The photovoltaic parameters of three devices (S1, S2, and S3) under different temperatures.
Table 5. The photovoltaic parameters of three devices (S1, S2, and S3) under different temperatures.
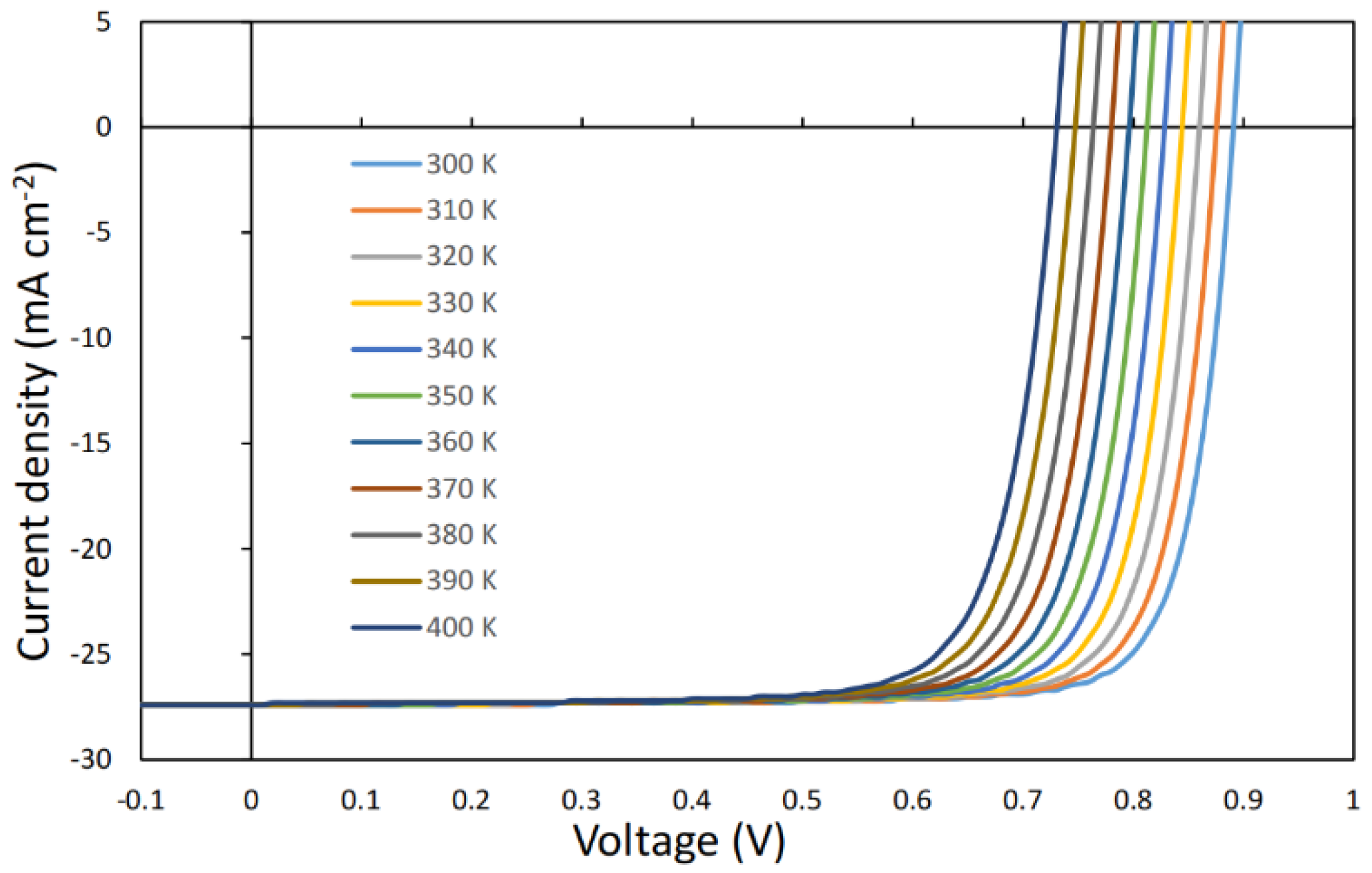
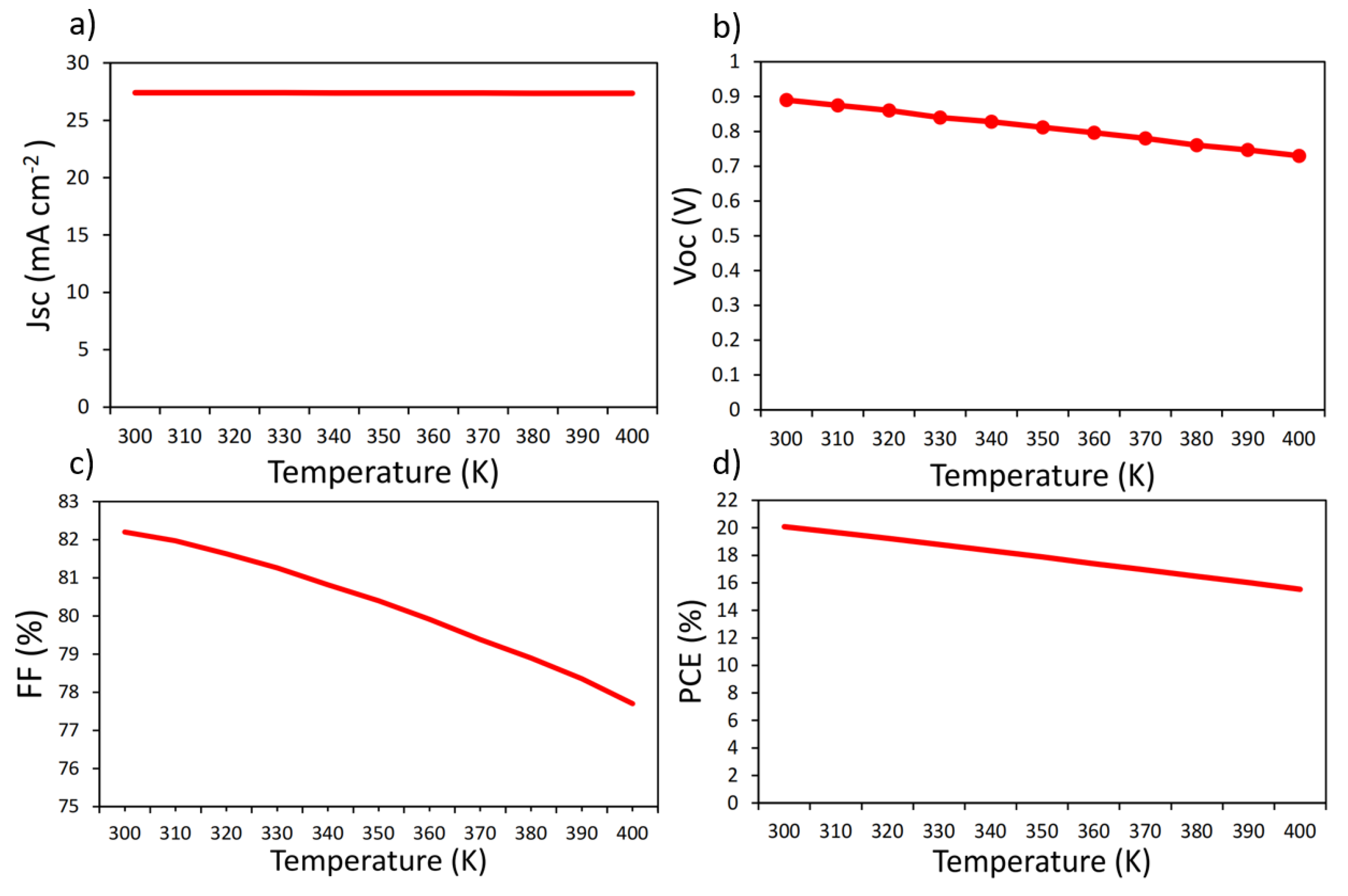
T(K) T(°C) Jsc(mA cm-2) Voc(V) FF(%) PCE(%)
S1 300 26.85 27.4 0.89 82.2 20.08
310 36.85 27.4 0.875 81.97 19.66
320 46.85 27.4 0.86 81.63 19.23
330 56.85 27.4 0.84 81.26 18.78
340 66.85 27.38 0.828 80.82 18.33
350 76.85 27.38 0.812 80.4 17.88
360 86.85 27.37 0.796 79.91 17.4
370 96.85 27.37 0.78 79.38 16.95
380 106.85 27.36 0.76 78.9 16.48
390 116.85 27.36 0.747 78.35 16.01
400 126.85 27.35 0.73 77.7 15.53
S2 300 26.85 27.43 0.89 82.3 20.11
310 36.85 27.43 0.875 82 19.68
320 46.85 27.42 0.86 81.6 19.25
330 56.85 27.42 0.84 81.2 18.8
340 66.85 27.41 0.83 80.8 18.35
350 76.85 27.41 0.81 80.4 17.9
360 86.85 27.41 0.8 79.9 17.43
370 96.85 27.4 0.78 79.4 16.96
380 106.85 27.4 0.76 78.9 16.5
390 116.85 27.38 0.75 78.3 16
400 126.85 27.38 0.73 78 15.55
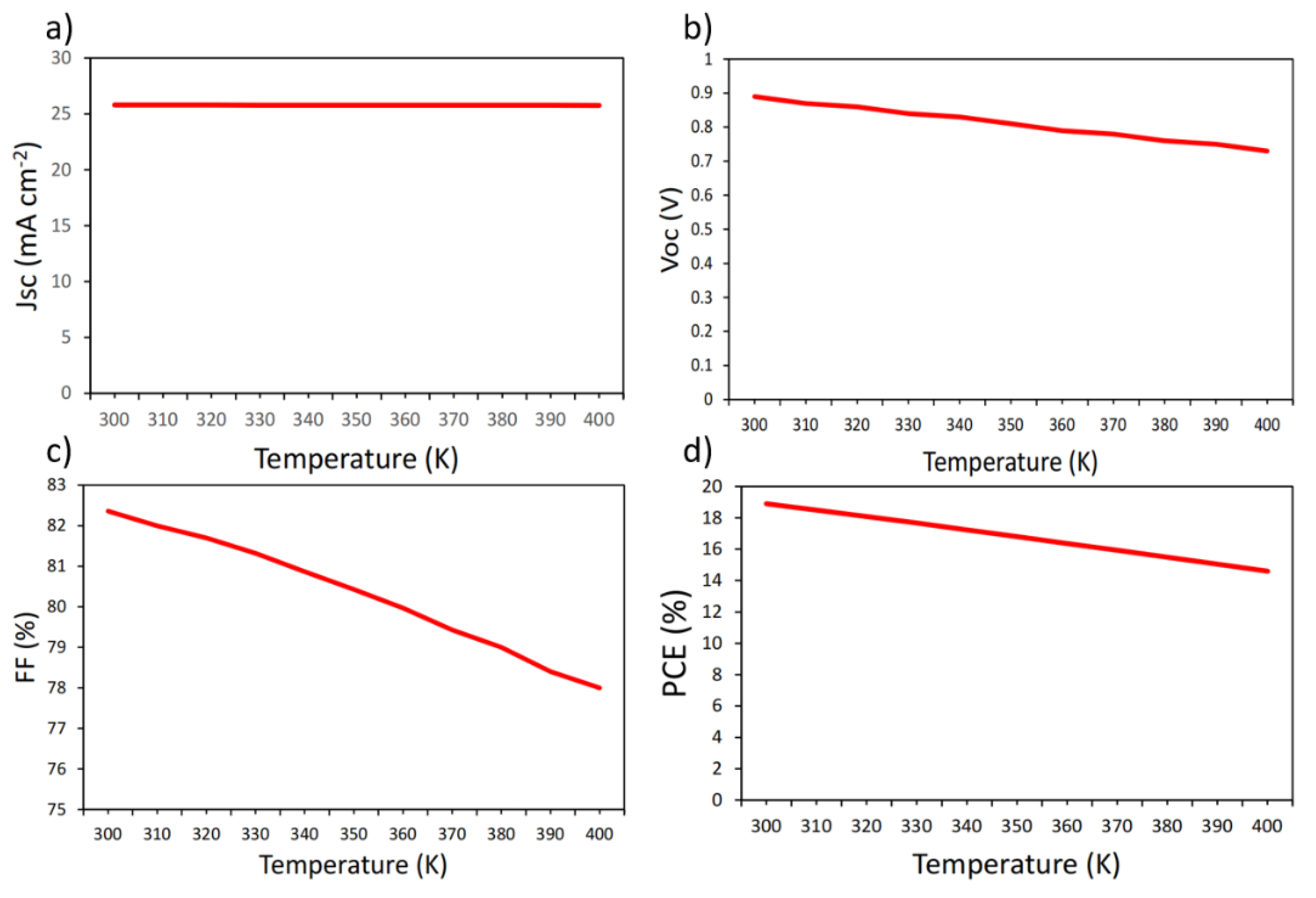
S3 300 26.85 25.8 0.89 82.36 18.9
310 36.85 25.8 0.87 82 18.5
320 46.85 25.8 0.86 81.7 18.08
330 56.85 25.79 0.84 81.32 17.67
340 66.85 25.79 0.83 80.87 17.23
350 76.85 25.78 0.81 80.43 16.81
360 86.85 25.78 0.79 79.97 16.37
370 96.85 25.77 0.78 79.43 15.93
380 106.85 25.77 0.76 79 15.5
390 116.85 25.77 0.75 78.4 15.05
400 126.85 25.76 0.73 78 14.6
Table 6. Results of the PCE loss ratio (%) due to the temperature increment.
Table 6. Results of the PCE loss ratio (%) due to the temperature increment.
PCE at 300K PCE at 350K Loss ratio %
Khan et al.[43] 5.75% 4.88% 15%
Anass et al.[31] 8% 7.4% 9%
Muhammad et al.[32] 6.82% 6.2% 9%
Kim et al. [25] 3.25% 2.7% 17%
Our study 20.11% 17.9% 11%
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated