A Fibration of Fermat Surface in Characteristic

Preprint

Article

A Fibration of Fermat Surface in Characteristic

Altmetrics

Downloads

Views

Comments

Xiaokun Zhong^*

This version is not peer-reviewed

Submitted:

26 July 2024

Posted:

27 July 2024

You are already at the latest version

Alerts

Abstract

Let S be a Fermat surface of degree 5 and let k be an algebraically closed field of characteristic p = 2. We give a fibration ƒ: S → P with upper limit 1 and lower limit k, and investigate the geometric properties of fiber of ƒ. Furthermore, we investigate the fibration-preserving automorphisms group Aut_{Pwith upper limit 1 and lower limit k}(S) of ƒ. We obtain that Aut_{Pwith upper limit 1 and lower limit k}(S) is a p-group of order 256.

Keywords:

Subject: Computer Science and Mathematics - Mathematics

MSC: 14G17; 14D06; 14J50

1. Introduction

Let k be an algebraically closed field and let S be the hypersurface in

P_{k}^{3}

defined by the equation

z_{0}^{5} - z_{1}^{5} = z_{2}^{5} - z_{3}^{5},

(1)

where

z_{0}, z_{1}, z_{2}, z_{3}

are the homogeneous coordinates.

The morphism

f : S \to P_{k}^{1}

is defined as follows:

f : (z_{0} : z_{1} : z_{2} : z_{3}) \mapsto \{\begin{matrix} z_{2}^{4} / z_{0}^{4}, if z_{0} = z_{1} and z_{2} = z_{3}, \\ (z_{0} - z_{1}) / (z_{2} - z_{3}), otherwise . \end{matrix}

(2)

When k is the complex numbers C, f is a fibration. It is well-known that the general fiber of f is a smooth curve. (see [1], Chapter III, Corollary 10.7). In [2,3,4], they investigate the fibration

f : S \to P_{C}^{1}

. For example, the general fiber of f is a smooth curve of genus 3. On the other hand, let

S_{λ}

denote the fiber over a point

λ \in P_{C}^{1}

, they obtain that

S_{λ}

is a singular fiber if and only if

λ

belongs to the following set

E : = {λ | λ^{5} = - 1 / 4, 1, o r - 4} \cup {0, \infty} .

(3)

However, when k is an algebraically closed field of positive characteristic, the situation will be different. The general fiber of a fibration may be singular (see [5]).

In this paper, k will be an algebraically closed field of characteristic 2. Although f remains a fibration, the general fiber of f is no longer smooth. In Section 2, we recall some necessary preliminaries. In Section 3, we investigate the geometric properties of fiber of f. We obtain that the following theorem.

Theorem 1.

(see Proposition 1, Proposition 2)

. Let k be an algebraically closed field of characteristic 2 and let S be a Fermat surface of degree 5 defined by the equation

(1)

. Let

f : S \to P_{k}^{1}

be a fibration defined by

(2)

. We obtain that

(i) for any

λ \in k

, the fiber

S_{λ}

has arithmetic genus 3.

(ii) the fiber

S_{λ}

is reducible if and only if

λ \in {c | c^{15} = 1} \cup {0, \infty} .

(4)

(iii) if

λ \notin {c | c^{15} = 1} \cup {0, \infty}

, then the fiber

S_{λ}

is a rational curve with a unique singular point

(1 : 1 : λ^{\frac{1}{4}} : λ^{\frac{1}{4}})

In Section 4, we investigate the fibration-preserving automorphisms group of f. More specifically, let

G : = {σ \in {Aut}_{k} (S) | \exists φ \in {Aut}_{k} (P_{k}^{1}) such that f \circ σ = φ \circ f}

(5)

and

{Aut}_{P_{k}^{1}} (S) : = {σ \in G | f \cdot σ = f}

. We have the following theorem.

Theorem 2.

(see Theorem 5, Theorem 6)

. Let H be the Sylow p-group of

{Aut}_{P_{k}^{1}} (S)

. We have

(i) for any

σ \in H

, there are some elements

a, b, c

and d in k such that

σ = (\begin{matrix} a & 1 + a & b & b \\ 1 + a & a & b & b \\ c & c & d & 1 + d \\ c & c & 1 + d & d \end{matrix}),

(6)

a^{4} = a

c = b^{4} = c^{16}

and

d^{4} = d

. Conversely, if σ is of the form as in

(6)

, then

σ \in H

(ii) the order of H is 256.

(iii)

{Aut}_{P_{k}^{1}} (S) = H

2. Preliminaries

In this section, let k be an algebraically closed field. Let S be a smooth projective surface, and C a smooth projective curve over k.

2.1. Fibration

We say

f : S \to C

is a fibration if f is a surjective morphism and

f_{*} O_{S} = O_{C}

Definition 1.

Let

f : S \to C

be a fibration and let

c \in C

be a point. Let

k (c)

be the residue field of c. Then the fiber of f over the point c is defined to be the fiber product

S_{c} : = S \times_{C} Spec k (c)

It is a fact that the topological space of

S_{c}

is homeomorphic to

f^{- 1} (c)

with the induced topology. (see [1], Chapter II, exercise 3.10)

2.2. Automorphism Group of $P_{k}^{1}$

Let

{GL}_{2} (k)

be the group of invertible

2 \times 2

matrices with entries in k, and

{PGL}_{2} (k) : = {GL}_{2} (k) / k^{*}

. It is known that

{PGL}_{2} (k) ≅ {Aut}_{k} (P_{k}^{1})

Theorem 3.

([6], Lemma 3.2 ). Let

s \in {PGL}_{2} (k)

be nontrivial and of finite order. Then

s^{p} = id

if and only if s has a unique fixed point in

P_{k}^{1}

Corollary 1.

Let H be a finite subgroup of

{PGL}_{2} (k)

. If H fixes at least two points of

P_{k}^{1}

, then H is a cyclic group with order prime to p.

Proof.

For any

s \in H

, if H fixes at least two points of

P_{k}^{1}

, then s fixes at least two points of

P_{k}^{1}

. By Theorem 3, the order of s is prime to p. This implies that the order of H is prime to p. Furthermore, H is a cyclic group (refer to [6], Proposition 4.5). □

Theorem 4.

([6], Proposition 4.7 ). If D is a finite subgroup of

{PGL}_{2} (k)

, then D fixes a unique point of

P_{k}^{1}

if and only if

D ≅ H ⋊ M

, where

H \subseteq D

is a nontrivial Sylow p-group and

M \subseteq D

is a cyclic group with order prime to p.

2.3. Automorphism Group of Fermat Surface of Degree 5

Let k be an algebraically closed field of characteristic

p = 2

and

q : = p^{2}

. Let S be the Fermat surface defined by the Equation (1). Then

{Aut}_{k} (S) = P U (4, q) : = {(a_{i j}) \in G L (4, F_{q^{2}}) | {(a_{i j})}^{t} (a_{i j}^{4}) = I} / {s c a l a r s}

(7)

(see [7], page 100, Theorem). Furthermore, one obtains that the order of

P U (4, q)

4^{6} \cdot (4^{2} - 1) (4^{3} + 1) (4^{4} - 1)

(see [8], page 8, Table 1).

3. The Fiber of f

In this section, let k be an algebraically closed field of characteristic

p = 2

and let S be the Fermat surface defined by the Equation (1). Note that the characteristic of k is 2, so

a + b = a - b

for any

a, b \in k

3.1. Reducible Fiber

Proposition 1.

For any

λ \in P_{k}^{1}

, the fiber

S_{λ}

is reducible if and only if

λ \in {c | c^{15} = 1} \cup {0, \infty} .

(8)

Proof.

When

λ \in {0, \infty}

, we obtain that

S_{λ}

is a union of four projective lines meeting in a point (see 3.1.1).

Now, let us suppose

λ \notin {0, \infty}

. Let

F (z_{0}, z_{1}, z_{2}) : = z_{2}^{4} + \frac{1}{λ^{3}} {(z_{0} + z_{1})}^{3} \cdot z_{2} + (λ + \frac{1}{λ^{4}}) {(z_{0} + z_{1})}^{4} + λ (z_{0}^{3} z_{1} + z_{0}^{2} z_{1}^{2} + z_{0} z_{1}^{3}) .

(9)

By definition,

(z_{0} : z_{1} : z_{2} : z_{3}) \in f^{- 1} (λ)

if and only if

\{\begin{matrix} F (z_{0}, z_{1}, z_{2}) = 0, \\ z_{0} + z_{1} = λ (z_{2} + z_{3}) \end{matrix}

(10)

Therefore, if

(z_{0} : z_{1} : z_{2} : z_{3}) \in f^{- 1} (λ)

, then

F (z_{0}, z_{1}, z_{2}) = 0

F (z_{0}, z_{1}, z_{2})

is reducible, then either

F (z_{0}, z_{1}, z_{2}) = (a_{0} + a_{1} z_{2} + a_{2} z_{2}^{2} + z_{2}^{3}) (b_{0} + z_{2})

(11)

for some

a_{0}, a_{1}, a_{2}, b_{0} \in k [z_{0}, z_{1}]

, or

F (z_{0}, z_{1}, z_{2}) = (α_{0} + α_{1} z_{2} + z_{2}^{2}) (β_{0} + β_{1} z_{2} + z_{2}^{2})

(12)

for some

α_{0}, α_{1}, β_{0}, β_{1} \in k [z_{0}, z_{1}]

In 3.1.2 and 3.1.3, we obtain that the necessary condition for

S_{λ}

to be reducible is that

λ^{15} = 1

. In 3.1.4, we obtain that

S_{λ}

is still a union of four projective lines meeting in a point if

λ^{15} = 1

In summary, the proof is complete. □

3.1.1. Case $λ \in {0, \infty}$

Let

E : = {(z_{0} : z_{1} : z_{2} : z_{3}) \in S | z_{0} = z_{1}, z_{2} \neq z_{3}}

By definition,

f^{- 1} (0) = E \cup {(1 : 1 : 0 : 0)}

. More specifically, if

(z_{0} : z_{1} : z_{2} : z_{3}) \in E

, then

z_{2}^{5} + z_{3}^{5} = z_{0}^{5} + z_{1}^{5} = 0

. Hence

0 = z_{2}^{5} + z_{3}^{5} = (z_{2} + z_{3}) (z_{2}^{4} + z_{2}^{3} z_{3} + z_{2}^{2} z_{3}^{2} + z_{2} z_{3}^{3} + z_{3}^{4})

. Combining this with the inequation that

z_{2} \neq z_{3}

, we obtain

z_{2}^{4} + z_{2}^{3} z_{3} + z_{2}^{2} z_{3}^{2} + z_{2} z_{3}^{3} + z_{3}^{4} = 0

. Hence

E = {(z_{0} : z_{0} : z_{2} : z_{3}) \in P_{k}^{3} | z_{2}^{4} + z_{2}^{3} z_{3} + z_{2}^{2} z_{3}^{2} + z_{2} z_{3}^{3} + z_{3}^{4} = 0 and z_{2} \neq z_{3}} .

(13)

Let

E^{'} : = {(z_{0} : z_{0} : z_{2} : z_{3}) \in P_{k}^{3} | z_{2}^{4} + z_{2}^{3} z_{3} + z_{2}^{2} z_{3}^{2} + z_{2} z_{3}^{3} + z_{3}^{4} = 0}

. Note that

E^{'} = E \cup {(1 : 1 : 0 : 0)}

, so

f^{- 1} (0) = E^{'}

. Let

{θ_{1}, θ_{2}, θ_{3}, θ_{4}}

be the solution set of the equation

z^{4} + z^{3} + z^{2} + z = 1

. We have

z_{2}^{4} + z_{2}^{3} z_{3} + z_{2}^{2} z_{3}^{2} + z_{2} z_{3}^{3} + z_{3}^{4} = (z_{2} + θ_{1} z_{3}) (z_{2} + θ_{2} z_{3}) (z_{2} + θ_{3} z_{3}) (z_{2} + θ_{4} z_{3})

. Hence

f^{- 1} (0) = ⋃_{i = 1}^{4} {(z_{0} : z_{0} : z_{2} : z_{3}) \in P_{k}^{3} | z_{2} + θ_{i} z_{3} = 0}

(14)

Therefore,

f^{- 1} (0)

is reducible and it has a unique singular point

(1 : 1 : 0 : 0)

. See the figure below.

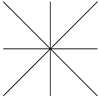
Similarly,

f^{- 1} (\infty) = ⋃_{i = 1}^{4} {(z_{0} : z_{1} : z_{2} : z_{2}) \in P_{k}^{3} | z_{0} + θ_{i} z_{1} = 0} .

(15)

It is reducible and it has a unique singular point

(0 : 0 : 1 : 1)

3.1.2. Case $F (z_{0}, z_{1}, z_{2}) = (a_{0} + a_{1} z_{2} + a_{2} z_{2}^{2} + z_{2}^{3}) (b_{0} + z_{2})$

Suppose

λ \notin {0, \infty}

. Note that

\begin{matrix} F (z_{0}, z_{1}, z_{2}) & = (a_{0} + a_{1} z_{2} + a_{2} z_{2}^{2} + z_{2}^{3}) (b_{0} + z_{2}) \\ = z_{2}^{4} + (b_{0} + a_{2}) z_{2}^{3} + (b_{0} a_{2} + a_{1}) z_{2}^{2} + (b_{0} a_{1} + a_{0}) z_{2} + b_{0} a_{0} . \end{matrix}

(16)

Combining this with (9), we obtain

\{\begin{matrix} a_{2} = b_{0}, \\ a_{1} = b_{0} a_{2} = b_{0}^{2}, \\ a_{0} = b_{0} a_{1} + \frac{1}{λ^{3}} {(z_{0} + z_{1})}^{3} = b_{0}^{3} + \frac{1}{λ^{3}} {(z_{0} + z_{1})}^{3}, \\ a_{0} b_{0} = (λ + \frac{1}{λ^{4}}) (z_{0}^{4} + z_{1}^{4}) + λ (z_{0}^{3} z_{1} + z_{0}^{2} z_{1}^{2} + z_{0} z_{1}^{3}) . \end{matrix}

(17)

Hence

a_{0} b_{0} = b_{0} \cdot [b_{0}^{3} + \frac{1}{λ^{3}} {(z_{0} + z_{1})}^{3}] = b_{0}^{4} + \frac{1}{λ^{3}} b_{0} {(z_{0} + z_{1})}^{3}

. We may assume

b_{0} = c_{0} z_{0} + c_{1} z_{1}

, where

c_{0}, c_{1} \in k

. Thus

\begin{matrix} a_{0} b_{0} & = b_{0}^{4} + \frac{b_{0}}{λ^{3}} {(z_{0} + z_{1})}^{3} \\ = (c_{0}^{4} + \frac{c_{0}}{λ^{3}}) z_{0}^{4} + (c_{1}^{4} + \frac{c_{1}}{λ^{3}}) z_{1}^{4} + \frac{c_{0} + c_{1}}{λ^{3}} (z_{0}^{3} z_{1} + z_{0}^{2} z_{1}^{2} + z_{0} z_{1}^{3}) . \end{matrix}

(18)

Combining this with (17), we obtain

\begin{matrix} (λ + \frac{1}{λ^{4}}) (z_{0}^{4} + z_{1}^{4}) + λ (z_{0}^{3} z_{1} + z_{0}^{2} z_{1}^{2} + z_{0} z_{1}^{3}) \\ = (c_{0}^{4} + \frac{c_{0}}{λ^{3}}) z_{0}^{4} + (c_{1}^{4} + \frac{c_{1}}{λ^{3}}) z_{1}^{4} + \frac{c_{0} + c_{1}}{λ^{3}} (z_{0}^{3} z_{1} + z_{0}^{2} z_{1}^{2} + z_{0} z_{1}^{3}) . \end{matrix}

(19)

Therefore,

\{\begin{matrix} c_{0}^{4} + \frac{c_{0}}{λ^{3}} = c_{1}^{4} + \frac{c_{1}}{λ^{3}} = λ + \frac{1}{λ^{4}}, \\ \frac{1}{λ^{3}} (c_{0} + c_{1}) = λ . \end{matrix}

(20)

This implies that

c_{0} + c_{1} = λ^{4}

, hence

0 = c_{0}^{4} + \frac{c_{0}}{λ^{3}} + c_{1}^{4} + \frac{c_{1}}{λ^{3}} = λ^{16} + λ

. Therefore,

λ^{15} = 1

3.1.3. Case $F (z_{0}, z_{1}, z_{2}) = (α_{0} + α_{1} z_{2} + z_{2}^{2}) (β_{0} + β_{1} z_{2} + z_{2}^{2})$

Suppose

λ \notin {0, \infty}

. Note that

\begin{matrix} F (z_{0}, z_{1}, z_{2}) & = (α_{0} + α_{1} z_{2} + z_{2}^{2}) (β_{0} + β_{1} z_{2} + z_{2}^{2}) \\ = z_{2}^{4} + (α_{1} + β_{1}) z_{2}^{3} + (α_{0} + β_{0} + α_{1} β_{1}) z_{2}^{2} + (α_{0} β_{1} + α_{1} β_{0}) z_{2} + α_{0} β_{0} . \end{matrix}

(21)

Combining this with (9), we obtain

\{\begin{matrix} α_{1} = β_{1}, \\ α_{0} = α_{1} β_{1} + β_{0} = β_{1}^{2} + β_{0}, \\ α_{0} β_{1} + α_{1} β_{0} = (β_{1}^{2} + β_{0}) β_{1} + β_{0} β_{1} = β_{1}^{3} = \frac{1}{λ^{3}} {(z_{0} + z_{1})}^{3}, \\ α_{0} β_{0} = β_{0} β_{1}^{2} + β_{0}^{2} = (λ + \frac{1}{λ^{4}}) (z_{0}^{4} + z_{1}^{4}) + λ (z_{0}^{3} z_{1} + z_{0}^{2} z_{1}^{2} + z_{0} z_{1}^{3}) . \end{matrix}

(22)

By (22),

β_{1}^{3} = \frac{1}{λ^{3}} {(z_{0} + z_{1})}^{3}

. Therefore, we may assume

β_{1} = \frac{θ}{λ} (z_{0} + z_{1})

, where

θ \in {z \in k | z^{3} = 1}

. We may assume

β_{0} = c_{0} z_{0}^{2} + c_{1} z_{0} z_{1} + c_{2} z_{1}^{2}

, where

c_{0}, c_{1}, c_{2} \in k

. Thus

\begin{matrix} α_{0} β_{0} & = β_{0} β_{1}^{2} + β_{0}^{2} \\ = (c_{0} z_{0}^{2} + c_{1} z_{0} z_{1} + c_{2} z_{1}^{2}) \cdot \frac{θ^{2}}{λ^{2}} {(z_{0} + z_{1})}^{2} + {(c_{0} z_{0}^{2} + c_{1} z_{0} z_{1} + c_{2} z_{1}^{2})}^{2} \\ = (c_{0}^{2} + \frac{c_{0} θ^{2}}{λ^{2}}) z_{0}^{4} + (c_{2}^{2} + \frac{c_{2} θ^{2}}{λ^{2}}) z_{1}^{4} + \frac{c_{1} θ^{2}}{λ^{2}} (z_{0}^{3} z_{1} + z_{0} z_{1}^{3}) + [\frac{(c_{0} + c_{2}) θ^{2}}{λ^{2}} + c_{1}^{2}] z_{0}^{2} z_{1}^{2} . \end{matrix}

(23)

Combining this with (22), we obtain

\{\begin{matrix} c_{0}^{2} + \frac{c_{0} θ^{2}}{λ^{2}} = c_{2}^{2} + \frac{c_{2} θ^{2}}{λ^{2}} = λ + \frac{1}{λ^{4}}, \\ \frac{c_{1} θ^{2}}{λ^{2}} = \frac{(c_{0} + c_{2}) θ^{2}}{λ^{2}} + c_{1}^{2} = λ . \end{matrix}

(24)

Hence

0 = c_{0}^{2} + \frac{c_{0} θ^{2}}{λ^{2}} + c_{2}^{2} + \frac{c_{2} θ^{2}}{λ^{2}} = (c_{0} + c_{2}) (c_{0} + c_{2} + \frac{θ^{2}}{λ^{2}})

. This implies that either

c_{0} + c_{2} = 0

c_{0} + c_{2} + \frac{θ^{2}}{λ^{2}} = 0

c_{0} + c_{2} = 0

, then

λ = \frac{c_{1} θ^{2}}{λ^{2}} = \frac{(c_{0} + c_{2}) θ^{2}}{λ^{2}} + c_{1}^{2} = c_{1}^{2}

by (24). It follows that

λ^{3} = c_{1} θ^{2}

and

λ = c_{1}^{2}

. Note that

θ^{3} = 1

, so

λ^{6} = c_{1}^{2} θ^{4} = λ θ

. Hence

λ^{15} = θ^{3} = 1

c_{0} + c_{2} + \frac{θ^{2}}{λ^{2}} = 0

, then

λ = \frac{c_{1} θ^{2}}{λ^{2}} = \frac{(c_{0} + c_{2}) θ^{2}}{λ^{2}} + c_{1}^{2} = \frac{θ^{4}}{λ^{2}} + c_{1}^{2} = \frac{θ}{λ^{2}} + c_{1}^{2}

by (24). In other words, we have

λ = \frac{c_{1} θ^{2}}{λ^{2}} = \frac{θ}{λ^{2}} + c_{1}^{2}

. This implies that

c_{1} = \frac{λ^{3}}{θ^{2}}

, hence

c_{1}^{2} = \frac{λ^{6}}{θ^{4}} = \frac{λ^{6}}{θ}

. Substituting this into

λ = \frac{θ}{λ^{2}} + c_{1}^{2}

, we obtain

λ^{10} + λ^{5} θ + θ^{2} = 0

. Note that

0 = θ^{3} + 1 = (θ + 1) (θ^{2} + θ + 1)

. If

θ = 1

, then

λ^{10} + λ^{5} + 1 = 0

, and hence

λ^{15} + 1 = (λ^{5} + 1) (λ^{10} + λ^{5} + 1) = 0

. Otherwise

θ^{2} + θ + 1 = 0

, as

λ^{10} + λ^{5} θ + θ^{2} = 0

, we obtain that either

λ^{5} = 1

λ^{5} = 1 + θ

. Therefore,

λ^{15} = 1

3.1.4. Case $λ^{15} = 1$

Note that

λ^{15} + 1 = (λ^{5} + 1) (λ^{10} + λ^{5} + 1)

. If

λ^{15} + 1 = 0

, then we obtain that either

λ^{5} + 1 = 0

λ^{10} + λ^{5} + 1 = 0

(i) Suppose

λ^{5} + 1 = 0

. Let

{θ_{0}, θ_{1}}

be the solution set of the equation

z^{2} + z + 1 = 0

. Then we have

F (z_{0}, z_{1}, z_{2}) = (z_{2} + λ^{4} z_{0}) (z_{2} + λ^{4} z_{1}) (z_{2} + λ^{4} θ_{0} z_{0} + λ^{4} θ_{1} z_{1}) (z_{2} + λ^{4} θ_{1} z_{0} + λ^{4} θ_{0} z_{1}) .

(25)

Hence

f^{- 1} (λ) = ⋃_{i = 1}^{4} {(z_{0} : z_{1} : z_{2} : z_{3}) \in P_{k}^{3} | F_{i} = 0 and z_{0} + z_{1} = λ (z_{2} + z_{3})},

(26)

where

F_{1} : = z_{2} + λ^{4} z_{0}, F_{2} : = z_{2} + λ^{4} z_{1}, F_{3} : = z_{2} + λ^{4} θ_{0} z_{0} + λ^{4} θ_{1} z_{1}

, and

F_{4} : = z_{2} + λ^{4} θ_{1} z_{0} + λ^{4} θ_{0} z_{1}

. Therefore,

f^{- 1} (λ)

is reducible and it has a unique singular point

(1 : 1 : λ^{4} : λ^{4})

(ii) Suppose

λ^{10} + λ^{5} + 1 = 0

. Let

{δ_{0}, δ_{1}}

be the solution set of the equation

z^{2} + λ^{9} z + λ^{13} = 0

. Let

F_{1} : = z_{2} + δ_{0} (z_{0} + z_{1}) + λ^{4} z_{1}, F_{2} : = z_{2} + δ_{1} (z_{0} + z_{1}) + λ^{4} z_{1}, F_{3} : = z_{2} + δ_{0} (z_{0} + z_{1}) + λ^{4} z_{0}

, and

F_{4} : = z_{2} + δ_{1} (z_{0} + z_{1}) + λ^{4} z_{0}

. Then we have

F (z_{0}, z_{1}, z_{2}) = \prod_{i = 1}^{i = 4} F_{i}

. Hence

f^{- 1} (λ) = ⋃_{i = 1}^{4} {(z_{0} : z_{1} : z_{2} : z_{3}) \in P_{k}^{3} | F_{i} = 0 and z_{0} + z_{1} = λ (z_{2} + z_{3})} .

(27)

Therefore,

f^{- 1} (λ)

is reducible and it has a unique singular point

(1 : 1 : λ^{4} : λ^{4})

3.2. Irreducible Fiber

By Proposition 1, if

λ \notin {c | c^{15} = 1} \cup {0, \infty}

, then the fiber

S_{λ}

is irreducible.

S_{λ}

is defined by

\{\begin{matrix} z_{0} + z_{1} = λ (z_{2} + z_{3}) \\ z_{2}^{4} + \frac{1}{λ^{3}} z_{2} {(z_{0} + z_{1})}^{3} + (λ + \frac{1}{λ^{4}}) (z_{0}^{4} + z_{1}^{4}) + λ (z_{0}^{3} z_{1} + z_{0}^{2} z_{1}^{2} + z_{0} z_{1}^{3}) = 0 \end{matrix}

(28)

Hence

S_{λ}

is isomorphic to the curve

C_{λ}

P_{k}^{2}

, where

C_{λ}

is defined by the equation

h_{λ} : = z_{2}^{4} + \frac{1}{λ^{3}} z_{2} {(z_{0} + z_{1})}^{3} + (λ + \frac{1}{λ^{4}}) (z_{0}^{4} + z_{1}^{4}) + λ (z_{0}^{3} z_{1} + z_{0}^{2} z_{1}^{2} + z_{0} z_{1}^{3}) = 0 .

(29)

Proposition 2.

(i) If

λ \notin {c | c^{15} = 1} \cup {0, \infty}

, then the fiber

S_{λ}

is a rational curve with a unique singular point

(1 : 1 : λ^{\frac{1}{4}} : λ^{\frac{1}{4}})

(ii) For any λ, the arithmetic genus

p_{a} (S_{λ})

is equal to 3.

Proof. (i) Let us consider the curve

C_{λ}

P_{k}^{2}

. We have

\{\begin{matrix} \frac{\partial h_{λ}}{\partial z_{2}} = \frac{1}{λ^{3}} {(z_{0} + z_{1})}^{3} \\ \frac{\partial h_{λ}}{\partial z_{1}} = (\frac{1}{λ^{3}} z_{2} + λ z_{0}) {(z_{0} + z_{1})}^{2} \\ \frac{\partial h_{λ}}{\partial z_{0}} = (\frac{1}{λ^{3}} z_{2} + λ z_{1}) {(z_{0} + z_{1})}^{2} \end{matrix}

(30)

By Jacobian criterion,

(1 : 1 : λ^{\frac{1}{4}})

is the unique singular point of

C_{λ}

. In other words,

(1 : 1 : λ^{\frac{1}{4}} : λ^{\frac{1}{4}})

is the unique singular point of

S_{λ}

Note that the arithmetic genus

p_{a} (C_{λ}) = \frac{(4 - 1) (4 - 2)}{2} = 3

, and

(1 : 1 : λ^{\frac{1}{4}})

is a triple singular point of

C_{λ}

. Hence the normalization of

C_{λ}

is a rational curve. Since

S_{λ}

is isomorphic to

C_{λ}

, we obtain that

S_{λ}

is a rational curve with a unique singular point

(1 : 1 : λ^{\frac{1}{4}} : λ^{\frac{1}{4}})

(ii) According to chapter III, corollary 9.10 in [1], the arithmetic genus of

S_{λ}

are all independent of

λ

. □

4. Subgroups of ${Aut}_{k} (S)$

In this section, let k be an algebraically closed field of characteristic

p = 2

and

q : = p^{2}

. Let S be the Fermat surface defined by the Equation (1). Note that

{Aut}_{k} (S) = P U (4, q^{2})

. Denoting

G : = {σ \in {Aut}_{k} (S) | \exists φ \in {Aut}_{k} (P_{k}^{1}) such that f \circ σ = φ \circ f}

and

{Aut}_{P_{k}^{1}} (S) : = {σ \in G | f \circ σ = f}

For any

σ = (a_{i j}) \in {Aut}_{P_{k}^{1}} (S)

, as

σ

preserves the fiber of f, we have

σ (f^{- 1} (0)) = f^{- 1} (0)

. In particular,

σ

fixes the unique singular point

(1 : 1 : 0 : 0)

f^{- 1} (0)

. Hence

(\begin{matrix} a_{11} & a_{12} & a_{13} & a_{14} \\ a_{21} & a_{22} & a_{23} & a_{24} \\ a_{31} & a_{32} & a_{33} & a_{34} \\ a_{41} & a_{42} & a_{43} & a_{44} \end{matrix}) (\begin{matrix} 1 \\ 1 \\ 0 \\ 0 \end{matrix}) = (\begin{matrix} 1 \\ 1 \\ 0 \\ 0 \end{matrix})

(31)

We obtain that

\{\begin{matrix} a_{11} + a_{12} = 1 \\ a_{21} + a_{22} = 1 \\ a_{31} + a_{32} = 0 \\ a_{41} + a_{42} = 0 \end{matrix}

(32)

Similarly,

σ

fixes the unique singular point

(0 : 0 : 1 : 1)

f^{- 1} (\infty)

. Hence

(\begin{matrix} a_{11} & a_{12} & a_{13} & a_{14} \\ a_{21} & a_{22} & a_{23} & a_{24} \\ a_{31} & a_{32} & a_{33} & a_{34} \\ a_{41} & a_{42} & a_{43} & a_{44} \end{matrix}) (\begin{matrix} 0 \\ 0 \\ 1 \\ 1 \end{matrix}) = (\begin{matrix} 0 \\ 0 \\ 1 \\ 1 \end{matrix})

(33)

We obtain that

\{\begin{matrix} a_{13} + a_{14} = 0 \\ a_{23} + a_{24} = 0 \\ a_{33} + a_{34} = 1 \\ a_{43} + a_{44} = 1 \end{matrix}

(34)

Combining (32) and (34), we have

σ = (\begin{matrix} a_{11} & 1 + a_{11} & a_{13} & a_{13} \\ 1 + a_{22} & a_{22} & a_{23} & a_{23} \\ a_{31} & a_{31} & a_{33} & 1 + a_{33} \\ a_{41} & a_{41} & 1 + a_{44} & a_{44} \end{matrix})

(35)

4.1. Sylow p-Group of ${Aut}_{P_{k}^{1}} (S)$

Let H be the Sylow p-group of

{Aut}_{P_{k}^{1}} (S)

. Let F be a general fiber of f. We have the following exact sequences:

1 \to {Aut}_{P_{k}^{1}} (S) \to {Aut}_{k} (F) .

(36)

By Proposition 2, F is a rational curve with a unique singular point. Hence

{Aut}_{k} (F) \subset {Aut}_{k} (P_{k}^{1}) ≅ PGL (2, k)

. By (36), we may regard

{Aut}_{P_{k}^{1}} (S)

as a subgroup of

{Aut}_{k} (F)

(hence of

{Aut}_{k} (P_{k}^{1})

). By Theorem 3 and Corollary 1, we obtain that

σ^{2} = id

for any

σ \in H

Let

σ = (a_{i j}) \in H

. As

σ^{2} = id

, we obtain that

(a_{i j}) (a_{i j}) = I

, and hence

{(a_{i j})}^{t} {(a_{i j})}^{t} = I

. On the other hand,

σ \in H

, hence

σ \in {Aut}_{k} (S) = P U (4, q^{2})

. This implies that

{(a_{i j})}^{t} (a_{i j}^{4}) = I

. Therefore, we have

(a_{i j}^{4}) = {(a_{i j})}^{t}

. In other words, we obtain that

\{\begin{matrix} a_{i j} = a_{j i}^{4} = a_{i j}^{16}, if i \neq j, \\ a_{i i} = a_{i i}^{4}, otherwise . \end{matrix}

(37)

Note that

σ

is also an element of

{Aut}_{P_{k}^{1}} (S)

, so

σ

has the form of (35). We obtain that

{(1 + a_{11})}^{4} = 1 + a_{22}

and

a_{11}^{4} = a_{11}

. This implies that

a_{11} = a_{11}^{4} = a_{22}

. Similarly, we have

a_{33} = a_{44}

a_{13} = a_{23}

and

a_{31} = a_{41}

. Therefore, we may assume

σ = (\begin{matrix} a & 1 + a & b & b \\ 1 + a & a & b & b \\ c & c & d & 1 + d \\ c & c & 1 + d & d \end{matrix})

(38)

where

a^{4} = a

c = b^{4} = c^{16}

and

d^{4} = d

Conversely, as

σ \cdot (\begin{matrix} z_{0} \\ z_{1} \\ z_{2} \\ z_{3} \end{matrix}) = (\begin{matrix} a (z_{0} + z_{1}) + b (z_{2} + z_{3}) + z_{1} \\ a (z_{0} + z_{1}) + b (z_{2} + z_{3}) + z_{0} \\ c (z_{0} + z_{1}) + d (z_{2} + z_{3}) + z_{3} \\ c (z_{0} + z_{1}) + d (z_{2} + z_{3}) + z_{2} \end{matrix}),

(39)

we obtain that

σ

preserves the fiber of f. Hence any element of the p-group of

{Aut}_{P_{k}^{1}} (S)

is of the form as in (38). We have proved the following theorem.

Theorem 5.

Let H be the Sylow p-group of

{Aut}_{P_{k}^{1}} (S)

. We have

(i) for any

σ \in H

, there are some elements

a, b, c

and d in k such that

σ = (\begin{matrix} a & 1 + a & b & b \\ 1 + a & a & b & b \\ c & c & d & 1 + d \\ c & c & 1 + d & d \end{matrix}),

(40)

a^{4} = a

c = b^{4} = c^{16}

and

d^{4} = d

. Conversely, if σ be of the form as in

(40)

, then

σ \in H

(ii) the order of H is 256.

Remark 1.

In particular,

(\begin{matrix} 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{matrix})

(41)

is a nontrivial element of H.

Remark 2.

Let F be a general fiber of f and let P be the unique singular point of F. By

(36)

, we may regard

{Aut}_{P_{k}^{1}} (S)

as a subgroup of

{Aut}_{k} (F)

. By Corollary 1 and the fact that H is nontrivial, we obtain that

{Aut}_{P_{k}^{1}} (S)

fixes a unique point P of F. By Theorem 4, we have

{Aut}_{P_{k}^{1}} (S) ≅ H ⋊ M

, where M is a cyclic group with order prime to p.

4.2. Subgroups of ${Aut}_{P_{k}^{1}} (S)$ with order prime to p

By Remark 4, we have

{Aut}_{P_{k}^{1}} (S) ≅ H ⋊ M

, where M is a cyclic group with order prime to p.

Theorem 6.

Let M as above. We obtain that

(i) M is trivial.

(ii)

{Aut}_{P_{k}^{1}} (S)

is a p-group of order 256.

Proof. (i) We may assume the order of M is r. Suppose

r \neq 1

. Let

ψ : = (a_{i j})

be a generator of M. Note that

ψ^{r} = {(a_{i j})}^{r} = I

and

{(a_{i j})}^{t} (a_{i j}^{4}) = I

, so

{(a_{i j})}^{r - 1} = {(a_{i j}^{4})}^{t}

. As

ψ

is an element of

{Aut}_{P_{k}^{1}} (S)

, we may assume

ψ

has the form of (35). Therefore,

ψ^{r - 1} = {(\begin{matrix} a_{11}^{4} & 1 + a_{11}^{4} & a_{13}^{4} & a_{13}^{4} \\ 1 + a_{22}^{4} & a_{22}^{4} & a_{23}^{4} & a_{23}^{4} \\ a_{31}^{4} & a_{31}^{4} & a_{33}^{4} & 1 + a_{33}^{4} \\ a_{41}^{4} & a_{41}^{4} & 1 + a_{44}^{4} & a_{44}^{4} \end{matrix})}^{t}

(42)

On the other hand, by Lemma 5, we may assume

ψ^{r - 1} = (\begin{matrix} c_{11} & 1 + c_{11} & c_{13} & c_{13} \\ 1 + c_{22} & c_{22} & c_{23} & c_{23} \\ c_{31} & c_{31} & c_{33} & 1 + c_{33} \\ c_{41} & c_{41} & 1 + c_{44} & c_{44} \end{matrix})

(43)

Combining (42) and (43), we obtain that

a_{11}^{4} = c_{11}

and

1 + a_{22}^{4} = 1 + c_{11}

. This implies that

a_{11}^{4} = c_{11} = a_{22}^{4}

, hence

a_{11} = a_{22}

. Similarly, we have

a_{33} = a_{44}

a_{13} = a_{23}

, and

a_{31} = a_{41}

. Therefore, we may assume

ψ = (\begin{matrix} a & 1 + a & b & b \\ 1 + a & a & b & b \\ c & c & d & 1 + d \\ c & c & 1 + d & d \end{matrix})

(44)

where

a, b, c, d \in k

, so

ψ^{2} = I

. Hence the order of M is 2, which is a contradiction.

Therefore,

r = 1

and M is trivial.

(ii) As M is trivial, we obtain that

{Aut}_{P_{k}^{1}} (S) = H

is a p-group. By Theorem 5, the order of

{Aut}_{P_{k}^{1}} (S)

is 256. □

Lemma 1.

Let

A = (\begin{matrix} a_{11} & 1 + a_{11} & a_{13} & a_{13} \\ 1 + a_{22} & a_{22} & a_{23} & a_{23} \\ a_{31} & a_{31} & a_{33} & 1 + a_{33} \\ a_{41} & a_{41} & 1 + a_{44} & a_{44} \end{matrix})

(45)

and

B = (\begin{matrix} b_{11} & 1 + b_{11} & b_{13} & b_{13} \\ 1 + b_{22} & b_{22} & b_{23} & b_{23} \\ b_{31} & b_{31} & b_{33} & 1 + b_{33} \\ b_{41} & b_{41} & 1 + b_{44} & b_{44} \end{matrix}) .

(46)

Then

A B = (\begin{matrix} c_{11} & 1 + c_{11} & c_{13} & c_{13} \\ 1 + c_{22} & c_{22} & c_{23} & c_{23} \\ c_{31} & c_{31} & c_{33} & 1 + c_{33} \\ c_{41} & c_{41} & 1 + c_{44} & c_{44} \end{matrix})

(47)

where

\{\begin{matrix} c_{11} = a_{11} b_{11} + (1 + a_{11}) (1 + b_{22}) + a_{13} (b_{31} + b_{41}), \\ c_{13} = a_{11} b_{13} + b_{23} (1 + a_{11}) + a_{13} (1 + b_{33} + b_{44}), \\ c_{22} = a_{22} b_{22} + (1 + a_{22}) (1 + b_{11}) + a_{23} (b_{31} + b_{41}), \\ c_{23} = a_{22} b_{23} + b_{13} (1 + a_{22}) + a_{23} (1 + b_{33} + b_{44}), \\ c_{33} = a_{33} b_{33} + (1 + a_{33}) (1 + b_{44}) + a_{31} (b_{13} + b_{23}), \\ c_{31} = a_{33} b_{31} + b_{41} (1 + a_{33}) + a_{31} (1 + b_{11} + b_{22}), \\ c_{44} = a_{44} b_{44} + (1 + a_{44}) (1 + b_{33}) + a_{41} (b_{13} + b_{23}), \\ c_{41} = a_{44} b_{41} + b_{31} (1 + a_{44}) + a_{41} (1 + b_{11} + b_{22}) . \end{matrix}

(48)

Remark 3.

By Theorem 6, for any nontrivial element

σ \in {Aut}_{k} (S)

with order prime to p, we obtain that σ does preserve the fiber of f.

Funding

This research received no external funding.

Data Availability Statement

Data are contained within the paper.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Hartshorne, R. Algebraic geometry. GTM. 52, Springer, 1977; pp. 92–273.
Matsumoto, Y. On the topological structure of the Fermat surface of degree 5. Kodai Mathematical Journal 1994, 17, 560–570. [Google Scholar] [CrossRef]
Ahara, K. On the topology of Fermat type surface of degree 5 and the numerical analysis of algebraic curves. Tokyo J.Math., 1993, 16, 321–340. [Google Scholar] [CrossRef]
Ahara, K.; Awata, I. On the global monodromy of a fibration of the Fermat surface of odd degree n. Tokyo J.Math. 2011, 34, 19–52. [Google Scholar] [CrossRef]
Bombieri, E.; Mumford, D. Enriques’ classification of surfaces in Char. p, II. Complex Analysis and Algebraic Geometry, Cambridge; Cambridge Univ Press, 1977; pp. 23–42. [Google Scholar]
Faber, X. Finite p-irregular subgroups of PGL₂(k). La Matematica 2023, 2, 479–522. [Google Scholar] [CrossRef]
Shioda, T. Arithmetic and geometry of Fermat curves. Algebraic Geometry Seminar, (Singapore 1987), World Sci. Publishing, Singapore, 1988, 95–102.
Gorenstein, D.; Lyons, R.; Solomon, R. The classification of the finite simple groups. Math. Surveys Monogr. 40, Amer. Math. Soc., Providence, RI, 1994. pp. 6–8.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Fibration of Fermat Surface in Characteristic

Abstract

1. Introduction

2. Preliminaries

2.1. Fibration

2.2. Automorphism Group of P k 1

2.3. Automorphism Group of Fermat Surface of Degree 5

3. The Fiber of f

3.1. Reducible Fiber

3.1.1. Case λ ∈ { 0 , ∞ }

3.1.2. Case F ( z 0 , z 1 , z 2 ) = ( a 0 + a 1 z 2 + a 2 z 2 2 + z 2 3 ) ( b 0 + z 2 )

3.1.3. Case F ( z 0 , z 1 , z 2 ) = ( α 0 + α 1 z 2 + z 2 2 ) ( β 0 + β 1 z 2 + z 2 2 )

3.1.4. Case λ 15 = 1

3.2. Irreducible Fiber

4. Subgroups of Aut k ( S )

4.1. Sylow p-Group of Aut P k 1 ( S )

4.2. Subgroups of Aut P k 1 ( S ) with order prime to p

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

2.2. Automorphism Group of $P_{k}^{1}$

3.1.1. Case $λ \in {0, \infty}$

3.1.2. Case $F (z_{0}, z_{1}, z_{2}) = (a_{0} + a_{1} z_{2} + a_{2} z_{2}^{2} + z_{2}^{3}) (b_{0} + z_{2})$

3.1.3. Case $F (z_{0}, z_{1}, z_{2}) = (α_{0} + α_{1} z_{2} + z_{2}^{2}) (β_{0} + β_{1} z_{2} + z_{2}^{2})$

3.1.4. Case $λ^{15} = 1$

4. Subgroups of ${Aut}_{k} (S)$

4.1. Sylow p-Group of ${Aut}_{P_{k}^{1}} (S)$

4.2. Subgroups of ${Aut}_{P_{k}^{1}} (S)$ with order prime to p