1. Introduction

2. Theoretical Background

2.1. Logistic Regression

Logistic regression is a statistical method used for analyzing a dataset in which there are one or more independent variables that determine an outcome. The outcome is measured with a dichotomous variable [16]. Logistic regression provides a method for modeling a binary response variables, which takes values 1 (success) and 0 (failures). The goal of logistic regression is to find the best fitting model to describe the relationship between the dichotomous characteristic of interest dependent variable and a set of independent variables.

2.1.1. Binary Logistic Regression

Logistic regression has had wide applications in traffic accident modelling. It is very useful when predicting accident fatalities using probabilistic systems to classify the probability as fatal or non fatal event. According to [17], the aforementioned are probability models independent of the distributions of predictors or explanatory variables. When p is the probability of the person being involved in a fatal accident and ${\beta }_i$ stands for regression coefficients having the feature $t_i$. The intercept is denoted by ${\beta }_0$. The logistic response function [17] is given as:

$$p={\displaystyle \frac{e^{{\beta }_0+{\sum }_{k=1}^n{\beta }_i{t}_i}}{1+e^{{\beta }_0+{\sum }_{k=1}^n{\beta }_i{t}_i}}}.$$

(1)

This is referred to as the logistic regression function [18]. This gives a likelihood of the response variable to be 1, given several predictor variables. Since it is non-linear, it is linearised by applying the logit response function. A formula for the logistic response function then becomes:

$${\displaystyle \frac{p}{1-p}}=e^{{\beta }_0+{\beta }_1{t}_1+{\beta }_2{t}_2+\cdots +{\beta }_p{t}_p}$$

(2)

The term ${\displaystyle \frac{p}{1-p}}$ in equation (2.2) is called the odds ratio of the event. Placing the natural logarithm on both sides, results in

$$log\left({\displaystyle \frac{p}{1-p}}\right)={\beta }_0+{\beta }_1{t}_1+{\beta }_2{t}_2+\cdots +{\beta }_p{t}_p$$

(3)

Since, the left hand side is a function of $t_1$, ⋯ , $t_p$ so equation (2.3) can be written as:

$$g\left(t_1,\cdots ,t_p\right)={\beta }_0+{\beta }_1{t}_1+{\beta }_2{t}_2+\cdots +{\beta }_p{t}_p$$

(4)

Equation $2.4$ can be used to establish the relationship between variables of interest. Maximum likelihood method is used to obtain coefficients in logistic regression. Hence a brief discussion is given. This technique evaluates the variables for a given statistic that results in a maximum likelihood distribution for the known likelihood distribution [16]. Equation $\left(2.8\right)$ is found by taking the exponential of an equation $\left(2.6\right)$. The log-likelihood function is produced by taking the natural log of an equation $\left(2.8\right)$. The critical endpoint of the log-likelihood function is obtained by equating the first derivative to zero.

$$\begin{array}{c}\hfill g\left(z_i\right)={\prod }_{i=1}^n{f}_i\left(z_i\right)={\prod }_{i=1}^n{p}_i^{z_i}{(1-p_i)}^{i-z_i}\end{array}$$

(5)

$$\begin{array}{c}\hfill \log g\left(z_i\right)=\left\}\right\}log{\prod }_{i=1}^n\left(\genfrac{}{}{0pt}{}{n_i}{z_i}\right)p_i^{z_i}{(1-p_i)}^{i-z_i}\end{array}$$

(6)

$$\log g\left(z_i\right)={\prod }_{i=1}^n{\left(e^{{\sum }_{k=0}^K{t}_{ik}{\beta }_k}\right)}^{z_i}{(1-\frac{e^{{\sum }_{k=0}^K{t}_{ik}{\beta }_k}}{1+e^{{\sum }_{k=0}^K{t}_{ik}{\beta }_k}})}^{n_i}$$

(7)

$$\log g\left(z_i\right)={\prod }_{i=1}^n\left(e^{z_i{\sum }_{k=0}^K{t}_{ik}{\beta }_k}\right){(1+e^{{\sum }_{k=0}^K{t}_{ik}{\beta }_k})}^{-n_i}$$

(8)

$$l\left(\beta \right)={\sum }_{k=1}^n{z}_i\left({\sum }_{k=0}^K{t}_{ik}{\beta }_k\right)-nlog(1+e^{{\sum }_{k=0}^K{t}_{ik}{\beta }_k})$$

(9)

$$\frac{\partial }{\partial {\beta }_k}{\sum }_{k=0}^K{t}_{ik}{\beta }_k=t_{ik}$$

(10)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\partial l\left(\beta \right)}{\partial {\beta }_k}}& ={\sum }_{i=1}^n{z}_i{t}_{ik}-n_i\frac{1}{1+e^{{\sum }_{k=0}^K{t}_{ik}{\beta }_k}}\frac{\partial }{\partial {\beta }_k}(1+e^{{\sum }_{k=0}^K{t}_{ik}{\beta }_k})\hfill & \end{array}$$

(11)

$$\begin{array}{ccc}& \hspace{1em}={\sum }_{i=1}^n{z}_i{t}_{ik}-n_i\frac{1}{1+e^{{\sum }_{k=0}^K{t}_{ik}{\beta }_k}}{e}^{{\sum }_{k=0}^K{t}_{ik}{\beta }_k}\frac{\partial }{\partial {\beta }_k}{\sum }_{k=0}^K{t}_{ik}{\beta }_k\hfill & \end{array}$$

(12)

$$\begin{array}{ccc}& ={\sum }_{i=1}^n{z}_i{t}_{ik}-n_i\frac{1}{1+e^{{\sum }_{k=0}^K{t}_{ik}{\beta }_k}}{e}^{{\sum }_{k=0}^K{t}_{ik}{\beta }_k}{t}_{ik}\hfill & \end{array}$$

(13)

$$\begin{array}{cc}& ={\sum }_{i=1}^n{z}_i{t}_{ik}-n_i{p}_i{t}_{ik}\hfill \end{array}$$

(14)

When Equation $2.14$ is equated to zero, it produces nonlinear equations, each with $m+1$ unknown variables [19]. Iteration is the method for resolving this problem.

2.1.2. Multinomial Logistic Regression

Multi-nomial logistic regression is an important method for analysing categorical data. It considers a nominal or ordinal response variable. Additionally, the model permits the approximation of three or more log odds [20]. Let K corresponds to the predictors for a dependent variable Z denoted by $T_1,T_2,\cdots ,T_k$, the model for log odds is [18]:

$$\mathrm{logit}\left[\mathrm{P}\left(\mathrm{Z}=1\right)\right]=\alpha +{\beta }_1{t}_1+{\beta }_2{t}_2+\cdots +{\beta }_k{t}_k$$

(15)

The alternative formula $\gamma \left(t\right)$ is given by:

$$\gamma \left(t\right)={\displaystyle \frac{e^{(\alpha +{\beta }_1{t}_1+{\beta }_2{t}_2+\cdots +{\beta }_k{t}_k)}}{1+e^{(\alpha +{\beta }_1{t}_1+{\beta }_2{t}_2+\cdots +{\beta }_k{t}_k)}}},$$

(16)

where ${\beta }_i$ indicates the impact of $t_i$ on the log odds that Z = 1. Let ${\gamma }_j$ represent the multinomial probability that belongs to the jth category. The multiple logistic regression model is given by :

$$log{\displaystyle \frac{{\gamma }_j\left(t_i\right)}{{\gamma }_k\left(t_i\right)}}={\alpha }_{0i}+{\beta }_{1j}{t}_{1i}+{\beta }_{2j}{t}_{2i}+\cdots +{\beta }_{pj}{t}_{pi},$$

(17)

with j = $1,2,\cdots ,(k-1)$, i = $1,2,\cdots ,n$. When the $\gamma$’s add to unity, this gives the result [18]:

$$log\left({\gamma }_j\left(t_i\right)\right)={\displaystyle \frac{e^{({\alpha }_{0i}+{\beta }_{1j}{t}_{1i}+{\beta }_{2j}{t}_{2i}+\cdots +{\beta }_{pj}{t}_{pi})}}{1+{\sum }_{j=1}^{k-1}{e}^{({\alpha }_{0i}+{\beta }_{1j}{t}_{1i}+{\beta }_{2j}{t}_{2i}+\cdots +{\beta }_{pj}{t}_{pi})}}}$$

(18)

2.1.3. Ordinal Logistic Regression

This type of regression has a dependent variable with at least three order levels. This differs from the binary logistic regression that takes only two values 0 and 1. The advantage of ordinal logistic regression is that it is capable of modelling at least two regression curves at the same time. The assumption in modelling with ordinal logistic regression is that the relationship between independent variables and logits are the same [21]. The coefficients of the independent variables do not differ significantly given that the logits are the same. The constant term ${\alpha }_k$ for each equation is different.

$$log\left({\displaystyle \frac{p_1}{1-p_1}}\right)={\alpha }_{k_1}+{\beta }^{\prime }T$$

(19)

$$log\left({\displaystyle \frac{p_1+p_2}{1-p_1-p_2}}\right)={\alpha }_{k_2}+{\beta }^{\prime }T$$

(20)

$$log\left({\displaystyle \frac{p_1+p_2+\cdots +p_k}{1-p_1-p_2-\cdots -p_k}}\right)={\alpha }_k+{\beta }^{\prime }T,$$

(21)

2.1.4. Baseline Category Logit Model

When ${\gamma }_j\left(\mathbf{t}\right)$ = $P\left(Z=j|\mathbf{t}\right)$ for a fixed setting t for independent variables, with ${\sum }_j{\gamma }_j\left(\mathbf{t}\right)=1$, for observations at that setting, the study considers the numbers at the J categories of Z as multinomial with probabilities, $\{{\gamma }_1\left(\mathbf{t}\right),\cdots ,{\gamma }_j\left(\mathbf{t}\right)\}$. logit models pair each dependent category with a baseline category given by :

$$log{\displaystyle \frac{{\gamma }_j\left(\mathbf{t}\right)}{{\gamma }_J\left(\mathbf{t}\right)}}={\alpha }_j+{\beta }^{\prime }T$$

(22)

where j = $1,2,\cdots ,(J-1)$, explain the effects of t on these (J-1) logits, the impact varies in line with the response paired with the baselines [18]. Since

$$log{\displaystyle \frac{{\gamma }_a\left(\mathbf{t}\right)}{{\gamma }_b\left(\mathbf{t}\right)}}=log{\displaystyle \frac{{\gamma }_a\left(\mathbf{t}\right)}{{\gamma }_J\left(\mathbf{t}\right)}}-log{\displaystyle \frac{{\gamma }_b\left(\mathbf{t}\right)}{{\gamma }_J\left(\mathbf{t}\right)}},$$

(23)

with categorical predictors, Pearson chi-square statistic and the likelihood ratio chi-square statistic goodness-of-fit statistics provide a mode check when data are not sparse [22].

2.1.5. Confidence Intervals for Logistic Regression

The odds ratio in logistic regression for the shortest width confidence interval was developed by [23]. The shortest width confidence interval has a smaller probability of covering the wrong odds ratio value compared with the standard confidence interval. Let the coefficient of logistic regression $\beta$ be estimated by maximum likelihood so that $\widehat{\beta }$ = ($\beta$, ${\delta }^2$) in a big sample. To achieve the shortest confidence interval for odds ratio = $e^{\beta }$ using $\widehat{\beta }$ assuming the variance is known. The $100(1-\alpha )$% confidence interval for $\beta$ is given by:

$$\begin{array}{c}\hfill \left(\widehat{\beta }-z_{1-{\displaystyle \frac{\alpha }{2}}}\sigma ,\widehat{\beta }+z_{1-{\displaystyle \frac{\alpha }{2}}}\sigma \right)\end{array}$$

(24)

and then exponentiates to obtain $100(1-\alpha )$% confidence interval for OR given by :

$$\begin{array}{c}\hfill \left(e^{\widehat{\beta }-z_{1-{\displaystyle \frac{\alpha }{2}}}\sigma },e^{\widehat{\beta }+z_{1-{\displaystyle \frac{\alpha }{2}}}\sigma }\right)\end{array}$$

(25)

where $z_{1-{\displaystyle \frac{\alpha }{2}}}$ is the $(1-{\displaystyle \frac{\alpha }{2}})$th quantile of the standard normal cdf, $z_{1-{\displaystyle \frac{\alpha }{2}}}$ = ${\varphi }^{-1}$$(1-{\displaystyle \frac{\alpha }{2}})$ where $\varphi$ is the cdf of the standard normal distribution. If $\alpha$ = 0.05 then $z_{1-{\displaystyle \frac{\alpha }{2}}}$ = $1.96$. The Wald CI with symmetric z values for OR is given by:

$$\begin{array}{c}\hfill \left(e^{\widehat{\beta }+z_1\sigma },e^{\widehat{\beta }+z_2\sigma }\right)\end{array}$$

(26)

where $z_1$<$z_1$ are such that ${\varphi }_{\left(z_2\right)}$ - ${\varphi }_{\left(z_1\right)}$ = 1- $\alpha$. The standard CI has the form $\left(2.22\right)$ with ${\varphi }_{z_2}$ = - ${\varphi }_{z_1}$. The following optimisation is obtained min$\left(e^{z_2\sigma }-e^{z_1\sigma }\right)$. According to [23], this optimisation problem reduces to the solution of the following system of equations for $z_1$ and $z_2$:

$$\begin{array}{c}\hfill {\varphi }_{\left(z_2\right)}-{\varphi }_{\left(z_1\right)}=1-\alpha \end{array}$$

(27)

$$\begin{array}{c}\hfill z_1+z_2=-2\sigma \end{array}$$

(28)

To overcome this system, they used Newton’s algorithm by updating the z-values as follows: $z_1^{\prime }=z_1+{\Delta }_1$, $z_2^{\prime }=z_2-{\Delta }_2$, where:

$$\begin{array}{c}\hfill {\Delta }_1={\displaystyle \frac{\delta -(z_1+z_2+2\sigma )\varphi \left(z_2\right)}{\varphi \left(z_2\right)+\varphi \left(z_1\right)}}\end{array}$$

(29)

$$\begin{array}{c}\hfill {\Delta }_2={\displaystyle \frac{\delta +(z_1+z_2+2\sigma )\varphi \left(z_1\right)}{\varphi \left(z_2\right)+\varphi \left(z_1\right)}}\end{array}$$

(30)

$$\begin{array}{c}\hfill \delta ={\varphi }_{\left(z_2\right)}-{\varphi }_{\left(z_1\right)}-1+\alpha \end{array}$$

(31)

starting from the standard values, $z_1$ = - $z_{1-{\displaystyle \frac{\alpha }{2}}}$ and $z_2$ = $z_{1-{\displaystyle \frac{\alpha }{2}}}$ and where $\varphi$ denotes the density of the standard variable. After $z_1$ and $z_2$ are determined the $100(1-\alpha )$% confidence interval for $OR$ is computed as $\left(e^{\widehat{\beta }+z_1\sigma },e^{\widehat{\beta }+z_2\sigma }\right)$.

For the standard confidence interval $z_1$ = ${\varphi }^{-1}\left({\displaystyle \frac{\alpha }{2}}\right)$ and $z_2$ = ${\varphi }^{-1}(1-{\displaystyle \frac{\alpha }{2}})$, and for optimal CI $z_1$ and $z_2$ are computed via iterations as a solution to an optimization problem. The result of the comparison of wrong coverage probabilities for standard and optimised 95% CI is shown in Figure $2.1$. Two scenarios are used one with $\sigma$ = 0.25 and the other with $\sigma$ = 0.4. The value of $O{R}_{true}$ = 1.2 in both cases. For the range of OR values the coverage of the wrong OR is smaller for the shortest with CI.

Figure 1. The probability of false coverage for the traditional Wald CI and the CI with shortest width: [23].

Figure 1. The probability of false coverage for the traditional Wald CI and the CI with shortest width: [23].

Confidence intervals can be determined using standard errors.

2.5. Machine Learning Methods

There are two main categories of machine learning, namely supervised learning and unsupervised learning. In supervised learning, the model learns patterns from a labelled dataset and the trained model is used to make predictions on unseen data. Unsupervised learning does not require a labelled dataset. The most commonly used machine learning include Random Forest and Artificial Neural Network. A brief discussion about them is given next.

2.5.1. Random Forest

According to [29], a random forest entails a predictor that consistitutes a collection of S randomised regression trees. For the j-th tree in the family, the value predicted at the query point $\mathbf{t}$ is indicated by $s_n(t,{\rho }_j,C_n)$, for j = $1,\cdots ,s$ where ${\rho }_j$ are independent random variables. $C_n$ stands for the training sample. Finite forest estimate formed by joined trees [29] given by :

$$s_{S;n}(t;{\rho }_1,\cdots ,{\rho }_m,C_n)={\displaystyle \frac{1}{S}}\sum _{j=1}^S{s}_n(t,{\rho }_j,C_n)$$

(48)

As S grows to infinity equation $\left(2.48\right)$ is obtained as:

$$s_n(t;c_n)={\mathbb{E}}_{\rho }\left[s_n(t,\rho ,C_n)\right],$$

(49)

$$\underset{t\to \infty }{lim}{s}_{n;S}(t;{\rho }_1,\cdots ,{\rho }_s,C_n)=s_n(t;C_n)$$

(50)

[30] states that a random forest algorithm uses the following parameters:

• $s_{try}$∈ (1, ⋯, p), which is the number of preselected directions for splitting
• $a_n$∈ (1, ⋯, n), which is the number of sampled data points in each tree.
• $q_n$∈ (1, ⋯, $a_n$), which is the number of leaves in each tree.

Additionally, [30] implemented the following random forest algorithm with a predicted value at $\mathbf{t}$. It consists of the input and output. The input has the training set denoted by $C_n$, with a number of trees $S>0$, $s_{try}$∈ (1, ⋯, p), $a_n$∈ (1, ⋯, n), $q_n$∈ (1, ⋯, $a_n$) and $\mathbf{t}$∈${[0;1]}^p$. For the output prediction of the random forest at $\mathbf{t}$ for j= 1, ⋯, S, the following procedures are followed [30].

• Uniformly chose $a_n$ in $C_n$ without replacement
• Set $P_0$ = ${[0;1]}^p$ partition on associated with the root of the trees
• For all 1 ≤≤$a_n$, set $P_L$= ∅
• Set $n_{nodes}$ = 1 and level = 0.
• while $n_{nodes}$<$q_n$ do if $P_{level}$ = ∅ ; then level = level + 1
• Let B be the first element in $P_{level}$ where B contains exactly one point then $P_{level}$ ← $P_{level}$ \$\left\{B\right\}$ $P_{level+1}$←$P_{level+1}$∪$\left\{B\right\}$
• Calculate the predicted value $s_n(t,{\Theta }_j,C_n$) at t equal to the average of the $Z_i$ falling in the cell of t in partition $P_{level}$∪$P_{level+1}$
• Calculate the random forest estimate $s_{S;n}(t;{\rho }_1,\cdots ,{\rho }_s,C_n)$ at the query point $\mathbf{t}$

2.5.2. Artificial Neural Network

It has neurons that can be expressed as

$$h_j\left(s\right)=\delta \left(w_j+\sum _{i=1}^n{w}_{ij}{t}_i\right)$$

(51)

where $\delta$ stands for non-linear function activation, $w_{ij}$ are the weights connecting neuron j to neuron i, $w_j$ is the bias and n is the total number of input nodes. A neural network that consists of three-layered is indicated in Figure $2.1$. The input layer pass on values t = $t_1,\cdots ,t_p$ to the second layer. The second layer has activation units $h_j$, and generates non-linear transformations as outputs. The third layer consists of an activation unit, and it makes use of weighted outputs obtained from the second layer and yields the predicted value which is the final output.

Figure 2. Artificial neural network : [31].

Figure 2. Artificial neural network : [31].

According to [32], perceptrons are used to design processing units of artificial neural networks. They are used to determine non-linear problems. Figure $2.2$ shows an input that has K nodes and a Node 0 representing the bias node. The J nodes stand for hidden layer and Node 0. I nodes stand for output layer with no bias node. A feedforward type network is used for the whole network. This means the network connections are allowed from a layer of a particular index to layers of a higher index [33]. Additionally, multilayer perceptron are often used in the testing phase and training phase. In the training phase, given a set of training data

Figure 3. Structure of multilayer perceptron: Source: [33].

Figure 3. Structure of multilayer perceptron: Source: [33].

Figure 4. How backpropagation works: Source: [33].

Figure 4. How backpropagation works: Source: [33].

$\left\{t\right(1),d(1\left)\right\},\cdots ,\left\{t\right(p),d(p\left)\right\},\cdots ,\left\{t\right(PT),d(PT\left)\right\}$ the target is to map $\left\{t\right(1\left)\right\}$ to $\left\{d\right(1\left)\right\}$. The Backpropagation algorithm is used to train the multilayer perceptron. A simple representation of the algorithm is illustrated in Figure $2.3$. From the figure, it could be considered that the output of the multilayer perceptron is equal to $t\left(p\right)$ applied across the input layer of the multilayer perceptron. The output of the multilayer perceptron which is the same as $d\left(p\right)$ an error function is constructed [33] and it can be written as:

$$\mathbb{E}\left(W\right)=\sum _{p=1}^{PT}\sum _{i=1}^I{\left[d_i^2\left(p\right)-y_i^2\left(p\right)\right]}^2,$$

(52)

where :

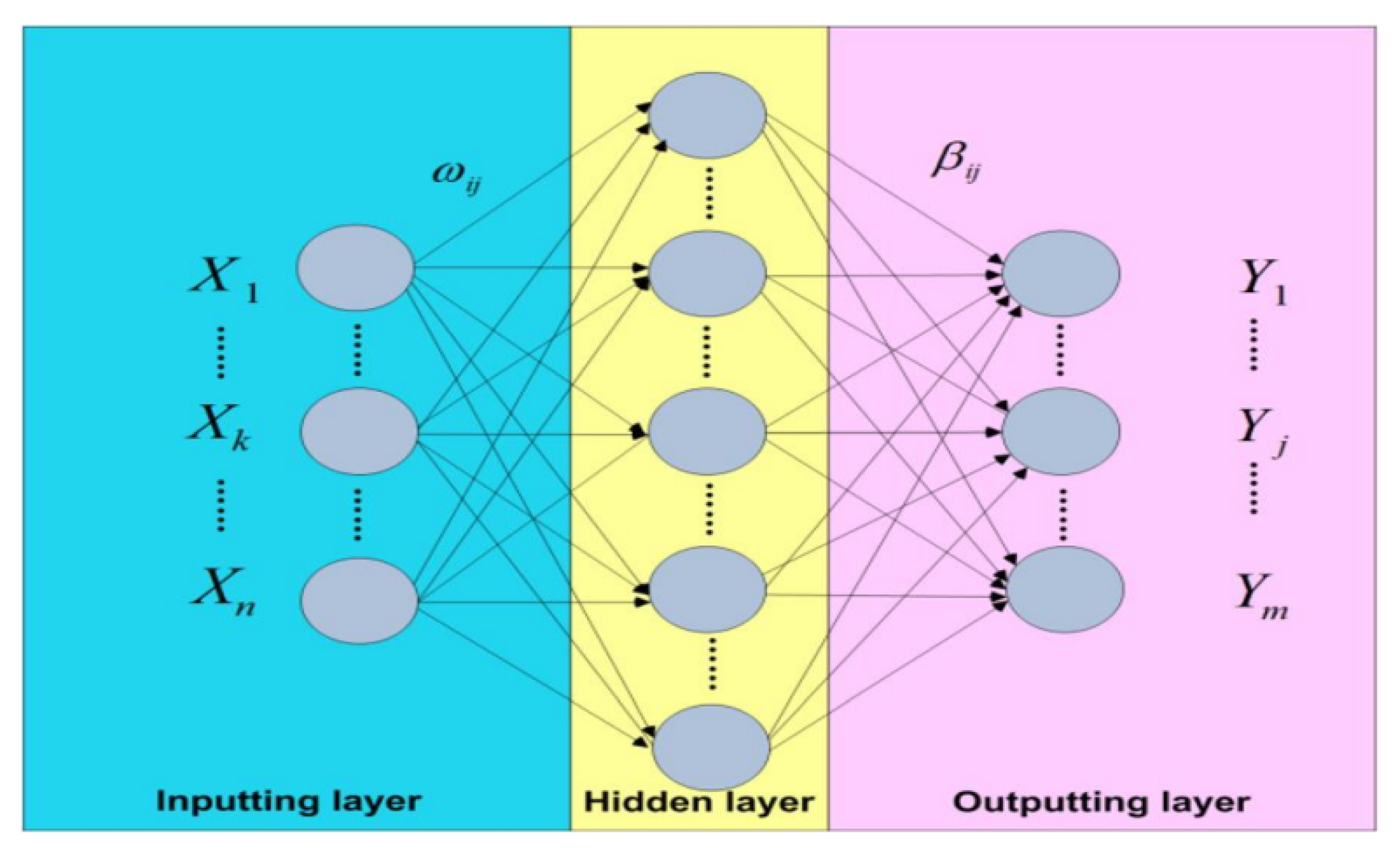
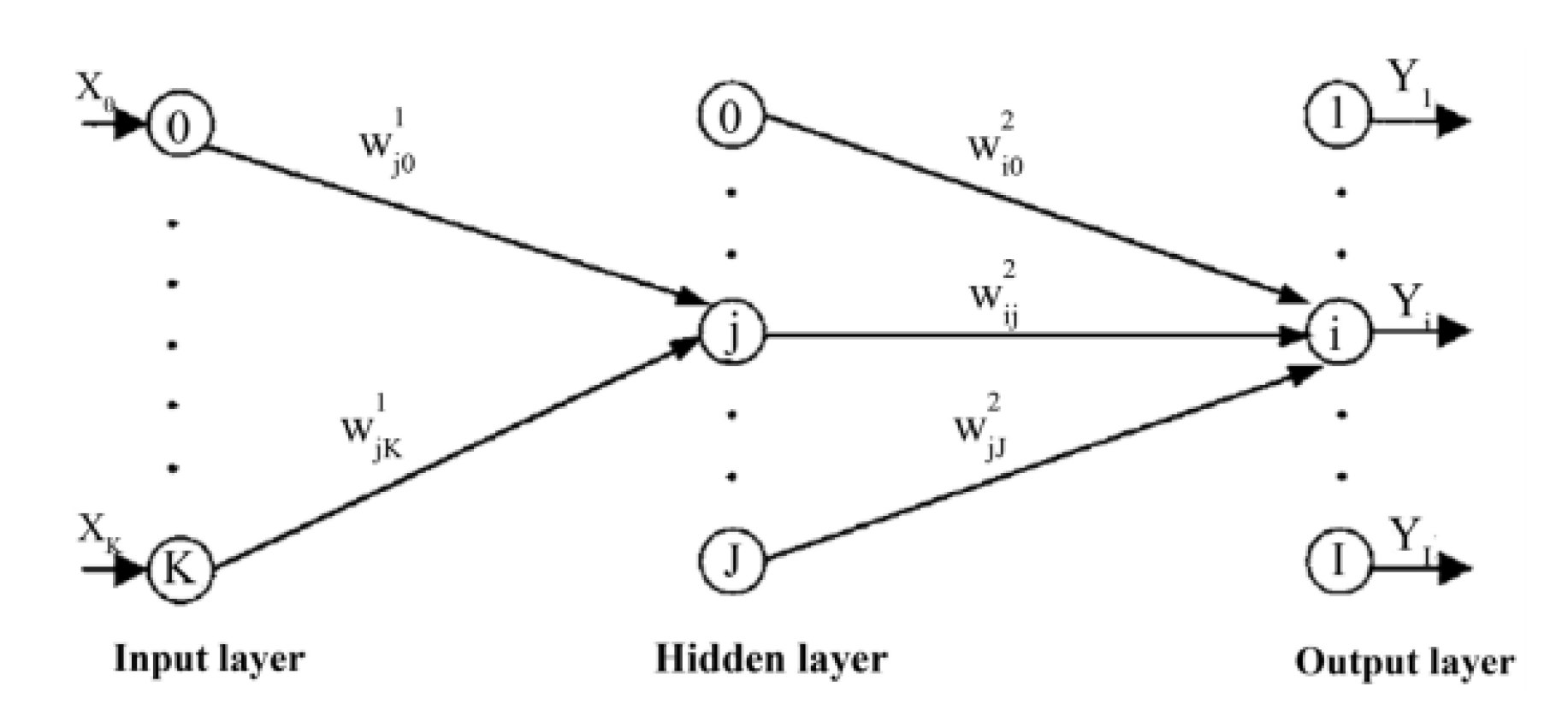
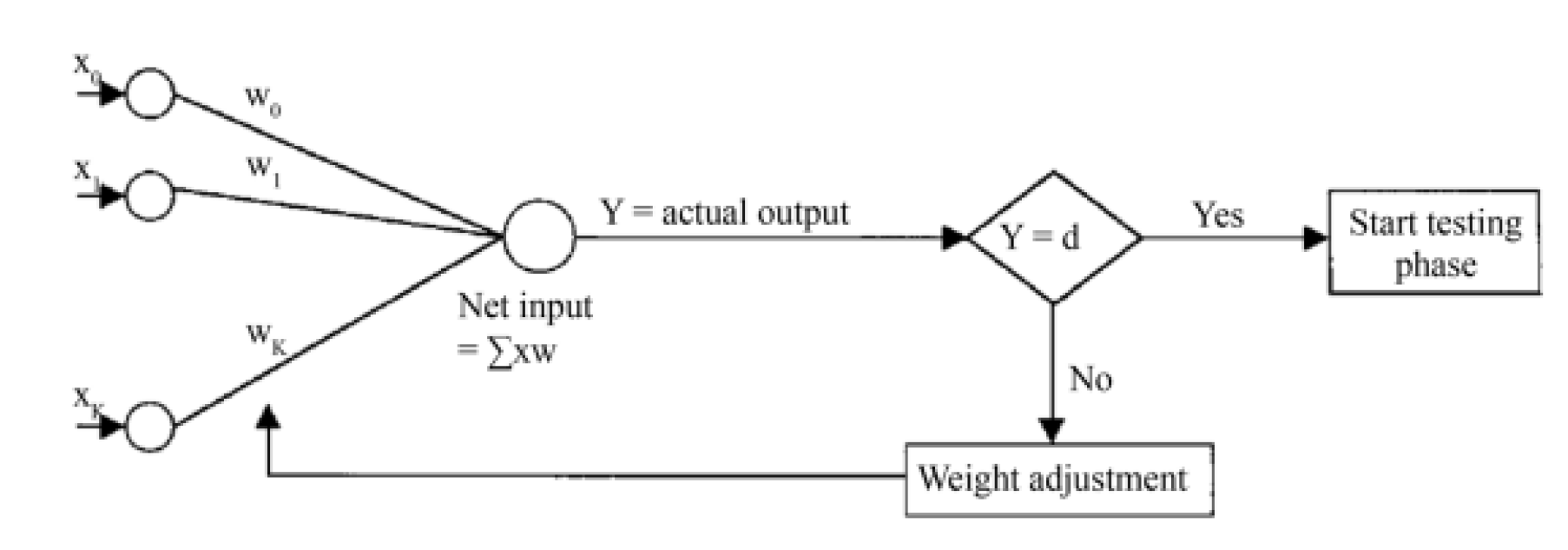
• $\mathbb{E}\left(W\right)$ = Error function to be minimised,
• W = the weight vector,
• $PT$ = the number of training patterns,
• I = the number of output nodes,
• $d_i^2\left(p\right)$ = the desired output of node i if the pattern p is introduced to the MLP,
• $y_i^2\left(p\right)$ = the actual output of node i if pattern p is introduced to the MLP

The actual output is taken closer to the desired output when the error function is reduced. Equation (2.52) is differentiated and optimisation techniques applied to perform the minimisation task. Gradient descent technique is given by:

$$\Delta W=-\eta \Delta \mathbb{E}\left(W\right),$$

(53)

where

• $\Delta W$ = the change of weight vector,
• $\eta$= the learning parameter and
• $\Delta \mathbb{E}\left(W\right)$ = the gradient vector $\mathbb{E}\left(W\right)$ concerning weight vector W

3. Literature Review

4. Materials and Methods

5. Data Analysis

5.2. Exploratory Data Analysis (EDA)

5.2.1. Handling Imbalances

The dependent variable, which is accident severity, was split up into non fatal and fatal classes. The fatal had 22 334 observations and the non fatal had 123 988 observations. There is a huge imbalance here. If one class has more observations than the other class, the results for classifying observations using probability will favour classes with more observations. To address the challenge of imbalance, the study employed the Upsampling method. The minority class size is increased by sampling with replacement and the size of classes will have an equal size. As a result, there will be fewer errors and the accuracy of the model will improve.

The exploration data analysis was conducted to evaluate associations among response variable and explanatory variables. The researcher adopted the accident dataset, which was recorded from the 1st of January 2014 until the 31st of December 2014. The total observation of the accident severity data was 146 322. The researcher used accident severity as the dependent variable and used, day of the week, number of vehicles (stands for vehicles involved in an accident in a given day), place of accident, road surface conditions, light conditions, weather conditions, speed limit, road type, and police attendance as the predictor variables. The days of the week were divided into two categories: weekends and weekdays. The variable light conditions was divided into day and night. The road surface conditions were classified as dry, snow, and wet. The time was categorised into four quarters. The types of roads were further classified into roundabouts, carriageways, one-ways/slips, and others.

On the other hand, weather conditions were divided into five categories: fine, rain, snow, fog/mist, and others. The urban or rural area variable was divided into two classes: urban and rural. The highest number of recorded traffic accident fatalities occurred on carriageways, which had 20 604 (92.25%). The weekdays accounted for 16 097 (72.07%) traffic accident fatalities. The variable weather conditions classified as fine had 18 869 (84.49%) traffic accident fatalities recorded. On the other hand, weather conditions classified as snowing recorded 40 (0.18%) traffic accident fatalities.

Table 1. Descriptive and inferential statistics.

Table 1. Descriptive and inferential statistics.

Category	Fatal	Non-Fatal	Row Total	Chi-square
	(f)(%)	(f)(%)	(f)(%)	P-value
Weekdays	16097(72.07%)	95264(85.55%)	111361(76.11%)	0.000
Weekends	6237 (27.93%)	28724 (82.16%)	34961 (23.89%)
Carriageway	20604 (92.25%)	110406 (84.27%)	131010 (89.54%)	0.000
One way/Slip	586 (2.62%)	3891 (86.91%)	4477 (3.06%)
Roundabout	1066 (4.77%)	9263 (89.68%)	10329 7.06%
Others	78 (0.35%)	428 (84.59%)	506 (0.35%)
Day	15595 (69.83%)	92476 (85.57%)	108071 (73.86%)	0.000
Night	6739 (30.17%)	31512 (82.38%)	38251 (26.14%)
Fine	18869 (84.49%)	101585 (84.34%)	120454 (82.32%)	0.000
Fog/Mist	140 (0.63%)	613 (81.41%)	753 (0.52%)
Raining	2718 (12.17%)	17280 (86.41%)	19998 (13.67%)
Snowing	40 (0.18%)	265 (86.89%)	305 (0.21%)
Other	567 (2.54%)	4245 (88.22%)	4812 (3.29%)
Dry	15658 (70.11%)	86361 (84.65%)	102019 (69.72%)	0.038
Snow	6354 (28.45%)	35567 (84.84%)	41921 (28.65%)
Wet	322 (1.44%)	2060 (86.48%)	2382 (1.63%)
Rural	9760 (43.70%)	40275 (80.49%)	50035 (34.20%)	0.000
Urban	12574 (56.30%)	83713 (86.94%)	96287 (65.81%)
Police Absent	1961 (8.78%)	24754 (92.66%)	26715 (18.26%)	0.000
Police Present	20373 (91.22%)	99234 (82.97%)	119607 (81.74%)
1 Quarter	5043 (22.58%)	29738 (85.50%)	34781 (23.77%)	0.000
2 Quarter	5666 (25.37%)	30177 (84.19%)	35843 (24.50%)
3 Quarter	5879 (26.32%)	31087 (84.10%)	36966 (25.26%)
4 Quarter	5746 (25.73%)	32986 (85.17%)	38732 (26.47%)

The p-values of chi-square of independence were all less than 5% level of significance, which implies that there is an association between the dependent variable and predictors. The results suggest that the predictors are candidates for explaining the accident severity.

This study categorised accidents into four quarters in order to examine seasonality effects. Table $5.1$ indicates that the third quarter recorded the most fatal traffic accidents, with 5 879 (26.32%) accidents, followed by the fourth quarter with 5 746 (25.73%) accidents. There were 5 043 (22.58%) accidents in the first quarter, and 5 666 (25.37%) accidents in the second quarter. There is a difference of 623 accidents between the first and second quarters. Table $5.1$ shows that there has been an increase in traffic accident fatalities from the first to the third quarter. On the other hand, Road type-related traffic accidents are very concerning since they are avoidable. If strict measures are put in place to prevent road accidents that cause death, the number of traffic fatalities could be reduced. Results show that 20 604 (15.73%) fatal accidents occurred on carriageway roads, followed by 1 066 (10.32%) at roundabouts. One way or Slip had more accidents than the others, with 78 traffic accidents.

It can be seen from the traffic accident fatalities by urban or rural area in Table $5.1$ that accidents happen more commonly in cities than in rural areas. This is because there is more volume of traffic in cities than in rural settings. The chances of an accident occurring are high when the traffic volume is also high. The predictor variable light conditions play a crucial role in analysing traffic accidents. There were two categories of light conditions, day and night. It was found that traffic accident fatalities occurred more often during the day than during the night. There are fewer accidents recorded at night as there is less traffic on the road compared to day time. The introduction of good road lighting could also be a contributing factor. In addition, [87] agrees to this point as one of the findings in their study was that night accidents can be reduced by the use of good road lighting. Since more people are usually working during the day, traffic is generally high during this time. Nights are associated with a high number of fatalities, despite fewer accidents occurring. This might be due to drunk driving. On the other hand, [87] mentioned that traffic volume is higher during daylight as a result, more traffic accident fatalities are recorded.

Variable road surface conditions contribute to the increased number of traffic accidents and deaths. Dry surface conditions is associated with the most traffic accident fatalities, with 15 658 (15.35%). Snow road surface conditions accounted for the second highest number of traffic fatalities accidents, with 6 354 (15.16%), followed by wet conditions, with 322 (13.52%). Wet roads may lead to more cautious driving than roads with dry surfaces, based on the results. Weather conditions impact on traffic accident fatalities were examined. A total of 18 869 (15.67%) traffic accident fatalities occurred in fine weather conditions. In addition, there were 2 718 (13.59%) accidents caused by the weather conditions, when it was raining. The number of accidents associated with snowfall was the lowest, with 305 in total. Fog or mist was responsible for 40 (18.59%) traffic accident fatalities.

5.3. Logistic Regression Analysis

The researcher conducted the stepwise regression approach for selecting the significant variables in explaining the severity of accidents. After determining the significant covariates, we fitted the binomial logistic regression model since we had a binary response. The methods that were explored in assessing the covariates were deviance and Akaike information criteria (AIC). The variable with the highest univariate AIC value and smallest deviance was first included, that was quarter and the other variables are consequently added based on how they influence the AIC and deviance value. From this result, it was observed that quarter, speed limit, road surface condition, day of the week, road type, light conditions, place of accident, number of vehicles and police attendance were significant.

Table 2. Stepwise regression approach for logistic regression model for traffic accident fatalities.

Table 2. Stepwise regression approach for logistic regression model for traffic accident fatalities.

Covariates	Df	Deviance	AIC
None		230649	230687
Quarter	3	230732	230764
The Speed limit	1	230742	230778
The Road surface condition	2	230788	230822
The Weather conditions	4	230819	230849
The Day of week	1	230848	230884
The Road type	3	231059	231091
The Light conditions	1	231046	231082
Place of accident	1	231304	231340
The Number of vehicles	1	232902	232938
Police attendance	1	234040	234076

5.4. Binomial Logistic Regression Model

Table $5.3$ shows the estimates, odds ratio, standard errors, z values and p-value for the predictor variables. The predictors for the logistic regression such as speed limit, and light conditions were statistically significant at 5% level since they had a p value less than $0.05$. The variables road type classified as others and weather condition classified as snowing had p vaues of $0.182964$ and $0.484654$, respectively. The p values are greater than $0.05$, hence they are insignificant. The odds ratio of 0.7200 for number of vehicles involved in traffic accident fatalities suggests that for every unit increase in the number of vehicles involved in a car accident, the likelihood of a traffic fatal accident decreases by 28%. The odds ratio of a person experiencing a fatal accident during the weekends is $1.2$ times that of weekdays. Traffic accident fatalities that occur on a slippery road have 17% less chance of resulting in a fatal accident compared to an accident that occurred in carriageways.

Table 3. Logistic regression for traffic accident fatalities.

Table 3. Logistic regression for traffic accident fatalities.

Covariates	Estimate	Odds Ratio	Sd	Z-Value	P-value
Intercept	-0.2110327	0.8097476	0.0326297	-6.468	0.0000
Number of Vehicles	-0.3284669	0.7200268	0.0070883	-46.339	0.0000
Day:Weekends	0.1610077	1.1746941	0.0114158	14.104	0.0000
Road Type:Slip	-0.1888540	0.8279073	0.0297239	-6.354	0.0000
Road Type Round About	-0.4055796	0.6665904	0.0210848	-19.236	0.0000
Road Type: Others	0.1125592	1.1191385	0.0845239	1.332	0.182964
Speed limit	0.0046902	1.0047012	0.0004875	9.621	0.0000
Light Conditions: Night	1.2657635	3.5457989	0.0118409	19.904	0.0000
Weather Conditions: Fog/Mist	-0.1769851	0.8377922	0.0674142	-2.625	0.008656
Weather Conditions: Raining	-0.2391297	0.7873128	0.0186169	-12.845	0.0000
Weather Conditions: Snowing	-0.0793410	0.9237249	0.1135330	-0.699	0.484654
Weather Conditions: Others	-0.1058903	0.8995233	0.0303448	-3.490	0.000484
Road Surface: Snow	-0.0155717	0.9845489	0.0147245	-1.058	0.290266
Road Surface: Wet	-0.5092450	0.6009491	0.0435462	-11.694	0.0000
Place of Accident: Urban	-0.3623045	0.6960704	0.0141845	-25.542	0.0000
Police Attendance Yes	0.8546232	2.3504886	0.0151043	56.581	0.0000
2nd Quarter	0.1260474	1.1343359	0.0148897	8.465	0.0000
3rd Quarter	0.1066344	1.1125274	0.0148262	7.192	0.0000
4th Quarter	0.0500855	1.0513610	0.0141083	3.550	0.000385

For every one unit increase in speed limit, we expect to see about 0.47% increase in the odds of experiencing a fatal accident. For light conditions, the parameter is equal to 1.2657635 and the odds occurring is 3.5457989. This means that the night travellers are 3.5457989 times more likely to be involved in a fatal accidents than those travelling during the day. There was an increase in traffic accident fatalities since the odds ratio was greater than one. Traffic accident fatalities that occurred in urban areas had an odds ratio of $0.6960704$ compared to rural areas. Since the odds ratio is less than one, this shows a decline in traffic accident fatalities as compared to rural area. The odds of experiencing a fatal accident in the presence of the police is $2.3504886$ times more likely to occur as compared to absence of police.

The Wald test was implemented to assess the achievement of the model. The null hypothesis assumes that there are no differences in accident severity using factors such as road type, light conditions, weather conditions, and road surface conditions drawn from an accident dataset. The alternative hypothesis is that there are differences in accident severity using factors such as road type, light conditions, weather conditions, and road surface conditions drawn from an accident dataset. The study rejects the null hypothesis since p < 0.05. The study concludes that there are differences in accident severity using factors such as road type, light conditions, weather conditions, and road surface condition drawn from an accident dataset since p = 0.000. The p values were less than 0.05 for the Wald test. Residuals and deviances were also used to assess models. The residual deviance obtained has a value of 230649 on 173565 degrees of freedom. On the other hand, the null deviance obtained has a value of 240639 on 173583 degrees of freedom. Since the residual deviance has a value less than the null deviance, this explains that the model is a better model compared to Random forest. The parameters are estimated using a method of maximum likelihood discussed under the theoretical background. Additionally, the pseudo $R^2$ value seems not to be good enough as the value is low.

5.5. Analysis of Variance (ANOVA) for Traffic Accident Fatalities

Table $5.4$ indicates the analysis of variance for accident severity. The ANOVA was conducted to assess the impact of each predictor on the regressor (accident severity). The results show that the explanatory variables are all statistically signficant since the corresponding p-values are less than 5% level of significance.

Table 4. Analysis of variance for the logistic regression for traffic accident fatalities.

Table 4. Analysis of variance for the logistic regression for traffic accident fatalities.

	Df	Deviance	Residual Df	P-value
The Number of Vehicles	1	1839.3	173582	0.000
The Day of Week	1	428.4	173581	0.000
The Road Type	3	588.9	173578	0.000
The Speed limit	1	2061.2	173577	0.000
The Light Conditions	1	262.3	173576	0.000
The Weather Conditions	4	414	173572	0.000
The Road Surface	2	128.3	173570	0.000
Place of Accident	1	750	173569	0.000
Police Attendance	1	3433.9	173568	0.000
Quarter	3	83.2	173565	0.000

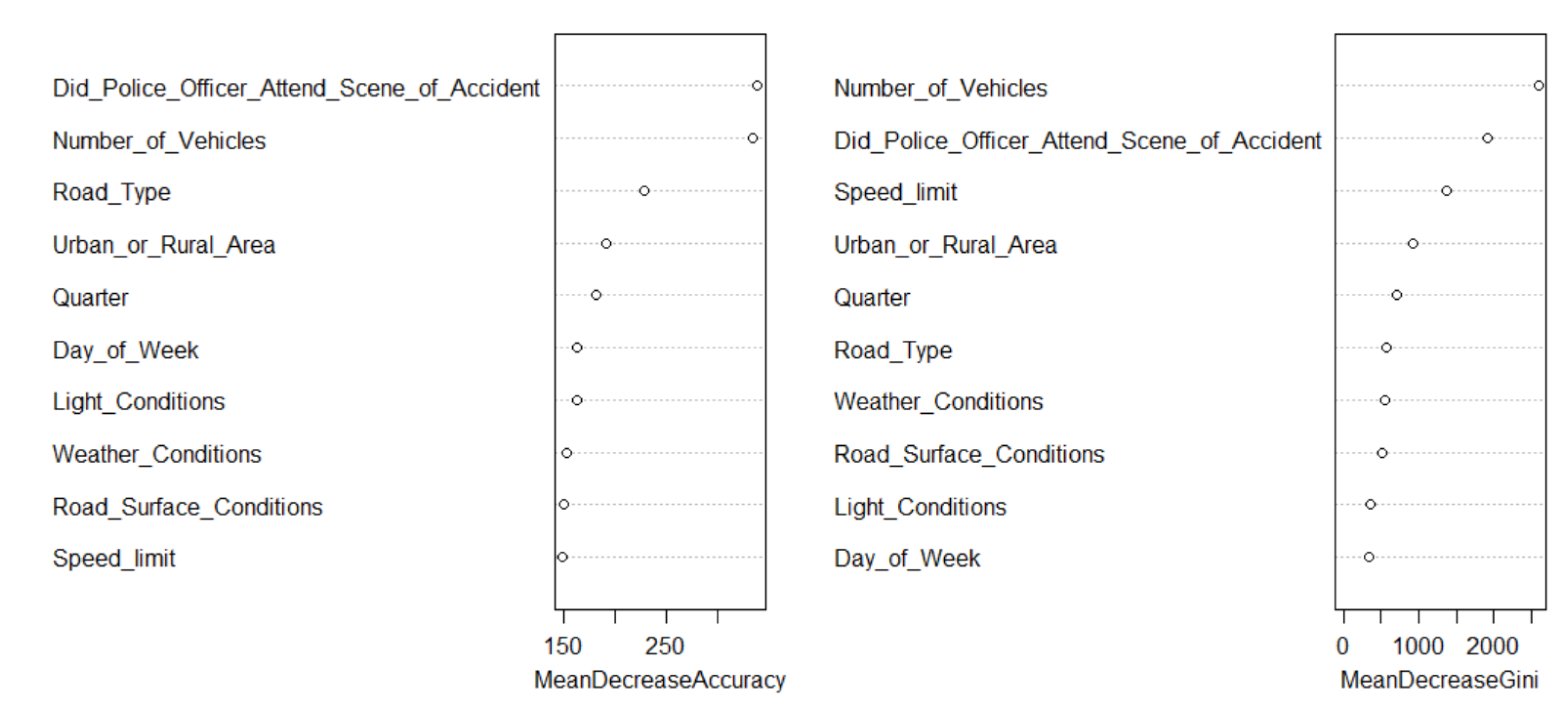
5.7. Random Forest Model

The random forest model of 500 trees was fitted with 10 variables being tried at each split. Table $5.5$ shows the mean decrease accuracy for each explanatory variable. The mean decrease accuracy expresses how much accuracy the model losses by excluding each explanatory variable. The variables number of vehicles, road type, police attendance, light conditions, place of accident and quarter are the top important variables. The speed limit and weather conditions were the least important variables. The speed limit had a mean decrease of $102.1669$, whereas weather conditions had a mean decrease of $103.2044$. Table $5.6$ shows the results of random forest model, including 500 number of trees. The Out Of Bag (OOB) performance error rate was 36.28%, suggesting that the random forest is a fair model.

Table 5. Feature selection for random forest model for traffic accident fatalities.

Table 5. Feature selection for random forest model for traffic accident fatalities.

Covariates	Mean Decrease Accuracy
The Number of Vehicles	248.5413
The Day of week	118.059
The Road Type	159.1584
The Speed limit	102.1669
The Light Conditions	119.8348
The Weather Conditions	103.2044
The Road Surface Conditions	108.9508
The Place of Accident	140.143
The Police Attendance	221.5322
The Quarter	120.894

Table 6. Random forest model for traffic accident fatalities: Confusion matrix.

Table 6. Random forest model for traffic accident fatalities: Confusion matrix.

Type of random tress: Classification
Number of trees : 500
OOB: Estimate of Error Rate: 36.28%
Confusion Matrix	0	1	class.error
0	55548	31244	0.3599871
1	31734	55058	0.3656328

Figure 5. Top features found as most important features in analysing traffic accident fatalities data.

Figure 5. Top features found as most important features in analysing traffic accident fatalities data.

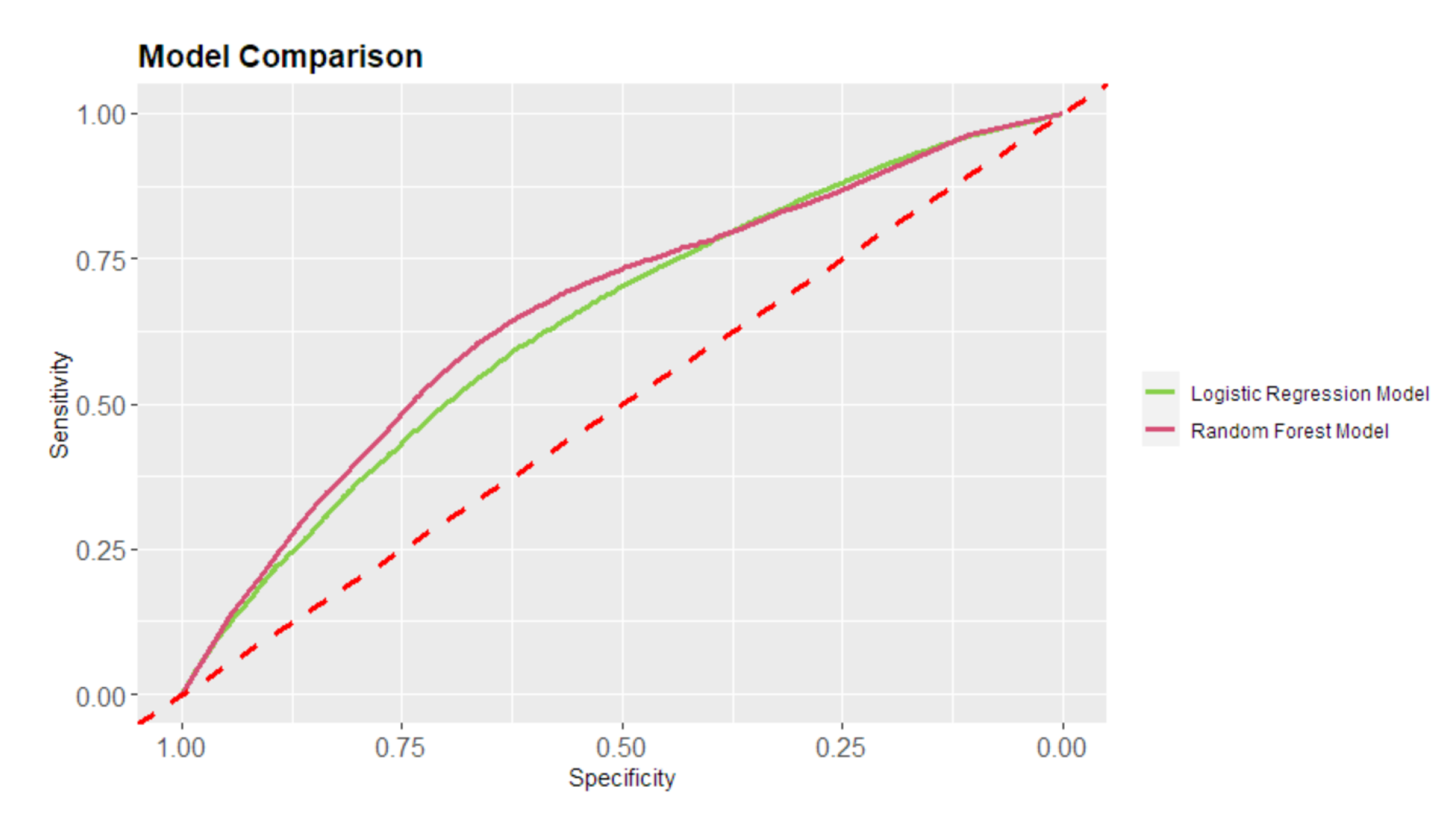
5.8. Model Performance Comparison for Random Forests and Logistic Regression

The target class, accident severity had two labels (Fatal, Non Fatal). The predictors of this classifier such as road surface conditions were used to fit the random forest model. Data was cross-validated by dividing 70% of the training data into 5 folds, and keeping 30% for testing. The metric measures that were adopted for the study were; accuracy, no information rate, kappa, Mcnemar’s test, sensitivity, specificity, gini index and area under the curve.

Table 7. Comparison of logistic regression and random Forests.

Table 7. Comparison of logistic regression and random Forests.

	Logistic Regression Model	Random Forest Model
Accuracy	0.7985	0.640
Recall	0.1935	0.6429
95% Confidence Interval	(0.7964, 0.8005)	(0.6376;0642
No Information Rate	0.8920	0.6021
Kappa	0.1147	0.1611
Mcnemar’s Test P-Value	0.0000	0.0000
Sensitivity	0.8620	0.9048
Precision	0.2736	0.9048
Specificity	0.2736	0.2395
Prevalence	0.8920	0.6021
Balanced Accuracy	0.5678	0.5721
Gini Index	0.2801	0.3179
F1 Score	0.2267	0.7517
AUC	0.64	0.6589

The logistic regression achieved an accuracy of 79.85%. This means 79.85% of the data is predicted correctly. The random forest achieved an accuracy of 64.01%. The results show that logistic regression is a better classifier for predicting accident severity since it had the highest accuracy percentage. The performance of the logistic regression was very close to random forest, with a small difference of 15.84%. However, the random forest model had higher sensitivity, 90.48%, Gini index of 31.79% and F1 Score, 75.17%. Logistic regression recorded both the highest specificity and no information rate with values of 27.36% and 89.20% respectively. Figure $5.2$ shows the receiver operating curve (ROC) comparing the two methods. When the area is big, mainly greater than 60% and the curve is above 50% diagonal line, it suggests that the model correctly predicts the accident severity.

Figure 6. ROC for logistic and random forest models comparing traffic accident fatalities.

Figure 6. ROC for logistic and random forest models comparing traffic accident fatalities.

Table $5.7$ indicates that for logistic regression and random forest, the AUC was significantly higher than 0.5. The random forest had a higher area under the curve of 65.89% compared to the logistic regression. Logistic regression was the most accurate classifier with the highest prevalence of 89.20% and recall of 19.35%.

5.9. Confidence Intervals

Two methods were used to find confidence intervals from the dataset. Confidence intervals estimates were obtained using the standard method discussed under the theoretical background. The second method used the shortest width CI for odds ratio (OR) in logistic regression based on a theorem by [23]. The two methods were discussed in the theoretical background section. From Table $5.8$, it can be seen that the predictors: number of vehicles, speed limit, and light conditions: Night do not contain 0. The 95% confidence intervals displayed show that light conditions had a minimum bound of $0.2125$ and highest bound of $0.2589$. The null hypothesis is given as $H_0$ = There is no association between the light conditions variable and the traffic fatal accident. The alternative hypothesis is given as $H_1$ = There is an association between the light conditions variable and the traffic fatal accident. The lower bound and the upper bound are less than one. Hence, light conditions are significant and had an influence on the increase in traffic accident fatalities. The predictor weather conditions snowing include 0 since it has a minimum bound of $-0.0091$ and highest bound of $0.0859$. This shows the parameter is statistically insignificant.

Looking at the 95% confidence interval, the variable urban has a significant effect on the traffic fatalities since the lower and upper bounds are $-0.3901$ and $-0.3345$, respectively. The 95% confidence interval for the variable "did the police officer attend the scene of the accident" had a minimum bound of $0.8250$ and highest bound of $0.8842$. This does not include zero and the positive values demonstrate that there is a greater risk of traffic fatal accidents. In summary, the fourth quarter result seems to be significant as the lower bound is $0.0224$ and the upper bound is $0.0777$. This is because zero is not included in this 95% confidence interval assuming normality. Looking at the variable speed limit with parameter estimate $\widehat{\beta }$ = 0.0046902 and $\sigma$ = $0.0004875$. The 95% CI intervals for shortest width for odds ratio (OR) in logistic regression are given by:

$$\begin{array}{ccc}\hfill 95\%\mathrm{CI}& =\left(e^{\widehat{\beta }-1.96\sigma },e^{\widehat{\beta }+1.96\sigma }\right)\hfill & \\ \hfill & =\left(e^{0.0046902-1.96\times 0.0004875},e^{0.0046902+1.96\times 0.0004875}\right)\hfill & \\ \hfill & =(1.003741683;1.005661667)\hfill \end{array}$$

The confidence intervals for speed limit do not include 1. This indicates that the speed limit is statistically significant. Additionally, the variable light conditions had a lower bound of 3.4644550 and an upper bound of 3.629052751. It does not contain 1 and we conclude that it is statistically significant.

Table 8. Wald CI and Shortest width CI results for traffic accident fatalities.

Table 8. Wald CI and Shortest width CI results for traffic accident fatalities.

Covaraites	Estimate	95% Shortest width CI	Std.Error	95% CI standard
Number of Vehicles	-0.3284669	0.7100925; 0.73010000	0.0070883	-0.3424; -0.3146
Day:Weekends	0.1610077	1.148702141; 1.2021274009	0.0114158	0.1386; 0.1834
Road Type:Slip	-0.1888540	0.7810525515; 0.8775729826	0.0297239
Road Type: Round About	-0.4055796	0.639604151; 0.6947151372	0.021084
Road Type: Others	0.1125592	0.9482779306; 1.320784719	0.0845239	-0.0531; 0.2782
Speed limit	0.0046902	1.003741683 ; 1.005661667	0.0004875	0.0037 ; 0.0056
Light Conditions: Night	1.2657635	3.46445501 ; 3.629052751	0.0118409	0.2125 ;0.2589
Weather Conditions: Raining	-0.2391297	0.759102227 ;0.816571684	0.0186169
Weather Conditions: Snowing	-0.0793410	0.7394373794 ; 1.153941738	0.1135330	-0.3019 ; 0.1432
Road Surface conditionaal: Snow	-0.0155717	0.9565409105 ; 1.013377002	0.0147245	-0.0444 ; 0.0133
Road Surface: Wet	-0.5092450	0.551785689; 0.654492961	0.0435462
Place of Accident: Urban	-0.3623045	0.676985029; 0.7156937836	0.0141845	-0.3901; -0.3345
Police Attendance Yes	0.8546232	2.281923601 ;2.42111366	0.0151043	0.8250 ;0.8842
4th Quarter	0.0500855	1.022686749 ;1.080839191	0.0141083	0.0224 ;0.0777

Table 9. Goodness of fit.

Table 9. Goodness of fit.

McFadden psedo R square	Cox and snell r square	Nagelkerke R square
0.04151248	0.05592391	0.07456521

Table 10. Wald test results for traffic accident fatalities.

Table 10. Wald test results for traffic accident fatalities.

Covaraites	Estimate	Wald ${\mathit{\chi }}^2$	DF	P-value
Intercept	-0.2110327	41.8	1	0.00
Number of Vehicles	-0.3284669	2147.3	1	0.0
Day:Weekends	0.1610077	198.9	1	0.00
Road Type:Slip	-0.1888540	40.4	1	0.00
Road Type Round About	-0.4055796	1.8	1	0.18
Road Type: Others	0.1125592	370.0	1	0.00
Speed limit	0.0046902	92.6	1	0.00
Light Conditions: Night	1.2657635	396.2	1	0.00
Weather Conditions: Fog/Mist	-0.1769851	6.9	1	0.0087
Weather Conditions: Raining	-0.2391297	12.2	1	0.00048
Weather Conditions: Snowing	-0.0793410	165.0	1	0.00
Weather Conditions: Others	-0.1058903	1	1	0.48
Road Surface: Snow	-0.0155717	1.1	1	0.29
Road Surface: Wet	-0.5092450	136.8	1	0.00
Place of Accident: Urban	-0.3623045	652.4	1	0.00
Police Attendance Yes	0.8546232	3201.5	1	0.00
2nd Quarter	0.1260474	71.7	1	0.0
3rd Quarter	0.1066344	51.7	1	0.00
4th Quarter	0.0500855	12.6	1	0.00039

6. Summary, Conclusions and Recommendations

References

1. Andeta, J.A. Road-traffic accident prediction model: Predicting the Number of Casualties, 2021.
2. Olsen, J.R.; Mitchell, R.; Ogilvie, D.; Team, M.S. Effect of a new motorway on social-spatial patterning of road traffic accidents: A retrospective longitudinal natural experimental study. PloS one 2017, 12, e0184047. [Google Scholar] [CrossRef] [PubMed]
3. Abubakar, I.; Tillmann, T.; Banerjee, A. Global, regional, and national age-sex specific all-cause and cause-specific mortality for 240 causes of death, 1990-2013: a systematic analysis for the Global Burden of Disease Study 2013. Lancet 2015, 385, 117–171. [Google Scholar]
4. Duncan, C.; Khattak, A.; Council, F. APPLYING THE ORDERED PROBIT MODEL TO INJURY SEVERITY IN TRUCK-PASSENGER CAR REAR-END COLLISIONS. Transportation Research Record 1998. [Google Scholar] [CrossRef]
5. Shankar, V.; Mannering, F.; Barfield, W. Effect of roadway geometrics and environmental factors on rural freeway accident frequencies. Accident Analysis & Prevention 1995, 27, 371–389. [Google Scholar]
6. Chen, M.; Zhou, L.; Choo, S.; Lee, H. Analysis of Risk Factors Affecting Urban Truck Traffic Accident Severity in Korea. Sustainability 2022, 14, 2901. [Google Scholar] [CrossRef]
7. Farmer, C.M.; Braver, E.R.; Mitter, E.L. Two-vehicle side impact crashes: the relationship of vehicle and crash characteristics to injury severity. Accident Analysis & Prevention 1997, 29, 399–406. [Google Scholar]
8. Subramanian, R. Passenger vehicle occupant fatality rates by type and size of vehicle; Citeseer, 2006.
9. Anvari, M.B.; Kashani, A.T.; Rabieyan, R. Identifying the most important factors in the at-fault probability of motorcyclists by data mining, based on classification tree models. International Journal of Civil Engineering 2017, 15, 653–662. [Google Scholar] [CrossRef]
10. Kumar, S.; Toshniwal, D. A data mining approach to characterize road accident locations. Journal of Modern Transportation 2016, 24, 62–72. [Google Scholar] [CrossRef]
11. Iranitalab, A.; Khattak, A. Comparison of four statistical and machine learning methods for crash severity prediction. Accident Analysis & Prevention 2017, 108, 27–36. [Google Scholar]
12. Bedard, M.; Guyatt, G.H.; Stones, M.J.; Hirdes, J.P. The independent contribution of driver, crash, and vehicle characteristics to driver fatalities. Accident Analysis & Prevention 2002, 34, 717–727. [Google Scholar]
13. Chang, L.Y.; Wang, H.W. Analysis of traffic injury severity: An application of non-parametric classification tree techniques. Accident Analysis & Prevention 2006, 38, 1019–1027. [Google Scholar]
14. KIM, S.H.; CHUNG, S.B.; SONG, K.H.; CHON, K.S. Development of an Accident Prediction Model using GLIM (Generalized Log-linear Model) and EB method: A case of Seoul. Journal of the Eastern Asia society for Transportation studies 2005, 6, 3669–3682. [Google Scholar]
15. Kim, J.H. Multicollinearity and misleading statistical results. Korean journal of anesthesiology 2019, 72, 558–569. [Google Scholar] [CrossRef] [PubMed]
16. Ahmed, L.A. Using logistic regression in determining the effective variables in traffic accidents. Applied mathematical Sciences 2017, 11, 2047–2058. [Google Scholar] [CrossRef]
17. Harrell, F.E. Regresión modeling strategies: whit applications to linear models, logistic regression, and survival analysis. Technical report, 2001.
18. Chatterjee, S.; Hadi, A.S. Regression analysis by example; John Wiley & Sons, 2015.
19. Czepiel, S.A. Maximum likelihood estimation of logistic regression models: theory and implementation. Available at czep. net/stat/mlelr. pdf 2002, 83. [Google Scholar]
20. Garson, D. Logistic Regression with SPSS. North Carolina State University. Public administration Program 2009. [Google Scholar]
21. Norušis, M.J. SPSS statistics 17.0: Statistical procedures companion; Prentice Hall/Pearson Education, 2008.
22. Agresti, A. Categorical Data Analysis. John Wiley & Sons. Inc., Publication 2002, 15, 24. [Google Scholar]
23. Dahiya, R.C.; Guttman, I. Shortest confidence and prediction intervals for the log-normal. The Canadian Journal of Statistics/La Revue Canadienne de Statistique 1982, pp. 277–291.
24. Mbachu, H.; Nduka, E.; Nja, M. Designing a pseudo R-Squared goodness-of-fit measure in generalized linear models. Journal of Mathematics Research 2012, 4, 148. [Google Scholar] [CrossRef]
25. Menard, S. Applied logistic regression analysis; Vol. 106, Sage, 2002.
26. Al-Ghamdi, A.S. Using logistic regression to estimate the influence of accident factors on accident severity. Accident Analysis & Prevention 2002, 34, 729–741. [Google Scholar]
27. Tsay, R.S. Multivariate time series analysis: with R and financial applications; John Wiley & Sons, 2013.
28. James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An introduction to statistical learning; Vol. 112, Springer, 2013.
29. Scornet, E.; Biau, G.; Vert, J.P. Supplementary materials for: Consistency of random forests. arXiv 2015, 1510. [Google Scholar]
30. Breiman, L. Random forests. Machine learning 2001, 45, 5–32. [Google Scholar] [CrossRef]
31. Louppe, G.; Wehenkel, L.; Sutera, A.; Geurts, P. Understanding variable importances in forests of randomized trees. Advances in neural information processing systems 26 2013. [Google Scholar]
32. Karayılan, T.; Kılıç, Ö. Prediction of heart disease using neural network. 2017 International Conference on Computer Science and Engineering (UBMK). IEEE, 2017, pp. 719–723.
33. Abdelwahab, H.T.; Abdel-Aty, M.A. Development of artificial neural network models to predict driver injury severity in traffic accidents at signalized intersections. Transportation Research Record 2001, 1746, 6–13. [Google Scholar] [CrossRef]
34. Guns, R.; Lioma, C.; Larsen, B. The tipping point: F-score as a function of the number of retrieved items. Information Processing & Management 2012, 48, 1171–1180. [Google Scholar]
35. Deng, X.; Liu, Q.; Deng, Y.; Mahadevan, S. An improved method to construct basic probability assignment based on the confusion matrix for classification problem. Information Sciences 2016, 340, 250–261. [Google Scholar] [CrossRef]
36. Berry, K.J.; Mielke Jr, P.W. A generalization of Cohen’s kappa agreement measure to interval measurement and multiple raters. Educational and Psychological Measurement 1988, 48, 921–933. [Google Scholar] [CrossRef]
37. Mandrekar, J.N. Receiver operating characteristic curve in diagnostic test assessment. Journal of Thoracic Oncology 2010, 5, 1315–1316. [Google Scholar] [CrossRef]
38. Japkowicz, N.; Stephen, S. The class imbalance problem: A systematic study. Intelligent data analysis 2002, 6, 429–449. [Google Scholar] [CrossRef]
39. Visa, S.; Ralescu, A. The effect of imbalanced data class distribution on fuzzy classifiers-experimental study. The 14th IEEE International Conference on Fuzzy Systems, 2005. FUZZ’05. IEEE, 2005, pp. 749–754.
40. Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: synthetic minority over-sampling technique. Journal of artificial intelligence research 2002, 16, 321–357. [Google Scholar] [CrossRef]
41. Ossiander, E.M.; Cummings, P. Freeway speed limits and traffic fatalities in Washington State. Accident Analysis & Prevention 2002, 34, 13–18. [Google Scholar]
42. Hauer, E. Statistical road safety modeling. Transportation Research Record 2004, 1897, 81–87. [Google Scholar] [CrossRef]
43. Anastasopoulos, P.C.; Tarko, A.P.; Mannering, F.L. Tobit analysis of vehicle accident rates on interstate highways. Accident Analysis & Prevention 2008, 40, 768–775. [Google Scholar]
44. Oppong, R.A. Statistical analysis of road accidents fatality in Ghana using Poisson regression. PhD thesis, 2012.
45. Anderson, M. Safety for whom? The effects of light trucks on traffic fatalities. Journal of health economics 2008, 27, 973–989. [Google Scholar] [CrossRef] [PubMed]
46. Ye, F.; Lord, D. Comparing three commonly used crash severity models on sample size requirements: Multinomial logit, ordered probit and mixed logit models. Analytic methods in accident research 2014, 1, 72–85. [Google Scholar] [CrossRef]
47. Caliendo, C.; Guida, M.; Parisi, A. A crash-prediction model for multilane roads. Accident Analysis & Prevention 2007, 39, 657–670. [Google Scholar]
48. Milton, J.; Mannering, F. The relationship among highway geometrics, traffic-related elements and motor-vehicle accident frequencies. Transportation 1998, 25, 395–413. [Google Scholar] [CrossRef]
49. Poch, M.; Mannering, F. Negative binomial analysis of intersection-accident frequencies. Journal of transportation engineering 1996, 122, 105–113. [Google Scholar] [CrossRef]
50. Shankar, V.; Milton, J.; Mannering, F. Modeling accident frequencies as zero-altered probability processes: an empirical inquiry. Accident Analysis & Prevention 1997, 29, 829–837. [Google Scholar]
51. Miaou, S. The relationship between truck accidents and geometric design of road sections: Poisson versus negative binomial regressions. Accident; Analysis and Prevention 1994, 26, 471–482. [Google Scholar] [CrossRef]
52. Valent, F.; Schiava, F.; Savonitto, C.; Gallo, T.; Brusaferro, S.; Barbone, F. Risk factors for fatal road traffic accidents in Udine, Italy. Accident Analysis & Prevention 2002, 34, 71–84. [Google Scholar]
53. Guo, L.; Ge, P.S.; Zhang, M.H.; Li, L.H.; Zhao, Y.B. Pedestrian detection for intelligent transportation systems combining AdaBoost algorithm and support vector machine. Expert Systems with Applications 2012, 39, 4274–4286. [Google Scholar] [CrossRef]
54. AKIN, H.B.; Şentürk, E. Bireylerin mutluluk düzeylerinin ordinal lojistik regresyon analizi ile incelenmesi-analysing levels of happiness of individuals with ordinal logistic analysis. Öneri Dergisi 2012, 10, 183–193. [Google Scholar]
55. Mussone, L.; Ferrari, A.; Oneta, M. An analysis of urban collisions using an artificial intelligence model. Accident Analysis & Prevention 1999, 31, 705–718. [Google Scholar]
56. Yan, X.; Yi, P.; Wu, C.; Zhong, M. ICTIS 2011. American Society of Civil Engineers, 2011.
57. Warner, P. Ordinal logistic regression. BMJ Sexual & Reproductive Health 2008, 34, 169–170. [Google Scholar]
58. Karayiannis, N.; Venetsanopoulos, A. ANNs: Learning Algorithms. Performance Evaluation and Applications. Kluwer Academic Publishers, Boston 1993.
59. Jadaan, K.S.; Al-Fayyad, M.; Gammoh, H.F. Prediction of road traffic accidents in jordan using artificial neural network (ANN). Journal of Traffic and Logistics Engineering 2014, 2. [Google Scholar] [CrossRef]
60. Brijesh Kumar, B.; Sourabh, P. Mining educational data to analyze students’ performance, 2011.
61. Kunt, M.M.; Aghayan, I.; Noii, N. Prediction for traffic accident severity: comparing the artificial neural network, genetic algorithm, combined genetic algorithm and pattern search methods. Transport 2011, 26, 353–366. [Google Scholar] [CrossRef]
62. Rezaie Moghaddam, F.; Afandizadeh, S.; Ziyadi, M. Prediction of accident severity using artificial neural networks. International Journal of Civil Engineering 2011, 9, 41–48. [Google Scholar]
63. Chibueze, O.T.; Nonyelum, O.F. Prediction of Solid Waste Generation Using Self-Organizing Map and Multilayer Perceptron Neural Networks. IUP Journal of Science & Technology 2010, 6. [Google Scholar]
64. Krishnaveni, S.; Hemalatha, M. A perspective analysis of traffic accident using data mining techniques. International Journal of Computer Applications 2011, 23, 40–48. [Google Scholar] [CrossRef]
65. Beshah, T.; Ejigu, D.; Abraham, A.; Snášel, V.; Krömer, P. Knowledge discovery from road traffic accident data in Ethiopia: Data quality, ensembling and trend analysis for improving road safety. Neural Network World 2012, 22, 215. [Google Scholar] [CrossRef]
66. Tavakoli Kashani, A.; Shariat-Mohaymany, A.; Ranjbari, A. A data mining approach to identify key factors of traffic injury severity. PROMET-Traffic&Transportation 2011, 23, 11–17. [Google Scholar]
67. Criminisi, A.; Shotton, J. Decision forests for computer vision and medical image analysis; Springer Science & Business Media, 2013.
68. Effati, M.; Thill, J.C.; Shabani, S. Geospatial and machine learning techniques for wicked social science problems: analysis of crash severity on a regional highway corridor. Journal of Geographical Systems 2015, 17, 107–135. [Google Scholar] [CrossRef]
69. Han, J.; Kamber, M.; Pei, J. Data mining concepts and techniques third edition. The Morgan Kaufmann Series in Data Management Systems 2011, 5, 83–124. [Google Scholar]
70. Pakgohar, A.; Tabrizi, R.S.; Khalili, M.; Esmaeili, A. The role of human factor in incidence and severity of road crashes based on the CART and LR regression: a data mining approach. Procedia Computer Science 2011, 3, 764–769. [Google Scholar] [CrossRef]
71. Al-Radaideh, Q.A.; Daoud, E.J. Data mining methods for traffic accident severity prediction. Int. J. Neural Netw. Adv. Appl 2018, 5, 1–12. [Google Scholar]
72. Li, X.; Lord, D.; Zhang, Y.; Xie, Y. Predicting motor vehicle crashes using support vector machine models. Accident Analysis & Prevention 2008, 40, 1611–1618. [Google Scholar]
73. Kadilar, G.O. Effect of driver, roadway, collision, and vehicle characteristics on crash severity: a conditional logistic regression approach. International journal of injury control and safety promotion 2016, 23, 135–144. [Google Scholar] [CrossRef]
74. Theofilatos, A.; Graham, D.; Yannis, G. Factors affecting accident severity inside and outside urban areas in Greece. Traffic injury prevention 2012, 13, 458–467. [Google Scholar] [CrossRef] [PubMed]
75. Potoglou, D.; Carlucci, F.; Cirà, A.; Restaino, M. Factors associated with urban non-fatal road-accident severity. International journal of injury control and safety promotion 2018, 25, 303–310. [Google Scholar] [CrossRef]
76. Christoforou, Z.; Cohen, S.; Karlaftis, M.G. Vehicle occupant injury severity on highways: An empirical investigation. Accident Analysis & Prevention 2010, 42, 1606–1620. [Google Scholar]
77. Herman, J.; Kafoa, B.; Wainiqolo, I.; Robinson, E.; McCaig, E.; Connor, J.; Jackson, R.; Ameratunga, S. Driver sleepiness and risk of motor vehicle crash injuries: a population-based case control study in Fiji (TRIP 12). Injury 2014, 45, 586–591. [Google Scholar] [CrossRef] [PubMed]
78. Wang, S.Y.; Chi, G.B.; Jing, C.X.; Dong, X.M.; Wu, C.P.; Li, L.P. Trends in road traffic crashes and associated injury and fatality in the People’s Republic of China, 1951–1999. Injury control and safety promotion 2003, 10, 83–87. [Google Scholar] [CrossRef] [PubMed]
79. Aarts, L.; Van Schagen, I. Driving speed and the risk of road crashes: A review. Accident Analysis & Prevention 2006, 38, 215–224. [Google Scholar]
80. Tefft, B.C. The Prevalence of Motor Vehicle Crashes Involving Road Debris, United States, 2011-2014. Age (years) 2016, 20, 10–1. [Google Scholar]
81. Clarke, D.; Ward, P.; Truman, W.; Bartle, C. Fatal vehicle-occupant collisions: An in-depth study. Road Safety Research Report 2007. [Google Scholar]
82. Chang, L.Y.; Mannering, F. Analysis of injury severity and vehicle occupancy in truck-and non-truck-involved accidents. Accident Analysis & Prevention 1999, 31, 579–592. [Google Scholar]
83. Rakha, H.; Van Aerde, M. Statistical analysis of day-to-day variations in real-time traffic flow data. Transportation research record 1995, pp. 26–34.
84. Pai, C.W.; Saleh, W. Exploring motorcyclist injury severity in approach-turn collisions at T-junctions: Focusing on the effects of driver’s failure to yield and junction control measures. Accident Analysis & Prevention 2008, 40, 479–486. [Google Scholar]
85. Anowar, S.; Yasmin, S.; Tay, R. Comparison of crashes during public holidays and regular weekends. Accident Analysis & Prevention 2013, 51, 93–97. [Google Scholar]
86. Kuhn, M.; Johnson, K.; Kuhn, M.; Johnson, K. Over-fitting and model tuning. Applied predictive modeling 2013, pp. 61–92.
87. Mokoma, L.D. Investigating pedestrian safety solutions on rural high-order roads. Case-study: R71 Polokwane. Master’s thesis, University of Cape Town, 2017.
88. Hawkins, R.K. Motorway traffic behaviour in reduced visibility conditions. Vision in Vehicles II. Second International Conference on Vision in VehiclesApplied Vision AssociationErgonomics SocietyAssociation of Optometrists, 1988.
89. De Pauw, E.; Daniels, S.; Thierie, M.; Brijs, T. Safety effects of reducing the speed limit from 90 km/h to 70 km/h. Accident Analysis & Prevention 2014, 62, 426–431. [Google Scholar]