Prerpints.org logo
Preprint
Article

Comparative Analysis of OSEM Parameters for Cardiac SPECT Imaging Across Multiple Camera Brands: A Monte Carlo Study

Altmetrics

Downloads

86

Views

60

Comments

0

supplementary.xlsx (577.17KB )

This version is not peer-reviewed

Applications in Image Analysis and Pattern Recognition

Submitted:

26 July 2024

Posted:

30 July 2024

You are already at the latest version

Alerts
Abstract
Background and Objective: To examine the effect of ordered subset expectation maximization (OSEM) parameters on the quantitative image quality of cardiac SPECT images in two different frequently used SPECT cameras and determine the optimal settings for producing images of best diagnostic quality. Another objective was to assess if different cameras produced a significant change in optimal parameters and levels of detectability. Methods: The optimization of OSEM iterative reconstruction algorithm was carried out by comparing image quality metrics, namely, contrast-to-noise ratio (CNR) and defect contrast across 12 OSEM subset-iteration combinations to find the best choice for cardiac perfusion SPECT images. Eight frames were reconstructed using the SIMIND Monte Carlo Simulation package. An activity of 370 MBq (10mCi) and projection acquisition interval of 20 seconds per projection were used. Attenuation (AC) and scatter corrections (SC) were performed in this study for all images. Results: The 16-2 subset-iteration combination yielded the highest CNR and defect contrast values for both cameras. The difference between CNR values for two cameras was found to be around 5% only. Conclusions: Monte Carlo simulations can be useful to investigate how quantitative image quality behaves with respect to reconstruction parameters and correction algorithms in a controlled environment. The found optimum is similar to values reported in previous findings. In this study, the use of different camera brands did not affect the optimum. The quantitative detectability measures were also very similar.
Keywords: 
Subject: Physical Sciences  -   Radiation and Radiography

1. Introduction

According to the World Health Organization, ischemic heart disease emerged as the leading cause of deaths, accounting for 16% of the total mortality [1]. Since the year 2000, it has exhibited the most substantial surge in death rates, with an increase of over 2 million deaths, reaching nearly 9 million deaths by 2019 [1]. Each year, around 17 million people around the world lose their lives due to cardiovascular diseases (CVD), particularly strokes and heart attacks [2]. Fortunately, such diseases can be diagnosed by performing myocardial perfusion imaging (MPI) using SPECT and other imaging modalities. The significance of MPI in the context of ischemic heart disease lies in its ability to noninvasively assess myocardial perfusion and diagnose CAD, which is crucial in understanding the widespread impact of ischemic heart disease, especially in the context of coronary artery blockages.
In nuclear imaging and emission tomography (ET), heart images can be obtained by Single photon emission tomography (SPECT) or positron emission tomography (PET). These techniques use radioactive substances to visualize various physiological aspects of the body [3]. ET is valuable for detecting tumors, pinpointing regions of the heart impacted by coronary artery disease and identifying brain areas influenced by drugs [3]. As the term "emission tomography" implies, this imaging approach combines two fundamental concepts: utilizing gamma-ray emission (known as the tracer principle) and creating three-dimensional internal body images (referred to as tomography) [3]. PET and SPECT primarily differ in the radioisotopes they use as tracers.
In SPECT studies, radiopharmaceuticals are labeled with single-photon emitters, which release one gamma-ray photon per radioactive decay event [3]. One example of this kind of radiotracer commonly used in SPECT myocardial perfusion imaging (MPI) is Technetium-99m. MPI is a firmly established, noninvasive imaging method extensively applied for assessing individuals with either a confirmed or suspected coronary artery disease (CAD) [4].
To obtain a cardiac perfusion image of diagnostic quality, different corrections and reconstruction techniques are utilized. SPECT images can be reconstructed using either the analytical filtered back projection (FBP) method or through iterative reconstruction (IR) using algebraic approaches [5]. The importance of these methods is in converting raw data into meaningful clinical images [5]. Lately, iterative reconstruction of images, specifically using the ordered subsets expectation maximization (OSEM) algorithm is the most used in clinical practice. Due to its iterative nature and computational superiority over other reconstruction techniques like conventional FBP, OSEM has helped in creating higher quality images in shorter durations [6,7,8].

1.1. Related Literature

Numerous studies utilize the OSEM algorithm for SPECT image reconstruction but only few discuss the topic of optimization of this algorithm in cardiac SPECT.
In a study by De Barros et al., the aim was to determine the optimal OSEM parameters for producing high-quality myocardial perfusion images, considering the relationship with patients' body mass index (BMI) [9]. They concluded that using four iterations and four subsets generated the highest diagnostic quality images across various BMI categories, while six iterations and four subsets were particularly effective for higher BMI levels, supporting precise diagnoses and effective treatment strategies [9]. Nevertheless, this study included only 28 patients, potentially limiting its generalizability, and focused on BMI without considering other variables like age or comorbidities. Additionally, no comparisons with a different reconstruction technique or another camera model were made.
On the other hand, a different study by Dheer et al. sought to optimize OSEM parameters for Tc-99m MIBI myocardial perfusion SPECT and compare them with FBP [10]. They concluded that four iterations and six subsets were optimal, with OSEM images reconstructed with a Butterworth filter being superior to FBP images [10]. However, this study did not account for the impact of BMI or other patient-specific factors, potentially introducing observer bias despite using kappa statistics. Moreover, it lacked a detailed analysis of the computational demands of different OSEM settings.
Overall, the results obtained in the two studies, although significant, did not depend on quantitative methods or image quality metrics, but rather on the evaluation of experienced physicians in the field, which leaves a gap for inconsistencies in the results due to probable human error.

1.2. Problem

It is possible that the optimal OSEM parameters could change for different brands due to several factors such as resolution and sensitivity or the design of the collimator, and the specific implementation of the OSEM algorithm by each manufacturer. Different camera brands utilize varying sensor technologies, resulting in different levels of image noise, which influences the optimal number of iterations needed to achieve the desired noise reduction. Similarly, variations in camera sensor resolutions mean that higher resolution images may require more iterations for comparable noise reduction. Additionally, while the core principles of OSEM remain consistent, the specific implementation by each manufacturer can differ, affecting the necessary number of iterations for optimal performance. Therefore, a simulation study investigating the optimal number of OSEM iterations for different SPECT camera brands would be useful.
Within SPECT imaging guidelines, specific reconstruction parameters are often outlined for filtered back projection (FBP), including details such as cut-off frequencies and filter orders tailored for rest and stress studies [10]. In instances where these parameters are not explicitly addressed in the guidelines, vendors may typically provide them. However, it's important to note that optimal OSEM reconstruction parameters are usually not indicated in the guidelines. This gap serves as the impetus for this study, which seeks to establish and optimize these parameters in hopes of establishing the optimal use of OSEM algorithm in MPI SPECT studies and find the answer to the question of how these values change according to the type of SPECT camera used.

1.3. Study Aim

The study aims to optimize the OSEM algorithm for SPECT cardiac perfusion imaging and examine the effect of different combinations of subsets and iterations on quantitative metrics such as the defect contrast percentage CNR. By using Simulating Medical Imaging Nuclear Detectors (SIMIND) Monte Carlo software to simulate two different SPECT systems, in conjunction with the XCAT phantom program to create normal and defective phantoms, the research seeks to define the best OSEM parameters for each of the cameras, thereby improving image quality and clinical utility. The study aims to enhance OSEM's role in cardiac imaging, leading to more accurate diagnoses and improved patient care.

2. Materials and Methods

2.1. Phantom

In this study, the 4D XCAT digital phantom, developed by Professor Paul Segars from Duke University, was used. The XCAT phantom program provides highly detailed anatomical models for both male and female subjects at the 50th percentile in terms of height, weight, and organ volumes [11]. This versatile software supports a wide range of medical imaging and research applications [11].
Using this program, a 4D voxelized male phantom that represent activity concentrations and attenuation coefficients of the torso organs was created. The arrangement of radioactivity levels across different organs was adjusted to replicate the typical distribution observed in SPECT images of a patient undergoing a Tc-99m Sestamibi study [12]. The following table (Table 1) displays the relative uptake ratios for the organs. In this study, the cardiac cycle was set to last for 1 second and distributed over 8 frames, which required generating a total of 16 3D phantom sets (activity and attenuation). Each phantom set was saved in a 256x256x256 array with a slice thickness and pixel size of 1.5 mm.

2.2. SIMIND and SPECT Systems

Two dual head SPECT cameras were simulated based on specifications of two typically used cameras, to produce images of the radiotracer distribution. Monte Carlo (MC) simulations were performed using the SIMIND (version 7.0.3) software for all frames of the phantom. SIMIND is a versatile Monte Carlo simulation code designed for modeling standard clinical Single-Photon Emission Computed Tomography (SPECT) cameras and has been rigorously validated against real SPECT cameras in many studies [13,14,15,16,17]. Table 2 demonstrates the intrinsic differences between the two camera models using 99m-Technetium as a radiotracer [18,19].
Moreover, although the two cameras exhibited greater similarities than disparities intrinsically, there were differences in the properties of their collimators and the dimensions of their crystals. Two gamma cameras with NaI (Tl) crystals acquired projection data with a radius of rotation of 20 cm. A low-energy high-resolution (LEHR) collimator was coupled with the cameras.

2.3. Reconstruction and Corrections

For each frame, twelve different processing runs were performed, one for each selected iteration/subset pair, with and without Poisson noise included in the projections. Reconstruction of images and application of OSEM and corrections was performed using CASTOR program. The twelve subset-iteration parameters with which the images were reconstructed are 2-4, 2-6, 2-8, 2-16, 2-32, 4-4, 4-6, 4-8, 4-12, 8-4, 8-6, 16-2. For each camera, 192 reconstructions were performed, with a total of 384 reconstructions. In the image’s reconstruction, the data were topographically visualized and processed in the three anatomical planes, with AMIDE (A Medical Image Data Analysis Tool). Both attenuation and scatter corrections were applied to all images.
Scatter correction was applied using the triple energy window (TEW) method in SIMIND. This approach utilizes three energy windows, including one centered around the photopeak. This method’s performance can be optimized and adjusted based on the location and width of these windows. It is important to note that the removal of scatter photons may increase Poisson noise, which can subsequently impact lesion detectability. Table 3 shows the settings used for TEW scatter correction.
In SIMIND and CASTOR, attenuation correction can be performed by including a switch during reconstruction, this switch was included in all reconstruction runs. SIMIND produces attenuation maps in units of cm-1.
Table 4. Acquisition parameters used in both camera models.
Table 4. Acquisition parameters used in both camera models.
Acquisition Parameter Value
Energy Resolution (% from 140keV) 9%
Intrinsic Resolution (mm) 0.95
Image Matrix Size 128x128
Pixel Size (mm) 3
Number of Projections 64
Angular Range 180° (RAO-LPO)

2.4. Filtering

In image processing, selecting the appropriate filter often involves finding a balance between reducing noise, suppressing fine details, enhancing contrast, and considering the spatial frequency pattern of the image data. In a myocardial perfusion study with 99mTc sestamibi, it has been found that optimal contrast between normal and defective myocardium could be achieved using the Butterworth filter, with cutoffs ranging from 0.3 to 0.5 and orders from 3 to 9 [5]. The Butterworth filter, widely used in nuclear medicine, is defined by two key parameters (Eq. 1): the cut-off frequency, representing the frequency where the filter function declines towards zero (fc), and the order (n), which determines the slope of the filter [20].
B f = 1 1 + f f c 2 n
This was further tested on simulated images across all frames and OSEM combinations to determine the exact order and cutoff frequency that would give the best SNR and CNR values. The optimal parameters were at an order of 3 and cut off frequency of 0.5. Interestingly, those parameters were the optimal for both cameras.

2.5. Image Quality Assessment

To quantitatively assess the relationship between image quality and OSEM parameters across the 8 frames, the CNR and SNR were calculated for the reconstructed images. To achieve this, three distinct regions of interest (ROIs) were set: the healthy part of left ventricular (LV) myocardium, the anterolateral lesion, and the background.
To limit variations in the results, the ROI selection depended mainly on the XCAT phantom that was developed. In other words, the mid slice of the short axis in the phantom files was selected and used to draw the ROI of the normal myocardium and the anterolateral lesion and then those ROIs were overlayed on the reconstructed images. This was done for each frame individually. The background ROI was set on the reconstructed image directly.
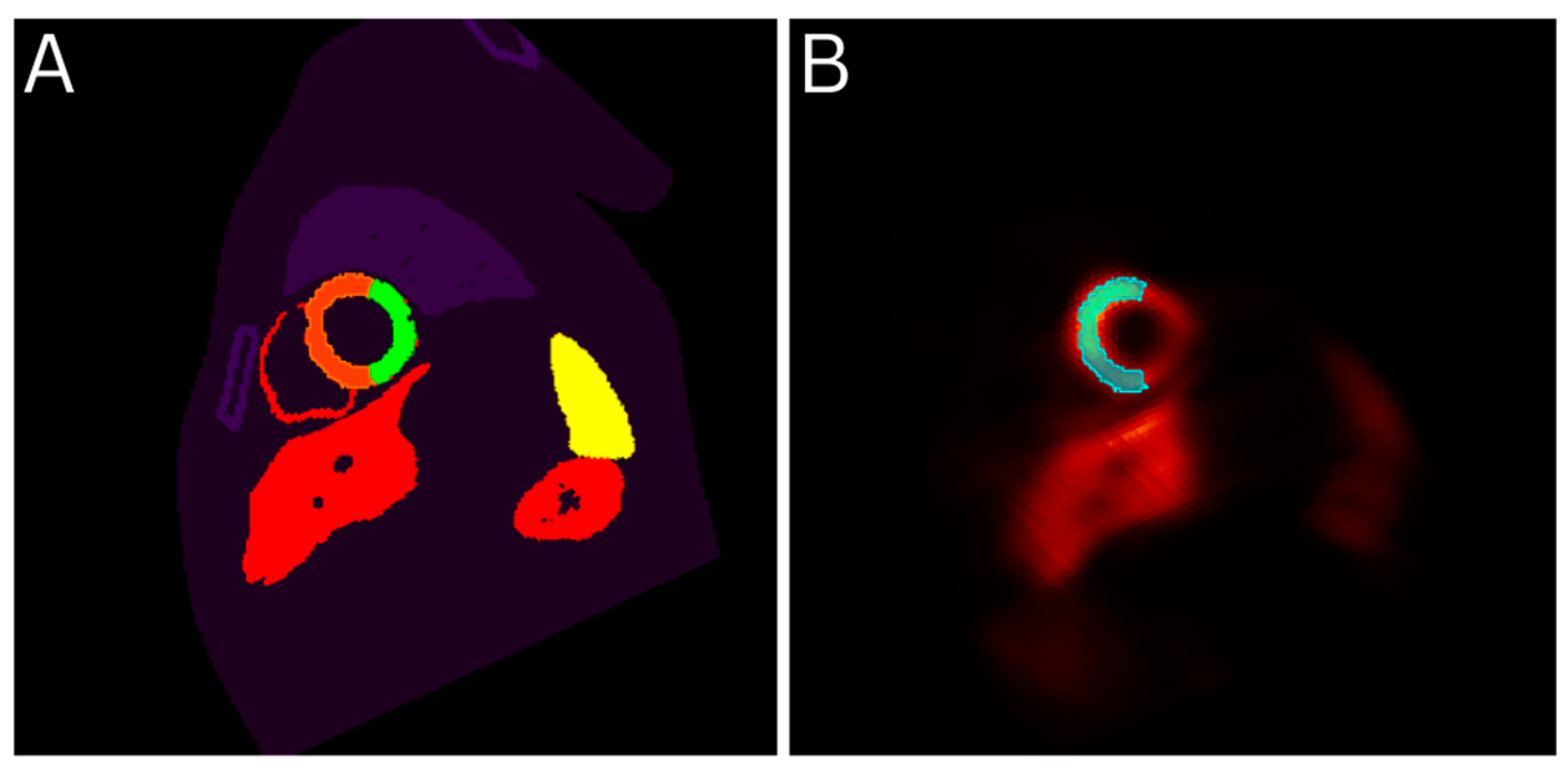
Preprints 113433 g001
Figure 1. ROI selection using the Phantom file as a template. Part A shows the XCAT phantom file for frame 6 with the healthy LV ROI drawn in orange and part B shows the reconstructed image of the same frame with the same ROI overlayed.
Figure 1. ROI selection using the Phantom file as a template. Part A shows the XCAT phantom file for frame 6 with the healthy LV ROI drawn in orange and part B shows the reconstructed image of the same frame with the same ROI overlayed.
Preprints 113433 g001
Defect Contrast, CNR and SNR were defined as shown below [4,21,22].
D e f e c t   C o n t r a s t   % = μ M Y O N o r m − μ M Y O D e f μ M Y O N o r m + μ M Y O D e f x   100 %
C N R = μ M Y O N o r m − μ M Y O D e f σ M Y O N o r m
S N R = μ M Y O N o r m σ B G
where µMYONorm is the mean voxel value on the healthy myocardial ROI, and µMYODef is the mean voxel value on the defective myocardial ROI µBG is the mean voxel value on the background ROI, and σBG is the standard deviation of voxel values on the background region of interest (ROI). The ROIs were selected for each frame individually on the mid slice of the short axis.

3. Results

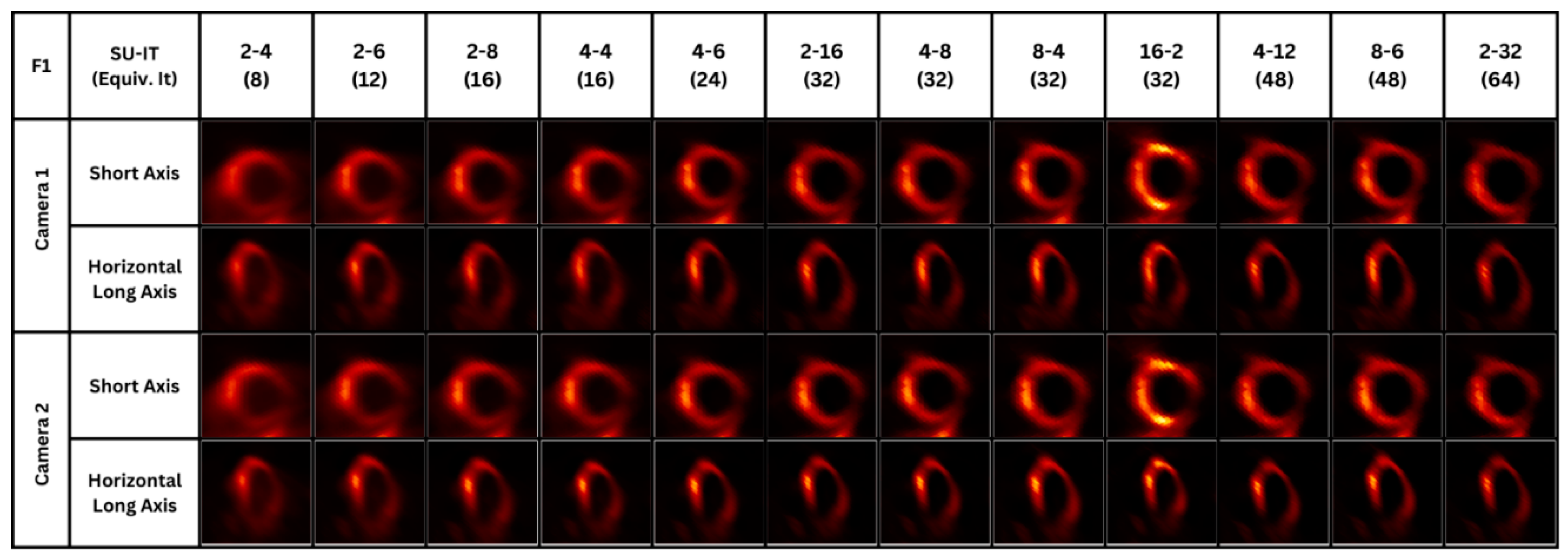
After obtaining the filtered images and selecting the ROIs, each image’s quality metrics were assessed. For each image, twelve OSEM parameters were considered, and with each parameter, a different CNR, SNR and contrast values were obtained. On the right, images of a single frame are shown for visual illustration of the differences between parameters across two heart planes. For each acquired image using Camera 1, the values obtained using a specific parameter were listed and compared to their corresponding values obtained using Camera 2.
Preprints 113433 g002
Figure 2. SPECT images using Camera 1 and Camera 2 with different OSEM parameters.
Figure 2. SPECT images using Camera 1 and Camera 2 with different OSEM parameters.
Preprints 113433 g002
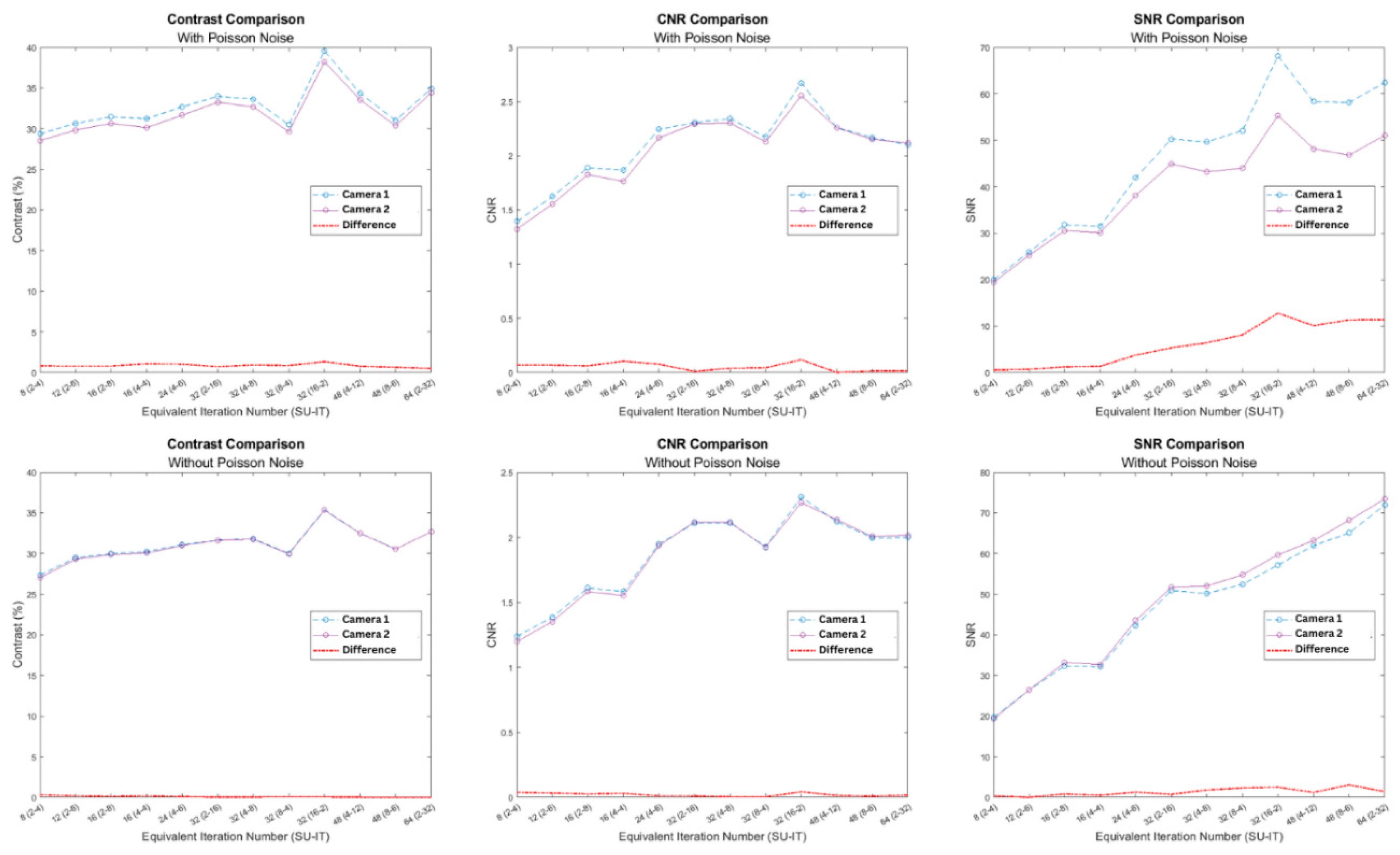
The results show an increasing trend in the values of the quality metrics as the number of iterations and subsets used in the OSEM reconstruction increased. Specifically, it is evident from the results shown in Figure 3, that for a specific subset number, as the number of iterations increased, the image quality kept improving. Moreover, Camera 1 results in higher contrast, CNR, and SNR values compared with Camera 2.

Statistical Analysis

Since SIMIND simulations consider the randomness of the photon interactions and therefore create different images each time, two simulations were made and reconstructed for each one frame to correctly capture the variance produced with the simulated images, resulting in a total of 16 simulations for each camera. The defect contrast, CNR, and SNR of the images were then ordered and ranked, and the Wilcoxon Signed-Rank Test was applied for statistical comparison. The test was two-tailed, and a p value of less than 0.05 was considered significant. Table 5 presents the average image quality metrics values obtained using both cameras across 16 images alongside the p-values for each comparison.

4. Discussion

4.1. Findings

After the quantitative assessment by CNR of the images produced by both cameras, the present study concludes that the utilization of the iterative OSEM algorithm with 16 subsets and 2 iterations generates images with the best diagnostic quality for patients with average BMI and body features, followed by the combination of 2 subsets and 32 iterations, in both cameras. Additionally, for CNR, the 4-8 combination is identified as the second-best parameter for both cameras. This shows that between the two camera models, the optimal OSEM parameter does not change. The comparison also shows a difference between the defect contrast and CNR values obtained from all twelve parameters using both cameras (Table 3). From Figure 3 and the quantitative results shown in Table 3, it can be seen that the difference between CNR values were small (~ 5%). Differences in SNR values were somewhat higher, but this may be due to various factors such as different background levels caused by differences in the collimators, spatial resolution, energy resolution etc.

4.2. Clinical Significance

The use of refined parameters appears to be crucial in facilitating the reconstruction of images with enhanced diagnostic accuracy, thereby ensuring precise diagnosis and subsequent suitable and efficient treatment for the patient. OSEM is widely used clinically, as it has been shown to be superior to FBP in most cases [23,24,25], but its optimal subsets and iteration numbers are yet to be determined and standardized for different types of SPECT imaging. This, alongside the trade-off between image quality and computational demand and processing time with each OSEM parameter, explains the significance of the research in this narrow topic and the need to establish the right reconstruction parameters for each type of SPECT imaging.

4.3. Comparison to Literature

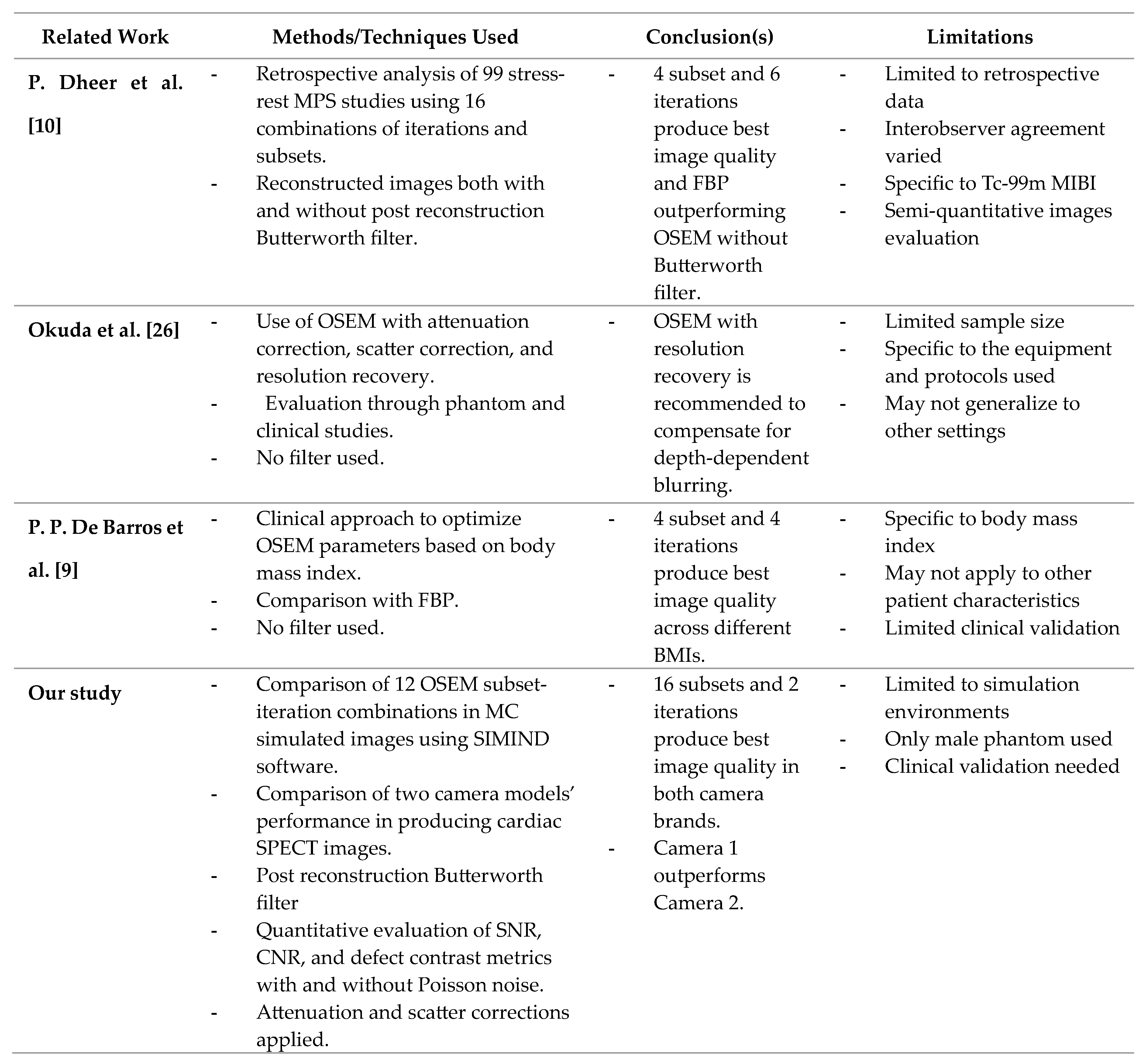
Unlike some studies, which rely on physician evaluations, the quantitative approach used in this study ensures more objective and reproducible results using controllable computational experiments.
De Barros et al. (2015) found that four iterations and four subsets produced the best images across various BMI categories, whereas Dheer et al. (2021) identified four iterations and six subsets as optimal, especially with a Butterworth filter. In both studies, the optimal OSEM parameters were determined based on the choice of physicians and the frequency with which that parameter was picked by different observers, in comparison with the rest of the parameters examined. Although the parameters included in this study were also assessed in the literature, quantitative assessment allows for a more accurate comparison between the parameters and their effect on image quality.
Additionally, this study differs from previous research using the more controllable Monte Carlo simulation method and using two different cameras to assess how the latter influences the optimal OSEM parameter settings and the defect detectability. Studying different cameras may also be helpful in standardizing images across clinics. In this case, we see that the optimal settings and defect detectability levels are similar while the images may have slightly differing SNR’s.
Table 6. Comparison with state-of-the-art studies and our study.
Table 6. Comparison with state-of-the-art studies and our study.
Preprints 113433 i001

4.4. Future Work and Limitations

It is important to note that the study is limited for its reliance on simulation environments, which are valuable but may not fully represent the complexities of real-world clinical settings. Moreover, only a male phantom was considered in this study, which leaves a space for uncertainty in the results when the patient is a female. Moreover, the computational power and time needed for optimizing OSEM, particularly concerning reconstruction with different pairs of subsets and iterations, should be noted. The study primarily explores the effects of different subsets and iterations within a specific parameter range, possibly leaving out various clinical scenarios. Therefore, clinical validation may be required to determine the practical applicability of the study's findings.
Future research should focus on validating the findings in clinical settings with a diverse patient population, including both male and female subjects. Additionally, exploring the optimization of OSEM parameters across different camera models and incorporating other patient-specific factors, such as age and comorbidities, could provide a more comprehensive understanding of the algorithm's performance.

5. Glossary

  • Ordered Subset Expectation Maximization (OSEM): An iterative reconstruction algorithm used to improve image quality in SPECT by optimizing the reconstruction process through subsets of data.
  • Single Photon Emission Computed Tomography (SPECT): A nuclear medicine tomographic imaging technique using gamma rays to provide 3D images of functional processes in the body.
  • Contrast-to-Noise Ratio (CNR): A metric used to quantify the contrast of an image relative to the background noise, indicating the detectability of features within the image.
  • Megabecquerel (MBq): A unit of radioactivity, representing one million disintegrations per second.
  • Attenuation Correction (AC): A process in imaging to correct for the reduction in signal strength as photons pass through different tissues, improving image accuracy.
  • Scatter Correction (SC): A method to reduce the effects of scattered photons in imaging, enhancing the quality and accuracy of the images.
  • Monte Carlo (MC): A statistical method used to model and simulate complex physical and mathematical systems, often used in medical imaging to simulate photon transport.
  • Myocardial Perfusion Imaging (MPI): A type of nuclear medicine procedure that illustrates the function of the heart muscle by showing blood flow through the myocardium.

Author Contributions

Albert Guvenis: Conceptualization, Resources, Supervision, Writing – Review & Editing. Ghassan Abojayab: Methodology, Software, Formal analysis, Validation, Writing - Original Draft, Visualization, Investigation.

Funding

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Acknowledgements

We would like to express our gratitude to Professor Paul Segars of Duke University for generously providing us with a free license for the XCAT phantom program to carry out our research.

Abbreviations

OSEM: Ordered Subset Expectation Maximization. SPECT: Single Photon Emission Computed Tomography. MC: Monte Carlo. CNR: Contrast-to-Noise Ratio. SIMIND: Simulating Medical Imaging Nuclear Detectors (MC Software). MBq: Megabecquerel. AC: Attenuation Correction. SC: Scatter Correction. MPI: Myocardial Perfusion Imaging.

References

  1. “Leading causes of death and disability 2000-2019: A visual summary.” https://www.who.int/data/stories/leading-causes-of-death-and-disability-2000-2019-a-visual-summary.
  2. World Health Organization: WHO, “Cardiovascular diseases EURO,” Feb. 10, 2022. https://www.who.int/europe/health-topics/cardiovascular-diseases#tab=tab_1.
  3. “Emission Tomography - 1st Edition | Elsevier Shop,” Oct. 25, 2004. https://shop.elsevier.com/books/emission-%20tomography/wernick/978-0-12-744482-6.
  4. T. Hosny, M. M. Khalil, A. A. Elfiky, and W. M. ElShemey, “Image quality characteristics of myocardial perfusion SPECT imaging using state-of-the-art commercial software algorithms: evaluation of 10 reconstruction methods,” PubMed, Dec. 15, 2020. https://pubmed.ncbi.nlm.nih.gov/33329938/.
  5. M. Lyra, A. Ploussi, M. Rouchota, and S. Synefia, “Filters in 2D and 3D cardiac SPECT image processing,” Cardiology Research and Practice, vol. 2014, pp. 1–11, Jan. 2014. [CrossRef]
  6. C. Trevisan et al., “Comparison between OSEM and FBP reconstruction algorithms for the qualitative and quantitative interpretation of brain DAT-SPECT using an anthropomorphic striatal phantom: implications for the practice,” Research on Biomedical Engineering, vol. 36, no. 1, pp. 77–88, Jan. 2020. [CrossRef]
  7. J. Ramon et al., “Investigation of dose reduction in cardiac perfusion SPECT via optimization and choice of the image reconstruction strategy,” Journal of Nuclear Cardiology, vol. 25, no. 6, pp. 2117–2128, Dec. 2018. [CrossRef]
  8. T. Yokei, H. Shinohara, and H. Onishi, “Performance evaluation of OSEM reconstruction algorithm incorporating three-dimensional distance-dependent resolution compensation for brain SPECT: A simulation study,” Annals of Nuclear Medicine, vol. 16, no. 1, pp. 11–18, Feb. 2002. [CrossRef]
  9. P. P. De Barros, L. F. Metello, T. S. C. Camozzato, and D. M. Da Silva Vieira, “Optimization of OSEM parameters in myocardial perfusion imaging reconstruction as a function of body mass index: a clinical approach,” Radiologia Brasileira/Radiologia Brasileira, vol. 48, no. 5, pp. 305–313, Oct. 2015. [CrossRef]
  10. P. Dheer, P. Gupta, S. Taywade, A. Passah, A. K. Pandey, and C. Patel, “Optimization of ordered subset expectation maximization parameters for image reconstruction in Tc-99m methoxyisobutylisonitrile myocardial perfusion SPECT and comparison with corresponding filtered back projection-reconstructed images,” Indian Journal of Nuclear Medicine, vol. 36, no. 1, p. 14, Jan. 2021. [CrossRef]
  11. CVIT - Center for Virtual Imaging Trials, “XCAT Phantom Program - CVIT - Center for Virtual Imaging Trials,” CVIT - Center for Virtual Imaging Trials, Oct. 10, 2022. https://cvit.duke.edu/resource/xcat-phantom-program/.
  12. W. P. Segars and B. M. W. Tsui, “Study of the efficacy of respiratory gating in myocardial SPECT using the new 4-D NCAT phantom,” IEEE Transactions on Nuclear Science, vol. 49, no. 3, pp. 675–679, Jun. 2002. [CrossRef]
  13. “Simind_Manual.pdf | Powered by Box.” https://lu.app.box.com/s/o5jwq2j0blrm99ll5b1ld1e4d59tmisa.
  14. J. E. Ejeh, J. A. Van Staden, and H. Du Raan, “Validation of SIMIND Monte Carlo Simulation software for modelling a Siemens Symbia T SPECT scintillation Camera,” in IFMBE proceedings, 2018, pp. 573–576. [CrossRef]
  15. G. Di Domenico et al., “Validation of SIMIND Monte Carlo for 99MTC and 177LU,” Research Square (Research Square), Jul. 2022. [CrossRef]
  16. Boolyen, M. et al. (2015) Verification of a Monte Carlo simulated Siemens Symbia SPECT/CT, European Journal of Medical Physics. Available at: https://www.physicamedica.com/article/S1120-1797(15)00243-4/fulltext.
  17. M. Dixon, “Development of a Monte Carlo simulation for SPECT Myocardial Perfusion Imaging,” UC Library, Jan. 2021. [CrossRef]
  18. “Symbia T Series SPECT/CT,” Siemens Healthineers USA. https://www.siemens-healthineers.com/en-us/molecular-imaging/spect-and-spect-ct/symbia-t.
  19. Selvamejia, “Infinia Hawkeye4 datasheet,” Scribd. https://www.scribd.com/document/170635359/Infinia-Hawkeye4-Datasheet.
  20. Rahimian, M. Etehadtavakol, M. Moslehi, and E. Y. K. Ng, “Myocardial Perfusion Single-Photon Emission Computed Tomography (SPECT) Image Denoising: A Comparative study,” Diagnostics (Basel), vol. 13, no. 4, p. 611, Feb. 2023. [CrossRef]
  21. M. J. Kortelainen, T. M. Koivumäki, M. J. Vauhkonen, and M. A. Hakulinen, “Dependence of left ventricular functional parameters on image acquisition time in cardiac-gated myocardial perfusion SPECT,” Journal of Nuclear Cardiology, vol. 22, no. 4, pp. 643–651, Aug. 2015. [CrossRef]
  22. Tantawy, H. M., Abdelhafez, Y. G., Helal, N. L., & Saad, I. E. (2020). Variation of Contrast Values for Myocardial Perfusion Imaging in Single-photon Emission Computed Tomography/Computed Tomography Hybrid Systems with Different Correction Methods. Journal of Clinical Imaging Science, 10, 58. [CrossRef]
  23. DePuey, E. G., Gadiraju, R., Clark, J., Thompson, L., Anstett, F., & Shwartz, S. C. (2008). Ordered subset expectation maximization and wide beam reconstruction “half-time” gated myocardial perfusion SPECT functional imaging: A comparison to “full-time” filtered backprojection. Journal of Nuclear Cardiology, 15(4), 547–563. [CrossRef]
  24. Søndergaard, H. M., Madsen, M. M., Boisen, K., Bøttcher, M., Schmitz, O., Nielsen, T. T., Bøtker, H. E., & Hansen, S. B. (2006). Evaluation of iterative reconstruction (OSEM) versus filtered back-projection for the assessment of myocardial glucose uptake and myocardial perfusion using dynamic PET. European Journal of Nuclear Medicine and Molecular Imaging, 34(3), 320–329. [CrossRef]
  25. Bai, J., Hashimoto, J., Suzuki, T., Nakahara, T., Kubo, A., Iwanaga, S., Mitamura, H., & Ogawa, S. (2001). Comparison of image reconstruction algorithms in myocardial perfusion scintigraphy. Annals of Nuclear Medicine, 15(1), 79–83. [CrossRef]
  26. Okuda, K., Nakajima, K., Yoneyama, H., Shibutani, T., Onoguchi, M., Matsuo, S., Hashimoto, M., & Kinuya, S. (2019). Impact of iterative reconstruction with resolution recovery in myocardial perfusion SPECT: phantom and clinical studies. Scientific Reports, 9(1). [CrossRef]
Preprints 113433 g003
Figure 3. The defect contrast, CNR, and SNR values across the OSEM parameters. The first row shows those values with Poisson noise included, while the 2nd row shows the results without Poisson noise.
Figure 3. The defect contrast, CNR, and SNR values across the OSEM parameters. The first row shows those values with Poisson noise included, while the 2nd row shows the results without Poisson noise.
Preprints 113433 g003
Table 1. Relative uptake ratios in an XCAT phantom for 99mTc-MIBI [12].
Table 1. Relative uptake ratios in an XCAT phantom for 99mTc-MIBI [12].
Organ(s) Relative Uptake Ratio
Heart Myocardium, Liver, and Kidneys 75
Spleen 60
Lungs 4
Stomach, Ribs, Spine, and Body 2
Table 2. Specifications of the two SPECT cameras [18,19].
Table 2. Specifications of the two SPECT cameras [18,19].
Parameter Camera 1 Camera 2
Crystal Crystal Thickness 0.95 mm 0.95 mm
Collimator Collimator Type LEHR LEHR
Hole Shape Hex Hex
Number of Holes 148,000 86,300
Hole Length 24.05 mm 35 mm
Hole Diameter 1.11 mm 1.5 mm
Septal Thickness 0.16 mm 0.2 mm
Septal Penetration 1.5% 0.3%
System System Sensitivity (@ 100 mm) 202 cpm/µCi 160 cpm/µCi
System Resolution (@ 100 mm) 7.5 mm 7.4 mm
Table 3. Energy windows used for photopeak and upper and lower windows for TEW scatter correction.
Table 3. Energy windows used for photopeak and upper and lower windows for TEW scatter correction.
Energy Window Window Width (Limits)
Upper window 2 (154-156 keV)
Lower window 2 (124-126 keV)
Photopeak window 28 (126-154 keV)
Table 5. Statistical comparison for the contrast, CNR, and SNR values.
Table 5. Statistical comparison for the contrast, CNR, and SNR values.
Metric Defect Contrast (%) Defect CNR SNR
Parameter C1 C2 Diff (%) p-value C1 C2 Diff (%) p-value C1 C2 Diff (%) p-value
2-4 29.390 28.552 2.90% 0.00112 1.395 1.324 5.37% 0.00044 19.999 19.435 2.90% 0.01129
2-6 30.669 29.847 2.74% 0.00078 1.624 1.555 4.42% 0.00044 25.960 25.249 2.82% 0.00446
2-8 31.484 30.664 2.67% 0.00078 1.891 1.828 3.44% 0.00064 31.825 30.573 4.10% 0.00320
4-4 31.241 30.145 3.64% 0.00064 1.869 1.764 5.95% 0.00044 31.478 30.113 4.53% 0.00271
4-6 32.713 31.673 3.27% 0.00078 2.242 2.167 3.58% 0.00053 41.930 38.158 9.89% 0.00135
2-16 34.002 33.266 2.22% 0.00112 2.307 2.295 0.50% 0.67912 50.279 44.954 11.85% 0.00044
4-8 33.653 32.706 2.89% 0.00112 2.345 2.304 1.78% 0.00446 49.653 43.225 14.87% 0.00044
8-4 30.519 29.637 2.94% 0.00161 2.172 2.128 2.15% 0.00271 52.133 44.012 18.45% 0.00044
16-2 39.610 38.244 3.53% 0.00053 2.673 2.555 4.62% 0.00078 68.162 55.383 23.07% 0.00044
4-12 34.375 33.591 2.34% 0.00135 2.267 2.260 0.10% 0.79599 58.353 48.223 21.01% 0.00044
8-6 31.043 30.371 2.19% 0.00613 2.170 2.152 0.74% 0.06267 58.171 46.828 24.22% 0.00044
2-32 34.929 34.416 1.52% 0.01306 2.107 2.119 0.81% 0.17881 62.441 51.072 22.26% 0.00044
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated