SMPTC3: Secure Multi-party Protocol Based Trusted Cross-chain Contracts

We propose an innovative approach called SMPTC3, designed specifically to enhance security and privacy in cross-chain transaction verification. This approach addresses multi-chain, multi-participant information exchange and large-scale cross-chain transfers, resisting various types of malicious attacks. We leverage the verifiability of cross-chain transactions based on smart contracts and innovatively transform transaction information into confidential sets, organizing them into quadratic secret polynomials. By utilizing secret sharing and random distribution techniques, we construct a secure multiparty computation method, tailored for cross-chain transactions. To enhance the efficiency of cross-chain transactions, we introduce cross-chain batch processing technology, grouping inter-chain transactions into cross-chain transaction sets. Unlike traditional distributed notary technologies, SMPTC3 designates honest participants as a cross-chain notary group, reducing the time required for redundant signature confirmations and significantly lowering the possibility of malicious notaries. Theoretical analysis and empirical experiments demonstrate that SMPTC3 is highly efficient in addressing cross-chain transaction security issues.

Keywords:

Subject: Computer Science and Mathematics - Information Systems

1. Introduction

Since Satoshi Nakamoto proposed the concept of blockchain [1], blockchain technology has realized a decentralized shared general ledger, which can be understood as a large-scale and decentralized distributed database, which is traceable, verifiable and not easy to be tampered with [2].

Recently, blockchain develops really fast, a large number of blockchain projects and their unique chain structures and tokens have been created, such as bitcoin blockchain [1] based on proof-of-work, Ethereum blockchain [3] transitioning from Proof-of-Work to Proof-of-Stake, the use of Proof-of-Stake [4,5,6], the use of Proof-of-Authority [7,8], and web3.0's hot consortium blockchains such as Hyperledger fabric, Corda, Quorum, which use consensus protocols such as PBFT [9,10] and Raft [11]. These chains do not communicate with each other in structure, which leads to great obstacles to the application and development of blockchain technology. Token and application data on the chain may form the data islanding effect of blockchain, so different blockchains need a unified method to transfer data and asset. Therefore, researchers put forward the concept of "cross-chain", which breaks the islanding effect among different blockchain projects and realizes interoperability between chains.

The current mainstream projects of cross-chain technology include Cosmos [12], Polkadot [13], Lightning Network [14], Fusion [15], Interledger [16], etc. The purpose is to realize asset exchange, information interaction and application collaboration between different blockchain platforms, reduce the difficulty of blockchain users and reduce the cross-chain transmission process. Table 1 shows the key attributes of some cross-chain projects.

The Problem. At present, cross-chain still relies on third-party centralized nodes and Relays. Even though Cosmos, Polkadot and cross-chain bridges [17,18] are proposed, which solve the inter-chain consensus protocol and some security problems, there is still the possibility of bridging chains doing evil. In 2019, Cosmos was found to have a re-entrustment loophole, which could immediately redeem guaranty tokens by replacing the Validator of parallel chain, resulting in early redemption of 7,250 Atom tokens with a value of about 43,500 US dollars, this event destroyed the fairness of the transaction. The Grandpa Consensus (GHOST-based Recursive Ancestor Deriving Prefix Agreement) Protocol used by Polkadot cannot tolerate Dos attacks. And there is the possibility that Nominators will do evil together [13]. In 2022, Lightning Network had a malicious channel attack problem, and after the uplink timed out. Malicious traders can still send bitcoin under the chain, causing theft.

And cross-chain bridge solutions focus on Two-blockchain interoperability, which doesn't suit the complex cross-chain requirements in multi-chain ecosystems. As depicted in Figure 1, suppose a user

U

, driven by investment motives, intends to exchange their assets

t_{1}

held on blockchain

C_{1}

for equivalent assets

t_{3}

on another blockchain

C_{3}

. However, given that both

t_{1}

and

t_{2}

aren’t stable currencies (potentially speculative coins), it requires converting

t_{1}

through cross-chain bridge

B_{1}

to obtain

t_{2}

on blockchain

C_{2}

(e.g., Ethereum's ETH). Subsequently, through

B_{2}

, converting

t_{2}

t_{3}

via cross-chain transfer. It's evident in this operational flow that

U

engages in two separate cross-chain transactions, resulting in a cumbersome process, and the multiple transactions incur additional operational costs.

Our approach. In blockchain cross-chain scenarios, involving collaboration among multiple parties may require computations involving sensitive information. Secret sharing can be employed to securely execute computations among multiple parties, ensuring that no private information from any party is disclosed. We propose SMPTC³ (Secure Multi-party Protocol Based Trusted Cross-chain Contracts) to implement a secure cross-chain interaction protocol, which is mainly aimed at large amount token transfer and cross-chain transmission of important private data. SMPTC³ does not need to trust any central committee or third-party node. It uses and improves the SMC [19,20,21,22,23] (secure multi-party computation) proposed by Yao to establish the trust between the participating chains, and defines the participating nodes as semi-honest adversaries to prevent the participating chain from doing evil. Meanwhile, participants can prove their identities without providing too much private data to ensure the privacy of cross-chain transactions. SMPTC³ embeds the improved SMC into the smart contract, and the cross-chain initiator C1 initiates the smart contract (SC) of the relay chain, and SC verifies whether the identities of C1 and other participants in the chain are true and reliable.

The SMPTC³ deploys a group of contracts, each situated on various participating chains, referred to as validator contracts. These validator contracts can invoke the validator contracts of other participating chains for cross-chain validation. They can also invoke sender and receiver contracts deployed across different chains to perform application-specific tasks. Depending on the application scenario, validator contracts may also require participating nodes to provide transaction information and Merkle proofs of smart contract states to ensure the atomicity of asset exchanges and the correctness of smart contracts. Figure 2 illustrates a hypothetical scenario of multi-chain asset exchange facilitated by SMPTC³. Initially, User U1 requests the validator contract to initiate a cross-chain transaction (step 1). To transfer asset, the validator contract invokes SClock and notifies participating users to lock their respective assets (step 2 and 3). Subsequently, the validator contract verifies the correctness and atomicity of the cross-chain transaction (step 5 and 6). Upon successful validation, it invokes SCmint to issue assets. To ensure transaction atomicity, SCmint can issue new assets only when users have locked assets on the chain. This necessitates SCmint to read the state of SClock (balance of U, step 4) from the relevant blockchain, which is not directly accessible in cross-chain transactions. This is achieved through validator contracts facilitating the transmission of block headers, transaction information, and correctness proofs between chains (step 5 and 6). SCmint can verify the correctness of user balances through the validator contract (step 7) and, upon successful verification, issue new assets to each user (step 8).

Apart from the aforementioned multi-chain asset transfer, SMPTC³ can also support applications such as multi-chain message interaction and multi-chain voting.

This design offers four benefits.

For large-amount token transfer and transmission of important private data in cross-chain, there is no need to verify its offline identity repeatedly, and its reliability is ensured through strict identity verification on the chain;
In multi-chain ecology, confidential information sharing or anonymous voting can be carried out for mutual distrust among members;
Prevent various types of attacks and avoid possible losses caused by loopholes in consensus protocol in the participating chain;
Due to the reliability of SMPTC³, there is no need for any additional security requirements beyond security logic of underlying blockchains, especially the third-party centralized nodes or the security committees in the relay chain;

Technical challenges. Although there are many theoretical researches [23,24] on secure multi-party computation at present, SMC is rarely used for blockchain cross-chain. Secondly, the two-party secure computation model is mostly used in the privacy protection methods on the chain, and whether the multi-party can resist collusion attack is an important problem for protocol security. Thirdly, the execution efficiency of complex computation tasks on ciphertext is very low and the communication cost is high. How to simplify the computation and communication cost in the cross-chain process has become a research challenge. Finally, when using SMC and blockchain, it should be noted that the participating nodes of the two technologies may overlap. Therefore, in practical application, it is necessary to consider that these overlapping situations can meet the security assumptions of the two technologies at the same time.

It is obviously infeasible to directly extend the inter-chain communication of secure two-party secure computation to multi-party, so we propose a novel scheme based on the original research results [19,20,25,26,27], presently available schemes include garbled circuit method [20,28,29], secret sharing method [30,31,32] and homomorphic encryption method [27,33]. We transform the private information of each participant into a secret set, and use the secret set for SMC. We find that in cross-chain, the set elements are regularly verifiable (traceability and immutability of blockchain), so the secure set is encoded into a special array, and the homomorphic encryption method is combined to solve the problem of SMC, to reduce the high computing cost and communication cost of traditional SMC. Then we use smart contract in EVM or chaincode in privacy channel by Fabric to ensure the information security of the computing process. Therefore, a secure cross-chain protocol with lower computation and communication cost is realized.

Our contribution. In this paper, we make the following contributions:

5.: In order to resist malicious attacks such as Sybil and Dos, we improve the homomorphic encryption method (P-ElGamal) and threshold signature method, and combine with the improved secure multi-party computation method (SMPTC³). The improved combination method can resist a variety of irresistible attacks of the original blockchain.
6.: We propose an improved multi-party security computation method (SMPTC³) for blockchain. Compared with the original method, it significantly reduces the computational complexity and communication complexity, so the SMPTC³ in this paper is efficient. And SMPTC³ can be applied to a variety of environments except blockchain.
7.: We convert the private data of multiple participants in different chains into secure sets. This method has great application value in cross-chain interaction, and can also provide a new secure transmission scheme for other cross-chain methods.
8.: SMPTC³ uses secure multi-party computation to solve collusion attacks and avoid relying on third-party central nodes or security committees for authentication. SMPTC³ is a novel cross-chain interaction protocol.
9.: Based on fabric, Ethernet and cosmos systems, we implement the multi-party participation model of SMPTC³ and verify it. Experiments show that this protocol has high performance.

2. Background

In this section we cover the background on blockchains, secure multi-party computation, and homomorphic encryption.

2.1. Blockchains

Blockchain [34,35] is a distributed shared ledger based on various technologies, and blockchain is essentially a distributed database with multi-participation and joint maintenance. Compared with centralized database management system, Blockchain system adopts decentralized or weakly centralized data management mode, There is no central node, All participating nodes can store data. The persistence of transactions is realized by the increasing data chain and decentralized consensus mechanism jointly maintained by participating nodes, which ensures the credibility of data based on verification, improves the query efficiency of participants and the data security of the system, and reduces the maintenance cost of the original database maintainer.

2.1.1. Cross-Chain

Cross-chain [2,36] can be understood as chain-to-chain communication protocols. Current cross-chain technologies include the following methods: Notary Schemes, Sidechains/Relays, Distributed Private Key Control, Hash-Locking, and Tight Coupling. Because cross-chain involves building trust between chains, there may be some problems, such as private data leakage in public chain, Sybil attack in consortium chain, and evil by third-party nodes. In the process of cross-chain, there may be more security problems due to the different consensus protocols of participating chains. The common solution is to use relay chain (cross-chain bridge [18,37]) to solve the problems of different consensus protocols, data leakage and third-party evil. However, at present, the relay chains are becoming centralized, and there is the possibility that the relay chains may do evil (Table 2 shows some cross-chain bridges security problem). Therefore, solving the trust problem between chains has become one of the key objectives of the research.

2.1.2. Smart Contracts

Smart contracts are event-driven, stateful computer programs deployed on shared distributed databases. The implementation of smart contract is not based on the trust of centralized third party, and its security is based on cryptography. Smart contracts based on blockchain support the creation of distrusted protocols. This means that the contract participants do not need to know or trust each other, but only make commitments through blockchain, which is consistent with secure multi-party computation. For example, the Ethereum smart contract consists of a contract code and two public keys. The first public key is provided by the contract creator, and the other public key is the contract itself, serves as a unique numeric identifier for each smart contract. All smart contract deployments are conducted through blockchain transactions, which will only be activated when external accounts (EOA) or other smart contracts invoke. Ethereum smart contract has the characteristics of certainty, non-tampering and distrust. Aiming at the trust problem in cross-chain process, it is one of the important means to express secure multi-party computing in the form of smart contract.

2.2. Secure Multi-Party Computation

2.2.1. Mathematical Definition

Assuming there are

n

participants

p_{1}, p_{2}, \dots, p_{n}

, each party has a private input data

x_{i}

, All participants calculate a function

f (x_{1}, x_{2}, \dots, x_{n})

together, and at the end of the calculation, each participant

p_{i}

can only get the output of private input data

x_{i}

, but can not get the input information and output information of other participants [38]. In secure multi-party computing, semi-honest model and malicious adversary model are usually used.

2.2.2. Honest Participants

Honest participants mean that, ideally, this kind of participants calculate strictly according to the requirements of the protocol, do not collect data privately, and do not have any malicious behaviors (attacking the protocol, refusing to participate in the protocol, stopping the protocol halfway, entering false data). This type of participant is ideal, but when designing a security model, it is generally assumed that there are no absolutely honest participants.

2.2.3. Semi-Honest Model

Semi-honest model is also called passive model [34] or honest-but-curious model, All participants in this kind of model are semi-honest, which refer to participants who calculate according to the requirements of the protocol during the calculation process, but these participants will record all the information collected during the protocol process and calculate the input information (private information) of other participants according to the collected information. Semi-honest participants do not actively attack protocols, but collect and record possible private information.

2.2.4. Malicious Adversary Model

In the malicious adversary model [39], some participants, as attackers, may use illegal input or malicious tampering input to calculate the private information of other participants, and may also refuse to participate in the protocol or stop the protocol halfway. Secure multi-party computation protocol based on malicious adversary model can meet the security requirements of semi-honest model.

2.3. Homomorphic Encryption

Because secure multi-party computation needs to ensure the privacy of data of each participant, it needs an encryption method with good homomorphism. ElGamal [27] has good multiplication homomorphism, as follows:

2.3.1. Key Generation

Given the security parameter

k

, the key generation algorithm generates a large prime number

p

with

k

bits and a generator

g

Z_{p}^{*}

, and randomly selects

x

as the secret key and the corresponding public key is

h = g^{x} \mod p

2.3.2. Encryption

To encrypt the message

M (M \in Z_{p}^{*})

, select the random number

r

and the ciphertext is

E_{p k} (M) = (c_{1}, c_{2}) = (g^{r} \mod p, {M h}^{r} \mod p)

2.3.3. Decryption

For ciphertext

E_{p k} (M) = (c_{1}, c_{2})

, decrypt it to

M = c_{2} {∙ c}_{1}^{- x} \mod p

2.3.4. Homomorphic Property

Encryption system has multiplicative homomorphism:

\begin{matrix} E_{p k} (M_{1}) {\times E}_{p k} (M_{2}) = (g^{r_{1}}, M_{1} h^{r_{1}}) \times (g^{r_{2}}, M_{2} h^{r_{2}}) \\ = (g^{r_{1} + r_{2}}, M_{1} {\times M}_{2} h^{r_{1} + r_{2}}) \\ = E_{p k} (M_{1} \times M_{2}) \end{matrix}

And the data encrypted by ElGamal

E_{p k} (M)

cannot get the original data

M

after decryption, so it is not completely decrypted, which can ensure that malicious nodes (semi-honest participants and malicious participants) in the chain can not obtain the private data of other participants, which is one of the important means in this paper.

3. Confidential Set and Secure Multi-party Computation for Cross-Chain

Firstly, the proposed solution in this paper does not require on-chain participants to encrypt transaction information in their sets using cryptographic algorithms. Since cryptographic algorithms consume significant computational power and communication costs, they are not suitable for cross-chain interactions. Therefore, the solution presented in this paper no longer employs cryptographic algorithms. Instead, it leverages mathematical methods for confidential computation, where participants communicate with each other only twice, establishing inter-chain trust locally. An essential feature of this solution is the elimination of the need to obtain and store public keys of other participants, preventing malicious activities by centralized transaction nodes or relay chains. This approach significantly reduces both computational and communication overhead.

3.1. Constructing Transaction Set

Assuming there are n participants on different chains, denoted as

p 1, p 2, \dots, p n (n \geq 3)

, collectively participating in a cross-chain transaction T, they collectively sign the transaction elements, including transaction signatures, sender identities, locked assets, transaction order, etc., denoted as

e_{1}, e_{2}, e_{3}, \dots, e_{m}

. These elements are hashed and packaged into sets:

X_{1} = \{x_{11}, x_{12}, \dots, x_{1 m}\} \dots X_{n} = {{x}_{n 1}, x_{n 2}, \dots, x_{n m}}

In order to ensure the confidentiality of the set information, each participant converts their set into polynomial form. They construct a quadratic secret polynomial by taking each element (hash value) of their set as a root parameter for the polynomial. The quadratic secret polynomials constructed by participants

p 1, p 2, \dots, p n

can be represented as:

f_{1} (x) = {{(x - x}_{11})}^{2} {{(x - x}_{12})}^{2} \dots {{(x - x}_{1 m})}^{2} \dots f_{n} (x) = {{(x - x}_{n 1})}^{2} {{(x - x}_{n 2})}^{2} \dots {{(x - x}_{n m})}^{2}

(1)

When

x = e

f_{i} (e) = 0

iff

e \in X_{i}

3.2. First Round of Participant Communication

The quadratic secret polynomials for participant

p_{i}, i \in [1, n]

can be organized as follows:

f_{i} (x) = \sum_{p = 0}^{2 m} e_{i p} x^{p}

(2)

The secret polynomials are then randomly divided into non-zero

t, 2 \leq t \leq n

shares such that:

f_{i} (x) = f_{i 1} (x) + \dots + f_{i t} (x)

(3)

Even if an adversary S on a certain chain obtains

t - 1

shares of the secret polynomial

p_{i}

1 < j < t

f_{i 1} (x) + \dots + f_{i (j - 1)} (x) + f_{i (j + 1)} (x) + \dots + f_{i t} (x)

(4)

From formula (3), it can be seen that

S

cannot obtain the complete secret polynomial. It is crucial to note that each share of the polynomial is non-zero and random, making equation (4) an indeterminate equation. Therefore, it is impossible to construct the complete quadratic secret polynomial

f_{i} (x)

. Even if

S

possesses the ability to reverse hash or use rainbow tables [40], they cannot obtain any element of the secret set

p_{i}

Due to the possibility of collusion attacks such as Sybil attacks and conspiracy attacks in a multi-chain environment, to enhance security, we introduce random sending and random number strategies.

Random Sending Strategy: As the sender, participant

p_{i}

randomly sends

t

shares of the polynomial to

t

recipients among the

n

participants

2 \leq t \leq n

, and t may include the sender

p_{i}

itself. Thus,

t

is not fixed, and the recipients are not certain whether other recipients have received the shares from the sender. This approach can also be used for cross-chain methods with relay chains and notary groups. In such cases,

t

shares of the polynomial are randomly sent to

t

relay chain nodes, forming a notary group, which then verifies and publicly discloses on the relay chain. The random sending strategy implies that even in a multi-chain environment, a witch attack or collusion attack cannot obtain the complete quadratic secret polynomial. Moreover, common consensus protocols have tolerances of 49% or 33%, while this scheme has a tolerance of 0%. Therefore, the tolerance of this scheme is lower than that of the consensus protocols used by each chain, eliminating the need for security guarantees at the underlying blockchain level.

Random Number Strategy [41]: To further enhance the security of this scheme, we introduce a random number strategy. Specifically, each share of the polynomial is assigned a random number

r_{i j}, r_{i j} \neq 0, i \in [1, n], j \in [1, t]

. To reduce the difficulty of verification and computational overhead in smart contracts, it is necessary to ensure:

\sum_{i = 1}^{n} \sum_{j = 1}^{t} r_{i j} = 0

(5)

From formulas (3), (4), and (5), it can be observed that with the introduction of the random number strategy, if

S

obtains an incomplete secret polynomial, the sum of some random numbers must be non-zero. This will significantly increase the decryption cost, greatly enhancing the security of the secret polynomial.

The first-round communication example among participant nodes is illustrated in Figure 3, involving six participant nodes labeled as A, B, C, D, E, F. In this initial communication round, each node divides its quadratic secret polynomial into three parts:

f_{A} = f_{A 1} + \dots + f_{A 3} \dots f_{D} = f_{D 1} + \dots + f_{D 3} \dots

Then each node randomly sends them to the cross-chain participant nodes.

The participants randomly distribute their respective secret polynomial fragments. As evident from nodes C, D, and F in the diagram, it's possible for a participant to distribute a fragment randomly to themselves. Meanwhile, as node B indicates, due to the random transmission strategy, a participant node might not receive any secret polynomial fragments.

3.3. Second Round of Participant Communication

After the first communication round, each participant

p_{i}

adds up all the partial polynomials they possess to form a new secret polynomial

h_{i} (x)

. Due to the random sending strategy,

h_{i} (x)

may be zero. After forming

h_{i} (x)

, the second communication protocol is initiated. Participant

p_{i}

sends the

h_{i} (x)

they own to every participant node involved in the cross-chain transaction. Upon receiving

h_{1} (x), h_{2} (x), \dots, h_{n} (x)

, participant

p_{i}

adds them up to create a new secret polynomial

F (x)

F (x) {= h}_{1} (x) + \dots + h_{n} (x)

(6)

From formulas (3), (5), and (6), the following computation process can be derived, resulting in formula (7).

\begin{matrix} F (x) = \sum_{i = 1}^{n} g_{i} (x) \\ = {(f}_{11} (x) + r_{11}) + \dots + {(f}_{n t} (x) + r_{n t}) # \\ = \sum_{i = 1}^{n} f_{i} (x) + \sum_{i = 1}^{n} \sum_{j = 1}^{t} r_{i j} \\ = f_{1} (x) + \dots + f_{n} (x) \end{matrix}

(7)

We provided the construction process of the secret polynomial in Protocol 1.

Protocol 1 Protocol 1 Constructing the Secret Polynomial

F (x)

Input: Transaction Elements

e_{1}, e_{2}, e_{3}, \dots, e_{m}

from each Participant

p_{i}

Output: Secret Polynomial

F (x)

1: Each participant

p_{i}

hashes and compiles their transaction elements

e_{1}, e_{2}, e_{3}, \dots, e_{m}

into a secret set

X_{i}

.
2:

p_{i}

constructs quadratic secret polynomials

f_{i} (x)

based on the elements in the secret set

X_{i}

.
3:

p_{i}

randomly divides

f_{i} (x)

into

t

parts. For each participant

p_{i}

and each polynomial fragment

f_{i j} (x)

, generate a random number

r_{i j}

such that

r_{i j} \neq 0

. These random numbers enhance security and ensure that

f_{i j} = (f_{i 1} (x) + r_{i 1}) + \dots + (f_{i t} (x) + r_{i t})

.
4:

p_{i}

randomly sends the t polynomial fragments to

t

participating nodes.
5: Participants

p 1, p 2, \dots, p n

collectively add up all the polynomial fragments to obtain

h_{1} (x), \dots, h_{n} (x)

, then broadcast it to all cross-chain participants.
6: Each node adds up all received polynomials

h_{1} (x), \dots, h_{n} (x)

to construct

F (x)

After the first round of communication, each participant consolidates all the secret polynomial fragments they own into a new secret polynomial, denoted as:

\begin{matrix} h_{A} = f_{B 1} + f_{C 2} + f_{D 3} + f_{E 2} # \\ h_{B} = \emptyset \\ \dots \\ h_{F} = f_{A 3} + f_{B 2} + f_{D 1} + f_{E 3} + f_{F 3} \end{matrix}

After the consolidation, each participant broadcasts the secret polynomial they possess to the participant network, ensuring that eventually, each participant has the complete secret polynomial F. Specially, as in the case of node B shown in Figure 3,

h_{B}

is zero, for the integrity and security of the protocol, B also needs to broadcast

h_{B}

to the network.

3.4. Secure Comparison

When the element

e_{i}

represents transaction verification information collectively possessed by all participants,

f_{i} (x)

can be transformed into the following form:

f_{i} (x) = {(x - e_{i})}^{2} S (x)

(8)

where

S (x)

is a

(2 m - 2)

-degree polynomial obtained by dividing

f (x)

{(x - e_{i})}^{2}

. Substituting e_i into equation (8), we get

f_{i} (x) = 0

, implying

F (x) = 0

. If a transaction element

e^{*}

is not a shared element, then

{(x - e^{*})}^{2} > 0

, and it follows that

f_{i} (x) > 0

, which implies

F (x) \neq 0

Each participant can substitute their transaction elements

e_{1}, e_{2}, e_{3}, \dots, e_{m}

into equation (7). If

F (e_{i}) = 0

, then

e_{i}

represents transaction information collectively owned by all participants. The smart contract can then make decisions based on predefined elements for comparison.

If the transaction elements possessed by each participant are accurately compared, operations such as cross-chain transfers are executed.

In Protocol 2, a secure multiparty computation scheme for transaction elements is provided.

Protocol 2 Secure Comparison Protocol

Input : F (x)

, e_{i}

Output: Verification Result
Procedure CompareElements (F(x), e_i)
For i=1 to m
If F(e_i)！=0
Then return False // Verification failed, indicating data tampering, terminate the cross-chain contract
Else
Continue
End if
End
Send transactions to Pools // Execute cross-chain transfer

4. Application Use Cases

A building block of cross-chain applications is ability to verify whether specific transactions exist on another blockchain and transactions atomicity. The existence of a transaction can be verified by receiver contract on the destination chain, acquired from user, third-party service, or validator contract (in this paper). This transaction

t r x

on source blockchain at block d can be obtained with Merkle proof. Subsequently, the receiver contract invokes updater contract to check if the Merkle proof of d from the source blockchain matches the one provided by the validator contract. The atomicity of multi-chain cross-chain transactions relies on a group of receiver contracts across all participating chains. This group of receiver contracts must collectively confirm the Merkle proof before proceeding, aiming for strong consistency and atomicity.

We present two application examples supported by SMPTC³, representing integral parts of Web 3.0:

4.1. Multi-Chain Asset Transfer

In Web 3.0, investment demands of individual users are expanding, often involving the transfer and exchange of cross-chain assets. Unlike miner node transfers of assets to high-yield mainstream blockchain networks, regular cross-chain bridges suffice for these scenarios. However, for individual users investing in potential coins or NFTs, regular cross-chain bridges entail complex multiple cross-chain transfers and high fees. Leveraging SMPTC³, users can employ a unified validator contract and pre-deployed locking contracts

{S C}_{l o c k}

and minting contract SCmint across multiple chains. The specific protocol involves the deployment of

{S C}_{v}

{S C}_{l o c k}

, and

{S C}_{m i n t}

in a multi-chain ecosystem. User

U_{1}

aims to swap their investment asset NFT

t_{1}

for an equivalent value in potential coin

t_{3}

. User

U_{2}

is willing to purchase

t_{1}

with an equivalent stable coin

t_{2}

, while User

U_{3}

has completed their investment and desires to exchange

t_{3}

for stable coin

t_{2}

. The detailed process is outlined in Figure 1.

4.2. Multi-Chain Information Interaction

Cross-chain message passing and data sharing involve sharing off-chain data across different blockchains, but simple bilateral cross-chain information exchange can't satisfy the current complexities of the blockchain ecosystem. Multi-chain information interaction satisfies this need. Message passing can be achieved by embedding messages into transactions. For example, to pass messages

m_{1}, m_{2}

from blockchain

C_{1}, C_{2} t o C_{3}

, a multi-chain transaction can be initiated, divided into two parts

{t r x}_{1}

and

{t r x}_{2}

. Users can embed messages

m_{1}

and

m_{2}

into

{t r x}_{1}

and

{t r x}_{2}

, respectively, sending them to

C_{3}

for verification and execution.

5. Trusted Cross-Chain Protocol for Two Participants

In this section, we aim to extend SMPTC³ to accommodate two participants and demonstrate through an example and security analysis that this approach is ineffective. Subsequently, we introduce a two-participant cross-chain verification method based on discrete logarithms.

5.1. Direct Extension of TMPC3 to Two Participants

In SMPTC³, the fundamental security assumption is

n \geq 3

, signifying multiple participants collectively executing cross-chain verification tasks. It allows participants to conceal data within secret polynomials and share them among other participants while ensuring the secrecy of data. However, a majority of cross-chain interaction scenarios are concentrated on two participants across two chains, i.e.,

n = 2

, from section 3.1, resulting in t=2, which can be derived from Equation (3):

\begin{matrix} f_{A} = f_{A 1} (x) + f_{A 2} (x) \\ f_{B} = f_{B 1} (x) + f_{B 2} (x) # \end{matrix}

The execution of the first round of communication leads to the transformation of Figure 3 into Figure 4:

Where:

h_{A} {+ h}_{B} - f_{B} = f_{A}

(9)

From equation (9), it can be observed that B can directly compute the complete quadratic secret polynomial of A. This makes Secret information of A highly susceptible to direct deduction, rendering the direct extension of SMPTC³ to two-party computation ineffective.

5.2. Two-Participant Cross-Chain Verification Method Based on Discrete Logarithms

In practical cross-chain scenarios involving two participants, the data source is determinate. Therefore, relying on random transmission based on quadratic secret polynomials becomes ineffective. Hence, leveraging discrete logarithms [41], we have designed a verification method (2PC3) tailored for Two-participant cross-chain scenarios.

As shown in Figure 5:

Two participants, A and B, first collectively agree on a large prime number

p

. Subsequently, each generates a large random number,

r_{a}

and

r_{b}

, respectively. Then, based on their respective sets

X_{A} = {x_{11}, x_{12}, \dots, x_{1 m}}

and

X_{B} = {x_{21}, x_{22}, \dots, x_{2 m}}

, they create

Y_{A}

and

Y_{B}

through the first round of discrete logarithm encryption and exchange these (steps 1 and 2). Following this, A and B individually perform the second round of discrete logarithm encryption to obtain

{Y_{B}}^{'}

and

{Y_{A}}^{'}

(step 3) and send these results to the verification contract (step 4). Upon successful comparison by the verification contract, a verification success message is sent to A and B (step 5).

The first round of discrete logarithm encryption is represented as:

\begin{matrix} y_{A i} | = {x_{1 i}}^{r_{a}} m o d p, x_{1 i} \in X_{A}, \\ y_{B i} | = {x_{2 i}}^{r_{b}} m o d p, x_{2 i} \in X_{B}, i \in [1, m] # # \end{matrix}

(10)

The second round of discrete logarithm encryption is represented as:

\begin{matrix} {y_{B i}}^{'} | = {y_{B i}}^{r_{a}} m o d p, y_{B i} \in Y_{B}, \\ {y_{A i}}^{'} | = {y_{A i}}^{r_{b}} m o d p, y_{A i} \in Y_{A}, i \in [1, m] # \end{matrix}

(11)

Derived from equations (9) and (10):

\begin{matrix} {y_{A i}}^{'} | = {x_{1 i}}^{r_{a} + r_{b}} m o d p # \\ {y_{B i}}^{'} | = {x_{2 i}}^{r_{a} + r_{b}} m o d p # \end{matrix}

(12)

From equation (11), if

X_{A} = X_{B}

, then

{Y_{A}}^{'} = {Y_{B}}^{'}

, where the exponents

r_{a}

and

r_{b}

along with the large prime number p are randomly generated. Hence, the encryption verification method used in this paper ensures semantic security. Due to the complexity of the discrete logarithm problem, deducing xi is almost impossible. Even in the presence of curious nodes on the chain or among participants, access to confidential information is unattainable.

Protocol 3 2PC3 Protocol

Input: Transaction Elements Set

X_{A}

and

X_{B}

from Participants

p_{A}

and

p_{B}

Output: Verification Result
1: Participants

p_{A}

and

p_{B}

jointly generate a large prime number

p

.
2:

p_{A}

and

p_{B}

each generate a large random number

r_{a}

and

r_{b}

.
3:

p_{A}

and

p_{B}

respectively perform the first round of discrete logarithm encryption on elements

x_{A i}

from set

X_{A}

and

x_{B i}

from set

X_{B}

, denoted as

y_{A i} = {x_{1 i}}^{r_{a}} m o d p, y_{B i} = {x_{2 i}}^{r_{b}} m o d p

, where

i \in [1, m]

, then forming confidential sets

Y_{A}

and

Y_{B}

.
4:

p_{A}

and

p_{B}

mutually exchange

Y_{A}

and

Y_{B}

.
5:

p_{A}

and

p_{B}

respectively perform the second round of discrete logarithm encryption on

Y_{B}

and

Y_{A}

, denoted as

{{y_{B i}}^{'} = {y_{B i}}^{r_{a}} m o d p, y}_{A i}^{'} = {y_{A i}}^{r_{b}} m o d p

, forming sets

{Y_{B}}^{'}

and

{Y_{A}}^{'}

.
6:

p_{A}

and

p_{B}

send

{Y_{B}}^{'}

and

{Y_{A}}^{'}

to the validator contract. After verification by the validator contract, the verification result is sent to the participants.

6. Implementation and Evaluation

The experiments for SMPTC3 are based on Fabric and the Ethereum test version Rinkeby (Geth) systems. The cross-chain contracts are implemented using Go and Solidity 3multi-party cross-chain algorithm from Chapter 3 and the two-party cross-chain algorithm from Chapter 5. Depending on the number of participants, the contract will automatically select the corresponding cross-chain solution(2PC or MPC). Based on the characteristics of blockchain cross-chain transactions (cross-chain information transmission also falls under cross-chain transactions), we use methods such as hashing and feature extraction to compute the transaction features, forming a verifiable high-privacy secret set. Then, based on the concept of Multi-Party Secure Computation (MPC) and combined with the communication characteristics of blockchain, we achieve communication and secure computation.

6.1. Experiment Setup

We conducted experimental tests using an Intel(R) Xeon(R) Gold 6354 CPU @ 3.00GHz and 504GB RAM. In accordance with requirements and industry standards, we report the average execution time and fees. The reported results are derived from the average of ten executions.

6.3. Security Test

We divided the participant nodes into four types: honest nodes, semi-honest adversaries, malicious adversaries, and downtime nodes. Based on these classifications, we set up four test scenarios: all honest nodes, an unspecified number of semi-honest adversaries, mostly honest nodes with one malicious adversary, and mostly honest nodes with one downtime node. Security testing was conducted with

(2, 3, 5)

participants, each scenario undergoing 100 actual tests, resulting in Figure 6.

From Figure 6, we can see that SMPTC³ can operate normally when all participants are honest nodes or when there are semi-honest adversaries. According to formulas (4-8), the semi-honest adversary model can only obtain partial fragments of the secret set and cannot acquire effective secret information. When there is a malicious adversary among the participants, SMPTC³ cannot pass the verification, and the cross-chain transaction will be abandoned, strictly ensuring the safety of cross-chain assets and information. Therefore, in malicious adversary environment, the number of successful verifications is zero. In the downtime node test environment, we divided it into two scenarios: one where the node downtime time exceeds the verification waiting time, and the other where the node recovers and re-responds to verification. Experimental tests show that if the node recovers from the crash and promptly responds and continues to participate honestly in verification, the verification task can still be successfully completed. This experiment demonstrates that SMPTC³ has good security and robustness, ensuring the safety of cross-chain assets and information.

6.3. Verify Time of SMPTC³

We measured the time overhead required for cross-chain transactions. For comparison with SMPTC³, we deployed conventional multi-signature notary mechanisms and sidechain mechanisms as control groups in the same experimental environment. Due to the complexity of multi-chain cross-chain scenarios, we designed the control group to achieve optimal experimental results, as shown in Figure 7. This ideal situation assumes there are only

n - 1

cross-chain operations (with

n

cross-chain participants, the maximum number of cross-chain operations could be

\frac{n (n - 1)}{2}

, and the minimum is

n - 1

After executing each set of experiments ten times and averaging the results, we obtained the data presented in Figure 8. As shown in Figure 8, the ideal verify time for the multi-signature notary mechanism and the sidechain mechanism increases linearly (

n

) with the number of participants. Given that the maximum number of cross-chain operations could be

\frac{n (n - 1)}{2}

, it is evident that the worst-case scenario will show a quadratic increase (

n^{2}

In contrast, for SMPTC³, the horizontal axis range of participants is

2 - 32

, and the overall trend remains horizontal. It is worth noting that with only two participants, verify time of SMPTC³ is slightly higher than in the multi-participant scenario. According to formulas (10-12), this is likely due to the computation time for exponential and modular operations. For multiple participants, as the number of participants increases, SMPTC³ verify time generally remains stable. However, when there are too many participants, such as

16 - 32

, the verify time slightly increases. As indicated by protocols 1 and 2, this is due to the increased communication and computation costs caused by the larger number of elements involved in the computation. But such situations are uncommon in practical applications and do not hold significant practical value.

In summary, SMPTC3 can effectively solve the complex problem of cross-chain interactions among multiple participants in practical applications. It also satisfactorily meets the basic requirements for two-party interactions.

7. Conclusions

The paper proposes an improved decentralized cross-chain method, SMPTC3, based on Multi-Party Secure Computation (MPC). The improved MPC method addresses the centralization issue inherent in traditional blockchain cross-chain methods, providing enhanced privacy and security. It innovatively solves the problem of multiple cross-chain operations in multi-chain ecosystems, significantly reducing the complexity of cross-chain interactions for multi-chain participants. Additionally, by leveraging the characteristics of blockchain technology, it extends MPC to Two-Party Secure Computation (2PC), meeting the basic cross-chain needs between two blockchains. Furthermore, SMPTC3 replaces the original cross-chain bridge solution, avoiding high cross-chain fees. Experimental results show that in blockchain cross-chain application scenarios, SMPTC3 effectively resolves issues that previously required multiple cross-chain operations through a single cross-chain interaction. For basic two-chain cross-chain requirements, its performance also surpasses that of previous methods. Unlike previous cross-chain bridge methods, SMPTC3 further reduces various costs associated with cross-chain interactions, thereby avoiding limitations on blockchain ecosystem performance due to cross-chain operations.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org, Figure S1: title; Table S1: title; Video S1: title.

Author Contributions

Conceptualization, G.Y. and T.N.; methodology, H.M. and X.L.; software, H.M. and M.Y.; validation, G.Y., T.N. and X.D.; formal analysis, G.Y. and X.L.; investigation, X.D. and M.Y.; resources, T.N.; data curation, H.M. and M.Y.; writing—original draft preparation, H.M..; writing—review and editing, T.N. and M.Y.; visualization, H.M.; supervision, H.M.; project administration, G.Y.; funding acquisition, all authors. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China (grant number 62072086, 62372097, and 61991404), and the Special Funds for Basic Scientific Research of Central Universities (grant number N2116005, N2116008, and N2416003).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The original contributions presented in this study are included in the Supplementary Materials, further inquiries can be directed to the corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

Nakamoto, S. Bitcoin: A peer-to-peer electronic cash system. Decentralized Business Review, 2008, 21260.
Mao, H.; Nie, T.; Sun, H.; Shen, D.; Yu, G. A Survey on Cross-Chain Technology: Challenges, Development, and Prospect. IEEE Access 2022, 11, 45527–45546. [Google Scholar] [CrossRef]
Wood, G.; et al. Ethereum: A secure decentralised generalised transaction ledger. Ethereum Project Yellow Paper 2014, 151, 1–32. [Google Scholar]
Bentov, I.; Pass, R.; Shi, E. Snow White: Provably Secure Proofs of Stake. IACR Cryptol. ePrint Arch. 2016, 919. [Google Scholar]
David, B.; Ga, P.; Kiayias, A.; Russell, A. Ouroboros praos: An adaptively-secure, semi-synchronous proof-of-stake protocol. Cryptology ePrint Archive 2017, 2017, 573. [Google Scholar]
Kiayias, A.; Russell, A.; David, B.; Oliynykov, R. Ouroboros: A provably secure proof-of-stake blockchain protocol. Annual International Cryptology Conference 2017, Springer, 357–388. [Google Scholar]
Angelis, S.; Aniello, L.; Baldoni, R.; Lombardi, F.; Margheri, A.; Sassone, V. PBFT vs Proof-of-Authority: Applying the CAP Theorem to Permissioned Blockchain. ITASEC 2018, 2018, 2058, 06. [Google Scholar]
Liu, X.; Zhao, G.; Wang, X.; Lin, Y.; Zhou, Z.; Tang, H.; Chen, B. MDP-Based Quantitative Analysis Framework for Proof of Authority. Conference on Cyber-Enabled Distributed Computing and Knowledge Discovery (CyberC) 2019, 227-236.
Li, Y.; Wang, Z.; Fan, J.; Zheng, Y.; Luo, Y.; Deng, C.; Ding, J. An Extensible Consensus Algorithm Based on PBFT. Conference on Cyber-Enabled Distributed Computing and Knowledge Discovery (CyberC) 2019, 17-23.
Wang, Y.; Song, Z.; Cheng, T. Improvement Research of PBFT Consensus Algorithm Based on Credit. Blockchain and Trustworthy Systems (BlockSys 2019), Springer, 2019, Vol. 1156, 47–59. [Google Scholar]
Wang, R.; Zhang, L.; Xu, Q.; Zhou, H. K-Bucket Based Raft-Like Consensus Algorithm for Permissioned Blockchain. 2019 IEEE 25th International Conference on Parallel and Distributed Systems (ICPADS) 2019, 996–999. [Google Scholar]
Kim, J.; Essaid, M.; Ju, H. Inter-Blockchain Communication Message Relay Time Measurement and Analysis in Cosmos. 2022 23rd Asia-Pacific Network Operations and Management Symposium (APNOMS) 2022, 1-6.
Abbas, H.; Caprolu, M.; Pietro, R. Analysis of Polkadot: Architecture, Internals, and Contradictions. 2022 IEEE International Conference on Blockchain (Blockchain) 2022, 61–70. [Google Scholar]
Zabka, P. ; Foerster, K-T. ; Schmid, S.; Decker, C. Empirical evaluation of nodes and channels of the lightning network. Pervasive and Mobile Computing 2022, 83, 101584. [Google Scholar]
Fusion Foundation. Fusion Whitepaper: An inclusive Cryptofinance platform based on blockchain. 2017.
Trestioreanu, L.; Cassagnes, C.; State, R. Deep dive into Interledger: Understanding the Interledger ecosystem. arXiv e-prints 2022.
LayerZero. https://layerzero.network/. 2022.
Xie, T.; Zhang, J.; Cheng, Z.; Zhang, F.; Zhang, Y.; Jia, Y.; Boneh, D.; Song, D. zkBridge: Trustless Cross-chain Bridges Made Practical. CCS 2022, 3003–3017. [Google Scholar]
Yao, A.C.-C. Protocols for Secure Computations. FOCS 1982, 1982, 160–164. [Google Scholar]
Yao, A.C.-C. How to Generate and Exchange Secrets. FOCS 1986, 1986, 162–167. [Google Scholar]
Goldwasser, S. Multi-Party Computations: Past and Present. PODC 1997, 1997, 1–6. [Google Scholar]
Dalskov, A.P.K.; Escudero, D.; Nof, A. Fast Fully Secure Multi-Party Computation over Any Ring with Two-Thirds Honest Majority. CCS 2022, 653–666. [Google Scholar]
Bayatbabolghani, F.; Blanton, M. Secure Multi-Party Computation. CCS 2018, 2018, 2157–2159. [Google Scholar]
Zhu, R.; Cassel, D.; Sabry, A.; Huang, Y. NANOPI: Extreme-Scale Actively-Secure Multi-Party Computation. CCS 2018, 2018, 862–879. [Google Scholar]
Freedman, M.J.; Hazay, C.; Nissim, K.; Pinkas, B. Efficient Set Intersection with Simulation-Based Security. Journal Cryptol. 2016, 29(1), 115–155. [Google Scholar] [CrossRef]
Cheon, J.H.; Jarecki, S.; Seo, J.H. Multi-Party Privacy-Preserving Set Intersection with Quasi-Linear Complexity. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2012, 95-A(8), 1366-1378.
El Gamal, T. A public key cryptosystem and a signature scheme based on discrete logarithms. IEEE Trans. Inf. Theory 1985, 31(4), 469–472. [Google Scholar] [CrossRef]
Goyal, V.; Mohassel, P.; Smith, A.D. Efficient Two Party and Multi Party Computation Against Covert Adversaries. EUROCRYPT 2008, 2008, 289–306. [Google Scholar]
Volgushev, N.; Schwarzkopf, M.; Getchell, B.; Varia, M.; Lapets, A.; Bestavros, A. Conclave: secure multi-party computation on big data. EuroSys 2019, 2019, 3:1–3:18. [Google Scholar]
Dolev, S.; Li, Y.; Sharma, S. Private and Secure Secret Shared MapReduce. DBSec 2016, 2016, 151–160. [Google Scholar]
Dahl, M.; Mancuso, J.; Dupis, Y.; Decoste, B.; Giraud, M.; Livingstone, I.; Patriquin, J.; Uhma, G. Private Machine Learning in TensorFlow using Secure Computation. CoRR abs/1810.08130, 2018.
Kumar, N.; Rathee, M.; Chandran, N.; Gupta, D.; Rastogi, A.; Sharma, R. Low: Secure TensorFlow Inference. IEEE Symposium on Security and Privacy 2020, 2020, 336–353. [Google Scholar]
Dong, Y.; Milanova, A.L.; Dolby, J. SecureMR: secure mapreduce computation using homomorphic encryption and program partitioning. HotSoS 2018, 2018, 4:1–4:13. [Google Scholar]
Bhushan, B.; Sinha, P.; Sagayam, K.M.; Andrew, J. Untangling blockchain technology: A survey on state of the art, security threats, privacy services, applications and future research directions. Computers & Electrical Engineering 2021, 90.
Wu, S.; Li, J.; Duan, F.; Lu, Y.; Zhang, X.; Gan, J. The Survey on the development of Secure Multi-Party Computing in the blockchain. 2021 IEEE Sixth International Conference on Data Science in Cyberspace (DSC), Shenzhen, China, 2021, 1-7.
Belchior, R.; Vasconcelos, A.; Guerreiro, S.; Correia, M. A Survey on Blockchain Interoperability: Past, Present, and Future Trends. ACM Computing Surveys 2021, 54, 1–41. [Google Scholar] [CrossRef]
Zhang, J.; Gao, J.; Li, Y.; Chen, Z.; Guan, Z.; Chen, Z. Xscope: Hunting for Cross-Chain Bridge Attacks. ASE 2022, 2022, 171:1–171:4. [Google Scholar]
Dou, J.; Liu, X.; Zhou, S.; Li, S. Efficient Secure Mutiparty Set Operations Protocols and Their Application. Chinese Journal of Computers 2018, 41, 1844–1860. [Google Scholar]
Goldreich, O. Foundations of cryptography: Volume 2, Basic applications. Cambridge University Press, London, UK, 2009.

Figure 1. Two cross-chain transactions based by cross-chain bridge.

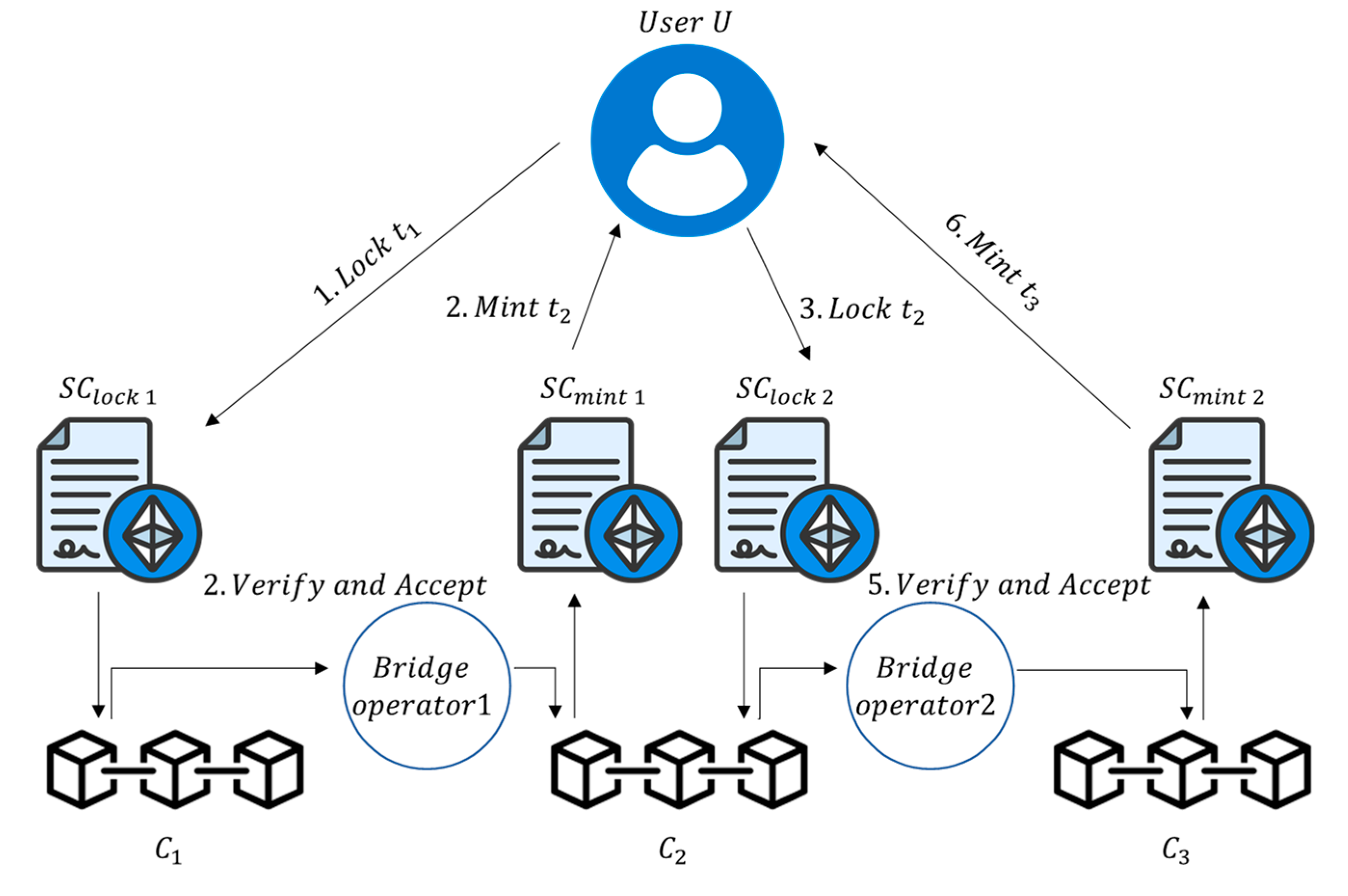
Figure 2. Multi-chain asset exchange by SMPTC3.

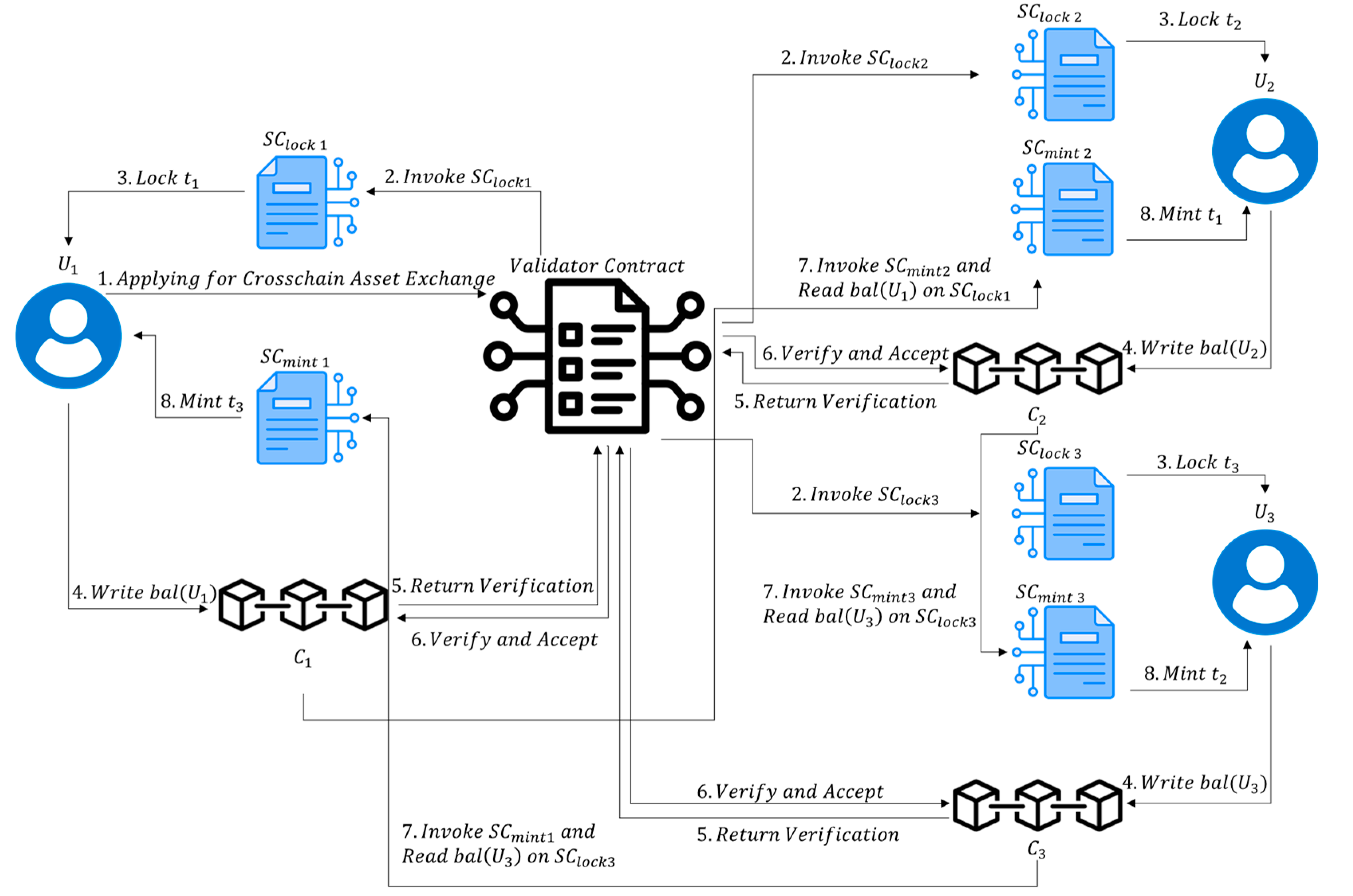
Figure 3. First-round communication example.

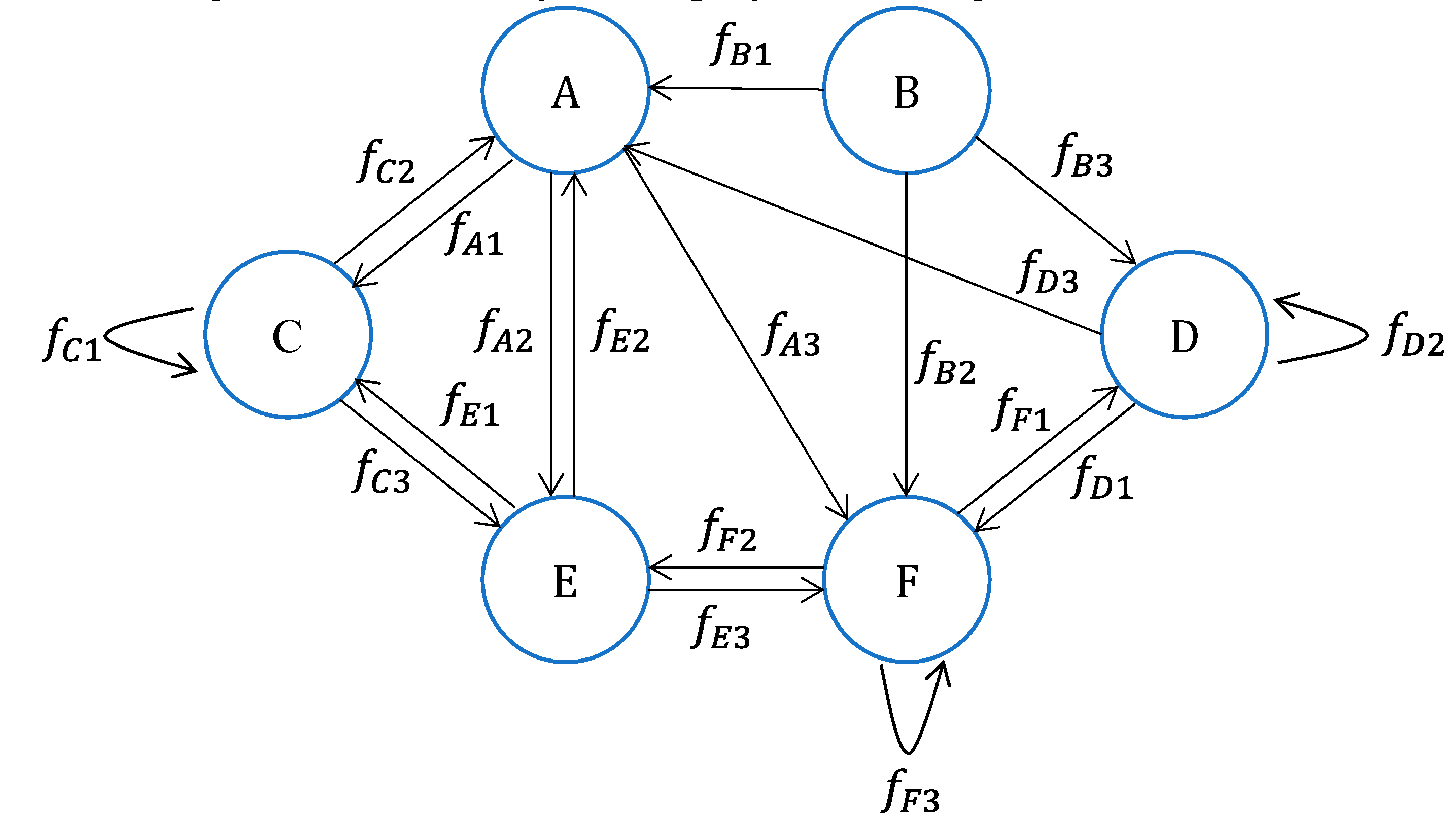
Figure 4. First-round communication on two participants.

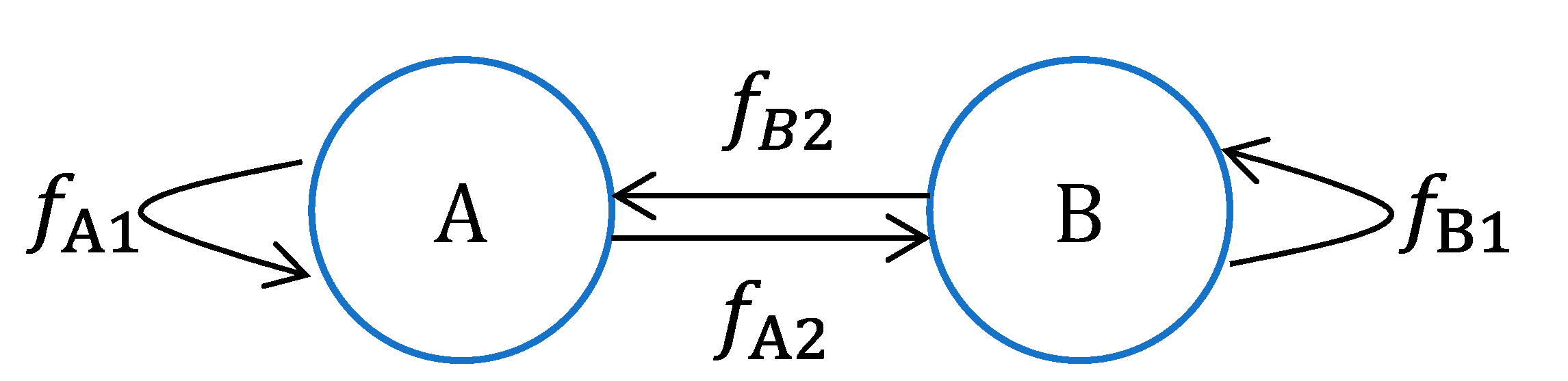
Figure 5. Verification method tailored for Two-participant(2PC3).

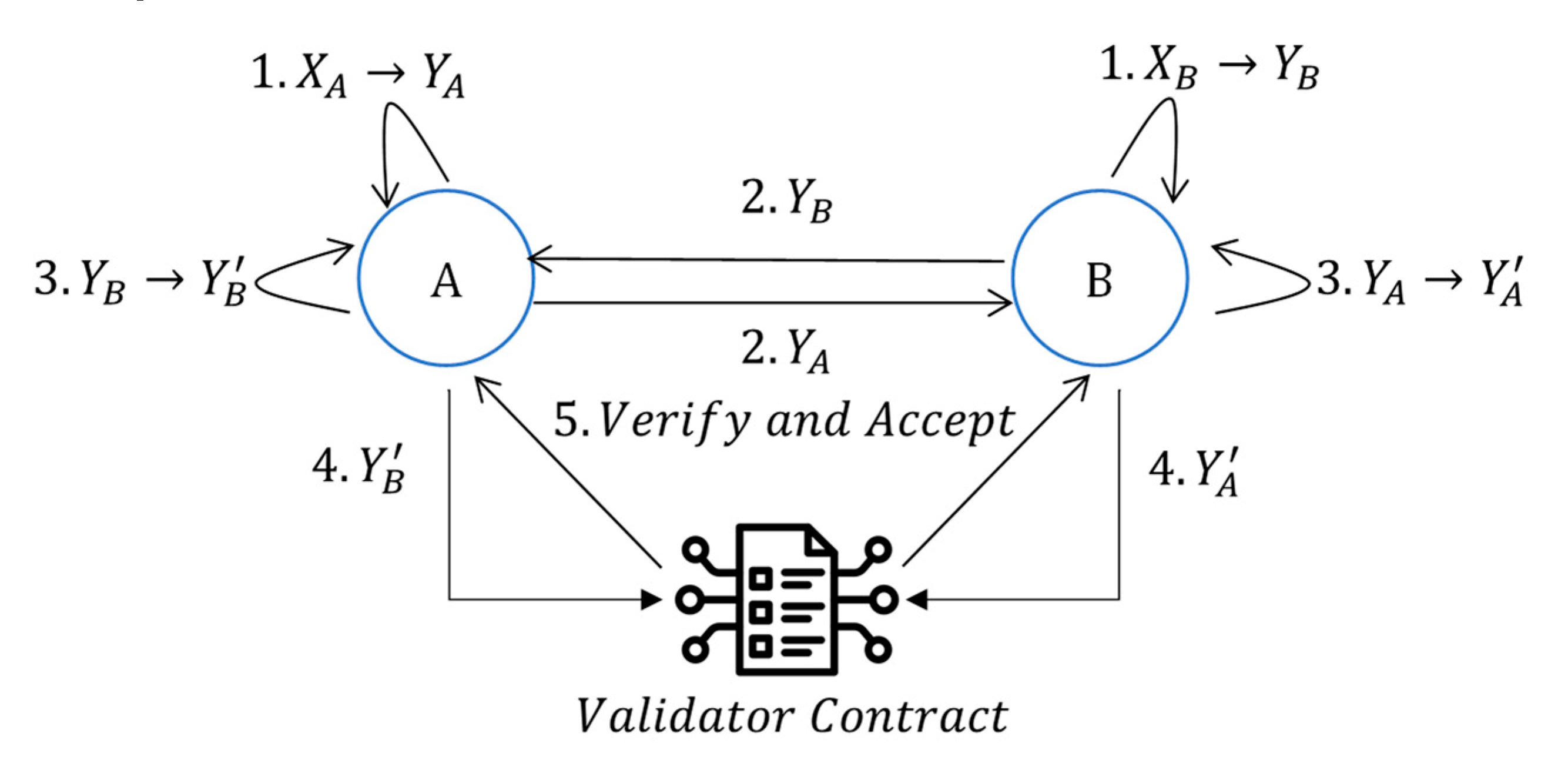
Figure 6. Security test results.

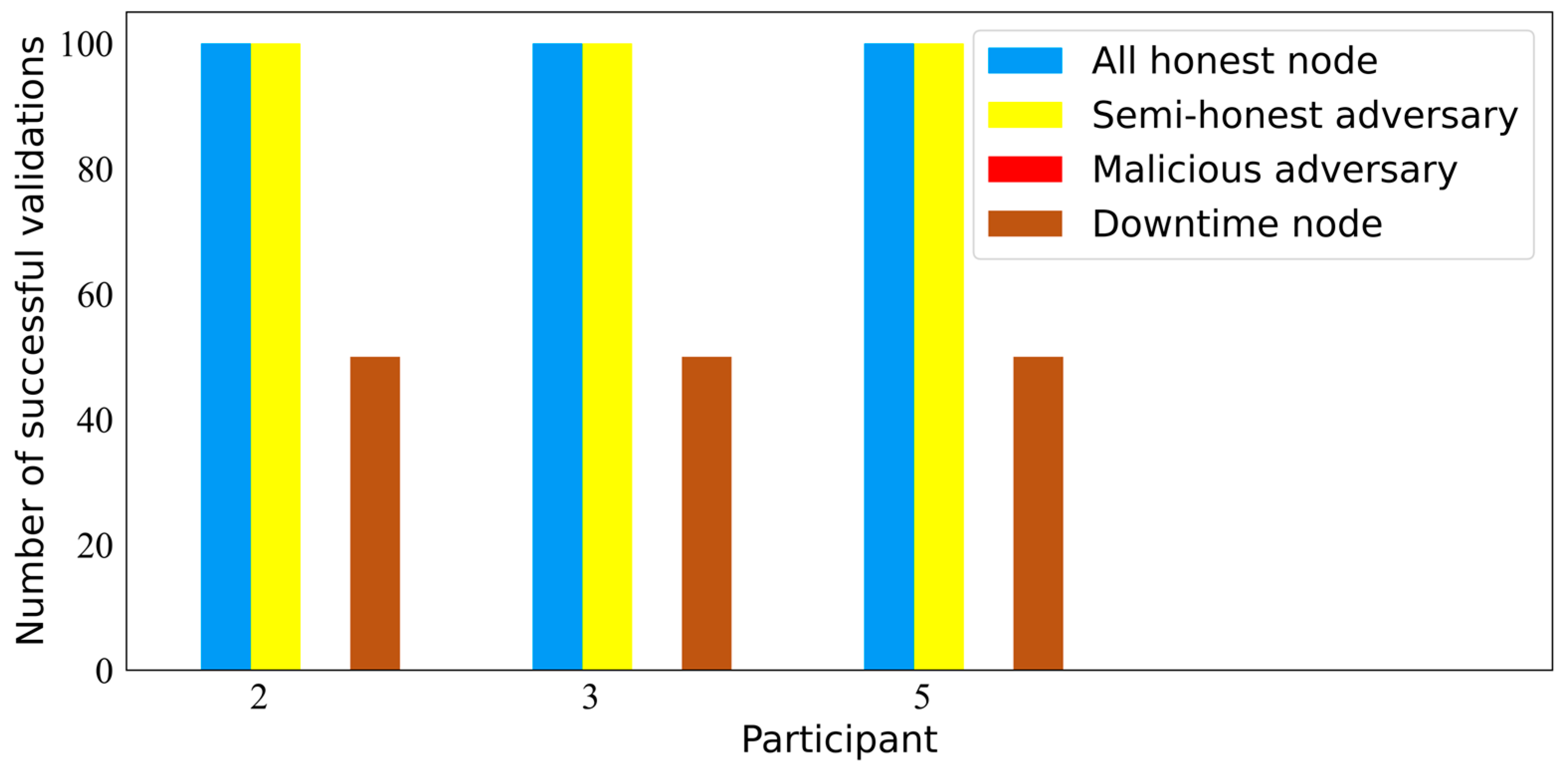
Figure 7. Ideal situation of the control group.

Figure 8. Verify time of SMPTC³ and conventional cross-chain methods.

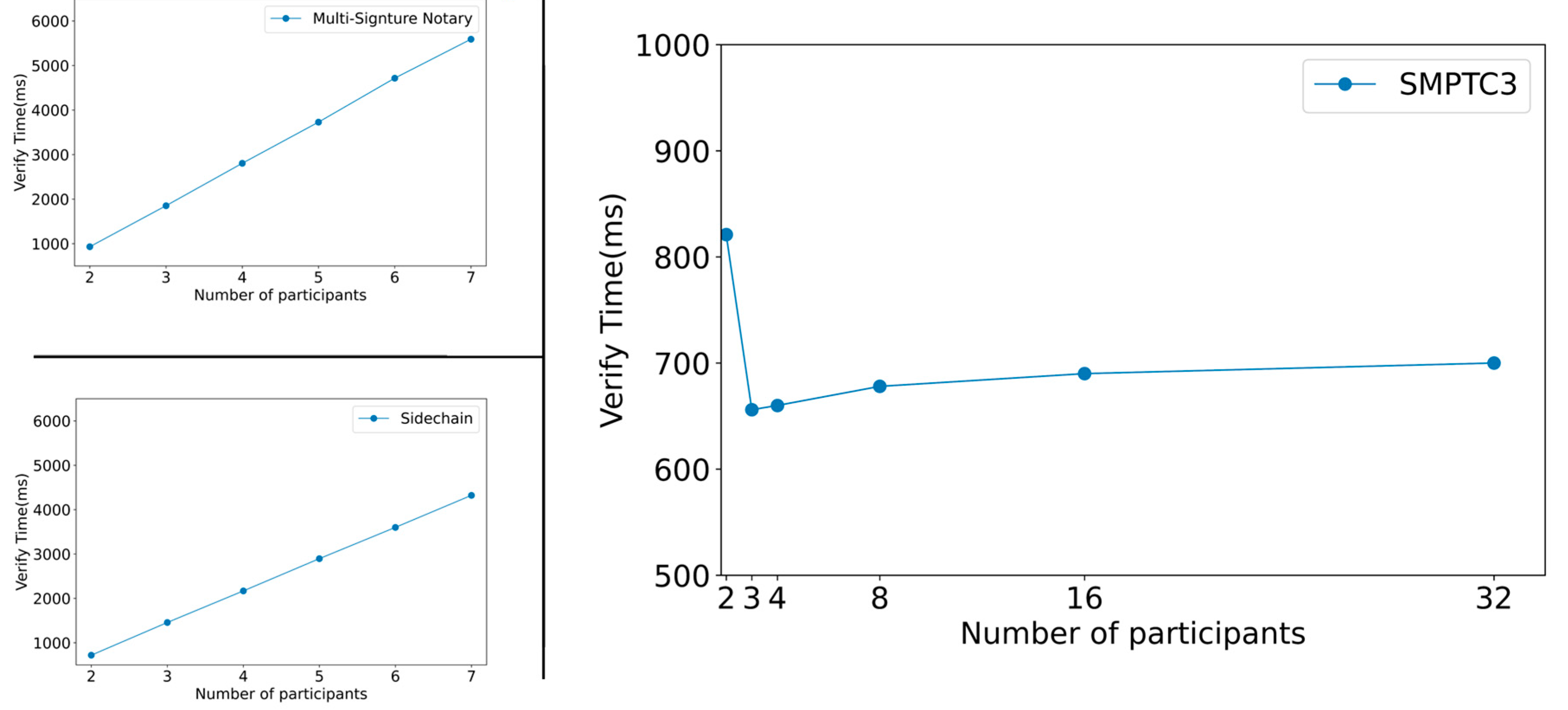
Table 1. Comparison of cross-chain projects.

Cross-Chain Project	Consensus	Cross-Chain Technology	Security	Transaction Speed
Cosmos	Tendermint BFT	IBC Protocol & Relays	Medium	Very High
Polkadot	Asynchronous BFT	Relays	Medium	Medium
Lighting Network	Following transactions chain	Channels	Medium	High
Fusion	PoW	DCRM	Medium	Medium
Interledger	Following transactions chain	Multi-Notary	Low	Medium

Table 2. Cross-chain bridges security problem.

Date	Victimization Agreement	Type of Attack	Operation Position
2021.07	Chainswap	Check for defects	After signing/cross-chain
2021.08	Poly Network	Hash collosion/check defect	signature
2022.01	Qubit Bridge	Incorrect setup/check defect	Before cross-chain
2022.01	Multichain	Interface compatibility issues	Before cross-chain
2022.02	Meter Bridge	Inspection defects	Before cross-chain
2022.02	Wormhole	Interface verification problem	signature
2022.03	Li Finance	Inspection defects	Before cross-chain
2022.03	Ronin Network	Validator control	signature

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer