Tensile Specimen Circular Grid Pattern and AI-Based Strain Calculation Method

During tensile testing of materials, strain measurement is conducted using either contact or non-contact methods. Contact methods offer high accuracy and precision but are limited by the specimen's thickness and dimensions, whereas non-contact methods minimize damage to thin specimens and allow measurements in various environments, though they require longer prep-aration and calculation times. This paper proposes a circular grid marking pattern and a strain prediction algorithm using artificial intelligence (AI), which simplifies the preparation process and allows strain prediction without additional equipment. The circular grid pattern can be ar-ranged in various configurations from 1×5 to 5×7, and a laser marker, which requires minimal time, was used to engrave the pattern on the specimen to shorten the preparation time. The AI model, trained on image-based data, enables strain calculation regardless of the specimen's gauge length and size, and allows measurement of local strain as well as gauge-length strain. The reliability of this concept was verified by applying it to tensile testing.

Keywords:

Subject: Engineering - Mechanical Engineering

1. Introduction

1.1. Research Background

Historically, the invention or development of new materials has driven the advancement of industrial technologies. Particularly, metal materials have long been used in various fields and continue to be subjects of ongoing research. Recently, in the mobility sector, where efficiency is paramount, composite or metal materials with high strength and stiffness are used [1]. However, defects such as fractures and wrinkles (cracks) in metal components can lead not only to personal injuries but also to significant economic losses. Therefore, to establish design safety standards for metal components, it is important to understand the physical properties of the formed shapes, such as thickness, springback, and residual stress [2]. Finite element analysis is commonly used to understand the physical properties occurring during the forming of metal materials. When the production conditions of the metal (such as composition and heat treatment) are standardized, the reliability of numerical results regarding the metal’s physical properties can be ensured through information obtained from extensive testing. However, for newly developed metals, material tests such as tensile tests are required to verify the reliability of numerical results by obtaining the material’s physical properties [3].

The tensile testing procedure involves mounting a specimen processed to standard specifications in a tester and measuring the stress and strain generated when it is subjected to tensile stress at a constant speed. Strain measurement methods can be divided into contact methods using gauges and non-contact methods using cameras or sensors. Contact measurement methods include mechanical extensometers that measure the displacement of physically moving parts, electrical resistance extensometers (strain gauges) that measure distance through resistance changes in attached resistors, and inductive extensometers that measure changes in induced current [4]. These extensometer-based contact measurement methods involve directly attaching gauges to the test specimen, acquiring displacement data through separate measurement equipment, and calculating strain by dividing this data by the initial length. Non-contact measurement methods include video measurement that tracks marking points on the specimen with high-speed cameras, laser measurement using laser beam reflection, digital image correlation (DIC) analyzing surface patterns of the specimen, and ultrasonic measurement using transmission and reception times of ultrasonic signals. Among these various non-contact measurement methods, DIC is particularly noteworthy because it allows 3D deformation measurement and data acquisition for multiple points, making it useful in diverse environments such as extreme temperatures and large deformations [5]. The DIC method analyzes the correlation of pixel values between two images to calculate strain from the changes in the pattern applied to the specimen’s surface [6,7]. As opposed to traditional methods that attach extensometers directly to the specimen, DIC provides additional detailed information, such as strain in the specimen’s width or thickness directions as well as the tensile direction (specimen length direction). Moreover, by capturing the entire specimen area with a camera during the test, deformation can be tracked at specific points, enabling measurement of local strain just before necking or fracture occurs [5].

Using mechanical extensometers involves attaching the equipment to the specimen during tensile testing, ensuring high-reliability measurements. This approach is less affected by changes in surrounding conditions such as ambient light or temperature. However, the measurement range of an extensometer may be exceeded by material elongation, and the measurement equipment specifications must be adjusted according to the material deformation. Furthermore, there is a critical issue when measuring the deformation of thin sheets: If the sheet’s thickness is less than the gap of the jig used for attaching the extensometer, measurement becomes impossible [8]. Strain gauges measure strain through electrical resistance, allowing the detection of fine deformations and applicability to various materials. However, unlike mechanical extensometers, they are significantly affected by temperature changes [9]. Inductive extensometers measure strain using electromagnetic induction, accurately detecting fine deformations like strain gauges, and can be used in high-temperature and extreme environments. However, they are affected by external electric fields, reducing the reliability of measurements in high-frequency environments. Furthermore, contact measurement methods measure material deformation by attaching gauges to the gauge length specified in the tensile specimen standards, making it difficult to accurately analyze the strain in areas where actual fracture occurs [10].

Unlike the contact measurement methods discussed previously, non-contact methods do not physically touch the specimen. Thus, they prevent deformation caused by the measuring instrument when measuring thin-sheet specimens. Additionally, they can measure regardless of the specimen’s shape and size and are usable under various environmental conditions, such as different temperatures and pressures and in vacuum [11]. However, non-contact methods require more expensive equipment than contact methods, such as high-speed and high-resolution cameras, lasers, and ultrasonic devices, in addition to image analysis software. Furthermore, optical devices are sensitive to surrounding optical conditions such as lighting, reflection, and dust. In particular, DIC requires high computing performance because it measures strain by analyzing correlations over the entire image area captured by the camera [5]. Additionally, to measure the strain on the tensile specimen surface using DIC, a speckle pattern must be applied to the specimen using spray, allowing the tracking of image changes. However, this application process is time consuming, and during the drying process, the paint may peel off depending on the specimen’s surface roughness and material properties, making measurement impossibleBottom of Form.

The technical issues of the various measurement methods discussed can be summarized as follows. Contact methods offer high accuracy and precision but are limited by the specimen’s thickness and dimensions. Non-contact methods minimize damage to thin specimens and allow measurements in various environments, but they require expensive equipment, are sensitive to environmental conditions, and involve lengthy preparation and calculation times. Therefore, a need exists for a strain measurement method that reduces calculation and preparation time and does not require additional equipment.

1.2. Literature Review

Because these contact and non-contact material property measurement methods have individual advantages and disadvantages concerning specimen shape, environment, time, and cost, many researchers have proposed ideas to overcome these drawbacks. Ko et al. [12] proposed a theoretical formula to predict the measurement performance of strain gauge sensors based on specimen deformation through experiments and finite element analysis, showing that measurement values can be predicted by finite element analysis. Some studies have been conducted to improve strain measurement accuracy at cryogenic temperatures. Tabin et al. [13] presented a dynamic analysis of specimen structures using clip-on extensometers in uniaxial tensile tests and proposed a method for calculating modal parameters and complex stiffness. Tabin [14] analyzed the time response of extensometers at cryogenic temperatures, confirming that it can affect the identification of mechanical parameters such as elongation. The results demonstrated that contact measurement methods could be used even in extreme environments such as cryogenic conditions. Xu et al. [15] proposed a method to split the laser beam into two independent sections to improve accuracy and resolution in laser measurement methods. This method exhibited no data loss even in large deformations and minimized uncertainties caused by changes in laser intensity. Kersemans et al. [16] proposed a method to measure the deformed specimen cross section using the harmonic ultrasonic backscatter polar scan (H-UBPS) method. This method demonstrated that the cross section of the specimen could be measured without sample preparation and achieved accuracy similar to commercial methods. Li et al. [17] proposed chain subset-based DIC technology and a modified second-order shape function (MSSF) to reduce calculation time in the existing DIC method for tensile test automation, showing that elastic modulus and stress–strain curves could be measured automatically. They proposed a tensile test method with higher measurement accuracy and reduced calculation time compared to traditional methods. Bulava et al. [18] proposed automation of strain measurement in tensile tests using a high-resolution camera. Images captured by the high-resolution camera were used to find the specimen through pattern matching, detect the specimen’s outline, measure deformation, and specify particular regions of interest (ROIs) to reduce calculation time.

Kim et al. [19] proposed a method to calculate the deformation of observed surfaces in tensile tests using in-situ scanning electron microscopy (SEM) and artificial intelligence (AI). The AI algorithm used, a super-resolution residual network (SRResNet), restored low-resolution in-situ SEM images to high-resolution images, improving strain measurement accuracy. Liu et al. [20] applied machine learning to predict the stress–strain curve of additively manufactured metamaterials. They used long short-term memory (LSTM) and convolutional neural networks (CNNs) to predict material properties based on the layered structure and process conditions, demonstrating the possibility of property prediction based on images. Shim et al. [21] captured the deformation patterns of surface particles of recycled composites to obtain image and strain data. They predicted the stress–strain curve and fracture path through deep-learning training on the image dataset, showing that mechanical properties of materials can be predicted without actual experiments, though the study was limited to recycled CFRTP (Carbon Fiber Reinforce Plastic) materials. Karathanasopoulos et al. [22] proposed an algorithm to identify fractures during tensile testing using a CNN. This method confirmed that using machine learning methods and image subset generation techniques can automatically locate fracture positions. Castro et al. [23] measured material strain using mechanochromic sensors and machine learning. They proposed a strain measurement method through image processing and a load prediction algorithm based on color changes due to applied loads. The results showed that material property data could be predicted using AI, although the study noted that data accuracy could decrease depending on the resolution of the mechanochromic sensors. Yang et al. [24] addressed the issue of reduced strain prediction accuracy and long calculation times in DIC measurements during sudden deformations or when the spray pattern tears by using deep learning to train contour images and compensate for lost measurement data. The results confirmed that previously lost strain data could be recovered. However, the proposed method assumes a uniform strain state across the entire specimen and cannot be applied when the specimen’s deformation is non-uniform. Lee [25] proposed a method to measure the strain between two marked points on the gauge length using the DIC technique. The method analyzed the movement distance of the marking points according to the specimen’s positioning angle in the image, confirming that measurement accuracy could decrease depending on the angle. However, Lee’s study could not measure local strain by marking the gauge length.

As is evident from these previous studies, contact measurement methods have been researched to ensure accuracy in extreme environments but remain challenging to apply to thin sheets [12,13,14]. Additionally, non-contact measurement methods have been studied to improve accuracy and reduce calculation times, but they still require preparatory work [15,16,17,18,19,20,21,22,23,24,25]. Many researchers have proposed methods to improve the accuracy and efficiency of DIC in strain calculation. Although DIC is considered the best method for material property measurement, the substantial preparation time required for spray pattern application still needs improvement. Moreover, accurately measuring the strain at the fracture site is crucial for predicting fracture behavior in metal materials [26], yet research in this area remains insufficient.

1.3. Motivation and Novelty

Traditional tensile testing methods involve significant time and cost due to preparatory work and equipment setup, limiting their usability in various environments. Therefore, a simplified and efficient method is required to enable usage without environmental limitations. Additionally, to improve strain prediction accuracy and minimize differences due to user proficiency, an automated process that minimizes user intervention is needed. Accurately predicting material behavior and fracture also requires identifying strain at the fracture point, not just at the gauge length.

Thus, this paper proposes a circular grid marking pattern and an AI-based strain prediction algorithm that simplifies the preparation process and allows strain prediction without additional equipment. To shorten the preparation time, the circular grid pattern is engraved on the specimen using a laser marker, which requires minimal time. Applying this method to tensile testing demonstrated the advantages of this study’s concept. The proposed circular grid marking pattern can be applied regardless of the specimen’s shape. Strain is measured using an image-based AI model, allowing calculation regardless of the specimen’s gauge length and size, and enabling the measurement of local strain as well as gauge-length strain. The strain predicted by the AI model is automatically used to calculate the stress–strain curve, elastic modulus, and elongation.

The structure of this paper is as follows. Section 2 introduces the theoretical background of the strain measurement calculation and method that utilizes the circular grid, as well as the image preprocessing and AI model used to detect only marking images and determine strain. Section 3 describes the tensile test procedure, including the shape and formation method of the circular grid pattern proposed in this study. The circular grid pattern’s strain prediction accuracy differences were analyzed according to specimen size and camera specifications. Section 4 explains the data generation method for training the proposed strain prediction algorithm and the AI training conditions. Section 5 covers the results and analysis of strain prediction accuracy with variations in the circular grid pattern, formation method, and AI training. Finally, Section 6 summarizes conclusions regarding the proposed circular pattern method and AI strain prediction.

2. Theoretical Background

2.1. Material Test

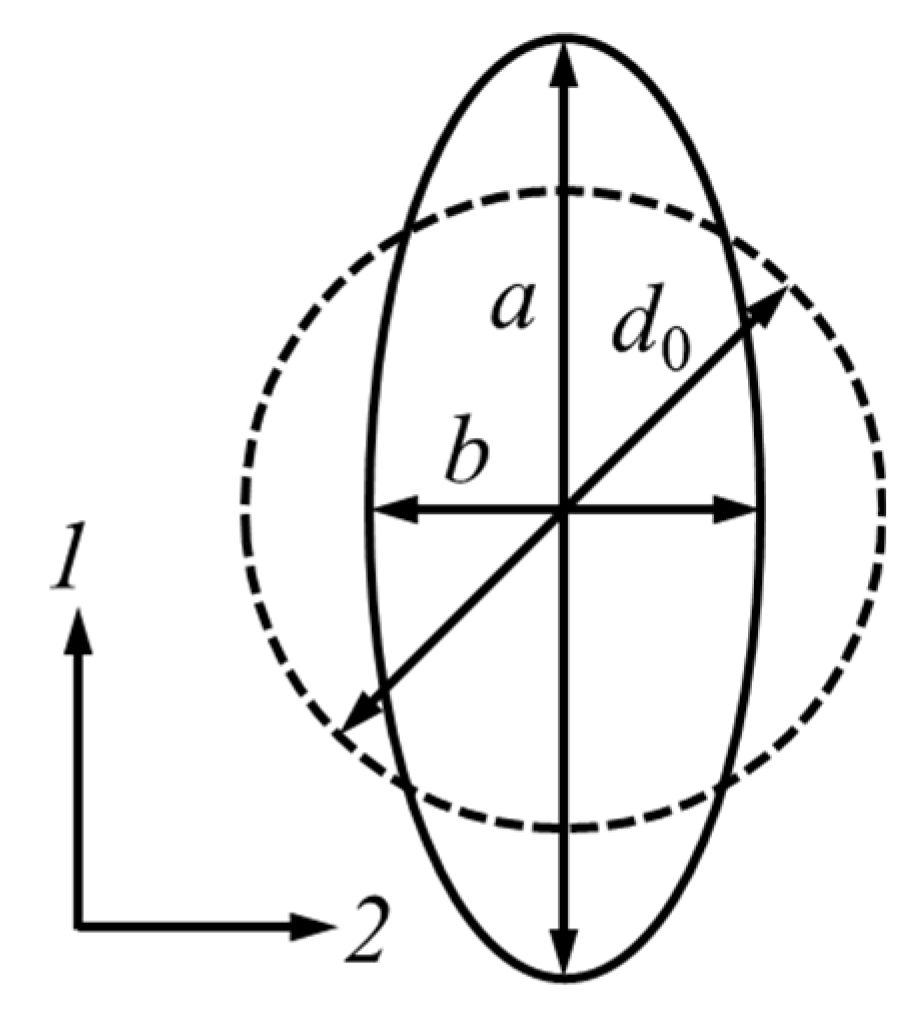
Formability refers to the ability or degree to which a material can undergo plastic deformation and is used to assess the material’s suitability for forming. To evaluate formability, tests are conducted to replicate the deformation modes that the material undergoes in actual processes, among which the tensile test is the most widely used method. The circular grid pattern proposed in this paper is applied for forming-limit tests [27,28,29]. As shown in Figure 1, the nominal and true strains of the deformed circles in the major (1) and minor (2) directions can be calculated using Equation (1). This paper proposes applying the circular grid pattern to tensile test specimens, considering only the major direction strain to calculate the stress–strain curve in tensile tests.

Engineering strain:

e_{1} = \frac{a - d_{0}}{d_{0}}, e_{2} = \frac{b - d_{0}}{d_{0}}

True Strain : ε_{1} = l n \frac{a}{d_{0}} = \ln (1 + e_{1}), ε_{2} = l n \frac{b}{d_{0}} = \ln (1 + e_{2})

(1)

2.2. DIC Measurement Method

The DIC method used to verify the proposed shape and prediction algorithm creates an irregular speckle pattern on the specimen, as shown in Figure 2, comparing pre-deformation and post-deformation images to calculate the entire specimen area. Compared to the traditional method of marking two points on the specimen and using an extensometer to measure strain, it provides detailed information such as directional strain and local strain. Additionally, because it captures images in real time during the test, it allows for tracking the deformation path and predicting the strain just before necking or fracture occurs.

2.3. Image Preprocessing

Image-based strain measurement methods are divided into 2D and 3D methods, with 3D DIC methods generally being applied for experiments. In this study, 2D was used to simplify the tensile test; because the material was a thin sheet, the difference between 2D and 3D was negligible, so thickness direction strain was ignored. The tensile test was recorded on video and images for the training data were generated from the test video, with necessary data extracted by image preprocessing.

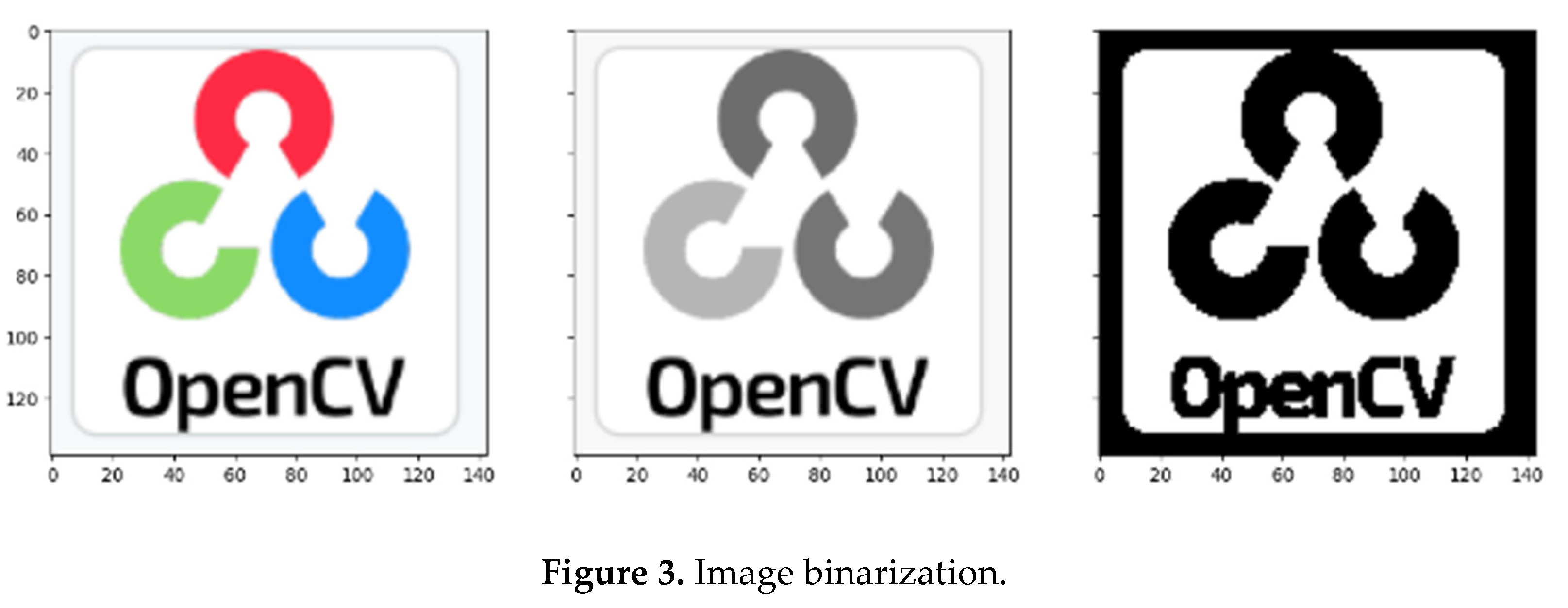
To extract only single circles from the circular grid pattern in the video recorded during the tensile test, image binarization was applied. Image binarization [30], as shown in Figure 3, converts the image into two colors, 0 and 255, and was applied in this study to reduce noise. Image binarization generally sets pixels above a certain threshold to 0 and the others to 255. In this case, the generated images had white objects on a black background. Given image A and structural element B, dilation and erosion are defined as in Equation (2). In Equation (2), B_z is the transformation of B by vector z, representing the symmetry of

\hat{B}

A ⨁ B = \{x| [{(\hat{B})}_{z} \cap A] \neq 0\} A ⊙ B = \{x| {(B)}_{z} \subseteq A\} A \circ B = (A ⨀ B) ⨁ B A ∙ B = (A ⨁ B) ⊙ B

(2)

After reducing noise and extracting only circles through image binarization, the image size typically consists of approximately 20×20 pixels. This size represents the pixel space where the circular pattern exists within a 1920×1080 size when adjusting the camera position considering the elongation of the material during the tensile test. The circular pattern exists in a relatively localized area compared to the image size, so even when captured at high resolution during the tensile test, only low-resolution images can be obtained. Super resolution was applied to obtain high-resolution images from these low-resolution images. Super resolution converts low-resolution images to high-resolution images through AI training, as shown in Figure 4 [31].

2.4. AI Training Model

AI algorithms that classify and predict specific values based on images generally use a CNN structure. A CNN is an artificial neural network comprising one or several convolutional layers and traditional artificial neural network layers, capable of extracting high-dimensional image information compared to conventional image processing methods. Unlike a fully connected neural network, a CNN maintains the shape of the input and output data for each layer, effectively recognizing features from adjacent images while preserving image spatial information. Using shared parameters for filters, it requires significantly fewer learning parameters compared to a general artificial neural network. Image classification and prediction algorithms based on CNN structures include Visual Geometry Group (VGG), ResNet, and MobileNet.

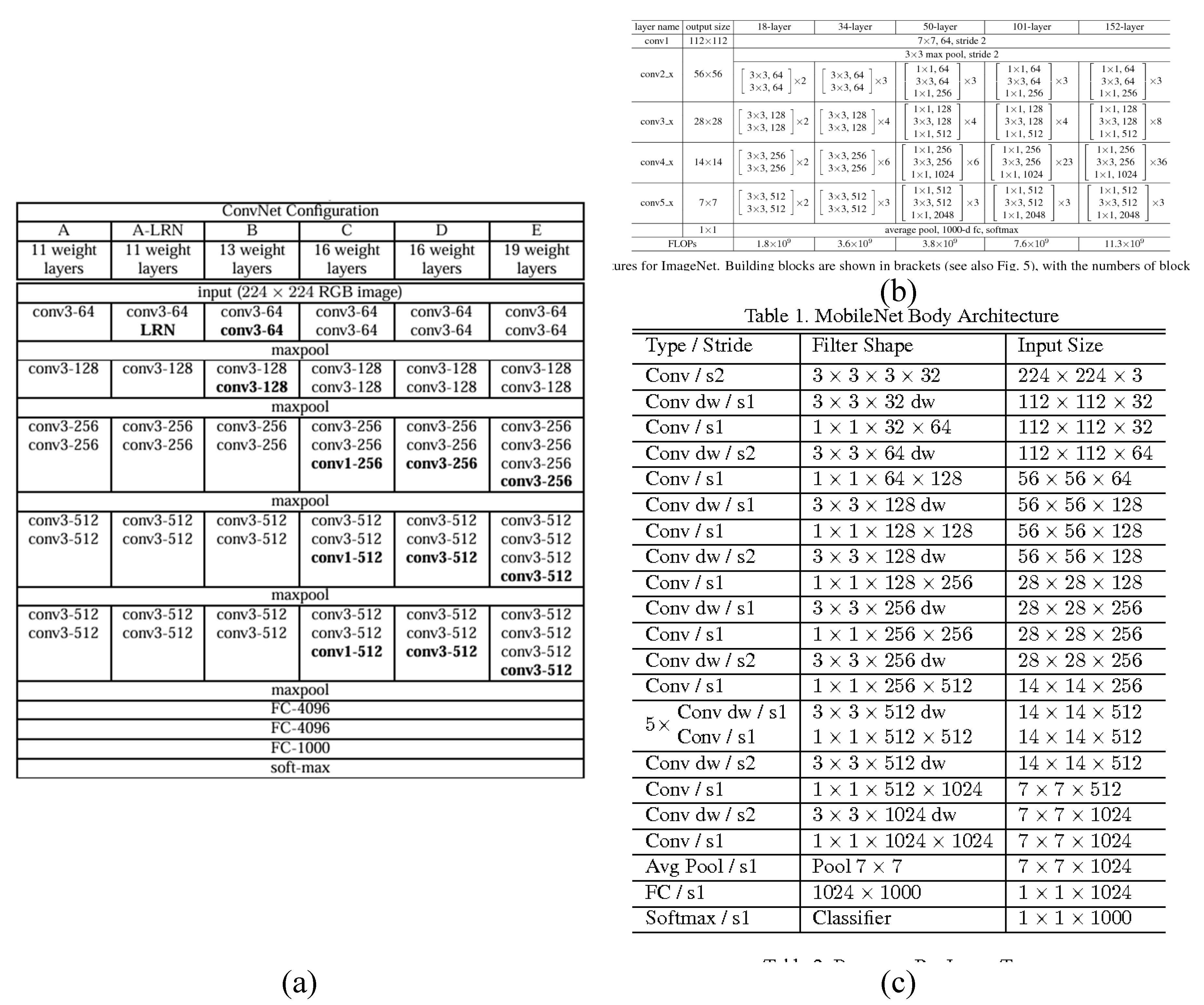
VGG [32] is distinguished as VGG16 or VGG19 according to the number of convolutional layers, with the model structure comprising C and E as shown in Figure 5a. It repeatedly applies convolutional layers with filtering techniques to the input image, the ReLU nonlinear activation function, and pooling layers that reduce the size of the image data. Then, the data are vectorized through the fully connected (FC) layer and normalized through the softmax activation function.

ResNet (Residual Network) [33], unlike VGG, is composed of blocks, as shown in Figure 5b. By residual mapping, which adds values that have passed through convolutional layers to those that have not, it mitigates overfitting and parameter vanishing problems as the layer depth increases [20]. ResNet’s layer structure uses convolutional layers with 7×7 filters and 3×3 max pooling.

MobileNetV2 [34] is a neural network designed for efficient computation in resource-constrained environments such as smartphones and other mobile devices, reducing the number of parameters and computation requirements compared to traditional CNNs. MobileNet applies depthwise separable convolutions, as shown in Figure 5c, which calculates spatial direction depth-wise convolutions and channel direction point-wise convolutions separately before combining them. Because different filters are applied to each channel, the number of output channels remains the same as the number of input channels.

3. Circular Grid Pattern

3.1. Circular Grid Pattern Shape

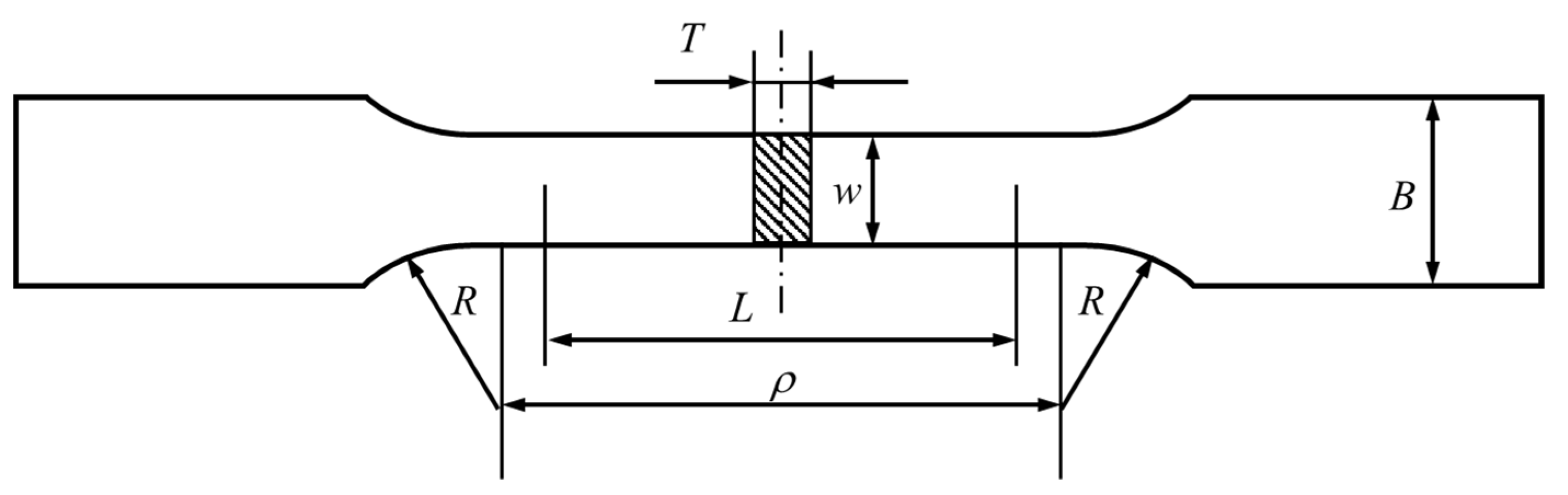
The tensile specimen used in this study applied the KS B 0801 standard, as shown in Figure 6. The material used was STS 304 3t. The specimen was processed using laser cutting.

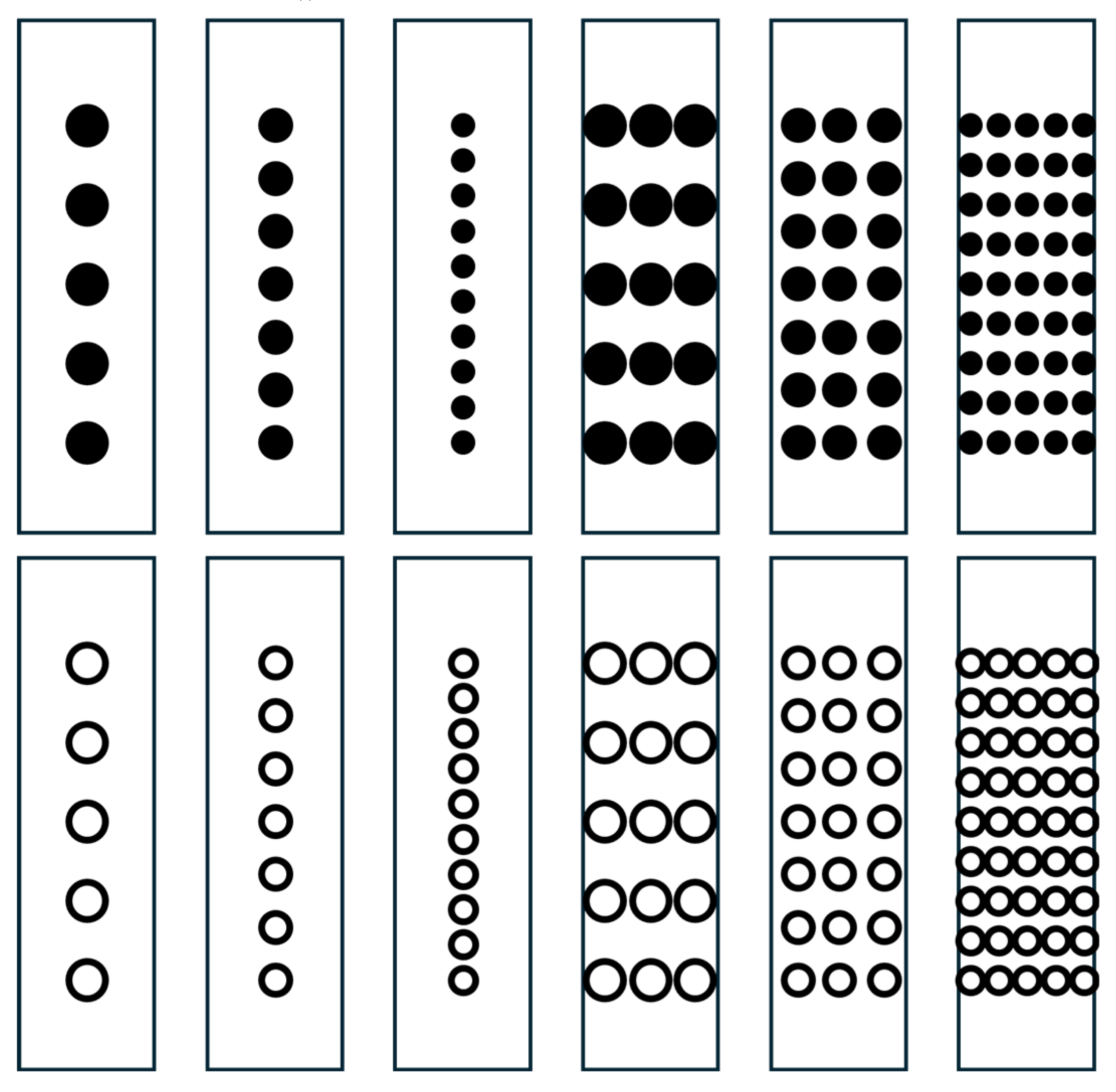
This paper proposes a circular grid pattern to replace the speckle pattern used in traditional DIC. The proposed circular grid pattern can measure strain from the gauge length to the local strain at the fracture site. As shown in Figure 7, the pattern consists of grids with circles arranged in configurations such as 1×5, 3×5, 1×7, and 5×7. The pattern position is based on the center of the parallel section of the tensile specimen. There must be at least one row, and at least three circular markings must be formed in the tensile direction. It should consist of at least two circles indicating the gauge length and one or more positioned at the specimen center. However, because fractures do not consistently occur at the center, at least five circular markings should be formed in the tensile direction to account for the fracture location. Accordingly, the 1×5 circular grid is the minimum pattern proposed in this study, and the minimum circle size can be selected on the basis of the material strain and camera specifications. This is a crucial factor because the area within the camera frame where the tensile specimen deforms must be specified, considering both the initial state and the deformation. The tensile specimen moves further from the camera as it strains, and the extracted tensile specimen area becomes a low-resolution image as the camera moves away. Hence, it is necessary to examine the minimum pixel size of the circle that can be calculated for strain.

3.2. Pattern Formation Method

The circular grid pattern can be represented using laser marking. Here, the laser marking was embossed, not affecting material behavior, and was engraved in black for clear distinction from the specimen in image processing. An ideal small fiber laser marker LG-20P was used for laser marking, with conditions of 300 mm/s and 50 Hz on the STS 304 surface.

4. Image Data and Training Procedure

4.1. Image Data Generation Method

Circular grid pattern images were extracted by recording the tensile test on video using a digital single-lens reflex (DSLR) camera. Additionally, to validate the proposed algorithm, data measured with the traditional DIC method were compared, and lighting was set up to capture images without reflections by reducing specimen reflection.

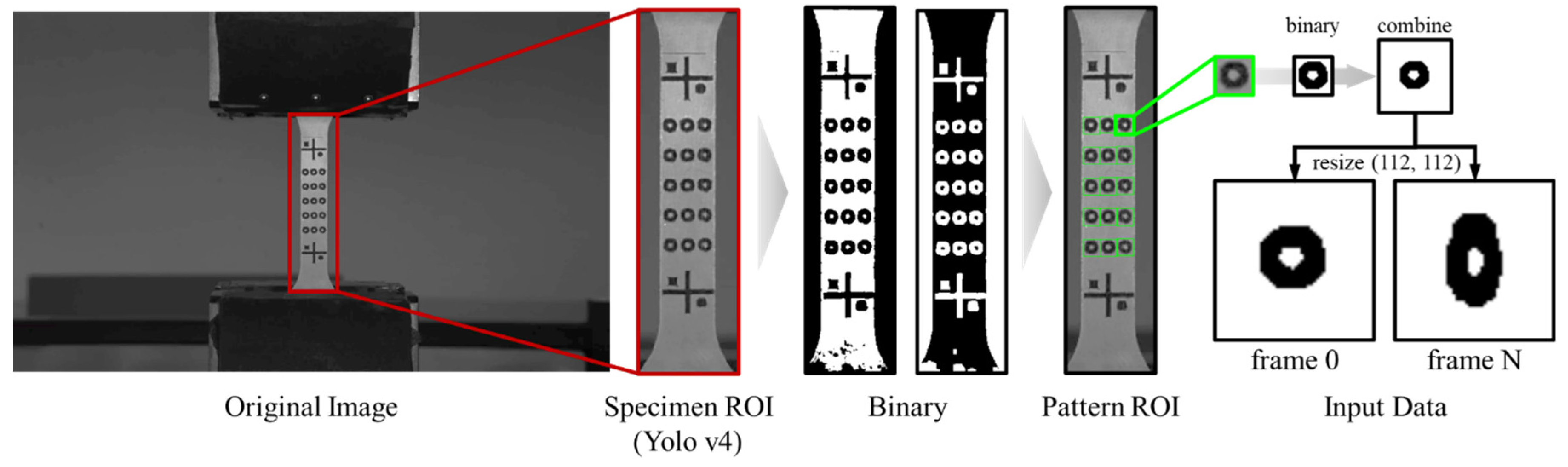
From the video of the tensile test process, circular image data were extracted from each frame. The procedure for extracting circular image data is shown in Figure 8, where the tensile specimen was identified using Yolo v4 training on the recorded original image, and the ROI of the detected tensile specimen was designated. Image binarization was applied for contour detection, and image inversion and morphological operations, specifically open operations, were performed to reduce unnecessary noise. To detect only the contours of the circular grid pattern, the pixel size detected was limited by the ratio of the gauge length to the circle diameter. As a result, the circular grid pattern was detected as shown in the pattern ROI of Figure 7, and the circular image ROI was obtained using the coordinates acquired at that time. The acquired circular ROI image was extracted from the original image to prevent information loss during the image preprocessing step that detects the circular pattern and was binarized for training application. The extracted circular images had different sizes depending on the size of each circle. For AI training, all images must be the same size, so the extracted circular images must be resized uniformly. Simply enlarging the extracted images to match the size can deform the circular image itself, leading to different results in strain calculations. To prevent this problem, the circle detected in the first frame of the video was designated as the initial circular image, and a white image twice the diameter of the circle was created. The binarized circular image was combined with the generated white image centered to create an image of the same size without losing the information about the circle size. Additionally, the images used for training were enlarged to a size of 112×112; because the resolution of the extracted circular image was low at about 20×20 pixels, super resolution was applied to obtain additional high-resolution images. From the images obtained through the preprocessing step, the initial circular image detected in the first frame and the circular images detected in frames 2 to N were used as input data for the AI application.

4.2. AI Training Procedure

In the strain prediction algorithm, the input data are the images of the undistorted circle from the initial frame and the distorted circles from subsequent frames, with the output being the corresponding strain values. Therefore, the length in the y-axis direction was measured for the image data obtained from image processing as described in Section 4.1, and each image was labeled with its strain. From the 6,450 data points obtained from tensile tests, 70% were used for training, 10% were classified as validation data, and the remaining were used as test data.

In AI, the accuracy of prediction results is determined by the coefficient of determination. The coefficient of determination is an indicator of how well the independent variables explain the dependent variable in a regression model; a higher coefficient indicates that the independent variables explain the dependent variable more effectively. The coefficient of determination is calculated as shown in Equation (3), where

y

is the observed value,

\bar{y}

is the mean of the observed values, and

\hat{y}

is the predicted value.

r^{2} = \frac{{\sum (\hat{y} - \bar{y})}^{2}}{{\sum (y - \bar{y})}^{2}}

(3)

5. Results and Discussion

5.1. AI Training Results

For strain prediction, algorithms with CNN structures were used, including VGG16, VGG19, ResNet50, and MobileNet, and the prediction accuracy of the four structures was compared. Among the AI algorithms compared, VGG16 had the highest coefficient of determination at 0.978. This result confirmed that the VGG structure is more suitable for strain prediction than other networks, as detailed in Table 1. AI training demonstrated that strain prediction based on images is sufficiently possible. This result confirmed that strain can be automatically calculated in tensile tests and that local strain can also be calculated.

5.2. Strain According to Resolution

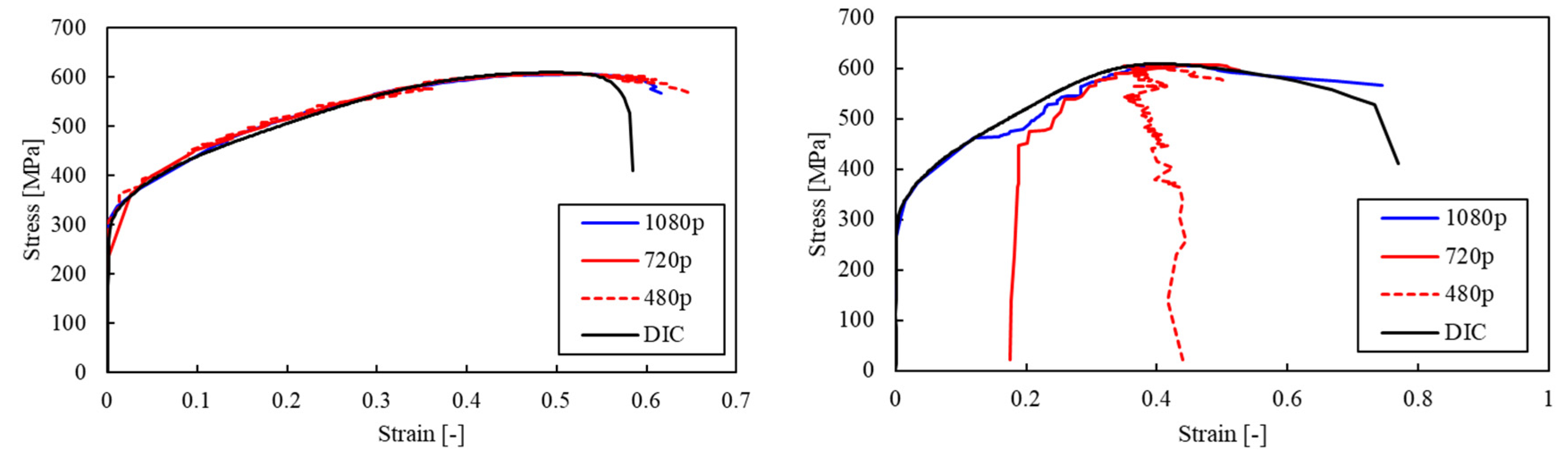
Tensile tests were conducted on the 3×5 circular grid array using STS 304 material. The video resolution during the tensile test was 1920×1080 (1080p), which was then changed to 1280×720 (720p) and 854×480 (480p) to analyze the impact of resolution on strain calculation. Strain was calculated for images at each resolution, and the stress–strain curves were compared, as shown in Figure 9. The graph shows that while calculating strain over the gauge length is not significantly affected by resolution, the accuracy of local strain calculations decreases as resolution decreases. Experiments confirmed that when the material elongation is 0.7, the image pixel size for the circle must be at least 10×10 pixels. To verify the proposed strain prediction algorithm, tensile test data for the predicted material was measured using a 3D DIC device; the calculated stress–strain curve is shown in Figure 9.

5.3. Discussion and Contributions

The measurement error between the existing method and the newly proposed method was sufficiently effective at less than 5%, verifying the validity of the proposed method and confirming that it could yield meaningful values. The minimum size criteria for the proposed circular pattern were established. This paper proposes a laser marking method, but other methods can be applied according to the operator’s needs.

The results show that compared to traditional tensile test methods, the equipment setup for the proposed method is easier and the preparation time is reduced, and the accuracy similar to that of existing methods. As a result, tensile test automation is feasible, and it is expected that a process for real-time application and versatility across various materials can be developed.

However, because this study was limited to steel materials and tensile tests, there are restrictions on applying it to various other materials and test methods. Additionally, noise was entirely removed from the dataset images for training, leading to reduced accuracy in noisy environments.

5. Conclusions

In this study, a 2D tensile test strain prediction algorithm without time and cost constraints was developed by applying image preprocessing and AI; the prediction accuracy of various algorithms was compared. The research process and results can be summarized as follows.

To reduce the preparation time for speckle pattern application in traditional DIC measurements, a new marking method is proposed, and an algorithm to predict strain based on this marking shape was suggested.

The strain prediction algorithm coefficients of determination were compared for the VGG16, VGG19, ResNet, and MobileNet AI structures; VGG16 exhibited the highest prediction accuracy.

As a result, tensile test automation was judged to be feasible, and it is expected that a process for real-time application and versatility across various materials can be developed.

Authorship contribution statement

Sarang Yi: Model design, Methodology, Software, Writing-original draft. Daeil Hyun: Writing-modification draft, Writing—review & editing. Seokmoo Hong: Supervision, Writing-modification draft, Writing—review & editing.

Acknowledgments

This work was supported by the research grant of the Kongju National University in 2023. FE results were obtained with a NVIDIA DGX STATION (Future Automotive Intelligent Electronics Core Technology Center, Cheonan, Republic of Korea)

Declaration of Competing Interest

The authors declared that there is no conflict of interest.

References

Trzepiecinski, T.; Najm, S.M. Current trends in metallic materials for body panels and structural members used in the automotive industry. Mater. 2024, 17, 590. [Google Scholar] [CrossRef]
Wiebenga, J.H.; Atzema, E.H.; An, Y.G.; Vegter, H.; van den Boogaard, A.H. Effect of material scatter on the plastic behavior and stretchability in sheet metal forming. J. Mater. Process. Technol. 2014, 214, 238–252. [Google Scholar] [CrossRef]
Banergee, D.K.; Iadicola, M.A.; Creuziger, A. Understanding deformation behavior in uniaxial tensile tests of steel specimens at varying strain rates. J. Res. Natl. Institute of Stand. Technol. 2021, 123. [Google Scholar] [CrossRef] [PubMed]
Schwarzkopf, E.A. Overview and comparison of noncontacting and traditional contacting extensometers. Evaluation of Existing and New Sensor Technologies for Fatigue, Fracture, and Mechanical Testing. Ed. Kang, J, McKeighan, PC, Dahlberg, G, & Kemmerer, R. 100 Barr Harbor Drive, PO Box C700, 2022. [CrossRef]
He, X.; Zhou, R.; Liu, Z.; Chen, S.Y.K.; Li, L. Review of research progress and development trend of digital image correlation. Multidiscipline model. Mater. Struct. 2024, 20, 81–114. [Google Scholar] [CrossRef]
Peters, W.H.; Ranson, W.F. Digital imaging techniques in experimental stress analysis. Opt. Eng. 1982, 21. [Google Scholar] [CrossRef]
Peters, W.H.; Ranson, W.F.; Sutton, M.A.; Chu, T.C.; Anderson, J. Application of digital correlation methods to rigid body mechanics. Opt. Eng. 1983, 22. [Google Scholar] [CrossRef]
Zhang, S.; Mao, S.; Arola, D.; Zhang, D. Characterization of the strain-life fatigue properties of thin sheet metal using an optical extensometer. Opt. Lasers. Eng. 2014, 60, 44–48. [Google Scholar] [CrossRef]
Gavrilenkov, S.I. Method of simulating temperature effect on sensitivity of strain gauge force sensor in non-uniform temperature field. AIP. Conf. Proc. 2019. [Google Scholar] [CrossRef]
Yoshihara, H.; Yoshinobu, M. Effects of specimen configuration and measurement method of strain on the sharacterization of tensile properties of paper. J. Wood. Sci. 2014, 287–293. [Google Scholar] [CrossRef]
Xu, Q.; Wang, X.; Yan, F.; Zeng, Z. Non-Contact extensometer deformation detection via deep learning and edge feature analysis. Des. Stud. Intell. Eng. 2023. [Google Scholar] [CrossRef]
Ko, M.; Lee, T. Performance Characteristics of Sensor Part in Extensometer Using Strain Gauge. Trans. Korean Soc. Mech. Engineers-A. 2019, 43, 201–208. [Google Scholar] [CrossRef]
Tabin, J.; Prącik, M. Methods for identifying dynamic parameters of clip-on extensometer–specimen structure in tensile tests. Meas. 2015, 63, 176–186. [Google Scholar] [CrossRef]
Tabin, J. Strain measurement by means of clip-on extensometers during discontinuous plastic flow at 4 K. Cryogenics, 2022, 123, 103451. [Google Scholar] [CrossRef]
Nie, X.; Song, B.; Loeffler, C.M. A novel splitting-beam laser extensometer technique for kolsky tension bar experiment. J. Dynamic Behav. of Mater. 2015, 1, 70–74. [Google Scholar] [CrossRef]
Kersemans, M.; Allaer, K.; Paepegem, W.V.; Abeele, K.V.D.; Pyl, L.; Zastavnik, F.; Sol, H.; Degrieck, J. A novel ultrasonic strain gauge for single-sided measurement of a local 3D strain field. Exp. Mech., 2014, 54, 1673–1685. [Google Scholar] [CrossRef]
Li, D.; Cheng, B.; Xiang, S.; Zhou, H. Integrative measurement method for tensile test based on DIC using modified second-order shape function. Meas. 2024, 226. [Google Scholar] [CrossRef]
Bulava, J.; Hargas, L.; Koniar, D. Contactless Material Tensil Testing Using a High-Resolution camera. Comput. 2022, 10, 121. [Google Scholar] [CrossRef]
Kim, S.J.; Min, H.G.; Park, J.H.; Kang, D.J. Application of deep learning method for time reduction and precision improvement in displacement measurement during in-situ SEM tensile test. Meas. 2024, in press. [Google Scholar] [CrossRef]
Liu, Q.; Wu, D. Machine learning and feature representation approaches to predict stress-strain curves of additively manufactured metamaterials with varying structure and process parameters. Mater. & Des. 2024, 241. [CrossRef]
Shim, Y.B.; Lee, I.Y.; Park, Y.B. Predicting the material behavior of recycled composites: Experimental analysis and deep learning hybrid approach. Compos. Sci. Technol. 2024, 249. [Google Scholar] [CrossRef]
Karathanasopoulos, N.; Hadjidoukas, P. Deep learning based automated fracture identification in material characterization experiments. Adv. Eng. Inform. 2024, 60. [Google Scholar] [CrossRef]
Castro, L.D.C.; Scabini, L.; Ribas, L.C.; Bruno, O.M.; Oliveira, O.N., Jr. Machine learning and image processing to monitor strain and tensile forces with mechanochromic sensors. Expert Syst. Appl. 2023, 212. [Google Scholar] [CrossRef]
Yang, R.; Li, Y.; Zeng, D.; Guo, P. Deep DIC: Deep learning-based digital image correlation for end-to-end displacement and strain measurement. J. Mater. Process Technol. 2022, 302. [Google Scholar] [CrossRef]
Lee, S. Analysis of tensile testing errors in metal thin film using the DIC method. Trans. Korean Soc. Mech. Eng. A, 2020, 44, 513–518. [Google Scholar] [CrossRef]
Kim, M.; Gu, B.; Hong, S. Determination of post-necking stress-strain relationship for zirconium low-oxidation based on actual cross-section measurements by DIC. J. Mech. Sci. Technol. 2020, 34, 4211–4217. [Google Scholar] [CrossRef]
Hsu, Q.C. Comparison of different analysis models to measure plastic strains on sheet metal forming parts by digital image processing. Int. J. Mach. Tools Manuf. 2003, 43, 515–521. [Google Scholar] [CrossRef]
Ibrahim, J.S.; Prasad, M.J.N.V.; Narasimhan, P.S.K. Effects of foil thickness to grain size (t/d) ratio and prestraining on tensile response, Microformability and Crystallographic texture of ultra-low carbon steel thin foils. Met. Mater. Int. 2024, 30, 348–359. [Google Scholar] [CrossRef]
Wankhede, P.; Narayanaswamy, N.G.; Kurra, S.; Priyadarshini, A. A portable device for single point strain analysis in sheet metal forming processes. HardwareX. 2022, 12. [Google Scholar] [CrossRef] [PubMed]
Joshi, O.S. Binary image processing for computation of connected components, image holes and Euler number using graph theory. 2018 International Conference on Advances in Communication and Computing Technology (ICACCT). 2018, 230–234. [Google Scholar] [CrossRef]
Dong, C.; Loy, C.C.; Tang, X. Accelerating the super-resolution convolutional neural network. Computer Vision-ECCV 2016, 2016, 391-407. [CrossRef]
Simonyan, K.; Zisserman, A. ; Very deep convolutional networks for large-scale image recognition. International Conference on Learning Representations. 2014. [Google Scholar] [CrossRef]
He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. 2016 IEEE Conference on Computer Vision and Pattern Recognition. 2015, 770–778. [Google Scholar] [CrossRef]
Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. MobileNets: Efficient convolutional neural networks for mobile vision applications. ArXiv. 2017. [Google Scholar] [CrossRef]

Figure 1. Major and minor direction strains of the circular grid pattern.

Figure 2. DIC measurement method.

Figure 3. Image binarization.

Figure 4. Example of super resolution application [31].

Figure 5. AI model structures: (a) VGG [32], (b) ResNet50 [33], and (c) MobileNetV2 [34].

Figure 6. Tensile specimen diagram.

Figure 7. Circular grid pattern examples.

Figure 8. Image preprocessing.

Figure 9. Comparison of DIC and strain prediction algorithm: (a) Gauge length, (b) local strain.

Table 1. AI training coefficient of determination.

Model Name	VGG16	VGG19	ResNet50	MobileNet
R²	0.978	0.974	0.9614	0.904

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer