Prerpints.org logo
Preprint
Article

An In-depth Evaluation of Educational Burst Games - in Relation to Learner Proficiency

Altmetrics

Downloads

87

Views

24

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

29 July 2024

Posted:

30 July 2024

You are already at the latest version

Alerts
Abstract
Game-based learning assessments lean on educational data mining approaches such as stealth assessments and quasi mixed-methods that help gather student learning proficiency. Rarely do we see approaches where student proficiency in learning is woven into the game's design. Educational Burst Games (EBGs) is a new approach to improving learning proficiency by designing fast-paced, short, repetitive, and skill-based games. They have the potential to be effective learning interventions both during instruction in the classroom and during after-school activities such as assignments and homework. Over five years we have developed two EBGs aimed at improving linear algebra concepts of undergraduate students. In this study, we provide results of an in-depth evaluation of the two EBGs developed with 45 participants that represent our target population. We discuss the role of EBGs and their design constructs such as pace and repetition, the effect of the format (2D vs. 3D), the complexity of the levels and the influence of prior knowledge on the learning outcomes.
Keywords: 
Subject: Computer Science and Mathematics  -   Algebra and Number Theory

1. Introduction

Educational technology has transformed how knowledge is acquired, making learning more interactive, engaging, and accessible. Among these innovations, educational burst games (EBGs) have emerged as a promising tool, leveraging the appeal of gaming to enhance learning outcomes [1]. Skill and drill games have had a long history of promoting proficiency in a particular subject area [2]. Math Bingo [3] replaces numbers with math problems in its bingo cards. Sentence Scramble [4] provides students with sentences that are scrambled and they have to arrange the words to be grammatically accurate. Science Memory Match [5] creates science cards with terms and definitions that students have to correctly match and Vocabulary Dominoes [6] uses words and their definitions as a matching strategy to connect the tiles. The common theme in the skill and drill games is the application of a learning strategy to an existing game mechanic (Bingo, Dominoes, etc.). EBGs include some skill and drill activity in the design of the game mechanic. However, what separates them is the inclusion of repetition and leveling-up similar to popular games such as Angry Birds and Peggle. The educational elements are then woven into EBGs to map the skill and the appropriate level of difficulty with proficiency or mastery of the subject matter. This study explores the effectiveness of EBGs in promoting learning proficiency, considering factors such as game complexity, format, and the learners’ prior knowledge.

2. Background

The integration of digital games in education has been extensively studied, showing varying impacts on motivation, engagement, and learning outcomes [7]. EBGs, characterized by their short duration and focus on repetitive learning tasks, offer unique advantages for educational settings. They align with cognitive theories suggesting repetition and engagement is critical for knowledge retention and skill acquisition [8].
Cognitive Load Theory [9] posits that learning is more effective when cognitive load is optimized. EBGs, with their brief and focused gameplay sessions, minimize extraneous cognitive load, allowing learners to concentrate on core educational content. Additionally, the theory of spaced repetition [10] supports the idea that information is more effectively retained when learning is distributed over time, a principle that EBGs naturally incorporate through their repetitive gameplay mechanics.
Research has shown that game-based learning (GBL) can significantly enhance student engagement and motivation [11,12]. Studies by Papastergiou [13] and Ke [14] have demonstrated the positive effects of digital games on learning outcomes in various subjects, including mathematics and language learning. However, the impact of game complexity, format, and prior knowledge on learning efficiency remains underexplored. This gap in research motivates the current study, aiming to provide insights into designing more effective EBGs for educational purposes. In prior work [15] we explored the relationship between combining inquiry-oriented learning (IOL) and game-based learning (GBL) where linear algebra concepts were discussed in classroom activities by the design of two EBGs. The study aimed to weave EBGs into an existing curricular framework for teaching linear algebra [16]. We then studied the effects of learning strategies that students employed due to the addition of the EBGs [17,18,19,20]. Our findings indicate that students can be directed to explore multiple strategies and critically evaluate the benefits when situated within the context of an EBG. For example, it was evident that strategies such as "Guess and Check" or "Mental Math" are nuanced and could have multiple meanings in their usage with the students. While the strategies are nuanced, EBGs help reinforce the proficiency levels of students through repetition and discussion of these strategies. However, questions remained in terms of the effect that EBGs have on increased proficiency in the subject matter and this study aims to help explore how effective EBGs can be in improving proficiency.
Studies on repetitive practice, such as those by Ericsson et al. [21] indicate that deliberate practice is key to achieving high levels of proficiency. Repetitive practice involves engaging in activities that require focused, repetitive efforts to improve performance. Ericsson’s research emphasizes that expert performance is largely the result of prolonged efforts to improve performance while negotiating motivational and external constraints. By repeatedly engaging with EBGs, learners can internalize and master the educational content more effectively. EBGs provide a structured yet flexible environment where learners can repeatedly practice and refine their skills, leading to improved proficiency over time.
Vygotsky’s [22] concept of the Zone of Proximal Development (ZPD) suggests that tasks should be within the learner’s capacity to be challenging yet achievable. The ZPD represents the difference between what a learner can do without help and what they can achieve with guidance and encouragement from a skilled partner. Investigating how varying levels of game complexity impact learner proficiency can provide insights into optimizing game design for educational purposes. EBGs can be tailored to progressively increase in difficulty, ensuring that learners are constantly challenged within their ZPD, which can enhance learning outcomes.
Research by Mayer and Moreno [23] on multimedia learning indicates that simpler visual presentations can facilitate better cognitive processing. Their Cognitive Theory of Multimedia Learning posits that learning is more effective when information is presented in a way that aligns with how human cognitive systems process information. Comparing 2D and 3D game formats can reveal whether simpler designs enhance learning efficiency by reducing cognitive load. EBGs designed in 2D formats may be easier for learners to navigate and understand, potentially leading to better learning outcomes compared to more complex 3D formats.
Theories of prior knowledge activation [24] emphasize that learners’ existing knowledge significantly impacts new learning. Prior knowledge provides a framework for understanding and assimilating new information. Assessing how prior knowledge influences proficiency in EBGs can help tailor these games to individual learner needs. For instance, EBGs can be designed with adaptive learning paths that account for the learner’s prior knowledge, ensuring that each learner receives personalized challenges that match their skill level.
Bandura’s [25] theory of self-efficacy highlights the importance of learners’ beliefs in their capabilities. Self-efficacy refers to an individual’s belief in their ability to succeed in specific situations or accomplish a task. Understanding how EBGs affect self-efficacy can provide valuable insights into their motivational and psychological benefits, potentially leading to more confident and capable learners. EBGs can enhance self-efficacy by providing immediate feedback, achievable goals, and opportunities for learners to experience success, thereby boosting their confidence and motivation to learn.
This study aims to fill the research gaps by systematically evaluating the impact of EBGs on learning proficiency, considering factors such as game complexity, format, and prior knowledge. Through this investigation, we hope to provide actionable insights for educators and game designers, ultimately enhancing the effectiveness of EBGs in educational settings. This study will address the following research questions.
  • Does quick repetitive gameplay (in burst games) help improve learner proficiency?
  • Does the complexity of the levels affect learner proficiency in burst games?
  • Does game format (2D vs 3D) affect learner proficiency in burst games?
  • Does prior domain knowledge influence learner proficiency (self-efficacy) or perceived ability?
  • How do the games impact self-efficacy or perceived ability?

3. Methods

The study was approved by the ASU IRB MOD00021448. A participatory design approach between computer science students in capstone course sequences working with math education and computer science faculty was used to develop the games. The games were iteratively developed by several capstone teams. As a result, the research team was able to iterate and build the games with very little cost. Two games titled Vector Unknown: 2D referred to as the “Bunny Game" and Vector Unknown: 3D Echelon Seas referred to as the “Pirate Game" were developed over the duration of five years. These two are hereby referred to in this article as game format, as being 2D or 3D.

3.1. Game Mechanics

VectorUnknown’s primary objective is to get the player’s character to a specified goal position. In the “Bunny Game", the player character is a bunny while in the “Pirate Game" the player character is a pirate. The objective is achieved by dragging and dropping two vectors into appropriate slots and then adjusting the vector’s scalars to create a linear combination that can get the player to the goal. The player is given a visual perspective of the game scene depending on the game format. There are a total of 3 levels in both the games. In level 1 and level 2, players are shown a line as a guide (shown in Figure 1 and Figure 2) to indicate the current output of their selected linear combination. In level 3, this line is removed as an added challenge for the players. A typical play-through involves the player starting the level, noting the goal position, trying out combinations of vectors and scalars until a solution is found, and then pressing the appropriate button to begin the movement. Thus a single play-though will take only a few minutes, conforming to the burst game paradigm. If the player reaches the goal position as a result of this movement, then they win the level. The scalars that manipulate the chosen vectors are handled via the “+” and “-” operators in the bunny game interface (Figure 1) or using sliders in the pirate game interface (Figure 2). The game tracks every operation of the player including the selection of vectors and the manipulation of scalars until they press the appropriate button (“GO” button in bunny game and “Submit” button in pirate game) and push that data for analysis.
There are a total of 3 levels in both the games with an increasing difficulty. Each level consists of a mathematical puzzle in which a player must move their avatar to a target location. To solve the puzzle, a player needs to drag and drop two vectors into appropriate slots and then adjust the vector’s factors (scalars) to create a linear combination that can get the player to the goal position. There are four available choices from which player can pick two. These choices consist of two pairs of linearly dependent vectors, i.e. vectors which are multiple of each other. For example, in Figure 1, the available choices are < − 1 , 0 > , < − 2 , 0 > , < − 1 , 1 > , < 6 , − 6 > , with < 6 , − 6 > and < − 2 , 0 > being selected by the player to reach the target position and their corresponding scalar coefficients being -1 and 3 respectively. In Figure 1 the choices < − 1 , 0 > and < − 2 , 0 > are linearly dependent as < − 2 , 0 > can be obtained by multiplying < − 1 , 0 > with a scalar 2. Similarly, < 6 , − 6 > can be obtained by multiplying < − 1 , 1 > with -6. This is done intentionally to have students make linearly independent vector choices when trying to solve the puzzles. The results of the player choices is the vector < − 12 , 6 > which is different from the goal of < − 8 , 6 > shown in Figure 1. In the first level, at least one of the vector pairs has x or y coordinate as zero, making it easier to reach the target position. For example, in the Figure 1 the pair < − 1 , 0 > , < − 2 , 0 > has y-coordinate as zero. In the second level, there are no zeros in either of the pair choices. However, in both the first and second levels, there is a guided path showing the trajectory that the player will follow on submitting the solution. In the third level, this guided path is absent and there are not zeros in either of the vector choices. This would push the player to use math instead of just guessing and checking the correct combination of scalars and vector. All the three levels are repeated 4 times with different vector choices and target goal in each repetition. These repetitions were termed as stages within levels. Thus, there were 3 levels with 4 stages i neach level. These are listed in Appendix ?? for the bunny game and Appendix ?? for the pirate game.

3.1.1. Bunny Game

Figure 1 shows the user interface in the bunny game that features four main sections of heads up display (HUD). A mini-map is located in the upper left corner of the interface, providing a top-down view of the game scene. It displays the X-Y axis in the 2D format that students typically associate with linear algebra. Next to the mini-map is the formula tab located on the right. Players can drag and drop the vector choices in the two blank slots located in this tab. Each slot has a scalar coefficient that players can adjust by using the plus and minus sign located below it. The results of player choices is computed and shown to the right of the equals sign. On pressing the “GO” button, the bunny initiates movement based on the result. Located below the formula tab is the game view-port which can be rotated using the arrow keys to get a better view of the axis. The view-port consists of a 2D grid with player and target locations mapped on it. The player character is depicted using a polygonal bunny model and the target location using a basket of eggs. In level 1 and 2, the trajectory that the bunny will follow based on the result is depicted using a red line. The path that has already been traversed in previous steps (in case goal was not reached) is shown in green. The upper right corner of the view-port displays the timer, showing the real time spent on the current level. To the left of the view-port lies the vector choices tab that shows four vector choice tiles. These choices can be dragged to the blank slots in the formula tab. It also displays the player’s current position which is origin by default ( < 0 , 0 > ). The goal position (coordinates of egg basket) are also displayed here. The bottom of this tab is used to track all the player choices
The game starts with a tutorial level (Figure 3) which is a brief walk-through of the game play mechanics and user interface used in the game. On completing the walk-through, player begins the level 1, followed by level 2 and level 3. Players can not skip a level and must complete them to advance to the next level.

3.1.2. Pirate Game

The 2D game evolved in a 3D format and followed similar design strategy, albeit adding an extra dimension into the mix. A narrative was also added to the game where the player is a pirate who is marooned on an island. By completing the levels the pirate can get the missing parts for his ship and sail away from the island.
The game starts with a tutorial level as well which is a brief narrative walk-through with a parrot named zeta (Figure 4) who tells them that the pirates need to scale various chasms in order to collect ship parts for rebuilding their ship. However, the tutorial level used only 1D vectors as opposed to 2D vectors (Figure 4). Zeta tells the players that they need to use combination of vectors and scalars in order to aim their grapple gun correctly to an anchored location. On completing the tutorial, player begins the level 1, followed by level 2 and level 3. Players can not skip a level and must complete them to advance to the next level. Once they cross all the chasms, they can obtain the sail needed for their ship.

3.2. Participants

The current study was conducted online with the help of zoom and qualtrics. The experiment protocol was approved by the ASU IRB STUDY00018334 and the experiment was conducted in accordance with the guidelines and regulations. A total of 45 participants completed the study. Participants were invited to a shared zoom session led by the researcher who walked them through the informed consent embedded in the qualtrics survey. Upon consenting, they filled the pre-survey which asked them about their previous experience and comfort level with linear vector algebra. It also asked them about their perceived skill (on a scale of 1-5) in how vectors and scalars work. Once pre-survey is completed, participants were taken to the next page which had details and the link to the game they will be playing. The order of play was randomized, therefore, some participants played the bunny game followed by the pirate game while others played in the reverse order. On finishing both the games, they were asked to fill a post-survey which asked them about their perceived skill after the game play and feedback, if any.
Preprints 113694 g005
Figure 5. The flowchart showing the participant workflow
Figure 5. The flowchart showing the participant workflow
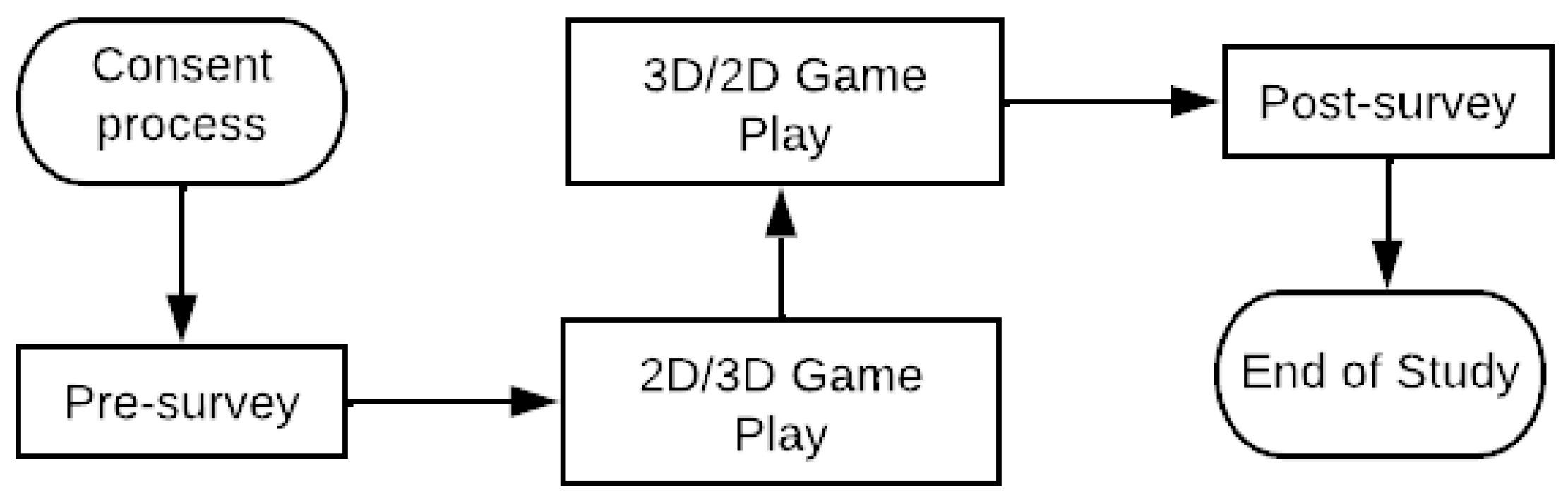
Preprints 113694 g005
Participants used their own computer for playing the game. Therefore, the game crashed sometimes for some players during the game play. Upon crash, their progress was not saved and they had to replay the game from the start. Therefore, in such a case, only the data for their first play-through was analysed. For example, if the game crashed while they were playing level 2.1, then the game play data until the level 2.1 was considered for analysis. The second attempt play-through data until level 2.1 was discarded. Therefore their game play data consisted of first attempts data until 2.1 and second attempt data from 2.1 to 3.4. There were a total of 16 participants whose 2D game data was corrupted in this manner, 5 whose 3D game got corrupted and 2 for whom both got corrupted.

3.3. Analytics to Support Learning Proficiency

A player can take multiple different approaches to reach the given target on a given level. Their approach may lead them towards or away from the target location. The steps that take them towards the target were classified as ideal steps and the steps that take them away from the target were classified as non-ideal steps. We used an algorithm that uses player data to classify a particular step as ideal or non-ideal. We provided four vectors as possible options. Of these four, two vectors were linearly dependent on the other two. Therefore, we presented two pairs of linearly dependent vectors. Let’s say the two vectors were A = < n , m > and B = < p , q > . Then their linearly dependent counterparts were C = k A and D = j B , Where n , m , p , q , k , j are scalars. The target position was generated so that it could be obtained by operating on the two linearly independent vectors. The goal position can be represented mathematically as x C + y D , where x and c are scalars. Depending on the vectors and scalars chosen by the student, their step could be ideal or non-ideal. The step that they took could be non-ideal for the following reasons:
  • If the step involved two linearly dependent vectors, i.e. choosing both A,C or B,D.
    -
    A and C are chosen as vectors
    -
    B and D are chosen as vectors
  • If the scalar is chosen such that it takes them away from the goal position. For example, if they choose A as an option and its corresponding scalar is adjusted in the direction opposite to where it should go. If the sign of the scalar is opposite to the sign of x k
    -
    sign of vector A’s scalar is different from sign of x k
    -
    sign of vector B’s scalar is different from sign of x
    -
    sign of vector C’s scalar is different from sign of y j
    -
    sign of vector D’s scalar is different from sign of y
This algorithm helps instructors determine whether students are guessing their solutions or attempting to cognitively use math while completing the levels. While Level 1 and 2 provides guided lines, the expectation is that students would easily correct their paths as soon as they see the direction they are headed. Level 3 would limit their guess and check abilities and they would have to rely more on their mental math skills.

4. Analysis

The raw data collected from the game consisted of the choices of scalars and vector at the every step. This raw data was used to determine if a particular step is ideal or not. The processed data consisted of total number of ideal and non-ideal steps used on a given level, which was used to compute the percentage of ideal steps (PIS) on that level. The learning proficiency was operationalized using this measure. Thus a higher percentage of ideal steps on a given level would indicate better learning proficiency as compared to a lower percentage.

4.1. Burst Game Effectiveness

The burst game effectiveness was evaluated for each level in both the games. In order to do so, the PIS was compared across the four stages within each level. A higher PIS in later stages would indicate the effectiveness of the burst game paradigm. Thus a total of 6 ANOVAs were carried out, 3 for each game, 1 for each level within a game.

4.2. Effect of Game Complexity

The levels became more complex as players progressed through the game. Level 1 was the least complex while level 3 was the most complex. PIS was averaged across the four stages of a given level to compute the average PIS for that level. The average PIS was then compared across the three levels in the game to evaluate the effect of complexity on the player proficiency. A total of two ANOVAs were conducted, 1 for each game format.

4.3. Effect of Game Format

PIS was averaged across all the three levels and four stages of each level to compute the average PIS for the overall game. The games were played in random order, where 29 participants played the 2D game followed by the 3D game while 16 participants played the 3D game followed by the 2D game. The order was considered another factor in this analysis and the comparison was conducted using the repeated-measures ANCOVA with order as between-subject and average PIS (2d vs 3d) as the within-subject factor.

4.4. Effect of Prior Knowledge

The pre-survey asked the participants to rate their perceived skill in the knowledge of vectors and scalars on a scale of 1 to 5. The average PIS calculated in the previous step is compared across these five groups to evaluate the effect of prior knowledge on the learning effectiveness.

5. Results

5.1. Burst Game Effectiveness

The mean PIS ( X ¯ ) and standard deviation ( s x ) of individual stages within levels was computed and indicated in Table 1. Table 2 lists the results of the 6 ANOVAs carried out, one for each level of the bunny and pirate games. These comparisons indicated that repetition caused significant performance different between the stages of level 2 in the bunny game and the level 1 & 3 of the pirate game. Figure 6 shows the box plots of different levels within these games. Box plot for the bunny game’s level 2 suggest that the median PIS was least in the stage 1 of this game and it improved in stage 2 while it was similar between stage 2 and 3. Stage 4 saw the maximum median PIS among the 4 stages of bunny game’s level 2.
The pirate game’s level 1 also demonstrated similar results where the median PIS was least in stage 1 and the most in stage 4, with stage 3 and 4 demonstrating similar PIS. The plots for level 3 of the pirate game also demonstrate similar results. However, there was no significant PIS difference within the rest of the bunny and pirate game levels which is also reflected in their box plots.

5.2. Effect of Game Complexity

No significant difference was observed in the mean PIS for the 2D game, F ( 2 , 88 ) = . 5632 , p = . 572 , η p 2 = . 01 . There was no significant difference in PIS for the 3D game either, F ( 2 , 88 ) = 1.5602 , p = . 216 , η p 2 = . 03 . Figure 7 shows the box plots for bunny and pirate game levels which supports these findings. These results suggest that the level complexity did not affect the learner performance ad there was no significant difference in PIS across different game levels.

5.3. Effect of Game Format

There was no significant interaction between the order and the game format, F ( 1 , 43 ) = . 82 , p = . 371 , η p 2 = . 019 . However, a significant difference due to the game format, F ( 1 , 43 ) = 8.57 , p = . 005 , η p 2 = . 166 . Subsequent post-hoc tests reveled no significant difference in the PIS due to order, F ( 1 , 43 ) = 0.23 , p = . 633 , η p 2 = . 005 . This suggests that it did not matter if the participants played the 2D game followed by the 3D game or in the reverse order. From the box plots in Figure 8 it appears that the median PIS was higher in the 2D game as compared to the 3D game.

5.4. Effect of Prior Knowledge

There was no significant difference observed in the 2D, F ( 4 , 40 ) = 2.419 , p = . 064 , η 2 = . 20 , and 3D game, F ( 4 , 40 ) = 2.116 , p = . 097 , η 2 = . 17 performance due to prior score. Figure 9 shows the box plots for average PIS across the 5 groups of participants who indicated their prior knowledge ranging from 1 to 5. However, the distribution of the groups was uneven across the 5 groups as indicated in the histogram in Figure 10.

6. Discussion and Limitations

This study investigated the impact of educational burst games (EBGs) on learning proficiency, examining factors such as game complexity, game format, and prior knowledge. Our findings revealed mixed support for the hypothesis that quick, repetitive gameplay enhances learner proficiency, aligning with the first principle of learning as stated by Bruner [26]. Some levels of the bunny and pirate game support this hypotheses while others do not. Of the 3 levels in bunny game, 1 support it while 2 out of 3 pirate game levels support it. Specifically, the increased proficiency observed in certain levels of the bunny and pirate games suggests that EBGs can indeed foster learning through repetitive gameplay mechanics. This is consistent with the work of SchimankeAuthor et al [27], who emphasized the value of repetition in educational games. However, they suggested that it might be better to space out the repetition and the games be designed with the spaced repetition approach instead of continuous repetition.
Contrary to our initial assumptions, the complexity of game levels did not significantly affect learning outcomes. This result challenges the common belief that more complex educational games provide better learning opportunities, suggesting instead that the core mechanics of burst games—regardless of complexity—sufficiently engage learners and contribute to proficiency. This finding are comparable to the conclusions of Wolfe [28], who reported that the learning is not linearly positively impacted by the game complexity. However, the results largely depend on how the complexity was manipulated and therefore these results must be interpreted with caution, considering the complexity implementation strategy in the game.
Our study also highlighted the superior effectiveness of 2D game formats over 3D formats in promoting learner proficiency irrespective of the order in which they were played. This is aligned with the Mayer and Moreno’s [23] Cognitive Theory of Multimedia Learning and supports the argument that simpler visual presentations in educational materials can facilitate better cognitive processing and learning outcomes. Thus, future game designs might benefit from prioritizing clarity and accessibility of content presentation over more complex, visually rich environments.
Interestingly, prior knowledge did not significantly influence learning outcomes within the game settings. This suggests that EBGs have the potential to level the playing field for learners with varying degrees of background knowledge, providing a valuable tool for inclusive education. This aligns with Premlatha and Geetha’s [29] findings on the adaptability of digital learning tools to diverse learning needs. However, this result is based on the self reported measure instead of an external assessment.
Our study’s insights are tempered by its limitations, including the small sample size and the reliance on self-reported measures of proficiency. Future research should aim for larger, more diverse participant pools and incorporate external assessments of learning outcomes to validate and expand upon our findings. Moreover, investigating the long-term retention of knowledge gained through EBGs could provide deeper insights into their educational value.

7. Conclusion

This study provides valuable insights into the effectiveness of educational burst games (EBGs) in enhancing learning outcomes across different subjects. Our findings highlight that while game complexity and prior knowledge do not significantly impact learning efficiency, the format of the game and its repetitive, engaging nature play crucial roles in educational achievement. The preference for 2D over 3D formats suggests a need for simplicity and focus in educational game design, emphasizing content delivery over graphical sophistication. Despite limitations, including a small sample size, this research underscores the potential of EBGs as accessible, inclusive tools for education. Future investigations should aim to broaden participant diversity, assess long-term knowledge retention, and refine game designs to maximize educational benefits. Through continued exploration, EBGs can significantly contribute to the evolving landscape of digital education, offering dynamic, effective learning experiences for diverse learners.

References

  1. Amresh, A.; Verma, V.; Salla, R. Educational Burst Games-A New Approach for Improving Learner Proficiency 2024.
  2. Abad Robles, M.T.; Collado-Mateo, D.; Fernández-Espínola, C.; Castillo Viera, E.; Gimenez Fuentes-Guerra, F.J. Effects of teaching games on decision making and skill execution: A systematic review and meta-analysis. International journal of environmental research and public health 2020, 17, 505. [Google Scholar] [CrossRef] [PubMed]
  3. Math Bingo. https://play.google.com/store/apps/details?id=com.jujusoftware.mathbingofree, 2024. [Online; accessed 9-April-2024].
  4. Vocabulary Spelling City. https://www.spellingcity.com/games/sentence-unscramble.html. [Online; accessed 9-April-2024].
  5. Science Lab Memory Matching Game by Petri & Pulp. https://www.amazon.com/Science-Memory-Matching-Petri-Pulp/dp/B08T8H52P7. [Online; accessed 9-April-2024].
  6. Vocabulary Dominoes: A Game for any Content Area. https://technologypursuit.edublogs.org/2017/06/03/vocabulary-dominoes-a-game-for-any-content-area/, 2017. [Accessed 09-04-2024].
  7. Yu, Z.; Gao, M.; Wang, L. The effect of educational games on learning outcomes, student motivation, engagement and satisfaction. Journal of Educational Computing Research 2021, 59, 522–546. [Google Scholar] [CrossRef]
  8. DeKeyser, R. Skill acquisition theory. In Theories in second language acquisition; VanPatten, B.; Williams, J., Eds.; 2020; pp. 83–104.
  9. Sweller, J. Cognitive load during problem solving: Effects on learning. Cognitive science 1988, 12, 257–285. [Google Scholar] [CrossRef]
  10. Ebbinghaus, H. Memory: A contribution to experimental psychology. Annals of neurosciences 2013, 20, 155. [Google Scholar] [CrossRef] [PubMed]
  11. Gee, J.P. What video games have to teach us about learning and literacy. Computers in entertainment (CIE) 2003, 1, 20–20. [Google Scholar] [CrossRef]
  12. Prensky, M. Fun, play and games: What makes games engaging. Digital game-based learning 2001, 5, 5–31. [Google Scholar]
  13. Papastergiou, M. Digital game-based learning in high school computer science education: Impact on educational effectiveness and student motivation. Computers & education 2009, 52, 1–12. [Google Scholar] [CrossRef]
  14. Ke, F. A case study of computer gaming for math: Engaged learning from gameplay? Computers & education 2008, 51, 1609–1620. [Google Scholar] [CrossRef]
  15. Amresh, A.; Verma, V.; Zandieh, M. Combining Game-Based and Inquiry-Oriented Learning for Teaching Linear Algebra. In Proceedings of the 2023 ASEE Annual Conference & Exposition; 2023. [Google Scholar]
  16. Zandieh, M.; Plaxco, D.; Williams-Pierce, C.; Amresh, A. Drawing on three fields of education research to frame the development of digital games for inquiry-oriented linear algebra. In Proceedings of the Proceedings of the 21st Annual Conference on Research in Undergraduate Mathematics Education; 2018. [Google Scholar]
  17. Bernier, J.; Zandieh, M. Comparing student strategies in a game-based and pen-and-paper task for linear algebra. The Journal of Mathematical Behavior 2024, 73, 101105. [Google Scholar] [CrossRef]
  18. Plaxco, D.; Mauntel, M.; Zandieh, M. Student Strategies Playing Vector Unknown Echelon Seas, a 3D IOLA Videogame. In Proceedings of the Proceedings of the Annual Conference on Research in Undergraduate Mathematics Education; 2023. [Google Scholar]
  19. Bernier, J.; Zandieh, M. Comparing student strategies in vector unknown and the magic carpet ride task. In Proceedings of the Proceedings of the Annual Conference on Research in Undergraduate Mathematics Education; 2022. [Google Scholar]
  20. Bettersworth, Z.; Smith, K.; Zandieh, M. Students’ written homework responses using digital games in Inquiry-Oriented Linear Algebra. In Proceedings of the Proceedings of the Annual Conference on Research in Undergraduate Mathematics Education; 2022. [Google Scholar]
  21. Ericsson, K.A.; Krampe, R.T.; Tesch-Römer, C. The role of deliberate practice in the acquisition of expert performance. Psychological review 1993, 100, 363. [Google Scholar] [CrossRef]
  22. Vygotsky, L.S. The development of higher psychological functions. Soviet Psychology 1977, 15, 60–73. [Google Scholar] [CrossRef]
  23. Mayer, R.E.; Moreno, R. Nine ways to reduce cognitive load in multimedia learning. Educational psychologist 2003, 38, 43–52. [Google Scholar] [CrossRef]
  24. Ausubel, D.P.; Novak, J.D.; Hanesian, H.; et al. Educational psychology: A cognitive view 1978.
  25. Bandura, A. Self-efficacy: The exercise of control; Macmillan, 1997.
  26. Bruner, R.F. Repetition is the first principle of all learning. Available at SSRN 224340 2001. [Google Scholar]
  27. Schimanke, F.; Mertens, R.; Vornberger, O. Spaced repetition learning games on mobile devices: Foundations and perspectives. Interactive Technology and Smart Education 2014, 11, 201–222. [Google Scholar] [CrossRef]
  28. Wolfe, J. The effects of game complexity on the acquisition of business policy knowledge. Decision Sciences 1978, 9, 143–155. [Google Scholar] [CrossRef]
  29. Premlatha, K.; Geetha, T. Learning content design and learner adaptation for adaptive e-learning environment: a survey. Artificial Intelligence Review 2015, 44, 443–465. [Google Scholar] [CrossRef]
Preprints 113694 g001
Figure 1. The red line (guided path) showing the player trajectory in the bunny game
Figure 1. The red line (guided path) showing the player trajectory in the bunny game
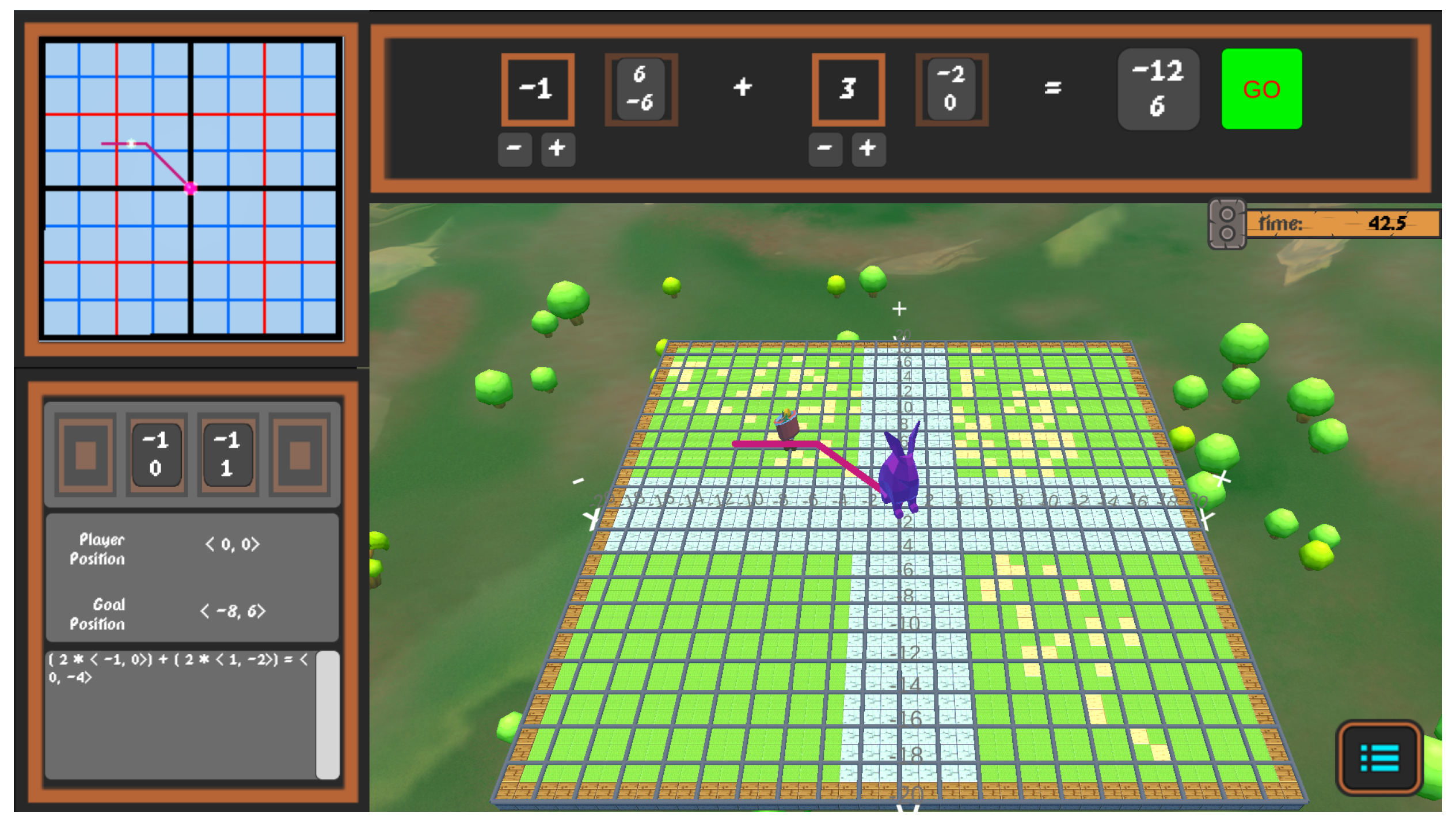
Preprints 113694 g001
Preprints 113694 g002
Figure 2. The guided path showing the player trajectory in the pirate game
Figure 2. The guided path showing the player trajectory in the pirate game
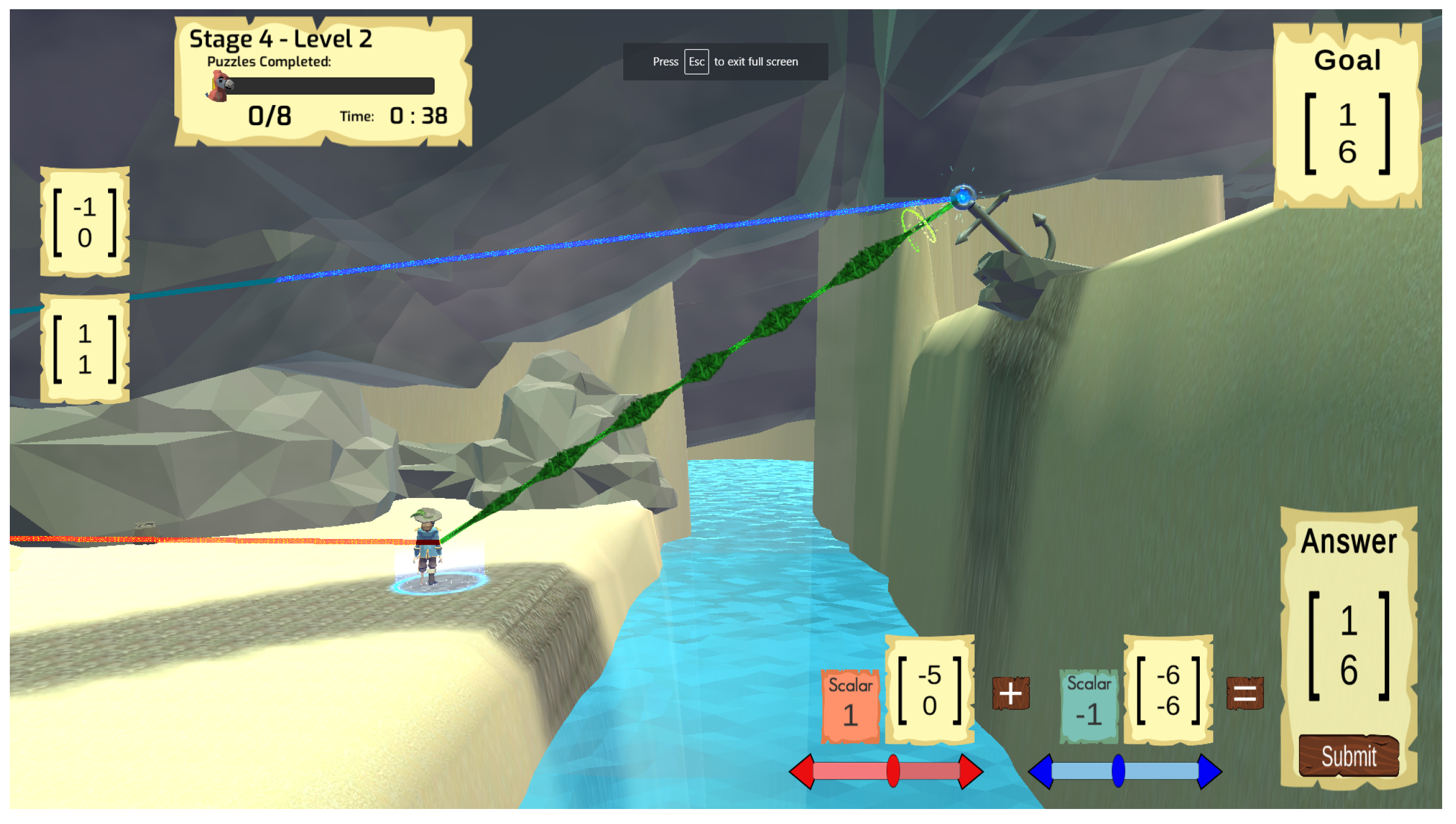
Preprints 113694 g002
Preprints 113694 g003
Figure 3. The tutorial level in the bunny game
Figure 3. The tutorial level in the bunny game
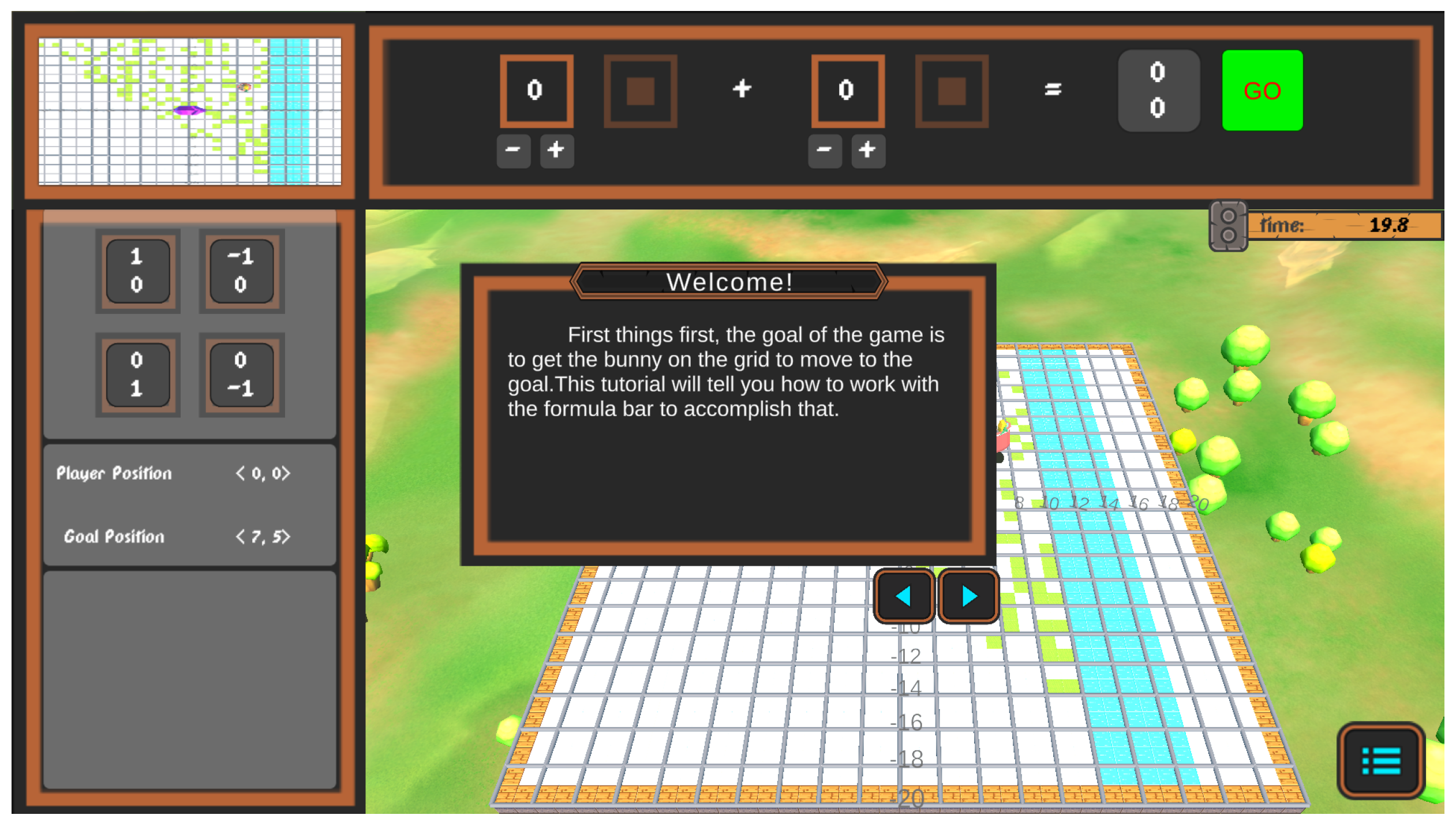
Preprints 113694 g003
Preprints 113694 g004
Figure 4. Tutorial level in the pirate game
Figure 4. Tutorial level in the pirate game
Preprints 113694 g004

Conversation with zeta Tutorial game play
Preprints 113694 g006
Figure 6. Box plots for bunny and pirate game’s individual levels
Figure 6. Box plots for bunny and pirate game’s individual levels
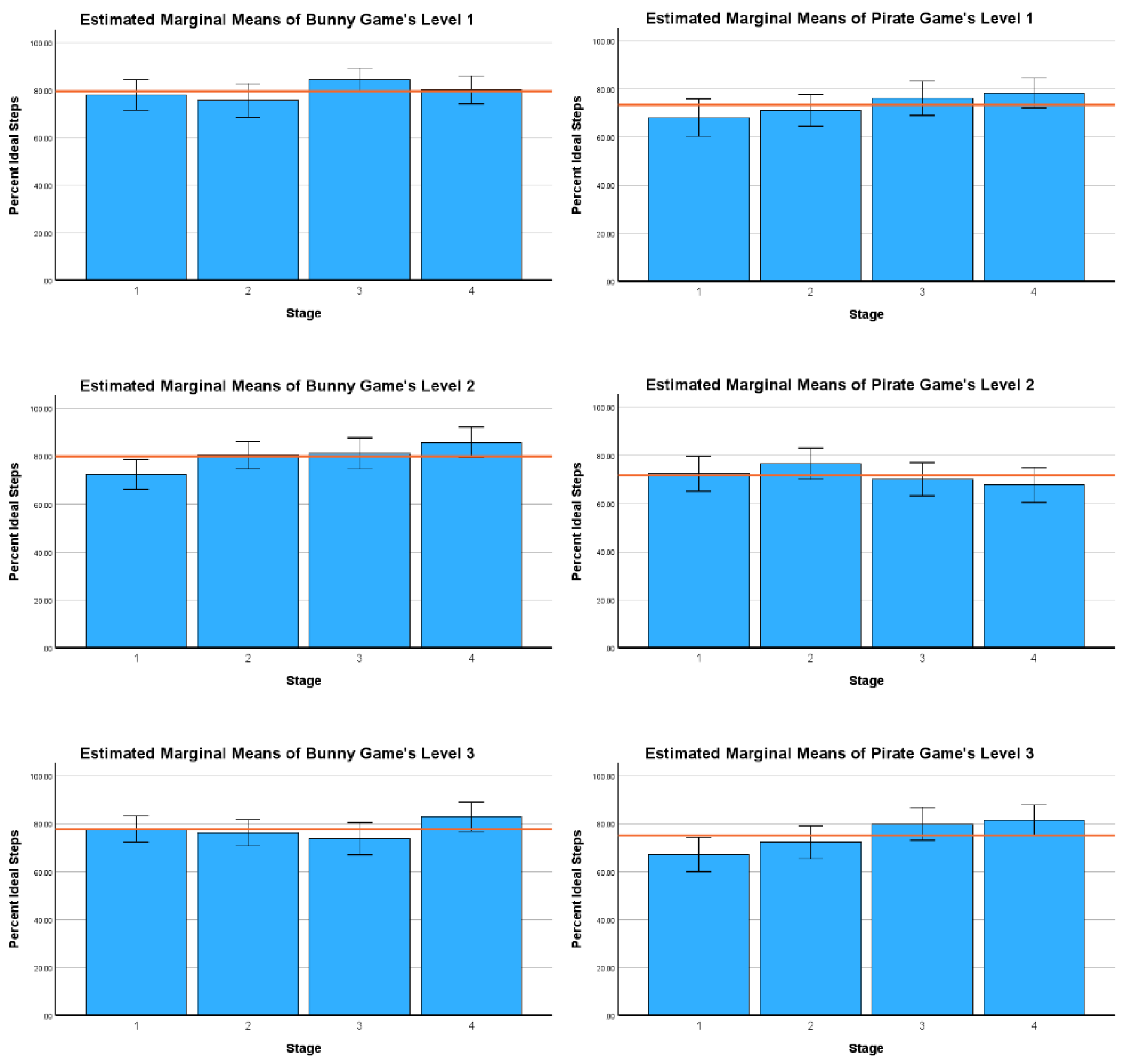
Preprints 113694 g006
Preprints 113694 g007
Figure 7. Averaged box plots for bunny and pirate game levels
Figure 7. Averaged box plots for bunny and pirate game levels
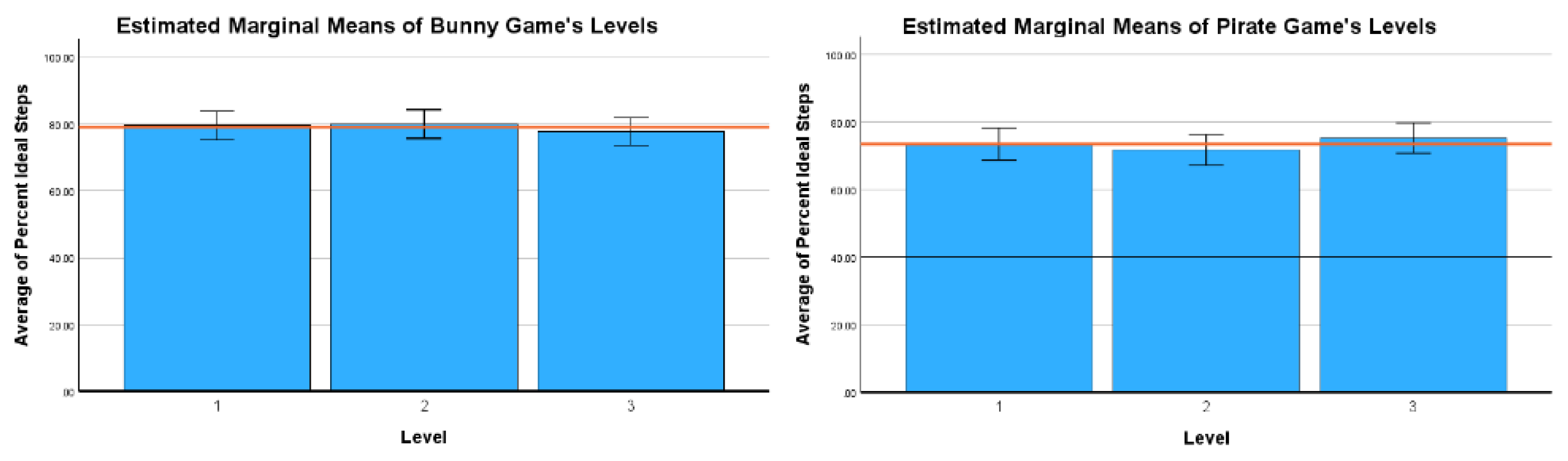
Preprints 113694 g007
Preprints 113694 g008
Figure 8. Averaged box plots for games based on game format and game-play order
Figure 8. Averaged box plots for games based on game format and game-play order
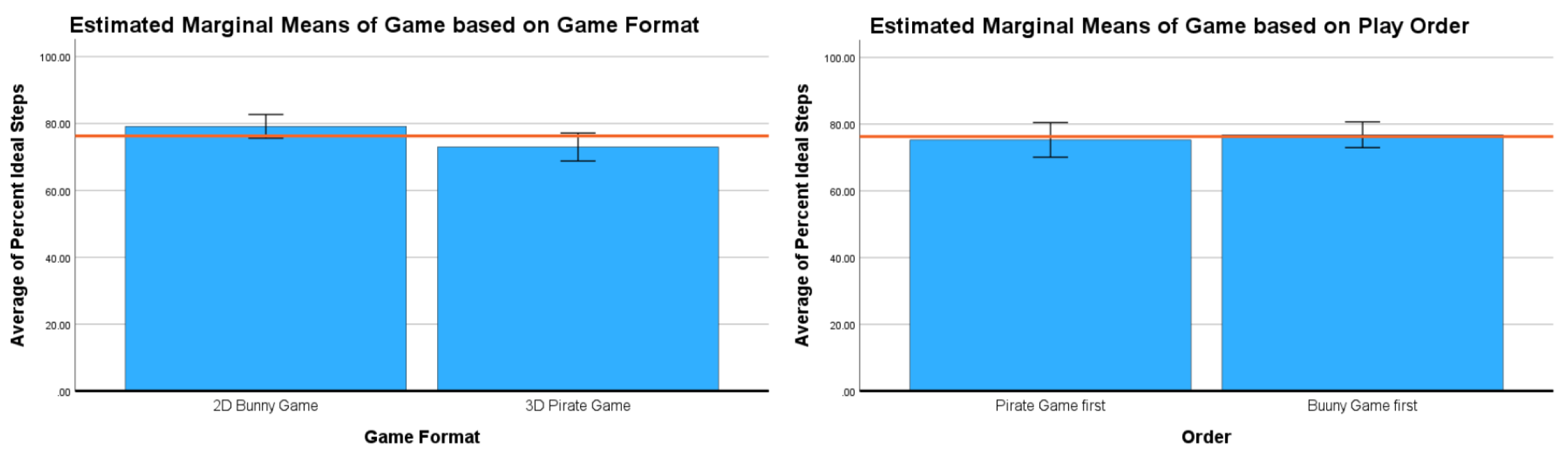
Preprints 113694 g008
Preprints 113694 g009
Figure 9. Averaged box plots for bunny and pirate game based on prior knowledge
Figure 9. Averaged box plots for bunny and pirate game based on prior knowledge
Preprints 113694 g009
Preprints 113694 g010
Figure 10. Histogram for bunny and pirate game based on prior knowledge
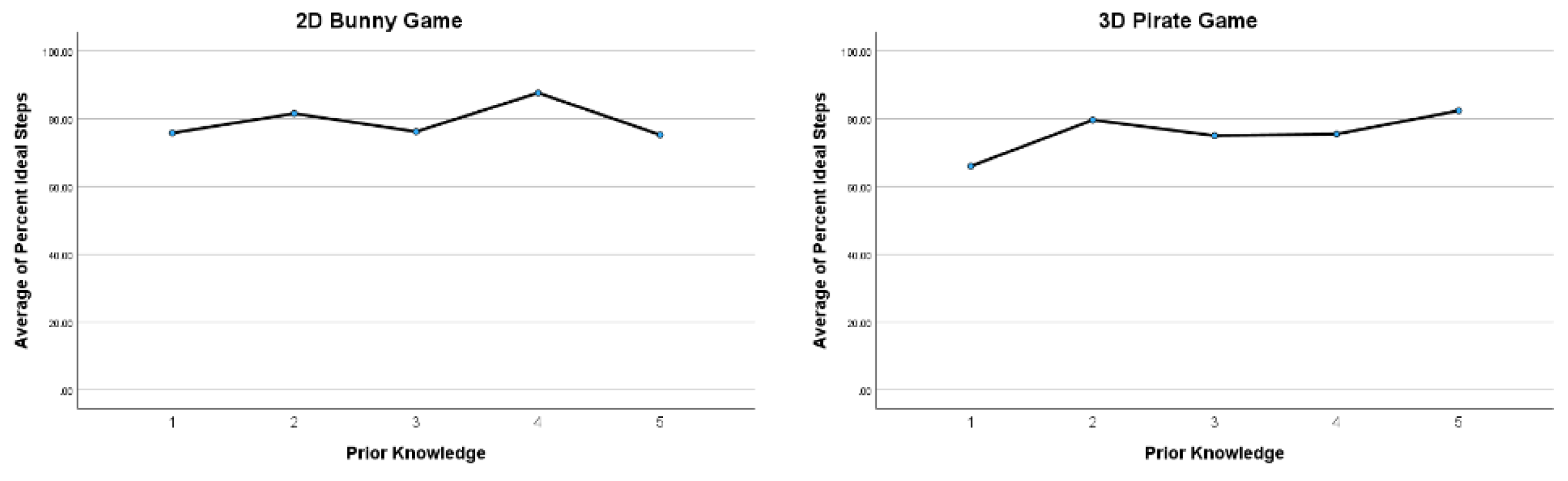
Figure 10. Histogram for bunny and pirate game based on prior knowledge
Preprints 113694 g010
Table 1. Mean and standard deviation of levels and stages in the games
Table 1. Mean and standard deviation of levels and stages in the games
2D 3D
Level Stage X ¯ s x X ¯ s x
1 1 75.73 23.52 68.15 25.97
2 78.03 21.14 71.12 21.78
3 84.45 17.01 76.15 23.60
4 80.18 19.90 78.36 21.00
2 1 72.43 20.80 72.44 24.23
2 80.41 18.91 76.57 21.89
3 81.15 21.98 70.14 23.07
4 85.83 21.44 67.74 24.12
3 1 77.83 18.09 67.19 23.78
2 76.24 18.56 72.27 22.86
3 73.83 22.65 79.96 22.83
4 83.00 20.18 81.44 21.30
Table 2. ANOVA results for comparing percent ideal steps within different stages of various game levels
Table 2. ANOVA results for comparing percent ideal steps within different stages of various game levels
Game format Level F ( 1 , 44 ) p η p 2
2D 1 1.88 .177 0.04
2 10.28 .003** 0.19
3 1.45 .235 0.03
3D 1 6.65 .013* 0.13
2 2.35 .132 0.05
3 13.02 .001*** 0.23
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated