Preprint
Article
Study on Leakage Assessment and Stability Analysis of Water Level Changes on Tunnels near Reservoirs
Altmetrics
Downloads
68
Views
21
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
29 July 2024
Posted:
31 July 2024
You are already at the latest version
Alerts
Abstract
The geological and hydrological conditions of tunnels near reservoirs are complex, and the impact of water level changes on the stability and leakage assessment of the lining structure is not considered in the current leakage evaluation. In order to construct an evaluation model for leakage level of tunnels near reservoirs, the influence of water level changes on tunnel stability and changes in environmental conditions on the leakage of tunnels were researched. Based on the AHP and extensibility theory, a hierarchical system for leakage assessment, incorporating values from nine indexes representing three aspects: geological conditions, hydrological conditions, and tunnel engineering. Numerical simulation was used to analyze the influence of water level changes. It was found that the water level change index greatly influences the displacement and stress distribution inside the tunnel structure. The leakage evaluation model was applied to the Tiebeishan Tunnel, resulting in a rating of 3, indicating medium-level leakage. Attention should be paid to water leakage in tunnels with changes in reservoir water levels. The leakage evaluation model for tunnels near reservoirs can effectively assess leakage levels under various conditions, providing a reference for safety assessments of tunnel leakage near reservoirs.
Keywords:
Subject: Engineering - Civil Engineering
1. Introduction
With the gradual improvement of China's comprehensive transportation system, tunnel engineering construction is in a phase of rapid development. However, complex geological conditions and operational environment can affect the structural performance of tunnels, disrupt normal traffic flow, and even jeopardize tunnel stability and road safety[1,2,3]. Extensive research has been conducted on tunnel structural safety evaluations, with both domestic and international researchers employing qualitative and quantitative methods to analyze and achieve notable results [4,5,6].
Hamidi et al. [7] conducted a safety assessment based on the Analytic Hierarchy Process for uncertain factors such as geological and geotechnical activities during tunnel construction. Hyun et al. [8] applied fault tree analysis to categorize risk factors into geological, design, construction, and management aspects, combining this with AHP to evaluate and analyze shield tunnel risks. S.W. Park et al. [9] evaluated the safety of common tunnel defects, categorizing tunnel lining structure conditions into five levels based on defined defect indicators. However, given the intricate and dynamic geological conditions in tunnels and underground engineering, waterproofing measures are influenced by construction conditions and external factors, thereby making leakage a critical factor impacting the safety of underground engineering.
In recent years, significant progress has been made in the research on tunnel leakage. Gong Xiaonan et al. [10] analyzed the types and causes of leakage in tunnels and underground engineering and proposed a concept of leakage prevention throughout the life cycle from the design and construction stages to the service period. The researchers discussed methods for detecting leakage, treatment measures, and innovative grouting materials, establishing a solid foundation for practical implementation and further research on leakage prevention in tunnel and underground engineering. Yang et al. [11] analyzed the interaction mechanisms between groundwater and surrounding rock using experimental and numerical simulation methods, investigating the disaster evolution process and patterns of karst cave water bursts in deep high-pressure tunnels. Li et al. [12] studied a risk assessment system for karst tunnel water inrush by combining Geographic Information Systems (GIS) with the Analytic Hierarchy Process (AHP), enabling real-time assessment of karst tunnel water inrush. Jiang Shiyu et al. [13] employed matter-element analysis and AHP to determine evaluation indicators based on geological and hydrological conditions, constructing a predictive model for tunnel water inrush disasters. Pan Haize[14] established a classification prediction and analysis model for tunnel seepage water diseases based on Distance Discriminant Analysis theory, conducting evaluations of seepage water disease levels using fuzzy comprehensive evaluation and BP neural network methods, and developing a visualization program, laying a theoretical foundation for preventing tunnel seepage water. These achievements have significantly advanced the understanding of tunnel seepage water diseases, detection methods, and safety assessments. However, there is limited research on the types of tunnel seepage water diseases near reservoir tunnels and their impact on structures.
Currently, several scholars have investigated the stress characteristics and drainage technologies of tunnels near reservoirs. Li et al.[15], focusing on subsea tunnels, discovered that both external water pressure and water inflow in the grouting area increase linearly with rising groundwater levels by comparing analytical and numerical solutions of pore pressure distribution and water inflow. Zhang et al.[16] examined the impact of different water storage conditions at the Longsheng Reservoir on the seepage and stress fields of tunnels near reservoirs during construction and operation, proposing potential risks and improvement measures. Shen Yanfeng[17] researched drainage schemes for tunnels near reservoirs, analyzing the effects of various schemes on water pressure distribution and lining stress, and evaluating the applicability of drainage and water-blocking schemes. Chen He[18], through on-site observation tests and three-dimensional numerical simulations, analyzed the stress and displacement changes in metro tunnel linings and surrounding rocks near reservoirs during water level fluctuations, guiding effective deformation and displacement control during operation.
In conclusion, existing research has not adequately considered the effects of external factors such as water level variations and water erosion on the safety assessment of leakage in tunnels near reservoirs. Addressing this gap, this paper analyzes the causes and influencing factors of tunnel leakage, investigates the effects of different reservoir water levels on tunnel structural stability, and establishes a hierarchical evaluation system for leakage in tunnels near reservoirs. Using the Tiebeishan Tunnel as a case study, a risk assessment of tunnel leakage diseases was conducted, and the preliminary discussion focused on the impact of factors such as changes in water pressure and water erosion on tunnel structure leakage.
2. Leakage Evaluation Model for Tunnels near Reservoirs
2.1. Analytic Hierarchy Process System
Base on the Analytic Hierarchy Process (AHP) and Extenics theory, a hierarchical model was constructed to determine the weight of each indicator, integrating qualitative and quantitative assessments for a comprehensive evaluation of tunnel leakage disease grades. During the model construction process, the rationality of the evaluation indicators directly influences the accuracy and applicability of the evaluation model. To achieve a combination of qualitative and quantitative evaluation of leakage, the hierarchical evaluation system for leakage in tunnels near reservoirs was established by referencing relevant domestic research on tunnel leakage and considering actual conditions of tunnel projects near reservoirs [19,20]. The primary goal of the model evaluation is to assess the risk of tunnel leakage near reservoirs, with secondary indicators including geological conditions, hydrological conditions, and tunnel engineering. Based on the actual situation, influential factor indicators corresponding to the secondary indicators were selected, totaling nine indicators as the basis for assessing the risk of tunnel leakage near reservoirs, as shown in Figure 1.
1.2. Classical Domain Matter Elements, Sectional Domain Matter Elements, and Target Matter Elements
Based on the matter-element theory and tunnel leakage evaluation indicators, the classical domain matter-element Rab, the node domain matter-element RP, and the target matter element R are determined as follows,
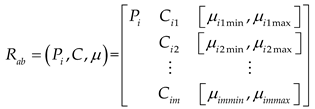
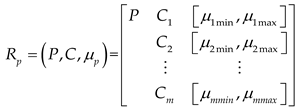
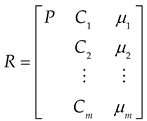 Where μ represents the value taken by the evaluation indicator C, which usually needs to be evaluated according to relevant norms, standards, or by professional technicians. The matter-element analysis method typically uses three elements: "object P," "characteristic C," and "value μ" to describe and form a triplet matter-element R = (P, C, μ).
Where μ represents the value taken by the evaluation indicator C, which usually needs to be evaluated according to relevant norms, standards, or by professional technicians. The matter-element analysis method typically uses three elements: "object P," "characteristic C," and "value μ" to describe and form a triplet matter-element R = (P, C, μ).

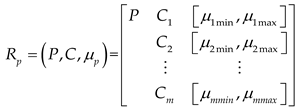

1.3. Selection of Status Values for Indicators and Consistency Check
To compare the importance of various evaluation indicators, the Saaty scale method is applied[21], as shown in Table 1, and the judgment matrix is as follow in Table 2.
Based on Table 2, the weight set of tunnel leakage evaluation indicators can be obtained, and the square root method is applied to calculate the weight values:
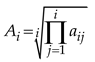 Where aij is the ith row and jth column element in the judgment matrix.
Where aij is the ith row and jth column element in the judgment matrix.
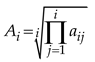
After normalization, the weight vectors of each indicator in the target model are obtained:
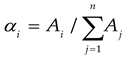 The maximum eigenvalue of the judgment matrix is calculated as follows:
The maximum eigenvalue of the judgment matrix is calculated as follows:
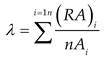 Where R is the judgment matrix; A is the normalized vector of Ai (α1α2…αi…αn); and n is the order of the judgment matrix.
Where R is the judgment matrix; A is the normalized vector of Ai (α1α2…αi…αn); and n is the order of the judgment matrix.
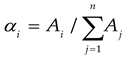
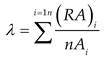
Finally, a consistency check is conducted, with the ratio expressed as follows:
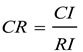 Where CI is the consistency index; CR is the consistency ratio; and RI is the random consistency index.
Where CI is the consistency index; CR is the consistency ratio; and RI is the random consistency index.
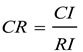
1.4. Correlation Calculation
The correlation degree of tunnel leakage levels is calculated based on the matter-element correlation matrix, as follows:
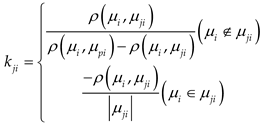
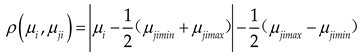
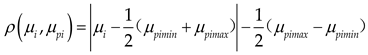 Where kji represents the correlation degree of evaluation indicator i concerning evaluation level j; μji is the value range of the classical domain, and μpi is the value range of the specific domain.
Where kji represents the correlation degree of evaluation indicator i concerning evaluation level j; μji is the value range of the classical domain, and μpi is the value range of the specific domain.
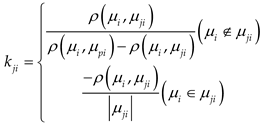
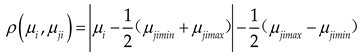
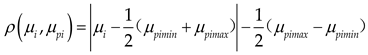
After determining the weight of each matter-element indicator in the evaluation model, the correlation degree of the evaluation indicators concerning the severity level of structural leakage is using the above formula. Consequently, the comprehensive correlation degree of each evaluation indicator concerning the evaluation level of the tunnel to be assessed is derived, as follows:
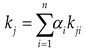 Where αi is the weight of each evaluation indicator in the matter-element model, and kji represents the correlation degree of evaluation indicator i concerning tunnel leakage level j.
Where αi is the weight of each evaluation indicator in the matter-element model, and kji represents the correlation degree of evaluation indicator i concerning tunnel leakage level j.
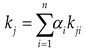
1.5. Determination of Water Seepage Levels
When all of the above parameters have been determined, the water leakage level of the target tunnel can be assessed:
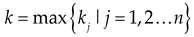
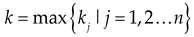
2. Effects of Water Level Changes on the Stability of Near-Reservoir Tunnels
2.1. Numerical Models
Using numerical simulation methods to explore the influence of different water levels on the stability of tunnels. The FLAC3D finite difference software was employed for modeling, with a model plane size of 75m x 75m x 10m. Figure 2 depicts the relative positions of the reservoir and the existing tunnel. The geological layers and lining were modeled using three-dimensional solid elements. The model had a buried depth of 25m, based on actual engineering conditions. The model adopts the lateral peripheral pressure loading mode with a constant load of 0.55MPa in the longitudinal direction, and the lateral pressure coefficient of 0.5. Based on on-site borehole analysis, the surrounding rock comprises 5m of highly weathered shale, 20m of weakly weathered shale (Grade IV), and 20m of slightly weathered limestone. Two types of boundary conditions were applied to the model's perimeter: fixed and free, with no constraints applied to the top surface. The porosity of the surrounding rock was set at 0.307, and the permeability coefficient was set at 2.5e-10 m²/(Pa·s). The seepage boundaries were impermeable on the two sides and the bottom of the model. The calculation parameters are detailed in Table 3.
Due to the reservoir being located beside the tunnel, the water level is inclined. Based on the survey data, simulations were conducted under four different conditions, with water levels set at 0m, 5m, 15m, and 25m, using the road surface as the reference point.
2.2. Calculation Results
2.2.1. Deformation Analysis
When the water level is at a high level of 25m, the deformation of the arch reaches its maximum. Under inclined water levels, the vertical displacement of the arch is the greatest, reaching 2.56mm at the water level of 25m, as shown in Figure 3. At the same time, the horizontal displacement of the right arch shoulder and side wall changes drastically, reaching 0.73mm, several times greater than the condition without considering the water level effect, as shown in Figure 4. The variation in the reservoir water level significantly affects the deformation of the surrounding rock. The monitoring points rapidly increased under water pressure in a short period, with the inner side displacement of the tunnel being larger than the outer side due to the bias effect of the inclined water level.
2.1.2. Stress Analysis
The principal stresses increase significantly with the rise of the reservoir water level. The maximum principal stress at the inner arch reaches 0.21MPa, and the compressive stress at the inner foot reaches 3.45MPa. At high water levels, the vertical stress at the inner foot reaches 3.22MPa, with the maximum horizontal stress at the foot reaching 0.98MPa. The horizontal stress is noticeably affected by water level changes, causing variations in stress distribution. Stress concentrations appear at the foot, shoulder, and arch, with the inner side of the water level having a larger stress concentration range than the outer side. The maximum vertical stress is at the foot, primarily due to the tunnel being in a biased pressure state from the tilted water level, as shown in Figure 5.
2.1.3. Plastic Zone Distribution
The variation in reservoir water levels affects the distribution of the plastic zone in the surrounding rock, with particularly changes observed in the inner arch and side walls. With the rise of reservoir water levels, the extension range and depth of the plastic zones in the inner arch and side walls increase markedly, while the plastic zone in the outer side walls and floor shows little change. Primarily due to the increasing water level, the pore water pressure increases, affecting the stress distribution of the surrounding rock, resulting in the continuous expansion of the plastic zone, as shown in Figure 6.
Through numerical calculations, it is found that tunnels near reservoirs are significantly affected by water level changes, reflected not only in the stress distribution and magnitude of the lining, but also in the increased deformation of the lining and surrounding rock with rising water levels. The deformation and cracking of the tunnel lining and surrounding rock can lead to a gradual increase in seepage pressure, thereby affecting the degree of water leakage within the tunnel. Therefore, the reservoir water level is one of the important factors influencing the leakage grade of tunnel structures.
3. Determination of Status Values for Water Leakage Evaluation Indicators
After determining the evaluation indicators, a method for classifying the relevant indicators of the tunnel is proposed. Supplementary and quantified evaluation criteria for each status indicator are determined, with the value range set from 0 to 4, detailed in Table 4, Table 5, Table 6, Table 7, Table 8, Table 9, Table 10, Table 11 and Table 12.
3.1. Surrounding Rock Classification
The comprehensive indicators of the surrounding rock are usually determined by its classification, considering factors such as strength, structural influence, and weathering condition. Based on the Rock Mass Rating (RMR) classification standards for rock geomechanics, a scheme for classifying the impact of tunnel leakage water is determined, as shown in Table 4.
Table 4.
Parameters of numerical calculation.
| Scale | Description of the technical situation |
| 1 | Score of RMR classification >80 |
| 2 | Score of RMR classification is between 60 and 80 |
| 3 | Score of RMR classification is between 40 and 60 |
| 4 | Score of RMR classification <40 |
3.2. Surrounding Rock Fracture
Indicators for rock mass joints and fractures are typically evaluated using the volume of joint number in the rock mass. The development degree of rock mass joints and fractures is used to classify the water leakage levels of tunnels, as shown in Table 5.
Table 5.
Evaluation criteria for surrounding rock fracture.
| Scale | Description of the technical situation |
| 1 | Volumetric joint count of the rock mass(jv) <10 lines/m3 |
| 2 | 10<Jv <20 lines/m3 |
| 3 | 20< Jv <30 lines/m3 |
| 4 | Jv >30 lines/m3 |
3.3. Overlying Relative Water Aquicludes
The indicator for the overlying relative aquiclude is evaluated by the thickness of the aquiclude. Aquicludes refer to impermeable layers, which are rock layers and soil layers with poor permeability, making it difficult for groundwater to pass through. The classification table for tunnel water leakage levels is determined, as shown in Table 6.
Table 6.
Evaluation criteria for relative water aquicludes.
| Scale | Relatively impermeable layer thickness |
| 1 | >6m |
| 2 | 3~6m |
| 3 | 0.5~3m |
| 4 | <0.5m |
3.4. Aquifer Permeability
The seepage performance of rock mass aquifers is an important indicator for evaluating tunnel seepage water, reflecting the permeability of the rock mass. The greater the permeability, the higher the likelihood of tunnel seepage water occurrence. The permeability index of the rock mass can be represented by the permeability coefficient of the rock mass. The classification table for tunnel water leakage levels is determined, as shown in Table 7.
Table 7.
Evaluation criteria for the aquifer permeability.
| Scale | Description of the technical situation |
| 1 | Permeability coefficient(K) <10-4 (cm/s) |
| 2 | Permeability coefficient (K) is between 10-4 and 0.5×10-3 (cm/s) |
| 3 | Permeability coefficient (K) is between 0.5×10-3 and 10-2 (cm/s) |
| 4 | Permeability coefficient(K) >10-2 (cm/s) |
3.5. Water Levels of Reservoirs
The groundwater level is closely related to the overlying water pressure and the burial depth of tunnels, and this relationship is not linear. Based on the analysis of the effects of different groundwater levels on tunnel structural displacement, stress, and plastic zones, the relative depth of tunnel burial to groundwater level is used to measure the impact of reservoir water levels on tunnel water leakage. The classification table is determined, as shown in Table 8.
Table 8.
Evaluation criteria for water level of reservoirs.
| Scale | Description of the technical situation |
| 1 | Relative height greater than design pavement elevation 0~5 (m) |
| 2 | Relative height greater than design pavement elevation 5~15 (m) |
| 3 | Relative height greater than design pavement elevation 15~25 (m) |
| 4 | Relative height greater than design pavement elevation >25 (m) |
3.6. Water Erosion
Water erosion significantly impacts the durability of concrete structures. The erosion indicators are affected by the external environment and different mineral compositions of the water. The classification table for the impact of tunnel water leakage is determined, as shown in Table 9.
Table 9.
Evaluation criteria for water erosion.
| Scale | Ph | Erosive CO2(mg/L) | Water Cl-(mg/L) |
| 1 | >6.5 | <15 | <100 |
| 2 | 5.0-6.5 | 15-30 | 100-500 |
| 3 | 4.0-5.0 | 30-60 | 500-5000 |
| 4 | <4.0 | >60 | >5000 |
3.7. Buried Depth of Tunnels
The greater the tunnel depth, the larger the catchment area, and the more groundwater groundwater supplied. Therefore, the average depth of the tunnel affects tunnel water leakage. For a specific tunnel, there is a minimum inflow depth that influences tunnel water leakage. The relative height of the minimum inflow depth can be used for evaluation. The classification table for the impact of tunnel water leakage is determined , as shown in Table 10.
Table 10.
Evaluation criteria for the buried depth of tunnels.
| Scale | Description of the technical situation |
| 1 | The tunnel depth is near the buried depth of the theoretical minimum water inflow. |
| 2 | The tunnel depth is less than the theoretical minimum water inflow. |
| 3 | The tunnel depth is greater than the theoretical minimum water inflow. |
| 4 | The tunnel depth is far greater than the theoretical minimum water inflow. |
3.8. Area of Tunnel Cross-Section
After tunnel excavation, the water pressure in the surrounding area decreases, acting like a drainage channel. Therefore, the larger the cross-sectional area of the tunnel, the more serious the water leakage. The classification table for the impact of tunnel water leakage is determined, as shown in Table 11.
Table 11.
Evaluation criteria for the cross section of tunnel.
| Scale | Description of the technical situation |
| 1 | Cross-sectional area <10 (m2) |
| 2 | 10<Cross-sectional area<30 (m2) |
| 3 | 30<Cross-sectional area<50 (m2) |
| 4 | Cross-sectional area >50 (m2) |
3.9. Tunnel Drainage Facilities for Water Leakage
Tunnel drainage systems span the design, construction, and operational service stages. The effectiveness of drainage facilities depends on whether the design is reasonable, construction quality meets standards, and regular inspections are conducted during the operational service stage. It also depends on whether issues are promptly identified and addressed. The classification table for the impact of tunnel drainage facilities on water leakage is determined as shown in Table 12.
Table 12.
Evaluation criteria for the drainage facilities.
| Scale | Description of the technical situation |
| 1 | Well-designed anti-drainage, standardized construction, regular maintenance |
| 2 | Well-designed anti-drainage, poor construction quality, regular maintenance |
| 3 | Well-designed anti-drainage, poor construction quality, irregular maintenance |
| 4 | Poor drainage protection design, poor construction quality, irregular maintenance |
4. Leakage Evaluation of Tiebeishan Tunnel
4.1. Surrounding Rock Classification Project overview
Tiebeishan tunnel, located within the Gaoliyingzi region on the Heida line in Fushun City, Liaoning Province, China, was built in 1989. The tunnel has a total length of 178 meters, a clear width of 7 meters, and a vertical clearance height of 5 meters. The geological conditions at the tunnel site are complex, with a maximum tunnel depth of 48 meters. The surrounding rock is composed of relatively stable granite gneiss. There is a fault zone trending from northwest to southeast passing 1 kilometer to the southeast. The joint fractures in the surrounding rock are well developed, causing varying degrees of surface water infiltration at the tunnel's entrance and exit sections, leading to the emergence of a certain amount of groundwater. Over the years, regular inspections have found serious water leakage problems in the tunnel, as shown in Figure 7. Consequently, major repairs have been undertaken on the drainage system to address these issues.
Figure 7.
Leakage diseases of tunnel: (a) water seepage; (b) water stain.

The spatial relationship between the tunnel and the reservoir is illustrated in Figure 8. The average distance between the tunnel and the reservoir is 128 meters, with the closest point being 8 meters from the water source. The Dahuofang Reservoir, which holds water year-round, has a controlled catchment area of 5,437 square kilometers and a total storage capacity of 21.81 billion cubic meters. The proximity of the tunnel to the reservoir, combined with the well-developed fractures in the surrounding rock, creates a water seepage pathway on the side of the tunnel nearest to the reservoir. Changes in the reservoir water level can affect the stress on the tunnel lining structure. Inspections have confirmed severe leakage problems in the tunnel, which, at their worst, can compromise the structural stability of the tunnel and traffic safety.
Figure 7.
Location of tunnel.
4.2. Determination of the Matter-Element Model
The classification of tunnel water leakage damage is divided into four categories: P1 for intact condition, P2 for minor leakage, P3 for moderate leakage, and P4 for severe leakage. After determining the classical domain and section domain of the matter-element model, the matter-element to be evaluated is determined based on the actual engineering situation of the Tiebeishan Tunnel.

4.3. Determination of Evaluation Indicator Weights and Consistency Tests
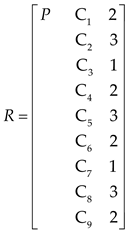
Based on the criterion of relative importance, a judgment matrix for the nine evaluation indicators in the matter-element evaluation model is formed, as shown in Table 13.
After establishing the judgment matrix, the weight for each indicator and the maximum eigenvalue of the judgment matrix are calculated by Equation (4), based on the square root method.
After calculation, the values for A1, A2, A3, A4, A5, A6, A7, A8 and A9 are 2.579, 2.579, 0.416, 0.717, 1.730, 0.728, 0.364, 0.373 and 2.819, respectively. The normalized weight vector for each evaluation indicator is:
A=(0.210,0.210,0.034,0.058,0.141,0.059,0.030,0.030,0.229)T
The maximum eigenvalue λ is 9.81. Therefore, the value of the consistency indicator can be derived from the following equation.
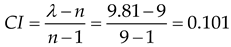
By calculating the stochastic consistency index RI as 1.46, followed by the following equation, the consistency ratio can be found.
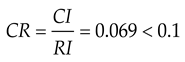
The result proves that the weight set meets the consistency test requirement. A is the calculated weight set of each matter-element, representing the weight accounted for by each evaluation indicator.
4.4. Correlation Calculation and Determination of Disease Levels
Based on the four levels of the tunnel disease degree classified in Section 4.2, combined with Equations (8) to (10), the correlation of each index is calculated. The specific process is as follows:
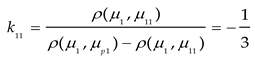
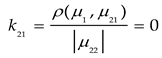
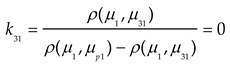
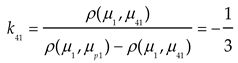 Where, kji represents the relevance of evaluation indicator i to evaluation level j. μji denotes the value range of the classical domain, and μpi denotes the value range of the section domain. ρ(μi,μji) is the distance from point μi to the interval (μjimin,μjimax), and ρ(μi,μpi) is the distance from point μi to the interval (μpimin,μpimax). The relevance matrix, which summarizes the relevance of each evaluation indicator to the different evaluation levels, is presented in Table 14.
Where, kji represents the relevance of evaluation indicator i to evaluation level j. μji denotes the value range of the classical domain, and μpi denotes the value range of the section domain. ρ(μi,μji) is the distance from point μi to the interval (μjimin,μjimax), and ρ(μi,μpi) is the distance from point μi to the interval (μpimin,μpimax). The relevance matrix, which summarizes the relevance of each evaluation indicator to the different evaluation levels, is presented in Table 14.
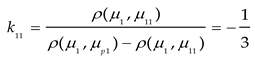
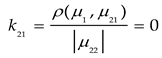
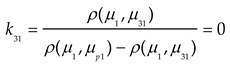
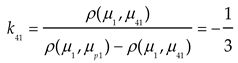
After calculating the correlation of each evaluation indicator regarding the four classes, based on Equation (11), the combined correlation of the disease classes of the evaluation model can be calculated as follows:
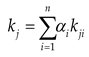
Calculation yields k1, k2, k3, k4 as -0.439, -0.191, -0.032, -0.228, according to the rating rules, the tunnel disease level is:
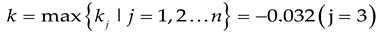
The evaluation grade of water leakage in the tunnel is Grade 3, indicating moderate water leakage.
4.5. Analysis of Evaluation Results
Based on the theories of extenics and the analytic hierarchy process, each evaluation indicator was quantified, and their importance and weight were calculated. Ultimately, the comprehensive correlation degree was determined, concluding that the leakage evaluation level of Tiebeishan Tunnel reached Level 3, indicating leakage. The evaluation model was found to align with the actual situation based on on-site inspection results and water leakage statistics. During inspections, severe cracks were observed in the tunnel lining structure, and issues like water leakage and efflorescence were noted during the rainy season, impacting traffic safety. This demonstrates that the established tunnel leakage evaluation model accurately reflects engineering realities and can serve as a valuable reference for similar projects.
4. Conclusion
- (1)
- Based on the existing methods for evaluating tunnel water leakage, the impact of external environmental changes on tunnels near reservoirs was considered. It is proposed that the leakage evaluation index should be divided into geological conditions, hydrological conditions and tunnel engineering aspects. Various factors influencing tunnel water leakage were analyzed, and a hierarchical evaluation index system for tunnel water leakage was proposed.
- (2)
- The changes in reservoir water level significantly affect the stability of tunnels. With increasing water levels, the displacements and stresses of the tunnel structure gradually increase, with the inner side of the water level experiencing significantly greater than the outer side. The plastic zone undergoes notable changes, and structural damage progresses from the inner side to the entire cross-section. Tunnels near reservoirs should focus on water level changes and implement targeted reinforcement measures to improve the stress state of tunnels.
- (3)
- Combining the qualitative and quantitative descriptions of leakage conditions, the evaluation indicators and value standards for water leakage were specified, based on Analytic Hierarchy Process (AHP) and the theory of extension. A hierarchical evaluation model for the leakage of tunnels near reservoirs was constructed.
- (4)
- The proposed leakage evaluation model was applied to the Tiebeishan Tunnel project. A judgment matrix was constructed, and the comprehensive relevance degree of the leakage grade was determined. The leakage level of the Tiebeishan tunnel is Grade 3, indicating moderate leakage. This application verified the rationality and applicability of the evaluation model.
Author Contributions
Conceptualization, methodology, software, writing—original draft preparation, Y.L.; writing—review and editing, Z.X.W. ; funding acquisition, validation, X.L.; supervision, data curation, writing—review, J.Y.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China (Grant No.52078306), and Doctoral Research Initiation of Foundation of Liaoning Province, China (No. 2023-BS-205), Funding Project of Northeast Geological S&T Innovation Center of China Geological Survey(NO. QCJJ2023-44), and Project of Transportation Science and Technology of Liaoning Province, China (No. 202341).
Data Availability Statement
Data were curated by the authors and are available upon request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Janda, T.; Šejnoha, M.; Šejnoha, J. Applying Bayesian Approach to Predict Deformations during Tunnel Construction. Num Anal Meth Geomechanics 2018, 42, 1765–1784. [Google Scholar] [CrossRef]
- Ye, F.; Qin, N.; Liang, X.; Ouyang, A.; Qin, Z.; Su, E. Analyses of the Defects in Highway Tunnels in China. Tunnelling and Underground Space Technology 2021, 107, 103658. [Google Scholar] [CrossRef]
- Qian, Q.-H. Scientific use of the urban underground space to construction the harmonious livable and beautiful city. Hazard control in tunnelling and underground engineering 2019, 1, 1–7. [Google Scholar]
- Coli, N.; Pranzini, G.; Alfi, A.; Boerio, V. Evaluation of Rock-Mass Permeability Tensor and Prediction of Tunnel Inflows by Means of Geostructural Surveys and Finite Element Seepage Analysis. Engineering Geology 2008, 101, 174–184. [Google Scholar] [CrossRef]
- Li, S.; Zhou, Z.; Li, L.; Xu, Z.; Zhang, Q.; Shi, S. Risk Assessment of Water Inrush in Karst Tunnels Based on Attribute Synthetic Evaluation System. Tunnelling and Underground Space Technology 2013, 38, 50–58. [Google Scholar] [CrossRef]
- Luciani, A.; Peila, D. Tunnel Waterproofing: Available Technologies and Evaluation Through Risk Analysis. Int J Civ Eng 2019, 17, 45–59. [Google Scholar] [CrossRef]
- Khademi Hamidi, J.; Shahriar, K.; Rezai, B.; Rostami, J.; Bejari, H. Risk Assessment Based Selection of Rock TBM for Adverse Geological Conditions Using Fuzzy-AHP. Bull Eng Geol Environ 2010, 69, 523–532. [Google Scholar] [CrossRef]
- Hyun, K.-C.; Min, S.; Choi, H.; Park, J.; Lee, I.-M. Risk Analysis Using Fault-Tree Analysis (FTA) and Analytic Hierarchy Process (AHP) Applicable to Shield TBM Tunnels. Tunnelling and Underground Space Technology 2015, 49, 121–129. [Google Scholar] [CrossRef]
- Park, S.W.; Shin, Y.S.; Oh, Y.S.; Ahn, S.R. A Guideline on Condition Assessment of Existing Old Railway Tunnels. Tunnelling and Underground Space Technology 2006, 21, 329–330. [Google Scholar] [CrossRef]
- Gong, X.N.; Guo, P.P. Prevention and mitigation methods for water leakage in tunnels and underground structures. China journal of highway and transport 2021, 34, 1–30. [Google Scholar] [CrossRef]
- Yang, W.; Fang, Z.; Wang, H.; Li, L.; Shi, S.; Ding, R.; Bu, L.; Wang, M. Analysis on Water Inrush Process of Tunnel with Large Buried Depth and High Water Pressure. Processes 2019, 7, 134. [Google Scholar] [CrossRef]
- Li, X.; Li, Y. Research on Risk Assessment System for Water Inrush in the Karst Tunnel Construction Based on GIS: Case Study on the Diversion Tunnel Groups of the Jinping II Hydropower Station. Tunnelling and Underground Space Technology 2014, 40, 182–191. [Google Scholar] [CrossRef]
- Jiang S Y, Chen J H, Li T, et al. Assessment and prediction of water gushing disaster risk in underwater tunnel. China Safety Science Journal, 2013, 23, 101–106. [CrossRef]
- Pan, H.Z. Study on groundwater disaster prevention and evaluation system of tunnel engineering; Southwest Jiaotong University: Cheng Du, 2009. [Google Scholar]
- Li, P.; Wang, F.; Long, Y.; Zhao, X. Investigation of Steady Water Inflow into a Subsea Grouted Tunnel. Tunnelling and Underground Space Technology 2018, 80, 92–102. [Google Scholar] [CrossRef]
- Zhang, B.; Wang, H.; Ye, Y.; Tao, J.; Zhang, L.; Shi, L. Potential Hazards to a Tunnel Caused by Adjacent Reservoir Impoundment. Bull Eng Geol Environ 2019, 78, 397–415. [Google Scholar] [CrossRef]
- Shen, Y.F. Analysis on fatigue of warm mix asphalt mixture. Urban Roads and Rridges & Flood Control 2021, 289-295+30. [CrossRef]
- Chen, H. Research on mechanical properties of subway tunnel structure and surrounding rock due to the water level fluctuation of adjacent water body; Hunan University of Science and Technology: Hu Nan, 2014. [Google Scholar]
- Sun, Z.; Zhang, D.; Fang, Q.; Wang, J.; Chu, Z.; Hou, Y. Analysis of Interaction between Tunnel Support System and Surrounding Rock for Underwater Mined Tunnels Considering the Combined Effect of Blasting Damage and Seepage Pressure. Tunnelling and Underground Space Technology 2023, 141, 105314. [Google Scholar] [CrossRef]
- Xin, C.-I.; Gao, B.; Sui, C.; Zhou, Y. Analysis of External Water Pressure on the Support and Lining of Deep Mountain Tunnels below High Water Tables. J. Highway Transp. Res. Dev. (English Ed.) 2014, 8, 61–66. [Google Scholar] [CrossRef]
- Band, P.; Shelake, A.; Gogate, N. AHP Approach for Risk Factors Prioritisation in Tunnel Construction. In Civil Engineering for Multi-Hazard Risk Reduction. IACESD 2023; Sreekeshava, K.S., Kolathayar, S., Vinod Chandra Menon, N., Eds.; Lecture Notes in Civil Engineering; Springer: Singapore, 2024; vol 457. [Google Scholar] [CrossRef]
Figure 1.
Leakage water evaluation system of tunnels near reservoirs.
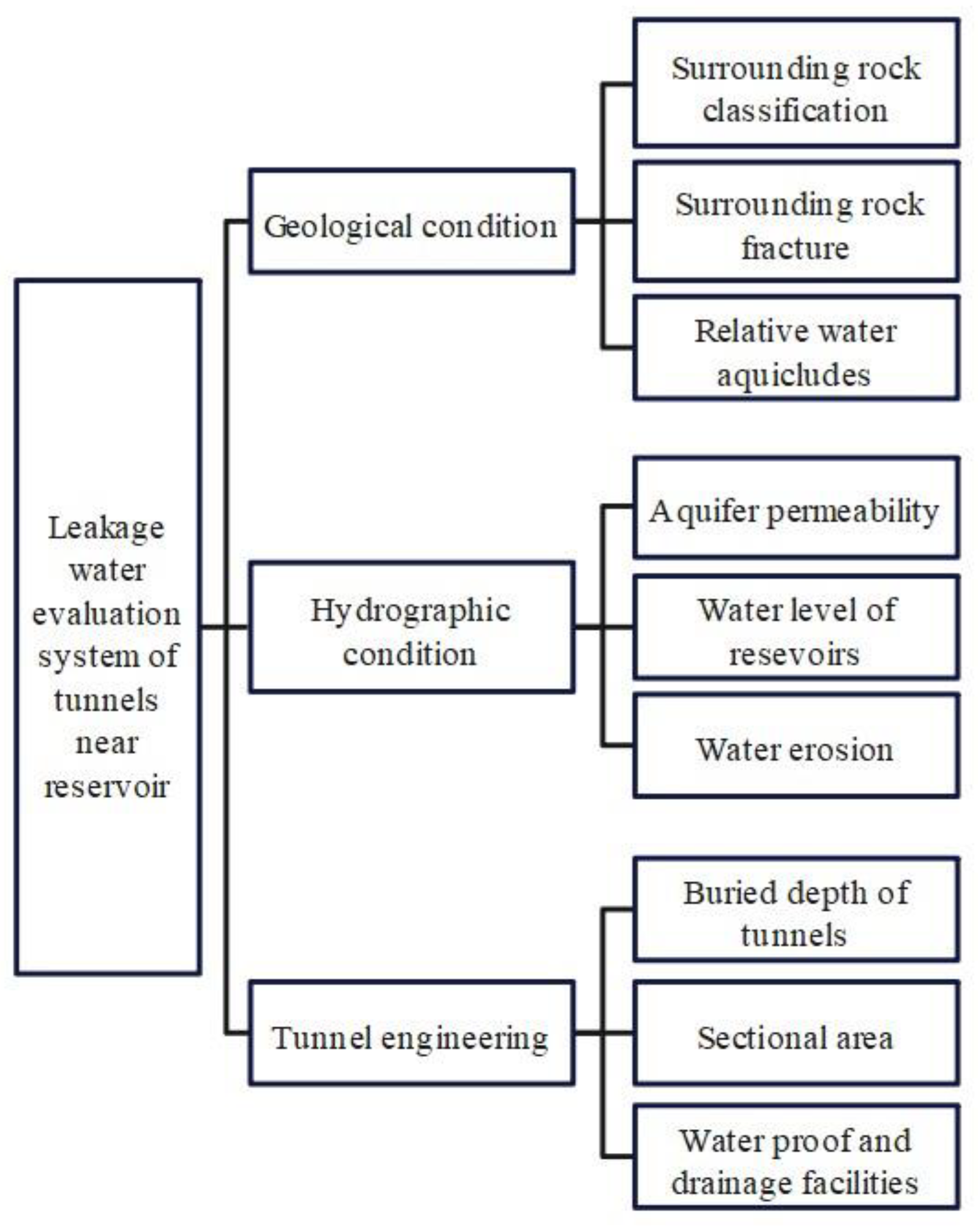
Figure 2.
Cross-section of the tunnel.
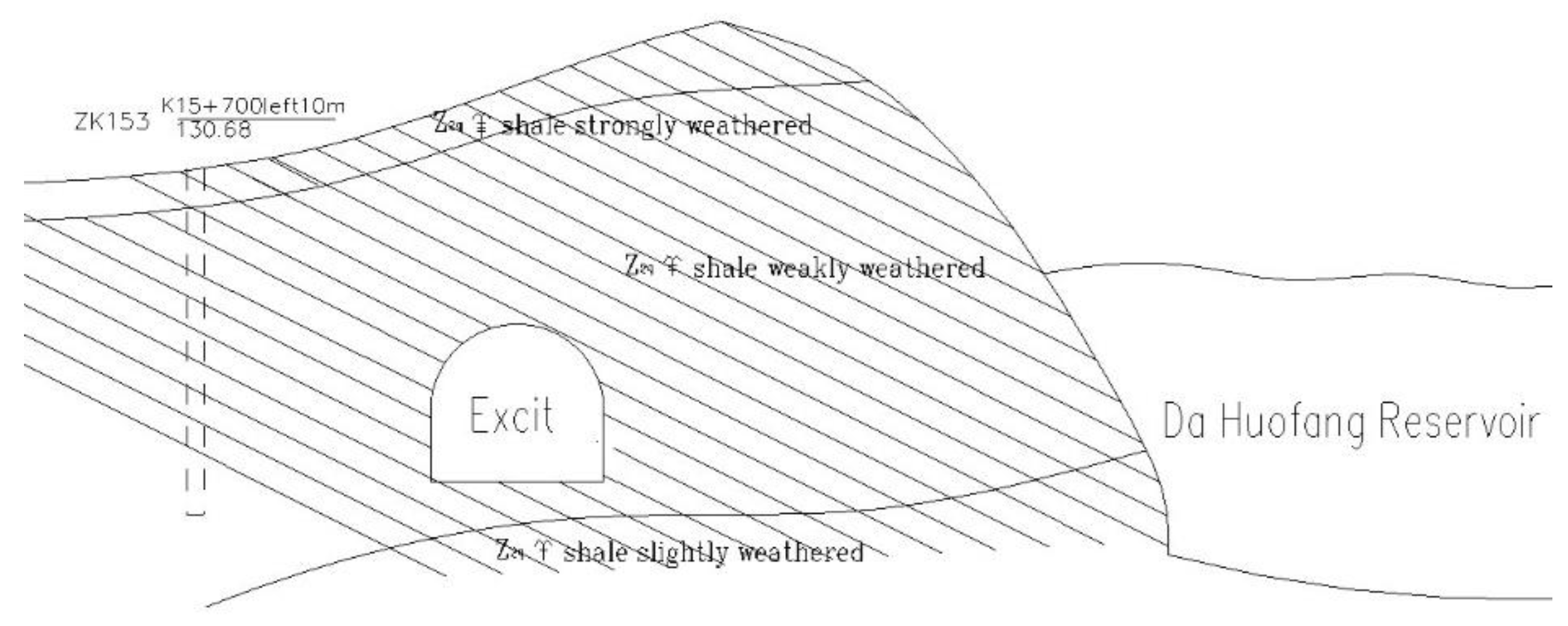
Figure 3.
Vertical deformation changes of different conditions.
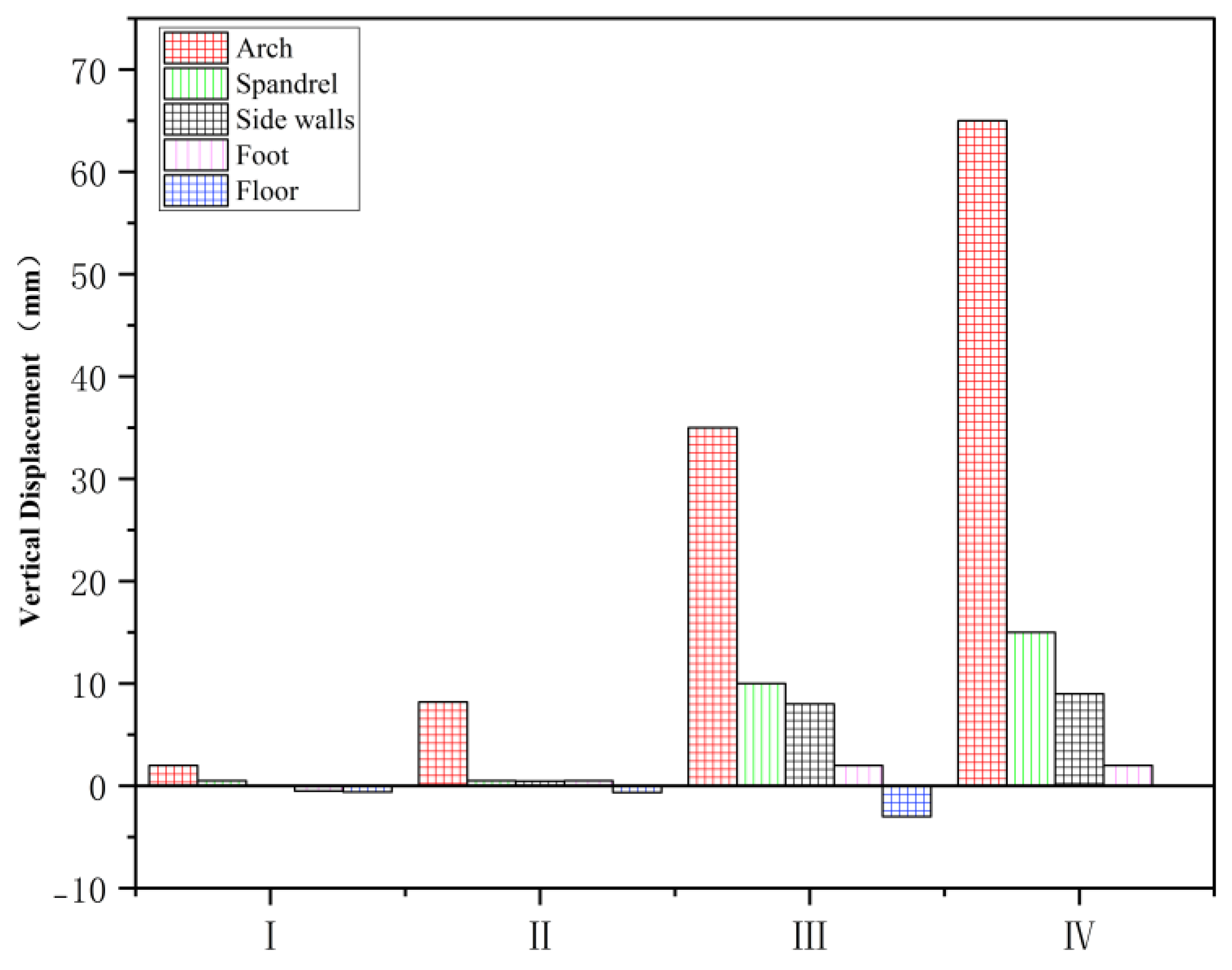
Figure 4.
Horizontal deformation changes of different conditions.
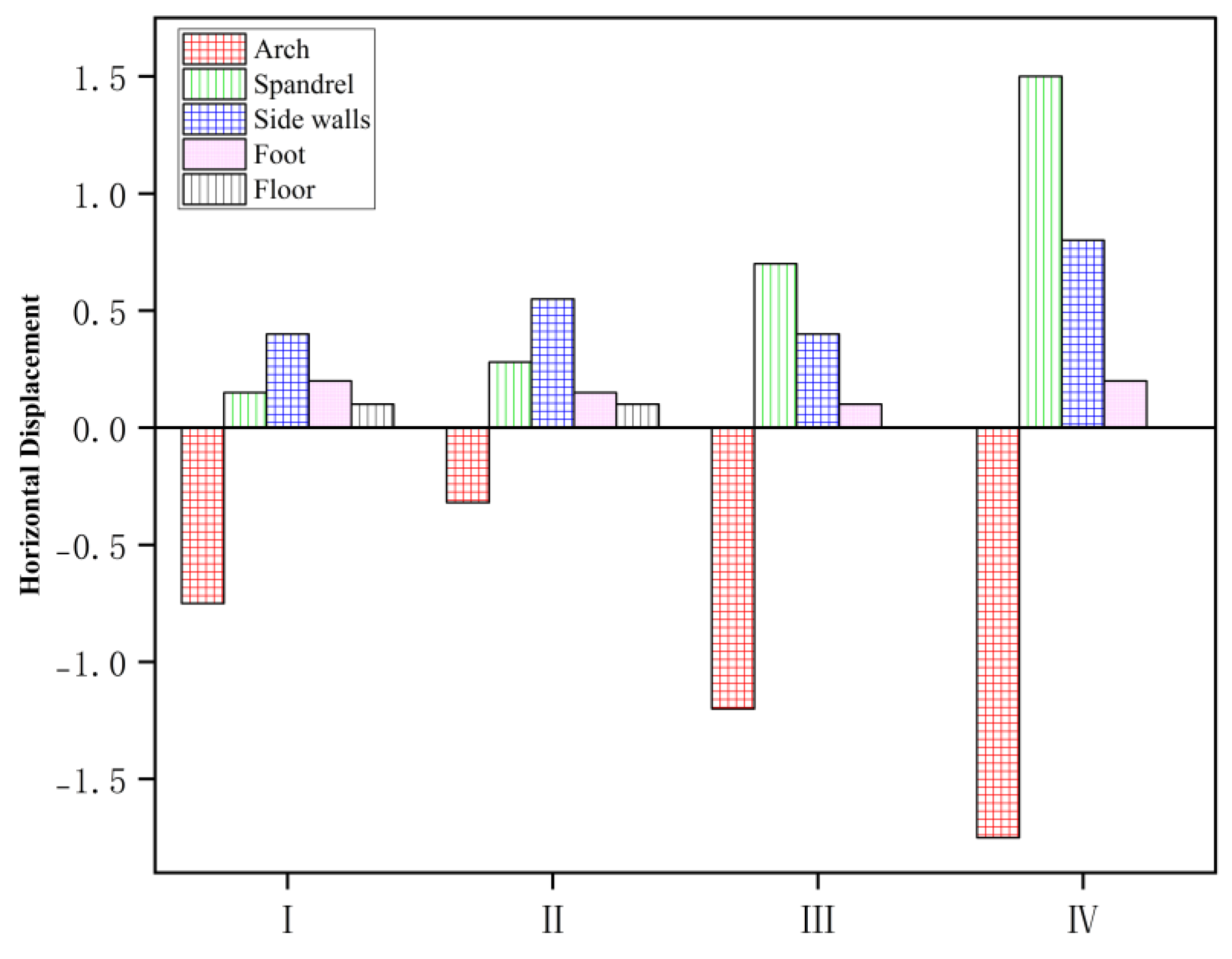
Figure 5.
Stress changes of different conditions.
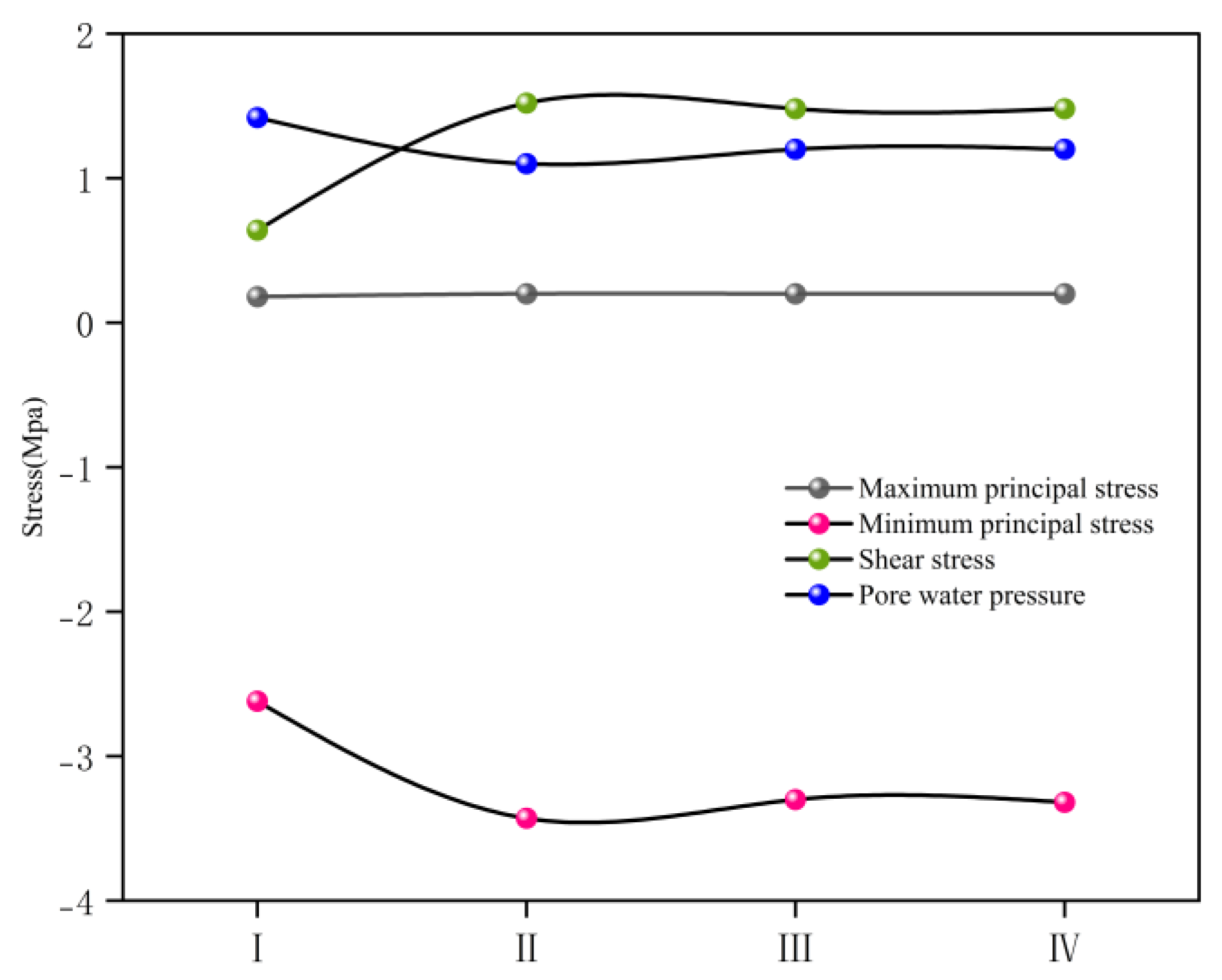
Figure 6.
Plastic zone of different conditions: (a) Condition Ⅰ; (b) Condition Ⅱ;(c) Condition Ⅲ(d) Condition Ⅳ.
Figure 6.
Plastic zone of different conditions: (a) Condition Ⅰ; (b) Condition Ⅱ;(c) Condition Ⅲ(d) Condition Ⅳ.
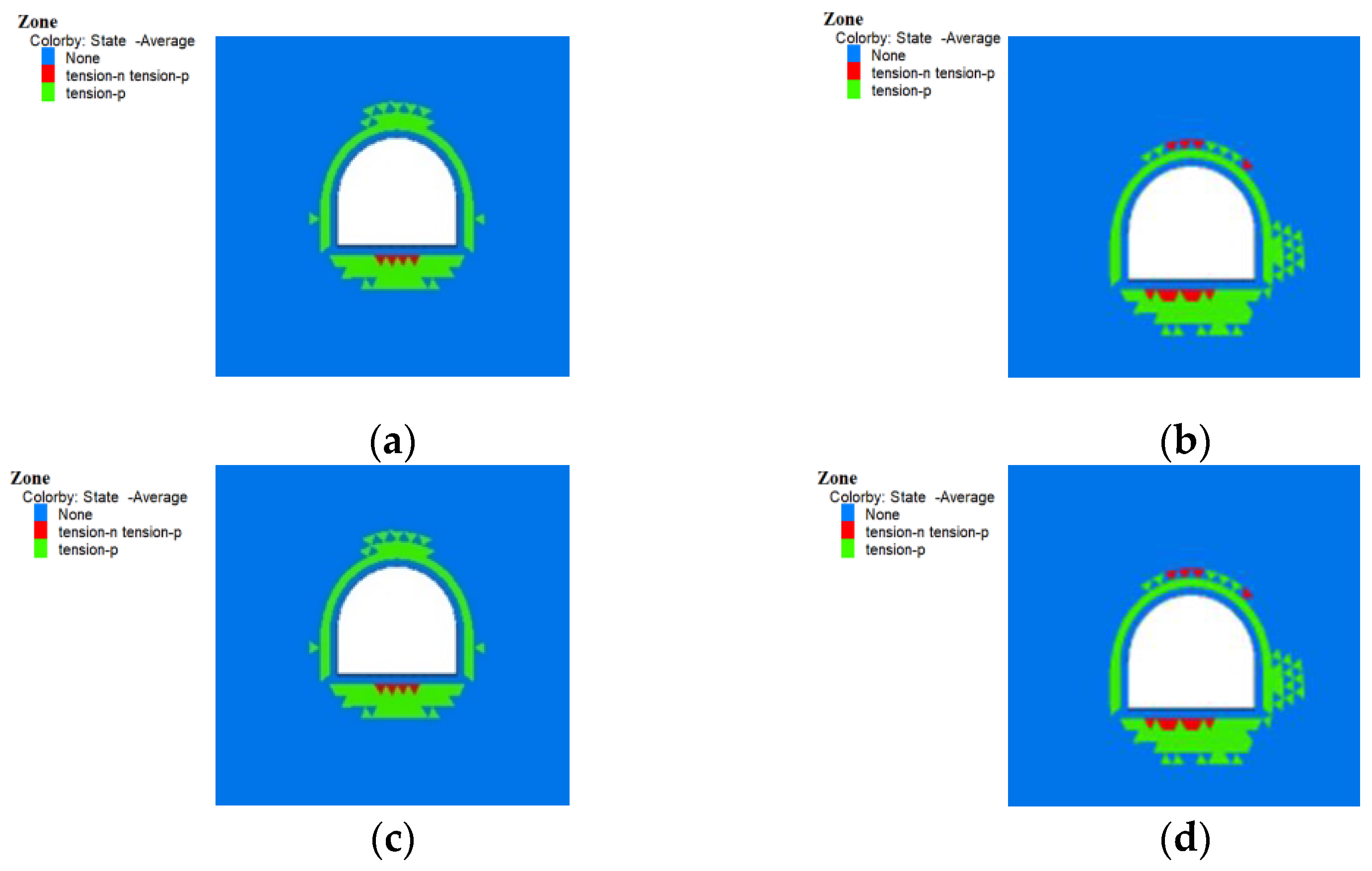
Table 1.
The meaning of each indicator scale.
| Scales | Comparative statement of importance |
| 1 | Compared to the same importance |
| 3 | One factor is slightly more important than the other |
| 5 | One factor is clearly more important than the other |
| 7 | One factor is more strongly important than the other |
| 9 | The extreme importance of one factor over another |
| 2,4,6,8 | Neighbourhood judgement median |
| 1/aij | When two factors are compared, if the former takes the above value for the latter, the latter takes the reciprocal of it |
Table 2.
General form of judgment matrix.
| R | C1 | C2 | … | Cn |
| C1 | 1 | a12 | … | a1n |
| C2 | 1/a12 | 1 | … | a2n |
| … | … | … | … | … |
| Cn | 1/ a1n | 1/ a2n | … | 1 |
Table 3.
Parameters of numerical calculation.
| Type | Density (g·cm-3) | Poisson's ratio | Elastic modulus (Pa) | φ (°) | c (MPa) |
| gravelly clay | 1.75 | 0.41 | 0.063e10 | 16.9 | 0.41 |
| weakly-slightly weathered metamorphic rocks | 1.9 | 0.38 | 0.15e10 | 25 | 0.35 |
| weak weathering | 2.09 | 0.32 | 0.47e10 | 33 | 0.45 |
| limestone | 2.4 | 0.28 | 1.3e10 | 44.5 | 1.1 |
| weak weathering | 2.3 | 0.2 | 3.15e10 | 54 | 1.8 |
Table 13.
Discriminant squares of tunnel structure disease evaluation model.
| R | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 |
| C1 | 1 | 1 | 6 | 3 | 2 | 5 | 7 | 4 | 1 |
| C2 | 1 | 1 | 6 | 3 | 2 | 5 | 7 | 4 | 1 |
| C3 | 1/6 | 1/6 | 1 | 1/3 | 1/5 | 1/3 | 3 | 1 | 1/5 |
| C4 | 1/3 | 1/3 | 3 | 1 | 1/4 | 1/3 | 3 | 3 | 1/5 |
| C5 | 1/3 | 1/2 | 5 | 4 | 1 | 5 | 5 | 5 | 1/3 |
| C6 | 1/5 | 1/5 | 3 | 3 | 1/5 | 1 | 2 | 2 | 1/5 |
| C7 | 1/7 | 1/7 | 1/3 | 1/3 | 1/5 | 1/2 | 1 | 3 | 1/6 |
| C8 | 1/4 | 1/4 | 1 | 1/3 | 1/5 | 1/2 | 1/3 | 1 | 1/5 |
| C9 | 1 | 1 | 5 | 5 | 3 | 5 | 6 | 5 | 1 |
Table 14.
Correlation degree of evaluation index on evaluation grade.
| Evaluation indicators | K1 | K2 | K3 | K4 |
| C1 | -1/3 | 0 | 0 | -1/3 |
| C2 | -2/3 | -1/2 | 0 | 0 |
| C3 | 0 | 0 | -1/2 | -2/3 |
| C4 | -1/3 | 0 | 0 | -1/3 |
| C5 | -2/3 | -1/2 | 0 | 0 |
| C6 | -1/3 | 0 | 0 | -1/3 |
| C7 | 0 | 0 | -1/2 | -2/3 |
| C8 | -2/3 | -1/2 | 0 | 0 |
| C9 | -1/3 | 0 | 0 | -1/3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







