Principles of Economic Externality Dynamics: The Economic Dynamics and the Standard Model (V)

Preprint

Article

Principles of Economic Externality Dynamics: The Economic Dynamics and the Standard Model (V)

Altmetrics

Downloads

107

Views

Comments

A peer-reviewed article of this preprint also exists.

Yingrui Yang^*

This version is not peer-reviewed

This preprints belongs to the Topic

The Impact of Artificial Intelligence on Research and Communication in the Social Sciences and Humanities

Submitted:

31 July 2024

Posted:

02 August 2024

You are already at the latest version

Alerts

Abstract

The present paper discusses the importance of economic externality and the economic phenomena involved. Section 1 draws on the framework of weak force theory in physics, we propose a new approach of dynamic analysis for economic externality. From a mesoscopic (intermediate scale) perspective, no distinction is made between the macro-demand and individual micro-buyers nor between the macro-supply and individual micro-sellers. Section 2 applies the isospin modeling method to construct two economic isospin models. One is between the achieving impulse and the fear-of-failure impulse, under the effect of economic externality. The other is between the market behavior and market residues, namely, market aftertaste. Section 3 discusses the microstructural properties of the market, including Dirac's equation and the market, Dirac -matrix notation, and the chirality and spin structure of market components. Section 4 discusses the helical structural characteristics of supply chains, including CPT theorems, Penrose zigzag helical processes, and several modeling directions of economic externality and buyer-seller interactions (weak interactions). Section 5 discusses the economic externality and the electroweak model, including extensive externality, externality mediations with Weinberg rotations, and economic analysis using lepton weak currents, including the analysis of lepton neutral weak currents. Finally, Section 6 provides a general discussion on the standard model of economic dynamics.

Keywords:

Subject: Social Sciences - Cognitive Science

-matrix notation, and the chirality and spin structure of market components. Section 4 discusses the helical structural characteristics of supply chains, including CPT theorems, Penrose zigzag helical processes, and several modeling directions of economic externality and buyer-seller interactions (weak interactions). Section 5 discusses the economic externality and the electroweak model, including extensive externality, externality mediations with Weinberg rotations, and economic analysis using lepton weak currents, including the analysis of lepton neutral weak currents. Finally, Section 6 provides a general discussion on the standard model of economic dynamics.

1. Introduction

Economic externalities, also known as the visible hand, are undoubtedly a significant aspect of economics. Delving into the dynamic mechanisms of economic externalities and establishing theoretical models holds substantial and practical significance. The prospects of a complex economy clearly depend on the degree of tacit cooperation between the visible hand and the invisible hand. Since the publication of Alfred Marshall's Principles of Economics, microeconomic theory has economics revolves around three concepts: price, supply, and demand. For an item to become a commodity, it must be assigned a price and have both supply and demand; this is referred to as having value and marketability. When there are buyers and sellers, a market is formed. In the market, there are no empty promises, and participants are collectively referred to as businesspeople. To conduct transactions, price negotiations are necessary. The price and its determination are ideally the result of bargaining between potential buyers and sellers. However, if a third external factor influences the price, it is referred to as an economic externality. For example, economic policies, including monetary or fiscal policies, or even a newly introduced market management mechanism, can all influence market prices as economic externalities. It is important to note that the economic externalities discussed here do not involve so-called "malicious externalities," as those pertain to business studies and are beyond the scope of this article.

Economic externalities require a dynamic model to deepen our understanding and surpass the current depiction of externalities in economics. The influence of economic externalities on market prices can be characterized using one of the four fundamental forces in physics, specifically the weak force. One physical model that characterizes this weak force is known as the isospin model, with its mathematical representation being the SU(2) symmetry group. Explaining why this is the case is the main focus of this paper.

In the history of modern physics, the concept of isospin was first proposed by Werner Heisenberg. The study of the weak force model originated from the research on particle decay by Tsung-Dao Lee and Chen-Ning Yang and was further developed through the gauge field theory research by Chen-Ning Yang and Robert Mills. This forms the backbone of the Standard Model of particle physics. It might be unexpected to Professor Yang that the gauge field theory model of the weak force has found elegant applications in the social sciences.

In previous work, we used quantum chromodynamics as a model framework to develop a strong force model for sub-economic dynamics. In this context, human economic impulses were assigned flavors, with the achievement impulse represented by the up quark and the fear impulse by the down quark, both sharing the SU(3) symmetry group. The strong force (or its mediator, the gluon) allows quarks to form bound states. The weak force can change the flavor of quarks, causing a quark bound state to decay. Similarly, economic externalities can alter the flavor of economic impulses, with both sharing the SU(2) symmetry group.

Previously, we used quantum electrodynamics as a model framework to develop the electromagnetic force model for market dynamics. In this model, the buying and selling intentions of market participants were given positive and negative market charges, analogous to positive and negative electric charges, to distinguish supply and demand. Both share the U(1) symmetry group.

In market dynamics, we defined a quantum version of the invisible hand and discussed the fluctuations of economic impulses in a liberal market mechanism within sub-economic dynamics. The economic issue in the dynamics of economic externalities is the visible hand, a central concept in Keynesian economics. The fluctuation of buying and selling intentions in the market and the changes in the flavor of economic impulses caused by economic externalities are causally related, manifesting as the interaction between Smith's invisible hand and Keynes's visible hand.

The second section of this paper applies the isospin model method to construct two economic isospin models. The first model deals with the isospin between economic achievement impulses and economic fear impulses under the influence of economic externalities. The second model deals with the isospin between market behavior and market aftertaste. The third section discusses the microscopic properties of the market, including the Dirac equation and the market, the Dirac matrix notation, and the chirality and helicity of market components. The fourth section discusses the helical structure between supply and demand, including the CPT theorem, Penrose's zig-zag helical process, and the modeling of economic externality effects (weak interactions). The fifth section discusses economic externalities and the electroweak model, covering topics such as externality mediators, coupling constants, the Weinberg angle, and neutral currents. The sixth section provides a general discussion on the Standard Model of economic dynamics.

The gauge field theory of weak dynamics also involves some more mathematical content, including Lagrangians, gauge transformations, gauge fields, covariant derivatives, and the Higgs mechanism. These topics are beyond the scope of this paper.

2. The Visible Hand and Isospin

2.1. The Visible Hand

The financial market changes rapidly; speculators may go long or short, and retail investors may buy or sell at a moment's notice. At such times, accounts are active. Funds may be abundant in an account, yet action may be withheld temporarily. At these times, accounts are inactive. However, an investor can change states at any time, either pouncing like a tiger entering the fray or withdrawing after a successful surprise attack. These market behaviors are influenced by changes in participants' psychology, often affected by economic externalities, known as the visible hand. How can these phenomena be modeled, and what is the underlying mathematical structure? This article will illustrate that this visible hand can be described by weak forces in physics. Correspondingly, such moments of hesitation can be modeled by the isospin dynamics in the sub-physical standard model, with the underlying mathematical structure being SU(2) symmetry.

Capital has its weaknesses, leading to financial crises, so market regulation is essential, which is basic knowledge. Hayek advocated for completely free financial markets in his book "Denationalization of Money," but for a considerable period in history, this could only be a beautiful myth. In a previous discussion, we talked about four conditions for economic rationality, namely the four requirements for perfect competitive markets, where the fourth condition is market regulation, which is an economic externality.

More broadly, society interacts with capital, and the dynamic relationship between social fairness and profit-seeking capital is the domain of political economics, which cannot be avoided. Due to war, the economic downturn of the early 20th century gave rise to the Keynesian school of economics, advocating for state power to use economic policies (including monetary and fiscal policies) to intervene in the economy, commonly referred to as the visible hand. Two years after the 2007 global financial crisis, the situation did not improve. Princeton economist Krugman (Nobel laureate) once asked, if there really is an invisible hand, why hasn't it come out to help us yet? In fact, the invisible hand is always elusive and travels hand in hand with the visible hand. In economic life, controlling inflation, adjusting interest rates, issuing government bonds, stabilizing prices, redistributing income, providing healthcare insurance, and so forth—all require the visible hand to play a role, all require timely intervention of economic policies, and all cannot do without the involvement of economic externalities.

Clearly, the various economic externalities described above will affect market prices in different ways. At the microeconomic level, the visible hand affects people's price perception. At the meso-economic level, economic externalities affect the economic behaviors of market participants. At the macroeconomic level, economic policies affect dynamic changes on the supply side and the demand side. We will see that economic policies have their preferences for intervention.

2.2. Weak Forces and Flavor Isospin

In the previous discussion, it was mentioned that economic impulses are characterized by quarks in particle physics. Quarks have flavor isospin, such as up quark (u) and down quark (d). Economic impulses similarly have flavor isospin, namely achievement impulse and fear impulse, represented by up quark and down quark respectively, still denoted as u and d. From this, we have:

Proposition 1:

Economic achievement impulse shares the same flavor isospin as the up quark, denoted as u.

Proposition 2:

Economic fear impulse shares the same flavor isospin as the down quark, denoted as d.

Quantum chromodynamics tells us that quarks are confined and can only exist in bound states. Similarly, we can consider bound states of economic impulses. The proton-type impulse bound state consists of two achievement impulses and one fear impulse, denoted as uud. The neutron-type impulse bound state consists of two fear impulses and one achievement impulse, denoted as ddu. Hence, we have:

Proposition 3:

The bound state composed of two economic achievement impulses and one economic fear impulse is called the proton-type impulse bound state, denoted as uud.

Proposition 4:

The bound state composed of two economic fear impulses and one economic achievement impulse is called the neutron-type impulse bound state, denoted as ddu.

Heisenberg noted that these two bound states, proton uud and neutron ddu, apart from the flavor isospin of one quark being different, have the same components and binding mode, akin to twins with different names, and they can transform into each other. This is known as isospin, denoted by

(\begin{matrix} u u d \\ d d u \end{matrix})

Proposition 5:

uud represents the proton-type impulse bound state dominated by achievement impulses with a secondary fear impulse, while ddu represents the neutron-type bound state dominated by fear impulses with a secondary achievement impulse. These two bound states form an isospin relationship, denoted as

Isospin dynamics analysis involves sourced analysis, with the source termed weak isospin charge, denoted as

I^{3}

. A neutron-type bound state, due to the action of weak forces, can decay into a proton-type bound state, i.e.,

I^{3} :

ddu → uud. It can be seen, that due to the weak charge's action, we effectively have d → u, meaning weak forces change the quark's flavor isospin. Economic externalities can be described by weak forces; the reason being that economic externalities can change the flavor isospin of economic impulses, transforming a fear impulse into an achievement impulse. Hence:

Proposition 6:

Economic externalities are a form of economic weak force, denoted as

I^{3}

. Economic weak force can act on economic impulses and change their flavor, expressed as

I^{3}

: d→u.

Proposition 7:

Due to the action of economic weak force, economic impulses with different flavors form isospin, which is denoted by Dirac spinor

(\begin{matrix} u \\ d \end{matrix}) .

As we mentioned earlier [1], quarks carry fractional electric charge. The upper quark carries

2 / 3

electric charge and the down quark carries

- 1 / 3

electric charge. It is not difficult to see that as a bound state, neutrons carry a zero charge, while protons carry an integer charge. In other words, considering the

market charge introduced in [2] above, the neutron economic impulse bound state is price-neutral, containing zero market charge, and its market performance is conservative and onlooker. On the other hand, the proton type of economic impulse bound state carries an integer market charge, and its market performance is aggressive. We understand that one of the means of promoting economic development is to revitalize the market, and this is precisely the meaning of economic externalities (such as economic policies) affecting market prices. We can see from the isospin model that economic externalities stimulate market behavior (both consumption and supply) by changing the flavor of an economic impulse. It is a psychological mechanism by which an impulse of economic fear becomes an impulse of economic achievement.

2.3. Isospin of Market Charge and Residual Taste

Just as in chess, market behavior always leaves a residual flavor. Here, it is necessary to briefly review the concept of market charge introduced earlier. Since Marshall's "Principles of Economics" (1890), microeconomics has been able to articulate around three basic concepts: price, supply, and demand. A demand consists of two components, namely buying intentions and desired goods. We have:

Proposition 8:

Let the market price be denoted as

γ

. Demand is composed of purchasing intentions and target goods. Purchasing intentions carry a negative market charge, denoted as

e^{-}

, and are fully sensitive to price

γ

. Similarly, supply consists of sales intentions and target goods. Sales intentions carry a positive market charge, denoted as

e^{+}

, and are likewise fully sensitive to price

γ

In market dynamics, positive and negative market charges are akin to positive and negative electric charges. A positron is the antiparticle of an electron. Assuming there is a price and a market, buying low and selling high is both economically rational and a natural inclination of market participants. Because buying and selling are always sensitive to price, whether to buy or not, to sell or not, market participants exhibit a hesitation phenomenon, referred to as spin. Spin hesitation is an intrinsic characteristic of market participants.

Engaging in buying and selling, discussing business, both parties have intentions to buy or sell, with shared goods goals. Based on individual buying and selling capabilities and market awareness, to facilitate market behavior, the bottom line is the negotiation of prices. Both buyers and sellers have the opportunity to trade, but not the obligation. Whether it's opening prices, inquiries, or negotiations, market participants have the right to hesitate, which is a fundamental principle of ordinary rationality.

In modern markets, in civilized society, it's common to buy rice and vegetables at supermarkets, or clothes, appliances, and daily necessities at shopping malls, as well as houses, cars, and various tickets like plane tickets, high-speed rail tickets, ballet tickets, or symphony concert tickets, all clearly priced. Payments can be made in cash, by card, or via transfer, with goods exchanged for money, accounts recognized and settled, and then both parties move on. Whatever psychological hesitation, cognitive thinking, reasoning, or decision-making occurred has already become the past. Money becomes a sunk cost. Traditional economics teaches us that economics is the study of efficiency, so forget about sunk costs. Assuming resources are scarce, economics itself seems only to study how to efficiently allocate scarce resources. Neoclassical economics warns us to follow the money and look forward. The so-called marginal analysis refers to whether investing an additional unit of scarce resources yields marginal income and marginal opportunity costs, each geometrically. If the former exceeds the latter, it is considered efficient, otherwise, it is considered inefficient. Here, "investing more" certainly looks forward. In terms of efficiency concepts alone, the corresponding mathematical concept is a derivative, and the corresponding physical concept is velocity.

However, from the perspective of economic psychology, do ordinary people completely refrain from contemplating after making a purchase? Did they get their money's worth? Today, if they happen upon a store promotion offering discounts (such as 30%, 50%, or even 70%), they might feel they made a good deal, experiencing some satisfaction, and may consider returning next time. Or, if they hear another store is selling the same item cheaper, they might feel they made a bad deal here and think not to return to this store next time. These are all remnants of market behavior. Although termed remnants, whether pondered deeply or lightly, they all involve mental effort and inevitably consume energy. Below, we will introduce how this consumer residue (likewise, supply residue) can be appropriately characterized by neutrinos from particle physics.

Economic externalities often play a significant role in creating market residue. For example, when the central bank adjusts interest rates, it has financial policy effects and even fiscal policy effects, impacting market prices. Persistent rate hikes can cause inflation, which in turn can lead to consumer dissatisfaction. This is a type of market residue, superficially seen as price residue, but deeper, it reflects policy residue.

Today, going out to refuel the car, after refueling, one can't help but sigh: gasoline prices have recently risen by nearly 30%. Maybe it's better to take public transportation from now on. This is demand-side consumer residue. Managing a farm, with intense competition, the fruits produced at home are increasingly difficult to sell at a good price. One can't help but think about switching to other productions. This is supply-side sales residue.

Weak interactions can change the flavor charge of quarks, causing a neutron to decay into a proton, i.e., ，

I^{3}

：

n \to p

. In fact, this only tells half of the story. The complete story is formulated by the following interaction formula,

I^{3} ： n \to p + e + V_{e}

where the symbols denote electrons and electron neutrinos. Under weak interactions, electrons and electron neutrinos form another kind of isospin, denoted as

(\begin{matrix} e \\ V_{e} \end{matrix})

Neutrinos in physics and market residue in economics are remarkably similar. Firstly, both have very low energy, akin to residual energy. Therefore, neutrinos are called physical residues. Furthermore, market residue naturally pertains to buying and selling residue. Neutrinos are denoted as

V_{e}

, and their footnote explains the close relationship between neutrinos and electrons. Additionally, neutrinos may or may not have mass, a topic still under debate in physics. As for market residue consequences, economics currently cannot confirm or deny them. Thus, both share a similar status in their respective fields. From this, we have:

Proposition 9.

In the dynamics of economic externalities, market residue is characterized by neutrinos, denoted as

V_{e}

, where e represents market charge. Similar to the earlier discussion on the isospin of electrons and electron neutrinos, we have,

Proposition 10.

Under the influence of economic externalities, market charge and market residue form an isospin, still denoted as

(\begin{matrix} e \\ V_{e} \end{matrix})

Neutrinos possess some unique properties. In gauge field theory, conventional mass concepts refer to Dirac mass, whereas neutrino mass refers to Majorana mass [5]. Moreover, neutrinos are their own antiparticles. These characteristics provide speculative reference space for further research into market residue.

2.4. Symmetry and Isospin Space

In mathematical terms, isospin dynamics satisfy SU(2) symmetry [6]. Weak isospin is characterized by two-dimensional Dirac spinors. In the language of group theory, this implies there are two basic representatives, thus its gauge symmetry can be described by the SU(2) symmetry group. This group has three generators, expressed by three Pauli matrices as follows,

σ_{1} = (\begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix}) ， σ_{2} = (\begin{matrix} 0 & - i \\ i & 0 \end{matrix}) ， σ_{3} = (\begin{matrix} 1 & 0 \\ 0 & - 1 \end{matrix})

This is called the isospin space. Similarly, we have:

Proposition 11:

The two types of isospins generated by economic externalities satisfy SU(2) symmetry and are characterized by three Pauli matrices as their isospin space. Here, the two types of isospins are respectively: economic impulse flavor charge isospin

(\begin{matrix} u \\ d \end{matrix})

market charge residue isospin

(\begin{matrix} e \\ V_{e} \end{matrix})

3. The Microeconomic Properties of the Market

In this section, we use concepts from microphysics to characterize the microeconomic properties of market components. It's important to note that this approach represents a transfer of knowledge from physics concepts but it does not imply any materialization of market phenomena. The aim of this study is to explore the interaction between economic externalities and markets, beginning with further consideration of the attributes of market components.

3.1. Dirac Equation and Markets

As stipulated in the propositions of the previous section, demand, supply, market sentiment, and economic impulses are characterized respectively by electrons, positrons, neutrinos, and quarks. These are all spin 1/2 fermions (commonly understood as matter particles). In earlier sections, we introduced the concept of wave functions for market components. Without considering interactions and external potential constraints for now, let

ψ

denote the free fermion wave function, whose dynamics are described by the Dirac equation:

i ℏ \frac{\partial ψ}{\partial t} = [c \vec{α} (- i ℏ \nabla) + β m c^{2}] ψ

Firstly, note that the above equation contains two constants: ℏ, the Planck constant, which informs us of the quantum nature of the Dirac equation, and

c

, the speed of light constant, which indicates the relativistic nature of this equation. In the context of this paper, relativistic means monetary, specifically that monetary dynamics have a quasi-light-like nature. Therefore, market components are sensitive to money, meaning they are price sensitive. These aspects were extensively discussed in the preceding papers [1,2,4]. The left side of the equation indicates it is a time-dependent Hamiltonian. Here,

\nabla

represents the gradient operator:

\vec{\nabla} = \frac{\partial}{\partial x} \hat{x} + \frac{\partial}{\partial y} \hat{y} + \frac{\partial}{\partial z} \hat{z}

Choosing a basis set, we have:

\vec{\nabla} = \frac{\partial}{\partial x^{1}} \hat{e_{1}} + \frac{\partial}{\partial x^{2}} \hat{e_{2}} + \frac{\partial}{\partial x^{3}} \hat{e_{3}}

Using the same basis set,

\vec{α}

is a vector which can be expanded as:

\vec{α} = α_{1} \hat{e_{1}} + α_{2} \hat{e_{2}} + α_{3} \hat{e_{3}}

In this equation, Dirac introduces two parameter matrices

\vec{α}

and β; their form and their magical effects will be seen shortly. The second term on the right side of the Dirac equation is the rest mass term; this can be clearly understood through the plane wave solutions of the wave function [6,7]. The role of this mass term, when interacting with market components and economic externalities, provides coupling constants [6]. The concept of coupling constants plays a foundational role in economic externality dynamics. Any economic externality cannot be too extreme; otherwise, it won't be accepted and thus won't be effective. As discussed earlier in a proceeding article [2], starting from the classical dynamics analysis of markets, the concept of market clearing point provides a common sense: market participants, while naturally rational in buying low and selling high, do not behave excessively. They neither demand exorbitant prices nor sell at rock-bottom prices, as it hampers transactions. The composure shown by market clearing point from market participants can thus be approximated as coupling constants between supply and demand. From the above discussion, we have

Proposition 12:

The market (free) spin

\frac{1}{2}

Fermion components are characterized by the Dirac equation.

Proposition 13:

The common knowledge of supply and demand regarding market prices is characterized by some coupling constants.

3.2. Dirac $γ$ Matrix Notation

In the Dirac equation, matrices β and

α_{i}

are defined by the Dirac

γ

matrices. We have:

γ^{0} = β

γ^{i} = β α_{i ，} i = 1 ， 2 ， 3 .

In Section 2.4, three Pauli matrices were introduced and rewritten as follows:

σ_{1} = (\begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix}) ， σ_{2} = (\begin{matrix} 0 & - i \\ i & 0 \end{matrix}), σ_{3} = (\begin{matrix} 1 & 0 \\ 0 & - 1 \end{matrix})

Clearly,

γ

is a 4×4 matrix. At the same time, we have the Dirac representation of chirality:

γ^{0} = (\begin{matrix} 0 & I \\ I & 0 \end{matrix}) = (\begin{matrix} \begin{matrix} 0 & 0 \\ 0 & 0 \end{matrix} & \begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix} \\ \begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix} & \begin{matrix} 0 & 0 \\ 0 & 0 \end{matrix} \end{matrix}),

γ^{5} = (\begin{matrix} - I & 0 \\ 0 & I \end{matrix}) = (\begin{matrix} \begin{matrix} - 1 & 0 \\ 0 & - 1 \end{matrix} & \begin{matrix} 0 & 0 \\ 0 & 0 \end{matrix} \\ \begin{matrix} 0 & 0 \\ 0 & 0 \end{matrix} & \begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix} \end{matrix}),

The marvel of the Dirac coefficient matrix lies in enforcing the anti-commutation relation,

\{γ^{u} ， γ^{v}\} = 2 g^{u v}

This is a necessary condition in Fermi statistics for spin

\frac{1}{2}

particles (such as electrons).

In classical quantum mechanics, the wave function is denoted by

φ

. In quantum field theory, the wave function is treated as a field, further considered as an operator, denoted as

ψ

. Its adjoint operator is denoted as

ψ^{†}

. This is known as the second quantization. The Dirac matrices defined above have the following important properties:

γ^{5} = i γ^{0} γ^{1} γ^{2} γ^{3}; {(γ^{5})}^{2} = I; {(γ^{5})}^{†} = γ^{5} .

Furthermore, when

ψ

is a spinor operator, its adjoint spinor is not simply

ψ^{†}

but characterized as

\bar{ψ} = ψ^{†} γ^{0}

. When

ψ

is treated as a particle,

\bar{ψ}

is characterized its antiparticle. Hence, the Lagrangian can be correspondingly written as:

L = i \bar{ψ} γ^{u} \partial_{u} ψ - m \bar{ψ} ψ

where

\bar{ψ}

represents the adjoint spinor. The notation

γ^{u} \partial_{u}

denotes the Einstein summation convention, which will be repeatedly used in subsequent descriptions. It's worth mentioning that the formula,

γ^{5} = i γ^{0} γ^{1} γ^{2} γ^{3},

has a clever solution in market dynamics. Organizing the terms in

γ^{0} γ^{1} γ^{2} γ^{3}

to express the eigenstates of demand spin as buy or don't buy, and supply spin as sell or don't sell, then

γ^{5}

represents the price. Before a transaction occurs, this is still a virtual bargaining process, so it must be complex with

i

3.2. The Chirality and Helicity of Market Components

To understand the contents of this section, it is necessary to supplement some textbook knowledge [7]. Like positrons, electrons, and neutrinos in physics, supply, demand, and market residues all have chirality in economic dynamics, which can be left-handed or right-handed. Thus, taking the left-handed state as the component

ψ_{L}

, and the right-handed state as the component

ψ_{R}

, a market component can be represented by the Weyl spinor as

ψ = (\binom{ψ_{L}}{ψ_{R}})

. By using Dirac matrix

γ_{5},

through the following equations, the component of left-hand spinor and the component of right-hand spimor can be solved as follows:

ψ_{L} = \frac{1}{2} (I - γ_{5}) ψ, ψ_{R} = \frac{1}{2} (I + γ_{5}) ψ

Here,

P_{L} = \frac{1}{2} (I - γ_{5}) a n d P_{R} = \frac{1}{2} (I + γ_{5})

are defined as chiral projection operators.

P_{L} ψ

and

P_{R} ψ

are eigenstates of

γ_{5}

, with eigenvalues -1 and +1 respectively. Thus,

γ_{5}

becomes a chiral operator, with its eigenstates being the left-handed and right-handed states of the Dirac spinor. The sensitivity of particle chirality lies in weak force dynamics, where the weak force interacts only with left-handed particles and right-handed antiparticles. Correspondingly, we have

Proposition 14:

Economic policies (including monetary and fiscal policies), as economic externalities, interact only with left-handed demand and right-handed supply.

Some explanations follow. First, a particle in motion has its direction of motion (its momentum direction) and its spin direction. When the direction of motion aligns with the spin direction, chirality corresponds to spin. We define spin up as left-handed and spin down as right-handed. Second, an antiparticle in motion can be considered as the time reversal of the corresponding particle. Under the same conditions, we define its spin up as right-handed and its spin down as left-handed. Third, the above statements hold true only for massless particles. For particles with mass, the spin direction and motion direction are not completely aligned but have deviations. Fourth, as Penrose explains [7], the instantaneous speed measured for an electron is always the speed of light, although the overall average speed of an electron is less than the speed of light. Therefore, for the sake of clarity in this context without causing misunderstanding, this text assumes that chirality aligns with spin. Fifth, recalling from the previous discussion [2], demand is characterized between buying and not buying by spin. We define buying as characterized by spin up (left-handed) and not buying as characterized by spin down (right-handed). Similarly, supply is characterized between selling and not selling by spin. We define selling as characterized by spin down (right-handed) and not selling as characterized by spin up (left-handed). In summary:

Proposition 15:

Effective economic policies interact with left-handed demand and right-handed supply to stimulate the economy and invigorate the market.

The concept to be introduced next is helicity. Helicity is a representation of the eigenstates of chirality, while chirality is a general representation of helicity. The background knowledge here pertains to spinor field in quantum field theory. A spinor field has four complex components, forming a four-dimensional complex space, which can be decomposed into two two-dimensional complex spaces, each rotating in the same manner with respect to the rotation of four-dimensional spacetime. These two- or four-dimensional complex vectors, which rotate with respect to the rotation of four-dimensional spacetime, are called spinors, and their field is called a spinor field. Specifically, here we are applying the physics of Weyl spinors [7] in market dynamics.

In quantum field theory, various particles are initially described by the language of gauge field theory, with no mass terms in their Lagrangian density functions. Later, when introducing the Higgs field (a scalar field), it explains how gauge particles acquire mass through the Higgs mechanism. In other words, it is presumed here that various gauge particles with spin 1/2, such as quarks, neutrinos, electrons, and positrons, are all massless. Massless spin 1/2 particles are described by the Weyl equation [7], written as follows:

\partial_{0} ψ = \pm σ^{i} \partial_{i} ψ

Considering the plane-wave solutions of this equation, one can derive:

ξ \equiv \frac{σ \cdot k}{|k|} = \pm 1

Among these, helicity, known as the particle's helicity, is the cosine of the angle between the particle's spin and its momentum direction. We know that three-dimensional momentum has three components, each multiplied by a Pauli matrix, denoted as σ · p. This is another expression of helicity.

As discussed earlier, in the process of negotiation, potential buyers represent demand while potential sellers represent supply. Before the actual transaction takes place, no consequences arise, and demand and supply can be considered temporarily massless. From a cognitive standpoint, both demand and supply have an intrinsic property of spin, manifested as hesitation between buying and not buying or selling and not selling. However, at the behavioral level, buyers must make decisions between buying and not buying, while sellers must decide between selling and not selling. In other words, as massless spin-market components, demand and supply each have two specific eigenstates. Thus, we have:

Proposition 16:

At the behavioral level of market activity, helicity is an inherent characteristic of both demand and supply.

4. The Helical Structure between Supply and Demand

4.1. CPT Theorem

History progresses in a spiral, and so does the economy, as well as the market. The market is where transactions take place, so how do transactions evolve in a spiral fashion, and how does economic externality influence them? Here, we first provide three possible inversion transformations. Financial markets are constantly changing—what changes? Buyers become sellers, sellers become buyers, reflecting the conjugated relationship between demand and supply. In quantum field theory, transforming a particle into its antiparticle is described by time reversal, known as the charge conjugation operator, denoted as

C

。We have

C | ψ⟩ = | \bar{ψ}⟩

. Specifically, the transformation

C

that turns a particle state with electric charge

q

into a particle state with electric charge

- q

is called electric charge conjugation. Additionally, there are the time reversal operator

T

and the space reversal (parity) operator P. Each of these changes the physical properties of particles, and each alone does not satisfy symmetry. However, when these three transformations are combined, they satisfy symmetry, known as the famous CPT theorem. These topics are beyond the scope of this article. The ever-changing nature of the market, the interplay between demand, supply, and prices should indeed satisfy the CPT theorem. Moreover, coupled with the impact of economic externalities, it clearly enriches the market's linkage mechanisms. The intricacies herein may be difficult to fully grasp in this section, but the intent is to explore the path.

4.2. Penrose's Zigzag Helicity Process

Considering the helicity of particles, particles can be described by a two-component wave function (i.e., Pauli spinors). The most vivid yet rigorous description of particle helicity that the author has encountered is Penrose's use of zigzag language in Chapter 25 of "The Road to Reality." [8] Likewise, in economic dynamics, demand is depicted by electrons, while supply is depicted by their antiparticles, positrons. Therefore, below we directly use zigzag language to discuss demand and supply.

Due to helicity, a demand can be separated into left-handed demand spinor and right-handed demand spinor, denoted sequentially as zig and zag. This reflects the two eigenstates of demand hesitating between buying and not buying. Similarly, a supply can be separated into left-handed supply spinor and right-handed supply spinor, denoted as

{z i g}^{'}

and

{z a g}^{'}

respectively. This reflects the two eigenstates of supply hesitating between not selling and selling. Expanding on this, demand to buy is noted as zig, demand not to buy as zag, supply not to sell as zig', and supply to sell as zag'.

In this interpretation, zig particles are the source of zag particles, and conversely, zag particles are the source of zig particles, with a coupling strength between them. In other words, zig and zag can be seen as a back-and-forth motion, where the forward zig motion is followed closely by the backward zag motion, and vice versa (see Figure 1, from Penrose [8]，p630).

It can be considered that zig has negative helicity, while zag has positive helicity. This process can extend but only to a finite length. For an increasing length zigzag process, its overall effect is equivalent to the overall movement of demand (or supply). For instance, a typical scenario is where a zig demand turns into a zag demand, then the zag demand turns back into a zig demand, and this zig demand again turns into a zag demand, repeating cyclically, forming a segment of finite length. This essentially describes a process of hesitation between buying and not buying (similarly, not selling and selling).

Using Penrose's zigzag notation, we can rewrite Proposition 14 as follows:

Proposition 14‘:

Economic policies (including monetary and fiscal policies), as economic externalities, only interact with left-handed zig and right-handed zag' occurrences (see Figure 2 from Penrose [8], p633).

Additionally, Penrose suggests that spin 1 massive particles can be described using three components: left-handed zig (helicity +1), right-handed zag (helicity -1), and spinless "zog" (helicity 0). Penrose argues that it is the zog particle that mediates weak interactions (i.e., economic externalities).

4.3. Modeling the Weak Interaction of Economic Externalities

We can now restate the proposition as follows: Effective economic policies stimulate the economy and invigorate the market through interactions with zig and zag', thereby adhering to the principle of economic externalities (weak interaction).

So, how do these interactions occur? We will introduce the famous Electroweak Model in Section 5. Here, let's first provide several other possible modeling directions.

Electrical attraction, the market is a place for doing business, where there is demand and supply, seemingly leading to prices and markets. However, markets do not always naturally occur; sometimes demand and supply are far apart, and other times they barely miss each other. Encounters between demand and supply or even transactions incur transaction costs. Markets are also not always efficient; market failure occurs when a free market cannot efficiently allocate goods and services, necessitating the introduction of economic externalities for regulation. For instance, if market failure is due to a monopoly, economic policies (including monetary policy, fiscal policy, or market regulations) need intervention. If market failure arises from outdated economic policies, new policies are required for correction. This is the interplay of the invisible hand and the visible hand. Here, we can consider the following modeling directions

First, the wave function model. The evolution of interactions between demand and supply can be viewed as a two-body problem. This can be modeled using the two-body wave functions from quantum mechanics, with economic externalities treated as potential energy.

Second, the photon and electric charges model: While likening market charges to electrical charges, demand to electrons, and supply to positrons is an effective modeling approach in market dynamics, the economic world differs from the material world where there are ubiquitous pairs of positive and negative electrons, constantly appearing and disappearing, perpetually renewing. However, in the economic world, there are no ready-made deals or buys that fall from the sky. Prices are similar to a photon field, guiding the trajectory of the market. Economic externalities influence market transactions through their impact on prices. An interaction between an electron and a positron generates one or more photons (to conserve energy), and photons create a new pair of electrons and positrons. This process can characterize the bargaining process in market dynamics.

Third, the Buy-Sell intention substitution model: In principle, externalities cannot command the market. So how do economic externalities influence the market? In physics, electrons and positrons (and neutrinos) are collectively referred to as leptons. Leptons have generational differences. Electrons and positrons

{(e}^{\pm})

, being light, belong to the first generation. There are heavier particles such as muons

μ^{\pm}

(2nd generation) and tauons （

τ^{\pm}

）, (3rd generation). Electrons and positrons interact with weak force mediators

(W^{\pm}

） to produce a pair of muons. This means weak force can convert a pair of low-mass positive and negative leptons into a pair of high-mass positive and negative leptons (see Figure 3).

Demand and supply each consist of two components: buying-selling intentions and target goods [2]. Buying-selling intentions carry market charges. Intentions can be categorized into weak, moderate, and strong generations. Thus, we have

Proposition 17.

Economic externalities can change the degree of buying and selling intentions, and can be modeled by the substitution effect of weak force on leptons.

Fourth, double helix model. Referring to Penrose's characterization of particle and antiparticle helicity with zigzag in 4.2, consider two Penrose helical chains: one is the demand zigzag helical chain, and the other is the supply zig'zag' helical chain. Meanwhile, we know that economic externalities sometimes have positive effects on the market and sometimes negative effects. Economic externalities can be categorized into positive externalities (H) and negative externalities (-H). Then, stipulate that zig and zag' are connected by H, and zag and zig' are connected by -H, denoted as H(zig, zag') and -H(zag, zig') respectively. Obviously, here economic externalities replace the role of hydrogen bonds, forming a dual helix trading model of trading similar to the DNA double helix structure.

This modeling approach has its potential advantages, potentially developing into a kind of cellular model. First, imagine a cell surface with a bilayer membrane, where the inner membrane carries DNA genetic codes structured as the dual helix chain built above. Secondly, one could design a Gödel numbering system responsible for self-reference and self-replication. In addition, its outer membrane carries mRNA, equivalent to the psychological traits and cognitive patterns of buyers or sellers, responsible for interacting with various external information enzymes to produce protein-based cognition. Douglas Hofstadter [9] refers to this cellular-like structure as molecular logic. In his book, "Gödel, Escher, Bach: Escher, Bach: An Eternal Golden Braid," he constructs a molecular model of a computer language and its operation (Chapter 16), which is an intricate and highly descriptive modeling method but beyond the scope of this article.

5. The Essence of Economic Externalities and the Electroweak Model

5.1. Philosophy of Externalities

We first need to embark on an economic philosophical inquiry: What is the essence of economic externality? The answer lies in market neutrality. In other words, it entails maintaining market neutrality, where the market does not lean towards demand nor towards supply. The market cannot be biased towards the demand side or the supply side; it must only exist as a unified entity encompassing both demand and supply. This understanding, seemingly commonplace, carries profound insights.

Market neutrality is not just the essence of the visible hand but also of the invisible hand. In earlier discussions [4], we defined the quantum version of the invisible hand as the uncertainty observed among market participants. This definition simultaneously establishes a global symmetry, implying that this hand remains unseen and constrains all market participants, whether buyers or sellers, under its uncertainty.

Superficially antagonistic, the visible hand and the invisible hand are fundamentally twins. They cooperate to sustain and perpetuate the market's vitality — the very life of the market. The essence of the market lies in demand and supply. The invisible hand is invariably linked to issues of market inequality, while the visible hand pertains to market fairness. Both manifest their existence through prices, representing two sides of the same coin. According to my interpretation of Georg Simmel's "Philosophy of Money," this duality of prices embodies the logic of the market, a kind of binary logic. The relationship between supply and demand constitutes the semantics of this binary logic. For both demand and supply, this market logic should be inherently unobservable. In other words, neither demand nor supply can manipulate the market.

For the market, each participant — whether buyer or seller — constitutes an element, not a subset. Therefore, all market participants, regardless of their position in demand or supply, exist in a symmetrical state. Only through this can the sustainability of the market be ensured, namely its conservation. This is akin to the market version of Noether's theorem: non-observable implies symmetry, and symmetry implies conservation.

Section 2 of this article discusses weak isospin dynamics, including the isospin between demand (or supply) and market residue. This model of isospin is analogous to the isospin of electrons (positrons) and neutrinos. The existence of electron-neutrino isospin predicts the existence of a neutral weak force mediator (boson, lepton), along with its corresponding neutral weak current. This is known as the isospin hypothesis. One of the subsequent contents aims to derive the neutral weak current and explain its dynamic implications for economic externalities.

In the previous article [2], market dynamics and sub-economic dynamics were discussed within the framework of free market assumptions, exploring how the invisible hand operates. Now, we investigate how the visible hand operates.

5.2. Weak Force Mediator and Weinberg Rotation

To illustrate this, we need to delve into some mathematical transformations and derivations. We will explain this in a relatively concise manner; readers not interested in these details can skip ahead to the conclusion.

Speaking in the language of mathematical group theory, the isospin space is two-dimensional, characterized by the SU(2) symmetry group, with two basic representations. According to the formula

n^{2} - 1, w h e n n = 2;

this group has three generators. Therefore, to maintain the invariance of the Lagrangian in weak isospin dynamics, three-gauge fields need to be introduced, denoted as

W_{μ}^{1} ， W_{μ}^{2} ， a n d W_{μ}^{3}

. These gauge fields themselves do not have direct physical meaning. However, they can derive physical meaning through the following transformations:

W_{μ}^{\pm} = \frac{1}{\sqrt{2}} (W_{μ}^{1} \mp {i W}_{μ}^{2}) ， W_{μ}^{0} = W_{μ}^{3} ，

W_{μ}^{1} = \frac{1}{\sqrt{2}} (W_{μ}^{+} + {i W}_{μ}^{-}) ， W_{μ}^{2} = \frac{i}{\sqrt{2}} (W_{μ}^{+} - W_{μ}^{-})

where

W_{μ}^{\pm}

are called the electrically charged weak mediator, while

W_{μ}^{0}

is called the electrically neutral weak mediator.

Now, referring back to the earlier discussion [2] on quantum electrodynamics and market dynamics satisfying the U(1) symmetry group, only one gauge field is needed. In the context of the combined U(1) and SU(2) gauge, weak hypercharge

Υ

is introduced. In the corresponding gauge transformations, the covariant derivative is defined as:

D_{μ} = \partial_{μ} + i g_{B} Υ B_{μ} + i g_{w} T^{i} W_{μ}^{i}

Here,

B_{μ}

and

W_{μ}^{i}

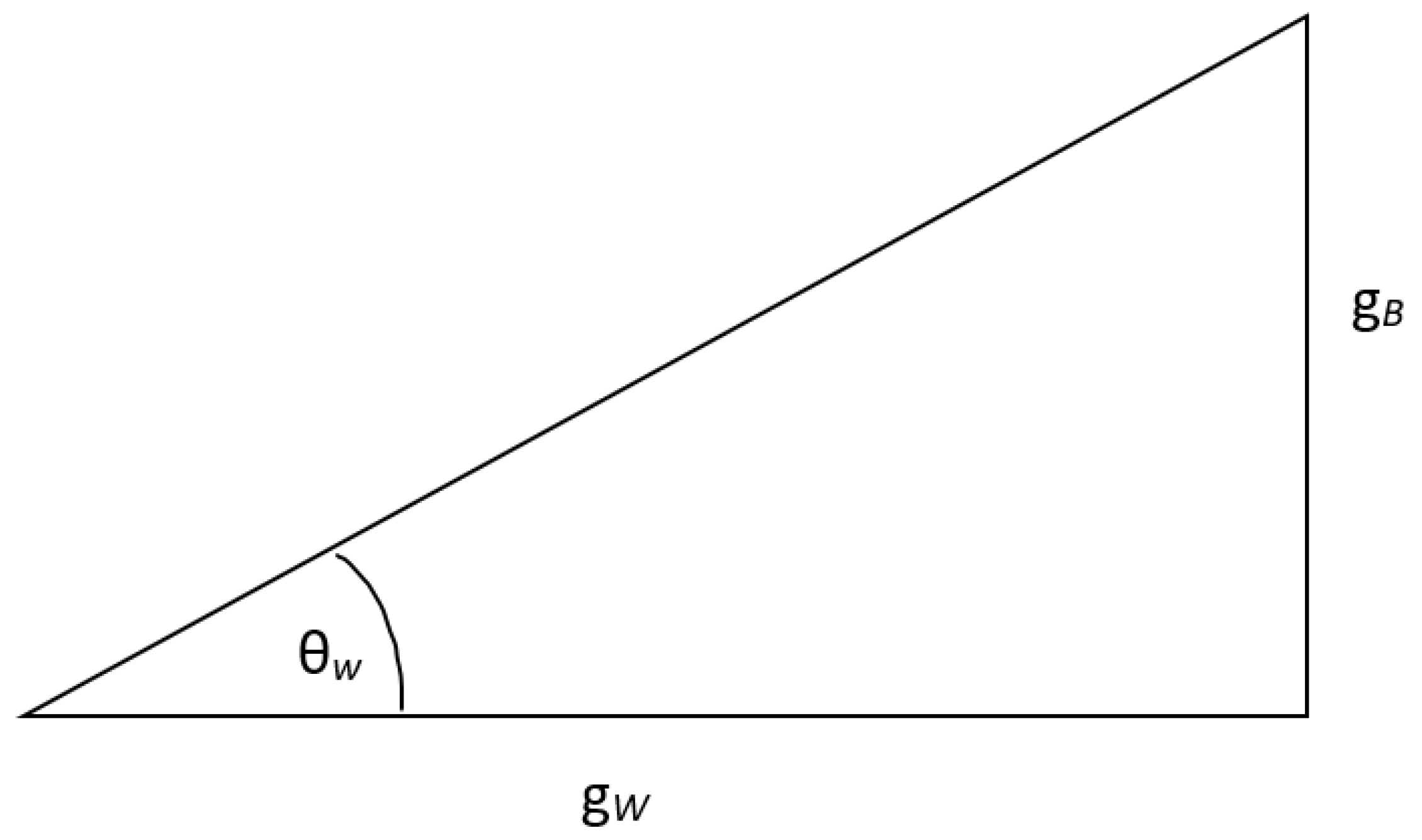
are gauge fields，while

g_{B}

and

g_{w}

are the corresponding coupling constants for the electron and weak bosons, respectively. With these two coupling constants, the Weinberg angle can be defined as:

t a n θ_{w} = \frac{g_{w}}{g_{B}}

which can be pictured below (see Figure 4 from McMahon [10], p229),

Note that

B_{μ}

and

W_{μ}^{0}

couple both are both charged leptons and neutrinos, but they themselves do not have direct physical meaning. However, unexpectedly, combining them using the Weinberg angle gives rise to direct physical significance. Therefore, we can define:

A_{μ} = \cos θ_{w} \cdot B_{μ} + \sin θ_{w} \cdot W_{μ}^{0}

Z_{μ} = - \sin θ_{w} \cdot B_{μ} + \cos θ_{w} \cdot W_{μ}^{0}

This rotation from

(B_{μ}

，

W_{μ}^{0})

(A_{μ}

，

Z_{μ})

is known as the Weinberg rotation. See Figure 4 for a schematic representation of the Weinberg angle.

As Zhengxing Wang [7] puts it: "The Weinberg rotation combines the seemingly physically meaningless gauge fields

B_{μ}

and

W_{μ}^{0}

to obtain the physical fields

A_{μ}

and

Z_{μ}

. It is truly ingenious. Just when it seems there's no way through, a bright path emerges from the darkness, making the Glashow-Weinberg-Salam model the most beautiful part of the Standard Model of particle physics."

Through the above rough mathematical reasoning, we finally theoretically identify

Z_{μ}

. This

Z_{μ}

particle does not change its electric charge when the weak interaction with charged leptons, hence it is electrically neutral. This is what electrically neutral signifies. In our discussion of externalities, we consider the visible hand to be neutral in market supply and demand, which is rooted in the electrically neutral attribute of

Z_{μ}

. Further explanation on this point will follow shortly.

5.3. Weak Hypercharge and Neutral Weak Current

The relationship between electric charge, weak hypercharge, and weak isospin charge is given by the following formulas,

Q = I^{3} + \frac{Υ}{2}

where

Q

represents the electric charge,

I^{3}

represents the weak isospin charge, and

Υ

represents the weak hypercharge. Weak hypercharge

Υ

and weak isospin charge

I^{3}

are mutually independent, hence

[Υ, \overset{⃑}{I}] = 0

. The role of weak isospin charge was introduced in Section 2. The relationship between electric charge and weak hypercharge is now understood as the interaction between charged leptons and weak force mediators. This interaction is known as the lepton weak current, generally expressed as:

J^{u i} = \sum_{e \to u, τ} (\bar{L_{e}}) γ^{u} τ^{i} L_{e}

where i = 1, 2, 3. Expanding this gives:

J^{u 1} = \sum_{e \to u, τ} ({\bar{v_{e}}}_{L}, \bar{e_{L}}) γ^{u} (\begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix}) (\binom{v_{e L}}{e_{L}}) = \sum_{e \to u, τ} ({\bar{e}}_{L} γ^{u} v_{e L} + {\bar{v}}_{e L} γ^{u} e_{L})

J^{u 2} = \sum_{e \to u, τ} ({\bar{v_{e}}}_{L}, \bar{e_{L}}) γ^{u} (\begin{matrix} 0 & - i \\ i & 0 \end{matrix}) (\binom{v_{e L}}{e_{L}}) = i \sum_{e \to u, τ} ({\bar{e}}_{L} γ^{u} v_{e L} - {\bar{v}}_{e L} γ^{u} e_{L})

J^{u 3} = \sum_{e \to u, τ} ({\bar{v_{e}}}_{L}, \bar{e_{L}}) γ^{u} (\begin{matrix} 1 & 0 \\ 0 & - 1 \end{matrix}) (\binom{v_{e L}}{e_{L}}) = \sum_{e \to u, τ} ({\bar{v}}_{e L} γ^{u} v_{e L} - {\bar{e}}_{L} γ^{u} e_{L})

where

J^{u 1}

and

J^{u 2}

are the charged lepton weak currents that change the electric charge, and

J^{u 3}

is the neutral lepton weak current that does not change the electric charge. The hypothesis of weak isospin space predicts the existence of the neutral lepton weak current.

The charged lepton weak current is coupled with the charged weak mediator

W^{\pm}

, while the neutral weak current can only couple with the electrically neutral weak mediator

Z^{0}

. Therefore, the discovery of the neutral lepton weak current

Z^{0}

particle confirms the hypothesis of weak isospin.

5.4. Lepton Weak Currents and Economic Externalities

First, let's distinguish three types of economic externalities: monetary policy, fiscal policy, and market regulations. Economic externalities are characterized by weak forces. Accordingly, we define monetary policy represented by the charged weak mediator

W^{+}

, fiscal policy by the charged weak mediator

W^{-}

, and market regulations by the electrically neutral weak mediator

Z^{0}

. As stated in the Section 2, demand is represented by the electron

e

, supply by the positron

\bar{e}

, and market sentiment (aftertaste) by the neutrino. Remembering these concepts allows us to interpret the three lepton weak currents within the framework of economic externality dynamics.

Each formula has three parts separated by two equal signs. On the left side of the formula is the name of this weak current. The middle of the formula shows the interaction (coupling) of the two isospins using matrices

γ^{u}

and corresponding Pauli matrices. On the right side is the state representation of this lepton weak current.

Note that in the right parentheses of the first two formulas,

J^{u 1} a n d J^{u 2},

there are four terms of mixed flow:

{\bar{e}}_{L} γ^{u} v_{e L} 、 {\bar{v}}_{e L} γ^{u} e_{L}

、

{\bar{e}}_{L} γ^{u} v_{e L}, a n d {\bar{v}}_{e L} γ^{u} e_{L}

. These mixed flows, as we have just seen, always associate electrons or positrons with neutrinos. According to the previous definitions, this means that economic policies, whether monetary or fiscal, always relate market supply and demand to market participants' experiences. Why do we need economic policies? Because there is always an imbalance between supply and demand in real markets, and consequently, there will always be fluctuations in market participants' experiences or sentiments. When people's market experiences and sentiments fluctuate dramatically, or when market supply and demand are excessively imbalanced, visible hands are needed to help, and economic policies play a mediating role.

Finally, the key is the third formula

J^{u 3}

.In the parentheses on the right side, we see two clean flows:

{\bar{v}}_{e L} γ^{u} v_{e L} a n d {\bar{e}}_{L} γ^{u} e_{L}

. In the former flow, there are only neutrinos and antineutrinos, and in the latter flow, there are only electrons and positrons. Mathematically, this is called trivialization, resulting in the orthogonalization of the neutrino flow and the electric flow. In physical terms, it is a type of neutral lepton weak current where charged particles remain unchanged, which means electrically neutral. So, what kind of economic externality separates market supply and demand from market sentiment? There is only one choice, which is market regulations. For market transactions, market regulations are actually externalities around us. Whether it's supply or demand, buying or selling, the essence of market regulations is to ensure fair prices. If this scope is exceeded, such as inflation, price monopolies, or market failures, economic policies like intervene. At the same time, market regulations strictly distinguish market supply and demand from market sentiment; only in this way can market conservation be ensured. Therefore, market regulations must be neutral in supply and demand.

Physicists tend to believe that the neutrino weak current reflects the essence of weak forces. According to our definition, market experiences and sentiments reflect the essence of economic externalities. Although market experiences and sentiments may be small, they can accumulate and eventually lead to changes in prices, driving the formation and implementation of economic policies. This demonstrates that human cognition is the most fundamental market externality, namely the weak force of the market.

6. General Discussion

This article first discusses the importance of economic externalities and then establishes two isospin models. These are preliminary contents of economic externality dynamics. Economic externality dynamics and its isospin models are constructed based on the concept structural framework of weak force theory and its isospin dynamics in particle physics. From the perspective of mathematical symmetry, the isospin model satisfies SU(2) symmetry. Earlier discussions on market dynamics [2] show that its model satisfies U(1) symmetry. In another earlier work [1], we also discusses sub-economic dynamics, whose model satisfies SU(3) symmetry. The symmetry expression of the standard model of particle physics is the direct product of three mathematical groups,

U(1)⊗SU(2)⊗SU(3).

So far, we have traversed most of the path in applying the standard model to construct the economic dynamics standard model.

The core of the particle physics standard model is gauge symmetry. The cost of this gauge symmetry is the masslessness of gauge particles, which is evidently unreasonable in physical terms. Particularly, the spontaneous symmetry breaking problem becomes more prominent upon discovering that gauge fields carrying weak force are indeed massive. The proposal of the Higgs mechanism fundamentally resolves this problem and thus becomes part of the standard model of particle physics. In economic dynamics, the ordinary rationality mechanism plays a role akin to the Higgs mechanism. From the perspective of theoretical physics, the standard model unifies in a certain sense the three natural forces: electromagnetic force, strong force, and weak force. From the perspective of economic philosophy, the standard model of economic dynamics unifies intentional cognitive power and consciousness power with external force.

Here, the logic is as follows. First, in market dynamics [2], buying and selling intentions carry market charges, cognitive fields are characterized by magnetic fields, and market dynamics use quantum electrodynamics as a reference framework of conceptual modeling. Second, in sub-economic dynamics [1], consciousness power plays a role akin to the strong force, characterized by strong force mediators, namely gluons, and sub-economic dynamics use quantum chromodynamics as a reference framework of conceptual modeling. Third, in the economic externality dynamics introduced in this article, economic external forces are characterized by weak force and use weak isospin dynamics as the conceptual model framework. To summarize, we have two standard models here, one is in physics, and another is in economics. They share the same gauge symmetries, which are characterized by the same mathematical symmetry groups.

The contents of weak force dynamics are very rich, providing many unexpected topics for discussion in economic externality dynamics. The gauge field theory of weak force dynamics also involves some more mathematized contents, including Lagrangian density function, gauge transformations, gauge fields and covariant derivatives, as well as the Higgs mechanism. Readers interested in these topics can refer to relevant articles or works by Tony Zee [5,6] or Zhengxing Wang [7].

Funding

This research received no external funding.

Acknowledgments

Thanks to Yongshi Wu, Yi Zhang, Xiao Xu, Hao Wu, and Zhangju Liu for their helpful discussions on physics concepts.

Conflicts of Interest

The author declare no conflict of interest.

References

Yang, Y. Principles of the sub-econ dynamics: The economic dynamics and the standard model (III). Sci. Econ. Soc. 2023, 41. [Google Scholar]
Yang, Y. Principles of the market dynamics: The economic dynamics and the standard model (II). Sci. Econ. Soc. 2023, 41. [Google Scholar]
Hayek, F.A. Denationalization of Money: The Argument Refined. 1990, Coronet Books Inc.
Yang, Y. Contents, methods and significance of the economic dynamics: The economic dynamics and the standard model (I). Sci. Econ. Soc. 2022, 40. [Google Scholar]
Tony Zee, Group Theory in a Nutshell for Physicists. 1965, Princeton University Press, Princeton.
Tony Zee, Quantum Field Theory in a Nutshell. 2010, Princeton University Press, Princeton.
Zhengxing Wang, Elementary Quantum Field Theory. 2008, Peking University Pres, Beijing.
Roger Penrose, The Road to Reality: A Complete Guide to the Laws of the Universe. Random House Inc., New York, 2005.
Douglas Hofstadter, Gödel, Escher, Bach: An Eternal Golden Braid. New York: Basic Books，Inc., 1995.
David McMahon, Quantum Field Theory. McGraw-Hill, 2008.

Figure 1.

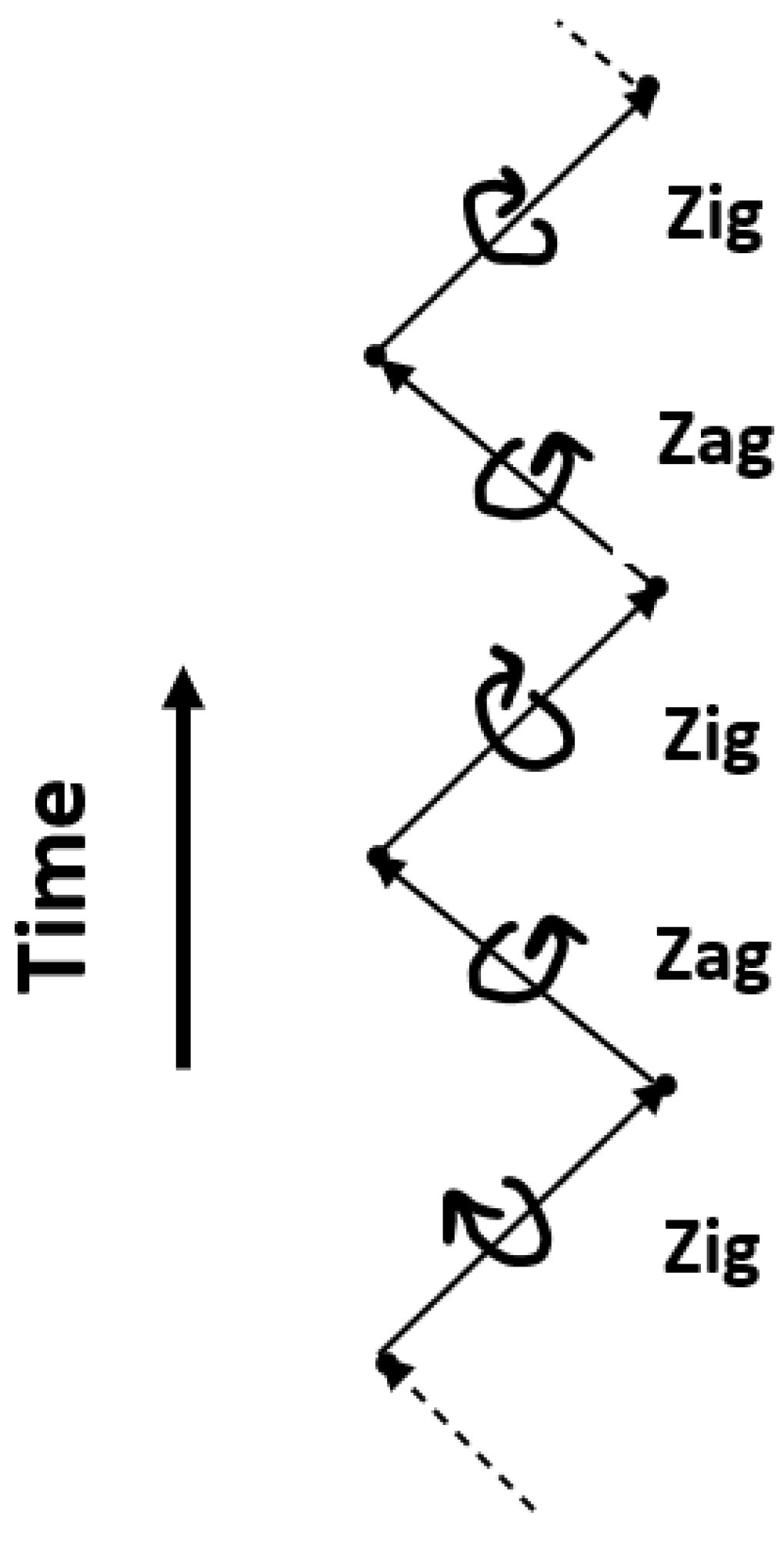
Figure 2.

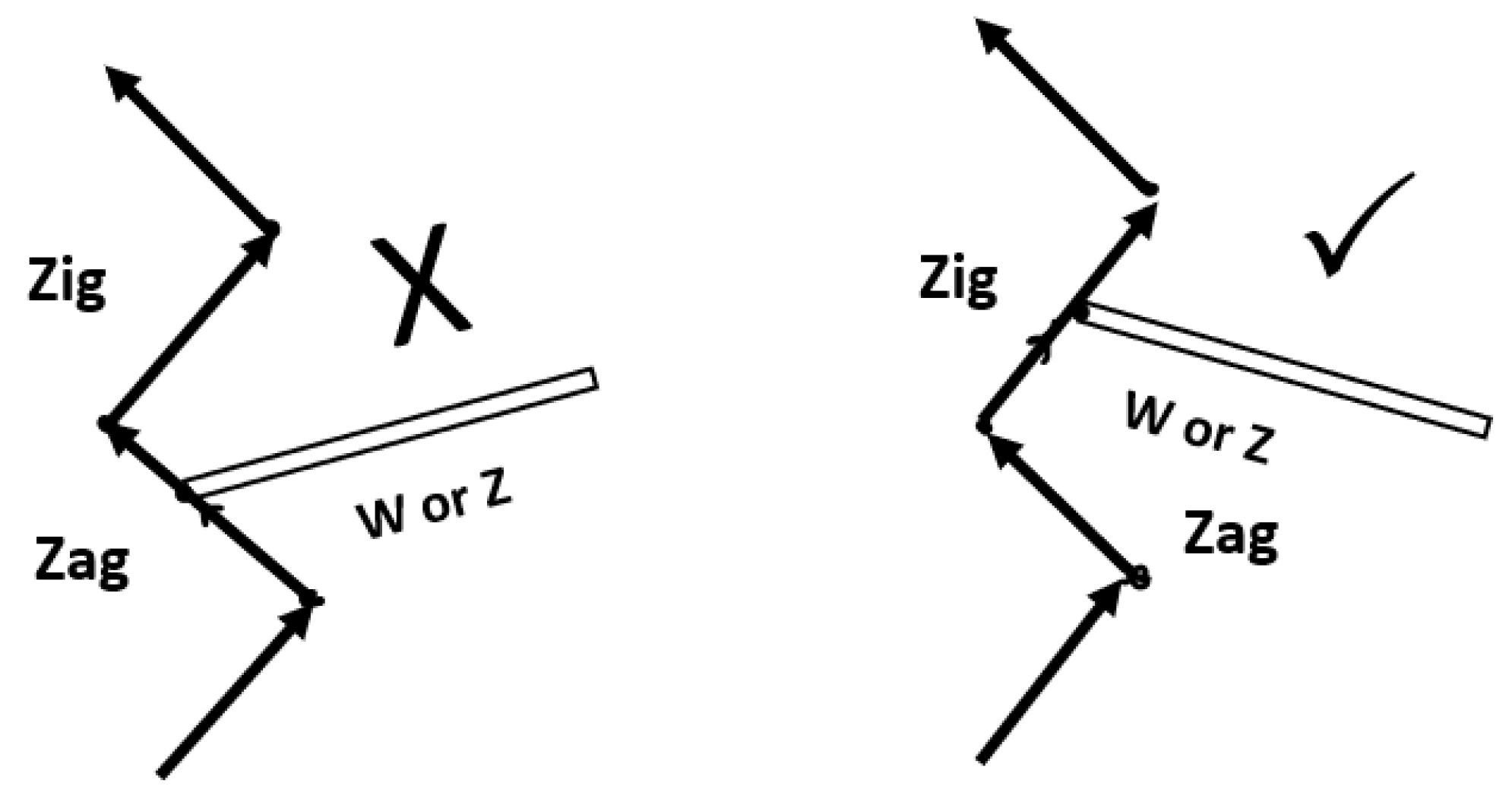
Figure 3.

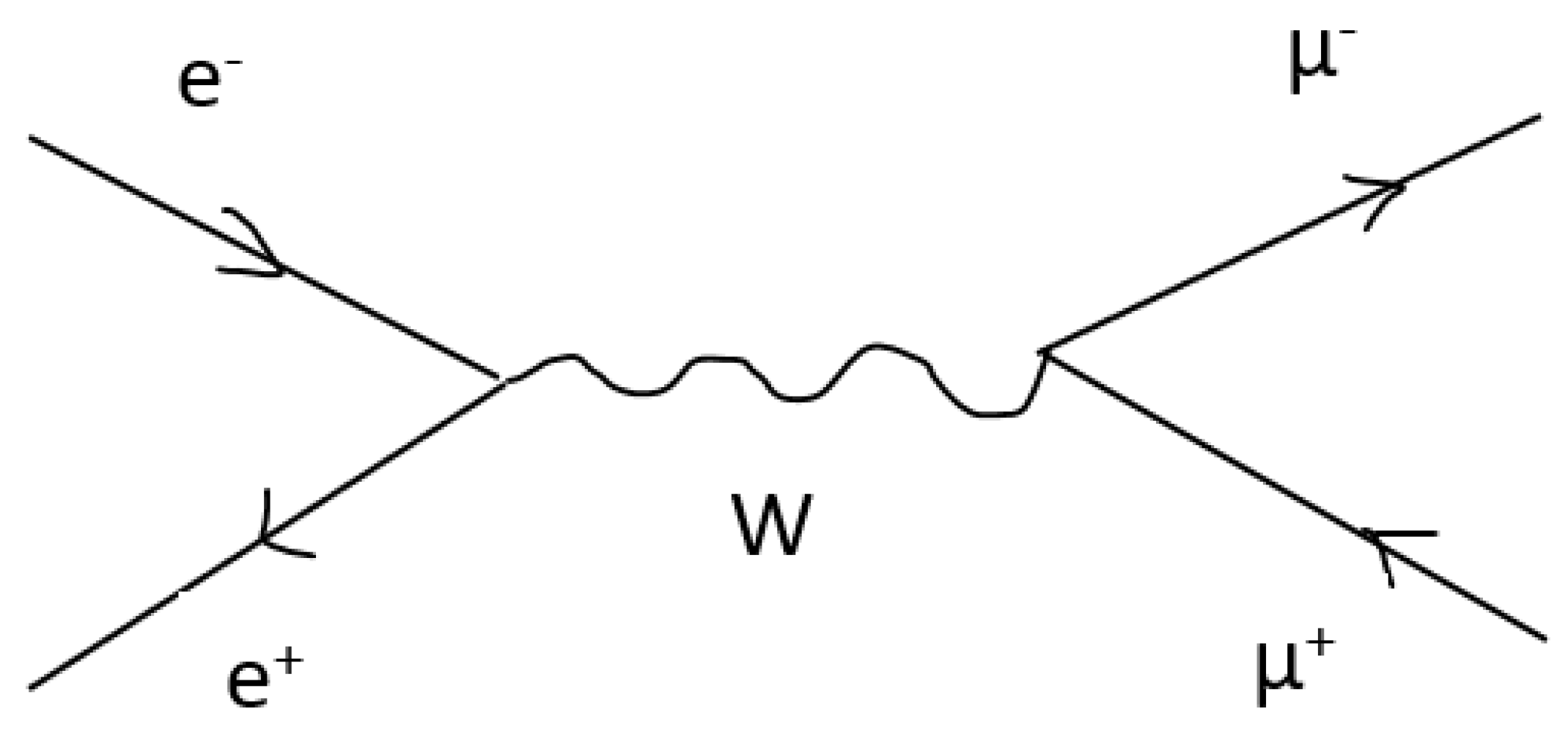
Figure 4.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Principles of Economic Externality Dynamics: The Economic Dynamics and the Standard Model (V)

Abstract

1. Introduction

2. The Visible Hand and Isospin

2.1. The Visible Hand

2.2. Weak Forces and Flavor Isospin

2.3. Isospin of Market Charge and Residual Taste

2.4. Symmetry and Isospin Space

3. The Microeconomic Properties of the Market

3.1. Dirac Equation and Markets

3.2. Dirac γ Matrix Notation

3.2. The Chirality and Helicity of Market Components

4. The Helical Structure between Supply and Demand

4.1. CPT Theorem

4.2. Penrose's Zigzag Helicity Process

4.3. Modeling the Weak Interaction of Economic Externalities

5. The Essence of Economic Externalities and the Electroweak Model

5.1. Philosophy of Externalities

5.2. Weak Force Mediator and Weinberg Rotation

5.3. Weak Hypercharge and Neutral Weak Current

5.4. Lepton Weak Currents and Economic Externalities

6. General Discussion

Funding

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

3.2. Dirac $γ$ Matrix Notation