Prerpints.org logo
Preprint
Review

Mechanical Behaviour of Breast Tissue: An In-Depth Systematic Review

Altmetrics

Downloads

138

Views

63

Comments

0

Submitted:

29 July 2024

Posted:

31 July 2024

You are already at the latest version

Alerts
Abstract
The breast holds significant importance in women's lactation process. The breast has diverse tissues such as glandular, Cooper’s ligament, lactiferous ducts, adipose, muscles, and skin with various mechanical properties. Most soft tissues exhibit nonlinear, viscoelastic, and anisotropic mechanical behaviour. Stiffness is one of the commonly used mechanical properties for measuring mechanical behaviour in soft tissues. However, this is typically used in simplifying cases where analysis is limited to within the linear elastic region. Young’s modulus is the prevailing measure for quantifying stiffness in tissues. This systematic review examines commonly used techniques for mechanically characterising breast soft tissues to close the gap in the literature. Additionally, this systematic review summarises the mechanical behaviour of the breast tissues available in the literature and highlights the uncovered areas to understand the mechanical behaviour of breast tissues fully. These include a) more mechanical behaviour studies, allowing more accurate modelling for other applications, b) Viscoelastic analysis studies, and c) mechanical analysis on other breast tissues, such as the lactiferous duct, also known as the milk duct. The data obtained in the review can be used as inputs in computational models to analyse the behaviour of the breast tissues.
Keywords: 
Subject: Engineering  -   Bioengineering

1. Introduction

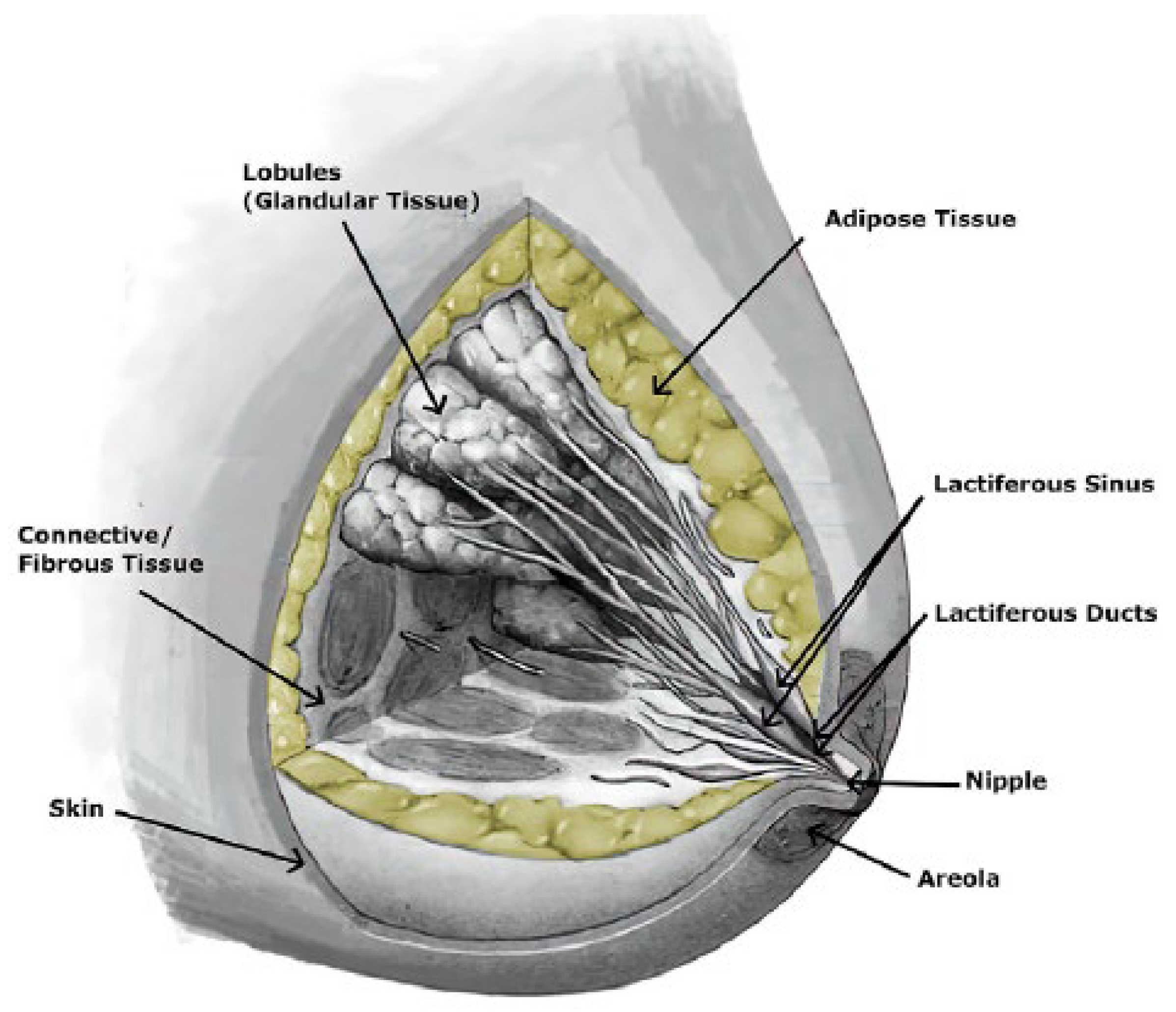
The breast is an organ associated with mammals and plays a crucial role in nurturing offspring [1]. A mammal is any member of a group of vertebrate animals in which the offspring are fed milk from the mother’s breast (mammary glands) [2]. The breast is essential as it plays a crucial role in lactation, which is a defining characteristic of the mammalian class [1,3]. It is a heterogeneous structure comprising various tissues, including glandular, adipose, and fibrous tissues (Figure 1) [4,5,6], which are responsible for the production and secretion of milk. The organ has varying proportions among individuals and dependent on age. Each woman’s breast is organised into lobes of glands known as lobules, containing excretory ducts that lead to the lactiferous sinus, extending from the central nipple-areolar complex. These lobes are embedded within fibrous and adipose tissues, accompanied by nerves, blood vessels, and lymphatic vessels [7].
The chest wall is substantially covered by the breast, with breast tissue potentially extending from the collarbone to the midpoint of the breastbone at the front. On the sides, breast tissue may extend into the armpit (root of the breast) and even reach as far as the latissimus dorsi muscle, which spans from the lower back to the arm’s humerus bone [8].
The composition of breasts varies among different women depending on differences in the amount of glandular, adipose, and connective tissue. These variances contribute to variations in breast firmness, as the ratio of adipose (fat) to connective tissue content plays a role. Moreover, the size and shape of breasts can fluctuate over time within the same woman due to factors such as changes during the menstrual cycle, pregnancy, post-weaning, and menopause [8]. Additionally, other than morphology and structure, the change in mechanical properties of a woman’s breast tissue is also due to factors such as menstrual cycle, menopause, lactation, age, etc. [7,9,10].
Moreover, a female breast primarily comprises the milk ducts, glandular lobules, adipose and the suspensory ligaments called Cooper’s ligaments, covered by muscle and skin [6]. Cooper’s ligaments are connective tissues that run from the pectoral fascia through and around breast tissues to the skin’s dermis. These ligaments keep the breast in place and maintain its shape [3,6]. From a mechanical point of view, connective tissues are typically considered essential for mechanical studies on soft tissues [5]. These tissues possess anisotropic, nonlinear, and time-dependent behavioural characteristics [11]. The stiffness of the tissue is greatly affected by the change in its structure. This is attributed to the higher sensitivity of Young’s modulus to structural change due to pathology such as cancer [12]. Young’s modulus is the prevailing measure for quantifying stiffness in tissues; it can be determined from the stress-strain curve as the slope by only considering the elastic region of the curve [3]. Moreover, Young’s modulus is dependent only on the material’s properties. Based on these assumptions, Young’s modulus can characterise tissues mechanically (Griffin et al. 2016). Additionally, the mechanical properties of breast tissues are characterised by viscoelasticity, primarily due to high collagen, which imparts viscous qualities to these tissues [13].
Although the breast comprises various tissues, adipose and glandular tissues are the primary ones. About 15-25 lobes of compound glands are embedded in fibrous and adipose tissues [8,14].

Literature Search Strategy

A systematic literature search was done to identify the mechanical characterisation of breast tissue publications. The literature search considered both human and animal studies. The Web of Science, IEEE, Science Direct, and Google Scholar databases were considered for the search. However, nothing related to the mechanical characterisation of breast tissues was found in the IEEE database. Most publications were found on the Web of Science and Science Direct databases. No exact number of publications from each database was noted. The following search terms were used as keywords: 1) Mechanical properties, 2) mechanical characterisation, 3) breast tissues, and 4) soft tissue. The synonyms for each term were added to increase the search findings.
The overall search strategy was structured as [(“breast tissues” OR “Mammary tissues”) AND (“mechanical properties” OR “mechanical behaviour”)]. The “OR” terms were used to find any synonyms within each category, while the “AND” terms were used to ensure that the search results included all key criteria.

Breast Tissue Mechanical Behaviours

The mechanical behaviour of soft tissues plays a crucial role in understanding the mechanisms underlying various diseases, particularly cancers and cardiovascular diseases [15]. Soft tissues exhibit complex mechanical properties that influence their response to physiological and pathological conditions. By studying these properties, researchers can gain insights into how diseases develop and progress [16]. For instance, the stiffness of cancerous tissues can differ significantly from that of healthy tissues, providing a potential biomarker for early detection. In cardiovascular diseases, the mechanical behaviour of blood vessels affects blood flow and pressure, which are critical factors in disease manifestation and progression. Therefore, analysing the mechanical properties of soft tissues not only enhances our understanding of disease mechanisms but also aids in the development of diagnostic and therapeutic strategies [17].
There exists an extensive array of testing techniques to characterise the mechanical properties of soft tissues [18]. Furthermore, the viscoelastic properties of the biological materials can be explored through standard creep and relaxation tests, as well as dynamic mechanical analysis. Additionally, these tests can be conducted under various deformation modes such as uniaxial tension or compression, equi-biaxial tension, pure or simple shear, planar tension, and multi-axial tension straining. 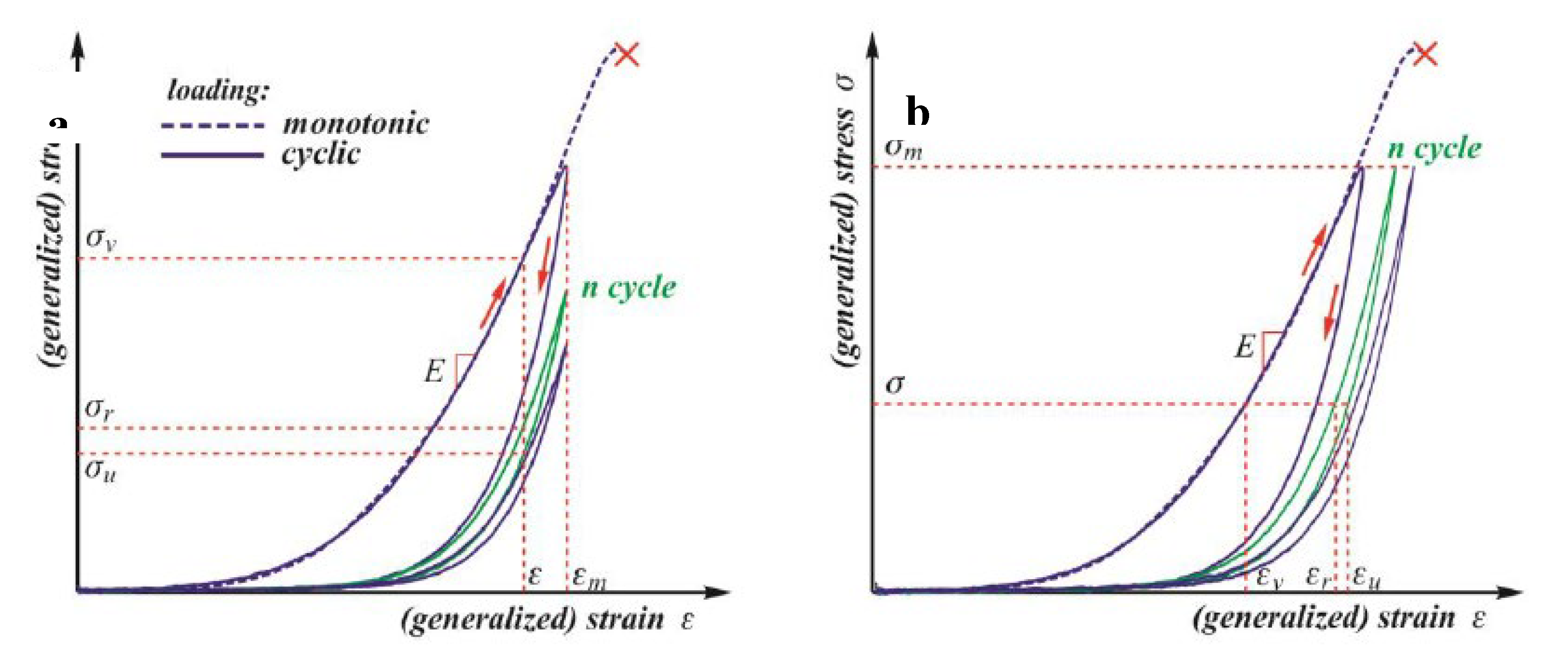Figure 2 illustrates the typical behaviour of soft tissues under monotonic and cyclic loading with three main curves under monotonic loading [18].
When subjected to monotonic loading, most soft tissues exhibit stress-strain curves that resemble a J-shape, characterised by three distinct phases. The most effective method to describe this pattern is by measuring the slope of the stress-strain curves and plotting it against the strain or stress. This approach forms the basis of the recognised Fung model, which explains the elastic behaviour of soft tissues. Nevertheless, under cycling loading, all biological soft tissues demonstrate a stress-softening phenomenon, initially observed in elastomers like natural and synthetic rubber, known as the Mullins effect. The primary challenge in qualitatively understanding this phenomenon lies in the variety of techniques used to quantify the degree of stress softening [18].
The mechanical characteristics of breast tissues are crucial for any attempt at biomechanical modelling and for designing biocompatible breast implants. Specifically, the interest is in the involved tissues’ elastic moduli and strength properties [8].
A comprehensive understanding of tissue-level behaviour is still lacking for the human breast [8,19]. Nevertheless, breast tissue exhibits nonlinear behaviour [20]. Moreover, most soft tissues exhibit nonlinear, viscoelastic, and anisotropic mechanical behaviour. This is primarily noticeable at large deformations [3]. Nevertheless, as a first approach, authors assume the soft tissue is elastic, isotropic, and nearly incompressible to determine the elastic modulus [21,22].
Different techniques, such as compression, tensile, and indentation, have been employed to determine the mechanical properties of various breast tissues [3]. Soft tissue’s mechanical characterisation would be in-vivo or in vitro [23]. Elastography is frequently employed in in-vivo experiments to investigate breast tissues. There are various elastography modalities, such as ultrasound (US), magnetic resonance (MR), or optical coherence tomography (OCT) elastography. These techniques indirectly measure the tissue’s stiffness by measuring the speed of shear waves propagating in the tissue of interest. The underlying concept is that shear-wave speed is related to tissue stiffness; shear waves travel faster in stiff tissues and slower in soft tissues. The previously mentioned techniques provide the capability to examine by imaging what once could only be examined by direct palpation, which is likely to open new opportunities to diagnose disease noninvasively. Moreover, besides stiffness, these elastography techniques can also measure other parameters such as shear-wave attenuation and tissue viscosity [24]. The researcher can utilise any of these modalities since they (modalities) yield similar results. While some researchers exclusively examined healthy breast tissues, including adipose and glandular tissues [25,26,27,28], others also considered diseased tissues, such as benign or malignant tumours [29]. [29] conducted the indentation test on the tumour specimen to produce force and displacement. Young’s modulus was determined through the iterative inversion technique that employs a finite element model of the piecewise homogeneous tissue in each iteration. From the study, the benign lesions and malignant tumours were found to be approximately five times and ten times stiffer than normal breast tissues, respectively.
Additionally, through mechanical testing and elastography, the instantaneous shear modulus for breast adipose samples usually ranges between 0.5 and 25 kPa [8,27,28,30]. The stiffness of the adipose tissue is dependent on the temperature. At 37   ℃ , adipose is more liquefied than at room temperature. Hence, the adipose modulus of elasticity is usually higher in in vitro than when the adipose is tested in in vivo [8,31].

Breast Skin

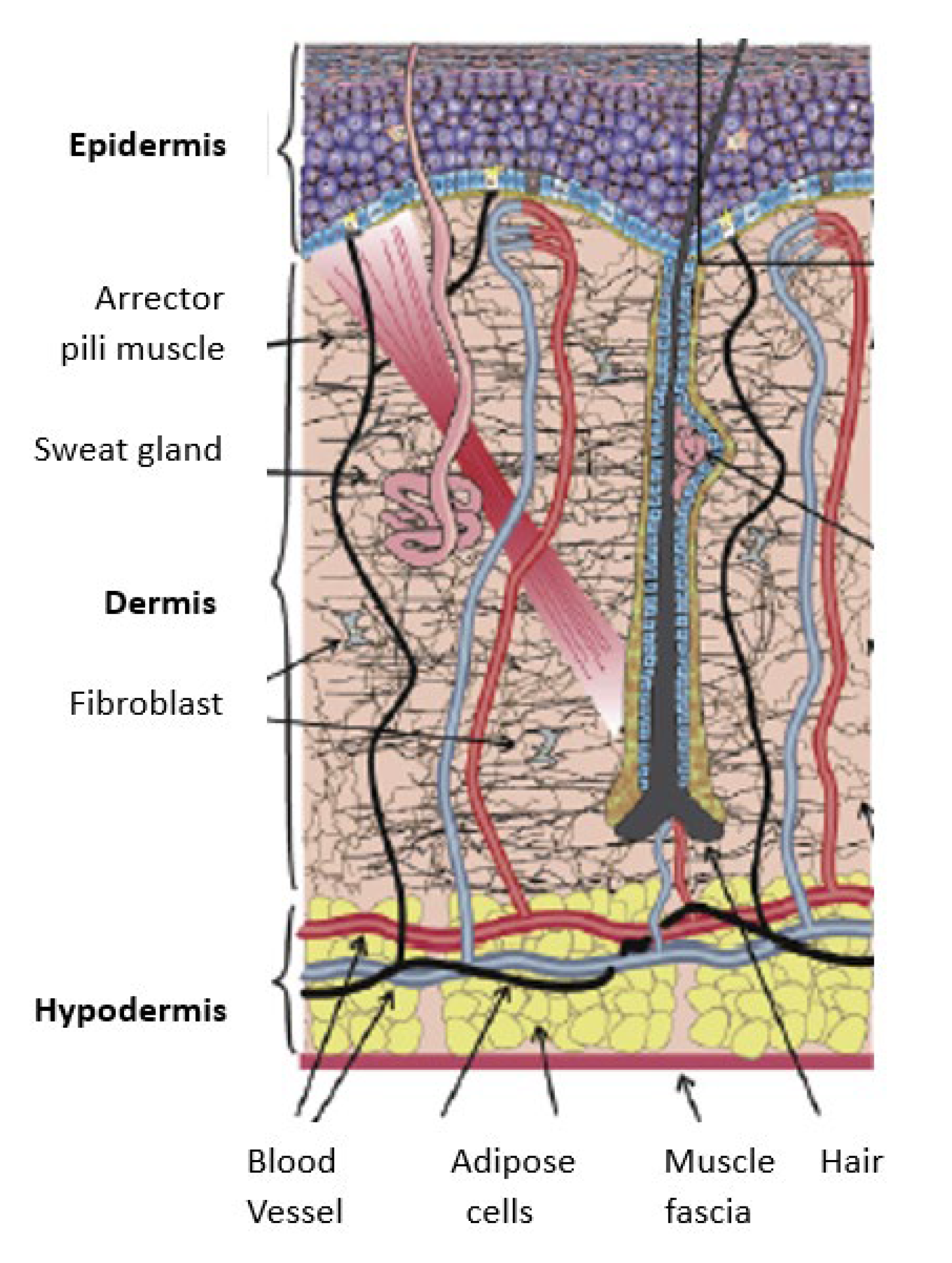
The skin comprises three layers: dermis, epidermis, and hypodermis (see Figure 3) [8,32]. The epidermis comprises a dead layer of cells called stratum corneum and has a thickness range of 50 – 100 µm. The dermis primarily comprises collagen and elastin fibers in a viscous medium made of water and glycoprotein. These fibers have different thicknesses with fibers in the deep dermis being thicker than the fibers of the upper dermis. Moreover, these fibers have a varying thickness of 1 to 3 mm. A collagen and elastin network within the dermis are arranged in various directions and subject to different prestress. The mechanical behaviour of the skin is determined by the deformation mechanism of collagen and elastin [33]. The hypodermis primarily comprises adipocytes, and its thickness differs from person to person [8].
Nevertheless, the epidermis comprises several layers, starting with the deepest layer, stratum basale, followed by the stratum spinosum, stratum granulosum, stratum lucidum, and the stratum corneum as the uttermost layer. Serving as the covering of the body, the epidermis plays a vital role in protecting the body from harm, maintaining hydration, generating new skin cells, and housing melanin, which determines skin colour [34]. Below the epidermis lies the dermis, which is intricately connected to the epidermis through the basal lamina (basement membrane). It comprises two interwoven layers of connective tissue – the papillary and reticular layers – the dermis accommodates sweat glands, hair follicles, muscles, sensory nerves, and bold vessels. The transition between these layers is seamless, lacking clear demarcation. The hypodermis is also referred to as subcutaneous fascia, constituting the deepest layer of the skin. It contains adipose and skin appendages such as hair follicles, sensory nerves, and blood vessels, contributing to insulation and cushioning beneath the dermis [35].
Preprints 113670 g003
Figure 3. Human skin structure [36].
Figure 3. Human skin structure [36].
Preprints 113670 g003
Like most soft tissues, human skin exhibits viscoelastic, nonlinear, and anisotropic mechanical behaviour. These mechanical properties vary with factors such as hydration, age, disease, and anatomical site. However, at 50% or less strains, the breast skin can be regarded as a linear isotropic material [8].
The surface (which includes the areola, nipple, and general skin cover) of the breast is enveloped by the skin [33,37], and the mechanical behaviour of the breast significantly influences the shape of the female breast. This is mainly attributed to the skin’s layered structure comprising the three previously mentioned layers [33].
The thickness of the skin is not uniform throughout the body; for example, the eyelids are thin, and the feet have thicker skin. The mechanical properties of the skin are influenced by its thickness, given the thicker dermis and more significant amounts of collagen and elastin. Accurate measurement of the mechanical properties of the skin requires concurrent measurement of its thickness. The primary objective is to non-invasively measure the biomechanical properties of breast skin in vivo through a simple, reliable, and reproducible method. Various non-invasive methods based on the mechanical models have been employed to determine both elastic and viscoelastic properties of human skin in vivo (suction test, optical coherence tomography (OCT), dynamic optical coherence elastography) [33,38].
[33], measured the elastic properties and thickness of the breast skin using the DermaLab suction-cup device and DermaScan ultrasound, respectively. The DermaLab suction-cup method works by positioning a small chamber on the surface of the skin and measuring the force required to deform the skin by a certain amount using gentle, gradual suction. The central part of the suction probe had a diameter of 10 mm. Two elevation sensors were placed at 1 mm and 2.5 mm from the skin’s surface. Double-sided tape secured the suction probe to the breast, creating a sealed chamber. Suction was applied by a vacuum pump to lift the skin to the desired elevation. The difference in suction pressure required to elevate the skin from elevation 1 to elevation two was recorded. Then, the modulus of elasticity was determined from the recorded pressure and strain data.
The time and suction pressure exerted over a predefined area of the skin were measured for a predefined fixed elevation of the skin. The average Young’s modulus of the breast skin was found to be 344 ± 88   k P a . The modulus range was 195 − 480 k P a . The 23 participants aged between 29 and 75 years were considered for the study.

1.2. Adipose

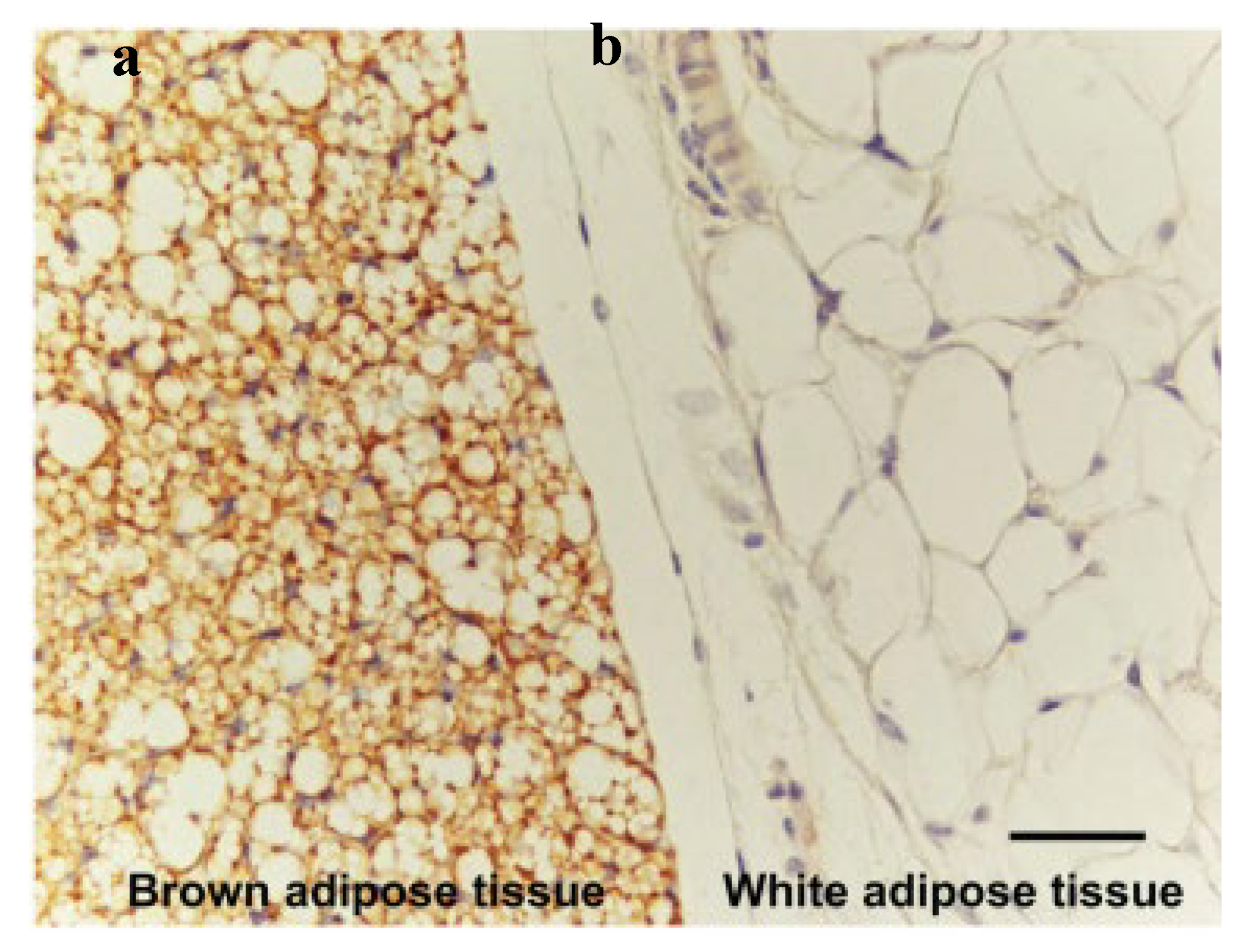
The adipose tissue, commonly known as fat, serves as a padding to protect other organs [1]. The breast comprises about 90% of adipose [20]. The adipose tissue is distinguished into white (with a single large lipid droplet) and brown (with many tiny lipid droplets), with white adipose being the predominant one in the human body. The distinguished names are based on the colour of the tissue when it is fresh and the cells’ morphology under the microscope (see Figure 4). Moreover, the amount of brown adipose tissue deteriorates in the first ten years of the human after birth; they are more present in the foetal stage. In the breast, the glandular tissue and the gap between the lobes are surrounded by the white adipose tissue. The adipose tissue plays an important role in the breast since the shape of the breast is mainly dependent on the amount of adipose tissue. Moreover, the amount of adipose is not constant due to different activities and different stages, such as pregnancy, lactation, and menopause [1]. When the woman reaches menopause, oestrogen levels drop, causing glandular tissue deterioration and eventually disappearing, leaving behind only adipose tissue, the suspensory ligaments, the superficial fascia, and skin. The structural support system of the breast, which includes the suspensory ligaments, the superficial fascia, and the skin, can also change its fibrous framework due to ageing and the effect of gravity. Breast ptosis (dropping) is always associated with loosening the superficial fascia, suspensory ligaments, and skin [8].
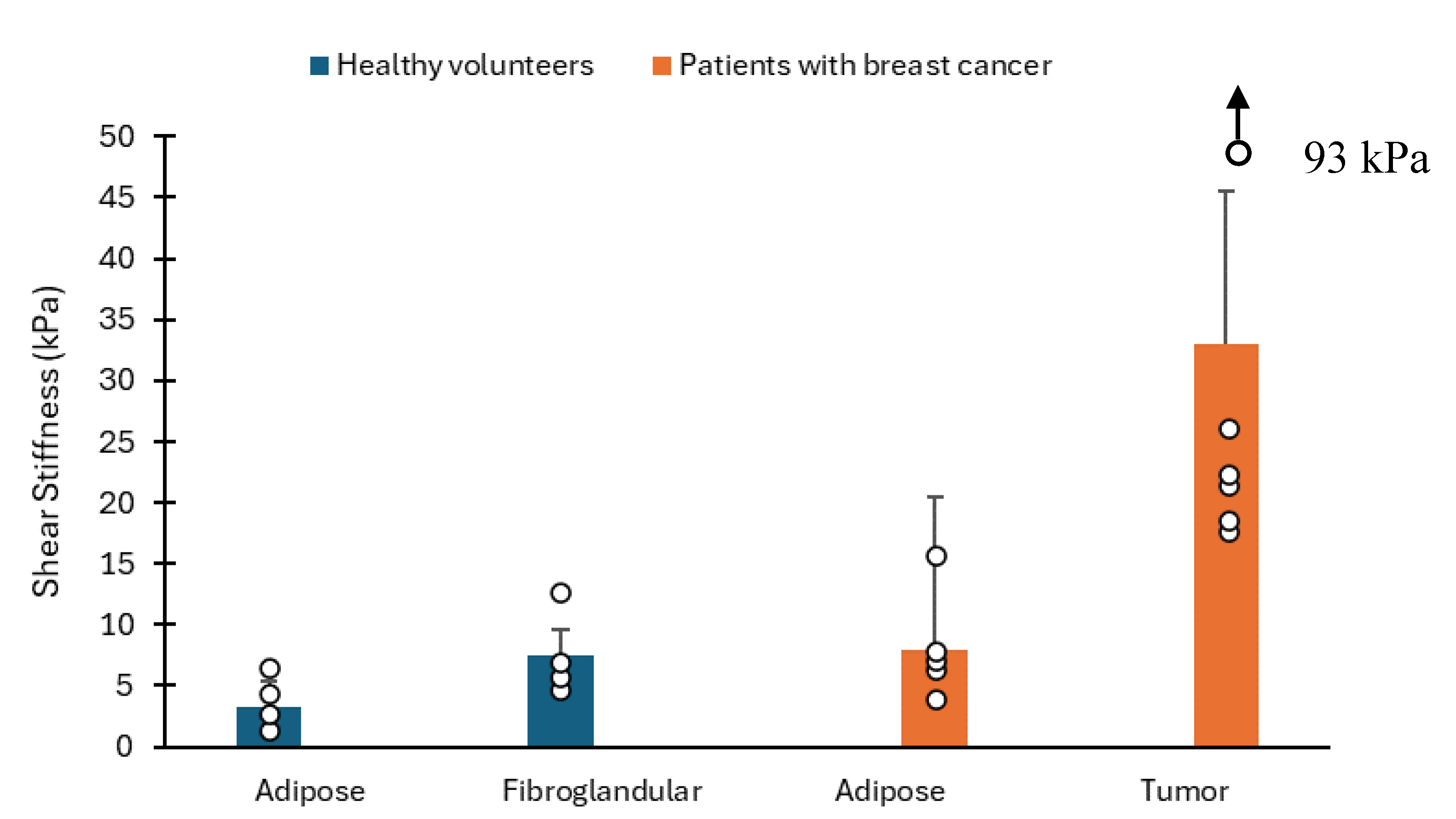
[27] conducted a study to assess the feasibility of MR elastography for breast tissue through phantom studies, imaging breast tumour specimens, and imaging healthy volunteers and a small group of patients with diagnosed breast cancer. Healthy volunteers were six, with ages ranging from 24 to 38 years, and patients with known breast malignancies were also six, with an age range of 43 – 69 years. The employed technique utilises vibrational stress to induce shear waves within the subject under examination. These shear waves’ minute cyclic displacements are captured using a motion-sensitive MR imaging technique. Subsequently, the images displaying wave propagation are processed to generate a quantitative representation of shear stiffness within the imaging plane. In all six volunteer studies, MR elastograms were generated from wave image data. These quantitative elastrograms revealed a moderate degree of variation in the shear stiffness of breast tissues, indicating slightly higher shear modulus values in fibroglandular tissues compared to adipose tissue (see Figure 5). The mean shear modulus values for adipose and fibroglandular tissues were found to be 3.3 ± 1.9 k P a a n d 7.7 ± 3.6 k P a , respectively.
[40] aimed to compare the linear elastic and hyperelastic characteristics of human decellularised adipose tissue (DAT) with those of normal breast adipose tissue. They conducted indentation tests to gather force-displacement data and utilised inverse finite element (FE) analysis to determine the elastic and hyperelastic parameters using Ogden, Arruda-Boyce, Yeoh, and the polynomial models by comparing the results with experimental data. Their findings indicated that DAT extracted from the breast exhibited a deformability similar to native normal tissue, with Young’s modulus of   3.46 ± 1.21 k P a aligning with the values reported in the literature for normal adipose breast tissue ( 3.25 ± 0.910 k P a ) [29].

1.2. Fibroglandular and Glandular Tissues

The glandular tissue of the breast contains the ducts and the lobules, which are the mil-producing glands [8]. [13], employed the torsion creep test to measure the nonlinear elastic properties of the fat, fibroglandular and muscle breast tissues and used the nonlinear flexible model to compare the results. The creep test is mainly utilised to measure the properties of materials by measuring the step response. The hog breast was considered for the study due to its similarity to the human breast. The load stress ranged from 0.1 k P a to 1 k P a , and strain data were recorded for 1 minute at each stress. One hundred eighty seconds interval was considered for the tests. The mean shear modulus of fibroglandular tissue was found to be 1.6 ( 1 0 ) 2 P a , which is 1.3 times that of fat tissue, while the mean shear modulus of muscle tissue was found to be 3.4 ( 1 0 ) 2   P a , that is, 3.4 times of fat tissue.
In a study by [41], the stiffness of fibroglandular tissues was compared with the overall volumetric density of the entire breast and local density. The observed stiffness was 2.3 ± 0.8 k P a , and it exhibited no correlation with age, breast volume, overall breast percent density, or local percent density (defined as the ratio between fibroglandular tissue area and the entire area).
[42], conducted a pilot study on the two layers of the breast, the lower layer and the upper layer. The lower layer comprised the fatty and fibroglandular tissues, while the upper layer comprised the skin. The VLASTIC method (whereby the aspiration device and the breast were put into contact) was used to estimate the tissue stiffness. The VLASTIC device comprises a syringe, a valve, connection tubes, and a 3D-printed resin cup, which rests on the tested breast skin. The VLASTIC method yields the negative pressure and the corresponding removed volume during quasi-static cyclic tests. The Pressure-Tissue Volume curves were collected using the VLATIC method. Then, the Inverse analysis of the Finite element model utilising ANSYS software was deployed to estimate Young’s moduli of the bilayer structure. Seven healthy women between the ages of 19 and 25 years were considered for the study, and the average Young’s moduli for the skin and fatty and fibroglandular tissue were found to be 56.3 ± 16.4 k P a and 3.04 ± 1.17 k P a , respectively.
Furthermore, [43] used the indentation test to measure the elastic properties of breast, adipose and glandular tissues. The stress-strain curve was analysed to attain Young’s modulus of the tissue by application of the indenter on the area of interest. The tissue elasticity was found to be 19.6 k P a , 8.7 k P a , and 4.9 k P a at varying temperatures, 5   ℃ , 22   ℃ , and 40   ℃ , respectively, during the preliminary experiment. Pig’s adipose was used for the preliminary tests. Then, the sample temperature was kept at a temperature of 37   ℃   to avoid the effect of temperature on the elasticity of the human tissue. The Young’s modulus for each tissue was determined at different stress ranges (0.0-0.2, 0.2-0.4, 0.4-0.6, 0.8-1.0, and 1.0-1.2 kPa). The maximum mean Young’s moduli of 17.3 ± 3.9 k P a and 15.4 ± 3.9 k P a of the breast adipose and glandular tissue were attained, respectively, in the stress range of 1.0 − 1.2 k P a .
Additionally, [44] considered the adipose, fibroglandular, and mixed breast tissues in their study to estimate the hyperelastic parameters of the 3rd-order Ogden, Veronda-Westman, Yeoh, and 5-term polynomial models. The indentation test was performed on the 72 healthy breast tissue samples (15 adipose, 17 mixed, and nine fibroglandular) obtained from reduction surgeries. All breast specimens were assumed to be isotropic. An inverse problem mathematical framework was followed, and the developed finite element (FE) model was utilised for an iteration of hyperelastic parameters. The hyperelastic parameters were updated at each iteration until a minimum difference between the indentation results (force-displacement) and simulation results or data from the FE model was attained. The study confirmed that mixed tissues were neither softer nor stiffer than the pure tissue types. Moreover, no significant differences were observed between adipose, fibroglandular, and mixed tissues.
[28] conducted manual segmentation and observed that the adipose was softer than the fibroglandular tissue. However, [29] conducted indentation tests on the adipose and fibroglandular tissues. The study found that adipose and fibroglandular had similar Young’s modulus.
[26] employed MR elastography to study typical breast tissues and determined the feasibility of this technique. They illuminated the tissues accurately with shear waves and effectively characterised the biomechanical properties of breast adipose and glandular tissue. The reported stiffness values were 2.45 ± 0.2 k P a and 0.43 ± 0.07 k P a for glandular and adipose tissue, respectively. Comparing both adipose tissue and glandular tissue, it is apparent that glandular tissue is stiffer than adipose tissue [25, 27, 28].

1.2. Cooper’s Ligaments (Connective Tissues)

Ligaments comprise densely arranged bundles of collagen fibres aligned in parallel to ensure structural stability. The fibroblasts are the primary cell types, and they are distributed among the collagen bundles [8]. Studying their mechanical properties (Cooper’s ligaments) is challenging, which may be attributed to the complexity of extracting them from the specimens and their delicate nature, making experimental handling difficult [3]. More experimental data is required to assess Cooper’s ligaments’ mechanical characteristics [42].
However, [45] conducted uniaxial tensile fracture tests on Cooper’s ligament samples extracted from a cadaver. The basic set-up of the uniaxial test on Cooper’s ligament is depicted in Figure 6. The experimental results were fitted with the Neo-Hookean hyperelastic constitutive model. Young’s mean modulus was 5.8 ± 4.2   M P a . The rupture strain and stress were 8.6 % ± 4.2 % and 1.9 ± 2.5 M P a , respectively. Furthermore, in the same study, Cooper’s ligaments were observed to be two to three orders of magnitude stiffer than breast adipose, muscle, and glandular tissue. The results from the performed uniaxial tensile tests on the cadaver were fitted to the hyperelastic constitutive model (Hookean model).
Additionally, [46] extended the study by [45] providing a detailed analysis of 28 uniaxial tensile tests and proposed anisotropic hyperelastic law to model the mechanical behaviour of Cooper’s ligaments. Three constitutive models (Triantafyllids, Holzapfel 2000, and “New model) were used to fit the experimental results. Ten ligaments were extracted from the cadaver (100 years old), 12 days after death. The pre-load in the range of 0.1 N was applied to the samples. The histology was done to determine the fiber orientation. The samples were immersed in the saline solution, and the temperature was kept at 37°C throughout the uniaxial tensile tests. The prepared samples were categorised into five groups (height/width ratio less than 5; higher than 5; thickness less than 0.063 mm; thickness ranging between 0.063 mm and 0.21 mm; thickness higher than 0.21 mm). The dual or “new” constitutive model was considered with one part representing the matrix (isotropic) and the other part representing the fibers (anisotropic). The neo-Hookean model was considered for the isotropic part, and the two models (Triantafyllidis and Abeyaratne model and Holzapfel 2000) were evaluated for the anisotropic part. The experimental results exhibited a notable dispersion, with a standard deviation of 5 MPa for Young’s modulus and 20 MPa for the tangent modulus. Moreover, the study found Young’s modulus ranging between 1 MPa and 10 MPa with a mode at 3 MPa.

Common Constitutive Models on Breast Tissues

Mechanical datasets of soft tissues are instrumental in advancing computational models that simulate disease conditions and predict tissue responses [17,47]. These datasets enable the creation of constitutive models that describe how tissues deform under various loads and conditions. Constitutive models are essential for developing realistic simulations of biological tissues, which can be used to test hypotheses and design medical devices. The mechanical behaviour data helps refine these models, making them more accurate and applicable to real-world scenarios [48].
Characterising and establishing constitutive models for soft tissues presents a formidable challenge, both in terms of theoretical development and parameter determination. Typically, investigations into soft tissues involve a combination of mechanical tests, morphological assessments, and computational modeling, all carried out at the meso scale, typically ranging from 3 to 10 mm in length [19].
A vast spectrum of material properties for breast tissues determined from the in-vitro experimental data was utilised in other studies to simulate the breast tissues with non-linear hyperelastic or linear elastic models. [49] conducted one of the first studies proposing the exponential stress-strain relationship for large deformation of mammary gland tissues using the in-vitro tissue sample. Other exponential constitutive models were proposed by [31,50].
Typically, to understand the mechanical behaviour of a specific material, a series of experiments are conducted. Once the results are attained, a model is required to fit these outcomes. The phenomenological approach suggests utilising strain energy functions that aim to match the data purely from a mathematical standpoint without considering the internal structure of the material; it treats it as a continuum. Usually, only one type of experimental test, such as a uniaxial test, is fitted. Consequently, while the computational model may behave as expected for this specific loading scenario, it might perform poorly under other types of loadings, such as shear stress. Many models struggle to accurately replicate a material’s behaviour under various loading conditions. Hence, it is crucial to understand which material model is being utilised, how it responds to different loading conditions, and the stress state the body will undergo in practice [1].
Numerous studies have been conducted to explore the mechanical properties of soft tissues, providing a rich body of knowledge that supports ongoing research [51]. These studies employ various experimental techniques and computational methods to characterize the mechanical behaviour, offering valuable insights into the biomechanical environment of tissues affected by diseases [52]. By continuously expanding and refining the mechanical datasets, researchers can improve the precision of computational models, ultimately contributing to better healthcare outcomes through improved diagnosis, treatment, and prevention strategies [17,53,54].
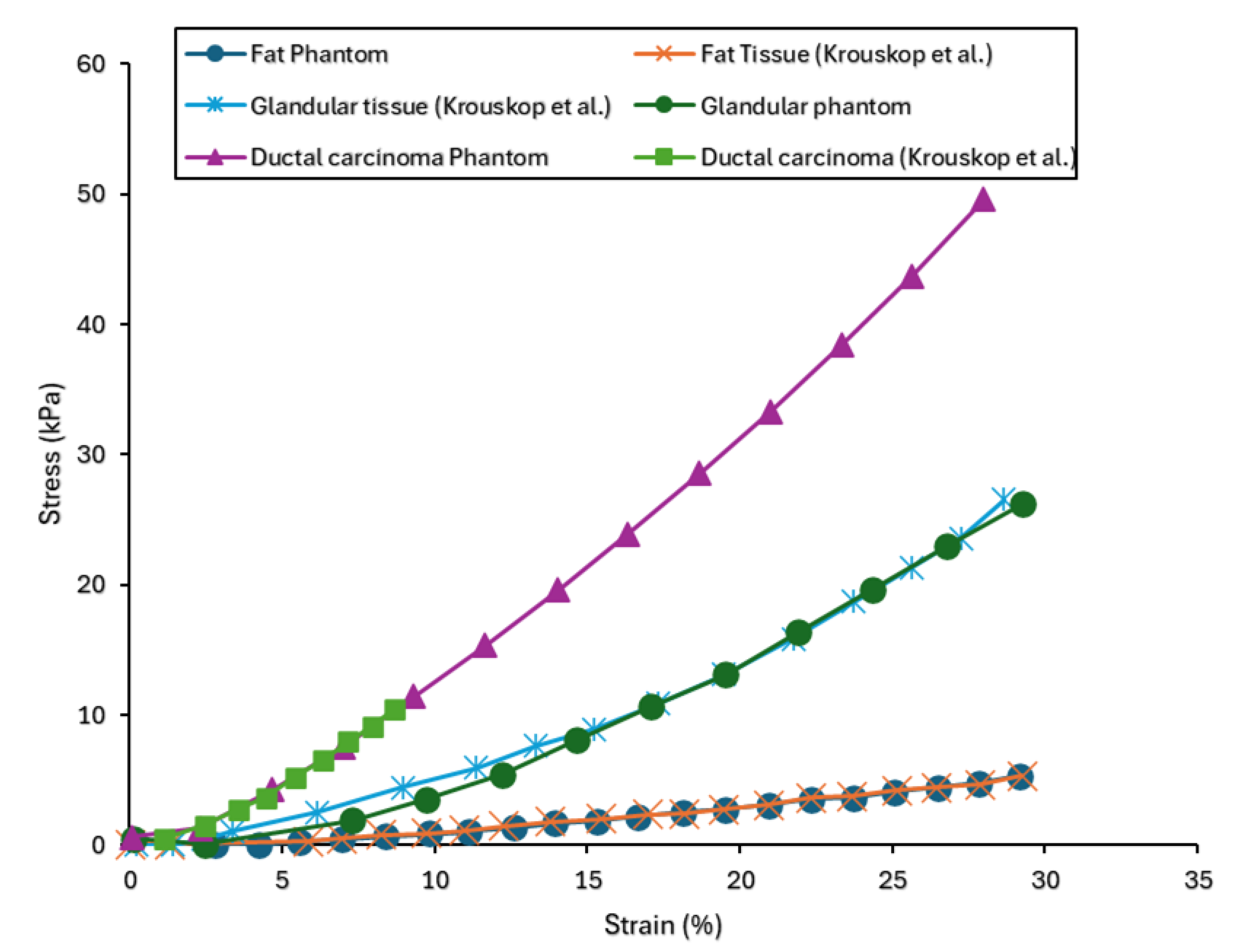
[55] conducted a study focusing on creating polymeric samples to replicate the mechanical properties of human breast tissues. Three types of breast tissue substitutes representing adipose, glandular, and ductal carcinoma tissues were developed and compared to the existing human breast tissue data from compression and relaxation tests. Additionally, stress relaxation tests were conducted on the fabricated tissue substitutes to analyse their viscoelastic behaviour. A finite strain viscoelastic model was proposed to characterise the mechanical response of these breast tissue substitutes, calibrated using experimental data. The data from breast tissue specimens found in the literature were then compared to the responses of the fabricated substitutes. Uniaxial data from the phantom tissues were compared to data from the compression of human breast tissues (glandular, adipose, and ductal carcinoma) [50]. Stress relaxation data for human breast adipose tissue from [56] was compared to the adipose substitute. The results of the uniaxial compression tests are depicted in Figure 7. Comparative analysis was conducted between the stress-strain response of adipose, glandular, and carcinoma phantoms and their respective biological tissue counterpart as documented in the literature [50]. From the experimental data, phantoms were observed to replicate the mechanical behaviour of their corresponding biological tissues. Specifically, for the adipose phantom, the average relative percentage difference between its stress response and the corresponding biological tissue from the literature was found to be 25 %. Similarly, the average percentage differences for the glandular and carcinoma phantoms were found to be 25% and 17%, respectively, suggesting strong agreement between the phantoms and their biological counterpart. Moreover, it was observed that the phantom responses across all three tissue types broadly fall within the error bars of the experimental data obtained from human breast tissues.
A thorough understanding of the breast anatomy and the mechanical characterisation of each breast tissue is vital to the accuracy of a breast constitutive model [14]. A mathematical model has the potential to replicate the mechanical properties exhibited by human and animal soft tissues [57]. Numerous hyperelastic models have been proposed in the literature, designed to mimic the behaviour of both rubber-like materials and biological materials. These models are developed to accurately replicate the characteristics observed in real-world materials [1]. However, there is still a notable absence of a comprehensive mathematical model capable of replicating the mechanical behaviour of soft tissues under different loading conditions such as compression, axial tension, biaxial tension, shear, etc [1,57]. Selecting an appropriate or suitable mathematical model to show the stress-strain response under various loading conditions is not straightforward [57]. Due to these challenges, some studies [58,59,60,61] have introduced mechanical behaviour approximations as linear elastic and hyperelastic material models. However, the applicability of these approximations is limited by strain rate, which influences the stress response [57]. Hence, it is essential to consider that hyperelastic models may only substitute a nonlinear viscoelastic model if the simulation does not involve load cycling, as seen in relaxation phenomena. This has recently been corroborated in bioengineering simulations [62], where viscoelastic properties are integrated into the relaxation step in the analysis of breast tissues by considering time that approaches infinity [57]. Additionally, the behaviour of the soft tissues subjected to large deformation is better defined by visco-hyperelastic models [63]. A strain energy model that uses the hyperelastic parameters to relate the strain energy of the isotropic material to deformation parameters is essential in estimating the hyperelastic parameters [44].
Initially, hyperelastic models were developed to characterise the stress-strain behaviour of elastomers, known for their highly nonlinear behaviour. From a solid mechanics perspective, the stress-strain relationship in many hyperelastic models can be derived from the Strain Energy Function (SEF), generally represented as W, which is a function of three invariants: I 1 ,   I 2 ,   a n d   I 3 , as shown in equation (1) [57].
W = f I 1 ;   I 2 ;   I 3
Furthermore, hyperelastic models involve distinct material constants, denoted as C i j , which differ based on the modelled material. Like many biological tissues, breast tissues show hyperelastic properties when subjected to deformation [44]. To model the nonlinear elastic behaviour of soft tissues, the hyperelastic strain energy functions are employed, with Mooney-Rivlin, Ogden, and Yeoh being the most widely used [64].
The Mooney -Rivlin model
The Mooney-Rivlin model, originally termed the Mooney model, was initially introduced by Money in 1940 and later reformulated in terms of invariants by Rivlin in 1948. It is recognised as one of the earliest hyperelastic models capable of effectively handling strains below 100% [65]. However, it fails to accurately capture the upturn (S-curve) observed in the force-extension relationship during uniaxial tests and the force-shear displacement relationship in shear tests. The mode’s expression for a compressible material is given by equation (2) [57, 65]:
W = C 10 I 1 − 3 + C 01 I 2 − 3 + 1 D 1 ( J e l − 1 ) 2
Where:
  • C 10 and C 01 represent material parameters.
  • J e l denotes the elastic volume ratio.
  • D 1 is a constant that characterises the compressibility of the material, typically determined from volumetric tests.
  • I 1 and I 2 refer to the first and second invariants [57].
For an incompressible material, such as rubber and soft tissues, the elastic volume ratio J e l equals 1, rendering the Money-Rivlin material model a suitable model for incompressible materials [57, 64]. The Money-Rivlin model encompasses various variants (Full polynomial, Biderman, Hynes-Wison, Yeoh, and Neo-Hookean model), each expanding upon the basic model through different methodologies [57] as described in the following sections.
Full polynomial Model
The full polynomial model (equation 4), referred to as the “Mooney-Rivlin” model or Full Polynomial model in literature, represents a Strain Energy Function (SEF) as a series, often truncated to second and third-order terms. Such truncations can constitute distinct models [66].
W = C i j ∑ i , j = 0 ∞ ( I 1 − 3 ) i ( I 2 − 3 ) j
Where i and j denote the strain tensor components, indicating the direction and interaction between different strain components in the material.
Moreover, this model is usually considered for large strain problems [66].
Biderman Model
Biderman model (equation 5) is a truncation of the series found in the Full Polynomial model, retaining only terms where i = 0 o r   j = 0 . It considers solely the first three terms for I 1 and one term for I 2 [57, 66, 67].
W = C 10 I 1 − 3 + C 01 I 2 − 3 + C 20 ( I 1 − 3 ) 2 + C 30 ( I 1 − 3 ) 3
The Haines-Wilson Model
The Hynes-Wilson model (equation 6) is another truncation derived from the Full Polynomial, which preserves only six terms of the series. This selection is made based on a comparison of invariants and principal stretches development of the strain energy function in the Full Polynomial model [66].
W = C 10 I 1 − 3 + C 01 I 2 − 3                                   + C 11 I 1 − 3 I 2 − 3 + C 02 ( I 2 − 3 ) 2 + C 20 ( I 1 − 3 ) 2         + C 30 ( I 1 − 3 ) 3
Yeoh Model
Yeoh model (equation 7), also referred to as the reduced polynomial model, focuses exclusively on the first invariant I 1 . Like other mentioned truncation models, the Yeoh model is derived from selecting particular terms from the series in the Full Polynomial model. It effectively captures the upturn of the stress-strain curve of rubber, offering a suitable fit across a broad strain range, and it can simulate various modes with limited data [67].
W = C i 0 ∑ i = 1 3 ( I 1 − 3 ) i
Neo-Hookean Model
The Neo-Hookean model (equation 8) was first proposed in 1943 and is considered the simplest hyperelastic model. It closely resembles Hooke’s law but as a hyperelastic model. It is a specific case of the Mooney-Rivlin model, unable to capture the upturn of the stress-strain curve when C 01 = 0 . This model proves helpful when material data is scarce, offering good approximations at small strains, up to 20% [57, 68].
W = C 10 I 1 − 3
The Neo-Hookean model is usually utilised to characterise the mechanical behaviour of breast soft tissues [11]
Ogden Model
Ogden model differs from the previous ones by relying on principal stretch ratios λ 1 ,   λ 2 ,   a n d   λ 3 rather than invariants. It effectively captures the stiffening phenomenon observed in the stress-strain curve and accurately represents rubber behaviour for extensive deformation ranges, up to 700%. However, it is advised against using this model with limited laboratory tests. Despite the challenges of determining material parameters, this model finds widespread application in addressing significant strain problems. The SEF for the Ogden model is defined by equation (9) [68].
W = ∑ n = 1 N μ n α n λ 1 α n + λ 2 α n + λ 3 α n − 3
Where n represents the number of Ogden terms, if n=1, the model is referred to as the one-term Ogden model [69].
Like the Full polynomial model, the Ogden model is also considered for large problems and is the most utilised model. However, it is difficult to determine the material parameters [66].
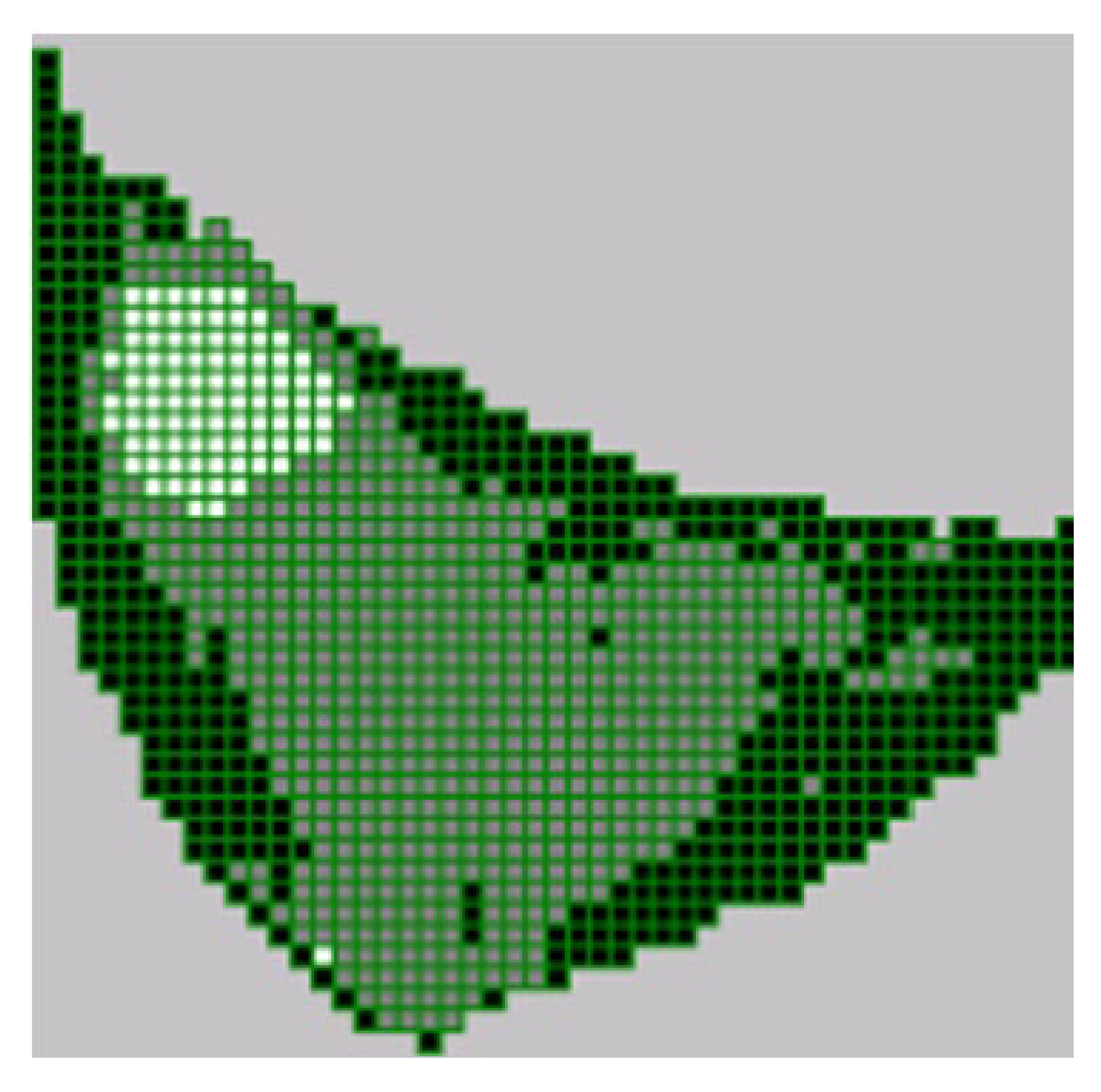
[70] developed a FEM model for simulating the deformation of the female breast during mammography compression. The Imageparser software was developed and employed to generate a FEM from 3-D medical images. Imageparser employs a semi-automatic technique to identify constituents within the image, including adjacent tissues and organs. The image segmentation is based on user-defined grayscale ranges and then meshes the tissues into elements of custom-defined sizes. By putting the generated FEM mesh into a FEM program such as ANSYS, mechanical deformation can be determined under specific boundary conditions and mechanical loadings. Due to the breast comprising various tissues with different mechanical properties, the breast tissues were segmented as new Regions of Interest (ROIs), utilising the grayscale classification of voxels. Corresponding grayscale ranges for different tissue types were identified by analysing the grayscale histogram. The voxels were mapped onto their respective categories based on the grayscale ranges. The adipose tissue was represented by a grayscale value range of 0 – 64, while parenchyma tissue (glandular tissue) was represented by a grayscale value range of 64 – 144. Moreover, the grayscale values from 144 – 256 represented the cancerous tissue. During the simulation of the breast tissues (adipose, glandular, and tumour tissues), the initial elastic moduli for adipose, glandular, and tumour tissues were 20 kPa, 35 kPa, and 100 kPa, respectively. These values were suggested by [50]. The number of voxels for each tissue element was counted to assign materials to elements. Thus, elements were mapped onto different tissues as depicted in Figure 8; black colour denotes adipose, grey denotes glandular, and the tumour is denoted by white colour. The Mooney-Rivlin nonlinear hyperelastic model was employed to describe the constitutive law for finite deformation. Considering the initial elastic moduli, the Mooney-Rivlin material constants were determined as: C 01 = 1.333 P a , C 10 = 2.000 P a for adipose; C 01 = 2333.3 P a , C 10 = 3500 P a for glandular; and C 01 = 6.667 P a , C 10 = 10.000 P a for the tumour tissue.
[71] introduced a method for real-time simulation of breast compression caused by two plates, which could be part of an X-ray mammogram or an MRI-guided biopsy device. The breast tissues (adipose, skin, and glandular) obtained from ten healthy participants with the age range of 34-90 years old were segmented from MR images. Ten authentic breast images were considered to simulate deformation offline with the finite element method (FEM) utilising the ANSYS software. The deformation results obtained through simulations were then imported into the three machine learning models (K-means clustering for each tissue, adipose, skin, and glandular). These models predicted breast deformation in real-time in less than 0.2 seconds with low mean error. Additionally, a similar material model was considered for all the participants, with a constant elastic constant for each tissue type. The model proposed by [72] was used for the skin. In addition, the hyperelastic model parameters previously determined by [70] were utilised to simulate the physical behaviour of glandular and breast adipose subjected to compression, employing a Mooney-Rivlin model for all three tissues (skin, glandular, and adipose).
Finally, the determined displacements following the simulation, including plate displacement and the proportions of skin, adipose, and glandular tissue from each breast, along with nodal coordinates and the allocation of elements to the breast tissues for each node, were used as inputs for training several machine learning models. These models were trained to learn the relationship between the mesh features and nodal displacements, enabling them to predict real-time deformations of the breast accurately, even for scenarios not encountered during the training process.

Tested Tissues

The adipose and glandular/fibroglandular are the breast tissues that have been investigated the most, and nothing was found on the lactiferous or milk duct, nipple, and areola regarding mechanical behaviour. The tissue studied the least was the connective tissue, Coper’s ligament. This fibrous tissue was studied collectively with glandular tissue to form fibroglandular tissue. Only one mechanical characterisation was done solely on Cooper’s ligaments. This may be attributed to the complexity of dissecting them.
The inverse framework was the most considerable technique for determining the parameters of the hyperelastic constitutive models.

Experimental Testing Methods

Conducting experimental tests has been an effective method for determining the properties of biological materials [1]. Despite the significant need, it remains a challenge to obtain reliable data on soft tissue properties and methods to measure these properties in the small in vitro tissue samples that are commonly available post-surgery [22].
The biomechanical properties measurement techniques of soft tissue samples include but are not limited to the ones discussed in this section. The following techniques were applied to the human breast. However, they could also be applied to other biological soft tissues in the body [22].
In the study by [50], a hydraulic system was utilised to apply low-frequency sinusoidal indentation loading to thin breast tissue slices. 142 normal tissue and tumour specimens were tested using different loading frequencies and levels of pre-compression. The slices were modelled as a semi-infinite elastic media under a uniform load from a circular indenter, for which a closed-form solution is available. It was observed that Young’s modulus of the breast tissues is slightly sensitive to different loading frequencies, it was found to increase by 1-10 fold with higher levels of pre-compression. However, a challenge with this geometry is that the tumour specimens tend to be small and normal tissues are often composed of heterogeneous regions of fibroglandular and adipose tissues. The force and the maximum displacement were recorded. Subsequently, the elastic modulus was determined (using equation 10), where E is the elastic modulus, q is the load density, a is the radius of the loaded area, v is the Poisson’s ratio, and w is the maximum displacement in the direction of the load. Moreover, the Poisson’s ratio value was considered 0.495 (for incompressible material).
E = 2 1 − v 2 q a w
[73] suggested a preparation method for small tissues. The method involved indenting a constrained cylindrical sample. The sample was constrained on its side boundaries using an external mould and a gelatin-agarose mixture to close the gaps between the tissue sample and the mould. To determine Young’s modulus, the slope of the force-displacement curve produced from the indentation test was converted to Young’s modulus with an empirically obtained conversion factor. This factor was then validated through finite element (FE) modelling. This method was proved unsuitable for breast tissues since shaping the breast tissue into the required cylindrical forms was unsuccessful due to the deformability nature of normal breast tissue. Moreover, fully constraining the side boundaries was found to be challenging. Failure to achieve this resulted in significant errors in the calculated Young’s modulus values.
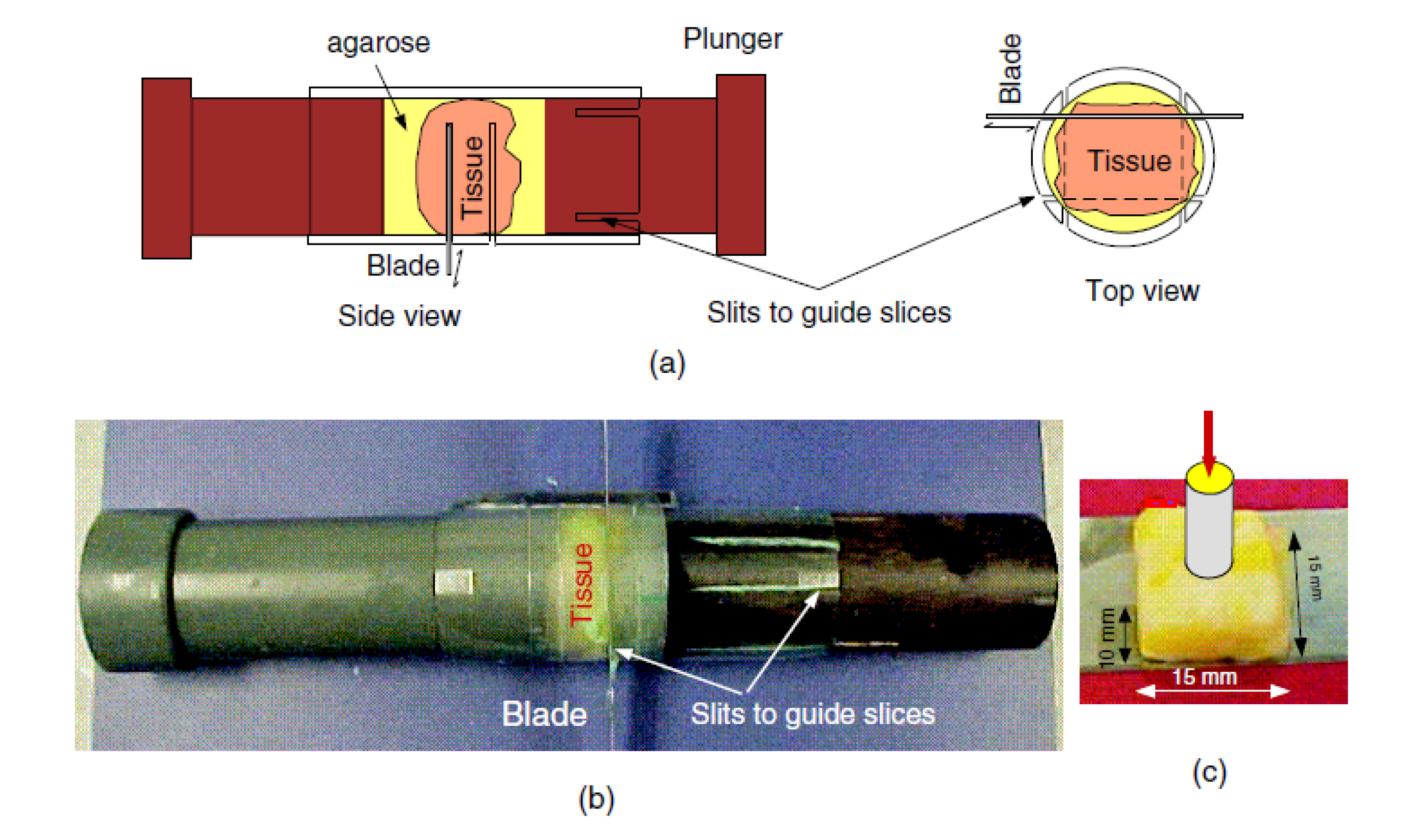
In the study conducted by [22], a method of precisely and consistently measuring the Young’s modulus in in vitro was introduced, adapting the technique initially proposed by [73] for small and significant soft samples. However, employing the uniform cylindrical samples, block-shaped samples were produced through cutting and the sides of the samples were not constrained. The indentation tests were carried out on the produced 15 x 15 x 10 m m 3 block-shaped specimens (see Figure 9 (c)). Additionally, a temperature apparatus was used to maintain the biological temperature of the tissue. The tissue was embedded within a 2.5 agarose solution. Subsequently, the encased tissue block was placed on top of a 10 mm layer of agarose solution at about 37   ℃ inside a small container. The agarose solution was poured gradually into the container until the tissue was submerged entirely, after which the agarose was allowed to solidify for 10 minutes. The top and bottom surfaces of the encased tissue sample were cut through agarose by a cylindrical cutting device (see Figure 9 (b)) without altering the volume of agarose. The other remaining sides of the block were cut through orthogonal slits. The conversion factor was estimated using two methods: experimental data and finite element (FE) simulation.
Equation 11 was used to determine the Young’s modulus. Where K is the conversion factor that depends solely on the object’s geometry and boundary conditions, E denotes Young’s modulus, and s represents the force-deformation slope produced from the indentation test. Moreover, k was estimated through FE modelling validated by calibrated samples.
E = k s
In the experimental method, a homogeneous 15 x 15 x 10cubed block shape sample made from plastisol PVC (M_F Manufacturing Company, Fort Worth, TX) with varying amounts of softener was used to calibrate the system (Figure 8). The same plastisol patches were used to produce cylindrical samples (7 mm radius and lengths of 60 – 85 mm). These cylindrical samples were used to measure each sample’s Young’s modulus. The uniaxial axial tests were conducted on the samples using the same system in Figure 10 but with some modifications to allow stretching of the cylindrical samples.
The ends of the samples were fixed to unplasticised polyvinyl chloride (PVC) discs attached to the actuator and load cell system. Each sample was initially pre-stretched with a 10 g force to ensure it was straight, using the piston as the reference point for deformation. Five cycles of sinusoidal stretching with a 2 mm amplitude and 0.1 Hz frequency were performed, producing linear force-displacement plots. This procedure was repeated twice for each sample. Therefore, the Young’s modulus for each was calculated from the attained force-displacement slope using equation 12,
E = l π r 2 F ∆ l
where l and r parameters are the cylindrical sample’s length and radius, respectively.
Following the measurement of Young’s modulus, each 15 x 15 x 10 m m 3 block was placed in the sample holder (see Figure 10). Five sinusoidal indentation cycles with a 0.5 mm amplitude and 0.1 Hz frequency were applied using a 2 mm radius indenter. The slope of the force-displacement (s) was determined. Then, the conversion factor (k) was calculated using equation 11 since the Young’s moduli of the samples were known from the previous experiment.
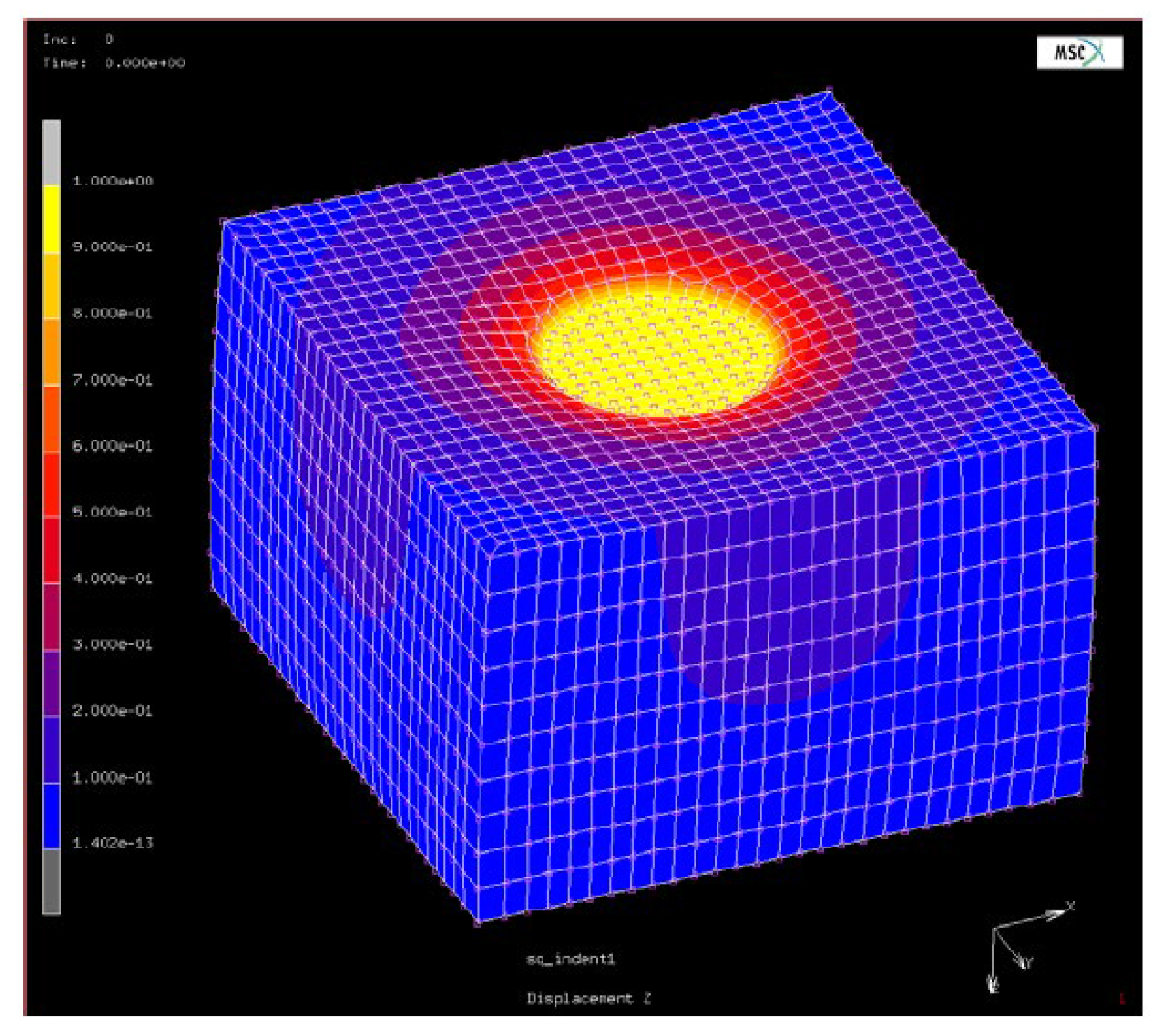
For FE simulations, a block of 15 x 15 x 10 m m 3 dimensions with an arbitrary modulus and Poisson’s ratio of v = 0.495 subjected to indentation was considered. Static loading corresponding to a 1.0 mm indentation with a 2.5 mm radius indenter was simulated with the indenter’s contact area and the bottom set to slipping boundary conditions. Figure 11 shows the deformed shape of the finite element model block. Similar to the experimental method, the force-displacement slope was attained, and the conversion factor was calculated using equation 10.
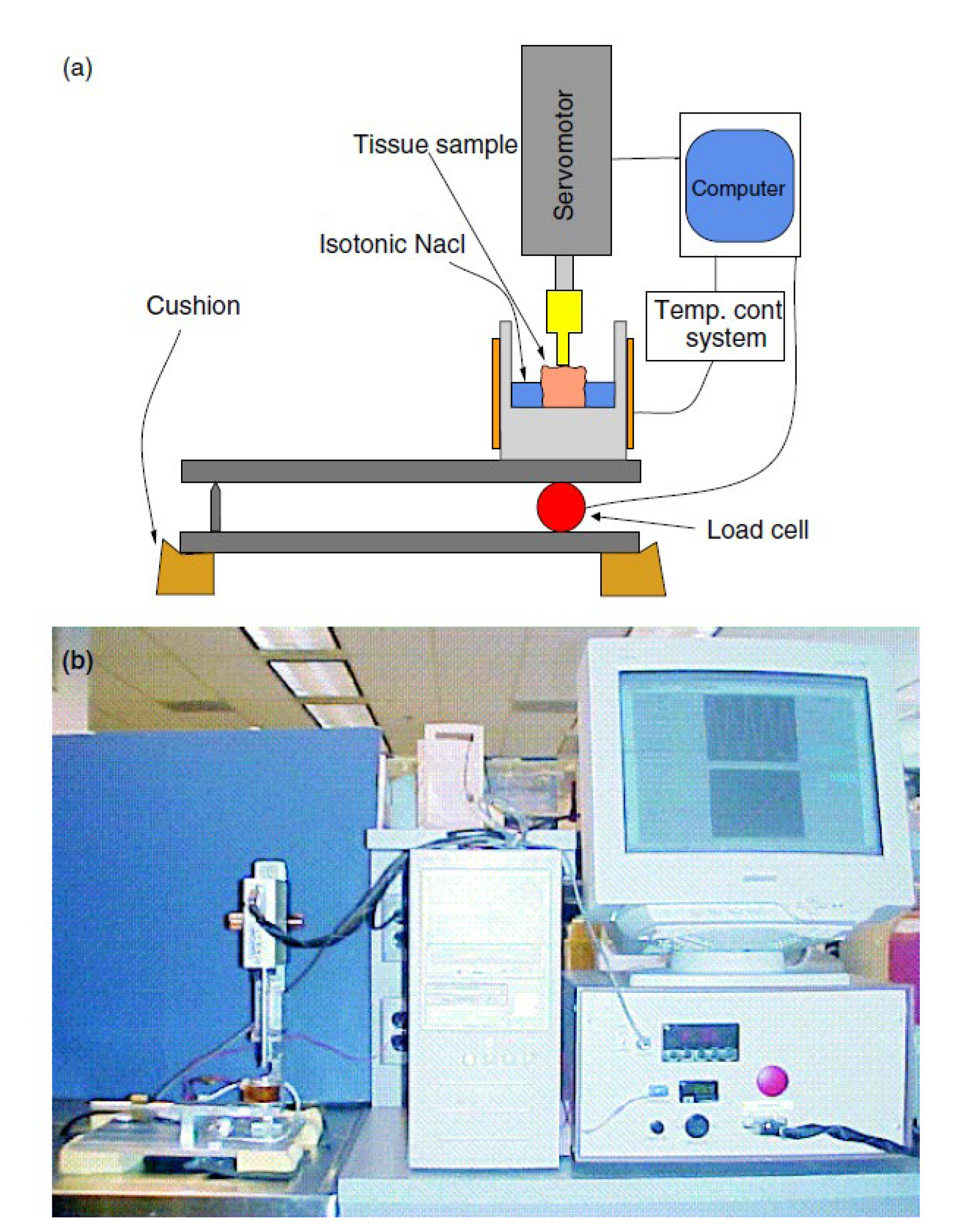
Furthermore, [22] measured the modulus of the breast tissue and compared it with the indentation technique. The adipose tissue specimen used in the indentation test was enclosed in a 30 x 30 x 37 mm cubed block of a 4% gelatin and 1.5 % agarose mixture. The enclosed tissue underwent an MRE experiment involving quasi-static sinusoidal compression applied using an MR-compatible device (Figure 12). The block was placed inside a birdcage coil and compressed by a piston driven by an ultrasonic MR-compatible motor. A 2-D spin-echo sequence with 256 x 128 resolution and 1 mm slice thickness was used to capture the sagittal MRI images of the block. Moreover, the block underwent sinusoidal compression at 1 Hz with a 1.5 mm amplitude, and displacement data were obtained using a STEAM pulse sequence with a repetition time (TR) to time to echo (TE) ratio (TR/TE = 950/12 ms) and a mixing time of 500 ms. The data were processed through an iterative MRE technique to calculate stress and update the elastic modulus. The tissue elasticity was then determined from a uniaxial compression test’s calculated ratio and known gelatin-agarose modulus.
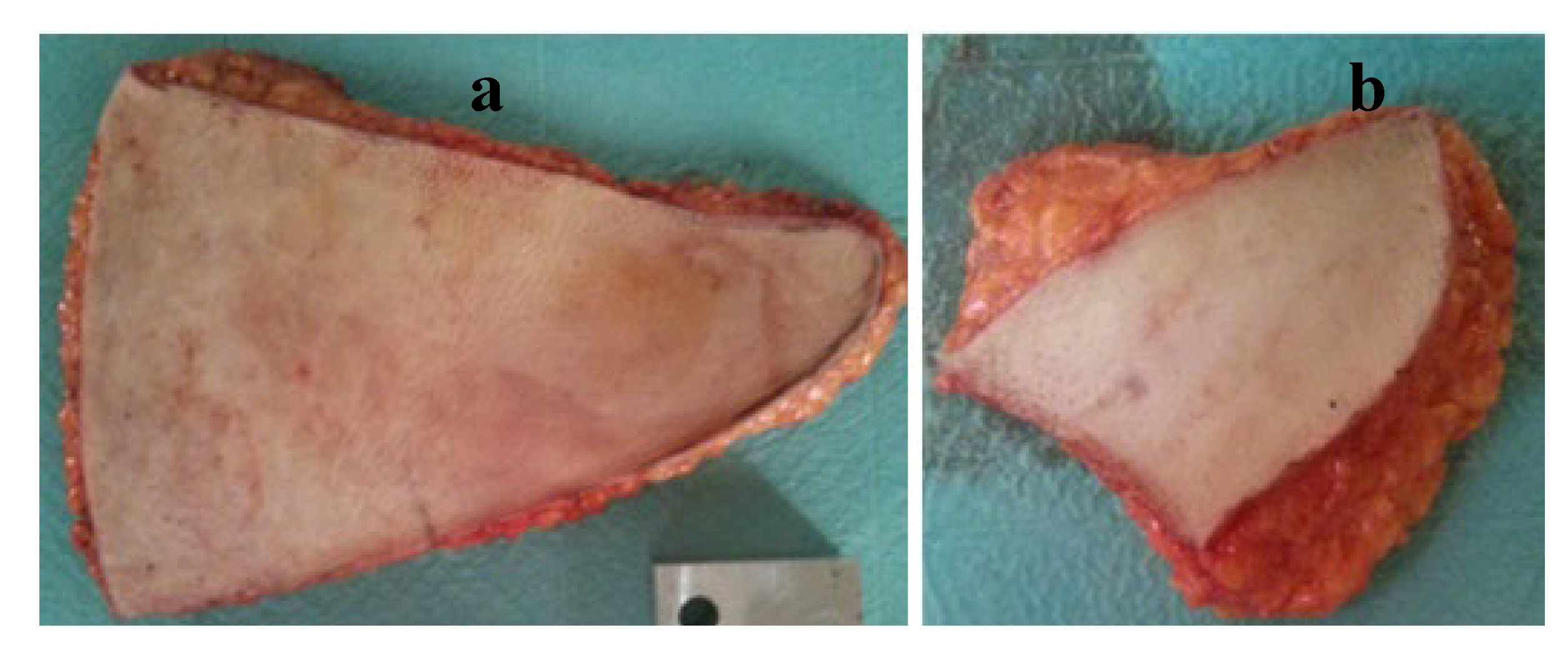
[1], conducted an indentation test on the breast and abdomen adipose tissues. The tissue samples were extracted from several patients with ages ranging between 42 and 57 years who underwent mastectomy surgery. Additionally, the mean age was 52.3 ± 6.9   years. 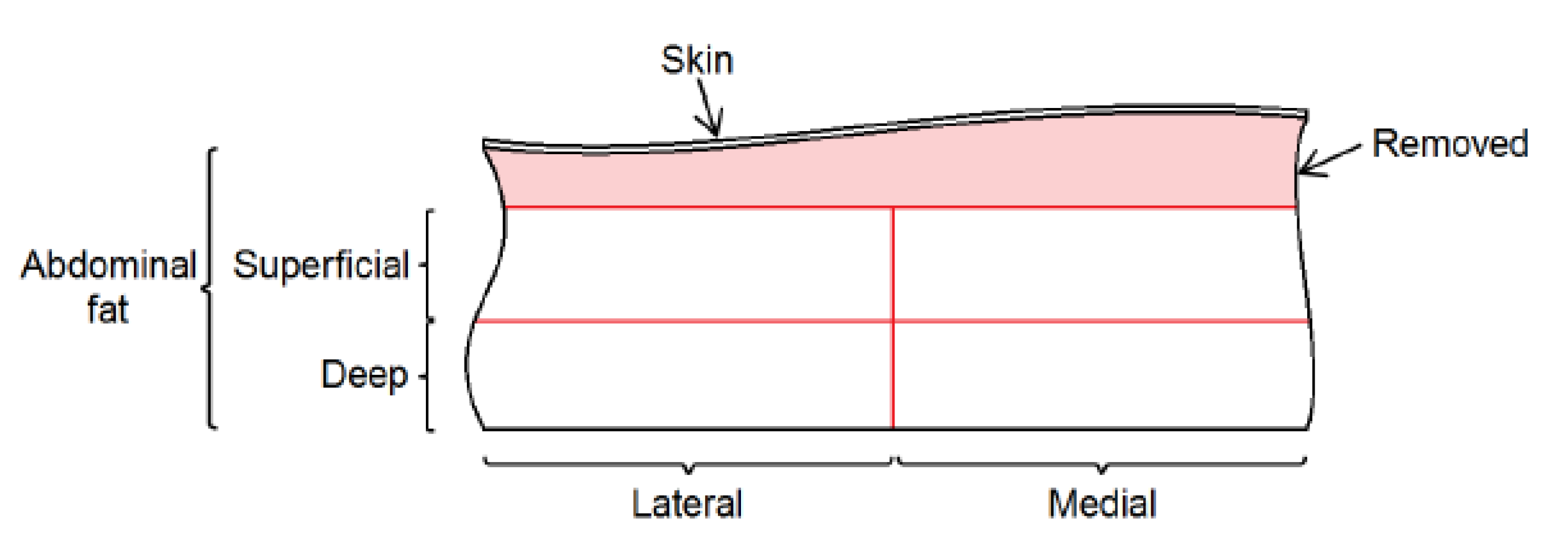The abdominal tissue utilised in the experiment constituted the portion not designated for reconstruction (Figure 13 (a)) while the breast tissue was sourced from the contralateral breast (Figure 13(b)). The tissue pieces were placed in a cool box with ice for preservation during transportation from the hospital to the laboratory. The skin was removed by cutting approximately a 5mm thickness of tissue. Abdominal tissue was further divided into superficial and deep slices, with each segment subsequently split into medial and lateral parts for analysis (see Figure 14). The slice thickness was ranging between 5 mm and 10 mm. For the breast sample, only superficial and deep divisions were considered due to size limitations. A meat slicer and a sharp knife were used to produce the cuts. 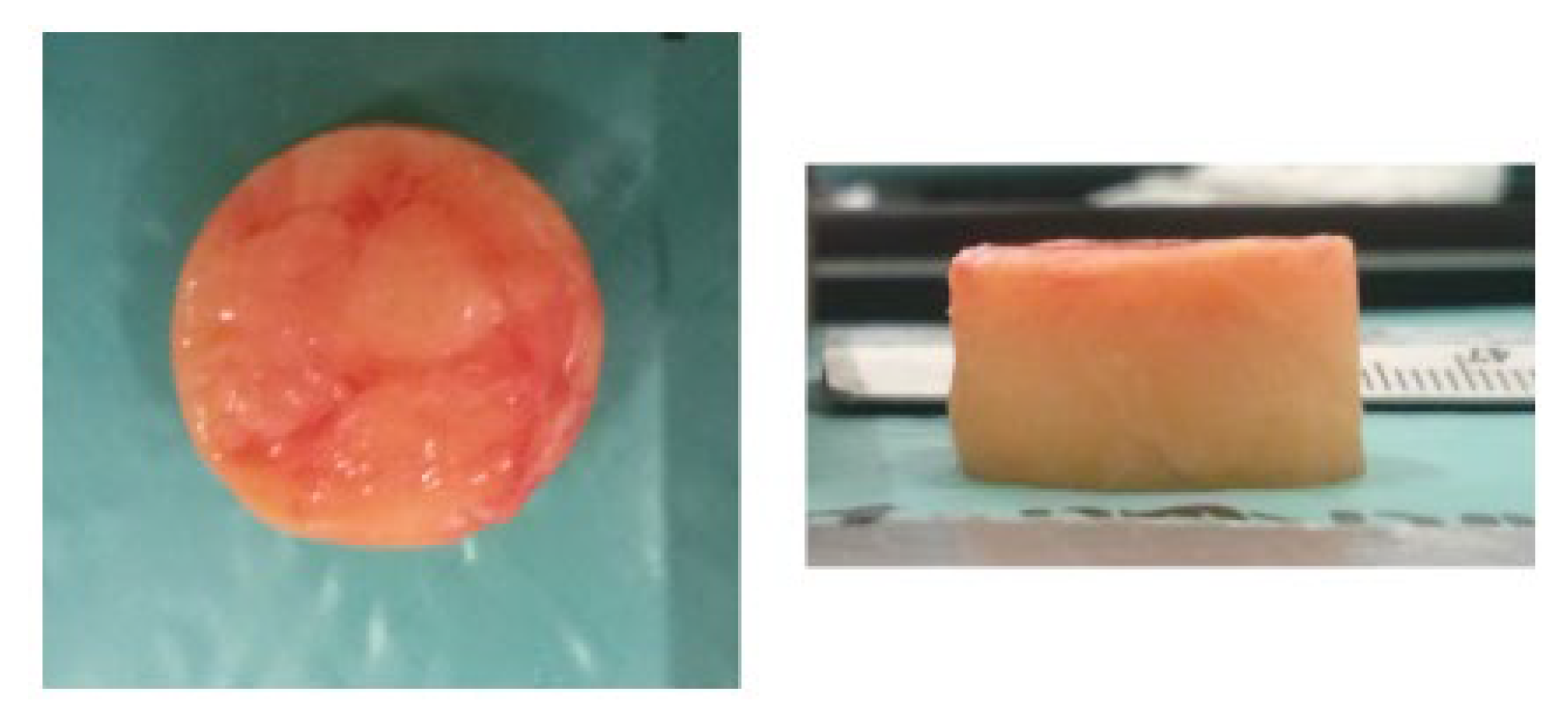The samples were frozen at − 20 ℃ to prevent tissue degradation. The cylindrical specimens for testing were produced from the slices utilising a hollow punch with a diameter of 19 mm. The extraction process necessitated frozen tissue to ensure cylindrical shape integrity. The prepared specimen is depicted in Figure 15. The specimens were placed in a saline solution at room temperature, permitting thawing. The specimens were subjected to a uniaxial compression test where they were compressed between two plates. The specimens were submerged in the saline solution throughout the tests, and the temperature was regulated using a heater and thermostat. During the uniaxial test, the force and displacement were recorded and later converted into stress and stretch. In this study, the mechanical properties of the adipose were determined by a quasi-linear viscoelasticity model.

Limitations

The basal cells and luminal Cells were not discussed in this paper. To fully understand the mechanical behaviour of the tissue, these cells should be considered. Moreover, the experimental aspect has yet to be discussed thoroughly.

Conclusions

This review was written to investigate the mechanical behaviour of the breast tissues and highlight what is missing in the literature regarding the mechanical characterisation of the breast tissues. The data obtained in the review can be used as inputs in computational models to analyse the behaviour of the breast tissues. Furthermore, a few studies have investigated the shear properties of the breast tissues, and no studies were found on the mechanical characterisation of the lactiferous duct.
From this review, it is apparent that glandular tissue is stiffer than adipose tissue. Moreover, the adipose tissue is the less stiff tissue in the breast, while Cooper’s ligaments are the stiffer tissue. However, Cooper’s ligaments were studied the least; this could be attributed to the complexity of dissecting it from the breast.
These findings on tissues stiffness within the breast have significant implications for both clinical practice and the development of medical devices. Healthcare providers can improve diagnostic accuracy, personalize treatment plans, and enhance patient outcomes by leveraging this knowledge of breast tissues. Concurrently, more advanced, tissue-specific tools and implants that better meet the needs of patients and clinicians can be created by medical device developers.
Understanding and modelling the mechanical properties of soft tissues is crucial for creating predictive computational models, which are vital for various fields such as medicine, tissue engineering, biology, cosmetics, and pharmaceuticals. Therefore, it is essential that the constitutive models accurately represent the key characteristics of these biological materials or tissues to ensure their suitability for specific applications.

Conflicts of Interest

No financial or personal relationships exist between the authors of this paper and any individuals or organisations that could influence or bias our work inappropriately.

References

  1. Calvo-Gallego, J.L., Experimental characterisation of breast tissues and its application to a numerical model of a healthy breast. 2016, University of Seville.
  2. Wei, Y.L., et al., Brain transcriptome analysis reveals genes involved in parental care behaviour in discus fish (Symphysodon haraldi). Gen Comp Endocrinol, 2021. 309: p. 113793. [CrossRef]
  3. Teixeira, A.M. and P. Martins, A review of bioengineering techniques applied to breast tissue: Mechanical properties, tissue engineering and finite element analysis. Front Bioeng Biotechnol, 2023. 11: p. 1161815. [CrossRef]
  4. Azar, F.S., D.N. Metaxas, and M.D. Schnall, A finite element model of the breast for predicting mechanical deformations during biopsy procedures, in Proceedings IEEE Workshop on Mathematical Methods in Biomedical Image Analysis. MMBIA-2000 (Cat. No.PR00737). 2000. p. 38-45.
  5. Chagnon, G., M. Rebouah, and D. Favier, Hyperelastic energy densities for soft biological tissues: A review. Journal of Elasticity, 2015. 120(2): p. 129-160. [CrossRef]
  6. Han, L., et al., Development of patient-specific biomechanical models for predicting large breast deformation. Physics in Medical & Biology, 2012. 57(2): p. 455-72. [CrossRef]
  7. Garcia, E., et al., A step-by-step review on patient-specific biomechanical finite element models for breast MRI to x-ray mammography registration. Med Phys, 2018. 45(1): p. e6-e31. [CrossRef]
  8. Gefen, A. and B. Dilmoney, Mechanic’s of the normal woman’s breast. Technology and Health Care, 2007. 15(4): p. 259-271.
  9. Babarenda Gamage, T., P. Nielsen, and M. Nash, Chapter 10 - Clinical applications of breast biomechanics. Biomechanics of Living Organs, 2017. 1: p. 215-242.
  10. Peurla, M., et al., Morphometric analysis of the terminal ductal lobular unit architecture in human breast. 2023.
  11. Mira, A., et al., A biomechanical breast model evaluated with respect to MRI data collected in three different positions. Clin Biomech (Bristol, Avon), 2018. 60: p. 191-199.
  12. Sarvazyan, A., Elastic properties of soft tissues, in Handbook of Elastic Properties of Solids, Liquids, and Gases. 2001, Academic Press.
  13. Tsukune, M., et al. Evaluation and comparison of the nonlinear elastic properties of the soft tissues of the breast. in 33rd Annual International Conference of the IEEE EMBS. 2011. Boston, Massachusetts USA.
  14. Ramião, N.G., et al., Biomechanical properties of breast tissue, a state-of-the-art review. Biomechanics and Modeling in Mechanobiology, 2016. 15(5): p. 1307-1323.
  15. Nemavhola, F., Study of biaxial mechanical properties of the passive pig heart: material characterisation and categorisation of regional differences. International Journal of Mechanical and Materials Engineering, 2021. 16(1): p. 6.
  16. Ngwangwa, H., et al., Determination of cross-directional and cross-wall variations of passive biaxial mechanical properties of rat myocardia. Processes, 2022. 10(4): p. 629.
  17. Masithulela, F., Bi-ventricular finite element model of right ventricle overload in the healthy rat heart. Biomedical Materials and Engineering, 2016. 27(5): p. 507-525.
  18. Kazakevičiūtė-Makovska, R., Biological soft tissues: Mechanical characterisation, data analysis, and model’s evaluation, in 20th International Conference Engineering mechanics 2014. 2014: Svratka, Czech republic. p. 288-291.
  19. Goodbrake, C., et al., On the Three-Dimensional Mechanical Behavior of Human Breast Tissue. Annals of Biomedical Engineering, 2022. 50(5): p. 601-613.
  20. Khaniki, H.B., et al., Hyperelastic structures: A review on the mechanics and biomechanics. International Journal of Non-Linear Mechanics, 2023. 148. [CrossRef]
  21. Delaine-Smith, R.M., et al., Experimental validation of a flat punch indentation methodology calibrated against unconfined compression tests for determination of soft tissue biomechanics. Journal of the Mechanical Behavior of Biomedical Materials, 2016. 60: p. 401-415.
  22. Samani, A., et al., Measuring the elastic modulus of ex vivo small tissue samples. Physics in Medicine & Biology, 2003. 48(14): p. 2183.
  23. Navindaran, K., J.S. Kang, and K. Moon, Techniques for characterizing mechanical properties of soft tissues. Journal of the Mechanical Behavior of Biomedical Materials, 2023. 138.
  24. Tang, A., et al., Ultrasound Elastography and MR Elastography for Assessing Liver Fibrosis: Part 1, Principles and Techniques. American Journal of Roentgenology, 2015. 205(1): p. 22-32.
  25. Chen, J., et al. Noncompressive MR elastography of breasts. in Proceedings of the International Society for Magnetic Resonance in Medicine. 2013.
  26. Lawrence, A.J., et al., Magnetic resonance elastography of the breast. Investigatve Radiology, 1998. 40: p. 412-420.
  27. McKnight, A., et al., MR elastography of breast cancer: Preliminary results. American Journal of Roentgenology, 2002. 178(6): p. 1411-1417.
  28. Van Houten, E.E., et al., Initial in vivo experience with steady-state subzone-based MR elastography of the human breast. J Magn Reson Imaging, 2003. 17(1): p. 72-85.
  29. Samani, A. and D. Plewes, An inverse problem solution for measuring the elastic modulus of intact ex vivo breast tissue tumours. Physics in Medicine & Biology, 2007. 52(5): p. 1274.
  30. Samani, A. and D. Plewes, A method to measuree the hyperelastic parameters of ex-vivo breast tissue samples. Physics in Medicine & Biology, 2004. 49(18): p. 4395-4405.
  31. Azar, F., D. Metaxas, and M. Schnall, A deformable Finite Element model of the breast for predicting mechanical deformations under external perturbations. Academic Radiology, 2001. 8(10): p. 965-975.
  32. Calleja-Agius, J. and M.P. Brincat, Effects of hormone replacement therapy on connective tissue: why is this important? Best Practice and Research Clinical Obstetrics and Gynaecology, 2009. 23(1): p. 121-7.
  33. Sutradhar, A. and M.J. Miller, In vivo measurement of breast skin elasticity and breast skin thickness. Skin Res Technol, 2013. 19(1): p. e191-9.
  34. Koster, M.I., Making an epidermis. Annals of the New York Academy of Sciences, 2009. 1170: p. 7-10.
  35. Arda, O., N. Goksugur, and Y. Tuzun, Basic histological structure and functions of facial skin. Clinics in Dermatology, 2014. 32(1): p. 3-13.
  36. Yagi, M. and Y. Yonei, Glycative stress and anti-aging: 7. Glycative stress and skin aging. Glycative Stress Research, 2018. 5(1): p. 50-54.
  37. McGhee, D.E. and J.R. Steele, Breast Biomechanics: What Do We Really Know? Physiology (Bethesda), 2020. 35(2): p. 144-156.
  38. Liang, X. and S.A. Boppart, Biomechanical properties of in vivo human skin from dynamic optical coherence elastography. IEEE Transactions on Biomedical Engineering, 2010. 57(4): p. 953-9.
  39. Ellis, J. Combat Obesity by Turning White Fat into Brown Fat. 2016; Available from: https://www.labroots.com/trending/genetics-and-genomics/4758/combat-obesity-white-fat-brown-fat.
  40. Omidi, E., et al., Characterization and assessment of hyperelastic and elastic properties of decellularized human adipose tissues. J Biomech, 2014. 47(15): p. 3657-63.
  41. Chen, J.H., et al., Evaluation of breast stiffness measured by ultrasound and breast density measured by MRI using a prone-supine deformation model. Biomark Res, 2019. 7: p. 20.
  42. Briot, N., et al., In vivo measurement of breast tissues stiffness using a light aspiration device. Clinical Biomechanics, 2022(99).
  43. Matsumura, T., et al., Measurement of elastic property of breast tissue for elasticity imaging, in 2009 IEEE International Ultrasonics Symposium. 2009, IEEE. p. 1451-1454.
  44. Dempsey, S.C.H., J.J. O’Hagan, and A. Samani, Measurement of the hyperelastic properties of 72 normal homogeneous and heterogeneous ex vivo breast tissue samples. J Mech Behav Biomed Mater, 2021. 124: p. 104794.
  45. Briot, N., et al., Ex-Vivo mechanical characterisation of the breast Cooper’s ligaments. Computer Methods in Biomechanics and Biomedical Engineering, 2020. 23(sup1): p. S49-S51.
  46. Briot, N., et al., Experimental characterisation and modelling of breast Cooper’s ligaments. Biomechanic and Modeling Mechanobiology, 2022. 21(4): p. 1157-1168.
  47. Masithulela, F.J., Computational biomechanics in the remodelling rat heart post myocardial infarction. 2016.
  48. Nemavhola, F., Fibrotic infarction on the LV free wall may alter the mechanics of healthy septal wall during passive filling. Biomedical Materials and Engineering, 2017. 28(6).
  49. Wellman, P.S., Tactile Imaging, in Engineering and Applied Sciences. 1999, Harvard University.
  50. Krouskop, T.A., et al., Elastic moduli of breast and prostate tissues under compression. Ultrasound Imaging, 1998. 20(4): p. 260-274.
  51. Nemavhola, F., Detailed structural assessment of healthy interventricular septum in the presence of remodeling infarct in the free wall–A finite element model. Heliyon, 2019. 5(6).
  52. Masithulela, F. The effect of over-loaded right ventricle during passive filling in rat heart: A biventricular finite element model. in ASME International Mechanical Engineering Congress and Exposition. 2015. Texas: American Society of Mechanical Engineers.
  53. Masithulela, F. Analysis of passive filling with fibrotic myocardial infarction. in ASME 2015 International Mechanical Engineering Congress and Exposition. 2015. Texas.
  54. Nemavhola, F., Biaxial quantification of passive porcine myocardium elastic properties by region. Engineering Solid Mechanics, 2017. 5(3): p. 155-166.
  55. Rao, S.N., et al., Mechanical response of polyacrylamide breast tissue phantoms: Formulation, characterization and modeling. Journal of Mechenical Behaviour of Biomedical Materials, 2022. 129: p. 105125.
  56. Calvo-Gallego, J.L., et al., Comparison of the viscoelastic properties of human abdominal and breast adipose tissue and its incidence on breast reconstruction surgery. A pilot study. Clinical Biomechanics 2020. 71: p. 37-44.
  57. Bustamante-Orellana, C., et al., Biomechanics of Soft Tissues: The Role of the Mathematical Model on Material Behavior, in Advances in Emerging Trends and Technologies. 2020. p. 301-311.
  58. Christensen, M.B., K. Oberg, and J.C. Wolchok, Tensile properties of the rectal and sigmoid colon: a comparative analysis of human and porcine tissue. SpringerPlus, 2015. 4(1).
  59. Gao, C. and H. Gregersen, Biomechanical and morphological properties in rat large intestine. 2000. p. 1089-1089-97.
  60. Liao, D., J. Zhao, and H. Gregersen, 3D Mechanical properties of the partially obstructed guinea pig small intestine. 2010. p. 2079-2079-86.
  61. Rubod, C., et al., Biomechanical Properties of Human Pelvic Organs. Urology, 2012. 79(4): p. 968.e17-968.e22.
  62. Calvo-Gallego, J.L., et al., Comparison of different constitutive models to characterize the viscoelastic properties of human abdominal adipose tissue. A pilot study. 2018. p. 293-293-302.
  63. Taylor, Z.A., et al., On modelling of anisotropic viscoelasticity for soft tissue simulation: numerical solution and GPU execution. Med Image Anal, 2009. 13(2): p. 234-44.
  64. Dwivedi, K.K., et al., A hyperelastic model to capture the mechanical behaviour and histological aspects of the soft tissues. Journal of Mechanical Behaviour of Biomedical Materials, 2022. 126: p. 105013.
  65. Hamza, M.N. and H.M. Alwan, Hyperelastic Constitutive Modeling of Rubber and RubberLike Materials under Finite Strain. Engineering & Technology Journal, 2010. 28(13): p. 2560-2575.
  66. Verron, E. and G. Marckmann, Comparison of Hyperelastic Models for Rubber-Like Materials. Rubber Chemistry and Technology, 2006. 79(5): p. 835-858.
  67. Shahzad, M., et al., Mechanical Characterization and FE Modelling of a Hyperelastic Material. Materials Research, 2015. 18(5): p. 918-924.
  68. Steinmann, P., M. Hossain, and G. Possart, Hyperelastic models for rubber-like materials: consistent tangent operators and suitability for Treloar’s data. Archive of Applied Mechanics, 2012. 82(9): p. 1183-1183-1217.
  69. Lohr, M.J., et al., An introduction to the Ogden model in biomechanics: benefits, implementation tools and limitations. Philosophical Transaction of the Royal Society A: Mathematical, Physicaland Engineering Science, 2022. 380(2234): p. 20210365.
  70. Yin, H.M., et al., ImageParser: a tool for finite element generation from three-dimensional medical images. BioMedical Engineering OnLine, 2004. 3(1).
  71. Martínez-Martínez, F., et al., A finite element-based machine learning approach for modeling the mechanical behavior of the breast tissues under compression in real-time. Computers in Biology and Medicine, 2017. 90: p. 116-124.
  72. Moes, N.C.C.M. and I. Horváth. Using finite elements model of the human body for shape optimization of seats: optimization material properties. in International Design Conference - Design 2002. 2002. Dubrovnik.
  73. Erkamp, R., et al., Measuring the elastic modulus of small tissue samples. Ultrason Imaging, 1998. 20(1): p. 17-28.
Preprints 113670 g001
Figure 1. Female Breast Anatomy [3].
Figure 1. Female Breast Anatomy [3].
Preprints 113670 g001
Preprints 113670 g002
Figure 2. Mechanical response of soft tissues subjected to (a) monotonic and quasi-static cycling loading to pre-scribed strain, and (b) pre-scribed stress [18].
Figure 2. Mechanical response of soft tissues subjected to (a) monotonic and quasi-static cycling loading to pre-scribed strain, and (b) pre-scribed stress [18].
Preprints 113670 g002
Preprints 113670 g004
Figure 4. Microstructures of (a) Brown adipose and (b) White adipose tissues [39].
Figure 4. Microstructures of (a) Brown adipose and (b) White adipose tissues [39].
Preprints 113670 g004
Preprints 113670 g005
Figure 5. MR elastography shear stiffness for adipose and fibroglandular breast tissues [27].
Figure 5. MR elastography shear stiffness for adipose and fibroglandular breast tissues [27].
Preprints 113670 g005
Preprints 113670 g006
Figure 6. Uni-axial test on Cooper’s ligament sample [46].
Figure 6. Uni-axial test on Cooper’s ligament sample [46].
Preprints 113670 g006
Preprints 113670 g007
Figure 7. Nominal stress-strain response of fat, glandular, and carcinoma phantoms [50].
Figure 7. Nominal stress-strain response of fat, glandular, and carcinoma phantoms [50].
Preprints 113670 g007
Preprints 113670 g008
Figure 8. The Breast Finite Element Analysis Mesh [70].
Figure 8. The Breast Finite Element Analysis Mesh [70].
Preprints 113670 g008
Preprints 113670 g009
Figure 9. (a) Cutting device, (b) Photo of an enclosed adipose sample when being cut, and (c)Photo of the block-shaped adipose tissue [22].
Figure 9. (a) Cutting device, (b) Photo of an enclosed adipose sample when being cut, and (c)Photo of the block-shaped adipose tissue [22].
Preprints 113670 g009
Preprints 113670 g010
Figure 10. The Indentation test Set-up (a) Schematic diagram and (b) Photo of the set-up [22].
Figure 10. The Indentation test Set-up (a) Schematic diagram and (b) Photo of the set-up [22].
Preprints 113670 g010
Preprints 113670 g011
Figure 11. FE model of a block-shaped adipose tissue sample subjected to indentation [22].
Figure 11. FE model of a block-shaped adipose tissue sample subjected to indentation [22].
Preprints 113670 g011
Preprints 113670 g012
Figure 12. Magnetic Resonance Compression Set-up [22].
Figure 12. Magnetic Resonance Compression Set-up [22].
Preprints 113670 g012
Preprints 113670 g013
Figure 13. (a) Abdominal Adipose sample, and (b) Breast adipose sample [1].
Figure 13. (a) Abdominal Adipose sample, and (b) Breast adipose sample [1].
Preprints 113670 g013
Preprints 113670 g014
Figure 14. Abdominal adipose Sample Division [1].
Figure 14. Abdominal adipose Sample Division [1].
Preprints 113670 g014
Preprints 113670 g015
Figure 15. Photo of the top and side view of the prepared cylindrical adipose specimen [1].
Figure 15. Photo of the top and side view of the prepared cylindrical adipose specimen [1].
Preprints 113670 g015
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated