Prerpints.org logo
Preprint
Article

Utilisation of Palm Frond Waste as Fuel for Co-firing Coal and Biomass in Tangentially Pulverized Coal Boiler Using Computational Fluid Dynamic (Cfd) Analysis

Altmetrics

Downloads

87

Views

42

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

30 July 2024

Posted:

30 July 2024

You are already at the latest version

Alerts
Abstract
Indonesia possesses significant biomass potential, including palm oil plantations. The palm oil industry has experienced rapid expansion, with a 7.67% growth rate over the past decade and an 11.09% annual increase in palm oil production. Co-firing (HT-FRD) is a beneficial technology for reducing exhaust gas emissions generated by coal-burning power stations. By utilizing Computational Fluid Dynamics (CFD), the study has modeled and evaluated co-firing palm frond residue (HT-FRD) with hydrothermal treatment into a 315 MWe boiler. In the simulation, six different HT-FRD co-firing ratios: 0%, 5%, 15%, 25%, 35%, and 50% were used to demonstrate the differences in combustion characteristics and emissions in the combustion chamber. The data indicates that HT-FRD co-firing can enhance temperature distribution, velocity, and unburned particles. All in all, co-firing conditions with 5% - 15% HT-FRD ratios appear to have the most favorable combustion temperature, velocity, and exhaust gas characteristics.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

In Indonesia, there has been a shift in Coal-Fired Power Plants (PLTU) from using high and medium-grade coal to low-grade coal. This policy change was primarily motivated by the comparatively lower cost of low-rank coal, which accounts for approximately 86.59% of the country's coal reserves [1]. The largest coal reserves in Indonesia consist of lignite and sub-bituminous coal, characterized by their low calorific value and higher sulfur content. Utilizing low-quality coal will affect all coal-fired power plant's operational reliability [2,3]. Unfortunately, the combustion of low-rank coal, which typically has a moisture content ranging from 40 to 50% (wet basis), presents challenges in Coal-Fired Power Plant boilers, leading to environmental issues and significant greenhouse gas emissions [4]. On the other hand, Indonesia possesses significant biomass potential, including palm oil plantations. The palm oil industry has experienced rapid expansion, with a 7.67% growth rate over the past decade and an 11.09% annual increase in palm oil production [5]. Unfortunately, the production of palm oil and the establishment of plantations have resulted in various environmental problems, such as greenhouse gas emissions, land conversion, and substantial agricultural waste production [6]. Such production generated solid waste, including fruit bunch peeling, palm shells, and fiber. Fiber frequently produces electricity and steam for milling [7]. To ensure the continuous cycling of nutrients and to mitigate soil erosion, it is usual practice to reuse peeled fruit bunches as mulch in the plantation. Compared to other types of solid waste, the mixed biomass of palm fronds (FRD) exhibits superior combustion performance, as indicated by higher Rmax and Tmax values, compared to other biomass mixtures [8].
Furthermore, using palm frond mixtures (FRD) can mitigate slagging-fouling risks, such as reducing the ash fusion temperature, deposition material, and sticky residue within the combustion chamber [9]. This process positively impacts the coal particle combustion, ensuring complete burning before entering the furnace exit [10,11]. There is a growing focus on utilizing biomass waste as an alternative to fossil fuels. Biomass co-firing is a promising technology that has the potential to substantially decrease CO2 emissions and improve the utilization of renewable energy sources in the overall energy system [12]. It is essential to consider the specific characteristics of each biomass when designing and selecting combustion chambers and boiler operating conditions [13]. Biomass can be employed in two distinct ways to produce electricity via combustion: dedicated combustion and co-firing. This method offers several advantages when we use co-firing in existing power plants, particularly coal-fueled ones. These advantages encompass enhanced combustion efficiency and reduced capital expenses [14]. Research on biomass co-firing has progressed rapidly, mainly through experiments and computational analysis. Detailed explanations have been given about the complex modeling of combustion technologies, including the simultaneous burning of coal and biomass [15].
The process of hydrothermal (HT) processing has been extensively researched as a means of converting biomass with a high moisture content into high calorific solid fuels [16,17,18,19]. Hydrothermal processing involves hydrolysis, condensation, decarboxylation, and dehydration reactions to convert biomass materials into carbon-rich solids under autogenous pressure at moderate temperatures (150 - 350 °C) [19]. Numerous studies have demonstrated that because hydrothermal biomass has higher carbon content, a higher calorific value, and is hydrophobic, it is more energy dense [20,21]. In addition, the hydrothermal method was deemed necessary for the treatment of palm biomass due to its high conversion efficiency, the abilityto treat biomass under wet conditions, its potential to produce various value-added products, and its ability to remove some inorganic constituents including potassium from the biomass, although it requires specialised equipment and complex process control [22,23,24].
Additionally, a number of studies have used computational fluid dynamics (CFD) with various biomasses to examine how coal and biomass co-firing behave against current traditional methods, such as olive waste [25], switch grass [26], pinewood [27], and the Cynara cardunculus [28]. The cofiring of various biomass and natural gas blends has also been modeled using CFD [29]. Co-firing of coal and recovered fuel [30]. and combustion of coal and biomass for oxy-fuel [31]. This investigation employs Computational Fluid Dynamics (CFD) as a highly accurate measurement technique to analyze the thermal performance of co-firing combustion [32]. Unfortunately, to the best of the authors' knowledge, no research has been discovered that discusses and elucidates the combustion characteristics of palm fronds and coal co-firing using numerical simulation on tangentially fired pulverized coal boilers. The main aim of this study is to investigate the process of burning palm fronds (FRD) and coal as a fuel in a 315 MW power plant to analyze the distribution of temperature, gas velocity, and flue gas composition of CO, CO2, and O2 in the combustion chamber.

2. Hydrothermal-Based Co-Firing System

Various techniques can be employed to integrate biomass with coal in combustion chambers and injection, including comilling, pregasification, and parallel co-firing. Compared to other strategies, the injection technique is the most efficient due to its lower capital costs and higher co-firing ratios [33]. Hence, the co-firing injection was selected for this analysis study. In this specific procedure, the palm fronds (FRD) are mixed with powdered coal and inserted into the combustion chamber following individual drying and grinding methods. (Figure 1) is a schematic diagram that demonstrates the fundamental principle of the FRD co-firing system. The raw FRD is dehydrated at temperatures ranging from 200 to 250 °C [34,35], typically taking several minutes to two hours.
This drying process aims to enhance the calorific value and properties of the FRD. Subsequently, the coal fuel is finely ground to the required particle size for efficient combustion within the boiler chamber. Following this, both fuel types are thoroughly mixed and injected into the combustion chamber and air, facilitated by respective heaters [36,37]. The superheater absorbs thermal energy from the combustion process, while the economizer generates steam specifically for the turbine. The flue gas, characterized by its comparatively low exergy level, is the fluidization gas in the bed to supply heat to the drying chamber. In this study, (Figure 2) presents a schematic representation of the combustion chamber employed, illustrating its dimensions, meshing layout, and the burner inlet located in the corner of the boiler. The dimensions of the boiler are 63.7 m in height, 13.7 m in width, and 36.2 m in length. It is utilized in a pre-existing coal-fired power plant with a 315 MWe power generation capacity.
The configuration and area of the boiler's combustion system were established through the commercial software SOLIDWORK 2020. Afterward, the process is proceeded by creating a simulation of the established system domain. In the case of co-firing simulation, the software ANSYS FLUENT 2023 R2 is utilized to calculate velocity distribution, temperature distribution, and exhaust gas composition. The simulation includes the fundamental equations (enthalpy, mass, and momentum), heat transfer radiative, turbulence, and reactions in the gaseous phase and particles. This method is optimal for quantifying fluid flow, heat and mass transfer, chemical reactions, and interactions between solids and fluids. The research examines the co-firing FRD and coal performance using the CFD method [32,38,39]. CFD modeling proves to be significantly more efficient in terms of time and cost than physical experimentation while also being safe and easily scalable. Consequently, it is frequently utilized to validate experimental approaches. The CFD analysis aims to clarify combustion processes, including combustion temperatures and resulting exhaust gas concentrations. This study employed unaltered coal as the standard for combustion. The coal and FRD flow rates are determined based on the specified FRD mass fraction. The study investigates five distinct FRD mass fractions: 0% (representing 100% coal), 5%, 15%, 25%, 35%, and 50%. Observations are made on the temperature distribution and gas concentration generated during co-firing.

2.1. Governing Equations

The Eulerian-Lagrangian approach is frequently used to simulate co-firing as a two-phase reaction flow involving solid and gas phases. This technique uses the Navier-Stokes equations to examine the gas phase, regarding the solid phase as a different entity. Newton's equations of motion are employed to determine the trajectory of each particle, while a spherical technique is employed to simulate the interactions between particles [40]. The energy and mass transfer calculation for each particle is conducted to determine factors such as temperature and gas concentration. This technique allows for a more accurate simulation by tracking the motion of every individual particle within the system. The interactions between the gaseous phase and solid particles encompass mass, momentum, and energy, performed using the particle source method within a cell. The particle's state undergoes modification as it traverses its trajectory [41,42]. Mathematical calculations in this approach are primarily governed by heat transfer and fluid flow. Fluid dynamics is classified as a flow with high viscosity; each governing equation can be expressed in the following fashion:
Mass continuity equation
D ρ D t + ρ ∇ . U → = 0
Momentum equation in the x component
ρ D u D t = − ∂ p ∂ x + ∂ τ x x ∂ x + ∂ τ y x ∂ y + ∂ τ z x ∂ z ρ f x
Momentum equation in the y component
ρ D v D t = − ∂ p ∂ y + ∂ τ x y ∂ x + ∂ τ y y ∂ y + ∂ τ z y ∂ z   ρ f y
Momentum equation in the z component
ρ D w D t = − ∂ p ∂ z + ∂ τ x z ∂ x + ∂ τ y z ∂ y + ∂ τ z z ∂ z   ρ f z
Energy equation
ρ D D t e + U 2 2 = ρ q + ∂ ∂ x k ∂ T ∂ x + ∂ ∂ y k ∂ T ∂ y + ∂ ∂ z k ∂ T ∂ z − ∂ ( u p ) ∂ x − ∂ ( v p ) ∂ y − ∂ w p ∂ z + ∂ u τ x x ∂ x + ∂ u τ y x ∂ y + ∂ u τ z x ∂ z + ∂ v τ x y ∂ x + ∂ v τ y y ∂ y + ∂ v τ z y ∂ z + ∂ w τ x z ∂ x + ∂ w τ y z ∂ y + ∂ w τ z z ∂ z + ρ f → U →
The fluid flow equations govern mathematical processes in quantitative physics calculations, specifically Computational Fluid Dynamics (CFD). The equations incorporate density, mass conservation, specific mass fraction, temperature, enthalpy, turbulent dissipation rate (ε), and turbulent kinetic energy (k) as essential factor fluids. It is assumed that the representation of viscous flow is achieved through fluid dynamics principles [43,44,45].

2.2. Turbulence

The combustion chamber flow in this study exhibits turbulence due to fluid inertia, complex geometry, and high flow rates. Turbulence plays a crucial role in the co-firing model within the combustion chamber as it significantly influences heat and mass transfer. The k-ε turbulence model is commonly used in computational fluid dynamics (CFD) modeling to calculate turbulent combustion flow. This study utilizes the k-ε model to solve the Reynolds-averaged Navier-Stokes (RANS) equations for co-firing modeling. The k-ε turbulence model is highly regarded for its effectiveness and user-friendly nature [33,46], making it a popular choice in numerous industrial applications [47]. This model's two primary equations govern the turbulent dissipation rate (ε) and turbulent kinetic energy (k). It can be articulated as follows:
Turbulent kinetic energy (k)
∂ ∂ t ρ k + ∂ ∂ x i ρ k u i = ∂ ∂ x j [ u + u t σ k ∂ k ∂ x j ] + P k + P b − ρ ε − Y M + S k
Turbulent dissipation rate (ε)
∂ ∂ t ρ ε + ∂ ∂ x i ρ ε u i = ∂ ∂ x j [ u + u t σ ε ∂ k ∂ x j ] + C 1 ε ϵ k ( P k + C 3 ε P b ) − ρ C 2 ε ε 2 k + S ε
The variables Pb, Ym, Pk, and μt denote long-term k production, turbulent viscosity, time effect, and the impact of variations in expansion on the overall energy dissipation rate, respectively. The equation determines the values:
μ t = ρ C μ k 2 ϵ
P k = − ρ u i '   u j ' ¯ ∂ u j ∂ x i
P b = β g i μ t P r t ∂ T ∂ x i
β = − 1 ρ ∂ ρ ∂ T p
Gi, T, and Prt are the gravitational acceleration, temperature, and turbulent Prandtl numbers.

2.3. Radiation

Solid particle combustion, including heating, ignition, and charcoal burning, relies on heat transfer through radiation. Therefore, it is essential to comprehend the rate and amount of volatile substances emitted during the devolatilization phase concerning temperature. The discrete ordinate (DO) radiation model is used in this simulation because it accurately considers the absorption of radiation heat during burning. The absorption coefficient is calculated using the weighted sum of grey gases model (WSGGM) with a fixed value of 0.6 [48,49]. To address the issue of radiation heat transfer, the study utilized the P-1 approach, which relies on the expansion of radiation intensity [46]. The radiation model can be mathematically represented in the following manner:
∇ . Γ ∇ G = a + a p G − 4 π ( a σ T 4 π + E p )
Γ = 1 / 3   ( a + a p + σ p )
G = 4   σ   T 4
a p = Lim V → 0 ⁡ ∑ n = 1 N ε p n A p n V
E p = Lim V → 0 ⁡ ∑ n = 1 N ε p n   A p n σ   T p n 4 π   V
σ p = Lim V → 0 ⁡ ∑ n = 1 N ( 1 − f p n ) ( 1 − ε p n ) A p n V
The variables Ap, σ, V, G, σp, and Ep The terms to be represented include absorption coefficient, incident radiation, Stefan-Boltzmann constant, particulate presence, particle scattering factor, equivalent emission, and volumes all contribute to the equivalent absorption coefficient. Furthermore, fpn, Tpn, εpn, and Apn denote the emissivity, scattering factor, projected area, temperature, and particle n.

2.4. Reaction Mechanisms Particle Phases

The co-firing of coal and HT-FRD is recognised as a unique gas-solid flow system that induces chemical reactions. The model known as Eulerian-Lagrangian incorporates hydrodynamics into the analysis [50,51]. Coal particles and FRD chips are modeled separately as a two-phase discrete model. The Rosin-Ramler distribution approach is adopted for the particle distribution model [52]. Various reactions take place within the particle phase, notably during charcoal combustion. Charcoal undergoes oxidation, producing carbon monoxide (CO), which is then released into the combustion chamber as a large amount of gas. Acknowledging that charcoal produced from biomass generally exhibits greater reactivity and a higher heating rate than charcoal obtained from coal is crucial. This study utilizes a cohesive and all-encompassing response mechanism to assess the process of charcoal combustion in the presence of air. The process combustion of FRD and coal can be described as follows [36]:
C h a r c o a l C + 0.5 O 2 → C O
C h a r F R D C + 0.5 O 2 → C O

2.5 Reaction Mechanisms Gas Phase

Throughout the devolatilization process, the volatile components from T-FRD and coal are disengaged and subsequently undergo a reaction with oxygen, facilitating additional combustion. The oxidation process of these volatile components is characterized by a two-step overall reaction mechanism in which CO plays a significant role [53,54]. The chemical composition and heat of formation of these components are determined through proximate and ultimate analyses. The Westbrook-Dryer mechanism provides insights into the reactions of volatile materials in the gas phase [55]:
C o a l : C 0.02 H 3.94 O 1.57 N 0.0278 S 0.0021 + 0.22 O 2 → C O + 1.97 H 2 O + 0.0138 N 2 + 0.0021 S O 2
H T F R D : C 1.05 H 2.32 O 0.92 N 0.0116 S 0.0011 + 1.17 O 2 → C O + 1.16 H 2 O + 0.0058 N 2 + 0.0011 S O 2
C O + 0.5 O 2 → C O 2
k = A   e − E i R T
All reactions in the gas or particle phases have their kinetic parameters listed in Table 1. The kinetic reaction rate coefficients are determined using equation (23), which is derived from the Arrhenius equation that incorporates the activation energy Ei [40,56,57]. It is presumed that the coal in question belongs to the lignite kind.

3. Materials

In this work, the coal used in the existing power plant, the coal and FRD particles used in this experiment are detailed in Table 2, which presents their composition. The coal is sourced from Kalimantan, Indonesia, especially known as LRC, and has a significantly high moisture content. On the other hand, the FRD is sourced from a palm oil mill in Sumatra, Indonesia. The FRD utilized in this study is the as-received FRD type, which has been drying.

4. Boundary condition

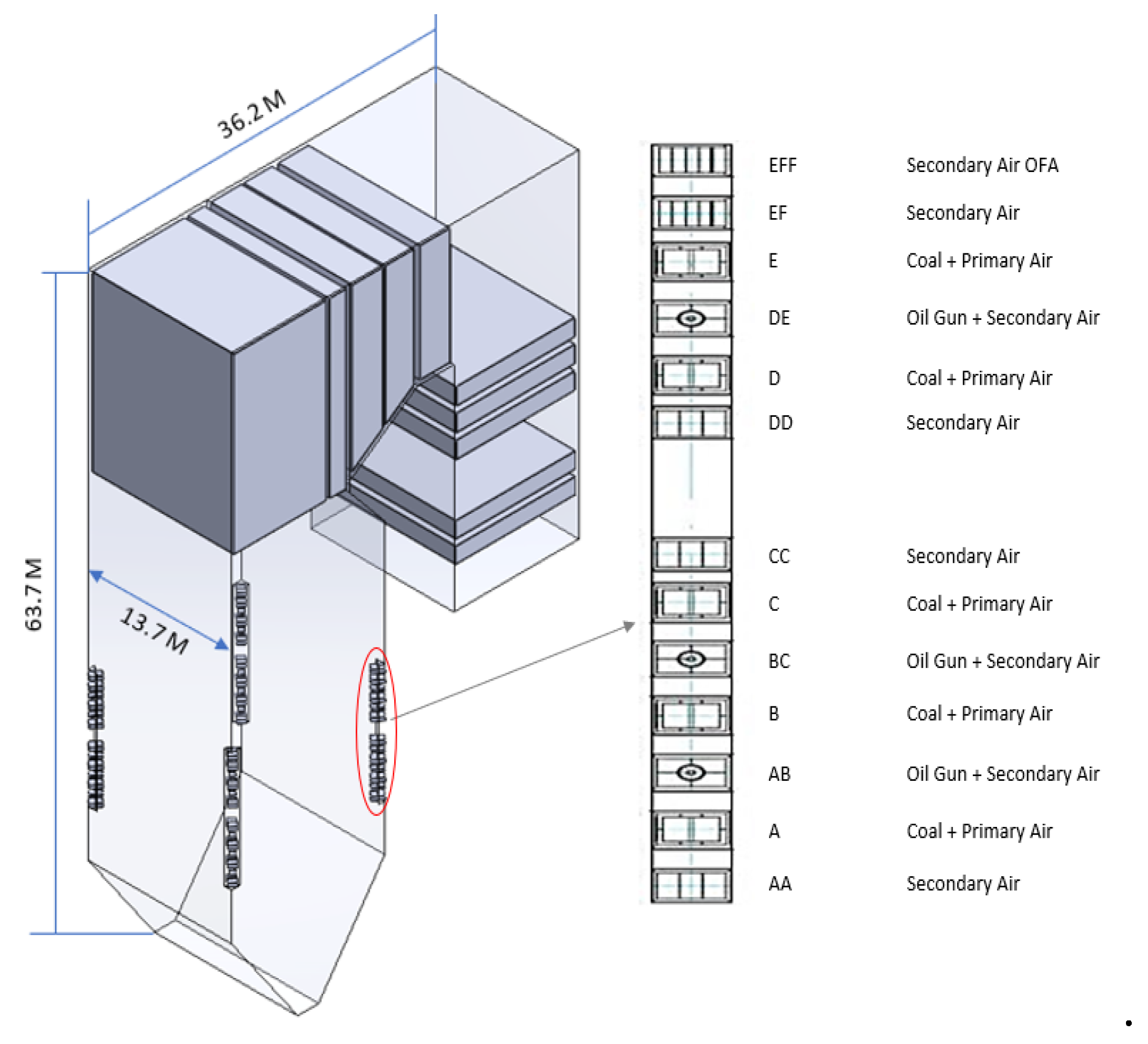
The simulation involves categorizing boundary conditions into four types: wall, mass flow inlet, pressure outlet, and interior. Figure 3 shows the simulation domain of co-firing coal and palm fronds in a tangentially pulverized coal boiler. The primary and secondary airflow at the inlet are subjected to mass flow inlet conditions, whereas the boiler outlet is subjected to pressure outlet conditions. The primary air is the fuel feeder gas that moves through the pipes alongside coal particles, and FRD is introduced into the furnace via burner inlets A, B, C, D, and E. However, in this simulation, burner E (standby) is not operated, so burner E is designated as a wall. Additional air gas, required for combustion, enters the furnace through burner inlets AA, AB, BC, CC, DD, DE, EF, and EFF, flowing through the outer pipe.
Each particle is viewed as a solid sphere ranging from 60 to 200 mesh (74-250μm), and the simulated power generator efficiently produces 315 MWe, achieving a fundamental combustion efficiency of 30%. Table 3 presents the boiler operating performance data. For the combustion simulation, the required amount of air is uniformly introduced into the chamber. The ratios of primary air, secondary air, and overfire air relative ratios remain unchanged compared to the scenario of pure coal combustion. Upon entering the combustion chamber, the particles undergo a series of ongoing events, which include heating, drying, devolatilization, combustion of gases and char, creation of pollutants, and emission of heat radiation [46,58]. The Coupled Algorithm, a method suitable for simulating complex geometries and multiple components, is employed to calculate the combined pressure and velocity of the Navier-Stokes equations. An analysis of the gas-solid two-phase flow is conducted using the Eulerian-Lagrangian technique. The Reynolds average Navier-Stokes (RANS) equations are solved in the Eulerian domain to conduct the gas phase modelling.
The coal characteristics and HT-FRD setup information at each burner location are presented in Table 4. Throughout the simulation, fuel is injected in varying proportions based on the HT-FRD mix ratio of 5-50% across 16 burners (A-D burner areas, while E burner remains on standby). The domain is represented in a 3D combustion chamber model with a mesh count of 737,426 unstructured tetrahedral cells. The CFD simulation tracks the spatial distribution of temperature, velocity, and concentrations of exhaust gases, including CO2, CO, and O2.

5. Grid Independence and Validating the Computational Fluid Dynamic (CFD) Simulation

An independent study is necessary to verify the accuracy of the data findings. The grid domain utilized should closely resemble real-world conditions.
Figure 4 and Figure 5 depict the variations in cell count and the comparison of the exit temperature at FEGT (Flue Gas Exit Temperature) for grid independence and validation. Under real-world conditions, the FEGT of the boiler's combustion chamber is measured at 1258.15 K. The simulation results, obtained with different cell counts of 474,764, 737,426, and 1,386,233, yield exit temperatures of 1368.51 K, 1258.51 K, and 1197.05 K, respectively. Consequently, when comparing the simulated FEGT gas temperature to the actual value, the error margin is 0.03% for the cell count 737,426

6. Results and discussion

6.1. Effects of Co-Firing HT-FRD on Distribution Temperature

Simulation approaches were used to investigate the impact of HT-FRD co-firing on the combustion parameters of a pulverized coal boiler. Figure 6 depicts 3D display model the temperature distribution within the combustion chamber for each HT-FRD co-firing, with different mixing ratios. The simulation findings reveal a slight variation in gas temperature distribution, increasing the proportion of HT-FRD combination, which generally results in a more vital flame, which leads to a more consistent temperature as the height within the combustion chamber increases. Greater volatility leads to accelerated heat evaporation from combustion within the combustion chamber to the external environment of the furnace.
This conclusion is supported by the temperature measurements in the FEGT region. Figure 7 illustrates the temperature distribution curve across the height of the furnace, ranging from the bottom ash to the furnace exit, for various ratios of HT-FRD co-firing.
The gas temperature distribution appears to be consistent across all co-firing ratios. There is a disparity in temperature between the combustion and OFA zones that goes all the way to the FEGT. As the biomass ratio increases, the maximum temperature falls from the primary combustion zone to the overfire air (OFA) zone.
However, in the FEGT section, the temperature rises with the HT-FRD co-firing ratio compared to pure coal. The highest combustion center temperature is found in the furnace section of the combustion chamber, with 0% HT-FRD mass fraction at 1711 K, followed by 15% 1688 K (decrease of 1.3%), 5% 1662 K (decrease of 2,9%), 25% 1656 K (decrease of 3,2%), 35% 1653 K (decrease of 3.4%), and 50% 1607 K (decrease of 6%). When using a 15% mass fraction of HT-FRD in co-firing, a greater combustion temperature is found than a 5% mass fraction. However, the difference is not regarded to be significant. The mean temperature of the gas at the exit of the combustion chamber flue (FEGT) for HT-FRD mass fractions of 0%, 5%, 15%, 25%, 35%, and 50% are 1258 K, 1457 K (increase of 15.8%), 1464 K (increase of 16.4%), 1436 K (increase of 14,2%), 1427 K (increase of 13.4%), and 1420 K (increase of 12,9%) respectively. The temperature distribution profile indicates the most favorable coal combustion and HT-FRD co-firing performance when the HT-FRD mixing ratio is 15%. The combustion process involves four stages: ash formation, char combustion, devolatilization, and drying. [59]. It is important to note that the combustion stages may vary for different fuels.
6.2. Effects of Co-Firing HT-FRD on Distribution Velocity
Figure 8 depict the mean velocity distribution throughout the combustion chamber for varying HT-FRD co-firing ratio. The velocity increases as the HT-FRD mass ratio increases across the combustion chamber.
The data presented in Table 2 indicates that HT-FRD particles exhibit higher volatile content moisture and lower than coal particles. Consequently, HT-FRD particles are swiftly dispersed throughout the combustion chamber, leading to devolatilization and an accelerated combustion process with an increased HT-FRD co-firing ratio. In the OFA zone, it can be seen that the velocity distribution increases up to 80%, for the 0% FRD mass ratio it is 7.77 m/s, followed by 5% at 13.77 m/s, 15% at 14.23 m/s, 25% at 14.06 m/s, 35% at 13.94 m/s, and 50% at 13.54 m/s.
Figure 9 demonstrates that the gas flow velocity in the combustion zone is rather consistent regardless of whether full coal or palm frond co-firing is used as fuel. This indicates that blending the fuels does not significantly affect the distribution of velocity. The rapid speed in this area indicates the ongoing combustion reaction. In the FEGT zones, the gas flow velocities in all circumstances exhibit a minor decrease as a result of the combustion process being reduced up to the flue gas. In addition, the gas flow velocity concentration remains relatively constant across varied co-firing mass ratio, indicating that the flow properties in the furnace are not greatly affected.

6.3. Effects of Co-Firing HT-FRD on Gas Emission CO2, CO, and O2

Figure 10 depict the distribution profiles of CO2 in the cross-section and the central location within the combustion chamber. The mean mass percentages of carbon dioxide CO2 in the flue gas at the exit of the combustion chamber (FEGT) the HT-FRD co-firing ratios resulted in a drop of up to 30.5%. Case 2 experienced a drop of 30.5% from 0.187 to 0.130. In case 3, there was a decrease of 25.1% from 0.187 to 0.140. Case 4 saw a decrease of 23.5% from 0.187 to 0.143. Case 5 had a decrease of 20.9% from 0.187 to 0.148. Finally, case 6 had a loss of 15% from 0.187 to 0.159. Therefore, a reduced ratio of thermal fuel replacement with biomass (HT-FRD) leads to a decreased concentration of carbon dioxide CO2 in the exhaust gases. Thus, a low HT-FRD co-firing ratio results in a lower CO2 concentration in the flue gas. The reactions illustrated in equations (18-22) primarily convert carbon into CO2. Consequently, coal possesses a higher carbon content than FRD. The inclusion of HT-FRD diminishes the carbon content while enhancing the volumetric heat capacity and the propensity of the flame to spin [60].
Figure 11 demonstrates that including biomass HT-FRD into the fuel in the combustion zone can gradually decrease flue gas emissions, particularly CO2, by reducing combustion reactions. The research demonstrates that the co-firing of palm frond biomass with coal can result in a reduction of CO2 emissions when compared to the complete combustion of coal. This suggests potential environmental advantages.
Figure 12 provide valuable insights into CO gas concentration traversing the combustion chamber during co-firing. Unlike total coal combustion, HT-FRD co-firing has properties that can increase the concentration of CO during combustion. An increase in the proportion of HT-FRD results in a higher level of CO concentration produced during the combustion process.
Nevertheless, augmenting the co-firing ratio of HT-FRD does not significantly alter the final result. The differing volatile matter levels between coal and HT-FRD can be considered as the cause of this outcome (as shown in Table 2), which are readily oxidized at high combustion temperatures, facilitating the formation of CO. Additionally, CO combines with the incoming O2 in the combustion to generate CO2.
Figure 13 shows that CO exhaust emissions increase with the addition of HT-FRD mass ratio, this indicates that the combustion is incomplete or part of the fuel is not burned out which results in increased CO gas in each zone. So that CO gas is not fully oxidised to CO2 in combustion.
Figure 14 depict the oxygen distribution profiles within the combustion chamber when co-firing at different HT-FRD ratios. An increased HT-FRD mass ratio leads to a reduction in oxygen concentration. Due to its higher oxygen content relative to coal, HT-FRD can be depleted alongside other flue gases during combustion. The O2 concentration exiting the combustion chamber at FEGT increased, for HT-FRD co-firing ratios of 0%, 5%, 15%, 25%, 35%, and 50% by 0.042, 0.084 (100% increase), 0.077 (83% increase), 0.075 (78.6% increase), 0.071 (69% increase), and 0.062 (47.6% increase), respectively.
Figure 15 depicts the O2 concentration curves as they move through the furnace during co-firing, with varying HT-FRD mass ratios.
In every instance, higher concentrations of O2 are seen in close proximity to the OFA zone, but they diminish gradually as the combustion reaction progresses. When comparing pure coal combustion to HT-FRD fuel combustion, it is observed that HT-FRD fuel can be decomposed quickly and the combustion produces high temperatures. Therefore, co-firing HT-FRD fuel can increase the consumption of oxygen concentration and reduce the amount of O2 remaining in the combustion zone.

7. Conclusions

The study investigated the potential of utilizing advanced FRD as a renewable energy source. Through modeling and evaluating the coal co-firing performance with HT-FRD using CFD analysis at various mixture mass ratios, it was found that a 5% HT-FRD mass ratio is the most optimal co-firing condition corresponding to the Coal-Fired Power Plants' actual conditions. It can be seen from the increase in combustion temperature in the FEGT zone by 16% from 1258 K to 1457 K, the velocity distribution increased by 80%, and the O2 concentration also increased by 100% from 0.042 to 0.084 mf. And most importantly, it can reduce CO2 emissions by 30% from 0.187 to 0.130 mf in the resulting exhaust gas. However, the addition of T-FRD produces a relatively high concentration of CO gas, which means that the freezing is not perfect. Attributed to the higher volatile matter HT-FRD content compared to coal. Incorporating this natural resource (FRD) can enhance the efficiency of utilizing renewable resources, mitigate environmental impacts, and prolong the operational lifespan of existing and future coal-fired power plants.

Author Contributions

This manuscript was written thanks to the contributions of all authors, each of whom collaborated in discussing the results, reviewing, and approving the final version of the manuscript.

Funding

The authors received no financial support for the research, authorship, and publication of this article.

Institutional Review Board Statement

Not applicable

Informed Consent Statement

Not applicable

Data Availability Statement

The datasets generated and/or analyzed during the current study are available from the corresponding author on reasonable request.

Acknowledgments

The authors gratefully recognize the financial assistance provided by the Center for Education Financing (BPPT) and Indonesia's endowment fund for education (LPDP) and the experts who made helpful ideas to improve the quality and substance of this research.

Conflicts of Interest

There are no potential conflicts of interest concerning the research, authorship, and publication of this article.

Abbreviation

Abbreviation Meaning
CFD computational fluid dynamics
CO2 carbon dioxide
CO carbon monoxide
FEGT furnace exit gas temperature
HT-FRD hydrothermal palm frond
OFA overfire air
O2 oxygen
RANS Reynolds average Navier-Stokes
PA primary air
SA secondary air

References

  1. PLN, ‘menteri energi dan sumber daya mineral republik indonesia keputusan menteri energi dan sumber daya mineral republik indonesia’, 2023.
  2. Aziz, M.; Oda, T.; Kashiwagi, T. Energy-Efficient Low Rank Coal Drying Based on Enhanced Vapor Recompression Technology. Dry. Technol. 2014, 32, 1621–1631. [Google Scholar] [CrossRef]
  3. Aziz, M.; Kansha, Y.; Kishimoto, A.; Kotani, Y.; Liu, Y.; Tsutsumi, A. Advanced energy saving in low rank coal drying based on self-heat recuperation technology. Fuel Process. Technol. 2012, 104, 16–22. [Google Scholar] [CrossRef]
  4. Liu, Y.; Aziz, M.; Kansha, Y.; Tsutsumi, A. A novel exergy recuperative drying module and its application for energy-saving drying with superheated steam. Chem. Eng. Sci. 2013, 100, 392–401. [Google Scholar] [CrossRef]
  5. Aziz, M.; Oda, T.; Kashiwagi, T. Design and Analysis of Energy-Efficient Integrated Crude Palm Oil and Palm Kernel Oil Processes. J. Jpn. Inst. Energy 2015, 94, 143–150. [Google Scholar] [CrossRef]
  6. Aziz, M.; Prawisudha, P.; Prabowo, B.; Budiman, B.A. Integration of energy-efficient empty fruit bunch drying with gasification/combined cycle systems. Appl. Energy 2015, 139, 188–195. [Google Scholar] [CrossRef]
  7. Basiron, Y. Palm oil production through sustainable plantations. Eur. J. Lipid Sci. Technol. 2007, 109, 289–295. [Google Scholar] [CrossRef]
  8. Darmawan, A.; Prida Putra, H.; Milky Kuswa, F.; Sholeh, M.; Aziz, M. Combustion characteristics during cofiring of palm empty fruit bunch, palm frond with bituminous coal. 2021.
  9. Hariana; Prabowo; Hilmawan, E. ; Kuswa, F.M.; Darmawan, A.; Aziz, M. A comprehensive evaluation of cofiring biomass with coal and slagging-fouling tendency in pulverized coal-fired boilers. Ain Shams Eng. J. 2023, 14, 102001. [Google Scholar] [CrossRef]
  10. S. Ihsan, Prabowo, W. A. Widodo, and I. N. A. Adi Saputra, ‘Numerical Investigation Effect of the addition of palm fronds on the burning of coal-fired boilers tangentially. in 2023 International Conference on Advanced Mechatronics, Intelligent Manufacture and Industrial Automation, ICAMIMIA 2023 - Proceedings, Institute of Electrical and Electronics Engineers Inc., 2023, pp. 261–265. [CrossRef]
  11. Gubba, S.; Ma, L.; Pourkashanian, M.; Williams, A. Influence of particle shape and internal thermal gradients of biomass particles on pulverised coal/biomass co-fired flames. Fuel Process. Technol. 2011, 92, 2185–2195. [Google Scholar] [CrossRef]
  12. Aziz, M.; Budianto, D.; Oda, T. Computational Fluid Dynamic Analysis of Co-Firing of Palm Kernel Shell and Coal. Energies 2016, 9, 137. [Google Scholar] [CrossRef]
  13. Fernando, R. Cofiring high ratios of biomass with coal. 2012.
  14. Koppejan, J.; Bv, B.; Kwant, K. Task 32 Biomass Combustion and Cofiring Task 32 Biomass Combustion and Cofiring Operating Agent. 2016.
  15. Griffifin, W.M.; Michalek, J.; Matthews, H.S.; Hassan, M.N.A. Availability of biomass residues for co-firing in peninsular Malaysia: Implications for cost and GHG emissions in the electricity sector. Energies 2014, 7, 804–823. [Google Scholar] [CrossRef]
  16. Novianti, S.; Nurdiawati, A.; Zaini, I.N.; Sumida, H.; Yoshikawa, K. Hydrothermal treatment of palm oil empty fruit bunches: an investigation of the solid fuel and liquid organic fertilizer applications. Biofuels 2016, 7, 627–636. [Google Scholar] [CrossRef]
  17. Lucian, M.; Fiori, L. Hydrothermal Carbonization of Waste Biomass: Process Design, Modeling, Energy Efficiency and Cost Analysis. Energies 2017, 10, 211. [Google Scholar] [CrossRef]
  18. Zaini, I.N.; Novianti, S.; Nurdiawati, A.; Irhamna, A.R.; Aziz, M.; Yoshikawa, K. Investigation of the physical characteristics of washed hydrochar pellets made from empty fruit bunch. Fuel Process. Technol. 2017, 160, 109–120. [Google Scholar] [CrossRef]
  19. Saqib, N.U.; Baroutian, S.; Sarmah, A.K. Physicochemical, structural and combustion characterization of food waste hydrochar obtained by hydrothermal carbonization. Bioresour. Technol. 2018, 266, 357–363. [Google Scholar] [CrossRef] [PubMed]
  20. Parshetti, G.K.; Hoekman, S.K.; Balasubramanian, R. Chemical, structural and combustion characteristics of carbonaceous products obtained by hydrothermal carbonization of palm empty fruit bunches. Bioresour. Technol. 2013, 135, 683–689. [Google Scholar] [CrossRef] [PubMed]
  21. Xiao, L.-P.; Shi, Z.-J.; Xu, F.; Sun, R.-C. Hydrothermal carbonization of lignocellulosic biomass. Bioresour. Technol. 2012, 118, 619–623. [Google Scholar] [CrossRef] [PubMed]
  22. Ibbett, R.; Gaddipati, S.; Davies, S.; Hill, S.; Tucker, G. The mechanisms of hydrothermal deconstruction of lignocellulose: New insights from thermal–analytical and complementary studies. Bioresour. Technol. 2011, 102, 9272–9278. [Google Scholar] [CrossRef] [PubMed]
  23. Román, S.; Nabais, J.; Laginhas, C.; Ledesma, B.; González, J. Hydrothermal carbonization as an effective way of densifying the energy content of biomass. Fuel Process. Technol. 2011, 103, 78–83. [Google Scholar] [CrossRef]
  24. Liu, Z.; Quek, A.; Hoekman, S.K.; Balasubramanian, R. Production of solid biochar fuel from waste biomass by hydrothermal carbonization. Fuel 2013, 103, 943–949. [Google Scholar] [CrossRef]
  25. Ma, L.; Gharebaghi, M.; Porter, R.; Pourkashanian, M.; Jones, J.; Williams, A. Modelling methods for co-fired pulverised fuel furnaces. Fuel 2009, 88, 2448–2454. [Google Scholar] [CrossRef]
  26. Gera, D.; Mathur, M.P.; Freeman, M.C.; Robinson, A. Effect of Large Aspect Ratio of Biomass Particles on Carbon Burnout in a Utility Boiler. Energy Fuels 2002, 16, 1523–1532. [Google Scholar] [CrossRef]
  27. Backreedy, R.; Fletcher, L.; Jones, J.; Ma, L.; Pourkashanian, M.; Williams, A. Co-firing pulverised coal and biomass: a modeling approach. Proc. Combust. Inst. 2005, 30, 2955–2964. [Google Scholar] [CrossRef]
  28. Pallarés, J.; Gil, A.; Cortés, C.; Herce, C. Numerical study of co-firing coal and Cynara cardunculus in a 350 MWe utility boiler. Fuel Process. Technol. 2009, 90, 1207–1213. [Google Scholar] [CrossRef]
  29. Yin, C.; Rosendahl, L.; Kær, S.K.; Condra, T.J. Use of numerical modeling in design for co-firing biomass in wall-fired burners. Chem. Eng. Sci. 2004, 59, 3281–3292. [Google Scholar] [CrossRef]
  30. Agraniotis, M.; Nikolopoulos, N.; Nikolopoulos, A.; Grammelis, P.; Kakaras, E. Numerical investigation of Solid Recovered Fuels’ co-firing with brown coal in large scale boilers – Evaluation of different co-combustion modes. Fuel 2010, 89, 3693–3709. [Google Scholar] [CrossRef]
  31. Bhuiyan, A.A.; Naser, J. CFD modelling of co-firing of biomass with coal under oxy-fuel combustion in a large scale power plant. Fuel 2015, 159, 150–168. [Google Scholar] [CrossRef]
  32. Bhuiyan, A.A.; Karim, M.R.; Naser, J. Modeling of Solid and Bio-Fuel Combustion Technologies. in Thermofluid Modeling for Energy Efficiency Applications, Elsevier Inc.: Amsterdam, The Netherlands, 2016; pp. 259–309. [CrossRef]
  33. Ranade, V.V.; Gupta, D.F. Computational Modeling of Pulverized Coal Fired Boilers. 2015.
  34. Aziz, M.; Oda, T.; Kashiwagi, T. Advanced Energy Harvesting from Macroalgae—Innovative Integration of Drying, Gasification and Combined Cycle. Energies 2014, 7, 8217–8235. [Google Scholar] [CrossRef]
  35. Li, W.; Guo, J.; Cheng, H.; Wang, W.; Dong, R. Two-phase anaerobic digestion of municipal solid wastes enhanced by hydrothermal pretreatment: Viability, performance and microbial community evaluation. Appl. Energy 2017, 189, 613–622. [Google Scholar] [CrossRef]
  36. Darmawan, A.; Budianto, D.; Aziz, M.; Tokimatsu, K. Retrofitting existing coal power plants through cofiring with hydrothermally treated empty fruit bunch and a novel integrated system. Appl. Energy 2017, 204, 1138–1147. [Google Scholar] [CrossRef]
  37. Xu, W.; Niu, Y.; Tan, H.; Wang, D.; Du, W.; Hui, S. A New Agro/Forestry Residues Co-Firing Model in a Large Pulverized Coal Furnace: Technical and Economic Assessments. Energies 2013, 6, 4377–4393. [Google Scholar] [CrossRef]
  38. Saputra, I.N.A.A. ; Prabowo; Setiyawan, A.; Kusuma, I.G.B.W.; Ihsan, S.; Hariana. 3D Simulation Combustion Characteristics Of EFB Biomass Co-Firing With Low Rank Coal In Pulverized Coal Boiler. in 2023 International Conference on Advanced Mechatronics, Intelligent Manufacture and Industrial Automation, ICAMIMIA 2023 - Proceedings, Institute of Electrical and Electronics Engineers Inc., 2023, pp. 370–374. [CrossRef]
  39. Karampinis, E.; Grammelis, P.; Agraniotis, M.; Violidakis, I.; Kakaras, E. Co--firing of biomass with coal in thermal power plants: technology schemes, impacts, and future perspectives. WIREs Energy Environ. 2013, 3, 384–399. [Google Scholar] [CrossRef]
  40. Wang, Y.; Yan, L. CFD Studies on Biomass Thermochemical Conversion. Int. J. Mol. Sci. 2008, 9, 1108–1130. [Google Scholar] [CrossRef]
  41. Bhuiyan, A.A.; Naser, J. Computational modelling of co-firing of biomass with coal under oxy-fuel condition in a small scale furnace. Fuel 2015, 143, 455–466. [Google Scholar] [CrossRef]
  42. Agosta, V.D. DAVID MIGDAL 1 A Source Flow Model for Continuum Gas-Particle Flow. 1967. Available Online: http://www.asme.
  43. Budianto, D.; Aziz, M.; Cahyadi; Oda, T. Numerical Investigation of Co-Firing of Palm Kernel Shell into Pulverized Coal Combustion. J. Jpn. Inst. Energy 2016, 95, 605–614. [Google Scholar] [CrossRef]
  44. Bhuiyan, A.A.; Naser, J. CFD modelling of co-firing of biomass with coal under oxy-fuel combustion in a large scale power plant. Fuel 2015, 159, 150–168. [Google Scholar] [CrossRef]
  45. Anderson, J.D. Governing Equations of Fluid Dynamics. 2009.
  46. Launder, B.I.S.B.E. Application Of the Energy-Dissipation Model Of Turbulence to the Calculation of Flow Near A Spinning Disc. Lett. Heat Mass Transf. 1974, 1, 131–138. [Google Scholar] [CrossRef]
  47. Majda, A.; Sethian, J. The Derivation and Numerical Solution of the Equations for Zero Mach Number Combustion. Combust. Sci. Technol. 1985, 42, 185–205. [Google Scholar] [CrossRef]
  48. Tabet, F.; Gökalp, I. Review on CFD based models for co-firing coal and biomass. Renew. Sustain. Energy Rev. 2015, 51, 1101–1114. [Google Scholar] [CrossRef]
  49. Jiang, Y.; Park, K.-H.; Jeon, C.-H. Feasibility Study of Co-Firing of Torrefied Empty Fruit Bunch and Coal through Boiler Simulation. Energies 2020, 13, 3051. [Google Scholar] [CrossRef]
  50. Oevermann, M.; Gerber, S.; Behrendt, F. Euler–Lagrange/DEM simulation of wood gasification in a bubbling fluidized bed reactor. Particuology 2009, 7, 307–316. [Google Scholar] [CrossRef]
  51. Smith, J.D.; Suo-Antilla, A.; Sreedharan, V. Transient LES based CFD modeling of coal-biomass co-firing combustion. Fuel Process. Technol. 2019, 193, 187–196. [Google Scholar] [CrossRef]
  52. Vesilind, P. The Rosin-Rammler particle size distribution. Resour. Recover. Conserv. 1980, 5, 275–277. [Google Scholar] [CrossRef]
  53. Yin, C.; Kaer, S.K.; Rosendahl, L.; Hvid, S.L. MODELING OF PULVERIZED COAL AND BIOMASS CO-FIRING IN A 150 KW SWIRLING-STABILIZED BURNER AND EXPERIMENTAL VALIDATION’.
  54. Rahman, M.N.; Othman, N.F.B. A Numerical Model for Ash Deposition Based on Actual Operating Conditions of a 700 MW Coal-Fired Power Plant: Validation Feedback Loop via Structural Similarity Indexes (SSIMs). CFD Lett. 2022, 14, 99–111. [Google Scholar] [CrossRef]
  55. Westbrook, C.K.; Dryer, F.L. Simplified Reaction Mechanisms for the Oxidation of Hydrocarbon Fuels in Flames. Combust. Sci. Technol. 1981, 27, 31–43. [Google Scholar] [CrossRef]
  56. Sami, M.; Annamalai, K.; Wooldridge, M. Co-firing of coal and biomass fuel blends. Prog. Energy Combust. Sci. 2001, 27, 171–214. [Google Scholar] [CrossRef]
  57. Ninduangdee, P.; Kuprianov, V.I.; Cha, E.Y.; Kaewrath, R.; Youngyuen, P.; Atthawethworawuth, W. Thermogravimetric Studies of Oil Palm Empty Fruit Bunch and Palm Kernel Shell: TG/DTG Analysis and Modeling. Energy Procedia 2015, 79, 453–458. [Google Scholar] [CrossRef]
  58. Rahman, M.N.; Yusup, S.; Fui, B.C.L.; Shariff, I.; Quitain, A.T. Oil Palm Wastes Co-firing in an Opposed Firing 500 MW Utility Boiler: A Numerical Analysis. CFD Lett. 2023, 15, 139–152. [Google Scholar] [CrossRef]
  59. Williams, A.; Pourkashanian, M.; Jones, J. The combustion of coal and some other solid fuels. Proc. Combust. Inst. 2000, 28, 2141–2162. [Google Scholar] [CrossRef]
  60. Khare, S.; Wall, T.; Farida, A.; Liu, Y.; Moghtaderi, B.; Gupta, R. Factors influencing the ignition of flames from air-fired swirl pf burners retrofitted to oxy-fuel. Fuel 2007, 87, 1042–1049. [Google Scholar] [CrossRef]
Preprints 113742 g001
Figure 1. Conceptual diagram of the hydrothermal treatment palm frond co-firing system (HT-FRD).
Figure 1. Conceptual diagram of the hydrothermal treatment palm frond co-firing system (HT-FRD).
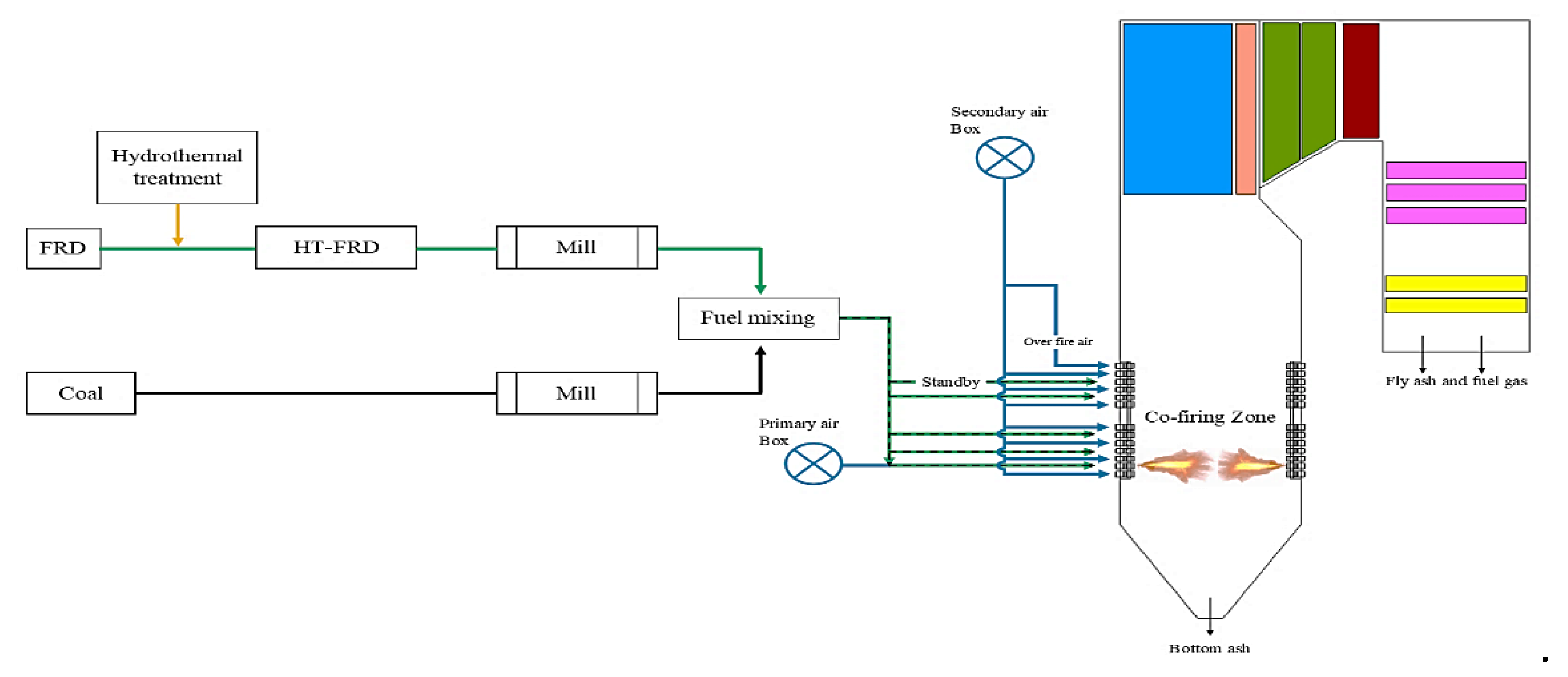
Preprints 113742 g001
Preprints 113742 g002
Figure 2. The design domain of a pulverized coal boiler simulation and the inlet burner [10,38].
Figure 2. The design domain of a pulverized coal boiler simulation and the inlet burner [10,38].
Preprints 113742 g002
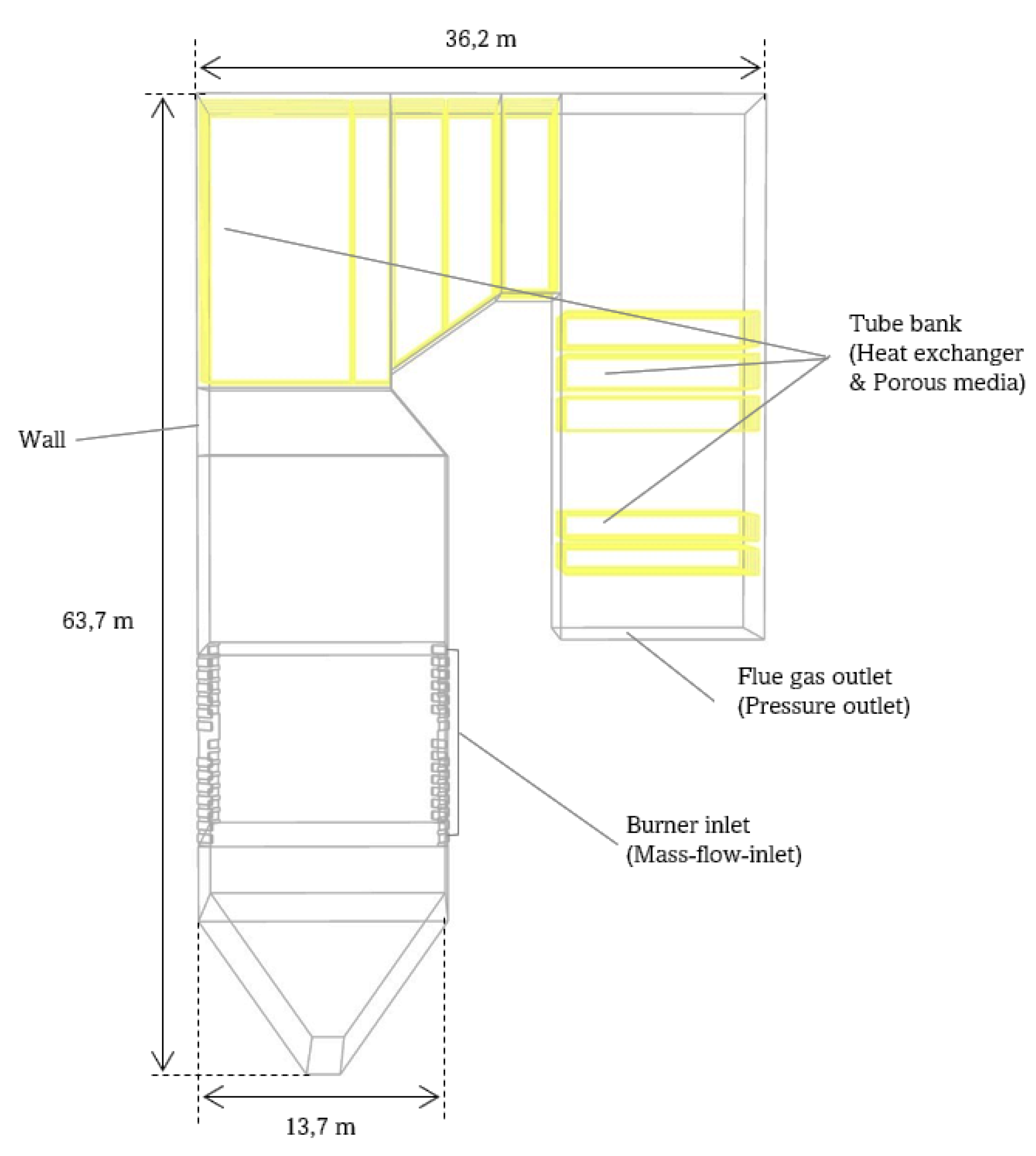
Preprints 113742 g003
Figure 3. Domain simulation of a pulverized coal boiler.
Figure 3. Domain simulation of a pulverized coal boiler.
Preprints 113742 g003
Preprints 113742 g004
Figure 4. Mesh model of the pulverized coal boiler.
Figure 4. Mesh model of the pulverized coal boiler.
Preprints 113742 g004
Preprints 113742 g005
Figure 5. Grid independence and validation based on FEGT.
Figure 5. Grid independence and validation based on FEGT.
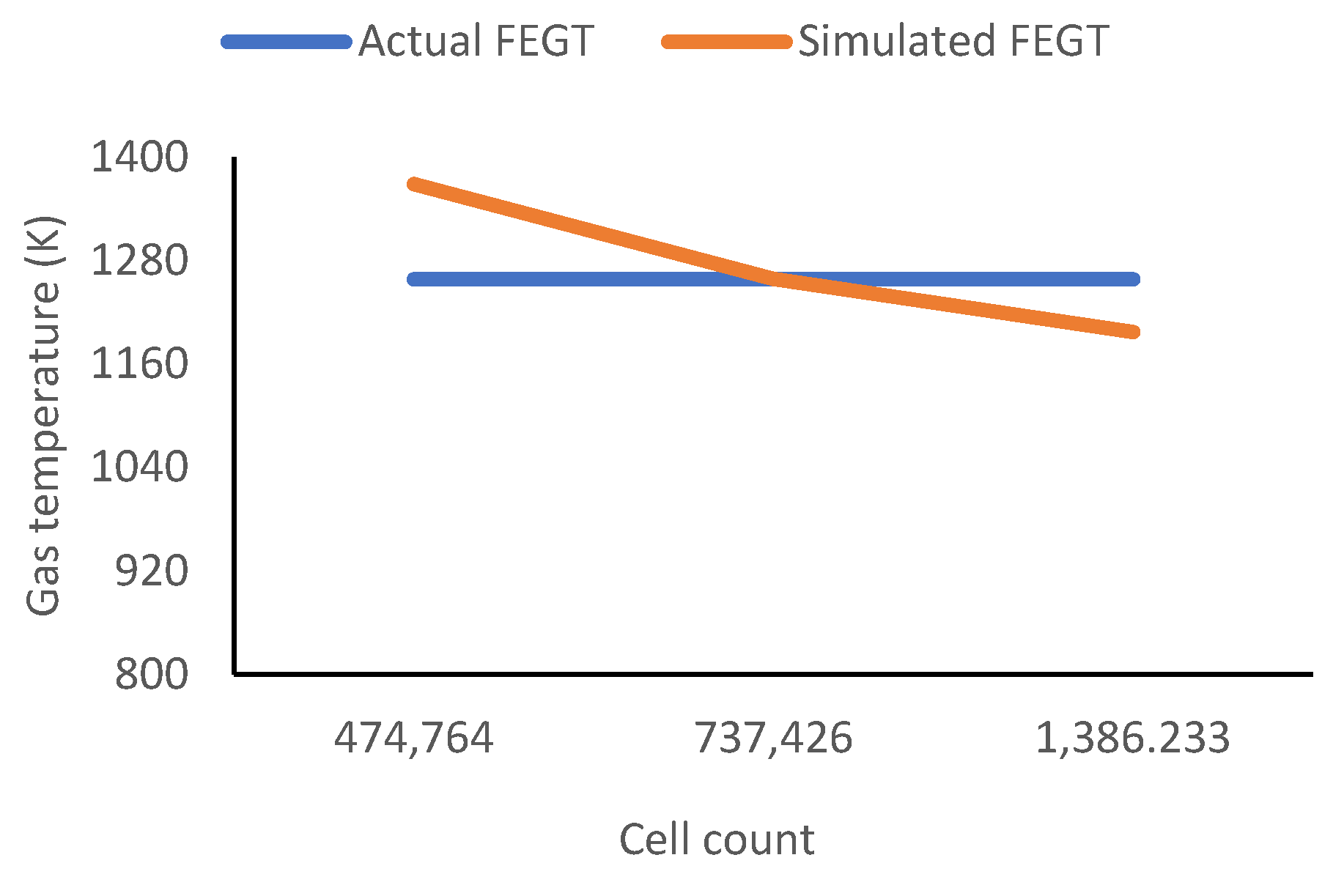
Preprints 113742 g005
Preprints 113742 g006
Figure 6. Temperature distribution under different blending ratios of HT-FRD across the furnace height.
Figure 6. Temperature distribution under different blending ratios of HT-FRD across the furnace height.
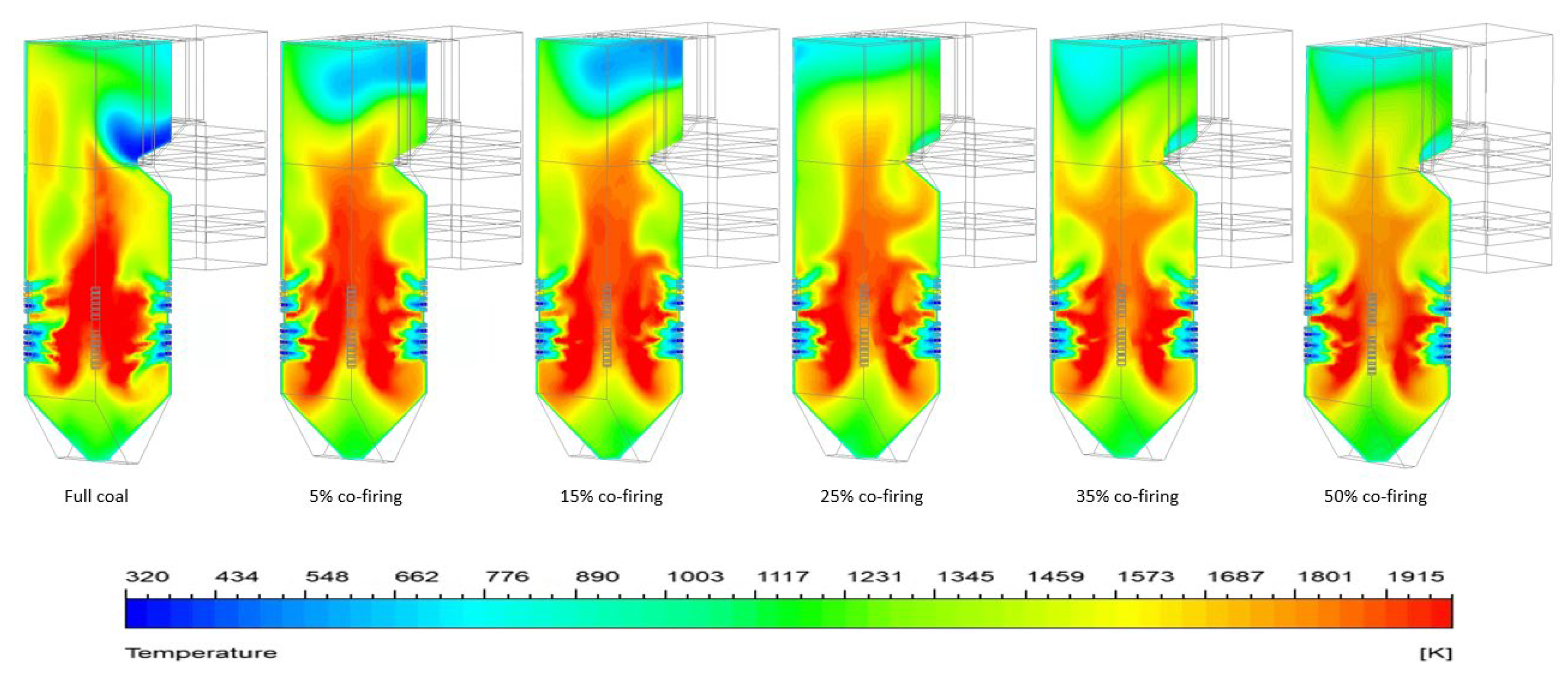
Preprints 113742 g006
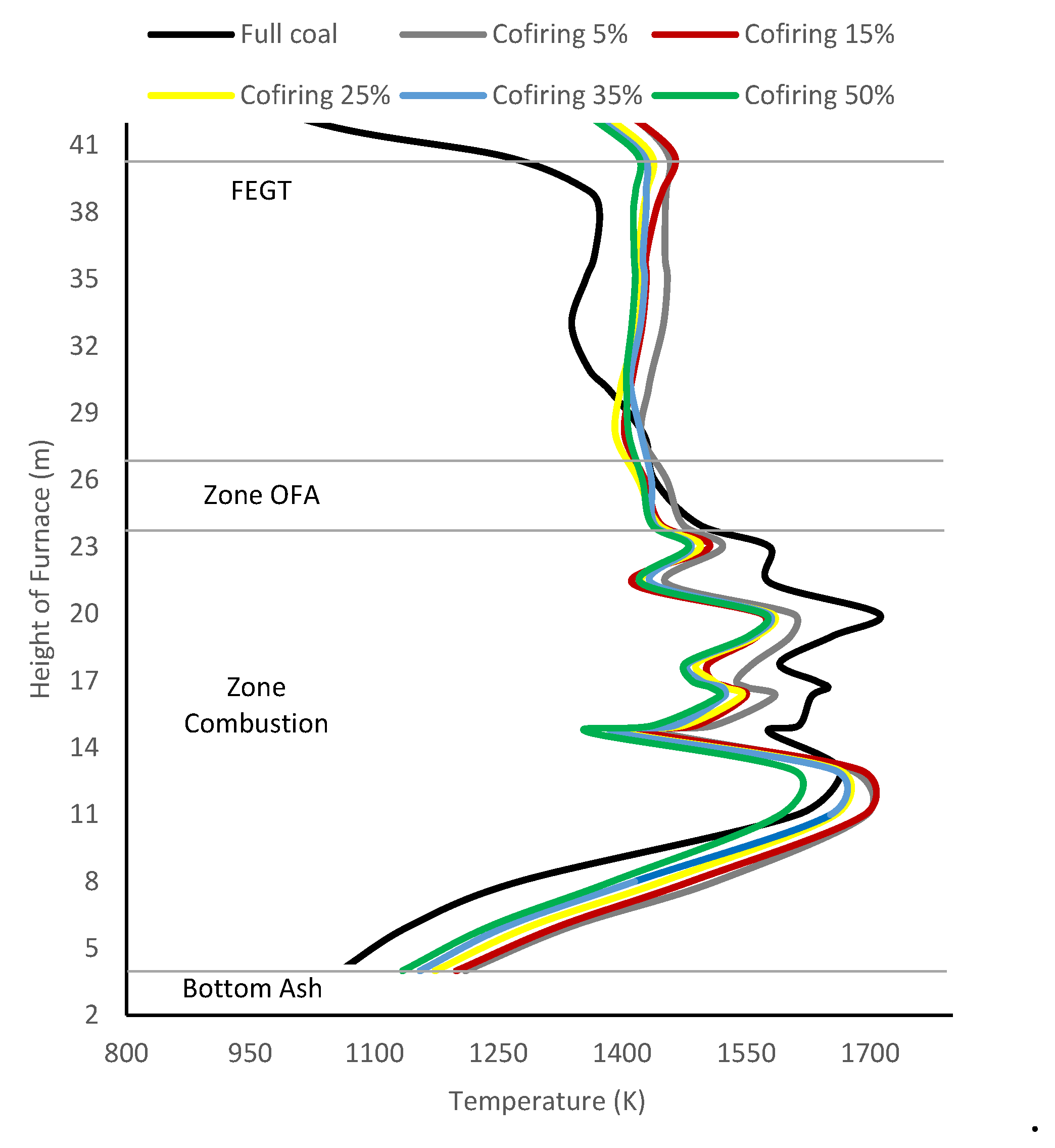
Preprints 113742 g007
Figure 7. Simulation gas temperature distribution under different blending ratios HT-FED across the furnace height.
Figure 7. Simulation gas temperature distribution under different blending ratios HT-FED across the furnace height.
Preprints 113742 g007
Preprints 113742 g008
Figure 8. Velocity distribution across the combustor for each HT-FRD co-firing ratio.
Figure 8. Velocity distribution across the combustor for each HT-FRD co-firing ratio.
Preprints 113742 g008
Preprints 113742 g009
Figure 9. Mean velocity distribution across the combustor for all evaluated mass fraction.
Figure 9. Mean velocity distribution across the combustor for all evaluated mass fraction.
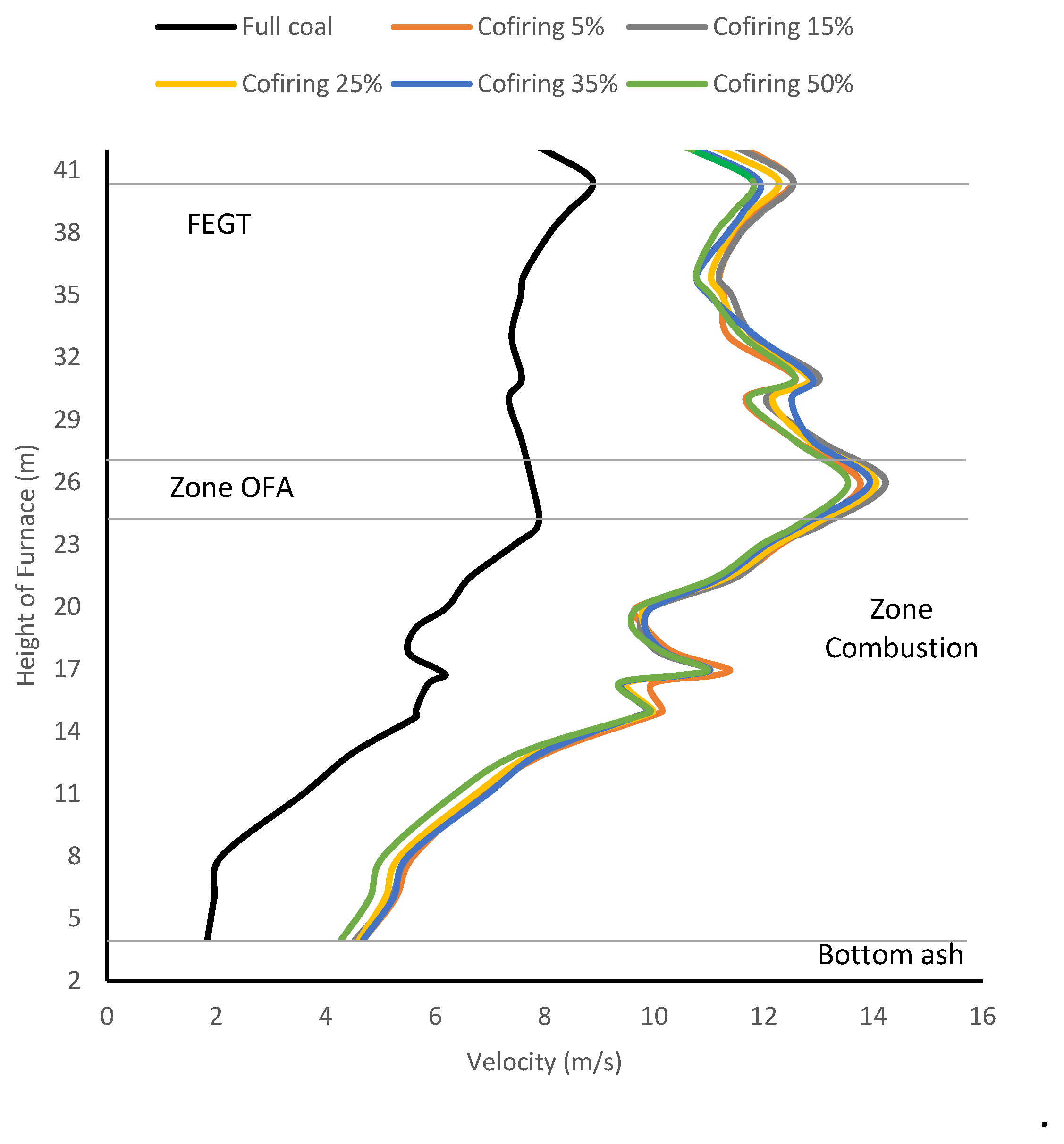
Preprints 113742 g009
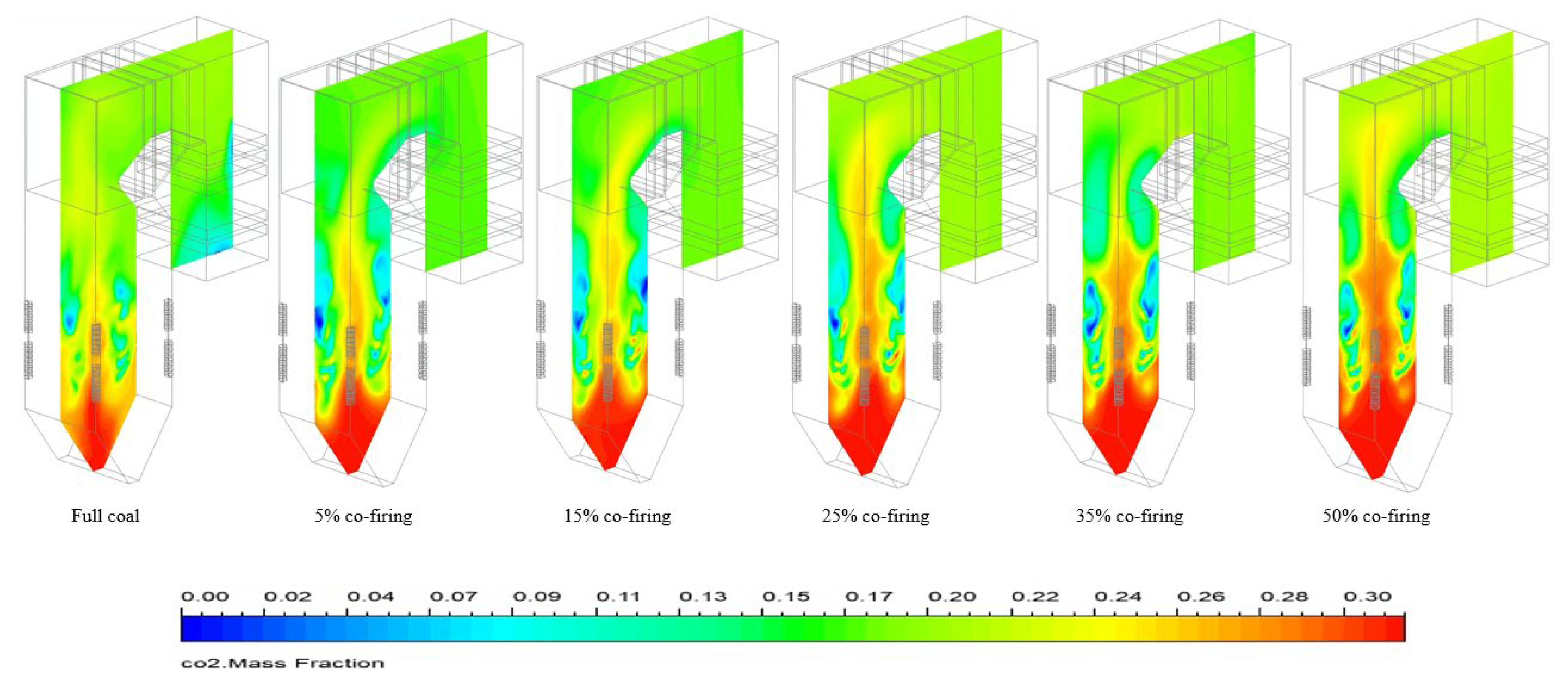
Preprints 113742 g010
Figure 10. CO2 distribution cross-sectional profile across the HT-FRD co-firing combustor ratios.
Figure 10. CO2 distribution cross-sectional profile across the HT-FRD co-firing combustor ratios.
Preprints 113742 g010
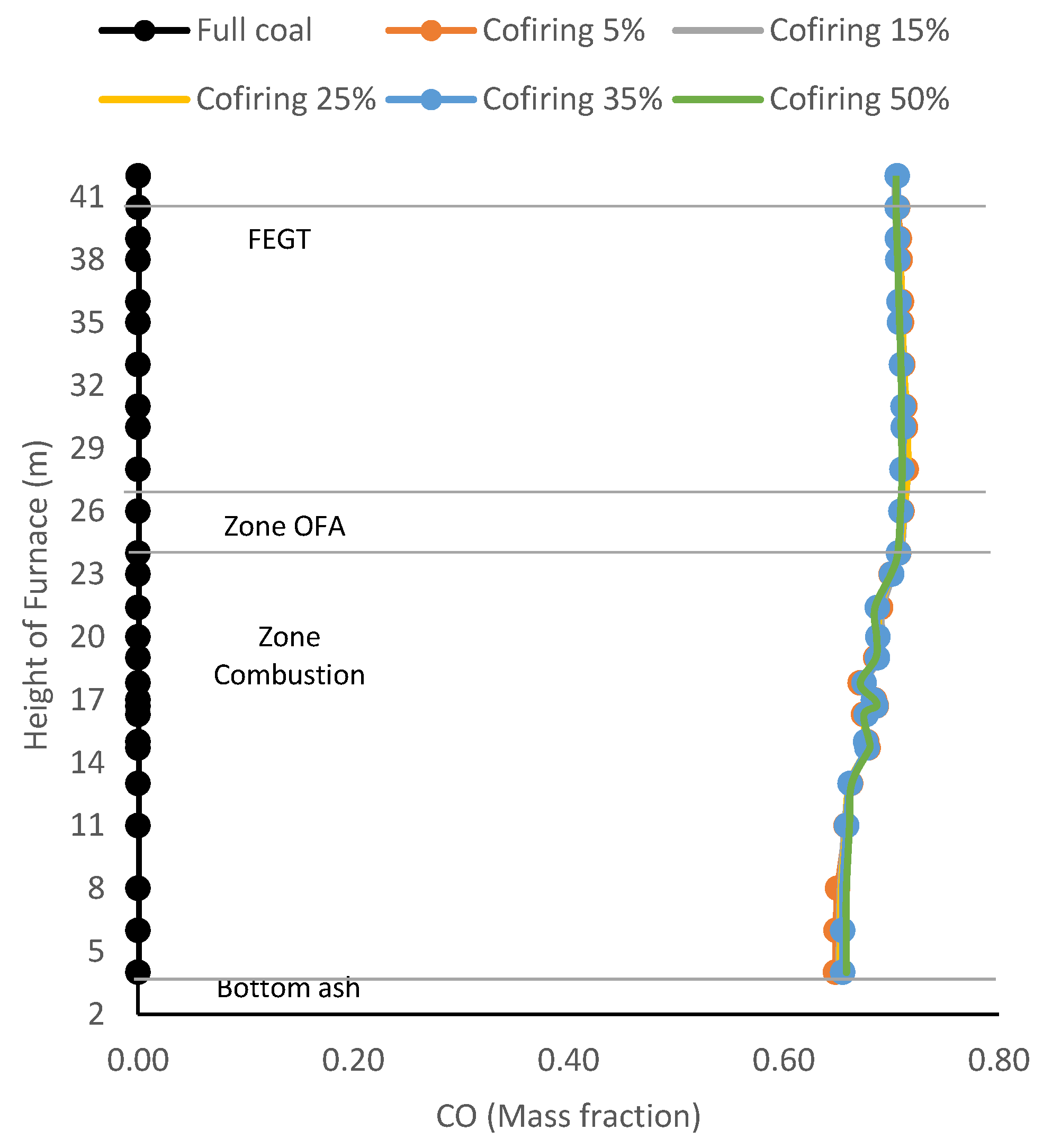
Preprints 113742 g011
Figure 11. CO2 distribution at the center across the height of HT-FRD co-firing combustor ratios.
Figure 11. CO2 distribution at the center across the height of HT-FRD co-firing combustor ratios.
Preprints 113742 g011
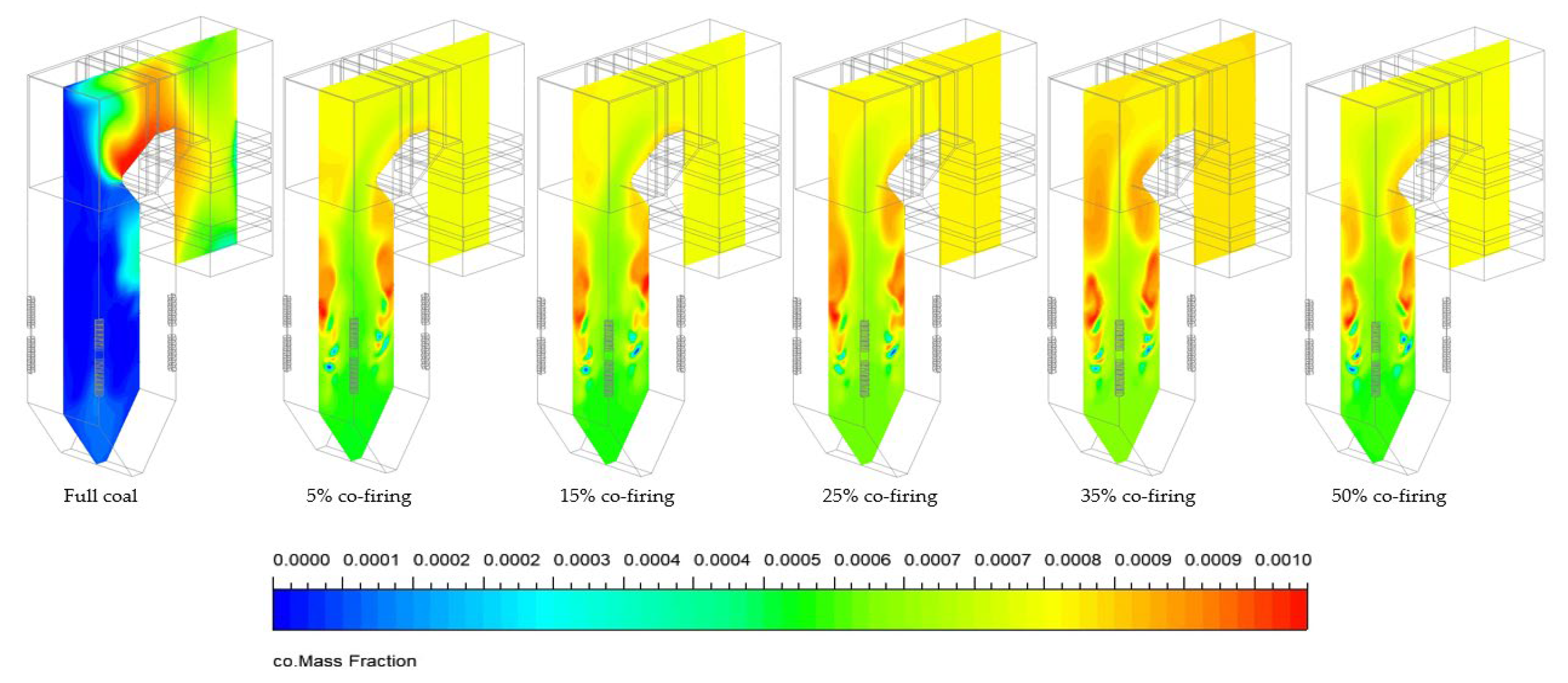
Preprints 113742 g012
Figure 12. CO distribution cross-sectional across the HT-FRD co-firing combustor ratios.
Figure 12. CO distribution cross-sectional across the HT-FRD co-firing combustor ratios.
Preprints 113742 g012
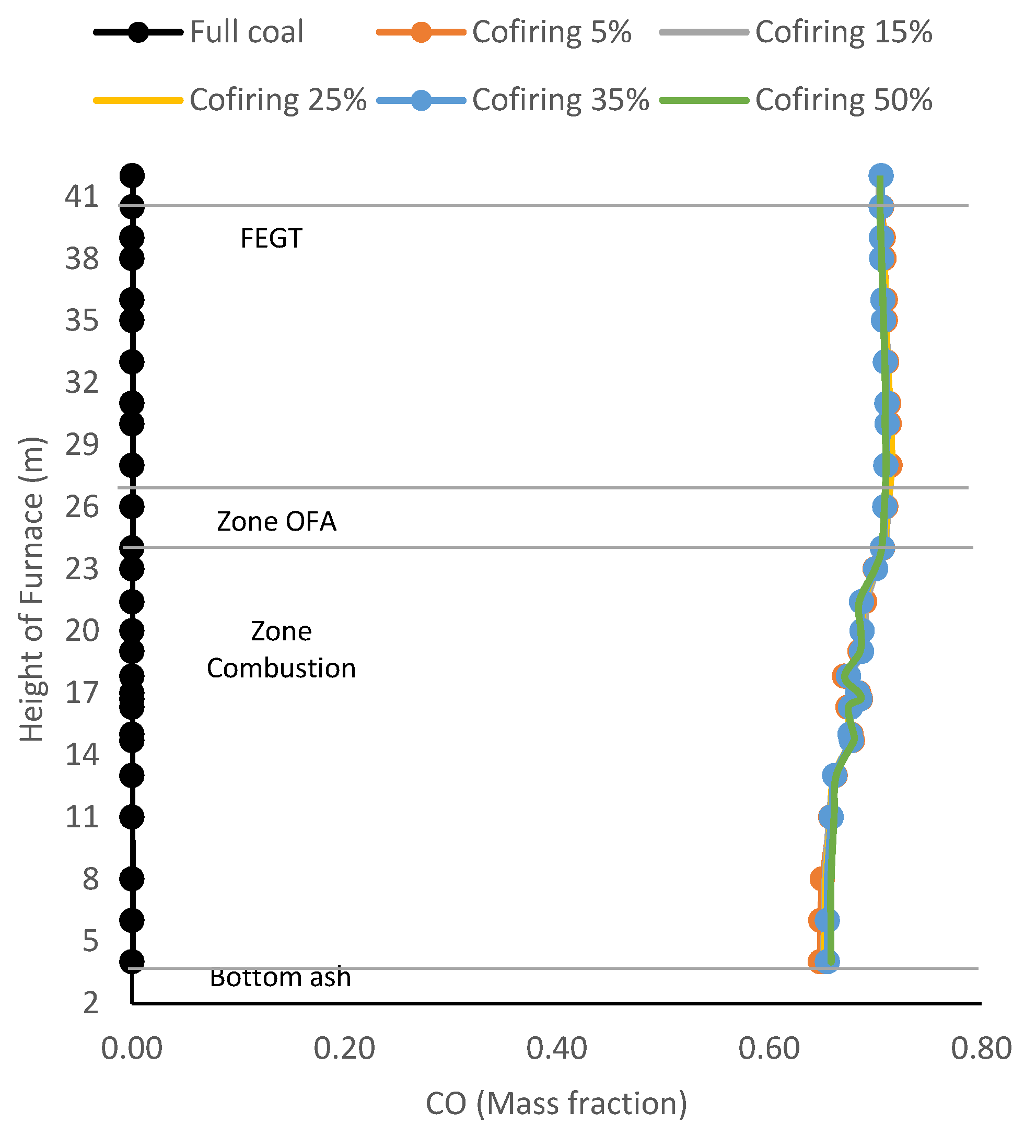
Preprints 113742 g013
Figure 13. CO distribution at the center across the height of HT-FRD co-firing combustor ratios.
Figure 13. CO distribution at the center across the height of HT-FRD co-firing combustor ratios.
Preprints 113742 g013
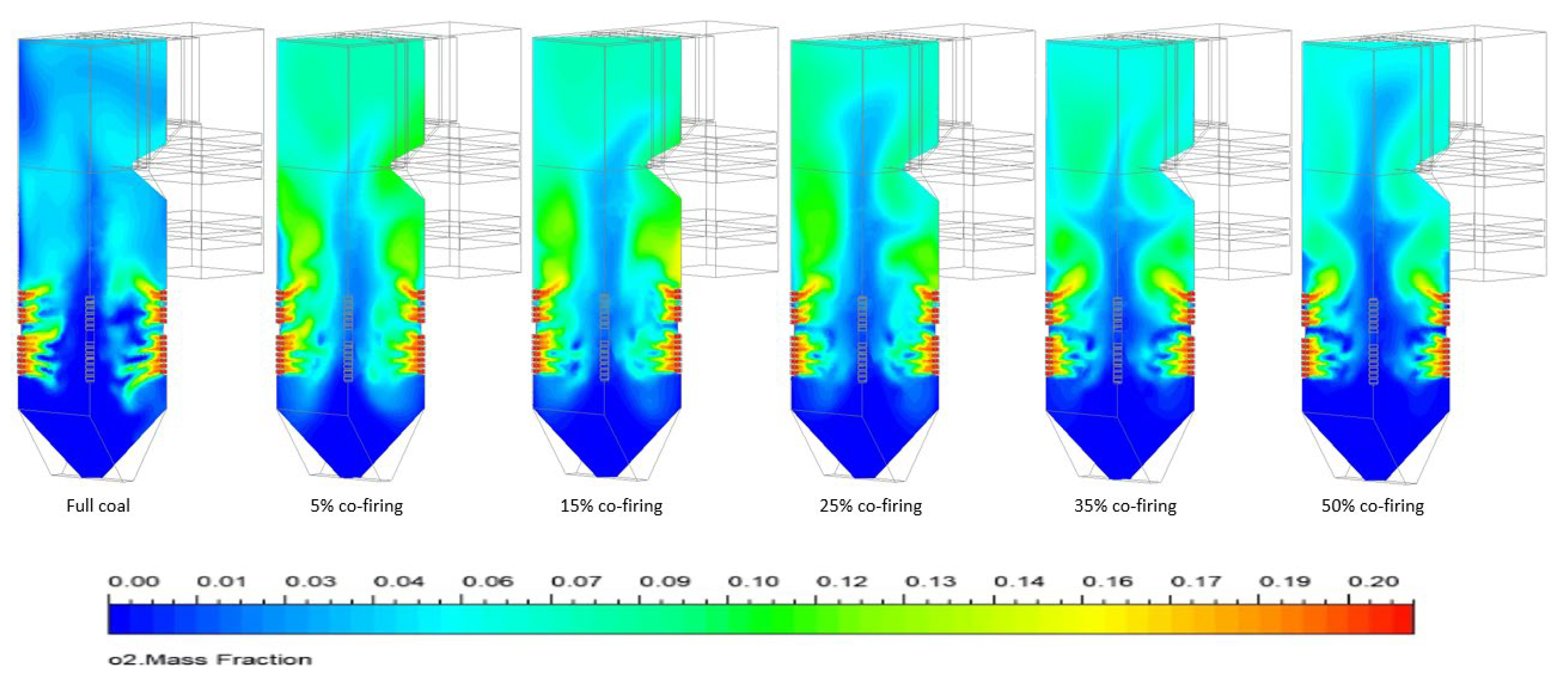
Preprints 113742 g014
Figure 14. O2 cross-sectional distribution across the HT-FRD co-firing combustor ratios.
Figure 14. O2 cross-sectional distribution across the HT-FRD co-firing combustor ratios.
Preprints 113742 g014
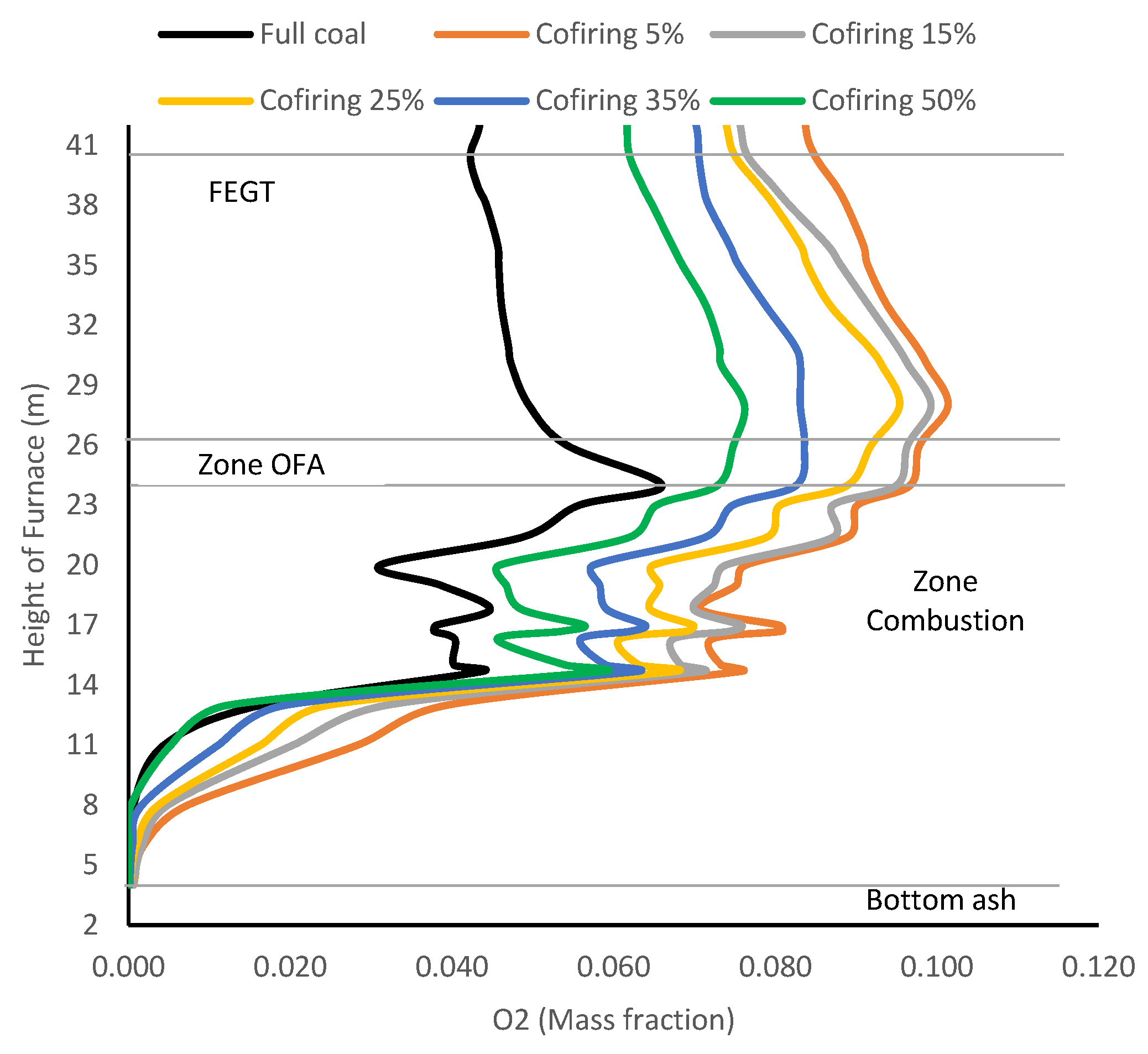
Preprints 113742 g015
Figure 15. O2 distribution at the center across the height of HT-FRD co-firing combustor ratios.
Figure 15. O2 distribution at the center across the height of HT-FRD co-firing combustor ratios.
Preprints 113742 g015
Table 1. Kinetic parameters are utilized in particle and gas phases for their respective reactions [40,56,57].
Table 1. Kinetic parameters are utilized in particle and gas phases for their respective reactions [40,56,57].
Equation Reaction A (s-1) Ei (J. kmol-1. K-1)
(18)
(19)
(20)
(21)
(22)		 2.0 x 1011
6.8 x 1015
3.0 x 108
1.9 x 1015
2.75 x 109 		4.4 x 107
1.67 x 108
1.26 x 108
1.27 x 108
8.47 x 107
Table 2. The composition of coal and oil palm fronds was utilized in this study [9].
Table 2. The composition of coal and oil palm fronds was utilized in this study [9].
Component Coal HT-FRD
Proximate analysis (as-received basis, wt %)
Volatile matter 33.76 77.81
Fixed carbon 32.31 14.29
Ash 2.50 2.09
Moisture 31.43 5.81
Ultimate analysis (dry ash-free basis, wt %)
Carbon (C) 46.96 44.37
Hydrogen (H) 3.29 5.51
Oxygen (O) 15.04 41.66
Nitrogen (N) 0.66 0.46
Sulfur (S) 0.12 0.10
Calorific value (as-received basis, Kcal/kg)
HCV 4452 3692
Table 3. Boiler parameters simulation.
Table 3. Boiler parameters simulation.
Item Boiler Operation Simulated
Case 1 2 3 4 5 6
Combustion type Pure coal Co-firing
HT-FRD bleeding ratio (%) 0 5 15 25 35 50
Fuel mills (burn zone) A B C D and E (standby)
Coal feed rates (kg/s) 10.54 10.01 8.96 7.91 6.85 5.27
Biomass feed rates (kg/s) - 0.53 1.58 2.64 3.69 5.27
PA a flow rate (kg/s) 97.62
SA a flow rate (kg/s) 190.74
OFA a flow rate (kg/s) 44.36
Temperature of PA (K) 326.9
Temperature of SA (K) 596.6
Temperature of OFA (K) 596.6
an overfire air (OFA), secondary air (SA), and primary air (PA).
Table 4. Setup point of coal and HT-FRD properties on each burner
Table 4. Setup point of coal and HT-FRD properties on each burner
Injection name Burner zone Temperature (K) Total Flow Rate (kg/s)
1 2 3 4 5 6
Coal- Injection A 329.8 11.14 10.59 9.47 8.36 7.24 5.57
B 329.2 11.24 10.67 9.55 8.43 7.30 5.62
C 330 10.90 10.36 9.27 8.18 7.09 5.45
D 330.7 8.88 8.44 7.55 6.66 5.77 4.44
E Standby
Frond- Injection A 329.8 - 0.56 1.67 2.79 3.90 5.57
B 329.2 - 0.56 1.69 2.80 3.93 5.62
C 330 - 0.55 1.64 2.73 3.82 5.45
D 330.7 - 0.44 1.33 2.22 3.11 4.44
E Standby
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated