Preprint
Article
On the Stabilizing Effect of Aspartate and Glutamate and Its Counteraction by Common Denaturants
Altmetrics
Downloads
72
Views
21
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
30 July 2024
Posted:
01 August 2024
You are already at the latest version
Alerts
Abstract
By performing DSC measurements on RNase A, we studied the stabilization provided by the addition of potassium aspartate or potassium glutamate, that leads to a significant increase in the denaturation temperature of the protein. The stabilization proves to be mainly entropic in origin. A counteraction of the stabilization provided by KAsp or KGlu is obtained by adding common denaturants such as urea, guanidinium chloride and guanidinium thiocyanate. A rationalization of experimental data is devised on the basis of a theoretical approach developed by one of us. The main contribution to the conformational stability of globular proteins comes from the gain in translational entropy of water and co-solute ions and/or molecules for the decrease in solvent-excluded volume associated with polypeptide folding (i.e., there is a large decrease in solvent-accessible surface area). The magnitude of this entropic contribution increases with the number density and volume packing density of the solution. The two destabilizing contributions come from the conformational entropy of the chain, that should not depend significantly on the presence of co-solutes, and from the direct energetic interactions between co-solutes and the protein surface in both the native and denatured states. It is the magnitude of the latter to discriminate between stabilizing and destabilizing agents.
Keywords:
Subject: Biology and Life Sciences - Biophysics
1. Introduction
It is well established that the conformational stability of globular proteins can be markedly modified by the addition to water of small co-solutes, both neutral and charged, which can be either stabilizing or destabilizing the native state. Even though a huge number of investigations, both experimental, computational and theoretical, have been performed, a complete molecular-level understanding is still lacking [1,2,3,4,5,6,7,8,9,10]. The common view is that stabilizing agents are preferentially excluded from the protein solvation shell, whereas destabilizing agents are preferentially accumulated in the protein solvation shell. It should be recognized that preferential exclusion or preferential accumulation are thermodynamic concepts, which do not provide an actual molecular mechanism [4].
Forty years ago, Arakawa and Timasheff reported that the addition of sodium glutamate, NaGlu, increased the thermal stability of hen egg white lysozyme and bovine serum albumin [11], causing a preferential hydration of the proteins. They interpreted these results in terms of an unfavorable Gibbs free energy of interaction of NaGlu with protein surfaces. This interesting finding was not followed by other experimental investigations until Record, Rayleigh and co-workers [12] made a careful study of the stabilization provided by potassium glutamate, KGlu, to the N-terminal domain of the ribosomal protein L9, and concluded that KGlu has a strong stabilizing action towards the folded state. According to the approach developed by Record, the KGlu stabilization originated from the unfavorable interactions of KGlu with both the hydrocarbon surface area and the amide surface area [13]; this proved to be an unusual situation, but a molecular-level explanation of such un-favorability was not provided. It should be noted that the Record’s approach is grounded on the additivity principle of energetic interactions, assuming the protein surface can be divided in two parts: the nonpolar hydrocarbon one and the polar amide one. This additivity principle cannot be taken for granted in the case of heteropolymers [14], such as globular proteins, consisting of different chemical groups, some of which are charged and more or less randomly dispersed on the surface, and some of which are able to make H-bonds with water molecules. Moreover, additivity should not hold in aqueous solutions containing ions such as aspartate and glutamate which, having three charges at pH 7.0 (two negative and one positive on the basis of the three pKa values), localized in different parts of the chemical structure, are involved in long-range Coulomb interactions (both attractive and repulsive).
In order to add something new and interesting to the puzzle, we decided to study the effect of both KAsp and KGlu on the conformational stability of a model globular protein, such as RNase A, by performing DSC measurements. The rationale was: (a) to directly measure the denaturation enthalpy and entropy changes that build up the denaturation Gibbs free energy change; (b) to verify if aspartate is a stabilizing agent, such as glutamate, a test that has not yet done, to the best of our knowledge. Moreover, we studied the counteraction of the stabilization afforded by KAsp and KGlu caused by the addition of denaturing agents, such as urea, guanidinium chloride, GdmCl, and guanidinium thiocyanate, GdmSCN, always performing DSC measurements. Experimental data are analyzed and discussed on the basis of a theoretical approach developed by one of us.
2. DSC Results
DSC measurements, shown in Figure 1, indicate that the temperature-induced denaturation of RNase A in 10 mM MOPS buffer with 100 mM NaCl, pH 7.0, is a reversible two-state process in all the considered aqueous solutions (i.e., the so-called re-heating criterion has been used to test the reversibility; the closeness to one of the CU values has been used to test the two-state cooperativity, see the fifth column of Table 1).
The Td values listed in the third column of Table 1 demonstrate that the protein thermal stability increases significantly on increasing the concentration of both KAsp and KGlu: Td passes from 63.5 °C in aqueous buffer solution to 72.7 °C in 1 M KAsp, and 72.3 °C in 1 M KGlu. These values imply that potassium aspartate and potassium glutamate are strong stabilizing agents of the folded state and their effect is closely similar; indeed, we found that Td = 66.2 °C in 1 M glucose, 67.2 °C in 1 M betaine, 67.6 °C in 1 M sucrose, 67.8 °C in 1 M TMAO, and 68.4 °C in 1 M trehalose [15,16]. It is worth underscoring that: (a) such a comparison is somewhat misleading because KAsp and KGlu are salts that dissociate in water, producing two ions, so that the actual molar concentration of co-solutes is larger than 1 M; (b) the presence of two ion types, one of which contains three charges, implies that long-range Coulomb interactions are operative.
As shown in Figure 2, the addition of denaturing agents, such as urea, GdmCl and GdmSCN, counteracts the stabilizing effect of KAsp and KGlu; for instance: (a) Td = 64.9 °C in 1.0 M KAsp + 1 M GdmCl, and 64.7 °C in 1 M KGlu + 1 M GdmCl; (b) Td = 58.0 °C in 1 M KAsp + 0.5 M GdmSCN, and 57.9 °C in 1 M KGlu + 0.5 M GdmSCN. These results confirm that counteraction is a general phenomenon independent of the chemical nature and structure of the stabilizing and destabilizing agents [15,16,17].
The values of the denaturation enthalpy change, ΔHd(Td), listed in the fourth column of Table 1, indicate that: (a) potassium aspartate and potassium glutamate, notwithstanding their marked ability to raise the Td value, do not cause a significant ΔHd(Td) increase; this is a strong indication that the stabilization provided by them has an entropic origin; (b) the addition of the denaturing agents, in particular GdmCl or GdmSCN, causes a significant ΔHd(Td)decrease. The present DSC data do not produce a linear plot of ΔHd(Td) versus Td, so it is not possible to obtain an estimate of ΔCp,d. However, the latter is needed to calculate the denaturation Gibbs free energy at 25 °C in all the considered aqueous solutions, starting from the experimental Td and ΔHd(Td) values. In a previous work, we obtained ΔCp,d = 6.4 ± 0.7 kJ K-1mol-1 from a ΔHd(Td) versus Td plot, consisting of 45 points coming from our own DSC measurements of RNase A in different aqueous solutions [16]. The latter ΔCp,d value has been used to calculate the ΔGd (25 °C) estimates reported in the fifth column of Table 1; the trend of these estimates is in line with that of the experimental Td values.
These experimental data need a reliable rationalization that has to come from a theoretical approach based on statistical mechanics.
3. Theoretical Approach and Its Application
It has been shown by one of us that the conformational stability of globular proteins in aqueous solutions can be rationalized by means of a theoretical approach, grounded on the assumption that polypeptide chains can populate two macrostates, the native one, N-state, and the denatured one, D-state. The approach singles out three fundamental contributions to the denaturation Gibbs free energy change, ΔGd [15,16,17,18,19,20]:
ΔGd = ΔΔGc – TΔSconf + ΔEa
The loss in translational entropy of solvent molecules associated with the increase in solvent-excluded volume upon denaturation. It is necessary to provide an explanation of what is the solvent-excluded volume effect to avoid misunderstandings. In a condensed state of the matter, such as a liquid, the space for the insertion of a solute molecule has to be created (i.e., the void space is a large fraction of the total volume, but it is partitioned in very small pieces, as a consequence of the size of liquid molecules, that prove to be not available for the insertion of a molecule). This means that reversible work has to be spent for cavity creation. The latter is a special process because it cannot be studied from the experimental point of view, but solely by means of theoretical approaches and computer simulations. The creation of a cavity (assumed to be spherical for simplicity), at a fixed position in a liquid, keeping constant temperature and pressure, causes an increase of the liquid volume equal to the van der Waals volume of the cavity it-self. However, the cavity existence produces a geometric constraint for the liquid (solvent and co-solute) molecules: the centers of the latter cannot enter the spherical shell between the van der Waals surface of the cavity and its solvent accessible surface area, otherwise the cavity would not exist, because its volume would be occupied. This geometric constraint produces a solvent-excluded volume effect for all the molecules or ions in the liquid system that are in continuous motion; this solvent-excluded volume effect leads to a significant decrease in the total number of available spatial configurations, and so in a loss of translational entropy of solvent and co-solute molecules. This reasoning implies that the magnitude of the solvent-excluded volume effect is proportional to solvent-accessible surface area of the cavity (i.e., of the inserted solute molecule). As a consequence, in the case of globular protein denaturation, this entropic contribution largely favors the N-state (i.e., water molecules push the polypeptide chain to collapse in order to gain translational entropy).
The entropic contribution due to the solvent-excluded volume effect can be calculated as the difference in the reversible work to create a cavity suitable to host the D-state and a cavity suitable to host the N-state:
ΔΔGc= ΔGc(D-state) – ΔGc(N-state)
Reliable ΔGc values can be calculated by means of the analytical relationship provided by classic scaled particle theory [21,22], SPT, assuming that simple geometric models can represent the two protein macrostates. Specifically, a sphere represents the N-state and a prolate spherocylinder represents the D-state, with a fundamental constraint. The sphere and the prolate spherocylinder must have the same van der Waals volume because experimental measurements indicate that the volume change associated with denaturation is a negligibly small quantity [23,24,25]. Clearly, even though the two objects have the same van der Waals volume, their water accessible surface area [26], WASA, is different (as their solvent-excluded volume):
in line with experimental findings that [27,28]:
WASA(prolate spherocylnder) > WASA(sphere)
WASA(D-state)
> WASA(N-state)
According to previous choices [15,16,17,20], the geometric features of the two objects are the following. The model protein has 138 residues so that its VvdW = 14137 Å3; the sphere representing the N-state has radius a = 15 Å and WASA = 3380 Å2 (note that, to calculate WASA, the radius assigned to water molecules is 1.4 Å, the customary one [26]); the prolate spherocylinder representing the D-state has radius a = 6 Å, cylindrical length l = 117 Å and WASA = 6128 Å2. The ΔGC values have been calculated by means of the following analytical relationship provided by classic SPT for a spherocylindrical cavity of radius a and cylindrical length l in a hard sphere fluid mixture (the pressure-volume term is neglected for its smallness at P = 1 atm) [19]:
where ξi = (π/6)·Σρ·σji, and ρj is the number density, in molecules per Å3, of the species j and σj is the corresponding hard sphere diameter; ξ3 = (π/6)⋅∑ρj⋅σj3 represents the volume packing density of the hard sphere fluid mixture (i.e., the volume fraction really occupied by solvent molecules and co-solute ions and molecules); by setting l = 0, the formula is that for a spherical cavity of radius a; by considering only one component, Eq. (5) is that for a hard sphere fluid.
ΔGC = RT·{-ln(1-ξ3) + [6ξ2/(1-ξ3)]a + [12ξ1/(1-ξ3)]a2 + [18ξ22/(1-ξ3)2]a2 +
+ [3ξ2/2(1- ξ3)]l + [6ξ1/(1-ξ3)]a·l + [9ξ22/(1-ξ3)2]a·l}
+ [3ξ2/2(1- ξ3)]l + [6ξ1/(1-ξ3)]a·l + [9ξ22/(1-ξ3)2]a·l}
Experimental values of the density of water [39] and all the considered aqueous salt solutions (measured by us), at 25 °C and 1 atm, have been used to perform calculations. The selected effective hard sphere diameters are: σ = 2.80 Å for water molecules [30,31]; 4.64 Å for urea molecules and 4.70 Å for Gdm+ ions (these two correspond to the diameter of the sphere possessing the same WASA of the molecule or ion [15]); 6.06 Å for Asp- ions and 6.37 Å for Glu- ions (these two correspond to the diameter of the sphere obtained by summing up the volume group contributions devised by Ben-Amotz and Willis [42]); 2.66 Å for K+ ions and 3.62 Å for Cl- ions (these come from the ionic radii fixed by Pauling [43]); 3.94 Å for SCN- ions, the same hard sphere diameter of carbon dioxide [15]. All these values are listed in Table 2.
The gain in conformational entropy of the polypeptide chain upon denaturation. It is straightforward to guess the sign of this entropic term, but it is very difficult to make a correct calculation. The N-state represents an ensemble of conformations confined in a small volume of the phase space, whereas the D-state represents a huge ensemble of fluctuating conformations occupying a significant fraction of the phase space. This implies that the conformational entropy change upon denaturation is a large positive quantity, favoring the stability of the D-state (i.e., there is a large gain in conformational degrees of freedom for the polypeptide chain upon denaturation). A reliable evaluation of this contribution needs the availability of realistic ensembles for the two macrostates, generated by means of large-scale computer simulations. Such a task has been undertaken by some research groups and it is possible to take advantage of their results [34,35,36]. Notwithstanding the complexity of the situation, it appears to be not wrong to assume that each residue gives the same independent contribution, ΔSconf(res) = 19 J K-1molres-1 [21,22,23,24]; so the overall conformational entropy term can be calculated as:
T·ΔSconf = T·Nres·ΔSconf(res)
It is interesting to note that Rose [37], by means of a simple calculation based on the accessible surface in the Ramachandran map, obtained ΔSconf(res) = 17.7 J K-1molres-1, close to the value reported above. The magnitude of the conformational entropy gain upon denaturation should depend little on the presence of co-solutes in the aqueous solution because these ions and molecules have weak interactions with proteins (in both the N-state and the D-state), due to the ubiquitous competition with water molecules. This reasoning implies that the T·ΔSconf term can be considered to be not affected by the presence of co-solutes [15,16,17].
A contribution accounting for the energetic interactions of the N-state and D-state with water molecules and co-solute ions and molecules, and the difference in intra-protein interactions between the two macrostates. This energetic term is given by:
ΔEa = Ea(D-state-water) – Ea(N-state-water) + ΔE(intra)
In aqueous solutions not containing co-solutes, the ΔEa values should be close to zero because an almost perfect balance for the energetic interactions between the N-state and the D-state is operative [20] (for instance, the gain in protein-water H-bonds upon denaturation corresponds to the loss of intra-protein H-bonds, in particular for the unfolding of secondary structure elements [38]). Fixing ΔEa = 0, and calculating the other two terms constituting the denaturation Gibbs free energy (see the first line in Table 3), it results that ΔGd = ΔΔGC – TΔSconf = 803 – 782 = 21 kJ mol-1 at 25 °C and 1 atm; the N-state of our model protein is more stable than the D-state. The obtained ΔGd value is reliable for a globular protein, because it corresponds to 152 J mol-1 per residue [39]; this indicates that the present “geometric” approach works well.
In the presence of co-solutes, the ΔEa values are negative, and their magnitude proves to be large in the case of denaturing agents [15,16,17]. The latter interact more favorably with protein surfaces than with water molecules, and tend to accumulate in the protein solvation shell, favoring denaturation. The ΔEa magnitude becomes so large on increasing the concentration of the denaturing agent to cause denaturation also around temperature. Reliable estimates of the ΔEa contribution are not simple to achieve because it is necessary to generate reliable conformational ensembles for the two macrostates, and to have good force-fields to describe all the feasible water-water, water-protein, water-cosolute, protein-cosolute interactions.
It is useful to apply this theoretical approach to the investigated binary and ternary aqueous solutions. The ΔGc values for both the N-state and the D-state, in all the considered aqueous solutions at 25 °C, have been calculated by means of Eq. (5), and are listed in the second and third columns of Table 3. The corresponding ΔΔGc = ΔGc(D-state) – ΔGc(N-state) values, reported in the fourth column of Table 3, are large and positive, indicating that the decrease in solvent-excluded volume associated with protein folding, is the main stabilizing contribution of the N-state (i.e., this contribution represents the most part of what is usually called the hydrophobic effect [19]). Moreover, the ΔΔGc‘ = ΔΔGc(other) – ΔΔGc(water) values, listed in the last column of Table 3, are all positive, indicating that: (a) the addition of all the considered co-solutes leads to an increase in the ΔGc magnitude; (b) it is not the ΔΔGc‘ sign that can discriminate between stabilizing and destabilizing agents. On the other hand, it is evident that the ΔΔGc‘ magnitude is significantly larger in the case of: (a) the two stabilizing agents, KAsp and KGlu (i.e., ΔΔGc‘ = 96 kJ mol-1 in 1 M KAsp, and 107 kJ mol-1 in 1 M KGlu); (b) all the ternary aqueous solutions (i.e., ΔΔGc‘ = 145 kJ mol-1 in 1 M KAsp + 1 M GdmCl, and 185 kJ mol-1 in 1 M KGlu + 1 M GdmCl). The explanation is provided by the numbers listed in the third column of Table 2, which allow the calculation of the molar density of such aqueous solutions, and by the numbers listed in the fourth column of Table 2, which represent the volume packing density of each solution. The result is that the ΔΔGc‘ magnitude is large when: (a) the overall molar density is not far from that of water (which has the largest molar density among all common liquids and solutions), and (b) the volume packing density is markedly larger than that of water (which has a small ξ3 value as a consequence of the small size of its molecules and its tetrahedral coordination). The latter two variables determine the magnitude of the solvent-excluded volume effect, which, in turn, determines the ΔGc magnitude.
Moreover, since the T·ΔSconf term has been assumed to be independent of the presence of co-solutes, the further distinction between stabilizing and destabilizing agents has to come from the ΔEa term. The latter is expected to be a negative quantity in all cases; but, its magnitude should be large in the case of destabilizing agents, as a consequence of favorable energetic attractions to protein surfaces (i.e., the difference between exposed and buried surfaces of globular proteins is small) made by urea molecules, Gdm+ and SCN- ions [40,41]. The occurrence of such favorable energetic attractions is strongly supported by the large number of “binding” sites for the above species found in several protein structures deposited in the Protein Data Bank, and carefully characterized [42,43,44]. In particular, the guanidinium and thiocyanate ions prove to be “sticky” [45], because their low charge density and large polarizability due to π-electrons allow the formation of good dispersion attractions with both polar and nonpolar moieties. In contrast, the aspartate and glutamate ions possess two negative charges and one positive charge at pH 7.0, localized in different parts of the chemical structure, that favor the formation of strong H-bonds with water molecules. This implies that aspartate and glutamate prefer to stay in water with respect to interact with protein surfaces. Indeed, the molar density and volume packing density of KAsp and KGlu aqueous solutions are large enough to cause a significant ΔGC increase that leads to a marked stabilization of the N-state. A simple analysis may be useful. On recognizing that the van der Waals volume of Asp- and Glu- is around 10 times larger than that of water, the conclusion should be that their presence causes a significant decrease in molar density. Such a decrease, however, does not happen because of the strong H-bonds established between Asp- and Glu- and water molecules (this is a manifestation of electrostriction caused by such ions). The large positive ΔΔGc‘ values in the ternary aqueous solutions are only partially offset by large negative ΔEa terms in the presence of 1 M urea, or 1 M GdmCl, or 0.5 M GdmSCN and, in fact, the Td values remain high (see Table 1).
4. Materials and Methods
4.1. Materials
Pancreatic ribonuclease, RNase A (Type XII-A), urea, GdmCl, GdmSCN, KAsp and KGlu were from Merck (Darmstadt, Germany). A buffer solution of 10 mM MOPS (3-(N-morpholino) propanesulfonic acid) with 100 mM NaCl at pH 7.0, was used. MOPS buffer was chosen for its low protonation enthalpy to reduce the pH temperature dependence. Chemicals for buffer were of analytical grade from Sigma and dissolved in Milli Q (Millipore, Bedford, MA, USA) water. Urea stock solutions were prepared, just before use, by weight in a 3 mL final volume calibrated flask. GdmCl and GdmSCN were purchased as a ready-to-use 8 M and 6 M buffered solutions, respectively. Protein stock solutions were extensively dialyzed against the buffer, and concentration determined by UV spectra using a sequence-based extinction coefficient of 9440 M-1cm-1 at 280 nm [46]. Samples for DSC measurements were prepared by mixing appropriate volumes of the protein stock solution with co-solute stock solutions, then diluting with buffer up to a fixed volume of 2 mL in a calibrated flask. Protein final concentration was kept constant at 1 mg mL-1.
4.2. Density Measurements
The density of binary (containing water and KAsp or KGlu), and ternary (containing water and both KAsp or KGlu and a denaturant) solutions was measured using a vibrating tube densimeter (Anton Paar 5000, Austria), which has an accuracy of 0.5 g dm-3, at a constant cell temperature of 25.000 ± 0.001 °C. Samples were prepared and measured in triplicate. For the preparation, a 2 mL calibrated flask was employed; the required amount of co-solute(s) was taken by weight, and then water was added until reaching the final volume.
4.3. Differential Scanning Calorimetry (DSC)
DSC measurements were done on a Nano-DSC (TA Instruments, USA), which has an active cell volume of 0.3 mL and works at a pressure of 3 atm. The scan speed was set at 1 °C min-1. Samples were prepared in a 3 mL calibrated flask, by adding the appropriate amount of protein and co-solute(s) and diluting with buffer until reaching the final volume. Each measurement was done in triplicate, measuring the appropriate blank (buffer or buffer plus co-solute) before the sample, and two scans were performed on each sample to check the reversibility of the thermal denaturation. The data was analysed using the Nano-Analyze software supplied by the manufacturer: the blank scan was subtracted by the sample scan and the excess heat capacity, <ΔCp>, was obtained by taking as baseline the linear temperature dependence of the heat capacity of the protein native state [47]. The calorimetric enthalpy change, ΔHd(Td) was obtained by integrating the area under the curve. Using the Nano-Analyze software, the experimental DSC curves were modelled according to the two-state reversible equilibrium to calculate the van’t Hoff enthalpy change, ΔHdvH(Td), and the cooperative unit, CU, defined as the calorimetric to van’t Hoff enthalpy ratio. A CU value close to 1 is a necessary condition to state that the observed transition is a cooperative two-state process [48,49]. The Gibbs free energy of denaturation at 25 °C, ΔGd(25 °C), has been calculated via the Gibbs-Helmholtz equation, using the Td, ΔHd(Td) and ΔCp,d values obtained from the measurements.
5. Conclusions
We have shown that KAsp and KGlu significantly stabilize the native state of RNase A with respect to the temperature-induced denaturation. This stabilization is counteracted by the addition of common denaturants, urea, GdmCl and GdmSCN. A rationalization of experimental data is provided by means of a theoretical approach.
Author Contributions
Conceptualization, PDV. and G.G.; methodology, G.I. and M.C.; investigation, G.I. and M.C.; data curation, P.D.V.; writing—original draft preparation, G.G.; writing—review and editing, M.C. and G.G.; project administration and funding acquisition, G.G.. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the project “IONHOF” funded by Ministero dell’Università e della Ricerca, MUR, ‘Progetti di Ricerca di Rilevante Interesse Nazionale (PRIN)’ Bando 2022 - grant 2022FTHZZ7 to Giuseppe Graziano.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Hofmeister, F. Zur Lehre von der Wirkung der Salze: Zweite Mittheilung. Arch. Für Exp. Pathol. Pharmakol. 1888, 24, 247–260. [Google Scholar] [CrossRef]
- Von Hippel, P.H.; Wong, K.-Y. On the Conformational Stability of Globular Proteins. J. Biol. Chem. 1965, 240, 3909–3923. [Google Scholar] [CrossRef]
- Baldwin, R.L. How Hofmeister Ion Interactions Affect Protein Stability. Biophys. J. 1996, 71, 2056–2063. [Google Scholar] [CrossRef]
- Schellman, J.A. Protein Stability in Mixed Solvents: A Balance of Contact Interaction and Excluded Volume. Biophys. J. 2003, 85, 108–125. [Google Scholar] [CrossRef]
- Batchelor, J.D.; Olteanu, A.; Tripathy, A.; Pielak, G.J. Impact of Protein Denaturants and Stabilizers on Water Structure. J. Am. Chem. Soc. 2004, 126, 1958–1961. [Google Scholar] [CrossRef]
- Mitra, L.; Smolin, N.; Ravindra, R.; Royer, C.; Winter, R. Pressure Perturbation Calorimetric Studies of the Solvation Properties and the Thermal Unfolding of Proteins in Solution—Experiments and Theoretical Interpretation. Phys. Chem. Chem. Phys. 2006, 8, 1249. [Google Scholar] [CrossRef]
- Godawat, R.; Jamadagni, S.N.; Garde, S. Unfolding of Hydrophobic Polymers in Guanidinium Chloride Solutions. J. Phys. Chem. B 2010, 114, 2246–2254. [Google Scholar] [CrossRef] [PubMed]
- Pegram, L.M.; Record, M.T. Thermodynamic Origin of Hofmeister Ion Effects. J. Phys. Chem. B 2008, 112, 9428–9436. [Google Scholar] [CrossRef] [PubMed]
- Record, M.T.; Guinn, E.; Pegram, L.; Capp, M. Introductory Lecture: Interpreting and Predicting Hofmeister Salt Ion and Solute Effects on Biopolymer and Model Processes Using the Solute Partitioning Model. Faraday Discuss 2013, 160, 9–44. [Google Scholar] [CrossRef]
- von Hippel, P.H. Changing the Stability of Macromolecular Surfaces by Manipulating the Aqueous Environment. Biophys. J. 2016, 111, 1817–1820. [Google Scholar] [CrossRef]
- Arakawa, T.; Timasheff, S.N. The Mechanism of Action of Na Glutamate, Lysine HCl, and Piperazine-N,N’-Bis(2-Ethanesulfonic Acid) in the Stabilization of Tubulin and Microtubule Formation. J. Biol. Chem. 1984, 259, 4979–4986. [Google Scholar] [CrossRef] [PubMed]
- Sengupta, R.; Pantel, A.; Cheng, X.; Shkel, I.; Peran, I.; Stenzoski, N.; Raleigh, D.P.; Record, M.T. Positioning the Intracellular Salt Potassium Glutamate in the Hofmeister Series by Chemical Unfolding Studies of NTL9. Biochemistry 2016, 55, 2251–2259. [Google Scholar] [CrossRef] [PubMed]
- Cheng, X.; Guinn, E.J.; Buechel, E.; Wong, R.; Sengupta, R.; Shkel, I.A.; Record, M.T. Basis of Protein Stabilization by K Glutamate: Unfavorable Interactions with Carbon, Oxygen Groups. Biophys. J. 2016, 111, 1854–1865. [Google Scholar] [CrossRef] [PubMed]
- Dill, K.A. Additivity Principles in Biochemistry. J. Biol. Chem. 1997, 272, 701–704. [Google Scholar] [CrossRef] [PubMed]
- Cozzolino, S.; Oliva, R.; Graziano, G.; Del Vecchio, P. Counteraction of Denaturant-Induced Protein Unfolding Is a General Property of Stabilizing Agents. Phys. Chem. Chem. Phys. 2018, 20, 29389–29398. [Google Scholar] [CrossRef] [PubMed]
- Cozzolino, S.; Tortorella, A.; Del Vecchio, P.; Graziano, G. General Counteraction Exerted by Sugars against Denaturants. Life 2021, 11, 652. [Google Scholar] [CrossRef] [PubMed]
- Vigorita, M.; Cozzolino, S.; Oliva, R.; Graziano, G.; Del Vecchio, P. Counteraction Ability of TMAO toward Different Denaturing Agents. Biopolymers 2018, 109, e23104. [Google Scholar] [CrossRef] [PubMed]
- Graziano, G. On the Molecular Origin of Cold Denaturation of Globular Proteins. Phys. Chem. Chem. Phys. 2010, 12, 14245. [Google Scholar] [CrossRef]
- Graziano, G. On the Mechanism of Cold Denaturation. Phys Chem Chem Phys 2014, 16, 21755–21767. [Google Scholar] [CrossRef]
- Pica, A.; Graziano, G. Shedding Light on the Extra Thermal Stability of Thermophilic Proteins. Biopolymers 2016, 105, 856–863. [Google Scholar] [CrossRef]
- Reiss, H. Scaled Particle Methods in the Statistical Thermodynamics of Fluids. In Advances in Chemical Physics; Prigogine, I., Ed.; Wiley, 1965; Vol. 9, pp. 1–84 ISBN 978-0-470-69910-2.
- Lebowitz, J.L.; Helfand, E.; Praestgaard, E. Scaled Particle Theory of Fluid Mixtures. J. Chem. Phys. 1965, 43, 774–779. [Google Scholar] [CrossRef]
- Royer, C.A. Revisiting Volume Changes in Pressure-Induced Protein Unfolding. Biochim. Biophys. Acta BBA - Protein Struct. Mol. Enzymol. 2002, 1595, 201–209. [Google Scholar] [CrossRef] [PubMed]
- Chalikian, T.V. Volumetric Properties of Proteins. Annu. Rev. Biophys. Biomol. Struct. 2003, 32, 207–235. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.R.; Makhatadze, G.I. Molecular Determinant of the Effects of Hydrostatic Pressure on Protein Folding Stability. Nat. Commun. 2017, 8, 14561. [Google Scholar] [CrossRef] [PubMed]
- Lee, B.; Richards, F.M. The Interpretation of Protein Structures: Estimation of Static Accessibility. J. Mol. Biol. 1971, 55, 379–IN4. [Google Scholar] [CrossRef] [PubMed]
- Miller, S.; Janin, J.; Lesk, A.M.; Chothia, C. Interior and Surface of Monomeric Proteins. J. Mol. Biol. 1987, 196, 641–656. [Google Scholar] [CrossRef]
- Creamer, T.P.; Srinivasan, R.; Rose, G.D. Modeling Unfolded States of Peptides and Proteins. Biochemistry 1995, 34, 16245–16250. [Google Scholar] [CrossRef] [PubMed]
- Kell, G.S. Density, Thermal Expansivity, and Compressibility of Liquid Water from 0.Deg. to 150.Deg.. Correlations and Tables for Atmospheric Pressure and Saturation Reviewed and Expressed on 1968 Temperature Scale. J. Chem. Eng. Data 1975, 20, 97–105. [Google Scholar] [CrossRef]
- Sorenson, J.M.; Hura, G.; Glaeser, R.M.; Head-Gordon, T. What Can X-Ray Scattering Tell Us about the Radial Distribution Functions of Water? J. Chem. Phys. 2000, 113, 9149–9161. [Google Scholar] [CrossRef]
- Graziano, G. Water: Cavity Size Distribution and Hydrogen Bonds. Chem. Phys. Lett. 2004, 396, 226–231. [Google Scholar] [CrossRef]
- Ben-Amotz, D.; Willis, K.G. Molecular Hard-Sphere Volume Increments. J. Phys. Chem. 1993, 97, 7736–7742. [Google Scholar] [CrossRef]
- Pauling, L. The Nature of the Chemical Bond and the Structure of Molecules and Crystals: An Introduction to Modern Structural Chemistry; 3. ed., 17. print.; Cornell Univ. Press: Ithaca, NY, 2010; ISBN 978-0-8014-0333-0. [Google Scholar]
- Baxa, M.C.; Haddadian, E.J.; Jumper, J.M.; Freed, K.F.; Sosnick, T.R. Loss of Conformational Entropy in Protein Folding Calculated Using Realistic Ensembles and Its Implications for NMR-Based Calculations. Proc. Natl. Acad. Sci. 2014, 111, 15396–15401. [Google Scholar] [CrossRef] [PubMed]
- Sharp, K.A.; O’Brien, E.; Kasinath, V.; Wand, A.J. On the Relationship between NMR-Derived Amide Order Parameters and Protein Backbone Entropy Changes: Measurement of Protein Backbone Entropy by NMR. Proteins Struct. Funct. Bioinforma. 2015, 83, 922–930. [Google Scholar] [CrossRef] [PubMed]
- Fogolari, F.; Corazza, A.; Fortuna, S.; Soler, M.A.; VanSchouwen, B.; Brancolini, G.; Corni, S.; Melacini, G.; Esposito, G. Distance-Based Configurational Entropy of Proteins from Molecular Dynamics Simulations. PLOS ONE 2015, 10, e0132356. [Google Scholar] [CrossRef] [PubMed]
- Rose, G.D. Reframing the Protein Folding Problem: Entropy as Organizer. Biochemistry 2021, 60, 3753–3761. [Google Scholar] [CrossRef] [PubMed]
- Rose, G.D. Protein Folding - Seeing Is Deceiving. Protein Sci. 2021, 30, 1606–1616. [Google Scholar] [CrossRef] [PubMed]
- Rees, D.C.; Robertson, A.D. Some Thermodynamic Implications for the Thermostability of Proteins. Protein Sci. 2001, 10, 1187–1194. [Google Scholar] [CrossRef]
- Zangi, R.; Zhou, R.; Berne, B.J. Urea’s Action on Hydrophobic Interactions. J. Am. Chem. Soc. 2009, 131, 1535–1541. [Google Scholar] [CrossRef] [PubMed]
- Lindgren, M.; Westlund, P.-O. On the Stability of Chymotrypsin Inhibitor 2 in a 10 M Urea Solution. The Role of Interaction Energies for Urea-Induced Protein Denaturation. Phys. Chem. Chem. Phys. 2010, 12, 9358. [Google Scholar] [CrossRef]
- Paladino, A.; Balasco, N.; Graziano, G.; Vitagliano, L. A Protein Data Bank Survey of Multimodal Binding of Thiocyanate to Proteins: Evidence for Thiocyanate Promiscuity. Int. J. Biol. Macromol. 2022, 208, 29–36. [Google Scholar] [CrossRef]
- Paladino, A.; Balasco, N.; Vitagliano, L.; Graziano, G. A Structure-Based Mechanism for the Denaturing Action of Urea, Guanidinium Ion and Thiocyanate Ion. Biology 2022, 11, 1764. [Google Scholar] [CrossRef] [PubMed]
- Paladino, A.; Vitagliano, L.; Graziano, G. The Action of Chemical Denaturants: From Globular to Intrinsically Disordered Proteins. Biology 2023, 12, 754. [Google Scholar] [CrossRef] [PubMed]
- Collins, K.D. Sticky Ions in Biological Systems. Proc. Natl. Acad. Sci. 1995, 92, 5553–5557. [Google Scholar] [CrossRef]
- Pace, C.N.; Vajdos, F.; Fee, L.; Grimsley, G.; Gray, T. How to Measure and Predict the Molar Absorption Coefficient of a Protein. Protein Sci. 1995, 4, 2411–2423. [Google Scholar] [CrossRef] [PubMed]
- Foglia, F.; Mandrich, L.; Pezzullo, M.; Graziano, G.; Barone, G.; Rossi, M.; Manco, G.; Del Vecchio, P. Role of the N-Terminal Region for the Conformational Stability of Esterase 2 from Alicyclobacillus Acidocaldarius. Biophys. Chem. 2007, 127, 113–122. [Google Scholar] [CrossRef]
- Zhou, Y.; Hall, C.K.; Karplus, M. The Calorimetric Criterion for a Two-State Process Revisited. Protein Sci. Publ. Protein Soc. 1999, 8, 1064–1074. [Google Scholar] [CrossRef]
- Chan, H.S. Modeling Protein Density of States: Additive Hydrophobic Effects Are Insufficient for Calorimetric Two-State Cooperativity. Proteins Struct. Funct. Genet. 2000, 40, 543–571. [Google Scholar] [CrossRef]
Figure 1.
DSC profiles of RNAse A in 10 mM MOPS + 100 mM NaCl buffer, pH 7.0, in the absence and presence of KAsp (panel A) or KGlu (panel B) at the indicated concentrations.
Figure 1.
DSC profiles of RNAse A in 10 mM MOPS + 100 mM NaCl buffer, pH 7.0, in the absence and presence of KAsp (panel A) or KGlu (panel B) at the indicated concentrations.
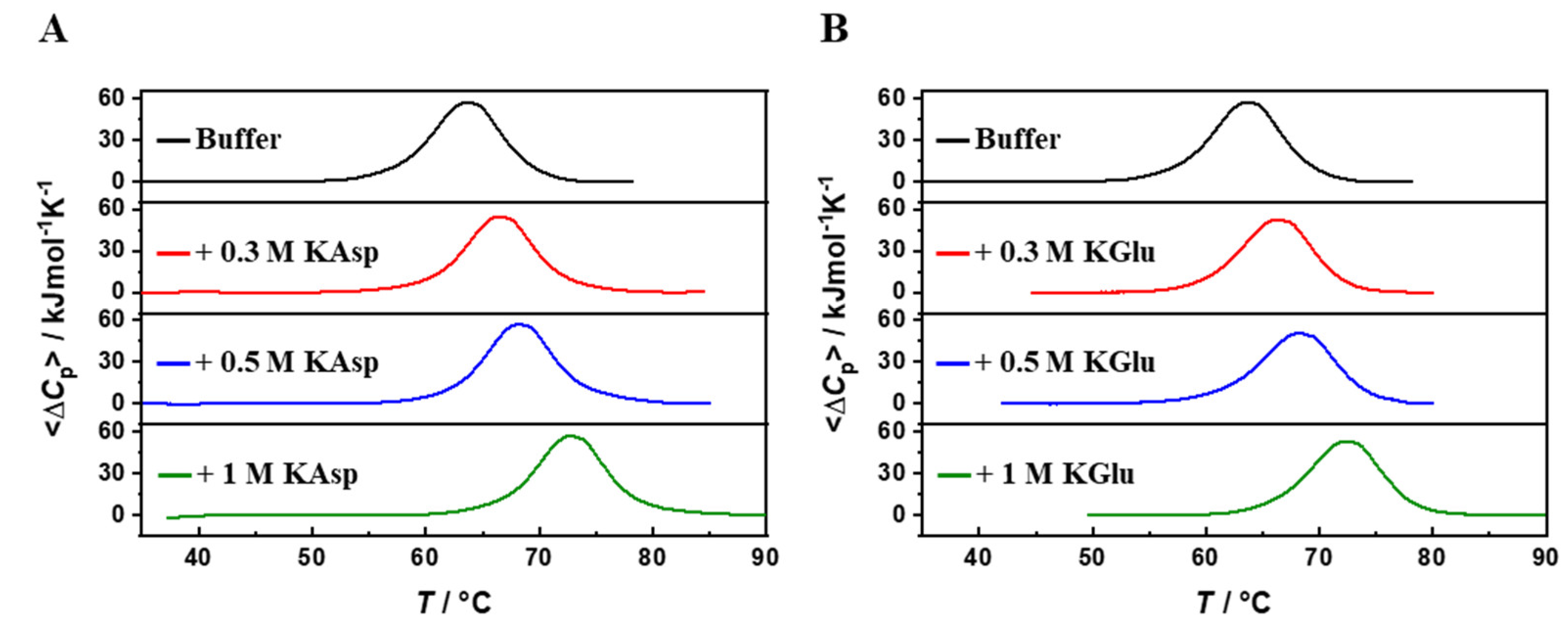
Figure 2.
DSC profiles of RNAse A in aqueous buffer, 1 M urea, 1 M KAsp plus 1 M urea, and 1 M KGlu plus 1 M urea (panel A); DSC profiles of RNAse A in aqueous buffer, 1 M GdmCl, 1 M KAsp plus 1 M GdmCl, and 1 M KGlu plus 1 M GdmCl (panel B); DSC profiles of RNAse A in aqueous buffer, 0.5 M GdmSCN, 1 M KAsp plus 0.5 M GdmSCN, and 1 M KGlu plus 0.5 M GdmSCN (panel C).
Figure 2.
DSC profiles of RNAse A in aqueous buffer, 1 M urea, 1 M KAsp plus 1 M urea, and 1 M KGlu plus 1 M urea (panel A); DSC profiles of RNAse A in aqueous buffer, 1 M GdmCl, 1 M KAsp plus 1 M GdmCl, and 1 M KGlu plus 1 M GdmCl (panel B); DSC profiles of RNAse A in aqueous buffer, 0.5 M GdmSCN, 1 M KAsp plus 0.5 M GdmSCN, and 1 M KGlu plus 0.5 M GdmSCN (panel C).
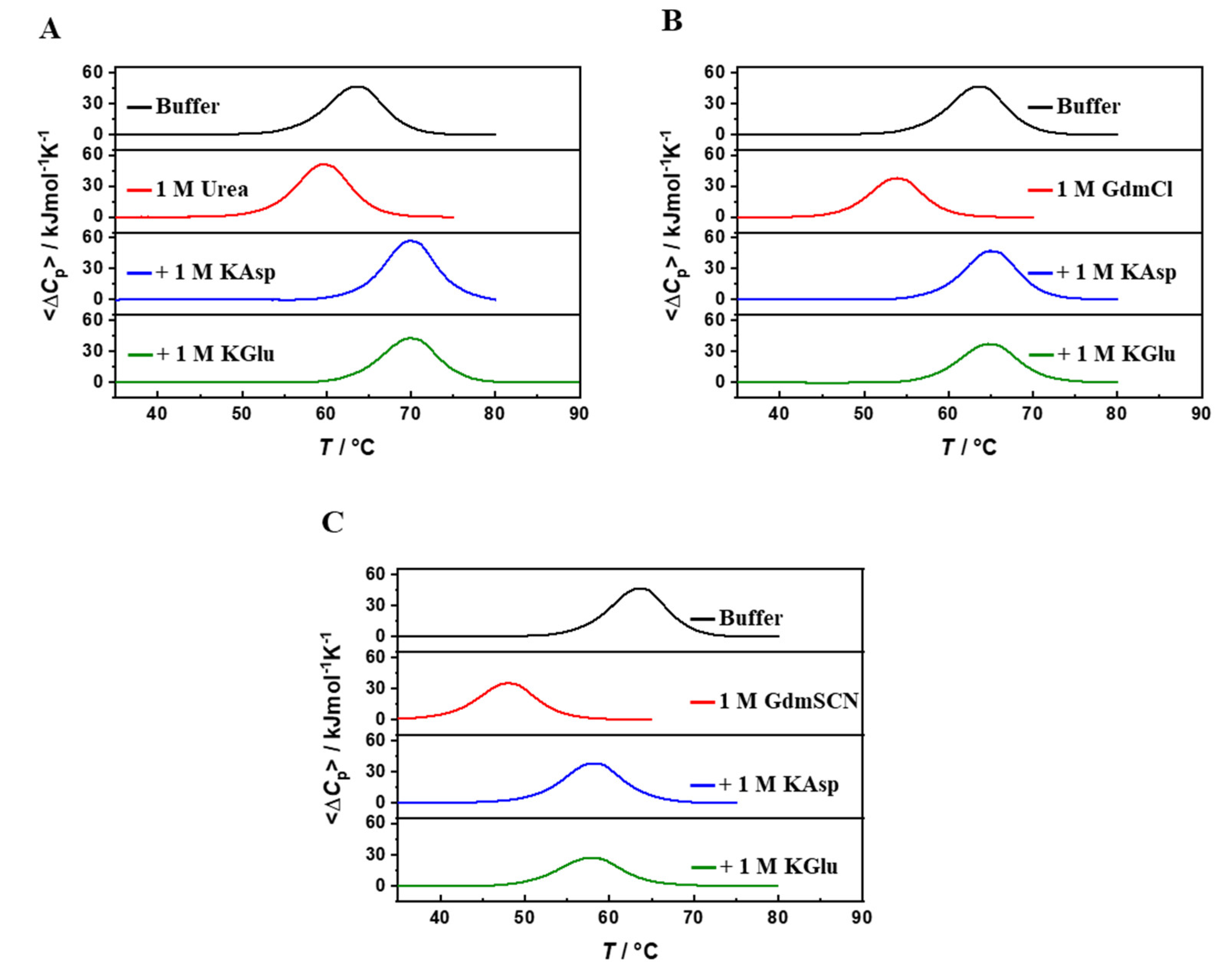
Table 1.
Thermodynamic parameters from the analysis of DSC curves for the temperature-induced denaturation of RNase A in the presence of different concentrations of potassium aspartate and potassium glutamate; and in the presence of 1 M concentration of one of the previous salts and some denaturing agents. CU is defined as the calorimetric to van’t Hoff enthalpy ratio.
Table 1.
Thermodynamic parameters from the analysis of DSC curves for the temperature-induced denaturation of RNase A in the presence of different concentrations of potassium aspartate and potassium glutamate; and in the presence of 1 M concentration of one of the previous salts and some denaturing agents. CU is defined as the calorimetric to van’t Hoff enthalpy ratio.
| Td/(°C) | ΔHd(Td) / kJ mol-1 | CU | ΔGd(25°C) / kJ mol-1 | |
|---|---|---|---|---|
| H2O | 63.5 | 464 | 0.99 | 38 |
| 0.3 M KAsp | 66.4 | 455 | 0.99 | 39 |
| 0.5 M KAsp | 68.2 | 480 | 0.97 | 42 |
| 1 M KAsp | 72.7 | 482 | 0.99 | 44 |
| 0.3 M KGlu | 66.3 | 485 | 0.97 | 42 |
| 0.5 M KGlu | 68.2 | 455 | 0.99 | 39 |
| 1 M KGlu | 72.2 | 480 | 0.97 | 44 |
| 1 M urea | 59.7 | 440 | 1.0 | 34 |
| 1 M KAsp + 1 M urea | 69.9 | 460 | 0.99 | 41 |
| 1 M KGlu + 1 M urea | 68.8 | 420 | 0.98 | 35 |
| 1 M GdmCl | 53.9 | 383 | 0.97 | 25 |
| 1 M KAsp + 1 M GdmCl | 64.9 | 400 | 0.99 | 31 |
| 1 M KGlu + 1 M GdmCl | 64.7 | 378 | 0.98 | 29 |
| 0.5 M GdmSCN | 47.9 | 320 | 0.96 | 17 |
| 1 M KAsp + 0.5 M GdmSCN | 58.0 | 352 | 0.96 | 24 |
| 1 M KGlu + 0.5 M GdmSCN | 57.9 | 360 | 0.97 | 25 |
Table 2.
Experimental values of the density and water molar concentration for pure water, and for considered binary and ternary aqueous solutions at 25 °C and 1 atm; values of the effective hard sphere diameters, σ assigned to all the species; values of the volume packing density, ξ3 for the solutions; values of the average effective hard sphere diameter, <σ> = ∑χj·σj, where χj is the molar fraction of the species j and σj is the corresponding hard sphere diameter.
Table 2.
Experimental values of the density and water molar concentration for pure water, and for considered binary and ternary aqueous solutions at 25 °C and 1 atm; values of the effective hard sphere diameters, σ assigned to all the species; values of the volume packing density, ξ3 for the solutions; values of the average effective hard sphere diameter, <σ> = ∑χj·σj, where χj is the molar fraction of the species j and σj is the corresponding hard sphere diameter.
| ρ / g L-1 | [H2O] / M | σ / Å | ξ3 | < σ> / Å | |
| H2O | 997 | 55.3 | 2.80 | 0.383 | 2.80 |
| 1 M KAsp | 1085 | 50.7 | 6.06 & 2.66 | 0.427 | 2.86 |
| 1 M K Glu | 1088 | 50.1 | 6.37 & 2.66 | 0.434 | 2.87 |
| 1 M urea | 1013 | 52.9 | 4.64 | 0.398 | 2.83 |
| 1 M KAsp + 1 M urea | 1099 | 48.2 | 6.06 & 2.66 & 4.64 | 0.441 | 2.90 |
| 1 M KGlu + 1 M urea | 1104 | 47.7 | 6.37 & 2.66 & 4.64 | 0.449 | 2.90 |
| 1 M GdmCl | 1024 | 51.5 | 4.70 & 3.62 | 0.404 | 2.85 |
| 1 M KAsp + 1 M GdmCl | 1109 | 46.7 | 6.06 & 2.66 & 4.70 & 3.62 | 0.447 | 2.91 |
| 1 M KGlu + 1 M GdmCl | 1112 | 46.1 | 6.37 & 2.66 & 4.70 & 3.62 | 0.458 | 2.92 |
| 0.5 M GdmSCN | 1011 | 52.8 | 4.70 & 3.94 | 0.392 | 2.83 |
| 1 M KAsp + 0.5 M GdmSCN | 1095 | 48.0 | 6.06 & 2.66 & 4.70 & 3.94 | 0.434 | 2.89 |
| 1 M KGlu + 0.5 M GdmSCN | 1101 | 47.5 | 6.37 & 2.66 & 4.70 & 3.62 | 0.442 | 2.90 |
Table 3.
Classic SPT estimates of the reversible work to create, in the reported aqueous solutions at 25 °C and 1 atm, cavities corresponding to the N-state (i.e., a sphere of 15 Å radius) and to the D-state (i.e., a prolate spherocylinder of 6 Å radius and 117 Å cylindrical length), respectively; values of ΔΔGC’ = ΔΔGC(co-solute) – ΔΔGC(water). All the numbers are in kJ mol-1 units; see text for further details.
Table 3.
Classic SPT estimates of the reversible work to create, in the reported aqueous solutions at 25 °C and 1 atm, cavities corresponding to the N-state (i.e., a sphere of 15 Å radius) and to the D-state (i.e., a prolate spherocylinder of 6 Å radius and 117 Å cylindrical length), respectively; values of ΔΔGC’ = ΔΔGC(co-solute) – ΔΔGC(water). All the numbers are in kJ mol-1 units; see text for further details.
| ΔGC(N) | ΔGC(D) | ΔΔGC | ΔΔGC’ | |
| H2O | 1072 | 1875 | 803 | - |
| 1 M urea | 1111 | 1942 | 831 | 28 |
| 1 M GdmCl | 1135 | 1984 | 849 | 46 |
| 0.5 M GdmSCN | 1085 | 1897 | 812 | 9 |
| 1 M KAsp | 1203 | 2102 | 899 | 96 |
| 1 M KAsp + 1 M urea | 1245 | 2176 | 931 | 128 |
| 1 M KAsp + 1 M GdmCl | 1269 | 2217 | 948 | 145 |
| 1 M KAsp + 0.5 M GdmSCN | 1207 | 2109 | 902 | 99 |
| 1 M KGlu | 1218 | 2128 | 910 | 107 |
| 1 M KGlu + 1 M urea | 1268 | 2215 | 947 | 144 |
| 1 M KGlu + 1 M GdmCl | 1323 | 2311 | 988 | 185 |
| 1 M KGlu + 0.5 M GdmSCN | 1228 | 2147 | 919 | 116 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







