Singular Value Decomposition of Elliptic Quaternion Matrices: Theory and Algorithms

In this study, we obtained results for the computation of eigen-pairs, singular value decomposition, pseudo-inverse, and the least square problem for elliptic quaternion matrices. Moreover, we established algorithms based on these results and provided illustrative numerical experiments to substantiate the accuracy of our conclusions. In the experiments, it was observed that the p-value in the algebra of elliptic quaternions and elliptic numbers directly affects the performance of the problem under consideration. Selecting the optimal p-value for problem-solving and the elliptic behavior of many physical systems make this number system advantageous in applied sciences.

Keywords:

Subject: Computer Science and Mathematics - Applied Mathematics

MSC: 11R52; 15A60; 15A18

1. Introduction

The singular value decomposition is a foundational aspect of matrix theory. In contrast to eigenvalue decomposition, which is limited to certain square matrices, singular value decomposition is applied to matrices of any size. Numerous results related to matrices, e.g., pseudo-inverses of matrices, solutions for least squares problems, and invariant norms under unitary transformations, can be derived from the principles of singular value decomposition. As a result, singular value decomposition is pivotal in the computation and analysis of matrices. In addition to its importance in the theoretical field, it appears in the solution of many problems in the applied fields, e.g., image processing, signal processing, principal component analysis, data compression, machine learning, deep learning, and computational mathematics, etc. Many researchers studied in these applied fields examine singular value decomposition methods. For example, Dian et al. presented a novel hyperspectral image and multispectral image fusion method based on the subspace representation and convolutional neural network denoiser. They obtained the subspaces via singular value decomposition of a high-resolution hyperspectral image [1]. Hashemipour et al. proposed a new lossy data compression framework centred on optimal singular value decomposition for big data compression [2]. Wang and Zhu focused on the implementation of data reduction algorithms such as SVD and principal component analysis in machine learning [3].

There is a generalization that includes three classes of 2-dimensional hypercomplex numbers [4]. The following is the definition of these numbers, known as generalized complex numbers:

q_{(g)} = q_{(g), r} + q_{(g), i} i,

where

q_{(g), r}, q_{(g), i} \in R, i \notin R

and

i^{2} = p (p \in R) .

Generalized Segre quaternions are generalized complex numbers extended to 4 dimensions. Generalized Segre quaternions are defined as follows:

q_{(G S)} = q_{(G S), r} + q_{(G S), i} i + q_{(G S), j} j + q_{(G S), k} k,

where

q_{(G S), r}, q_{(G S), i}, q_{(G S), j}, q_{(G S), k} \in R, i, j, k \notin R

. The multiplication rules for

i, j

and k units are given in the table below:

Table 1. Multiplication rules of

i, j

and k units.

Table 1. Multiplication rules of

i, j

and k units.

	i	j	k
i	p	k	$p j$
j	k	1	i
k	$p j$	i	p

Based on the value of p, generalized complex numbers and Segre quaternions are classified as follows [5]:

Every number system in Table 2 has various scientific and technological applications. Problems in non-Euclidean geometries are solved by hyperbolic complex numbers and hyperbolic quaternions [6]. In domains like robotic control and spatial mechanics, parabolic complex (dual) numbers and parabolic quaternions are employed [7]. On the other hand, as numerous physical systems demonstrate elliptical behavior, the practical applications of elliptic complex numbers and elliptic quaternions in applied science are noteworthy. For example, Ozdemir defined elliptic quaternions (non-commutative) and generated an elliptical rotation matrix for the motion of a point on an ellipse through some angle about a vector using those quaternions [8]. Dundar et al. studied elliptical harmonic motion, which is the superposition of two simple harmonic motions in perpendicular directions with the same angular frequency and phase difference of

\frac{π}{2}

by using elliptic complex numbers [9]. Derin and Gungor proposed the generalization of gravity, including the Proca-type and gravitomagnetic monopole by means of elliptic biquaternions [10]. Catoni et al. introduced algebraic properties and the differential conditions of elliptic quaternionic systems [5]. Additionally, Catoni et al. studied the constant curvature spaces associated with the geometry generated by elliptic quaternions. They formulated geodesic equations within the context of Riemann geometry [11]. Gua et al. defined the elliptic quaternionic canonical transform and investigated Parseval’s theorem with the help of this transform [12]. Yuan et al. obtained the Hermitian solutions of the elliptic quaternion matrix equation

(A X B, C X D) = (E, G)

[13]. Tosun and Kosal characterized the existence of the solution to Sylvester s-conjugate elliptic quaternion matrix equations. They obtained the solution explicitly using a real representation of an elliptic quaternion matrix [14]. Gai and Huang developed a new convolutional neural network with elliptic quaternion values. They conducted extensive experiments on colour image classification and colour image denoising to evaluate the performance of the proposed convolutional neural network [15]. Guo et al. studied the problem of solutions to Maxwell’s equations of elliptic quaternions using a real representation of elliptic quaternion matrices [16]. Atali et al. obtained the elliptic quaternionic least-squares solution with the minimum norm of the elliptic quaternion matrix equation

A X = B

. Furthermore, leveraging the insights derived from their theories, they developed a novel color image restoration model known as the elliptical quaternionic least squares restoration filter [17].

As observed, the elliptic quaternions and their matrices find numerous practical applications in various branches of applied sciences. Thus, further study of the theoretical properties and numerical computations of elliptic quaternions and their matrices is becoming increasingly necessary. In this regard, we have derived outcomes concerning the computation of eigen-pairs, singular value decomposition, pseudo-inverse, and least square solutions with the minimum norm for elliptic quaternion matrices. Additionally, algorithms have been formulated based on these results, accompanied by illustrative numerical experiments to validate our findings’ precision empirically.

Within the context of this paper, the following notations will be employed. Let

R

C

C_{p}

, and

H_{p}

denote the sets of real numbers, complex numbers, elliptic complex numbers, and elliptic quaternions, respectively.

R^{m \times n}

C^{m \times n}

C_{p}^{m \times n}

, and

H_{p}^{m \times n}

denote the set of all

m \times n

matrices on

R

C

C_{p}

and

H_{p}

, respectively. We will also denote elliptic complex numbers as EC numbers and elliptic quaternions as EQs for short. The notation to be used to represent numbers throughout the study is given in the table below.

Moreover, all computations in this study are performed using the MATLAB 2024a (64bit) on an Intel(R) Xeon(R) CPU E5-1650 v4 @3.60GHz (12 CPUs)/16GB (DDR3) RAM computer.

2. Preliminaries

An EC number

q_{(e)}

is denoted by

q_{(e)} = q_{(e), r} + q_{(e), i} i

where

i^{2} = p < 0

and

q_{(e), r}, q_{(e), i}, p \in R

. The conjugate and norm of

q_{(e)} \in C_{p}

are defined as

\bar{q_{(e)}} = q_{(e), r} - q_{(e), i} i and {∥q_{(e)}∥}_{p} = \sqrt{q_{(e), r}^{2} - p q_{(e), i}^{2}},

respectively [18]. The multiplication of EC numbers

q_{1, (e)} = q_{1, (e), r} + q_{1, (e), i} i

and

q_{2, (e)} = q_{2, (e), r} + q_{2, (e), i} i

is defined as

q_{1, (e)} q_{2, (e)} = (q_{1, (e), r} q_{2, (e), r} + p q_{1, (e), i} q_{2, (e), i}) + i (q_{1, (e), r} q_{2, (e), i} + q_{2, (e), r} q_{1, (e), i}) .

An EC matrix

Q_{(e)}

is denoted as

Q_{(e)} = Q_{(e), r} + Q_{(e), i} i

where

i^{2} = p < 0

p \in R

, and

Q_{(e), r}

Q_{(e), i} \in R^{m \times n}

. The conjugate, transpose, conjugate transpose and Frobenius norm of

Q_{(e)}

C_{p}^{m \times n}

are defined by

\bar{Q_{(e)}} = Q_{(e), r} - Q_{(e), i} i

Q_{(e)}^{T} = Q_{(e), r}^{T} + Q_{(e), i}^{T} i, Q_{(e)}^{*} = Q_{(e), r}^{T} - Q_{(e), i}^{T} i,

and

∥ Q_{(e)} ∥_{p} = \sqrt{∥ Q_{(e), r} ∥^{2} - p {∥ Q_{(e), i} ∥}^{2}}

, respectively. The multiplication of the EC matrices

Q_{1, (e)} = Q_{1, (e), r} + Q_{1, (e), i} i

and

Q_{2, (e)} = Q_{2, (e), r} + Q_{2, (e), i} i

is defined as

Q_{1, (e)} Q_{2, (e)} = (Q_{1, (e), r} Q_{2, (e), r} + p Q_{1, (e), i} Q_{2, (e), i}) + i (Q_{1, (e), r} Q_{2, (e), i} + Q_{2, (e), r} Q_{1, (e), i}) .

An EQ

q_{(E)}

is denoted as

q_{(E)} = q_{(E), r} + q_{(E), i} i + q_{(E), j} j + q_{(E), k} k

where

i^{2} = k^{2} = p < 0

j^{2} = 1

i j = j i = k

j k = k j = i

k i = i k = p j

, and

q_{(E), r}, q_{(E), i}, q_{(E), j}, q_{(E), k}, p \in R

[5,18]. An EQ

q_{(E)}

is denoted in the forms:

q_{(E)} = (q_{(E), r} + i q_{(E), i}) + (q_{(E), j} + i q_{(E), k}) j = q_{(e), 1} e_{1} + q_{(e), 2} e_{2}

where

q_{(e), 1} = (q_{(E), r} + q_{(E), j}) + (q_{(E), i} + q_{(E), k}) i

and

q_{(e), 2} = (q_{(E), r} - q_{(E), j}) + (q_{(E), i} - q_{(E), k}) i,

are an EC numbers and

e_{1} = \frac{1 + j}{2}, e_{2} = \frac{1 - j}{2} .

Clearly,

e_{1} e_{2} = 0, e_{1} + e_{2} = 1

e_{1}^{2} = e_{1}

and

e_{2}^{2} = e_{2} .

As a result,

e_{1}

and

e_{2}

are disjoint idempotent units.

The multiplication of the two EQs

q_{1, (E)} = q_{1, (e), 1} e_{1} + q_{1, (e), 2} e_{2}

and

q_{2, (E)} = q_{2, (e), 1} e_{1} + q_{2, (e), 2} e_{2}

is defined by

\begin{matrix} q_{1, (E)} q_{2, (E)} = (q_{1, (e), 1} q_{2, (e), 1}) e_{1} + (q_{1, (e), 2} q_{2, (e), 2}) e_{2} . \end{matrix}

The conjugate and norm of the EQ

q_{(E)} = q_{(e), 1} e_{1} + q_{(e), 2} e_{2}

are defined by

\bar{q_{(E)}} = \bar{q_{(e), 1}} e_{1} + \bar{q_{(e), 2}} e_{2}

and

{∥q_{(E)}∥}_{p} = \frac{1}{\sqrt{2}} \sqrt{({∥q_{(e), 1}∥}_{p}^{2} + {∥q_{(e), 2}∥}_{p}^{2})},

respectively.

An EQ matrix

Q_{(E)}

is represented

\begin{matrix} Q_{(E)} = Q_{(E), r} + Q_{(E), i} i + Q_{(E), j} j + Q_{(E), k} k = (Q_{(E), r} + Q_{(E), i} i) + j (Q_{(E), j} + Q_{(E), k} i) \\ = Q_{(e), 1} e_{1} + Q_{(e), 2} e_{2} \end{matrix}

(1)

where

Q_{(e), 1} = (Q_{(E), r} + Q_{(E), j}) + (Q_{(E), i} + Q_{(E), k}) i

and

Q_{(e), 2} = (Q_{(E), r} - Q_{(E), j}) + (Q_{(E), i} - Q_{(E), k}) i

are EC matrices and

Q_{(E), r}, Q_{(E), i}, Q_{(E), j}, Q_{(E), k} k \in R^{m \times n}

[14,17]. The multiplication of the two EQ matrices

Q_{1, (E)} = Q_{1, (e), 1} e_{1} + Q_{1, (e), 2} e_{2}

and

Q_{2, (E)} = Q_{2, (e), 1} e_{1} + Q_{2, (e), 2} e_{2}

is defined by

\begin{matrix} Q_{1, (E)} Q_{2, (E)} = (Q_{1, (e), 1} Q_{2, (e), 1}) e_{1} + (Q_{1, (e), 2} Q_{2, (e), 2}) e_{2} . \end{matrix}

The conjugate, transpose, conjugate transpose, and Frobenius norm of EQ matrix

Q_{(E)} = Q_{(e), 1} e_{1} + Q_{(e), 2} e_{2} \in H_{p}^{m \times n}

are defined by

\bar{Q_{(E)}} = \bar{Q_{(e), 1}} e_{1} + \bar{Q_{(e), 2}} e_{2}

Q_{(E)}^{T} = Q_{(e), 1}^{T} e_{1} + Q_{(e), 2}^{T} e_{2}

Q_{(E)}^{*} = \bar{Q_{(e), 1}^{T}} e_{1} + \bar{Q_{(e), 2}^{T}} e_{2}

and

\begin{matrix} {∥Q_{(E)}∥}_{p} = \frac{1}{\sqrt{2}} \sqrt{({∥Q_{(e), 1}∥}_{p}^{2} + {∥Q_{(e), 2}∥}_{p}^{2})} . \end{matrix}

3. Eigenvalues and Eigenvectors, Singular Value Decomposition, Pseudo-Inverse, and Least Squares Problem for EQ Matrices

3.1. EC Matrices

The lemmas that will be given in this subsection and will be used in the proofs of theorems regarding EQ matrices have been obtained through the following isomorphisms and their inverses:

\begin{matrix} η_{p} : C_{p} \to C \\ q_{(e)} = q_{(e), r} + i q_{(e), i} \to η_{p} (q_{(e)}) = q_{(c)} = q_{(e), r} + I \sqrt{- p} q_{(e), i} \end{matrix}

and

\begin{matrix} H_{p} : H_{p}^{m \times n} \to H^{m \times n} \\ Q_{(e)} = Q_{(e), r} + Q_{(e), i} \to H_{p} (Q_{(e)}) = Q_{(c)} = Q_{(e), r} + I \sqrt{- p} Q_{(e), i} \end{matrix}

where I represents the complex unit (

I^{2} = - 1

) [4].

Lemma 1.

A polynomial function of degree N with EC number coefficients presented by

f_{p} (x_{(e)}) = x_{(e)}^{N} + q_{(e), N - 1} x_{(e)}^{N - 1} + \dots + q_{(e), 1} x_{(e)} + q_{(e), 0}

has exactly N zeros in the set of EC numbers.

Lemma 2.

Let

Q_{(e)} \in C_{p}^{n \times n}

. An EC matrix

Q_{(e)}

is nonsingular if and only if the complex matrix

H_{p} (Q_{(e)})

are nonsingular. If

H_{p} (Q_{(e)})

are nonsingular, then

Q_{(e)}^{- 1} = Re ({(H_{p} (Q_{(e)}))}^{- 1}) + \frac{i}{\sqrt{- p}} Im ({(H_{p} (Q_{(e)}))}^{- 1}) .

Lemma 3.

Let

Q_{(e)} \in C_{p}^{m \times n}

. Then

r a n k (Q_{(e)}) = r a n k (H_{p} (Q_{(e)})) .

Lemma 4.

Let the eigenvalues of an complex matrix

H_{p} (Q_{(e)})

be denoted by

λ_{H_{p} (Q_{(e)})}

, and let the corresponding eigenvectors be represented by

x_{H_{p} (Q_{(e)})} .

Then, the eigenvalues of the EC matrix

Q_{(e)} \in C_{p}^{n \times n}

are given by

λ_{(e)} = Re (λ_{H_{p} (Q_{(e)})}) + \frac{i}{\sqrt{- p}} Im (λ_{H_{p} (Q_{(e)})})

and the corresponding eigenvectors are given by

x_{(e)} = Re (x_{H_{p} (Q_{(e)})}) + \frac{i}{\sqrt{- p}} Im (x_{H_{p} (Q_{(e)})}) .

The converse of this lemma is also true.

Lemma 5.

Let

Q_{(e)} \in C_{p}^{m \times n}

be an EC matrix. The pseudo-inverse of

Q_{(e)}

, denoted by

{(Q_{(e)})}^{†}

, is given by

{(Q_{(e)})}^{†} = Re ({(H_{p} (Q_{(e)}))}^{†}) + \frac{i}{\sqrt{- p}} Im ({(H_{p} (Q_{(e)}))}^{†})

where

{(H_{p} (Q_{(e)}))}^{†}

is the pseudo-inverse of the complex matrix

H_{p} (Q_{(e)})

Lemma 6.

Let

Q_{(e)} \in C_{p}^{m \times n}

. Suppose that the singular value decomposition of the complex matrix

H_{p} (Q_{(e)})

is given by

H_{p} (Q_{(e)}) = U_{(c)} Σ V_{(c)}^{*} .

Then, the singular value decomposition of the EC matrix

Q_{(e)}

Q_{(e)} = (Re (U_{(c)}) + \frac{i}{\sqrt{- p}} Im (U_{(c)})) Σ {(Re (V_{(c)}) + \frac{i}{\sqrt{- p}} Im (V_{(c)}))}^{*}

where Σ is a real matrix. The converse of this statement is also true.

Lemma 7.

Let

Q_{(e)} \in C_{p}^{m \times n}

. Suppose that

H_{p} (Q_{(e)}) = U_{(c)} Σ V_{(c)}^{*} .

In this case, the pseudo-inverse of EC matrix

Q_{(e)}

is given by

{(Q_{(e)})}^{†} = (Re (V_{(c)}) + \frac{i}{\sqrt{- p}} Im (V_{(c)})) Σ^{†} {(Re (U_{(c)}) + \frac{i}{\sqrt{- p}} Im (U_{(c)}))}^{*} .

Lemma 8.

Let

Q_{1, (e)} \in C_{p}^{m \times n}

and

Q_{2, (e)} \in C_{p}^{m \times q}

. Suppose that

H_{p} (Q_{1, (e)}) = U_{(c)} Σ V_{(c)}^{*} .

In this case, the least squares solution with the minimum norm

X_{(e)}

of the EC matrix equation

Q_{1, (e)} X_{(e)} = Q_{2, (e)}

is given by

X_{(e)} = (Re (V_{(e)}) + \frac{i}{\sqrt{- p}} Im (V_{(e)})) Σ^{†} {(Re (U_{(e)}) + \frac{i}{\sqrt{- p}} Im (U_{(e)}))}^{*} Q_{2, (e)} .

3.2. EQ Matrices

Let

Q_{(E)} = Q_{(e), 1} e_{1} + Q_{(e), 2} e_{2} \in H_{p}^{m \times n}

. Since

e_{1}

and

e_{2}

are disjoint idempotent units here, the mathematical properties associated with EQ matrices are closely related to EC matrices

Q_{(e), 1}, Q_{(e), 2}

. In this subsection, results related to eigen-pairs, singular value decomposition, pseudo-inverse, and least squares solution with the minimum norm for EQ matrices have been derived from this fact.

Definition 1.

A monic polynomial of degree N with EQ variables

x_{(E)}

is expressed as

f_{p} (x_{(E)}) = x_{(E)}^{N} + q_{(N - 1), (E)} x_{(E)}^{N - 1} + \dots + q_{1, (E)} x_{(E)} + q_{0, (E)},

where

q_{(N - 1), (E)}, q_{(N - 2), (E)}, . . ., q_{1, (E)}, q_{0, (E)}

are EQ coefficients.

Theorem 1.

A polynomial function

f_{p} (x_{(E)})

with degree N has exactly

N^{2}

zeros in the set of EQs.

Proof.

The polynomial

f_{p} (x_{(E)})

can be written in the form

\begin{matrix} f_{p} (x_{(E)}) & = & {(x_{(e), 1} e_{1} + x_{(e), 2} e_{2})}^{N} + (q_{(N - 1), (e), 1} e_{1} + q_{(N - 1), (e), 2} e_{2}) {(x_{(e), 1} e_{1} + x_{(e), 2} e_{2})}^{N - 1} \\ + \dots + (q_{1, (e), 1} e_{1} + q_{1, (e), 2} e_{2}) (x_{(e), 1} e_{1} + x_{(e), 2} e_{2}) + (q_{0, (e), 1} e_{1} + q_{0, (e), 2} e_{2}) \\ = & ({(x_{(e), 1})}^{N} + (q_{(N - 1), (e), 1}) {(x_{(e), 1})}^{N - 1} + \dots + (q_{1, (e), 1}) (x_{(e), 1}) + q_{0, (e), 1}) e_{1} + \\ ({(x_{(e), 2})}^{N} + (q_{(N - 1), (e), 2}) {(x_{(e), 2})}^{N - 1} + \dots + (q_{1, (e), 2}) (x_{(e), 2}) + q_{0, (e), 2}) e_{2} \\ = & f_{p} (x_{(e), 1}) e_{1} + f_{p} (x_{(e), 2}) e_{2}, \end{matrix}

where

f_{p} (x_{(e), 1})

and

f_{p} (x_{(e), 2})

are polynomials of degree N with EC number coefficients and values. Since these polynomials have at most N zeros each, the EQ-valued polynomial

f_{p} (x_{(E)})

has at most

N^{2}

roots.

Theorem 2.

An EQ matrix

Q_{(E)} = Q_{(e), 1} e_{1} + Q_{(e), 2} e_{2} \in H_{p}^{n \times n}

is nonsingular if and only if the EC matrices

Q_{(e), 1}, Q_{(e), 2} \in C_{p}^{n \times n}

are nonsingular. If

Q_{(e), 1}, Q_{(e), 2} \in C_{p}^{n \times n}

are nonsingular, then

Q_{(E)}^{- 1} = Q_{(e), 1}^{- 1} e_{1} + Q_{(e), 2}^{- 1} e_{2} .

Proof.

Let’s assume that

Q_{(E)} = Q_{(e), 1} e_{1} + Q_{(e), 2} e_{2} \in H_{p}^{n \times n}

is nonsingular and

Q_{(E)}^{- 1} = P_{(e), 1}^{} e_{1} + P_{(e), 2}^{} e_{2}

is inverse of

Q_{(E)}

. In this case,

Q_{(E)} Q_{(E)}^{- 1} = (Q_{(e), 1} P_{(e), 1}^{} e_{1} + Q_{(e), 2} P_{(e), 2}^{} e_{2}) = I_{n} e_{1} + I_{n} e_{2}

holds. By this fact,

Q_{(e), 1} P_{(e), 1}^{} = I_{n} a n d Q_{(e), 2} P_{(e), 2}^{} = I_{n}

are obtained. Then, we get

Q_{(e), 1}^{- 1} = P_{(e), 1}^{} a n d Q_{(e), 2}^{- 1} = P_{(e), 2}^{} .

Conversely, let’s assume that

Q_{(e), 1}, Q_{(e), 2} \in C_{p}^{n \times n}

are nonsingular EC matrices. In this case,

(Q_{(e), 1} e_{1} + Q_{(e), 2} e_{2}) (Q_{(e), 1}^{- 1} e_{1} + Q_{(e), 2}^{- 1} e_{2}) = I_{n} e_{1} + I_{n} e_{2}

holds. Consequently,

Q_{(E)} = Q_{(e), 1} e_{1} + A_{(e), 2} e_{2} \in H_{p}^{n \times n}

is nonsingular and

Q_{(E)}^{- 1} = Q_{(e), 1}^{- 1} e_{1} + Q_{(e), 2}^{- 1} e_{2}

is valid.

Theorem 3.

Let

Q_{(E)} = Q_{(e), 1} e_{1} + Q_{(e), 2} e_{2} \in H_{p}^{n \times n}

. Suppose that

λ_{(e), 1}

and

λ_{(e), 2}

are eigenvalues of EC matrices

Q_{(e), 1}

and

Q_{(e), 2}

corresponding to the eigenvectors

x_{(e), 1}

and

x_{(e), 2},

respectively. Then

λ_{(E)} = λ_{(e), 1} e_{1} + λ_{(e), 2} e_{2}

is an eigenvalue of

Q_{(E)}

corresponding to the eigenvector

x_{(E)} = x_{(e), 1} e_{1} + x_{(e), 2} e_{2}

and its converse is also true.

Proof.

Suppose

(λ_{(e), 1}, x_{(e), 1})

and

(λ_{(e), 2}, x_{(e), 2})

are eigen-pairs of EC matrices

Q_{(e), 1}

and

Q_{(e), 2}

, respectively. Then,

\begin{matrix} Q_{(E)} x_{(E)} = Q_{(E)} (x_{(e), 1} e_{1} + x_{(2), 2} e_{2}) & = & (Q_{(e), 1} e_{1} + Q_{(e), 2} e_{2}) (x_{(e), 1} e_{1} + x_{(e), 2} e_{2}) \\ = & Q_{(e), 1} x_{(e), 1} e_{1} + Q_{(e), 2} x_{(e), 2} e_{2} \\ = & λ_{(e), 1} x_{(e), 1} e_{1} + λ_{(e), 2} x_{(e), 2} e_{2} \\ = & (λ_{(e), 1} e_{1} + λ_{(e), 2} e_{2}) (x_{(e), 1} e_{1} + x_{(e), 2} e_{2}) = λ_{(E)} x_{(E)} . \end{matrix}

Thus,

(λ_{(E)}, x_{(E)})

is an eigen-pairs of

Q_{(E)}

. Conversely, assume that

(λ_{(E)}, x_{(E)})

is an eigen-pairs of

Q_{(E)}

. Then, we get

Q_{(E)} x_{(E)} = λ_{(E)} x_{(E)}

and

Q_{(e), 1} x_{(e), 1} e_{1} + Q_{(e), 2} x_{(e), 2} e_{2} = λ_{(e), 1} x_{(e), 1} e_{1} + λ_{(e), 2} x_{(e), 2} e_{2}

which implies

Q_{(e), 1} x_{(e), 1} = λ_{(e), 1} x_{(e), 1} and Q_{(e), 2} x_{(e), 2} = λ_{(e), 2} x_{(e), 2} .

Corollary 1.

Let

Q_{(E)} = Q_{(e), 1} e_{1} + Q_{(e), 2} e_{2} \in H_{p}^{n \times n}

. Since EC matrices

Q_{(e), 1}

and

Q_{(e), 2}

have at most n eigenvalues, the EQ matrix

Q_{(E)}

has at most

n^{2}

eigenvalues.

Theorem 4.

Let

Q_{(E)} = Q_{(e), 1} e_{1} + Q_{(e), 2} e_{2} \in H_{p}^{m \times n}

. Suppose that singular value decompositions of

Q_{(e), 1}

and

Q_{(e), 2}

are

Q_{(e), 1} = U_{(e), 1} Σ_{1} V_{(e), 1}^{*}

and

Q_{(e), 2} = U_{(e), 2} Σ_{2} V_{(e), 2}^{*}

, respectively. Then, the singular value decomposition of EQ matrix

Q_{(E)}

is given by

Q_{(E)} = U_{(E)} Σ_{(E)} V_{(E)}^{*}

where

Σ_{(E)} = Σ_{1} e_{1} + Σ_{2} e_{2}, U_{(E)} = U_{(e), 1} e_{1} + U_{(e), 2} e_{2}

and

V_{(E)} = V_{(e), 1} e_{1} + V_{(e), 2} e_{2}

such that

U_{(E)}

and

V_{(E)}

are unitary matrices.

Proof.

Let the singular value decompositions of

Q_{(e), 1}

and

Q_{(e), 2}

Q_{(e), 1} = U_{(e), 1} Σ_{1} V_{(e), 1}^{*}

and

Q_{(e), 2} = U_{(e), 2} Σ_{2} V_{(e), 2}^{*}

, respectively. Then, the singular value decomposition of

Q_{(E)}

is as follows:

\begin{matrix} Q_{(E)} = Q_{(e), 1} e_{1} + Q_{(e), 2} e_{2} & = & (U_{(e), 1} Σ_{1} V_{(e), 1}^{*}) e_{1} + (U_{(e), 2} Σ_{2} V_{(e), 2}^{*}) e_{2} \\ = & (U_{(e), 1} e_{1} + U_{(e), 2} e_{2}) (Σ_{1} e_{1} + Σ_{2} e_{2}) {(V_{(e), 1} e_{1} + V_{(e), 2} e_{2})}^{*} \\ = & U_{(E)} Σ_{(E)} V_{(E)}^{*} \end{matrix}

where

\begin{matrix} U_{(E)} U_{(E)}^{*} & = & (U_{(e), 1} e_{1} + U_{(e), 2} e_{2}) {(U_{(e), 1} e_{1} + U_{(e), 2} e_{2})}^{*} \\ = & U_{(e), 1} U_{(e), 1}^{*} e_{1} + U_{(e), 2} U_{(e), 2}^{*} e_{2} \\ = & I_{n} e_{1} + I_{n} e_{2} = I_{n}, \\ V_{(E)} V_{(E)}^{*} & = & (V_{(e), 1} e_{1} + V_{(e), 2} e_{2}) {(V_{(e), 1} e_{1} + V_{(e), 2} e_{2})}^{*} \\ = & V_{(e), 1} V_{(e), 1}^{*} e_{1} + V_{(e), 2} V_{(e), 2}^{*} e_{2} \\ = & I_{n} e_{1} + I_{n} e_{2} = I_{n}, \end{matrix}

and

Σ_{(E)}

is hyperbolic matrix. (

Σ_{(E)}

is real matrix if and only if

Σ_{1} = Σ_{2} .

) □

Corollary 2.

Let

Q_{(E)} = Q_{(e), 1} e_{1} + Q_{(e), 2} e_{2} \in H_{p}^{m \times n}

. Then

r a n k (Q_{(E)}) = max (r a n k (Q_{(e), 1}), r a n k (Q_{(e), 1})) = max (r a n k (Σ_{1}), r a n k (Σ_{2})) .

Corollary 3.

Let

Q_{(E)} = Q_{(e), 1} e_{1} + Q_{(e), 2} e_{2} \in H_{p}^{m \times n}

be the singular value decomposition of an EQ matrix in the form

Q_{(E)} = U_{(E)} Σ_{(E)} V_{(E)}^{*} .

Then, the pseudo-inverse of

Q_{(E)}

Q_{(E)}^{†} = V_{(E)} Σ_{(E)}^{†} U_{(E)}^{*}

where

Σ^{†} = Σ_{1}^{†} e_{1} + Σ_{2}^{†} e_{2}

and

Σ_{1}, Σ_{2} \in R^{m \times n} .

Theorem 5.

The least squares solution with the minimum norm of the EQ matrix equation

Q_{1, (E)} X_{(E)} = Q_{2, (E)}

X_{(E)} = Q_{1, (E)}^{†} Q_{2, (E)} = V_{(E)} Σ_{(E)}^{†} U_{(E)}^{*} Q_{2, (E)} .

where

Q_{1, (E)} \in H_{p}^{m \times n}

and

Q_{2, (E)} \in H_{p}^{m \times q}

Proof.

The least squares solution with the minimum norm of the EQ matrix equation

Q_{1, (E)} X_{(E)} = Q_{2, (E)}

X_{(E)}

. Then we get

{∥Q_{1, (E)} X_{(E)} - Q_{2, (E)}∥}_{p} = min

and

\begin{matrix} {∥Q_{1, (E)} X_{(E)} - Q_{2, (E)}∥}_{p}^{2} & = & {∥(Q_{1, (e), 1} e_{1} + Q_{1, (e), 2} e_{2}) (X_{(e), 1} e_{1} + X_{(e), 2} e_{2}) - (Q_{2, (e), 1} e_{1} + Q_{2, (e), 2} e_{2})∥}_{p}^{2} \\ = & {∥(Q_{1, (e), 1} X_{(e), 1} e_{1} + Q_{1, (e), 2} X_{(e), 2} e_{2}) - (Q_{2, (e), 1} e_{1} + Q_{2, (e), 2} e_{2})∥}_{p}^{2} \\ = & {∥(Q_{1, (e), 1} X_{(e), 1} - Q_{2, (e), 1}) e_{1} + (Q_{1, (e), 2} X_{(e), 2} - Q_{2, (e), 2}) e_{2}∥}_{p}^{2} . \end{matrix}

From Eq. (), we have

{∥Q_{1, (E)} X_{(E)} - Q_{2, (E)}∥}_{p}^{2} = \frac{1}{2} ({∥Q_{(e), 1} X_{(e), 1} - Q_{2, (e), 1}∥}_{p}^{2} + {∥Q_{1, (e), 2} X_{(e), 2} - Q_{2, (e), 2}∥}_{p}^{2}) .

Hence,

{∥Q_{1, (E)} X_{(E)} - Q_{2, (E)}∥}_{p} = min .

if and only if

{∥Q_{1, (e), 1} X_{(e), 1} - Q_{2, (e), 1}∥}_{p} = min ., and {∥Q_{1, (e), 2} X_{(e), 2} - Q_{2, (e), 2}∥}_{p} = min .

{∥Q_{1, (e), 1} X_{(e), 1} - Q_{2, (e), 1}∥}_{p} = min,

then

X_{(e), 1} = Q_{1, (e), 1}^{†} Q_{2, (e), 1}

and similarly,

X_{(e), 2} = Q_{1, (e), 2}^{†} Q_{2, (e), 2}

where

Q_{1, (e), 1}^{†} = V_{(e), 1} Σ_{1} U_{(e), 1}^{*} and Q_{1, (e), 2}^{†} = V_{(e), 2} Σ_{2} U_{(e), 2}^{*} .

Therefore, the least squares solution of the equation

Q_{1, (E)} X_{(E)} = Q_{2, (E)}

\begin{matrix} X_{(E)} & = & (V_{(e), 1} Σ_{1} U_{(e), 1}^{*} Q_{2, (e), 1}) e_{1} + (V_{(e), 2} Σ_{2} U_{(e), 2}^{*} Q_{2, (e), 2}) e_{2} \\ = & ((V_{(e), 1} Σ_{1} U_{(e), 1}^{*}) e_{1} + (V_{(e), 2} Σ_{2} U_{(e), 2}^{*}) e_{2}) (Q_{2, (e), 1} e_{1} + Q_{2, (e), 2} e_{2}) \\ = & (V_{(e), 1} e_{1} + V_{(e), 2} e_{2}) (Σ_{1} e_{1} + Σ_{2} e_{2}) (U_{(e), 1}^{*} e_{1} + U_{(e), 2}^{*} e_{2}) (Q_{2, (e), 1} e_{1} + Q_{2, (e), 2} e_{2}) \\ = & V_{(E)} Σ_{(E)}^{†} U_{(E)}^{*} Q_{2, (E)} = Q_{1, (E)}^{†} Q_{2, (E)} \end{matrix}

which completes the proof.

3.2.1. Algorithms

The following algorithms delineate the computational procedures for determining eigen-pairs, singular value decomposition, pseudo-inverse computation, and the derivation of least squares solution with the minimum norm for EQ matrices.

Algorithm 1:Eigen-pairs of

Q_{(E)} \in H_{p}^{n \times n}

1:: Start
2:: Input $Q_{(E), r}, Q_{(E), i}, Q_{(E), j}, Q_{(E), k}$ and p
3:: Form $Q_{(e), 1}$ and $Q_{(e), 2}$ according to Eq. (1)
4:: Compute $λ_{(e), 1}$ and $λ_{(e), 2}$ according to Lemma 4 and Theorem 3
5:: Compute $x_{(e), 1}$ and $x_{(e), 2}$ according to Lemma 4 and Theorem 3
6:: Form $λ_{(E)} = λ_{(e), 1} e_{1} + λ_{(e), 2} e_{2}$
7:: Form $x_{(E)} = x_{(e), 1} e_{1} + x_{(e), 2} e_{2}$
8:: Output $λ_{(E)}$ and $x_{(E)}$
9:: End

Algorithm 2:Singular Value Decomposition of

Q_{(E)} \in H_{p}^{m \times n}

1:: Start
2:: Input $Q_{(E), r}, Q_{(E), i}, Q_{(E), j}, Q_{(E), k}$ and p
3:: Form $Q_{(e), 1}$ and $Q_{(e), 2}$ according to Eq. (1)
4:: Compute $Q_{(e), 1} = U_{(e), 1} Σ_{1} V_{(e), 1}^{*}$ and $Q_{(e), 2} = U_{(e), 2} Σ_{2} V_{(e), 2}^{*}$ according to Lemma 6
5:: Form $U_{(E)} = (U_{(e), 1} e_{1} + U_{(e), 2} e_{2}), Σ_{(E)} = (\sum_{1} e_{1} + \sum_{2} e_{2}),$ and $V_{(E)} = (V_{(e), 1} e_{1} + V_{(e), 2} e_{2})$
6:: Output $U_{(E)}, Σ_{(E)}, V_{(E)}$
7:: End

Algorithm 3:Pseudo-inverse of

Q_{(E)} \in H_{p}^{m \times n}

1:: Start
2:: Run the Algorithm 2 for EQ matrix $Q_{(E)}$
3:: Form $Q_{(E)} = U_{(E)} \sum_{(E)} V_{(E)}^{*}$
4:: Compute $Q_{(E)}^{†} = V_{(E)} Σ_{(E)}^{†} U_{(E)}^{*}$
5:: Output $Q_{(E)}^{†}$
6:: End

Algorithm 4:Least Squares Solution with the Minimum Norm of

Q_{1, (E)} X_{(E)} = Q_{2, (E)}

1:: Start
2:: Input $Q_{1, (E), r}, Q_{1, (E), i}, Q_{1, (E), j}, Q_{1, (E), k},$ $Q_{2, (E), r}, Q_{2, (E), i}, Q_{2, (E), j}, Q_{2, (E), k}$ and p
3:: Run the Algorithm 3 for EQ matrix $Q_{1, (E)}$
4:: Compute $X_{(E)} = Q_{1, (E)}^{†} Q_{2, (E)} = V_{(E)} Σ_{(E)}^{†} U_{(E)}^{*} Q_{2, (E)}$
5:: Output $X_{(E)}$
6:: End

3.2.2. Numerical Examples

Example 1.

Given the EQ matrices

Q_{1, (E)}

and

Q_{2, (E)}

as follows:

Q_{1, (E)} = (\begin{matrix} 9 + i - 7 j + 2 k & 2 - 7 i + j + 5 k & 8 - 4 i + 7 j - 4 k \\ 5 + 8 i - j + 4 k & 4 + 7 i + j - k & 9 - 6 i - 3 j + 8 k \\ 8 + 9 i + 3 j - 4 k & 9 - 2 i + 8 j + 2 k & 6 - 5 i + 9 j - 6 k \end{matrix}),

and

Q_{2, (E)} = (\begin{matrix} 7 + 2 i + 3 j + k \\ 7 - 6 i + j + 4 k \\ 3 + 3 i - 5 j - 8 k \end{matrix}) .

Let’s find the least squares solution with the minimum norm by using Algorithms 2, 3, and 4 for

p = - 0.5

. By the Algorithm 2, we get the singular value decomposition of EQ matrix

Q_{1, (E)}

as follows:

Σ = (\begin{matrix} 27.1507 + 5.1850 j & 0 & 0 \\ 0 & 13.3956 - 3.6604 j & 0 \\ 0 & 0 & 3.5511 + 0.0727 j \end{matrix}),

U = (\begin{matrix} - 0.5887 - 0.0895 i + 0.1905 j - 0.1797 k & 0.5737 + 0.2198 i + 0.2880 j - 0.0213 k & - 0.1504 - 0.0811 i + 0.3531 j + 0.1408 k \\ - 0.2573 - 0.4628 i + 0.0895 j - 0.0090 k & - 0.2014 - 0.8270 i + 0.0050 j + 0.3648 k & 0.1490 + 0.6752 i + 0.1013 j + 0.4671 k \\ - 0.4969 - 0.4443 i - 0.2639 j + 0.0273 k & - 0.1356 + 0.2676 i - 0.1680 j - 0.2529 k & - 0.1172 + 0.4220 i - - 0.326 j - 0.7217 k \end{matrix}),

and

V = (\begin{matrix} - 0.6674 + 0.2309 j & - 0.1204 - 0.3768 j & 0.5534 + 0.1965 j \\ - 0.3280 - 0.3659 i - 0.1703 j + 0.0553 k & - 0.4857 + 0.1440 i - 0.0426 j + 0.0036 k & - 0.3596 - 0.6220 i - 0.2807 j + 0.5391 k \\ - 0.2692 - 0.5713 i - 0.2100 j - 0.1815 k & 0.4859 - 0.3190 i + 0.1157 j + 0.7682 k & - 0.1476 - 0.1702 i + 0.2676 j + 0.0299 k \end{matrix}) .

By Algorithms 2 and 3, the least squares solution and minimum norm are found as

\begin{matrix} X_{(E)} = & Q_{1, (E)}^{†} Q_{2, (E)} = V_{(E)} Σ_{(E)}^{†} U_{(E)}^{*} Q_{2, (E)} \\ = & (\begin{matrix} 0.7612 - 1.5582 i - 0.1979 j - 0.5332 k \\ - 1.4757 - 0.2366 i + 0.1496 j + 1.2282 k \\ 0.0461 + 0.2919 i + 0.4652 j - 0.0282 k \end{matrix}) \end{matrix}

and

∥Q_{1, (E)} X_{(E)} - Q_{2, (E)}∥ = 1 . 1801 \times 1 0^{- 14},

respectively.

Example 2.

Let’s define the dimensions of the EQ matrices

Q_{1, (E)}

and

Q_{2, (E)}

given by:

\begin{matrix} g = 1 : 1 : 20, m = 50 g, \\ Q_{1, (E)} = r a n d (m, m) + r a n d (m, m) i + r a n d (m, m) j + r a n d (m, m) k, \\ Q_{2, (E)} = r a n d (m, 1) + r a n d (m, 1) i + r a n d (m, 1) j + r a n d (m, 1) k . \end{matrix}

Then, the errors (or minimum norms) corresponding p and m-values are shown in Figure 1. Here, Algorithm 4 was executed for each m-value, iterating over each p-value in the range

- 1 \leq p \leq - 0.1

with a step size of

0.1

. The minimal errors were identified and highlighted on the surface plot with red dots.

Also, we compare our new proposed Algorithm 4 and the Algorithm documented by Atali et al. in [17], focusing on CPU time and error metrics. The experimental results of this comparison are depicted in Figure 2 (CPU times) and Figure 3 (Errors).

and

Figure 2 and Figure 3 show that our proposed algorithm outperforms the algorithm presented by Atali et al. in [17] regarding computational efficiency and accuracy.

4. Conclusion

In this research, we derived outcomes for determining eigen-pairs, performing singular value decomposition, obtaining pseudo-inverse, and finding the least squares solution with the minimum norm for EQ matrices. Additionally, we developed algorithms grounded on these outcomes and presented illustrative numerical instances to validate our results.

This number system is more useful in the applied sciences since it allows one to select the ideal p-value suited for the type of problem in EQs, considering the elliptical behaviour of many physical systems. As a result, the use of EQs in today’s critical technology fields - information security, data analytics, simulation technologies, robotics, signal processing, image processing, artificial intelligence, and machine learning - will effectively solve many problems related to time, memory, and performance.

Author Contributions

Conceptualization, H. H. K.; Formal analysis, E. K.; H. H. K., E. K. and B. Ç. wrote the main manuscript text. All authors reviewed the manuscript. All authors have read and agreed to the published version of the manuscript.

Data Availability Statement

The data used to support the findings of this study are available from the corresponding author upon request.

Acknowledgments

This paper was supported by the Scientific and Technological Research Institution of TÜRKİYE (TUBITAK-1002-a-121F289). We thank TÜBİTAK for their support.

Conflicts of Interest

The authors declare no competing interests.

References

Dian, R.; Li, S.; Kang, X. Regularizing hyperspectral and multispectral image fusion by CNN denoiser. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32(3), 1124–1135. [Google Scholar] [CrossRef] [PubMed]
Hashemipour, N. et al. Optimal Singular value decomposition based big data compression approach in smart grids. IEEE Trans. Ind. Appl. 2021, 32(3), 1124–1135. [Google Scholar]
Wang, Y. C.; Zhu, L. Research and implementation of SVD in machine learning. 2017 IEEE/ACIS 16th International Conference on Computer and Information Science 2017, 471–475.
Harkin, A. A.; Harkin, J. B. Geometry of generalized complex numbers. Math. Mag. 2004, 77(2), 118–129. [Google Scholar] [CrossRef]
Catoni, F.; Cannata, R.; Zampetti, P. An introduction to commutative quaternions. Adv. Appl. Clifford Algebr. 2006, 16, 1–28. [Google Scholar] [CrossRef]
Yaglom, I. M. A Simple non-Euclidean geometry and its physical basis; Springer-Verlag, New York; 1979.
Condurache, D.; Burlacu, A. Dual tensors based solutions for rigid body motion parameterization. Mech Mach Theory 2014, 74, 390–412. [Google Scholar] [CrossRef]
Özdemir, M. An alternative approach to elliptical motion. Adv. Appl. Clifford Algebras 2016, 26, 279–304. [Google Scholar] [CrossRef]
Dundar, F. S.; Ersoy, S.; Pereira, N. T. S. Bobillier formula for the elliptical harmonic motion. An. St. Univ. Ovidius Constanta 2018, 26, 103–110. [Google Scholar] [CrossRef]
Derin, Z.; Gungor, M. A. Elliptic biquaternionic equations of gravitoelectromagnetism. Math. Methods Appl. Sci. 2022, 45(8), 4231–4243. [Google Scholar] [CrossRef]
Catoni, F.; Cannata, R.; Zampetti, P. An introduction to constant curvature spaces in the commutative (Segre) quaternion geometry. Adv. Appl. Clifford Algebr. 2006, 16(2), 85–101. [Google Scholar] [CrossRef]
Guo, L.; Zhu, M.; Ge, X. Reduced biquaternion canonical transform, convolution and correlation Signal Processing 2011, 91(8), 2147–2153.
Yuan, S.F.; Tian, Y.; Li, M. Z. On Hermitian solutions of the reduced biquaternion matrix equation (AXB,CXD)=(E,G). Linear Multilinear Algebra, 2020, 68(7), 1355–1373.
Tosun, M.; Kosal, H. H. An algorithm for solving the Sylvester s-conjugate elliptic quaternion matrix equations. In Š. Hošková-Mayerová, C. Flaut, F. Maturo (Eds.), Algorithms as a Basis of Modern Applied Mathematics, Springer International Publishing, 2021; pp. 279–292.
Gai, S.; Huang, X. Reduced biquaternion convolutional neural network for color image processing, IEEE Trans. Circuits Syst. Video Technol., 2022, 32(3), 1061–1075.
Guo, Z. ; Zhang, D;. Vasiliev, V. I.; Jiang, T. Algebraic techniques for Maxwell’s equations in commutative quaternionic electromagnetics, The European Physical Journal Plus, 2022, 137(5), 577–1075.
Atali, G.; Kosal, H. H.; Pekyaman, M. A new image restoration model associated with special elliptic quaternionic least-squares solutions based on LabVIEW, J. Comput. Appl. Math., 2023, 425, 115071. [Google Scholar] [CrossRef]
Catoni, F, et al., The mathematics of Minkowski space–time: with an introduction to commutative hypercomplex numbers, Birkhäuser, Basel; 2008.

Figure 1. Errors corresponding p and m-values.

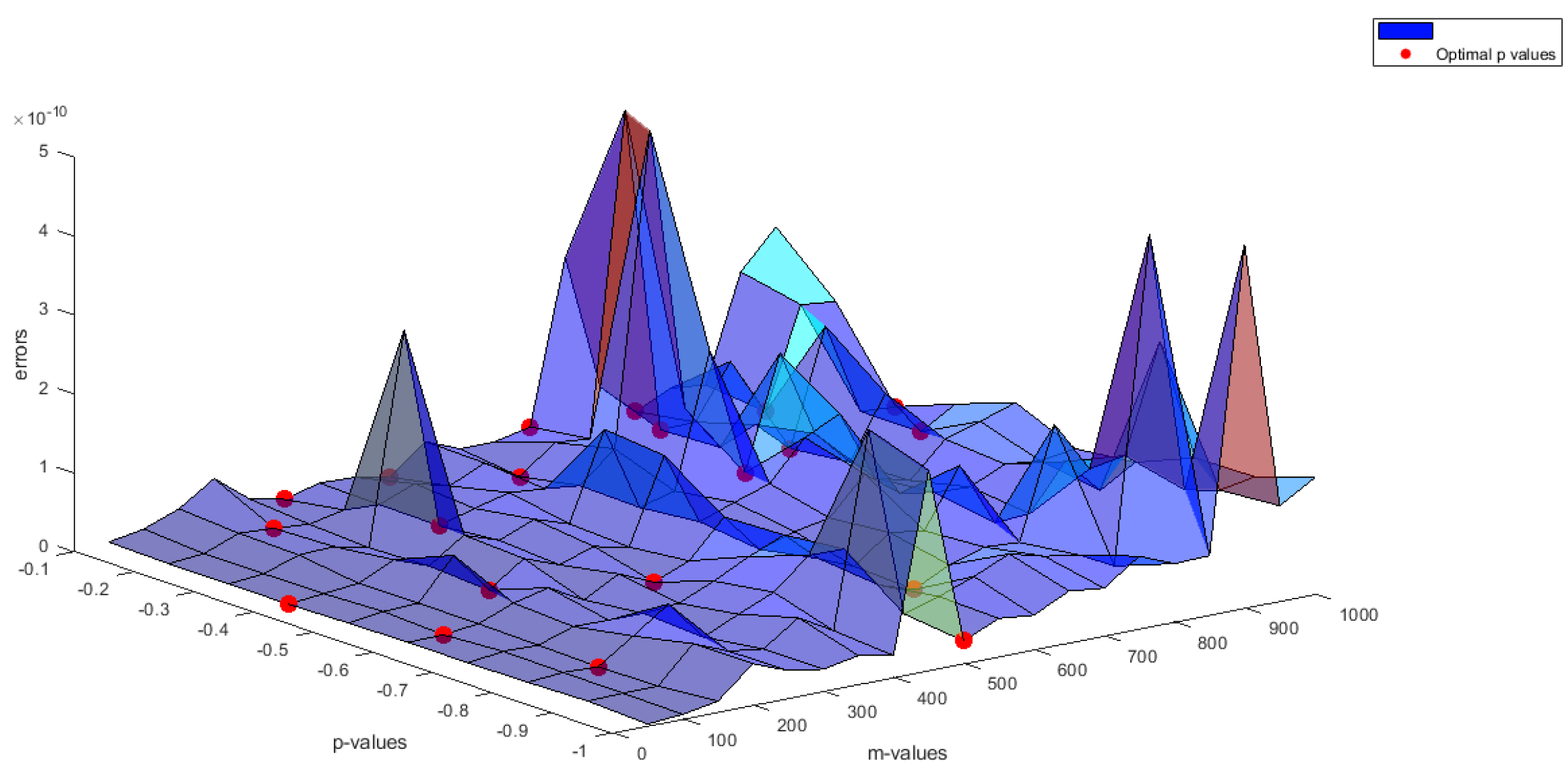
Figure 2. CPU times according to m and optimal

p -

values.

Figure 2. CPU times according to m and optimal

p -

values.

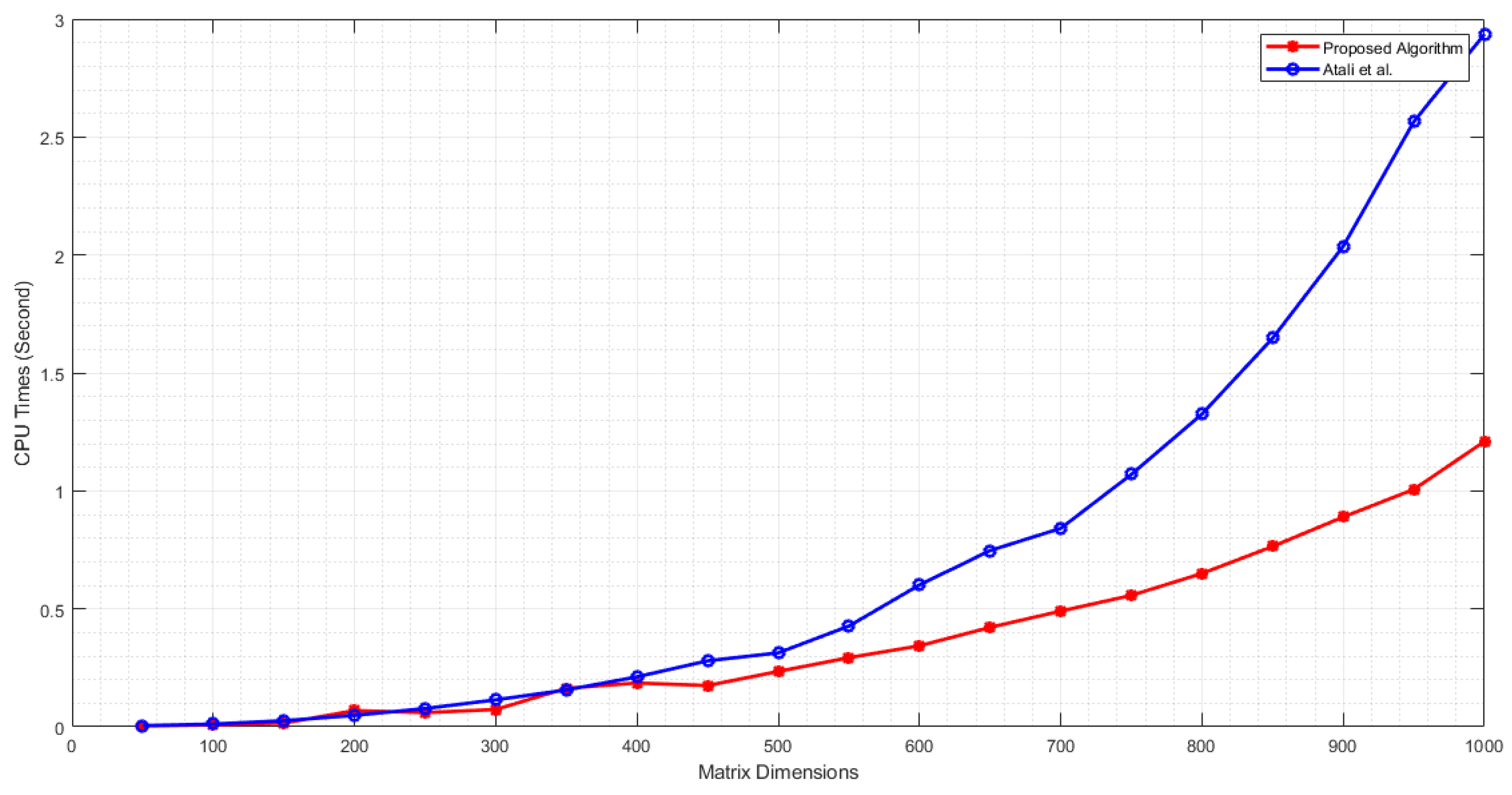
Figure 3. Errors according to m and optimal

p -

values.

Figure 3. Errors according to m and optimal

p -

values.

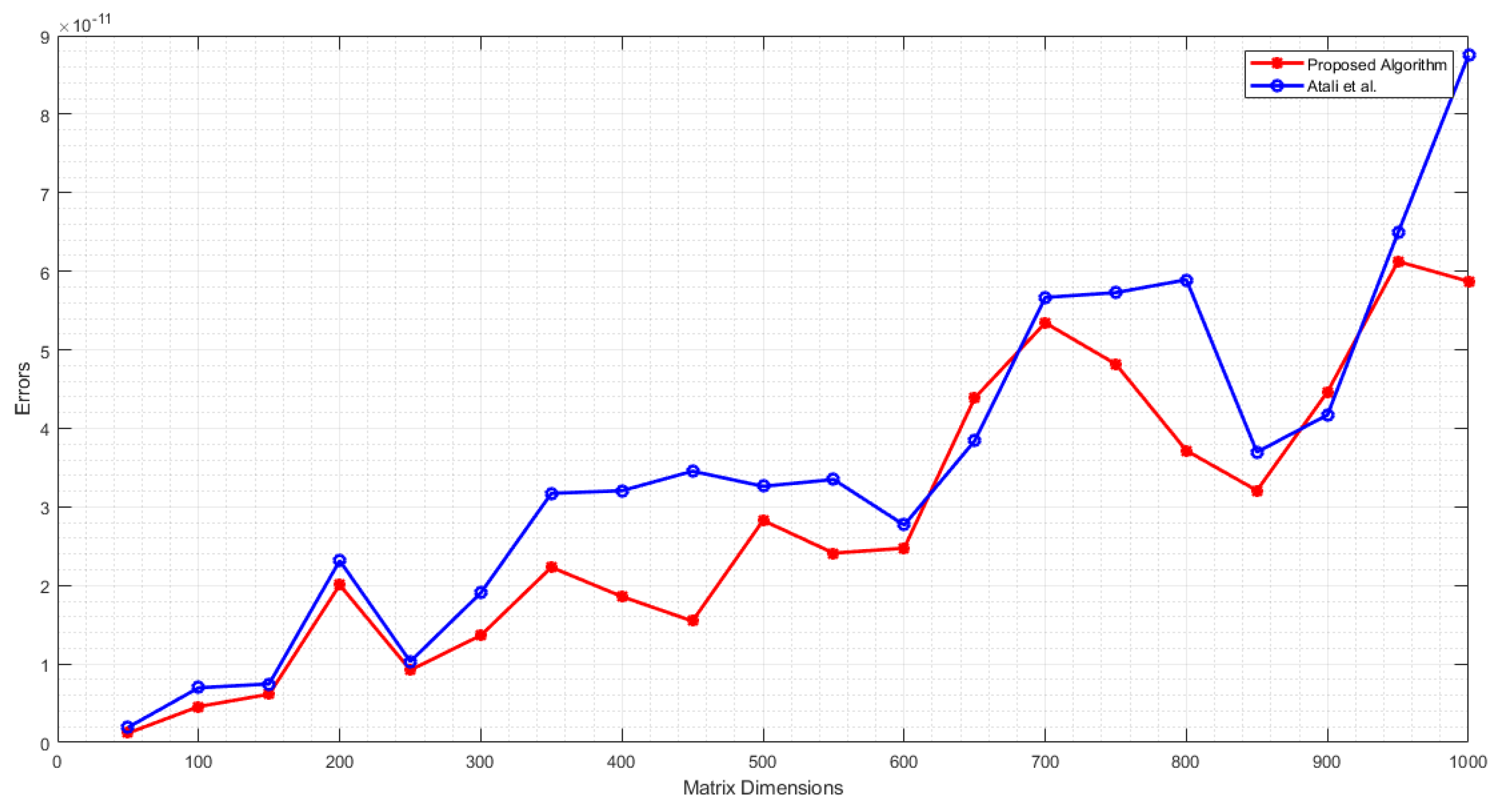
Table 2. Classification of numbers.

	$p > 0$	$p = 0$	$p < 0$
Generalized complex numbers	Hyperbolic complex numbers	Parabolic complex numbers	Elliptic complex numbers
Generalized segre quaternions	Hyperbolic quaternions	Parabolic quaternions	Elliptic quaternions

Table 3. Notations.

	$□ = c$	$□ = e$	$□ = E$
$q_{(□)}$	Complex number	Elliptic complex number	Elliptic quaternion
$Q_{(□)}$	Complex matrix	Elliptic complex matrix	Elliptic quaternion matrix

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Singular Value Decomposition of Elliptic Quaternion Matrices: Theory and Algorithms

Abstract

1. Introduction

2. Preliminaries

3. Eigenvalues and Eigenvectors, Singular Value Decomposition, Pseudo-Inverse, and Least Squares Problem for EQ Matrices

3.1. EC Matrices

3.2. EQ Matrices

3.2.1. Algorithms

3.2.2. Numerical Examples

4. Conclusion

Author Contributions

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe