Primordial Axion Stars and Galaxy Halos Formation

Preprint

Article

Primordial Axion Stars and Galaxy Halos Formation

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Alexander I Nesterov^*

This version is not peer-reviewed

Submitted:

01 August 2024

Posted:

02 August 2024

You are already at the latest version

Alerts

Abstract

Primordial axion stars, hypothetical stars formed from axions, could play an essential role in forming galaxy halos. These stars could have originated in the early universe shortly after the Big Bang. We show that while “normal” axions coalesce into a gravitationally bound Bose-Einstein condensate, forming a dense object - an axion star, the ultralight axions could act as the initial seeds for galaxy halos.

Keywords:

Subject: Physical Sciences - Particle and Field Physics

Introduction

The axions are one of the favorite cold dark matter (CDM) candidates [1,2,3,26]. Initially, they were invented to solve the strong

CP

problem: Why does quantum chromodynamics (QCD) not break the

CP

-symmetry? The Peccei-Quinn (PQ) theory, solving this problem, leads to the existence of very light axions [4,5,6,7]. Since the axions have a tiny mass and extraordinarily weak coupling to matter and radiation, it would be challenging to detect them. Efforts toward detecting axions include a wide range of technologies [8,9,10].

The massless axion arises due to a spontaneous breaking of the

U {(1)}_{PQ}

symmetry. The axion acquires a mass during the QCD phase-transition, following the PQ phase-transition. In terms of the axion decay constant,

f_{a}

, the axion mass induced by QCD instantons can be written as

m \approx 6 μ eV (10^{12} GeV / f_{a})

[11,12]. More precise estimation of the axion mass yields [13]

\begin{matrix} m_{a} \approx 5.7 μ eV (\frac{10^{12} GeV}{f_{a}}) . \end{matrix}

(1)

Cosmological and astrophysical constraints restrict the value of the decay constant and leave the allowed QCD axion mass window as

6 μ eV ⩽ m ⩽ 2000 μ eV

[14]. Recent calculations of the axion mass, based on high-temperature lattice QCD, lead to the more narrow window:

50 [μ eV] ⩽ m ⩽ 1.5 \cdot 10^{3} [μ eV]

[15]. The axions with the mass range

10^{- 33} eV ≲ m ≲ 10^{- 18} eV

are known as ultralight axions (ULAs). The mass of ULA’s can be estimated as follows [16,17]:

m_{a} = 5.3 \times 10^{- 19} eV {(\frac{10^{16} GeV}{f_{a}})}^{4}

(2)

There are two sources of cold light axions: vacuum misalignment and string decay and domain-wall decay [11]. In the first case, inflation occurs after the PQ phase transition. The axion field is homogenized over enormous distances, and the vacuum misalignment yields axions with the zero-momentum mode and zero velocity dispersion. In the second scenario, the axion field will have random values in different causally connected universe volumes when the PQ phase transition occurs after inflation. This results in the appearance of a network of cosmic strings. The strings disappear after the QCD phase transition, radiating massive axions with momentum of order the Hubble expansion rate. The cold LAs, produced by string decay, have a wide distribution of momentums in their vacuum state and an extremely small velocity dispersion of their excitations [18,27,34]. Primordial axion stars formed by axions with mass

m_{a} \sim 10^{- 6}

eV, also known as axion clumps, are formed in the early universe shortly after the Big Bang when axions condensed into a dense, gravitationally bound Bose-Einstein condensate. These clumps can range in size and mass, potentially forming compact objects with significant gravitational influence [19,20,21,22,23,29,31].

In modern understanding of galaxy formation, every galaxy forms within a dark matter halo. The formation of galaxy halos is a critical aspect of galaxy formation, providing the gravitational scaffold around which baryonic matter (ordinary matter) accumulates to form stars and galaxies. Primordial axion stars, formed in the early universe, could act as seeds for the formation of larger structures, leading to the formation of galaxies surrounded by halos. Their gravitational influence would attract surrounding dark matter and baryonic matter, facilitating the growth of density perturbations that eventually lead to galaxy formation.

In this paper, we study the formation of the DM stars by ULAs and the relationship between primordial axion stars and galaxy halos. We show that ULA stars, with a size and mass comparable with observable data for typical galaxies of our universe, are formed in the radiation-dominated era.

The paper is organized as follows. Section 1 discusses the cosmological production of axions and the formation of axion stars. In Section 2, we introduce a non-relativistic model describing axion Bose-Einstein condensate. Section 3 summarizes the results obtained and discusses possible generalizations of our approach. Throughout the paper, we use the natural unit convention,

ℏ = c = 1

1. Cosmological Production of Axions

We assume the universe is described by

Λ

CDM model [35,36]. In this model, the universe comprises photons, neutrinos, ordinary (baryon) matter, cold dark matter, and dark energy. The latter is defined by the cosmological constant,

Λ

, and is responsible for the observable acceleration in the expansion of our universe. The axion DM can be described by a model with the action given by [11,37,38],

\begin{matrix} S = \int \sqrt{- g} d^{4} x (\frac{1}{2} g^{μ ν} ϕ_{, μ} ϕ_{, ν} - V (ϕ)) . \end{matrix}

(3)

The corresponding equation of motion is the Klein-Gordon equation:

□ ϕ = - \frac{\partial V (ϕ)}{\partial ϕ} .

(4)

Qualitatively the potential

V (ϕ)

, generated by QCD instantons, may be written as [5,11]

\begin{matrix} V (ϕ) = {(m_{a} f_{a})}^{2} (1 - cos (ϕ / f_{a})), \end{matrix}

(5)

where

m_{a}

is the axion mass. The potential

V (ϕ)

is the periodic function with a period defined by a shift-invariance,

ϕ \to ϕ + 2 π f_{a}

. There are N degenerate vacua, and the axion field has a range

0 < ϕ < 2 π f_{a}

[11].

1.1. Non-Relativistic Limit of the Klein-Gordon Equation

In the non-relativistic limit, the Klein-Gordon equation has the form of the Schrödinger equation with the effective potential describing the interacting forces in the system in the non-relativistic limit [20,21,24,39,40]. Writing,

ϕ = \frac{1}{2 \sqrt{m_{a}}} (ψ e^{- i m_{a} t} + ψ^{*} e^{i m_{a} t}),

(6)

one can show that the non-relativistic theory is described by the effective action for the complex field

ψ

(see Appendix for detail):

\begin{matrix} S_{eff} = \int d^{4} x (\frac{i}{2} (ψ^{*} \dot{ψ} - {\dot{ψ}}^{*} ψ) - \frac{1}{2 m_{a}} \nabla ψ^{*} \cdot \nabla ψ - V_{eff} (ψ^{*} ψ) - \frac{1}{8 π G} \nabla Φ \cdot \nabla Φ - m_{a} ψ^{*} ψ Φ), \end{matrix}

(7)

where

Φ (r)

is the Newtonian gravitational potential, and

V_{e f f} (| ψ |)

is the effective potential obtained as the non-relativistic limit of the instanton potential Eq. (5). The equations of motion are given by

\begin{matrix} \begin{matrix} i \frac{\partial ψ}{\partial t} = - \frac{1}{2 m} \nabla^{2} ψ + m_{a} Φ ψ + \frac{\partial V_{eff}}{\partial ψ^{*}} ψ, \\ \nabla^{2} Φ = 4 π G m_{a} {| ψ |}^{2} . \end{matrix} \end{matrix}

(8)

For the axion field, the effective instanton non-relativistic potential potential was derived in Refs. [39,41] and takes the form

\begin{matrix} V_{eff} (ψ^{*} ψ) = \frac{1}{2} m_{a} ψ^{*} ψ + m_{a}^{2} f_{a}^{2} [1 - J_{0} (n^{1 / 2})], \end{matrix}

(9)

where

J_{0} (z)

is a Bessel function,

n = ψ^{*} ψ / n_{0}

and

n_{0} = m_{a} f_{a}^{2} / 2

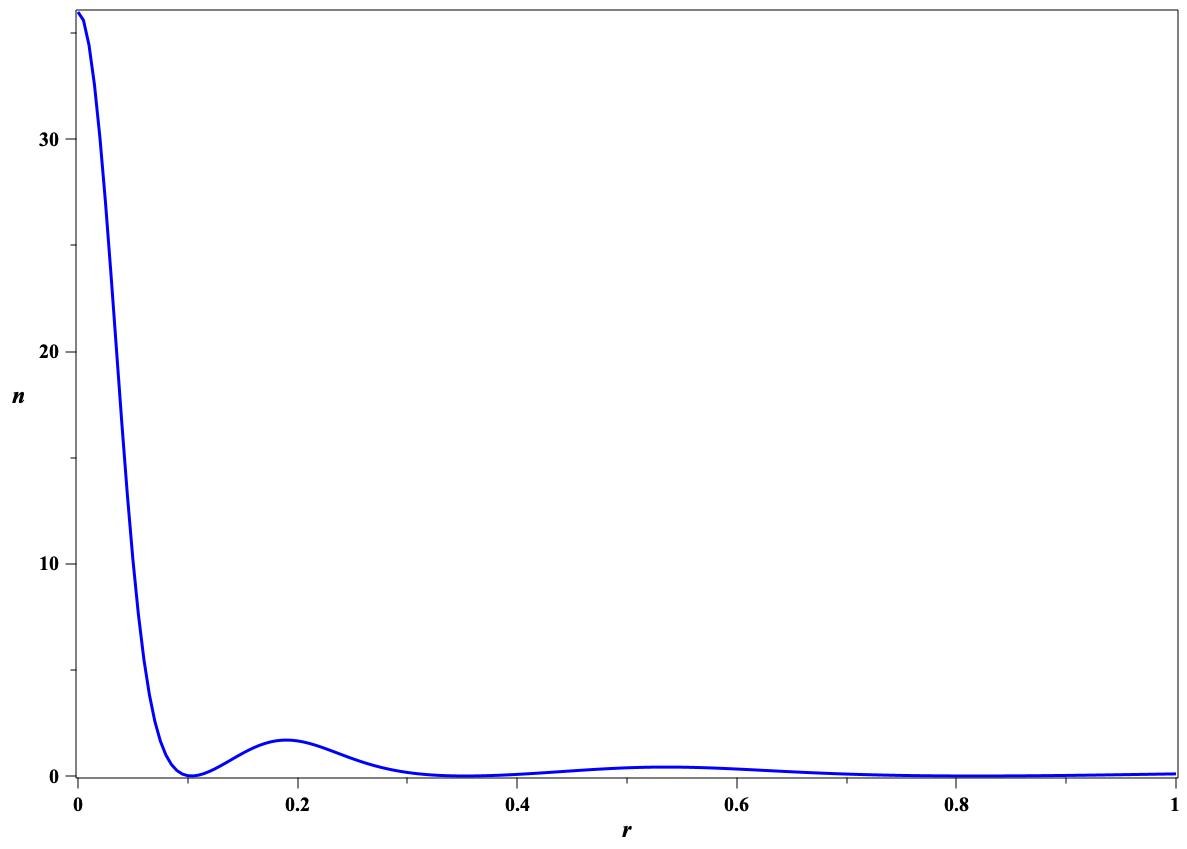
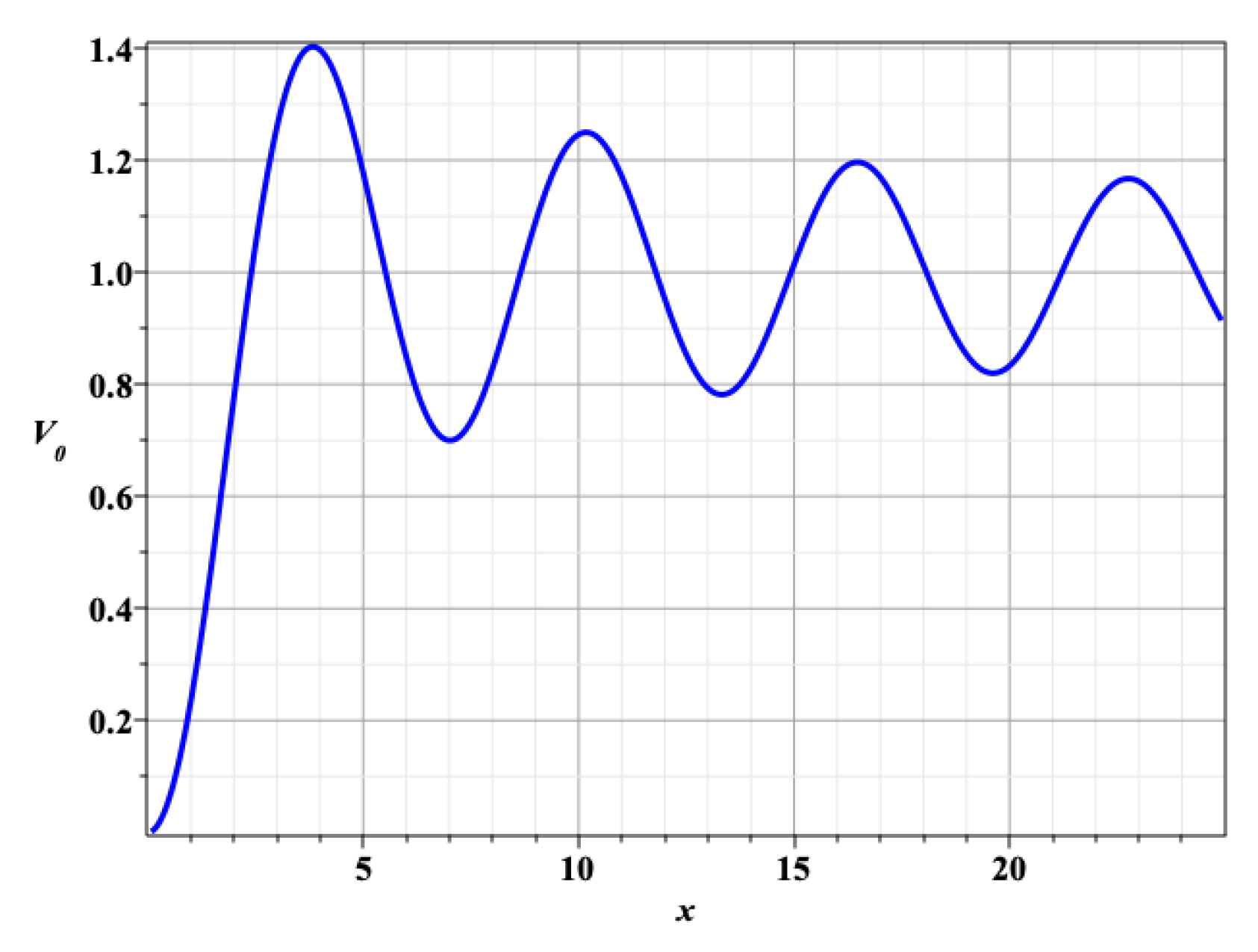
Figure 1 represents the normalized effective potential,

V_{0} (x) = 1 - J_{0} (x)

, with the first term subtracted:

\begin{matrix} V_{0} = \frac{1}{2 m n_{0}} (V_{eff} - \frac{1}{2} m_{a} ψ^{*} ψ) \end{matrix}

(10)

The stable solutions for the axion stars with

n ≫ 1

(dense stars) correspond to the minima of the effective potential [20].

1.2. Formation of Axion Stars

Axion stars are characterized by their high density and stability, maintained by a balance between gravitational attraction and quantum pressure due to the axions’ wave-like nature. They can be categorized into two types:

Dilute Axion Stars ( $n_{c o r e} ≪ 1$ ). These stars are less dense and more extended, and insert "their size is determined by "their size is determined by the axion mass and self-interaction strength.
Dense Axion Stars ( $n_{c o r e} ≳ 1$ ). These are more compact and can undergo complex dynamical processes, including potential collapse into black holes and phase transition to the dilute stars under certain conditions.

The stability and structure of axion stars are determined by the balance between gravitational attraction and the quantum pressure arising from the Heisenberg uncertainty principle.

2. Model

The non-relativistic axions can form a Bose-Einstein condensate (BEC). The equations that describe a static BEC of axions can be obtained by considering an axion field

ψ (r, t)

whose time dependence is

ψ (r) exp (- i μ t)

, where

μ

is the chemical potential [20]. They can be expressed conveniently as coupled equations for

ψ (r)

and the gravitational potential

Φ (r)

\begin{matrix} \begin{matrix} \nabla^{2} \hat{ψ} = & 2 m_{a}^{2} (Φ - \frac{μ}{m_{a}} - \frac{1}{2} + \frac{J_{1} (| \hat{ψ} |)}{| \hat{ψ} |}) \hat{ψ}, \\ \nabla^{2} Φ = & 4 π G m_{a} n_{0} {| \hat{ψ} |}^{2}, \end{matrix} \end{matrix}

(11)

where

\hat{ψ} = ψ / \sqrt{n_{0}}

G = 1 / m_{p}^{2}

, and

m_{p}

denotes the Planck mass (

m_{p} = 1.2 \cdot 10^{19} GeV

). To further simplify matters, we rescale coordinates and functions:

r \to r^{*} = r / r_{0}

ψ \to ψ (r^{*})

and

Φ \to γ Φ (r^{*})

, where

r_{0} = γ / m_{a}

and

γ = m_{p} / f_{a}

Hereafter, we drop *’s in rescaled functions and parameters. Then, the dimensionless equations can be recast as follows:

\begin{matrix} \begin{matrix} \nabla^{2} \hat{ψ} = & 2 (Φ - γ ε) \hat{ψ}, \\ \nabla^{2} Φ = & 4 π | \hat{ψ} |^{2}, \end{matrix} \end{matrix}

(12)

where

\begin{matrix} ε = \bar{μ} + \frac{1}{2} - \frac{J_{1} (| \hat{ψ} |)}{| \hat{ψ} |}, \end{matrix}

(13)

and we set

\bar{μ} = μ / m_{a}

In Table 1, we present various length and mass scales to facilitate recalculation in physical units. In particular, the mass of the axion star can be obtained using the formula:

\begin{matrix} M = 3 M_{0} \int {| \hat{ψ} |}^{2} d^{3} V^{*}, \end{matrix}

(14)

where the integration is performed over dimensionless variables

r^{*}

, and

M_{0} = 4 π n_{0} r_{0}^{3} / 3

Our model is based on the previous studies of the rotating axion stars made in [20,22,23,40,42]. In general

ψ

may consist of a superposition of various spherical harmonics

Y_{l}^{m}

\begin{matrix} \hat{ψ} (r, θ, φ) = \sum_{ℓ = 0}^{\infty} \sum_{m = - l}^{ℓ} f_{ℓ}^{m} r^{ℓ} Y_{ℓ}^{m} (θ, φ) . \end{matrix}

(15)

For simplicity, we assume the following ansatz:

\hat{ψ} (r, θ, ϕ) = R (r) Y_{l}^{m} (θ, φ) .

(16)

After substitution of

\hat{ψ} (r, θ, ϕ)

, one can rewrite Eq. (12) as

\begin{matrix} \begin{matrix} Δ_{r} R - \frac{l (l + 1)}{r^{2}} R = 2 (Φ - γ \bar{μ} - \frac{γ}{2} + \frac{γ J_{1} (R | Y_{l}^{m} |)}{R | Y_{l}^{m} |}) R, \\ \nabla^{2} Φ = 4 π R^{2} {| Y_{l}^{m} |}^{2}, \end{matrix} \end{matrix}

(17)

where

Δ_{r}

denotes the radial part of the Laplacian,

\begin{matrix} Δ_{r} = \frac{1}{r^{2}} \frac{\partial}{\partial r} (r^{2} \frac{\partial}{\partial r}) . \end{matrix}

(18)

Note that (17) still depends on angular variables

θ

and

φ

. Therefore, following [40], we take the angular average of these equations. rgb]1,0,0We define the angular averaged gravitational potential and use the normalization of the spherical harmonics:

\begin{matrix} \tilde{Φ} = \frac{1}{4 π} \int Φ (r, θ, φ) d Ω, \int Y_{ℓ}^{m} Y_{ℓ^{'}}^{m^{'} *} d Ω = δ_{ℓ ℓ^{'}} δ_{m m^{'}} ., \end{matrix}

(19)

\begin{matrix} J_{l}^{m} = \frac{1}{4 π} \int \frac{J_{1} (R | Y_{l}^{m} |)}{R | Y_{l}^{m} |} d Ω . \end{matrix}

(20)

Then, we obtain for angular averaged potentials the following equations of motion:

\begin{matrix} Δ_{r} R = & 2 (\tilde{Φ} + \frac{l (l + 1)}{2 r^{2}} - γ \bar{μ} - \frac{γ}{2} + γ J_{l}^{m})) R, \end{matrix}

(21)

\begin{matrix} Δ_{r} \tilde{Φ} = & R^{2} . \end{matrix}

(22)

For

l = 0, 1

, we have obtained the analytical expressions for

J_{l}^{m}

. The computation yields:

\begin{matrix} J_{1}^{0} = J_{0} (a_{0} R) - \frac{J_{1} (a_{0} R)}{a_{0} R} + \frac{π}{2} (J_{1} (a_{0} R) H_{0} (a_{0} R) - J_{0} (a_{0} R) H_{1} (a_{0} R)), \end{matrix}

(23)

\begin{matrix} J_{1}^{\pm 1} = \frac{1 - cos (a_{1} R)}{a_{1}^{2} R^{2}}, J_{0}^{0} = \frac{J_{1} (R)}{R}, \end{matrix}

(24)

where

a_{0} = \sqrt{3 / 4 π}

a_{1} = \sqrt{3 / 8 π}

and

H_{n} (z)

denotes the Struve function.

For a given function

R (r)

, the gravitational potential can be obtained due to the integration of Eq. (). The solution can be written as follows:

\begin{matrix} \tilde{Φ} (r) = - \frac{1}{r} \int_{0}^{r} x^{2} R^{2} (x) d x - \int_{r}^{r_{h}} x R^{2} (x) d x, \end{matrix}

(25)

where

r_{h}

is the radius of the star. From here it follows that

\tilde{Φ} (0) = {\tilde{Φ}}_{0}

and

Φ^{'} (0) = 0

, where

\begin{matrix} {\tilde{Φ}}_{0} = - \int_{0}^{r_{h}} x R^{2} (x) d x . \end{matrix}

(26)

We impose the following boundary conditions to solve numerically the coupling system of the differential equations (21) - ():

\begin{matrix} R (0) = R_{0}, R {(0)}^{'} = R_{1}, \tilde{Φ} (0) = Φ_{0}, {\tilde{Φ}}^{'} (0) = 0 . \end{matrix}

(27)

The radius of the axion star is obtained as the solution of the equation:

\begin{matrix} \tilde{Φ} (r_{h}) = - \frac{M^{*} (r_{h})}{r_{h}}, \end{matrix}

(28)

where

M^{*} (r_{h}) = \int_{0}^{r_{h}} x^{2} R^{2} (x) d x

is the scaled mass of the star,

M^{*} = M / M_{0}

, and

\begin{matrix} \tilde{Φ} (r_{h}) = - \frac{1}{r_{h}} \int_{0}^{r_{h}} x^{2} R^{2} (x) d x . \end{matrix}

(29)

The chemical potential is subject to the boundary conditions:

\begin{matrix} \bar{μ} = [\frac{1}{γ} (\tilde{Φ} + \frac{l (l + 1)}{2 r^{2}}) + J_{l}^{m} - \frac{1}{2}] |_{r = r_{h}} = 0 \end{matrix}

(30)

3. Results and Discussion

Following the procedure outlined in Sect. Section 2 we have solved numerically the equations of motion (19) - () for the axion mass,

m_{a} = 5.3 \cdot 10^{-} 19

eV, and the boundary conditions presented below.

Dense stars:

$\begin{matrix} R (0) = 6, R {(0)}^{'} = 0, Φ (0) = - 1.5, Φ^{'} (0) = 0, (l = 0, m = 0) . \end{matrix}$
Dilute stars:

$\begin{matrix} R (0) = 0.1, R {(0)}^{'} = 0, Φ (0) = - 0.065, Φ^{'} (0) = 0, (l = 0, m = 0), \\ R (0) = 0, R {(0)}^{'} = 10, Φ (0) = - 0.001, Φ^{'} (0) = 0, (l = 1, m = 0), \\ R (0) = 0, R {(0)}^{'} = 0.12, Φ (0) = - 0.5, Φ^{'} (0) = 0, (l = 1, m = \pm 1) . \end{matrix}$

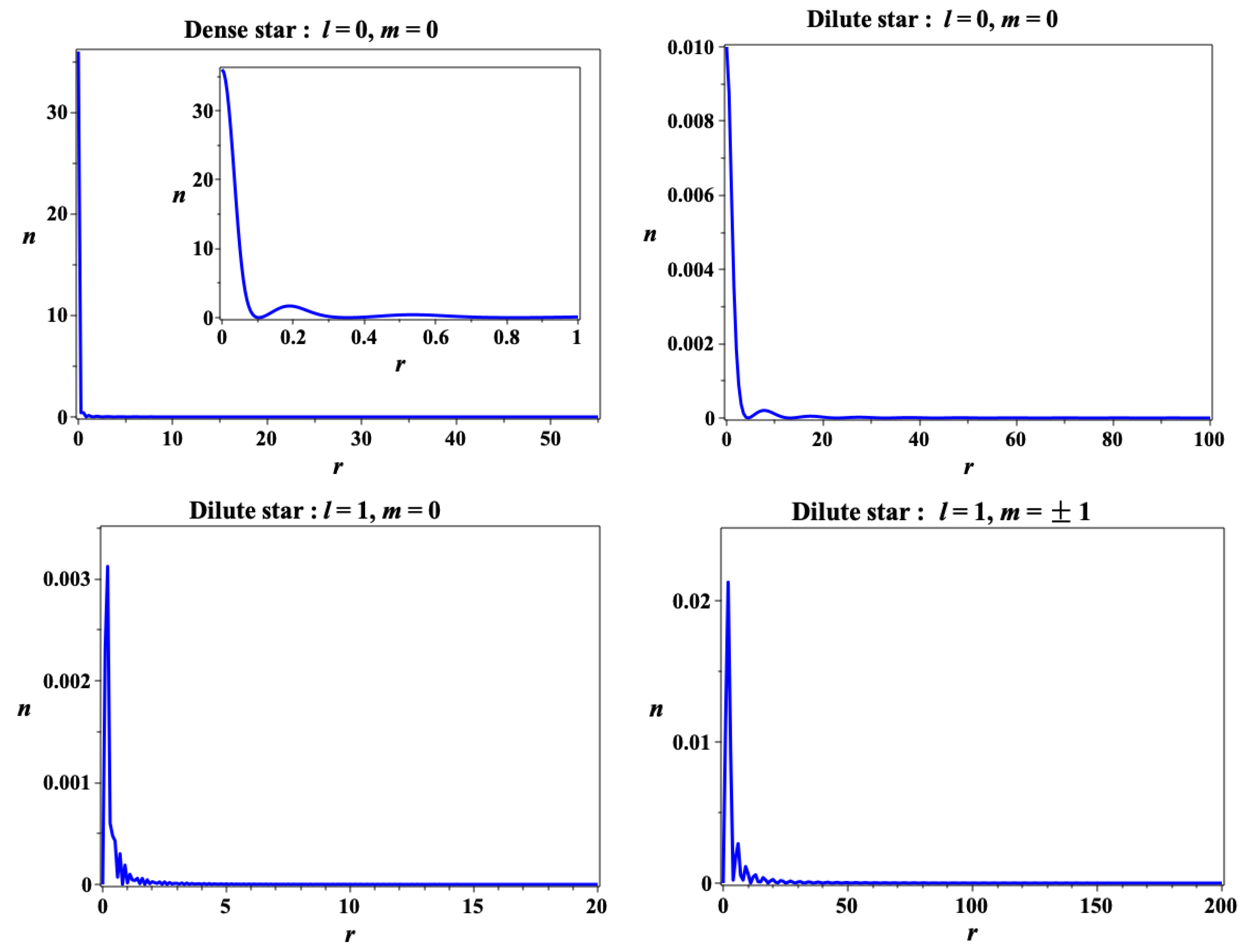
The results are summarized in Figure 2 and Table 2. To obtain the redshift, we use the relation

z = n_{h} / n_{D M}

, where

n_{D M} = {\bar{ρ}}_{DM} / m_{a}

is the average density of DM obtained from the data presented in Refs. [39,43]:

{\bar{ρ}}_{DM} = 1.3 \times 10^{- 6} GeV / {cm}^{3}

. As follows from Table 2, the formation of the axion stars begins in the radiation-dominated era, which, according to the

Λ

CDM model, corresponds to redshift

z \approx (5.244 \cdot 10^{3} - 1.47 \cdot 10^{11}

The mass of galaxies can vary significantly depending on their type and size:

Dwarf Galaxies: $M \approx (10^{7} - 10^{9}) M_{⊙}$ .
Spiral Galaxies: $M \approx (10^{10} - 10^{12}) M_{⊙}$ .
Elliptical Galaxies: $M \approx (10^{12} - 10^{13}) M_{⊙}$ .

Considering the distribution of different types of galaxies, the average mass of galaxies in our universe can be roughly estimated as follows:

M \approx 10^{11} M_{⊙}

. As one can see, the mass of axion stars presented in Table 2 is inside the range of the observable data.

The current size of the axion stars can obtained using the relation:

d = 2 z r_{h}

. We obtain

$d = 52.2$ kpc ( $M = 1.57 \cdot 10^{10} M_{⊙}$ )
$d = 76.4$ kpc ( $M = 3.43 \cdot 10^{9} M_{⊙}$ )
$d = 2.52$ kpc ( $M = 4 \cdot 10^{7} M_{⊙}$ )
$d = 8.3$ kpc ( $M = 3.92 \cdot 10^{10} M_{⊙}$ )

These results are in agreement with an estimation of the halo size for typical galaxies:

Spiral Galaxies: 61.3 to 92 kpc in diameter
Elliptical Galaxies: 92 to 306.6 kpc in diameter
Dwarf Galaxies: up to 9.2 kpc in diameter

Primordial ULA stars offer potential insights into the nature of dark matter and its role in galaxy formation. As axion stars accrete additional axions, they contribute to the overall density of dark matter halos. This increased density can enhance the gravitational potential of the halo, making it more effective at attracting and retaining baryonic matter. By acting as seeds for structure formation, primordial axion stars could play a pivotal role in the formation of galaxies and shape the universe as we observe it today. Further research is needed to understand their properties, but their potential impact on our understanding of the universe is profound.

Funding

This research received no external funding.

Data Availability Statement

No new data were created or analyzed in this study.

References

Kawasaki, M.; Nakayama, K. Axions: Theory and Cosmological Role. Annual Review of Nuclear and Particle Science 2013, 63, 69–95. [Google Scholar] [CrossRef]
Feng, J.L. Dark Matter Candidates from Particle Physics and Methods of Detection. Annual Review of Astronomy and Astrophysics 2010, 48, 495–545. [Google Scholar] [CrossRef]
Bertone, G.; Hooper, D. History of dark matter. Rev. Mod. Phys. 2018, 90, 045002. [Google Scholar] [CrossRef]
Peccei, R.; Quinn, H. CP Conservation in the Presence of Pseudoparticles. Phys. Rev. Lett. 1977, 38, 1440–1443. [Google Scholar] [CrossRef]
Peccei, R.D.; Quinn, H.R. Constraints imposed by CP conservation in the presence of pseudoparticles. Phys. Rev. D 1977, 16, 1791–1797. [Google Scholar] [CrossRef]
Weinberg, S. A New Light Boson? Phys. Rev. Lett. 1978, 40, 223–226. [Google Scholar] [CrossRef]
Wilczek, F. Problem of Strong P and T Invariance in the Presence of Instantons. Phys. Rev. Lett. 1978, 40, 279–282. [Google Scholar] [CrossRef]
Rosenberg, L.J. Dark-matter QCD-axion searches. Proceedings of the National Academy of Sciences 2015, 112, 12278–12281. [Google Scholar] [CrossRef]
Arvanitaki, A.; Huang, J.; Van Tilburg, K. Searching for dilaton dark matter with atomic clocks. Phys. Rev. D 2015, 91, 015015. [Google Scholar] [CrossRef]
Arvanitaki, A.; Dimopoulos, S.; Van Tilburg, K. Sound of Dark Matter: Searching for Light Scalars with Resonant-Mass Detectors. Phys. Rev. Lett. 2016, 116, 031102. [Google Scholar] [CrossRef]
Sikivie, P. , Cosmology. In Axions: Theory, Cosmology, and Experimental Searches; Kuster, M., Raffelt, G., Beltrán, B., Eds.; Springer Berlin Heidelberg: Berlin, Heidelberg, 2008; pp. 19–50. [Google Scholar]
Chang, S.; Hagmann, C.; Sikivie, P. Studies of the motion and decay of axion walls bounded by strings. Phys. Rev. D 1998, 59, 023505. [Google Scholar] [CrossRef]
di Cortona, G.G.; Hardy, E.; Vega, J.P.; Villadoro, G. The QCD axion, precisely. Journal of High Energy Physics 2016, 2016, 34. [Google Scholar] [CrossRef]
Kim, J.E.; Carosi, G. Axions and the strong CP problem. Rev. Mod. Phys. 2010, 82, 557–601. [Google Scholar] [CrossRef]
Borsanyi, S.; Fodor, Z.; Guenther, J.; Kampert, K.H.; Katz, S.D.; Kawanai, T.; Kovacs, T.G.; Mages, S.W.; Pasztor, A.; Pittler, F.; et al. Calculation of the axion mass based on high-temperature lattice quantum chromodynamics. Nature 2016, 539, 69–71. [Google Scholar] [CrossRef] [PubMed]
Marsh, D.J.E. Axion cosmology. Physics Report 2016, arXiv:astro-ph.CO/1510.07633]643, 1–79. [Google Scholar] [CrossRef]
Kim, J.E.; Marsh, D.J.E. An ultralight pseudoscalar boson. Phys. Rev. D 2016, 93, 025027. [Google Scholar] [CrossRef]
Yamaguchi, M.; Kawasaki, M.; Yokoyama, J. Evolution of Axionic Strings and Spectrum of Axions Radiated from Them. Phys. Rev. Lett. 1999, 82, 4578–4581. [Google Scholar] [CrossRef]
Jetzer, P. Boson stars. Physics Reports 1992, 220, 163–227. [Google Scholar] [CrossRef]
Braaten, E.; Mohapatra, A.; Zhang, H. Dense Axion Stars. Phys. Rev. Lett. 2016, 117, 121801. [Google Scholar] [CrossRef]
Braaten, E.; Zhang, H. Colloquium: The physics of axion stars. Rev. Mod. Phys. 2019, 91, 041002. [Google Scholar] [CrossRef]
Schiappacasse, E.D.; Hertzberg, M.P. Analysis of dark matter axion clumps with spherical symmetry. Journal of Cosmology and Astroparticle Physics 2018, 2018, 037–037. [Google Scholar] [CrossRef]
Visinelli, L.; Baum, S.; Redondo, J.; Freese, K.; Wilczek, F. Dilute and dense axion stars. Physics Letters B 2017, 777. [Google Scholar] [CrossRef]
Eby, J.; Mukaida, K.; Takimoto, M.; Wijewardhana, L.C.R.; Yamada, M. Classical nonrelativistic effective field theory and the role of gravitational interactions. Phys. Rev. D 2019, 99, 123503. [Google Scholar] [CrossRef]
Chavanis, P.H. Phase transitions between dilute and dense axion stars. Phys. Rev. D 2018, 98, 023009. [Google Scholar] [CrossRef]
O’Hare, C.A.J. Cosmology of axion dark matter. PoS 2024, arXiv:hep-ph/2403.17697]COSMICWISPers, 040. [Google Scholar] [CrossRef]
Diez-Tejedor, A.; Marsh, D.J. Cosmological production of ultralight dark matter axions. arXiv preprint arXiv:1702.02116 arXiv:1702.02116 2017.
Du, X.; Behrens, C.; Niemeyer, J.C.; Schwabe, B. Core-halo mass relation of ultralight axion dark matter from merger history. Phys. Rev. D 2017, 95, 043519. [Google Scholar] [CrossRef]
Eby, J.; Leembruggen, M.; Street, L.; Suranyi, P.; Wijewardhana, L.C.R. Global view of QCD axion stars. Phys. Rev. D 2019, 100, 063002. [Google Scholar] [CrossRef]
Eby, J.; Leembruggen, M.; Street, L.; Suranyi, P.; Wijewardhana, L.C.R. Approximation methods in the study of boson stars. Phys. Rev. D 2018, 98, 123013. [Google Scholar] [CrossRef]
Bautista, B.; Degollado, J.C. Static axion stars revisited. Frontiers in Astronomy and Space Sciences 2024, 11. [Google Scholar] [CrossRef]
Musoke, N.; Hotchkiss, S.; Easther, R. Lighting the Dark: Evolution of the Postinflationary Universe. Phys. Rev. Lett. 2020, 124, 061301. [Google Scholar] [CrossRef] [PubMed]
Wechsler, R.H.; Tinker, J.L. The Connection Between Galaxies and Their Dark Matter Halos. Annual Review of Astronomy and Astrophysics 2018, 56, 435–487. [Google Scholar] [CrossRef]
Lee, Jae-Weon. Brief History of Ultra-light Scalar Dark Matter Models. EPJ Web Conf. 2018, 168, 06005. [Google Scholar] [CrossRef]
Frieman, J.A.; Turner, M.S.; Huterer, D. Dark Energy and the Accelerating Universe. Annual Review of Astronomy and Astrophysics 2008, 46, 385–432. [Google Scholar] [CrossRef]
Ryden, B. Introduction to Cosmology; Cambridge University Press: New York, NY, USA, 2017. [Google Scholar]
Marsh, D.J. Axion cosmology. Physics Reports 2016, 643, 1–79. [Google Scholar] [CrossRef]
Hui, L.; Ostriker, J.P.; Tremaine, S.; Witten, E. Ultralight scalars as cosmological dark matter. Phys. Rev. D 2017, 95, 043541. [Google Scholar] [CrossRef]
Braaten, E.; Mohapatra, A.; Zhang, H. Nonrelativistic Effective Field Theory for Axions. Phys. Rev. 2016, arXiv:hep-ph/1604.00669]D94, 076004. [Google Scholar] [CrossRef]
Davidson, S.; Schwetz, T. Rotating drops of axion dark matter. Phys. Rev. D 2016, 93, 123509. [Google Scholar] [CrossRef]
Eby, J.; Suranyi, P.; Vaz, C.; Wijewardhana, L.C.R. Axion Stars in the Infrared Limit. JHEP 2015, arXiv:hep-th/1412.3430]03, 080. [Google Scholar] [CrossRef]
Miniati, F.; Gregori, G.; Reville, B.; Sarkar, S. Axion-Driven Cosmic Magnetogenesis during the QCD Crossover. Phys. Rev. Lett. 2018, 121, 021301. [Google Scholar] [CrossRef] [PubMed]
Olive, K. Review of Particle Physics. Chinese Physics C 2014, 38, 090001. [Google Scholar] [CrossRef]
Planck Collaboration et al. A &A 2020, 641, A1. [CrossRef]

Figure 1. Effective potential:

V_{0} = 1 - J_{0} (x)

Figure 1. Effective potential:

V_{0} = 1 - J_{0} (x)

Figure 2. Axion field density, n, vs. dimensionless radial variable r (

m_{a} = 5.3 \cdot 10^{- 19}

eV). Inset: zoom of the main graph.

Figure 2. Axion field density, n, vs. dimensionless radial variable r (

m_{a} = 5.3 \cdot 10^{- 19}

eV). Inset: zoom of the main graph.

Table 1. Acronyms:

f_{a}

- Coupling constant;

M_{⊙}

- sun mass;

n_{D M}

- dark matter density.

Table 1. Acronyms:

f_{a}

- Coupling constant;

M_{⊙}

- sun mass;

n_{D M}

- dark matter density.

Axion mass [eV]	$f_{a}$ [GeV]	$r_{0}$ [pc]	$M_{0}$ [ $M_{⊙}$ ]	$n_{0}$ [ $1 / c m^{3}$ ]	$n^{*} = n_{D M} / n_{0}$
$5.3 \cdot 10^{- 23}$	$10^{17}$	12	$3.59 \cdot 10^{14}$	$3.45 \cdot 10^{43}$	$7.11 \cdot 10^{- 19}$
$5.3 \cdot 10^{- 19}$	$10^{16}$	$1.2 \cdot 10^{- 3}$	$3.59 \cdot 10^{8}$	$3.45 \cdot 10^{45}$	$7.11 \cdot 10^{- 23}$
$5.7 \cdot 10^{- 6}$	$10^{12}$	$1.12 \cdot 10^{- 18}$	$3.34 \cdot 10^{- 19}$	$3.71 \cdot 10^{46}$	$6.15 \cdot 10^{- 39}$

Table 2. Results of numerical computation.

Angular	Axion mass $m_{a} = 5.3 \cdot 10^{- 19}$ eV
momentum	Star radius, $r_{h}$	Star mass	Density, $n_{h}$	Redshift, z
$l = 0$ , $m = 0$	55 [ 0.06 pc]	43.8 [ $1.57 \cdot 10^{10} M_{⊙}$ ]	$5.86 \cdot 10^{- 6}$	$4.35 \cdot 10^{5}$
$l = 0$ , $m = 0$	350 [ 0.48 pc]	9.56 [ $3.43 \cdot 10^{9} M_{⊙}$ ]	$3.58 \cdot 10^{- 8}$	$7.96 \cdot 10^{4}$
$l = 1$ , $m = 0$	410 [ 0.49 pc]	0.11 [ $4 \cdot 10^{7} M_{⊙}$ ]	$1.21 \cdot 10^{- 12}$	2572
$l = 1$ , $m = \pm 1$	550 [ 0.66 pc]	109.5 [ $3.92 \cdot 10^{10} M_{⊙}$ ]	$1.77 \cdot 10^{- 11}$	6291

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Primordial Axion Stars and Galaxy Halos Formation

Abstract

Introduction

1. Cosmological Production of Axions

1.1. Non-Relativistic Limit of the Klein-Gordon Equation

1.2. Formation of Axion Stars

2. Model

3. Results and Discussion

Funding

Data Availability Statement

References

MDPI Initiatives

Important Links

Subscribe