Prerpints.org logo
Preprint
Article

Efficient Forward Modeling of Gravitational Fields in Spherical Harmonic Domain with Application to Lunar Topography

Altmetrics

Downloads

114

Views

36

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

29 July 2024

Posted:

01 August 2024

You are already at the latest version

Alerts
Abstract
Gravity forward modeling as a basic tool has been wildly used to topography correction and 3D density inversion. The source region is usually discretized into tesseroid (i.e., spherical prism) to consider the influence of the curvature of planets in global or large-scale problems. Traditional gravity forward modeling methods in spherical coordinates, including the Taylor expansion and Gaussian-Legendre quadrature, are all based on spatial domain, which are mostly low computational efficiency. This study proposes a high-efficient forward modeling method of gravitational fields in spherical harmonic domain, in which the gravity anomalies and gradient tensors can be expressed as spherical harmonic synthesis form of spherical harmonic coefficients of 3D density distribution. A homogeneous spherical shell model has been used to test its effectiveness compared with traditional spatial domain methods. It demonstrates that the computational efficiency of the proposed spherical harmonic domain method has improved by four orders of magnitude and with a similar level of computational accuracy compared with the optimized 3D GLQ method. Finally, the proposed forward method is applied to topography correction of the Moon. The results show that the gravity response of the topography by our method is close to that of the optimized 3D GLQ method, and is also consistent with previous results.
Keywords: 
Subject: Environmental and Earth Sciences  -   Geophysics and Geology

1. Introduction

Forward modeling of gravitational fields plays an important role in data processing and geological interpretation in gravity exploration. It has been wildly used to calculate the gravity responses of topography, sedimentary layer, crystalline layer and Moho interface [1,2,3,4,5]. Then these effects can be removed from the free-air gravity anomaly to get the residual gravity anomaly that only produced by the inhomogeneity of the upper mantle of the lithosphere [6,7,8,9]. In addition, gravity forward modeling, as the core of iteration of 3D density inversion, is typically employed in mineral resources exploration [10,11,12] and lithospheric density structures of planetary interiors [13,14,15]. However, traditional gravity forward methods are mostly based on Cartesian coordinate system [16,17]. In recent years, with the development of satellite gravity, more and more high-precision and resolution gravity field models have been applied to the study of 3D density structures and evolution history of the Earth [18,19], the Moon [20,21,22] and Mars [23,24]. Therefore, gravity forward methods and relative methods of data processing and inversion should be changed from Cartesian coordinate system to spherical coordinates.
Gravity forward modeling in spherical coordinates can be carried out in spatial domain and spherical harmonic domain (i.e., frequency domain). In spatial domain, we usually divide the study region into some spherical prisms, i.e., tesseroids [25]. The gravity responses of these tesseroids can be obtained by the accumulation of gravity signal generated by each tesseroid. However, the 3D Newton’s integral of the tesseroid is usually hard to be solved analytically except for the case that the source regions are sphere and sphere shell with constant density [26]. Therefore, numerical integration methods are alternatively more common to tackle this issue, e.g., the Taylor series expansion [27,28] and the 2D/3D Gauss-Legendre quadrature (GLQ) method [29,30,31]. However, these numerical methods always lead to absolutely wrong results when the observation points are close to tesseroids. Uieda et al. [32] proposed an adaptive discretization method that has greatly increased the computational precision ensuring the relative error less than 0.1%. In addition, the computational efficiency will be another severe issue for large-scale or global gravity forward and inversion especially when the discretization is fine. Recently, some strategies, e.g., the kernel matrix equivalent storage [4,33] and the fast kernel-vector multiplication [5,34] have been proposed which decreased the computing time by three orders of magnitude compared with traditional method. Though the issues on computational efficiency and accuracy of these methods in spatial domain have been well settled, global and regional gravitational fields are now more commonly released in the form of spherical harmonic coefficients which makes it difficult for these spatial domain methods to simulate the gravity responses with specified degrees and orders. However, this will be very simple for the spherical harmonic domain methods.
Spherical harmonics are special functions defined on the surface of a sphere that form an orthogonal basis set for square-integrable functions, by which non-singular spectra expressions for gravity anomalies and gradients are derived based on the sums of spherical harmonic coefficients of gravitational field models [35,36]. Similar to the Parker’s formula [37] and the interface iterative inversion method [38] in Cartesian coordinate, Wieczorek and Phillips [39] derived the formula for calculating gravity anomaly of single undulating interface with constant density and the iterative inversion method of density interface in spherical harmonic domain, which were used to lunar topography correction and estimation of lunar crustal thickness [40,41]. This method is high-efficient and suitable for gravity correction using high-order and high-resolution terrain models, and gravity inversions of a single density interface. However, the binomial series expansion in this method has great effect to computational accuracy and convergence in inversion. Root et al. [42] proposed a correction to mitigate this erroneous behavior, by which it is applied to gravity forward modeling of Earth’s density structures. Instead of implementing the binomial expansion of the product of topographic relief and 2D density distribution in Wieczorek and Phillips [39], Šprlák et al. [43,44] present an innovative approach to construct the gravitational potential spectra in spherical coordinates using the discrete Fourier transform. In addition to topography corrections, these spherical harmonic domain methods have been also widely used in the calculation of gravity disturbances of lithosphere from crustal models with variable density distributions [2,8,45]. Although forward modeling methods of the gravity anomaly have been extensively studied and applied, studies on spherical harmonic spectra of gravitational gradient tensors remain comparatively rare. Besides, there are few studies on gravity forward and inversion modeling of 3D density anomalies by using the spherical harmonic methods [46].
To adapt to the requirement of gravity forward and inversion of 3D density anomalies with arbitrary degrees and orders, this study proposes an efficient forward modeling method of gravitational field in spherical harmonic domain, in which the gravity anomalies and gradient components are expressed as a form of spherical harmonic synthesis of spherical harmonic coefficients of arbitrary 3D density distributions. Two synthetic models demonstrate that the proposed method has improved the computational efficiency by four orders of magnitude and with a similar level of computational accuracy compared with the optimized 3D GLQ method [4,5]. Finally, we apply this method to calculated the topography correction and Bouguer gravity anomaly of the Moon.

2. Theory and Methods

2.1. Spatial Domain Forward Modeling Method

In spherical coordinates, the global spherical shell is typically discretized into tesseroids [25], and observation points are on a spherical surface aligning with the tesseroids mesh, as shown in Figure 1.
Here we define a local north-oriented frame (LNOF) where z-axis points to upward in geocentric radial direction, x-axis towards the north and y-axis directs to the east. We suppose that P (r, φ, λ) is an arbitrary observation point and Q (rʹ, φʹ, λʹ) is the center position of an arbitrary tesseroid bounded by (r1, r2), (φ1, φ2), and (λ1, λ2) in three directions, where r, φ and λ (also for rʹ, φʹ and λʹ) are geocentric radius, latitude, and longitude, respectively. Therefore, the gravitational potential on point P by tesseroid Q with homogeneous density ρ can be written as Newton’s integral [28,31,32]:
V ( r , φ , λ ) = G ρ ∫ r 1 r 2 ∫ φ 1 φ 2 ∫ λ 1 λ 2 r ′ 2 cos φ ′ ℓ d r ′ d φ ′ d λ ′
where G is the gravitational constant; l is the distance between P and Q:
ℓ = r ′ 2 + r 2 − 2 r ′ r cos ψ cos ψ = sin φ sin φ ′ + cos φ cos φ ′ cos ( λ ′ − λ )
According to the coordinate transformation relationship between the geocentric spherical coordinates and the local rectangular coordinates [27,31], it is easy to obtain their partial derivatives of V to r, φ and λ, then the gravitational accelerations gα and gradient tensors gαβ can be obtained by their combinations [47,48], where α, β∈(x, y, z):
[ g α ] = [ g x g y g z ] T = [ 1 r ∂ V ∂ φ 1 r cos φ ∂ V ∂ λ ∂ V ∂ r ] T
[ g α β ] = [ 1 r 2 ( ∂ 2 V ∂ φ 2 + r ∂ V ∂ r ) 1 r 2 cos φ ( ∂ 2 V ∂ φ ∂ λ + tan φ ∂ V ∂ λ ) 1 r ( ∂ 2 V ∂ φ ∂ r − 1 r ∂ V ∂ φ ) 1 r 2 cos φ ( ∂ 2 V ∂ φ ∂ λ + tan φ ∂ V ∂ λ ) 1 r 2 cos 2 φ ( ∂ 2 V ∂ 2 λ + r cos 2 φ ∂ V ∂ r − cos φ sin φ ∂ V ∂ φ ) 1 r cos φ ( ∂ 2 V ∂ r ∂ λ − 1 r ∂ V ∂ λ ) 1 r ( ∂ 2 V ∂ φ ∂ r − 1 r ∂ V ∂ φ ) 1 r cos φ ( ∂ 2 V ∂ r ∂ λ − 1 r ∂ V ∂ λ ) ∂ 2 V ∂ 2 r ]
The gravitational potential, three components of anomalies, and gradient tensors can be further rearranged as [32]:
V ( r , φ , λ ) = G ρ ∫ r 1 r 2 ∫ φ 1 φ 2 ∫ λ 1 λ 2 1 ℓ κ ⋅ d r ′ d φ ′ d λ ′ ,
g α ( r , φ , λ ) = G ρ ∫ r 1 r 2 ∫ φ 1 φ 2 ∫ λ 1 λ 2 Δ α ℓ 3 κ ⋅ d r ′ d φ ′ d λ ′ ,
g α β ( r , φ , λ ) = G ρ ∫ r 1 r 2 ∫ φ 1 φ 2 ∫ λ 1 λ 2 ( 3 Δ α Δ β ℓ 5 − δ α β ℓ 3 ) κ ⋅ d r ′ d φ ′ d λ ′ ,  
where δαβ is Kronecker’s delta (δαβ = 1, if α = β and δαβ = 0, if α ≠ β), and
Δ x = r ′ [ cos φ sin φ ′ − sin φ cos φ ′ cos ( λ ′ − λ ) ]     Δ y = r ′ cos φ sin ( λ ′ − λ ) Δ z = r ′ cos ψ − r κ = r ′ 2 cos φ ′
There is no analytical solution of Equations (5) – (7) since they contain elliptical integrals about φ' and λ'. Therefore, we should adopt numerical integration methods to solve it. Since the 3D GLQ method is numerically better than the Taylor series expansion method [31], we choose the 3D GLQ to represent the spatial domain method. For simple, taking one-dimensional GLQ as an example, a line integral of continuous function f(x) in [a, b] interval can be expressed as:
∫ a b f ( x ) d x ≈ b − a 2 ∑ k = 0 N W k f ( b − a 2 x k + a + b 2 )
where N is the number of Gaussian nodes; xk and Wk are the k-th Gaussian node and Gaussian coefficient in [1,1] interval, respectively, where the commonly used Gaussian nodes and coefficients are given by Wild-Pfeiffer [31]. In the following comparison, we use two Gaussian nodes to fit the trade-off between computational accuracy and efficiency.
We note that if we simply use this 3D GLQ method to gravity forward modeling of tesseroids, its computational efficiency and accuracy will be very low, especially when observation points are close to the top of tesseroids and when the source region is discretized finely. Therefore, we will employ the optimal methods of adaptive discretization by Uieda et al. [32] and kernel matrix equivalent storage by Zhao et al. [5] for comparison with the new proposed method in the next section.

2.2. Forward Method in Spherical Harmonic Domain

The gravitational field outside the Earth satisfies Laplace equation, so it can also be expressed as spherical harmonic expansion. Based on this theory, here we firstly derive the equations of the gravitational field of a single-layer spherical shell model in the form of spherical harmonic expressions, and then the expressions of 3D source region are obtained by accumulation of each layer. The gravitational potential in Equation (1) can be reshaped as:
V ( r , φ , λ ) = G ∬ S ∫ r ′ ρ ( r ′ , φ ′ , λ ′ ) ℓ ( r , φ , λ ; r ′ , φ ′ , λ ′ ) d S d r ′
where S denotes the range of spherical integral.
The gravitational potential V and 3D density distribution ρin Equation (10) can be written in the form of normalized spherical harmonic functions according to the spherical harmonic expansion theory [49]:
V ( r , φ , λ ) = ∑ l = 0 L ∑ m = 0 l [ V ¯ l m 1 ( r ) R ¯ l m ( φ , λ ) + V ¯ l m 2 ( r ) T ¯ l m ( φ , λ ) ]
ρ ( r ′ , φ ′ , λ ′ ) = ∑ l = 0 L ∑ m = 0 l [ ρ ¯ l m 1 ( r ′ ) R ¯ l m ( φ ′ , λ ′ ) + ρ ¯ l m 2 ( r ′ ) T ¯ l m ( φ ′ , λ ′ ) ]
where V ¯ l m 1 ( r ) and V ¯ l m 2 ( r ) are fully normalized spherical harmonic coefficients of the gravitational potential with degree l and order m on a sphere surface with radius r; ρ ¯ l m 1 ( r ′ ) and ρ ¯ l m 2 ( r ′ ) are fully normalized spherical harmonic coefficients of the 2D density distribution on a layer with radius rʹ; L is the maximum spherical harmonic degree; R ¯ l m ( φ , λ ) and T ¯ l m ( φ , λ ) are fully normalized spherical harmonic functions which can be written as [49]:
R ¯ l m ( φ , λ ) = P ¯ l m ( sin φ ) cos m λ T ¯ l m ( φ , λ ) = P ¯ l m ( sin φ ) s i n m λ
where P ¯ l m ( sin φ ) is the 4π fully-normalized associated Legendre function.
The Green function (1/l) in Equation (10) is the key to spherical harmonic domain methods which can be expressed as [49]:
1 ℓ = 1 r ∑ l ∞ ( r ′ r ) l 1 2 l + 1 ∑ m = 0 l [ R ¯ l m ( φ , λ ) R ¯ l m ( φ ′ , λ ′ ) + T ¯ l m ( φ , λ ) T ¯ l m ( φ ′ , λ ′ ) ] ,         r > r ′
We should note that the infinite series in Equation (14) only converge uniformly for any observation points that are r > rʹ, i.e., the observation points need to be outside of the source region. Substituting Equations (11), (12) and (14) into (10), and employing the orthogonal characteristic of spherical harmonic functions, we get:
V ¯ l m 1 ( r ) = G ∫ r ′ 4 π r ′ 2 l + 1 ( r ′ r ) l + 1 ρ ¯ l m 1 ( r ′ ) d r ′ V ¯ l m 2 ( r ) = G ∫ r ′ 4 π r ′ 2 l + 1 ( r ′ r ) l + 1 ρ ¯ l m 2 ( r ′ ) d r ′
Equation (15) shows that spherical harmonic coefficients of gravitational potential are calculated according to the radial integration of spherical harmonic coefficients of 3D density distribution, which is the core of gravity forward modeling in spherical harmonic domain. By substituting Equation (15) into (10), we can get spherical harmonic expressions of gravitational potential on a sphere with a given radius r outside the source region:
V ( r , φ , λ ) = 4 π G ∑ l = 0 L ∑ m = 0 l ∫ r ′ r ′ 2 l + 1 ( r ′ r ) l + 1 [ ρ ¯ l m 1 ( r ′ ) R ¯ l m ( φ , λ ) + ρ ¯ l m 2 ( r ′ ) T ¯ l m ( φ , λ ) ] d r ′
According to Equations. (3) and (4), we can obtain the spherical harmonic expressions of gravitational acceleration and gradient tensors:
g x ( r , φ , λ ) = 4 π G ∑ l = 0 L ∑ m = 0 l ∫ r ′ 1 2 l + 1 ( r ′ r ) l + 2 [ ρ ¯ l m 1 ( r ′ ) cos m λ + ρ ¯ l m 2 ( r ′ ) s i n m λ ] ∂ P ¯ l m ( sin φ ) ∂ φ d r ′
g y ( r , φ , λ )   = 4 π G ∑ l = 0 L ∑ m = 0 l ∫ r ′ 1 ( 2 l + 1 ) cos φ ( r ′ r ) l + 2 m [ − ρ ¯ l m 1 ( r ′ ) sin m λ + ρ ¯ l m 2 ( r ′ ) cos m λ ] P ¯ l m ( sin φ ) d r ′
g z ( r , φ , λ ) = − 4 π G ∑ l = 0 L ∑ m = 0 l ∫ r ′ l + 1 2 l + 1 ( r ′ r ) l + 2 [ ρ ¯ l m 1 ( r ′ ) R ¯ l m ( φ , λ ) + ρ ¯ l m 2 ( r ′ ) T ¯ l m ( φ , λ ) ] d r ′
g x x ( r , φ , λ ) = 4 π G ∑ l = 0 L ∑ m = 0 l ∫ r ′ 1 r ( 2 l + 1 ) ( r ′ r ) l + 2 [ ρ ¯ l m 1 ( r ′ ) cos m λ + ρ ¯ l m 2 ( r ′ ) s i n m λ ] ⋅                                                                                                                                     [ ∂ 2 P ¯ l m ( sin φ ) ∂ φ 2 − ( l + 1 ) P ¯ l m ( sin φ ) ] d r ′
g x y ( r , φ , λ ) = 4 π G ∑ l = 0 L ∑ m = 0 l ∫ r ′ 1 r ( 2 l + 1 ) ( r ′ r ) l + 2 m [ − ρ ¯ l m 1 ( r ′ ) sin m λ + ρ ¯ l m 2 ( r ′ ) cos m λ ] ⋅                                                                                                                                       [ ∂ P ¯ l m ( sin φ ) cos φ ∂ φ + tan φ cos φ P ¯ l m ( sin φ ) ] d r ′
g x z ( r , φ , λ ) = − 4 π G ∑ l = 0 L ∑ m = 0 l ∫ r ′ l + 2 r ( 2 l + 1 ) ( r ′ r ) l + 2 [ ρ ¯ l m 1 ( r ′ ) cos m λ + ρ ¯ l m 2 ( r ′ ) s i n m λ ] ∂ P ¯ l m ( sin φ ) ∂ φ d r ′
g y y ( r , φ , λ ) = − 4 π G ∑ l = 0 L ∑ m = 0 l ∫ r ′ 1 r ( 2 l + 1 ) ( r ′ r ) l + 2 [ ρ ¯ l m 1 ( r ′ ) cos m λ + ρ ¯ l m 2 ( r ′ ) s i n m λ ] ⋅                                                                                                                                                     [ m 2 P ¯ l m ( sin φ ) cos 2 φ + ( l + 1 ) P ¯ l m ( sin φ ) + tan φ ∂ P ¯ l m ( sin φ ) ∂ φ ] ∂ P ¯ l m ( sin φ ) ∂ φ d r ′
g y z ( r , φ , λ ) = − 4 π G ∑ l = 0 L ∑ m = 0 l ∫ r ′ l + 2 r ( 2 l + 1 ) ( r ′ r ) l + 2 m [ − ρ ¯ l m 1 ( r ′ ) sin m λ + ρ ¯ l m 2 ( r ′ ) cos m λ ] P ¯ l m ( sin φ ) cos φ d r ′
g z z ( r , φ , λ ) = 4 π G ∑ l = 0 L ∑ m = 0 l ∫ r ′ ( l + 1 ) ( l + 2 ) r ′ ( 2 l + 1 ) ( r ′ r ) l + 3 [ ρ ¯ l m 1 ( r ′ ) cos m λ + ρ ¯ l m 2 ( r ′ ) sin m λ ] P ¯ l m ( sin φ ) d r ′
Equations (17) – (25) contain the singular terms of 1/cosφ and 1/cos2φ when φ is closing to the pole. In addition, some equations include the terms of derivatives of P ¯ l m ( sin φ ) . These mathematical problems have been well solved by previous studies [35,36,50], so here we will not focus on it.
The above Equations (17) – (25) are only theoretical expressions in the form of continuous radial integral. It is hard to calculate spherical harmonic coefficients of continuous density distribution in actual forward modeling. Therefore, the 3D spherical shell model will be divided into several density layers in the depth direction, and each density layer will be approximated by numerical integration. Finally, the gravitational fields generated by all layers will be summed. Supposing that a spherical shell model with a radius interval of [ra, rb] is evenly divided into Nz layers with the thickness of each layer ∆r = (rb − ra)/Nz, the center radius of each layer of the spherical shell is:
r ′ k = r a + ( k − 0.5 ) × Δ r ,           k = 1 , 2 , ⋯ , N z
Though the 3D source region has been divided into multi-layer spherical shells, ρ ¯ l m 1 ( r ′ ) and ρ ¯ l m 2 ( r ′ ) are still continuous functions of r'. Assuming that the radial subdivision interval ∆r is small enough, then the density distribution on the k-th layer can be seen as a constant equal to its center density. Therefore, the above equations can be numerically solved, taking the commonly used V, gz and gzz components as examples:
V ( r , φ , λ ) = 4 π G ∑ k = 1 N z ∑ l = 0 L ∑ m = 0 l [ ρ ¯ l m 1 ( r ′ k ) R ¯ l m ( φ , λ ) + ρ ¯ l m 2 ( r ′ k ) T ¯ l m ( φ , λ ) ] ( 2 l + 1 ) ( l + 3 ) r l + 1 [ ( r ′ k + 1 2 Δ r ) l + 3 − ( r ′ k − 1 2 Δ r ) l + 3 ]
g z ( r , φ , λ ) = - 4 π G ∑ k = 1 N z ∑ l = 0 L ∑ m = 0 l ( l + 1 ) [ ρ ¯ l m 1 ( r ′ k ) R ¯ l m ( φ , λ ) + ρ ¯ l m 2 ( r ′ k ) T ¯ l m ( φ , λ ) ] ( 2 l + 1 ) ( l + 3 ) r l + 2 × [ ( r ′ k + 1 2 Δ r ) l + 3 − ( r ′ k − 1 2 Δ r ) l + 3 ]
g z z ( r , φ , λ )       = 4 π G ∑ k = 1 N z ∑ l = 0 L ∑ m = 0 l ( l + 1 ) ( l + 2 ) [ ρ ¯ l m 1 ( r ′ k ) R ¯ l m ( φ , λ ) + ρ ¯ l m 2 ( r ′ k ) T ¯ l m ( φ , λ ) ] ( 2 l + 1 ) ( l + 3 ) r l + 3 × [ ( r ′ k + 1 2 Δ r ) l + 3 − ( r ′ k − 1 2 Δ r ) l + 3 ]
According to Equations. (27) – (29), the steps of gravitational forward modeling of 3D spherical shell model in spherical harmonic domain are clear. We firstly expand density distributions of each layer into spherical harmonic coefficients which are multiplied by the coefficients of corresponding degree and order. Next, gravitational responses of each layer can be obtained by spherical harmonic synthesis of the result in the first step. Finally, these gravity effects of each layer are summed. For more specificity, Table 1 shows detailed procedures of our method with gz component as example.
Similar to the procedures of gravitational forward modeling in Cartesian coordinate system that based on FFT [51,52], the forward modeling in spherical harmonic domain need also the spherical harmonic forward and inverse transformations. Therefore, the computational efficiency of spherical harmonic transformations dominates the efficiency of spherical harmonic based methods. Wieczorek and Meschede [53] released a software package SHTOOLS (https://shtools.github.io/SHTOOLS/), in which the Fourier transform software FFTW [54] and the OpenMP parallel program under the “DUCC” library (https://github.com/litebird/ducc) are employed by default to greatly improved the computational efficiency of spherical harmonic expansion and synthesis. In this study, 3D gravity forward modeling in spherical harmonic domain is performed under the SHTOOLS software system as expressed in the steps 2 and 4 in Table 1.

3. Synthetic Forward Model Tests

3.1. Sphere Shell Model

Here we firstly design a simple spherical shell model to testify the efficiency of our method compared with 3D GLQ methods. A homogeneous spherical shell with density of 500 kg/m3 and thickness of 100 km ranging from 1638 to 1738 km, as shown in Figure 2, is divided into small tesseroids with varying intervals ranging from 0.25° to 20° and 1 layer in depth. The gravitational fields are calculated and compared at 10 km height above the top surface of the shell model with observation points aligning with the tesseroid mesh. The analytical solution of the gravitational field of the sphere shell is calculated by the difference of gravity responses of two spheres with different radii [27].
We calculate the gz and gzz at different mesh intervals (i.e., different mesh scales) using adaptive discretization method by Uieda et al. [32] and kernel matrix equivalent storage method by Zhao et al. [5], and this proposed spherical harmonic domain method, with their relative computational time shown in Figure 3. The absolute errors of gz and gzz by the spatial domain method and our proposed spherical harmonic domain method are shown in Figure 4. In addition, we also show the comparison of computational time and the maximum relative error of gz and gzz when the mesh interval is 0.25° (i.e., the discretization is 720 × 1440 × 1) in Table 2.
Figure 3 shows that the computational time increases rapidly with the decreases of mesh interval (i.e., with the increases of total number of tesseroids). Specifically, the computational efficiency by the proposed spherical harmonic domain method is increased by 3 and 6 orders of magnitude compared with the methods of Zhao et al. [5] and of Uieda et al. [32], respectively, for the gz component when the mesh interval is less than 3° (Figure 3a). As for the gzz component, the improvements of computational efficiency are more obvious, which are 4 orders and 7 orders of magnitude (Figure 3b), respectively. These improvements on the computational efficiency are quantified in Table 2, where the absolute computational times by the spatial domain methods are extremely long, while the computational time by the proposed spherical harmonic domain method is acceptable and suitable to global 3D gravity inversion.
As for computational accuracy, Figure 4 shows absolute errors of gz and gzz by both the spatial and spherical harmonic domain methods vary with latitude. Also, it is obviously that absolute errors by the proposed spherical harmonic domain method (Figure 4b and d) are lower than that by the spatial domain method (Figure 4a and c). Specifically, the maximum relative error of the gz component by the proposed spherical harmonic domain method is decreased by 3 orders of magnitude compared with that by the spatial domain method, as shown in Table 2, while the improvement on the accuracy for the gzz component is about two orders of magnitude.

3.2. Complex Synthetic Model

Here we design a more complex synthetic model to further test the effectiveness of the proposed method. The model is a spherical shell with a thickness of 100 km ranging from 1638 km to 1738 km, which is evenly discretized into 360 × 720 × 10 tesseroids (i.e., with a mesh interval of 0.5° in horizontal direction and ten layers in depths) with their density anomalies varying as:
ρ ( r , φ , λ ) = ( 1738 − r ) ⋅ [ sin ( 2 φ ) ⋅ sin ( 2 λ ) ]
The density distribution of this model on a layer with its radius of r = 1682.5 km is shown in Figure 5. The gravitational fields are calculated on a spherical surface at 10 km above the top surface of this model. Figure 6 shows the gz and gzz of this model by the spatial domain method, and the differences between it and the proposed spherical harmonic domain method.
Although it is difficult for this complex model to have an analytical solution, the results by the spatial domain method with adaptive discretization strategy [32] can be regarded as standards for comparison. It can be seen in Figure 6 that the gz and gzz by the proposed spherical harmonic domain method are very close to (a) and (b) by the spatial domain method, with the biggest differences for gz (c) and gzz (d) between the two methods lower than 0.5 mGal and 5.0 E, respectively, which proves the effectiveness of our method.

4. Application to Lunar Topography Correction

Bouguer gravity anomaly is the comprehensive reflection of all density anomalies after removing the influence of topography from the free-air anomaly, which has been widely used in 3D gravity inversion to reveal the density structure and deformation mechanism of the lithosphere. In addition, Bouguer anomalies are also the basis for other gravity corrections, such as residual gravity anomalies used for Moho interface inversion by removing the gravity responses of sedimentary layers, crystalline crust layers and deep mantle effects from Bouguer anomalies. Here we employ the proposed method to calculate the gravity response of the lunar topography and then obtain the Bouguer gravity anomaly.
The latest lunar gravitational field model GL1500E [21] is used here to calculate the free-air gravity anomaly. This model is expressed in the form of spherical harmonic coefficients, where different degrees and orders represent gravity anomalies with different spatial resolutions [55]. In this study, the free-air gravity is obtained with truncated degrees of 450 equivalent to a horizontal resolution of 0.4° × 0.4° by using spherical harmonic synthesis methods [56]. Considering that the observation data are usually extended upwards to a certain height in inversions to reduce the influence of the noise in data [57], so we calculate the free-air gravity anomaly on a surface of r = 1,748 km which is 10 km height above the reference radius, as shown in Figure 7a.
Next, we evaluate gravity responses of the lunar topography. The lunar topography map (Figure 7b) is obtained by spherical harmonic synthesis of the model LRO_LTM05_2050 [58] using the same degrees of coefficients as the free-air gravity anomaly to keep consistency. Considering that our method is suitable for uniform layered shells which is inconsistent with the topography model, so it is necessary to discrete the terrain to plenty of tesseroids with constant thickness for each layer to reduce the error of fitting the terrain using tesseroids. Figure 7b shows the lunar topography ranges from −9.29 to 9.63 km, so we construct a spherical shell that slightly higher than the topography ranging from −10.00 to 10.00 km to cover the topography, and then this spherical shell is evenly divided into 400 thin layers with an interval of 0.05 km, as shown in Figure 8. Next, we need to judge the relationship between the depth of the geometric center of each tesseroid and the terrain. If the tesseroid is covered by the terrain, the correction density of this tesseroid is assigned as 2560 kg/m3 (for mountain) or −2560 kg/m3 (for basin), otherwise 0 kg/m3. The topography correction is also calculated on a surface of r = 1748 km consistent with the free-air gravity. Figure 9 shows the gravity effects of the lunar topography calculated by the spatial domain method, and the differences between it and the proposed method.
Figure 9 shows that the gravity effect of the lunar topography by the proposed method is similar to the result that by the spatial domain method which further proves the effectiveness and practicality of our method. The computational times of the topography corrections by our method and the spatial domain method are 88.69 s and 48789.98 s, respectively, indicating the high efficiency of the proposed method. However, the advantage of our method in terms of computational efficiency is slightly weakened in this application compared with that in the synthetic example in Section 3. This is because the premise of the proposed method is that all tesseroids of each layer have the same thickness. Therefore, when calculating terrain correction, the entire terrain needs to be divided into several thin layers (e.g., 400 layers in this example).
We remove gravity responses of topography from the free-air gravity to get the Bouguer gravity anomaly. Since the results of topography corrections by the spatial domain method and the proposed method are nearly close, here we just show Bouguer gravity anomaly that by the proposed method in Figure 10a. The Bouguer gravity anomaly in Figure 10a ranges from −500 mGal to 900 mGal, where the positive high anomalies are mainly distributed in most mascon basins and the South Pole-Aitken basin, while the negative anomalies are distributed on the Highland on the farside of the Moon. It can be found that the Bouguer gravity anomaly in Figure 10a is very close to the Bouguer result of Liang et al. [14], and the only difference between them is that the latter one used spherical harmonic coefficients with degrees and orders less than 60 to calculate the free-air gravity anomaly and the topography correction, with makes its resolution much lower than that of in this paper. However, the features of the Bouguer gravity anomaly in Figure 10a are very different from the results of Neumann et al. [56] and Zhao et al. [5]. It is obviously that the positive and negative Bouguer anomalies in Figure 10a display obvious asymmetries between nearside and farside of the Moon as well as between the northern and southern hemispheres. As for the results in Neumann et al. [56] and Zhao et al. [5] as shown in Figure 10b, positive high anomalies are significantly distributed beneath most mascon basins with less significant negative anomalies scattering around the positive anomalies (i.e., mascon basins). This is because they used 6−450 degrees and orders of spherical harmonic coefficients to calculate the free-air gravity anomaly and the topography correction, where the effect of the hemispheric asymmetry and the South Pole-Aitken impact has been naturally removed by discarding the signal with degrees and orders less than 6.

4. Discussion

The topography correction by spatial domain methods is essentially a forward modeling to evaluate gravity responses of the terrain observed on a surface with certain height. In this way, the obtained topography correction contains all degrees and orders of signals. If to calculate the Bouguer gravity anomaly with desired degrees and orders, the topography correction should be calculated with the same degrees and orders which is generally difficult for the spatial domain method. However, this is very easy for spherical harmonic domain methods. As shown in Equations. (16)−(25), the gravity effects of the topography within desired degrees and orders are directly calculated by spherical harmonic synthesis.
We note that topography correction is only an application example of the proposed method. More generally, this method can be served as a forward kernel for iterative inversion of 3D gravitational field in spherical coordinate system, which can greatly improve the computational efficiency of inversion modeling. In addition, we should also note that the proposed spherical harmonic domain method is only applicable to global forward modeling since the spherical harmonic functions are defined on a sphere. However, gravity anomaly and density structures on local region are usually more concerned than the global scale. For this case, the spherical cap harmonic analysis will be a good choice for the local gravitational field [59−61]. The proposed spherical harmonic domain method in this paper can also be analogized to the spherical cap harmonic analysis for local gravity forward and inversion modeling.

5. Conclusions

This study presented a high-efficient gravitational forward modeling method in spherical coordinate system based on spherical harmonic transform, in which the gravity anomalies and gradient tensors can be expressed as spherical harmonic synthesis form of spherical harmonic coefficients of 3D density distribution. Two synthetic forward examples demonstrated that the computational efficiency of the proposed method has improved by four orders of magnitude and with a similar level of computational accuracy compared with the optimized 3D GLQ method. The verified gravity forward method is then applied to calculate the topography correction and the Bouguer gravity anomaly of the Moon using the latest high-resolution gravitational field model and topography model. The result shows that the gravity effect of the lunar topography by the proposed method is similar to the result that by the spatial domain method. The computational efficiency of the topography correction is relatively lower than the synthetic forward examples because that the terrain should be evenly discretized into many thin layers to satisfy the requirement of the proposed forward method. In addition, the proposed method can calculate topography correction and Bouguer gravity anomaly with any desired degrees and orders, which is generally different for the spatial domain method. However, we should note that the proposed spherical harmonic domain method is only applicable to global gravity forward modeling, which may be analogized and applied to the spherical cap harmonic analysis for local gravity forward and inversion modeling.

Author Contributions

Conceptualization, G.Z.; methodology, G.Z.; software, S.L.; validation, G.Z. and S.L.; formal analysis, S.L.; investigation, S.L.; resources, G.Z.; data curation, G.Z.; writing—original draft preparation, S.L.; writing—review and editing, G.Z.; visualization, G.Z.; supervision, G.Z.; project administration, G.Z.; funding acquisition, G.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This research is supported by the National Natural Science Foundation of China (Grant No. 42204090) and the Natural Science Foundation of Sichuan Province (Grant No. 2023NSFSC0253).

Data Availability Statement

The data and codes for this paper are freely available at the website: https://doi.org/10.6084/m9.figshare.23790705.v1 [62].

Acknowledgments

All projected figures are drawn using the Generic Mapping Tools [63].

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Roy, and L. Wu. Generalized Gauss-FFT 3D forward gravity modeling for irregular topographic mass having any 3D variable density contrast. Computers & Geosciences 2023, 172, 105297. [Google Scholar]
  2. R. Tenzer, K. Hamayun, and P. Vajda. Global maps of the CRUST 2.0 crustal components stripped gravity disturbances. Journal of Geophysical Research: Solid Earth 2009, 114, B5. [Google Scholar]
  3. R. Tenzer, V. Gladkikh, P. Novák, and P. Vajda. Spatial and spectral analysis of refined gravity data for modelling the crust–mantle interface and mantle-lithosphere structure. Surveys in geophysics 2012, 33, 817–839. [Google Scholar] [CrossRef]
  4. G. Zhao, B. Chen, L. Uieda, J. Liu, M. K. Kaban, L. Chen, and R. Guo. Efficient 3-D large-scale forward modeling and inversion of gravitational fields in spherical coordinates with application to lunar mascons. Journal of Geophysical Research: Solid Earth 2019, 124, 4157–4173. [Google Scholar] [CrossRef]
  5. G. Zhao, J. Liu, B. Chen, M. K. Kaban, and J. Du. 3-D Density Structure of the Lunar Mascon Basins Revealed by a High-Efficient Gravity Inversion of the GRAIL Data. Journal of Geophysical Research: Planets 2021, 126, e2021JE006841. [Google Scholar] [CrossRef]
  6. M. K. Kaban, W. D. Mooney, and A. G. Petrunin. Cratonic root beneath North America shifted by basal drag from the convecting mantle. Nature Geoscience 2015, 8, 797–800. [Google Scholar] [CrossRef]
  7. M. K. Kaban, W. Stolk, M. Tesauro, S. El Khrepy, N. Al-Arifi, F. Beekman, and S. A. Cloetingh. 3D density model of the upper mantle of Asia based on inversion of gravity and seismic tomography data. Geochemistry, Geophysics, Geosystems 2016, 17, 4457–4477. [Google Scholar] [CrossRef]
  8. R. Tenzer, and W. Chen. Mantle and sub-lithosphere mantle gravity maps from the LITHO1. 0 global lithospheric model. Earth-Science Reviews 2019, 194, 38–56. [Google Scholar] [CrossRef]
  9. G. Zhao, J. Liu, B. Chen, M. K. Kaban, and X. Zheng. Moho beneath Tibet based on a joint analysis of gravity and seismic data. Geochemistry, Geophysics, Geosystems 2020, 21, e2019GC008849. [Google Scholar] [CrossRef]
  10. Boulanger, and M. Chouteau. Constraints in 3D gravity inversion. Geophysical prospecting 2001, 49, 265–280. [Google Scholar] [CrossRef]
  11. J. Liu, J. Zhang, L. Jiang, Q. Lin, and L. Wan. Polynomial-based density inversion of gravity anomalies for concealed iron-deposit exploration in North China. Geophysics 2019, 84, B325–B334. [Google Scholar] [CrossRef]
  12. J. Kamm, I. A. Lundin, M. Bastani, M. Sadeghi, and L. B. Pedersen. Joint inversion of gravity, magnetic, and petrophysical data—A case study from a gabbro intrusion in Boden, Sweden. Geophysics 2015, 80, B131–B152. [Google Scholar] [CrossRef]
  13. Y. Deng, W. Levandowski, and T. Kusky. Lithospheric density structure beneath the Tarim basin and surroundings, northwestern China, from the joint inversion of gravity and topography. Earth and Planetary Science Letters 2017, 460, 244–254. [Google Scholar] [CrossRef]
  14. Q. Liang, C. Chen, and Y. Li. 3-D inversion of gravity data in spherical coordinates with application to the GRAIL data. Journal of Geophysical Research: Planets 2014, 119, 1359–1373. [Google Scholar] [CrossRef]
  15. Y. Zhong, Z. Ren, J. Tang, Y. Lin, B. Chen, Y. Deng, and Y. Jiang. Constrained gravity inversion with adaptive inversion grid refinement in spherical coordinates and its application to mantle structure beneath Tibetan Plateau. Journal of Geophysical Research: Solid Earth 2022, 127, e2021JB022916. [Google Scholar] [CrossRef]
  16. X. Li, and M. Chouteau. Three-Dimensional Gravity Modeling In All Space. Surveys in Geophysics 1998, 19, 339–368. [Google Scholar] [CrossRef]
  17. D. Nagy, G. Papp, and J. Benedek. The gravitational potential and its derivatives for the prism. Journal of Geodesy 74, no. 7- 2000, 8, 552–560.
  18. Förste, S. Bruinsma, F. Flechtner, O. Abrykosov, C. Dahle, J. Marty, J. Lemoine, R. Biancale, F. Barthelmes, and K. Neumayer, "EIGEN-6C3-The latest Combined Global Gravity Field Model including GOCE data up to degree and order 1949 of GFZ Potsdam and GRGS Toulouse." G51A-0860.
  19. N. K. Pavlis, S. A. Holmes, S. C. Kenyon, and J. K. Factor. The development and evaluation of the Earth Gravitational Model 2008 (EGM2008). Journal of geophysical research: solid earth 2012, 117, no–B4. [Google Scholar]
  20. S. Goossens, K. Matsumoto, Q. Liu, F. Kikuchi, K. Sato, H. Hanada, Y. Ishihara, H. Noda, N. Kawano, and N. Namiki. Lunar gravity field determination using SELENE same-beam differential VLBI tracking data. Journal of Geodesy 2011, 85, 205–228. [Google Scholar] [CrossRef]
  21. S. Konopliv, R. S. Park, D. N. Yuan, S. W. Asmar, M. M. Watkins, J. G. Williams, E. Fahnestock, G. Kruizinga, M. Paik, and D. Strekalov. High-resolution lunar gravity fields from the GRAIL primary and extended missions. Geophysical Research Letters 2014, 41, 1452–1458. [Google Scholar] [CrossRef]
  22. M. T. Zuber, D. E. Smith, M. M. Watkins, S. W. Asmar, A. S. Konopliv, F. G. Lemoine, H. J. Melosh, G. A. Neumann, R. J. Phillips, and S. C. Solomon. Gravity field of the Moon from the Gravity Recovery and Interior Laboratory (GRAIL) mission. Science 2013, 339, 668–671. [Google Scholar]
  23. Genova, S. Goossens, F. G. Lemoine, E. Mazarico, G. A. Neumann, D. E. Smith, and M. T. Zuber. Seasonal and static gravity field of Mars from MGS, Mars Odyssey and MRO radio science. Icarus 2016, 272, 228–245. [Google Scholar] [CrossRef]
  24. S. Konopliv, R. S. Park, and W. M. Folkner. An improved JPL Mars gravity field and orientation from Mars orbiter and lander tracking data. Icarus 2016, 274, 253–260. [Google Scholar] [CrossRef]
  25. E. G. Anderson. The effect of topography on solutions of Stokes' problem. UNSW Sydney, 1976.
  26. X. L. Deng, and N. Sneeuw. Analytical Solutions for Gravitational Potential up to Its Third-order Derivatives of a Tesseroid, Spherical Zonal Band, and Spherical Shell. Surveys in Geophysics 2023, 44, 1125–1173. [Google Scholar] [CrossRef]
  27. T. Grombein, K. Seitz, and B. Heck. Optimized formulas for the gravitational field of a tesseroid. Journal of Geodesy 2013, 87, 645–660. [Google Scholar] [CrossRef]
  28. Heck, and K. Seitz. A comparison of the tesseroid, prism and point-mass approaches for mass reductions in gravity field modelling. Journal of Geodesy 2007, 81, 121–136. [Google Scholar] [CrossRef]
  29. M. Asgharzadeh, R. Von Frese, H. Kim, T. Leftwich, and J. Kim. Spherical prism gravity effects by Gauss-Legendre quadrature integration. Geophysical Journal International 2007, 169, 1–11. [Google Scholar] [CrossRef]
  30. F. Ouyang, L.-w. Chen, and Z.-g. Shao. Fast calculation of gravitational effects using tesseroids with a polynomial density of arbitrary degree in depth. Journal of Geodesy 2022, 96, 97. [Google Scholar] [CrossRef]
  31. F. Wild-Pfeiffer. A comparison of different mass elements for use in gravity gradiometry. Journal of Geodesy 2008, 82, 637–653. [Google Scholar] [CrossRef]
  32. L. Uieda, V. C. Barbosa, and C. Braitenberg. Tesseroids: Forward-modeling gravitational fields in spherical coordinates. Geophysics 2016, 81, F41–F48. [Google Scholar] [CrossRef]
  33. X. Zeng, X. Wan, M. Lin, and W. Wang. Gravity field forward modelling using tesseroids accelerated by Taylor series expansion and symmetry relations. Geophysical Journal International 2022, 230, 1565–1584. [Google Scholar] [CrossRef]
  34. X. Wang, J. X. Wang, J. Liu, and J. Li. Fast 3D magnetic anomaly forward modelling based on integral equation. IEEE Transactions on Geoscience and Remote Sensing, 2023.
  35. M. Eshagh. Non-singular expressions for the vector and the gradient tensor of gravitation in a geocentric spherical frame. Computers & Geosciences 2008, 34, 1762–1768. [Google Scholar]
  36. M. Petrovskaya, and A. Vershkov. Non-singular expressions for the gravity gradients in the local north-oriented and orbital reference frames. Journal of Geodesy 2006, 80, 117–127. [Google Scholar] [CrossRef]
  37. R. Parker. The rapid calculation of potential anomalies. Geophysical Journal International 1973, 31, 447–455. [Google Scholar] [CrossRef]
  38. W. Oldenburg. The inversion and interpretation of gravity anomalies. Geophysics 1974, 39, 526–536. [Google Scholar] [CrossRef]
  39. M. A. Wieczorek, and R. J. Phillips. Potential anomalies on a sphere: Applications to the thickness of the lunar crust. Journal of Geophysical Research: Planets 103, 1, 1715-1724.
  40. Y. Ishihara, S. Y. Ishihara, S. Goossens, K. Matsumoto, H. Noda, H. Araki, N. Namiki, H. Hanada, T. Iwata, S. Tazawa, and S. Sasaki. Crustal thickness of the Moon: Implications for farside basin structures. Geophysical Research Letters 36, 2009.
  41. M. A. Wieczorek, G. A. Neumann, F. Nimmo, W. S. Kiefer, G. J. Taylor, H. J. Melosh, R. J. Phillips, S. C. Solomon, J. C. Andrews-Hanna, and S. W. Asmar. The crust of the Moon as seen by GRAIL. Science 2013, 339, 671–675. [Google Scholar]
  42. Root, P. Novák, D. Dirkx, M. Kaban, W. van der Wal, and L. Vermeersen. On a spectral method for forward gravity field modelling. Journal of Geodynamics 2016, 97, 22–30. [Google Scholar] [CrossRef]
  43. Sprlak, M. , Han, S., -C., Featherstone, W., and E.. Forward modelling of global gravity fields with 3D density structures and an application to the high-resolution (similar to 2 km) gravity fields of the Moon. Journal of Geodesy, 2018.
  44. M. Šprlák, S.-C. Han, and W. Featherstone. Spheroidal forward modelling of the gravitational fields of 1 Ceres and the Moon. Icarus 2020, 335, 113412. [Google Scholar] [CrossRef]
  45. M. Rexer, C. Hirt, S. Claessens, and R. Tenzer. Layer-Based Modelling of the Earth's Gravitational Potential up to 10-km Scale in Spherical Harmonics in Spherical and Ellipsoidal Approximation. Surveys in Geophysics 2016, 37, 1–40. [Google Scholar]
  46. G. Ramillien. Density interface topography recovered by inversion of satellite gravity gradiometry observations. Journal of Geodesy 2017, 91, 881–895. [Google Scholar] [CrossRef]
  47. Álvarez, M. Gimenez, C. Braitenberg, and A. Folguera. GOCE satellite derived gravity and gravity gradient corrected for topographic effect in the South Central Andes region. Geophysical Journal International 2012, 190, 941–959. [Google Scholar] [CrossRef]
  48. S. Casotto, and E. Fantino. Gravitational gradients by tensor analysis with application to spherical coordinates. Journal of Geodesy 2009, 83, 621–634. [Google Scholar] [CrossRef]
  49. B. Hofmann-Wellenhof, and H. Moritz, Physical geodesy: Springer Science & Business Media, 2006.
  50. J. Du, C. Chen, V. Lesur, and L. Wang. Non-singular spherical harmonic expressions of geomagnetic vector and gradient tensor fields in the local north-oriented reference frame. Geoscientific Model Development Discussions 2014, 7, 8477–8503. [Google Scholar]
  51. L. Wu, and G. Tian. High-precision Fourier forward modeling of potential fields. Geophysics 2014, 79, G59–G68. [Google Scholar] [CrossRef]
  52. G. Zhao, B. Chen, L. Chen, J. Liu, and Z. Ren. High-accuracy 3D Fourier forward modeling of gravity field based on the Gauss-FFT technique. Journal of Applied Geophysics 2018, 150, 294–303. [Google Scholar] [CrossRef]
  53. M. A. Wieczorek, and M. Meschede. SHTools: Tools for working with spherical harmonics. Geochemistry, Geophysics, Geosystems 2018, 19, 2574–2592. [Google Scholar] [CrossRef]
  54. M. Frigo, and S. G. Johnson. The Design and Implementation of FFTW3. Proceedings of the IEEE 2005, 93, 216–231. [Google Scholar] [CrossRef]
  55. P. Ditmar, J. Kusche, and R. Klees. Computation of spherical harmonic coefficients from gravity gradiometry data to be acquired by the GOCE satellite: regularization issues. Journal of Geodesy 2003, 77, 465–477. [Google Scholar] [CrossRef]
  56. G. A. Neumann, M. T. Zuber, M. A. Wieczorek, J. W. Head, D. M. Baker, S. C. Solomon, D. E. Smith, F. G. Lemoine, E. Mazarico, and T. J. Sabaka. Lunar impact basins revealed by Gravity Recovery and Interior Laboratory measurements. Science advances 2015, 1, e1500852. [Google Scholar]
  57. Y. Li, and D. W. Oldenburg. 3-D inversion of magnetic data. Geophysics 1996, 61, 394–408. [Google Scholar] [CrossRef]
  58. E. Smith, M. T. E. Smith, M. T. Zuber, G. A. Neumann, F. G. Lemoine, E. Mazarico, M. H. Torrence, J. F. McGarry, D. D. Rowlands, J. W. Head III, and T. H. Duxbury. Initial observations from the lunar orbiter laser altimeter (LOLA). Geophysical Research Letters 37, 2010.
  59. G. Haines. Spherical cap harmonic analysis. Journal of Geophysical Research: Solid Earth 90, no. B 1985, 3, 2583–2591.
  60. M. Korte, and R. Holme. Regularization of spherical cap harmonics. Geophysical Journal International 2003, 153, 253–262. [Google Scholar] [CrossRef]
  61. Thébault, J. Schott, and M. Mandea. Revised spherical cap harmonic analysis (R-SCHA): Validation and properties. Journal of Geophysical Research: Solid Earth 2006, 111, B1. [Google Scholar]
  62. Zhao, S. Liang. High-Efficient Forward Modeling Method of Gravitational Fields in Spherical Harmonic Domain with Application to Lunar Topography. figshare. Dataset. 2024. [CrossRef]
  63. P. Wessel, J. Luis, L. Uieda, R. Scharroo, F. Wobbe, W. H. Smith, and D. Tian. The generic mapping tools version 6. Geochemistry, Geophysics, Geosystems 2019, 20, 5556–5564. [Google Scholar]
Preprints 113594 g001
Figure 1. Sketch map of discretization of a global spherical shell (a) and its observation points (b).
Figure 1. Sketch map of discretization of a global spherical shell (a) and its observation points (b).
Preprints 113594 g001
Preprints 113594 g002
Figure 2. Sketch map of a single layer global spherical shell model with radius ranging from 1638 to 1738 km, and density ρ = 1000 kg/m3. The observation point P is located on a sphere with the height h from the outer sphere.
Figure 2. Sketch map of a single layer global spherical shell model with radius ranging from 1638 to 1738 km, and density ρ = 1000 kg/m3. The observation point P is located on a sphere with the height h from the outer sphere.
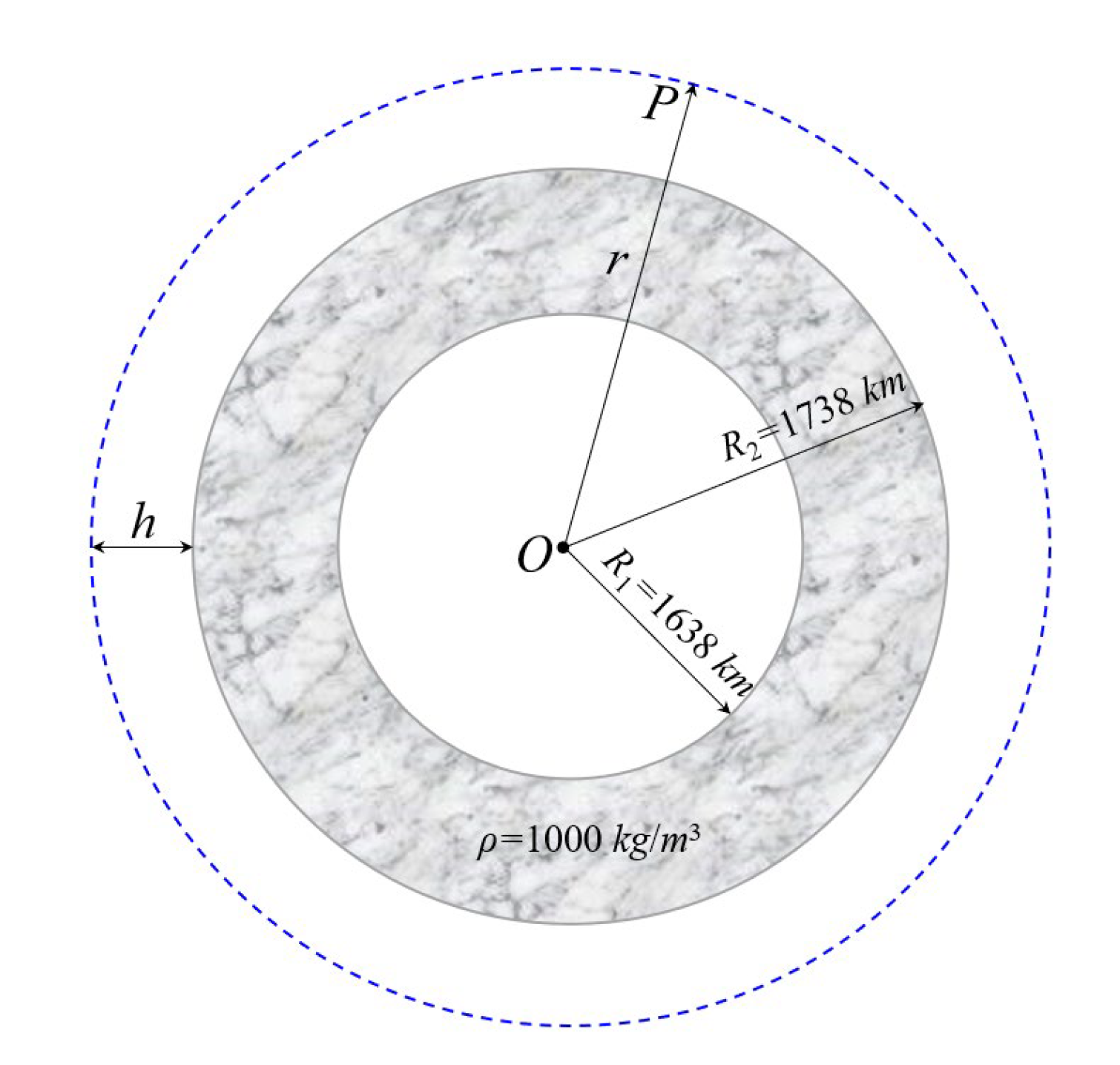
Preprints 113594 g002
Preprints 113594 g003
Figure 3. Comparison of relative computational times of (a) gz and (b) gzz by the two spatial domain methods and the proposed method.
Figure 3. Comparison of relative computational times of (a) gz and (b) gzz by the two spatial domain methods and the proposed method.
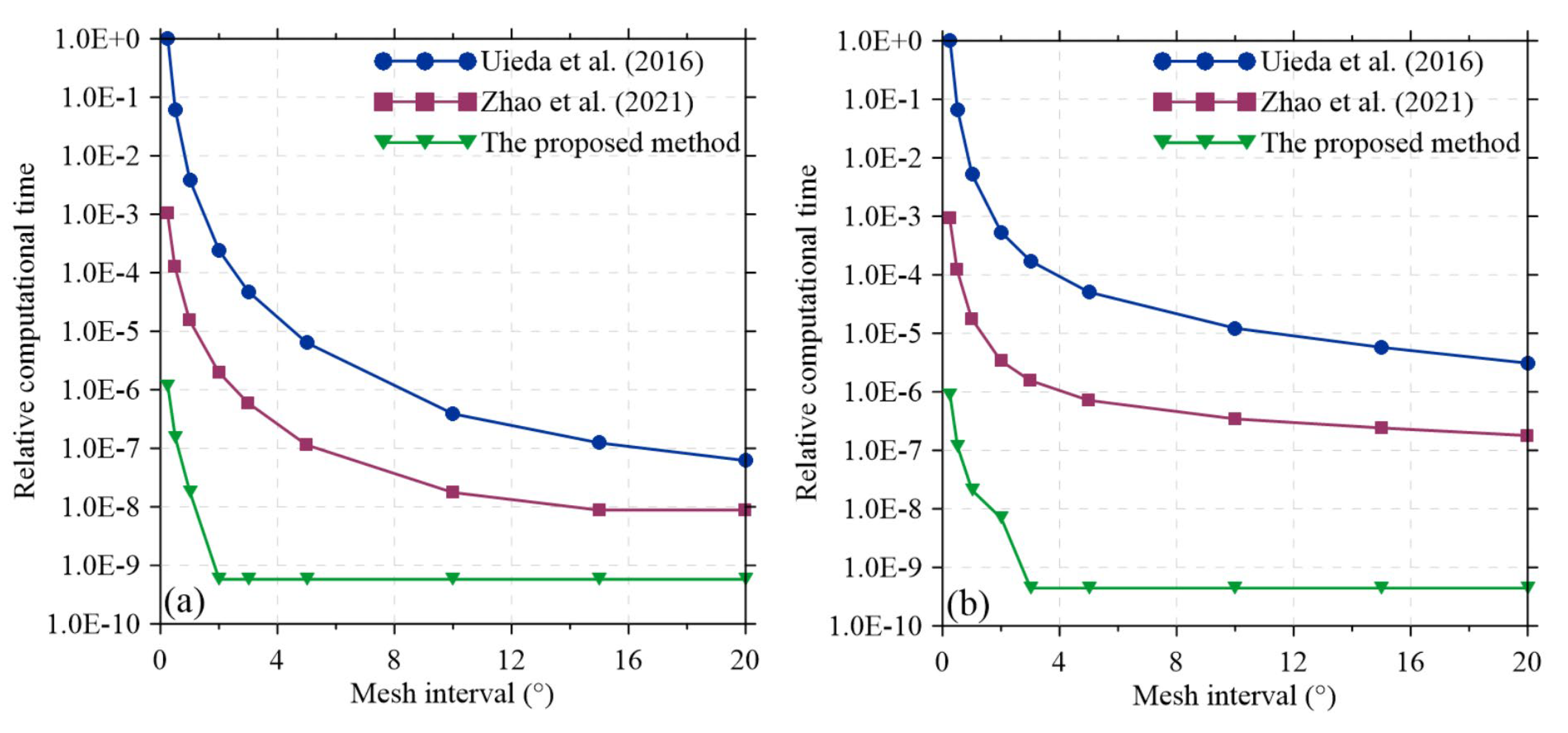
Preprints 113594 g003
Preprints 113594 g004
Figure 4. Distribution of absolute error of gz in (a) and (b), and gzz in (c) and (d), where (a) and (c) are derived from the spatial domain methods, (b) and (d) are from the proposed spherical harmonic domain method.
Figure 4. Distribution of absolute error of gz in (a) and (b), and gzz in (c) and (d), where (a) and (c) are derived from the spatial domain methods, (b) and (d) are from the proposed spherical harmonic domain method.
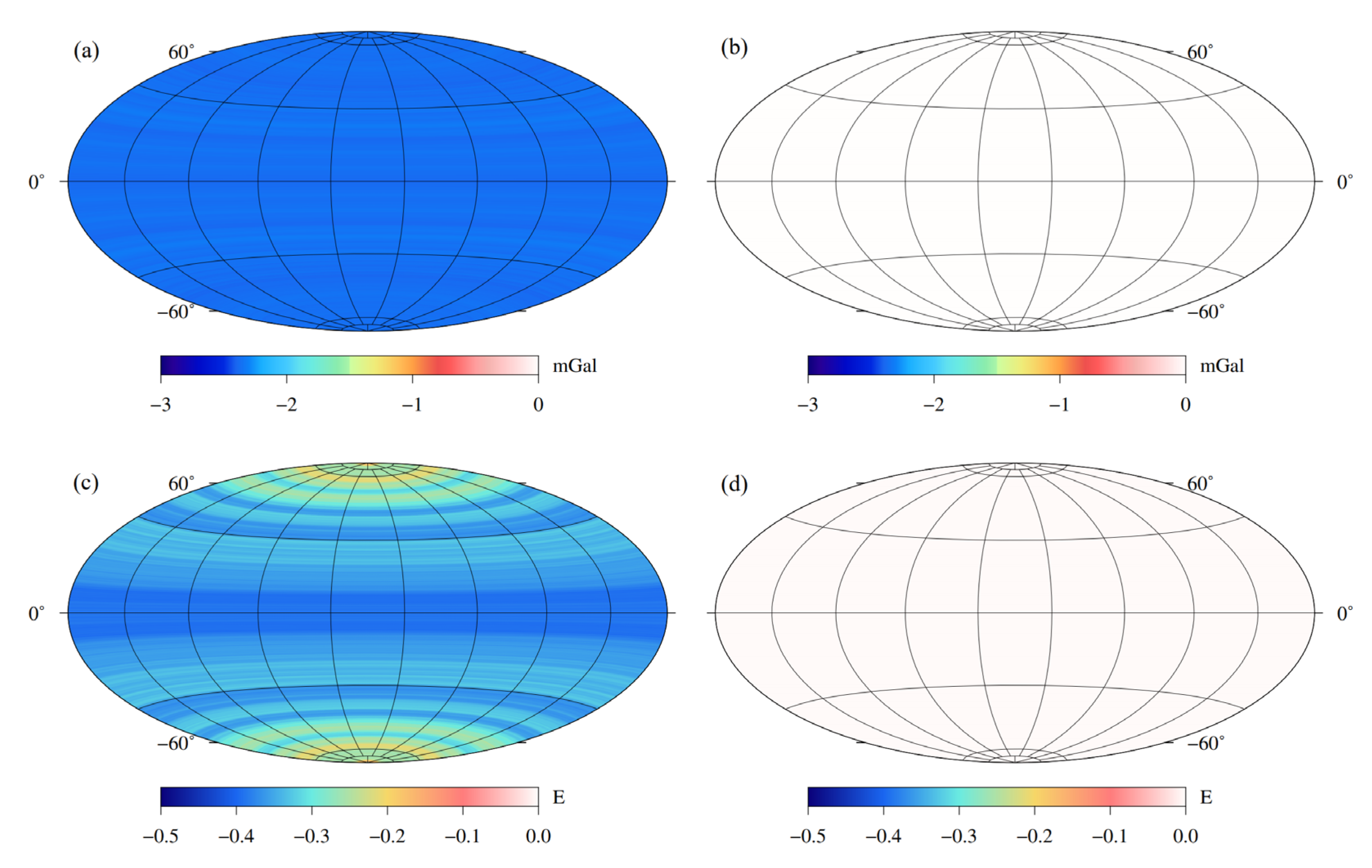
Preprints 113594 g004
Preprints 113594 g005
Figure 5. Density distribution of the complex synthetic model at the radius of 1682.5 km.
Figure 5. Density distribution of the complex synthetic model at the radius of 1682.5 km.
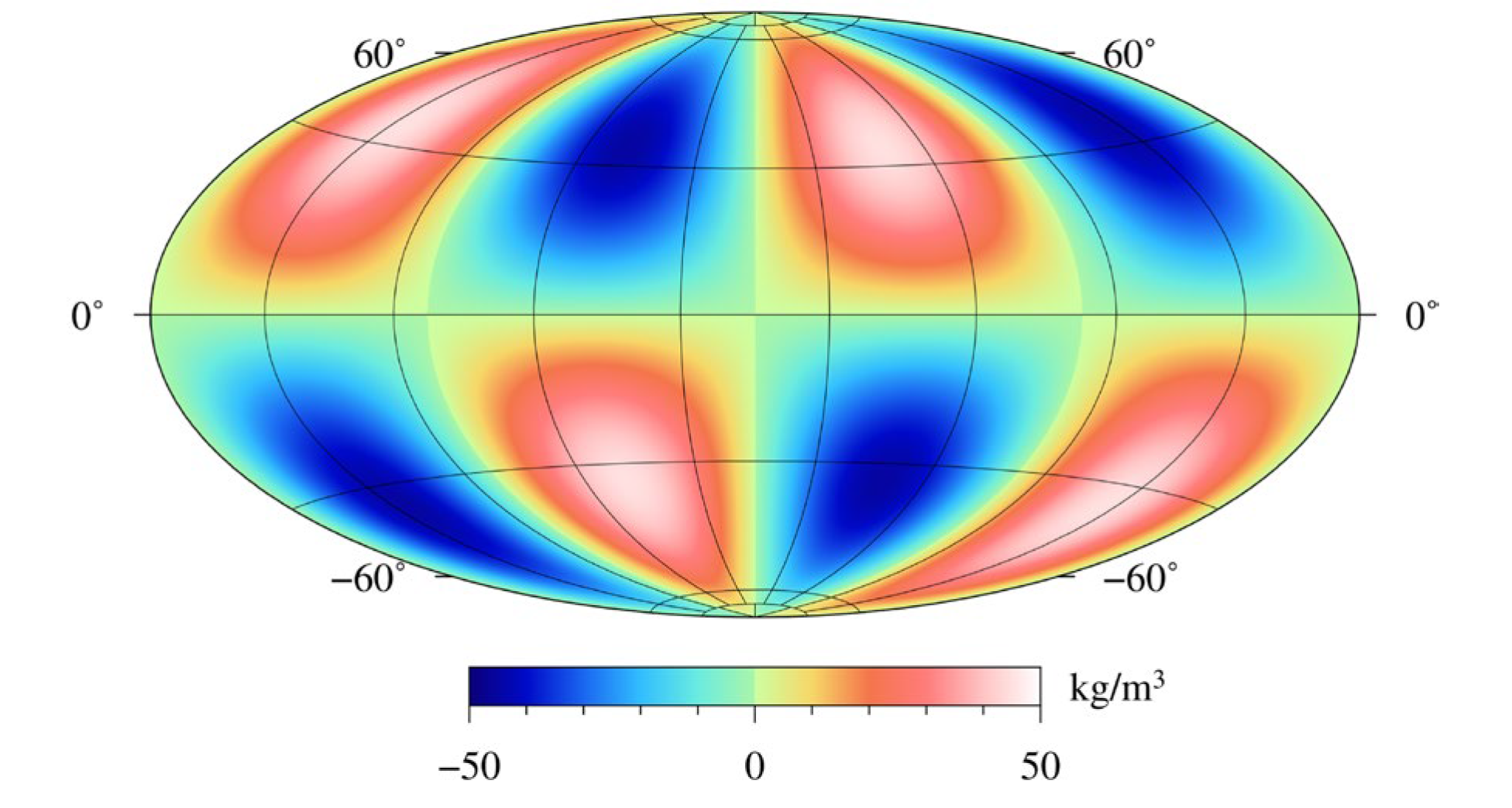
Preprints 113594 g005
Preprints 113594 g006
Figure 6. The gravitational responses of gz in (a) and gzz in (b) of this complex model derived from the spatial domain methods, with (c) and (d) the differences of gz and gzz between the two methods, respectively.
Figure 6. The gravitational responses of gz in (a) and gzz in (b) of this complex model derived from the spatial domain methods, with (c) and (d) the differences of gz and gzz between the two methods, respectively.
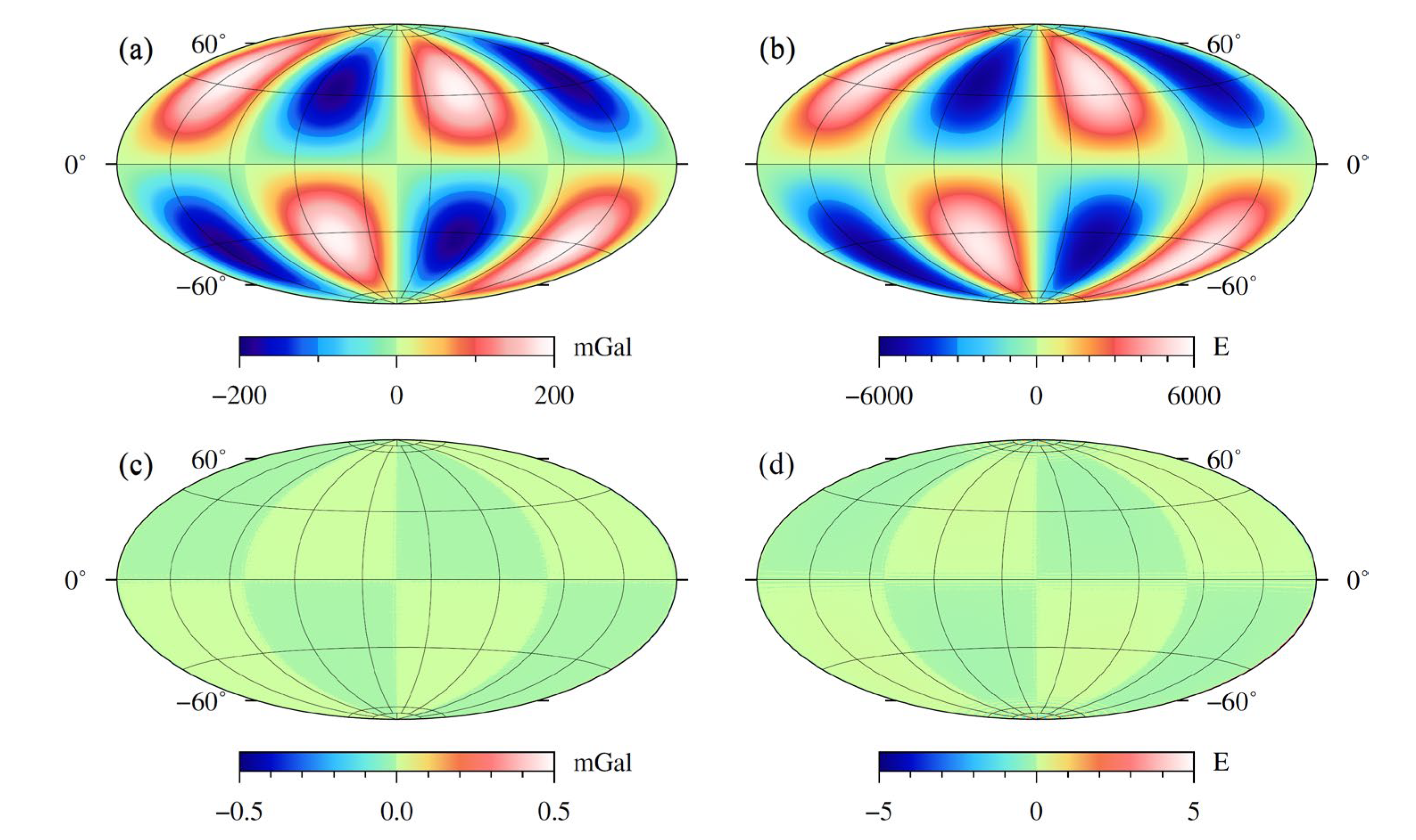
Preprints 113594 g006
Preprints 113594 g007
Figure 7. (a) Free-air gravity anomaly at 10 km height; (b) topography of the Moon.
Figure 7. (a) Free-air gravity anomaly at 10 km height; (b) topography of the Moon.
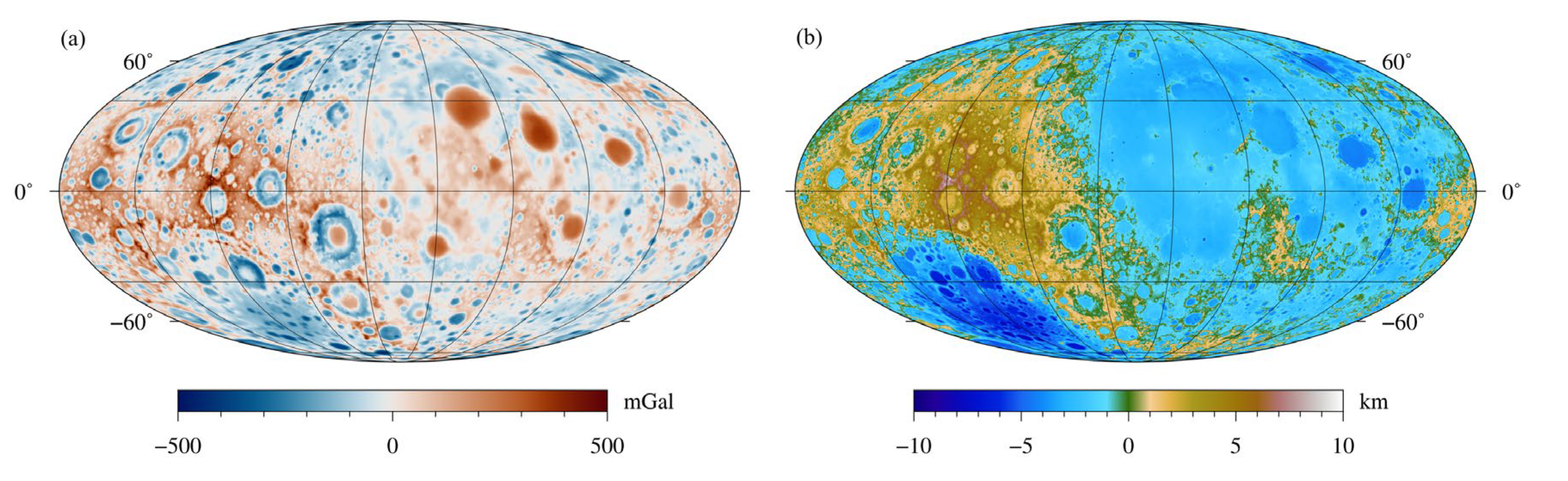
Preprints 113594 g007
Preprints 113594 g008
Figure 8. Sketch map of the discretization of the terrain in radial direction. The dark gray represents mountains with a correction density of 2560 kg/m3, while the light blue represents basins with a correction density of −2560 kg/m3. Red dots indicate that the tesseroids are outside the terrain with a correction density of 0 kg/m3, while blue dots indicate that the tesseroids are inside the terrain.
Figure 8. Sketch map of the discretization of the terrain in radial direction. The dark gray represents mountains with a correction density of 2560 kg/m3, while the light blue represents basins with a correction density of −2560 kg/m3. Red dots indicate that the tesseroids are outside the terrain with a correction density of 0 kg/m3, while blue dots indicate that the tesseroids are inside the terrain.
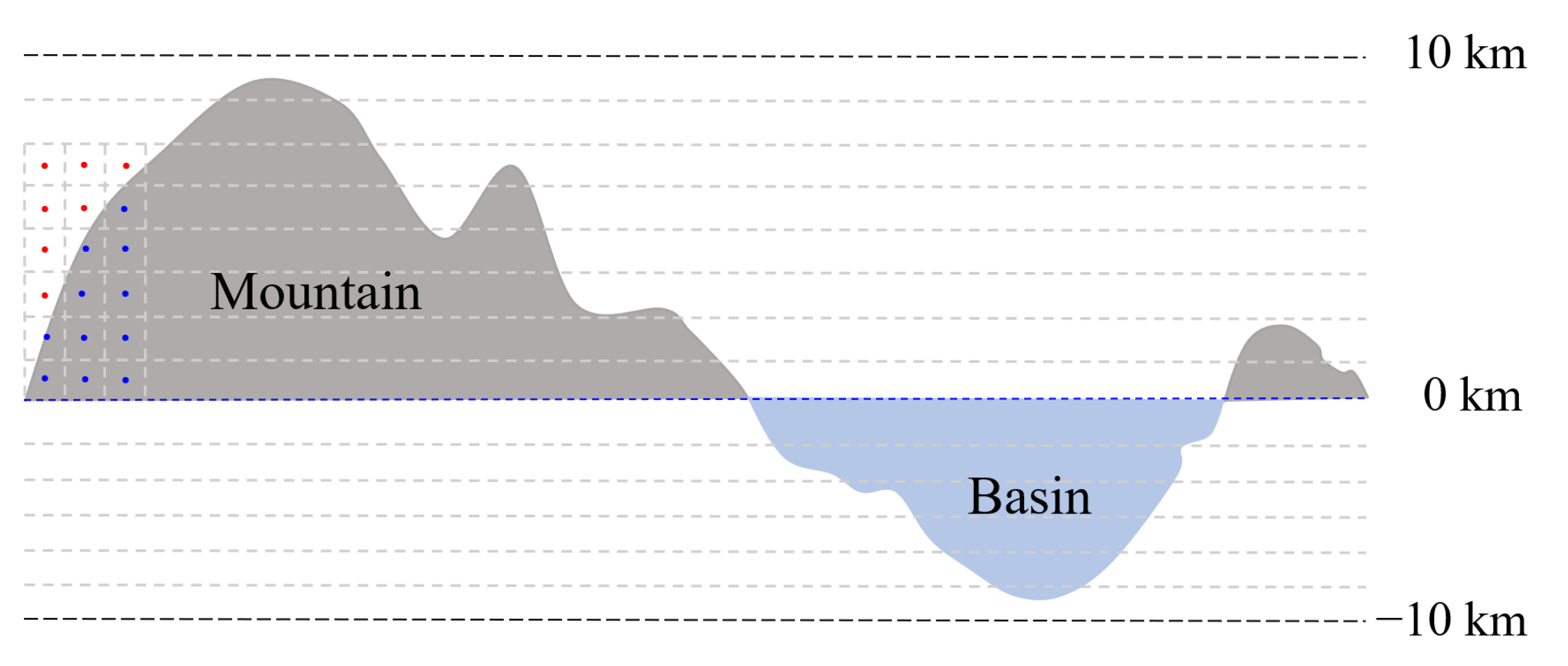
Preprints 113594 g008
Preprints 113594 g009
Figure 9. Gravity effects of the lunar topography calculated by (a) the spatial domain method and (b) the proposed spherical harmonic domain method.
Figure 9. Gravity effects of the lunar topography calculated by (a) the spatial domain method and (b) the proposed spherical harmonic domain method.
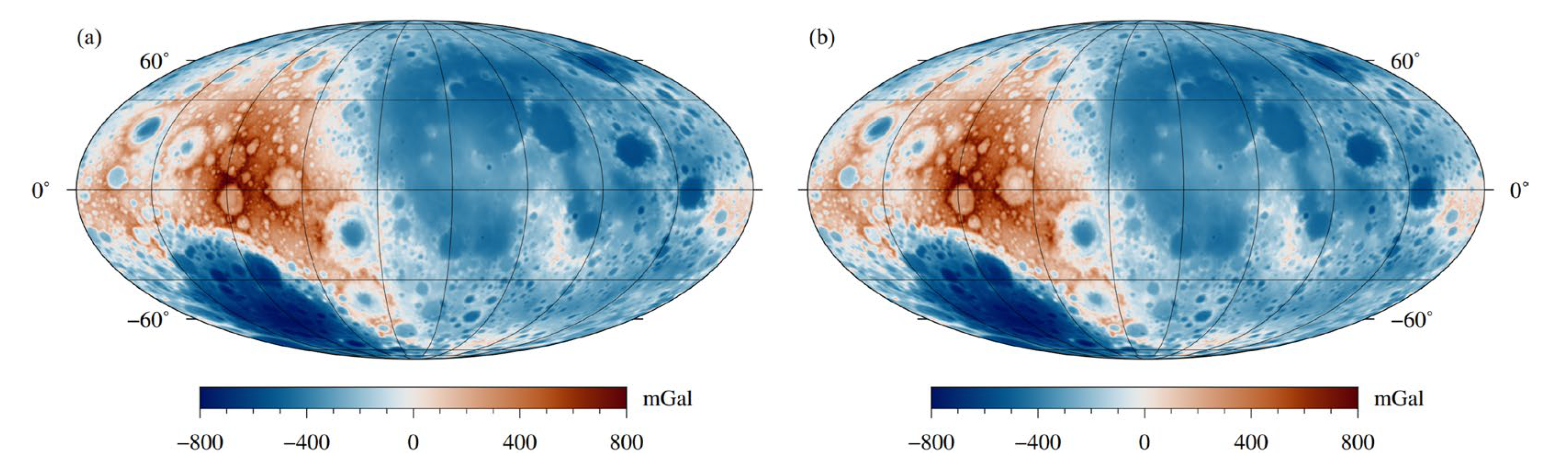
Preprints 113594 g009
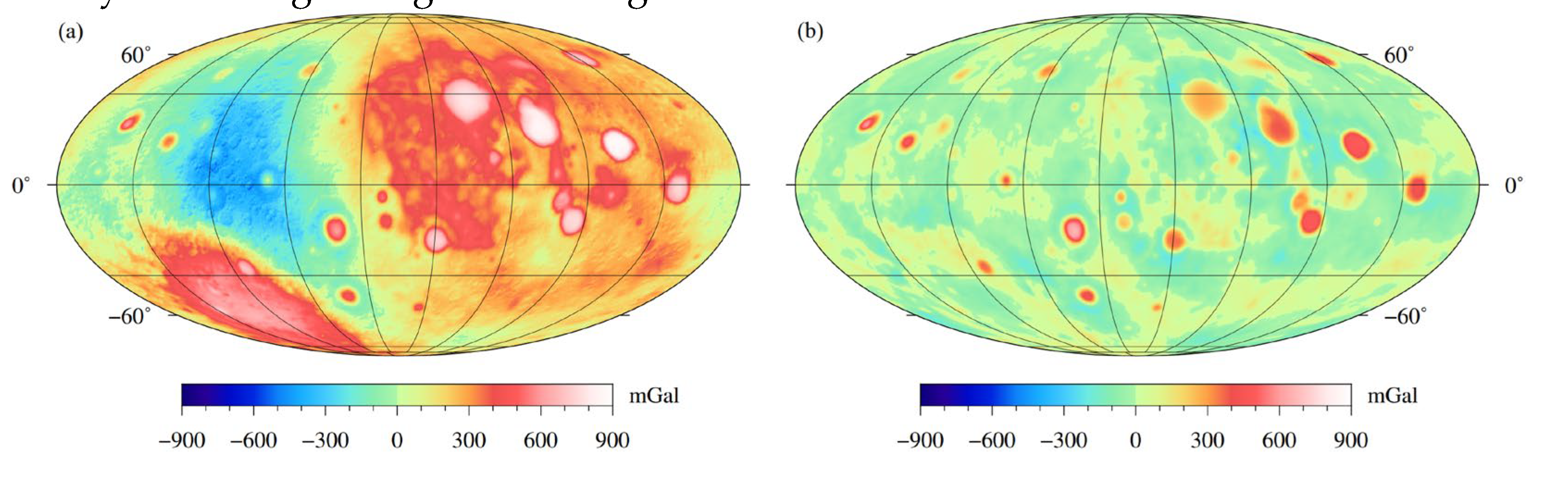
Preprints 113594 g010
Figure 10. (a) Bouguer anomaly by removing the topography correction in Figure 9a from the free-air gravity anomaly in Figure 7a; (b) Bouguer gravity anomaly obtained by using 6−450 degrees of spherical harmonic coefficients.
Figure 10. (a) Bouguer anomaly by removing the topography correction in Figure 9a from the free-air gravity anomaly in Figure 7a; (b) Bouguer gravity anomaly obtained by using 6−450 degrees of spherical harmonic coefficients.
Preprints 113594 g010
Table 1. Procedures of the proposed method for gz component.
Table 1. Procedures of the proposed method for gz component.
Algorithm: Gravity forward modeling in spherical harmonic domain
Input: 3D density distributions of each layer
1. Do k = 1 to Nz, and initialize gz = 0
 2. Calculate ρ ¯ l m 1 ( r ′ k ) and ρ ¯ l m 2 ( r ′ k ) ;
 3. Multiply the factor ( l + 1 ) ( 2 l + 1 ) ( l + 3 ) r l + 2 [ ( r ′ k + 1 2 Δ r ) l + 3 − ( r ′ k − 1 2 Δ r ) l + 3 ] to step 1;
 4. Spherical harmonic synthesis of the result in step 3 to get gz(k);
 5. gz = gz + gz(k);
6. End Do
Output: 2D distribution of gz component.
Table 2. Comparison of computational time and the maximum relative errors of gz and gzz by the two spatial domain methods and the proposed method when the mesh interval is 0.25°. The test is implemented with Intel Core i7−11800H CPU and 16 GB RAM.
Table 2. Comparison of computational time and the maximum relative errors of gz and gzz by the two spatial domain methods and the proposed method when the mesh interval is 0.25°. The test is implemented with Intel Core i7−11800H CPU and 16 GB RAM.
Methods Computational time (s) Maximum relative error (%)
gz gzz gz gzz
Uieda et al. [32] 1850759.53 2256446.96 3.12E-02 5.15E-04
Zhao et al. [5] 1880.19 2148.41 3.12E-02 5.15E-04
The proposed method 1.96 1.96 6.15E-06 3.38E-06
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated