Prerpints.org logo
Preprint
Article

Line Loss Comprehensive Evaluation Management System Based on Knowledge Graph

Altmetrics

Downloads

53

Views

22

Comments

0

This version is not peer-reviewed

Submitted:

01 August 2024

Posted:

02 August 2024

You are already at the latest version

Alerts
Abstract
This study constructs a comprehensive line loss management evaluation knowledge graph, considering the impact of various factors such as power grid structure characteristics, equipment's physical parameters, power grid operation characteristics, electricity consumption features, and natural conditions. It establishes the association between line loss characteristics and line loss retrieval and configures the data source for line loss management evaluation indicators. Based on Principal Component Analysis (PCA), this study selects comprehensive evaluation indicators for line loss management, verifies the rationality of the indicators, and proposes an integrated evaluation method for municipal power grid line loss management. A full-process composite evaluation method based on DEMATEL-Entropy Weight-TOPSIS is constructed, and the accuracy of the evaluation method is verified through ablation experiments. The TOPSIS analysis method is applied to empirical research on cross-sectional data from a city in Guangxi from 2012 to 2022 to validate the evaluation system's effectiveness, scientific nature, and objectivity. The case analysis shows that the line loss evaluation index system established in this paper effectively reduces the redundancy of line loss data and can objectively and rationally reflect the actual status of line loss management work, serving as a basis for decision-making in future line loss management evaluations.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

Achieving carbon peak and neutrality is a major strategic decision made by the state to coordinate domestic and international situations, and line loss management is of great importance to the development of the country and the power grid. Reducing line loss can improve the efficiency of the power system, reduce power loss, improve the quality of power supply, and reduce the operating costs of the power grid. This not only facilitates the sustainable development of the power industry but also ensures the country's energy security and economic development [1]. At the same time, line loss management can also promote technological progress and innovation in the power industry, driving the power industry towards intelligent, digital, efficient, and green development and enhancing the competitiveness and core competitiveness of the power industry [2,3]. The line loss management evaluation methods and indicators used by power grid companies have different focuses. Reference [4] constructs a comprehensive evaluation system for line loss management of the power grid, combining subjective and objective weights to score indicators, ensuring the authenticity and reliability of the indicator scores. Reference [5], based on the evaluation system for transformer interval line loss reduction strategies, establishes a line loss calculation model using convolutional neural networks to more accurately assess the line loss levels in the distribution transformer area. Zhong Xiaoqiang et al [6] trained with multiple dimensional electrical characteristic parameters of the substation area as inputs to obtain the corresponding deep learning line loss rate calculation model.
For the research above methods, whether using the comprehensive line loss rate as the evaluation standard or using the comprehensive line loss rate as the main criterion and the voltage-level line loss rate and the active line loss rate as supplementary criteria [7], the selection of indicators is either one-sided, without exploring the characteristics of line loss, or focuses on the analysis of line loss faults in the distribution network, or focuses on data analysis on the transformer side and the user side [8]. More consideration must be given to the dimensionality of line loss indicators and the extraction of knowledge from data of different structures [9]. At the same time, there needs to be a more comprehensive evaluation of the entire process of line loss in the power grid field. Some evaluation systems need to be more active in pursuing objective data results and discussing the impact of subjective human factors [10,11]. In addition, some analytical methods only choose subjective analyses based on expert evaluation, such as the Analytic Hierarchy Process or the Delphi method, making data detection susceptible to personal authority influence and lacking universality [12]. Therefore, a complete and refined line loss comprehensive evaluation management system based on a knowledge graph is essential.

2. Materials and MethodsConstructing the Knowledge Map of Line Loss Comprehensive Evaluation Management

In response to the issues of chaotic line loss indicators and unclear characteristics of these indicators, it is necessary to go through two steps in the knowledge graph: knowledge acquisition and knowledge extraction. In power systems with a complex knowledge structure, researchers have recently begun to use knowledge graphs to visualize knowledge and improve the efficiency of knowledge utilization. Rui Liu et al. [13], based on the complexity and real-time changes of power system operations and maintenance, proposed a process of multiple data handling, knowledge representation learning, and graph construction but did not point out its role in improving the operational efficiency of the power system in reference schemes and decision guidance; Chen Qian et al. [14] conducted a systematic review and summary of the application of Knowledge Graphs (KG) in fault diagnosis and handling in power systems, aiming to provide ample and comprehensive guidance for further research in this field; Chen Junbin et al. [15] reviewed the development of knowledge graph technology from aspects such as knowledge extraction, knowledge representation learning, knowledge mining, knowledge reasoning, knowledge fusion, and the application of knowledge graphs. They introduced the application and prospects of knowledge graphs in the scheduling operation of power systems in terms of assisting in optimized decision-making, vertical risk control, operational pattern analysis, optimizing model improvement experience, and superparameter tuning. However, they noted that there still needs to be more examining data correlation.
Existing research on domain-specific knowledge graphs shows varied technical architectures but commonly includes knowledge extraction, fusion, and processing [16]. This paper uses Principal Component Analysis (PCA) for dimensionality reduction, feature extraction, data compression, and noise reduction on extensive indicator sets. The line loss evaluation entity graph integrates the power grid's network topology, planned losses, and management-related losses, facilitating entity querying and matching for the evaluation logic graph.
Guided by the principal component analysis in selecting indicator elements, the generation of the evaluation logic graph is directed [17]. The evaluation logic graph defined in this paper is a networked and structured expression of specific evaluation logic emphasized in the traditional evaluation system, such as evaluation indicators, indicator weights, and comprehensive evaluation criteria. According to the evaluation elements defined by the data model, the generation of the evaluation logic graph is guided by applying technical methods such as natural language processing, knowledge extraction, and information structuring. This allows for obtaining specific content such as the definition of evaluation indicators, indicator calculation methods, the design process of indicator weights, and evaluation criteria models.
The Figure 1 illustrates the construction process of the comprehensive line loss evaluation management knowledge graph.

3. Calculation and Analysis of Data in Line Loss Comprehensive Evaluation Management Entity Map

3.1. Regional Sample Acquisition and Verification

The widespread application of intelligent technologies such as information storage in power systems, along with the full-scale promotion of intelligent collection devices like smart meters in distribution networks, has enabled power grid enterprises to access an ever-increasing scale of electric power data. This provides robust support for acquiring sample data for line loss analysis [18]. The trend of regional line loss changes is influenced by factors such as line aging, circuit equipment, and user behavior, making the regional line loss changes highly complex. While line losses may appear to lack a discernible pattern, specific characteristic patterns of change within are known as chaotic features. The obtained sample data can be divided into static and dynamic data. Static data include the supply area, transformer model, number of conductors, line length, supply radius, rated capacity, residential households, non-residential households, theoretical line loss of the substation area, and reasonable range. Dynamic data include the supply quantity and the amount of lost electricity [19].
In the collected data samples, due to disturbances such as manual meter reading errors and collection equipment abnormalities, some data exhibit unreasonable formats and values. Therefore, before data processing, some data are excluded based on the attributes of the sample data and the line loss characteristic information they reflect.

3.2. Data Outlier Handling and Planning Are Unified

During the data collection process for electricity usage by metering equipment, unexpected factors such as statistical errors and equipment malfunctions can lead to anomalies or missing parameters in the data preserved by the power system. The incorporation of these anomalous data can affect the training of subsequent line loss calculation models, necessitating appropriate corrective measures. To identify anomalous data, this chapter, based on the characteristics of the data, assumes that dynamic data, such as electricity consumption, do not fluctuate significantly over the same period and can approximately satisfy the following formula [20]:
x t − 1 − x t = x t − x t + 1
For the collected dynamic data, the data set is set to X = x 1 , x 2 , … , x t − 1 , x t , x t + 1 , and the formula is used to calculate the t + 1 time value, and the calculated value is compared with the collected real value. If the difference between the real value and the calculated value exceeds the set threshold, the moment is an abnormal value, and the next abnormal value processing operation is performed.
Suppose that there is an abnormal value x i in a data sequence, take k adjacent points before and after the abnormal value ( k value is selected according to the actual situation, generally odd and not more than 20), and then calculate the average value as the correction value, the calculation is as follows:
x i = x i − k + ⋯ + x i − 1 + x i + 1 + ⋯ x i + k 2 K
In order to eliminate the difference of orders of magnitude, the values are mapped to [0,1] on the premise of retaining the numerical attributes. The commonly used processing methods are deviation standardization method and z-score standardization method. In this paper, the deviation standardization method is used to process the data, which not only retains the relationship existing in the original data, but also eliminates the influence of dimension and data value range on the subsequent analysis. Due to the large number of sample parameters obtained in the station area and the large difference in the order of magnitude between different parameters, the characteristic parameters can be standardized according to the formula to construct a standardized set X ∗ :
X ∗ = x i − x i − m i n x i − m a x − x i − m i n i = 1 , 2 , … , n

3.3. Knowledge Fusion Based on Principal Component Analysis

Knowledge fusion is the process of eliminating redundant and ambiguous information to provide a more comprehensive and high-quality knowledge graph. Knowledge fusion includes coreference resolution, entity disambiguation, and knowledge integration. Electrical energy loss occurs at various stages such as power transmission, transformation, distribution, and consumption. However, the complex topological structure and various abnormal line losses lead to confusion in line loss indicators. In the comprehensive evaluation knowledge graph of the power distribution network, knowledge integration involves merging the existing structured database of the power distribution network with the extracted comprehensive evaluation knowledge [21].
Based on the requirements above, this paper introduces a line loss feature indicator screening based on Principal Component Analysis (PCA), mapping the line loss feature quantities from a low-dimensional state space to a high-dimensional space to better explore the relationships between the feature quantities. In the process of knowledge extraction and knowledge fusion within the knowledge graph, based on the analysis mentioned above, each indicator is analyzed for its impact factors on the line loss rate, and the PCA method is used for the dimensionality reduction of the indicators [22]; finally, a composite evaluation method is adopted to construct the evaluation process, and then the classification evaluation prediction accuracy of the evaluation index system in the evaluation is calculated, thereby obtaining the impact coefficients of each indicator under this method.
As an important statistical method [23], principal component analysis can transform multi-index problems into fewer comprehensive indicators. For the sample space of order N × P , there are N samples, each sample contains P -dimensional indicators, and the matrix is expressed as :
X = x 11 x 12 ⋯ x 1 p x 21 x 22 ⋯ x 2 p ⋮ ⋮ ⋮ x N 1 x N 2 … x N p
The cumulative variance contribution rate of the first n principal components is:
ρ = ∑ i = 1 n λ i / ∑ j = 1 P λ j
When ρ ≥ 0.70, it can be considered that the first n principal components cover most of the information in the original data. Taking the contribution rate of each principal component as the weight, the comprehensive evaluation index is :
f = α 1 y 1 + α 2 y 2 + ⋯ + α n y n
In the formula : n is the number of principal components adopted ; α j is the contribution rate of the j principal component. The higher the comprehensive index of line loss is, the higher the base of line loss rate is due to various objective factors such as power grid structure, equipment status, load level and so on, which should be considered in evaluating its line loss management level.
Figure 2 illustrates the knowledge fusion based on principal component analysis, which has constructed a line loss index system. This system ensures that, with minimal loss of information, multiple indicators are transformed into a few comprehensive indicators through multivariate statistical analysis. After the selection is completed, the comprehensive indicators are called principal components, where each principal component is a linear combination of the original variables, and each principal component is unrelated to each other, making the principal components have superior performance compared to the original variables.

4. Construction of Line Loss Comprehensive Evaluation Management Logic Diagram

The line loss indicator system screened based on Principal Component Analysis has different focuses for each indicator. At the same time, these indicators may not fully address the actual municipal power grid line loss management system. In practical applications, it is often necessary to assign weights to each indicator to reflect the objectivity of the indicator evaluation results. There are differences in the evaluation indicators among different evaluation systems; some evaluation methods tend to be subjective to experts, while others are overly objective. Given the extensive and complex nature of existing line loss management, which can lead to data redundancy and bias, this paper proposes a composite evaluation method for line loss indicators based on a knowledge graph [24,25].
Faced with the above issues, this paper chooses to integrate the single evaluation method of line loss indicators, integrating the evaluation ideas between methods to achieve an "organic combination." The evaluation logic knowledge graph presents the abstract knowledge of power grid line losses in a composite evaluation manner, dividing the evaluation logic knowledge graph into three parts: evaluation index content, weight logic, and evaluation logic. This study's line loss evaluation target indicators can generally be divided into four dimensions: planning, management, operation, and technology. Evaluation results across different dimensions may exhibit extreme and outlier values, causing certain deviations in the overall indicator evaluation results. Therefore, this paper constructs a composite evaluation framework based on the DEMATEL subjective weighting method and the Entropy-Weight and TOPSIS objective weighting methods.

4.1. Fuzzy DEMATEL Method

DEMATEL (Decision-Making Trial and Evaluation Laboratory) method, called 'Decision-Making Trial and Evaluation Laboratory, 'is a method of system analysis based on graph theory and matrix. This method was proposed by Gabus and Fontela in 2010. The triangular fuzzy number in the fuzzy set theory is introduced to improve the DEMATEL method, which avoids the subjective differences of experts, quantifies the relationship between factors, deals with the fuzziness of the evaluation process, and ensures that the weight results are accurate and true.
By analyzing the logical relationship between the various elements in the system and the direct influence relationship between the phases, the degree of influence of each factor on other factors and the degree of influence are calculated, and the degree of cause and center of the sea factors are calculated. [26].
In [27,28], the influence degree D i and the influence degree C i of each factor are calculated by the comprehensive influence matrix Y ; and the centrality M i and the cause degree R i The centrality M i represents the importance of the index in the system. The greater the centrality is, the more important the index is. Finally, the subjective weights of the DEMATEL method can be obtained from the centrality M i :
w z i = M i ∑ i = 1 n M i
In the formula, d j represents the information entropy redundancy of the index j, and w j represents the weight of each index.

4.2. Entropy Weight Method Objective Weighting

Claude Elwood Shannon first introduced entropy in information theory, and it has since been widely applied in various fields such as engineering technology and socio-economics[29]. The entropy weight method can determine objective weights based on the variability of line loss indicators. Generally speaking, the smaller the information entropy of an indicator, the greater the variability of its value, the more information it provides, and the greater its role in comprehensive evaluation, hence its more significant weight. Conversely, the larger the information entropy of an indicator, the smaller the variability of its value, the less information it offers, and the smaller its role in comprehensive line loss evaluation, resulting in a smaller weight [29].
e j = − k ∑ i = 1 n p i j ln p i j , j = 1 , … , m
In the formula, e j represents the entropy value of the jth index, and p i j sample value accounts for the proportion of the index.
w j = 1 − e j ∑ j = 1 m e j , j = 1 , … , m
In the formula, d j represents the information entropy redundancy of the index j, and w j represents the weight of each index.

4.3. Combined Evaluation Analysis Based on DEMATEL-Entropy Weight-TOPSIS

The DEMATEL method is proposed for filtering the main elements of complex systems and simplifying the process of system structure analysis[30]. This methodology fully utilizes the experience and knowledge of experts to deal with complex issues, especially for systems with uncertain relationships between elements. However, the DEMATEL evaluation is more inclined towards subjective expert factors and is susceptible to personal biases. Therefore, the Entropy-Weight objective weighting method is proposed. The Entropy-Weight method can objectively reflect the differences and importance among various indicators, providing more accurate computational results. However, indicators must conform as closely as possible to a normal distribution, do not handle outliers well, and do not account for the interdependencies between indicators. Thus, based on an analysis of the connotations of low-carbon competitiveness, this paper integrates multiple evaluation approaches, combining subjective and objective evaluation methods, and applies a composite of various evaluation methods. This integration aims to complement each other, enabling a comprehensive, scientific, and objective assessment of regional line loss competitiveness, ensuring that the indicator weights reflect the objectivity of the data, and guarantee the predictability of the indicator system.
The TOPSIS (Technique for Order Preference by Similarity to an Ideal Solution) method is a sorting technique that approximates an ideal solution. It ranks a finite set of evaluation objects based on their closeness to an idealized target, making it a commonly used and effective evaluation method in multi-criteria decision analysis [30]. Because this method can objectively rank evaluation objects in a scientifically sound and reasonable manner, scholars have widely adopted it for evaluating sample data. However, the conventional TOPSIS method does not consider the weights of individual indicators; instead, it uses a one-dimensional qualitative approach that averages the weights of evaluation indicators for ranking. This can lead to a deviation between the evaluation results and objective values. This paper will use the weighted TOPSIS method, based on the combined subjective and objective weight results calculated earlier in the paper, to construct a DEMATEL-Entropy Weight-TOPSIS evaluation approach. This approach will be used to calculate the scores for the competitiveness of line loss in Nanning City over the years, with the specific calculation process as follows:
With the same trend and index dimensionless for positive and negative indicators, the normalized formula is :
a i j = ( x i j − min x i j ) / ( max x i j − min x i j )
Calculate the distance between each evaluation object and the optimal scheme and the worst scheme D i + and D i − :
D i + = ∑ j = 1 m w j   ( a i j − a i j + ) 2
D i − = ∑ j = 1 m w j   ( a i j − a i j − ) 2
Calculate the closeness of each evaluation object to the optimal scheme and the worst scheme C i :
C i = D i − D i + + D i −
The content of the evaluation index part involves relationships between various index entities that are primarily parallel or inclusive. The specific attributes of each index include the calculation method, actual value, index weight, and corresponding evaluation. The data for index calculation can be obtained through data collection and preprocessing methods. For instance, when calculating indices such as the proportion of overloaded lines, voltage qualification rate, power supply reliability, and fault outage rate, information such as the total number of lines, number of users, outage conditions of each user, and voltage status at voltage monitoring points is required. Information such as the total number of lines and the number of users is stored in the power grid equipment database and user information database, and can be directly retrieved from the database. The voltage status at voltage monitoring points and other required information must be derived from historical data through statistical calculations. Descriptive statistical methods can be utilized, and corresponding programs can be developed to achieve this.

 V. Construction of Line Loss Comprehensive Evaluation Management Case Map 

The comprehensive evaluation case graph of the power grid stores historical evaluation case information for the area, providing case characteristics such as historical evaluation targets, content, methods, models, and historical performance of various indices. This enables the calculation of similarity between cases over different time periods, facilitating performance comparison of the distribution network across temporal dimensions. On one hand, it can uncover potential issues, and on the other hand, cases with high similarity can provide reference for the current evaluation task.

5.1. Line Loss Index Model Based on Principal Component Analysis

Guangxi Power Grid Corporation, adhering to the "Line Loss Management Measures" required by China Southern Power Grid, divides the evaluation process into four levels: planning for loss reduction, management for loss reduction, operation for loss reduction, and technology for loss reduction, covering the entire process of line loss management. Line loss management, as a comprehensive indicator reflecting the high-quality development level of the power grid, involves professions such as power grid planning and construction, technology, operation, and marketing, which is equivalent to a "comprehensive physical examination" for the power grid. Traditional line loss rate statistics are affected by the inconsistency of meter reading periods, resulting in large monthly fluctuations and significant deviations between analysis conclusions and actual conditions, making the "physical examination report" not precise enough, and thus "prescribing medicine" becomes difficult. To address this challenge, Nanning Power Supply Bureau has fully implemented an innovative management of comprehensive line loss in the same period this year, relying on the unified meter reading cycle of supply and sales electricity quantity and "big data" support. For the first time, the comprehensive line loss rate of "day, month, and year" for power grid equipment has achieved index regression to the true and visual monitoring, realizing the modeling and analysis of the operating loss of the entire main grid and distribution grid equipment. Accurately finding the "problem" allows for precise measures for loss reduction, achieving the management effect of "lifting the Earth with a fulcrum."
To demonstrate the practicality of the indicator selection method in this paper, 104 sets of line loss indicator data from municipal power grid enterprises of the Southern Power Grid are taken as an example. The comprehensive line loss rate and the industry's evaluation of power grid enterprises' line loss are used to divide the 104 sets of data into 44 Class A enterprises and 60 Class B enterprises, and the composite evaluation analysis method is selected for verification.
The case study uses statistical calculation data of 104 power supply enterprises' line loss reduction impact indicators, each sample containing 13 indicators in four major categories: planning for loss reduction, management for loss reduction, operation for loss reduction, and technology for loss reduction. The cumulative contribution rate of these 37 principal components has reached 100.00%, and the cumulative contribution rate of the first 13 principal components has reached 70.211%, calculating the comprehensive line loss reduction indicators for each city. As shown in Table 1, after standardizing the sample data and performing principal component analysis, the contribution rates of each principal component are obtained.
The cumulative variance contribution rate of the 13 principal components reaches 70.211%, representing more than 70.211% of the characteristic information of the line loss indicators. The line loss impact factors selected through principal component analysis can be divided into four major categories: planning dimension indicators account for 17.7% of the characteristic information, management dimension indicators account for 44.5%, operational dimension indicators account for 18.2%, and technical dimension indicators account for 19.6%, totaling 13 indicators. The feature extraction of line loss based on principal component analysis retains the features that contribute the most to the variance in the dataset. Replacing 37 indicators with 13 indicators greatly reduces the computational load and provides a scientific evaluation of objective phenomena. For detailed cumulative contribution rates of the 37 principal components, see Appendix I.

5.2. Data Analysis and Experimental Platform

There are as many as 3.05 million users in the local city. The traditional customer electricity accurate portrait and collection management is very difficult and has a long cycle. Based on the basic data of Nanning from 2014 to 2017, this paper uses the DEMATEL-Entropy Weight-TOPSIS combination evaluation method to conduct an empirical study on the whole process of line loss management evaluation system. Based on the above subjective and objective combination of weight determination methods, this paper will follow the scientific, objective and reasonable evaluation ideas, on the basis of specific data analysis, according to the expert assignment weight, to ensure that the index weight determination in the design index system is scientific, and the index data weight is objective and reasonable. Therefore, the weight W and W i obtained by the expert assignment of the subjective evaluation method, the weight W ' and W i ' of the objective evaluation method, according to the weight ratio W ∶ W ' = 1 ∶ 1 and W i ∶ W i ' = 1 ∶1, the weighted average is carried out again, and the weight of each evaluation index in the evaluation index system is finally calculated.

5.3. Ablation Experiment Based on DEMATEL-Entropy Weight-TOPSIS Whole Process Combination Evaluation Method

An ablation experiment simulation was conducted on the model to verify the effectiveness of each part of the predictive model proposed in this paper, DEMATEL-Entropy Weight-TOPSIS. There are two ablation experiments, each removing the structures of DEMATEL and Entropy Weight, respectively. Therefore, the evaluation methods involved in this paper's ablation prediction comparison are DEMATEL-TOPSIS evaluation and Entropy Weight-TOPSIS evaluation, respectively. These evaluation methods retain the comparison of the distance between each scheme and the ideal solution to judge the superiority or inferiority of the schemes and analyze the impact of various line loss indicators on enterprises from a horizontal perspective.
Using the entropy value method for weight assignment in the ablation experiment can improve the drawbacks of the traditional subjective human weight assignment in the TOPSIS method. It can also avoid the distortion of the evaluation results caused by too much human interference. The TOPSIS method does not require too many evaluation samples. It can fully and objectively reflect the advantages and disadvantages of various evaluation schemes through the information from the original data.
To address the impact of the interaction among comprehensive evaluation indicators on the system evaluation, the DEMATEL method was used to solve the relationships between indicators. Experts in the power industry were invited to distinguish the indicators into cause factors and result factors. A total of 50 experts with rich theoretical knowledge and field experience were invited as research subjects to score the degree of mutual influence between various risk factors according to the rules.
Table 2. Influencing factors of fuzzy dematel analysis.
Table 2. Influencing factors of fuzzy dematel analysis.
Target Impact f: Affected e; Center Cloud Z sort Reason y; Factor attributes
Main variable capacity-to-load ratioU11 1.374 0.740 2.114 10 0.634 Cause factors
The pass rate of reactive power configuration of substationU12 1.213 1.807 3.020 7 -0.594 Result factors
Unplanned outage rate of distribution linesU13 0.814 0.809 1.622 13 0.005 Cause factors
Public change outage rateU14 1.990 1.128 3.117 5 0.862 Cause factors
The proportion of old low-voltage energy metersU21 1.088 1.447 2.535 9 -0.359 Result factors
The proportion of automatic meter readingU22 0.730 1.107 1.836 11 -0.377 Result factors
Data acquisition integrity rate of four types of terminalsU23 1.214 0.561 1.775 12 0.653 Cause factors
The rate of emergency repair orders for hundreds of householdsU24 2.079 1.268 3.347 2 0.811 Cause factors
Electricity sales growth rateU25 0.962 1.845 2.807 8 -0.883 Result factors
The success rate of automatic execution of fee controlU26 0.881 2.165 3.046 6 -1.184 Result factors
Power factor pass rateU31 1.132 2.190 3.322 4 -1.185 Result factors
Availability rate of substation reactive power compensation deviceU41 1.434 2.028 3.462 1 -0.594 Result factors
Energy-saving main variable ratioU42 1.910 1.436 3.346 3 0.474 Cause factors
The whole process line loss management data of Nanning City was selected as a sample, and a total of 10 experts were selected to score the line loss management level indicators of the project by means of independent scoring by experts. According to the scoring matrix, the weight is calculated using the entropy weight method. The weight of each index in the comprehensive evaluation index system of line loss management is shown in the following Table 3 Entropy Weight Analyze the influencing factors.

5.4. Comparison and Post-Test of Comprehensive Evaluation Results of Line Loss under Ablation Evaluation Method

Based on the standardized raw data and the comprehensive indicator weights from the fuzzy DEMATEL method and Entropy Weight method presented in Table 2 and Table 3, the TOPSIS algorithm model was applied. Utilizing Equation 12, the Euclidean distance of the positive and negative ideal solutions for the line loss reduction management capability was calculated. Subsequently, Equation 13 was used to determine the target layer closeness degree of 11 electric power companies in 2021 for line loss management capability, and the companies were ranked according to the degree of closeness, as shown in Table 4. The scores from the ablation experiment based on the DEMATEL-Entropy Weight-TOPSIS model are presented in the table below.
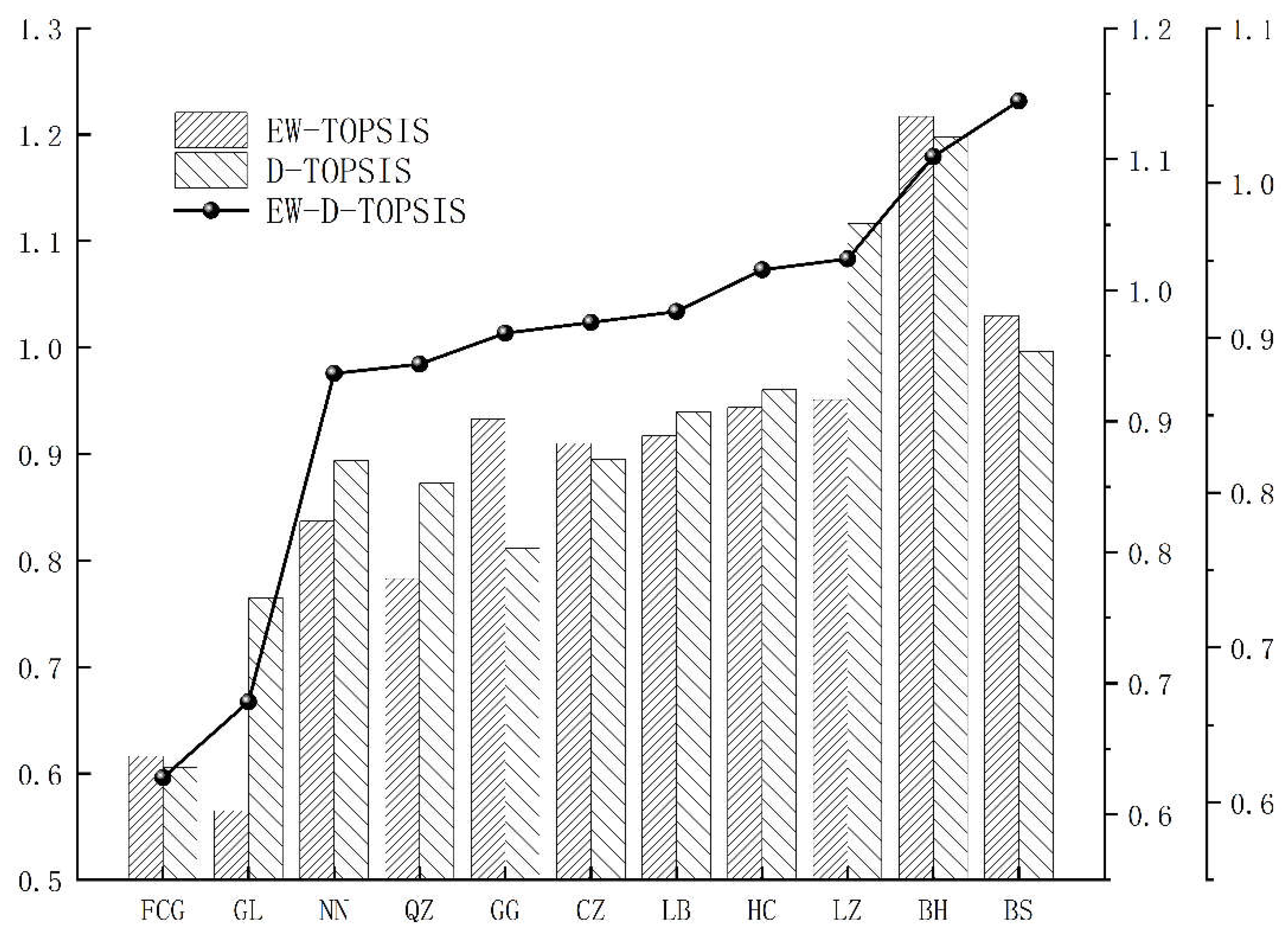
As shown in Figure 3 above, the rank correlation coefficient is used for testing. The rank correlation coefficient, also known as the rank correlation coefficient, is a statistic obtained by ranking the sample values of the two elements in the order of the size of the data and replacing the actual data with the order of the sample values of each element.
p = 1 − 6 n ( n 2 − 1 ) ∑ i = 1 n d i 2
In the case of n > 8, the t-test is performed on the rank correlation coefficient ρ. The test statistic is :
t = n − 2 p / 1 − p 2
If t ≤ t n / 2 ( n − 2 ) , it can be considered that the results of the ablation evaluation method are not closely related to the results of the analysis, otherwise the results of the combined evaluation are closely related to the results of the original method.
The rank correlation coefficients of the original combination evaluation results with DEMATEL-TOPSIS method and Entropy Weight-TOPSIS method are 0.9512,0.8593 and 0.6440 respectively. The corresponding t values were 16.6018, 14.0463 and 13.5327, respectively. The test critical value corresponding to the significant level a = 0.05 is t a / 2 ( n − 2 ) = t 0.025 ( 29 ) = 2.045 , which is easy to judge that the results of DEMATEL-Entropy Weight-TOPSIS combination evaluation are closely related to the results of expert evaluation.
The 2021 sample enterprises' line loss management capability assessment scores showed varying degrees of difference. Through clustering and stratification, enterprises with more robust line loss management capabilities scored above 0.92, while those with weaker capabilities scored below 0.7, with the rest falling into the medium category. The enterprises with a strong gradient of line loss management capability include four listed companies: BS, BH, LZ, and HC. Among them, BS enterprise had the highest comprehensive score for line loss management capability in 2021, indicating that it is generally ideal. LB's line loss management capability score was 0.917, placing it in the second tier, with a general strength in line loss management capability, and the total number of enterprises in the second tier accounted for 45.4% of the research sample. The lowest comprehensive score was obtained by GL company, with a score of 0.616, a difference of 0.437 points from the top-scoring enterprise, indicating a significant difference in management capability and considerable room for improvement in line loss management.
D.  Based on DEMATEL-Entropy Weight-TOPSIS, the evaluation system of line loss management in the whole process of a city in Guangxi is studied.
According to the established evaluation indicator system, data was collected and processed through data verification and proportion calculation to obtain the values of secondary indicators. The optimal values for positive and negative indicators were set to 1 and 0, respectively, while the optimal value for interval indicators was taken as the specified maximum value. The acceptable values were determined by national standards, industry standards, or specifications, as well as expert experience.
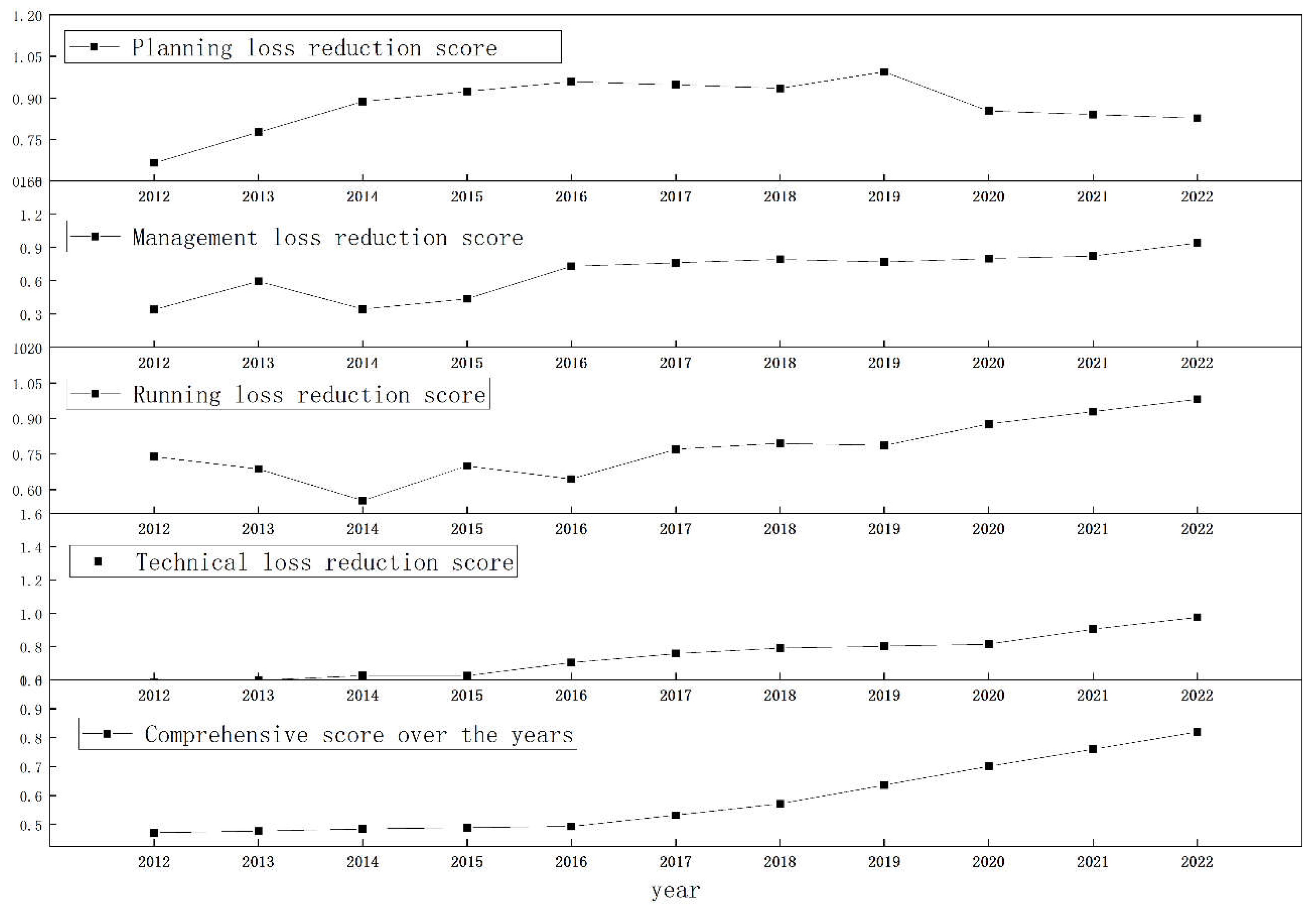
As shown in Table 5 and Figure 4, from 2012 to 2022, the overall trend of the full-process line loss management in Nanning City showed an upward trend. The development was relatively flat from 2012 to 2016, rapidly increasing after 2016, indicating a positive trend in line loss management. The reason for the relatively flat development from 2014 to 2016 was that although the competitiveness of management loss reduction and planning loss reduction continued to rise steadily, operational loss reduction decreased by about 23.7%, significantly lowering the line loss management competitiveness score. In 2016, the competitiveness of urban management loss reduction decreased by about 15.3% compared to 2015, which constrained the development of line loss management in Nanning City, leading to a decrease in the overall low-carbon competitiveness score for these two years. At the same time, as shown in Table 3 and Figure 3, the operational loss reduction showed a fluctuating development from 2014 to 2017, with an overall slight downward trend; the development trend of technical loss reduction was good, roughly showing an upward trend since 2014, which is consistent with the national grid loss technology development situation;. However, the score of the planning loss reduction competitiveness indicator was not very stable, the overall change was insignificant.
The visualization and analysis of the case graph compared with the existing comprehensive line loss management of the Southern Power Grid show that the knowledge graph provides managers with more comprehensive and accurate data support after intelligently integrating and analyzing data sources. Compared with the single data report analysis of traditional methods, comprehensive evaluation can associate multiple data sources, helping managers to better understand the essence of line loss issues. The knowledge graph can also update data and knowledge in real-time, achieving intelligent line loss evaluation and management, reducing the requirements for manual intervention compared to the past, and improving management efficiency and accuracy, greatly enhancing the determination speed of comprehensive line loss evaluation management. At the same time, the knowledge graph can use data mining and predictive analysis techniques to provide early warning and forecasting for line loss issues, discovering potential risk in advance.
  • Conclusion
This paper constructs a comprehensive evaluation system of line loss based on a knowledge graph. The main conclusions are as follows:
A new comprehensive line loss evaluation management knowledge graph has been constructed and divided into three modules to effectively address existing line loss characteristics, providing a more refined and detailed description of the analysis when selecting indicators than traditional graph libraries.
A new comprehensive evaluation management system for line loss reduction has been proposed based on the indicator extraction of the line loss management knowledge graph, from which four categories and 13 types of indicators are selected to build a comprehensive evaluation model for line loss reduction. This model more comprehensively reflects the correlation between indicators, achieving precise positioning of existing problems and reducing the issue of redundant computation due to similar line loss problems.
A composite evaluation method based on DEMATEL-Entropy Weight-TOPSIS has been proposed, and the reliability of the evaluation method has been verified through ablation experiments. After the case analysis of line loss in Nanning City, the authenticity and reliability of the evaluation system were tested, which allowed us to more accurately judge the advantages and disadvantages of the indicator system and reduce the probability of misjudgment.
The paper has researched the comprehensive evaluation management system for line loss reduction. With the increasing scale of distribution networks and the increasing complexity of line loss situations, line losses in the same area may also exhibit periodic changes due to users' electrical characteristics and patterns within the region. Therefore, accurately grasping the true situation of regional line losses requires further research.

Author Contributions

Conceptualization, B.L. and W.W.; methodology, W.W.; software, W.W.; validation, B.L., W.W., formal analysis, W.W.; investigation, W.W.; resources, B.L.; data curation, B.L.; writing—original draft preparation, W.W.; writing—review and editing, W.W.; visualization, W.W.; supervision, B.L.; funding acquisition, B.L. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported in part by the Natural Science Foundation of Guangxi Province under grant 2020GXNSFAA297117.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data used in this study were obtained from China Southern Power Grid and have been licensed for sharing with other researchers upon request. Restrictions may apply to the availability of these data, which were used under license for this study and are not publicly available. Data are, however, available from the authors upon reasonable request and with permission from China Southern Power Grid.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. X. Ivan Li, H. Zhu and L. Zhang, "Review on China's National Carbon Market and Analysis for Commercial Development Potential of Carbon Capture, Utilization and Storage in China," 2022 IEEE PES Innovative Smart Grid Technologies - Asia (ISGT Asia), Singapore, Singapore, 2022, pp. 804-807.
  2. W. Wang, S. Song, Y. Teng, W. Wang, L. Sun, and J. Wang, "Research on Line Loss Diagnosis and Management Method Based on Big Data Technology," in 2020 Chinese Control And Decision Conference (CCDC), 22-24 Aug. 2020 2020, pp. 5524-5529. [CrossRef]
  3. B. Chen, K. Xiang, L. Yang, Q. Su, D. Huang, and T. Huang, "Theoretical Line Loss Calculation of Distribution Network Based on the Integrated Electricity and Line Loss Management System," in 2018 China International Conference on Electricity Distribution (CICED), 17-19 Sept. 2018 2018, pp. 2531-2535. [CrossRef]
  4. J. Yu, Y. Chen, J. Zhao, and L. Yan, "Comprehensive evaluation system of rural area network line loss management," in 2018 Chinese Control And Decision Conference (CCDC), 9-11 June 2018 2018, pp. 6464-6469. [CrossRef]
  5. W. Hu, Q. Guo, W. Wang, W. Wang, and S. Song, "Loss reduction strategy and evaluation system based on reasonable line loss interval of transformer area," Applied Energy, vol. 306, p. 118123, 2022/01/15/ 2022. [CrossRef]
  6. X. Zhong,J Chen,M Jiang,X Zheng, “A Line Loss Analysis Method Based on Deep Learning Technique for Transformer District” Power System Technology. 2020;44(02):769–74.
  7. B. Li, Y. Tan, Q. Guo, and W. Wang, "Application of Comprehensive Evaluation of Line Loss Lean Management Based on Big-Data-Driven Paradigm," Sustainability, vol. 15, no. 15. [CrossRef]
  8. Z. Tang et al., "Research on Short-Term Low-Voltage Distribution Network Line Loss Prediction Based on Kmeans-LightGBM," Journal of Circuits, Systems and Computers, vol. 31, no. 13, p. 2250228, 2022/09/15 2022. [CrossRef]
  9. W. Hu, Q. Guo, W. Wang, W. Wang, and S. Song, "Loss reduction strategy and evaluation system based on reasonable line loss interval of transformer area," Applied Energy, vol. 306, p. 118123, 2022/01/15/ 2022. [CrossRef]
  10. W. Zongbao, "A Line Loss Management Method Based on Improved Random Forest Algorithm in Distributed Generation System," Distributed Generation & Alternative Energy Journal, vol. 37, no. 1, pp. 1-22, 08/27 2021. [CrossRef]
  11. L. Liu, "Application of power metering automation in online loss management," Journal of Physics: Conference Series, vol. 2310, p. 012077, 10/01 2022. [CrossRef]
  12. Y. Qin, H. Cui, and M. Zhang, "An Identification Method of Metering Anomaly Based on Line Loss Analysis of Low Voltage Station," in Journal of Physics: Conference Series, 2022, vol. 2399, no. 1: IOP Publishing, p. 012046.
  13. R. Liu, R. Fu, K. Xu, X. Shi, and X. Ren, "A Review of Knowledge Graph-Based Reasoning Technology in the Operation of Power Systems," Applied Sciences, vol. 13, no. 7. [CrossRef]
  14. Q. Chen, Q. Li, J. Wu, C. Mao, G. Peng, and D. Wang, "Application of knowledge graph in power system fault diagnosis and disposal: A critical review and perspectives," Frontiers in Energy Research, vol. 10, p. 988280, 2022.
  15. J. Chen, G. Lu, Z. Pan, T. Yu, M. Ding, and H. Yang, "Research review of the knowledge graph and its application in power system dispatching and operation," Frontiers in Energy Research, vol. 10, p. 896836, 2022.
  16. S. Liang, "Knowledge graph embedding based on graph neural network," in 2023 IEEE 39th International Conference on Data Engineering (ICDE), 2023: IEEE, pp. 3908-3912.
  17. L. Zheng, Z. Zheng, Y. Chen, and A. Qi, "Environmental protection evaluation of new inorganic non-metallic building materials based on principal component analysis," International Journal of Materials and Product Technology, vol. 67, no. 2, pp. 178-193, 2023.
  18. J. D. Wendt, R. Wells, R. V. Field, and S. Soundarajan, "On data collection, graph construction, and sampling in twitter," in 2016 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining (ASONAM), 2016: IEEE, pp. 985-992.
  19. X. Wu and G. Li, "Intelligent Agricultural Data Collection and Analysis System Based on Internet of Things," in 2023 IEEE 2nd International Conference on Electrical Engineering, Big Data and Algorithms (EEBDA), 2023: IEEE, pp. 506-509.
  20. M. Sharma and R. Gupta, "The Significance of using Data Extraction Methods for an Effective Big Data Mining Process," 2023 2nd International Conference for Innovation in Technology (INOCON), Bangalore, India, 2023, pp. 1-4.
  21. J. Cui, G. Li, M. Yu, L. Jiang, and Z. Lin, "Aero-engine fault diagnosis based on kernel principal component analysis and wavelet neural network," in 2019 Chinese Control And Decision Conference (CCDC), 2019: IEEE, pp. 451-456.
  22. Garniwa, "Principal component analysis and cluster analysis for development of electrical system," in 2017 15th International Conference on Quality in Research (QiR): International Symposium on Electrical and Computer Engineering, 2017: IEEE, pp. 439-443.
  23. Y. Pei, "Linear principal component discriminant analysis," in 2015 IEEE International Conference on Systems, Man, and Cybernetics, 2015: IEEE, pp. 2108-2113.
  24. Z. Xu and J. Wu, "Comprehensive evaluation model of smart city economic management efficiency based on multidimensional data mining," in 2021 International Conference of Social Computing and Digital Economy (ICSCDE), 2021: IEEE, pp. 92-95.
  25. X. Cheng, M. Yu, M. Liu, R. Huang, L. Xie, and H. Tan, "Research on comprehensive performance evaluation method of smart energy meter," in 2018 3rd International Conference on Mechanical, Control and Computer Engineering (ICMCCE), 2018: IEEE, pp. 450-455.
  26. T. Wang, Y. Sun, X. Song, Z. Wang, Y. Ren, and W. Xu, "Analysis on Causes of Train Operation Conflicts in High-Speed Railway Based On Fuzzy DEMATEL-ISM," in 2020 Chinese Automation Congress (CAC), 2020: IEEE, pp. 2318-2323.
  27. P. Bashardoost, F. Nasirzadeh, and N. N. Mohtashemi, "An integrated fuzzy-DEMATEL approach to project risk analysis," in 2018 7th International Conference on Industrial Technology and Management (ICITM), 2018: IEEE, pp. 411-416.
  28. Y. Wang, L. Tian, and Z. Chen, "A reputation bootstrapping model for e-commerce based on fuzzy dematel method and neural network," IEEE Access, vol. 7, pp. 52266-52276, 2019.
  29. J. Qi, J. Liu, Z. Liu, and K. Wang, "Evaluation Method of Power Channel Operation Quality Based on Entropy Weight Method," in 2023 3rd International Conference on New Energy and Power Engineering (ICNEPE), 2023: IEEE, pp. 1014-1017.
  30. Z. Zhu, J. Pan, and X. Liu, "Optimal Ordering and Transportation Model Design Based on BP Neural Network and Entropy Weight TOPSIS," in 2021 IEEE Conference on Telecommunications, Optics and Computer Science (TOCS), 10-11 Dec. 2021 2021, pp. 500-503. [CrossRef]
Preprints 114035 g001
Figure 1. Knowledge graph of line loss comprehensive evaluation management.
Figure 1. Knowledge graph of line loss comprehensive evaluation management.
Preprints 114035 g001
Preprints 114035 g002
Figure 2. Construction of line loss index system based on principal component analysis.
Figure 2. Construction of line loss index system based on principal component analysis.
Preprints 114035 g002
Preprints 114035 g003
Figure 3. DEMATEL-Entropy Weight-TOPSIS Model Ablation Study Scores.
Figure 3. DEMATEL-Entropy Weight-TOPSIS Model Ablation Study Scores.
Preprints 114035 g003
Preprints 114035 g004
Figure 4. TOPSIS Historical Comprehensive Scores and Scores of Each First-Level Indicator.
Figure 4. TOPSIS Historical Comprehensive Scores and Scores of Each First-Level Indicator.
Preprints 114035 g004
Table 1. Eigenvalues and variance contribution of the principal component analysis method.
Table 1. Eigenvalues and variance contribution of the principal component analysis method.
成分 Explanation of total variance
Amount to Percentage of variance Cumulative %
Main variable capacity-to-load ratio 3.858 10.428 10.428
The pass rate of reactive power configuration of substation 2.933 7.926 18.354
Unplanned outage rate of distribution lines 2.854 7.712 26.067
Public change outage rate 2.448 6.617 32.684
The proportion of old low-voltage energy meters 2.130 5.758 38.441
The proportion of automatic meter reading 1.936 5.232 43.673
Data acquisition integrity rate of four types of terminals 1.870 5.053 48.727
The rate of emergency repair orders for hundreds of households 1.651 4.461 53.188
Electricity sales growth rate 1.550 4.189 57.376
The success rate of automatic execution of fee control 1.346 3.637 61.013
Power factor pass rate 1.174 3.173 64.187
Availability rate of substation reactive power compensation device 1.167 3.155 67.341
Energy-saving main variable ratio 1.062 2.870 70.211
Table 3. Entropy Weight Analyze the influencing factors.
Table 3. Entropy Weight Analyze the influencing factors.
First-level indicators First-level weight Secondary indicators Second-level weight Comprehensive weight
Planned loss reduction 0.2532 Main variable capacity-to-load ratio 0.0366 0.0093
The pass rate of reactive power configuration of substation 0.2476 0.0627
Unplanned outage rate of distribution lines 0.2117 0.0536
Public change outage rate 0.5041 0.1276
Manage loss reduction 0.4792 The proportion of old low-voltage energy meters 0.2866 0.1373
The proportion of automatic meter reading 0.0131 0.0063
Data acquisition integrity rate of four types of terminals 0.2866 0.1373
The rate of emergency repair orders for hundreds of households 0.2460 0.1179
Electricity sales growth rate 0.1678 0.0804
The success rate of automatic execution of fee control 0.5006 0.1340
Operation loss reduction 0.1377 Power factor pass rate 0.4356 0.1166
Technical loss reduction 0.1299 Availability rate of substation reactive power compensation device 0.0136 0.0037
Energy-saving main variable ratio 0.0502 0.0134
Table 4. DEMATEL-Entropy Weight-TOPSIS Model Ablation Study Scores.
Table 4. DEMATEL-Entropy Weight-TOPSIS Model Ablation Study Scores.
region EW-TOPSIS billing D-TOPSIS billing EW-D-TOPSIS billing
BS 1.03 2 0.953 3 1.053 1
BH 1.217 1 1.117 1 1.017 2
CZ 0.91 7 0.871 6 0.91 6
FCG 0.616 10 0.636 11 0.616 11
GG 0.933 5 0.803 9 0.903 7
GL 0.565 11 0.765 10 0.665 10
HC 0.944 4 0.924 4 0.944 4
LB 0.917 6 0.907 5 0.917 5
LZ 0.951 3 1.051 2 0.951 3
NN 0.837 8 0.87 7 0.877 9
QZ 0.783 9 0.853 8 0.883 8
Table 5. Topsis comprehensive score over the years and each secondary index score table.
Table 5. Topsis comprehensive score over the years and each secondary index score table.
Topsis score Comprehensive score over the years Planning loss reduction score Management loss reduction score Running loss reduction score Technical loss reduction score
2012年 0.4704 0.6654 0.3402 0.7388 0.5866
2013年 0.4775 0.7764 0.5938 0.6866 0.5954
2014年 0.4846 0.8874 0.3448 0.5544 0.6248
2015年 0.489 0.9232 0.4379 0.6995 0.6244
2016年 0.4934 0.959 0.731 0.6446 0.7024
2017年 0.5323 0.947 0.7626 0.7699 0.7566
2018年 0.5712 0.935 0.7942 0.7952 0.7892
2019年 0.636 0.9943 0.7711 0.7857 0.8012
2020年 0.7008 0.8536 0.8002 0.8762 0.8132
2021年 0.76 0.8401 0.8224 0.9284 0.9044
2022年 0.8192 0.8266 0.9428 0.9806 0.9748
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated