Prerpints.org logo
Preprint
Article

Comparative Performance Assessment between Incompressible and Compressible Solvers to Simulate a Cavitating Wake

Altmetrics

Downloads

104

Views

33

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

01 August 2024

Posted:

01 August 2024

You are already at the latest version

Alerts
Abstract
The cavitating wake behind a wedge has been simulated employing both incompressible and compressible solvers with the purpose of comparing their performance. To develop the compressible solver, the ZGB cavitation model for incompressible flows has been modified to consider the compressibility effects. First, the equations of state for the vapor and liquid phases have been implemented. Then, a pressure limit and absorbing boundary conditions have been set to prevent a non-physical pressure field. To test the developed compressible solver, a series of verification tests have been conducted comprising a 1D sod cavitating tube and the cavitating vortex shedding behind a circular body at laminar flow conditions. After that, the incompressible and the validated compressible solvers have been applied to simulate the cavitating wake behind a wedge. The obtained results show similar predictions with the two solvers in terms of pressure, vortex shedding frequency and instantaneous and average vapor volume fraction profiles. Moreover, it is interesting to note that the components of the fluid force fluctuations on the body at the lowest frequencies, as predicted by both solvers, are indistinguishable. However, the higher frequency fluctuations of the forces tend to be better resolved and amplified when the compressibility is considered. Overall, both flow solvers have provided comparable cavitation phenomena, yielding results well aligned with experimental observations.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

Vortical flow structures and cavitation are two common phenomena encountered in hydraulic machinery. As the fluid passes the fixed vanes, the guide vanes or the runner blades, it creates complex wake flow patterns that might develop in what is known as a vortex street. The resulting alternating shed vortices induce force fluctuations on the solids and provoke vortex-induced vibrations which may induce severe fatigue damage. In addition, vaporous cavities will be initiated and persist inside the center of the alternating shed vortices if the ambient pressure is low enough [1]. As these cavities move to the high-pressure region and collapse, they might also induce severe material erosion on adjacent surfaces. It is well known that the occurrence and development of cavitation can strongly alter the dynamic behavior of vortex street flows [2,3,4,5]. For example, it has been reported that cavitation tends to enhance the amplitude of the vortex-induced vibrations [4]. Therefore, further exploration of the effect of cavitation on the vortex street flow is essential to mitigate the damage caused by the cavitation and/or vortex-induced vibrations.
Currently, the computational fluid dynamic (CFD) method has been proved to provide detailed insights into complex flow fields, particularly in cases involving cavitation. Various numerical approaches, each with different levels of complexity, are available to simulate the cavitating flow. For a comprehensive review of the cavitation modeling approaches, see Niedźwiedzka et al. [6] and Folden and Aschmoneit [7]. Among these numerical models, the transport equation model (TEM) is one of the most widely used which includes an additional transport equation for the vapor phase volume fraction and a source term that accounts for mass transfer between phases. Without considering fluid compressibility, TEM-based simulations can effectively capture the transition from sheet to cloud cavitation, driven by a liquid re-entrant jet across different geometries [8,9,10], aligning well with experimental observations [11,12,13,14,15]. Conversely, the transition from the sheet cavitation to the cloud cavitation can be dominated by the condensation shock [16,17,18], which is highly related to the fluid compressibility of the mixture. Coupled with the equation of state for the liquid and vapor, TEM can successfully capture the condensation shock and its impact on the transition from sheet cavitation to cloud cavitation[10,18,19,20,21].
For the developed cavitation within the vortex street flows, bubble-vortex interactions alter the growth and collapse dynamics of cavitation [22,23,24,25,26]. This makes the roles for fluid compressibility in cavitating vortex street flows distinct from those observed in unsteady cloud cavitation. Previous numerical investigations have highlighted the impact of fluid compressibility on cavitating vortex street flows, particularly at extremely low cavitation numbers. For example, Brandao and Mahesh [27] have numerically captured the condensation shock on the surface of the circular cylinder where cavitation is highly developed. Additionally, Kim et al. [28] confirmed that fluid compressibility can alter the morphology of fully developed cavities when the cavitation number is less than half of the cavitation inception number. However, the effects of fluid compressibility on the dynamics of vortex street flows have received limited attention, especially at intermediate cavitation numbers.
The aim of this study is to demonstrate the influence of fluid compressibility on the dynamics of a cavitating vortex street by numerically resolving the cavitating flow field using both incompressible and compressible cavitation solvers. This paper is composed of five sections. Following this introduction, the second section explains the governing equations. The third section details the corresponding numerical treatment. In the fourth section, the implemented numerical solvers are validated, and the results from both the incompressible and compressible solvers are compared. Finally, the fifth section presents the conclusions and summarizes the results.

2. Governing Equations

2.1. Mass Conservation Equation

The equation for the conserved mass without external mass source is given by:
∂ ρ / ∂ t + ∇ · ρ u = 0
here, ρ is the density, u is the velocity, and t is the time. This equation is valid for both incompressible and compressible flows.

2.2. Momentum Conservation Equation

In an inertial reference frame, the conserved momentum equation can be written as follows:
∂ ρ u / ∂ t + ∇ · ρ u u = − ∇ p + ∇ · τ
where p is the pressure and τ is the stress tensor which is defined as:
τ = μ ∇ u + ∇ u T − 2 / 3 ∇ · u I
here, μ is the fluid molecular viscosity and I is the unit tensor.

2.3. Realizable k -Epsilon Delayed Detached Eddy Simulation (DDES) Model

In the realizable k -epsilon DDES model, the governing equation for the turbulence kinetic energy, k , can be written as follows:
∂ ρ k / ∂ t + ∇ · ρ u k = P k − Y k * + ∇ · μ + μ t / σ k ∇ k            
where ε is the dissipation, P k is the generation term of k , μ t is the turbulent viscosity and σ k is the turbulent Prandtl number.Furthermore, the dissipation of turbulent kinetic energy, Y k * , is given by:
Y k * = ρ k 3 2 l d e s
where
l d e s = m i n ⁡ l r k e , l l e s ; l r k e = k 3 2 ε ; l l e s = C d e s Δ m a x
here, Δ m a x is the maximum length of the cell edge and C d e s = 0.61 is the model constant. If l r k e   = l l e s , l d e s is replaced by the following functions:
l d e s = l r k e − f y m a x 0 , l r k e − C d e s Δ m a x
f y = 1 − t a n h ⁡ 20.0 r y 3
r y = μ + μ t / ρ u : u κ y 2
where y represents the wall distance and κ = 0.41.

2.4. Cavitation Modelling

The volume fraction transport equation for the vapor volume fraction, α v , is given by:
∂ ρ v α v / ∂ t + ∇ · ρ v α v u = m ˙
The ρ and μ , of the fluid mixture are defined, respectively, as:
ρ = α v ρ v + 1 − α v ρ l
μ = α v μ v + 1 − α v μ l
where ρ v and ρ l are the water and vapor densities, respectively, μ v and μ l are the water and vapor dynamic viscosities, respectively.
The mass transfer rate between the liquid and vapor due to the cavitation is modelled with a source term, m ˙ , presented in equation (10). If the effects of viscosity, non-condensable gas, surface tension, and second-order derivation are neglected, the Rayleigh-Plesset equation can be simplified and written as:
R ˙ = 2 P r e f − p v 3 ρ l
where p is the saturated vapor pressure and R is the bubble radius.
Assuming that the distribution of the nucleation inside the flow field is uniform and independent of the flow structures, then the relationship between the bubble radius, R , and α v is given by:
α v = n 4 π 3 R 3
where n is the number of nucleation per unit volume. Then, m ˙ is calculated by:
m ˙ = ρ v α ˙ v = n ρ v 3 4 π 3 R 2 R ˙
By submitting n given by equations (13) and (14) into equation (15), m ˙ can be expressed as:
m ˙ = 3 ρ v α v R 2 P r e f − p v 3 ρ l
In the vaporization process, the nucleation site density must decrease as the vapor volume fraction increases. To model this process, α needs to be replaced with 1 − α v α nuc in equation (16). Then, the final ZGB cavitation model [29] is presented as follows:
m ˙ = F c 3 α v ρ v R 0 2 3 p − p v ρ l                                             p > p v F v 3 ρ v 1 − α v α nuc R 0 2 3 p v − p ρ l                   p < p v
where p v is the saturated vapor pressure. The initial value of the bubble radius is R = 1 μ m , the nucleation site of the volume fraction α nuc = 5 × 10 − 4 . Here, the optimal empirical condensation and vaporization coefficients have been selected as F c = 0.001 and F v = 50.0 , respectively.

2.5. Equation of State

The density of the compressible liquid phase can be computed using the Tait equation [20,30]:
ρ p l = ρ l , s a t p + B p v + B 1 / N
and the corresponding sound speed is defined as
c p l = ∂ p ∂ ρ = N ρ l , s a t p v + B p + B p v + B N − 1 / N
where B is the water bulk modulus, 3.1 × 10 8 Pa, ρ l , s a t is the liquid density at p v , 998.18 kg/m3, and N is a model constant equal to 7.15.
The density of the compressible vapor phase using the polytropic equation of state [31] can be written as:
ρ p v = p / C v 1 / n
and the corresponding sound speed is:
c p v = ∂ p ∂ ρ = C v n p / C v n − 1 / n
where the model constant C v can be estimated from a density of 0.017 kg/m3 at p v . The polytropic exponent n for an adiabatic assumption is 1.4.

2.6. Sponge Layer Conditions

Up to date, although the use of the pressure-based method has achieved notable success in a wide range of compressible cavitating flows [32,33], several unresolved numerical difficulties remain, particularly concerning the determination of the inlet and outlet boundary conditions in CFD simulations. Typically, such calculations are conducted on a truncated domain of the entire system and the standard inlet/outlet boundary conditions may fail to allow some of the flow features to leave the computational domain as physically expected. For that reason, artificial treatments of the truncated domains are required to avoid pressure waves reflected at the boundaries. Therefore, the sponge layer has been adopted for its flexibility and simplicity [34]. The set of formulas of the sponge layer based on the pressure and velocity for the pressure-based method is given as follows:
∂ ρ / ∂ t + ∇ · ρ u = σ x ∂ ρ ∂ p p = p r e f p r e f − p
∂ ρ u / ∂ t + ∇ · ρ u u + p I − τ = σ x ρ u r e f − u
where the subtitle “ref” refers to a target value of the flow variable and σ x is the function of the damping coefficient, which is defined as:
σ x = 3 α p o l x / L β p o l 2 ∆ t γ p o l
here, α p o l = 1.0 , β p o l = 3.0 , γ p o l = 1.0 and x is the distance from the leading edge of the sponge layer and L is the length of the sponge layer, as shown in Figure 1.

3. Numerical Method

In this section, the governing equations are discretised using the Finite Volume Method (FVM) over the collocated unstructured mesh. More attention will be paid to the numerical algorithm for the pressure-based multiphase solver with/without consideration of fluid compressibility using the predefined macro “DEFINE_LINEARIZED_MASS_TRANSFER” inside the ANSYS Fluent® platform.

3.1. Incompressible Mixture/VOF Model

Without consideration of fluid compressibility, the fluid densities are constant. The numerical algorithm for the mass conservation and volume fraction transport equation with linearized source terms is detailed in the following subsection.

3.1.1. Volume Continuity Equation

To guarantee mass conservation and numerical stability, the pressure-correction equation is based on the total volume continuity instead of the mass conservation equation.
1 ρ v ∂ ρ v α v / ∂ t + ∇ · ρ v α v u − m ˙ + 1 ρ l ∂ ρ l α l / ∂ t + ∇ · ρ l α l u + m ˙ = 0
Integrating equation (25) over a control volume, the discretized form of the volume continuity is given by:
1 ρ v ρ v α v − ρ v α v 0 ∆ t d V + ∑ f ρ v α v u f A f + 1 ρ v ρ l α l − ρ l α l 0 ∆ t d V + ∑ f ρ l α l u f A f = 1 ρ v − 1 ρ l m ˙ * − ∂ m ˙ ∂ p * p * − p v + ∂ m ˙ ∂ p * 1 ρ v − 1 ρ l ⏟ d s / d p p − p v
where d V is the volume of the control cell, A f is the face area vector within the control volume, ρ v α v u f and ρ l α l u f are the vapor and liquid mass fluxes, respectively. On the collocated grid, the phase mass flux is computed using a Rhie–Chow interpolation.
More importantly, the term d s / d p is the linearized mass transfer related to the pressure for the pressure correction equation, which can enhance the numerical stability of the cavitation simulation.

3.1.2. Second phase Fraction Equation

In ANSYS Fluent®, only the transport equation for the second phase volume fraction is solved using the VOF or mixture model. Normally, the vapor phase is set to be the second phase. Thus, the vapor volume fraction is obtained with the vapor phase continuity equation as presented in equation (10). Correspondingly, the discretized form of the equation can be written as follows:
1 ρ v ρ v α v − ρ v α v 0 ∆ t d V + ∑ f ρ v α v u f A f = m ˙ ρ v d V
Assuming that the mass source term m ˙ can be rewritten as the function of α v and α l :
m ˙ ρ v = m ˙ 0 + S l α l − S v α v
With linearized the mass source term m ˙ , the equation (27) can be rewritten as:
1 ρ v ρ v α v − ρ v α v 0 ∆ t d V + ∑ f ρ v α v u f A f = S c + S p α v d V
where
S c = m ˙ 0 + S l S p = − S v + S l
here, S p is the linear part of the source term m ˙ , and S c is the part of m ˙ which cannot be linearized.

3.2. Compressible Mixture/VOF Model

In this section, the robust numerical algorithm for multiphase flows to handle fluid compressibility is introduced [32]. With the SIMPLE method, velocity and density fields can be decomposed into two parts as follows:
ρ v = ρ v * + ρ v ' = ρ v * + ∂ ρ v * ∂ p p ' ρ l = ρ l * + ρ l ' = ρ l * + ∂ ρ l * ∂ p p ' u = u * + u '
where “ * ” indicates the tentative values and “ ' ” indicates the variable correction.

3.2.1. Volume Continuity Equation

Unlike the incompressible pressure-correction equation, the phase masses for vapor and liquid, ρ v α v and ρ l α l , respectively, and the phase flux terms for vapor and liquid, ρ v α v u and ρ l α l u , respectively,are computed with the following expressions:
  ρ v α v = ρ v * α v + ∂ ρ v * ∂ p p ' α v ρ l α l = ρ l * α l + ∂ ρ l * ∂ p p ' α l
  ρ v α v u = ρ v * + ρ v ' α v u * + u ' = ρ v * u * α v + ∂ ρ v * ∂ p p ' u * α v + ρ v * u ' α v + ρ v ' α v u ' ⏟ h i g h − o r d e r ρ l α l u = ρ l * + ρ l ' α l u * + u ' = ρ l * u * α l + ∂ ρ l * ∂ p p ' u * α l + ρ l * u ' α l + ρ l ' α l u ' ⏟ h i g h − o r d e r
Normally, the high-order correction terms in equation (33) are omitted due to their small magnitude compared with the rest of terms and their negligible influence on the resolved field. Then the discretised form of the volume continuity can be written as:
1 ρ v ρ v * α v * + ∂ ρ v * ∂ p p ' − ρ v 0 α v 0 ∆ t d V + ∑ f ρ v , f * u * α v + ∂ ρ v * ∂ p f p ' u * α v + ρ v , f * u ' α v A f + 1 ρ l ρ l * α l * + ∂ ρ l * ∂ p p ' − ρ l 0 α l 0 ∆ t d V + ∑ f ρ l , f * u * α l + ∂ ρ l * ∂ p f p ' u * α l + ρ l , f * u ' α l A f = 1 ρ v − 1 ρ l m ˙ * − ∂ m ˙ ∂ p * p * − p v + + ∂ m ˙ ∂ p * 1 ρ v − 1 ρ l ⏟ d s / d p p − p v
where ρ v , f * u * α v is the phase mass flux at the cell face.
The above equation not only couples the pressure and velocity but also involves the interaction between the flow field and the mass transfer source term. Note that the terms ∂ ρ v * ∂ p and ∂ ρ l * ∂ p are related to the effect of the vapor and liquid compressibility on the pressure correction, respectively. By default, these terms are approximated by the upwind scheme. The compressibility-related term in the transient term and mass transfer source term can be easily linearized, which can significantly enhance the numerical stability without affecting the final solution.

3.2.2. Second Phase Fraction Equation

With consideration of the compressible effect of the second phase, the discretised form of the volume fraction equation can be written as follows when the second phase is the vapor:
1 ρ v ρ v α v − ρ v 0 α v 0 ∆ t d V + ∑ f ρ v , f α v u f A f = S c + S p α v d V
And the left-hand side of the equation can be rewritten as:
α v − α v 0 ∆ t d V + ∑ f α v u f A f = S c + S p α v d V + − ρ v − ρ v 0 ρ v α v 0 d V ∆ t + ∑ f ρ v − ρ v , f ρ v α v u f A f ⏟ e x p a n s i o n   s o u r c e
where the last term is the expansion source term accounting for the effect of fluid compressibility on the volume conservation equation. It is composed of two parts: one corresponding to the transient term and the other one to the advection term.

3.3. Pressure Limits

As we know, the pressure-based solver can provoke an unbounded pressure field, e.g. negative pressure field. For the compressible flow, it is necessary to limit the pressure since the obtained negative pressure field is out of the predefined range for the fluid material. However, limiting the pressure is a challenging numerical issue, which will lead to a decrease in the convergence rate and to numerical instability. In the case of the multiphase compressible flows, the situation will be more severe. As mentioned by Li and Vasquez [32], it is difficult to directly limit the pressure above zero in the region where only a negligible amount of gas is present. In such a case, the limitation of the pressure must consider the effect of the local flow characteristic. According to the pressure-limited method proposed by Li and Vasquez [32], the fluid density is computed using the barotropic law with a pre-described pressure limit when the local pressure turns negative. For instance, the Tait equation for the compressible liquid density with the pressure-limited can be rewritten as:
ρ p l = ρ l , s a t m a x ⁡ p , p l i m + B p v + B 1 / N
and the corresponding sound speed with the pressure-limited is defined as
c p l = ∂ p ∂ ρ = N ρ l , s a t p v + B m a x ⁡ p , p l i m + B p v + B N − 1 / N
where   p l i m is the pre-described pressure limit.

4. Validation

4.1. Case1: 1-D Two-Phase Time-Dependent Test Case

In this section, the compressible cavitation model is used to describe the effects of a density reduction below the density value of the saturated liquid induced by two symmetrical expansion waves as in the numerical setup defined by Schmidt [35]. The domain consists of a 1-D tube with a length of 1 m. At time t = 0 s, the tube is full of pure liquid water, and the pressure is constant with a value of p = 0.9 bar. The velocity field is assumed to jump at x = 0.5 m from the left velocity, u L = - 10 m/s, to the right velocity, u R = 10 m/s, to force the phase change from liquid to vapor to occur. Furthermore, the domain has been divided into 1000 cells and the time integration has been performed using the first-order implicit scheme with a time step ∆ t = 1∙10-7 s.
To verify the implementation of the compressible cavitation model, the current numerical results have been compared with the ones obtained by Schmidt [35]. Figure 2 presents the pressure, the velocity, the vapor volume fraction, and the sound speed distributions along the tube at time t   = 1.5∙10-4 s using the present compressible cavitation model and the results obtained by Schmidt [35]. Without experiencing numerical oscillations in regions with high gradients, the current implemented solver is proved to be numerically stable. Furthermore, the distribution of the flow quantities along the tube is almost identical between the current ones and the those extracted from the reference simulation. The precise agreement between both sets of results demonstrates the validity of the implemented compressible cavitation model.

4.2. Case2: Cavitating Flow over a Circular Cylinder

The present simulations of the non-cavitating and cavitating flows over a stationary cylinder have been performed with a large 2D computational domain of dimensionless dimensions relative to the cylinder diameter, D, in the horizontal and vertical ranges -50 ≤ x / D ≤ 50 and -50 ≤ y / D ≤ 50, respectively, to avoid the effect of the domain boundaries, as depicted in Figure 3. The cylinder has been located in position (0, 0) and the number of grid elements in the circumferential and radial directions are 480 and 220, respectively. The symbol, θ , represents the angle around the cylinder surface measured from its front stagnation point. The inflow condition of u = u r e f and the pressure condition of p = p r e f has been set at the boundaries located at x / D =-50 and x / D =50, respectively, while the symmetry condition has been used at the top and bottom boundaries.
The drag and lift coefficients, denoted as C D and C L , have been defined as:
C D = F x 1 2 ρ l U r e f 2 D
C L = F y 1 2 ρ l r e f 2 D
where F x and F y are the streamwise and transverse components of the force acting on the cylinder surface, respectively, and U r e f is the free-stream velocity.
The unsteady vortex shedding case has been calculated for liquid water at R e =200 as in previous studies [36,37,38,39,40,19,41,42]. Vortices are generated on the cylinder surface and detach alternatively from its upper and lower surfaces which results in fluctuations of C D and C L as shown in Figure 4. The time-average value of C D , denoted as C D , a v , the maximum value of C L , denoted as C L , m a x , and the S t value are listed in Table 1 and compared with published data obtained by different authors using different meshes and methods. It is confirmed that the present results match well with the reference values.
Simulations are extended to cavitation conditions at σ   = 1.0. As shown in Figure 5, the oscillating flow around the cylinder results in C D and C L fluctuations. The corresponding C D , a v , C L , m a x , and S t values are listed in Table 2 and compared with previous results obtained by other authors. As the liquid pressure decreases to p v , cavitation occurs around the lateral surface of the cylinder and then the vaporous bubbles detach from the cylinder surface and travel within the shed vortices. The positive velocity divergence caused by the appearance of cavitation leads to the vorticity dilatation, thus elongating and weakening the shed vortices [19]. Therefore, the computed shedding frequencies are reduced to S t   = 0.17, which are comparable to the corresponding predictions of 0.16 reported by Seo et al. [38] and Gnanaskandan and Mahesh [19], and of 0.177 reported by Hong and Son [42]. Moreover, Figure 6 compares the instantaneous vorticity contour colored with vapor volume fraction at σ =1.0 obtained by Gnanaskandan and Mahesh [19] and the present method, showing similar results.

5. Results

5.1. Computational Domain and Boundary Conditions

Figure 7 shows the dimensions of the computational domain to simulate the flow around a wedge which are the same as the ones used in the experimental setup presented by Wu et al. [5] . The cross-section of the tunnel is rectangular and its width is 4D, where D is the height of the wedge base which equal to 0.019 m. The span of the wedge is 4D. For the incompressible cavitation case, the inlet is located at 13.5D upstream from the wedge trailing edge plane and the outlet is at 19.5D downstream from it. For the compressible cavitating simulation the fluid domain is extended to implement the sponge layers at the inlet and outlet boundaries which are located 25.9D upstream and 36.6 D downstream of the trailing edge, respectively.
The flow around the wedge has been simulated using the DDES model to capture the globally unstable flow characteristics. Such flow has the feature that the turbulence in the separated zone is independent of the turbulence within the incoming attached boundary layer [43]. This flow feature can require to reduce significantly the mesh resolution. Following the suggestions provided by ANSYS Fluent® [43], more than 20 cells per characteristic length, D, are sufficient to resolve the main flow instability. Furthermore, an isotropic cell (Δx = Δy = Δz) has been used in the area near the trailing edge of the wedge to avoid the numerical error resulting from cells with too large aspect ratios. To assess the effects of mesh refinement on the calculations, three meshes with different refinements have been tested as listed in Table 3. The topology of mesh M1 around the wedge is depicted in Figure 8(a) and 8(b).
For the non-cavitating case, the inlet boundary condition has been set as a uniform inflow velocity, U r e f =6 m/s, and the outlet type boundary condition has been set as shown in Figure 9(a). For the cavitation case at σ   = 1.9, the corresponding total pressure has been specified at the inlet boundary condition and the fixed mass flowrate boundary condition has been fixed at the outlet. To absorb the pressure wave generated by the compressible fluid and avoid reflections, sponge layer boundaries have been added at the inlet and outlet areas [34], as depicted in Figure 9(b). The specific values of the different boundary conditions for the two operating conditions without and with cavitation are detailed in Table 4.
All the simulations have been run with ANSYS Fluent® using the Bounded Central Difference (BCD) advected scheme and a time step of Δ t =5×10-5 s where the corresponding advected Courant number is below 1 behind the wedge.

5.2. Verification and Validation of the Non-Cavitating Case

Figure 10 shows the spectra of the simulated lift coefficient calculated using FFT for the three different grid refinements at non-cavitation conditions with the compressible model. It can be seen that for all the meshes the same maximum frequency peak is obtained with similar amplitude even when the coarse mesh is used. Therefore, to save computational resources, the mesh M1 has been selected and used for the following analysis.
As presented in Figure 10, the main frequency peak corresponding to the vortex shedding frequency is found around 91 Hz which y is in good agreement with the value of 90 Hz obtained by Wu et al. [5].
The numerically obtained C p on the surface of the wedge is plotted in Figure 11. Here, the position at y = ± 0.5 D corresponds to the two vertices at the truncated trailing edge. It can be seen that, at the centerline of the base of the wedge, the value of C p = -1.5 is exactly the same as the experimental value reported by Wu et al. [5]. Therefore, it can be concluded that, in the non-cavitating case, the current numerical solution of the unsteady flow field provides a reasonable resemblance to the flow conditions measured during the experiment carried out by Wu et al. [5].

5.3. Assessment of the Compressible Cavitation Model

Using the validated incompressible and compressible modelling approaches presented in the previous sections, the cavitating wake behind the wedge at U r e f =6 m/s and σ   = 1.9, has been calculated numerically to demonstrate the effects of fluid compressibility on the dynamics of the cavitating vortex shedding behind the wedge.

5.3.1. Pressure on the Wedge Surface

Figure 12 compares the mean values of C p on the wedge surface using both the incompressible and the compressible cavitation solvers and it can be seen that the results are exactly the same. Moreover, , the numerical C p of -1.4 at the centreline of the base of the wedge is in good agreement with the experimental value of -1.45 obtained by Wu et al. [5].

5.3.2. Unsteady Loads on the Wedge Surface

For comparison, Figure 13 shows the time histories of C L and their spectra with the incompressible and compressible cavitation solvers for σ   = 1.9. It can be seen that both solvers predict the same value of 210 Hz for the vortex shedding frequency behind the wedge. Such result is in good agreement with the dominant frequency reported by Wu et al. As shown in Figure 13(b), the shape and amplitudes of the spectra obtained with the incompressible and compressible cavitation solver are quite similar for the lower frequencies below 800 Hz. However, at high frequencies above 1000 Hz, the spectra obtained with the incompressible cavitation solver present lower amplitude values than with the compressible cavitation solver. It is interesting to note that similar results have also been observed in the investigation of cloud cavitation around the hydrofoil conducted by Wang et al. [20].

5.3.3. Cavitation Structures

Figure 14 shows visualization of the 3D cavitation structures inside the shed vortices using iso-surface plots with the numerical results obtained with both the incompressible and the compressible cavitation solvers. And they are compared in the same figure with the photographs taken during the experimental tests carried out by Wu et al. [5]. It can be seen that the first few pairs of spanwise vortex cores (identified with the Q criterion) are filled with vapor, and that these cavity structures (represented with iso-surfaces of α v = 0.05) are advected downstream. Furthermore, the relative positions of the vortices and the spacings obtained with the incompressible and compressible cavitation models are quite similar and they align well with the experimental results.
Figure 15 shows the simulated instantaneous field of α v in the cavitating wake at different instants of time obtained with the incompressible (Incomp.) and compressible (Comp.) cavitation solvers at σ = 1.9 as well as the experimental (Exp.) images reported by Wu et al. [5] using time-resolved X-ray densitometry. All of them show clearly the periodically shed vortices at the vortex shedding frequency. The evolution of the cavitation structures with time confirms that the periodic shedding is governed by the alternating shedding vortex street behind the wedge. In each shedding period, a cavity starts to form and fill the center of the shed vortex. Then, the cavitating vortex is advected from the attached boundary layer and shed from the trailing edge. The alternating cavitating shedding vortices form the vortex street behind the wedge. The comparison between numerical results using incompressible and compressible cavitation solvers and the experimental results indicates that both cavitation solvers can capture the main flow characteristics in terms of the cavities morphology and their relative position as it can be seen in Figure 15(a) and Figure 15(c).
Figure 16 shows the time average void fraction field calculated with the incompressible (Incomp.) and compressible (Comp.) cavitation solvers and the experimental results. It can be seen that the simulations with two different cavitation solvers produce almost indistinguishable mean and RMS void fraction fields behind the wedge. The shape of mean cavity structures obtained numerically is comparable to the pattern observed in the experimental image. Note that, there is a downstream offset in the mean and RMS void fraction fields between the numerical and the experimental results that may be due to the low numerical resolution of the locally unstable flow structures within the detachment area.

6. Conclusions

In this study, the numerical results predicted by with an incompressible and a compressible cavitation model have been compared to assess the effects of the fluid compressibility on the characteristics and dynamics of the cavitating flow behind a wedge. For validation, the experimental results obtained by Wu et al. [5] for a cavitating wake behind a wedge have been taken as a reference. It has been found that both solvers capture the dynamics of the cavitating vortex street and give similar results in terms of mean pressure, lift and drag forces as the experimental ones. The main difference has been found on the frequency content of the fluid force fluctuations:
  • For low frequencies up to 800 Hz, both solvers predict similar amplitudes.
  • For higher frequencies above 1000 Hz, the compressible solver predicts larger amplitudes.
Moreover, regarding the prediction of the dominant vortex shedding frequency and the instantaneous and mean void fraction fields, the simulations performed with both solvers have provided almost identical results.
To summarize, it has been confirmed that the proposed compressibility solver is able to predict the cavitating vortex shedding behind a wedge.

Author Contributions

Conceptualization, Jian Chen and Linlin Geng.; methodology, Jian Chen.; software, Jian Chen and Xavier Escaler; validation, Esteve Jou and Xavier Escaler; formal analysis, Jian Chen and Linlin Geng; investigation, Jian Chen and Linlin Geng; resources, Esteve Jou and Xavier Escaler; data curation, Esteve Jou and Xavier Escaler; writing—original draft preparation, Jian Chen; writing—review and editing, Xavier Escaler; visualization, Esteve Jou; supervision, Xavier Escaler; funding acquisition, Linlin Geng and Xavier Escaler. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Jiangsu Province Science Foundation for Youths, grant number BK20220538 and Jiangsu University, grant number 21JDG052.

Data Availability Statement

All data generated or analyzed during this study are included in this article.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Franc, J.P.; Michel, J.M. Fundamentals of Cavitation; Springer science & Business media, 2006.
  2. Young, J.O.; Holl, J.W. Effects of Cavitation on Periodic Wakes behind Symmetric Wedges. 1966.
  3. Belahadji, B.; Franc, J.P.; Michel, J.M. Cavitation in the Rotational Structures of a Turbulent Wake. Journal of Fluid Mechanics 1995, 287, 383–403. [Google Scholar] [CrossRef]
  4. Ausoni, P.; Farhat, M.; Escaler, X.; Egusquiza, E.; Avellan, F. Cavitation Influence on von Kármán Vortex Shedding and Induced Hydrofoil Vibrations. Journal of Fluids Engineering 2007, 129, 966–973. [Google Scholar] [CrossRef]
  5. Wu, J.; Deijlen, L.; Bhatt, A.; Ganesh, H.; Ceccio, S.L. Cavitation Dynamics and Vortex Shedding in the Wake of a Bluff Body. Journal of Fluid Mechanics 2021, 917, A26. [Google Scholar] [CrossRef]
  6. Niedźwiedzka, A.; Schnerr, G.H.; Sobieski, W. Review of Numerical Models of Cavitating Flows with the Use of the Homogeneous Approach. Archives of thermodynamics 2016, 37. [Google Scholar] [CrossRef]
  7. Folden, T.S.; Aschmoneit, F.J. A Classification and Review of Cavitation Models with an Emphasis on Physical Aspects of Cavitation. Physics of Fluids 2023, 35, 081301. [Google Scholar] [CrossRef]
  8. Coutier-Delgosha, O.; Reboud, J.L.; Delannoy, Y. Numerical Simulation of the Unsteady Behaviour of Cavitating Flows. International Journal for Numerical Methods in Fluids 2003, 42, 527–548. [Google Scholar] [CrossRef]
  9. Ji, B.; Luo, X.; Arndt, R.E.A.; Wu, Y. Numerical Simulation of Three Dimensional Cavitation Shedding Dynamics with Special Emphasis on Cavitation–Vortex Interaction. Ocean Engineering 2014, 87, 64–77. [Google Scholar] [CrossRef]
  10. Gnanaskandan, A.; Mahesh, K. Large Eddy Simulation of the Transition from Sheet to Cloud Cavitation over a Wedge. International Journal of Multiphase Flow 2016, 83, 86–102. [Google Scholar] [CrossRef]
  11. Arndt, R.E.A. Cavitation in Fluid Machinery and Hydraulic Structures. Annual Review of Fluid Mechanics 1981, 13, 273–326. [Google Scholar] [CrossRef]
  12. Callenaere, M.; Franc, J.P.; Michel, J.M.; Riondet, M. The Cavitation Instability Induced by the Development of a Re-Entrant Jet. Journal of Fluid Mechanics 2001, 444, 223–256. [Google Scholar] [CrossRef]
  13. Kawanami, Y.; Kato, H.; Yamaguchi, H.; Tanimura, M.; Tagaya, Y. Mechanism and Control of Cloud Cavitation. Journal of Fluids Engineering 1997, 119, 778–794. [Google Scholar] [CrossRef]
  14. Laberteaux, K.R.; Ceccio, S.L. Partial Cavity Flows. Part 1. Cavities Forming on Models without Spanwise Variation. Journal of Fluid Mechanics 2001, 431, 1–41. [Google Scholar] [CrossRef]
  15. Leroux, J.-B.; Astolfi, J.A.; Billard, J.Y. An Experimental Study of Unsteady Partial Cavitation. Journal of Fluids Engineering 2004, 126, 94–101. [Google Scholar] [CrossRef]
  16. Wu, J.; Ganesh, H.; Ceccio, S. Multimodal Partial Cavity Shedding on a Two-Dimensional Hydrofoil and Its Relation to the Presence of Bubbly Shocks. Experiments in Fluids 2019, 60, 1–17. [Google Scholar] [CrossRef]
  17. Ganesh, H.; Mäkiharju, S.A.; Ceccio, S.L. Bubbly Shock Propagation as a Mechanism for Sheet-to-Cloud Transition of Partial Cavities. Journal of Fluid Mechanics 2016, 802, 37–78. [Google Scholar] [CrossRef]
  18. Bhatt, A.; Ganesh, H.; Ceccio, S.L. Partial Cavity Shedding on a Hydrofoil Resulting from Re-Entrant Flow and Bubbly Shock Waves. Journal of Fluid Mechanics 2023, 957, A28. [Google Scholar] [CrossRef]
  19. Gnanaskandan, A.; Mahesh, K. Numerical Investigation of Near-Wake Characteristics of Cavitating Flow over a Circular Cylinder. Journal of Fluid Mechanics 2016, 790, 453–491. [Google Scholar] [CrossRef]
  20. Wang, C.; Wang, G.; Huang, B. Characteristics and Dynamics of Compressible Cavitating Flows with Special Emphasis on Compressibility Effects. International Journal of Multiphase Flow 2020, 130, 103357. [Google Scholar] [CrossRef]
  21. Vaca-Revelo, D.; Gnanaskandan, A. Numerical Assessment of the Condensation Shock Mechanism in Sheet to Cloud Cavitation Transition. International Journal of Multiphase Flow 2023, 169, 104616. [Google Scholar] [CrossRef]
  22. Katz, J. Cavitation Phenomena within Regions of Flow Separation. Journal of Fluid Mechanics 1984, 140, 397–436. [Google Scholar] [CrossRef]
  23. O’Hern, T.J. An Experimental Investigation of Turbulent Shear Flow Cavitation. Journal of Fluid Mechanics 1990, 215, 365–391. [Google Scholar] [CrossRef]
  24. Iyer, C.O.; Ceccio, S.L. The Influence of Developed Cavitation on the Flow of a Turbulent Shear Layer. Physics of Fluids 2002, 14, 3414–3431. [Google Scholar] [CrossRef]
  25. Choi, J.; Ceccio, S.L. Dynamics and Noise Emission of Vortex Cavitation Bubbles. Journal of Fluid Mechanics 2007, 575, 1–26. [Google Scholar] [CrossRef]
  26. Agarwal, K.; Ram, O.; Lu, Y.; Katz, J. On the Pressure Field, Nuclei Dynamics and Their Relation to Cavitation Inception in a Turbulent Shear Layer. Journal of Fluid Mechanics 2023, 966, A31. [Google Scholar] [CrossRef]
  27. Brandao, F.L.; Bhatt, M.; Mahesh, K. Numerical Study of Cavitation Regimes in Flow over a Circular Cylinder. Journal of Fluid Mechanics 2020, 885, A19. [Google Scholar] [CrossRef]
  28. Park, S.; Seok, W.; Park, S.T.; Rhee, S.H.; Choe, Y.; Kim, C.; Kim, J.H.; Ahn, B.K. Compressibility Effects on Cavity Dynamics behind a Two-Dimensional Wedge. Journal of Marine Science and Engineering 2020, 8. [Google Scholar] [CrossRef]
  29. Zwart, P.; Gerber, A.G.; Belamri, T. A Two-Phase Flow Model for Predicting Cavitation Dynamics. In Proceedings of the Fifth International Conference on Multiphase Flow; January 1 2004.
  30. Egerer, C.P.; Schmidt, S.J.; Hickel, S.; Adams, N.A. Efficient Implicit LES Method for the Simulation of Turbulent Cavitating Flows. Journal of Computational Physics 2016, 316, 453–469. [Google Scholar] [CrossRef]
  31. Tong, S.-Y.; Zhang, S.; Wang, S.-P.; Li, S. Characteristics of the Bubble-Induced Pressure, Force, and Impulse on a Rigid Wall. Ocean Engineering 2022, 255, 111484. [Google Scholar] [CrossRef]
  32. Li, H.; Vasquez, S.A. Numerical Simulation of Steady and Unsteady Compressible Multiphase Flows. In Proceedings of the ASME 2012 International Mechanical Engineering Congress and Exposition; American Society of Mechanical Engineers Digital Collection, October 8 2013; pp. 2239–2251.
  33. Brunhart, M.; Soteriou, C.; Gavaises, M.; Karathanassis, I.; Koukouvinis, P.; Jahangir, S.; Poelma, C. Investigation of Cavitation and Vapor Shedding Mechanisms in a Venturi Nozzle. Physics of Fluids 2020, 32, 083306. [Google Scholar] [CrossRef]
  34. Mani, A. Analysis and Optimization of Numerical Sponge Layers as a Nonreflective Boundary Treatment. Journal of Computational Physics 2012, 231, 704–716. [Google Scholar] [CrossRef]
  35. Schmidt, S.J. A low Mach number consistent compressible approach for simulation of cavitating flows, Technical University of Munich: Munich, Germany, 2015.
  36. Braza, M.; Chassaing, P.; Minh, H.H. Numerical Study and Physical Analysis of the Pressure and Velocity Fields in the near Wake of a Circular Cylinder. Journal of Fluid Mechanics 1986, 165, 79–130. [Google Scholar] [CrossRef]
  37. Ding, H.; Shu, C.; Yeo, K.S.; Xu, D. Numerical Simulation of Flows around Two Circular Cylinders by Mesh-Free Least Square-Based Finite Difference Methods. International Journal for Numerical Methods in Fluids 2007, 53, 305–332. [Google Scholar] [CrossRef]
  38. Seo, J.H.; Moon, Y.J.; Shin, B.R. Prediction of Cavitating Flow Noise by Direct Numerical Simulation. Journal of Computational Physics 2008, 227, 6511–6531. [Google Scholar] [CrossRef]
  39. Harichandan, A.B.; Roy, A. Numerical Investigation of Flow Past Single and Tandem Cylindrical Bodies in the Vicinity of a Plane Wall. Journal of Fluids and Structures 2012, 33, 19–43. [Google Scholar] [CrossRef]
  40. Qu, L.; Norberg, C.; Davidson, L.; Peng, S.-H.; Wang, F. Quantitative Numerical Analysis of Flow Past a Circular Cylinder at Reynolds Number between 50 and 200. Journal of Fluids and Structures 2013, 39, 347–370. [Google Scholar] [CrossRef]
  41. Kim, K.H.; Choi, J.I. Lock-in Regions of Laminar Flows over a Streamwise Oscillating Circular Cylinder. Journal of Fluid Mechanics 2019, 858, 315–351. [Google Scholar] [CrossRef]
  42. Hong, S.; Son, G. Numerical Simulation of Cavitating Flows around an Oscillating Circular Cylinder. Ocean Engineering 2021, 226, 108739. [Google Scholar] [CrossRef]
  43. Menter, F.R. Best Practice: Scale-Resolving Simulations in ANSYS CFD; ANSYS Germany GmbH, 2015.
Preprints 114062 g001
Figure 1. Schematic of the sponge layer implementation.
Figure 1. Schematic of the sponge layer implementation.
Preprints 114062 g001
Preprints 114062 g002
Figure 2. Comparison of flow quantities obtained with the present model and the simulation by Schmidt (2015) at time t   = 1.5∙10-4 s for the 1-D two-phase time-dependent case.
Figure 2. Comparison of flow quantities obtained with the present model and the simulation by Schmidt (2015) at time t   = 1.5∙10-4 s for the 1-D two-phase time-dependent case.
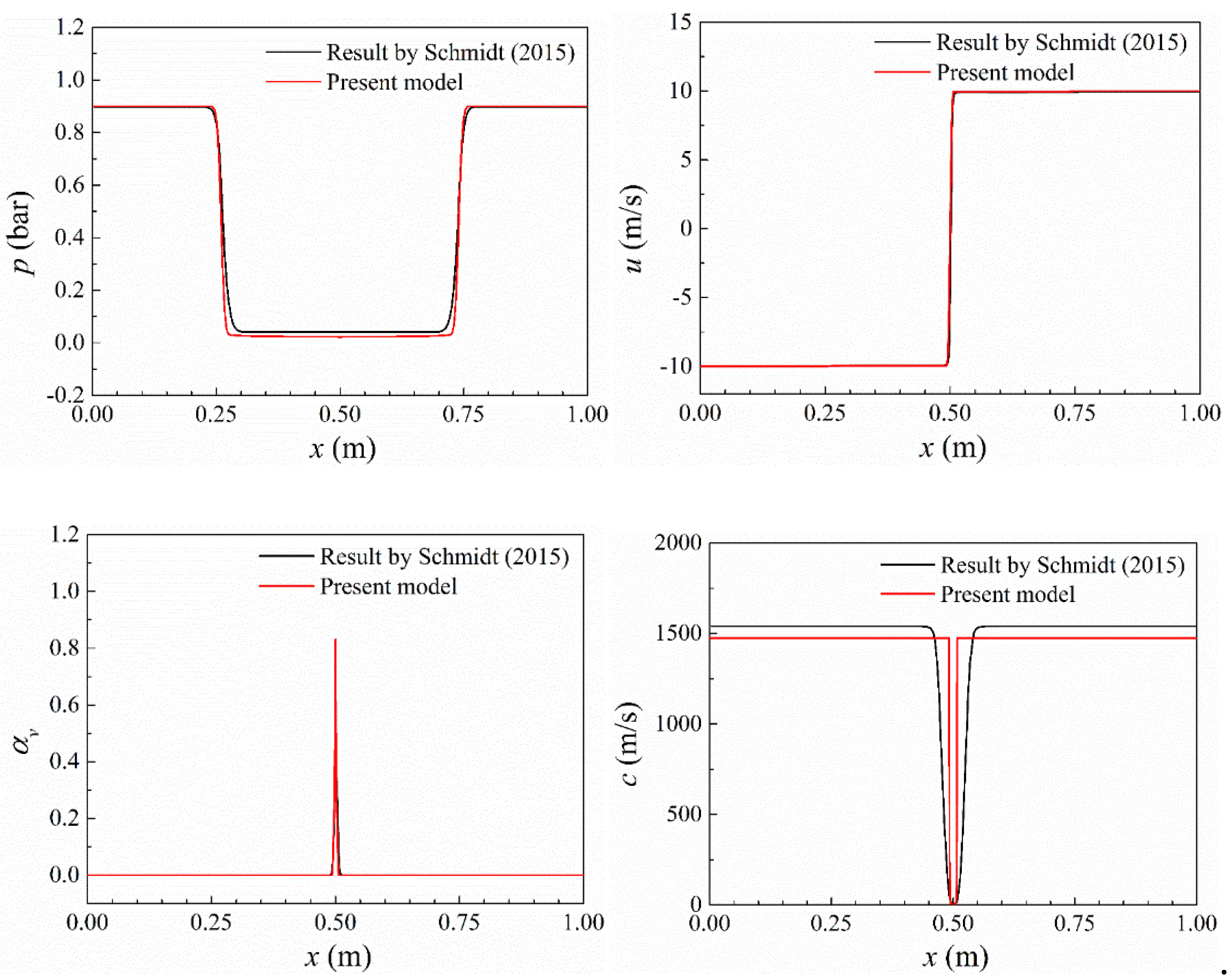
Preprints 114062 g002
Preprints 114062 g003
Figure 3. Details of the computational meshes around the circular cylinder: (a) whole domain and (b) region near the circular cylinder.
Figure 3. Details of the computational meshes around the circular cylinder: (a) whole domain and (b) region near the circular cylinder.
Preprints 114062 g003
Preprints 114062 g004
Figure 4. Time history of C D and C L for the non-cavitation regime.
Figure 4. Time history of C D and C L for the non-cavitation regime.
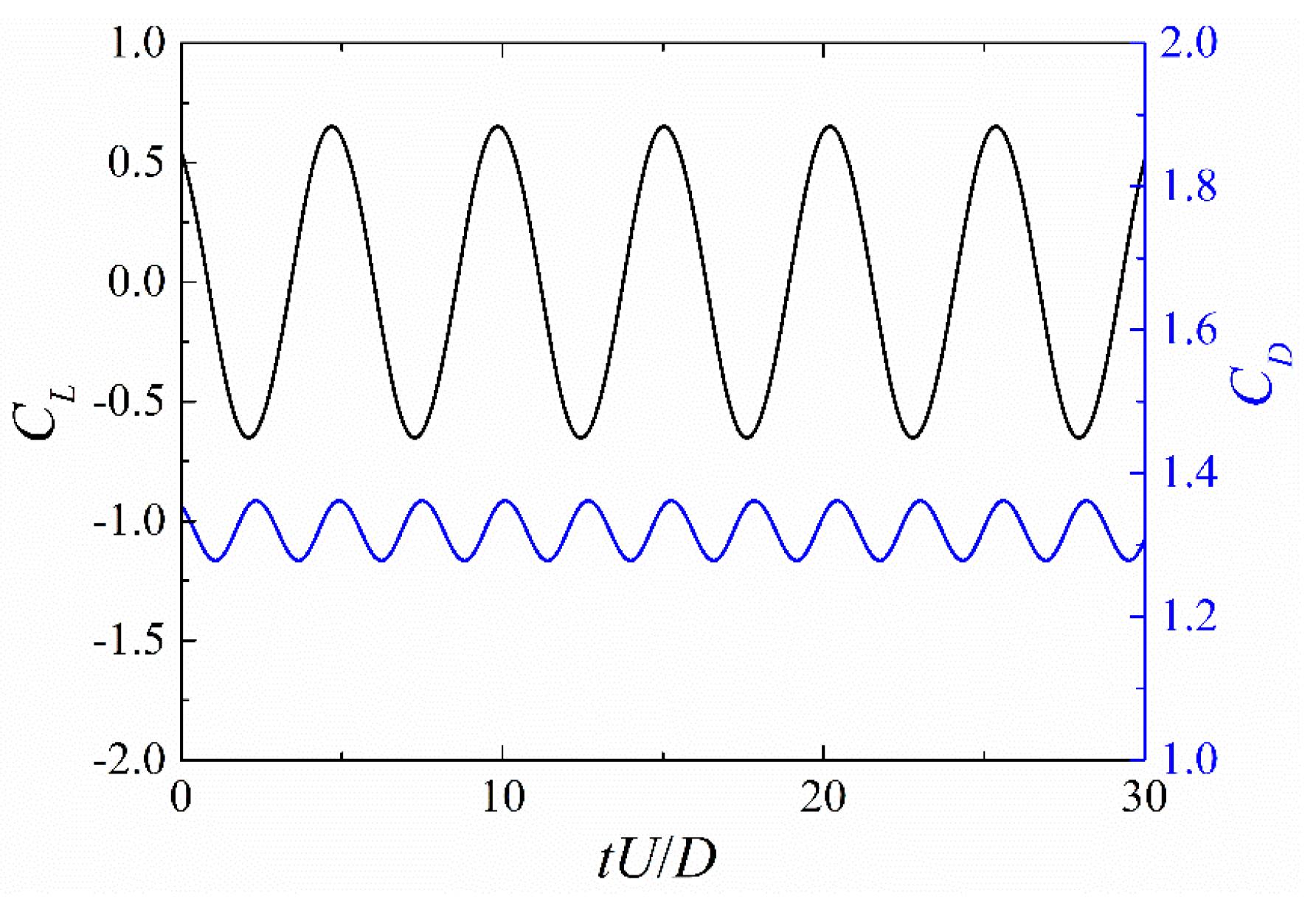
Preprints 114062 g004
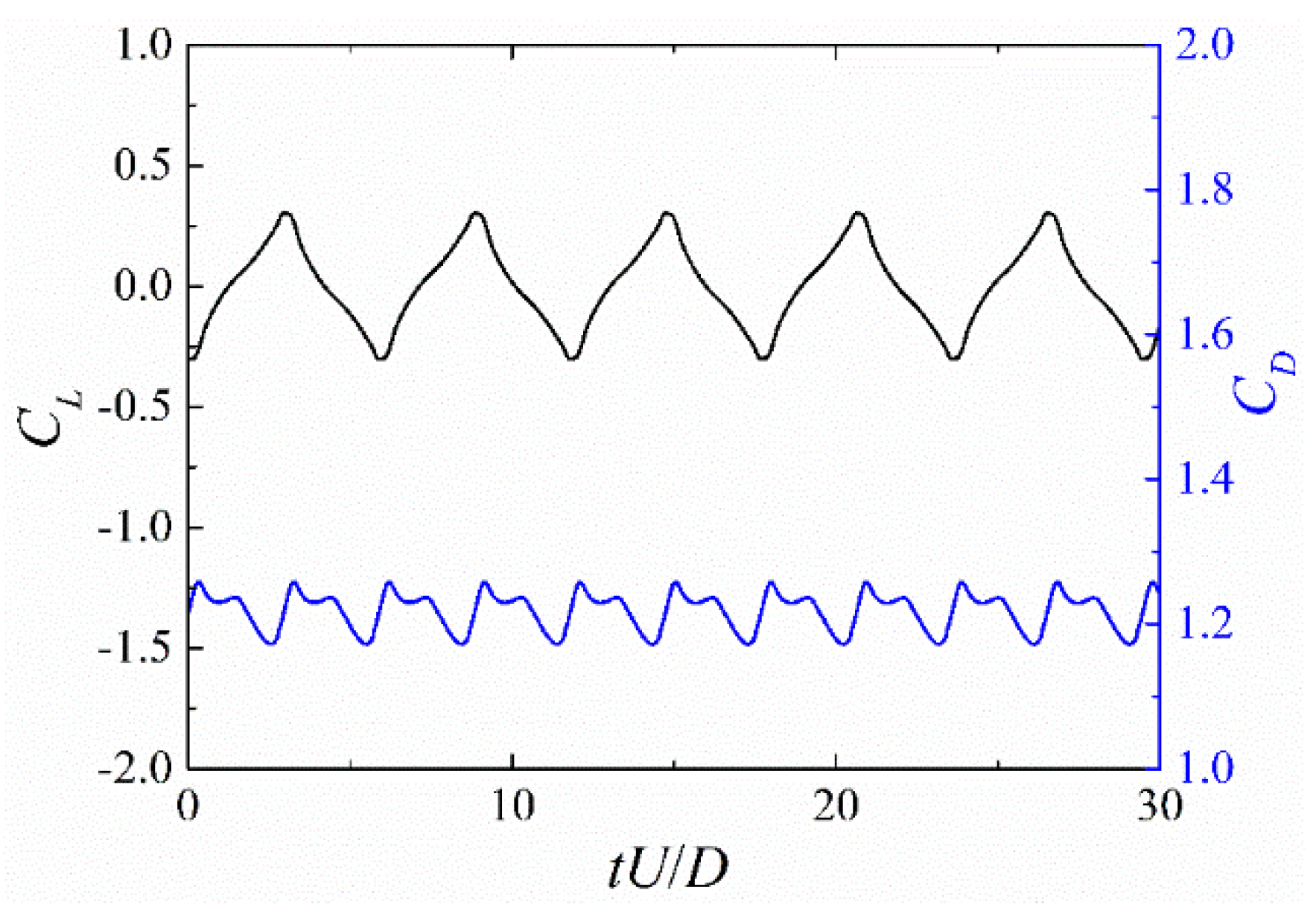
Preprints 114062 g005
Figure 5. Time history of C D and C L for the cavitation regime at σ =1.0.
Figure 5. Time history of C D and C L for the cavitation regime at σ =1.0.
Preprints 114062 g005
Preprints 114062 g006
Figure 6. Comparison of the instantaneous vorticity contour colored with vapor volume fraction at σ =1.0 between (a) Gnanaskandan and Mahesh [19] and (b) the current results.
Figure 6. Comparison of the instantaneous vorticity contour colored with vapor volume fraction at σ =1.0 between (a) Gnanaskandan and Mahesh [19] and (b) the current results.
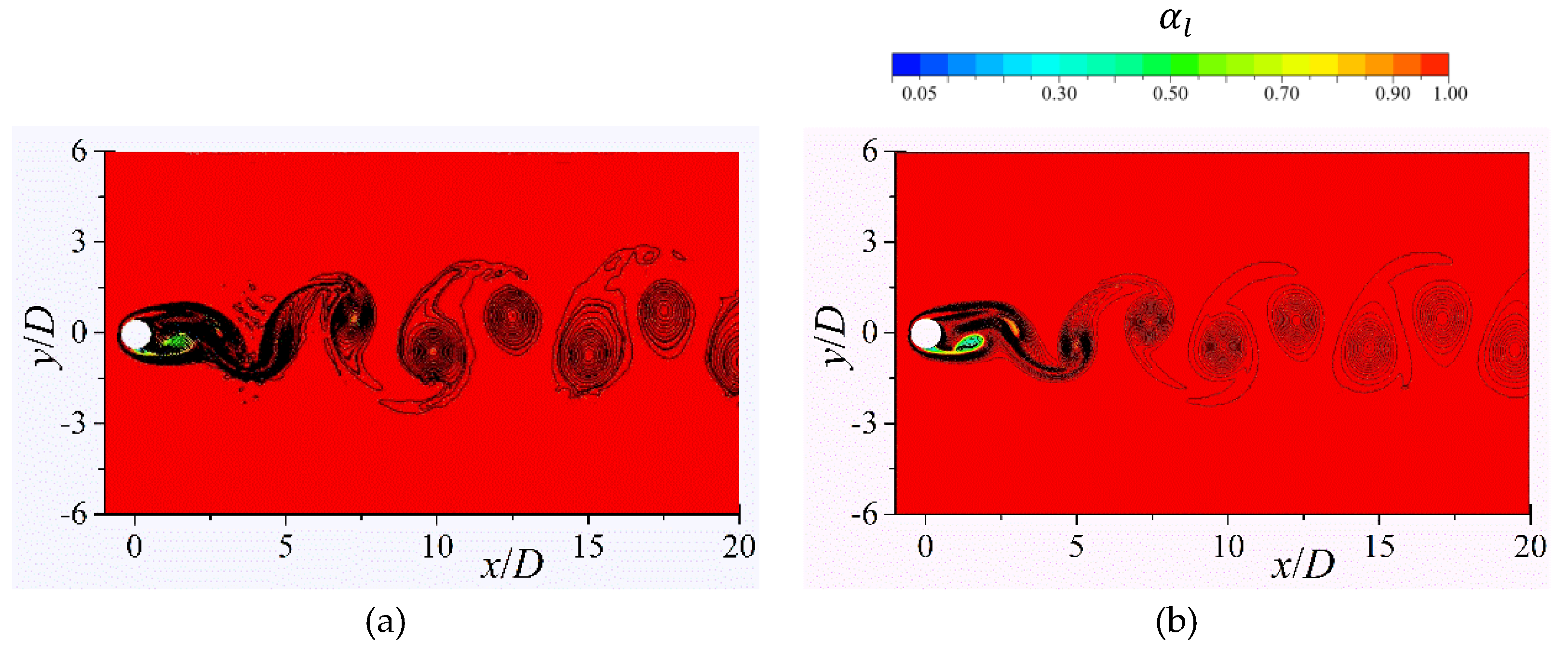
Preprints 114062 g006
Preprints 114062 g007
Figure 7. Computational domain for (a) the incompressible and (b) the compressible cavitation models.
Figure 7. Computational domain for (a) the incompressible and (b) the compressible cavitation models.
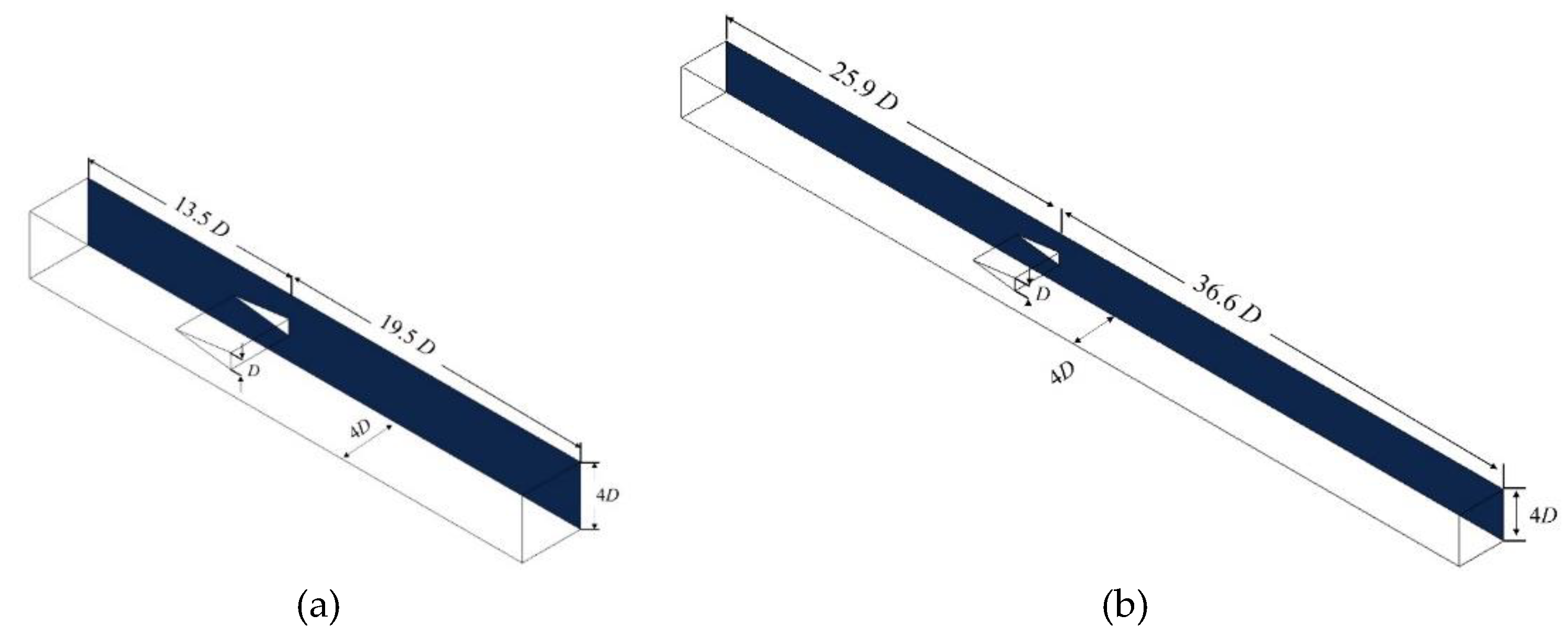
Preprints 114062 g007
Preprints 114062 g008
Figure 8. Views of the mesh topology around the wedge from (a) the side and (b) the top.
Figure 8. Views of the mesh topology around the wedge from (a) the side and (b) the top.
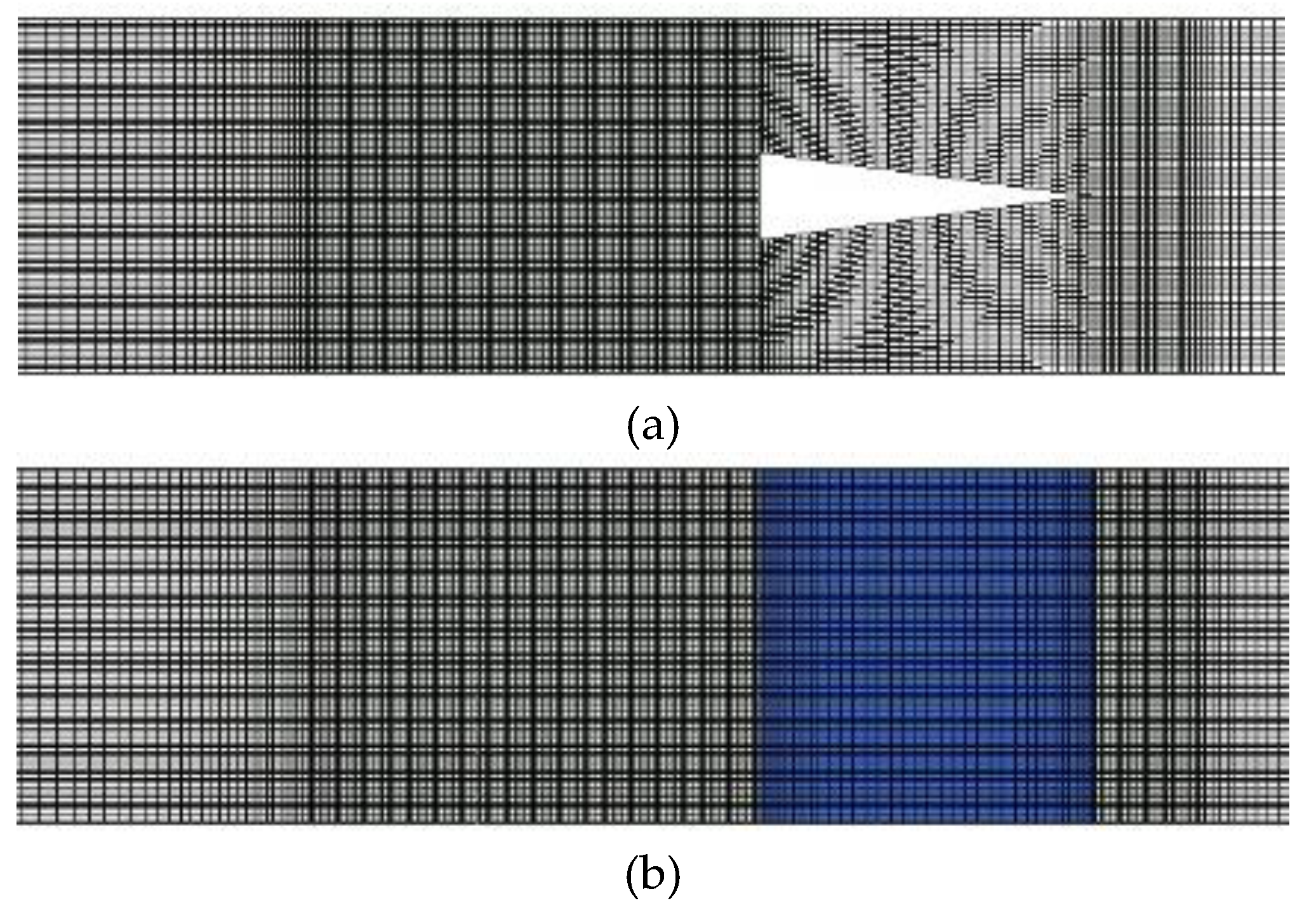
Preprints 114062 g008
Preprints 114062 g009
Figure 9. Fluid domain and boundary conditions defined to simulate the cavitating flow behind the wedge using an (a) incompressible cavitation model and a (b) compressible cavitation model.
Figure 9. Fluid domain and boundary conditions defined to simulate the cavitating flow behind the wedge using an (a) incompressible cavitation model and a (b) compressible cavitation model.
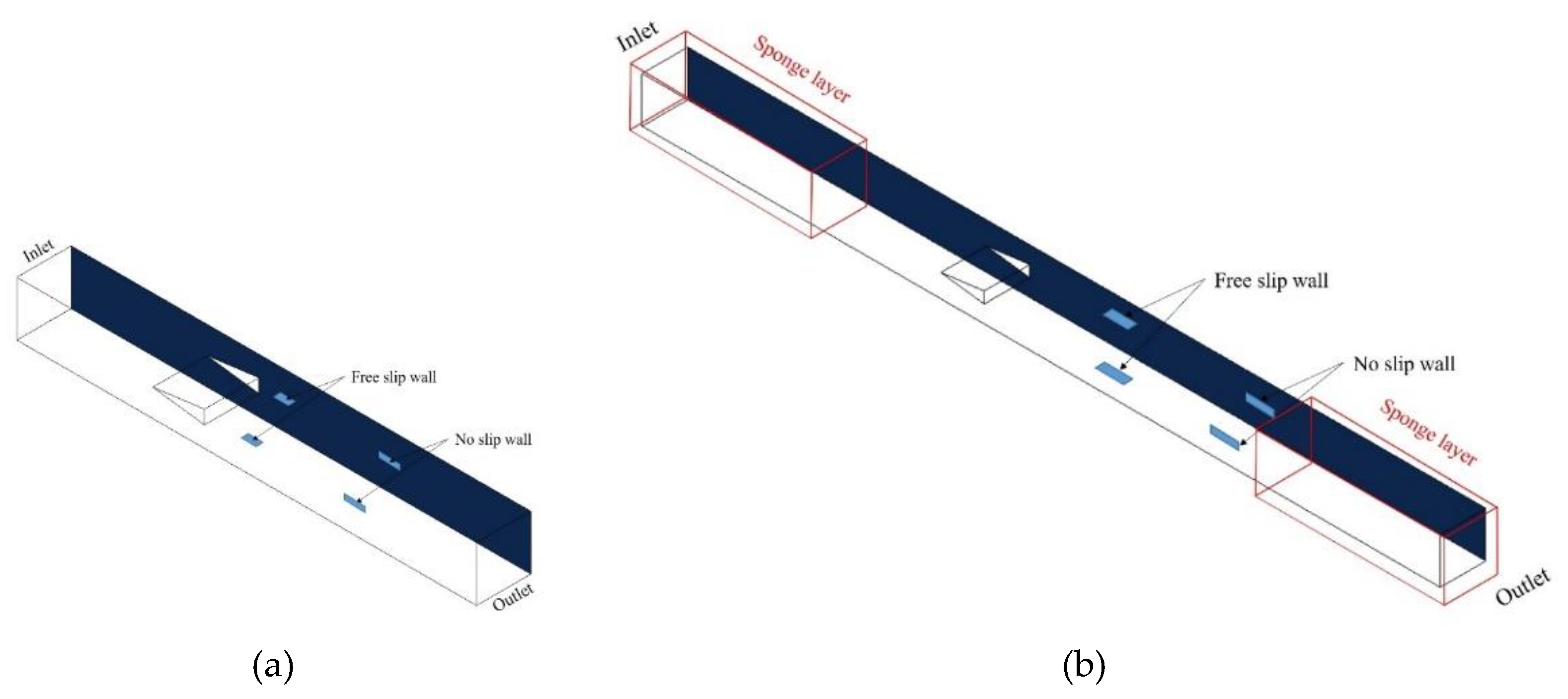
Preprints 114062 g009
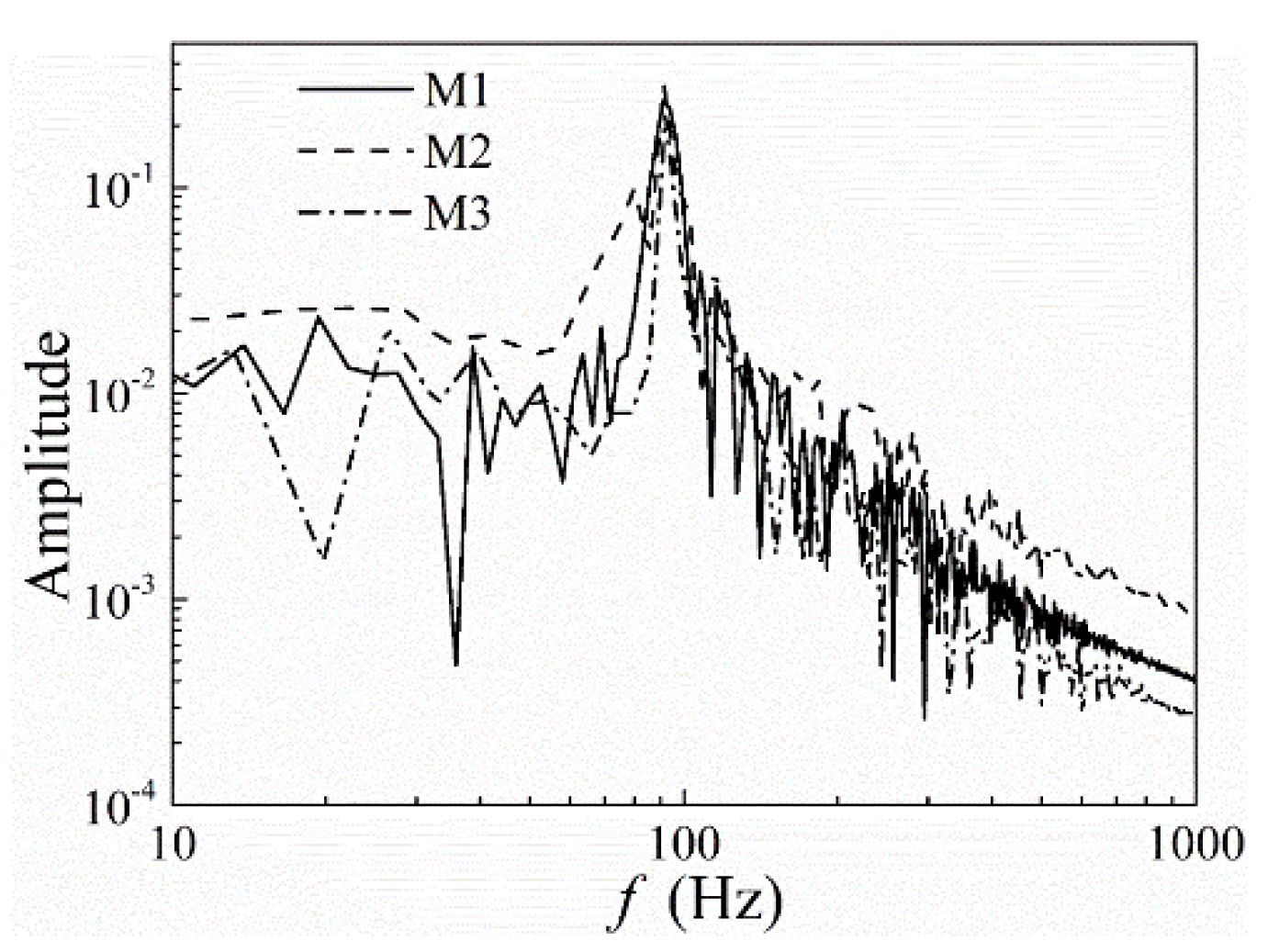
Preprints 114062 g010
Figure 10. Spectra of the lift coefficient for three different mesh refinements in the case of no-cavitation.
Figure 10. Spectra of the lift coefficient for three different mesh refinements in the case of no-cavitation.
Preprints 114062 g010
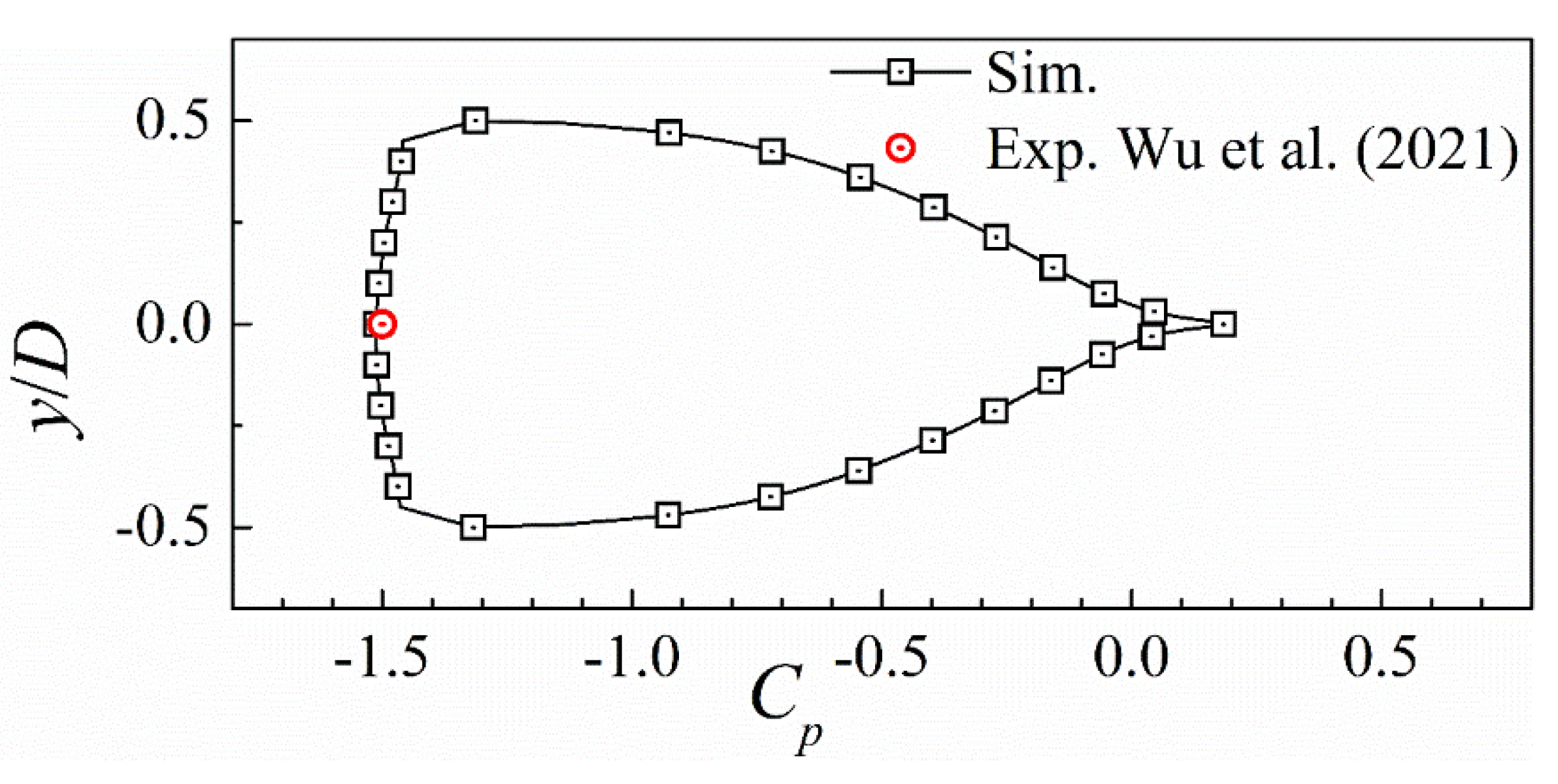
Preprints 114062 g011
Figure 11. Simulated versus measured C p values around the surface of the wedge at the non-cavitating condition.
Figure 11. Simulated versus measured C p values around the surface of the wedge at the non-cavitating condition.
Preprints 114062 g011
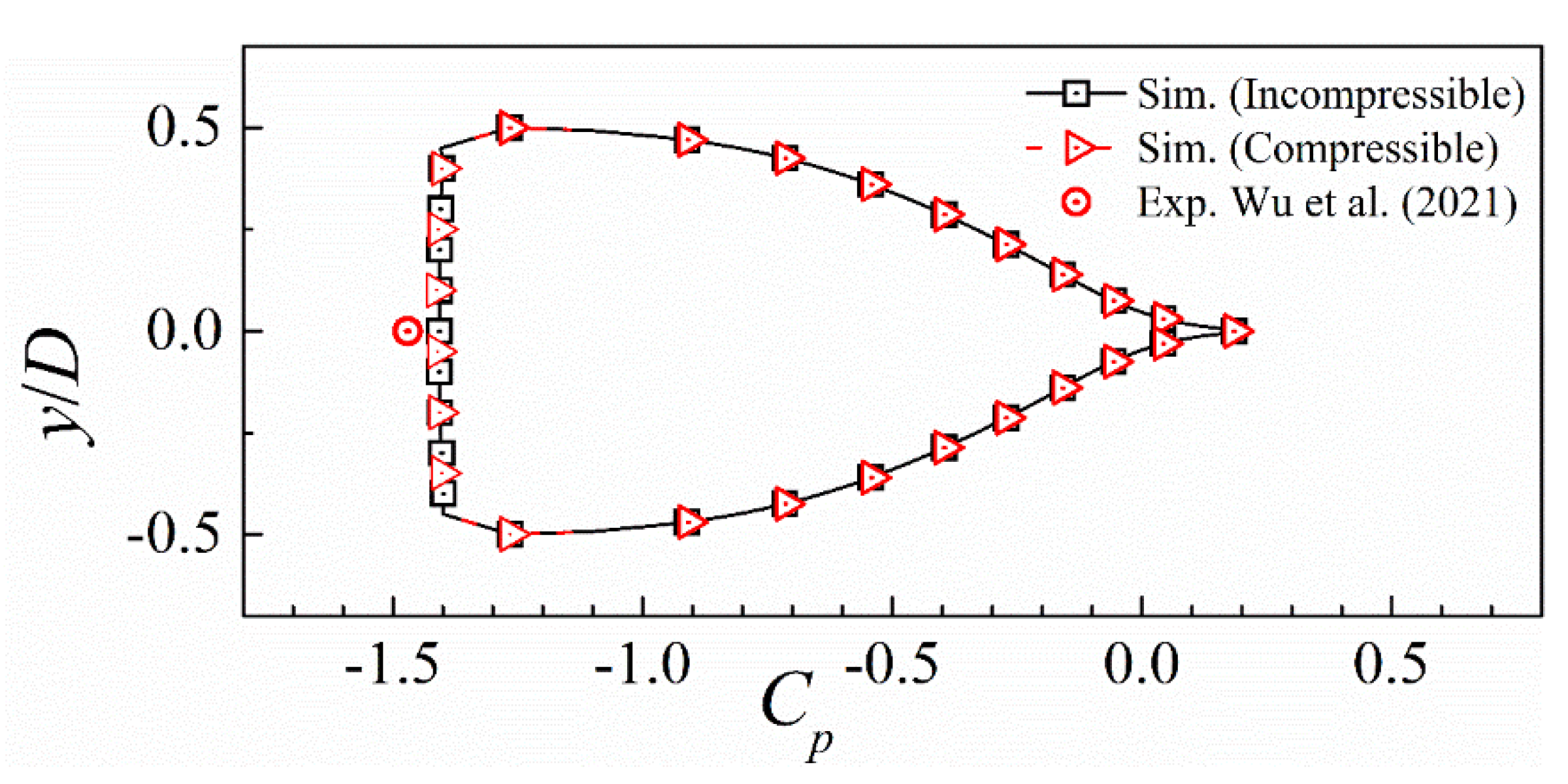
Preprints 114062 g012
Figure 12. Simulated versus measured C p values around the surface of the wedge using the incompressible and compressible cavitation models at cavitation conditions with σ = 1.9.
Figure 12. Simulated versus measured C p values around the surface of the wedge using the incompressible and compressible cavitation models at cavitation conditions with σ = 1.9.
Preprints 114062 g012
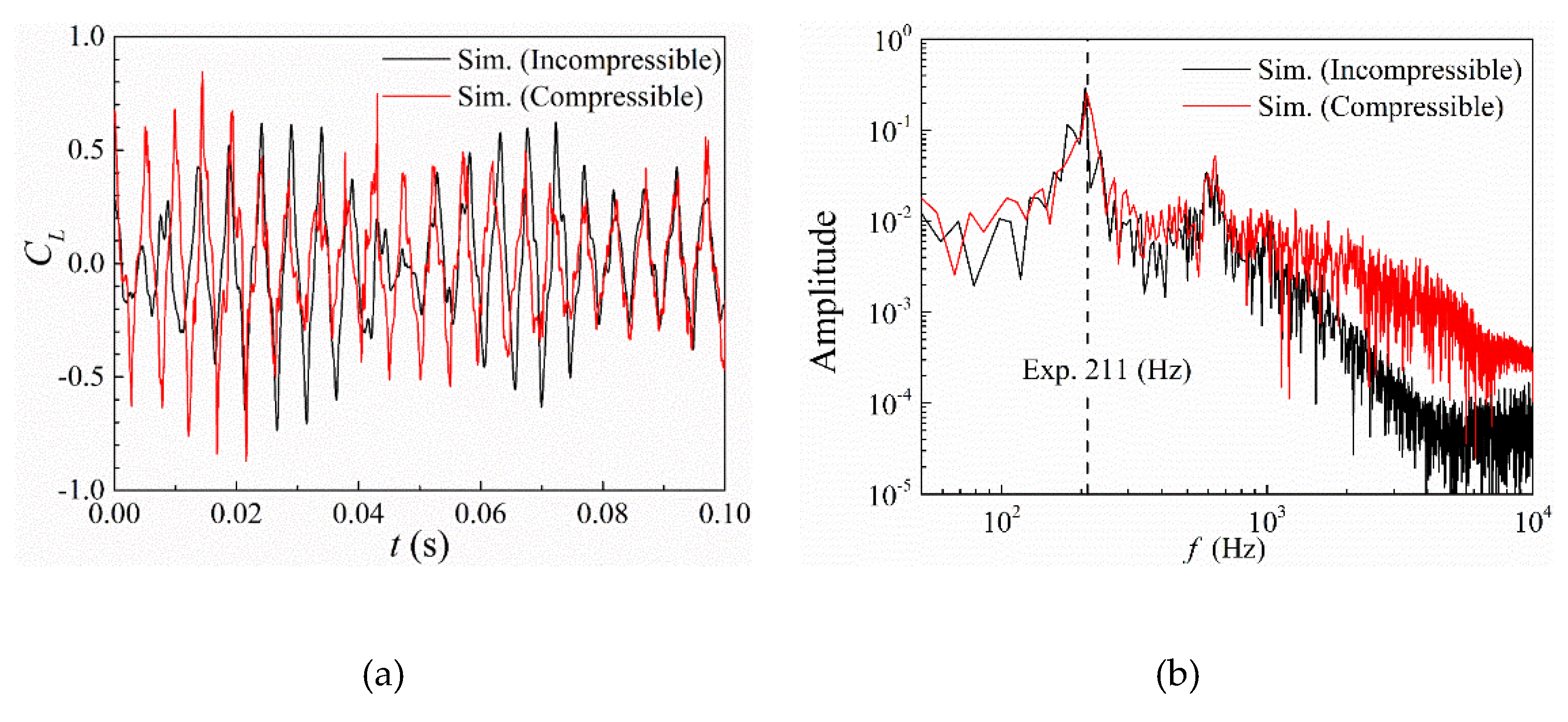
Preprints 114062 g013
Figure 13. (a) Lift coefficient time histories and (b) corresponding spectra with the incompressible and the compressible cavitation models for σ =1.9.
Figure 13. (a) Lift coefficient time histories and (b) corresponding spectra with the incompressible and the compressible cavitation models for σ =1.9.
Preprints 114062 g013
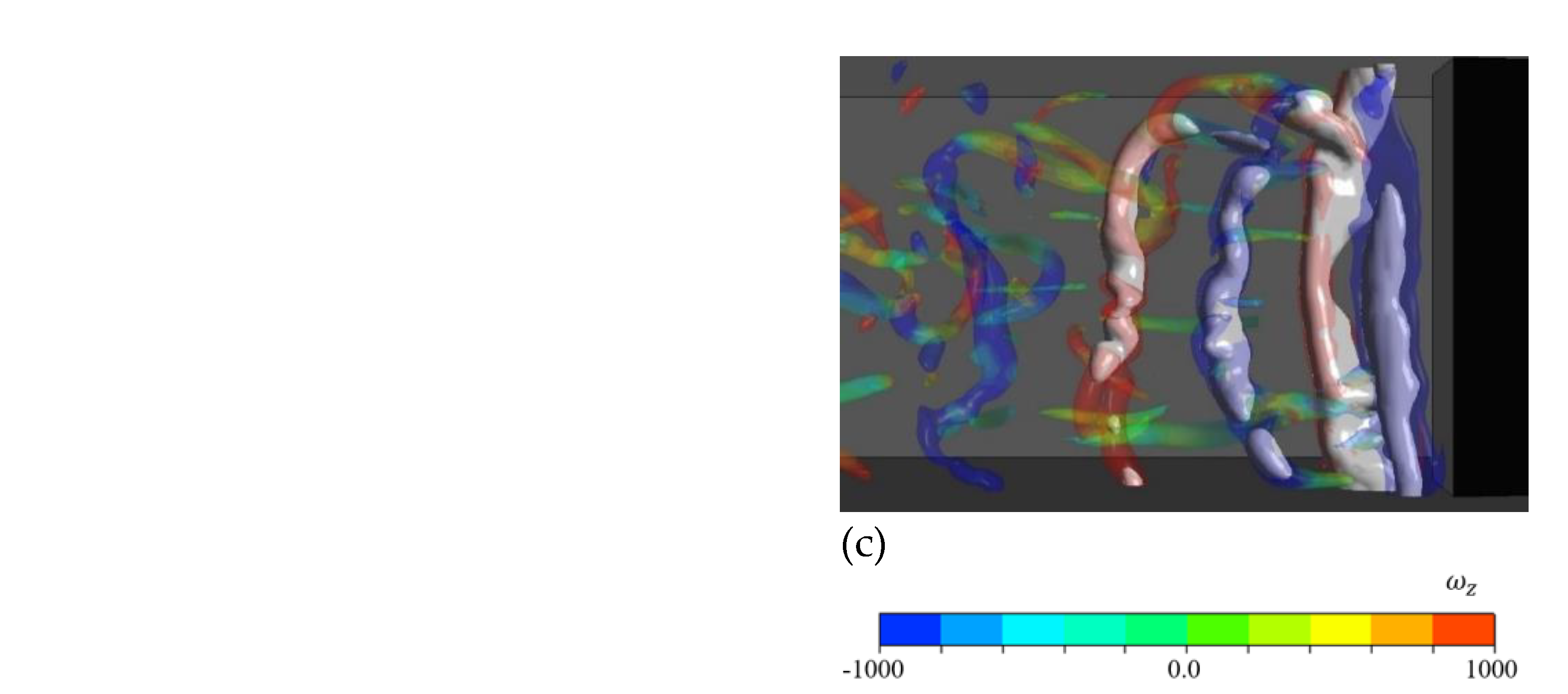
Preprints 114062 g014aPreprints 114062 g014b
Figure 14. Comparisons of (a) the experimentally [5] and the numerically obtained cavity structures using (b) the incompressible and (c) the compressible cavitation models at σ =1.9. The vortical structures are identified with an iso-surface of α v = 0.05 and the vorticity level is indicated with the Q criterion.
Figure 14. Comparisons of (a) the experimentally [5] and the numerically obtained cavity structures using (b) the incompressible and (c) the compressible cavitation models at σ =1.9. The vortical structures are identified with an iso-surface of α v = 0.05 and the vorticity level is indicated with the Q criterion.
Preprints 114062 g014aPreprints 114062 g014b
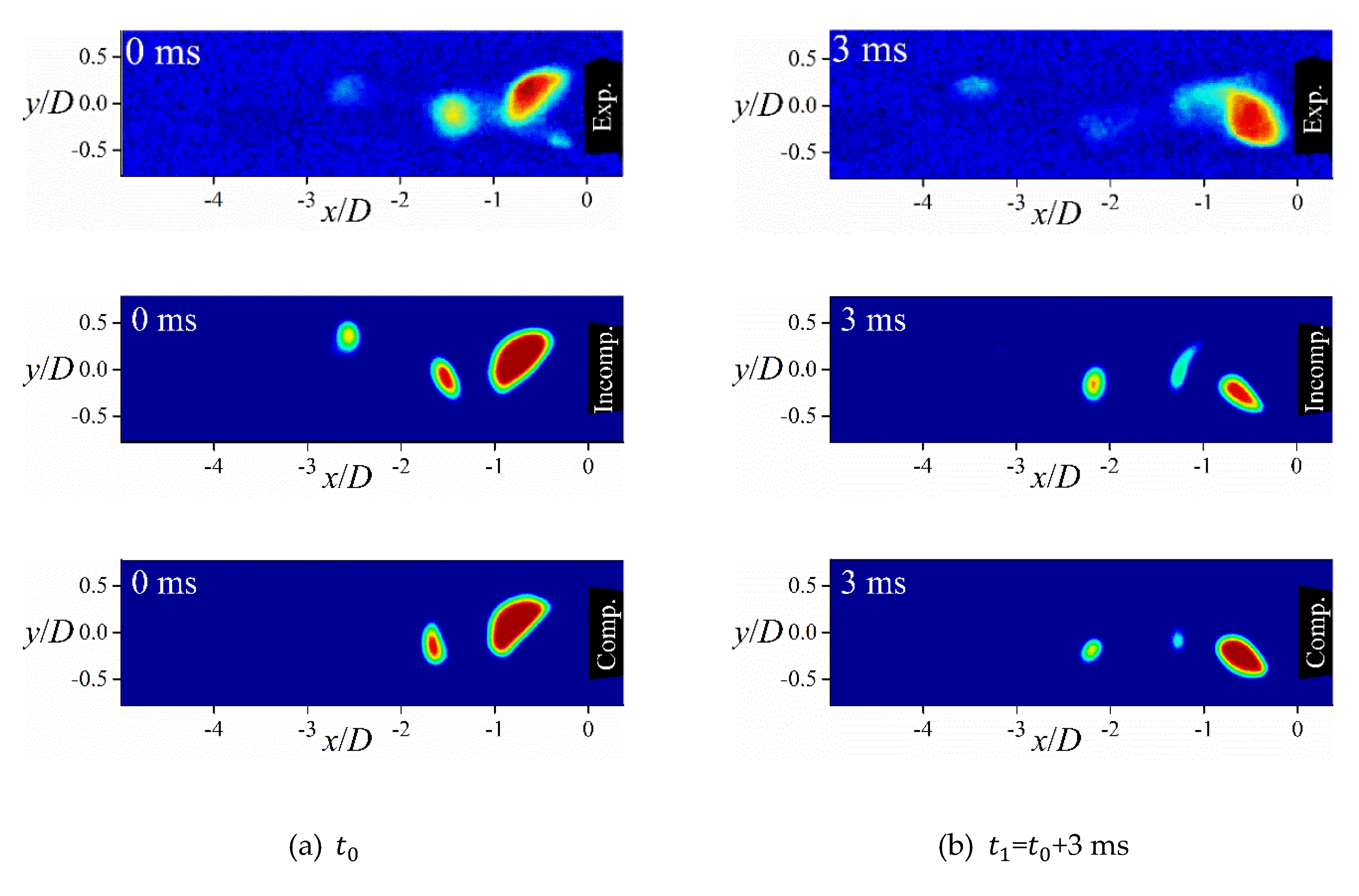
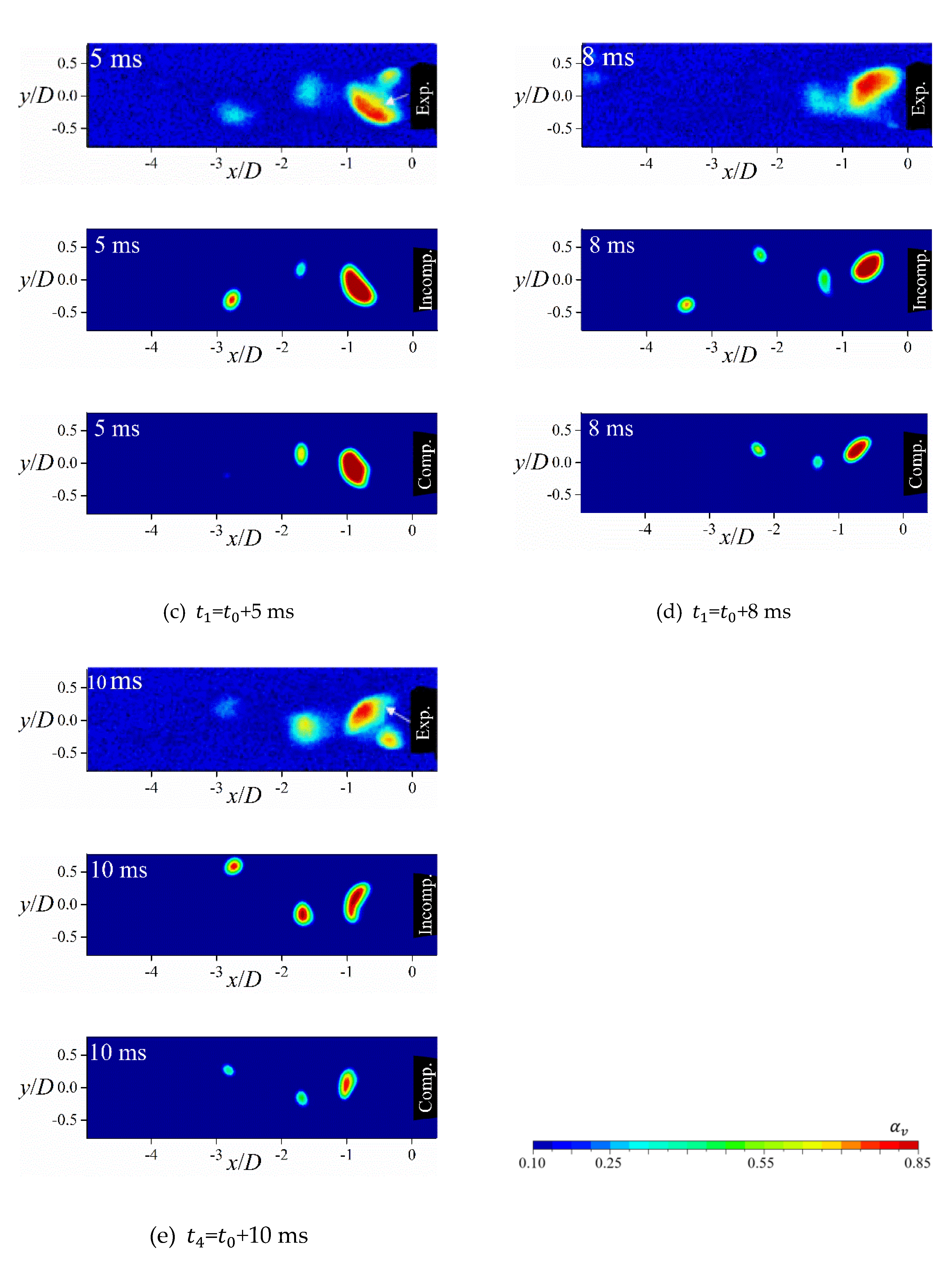
Preprints 114062 g015aPreprints 114062 g015b
Figure 15. Comparisons of the experimentally (Exp.) [5] and numerically obtained void fraction contour plots at different instants of time during the vortex shedding using the incompressible (Incomp.) and the compressible (Comp.) cavitation model at σ =1.9.
Figure 15. Comparisons of the experimentally (Exp.) [5] and numerically obtained void fraction contour plots at different instants of time during the vortex shedding using the incompressible (Incomp.) and the compressible (Comp.) cavitation model at σ =1.9.
Preprints 114062 g015aPreprints 114062 g015b
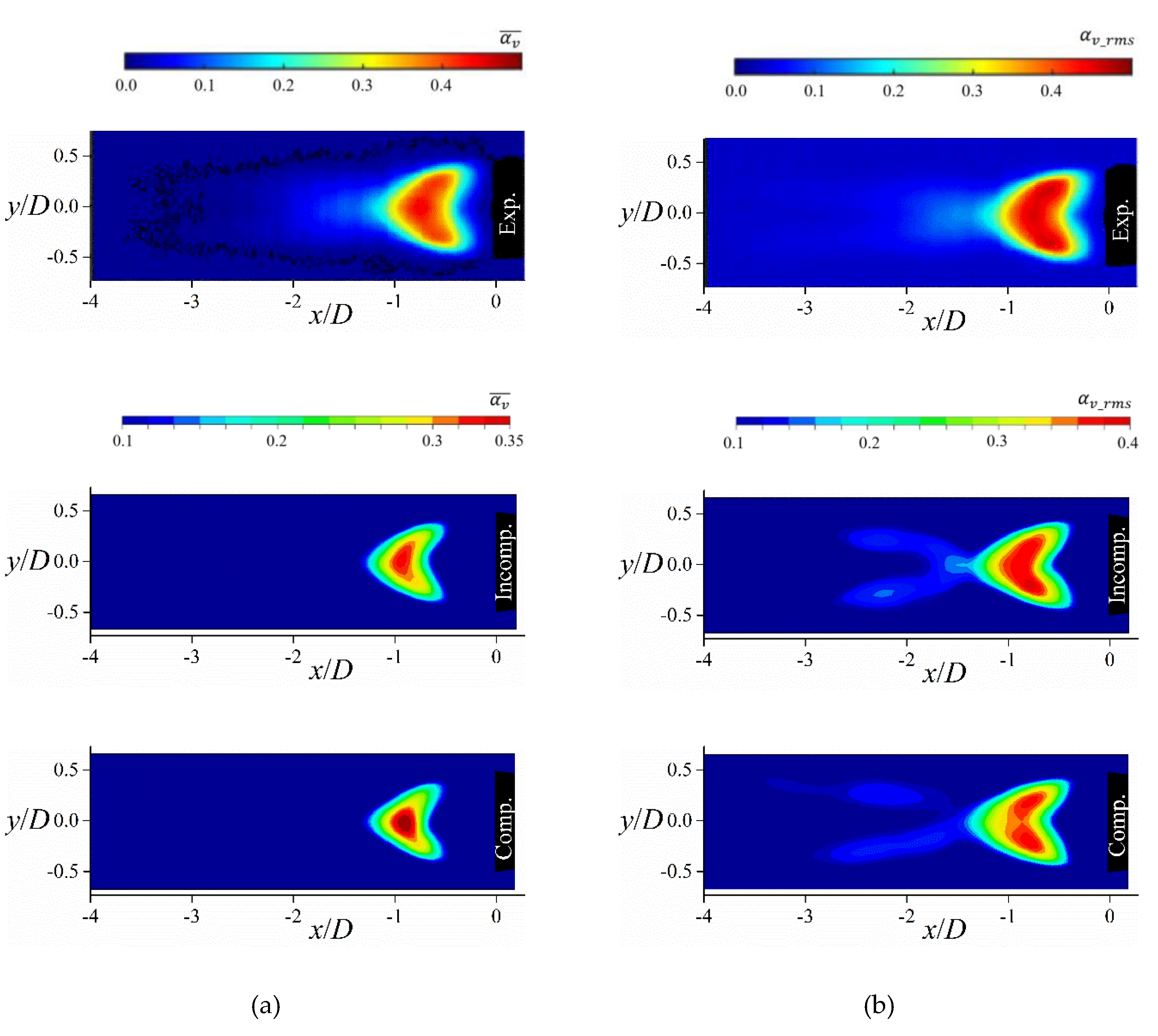
Preprints 114062 g016
Figure 16. Comparisons of the experimentally (Exp.) [5] and numerically obtained time average (a) and (b) RMS void fraction fields using the incompressible (Incomp.) and the compressible (Comp.) cavitation models at σ =1.9.
Figure 16. Comparisons of the experimentally (Exp.) [5] and numerically obtained time average (a) and (b) RMS void fraction fields using the incompressible (Incomp.) and the compressible (Comp.) cavitation models at σ =1.9.
Preprints 114062 g016
Table 1. Comparison of C D , a v , C L , m a x , and S t values between the current simulation and the results previously published by other authors for a circular cylinder at R e   = 200 without cavitation.
Table 1. Comparison of C D , a v , C L , m a x , and S t values between the current simulation and the results previously published by other authors for a circular cylinder at R e   = 200 without cavitation.
C D , a v C L , m a x S t
Braza et al. [36] 1.40 0.75 0.20
Ding et al. [37] 1.35 0.66 0.196
Seo et al. [38] 1.08 0.60 0.19
Harichandan and Roy [39] 1.32 0.60 0.194
Qu et al. [40] 1.32 0.66 0.196
Gnanaskandan et al. [19] - - 0.198
Kim and Choi [41] 1.35 0.70 0.197
Hong and Son [42] 1.32 0.66 0.194
Current simulation 1.32 0.65 0.194
Table 2. Comparison of C D , a v , C L , m a x , and S t values between the current simulation and the results previously published by other authors for a circular cylinder at R e = 200 at σ   = 1.0.
Table 2. Comparison of C D , a v , C L , m a x , and S t values between the current simulation and the results previously published by other authors for a circular cylinder at R e = 200 at σ   = 1.0.
C D , a v C L , m a x S t
Seo et al. [38] 1.08 0.42 0.16
Gnanaskandan and Mahesh [19] 1.10 0.56 0.16
Hong and Son [42] - - 0.177
Current simulation 1.22 0.30 0.17
Table 3. Characteristic parameters of the different meshes considered for the sensitivity test.
Table 3. Characteristic parameters of the different meshes considered for the sensitivity test.
Name Number of cells D /Δx
M1 1.39×106 20
M2 2.75×106 26
M3 4.13×106 30
Table 4. Specific values of the boundary conditions for the non-cavitation and cavitation conditions.
Table 4. Specific values of the boundary conditions for the non-cavitation and cavitation conditions.
σ Inlet boundary Value Outlet boundary Value Top wall Bottom wall Other walls
Non cavitation Fixed velocity 6 m/s Outlet - FSW FSW NSW
1.9 Total pressure 54540 Pa Mass flowrate 34.66 kg/s FSW FSW NSW
Free slip wall: FSW No slip wall: NSW.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated