The Symmetry Group of the Grand Antiprism

Preprint

Article

The Symmetry Group of the Grand Antiprism

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Barry Monson^*

This version is not peer-reviewed

Submitted:

01 August 2024

Posted:

02 August 2024

You are already at the latest version

Alerts

Abstract

The grand antiprism A is an outlier among the uniform 4-polytopes, since it is not obtainable from Wythoff’s construction. Its symmetry group G(A) has been incorrectly described as [[10,2+,10]] or even as an `ionic diminished Coxeter group’. In fact, G(A) is another group of order 400, namely the group ±[D10×D10]·2, in the notation of Conway and Smith.

Keywords:

Subject: Computer Science and Mathematics - Geometry and Topology

1. Introduction

A convex d-polytope

Q

in Euclidean space is uniform if its symmetry group

G (Q)

is transitive on its vertices, and if, furthermore, each facet of

Q

is uniform. To initiate this recursive condition in a geometrically pleasing way, we agree that a uniform polygon should be regular.

It is easy to see that all edges of

Q

have the same length. However, for

d ⩾ 3

Q

may well have different kinds of facets. For example, the pentagonal antiprism

P_{5}

on the right in Figure 1 is bounded by two regular pentagons

{5}

and ten equilateral triangles

{3}

. A regular polytope

Q

, which by definition has a symmetry group transitive on flags, is certainly uniform. Consider the regular tetrahedron

{3, 3}

, also in Figure 1.

In ordinary space

E^{3}

, the uniform convex polyhedra include the five Platonic solids, the thirteen Archimedean solids, as well as n-gonal prisms and antiprisms, for

n ⩾ 3

. There is a little redundancy here: the 3-gonal antiprism and 4-gonal prism have more symmetry than first expected, being the regular octahedron

{3, 4}

and cube

{4, 3}

, respectively. For an excellent discussion of these polyhedra, their groups, as well as uniform tessellations of the plane, we refer to Coxeter’s paper [7]. After a remarkable break starting with World War II, Coxeter explored uniform polytopes of higher dimension in two follow-up articles [9,10] appearing in the 1980s. An essential tool throughout is Wythoff’s construction for uniform polytopes.

In [9], we find a discussion of the grand antiprism

A

, discovered by J. H. Conway and M. Guy in 1965 [4]. This remarkable object is the only uniform 4-polytope which cannot be constructed by Wythoff’s construction, even accepting Coxeter’s extension of the method to rotation groups. Coxeter also described the symmetry group

G (A)

[[10, 2^{+}, 10]] ≃ G^{4, 4, 10} .

In fact, this is the wrong group of order 400, an error which has percolated into the literature.

In Section 2 we use Wythoff’s construction to construct the 600-cell

S

, then find

A

inscribed in it. A correct description of the symmetry group

G (A)

(as a semidirect product

[5, 2, 5] ⋊ C_{4}

) appears in Proposition 1. Actually, this was already derived in a slightly different way in [17]. Nevertheless, that paper still seems to suggest

[[10, 2^{+}, 10]]

as the group.

Now the finite subgroups of

G O_{4} (R)

have been variously classified, but it seems that the catalogue recently appearing in [5] is complete and corrects small errors or oversights in earlier attempts, such as that in [14]. In order to help the reader understand all this, we have reviewed in Section 4 how unit quaternions are used to describe isometries in

E^{3}

and

E^{4}

. At the end of this long but necessary digression, we show in Example 3 that

G (A) ≃ \pm [D_{10} \times D_{10}] \cdot 2,

here using the notation of [5].

2. The 600-cell $S = {3, 3, 5}$ and the Grand Antiprism $A$

A useful way to understand the grand antiprism

A

is to see it inscribed in the 600-cell

S = {3, 3, 5}

, so we begin by describing the latter regular 4-polytope. The symmetry group

G (S)

is the (linear) Coxeter group

H_{4} = [3, 3, 5]

, with generating reflections

r_{0}, r_{1}, r_{2}, r_{3}

corresponding to the nodes of the diagram

◯ • \frac{3}{} • \frac{3}{} • \frac{5}{} •

(1)

The ring decorating the first node is an instruction to perform Wythoff’s construction. In this instance, we choose a non-zero base vertex

v

fixed by

r_{1}, r_{2}, r_{3}

. The regular polytope

S

is then the convex hull of the

H_{4}

-orbit of

v

If, as in [18], we identify an involutory isometry like

r_{j}

with its fixed space, or mirror, we see that

v

spans the Wythoff space

W = r_{1} \cap r_{2} \cap r_{3}

(2)

corresponding to the unringed nodes in diagram (1).

A linear Coxeter group like

H_{4}

has special properties which serve to make the construction recursive. In particular, the subgroup of

H_{4}

which fixes W pointwise is generated by the reflections indicated in (2). Thus the number of vertices in

S

is the index of the subgroup

〈 r_{1}, r_{2}, r_{3} 〉

. Furthermore, this subgroup is itself the Coxeter group

[3, 5]

corresponding to the diagram obtained by deleting the first node:

\cdot ◯ • \frac{3}{} • \frac{5}{} •

(3)

We conclude that there are

14400 / 120 = 120

vertices. The diagram in (3) arises by transferring the ring in (1) to the second node. This means that the vertex-figure at each vertex of

{3, 3, 5}

is a regular icosahedron

{3, 5}

. The orthogonal projection behind Figure 2 maps

v

to the centre of this isosahedron. The red edges

v u

and

v w

serve as a reminder that

v

lies outside the hyperplane supporting the vertex-figure. We shall soon see that

. . . w v u . . .

is really part of a planar decagon.

One can read much more from the diagram (1). For instance, just by deleting the right-most node, we find that all facets of

S

are regular tetrahedra

{3, 3}

, and that there are

600 = 14400 / 24

of them.

We now draw on [11] and [8] to give a more explict description of both

S

and its group

H_{4}

(as a subgroup of

G O_{4} (R)

). Depending on our algebraic needs, it will be useful at times to regard a point

x = (x_{0}, x_{1}, x_{2}, x_{3}) \in E^{4}

as either a pair

(u, v)

of complex numbers (so

u = x_{0} + x_{1} ı, v = x_{2} + x_{3} ı

) or as a single quaternion

x_{0} + x_{1} i + x_{2} j + x_{3} k = u + v j

. In this spirit, we find in [11] a description of the 120 vertices of

S

as pairs of complex numbers. We need

ϵ = exp (π / 10)

and the related angle

λ = \frac{1}{2} arctan 2 ≐ 31 . 72^{\circ}

, so that

cos λ = τ^{\frac{1}{2}} 5^{- \frac{1}{4}}

sin λ = τ^{- \frac{1}{2}} 5^{- \frac{1}{4}}

, with

τ = (1 + \sqrt{5}) / 2

the Golden ratio.

Here then are the 120 vertices of

S

in a slight modification of Coxeter’s notation. The parameters

μ, ν

are residues modulo 10:

2 μ + 1 | \underset{̲}{} = (ϵ^{2 μ + 1}, 0), \underset{̲}{} | 2 ν + 1 = (0, ϵ^{2 ν + 1})

(4a)

2 μ | 2 ν = (ϵ^{2 μ} cos λ, ϵ^{2 ν} sin λ) (μ + ν even)

(4b)

2 μ | 2 ν = (ϵ^{2 μ} sin λ, ϵ^{2 ν} cos λ) (μ + ν odd)

(4c)

Remark 1.

We have indeed 120 points of norm 1 in

E^{4}

. Since

S

is centrally symmetric, the vertices occur in 60 antipodal pairs. A special property of

S

is that each pair is normal to a hyperplane of symmetry for the polytope. These 60 reflections comprise the single conjugacy class of reflections in

H_{4}

. Thus (in 14400 ways) we can extract from the vertices a simple system of roots for

H_{4}

[15, Chapter 1.3]. That is, we can find four vertices to serve as `outer’ unit normals

n_{j}

for the mirrors of the generating reflections

r_{j}

, (

j = 0, 1, 2, 3

). We choose

n_{0} = 7 | \underset{̲}{}, n_{1} = 16 | 2, n_{2} = \underset{̲}{} | 9, n_{3} = \underset{̲}{} | 17 .

(5)

Note, for instance, that

r_{0} : (u, v) \mapsto (- \bar{u} ϵ^{14}, v) .

A suitable base vertex (fixed by

r_{1}, r_{2}, r_{3}

) is then

v = 1 | \underset{̲}{}

. The base edge joins

v

u = (v) r_{0} = 3 | \underset{̲}{}

. Clearly, the angle between (vectors)

v, u

2 π / 10

, and each edge of

S

has length

2 sin \frac{π}{10} = τ^{- 1} .

There is now enough algebraic detail in place for the reader to check, with effort, our subsequent calculations. (We often seek refuge in GAP [1].) □

First off, the central symmetry

x \mapsto - x

factors as

z = {(r_{0} r_{1} r_{2} r_{3})}^{15}

H_{4}

[8]. The icosahedral vertex-figure at

v

, say, has its own central symmetry

{(r_{1} r_{2} r_{3})}^{5}

. Using Figure 2 and our earlier calculations, we see [11] that

s = {(r_{1} r_{2} r_{3})}^{5} r_{0}

(6)

cyclically moves

. . . w v u . . .

one step along a planar convex decagon A (contained in the 1-skeleton of

S

). We note that

s : (u, v) \mapsto (u ϵ^{2}, - v) .

Comparing (4a), we see that the vertices

2 j + 1 | \underset{̲}{}

of A lie in the

x_{0} x_{1}

-plane, while the vertices

\underset{̲}{} | 2 j + 1

of an orthogonal convex decagon B lie in the

x_{2} x_{3}

-plane.

Remark 2.

Since the icosahedron has 6 pairs of antipodal vertices, each vertex of

S

lies on 6 planar decagons, and altogether there are 72 such decagons. Furthermore, one can select 12 vertex-disjoint decagons to exhaust the vertices of

S

. The 12 circumcircles belong to a Hopf fibration of

S^{3}

[11, Section 4.9]. □

Definition 1.

The grand antiprism

A

is the convex hull of the 100 vertices of

S

which remain after deleting two orthogonal decagons.

Let us remove A and B, leaving the points

2 μ | 2 ν

. Since

S

is inscribed in

S^{3}

, these 100 points survive as the vertices of their convex hull

A

. To survey the facets of

A

, we consult [11, Section 4.6, Exercise 2].

Each edge of the decagon A is surrounded in

S

by 5 tetrahedral facets; and a vertex such as

v

is common to 10 further tetrahedra whose bases form a belt running in zig-zag fashion around the middle of the icosahedral vertex-figure, as in Figure 2. In this way A and B each meet 150 tetrahedra. These 300 facets of

S

are lost when we construct

A

If we first remove

v

from

S

, its icosahedral vertex-figure (Figure 2) becomes a facet of the new convex hull. If we next remove

u, w

adjacent to

v

, we further truncate this icosahedron back to the pentagonal antiprism

P_{5}

whose lateral triangles are those in the belt just described. In this way, the facets of

A

include a ring

R_{A}

of 10 copies of

P_{5}

. One pentagonal face on an antiprism arising this way has vertices

2 μ | 0, 2 μ | 4, 2 μ | 8, 2 μ | 12, 2 μ | 16 (μ even),

while the other pentagon is

2 μ + 2 α | 2, 2 μ + 2 α | 6, 2 μ + 2 α | 10, 2 μ + 2 α | 14, 2 μ + 2 α | 18,

with

α

alternating

\pm 1

as we run round the ring. The 50 vertices of

R_{A}

are the points

2 μ | 2 ν

with

μ + ν

even, from (4b). The symmetry s in (6) moves

R_{A}

one step along itself.

The complementary ring

R_{B}

derived from B is disjoint from

R_{A}

and provides 10 more copies of

P_{5}

. Its 50 vertices are the points

2 μ | 2 ν

, with

μ + ν

odd, found in (4c).

The 100 triangular faces in each ring form a non-regular toroidal map of Schläfli type

{3, 6}

[11]. Each triangle on

R_{A}

is the base of a tetrahedral facet of

S

whose apex is on

R_{B}

. In this way,

A

inherits 100 tetrahedral facets, let us say of type A. In complementary fashion,

A

acquires from

S

the 100 tetrahedral facets of type B. The final 100 facets of

A

are tetrahedra of type

A B

. Each has one edge on

R_{A}

with the opposite edge on

R_{B}

. Tetrahedra of type

A B

have vertices

2 μ | 2 ν, 2 μ | 2 ν + 2, 2 μ + 2 | 2 ν, 2 μ + 2 | 2 ν + 2 (any μ, ν) .

(7)

Altogether,

A

has 500 edges, 20 regular pentagons and 700 equilateral triangles as faces of lower rank. Each vertex-figure is non-uniform and arises as the convex hull of the 10 points which remain when an edge is deleted from an icosahedron

{3, 5}

It is still not quite clear that

A

is uniform, so we take a close look at its symmetry group

G = G (A)

. Notice that G is a subgroup of

H_{4}

. It coincides with the (set-wise) stabilizer of the decagons

{A, B}

Let

K ⩽ G

be the subgroup that takes A into A (and thus B into B). First of all, K contains every reflection r in a hyperplane orthogonal to a pair of antipodal vertices of A. This r induces a reflection symmetry of A while fixing B pointwise; and the five reflections coming from A this way generate a dihedral group of order 10.

In addition, the central symmetry

z \in K

, so K contains

r z

, which also acts by reflection on A, though as a half-turn on B. (One can view

r z

as a half-turn about a vertex of A in the 3-space spanned by A and some vertex of B.)

Let us choose the new reflection r to have normal

n = 15 | \underset{̲}{}

. Then

D (A) = 〈 r_{0}, r z 〉

acts on A as the full dihedral symmetry group

D_{20}

of order 20, though half its elements act as half-turns on B. Similarly, we have

D (B) = 〈 r_{2} z, r_{3} 〉 ≃ D_{20}

acting on decagon B.

Note that

z = {(r_{0} r z)}^{5} = {(r_{2} z r_{3})}^{5} \in D (A) \cap D (B)

. These two dihedral groups commute with one another and intersect in a centre

〈 z 〉

of order 2. Thus K has order 200.

In [9, p. 590], Coxeter observed that

K ≃ [10, 2^{+}, 10] = 〈 a_{0}, a_{1} a_{2}, a_{3} 〉,

(8)

the `ionic’ subgroup of the Coxeter group

[10, 2, 10] = 〈 a_{0}, a_{1}, a_{2}, a_{3} 〉

with diagram

• \frac{10}{} • • \frac{10}{} • .

(Compare [9, p. 569] and [16, p. 239]. The whimsical adjective `ionic’ comes from the fact that the reflections

a_{j}

have determinant

- 1

, so that words of even length like

a_{1} a_{2}

give determinant

+ 1

, thereby reducing the `negative charge’.)

To verify (8), first take

a_{0} = r_{0}, a_{3} = r_{3}

; but let

a_{1}

be the reflection acting on A as

r z

but fixingB. Likewise let

a_{2}

act as

r_{2} z

on B but fix A. (Note that

a_{1}, a_{2}

do not belong to G.) We get (8) upon noting that

a_{1} a_{2} = r r_{2} z

It is curious that with the involutory generators

a_{0}, a_{1} a_{2}, a_{3}

, K is isomorphic to the full automorphism group of the regular map

{10, 10 | 2}

[12, Section 8.5].

Any

g, h \in G

which take A to B must also take B to A, so

g h \in K

. Thus G has order 400. The crucial question is how G extends K.

In [9, Section 2.8], Coxeter describes a half-turn t which is meant to do the job. Certainly various half-turns t swap A and B. However, no such t can lie in G (or in

H_{4}

)! To verify this, we note that the supposed half-turn would have to map

(u, v)

to either

(v y^{- 1}, u y)

(\bar{v} y, \bar{u} y)

, for some complex number y of norm 1. But

0 | 0 = (cos λ, sin λ)

must map to some

2 μ | 2 ν = (ϵ^{2 μ} sin λ, ϵ^{2 ν} sin λ)

, with

μ + ν

odd. We would need

ϵ^{2 μ \pm 2 ν} = 1

, which is impossible for

μ + ν

odd.

If we do move sideways and adopt the half-turn

t : (u, v) \mapsto (\bar{v} y, \bar{u} y)

, with

y = ϵ^{4}

, then we have an involution which (by conjugation) swaps

a_{0}, a_{3}

while fixing

a_{1} a_{2}

. This is just what is needed to `double’ the group

K ≃ [10, 2^{+}, 10]

and so arrive at

[[10, 2^{+}, 10]] ≃ G^{4, 4, 10} .

(See [16, pp. 255ff] and [9, p. 590].) The group on the left denotes the semidirect product

[10, 2^{+}, 10] ⋊ 〈 t 〉

, which indeed is isomorphic to

G^{4, 4, 10}

, one of a family of groups defined by a special sort of presentation [12, p. 96]. In this case, in terms of the generators

a = a_{1} a_{2} a_{0}, b = a_{0} t, c = t a_{0} a_{1} a_{2}

, we have defining relations

a^{10} = b^{4} = c^{4} = {(a b)}^{2} = {(b c)}^{2} = {(c a)}^{2} = {(a b c)}^{2} = 1

[9, Equation 2.39]. Note that

〈 t, a_{2} 〉 ≃ D_{8}

. Since

G (A)

has no such subgroup, we confirm once more that

G (A)

cannot be

[[10, 2^{+}, 10]]

On the other hand, we can exhibit a symmetry

p \in H_{4}

of period 4 which swaps A and B. Taking

μ = 0, ν = 1

in (7), we see that

0 | 2, 0 | 4, 2 | 4, 2 | 2

(9)

are vertices of a facet of type

A B

for

A

. This regular tetrahedron is a facet of

S

, so it admits the Petrie symmetry p which cyclically permutes the vertices as they appear in (9). Thus p has order 4, and in fact also permutes the roots

n_{0}, n_{3}, n, n_{2}

in a 4-cycle. Moreover, p swaps A and B, and

p \in G (A)

It is now finally clear that

G (A)

is vertex-transitive, so that

A

really is uniform!

Note that the subgroup

〈 r_{0}, r, r_{2}, r_{3} 〉

of K is the linear Coxeter group

[5, 2, 5]

of order 100. Conjugation by p in G will transform its generators in a 4-cycle

(r_{0}, r_{3}, r, r_{2})

. Furthermore,

p^{2}

lies in K but not in its subgroup

[5, 2, 5]

. We have

Proposition 1.

The grand antiprism is uniform. Its symmetry group

G (A)

is the semidirect product

[5, 2, 5] ⋊ C_{4} .

Remark 3.

It is easy to check that

G (A)

has defining relations

r^{2} = p^{4} = {(p^{- 2} r p^{2} r)}^{5} = {(p^{- 1} r p r)}^{2} = 1 .

The group

G (A)

was correctly described as such a semidirect product in [17, Section 2]. The authors there used quaternion methods, which we turn to in Section 4. However, they seem to continue the mislabelling of

G (A)

as `the ionic diminished Coxeter group

[10, 2^{+}, 10]

’.

Considering the toroidal maps on the surfaces of the rings

R_{A}, R_{B}

, it is quite natural that the symmetry p is induced by an affine function of the vertex symbols:

p : 2 μ | 2 ν \mapsto (2 ν - 2) | (4 - 2 μ) (mod 20) .

□

We conclude this section by describing the subgroups of

G (A)

which preserve some substructures of

A

The vertex

2 | 2

is typical and is fixed in

G (A)

by the subgroup

〈 r_{0}, r_{3} 〉 ≃ C_{2} \times C_{2}

The point

2 | 2

belongs to 2 facets of type B. One of these has base triangle

0 | 2, 2 | 4, 4 | 2

R_{B}

and is fixed in

G (A)

〈 r_{0} 〉

. Each tetrahdron of type A or B in

A

has, in this way, a stabilizer generated by a single reflection.

However, a tetrahedron of type

A B

has a stabilizer of order 4 generated by a Petrie symmetry, just as p does for the tetrahedron with the vertices in (9).

It is clear that

G (A)

acts transitively and faithfully on the 20 pentagonal antiprisms. Thus each such facet must inherit its full symmetry group of order 20 from

G (A)

. For instance, the group of the pentagonal antiprism with vertices

	$2 \| 2$		$2 \| 6$		$2 \| 10$		$2 \| 14$		$2 \| 18$
$0 \| 0$		$0 \| 4$		$0 \| 8$		$0 \| 12$		$0 \| 16$		$0 \| 0$

is generated by the reflection

r_{3}

and the half-turn

h = p^{2}

about the centre of the edge

2 | 2 0 | 4

. (The reflection

r_{0}

fixes the upper pentagon point-wise but maps the pentagonal antiprism itself to one of its neighbours in the ring

R_{A}

.) We refer to Section 3 for more on the symmetry group

[5, 2^{+}]

for a pentagonal antiprism.

From the action of

G (A)

on the 20 antiprismatic facets we obtain this faithful permutation representation:

\begin{matrix} r & \mapsto & (1, 10) (2, 9) (3, 8) (4, 7) (5, 6) \\ p & \mapsto & (1, 12) (2, 11, 10, 13) (3, 20, 9, 14) (4, 19, 8, 15) (5, 18, 7, 16) (6, 17) \end{matrix}

Note that

{(r p)}^{2} \mapsto (1, 2, 3, 4, 5, 6, 7, 8, 9, 10) (11, 12, 13, 14, 15, 16, 17, 18, 19, 20)

simultaneously rotates each ring through a tenth of a turn.

3. More on Wythoff’s Construction

In [6] Coxeter extended Wythoff’s construction to general Coxeter groups G of finite or affine type, with nodes of the diagram ringed in any way. (See also [7 Section 1.5], [9, Section 2.4] and [11, Section 2.4].) All this is aimed at enumerating uniform polytopes and tessellations in Euclidean space. Actually, Coxeter also employed a variant of the construction based on just the rotation subgroup

G^{+}

, indicated by replacing all nodes in the diagram by empty rings. The choice of base vertex

x

required to guarantee uniformity is now trickier and sometimes impossible, although the construction always works in

E^{3}

. In particular, the n-gonal antiprism

P_{n}

is produced by the diagram

◯ \frac{n}{} ◯ ◯

(10)

The underlying Coxeter group

G = [n, 2]

has order

4 n

, so

G^{+}

has order

2 n

and indeed is isomorphic to the dihedral group

D_{2 n}

(of order

2 n

). We have

G^{+} = 〈 q, h 〉

, where q is a rotation through

2 π / n

about some axis l, while h is a half-turn about an axis m meeting l at right angles. A base vertex

x

can now be chosen to produce a pair of regular n-gons separated by a belt of

2 n

equilateral triangles running in zig-zag fashion. The pentagonal antiprism (

n = 5

) is illustrated in Figure 1. For

n > 3

the full symmetry group of the antiprism does have order

4 n

but is not quite the group G. Instead,

G (P_{n})

is the group

[2 n, 2^{+}]

, once more following the notation of [16, Section 11.4] and [9]. Beginning with the larger Coxeter group

[2 n, 2] = 〈 u_{0}, u_{1}, u_{2} 〉

, we need the ionic subgroup

[2 n, 2^{+}] = 〈 u_{0}, u_{1} u_{0} u_{1}, u_{1} u_{2} 〉,

of order

4 n

. In fact, as we saw in Section 2, we find that this group is generated by the reflection

u_{0}

and the half-turn

u_{1} u_{2}

. When n is odd, this group actually is isomorphic to

[n, 2]

, though geometrically different.

Remark 4.

We noted earlier that Wythoff’s construction, including the extension to rotation groups, gives all uniform polyhedra in

E^{3}

. In [4], Conway and Guy apparently used a local approach to construct all uniform 4-polytopes [9, p. 588]: they computed the dihedral angles for all uniform polyhedra, then tried to assemble these facets so that around each edge the dihedral angles sum to less than

2 π

. They found that only one uniform polytope in

E^{4}

, the grand antiprism, eludes the more general Wythoff’s construction. This is simply because

G (A)

is neither a Coxeter group nor a rotation subgroup.

The grand antiprism is discussed in [3], with some useful figures. However, I could not find there a description of the group, although Conway surely knew all about it. Nor can I find that he wrote about the group elsewhere, so it was Coxeter who initiated the discussion in [9].

There are also some very fine illustrations in the Wikipedia article Grand Antiprism. However, at the time of writing, that article also mislabels the group

G (A)

. □

Remark 5.

One can actually use the method to manufacture a vertex-transitive polytope

Q

by applying the `incorrect’ group

G = [[10, 2^{+}, 10]]

to the same base vertex

0 | 0

, as for

A

. The orbit still has size 100, containing the vertices of ring

R_{A}

along with their images under the spurious half-turn t. We seem to obtain the points described in (4b) and (4c); however, we must now take

μ + ν

even in both cases. The convex hull

Q

of this orbit still has the 100 vertices; but it cannot be uniform since it has edges of different lengths. For instance, there is an edge of length

τ^{- 1}

Q

from

0 | 4

0 | 0

, just as in

A

. However, there is also a slightly longer edge of length

2^{\frac{1}{2}} τ^{- \frac{1}{2}} 5^{- \frac{1}{4}}

from

0 | 4

to the new vertex

(2 | 2) t

The geometric effect of the spurious half-turn t is to map each pentagon from ring

R_{A}

to a pentagon coplanar and concentric with a pentagon in ring

R_{B}

, but turned a half-turn with respect to the latter. We see again why t cannot lie in

H_{4}

Disappointed, we conclude that there is no undiscovered uniform 4-polytope missed by Conway and Guy! □

4. Quaternions and Finite Isometry Groups in $E^{4}$

In order to locate

G (A)

, or

[[10, 2^{+}, 10]]

for that matter, in a catalogue of all finite isometry groups on

E^{4}

, that is, within the finite subgroups of

G O_{4} (R)

, we need some tools from the algebra of quaternions. We follow [5, Chapter 4] and [11, Chapter 6].

Recall first that the conjugate of

x = x_{0} + x_{1} i + x_{2} j + x_{3} k \in E^{4}

\tilde{x} = x_{0} - x_{1} i - x_{2} j - x_{3} k

, for which we have

\tilde{x z} = \tilde{z} \tilde{x}

. The norm or squared length of

x

N (x) = x \tilde{x} = \tilde{x} x,

which, crucially, is multiplicative. For a unit quaternion

x

we have

x^{- 1} = \tilde{x}

The group

P

of unit quaternions (also known as

{Spin}_{3}

) is a double cover of

S O_{3} (R)

[11, 6.43]. To see this we first identify

E^{3}

with the space of pure quaternions

z

(for which

z_{0} = 0

). Note that

z^{2} = - N (z)

For each

a \in P

, one can find a unit pure quaternion

u

and then a unique angle

α

(

0 ⩽ α ⩽ π

), so that

a = exp (α u) : = cos (α) + sin (α) u .

Next we observe that the mapping of pure quaternions given by

[a] : z \mapsto \tilde{a} z a, (z \in E^{3})

effects a rotation through angle

2 α

about the axis spanned by

u

. Noting that we compose such mappings left to right, we have

Proposition 2.

There is a

2 : 1

surjection

\begin{matrix} P & \to & S O_{3} (R) \\ a & \mapsto & [a] \end{matrix}

The kernel of this epimorphism is

\pm 1

A finite multiplicative group of quaternions must be a subgroup of

P

. Using Proposition 2 and the known classification of finite rotation groups in

E^{3}

, we easily verify that the finite groups of quaternions are those described in Table 1.

From [5, Theorem 12] we have the generators

a = (- 1 + i + j + k) / 2

b_{T} = i

b_{O} = (j + k) / \sqrt{2}

and

b_{I} = (i + τ^{- 1} j + τ k) / 2

Example 1.

For the moment, let us view the vertices of

S

as unit quaternions. Since the identity quaternion is not one of these, we do not quite have a multiplicative group. However, if we premultiply vertices by

v^{- 1}

(essentially

ϵ^{- 1}

), then we do get the binary icosahedral group

2 I = 〈 5, 3, 2 〉

. The notation is a reminder that this group is a double cover of the icosahedral group

(5, 3, 2) = {[5, 3]}^{+}

, of order 60. Consider also quaternions

u = 3 | \underset{̲}{}, z = 4 | 0

. Then the two generators

d = v^{- 1} u, e = v^{- 1} z

satisfy the defining relations

d^{5} = e^{3} = {(d e)}^{2}

for

〈 5, 3, 2 〉

[11, Chapter 6.5]. Derived as they are from (4), these alternate generators are a bit messier than

a, b_{I}

from Table 1:

\begin{matrix} d & = & \frac{1}{2} (τ + 5^{\frac{1}{4}} τ^{- \frac{1}{2}} i), \\ e & = & \frac{1}{2} (1 + 5^{- \frac{1}{4}} τ^{\frac{3}{2}} i + j - 5^{- \frac{1}{4}} τ^{- \frac{3}{2}} k) . \end{matrix}

□

Let us move on to

E^{4}

. The reflection in the hyperplane orthogonal to the unit quaternion

a

is described by the mapping

z \mapsto - a \tilde{z} a,

which we denote by

* [- \tilde{a}, a

]. (Recall that

\tilde{a} = a^{- 1}

.) It follows that any direct isometry on

E^{4}

can be described as

[l, r] : z \mapsto \tilde{l} z r, z \in E^{4} .

The notation is meant to suggest a pair of left and right unit quaternions, and so we need the direct product

Δ = P \times P .

Proposition 3.

There is a

2 : 1

surjection

\begin{matrix} Δ & \to & S O_{4} (R) \\ (l, r) & \mapsto & [l, r] \end{matrix}

The kernel of this epimorphism is

\pm (1, 1)

Any opposite symmetry is likewise described by

* [l, r] : z \mapsto \tilde{l} \tilde{z} r, z \in E^{4} .

For instance, ordinary conjugation is given by either

* [1, 1]

* [- 1, - 1]

. (This effects a central symmetry in the real subspace of pure quaternions.)

To put all this in one package, it is useful to extend

Δ

by an involution, which we label * and which acts on

Δ

by swapping entries:

* (l, r) * = {(l, r)}^{*} = (r, l) .

Using the semidirect product

Δ^{'} = Δ ⋊ C_{2} = (P \times P) ⋊ 〈 * 〉,

we now have a

2 : 1

epimorphism

\begin{matrix} Δ^{'} & \to & G O_{4} (R) \\ (l, r) & \mapsto & [l, r], \\ (l, r) & \mapsto & * [l, r], \end{matrix}

still with kernel

\pm (1, 1)

These results provide the first step to determining all geometrically distinct finite subgroups G of

G O_{4} (R)

. We must first find finite subgoups H of

Δ

if we seek subgroups

G^{+}

S O_{4} (R)

. Clearly, H is a subdirect product of some

L_{*} \times R_{*}

, where the left and right groups

L_{*}, R_{*}

are, up to conjugacy, amongst the finite groups listed in Table 1. In fact, we could assume, if it helps, that

L_{*}, R_{*}

are just as given in the Table; and we can further assume

(- 1, - 1) \in L_{*} \times R_{*}

, though this need not be so for H. To organize the many possibilities, we can use Goursat’s Theorems on subdirect products, as described for instance in [2]. The upshot is that the H’s are parametrized by triples

(K_{L_{*}}, K_{R_{*}}, θ)

such that the normal subgroups

K_{L_{*}} ⊴ L_{*}

and

K_{R_{*}} ⊴ R_{*}

admit an isomorphism

θ : L_{*} / K_{L_{*}} \to R_{*} / K_{R_{*}} .

Then

H = {(l, r) \in L_{*} \times R_{*} : (l K_{L_{*}}) θ = r K_{R_{*}}} .

The group

G^{+}

has order

\frac{| L_{*} | \cdot | R_{*} |}{e_{*} f_{*}},

where

f_{*} = [L_{*} : K_{L_{*}}] = [R_{*} : K_{R_{*}}]

is the order of the common quotient, and

e_{*} \in {1, 2}

is the order of

H \cap 〈 (- 1, - 1) 〉

The actual cases are bewildering and are outlined in [5]. In those Tables of groups

G^{+}

, typical entries look like

\pm \frac{1}{f} [A \times B] or + \frac{1}{f} [A \times B],

for the so-called `diploid’ or `haploid’ cases, respectively, for which the central symmetry z does or does not lie in the group.

The convention in the Tables is that

A, B

denote subgroups of

S O_{3} (R)

, not their quaternionic covers

L_{*}, R_{*}

. Likewise, we used

f_{*}

above rather than f, since in some cases (not of concern here), one has

f = f_{*} / 2

If we seek a finite subgroup G of

G O_{4} (R)

with opposite isometries, then we work in

Δ^{'}

and adjoin to one of the subdirect products

H ⩽ L_{*} \times R_{*}

some element

* (a, b)

. Here there are simplications, mainly because

L_{*} ≃ R_{*}

is forced. If desired, we can even take

L_{*} = R_{*}

. Up to conjugacy in

Δ^{'}

there can be various choices for

* (a, b)

, though often

* (1, 1)

is usable. The finite subgroups of this kind in

G O_{4} (R)

are listed in Table 4.3 of [5].

We shall look more closely only at a few of the “diploid, achiral groups”, which appear in [5] as

G = \pm \frac{1}{f} [A \times A] \cdot 2,

though perhaps with some decorations to distinguish, for instance, choices for

* [a, b]

. In such cases,

L_{*} = 2 A

e_{*} = 2

and

f = f_{*}

, so the order is

\frac{{4 | A |}^{2}}{f} .

(11)

We have reviewed all this machinery just so that the reader can make sense of the following brief results. It can take a great deal of work to fit a well-known linear group into the scheme underlying the Tables in [5].

Example 2.

From the very first entry in [5] we have

H_{4} = [3, 3, 5] = \pm [I \times I] \cdot 2 .

The “

\cdot 2

” indicates that we have doubled the order of the rotation group

{[3, 3, 5]}^{+}

by adjoining an opposite symmetry, in fact,

* [1, 1]

. We have

L_{*} = R_{*} = 2 I

, so

A = B = I

, the icosahedral group of order 60. The parameter

f = f_{*} = 1

, and

K_{L_{*}} = K_{R_{*}} = 2 I

, with θ trivial. The order of

H_{4}

does indeed equal

4 \cdot 60^{2} = 14400

from (11).

Now compare this with our construction of

H_{4}

in Section 2. There we chose the basic roots

n_{j}

in (5) for the generating reflections

r_{j}

. Thus

r_{j} = * [n_{j}^{- 1}, n_{j}]

, so that the subgroup of direct isometries

H_{4}^{+}

is generated by rotations

s_{j} : = r_{j - 1} r_{j} = [- n_{j - 1} n_{j}^{- 1}, - n_{j - 1}^{- 1} n_{j}], (j = 1, 2, 3) .

We find that

R_{*}

is the binary icosahedral group generated by quaternions

d, e

in Example 1. But now

L_{*}

is the conjugate subgroup

v R_{*} v^{- 1}

P

. This has no effect on the conjugacy class of

H_{4}

G O_{4} (R)

. □

Example 3.

The rotations

s_{2} = r_{1} r_{2}, s_{3} = r_{2} r_{3}

H_{4}

generate a copy of the icosahedral group

I = {[3, 5]}^{+}

. From Figure 2, we see that I contains the dihedral group

D_{10}

, generated for instance by

s_{3}

, rotation through

2 π / 5

about

u

, and our half-turn

h = s_{2} s_{3}^{- 2} s_{2}^{- 1} s_{3} s_{2}^{- 1}

about the midpoint of edge

2 | 2 0 | 4

. (This edge belongs to the Petrie polygon preserved by

s_{3}

in Figure 2.)

Lift to the binary icosahedral group

R_{*} = 〈 a_{2}, a_{3} 〉

of Example 2, now generated by

a_{2} = - n_{1}^{- 1} n_{2}, a_{3} = - n_{2}^{- 1} n_{3}

. This group of order 120 contains the dicyclic group

〈 5, 2, 2 〉 = 〈 a_{3}, b 〉

of order 20, where

b = a_{2} a_{3}^{- 2} a_{2}^{- 1} a_{3} a_{2}^{- 1} .

But from the previous Example we now know that

L_{*} = v R_{*} v^{- 1}

contains its own copy

〈 v a_{3} v^{- 1}, v b v^{- 1} 〉

of the dicyclic group. Thus

L_{*} \times R_{*}

contains the direct product of commuting dicyclic groups. This group of order 400 projects to the rotation group

\pm [D_{10} \times D_{10}]

of order 200 in

S O_{4} (R)

[5]. We can adjoin the opposite symmetry

* [1, 1]

to finally see that

G (A) ≃ \pm [D_{10} \times D_{10}] \cdot 2,

(so take

p = 5

in line 19 of [5]).

We see that

G (A)

appears as a subgroup of

H_{4}

in a quite natural way. Indeed, this is essentially the approach taken in [17]. However, as mentioned earlier, the mislabelling of

G (A)

is at least suggested there. □

Example 4.

We will not include the details needed to correctly classify our unneeded `ionic diminished Coxeter group’:

[[10, 2^{+}, 10]] ≃ \pm \frac{1}{4} [D_{20} \times {\bar{D_{}}}_{20}] \cdot 2

(line 21 of [5, Table 4.3]). The adjoined opposite symmetry can again be taken to be

* [1, 1]

. The bar in

{\bar{D_{}}}_{20}

is merely a notational device signalling the fact that

D_{4} ≃ C_{2} \times C_{2}

is special among dihedral groups in having automorphisms freely permuting the non-identity elements. See [5, p. 50 and footnote 3] for more. □

Remark 6.

Conway and Smith describe in [5, Chapter 4.5] errors or omissions in previous catalogues of the isometry groups in

E^{4}

. Perhaps the best known earlier enumeration of the groups is that of Du Val in [14, Sections 21–22]. Apparently, there are some redundancies to be found there.

□

5. Some Final Comments and Thanks

The grand antiprism has been examined elsewhere, generally in wider discussions of uniform 4-polyopes. We mention, for instance, [19,21] and [13]. This last paper employs subrootsystems for the group

H_{4}

, rather as in [17], but with a broader look that takes in other uniform polytopes, such as the snub 24-cell.

Our work on the grand antiprism is an offshoot of a more extensive investigation into abstract regular 4-polytopes whose automorphism groups are subgroups of low index in some orthogonal group

O (d, p, e)

over a finite field

G F (p)

[20]. (The parameter

e = \pm 1

flags the Witt index for the corresponding d-dimensional orthogonal geometry.) For instance,

H_{4} ≃ O_{1} (4, 5, + 1)

, the subgroup generated by reflections whose roots have square spinor norm. From [20, Equation (14)], we find a similarly structured group and accompanying geometry whenever

p \equiv 1 (mod 4)

. Moreover, we get an abstract regular 4-polytope with tetrahedral facets and

p^{3} - p

vertices. Inscribed in it, we must find a relative of the grand antiprism. But, of course, this abstract 4-polytope will not have a familiar convex realization.

We still do not properly understand the presentations of such orthogonal groups, when ones hands are tied (as they will be!) by using just 4 generating reflections. This in turn is necessary for an understanding of the universal regular polytopes whose facets are tetrahedra and whose vertex-figures are certain naturally occuring maps of type

{3, p}

[20, Conjectures 1,2,3].

Finally, let me here thank Peter McMullen for his input, in particular for suggesting the use of the subgroup K in Section 2 as a way to more easily understand the structure of

G (A)

References

The GAP Group, GAP – Groups, Algorithms, and Programming, Version 4.11.1. http://www.gap-system.org, 2021.
K. Bauer, D. Sen, and P. Zvengrowski, A generalized goursat lemma, Tatra Mt. Math. Publ., 64 (2015), pp. 1–19.
J. H. Conway, H. Burgiel, and C. Goodman-Strauss, The Symmetries of Things, A K Peters, Ltd., Wellesley, Mass., 2008.
J. H. Conway and M. Guy, Four-dimensional archimedean polytopes, in Proceedings of the Colloquium on Convexity, Copenhagen 1965, Kobenhavns University Mathematics Institute, pp. 38–39.
J. H. Conway and D. A. Smith, On Quaternions and Octonions, A K Peters, Natick, Mass., 2003.
H. S. M. Coxeter, Wythoff’s construction for uniform polytopes, Proc. London Math. Soc., 38 (1935), pp. 327–339. (Reprinted in The Beauty of Geometry: Twelve Essays, Dover, NY, 1999).
H. S. M. Coxeter, Regular and semi-regular polytopes. I, Math. Z., 46 (1940), pp. 380–407. (Reprinted in Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by Sherk, F.A, McMullen, P., Thompson, A.C. and Weiss, A.I., Wiley-Interscience, New York, 1995, pp 251–278).
H. S. M. Coxeter, Regular Polytopes, Dover, New York, 3rd ed., 1973.
H. S. M. Coxeter, Regular and semi-regular polytopes. II, Mathematische Zeitschrift, 188 (1985), pp. 559–591.
, Regular and semi-regular polytopes. III, Math. Z., 200 (1988), pp. 3–45.
H. S. M. Coxeter, Regular Complex Polytopes, Cambridge University Press, Cambridge, UK, 2nd ed., 1991.
H. S. M. Coxeter and W. O. J. Moser, Generators and Relations for Discrete Groups, Springer, New York, 3rd ed., 1972.
P.-P. Dechant, Clifford spinors and root system induction: H₄ and the grand antiprism, Adv. Appl. Clifford Algebr., 31 (2021), pp. Paper No. 57, 35.
P. Du Val, Homographies, Quaternions and Rotations, Oxford University Press, Oxford.
J. E. Humphreys, Reflection Groups and Coxeter Groups, Cambridge University Press, Cambridge, UK, 1990.
N. W. Johnson, Geometries and Transformations, Cambridge Univ. Press, Cambridge, UK, 2018.
M. Koca, M. A. Ajmi, and N. O. Koca, Grand antiprism and quaternions, J. Phys. A: Math. Theor., 42 (2009).
P. McMullen and E. Schulte, Abstract Regular Polytopes, vol. 92 of Encyclopedia of Mathematics and its Applications, Cambridge University Press, Cambridge, UK, 2002.
M. Möller, 4-dimensionale archimedische Polytope, Results Math., 46 (2004), pp. 271–360.
B. Monson and E.Schulte, Reflection groups and polytopes over finite fields- II, Advances in Applied Mathematics, 38 (2007), pp. 327–356.
R. Nicolovius, Untersuchungen der vierdimensionalen Archimedischen Polytope, Mitt. Math. Ges. Hamburg, 27 (2008), pp. 91–116.

Figure 1. The tetrahedron and pentagonal antiprism.

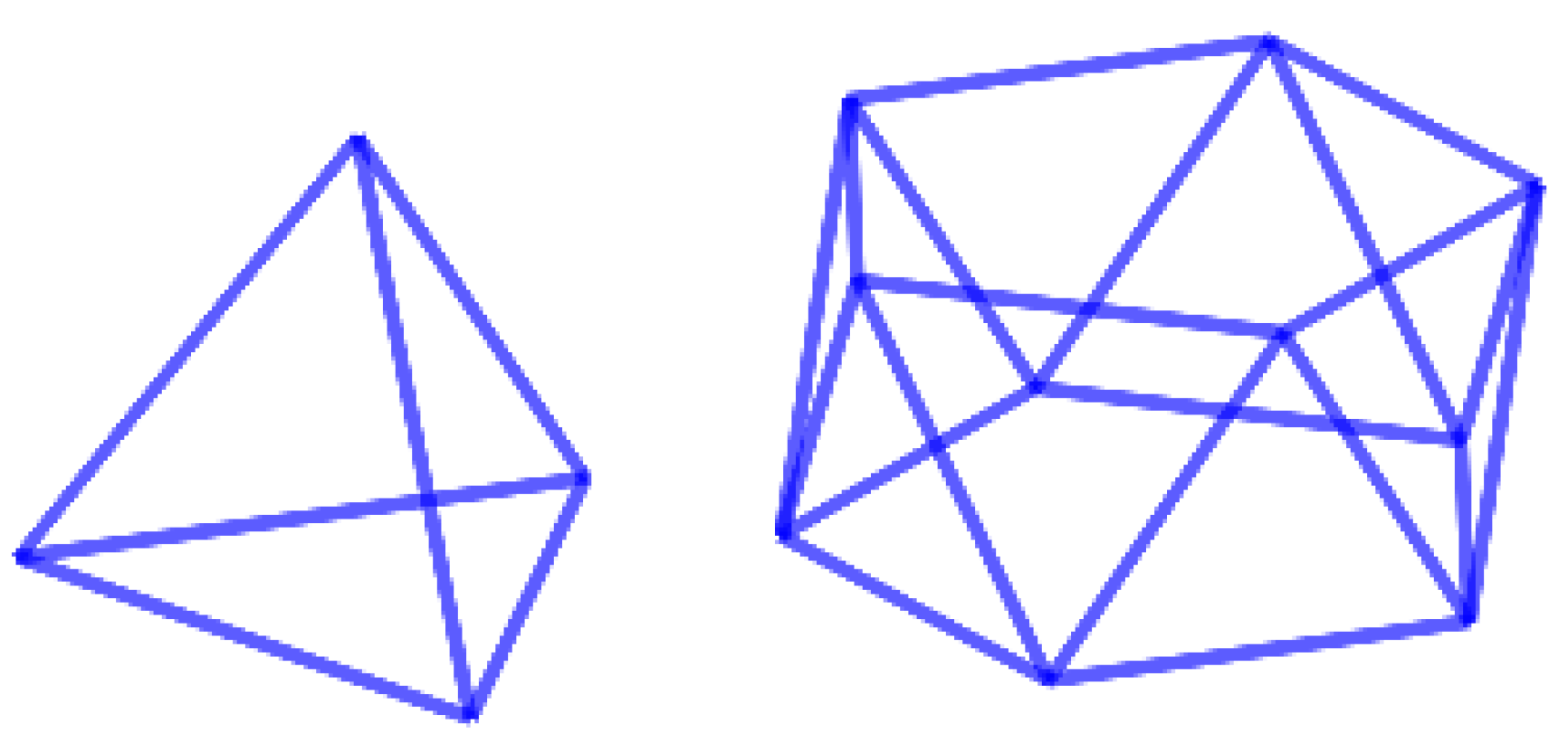
Figure 2. The vertex-figure for

v = 1 | \underset{̲}{}

S

Figure 2. The vertex-figure for

v = 1 | \underset{̲}{}

S

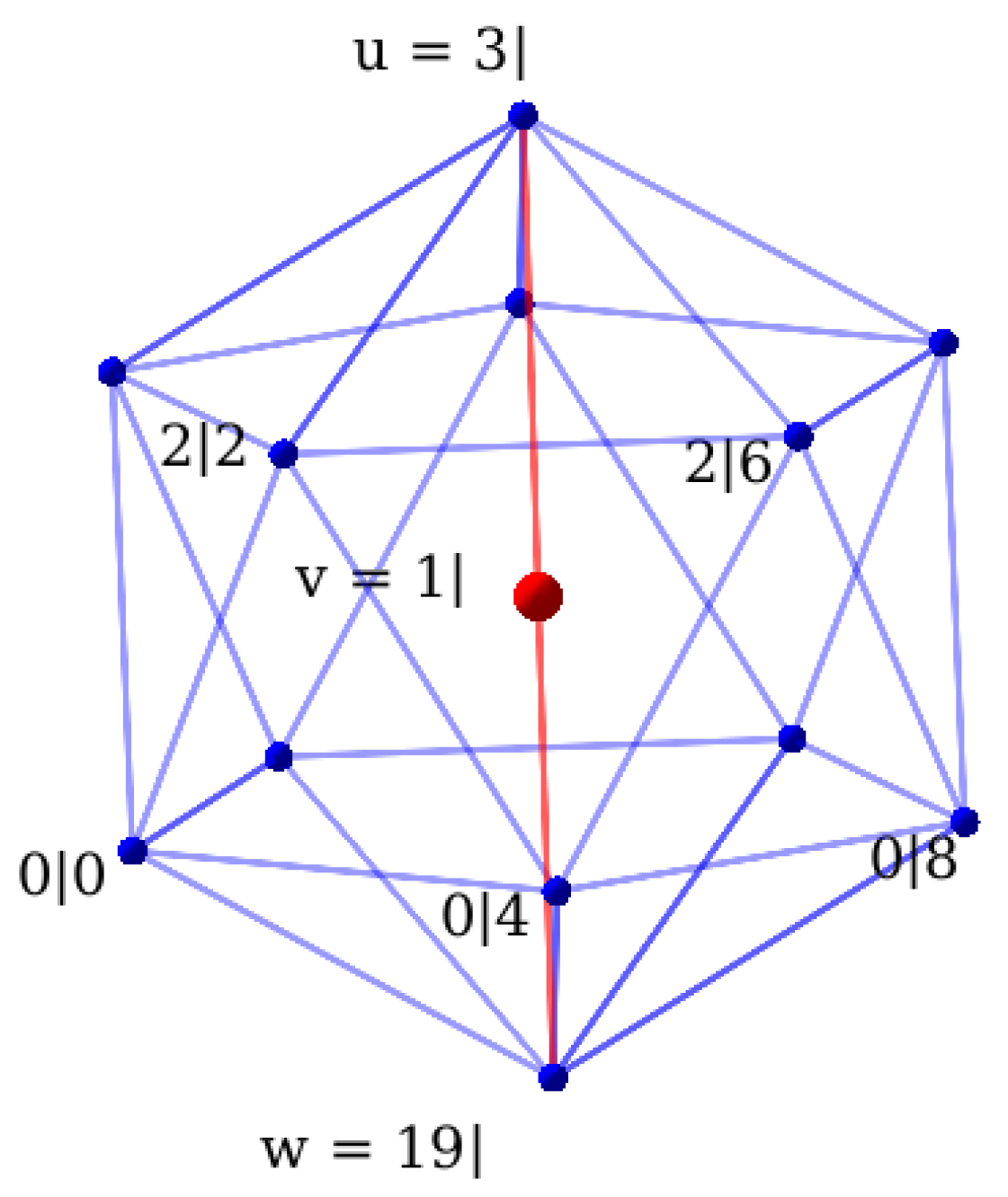
Table 1. The finite groups of quaternions

Name	Conway	Coxeter	Order	Convenient
	notation	notation		generators
cyclic (even order $2 m$ )	$2 C_{m}$	$〈 m, m, 1 〉 = C_{2 m}$	$2 m$	$exp (π i / m)$
cyclic (odd order m)	$1 C_{m}$	$C_{m}$	m	$exp (2 π i / m)$
dicyclic	$2 D_{2 m}$	$〈 m, 2, 2 〉$	$4 m$	$exp (π i / m), j$
binary tetrahedral	$2 T$	$〈 3, 3, 2 〉$	24	$a, b_{T}$
binary octahedral	$2 O$	$〈 4, 3, 2 〉$	48	$a, b_{O}$
binary icosahedral	$2 I$	$〈 5, 3, 2 〉$	120	$a, b_{I}$

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

	$2 \| 2$		$2 \| 6$		$2 \| 10$		$2 \| 14$		$2 \| 18$
$0 \| 0$		$0 \| 4$		$0 \| 8$		$0 \| 12$		$0 \| 16$		$0 \| 0$

The Symmetry Group of the Grand Antiprism

Abstract

1. Introduction

2. The 600-cell S = { 3 , 3 , 5 } and the Grand Antiprism A

3. More on Wythoff’s Construction

4. Quaternions and Finite Isometry Groups in E 4

5. Some Final Comments and Thanks

References

MDPI Initiatives

Important Links

Subscribe

2. The 600-cell $S = {3, 3, 5}$ and the Grand Antiprism $A$

4. Quaternions and Finite Isometry Groups in $E^{4}$