Prerpints.org logo
Preprint
Review

Dual-band Passive Beam-Steering Antenna Technologies for Low Power Satellite Communication and Modern Wireless Systems: A Review

Altmetrics

Downloads

211

Views

48

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

01 August 2024

Posted:

06 August 2024

You are already at the latest version

Alerts
Abstract
Efficient beam steerable high-gain antennas enable high-speed data rates over long-distance networks, including wireless backhaul, satellite communications (SATCOM), and SATCOM On-the-Move. These characteristics are essential for advancing contemporary wireless communication networks, particularly within 5G and beyond. Various beam-steering solutions have been proposed in the literature, with passive beam-steering mechanisms employing planar metasurfaces emerging as cost-effective, power-efficient, and compact options. These attributes make them well-suited for use in confined spaces, large-scale production and widespread distribution to meet the demands of the mass market. Utilizing a dual-band antenna terminal setup is often advantageous for full duplex communication in wireless systems. Therefore, this article presents a comprehensive review of the dual-band beam steering techniques for enabling full-duplex communication in modern wireless systems, highlighting their design methodologies, scanning mechanisms, physical characteristics, and constraints. Despite the advantages of planar metasurface-based beam steering solutions, literature on dual-band beam steering antennas supporting full duplex communication is limited. This review article identifies research gaps and outlines future directions for developing economically feasible passive dual-band beam-steering solutions for mass deployment.
Keywords: 
Subject: Engineering  -   Telecommunications

1. Introduction

With an ever-increasing demand for seamless global connectivity, the satellite terminal market has experienced exponential growth [1]. This surge is additionally driven by the rapid advancement of technologies such as the Internet of Things (IoT), communication on the move (COTM), in-flight internet connectivity, maritime and offshore connectivity, and efforts to bridge the connectivity gap in underserved areas. The integration of IoT in the aviation industry is poised to revolutionize operations, leveraging satellite communication (SATCOM) for real-time data transmission and reception among IoT systems and components. From providing internet access in remote regions to facilitating emergency services in critical situations, SATCOM has the potential to benefit many sectors. As per International Telecommunication Union (ITU) reports, ≈ 67 % of the world population is using the internet, out of which 59 % of web traffic worldwide is through mobile devices [2,3]. In such scenarios, satellite communication is the most appropriate solution for mobile connectivity when terrain, line-of-sight or distance restricts connectivity via the standard terrestrial networks. Wireless telecommunication providers intend to utilize more and more nodes from the SATCOM to extend the coverage provided by the terrestrial networks in sparsely populated regions [4,5,6]. The necessity for ubiquitous connectivity for some of the platforms in the present-day communication landscape is clearly illustrated in Figure 1.
Some of the typical commercial communication satellite systems include Iridium-NEXT, LeoSat, OneWeb, Starlink, O3B, and Kuiper [7,8]. Most satellite communication networks utilize low-earth orbit (LEO) and medium-earth orbit (MEO) satellites, which are preferred over geostationary satellites (GEO) due to their proximity to Earth. This proximity results in lower power consumption and lower latency [9,10,11]. These LEO satellites utilize Ku/Ka bands for full-duplex communication. Since LEO satellites are non-stationary, beam-steering antennas are employed to maintain connectivity with the satellite by constantly switching beams from one satellite to another. Moreover, medium-to-high gain antennas are required since they can close the link budget with lesser transmission power, reducing the power burden on the radio frequency (RF) system [12].
Based on the steering principles involved, beam steering antennas can be broadly classified as mechanical and electrical. [13]. Electrical antenna systems can be further classified as phased arrays or beamforming antennas, including digital, hybrid and analog beamforming [13,14]. Steering antenna systems have also been classified in the literature based on their size [15] and system properties [16].
In mechanical beam steering, the complete antenna system is physically rotated with the help of electric motors to direct the beam in any direction. High-gain antennas such as reflector dishes or arrays of horns are typical examples of mechanically steered antennas [5,17]. Various mechanical steering antennas for SATCOM On-The-Move (SOTM) are commercially available [18]. Although mechanical steering methods maintain antenna gain and offer flexible steering ranges, such systems are undesirable in certain applications due to antenna weight and size, weather effects, and steering speeds. Some of the mechanical steering systems are bulky and expensive. Power requirements are also increased when the complete system has to be rotated. Such designs may not be feasible when the whole system has to be incorporated into a smaller space to reduce the payload. Likewise, for mobile platforms such as cars, trains, or aircraft, integrating a mechanically rotating system proves impractical. In these scenarios, where aerodynamic considerations are paramount, compact and planar antenna systems reign supreme over their bulkier, mechanically rotated counterparts.
The other technique uses phased arrays, an electrical beam steering technique that can provide adaptive beam scanning and beam shaping capabilities [19]. The currently available active RF-based electrical steering antennas, including [20,21], utilize electrical beam steering by incorporating active metasurfaces for full-duplex shared aperture antenna operation. Several other antenna systems are available for SOTM and COTM [22,23]. Although electrical beam steering systems provide faster scanning speed and compact antenna designs, they require complex feed networks, heat sinks and greater power than passive systems.
Lately, there has been a notable increase in research interest in metasurface-based beam steering techniques [24,25,26,27]. These techniques are particularly attractive because they offer cost-effective solutions for planar antennas well-suited for large-scale deployment. Metasurface-based beam steering techniques function similarly to phased arrays, but instead of using RF phase shifters, they employ phase delay unit cells [28,29] or phase rotation unit cells [30]. This innovation enables flexible beam manipulation while reducing the complexity associated with conventional phased-array implementations. The classification of various beam steering techniques is illustrated in Figure 2.
The fundamental component in a passive metasurface-based beam steering system is the phase-gradient metasurface (PGM). Unlike previously reported articles on beam steering antennas, this article provides a comprehensive review in terms of the following key features that have not been consolidated in previous review articles.
  • The review encapsulates passive beam steering techniques focusing on full-duplex systems incorporating passive metasurfaces.
  • Since the first step in designing a passive metasurface is finalizing the phase shifting cell, a subwavelength element that repeats periodically/aperiodically over the entire surface, careful design and selection are crucial and require deliberation. Therefore, the focus of this article is the design and analysis of different dual-band phase transformation cell topologies available in the literature, with the pros and cons of each on the system-level parameters. This analysis aims to provide a valuable resource for designers beginning the development of dual-band PGMs used in various applications such as dual-band beam-steering, dual-band phase correction, and dual-band lenses.
Given the emphasis on designing and developing dual-band PGMs, we briefly discuss the steering mechanisms that incorporate dual-band PGMs to provide context. These steering mechanisms can be categorized into three main types: transmitarrays (TAs)-based beam steering, reflectarrays (RAs)-based beam steering, and near-field meta-steering (NFMS). A brief overview of these techniques is provided in the following subsequent section. The rest of the paper is organized as follows: Section II briefly overviews the steering technologies incorporating phase-gradient metasurfaces. Section III discusses various unit cell topologies. This is followed by an analysis of the challenges associated with dual-band unit cell design and a review of different approaches implemented to address these challenges. Finally, the paper provides a summary and concludes with a comparison of existing passive dual-band metasurfaces an integeral part of passive beam-steering antenna systems.

2. Dual-Band Metasurface Based Beam-Steering Techniques

The antenna systems utilizing metasurfaces or metamaterials discussed in the literature can be broadly classified as RAs, TAs, and NFMS. Dual-band beam-steering with RAs has mostly been achieved by utilizing reconfigurable RAs or a combination of RAs and phased arrays. On the other hand, the other two techniques use strategically designed metasurfaces to achieve dual-band beam steering capability. Beam-steering in TAs is implemented either by feed translation/rotation or by rotating the transmitarrays. In the case of NFMS systems, two PGMs are independently rotated synchronously or asynchronously parallel to the antenna axis and placed in the near-field of the antenna to achieve beam steering. This section briefly describes these three popular techniques along with state-of-the-art antenna systems. The inherent challenges associated with each approach are also discussed subsequently.

2.1. Reflectarray-Based Beam-Steering

Introduced initially in 1963 [31], reflectarrays are a type of antenna that combines the attributes of reflector antennas with array antenna principles. It consists of a feed antenna illuminating a reflecting surface. The feed is usually a horn antenna placed at a focal distance from the reflecting surface. In reflectarrays, planar metasurfaces are mostly used to emulate the behavior of a curved reflector. These metasurfaces comprise an array of scatterers that produce a predefined phase shift to compensate for the path lengths of a radiated wave from the feed placed at the focal length from the surface. As a result, the beam can be tilted in any direction based on the arrangement of the phase-shifting scatterers. A comparative analysis of passive mechanically reconfigurable single band reflectarrays was given in [32]. Reconfigurable reflectarrays that comprise a combination of active and passive metasurfaces have been presented in [33]. However, beam-steering was not explored. Dual-band beam steering has been made possible with reconfigurable reflectarrays or a hybrid of active and passive reflectarrays that can change the phase shift of cells to make adaptive beam steering possible. Such reflectarrays have been reported in [34,35,36,37,38].

2.2. Transmitarrays-Based Beam-Steering

Recently, another class of antennas known as transmitarrays has gained significant research focus, enabling the design of highly directive antennas with beam-steering capabilities. They incorporate passive metasurfaces with properties similar to those of a lens but are planar and fabricated using printed circuit board (PCB) technology. Compared to lens antennas, they are lightweight, conformable, and reconfigurable (in beam shape, direction, and polarization) [39]. Similarly to a reflectarray, in transmitarrays, a feed source is placed at the focal point of the metasurface. Dual-band beam-steering transmitarrays have been reported in [40,41,42,43,44,45,46,47,48,49,50,51,52]. In most steering mechanisms, in-plane feed translation or feed rotation has been used to steer the beam, requiring additional feed displacement arrangements [40,49,50,51]. In some transmitarrays, the rotation of the dual-band metasurface has been used [41]. In [40], an optimal approach for designing a dual-frequency band transmitarray was presented, exhibiting a measured gain of 24 dBi at 20 GHz and 27 dBi at 30 GHz. The consistent beam direction in both frequency bands with steering confirmed the full-duplex operation in the dual-frequency bands. In [50], the dual-band transmitarray operating at Ka-band, with a gain of 28.3 dBi and 28.4 dBi at the two frequency bands of 20 GHz and 30 GHz, was presented. Another dual-band beam-steering transmitarray using planar metasurfaces was presented in [41]. The metasurface comprised the double square loop resonant elements in the multi-layer unit cell providing a steering range of around ± 50 ∘ , with the peak gain of 19.8 dBi at 14 GHz and 16.7 dBi at 8 GHz, respectively. The concept of beam steering with independent phase control using a folded transmitarray was presented in [42]. The unit cell provided independent phase control for the dual frequency bands utilising polarization conversion from linear to different circular polarization (RHCP and LHCP). Several types of multilayer dielectric, composite, and metallic phase-shifting surfaces or metasurfaces have been reported in the literature with linear- and circular-polarization-compatible unit cells.

2.3. Near-Field Meta-Steering Systems

One disadvantage of a transmitarray is its lateral height because the feed is placed at a specific distance equivalent to the focal length from the metasurfaces. Another technology known as Near-Field Meta-Steering (NFMS) was proposed in [25] to reduce the total lateral height of the antenna and to avoid feed displacement for steering the beam. The design presented in [25] was for single-frequency band operation. Several modifications of single band NFMS have also been presented in [53,54,55,56]. Later, NFMS systems supporting full-duplex communication were presented in [57]. In NFMS, the metasurfaces are placed within the near-field of a high-gain antenna system. The rotation of these metasurfaces about their axis in parallel to the antenna axis enables beam steering.

2.4. A Comparative Analysis of Antenna Beam-Steering Based on RAs, TAs and NFMS

Figure 3 illustrates the three different steering techniques discussed earlier in this section, showcasing the difference in steering methods based on their structure and operating principles.
In RAs, the reflection magnitude of the metasurface is always 1 (0 dB) due to the reflections of the entire incident wave from a metal ground plane; thus, only the reflection phase of the elements can be controlled. RAs also suffer from feed blockage issues [58]. Furthermore, most reflectarrays have a bandwidth limitation of around 10% or less [58]. The feed must also be maintained at a specific distance from the reflecting surface to achieve better aperture illumination and higher gain. One advantage of RAs is that they can combine the positive features of both reflectors and phased arrays without needing additional phase shifters or power dividers [59].
The issue of feed blockage is resolved in TAs as the metasurfaces are used in transmission mode, allowing planar beam-steering antenna system designs for single-band, broadband, and dual-band applications with high gain while maintaining the pattern shape during beam steering. One disadvantage associated with TAs involving the feed-tuning technique is pattern degradation due to phase alteration during feed displacement. Another disadvantage is the requirement of placing the metasurface at a focal distance from the feed to maintain the F/D ratio, which notably hinders size reduction in TAs.
An advantage of NFMS systems over TAs is a significantly reduced overall system height since the metasurfaces are placed in the near-field region of the antenna. That said, dual-band high-gain NFMS systems are not as extensively explored in the literature compared to TAs. One future research direction could be to investigate dual-band and broadband NFMS systems for high-gain applications suitable for SATCOM On-The-Move applications.
In the three steering mechanisms discussed in this section, the fundamental component of the system facilitating beam steering is a free-standing metasurface placed at various locations with respect to the feed, distinguishing the steering mechanisms from one another. In a reflectarray, such a surface is used in reflection mode with a reflection coefficient close to 1 (0 dB), while in transmitarrays or NFMS systems, highly transmitting metasurfaces are used with a transmission coefficient close to 1 (0 dB). This review article further discusses various passive highly transmissive dual-band metasurfaces used in the literature to design the full-duplex beam-steering antenna systems, i.e., TAs-based beam-steering antennas and NFMS systems. These dual-band metasurfaces have been referred to as Phase Shifting Surface (PSS) [60,61,62], Phase-Gradient Metasurface [26,63], time delay metasurface [25], discrete lens, planar lens, and flat lens [24,40] in literature. In this article, these metasurfaces have consistently been referred to as phase-gradient metasurfaces.

3. Passive Dual-Band Phase-Gradient Metasurfaces

Metamaterials are artificially engineered materials created using sub-wavelength elements, known as meta-atoms or unit cells [64]. Metasurfaces are the planar alternative to metamaterials and are sometimes referred to as 2D electromagnetic surfaces [65]. Metasurfaces are used for various applications, such as polarization conversion, filtering, designing phase-shifting surfaces and phase-gradient metasurfaces [24,26]. Passive phase-gradient metasurfaces are freestanding surfaces with a saw-tooth phase profile in a specific direction while maintaining a constant phase in the orthogonal direction. An array of distinct cells (periodically repeated in one of the directions, either x or y, while aperiodic in the orthogonal direction) determines this phase gradient, with each cell designed to provide a predetermined transmission phase shift to a normally incident electromagnetic wave. In some applications, the amplitude of the near-electric field can also be manipulated using these cells. We can refer to the antenna array theory to understand the working principle behind the PGMs. As per the antenna array theory [66], if several discrete identical radiating elements are arranged in a straight line, the field radiated by such an array can be given by Equation (1). in its simplest form.
E array = E sin gle element at reference point × Array factor
where E a r r a y represents the total electric field. The array factor depends on the number of elements (N), the geometrical properties of the elements, their spacing (d), their relative magnitudes and their relative phase. When all the array elements are identical, with equal magnitude and a progressive phase delay among the adjacent elements, the array is called a uniform linear array. For a uniform linear array, the array factor (AF) is given by Equation (2).
A F ( θ ) = sin N k d 2 sin θ sin k d 2 sin θ ,
where d is the spacing between the elements, k is the free space wave-number, and N is the total number of elements. The maxima of the beam occurs at k d s i n θ = 2 m π , where m = 0 , ± 1 , ± 2 , ± 3 , . . . . Secondary maxima, known as the grating lobes, occur in array antennas when the inter-element spacing is large relative to the operating wavelength. These lobes occur at an angle away from the main beam, and their angular position can be calculated using Equation (3).
θ g = sin − 1 m λ d
The following condition must be satisfied to avoid the grating lobes in the visible region ( θ = ± 90 ∘ ) given in Equation (4).
d λ ≤ 1 − 1 N
To direct the radiated beam away from the broadside direction, all the antenna elements are fed with a signal that has been phase-shifted. This is done so that the phase shift between adjacent antenna elements remains constant, denoted by ϕ s t e p . For example, if we want to tilt the radiated beam at an angle θ o away from the broadside direction, ϕ s t e p between adjacent elements can be set as ϕ s t e p = k d sin θ o . One method to achieve a constant phase shift among adjacent elements is directly exciting the feed with phase-shifted signals, often utilizing active phase shifters. Alternatively, the feed length (microstrip or strip-line length) can be adjusted so that each element receives a phase-shifted input.
Similarly to antenna arrays, in the case of passive phase-gradient metasurfaces, if an array of cells on the surface is arranged such that the phase difference between adjacent cells remains constant, denoted by ϕ s t e p , the incident beam on the surface can be tilted to an angle θ o away from the broadside direction, depending on this phase gradient. In Figure 4, we observe how an array of cells with an element-to-element phase difference equal to ϕ s t e p resembles a metasurface comprised of cells with a gradient phase profile. The fundamental phase-shifting element in the phase-gradient metasurface is a sub-wavelength cell. Based on structure and composition, the different types of cells available in the literature can be broadly classified, as shown in Figure 5.
The first step in designing any metasurface is to find a suitable phase transformation cell topology. Since a phase-shifting cell is a fundamental element that is repeated with variations in its geometric properties on the surface, the overall performance of the antenna system greatly depends on the design and analysis of the cell. This phase shifting cell is initially simulated using periodic boundary conditions in the x and y directions while assuming Floquet mode excitation in the z direction to analyze its transmission coefficient phase and magnitude response and hence is referred to as a unit cell when simulated with periodic boundary conditions. Floquet mode excitation in the CST- Microwave Studio (MWS) is shown in Figure 6. The different types of dual-band unit cells that have been used in the literature using the different structural topolgies are shown in Figure 7.

3.1. All-Dielectric Unit Cells

All-dielectric unit cells have been explored in [68,69,70,71,72] for various beam steering and phase correction applications. Dual-frequency or multi-wavelength meta-molecules were presented in [67]. A hexagonal unit cell operating at two different frequencies and providing independent phase control was designed using four nano-posts placed at the center of the hexagonal cell. Three nanoposts were used to control the cell response at the higher frequency, while one nanopost was used to control the response at the lower frequency. The diameter of the nano-posts was varied to achieve phase variation, keeping their length constant. Using a holey substrate, a dual-band all-dielectric unit cell was also reported in [73] for dual-band phase correction in transmitarrays. However, the structure may not be suitable for designing phase-gradient metasurfaces. A crucial obstacle exists in creating all-dielectric dual-frequency metasurfaces. While several designs necessitate more significant physical footprints, others involve complex machining operations, presenting substantial challenges in the manufacturing process. In addition, the design of all-dielectric unit cells to achieve dual-frequency band capabilities may raise problems regarding feasibility.

3.2. All-Metallic Unit cells

Single band all-metallic unit cells were also explored in [53,56,73,74,75], eliminating the need for expensive laminates in all-dielectric or composite (metal-dielectric printed) structures. The first dual-band all metallic phase gradient near-field meta-steering antenna was reported in [57] utilizing dual-band all metallic unit cells incorporating a modified swastika slot in the middle for phase adjustment at one frequency band of operation while half swastika slots in the corners for the other frequency band’s phase tuning. Overall, four metal and dielectric layers separated by air gaps were utilized.
However, limitations of these structures include narrow operation bandwidth, losses due to the conductivity of metallic layers, expensive manufacturing, and polarization dependence. Moreover, most of these cells are fabricated by cutting slots in the metal sheets using the concentrated heat of high-power lasers. When subjected to high-intensity heat, the metal sheets may deform, which can be a significant obstacle in extending such designs for highly directive ( > 30 ) dBi applications. Most of the all-metal structures are in the form of mesh, which may become very thin for higher frequencies, and bending of the surface may be another issue when using such unit cells.

3.3. Composite Metal-Dielectric Unit Cells

Composite (metal-dielectric) unit cells are made up of both metal and dielectric material. A detailed analysis of the choice of resonating element for such unit cells was presented in [76]. Multilayer printed unit cells can be used to design the metasurfaces. For implementing metasurface, only those cells that offer high transmission magnitude, ideally less than -1 dB, are selected. However, when the complete phase range is impossible using only -1 dB cells, a few cells with up to -3 dB transmission magnitude can also be selected. According to the detailed analysis of metasurfaces conducted in [77], the transmission phase of any single layer (one conductor layer placed over a dielectric substrate) surface is a function of substrate electrical thickness β h d , where β is the phase constant ( β = 2 π ϵ r λ 0 ) and h d is the height of the substrate. With a single-layer unit cell, the maximum phase range that can be achieved regardless of the implemented metallic element shape is 54 ∘ with a transmission coefficient magnitude within -1 dB and 90 ∘ with a transmission coefficient magnitude greater than -3 dB. To increase the phase range, the number of layers must be increased.
Wide-band dual resonant double square ring unit cells were presented in [78]. The unit cell structure had four metal-dielectric layers separated by an air gap. Adding the inner rings increased the achievable phase range and improved the 1 dB gain bandwidth by 7.5%. For any selected unit cell geometry, the phase range of a multi-layer unit cell structure depends on the substrate material, the number of layers, and the spacing between the layers. A minimum 3-layer structure with two dielectric layers and three metal layers is required to provide a phase range of 360 ∘ , which also comes at the cost of a reduced transmission coefficient magnitude of -3 dB. Increasing the number of layers increases the phase range with transmission coefficient magnitude closer to 0 and more significant than -1 dB. It was also deduced that the electrical thickness of a substrate β h d should be at least 90 degrees at the resonant frequency to achieve the maximum transmission phase range [77]. The complete analysis of two-, three-, and four-layer FSSs was given for different relative permittivity values. It was concluded that the height of the dielectric layer should be selected according to the required phase range and the dielectric permittivity. If β h d is decreased below 90 degrees, the phase range is reduced to 120 degrees. If β h d increases above 90 degrees, the transmission phase range is reduced to 240 degrees. For a three-layer FSS, with the increase in relative permittivity, the phase range increases. For ϵ r = 4 . 7 and | S 21 | ≥ − 3 d B , a transmission phase range of 360 degrees can be achieved with a four-layer unit cell with a reasonable transmission magnitude of | S 21 | ≥ − 1 d B . The analysis included conducting experiments with different shapes of unit elements.
The main challenge in building a thin and lightweight metasurface is to achieve a complete 360-degree phase range while minimizing the number of layers. This optimization is essential to reduce the design expense. To design a dual-band beam steering system, the unit cell should be able to resonate in two different frequency bands. Many structures reported in the literature focus solely on dual-band metasurface design without addressing the beam steering aspect. Designing a dual-band unit cell for a dual-band phase-gradient metasurface is more challenging than designing a single-band PGM, primarily due to the need for independent 360 ∘ phase range coverage required at the dual frequency bands, which is often achieved by varying the dimensions/rotation angle of resonant elements of the cell.
Most cells reported in the literature are selected based on identifying phase pairs that simultaneously provide the required phase for both frequencies while maintaining a high transmission magnitude. However, this process is time-consuming, involving rigorous parameter sweep simulations where cell parameters are varied to analyze the phase response at both frequencies. This generates datasets with the maximum possible phase combinations for two frequencies with a high transmission coefficient magnitude. The highly transmitting cells are then selected from these generated datasets depending upon the required phase profile of the metasurface. Such dual-band PGMs have been reported in [40,43,52] where the phase shift through the cell is tuned either by varying the length or width of the geometric shape within the cell or by rotating the shape itself at various angles within the cell. In [40], phase tuning was achieved using phase delay (PD) unit cells, and a generic methodology to reduce the complexity of dual-band metasurface was presented. This work was an extension of the work presented earlier in [79,80]. The PD unit cell structure reported in [81] was combined with the PD cell reported in [82] to design the dual band unit cell. According to [81], the cell corresponding to the frequencies f 1 and f 2 can be designed using square loops corresponding to the lower frequency and square patches corresponding to the higher frequency. Using square patch and loop as resonant elements in the dual frequency bands, [40] further suggested that if the frequency in the two bands is selected to maximize the greatest common divider between them, it will result in fewer non-repeated cells to achieve 360 ∘ independent phase wrapping at the dual frequency bands. In the given analysis, the cell period was λ / 4 × λ / 4 for the lower frequency band and λ / 3 × λ / 3 at the higher frequency band. The square patch within the unit element controls the phase at a higher frequency, and a square ring controls the phase at a lower frequency band. The reported unit cell was a seven-layer structure, and cell sizes were optimized to obtain the specific dimensions, giving required phases with high transmission coefficient magnitudes for both bands. Along with the time-consuming cell selection process discussed previously, another design limitation was utilizing seven metal and six dielectric layers, leading to a thicker metasurface. These layers were also bonded together, increasing the overall cost and complexity of the design and fabrication process. A comparison of the response of PD and phase rotation (PR) unit cells in terms of the scattering parameters of the surface was also discussed in [83]. The paper compared the working principles of PD and PR cells, their effect on the polarization of incident waves, and their design complexity.
In another study, a dual-band cell was introduced with circular polarization, operating at frequencies of 20 GHz and 30 GHz [50]. The unit cells designed for each frequency allowed independent phase variation at the respective bands, achieved by adjusting distinct cell parameters separately. To achieve this, the resonating element for the higher frequency band was strategically positioned at the corners of each cell. This placement ensured that when the cells were arranged in a periodic lattice, they formed complete resonating elements. In contrast, the resonating element was placed in the center of each cell for the lower frequency band. This approach of interleaving the resonating elements specific to different frequency bands reduced the computational time required compared to previous techniques that aimed to identify common phase pairs. The overall structure of the proposed design consisted of three layers, comprising three metal and three dielectric layers, with dual-polarized slot elements. Beam steering was achieved by translational sliding of the transmit array relative to the feeder. The proposed unit cell design was also converted to an all-metallic structure, eliminating the requirement of expensive laminates and making the cell suitable for high-temperature applications. The same approach of strategically positioning the resonant elements within the unit cell to achieve independent frequency tuning at the dual frequency bands has also been utilized in [42,45,51]. Interleaved cells, however, acquire more space. Arranging the elements in a gradient metasurface while avoiding corner discontinuities can also be challenging.
A linearly polarized unit cell with vertical and horizontal dipoles corresponding to the dual frequency bands was also utilized to design a dual-band transmitarray for wide beam scanning in [51]. The proposed design can be used for the uplink and downlink Ka-bands. Beam scanning of ± 40 ∘ and ± 30 ∘ was achieved independently at the two frequency bands. The results suggested that the transmitted beam can be scanned over 80 ∘ for 19 . 5 GHz and 65 ∘ for 29 GHz in elevation with only 2 dB scan loss in the peak gain. Displacement of the feed horn antenna at the focal distance from the surface was proposed for tilting the beam. Another similar dual-band unit cell with double horizontal and vertical dipoles was reported in [46].
Another dual-band design allowing independent phase tuning through the cell at dual frequency bands was reported in [49]. The reported cell was a single-layered substrate meta-atom. The two metallic layers at the top and bottom of the substrate layer were composed of a modified Jerusalem cross-resonator seated in a circular hole, a modified complementary split-ring resonator, and a ring connector. The modified Jerusalem cross resonator was used to tailor the phase of the cell at the lower frequency band f L . In contrast, the modified complementary split-ring resonator was utilized to tailor the phase at the higher frequency band f H . In this case, the PR technique independently tunes the phase response at the dual frequency bands. In [41], a dual-band lens was implemented, operating in orthogonal polarization for the X-band and Ku-band. A rectangular dual-band cell with two orthogonal rectangular patches printed on four metal layers separated by three dielectric layers was used. At f L =8 GHz, a y-polarized feed was used, with the resonant elements’ dimensions parallel to the y-direction tuned for phase control. At f H =14 GHz, an x-polarized feed was used, with the resonant elements’ dimensions parallel to the x-axis being tuned for phase adjustment.
Recently, another dual-band cell with independent frequency tuning was reported in [84]. The unit cell consisted of four metal layers and four dielectric layers of a thin substrate. It was composed of interleaved square slot and cross slot resonant elements, following the orthogonal principle of resonance to allow independent phase tuning at the dual frequency bands.
The composite unit cells reported in this section provide more design flexibility and wider bandwidth at the dual frequency bands of operation. Moreover, such PGMs can be precisely fabricated at higher frequency bands using the standard printed circuit board fabrication techniques. However, high-performance laminates are costly. The dielectric electric field breakdown threshold is also lower than that of metals, making it less feasible for space applications or where environmental conditions are harsh [57,84].

4. A Comparison of Different Dual-Band Phase-Transformation Cells

Figure 8 summarizes the techniques previously used to design a dual-band PGMs incorporated into a transmitarray or near-field metasurface (NFMS) to achieve beam steering.
Based on the literature review presented above, a comparison of different relevant unit cell topologies used for phase correction or beam steering is presented in Table. Table 1. The unit cell topologies investigated in this work extend beyond those specified in Table 1. However, our focus remains on those relevant to dual-band passive phase-gradient metasurface design. The survey reveals that the independent performance of the unit cell in each frequency band provides greater flexibility in the design of TAs or NFMS for full-duplex steering applications. When the unit cell’s response is independent at the two frequency bands, it allows for arbitrary beam direction. Coincident beam direction at the dual frequency bands is preferred in full-duplex communication systems. In such cases, a cell with an independent phase response can help avoid tedious and time-consuming phase optimization techniques. Dual-polarized cells are also preferred over linear-only polarization since they can accommodate any polarization, circular, linear, or slant.
The summary presented in the Table 1 shows that achieving an independent phase response across a broader frequency range is a relatively underexplored area. Many dual-band cell topologies rely on optimizing phase pairs at specific frequency bands, necessitating a lengthy design process. Moreover, when the frequency separation is large, the interleaved placement of resonant elements at the dual frequency bands results in larger cells at the higher frequency band. Grating lobes start to appear for different wave-incidence angles if the cell size is greater than half the wavelength.

5. Conclusions

Beam steering is essential in the modern communication landscape dominated by technologies like SATCOM and COTM. Mass-produced, cost-effective solutions are necessary to meet the expanding consumer base. Beam steering antennas based on passive planar metasurfaces offer compact, low-profile, and cost-effective solutions with steering capabilities similar to phased arrays but without the need for active RF components that require heat sinks and complex feed networks. These planar metasurfaces, specifically known as phase-gradient metasurfaces, enable precise control over the direction of electromagnetic waves by incorporating passive phase-shifting/phase-transforming cells. This article presents a comprehensive analysis of various design techniques found in the literature for dual-band phase-shifting cells in PGMs. These designs aim to enable full duplex communication using a single shared aperture.
Since the fundamental element in a PGM is a phase-transforming cell, selecting a suitable dual-band unit element is crucial to ensure the desired performance of the overall steering antenna system. The dual-band cells described in the literature have been comprehensively classified on the basis of their structure in this article. Furthermore, to achieve dual-band resonance, three main techniques have been utilized in the reported designs for the selection and tuning of resonant shapes within the cells.
  • Optimized Phase Pair [40,41,79]: This technique may result in the design of concentric cells and smaller unit cells but requires more optimization and complex computations with larger datasets.
  • Interleaved Resonant Elements [42,45,46,47,48,50,51,52,57,67,84,85]: Enables independent tuning but may result in larger cell sizes that may lead to phase quantization error or grating lobes particularly at higher frequency band. The placement of cells to form the PGM needs careful investigation to avoid corner element shape discontinuities. Smaller unit cell topologies needs to be explored to design a PGM that can allow better resolution in phase correction/tunning and enhance the overall steering range of the antenna system.
  • Layer Separation [43,86]: This approach may lead to an increased number of layers.
  • Concentric Cell [49]: The designed cell has a modified Jerusalem cross resonator and a modified complementary split ring resonator to tune transmission properties at two frequencies independently. The overall cell is concentric but at the cost of complex geometry for the overall cell.
Nevertheless, each technique has its own advantages and disadvantages, necessitating careful consideration in metasurface design. From analyzing various unit cell topologies, several research gaps have been identified.
All-metallic phase-shifting cells, suitable for space applications, allow operation under high power without requiring expensive laminates. However, these structures suffer from narrow bandwidth. Exploring waveguide-based dual-band all-metallic phase-shifting cells could offer higher bandwidth along with improved structural rigidity.
Composite metal-dielectric phase-shifting unit cells can provide an improved bandwidth response, but most of these composite cells require multiple layers of metal and dielectric to achieve maximum phase range at dual frequency bands, increasing the overall thickness of the structure. Dual-band subwavelength cells with fewer metal-dielectric layers that can offer a better phase range while reducing the number of alternating layers can be further explored. The incident field for the majority of feed antennas is concentrated at the center, high transmission magnitude cells can be placed in the center, while low transmission magnitude cells with desired phase shifts can be positioned towards the periphery. This approach of amplitude tapering, coupled with height reduction, can be explored to achieve better performance. Moreover, most dual-band cells have been optimized for normal angles of incidence. The stability of a unit cell’s response under oblique angles of incidence at the two frequency bands needs further investigation.
Although several variations of passive metasurfaces have been reported, reconfigurability, as seen in active reflectarrays, has not been extensively explored. Further research into reconfigurable metasurfaces is needed to dynamically control the beam direction.
In summary miniaturization of cells, while maintaining independent dual frequency response and achieving a wider bandwidth in dual frequency bands, remains a significant challenge for designing shared aperture antennas based on passive metasurfaces that can provide compact and cost-effective solutions with lower power consumption for the future communication systems catering the ever increasing demands for global connectivity.

Author Contributions

The original draft was prepared by M.I. Nabeel and K.Singh, funding acquisition for this publication was done by K. Singh, the research was supervised by M. U. Afzal, D. N Thalakotuna and K. P Esselle. All authors have contributed towards the review and editing of this article. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the International Research Scholarship (IRS) and the Faculty of Engineering and IT Scholarship (FEIT) by the University of Technology Sydney (UTS).

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
SATCOM Satellite Communications
COTM Communication on the move
ITU International Telecommunication Union
LEO Lower Earth Orbit
MEO Medium Earth Orbit
GEO Geostationary Earth Orbit
PGM Phase Gradient Metasurface
RF Radio Frequency
SOTM SATCOM on the Move
NFMS Near Field Meta-Steering
RA Reflectarray
TA Transmitarray
RHCP Right Hand Circularly Polarized
LHCP Left Hand Circularly Polarized
PSS Phase Shifting Surfaces
MWS Microwave Studio
PD Phase Delay
PCB Printed Circuit Board
PR Phase Rotation

References

  1. Skyquest. Satellite Data Services Market Insights. https://www.skyquestt.com/report/satellite-data-services-market.
  2. Fortune Business Insight. Fortune Business Insights: Satcom Market. https://www.fortunebusinessinsights.com/satellite-communication-satcom-market-102679.
  3. statista. Internet usage worldwide - Statistics & Facts. https://www.statista.com/topics/1145/internet-usage-worldwide/#topicOverview.
  4. straitsresearch. Satellite Communication Market. https://straitsresearch.com/report/satellite-communication-market#:~:text=Market%20Overview,period%20(2022%E2%80%932030).
  5. You, R.; Gao, W.; Wu, C.; Li, H. Technologies for spacecraft antenna engineering design; Springer, 2021.
  6. Viasat. Satellite communications in 2024: The ins and outs. https://news.viasat.com/blog/corporate/satellite-communications-in-2024-the-ins-and-outs.
  7. Huang, J.; Cao, J. Recent development of commercial satellite communications systems. Artificial intelligence in China: Proceedings of the international conference on artificial intelligence in China. Springer, 2020, pp. 531–536.
  8. imarc. Top Players in the Satellite Communication (SATCOM) Market. https://www.imarcgroup.com/satellite-communication-companies.
  9. RF Wireless World. Advantages and Disadvantages of LEO orbit. https://www.rfwireless-world.com/Terminology/Advantages-and-Disadvantages-of-LEO-orbit.html .
  10. Lockie, D.G.; Thomson, M. Spacecraft antennas and beam steering methods for satellite communciation system, 1997. US Patent 5,642,122.
  11. Osoro, O.B.; Oughton, E.J. A techno-economic framework for satellite networks applied to low earth orbit constellations: Assessing Starlink, OneWeb and Kuiper. IEEE Access 2021, 9, 141611–141625. [CrossRef]
  12. He, Y.; Yang, F.; Han, G.; Li, Y. High-throughput SatCom-on-the-move antennas: technical overview and state-of-the-art. Digital Communications and Networks 2023. [CrossRef]
  13. Uchendu, I.; Kelly, J.R. Survey of beam steering techniques available for millimeter wave applications. Progress in electromagnetics research B 2016, 68, 35–54. [CrossRef]
  14. Zarb-Adami, K.; Faulkner, A.; De Vaate, J.B.; Kant, G.; Picard, P. Beamforming techniques for large-N aperture arrays. 2010 IEEE International Symposium on Phased Array Systems and Technology. IEEE, 2010, pp. 883–890.
  15. Esselle, K.; Singh, K.; Thalakotuna, D.; Koli, M.N.Y.; Ahmed, F. Beam-steering antenna technologies for space-related applications. 2023 17th European Conference on Antennas and Propagation (EuCAP). IEEE, 2023, pp. 1–5.
  16. Ahmed, F.; Singh, K.; Esselle, K.P. State-of-the-art passive beam-steering antenna technologies: Challenges and capabilities. Ieee Access 2023. [CrossRef]
  17. Rudge, A.; Withers, M. New technique for beam steering with fixed parabolic reflectors. Proceedings of the Institution of Electrical Engineers. IET, 1971, Vol. 118, pp. 857–863.
  18. EM solutions. Em solutions. https://www.emsolutions.com.au/products-and-solutions/sotm/.
  19. Boriskin, A.; Sauleau, R. Aperture antennas for millimeter and sub-millimeter wave applications; Springer, 2018.
  20. Sazegar, M.; Nassar, I.; Eylander, C.; Momeni, A.; Eylander, B.; Stevenson, R. Ku-Band SATCOM User Terminal With Complete Beam Steering Using a Shared Aperture Metasurface for Full-Duplex Operation. 2023 17th European Conference on Antennas and Propagation (EuCAP). IEEE, 2023, pp. 1–3.
  21. Kymeta Corporation. Kymeta Terminal. https://www.kymetacorp.com/products/terminal/.
  22. ThinKom Solutions. ThinKom. https://www.thinkom.com/technology.
  23. Kymeta Corporation. Starlink for Homes. https://www.starlink.com/residential?utm_source=google&utm_medium=paid&utm_campaign=lf_au_res_egn_src_ggl_brd_stk-pe&utm_content=694470362766&utm_term=starlink&utm_id=&gad_source=1&gclid=EAIaIQobChMI18yNvuW5hQMVlhitBh2UggomEAAYASAAEgLbEPD_BwE.
  24. Gagnon, N. Phase shifting surface (PSS) and phase and amplitude shifting surface (PASS) for microwave applications; University of Ottawa (Canada), 2011.
  25. Afzal, M.U.; Esselle, K.P. Steering the beam of medium-to-high gain antennas using near-field phase transformation. IEEE Transactions on Antennas and Propagation 2017, 65, 1680–1690. [CrossRef]
  26. Akbari, M.; Farahani, M.; Ghayekhloo, A.; Zarbakhsh, S.; Sebak, A.R.; Denidni, T.A. Beam tilting approaches based on phase gradient surface for mmWave antennas. IEEE Transactions on Antennas and Propagation 2020, 68, 4372–4385. [CrossRef]
  27. Singh, K.; Ahmed, F.; Esselle, K. Electromagnetic metasurfaces: Insight into evolution, design and applications. Crystals 2022, 12, 1769. [CrossRef]
  28. Singh, K.; Afzal, M.U.; Kovaleva, M.; Esselle, K.P. Controlling the most significant grating lobes in two-dimensional beam-steering systems with phase-gradient metasurfaces. IEEE Transactions on Antennas and Propagation 2019, 68, 1389–1401. [CrossRef]
  29. Singh, K.; Afzal, M.U.; Esselle, K.P. Designing efficient phase-gradient metasurfaces for near-field meta-steering systems. IEEE Access 2021, 9, 109080–109093. [CrossRef]
  30. Zhao, X.; Yuan, C.; Liu, L.; Peng, S.; Zhang, Q.; Zhou, H. All-metal transmit-array for circular polarization design using rotated cross-slot elements for high-power microwave applications. IEEE Transactions on Antennas and Propagation 2017, 65, 3253–3256. [CrossRef]
  31. Berry, D.; Malech, R.; Kennedy, W. The reflectarray antenna. IEEE Transactions on Antennas and Propagation 1963, 11, 645–651. [CrossRef]
  32. Mirmozafari, M.; Zhang, Z.; Gao, M.; Zhao, J.; Honari, M.M.; Booske, J.H.; Behdad, N. Mechanically reconfigurable, beam-scanning reflectarray and transmitarray antennas: A review. Applied Sciences 2021, 11, 6890. [CrossRef]
  33. Budhu, J.; Grbic, A.; Michielssen, E. Dualband stacked metasurface reflectarray. 2020 IEEE International Symposium on Antennas and Propagation and North American Radio Science Meeting. IEEE, 2020, pp. 821–822.
  34. Baladi, E.; Xu, M.Y.; Faria, N.; Nicholls, J.; Hum, S.V. Dual-band circularly polarized fully reconfigurable reflectarray antenna for satellite applications in the Ku-band. IEEE Transactions on Antennas and Propagation 2021, 69, 8387–8396. [CrossRef]
  35. Teng, M.; Yu, S.; Kou, N. A Dual-Band Beam Steering Array Antenna With Integration of Reflectarray and Phased Array. IEEE Antennas and Wireless Propagation Letters 2023. [CrossRef]
  36. Nam, Y.H.; Kim, Y.; Lee, S.G.; Lee, J.H. Hybrid reflectarray antenna of passive and active unit cells for highly directive two-direction beam steering. IEEE Access 2022, 11, 6299–6304. [CrossRef]
  37. Luo, Q.; Gao, S.; Li, W.; Sobhy, M.; Bakaimi, I.; de Groot, C.K.; Hayden, B.; Reaney, I.; Yang, X. Multibeam dual-circularly polarized reflectarray for connected and autonomous vehicles. IEEE Transactions on Vehicular Technology 2019, 68, 3574–3585. [CrossRef]
  38. Chi, P.L.; Cheng, Y.H.; Yang, T. Novel Dual-Frequency Independent Beam-Scanning Reflectarray. 2023 IEEE International Symposium on Antennas and Propagation and USNC-URSI Radio Science Meeting (USNC-URSI). IEEE, 2023, pp. 1337–1338.
  39. Dussopt, L. Transmitarray antennas. Aperture Antennas for Millimeter and Sub-Millimeter Wave Applications 2018, pp. 191–220.
  40. Matos, S.A.; Lima, E.B.; Silva, J.S.; Costa, J.R.; Fernandes, C.A.; Fonseca, N.J.; Mosig, J.R. High gain dual-band beam-steering transmit array for satcom terminals at Ka-band. IEEE Transactions on Antennas and Propagation 2017, 65, 3528–3539. [CrossRef]
  41. Zeng, Q.; Xue, Z.; Ren, W.; Li, W. Dual-band beam-scanning antenna using rotatable planar phase gradient transmitarrays. IEEE Transactions on Antennas and Propagation 2020, 68, 5021–5026. [CrossRef]
  42. Lei, H.; Liu, Y.; Jia, Y.; Yue, Z.; Wang, X. A low-profile dual-band dual-circularly polarized folded transmitarray antenna with independent beam control. IEEE Transactions on Antennas and Propagation 2021, 70, 3852–3857. [CrossRef]
  43. Naseri, P.; Mirzavand, R.; Mousavi, P. Dual-band circularly polarized transmit-array unit-cell at X and K bands. 2016 10th European Conference on Antennas and Propagation (EuCAP). IEEE, 2016, pp. 1–4.
  44. Naseri, P.; Matos, S.A.; Costa, J.R.; Fernandes, C.A.; Fonseca, N.J. Dual-band dual-linear-to-circular polarization converter in transmission mode application to K/Ka--band satellite communications. IEEE Transactions on Antennas and Propagation 2018, 66, 7128–7137. [CrossRef]
  45. Wang, P.; Ren, W.; Zeng, Q.; Xue, Z.; Li, W. Dual-band beam-scanning antenna at ka-band by rotation of two transmitarrays. IEEE Antennas and Wireless Propagation Letters 2022, 21, 1792–1796. [CrossRef]
  46. Aziz, A.; Zhang, X.; Yang, F.; Xu, S.; Li, M. A dual-band orthogonally polarized contour beam transmitarray design. IEEE Transactions on Antennas and Propagation 2021, 69, 4538–4545. [CrossRef]
  47. Bagheri, M.O.; Hassani, H.R.; Rahmati, B. Dual-band, dual-polarised metallic slot transmitarray antenna. IET Microwaves, Antennas & Propagation 2017, 11, 402–409.
  48. Pham, K.T.; Sauleau, R.; Fourn, E.; Diaby, F.; Clemente, A.; Dussopt, L. Dual-band transmitarrays with dual-linear polarization at Ka-band. IEEE Transactions on Antennas and Propagation 2017, 65, 7009–7018. [CrossRef]
  49. Wang, S.; Chen, Y.; Gao, J.; Zhai, G.; Ding, J. Ultrathin Dual-Band Wide-Angle Beam Scanning Metalens Based on High-Efficiency Meta-Atom. Advanced Photonics Research 2022, 3, 2100186. [CrossRef]
  50. Hasani, H.; Silva, J.S.; Capdevila, S.; García-Vigueras, M.; Mosig, J.R. Dual-band circularly polarized transmitarray antenna for satellite communications at (20, 30) GHz. IEEE Transactions on Antennas and Propagation 2019, 67, 5325–5333. [CrossRef]
  51. Pham, T.K.; Guang, L.; González-Ovejero, D.; Sauleau, R. Dual-band transmitarray with low scan loss for satcom applications. IEEE Transactions on Antennas and Propagation 2020, 69, 1775–1780. [CrossRef]
  52. Hasani, H.; Silva, J.S.; Mosig, J.R.; Garcia-Vigueras, M. Dual-band 20/30 GHz circularly polarized transmitarray for SOTM applications. 2016 10th European Conference on Antennas and Propagation (EuCAP). IEEE, 2016, pp. 1–3.
  53. Singh, K.; Afzal, M.U.; Esselle, K.P. Efficient Near-Field Meta-Steering Systems for Connectivity-On-The-Move Applications using Hybrid Metasurfaces. 2022 IEEE International Symposium on Antennas and Propagation and USNC-URSI Radio Science Meeting (AP-S/URSI). IEEE, 2022, pp. 641–642.
  54. Koli, M.N.Y.; Afzal, M.U.; Esselle, K.P. Increasing the gain of beam-tilted circularly polarized radial line slot array antennas. IEEE Transactions on Antennas and Propagation 2022, 70, 4392–4403. [CrossRef]
  55. Ahmed, F.; Afzal, M.U.; Hayat, T.; Esselle, K.P.; Thalakotuna, D.N. A near-field meta-steering antenna system with fully metallic metasurfaces. IEEE Transactions on Antennas and Propagation 2022, 70, 10062–10075. [CrossRef]
  56. Baba, A.A.; Hashmi, R.M.; Attygalle, M.; Esselle, K.P.; Borg, D. Ultrawideband beam steering at mm-wave frequency with planar dielectric phase transformers. IEEE Transactions on Antennas and Propagation 2021, 70, 1719–1728. [CrossRef]
  57. Ahmed, F.; Afzal, M.U.; Esselle, K.P.; Thalakotuna, D.N. Novel Dual-Band Phase-Gradient Metascreen and Dual-Band Near-Field Meta-Steering Antenna. IEEE Transactions on Antennas and Propagation 2024. [CrossRef]
  58. Ettorre, M.; Pavone, S.; Casaletti, M.; Albani, M.; Mazzinghi, A.; Freni, A. Aperture Antennas for Millimeter and Sub-Millimeter Wave Applications. Cham: Springer 2018, pp. 243–288.
  59. Huang, J. Analysis of a microstrip reflectarray antenna for microspacecraft applications. The Telecommunications and Data Acquisition Report 1995.
  60. Gagnon, N.; Petosa, A.; McNamara, D.A. Printed hybrid lens antenna. IEEE transactions on antennas and propagation 2012, 60, 2514–2518. [CrossRef]
  61. Gagnon, N.; Petosa, A. Using rotatable planar phase shifting surfaces to steer a high-gain beam. IEEE transactions on antennas and propagation 2013, 61, 3086–3092. [CrossRef]
  62. Gagnon, N.; Petosa, A.; McNamara, D.A. Thin microwave quasi-transparent phase-shifting surface (PSS). IEEE transactions on antennas and propagation 2010, 58, 1193–1201. [CrossRef]
  63. Ding, F.; Pors, A.; Bozhevolnyi, S.I. Gradient metasurfaces: a review of fundamentals and applications. Reports on Progress in Physics 2017, 81, 026401. [CrossRef] [PubMed]
  64. Bose, J.C. On the rotation of plane of polarisation of electric wave by a twisted structure. Proceedings of the Royal Society of London 1898, 63, 146–152.
  65. Ali, A.; Mitra, A.; Aïssa, B. Metamaterials and metasurfaces: A review from the perspectives of materials, mechanisms and advanced metadevices. Nanomaterials 2022, 12, 1027. [CrossRef] [PubMed]
  66. Balanis, C.A. Antenna theory: analysis and design; John wiley & sons, 2016.
  67. Arbabi, E.; Arbabi, A.; Kamali, S.M.; Horie, Y.; Faraon, A. Multiwavelength polarization-insensitive lenses based on dielectric metasurfaces with meta-molecules. Optica 2016, 3, 628–633. [CrossRef]
  68. Baba, A.A.; Hashmi, R.M.; Esselle, K.P.; Weily, A.R. Compact high-gain antenna with simple all-dielectric partially reflecting surface. IEEE Transactions on Antennas and Propagation 2018, 66, 4343–4348. [CrossRef]
  69. Afzal, M.U.; Esselle, K.P.; Lalbakhsh, A. A methodology to design a low-profile composite-dielectric phase-correcting structure. IEEE antennas and wireless propagation letters 2018, 17, 1223–1227. [CrossRef]
  70. Afzal, M.U.; Esselle, K.P.; Zeb, B.A. Dielectric phase-correcting structures for electromagnetic band gap resonator antennas. IEEE Transactions on Antennas and Propagation 2015, 63, 3390–3399. [CrossRef]
  71. Jain, S.; Abdel-Mageed, M.; Mittra, R. Flat-lens design using field transformation and its comparison with those based on transformation optics and ray optics. IEEE Antennas and Wireless Propagation Letters 2013, 12, 777–780. [CrossRef]
  72. Emara, M.K.; Tomura, T.; Hirokawa, J.; Gupta, S. Fabry–Pérot-Based Compound All-Dielectric Huygens’ Structure for Circularly Polarized Millimeter-Wave Beamforming. IEEE Antennas and Wireless Propagation Letters 2020, 19, 1784–1788. [CrossRef]
  73. Al-Nuaimi, M.K.T.; Hong, W.; Zhang, Y. Design of high-directivity compact-size conical horn lens antenna. IEEE Antennas and Wireless Propagation Letters 2014, 13, 467–470. [CrossRef]
  74. Eskandari, H.; Albadalejo-Lijarcio, J.L.; Zetterstrom, O.; Tyc, T.; Quevedo-Teruel, O. H-plane horn antenna with enhanced directivity using conformal transformation optics. Scientific Reports 2021, 11, 14322. [CrossRef]
  75. Holzman. A highly compact 60-GHz lens-corrected conical horn antenna. IEEE antennas and wireless propagation letters 2004, 3, 280–282. [CrossRef]
  76. Munk, B.A. Frequency selective surfaces: theory and design; John Wiley & Sons, 2005.
  77. Abdelrahman, A.H.; Yang, F.; Elsherbeni, A.Z.; Nayeri, P.; Balanis, C.A. Analysis and design of transmitarray antennas 2017.
  78. Ryan, C.G.; Chaharmir, M.R.; Shaker, J.; Bray, J.R.; Antar, Y.M.; Ittipiboon, A. A wideband transmitarray using dual-resonant double square rings. IEEE Transactions on antennas and propagation 2010, 58, 1486–1493. [CrossRef]
  79. Matos, S.A.; Lima, E.B.; Costa, J.R.; Fernandes, C.A.; Fonseca, N.J. Generic formulation for transmit-array dual-band unit-cell design. 2017 11th European Conference on Antennas and Propagation (EUCAP). IEEE, 2017, pp. 2791–2794.
  80. Lima, E.B.; Matos, S.A.; Costa, J.R.; Fernandes, C.A.; Fonseca, N.J. Circular polarization wide-angle beam steering at Ka-band by in-plane translation of a plate lens antenna. IEEE Transactions on Antennas and Propagation 2015, 63, 5443–5455. [CrossRef]
  81. Ebrahimi, A.; Withayachumnankul, W.; Al-Sarawi, S.; Abbott, D. Design of dual-band frequency selective surface with miniaturized elements. 2014 International Workshop on Antenna Technology: Small Antennas, Novel EM Structures and Materials, and Applications (iWAT). IEEE, 2014, pp. 201–204.
  82. Li, M.; Behdad, N. Wideband true-time-delay microwave lenses based on metallo-dielectric and all-dielectric lowpass frequency selective surfaces 2013. 61, 4109–4119.
  83. Naseri, P.; Matos, S.A.; Costa, J.R.; Fernandes, C.A. Phase-Delay Versus Phase-Rotation Cells for Circular Polarization Transmit Arrays—Application to Satellite Ka-Band Beam Steering. IEEE Transactions on Antennas and Propagation 2018, 66, 1236–1247. [CrossRef]
  84. Nabeel, M.I.; Afzal, M.U.; Singh, K.; Thalakotuna, D.N.; Esselle, K.P. Dual-Band Printed Near-Field Metasurface with Independent Phase Transformation for Enhanced Antenna Gain. IEEE Antennas and Wireless Propagation Letters 2024. [CrossRef]
  85. Mutluer, E.; Döken, B.; Kartal, M. A dual-band frequency selective surface design for satellite applications. 2018 18th Mediterranean Microwave Symposium (MMS). IEEE, 2018, pp. 43–46.
  86. Chaharmir, M.R.; Shaker, J. Design of a multilayer X-/Ka-band frequency-selective surface-backed reflectarray for satellite applications. IEEE Transactions on Antennas and Propagation 2015, 63, 1255–1262. [CrossRef]
Preprints 114010 g001
Figure 1. The modern wireless communication landscape.
Figure 1. The modern wireless communication landscape.
Preprints 114010 g001
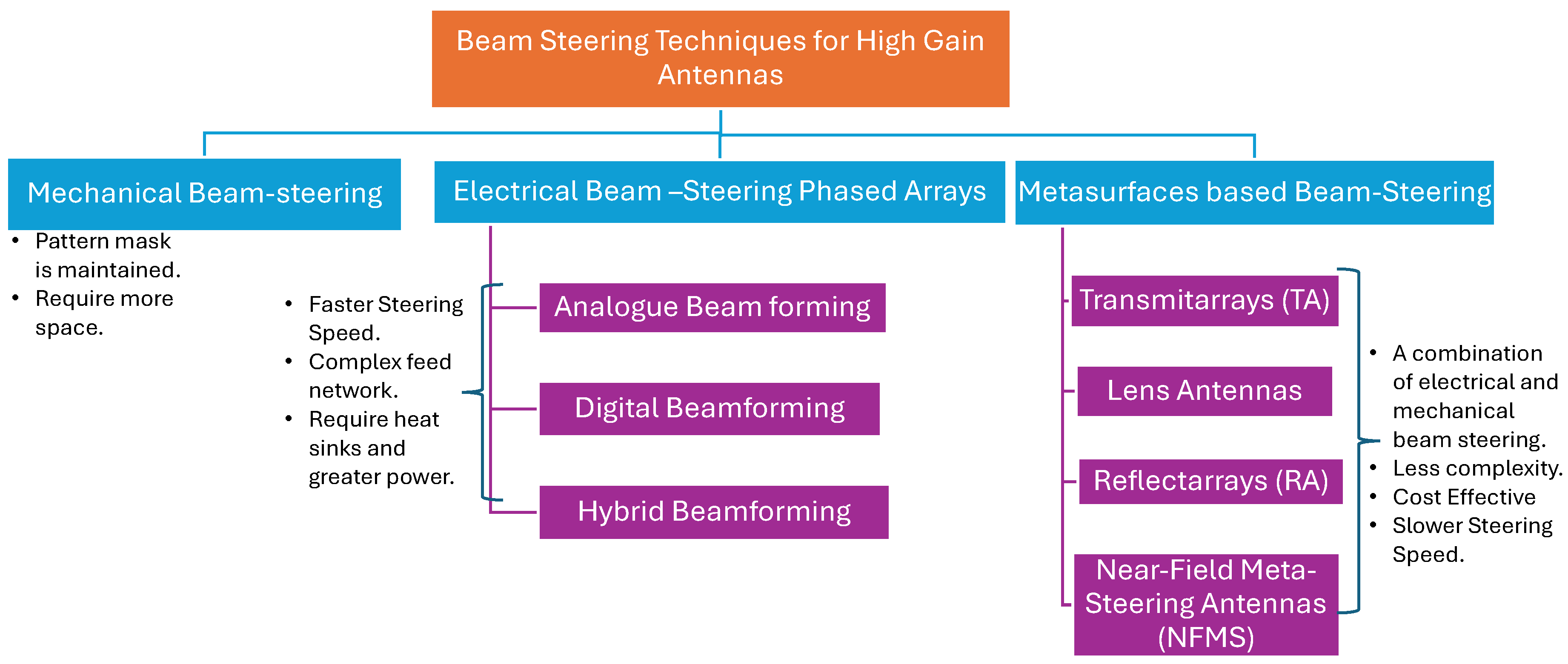
Preprints 114010 g002
Figure 2. Classification of beam-steering techniques.
Figure 2. Classification of beam-steering techniques.
Preprints 114010 g002
Preprints 114010 g003
Figure 3. Dual-band metasurface based beam-steering techniques.
Figure 3. Dual-band metasurface based beam-steering techniques.
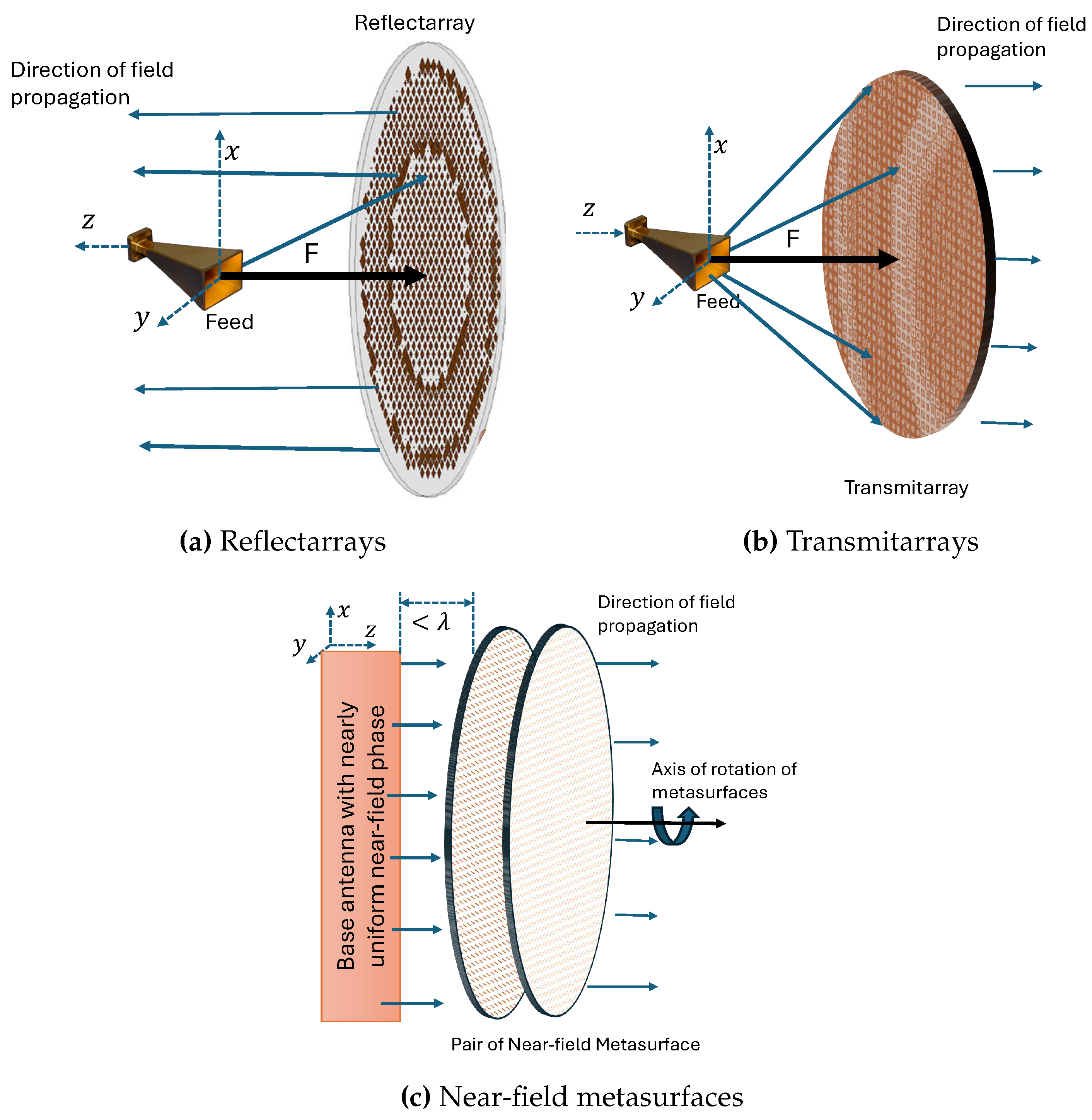
Preprints 114010 g003
Preprints 114010 g004
Figure 4. Analogy between an antenna array and array of cells arranged in a metasurface to exhibit a transmission phase gradient.
Figure 4. Analogy between an antenna array and array of cells arranged in a metasurface to exhibit a transmission phase gradient.
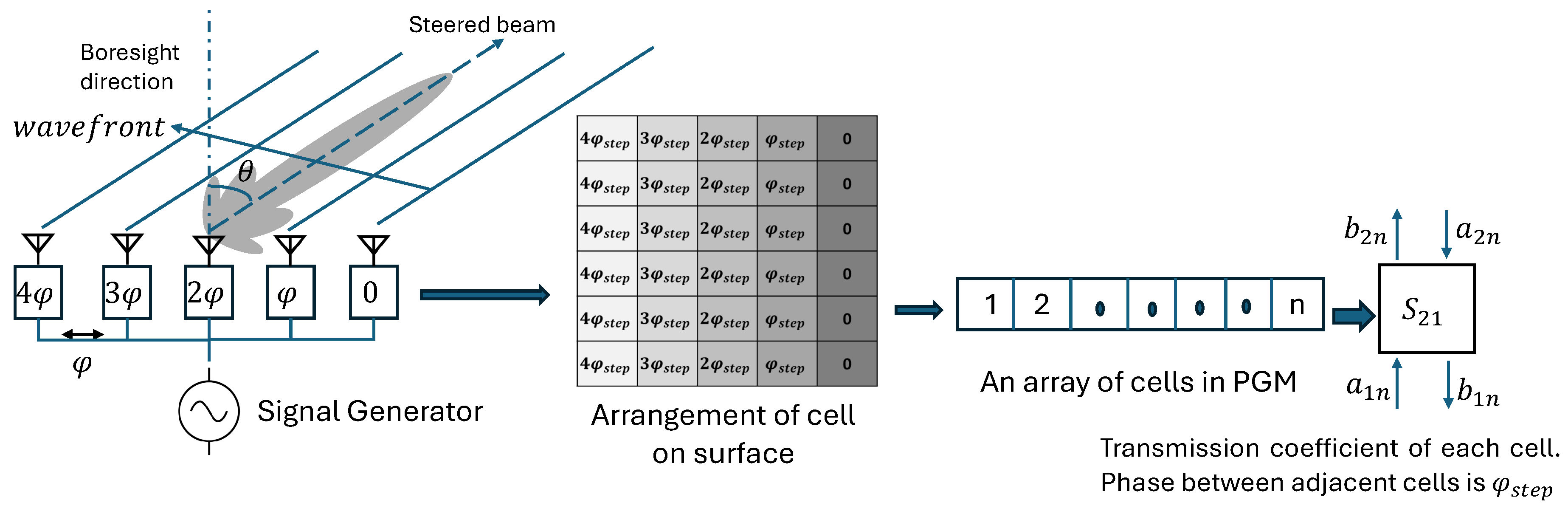
Preprints 114010 g004
Preprints 114010 g005
Figure 5. Different phase transformation cell topologies based on their implemented structure. (a) An all dielectric multiwavelength cell [67], (b) A dual-band all metal cell [57] and (c) a dual band composite cell [40].
Figure 5. Different phase transformation cell topologies based on their implemented structure. (a) An all dielectric multiwavelength cell [67], (b) A dual-band all metal cell [57] and (c) a dual band composite cell [40].
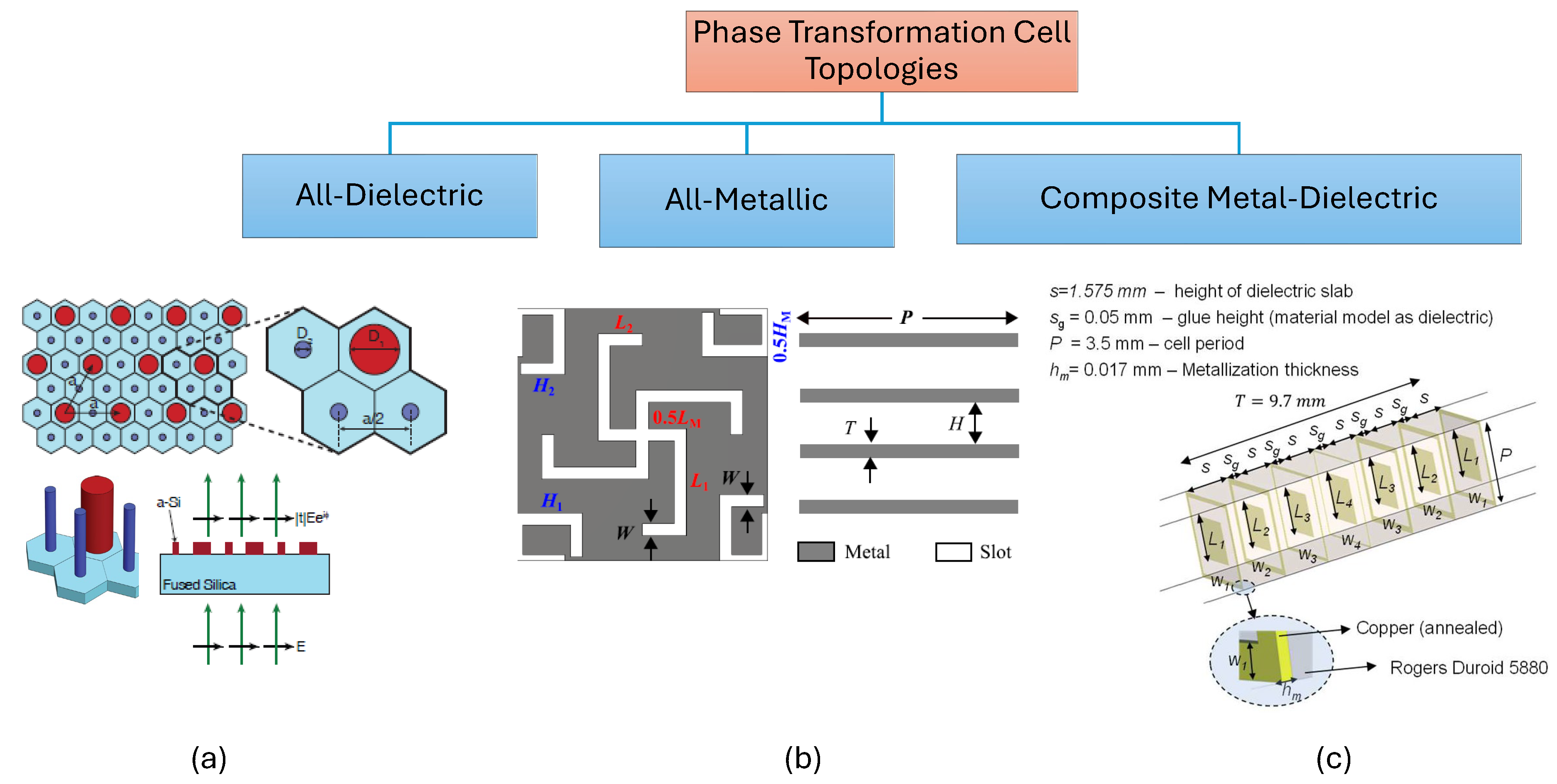
Preprints 114010 g005
Preprints 114010 g006
Figure 6. Unit cell simulations in CST, Periodic in x and y axis, open in z axis with Floquet mode excitation.
Figure 6. Unit cell simulations in CST, Periodic in x and y axis, open in z axis with Floquet mode excitation.
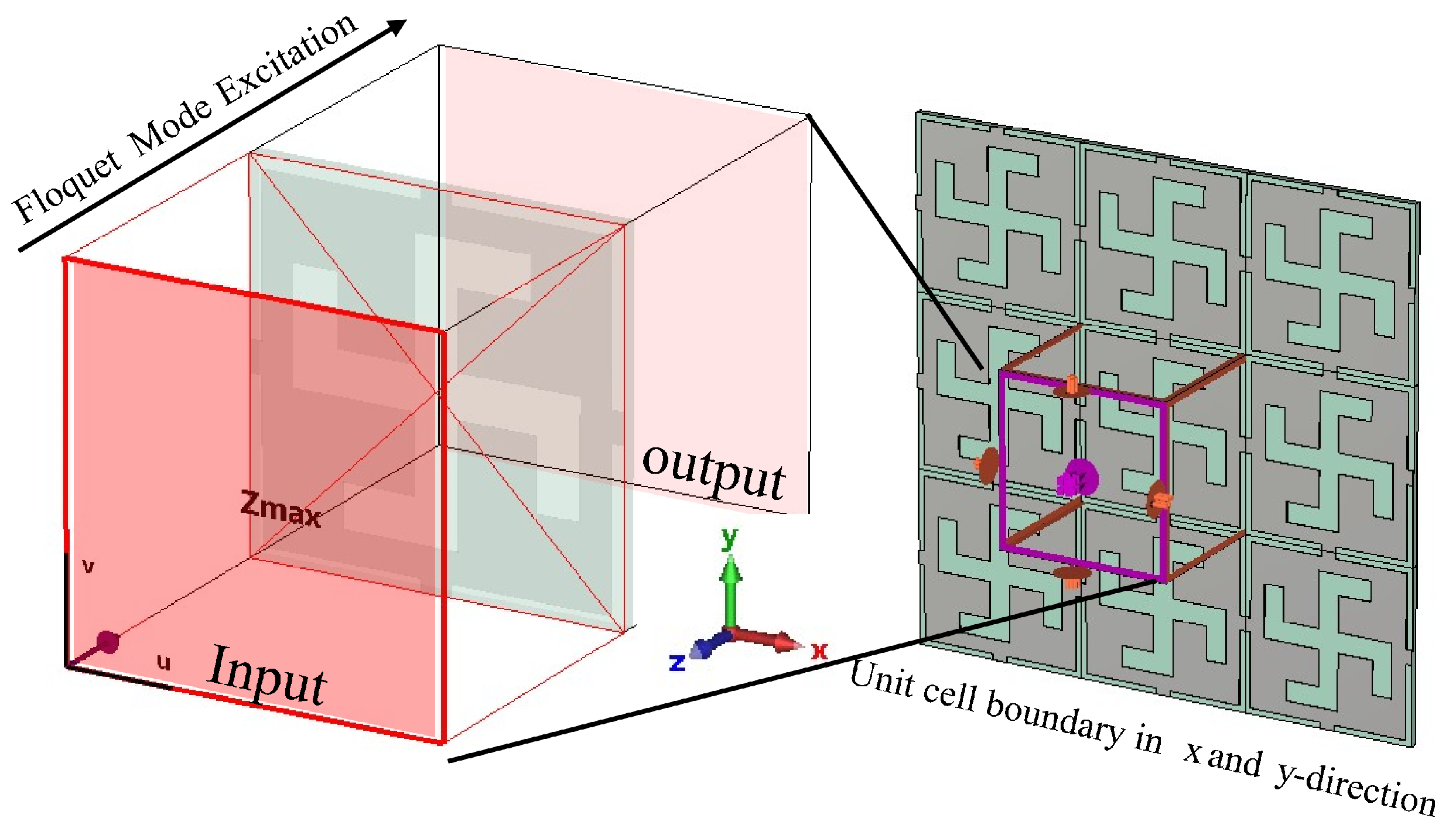
Preprints 114010 g006
Preprints 114010 g007
Figure 7. Different types of dual-band phase shifting cells. (a) Multilayer cells based on the selection of optimized phase pairs corresponding to the desired response in the dual-frequency bands, (b) interleaving resonant elements corresponding to each frequency, (c) dual-band phase rotation cell, and (d) a concentric cell using orthogonal polarized modified split rings and Jerusalem cross.
Figure 7. Different types of dual-band phase shifting cells. (a) Multilayer cells based on the selection of optimized phase pairs corresponding to the desired response in the dual-frequency bands, (b) interleaving resonant elements corresponding to each frequency, (c) dual-band phase rotation cell, and (d) a concentric cell using orthogonal polarized modified split rings and Jerusalem cross.
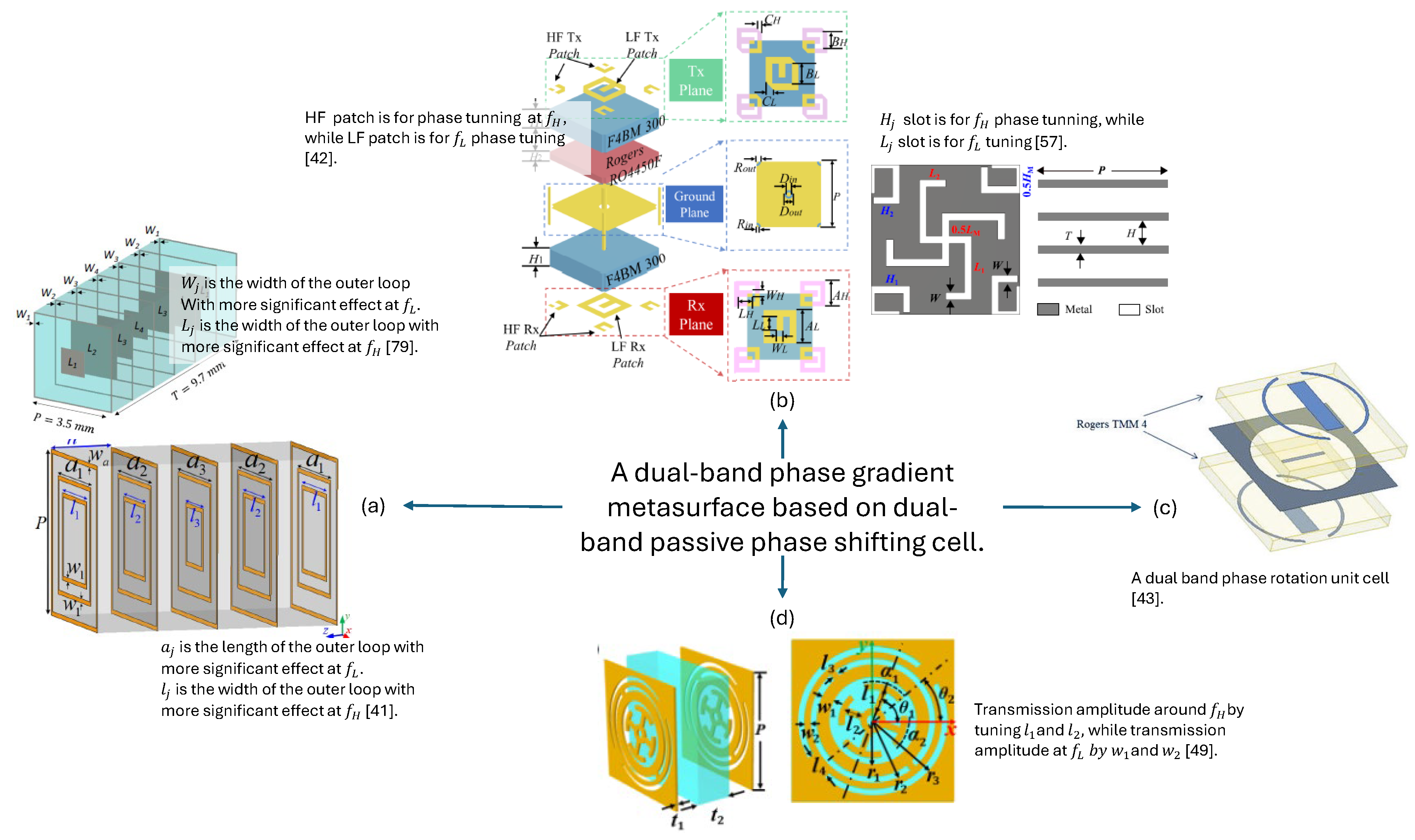
Preprints 114010 g007
Preprints 114010 g008
Figure 8. Summary of techniques to design a dual-band unit cell for passive phase-gradient metasurfaces.
Figure 8. Summary of techniques to design a dual-band unit cell for passive phase-gradient metasurfaces.
Preprints 114010 g008
Table 1. Specifications of resonant elements in various references.
Table 1. Specifications of resonant elements in various references.
Ref Resonant Element Topology Number of Layers Cell Size Frequency Capability Polarization   Phase Control
[78] Double Square Loop Composite separated by air gap 4 0.6 λ Wideband (29-32 GHz) CP NA
[85] 4-arm structure for one band, 4-leg structure for other-band Composite One metal and one dielectric layer 0.2 λ L Dual-band Ku/Ka (14.1-16 GHz and 29.2-36.8 GHz) Dual Separate tuning of elements by length variation
[86] Cross dipole for higher frequency, backed by square loops for lower frequency Composite interleaved structure Five dielectric and seven metal layers 0 . 3 λ L and 0 . 4 λ H Dual Band (20,30 GHz) CP NA
[52] Split ring center elements for lower frequency, quarter split circle at corners for higher frequency Composite Five metal and four dielectric layers 0.53 λ L and 0.8 λ H Dual Band (20,30 GHz) CP Independent phase tuning by rotation of split rings
[79] Square Patch Middle and square loop mentions shape against design frequ Composite seven metal and six dielectric layers 0.35 λ H Dual Band (20,30 GHz) CP Optimal Phase Pair Selection
[42] High frequency and low frequency patches Composite Three metal & two dielectric layers, bonded together 0.49 λ L and 0.6 λ H Dual band (12,15 GHz) Dual CP NA
[50] Swastika cross slot for lower frequency, half cross slot on cell corners for higher frequency Composite, Thin substrate separated by air gap Three metal and three dielectric layers 0.53 λ H Dual band (20,30 GHz) CP Independent Frequency tuning by length variation
[41] Three concentric square loops Composite structure, bonded layers Five metal & four dielectric layers 0.38 λ H Dual band (8,14 GHz) CP Optimum Phase pair by length variation
[51] Vertical and Horizontal Dipoles Composite Bonded Layers Three metal and three dielectric layers 0.58 λ H Dual-band (20,30 GHz) LP Independent frequency tuning as the resonating elements are cross-polarized
[47] Cross slot and magnetic dipole slot All metal Three metal layers 0.33 λ H Dual-band (11, 12.5 GHz) CP Independent frequency tuning as the resonating elements are cross-polarized
[57] Modified swastika slot in the middle for LF, and half swastika slot in corners for HF All metal, separated by air gap Four metal layers 0.5 λ H Dual-band (Ku) CP Optimum phase pair with partially independent phase response
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated