Preprint
Article
Machine Learning Monte Carlo Approaches and Statistical Physics Notions to Characterize Bacterial Species in Human Microbiota
Altmetrics
Downloads
111
Views
35
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
01 August 2024
Posted:
02 August 2024
You are already at the latest version
Alerts
Abstract
Recent studies have shown correlations between the microbiota's composition and various health conditions. Machine learning (ML) techniques are essential for analyzing complex biological data, particularly in microbiome research. ML methods help analyze large datasets to uncover microbiota patterns and understand how these patterns affect human health. This study introduces a novel approach combining statistical physics with the Monte Carlo (MC) methods to characterize bacterial species in the human microbiota. We assess the significance of bacterial species in different age groups by using notions of statistical distances to evaluate species prevalence and abundance across age groups and employing MC simulations based on statistical mechanics principles. Our findings show that the microbiota composition experiences a significant transition from early childhood to adulthood. Species such as Bifidobacterium breve and Veillonella parvula decrease with age, while others like Agathobaculum butyriciproducens and Eubacterium rectale increase. Additionally, low-prevalence species may hold significant importance in characterizing age groups. Finally, we propose an overall species ranking by integrating the methods proposed here in a multicriteria classification strategy. Our research provides a comprehensive tool for microbiota analysis using statistical notions, ML techniques, and MC simulations.
Keywords:
Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning
1. Introduction
Machine learning (ML) techniques are fundamental in analyzing extensive, complex biological data from different areas of biological science [1]. These advanced computational methods are precious in microbiome research, enabling the integration and interpretation of vast datasets to uncover intricate patterns and relationships within the microbiota. The microbiota, the community of microorganisms that colonizes the human body, is considered to affect a wide range of physiological processes, from immunity to digestion, and plays a crucial role in determining human health [2,3,4]. An ever-increasing number of studies have highlighted the possible correlation between the abundance, variability, and richness of bacterial species belonging to the human microbiota and many health disorders and/or diseases [3,5,6,7]. In this context, investigating in depth the human gut microbiota composition and its correlation with the different host intrinsic parameters, such as age, gender, health condition, and lifestyle, could be crucial for better understanding the main factors that might impact the individuals’ health status [6,7].
The study of the human microbiota was made possible by developing modern next-generation sequencing techniques, which allow the precise and in-depth identification of the microbial populations that inhabit the human body [8,9]. However, these modern techniques, such as the 16S rRNA gene profiling and shotgun metagenomic sequencing, require sophisticated and advanced technological approaches capable of analyzing large and complex databases and identifying subtle patterns within them. Despite these advancements, there currently needs to be a unified statistical methodology for analyzing metagenomic data, leading to significant variability in the approaches used. In this context, the development of MLs has provided powerful tools to address this challenge, allowing us to extract useful information from large microbiota databases and develop models to predict the abundance of bacterial species in response to various factors.
In this study, we evaluate a new approach by integrating statistical physics notions with the machine learning Monte Carlo (MC) method to characterize bacterial species in the human microbiota. Specifically, in addition to classic statistical classification strategies such as species prevalence and abundance, we introduce and utilize different statistical distance notions to assess how much the average occurrence of a species in the age group samples deviates from the general average across groups. Then, we use MCs, which are computational algorithms based on repeated random sampling to obtain numerical results [10], widely used in various fields of biology [11,12], ecology [13], and physics [14]. MCs are random numerical experiments on a computer where we can observe the outcomes of these experiments, and they are instrumental when dealing with complex systems with high uncertainty or randomness, such as bacterial species sampling. We perform MCs whose rationale is based on the concepts of the microcanonical and canonical ensembles in statistical mechanics [15]. MCs allow us to find the statistical significance of bacterial species for age groups by comparing their empirical prevalence with that of the numerical experiment. Last, since we evaluate the importance of bacterial species in the age groups with different classification strategies, we propose a further analysis to obtain an overall species ranking by evaluating the results of the different strategies together.
This manuscript offers new methodological approaches and insight into classifying important species in biology. It can be useful for solving classification problems in empirical databases using machine learning Monte Carlo simulation.
2. Methods
2.1. Database
The data used in this study were obtained from publicly available datasets regarding the human gut microbiota across different life stages. These comprehensive datasets included samples from various regions worldwide, providing a diverse and representative overview of the global human gut microbiota [16]. In detail, this study included a total of 5,896 sequenced fecal samples collected from 71 public bioprojects across 34 different countries. The datasets included sequenced fecal samples collected from healthy individuals ranging from birth to over 100 years old, with a robust statistical representation of all the different age groups. The collected samples, as reported in the previous manuscript [16], were used to assess the microbiota composition at the species level through the METAnnotatorX2 software following the standard filtering parameters reported in the manual with Homo sapiens reads removal [17]. Moreover, the samples included in the analysis were categorized into four age groups, that is, G1 (0–4 years), G2 (5–17 years), G3 (18–64 years), and G4 (65 years and older), following the guidelines provided by the World Health Organization (WHO) [18].
2.2. Statistical Analyses
Average Occurrences
The columns of the matrix database represent bacterial species; the rows of the database are the human fecal samples. The element of indicates the relative abundance of the species in the sample . Figure 1A depicts a simple example of the database used here.
The average occurrence of the species among all samples is:
Where is the total number of samples; we can call the average weighted occurrence. estimates how much of a bacterial species is present among all samples. The average weighted occurrence is commonly called the ‘relative average abundance’ of bacterial species [16,19].
The samples are divided by age into four groups. We compute as the average occurrence of species within group and call it the average weighted occurrence (AWO).
In formula:
Where is the total number of samples of the group . provides an estimate of how much a bacterial species is present among the group samples. For this, it furnishes a first and simple estimate of how a bacterial species is present within a given age range of the subjects examined.
Second, we convert the species abundances into simple occurrences (presence/absence). We call this new database the occurrences matrix . For this, is a binary matrix in which the elements of the species/columns are 0 (no occurrence) and 1 (occurrence) (Figure 1B). The element of the matrix is 1 if the species occurs in sample and 0 otherwise.
The average species occurrence among all samples in the matrix is:
We can call the average binary occurrence (ABO), whereas it is usually called the ‘prevalence’ of the bacterial species [16,19].
Then, we compute , the average binary occurrence of species within group . For each column , we divide the total number of 1 occurring within group by the total number of samples. represents the average occurrence among the sample of the species within group .
In formula:
Where is the total number of samples of the group , since this average is computed considering the simple presence-absence of species occurrence in the sample. and estimates how frequent it is to find a particular bacterial species among samples without considering the relative abundance of the species in the sample.
Relative Distances
We compute the distance between the observed () and the expected () species occurrence within each group. We define this distance as the relative deviation of the average species occurrence within the group from the average species occurrence among groups (among all samples). This is represented by the ratio:
Where indicates the average species occurrence within a group, and is the average species occurrence among all samples (among groups).
The average weighted occurrence among all samples represents the expected occurrence. The average weighted occurrence of species within group represents the observed occurrence.
The weighted distance becomes:
The higher the distance , the higher the difference between the observed and the expected species occurrence within the group . From now on, is the relative weighted distance (RWD). We can see this distance as the relative deviation of the relative average abundance within the group (observed occurrence) concerning the relative average abundance across all samples (expected occurrence).
We can translate Equation 6 using the binary occurrence. The average binary occurrence among samples represents the expected occurrence. The average binary occurrence of species within group represents the observed occurrence. We call this the relative binary distance (RBD), and it is computed as follows:
This statistical distance is the relative deviation of the species prevalence within the group (observed occurrence) concerning the prevalence across all groups (expected occurrence).
Let’s consider how the RBD and RWD distances evaluate specific cases of species occurrence.
We start with the case of a bacterial species occurring only within a group.
The average binary occurrence of the species is:
And the average binary occurrence of the species within group is:
Substituting Eqs. 8 and 9 in Eq. 7 of the relative binary distance, we obtain:
Reversing the denominator:
In the case the species occurs only in group , we have the equivalence between the prevalence within the group and across all groups:
And:
For this, Eq. 11 results:
Eq. 12 indicates that if a bacterial species occurs only within group , the value of the distance RBD is only determined by the ratio, that is, the ratio between the total number of samples and the number of samples in group . The last outcome implies that species with different prevalences that occur only within a group will return the same RBD value. In this case, species with different occurrences have the same distance, and the RBD is not able to discriminate their importance in characterizing the group. This implies that Eq. 12 also provides the RBD maximum value. Figure 1 depicts an example of RBD computation for species that occur only within a group. From Figure 1B, we calculate the RBD values for species S1 and S6 for group G1; we compute and .
Using Eq. 6 for species S1, we have:
And for species S6:
Even though the occurrences are different, and species S6 is more frequent than S1 in group 1, the RBD value is the same.
Let’s consider the case of a bacterial species that does not occur within a group. In this case, and Eq. 6 results:
This result implies that all the species not occurring within a group will return the RBD value , and that is also the minimum value. RBD is constrained in the interval [-1,1]. It is easy to show that the maximum and the minimum values derived in Equations 12 and 13 for RBD are also the limits of the weighted counterpart RWD.
We can introduce a second-order hierarchy to rank the ties to solve the RWD and RBD problem of presenting ties in species ranking when species occur only within a group. For example, in the case of ties, we can rank the species presenting the same RWD and RBD values using measures of their average occurrence within the group; for example, we can use the relative abundance and the prevalence of the species in the group as a second-order criterion to rank ties. Therefore, species are first ranked according to their relative distance, thus assessing their statistical distance from the overall average occurrence, and then according to their average occurrence within the group. We can choose the ranking strategy to solve ties with the rationale that we prefer for the problem at hand. For example, suppose we want to prioritize the number of times a species appears, i.e., its prevalence. In this case, we can use the average binary occurrence as a second-order criterion to rank ties. If we want to prioritize the abundance of a species in the sample, i.e., the relative species abundance, we can adopt its average weighted occurrence as a second-order criterion to rank ties. The selection of the second-order ranking criterion should be guided by the rationale that aligns most closely with the objectives of the analysis. In this research, we rank ties using the species binary occurrence. In Figure 2, we furnish an example of a second-order rank methodology for solving ties.
Inside-Outside Distances
Then, we used a second type of distance by computing the difference between the species occurrence inside the group and the species occurrence outside the group, that is:
Where is the average weighted occurrence of species within group and is the average weighted occurrence of species outside group . Since is the difference between the inside and outside average species occurrence, we refer to as the inside-outside weighted distance (IOWD). In other terms, IOWD is the difference between the relative species abundance within the group and the relative species abundance outside the group.
We can modify Eq. 14 using the species binary occurrence and defining the inside-outside binary distance (IOBD):
here, is the average binary occurrence of species within group , and is the average binary occurrence of species outside group . IOBD is the difference between the species prevalence within the group and the species prevalence outside the group.
We can compute the range limits for the outside-inside distances. Let us take Eq. 14, giving the IOWD. The maximum value occurs satisfying the three conditions: i) species occurs only within a group (, species does not occur outside the group ), ii) species occurs in all the samples of group , and iii) species abundances equal 1 (i.e., , meaning that is the only bacterial species in the sample ). These three conditions lead to , and the maximum IOWD becomes .
At the opposite end, the minimum value occurs when i) the species does not occur in the group (), ii) species occurs in all the samples outside group , and iii) species abundances outside group equal 1. These three conditions lead to , and the minimum IOWD becomes . It is easy to show that the minimum and the maximum values for IOBD in Eq. 15 are the same as those derived above for the IOWD. The minimum and the maximum values for Eq. 14 require , thus demonstrating that Eqs. 14 and 15 return the same range limits [1,-1]. The distances computed using Eqs. 14 and 15 do not present the ties problem in ranking, as we find for RBD and RWD. The species producing IOWD and IOBD values corresponding to the closed interval [1,-1] range limits have the same occurrences among samples. This means that they present identical columns in the bacterial species database, so having the same IOWD and IOBD is a proper way to evaluate their importance.
The inside-outside distances can adequately evaluate the case of ranking ties shown above for the relative distances RBD and RWD. As we did above for RBD and RWD, we computed IOBD for species S1 and S6 for group G1 in Figure 1; we computed and .
Using Eq. 15 for species S1, we have:
And for species S6:
The result demonstrates that the inside-outside distance can discriminate species that occur only within a group but with different occurrences. This property may be necessary when a bacterial species database presents many species occurring only in one group.
2.3. Montecarlo Numerical Simulations
Microcanonical Simulation
We first perform a Microcanonical Monte Carlo (MM) numerical simulation. The MM simulation keeps the total number of elements (occupied sites) fixed in every random assignment of occurrences. The word microcanonical arises from the microcanonical ensemble in statistical mechanics [15], and it was extended to non-thermodynamical problems, such as percolation theory [14]. In percolation theory, the microcanonical approach to percolation focuses on the behavior of individual sites within the lattice [14]. It is based on the idea of considering all the microstates (i.e., the possible configurations) of a system with the same total number of occupied sites and assigning the same probability to each of them. In other words, the microcanonical ensemble assumes that the only information known about the system is the total number of occupied sites.
In detail, the microcanonical approach consists of randomizing the columns of matrix (Figure 1B) by permuting each species binary occurrence column. The microcanonical randomization preserves the total number of 1 and 0 in the column, thus fixing the total number of binary occurrences. We iterate the process 106 times.
Canonical Simulation
Then, we perform a Canonical Monte Carlo (CM) numerical simulation. We fix the probability of having a species occurrence in every random assignment of occurrences. The word canonical, too, arises from the canonical ensemble in statistical mechanics [15], and it was extended to percolation theory [14]. Consider a lattice with a finite number of sites where each site can be occupied or empty. The canonical approach assigns an occupation probability to each site; is the probability of having an empty site. For these reasons, unlike the microcanonical approach, the canonical approach preserves only the probability of occupied sites. In the canonical approach, the total number of occupied sites can vary between simulations [14].
In our canonical MC simulation, we compute the average occurrence among samples for each species . To do this, we divide the total number of 1 by the total number of samples. This computation returns the average binary occurrence (or prevalence) in Equation 3. represents the probability to finding species among samples. The probability represents the probability of not finding species among samples. Using probability , we can sort the occurrences from a binomial distribution. We assign 1 with probability and 0 with probability in each element of the randomized matrix. The canonical-like randomization preserves the average number of occurrences (at least for a higher number of iterations). We iterate the process 106 times.
Monte Carlo Statistical Analyses
To evaluate the significance of the MC outcomes, we follow this scheme. 1) We compute , which is the average occurrence among samples of finding the species within group of the randomized matrix. Last, to evaluate the probability of having the observed average occurrence by chance, we count how many times , and divide this value by the total number of iterations (). We obtain a p-value indicating the probability of having, by chance, a higher species occurrence within the group.
Therefore, we can compute , which indicates the significance of observing species in group by chance, as follows:
Where is the Kronecker delta function for which , and the total number of MC simulations (106).
In the case of ties, which are species presenting the same p-value, we rank these ties according to the prevalence of the species. We performed the numerical MC simulations and the statistical analyses using the software R version 4.3.1, with packages MASS and openxlsx. The MC simulations were coded in parallel using the R programming language with doParallel and foreach modules and executions iterated 1 million times took approximately 60 hours on 64 cores and 200 GB ram. We performed the numerical simulations using the High Performance Computing (HPC) cluster of the University of Parma and the CINECA supercomputer Galileo100.
Table 1 lists the bacterial species classification strategies used in this research with formula and meaning.
3. Results and Discussion
3.1. Average Occurrence
In Figure 3, in the top row, we plot the frequency distribution of the binary occurrence of species (prevalence). The species prevalence is highly skewed with a long right tail, considering all samples together (Figure 3A, chart ‘All’) and the prevalence within the groups (Figure 3B). The highly skewed distribution with a long right tail indicates that the database presents few species occurring in most of the samples, and most of the bacterial species show minor occurrences, i.e., most of the species are rare. Table 2 shows the ten most common species (greater prevalence) with their relative binary occurrence values. As we can see, for groups G2, G3, and G4, most of the species with the highest prevalence occur in more than 80% of the sample. Only for group G1, the most common species show a prevalence lower than 0.75. Figure 3A depicts the scatterplots of the average weighted occurrence () vs. average binary occurrence (). We find a positive correlation between them for both the average among all samples (Figure 3A, chart “All”) and within the groups (Figure 3C, charts G1, G2, G3, G4). Computing the Pearson correlation coefficient [20] to quantify the correlation between and , we obtain the values = 0.667 for all the samples and = {0.674, 0.640, 0.627, 0.674} for each group, respectively. The Pearson correlation outcomes indicate a positive correlation between the variables; when increases, also increases. Despite the good correlation, there are some less correlated points, showing how the prevalence of bacterial species is not always correlated with their relative species abundance (or weighted occurrence). This discrepancy highlights the complex nature of microbial ecosystems, where a highly prevalent taxa within a population does not necessarily dominate in abundance. Previous research has demonstrated that the gut microbiota undergoes significant taxonomic and functional shifts influenced by various factors, including age, diet, and health status [21,22].
Table 2.
Ten most common species for each group with its prevalence (relative binary occurrence).
| G1 | G2 | G3 | G4 | ||||
|---|---|---|---|---|---|---|---|
| Bifidobacterium longum | 0.73 | Bacteroides unknown_species | 0.98 | Blautia unknown_species | 0.99 | Blautia unknown_species | 0.98 |
| Escherichia coli | 0.65 | Blautia unknown_species | 0.98 | Ruminococcus unknown_species | 0.98 | Ruminococcus unknown_species | 0.98 |
| Blautia unknown_species | 0.61 | Ruminococcus unknown_species | 0.97 | Clostridium unknown_species | 0.97 | Eubacterium unknown_species | 0.96 |
| Clostridium unknown_species | 0.61 | Clostridium unknown_species | 0.96 | Eubacterium unknown_species | 0.97 | Clostridium unknown_species | 0.96 |
| Bacteroides unknown_species | 0.61 | Bacteroides uniformis | 0.94 | Roseburia unknown_species | 0.96 | Faecalibacterium unknown_species | 0.95 |
| Ruminococcus unknown_species | 0.58 | Eubacterium unknown_species | 0.94 | Faecalibacterium prausnitzii | 0.96 | Roseburia unknown_species | 0.94 |
| Bacteroides uniformis | 0.57 | Roseburia unknown_species | 0.93 | Faecalibacterium unknown_species | 0.96 | Faecalibacterium prausnitzii | 0.94 |
| Blautia wexlerae | 0.57 | Faecalibacterium unknown_species | 0.92 | Eubacterium rectale | 0.93 | Enterocloster unknown_species | 0.9 |
| Flavonifractor plautii | 0.54 | Faecalibacterium prausnitzii | 0.92 | Bacteroides unknown_species | 0.93 | Bacteroides uniformis | 0.88 |
| Ruminococcus gnavus | 0.51 | Blautia wexlerae | 0.91 | Enterocloster unknown_species | 0.91 | Bacteroides unknown_species | 0.88 |
Table 3.
Twenty species of highest rank for the group G1 for each ranking strategy.
| ABO | AWO | RBD | RWD | IOBD | IOWD | MM | CM |
|---|---|---|---|---|---|---|---|
| Bifidobacterium longum | Bifidobacterium longum | Methylobacterium unknown_species | Microbacterium oleivorans | Bifidobacterium breve | Bifidobacterium longum | Bifidobacterium longum | Bifidobacterium longum |
| Escherichia coli | Escherichia coli | Cutibacterium avidum | Neisseria meningitidis | Bifidobacterium longum | Escherichia coli | Escherichia coli | Escherichia coli |
| Blautia unknown_species | Bifidobacterium breve | Vibrio harveyi | Rhizobium daejeonense | Erysipelatoclostridium ramosum | Bifidobacterium breve | Ruminococcus gnavus | Ruminococcus gnavus |
| Clostridium unknown_species | Bifidobacterium bifidum | Actinomyces urogenitalis | Rubrobacter unknown_species | Bifidobacterium bifidum | Bifidobacterium bifidum | Bifidobacterium unknown_species | Bifidobacterium unknown_species |
| Bacteroides unknown_species | Bacteroides uniformis | Staphylococcus hominis | Scandinavium goeteborgense | Veillonella parvula | Bacteroides fragilis | Bifidobacterium breve | Bifidobacterium breve |
| Ruminococcus unknown_species | Bacteroides fragilis | Nocardia nova | Serratia nematodiphila | Ruminococcus gnavus | Veillonella parvula | Bifidobacterium bifidum | Bifidobacterium bifidum |
| Bacteroides uniformis | Phocaeicola dorei | Acinetobacter lwoffii | Acidovorax oryzae | Veillonella unknown_species | Ruminococcus gnavus | Bifidobacterium pseudocatenulatum | Erysipelatoclostridium ramosum |
| Blautia wexlerae | Blautia wexlerae | Streptococcus peroris | Cloacibacterium normanense | Enterococcus faecalis | Enterococcus faecalis | Erysipelatoclostridium ramosum | Eggerthella lenta |
| Flavonifractor plautii | Ruminococcus gnavus | Azoarcus communis | Frigoribacterium unknown_species | Clostridium innocuum | Bifidobacterium pseudocatenulatum | Eggerthella lenta | Veillonella parvula |
| Ruminococcus gnavus | Bifidobacterium pseudocatenulatum | Acidovorax oryzae | Gleimia unknown_species | Veillonella atypica | Phocaeicola dorei | Veillonella parvula | Clostridium innocuum |
| Bifidobacterium unknown_species | Prevotella copri | Mycolicibacterium elephantis | Herbaspirillum huttiense | Eggerthella lenta | Parabacteroides distasonis | Clostridium innocuum | Enterocloster bolteae |
| Eubacterium unknown_species | Veillonella parvula | Serratia liquefaciens | Afipia broomeae | Klebsiella michiganensis | Erysipelatoclostridium ramosum | Enterocloster bolteae | Veillonella unknown_species |
| Phocaeicola vulgatus | Parabacteroides distasonis | Micromonospora endophytica | Aggregatibacter kilianii | Hungatella effluvii | Klebsiella pneumoniae | Veillonella unknown_species | Coprococcus phoceensis |
| Bacteroides thetaiotaomicron | Enterococcus faecalis | Myxococcus xanthus | Agreia unknown_species | Haemophilus unknown_species | Staphylococcus epidermidis | Streptococcus unknown_species | Haemophilus parainfluenzae |
| Bifidobacterium breve | Phocaeicola vulgatus | Micrococcus yunnanensis | Lysobacter enzymogenes | Lactobacillus rhamnosus | Bifidobacterium dentium | Coprococcus phoceensis | Hungatella effluvii |
| Faecalibacterium unknown_species | Faecalibacterium unknown_species | Ralstonia pickettii | Mannheimia unknown_species | Enterocloster bolteae | Enterobacter hormaechei | Haemophilus parainfluenzae | Intestinibacter bartlettii |
| Roseburia unknown_species | Anaerostipes hadrus | Metakosakonia unknown_species | Massilia unknown_species | Veillonella infantium | Blautia wexlerae | Hungatella effluvii | Enterococcus faecalis |
| Faecalibacterium prausnitzii | Collinsella aerofaciens | Neisseria flavescens | Achromobacter insuavis | Haemophilus parainfluenzae | Haemophilus haemolyticus | Intestinibacter bartlettii | Veillonella atypica |
| Enterocloster unknown_species | Bifidobacterium adolescentis | Streptomyces albidochromogenes | Alicycliphilus denitrificans | Coprococcus phoceensis | Haemophilus parainfluenzae | Enterococcus faecalis | Haemophilus unknown_species |
| Phocaeicola dorei | Eubacterium rectale | Cutibacterium unknown_species | Micrococcus luteus | Sellimonas intestinalis | Veillonella atypica | Veillonella atypica | Phocaeicola sartorii |
We draw the scatterplots of the species occurrences across all samples vs. species occurrences within groups for both binary (prevalence, Figure 3D) and weighted (relative abundance, Figure 3D) occurrences. The scatterplots in Figure 3D allow us to visually identify which species are prevalent in the group compared to their presence across all groups. The points above the bisector line indicate species with an average occurrence within a group higher than the average occurrence among groups (among all samples). On the contrary, points below the bisector line indicate species that occur less within the group than considering all samples. Points on the bisector lines indicate similar average species occurrence within and across groups.
3.2. Statistical Distance Notions
Figure 4 compares the group species prevalence () for the 50 species with the highest , and the value for the species with the highest statistical distance values, RBD and IOBD. We find a significant difference between the values for the 50 species ranked by the average binary occurrence ABO (Figure 4 black line, top row) and ranked by the relative binary distance RBD (Figure 4 red line, top row). The values for the first 50 species ranked by ABO are above 0.6 for all groups, whereas the values for the first 50 species ranked by RBD are very low (<0.1). This result indicates that species with a higher RBD in the group may exhibit a low prevalence in the same group. The high RBD exhibited by species with a very low average occurrence in the group would suggest that species with a very low prevalence within the group may be highly characteristic of the group.
Nevertheless, as noted in the ‘Relative distances’ section of the Methods, when a bacterial species is exclusively found within a group, the RBD value is calculated as the ratio of the total number of samples to the group’s sample size (Eq. 12). Consequently, species exclusive to a single group will exhibit identical RBD values regardless of their varying prevalence within that group. To elucidate this issue, we determined the number of group-exclusive species among the top 50 species ranked by both RBD and RWD, revealing counts of 50, 5, 50, and 27 species for groups G1, G2, G3, and G4, respectively. This result unveils that many species with the highest RWD and RBD ranking are exclusively present within the groups (for groups G1 and G3, all the first 50 species are exclusive to the groups). The RWD and RBD distances return rank ties for species that occur only in one group; therefore, RWD and RBD cannot discriminate the relative importance of these species. These latest results indicate how the statistical distances RWD and RBD may present problems in selecting the most characteristic species of a group in our database.
Then, we find a reduced difference between the values for the 50 species ranked by prevalence (average binary occurrence ABO, Figure 4 black line, bottom row) and ranked by the inside-outside binary distance IOBD (Figure 4 red line, bottom row). However, we observe that the variability for species ranked by IOBD is very high. Some bacterial species have a high occurrence, while others close in rank show a much lower occurrence. This result indicates that low-prevalence species within the group may instead have a high statistical distance between the average occurrence inside and outside the group, meaning that they are much more prevalent in the group compared to their occurrence in the other groups. These species may be good candidates to characterize the group. Figure 4 shows an interesting pattern for the group G1. G1 shows the highest difference between the values of the species with the highest occurrence and the values of the species with the highest IOBD. Differently from the other groups, G1 is characterized by a set of bacterial species that occur preferentially in G1, that is, bacterial species that show a higher difference between their prevalence in individuals of young age and their prevalence in older ages. In detail, the ten species ranked by IOBD mainly belong to six different genera, i.e., Bifidobacterium, Clostridium, Enterococcus, Erysipelatoclostridium, Ruminococcus, and Veillonella, which are typical of the infant microbiota and consistent with previous results obtained from the pooled analysis of these datasets [16]. In particular, the highest-ranked species are Bifidobacterium bifidum, Bifidobacterium breve, and Bifidobacterium longum, which are widely recognized as primary colonizers of the infant gut, confirming the validity of the statistical approach used.
The IOWD and IOBD distances show some advantages concerning the relative distances RWD and RBD. We compute the number of species that occur only within a group in the first 50 species ranked by IOWD and IOBD, discovering that no species occur only within a group for both ranking strategies. Further, we outline that the IOBD and IOWD distances do not create ties when species occur only in one group. If a species occurs only in group , the average occurrence outside group is . Consequently, Eq. 15 becomes , indicating that the statistical distance IOBD is the average occurrence of the species within group . The same reasoning can be applied to IOWD computed in Eq. 14, and the IOWD value for species occurring only in one group becomes . These results ensure no ties for species with different occurrence values in the IOBD and IOWD species rank.
3.3. Montecarlo Simulations
Figure 5 depicts the scatterplots for each group of the species binary occurrence vs. the MCs binary occurrence outcomes for both microcanonical and canonical approaches. The x-axis () represents the MCs simulation outcomes of the species occurrences, and the y-axis represents the empirical/observed () occurrences of the species (prevalence). The bisector line indicates the perfect agreement between the species’ empirical and simulated occurrences. Points above the bisector line are bacterial species with empirical occurrences higher than the simulated ones; however, species below the bisector line present simulated occurrences higher than empirical ones. Group G1 presents many of the most prevalent species below the bisector line concerning the other groups. Differently, other groups (G2, G3, and G4) present many of the more prevalent species above the bisector line.
Figure 6A outlines the 20 bacterial species with the highest difference between the observed occurrence () and the simulated occurrence () in G1 by green points. These species are the most distant above the bisector line, indicating their empirical occurrence in G1 is higher than in the simulated one. The higher observed occurrence indicates that these bacterial species appear much more frequently in G1 than expected by chance, indicating their high prevalence in the microbiota of individuals in G1. We call these taxa ‘the characterizing species’ of G1. On the contrary, black points are the twenty bacterial species with the lowest difference between the observed occurrence () and the simulated occurrence () in group 1 (G1). They are ‘rare species’, lying with the highest distance below the bisector line, unveiling that their simulated occurrence in G1 is higher than the empirical one.
Figure 6B shows that the rare bacterial species with low occurrence in G1 (black points) lie distant above the bisector line in groups G2, G3, and G4, indicating that these bacterial species present a higher observed occurrence than expected by chance in G2, G3, and G4.
Group 1 is the set of younger individuals. The age of individuals increases from G1 to G4. The results of MCs tell us from a numerical-statistical perspective that when age increases, there is a clear transition of the species composition in the microbiota of individuals. The G1 characterizing species that in the G1 plot lie above the bisector line (Figure 6) in G2 are superimposed on the bisector line, indicating that their occurrences do not deviate from what is expected by chance. Then, in G3 and G4, the characterizing species are clearly below the bisector line, showing that their empirical occurrence in the group is lower than expected by chance. This pattern demonstrates that the transition emerges passing from G1 to G3 and that G2 represents the transition age group.
Figure 7 shows the average binary occurrence in the group () for the first 10 characterizing bacterial species with the highest difference between and in G1. The average binary occurrence in G1 () is generally high and decreases in the other groups (Figure 7, top row). Three characterizing bacterial species, Veillonella dispar, Enterococcus faecalis, and Hydrogenoanaerobacterium unknown_species, present , outlining how the MCs unveil that species of lower prevalence can be essential to characterize the microbiota of the age group. Figure 7 bottom row depicts for the first rare species in G1, that is, species minimizing the difference between Obs and Sim in G1. of the rare species identified by the MCs simulations in G1 are very low, and they quickly increase in the other higher age groups, showing that these rare species in G1 become dominant in the microbiota with age increases. These results reflected the fluctuation and the adaptation of the intestinal microbiota during the human life span. In fact, species like Bifidobacterium breve, Bifidobacterium longum, and Veillonella parvula are predominant in the infant gut microbiota and decrease as individuals age. Interestingly, Bifidobacterium longum, Ruminococcus gnavus, and Clostridium innocuum decrease less significantly, indicating that these taxa remain present in adults. Conversely, certain bacterial species, such as Agathobaculum butyriciproducens, Eubacterium rectale, and Coprococcus, are found to have a low prevalence in infants and increase significantly in adults. This dynamic change aligns with findings in the literature, which indicate that gut microbiota composition evolves with age due to varying physiological stages and dietary habits. Species Eubacterium rectale presents a higher prevalence in G1 () than many characterizing species (see panels G1, Figure 7), demonstrating how the simple prevalence of bacterial species may not be a reliable proxy for their importance in characterizing age groups.
The results from the two different approaches to the MCs are similar. Figure A1 in the Supplementary material file shows the scatterplots of the p-values carried out with the microcanonical approach against the p-values obtained from the canonical approach for each age group. The p-values of the two MC approaches are correlated, demonstrating that the two approaches yield similar significance values for the occurrence of the bacterial species.
Figure 8 illustrates the scatterplots of the group prevalence () vs. the MCs simulated p-value for the same group (p-val) for both microcanonical and canonical approaches. The points lying on the x-axis indicate bacterial species with very low and significant p-values (p-value<0.05). These are species for which it is highly unlikely to obtain their empirical occurrence by chance with the MCs. In other words, these species preferentially occur within a group if comparing their occurrence in other groups. On the contrary, species with a p-value approaching 1 are bacterial species that are likely to present an MCs simulation occurrence in the group higher than the empirical occurrence in the same group; that is, they are species that do not preferentially occur in the group. It should be noted that many species with p-value present a very high occurrence in the group. For example, there are many species in group G1 with and with p-value; that is, they occur in more than half of the samples in the group, but it is very likely to obtain these occurrences by chance. Thus, they are not significant for MC simulations. This result suggests that the simple species prevalence in a group is insufficient to identify the more critical bacterial species for a particular age group.
3.4. Species Rank Correlations
We analyze the species rank correlations among classification strategies by computing the number of common bacterial species in the first 50 species for each rank. The set defines the first 50 bacterial species for strategy , and defines the first 50 bacterial species for strategy ; the cardinality of the intersection between the two species set returns the number of common species between the ranks. Table 4 depicts the species rank intersection for the first 50 species ranked by each strategy for each group. The relative distances RBD and RWD do not share common species with the other strategies, showing how these two strategies, which give high importance to species, including rare ones, that occur solely within a group, return peculiar species rankings. Most importantly, the G1 differs from all other groups, unveiling the lowest overlap between the ranks provided by the MCs simulations and the ranks based on species occurrence (ABO and AWO). In G1, the MCs present 13 (MM) and 12 (CM) common species with the highest occurrence species rank (ABO). In G2, G3, and G4, the MCs present more than 48 common species in common with the highest occurrence species rank (ABO). This result has two main implications. On the one hand, it demonstrates how group G1 differs from all others in terms of bacterial species composition. Additionally, the MCs identify bacterial species as highly important for group 1, which may not necessarily be of high binary or weighted occurrence within the group. Therefore, MC simulation approaches may be a valuable tool for gathering additional information on the importance of bacterial species for age groups.
3.5. Overall Ranking
In this article, we propose eight classification strategies using different rationales for identifying and ranking the characterizing bacterial species for the different age groups. The different strategies furnish different species ranking. Therefore, we perform a last analysis to obtain an overall species ranking by evaluating the results of the different strategies together. We count the frequency of each bacterial species appearing in the first ten species in each strategy, leading to a comprehensive rank evaluation. The results of this analysis are in Table 5. Table A1, Table A2, Table A3 and Table A4 depict the overall ranking computing for each group.
Table 5 lists the ten species with the highest score according to the overall ranking for each group, with the percentage indicating the fraction of time the species is ranked within the first ten species for each ranking strategy. For example, 75% indicates that the species is ranked in the first ten species in 75% of the cases, i.e., it figures in 6 over the 8 ranking strategies. For instance, Bifidobacterium longum, B. breve, and Ruminococcus gnavus are prevalent in younger individuals (G1), while species such as Faecalibacterium prausnitzii and Eubacterium rectale become more significant in older groups (G3 and G4). This transition aligns with the literature, indicating that gut microbiota composition evolves with age due to varying physiological stages and dietary habits.
An overall ranking, that is, a multicriteria approach to find and classify important bacterial species for each age group, can be helpful when each criterion to rank species accounts for specific and important information about species occurrence in the sample database. For example, we are interested in evaluating both the binary occurrence and the sample abundance. In that case, we have to consider notions of statistical distance focusing on the species’ prevalence and abundance together. On the other hand, when the information for the classification problem we need to solve is specific and exhaustive, using a multicriteria approach is not recommended, as it would confuse the bacterial species classification with information derived from other classification methods based on different rationales.
Finally, using a multicriteria approach can help discover ‘eccentric criteria’ that provide results utterly different from the results set of other criteria. Table A1, Table A2, Table A3 and Table A4 show that RBD and RWD provide a species ranking that differs from all other strategies. This evidence suggests that RBD and RWD may have classification issues with the database under examination.
4. Conclusion
This manuscript proposes and tests different classification strategies to characterize important bacterial species in human microbiota for different age groups. First, in addition to the classic statistical notions of species prevalence and abundance, we introduce different notions of statistical distance to classify important species for each age group. Among the approaches used, RBD and RWD appear less effective, as they return many rank ties for species of different prevalence, and they frequently rank species of a negligible prevalence within the group. The other statistical distance notions IOBD and IOWD return more reliable results. On the one hand, they do not return ties for species of different prevalence; on the other hand, IOBD and IOWD prioritize both low- and high-occurrence species within the group, suggesting that low-prevalence species within the group may hold greater significance to the group’s identity. These species may be good candidates to characterize the group.
Then, we perform machine learning Monte Carlo simulations based on the physics concepts of the microcanonical and canonical ensembles in statistical mechanics to characterize the bacterial species. MCs furnish important outcomes. First, the MCs tell us from a numerical-statistical perspective that when age increases, there is a clear transition of the species composition in the microbiota of individuals. The transition emerges, passing from G1 (0–4 years) to G3 (18–64 years), and G2 (5–17 years) represents the transition age group. MCs finding demonstrates that the microbiota changes throughout the whole period, from early childhood to adolescence, and stabilizes in adulthood. Some species, such as Bifidobacterium breve and Veillonella parvula, are predominant in infants but decrease with age, while others, like Agathobaculum butyriciproducens and Eubacterium rectale, increase. The two MC approaches used yielded similar results, demonstrating the robustness of the findings.
Second, MCs show that low-prevalence species may be statistically significant in characterizing the age group, unveiling how the simple prevalence of a bacterial species in the age group may not be a comprehensive proxy for its importance. Third, MCs are a useful tool for identifying species for the age group by simply computing the bacterial species, maximizing the difference between empirical prevalence and simulated one. These species with a very high difference between empirical and simulated prevalence are very unlikely to occur in the group by chance, and for this, they are highly significant for the age group.
Last, we perform an overall species ranking by evaluating the different classification strategies together. The analyses consider how often the species fall within the first ten species for each ranking strategy. For example, 75% indicates that the species is ranked in the first ten species 75% of the time, i.e., it figures 6 times over the eight ranking strategies. In this way, we obtain a species classification that considers the abundance of bacterial species in the groups from different statistical points of view. The overall ranking can be viewed as a multicriteria statistical classification strategy that can be helpful when comparing multiple factors or criteria. It is advantageous when the strategies are, in some measure, incommensurable criteria that consider different aspects of the bacterial species occurrence in the samples.
The results presented here can help guide future research in microbial ecology and human health by providing a robust framework for identifying key bacterial species across various contexts, such as the role of the microbiota in health and disease. This approach simplifies and enhances the identification of key bacterial players, potentially improving our ability to analyze and interpret complex microbiome data.
Fundings
This research is funded by Ecosister project, funded under the National Recovery and Resilience Plan (NRRP), Mission 4 Component 2 Investment 1.5 - Call for tender No. 3277 of 30/12/2021 of Italian Ministry of University and Research funded by the European Union – NextGenerationEU Award Number: Project code ECS00000033, Concession Decree No. 1052 of 23/06/2022 adopted by the Italian Ministry. We acknowledge the CINECA award under the ISCRA initiative for the availability of high-performance computing resources and support. This study was also supported by Fondazione Cariparma as part of the Parma Microbiota project and “Characterization of the Metabolic Potential of the Human Microbiota in European Populations” project (2023-0555). Part of this research is conducted using the high-performance computing facility of the University of Parma.
References
- Xu, C.; Jackson, S.A. Machine Learning and Complex Biological Data. Genome Biol 2019, 20. [Google Scholar] [CrossRef] [PubMed]
- Valdes, A.M.; Walter, J.; Segal, E.; Spector, T.D. Role of the Gut Microbiota in Nutrition and Health. BMJ 2018, 361, k2179. [Google Scholar] [CrossRef] [PubMed]
- Hou, K.; Wu, Z.-X.; Chen, X.-Y.; Wang, J.-Q.; Zhang, D.; Xiao, C.; Zhu, D.; Koya, J.B.; Wei, L.; Li, J.; et al. Microbiota in Health and Diseases. Signal Transduct Target Ther 2022, 7, 135. [Google Scholar] [CrossRef] [PubMed]
- Rooks, M.G.; Garrett, W.S. Gut Microbiota, Metabolites and Host Immunity. Nat Rev Immunol 2016, 16, 341–352. [Google Scholar] [CrossRef] [PubMed]
- Maciel-Fiuza, M.F.; Muller, G.C.; Campos, D.M.S.; do Socorro Silva Costa, P.; Peruzzo, J.; Bonamigo, R.R.; Veit, T.; Vianna, F.S.L. Role of Gut Microbiota in Infectious and Inflammatory Diseases. Front Microbiol 2023, 14, 1098386. [Google Scholar] [CrossRef] [PubMed]
- Milani, C.; Ticinesi, A.; Gerritsen, J.; Nouvenne, A.; Andrea Lugli, G.; Mancabelli, L.; Turroni, F.; Duranti, S.; Mangifesta, M.; Viappiani, A.; et al. Gut Microbiota Composition and Clostridium Difficile Infection in Hospitalized Elderly Individuals: A Metagenomic Study. Sci Rep 2016, 6. [Google Scholar] [CrossRef] [PubMed]
- Mancabelli, L.; Milani, C.; Lugli, G.A.; Turroni, F.; Mangifesta, M.; Viappiani, A.; Ticinesi, A.; Nouvenne, A.; Meschi, T.; Van Sinderen, D.; et al. Unveiling the Gut Microbiota Composition and Functionality Associated with Constipation through Metagenomic Analyses. Sci Rep 2017, 7. [Google Scholar] [CrossRef] [PubMed]
- Wensel, C.R.; Pluznick, J.L.; Salzberg, S.L.; Sears, C.L. Next-Generation Sequencing: Insights to Advance Clinical Investigations of the Microbiome. J Clin Invest 2022, 132. [Google Scholar] [CrossRef] [PubMed]
- Gao, B.; Chi, L.; Zhu, Y.; Shi, X.; Tu, P.; Li, B.; Yin, J.; Gao, N.; Shen, W.; Schnabl, B. An Introduction to next Generation Sequencing Bioinformatic Analysis in Gut Microbiome Studies. Biomolecules 2021, 11, 530. [Google Scholar] [CrossRef] [PubMed]
- Robert 1961-, C.P.; Casella, G. Monte Carlo Statistical Methods; Springer texts in statistics; Second edition.; Springer New York: New York, NY, 2004; ISBN 9781475741452. [Google Scholar]
- Manly, B.F.J. Randomization, Bootstrap and Monte Carlo Methods in Biology; Chapman and Hall/CRC, 2018; ISBN 9781315273075.
- Montepietra, D.; Bellingeri, M.; Ross, A.M.; Scotognella, F.; Cassi, D. Modelling Photosystem i as a Complex Interacting Network: Modelling the Photosynthetic System i as Complex Interacting Network. J R Soc Interface 2020, 17. [Google Scholar] [CrossRef] [PubMed]
- Soldaat, L.L.; Pannekoek, J.; Verweij, R.J.T.; van Turnhout, C.A.M.; van Strien, A.J. A Monte Carlo Method to Account for Sampling Error in Multi-Species Indicators. Ecol Indic 2017, 81, 340–347. [Google Scholar] [CrossRef]
- Newman, M.E.J.; Ziff, R.M. Efficient Monte Carlo Algorithm and High-Precision Results for Percolation; 2000.
- Kerson Huang STATISTICAL_MECHANICS_2ND_ED; Wiley India Pvt. Limited, Ed.; 2nd ed.; 2008.
- Mancabelli, L.; Milani, C.; De Biase, R.; Bocchio, F.; Fontana, F.; Lugli, G.A.; Alessandri, G.; Tarracchini, C.; Viappiani, A.; De Conto, F.; et al. Taxonomic and Metabolic Development of the Human Gut Microbiome across Life Stages: A Worldwide Metagenomic Investigation. mSystems 2024, 9. [Google Scholar] [CrossRef] [PubMed]
- Milani, C.; Lugli, G.A.; Fontana, F.; Mancabelli, L.; Alessandri, G.; Longhi, G.; Anzalone, R.; Viappiani, A.; Turroni, F.; van Sinderen, D.; et al. METAnnotatorX2: A Comprehensive Tool for Deep and Shallow Metagenomic Data Set Analyses. mSystems 2021, 6, e0058321. [Google Scholar] [CrossRef] [PubMed]
- Bull, F.C.; Al-Ansari, S.S.; Biddle, S.; Borodulin, K.; Buman, M.P.; Cardon, G.; Carty, C.; Chaput, J.-P.; Chastin, S.; Chou, R.; et al. World Health Organization 2020 Guidelines on Physical Activity and Sedentary Behaviour. Br J Sports Med 2020, 54, 1451–1462. [Google Scholar] [CrossRef] [PubMed]
- Lugli, G.A.; Mancabelli, L.; Milani, C.; Fontana, F.; Tarracchini, C.; Alessandri, G.; van Sinderen, D.; Turroni, F.; Ventura, M. Comprehensive Insights from Composition to Functional Microbe-Based Biodiversity of the Infant Human Gut Microbiota. NPJ Biofilms Microbiomes 2023, 9, 25. [Google Scholar] [CrossRef] [PubMed]
- Pearson, K. VII. Note on Regression and Inheritance in the Case of Two Parents. Proceedings of the Royal Society of London 1895, 58, 240–242. [Google Scholar] [CrossRef]
- Lozupone, C.A.; Stombaugh, J.I.; Gordon, J.I.; Jansson, J.K.; Knight, R. Diversity, Stability and Resilience of the Human Gut Microbiota. Nature 2012, 489, 220–230. [Google Scholar] [CrossRef]
- Consortium, H.M.P. Structure, Function and Diversity of the Healthy Human Microbiome. Nature 2012, 486, 207–214. [Google Scholar] [CrossRef]
Figure 1.
Bacterial species database example. Rows are fecal samples (C1, C2,…,C3). Columns are bacterial species (S1, S2,…,S6). Rows/samples are shared in four groups by age (G1, G2, G3, G4). (A) Matrix database , in which each cell indicates the relative abundance of bacterial species (column) in the sample (row). (B) Matrix database , in which each cell indicates the presence/absence of a bacterial species (column) in the sample (row).
Figure 1.
Bacterial species database example. Rows are fecal samples (C1, C2,…,C3). Columns are bacterial species (S1, S2,…,S6). Rows/samples are shared in four groups by age (G1, G2, G3, G4). (A) Matrix database , in which each cell indicates the relative abundance of bacterial species (column) in the sample (row). (B) Matrix database , in which each cell indicates the presence/absence of a bacterial species (column) in the sample (row).
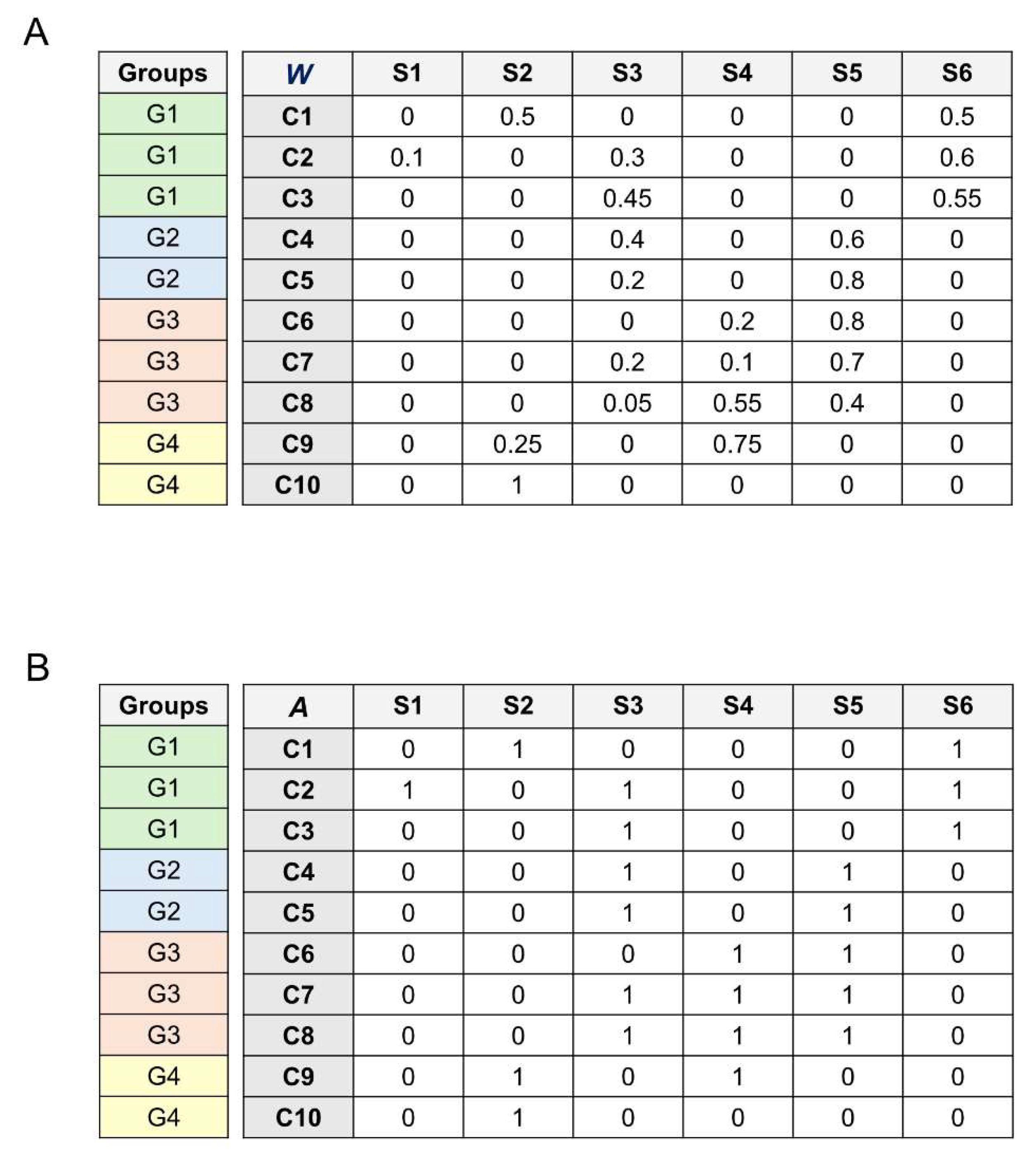
Figure 2.
simple bacterial species database example showing ties in the relative distance ranking strategies. Rows are fecal samples (C1, C2,…,C3). Columns are bacterial species (S1, S2,…,S6). Rows/samples are shared in four groups by age (G1, G2, G3, G4). (A) species database in which all three species occur only within group G1. (B) RWD strategy ranking and values. (2nd column) As we can see, the RWD value is the same for S1, S2 and S3. (3rd column) When using the weighted average occurrence as a second-order criterion, the ranking becomes S3, S2, and S1. (4th column) When adopting the binary average occurrence as a second-order criterion, the ranking becomes S3, S1, S2. We give the RWD values and the second-order ranking values within brackets.
Figure 2.
simple bacterial species database example showing ties in the relative distance ranking strategies. Rows are fecal samples (C1, C2,…,C3). Columns are bacterial species (S1, S2,…,S6). Rows/samples are shared in four groups by age (G1, G2, G3, G4). (A) species database in which all three species occur only within group G1. (B) RWD strategy ranking and values. (2nd column) As we can see, the RWD value is the same for S1, S2 and S3. (3rd column) When using the weighted average occurrence as a second-order criterion, the ranking becomes S3, S2, and S1. (4th column) When adopting the binary average occurrence as a second-order criterion, the ranking becomes S3, S1, S2. We give the RWD values and the second-order ranking values within brackets.
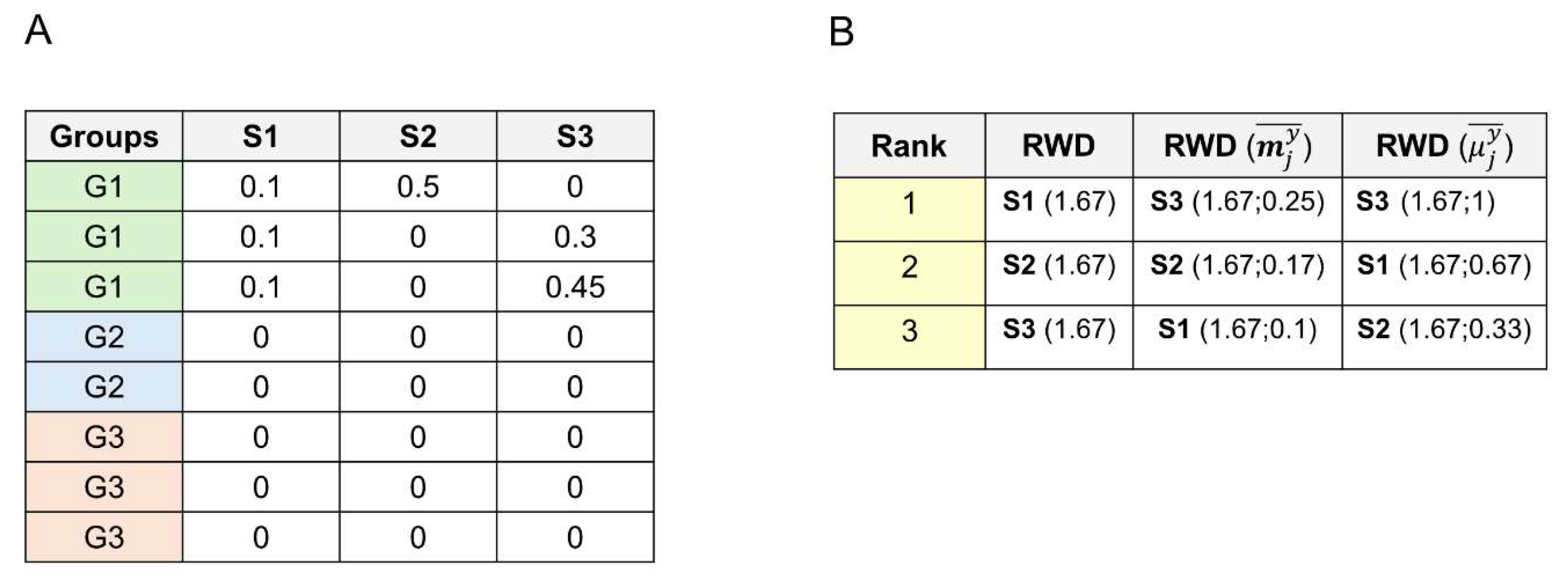
Figure 3.
(A) Left panel: bacterial species binary occurrence frequency distributions for all samples (All); X-axis: species binary occurrence; y-axis: frequency of the occurrence value. The x-axis is normalized by the total number of samples for each plot; in this way, the occurrence may range from 0 (no occurrence) to 1 (the species occurs in all the samples). Right panel: scatterplots of the average weighted occurrence () vs. average binary occurrence () for all samples. (B) Bacterial species binary occurrence frequency distributions for groups age (G1, G2, G3, G4). (C) Scatterplots of the average weighted occurrence () vs. average binary occurrence () for groups age (G1, G2, G3, G4). (D) Scatterplots of the average binary occurrence within group () vs. the average binary occurrence () for groups age (G1, G2, G3, G4). (E) Scatterplots of the average weighted occurrence within group () vs. the average weighted occurrence () for groups age (G1, G2, G3, G4).
Figure 3.
(A) Left panel: bacterial species binary occurrence frequency distributions for all samples (All); X-axis: species binary occurrence; y-axis: frequency of the occurrence value. The x-axis is normalized by the total number of samples for each plot; in this way, the occurrence may range from 0 (no occurrence) to 1 (the species occurs in all the samples). Right panel: scatterplots of the average weighted occurrence () vs. average binary occurrence () for all samples. (B) Bacterial species binary occurrence frequency distributions for groups age (G1, G2, G3, G4). (C) Scatterplots of the average weighted occurrence () vs. average binary occurrence () for groups age (G1, G2, G3, G4). (D) Scatterplots of the average binary occurrence within group () vs. the average binary occurrence () for groups age (G1, G2, G3, G4). (E) Scatterplots of the average weighted occurrence within group () vs. the average weighted occurrence () for groups age (G1, G2, G3, G4).
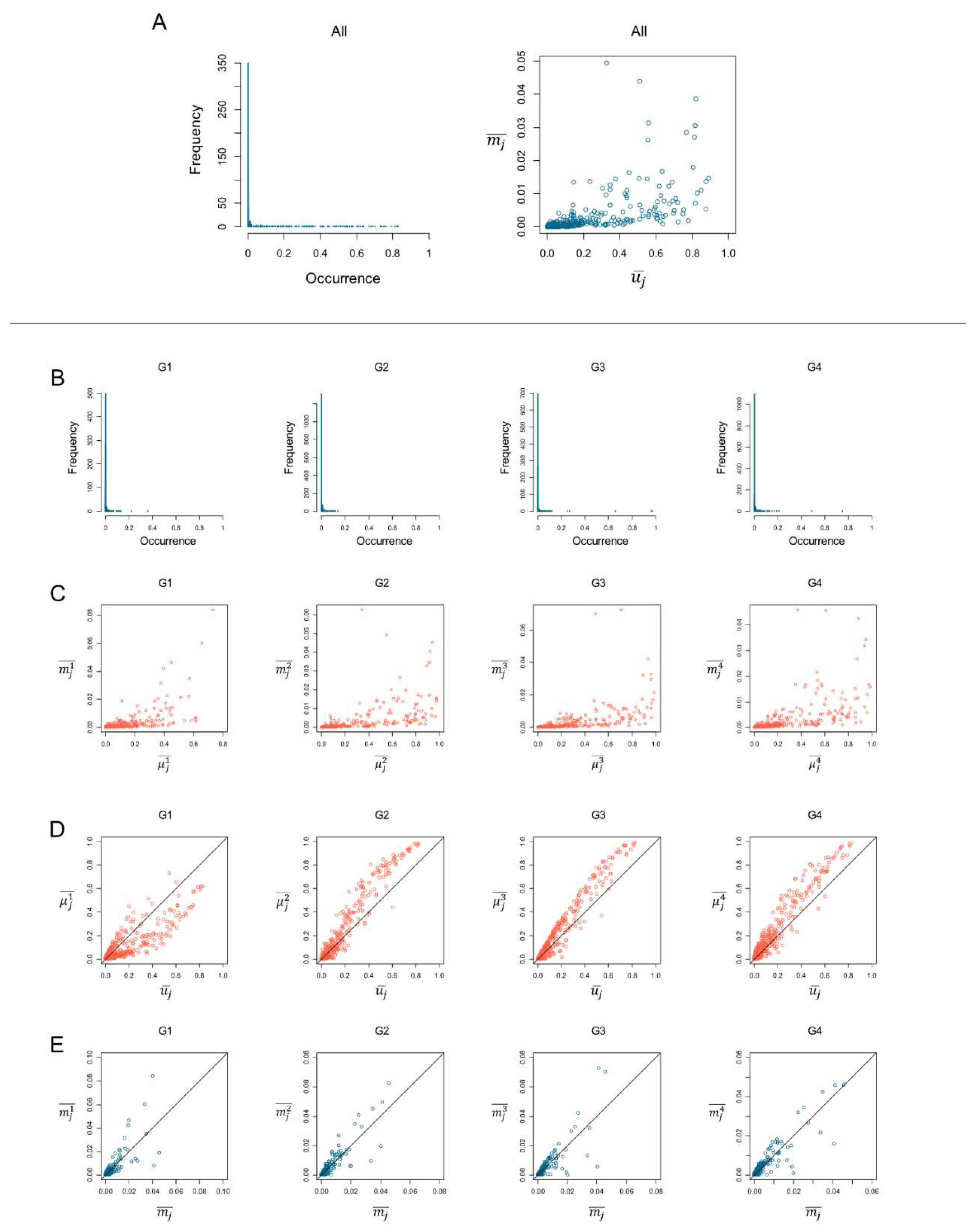
Figure 4.
Comparison between species average binary occurrence for each group () and the notions of statistical distance. Top row: first 50 species ranked by average binary occurrence ABO (black line) and relative binary distance RBD (red line); bottom row: first 50 species ranked by average binary occurrence ABO (black line) and inside-outside binary distance IOBD (red line).
Figure 4.
Comparison between species average binary occurrence for each group () and the notions of statistical distance. Top row: first 50 species ranked by average binary occurrence ABO (black line) and relative binary distance RBD (red line); bottom row: first 50 species ranked by average binary occurrence ABO (black line) and inside-outside binary distance IOBD (red line).
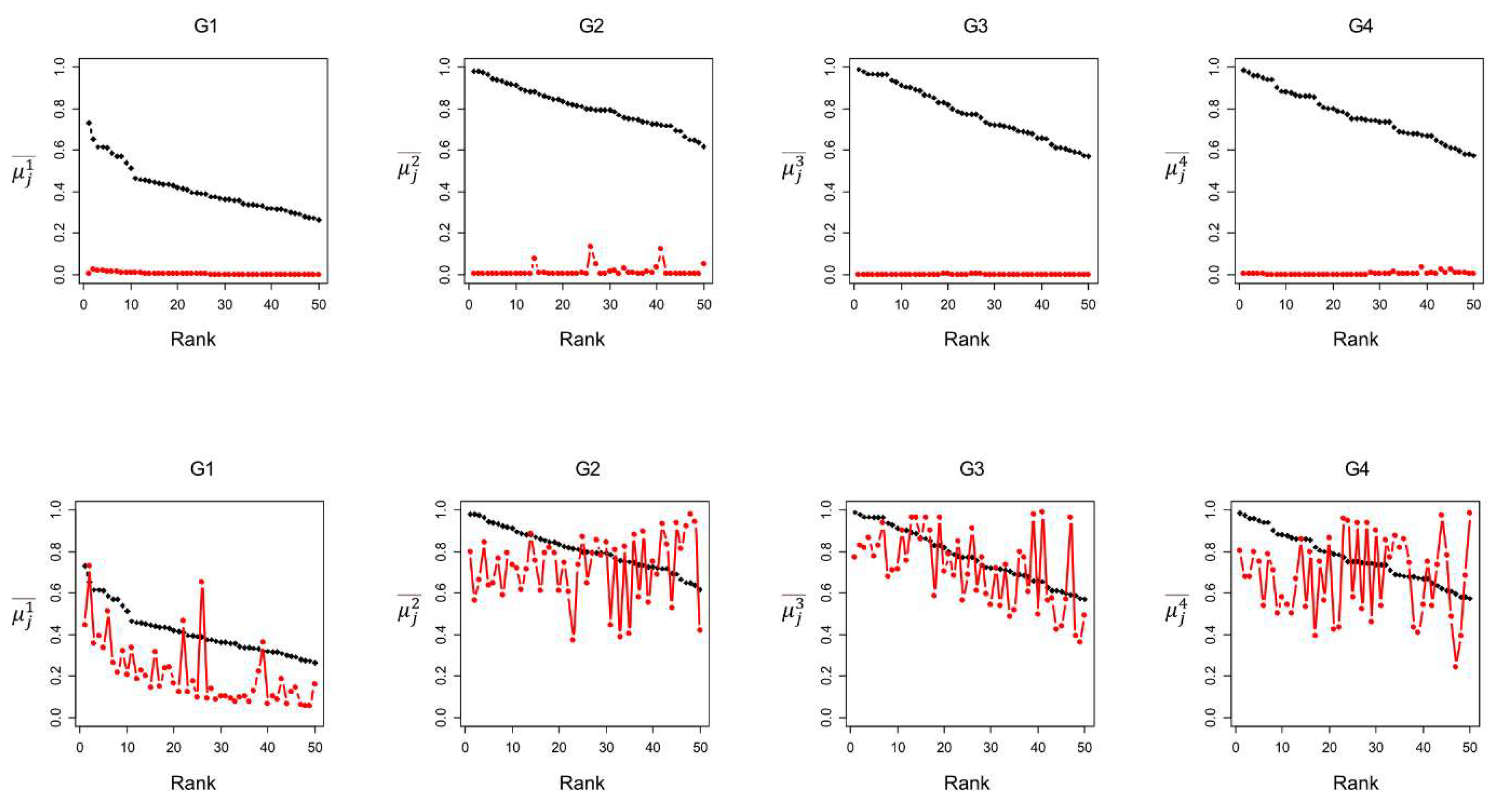
Figure 5.
Scatterplots of the species binary occurrence (presence/absence in the sample) for each group. Y-axis () represents the Monte Carlo (MC) simulation outcomes of the species occurrences; x-axis () represents the empirical (observed) occurrences of the species. (A) Microcanonical MC simulations; (B) canonical MC simulations. Columns depict the scatterplots for the four groups by age (G1, G2, G3, G4). The bisector lines indicate the complete agreement between the empirical and the simulated occurrences.
Figure 5.
Scatterplots of the species binary occurrence (presence/absence in the sample) for each group. Y-axis () represents the Monte Carlo (MC) simulation outcomes of the species occurrences; x-axis () represents the empirical (observed) occurrences of the species. (A) Microcanonical MC simulations; (B) canonical MC simulations. Columns depict the scatterplots for the four groups by age (G1, G2, G3, G4). The bisector lines indicate the complete agreement between the empirical and the simulated occurrences.
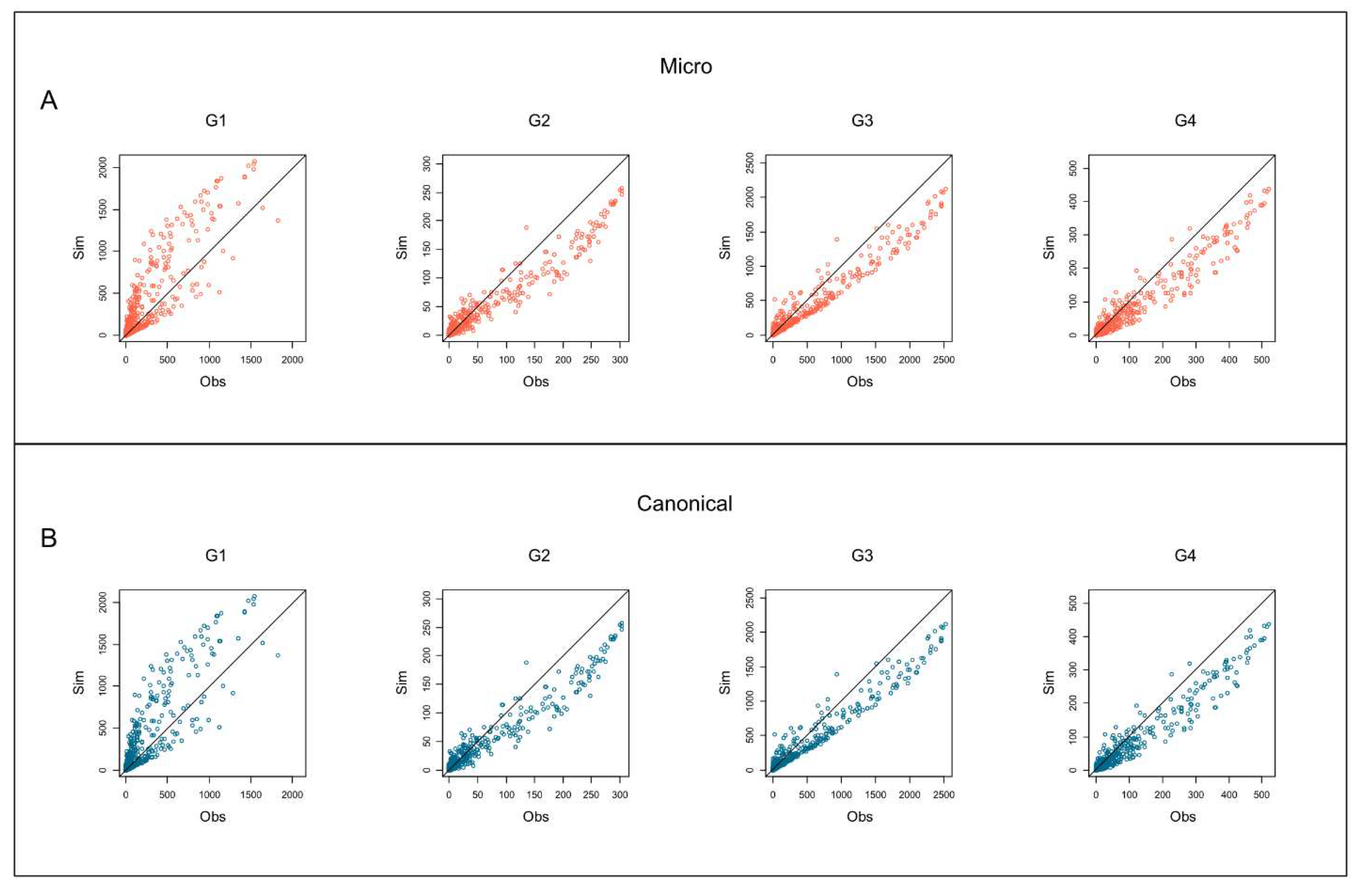
Figure 6.
(Panel A) Scatterplots of the observed species binary occurrence () and the simulated occurrence () in group 1 (G1) for the microcanonical Monte Carlo approach. We outline the points in green for the 20 bacterial species with the highest difference between and . These ‘characterizing species’ are the more distant below the bisector line in chart G1, indicating that the observed (empirical) occurrence in group 1 is higher than the simulated one. The points in black are the 20 bacterial species with the lowest difference between the observed occurrence () and the simulated occurrence () in group 1 (G1). These are the ‘rare species’ that are the more distant above the bisector line in chart G1, indicating that the simulated occurrence in G1 is higher than the empirical one. (Panel B) Scatterplots of the species binary occurrence for each group, where green points are the 20 bacterial species with the highest difference between and , and black points are the 20 bacterial species with the lowest difference between and .
Figure 6.
(Panel A) Scatterplots of the observed species binary occurrence () and the simulated occurrence () in group 1 (G1) for the microcanonical Monte Carlo approach. We outline the points in green for the 20 bacterial species with the highest difference between and . These ‘characterizing species’ are the more distant below the bisector line in chart G1, indicating that the observed (empirical) occurrence in group 1 is higher than the simulated one. The points in black are the 20 bacterial species with the lowest difference between the observed occurrence () and the simulated occurrence () in group 1 (G1). These are the ‘rare species’ that are the more distant above the bisector line in chart G1, indicating that the simulated occurrence in G1 is higher than the empirical one. (Panel B) Scatterplots of the species binary occurrence for each group, where green points are the 20 bacterial species with the highest difference between and , and black points are the 20 bacterial species with the lowest difference between and .
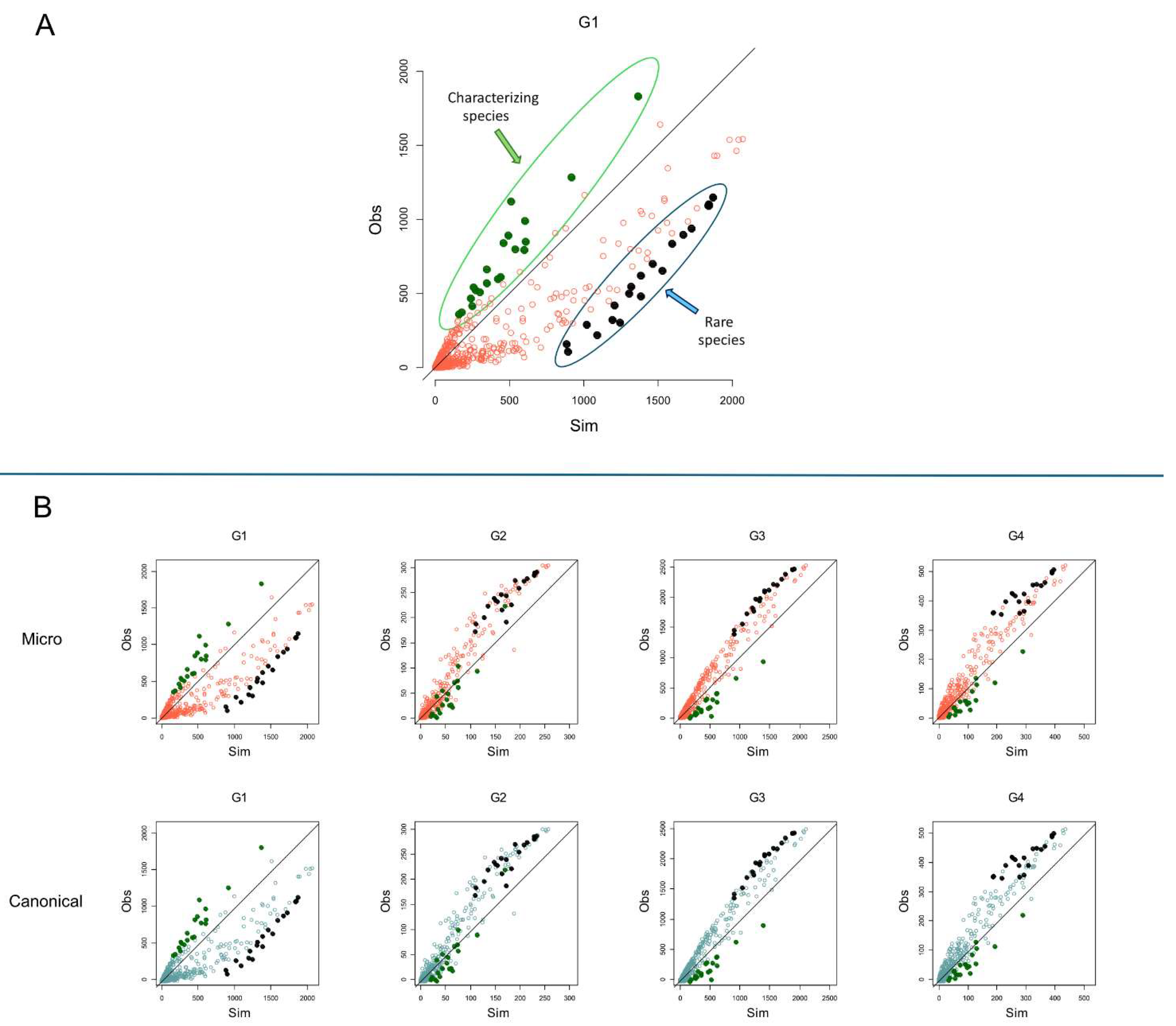
Figure 7.
First row: Barplots of the average binary occurrence in the group () for the 10 bacterial species with the highest difference between the observed occurrence () and the simulated occurrence () in group 1 (G1). These are characterizing species lying more distant above the bisector line in Figure 6, indicating that the simulated occurrence in group 1 is lower than the empirical one. Second row: Barplots of the average binary occurrence in the group () for the ten bacterial species with the lowest difference between the observed occurrence () and the simulated occurrence () in group 1 (G1). These are rare species lying more distant below the bisector line in Figure 6, indicating that the simulated occurrence in group 1 is higher than the empirical one.
Figure 7.
First row: Barplots of the average binary occurrence in the group () for the 10 bacterial species with the highest difference between the observed occurrence () and the simulated occurrence () in group 1 (G1). These are characterizing species lying more distant above the bisector line in Figure 6, indicating that the simulated occurrence in group 1 is lower than the empirical one. Second row: Barplots of the average binary occurrence in the group () for the ten bacterial species with the lowest difference between the observed occurrence () and the simulated occurrence () in group 1 (G1). These are rare species lying more distant below the bisector line in Figure 6, indicating that the simulated occurrence in group 1 is higher than the empirical one.
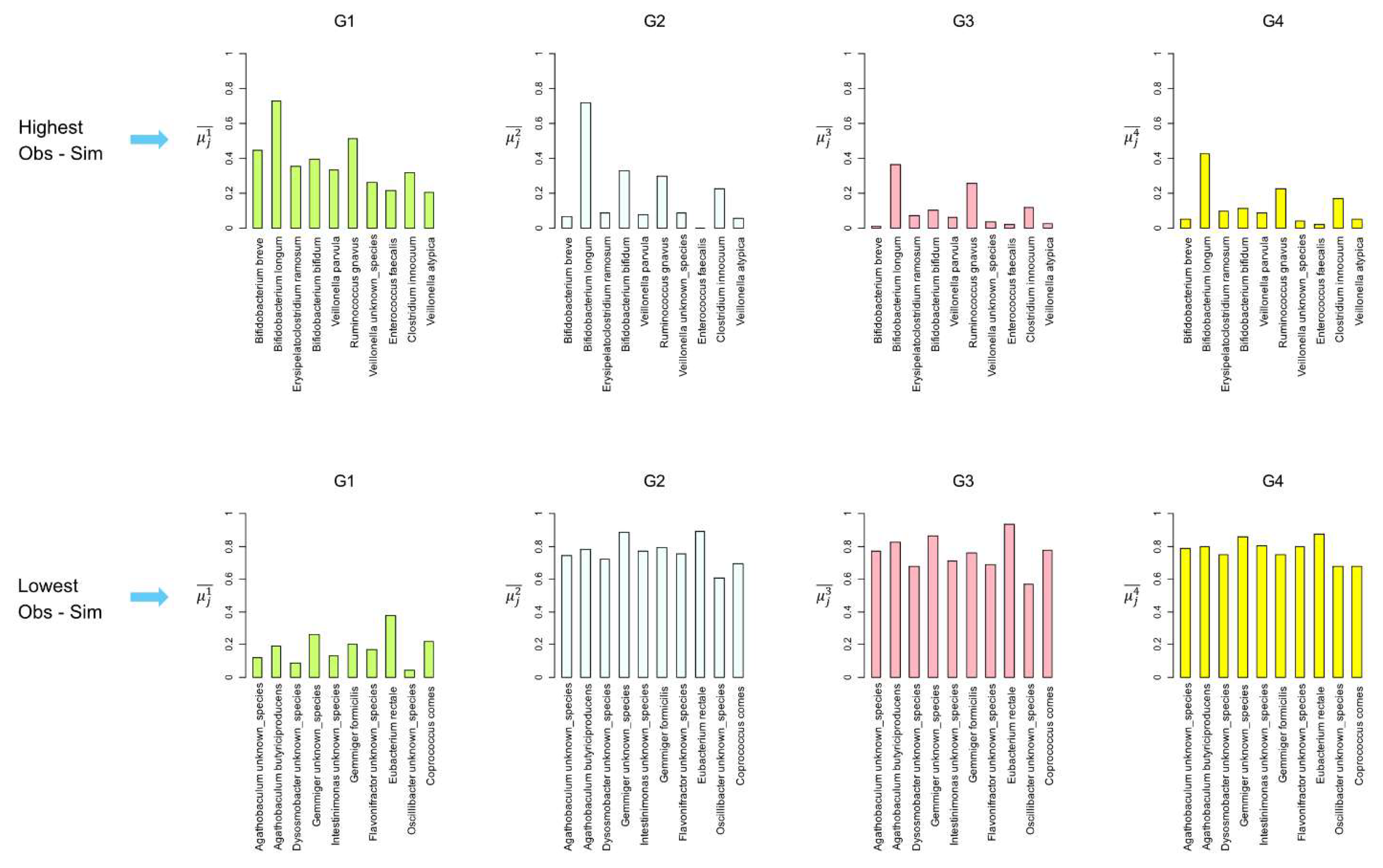
Figure 8.
Scatterplots of the species average binary occurrence for each group () vs. the Monte Carlo (MC) p-value (p-val) to obtain the occurrence by chance. (A) Microcanonical MC simulations; (B) Canonical MC simulations. Columns depict the scatterplots for the four groups by age (G1, G2, G3, G4).
Figure 8.
Scatterplots of the species average binary occurrence for each group () vs. the Monte Carlo (MC) p-value (p-val) to obtain the occurrence by chance. (A) Microcanonical MC simulations; (B) Canonical MC simulations. Columns depict the scatterplots for the four groups by age (G1, G2, G3, G4).
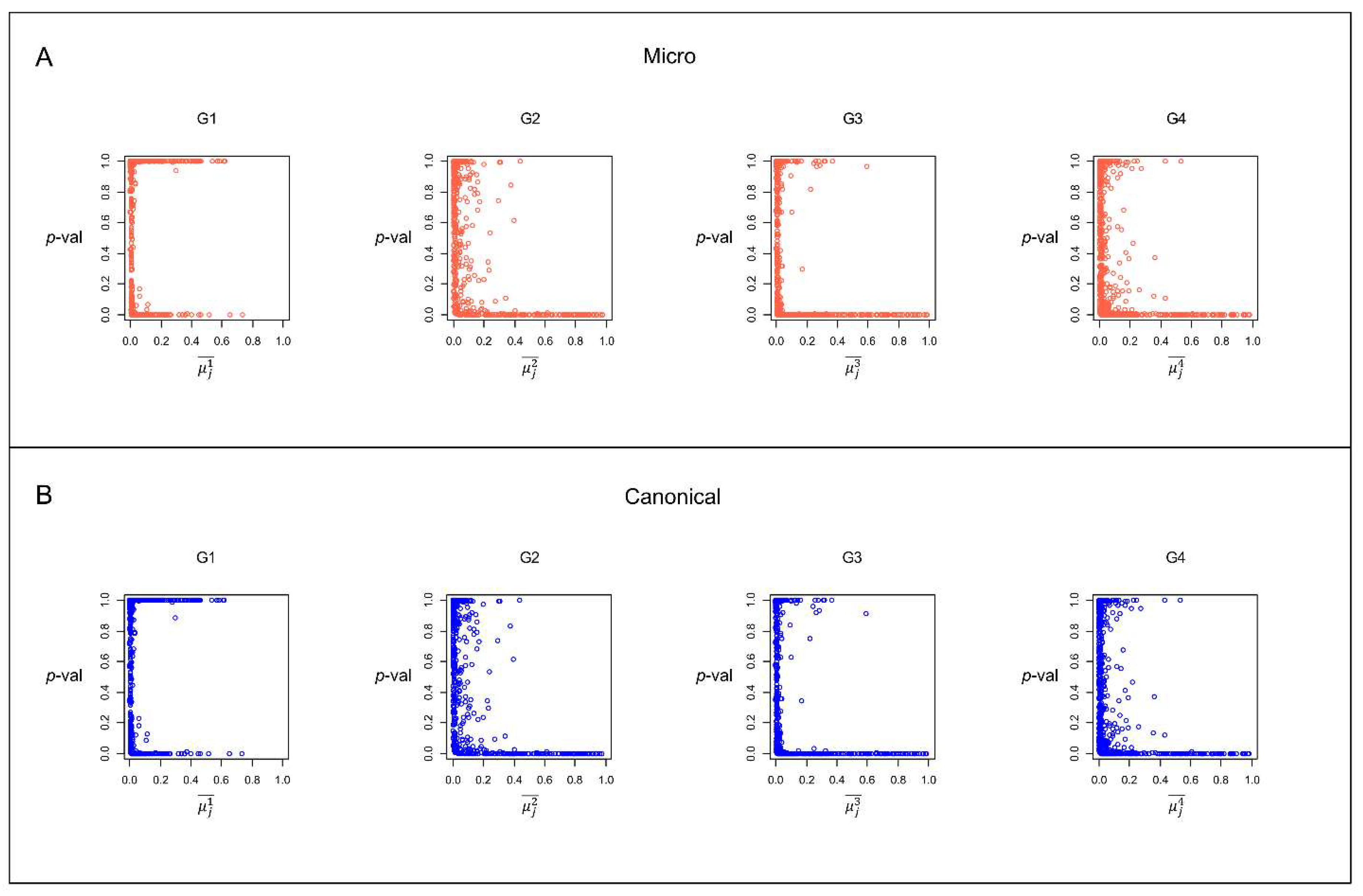
Table 1.
List of the bacterial species ranking strategies.
| Strategy | Acronym | Formula | Meaning | |
|---|---|---|---|---|
| Average weighted occurrence | AWO | of indicates the relative abundance of the species in the sample ; is the total number of samples of the group . | Weighted abundance of a species in a group. | |
| Average binary occurrence | ABO | of indicates the presence of the species in the sample ; is the total number of samples of the group . | Binary abundance of a species in a group, commonly called 'species prevalence'. | |
| Relative weighted distance | RWD | is the average weighted occurrence within group ; is the average weighted occurrence among all samples. | Relative deviation of the average weighted abundance of a species in the group from the overall mean. | |
| Relative binary distance | RBD | is the average binary occurrence within group ; is the average binary occurrence among all samples. | Relative deviation of the average binary abundance of a species in the group from the overall mean. | |
| Inside-outside weighted distance | IOWD | is the average weighted occurrence of species within group ; is the average weighted occurrence of species outside group . | Difference between the average weighted abundance of a species within and outside a group | |
| Inside-outside binary distance | IOBD | is the average occurrence of species within group ; is the average occurrence of species outside group . | Difference between the average binary abundance of a species within and outside a group | |
| Micro-canonical Monte Carlo | MM | average occurrence of species within group of the randomized matrix, is the average binary occurrence within group ; is the Kronecker delta function for which , and the total number of simulations. | Evaluates the probability to have a species abundance within a group by permuting its binary occurrence. | |
| Canonical Monte Carlo | CM | average occurrence of species within group of the randomized matrix, is the average binary occurrence within group ; is the Kronecker delta function for which , and the total number of simulations. | Evaluates the probability to have a species abundance within a group by sorting the binary occurrence at random. | |
Table 4.
Species rank intersection for the first 50 species ranked by each strategy for each group. Element of tables indicates the species overlapping between the rank set of strategy and the rank set of strategy , that is .
Table 4.
Species rank intersection for the first 50 species ranked by each strategy for each group. Element of tables indicates the species overlapping between the rank set of strategy and the rank set of strategy , that is .
| G1 | G2 | ||||||||||||||||
| ABO | AWO | RBD | RWD | IOBD | IOWD | MM | CM | ABO | AWO | RBD | RWD | IOBD | IOWD | MM | CM | ||
| ABO | 50 | 33 | 0 | 0 | 13 | 21 | 1 | 7 | ABO | 50 | 30 | 0 | 0 | 37 | 25 | 22 | 22 |
| AWO | 0 | 50 | 0 | 0 | 16 | 30 | 2 | 9 | AWO | 0 | 50 | 0 | 0 | 29 | 32 | 24 | 24 |
| RBD | 0 | 0 | 50 | 5 | 0 | 0 | 8 | 3 | RBD | 0 | 0 | 50 | 37 | 0 | 0 | 3 | 3 |
| RWD | 0 | 0 | 0 | 50 | 0 | 0 | 2 | 1 | RWD | 0 | 0 | 0 | 50 | 0 | 1 | 4 | 4 |
| IOBD | 0 | 0 | 0 | 0 | 50 | 27 | 5 | 20 | IOBD | 0 | 0 | 0 | 0 | 50 | 31 | 27 | 27 |
| IOWD | 0 | 0 | 0 | 0 | 0 | 50 | 4 | 13 | IOWD | 0 | 0 | 0 | 0 | 0 | 50 | 26 | 26 |
| MM | 0 | 0 | 0 | 0 | 0 | 0 | 50 | 20 | MM | 0 | 0 | 0 | 0 | 0 | 0 | 50 | 50 |
| CM | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 50 | CM | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 50 |
| G3 | G4 | ||||||||||||||||
| ABO | AWO | RBD | RWD | IOBD | IOWD | Micro | Canon | ABO | AWO | RBD | RWD | IOBD | IOWD | MM | CM | ||
| ABO | 50 | 35 | 0 | 0 | 38 | 29 | 3 | 6 | ABO | 50 | 31 | 0 | 0 | 31 | 24 | 15 | 15 |
| AWO | 0 | 50 | 0 | 0 | 27 | 34 | 4 | 10 | AWO | 0 | 50 | 0 | 0 | 21 | 28 | 16 | 16 |
| RBD | 0 | 0 | 50 | 14 | 0 | 0 | 0 | 0 | RBD | 0 | 0 | 50 | 40 | 0 | 0 | 0 | 0 |
| RWD | 0 | 0 | 0 | 50 | 0 | 0 | 0 | 0 | RWD | 0 | 0 | 0 | 50 | 0 | 0 | 0 | 0 |
| IOBD | 0 | 0 | 0 | 0 | 50 | 32 | 5 | 6 | IOBD | 0 | 0 | 0 | 0 | 50 | 27 | 19 | 19 |
| IOWD | 0 | 0 | 0 | 0 | 0 | 50 | 5 | 9 | IOWD | 0 | 0 | 0 | 0 | 0 | 50 | 16 | 17 |
| MM | 0 | 0 | 0 | 0 | 0 | 0 | 50 | 42 | MM | 0 | 0 | 0 | 0 | 0 | 0 | 50 | 48 |
| CM | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 50 | CM | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 50 |
Table 5.
The 10 highest rank species according to the overall ranking. The percentage beside each species indicates the fraction of occurrences of the species within the first ten species for each ranking strategy. For example, 75% indicates that the species is ranked in the first ten species 70% of times, i.e., it figures 6 times over the 8 ranking strategies.
Table 5.
The 10 highest rank species according to the overall ranking. The percentage beside each species indicates the fraction of occurrences of the species within the first ten species for each ranking strategy. For example, 75% indicates that the species is ranked in the first ten species 70% of times, i.e., it figures 6 times over the 8 ranking strategies.
| Rank | G1 | G2 | G3 | G4 | ||||
| 1 | Bifidobacterium longum | 75% | Bacteroides unknown_species | 62.5% | Faecalibacterium prausnitzii | 75% | Intestinimonas unknown_species | 63% |
| 2 | Bifidobacterium breve | 75% | Faecalibacterium prausnitzii | 62.5% | Faecalibacterium unknown_species | 75% | Faecalibacterium prausnitzii | 63% |
| 3 | Ruminococcus gnavus | 75% | Faecalibacterium unknown_species | 62.5% | Eubacterium rectale | 75% | Faecalibacterium unknown_species | 63% |
| 4 | Escherichia coli | 62.5% | Ruminococcus unknown_species | 62.5% | Eubacterium unknown_species | 75% | Ruminococcus unknown_species | 63% |
| 5 | Bifidobacterium bifidum | 62.5% | Bacteroides uniformis | 62.5% | Roseburia unknown_species | 75% | Bacteroides uniformis | 63% |
| 6 | Veillonella parvula | 62.5% | Eubacterium rectale | 62.5% | Roseburia inulinivorans | 75% | Gemmiger unknown_species | 63% |
| 7 | Enterococcus faecalis | 62.5% | Phocaeicola vulgatus | 62.5% | Blautia unknown_species | 63% | Blautia unknown_species | 50% |
| 8 | Erysipelatoclostridium ramosum | 50% | Blautia unknown_species | 50% | Ruminococcus unknown_species | 63% | Agathobaculum butyriciproducens | 50% |
| 9 | Veillonella atypica | 50% | Parabacteroides unknown_species | 50% | Lachnospira unknown_species | 63% | Eubacterium rectale | 50% |
| 10 | Haemophilus parainfluenzae | 50% | Gemmiger unknown_species | 50% | Gemmiger unknown_species | 63% | Eubacterium unknown_species | 50% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated









