The Impact of Adversarial Attacks on a Computer Vision Models Perception of Images

Preprint

Article

The Impact of Adversarial Attacks on a Computer Vision Models Perception of Images

Altmetrics

Downloads

Views

Comments

This version is not peer-reviewed

Submitted:

01 August 2024

Posted:

05 August 2024

You are already at the latest version

Alerts

Abstract

Image clustering and classification are fundamental tasks in computer vision, critical for applications overlap image retrieval, object recognition, and image classification. However, the robustness of clustering algorithms against adversarial attacks remains interesting topic. In this paper, we investigate how adversarial attacks on image classification algorithms impact Image Clustering, similarity obtained using the Dot Product, KNN, HNSW algorithms and model Gradient-Weighted Class Activation Mapping (Grad-CAM). In our work was proposed a targeted study of the impact of adversarial attacks on the clustering ability of ResNet50 under various adversarial scenarios. Was used ResNet50 as the basis for the experiments, a widely used architecture known for its effectiveness in image classification. This network was subjected to various adversarial attacks in order to understand how these perturbations affect its clustering capabilities. By thoroughly examining the resultant clustering outcomes under different attack scenarios, we aim to uncover vulnerabilities and nuances inherent in clustering algorithms and similarity metrics when confronted with adversarial input.

Keywords:

Subject: Computer Science and Mathematics - Security Systems

1. Introduction

Recent years, the field of computer vision has witnessed remarkable advancements, leading to the development of powerful models capable of accurately recognizing and interpreting visual information. These models have found applications in diverse domains, ranging from autonomous driving and medical imaging to security and surveillance systems. However, amidst these advancements, a growing concern has emerged regarding the vulnerability of such models to adversarial attacks.

Adversarial attacks refer to the deliberate manipulation of input data with the aim of deceiving machine learning models into producing incorrect outputs. These attacks pose a significant threat to the reliability and security of computer vision systems, potentially leading to erroneous decisions with far-reaching consequences. Understanding the impact of adversarial attacks on the perception of images by computer vision models has thus become a pressing research area.

The history of adversarial attacks can be traced back to the pioneering work of Szegedy et al., where they first demonstrated the existence of small, imperceptible perturbations that could cause deep neural networks to misclassify images. Since then, adversarial attacks have garnered increasing attention from researchers, leading to the development wide range of attack strategies and defense mechanisms.

In this paper, we are going to show the impact of adversarial attacks, on the perception of images by computer vision models. We investigate how these attacks influence the performance of state-of-the-art model ResNet-50 [1] across various tasks, including image classification, object detection, and semantic segmentation. Through comprehensive experiments and analysis, we aim to shed light on the vulnerabilities of computer vision systems to adversarial manipulation and explore potential strategies to enhance their robustness in real-world scenarios.

2. Attacks in Question

Among the various adversarial attack methods, the Fast Gradient Sign Method (FGSM) [2] and Projected Gradient Descent (PGD) [3] have emerged as prominent techniques due to their effectiveness and simplicity. FGSM generates adversarial perturbations by taking a single step in the direction of the gradient of the loss function with respect to the input. The “fast gradient sign method” of generating adversarial examples was written as:

η = ε sgn (\nabla_{x} L (θ, x, y))

2.1. Projected Gradient Descent

Despite its simplicity, the FGSM method has proven to be highly effective in creating adversarial examples. However, the PGD method [3], proposed by Madry et al., builds on the idea of the FGSM by applying small perturbations iteratively within a bounded epsilon neighborhood of the original input, its results in more robust adversarial examples. This method can be described by the following equation:

x^{t + 1} = Π_{x + S} (x^{t} + α sign (\nabla_{x} L (θ, x, y)))

2.2. Carlini & Wagner Attack

The Carlini&Wagner (CW) [4] adversarial attack is a highly efficient and effective method introduced by Nicholas Carlini and David Wagner. This attack optimizes an objective function to minimize the amount of perturbation required to misclassify an input. This process is achieved by solving an optimization problem. The attack can be adapted to different distance metrics, such as

L_{0}

L_{2}

, and

L_{\infty}

, allowing for the creation of various types of perturbations. In our work, we considered this attack with the

L_{2}

metric. This method works by optimizing the following expression and search for w that solves:

minimize {∥\frac{1}{2} (tanh (w) + 1) - x∥}_{2}^{2} + c \cdot f (\frac{1}{2} (tanh (w) + 1)

With given x, a target class t, model output

Z (x)

and f defined as:

f (x^{'}) = max (max \{Z {(x^{'})}_{i} : i \neq t\} - Z {(x^{'})}_{t}, - κ)

2.3. Basic Iterative Method for FGSM

The Basic Iterative Method (BIM) [5] is an adversarial attack technique that builds upon the Fast Gradient Sign Method (FGSM) in order to enhance its effectiveness. BIM generates adversarial examples by applying multiple small perturbations to the input image iteratively, instead of using a single step as in FGSM. At each iteration, the method adjusts the image in the direction of the gradient of the loss function, gradually accumulating perturbations until a desired level of adversarial strength is achieved. This iterative process allows BIM to create more accurate and powerful adversarial examples compared to FGSM, and can be described with:

X_{0}^{a d v} = X,

X_{N + 1}^{a d v} = C l i p p_{X, ϵ} \{X_{N}^{adv} + α sign (\nabla_{X} J (X_{N}^{adv}, y_{true}))\}

2.4. Elastic-Net Attack

The Elastic-Net Adversarial Attack (EAD) [6], developed by Pin-Yu Chen and others, is a tricky adversarial attack technique that combines the advantages of both

L_{1}

and

L_{2}

-based approaches. This attack generates adversarial samples by solving an optimization problem that aims to minimize the classification certainty while incorporating an elastic net regularization term. This term combines the

L_{1}

regularization, which promotes sparsity in the perturbation, and the

L_{2}

regularization, which ensures that the overall perturbation is small. If given an input image

x_{0}

with its correct label

t_{0}

, we define an adversarial example x as an input that has the same target class as

t \neq t_{0}

. We can define the loss function

f (x)

for these targeted attacks as:

f (x, t) = max \{max_{j \neq t} {[Logit (x)]}_{j} - {[Logit (x)]}_{t}, - κ\}

2.5. Expectation Over Transformation PGD

Expectation Over Transformation (EOT) [7], combined with Projected Gradient Descent (PGD), is an advanced adversarial attack technique that generates robust adversarial examples. These examples remain effective even under various input transformations, such as rotation, translation, or noise. EOT accounts for input variability by averaging the adversarial loss across a distribution of transformations. PGD then minimizes this expected loss iteratively, ensuring that the adversarial perturbations remain effective despite transformations. This makes the attack resilient and versatile, producing adversarial examples that consistently deceive machine learning models in real-world scenarios. EOTPGD works by estimating the real gradient of the network as the average of the gradients over multiple random vectors

ϵ

, one can obtain a more stable and therefore efficient attack:

{\hat{x}}_{t + 1} \leftarrow Π_{x + S} [{\hat{x}}_{t} + η \underset{ϵ}{E} ({\nabla_{x} L (f (x; w, ϵ), \hat{y})|}_{x = {\hat{x}}_{t}})]

2.6. JitteR-Based Attack

A Jitter-based [8] adversarial attack is a method that enhances the effectiveness of adversarial samples by introducing small, randomized transformations, or jitters, to the input image during the attack. These transformations could include minor shifts, rotations, or additions of noise. By applying these jittering transformations iteratively while generating the adversarial perturbation, the attack ensures that the generated samples remain effective even in the presence of such variations. This approach increases the robustness of the adversarial samples against defenses that are based on input transformations, thereby making the attack more powerful and versatile at evading detection by machine learning algorithms.

L_{J i t t e r} = \{\begin{matrix} \frac{| | \hat{z} - Y + N (0, σ) {| |}_{2}}{{| | γ | |}_{p}} & if misclassified \\ | | \hat{z} - Y + N (0, σ) {| |}_{2} & if not misclassified yet \end{matrix}

3. The Impact of Adversarial Attacks on Grad-CAM in Classification Task

The Grad-CAM (Gradient-Weighted Class Activation Mapping) [9] is a technique that aims to visualize the areas of an image that contribute significantly to the model’s classification decision. This technique highlights these areas, making it easier for users to understand which parts of the image are important to the model’s prediction. However, the effectiveness of Grad-CAM in the presence of adversarial attacks has not been fully explored. Adversarial attacks can alter the visual appearance of an image while maintaining its overall structure, potentially misleading attention mechanisms like Grad-CAM.

In this section, we examine the impact of adversarial attacks on Grad-CAM for a classification task. To investigate this question, we conduct experiments using a well-established benchmark dataset ImageNet-1k, and evaluate the performance of Grad-CAM under various adversarial attack scenarios. We employ commonly used methods for generating adversarial examples, such as FGSM (an iterative variant called BIM), PGD, CW, EAD with

L_{\infty}

norm, EOTPGD and Jitter attacks to create adversarial instances. For each method, we generate perturbations and assess their effect on the output of Grad-CAM.

Based on the resulting visualizations from the final layer of the neural network, it can be concluded that various attacks have distinct effects on different layers of the network. As shown in Figure 1a, FGSM and Jitter-based attacks cause the model’s focus to become blurred, while still remaining on the most significant part of the original image. In other cases, however, the attack causes a shift in attention away from the important region of the image. At the same time, a study of the visual representation of the attention patterns of the initial layers of the neural network Figure 1b indicates that the previously identified FGSM and Jitter-based adversarial attacks cause a lesser degree of alteration in the perception of affected images by the initial layers compared to other types of attacks.

4. The Impact of Adversarial Attacks on Image Clustering Visualization

The t-SNE [10] algorithm has been used in this work to visualize image clusters. t-SNE, or t-distributed Stochastic Neighbor Embedding, is a powerful technique that is commonly used in machine learning and data visualization to reduce the dimensionality of high-dimensional datasets. It was developed by Laurens van der Maaten and Geoffrey Hinton and has been widely adopted for embedding and visualizing complex data sets, including those used in computer vision applications.

t-SNE works by first calculating pairwise similarities between data points in a high-dimensional space. These similarities are typically calculated using a Gaussian kernel which measures the similarity between two data points based on their Euclidean distance in the original space. The similarity between data point

x_{j}

and data point

x_{i}

is the conditional probability,

p_{j ∣ i}

which is described by the following equation:

p_{j ∣ i} = \frac{exp (- {∥x_{i} - x_{j}∥}^{2} / 2 σ_{i}^{2})}{\sum_{k \neq i} exp (- {∥x_{i} - x_{k}∥}^{2} / 2 σ_{i}^{2})}

Next, t-SNE constructs a probability distribution over pairs of points in the high-dimensional space, with probabilities proportional to the similarity values calculated earlier. It then defines a similar probability distribution over pairs of points in a lower-dimensional space, typically two or three dimensions, which represents the embedding space. This low-dimensional counterparts are denoted as

y_{i}

and

y_{j}

q_{j ∣ i} = \frac{exp (- {∥y_{i} - y_{j}∥}^{2})}{\sum_{k \neq i} exp (- {∥y_{i} - y_{k}∥}^{2})}

The goal of t-SNE is to minimize the difference between these two probability distributions, which is known as the Kullback-Leibler (KL) divergence. This is accomplished by iteratively altering the position of data points in a lower-dimensional space until the embedding accurately reflects the similarities between data points in the original high-dimensional space. This goal can be expressed by the following equation:

C = \sum_{i} K L (P_{i} | | Q_{i}) = \sum_{i} \sum_{j} p_{j ∣ i} log \frac{p_{j ∣ i}}{q_{j ∣ i}}

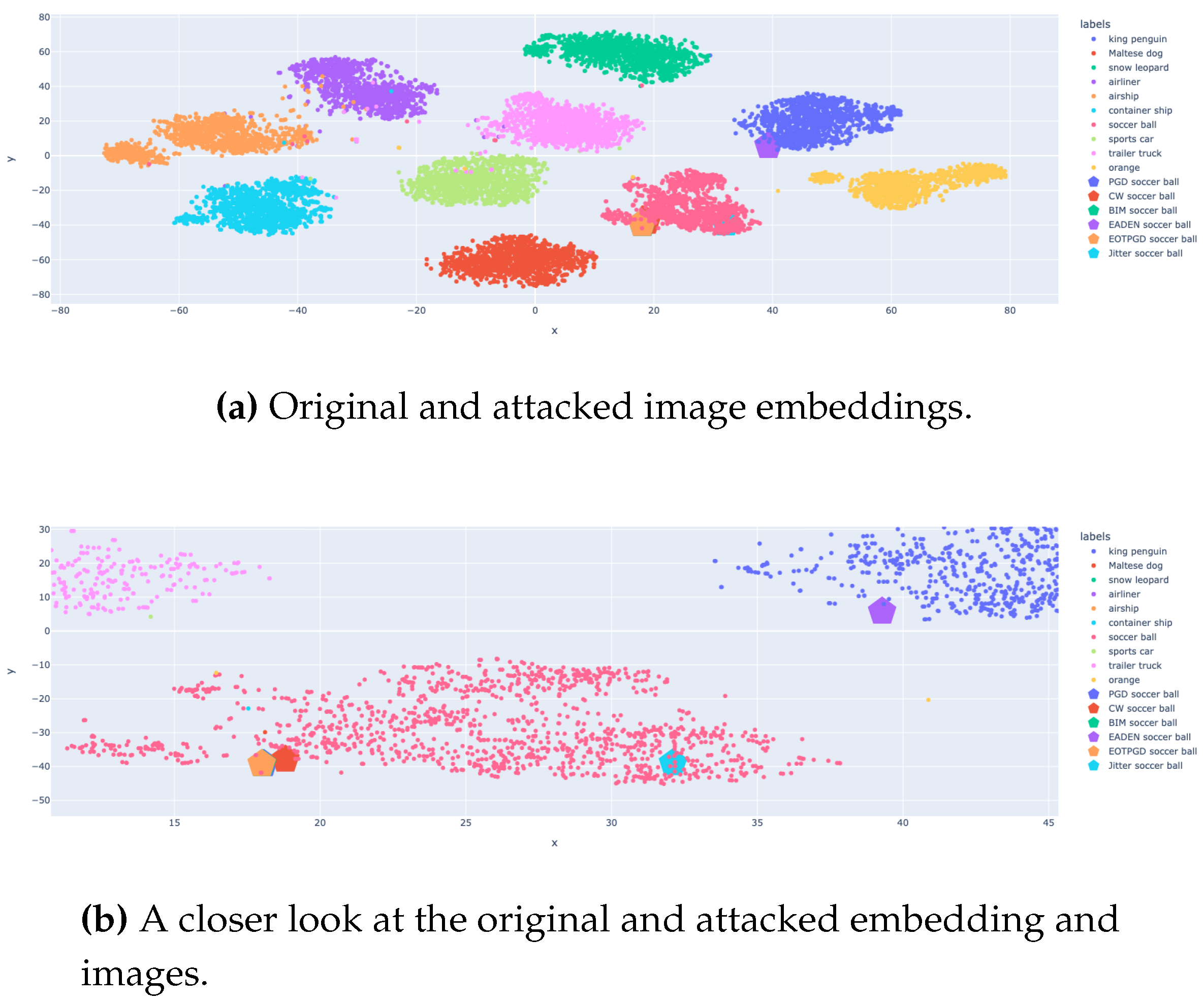
Visualisation with using t-SNE shown on Figure 2a where images with the "king penguin" class were attacked by various adversarial algorithms to change the class of the original image to "soccer ball". Upon closer examination of the t-SNE visualization of the resulting embeddings shown on Figure 2b, the image generated by the PGD algorithm falls within the same cluster as the original image. Additionally, the embedding generated during the attack using the Jitter algorithm has been separated from the overall group of attacked images. The rest of the attacks formed a dense cluster from which the CW algorithm was slightly separated.

5. The Impact of Adversarial Attacks on Image Clustering

5.1. Dot Product

The dot product is a fundamental operation in algebraic mathematics that allows for the assessment of the similarity between vectors in a given space. An example of the dot product values generated by the ResNet50 model is presented in Table 1. This table includes dot products and their differences for pairs of images consisting of the original image, a random image, an image from the same class, and images that have been manipulated using various algorithms.

Additionally, examples of the differences in dot products between these various image types are provided. As you can observe, the Jitter attack proved to be the most efficient when using a dot product metric. Based on the results obtained, even considering the high level of confidence that the model has in its incorrect classification of adversarial examples, there is often a noticeable difference in the dot products of attacked and pure images in most cases.

5.2. K-Nearest Neighbors Algorithm

The K-Nearest Neighbors (KNN) [11] algorithm begins by storing an entire training dataset. When a new data point requires classification or value prediction, the algorithm calculates the distance between that point and each point in the training set using a variety of distance metrics, including Euclidean, Manhattan, and Minkowski. Euclidean distance is the most commonly used metric, including it is used in this work.

Once the distances have been calculated, the algorithm determines the k data points that are nearest to the new input. The value of k, which should be a positive integer, plays a significant role in the algorithm, as it specifies the number of nearest neighbors to be considered. A small value for k makes the algorithm more sensitive to noise, whereas a large value may smooth out the decision boundary too much, potentially affecting the model’s accuracy.

For classification problems, the new data instance is assigned to the class that is most commonly represented among its k closest neighbors. This majority vote process makes the algorithm non-parametric, meaning that it does not make any underlying assumptions about the distribution of the data. For regression problems, the algorithm computes the average of the target values of its k closest instances to predict the target value for the given new instance.

In this paper, we clustered the attacked images using KNN algorithm with Euclidean distance as the similarity metric. Table 2 presents the Attack Success Rate (ASR) of various algorithms, including KNN classification. As can be seen, the ASR for KNN is quite high, indicating that this technique is effective at defending against attacks. The EADEN and EOTPGD algorithms show lower ASRs, which may be due to changes in the optimization metric during the last two attacks. This could be related to changes in how the algorithms handle infinity metrics. The CW algorithm also shows a lower ASR, which could be attributed to its purpose of minimizing perturbations. W may also notice that ResNet50 performs poorly when classifying all of the attacked images.

5.3. Hierarchical Navigable Small World

The Hierarchical Navigable Small World (HNSW) [12] algorithm is an advanced technique used for approximate nearest neighbor searching, which is essential in various fields such as information retrieval, computer vision, and recommender systems. This algorithm is specifically designed to handle large datasets efficiently by creating a multi-level graph structure that enhances the speed of search and retrieval processes.

The HNSW algorithm is based on the concept of small-world networks, which are characterized by the fact that most nodes can be reached from any other node by a small number of connections, regardless of the size of the network. This property allows us to create a graph in which each node represents a data point and edges are drawn between nodes based on their similarity in the feature space. The construction process of the HNSW algorithm involves multiple layers. Each layer represents a coarser approximation of the original data, with the goal of finding a balance between accuracy and computational efficiency. By using this approach, the algorithm can efficiently navigate through complex data sets and find meaningful patterns.

The top level of the HNSW data structure contains a small subset of data points, which makes it easier to quickly navigate. As one progresses through the levels, the graph becomes more dense, containing more data points and providing greater granularity. This hierarchical organization allows for a trade-off between search speed and accuracy, since the algorithm can quickly traverse the upper levels and then refine its search in the deeper levels.

To perform a search, the HNSW algorithm begins at the top level with a randomly selected starting point and employs a greedy search strategy to progressively narrow the search space until it reaches the query location. At each iteration, the algorithm examines the neighboring nodes of the current position and selects the one with the shortest distance to the query. The process continues iteratively until the bottom level is reached, where a finer-grained search is conducted in order to locate the nearest matches with greater precision.

This paper examines the impact of adversarial attacks on the HNSW algorithm with different similarity metrics the first of which is cosine similarity:

d = 1.0 - \frac{\sum (A_{i} * B_{i})}{\sqrt{\sum A_{i}^{2} * \sum B_{i}^{2}}} .

As you can see in Table 2, this metric has a fairly low resistance to adversarial attacks.

The squared

L_{2}

d = \sum ({(A_{i} - B_{i})}^{2})

measure was also used as a similarity metric. As you can see in the same table, this measure shows the worst results, when using it, all attacks were successful, this is due to the use of L2 measures when generating adversarial examples.

In the end, inner product:

d = 1.0 - \sum (A i * B i)

metric showed itself in the best way. When using this metric, the ASR of the algorithms remains the smallest, which makes it the best choice for systems operating under the threat of adversarial attacks.

6. Conclusion

In this study, we comprehensively examined the impact of adversarial attacks on image clustering and classification, with a particular focus on the robustness of these methods under adversarial conditions. We focused on the ResNet50 model, utilizing various adversarial attack techniques including FGSM, PGD, CW, BIM, EADEN, EOTPGD, and Jitter attacks. By examining the effects of these attacks through Grad-CAM visualizations, dot product similarity measures, KNN clustering, and HNSW clustering, we uncovered critical insights into the vulnerabilities and resilience of clustering algorithms when faced with adversarial perturbations.

Our research has shown that adversarial attacks can significantly distort the model’s perception of images, impacting both the Grad-CAM visualizations and the clustering outcomes. Grad-CAM visualizations showed that attacks like FGSM and Jitter-based methods could blur the model’s focus, yet the important regions of the image remained partially identifiable. Other attacks, however, redirected the model’s attention away from these significant regions, highlighting the varied effects different attacks can have.

The KNN algorithm showed a high attack success rate, indicating that it is quite effective in clustering adversarial examples separately from pure images. This suggests that KNN could serve as a robust defense mechanism against certain types of adversarial attacks. Similarly, the HNSW algorithm, particularly with the inner product similarity metric, demonstrated resilience against adversarial perturbations. The inner product metric achieved the lowest attack success rate, making it the most effective similarity measure in our tests.

Acknowledgments

This research was funded by the Ministry of Science and Higher Education of the Russian Science Foundation (Project “Goszaadanie” No.075-00003-24-02, FSEE-2024-0003).

References

He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition, 2015. arXiv:cs.CV/1512.03385.
Goodfellow, I.J.; Shlens, J.; Szegedy, C. Explaining and Harnessing Adversarial Examples, 2015. arXiv:stat.ML/1412.6572.
Madry, A.; Makelov, A.; Schmidt, L.; Tsipras, D.; Vladu, A. Towards Deep Learning Models Resistant to Adversarial Attacks, 2019. arXiv:stat.ML/1706.06083.
Carlini, N.; Wagner, D. Towards Evaluating the Robustness of Neural Networks, 2017. arXiv:cs.CR/1608.04644.
Kurakin, A.; Goodfellow, I.; Bengio, S. Adversarial examples in the physical world, 2017. arXiv:cs.CV/1607.02533.
Chen, P.Y.; Sharma, Y.; Zhang, H.; Yi, J.; Hsieh, C.J. EAD: Elastic-Net Attacks to Deep Neural Networks via Adversarial Examples, 2018. arXiv:stat.ML/1709.04114.
Zimmermann, R.S. Comment on "Adv-BNN: Improved Adversarial Defense through Robust Bayesian Neural Network", 2019. arXiv:cs.LG/1907.00895.
Schwinn, L.; Raab, R.; Nguyen, A.; Zanca, D.; Eskofier, B. Exploring Misclassifications of Robust Neural Networks to Enhance Adversarial Attacks, 2021. arXiv:cs.LG/2105.10304.
Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-CAM: Visual Explanations from Deep Networks via Gradient-Based Localization. International Journal of Computer Vision 2019, 128, 336–359. [CrossRef]
van der Maaten, L.; Hinton, G. Visualizing Data using t-SNE. Journal of Machine Learning Research 2008, 9, 2579–2605.
Fix, E.; Hodges, J. Discriminatory Analysis: Nonparametric Discrimination: Consistency Properties; USAF School of Aviation Medicine, 1951.
Malkov, Y.A.; Yashunin, D.A. Efficient and robust approximate nearest neighbor search using Hierarchical Navigable Small World graphs, 2018. arXiv:cs.DS/1603.09320.

Figure 1. Comparing pure images with images that have been attacked by FGSM and PGD methods.

Figure 2. Clustering pure images and images that was attacked with different methods. Labels was changed from "king penguin" to "soccer ball".

Table 1. Similarities for attacked and different classes of pure images.

Attack type	dot product with random class image	dot product with original class image	diff rnd and original	dot product with target class image	diff rnd and targeted
PGD	427.38	639.34	211.95	521.20	93.81
CW	376.59	569.24	192.65	430.78	54.18
BIM	415.03	582.20	167.18	450.36	35.33
EADEN	439.24	779.36	340.12	553.97	114.73
EOTPGD	381.65	565.35	183.69	471.10	89.45
Jitter	413.08	581.48	168.40	588.21	175.14

Table 2. Attack success rates on different clustering algorithms.

Attack type	KNN over embeddings using $L_{2}$	Model output	HNSW with cosine similarity	HNSW with $L_{2}$ similarity	HNSW with $i p$ similarity
PGD	1.0	1.0	1.0	1.0	0.25
CW	0.63	1.0	0.95	1.0	0.11
BIM	1.0	1.0	1.0	1.0	0.37
EADEN	0.0	1.0	0.57	1.0	0.14
EOTPGD	0.89	1.0	0.95	1.0	0.21
Jitter	1.0	1.0	1.0	1.0	0.5

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

The Impact of Adversarial Attacks on a Computer Vision Models Perception of Images

Abstract

1. Introduction

2. Attacks in Question

2.1. Projected Gradient Descent

2.2. Carlini & Wagner Attack

2.3. Basic Iterative Method for FGSM

2.4. Elastic-Net Attack

2.5. Expectation Over Transformation PGD

2.6. JitteR-Based Attack

3. The Impact of Adversarial Attacks on Grad-CAM in Classification Task

4. The Impact of Adversarial Attacks on Image Clustering Visualization

5. The Impact of Adversarial Attacks on Image Clustering

5.1. Dot Product

5.2. K-Nearest Neighbors Algorithm

5.3. Hierarchical Navigable Small World

6. Conclusion

Acknowledgments

References

MDPI Initiatives

Important Links

Subscribe