Prerpints.org logo
Preprint
Communication

Offsetting Dense Particle Sedimentation in Microfluidic Systems

Altmetrics

Downloads

151

Views

86

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

08 August 2024

Posted:

12 August 2024

You are already at the latest version

Alerts
Abstract
Sedimentation is an undesirable phenomenon that complicates the design of microsystems that exploit dense microparticles as delivery tools, especially in biotechnological applications. It often informs the integration of continuous mixing modules, consequently impacting system footprint, cost, and complexity. The impact of sedimentation is significantly worse in systems designed with the intent of particle metering or binary encapsulation in droplets. Circumventing this problem involves the unsatisfactory adoption of gel microparticles as an alternative. This paper presents two solutions – a hydrodynamic solution that changes the particle sedimentation trajectory relative to a flow-rate dependent resultant force; and induced hindered settling (i-HS), which exploits Richardson-Zaki (RZ) corrections of Stokes’ law. The hydrodynamic solution was validated using a multi-well fluidic multiplexing and particle metering manifold. Computational image analysis of multiplex metering efficiency using this method showed an average reduction in well-to-well variation in particle concentration from 45% (Q = 1 mL/min, n = 32 total wells) to 17% (Q = 10 mL/ min, n = 48 total wells). By exploiting a physical property (cloud point) of surfactants in the bead suspension in vials, the i-HS achieved 58% reduction in the sedimentation rate. This effect results from surfactant phase change, which increases the turbidity (transient increase in particle concentration), thereby exploitingthe RZ theories. Both methods can be used independently or synergistically to eliminate bead settling in microsystems or minimize particle sedimentation.
Keywords: 
Subject: Engineering  -   Bioengineering

1. Introduction

Interest in using microparticles as delivery systems in various technologies has been widely researched, especially in combination with microdroplets for biological applications [1,2,3,4,5,6]. This is partly due to the high surface-to-volume ratio and the ease of immobilizing bio-recognition molecules on these materials, as well as the potential for compartmentalized single-molecule assays[7,8]. Unfortunately, challenges with bead settling confound these applications[3,6,9]. Offsetting particle density poses a challenge when loading microparticles into encapsulation devices because the higher-density particles sediment in the fluidic channels, causing a non-homogeneous distribution of microparticles in droplets. One method of resolving this challenge involves suspending the particles in equally dense fluids or introducing humectants such as glycerol [3,10]. However, an adequate amount of the humectants for increased bead buoyancy may be required at concentrations that may be inhibitory to the intended bio-applications, such as nucleic acid amplification technologies [11]. Researchers have also circumvented sedimentation problems by using gel beads [12,13,14,15]. While these have been used successfully in ensuring the binary distribution of beads in droplets without sedimentation issues, their non-Newtonian rheological properties make them difficult to handle. The use of channels with aspect ratios close to the particle diameter is another method for maintaining a single streamline, ensuring that only one particle is queried by the continuous phase at the point of encapsulation. However, considering that these beads are hard-shelled, their packing density may prohibit the possibility of closed packing in narrow channels. Additionally, since sedimentation velocity depends on the mass and size of the particles, the use of smaller particles is also an option; however, this may impact the capacity to carry an adequate amount of biomolecules of interest. Price and Paegel [3] presented a potentially simple solution by exploiting the sedimentation potential of the beads using a hopper system. However, they found that it took 0.8 h (17 µm TetanGel resin beads) and 3.8 h (2.8 µm magnetic beads) to introduce the beads before single-bead encapsulation. Kim et al. [2] successfully developed a pneumatic system that was capable of trapping and releasing beads, thus creating a deterministic encapsulation of a defined number of beads per droplet. This system, however, involves complex implementations of pumps and valves, thus making it unfit for low-cost and low-complexity applications. Mechanical agitation has also been successfully adopted; however, this complicates the system and could make integration into a unified product difficult. Applications requiring equal spatial distribution of particles are also impacted by sedimentation, which is compounded by non-slip conditions in laminar flow between parallel plates. For particles in such systems, wall lift and drag forces have been shown to depend on shear rate, especially at very low Reynold’s numbers [16]. In this paper, simplistic solutions to sedimentation, which can be applied to most particle-based systems, are exemplified in two different forms. A flow rate-dependent method that alters the sedimentation trajectory of suspended particles was applied to a microfluidic particle metering system while induced hindered settling was applied to particles in suspension.

2. Materials and Methods

2.1. Design and Frication of Fluid-Metering Chip

The chip was designed as a 16-well manifold for fluid and particle metering devices in which the metering chambers are separated from a lower storage chamber by a capillary valve (Figure 1A). Having both chambers was necessary to prevent one of the consequences of manifold systems, which is sequential filling. This would entail that each well will be filled to the brim before the next, thereby leaving no headspace to allow further fluid manipulations such as mixing. The lower storage chambers were perforated at positions modeled to give a convex meniscus at the approximate intended fill volume. To achieve this on a 3D plane, a 60o hemisphere mimicking the hydrophilic contact angle between the chip surface and the buffer was used to cut an extrusion of the 3D-model infill until the desired fill volume was achieved on the model (Figure 1B). During assembly, the perforations were plugged with polytetrafluoroethylene (PTFE) membranes such that wicking of the metered volume into the membranes triggered an increase in the chamber pressure thereby preventing further emptying of the top metering chamber (Figure 1C). All 3D models were designed using SolidWorks (Dassault Systèmes) and printed using ProFLuidics 285D digital light processing (DLP) 3D printer (CADworks3D). The design files are included as supplementary file (Sf1).
As illustrated in Figure 1D above, a consequence of increased number of metering wells, n, is an increase in length of the flow path, l, which consequently leads to a particle concentration gradient, in which the first well (Figure 1D-ii) contains a significantly greater concentration of suspended particles than the nth well due to bead settling. This challenge necessitates the need for a mechanism of counteracting or reducing the sedimentation of the beads to improve metering efficiency (Figure 1D-ii&iii).

2.2. Hydrodynamic Interruption of Sedimentation

The interaction of particles of different sizes and shapes have been the subject of many research, especially in environmental studies. However, there is a dearth of empirical demonstration of hydrodynamic interruption of particle sedimentation, especially in microfluidic systems. Here, the fabricated fluidic and particle-metering chips were used to demonstrate this phenomenon. The fabricated chips were connected to a syringe pump (Legato, KD Scientific) via a modified Eppendorf tube which held the bead suspension. For each experimental run, the syringe pump was programmed to run at a defined, arbitrarily chosen volumetric rate, Q = 1, 3.5, 5, and 10mL/ min until the feed channel was completely emptied. Each experimental condition was replicated (for Q=1mL/min, n=2; for Q = 3.5, 5 and 10 mL/ min, n=3) to determine the reproducibility of the results. Before each run, the bead vial was vortexed to ensure uniform bead distribution; and then loaded into the bead vial. Visual data were collected using Canon M50 Mark II mirrorless camera at 60 frames/ sec for computational image analysis via the algorithm below.

2.3. Induced Hindered Settling (i-HS)

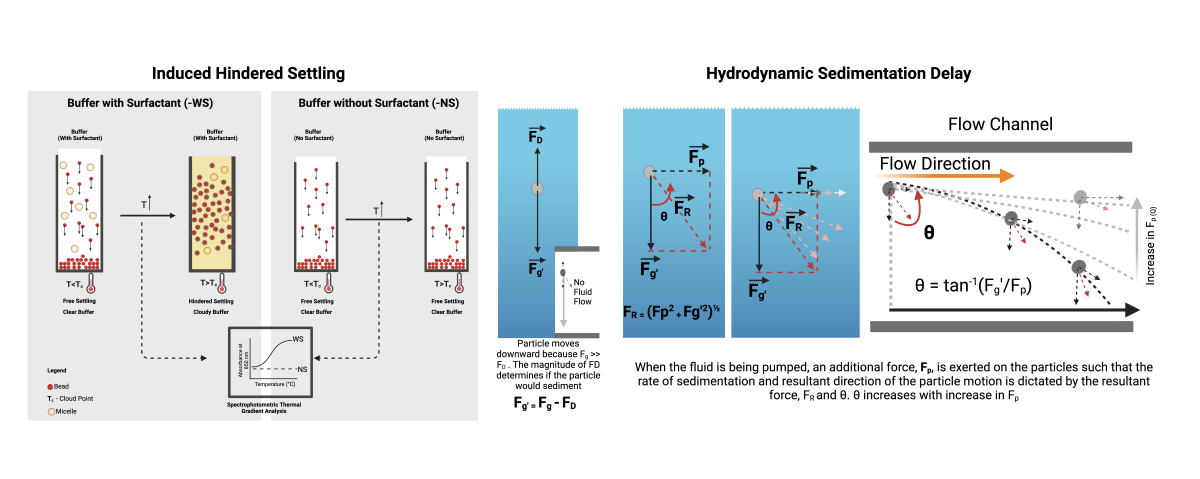
The Richardson–Zaki modification of Stokes’ law[17,18](equation 1) shows that at higher particle concentrations, the particle settling velocity decreases due to particle–particle interactions. This principle suggests that if we could increase the particle concentration in the buffer, we could delay or overcome particle settling. For biomedical applications, however, the particle concentrations are predetermined empirically for optimal performance and cost reasons and, as such, cannot be indefinitely increased to exploit the Richardson–Zaki principle. This principle could be exploited only if there was a way to transiently increase the particle concentration (or increase the turbidity of the particle-suspending solution) without introducing additional particles. This is the basis of the i-HS alternative.
V t V 0 = ( 1 − ⌀ ) n
Where V t = settling velocity in turbid fluid,
V 0 = settling velocity in clear fluid,
n = exponent of reduction in settling velocity,
⌀ = volume fraction of suspended particles in the fluid (turbidity)
To ascertain the feasibility of the i-HS, the cloud point of the surfactant in proprietary bead suspension buffer was exploited. As a preliminary analysis of this concept, the buffer was modified with and without ECOSURF EH-9 and designated with the prefixes -WS and -NS, respectively, and analysed via a spectrophotometric thermal gradient (STG) using Agilent BioTek Epoch 2 in a 96-well plate (Figure 5). Hypothetically, an increase in the turbidity of the -WS buffer relative to the turbidity of the -NS buffer would signal the feasibility of the concept.
Subsequently, bead suspensions of the same concentration as in previous experiments were added to clear glass vials and grouped according to the experimental protocol (Figure 5). This setup enabled the investigation of the effect of the surfactant cloud point on bead settling. Test temperatures which can be tolerated by downstream processes (50±100C), and at which cloud point was induced were chosen from different temperature points on the STG data. Raw STG data is included as supplemetary data, SD1.

2.4. Data Acquisition and Analysis

Replicate (n=12) turbidimetric measurements at different temperatures and data collection were achieved using a spectrophotometer at a near-infrared (NIR) wavelength of 850 nm. For bead settling experiments, heating of the glass vials for bead settling was performed using a Benchmark Multitherm shaker and cooling device. Visual data in the form of video recordings (Canon M50 Mark II Mirrorless camera at 60 frames per second) were collected for the assessment of bead settling and suspension homogeneity in the vials. Each test was run in duplicates.
The collected videos were analysed using the Python computer vision library (OpenCV) following the algorithm shown in Figure 2. To determine the bead settling velocity in the vials, the intensity of the pixels within the region of interest (region covered by the bead suspension) was monitored throughout the video timeline. By monitoring the pixel intensity over time, the presence and later absence of beads within a pixel signals the settling of the beads. The sedimentation rate was determined as the rate of change of gray value (Equation 2).
∂ G ∂ t = − V s
Where ∂ G ∂ t = rate of change of gray values over time, ∂ G ∂ z = rate of change of gray values with respect to height, V s = sedimentation rate.
The pixel intensity (mean gray value) refers to the brightness of a pixel in an image. From the grayscale images, the intensity was measured on a scale of 0–255, where 0 represents black and 255 represents white. The mean gray values correspond to the concentration of the beads or the homogeneity of the bead suspension.

3. Results

3.1. Fabrication of Particle Metering Chip

To prevent premature emptying of the top metering wells, the dimensions of the feed channel were modeled using SolidWorks Flow Simulations software (Dassault Systèmes). The capillary stop valves were designed to have a Laplace pressure of 403 Pa calculated using equation 1.
Δ P = 2 * γ 1 w + 1 h cos θ c
Where θ c = f l u i d c o t a c t a n g l e = 2 , w = v a l v e w i d t h = 0.5 m m , h = v a l v e h e i g h t = 1.25 m m , γ = γ water s u r f a c e t e n s i o n = 0.072 N / m
After printing, the geometric conformance of the 3D-printed capillary valves to the CAD model was determined using optical metrology (Keyence). This was determined to be 0.49±0.02mm (n=10), thus conforming with the design parameters (equation 3).
A major consequence of manifold splitting results from the interaction between the buffer, the shared walls between wells, the material surface properties, and the flow regime (Figure4). This interaction led to an undesired siphon effect whereby asynchronously emptied wells drew fluid from neighboring wells, leading to metering inefficiencies. This was resolved by reprogramming the flow regime to ensure synchronous emptying of the wells via an instantaneous increase in Laplace pressure (Figure 4 iv).

3.2. Hydrodynamic Interruption of Sedimentation

As shown in Figure 5A, at a volumetric flow rate of Q = 1 mL/min, much of the beads eluted early in the experimental run, forcing the mean gray value (MGV) of wells 1 through 7 to be significantly lower (higher bead concentration) than that of wells 8–16 (Figure 5C). Pairwise comparisons (Student’s t test, alpha = 0.05) of the MGVs of the 16 wells from Q=1 mL/min to the other tested Qs revealed a significant difference between them, with p values <0.0001 (Figure 5B). While increasing Q from 3.5 mL/min to 10 mL/min did not significantly affect the average concentration of the beads (p values: Q3.5 – Q10 = 0.107; Q5 – Q10 = 0.231; Q3.5 – Q5 = 0.675), analyses of the data from each flow rate showed improved bead distribution (Figure 5C). For Q = 3.5 mL, wells 14–16 had significantly lower bead concentrations; for Q = 5mL/min, wells 15 and 16 had significantly lower bead concentrations; and for Q = 10 mL/min, only well 16 had a significantly lower bead concentration. Details of the analysis can be found in the video data, SD2.

3.3. Sedimentation Offset Via Induced Hindered Settling

Phase separation in the particle suspension buffer was induced and confirmed via spectrophotometric analyses, which showed a temperature-driven increase in turbidity (Figure 6A). Since this change is reversible[19], it offers a perfect solution for increasing the probability of particle-particle interactions and, consequently, hindering settling. Incubation of the WS buffer at 55 ∘ C resulted in a ~45% increase in turbidity (Figure 6B).
As shown in Figure 6C&D, this phenomenon translated to a reduction in bead settling velocity. In accordance with the theory of hindered settling, an increase in the bead suspension buffer temperature and, consequently, the cloud point of the surfactant reduced the sedimentation rate of the beads by 58% (Figure 6 D&E). Continuous or controlled heating of the beads in a vial (Figure7) showed similar result of improved particle metering (data not shown). Notably, the presence of surfactants, while necessary for fluid flow, increases the bead settling velocity as shown in Figure 6C-E – WS_RT (slope = 0.4341) vs NS_RT (slope = 0.2744). As shown in Figure 6E, there was no significant difference in sedimentation rate between -NS buffer at room temperature and one heated to 46oC (NS_46°C vs NS_RT); however, increasing the heating temperature to 55°C led to an increase in the rate of sedimentation (NS_46 – slope:0267, NS_55 – slope:0.296).

4. Discussion

4.1. Hydrodynamic Interruption of Particle Sedimentation

Particle sedimentation occurs because of the action of gravitational pull on the particles. The rate at which particles sediment, V s , is influenced by factors such as particle volume and the density of the suspending fluid.
V s = g 2 r 2 9 η 0 ( m p v p − ρ f )
V s = Sedimentation velocity at infinite dilution, r = particle radius, η 0 = viscosity of suspending fluid, m p = mass of particle, v p = volume of particle, ρ f = density of suspending fluid, g = |g| = 9.8 m / s 2 .
These, in turn, also influence the drag force, ( F d ), which in simple terms, the drag force refers to the resistance force exerted by a fluid to the downward motion of the particles.
F d = 1 2 [ ρ f C d A V s 2 ]
where F d = d r a g f o r c e , V = p a r t i c l e v e l o c i t y , A = p a r t i c l e a r e a , C d = d r a g c o e f f i c i e n t = 24 Re for spheres [20], therefore:
F d = 12 [ ρ f A V s 2 Re ]
Substituting g 2 r 2 9 η 0 m p v p − ρ f for V s in Equation (5)
F d = 12 [ ρ f A [ g 2 r 2 9 η 0 ( m p v p − ρ f ) ] 2 Re ] W h e r e R e = R e y n o l d ′ s n u m b e r
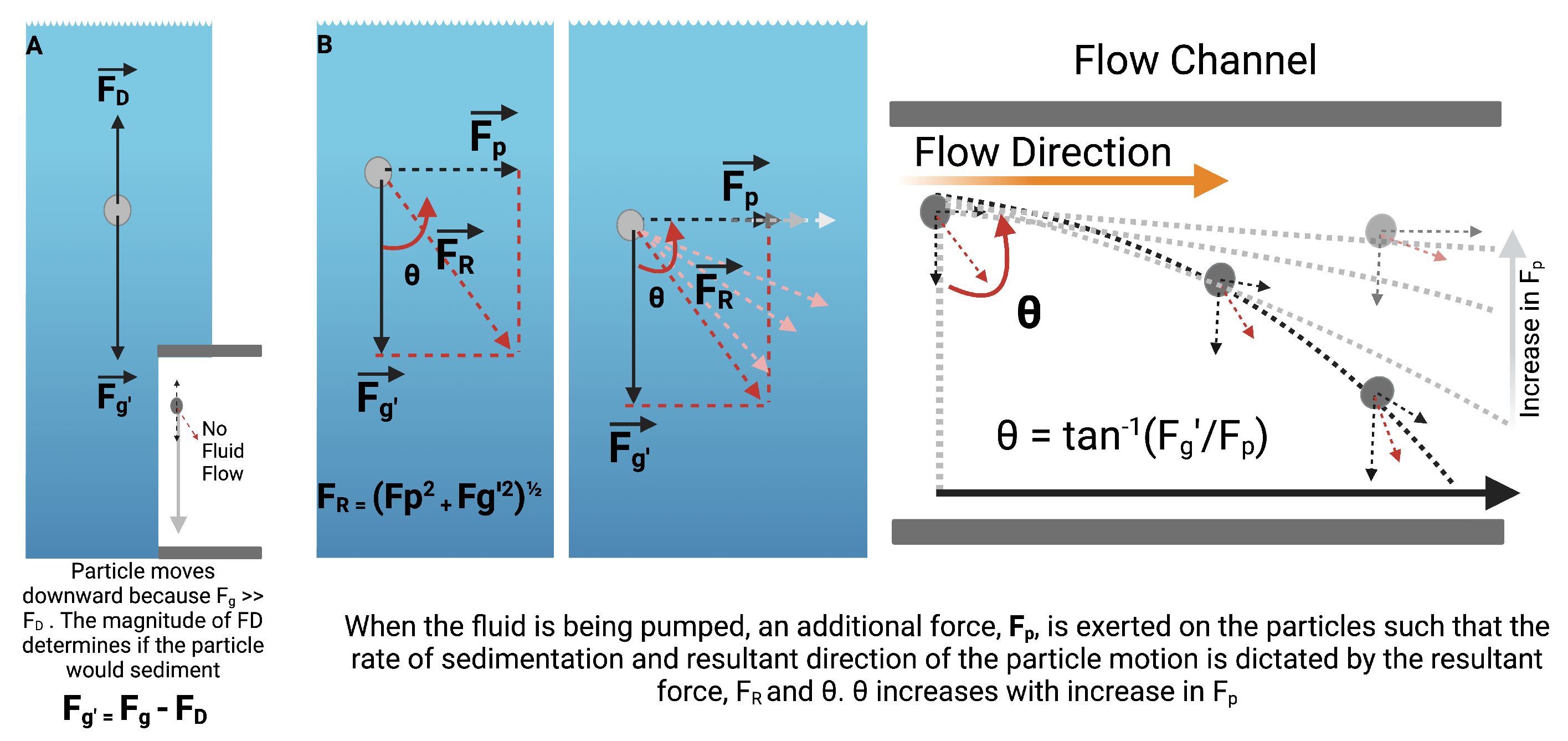
As shown in equation 5, several factors contribute to the drag force exerted on the particles. Consider particles at steady state, as illustrated in Figure 7, the particles sediment in response to the resultant of opposing forces, drag force and gravity.
F g ′ = F g − F d
However, in fluidic state, the rate and direction of sedimentation is largely determined by the magnitude if the force, F p applied to the particle due to pumping.
Since the deviation of the particle from a straight downward sedimentation is given by:
θ = tan − 1 ( F g ′ F p )
Theoretically, at constant |g’|, increasing F p would result in a concomitant increase in θ towards 900.
lim F p → ∞ θ ( F p ) = 90 0
∫ F p ∞ d θ d F p d F p = 90 ∘ − θ F p
Considering this theory, since F p = ma, where m=mass; and a = acceleration = Fluid Velocity time , F p
can be increased via the volumetric flow rate.
Empirical findings from the data above validate the working theory as stated in equations 9-11; thus, as the acceleration of the beads in solution increase as a result of the increase in Q of the suspending fluid, gravitational pull on the particles is counteracted. The particles therefore remain homogenized in solution long enough to be evenly distributed. This method, although simplistic and easy to implement in most systems, may be impractical for shear-averse processes where high flow rates (deviation from laminar flow) could impact the structural integrity of the suspended particles. Additionally, as shown in Figure 5B, increasing Q beyond a certain threshold yields very minimal improvement, which may not justify the high volumetric flow rate requirement. These limitations therefore necessitate the need for a more shear-tolerant alternative that would not only alter the sedimentation trajectory but also significantly reduce it.

4.2. Induced Hindered Settling

Although ECOSURF EH-9 has a cloud point of 640C at 10 wt% actives aqueous solution, spectrophotometric thermal gradient data (Figure 6A) shows that at 0.1 wt%, turbidimetric changes could be initiated at temperatures lower than the cloud point. This finding improves on the existing knowledge that heating solutions containing non-ionic surfactants to temperatures above the surfactant cloud point (Tc) could induce a phase change[21]. While the exact role of the salts in the proprietary buffer on the lower cloud point was not explored, data from [22] suggests that the cloud point of non-ionic surfactants could be lowered via the addition of salts. Figure 6A also shows a biphasic change in buffer turbidity relative to temperature increase. The primary reason for this biphasic relationship could not be determined from secondary data, however, a thermally-induced phase change due to surfactant cloud point could explain increase in turbidity. This phase change results in the formation of surfactant micelles that interact with the particles, thereby conforming to the Richardson–Zaki theory. Although this phase change can also be induced chemically via the addition of ionic surfactant and electrolytes, for this application, micellar aggregation occurred because of thermally induced reduction in the hydration of oxyethylene oxygen in hydrophilic groups, which leads to micellar aggregation. This phenomenon has been widely adopted in environmental studies and in separation science as a form of cloud point extraction (CPE)[21,23,24,25,26]. While encouraging, most applications requiring microparticle manipulation may not be tolerant to heating. For such applications, the choice of surfactants with cloud points closer to tolerable temperatures or chemical tuning[22] of the surfactant cloud point may be ideal.

5. Conclusions

Various biomedical applications, especially in microfluidic systems, require microparticle handling. The development of specialized devices for continuous mixing or a complete switch to gel beads has been mostly adopted due to the challenge of bead settling. However, these factors increase the cost and complexity of the system. This paper presents two simplistic solutions, hydrodynamic and i-HS solutions. Both solutions exploit rudimentary components in biomedical platforms, thereby not adding to the cost. While they can be applied independently, they can also be combined to achieve a uniform distribution of particles of various sizes or to lower their settling velocity for fluidic applications. This was successfully applied in particle metering and distribution manifold (data not shown). A limitation of both systems is the requirement for an initial homogenization step and continued heating for the i-HS (optional). Moreso, thermal induction of hindered settling as demonstrated in this research may not be ideal for most biomedical systems. However, thermal i-HS may not be necessary considering the possibility of non-thermal cloud point tuning [22]. These principles can be adopted in particle-laden flows involving the need for mechanistic encapsulation of microparticles.

Data Availability Statement

All requisite data and design files are included in the supplementary data folder.

Acknowledgments

This work was supported by the Department of Health and Social Care-funded Centre for Antimicrobial Optimisation (CAMO) at Imperial College London; the Wellcome Trust CAMO-Net programme [226691/Z/22/Z]; Wellcome Trust Innovator Award [215688/Z/19/Z]; the NIHR Imperial Biomedical Research Centre; the NIHR [134694] using UK aid from the UK Government to support global health research. J.R.M. is affiliated with the NIHR Health Protection Research Unit (HPRU) in Healthcare Associated Infections and Antimicrobial Resistance at Imperial College London in partnership with the UK Health Security Agency, in collaboration with, Imperial Healthcare Partners, the University of Cambridge and the University of Warwick. The views expressed in this publication are those of the authors and not necessarily those of the NHS, the National Institute for Health Research, the Department of Health and Social Care, or the UK Health Security Agency.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Iwai, K.; Sochol, D.R.; Lin, L. A bead-in-droplet solution exchange system via continuous flow microfluidic railing. 2013 IEEE 26th International Conference on Micro Electro Mechanical Systems (MEMS) 2013, pp. 1203–1206.
  2. Kim, H.; Choi, I.H.; Lee, S.; Won, D.J.; Oh, Y.S.; Kwon, D.; Sung, H.J.; Jeon, S.; Kim, J. Deterministic bead-in-droplet ejection utilizing an integrated plug-in bead dispenser for single bead-based applications. Scientific Reports 2017, 7, 1–9. [Google Scholar] [CrossRef] [PubMed]
  3. Price, A.K.; Macconnell, A.B.; Paegel, B.M. Microfluidic bead suspension hopper. Analytical Chemistry 2014, 86, 5039–5044. [Google Scholar] [CrossRef] [PubMed]
  4. Myers, K.K.; Herich, J.P.; Chavez, J.E.; Berkey, K.G.; Loi, A.J.; Cleveland, P.H. A Novel Method to Gently Mix and Uniformly Suspend Particulates for Automated Assays. SLAS Technology 2021, 26, 498–509. [Google Scholar] [CrossRef] [PubMed]
  5. Wang, C.H.; Lien, K.Y.; Wu, J.J.; Lee, G.B. A magnetic bead-based assay for the rapid detection of methicillin-resistant Staphylococcus aureus by using a microfluidic system with integrated loop-mediated isothermal amplification. Lab on a Chip 2011, 11, 1521–1531. [Google Scholar] [CrossRef] [PubMed]
  6. Anyaduba, T.D.; Otoo, J.A.; Schlappi, T.S. Picoliter Droplet Generation and Dense Bead-in-Droplet Encapsulation via Microfluidic Devices Fabricated via 3D Printed Molds. Micromachines 2022, 13, 1946. [Google Scholar] [CrossRef] [PubMed]
  7. Sassolas, A.; Hayat, A.; Marty, J.L. Immobilization of enzymes on magnetic beads through affinity interactions. Methods in Molecular Biology 2013, 1051, 139–148. [Google Scholar] [CrossRef] [PubMed]
  8. Vashist, S.K.; Luong, J.H. Antibody Immobilization and Surface Functionalization Chemistries for Immunodiagnostics; Elsevier, 2018; pp. 19–46. [Google Scholar] [CrossRef]
  9. Poles, M.; Meggiolaro, A.; Cremaschini, S.; Marinello, F.; Filippi, D.; Pierno, M.; Mistura, G.; Ferraro, D. Shaking Device for Homogeneous Dispersion of Magnetic Beads in Droplet Microfluidics. Sensors 2023, 23. [Google Scholar] [CrossRef] [PubMed]
  10. Banerjee, U.; Jain, S.K.; Sen, A.K. Particle encapsulation in aqueous ferrofluid drops and sorting of particle-encapsulating drops from empty drops using a magnetic field. Soft Matter 2021, 17, 6020–6028. [Google Scholar] [CrossRef] [PubMed]
  11. Anyaduba, T. Primer Payload System for Higher-Order Multiplex LAMP: Design and Development of Unit Processes. KGI Theses and Dissertations 2021. [Google Scholar]
  12. Shintaku, H.; Kuwabara, T.; Kawano, S.; Suzuki, T.; Kanno, I.; Kotera, H. Micro cell encapsulation and its hydrogel-beads production using microfluidic device. Microsystem Technologies 2007, 13, 951–958. [Google Scholar] [CrossRef]
  13. Klein, A.M.; Mazutis, L.; Akartuna, I.; Tallapragada, N.; Veres, A.; Li, V.; Peshkin, L.; Weitz, D.A.; Kirschner, M.W. Droplet barcoding for single-cell transcriptomics applied to embryonic stem cells. Cell 2015, 161, 1187–1201. [Google Scholar] [CrossRef] [PubMed]
  14. Zilionis, R.; Nainys, J.; Veres, A.; Savova, V.; Zemmour, D.; Klein, A.M.; Mazutis, L. Single-cell barcoding and sequencing using droplet microfluidics. Nature Protocols 2017, 12, 44–73. [Google Scholar] [CrossRef] [PubMed]
  15. Clark, I.C.; Abate, A.R. Microfluidic bead encapsulation above 20 kHz with triggered drop formation. Lab on a Chip 2018, 18, 3598–3605. [Google Scholar] [CrossRef] [PubMed]
  16. Ekanayake, N.I.; Berry, J.D.; Stickland, A.D.; Dunstan, D.E.; Muir, I.L.; Dower, S.K.; Harvie, D.J. Lift and drag forces acting on a particle moving with zero slip in a linear shear flow near a wall. Journal of Fluid Mechanics 2020, 904. [Google Scholar] [CrossRef]
  17. Riuxardson, J.F.; Zaki, W.N. The sedimentation of a suspension of uniform spheres under conditions of viscous flow.
  18. Zhu, Z.; Wang, H.; Peng, D.; Dou, J. Modelling the hindered settling velocity of a falling particle in a particle-fluid mixture by the Tsallis entropy theory. Entropy 2019, 21. [Google Scholar] [CrossRef] [PubMed]
  19. Ghaedi, M.; Shokrollahi, A.; Mehrnoosh, R.; Hossaini, O.; Soylak, M. Combination of cloud point extraction and flame atomic absorption spectrometry for preconcentration and determination of trace iron in environmental and biological samples. Central European Journal of Chemistry 2008, 6, 488–496. [Google Scholar] [CrossRef]
  20. Mariusz, R.; Ewelina, L. MODELING OF THE SEDIMENTATION PROCESS OF MONODISPERSE SUSPENSION. International Journal of Computational Methods and Experimental Measurements 2022, 10, 50–61. [Google Scholar] [CrossRef]
  21. Miyake, M.; Yamashita, Y. Molecular Structure and Phase Behavior of Surfactants. Cosmetic Science and Technology: Theoretical Principles and Applications 2017, pp. 389–414. [CrossRef]
  22. Cloud Point of Non-Ionic Surfactants – METTLER TOLEDO.
  23. Nazar, M.F.; Shah, S.S.; Eastoe, J.; Khan, A.M.; Shah, A. Separation and recycling of nanoparticles using cloud point extraction with non-ionic surfactant mixtures. Journal of Colloid and Interface Science 2011, 363, 490–496. [Google Scholar] [CrossRef] [PubMed]
  24. Duester, L.; Fabricius, A.L.; Jakobtorweihen, S.; Philippe, A.; Weigl, F.; Wimmer, A.; Schuster, M.; Nazar, M.F. Can cloud point-based enrichment, preservation, and detection methods help to bridge gaps in aquatic nanometrology? Analytical and Bioanalytical Chemistry 2016, 408, 7551–7557. [Google Scholar] [CrossRef] [PubMed]
  25. Na, G.C.; Yuan, B.O.; Stevens, H.J.; Weekley, B.S.; Rajagopalan, N. Cloud point of nonionic surfactants: Modulation with pharmaceutical excipients. Pharmaceutical Research 1999, 16, 562–568. [Google Scholar] [CrossRef]
  26. Al-Saadi, M.R.; Al-Garawi, Z.S.; Thani, M.Z. Promising technique, cloud point extraction: Technology & applications. Journal of Physics: Conference Series, 2021. [Google Scholar]
Preprints 114716 g001
Figure 1. Minimal illustrations of the chip sub-units showing critical design elements. Di Illustration of the fluidic metering device showing the shared feed channel and the tributary wells (outflow channels).ii Illustration of undesirable iii desirable effect of bead settling as a result of sedimentation across the feed channel of length, l.
Figure 1. Minimal illustrations of the chip sub-units showing critical design elements. Di Illustration of the fluidic metering device showing the shared feed channel and the tributary wells (outflow channels).ii Illustration of undesirable iii desirable effect of bead settling as a result of sedimentation across the feed channel of length, l.
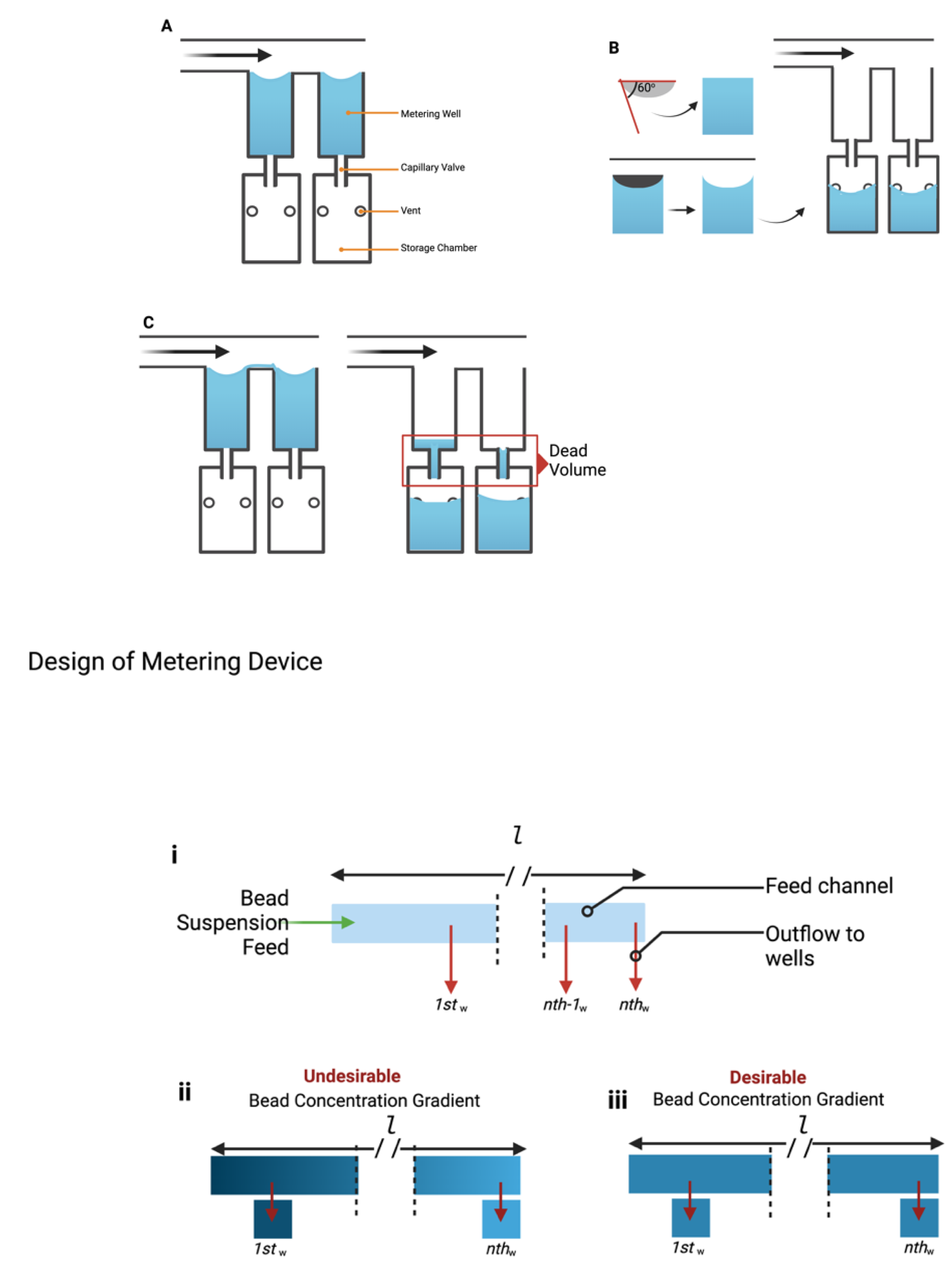
Preprints 114716 g001
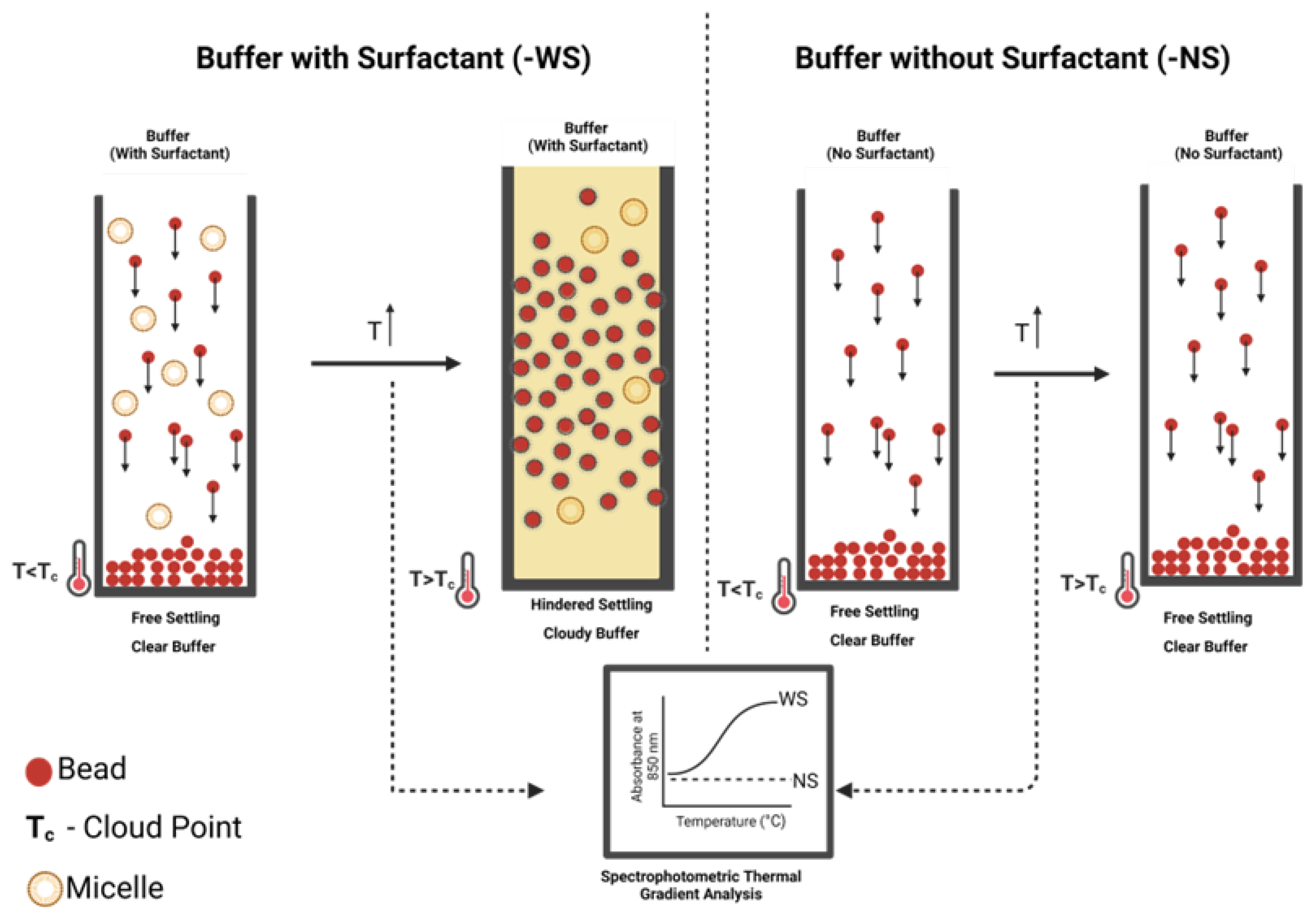
Preprints 114716 g002
Figure 2. Schematic representation of the induced hindered settling and spectrophotometric thermal gradient analytical protocol.
Figure 2. Schematic representation of the induced hindered settling and spectrophotometric thermal gradient analytical protocol.
Preprints 114716 g002
Preprints 114716 g003
Figure 3. Still and video image processing algorithm for feature extraction and numerical data retrieval.
Figure 3. Still and video image processing algorithm for feature extraction and numerical data retrieval.
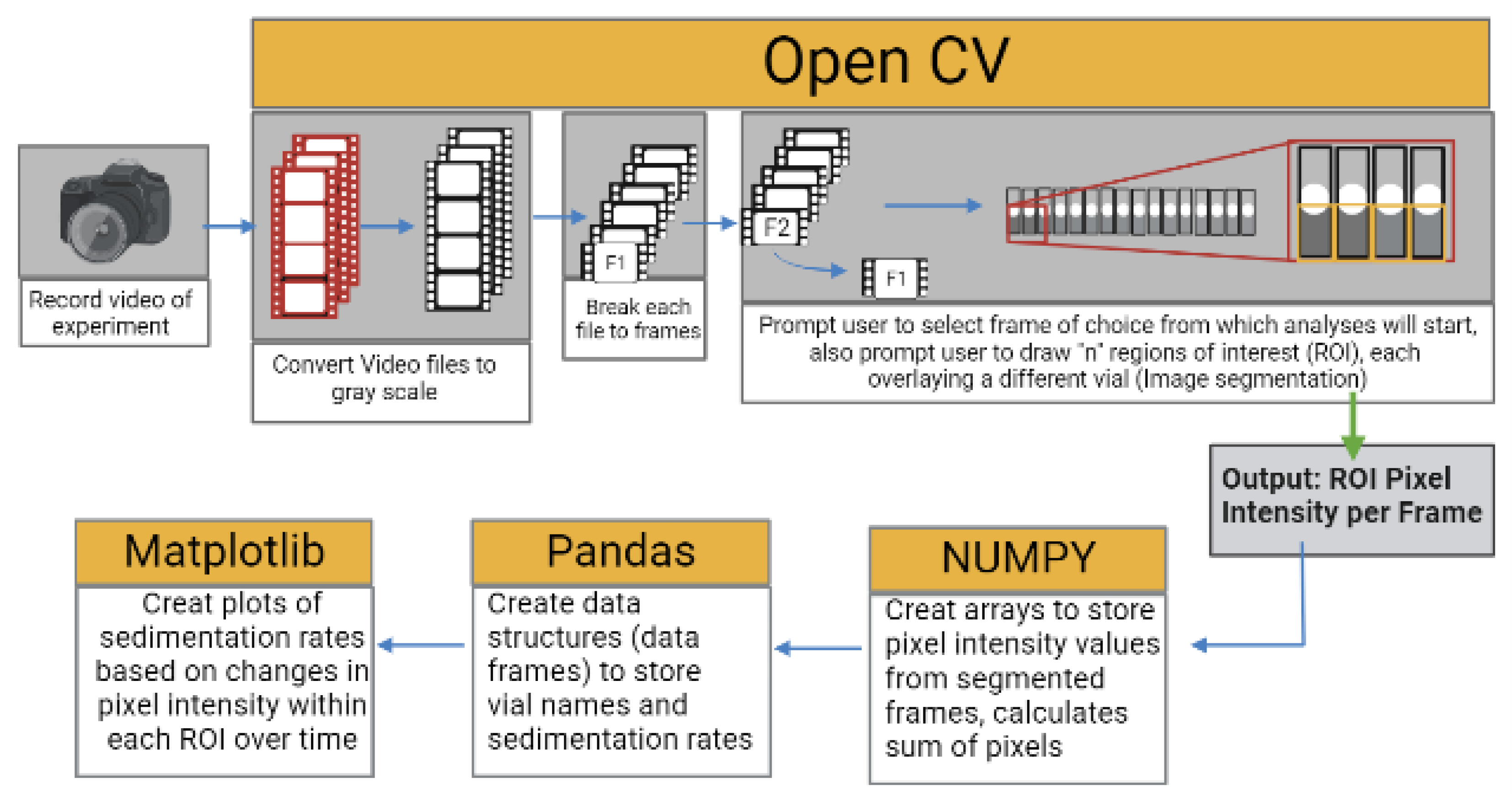
Preprints 114716 g003
Preprints 114716 g004
Figure 4. i-iii shows the effect of asynchronous emptying of the metering wells. iv shows the pump ramp program:[2] Ramp from 0.1mL/ min to 1mL/ min in 5 secs [3] Hold at 1mL/ min for 72 secs (72secs is the time required to completely empty the surrogate elution chamber – per my setup - + time to empty the feed well ) [4] Ramp from 1mL/ min to 10 mL/ min in 5secs (5 secs – arbitrarily chosen – being careful to ensure the syringe pump could handle that ramp) [5] Hold at 10 mL/ min for 6 secs (10 mL/ min for 6 seconds ensures 690 µL is pushed from the all metering wells while keeping the unit pressurized). The positive pressure is important momentarily to ensure all wells are emptied simultaneously.
Figure 4. i-iii shows the effect of asynchronous emptying of the metering wells. iv shows the pump ramp program:[2] Ramp from 0.1mL/ min to 1mL/ min in 5 secs [3] Hold at 1mL/ min for 72 secs (72secs is the time required to completely empty the surrogate elution chamber – per my setup - + time to empty the feed well ) [4] Ramp from 1mL/ min to 10 mL/ min in 5secs (5 secs – arbitrarily chosen – being careful to ensure the syringe pump could handle that ramp) [5] Hold at 10 mL/ min for 6 secs (10 mL/ min for 6 seconds ensures 690 µL is pushed from the all metering wells while keeping the unit pressurized). The positive pressure is important momentarily to ensure all wells are emptied simultaneously.
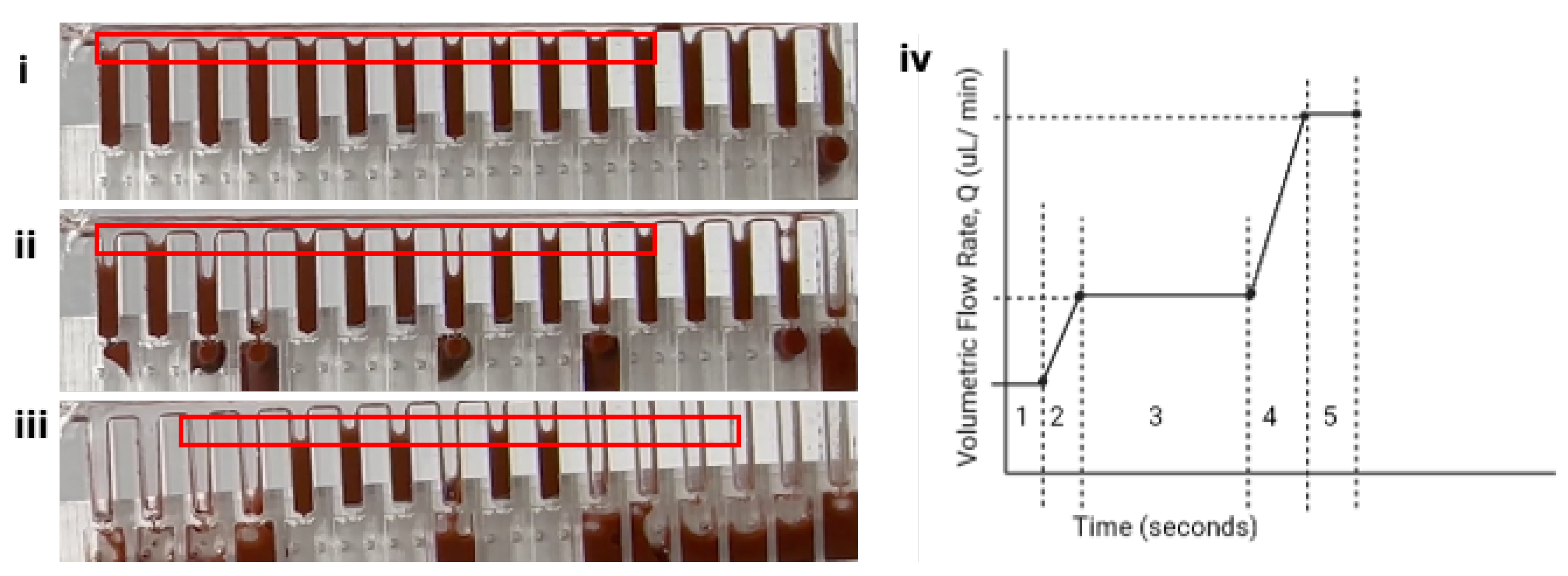
Preprints 114716 g004
Preprints 114716 g005
Figure 5. A Distribution pattern of suspended beads in response to changes in the volumetric flow rate. B . Comparison of the effect of flow rate on the mean bead concentration C . Pairwise comparison of well-to-well bead concentrations.
Figure 5. A Distribution pattern of suspended beads in response to changes in the volumetric flow rate. B . Comparison of the effect of flow rate on the mean bead concentration C . Pairwise comparison of well-to-well bead concentrations.
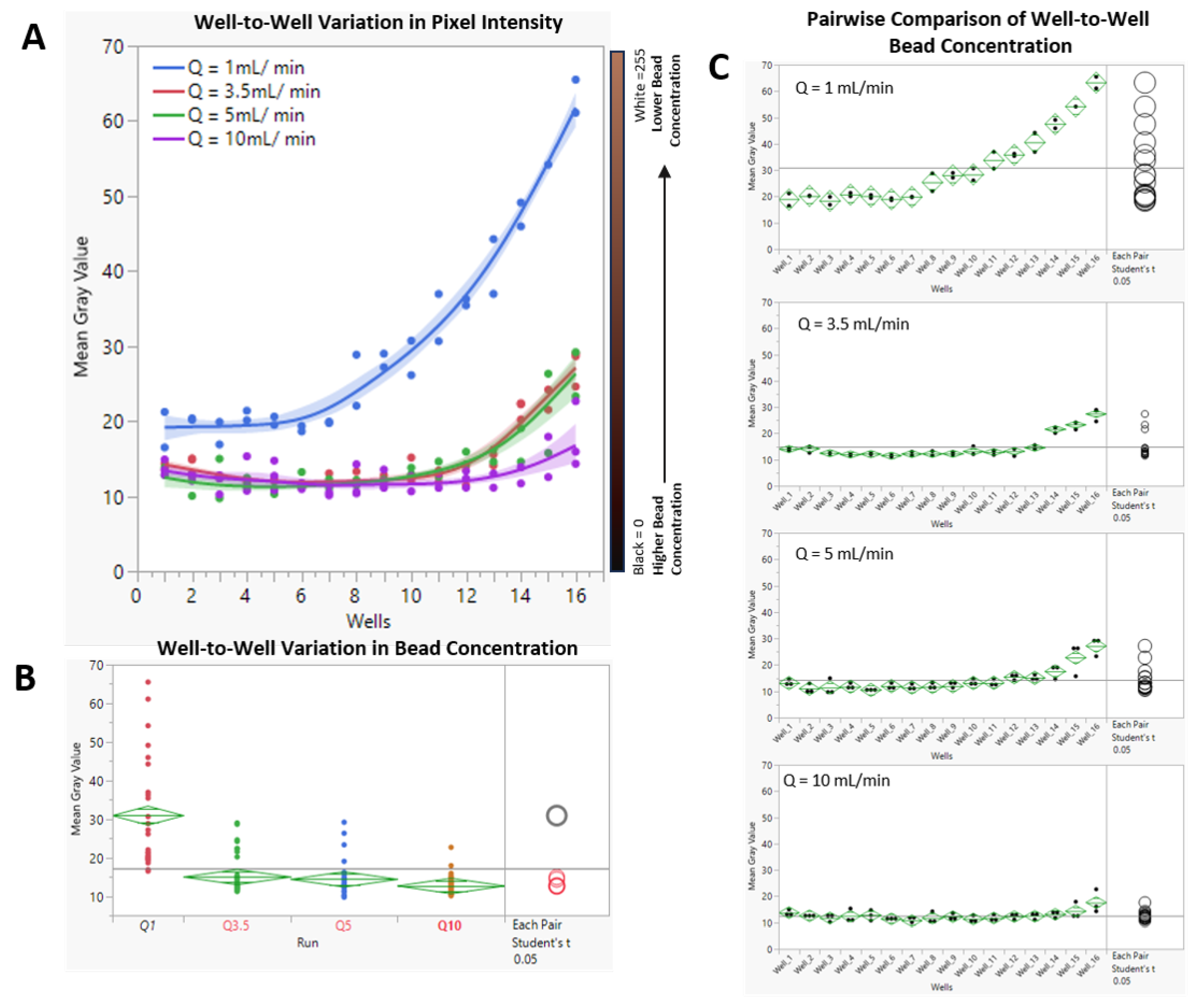
Preprints 114716 g005
Preprints 114716 g006
Figure 6. A . Spectrophotometric thermal gradient (STG) analysis of buffers with (-WS) and without (-NS) surfactants. B. Pairwise comparison of STG results. C. Timelapse images showing bead sedimentation in glass vials. D. XY plots of different experimental conditions showing the temporal rate of change in pixel intensity. E. Analysis of means (ANOM) of the sedimentation gradients ( α = 0.05). Video data of the experimental setup is included in SD3.
Figure 6. A . Spectrophotometric thermal gradient (STG) analysis of buffers with (-WS) and without (-NS) surfactants. B. Pairwise comparison of STG results. C. Timelapse images showing bead sedimentation in glass vials. D. XY plots of different experimental conditions showing the temporal rate of change in pixel intensity. E. Analysis of means (ANOM) of the sedimentation gradients ( α = 0.05). Video data of the experimental setup is included in SD3.
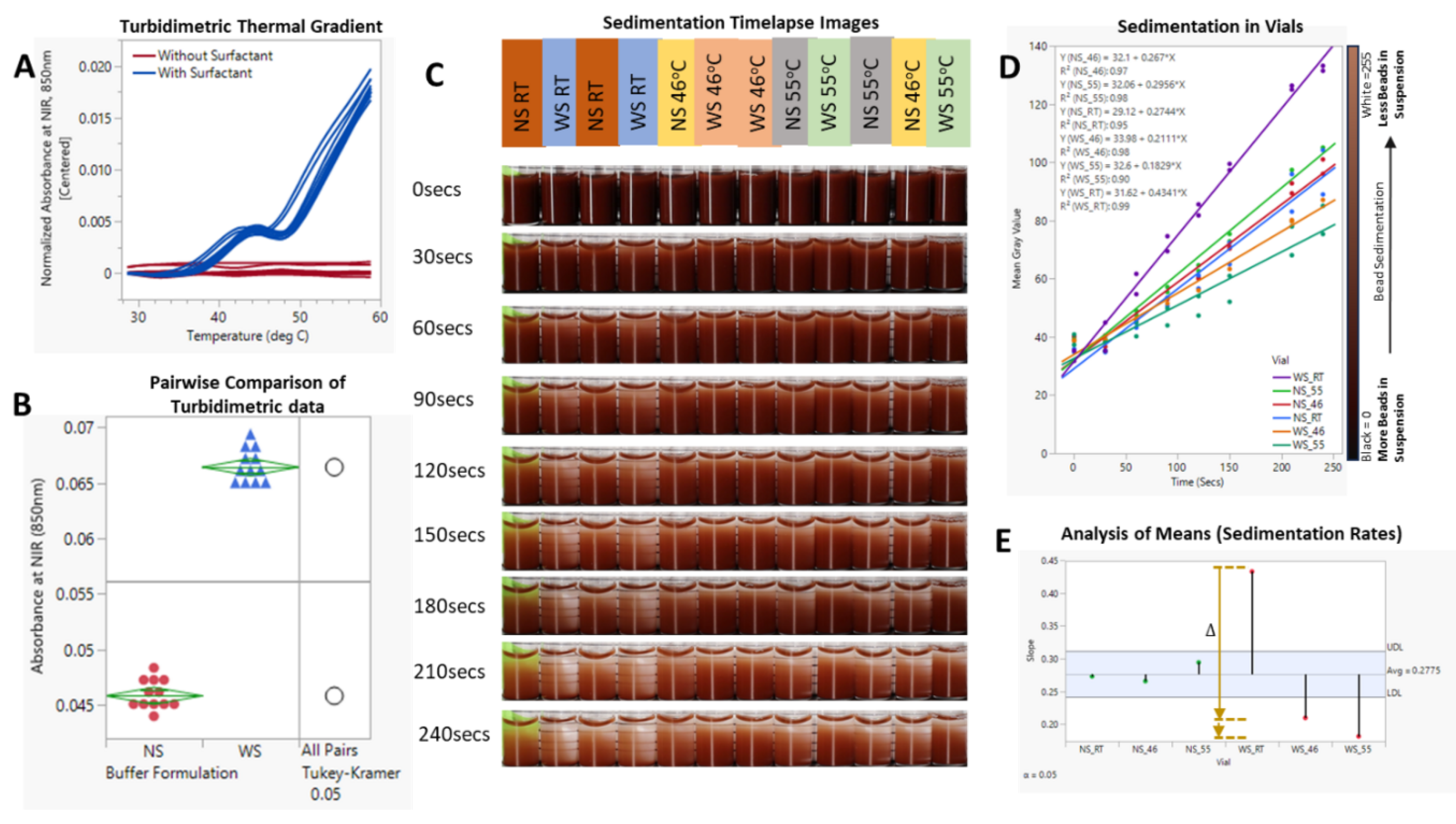
Preprints 114716 g006
Preprints 114716 g007
Figure 7. Working Theory for Hydrodynamic Interruption of Particle Sedimentation.
Figure 7. Working Theory for Hydrodynamic Interruption of Particle Sedimentation.
Preprints 114716 g007
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated