Prerpints.org logo
Preprint
Article

Theoretical Models of Multiple Failure Mechanisms in Rock Materials

Altmetrics

Downloads

70

Views

15

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

02 August 2024

Posted:

06 August 2024

You are already at the latest version

Alerts
Abstract
Rock materials failures are accompanied by the co-existence of various failure mechanisms, in-cluding rock fracturing, shearing, and compaction yield. These mechanisms manifest macro-scopically as multiple failure modes and nonlinear strength characteristics related to stress levels. Considering the limitations of current rock mechanics strength theories, which are primarily derived from single failure mechanisms, this study evaluates the applicability of alternative strength theories. Based on the extensional-strain criterion and the PMC (Paul-Mohr-Coulomb) model, a piecewise linear strength model was proposed that is suitable for analyzing multiple failure mechanisms in rocks and revealing the intrinsic mechanisms of multi-mechanism rock material failure. A multiple failure mechanism strength model in the form of inequalities was proposed, using the generalized shear stress, mean stress, and stress Lode angle as parameters. Strength tests conducted on sandstone and granite rock material samples under different stress conditions revealed distinct piecewise linear strength characteristics for both rock types, vali-dating the rationality and applicability of the multiple failure mechanism model. The findings construct a multi-mechanism failure model for rocks, providing enhanced predictive capabilities and aiding in the prevention of rock structural failures.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

Rock failure processes can exhibit significant nonlinear behavior and characteristic failure mechanism transitions. During these processes, various failure mechanisms such as rock extension, shearing, and compaction yields can co-exist. Furthermore, rocks exhibit different failure modes under different confining pressures. For example, under tensile stress or low-pressure conditions, rocks may exhibit tensile failure. As the pressure gradually increases, the failure mode transitions from tensile to shear failure. At higher stress levels in deeper regions, the failure mode shifts from conventional shear failure to pore collapse failure. Thus, rocks transition between multiple failure modes, including tensile failure, shear failure, and compaction-shear yield.
Paul (1968) considered the influence of the intermediate principal stress on the Mohr-Coulomb model and proposed an expression involving three principal stresses [1,2]. Three parameter constants were determined for the stress states of uniaxial compression, uniform triaxial (isotropic) extension, and uniaxial extension. Meyer and Labuz further developed this into the PMC strength model [3]. They discussed the transformation characteristics of failure mechanisms in rock materials based on the PMC model and examined the shape of dodecagonal PMC failure surfaces. Two failure planes were fit to describe the nonlinear failure surface, which led to the development of the dodecahedral PMC model. This model allows for the observation of changes in the shape of the failure surface with increasing mean stress, characterizing the transition of rock material failure from tensile failure to shear failure as the stress conditions increase.
For the material parameters, Makhnenko et al. proposed a plane fitting method that minimizes the sum of the squared orthogonal distances between data points and the failure surface [4], whereas Zeng et al. suggested using the least squares method to fit parameters [5]. Asem et al. introduced a simplified PMC model that assumes the same friction angle under both tensile and compressive conditions and reduces the dodecagonal PMC model by two parameters; in other words, the resulting model has only four parameters [6].
Under tensile stress or low-pressure conditions, the rock failure mode is a tensile failure. Rocks undergo splitting failure under uniaxial stress or low confining pressure conditions with no tensile stress on the failure plane. Stacey (1981) proposed the extensional-strain criterion to explain the brittle failure mechanisms of deep quartzites in South Africa [7]. The results indicate that for materials exhibiting linear deformation behavior, the onset and depth of failure can be correlated with extensional strain.
This study characterizes rock failure under tensile and tensile-shear conditions using the extensional-strain criterion and describes compressive-shear failure based on the PMC model. A unified strength model under the influence of multiple failure mechanisms was then derived. By analyzing field and laboratory test data, a theoretical model suitable for multiple failure mechanisms in rocks was proposed, which revealed intrinsic low-strength rock failure mechanisms.

2. Related Work

2.1. PMC Model

In 1968, Paul considered the influence of the intermediate principal stress and proposed the PMC model [1,2]. In 2013, Meyer and Labuz developed this concept into the PMC strength model, and the expression for principal stresses is as follows [3]:
A σ 1 + B σ 2 + C σ 3 = 1
where A, B, and C are material constants, and σ1, σ2, and σ3 represent the three principal stresses. When B = 0, Equation (1) becomes the MC (Mohr-Coulomb) strength criterion.
A = 1 − sin ⁡ φ c 2 sin ⁡ φ c ⋅ 1 V 0
B = sin ⁡ φ c − sin ⁡ φ e 2 sin ⁡ φ c sin ⁡ φ e ⋅ 1 V 0
C = − 1 + sin ⁡ φ e 2 sin ⁡ φ e ⋅ 1 V 0
where φc and φe are the internal friction angles during compression and extension, respectively, and V0 is the theoretical triaxial tensile strength.
By substituting the three parameters A, B, and C into Equation (1), they can be expressed in terms of the two internal friction angles and the vertex as follows:
1 − sin ⁡ φ c 2 sin ⁡ φ c ⋅ σ 1 V 0 + sin ⁡ φ c − sin ⁡ φ e 2 sin ⁡ φ c sin ⁡ φ e ⋅ σ 2 V 0 − 1 + sin ⁡ φ e 2 sin ⁡ φ e ⋅ σ 3 V 0 = 1
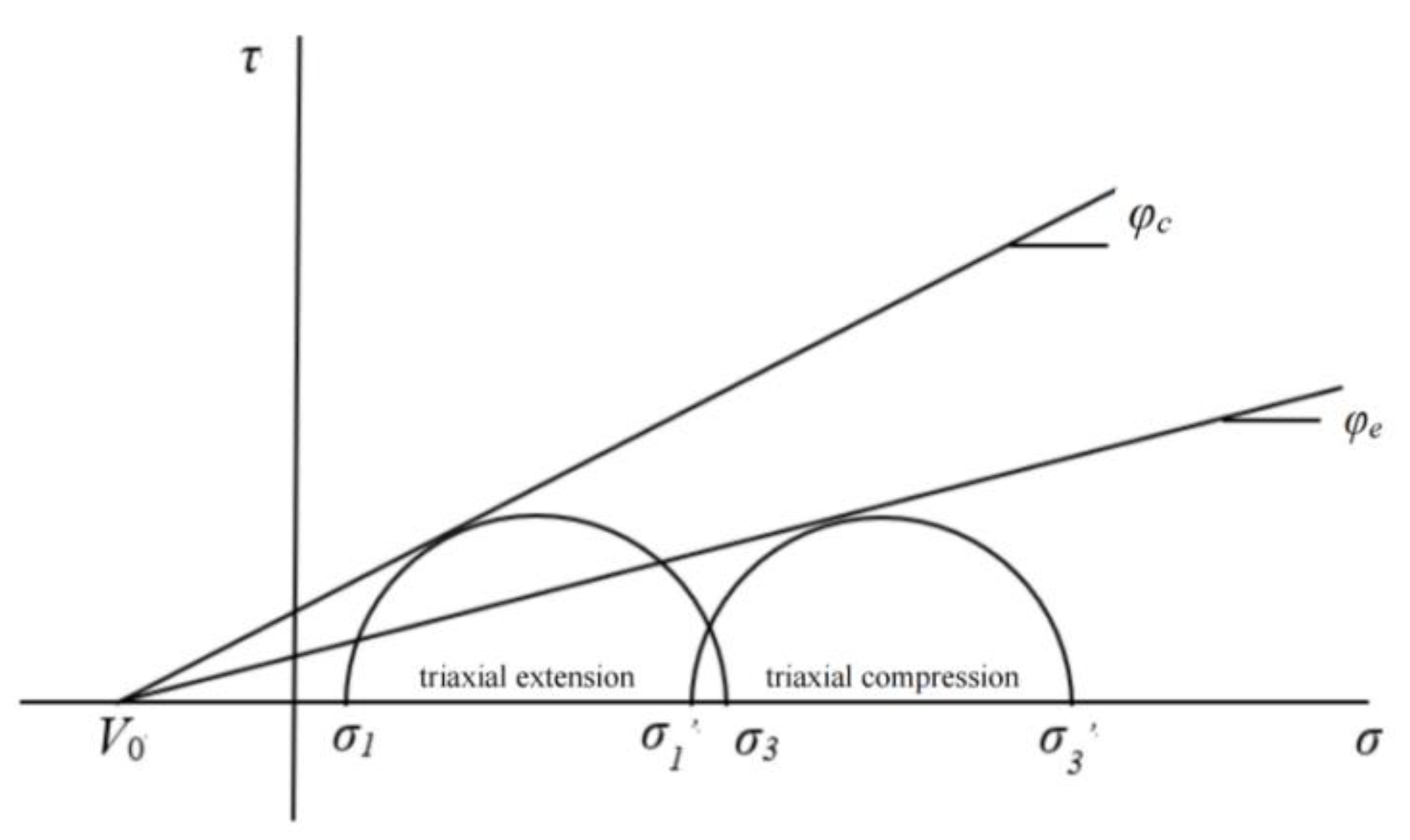
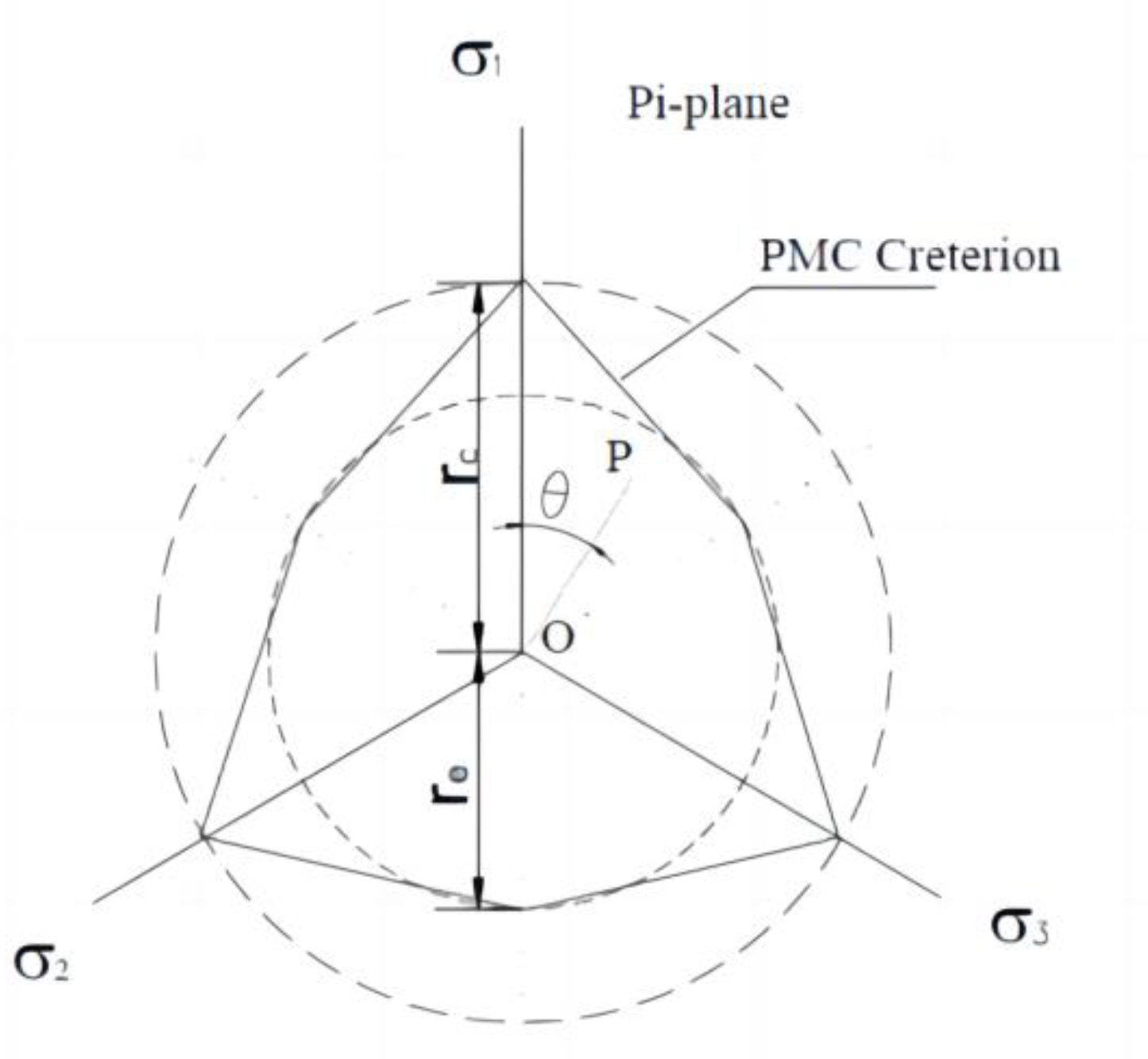
The PMC failure model constructs a failure surface in the principal stress space with a common vertex V0. The PMC criterion accounts for the influence of the intermediate principal stress by using the different friction angles of rock materials under compression and tension. The multiaxial linear failure criterion includes three principal stresses. These three material parameters can be obtained using conventional triaxial tests on rocks. The PMC model failure envelope is shown in Figure 1.
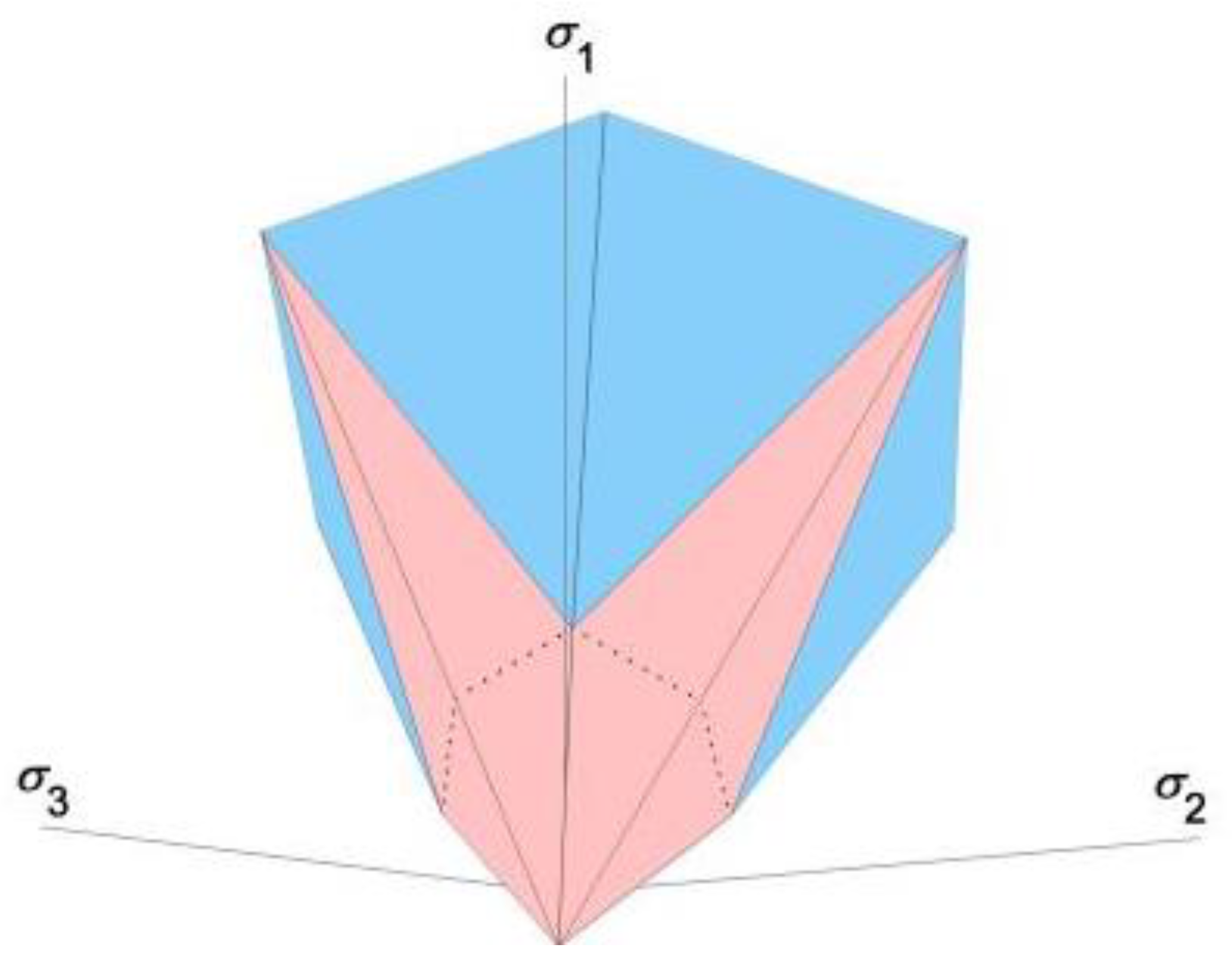
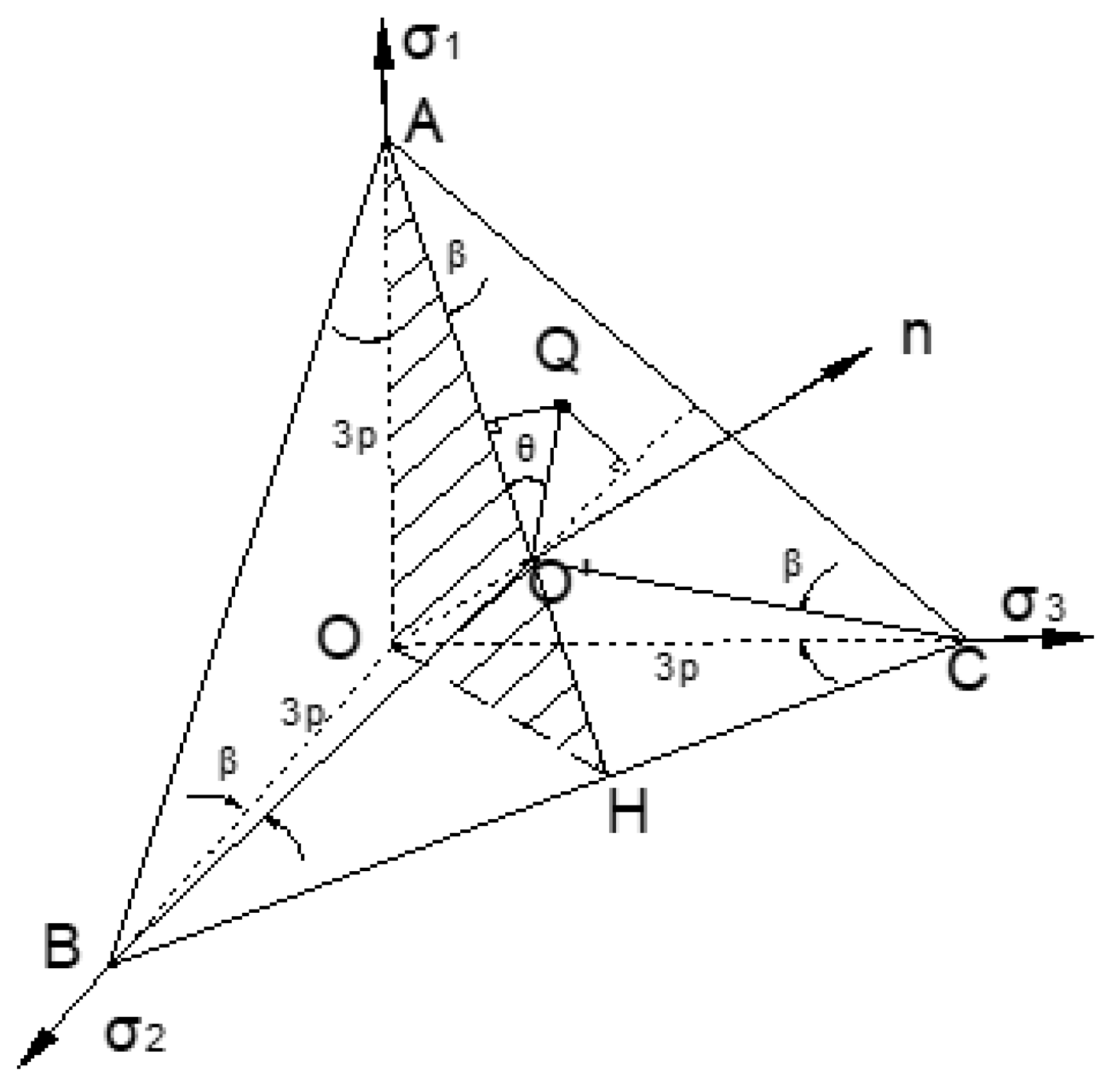
To capture the transition characteristics of failure mechanisms in geotechnical materials, the Labuz team developed a dodecahedral PMC model based on the PMC framework [3]. The PMC failure criterion constructs a dodecagonal failure surface in a piecewise linear manner by fitting two planes (Figure 2), which can be approximately regarded as a nonlinear failure surface. This model characterizes the mechanism by which rock materials transition from tensile to shear failure under increasing stress conditions.

2.2. Extensional-Strain Criterion and Brittle Failure

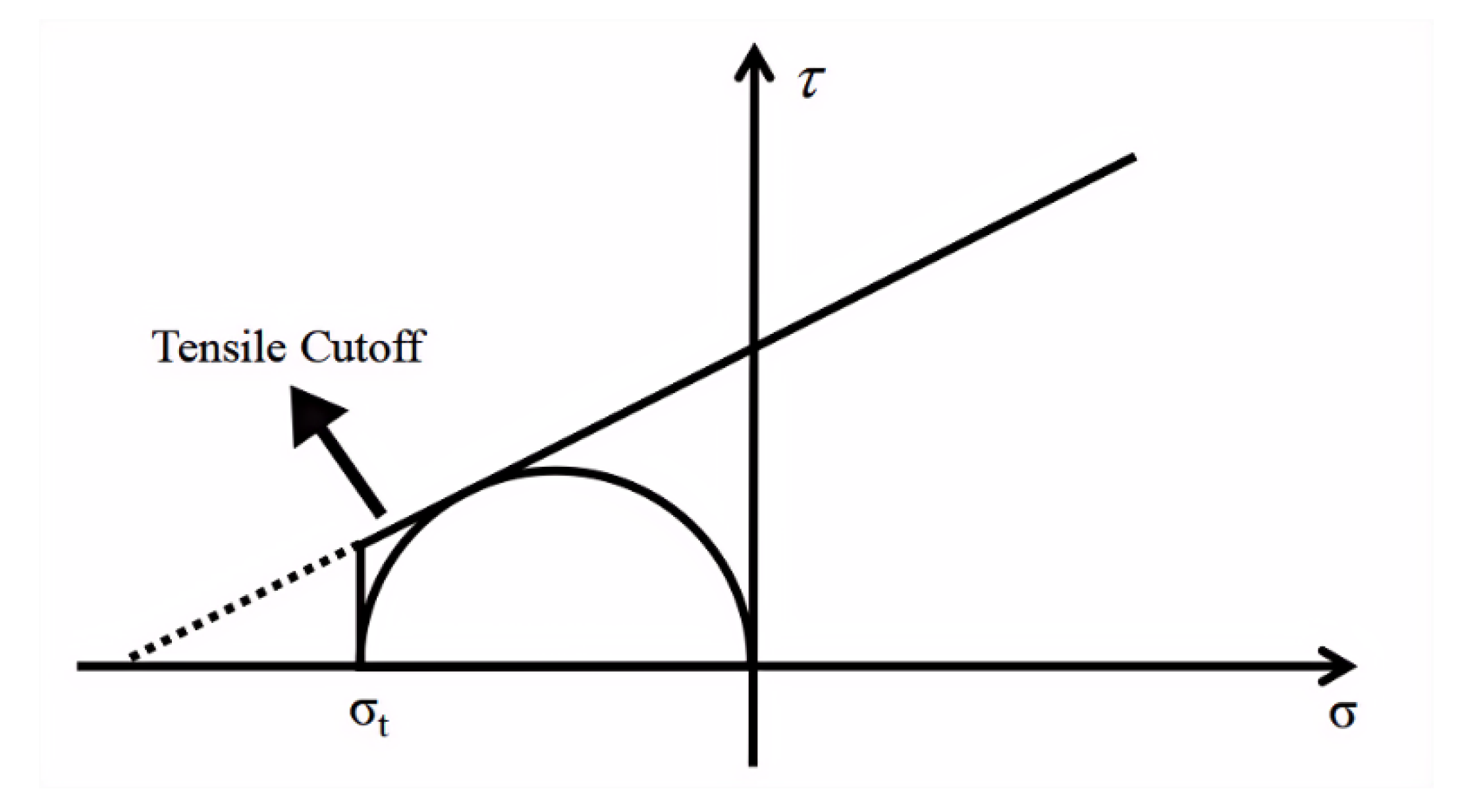
Rocks exhibit different failure modes under different confining pressures. Under tensile stress or low-pressure conditions, rocks primarily undergo tensile failure, not shear failure. However, the MC and PMC models only include failure criteria under compressive and pure shear stress conditions and do not address failure criteria under tensile-shear conditions [8]. Therefore, using the MC criterion to calculate rock failure under tensile or low-stress levels often results in significant errors. To address this issue, Paul (1961) modified the single inclined line of the MC criterion to an inclined line and a vertical line tangent to the uniaxial tensile stress circle, forming a two-segment linear strength curve known as the tensile cutoff criterion. The modified failure criterion is shown in Figure 3 [9], where σt represents the measured tensile strength. However, while the dodecagonal PMC model can characterize the mechanism of rock material transitioning from tensile failure to shear failure as stress conditions increase, it cannot represent the failure mechanism of rocks under tensile-shear conditions. Therefore, it is necessary to study the tensile-shear failure criterion of rocks and establish a connection with the PMC strength model.
Numerous scholars have investigated the strength criteria of rocks under tensile-shear conditions, and the resulting models can be roughly classified into hyperbolic models, parabolic models, and models based on the Hoek-Brown criterion [10,11,12,13,14,15,16]. However, relatively few studies have been conducted on this topic, and consequently, experimental data are lacking. Therefore, the tensile-shear constitutive models and failure criteria currently lack adequate support. Stacey (1981) predicted the brittle failure mechanisms of deep massive quartzites in South Africa using the extensional-strain criterion [7]. The results indicate that for materials exhibiting linear deformation behavior, failure may be related to extensional strain. The extensional strain of rocks can be calculated using the generalized Hooke's law, as follows:
ε 1 = 1 E [ σ 1 − μ ( σ 3 + σ 2 ) ] ε 2 = 1 E [ σ 2 − μ ( σ 1 + σ 3 ) ] ε 3 = 1 E [ σ 3 − μ ( σ 1 + σ 2 ) ]
where μ is the Poisson's ratio; E is the elastic modulus; and ε1, ε2, and ε3 are the first, second, and third principal strains, respectively. According to the extensional-strain criterion, when the minimum principal stress-strain exceeds the critical strain, the rock undergoes tensile failure. When ε 3 < 0 , the specimen experiences tensile strain, and when ε 3 > 0 , the specimen experiences compressive strain.

3. Methodology

3.1. Proposal of the PMC Model Considering Extensional Strain

Based on the dodecagonal PMC model, a failure surface was added that considers the extensional-strain criterion. A three-segment strength formula that accounts for both tensile-shear and compressive-shear failures is proposed. This model can be expressed using the three principal stresses as follows:
A ' σ Ⅰ + B ' σ Ⅱ + C ' σ Ⅲ = 1
where, Aʹ, Bʹ, and Cʹ are material constants; σ1, σ2, and σ3 are the maximum, intermediate, and minimum principal stresses, respectively. For the failure surface, based on the generalized Hooke's law, the failure conditions can be obtained as follows:
ε 1   o r   ε 2   o r   ε 3 = ε c
where the critical strain ε c = − σ t / E and is the tensile strength, μ is the Poisson's ratio, and E is the elastic modulus. When σ Ⅲ − μ ( σ Ⅰ + σ Ⅱ ) < 0 , the rock is in the tensile failure stage or transitioning from tensile to shear failure. According to the extensional-strain criterion, when ε 1 = ε c , the rock undergoes tensile failure, and the following can be derived:
− σ t = σ Ⅲ − μ ( σ Ⅰ + σ Ⅱ )
According to Equations (8) and (9):
A ' = B ' = − μ σ t
C ' = − 1 σ t
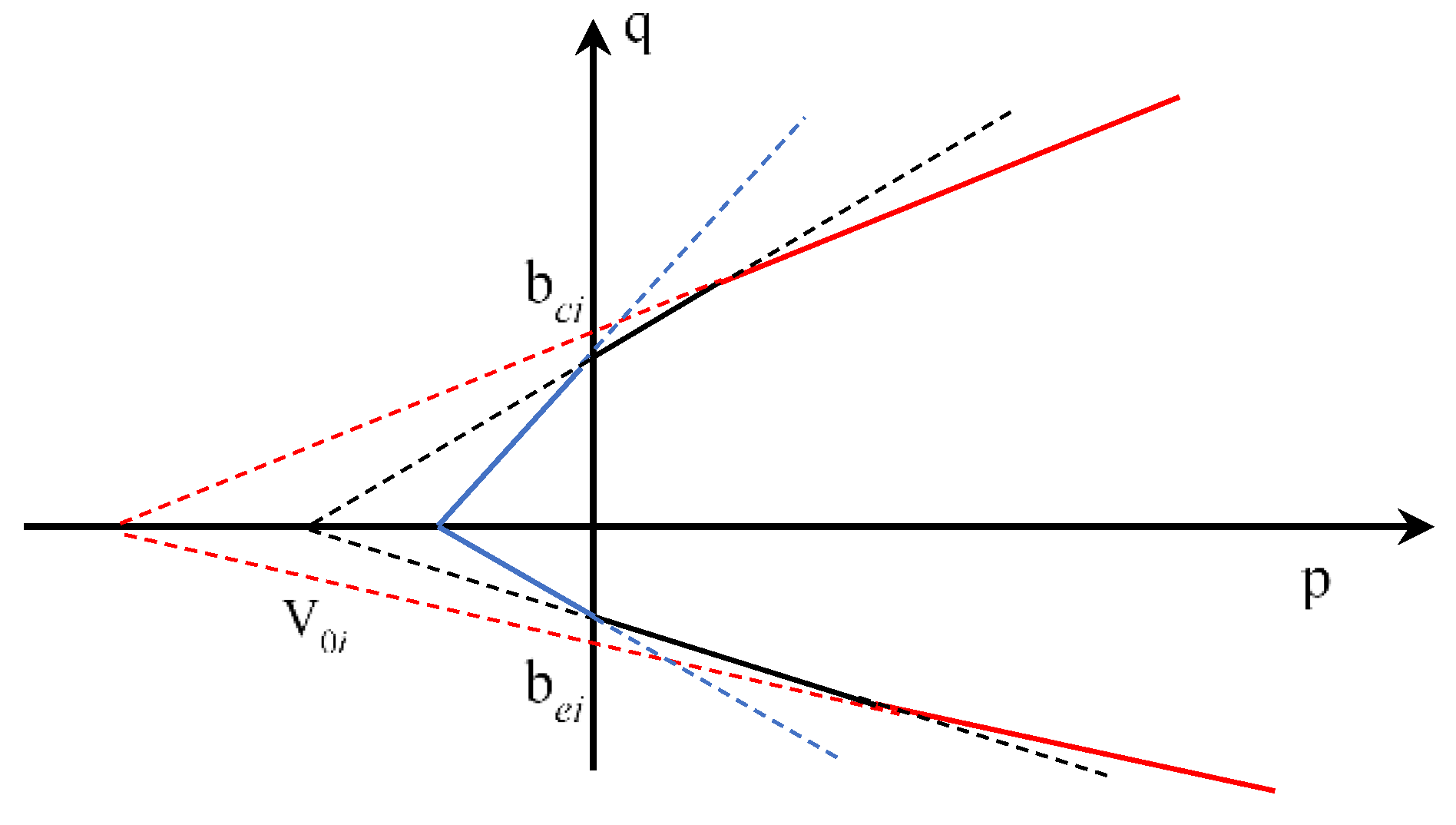
The three-segment linear form of the strength criterion can fundamentally satisfy the fitting of the transformation of rock failure mechanisms. Tensile or tensile-shear failure under tensile stress or low pressure is characterized by the extensional-strain criterion; as the pressure gradually increases, the rock failure mode transitions from tensile failure to shear failure; under higher stress levels, the rock failure mode transitions to conventional shear failure, as shown in Figure 4.
In the p-q plane, where the horizontal axis represents the mean stress p and the vertical axis represents the generalized shear stress q, the conventional PMC linear strength intersects the q axis at bci and bei and intersects the p axis at V0i. In the p-q plane, Equation (7) can be written as follows:
q = b θ i V 0 i p + b θ i = b θ i p V 0 i + 1
where bθi is the intercept of the conventional PMC linear strength line in the p-q plane, and V0i is its root.
By fitting the failure curve using a piecewise linear approach, a PMC strength formula that considers extensional strain can be obtained. In the p-q plane, the formula can be written as follows:
q c n = min ⁡ b c n p V 0 i + 1        
q e n = min ⁡ b e n p V 0 i + 1        
where n represents the failure mechanism number and qc(n) and qe(n) are the critical shear stress values under different failure mechanisms. Similarly, bcn and ben represent the intercepts of the PMC linear strength lines on the p-q plane under different failure mechanisms, and V0i represents their roots.

3.2. Unified Equation of the Multiple Failure Mechanism Model

Equation (14) is presented in the form of intercepts and other data, without specific expressive significance. For spatial loading, the influence of the Lode angle should be considered. Therefore, under the premise of spatial loading, deriving a model for multiple failure mechanisms is more effective. Based on the PMC criterion, a general model is proposed to obtain different solutions under various failure mechanisms.
In the PMC model, the strength from the meridional plane is extended to the stress space as follows:
f = σ 1 1 − s i n φ c 2 s i n φ c + σ 2 s i n φ c − s i n φ e 2 s i n φ c s i n φ e − σ 3 1 + s i n φ e 2 s i n φ e − V 0 = 0
where V0 is the assumed strength under triaxial equal tensile conditions; φc is the internal friction angle under triaxial compression; and φe is the internal friction angle under triaxial extension. The triaxial compression and extension strength lines at the same V0 point can be considered a set, where n denotes the failure mechanism number. The definition of the stress Lode angle is shown in Figure 5. The Lode angle (0° ≤ θ ≤ 60°) is the rotation angle from the maximum principal stress axis (θ = 0°) to the minimum principal stress axis.
The maximum radius on the π-plane corresponds to the rc value under triaxial compression, and the minimum radius corresponds to the re value under triaxial extension. Let the stress state at any point on this π-plane be (p, q, θ), where p is the mean stress, q is the generalized shear stress, and θ is the Lode angle. The relationship with the principal stresses is as follows:
p = σ 1 + σ 2 + σ 3 3
q = ( σ 1 − σ 2 ) 2 + ( σ 2 − σ 3 ) 2 + ( σ 3 − σ 1 ) 2 2
As shown in Figure 5, with the centroid O of the π-plane as the center, the distance from any point on the plane to the center represents the magnitude of the deviatoric stress in the stress space. Taking the meridional plane as an example, its radius is determined as follows:
r θ = ( p + V 0 ) tan ⁡ φ θ
where rθ and φθ are the radius and the corresponding internal friction angle on the π-plane when the Lode angle is θ, and the connection line between the stress point and the far point is the slope line. When the stress state is triaxial compression, φθ = φc; when it is triaxial extension, φθ = φe.
On the π-plane, through the stress point (p, q, θ), perpendicular lines are drawn to the three coordinate axes, intersecting the axes at the points ( σ I ` , 0, 0), (0, σ I I ` , 0), and (0, 0, σ I I I ` ). Here, σ I ` ​, σ I I ` , and σ I I I ` represent the principal stresses, but their magnitudes are not determined. In the quadrant shown in Figure 5, the order of the coordinates on the three axes is σ1 > σ2 > σ3. Roman numerals were used to indicate the order of the principal stress values. Thus:
σ I ‵ = r θ cos ⁡ θ
σ I I ‵ = r θ cos ⁡ ( 6 0 ° − θ )
The relationship between the line segment on the π-plane and the principal stress space coordinates is shown in Figure 6. The length of the AH line segment is the height h of the equilateral triangle of the slope plane, and the intercepts of the slope plane along the three coordinate axes are all 3p. The geometric relationship yields:
σ 1 σ I ' + h 3 = 3 p h
Since the π-plane is an equilateral plane, h = 3 6 2 p . Substituting this into the equation yields σ 1 = 6 3 σ I ' + p , and substituting into Equation (19) results in the following:
σ 1 = 6 3 r θ cos ⁡ θ + p
Similarly, the following can be obtained:
σ 2 = p − 6 3 σ I I I ‵ = p − 6 3 r θ cos ⁡ ( 6 0 ° − θ )
In the equation, p represents the mean stress. Since the principal stresses on the π-plane are equal, the stress value on the σ3 axis corresponds to the intermediate principal stress, which is as follows:
σ 3 = 3 p − σ 1 − σ 2 = p − 6 3 r θ cos ⁡ θ − cos ⁡ 6 0 ∘ − θ = p − 6 3 r θ cos ⁡ 6 0 ∘ + θ
Substituting Equations (22) to (24) into Equation (15) and rearranging yields results in the following:
6 3 r θ [ cos ⁡ θ ⋅ 1 − s i n φ c 2 s i n φ c − cos ⁡ 6 0 ∘ + θ ⋅ s i n φ c − s i n φ e 2 s i n φ c s i n φ e + cos ⁡ 6 0 ∘ − θ ⋅ 1 + s i n φ e 2 s i n φ e ] − p + V 0 = 0
The relationship between the π-plane and the principal stress space shows that:
r θ = ( p + V 0 ) tan ⁡ φ θ = 2 3 q
In the equation, q is the generalized shear stress. Substituting Equation (26) into Equation (25) yields:
2 3 q [ cos ⁡ θ ⋅ 1 − s i n φ c 2 s i n φ c − cos ⁡ 6 0 ∘ + θ ⋅ s i n φ c − s i n φ e 2 s i n φ c s i n φ e + cos ⁡ 6 0 ∘ − θ ⋅ 1 + s i n φ e 2 s i n φ e ] − p + V 0 = 0
Which can be rearranged as follows:
q = 6 s i n φ c s i n φ e p + V 0 2 3 s i n φ c s i n θ − 2 s i n φ c s i n φ e cos ⁡ 6 0 ∘ + θ + 2 3 s i n φ e sin ⁡ 6 0 ∘ − θ
When θ = 0°, the stress state corresponds to conventional triaxial compression. From Equation (28), the following expression is obtained:
q = 6 sin ⁡ φ c 3 − sin ⁡ φ c ( p + V 0 )
When θ = 60°, the stress state corresponds to triaxial extension. From Equation (28), the following is obtained:
q = 6 sin ⁡ φ e 3 + sin ⁡ φ e ( p + V 0 )
The calculation results are consistent with those obtained from the PMC strength Equation (15). Therefore, based on Equation (28), the general formula for the strength criterion in stress space under the coupled influence of multiple failure mechanisms can be derived as:
q = m i n 6 s i n φ c i s i n φ e i p + V 0 2 3 s i n φ c i s i n θ − 2 s i n φ c i s i n φ e i cos ⁡ 6 0 ∘ + θ + 2 3 s i n φ e i sin ⁡ 6 0 ∘ − θ ( i = 1 , . . . , n )
where q is the generalized shear stress; p is the mean stress; θ is the stress Lode angle (with the axis of the maximum principal stress as 0°); φc is the internal friction angle under triaxial compression; φe is the internal friction angle under triaxial extension; V0 is the assumed strength under triaxial equal tensile conditions; and n is the failure mechanism group.
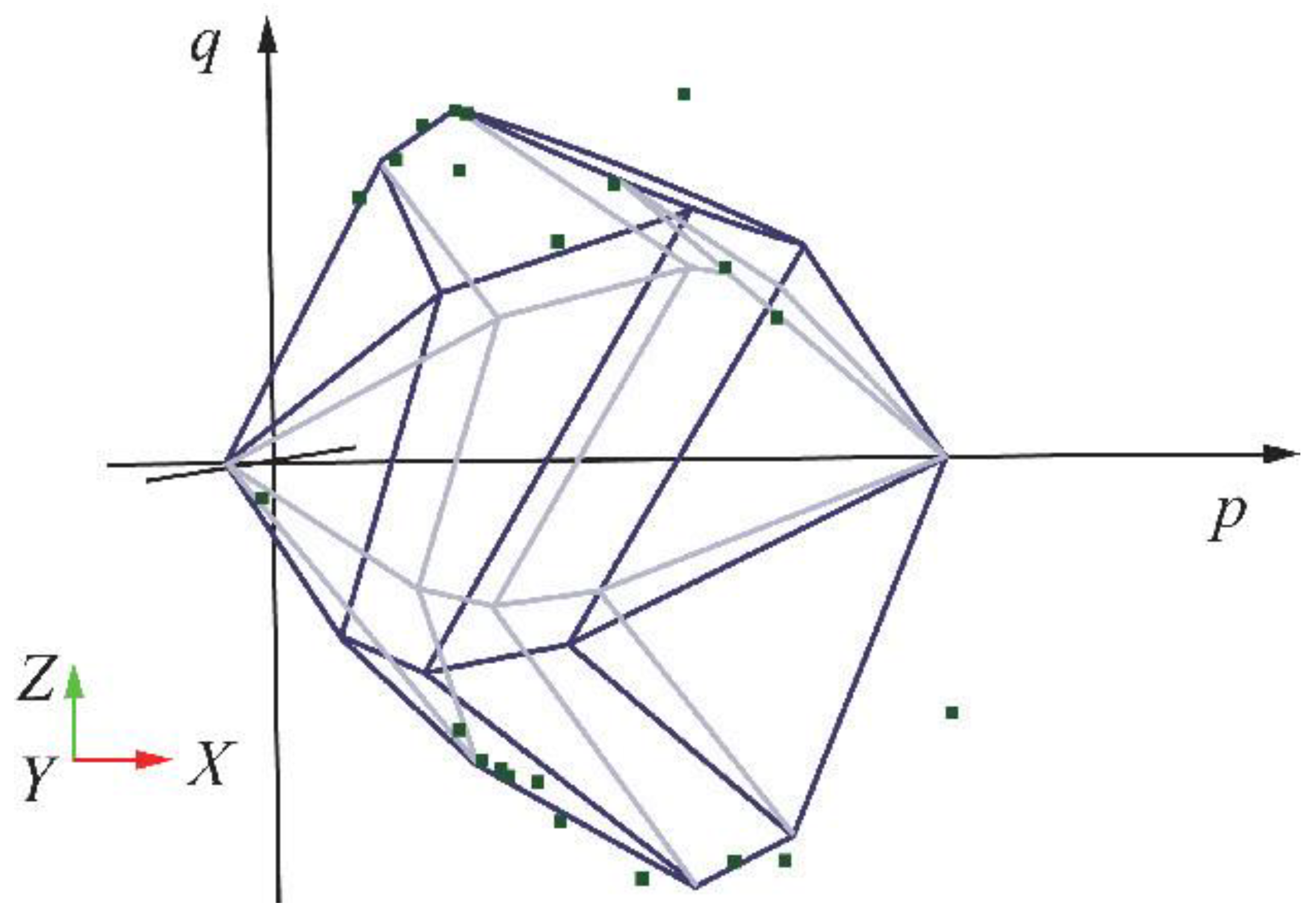
When n = 1, the formula corresponds to the conventional PMC model; when n ≥ 2, the formula represents the multiple failure mechanism model. Specifically, when forming a yield model similar to a "cap" the shear strength envelope can effectively explain the pore collapse phenomenon in porous rocks. Based on the data reported by Folta et al., the data fitting curve can be obtained as shown in Figure 7 [17]:

3.3. Parameter Fitting Method

Zeng et al. proposed a new fitting method based on the transformation of stress invariant relationships in the p-q plane [5,18]. They derived a parameter acquisition method for a multiple failure mechanism model based on this approach.
In a π-plane, any given stress state can be represented in cylindrical coordinates (rθ, θ, ρ). A schematic of the PMC failure surface in the π-plane when p = 0 is shown in Figure 8.
represents the failure envelope line. θ represents the Lode angle and rθ is the radius of the π-plane corresponding to the Lode angle θ and the slope line’s apical angle. rc is the intercept in the axisymmetric compression line and re represents the intercept in the multiaxial line.
The intercept bθ needs to be defined, and a relationship should be established between bθ and rθ. The failure envelope line y = k x + r c in the rectangular coordinate system can be expressed in terms of rθ and θ as follows:
r θ cos ⁡ θ = k ⋅ r θ sin ⁡ θ + r c
where θ represents the Lode angle and rθ is the radius of the π-plane corresponding to the Lode angle θ and the slope line’s apical angle. rc is the intercept in the axisymmetric compression line. In the π-plane, k is the slope of the line, and rθ is as follows:
r θ = r c cos ⁡ θ − k sin ⁡ θ
In any π-plane, the relationship between rθ and qθ can be obtained through the second stress invariant J2 as follows:
r θ = 2 3 q θ
where qθ is the shear stress in the direction of rθ. In the multiaxial line, qθ = bθ; in the axisymmetric compression line, qθ = bc, where bc is the shear stress intercept in the axisymmetric compression line. In the axisymmetric extension line, qθ = bθ. Therefore, rθ can be written as:
r θ = 2 3 b θ r c = 2 3 b c r e = 2 3 b e
In the formula, be represents the shear stress intercept in the axisymmetric extension line, and re represents the intercept in the multiaxial line. Substituting Equation (35) into Equation (33) yields be as follows:
b θ = b c cos ⁡ θ − k sin ⁡ θ
In the p-q plane, Equation (36) represents the functional relationship of the intercept bθ and the unknown variable k needs to be determined. In the π-plane, where the failure line passes through the axisymmetric extension point (rθ = re, θ = 60°), Equation (32) can be written as:
r e = 3 ⋅ k ⋅ r e + 2 r c
Considering Equation (35), the ratio α = r c r e can be written as:
α = r c r e = 2 3 ⋅ b c 2 3 ⋅ b e = b c b e
Substituting Equation (38) into Equation (37) yields:
k = 1 − 2 α 3
Knowing the expressions for bθ and k, the general Equation (39) for the PMC criterion in the p-q plane can be written as:
b c V 0 p + k q sin ⁡ θ + b c = q cos ⁡ θ
According to Equation (40), a linear equation system can be constructed using the data from axial compression, extension, and multiaxial tests, with θ under various conditions. In some studies, θ is equivalent to the Lode angle, but differences exist. The original definition of the Lode angle ranges from −30° to 30°, but in the coordinate system, θ ranges from 0° to 360°. However, θ ranging from 0° to 60° is sufficient for isotropic expressions. Whereas θ = 0° corresponds to axisymmetric compression and θ = 60°corresponds to axisymmetric extension. The θ value in multiaxial stress states can be calculated from the principal stresses as follows:
tan ⁡ θ = 3 σ Ⅱ − σ Ⅲ 2 σ І − σ Ⅱ − σ Ⅲ
where, σ Ⅰ ,   σ Ⅱ , and σ Ⅲ represent the maximum, intermediate, and minimum principal stresses, respectively. Strength data under axisymmetric and multiaxial conditions are expressed as σ І ,     σ П ,   a n d   σ Ш , and by substituting these into Equation (40), the p, q, and θ for each stress state can be determined. Using these three parameters, a system of linear equations A·x = B is generated:
p 1 q 1 sin ⁡ θ 1 1 p 2 q 2 sin ⁡ θ 2 1 ⋮ ⋮ ⋮ p n q n sin ⁡ θ n 1 b c V 0 k b c = q 1 cos ⁡ θ 1 q 2 cos ⁡ θ 2 ⋮ q n cos ⁡ θ n
where A is the rectangular data matrix, x is the parameter vector, and B is the data vector.
Using the least squares method to solve Equation (42), bc/V0, k, and b are obtained. According to the expressions for the axisymmetric compression and extension lines in the p-q plane, φc and φe are calculated as follows:
sin ⁡ φ c = 3 b c 6 V 0 + b c sin ⁡ φ e = 3 b e 6 V 0 − b e
Thus, the material parameters φc , φe, and V0 of the general formula for the strength criterion in stress space under the coupled influence of multiple failure mechanisms (Equation 31) can be solved.

4. Experiments

4.1. Experimental Conditions

Experiments were conducted on Sichuan yellow sandstone and deep granite from the Jinchuan No. 2 mining area. High-pressure triaxial compression tests were performed using the TAW-2000 microcomputer-controlled electro-hydraulic servo rock triaxial testing machine and the portable self-sealing rock triaxial test high-pressure chamber pressurization system.
Standard rock mechanics specimens with dimensions of φ30 mm × 60 mm were prepared (Figure 9).
(a) (b)
This conventional triaxial test relies on two independent loading systems and therefore cannot use the system settings to load axial and confining pressures simultaneously at the same rate. To ensure quasi-static conditions and reduce experimental error, an independent stepwise loading method for axial and confining pressures was adopted. The stepwise loading procedure is shown in Table 1. During the experiment, axial loading was initially controlled by stress, with a loading rate of 100 N/s. After reaching the hydrostatic pressure state, the radial pressure was maintained at a constant level throughout the experiment. Axial loading was then continued at the same rate until approximately 50% of the peak strength was reached, at which point it was switched to deformation control with a loading rate of 0.03 mm/min. During confining pressure loading, coarse control was first applied, with a loading rate of 1 MPa/s. When approaching 5 MPa of the hydrostatic pressure state, fine control was applied using a micro-adjustment handwheel, with a loading rate of 0.2 MPa/s.

4.2. Experimental Results

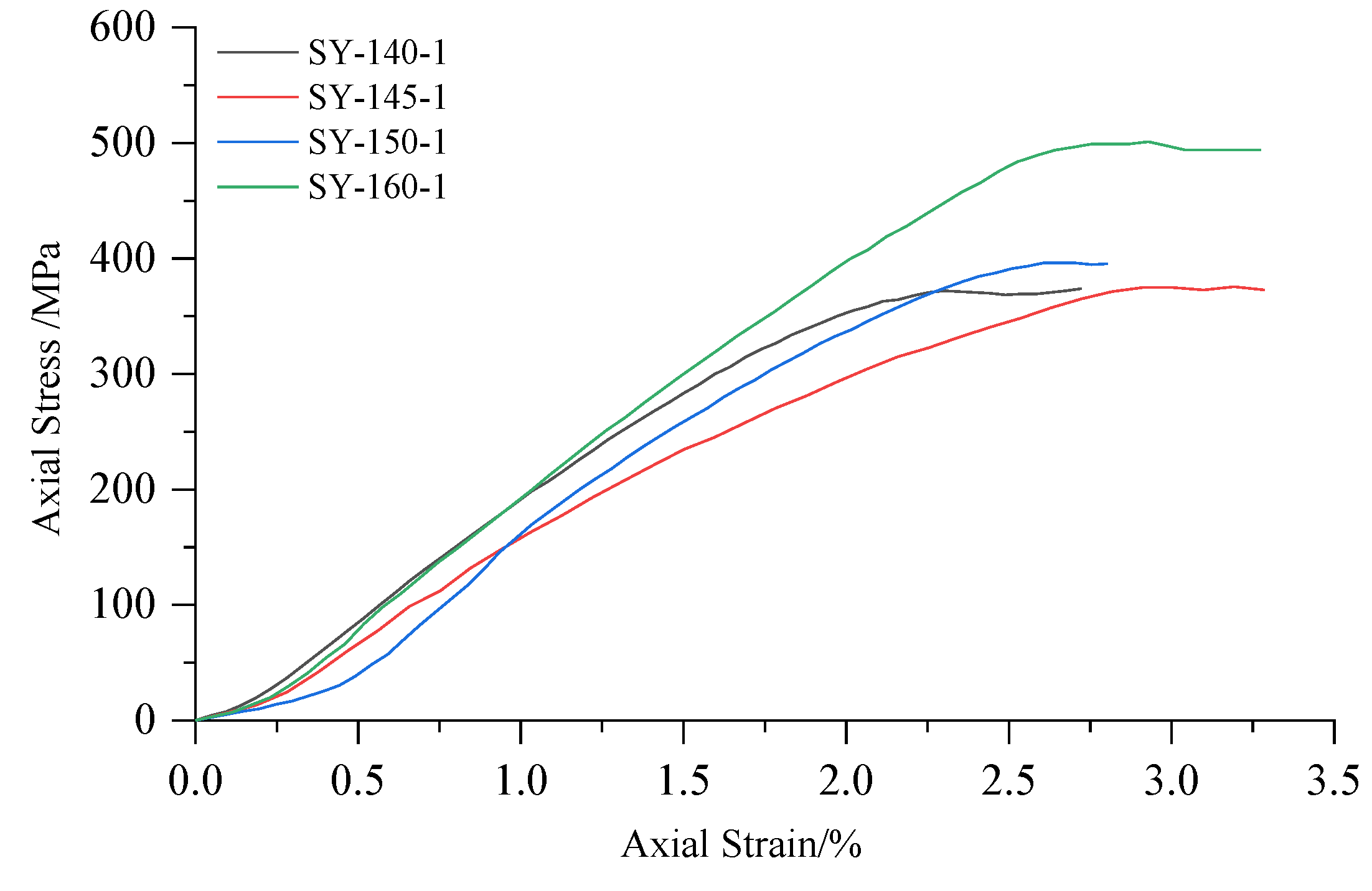
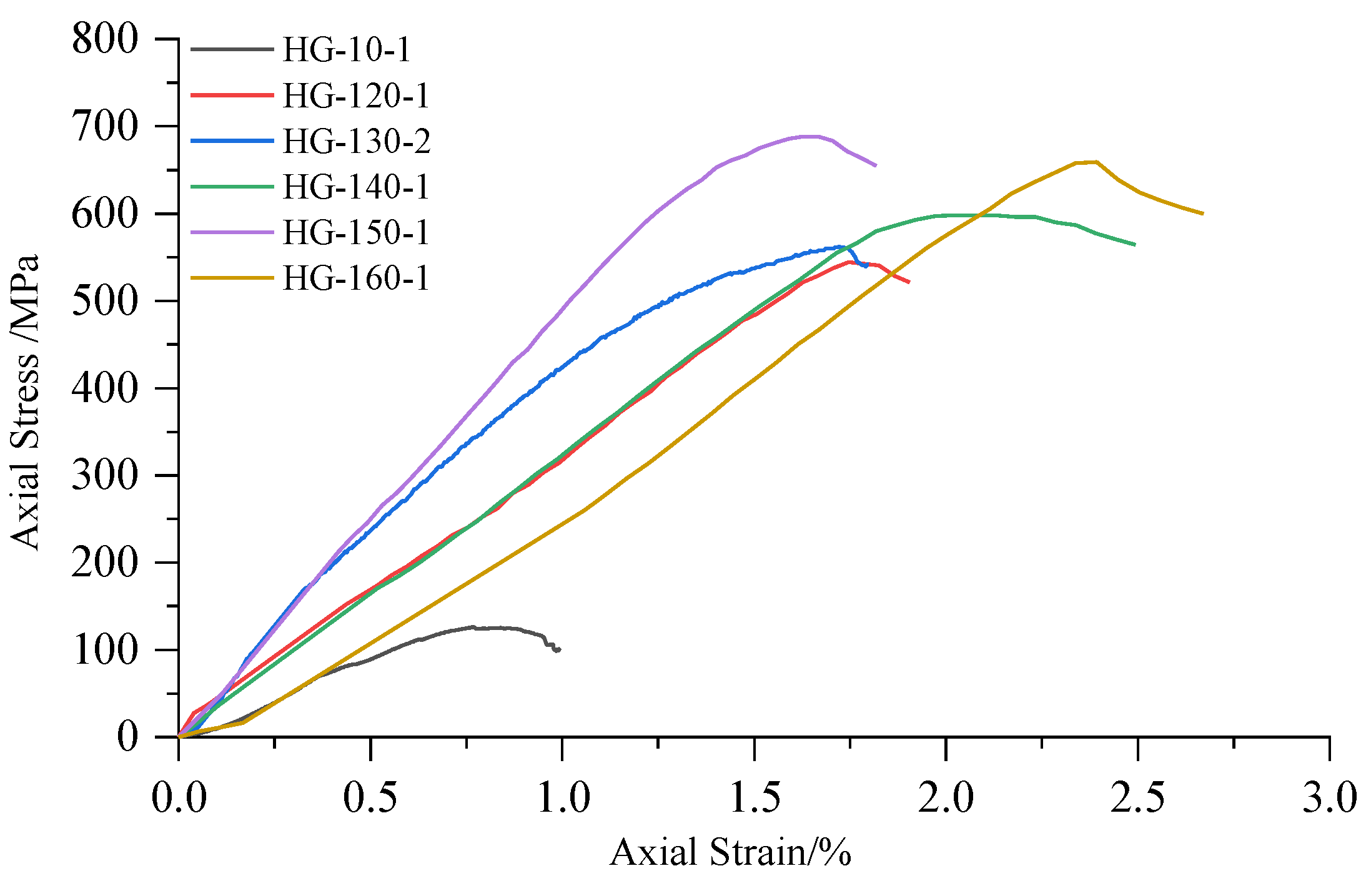
High-confining pressure conventional triaxial tests were conducted on Sichuan yellow sandstone and Jinchuan granite using the above stepwise loading scheme. For the Sichuan sandstone, 16 groups of different confining pressures ranging from 0 to 170 MPa were set, whereas for the Jinchuan granite, 13 groups of different confining pressures ranging from 0 to 160 MPa were set. The stress-strain curves for each rock sample during the tests are shown in Figure 10 and Figure 11. The data for principal stress, mean stress and deviatoric stress at failure are presented in Table 2. The failure modes of the samples are shown in Figure 12 and Figure 13. Both the Sichuan yellow sandstone and Jinchuan granite exhibited similar failure mode trends with increasing confining pressure: under low confining pressure, the failure is primarily shear failure, with the angle of the failure plane decreasing as the confining pressure increases; whereas under higher confining pressure, the angle continues to decrease, gradually exhibiting a trend towards compressive-shear failure.

4.3. Applicability of the PMC Model for Strength with Multiple Failure Mechanisms

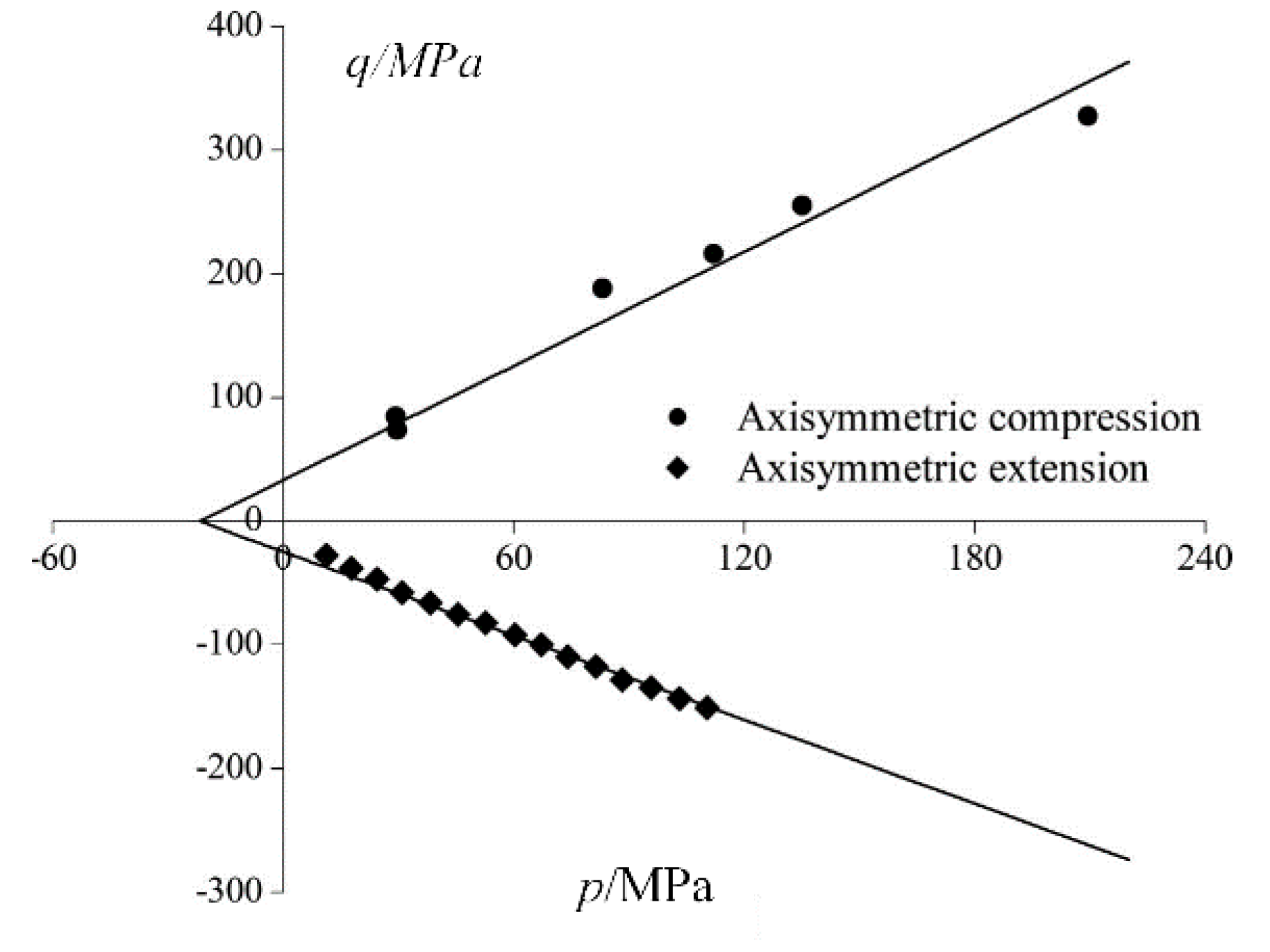
When n = 1, analysis is conducted using Berea sandstone experimental data (Bobich) (Table 3) [19]. The fitted failure surface in the p-q plane with the experimental data (conventional triaxial compression tests and conventional triaxial extension tests) is shown in Figure 14. The negative axis of q represents triaxial extension tests, and the positive axis of q represents triaxial compression tests. The PMC criterion fitting results closely match the experimental results, and the friction angle in conventional triaxial compression tests is smaller than in conventional triaxial extension tests. The difference between φc and φe illustrates the influence of the intermediate principal stress.
When n = 2, the experimental data for Jinchuan granite samples is analyzed. To ensure V0(1) ≥ V0(2), the region is divided into two segments: p ≥ 200 MPa and p ≤ 200 MPa. The six-parameter PMC model fitting results are shown in Table 4. The six-parameter PMC model for granite in the p-q plane is shown in Figure 15. The granite strength exhibits distinct piecewise linear characteristics, which can be fitted using the six-parameter PMC model. However, due to the lack of triaxial extension test data, this model is only applicable to the transitional stage of tensile-shear failure in rocks and cannot characterize the tensile failure mode of granite.
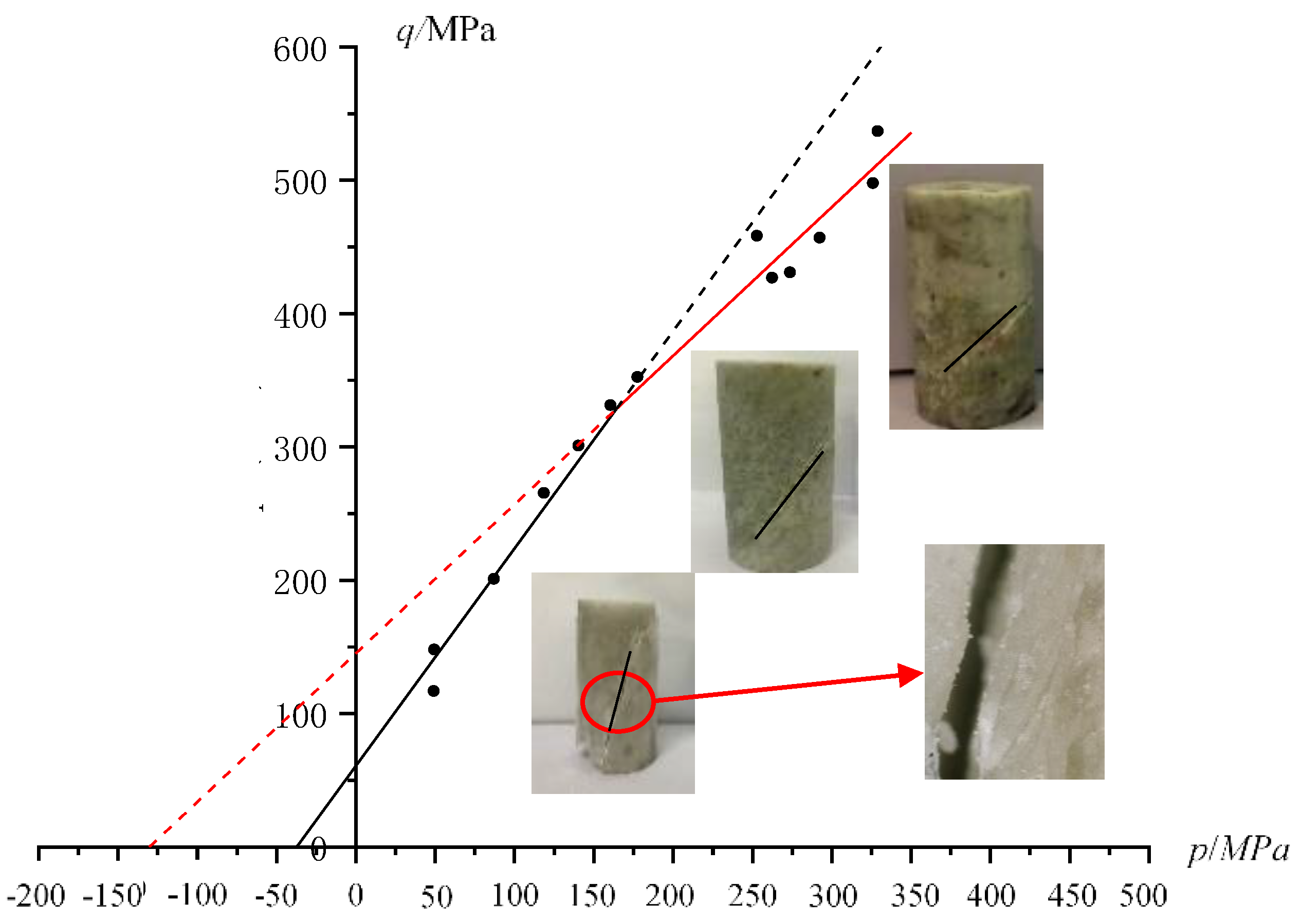
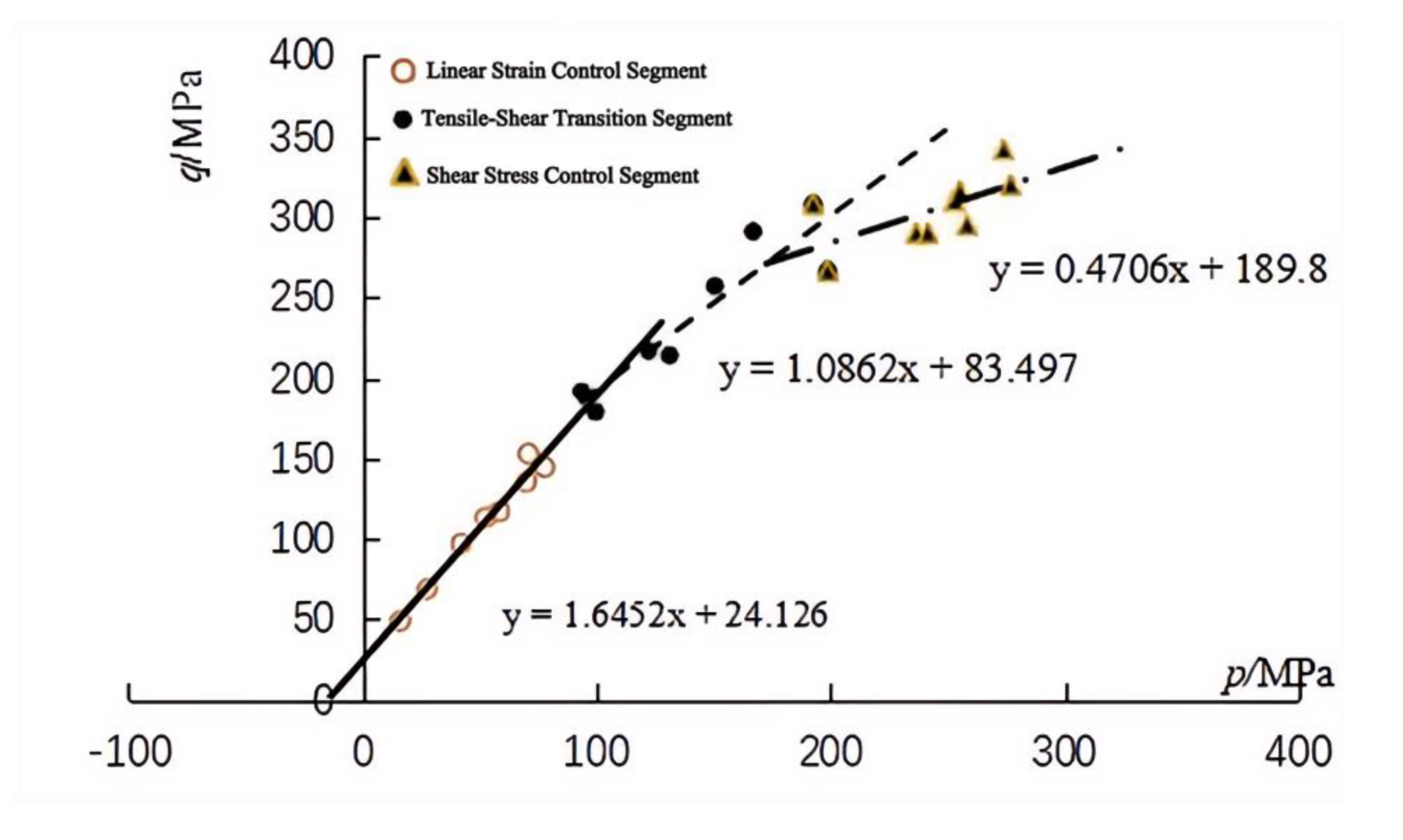
When n ＞ 2, the experimental data for Sichuan yellow sandstone samples is analyzed, and the fitting results are shown in Table 5. The fitted PMC failure surface with the experimental data in the p-q plane is shown in Figure 16. The strength of the yellow sandstone exhibits distinct piecewise strength characteristics, which conform to strength patterns under the influence of multiple failure mechanisms (Figure 16).

5. Conclusions

(1) In light of the limitations of traditional rock strength theories, which consider only the impact of a single failure mechanism, and recognizing that tensile and splitting failures of rocks under low-stress conditions conform to the maximum elongation strain theory while shear-type failures occur at high-pressure levels, a multiple failure mechanism theory model for rocks has been proposed based on the PMC piecewise linear model. This model establishes a unified expression for multiple failure modes in the form of inequalities. Experimental verification has demonstrated that this criterion can effectively achieve nonlinear fitting for granite, sandstone, and other rock types.
(2) The rock multiple failure mechanism theory model's failure criterion can encompass the MC strength theory, the PMC strength model, and the 12-sided PMC model. It can also be extended to derive the asymmetric PMC-BPMC model, which considers isotropic yield. By integrating the principles of plastic flow rules and hardening laws, the model can be expanded to analyze and explain the mechanisms of pore collapse phenomena in rocks under high pressure, corresponding to the specialized "cap" yield model mentioned in the text.
(3) Using experimental data from Jinchuan granite and Sichuan yellow sandstone, the rock multiple failure mechanism theory model was fitted for n = 1 (considering only shear failure), n = 2 (considering the transition from shear failure to tensile failure), and n ＞ 2 (coexistence of tensile and shear failure). The results indicate that the rock strength exhibits distinct segmented strength characteristics, consistent with the strength patterns under the influence of multiple failure mechanisms. This validates the applicability of the multiple failure mechanism theory model to rock materials. However, since this study only considers generalized shear stress, mean stress, and stress Lode angle parameters in the rock failure process, other minor stress influences and environmental factors were not discussed, presenting certain limitations.

Author Contributions

Conceptualization, Shiqi Li; Yuan Li; Dongjue Fan and Liang Zhao; Software, Shiqi Li and Yuan Li; Research, Shiqi Li and Yuan; Abstract, Shiqi Li and Yuan Li; Validation, Yuan Li; Formal analysis, Shiqi Li and Liang Zhao; Data curation, Shiqi Li; Litian Zhang and Dongjue Fan; Original draft, Shiqi Li and Litian Zhang ; Review & editing, Yuan Li; Literature review, Shiqi Li and Yuan Li; Figures: Yuan Li and Shiqi Li; Tables: Shiqi Li and Yuan Li; Translation: Shiqi Li and Litian Zhang; Funding: Yuan Li. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Key R&D Program of China (grant number 15013130).

Data Availability Statement

The authors have not obtained permission to publish the data. Therefore, the data can be obtained from the corresponding author upon reasonable request.

Acknowledgments

Experimental equipment and technical support were provided by the University of Science and Technology Beijing. Data support was provided by Litian Zhang, a master's graduate from the University of Science and Technology Beijing.

Conflicts of Interest

The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. Paul, B. Generalized pyramidal fracture and yield criteria. Int. J. Solids Struct. 1968, 4, 175–196. [Google Scholar] [CrossRef]
  2. Paul, B. Macroscopic criteria for plastic flow and brittle fracture. Fracture 1968, 2, 313–496. [Google Scholar]
  3. Meyer, J.P.; Labuz, J.F. Linear failure criteria with three principal stresses. Int. J. Rock Mech. Min. Sci. 2013, 60, 180–187. [Google Scholar] [CrossRef]
  4. Makhnenko, R.; Labuz, J. Plane strain testing with passive restraint. Rock Mech. Rock Eng. 2014, 47, 2021–2029. [Google Scholar] [CrossRef]
  5. Zeng, F.; Li, Y.; Labuz, J.F. Paul-Mohr-Coulomb failure criterion for geomaterials. J. Geotech. Geoenviron. Eng. 2018, 144, 06017018. [Google Scholar] [CrossRef]
  6. Dehler, W.; Labuz, J.F. Stress path testing of an anisotropic sandstone. J. Geotech. Geoenviron. Eng. 2007, 133, 116–119. [Google Scholar] [CrossRef]
  7. Stacey, T.R. A simple extension strain criterion for fracture of brittle rock. In Int. J. Rock Mech. Min. Sci. Geomech. Admin. 1981, 18, 469–474. [Google Scholar] [CrossRef]
  8. Huang, S. Study on mechanical model of brittle rock under high stress condition and its engineering applications. Institute of Rock and Soil Mechanics. Graduate School of Chinese Academy of Sciences; Wuhan Institute of Geotechnical Mechanics: Wuhan, China, 2008. [Google Scholar]
  9. Paul, B. A modification of the coulomb-mohr theory of fracture. J. Appl. Mech. 1961, 28, 259–268. [Google Scholar] [CrossRef]
  10. Zhou, H. M.; Xiong, S. H.; Liu, X. H.; Yang, Z. H.; Kong, X. H. In-situ tension-shear tests and strength criterion studies on TGP shiplock slope rock mass. Yanshilixue Yu Gongcheng Xuebao. Chin. J. Rock Mech. Eng. 2005, 24, 4418–4421. [Google Scholar]
  11. Sun, J. Theory and Practice of Underground Engineering Design; Shanghai Science and Technology Publishing House: Shanghai, China, 1996. [Google Scholar]
  12. Zhou, H.M.; Xu, P.; Sheng, Q.; YU, Y. Application of new technology of rock mechanics test in TGP. J. Yangtze River Sci. Res. Inst. 2001, 18, 68. [Google Scholar]
  13. Liu, F.Z. Study on mechanical property of rock in tension and tension shear state. J. Yangtze River Sci. Res. Inst. 1996, 13, 35. [Google Scholar]
  14. Zhu, Z.L.; Li, J.L.; Wang, K.P. Experimental research on rock tension-shear strength and creep rupture related to the three gorges project. J. Univ. Hydraul. Electr. Eng. (Yichang) 1998, 20, 16–19. [Google Scholar]
  15. Jianlin, L. Experimental study on rheological properties of rock in tension and shear. J. Geotech. Eng. 2000, 22, 299–303. [Google Scholar]
  16. Li, P.; Yin, Y. Modification of Drucker-Prager criterion in tensile shear region. Chin. J. Rock Mech. Eng. 2010, 29, 3029–3033. [Google Scholar]
  17. Folta, B.L. Strength Testing Under Multi-axial Stress States; University of Minnesota: Minneapolis, MN, USA, 2016. [Google Scholar]
  18. Labuz, J.F.; Zeng, F.; Makhnenko, R.; Li, Y. Brittle failure of rock: A review and general linear criterion. J. Struct. Geol. 2018, 112, 7–28. [Google Scholar] [CrossRef]
  19. Bobich, J.K. Experimental Analysis of the Extension to Shear Fracture Transition in Berea Sandstone; Texas A&M University, College Station: TX, USA, 2005. [Google Scholar]
Preprints 114145 g001
Figure 1. PMC model failure envelope. The internal friction angles during compression and extension are φc and φe respectively. V0 is the theoretical triaxial tensile strength. The three principal stresses are σ1, σ2, and σ3.
Figure 1. PMC model failure envelope. The internal friction angles during compression and extension are φc and φe respectively. V0 is the theoretical triaxial tensile strength. The three principal stresses are σ1, σ2, and σ3.
Preprints 114145 g001
Preprints 114145 g002
Figure 2. Dodecagonal PMC model. The dodecagonal failure surface, constructed in a piecewise linear manner by fitting two failure planes. The three principal stresses are σ1, σ2, and σ3.
Figure 2. Dodecagonal PMC model. The dodecagonal failure surface, constructed in a piecewise linear manner by fitting two failure planes. The three principal stresses are σ1, σ2, and σ3.
Preprints 114145 g002
Preprints 114145 g003
Figure 3. Schematic diagram of stretch truncation. The single inclined line of the MC criterion is modified to an inclined line and a vertical line tangent to the uniaxial tensile stress circle, forming a two-segment linear strength curve known as the tensile cutoff criterion. σt represents the measured tensile strength.
Figure 3. Schematic diagram of stretch truncation. The single inclined line of the MC criterion is modified to an inclined line and a vertical line tangent to the uniaxial tensile stress circle, forming a two-segment linear strength curve known as the tensile cutoff criterion. σt represents the measured tensile strength.
Preprints 114145 g003
Preprints 114145 g004
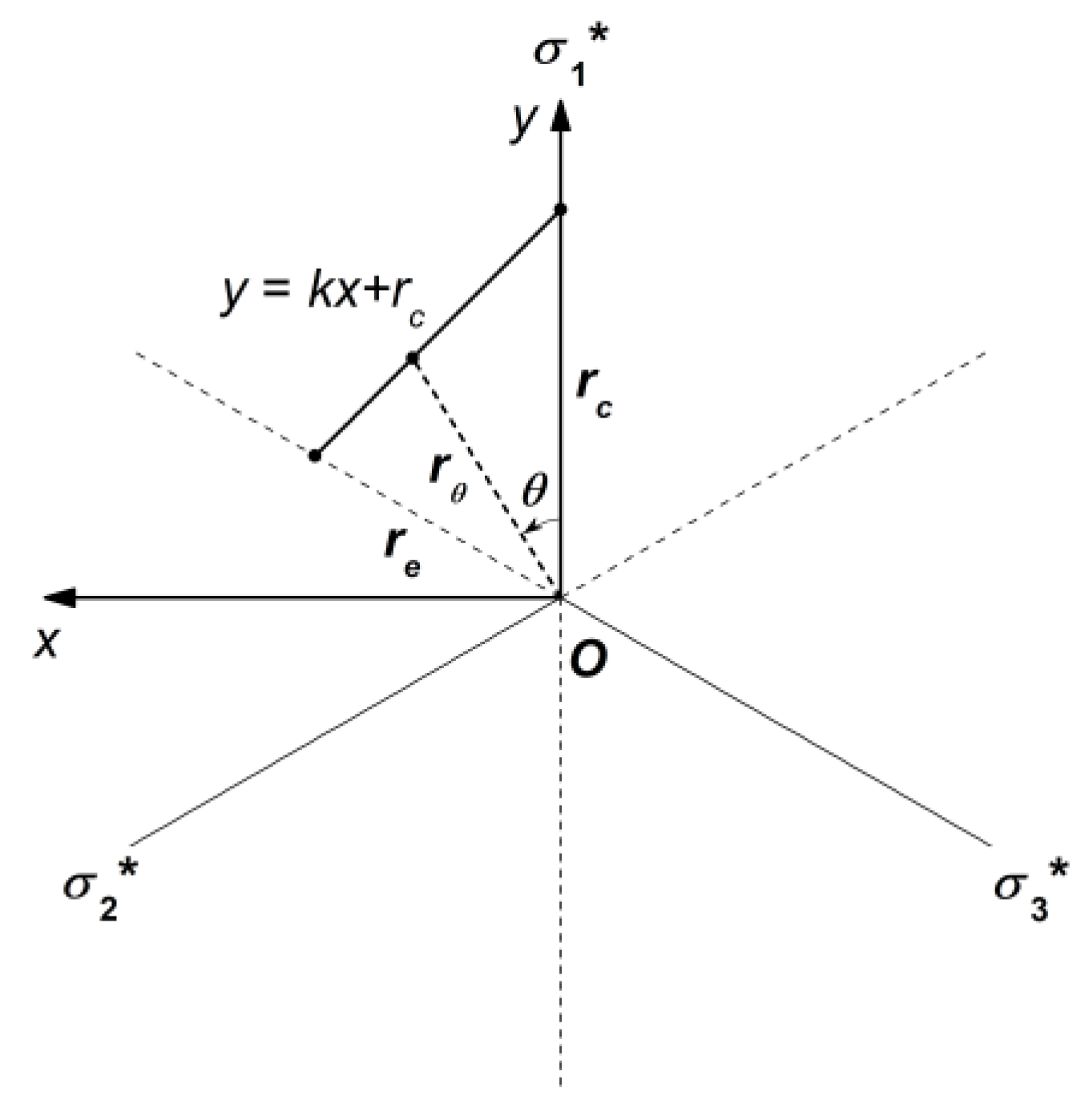
Figure 4. Extensional-strain criterion p-q plane schematic diagram. The linear forms represent the rock failure modes, from left to right: tensile failure, transition from tensile failure to shear failure, and conventional shear failure. The parameters in the figure, such as root and intercept, do not have specific meanings.
Figure 4. Extensional-strain criterion p-q plane schematic diagram. The linear forms represent the rock failure modes, from left to right: tensile failure, transition from tensile failure to shear failure, and conventional shear failure. The parameters in the figure, such as root and intercept, do not have specific meanings.
Preprints 114145 g004
Preprints 114145 g005
Figure 5. Relationship of the stress Lode angle and the π-plane. The maximum radius on the plane corresponds to the rc value under triaxial compression, and the minimum radius corresponds to the re value under triaxial extension. θ represents the Lode angle.
Figure 5. Relationship of the stress Lode angle and the π-plane. The maximum radius on the plane corresponds to the rc value under triaxial compression, and the minimum radius corresponds to the re value under triaxial extension. θ represents the Lode angle.
Preprints 114145 g005
Preprints 114145 g006
Figure 6. Relationship between the spatial and deviatoric stress radius on the π-plane. The length of the AH line segment is the height h of the equilateral triangle of the slope plane, and the intercepts of the slope plane along the three coordinate axes are all 3p. θ represents the Lode angle.
Figure 6. Relationship between the spatial and deviatoric stress radius on the π-plane. The length of the AH line segment is the height h of the equilateral triangle of the slope plane, and the intercepts of the slope plane along the three coordinate axes are all 3p. θ represents the Lode angle.
Preprints 114145 g006
Preprints 114145 g007
Figure 7. Model shape and data fitting in p-q space. The "cap" shaped shear strength envelope during pore collapse in rocks.
Figure 7. Model shape and data fitting in p-q space. The "cap" shaped shear strength envelope during pore collapse in rocks.
Preprints 114145 g007
Preprints 114145 g008
Figure 8. Schematic showing the PMC failure surface in the π plane with polar and orthogonal coordinate systems when p = 0. y = k x + r c
Figure 8. Schematic showing the PMC failure surface in the π plane with polar and orthogonal coordinate systems when p = 0. y = k x + r c
Preprints 114145 g008
Preprints 114145 g009
Figure 9. Prepared rock samples used to assess the multiple failure mechanisms. (a) Sichuan Yellow Sandstone; (b) Jinchuan granite.
Figure 9. Prepared rock samples used to assess the multiple failure mechanisms. (a) Sichuan Yellow Sandstone; (b) Jinchuan granite.
Preprints 114145 g009
Preprints 114145 g010
Figure 10. Stress-strain curves of Sichuan yellow sandstone in conventional triaxial compression tests.
Figure 10. Stress-strain curves of Sichuan yellow sandstone in conventional triaxial compression tests.
Preprints 114145 g010
Preprints 114145 g011
Figure 11. Stress-strain curves of Jinchuan granite in conventional triaxial compression tests.
Figure 11. Stress-strain curves of Jinchuan granite in conventional triaxial compression tests.
Preprints 114145 g011
Preprints 114145 g012
Figure 12. Failure modes of Sichuan yellow sandstone: (a) SY-0-1; (b) SY-10-1; (c) SY-20-1; (d) SY-30-1; (e) SY-40-1; (f) SY-50-1; (g) SY-60-2; (h) SY-65-1; (i) SY-70-1; (j) SY-90-1; (k) SY-110-2; (i) SY-140-2; (m) SY-145-1; (n) SY-150-1; (o) SY-160-1; (p) SY-170-1. (a) to (p) show the failure plane angles with gradually increasing confining pressure.
Figure 12. Failure modes of Sichuan yellow sandstone: (a) SY-0-1; (b) SY-10-1; (c) SY-20-1; (d) SY-30-1; (e) SY-40-1; (f) SY-50-1; (g) SY-60-2; (h) SY-65-1; (i) SY-70-1; (j) SY-90-1; (k) SY-110-2; (i) SY-140-2; (m) SY-145-1; (n) SY-150-1; (o) SY-160-1; (p) SY-170-1. (a) to (p) show the failure plane angles with gradually increasing confining pressure.
Preprints 114145 g012
Preprints 114145 g013
Figure 13. Failure modes of Jinchuan granite: (a) HG-0-1; (b) HG-10-1; (c) HG-20-1; (d) HG-30-1; (e) HG-40-2; (f) HG-50-1; (g) HG-60-1; (h) HG-100-1; (i) HG-120-1; (j) HG-130-2; (k) HG-140-1; (i) HG-150-1; (m) HG-160-1. (a) to (m) show the failure plane angles with gradually increasing confining pressure.
Figure 13. Failure modes of Jinchuan granite: (a) HG-0-1; (b) HG-10-1; (c) HG-20-1; (d) HG-30-1; (e) HG-40-2; (f) HG-50-1; (g) HG-60-1; (h) HG-100-1; (i) HG-120-1; (j) HG-130-2; (k) HG-140-1; (i) HG-150-1; (m) HG-160-1. (a) to (m) show the failure plane angles with gradually increasing confining pressure.
Preprints 114145 g013
Preprints 114145 g014
Figure 14. Experimental results obtained for the Berea sandstone. The negative axis of q represents triaxial extension tests, and the positive axis of q represents triaxial compression tests.
Figure 14. Experimental results obtained for the Berea sandstone. The negative axis of q represents triaxial extension tests, and the positive axis of q represents triaxial compression tests.
Preprints 114145 g014
Preprints 114145 g015
Figure 15. Six-parameter PMC model for granite on the p-q plane. The six parameters represent the failure mechanism number n for n = 1 and n = 2 as φc, φe, and V0. The piecewise linear relationship shown in the figure represents the results of the PMC six-parameter fitting. The diagram in the figure illustrates the cracking of Jinchuan granite, with the cracking plane angles gradually increasing from lower left to upper right as the confining pressure increases.
Figure 15. Six-parameter PMC model for granite on the p-q plane. The six parameters represent the failure mechanism number n for n = 1 and n = 2 as φc, φe, and V0. The piecewise linear relationship shown in the figure represents the results of the PMC six-parameter fitting. The diagram in the figure illustrates the cracking of Jinchuan granite, with the cracking plane angles gradually increasing from lower left to upper right as the confining pressure increases.
Preprints 114145 g015
Preprints 114145 g016
Figure 16. Fitting the failure strength of yellow sandstone with multiple mechanisms. The diagram shows the comparison between the PMC fitted failure surface and the experimental data curves in the p-q plane.
Figure 16. Fitting the failure strength of yellow sandstone with multiple mechanisms. The diagram shows the comparison between the PMC fitted failure surface and the experimental data curves in the p-q plane.
Preprints 114145 g016
Table 1. Comparison table of the axial load and axial stress under step loading.
Table 1. Comparison table of the axial load and axial stress under step loading.
σ/MPa P/kN σ/MPa P/kN σ/MPa P/kN
5 3.5 65 45.5 125 87.5
10 7 70 49 130 91
15 10.5 75 52.5 135 94.5
20 14 80 56 140 98
25 17.5 85 59.5 145 101.5
30 21 90 63 150 105
35 24.5 95 66.5 155 108.5
40 28 100 70 160 112
45 31.5 105 73.5 165 115.5
50 35 110 77 170 119
55 38.5 115 80.5 175 122.5
60 42 120 84 180 126
Table 2. Summary of the conventional triaxial compression analysis of Sichuan yellow sandstone and Jinchuan granite.
Table 2. Summary of the conventional triaxial compression analysis of Sichuan yellow sandstone and Jinchuan granite.
Number Wave Velocity/km/s σ2/MPa σ3/MPa σ1/MPa p/MPa q/MPa θ l /°
SY-0-1 1.43 0 0 49 16 49 −30
SY-10-1 1.58 10 10 107 42 97 −30
SY-20-1 1.69 20 20 173 71 153 −30
SY-30-1 1.42 30 30 222 94 192 −30
SY-40-1 1.54 40 40 219 100 179 −30
SY-50-1 1.43 50 50 267 122 217 −30
SY-60-2 1.5 60 60 274 131 214 −30
SY-65-1 1.52 65 65 322 151 257 −30
SY-70-1 1.46 70 70 361 167 291 −30
SY-90-1 1.46 90 90 398 193 308 −30
SY-110-2 1.72 110 110 377 199 267 −30
SY-140-2 1.43 140 140 430 237 290 −30
SY-145-1 1.61 145 145 477 256 332 −30
SY-150-1 1.46 150 150 460 253 310 −30
SY-160-2 1.62 160 160 502 274 342 −30
SY-170-1 1.45 170 170 490 277 320 −30
HG-0-1 8.78 0 0 148 49 148 −30
HG-10-1 8.33 10 10 127 49 117 −30
HG-20-1 8.56 20 20 221 87 201 −30
HG-30-1 8.33 30 30 296 119 266 −30
HG-40-2 8.45 40 40 341 140 301 −30
HG-50-1 8.78 50 50 381 160 331 −30
HG-60-1 8.36 60 60 413 178 353 −30
HG-100-1 7.89 100 100 559 253 459 −30
HG-120-1 8.33 120 120 547 262 427 −30
HG-130-2 8.38 130 130 561 274 431 −30
HG-140-1 8.82 140 140 597 292 457 −30
HG-150-1 7.14 150 150 687 329 537 −30
HG-160-1 8.33 160 160 658 326 498 −30
Table 3. PMC model fitting results.
Table 3. PMC model fitting results.
Material φc /° φe /° V0 /kPa
Berea Sandstone 37.7 44.2 21.7
Table 4. Parameters used in the Jinchuan granite PMC model.
Table 4. Parameters used in the Jinchuan granite PMC model.
Failure mechanism number n φc /° φe /° V0 /kPa
1 42.853 42.853 27.712
2 28.020 28.020 130.953
Note: Due to the lack of triaxial extension and true triaxial tests, only triaxial compression data is used for fitting; therefore, φc= φe.
Table 5. Strength parameters of sandstone under the influence of multiple failure mechanisms.
Table 5. Strength parameters of sandstone under the influence of multiple failure mechanisms.
Failure mechanism number n V0
/MPa		 φc
/°		 φe
/°
1 (low-pressure failure segment) 14.66 40 40
2 (transition segment) 76.87 27 27
3 (high-pressure failure segment) 403.31 13 13
Note: Due to the lack of triaxial extension and true triaxial tests, only triaxial compression data is used for fitting; therefore, φc = φe​.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated