Three-dimensional Fuzzy Modeling for Nonlinear Distributed Parameter Systems Using Simultaneous Perturbation Stochastic Approximation

Many systems in the manufacturing industry have spatial distribution characteristics, which correlate with both time and space. Such systems are known as distributed parameter systems (DPS). Due to the spatiotemporal coupling characteristics, the modeling of such systems is quite complex. The paper presents a new approach for three-dimensional fuzzy modeling using Simultaneous Perturbation Stochastic Approximation (SPSA) for nonlinear DPS. The Affinity Propagation clustering approach is utilized to dynamically determine the optimal number of fuzzy rules and construct a collection of preceding components for three-dimensional fuzzy models. Fourier space base functions are used in the resulting components of three-dimensional fuzzy models, and their parameters are learned by the SPSA algorithm. The proposed three-dimensional fuzzy modeling technique was utilized on a conventional DPS within the semiconductor manufacturing industry, with the simulation experiments confirming its efficacy.

Keywords:

Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning

1. Introduction

The spatial distribution characteristics are widely present in many manufacturing industries such as petroleum, chemical, steelmaking, and rolling. The dynamic characteristics of the system change with time and space, and this type of system is called a distributed parameter system (DPS)[1]. The dynamic characteristics of DPS are usually described by partial differential equations and integral equations. Traditionally, the spatial distribution characteristics of such systems are often ignored, and the inherent DPS is approximated as lumped parameter systems (LPS), and then are modeled and controlled using the mature lumped parameter methods. With the development of the times, people’s requirements for product quality are gradually increasing. With the advancement of sensors, actuators, and computing technology, the modeling, control, and optimization techniques of DPS have received increasing attention in the fields of science and engineering. For practical use in areas like optimization, control design, analyzing, and numerical simulations of DPS[2], it is necessary to use an appropriate mathematical model to describe its dynamic characteristics. Therefore, the modeling of DPS has become a very important research field.

The modeling methods for DPS can usually be divided into: mechanism modeling with known partial differential equations and grey box/black box modeling with unknown partial differential equations. Mechanism modeling is the process of obtaining partial differential equations for DPS from the point of view of physical or chemical reaction knowledge of the system, such as thermal energy balance, material balance, or momentum balance relationships. Considering the complexity of calculations and the restricted quantity of sensors and actuators, modeling such systems further requires the use of spectral methods[1], finite element[3], finite difference techniques, etc., to simplify the essentially infinite dimensional system into a finite dimensional system[4]. Nonetheless, in real-world scenarios, it will be challenging to obtain accurate mathematical descriptions of the system through mechanism modeling method due to incomplete knowledge of physical and chemical processes. The second modeling method is based on data, including gray box modeling and black box modeling[5]. The model expressed by partial differential equations of the system is established through prior knowledge, and the unknown parameters of the model are obtained by identification from the input/output data of the system. This method is called grey box modeling. Directly identifying the structure and parameters of a system from input/output data is called black box modeling. In practical applications, black box modeling has a wider range of applications. How to extract the relationship between system inputs/outputs with spatial distribution characteristics from data is currently a challenge in modeling research.

In recent decades, researchers have conducted continuous research on black box modeling of DPS. Most methods decompose variables into a series of spatial functions and temporal coefficients[6], and then reconstruct the system. Traditional methods usually pre-set spatial functions, such as Jacobian polynomials, spline functions, etc., and prior knowledge also dictates the quantity of spatial functions. The time coefficients are estimated using traditional modeling methods for LPS. In the past 20 years, spatial functions have been estimated using the Karhunen-Loève (KL) decomposition method[7,8]. The time coefficient is still estimated using traditional modeling methods for LPS. In practical applications, essentially infinite dimensional systems require model simplification to obtain lower order ordinary differential equations. However, model simplification can lead to unmodeled dynamics and unknown nonlinearity[9].

Intelligent methods like neural networks and fuzzy systems have been incorporated into DPS modeling as well. References [8,10,11] combined neural networks with space-time separation methods and achieved good experimental results on parabolic DPS modeling problems. Wang et al. [10] used a nonlinear PCA method to obtain space base functions. After space-time separation and dimension reduction, a neural network was used to identify the time coefficients. Zhang et al.[11] used the PCA algorithm to obtain space base functions. After space-time separation and dimension reduction, the time model was decomposed into linear and nonlinear parts. The ARX model was used to model the linear part, and the RBF neural network was employed to model the nonlinear part. Fan et al.[8] used the KL decomposition method to obtain space base functions. After space-time separation and dimension reduction, a mixed time series model of long short-term memory network and multi-layer perceptron was used to model the time coefficients. However, the aforementioned modeling methods still require dimension reduction.

Three-dimensional fuzzy modeling[9,12] is a new type of DPS modeling method that has developed in the past five years. In three-dimensional fuzzy model, the functions of space-time separation and space-time reconstruction are naturally integrated into three-dimensional fuzzy rules. In each three-dimensional fuzzy rule, space-time separation is naturally achieved, where the preceding component is computed as the time factor and the resulting component is regarded as the space base function. In the combination operation of multiple excited three-dimensional fuzzy rules, space-time reconstruction is naturally achieved. Compared with traditional modeling methods of distributed parameter systems, three-dimensional fuzzy modeling method has two advantages: it does not rely on model dimension reduction and has language interpretability.

At present, the three-dimensional fuzzy model has been applied in the modeling of DPS such as rapid thermal processing and chemical reactors. Zhang et al.[9] introduced a three-dimensional fuzzy modeling approach utilizing clustering and support vector regression, where nearest neighbor clustering (NNC) method and similarity analysis technique were employed for mining and condensing the initial preceding components in the three-dimensional fuzzy rules, and support vector regression machines are employed to acquire knowledge about the space base functions of the resulting components in the three-dimensional fuzzy rules. However, the clustering results of the NNC algorithm are influenced by the initial representative point selection, and the structural simplification process is very cumbersome. Zhang et al.[12] proposed a method for three-dimensional fuzzy modeling that utilizes KL decomposition to derive space base functions for the resulting sets of the three-dimensional fuzzy rule. The resulting sets consist of a restricted amount of space base functions with higher weights. This method pertains to the scope of dimension reduction and results in dynamic characteristics that have not been modeled.

Based on the above discussion, this paper introduces an innovative three-dimensional fuzzy modeling method for DPS. Utilizing the Affinity Propagation (AP) clustering algorithm, the preceding components of the fuzzy rule are derived within the three-dimensional fuzzy modeling framework. By considering every data point as a potential class representative point, the AP algorithm circumvents the issue of clustering outcomes being constrained by the choice of initial class representative points. Unlike existing methods such as KL decomposition or support vector regression to learn space base functions, this paper sets the Fourier space base function as the resulting component of three-dimensional fuzzy rules. The construction of Fourier space base functions is simple and can better approximate the actual spatial distribution characteristics. Furthermore, the parameters of the Fourier space base function are fine-tuned using the simultaneous perturbation stochastic approximation (SPSA) algorithm.

The key innovations of this study are outlined below:

1) The AP clustering approach is utilized to dynamically determine the most suitable quantity of fuzzy rules and construct preceding sets for the three-dimensional fuzzy model.

2) The Fourier space base functions are initially introduced as the resulting sets of the three-dimensional fuzzy model.

3) The SPSA technique is employed to dynamically update the coefficients of Fourier space base functions for the three-dimensional fuzzy model.

This paper is outlined as follows. The second section offers problem description. The third section offers an in-depth explanation of the three-dimensional fuzzy modeling method. The fourth section applies the proposed modeling method to a rapid thermal chemical vapor deposition system. In the final section, the conclusion is given.

2. Problem Description

2.1. Mathematical Description of Distributed Parameter Systems and Its Characteristics

Numerous processes, like the industrial chemical reaction[1], semiconductor production[14], transmission in cure or reflow processes[15] and Lithium-ion Battery Thermal Process[16,17], are spatially distributed in practice. They can be depicted using the subsequent mathematical formula:

\begin{matrix} \begin{matrix} \frac{\partial^{m} w (f, t)}{\partial t^{m}} = Υ w (f, t) + ℏ (w) + λ b (f) Q (t) \\ l_{a} \leq f \leq l_{b}, t \geq 0 \\ m = 1 or 2 \end{matrix} \end{matrix}

(1)

where,

w (f, t)

represents the output;

ℏ (w)

is a nonlinear function;

Υ

is linear space differential operator, which includes first or second order spatial derivatives (

\partial / \partial f, \partial^{2} / \partial f^{2}

), and is dense in Hilbert space;

λ

is a constant vector;

Q = [q_{1} q_{2} \dots q_{\underset{̲}{L}}] \in R^{1 \times \underset{̲}{L}}

is manipulating input vector (i.e. multiple control sources);

b (f) = {[b_{1} (f) b_{2} (f) \dots b_{\underset{̲}{L}} (f)]}^{T} \in R^{\underset{̲}{L}}

is a known smooth function about f, which describes the distribution of Q in the spatial domain

\bar{F} \subset [l_{a}, l_{b}]

Usually, boundary and initial conditions also restrict the system depicted in the Equation (1). As an illustration, at t=1, the boundary and initial conditions can be depicted in the following equations:

\begin{matrix} \begin{matrix} \frac{\partial w (l_{a}, t)}{\partial f} = g_{a} (w (l_{a}, t), Q (t)) \\ \frac{\partial w (l_{b}, t)}{\partial f} = g_{b} (w (l_{b}, t), Q (t)) \end{matrix} \end{matrix}

(2)

\begin{matrix} \begin{matrix} w (f, 0) = w_{0} (f) \end{matrix} \end{matrix}

(3)

where,

g_{a} (w (l_{a}, t), Q (t))

is dependent on

w (l_{a}, t)

and

Q (t)

, and

g_{b} (w (l_{b}, t), Q (t))

is dependent on

w (l_{b}, t)

and

Q (t)

;

w_{0} (f)

is a known function.

This type of system has spatiotemporal coupling characteristics and is an infinite dimensional system.

w (f, t)

can be spatiotemporally separated into an infinite weighted sum of space base functions and time coefficients, as shown in Equation (4).

\begin{matrix} \begin{matrix} w (f, t) = \sum_{i = 1}^{\infty} w_{i} φ_{i} (f) \end{matrix} \end{matrix}

(4)

Practically, it is necessary to utilize a finite quantity of sensors positioned at

f_{1}, f_{2}, \dots, f_{p}

; therefore,

\bar{F} = [f_{1}, f_{2}, \dots, f_{P}]

w (\bar{F}, t) = [w (f_{1}, t), w (f_{2}, t), \dots, w (f_{p}, t)]

represents the output in space. The data-driven modeling challenge for the DPS, as outlined in Equations (1) - (3), entails the task of determining a spatiotemporal coupled model using the input

{Q (k)}_{k = 1}^{K}

and the output

{\{w (f_{i}, k)\}}_{i = 1, k = 1}^{P, K}

, where K is the time length. Essentially, systems with an infinite number of dimensions will be converted into the systems with a finite number of dimensions. When the mechanism model described in Equations (1) - (3) is unknown, utilizing the KL decomposition technique, the system’s space base function can be derived from the gathered data set

\bar{S} = {\{Q (k) w (f_{i}, k)\}}_{i = 1, k = 1}^{P, K}

. Then,

w (f, t)

can be approximately depicted as Equation (5).

\begin{matrix} \begin{matrix} w_{n} (f, t) = \sum_{i = 1}^{n} w_{i} φ_{i} (f) \end{matrix} \end{matrix}

(5)

The time coefficient in Equation (5) can be identified using traditional methods.

However, the modeling approach of DPS using KL decomposition unavoidably results in neglected dynamic features and uncertainties in the identified model due to the decrease of dimensions.

2.2. Three-dimensional Fuzzy Modeling

The three-dimensional fuzzy system[18] was first established in 2007 and has since been used in the domain of DPS control[19]. Recently, there has been effective development of the three-dimensional fuzzy system for modeling DPS. The relevant theory of three-dimensional fuzzy system and black box modeling theory were combined to form a three-dimensional fuzzy modeling framework as shown in Figure 1[9]. Unlike traditional modeling methods, the three-dimensional fuzzy modeling method can model a DPS without reduction dimension.

Assume that K and J represent the order of the input variable

Q (k)

and output variable

w (\bar{F}, k)

, respectively. Input variables of three-dimensional fuzzy system are

{Q (k - 1), Q (k - 2), \dots, Q (k - K)}

and

{w (\bar{F}, k), w (\bar{F}, k - 1), \dots, w (\bar{F}, k - J)}

. The three-dimensional fuzzy rule is given as shown in Equation (6).

\begin{matrix} \begin{matrix} {\bar{V}}_{l} : \\ if w (\bar{F}, k - 1) is {\bar{O}}_{1 l} and \dots and w (\bar{F}, k - J) is {\bar{O}}_{J l} \\ and q_{1} (k - 1) is Q_{1}^{1 l} and \dots and q_{1} (k - K) is Q_{1}^{K l} \\ ⋮ \\ and q_{\underset{̲}{L}} (k - 1) is Q_{\underset{̲}{L}}^{1 l} and \dots and q_{\underset{̲}{L}} (k - K) is Q_{\underset{̲}{L}}^{K l} \\ then w (\bar{F}, k) is φ_{l} (\bar{F}) \end{matrix} \end{matrix}

(6)

where

φ_{l} (\bar{F})

is a space base function,

{\bar{O}}_{s l}

is a three-dimensional fuzzy set,

Q_{g}^{h l}

is a conventional fuzzy set,

s = 1, 2, \dots, J, h = 1, 2, \dots, K, g = 1, 2, \dots, \underset{̲}{L}, l = 1, 2, \dots, \bar{Z}

\bar{Z}

indicates the count of fuzzy rules.

For any three-dimensional fuzzy rule

{\bar{V}}_{l} (l = 1, 2, \dots, \bar{Z})

, its preceding set ‘

if w (\bar{F}, k - 1) i s {\bar{O}}_{1 l} and

\dots and q_{\underset{̲}{L}} (k - K) is Q_{\underset{̲}{L}}^{K l}

’ corresponds to the time coefficient

w_{l}

. The resulting set ‘

then w (\bar{F}, t) is φ_{l} (\bar{F})

’ corresponds to the space base function

φ_{l} (F)

, and space-time separation is ingeniously achieved through three-dimensional fuzzy rules. If

Z^{'}

three-dimensional fuzzy rules are excited, the time coefficients and space base functions of

Z^{'}

three-dimensional fuzzy rules will naturally realize space-time reconstruction. The final result is

\sum_{l = 1}^{Z^{'}} w_{l} φ_{l} (\bar{F})

The three-dimensional fuzzy modeling framework can be divided into three parts.

(1) Acquire the preceding set of fuzzy rules in order to derive temporal coefficients.

(2) Acquire knowledge about the space base functions of the resulting set.

(3) Obtain predicted output through space-time reconstruction.

The study will explore an innovative approach to three-dimensional fuzzy modeling within this specific framework.

3. SPSA Learning Based Three-Dimensional Fuzzy Modeling

3.1. Modeling Methodology

As for an unknown DPS system, space base functions are frequently calculated by KL decomposition technique. However, implementing the KL decomposition technique is bound to result in the simplification of models. The three-dimensional fuzzy model has the innate ability to amalgamate space-time separation and space-time reconstruction into three-dimensional fuzzy rules and thereafter avoids the model reduction.

In this study, a novel SPSA learning based three-dimensional fuzzy model methodology is proposed, the scheme of which is shown in Figure 2.

The modeling methodology is divided into two parts, namely, learning for preceding components of three-dimensional fuzzy rules and learning for resulting components of three-dimensional fuzzy rules. In the first part, by using AP clustering, preceding components of three-dimensional fuzzy rules are learned. In the second part, the Fourier function is initially selected as the space base function as the resulting components of the three-dimensional fuzzy rule. Then the SPSA method is used to determine the coefficients of the Fourier space base function adaptively. Three distinct characteristics are evident in the SPSA learning based three-dimensional fuzzy modeling method as blow.

1) AP clustering is employed to manage a collection of spatiotemporal data and extract the preceding components of three-dimensional fuzzy rules in an adaptable manner, without the need to define the number of clusters.

2) The Fourier space base functions are investigated in three-dimensional fuzzy modeling.

3) SPSA algorithm is used to acquire optimal parameters of Fourier space base functions.

3.2. AP Clustering Learning for Preceding Components of Three-dimensional Fuzzy Rule

Frey and Dueck introduced Affinity Propagation (AP) Clustering[13], a novel clustering technique, in 2007. It can handle with large-scale data sets in a short period of time without initializations of cluster number and cluster core. The process of AP clustering involves initially selecting specific samples known as exemplars, followed by linking each sample on the left to its closest examples. Two kinds of message, namely responsibility and availability, are passed in AP clustering. Let

V = {[r (i, ν)]}_{n \times n}

be responsibility matrix,

A = {[a (i, ν)]}_{n \times n}

be the availability matrix, and

S = {[s (i, ν)]}_{n \times n}

be the similarity matrix. The responsibility

r (i, ν)

reflects how strongly the sample i want to choose the candidate exemplar

ν

as its exemplar. The presence of

a (i, ν)

mirrors the collective data demonstrating the appropriateness of sample i in selecting candidate

ν

as the exemplar. The similarity

s (i, ν)

represents the degree of similarity between the sample i and its nearest exemplar

ν

. Then, the message between V and A is propagated so that the sample similarity S in the cluster is the largest and the sample similarity between the clusters is the smallest. The detailed algorithm description is presented in Appendix A and the algorithm procedure is shown in Figure A.1 of Appendix A.

For a spatiotemporal data set

\bar{S}

from DPS, AP clustering algorithm is employed to cluster the dataset

\bar{S}

Z^{'}

clusters. Each cluster corresponds to the preceding components of a three-dimensional fuzzy rule. Hence, the preceding components of

Z^{'}

three-dimensional fuzzy rules are achieved. Assumed that

o^{1}, \dots, o^{Z^{'}}

with

o^{i} = (o_{χ}^{i}, o_{c}^{i})

are

Z^{'}

cluster cores. These cores will guide to construct the preceding components of

Z^{'}

three-dimensional fuzzy rules. Utilizing a Gaussian type membership function, the cluster’s core

o^{i}

aligns with the Gaussian type MFs’ center in the preceding components, while

o_{χ}^{i}

and

o_{c}^{i}

represent the centers of three-dimensional MFs and conventional MFs, respectively.

The breadth of Gaussian type membership function can be computed according to the interval range of the input variables from the input data set. Regarding the spatial output variable

w (\bar{F}, k)

, the breadth of the Gaussian type three-dimensional MF at an identical spatial point is calculated as in (7).

\begin{matrix} \begin{matrix} σ_{w} (f_{j}) \approx max (\frac{w^{max} (f_{j}) - w^{min} (f_{j})}{η}) \\ η \in [0.01, 2] \end{matrix} \end{matrix}

(7)

where

w^{max} (f_{j})

and

w^{min} (f_{j})

represent the highest and lowest

w (\bar{F}, k)

values at the sensor’s location

f = f_{j}

;

η

is a variable set by the users.

Regarding the variable

Q (k)

, the breadth of the conventional Gaussian MF is outlined below.

\begin{matrix} \begin{matrix} σ_{Q} = [\begin{matrix} σ_{μ_{1}} & \dots & σ_{μ_{\underset{̲}{L}}} \end{matrix}] \end{matrix} \end{matrix}

(8)

where

σ_{μ_{i}} = \frac{q_{i}^{max} - q_{i}^{min}}{η_{i}}

η_{i} \in [0.01, 2]

;

q_{i}^{max}

and

q_{i}^{min}

represent the highest and lowest values of the ith input variable;

η_{i}

is a variable set by the users;

i = 1, 2, \dots, \underset{̲}{L}

The coefficients

η

in Equation (7) and

η_{i}

in Equation (8) can be modified based on the present situation.

3.3. SPSA Learning for Resulting Components of Three-dimensional Fuzzy Rule

3.3.1. Fourier Space Base Function

Space base function is crucial to the performance of the modeling[6]. In three-dimensional fuzzy modeling, KL decomposition technique and SVR have been used to estimate space base functions. Traditional DPS modeling approaches allow for the selection of fixed form functions, including Spline functions, Legendre polynomials, and Jacobi polynomials[6], as space base functions, in addition to KL decomposition estimation. In this study, Fourier space base functions are taken as the resulting components of three-dimensional fuzzy rules. Spatial dynamics of a DPS can be represented by multiple Sine waves and Cosine waves with different amplitude and frequency. A Fourier space base function is expressed as in (9).

\begin{matrix} \begin{matrix} φ_{l} (\bar{F}) = a_{i} sin (b_{l} \bar{F}) + c_{l} cos (b_{l} \bar{F}) + d_{l} \\ (l = 1, 2, \dots, Z^{'}) \end{matrix} \end{matrix}

(9)

Therefore, the variable

w (\bar{F}, k)

can be expressed as a linear sum of Fourier space base functions, with each space base function multiplied by its corresponding time coefficient, which is shown as in (10).

\begin{matrix} \begin{matrix} w (\bar{F}, k) = \sum_{l = 1}^{Z^{'}} ψ^{l} (k) φ_{l} (\bar{F}) \end{matrix} \end{matrix}

(10)

\begin{matrix} \begin{matrix} ψ^{l} (k) = \sum_{h = 1}^{P} a_{h}^{l} \prod_{s = 1}^{J} E_{A} \times \prod_{i = 1}^{\underset{̲}{L}} \prod_{g = 1}^{K} E_{B} \\ E_{A} = exp (- {((w (f_{h}, k - s) - c_{s h}^{l}) / σ_{s h}^{l})}^{2}) \\ E_{B} = exp (- {((q_{i} (k - g) - d_{i}^{g l}) / δ_{i}^{g l})}^{2}) \end{matrix} \end{matrix}

(11)

where

ψ^{l} (t)

is called as fuzzy basis function[19] in the context of three-dimensional fuzzy system, also called time coefficient in a three-dimensional fuzzy model;

c_{s h}^{l}

and

σ_{s h}^{l}

are denoted as central point and breadth of the Gaussian type three-dimensional fuzzy set

{\bar{O}}_{s l}

at the hth sensor position;

d_{i}^{g l}

and

δ_{i}^{g l}

represent the central point and breadth of the conventional Gaussian fuzzy set

Q_{i}^{g l}

;

a_{h}^{l}

represents the weight assigned to the hth sensor location.

The SPSA method will be used to learn the coefficients of the Fourier space base function.

3.3.2. Parameter Learning Using SPSA Algorithm

The SPSA [20] is a highly effective technique for optimizing complex nonlinear problems. It possesses a robust theoretical basis and is frequently more effective and simpler to execute compared to widely recognized techniques like simulated annealing or genetic algorithms.In contrast with gradient descent method, SPSA does not necessitate the direct measurement of the gradient of the target function. Instead, it just requires two measurements of the target function at every iteration to approximate the gradient, regardless of the complexity of the optimization problem.The two measurements are obtained by randomly and simultaneously altering all the variables in the problem in a correct manner, which is known as “simultaneous perturbation”.

In this study, in each iteration the approximation gradients of all parameters of Fourier space base functions are computed by two randomly disturbed measurements of target functions. Let

{\hat{ϑ}}_{k} = [a_{1, k}, b_{1, k}, c_{1, k}, d_{1, k}, a_{2, k}, b_{2, k}, c_{2, k}, d_{2, k}, \dots, a_{Z^{'}, k,}, b_{Z^{'}, k}, c_{Z^{'}, k}, d_{Z^{'}, k}] \in R^{{4 Z}^{'}}

be all the parameters at the kth iteration, where

a_{i, k}, b_{i, k}, c_{i, k}

and

d_{i, k}

are parameters of ith space base function at the kth iteration. The target function is described as the L2 norm of the difference between the spatial output

w (\bar{F}, t)

and the predicted spatial output

\hat{w} (\bar{F}, t)

as follows.

\begin{matrix} \begin{matrix} J (\hat{ϑ}) = \frac{1}{2} \sum_{i = 1}^{n} {(w_{i} (\bar{F}, t) - {\bar{w}}_{i} (\bar{F}, t))}^{2} \end{matrix} \end{matrix}

(12)

The algorithm of SPSA is described as follows.

Step 1: Initialization and selection of coefficients

Initialize the timer number as

k = 0

. Select an initial estimate

{\hat{ϑ}}_{0}

and choose non-negative constants b, d, A,

α

, and

β

for SPSA algorithm. Then, calculate sequences

b_{k}

and

d_{k}

as in (13) and (14).

\begin{matrix} \begin{matrix} b_{k} = b / {(A + k + 1)}^{α} \end{matrix} \end{matrix}

(13)

\begin{matrix} \begin{matrix} d_{k} = d / {(k + 1)}^{β} \end{matrix} \end{matrix}

(14)

Step 2: Simultaneous perturbation vector generation

Create a random perturbation vector

Δ_{k}

in a

4 Z^{'}

-dimensional space, where each component of

Δ_{k}

is individually produced from a zero-mean probability distribution that satisfies the specified constraints in [20]. Here, we use Bernoulli

\pm 1

distribution, which means that there is an equal probability of 0.5 for each event of

\pm 1

Step 3: Evaluation of the cost function

Calculate two values of the cost function

J (\hat{ϑ})

by perturbing the current

{\hat{ϑ}}_{k}

simultaneously:

J ({\hat{ϑ}}_{k} + d_{k} Δ_{k})

and

J ({\hat{ϑ}}_{k} - d_{k} Δ_{k})

, where

d_{k}

and

Δ_{k}

are obtained from Step 1 and Step 2, respectively.

Step 4: Approximation of the gradient

Compute the simultaneous perturbation estimate for the gradient

g ({\hat{ϑ}}_{k})

\begin{matrix} \begin{matrix} {\hat{g}}_{k} ({\hat{ϑ}}_{k}) = \frac{J (\hat{ϑ} k + d_{k} Δ_{k}) - J ({\hat{ϑ}}_{k} - d_{k} Δ_{k})}{2 d_{k}} [\begin{matrix} {Δ_{k 1}}^{- 1} \\ {Δ_{k 2}}^{- 1} \\ ⋮ \\ {Δ_{k p}}^{- 1} \end{matrix}] \end{matrix} \end{matrix}

(15)

where

Δ_{k i}

represents the ith element of the

Δ_{k}

vector.

Step 5: Revision of the $ϑ$ estimation

\begin{matrix} \begin{matrix} {\hat{ϑ}}_{k + 1} = {\hat{ϑ}}_{k} - b_{k} {\hat{g}}_{k} ({\hat{ϑ}}_{k}) \end{matrix} \end{matrix}

(16)

Using (16) to modify

{\hat{ϑ}}_{k}

to a fresh value

{\hat{ϑ}}_{k + 1}

Step 6: Iterating or terminating

Go back to Step 2 and substitute k with

k + 1

. Terminate the algorithm if there is minimal variation in several consecutive iterations or if the maximum number of iterations has been reached.

3.3.3. Three-dimensional Fuzzy Modeling Flowchart

The proposed three-dimensional fuzzy modeling is designed in seven stages, as illustrated in Figure 3.

Stage 1: Set up the elements of a three-dimensional fuzzy model, consisting of the structure of three-dimensional fuzzy rules, the method of three-dimensional fuzzification, the method of defuzzification, various types of fuzzy operators, and other related components.

Stage 2: Assign the Fourier space base functions, as depicted in Equation (9), to the resulting components of the three-dimensional fuzzy rules.

Stage 3: Create a collection of spatial and temporal input-output data from a DPS.

Stage 4: Cluster the spatiotemporal data using AP clustering algorithm.

Stage 5: Create the preceding components of three-dimensional fuzzy rules based on the clusters identified in Stage 4.

Stage 6: Utilizing the SPSA technique to determine the parameters of the Fourier space base functions in resulting components of three-dimensional fuzzy rules.

Stage 7: Combine the preceding components from Stage 5 with the resulting components of three-dimensional fuzzy rules to form the entire three-dimensional fuzzy rule foundation.

A three-dimensional fuzzy model is obtained after the completion of a seven-stage design process.

4. Application to RTCVD System

4.1. RTCVD System

Figure 4 displays the schematic of the rapid thermal chemical vapor deposition (RTCVD) system.

A 6-inch silicon wafer is positioned on a revolving support inside the system’s chamber and subjected to heat from a heating system. The heating system consists of three Lamp banks. Lamp bank 1 uniformly warms the whole surface area of the wafer, Lamp bank 2 specifically heats the periphery of the wafer, and Lamp bank 3 equally heats the wafer as a whole. The Figure 5 displays the incident radiation flux emitted by the heating lights. A 10% concentration of silane gas (SiH4) is fed into the reactor. SiH4 undergoes decomposition to produce silicon (Si) and hydrogen gas (H2). A layer of polysilicon, with a thickness of 0.5

μ m

, is applied onto the wafer by depositing it at temperatures of about 800K or more, which takes about 1 minute. During wafer processing, the support is turned to ensure that the temperature is evenly distributed in the azimuthal direction. Due to the thinness of the silicon wafer, all changes in temperature along the azimuth direction are disregarded. Hence, it is necessary to maintain consistent temperature distribution over the wafer radius in order to achieve a homogeneous deposition of polysilicon on the wafer. This may be achieved by regulating the power supplied to the three zones of lighting groups. A one-dimensional space model of the thermal dynamics may be expressed as the following PDE [21,22]:

\begin{matrix} \begin{matrix} \begin{matrix} \partial T_{f}^{'} / \partial k^{'} = & κ_{0} [(1 / f^{'}) \partial T_{f}^{'} / \partial f^{'} + \partial^{2} T_{f}^{'} / \partial f^{' 2}] \\ + σ_{0} (1 - T_{f}^{' 4}) + ω_{f} ϱ_{1} (f^{'}) q_{1} \\ + ω_{f} ϱ_{2} (f^{'}) q_{2} + ω_{f} ϱ_{3} (f^{'}) q_{3} \end{matrix} \end{matrix} \end{matrix}

(17)

Constrained by the specified border conditions.

\begin{matrix} \begin{matrix} \{\begin{matrix} \partial T_{f}^{'} / \partial f^{'} = σ_{e d} (1 - T_{f}^{' 4}) + ϱ_{e d} q_{2} & when f^{'} = 1 \\ \partial T_{f}^{'} / \partial f^{'} = 0 & when f^{'} = 0 \end{matrix} \end{matrix} \end{matrix}

(18)

where the non-dimensional wafer temperature, denoted by

T_{f}^{'} = T_{f} / T_{a m b}

, represents the ratio of the actual wafer temperature

(T_{f})

to the ambient temperature

(T_{a m b})

, which is 300K. The non-dimensional time, denoted by

k^{'} = k / τ

, represents the ratio of the actual time

(k)

τ

, which is

2.9 s

. The non-dimensional radius position, denoted by

f^{'} = f / V_{f}

, represents the ratio of the actual radius position

(f)

to the wafer radius

(V_{f})

, which is

7.6 c m

. The variables

q_{1}

q_{2}

and

q_{3}

represent the percentage of the light source power. The variables

ϱ_{1} (f^{'})

ϱ_{2} (f^{'})

ϱ_{3} (f^{'})

represent the wafer incident radiation flux from the three-zone warming lights, respectively. The parameters in (17) through (18) are listed as follows:

\begin{matrix} \begin{matrix} κ_{0} = 0.0021, σ_{0} = 0.0012, σ_{e d} = 0.0037 \\ ϱ_{e d} = 4.022, ω_{f} = 0.0256 \end{matrix} \end{matrix}

The RTCVD system is a complex system that exhibits both spatial and temporal characteristics and has an unlimited number of dimensions. For practical purposes, a certain number of sensors must be used. Assume that sensors positioned at

f_{1}, f_{2}, \dots, f_{P}

are employed to gauge the system’s output. Consider

\bar{F}

as the spatial domain, where

\bar{F}

is a vector containing the elements

f_{1}, f_{2}, \dots, f_{P}

. Let

w (\bar{F}, k)

be a vector denoted by

w (f_{1}, k), w (f_{2}, k), \dots, w (f_{P}, k)

, where

w (f, k) = T_{f} (f, k)

. The temporal input

Q (k)

is defined as

[q_{1} (k) q_{2} (k) q_{3} (k)]

, where

k \in R

is the time variable. The objective of the modeling problem is to determine a spatiotemporal model based on the input

{Q (k)}_{k = 1}^{K}

and the output

{\{w (f_{i}, k)\}}_{i = 1, k = 1}^{P, K}

, where K represents the duration of time.

In practical operation, 11 sensors are placed evenly along the radial direction. To simulate the impact of noise, 11 independent sets of Gaussian white noise signals were added to the data collected from 11 sensors. The average value is zero and the standard deviation is

σ (f) = A_{d} (f) n_{d}

A_{d} (f) = (max (w (f, t)) - min (w (f, t))) / 3

n_{d} = 0.2 %

4.2. SPSA Learning Based Three-dimensional Fuzzy Modeling

In order to obtain sufficient dynamic information of the system, interference signals with amplitudes not exceeding 10% are added to the manipulated input variables

q_{1}

q_{2}

, and

q_{3}

, respectively. Thus, the three manipulated input variables affected by interference signals, namely the excitation signals, can be given by the following Equation (19).

\begin{matrix} \begin{matrix} q_{1} (t) = q_{1 a} + Δ_{1 a} * q_{1 a} * rand () * S_{r} \\ q_{2} (t) = q_{2 a} + Δ_{2 a} * q_{2 a} * rand () * S_{r} \\ q_{3} (t) = q_{3 a} + Δ_{3 a} * q_{3 a} * rand () * S_{r} \\ S_{r} = sign (rand () - 0.5) \end{matrix} \end{matrix}

(19)

where

q_{1 a}

q_{2 a}

and

q_{3 a}

are steady-state inputs at a furnace temperature of

1000 K

Δ_{1 a}

Δ_{2 a}

and

Δ_{3 a}

are the disturbance amplitude of

q_{1 a}

q_{2 a}

and

q_{3 a}

. In this study,

q_{1 a}

q_{2 a}

and

q_{3 a}

are 0.2028, 0.1008 and 0.2245, respectively,

Δ_{1 a}

Δ_{2 a}

and

Δ_{3 a}

are set to

10 %

A sample interval of 0.5 seconds was established in this investigation. The entire simulation time period was 7000 seconds. Therefore, 14000 samples were generated, in which 600 samples were randomly selected for training experiments and then 300 samples were randomly selected for testing experiments.

In this study, for simplicity,

J = 1

and

K = 1

were chosen. Thus, the dataset can be written as Equation (20).

\begin{matrix} \begin{matrix} S = \{χ^{k}, w_{f}^{k}\} = \{(χ_{f}^{k}, χ_{q}^{k}), w_{f}^{k} ∣ χ_{f}^{k} \in R^{11 \times 1}, \\ χ_{q}^{k} \in R^{1 \times 3}, w_{f}^{k} \in R^{11 \times 1}, k = 1, \dots, 600\} \end{matrix} \end{matrix}

(20)

where

\begin{matrix} \begin{matrix} χ^{k} = (χ_{f}^{k}, χ_{q}^{k}) \\ χ_{f}^{k} = [w (\bar{F}, k - 1)] \\ χ_{q}^{k} = [q_{1} (k - 1), q_{2} (k - 1), q_{3} (k - 1)] \\ w_{f}^{k} = w (\bar{F}, k) = {[w (f_{1}, k), \dots, w (f_{11}, k)]}^{T} \end{matrix} \end{matrix}

For

χ^{k}

in the dataset S, AP clustering is used. The AP method sets the coefficient of dampness

λ

to 0.9 and the reference degree P to 0.5. Following the process of clustering learning, a total of Seven fuzzy rules and their accompanying clustering cores were successfully acquired. Equation (7) shows the breadth setting of the Gaussian spatial membership function, whereas Equation (8) shows the breadth setting of the conventional Gaussian membership function.

This paper uses Fourier space base functions to represent the fuzzy rule resulting set, and applies the SPSA method to improve the coefficients of Fourier space base functions.

In the SPSA algorithm, the relevant parameter settings are as follows:

α = 0.602

β = 0.101

i t e r_{max} = 50000

A = 5000

d = 0.003

b = 0.015

Based on the learning results of the AP algorithm, it is evident that there are a total of 7 fuzzy rules, so the parameter dimension that needs to be adjusted is 28, and the optimization range control of the parameters is

[- 10, 10]

. The end point criterion is defined as either reaching the maximum number of iterations or when the change in iteration becomes less than 0.00001 for five consecutive occasions.

The initial value of

{\hat{ϑ}}_{0}

is obtained through gradient descent algorithm, as shown in Equation (21).

\begin{matrix} \begin{matrix} [0.0376 & 29.4590 & - 0.0307 & - 1.1126 \\ - 0.0343 & 26.6246 & - 0.0037 & 0.7921 \\ - 0.0272 & 26.6246 & - 0.0464 & 0.1736 \\ 0.0048 & 25.0165 & 0.0339 & 0.4068 \\ 0.0007 & 18.4397 & - 0.0079 & 0.9764 \\ 0.0016 & 18.4623 & - 0.0041 & - 0.0672 \\ - 0.0323 & - 8.0553 & - 0.0381 & 0.2669] \end{matrix} \end{matrix}

(21)

By using the SPSA algorithm, the optimal parameters for the Fourier space base function of the fuzzy rule resulting set can be obtained.

For the convenience of observation, Figure 6 shows seven space base functions.

The seven three-dimensional fuzzy rules derived from the data are listed as follows:

{\bar{V}}_{1} :

w (\bar{F}, k - 1)

is very Positive Large and

q_{1} (k - 1)

is Positive Small and

q_{2} (k - 1)

is Positive Large and

q_{3} (k - 1)

is very Positive Large, then

w (\bar{F}, k)

is [0.8147 0.9058 0.1270 0.9134 0.6324 0.0975 0.2785 0.5469 0.9575 0.9649 0.1576].

{\bar{V}}_{2} :

w (\bar{F}, k - 1)

is more than Zero and

q_{1} (k - 1)

is less than Positive Medium and

q_{2} (k - 1)

is Positive Small and

q_{3} (k - 1)

is Positive Medium, then

w (\bar{F}, k)

is [6.7941 6.7002 3.3976 5.6020 0.9932 2.9523 6.4101 5.5455 6.7164 4.5902 0.2500].

{\bar{V}}_{3} :

w (\bar{F}, k - 1)

is less than Positive Small and

q_{1} (k - 1)

is more than Postive Medium and

q_{2} (k - 1)

is more than Zero and

q_{3} (k - 1)

is very Positive Large, then

w (\bar{F}, k)

is [12.7369 -14.0099 -10.1810 -11.3661 -11.1470 -5.8834 -9.8322 -2.5678 -10.5907 -0.4775 -4.1538].

{\bar{V}}_{4} :

w (\bar{F}, k - 1)

is very Positive Large and

q_{1} (k - 1)

is Positive Large and

q_{2} (k - 1)

is slightly Positive Small and

q_{3} (k - 1)

is Positive Large, then

w (\bar{F}, k)

is [0.4617 0.9713 8.2346 6.9483 3.1710 9.5022 0.3445 4.3874 3.8156 7.6552 7.9520].

{\bar{V}}_{5} :

w (\bar{F}, k - 1)

is more than Positive Medium and

q_{1} (k - 1)

is Positive Large and

q_{2} (k - 1)

is more than Zero and

q_{3} (k - 1)

is Positive Medium, then

w (\bar{F}, k)

is [1.8687 4.8976 4.4559 6.4631 7.0936 7.5469 2.7603 6.7970 6.5510 1.6261 1.1900].

{\bar{V}}_{6} :

w (\bar{F}, k - 1)

is more than Positive Medium and

q_{1} (k - 1)

is Positive Medium and

q_{2} (k - 1)

is slightly Positive Small and

q_{3} (k - 1)

is very Positive Large, then

w (\bar{F}, k)

is [-2.4918 -4.7987 -1.7019 -2.9263 -1.1191 -3.7563 -1.2755 -2.5298 -2.5673 -2.3571 -3.125].

{\bar{V}}_{7} :

w (\bar{F}, k - 1)

is Positive Large and

q_{1} (k - 1)

is Positive Small and

q_{2} (k - 1)

is Positive Small and

q_{3} (k - 1)

is less than Positive Medium, then

w (\bar{F}, k)

is [-1.2263 -0.4110 -1.1889 -0.7443 -1.0026 -0.4407 -1.3535 -1.6484 -2.6840 -1.4376 -0.6583].

Finally, the complete three-dimensional fuzzy modeling of RTCVD has been achieved. The abbreviation for the suggested three-dimensional modeling technique, which combines AP clustering with Fourier space base functions, is AP Fourier SPSA-3D fuzzy modeling.

The simulation results of AP-Fourier-SPSA-3D are shown in the following figures. The predicted result of the model in the training data is displayed in Figure 7, while the discrepancies between the expected and actual values are illustrated in Figure 8. Figure 9 displays the anticipated outcome of the procedure in the test data, whereas Figure 10 illustrates the flaws in the predictions. The root mean square error (RMSE) performance indices are shown in Table 1.

4.3. Simulation Comparison

In this study, three modeling methods were selected for comparison: KL-LS[23] and NNC-SVR-3D[9]. The KL-LS modeling approach utilizes the KL decomposition technique to compute space functions and decrease model dimensions. Subsequently, the least squares identification method is employed to determine low dimensional temporal coefficients. NNC-SVR-3D fuzzy modeling method is to use nearest neighbor clustering algorithm to learn the preceding components of three-dimensional fuzzy rules, which is reduced with the use of a similarity assessing approach, and use multiple single output support vector machines to learn the space base functions of the resulting components. Additionally, gradient descent approach is utilized to determine the coefficients of Fourier space base function for the suggested three-dimensional fuzzy modeling based on AP clustering and Fourier space base function, which is abbreviated as AP-Fourier GD-3D.

The prediction errors of KL-LS model, NNC-SVR model on training data and test data can be seen in Figure 11 and Figure 12, Figure 13 and Figure 14, respectively. The time normalized absolute errors

T N A E (f) = \sum | e (f, k) | / \sum Δ k

of these models on training and test data are shown in Figure 15 and Figure 16, respectively. The RMSE performance indexes of these models are shown in Table 1.

From Table 1 and Figure 7 to Figure 16, it can be evident that the three-dimensional fuzzy models outperform the KL-LS model. The KL-LS modeling method is traditional modeling methods based on KL decomposition, which require dimension reduction. Consequently, this will unavoidably result in the emergence of unmodeled dynamic characteristics and uncertainties. The suggested three-dimensional modeling approach seamlessly merges space-time separation and space-time reconstruction, eliminating the necessity for reducing dimensions. In three three-dimensional fuzzy models, the proposed AP-Fourier SPSA-3D model has better performance. It discloses that the Fourier space base function has better spatial characteristics to disclose the spatial relationship of the DPS system, the AP clustering algorithm can adaptively select cluster cores and its numbers based on the distribution characteristics of data, and SPSA algorithm can successfully avoid getting stuck in local optima.

Table 1. Comparison of RMSE among AP-Fourier-SPSA-3D, AP-Fourier-GD-3D,

NNC-SVR-3D and KL-LS

Table 1. Comparison of RMSE among AP-Fourier-SPSA-3D, AP-Fourier-GD-3D,

NNC-SVR-3D and KL-LS

model	AP-Fourier-SPSA-3D	AP-Fourier-GD-3D	NNC-SVR-3D	KL-LS
Training data	0.9229	0.9899	1.2862	2.4481
Test data	0.9027	0.9558	1.2214	2.2903

5. Conclusions

The study introduced a three-dimensional fuzzy modeling technique using SPSA learning for DPS, which widely exists in the manufacturing industry. On the three-dimensional fuzzy modeling framework, AP clustering was used to learn the preceding components, and adaptively determine the quantity of fuzzy rules. The three-dimensional fuzzy model used the Fourier space base function as the resulting components, while the SPSA method was employed to dynamically acquire the coefficients of the Fourier space base function. The suggested approach was implemented on a conventional distributed parameter system in the semiconductor manufacturing industry. The simulation experiment demonstrates the superiority of the three-dimensional fuzzy modeling method over the conventional space-time separation modeling method. Additionally, it shows that the Fourier space base function is more effective in revealing the spatial distribution characteristics of distributed parameter systems compared to the spatial function obtained through KL decomposition.

Author Contributions

Conceptualization, Tangchen Wang; Data curation, Shaopu Wang; Formal analysis, Chong Cheng; Funding acquisition, Xianxia Zhang; Investigation, Chong Cheng; Methodology, Xianxia Zhang; Project administration, Xianxia Zhang; Resources, Shaopu Wang; Software, Tangchen Wang; Supervision, Xianxia Zhang; Validation, Chong Cheng; Visualization, Shaopu Wang; Writing – original draft, Tangchen Wang; Writing – review \ editing, Xianxia Zhang.

Funding

This work was supported by the project from the National Natural Science Foundation of China under Grant 62073210.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

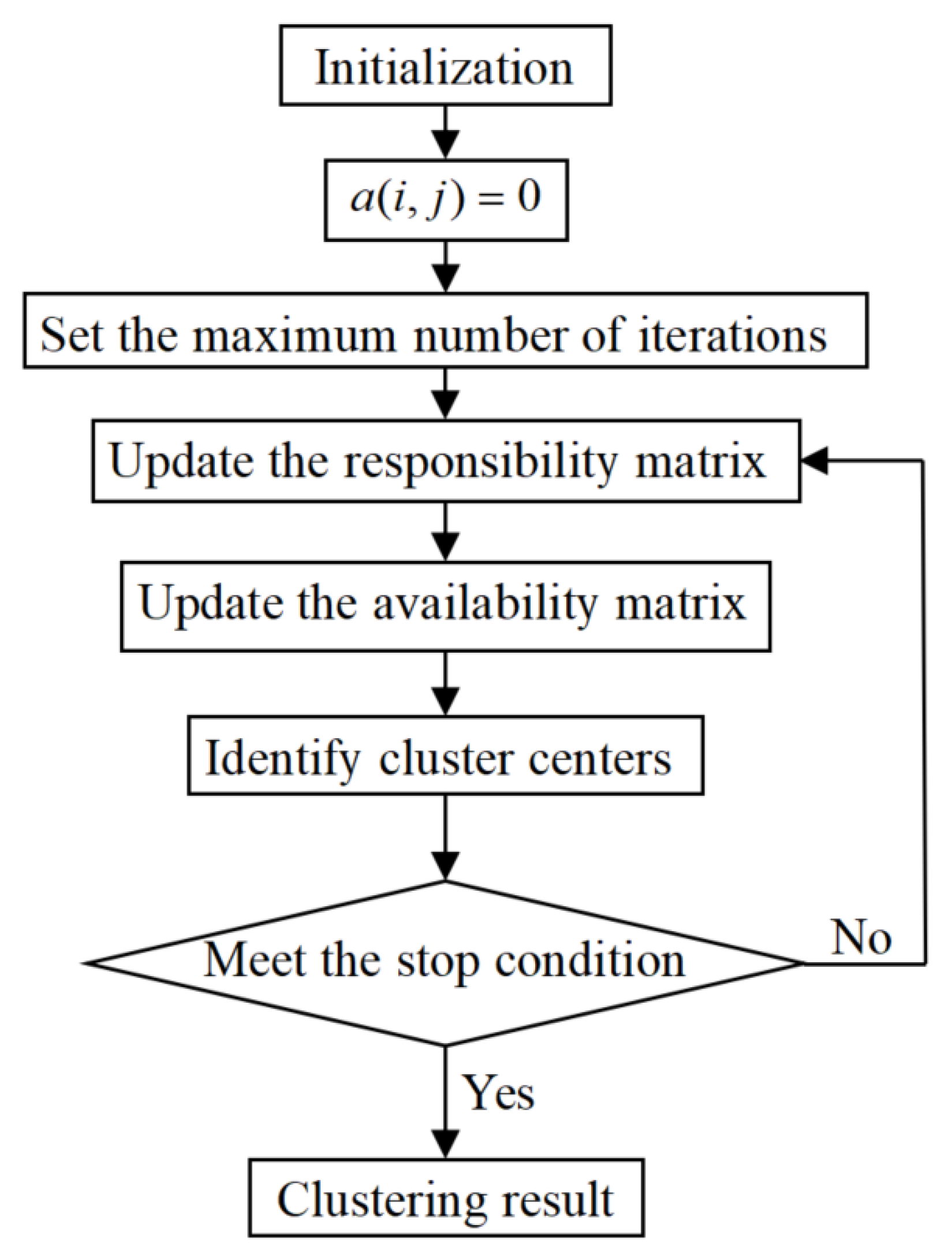
Appendix A

Appendix Algorithm Description of AP Clustering and Its Flow Chart

Assumed that

\tilde{E} = \{{\tilde{E}}_{1}, \dots, {\tilde{E}}_{Z}\}

is a data set,

{\tilde{E}}_{i} \in R^{n}

(

i = 1, \dots, Z

). The procedure of AP clustering is described as below and its process diagram is displayed in Figure A.1.

Step 1: Calculate the similarity matrix S of the data pair. The similarity between any two sample points

{\tilde{E}}_{i}

and

{\tilde{E}}_{ν}

is measured by the negative Euclidean distance:

s (i, ν) = - {∥{\tilde{E}}_{i} - {\tilde{E}}_{ν}∥}^{2}

. Then, the similarity matrix S is normalized as in (A.1)

\begin{matrix} \begin{matrix} S = \frac{S - min (min (S))}{max (max (S) - min (min (S)))} \end{matrix} \end{matrix}

(A.1)

Step 2: Set the maximum number of iteration T, damping factor

λ

, and reference degree

p (ν) = s (ν, ν) = m e d i a n (s (i, ν))

Step 3: Update the responsibility matrix, the update rule is given as follows.

\begin{matrix} \begin{matrix} r (i, ν) \leftarrow s (i, ν) - max_{ν^{'} \neq ν} (a (i, ν^{'})) + s (i, ν^{'}) \end{matrix} \end{matrix}

(A.2)

\begin{matrix} \begin{matrix} r (ν, ν) = p (ν) - max_{j \neq ν} {a (ν, j) + s (ν, j)} \end{matrix} \end{matrix}

(A.3)

Using damping factor

λ

, the responsibility matrix

V^{(ν)}

at the kth iteration is updated as in (A.4 10)

\begin{matrix} \begin{matrix} V^{(k)} = (1 - λ) V^{(k)} + λ V^{(k - 1)} \end{matrix} \end{matrix}

(A.4)

Step 4: Update the availability matrix, the update rules are given as follows

\begin{matrix} \begin{matrix} a (i, ν) \leftarrow min {0, r (ν, ν) + \\ \sum_{i^{'} \notin {i, ν}} max (0, r (i^{'}, ν))} \end{matrix} \end{matrix}

(A.5)

\begin{matrix} \begin{matrix} a (ν, ν) \leftarrow \sum_{i^{'} \neq ν} max (0, r (i^{'}, ν)) \end{matrix} \end{matrix}

(A.6)

Using damping factor

λ

, the availability matrix

A^{(j)}

at the jth iteration is updated as in (A.7)

\begin{matrix} \begin{matrix} A^{(j)} = (1 - λ) A^{(j)} + λ A^{(j - 1)} \end{matrix} \end{matrix}

(A.7)

Step 5: The decision matrix is obtained by summing the availability matrix and the responsibility matrix. Find out the point in the decision matrix where the diagonal is greater than 0 as the cluster representative center. The sample points are classified according to the distance between the sample points and the cluster representative points.

Step 6: Determine the number of iterations and the iteration stop condition, and assign the data points to the corresponding cluster centers.

References

Christofides, P. D.; Chow, J. Nonlinear and Robust Control of PDE Systems: Methods and Applications to Transport-Reaction Processes. Appl. Mech. Rev. 2002, 55, B29–B30. [Google Scholar] [CrossRef]
Wang, Z. P.; Wu, H. N.; Chadli, M. H_∞ Sampled-Data Fuzzy Observer Design for Nonlinear Parabolic PDE Systems. IEEE Trans. Fuzzy Syst. 2020, 29, 1262–1272. [Google Scholar] [CrossRef]
Braess, D.; Schumaker, L. L. Finite Elements: Theory, Fast Solvers, and Applications in Elasticity Theory; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
Lu, X. J.; Zou, W.; Huang, M. H. A Novel Spatiotemporal LS-SVM Method for Complex Distributed Parameter Systems with Applications to Curing Thermal Process. IEEE Trans. Ind. Inf. 2016, 12, 1156–1165. [Google Scholar] [CrossRef]
Wang, M. L.; Li, N.; Li, S. Y. Model-Based Predictive Control for Spatially-Distributed Systems Using Dimensional Reduction Models. Int. J. Autom. Comput. 2011, 8, 1–7. [Google Scholar] [CrossRef]
Li, H. X.; Qi, C. K. Modeling of Distributed Parameter Systems for Applications—A Synthesized Review from Time-Space Separation. J. Process Control 2010, 20, 891–901. [Google Scholar] [CrossRef]
Li, H. X.; Qi, C. K. Spatio-Temporal Modeling of Nonlinear Distributed Parameter Systems: A Time/Space Separation Based Approach; Springer Science & Business Media: Berlin, Germany, 2011. [Google Scholar]
Fan, Y. J.; Xu, K. K.; Wu, H.; Zheng, Y.; Tao, B. Spatiotemporal Modeling for Nonlinear Distributed Thermal Processes Based on KL Decomposition, MLP and LSTM Network. IEEE Access 2020, 8, 25111–25121. [Google Scholar] [CrossRef]
Zhang, X. X.; Zhao, L. R.; Li, H. X.; Ma, S. W. A Novel Three-Dimensional Fuzzy Modeling Method for Nonlinear Distributed Parameter Systems. IEEE Trans. Fuzzy Syst. 2018, 27, 489–501. [Google Scholar] [CrossRef]
Wang, M. L.; Qi, C. K.; Yan, H. C.; Shi, H. B. Hybrid Neural Network Predictor for Distributed Parameter System Based on Nonlinear Dimension Reduction. Neurocomputing 2016, 171, 1591–1597. [Google Scholar] [CrossRef]
Zhang, R. D.; Tao, J. L.; Lu, R. Q.; Jin, Q. B. Decoupled ARX and RBF Neural Network Modeling Using PCA and GA Optimization for Nonlinear Distributed Parameter Systems. IEEE Trans. Neural Netw. Learn. Syst. 2016, 29, 457–469. [Google Scholar] [CrossRef] [PubMed]
Zhang, X. X.; Fu, Z. Q.; Li, S. Y.; Zou, T.; Wang, B. A Time/Space Separation Based 3D Fuzzy Modeling Approach for Nonlinear Spatially Distributed Systems. Int. J. Autom. Comput. 2018, 15, 52–65. [Google Scholar] [CrossRef]
Frey, B. J.; Dueck, D. Clustering by Passing Messages Between Data Points. Science 2007, 315, 972–976. [Google Scholar] [CrossRef]
Deng, H.; Li, H. X.; Chen, G. Spectral-Approximation-Based Intelligent Modeling for Distributed Thermal Processes. IEEE Trans. Control Syst. Technol. 2005, 13, 686–700. [Google Scholar] [CrossRef]
Meng, X. B.; Chen, C. L. P.; Li, H. X. Confidence-Aware Multiscale Learning for Online Modeling of Distributed Parameter Systems with Application to Curing Process. IEEE Trans. Ind. Electron. 2023, 70, 9432–9440. [Google Scholar] [CrossRef]
Wei, P.; Li, H. X. Two-Dimensional Spatial Construction for Online Modeling of Distributed Parameter Systems. IEEE Trans. Ind. Electron. 2022, 69, 10227–10235. [Google Scholar] [CrossRef]
Feng, Y.; Zhu, X. Y.; Wang, Y. N.; Wang, B. C.; Zhang, H.; Wu, Z. G.; Yan, H. C. PDE Model-Based On-Line Cell-Level Thermal Fault Localization Framework for Batteries. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 2507–2516. [Google Scholar] [CrossRef]
Li, H. X.; Zhang, X. X.; Li, S. Y. A Three-Dimensional Fuzzy Control Methodology for a Class of Distributed Parameter Systems. IEEE Trans. Fuzzy Syst. 2007, 15, 470–481. [Google Scholar] [CrossRef]
Zhang, X. X.; Jiang, Y.; Li, H. X.; Li, S. Y. SVR Learning-Based Spatiotemporal Fuzzy Logic Controller for Nonlinear Spatially Distributed Dynamic Systems. IEEE Trans. Neural Netw. Learn. Syst. 2013, 24, 1635–1647. [Google Scholar] [CrossRef] [PubMed]
Spall, J. C. Introduction to Stochastic Search and Optimization: Estimation, Simulation, and Control; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
Theodoropoulou, A.; Adomaitis, R. A.; Zafiriou, E. Model Reduction for Optimization of Rapid Thermal Chemical Vapor Deposition Systems. IEEE Trans. Semicond. Manuf. 1998, 11, 85–98. [Google Scholar] [CrossRef]
Adomaitis, R. A. A Reduced-Basis Discretization Method for Chemical Vapor Deposition Reactor Simulation. Math. Comput. Model. 2003, 38, 159–175. [Google Scholar] [CrossRef]
Qi, C. K.; Li, H.-X. A Karhunen-Loève Decomposition-Based Wiener Modeling Approach for Nonlinear Distributed Parameter Processes. Ind. Eng. Chem. Res. 2008, 47, 4184–4192. [Google Scholar] [CrossRef]

Figure 1. Framework of three-dimensional fuzzy model (three-dimensional abbreviated as 3D)

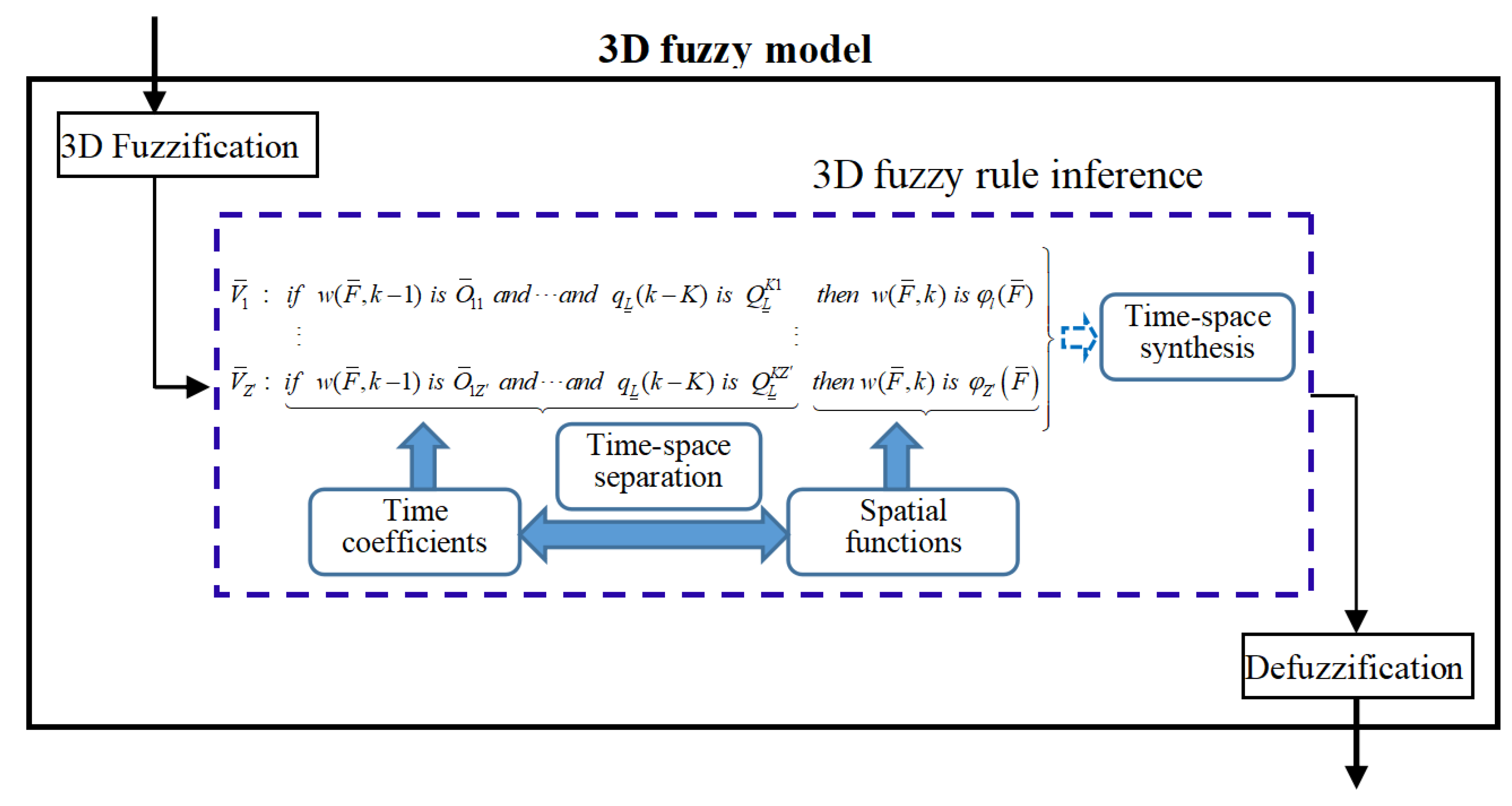
Figure 2. Scheme of SPSA learning based three-dimensional fuzzy modeling

Figure 3. Flowchart of SPSA learning based three-dimensional fuzzy modeling (three-dimensional abbreviated as 3D)

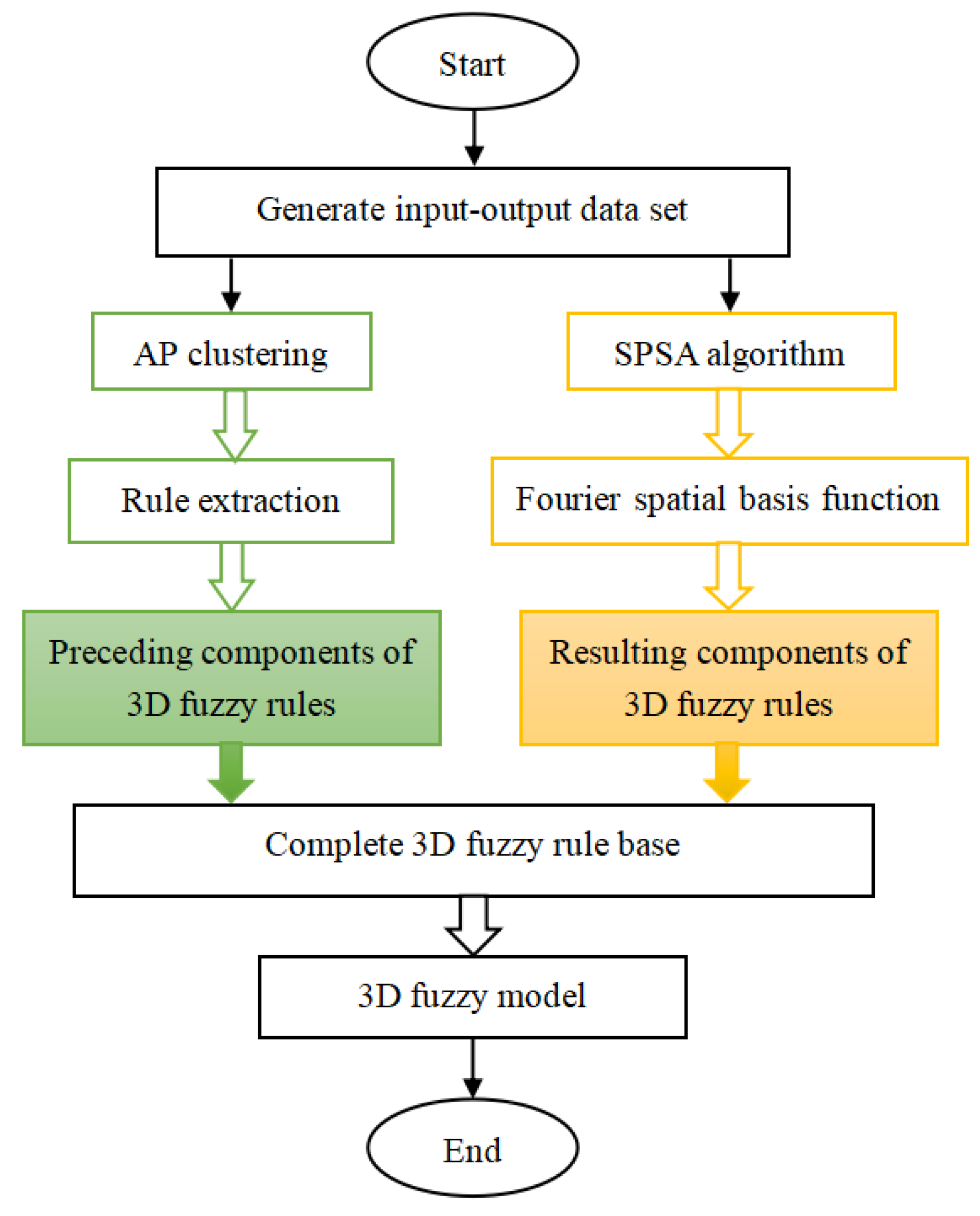
Figure 4. Sketch for RTCVD system

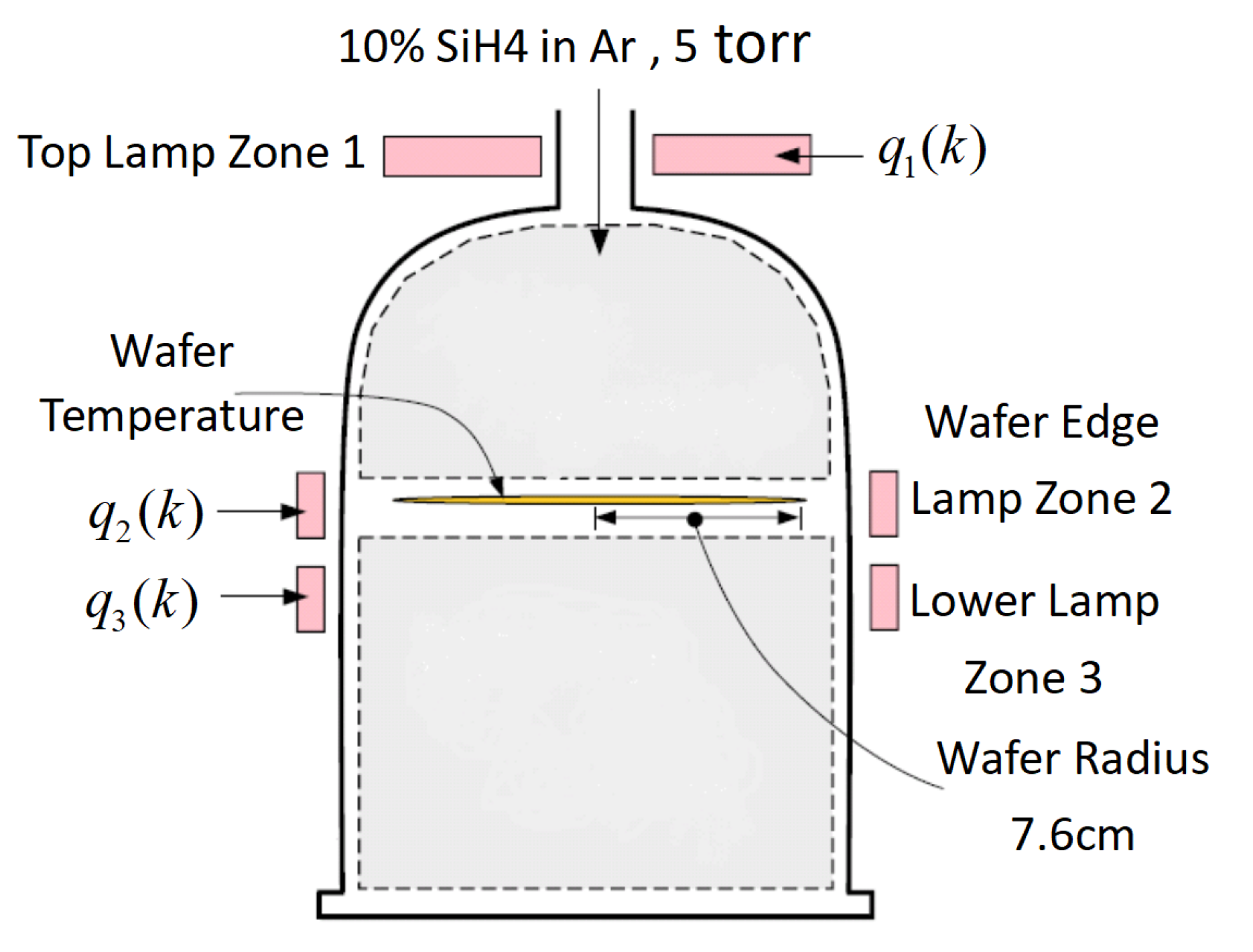
Figure 5. Radiation flux distribution of Lamp banks 1, 2, and 3

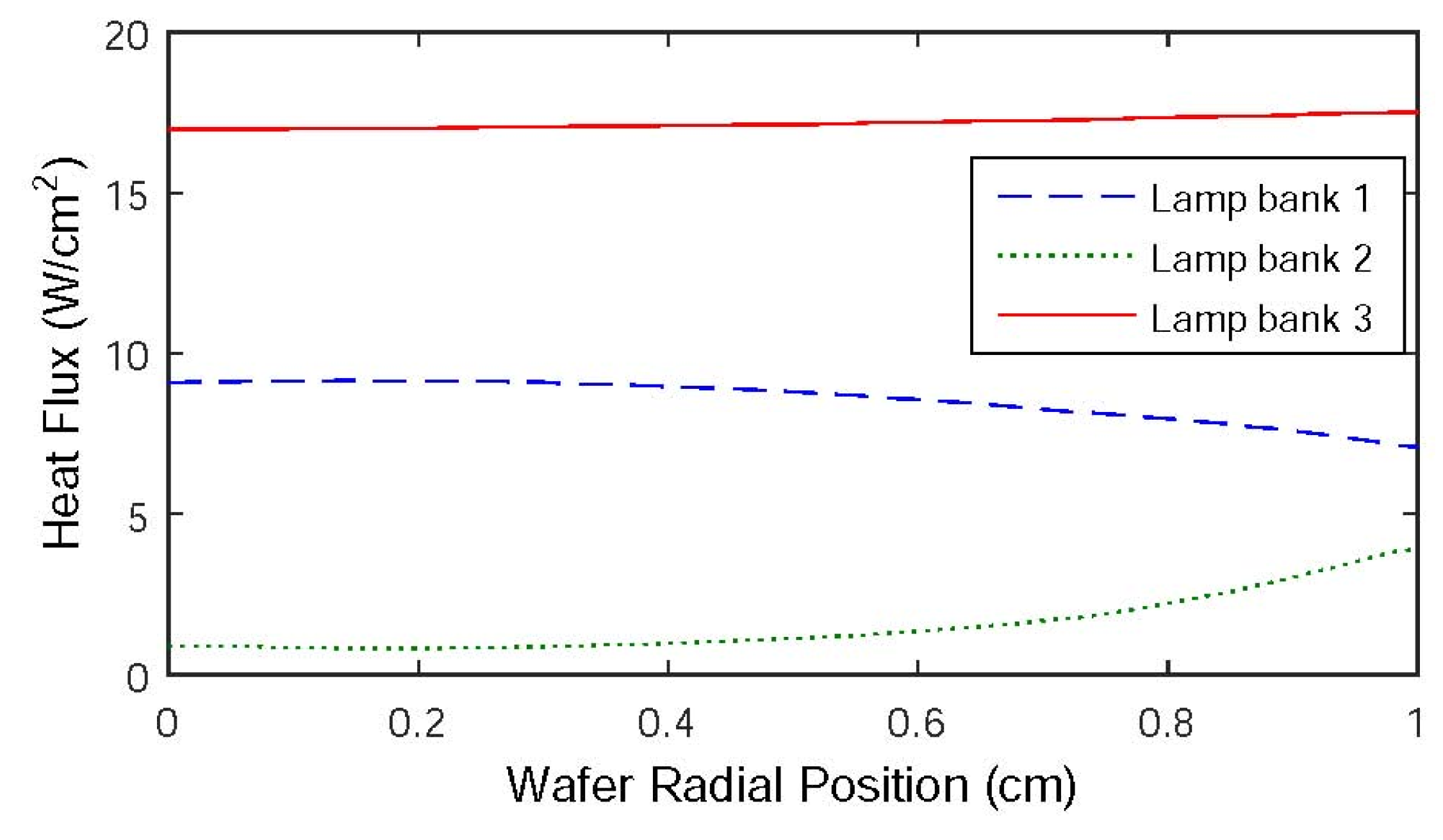
Figure 6. Seven space base functions learned by SPSA algorithm

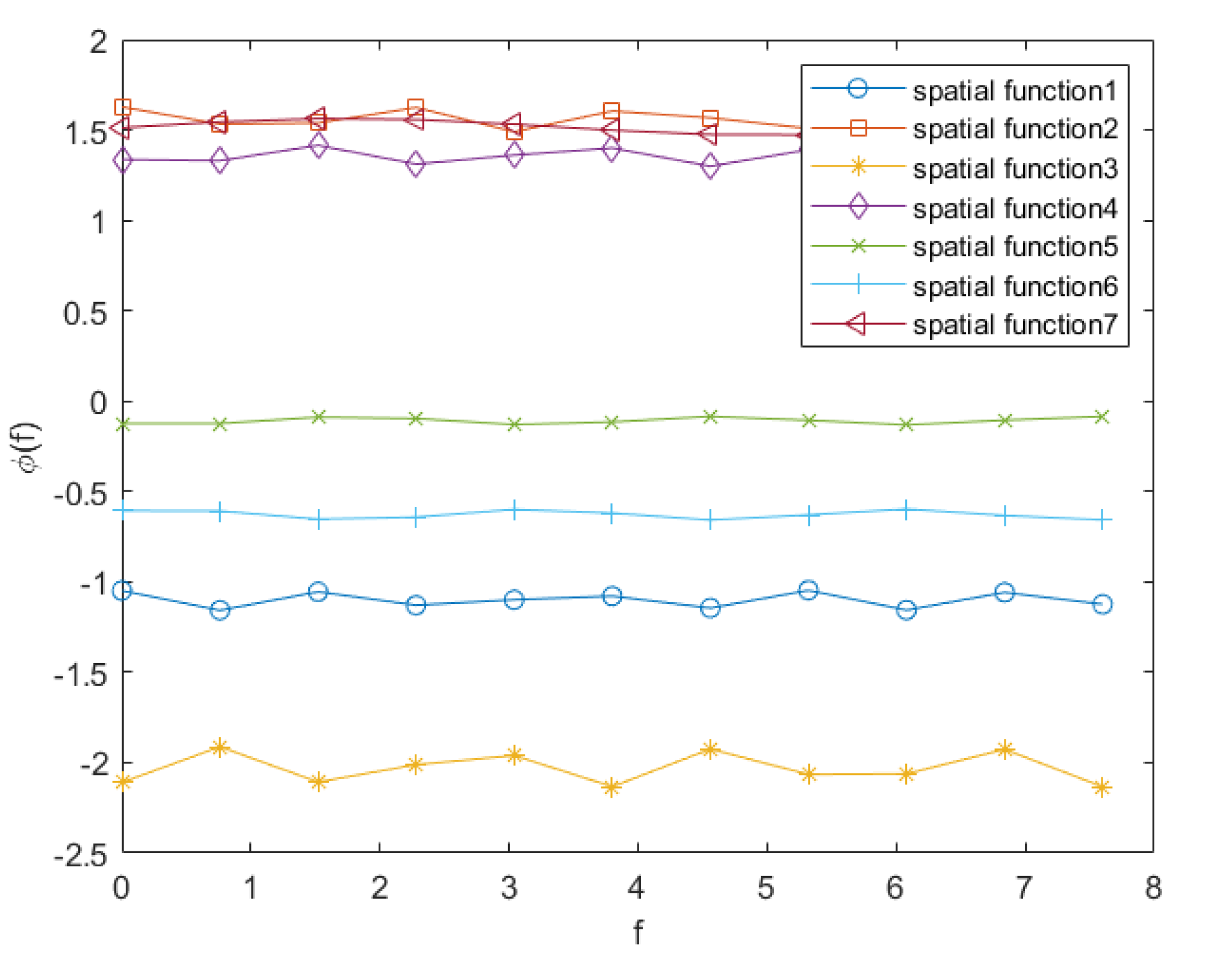
Figure 7. The predicted process output of the AP-Fourier-SPSA-3D model in training data

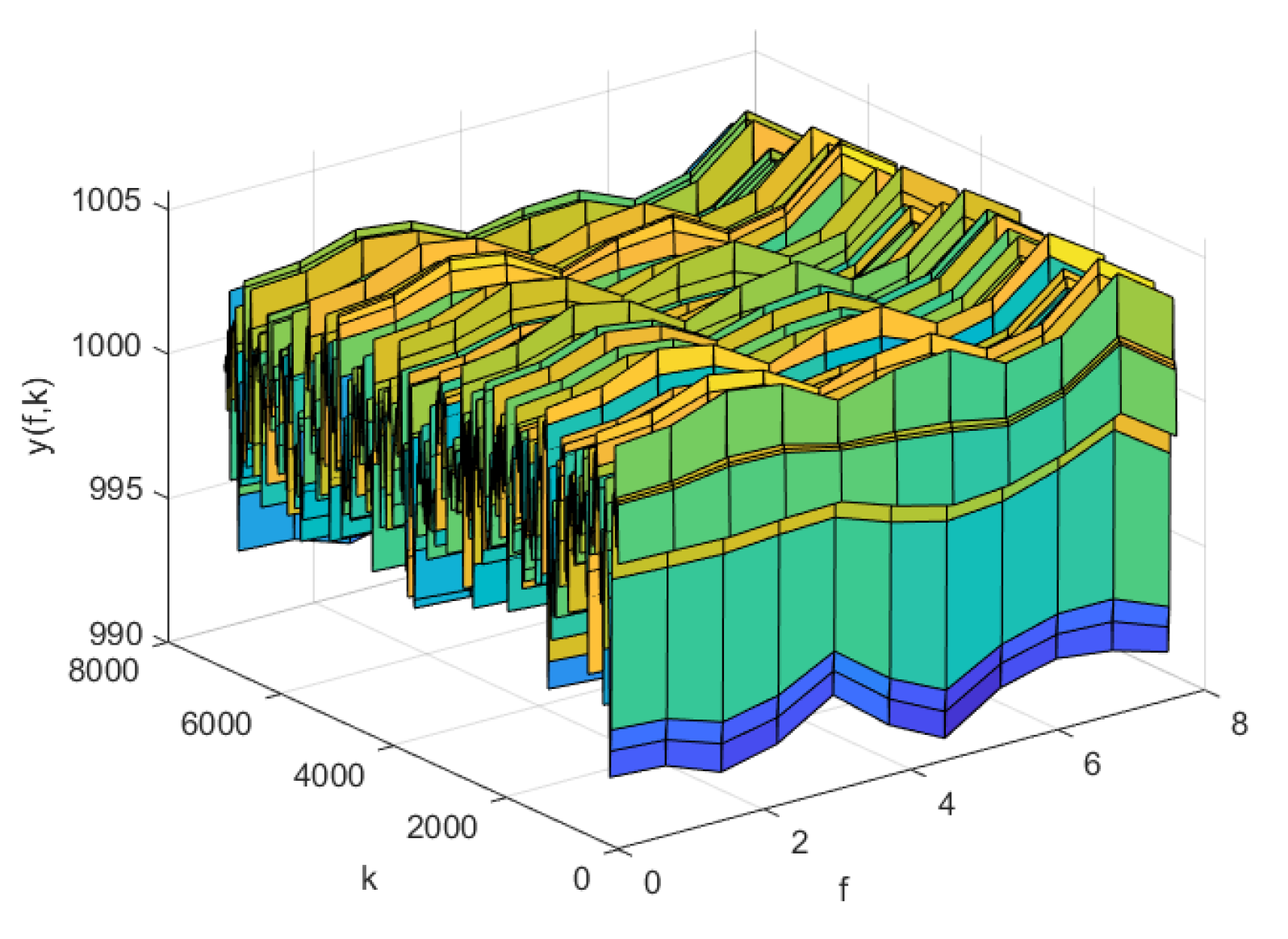
Figure 8. The predicted errors of the AP-Fourier-SPSA-3D model in training data

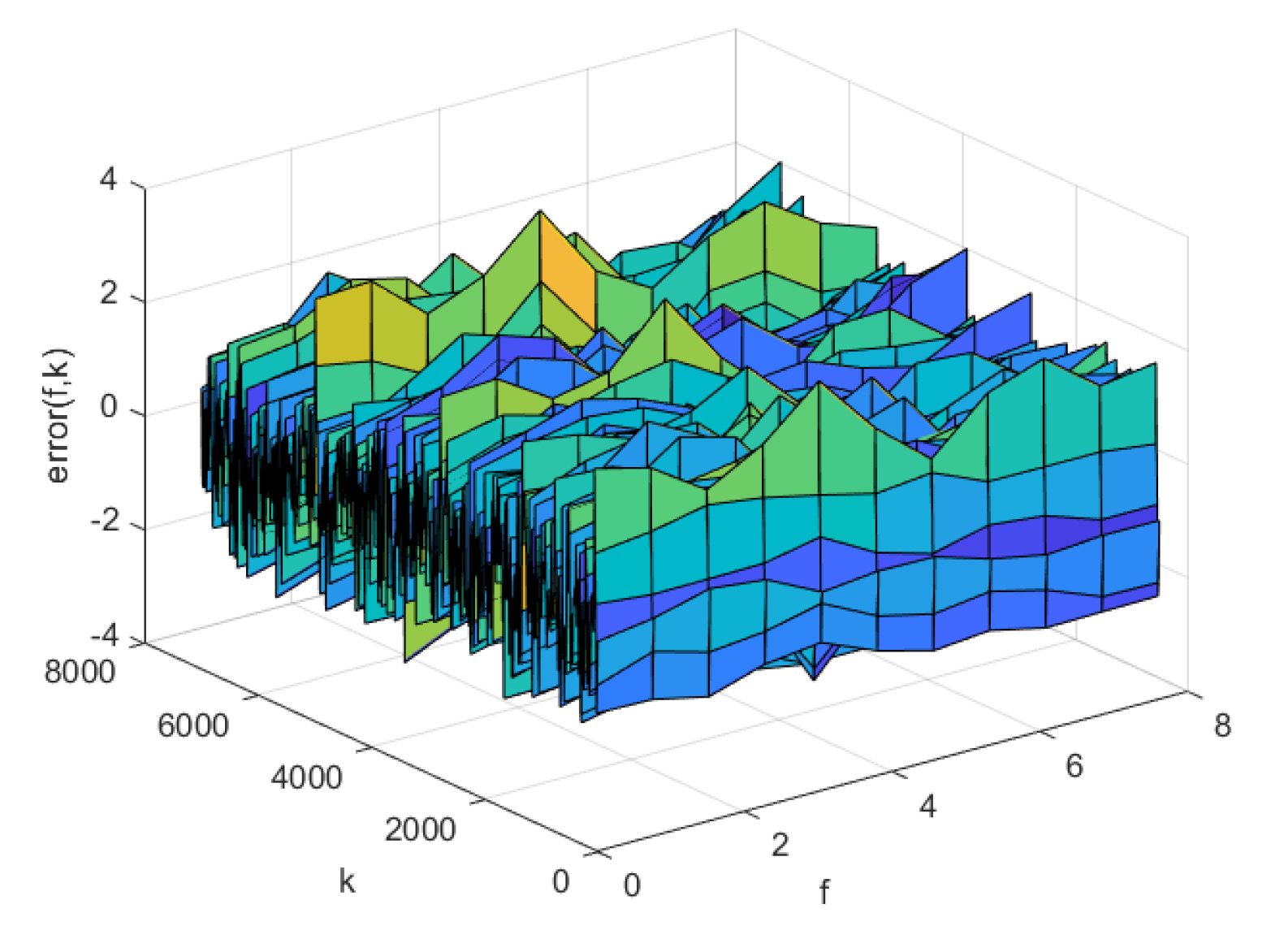
Figure 9. The predicted process output of the AP-Fourier-SPSA-3D model in test data

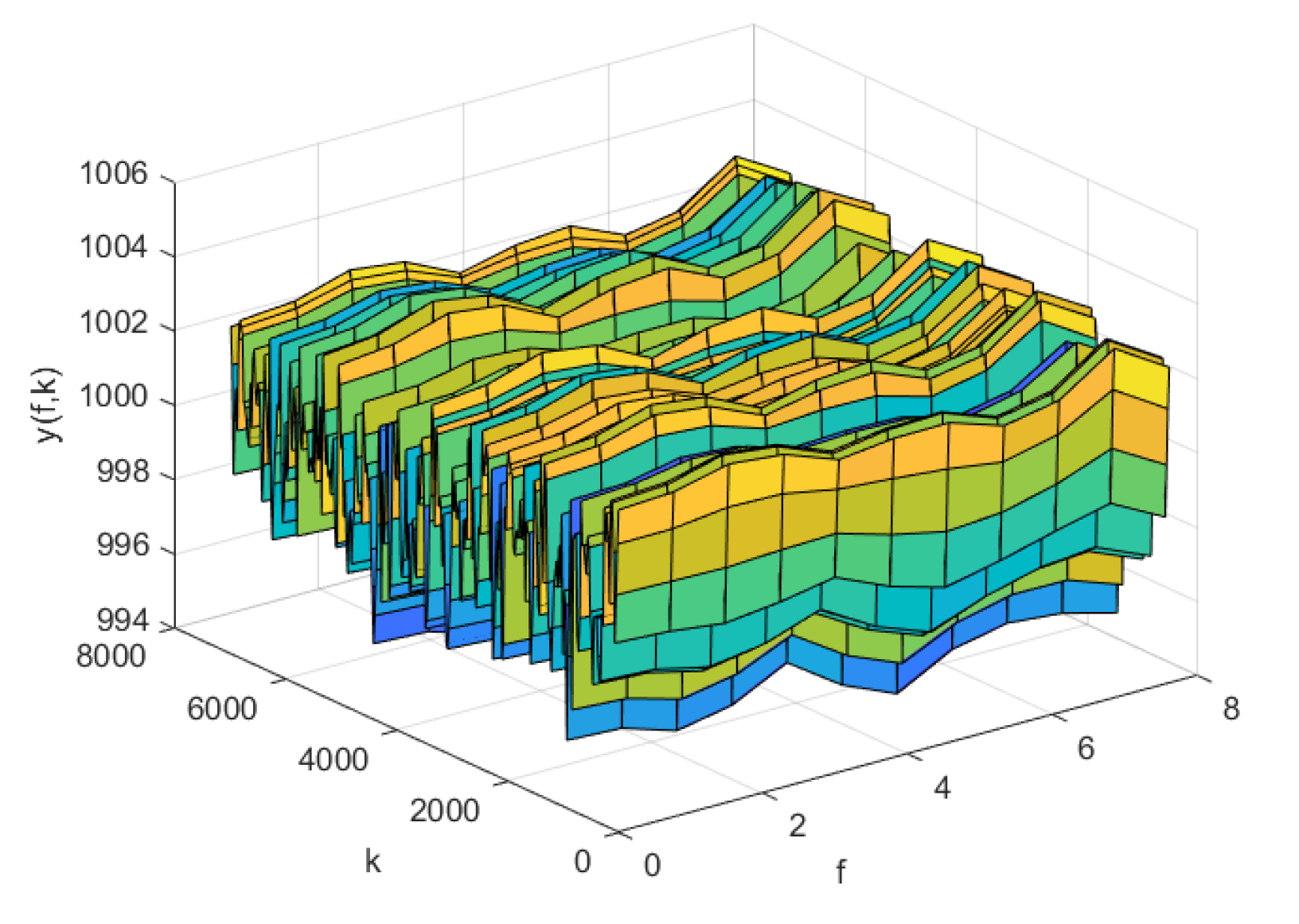
Figure 10. The predicted errors of the AP-Fourier-SPSA-3D model in test data

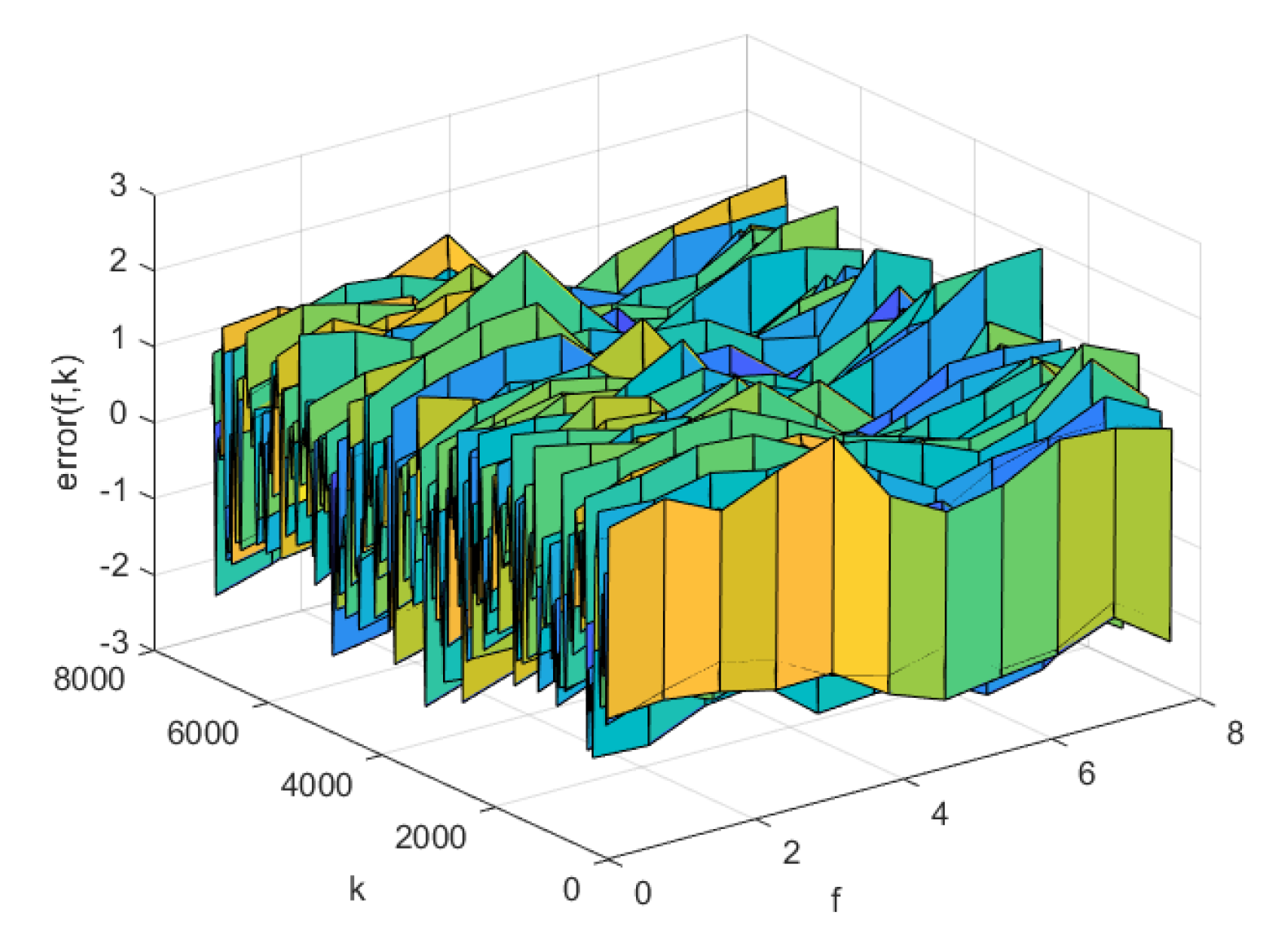
Figure 11. Prediction error of KL-LS model on training set

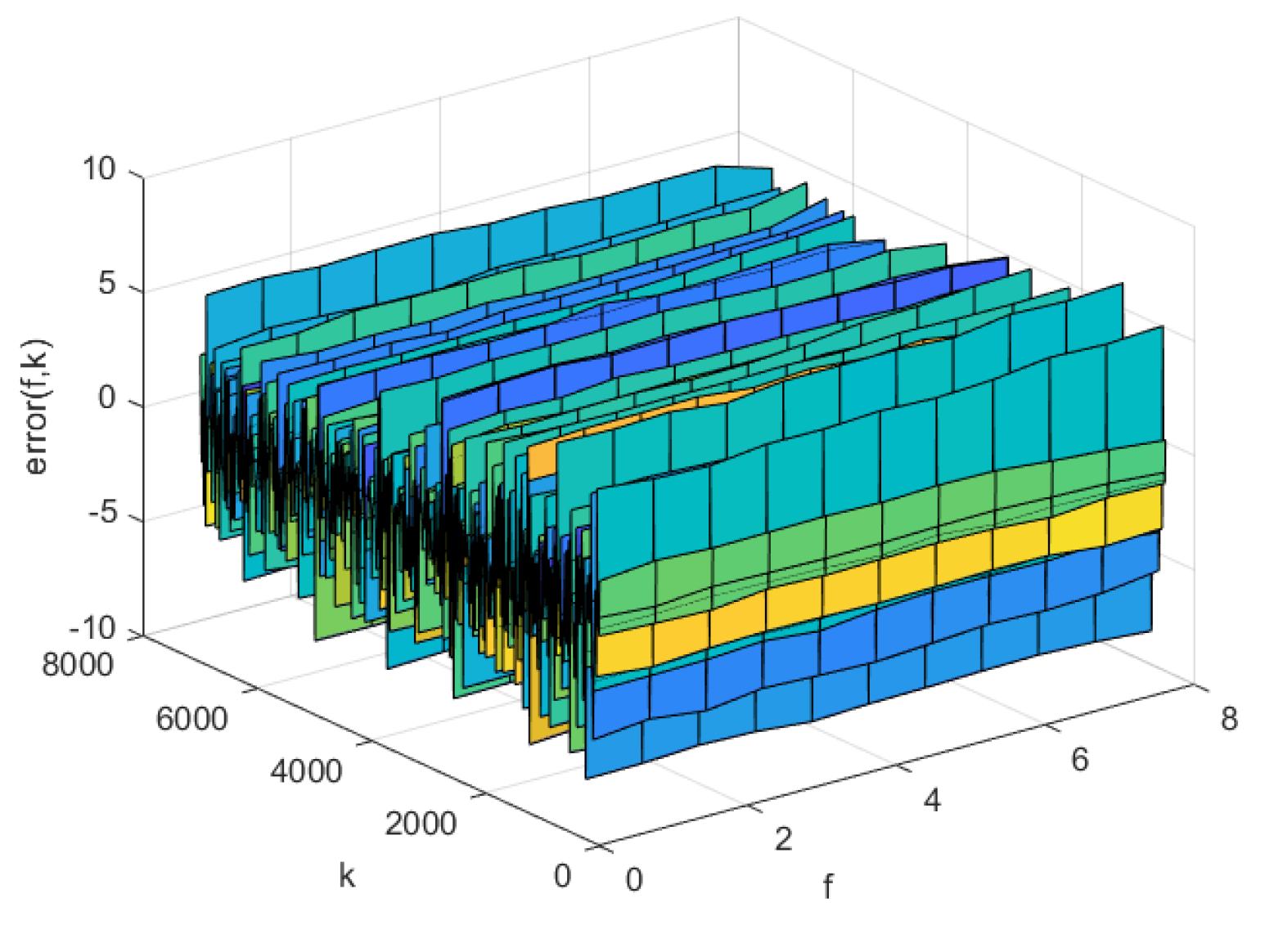
Figure 12. Prediction error of KL-LS model on test set

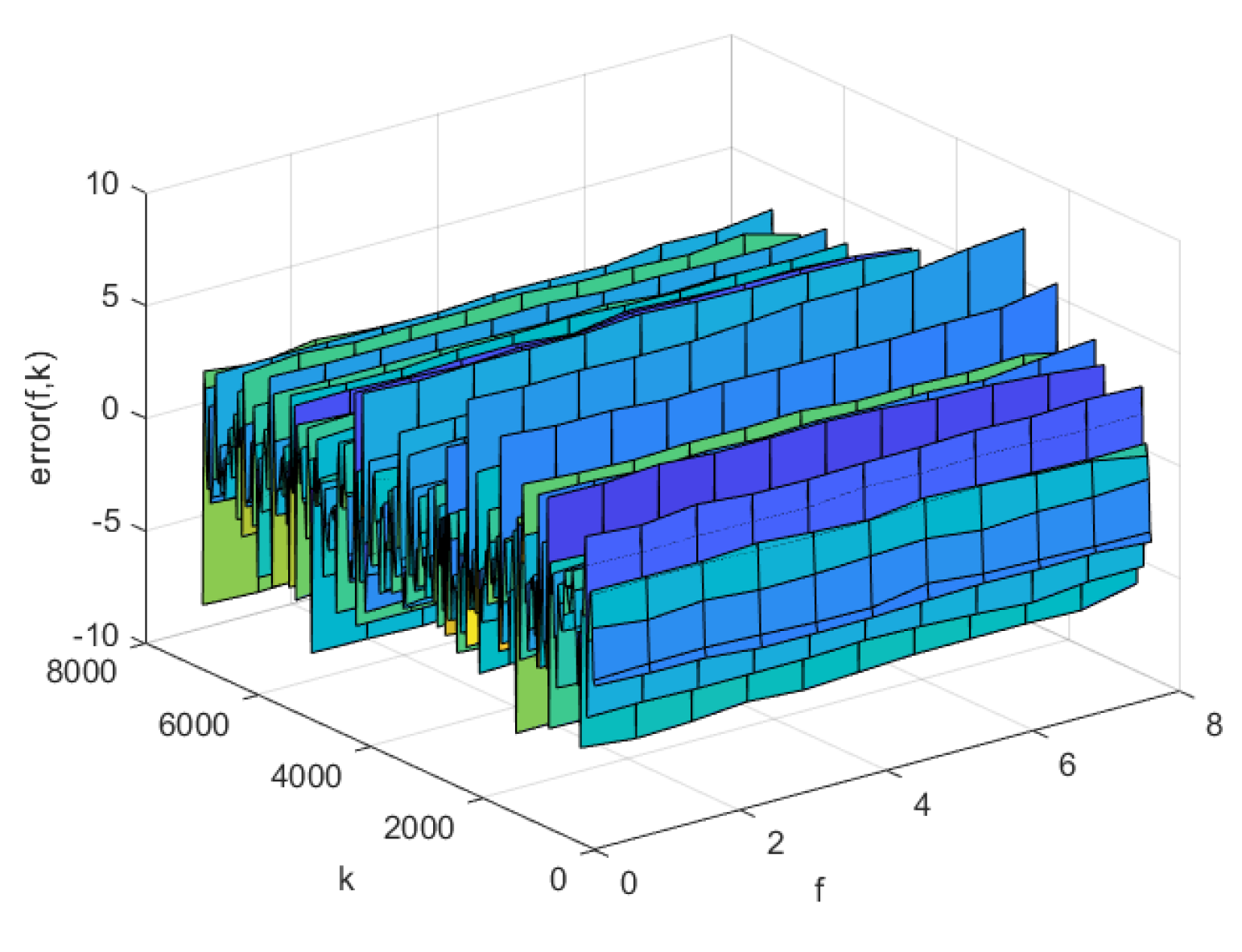
Figure 13. Prediction error of NNC-SVR-3D model on training set

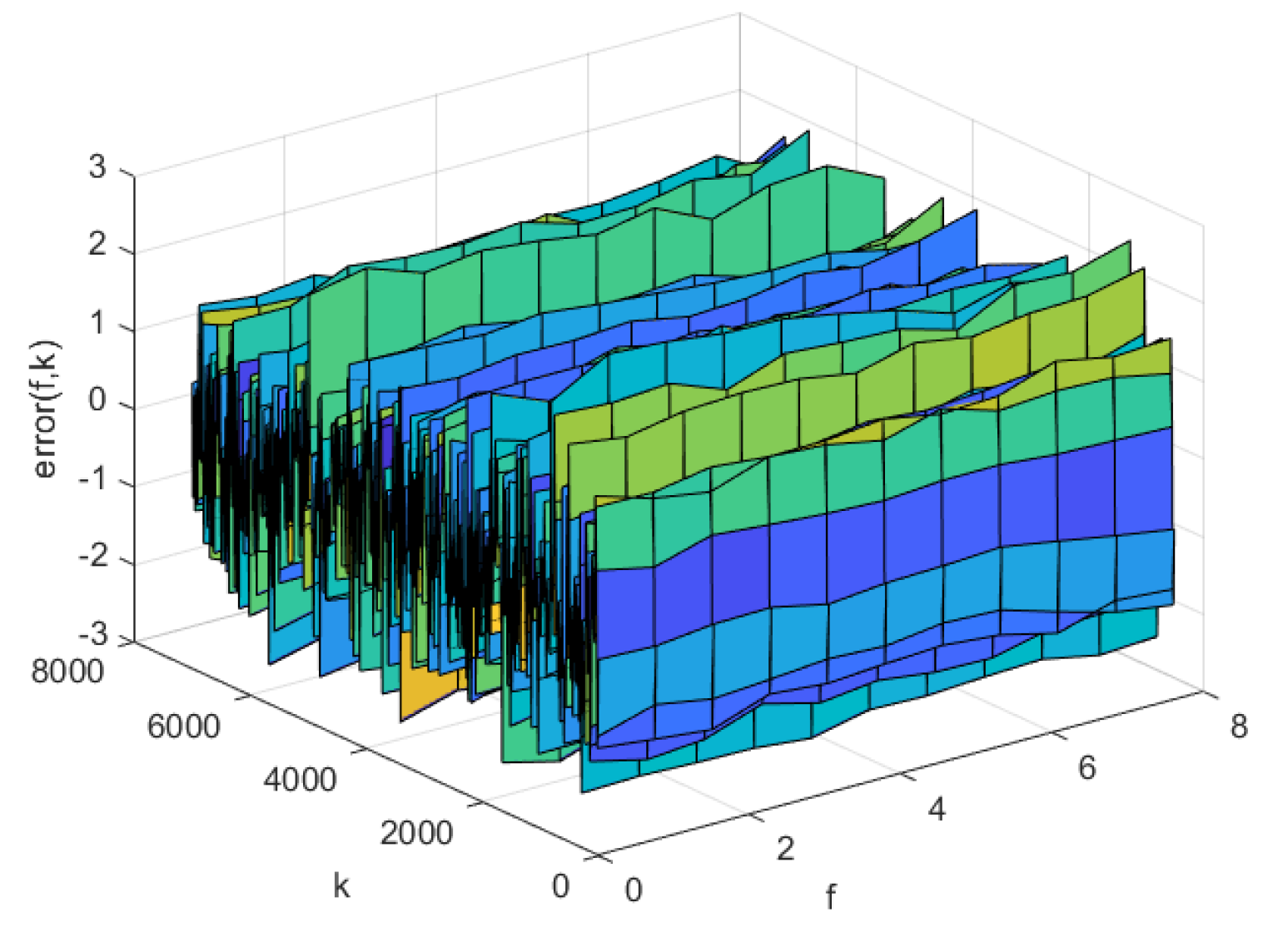
Figure 14. Prediction error of NNC-SVR-3D model on training set

Figure 15. TNAE of four models on training data

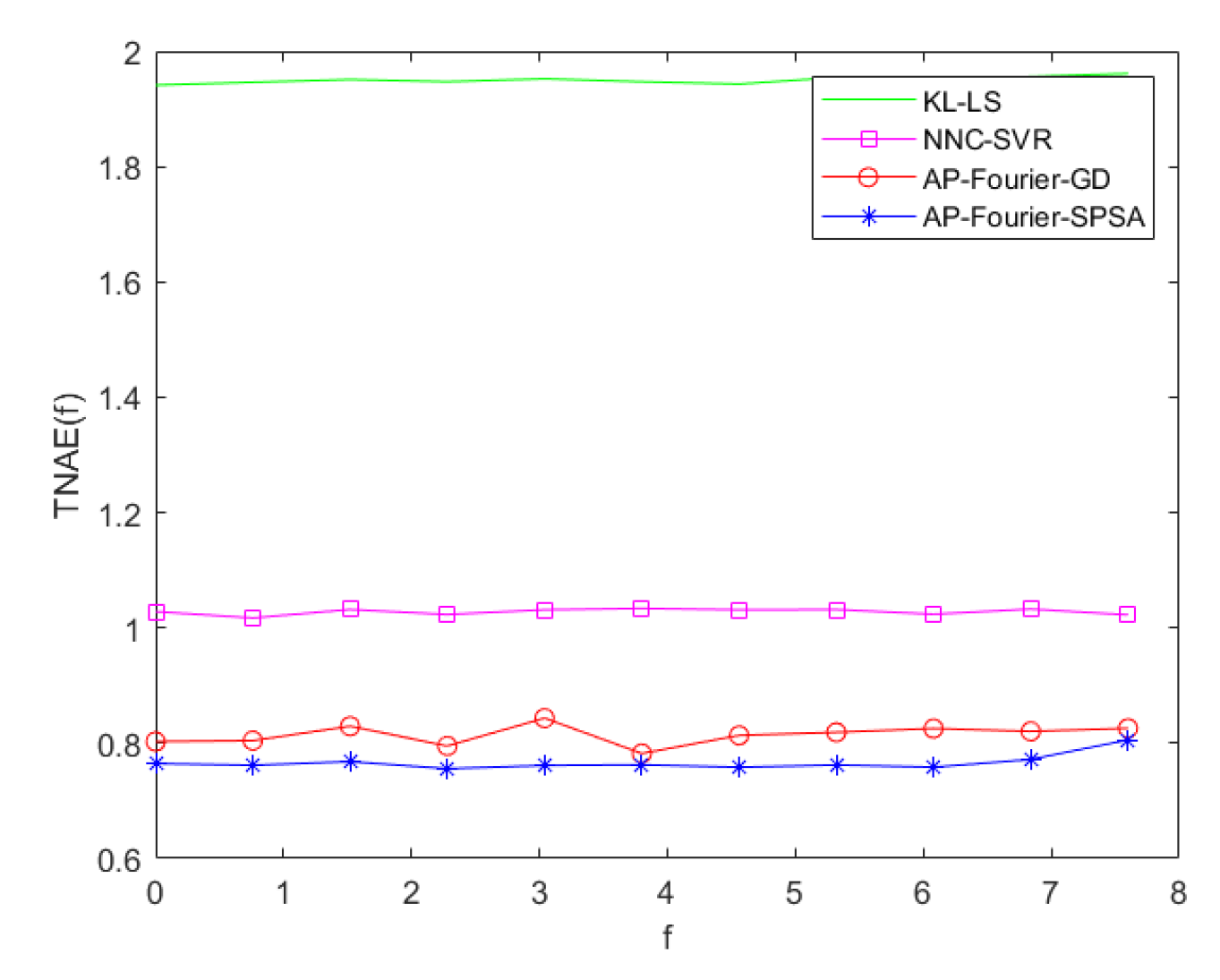
Figure 16. TNAE of four models on test data

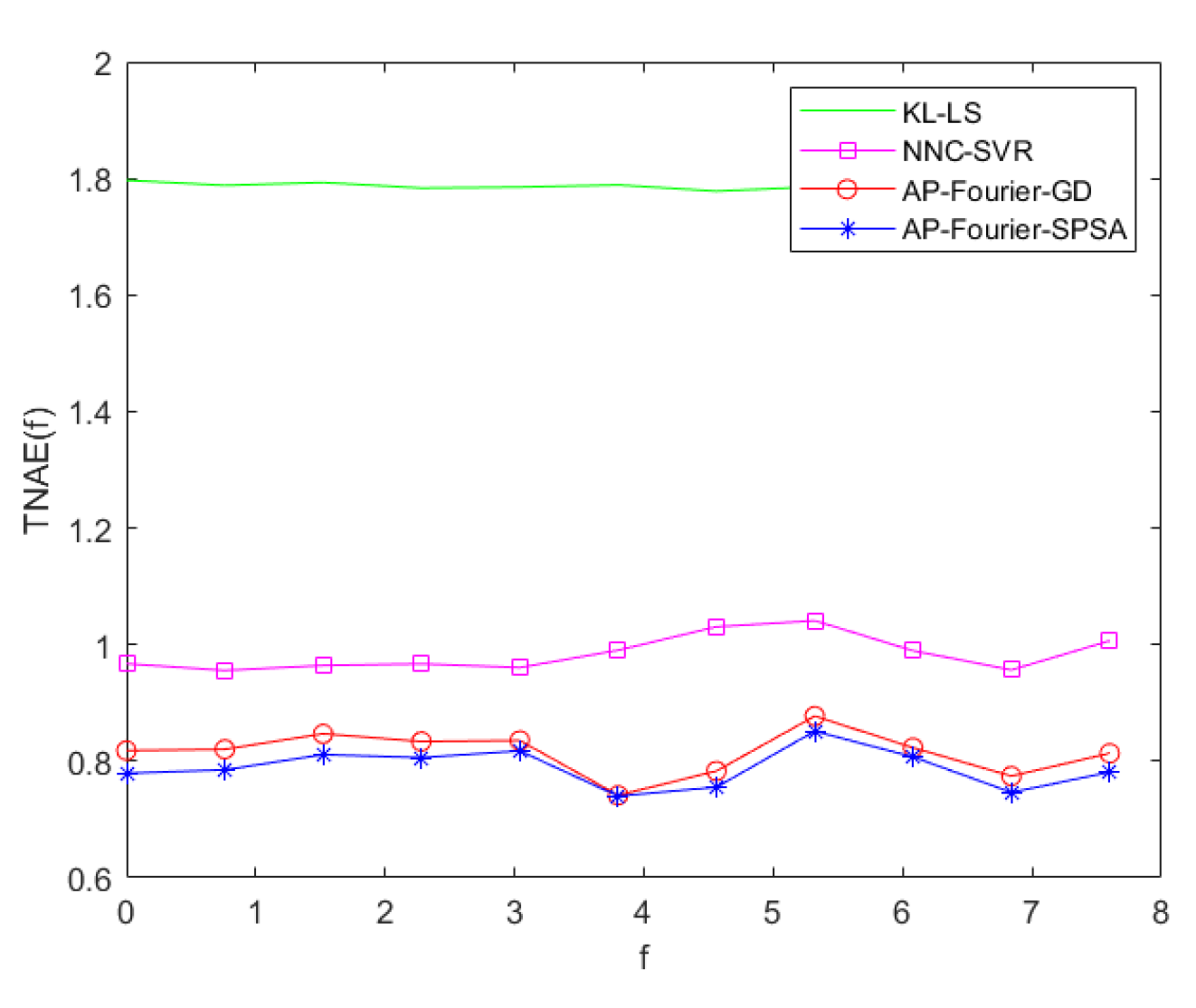
Figure 17. Flow chart of AP clustering algorithm

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Three-dimensional Fuzzy Modeling for Nonlinear Distributed Parameter Systems Using Simultaneous Perturbation Stochastic Approximation

Abstract

1. Introduction

2. Problem Description

2.1. Mathematical Description of Distributed Parameter Systems and Its Characteristics

2.2. Three-dimensional Fuzzy Modeling

3. SPSA Learning Based Three-Dimensional Fuzzy Modeling

3.1. Modeling Methodology

3.2. AP Clustering Learning for Preceding Components of Three-dimensional Fuzzy Rule

3.3. SPSA Learning for Resulting Components of Three-dimensional Fuzzy Rule

3.3.1. Fourier Space Base Function

3.3.2. Parameter Learning Using SPSA Algorithm

3.3.3. Three-dimensional Fuzzy Modeling Flowchart

4. Application to RTCVD System

4.1. RTCVD System

4.2. SPSA Learning Based Three-dimensional Fuzzy Modeling

4.3. Simulation Comparison

5. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

Appendix A

Appendix Algorithm Description of AP Clustering and Its Flow Chart

References

MDPI Initiatives

Important Links

Subscribe