Preprint
Article
Synergizing Phenomenological and AI-Based Models with Industrial Data to Develop Soft Sensors for a Sour Water Treatment Unit
Altmetrics
Downloads
93
Views
27
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
02 August 2024
Posted:
06 August 2024
You are already at the latest version
Alerts
Abstract
Sour waters are one of the main aqueous byproducts generated during petroleum refining and require processing in Sour Water Treatment Units (SWTUs) to remove contaminants such as H₂S and NH₃ in compliance with environmental legislations. Therefore, monitoring the composition of SWTU effluents, including acid gas, ammoniacal gas, and treated water, is essential. This study aims to present an AI (artificial intelligence) hybrid-based methodology to develop soft sensors capable of real-time prediction of H₂S and NH₃ mass fractions in the effluents of SWTUs and validate them using real data from industrial units. Initially, a new database based on the dynamic simulation of a two stripping columns SWTU phenomenological model, developed in Aspen Plus Dynamics® V10, was generated, aiming at non-faulty runs, unlike our previous work [1]. Ensemble methods (Decision Trees), such as Gradient Boosting and Random Forest, and Support Vector Machines were compared for soft sensor creation using these simulated data. The best outcome was the development of six soft sensors based on Random Forest with R² greater than 0.87, MAE less than 0.12, MSE less than 0.17, and RMSE less than 0.41. Variable importance analysis revealed that the temperature of the second stage of Column 1 significantly influences the thermodynamic equilibrium of H₂S and NH₃ separation from sour waters, being critical for five of the six soft sensors. After this initial stage using data from the phenomenological model, data from an industrial-scale SWTU were used to develop real soft sensors. The results proved the effectiveness of the conjugated use of physical model and industrial data approach in the development of soft sensor for two-column SWTUs.
Keywords:
Subject: Engineering - Chemical Engineering
1. Introduction
One of the most important challenges of our times is to reduce the climate impacts of industrial processes. The reduction of harmful gas emissions and the prevention of soil and water contamination play an important role in that purpose.
In the context of petroleum refining process, steam and water streams are used in various units such as hydroprocessing, delayed coking, and fluidized catalytic cracking, just to name a few systems. One of the effluents from these units is referred to as sour water, as it is contaminated with various weak electrolytes such as phenol, ammonia (NH₃), hydrogen sulfide (H₂S), and possible traces of carbon dioxide (CO₂) [2].
After the refining stage, sour water is directed to the Sour Water Treatment Unit (SWTU) to reduce contaminant levels, focusing primarily on the removal of NH₃ and H₂S. The stream undergoes a stripping process, being subjected to a heating and rectification system where the necessary heat is provided to reduce the partial pressures of gases and separate the contaminants [3].
This process is usually carried out with two columns when ammonia concentration in sour water is high, as illustrated in Figure 1. In this configuration, the first column produces a top stream rich in H₂S, known as acid gas, which is directed to the Sulfur Recovery Unit (SRU). The second column is responsible for separating the bottom output from the first one into two streams: a top stream rich in NH₃, known as ammoniacal gas, which is sent to the ammonia incinerator, and a bottom stream referred to as treated water.
According to the Brazilian environmental legislation, at least 90% of the incoming H₂S load in sour water must be removed and sent to the Sulfur Recovery Unit (SRU). This is a critical point in the process because if H₂S residues are sent to the second column, they will be eliminated along with ammoniacal gas (NH₃), producing SOX, which is environmentally undesirable as it contributes to air pollution and is a precursor to acid rain [4,5,6]. Nevertheless, a high efficiency in H₂S removal can have negative consequences on the operation of the Sulfur Recovery Unit (URE). An increase in H₂S removal can lead to an increase in NH₃ concentration in the acid gas, causing operational issues in the unit. This problem may result in efficiency loss due to line blockages and the formation of NOx, a compound highly detrimental to the environment and public health, as it is also a precursor to acid rain and photochemical smog [7,8].
Therefore, maintaining a high H₂S recovery in the first tower while simultaneously reducing the NH₃ content in the acid gas represents conflicting goals and characterizes an operation with a narrow tolerance range for units with this configuration. Furthermore, small disturbances that may cause variations in the STWU feed streams composition can result in faults that ultimately lead to the emission of environmentally harmful compounds above regulatory limits.
Currently, a major operational challenge is to monitor the effluent composition of these units online. Soft sensors play an important role to solve these difficulties. Soft sensors are mathematical models or algorithms that allow estimating the value of a variable of interest based on available process information, without the need for direct measurements of that variable [9]. They can be employed for real-time monitoring of process variables, enabling trends and anomalies identification, triggering alerts and notifications when potential problems are detected. Additionally, they offer substantial cost savings compared to traditional sensors, as they eliminate the need for physical installation and maintenance and are not affected by obsolescence due to corrosion in industrial environments [10]. Soft sensors can also assume the role of physical sensors in situations of unexpected failure. This ensures that operators have continuous access to the necessary information to monitor and control processes, reducing the risk of unplanned disruptions due to lack of essential information [2]. Finally, for process control applications, they eliminate the measurement delay issues associated to complex laboratory analyses [11]. Thus, the development of soft sensors for a SWTU is an advantageous solution for investment and precision issues compared to online analyzers and laboratory analyses.
There are three main approaches used to estimate variables based on other measurements. These are i) model-driven (or white-box) in which a model based on fundamental principles is employed; ii) data-driven (or black-box) that relies solely on historical process data, allowing models to be created using Machine Learning techniques; and iii) gray-box, which is a combination of the two previous methods [12,13].
The main objective of the present study was the development of soft sensors for predicting the composition of all main effluents from a SWTU with a two striping tower configuration using a gray-box or hybrid approach.
In the initial phase of the investigation, a new database was developed to support this research, utilizing a modified version of the dynamic model of a SWTU with two stripping columns previously developed in Aspen Plus Dynamics® V10 by [1]. Ensemble methods (decision trees) such as Gradient Boosting [14] and Random Forest [15,16], along with Support Vector Machines [17,18], were initially compared for soft sensor creation, using the simulated data generated by the phenomenological model. Subsequently, six models were developed to predict H₂S and NH₃ concentrations in each output stream of the unit. The input variables for each soft sensor were determined and analyzed.
In the second part of the work, the methodology was validated by applying it to a real industrial-scale unit. The goal was to utilize the available information about the process provided by the phenomenological model to enhance and calibrate the data-driven AI-based model. This approach allowed the combination of theoretical understanding with the flexibility of data-driven modeling. Compared to other techniques that implicitly integrate machine learning techniques with physical equations [19], the present proposal aims to be more intuitive and natural, as the intention was to develop a tool to assist the operator in a human-centred Industry 5.0 context [20].
Although developments in soft sensors for other wastewater treatments are more common [21], the number of applications specifically addressing SWTUs is scarce. In [22], soft sensor models were developed to estimate the removal efficiency of H₂S in a SWTU. The collected data spanned a two-year operational period of a sour water stripper processing non-phenolic acid water. Only steady-state data were employed, so that a total of 144 different operating conditions were considered. A simplified phenomenological approach developed in AspenOne® and a linear statistical model did not show reliability in the results obtained. On the other hand, a multilayered perceptron (MLP) neural network proved suitable for the desired application. In [23], a semi-supervised learning approach based on deep neural networks was employed to develop two soft sensors for estimating the concentrations of H₂S and NH₃ in the wastewater of a SWTU with only one column. The study addresses the difficulty of labeling data, as, in certain industrial scenarios, input variables are constantly measured, while output variables are quantified only once or twice a day. The results of the deep neural network-based sensors used were compared with MLP network models. The sensors developed with deep neural networks exhibited better performance and proved to be an effective strategy for industrial applications where a shortage of labeled data can significantly impact the performance of data-driven soft sensors.
The present work has been divided into six sections. Section 1 encompasses the motivation, objective, and a review of previous works. Section 2 presents the phenomenological model used. Section 3 provides a detailed description of the methodology for developing the database and soft sensors, based on the phenomenological model. In Section 4, the results for a real industrial SWTU are presented and discussed. Finally, Section 5 addresses the conclusions.
2. Materials and Methods
2.1. The Phenomenological Model
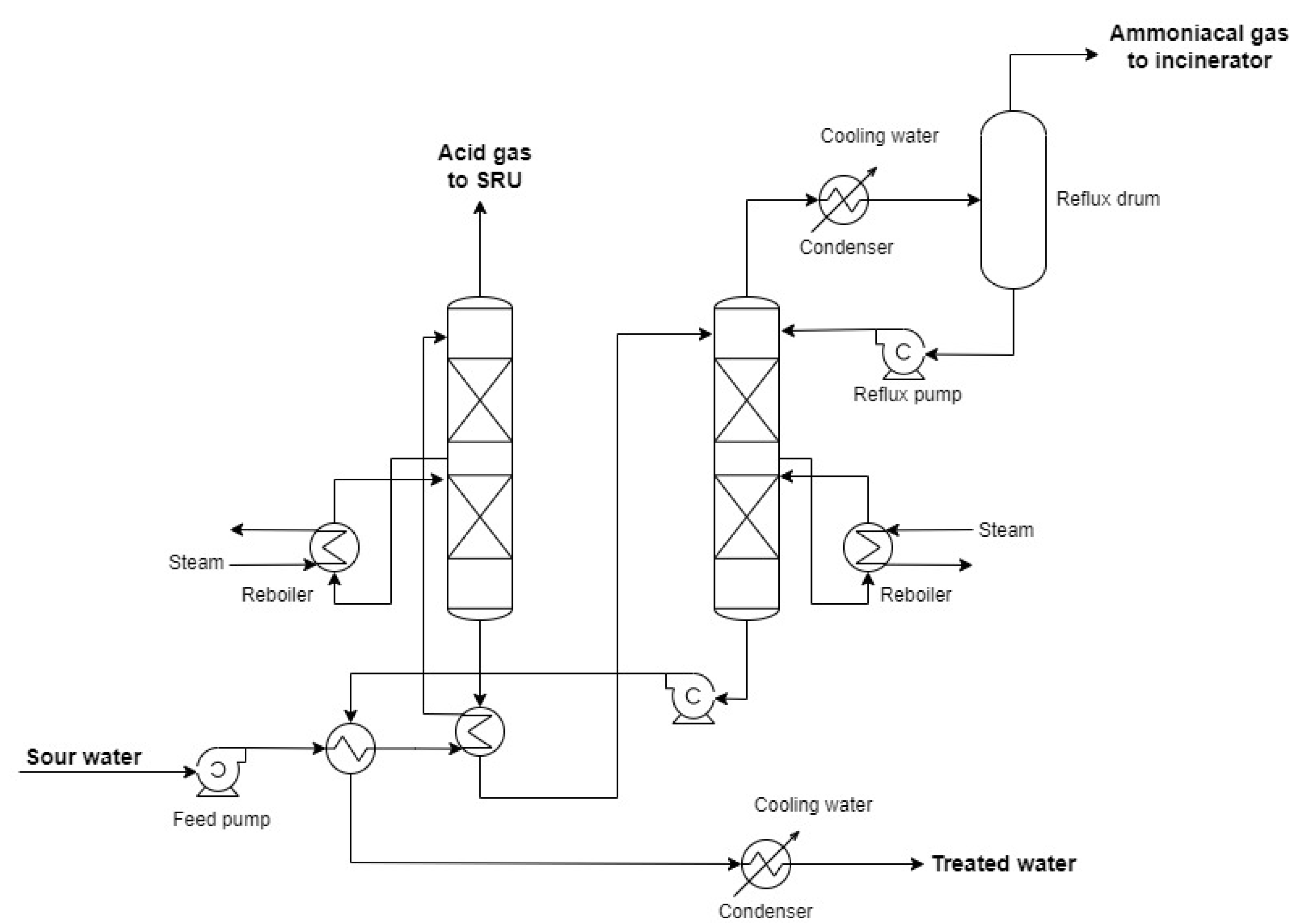
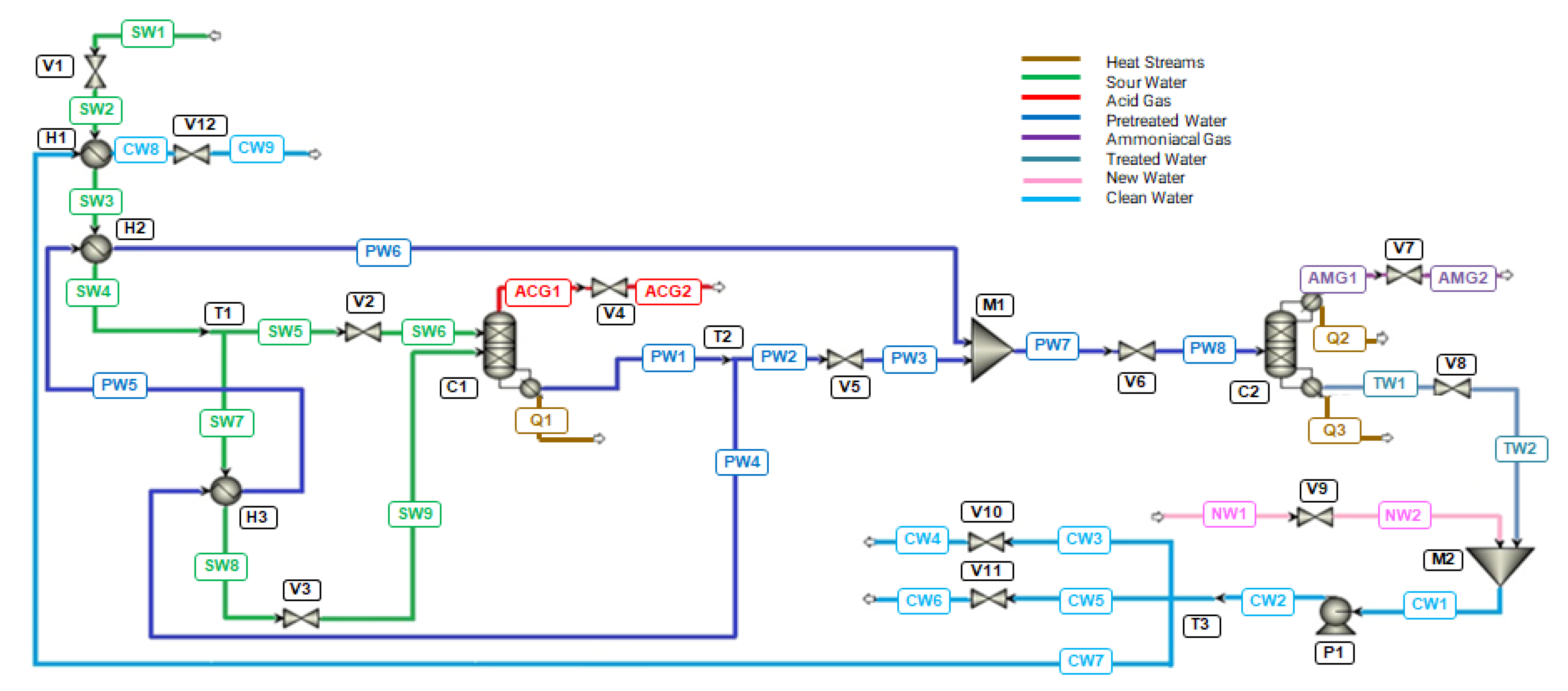
In [1], the author conducted the dynamic simulation of a SWTU in Aspen Plus Dynamics® V10 using the Gas Process Association Sour Water Equilibrium (GPSWAT) model, considered the most suitable for sour water applications. In this simulation, there are thirty-four material streams and seven different compositions, three heat streams, and twenty-three pieces of equipment: twelve valves, three heat exchangers, three splitters, two mixers, one pump, and two columns. The block diagram in Figure 2 summarizes all the streams and key equipment in the simulation, where H1, H2, and H3 are the heat exchangers, and C1 and C2 are the stripping columns.
The seven different compositions described in the process are sour water, which is the incoming stream to be treated; acid gas, which is the overhead stream from the first column rich in H₂S; ammoniacal gas, which is the overhead stream from the second column rich in NH₃; pre-treated water, which is the bottom stream from the first column, hence rich in NH₃; treated water, which is the bottom stream from the second column, containing small amounts of dissolved H₂S and NH₃ contaminants; new water, which is an aqueous stream without contaminants, and finally, clean water, which is the mixture of new water with treated water. Table 1 correlates the abbreviations of these streams with their compositions.
The two input streams of the process are SW1 and NW1, while the five output streams are ACG2, AMG2, CW4, CW6, and CW9. SW1 is the sour water to be treated, and NW1 is the new uncontaminated water source that dilutes the treated water stream after passing through the two columns. Table 2 displays the physical properties of the input streams.
These streams had their mass flow described as a function of SW1, defined as SW1F. These values were anonymized due to the confidentiality of information that originated the simulations developed by [1].
Finally, ACG2 and AMG2 are the outputs of acid gas and ammoniacal gas, respectively. CW4, CW6, and CW9 are the outputs of clean water with the same composition.
The simulation begins with the SW1 stream, which is preheated in heat exchangers H1 and H2 through energy integration with streams CW7 and PW5, respectively, becoming SW4. SW4 is divided into SW5 and SW7. SW5 becomes SW6 after passing through valve V2 and enters the top of column C1. SW7 is preheated once again in heat exchanger H3 through energy integration with PW4 and becomes SW9 after passing through valve V3, subsequently entering the lower feed of column C1. Therefore, streams SW6 and SW9 feed C1.
Column C1 is heated by the thermal load Q1 from the reboiler, separating the overhead stream ACG1 (acid gas) from the bottom stream PW1 (pre-treated water). ACG1, after valve V4, becomes ACG2 and is removed from the system, while PW1 is split into two streams: PW2 and PW4. PW4 is cooled in heat exchanger H3 through energy integration with SW7 and becomes PW5. PW5 is further cooled in H2 through energy integration with SW3 and becomes PW6. PW2 becomes PW3 after passing through valve V5 and is mixed with PW6, forming PW7. It is noteworthy that PW7 has the same mass flow as PW1, as the streams that split reunite without losses. After valve V6, PW7 becomes PW8 and enters the feed of column C2.
Column C2 has a condenser and a reboiler, with thermal loads Q2 and Q3, respectively. The overhead stream from Column 2 is AMG1 (ammoniacal gas), and the bottom stream is TW1 (treated water). AMG1, after valve V7, becomes AMG2 and is removed from the system. TW1, after valve V8, becomes TW2. TW2 is mixed with NW2, becoming clean water (CW1). After passing through pump P1, CW1 is then called CW2. CW2 is divided into three streams: CW3, CW5, and CW7. CW3, after valve V10, becomes CW4 and is removed from the system. CW5, after passing through valve V11, becomes CW6 and is removed from the system. Meanwhile, CW7 is cooled in heat exchanger H1 through energy integration with SW2, becoming CW8. CW8, after valve V12, becomes CW9 and is removed from the system. A more complete view of the process is in Figure 3, showing the static simulation developed by [1].
There are two 'RadFrac' type columns and three 'HeatX' type heat exchangers in the simulation. Column C1 consists of 5 stages, and Column C2 consists of 6 stages. The feed occurs at stages 1 (SW6) and 2 (SW9) in C1, and at stage 2 (PW8) in C2. The two mixers were configured to receive both liquid and vapor phases. Valves V4 and V7 were configured only to receive vapor, while the other valves accept only the liquid phase. All valves have an associated pressure drop.
The dynamic model by [1] includes 14 controllers added to ensure the operability and stability of the process, as well as aid in the convergence of the dynamic simulation. The controllers in the simulation are: two for pressure at the tops of the columns, four for level at the bottom and top of the columns, three for temperature, including one before the first column and one in its second stage, and another at the top of the second column; four mass flow controllers, two before the first column and two after the second column; and an integrated control of mass flow and thermal load in the second column. Table 3 describes the controlled and manipulated variables for each of these controllers.
The tuning of the controllers was performed based on general rules described in the literature and through expert advice from the industry [1].
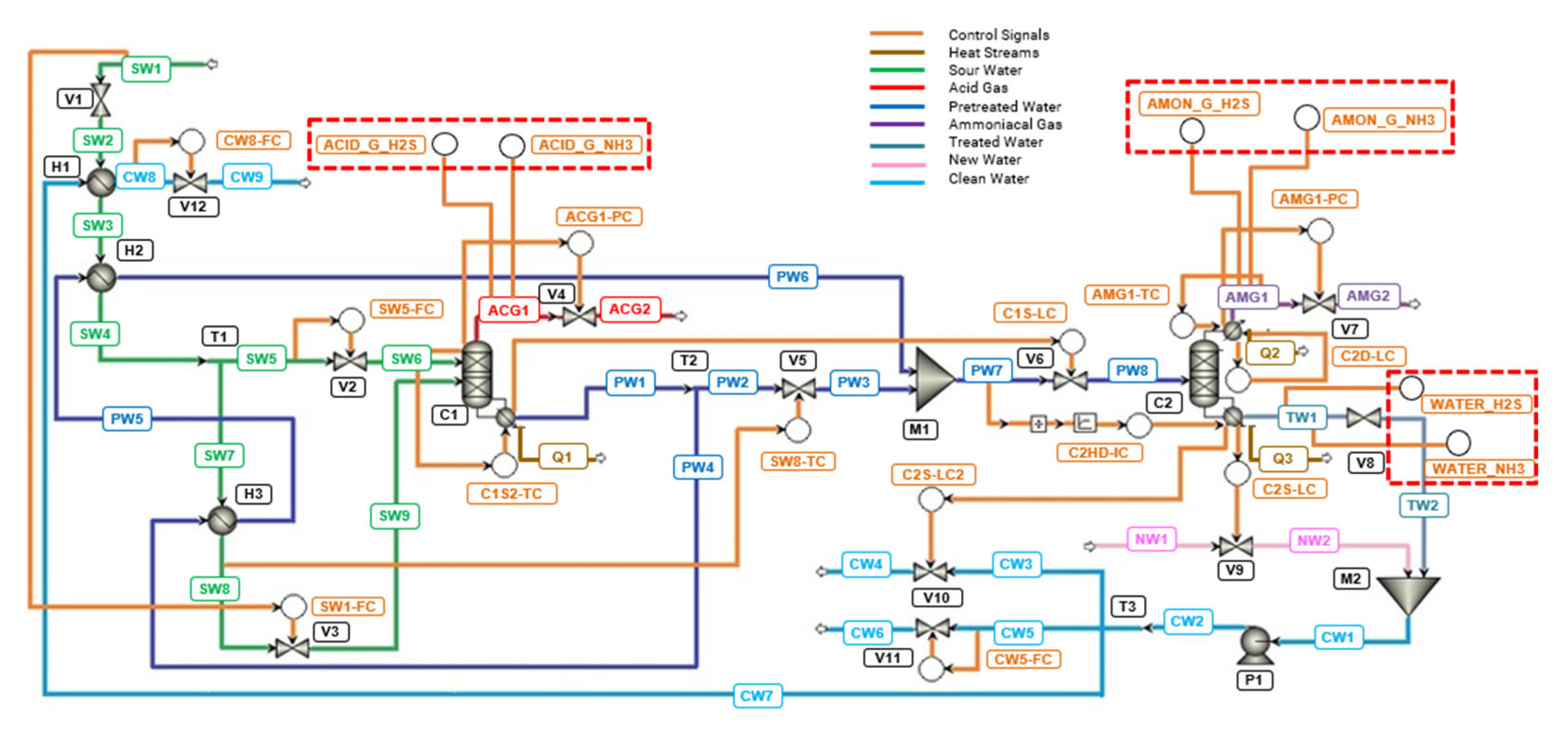
The first step in creating the new database for the development of soft sensors involved the inclusion of six controllers not previously used in the dynamic simulation of the SWTU with two stripping columns by [1].
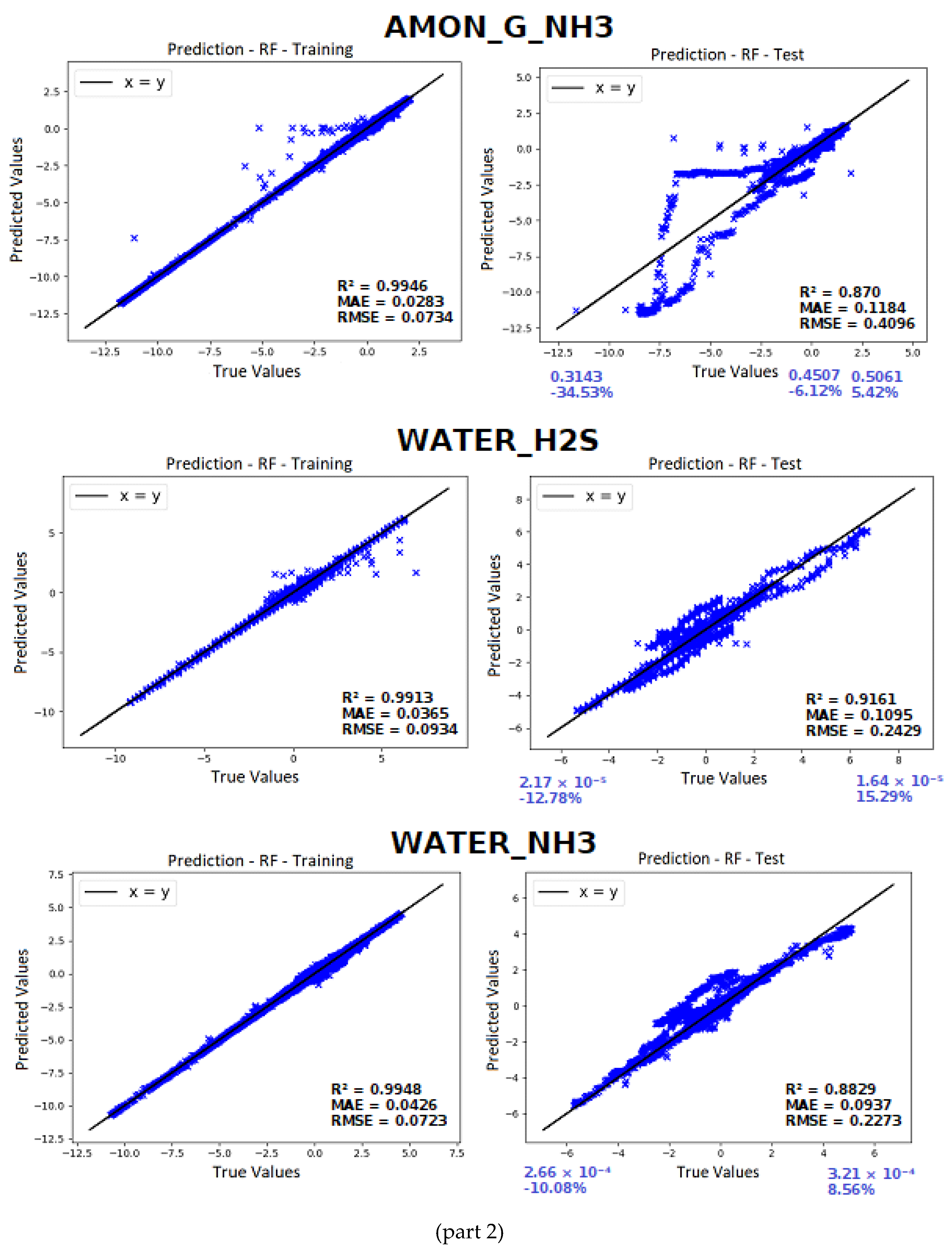
Among these controllers, two were incorporated into the acid gas stream (ACG1) at the top of Column 1 (ACID_G_H₂S and ACID_G_NH₃), another two were added to the ammoniacal gas stream (AMG1) at the top of Column 2 (AMON_G_H₂S and AMON_G_NH₃), and two more (WATER_H₂S and WATER_NH₃) were introduced into the treated water stream (TW1) withdrawn from the bottom of Column 2. The six new controllers can be seen in Figure 4, along with the original simulation controllers.
To enable the collection of dynamic data for the fractions of H₂S and NH₃ in the effluents described, the PID (Proportional, Integral, Derivative) controllers included were adjusted with a gain of 0, an integral time of 1 minute, and a derivative time of 0. This configured them to operate solely as 'indicators', without effectively performing control functions during the simulation, only storing the dynamic data.
2.2. Development of the Database and Phenomenological Study of the Process
The simulations, calculations, and codes were developed and executed on a computer with an Intel(R) Core™ i5 7200U, with a CPU@ 2.50 GHz 2.70 GHz processor, 8.00 GB installed memory (RAM), and Windows 10 64-bit operating system. The dynamic simulation of the SWTU was performed using Aspen Plus Dynamics® V10. All data processing and Artificial Intelligence algorithms were implemented in Python 3.11.4 within the integrated development environment Visual Studio Code 1.79.2. The libraries numpy (1.25.2), matplotlib (2.0.2), joblib (1.3.2), scikit-learn (0.19.0), pandas (2.1.0), seaborn (0.12.2), and optuna (3.3.0) were extensively used.
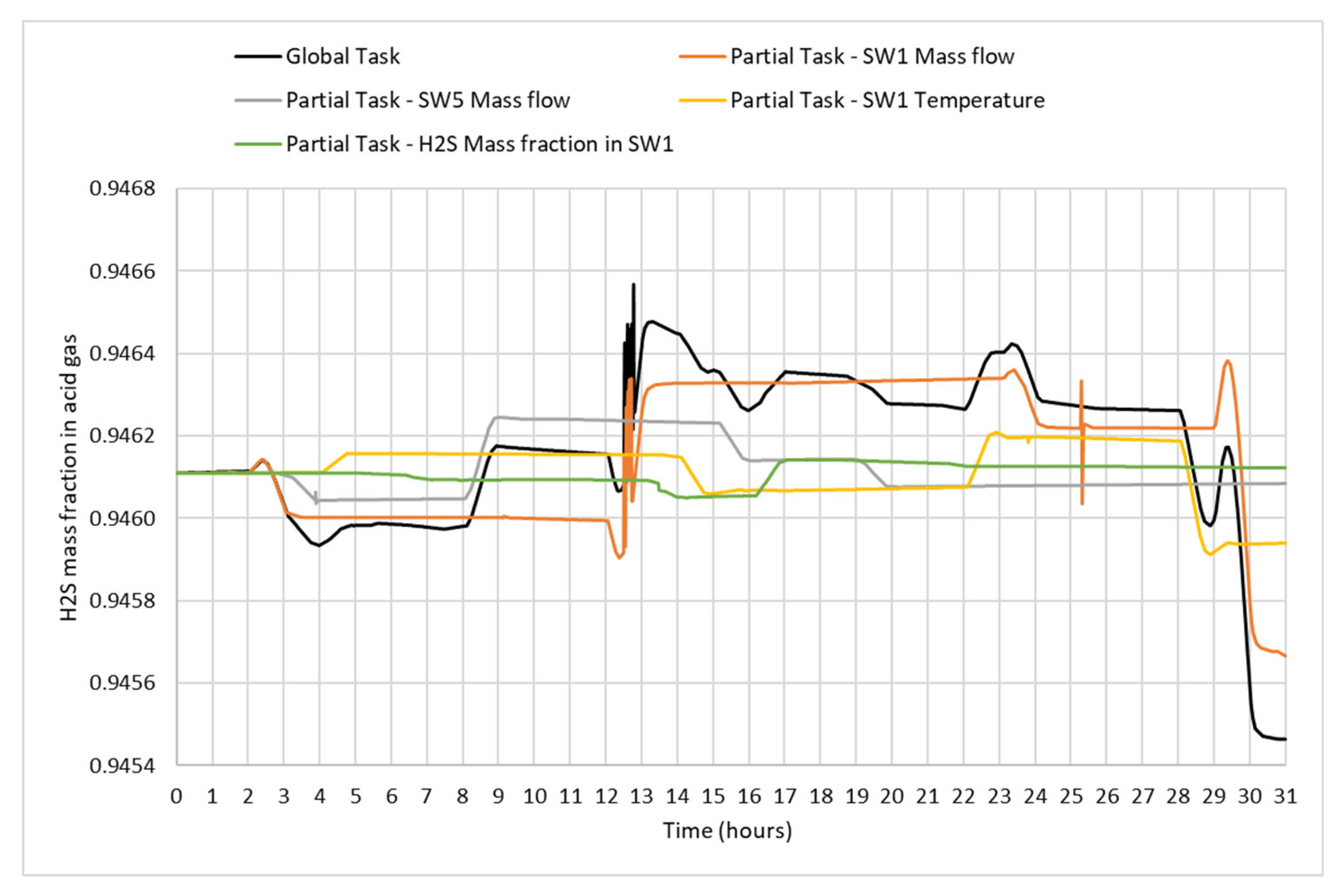
The dynamic simulation, after the changes discussed in Section 2 and illustrated in Figure 4, was tested in various scenarios of normal operation with disturbances in five variables of interest, namely, SW1 mass flow rate, SW5 mass flow rate, SW1 temperature, and NH₃ and H₂S mass fractions in SW1. These variables were chosen because they are input process variables that could undergo variations in a real process. SW1 is the sour water entering the system for treatment, and SW5 represents 10% of SW1, which, after passing through the heat exchangers, enters the top of column C1. Normal operation is characterized when events such as complete valve opening or closing, overflows, or lack of level in the columns do not occur.
2.3. Comparison of Artificial Intelligence Algorithms
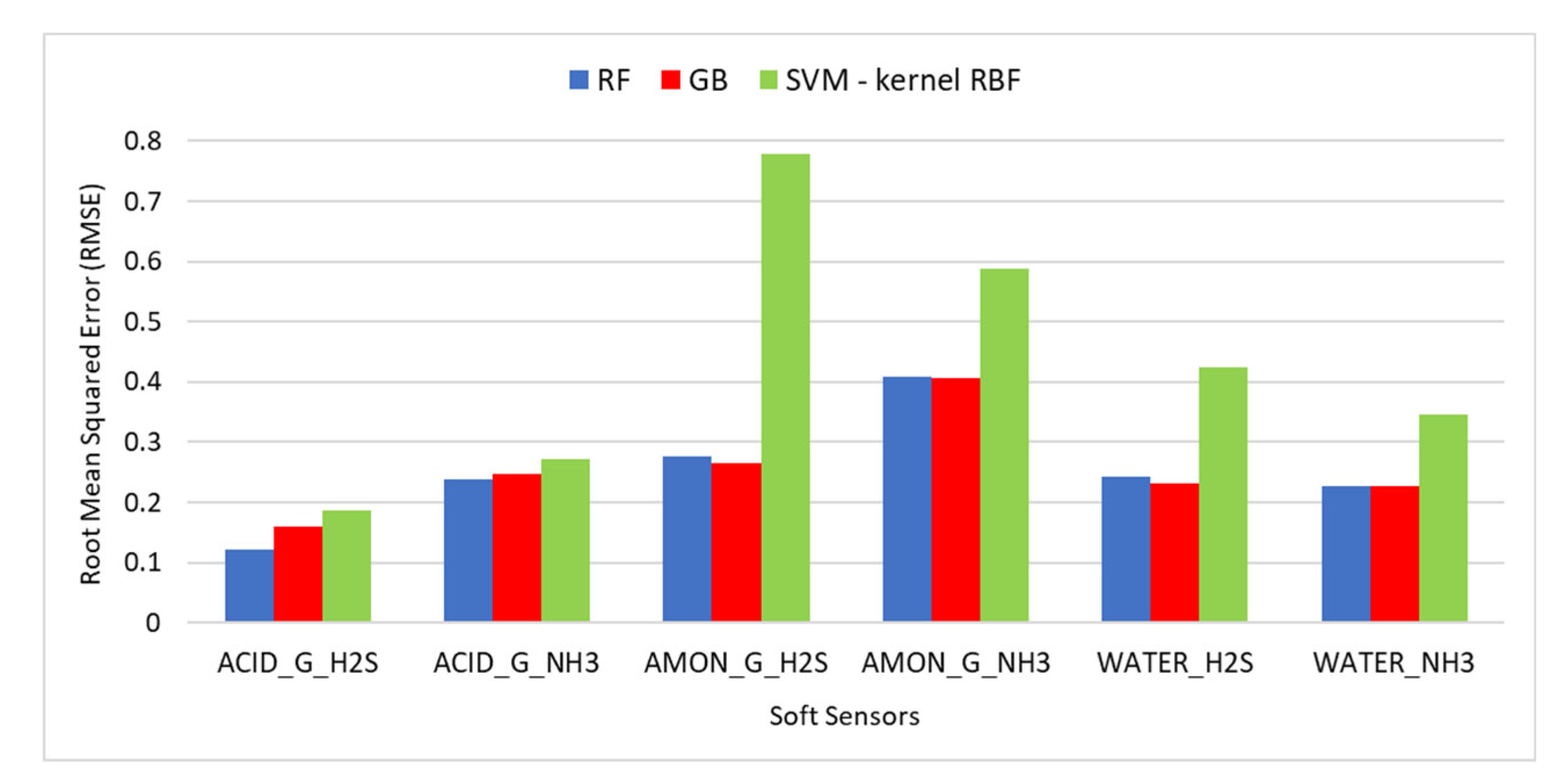
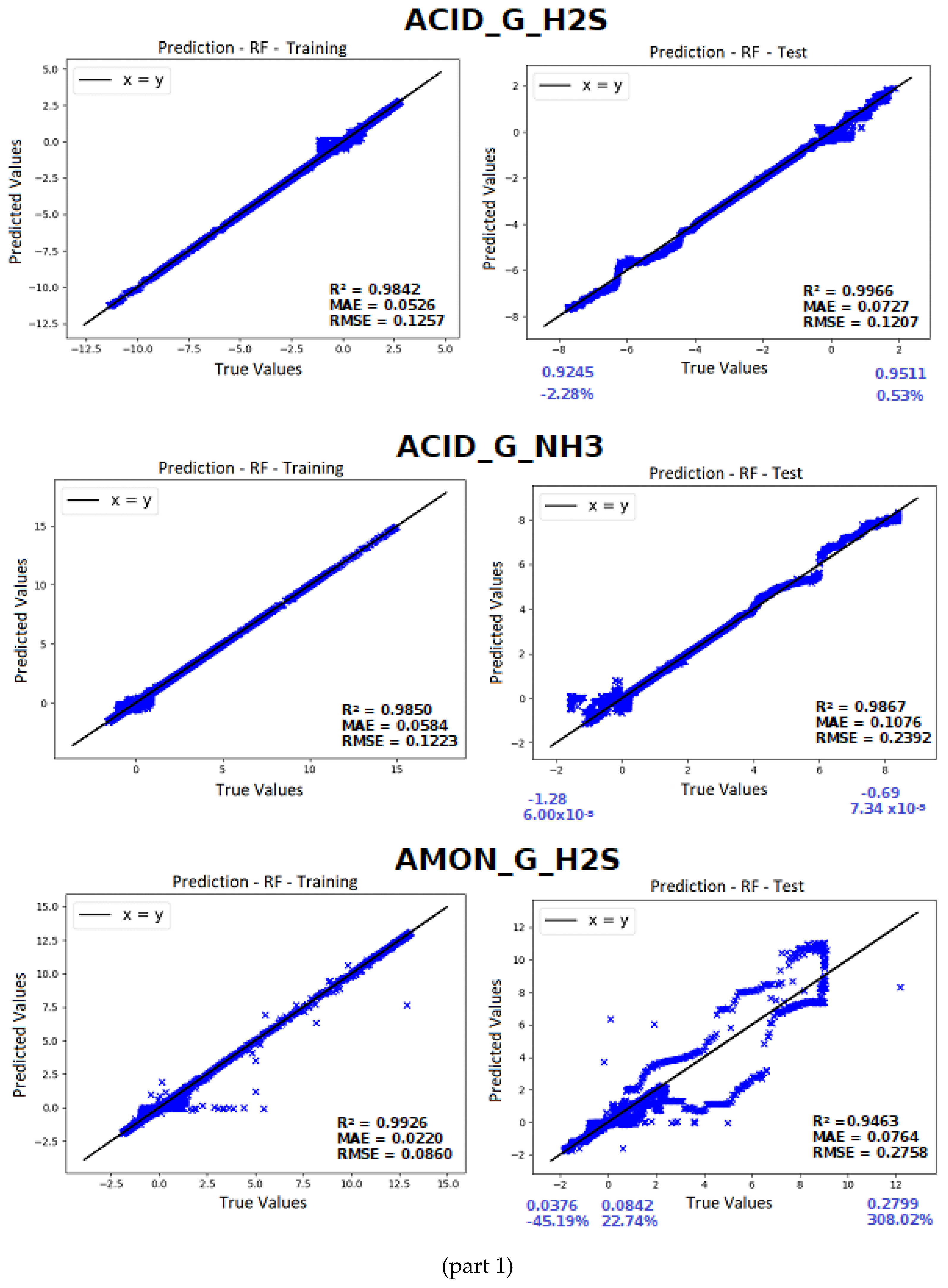
To create the six soft sensors, AI tools such as Random Forests, Gradient Boosting, and SVM with linear and RBF kernels models were evaluated using the same training and test datasets. The methods of Gradient Boosting (GradientBoostingRegressor function), Random Forest (RandomForestRegressor) and SVM (SVR function, linear and RBF kernels) from the scikit-learn library (version 0.19.0) were employed. These kernels were chosen because they demonstrated the best results and the shortest computational times in a previous study [24].
Optuna library was used for hyperparameter optimization of the RF algorithm, aiming to obtain the most effective and accurate model for each of the six sensors. The optimized hyperparameters included the number of estimators (rf_n_estimators), representing the number of trees in the forest, the maximum depth of the trees (rf_max_depth), and the minimum number of samples required to form a leaf (terminal node) of the tree (rf_min_samples_leaf). The lower and upper limits were defined for each of the RF hyperparameters and are shown in Table 4. This methodology enhances the efficiency of the optimization by eliminating the need to consider extreme or impractical values and helps to prevent overfitting or underfitting issues in the model and resulting in computational time savings. Similarly, the number of iterations (or number of trials) for the hyperparameter optimization process was set to 40.
Analogously to the RF, the same hyperparameters mentioned in Table 4 were optimized for the GB algorithm using the same limits and number of iterations, while for the SVM models, there was no optimization of the hyperparameters (C and gamma), as optimizing them did not yield significant gains as shown by [24].
Data processing takes place after storing the dynamic data from all 20 controllers after each simulation (or simply 'run'). Concatenating this information within normal operation resulted in the development of the database, which was later divided into training and testing data to be used in the development of AI-based soft sensors. To guarantee the representativeness and efficient training of the models, it was ensured that each database had at least one example of each simulation in normal operation. Additionally, all data related to a single run were consolidated in the same database to prevent data leakage, especially considering that the simulations contain temporal data. Furthermore, data shuffling, separation into inputs and outputs, as well as normalization were performed.
After dividing the database, the training set consisted of 45,483 samples (59%), while the test set contained 31,525 samples (41%). The listing with the description of each simulation that composed each set can be found in Table 5 and Table 6.
To clarify the division of runs between training and testing databases, each database contains one example of each simulation. Although they share the same description, each simulation is unique, featuring various versions in terms of intensity, amplitude, and timing of the disturbances. The normalized database can be found in [29].
2.4. Soft sensors using Random Forests
A RF model was developed for each of the six virtual sensors: ACID_G_H₂S, ACID_G_NH₃, AMON_G_H₂S, AMON_G_NH₃, WATER_H₂S, and WATER_NH₃. Each algorithm was trained, validation was conducted with 20% of the training data, and the final evaluation of the best model for each sensor was performed using the test data. Hyperparameter optimization was conducted for all sensors using the lower and upper limits specified in Table 4.
2.5. Global Analysis of the Importance of Variables and Phenomenological Study of the Process
The randomForest package provides valuable information for phenomenologically evaluating a process: the measurement of the Importance of Predictor Variables (Variable Importance – VI). The significance of a variable arises from its complex interaction with other variables. The algorithm assesses the importance of a variable by observing the extent to which the prediction error increases when the data for that variable is altered, while keeping all other variables unchanged. The necessary calculations are conducted tree by tree as the random forest is constructed [25]. This functionality enables the reduction of the dataset of interest by eliminating less important variables, ensuring the simplification and optimization of the model, along with a reduction in computational processing time [26,27].
Therefore, an analysis of the most relevant variables was conducted for each of the sensors. Variables with importance below 2% were excluded, and the predictive capacity of the retrained sensors was evaluated using the same presented metrics (R2, MAE, and RMSE). This reduction of the input dataset, achieved by removing less important variables, enables the simplification and optimization of the model, thus increasing the analysis speed.
2.6. Implementation to a real SWTU
In this section the knowledge gained with the approach based on the phenomenological model is employed to develop random forest models using data from a real SWTU of a Brazilian oil refinery. The chosen unit for this development has the same flowsheet configuration of the simulated plant, making it possible to use the same inputs as in the simulated modelling.
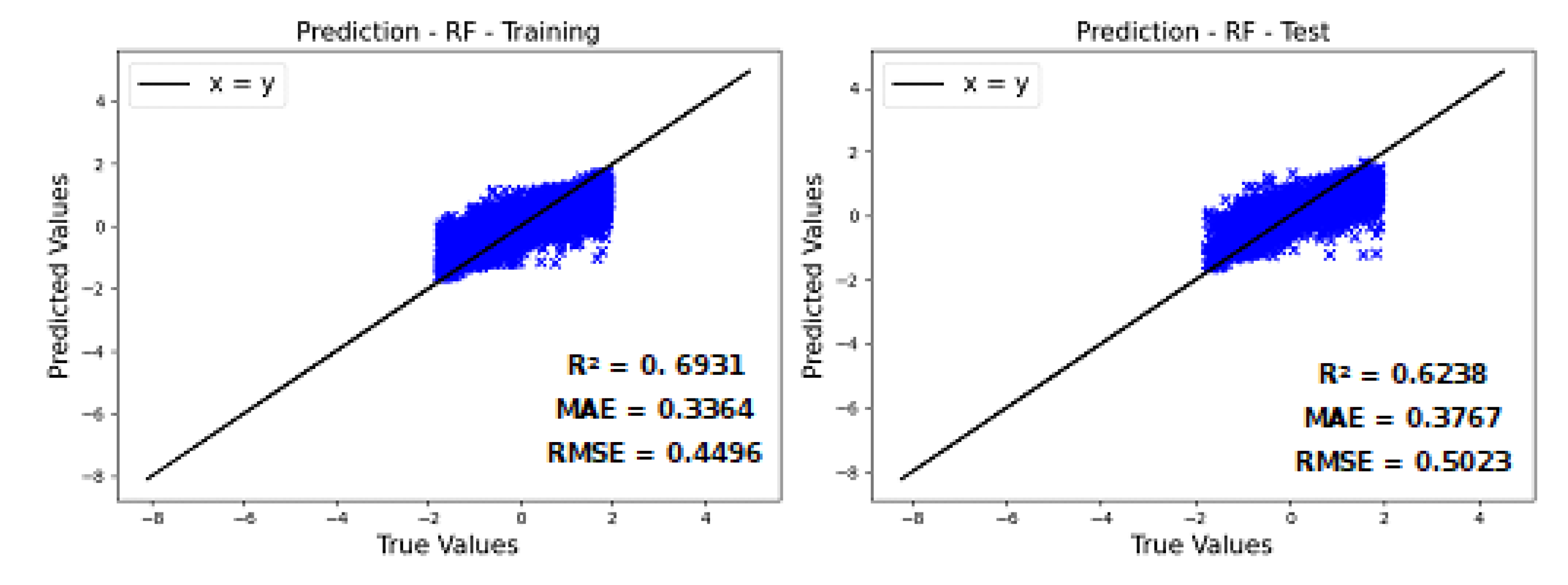
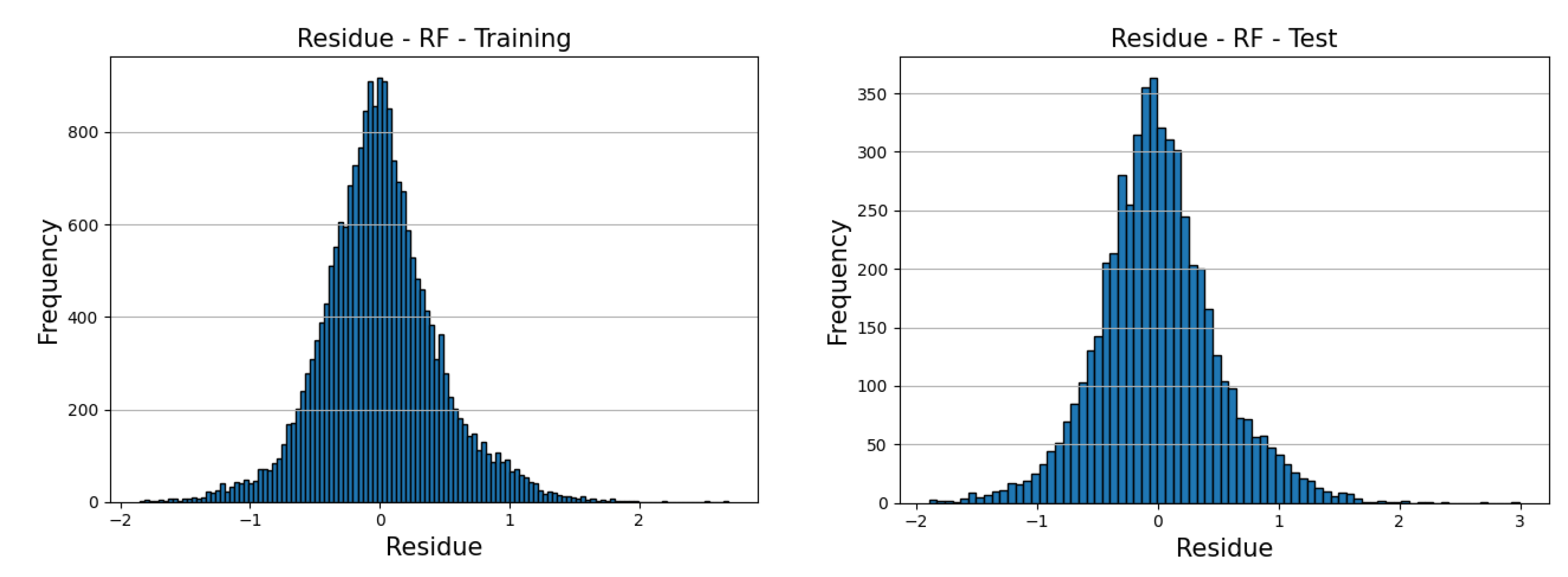
The WATER_NH₃ sensor was selected for modeling. For this sensor, the plant utilizes an online analyzer that produces results approximately every 20 minutes. Unfortunately, analysis for acid and ammoniacal gases were not conducted on the site and only a limited number of laboratory results were available for H₂S on treated water. This was expected due to the hazards involved in sampling acid gas and that H₂S is not a primary concern on treated water given that H₂S is easier to remove than NH₃ in the second column, making more sense to control only the NH₃ content on treated water.
Even though the online analyzer generates results every 20 minutes, it is worth to mention that any control application to be implemented on the plant would need information at least on a minute basis, justifying the importance of modeling this kind of sensor even in a plant with online analyzer.
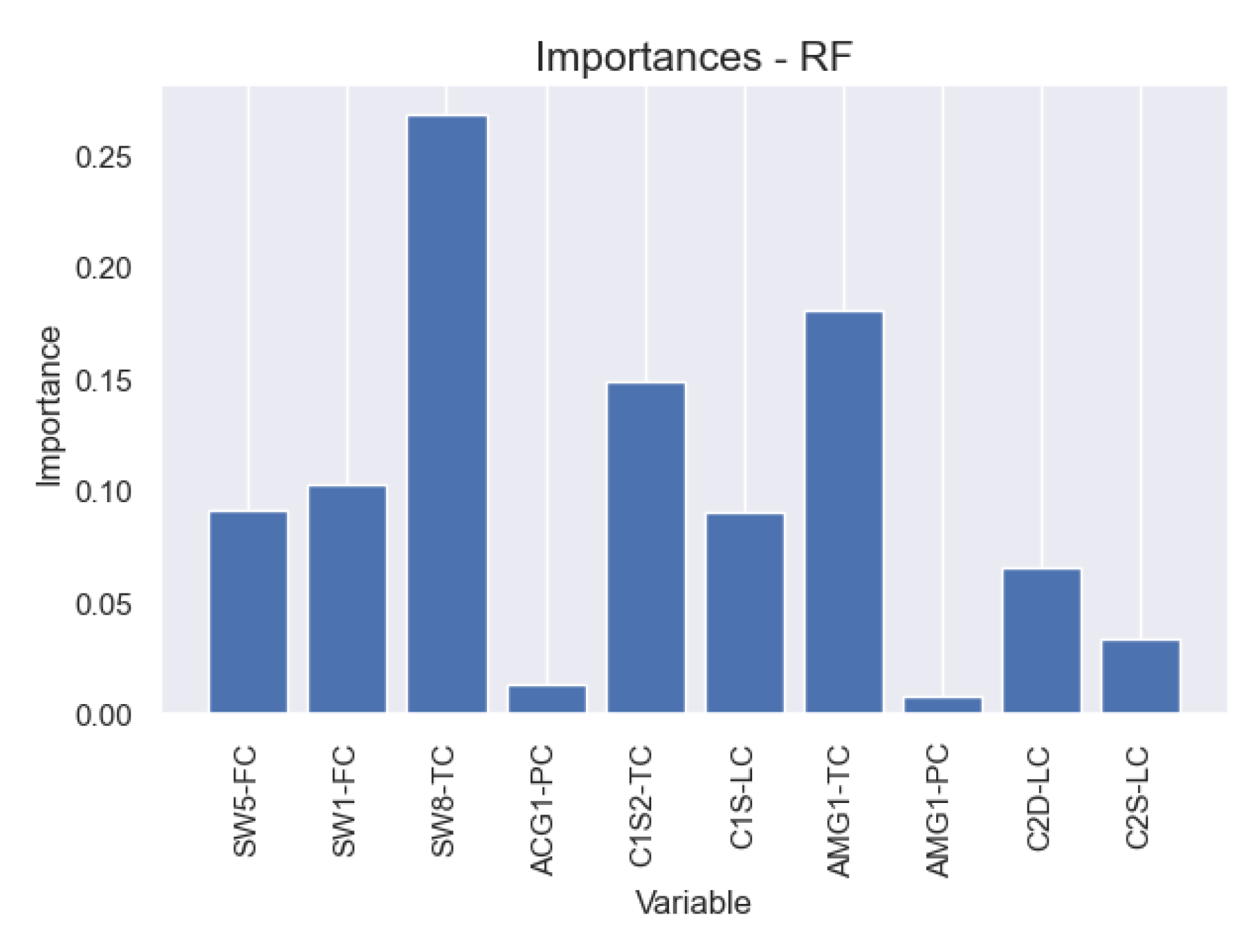
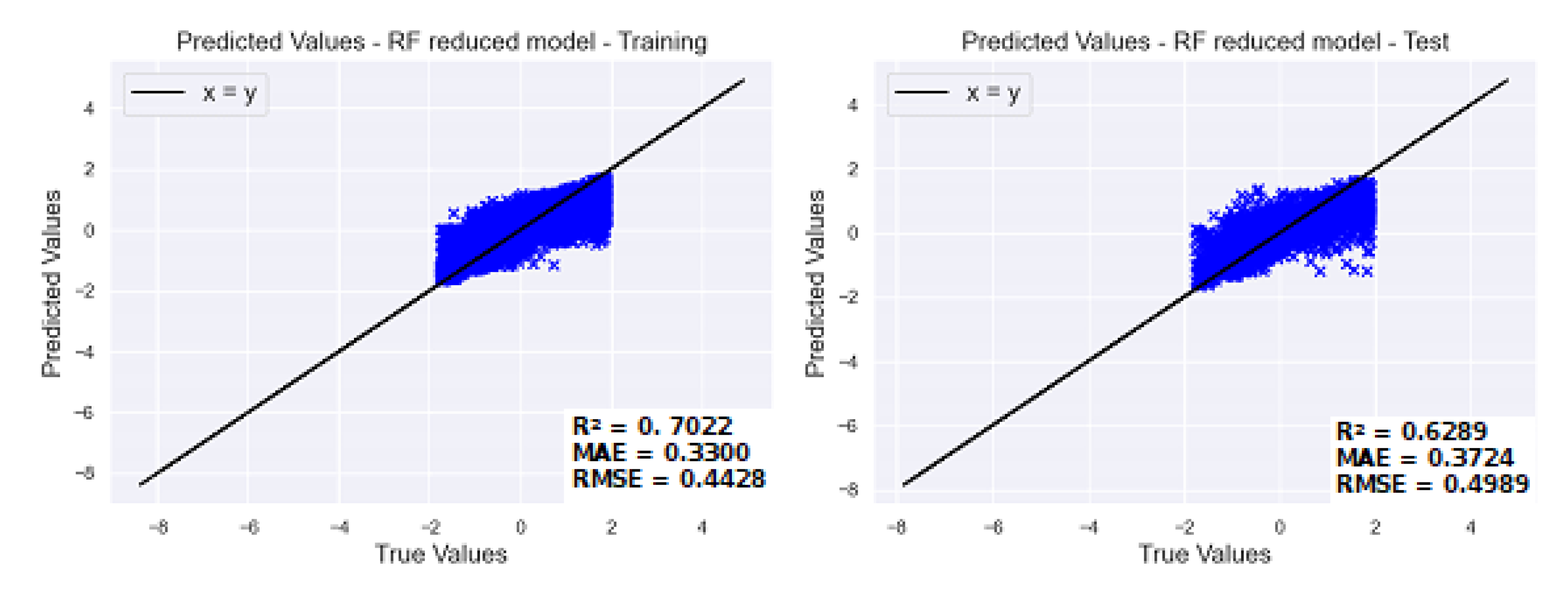
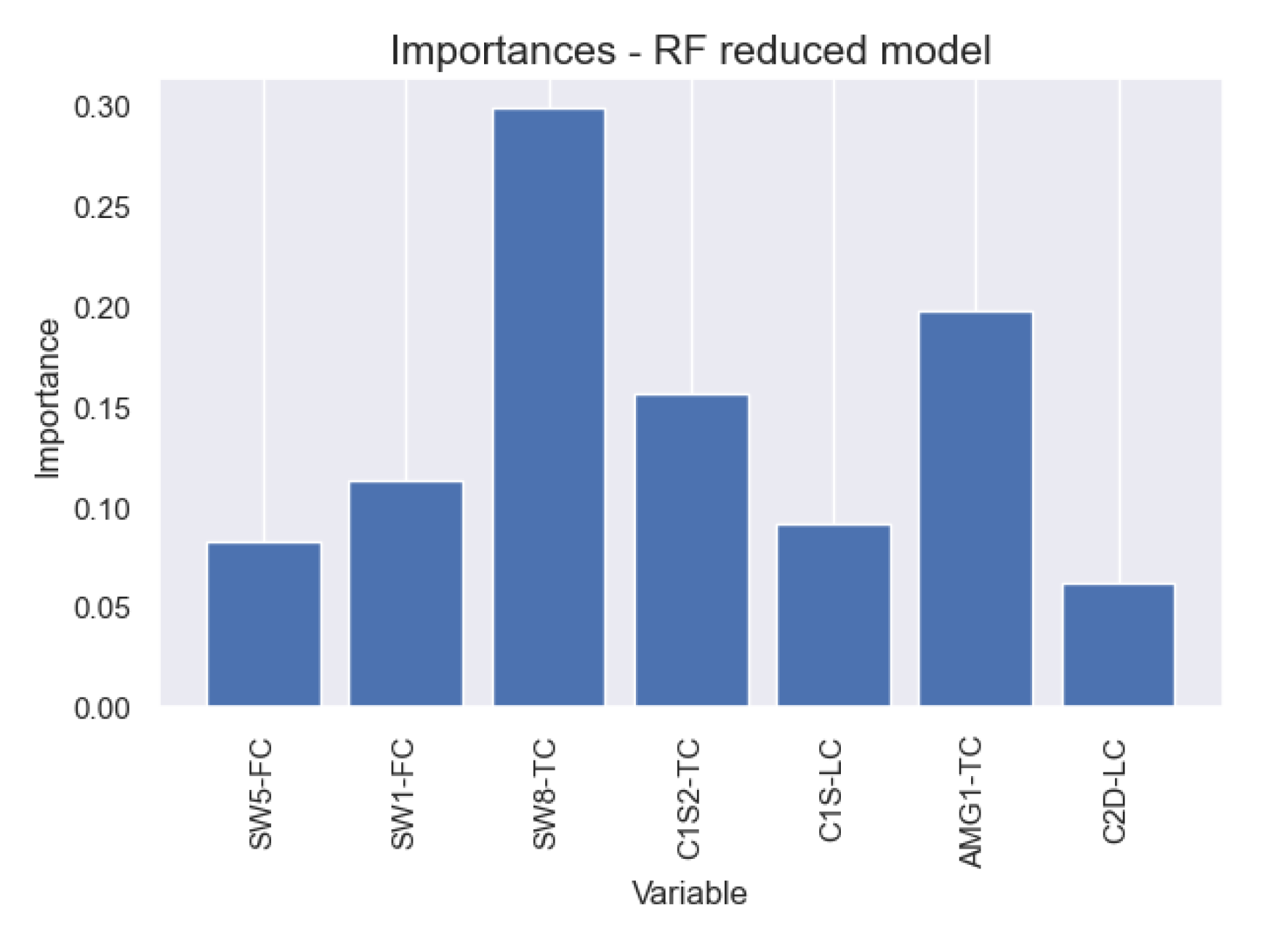
Given that operating conditions of the industrial plant did not precisely match the intervals used in the simulation runs, it was not prudent to use directly the models obtained with simulation data. Therefore, the sensor was retrained with real plant data. Variables SW5-FC, SW1-FC, SW8-TC, ACG1-PC, C1S2-TC, C1S-LC, AMG1-TC, AMG1-PC, C2D-LC, C2S-LC were considered as input variables. Variables CW8_FC, C2HD-IC, CW5-FC were not included as these measurements were not available in the real plant.
The first step of data acquisition involved retrieving results from the analyzer, starting from its installation date, covering a period of 22 months, yielding 40,338 results. Subsequently, rather than acquiring input data, at the same timestamps of the analyzer results, they were collected applying a 20-minute time average prior to those timestamps. This approach is due to the need to minimize not only the effects of dynamic and dead times but also disturbances characteristics of any industrial plant. It is believed that using the input values on exactly the timestamps of the analyzer results would not correctly represent the information that generated the outputs.
Before modelling, an interquartile range method was applied to remove outliers. The scale value used was 1.7, which means that this procedure discarded any value greater than 3 standard deviations from the respective mean. The final useful data were composed of 21,433 rows. The data were normalized using the method StandardScaler from python scikit-learn module. The normalized data were split into 10% for test and 90% for training from which 20% was reserved for validation.
Model training was executed with the same methodology used in training with simulated data, which consisted of using python’s Optuna library to explore the hyperparameters of Random Forest Regressor, i.e., rf_min_samples_leaf (1 to 10), rf_max_depth (5 to 10) and rf_n_estimators (1 to 50). The best model hyperparameters were, respectively, 1, 10 and 48.
3. Results
3.1. Development of the Database and Phenomenological Study of the Process
A preliminary study of integration methods [28] revealed that the standard Implicit Euler integrator was the most suitable when compared to other available options, such as Runge-Kutta 4 and Gear integration methods. The observed integration errors could be attributed to the inherent complexity of the differential equations in the system.
The initial strategy for building the database was to develop a global run consisting of 4 random disturbances ranging between +1% and -1% of the set point value for each of the five variables subjected to disturbances. Simultaneously, partial runs were developed that featured only the disturbances of a specific variable at the same time they occurred in the global run. That is, the partial run of the mass flow rate of SW1, for example, refers to the global run in which all disturbances not related to the mass flow rate of SW1 were removed from the programmed task.
The results from the global run, which includes random disturbances ranging from -1% to +1%, along with their respective partial runs, are shown in Figure 5. Similar studies were also conducted for the other effluent streams, considering H₂S and NH₃ [28]. After interpreting the simulations, it is concluded that the mass flow rates of SW1 and SW5, and the temperature of SW1, are extremely important variables for the thermodynamic separation process in the two stripping columns. This is because they directly interfere with the fractions of H₂S and NH₃ in the acid gas (effluent from Column 1), ammoniacal gas, and treated water (effluents from Column 2). This is a consistent result, as these are characteristics linked to the input stream of the process.
However, despite the applied deviations, it was observed that the disturbances caused only a slight variation in the fractions of H₂S and NH₃ in the effluents, especially in the H₂S fraction of the acid gas, which presented only a 0.12% variation. This result was not ideal, as it would imply low variability in the data subsequently used in the soft sensors training.
Therefore, new global runs were developed with substantially more intense disturbances (ranging from -25% to +30% of the set point value) for each of the five variables studied individually, while maintaining disturbances between +1% and -1% for the other input variables. The objective was to achieve, at least, a 1% variation in the H₂S fraction of the acid gas and to keep the simulation within normal operation. Furthermore, the aim was also to determine which of the analyzed variables were most relevant to the variation in H₂S fraction.
The global runs with increased magnitude disturbances in the SW1 mass flow rate, SW5 mass flow rate, SW1 temperature, and NH₃ and H₂S mass fractions in SW1 still showed a small variation in acid gas H₂S fraction, as displayed in Table 7. On the other hand, the global run of the mass flow rate of SW5 proved to be more effective among all. Therefore, a new global run was created for the mass flow rate of SW5 with disturbances of higher magnitude than the previous ones (ranging from -30% to +40% of the set point value for the variable), resulting in a 1% variation in acid gas H₂S fraction, while keeping normal operation.
Aiming at further expanding the database diversity and contributing to the future development of more robust sensors, an exploratory analysis was conducted within the dynamic simulation to identify the variable with the greatest potential to modify the H₂S fraction in the acid gas. The attempt was to 'trick' the controller's set point to understand how the other variables in the system would be affected. For this purpose, a splitting element was added to the simulation, where Input 1 was the mass fraction of H₂S in the acid gas stream, and the Output was the Remote Set Point (SP) of the ACID_G_H₂S controller. While the simulation was running, the value of Input 2 was altered to set a new SP outside the normal operation of the controller so that the responses of the other variables involved in the process could be evaluated.
After the test, it was identified that the variable most affected by the change was the temperature of the second stage of Column 1, a variable controlled by the C1S2-TC controller. Based on this, new runs were generated with a focus solely on evaluating this variable. One of them consisted of a gradual ramp-up of the temperature of the second stage of Column 1, by applying only positive disturbances (between 2% to 15%) to the set point of the C1S2-TC controller. This resulted in a variation of the H₂S fraction in the acid gas of 2.3%, which is more than double of the value obtained thus far.
3.2. Comparison of Artificial Intelligence Algorithms
Figure 7 shows the comparison of the coefficient of determination (R²) among the three evaluated methods (RF, GB, and SVM) for each of the six sensors, while in Figure 8, the comparison of the Root Mean Square Error (RMSE) is presented.
An initially relevant conclusion was that the SVM method using the linear kernel did not fit well to the data from the developed database, as it is evident from the prediction shown in Figure 8. Additionally, the computational time for processing the ACID_G_H₂S sensor algorithm was significantly higher, exceeding 20 minutes. The coefficient of determination (R²) obtained was 0.9388, which is lower than the results achieved by other methods as shown in Figure 7. Therefore, the linear kernel and its results were discarded and, in Figure 7 and Figure 8, only the data related to the SVM method with RBF kernel were presented.
From Figure 6 and Figure 7, it became evident that the R² and RMSE metrics, for all SVM sensors, showed poorer performance compared to the other two methods. Additionally, it is important to emphasize that this method does not provide information about variable importance, a significant aspect for understanding the process. On the other hand, the metrics for GB are very similar to those found for RF in all sensors. In addition to the metrics, the prediction and residuals graphs, and the overall results of variable importance are very similar for both methods. These results were not presented in this section to avoid hindering the readability, but they can be found in [28].
Figure 6.
Comparison of the coefficient of determination (R²) among RF, GB, and SVM with RBF kernel models.
Figure 6.
Comparison of the coefficient of determination (R²) among RF, GB, and SVM with RBF kernel models.
Figure 7.
Comparison of the root mean square error (RMSE) among RF, GB, and SVM with RBF kernel models.
Figure 7.
Comparison of the root mean square error (RMSE) among RF, GB, and SVM with RBF kernel models.
Figure 8.
Prediction of the ACID_G_H₂S sensor using SVM - linear kernel.
3.3. Soft Sensors Using Random Forests
The hyperparameter optimization results are detailed in Table 8. The most effective model for all sensors required the maximum tree depth (rf_max_depth), which is 10. A decision was made not to increase this number to avoid overly complex models. As for the other hyperparameters, i.e., number of trees (rf_n_estimators) and number of samples to split a node (rf_min_samples_leaf), intermediate values were typically obtained, except for two cases: rf_min_samples_leaf in AMON_G_NH₃ and WATER_H₂S.
For the evaluation of all sensors, predictions can be assessed in Figure 9, where the true values from the training and test databases were compared with the values predicted by the sensor. It is evident that most sensors exhibit excellent data prediction capability, due to the high R² values. Furthermore, the low error values for MAE (Mean Absolute Error) and RMSE (Root Mean Squared Error) suggest that the models can make accurate predictions, and the individual predictions are generally very close to the actual values.
The sensors to predict H₂S and NH₃ in acid gas have shown better performance than the others. The reliable prediction range of acid gas NH₃ fraction is notably broader when compared to the range of the H₂S fraction, which varies between -2.28% and 0.53% of normal operation. This behavior is supported by the results observed in Table 5, where the acid gas H₂S fraction varied by approximately -2.17%, while the NH₃ fraction varied around 143.81% during the temperature increase in the second stage of column 1 from 120.3 to 141.9°C.
This highlights that, in the evaluated normal operating situations, the acid gas NH₃ mass fraction is notably more sensitive to disturbances, especially concerning the temperature of the second stage of the first stripping column. On the other hand, the acid gas H₂S mass fraction is more stable, showing smaller variations in the presence of disturbances. This analysis emphasizes the relative importance of these two variables in the contaminants separation process and provides valuable insights for process control and optimization.
Initially, when analyzing the metrics in conjunction with the prediction of the AMON_G_H₂S sensor, it is observed that, unlike what happened with the acid gas sensors, the results for the training dataset were quite different from those found for the test dataset. Despite the R² value between the two sets showing only a slight absolute decrease of 4.89%, the results of MAE, MSE, and RMSE for the test set exhibited a significant absolute increase when compared to the training one. A sort of data hysteresis was observed in the test results, which was not as evident in the training ones.
This hysteresis indicated that the model predicted different values of H₂S fraction in ammoniacal gas for the same observed value present in the test set. On the other hand, the reverse was also observed, where the same value was predicted for different and distant observed values. This hysteresis is likely to have occurred due to the transient dependence on the previous state, influencing the current state.
In order to better evaluate this behavior, each of the 12 simulations from the test bank listed in Table 7 was tested individually. The best model, already optimized for the AMON_G_H₂S sensor, was used to assess the contribution of each simulation to the overall model. Examining each simulation in isolation revealed that the dataset from Run 7 played a role in the hysteresis of the results, leading to less precise predictions within the range of values from 0.86 to 12.17, as depicted in Figure 10. Notably, this specific simulation accounts for only 11% of the test dataset. Consequently, the remaining 89% of the data appears to have contributed to the model attaining a high R² value of 0.9463. Meanwhile, the dispersion caused by the 11% of data from Run 7 was apparent primarily in error metrics like MAE, MSE, and RMSE.
Similar to the AMON_G_H₂S sensor, the results for the AMON_G_NH₃ sensor exhibited notable differences between the training and test sets. As before, it became evident that the dataset from Run 7 contributed to the hysteresis of the results, leading to less accurate predictions in the range of values from -11.56 to -1.89. As previously highlighted, this specific simulation represents only 11% of the comprehensive test set. Nevertheless, these data significantly impacted not only the R² value but also error metrics, including MAE, MSE, and RMSE, obtained for the AMON_G_NH₃ sensor, resulting in the lowest R² among all sensors following the evaluation with the test set.
The predictive performance of this sensor demonstrated only a reasonable quality in comparison to the top-performing acid gas sensors developed. The R² value for the training set marginally surpassed that of the acid gas sensors, while for the test set, it exhibited a slight decrement. Conversely, the error results were found to be comparable to those observed for the ACID_G_NH₃ sensor.
The analysis of the WATER_NH₃ sensor revealed a slightly lower coefficient of determination (R²) for the test set compared to its counterpart, the WATER_H₂S sensor. However, it is noteworthy that error metrics such as MAE, MSE, and RMSE yielded, in most cases, more favorable results for the WATER_NH₃ sensor in both the training and test datasets. These findings suggest that, although the WATER_NH₃ sensor may have a relatively lower capacity to explain the variation in input data, its predictions are more accurate in terms of proximity to actual values.
3.4. Global analysis of the Importance of Variables and Phenomenological Study of the Process
For four out of the six developed sensors, the reduction generally led to metrics improvements, except for the AMON_G_H₂S and WATER_NH₃ sensors. In the case of the AMON_G_H₂S sensor, the MAE values increased by around 13.22%, which is still considered acceptable for practical use. This allows for the removal of variables without compromising the model's performance for this sensor. However, for the WATER_NH₃ sensor, error metrics increased substantially, with the MAE, for example, rising by approximately 90.72%. Therefore, unlike the other sensors, WATER_NH₃ requires the use of the original set of input variables to maintain the confidence of the results.
The complete analysis is summarized in Table 9, which shows the selected variables and the reduction in RMSE for the test data compared to the prediction before variable reduction.
The results found in Table 9 reinforce that the process of removing H₂S and NH₃ contaminants from sour waters is largely dependent on temperature. All temperature measurements in the simulation (highlighted in Table 9) – in the first column feed stream (SW8), the second stage of Column 1 (C1S2), and ammoniacal gas (AMG) – emerged as important variables among the six virtual sensors, indicating the fundamental role of temperature in controlling the thermodynamic separation process of H₂S and NH₃.
3.5. Implementation to a Real SWTU
In Figure 10 the model results are presented as well as their metrics. Additionally, Figure 11 presents the residual values for both the training and testing datasets. It is noticeable that the distribution of these residuals closely aligns with the symmetry of a normal distribution curve. It means that the model's predictions are consistently accurate across a range of values, with errors evenly distributed on either side of the mean. This symmetry suggests that the model does not systematically overestimate or underestimate the observed data.
An analysis of the most relevant variables was conducted for the sensor. Figure 12 presents the variable importances resulting from the random forest modelling considering all the ten available measurements as inputs.
Figure 12 evidences the reduced importance of ACG1-PC and AMG1-PC (< 2%). This was not primarily expected as AMG1-PC has great importance for the WATER_NH₃ sensor modeled with simulated data. Nonetheless, it was noted that the acquired pressure data for the real SWTU had the lowest coefficient of variation compared to other variables (i.e., ACG1-PC, 3,38%, and AMG1-PC, 2,00%, while C1S2-TC, 7,50% and AMG1-TC, 6,26%). This greater stability in pressure readings may explain the lower significance of ACG1-PC and AMG1-PC in real data modelling.
Hence, a reduced model was produced excluding these variables from the input data. Figure 13 shows the predictions for this simplified model, also including the metrics. It was possible to achieve slightly better results removing the inputs with marginal importance. Finally, Figure 14 shows the final input variables importances, where the three most important variables are temperatures.
4. Discussion
4.1. Development of the Database and Phenomenological Study of the Process
Due to its detected relevance, the influence of the temperature of the second stage of Column 1 on the separation process of contaminants NH₃ and H₂S was evaluated during the simulation at specific points. The total mass flow rate of the acid gas stream (ACG1) was verified to calculate the recovery of H₂S in the acid gas. The information obtained from this simulation can be found in Table 10.
Through the dynamic data and information from Table 10, it was possible to prepare Figure 15. The results obtained highlighted that the H₂S removal efficiency increases with the rise in the temperature of the second stage of Column 1, particularly until achieving approximately 90% recovery, a value required by Brazilian environmental legislation. Beyond this point, it is noted that the continuous increase in column temperature results in small increments in the variation of H₂S recovery. On the other hand, a more pronounced vaporization of NH₃ begins, leading to an acid gas with a higher ammonia content. Elevated levels of NH₃ in the acid gas sent to the SRU can result in deposits of ammonium salts in the cold spots of the unit and an increase in NOx emissions, which is environmentally undesirable.
Thus, the need for effective control over the first column thermal load is emphasized to prevent H₂S recovery efficiency over-specification and unnecessary energy expenditure in the reboiler. This analysis highlights the potential optimization gain of a process with soft sensors to analyze compositions of effluents from a SWTU.
4.2. Comparison of Artificial Intelligence Algorithms
Based on the results comparison, it became clear that GB is an equivalent method to RF, and SVM proves to be less accurate in modeling the specific database. Therefore, the RF models were selected, and all subsequent analyses of virtual sensors were conducted based on this algorithm. This method also proved to be the most effective choice for the dataset of [1], achieving an accuracy of 95.2% after variable reduction in the Fault Detection and Diagnosis (FDD) study of the same SWTU.
4.3. Global Analysis of the Importance of Variables and Phenomenological Study of the Process
The temperature of the second stage in Column 1 (C1S2) was identified as the most significant in five out of the six virtual sensors. This result emphasizes that this is a critical process variable, which should be constantly monitored, as it affects both the recovery of H₂S in the acid gas from the first column and, consequently, the recovery of NH₃ in the ammoniacal gas from the second column. Additionally, it corroborates with the results found in Section 3.1, where the findings indicated the need for effective control over the thermal load of the first column to prevent over-specification of the H₂S recovery efficiency. This, besides causing unnecessary energy expenditure in the reboiler, can lead to operational issues in the SRU due to an increase in acid gas NH₃ content.
The controller C1S2-TC acts on the thermal load of C1’s reboiler, which is the manipulated variable, to regulate the temperature of the C1’s second separation stage. Consequently, it is consistent that the SW5 mass flow (i.e., the stream entering C1’s first stage) and SW8 temperature (i.e., the temperature of stream entering C1’s second stage) are considered important. Disturbances in the mass flow or temperature of streams feeding the first column will directly affect the thermal load of C1’s reboiler, as it will work to maintain the thermodynamic equilibrium within the column.
Evaluating the effluents from Column 2 (i.e., ammoniacal gas and treated water), a significant influence of temperature is also observed, as indicated by the temperatures of ammoniacal gas (AMG) and C1’s second stage (C1S2). Additionally, the pressure of ammoniacal gas (AMG) emerges as an important variable in both AMON_G_H₂S and WATER_NH₃. This is due to the need to maintain a lower pressure in Column 2 than in Column 1, to facilitate the selective removal of NH₃ in the ammoniacal gas, resulting in lower levels of NH₃ in the treated water. Deviations from this pressure balance could potentially increase both the H₂S fraction in the ammoniacal gas and the NH₃ fraction in the treated water, which are undesirable for the process.
The bottom level of Column 1 (C1S) emerges as an essential variable for the AMON_G_NH₃ sensor. The associated controller, C1S-LC, directly modulates the opening percentage of valve V6, regulating the flow of pre-treated water entering Column 2. The mass within the column significantly impacts the thermal load needed to maintain thermodynamic separation equilibrium. This factor is essential to achieve the maximum possible concentration of NH₃ in the ammoniacal gas, representing the primary objective of Column 2 operation.
Finally, it is important to highlight that, among the 13 variables analyzed, only 6 were considered important for five out of the six virtual sensors developed. This observation suggests that modeling for these sensors in different SWTUs can be simplified by using only the 6 essential variables as main inputs, aiming to optimize resources and seek improvements in the achieved results. However, this does not apply to the WATER_NH₃ sensor.
5. Conclusions
The first contribution of this study involves the modifying a phenomenological model of a two-column SWTU based on [1]. New simulated data were then generated for sensor development, expanding the Aspen Plus Dynamics® V10 model with six additional controllers for acid gas, ammoniacal gas, and treated water effluents. This resulted in a new database comprising 30 simulations, over 77 thousand samples, set to be publicly shared as a benchmark for virtual sensor development studies.
The data generation involved applying disturbances to five input variables: mass flow of SW1 and SW5, temperature of SW1, and mass fractions of H₂S and NH₃ in SW1. Some key finding using the phenomenological investigation indicates that the operational variable most influencing the H₂S fraction in the acid gas is the temperature of the second stage of Column 1. It is also observed that increasing this temperature improves the recovery of H₂S in the acid gas. However, additional increments in the temperature of Column 1, after the system achieves 90% recovery as required by Brazilian environmental legislation, result in minimal gains in H₂S removal efficiency and pronounced volatilization of NH₃ in the acid gas, which may lead to operational issues in the SRU. This highlights the importance of precise control of thermal load in the first column to optimize the process and the possibility of using virtual sensors to analyze effluents from an SWTU and may be characterized as a contribution of this work as well.
A third contribution of this manuscript is the comparative analysis of the RF, GB, and SVM algorithms, which revealed that the first two are equivalent, exhibiting very similar metrics, while the SVM method with RBF kernel showed the worst performance. Thus, RF was chosen as the standard AI methodology for the development of virtual sensors.
This leads to the core advancement of this research which is the development of six soft sensors (ACID_G_H₂S, ACID_G_NH₃, AMON_G_H₂S, AMON_G_NH₃, WATER_H₂S, and WATER_NH₃). All sensors exhibited a coefficient of determination (R²) greater than 0.87 and RMSE less than 0.41 before reducing the input variables. The study of Variable Importance showed that the sensors continued to present good metrics after the exclusion of the input variables with a contribution of less than 2%, proving useful for improving computational processing time without compromising model performance. The only exception was the WATER_NH₃ sensor, which revealed the need for the original set of input variables to maintain result reliability. The overall analysis of Variable Importance highlighted the significant influence of temperature on the process of removing H₂S and NH₃ contaminants from sour waters. The results indicated that all temperature variables were relevant for controlling the thermodynamic separation process of these compounds, with the temperature of the second stage of Column 1 being particularly important.
The fifth contribution of this work is particularly challenging as it validated the approach through its application to a real-world process. In this case, the application referred to a industrial unit where there was available data for the NH₃ fraction in treated water. The developed algorithms were applied to the actual unit data, yielding highly satisfactory results with residuals exhibiting a normal distribution. This is noteworthy, considering that the data originated from process historians, thus being subject to treatments (such as compression and exception handling) that impact their intrinsic variability, making modeling more challenging.
The soft sensors developed here serve for multiple purposes, including monitoring, control, and 'what-if' analysis. The approach adopted considered the synergistic use of a phenomenological and AI-based models. The simulation study provided valuable physical insights, guiding the selection of the most appropriate input variables for the empirical simplified models. As a result, the most significant advancement achieved here is the facilitation of soft sensors development for any SWTU with the presented configuration.
Author Contributions
Conceptualization, Príamo Melo Jr. and Maurício de Souza Jr.; Data curation, Danielle Queiroz , Francisco Davi Rodrigues and Júlia Nogueira; Formal analysis, Júlia Nogueira, Príamo Melo Jr. and Maurício de Souza Jr.; Investigation, Danielle Queiroz , Francisco Davi Rodrigues and Júlia Nogueira; Methodology, Júlia Nogueira, Príamo Melo Jr. and Maurício de Souza Jr.; Resources, Júlia Nogueira and Maurício de Souza Jr.; Software, Danielle Queiroz , Francisco Davi Rodrigues and Júlia Nogueira; Supervision, Príamo Melo Jr. and Maurício de Souza Jr.; Validation, Francisco Davi Rodrigues ; Writing – original draft, Danielle Queiroz and Francisco Davi Rodrigues ; Writing – review & editing, Júlia Nogueira, Príamo Melo Jr. and Maurício de Souza Jr..
Funding
Professor Maurício B. de Souza Jr. is grateful to financial support from CNPq (Grant No. 311153/2021-6) and Fundação Carlos Chagas Filho de Amparo à Pesquisa do Estado do Rio de Janeiro (FAPERJ) (Grant No. E-26/201.148/2022).
Data Availability Statement
The following supporting information can be downloaded at: https://github.com/danigradin/UTAA_Soft_Sensors, Database for UTAA Soft Sensors, reference [29].
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results”.
References
- NOGUEIRA, J. N. P.; MELO, P. A.; SOUZA JR., M. B. Faulty scenarios in sour water treatment units: Simulation and AI-based diagnosis. Process Safety and Environmental Protection, v. 165, p. 716-727, 2022.Author 1, A.; Author 2, B. Title of the chapter. In Book Title, 2nd ed.; Editor 1, A., Editor 2, B., Eds.; Publisher: Publisher Location, Country, 2007; Volume 3, pp. 154–196. [Google Scholar]
- HO, C.-D.; CHEN, Y.-H.; CHANG, C. M.; CHANG, H. Evaluation of Process Control Schemes for Sour Water Strippers in Petroleum Refining. Processes, v. 9, 363, 2021.
- SOARES, A. de F.; PENTEADO, E. D.; DINIZ, A. A. R.; KOMESU, A. Influence of operational parameters in sour water stripping process in effluents treatment. Journal of Water Process Engineering, v. 41, 2021.
- Brazil, Ministry of the Environment, N.E.C., Resolution number 382 of December 26, 2006. Official Gazette, No. 01 of January 2, section 1, 2007.
- QUINLAN, M. , HATI, A., Processing NH3 Acid Gas in Sulphur Recovery Unit, Gas, p. 45–55, 2010.
- CONAMA (National Environmental Council). RESOLUTION No. 436, OF DECEMBER 22, 2011. Available at https://www.udop.com.br/download/legislacao/meio/institucional_site_juridico/Conama_Resolucao%20436.pdf (in Portuguese). Accessed on February 20th, 2023.
- EAP (United States Environment Protection Agency). What is Acid Rain? 2021. Available at https://www.epa.gov/acidrain/what-acid-rain. Accessed on February 20, 2023.
- COLBECK, I.; MACKENZIE, A. R. Air Pollution by Photochemical Oxidants. Amsterdam [The Netherlands]; New York: Elsevier, 1994.
- KADLEC, P.; GABRYS, B.; STRANDT, S. Data-Driven Soft Sensors in the Process Industry, Computers and Chemical Engineering, v. 33, p. 795–814, 2009. [CrossRef]
- BARROS, D. J. S. Investigation of the effect of process variables on H2S removal efficiency in a two-stage sour water treatment Unit. Master’s thesis (In Portuguese). PPGEQ – UFPR, 2016.
- JOUCOWSKI. J.; Ndiaye, P. M.; Corazza, M. L.; Lenzi, M. K. Inferring Light-cycle-oil Stream Properties Using Soft Sensors, Chemical and Biochemical Engineering Quarterly, v. 27 (3), p. 289–296, 2013.
- FORTUNA, L., GRAZIANI, S., RIZZO, A., XIBILIA, M. G., OTHERS. Soft sensors for monitoring and control of industrial processes, v. 22. Springer, 2007.
- LIN, B., RECKE, B., KNUDSEN, J. K., JØRGENSEN, S. B. A systematic approach for soft sensor development, Computers & chemical engineering, v. 31, n. 5-6, p. 419– 425, 2007.
- ZHOU, Z.H. Ensemble Methods: Foundations and Algorithms. Abingdon-on-Thames: Taylor & Francis, 2012.
- BREIMAN, L.; FRIEDMAN, J.; STONE, C.; et al. Classification and Regression Trees. Taylor & Francis, 1984.
- BREIMAN, L. Random Forests. Machine Learning, v. 45, p. 5–32, 2001.
- TRAVALIS, T. B.; INCE, H. Support vector machine for regression and applications to financial forecasting. In: Proceedings of the IEEE-INNS-ENNS International Joint Conference on Neural Networks. IJCNN 2000. Neural Computing: New Challenges and Perspectives for the New Millennium, Como, Italy, p. 348-353, v. 6, 2000.
- IVANCIUC, O., Applications of Support Vector Machines in Chemistry. In: Reviews in Computational Chemistry, chapter 6, p. 291-400, John Wiley & Sons, Ltd., 2007.
- QUEIROZ, L. H.; SANTOS, F. P.; OLIVEIRA, J. P.; SOUZA; M. B. Physics-Informed deep learning to predict flow fields in cyclone separators, Digital Chemical Engineering, v. 1, 100002, 2021.
- OFFERMANS, T; SZYMANSKA, E.; SOUZA, F. A. A.; JANSEN, J. J. Process expert knowledge is essential in creating value from data-driven industrial soft sensors, Computers & Chemical Engineering, v. 83, 108602, 2024.
- BAGHERI, M.; MIRBAGHERI, S. A.; EHTESHAMI, M., BAGHERI, Z. Modeling of a sequencing batch reactor treating municipal wastewater using multi-layer perceptron and radial basis function artificial neural networks, Process Safety and Environmental Protection, v. 93, p. 111–123, 2015. [CrossRef]
- BARROS, D. J. S., BARROS, E. S., ZANOELO, E. F., Soft-sensor models to estimate the efficiency of H2S removal from an oil refinery stream of nonphenolic sour water, Chemical Engineering Communications, v. 205, p. 1050–105, 2018. [CrossRef]
- GRAZIANI, S.; XIBILIA, M. G. A deep learning based soft sensor for a sour water stripping plant. In: IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Turin, Italy, 2017.
- NOGUEIRA, J. N. P. Fault Detection and Diagnosis of a Two-Column Sour Water Treatment Unit Based on Artificial Intelligence Algorithms. M.Sc. Thesis, UFRJ, EPQB, 2021.
- LI, A.; WIENER, M. Classification and Regression by Randomforest. R News, v. 2, p. 18-22, 2002.
- BELGIU, M.; DRAGUT, L. Random Forest in remote sensing: A review of applications and future directions, ISPRS Journal of Photogrammetry and Remote Sensing, v. 114, p. 24–31, 2016.
- SPEISER, J. L., MILLER, M. E., TOOZE, J., IP, E. A comparison of random forest variable selection methods for classification prediction modeling, Expert Systems with Applications, v. 134, p. 93–101, 2019.
- QUEIROZ, D. G., Development of Virtual Sensors for Prediction the Composition of Effluents From a Sour Water Treatment Unit. Monograph for the bachelor’s degree in chemical engineering (in Portuguese), Federal University of Rio de Janeiro, 2023b.
- QUEIROZ, D. G., A Database for UTAA Soft Sensors. Available at https://github.com/danigradin/UTAA_Soft_Sensors, 2023a. Accessed on May 1, 2024.
Figure 1.
Simplified scheme of an Acid Water Treatment Unit with two columns based on [5].
Figure 1.
Simplified scheme of an Acid Water Treatment Unit with two columns based on [5].
Figure 2.
Block diagram of [1] process simulation.
Figure 2.
Block diagram of [1] process simulation.
Figure 3.
[1] static process simulation.
Figure 3.
[1] static process simulation.
Figure 4.
Adaptation of the dynamic simulation by [1] with the inclusion of the new six controllers: ACID_G_H₂S, ACID_G_NH₃, AMON_G_H₂S, AMON_G_NH₃, WATER_H₂S, and WATER_NH₃.
Figure 4.
Adaptation of the dynamic simulation by [1] with the inclusion of the new six controllers: ACID_G_H₂S, ACID_G_NH₃, AMON_G_H₂S, AMON_G_NH₃, WATER_H₂S, and WATER_NH₃.
Figure 5.
Important variables for determining the fraction of H₂S in the acid gas.
Figure 9.
(Part 1): Prediction sensors using RF with training and test data. Models metrics are presented on the respective plots. The denormalized validated interval is in blue in the axis, along with the relative interval considering the normal operation value as parameter. (Part 2): Prediction sensors using RF with training and test data. Models metrics are presented on the respective plots. The denormalized validated interval is in blue in the axis, along with the relative interval considering the normal operation value as parameter.
Figure 9.
(Part 1): Prediction sensors using RF with training and test data. Models metrics are presented on the respective plots. The denormalized validated interval is in blue in the axis, along with the relative interval considering the normal operation value as parameter. (Part 2): Prediction sensors using RF with training and test data. Models metrics are presented on the respective plots. The denormalized validated interval is in blue in the axis, along with the relative interval considering the normal operation value as parameter.
Figure 10.
Prediction of the WATER_NH₃ sensor with data of real SWTU using RF: training (left) and test data (right).
Figure 10.
Prediction of the WATER_NH₃ sensor with data of real SWTU using RF: training (left) and test data (right).
Figure 11.
Training (left) and test (right) prediction residue.
Figure 12.
Variable importance for the sensor based on random forest model obtained with data from real SWTU.
Figure 12.
Variable importance for the sensor based on random forest model obtained with data from real SWTU.
Figure 13.
Prediction of the WATER_NH₃ sensor with reduced dataset of real SWTU using RF with training (left) and test data (right).
Figure 13.
Prediction of the WATER_NH₃ sensor with reduced dataset of real SWTU using RF with training (left) and test data (right).
Figure 14.
Variable importance for the sensor based on random forest model obtained with reduced data from real SWTU.
Figure 14.
Variable importance for the sensor based on random forest model obtained with reduced data from real SWTU.
Figure 15.
Relationship between H₂S recovery in the acid gas and temperature of the 2nd stage of Column 1.
Figure 15.
Relationship between H₂S recovery in the acid gas and temperature of the 2nd stage of Column 1.
Table 1.
Legend of the streams in the dynamic simulation by [1].
Table 1.
Legend of the streams in the dynamic simulation by [1].
| Abbreviation | Stream composition |
| SW | Sour Water |
| PW | Pretreated Water |
| TW | Treated Water |
| NW | New Water |
| CW | Clean Water |
| ACG | Acid Gas |
| AMG | Ammoniacal Gas |
Table 2.
Physical properties of the input streams of the system.
| Proprerty | Unity | SW1 | NW1 |
| Temperature | °C | 38.8 | 122.4 |
| Pressure | bar | 10.33 | 2.29 |
| Mass flow | t/h | SW1F | 38.5% de SW1F |
| Mass fraction of H2O | - | 0.9928 | 1.0000 |
| Mass fraction of NH₃ | - | 0.0032 | 0.0000 |
| Mass fraction of H₂S | - | 0.0040 | 0.0000 |
dimensionless
Table 3.
14 controllers present in the dynamic simulation by [1].
Table 3.
14 controllers present in the dynamic simulation by [1].
| Controller | Controlled variable | Manipulated variable |
| SW1-FC | SW1 Mass Flow Rate | V3 Opening % |
| SW5-FC | SW5 Mass Flow Rate | V2 Opening % |
| CW5-FC | CW5 Mass Flow Rate | V11 Opening % |
| CW8-FC | CW8 Mass Flow Rate | V12 Opening % |
| SW8-TC | SW8 Temperature | V5 Opening % |
| C1S2-TC | C1 2nd Stage Temperature | C1 Reboiler Load |
| AMG1-TC | AMG1 Temperature | C2 Condenser Load |
| C1S-LC | C1 Bottom Level | V6 Opening % |
| C2D-LC | C2 Reflux Drum Level | Mass Flow Rate of C2 Reflux Drum |
| C2S-LC | C2 Bottom Level | V9 Opening % |
| C2S-LC2 | C2 Bottom Level Safeguard | V10 Opening % |
| ACG1-PC | AGC1 Pressure | V4 Opening % |
| AMG1-PC | AMG1 Pressure | V7 % Opening % |
| C2HD-IC | Ratio between the C2 Reboiler Load and PW7 Mass Flow Rate | C2 Reboiler load |
Table 4.
Lower and upper limits defined for each hyperparameter.
| Hyperparameters | Limits |
| rf_n_estimators | 1 to 50 |
| rf_max_depth | 5 to 10 |
| rf_min_samples_leaf | 1 to 10 |
Table 5.
Listing of the runs present in the training database.
| Training Database | |
| Run | Description |
| 1 | Global run with disturbances between -1% and +1% on the set points of the 5 standard variables – version A |
| 2 | Global run with disturbances between -30% to 40% of the set point of the mass flow rate of SW5 – version A |
| 3 | Global run with more numerous disturbances between -30% to 40% of the set point of the mass flow rate of SW5 – version A |
| 4 | Global run with disturbances between -25% to 30% in the temperature of SW1 – version A |
| 5 | Global run with disturbances between -25% to 30% in the H₂S mass fraction in SW1 – version A |
| 6 | Global run with disturbances between -25% to 30% in the NH₃ mass fraction in SW1 – version A |
| 7 | Global run with positive disturbances in a gradually increasing ramp in the temperature of the 2nd stage of C1 – version A |
| 8 | Global run with random positive and negative disturbances in the temperature of the 2nd stage of C1 – version A |
| 9 | Partial run of the mass flow rate of SW1 – version A |
| 10 | Partial run of the mass flow rate of SW1 – version B |
| 11 | Partial run of the mass flow rate of SW5 – version A |
| 12 | Partial run of the mass flow rate of SW5 – version B |
| 13 | Partial run of the temperature of SW1 – version A |
| 14 | Partial run of the temperature of SW1 – version B |
| 15 | Partial run of the NH₃ mass fraction in SW1 – version A |
| 16 | Partial run of the NH₃ mass fraction in SW1 – version B |
| 17 | Partial run of the H₂S mass fraction in SW1 – version A |
| 18 | Partial run of the H₂S mass fraction in SW1 – version B |
Table 6.
Listing of the runs present in the test database.
| Test Database | |
| Run | Description |
| 1 | Global run with disturbances between -1% and +1% on the set points of the 5 standard variables – version B |
| 2 | Global run with disturbances between -30% to 40% of the set point of the mass flow rate of SW5 – version B |
| 3 | Global run with disturbances between -25% to 30% in the temperature of SW1 – version B |
| 4 | Global run with disturbances between -25% to 30% in the H₂S mass fraction in SW1 – version B |
| 5 | Global run with disturbances between -25% to 30% in the NH₃ mass fraction in SW1 – version B |
| 6 | Global run with positive disturbances in a gradually increasing ramp in the temperature of the 2nd stage of C1 – version B |
| 7 | Global run with random positive and negative disturbances in the temperature of the 2nd stage of C1 – version B |
| 8 | Partial run of the mass flow rate of SW1 – version C |
| 9 | Partial run of the mass flow rate of SW5 – version C |
| 10 | Partial run of the temperature of SW1 – version C |
| 11 | Partial run of the NH₃ mass fraction in SW1 – version C |
| 12 | Partial run of the H₂S mass fraction in SW1 – version C |
Table 7.
Variations in acid gas H₂S mass fraction for each global run.
| Global runs | Variation in acid gas H₂S mass fraction |
| SW1 mass flow rate | 0.15 |
| SW5 mass flow rate | 0.66 |
| SW1 temperature | 0.29 |
| H₂S mass fraction in SW1 | 0.24 |
| NH₃ mass fraction in SW1 | 0.12 |
Table 8.
Optimized Hyperparameters for the sensors using RF.
| Sensor | Hyperparameters | Optimal value |
| ACID_G_H₂S | rf_min_samples_leaf | 6 |
| rf_n_estimators | 33 | |
| ACID_G_NH₃ | rf_min_samples_leaf | 3 |
| rf_n_estimators | 47 | |
| AMON_G_H₂S | rf_min_samples_leaf | 3 |
| rf_n_estimators | 30 | |
| AMON_G_NH₃ | rf_min_samples_leaf | 1 |
| rf_n_estimators | 30 | |
| WATER_H₂S | rf_min_samples_leaf | 1 |
| rf_n_estimators | 34 | |
| WATER_NH₃ | rf_min_samples_leaf | 2 |
| rf_n_estimators | 47 |
Table 9.
Global analysis of the importance of variables in all sensors after reduction.
| Variables/ Sensors | ACID_G_H₂S | ACID_G_NH₃ | AMON_G_H₂S | AMON_G_NH₃ | WATER_H₂S | WATER_NH₃ |
| CW8_FC | ||||||
| SW5-FC | X | X | ||||
| SW1-FC | ||||||
| SW8-TC | X | X | ||||
| ACG1-PC | ||||||
| C1S2-TC | X | X | X | X | X | |
| C1S-LC | X | |||||
| AMG1-TC | X | X | X | |||
| AMG1-PC | X | X | ||||
| C2D-LC | ||||||
| C2S-LC | ||||||
| C2HD-IC | ||||||
| CW5-FC | ||||||
| MAE % change | -22.69 | -13.48 | +13.22 | -10.72 | -9.41 | +90.72 |
Table 10.
Results of the exploratory analysis on the temperature variable of the second stage of Column 1.
Table 10.
Results of the exploratory analysis on the temperature variable of the second stage of Column 1.
| Time (h) | Acid gas H₂S mass fraction | Acid gas NH₃ mass fraction | Temperature in the 2nd stage of C1 (°C) | Acid gas H₂S recovery (%) | Variation between the recovery values (%) |
| 2.00 | 0.9476 | 7.67x10-5 | 120.30 | 81.25 | - |
| 7.30 | 0.9461 | 8.19x10-5 | 123.32 | 89.54 | 9.25 |
| 15.00 | 0.9445 | 8.79x10-5 | 126.65 | 91.10 | 1.71 |
| 30.00 | 0.9395 | 1.10x10-4 | 132.94 | 92.68 | 1.70 |
| 45.00 | 0.9360 | 1.28x10-4 | 136.21 | 93.18 | 0.54 |
| 60.00 | 0.9277 | 1.82x10-4 | 141.54 | 93.83 | 0.70 |
| 70.00 | 0.9270 | 1.87x10-4 | 141.90 | 93.85 | 0.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated