Prerpints.org logo
Preprint
Article

Eight-Bar Elbow Joint Exoskeleton Mechanism

Altmetrics

Downloads

122

Views

40

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

02 August 2024

Posted:

06 August 2024

You are already at the latest version

Alerts
Abstract
This paper deals with the design and kinematic analysis of a novel mechanism for the elbow joint of an upper-limb exoskeleton, with the aim of helping operators, in terms of effort and physical resistance, in carrying out heavy operations. In particular, the proposed eight-bar el-bow joint exoskeleton mechanism consists of a motorized Watt I six-bar linkage and a suitable RP dyad, which connects mechanically the external parts of the human arm with the corre-sponding forearm by hook and loop velcro and thus, helping their closing relative motion for lifting objects during repetitive and heavy operations. This relative motion is not a pure rotation and thus, the upper part of the exoskeleton is fastened to the arm, while the lower part is not rigidly connected to the forearm, but through a prismatic pair which allows both rotation and sliding along the forearm axis. Instead, the human arm is sketched by means of a crossed four-bar linkage, which coupler link is considered as attached to the glyph of the prismatic pair, that is fastened to the forearm. Therefore, the kinematic analysis of the whole ten-bar mecha-nism, which is obtained by joining the Watt I six-bar linkage and the RP dyad to the crossed four-bar linkage, is formulated to investigate the main kinematic performance and for design purposes. The proposed algorithm has given several numerical and graphical results. Finally, a double-parallelogram linkage, as particular case of the Watt I six-bar linkage, was considered in combination with the RP dyad and the crossed four-bar linkage, by giving a first mechanical de-sign and a 3D printed prototype.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

Exoskeletons design, in particular for devices like upper limb exoskeletons, is aimed to carefully replicate the human joint movements. Achieving this accuracy involves understanding the kinematics of the human body and translating it into appropriate mathematical models. This, together with an adequate fit, size and weight, determine the goodness of the designed device itself. In order to be able to design these devices, it is therefore necessary to first understand what the real movements are and make an appropriate schematization. In particular, the human arm is composed of three joints: the shoulder, the elbow and the wrist. From a kinematic point of view, the human arm can be schematized with an open kinematic chain with 7 degrees of freedom (DOF), as reported in [1,2]. Specifically, there are 3 DOF in the shoulder (ball and socket joint), 1 DOF in the elbow (revolute joint) and 3 DOF in the wrist (spherical joint). Among the upper limb exoskeletons there are many examples of 7 DOF kinematic chains, which try to reproduce the real kinematic scheme of the human arm [3,4], but there are also examples of kinematic chains with a lower number of degrees of freedom, such as those at 3 DOF [5,6] or 6 DOF [7,8]. Over the years, exoskeletons have undergone considerable variations not only in terms of choice of kinematic chain, but also in terms of fields of application. In fact, historically they are born in the military field with the aim of increasing the performance of soldiers in terms of resistance and strength, but are widely used both in the rehabilitation and in the industrial fields. In particular, in the rehabilitation sector, upper limb exoskeletons have undergone considerable development in the last decade [9,10,11,12,13,14]. Exoskeletons for upper limb also differ in relation to the actuation system. Considering that they can also be totally passive or underactuated, most of them have electric actuation [15], even if there are also examples of exoskeletons that have a pneumatic actuation [16]. In the design of upper limb exoskeletons, different types of mechanisms are used. They typically present serial kinematic chains, but there are also examples of exoskeletons that have parallel architectures [17], rather than the presence of gears [18] or tendon-driven systems [19,20].
In recent years, it is also possible to find an effort in the design of systems that are as anthropomorphic, as possible, as proposed by Bai in [21] regarding the shoulder joint which approximates a spherical motion. The synthesis of a spherical rigid body guidance for five-poses can be found in [22]. Furthermore, soft robotics has been gaining traction in the field of exoskeletons. Soft robotic exosuits provide a comfortable and portable alternative to rigid exoskeletons for upper limb support, enhancing user comfort and freedom of movement, as reported in [23].
Also, with regard to the elbow, there are several solutions that try to consider the fact that it cannot strictly be represented with a simple revolute joint [24,25,26,27,28,29]. It is clear that in order to design a mechanism that is able to approximate as faithfully as possible the real movement of the human elbow, it is necessary to perform an accurate analysis of the movement. For this purpose, centrodes which represent the exact law of motion that the designer wants to approximate, are useful.
In literature, Beadle and O'Brien conducted the first experiments on the experimental detection of the human elbow centrodes [30], taking inspiration from Freudenstein, who years earlier had pioneered the usefulness of centrodes in the analysis of human knee movement [31]. The use of centrodes as a kinematic analysis tool can be found in different fields of engineering. As proposed by the authors in [32], centrodes can be used as an analysis tool to validate a knee joint exoskeleton mechanism accuracy. They can also be used to investigate the kinematic characteristics of classical mechanisms, such as the slider-crank mechanism [33], but their field of application is transversal and also related to other sectors, such as machine tools [34]. This analysis tool, combined with that of the Bresse circles [35,36,37] can be very useful for the designer when designing new devices.
The subject of this paper is the design and the kinematic analysis of a novel eight-bar elbow joint exoskeleton mechanism that is composed by a motorized Watt I six-bar linkage and a suitable RP dyad, which connects mechanically the external parts of the human arm with the corresponding forearm by hook and loop velcro. Moreover, the human arm is sketched by means of a crossed four-bar linkage, which coupler link is considered as attached to the glyph of the prismatic pair, that is fastened to the forearm.
Therefore, the kinematic analysis of the whole ten-bar mechanism, is formulated to investigate the main kinematic performance and for design purposes. The proposed algorithm has given several numerical and graphical results and finally, a double-parallelogram linkage was considered in combination with the RP dyad and the crossed four-bar linkage, by giving a first mechanical design and a 3D printed prototype.
The main benefits of the proposed eight-bar elbow joint exoskeleton mechanism are:
-
A natural coupling with the human arm;
-
Wearable by workers of different arm sizes;
-
One motor only;
-
A comfortable motor installation under the human arm.

2. Ten-Bar Exoskeleton Elbow Joint Mechanism

The whole one DOF upper-limb exoskeleton mechanism that includes the kinematic sketch of the human arm is represented by the ten-bar mechanism of Figure 1, which consists of the proposed eight-bar elbow joint exoskeleton mechanism and the crossed four-bar linkage. In particular, the first is composed by the Watt I six-bar linkage, which links are numbered by 1 to 6, and the RP dyad of members 6 (coupler), 7 (piston) and 8 (glyph). When the eight-bar elbow joint exoskeleton mechanism is worn, links 1 and 8 are fastened by hook and loop velcro to the arm and forearm, respectively.
The human elbow joint is made up of three bones: the upper arm bone (humerus) and two forearm bones (ulna and radius), which can be sketched by a crossed four-bar linkage of links 1 (arm) and 8 (forearm), along with the crossed links 9 and 10. In fact, the relative motion is not a pure rotation and thus, the upper part of the exoskeleton is fastened to the arm, while the lower part is not rigidly connected to the forearm.
The macroscopic movement of the elbow is actually the result of the interaction between the ends of the bony segments of the arm and forearm in contact. They can be thought of as conjugate surfaces: the relative movement between these two represents the effective motion law of the elbow. If one approaches the movement of the elbow as a plane movement, the projections of these surfaces on it are two curves, which represent the centrodes, whose point of contact is the instantaneous center of rotation. The use of a crossed-four-bar linkage allows to have the position of the instantaneous center of rotation of the coupler link 8 (glyph) close to that of the forearm with respect to the arm.
Applying Grubler's formula, one has
N = 3   ( n − 1 ) − 2 l = 27 − 13 ⋅ 2 = 1   DOF
where N, n and l are the numbers of the degrees of freedom, of the rigid links and of the lower kinematic pairs, respectively.
In the following the kinematic analysis of the human elbow-joint and its exoskeleton is formulated.

3. Kinematic Analysis

The kinematic analysis of the one DOF ten-bar mechanism of Figure 2 is developed by first considering separately the Watt I six-bar linkage A0ABB0-BCDE and the crossed four-bar linkage M0MNN0, respectively, and then, joining them at H point to analyze the whole ten-bar mechanism. This chapter is organized in the following three sub-sections:
  • 3.1 – Watt I six-bar linkage
  • 3.2 – Crossed four-bar linkage
  • 3.3 – Ten-bar mechanism

3.1. Watt I Six-Bar Linkage

The main part of the proposed elbow joint exoskeleton mechanism is the Watt I six-bar linkage of Figure 3a, which includes the vector loops of both four-bar linkages A0ABB0 and BCDE by giving the following vector equations:
r 2 + r 31 − r 1 − r 41 = 0 r 42 + r 5 − r 32 − r 6 = 0
where vectors ri are expressed by r i = r i cos θ i i + r i sin θ i j for i = 1, …, 6, where i and j are the unit vectors of the X and Y-axes. The same is for the vectors r31, r32, r41 and r42 which second subscript number refers to loops 1 and 2, respectively.
The ICs (instantaneous centers of rotation) P3, P5 and P6 of the coupler links 3, 5 and 6, respectively, have been determined by applying the Aronhold-Kennedy theorem, according to the graphical constructions of Figure 3b.
Thus, the first of Eqs. (2) gives
A sin θ 3 + B cos θ 3 + C = 0
which can be solved as follows
θ   3 = 2 t a n − 1 − A + σ A   2 − C   2 + B   2 C − B
where σ is equal to ±1 according to the assembly mode.
The coefficients A, B and C are obtained as function of the driving angle θ 2 by
A = 2     r   2     r 31 sin θ 2 B = 2     r 31 r   2 cos θ 2 − r 1 C = r   1 2 + r   2 2 + r   31 2 − r   41 2 − 2     r   1   r 2 cos θ 2
Moreover, solving the first of Eq. (2) with respect to θ 4, one has
θ 4 = tan   − 1   r 31 sin θ 3 + r 2 sin θ 2 r 2 cos θ 2 + r 31 cos θ 3 − r 1
From the first of Eqs. (2), the angular velocities ω3 and ω4 can be obtained as follows
ω   4 = r 2 sin θ 2 − θ 3 r 41 sin θ 4 − θ 3 ω   2 ω   3 = r 2 sin θ 2 − θ 4 r 31 sin θ 4 − θ 3 ω   2
where the angles θ 3 and θ 4 are given by Eqs. (4) and (6), respectively.
Similarly, from the second of Eqs. (2), one has
θ 6 = 2 t a n − 1 − D + σ D   2 − F   2 + E   2 F − E
which the coefficients D , E and F are given by
D = 2     r 32     r 6 sin θ 3 − 2     r 42   r 6 sin θ 4 E = 2     r 32   r 6 cos θ 3 − 2   r 42   r 6 cos θ 4 F = r   42 2 + r   32 2 + r   6 2 − r   5 2 − 2     r   42   r 32 cos θ 3 cos θ 4 − 2     r   42   r 32 sin θ 3 sin θ 4
Thus, solving with respect to θ 5, one has
θ   5 = tan − 1     r 32 sin θ 3 + r 6 sin θ 6 − r 42 sin θ 4 r 32 cos θ 3 + r 6 cos θ 6 − r 42 cos θ 4
From the second of Eqs. (2), the angular velocities ω 5 and ω 6 are obtained as follows
ω   5 = ω 3   r 32 sin θ 6 − θ 3 − ω 4   r 42 sin θ 6 − θ 4 r 5 sin θ 6 − θ 5
ω   6 = ω 3   r 32 sin θ 5 − θ 3 − ω 4   r 42 sin θ 5 − θ 4 r 6 sin θ 6 − θ 5
The velocity vectors vA, vB, vC, vD and vE of points A, B, C, D and E, respectively, are obtained by assuming the following in vector forms:
v A = ω   2 − r 2   sin θ 2 , r 2   cos θ 2     T v B = ω   4 − r 4   sin θ 4 , r 4   cos θ 4     T v C = v B X − r 32   ω 3 sin θ 3 , v B Y + r 32   ω 3 cos θ 3     T v D = v C X − r 6   ω 6 sin θ 6 , v C Y + r 6   ω 6 cos θ 6     T v E = v B X − r 42   ω 4 sin θ 4 , v B Y + r 42   ω 4 cos θ 4     T
where T indicates the transpose matrix.
Finally, the velocity vector vH6 of the point H, as belonging to the coupler link 6, is given by
v H 6 = v C X + ω 6 d 1 + d 3   sin θ 6 − ω 6   d 2 cos θ 6 , v C Y − ω 6 d 1 + d 3   cos θ 6 − ω 6   d 2 sin θ 6   T

3.2. Crossed Four-Bar Linkage

The crossed four-bar linkage of Figure 4a, which includes the corresponding vector loop of the linkage M0MNN0, sketches the human elbow joint, while Figure 4b shows the graphical construction for determining the ICs of each link.
Therefore, the following vector-loop equation is obtained
r 10 + r 8 − r 9 − r 11 = 0
where r i = r i cos θ i i + r i sin θ i j for i = 8, …, 11.
Thus, one has
G s i n θ 8 + H cos θ 8 + I = 0
which can be solved by giving
θ 8 = 2 t a n − 1 − G + σ G   2 − I   2 + H   2 I − H
where σ is equal to ±1 according to the assembly mode.
The coefficients G , H and I are given as function of the driving crank angle θ 10 by
G = 2     r 10     r 8 sin θ 10 H = 2     r 8 r 10 cos θ 10 − r 11 I = r   11 2 + r   10 2 + r   8 2 − r   9 2 − 2     r   10   r 11 cos θ 10
Moreover, Eq. (15) can be solved with respect to θ 9 by giving
θ   9 = tan − 1 r 11 sin θ 11 + r 8 sin θ 8 − r 10 sin θ 10 r 11 cos θ 11 + r 8 cos θ 8 − r 10 cos θ 10
From the Eq. (15), the angular velocities ω8 and ω9 are obtained as follows
ω   8 = r 10 sin θ 10 − θ 9 r 8 sin θ 9 − θ 8 ω   10 ω   9 = r 10 sin θ 10 − θ 8 r 9 sin θ 9 − θ 8 ω   10
The velocity vectors of points M and N are given by
v M = ω     10 − r 10   sin θ 10 , r 10   cos θ 10   T v N = ω   9 − r 9   sin θ 9 , r 9   cos θ 9     T

3.3. Ten-Bar Mechanism

The formulation that has been developed in the previous two sub-sections is now combined in order to obtain a general algorithm for the kinematic analysis of the whole ten-bar mechanism. Additional kinematic considerations are applied by using the Aronhold-Kennedy theorem, as shown in Figure 5. In particular, the ICs P6, P8 and P68 are of interest in order to express the velocity vectors vH6 and vH8 of point H, as belonging to the coupler links 6 and 8, respectively, along with their relative velocity vector vH68.
Thus, one has
v H 6 = v H 8 + v H 68
where each velocity vector is given by
v H 8 = ω       8 × P   8   H v H 6 = ω     6 × P   6   H v H 68 = ω     68 × P   68   H
Therefore, in scalar form, one has
ω       6   P     6 P     6     8 =     ω       8   P     8 P     6     8
where P     6 P     6     8 and P     8 P     6     8 are the distances of the ICs P6 and P8 with respect to P68.
The angular velocity   ω       8   of the coupler link 8 of the four-bar linkage is now related to that of the coupler link 6 of the Watt I six-bar linkage by means of the ICs P6, P8 and P68.

4. Graphical and Numerical Results

The proposed formulation for the kinematic analysis of the ten-bar mechanism, which includes both the eight-bar elbow joint exoskeleton mechanism and the human elbow joint mechanism, has been implemented in Matlab for validation purposes.
In fact, Figure 6 and Figure 7 show the results for the crank angles θ 2 = 255° and θ 2 = 290° by giving the angular velocities of all moving links and the linear velocities of points A, B, C, D, E, H, M and N. The geometric input data are reported in Table 1, where the link lengths of the Watt I six-bar linkage, have been chosen in such a way to be compatible with the application as elbow-joint exoskeleton mechanism and with the aim to validate in general the proposed kinematic analysis algorithm.
The results of the proposed algorithm for the input data of Table 1 and the driving angular velocity ω 2 = 1 rad/s, are reported in Table 2 and Table 3.

5. Application and Prototype

The proposed general formulation for the kinematic analysis of the ten-bar mechanism of Figure 2 can be used to analyze and design a suitable eight-bar elbow joint exoskeleton mechanism of different shapes and sizes. In particular, the case of when the Watt I six-bar linkage becomes a double-parallelogram linkage and the crossed four-bar linkage becomes an anti-parallelogram linkage, is now considered and the whole mechanism takes the shape of Figure 8a, according to the application that is sketched in Figure 8b.
Thus, by running the same Matlab program, the results of Figure 9 and Figure 10 have been obtained for the crank angles θ 2 = 300° and θ 2 = 252°, respectively. The geometric input data are reported in Table 4, along with the input angular velocity ω2 = 1 rad/s. The obtained results are reported in Table 5 and Table 6.
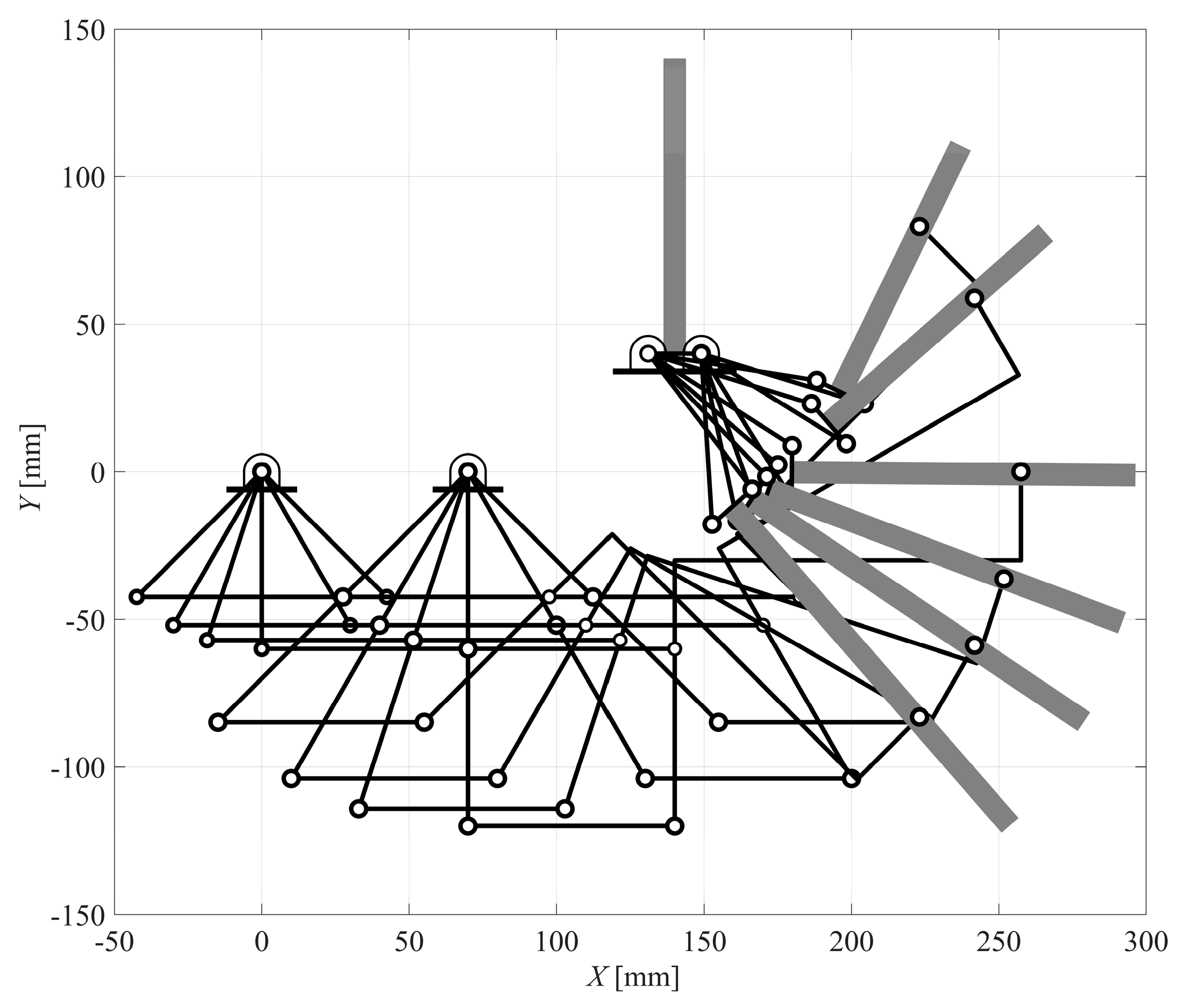
The mechanical design of the proposed ten-bar mechanism has been developed in order to build and test under a kinematic point of view, the first 3D printed planar prototype of Figure 11, which shows a step by step sequence of the closing motion, in comparison with the corresponding Matlab graphical results. Similarly, the whole sequence is shown in Figure 12.

6. Conclusions

A novel eight-bar elbow joint exoskeleton mechanism, which consists of a motorized Watt I six-bar linkage and a suitable RP dyad, has been proposed and a suitable algorithm for the kinematic analysis of the whole one DOF ten-bar mechanism that includes the human elbow joint mechanism, has been formulated for designing elbow joint exoskeleton mechanisms of different shapes and sizes. A first planar prototype has been designed and built by means of a 3D printer.
The dynamic analysis in load conditions of the proposed exoskeleton closing motion, along with the actuation and control, will be a part of the next developments.

Funding

This research activity of title EXOSKELETON (Development of an elbow/knee joint kinematic) was funded by the IIT (Italian Institute of Technology) of Genoa, within a Research Contract, which was stipulated with DICEM (Dept. of Civil & Mechanical Engineering) of the University of Cassino & Southern Lazio (Italy) in the years 2018/19.

References

  1. Zatsiorsky, V.M.; Kinematics of Human Motion, Human Kinetics: Champaign, IL, 1998.
  2. Klopčar, N.; Tomšič, M.; Lenarčič, J. A kinematic model of the shoulder complex to evaluate the arm-reachable workspace. Journal of Biomechanics, 2007, 40(1), pp. 86–91. [CrossRef]
  3. Rosen, J.; Perry, J. Upper limb powered exoskeleton. International Journal of Humanoid Robotics 2007, 04(03), pp. 529–548.
  4. Naidu, D.; Stopforth, R.; Bright, G.; Davrajh, S. A 7 DOF exoskeleton arm: Shoulder, elbow, wrist and hand mechanism for assistance to upper limb disabled individuals. In Proceedings of the IEEE Africon '11, Victoria Falls, Zambia; 2011; pp. 1–6. [Google Scholar]
  5. Kiguchi, K.; Rahman, M.H.; Sasaki, M.; Teramoto, K. Development of a 3DOF mobile exoskeleton robot for human upper-limb motion assist. Robotics and Autonomous Systems 2008, 56(8), pp. 678–691. [CrossRef]
  6. Wang, X.; Song, Q.; Wang, X.; Liu, P. Kinematics and Dynamics Analysis of a 3-DOF Upper-Limb Exoskeleton with an Internally Rotated Elbow Joint. Appl. Sci. 2018, 8, 464. [Google Scholar] [CrossRef]
  7. Lu, J.; Chen, W.; Tomizuka, M. Kinematic design and analysis of a 6-DOF upper limb exoskeleton model for a brain-machine interface study. IFAC Proceedings Volumes 2013, 46(5), pp. 293–300. [CrossRef]
  8. Chen, Y.; Ge, L.; Yanhe, Z.; Jie, Z.; Hegao, C. Design of a 6-DOF upper limb rehabilitation exoskeleton with parallel actuated joints. Bio-Medical Materials and Engineering 2014, 24(6), pp. 2527–2535.
  9. Caldwell, D.; Tsagarakis, N.; Kousidou, S.; Costa, N.; Sarakoglou, I. “Soft” exoskeletons for upper and lower body rehabilitation — design, control and testing. International Journal of Humanoid Robotics 2014, 4(03), pp. 549–573.
  10. Vertechy, R.; Frisoli, A.; Dettori, A.; Solazzi, M.; Bergamasco, M. Development of a new exoskeleton for upper limb rehabilitation. In Proceedings of the 2009 IEEE International Conference on Rehabilitation Robotics, Kyoto, Japan; 2009; pp. 188–193. [Google Scholar]
  11. Tsai, B.C.; Wang, W.W.; Hsu, L.C.; Fu, L.C.; Lai, J.S. An articulated rehabilitation robot for upper limb physiotherapy and training. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan; 2010; pp. 1470–1475. [Google Scholar]
  12. Lugo-Villeda, M.A.; Ruiz-Sanchez, F.J.; Dominguez-Ramirez, O.A.; Parra-Vega, V. Robotic Design of an Upper Limb Exoskeleton for Motion Analysis and Rehabilitation of Paediatric Neuromuscular Disorders. In Proceedings of Converging Clinical and Engineering Research on Neurorehabilitation. Biosystems & Biorobotics, vol 1. Springer, Berlin, 2013, pp. 265-269.
  13. Maciejasz, P.; Eschweiler, J.; Gerlach-Hahn, K.; Jansen-Troy, A.; Leonhardt, S. A survey on robotic devices for upper limb rehabilitation. Journal of NeuroEngineering and Rehabilitation, 2014, 11(1). [CrossRef]
  14. Zeiaee, A.; Soltani-Zarrin, R.; Langari, R.; Tafreshi, R. Design and kinematic analysis of a novel upper limb exoskeleton for rehabilitation of stroke patients. In Proceedings of the 2017 International Conference on Rehabilitation Robotics (ICORR), London, UK; 2017; pp. 759–764. [Google Scholar]
  15. Gull, M.A.; Bai, S.; Bak, T. A Review on Design of Upper Limb Exoskeletons. Robotics 2020, 9, 16. [Google Scholar] [CrossRef]
  16. Tsagarakis, N.; Caldwell, D. G.; Medrano-Cerda, G. A. A 7 DOF pneumatic muscle actuator (PMA) powered exoskeleton. In Proceedings of 8th IEEE International Workshop on Robot and Human Interaction. RO-MAN '99 (Cat. No.99TH8483), Pisa, Italy, 1999, pp. 327-333.
  17. Stanišić, M.M.; Goehler, C.M. Reproducing human arm motion using a kinematically coupled humanoid shoulder–elbow complex. Applied Bionics and Biomechanics 2008, 5(4), pp. 175–185.
  18. Xiao, Y.; Zhu, Y.; Wang, X.; Zhao, Y.; Ding, Q. Configuration optimization and kinematic analysis of a wearable exoskeleton arm. In Proceedings of the 2017 International Conference on Robotics and Automation Sciences (ICRAS), Hong Kong, China; 2017; pp. 124–128. [Google Scholar]
  19. Ma, R.; Tang, Z.; Gao, X.; Ni, W. Mechanism Design and Kinematics Analysis of an Original Cable-driving Exoskeleton Robot. 2018 2nd IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Xi'an, China, 2018, pp. 1869-1874.
  20. Dežman, M.; Asfour, T.; Ude, A.; Gams, A. Mechanical design and friction modelling of a cable-driven upper-limb exoskeleton. Mechanism and Machine Theory 2022, 171(1):104746. [CrossRef]
  21. Bai, S.; Christensen, S.; Islam, M. R. U. An upper-body exoskeleton with a novel shoulder mechanism for assistive applications. In Proceedings of the 2017 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Munich, Germany; 2017; pp. 1041–1046. [Google Scholar]
  22. Figliolini, G.; Lanni, C.; Kaur, R. ; Kinematic Synthesis of Spherical Four-bar Linkages for Five-Poses Rigid Body Guidance. In Uhl T. (eds) Advances in Mechanism and Machine Science. IFToMM WC 2019. Mechanisms and Machine Science, vol 73. Springer, Cham, 2019, pp. 639-648. [CrossRef]
  23. Bardi, E.; Gandolla, M.; Braghin, F.; Resta, F.; Pedrocchi, A.L.G.; Ambrosini, E. Upper Limb Soft Robotic Wearable Devices: A Systematic Review. J. of NeuroEngineering Rehabil. 2022, 19, article number 87. [CrossRef]
  24. Matsumoto, Y.; et al. Development of an elbow-forearm interlock joint mechanism toward an exoskeleton for patients with essential tremor. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA; 2014; pp. 2055–2062. [Google Scholar]
  25. Manna, S.K.; Dubey, V.N. A mechanism for elbow exoskeleton for customised training, In Proceedings of 2017 International Conference on Rehabilitation Robotics (ICORR), London, UK, 2017, pp. 1597-1602.
  26. Canesi, M.; Xiloyannis, M.; Ajoudani, A.; Biechi, A.; Masia, L. Modular one-to-many clutchable actuator for a soft elbow exosuit. In Proceedings of IEEE Int. Conf. Rehabil. Robot., 2017 July; 2017, pp. 1679-1685.
  27. Song, H.; Kim, Y.S.; Yoon, J.; Yun, S.H.; Seo, J.; Kim, Y.J. Development of Low-Inertia High-Stiffness Manipulator LIMS2 for High-Speed Manipulation of Foldable Objects. In Proceedings of 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 2018, pp. 4145-4151.
  28. Zhang, S.; Fu, Q.; Guo, S.; Fu, Y. A Telepresence System for Therapist-in-the-Loop Training for Elbow Joint Rehabilitation. Appl. Sci. 2019, 9, 1710. [Google Scholar] [CrossRef]
  29. Liu, Y., Wang, D., Yang, S. et al. Design and experimental study of a passive power-source-free stiffness-self-adjustable mechanism. Front. Mech. Eng. 2021, 16, 32–45. [CrossRef]
  30. Beadle, C.W.; O’Brien, M.E. Kinematic analysis of the human elbow. Orthotics and Prosthetics 1976, 31(2), pp. 31-31.
  31. Freudenstein, F.; Woo, L.S. Kinematics of the human knee joint. The Bulletin of Mathematical Biophysics 1969, 31(2), pp. 215–232.
  32. Tomassi, L.; Lanni, C.; Figliolini, G.; A Novel Design Method of Four-Bar Linkages Mimicking the Human Knee Joint in the Sagittal Plane. Niola V., Gasparetto A., Quaglia G., Carbone G. (Eds.), In Proceedings of Advances in Italian Mechanism Science. IFToMM Italy 2022, Naples, Italy, Mechanism and Machine Science, 2022, vol. 122 MMS, pp. 586-592, Springer, Cham. [CrossRef]
  33. Figliolini, G.; Lanni, C.; Tomassi, L.; First and Second Order Centrodes of Slider-Crank Mechanisms by Using Instantaneous Invariants, Altuzarra O., Kecskeméthy A., (Eds), Springer Proc. in Advances Robotics, 18th Intern. Symposium on Advances in Robot Kinematics (ARK 2022) Bilbao, Spain, 2022, vol. 24 SPAR, Springer, pp. 303 – 310. [CrossRef]
  34. Figliolini, G.; Lanni, C.; Sorli, M.; Kinematic analysis and centrodes between rotating tool with reciprocating motion and workpiece. Niola V., Gasparetto A., Quaglia G., Carbone G., (Eds), In Proceedings of Advances in Italian Mechanism Science. IFToMM Italy 2022, Mechanisms and Machine Science, Naples, Italy, 2022, vol. 122 MMS, pp.54-60. [CrossRef]
  35. Lanni, C.; Figliolini, G.; Tomassi, L.; Higher-Order Centrodes and Bresse’s Circles of Slider-Crank Mechanisms, In Proceedings of the ASME 2023 IDETC-CIE2023, Boston, Massachusetts, August 20-23, Vol.8, 2023, article number v008t08a012. [CrossRef]
  36. Figliolini, G.; Lanni, C.; Tomassi, L.; Kinematic Analysis of Slider – Crank Mechanisms via the Bresse and Jerk’s Circles. In Proceedings of XXIV AIMETA Conference 2019, Carcaterra A., Graziani G., Paolone A. (Eds)., Rome, Italy, 2020, pp.278-284. [CrossRef]
  37. Figliolini, G.; Lanni, C.; Cirelli, M.; Pennestrì, E.; Kinematic Properties of nth-order Bresse Circles Intersections for a Crank-Driven Rigid Body. Mechanism and Machine Theory 2023, vol. 190, article number 105445. [CrossRef]
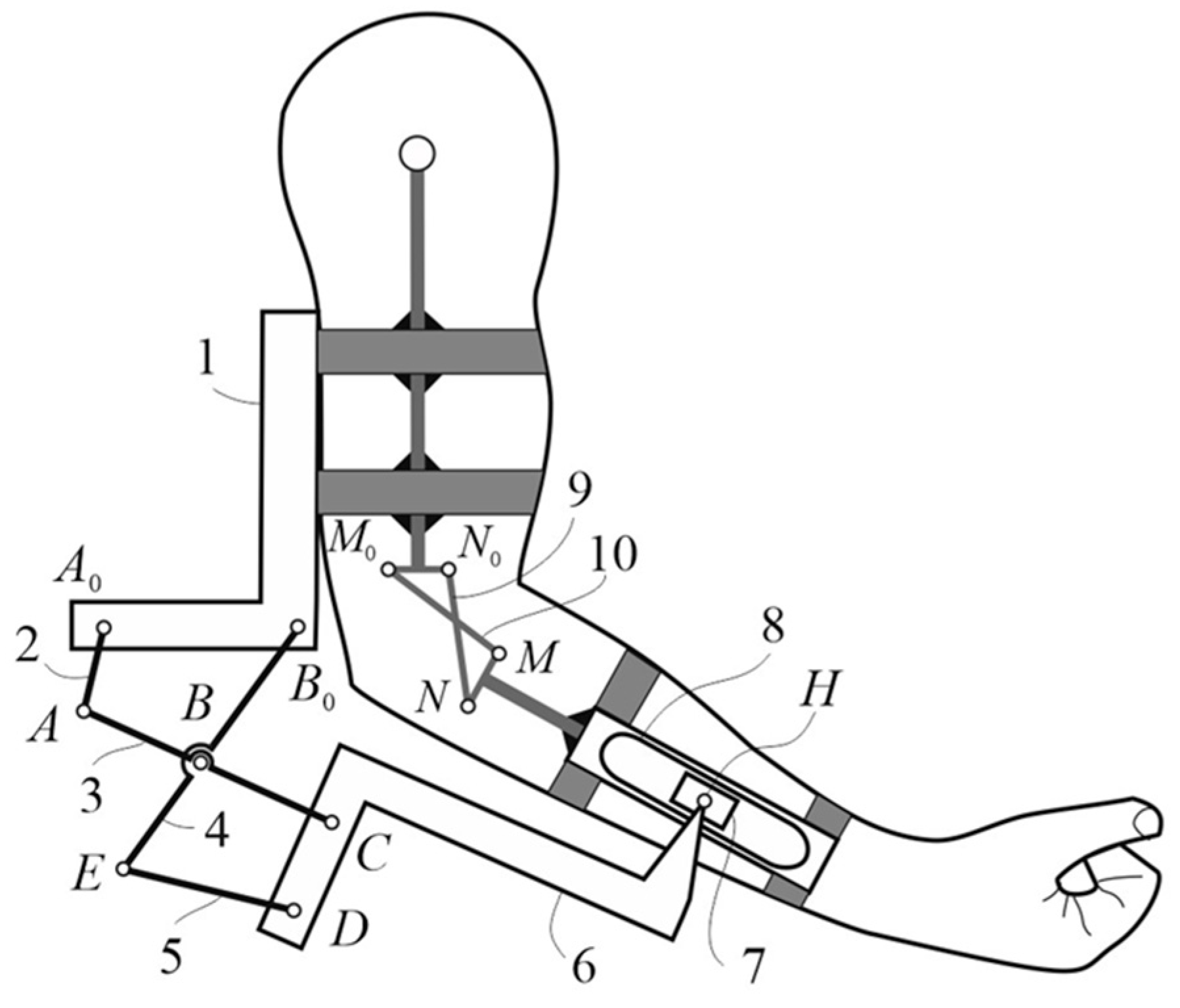
Preprints 114206 g001
Figure 1. Ten-bar exoskeleton elbow joint mechanism.
Figure 1. Ten-bar exoskeleton elbow joint mechanism.
Preprints 114206 g001
Preprints 114206 g002
Figure 2. Ten-bar mechanism.
Figure 2. Ten-bar mechanism.
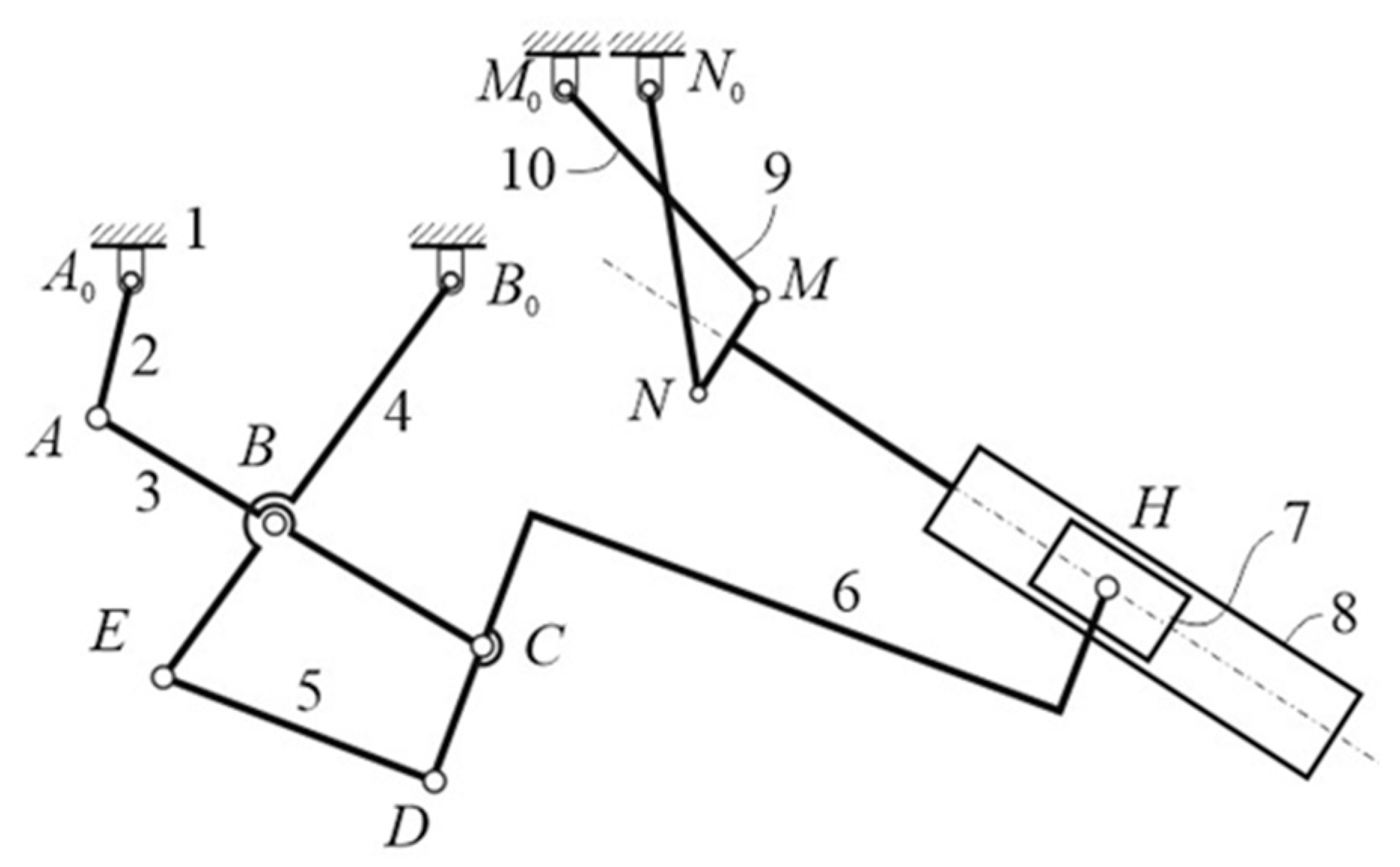
Preprints 114206 g002
Preprints 114206 g003
Figure 3. Watt I six-bar linkage: (a) vector loops; (b) ICs.
Figure 3. Watt I six-bar linkage: (a) vector loops; (b) ICs.
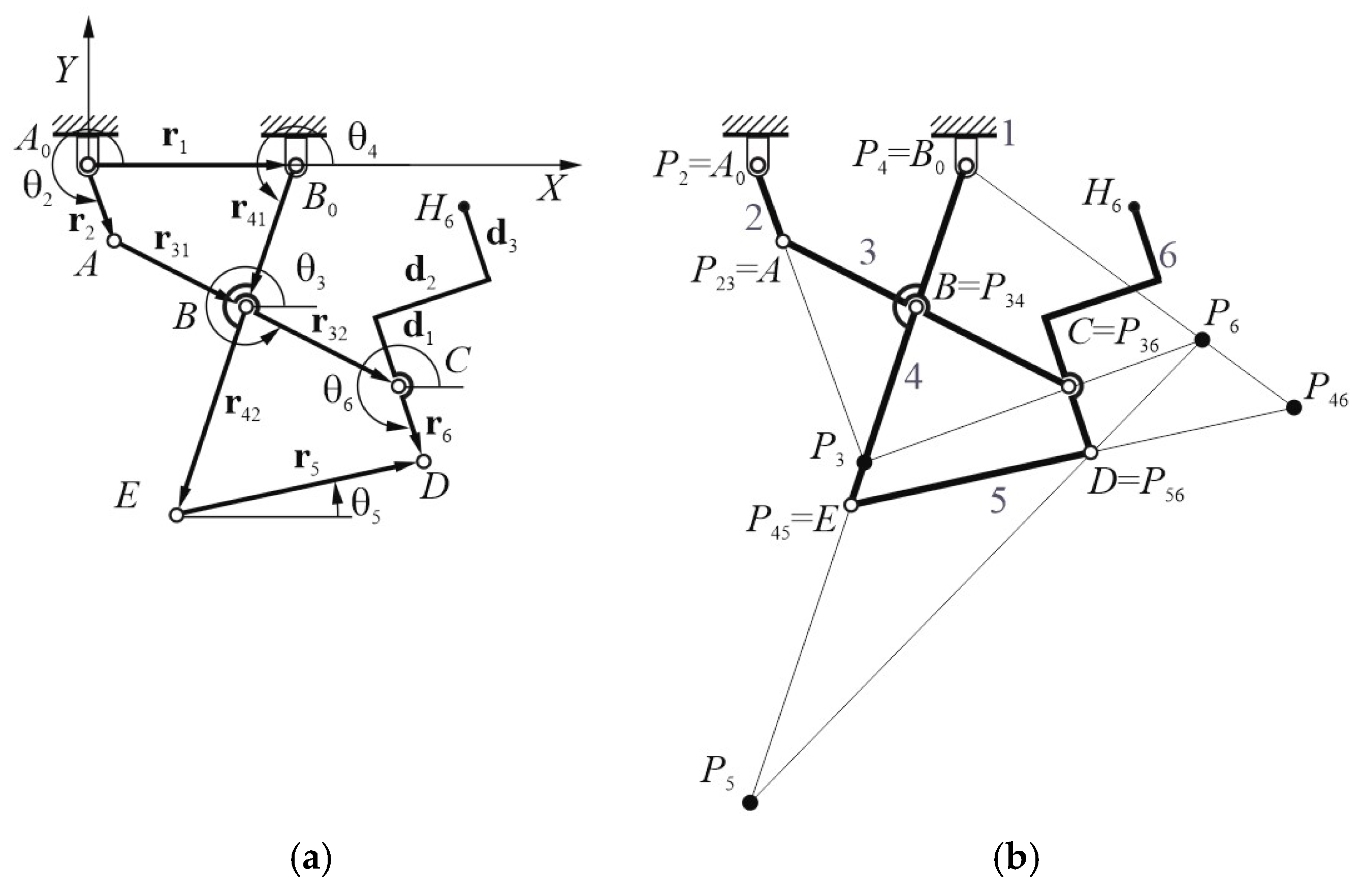
Preprints 114206 g003
Preprints 114206 g004
Figure 4. Crossed four-bar linkage: (a) vector loop; (b) ICs.
Figure 4. Crossed four-bar linkage: (a) vector loop; (b) ICs.
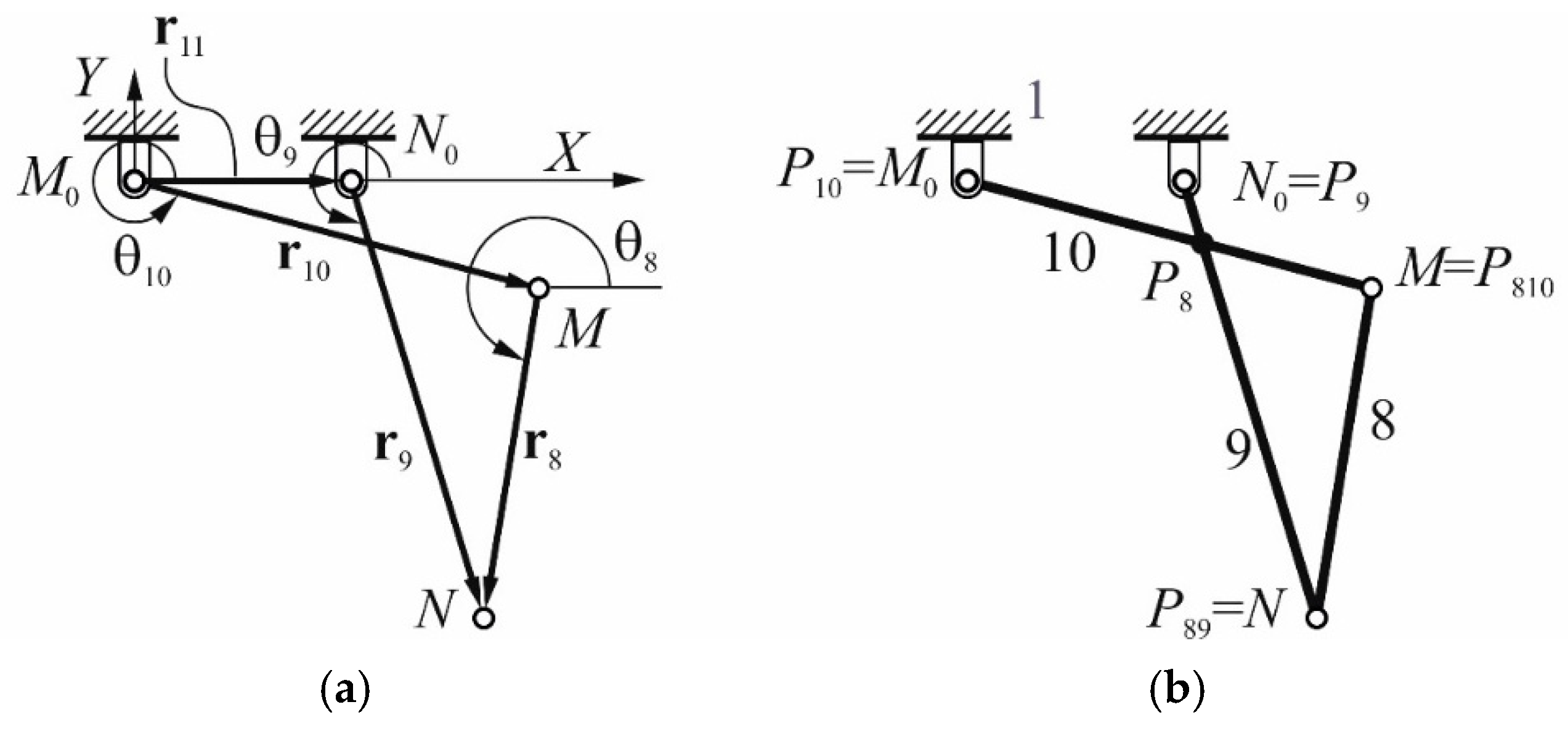
Preprints 114206 g004
Preprints 114206 g005
Figure 5. Ten-bar mechanism: ICs.
Figure 5. Ten-bar mechanism: ICs.
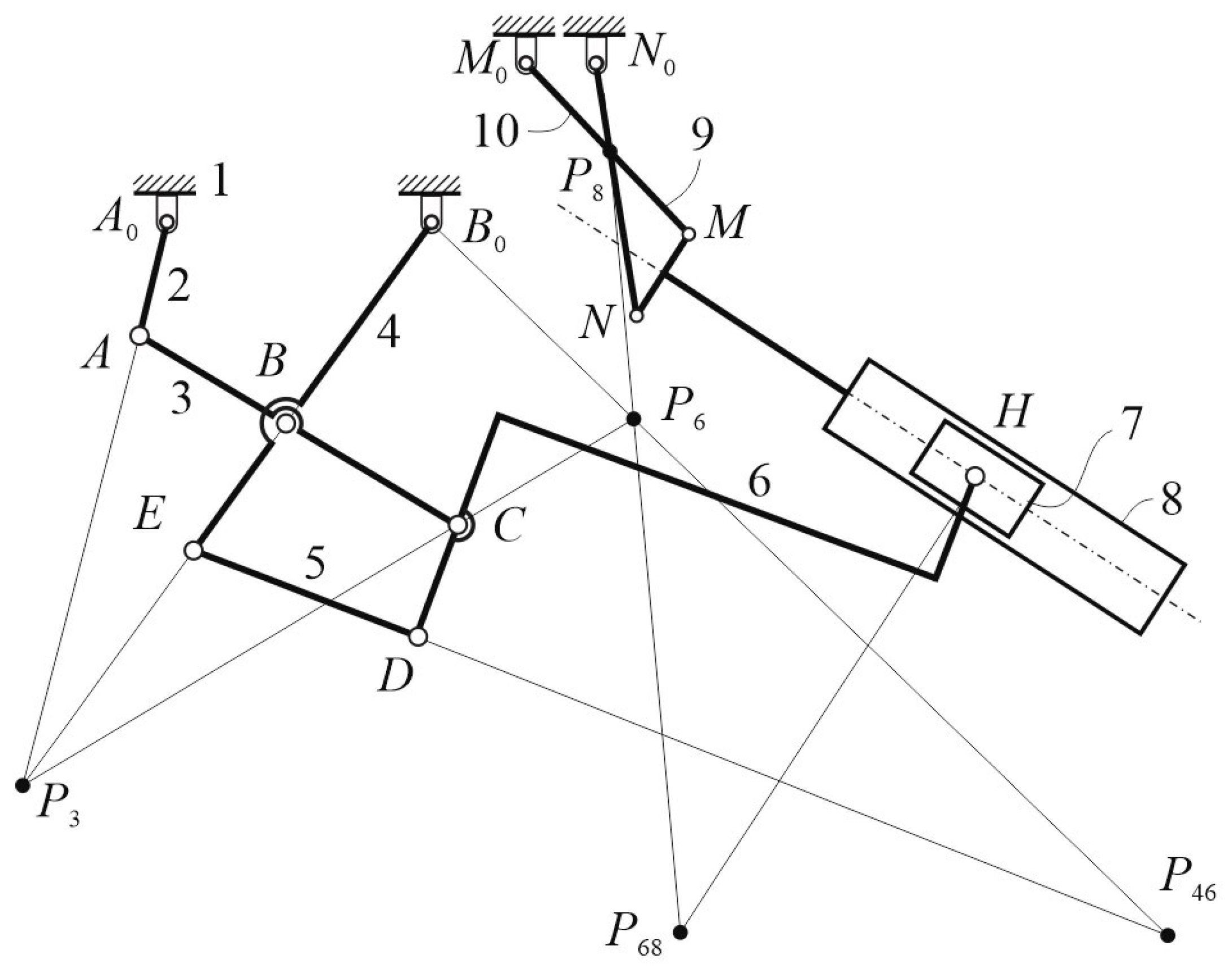
Preprints 114206 g005
Preprints 114206 g006
Figure 6. Ten-bar mechanism: result for a crank angle θ2 = 255° of A0A.
Figure 6. Ten-bar mechanism: result for a crank angle θ2 = 255° of A0A.
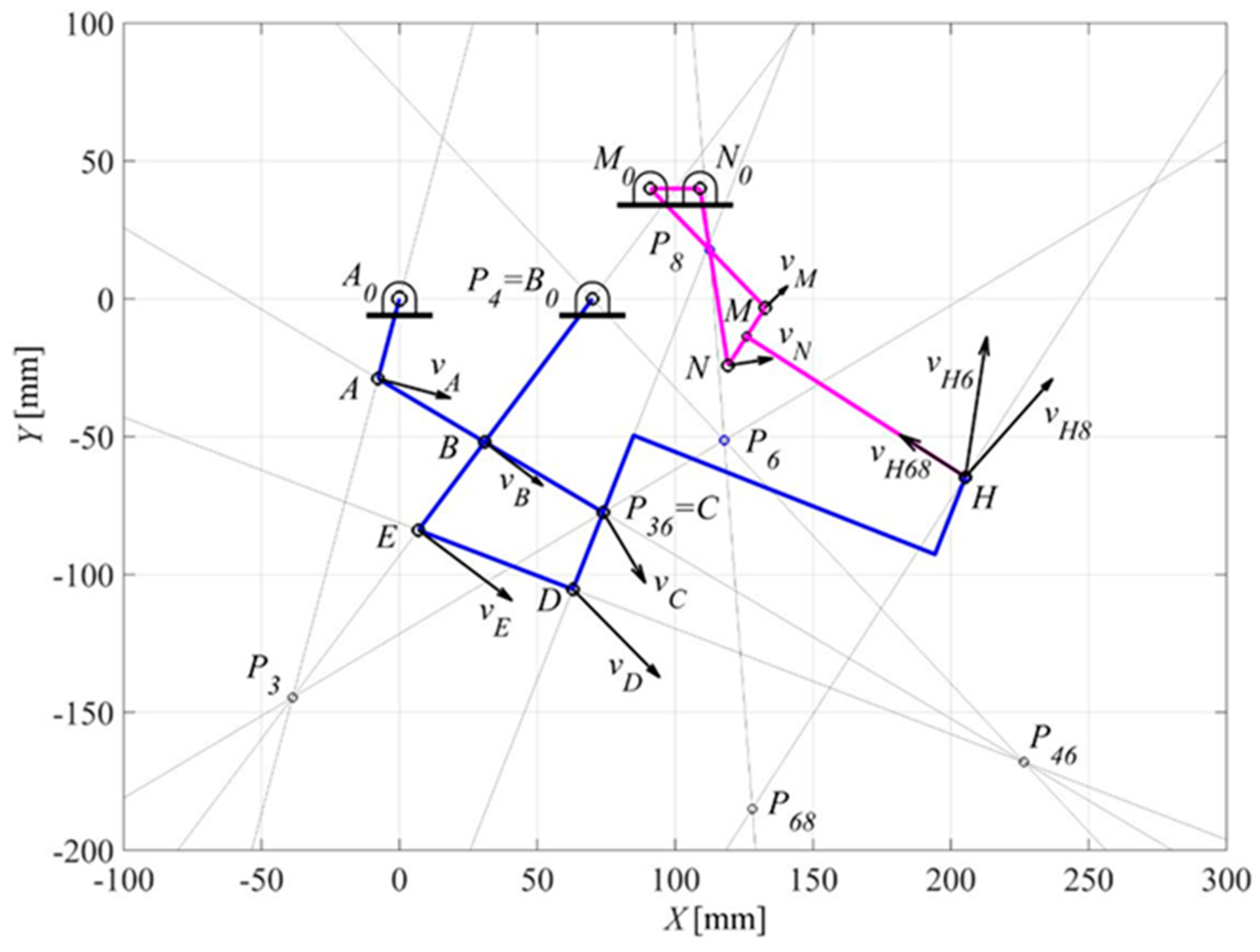
Preprints 114206 g006
Preprints 114206 g007
Figure 7. Ten-bar mechanism: result for a crank angle θ2 = 290° of A0A.
Figure 7. Ten-bar mechanism: result for a crank angle θ2 = 290° of A0A.
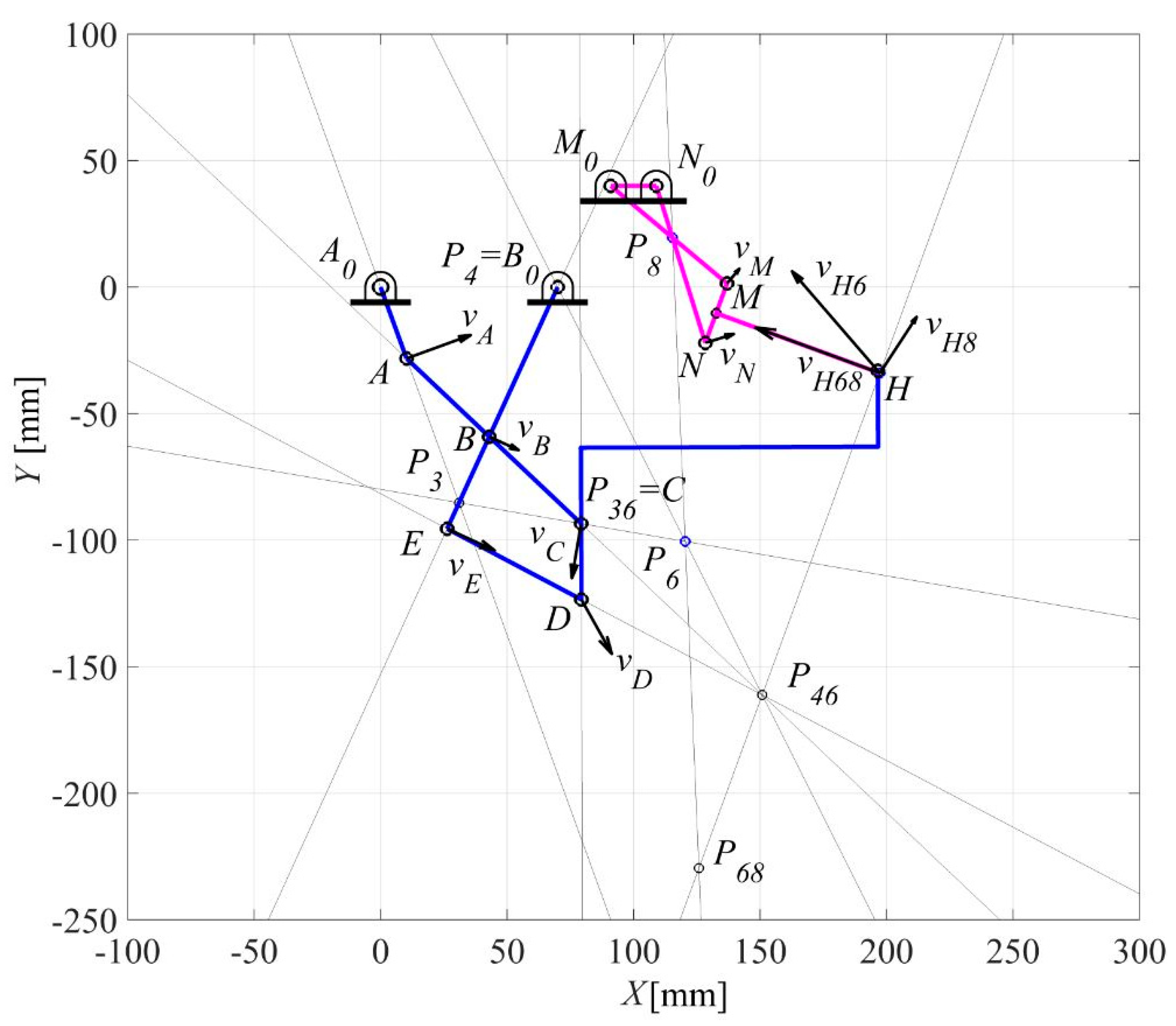
Preprints 114206 g007
Preprints 114206 g008
Figure 8. Ten-bar elbow joint exoskeleton mechanism: (a) kinematic sketch; (b) application.
Figure 8. Ten-bar elbow joint exoskeleton mechanism: (a) kinematic sketch; (b) application.
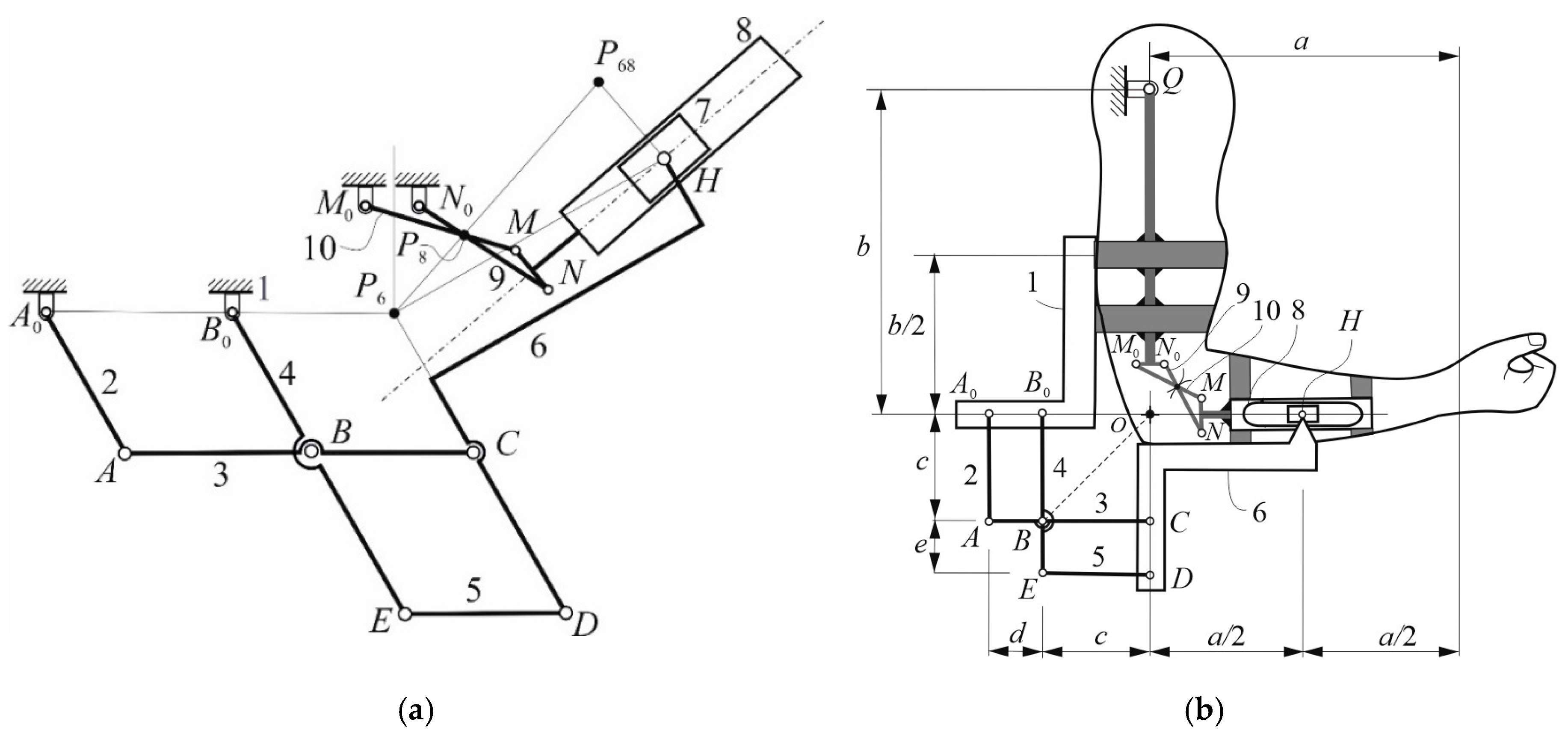
Preprints 114206 g008
Preprints 114206 g009
Figure 9. Ten-bar linkage for the upper-limb exoskeleton: result for a crank angle θ2 = 300° of A0A.
Figure 9. Ten-bar linkage for the upper-limb exoskeleton: result for a crank angle θ2 = 300° of A0A.
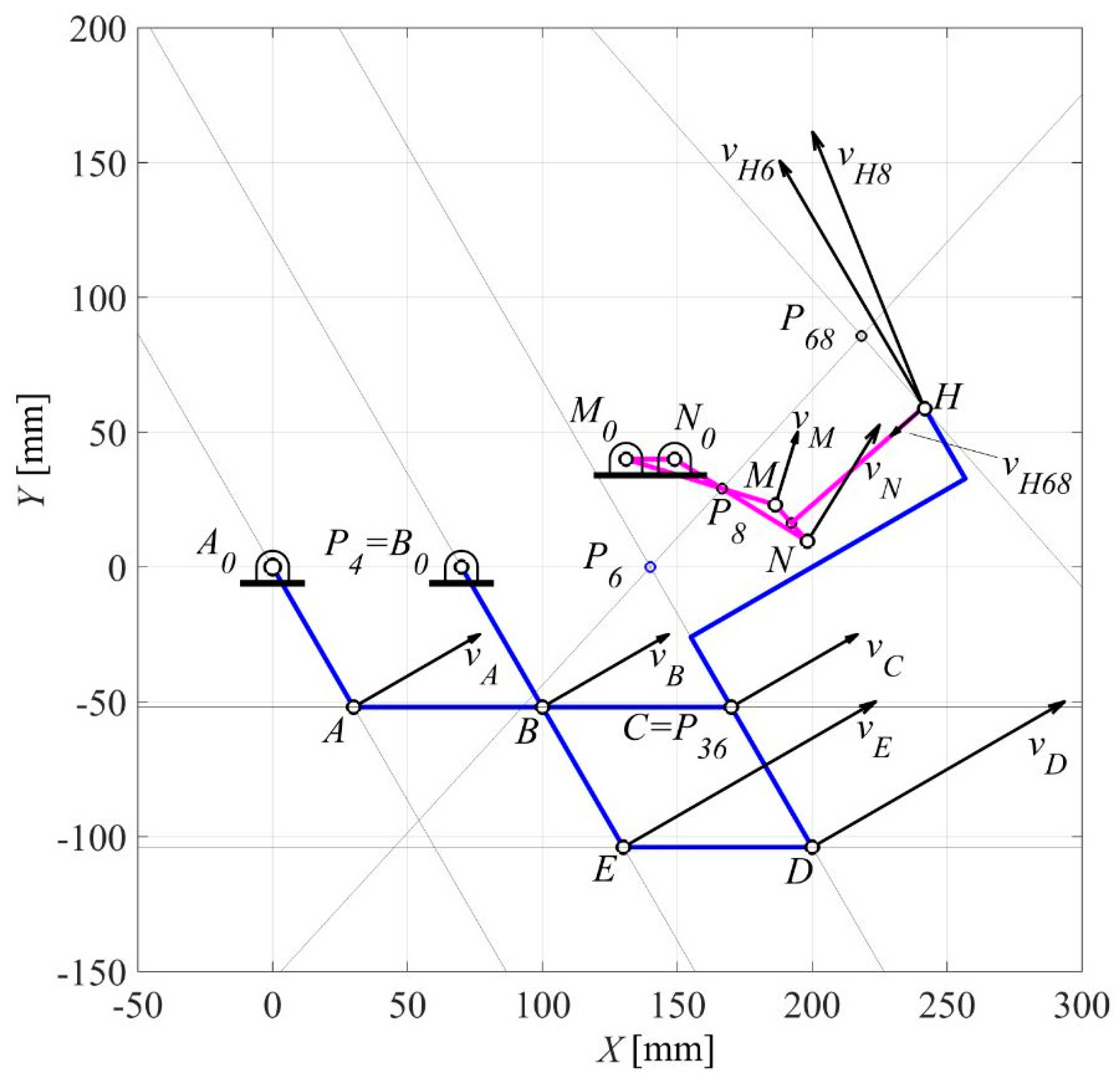
Preprints 114206 g009
Preprints 114206 g010
Figure 10. Result for a crank angle θ 2 = 252° of A0A for ten-bar linkage.
Figure 10. Result for a crank angle θ 2 = 252° of A0A for ten-bar linkage.
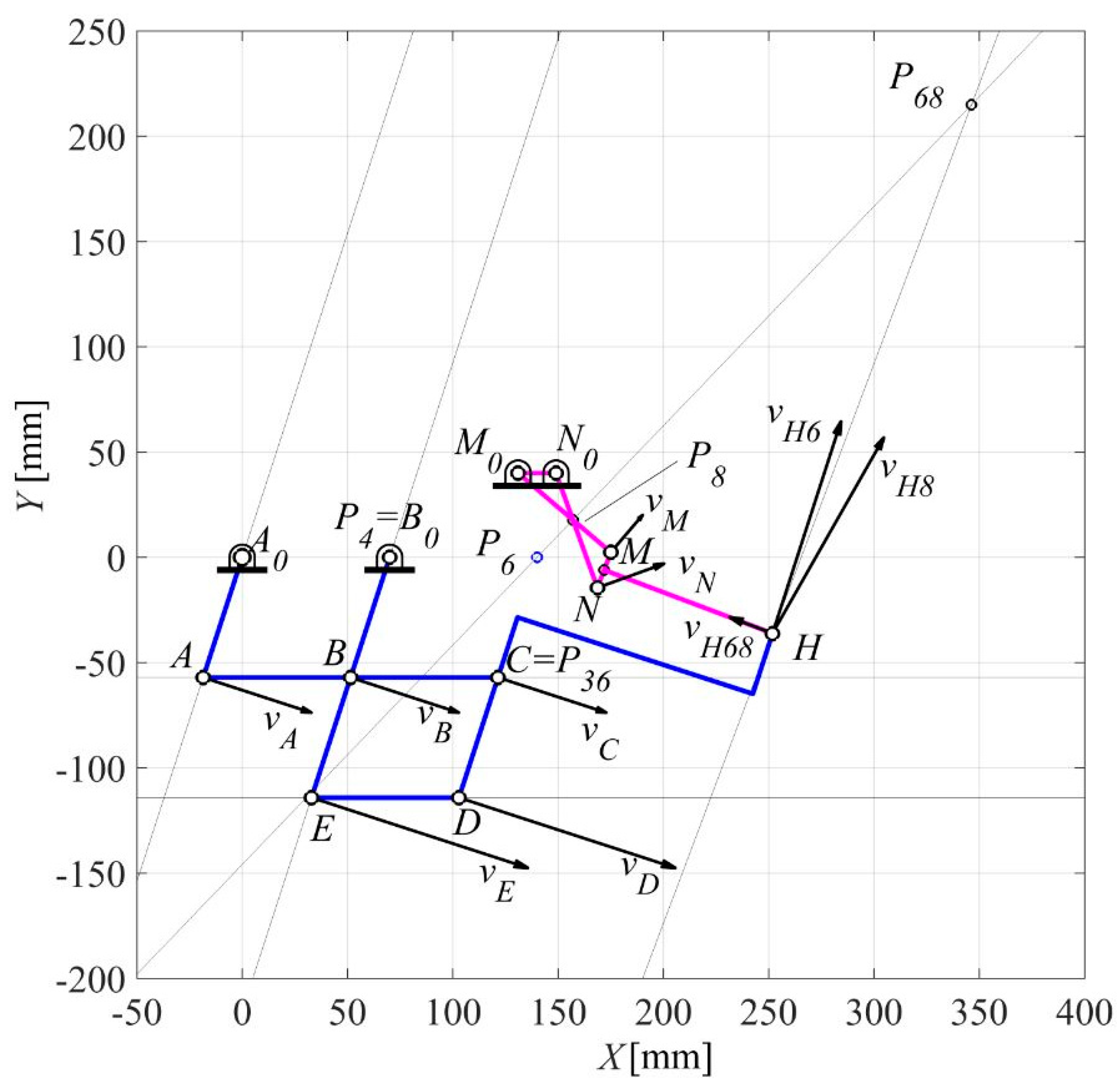
Preprints 114206 g010
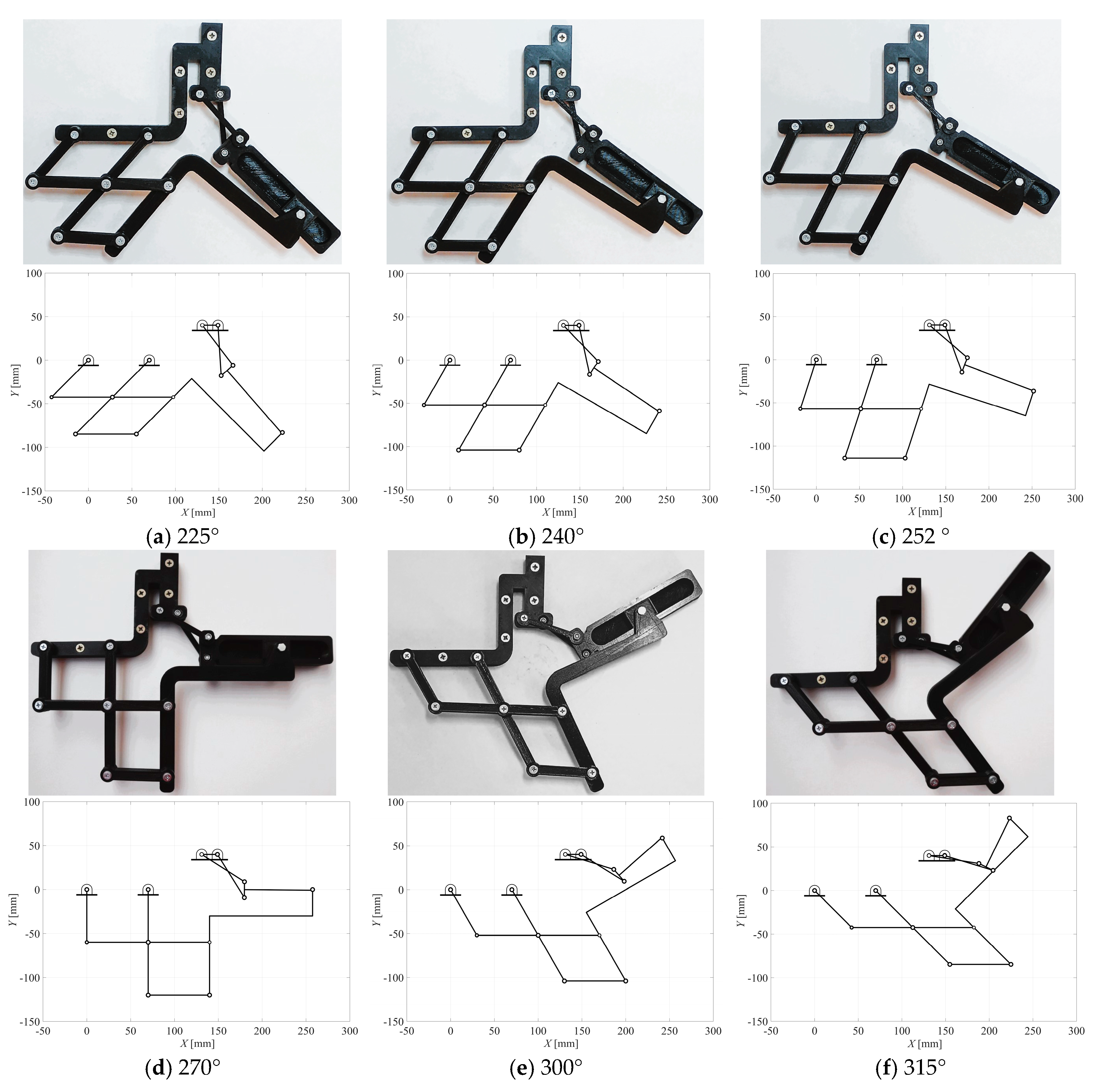
Preprints 114206 g011
Figure 11. Ten-bar mechanism and 3D printed prototype for different configurations of crank angles θ 2: (a) 225°; (b) 240°; (c) 252°; (d) 270°; (e) 300°; (f) 315°.
Figure 11. Ten-bar mechanism and 3D printed prototype for different configurations of crank angles θ 2: (a) 225°; (b) 240°; (c) 252°; (d) 270°; (e) 300°; (f) 315°.
Preprints 114206 g011
Preprints 114206 g012
Figure 12. Whole sequence of the ten-bar mechanism closing motion.
Figure 12. Whole sequence of the ten-bar mechanism closing motion.
Preprints 114206 g012
Table 1. The geometric input data in the case of Figure 6 and Figure 7.
Table 1. The geometric input data in the case of Figure 6 and Figure 7.
r1 [mm] r2 = r6 [mm] r31 [mm] r32 [mm] r41 [mm] r42 [mm]
70 30 45 50 65 40
r8 [mm] r9 [mm] r10 [mm] r11 [mm] d1 = d3 [mm] d2 [mm]
25 65 60 18 30 117.50
Table 2. Output linear velocities of all significant points for the case of Figure 6 and Figure 7.
Table 2. Output linear velocities of all significant points for the case of Figure 6 and Figure 7.
θ 2 [deg] vA [mm/s] vB [mm/s] vC[mm/s] vD[mm/s] vE[mm/s]
255 [28.978, −7.765]T [23.220, −17.463]T [16.82, −28.239]T [34.78, −35.324]T [37.509,− 28.21]T
290 [28.191, 10.261]T [12.906, − 5.905]T [−4.077, −23.86]T [13.328, −23.80]T [20.848, − 9.538]T
vH6 [mm/s] vH8 [mm/s] vH68 [mm/s] vM [mm/s] vN [mm/s]
255 [8.648, 56.278]T [34.933, 39.356]T [−26.38, 16.937]T [8.853, 8.549]T [17.782, 2.818]T
290 [−39.128, 44.18]T [16.092, 24.658]T [−54.675, 20.00]T [5.443, 6.483]T [12.502, 3.904]T
Table 3. Output angular velocities of all moving links for the case of Figure 6 and Figure 7.
Table 3. Output angular velocities of all moving links for the case of Figure 6 and Figure 7.
θ2 [deg] ω3 [rad/s] ω4 [rad/s] ω5 [rad/s] ω6 [rad/s] ω8 [rad/s] ω9 [rad/s] ω10 [rad/s] ω11 [rad/s]
255 − 0.251 0.447 − 0.127 0.644 0.424 0.277 0.205 0.219
290 − 0.4944 0.2183 − 0.2688 0.5802 0.3007 0.2015 0.1411 0.2795
Table 4. The geometric input data in the case of Figure 9 and Figure 10.
Table 4. The geometric input data in the case of Figure 9 and Figure 10.
R1 = r31 = r32 = r5 [mm] r2 = r41 = r42 = r6 [mm] r8 = r11 [mm] r9 = r10 [mm] d1 = d3 [mm] d2 [mm]
70 60 18 57.90 30 117.50
Table 5. Output linear velocities of all significant points for the case of Figure 9 and Figure 10.
Table 5. Output linear velocities of all significant points for the case of Figure 9 and Figure 10.
θ 2 [deg] vA = vB =vC[mm/s] vD = vE[mm/s]
300 [51.962, 30.000]T [112.583,65.000]T
252 [57.063, − 18.5410]T [13.328,−23.804]T
vH6 [mm/s] vH8 [mm/s] vH68 [mm/s] vM [mm/s] vN [mm/s]
300 [−58.750, 101.758]T [−45.816, 103.288]T [−13.556, −11.892]T [9.158, 29.955]T [29.650, 47.93]T
252 [36.309, 111.749]T [58.722, 103.305]T [−22.609, 8.507]T [16.74, 19.605]T [35.108,12.69]T
Table 6. Output angular velocities of all moving links for the case of Figure 9 and Figure 10.
Table 6. Output angular velocities of all moving links for the case of Figure 9 and Figure 10.
θ2 [deg] ω 3 = ω 5 [rad/s] ω 4 = ω 6 [rad/s] ω8 [rad/s] ω9 [rad/s] ω10 [rad/s] ω11 [rad/s]
300 0 1 1.514 0.973 0.541 − 0.514
252 − 0.4944 0.2183 1.0901 0.6448 0.4453 − 0.0901
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated