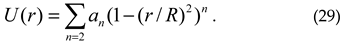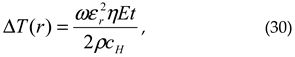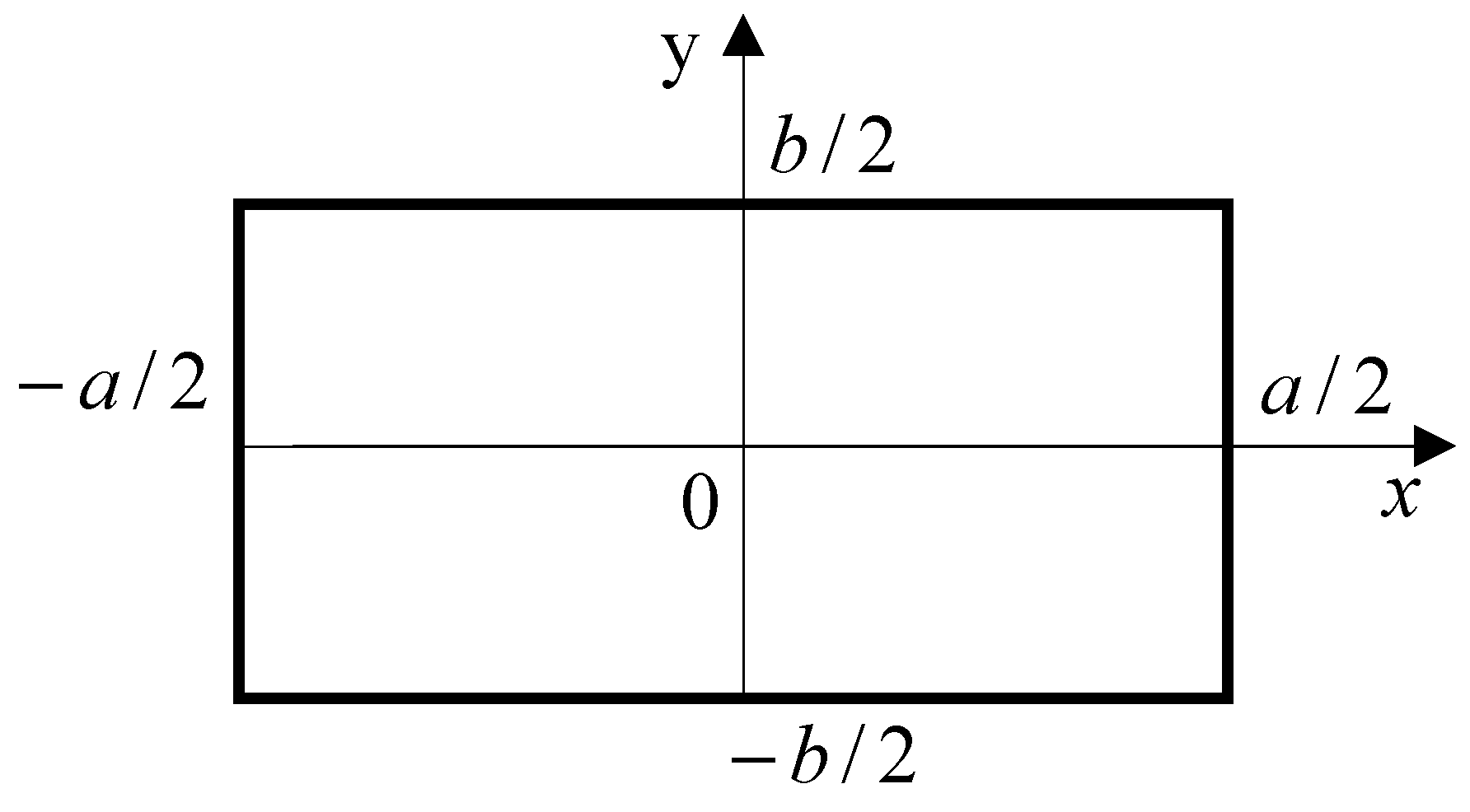Conclusions
In the classical acoustic resonance interpretation, LDR of a planar defect, like a delamination, can be perceived as a resonance of an oscillator activated by a standing wave formation due to constructive interference of the flexural waves. The generic structure of the LDR frequency developed as a function proportional to the defect depth, reciprocal to the square of its size has been validated for various shape delaminations by using closed form calculations via classical Rayleigh’s method.
The flexural wave encounter with an out-of-plane crack is shown to be accompanied by the mode conversion to the edge wave propagating along the crack faces. The latter manifests similar dispersion behaviour to that of the low-frequency A0–mode along with characteristic slow decay as a function of the distance from the crack face. At certain frequencies, the edge waves in the crack interfere constructively and the crack also falls into the LDR with characteristic decay of the wave amplitude as a function of the distance from the edge.
3D-defects, like porous bubbles in solid materials manifest sharp resonances of breathing mode (LDR) in the high-kHz frequency range followed by a periodic series of the higher-order vibration modes. According to the analysis developed, the resonance frequencyfor the breathing mode is reciprocal to the pore radius R so that it can be assessed by the value of the parameter for a particular pore. This product is envisaged and experimentally verified to lie in the range between 0.5 and 0.72, where is the sound velocity in air.
The excitation at the LDR frequency readily moves the pore vibration to the nonlinear regime manifested by wide nonlinear spectra that contain multiple higher harmonics. The bubble nonlinearity combined with their resonance also results in efficient higher harmonic generation for excitation at subharmonics of LDR frequencies (subharmonic resonance).
The experimental methodology of laser vibrometry is successfully applied to a search of LDR and imaging of defects in a variety of composite materials. LDR with local resonance “amplification” of the vibration amplitude as high as ~ 20-40 dB are generally measured for various types of realistic defects in CFRP. A strong frequency selectivity of LDR implies an opportunity of detecting a certain defect among a multitude of other defects. The ultrasonic excitation at LDR frequencies generally enables to visualize only a part of the defect while a wideband excitation which covers a number of the higher-order LDR visualizes clearly a total shape of the defect.
An activation of LDR enables to route the input acoustic energy directly to the defect that dramatically increases its vibration amplitude and shifts into nonlinear regime. Nonlinear acoustics is a promising NDT technology for diagnostics of damage based on the wave frequency conversion (e.g. generation of higher harmonics, mixing frequencies, etc.). Such “classical” nonlinear modes correspond to nonlinear terms in non-Hookian equation of state of the material. They use the excitation at the fundamental LDR frequency while the nonlinear images usually demonstrate a higher contrast than the fundamental LDR image.
The concept of LDR combined with the defect nonlinearity identifies it as a nonlinear oscillator and results in qualitatively new “non-classical” features characteristic of nonlinear (combination frequency, subharmonic) and parametric resonances.
A low ultrasound-heat conversion is a major shortcoming of NDT thermosonic techniques which is usually taken for granted without an effort to be optimized. According to the analysis presented, it is a quadratic function of LDR amplification factor that enables to increase the acousto-thermal efficiency by orders of magnitude. As a result, the case studies of LDR thermosonics for simulated and realistic defects (delaminations, impacts, cracks) confirm the feasibility of high contrast imaging in the mW-power range. Further enhancement of sensitivity and SNR of thermosonic images is achieved by using LDR in the lock-in image mode. This enables to proceed to remote thermosonic imaging by using an ACU excitation of defects.
A local standing wave vibration developed in the defect area via LDR has been also shown to result in the resonant air-coupled emission (RACE) emanating from this area in ambient air. The resonant rise in radiation efficiency enables to reduce an input signal in contact excitation mode and opens an opportunity for remote activation-reception of airborne radiation.
A different experimental approach which does not require preliminary knowledge of LDR frequency is based on a wideband acoustic activation by using a noise-like input signal. Provided the excitation bandwidth includes an LDR frequency the defect resonance is developed and a RACE signal is generated. The noisy mode of RACE is applicable to simultaneous imaging of any and all defects whose LDR frequencies occur within the bandwidth of acoustic excitation.
The case studies confirmed RACE applicability to imaging of serious defects in composites (including BVID) with modest restrictions on the microphone distance from the defect.
Unlike 2D-RACE scanning of flat specimens, the use of industrial robots provides fully autonomous detecting and imaging of the defects in complicated shape components. The robotic RACE scanning combined with wideband noisy excitation proves the feasibility of simultaneous imaging of multiple defects without prior search for LDR frequencies.
A new full-field RACE imaging method with an array of microphones as a receiver avoids the drawback of time-consuming scanning modes and is used for detection and imaging of defects. The case studies of the full-field RACE mode with acoustic camera array validate imaging of various defects in composites. The RACE approach simplifies integration of the proposed NDT imaging system which includes only inexpensive fully acoustic instrumental components.
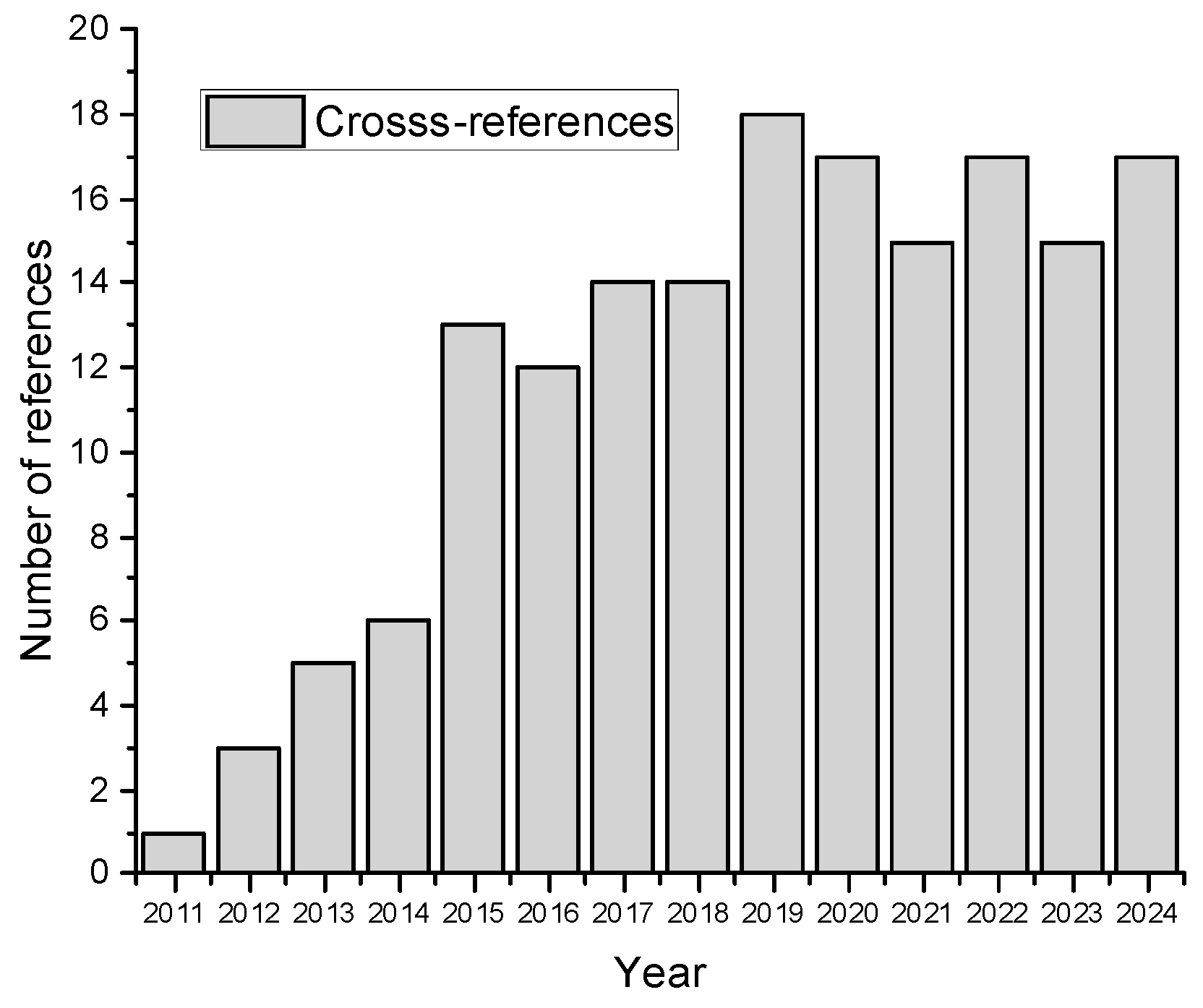
Figure 1.
Annual citing of LDR topic.
Figure 1.
Annual citing of LDR topic.
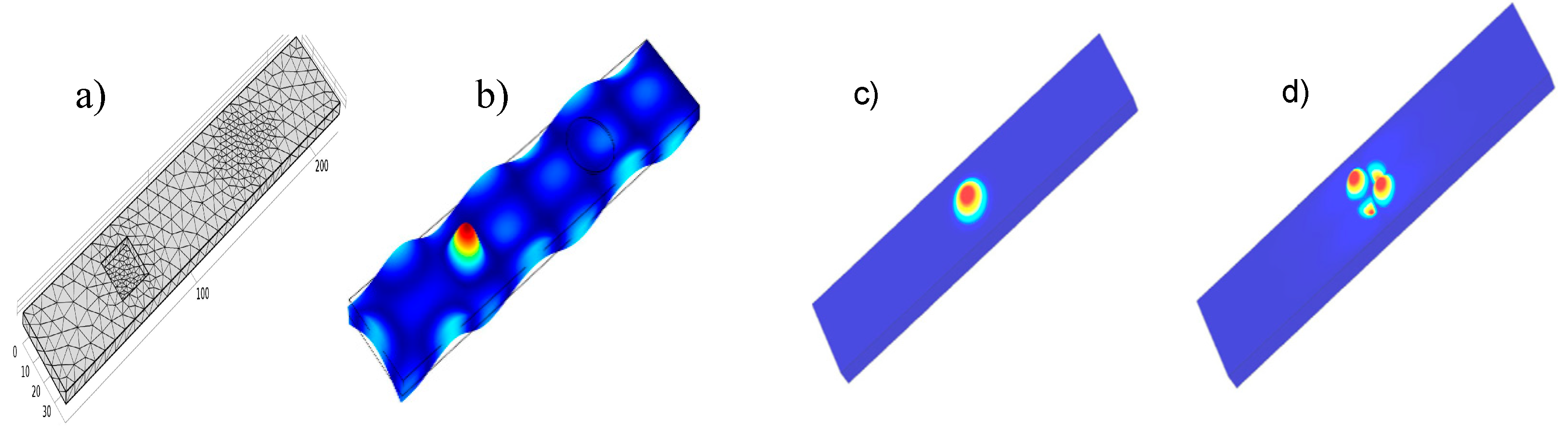
Figure 2.
FEM mesh (a) and fundamental LDR vibration pattern at f0 = 8255 Hz (b) for 2x2 cm2 square FBH in a PMMA plate; A fundamental LDR (10.4 kHz) (c) and higher-order LDR (23.25 kHz) (d) for a circular FBH (radius 1 cm, depth 2 mm) in a PMMA plate (thickness 3 mm).
Figure 2.
FEM mesh (a) and fundamental LDR vibration pattern at f0 = 8255 Hz (b) for 2x2 cm2 square FBH in a PMMA plate; A fundamental LDR (10.4 kHz) (c) and higher-order LDR (23.25 kHz) (d) for a circular FBH (radius 1 cm, depth 2 mm) in a PMMA plate (thickness 3 mm).
Figure 3.
Layout of rectangular delamination.
Figure 3.
Layout of rectangular delamination.
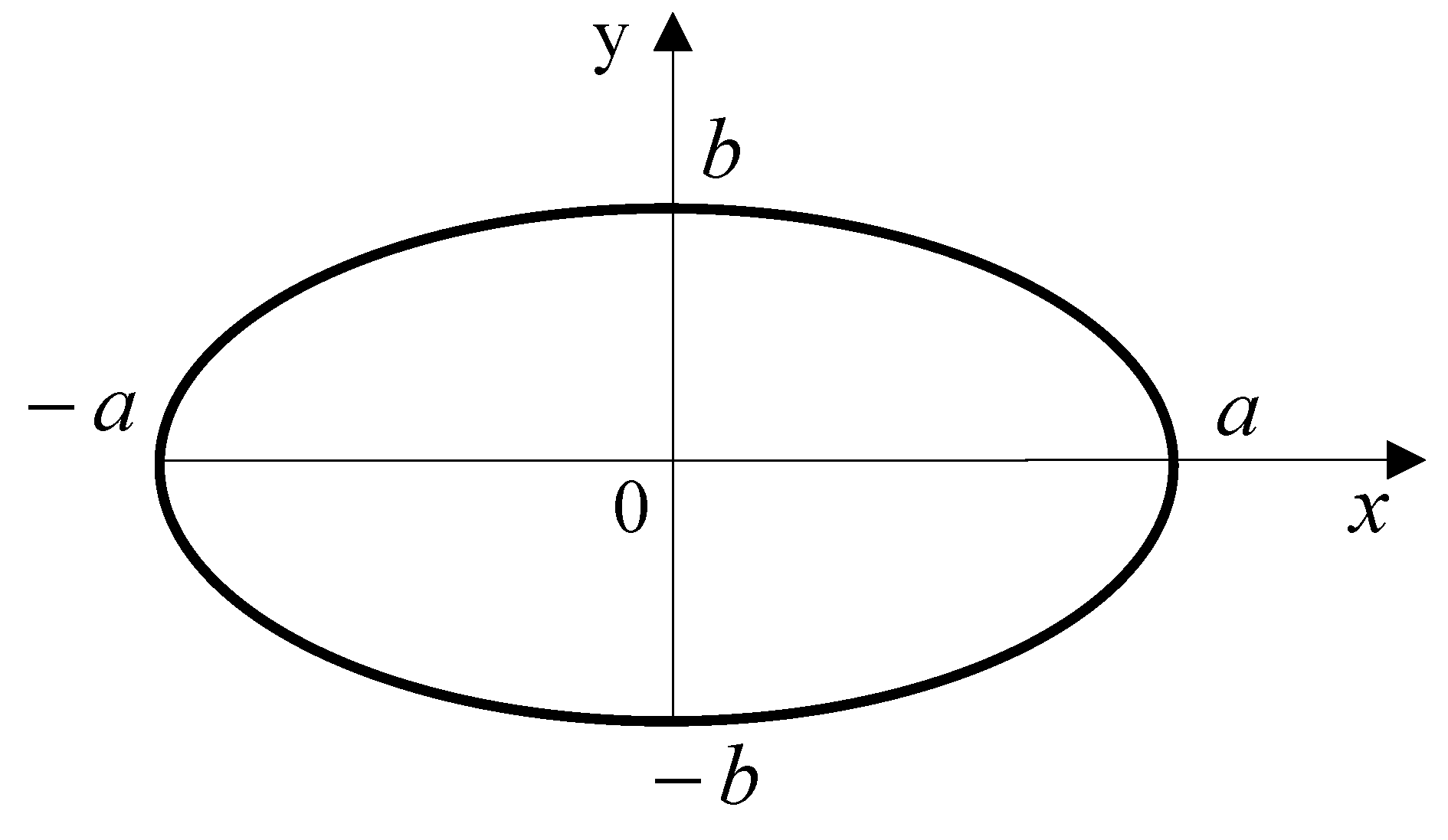
Figure 4.
Layout of elliptical delamination.
Figure 4.
Layout of elliptical delamination.
Figure 5.
LDR frequency response (b), vibration pattern at f0=14625 Hz (c) for rectangular FBH in PMMA (a).
Figure 5.
LDR frequency response (b), vibration pattern at f0=14625 Hz (c) for rectangular FBH in PMMA (a).
Figure 6.
LDR frequency response (b), vibration pattern at f0=16000 Hz (c) for a square FBH in PMMA PPMMAPMMA (a).
Figure 6.
LDR frequency response (b), vibration pattern at f0=16000 Hz (c) for a square FBH in PMMA PPMMAPMMA (a).
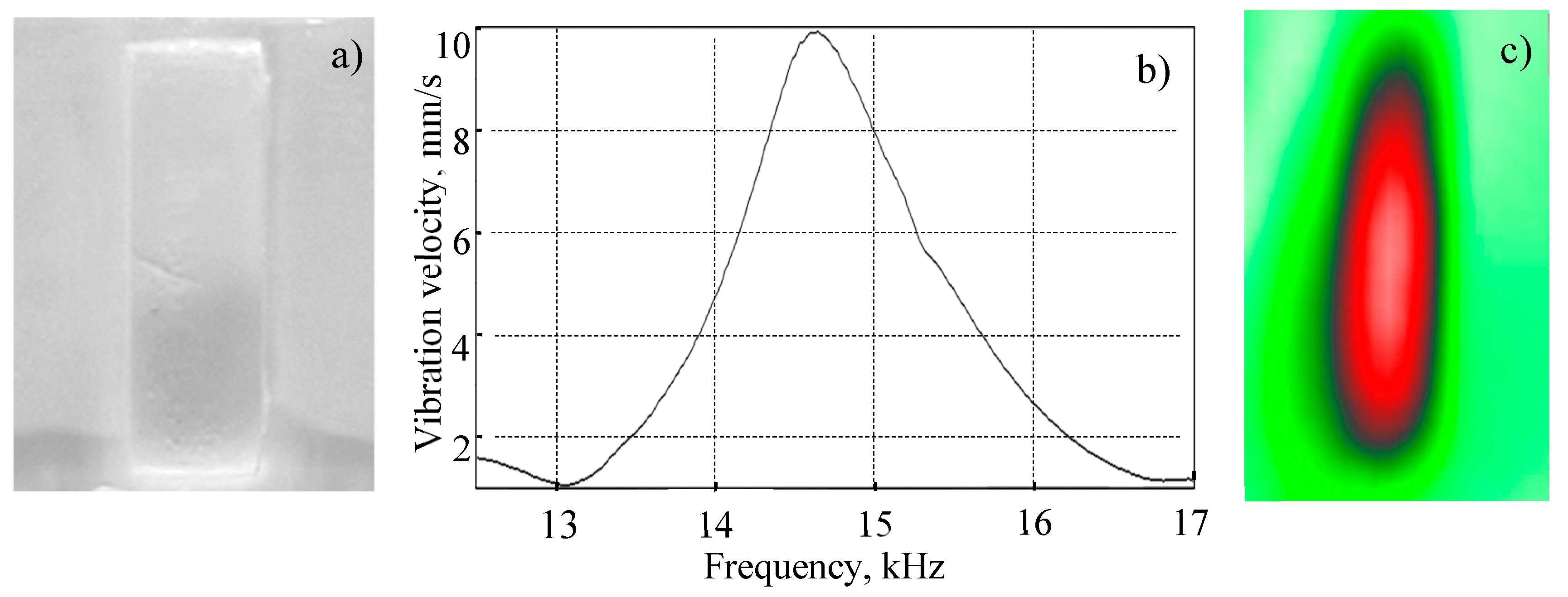
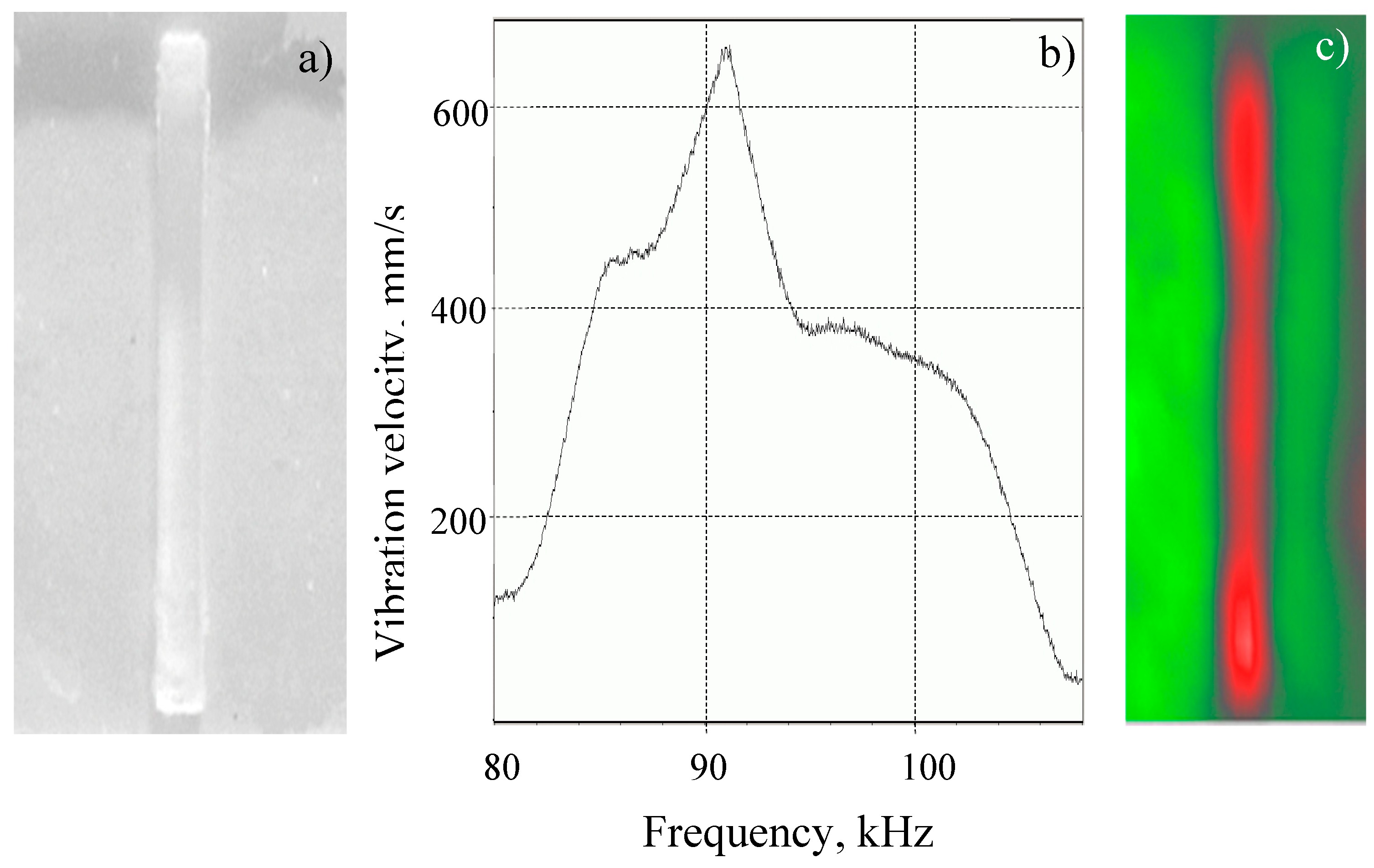
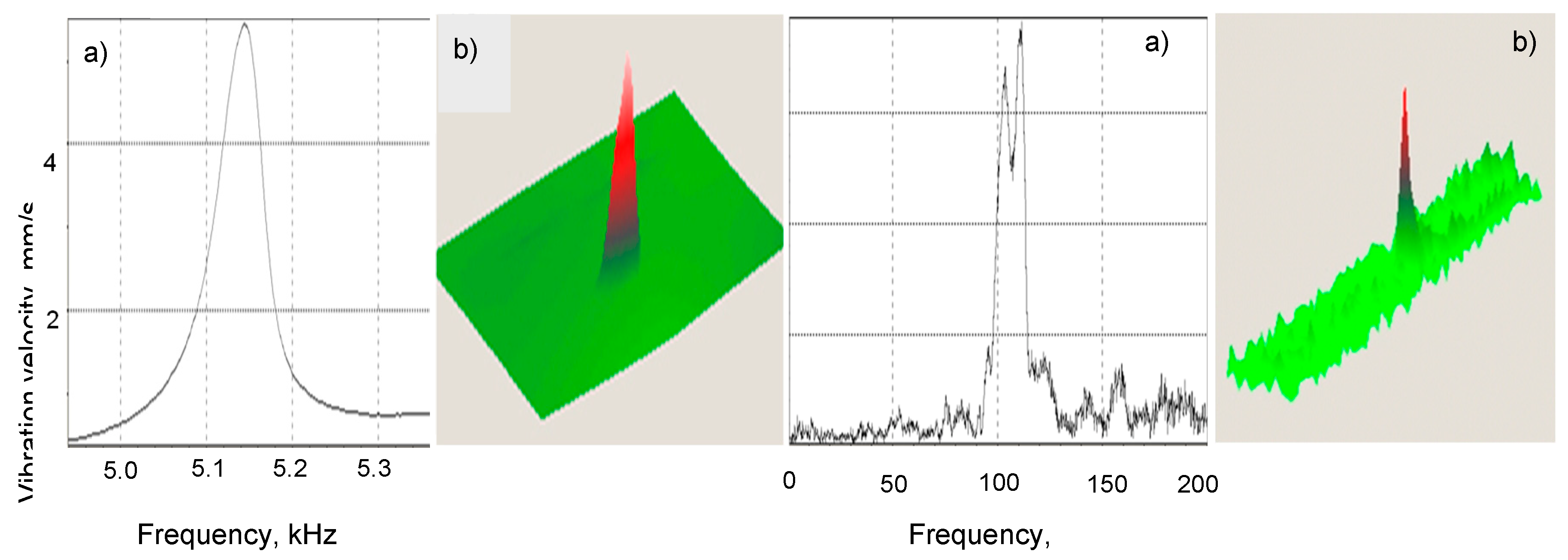
Figure 7.
Notch FBH (a): LDR frequency response (b) and LDR vibration image at f0 = 91000 Hz (c).
Figure 7.
Notch FBH (a): LDR frequency response (b) and LDR vibration image at f0 = 91000 Hz (c).
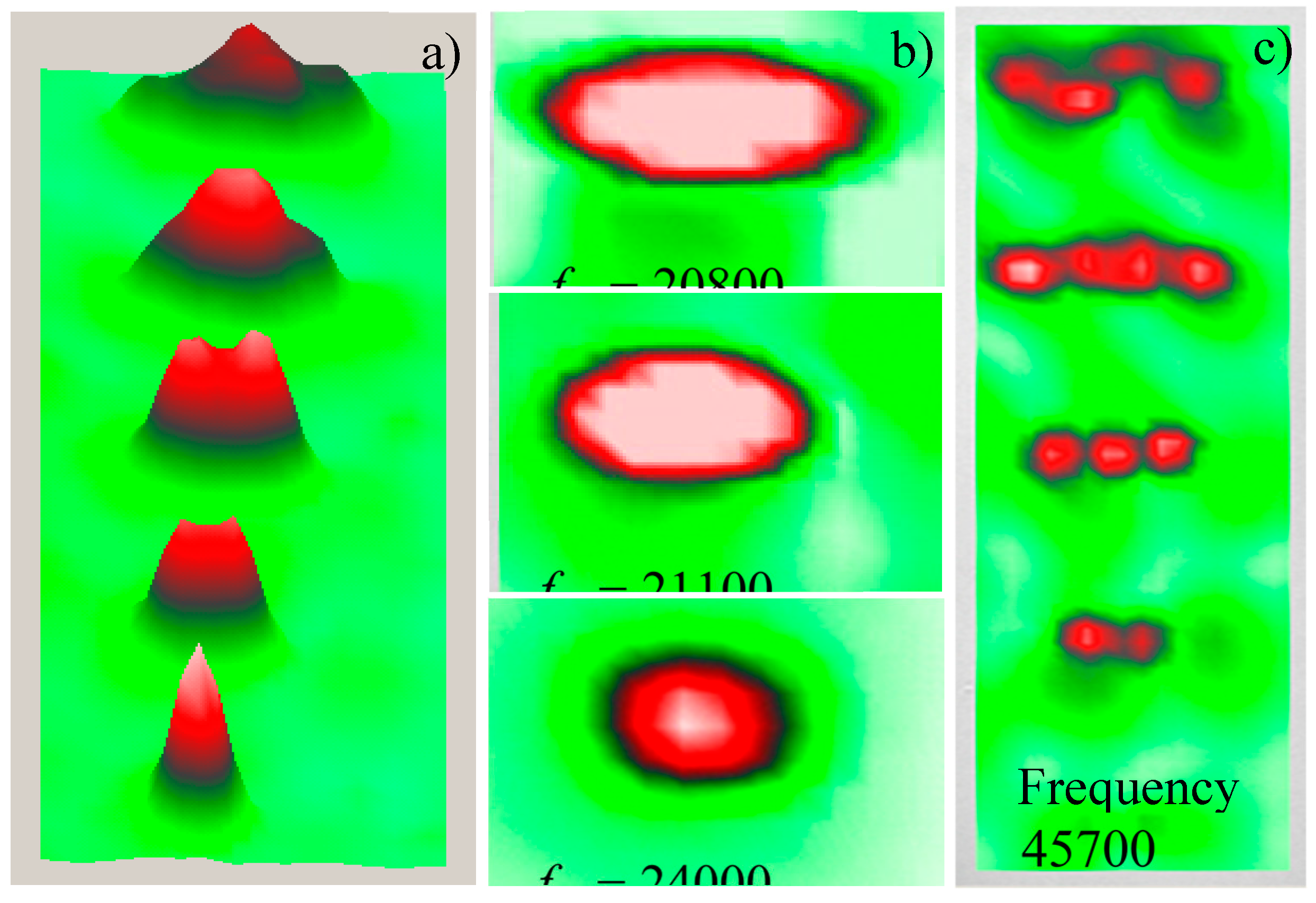
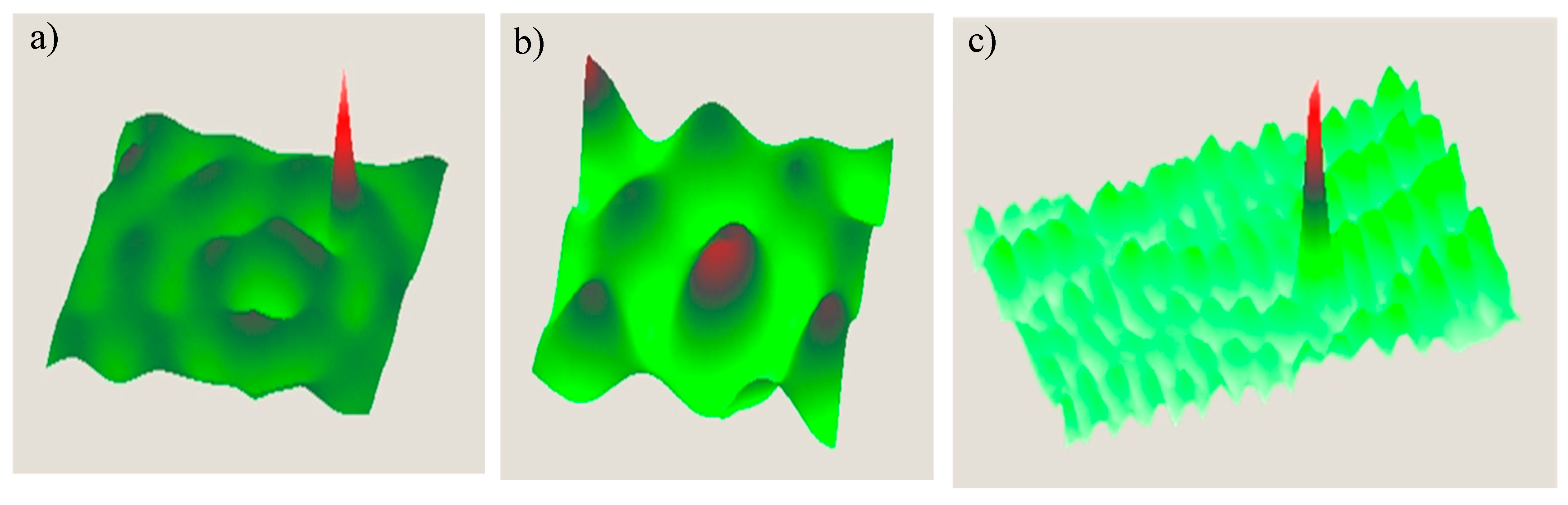
Figure 8.
Vibration images for various modes of LDR excitation in the set of elliptical FBH: Wideband (a), separate fundamental LDR frequencies (b), and higher-order mode excitation for 4 elliptical FBH (c).
Figure 8.
Vibration images for various modes of LDR excitation in the set of elliptical FBH: Wideband (a), separate fundamental LDR frequencies (b), and higher-order mode excitation for 4 elliptical FBH (c).
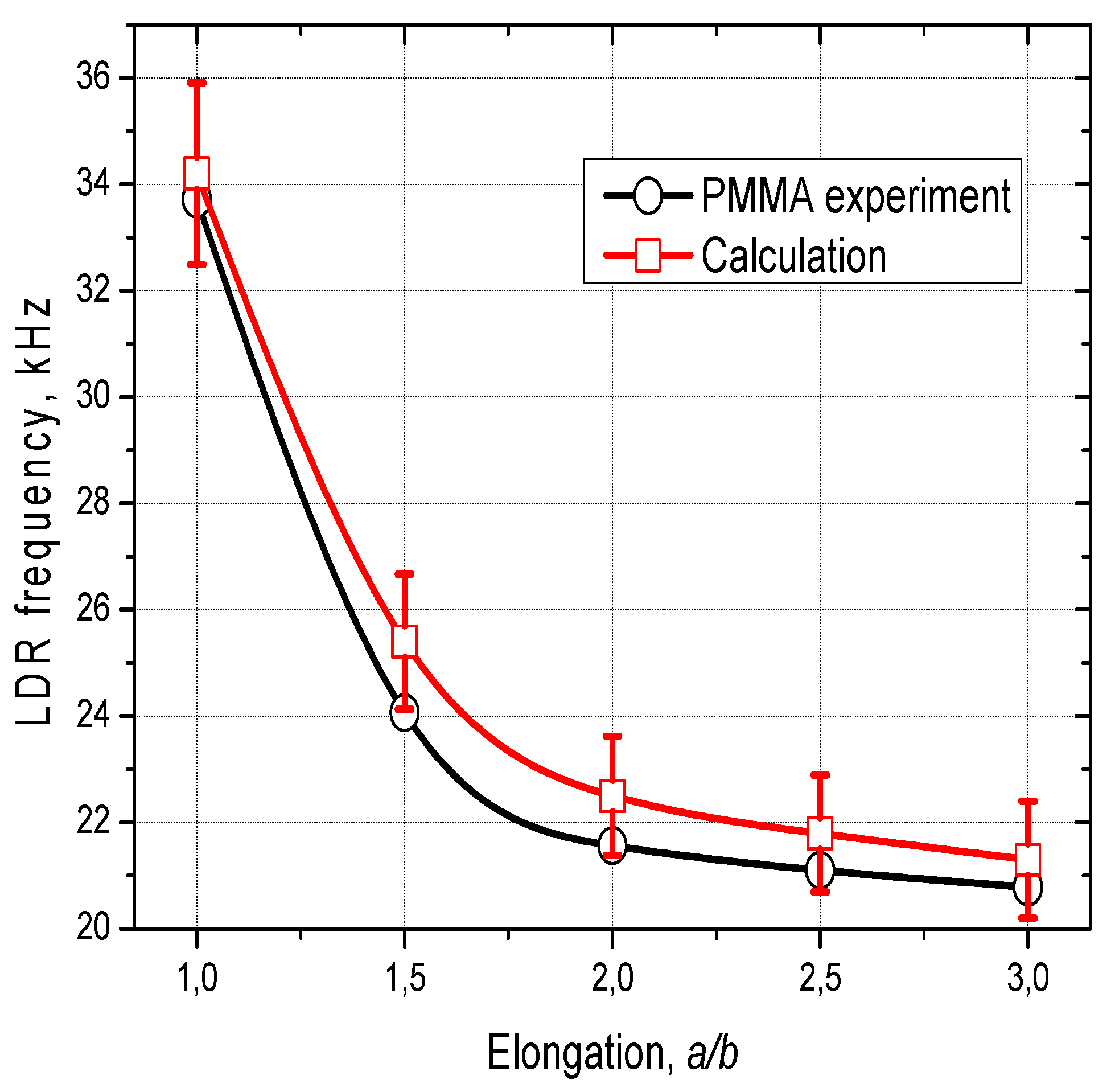
Figure 9.
Measured LDR frequencies of elliptical FBH vs the values calculated from (15).
Figure 9.
Measured LDR frequencies of elliptical FBH vs the values calculated from (15).
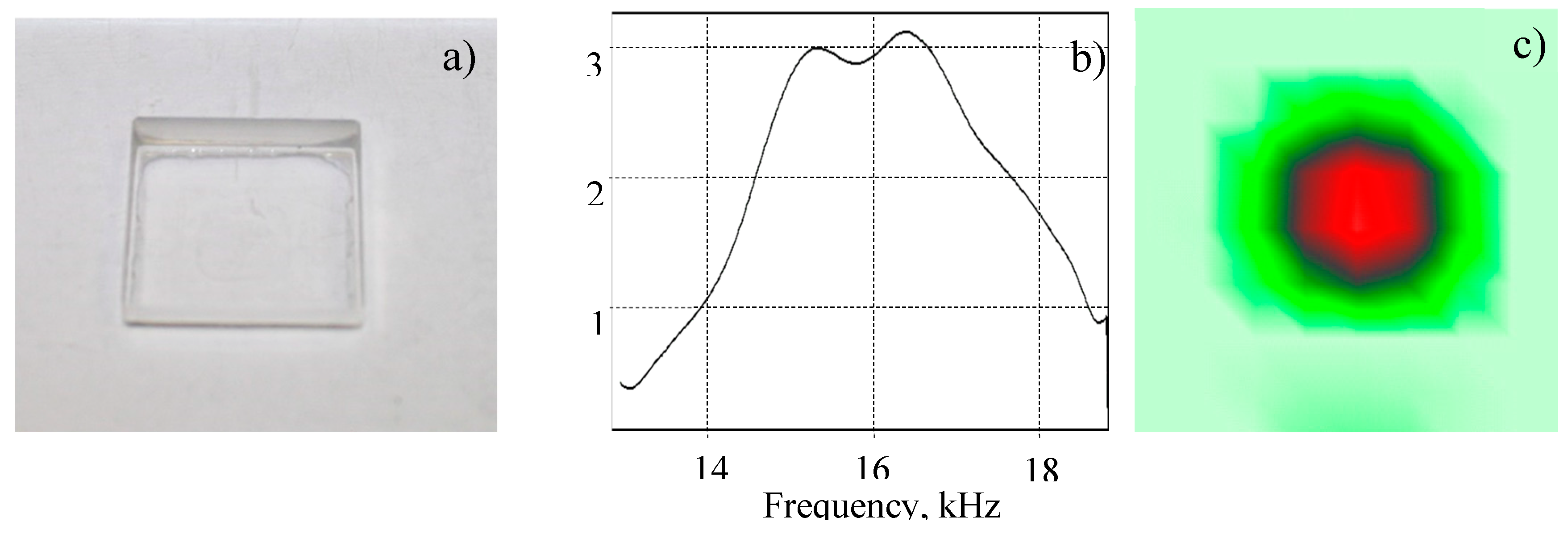
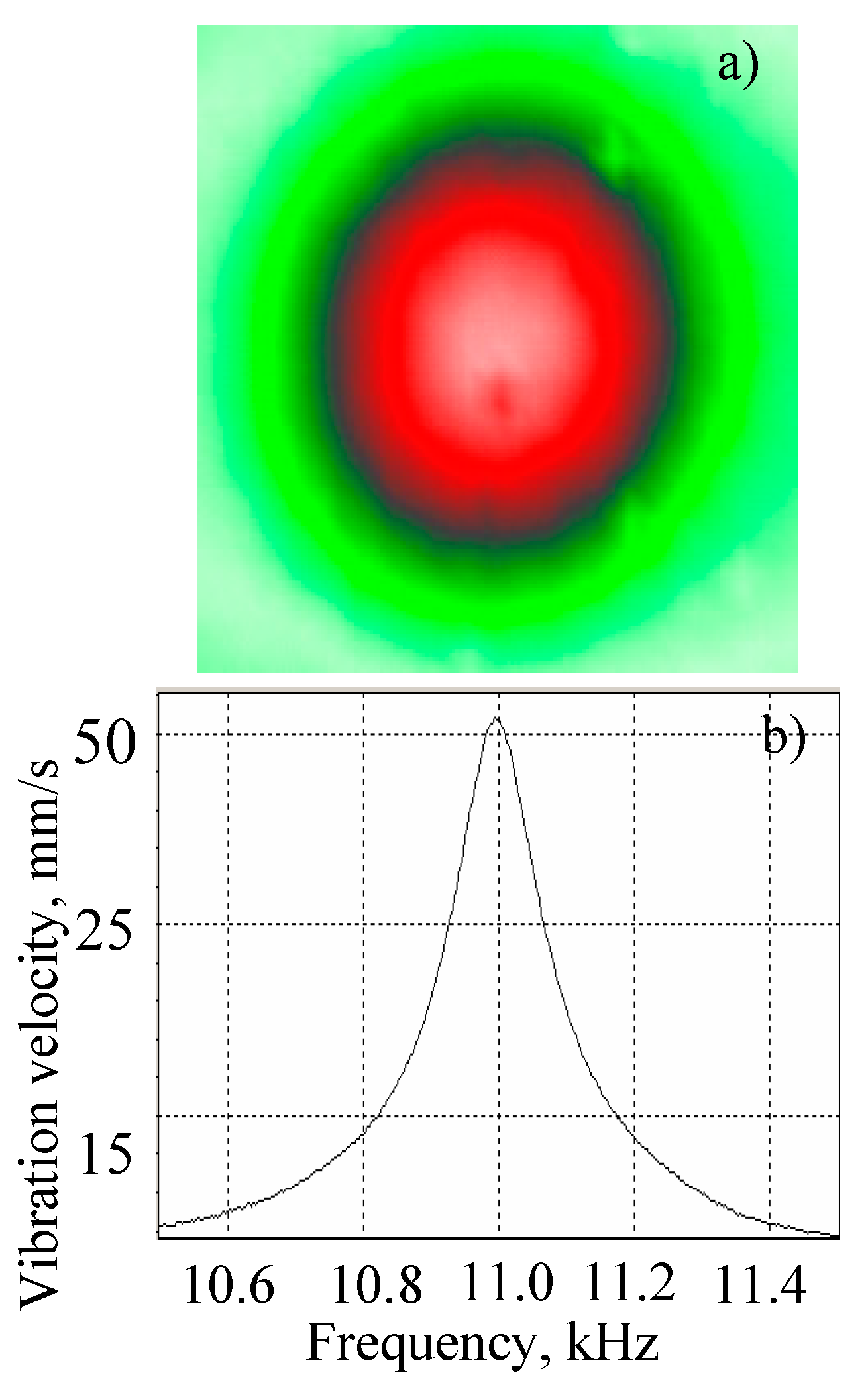
Figure 10.
LDR image (a) frequency response (b) for a circular FBH in PMMA (a).
Figure 10.
LDR image (a) frequency response (b) for a circular FBH in PMMA (a).
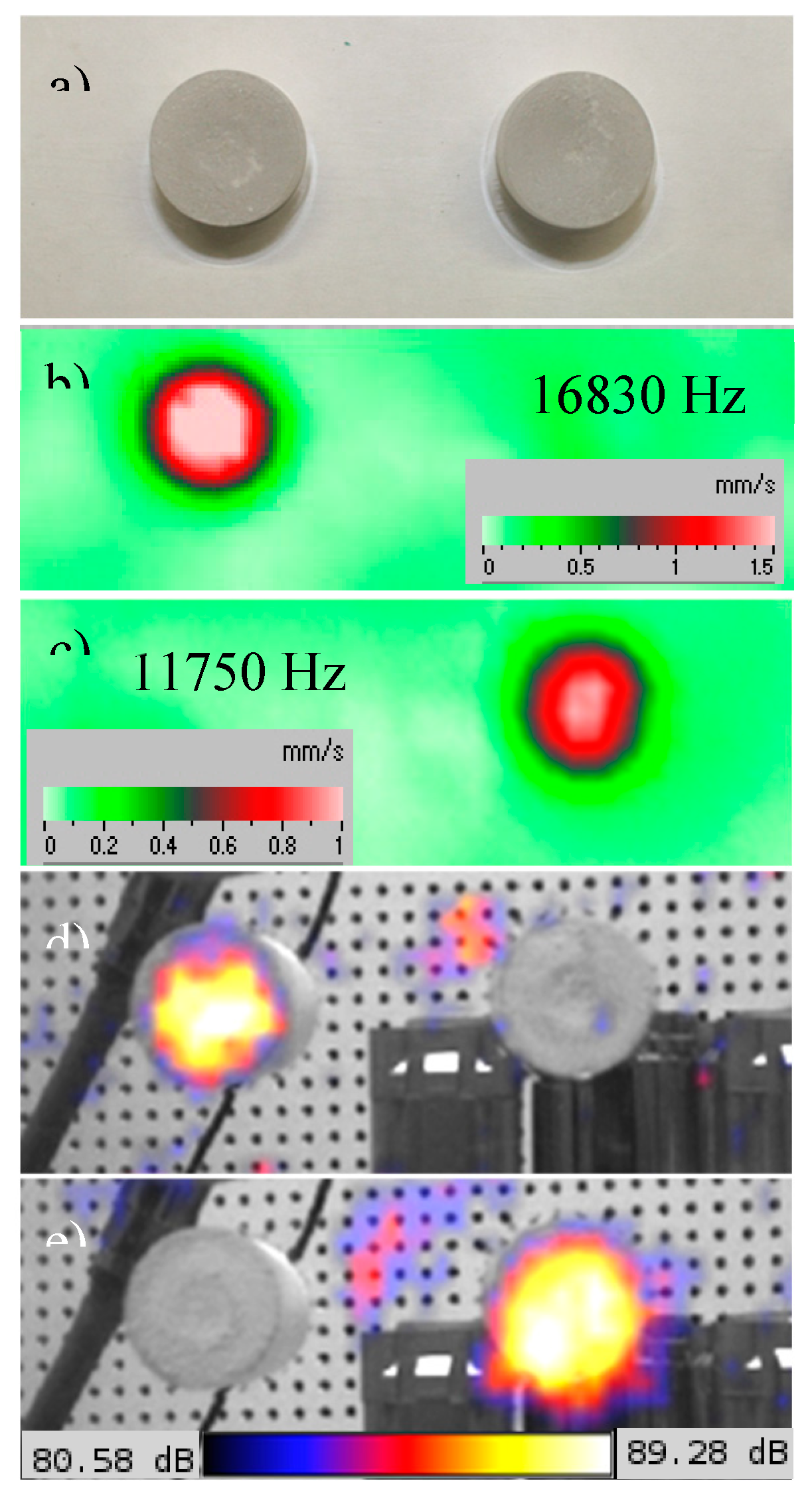
Figure 11.
LDR frequency responses (a) and vibration patterns (b) for two different impact damages in CFRP plates.
Figure 11.
LDR frequency responses (a) and vibration patterns (b) for two different impact damages in CFRP plates.
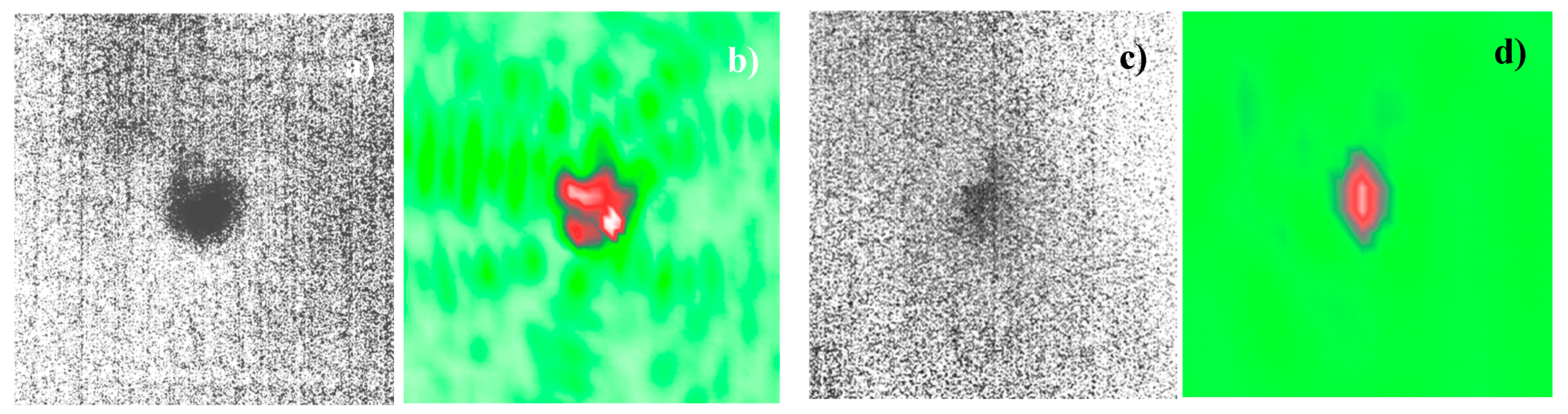
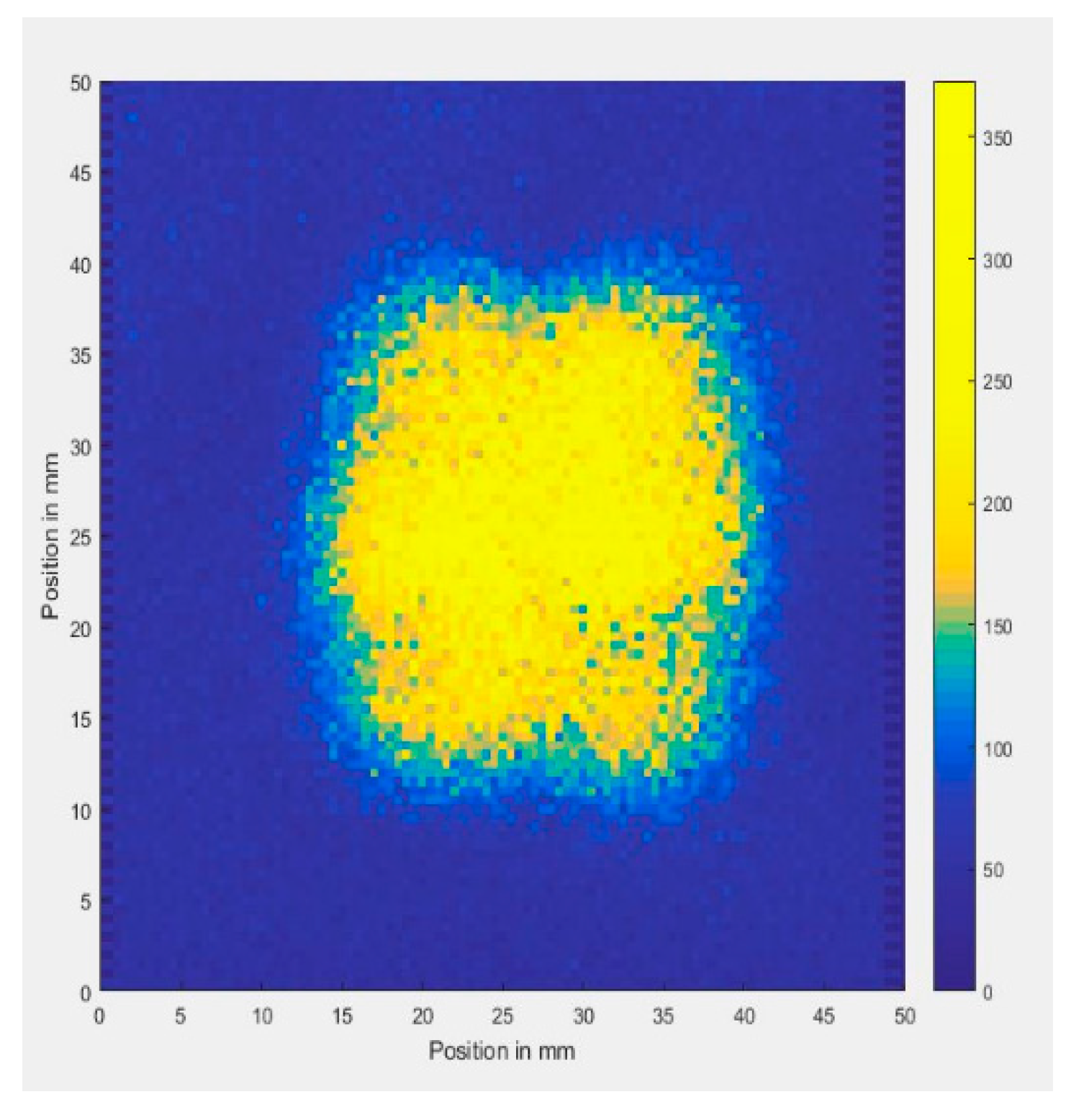
Figure 12.
a, b, c. LDR imaging of heat damage in CFRP: a) excitation matched to LDR frequency (48.5 kHz); b) 30 kHz excitation. c) LDR image (91.16 kHz) of 7x7 mm2 delamination in CFRP plate.
Figure 12.
a, b, c. LDR imaging of heat damage in CFRP: a) excitation matched to LDR frequency (48.5 kHz); b) 30 kHz excitation. c) LDR image (91.16 kHz) of 7x7 mm2 delamination in CFRP plate.
Figure 13.
(a-c). Frequency selective LDR imaging of heat damaged areas in CFRP plate (a): separate imaging of defects by matching their LDR frequencies (b-c); imaging of both defects in a wideband excitation mode.
Figure 13.
(a-c). Frequency selective LDR imaging of heat damaged areas in CFRP plate (a): separate imaging of defects by matching their LDR frequencies (b-c); imaging of both defects in a wideband excitation mode.
Figure 14.
Effect of the higher-order LDR: image of a square inset in CFRP plate at fundamental LDR (8980 Hz) (a), higher-order LDR (15600 Hz (b)), (27250 Hz (c)), and in a wideband (1-100 kHz) excitation mode (d).
Figure 14.
Effect of the higher-order LDR: image of a square inset in CFRP plate at fundamental LDR (8980 Hz) (a), higher-order LDR (15600 Hz (b)), (27250 Hz (c)), and in a wideband (1-100 kHz) excitation mode (d).
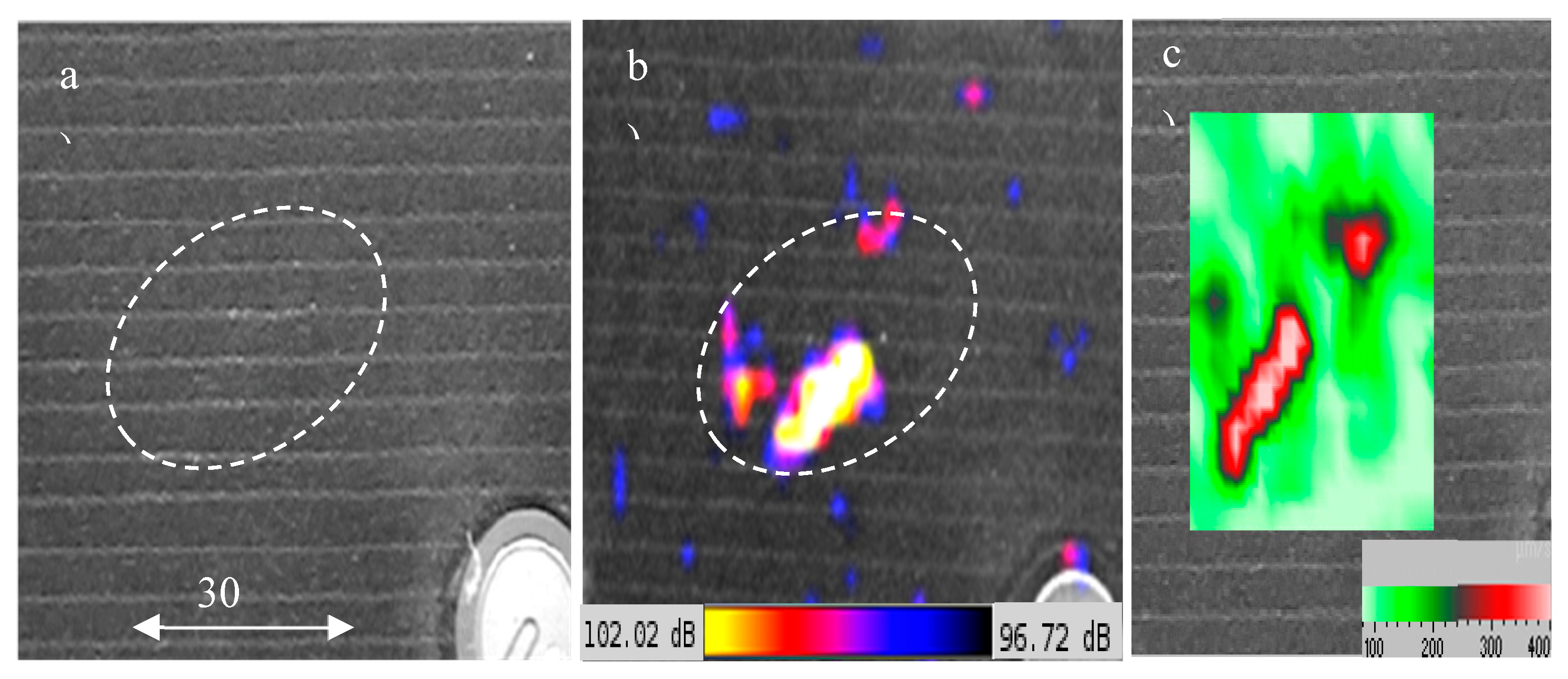
Figure 15.
The cracks tested in concrete plate N1, N2 correspondingly.
Figure 15.
The cracks tested in concrete plate N1, N2 correspondingly.
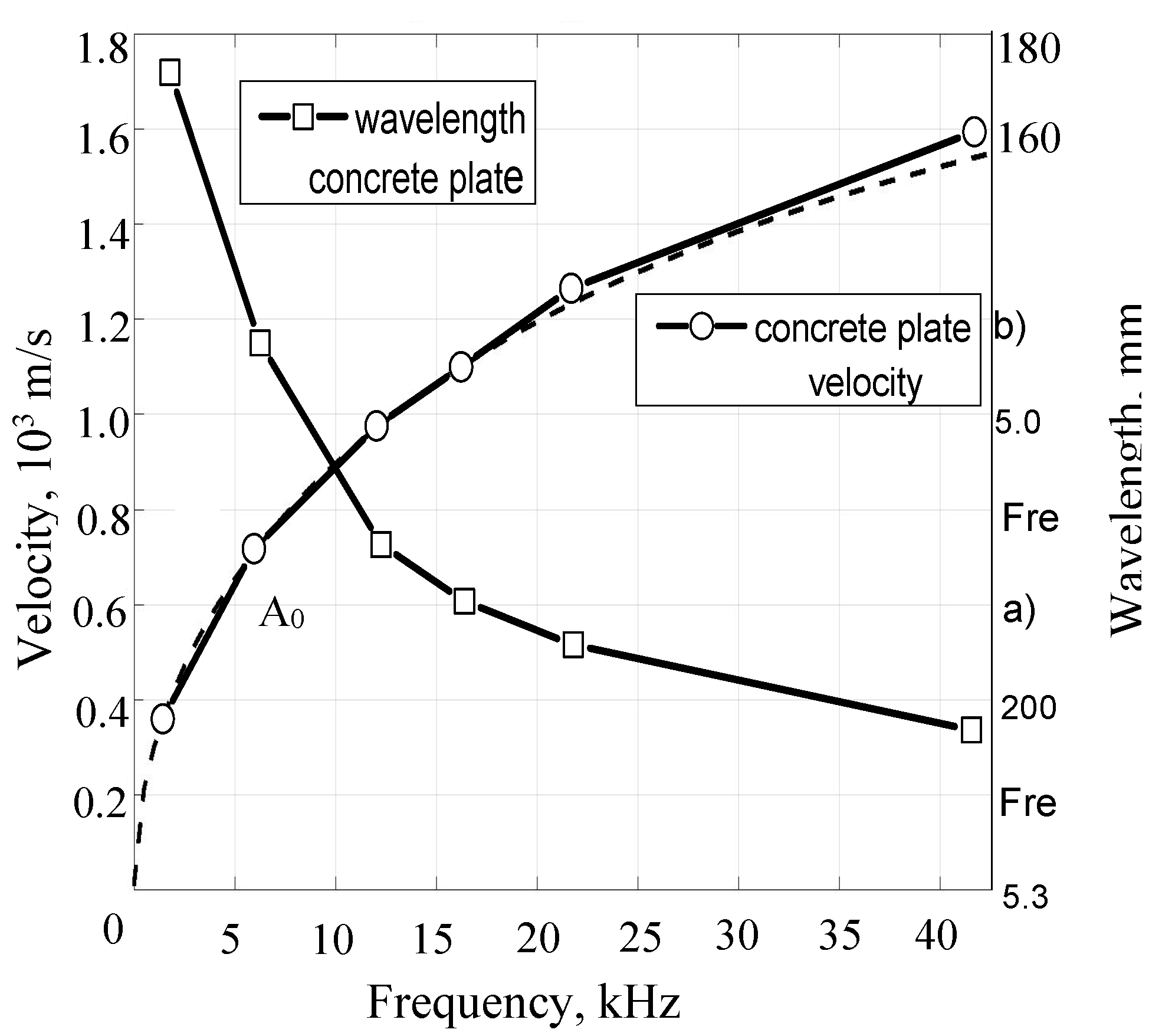
Figure 16.
FW (EW) wavelengths measured and dispersion curves calculated in concrete.
Figure 16.
FW (EW) wavelengths measured and dispersion curves calculated in concrete.
Figure 17.
LDR of EW in concrete crack N1.
Figure 17.
LDR of EW in concrete crack N1.
Figure 18.
Various types of LDR for crack N2 in concrete: partial LDR at opposite crack faces (a, b); higher-order LDR (c, d); superposition of the LDR in wideband (1-20 kHz) activation mode (e).
Figure 18.
Various types of LDR for crack N2 in concrete: partial LDR at opposite crack faces (a, b); higher-order LDR (c, d); superposition of the LDR in wideband (1-20 kHz) activation mode (e).
Figure 19.
CT-scans of the specimens with the reconstructed pores N1 – N3 (left) and magnification of pores N2 – N4 (right).
Figure 19.
CT-scans of the specimens with the reconstructed pores N1 – N3 (left) and magnification of pores N2 – N4 (right).
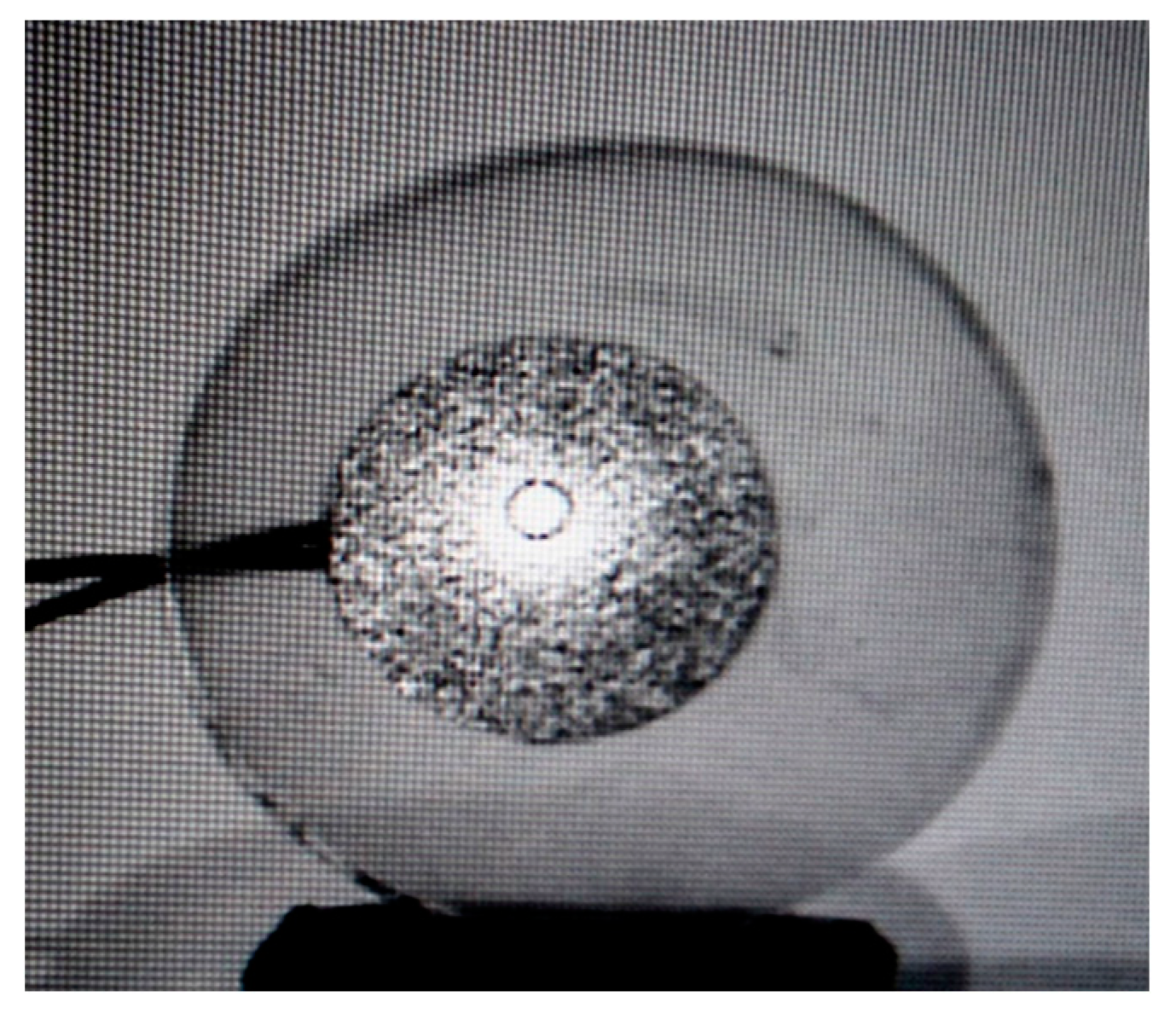
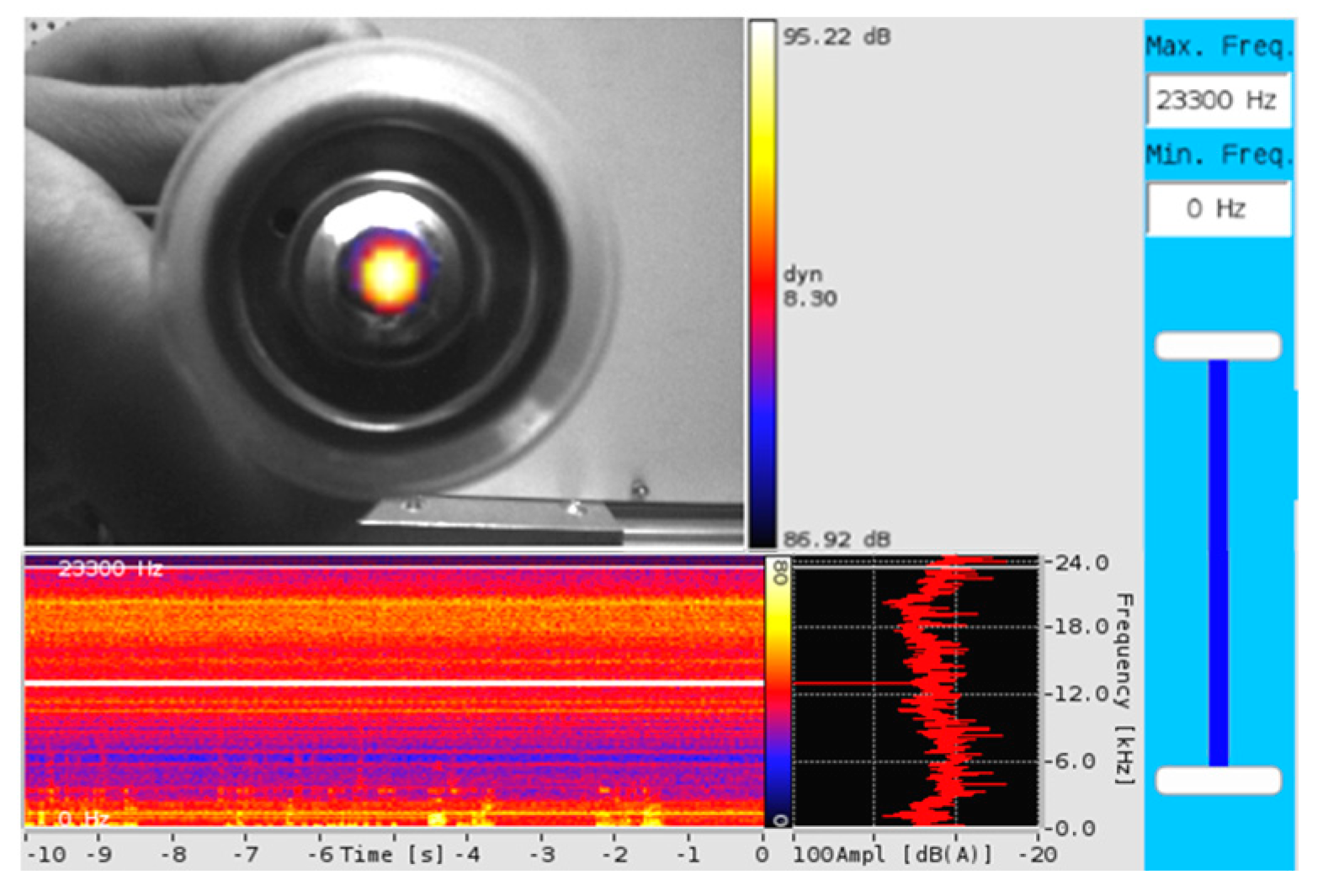
Figure 20.
Laser beam probing of spherical pore vibrations via flat bottom of transparent specimen.
Figure 20.
Laser beam probing of spherical pore vibrations via flat bottom of transparent specimen.
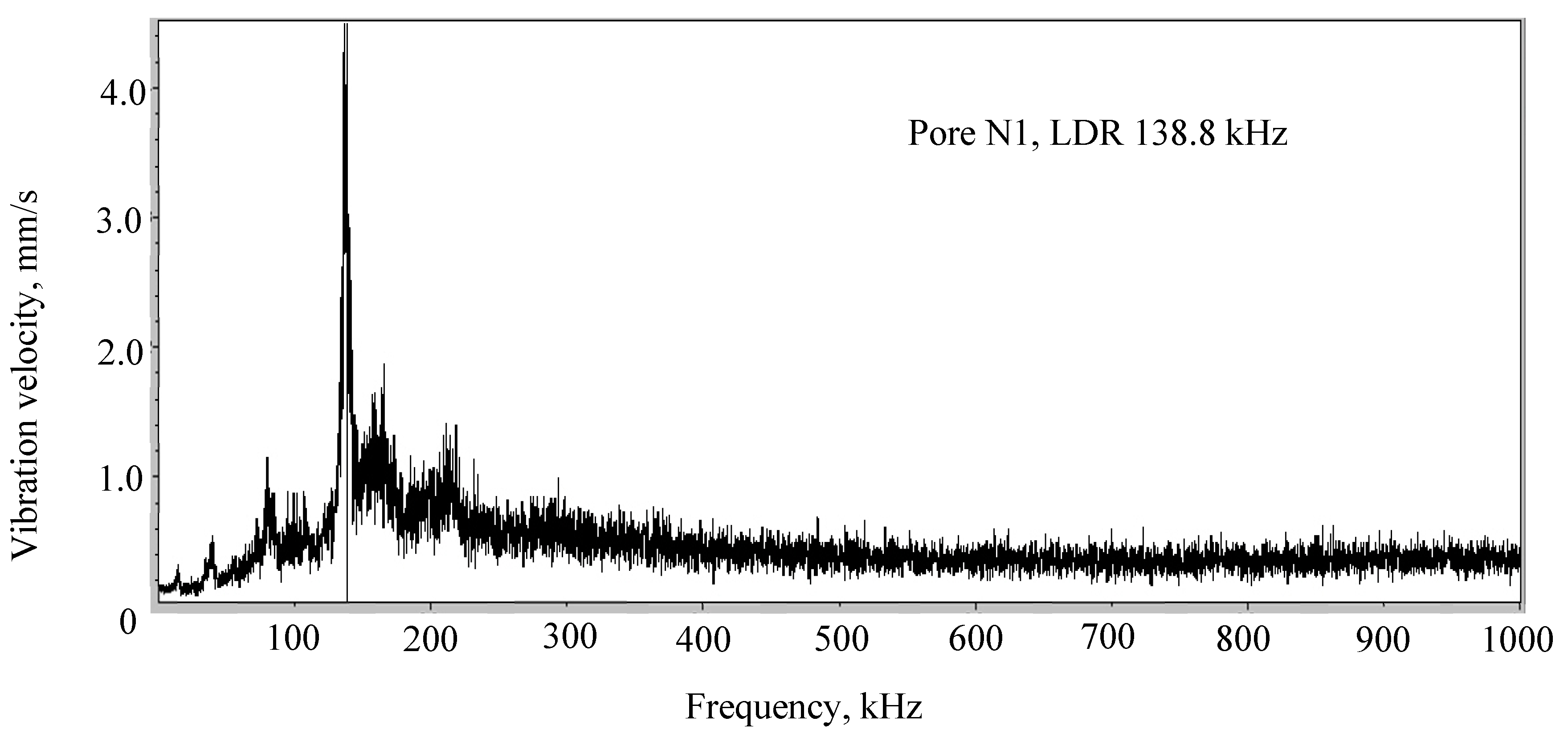
Figure 21.
LDR FR measured for bubble N1.
Figure 21.
LDR FR measured for bubble N1.
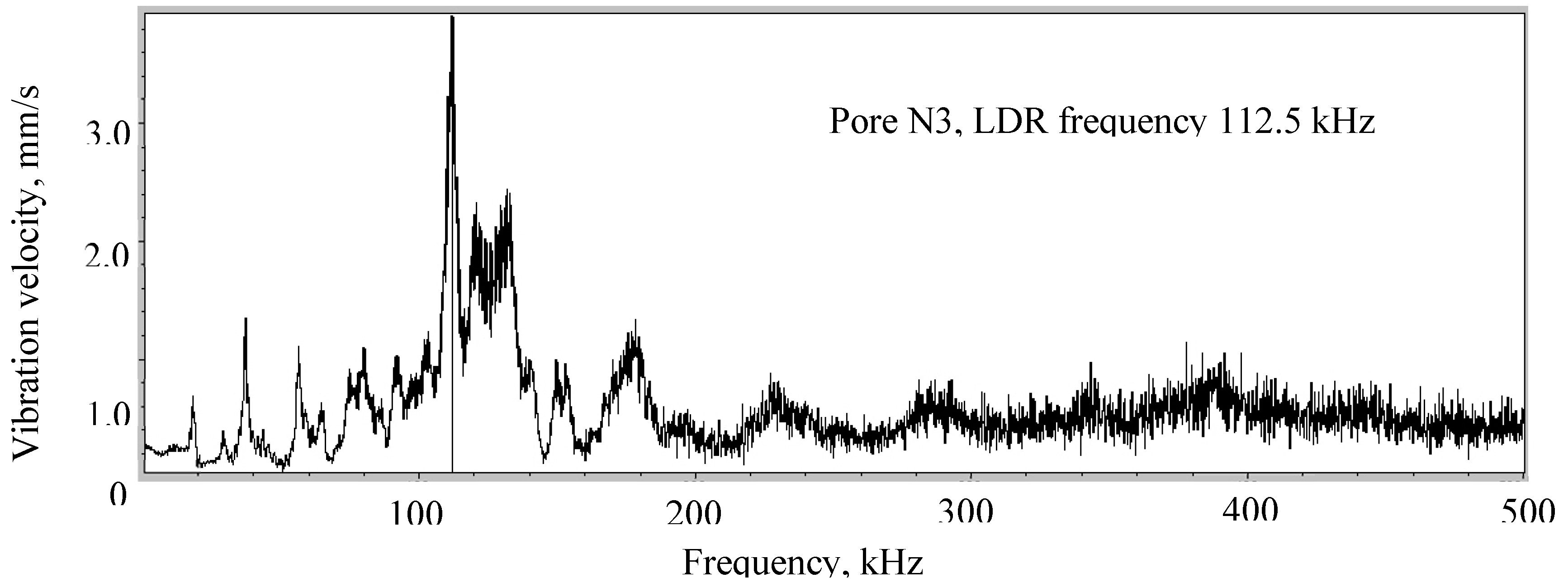
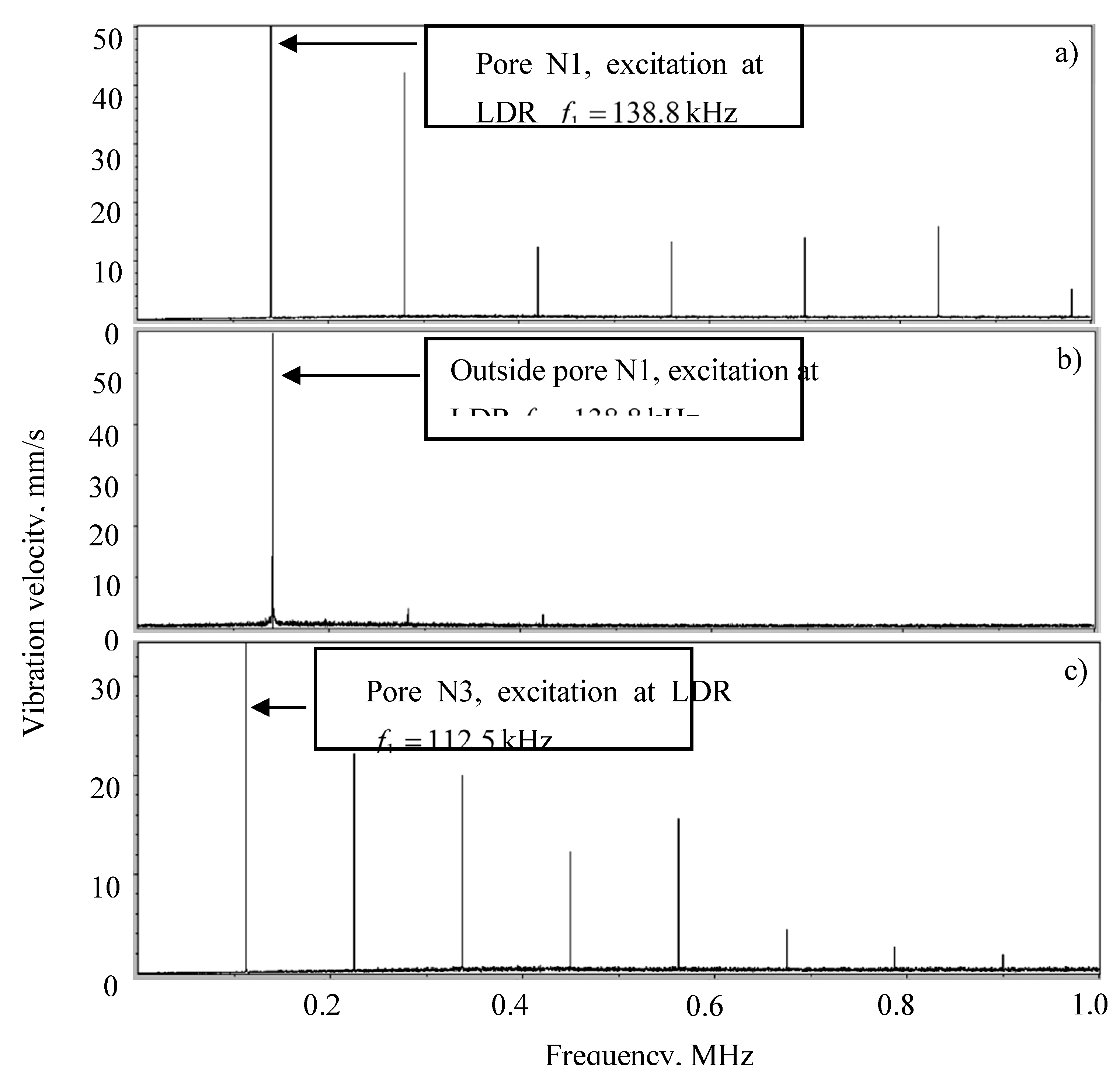
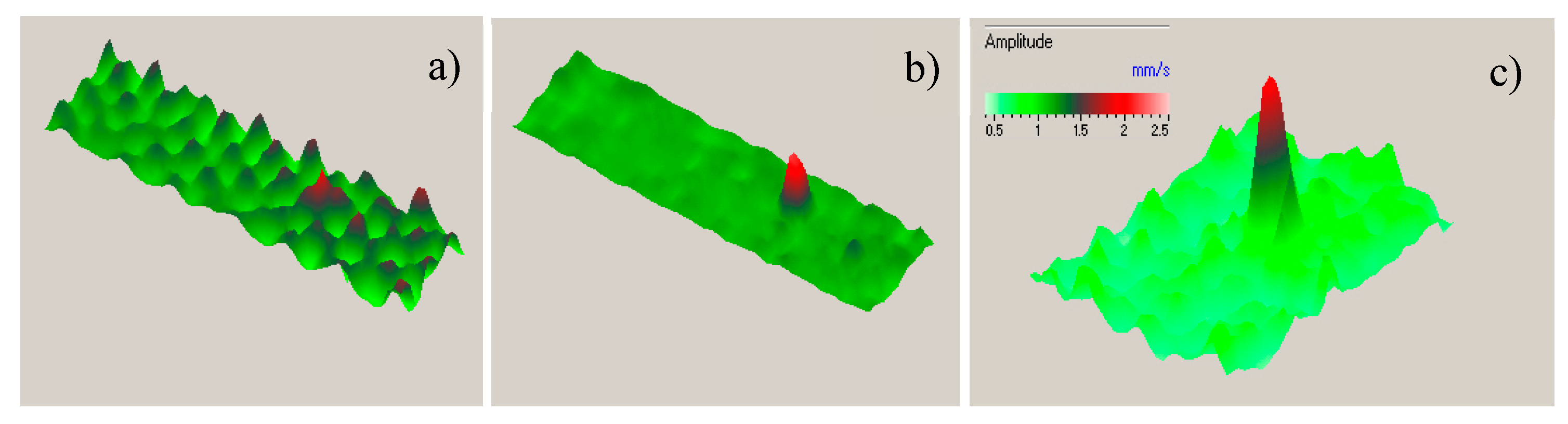
Figure 24.
Higher harmonics inside pore N1 (a); outside pore N1 (b) and in pore N3 (c) for excitations at bubble LDR frequencies.
Figure 24.
Higher harmonics inside pore N1 (a); outside pore N1 (b) and in pore N3 (c) for excitations at bubble LDR frequencies.
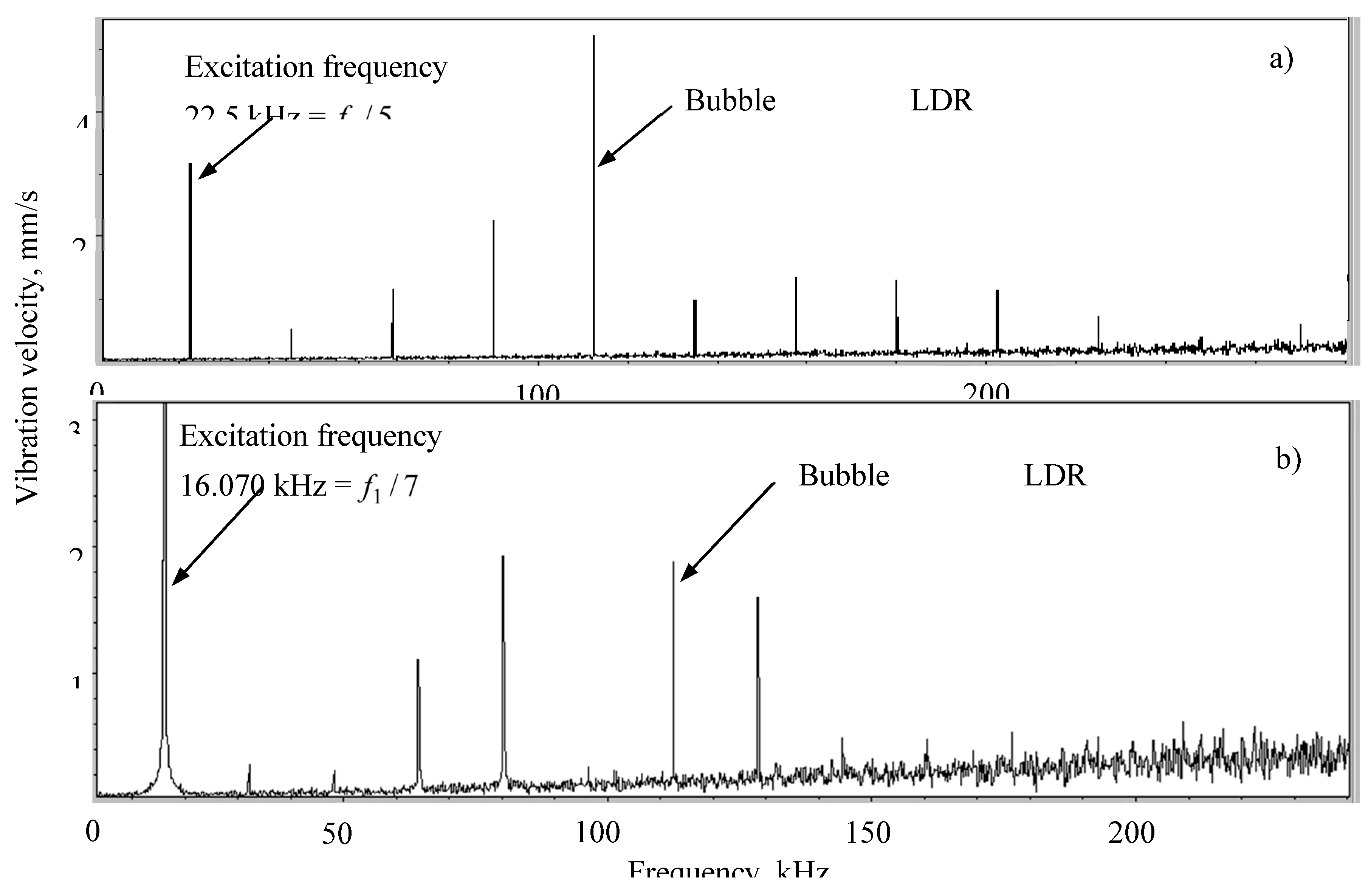
Figure 25.
Effect of subharmonic resonance of selected higher harmonics in specimen N3 excitation at the subharmonic frequency f1/5 (a) and f1/7 (b).
Figure 25.
Effect of subharmonic resonance of selected higher harmonics in specimen N3 excitation at the subharmonic frequency f1/5 (a) and f1/7 (b).
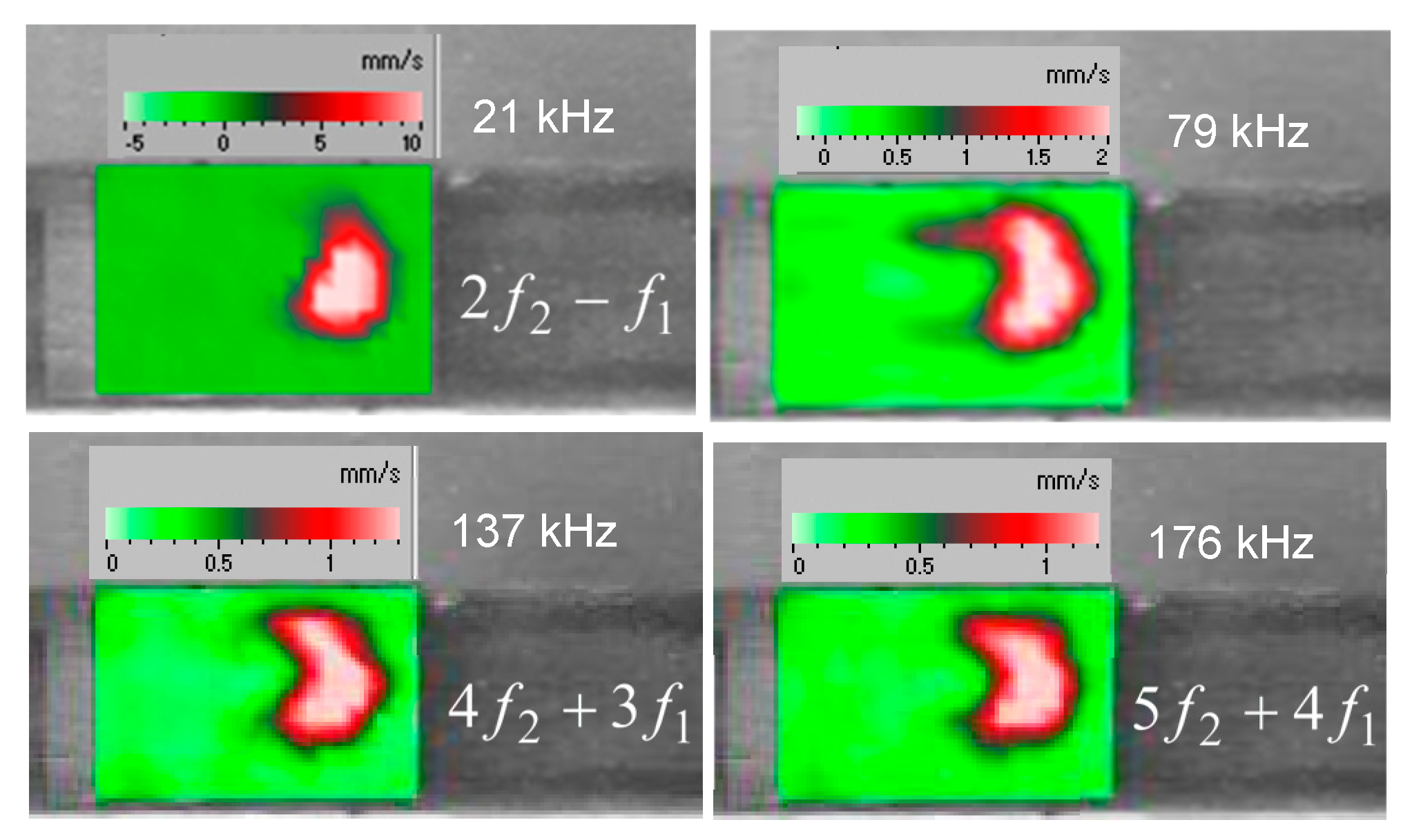
Figure 26.
Nonlinear defect imaging via classical modes: Linear (36.77 kHz, a) and second harmonic (73.53 kHz, b) LDR imaging of a delamination in GFRP specimen; Sum-frequency image of the impact-induced damage (~5x5mm2) in a CFRP plate.
Figure 26.
Nonlinear defect imaging via classical modes: Linear (36.77 kHz, a) and second harmonic (73.53 kHz, b) LDR imaging of a delamination in GFRP specimen; Sum-frequency image of the impact-induced damage (~5x5mm2) in a CFRP plate.
Figure 27.
Imaging of elliptical delamination in GFRP at various-order mixing frequencies for 19 kHz and 20 kHz primary waves.
Figure 27.
Imaging of elliptical delamination in GFRP at various-order mixing frequencies for 19 kHz and 20 kHz primary waves.
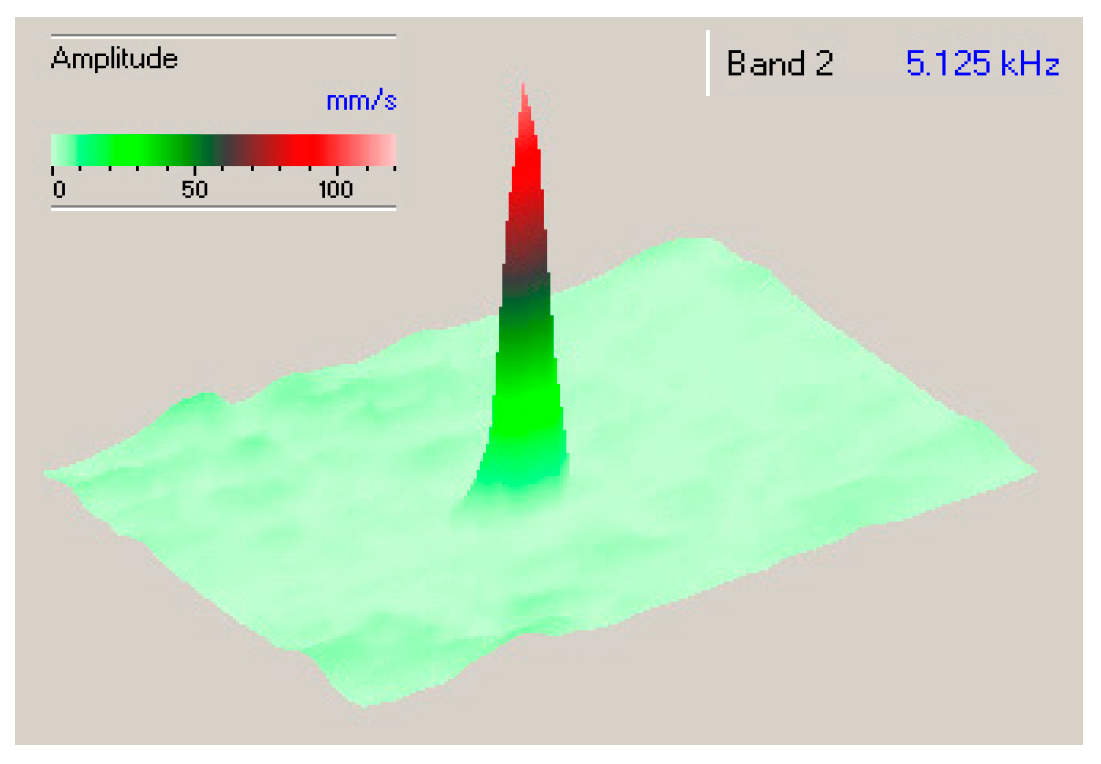
Figure 28.
Subharmonic LDR imaging of impact damage in a CFRP plate: Input 10250 Hz; output 5125 Hz.
Figure 28.
Subharmonic LDR imaging of impact damage in a CFRP plate: Input 10250 Hz; output 5125 Hz.
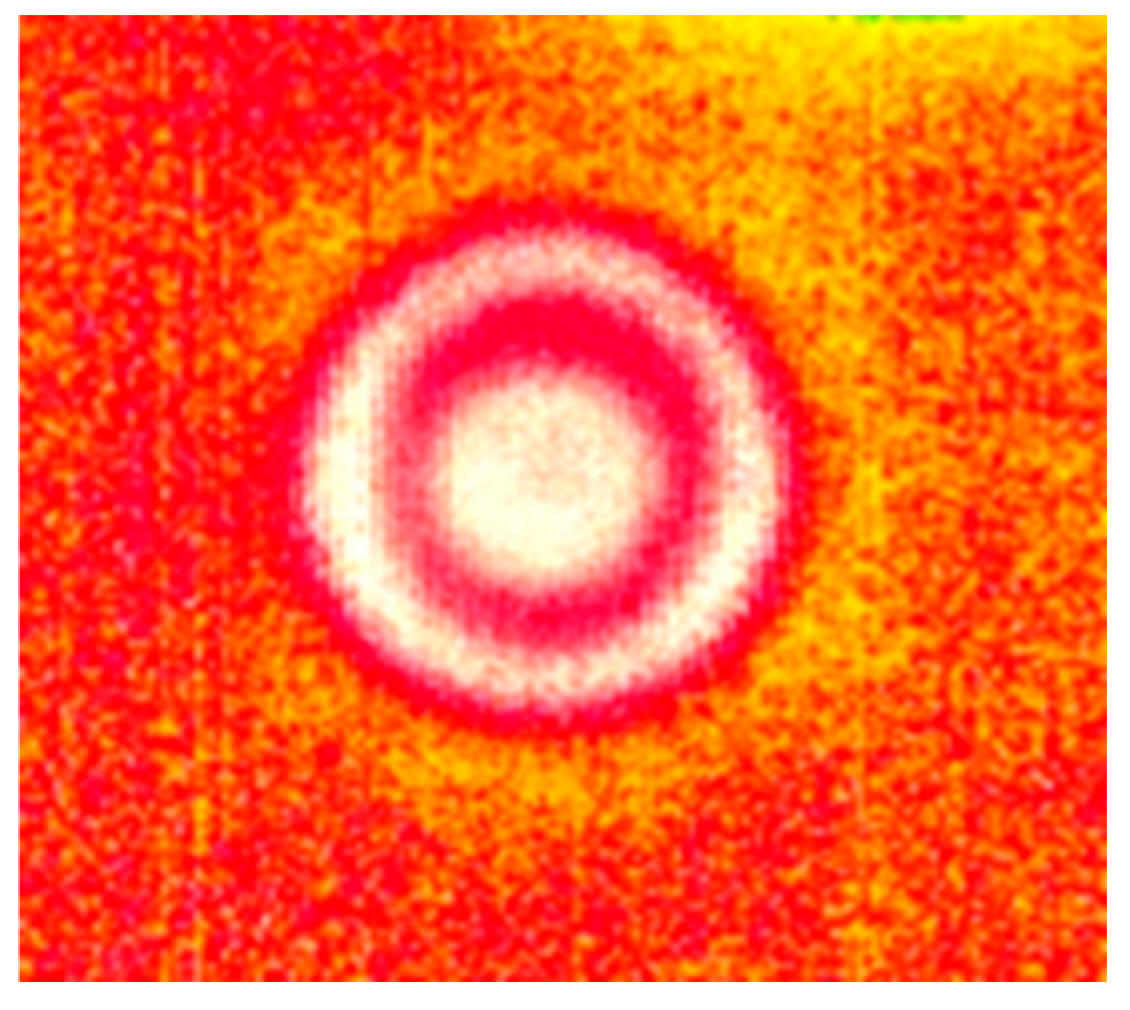
Figure 29.
Temperature pattern generated by LDR vibrations in a circular FBH.
Figure 29.
Temperature pattern generated by LDR vibrations in a circular FBH.
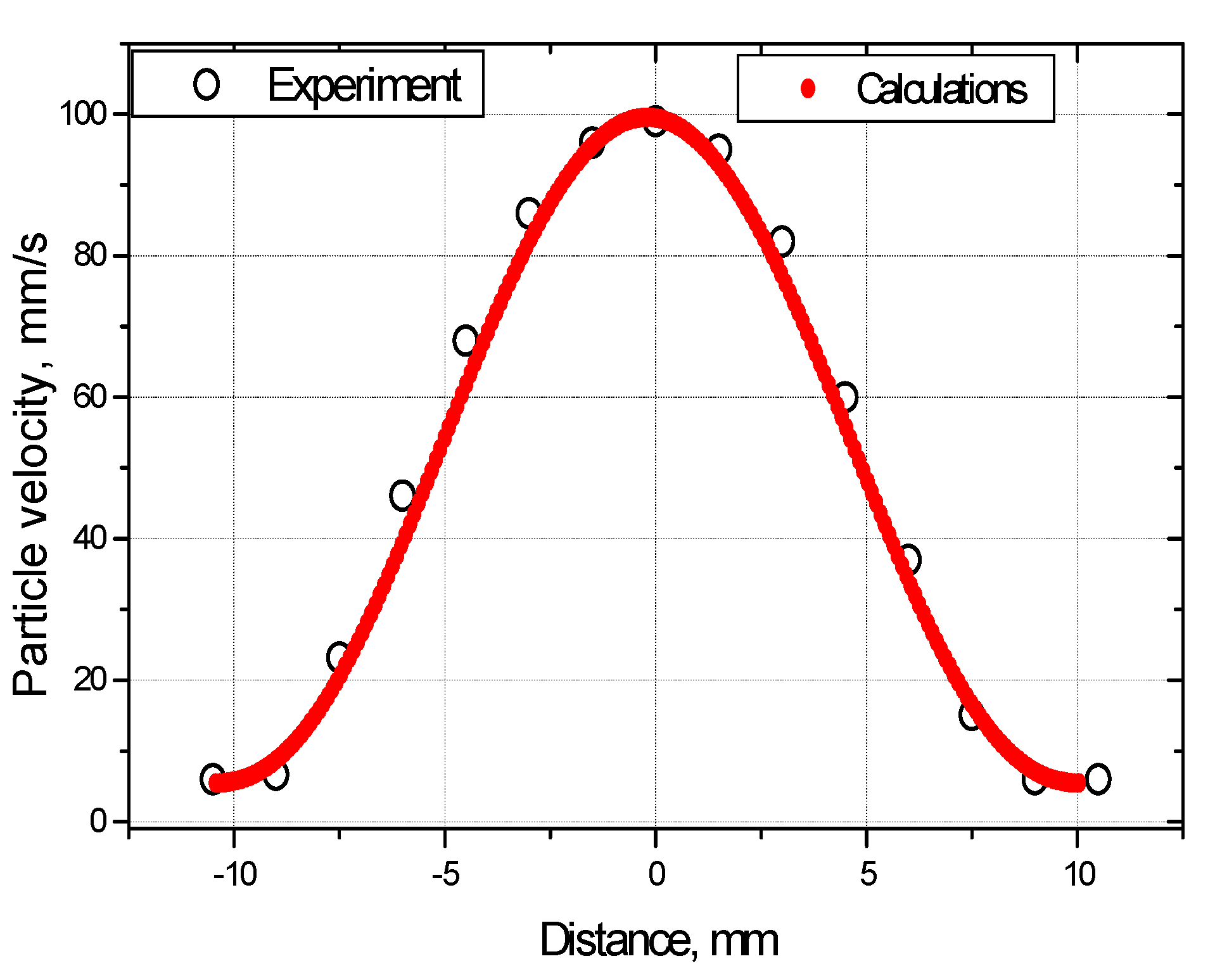
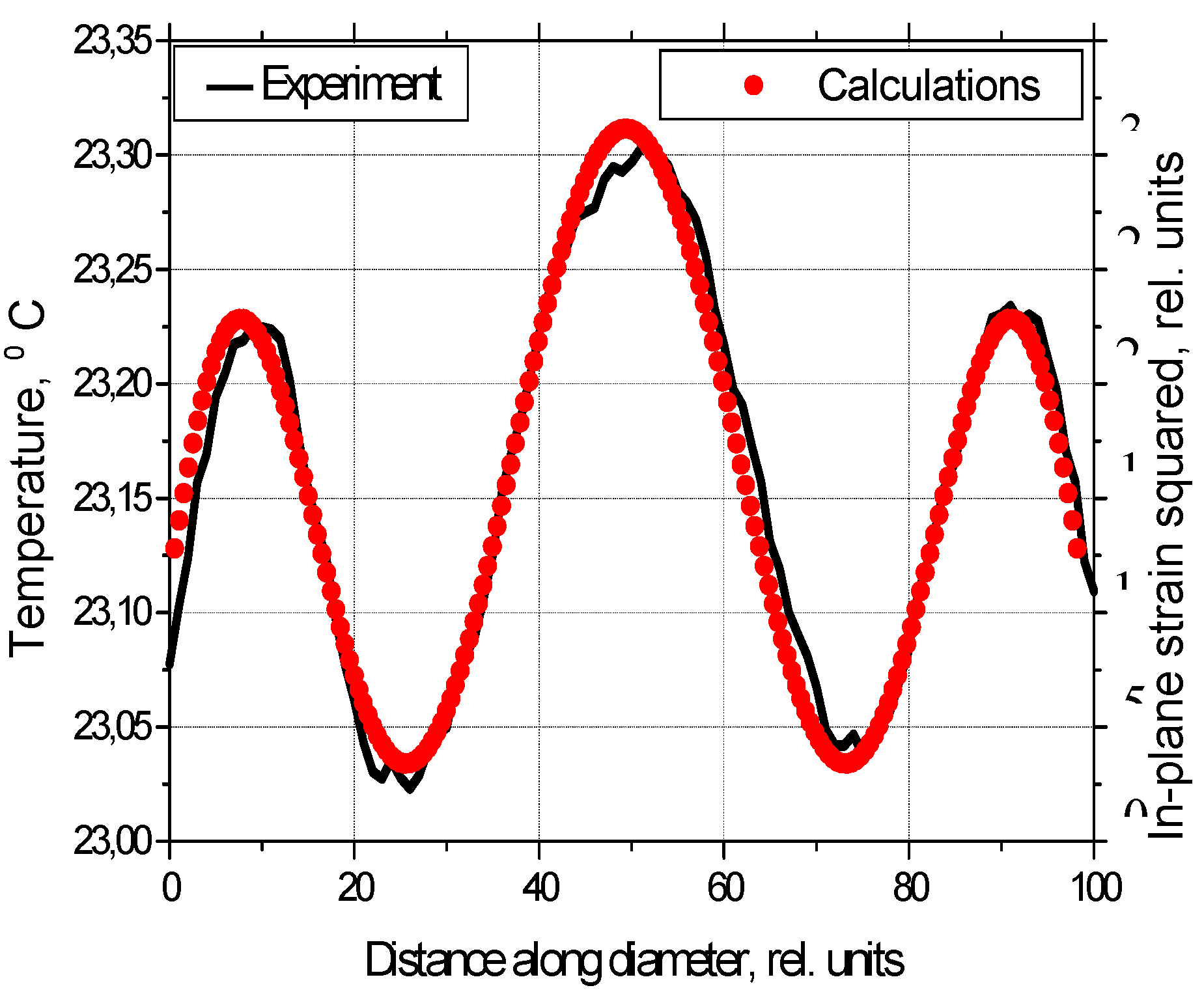
Figure 31.
Temperature patterns generated by LDR vibrations in a circular FBH: measured and calculated from Eq. (30).
Figure 31.
Temperature patterns generated by LDR vibrations in a circular FBH: measured and calculated from Eq. (30).
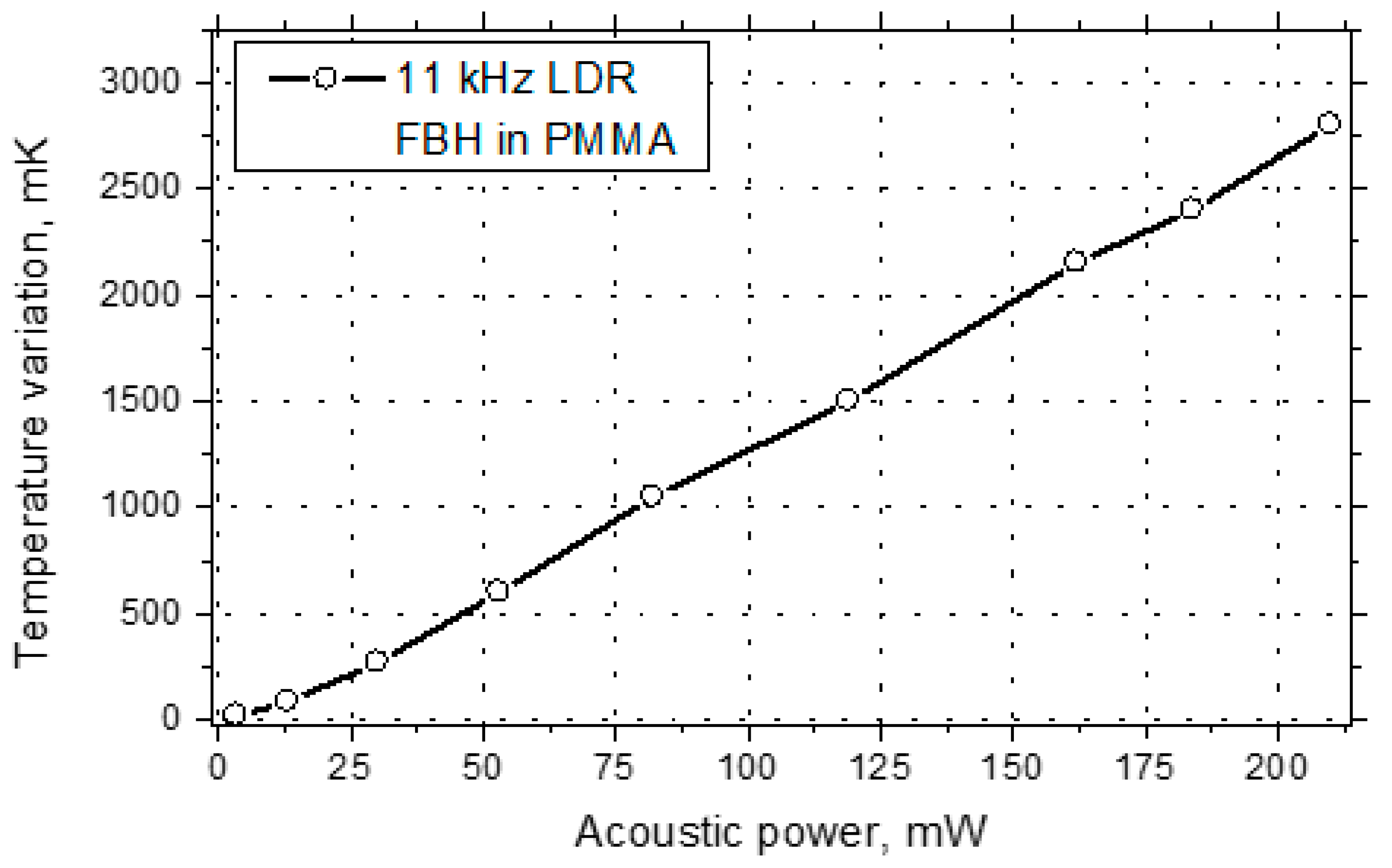
Figure 32.
Temperature response of FBH as a function of input acoustic power at LDR frequency 11 kHz.
Figure 32.
Temperature response of FBH as a function of input acoustic power at LDR frequency 11 kHz.
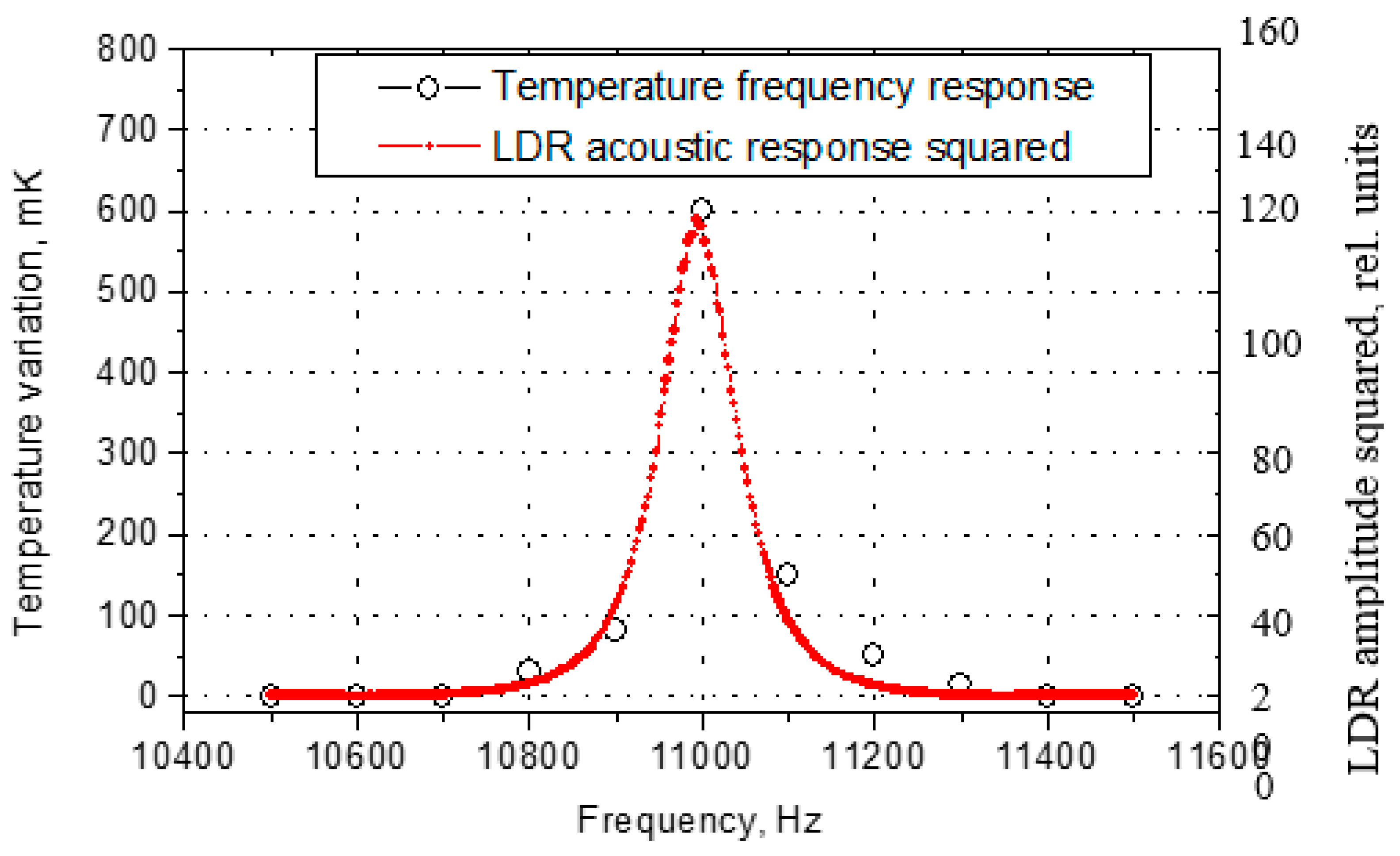
Figure 33.
Temperature and acoustic response squared for FBH as a function of driving frequency.
Figure 33.
Temperature and acoustic response squared for FBH as a function of driving frequency.
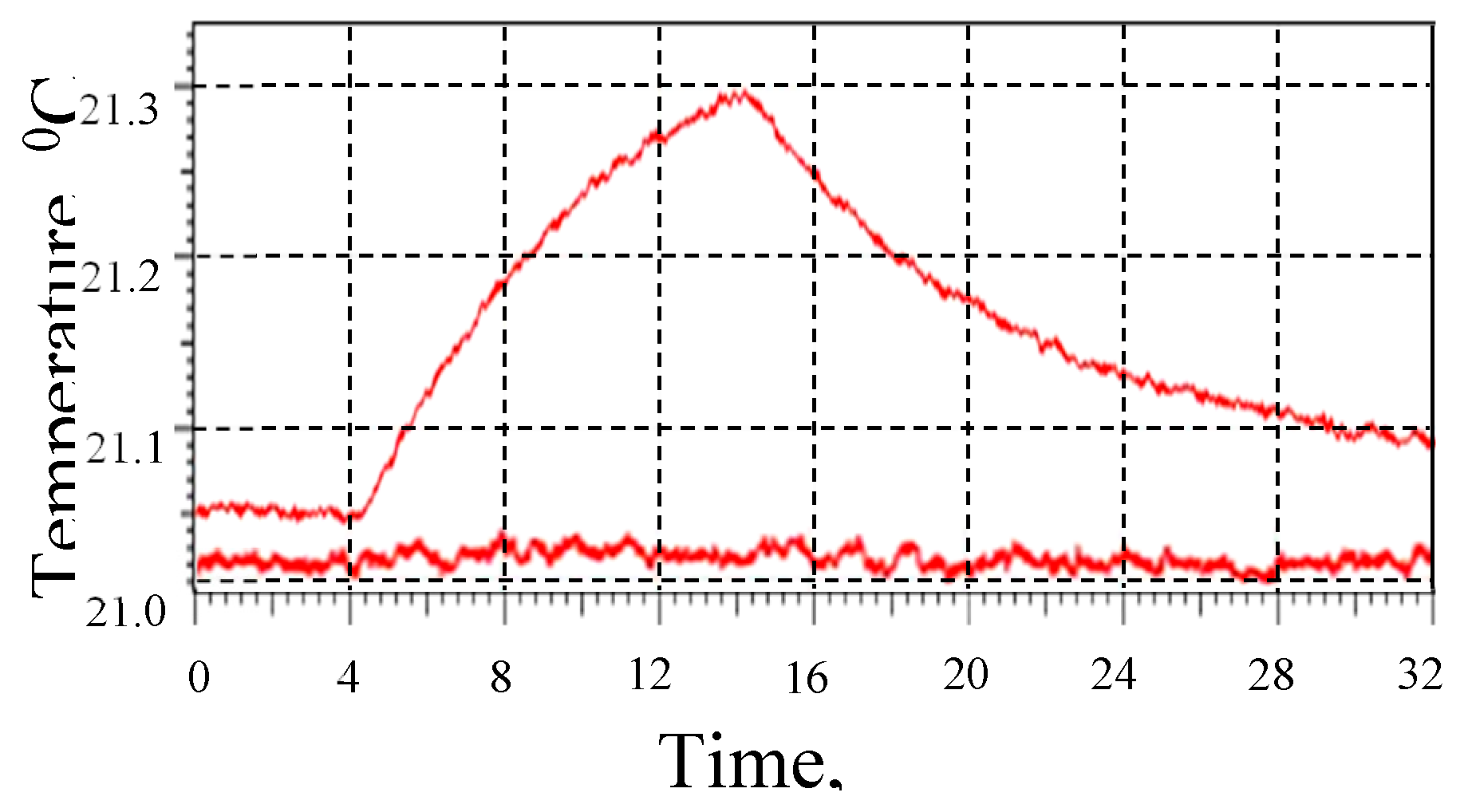
Figure 34.
Temperature response of a rectangular insert in CFRP plate at LDR frequency (8980 Hz, upper curve) and outside LDR (lower curve, 8000 Hz).
Figure 34.
Temperature response of a rectangular insert in CFRP plate at LDR frequency (8980 Hz, upper curve) and outside LDR (lower curve, 8000 Hz).
Figure 35.
Laser vibrometry (a, b) and thermosonic (c, d) images of a rectangular insert in CFRP plate at fundamental LDR frequency (8980 Hz, (a, c)) and at higher-order LDR (15600Hz, (b, d)).
Figure 35.
Laser vibrometry (a, b) and thermosonic (c, d) images of a rectangular insert in CFRP plate at fundamental LDR frequency (8980 Hz, (a, c)) and at higher-order LDR (15600Hz, (b, d)).
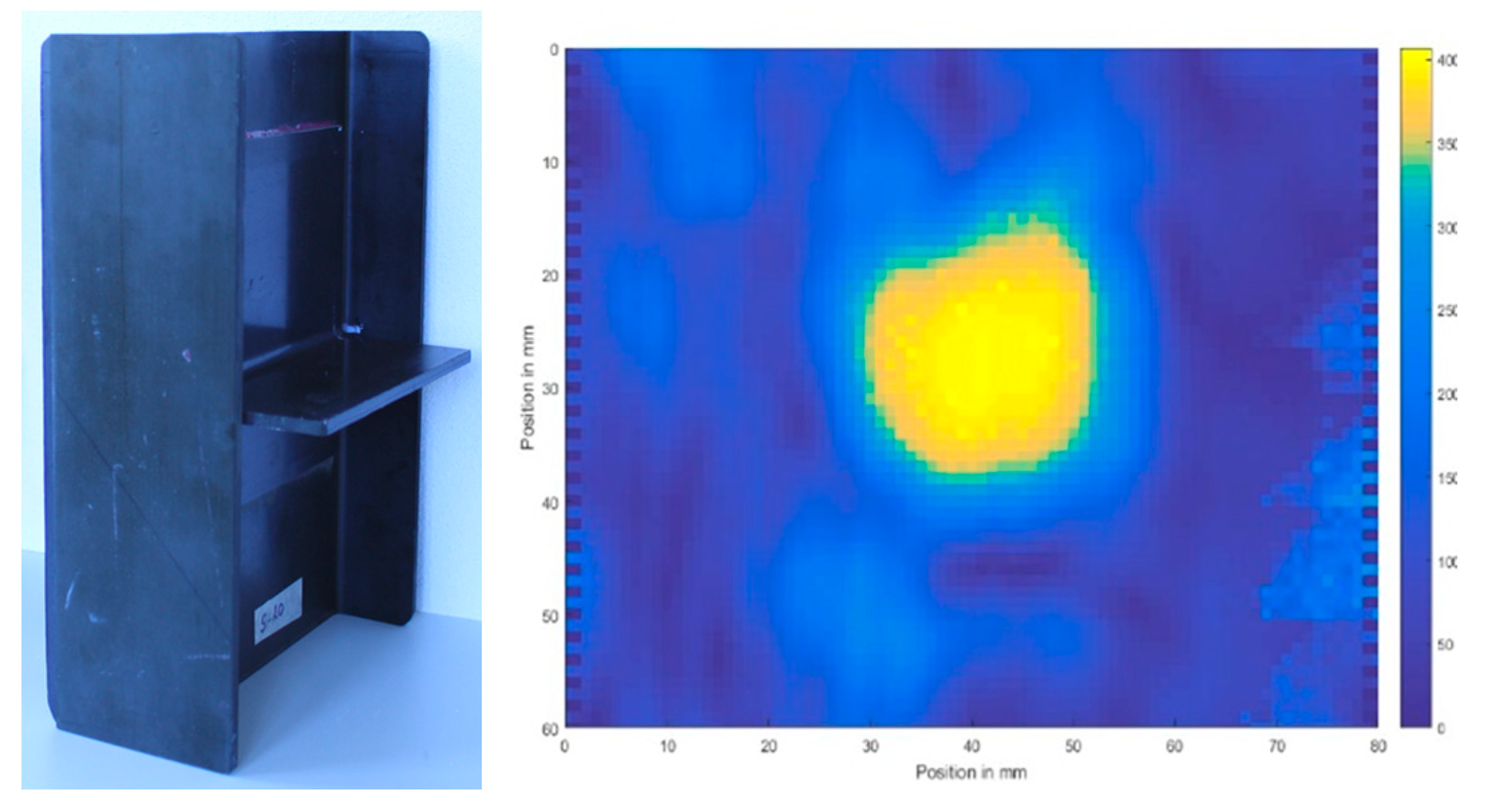
Figure 36.
Laser vibrometry (b) and LDR thermography (c) imaging of fatigue crack between the rivet holes (dotted area in zoomed optical image (a)) in aluminum aviation component.
Figure 36.
Laser vibrometry (b) and LDR thermography (c) imaging of fatigue crack between the rivet holes (dotted area in zoomed optical image (a)) in aluminum aviation component.
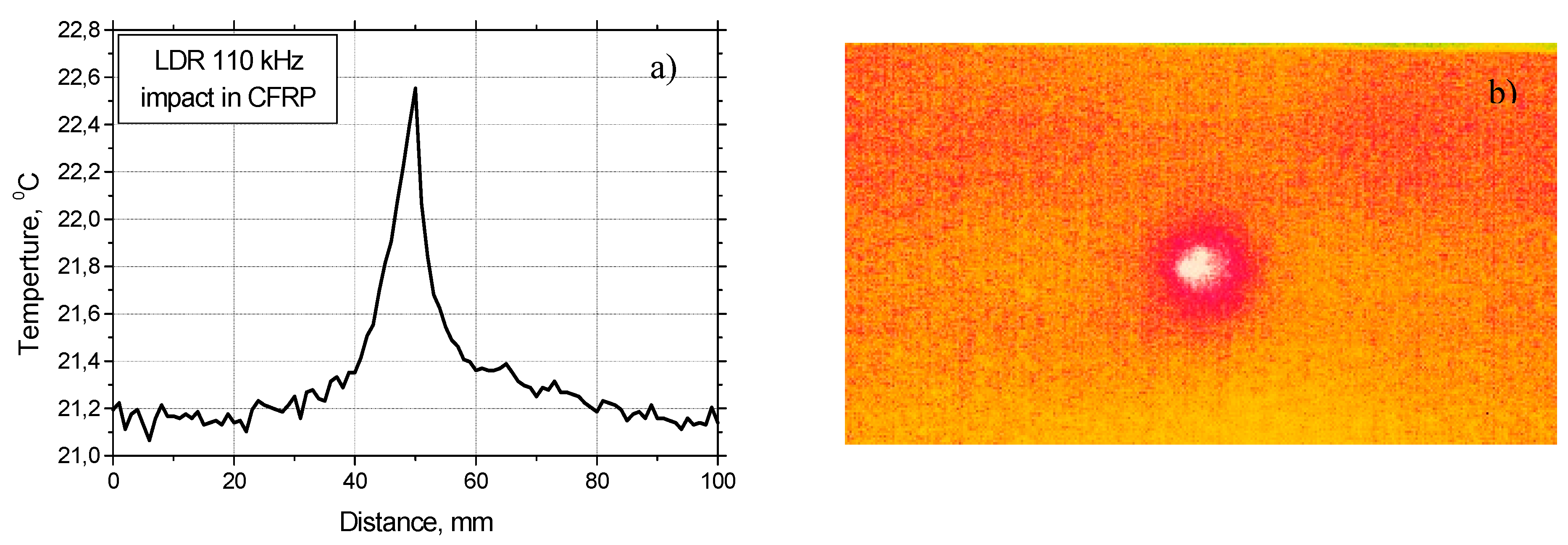
Figure 37.
LDR thermosonic imaging of ~(5x5 mm2) impact damage area in a CFRP plate (b); quantified temperature contrast of the image (a).
Figure 37.
LDR thermosonic imaging of ~(5x5 mm2) impact damage area in a CFRP plate (b); quantified temperature contrast of the image (a).
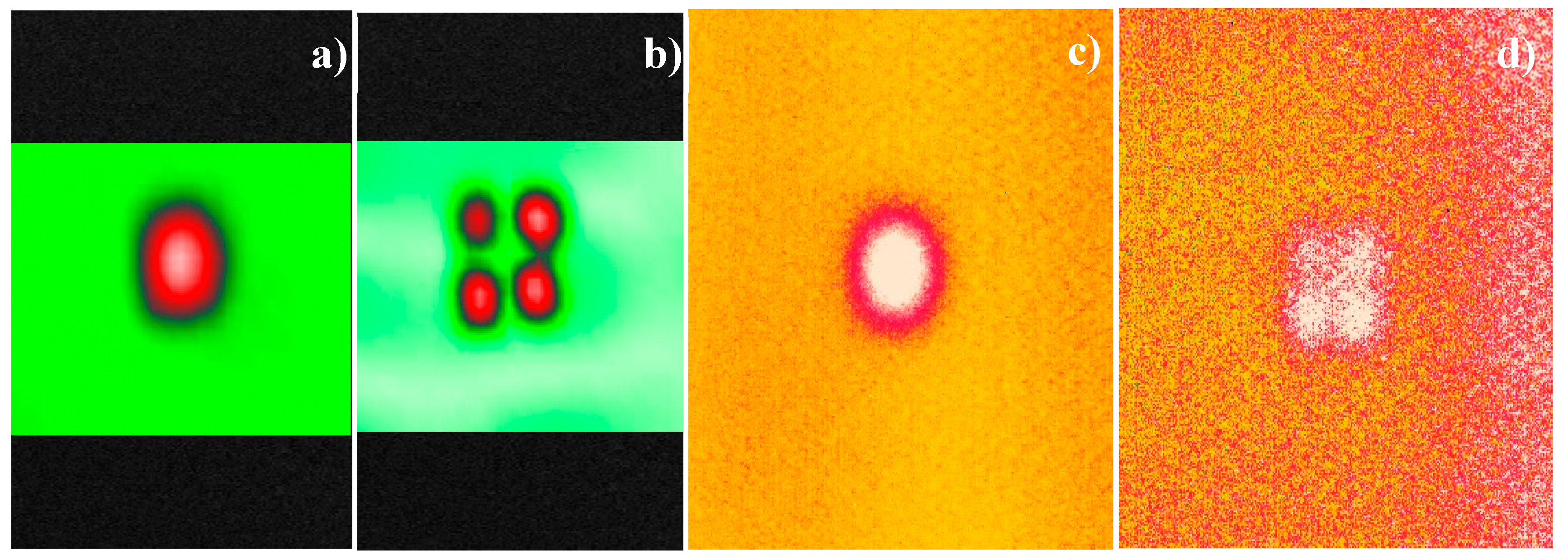
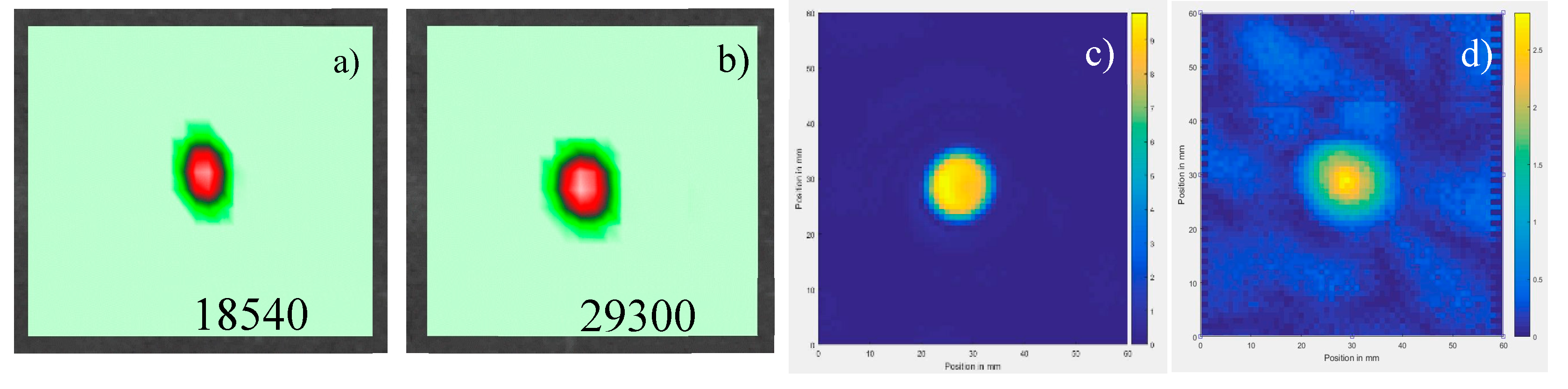
Figure 38.
LDR thermosonic imaging of FBH in PMMA plate at LDR frequency 7670 Hz: (a) - amplitude lock-in (lock-in frequency 0.05 Hz) image (acoustic input ~200 W); (b) – temperature image at input power ~ 2 mW.
Figure 38.
LDR thermosonic imaging of FBH in PMMA plate at LDR frequency 7670 Hz: (a) - amplitude lock-in (lock-in frequency 0.05 Hz) image (acoustic input ~200 W); (b) – temperature image at input power ~ 2 mW.
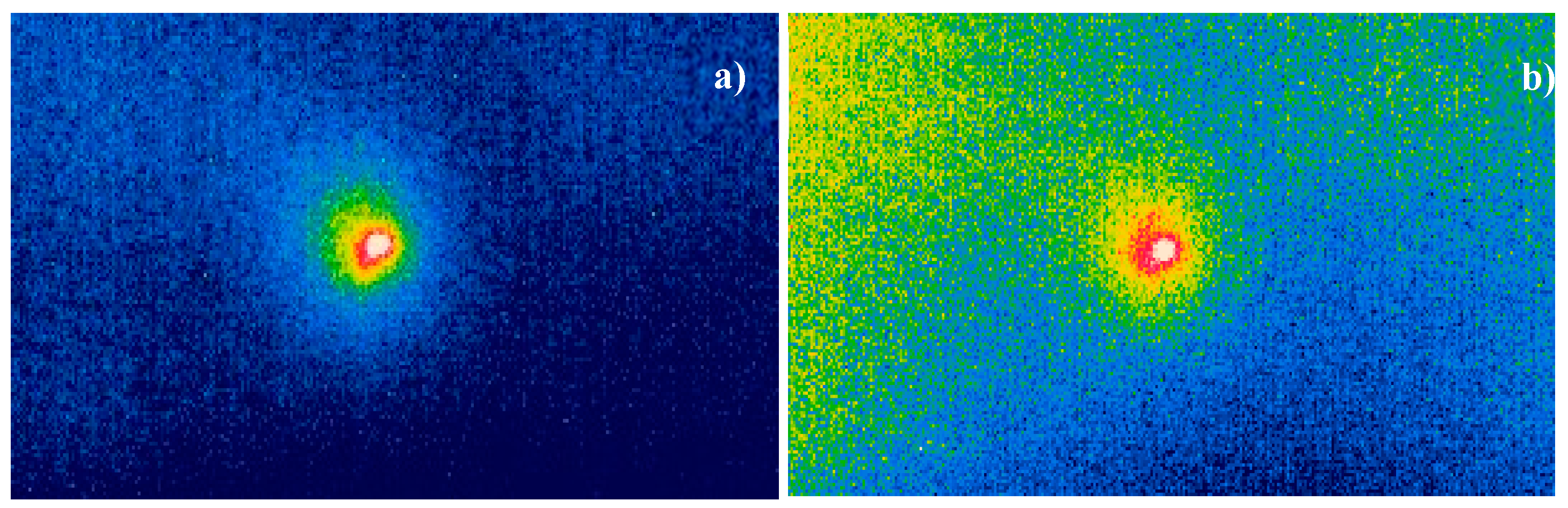
Figure 39.
LDR thermosonic imaging of an impact (~5x5 mm2) in CFRP plate: amplitude lock-in image (a) at ~ 1mW input acoustic power; (b) – temperature image at ~16 mW input power.
Figure 39.
LDR thermosonic imaging of an impact (~5x5 mm2) in CFRP plate: amplitude lock-in image (a) at ~ 1mW input acoustic power; (b) – temperature image at ~16 mW input power.
Figure 40.
“Through-transmission” non-contact ACU thermosonics set-up (a); temperature response of FBH to 50 mW ACU excitation at LDR frequency 50.2 kHz (b).
Figure 40.
“Through-transmission” non-contact ACU thermosonics set-up (a); temperature response of FBH to 50 mW ACU excitation at LDR frequency 50.2 kHz (b).
Figure 41.
Noncontact ACU LDR thermosonic (a, c) and laser vibrometry (b, d) imaging of an impact area (~12 mm diameter) in CFRP plate at different frequencies: (a), (b) - ACU excitation at LDR frequency of 69.6 kHz; (c), (d) – ACU frequency 69 kHz.
Figure 41.
Noncontact ACU LDR thermosonic (a, c) and laser vibrometry (b, d) imaging of an impact area (~12 mm diameter) in CFRP plate at different frequencies: (a), (b) - ACU excitation at LDR frequency of 69.6 kHz; (c), (d) – ACU frequency 69 kHz.
Figure 42.
Airborne field above CFRP specimen with an impact: a) non-resonant case (45 kHz excitation); b) LDR case at 61.2 kHz excitation.
Figure 42.
Airborne field above CFRP specimen with an impact: a) non-resonant case (45 kHz excitation); b) LDR case at 61.2 kHz excitation.
Figure 43.
Experimental setup of RACE imaging system.
Figure 43.
Experimental setup of RACE imaging system.
Figure 44.
Laser vibrometry LDR images of FBH in CFRP (a, b) and RACE images at the same frequencies (c, d).
Figure 44.
Laser vibrometry LDR images of FBH in CFRP (a, b) and RACE images at the same frequencies (c, d).
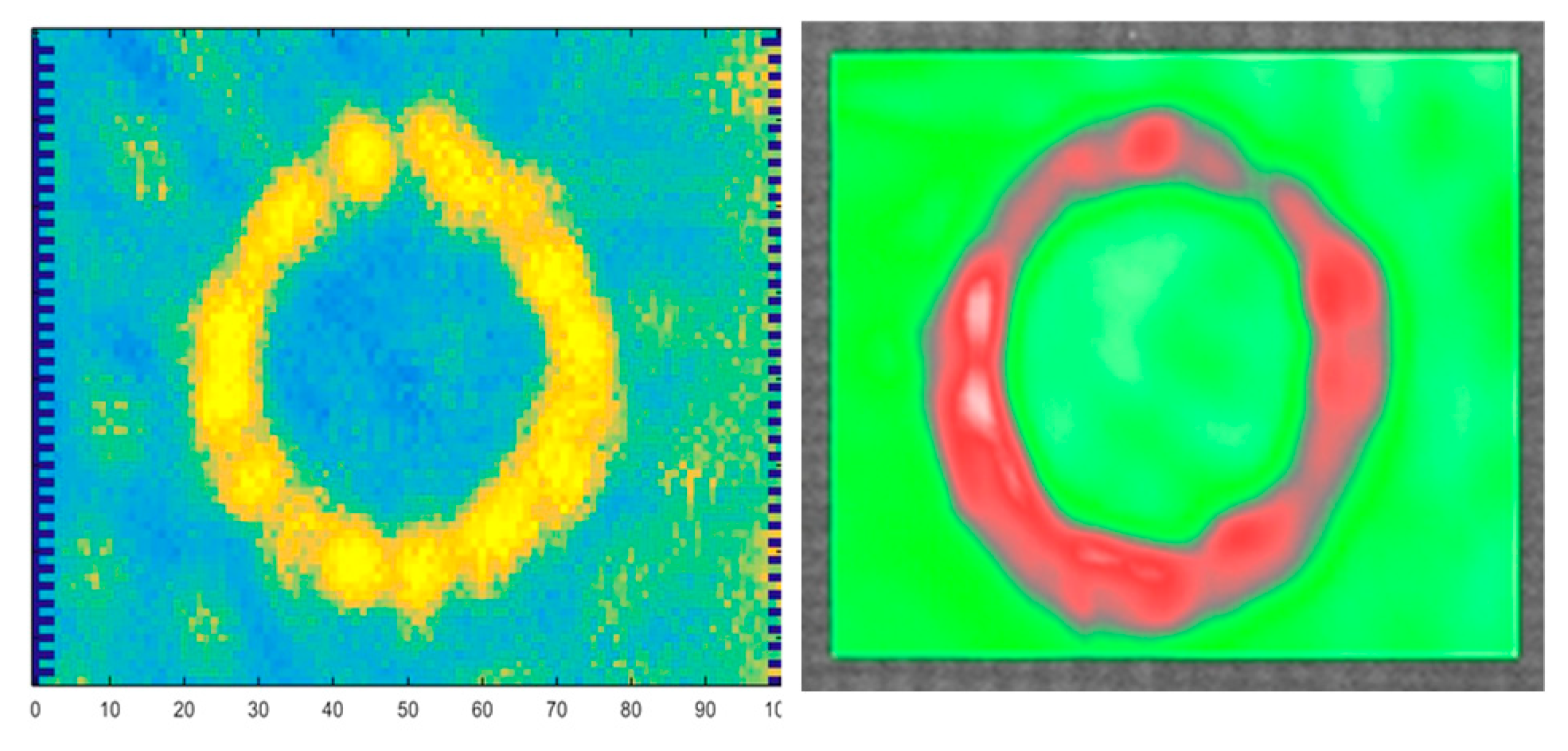
Figure 45.
RACE imaging of 20x20 mm2 disbond in adhesive joint (right) of CFRP spar specimen (left). LDR frequency of the defect is 15250 Hz.
Figure 45.
RACE imaging of 20x20 mm2 disbond in adhesive joint (right) of CFRP spar specimen (left). LDR frequency of the defect is 15250 Hz.
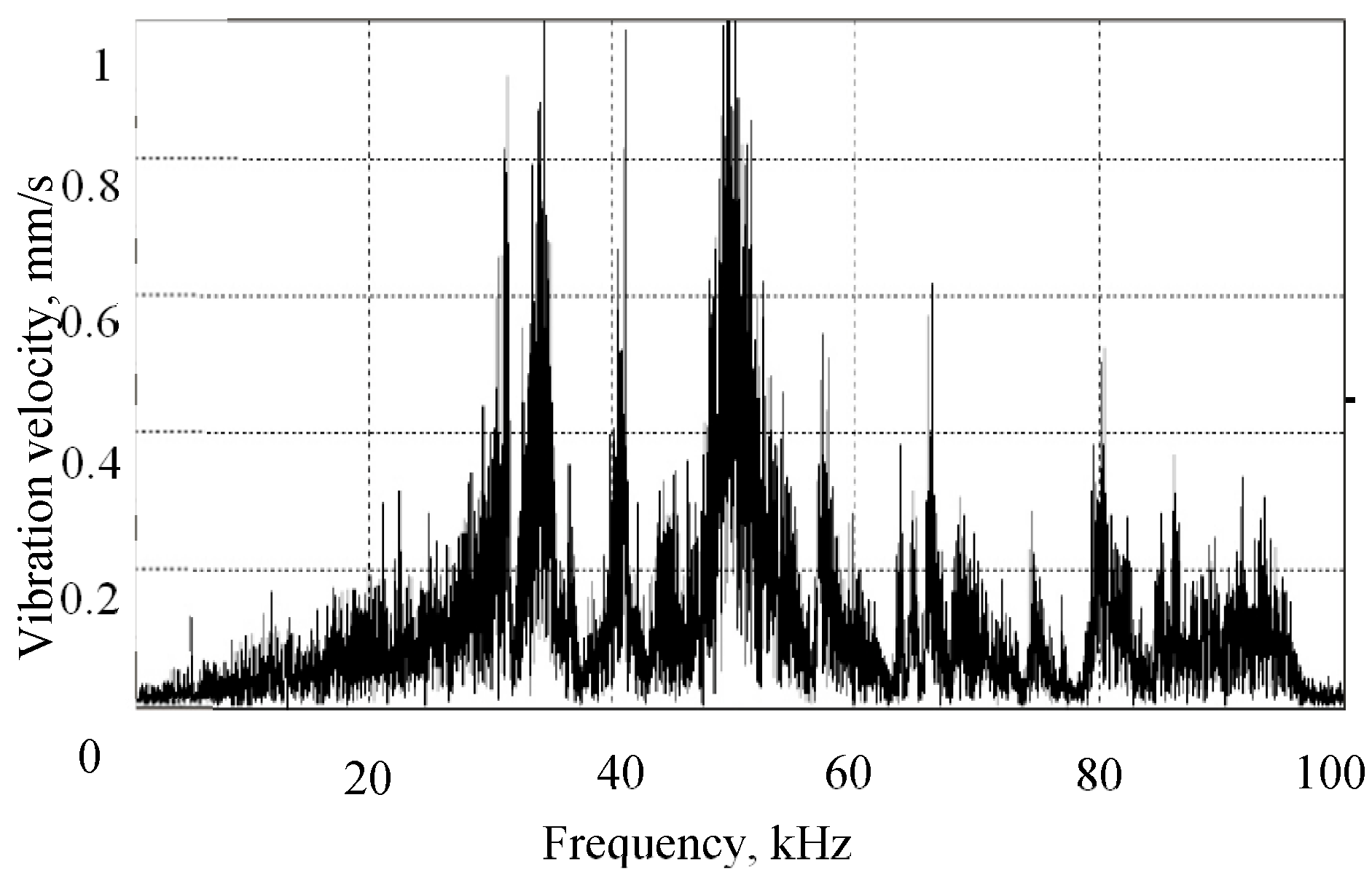
Figure 46.
Acoustic spectrum generated by a piezo-transducer for a noise input voltage.
Figure 46.
Acoustic spectrum generated by a piezo-transducer for a noise input voltage.
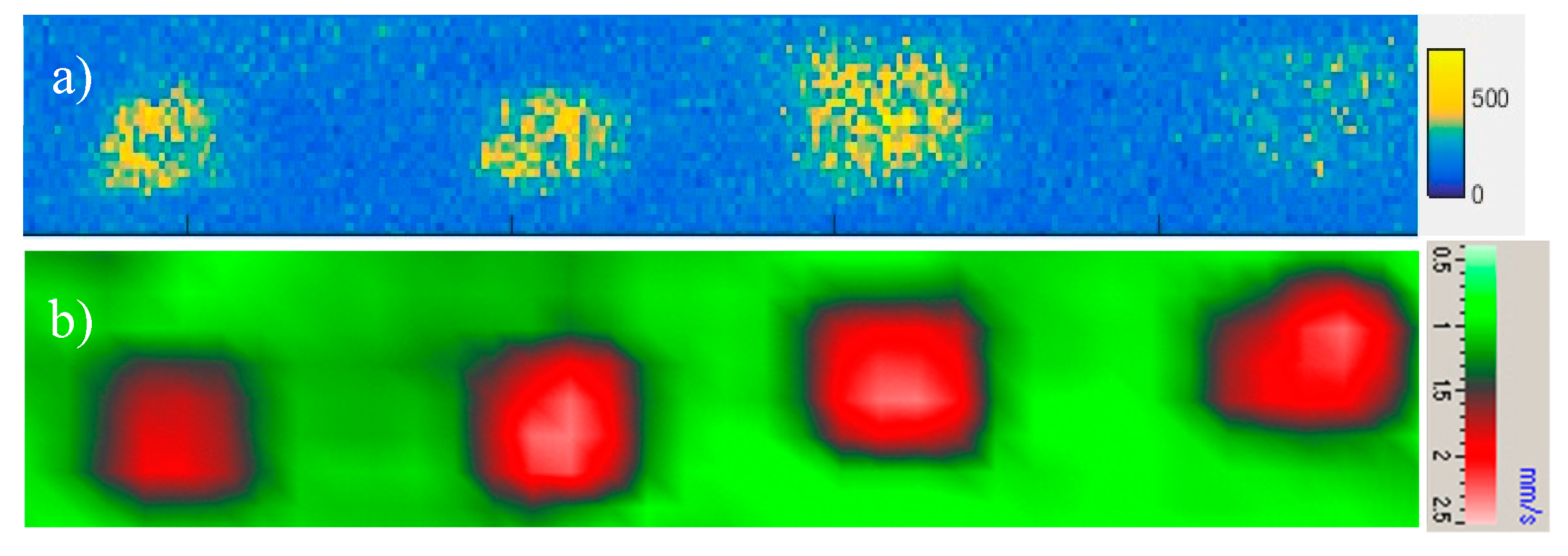
Figure 47.
Multiple defect imaging in noisy mode of RACE: 4 circular FBH of different depths (a) and 4 square inserts at various depths (b) in CFRP plates.
Figure 47.
Multiple defect imaging in noisy mode of RACE: 4 circular FBH of different depths (a) and 4 square inserts at various depths (b) in CFRP plates.
Figure 48.
Zoom-in image of the square insert in CFRP plate obtained in a noisy mode of RACE.
Figure 48.
Zoom-in image of the square insert in CFRP plate obtained in a noisy mode of RACE.
Figure 49.
Noisy RACE (left) and wideband laser vibrometry (right) images of a Teflon ring embedded in (400x400x2 mm3) CFRP plate.
Figure 49.
Noisy RACE (left) and wideband laser vibrometry (right) images of a Teflon ring embedded in (400x400x2 mm3) CFRP plate.
Figure 50.
Robotic scanning setup.
Figure 50.
Robotic scanning setup.
Figure 51.
Noisy mode of LDR imaging for 4 inserts in CFRP: RACE imaging (a), wideband laser vibrometry (b).
Figure 51.
Noisy mode of LDR imaging for 4 inserts in CFRP: RACE imaging (a), wideband laser vibrometry (b).
Figure 52.
SoundCam setup for fullfield RACE imaging.
Figure 52.
SoundCam setup for fullfield RACE imaging.
Figure 53.
The interface of SoundCam and full-field image of acoustic field for piezo-transducer (frequency 13100 Hz).
Figure 53.
The interface of SoundCam and full-field image of acoustic field for piezo-transducer (frequency 13100 Hz).
Figure 54.
Comparison between scanning vibrometry (b, c) and full-field RACE images (d, e) for a pair of FBH in Plexiglas plate (a) activated at different LDR frequencies.
Figure 54.
Comparison between scanning vibrometry (b, c) and full-field RACE images (d, e) for a pair of FBH in Plexiglas plate (a) activated at different LDR frequencies.
Figure 55.
20 J impact-induced BVID in non-crimp fabric CFRP plate (a) with vibrometry image at LDR frequency 32200 Hz (c) and full-field visualization using acoustic camera (b).
Figure 55.
20 J impact-induced BVID in non-crimp fabric CFRP plate (a) with vibrometry image at LDR frequency 32200 Hz (c) and full-field visualization using acoustic camera (b).
Table 1.
LDR for pores N1-N3.
Table 1.
LDR for pores N1-N3.
| Pore |
(kHz) |
|
| N1 |
138.8 |
0.66c |
| N2 |
124.06 |
0.63c |
| N3 |
112.5 |
0.61c |