Water and the Origin of Life

Marc Henry

doi:10.20944/preprints202408.0414.v1

Submitted:

06 August 2024

Posted:

06 August 2024

You are already at the latest version

Abstract

This article reviews all the major stages in the origins of life. From the emergence of matter in the initial Big Bang to the modern, civilized human being. On an immaterial level, it is proposed and explained how consciousness necessarily takes precedence over matter. Next, we explain how consciousness, with its ability to process information, selected the water molecule to breathe life into the periodic table of elements. We also explain why the notion of entropy allows us to evolve: "Die Entropie der Welt strebt einem Maximum zu" (second principle) and, therefore, takes precedence over the notion of energy, which, on the contrary, encourages us to preserve what we have: "Die Energie der Welt bleibt konstant" (first principle). This is followed by a discussion of the importance of quantum coherence and the need to rely on a second quantization formalism for a proper understanding of the physical-biochemical properties of water. Moreover, throughout the argument developed on the best and most fundamental things science has to offer, care is taken to link this knowledge to the great philosophies of the West (Greece), the East (China, India) or even to practices of a shamanic nature (Africa, America). Hence, finally, the proposal to reconsider all musical practice within the framework of the diapason of water at a frequency of 429.62 Hz, as well as all therapeutic practice on the basis of seven clearly identified and established frameworks of thought.

Keywords:

Water

;

Life

;

Consciousness

;

Membranes

;

Music

;

Diapason

;

Greek philosophie

;

Chinese philosophy

;

Ayurveda

;

Medicine

;

Shamanism

;

Information

;

Exformation

;

7 frames of thinking

Subject:

Biology and Life Sciences - Life Sciences

1. Introduction

This paper suggests that life is an inevitable phenomenon from the moment three ingredients mix: water, mineral ions derived from the elements (Na, K, Mg, Ca, B, V, Cr, Mn, Fe, Co, Ni, Cu, Zn, Mo, Si, P, S, Se, F, Cl, I) and organic matter based on the quadrette (C, H, O, N). As it is stars that synthesize atomic nuclei and electrons that neutralize the positive electric charges of these nuclei, life can only be a phenomenon of a profoundly quantum nature. And, as the water molecule is by far the largest constituent of a cell, the theory of relativity also comes into play. Because to understand this substance with the formula H₂O, we need to call on the quantum physics of second quantization fields, and not on the quantum physics of first quantization. Finally, one last science is absolutely necessary to explain the complexity of the living world: the thermodynamics of irreversible processes [1,2]. These different ingredients are, more often than not, largely ignored by conventional biologists, who see the living cell as an object obeying the laws of classical physics: Newton's equations for the mechanical aspect and Maxwell's equations for the electromagnetic aspect. As for the reactivity aspect, it draws heavily on the thermodynamics of chemical equilibria, focusing on the notion of energy. The entropy aspect is only taken into account to model chemical potential via the notions of enthalpy H(P,V) and "free" energies known as Gibbs G(T,P) or Helmholtz F(T,V). Because of these theoretical limitations, one phenomenon closely linked to life remains a profound mystery: consciousness. While consciousness is clearly manifest in human beings, there is growing evidence to suggest that it also exists in animals, plants and even in the single-celled world of bacteria.

Here, we propose to place biology in a quantum, relativistic and entropic framework, while including the phenomenon of consciousness from the outset. This has, of course, already been done and published in previous scientific articles, where all the technical and scientific details can be found. Our aim, therefore, is not to repeat what has already been said, but rather to glue the pieces together to provide a coherent overview of the inexorability of the vital phenomenon, both in its purely material (mechanical or chemical) and immaterial aspects (electromagnetism or psyche via the notion of consciousness). Let it be clear that we have no pretension of asserting that this is a theoretically demonstrated and experimentally validated vision. Rather, it is a synthetic proposal designed to orient future biological research on a clear physicochemical basis, in line with the laws of modern physics. In other words, it's a paradigm shift that places the quantum vacuum and its interfacial material agent, the water molecule, at the center of the game, rather than on its periphery as a mere filler for the holes created by organic and/or inorganic matter. So don't be overly surprised if we start with some basic physics notions. For, like a painter faced with a blank canvas or a musician faced with an empty score, a framework must be put in place so as not to spill over into purely philosophical or religious considerations. Because, as soon as we talk about consciousness, religion is not far away... And so, it's imperative to put in place solid safeguards rooted in science and not in dogmatism of any kind. Once the framework is in place, it's time to fill it with a palette that draws on tangible, weighable matter, of course, but also on non-matter (imponderable waves and fields) and the mixed concept of information, which is equally weighable (entropy) and imponderable (memory, consciousness).

We're well aware that the origin of life is an intensely debated subject, both in science and in religion. Indeed, for some, life may well be the result of extraterrestrial intervention. If this were the case, everything we say here would obviously be wrong and biased by our anthropocentric nature. Our first working hypothesis will therefore be to assume that, since the appearance of planet Earth in the solar system, no extraterrestrial life form has come to put its grain of salt and interfere with the basic physicochemical processes as we are about to describe them as simply and succinctly as possible. In this review, we will also attempt to blend the scientific and philosophical approaches. After all, there's no guarantee that science is the best route to knowledge. It's up to each and every one of us to decide and choose what suits us best, in the light of what we're about to present.

Matter, Elements, Emptiness and Movement

The city of Miletus Ionia (Asia Minor) was the cradle of a monistic philosophy which explained, in a language accessible to all, that there was a single primordial substance or element. This primordial substance contained within itself a principle that created the visible world: movement. As everything was matter for the Milesians, including the soul or thought (ψυχὴ, psychê), the question of emptiness didn't even arise. For Thales of Miletus, the founder of this way of thinking, the primary, animate element is the water of the River Oceanos (Ωκεανος), hence the idea of an Earth floating on an ocean. Thales sees water as the permanent basic element that ensures the constitution and transformation of all things. His apothegm is that "All is water, all is one". According to Diogenes Laërtius (c.300 C.E.), it was Thales who first enunciated the precept "Gnothi Seauton" (Γνῶθι σεαυτόν) meaning "know thyself", which is engraved at the entrance to the temple of Delphi at the foot of Mount Parnassus. We see here, then, the close link that exists, from the outset, between life in the form of pure consciousness or cells, and liquid water.

Anaximander of Miletus, a disciple of Thales, prefers to place the origin of all things in perpetual circular motion, which cannot be preceded by anything else. Thus, in the beginning, matter appears in the form of a neutral element more subtle than water but denser than air, which Anaximander calls Apeiron (Aπειρον). This Apeiron is imperceptible to the senses and unbounded. It can be resolved into a pair of states: hot/cold on the one hand and dry/wet on the other. Each world thus adopts a spherical shape with a cold central core (Earth) surrounded by wet (Water), then dry (Air) and finally hot (Fire). Like Anaximander, Anaximenes of Miletus wanted to place movement at the origin of things, but he was looking for something that could be perceived by the physical senses, and which was unbounded and in perpetual agitation. Since the element Air possesses all these qualities, he posited that "everything comes from air, and everything returns to it". This view that, without air, there would be no life resonates today in the fundamental division between living beings that breathe air and those that can live in anaerobic conditions.

In 494 B.C.E., the city of Milet was taken and ravaged by the Persians, putting an end to the development of the empiricist and monistic Milesian philosophy. However, this philosophy was to be found again, still in Ionia, but further north in the city of Clazomenae, in a dualistic form from which Socrates, Plato and Aristotle drew. And, by the same token, all our contemporary thought. Anaxagoras of Clazomenae posited that "nothing is born and nothing perishes, but things that already exist combine and then separate again". The novelty introduced by Anaxagoras is Intelligence or Spirit (Νοῦς, Nous), an infinite non-material thing quite distinct from the Milesian material psyche, which is the initial driving force, the very principle of movement. This spirit is non-limited and allied to nothing. But it exists on its own, possessing the capacity to discriminate, not to generate. It has the ability to rotate material principles (Υλη, Hylê) called homeomeres, which are infinite in number and infinitely small at the same time. It follows from this that the void cannot exist for Anaxagoras. The Spirit (Νοῦς) separating itself from the Whole (Παν, Pan) at one point thus triggers a whirling movement (Περιχωρησις, perichoresis) that gradually spreads throughout the Universe and continues to do so to this day. Under the effect of Νοῦς, heavier bodies, like earth, are carried downwards. The lighter ones, like fire or ether (αἰθειν, aithein), move upwards. Air and water are in the middle.

Between the cities of Milet and Clazomenae lies the town of Colophon, where the bard Xenophanes of Colophon sang the praises of a single God. One great whole, present in all things, being both ψυχη and νοῦς. For Xenophanes, mud, a mixture of earth and water, is the origin of the universe, which has no beginning and no end. Man, like the universe, is a mixture of earth and water. South of Colophon and north of Miletus, we find another poet, Heraclitus of Ephesus, known as "the obscure" because he was particularly difficult to understand. Indeed, Heraclitus was one of the first philosophers to use symbolic language, where logos (Λογος, logos) implies an underlying harmony of opposites. This implies, metaphorically speaking, the laws of eternal (αἰωνα, aiona) change. From all things the one and from the one all things. For Heraclitus, all matter comes from fire and will return to fire, the archetype of the eternally changing substratum. Fire is eternally alive, because it has always existed and always will. All becoming is the fruit of discord (ἐριν, érin) and necessity (χρεων, khreon). Heraclitus was the first to give a creative image of time. His favorite image is that of the river seen as a dynamic system in perpetual change. But one that nevertheless possesses its own law of organization and existence. Since nothing is permanent and everything is movement, Heraclitus' apophthegm would be "Πάντα ῥεῖ, Penta rhei".

Empedocles of Akragas was the last "empiricist" philosopher, heir to the Ionian tradition. For his part, he sought an adequacy between sensory perception and the intrinsic reality of Nature (Φυσεως, Phuseôs). For Empedocles, it is the senses that teach the true nature of things. Like many of his colleagues, he took the view that nothing can absolutely come into existence from nothingness, and that what is cannot perish. The Whole (το Παν, to Pan) is seen as an absolute continuum that leaves no room for the void, and is expressed in a fourfold reality (fire, air, water and earth), which are the "roots of all things". Each root (στοιχεια, stoikheia) displays the property of quantitative invariance. In order to provide the necessary impetus for the movement without which all creation would be impossible, Empedocles also considers two complementary "producing causes" to explain the transformation of roots. On the one hand, attraction (φιλια, philia) unites the multiple into one. On the other, repulsion (νεικος, neikos) divides the one into the many. Attraction reigns over Sphairos. That is, the sphere of the intelligible. Whereas repulsion reigns over the Cosmos. In other words, the sensible world. As with Anaxagoras, roots assemble and dissociate according to a law of conservation of content, generating variable forms. All creation is the fruit of chance encounters and the necessity of symmetries imposed by repulsion. But with a memory (ἀναμνησις, anamnêsis) that leads roots to seek each other out in order to find each other again thanks to attraction.

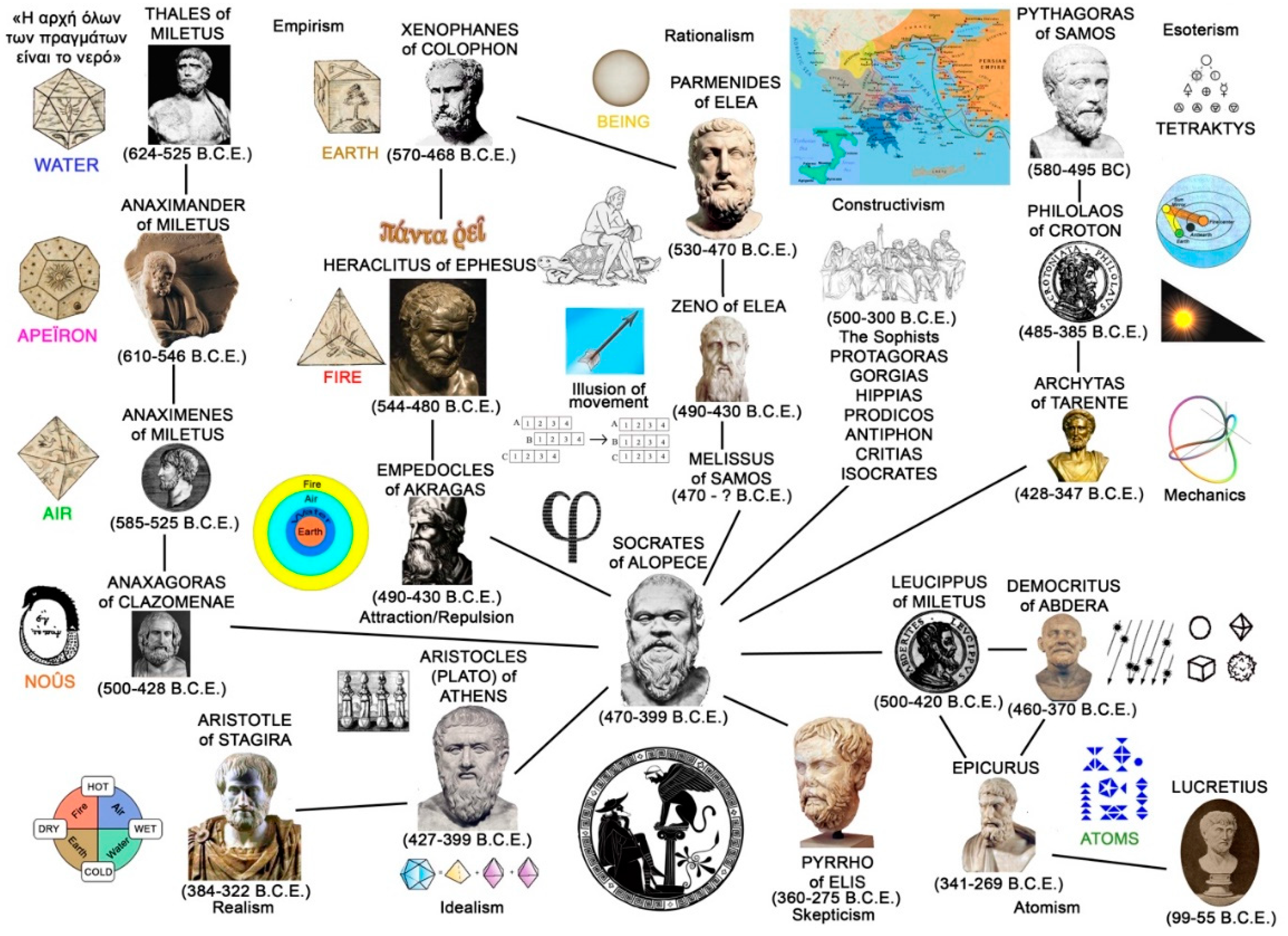
Figure 1, on the left, summarizes these different empiricist philosophies, in which emptiness (Apeiron), consciousness (Nous), matter (Water, Air, Earth), energy (Fire) and force (Attraction/Repulsion) play, in turn, the role of creative principle. In 540 B.C.E., the Persian conquest forced the Ionians to flee to the far west and found the city of Elea. It was here that Parmenides posited that there are two paths to knowledge. The first is the path of Truth (ἀληθειης, aleitheiês) based on reason. It corresponds to the intrinsic state of nature, a state totally independent (objective) of its observer. Thus, it is with Parmenides that a driving principle (ψυχη, psykhê) appears, capable of giving life (ζωη, Zoê), spirit (νους, nous) and thought (φρονησις, phronêsis) to any material structure. The consequence is that there is a single, eternal (ἀτελεστον, ateleston) and immobile (ἀτρεμες, atremes) Being (το ἐον, to eon). In short, something that is uncreated (ἀγενητον, agenêton) and also imperishable (ἀνωλεθρον, anôlethon). And, which preserves itself no matter what, allowing us, by reference, to reason about the world. Moreover, Being is non-divisible (οὐλομελε, oulomele, global, without separate members) and homogeneous (ὁμοιον, omoion). Consequently, Being is continuous and One, and therefore emptiness does not exist. Since Being possesses all attributes, it possesses in particular the attribute of being the limit. And, as such, it cannot be infinite. Thus, this completed Being that fixes eternal permanence is clearly opposed to Anaximander's infinite Apeiron, generator of intrinsic change.

The second path to truth is the path of opinion (δοξῶν, doxôn) based on the senses. This path, which we must be wary of, is opposed to the path of truth, which is sure. So, while Being is, opinion teaches Non-Being. To the eternity of Being and its permanence, it opposes birth, death and change. Similarly, instead of the immobility and globality of Being, opinion makes us believe in the locality of movement. To the present, it opposes the past and the future, and to unity, variety. Finally, to the homogeneity and continuity of Being, opinion shows us the heterogeneity and discontinuity of the world. For his part, Zeno of Elea was a fervent disciple of Parmenides. It was he who invented dialectics with his reasoning by the absurd, reductio ad absurdum, to counter the attacks of his master Parmenides' opponents. Zeno thus posed 4 paradoxes (dichotomy, Achilles and the tortoise, arrow and stadium) in relation to the infinite divisibility of space and time. The conclusion of Zeno's four paradoxes is clear: whatever hypotheses imply the continuity or discontinuity of time and space; it is impossible to account for motion. And, therefore, motion is an illusion. Parmenides' arguments on the rational necessity of believing that Being exists and conserves itself were also taken up by Melissus of Samos. But Melissus questions the spatial finiteness of this Being, concluding that the spherical, perfect, homogeneous and immobile nature of Being is non-limited.

In opposition to Parmenides' realism, there was also the esoteric school of Pythagoras of Samos, a mystico-religious philosopher and contemporary of Zarathustra (628-551 B.C.E.), Buddha (563-483 B.C.E.) and Confucius (551- 479 B.C.E.). Around 530 B.C.E., he founded a politico-religious school in Crotone (southern Italy), teaching musical harmony, metallurgy, the rule of proportion in painting, sculpture and architecture, and the existence of biological, meteorological and astronomical cycles. Nothing Pythagoras taught was to be written down or divulged to the uninitiated. There were two classes of initiates, the mathematicians (μαθηματικοι, mathêmatikoi), privileged students in the knowledge of the Master's thoughts. And, acousmaticians (ἀκουσματικο, acousmatiko), listeners capable of knowing a little of this teaching. The Τετρακτυς, a triangle formed from the first four integers, the sum of which is the Decade, the sacred number, was the sign of belonging to the Pythagorean group, for whom "All is number". Unlike Parmenides, the interval filled by the void played just as important a role as the One. The role of the void was to distinguish numbers, their nature, their elements, their parts, their individuality. As the void fills everything, penetrates everything, embraces everything, it could very well be a reality, a primordial principle on a par with the One. The existence of even (2n = n+0+n) and odd (2n+1 = n+1+n) numbers led to a logical grouping of concepts: One (εν, en), Odd (περιττον, peritton), Male (αρρεν, arren), Rectilinear (ευθη, euthê), Square (τετραγωνον, tetragônon), Limited (περας, peras), Good (αγαθον, agathon), Luminous (φως, phos), Straight (δεξιον, dexion) or Motionless (ηρεμουν, êremoun). In contrast, there were Many (και πληθον, kai plêthon), Even (και αρτιον, kai artion), Female (και θυλη, kai thulê) Curved (και καμπυλον, kai kampulon), Rectangular (και ετερομηκες, kai eteromêkes), Unlimited (και απειρον, kai apeiron) Evil (και κακον, kai kakon), Dark (και σκοτον, kai skotos), Left (και αριστερον, kai aristeron) or Mobile (και κινουμενουν, kai kinoumenoun). For the Pythagoreans, there was also an immaterial soul (ψυχη, psychê) with the memory of past lives (ἀναμνησις anamnesis) quite distinct from the physical body.

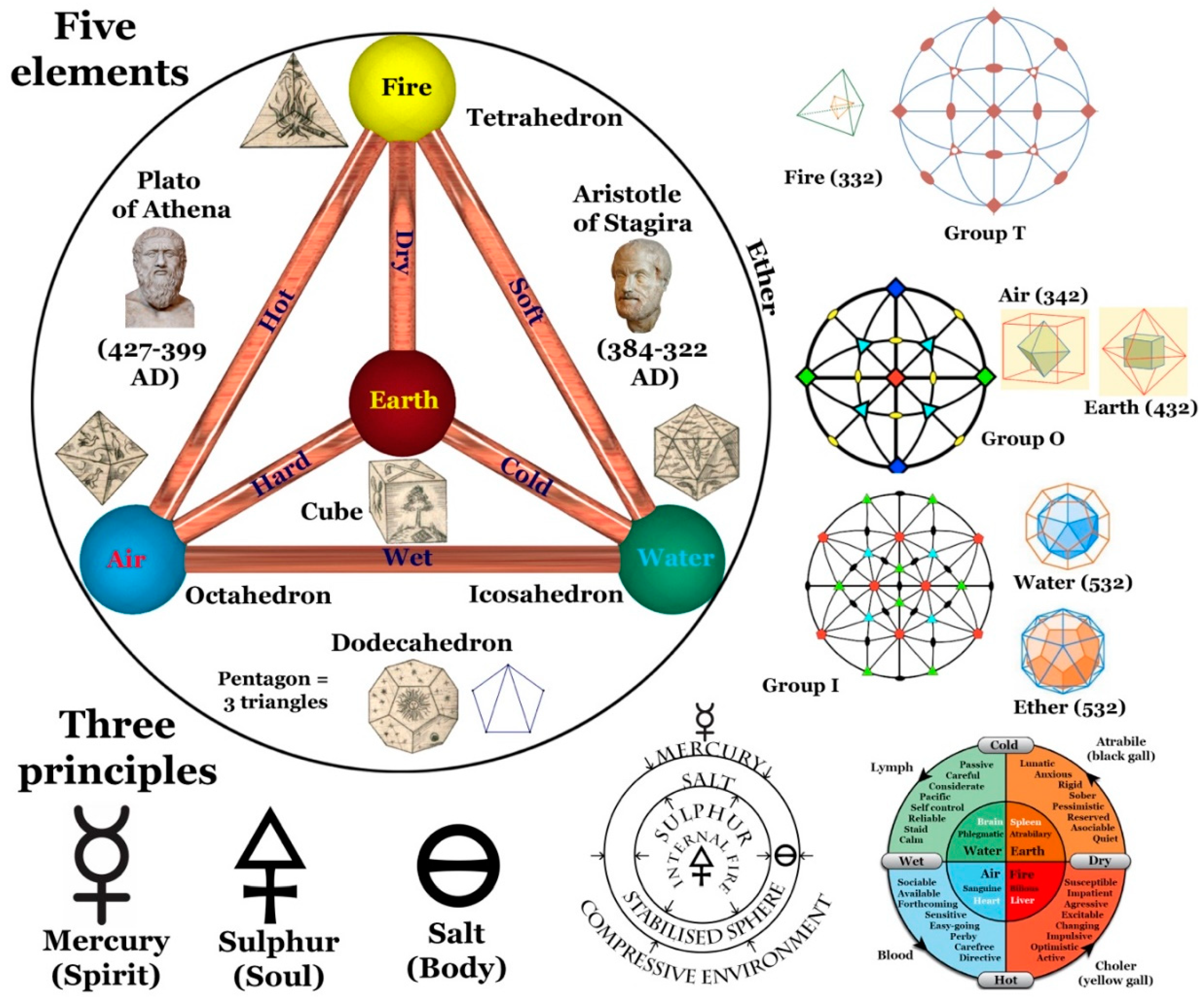
Philolaus was a pupil of Pythagoras, the only survivor of the fire at the Crotone School around 450 B.C.E. He was the first to associate the tetrahedron with fire, the octahedron with air, the icosahedron with water and the cube with earth. It was he who first associated the tetrahedron with fire, the octahedron with air, the icosahedron with water and the cube with earth, and the dodecahedron with a fifth element, ether. Archytas, a pupil of Philolaus, defined arithmetic, geometric and harmonic progressions as the foundations of musical rules. He also placed himself at the end of the sky delimited by the fixed stars, and asked himself whether it was possible to extend his hand or a stick. Since nothing seemed to stand in the way of this gesture, he deduced that, despite its apparent perfection, the Universe could only be infinite.

For Parmenides, emptiness and motion do not exist, whereas for Heraclitus, emptiness and motion are real things. Atomism arose from the desire of the philosopher Leucippus to reconcile the views of Parmenides and Heraclitus. He described the Universe in terms of a vacuum and microscopic, inseparable, unalterable Parmenidean worlds - atoms. Concerned with symmetry, Leucippus thus gave Being, seen as an atom, the attribute of Fullness, and Non-Being, that of the Void (κενον, kenon) existing between atoms. The One thus remains unique, but due to the existence of the Void, it can divide into a multitude of fragments of infinitely varied forms. These "atoms", inseparable and invisible because of their smallness, are in perpetual motion. This brilliant idea was taken up by Democritus of Abdera, whose philosophy is known to us thanks to Epicurus, the last representative of Greek philosophy, and Lucretius, a great admirer of Epicurus. For Democritus: "Nothing comes from nothing; nothing that exists can be annihilated. All change is the aggregation or disintegration of parts. Nothing happens by chance, but everything has its reason and its necessity”. Atoms are infinite in number and infinitely diverse in form. Falling eternally through immense space, the largest and fastest collide with the smallest. The resulting lateral movements and whirlpools (δινήν, dinên) are the beginning of the world's formation. It follows that the World had no beginning and will have no end. Nor is there any indication that there is only one world. The soul, on the other hand, is made up of subtle, smooth, round atoms, similar to those of fire. These atoms are the most mobile of all, and from their movement, which penetrates the whole body, come the phenomena of life. No cause, no force was required to impose their initial movement on the atoms. For their movement is eternal, both in the past and in the future.

While Democritus takes matter and emptiness as his starting point, the first sophist, Protagoras (c.490 – c.420 B.C.E.), no longer takes the object, external nature, as his starting point, but rather sensation. For a sophist, for a given event, there are as many protagonists as there are opinions, each constituted by what he or she has experienced. Thus, "man is the measure of all things, of those that are, of their existence, of those that are not, of their non-existence". No single opinion can bring together all lived experiences. So, there is no truth in itself. There are only truths particular to each individual. The sophist Gorgias (483 – 375 B.C.E.) went beyond Protagoras' pessimism, moving towards nihilism. He does this via three principles: first, that there is nothing. The second, that even if there is something, that something is unknowable to man. And thirdly, that even if this something is knowable, it cannot be divulged or communicated to others.

By shifting the debate from the object to the subject, the sophists' way of thinking would of course send shockwaves through all Greek thought. This would prompt Socrates to assert ironically that "all I know is that I know nothing" (Ἓν οἶδα ὅτι οὐδὲν οἶδα, En oida oti ouden oida). It's also an ethical injunction to look inward: "Know thyself". Becoming aware of one's ignorance is the indispensable first step on the path to knowledge. Just as the emptiness of matter enables us to distinguish between all things, the emptiness of ideas enables us to distinguish between science (επιστήμη, epistêmê) and opinion or belief (doxa). Socrates claims to know nothing, to have nothing to teach. For him, only dialogue (διάλογος, dialogos) between two consciences, two reasons, two logos can bring forth novelty and enable mutual enrichment. So, we can no longer content ourselves with poetic fragments in the style of Heraclitus or Parmenides. Since Socrates, thinkers' assertions have had to be justified by rigorous arguments. That's because they have to be put through the Socratic maieutic sieve. Hence the birth of the scientific way of thinking, a formidable tool at the service of certainty. That there is an order of reality that transcends both the senses and the opinions of reason that interpret them. This dogmatism underpins virtually all philosophies, whether pre-Socratic, as in Thales, Parmenides or Pythagoras, or post-Socratic, as in Plato and Aristotle. Dogmatism reached its most perfect and well-defined form in the Middle Ages with Saint Thomas of Aquinas (1227 E.C. – 1274 E.C.).

To oppose all dogmatic positions, Pyrrho of Elea, whose philosophy was handed down to us by Sextus Empiricus (160-210 C.E.), claimed that nothing is certain. And that every proposition could be opposed by an equally probable contrary proposition. Therefore, the wise man must stick to examination and abstain from judgment (ἐποχή, epoché) (σκέψεις, skepsis). Hence the name skeptics, followers of the no-yes, no-no philosophy. Skeptics distinguish between good things, bad things and indifferent things, based on what appears to them. The skeptic denounces the vanity of any dogmatic search for causes. He is thus a precursor of the positivist, who holds to scientific knowledge alone, without any value judgments. In the end, it was the Socratic maieutic that enabled us to move beyond the nihilistic discourse of the sophists and the abstention from judgment of the skeptics. But above all, it crystallized the debate between the supporters of emptiness (Pythagoras and the atomists) and the opponents of emptiness (Empedocles and Anaxagoras) in favor of the latter.

Plato born Aristocles, who met Socrates at the age of 20, was shocked by the latter's death. In fact, Socrates calmly drank a lethal decoction of hemlock after being sentenced to death by the People's Court of Athens for impiety and corruption of youth. Plato wondered how false speeches could be more persuasive than true ones. He used the allegory of the Cave to explain his tripartite vision of nature. There are the intelligible forms, the ideas (εἶδος, eidos), which are the immutable models of sensible things. These ideas are merely the images of intelligible forms projected onto a spatial medium. In other words, a material on which the action of the demiurge is exerted, enabling sensible things to appear. Plato believes in the existence of non-being, like Leucippus and Democritus. But he never quotes Democritus, for whom non-being is identified with emptiness (κενόν, kenon). Plato rejects this concept. He speaks of something that is both a receptacle and a material. A thing capable of mediating between the sensible and the intelligible, and which he calls extent (la chora, χώρα). Extent, then, is not empty space, but the permanent matter of the universe. Thus, Plato agreed with Socrates that the general, as one and stable, can alone be the object of science. He also agreed with Heraclitus that the sensible world was in a state of perpetual change. His world of ideas corresponded to the Eleatian definition of being: one, unchanging, free from multiplicity and change. But at the same time, he agreed with Democritus (without ever naming him) on the multiplicity of things.

Plato's pupil, Aristotle, recognized that the goal of science is to know the principles and causes of being. But Aristotle rejected the idea of a universal separate from individuals. For, as the idea is outside things, to know the idea is not to know the thing. Here, there's no question of substituting another intelligible world for the sensible one. Rather, we simply need to determine the point of view from which we must consider the sensible world in order to find it intelligible. Aristotle thus sees philosophy as the science of being in general. Physics, on the other hand, is the science of material beings in motion, or capable of receiving motion. Aristotle thus contrasts form, which particularizes, with ideas, which generalize. He posits that being is composed of an indeterminate material cause (cf. Pythagorean even numbers) that exists in potential. And, this material cause is associated with an essential or formal cause that exists in act (cf. Pythagorean odd numbers). Matter (ὕλη, hylê) and form (μορφή, morphê) are therefore, along with privation, the principles that coexist in substance (ουσία, ousia). But, which can only be isolated by abstraction. So, unlike Plato, who identifies matter and extent in a theory of the appearance of sensible forms from pre-existing intelligible forms, Aristotle develops a theory of matter as the substratum of change. For Aristotle, the act is the realization of the possible, which requires a driving cause that generates movement. And a final cause that stops it in its tracks. This movement is considered continuous and infinitely divisible. It can occur in three ways: spatial displacement (A → A), displacement in quantity A by evolution (∆A), displacement in quality by alteration (A → B). Hence the Aristotelian apothegm: "Everything moved is necessarily moved by something". But there can't be an infinite series of principles. We must therefore necessarily stop at a first cause, God, who communicates motion without having received it. From this first principle, there is an infinite chain of causes and effects in time (displacement), in magnitude (evolution) and in the succession of beings (alteration). Like his master Plato, Aristotle fought against the idea that the void could exist. The basic idea stemmed from the fact that "the quantity that surpasses another quantity is composed, first of the quantity by which it surpasses the other, and then of the very quantity it surpasses". Thus, 5 = 3 + 2, where 3 is the quantity separating 5 from 2, which is the quantity surpassed. But if I write that 5 = 5 + 0, the latter appears to be composed of itself and nothing, which is rather awkward. The void can have no proportion to the full, so it doesn't exist. This leads us to regard the void as a non-being, suggesting that it is a privation rather than something in itself.

Water, Water, Everywhere

It was important to review the philosophies behind the development of our "modern" science. It's no exaggeration to say that, before Aristotle, there was a veritable ferment of ideas. Then, from Aristotle onwards, this ferment came to an abrupt halt. The reason for this abrupt halt is the idea that, if the void exists, it can only be a deprivation of matter. And not a thing in itself existing independently of matter. Worse still, the very idea that the vacuum could create matter was simply inconceivable. The basic question was: "Why is there something rather than nothing? This totally echoes the question that interests us here: "How could life have arisen from non-living things? As these are very difficult questions, the temptation is great to invoke the existence of an immaterial divinity that substitutes for the void, or is the only one capable of procuring life. Let's now take a look at modern science. According to Figure 1, there are five main currents of thought:

i): The pre-Socratic Empiricist movement, based on the theory of the four elements (Earth/Water/Air/Fire) and beginning with Thales and Xenophanes. This trend was taken up in part by post-Socratic Aristotelian realism.
ii): Pre-Socratic esotericism (Tetrahedron, Octahedron, Cube, Icosahedron, Dodecahedron). This trend begins with Pythagoras and continues with Socrates towards Platonic idealism (ideas). Or towards Aristotelian realism (duality of matter and form), where emptiness is deprivation.
iii): The pre-Socratic Rationalist movement, which denies movement and therefore emptiness. Since, without emptiness, there can be no movement. This trend derives from the ideas of Parmenides. It culminates in the idea that Being can only be limitless, and therefore infinite.
iv): The pre-Socratic constructivist trend, which puts the human being at the center of the game. This trend asserts that there can be no absolute truth. Since the human being is the measure of all things. This gave rise to post-Socratic skepticism, in which observation is all that counts. Since the void cannot be observed, it does not exist.
v): The post-Socratic Atomist movement, which takes up the starting point of rationalism. But here, instead of denying the existence of motion, since it is clearly observable, we deduce that the void must also exist. Hence, atoms of matter moving in a non-material vacuum.

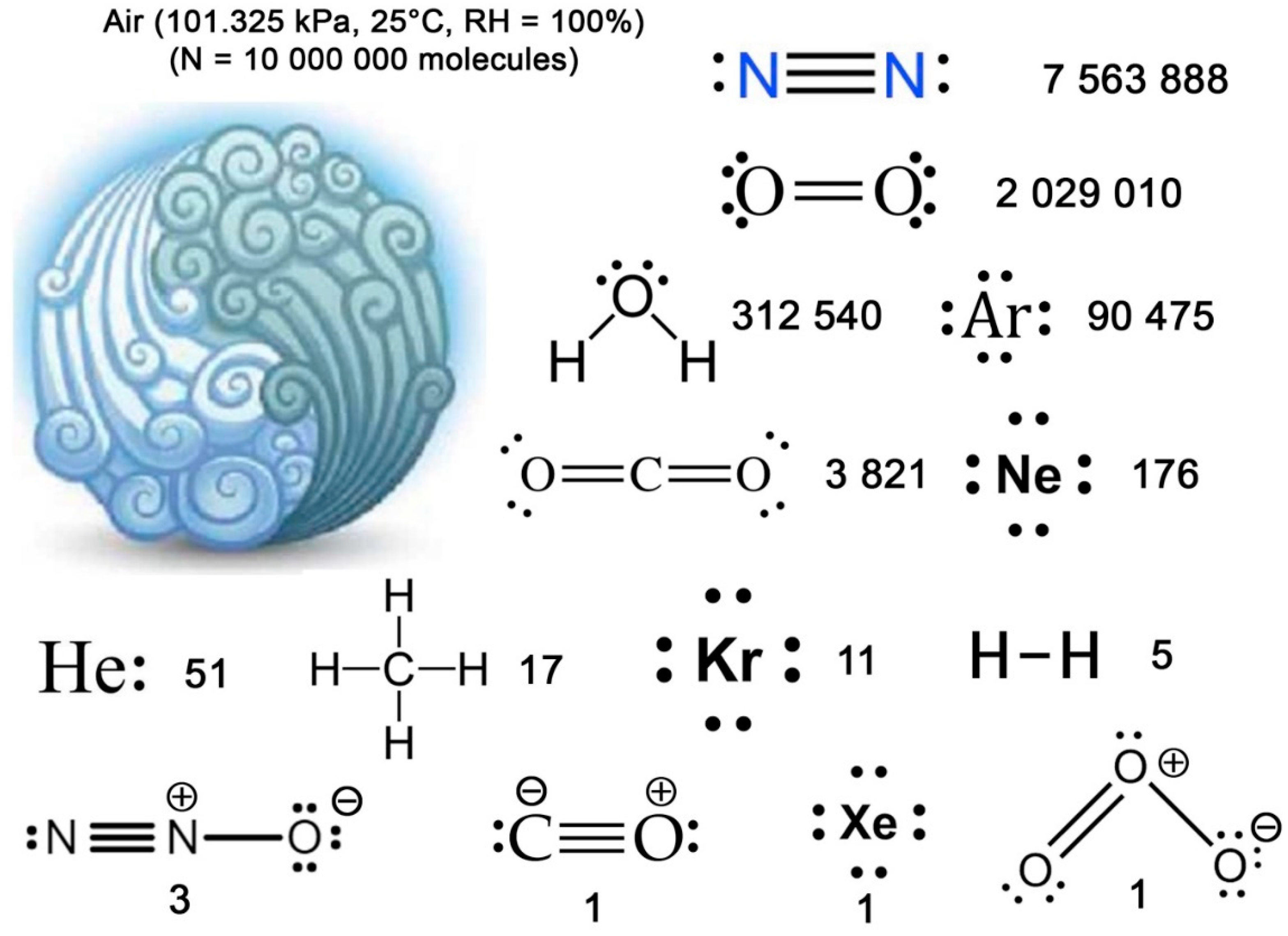
First of all, it's clear that the empiricist trend is problematic. We know today that, under ambient conditions of temperature (T = 20°C) and pressure (P = 101.325 kPa), air always contains water. Figure 2 summarizes what we know today about this element called "air". For simplicity's sake, we've chosen to use only whole numbers. To do this, we have taken the composition of a dry atmosphere [3] and calculated the quantity of water vapor present in the air at a temperature of 25°C, a pressure of 101,325 Pa and a relative humidity of 100%. That is, P(air) = 98,158 Pa and P(H₂O) = 3,167 Pa [4]. We then calculated the number of each of the fourteen molecules present in the atmosphere, for a total of 100,000 air molecules. This shows that the water molecule comes in third place, just after the oxygen molecule. Of course, we've assumed a relative humidity of 100%. So here we have the maximum number of water molecules that can be present at 25°C at sea level. But even in a hot desert, there will always be some humidity, up to 2%. With such relative humidity, we calculate P(air) = 101,324 Pa and P(H₂O) = 0.634 Pa [4], which still corresponds to 63 water molecules compared with one Xenon molecule and 182 Neon molecules. Water is thus becoming very rare, but is still very much present. In other words, it's completely unrealistic to consider air without a single molecule of water in it. Of course, this fundamental fact disqualifies air as an elementary constituent of all matter. After all, there will always be a non-zero quantity of water in air.

The same applies to the "element" Earth. Figure 3 shows the total amount of water present on planet Earth. Here too, imagining a totally anhydrous earth is totally unrealistic. There will always be moisture in the earth's soil. For comparison with Figure 2, we have considered an average soil composition. Once again, we calculated the molar fractions of the main elements and the proportion of water molecules. For the calculation, a typical soil was assumed to be 50% void and 50% dry matter. The 50% void contains either air (25%) or water (25%). For the inorganic solid part based on the elements (Si, Al, O, H + Fe, Mn, Ca, Mg, Na, Cl), we took a mixture of sand (40%), silt (40%) and clays (20%). The sand and silt are essentially composed of quartz with the formula SiO₂ and a molar mass of 60.08 Da. For the clay we have instead a kaolinite Al₂Si₂O₅(OH)₄ with a molar mass of 258 Da. Hence an average molar mass of 60.08×0.8 + 258×0.2 = 99.7 Da for the dry soil. A typical value for organic matter is 14 mg per gram of dry soil [5]. If we assume that this organic fraction is essentially a mixture of equal mass of amino acids belonging to proteins (average molar mass 110 Da per amino acid) and glucose (molar mass 180.156 Da), we calculate an average molar mass of 137 Da. Consequently, for a soil with a density of 2.66 g·cm⁻³ and 50% porosity, we would expect to find 1.33 g of dry mineral matter with an average molar mass of 99.7 Da in a volume of 1 cm³ when saturated with water. Then, 0.25 cm³ = 0.25 g of water with a molar mass of 18.01 Da. And again, 0.25 cm³ = 0.27925 mg of air with an average molar mass of 28.97 Da. And, finally, 18.62 mg of organic matter with an average molar mass of 137 Da. Hence the figures shown in Figure 3.

We can see that when we hold a handful of earth in our hand, we're essentially holding an equimolar mixture of water and matter, with very little air. And let's suppose that this air is flushed away by substituting water during a heavy rainfall, for example. We would then obtain, still for 10,000 molecules of "Earth": 6,732 molecules of water, 3,235 molecules of mineral rock and 55 molecules of organic matter. The conclusion is that what we call "earth" is more water than rock. This is why plants can grow even when no liquid water is visible. Hence the term "morphogenic" water [6]. This is a reminder of the fundamental fact that water can be found in vast quantities in a wide variety of forms. But, without revealing that they are, molecularly speaking, essentially just water. Indeed, the term "morphogenic" was coined from two Greek roots. On the one hand, the root "morphos", meaning "form". On the other, the root "genos", meaning "creator". So, morphogenic water is the water that gives rise to all the forms we can observe in the natural world around us. To convince yourself of this, all you have to do is thoroughly dehydrate any material form. It will then be reduced to powder. The only exceptions are materials formed from mineral particles such as quartz or clay, where water is not found inside the crystalline structures, but rather on the outside. In this case, it is possible to retain the original shape throughout the dehydration process, to obtain totally anhydrous glasses or ceramics.

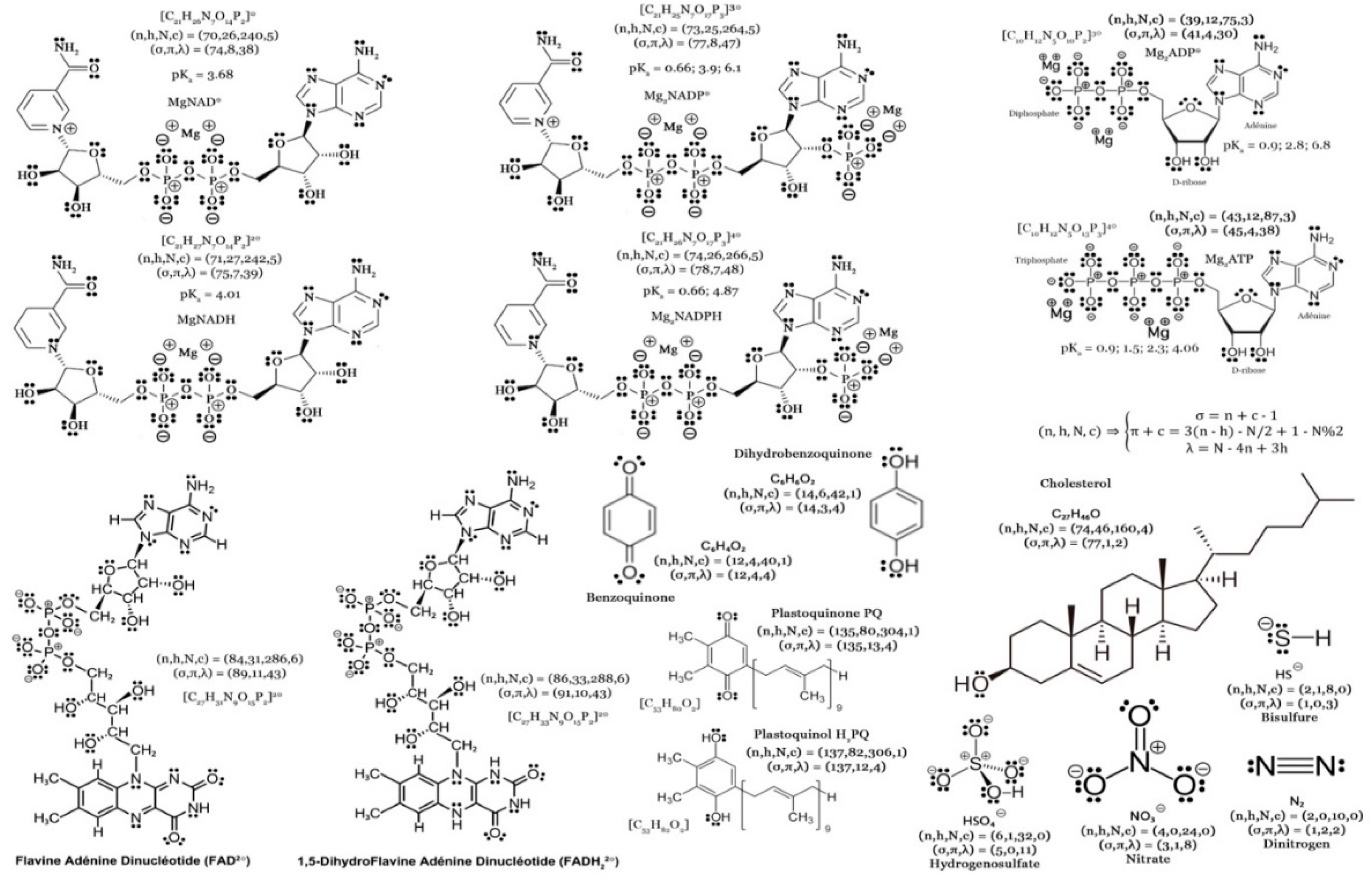
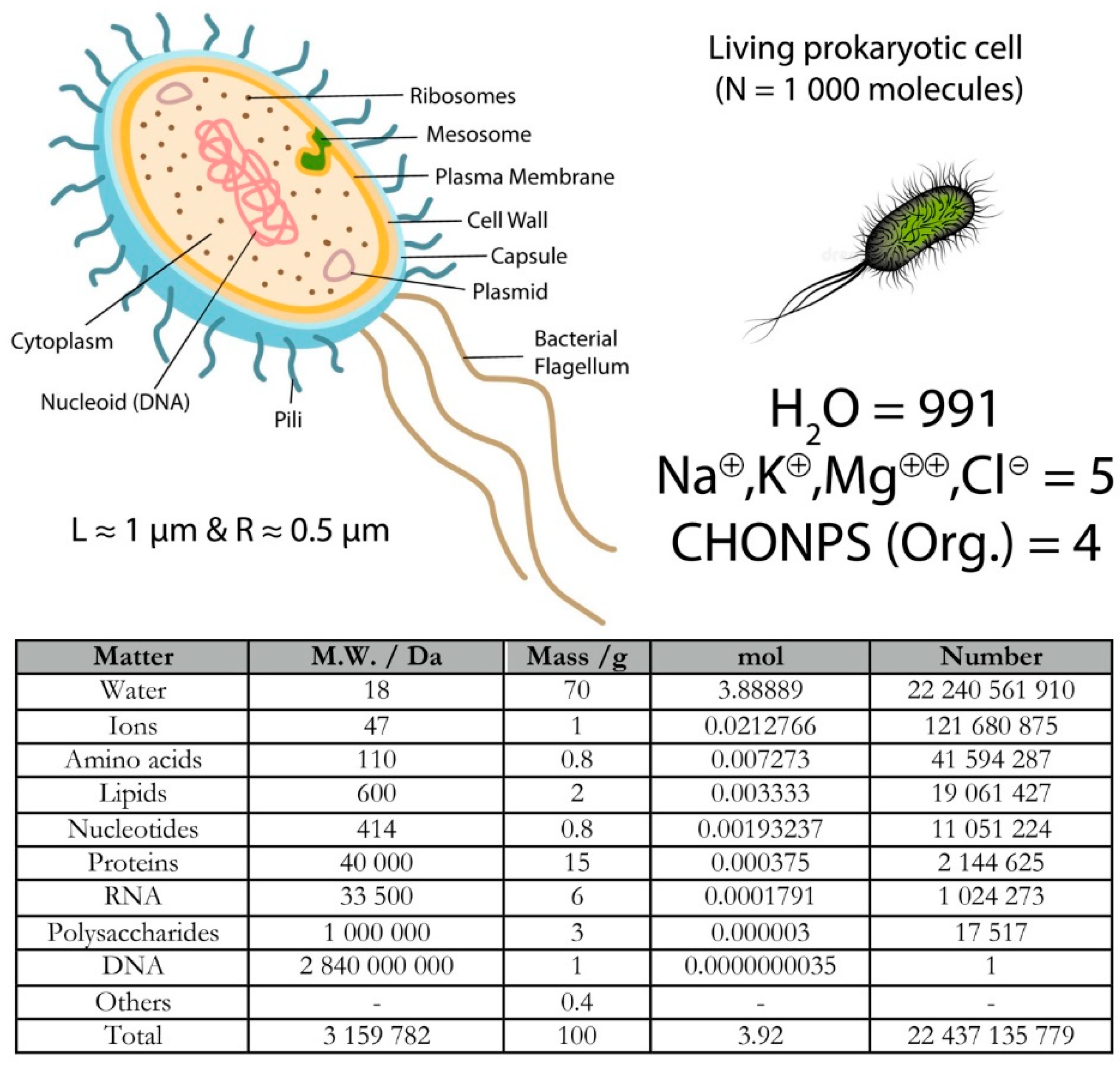
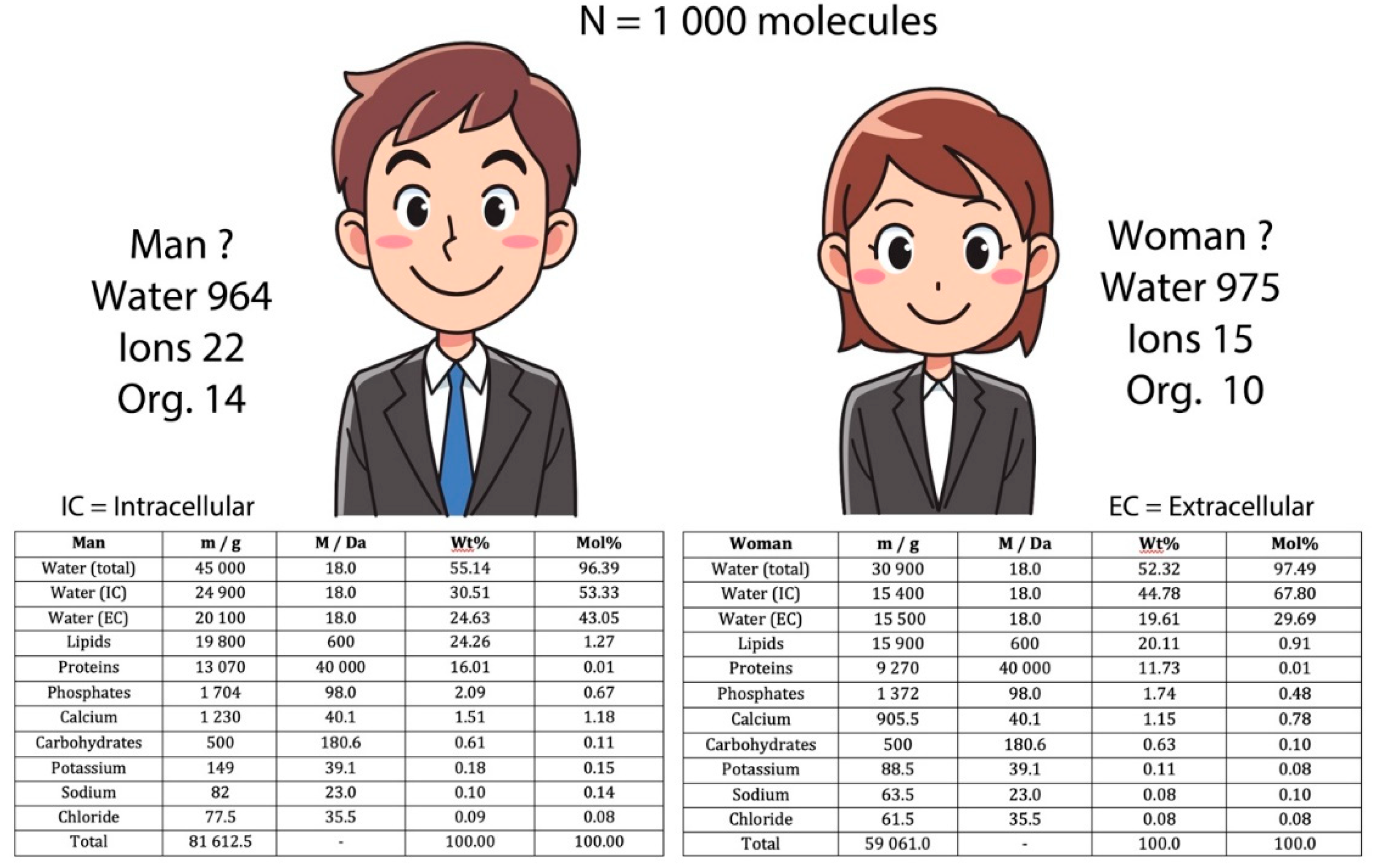
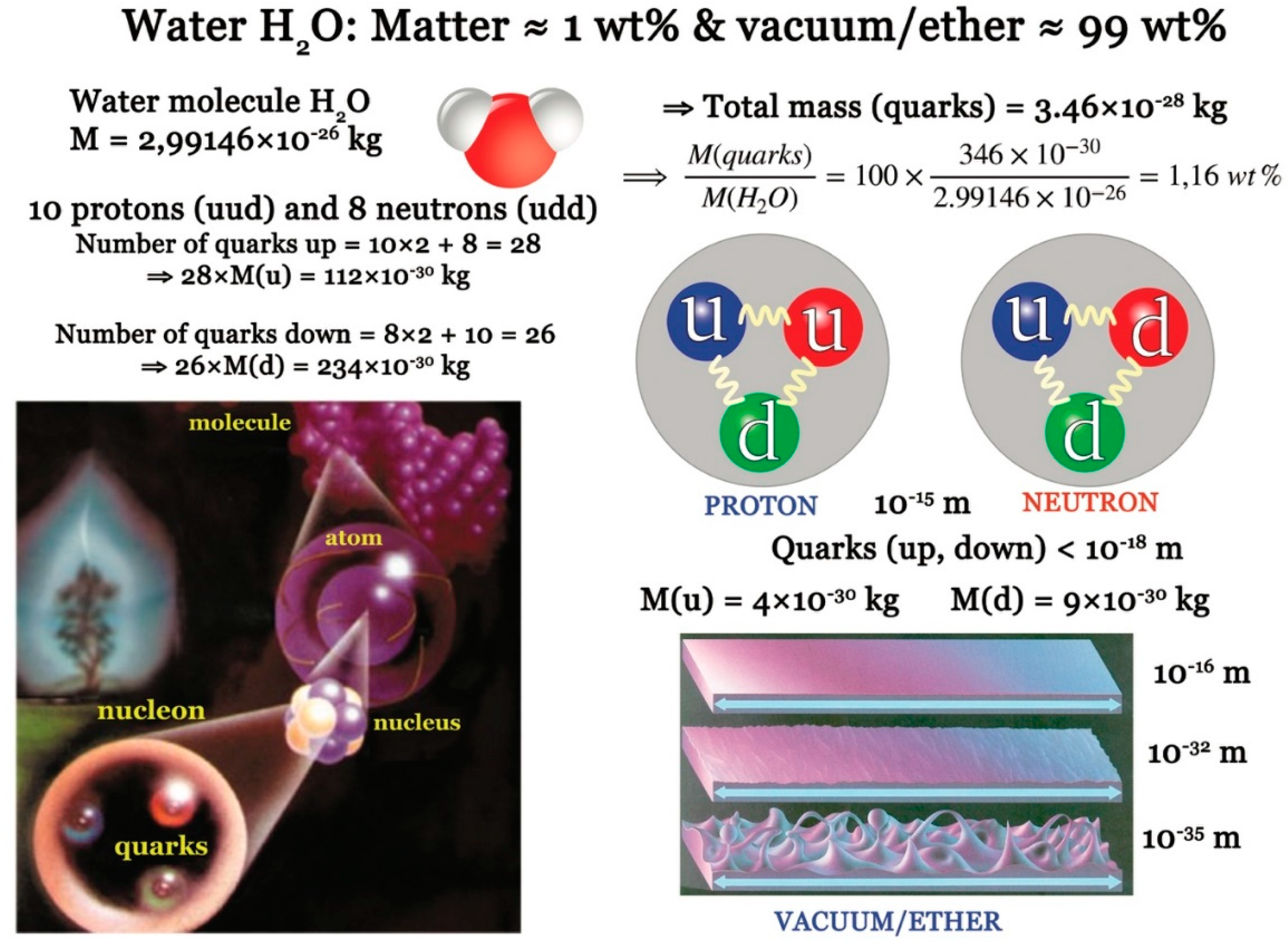
Let's take a look at an extreme case of an object that, from the outside, doesn't look like water. Yet it is essentially water. I'm talking here about a living cell of the prokaryotic type (see Figure 4). Take a bacterium like Escherichia Coli. What we see is a cylindrical body covered with very fine hairs. Several flagella emerge from the cylinder, enabling the bacterium to move around independently. In short, we're dealing with a living being, not inert matter subject to external disturbances. Now, let's take a look at what we find inside this bacterium (see the table accompanying the figure). This table lists the main constituents and their relative proportions [7]. And, as we've become accustomed to doing, let's transform all the measured masses into moles. The result is indisputable. This living thing is 99.1 mol% water. In other words, if we count to 1,000, we'll find 991 water molecules, 5 mineral ions and 4 molecules based on highly varied combinations of carbon, hydrogen, oxygen, nitrogen, phosphorus or sulfur (CHONPS). In other words, E. Coli bacteria can be summed up as a drop of slightly salty water "polluted" by a few rare organic molecules. Or, if you prefer, that all biology books, no matter how thick, speak, in fine, of only 4‰ of the matter present. All the rest, or 994‰ of the matter is a matter of water containing minerals.

This applies to all living beings. Take a human being, for example. If we look inside and out, we see skin, organs and bones. But if we take into account that all these objects are made up of cells, we would expect water to be the predominant molecule. Figure 5 lists the molecules present in a human body. The relative molar proportions totally confirm this point of view. Thus, a man, boils down to 964 mol‰ of water molecules containing 22 mol‰ of dissolved minerals and 14 mol‰ of molecules based on the CHONPS elements. For women, it's slightly different. There's a little more water (975 mol‰) and a little less minerals (15 mol‰) or organic molecules (10 mol‰). So, there's an awful lot of water in a male or female human being. In fact, the novelty for bodies made of eukaryotic cells, compared to a simple prokaryotic bacterium, is that there are two types of water: immobile intracellular water and extracellular water that moves. And it's in this respect that men differ from women. In a man there is much less intracellular water (533 mol‰) than in a woman (678 mol‰). Which means, of course, that we have the opposite situation for extracellular water: 431 mol‰ in men versus 297 mol‰ in women. In other words, the sexualization of human beings is primarily linked to water, more than to the shape of organs or the XX or XY nature of chromosomes. Hence the illusion of being able to change sex via surgery (organs) or genetic manipulation of chromosomes. Whatever we do, a man will always have more extracellular water than a woman.

Chinese Philosophy and Tao

Returning now to Figure 1, we can greatly simplify the Western materialistic vision of nature. Indeed, we now know that there are only two fundamental "elements" to consider: Water and Fire. And it's at this precise point that we should forget Western science for a moment. In the East, other, perhaps more relevant philosophies have emerged. I'm obviously thinking here of the Chinese civilization summarized in Figure 6. But first, a few dates. Figure 1 shows that in Greece, everything began in the first millennium B.C.E.

Chinese culture began as early as the third millennium B.C.E., with the Longshan culture (3000 - 1900 B.C.E.) in the lower basin of the Yellow River (Huang He). During the same period, in Europe, the Bronze Age began in Greece and the Aegean Sea (3500 - 2000 B.C.E.). In the Near East, the Jiroft civilization flourished in Iran (3200 - 2100 B.C.E.), followed by the Archaic dynasties of Mesopotamia (2900 - 2340 B.C.E.). The Indian subcontinent saw the blossoming of the Indus Valley civilization in India and Pakistan (2600 - 1900 B.C.E.). In America, vast cultural and religious complexes were built on the central coast of Peru (2600-1800 B.C.E.). Lastly, Africa saw the construction of the great pyramids in Egypt (2700-2000 B.C.E.).

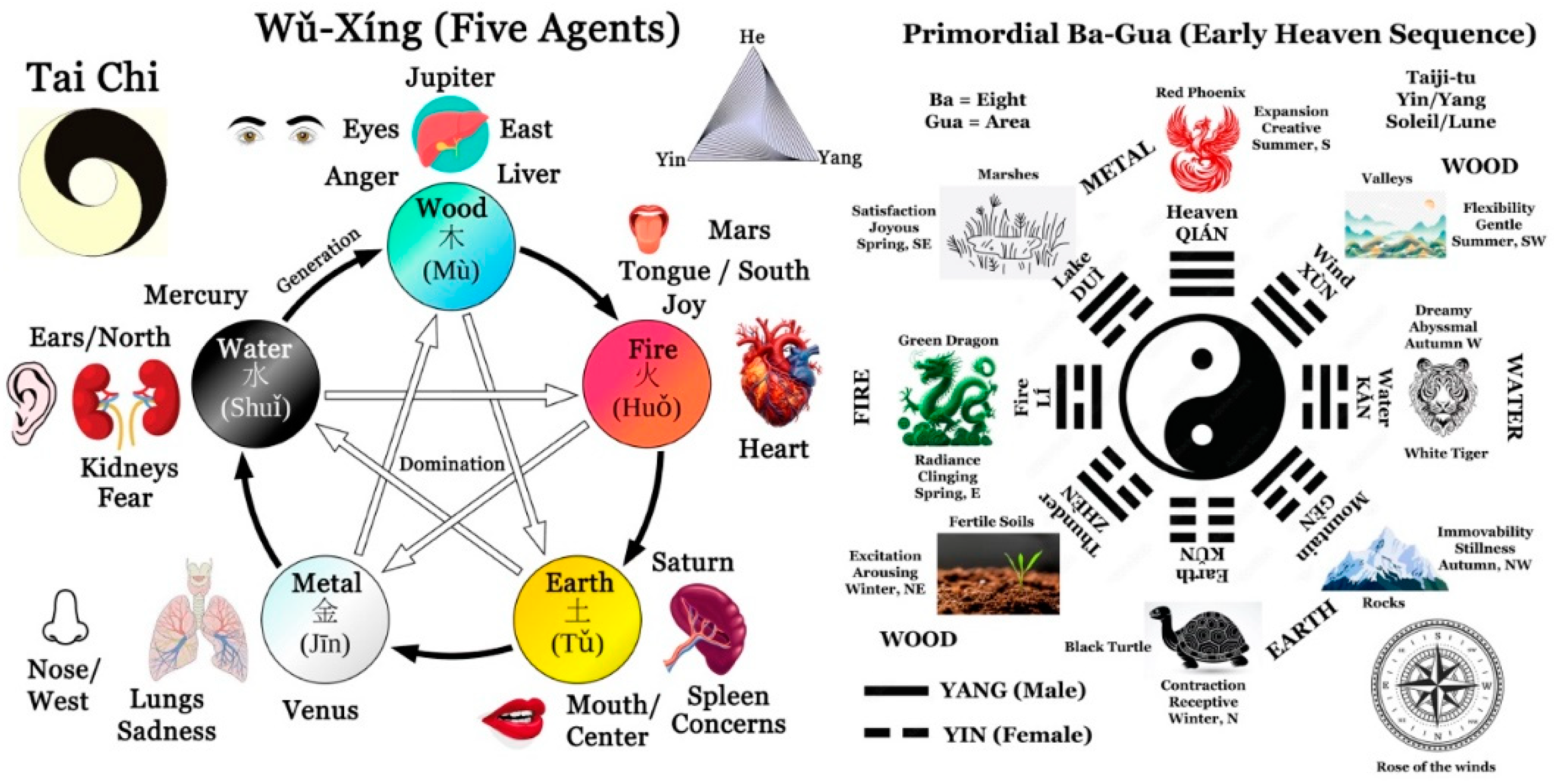
All this is to realize that Chinese culture far precedes Western culture, where the notion of elements refers to concepts of form, substance and quality. In China, on the other hand, we tend to speak of agents of transformation, and therefore of processes or changes. And these changes refer to the cosmos, the terrestrial world and human nature. To sum up. In China, we assume the existence of a fundamental principle forming and animating the universe, breathing life into it, the 1, called Tao. Tao then creates the yin-yang pair associated with the number 2. Yang is a masculine, sonorous principle (music) symbolized by the Sun, associated with all that is bright, luminous, hot (gas) and always in motion. In contrast, Yin is feminine and silent (rite), symbolized by the Moon, associated with all that is dark, obscure, cold (solid) and at rest. But because of the Tao in the background, Yang and Yin are by no means static principles. On the contrary, they are dynamic entities that allow Ch'i or Q'ì to circulate. When Ch'i circulates, what is light and clear tends to rise towards the sky. What's dark and heavy, on the other hand, tends to fall to the ground. A well-known symbol of this dynamic Yin/Yang duality is the "Tàji Tú", which features two spirals of opposite chirality. One is white, the other black. But both are interlocked, with black and white dots superimposed. Hence the dynamic, since at any moment the white spiral can become black and vice versa.

Of course, such a constantly shifting Yin/Yang dynamic calls for a state of balance and harmony, "He", associated with the number 3 and the geometric figure of the triangle. Hence the saying: "Never two without three". There are two ways of representing this ternary principle. The first is in the form of the "Tai Chi" symbol, represented by a white center around which two spirals wind, one yellow, turning to the left, the other black, turning to the right. Here, the dynamic has been stabilized by the presence of the Tai Chi center. The second representation is an equilateral triangle. Here, the base symbolizes the Yin/Yang duality and the third vertex the "He", achieving a perfectly balanced synthesis between the two opposing vertices. Of course, the perfect ternary symmetry evokes the idea that the "He", "Yin" and "Yang" aspects are totally indistinguishable, forming a unity that recalls the existence of the "Tao". If the Yin/Yang pair refers to the Earth/Sky pair, the Yin/He/Yang triplet indicates that between Heaven and Earth, there is a middle ground. And that this middle ground, symbolizing the harmony of the Earth/Sky pair, could very well be the human being. Hence the existence of three types of "energy". The first, Yang (Ch'i), is of a respiratory nature, breathing life into us. The second, Yin (Jing), is of a sexual nature, authorizing reproduction. And the third, He (Chen), is spiritual in nature, animating the immortal soul of every human being.

In Taoist philosophy, everything that is 1, 2 or 3 is invisible and inaccessible to the human senses. This is why the summits of Chinese pyramids are always truncated to symbolize such inaccessibility. For, as explained in the Tao Te Ching, the number 3 is capable of producing all things: "The Tao produced One; One produced Two; Two produced Three; Three produced All things. All things leave behind them the Obscurity (out of which they have come), and go forward to embrace the Brightness (into which they have emerged), while they are harmonized by the Breath of Vacancy." [9].

Among them, the very first, the number 4, restores the dynamic introduced by the number 2. But this new dynamic is an accessible movement of earthly nature represented by the four cardinal points (South, West, North and East). And each of these four cardinal points is associated with a legendary animal associated with the four seasons. With one pair (South/North) represented by the Red Phoenix (Summer)/Black Turtle (Winter) pair, which is associated with a duality of Heaven (Yang) and Earth (Yin). A second pair (West/East), represented by the White Tiger (Autumn)/Green Dragon (Spring) pair, is associated with the duality of Water (Yin) and Fire (Yang). It is at this precise point, the Water/Fire duality, that Chinese and Greek philosophers find themselves on the same wavelength. This also applies to the other pair, which is formulated as Heaven/Earth in China and Air/Earth in Greece. And isn't Air in Heaven, the opposite of Earth?

The difference between the two philosophies is that the four Greek elements emerge from virtually nowhere. The four cardinal directions, on the other hand, have the Yin/Yang duality and the unity of the Tao as their backdrop. From this point of view, Chinese philosophy appears far more rational and convincing than Greek philosophy. But it's also the way it follows the numerical progression that makes it even more convincing. For example, for the number 5, we tend to think of the five "elements" of Wu-Xing (five-pointed star). But this would be a serious mistake. The temptation is great, since three of these agents (Fire, Water and Earth) coincide with three of the Greek elements. Only Air is eliminated from the Chinese pentacle. The reason is simple, since Air actually appears in the form of Heaven in the number 4, which precedes the number 5. It would therefore be totally illogical to include it again at this higher level. So, how do we understand these 5 agents?

The idea is to understand that the number 4 is intimately associated with life on Earth. The Earth is dark, while the Sky is clear and luminous when the Sun shines. And, as chapter 42 of the Tao Te Ching makes clear, all things tend to move from darkness to light. As the number 4 is associated with the Earth, it's only logical that it should tend towards the next level up, the number 5, which must therefore be associated with Heaven. And what do we see moving in the sky apart from the Sun (Yang) and Moon (Yin)? The answer, of course, is the stars. But a careful observer of the heavens will note that these "stars", observable as points of light, are of two types. The vast majority of these points of light form unchanging patterns in time, called "constellations", which move as a whole through rotation. On Earth, however, everything is in constant motion, thanks to the harmony brought about by the breathing of the void. So, all we have to do is search the sky to see if there are any luminous points animated by the breathing of the void, never occupying the same place from night to night. If so, this could hold the key to the successor of the number 4.

And, indeed, all is well, for there are exactly five points of light moving against a fixed, unchanging background of stellar constellations. These are, of course, the five planets of the solar system visible to the naked eye. Starting with the Sun: Mercury, Venus, Mars, Jupiter and Saturn. Symbolically, the number 5 refers to the letter X, formed by two inclined branches meeting at a point. This letter also appears if we project a square-based pyramid from its apex, where the four triangular faces meet. The number Five thus reveals a center, whereas the number Three revealed a median. It is, therefore, a higher degree of harmony that brings stability. Such a center, organizing two pairs of opposing Yin/Yang polarity, is obviously reminiscent of the undifferentiated Tao. Here we find the attributes of the planet Mercury, whose sex is both male (Yang) and female (Yin). Mercury, i.e. intelligence, is therefore an organizing center between the pair Mars (Yang) and Venus (Yin) on the one hand, and the pair Jupiter (Yang) and Saturn (Yin) on the other. But we can also refer to the organizing center of the human heart. And here, the pair of opposites becomes the pair Kidneys (Yin) and Spleen (Yang) on the one hand, and the second pair Lungs (Yin) and Liver (Yang) on the other.

As you may have gathered, in Chinese philosophy, even numbers are dynamic in nature. They therefore belong to the earthly realm. In contrast, odd numbers are static in nature, belonging to the celestial realm with its unchanging stellar constellations. So, the successor to the number 5 must refer to a higher level of terrestrial organization. A level where we expect to find the dynamic impetus of the number 2. On the other hand, the harmony brought about by the number Five, symbolized by the letter X, must not be broken. There's only one solution: the octahedron, a geometric figure with six vertices and eight triangular faces, which, like the square-based pyramid, is again represented in projection by the letter X. This new figure, or geometry, allows us to achieve a perfect balance between the three directions of the earth: Right/Left, Front/Back and Top/Bottom. The Six figure thus organizes the dynamic exchanges between Heaven and Earth, shaping the world in which life expresses itself.

With the number Seven, we find celestial stability in the form of a new organizing center. Geometrically speaking, we add a center to the octahedron, where the three directions defined by the number Six intersect (7 = 1 + 6). This organizing center is the spark of life that can either start or stop. Here we find the Yin/Yang fusion expressed through the pairing of Life (Yang) and Death (Yin). To be alive is to accept that we must die one day. But, at the same time, it means admitting that it is always possible to be reborn if you have died. The number Seven represents the attainment of a perfection that can be seen in the celestial image: Sun, Moon, Mercury, Venus, Mars, Jupiter and Saturn, i.e. 7 = 2 + 5. But also in the earthly image: Heaven, Middle, Earth, Spring, Summer, Autumn, Winter, i.e. 7 = 3 + 4.

The number Eight represents the distribution and terrestrial organization of the formidable vital energy underpinned by the number Seven (8 = 7 + 1). But it's also the number of double differentiation (8 = 4 + 4), symbolized by the eight-pointed compass rose. The four intermediate directions (SE, NE, NW, SW) here refer to the fact that when the Earth accumulates, mountains are created by the accumulation of rocks. Between two mountains, there's usually a valley in which the air is set in motion, generating wind. Mutually-reinforcing winds can lead to thunderstorms, with thunder and lightning shattering rocks and transforming them into fertile soil. Last but not least, mountains facilitate the condensation of water in the form of snow on high ground, which then melts and gathers in the deepest valleys to form lakes or marshes. The result is a new, clearly terrestrial quaternity (Mountain/Vent/Thunder/Lake) rotated by 45° in relation to the quaternity (South/East/North/West) expressed in the Sky. This is where we find the primordial Ba Gua or Pa Kua of Taoism or Feng Shui. This geometric figure of octagonal symmetry can also be deduced from the 8 trigrams of the Yi Jing, as shown in Figure 6 on the right. This figure expresses geometrically the numerical identity 2³ = 2×2×2 = 8. Another geometric figure, the cube with its 8 vertices, expresses a double quaternity (8 = 4 + 4) indistinguishable from the square when projected onto a plane along one of its 6 square faces.

Ba Gua is a tool for checking whether qi (or chi) is flowing properly through the body. As the number eight is associated with healing, this is another tool for rebalancing the energies circulating in the house where you live. In Taoism, we find here all eight immortals. These embody the dynamism associated with victory over earthly death (number 4), through perfect union with the essence of life (another extra- or intra-terrestrial number 4). All this through eight figures representative of Chinese society:

-: The military man, Zhon LiQuin, leader of the group, who uses his fan to resurrect dead people.
-: The woman, He XiangGu, holding in her hand a lotus that represents spiritual fulfillment and watches over the family's health.
-: The vigilante, Lü DongBing, an alchemist who, with his sword, symbolizes moral rectitude combined with knowledge and wisdom. He is the patron saint of poets.
-: The beggar, Lan CaiHe, holding a basket of flowers, symbolizing happiness and longevity. He is the patron saint of gardeners.
-: The scholar, Han XiangZi, writer and civil servant, always carries a flute. He is therefore the patron saint of musicians.
-: The ugly, shaggy, bedraggled cripple, Tie GuaiLi. He holds a gourd, symbol of immortality, filled with the elixir of long life. He is the patron saint of the sick.
-: The old man, Zhang GuoLao, who wards off evil spirits with his "YuGu" cylindrical drum. He is the patron saint of painters.
-: The great nobleman, Cao GuoJiu, who purifies the world with his two jade plates. He is the patron saint of actors.

After the earthly number Eight, symbolizing the possibility of rebirth after death, we move on to the number Nine, which brings us back to celestial stability. Geometrically, we again consider the cube, but, as before, we include the center (9 = 8 + 1). The immaterial celestial aspect of the number 9 is symbolized by the nine orifices of the human body: 2 eye cavities, 2 ear cavities, 2 nasal cavities, 1 mouth, 1 vagina in women or 1 urethra in men and, finally, 1 anus (9 = 2×3 + 3 = 6 + 3). The Nine thus asserts itself as a complete completion, a finishing touch, the completion of the One. Nine thus represents the exhaustion of numbers. It symbolizes the achievement of completeness. For everything has been deployed, organized and completed. Hence, in humans, the 9 months of pregnancy, or, in cats, the 9 weeks before giving birth.

Nine therefore symbolizes the greatest expression of Yang. But, at the same time, its exhaustion. Hence the need to return to unity, symbolized by the number 10 (10 = 1 + 0 = 1). A number that can be associated with Wu-Xing and its 5 agents: Wood, Fire, Earth, Metal and Water. Note that three of the five agents (Earth, Water and Fire) are also present in the octagonal Ba Gua. So, for the latter, we can also consider that the wood element splits into a pair (Wind, Thunder) and the metal element into a pair (Lake, Sky). This leaves two opposing pairs (fire, water) and (earth, mountain), i.e. 8 = 4×2 instead of 4 + 4.

But in Wu-Xing, the 5 agents are involved in 5 cycles of creation and 5 cycles of domination (Figure 6 left), i.e. 10 = 5×2 = 5 + 5. On a strictly numerical level, we can appreciate the elegant solution to the crisis generated by the number 5 and the basic instability linked to the number 2, i.e. 10 = 5×2 or 7 = 5 + 2. It's well known, but it's worth remembering. So, to create fire, you need wood, and once burnt the wood will have generated ashes, i.e. earth. These ashes are made up of metal cations, which when buried in the ground can be reduced to metal. When the metal comes to the surface, drops of water appear. This water is necessary for the wood to grow again. It's all perfectly logical, and there's no divinity involved in the process of creating one element from another. The result is a 5-stage generation cycle in the shape of a regular pentagon.

But alongside this Yin cycle of generation, there's also a Yang cycle of domination, which takes the dual form of the star pentagon. Thus, fire dominates metal, since it melts it. Metal in turn dominates wood, as it enables it to be cut into pieces. Wood dominates earth, as it lifts and pierces it as it grows. Earth dominates water, as it channels it and prevents it from flowing away. Finally, water dominates fire, since it can extinguish it.

All this is of course applicable to the human body. Figure 6 shows the analogy between the 5 agents, i.e. the 5 main organs (Heart, Spleen, Lungs, Kidneys and Liver) of a Yin nature. Here, the Liver communicates its energy to the Heart, which in turn communicates it to the Spleen, which passes it on to the Lung, which sends it to the Kidney, before returning to the Liver. Alternatively, this is the Yang cycle of the 5 emotions. Thus, joy dominates sadness, since it makes it disappear. And when you're angry, becoming sad makes the anger disappear. Anger, on the other hand, is a reaction to the presence of worries. These are eliminated as soon as we become afraid. And, finally, as soon as you're afraid, you can't be happy, which brings us back to where we started. Through this type of correspondence and the two movements of generation and domination, it is possible to cure a large number of illnesses, both physical and psychological. For this, natural derivatives of minerals, plants or animals are used.

And What About the Vacuum?

The main advantage of Chinese philosophy over Greek philosophy is that the two antagonistic pairs Water/Fire and Heaven (Air)/Earth do not emerge from nothing. They originate in an undifferentiated unity, the Tao, which is simultaneously feminine and masculine in nature. On the other hand, the notion of emptiness escapes Taoism altogether. The term "undifferentiated" refers to something that exists and is not empty. In other words, Chinese arithmetic starts with the number 1 and forgets the number 0. Yet, as we saw above, to explain the movement of atoms, Greek philosophy needs the void. If you prefer, the notion of negative quantity has no place in Chinese philosophy. It's all about the positive, the tangible, the manifest. Concepts born of three things imperceptible to our five senses, but also "full". The unity of the Tao, the duality of Yin/Yang and the median term, He harmony, which leads to the possibility of creating everything via a trinity.

As already mentioned, modern science validates the atomic theory of matter. And, therefore, the underlying notion of emptiness, which is absent from Taoism. Hence the rejection of this elegant vision of the structure of the visible universe, where there is no place for the void. This is particularly striking in medicine, where in the West, all illness is treated with chemical molecules made up of atoms, and not according to Taoist philosophy based on an intangible Yin/Yang duality. In this section, I propose to show that, via the science known as quantum field physics, or second quantization physics, we can forget the notion of the atom. And that, fundamentally, everything is a matter of a vacuum capable of vibrating.

The best way to introduce the subject is to return to the atom, the elementary constituent of all matter. In chemistry, these ideas are finalized in the periodic table of elements drawn up by the chemist Dmitri Mendeleev (Figure 7). But let's forget this table for a moment, and focus on the first box bearing the symbol "H" for the hydrogen atom. At the beginning of the twentieth century, just when we thought we had completely elucidated the nature of matter, a terrible crisis arose. This crisis was linked to the discovery of a tiny particle of matter that explained the existence of electrical and magnetic phenomena: the electron. This particle of matter in fact carries a negative elementary electric charge -e = -1.602 176 634×10⁻¹⁹ C. These "electrons" were discovered in 1899 by British physicist Sir Joseph John Thomson (1856-1940). His discovery was rewarded with the Nobel Prize in Physics in 1906.

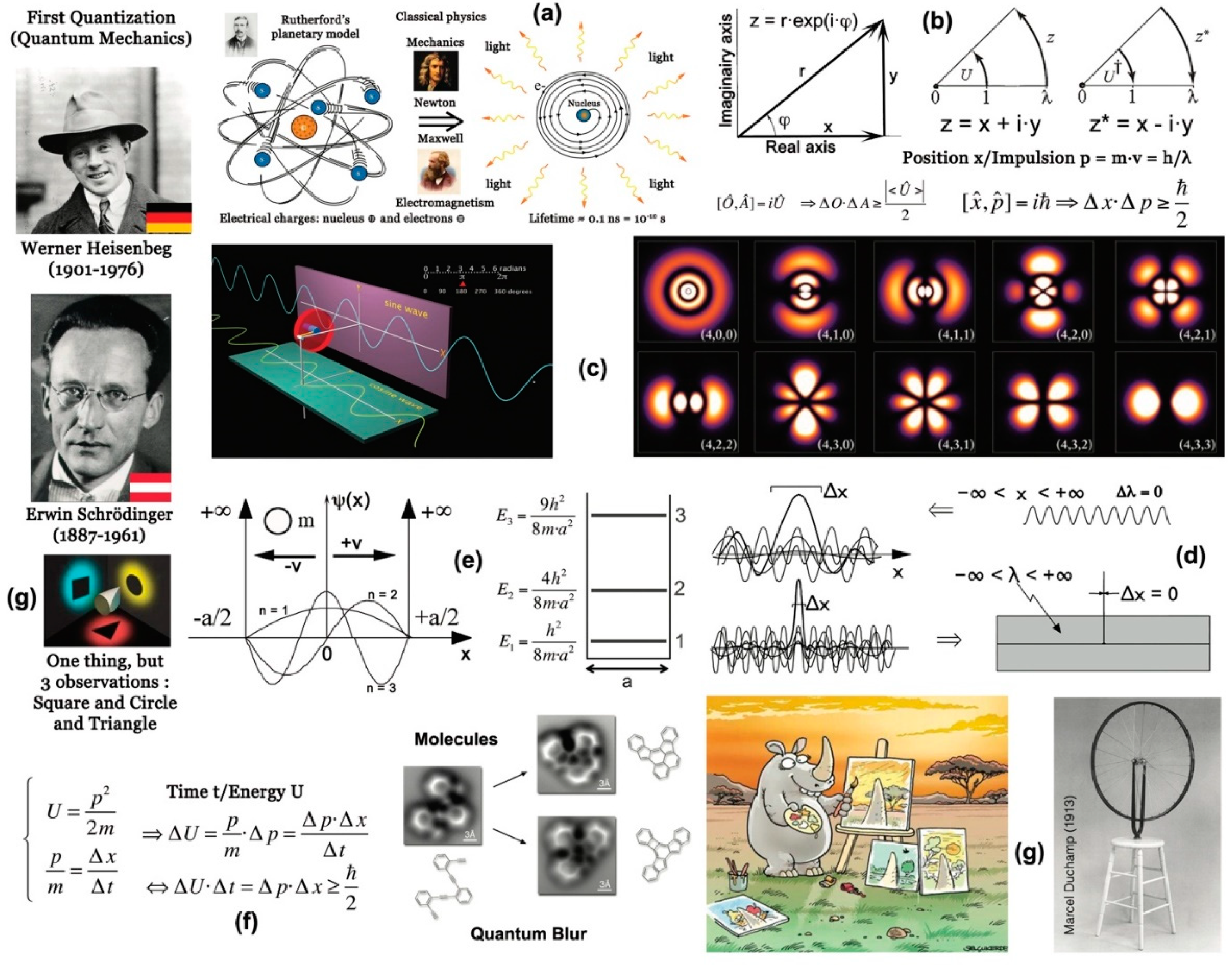
Then, in 1911, New Zealand physicist and chemist Ernest Rutherford (1871-1937), the father of nuclear physics, discovered the atomic nucleus, which carries an electric charge of the opposite sign to that of the electron, and is therefore positive. In 1914, he hypothesized that the nucleus of hydrogen, the lightest known atom, was made up of a single, positively-charged particle, which he named the proton. In 1914, we learned that the most abundant atom in the universe, the source of all other elements synthesized in the heart of stars, is composed of a single proton with a positive charge +e. Around this proton "orbits" a single electron of opposite electric charge -e. All is well. Except, of course, for Coulomb's law, the validity of which cannot be called into question. This law stipulates that two electric charges of opposite sign must attract each other. And this, with a force proportional to the inverse of the square of the distance separating the two charges. And that's the end of the matter. Because of this law, the hydrogen atom simply cannot exist! If, by any chance, a proton with a positive electric charge sees an electron with a negative electric charge in its vicinity, it will inevitably attract it to itself (see Figure 8, top left). And, in the end, the only stable configuration will be a proton that has swallowed an electron, i.e. a neutron n°. This second particle does exist, but was not discovered until 1932 by British physicist James Chadwick (1891-1974).

In 1914, such instability came as a great surprise. And, above all, we were totally unable to explain the electron cloud's size of around 0.1 nm = 10⁻¹⁰ m. A huge value compared to the size of the nucleus, which is around 1 fm = 10⁻¹⁵ m. A very mysterious force seemed to hold the electron in an orbit far away from the nucleus, preventing it from crashing into it. To understand the scale of the problem, the nucleus, which concentrates all the atom's mass, has a volume of 10⁻⁴⁵ m³. This compares with a volume of 10⁻³⁰ m³ for the electron cloud. In short, 99.9999999999999% of an atom is empty space! So why so much vacuum? The atom would appear stable instead of imploding on itself. And, not with a lifetime of the order of 0.1 ns = 10⁻¹⁰ seconds. And, releasing an enormous amount of light.

However, there was a hint that the situation wasn't quite so catastrophic. In fact, according to Maxwell's theory, the "vacuum" didn't seem quite empty. Since, to allow the propagation of light, it had to possess an electrical impedance Z₀ = µ₀·c ≈ 377 Ω, with µ₀ = 4π·10⁻⁷ kg·m·A⁻²·s⁻² (magnetic permeability of the vacuum) and c = 299,792,458 m·s⁻¹ (propagation speed of light in vacuum). A new science was indeed about to be born. And it's best to quote the revealing words of French mathematician Henri Poincaré (1854-1912): "One of the most astonishing discoveries that physicists have announced in recent years is that matter does not exist...". [10].

First Quantification

The solution to the mystery arrived in 1924 with the advent of quantum mechanics. But rather than rehash the well-known history, let's jump straight to the founding principle of this science, known as "contextuality". This was stated in 1946: "There is no such thing as a state variable" [11]. Remember that every value of a state variable, such as the internal energy U in thermodynamics or the Hamilton function H in mechanics, corresponds to an exactly defined value for every other variable. The Février-Destouches theorem [11] therefore dictates that if an observable system possesses a state variable, then statements of measurement results on this system must follow classical Aristotelian Boolean logic. Namely: identity, contradiction and excluded third. In such a case, determinism is said to exist, since all quantities are simultaneously measurable. Hence the use of so-called "real" numbers, which open up the possibility of differential and integral calculus, unlike "integer" numbers where this kind of calculation is impossible. This is the situation encountered in classical Newtonian or relativistic physics, thermodynamics or electromagnetism (Maxwell's equations).

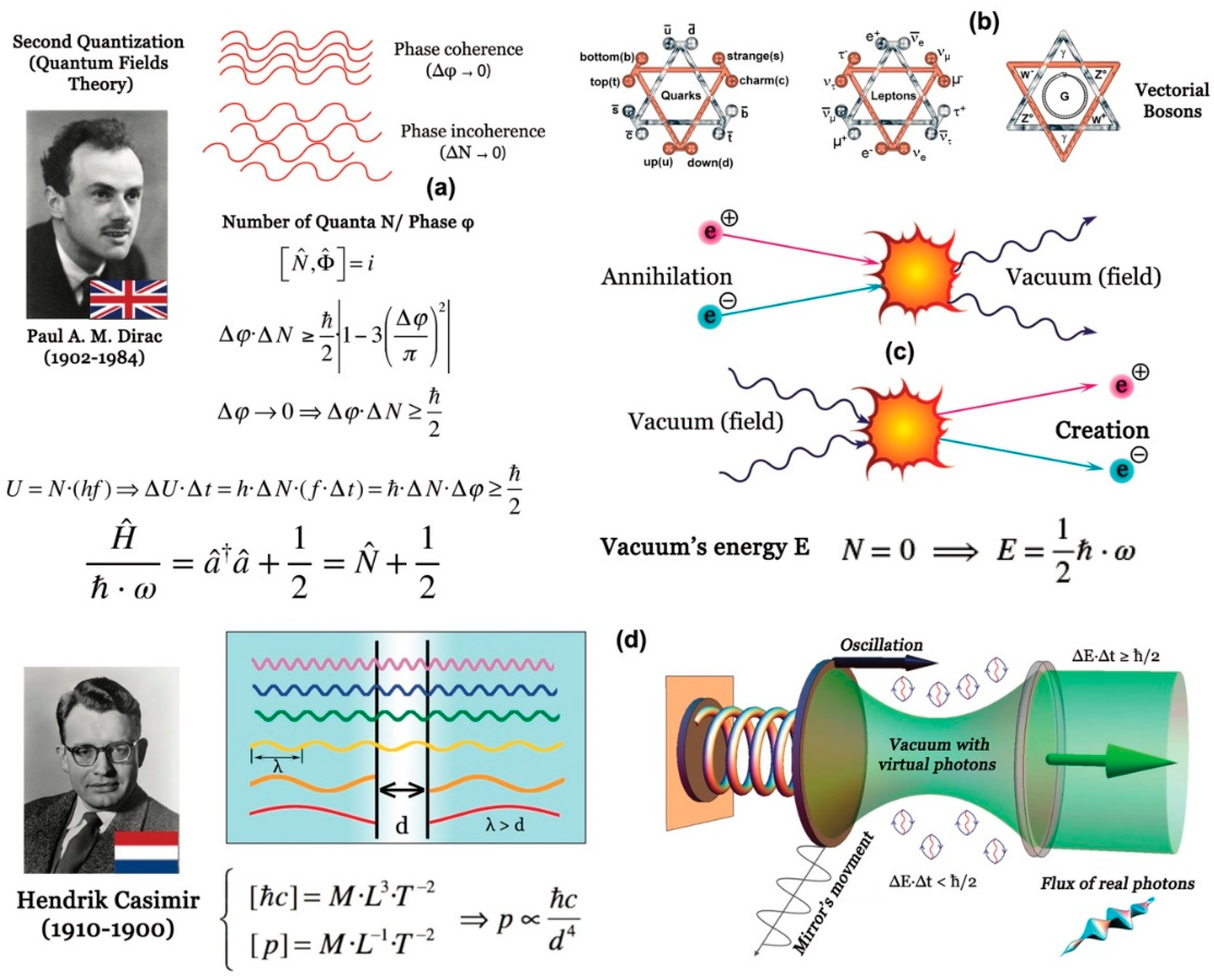
And it's precisely at this level that something very remarkable happens. For, many natural things are measured with integers, not real numbers. So, when a cell divides, you get two cells, then four, then eight and so on. You'll never get 3.1416 cells. Similarly, an apple tree will always yield an integer number of apples, and a family will always be made up of an integer number of individuals. And, above all, when a hydrogen atom is excited, it emits only certain frequencies that can be indexed by integers. Between two emission lines, there is only darkness, no light. In the same way, between the number 1 and the number 2, there's nothing at all, just emptiness. And, as we saw above, an atom is, in fact, essentially empty, containing a whole number of protons, neutrons and electrons.

The triumphant physics of the entire nineteenth century was based on the use of infinitely divisible real numbers. It is perfectly incapable of explaining the integers used by spectroscopists to index the absorption or emission lines of atoms. And it was this same physics which, in 1914, forbade these very atoms to exist. There was only one way out: give up on real numbers and develop a new physics in which integers would play a leading role. Integers have been used since the dawn of time to count and answer the question: "How many ..."? And the Latin word for "how many" is "quantum". Hence the name "quantum mechanics" for this new physics that was to restore stability to the atom. And explain why they respond with discontinuous integers. The father of this quantum theory was the German physicist Max Planck (1858-1947).

The latter was obsessed with the problem of the ultraviolet catastrophe in the radiation spectrum of the "black body". In fact, we knew that at low temperatures a black body could emit in the infrared. At very high temperatures (T > 10,000 K), its color ranges from red to blue. The problem was that it never emitted in the ultraviolet at room temperature (T ≈ 300 K), as predicted by Maxwell's theory. Something forced the radiation density to decrease exponentially with temperature. And, there was nothing in Maxwell's equations to identify that something. All that was known was that, at low temperatures, experiments showed that radiation density increased with the square of the frequency. And, that this experimental fact was well and truly predicted by Maxwell's theory.

We were therefore faced with a theory that was both true and false. Planck, in a flash of genius, wondered whether it wasn't the calculation procedure, involving the calculation of an integral, that needed to be called into question. Integral calculation presupposes the use of real numbers. What would happen if we used integers instead of real numbers to index light emission frequencies? So, Planck replaced the integration procedure with the calculation of an infinite but convergent series. This time, the solution obtained was perfectly in line with the experimental curves. What's more, at low frequencies, we find the radiation density predicted by Maxwell's theory. At high frequencies, we find an exponential decay that avoids the ultraviolet catastrophe.

In doing so, a new universal constant, Planck's constant (symbol h ≈ 663 zJ·fs = 6.63×10⁻³⁴ J·s), had just made a sensational appearance in physics. Now, it turns out that this constant has the dimension of an action, M·L²·T⁻¹, a well-known quantity in Lagrangian mechanics. Here, to predict the trajectory of a moving object, we seek to minimize its action integral. From a practical point of view, action is defined as energy E multiplied by time ∆t. But since the inverse of a duration measured in seconds is a frequency f measured in hertz (Hz), it follows that we can write: E = h·f. Here, energy is no longer seen as something dependent on mass and velocity, but rather as something associated with vibration. And, in the case of light, what vibrates are immaterial entities, the electric field E or the magnetic induction B. The conceptual leap then is to think that, as an atom is essentially made up of a vacuum, the latter would be more a vibration of the vacuum than a material thing. In short, everything in nature would be vibration rather than matter... And then, the integer n would express the idea that, in nature, any change implies the involvement of, at the very least, a quantum of action h, perhaps more (n×h) but never less (n ≥ 1).

This is where we need to return to the Février-Destouches theorem. Since, in order to have the right to manipulate real numbers, there must be a state variable. On the other hand, as soon as there are quantities that are not simultaneously measurable in law, there can be no state variable. Essential indeterminism then arises, as certain pairs of propositions cannot be joined by the conjunction and (∧) according to the rules of classical propositional calculus. In this case, it is necessary to use complementarity logic rather than Boolean logic. The practical consequence is that we must then abandon the use of real numbers and instead use an algebra based on complex numbers.

Now, a complex number is actually a pair of real numbers, the first called the "real part" and the second the "imaginary part". In other words, while the real number is represented by a straight line, the complex number is represented by a plane. And what can you do in a plane that you can't do on a straight line? Answer: you can rotate. Basically, real numbers allow you to make translations, while complex numbers allow you to make rotations. And, of all the possible rotations, there's one in particular that takes the real number line in a perpendicular direction. This rotation, represented by the symbol "i", has the following property: i² = i×i = -1. The fact that we get the number -1 after squaring is due to the fact that if we turn twice by an angle of 90° in the same direction, we end up on the starting straight line. But if this straight line was oriented to the right, it ends up oriented to the left after the double 90° rotation. Hence the -1 sign. To get the axis back to its original orientation, we therefore need to perform the operation i 4 times: i⁴ = i²×i² = (-1)×(-1) = 1. There's nothing mysterious about this once you've understood that a complex number, z = x + i·y, is a two-dimensional number. And not a one-dimensional number like a real number. The operation known as "conjugation", which consists in changing the sign in front of the symbol "i", means that the rotation must be in the opposite direction, i.e. from right to left.

But complex numbers z = x + i·y also have another, non-Cartesian representation, known as "polar". Here, the same number z can also be seen as an arrow having a certain length r and making a certain angle φ with the axis measuring the real part. Furthermore, when the arrow rotates with a constant angular velocity, the movement of its tip projected along two perpendicular directions generates two vibrations 90° out of phase with each other. In other words, the real part x corresponds to a cosine function, while the imaginary part y corresponds to a sine function, i.e. z = x + i·y = r×exp(iφ) = r·cos φ + i·sin φ. Consequently, to assert that "everything is vibration" is to admit that physical reality must be described with complex numbers rather than real numbers. It then follows, according to the Février-Destouches theorem, that there is no such thing as a state variable. In other words, this means that, in law, there are two quantities that cannot be measured simultaneously. This gives rise to an essential indeterminacy, which implies that certain forecasts are subject to error, and must therefore be expressed in terms of probabilities rather than certainties.

All that remains is to find this pair of non-simultaneously measurable quantities. To do this, we simply need to forget the notion of energy for a moment and focus on the concept of entropy S, a physical quantity introduced in 1854 by Prussian physicist Rudolf Clausius (1822-1888). For, thanks to Clausius, we have the second principle of thermodynamics, which states that during any material transformation, the entropy of a system can only increases: ∆S = ∆Q/T ≥ 0. Here ∆Q is the amount of heat exchanged during the transformation and T the absolute temperature measured in Kelvin (K). Behind this inequality lies the fundamental principle that heat always flows from the hot body to the cold body. The opposite process, in which the cold body spontaneously gives up heat to the hot body, can never be observed.

But, thanks to the kinetic theory of gases, we know that all matter is made up of atoms in motion for a certain temperature T ≥ 0. Now, according to the laws of mechanics, every atom is defined by its position q and by its momentum p = m·v, where m is a mass moving at velocity v. This is called a "microstate". And for a macrostate characterized by a given volume V and temperature T, there exists a set of microstates W, all compatible with the macrostate in question. Thus, in 1875, Austrian physicist Ludwig Boltzmann (1844-1906) established a link between the entropy S of a system and its number of accessible microstates: S = k_B·Ln W, where k_B = 1.380649×10⁻²³ J·K⁻¹ is a universal constant which Max Planck called Boltzmann's constant in 1900.

Now, due to Brownian motion any atom is equiprobably located at any point of a certain volume V = L³. Hence a positional indeterminacy ∆q = L along x, y or z directions. This corresponds to a number of positional states W_q ∝ V^N = (∆q)^3N. On the other hand, the kinetic theory of gases gives us the probability density of observing a certain velocity v at a temperature T. This, with a width at half-height which is therefore, a good measure of the indeterminacy on velocities ∆v. Hence an indeterminacy on the momentum ∆p = m·∆v, corresponding to a number of dynamic states W_p ∝ (∆p)^3N. Total indeterminacy in terms of positions and quantities of motion will therefore be given by the product W_q·W_p = (∆q·∆p)^3N. Note that the product of a position L and a momentum M·L·T⁻¹ is homogeneous with an action M·L²·T⁻¹. We have just seen that there is a minimal action, h, for a change to be observed. So, by dividing the product W_q·W_p by this quantum of action, we obtain the total number of microstates W = (∆q-∆p/h)^3N compatible with the macrostate under consideration. It follows logically from this that :

S = k_B·Ln(∆q-∆p/h)^3N ≥ 0 ⇒ 3N·k_B·Ln(∆q·∆p/h) ≥ 0 ⇒ ∆q·∆p/h ≥ 1 ⇔ ∆q·∆p ≥ h

A fundamental "indeterminacy" relationship between position and impulse is thus obtained. It's then easy to derive another one, linking time t and energy U (Figure 8, right). We can clearly see how the existence of the action quantum h alone ensures the existence of pairs of non-simultaneously measurable quantities. Although h is very small, its value is not zero. It is therefore impossible to have simultaneously: ∆q = ∆p = ∆U = ∆t = 0. Since the pairs (p, q) or (U, t) are not simultaneously measurable with infinite precision, there can be no state variable associated with the quantities p, q, U and t. And, according to the Février-Destouches theorem, this absence of a state variable means that the Boolean logic associated with real numbers must be abandoned. Instead, we adopt the wave logic associated with complex numbers. Hence the need for "wave" mechanics based on the algebra of complex numbers rather than the algebra of real numbers.

Figure 8 shows another way of understanding this famous wave-corpuscle duality. Consider a perfectly monochromatic wave with wavelength λ = h/p = h/m·v, i.e. (∆p = 0). The immediate consequence is that it is then impossible to locate it precisely, since it repeats identical to itself to infinity. Now, let's consider the addition of a number of vibrations that don't have quite the same wavelengths. We see that at the origin (x = 0), all waves are in phase. The more waves of different frequencies are added together, the greater the amplitude. Elsewhere, due to phase shifts, amplitudes only decrease. In the end, after adding an infinite number of vibrations, all the amplitude is now concentrated at the origin, with no spread to the right or left (∆x = 0). The constituent waves have thus been transformed into a perfectly localizable corpuscle.

In short, the introduction of the action quantum h solves not only the problem of the ultraviolet catastrophe, but also the problem of the atom's instability. Indeed, we know that the nucleus has a size of 1 fm. So, let's suppose that an electron with a negative electrical charge happens to wander onto the positively charged nucleus. The indeterminacy about its position then becomes very small ∆q ≈ 10⁻¹⁵ m. But, then, the minimum indeterminacy on its momentum is: ∆p ≈ h/∆q. Now, we know that the energy of attraction between proton and electron at a distance d is worth E = e²/4πε₀d ≈ -231(zJ)/d(nm). So, with d = 10⁻⁶ nm, it comes E = -231 fJ. Now, an electron with mass m_e ≈ 10⁻³⁰ kg and able to possess momentum ∆p = h/∆q, has a minimum kinetic energy: K_min = h²/2m_e·∆q² ≈ 33×10⁶ fJ. In other words, the kinetic energy of repulsion here is a hundred thousand times greater than the energy of attraction! Under such conditions, the electron has absolutely no chance of staying on the nucleus. But can it go very far? No, of course not, because as it moves further away, the indeterminacy of its position increases, which mechanically diminishes the indeterminacy of its momentum. For example, if the electron finds itself at a distance of 1 nm = 10⁻⁹ m, its minimum kinetic energy becomes: K_min = h²/2m_e·∆q² ≈ 2.2 zJ compared to an attraction energy of -231 zJ. Here, attraction clearly wins out...

This shows that for the electron of the hydrogen atom, the equilibrium distance where attraction and repulsion compensate each other must be close to 10 pm = 10⁻¹¹ meters. For, at this distance we find K_min ≈ 22 aJ against E ≈ -23 aJ. In fact, a more rigorous quantum calculation gives a₀ ≈ 53 pm for the size of a hydrogen atom. Thanks to quantum action, furnaces no longer emit gamma rays and atoms regain the right to exist. In short, the world, as we observe it, finds its meaning and familiarity. However, the price of a stable atomic world is high. We have to give up using real numbers, however attractive they may be. Everything has to be thought of in terms of complex numbers with a real part and an imaginary part. But, as the term implies, this means that part of reality becomes unobservable on principle. To recover observable real numbers, we need to eliminate this imaginary part. In concrete terms, this means that once you've rotated to the left and left observable reality, you need to rotate to the right to return to observable reality. Mathematically speaking, this means evaluating the product z·z*, so that all that remains is the square of the modulus of the number z, which is obviously a real number. And, as a complex number can also be seen as a probability wave, we find a wave-like unreality (complex number) coexisting with a corpuscular reality (real number).

In other words, when no attempt is made to observe the system, it evolves with a complex probability amplitude generally denoted ψ(x,y,z,t). However, as soon as a measurement is made on this system (observation), this wave function collapses to give an observable probability density ψ(x,y,z,t)×ψ*(x,y,z,t). Consequently, although the object is first and foremost a wave, we can only observe a world made up of particles whose motion obeys the rules of probability calculus. In mathematical terms, this means that each physical quantity must be associated not with a real number, but with a quantum operator denoted Ô, for example. This operator can act on any function ψ(x,y,z,t), giving a new function ψ'(x,y,z,t) = Ô·ψ(x,y,z,t) = λ·ψ(x,y,z,t), where λ is a real number, called the "eigenvalue" of the Ô operator. It is this real eigenvalue λ that can be measured experimentally. And, which can be indexed by an integer n. And, suppose there exists another operator Â such that [Ô,Â] = Ô·Â – Â·Ô = i·Û. Here, Û is the "commutator" operator. Then, the product of the quantum indeterminacy on the quantity Ô (∆O) by that on the quantity Â (∆A) will be such that ∆O·∆A ≥ ½|U| (Heisenberg's uncertainty principle). Applied to the two quantities position and momentum, this gives ∆p·∆x ≥ ℏ/2, with ℏ = h/2π.

There's another, more imaginative way of understanding the appearance of integers in a world of continuity. In fact, we've known since antiquity, and since the work of Pythagoras, that behind every vibrating string there are whole numbers. These are called harmonics. They are what make music so original. In music, this integer n indicates the number of times the string's amplitude of vibration cancels out between its left and right ends. Note that an electron confined in a potential well of width a (Figure 8) behaves, in fact, rather like a vibrating string of fixed length. Except that in 3 dimensions, as in the case of the hydrogen atom, triplets of integers are needed to characterize all the vibrational states allowed (see the interference diagrams in Figure 8, left). So, rather than seeing a corpuscle endowed with mass m, velocity v, momentum p = m·v and energy E, we'll speak instead of its wavelength λ = h/p, frequency f = v/λ or pulsation ω = 2π·f or phase φ. Note, moreover, that this phase has no corpuscular equivalence, since it exists only when complex numbers are considered. Physically speaking, it's an angle that lies between zero and 2π and allows us to account for the interference properties that exist only with waves. As phase is linked to a complex number, it is impossible to measure it, unlike frequency, which is linked to a real number called "energy", and wavelength, which is linked to a real number called "momentum".

A first crucial consequence of the finitude of the quantum of action is that an observer never sees the world as it is. He always sees a world modified by his presence. An example of this is the image of an artist rhinoceros who wants to paint the landscape he observes (Figure 8, bottom). Of course, he'll never be able to paint the landscape as it is. After all, there's always a rhinoceros horn stuck in the background. If the horn isn't there, we can legitimately deduce that it wasn't a rhinoceros that painted the landscape. Whenever we observe, there will always be a clue somewhere in the measurements to show that an observer was indeed there. And that his presence has modified the landscape.

A second consequence is that, above a certain size scale, there will always be a quantum blur. In other words, if we try to observe too much detail, we won't see anything. This is of course linked to the wave-corpuscle duality, but applied to light and not to matter. Indeed, Maxwell's deterministic equations validate without any possible discussion the idea that light is a wave of electromagnetic nature. But, in fact, light is only a wave when it propagates without interacting with matter. On the other hand, as soon as it interacts, it can only do so as a corpuscule ("photoelectric" effect). Hence the existence of zero-mass "corpuscles" of light called "photons", invented by German physicist Albert Einstein (1879-1955).

So, suppose we're looking to see the trajectory of an electron of mass m_e gravitating around a proton as in the hydrogen atom. In quantum mechanics, the mean electron orbital size depends on the square of an integer n and the Sommerfeld constant α ≈ 1/137, i.e. <r> = ℏ·n²/(α·m_e·c), with ℏ= h/2π. Moreover, the average binding energy <E> at this distance <r>, on the other hand, varies as <E> = ½·(α/n)²·m_e·c². Now, to make the observation, I need a light source. Because, if I don't illuminate my system, I won't see anything! And, to "see" the electron, the light must interact with it. Obviously, this presupposes a shock between the photon sent and the electron. So, there's a transfer of some momentum ∆p = h/λ, where λ = c/f is the wavelength associated with the photon of energy E = h·f. This transfer of momentum between photon and electron corresponds to an increase in the electron's kinetic energy ∆K ≈ (∆p)/2m²_e ≈ h²/(2m_e·λ² ). On the other hand, if I don't want my photon to be diffracted, the photon's wavelength must be much smaller than the mean radius <r> of the electron orbit, a condition for having a sharp image. I can therefore hope at best that λ ≈ <r>, which will lead to a kinetic energy transfer ∆K ≈ 4π²·<E>/n². So, for n = 1, I'm therefore imparting to the electron a kinetic energy some 36 times greater than its binding energy, removing any hope of observing its supposed trajectory. As a result, the atomic world will remain veiled from us forever.

How can something full of "emptiness" be perceived as a hard, impenetrable object? To understand this, I'd turn to an object called Roue de bicyclette, made in 1913 by French artist Marcel Duchamp (1887-1968). It's a bicycle wheel mounted on a stool. Here, if the wheel is stationary, it's easy to pass your hand through its spokes without injury. And, therefore, apprehend the vacuum that constitutes it. But in quantum physics, the state of rest does not exist, because of the finiteness of the quantum of action. So, the wheel is constantly turning "in a vacuum". But once the wheel is spinning at a sufficiently high frequency, it's impossible to pass your hand between the spokes without hurting yourself. Thus, an object full of "emptiness" has become, through the magic of movement, a hard, impenetrable thing. This analogy explains how an atom can be "empty" and behave like a hard, impenetrable thing in measurements, if its vibratory frequency is high enough. It's also worth noting that this same emptiness is found in the spectrum of light frequencies emitted by an atom when excited by electromagnetic radiation. Hence the famous "quantum leaps", in flagrant opposition to the Aristotelian credo, "Natura non facit saltus".

It's worth noting that there's nothing in quantum mechanics to specify at what size scale we should switch from quantum probabilism to strict classical determinism. All we know is that even molecules with a molar mass as high as 7,000 daltons (Da) still behave like probability waves. And not as objects with deterministic behavior. Consider that the molar mass of a water molecule is barely 18 Da. The average molar mass of an amino acid, the basic building block of every protein, is 110 Da. The average molar mass of a nucleotide, the building block of DNA, is 300 Da. Even the molar mass of a phospholipid, the main constituent of cell membranes, is just 775 Da. In short, every molecule in a living cell must be seen as a probability wave. But, strangely enough, biologists are still not trained in this quantum physics, even though it has been fully formalized since 1926!

The essential reason is that the quantum phase φ cannot be measured. Only a phase difference ∆φ can give rise to observable effects. In fact, this is in no way specific to quantum mechanics. For, when we send out an electromagnetic wave, the latter brings energy via the square of the electric field E or the square of the magnetic flux density B. But the fields E and B are also associated with a scalar potential V and a vector potential A, which are only defined to within one integration constant. Only potential differences can therefore be measured, just as only phase differences can be observed, in the form of interference patterns. In the Aharonov-Bohm effect, for example, an interference pattern is obtained when an electron beam split into two secondary beams passes through a region where the magnetic flux density B is zero, but the associated vector potential A is non-zero [13].

In conclusion, there's an important difference between a deterministic point of view using only real numbers and a quantum point of view requiring the use of complex numbers. So, if a deterministic physicist wants to know the position of a particle, he'll say: "It's here at position x and time t". In contrast, a quantum physicist would say: "It is necessarily somewhere, and let x be the result of measuring its most probable position at time t". The quantum physicist is therefore careful to distinguish between three concepts: the state, noted |a>, characterized by a label, the operator Â associated with the measurement process and the result, a, of the measurement: Â|a> = a·|a>. Note that complex numbers are used here in the definition of the Â operator, but that the so-called "eigenvalue", a, is a real number. On a practical level, the Â operator is either a square matrix (Heisenberg representation) or a differential operator (Schrödinger representation). In the Heisenberg representation, the state |a> is identified with a vector evolving in a discrete, infinite-dimensional space. In Schrödinger's representation, on the other hand, it is a wave function ψ(x, y, z, t). In fact, it doesn't matter - both representations lead to the same end result.

Second Quantization

The first quantification explains the stability of the atom. And, therefore, the stability of the observable world. You might think that we've reached the end of the road. In fact, this is not true. For there remains the thorny problem of the size scale at which we leave the probabilistic framework of the atomic and molecular world to return to the deterministic framework of macroscopic objects familiar to our 5 physical senses. As we've already said, there's nothing in the formalism that allows us to set such a limit. Worse still, there are phenomena (superfluidity or superconductivity) where matter behaves quantum-like even on a macroscopic scale. Here, we usually get away with saying that this only concerns very low temperatures. Except that superconductors also seem to exist at high critical temperatures... In short, some physicists would like quantum physics to remain confined to very small scales.

But, as we shall see, this is impossible. The starting point was mentioned earlier. When we saw that a vacuum vibrating at very high frequencies could be perceived as something hard and impenetrable. In fact, rather than talking about a vacuum, it would be better to talk about "ether". Greek philosophy already spoke of it. The existence of the ether is therefore nothing new in itself. In fact, the notion was taken up by German philosopher Immanuel Kant (1724-1804) in 1755. He assumed the existence of an elementary substance filling space, within which all bodies could be resolved. Following the general development of physics from Descartes to Euler, Kant assumes that this substance is closer to force or energy than to matter. Except that, being more subtle, it is more difficult to detect with instruments. Then, from 1788/9, he had the audacity to dematerialize his ether and make it a fundamental transcendental material. The ether was therefore not a body, as it could change neither place nor form.

In the nineteenth century, the ether came back into play following the establishment of Maxwell's equations. For light to be an electromagnetic transverse wave, it had to be able to vibrate a physical ether that was supposed to fill the vacuum. But this ether had to be both extremely tenuous and stiffer than steel to justify light's extremely high propagation speed (c = 298,792,458 m·s⁻¹). To verify the existence of this ether, American physicists Albert Michelson (1852-1931) and Edward Morley (1838-1923) studied, between 1881 and 1889, if variations in the speed of light could be detected, using a device based on light interference. But the final result was that no variations could be observed; i.e. the speed of light always remained constant. Albert Einstein used this crucial result as a basis for deducing, in 1905, that the ether did not exist. Only the vacuum existed.

Unfortunately for Einstein, this conclusion was far too hasty, as his analysis had ignored the phenomenon of gravitation. So, ten years later, in 1915, as part of his theory of general relativity, he realized that masses could bend this supposedly empty space-time! Here's what he wrote in a speech delivered on May 5, 1920 at the Reich University in Leiden [14]:

"In summary, we can say: According to the general theory of relativity, space is endowed with physical qualities; so, in this sense an ether exists. According to the general theory of relativity, space without ether is unthinkable; Because in such a system there would not only be no propagation of light, but also no possibility of the existence of scales and clocks, and therefore no spatial-temporal distances in the sense of physics. However, this ether must not be thought of as having the characteristic property of ponderable media of consisting of parts that can be traced through time; the concept of movement may not be applied to him.".

So, after all, Kant was right and the ether does exist. In this new way of thinking, matter doesn't exist in its own right. On the other hand, it can always be created or annihilated from this relativistic ether. In quantum physics, any state of energy E can be associated with a frequency f = E/h. Each state also has a quantum phase. Each state also has a quantum phase φ = ω·t = 2πf·t =2πE·t/h. Consider then the total energy E associated with a total number of quanta N: E = N·h·f. It follows that any fluctuation in energy ∆E lasts for a period of time ∆t = ∆φ/2πf. This therefore corresponds to a fluctuation in the number of quanta ∆N = ∆E/h·f. Now, we have seen (Figure 8) that ∆E·∆t ≥ ℏ/2. It therefore follows that ∆N·hf·∆φ/2πf ≥ ℏ/2, or after simplification: ∆N·∆φ ≥ ½. We have thus achieved our goal. For, let's remember, the quantum phase is an unobservable entity and therefore immaterial in nature. Similarly, the number N can designate both a number of particles, which are, after all, immaterial probability waves when unobserved, and a number of photons, equally immaterial. As for the factor ½, this is a pure number with no physical content that will take the same value in an atom as in a galaxy.

Consequently, we've just found a new pair of variables (N, φ), where precise knowledge of one lead to complete indeterminacy of the other. And, once again, according to the Février-Destouches theorem, if there is a pair of non-simultaneously measurable quantities, we must once again renounce determinism and adopt the probabilistic point of view. Except, this time, the indeterminacy relation no longer involves a ridiculously small quantum of action. In short, there are no size or temperature limits. In this new way of thinking, quantum physics must be applied to all scales, from the smallest particle to the entire universe.

Let's take a closer look at how this new way of thinking works. As indicated, we've abandoned the principle of conservation of mass, so dear to Lavoisier. In fact, this is permissible insofar as we place ourselves in a relativistic framework. For mass m is an independent attribute of energy E only within the framework of the Galilean mechanics group Gal(3,1). As soon as we work with the relativistic Poincaré group ISO(3,1), we're dealing with an overgroup of Gal(3,1). In ISO(3,1), mass and energy are two equivalent ways of describing the same property of inertia with respect to motion, since E = m·c². In practical terms, this means that, on the scale of an elementary particle, it is possible to make it appear from the quantum ether. For, as Figure 9 shows, this ether must be seen, on a scale of 10⁻³⁵ meters, as a medium filled with energy fluctuations, of average amplitude ∆E.

Hence the possibility of creating any mass ∆m = ∆E/c², as soon as the ether fluctuation is large enough. Such a particle that magically emerges from the ether is called a "virtual" particle. Now, for such a fluctuation to remain unobservable, i.e. virtual, it suffices that ∆N·∆φ ≤ ½. Either, ∆E·∆t < ℏ/2, or ∆m ≤ ℏ/2c²·∆t. This shows us that a virtual particle of mass ∆m can be created from the ether, provided its lifetime is ∆t ≤ ℏ/2∆m·c². Furthermore, since ∆x = c·∆t, the size scale ∆x at which a virtual particle can be created is such that ∆x ≤ ℏ/2∆m·c. Let's translate this, using complex numbers, the only ones allowed in quantum physics. So, let's consider a quantum state, denoted |n>, which contains a number n of quanta. Let â be the so-called "creation" operator, capable of creating a new state of the ether, denoted |n+1> now containing (n+1) quanta.

Now let's take a look at complex numbers rather than real numbers. For, as Figure 8 shows, creating a virtual particle from the ether with a complex probability amplitude z, means that there necessarily exists a conjugate amplitude z*, where the rotation is reversed. There is therefore a so-called "adjoint" annihilation operator, â† (read "a-dagger"), which returns to the starting state by annihilating the quanta that had just been created. This operator can thus bring the ether back to its fundamental state, denoted |0>. At this point, it is impossible to go any further and destroy the ether, i.e. â†|0> = 0. This means that a vacuum can never be annihilated, since it is impossible to be less than nothing. Consequently, the ether is the only tangible, indestructible reality that fills the entire universe and is the source of everything.

Now, by combining these two creation â and annihilation â† operators, we can create a third, â†·â that leaves the ether in its |n> state. Very simply, this new operator allows us to count quanta, one by one. As these notions may seem very abstract, let's return to the problem of atomic stability. In the context of the first quantization, matter is indestructible. And, as we've already seen, the indeterminacy relation ∆x·∆p ≥ ℏ/2 prevents the electron from merging with the nucleus. To be more precise, it's the same electron that spirals towards the nucleus or flees it as a result of the impossibility of being confined to a very small volume. In second quantization, things are very different. In this relativistic world, there are two types of particles. The first type is called matter and the second type is called antimatter. This stems from the fact that for a particle at rest (p = 0), there are two states, one with positive energy, E = +m₀·c², and the other with negative energy, E = -m₀·c². So, if there is an electron with electric charge -e, there must also exist a positron of the same mass, but with positive electric charge +e. And, when an electron meets a positron, they can annihilate each other to give back vacuum and release an energy equal to the sum of the disintegrated masses, i.e. 2m₀.

Let's now investigate at what size scale ∆x it is possible to create such an electron/positron pair via a fluctuation in the ether. Here, we have ∆m = 2m₀ ≈ 2×10⁻³⁰ kg, and so it will suffice that ∆x ≤ ℏ/4m₀·c ≈ 8.33×10⁻¹⁴ m. Consequently, an electron spiraling towards a nucleus with a maximum size of 10⁻¹⁴ m won't have time to reach it. Because, before it does, there's a good chance it will encounter an electron/positron pair from the fluctuations of the quantum ether. The falling electron can then be annihilated by the positron emerging from the ether. The electron leaving the ether, which was virtual, now becomes real. It can then use the kinetic energy of confinement to escape the attraction of the nucleus. In short, this creates the illusion that it's the same electron that falls and leaves again.

For indistinguishability is one of the other charms of quantum physics. If you're faced with two electrons that are identical in every way, it's impossible to know which one is on the left and which one is on the right. To find out, you have to observe them. And if, by any chance, you don't observe them, they may very well exchange positions! Basically, this means that an atom is a dynamic structure that constantly disintegrates and reintegrates at a very high frequency. The characteristic time of this process is given by ∆t = ∆x/c ≈ 3×10⁻²² seconds. So, Marcel Duchamp's bicycle wheel spins so fast that, on our scale of seconds, we have the impression of stable, hard and impenetrable atoms. In fact, this is an illusion, since all we have is ether vibrating at very high frequency.

In fact, this process of permanent creation/annihilation also applies to the atomic nucleus. To say that it's made up of protons and neutrons is a misnomer. For it, too, is an even higher-frequency vibration of the ether. In fact, there are particles called "pions" that exist in three "flavors". There's the negative pion, denoted π-, with mass ∆m = 2.51×10⁻²⁸ kg which is capable when it encounters a proton of transforming it into a neutron. Knowing that ℏ/2c ≈ 1.7×10⁻⁴³ m·kg⁻¹, this can occur spontaneously via an ether fluctuation as soon as ∆x ≈ 6.8×10⁻¹⁵ meters for a duration ∆t = ∆x/c ≈ 2.3×10⁻²³ seconds. Since the positive pion, denoted π+, is the antiparticle of the negative pion, any neutron can, after encountering a positive pion, become a proton on the same size and time scales. Finally, there is also a neutral pion, denoted π° with mass ∆m = 2.43×10⁻²⁸ kg, which is capable, when it encounters a neutron, of transforming it into another neutron. Or transmute a proton into another proton, again on the same size and time scales.

The atomic nucleus is therefore no more material than its direct descendant, the atom. It simply vibrates on a smaller scale and at a higher frequency than the atom. And, of course, since every molecule is made up of atoms, it too is a vibratory structure of the ether. We can thus move up the scale to arrive at the entire universe, which observed at a size scale of 10⁻¹⁵ meters and a time scale of 10⁻²³ seconds doesn't stop, at the level of its elementary components, disintegrating and rebuilding itself. What's remarkable is that, in spite of this, we observe large-scale structures that can exist over very long durations. Figure 9 shows that while these energetic fluctuations in the ether are not directly observable, they do have tangible, observable effects (Lamb effect and static or dynamic Casimir effects).

The static Casimir effect can be understood by looking at two boats placed side by side in a harbor. As the water in the harbor is constantly agitated, long-wave ripples are excluded from the space between two hulls. This is not the case for short-wave ripples. As a result, the two boats move closer together, requiring tires to prevent them from colliding. The same effect occurs in the quantum vacuum, where two mirrors highlight the spontaneous approach. In the dynamic Casimir effect, on the other hand, light can be made to emerge from this vacuum. All it takes is for one of the two mirrors to oscillate at a certain frequency relative to the second, immobile mirror. All this shows that this quantum world, unobservable in principle, is nonetheless capable of having very tangible and real effects.

This brings us directly to the notion of coherence, which is the other facet of these relativistic vibrations of an ether. For so far, we've essentially been talking about the indeterminacy aspect of the number of particles, ∆N, involved in the condition of visibility, ∆N·∆φ ≥ ½, or invisibility (ether), ∆N·∆φ < ½. We must therefore, now turn to the coherence aspect via indeterminacy on the quantum phase, ∆φ. This is, of course, much more difficult since the quantum phase, φ, is, in itself, fundamentally unobservable. Indeed, only phase differences (interference) can be observed.

This brings us directly to the notion of the quantum field. To help visualize the concept, we can take as an example a wheat field made up of a large number N of wheat ears. Each ear has an amplitude (its height) and a phase φ (its orientation relative to the ground). Energy is also required, in this case the wind, which can blow over the wheat field with varying degrees of force. This situation already makes it clear that there are two states for the field. A state in which there is no wind, and a state in which the wind blows with a certain force. When the wind is zero, it's easy to count the ears (∆N = 0). The consequence is that the orientation of the ears of corn can be arbitrary (∆φ → ∞). But, if now the wind blows, some ears all take the same direction (∆φ → 0), and it becomes impossible to count them (∆N → ∞). In fact, the field as a whole is traversed by these magnificent coherence waves that make it undulate in a quite striking way.

This shows us that phase coherence is a phenomenon that can be demonstrated on our macroscopic scale. In any case, there are always two states. The first state is the one in which things can be counted, because there is no coherent collective motion. The second is where coherent collective movements appear, making it very difficult, if not impossible, to count things. In this case, well-defined spatial or temporal structures appear, which merely reflect the underlying phase coherence. And this coherence can occur at any size scale. For example, at the scale of the infinitely large, a galaxy is simply a coherent field of stars, while the night sky is an incoherent field of the same stars. Now, on the scale of the infinitely small, the atomic nucleus is a coherent field of protons and neutrons, while the nuclear explosion is an incoherent field of these same nucleons.

Similarly, a molecule can be seen as a coherent field of atoms, whereas a mixture of dioxygen and dihydrogen is an incoherent field of the same atoms. In fact, as soon as the size scale becomes atomic or molecular, we speak of a quantum field. It is then imperative to use complex numbers to describe the behavior of atoms or molecules (wave/corpuscle duality). For macroscopic examples, we can use real numbers and simply speak of "fields", as soon as we consider a large number of objects as a whole.

Ether in Indian and Greek philosophy

We've just seen that modern Western science validates the idea that the only real component of the universe is the relativistic ether. What's more, the physics of second quantization introduces a mathematical formalism based on three operators, capable of creating, conserving and destroying all matter. This brings us to an ancient civilization which, almost word for word, embodies everything that modern physics has patiently developed since 1927, when physicist Paul Adrien Maurice Dirac perfected the formalism of quantum electrodynamics (see Figure 9).

This Indian civilization began in the Neolithic period as early as 7,000 B.C.E. The archaeological site of Mehrgarh in Pakistani Baluchistan, west of the Indus Valley, already bears witness to agricultural practices. Between 5500 B.C.E. and 4800 B.C.E., pottery appeared, along with a ceramic and metallurgical industry. The site was deserted around 2600 B.C.E. - 2000 B.C.E., after the appearance of the Indus Valley civilization. This civilization concentrated around the city of Harappa between 3,000 B.C.E. and 1,600 B.C.E. (Bronze Age) in what is today the Punjab in Pakistan. Then, during the period from 1,500 B.C.E. to 600 B.C.E., Vedism appeared, and the Shruti literature of "revealed knowledge" flourished. This literature was initially oral, and took shape with the writing of the four Vedas. The first was the Rigveda or Veda of stanzas. This was followed by the Yajurveda, or Veda of formulas, and the Samaveda, or Veda of melodies. Finally comes the Atharvaveda, specifically dedicated to the knowledge and use of the mineral, plant and animal worlds for healing. It was this fourth Veda that gave birth to Ayurveda. Around 500 B.C.E., the Buddhist period gave a strong impetus to the exploration of Ayurveda. Then, between 600 B.C.E. and 500 C.E., the Brahminic religion, also known as ancient Hinduism, developed. During this period, society was divided into four castes (varna): priests (Brahmins), priests, teachers and lawyers. Even later, around 100-300 C.E., the "Sanatana dharma", meaning "eternal law", developed, laying the foundations of modern Hinduism. Then, around the year 1000 C.E., the "Yoga" school of Hinduism appeared.

Early Hindu cosmology bears a strong resemblance to Chinese cosmology. At the very beginning, there is only Brahman or Prajapati, the Absolute, the undifferentiated One, without beginning or end, the Hindu equivalent of the Chinese Tao. Impossible, then, to represent him, for he is not a divinity. The best way to think of Brahman is as a vibration, a primordial sound, the creator of all things. This sound is pronounced AUM or Ôm (Figure 10). Then, if we take the pronunciation Ôm, Brahman splits in two, giving rise to Prâna on the one hand, the energy equivalent to Chinese "Yang", and Akasha on the other, the substance equivalent to Chinese "Yin". Then comes the Trimurti, which corresponds to the ternary AUM structure of the fundamental vibration. Here we find three deities: Brahma the creator (initial letter 'A'), Shiva the destroyer (final letter 'M') and Vishnu the preserver (middle letter 'U'). It's at this level that there's a strong resonance with quantum field physics (Figure 10). Since quantum field physics has three basic operators. The one that creates a new |n+1> state from the |n> state. The one that annihilates this state to return to the starting state. And finally, the one that maintains the initial state |n>.

Just as in China, where anything can be created from the number 3, this divine ternary structure AUM has many variations in India. For example, one of them corresponds to the three "Gunas" of yoga: Rajas (activity, desire), Sattva (purity, knowledge) and Tamas (darkness, destruction). Here, the sound "AUM" is supposed to maintain the balance between these three Gunas. As in China, odd numbers are associated with stable things. Of these, the two following 3 - 5 and 7 - play a prominent role.

For example, the primordial sound AUM (Figure 10) can be analyzed according to 5 states. Three earthly states, waking, sleeping and dreaming, beneath a fourth state (veil symbolizing spirit). And, masking a fifth ultimate reality, consciousness. According to Ayurveda, there is a "Pancha Maha Bhutas", with the word "Pancha" meaning the number "5", the word Maha meaning "great" and the word Bhutas meaning "Substances". This expression can therefore be translated as the 5 fundamental categories of substances or 5 primordial states of matter. Consequently, the universe, like man, is made up of five fundamental elements, "mahabutas" (Figure 10). Three of these are shared with the Chinese: fire, water and earth. But here, air replaces wood and ether replaces metal. It would seem, then, that the Hindus understood that wood was in fact nothing more than solidified air (CO₂). Similarly, they would have understood that metal could come from the earth, but also fall from the sky, in the form of meteorites. So, as in China, there are 5 elements, at the cost of a few changes in order to involve extraterrestrial matter, absent from purely terrestrial Chinese philosophy.

Ayurveda's great originality lies in its introduction of a principle of stability via a trinity of 3 "doshas". Ether, acting on air, generates the wind "Vâta", authorizing the movement of matter. Fire, acting in concert with water, generates steam "Pitta", capable of digesting or transforming all forms of matter. Finally, earth, acting in concert with water, generates the mud "Kâpha", which enables things to link together to achieve a state of equilibrium. The result is the number 8 (5 + 3 = 8), which is even and therefore unstable. Hence the need for reincarnation (death followed by rebirth), which provides the opportunity to heal the karma accumulated in a previous life.

On the other hand, to divide a pentagon into 3 pieces, quadrilaterals must be used. So, each dosha is quaternary in nature, meaning that something is in progress via their action on the 5 elements. This gives rise to the 5x4 = 20 "adi gunas", pairs of opposites attributed to substances or even circumstances. This describes our apprehension of the world and helps us to restore our balance and health when it is disturbed. And, as in Chinese medicine, natural derivatives of minerals, plants or animals are used to restore the disturbed balance.

On the other hand, unlike Chinese philosophy, Hindu philosophy is also obsessed with the number 7, associated with the idea of perfection. Thus, the universe is likened to a cosmic egg floating on a primeval ocean, stratified into 7 domains. In the upper zone we find 3 regions, forming the Bhumi, where matter reigns (Earth, Atmosphere and Sky). And above this, we find 4 celestial regions (Svarga) where there is only light. A total of 4 + 3 = 7 domains. In its lower zone (Patala), the egg contains 7 regions filled with jewels and lakes. But the last and seventh region is populated by demons and snakes (Nagas). The Earth itself is made up of 7 continents surrounded by 7 seas.

The number 7 is also found in yoga, in the form of the seven chakras. Logically, yoga associates the 5 Ayurvedic elements with the first five chakras. And, just as logically, to achieve a certain kind of beauty, the sixth chakra is associated with light. And to achieve perfection, a seventh chakra is evoked. This allows us to see the world as a unity in which the elements and light have no existence of their own. Rather, they exist only because they are in constant relationship with one another via an underlying unity. For Buddhists, this unity is called "emptiness", but the basic idea remains the same. Thus, the union of beauty (6) and unity (1) naturally leads to a form of perfection (7 = 6 + 1).

But where Hindus differ from the Chinese is in mathematics. For it was they who invented the number zero to represent the absence of quantity, i.e. emptiness (shunya). More precisely, the Chinese, but also the Babylonians, were aware of zero as a position. Around 400 B.C.E., the Babylonians used two small square brackets to indicate that a place in a number was vacant. This made it possible to distinguish the number 27 from the number 207. However, it was impossible to distinguish between 27 and 270, and it was in this ability to distinguish between these two numbers that the Hindu originality lay. In 628 C.E., the mathematician Brahmagupta defined zero (shunya, meaning "void" or "nothingness" in Sanskrit) as the subtraction of a number by itself, i.e. a - a = 0. Hence: a + 0 = a, a - 0 = a and a×0 = 0. He even understands that division by zero leads to infinity. Indeed, in Buddhist philosophy, the concept of "shunya" is central to achieving nirvana, hence the great innovation of seeing zero as a number in its own right and not as an empty position in a non-zero number. Until 2018, the oldest representation of the number 0 was an inscription on a temple wall in Gwalior, India. Since then, carbon-14 dating of an ancient text known as the "Bakhshali manuscript" has pushed back the date of the explicitly symbolized zero by 500 years. In this text, hundreds of zeros are indicated by a dot, a symbol that later evolved into the current representation of a circle with nothing in the middle.

It's amusing to note that zero, as a number, didn't exist in Europe until the X^e century C.E.. So, when the Gregorian calendar was developed in the VI^e century C.E., we went directly from year -1 to year +1. Hence the historians' calendar, in which the year 0 does not exist, which differs from the astronomers' calendar, which has a year zero. In ephemeris calculations, the year zero is the one immediately preceding the first year of the Christian era, i.e. year -1. The presence of zero means that a period extending from a date in year m to the same date in year n has a duration of n-m years. Thus, the time interval separating March 1st of year -1 from March 1st of year +1 in the astronomical calendar lasts two years. In contrast, the interval between these same dates in a calendar without a zero year (such as the Revolutionary, Gregorian or Julian calendars) lasts just one year. This is why we entered the 3rd millennium on January 1, 2001, rather than January 1, 2000, when we were still in the 2nd millennium, which ended at midnight on December 31, 2000.

Unlike the Greeks, who hardly ever went beyond 10,000, the Hindus had names for numbers that could be gigantic, such as 10¹⁷ or 10⁵³. This was because, mathematically speaking, the inverse of the number zero corresponds to infinity: 1/0 = ∞. As a result, irrational numbers like √2, didn't scare them in the least. Thus, in 800 B.C.E., the Indian mathematician Baudhayana enumerated the theorem unjustly attributed to Pythagoras as follows: "The area produced by the diagonal of a rectangle is equal to the sum of the area produced by it on two sides". He even gives an approximate value for the length of this diagonal: "The measure must be increased by a third and decreased by a quarter. This is its diagonal approximately." Or, in modern notation: √2 ≈ 1 + 1/3 + 1/3×4 -1/3×4×34 = 577/408 ≈ 1.414216, to be compared with the exact value rounded to six decimal places: 1.414214. Finally, he also gives a way of finding a circle whose area is the same as that of a square: "Draw half its diagonal about the center towards the East-West line; then describe a circle together with a third part of that which lies outside the square."

The Ether in Greek Culture

Today, we know that the peoples of western India are all descended from "Indo-European" ancestors. So, it's perfectly logical that the 5 elements of Greek philosophy are absolutely identical to those of Ayurveda: ether, fire, air, water and earth. However, with the Greeks, one of these 5 elements, ether, was given a special status. At this point, it's worth returning to Plato's philosophy (Figure 11). For this philosopher, each element could be associated with a regular polyhedron, and everything had to be made up of triangles to ensure stability. The simplest solid was the 4-vertex tetrahedron, formed by assembling 4 equilateral triangles. Now, 4 is the number of action, of unstoppable progress. Plato therefore logically associated this solid with the element of fire, which always tends to spread. The second solid with the fewest triangles was the octahedron, with 8 equilateral triangular faces. Here we find the number 4 of action in the fact that 8 = 4x2 and that each vertex is formed by the meeting of 4 triangles. The notion of beauty was also present in the fact that an octahedron has 6 vertices. What element could be more stable than fire, yet always in motion: air, of course.

Still in terms of triangles, the next solid was the cube, with 6 square faces and 8 vertices, each vertex being common to 3 faces. To form the square, two isosceles triangles had to be associated by their hypotenuse. A cube is therefore made up of 6x2 = 12 isosceles triangles. As 1 + 2 = 3, the cube was clearly associated with something very stable and a source of beauty: the element earth (crystals). The fourth solid was the icosahedron, formed of 20 equilateral triangles with 5 triangles at each of the 12 vertices. Here we find the numbers 2 (2 + 0 = 2), 5 and 3 (1 + 2 = 3), i.e. something both stable (3) and unstable (2), a source of permanent crisis (5). Water, with its irresistible tendency to flow while remaining at rest in a watertight container, fit the bill perfectly.

Plato could therefore be very pleased with such a correspondence. But his mathematical science told him that there was a fifth solid made up of 12 regular pentagons with 3 faces meeting at each of the 20 vertices. As with the squares of the cube, he had to cut a pentagon into triangles. This was made possible by 2 identical isosceles triangles and a third one different from the first two (see Figure 11). A pentagonal dodecahedron thus had 12x3 = 36 triangles; a number reducible to the number 9 (3 + 6 = 9). This last solid had to evoke something new, something different from the other 4. The decision was therefore taken to conceal the existence of this fifth element, which corresponded to what Plato called "quintessence", and what Aristotle called "ether". Only the initiated knew about this fifth element, while the uninitiated were content with the other 4 material elements.

Indeed, for Plato, the number of action is 4, while 5 is the number of crisis. So, as we've seen, the Chinese identify 4 elements (wood, fire, metal, water) with 4 seasons (spring, summer, autumn, winter) and 4 cardinal points (east, south, west, north). But they don't stop there, invoking the center of the cardinal cross for their fifth element, earth. This, of course, obliges them to introduce a fifth season: the end of summer, known in the West as "Indian summer". For his part, Plato found it more logical to reject the center outside the earth, thus retaining only 4 cardinal points for orientation on the earth's surface and 4 seasons. From then on, the crisis linked to the number 5 becomes external and spiritual for Plato and the Hindus, with a race to the spiritual directed towards a quintessence outside ourselves. For the Chinese, on the other hand, this crisis is more earthly and oriented towards the material.

The problem with this view is that, apparently, there's nothing beyond quintessence. For Pythagoras, it was quite clear that the crisis of 5 meant moving towards beauty (6) and perfection (7). This philosophy of quintessence (5 = 4 + 1) lacked a principle for achieving perfect earthly stability (3) (7 = 4 + 3). This is obviously in stark contrast to the Eastern solution (7 = 5 + 2), where perfection is sought within us (via the notion of center), and not outside us in an inaccessible quintessence. This was also different from the Hindu solution, which united beauty and unity (7 = 6 + 1). In fact, on a purely religious level, the solution (5 = 4 + 1) went very well with the existence of an inaccessible "God" (1) sending his "Son" to earth to be crucified (4). And then there was a whole concept of medicine, humourism, also based on the number 4 (Figure 11).

How do you introduce the number 3 under these conditions? Paracelsus provided the solution, introducing a "tria prima" (sulfur, mercury and salt). These three principles are obviously reminiscent of the 3 Ayurvedic doshas, reintroduced here in a Westernized version. Within this ternary, the mercurial principle acts as a compressive force from the outside (soul). To balance this external pressure, the sulfuric principle acts, in contrast, as an expanding force from within (spirit). The result is a state of equilibrium in the personality that can be modulated by the salt (body). This union of the material (4 elements) and the spiritual (3 principles) enables a certain form of perfection to be achieved once again (7 = 4 + 3).

But this totally idealistic vision of nature was opposed by the materialistic vision of Democritus. Plato hated Democritus so much that, after his death, he planned to burn all his books. For Democritus, there are only two primary elements: atoms and the void. Atoms, which form matter, are indivisible and invariable, eternal and perpetually in motion. They differ only in shape, size, position and order. All bodies are combinations of atoms, and their separation leads to their destruction. It could be said that atoms are avatars of the Chinese Yang, with the void playing the role of Yin, and bodies formed of atoms demonstrating the existence of a He, a harmony, via the bond that unites two atoms to each other (chemical bond). For Democritus, the soul is made up of fiery, light, spherical atoms and disappears after death. There is therefore no life in the afterlife, and no organizing God. There are only countless atoms eternally moving in the infinite void. Without too much exaggeration, Plato can be said to have been the precursor of fascism, which requires the presence of leaders with all the power to direct a people of slaves. Democritus, on the other hand, was a representative of ancient democracy, and a fierce opponent of slave aristocracy. Hence Plato's hatred of Democritus. Epicurus and later Lucretius tried to propagate Democritus' materialism. But it was Plato's idealism, taken up by Aristotle, that triumphed until the advent of quantum physics, which rehabilitated atoms and their intrinsic emptiness.

In the Beginning Was Emptiness...

To talk about the origin of life, it's imperative to understand that, just like our universe, life has non-material, even spiritual aspects as well as purely material ones. While this is particularly obvious in humans, it is much less so in bacteria. For simplicity's sake, these two inseparable aspects of the vital phenomenon will be labelled: "matter" for everything visible and tangible, and "consciousness" for everything invisible and immaterial.

It would be a serious methodological error not to take into account this fundamental duality between matter and consciousness. In fact, we are naive enough to believe that the difficulties we encounter when we try to talk about the origin of life are intimately linked to our failure to take this fundamental duality into account. But that's far from enough. For it is also imperative to understand that consciousness is not an emergent property of matter. This follows from the observation of the logical postulate that any phenomenon pre-existing another can participate in the creation of the latter, whereas the opposite is impossible. Indeed, if we accept this basic postulate, then we can only arrive at the logical conclusion that the space-time-matter framework used by conventional science is capable of emerging from a non-local consciousness according to a precise hierarchical cascade [15]. And if we wish to transcend this fundamental duality, there is only one concept that can do so without any contradictions: the concept of the void, or rather the ether. Hence the need, before speaking of consciousness or matter, to have a precise idea of the nature of this ether at the origin of all things and all thought. And to make a clear distinction between the three concepts of nothingness, emptiness/ether and vacuity.

In fact, nothingness is easily identified with "nothing", i.e. with the set of things that are impossible. An example of nothingness is the statement that 1 + 1 = 3. If such a thing were true, then the world as we know it simply couldn't exist. For our living world to exist, it is imperative that 1 + 1 = 2, and nothing else. This may seem obvious, but it's precisely because it's obvious that this basic fact is so often overlooked. And, as soon as something is concealed, there's the danger of "talking about nothing". In fact, we can recognize in the identity 1 + 1 = 2, the notion of identical reproduction leading to growth, a notion that applies just as much to an idea as to a living cell.

Let's move on to the notion of emptiness/ether, which is very clearly distinguished from the notion of nothingness. To be empty is not to be "nothing", but rather to be "primitive", i.e. to be "at the origin" of something quite concrete. To take the previous example, I can easily create emptiness by assuming that 1 - 1 = 0. Here we find the notion of sexual reproduction by birth. Two very concrete and differentiated things (1 and -1) decide to unite intimately to create an entirely new thing (0) that cannot be identified with the two "parents".

Finally, there's the notion of vacuity. To grasp this new notion, which is neither "nothing" nor "emptiness", I'll refer to set theory and the so-called "Peano-Cantor" construction (Figure 12). This construction assumes that the empty set, denoted ∅, exists. And, as it contains no elements, its number of elements, or cardinal, is zero. If you prefer, I'm dealing with the previous "new" thing, but one that hasn't yet materialized. Aristotle would say that it exists "in potential". Nowadays, we'd say it exists "in consciousness". Let us now consider the set A, which contains the empty set as its only element, and is therefore of cardinal 1. The two sets ∅ and A are clearly different in nature, since A contains one element ∅ while ∅ contains nothing at all! Aristotle would say that the "new" thing now exists "in act" whereas a contemporary scientist would speak of existence in the form of a cell. In concrete terms, set A can be seen as a drawer containing an empty bag, and so cannot itself be empty, since it contains a bag... So, we do indeed have two things, an empty bag and a drawer containing this empty bag, which makes it possible to define a new set B of cardinal 2 formed by the union of these two different elements. True, but this new set B, added to the first two, Ø and A, in turn defines a new set of cardinal 3 and so on ad nauseam (see Figure 12).

This ingenious construction shows that emptiness, by virtue of its very existence, is capable of generating an infinite number of things, all of which are hollow shells fitted together like a set of Russian dolls. It is this interlocking of empty things that we refer to as "vacuity". It doesn't matter whether you use the column on the left, which, with its succession of different letters, masks the nesting and emptiness of things, or the column on the right, which shows that all you need is one powerfully creative thing: the empty whole Ø. In fact, it doesn't really matter which labels we choose to place at each stage of the interlocking process, because all this applies to everything, material or spiritual. The construction of Peano-Cantor is in fact summed up very well by the Zen koan "Mu Soku Wu, Wu Soku Mu", which could be translated as "From the void everything can spring, and this everything can always return to the creative void".

The Peano-Cantor construction teaches us that we can very well be both empty (Ø) and non-empty, i.e. an arbitrary nesting of equally empty things. In this way, we experience the non-duality that is the very essence of vacuity, and which corresponds to the Western ouroboros, the ensô of Zen Buddhism or the ying/yang symbol of Taoist philosophy (see Figure 12). There are also ribbons that have only one side, such as the Moebius ribbon, or the Klein bottle, which has neither inside nor outside. Vacuity can be reduced neither to a self nor to a lack of self. As a middle way, vacuity is a way of not being trapped either in the idea that things exist, or in the idea that things don't exist. Existence and non-existence are a dualism that is imbued in our concepts and our ways of thinking and speaking. To be empty, then, is not to be non-existent. It is to be devoid of permanent identity.

So, to speak of a thing, you need at least three words: two words to describe the thing and the non-thing, and a third word to unite the thing and the non-thing into a meta-thing, a substance that lies behind the thing, but is neither the thing nor the non-thing. Chinese philosopher Lao Tzu's Tao-te-king XLII-1 is very clear on this point:

"The Tao produced One, One produced Two, Two produced Three, Three produced ten thousand beings...". If you're uncomfortable with Eastern philosophies, you may also refer Plato's Timaeus. In this work, Plato speaks of expanse (la chôra, χώρα), the permanent matter of the universe, which participates simultaneously in the sensible and the intelligible. We thus find the principle of identity (A: the Model, which is always identical to itself), the principle of contradiction (non-A: the copy, different from the Model), and the chôra, which is neither the Model nor its copy, but is of a "third kind", neither A nor non-A. Which ultimately remains unintelligible, by reason of the excluded third. For it is this reason that rejects the notion of the included third symbolized by the chôra, forcing us to make do with the Aristotelian place (τόπος, topos) that suits the disjunctive logic of the excluded third perfectly. The chôra can thus be seen as the milieu in which the becoming occurs [16]. It should also be remembered that, as early as the III^e century C.E., Indian logicians developed tetralemmes which, on the contrary, allow the inclusion of the third party according to four lemmas: 1. A (affirmation); 2. non-A (negation); 3. neither A nor non-A (neither affirmation nor negation); 4. both A and non-A (both affirmation and negation). In a more scientific sense, the problem of vacuity or chôra reappears fully in quantum physics in the form of wave-corpuscle duality, which must be understood as non-duality, in the sense discussed above.

In fact, it took a long time to accept the existence of the vacuum and, above all, the fact that the vacuum and matter are two facets of the same reality. Indeed, it's matter which, by its presence, defines where there's a void and where there isn't. And it's the void which, in turn, by its presence or absence, gives meaning to the void. And it's the void which, in turn, by its presence or absence, gives meaning and form to matter. Remove the void and all becomes shapeless chaos. For behind the existence of the void lies the notion of movement. And how do we recognize that something is alive? By the fact that it has an autonomous movement with no apparent motor. Another crucial point is that all living matter is essentially made up of a single substance: water. And behind this substance lies the vacuum. Indeed, according to the Standard Model, which counts the material and non-material particles that populate the universe, there are, on the one hand, quarks, the constituents of atomic nuclei. On the other hand, electrons neutralize the positive electric charge brought by protons formed by the "uud" combination (Figure 13). And there's another "udd" combination, with zero electric charge, which defines the neutron. However, when we calculate the mass balance between the quarks and electrons making up the water molecule and the molecule itself, it's clear that these "observable" particles make up only 1.2% of the total mass. In other words, 98.8% of the mass of a water molecule comes from the vacuum or ether that constitutes it.

Such a fact is obviously shocking to a mind firmly anchored in matter. For an Indian mind, however, it's a no-brainer. In fact, it's self-evident. And, as soon as one wishes to associate the ether with a tangible reality, it becomes impossible to evacuate consciousness from the problem of the origin of life. And since the ether is empty of matter, while being something in itself, capable of creating all matter, the only thing it is capable of containing is information. And what does consciousness do? It manipulates information. Let's take a closer look.

Consciousness and Mathematics

It was proved in 1913 by the American mathematician Henry Maurice Sheffer (1882-1964) that Boolean algebra could be defined using a single binary operator called NAND (non-conjunction). Such an operator can be represented by an ascending bar (↑) or "Sheffer bar". Figure 14 summarizes what's going to be said here. This rather remarkable property has made NAND gates crucial to modern digital electronics, enabling the manufacture of flash memory and the design of high-performance computing processors. Since all binary logic operations can be encoded with this single logic connector. Recall that if P and Q are two true or false propositions (binary logic), then v(P↑Q) = 1 in all cases unless v(P) = v(Q) = 1, in which case v(P↑Q) = 0. In this framework, if P represents any statement such as "I am", three primitive concepts immediately emerge:

-: Negation: ¬P = P↑P or "I am not".
-: The tautology: ⊤ = (¬P↑P) = P↑P↑P or "I am what I am".
-: The contradiction: ⊥ = ¬⊤ = (⊤↑⊤) = P↑P↑P↑P↑P or "I am what I am not".

Our starting point, then, is that these three concepts form the basis of all identification principles, i.e. of all consciousness. Negation allows us to define our exterior, and tautology our interior. Contradiction, on the other hand, posits the existence of incompleteness. In other words, there are, as a matter of principle, propositions that are undecidable on the sole level of logic, in accordance with Gödel's theorem of 1931. The other attributes of consciousness then follow logically as soon as we apply the operation of non-conjunction to two different statements P and Q. First and foremost, we can, for example, give a precise meaning to the notion of causality in the form of a principle of implication:.

- Implication: (P⇒Q) = P↑(P↑Q)

If we pose Q = P, we find the tautology in a new form (P ⇒ P), which can be translated as "If I, then I". Above all, causality allows us to posit the existence of time as an endless chain of causes (P) and effects (Q). Irreversibility is naturally introduced here by the fact that the truth table of (P ⇒ Q) is different from that of (Q ⇒ P). Implication also uncovers another crucial attribute of consciousness, inhibition in the form:

- Inhibition: (P⊣Q) = (P⇒Q) ↑ (P⇒Q) = [P↑(P↑Q)]↑[P↑(P↑Q)]

Note that Implication and Inhibition are dual notions since we can write: (P⇒Q) = (P⊣Q) ↑ (P⊣Q)

Causality thus posits the existence, in principle, of an active, expansive "Yang" mode operating by implication. This mode complements a passive, contractive "Yin" mode operating by inhibition. From a neuronal point of view, this means the existence of two modes of autonomy: sympathetic or active, and parasympathetic or inhibitory. As well as alternating between a waking state (active consciousness) and a sleeping state (passive consciousness).

Another attribute of consciousness is its ability to distinguish between what is similar (equivalence) and what is different (incompatibility):

-: Equivalence: (P ⇔ Q) = [(P↑P)↑(Q↑Q)↑(P↑Q)]
-: Incompatibility: (P⊕ Q) = (P↑P)↑(Q↑Q)↑(P↑Q)↑(P↑P)↑(Q↑Q)↑(P↑Q)

For completeness, consciousness also possesses the ability to bring things together (synthesis) according to an operation of conjunction (P∧Q) = (P↑Q)↑(P↑Q). Or, on the contrary, to separate them (analysis) according to a disjunction operation (Q∨P) = (P↑P)↑(Q↑Q). It is obviously quite remarkable that all these attributes of consciousness derive from the givenness of a single logical operation: non-conjunction. From a symbolic point of view, this non-conjunction, a fundamental attribute of consciousness, has been repeatedly represented in the form of the Ouroboros, the snake that bites its own tail. Its circular shape clearly defines an exterior (negation), an interior (tautology) and a fundamental incompleteness. The beginning coincides with the end (contradiction). The tautological aspect of consciousness can be summed up by the statement: "Only consciousness can be conscious".

In this respect, it should be noted that consciousness is capable of proceeding according to three different types of logic, depending on the meaning given to contradiction. There is the classical mode of thought, which allows reasoning by the absurd and deduces from a contraction (¬P⇒⊥) that P or ¬¬P are valid (elimination of double negation) [17]. This is the rational and coherent way of thinking of active consciousness, based on Boolean algebra.

The second way of thinking is intuitionistic logic [18]. It conforms to a quantum way of thinking that posits that contradictions exist (such as wave/corpuscle duality, for example). But, that from a contradiction that is false by nature, we can deduce any proposition (⊥⇒P). This principle of explosion, characteristic of Heyting algebras, is at the root of notions such as the big bang for inert matter. Or biodiversity for living matter. In the intuitionist mode, the double negation has an autonomous status different from that of the assertion (on the other hand, it is always true that ¬¬¬P = ¬P). This is the unconscious way of thinking that makes the decoding of dreams so difficult for active consciousness.

The third way of thinking is that of minimal logic, which provides no special treatment for contradiction [19]. As a result, minimal logic makes no distinction between the formula ⊥ and any other formula F. In fact, if we assign no special role to contradiction, we can make any formula F play the role of this contradiction, by defining negation as P ⇒ F. Here we recognize a highly original mode of thinking for consciousness, where everything is affirmed and nothing is denied, which we could therefore call "full consciousness".

Information

As the Palo Alto school of psychology, funded by Gregory Bateson, has shown, it is absolutely impossible not to communicate [20]. In fact, any silence or omission can have far-reaching consequences. To raise our level of consciousness, we need to be able to communicate, i.e. exchange information using a language that can be either digital or analog. Information is therefore not a primary trait of consciousness, but always a secondary effect of conscious (digital) and reflective (analog) sensitivity. Hence the conclusion: Consciousness precedes the notion of information, and is therefore hierarchically superior to it.

This leads us to consider two levels of language: "object language", which speaks of concrete objects, and "metalanguage", which takes language itself as its object. While object language is particularly well-suited to digital communication in terms of content, it is in fact totally devoid of meaning. Hence the role of metalanguage, which is a language designed to give meaning to object language. And this in the context of analog, not just digital, communication. This is also in line with Gödel's incompleteness theorem, which states that there is no such thing as a self-contained language. So, to define the truth of an object-language L, we need to go up to the ML level (metalanguage), which alone has the resources to refer to all the expressions of L. The truth for L is therefore to be found in ML and not in L. Similarly, the truth for ML will be found in MML up to a regression to infinity.

In other words, a language cannot contain an adequate predicate of truth for itself. And the definition of truth cannot be defined within it. Truth must be defined in a higher language. All communication has two aspects: content (or passive information) and relation (or active information). And, as the relation orders the content, the relation can only be a meta-communication. It's also important to understand that, in any communication, one of the subjects may have more information at his disposal than the other. Even if the latter thinks he has just as much. So, it's dangerous to believe that the other has the same amount of information as yourself. But also, that they will draw the same conclusions. The problem with analog messages is that they lack many of the elements that make up the morphology and syntax of digital language. It's up to the translator to insert the missing elements. When translating analog material into digital, we need to introduce the logical truth functions that are absent from communication in the analog mode. This is particularly true of negation, which, as we have seen, does not exist in minimal logic and underpins communication in the active analog mode. All communication exchanges are therefore symmetrical or complementary, depending on whether they are based on equality or difference.

Moreover, in any cognitive act, we need to distinguish between the fact of perceiving (passive information or digital object language) and the fact of understanding what we have perceived (active information or analogical metalanguage). Active information brings us back to the notion of meaning, which can be defined as information in a context. It is also possible to assert that "A bit of information is definable as a difference which makes a difference" [21]. Although so similar in nature that they are often confused in common parlance, passive and active information do not act at the same level. From a thermodynamic point of view, we find this duality of information in entropy, which measures the quantity of information available at a digital level [22]. The other partner is complexity or thermodynamic depth, which corresponds to the quantity of information rejected at an analog level during the process leading to the physical materialization of an object [23].

Here we find the notion of exformation processed by consciousness but not transmitted, which defines context [24]. Since it is meaning that gives information its value, active information (meaning, exformation) is chronologically prior to passive information (content) and therefore hierarchically superior to it. By recognizing this fundamental duality in the notion of information, we reconcile the two interpretations of entropy: thermodynamic according to Shannon-Von Neumann, defined at the digital level of object language. And cybernetic according to Wiener-Schrödinger, defined at the analog level of metalanguage [25]. The mistake not to be made here is to believe that we can obtain meaning (cybernetic entropy) simply by changing the sign of nonsense (thermodynamic entropy). We must also reject the equation of entropy with disorder and negentropy with order, because disorder is not in matter but in the consciousness of the observer of matter. Entropy and information cannot be defined without context. Information measures our degree of surprise, and there are more surprises in disorder than in order. Something that doesn't surprise us is necessarily orderly. So, information is only clearly defined when we explain what we mean by order. One of the consequences of Gödel's incompleteness theorem is that it is impossible to know whether there is order in disorder. The notions of order and disorder are therefore subjective, since they are situated at the level of metalanguage and not object language.

Energy or Entropy?

In thermodynamics, entropy is identified with the energy available per degree of freedom (position or motion) via Boltzmann's constant. While, according to the first principle, the energy of the universe is constant, its entropy can only increase during the spontaneous transformations of closed physical systems. This is achieved through the production of heat, so that energy can be distributed over the greatest possible number of degrees of freedom available in the system under consideration. However, it is information that is responsible for this process [26]. Any flow of entropy (or information) allows structures to emerge through self-organization [27]. It follows logically, then, that it is information/entropy that channels energy towards ever more harmonious complexity (meaning) and, ultimately, towards life. We can thus affirm that the role of information is chronologically prior and therefore hierarchically superior to that of energy.

Physicist John Archibald Wheeler's position that everything in the universe is made of information, "It from bit", therefore seems perfectly legitimate [28]. It should also be noted that the duality observed at the level of language and information is also found at the level of energy. In relativistic theory, mass m and energy E are equivalent according to the famous Poincaré-Einstein equation, E = m·c², where c is the speed of light in a vacuum. On the other hand, quantum theory teaches us that this same energy can also be seen as a frequency according to the Planck-Einstein relation, E = h·f, where h is the quantum of action. It follows that any mass can be interpreted as a vibration, and vice versa. Since time, seen as a succession of causes and effects, is prior to information, itself prior to energy, we can deduce that: matter, which is characterized by a non-zero mass at rest seen as energy, has a hierarchical status inferior to energy seen as the inverse of time (frequency).

Material bodies are therefore logically at the bottom of our hierarchy. This means that the neuron, which is the material structure processing information by means of energy in every living being, is also at the bottom of the hierarchy. It cannot therefore generate the consciousness that lies at the top of the hierarchy. We have thus demonstrated that consciousness predates meaning, which predates information, which predates energy, which predates the material neuron. Moreover, consciousness operates according to three logics (classical, intuitionistic and minimal). The neuron, on the other hand, is found in the brain, intestines and heart, and operates at the level of digital object language, obeying classical logic. It follows, therefore, that the neuron is not the only channel for the expression of consciousness. Intuitionist logic, which posits that any proposition can be deduced from a contradiction, accounts for the creativity of consciousness when it expresses itself through the energy/matter channel. Similarly, the body, which is incapable of lying, necessarily uses the third analogical channel of expression, which operates according to a minimal logic, since here the concept of negation simply doesn't exist. To localize consciousness at the level of a single organ, the brain, is therefore a perfectly illogical attitude, given the proposed hierarchy based on the existence of a single logical connector, the non-conjunction, authorizing three modes of handling contradiction.

Water and Information

Upstream, we have the consciousness capable of processing information, and downstream, we have the living cell, made up essentially of water at over 99 mol%. This naturally raises the question of whether water might act as an interface between vacuum/ether information and biological information. As this point has already been dealt with in another paper [29], we will restate only the essentials here. Establishing conceptual and logical links between consciousness and information also has the advantage of providing an obvious and simple explanation for the appearance of quantum physics in the visible universe. What's more, the three notions of particles, fields and information fit perfectly with the three types of consciousness (digital, analog and non-dual). Now, a question that has a crucial bearing on our understanding of consciousness is: what happens after death? The father of electromagnetism, James Clerk Maxwell, made it clear on his deathbed that he felt what he had done had been done by something greater than himself.

At this stage, the idea is to propose that this thing inside us that goes far beyond us is the information available in the void/ether. Information accessible through our three forms of consciousness (digital, analog and non-dual). To demonstrate this, we need only refer to group theory. In modern physics, every law can be seen as a consequence of the existence of an underlying symmetry group. And, when we look for the symmetry group that leaves Maxwell's famous equations invariant, we come across the ISO(4,2)⊗U(2)⊗U(2) group characterized by 6×5/2 + 2² + 2² = 23 generators. What interests us here are the 15 infinitesimal generators of the ISO(4,2) subgroup, where the acronym ISO stands for "Inhomogeneous Special Orthogonal" group. Among them are the seven generators of the Gal(3,1) subgroup underlying Galilean physics: three spatial translations, three spatial rotations and one translation in time. The (3,1) doublet thus refers to the fact that we live in a three-dimensional space (3) to which a temporal dimension (1) has been added. In short, to describe any purely mechanical phenomenon, it's imperative to consider a triplet of real numbers (x, y, z). This allows us to distinguish, in space, between right and left (x-axis), front and back (y-axis) and up and down (z-axis). But that's not enough. We also need to add another real number to distinguish between past, present and future (time t). The fact that this fourth coordinate is not integrated with the other three is linked to the fact that time always flows from the past to the future and never in the opposite direction.

The French mathematician Henri Poincaré then added 3 other generators leading to the ISO(3,1) Lorentz subgroup. This, in the form of three Lorentz boosts mixing each of the three spatial coordinates (x, y, z) with the temporal coordinate (t). The consequence is that space and time can now mix. Hence the relativistic notion of space-time. But, to preserve the impossibility of going back in time, the time coordinate becomes the imaginary part of a complex number describing this mixture of space and time. In practical terms, this means that we have now unified mechanical and electromagnetic phenomena. It also means that we've gone from three Casimir invariants for Gal(3,1): mass (spatial translations), energy (temporal translation) and spin (spatial rotations), to just two: mass/energy with E = m·c² and spin, for ISO(3,1). But the fact is that there is an ISO(4,2) supergroup including ISO(3,1) as a subgroup. As its symbol indicates, this supergroup adds a fourth space coordinate s and a second time coordinate ψ, associated with five new infinitesimal generators. The first generator corresponds to dilation in space or time, and the other four to conformal symmetries that preserve angles between two arbitrary directions.

The new spatial coordinate s is used to specify the size scale (small/large) at which the system under study is considered. For space, this corresponds to the number of particles in an inert system. Or the number of cells in a living system. So, for a crystal, you only need to define the crystal lattice to know everything. Whereas for a living being, it's the cell that suffices. For time, this scale coordinate means that it's enough to limit ourselves to a frequency range covering an octave (factor 2). Hence the fact that transposing from octave to octave does not change the musical rendering. Now we need also to know what the second time coordinate ψ represents. And it's here that I propose to bring consciousness into play. So, in addition to time t, measured by a clock, there would be time ψ measured by consciousness. Roughly speaking, ψ would indicate at what level of reincarnation and therefore at which information level we are located in the void/ether. Unlike the other five coordinates, this is a matter of proposition and speculation, not certainty. But it is precisely the purpose of this paper to see how far we can go with such a hypothesis.

We therefore consider our universe to form a 6D continuum (6 = 4+2) with four spatial coordinates (abscissa, ordinate, coordinate, scale) and two temporal coordinates (time and level of information/consciousness). What motivates us here is that the characteristic of time is that it cannot be reversed. And, by the same token, the level of information cannot be reversed. For, according to Shannon's theory, this level is defined by I = Σ_i p_i·ln p_i, where p_i represents the probability of having a certain piece of information i among a whole set of information. Similarly, we know that in statistical thermodynamics, the entropy of a system is defined as S = k_B ×Σ_i p_i·ln p_i , where now p_i represents the probability of observing a certain microstate (x, y, z, t) in space and time. And, just as it is impossible to go back in time, it is, in fact, impossible to decrease the entropy of the universe, which can only increase. The k_B constant (Boltzmann's constant) is here simply a scaling constant, allowing us to determine whether we are working with matter or with pure information via consciousness. There are thus two dimensions for time, one, t, associated with energy E, and the other, ψ, associated with entropy/information S.

In summary, we propose the existence of three types of continuums noted M⁴, C⁵ and V⁶ hereafter. The M⁴ continuum corresponds to Minkowski’s spacetime limited to the quadruplet (x, y, z, i·c·t). The C⁵ continuum is a conformally symmetrical space characterized by five coordinates (x, y, z, i·c·t, s), the last coordinate (s) referring to a position in the size scale (small/large). From a mathematical point of view, by combining the dilation symmetry operation with the translation and rotation symmetries, it is possible to construct a mass-conjugate quantum eigentime operator. This coordinate makes then it possible to speak of birth and death in an absolute sense. It is thus meaningful to assert that a given mass appeared here (place of birth) at a precise moment (date of birth) and disappeared there (place of death) at a later moment (date of death). And all this can be repeated ad nauseam.

Whether we're in M⁴ or C⁵, we're still describing the observable universe at an object-oriented level. The existence of a larger embedding space V⁶, would allow a supra-consciousness to operate on a virtual information field. Another crucial point is that the use of dilation symmetry operators may also be linked to the fact that a conscious being is free to operate changes of measurement units without altering the observed system. In short, all units are equal... The fact that the information field V⁶ is fundamentally scale-invariant is just another way of saying that space, time and matter don't exist by themselves. Hence the not-so-surprising assertion that matter is a mere illusion and doesn't exist in its own right. There is therefore a fundamental equation W = k_B·T = h·f = m·c² = e·U = (2h·α/e)·I = G·m²/D, indicating that matter can always be associated with the same energy W via interactions of a thermal, vibratory, mechanical, electrical (voltage U), magnetic (electric current I) and gravitational (mass m and distance D) nature. This, with a set of universal constants k_B = 0.0138 zJ·K⁻¹, h = 663 zJ·fs, c = 299,792,458 m·s⁻¹, e = 0.16 aC, α = 1/137 and G = 66.7384 pJ·kg⁻²·m, valid whatever the scale of observation.

For quantum physics, this suggests introducing a new scale wave function ψ(x,y,z,t,s) taking its values not only in space (x,y,z) and time (t) but also in scale (s). Now, by squaring the amplitude of such a scale wave ψ(x,y,z,t,s)·ψ*(x,y,z,t,s), we should obtain the probability of observing the mass of a system at any scale of observation. Using quantum scale operators, it is then possible to write a generalized Schrödinger equation whose solutions are waves propagating with time in scale as well as in space. We then find that the square of the ratio of the amplitudes of the fastest pair of these scale waves (the first two harmonics), is related by a universal constant N = ¼exp(4π²/ln2) ≈ 10²⁴. This justifies the order of magnitude of Avogadro's constant N_A = 6.022×10²³ mol⁻¹, which sets the size of atoms in relation to that of macroscopic bodies. The inclusion of other harmonics in the description slightly modifies the value, but not the exponent.

In other words, V⁶ must be seen as an entity that exists beyond space, time and matter and is the ultimate source of all types of reality. It would contain in the form of bit strings all past, present and future events in our universe. The ether of general relativity is therefore the physical substate of V⁶ on which it is physically possible to write or read bits of information as on any type of memory. In other words, everything is possible in V⁶, even the non-physical things that are commonly visualized during dreams as chimeras, monsters or other nonsense for the conscious "self" evolving in a C⁵ subspace. The ether V⁶ is also the repository of all mathematical ideas, all scientific theories, all works of art, all pieces of music, all deities - in other words, the common source of inspiration for everyone involved in art, science or spirituality.

With regard to the mechanism for reading from or writing to such an ether, we can refer to quantum-loop gravity by stating that the ether can exist in two distinct states: looped (bit 1) or unlooped (bit 0). It is also possible to define a quantum of spatial area A_P = ħ·G/c³ (where ħ = h/2π is Dirac's constant) and therefore also a quantum of length L_P = A_P^½ = (ħ·G/c³)^½ as well as a quantum of temporal area t_P ² = A_P/c². Knowing the age of the universe t_U = 4.3×10¹⁷ s, it follows that the memory capacity of our universe C⁵ embedded in the ether V⁶ is currently about M = (c·t_U/L_P)⁴ = c¹⁰·t_U⁴/(ħ·G)² ≈ 10²⁴⁴ bits. Alternatively, the ether of general relativity can be replaced by the vacuum of quantum theory. At the level of the information stored in V⁶, this doesn't matter. However, after projection into a subspace C⁵, where energy matters, the two points of view don't agree. This stems from the fact that mass M scales with length L in general relativity (M = G·L/c²) while it scales with the inverse of a length (M = h·c/L) in quantum physics. Hence the difficulty of marrying these two theories together.

That said, we can now turn to the crucial role played by the water molecule in this picture. First of all, the distinction between inert and living things lies in the ability of a given material system to explore the fifth dimension. This, by allowing changes in size through a metabolism that enables duplication. And, to memorize what has been acquired by being able to process information (consciousness) in a sixth dimension. In contrast, an inert thing is limited in its evolution by the M⁴ subspace. It follows that, neurons, being made of matter, surely hold in M⁴ a form of local consciousness, the conscious "self", embedded in a supra-consciousness that extends in V⁶ far beyond the brain, heart or gut. What's more, the neurons acting at the level of object-oriented language obey Boolean binary logic. Consequently, there should be at least one other channel of expression involving the whole body obeying intuitionistic logic (meta-consciousness). Finally, a third channel could also be identified, involving the mind/body combination in the V⁶ field and obeying minimal logic where negation simply doesn't exist.

On the other hand, there is experimental evidence that water is capable of storing, in the form of an electromagnetic signal, the information needed to produce, from separate nucleotides, a molecule as complex as DNA [30,31,32,33]. For some ten years, this claim always came from the same research group, until an independent group confirmed such a possibility [34]. Obviously, in a M⁴ continuum, such a claim appears, on a theoretical level, totally unfounded. But, in a V⁶ continuum, nothing very surprising. The mechanism authorizing such a phenomenon was put forward as early as 1988 [35] and refined in 1995 [36], then in 2012 [37], and finally amended definitively in 2018 [38]. We briefly recall it here.

The starting point is the possibility of generating an attractive force between two mirrors proportional to the inverse of the power of four of their distance d (static Casimir effect) [39]. Such a force (Figure 9d) arises from the exclusion of all wavelengths greater than d. In another experiment, unobservable virtual photons filling the quantum ether can be transformed into real photons (dynamic Casimir effect) [40]. All we need to do is set one of the two mirrors in relativistic motion (Figure 9d). The existence of such virtual photons within the quantum ether is ensured via the existence of an operator N. An operator whose eigenvalues correspond to the number of quanta with pulsation ω = ∆φ/∆t, where φ is the unobservable quantum phase angle related to the internal state of each quantum.

Under these conditions, the reduced Hamiltonian can be written: H/ħω = N + ½. Hence, when the quantum field is in its ground state (empty), the existence of a so-called "zero-point" energy ZPE = ½ħω, with ω = ∆φ/∆t and corresponding to N = 0. [41] Moreover, there is non-commutation between the quantum number operator N and the phase angle operator Θ: [N,Θ] = -i. There is therefore an indeterminacy relation ∆N×∆φ ≥ ½, responsible for quantum coherence at all scales, including a macroscopic one [42,43]. And, with W = N×ħω or ∆W = ħω×∆N, any uncertainty ∆N, such that ∆N·∆φ ≥ ½, leads to an energy uncertainty such that ∆W·∆t ≥ ½. It is therefore possible, in quantum field theory, to temporarily violate the sacrosanct principle of energy conservation. But, only for a short time ∆t < ħ/∆W.

These considerations apply, of course, to all types of matter. Matter seen not by a chemical formula, but rather, equivalently, by its frequency spectrum. Such a spectrum is easy to obtain thanks to a whole range of different spectroscopic techniques. The question that now arises is to once again consider the water molecule, the most abundant molecule in the universe. But, no longer with its formula H₂O, but, rather, via the frequency spectrum associated with such a stoichiometric formula [42] (Figure 15a). The interest here is that the water molecule is a very small entity, with a diameter close to 0.3 nanometers. Consequently, the energy levels of the first excited states do not form a continuum, but rather a ladder with widely spaced rungs. Thus, there is a first excited level at an energy ∆W = 1120 zJ, for an ionization energy of 2022 zJ. This level, however, cannot be used, as it corresponds to anti-bonding states of the O-H bond. If it were used, there would be a non-negligible risk of OH• hydroxyl radicals appearing.

The idea is therefore, in order to achieve virtual excitations using vacuum energy, to use non-bonding Rydberg levels located on the oxygen atom, of the 5d orbital type. This is because such a level, located at an energy ∆W = 1934 zJ above the ground state of the water molecule, is capable of giving a coherence gap of the same order of magnitude as the energy of the hydrogen bond [29]. Hence a self-excitation wavelength λ(μm) = 198.645/∆W(zJ), i.e. λ ≈ 0.1 μm = 100 nm and a lifetime ∆t < ħ/∆W = 106/1937 fs ≈ 10⁻¹⁶ s, since ħ ≈ 106 zJ-fs. Now, the power P radiated by an electron of mass m_e ≈ 10⁻³⁰ kg subjected to acceleration a and velocity v = a·τ_e, is written P = (m_e·a)·v = ⅔·ħ·(a/c)², with α ≈ 1/137, Sommerfeld's fine structure constant. Hence a characteristic relaxation time τ_e = ⅔α·ħ/(m_e·c²) ≈ 10⁻²³ s, since m_e·c² ≈ 82 fJ. The number of water molecules affected by such virtual excitation extracted from the vacuum during a time lapse ∆t ≈ 10⁻¹⁶ s, is therefore: ∆N ≈ 10⁻¹⁶/10⁻²³ = 10⁷. This also means that the maximum uncertainty on the phase angle φ common to these N_CD ≈ 10 million water molecules forming a "coherence domain" (CD) of size λ is such that ∆φ ≈ ½∆N, i.e. ∆φ < 5×10⁻⁸ rad. On the other hand, in order to minimize the increased electron repulsions via these excited states, this cannot occur in volume, but rather in the vicinity of any 2D interface [43].

More precisely, Figure 15b shows that when a water molecule in its gaseous state interacts with the quantum vacuum via one of its excited states, the diameter of its electron cloud increases. Here, the only possibility is to wait long enough for relaxation back to the ground state. The energy required for excitation is then returned to the vacuum. In the liquid state, however, the scenario is different. Here, van der Waals forces mean that molecules are relatively close together. As a result, if a water molecule becomes excited, it expands as expected. But its electron cloud then overlaps that of a neighboring molecule. And, as a result of this partial overlap, quantum entanglement can occur, leading to the possibility of cross-relaxation. In other words, instead of returning the borrowed photon to the vacuum, it is transferred to the water molecule entangled near van der Waals. The first molecule thus relaxes, while the second in turn becomes excited (Figure 15c). Of course, this mechanism doesn't stop there, which means that the initial photon borrowed from the vacuum passes from molecule to molecule, without returning there. Except that, after around 10 million transfers, the process reaches its limits, and the vacuum ultimately reclaims the photon it was kind enough to supply to the first water molecule. In short, some 10 million molecules, for a brief moment, shared the same photon extracted from the vacuum. And, as a result of this sharing, the quantum vacuum was able to act as a "glue" between around 10 million water molecules (coherence domain). Figure 15d shows how this glue can be represented within the framework of a second quantization formalism, via so-called "virtual" photons circulating ceaselessly between water molecules, thereby rendering them totally indistinguishable and united by the same quantum phase.

As this is very technical, we could also say that there is a perpetual game of soccer between the vacuum, which plays the role of playing field and referee, the water molecules, which are the players, and the photons, which play the role of balloons. In classical physics, there's obviously nothing equivalent, hence the invention of an ad-hoc term, where this "glue" is called the "hydrogen bond". In short, a simple word to translate this subtle, perpetual interplay involving vacuum, light and matter. That's why this glue is found not only in liquid water, but also in a large number of biological molecules (DNA, RNA, proteins, sugars) fundamental to life. As water and biopolymers use exactly the same glue, it's no exaggeration to say that "water is life".

Therefore, if scientists were serious and consistent, they would integrate all the available data acquired during years of theoretical and experimental toil on liquid water, the water that wets, quenches and gives life (Figure 15e). Yes, we're a long way from the formula H₂O. Let's recap: H for hydrogen, D for deuterium, T for tritium and O for oxygen with 3 digits 16, 17 or 18 indicating which isotopologue we're dealing with. Next, the arrows indicate the spin state of the H, D or T atoms (ortho or para water). The dots '.' stand for aqueous physical vacuum, something different from nothingness. The Greek letter γ stands for the coherent glue or "hydrogen bond" between water molecules. Whereas the letter γ' stands for the coherent glue of a covalent nature between different types of atoms. Finally, the positive charge (hydronium ion H₃O^⊕) appears as soon as an oxygen atom is surrounded by three γ' glues and a single γ glue. Whereas it's the negative charge that appears if that same oxygen atom is surrounded by three γ glues and a single γ' glue (hydroxide ion OH^⊖). In pure, neutral water, these two ions are always in equal amounts, hence pH = 7. And, if there's an imbalance, we speak of an "acidic" (excess of H₃O^⊕ ions) or "basic" (excess of OH^⊖ ions) medium. It's important to realize, however, that as soon as these species are no longer in exactly equal concentration, the thing we're manipulating is no longer water, but something else we call "acid" or "base". Scientifically speaking, the drawing represents what is known as a "coherence domain", which may contain several million water molecules, although there are barely 17 represented.

And for those who still have trouble visualizing what a coherence domain is, there's Figure 15f. Here, the same phenomenon is reproduced on a macroscopic scale, with grains of sand playing the role of water molecules and a vibrating plate playing the role of the quantum vacuum. But it's also true of starlings in the sky or schools of fish. In the case of starlings (water molecules), air plays the role of the quantum vacuum, the vibratory support. For schools of fish (water molecules), it's seawater itself that once again plays the role of quantum vacuum, a vibratory support. Let's now look at the practical consequences of this new way of thinking about hydrogen bonding.

Thus, a mammalian cell has a mass m ≈ 1 ng [44], for a volume of 10⁻⁹ cm³, a diameter D ≈ 12 μm and a surface area A ≈ π·D² ≈ 500 μm². As already mentioned, such a cell is made of more than 99 mol% morphogenic water of density d ≈ 1 g·cm-³. Furthermore, such a cell is covered by a hydration shell strongly associated with its lipid bilayer. If these water molecules are excited by vacuum/ether at λ ≈ 0.1 μm, the number of coherence domains is worth N_DC = 2·A/λ² ≈ 2×500/0.01 = 100,000. The factor two takes into account both extracellular and intracellular water shells. Depending on what is embedded in such a lipid bilayer, there may be regions where coherence is activated (bit 1). And other regions where coherence is absent (bit 0). Hence the possibility of encoding information. Furthermore, a coherence gap δW ≈ 42 zJ [37], corresponds to an associated wavelength λ(μm) = 198.645/42 ≈ 4.7 μm, falling in the infrared region of the electromagnetic spectrum. The energy required to modify the coherence state in these aqueous domains could therefore very well be supplied by the sun/earth couple. For, the Sun illuminates the Earth at 0.5 μm with re-emission by the latter at around 10 μm.

This is also in line with the observation that any hydrophilic surface has an exclusion zone (EZ-water) that converts IR radiation into an electrical potential [45]. In other words, the water layers surrounding a cell can store information that can be written, erased or read using infrared radiation. Knowing that 1 byte = 8 bits, the total memory capacity of these water layers is estimated at N_DC /8 ≈ 10 ko. With 3.72×10¹³ cells in a human body [44], the memory capacity of the membranes would therefore be close to 3.72×10¹⁷ bytes = 372 Po. We can also consider the reference value of 36 liters of water, average between men and women in the adult white American population (20-79 years) [46]. However, the hydration shell of intracellular biopolymers consists of a maximum of four water monolayers [41], i.e. a thickness of around 1 nm, since a water molecule has a diameter of around 0.3 nm. Hence a volume V_DC ≈ 1×100×100 = 10⁴ nm³ per coherence domain and therefore 8×10⁴ nm³ per byte of information. Since 1 L = 10²⁴ nm³, we find for 36 L of intracellular and extracellular water or interstitium [47] a total of: 36×10²⁴/8×10⁴ bytes = 450 Eo.

In addition to cell membranes and interstitium, consider the human intestine, known to contain around 3.8×10¹³ prokaryotes [48]. A prokaryotic cell has a diameter ten times smaller than that of a eukaryotic cell, i.e. a surface area 100 times smaller (A' = A/100 = 5 µm²). Hence a storage capacity at λ = 0.1 µm estimated at 2A'/8λ² ≈ 10/(8×0.01) = 125 bytes. Therefore, for the human intestine we find a total of 3.8×125×10¹³ = 4.75×10¹⁵ bytes = 4.75 Po. And, with around 5×10³⁰ prokaryotes on earth [49], we find a total of 6.25×10³² bytes. By comparison, for a total of 8.1×10⁹ human beings in 2024 [50], each carrying 4.5×10²⁰ bytes in their bodies, we only get a total of M(t) = 4.5×8.1×10²⁹ bytes = 3.645×10³⁰ bytes.

But for consciousness, memory capacity is not enough. For, one must also take into account the bandwidth BW(t) = dM(t)/dt [51]. And, for a human being we find BW(t) ≈ 1 Mo·s⁻¹, coming mainly from the sense of vision [24], or for about 100 years of existence about 3,156×10⁹ s, and therefore a total of 3,156×10⁹×10⁶ = 3,156×10¹⁵ bytes ≈ 3.2 Po. This corresponds to just 1% of the memory capacity of the body's membranes. Even assuming a bandwidth of external stimuli of 100 Go·s⁻¹ corresponding to all that's possible to record during an entire human lifetime [29], we find 32×10¹⁸ bytes = 32 Eo, or just 10% of the body's 450 Eo. Hence, the consciousness that is required to make sense of this raw data stored in every human body and define what is usually referred to as "context" [52]. The role of the conscious "I" is to discard a large part of this context that is not transmitted (exformation) [24]. And we know that the average water turnover of a sedentary adult is 3256 mL per day, or 37 μL·s⁻¹ [53]. So, if water is indeed the information carrier in the human body, we calculate a bandwidth of BW(t) = 37×10¹⁸/8×10⁴ = 462.5 To·s⁻¹, since V_CD = 10⁴ nm³ and 1 μL = 10¹⁸ nm³. This value is 12 times lower than the global Internet traffic estimated for the year 2025 at 181 Zo [54], i.e. 181×10²¹/3.156×10⁷ ≈ 5.735 Po·s⁻¹. However, we can also consider the movement of water inside the body, independent of external losses. Now, in Homo Sapiens, blood is distributed to cells by around 10⁹ capillaries of internal diameter D_C = 3.5 μm for a total cross-sectional area of A_C = 6 m² [55]. On the other hand, the largest artery of the heart is the aorta with a mean diameter D_A = 30 mm [56] associated with a mean blood flow velocity v_A = 76 cm·s⁻¹ [57]. Knowing that ¼π·D_A²·v_A = A_C·v_C = 537 cm³·s⁻¹ = 537×10²¹ nm³·s⁻¹, i.e. v_C = 89.5 cm·s⁻¹, it follows that BW(t) = 537×10²¹/8×10⁴ = 6.7 Eo·s⁻¹, throughput 1000 times greater than the entire global internet forecast for the year 2025.

Clearly, the most likely place where such information flows exist is in cell membranes. This means that any cell membrane could be the host of a local consciousness, and intelligence is expected in amoebae, for example, as has been observed experimentally with the plasmodium mold Physarum polycephalum [58]. This mold has also been shown to be able to anticipate periodic events [59]. Since the osmotic coefficient of permeability of a lipid bilayer for water is around 100 μm·s⁻¹ [60], it comes for a surface area A(prokaryote) = 5 μm² a bandwidth BW(t) = 5×100×10⁹/8×10⁴ = 6.25 Mo·s⁻¹. So, for all terrestrial prokaryotes, we expect: BW_pro (t) = 5×6.25×10³⁶ ≈ 3.1×10³⁷ bytes·s⁻¹. By comparison, humanity as a whole is characterized by BW_hum (t) = 6.7×10¹⁸×7.7×10⁹ ≈ 5.2×10²⁸ bytes·s⁻¹. In other words, the human contribution to the earth's global consciousness is just one part per billion (ppb). In fact, in view of these enormous bandwidths, it should be obvious that we're talking here about consciousness at an object-oriented, i.e. largely unconscious, level. Consequently, for the blood circulating in our capillaries, we can speak of a personal unconscious, or even Freud's "id" [61]. Whereas for the water that circulates on the membranes of prokaryotes, we are probably confronted with Jung's collective unconscious [62].

When it comes to consciousness at a meta-level, we leave the object-oriented digital mode and land in an analog mode associated with muscular movements or with electromagnetic signals emitted by the brain, gut and heart. However, we know from the invariance of Maxwell's equations under the symmetry operations of the ISO(4,2)⊗U(2)⊗U(2) mathematical group that all electromagnetic reality should be embedded in an ether V⁶. Fitting consciousness into the restrictive framework of a Minkowski M⁴ space is generally perceived as a "difficult problem" [63]. And then there's also the free will of living beings, which can be described as a "difficult issue" [64].

In the ether V⁶, on the other hand, there should be no problems or difficult issues related to consciousness. Here, each conscious being occupies a certain volume with highly significant bits that never change and other bits that can be reconfigured according to experiences on a C⁵ hyper-surface at a given location (coordinates x-, y-, z-), at a given moment (coordinate t-) and at a given scale in space and time (coordinate s-). Using the language of group theory, reducing reality to a space C⁵ means separating the group ISO(4,2) having infinitesimal generators describing an external world, from the group U(2)⊗U(2) having finite generators and describing the internal world of elementary particles (strong and weak interaction). Consequently, our approach is consistent with physicalism as well as dualism.

As explained above, the s-coordinate of C⁵ is crucial in differentiating between living things and inert things. Thus, a rock has an existence in space and time at a given scale, but lacks software in V⁶ enabling it to develop on its own. In other words, for inert matter, space V⁶ and its subspace M⁴ seem to be completely disconnected due to too low a water content. A seed, on the other hand, also has an existence in M⁴. But, more importantly, it possesses in V⁶ a small ROM containing downloadable instructions on how to grow over time. Such a ROM enables it to change size, optimally managing matter and energy via metabolism. At birth, the necessary information stored in V⁶'s ethereal substance is transferred as ROM to DNA and as RAM to the hydration shells of membranes and biopolymers. On death, the information is transferred to the hydration shells of the terrestrial microbiota or animals that have devoured the living being. The same applies to animals, but here the ROM in V⁶ can be updated via their metabolism in C⁵. This is precisely why animals, unlike plants, have the ability to move in C⁵ in search of food. As animals, humans are also able to reconfigure their software in V⁶ thanks to their metabolism in C⁵. However, they have the additional ability to do so after mentally focusing their attention (through meditation, for example) on a particular set of bits in V⁶ in a state generally referred to as "mindfulness".

This would mean that humans have the ability to mentally access the internal world of matter covered by U(2)⊗U(2) symmetry. Whereas animals are condemned to use only the ISO(4,2) part of reality. As the generators of the U(2)⊗U(2) group are integrative and differential in nature, they couple the macrocosm with the microcosm at all scales. Further work is therefore needed to fully understand their role in nature. During the exchange of information between space V⁶ and hyper-surface C⁵, the conscious being has the feeling of being traversed by a pure energy that could be identified with the "Prana" or "Qi" of Eastern civilizations. Such an information-driven flow would be perceived as entropy by a Western mind. Consequently, the shift in scale can only be experienced as energy, as the presence of matter locally breaks the ISO(4,2) symmetry, reducing it to ISO(3,1) with the appearance of a force called gravitation necessary to restore full symmetry on a global scale.

This modeling of the phenomenon of consciousness appears, therefore, intimately linked to gravitation, as proposed by the Orch-R model of consciousness [65]. Such a reduction from ISO(4,2) symmetry in C⁵ to ISO(3,1) symmetry in M⁴ can be identified with the collapse of the wave function in quantum physics. As cognitive neuroscientist Marcel Kinsbourne quotes: "What makes any problem difficult is that something false but attractive stands in its way" [64]. Here, the thing that is false but attractive is obviously the fact that matter exists by itself. As explained earlier, the fact that matter does not exist and is an illusion has been lucidly perceived by great scientists such as Henri Poincaré, Max Planck, Werner Heisenberg, Erwin Schrödinger and John Wheeler. In our approach, Einstein's call to think at a higher level [66] means replacing the ISO(3,1) group with its ISO(4,2) supergroup.

Of course, Eastern philosophies did not wait for the discovery of group theory or quantum physics to reach the conclusion that matter was an illusion and that ultimate reality was to be found in consciousness. Fortunately, Western science, based on powerful mathematical models, comes to exactly the same conclusion. These considerations are also fully in line with Hinduism's concept of multiple lives. For, here, karma corresponds to the traces left in V⁶ by conscious beings experiencing multiple life forms in C⁵. It is also consistent with shamanism, with V⁶ becoming the spirit world. More generally, this is consistent with all altered states of consciousness where one has direct access to the invisible reality of V⁶ without having to experience death, the "normal" gateway to it automatically. Another consequence is that near-death experiences (NDEs) or out-of-body experiences (OBEs) should be seen as actual journeys into V⁶ with the help of consciousness. And, not, as unreal mental images generated by an oxygen-starved brain. Finally, all this points to at least three different ways of healing when you're ill. Healing can happen in M⁴ through the use of material drugs or stimuli of an electromagnetic nature (for example). Healing can also occur in C⁵ due to water's ability to store or transmit various and sundry information. Finally, healing can also occur in V⁶ via purely informational means involving consciousness (placebo effect, among others).

The Origin of Life

Now we come to the crux of this paper. How can we understand the phenomenon of life in 2024? Figure 16 summarizes the main point. The central idea defended here is that consciousness gave birth to life, and not the other way round. However, a certain number of stages are necessary to go from the very beginning - consciousness - to the final end - life on earth. And among the five intermediate stages, the immaterial concept of information and that material thing called "water" appear to be closely linked. To imagine life without consciousness is simply impossible. And, whatever the context - bacterium, plant, animal or human being - each entity participates in its own way and with its own skills in raising the overall level of consciousness of this planet called "Earth". In the foregoing, we've already shown that each entity on Earth can be assigned a bandwidth expressed in bytes per second. And this information is never lost. Rather, it is stored in the ether, also known as the "quantum vacuum", according to the state of coherence (bit 1) or incoherence (bit 0) of a Planck cell. The existence of such cells is assured by two theories central to contemporary physics: quantum physics and general relativity.

Within this framework, it is possible to identify five "fundamental dimensions": mass M, length L, time T, temperature Θ and electric charge Q. And, opposite these five fundamental dimensions, we can contrast five universal constants:

-: The universal gravitational constant: [G] ≡ M⁻¹·L³·T⁻²
-: The quantum of action, also known as Planck's constant: [h] ≡ M·L²·T⁻¹
-: The speed of light in the vacuum/ether: [c] = L·T⁻¹
-: The entropy quantum, also known as Boltzmann's constant: [k_B ] = M·L²·T⁻²·Θ⁻¹
-: Coulomb's constant: [k_C ] = M·L³·T⁻²·Q⁻²

The constant [G] is used to describe the interaction between immobile masses. The action quantum [h] describes the interaction between moving masses with a certain velocity v. The constant [c] tells us that there are light "particles" (photons) with no mass, but with a very characteristic speed limit. The entropy quantum [k_B] guarantees the existence of something called "heat", capable of setting masses in motion spontaneously and not initiated by shocks between masses. Finally, Coulomb's constant [k_C] guarantees the existence of charges responsible for non-mechanical, non-luminous or non-calorific phenomena such as electricity (immobile charges) or magnetism (moving charges). The latter constant is linked to the existence of a quantum of charge e such that e² = αℏc/k_C, where ℏ = h/2π and α is a dimensionless pure number such that 1/α = 137.03599911..., called the "Sommerfeld constant". This constant [k_C ], in turn, is intimately related to the so-called "ether permittivity", denoted ε₀, with 1/k_C = 4πε₀. Note that we prefer the term "ether" here to its equivalent the word "vacuum", which can give the unfortunate impression that there's nothing there. For, in fact, in this void/ether, there is indeed something that is information, but which is neither visible, nor tangible to the physical senses. Consciousness is the only way to access this information, provided we have a communication interface - which, in the material world, is provided by water.

Everything is therefore in place to divide the vacuum/ether into elementary cells called "Planck cells" with an "elementary" area A_P = ℏG/c³ or an elementary volume V_P = [(ℏG/c)^½ ]³ depending on whether we're at a matter/ether interface (A_P ) or in pure ether (V_P ). For, as explained above, in modern physics, matter has no existence of its own, being merely a more or less intense excitation of the underlying ether that permeates everything material or non-material. As Figure 16 reveals, a chain of seven key concepts underpins everything that can happen in our universe. From immaterial consciousness to material life. First, there's the basic substrate: the ether or quantum vacuum, whichever you prefer to call it. Then, this ether is merely a substrate for this thing we call "information", which can exist in two states: "true = 1" or "false = 0". The size scale here is L_P = (ℏG/c)^½ = 1.616×10⁻³⁵ m. Even if the size scale seems extraordinarily small, thought allows us to imagine the existence of an arbitrary number of perfectly unobservable quantum blocks of even smaller size. However, even at this size, we can assume that the laws of quantum physics remain valid. And so, as soon as a Planck cell encodes the bit "1", then all the constituent sub-blocks all share the same quantum phase (coherence). On the other hand, if bit "0" is encoded, there is no phase correlation between the various sub-blocks (incoherence). Note that at this stage, this information is in its raw state, totally devoid of meaning. But if, at this level, the true or false states of Planck cells cannot be measured individually, it is still possible to associate a global total information quantity I = Σ_i (p_i ×Ln p_i) by assigning each cell a probability p_i of being, for example, in a "true" state. Then, by multiplying this sum I by the entropy quantum k_B, we recover an entropy of a more thermodynamic nature. This assumes that there is matter in motion somewhere, so that we can define a temperature T, via the average kinetic energy of the particles making up this decorative matter.

To move towards life, we must now, via consciousness, give meaning to this raw information, i.e. define a context. A context is also information. But it's information that's not intended to be transmitted. Hence another name, exformation, which is information that remains in the ether with the cloud of the entity who will play the role of transmitter. And this is where it all happens. The basic tool for sorting out what is to be transmitted and what is not is the Sheffer bar, a binary logical operation that can be considered the primary source of all other logical operations. This is where the notion of energy comes in, because this sorting doesn't happen by itself. It requires work and a certain level of activity, not only in the mathematical sense, but also in the thermodynamic sense (concentration gradients). Hence another piece of information, carefully processed and purified, worthy of being transmitted to a receiver that can only be water. For this substance is material in nature, making up 99.1 mol% of all living cells.

For, if an information receiver is to be present, the best thing is for it to envelop, like its ancestor, the ether, anything that isn't water. This automatically solves the problem of which direction to send the information calculated by the consciousness. In fact, whatever the direction, there will always be water to receive and store this information. And here again, great economy of means. It's the same phase coherence mechanism as for the mother ether. We've just changed scale. Instead of manipulating immaterial sub-domains of a Planck cell, we manipulate coherence domains made of water molecules, as seen previously. Anyway, in both cases (ether and water) we can memorize a sequence of numbers 0 and/or 1. The only difference is that this can be done in 3D for ether, but only in 2D for water. So, what we're referring to here is "morphogenic" water. And not water with the formula H₂O. That's why this H₂O formula is drawn with thick letters in non-uniform colors, to clearly suggest that this is not ultrapure liquid water. Ideally, of course, the water should be attached to lipid membranes, which can form by self-assembly as soon as a material of an oily nature is dispersed in liquid water. But this is not mandatory. For, it can also be any gas/water interface involving one or more gaseous substances (air) mixed with water. The only difference is that the information stored in lipid bilayers is far more stable than that stored in gas/water interfaces, which disappear rapidly as soon as the temperature rises too high.

Ultimately, it is this informed morphogenic water that gives rise to all the extremely sophisticated nanostructures found in a living cell. All wrapped up in a membrane bilayer that clearly differentiates between intracellular and extracellular media. After all, it's all water: 964 mol‰ for a man and 975 mol‰ for a woman. The rest of the story involves concentration gradients involving one or more of the 19 ions encountered in a cell. More particularly, the pair Na⊕ in the extracellular medium and K⊕ in the intracellular medium is used to generate a membrane electrical potential. It's worth noting that organic matter only appears in the very last place. And, that among all possible and imaginable molecules, two appear absolutely vital and inescapable. These two kinds of molecules correspond to proteins embedded in the lipid bilayer. The role the first one is to form a tunnel able to transfer water from the intracellular to the extracellular environment and vice versa. These tunnels are called "aquaporins". The other kind will also act as a tunnel. But here, to allow inorganic ions to pass through the lipidic barrier. This, in order to modulate membrane electrical potentials as effectively as possible. This second kind of tunnel is called an "ion pump". So, with just a few proteins, the basic blueprint of life is in place. The rest is simple decoration, which will evolve over time to become ever more efficient and effective.

With such a background in mind, it appears that biology is currently plagued by several fossil concepts that may be responsible for this difficulty in elucidating the basic mechanisms of life. A careful examination of the origins of thermodynamics has identified these fossil concepts [2]:

-: Assumption that heat is a form of energy.
-: Equating entropy with disorder.
-: Equating death with states of maximum entropy.
-: Assimilation of Adenosine Tri-Phosphate (ATP) into the energy currency of living cells.
-: Non-recognition of entropy as a state function of the entire universe.
-: Belief that so-called "free" energies are a form of energy.
-: Ignorance of the basic principles of quantum physics, and in particular of the importance of intrinsic spin.
-: Confusion between three different forms of reversibility.
-: Failure to recognize that irreversibility lies at the heart of living systems.

Basically, these fossil concepts have been safely tucked away in a cupboard. Then, remains the fact that life is deeply rooted, through the concept of entropy, in quantum physics on the one hand and cosmology on the other. This is in perfect accord with everything we've just said. Namely, that life is not an emergent property of matter. Rather, it has always been a fundamental property of a universe filled with particles and fields subject to consciousness. It was therefore proposed to retain only Ludwig Boltzmann's clear definition of entropy. The latter is expressed only in terms of the multiplicity of microstates Ω, S = k_B ×Ln Ω with a second principle expressed in its most general possible form. Form applicable to any type of macro-state, i.e., ∆S(universe) ≥ 0.

Concerning entropy, we recall that this concept was coined in the mid-nineteenth century to predict how a chemical system comes to undergo spontaneous evolution over time. The problem is that the so-called "second principle" (∆S ≥ 0) designates the gaseous state as the final product of all evolution in a closed system. This is perfectly at odds with direct observation of biological systems. For the latter undergo spontaneous evolution from a gaseous state characterized by maximum entropy towards highly complex structures, displaying considerably lower entropies. Hence an apparent violation of the sacrosanct second principle of thermodynamics. However, it's also perfectly permissible to consider the Earth as an open system rather than a closed one. If this were the case, it would be capable of undergoing a spontaneous (local) decrease in entropy. But only if the excess entropy could be effectively exported to the entire universe via infrared photons imperceptible to the human senses [2]. If the entropy exported in the form of invisible infrared radiation is much higher than the entropy decrease observed on Earth, then the appearance of life on this planet becomes fully compliant with the second law.

The consequences of such a broader viewpoint, taking into account all types of process (reversible and irreversible), have been studied in depth [1] and will not be repeated here. The central idea is that the first condition for the spontaneous appearance of life on Earth is the existence of a metabolism, taking the form of thermodynamic cycles capable of generating large amounts of entropy by degrading low-entropy molecular systems (food) into high-entropy molecular compounds (waste). Two possible cycles have been identified, based on the very low entropy of the Earth's metallic core. This, in order to generate reducing gases (such as H₂, CO, NH₃ or H₂S) thanks to the low entropy of solar radiation (food). And, simultaneous production, as waste products, of solid minerals (serpentine, metal sulfides, magnetite or even goethite) or gases such as water vapor or carbon dioxide. The large entropy flux generated by these processes can then be used to build low-entropy molecular systems based on reduced carbon species and soluble phosphates, which are observed in all living cells [2]. Another consequence of this approach is the recognition of the ubiquitous role played by water in all aspects of life, through the concept of "water activity".

End of Meteorite Bombardment (3900 Myr)

Three major events have marked the evolution of the Universe. The first is the Big Bang, which saw the appearance of matter and light in the form of stars. And a star is basically something that burns hydrogen to form the atoms that make up all matter. However, hydrogen isn't really an atom, since it has no nucleus. Let’s recall here that a nucleus is defined as an assembly of protons and neutrons. And while deuterium D is indeed an atom with a nucleus, its lighter isotope H is not, since it has no neutrons. In fact, the hydrogen atom is an assembly of two elementary particles. One is made up of quarks (the proton p^⊕) and the other is the electron (e^⊝), which is a lepton. Quarks and leptons are themselves creatures of the ether (or, if you prefer, of the quantum vacuum), created by a fluctuation which, for want of a better term, will be assumed to be random. This is fundamental, because this simple fact will confer on chemical combinations of the H₂ or indeed H₂O type, quite original properties. This, compared to other molecules with only 2 or 3 constituent atoms. Because, as we saw above, beyond 3, we leave the sphere of "elementary" processes generating "motion" to enter that of processes generating very diverse and varied "structures".

At the very beginning of this article, we saw that to ensure stability, it's imperative to obey a ternary logic of the thesis - antithesis - synthesis type. For example, we know (Figure 7) that hydrogen and oxygen are the two most abundant elements (green boxes) in the universe, and thus, on Earth. And, what happens when a dihydrogen molecule H₂ (thesis) meets a dioxygen molecule O₂ (antithesis)? You do get a triatomic synthesis, in the form of two H₂O water molecules. Hence, it's not possible to have life without this really extraordinary substance that is water. But that's not enough. To store information, water has to be morphogenic. So, it must also contain, at the very least, air bubbles if consciousness is to unfold in all three spatial dimensions. The price to pay, however, is low stability in relation to outside temperature. If, on the other hand, we move into two dimensions, by attaching the water to a non-gaseous lipidic surface, then we can develop hardware systems capable of storing information permanently. But only if the temperature is neither too high nor too low. Hence the second event, the formation of the solar system following an accident 4.5 billion years ago. But, also, the choice of planet Earth, both close enough (thesis) and far enough (antithesis) from a star (Earth-Sun system). And, of course, the choice of water as the ultra-majority constituent of all life forms (at least 96 mol% in humans).

If we accept that life does not escape the constraints imposed by physics, we would expect any form of life to express itself within a framework that allows:

Control of space (meter), which requires the use of membranes.

Control of time (seconds), which requires genes.

Control of mass kilogram), which implies the existence of a metabolism.

Control of electrical charge (amperes) via membranes allowing concentration gradients for ionic species.

Control of temperature (kelvin) to initiate polymerization reactions.

Control of the number of molecules (mole) via membranes, genes and metabolism.

Control of light flux (candela) via chromophores (photosynthesis).

Hence the close symbiosis between three prerequisites:

i): Membranes that provide the awareness of existence in relation to an external environment. Hence the need to know how to manage lipids.
ii): Genes that enable experience to be passed on to new generations at physical death. Here, it's the management of nucleic acids capable of supporting a genetic code that comes into play.
iii): A metabolism that allows us to build ourselves from the information contained in our genes, from birth to death. As we shall see, this requires mastery of phosphorylation.

Now, let’s suppose that these three prerequisites have been fulfilled. How do we develop, now, non-gaseous interfaces that can immobilize these water molecules, which are just waiting to move? The answer lies in creating nanostructures, via covalent interactions, based on other sufficiently abundant elements such as carbon, nitrogen or sulfur (Figure 7). About 3900 Myr ago, the relentless bombardment of the Earth by meteorites finally came to an end. At this time, carbon is found in the air in the form of methane CH₄, carbon monoxide CO, and carbon dioxide CO₂. For nitrogen, again in the air, we have dinitrogen N₂, ammonia NH₃ giving rise to the ammonium cation NH₄^⊕ in water or hydrogen cyanide HCN which, in water, gives rise to the cyanide anion CN^⊝. Finally, there's sulfur, found in air either as hydrogen sulfide H₂S, or as the hydrogen sulfide anion or bisulfide HS^⊝ in water (sea ≈ 10⁻² M).

Five other highly abundant elements with a strong affinity for water complete the picture: sodium (Na), potassium (K), magnesium (Mg), calcium (Ca) and chlorine (Cl). Unsurprisingly, elements with a metallic character will end up as cations (thesis): sodium Na^⊕ (>10⁻¹ M), potassium K^⊕ (≈10⁻² M), calcium Ca²^⊕ (≈ 10⁻³ M) and magnesium Mg²^⊕ (≈10⁻² M). While chlorine, a non-metal, would form the chloride anion Cl^⊝ (>10⁻¹ M). With these four metallic species (Na, K, Mg, Ca) and the six non-metallic elements (C, H, O, N, S, Cl), we have 10 of the 11 elements absolutely essential to life (red circles in Figure 7). The eleventh element, phosphorus, which is also absolutely essential, is less abundant than the other ten (yellow). Above all, it is rarely found in the air, even though it is also a non-metal. Its preferred place is therefore water in the form of HPO₄²^⊝ phosphate anions (<10⁻⁵ M).

Then there are also the 14 elements that are essential to life, but only in trace amounts. They are marked with a blue square in Figure 7. And finally, the 7 elements marked with a white triangle, which are only essential for certain species [67]. Here, with regard to the origin of life, within a reducing atmosphere, we would highlight in particular:

-: Iron in the form of ferrous Fe²^⊕ ions (≈ 10⁻⁷ M)
-: The divalent cations Mn²^⊕ (≈ 10⁻⁷ M) and Zn²^⊕ (≈ 10⁻¹² M)
-: Monovalent cations Cu^⊕ (≈ 10⁻²⁰ M); Co^⊕ (≈ 10⁻¹³ M) and Ni^⊕ (≈ 10⁻¹² M)
-: Thiolates anions such as MoS₄²^⊝ (≈ 10⁻¹⁰ M) and WS₄²^⊝ (≈ 10⁻⁹ M)
-: Vanadates VO²^⊕ (≈ 0.3×10⁻⁷ M)

These elements, along with perhaps one or two others, are the only ones of interest in possible initial organic systems, with sulfide-rich anoxygenic seawater.

Now, there must necessarily have been a primitive organization of all this prebiotic chemistry before reproductive life. Because reproductive life requires a code that can only "code" a pre-existing system. On the one hand, we have lipids and proteins (metabolism), which clearly act as "material". On the other, we have nucleic acids (replication), which can act as "software". And then, to play the role of electricity circulating between the components, we have everything we need in the way of water holding dissolved inorganic ions. Hence, the third event, the appearance of life on Earth 3.9 to 3.5 Gyr ago.

If we think of the ternary relationship between proteins (thesis), nucleic acids (antithesis) and metabolism (synthesis), the same problem immediately arises. Protein synthesis cannot have taken place in solution, because in order to condense two amino acids, a water molecule must be eliminated:

R-NH₂ + HO-CO-R' = R-NH-OC-R' + H₂O

The simple law of mass action therefore prohibits the formation of any chemical bond of a peptide nature in water. The same constraint also applies to the phosphodiester bond that produces polynucleotides:

MgO₃P-O-Cb-OH + (HO)-Cb-O-PO₂K = MgO₃P-O-Cb-O-KPO₂-O-Cb + H₂O

Here, the symbol Cb represents a carbohydrate (sugar) such as ribose (RNA) or deoxyribose (DNA). RNA and DNA are also molecules capable of replication (replicators), and can code for proteins via a genetic code. Finally, no metabolism would be possible without the phosphorylation reaction, which also eliminates a molecule of water:

MgO₃P-OH + HO-X = MgO₃P-O-X + H₂O

Here, X can be an amino acid, any small molecule bearing a hydroxyl function, or even another phosphorus derivative to obtain a polyphosphate. Fortunately, nature has found a universal solution to enable all these reactions, crucial for any living being, to take place. The idea is actually quite simple: all that's needed is to create compartments isolated from the surrounding aqueous environment. And this need must have arisen even before the need to refer to codes. A code will only become essential when it comes to reproduction, whereas to live, the code is useless. Consequently, the appearance of a code that guarantees continuity requires that the system already has sufficient persistence to give it time to evolve.

And to make these compartments, nature has fallen back on the eternal recipe of the ternary, but here applied to very special molecules: fatty acids. For it is a fact that any covalent association between a hydrophilic molecule (polar head, thesis) and another hydrophobic one (tail, antithesis) can give rise, via self-assembly reactions, to extremely sophisticated nanostructures (synthesis) (Figure 17) [68]. Of course, these systems become self-assembled thanks to non-covalent forces (van der Waals forces, hydrogen bonds) that are intrinsically weak compared with chemical bonds of a covalent nature. But they have the great advantage of being cooperative. In other words, as the number of self-assembled objects in a nanostructure increases, so does the probability of adding a new object of the same kind.

Now, how can we make fatty acids under prebiotic conditions? This is where we need to talk a little bit about serpentinites, which are water-rich rocks composed mainly of minerals from the serpentine group (chrysotile, lizardite and antigorite). They are found on almost every continent. Such a rock with the formula Mg₃Si₂O₅(OH)₄ is obtained as a result of the relatively low-temperature hydration of peridotite, the main rock of the upper mantle, composed of magnesium-rich olivine and orthopyroxene (Figure 18). Ultramafic rocks and serpentinites are abundant in the oldest Archean greenstone belts (3.81-3.70 Ga) on Earth. Serpentinization is a natural process that releases hydrogen and other reduced gases, creating a unique deep-sea ecosystem [69]. It is thus assumed that this serpentinization reaction would have provided favorable environments for the abiotic production of lipid chains or amino acids. All that's needed is for seawater to come into contact with the oceanic crust at hydrothermal vents with temperatures ranging from 100°C to 400°C via fissures and crevasses. The chemical constituents of the seawater involved in this serpentinization are water and carbon dioxide dissolved as bicarbonate ions. While the constituents of the earth's crust are ferrous ions contained in olivines. Accordingly, seismic data indicate that fluids can percolate to depths of 500 m below the seafloor, reaching temperatures of between 150°C and 200°C.

Under these conditions, the ferrous Fe²^⊕ ion in rocks is capable of reducing water to produce ferric ions in the form of magnetite Fe₃O₄ or goethite (FeOOH), with wastes as brucite Mg(OH)₂ and "serpentine". It was thus estimated that one cubic meter of olivine could deliver around 500 moles of dihydrogen during serpentinization. Morever, the vast majority of rocks making up the Earth's oceanic crust consist of olivine or pyroxene, minerals which can also take part in the serpentinization reaction. This serpentinization reaction therefore most likely occurred as soon as there were oceans on Earth. What's more, it has been estimated that the total volume of the Earth's oceans passes through its hydrothermal vents every 100,000 years or so. So, the vast number of ferrous ions that make up the earth's electron reservoir for producing dihydrogen via serpentinization is in no danger of being depleted. Serpentinization delivers and has always delivered a non-negligible quantity of dihydrogen that can be used as a source of electrons for the primary production of organic matter in undersea ecosystems. With hydrothermal vents, we also know that serpentinization can geochemically reduce carbon dioxide into methane CH₄. This same geochemical process could therefore have perfectly fostered an energy metabolism based on chemical reactions involving carbon compounds and releasing large amounts of entropy as found in methanogenic or acetogenic bacteria. These reactions could also have been accelerated by cofactors and enzymes. Serpentinization can occur in both hot, acidic black smokers and colder, alkaline vents. These two types of hydrothermal vents could therefore have offered pH gradients that were quite similar to those present in hadean oceans. The lower temperature in the vicinity of the vents could provide favorable conditions to support abiotic synthesis and accumulation of reduced carbon compounds.

Hence the possibility that the following molecules, crucial for all metabolism, appeared around 4 billion years ago (Figure 18): methane (CH₄), formaldehyde H₂CO (H₂C=:O:), hydrocyanic acid HCN (H-C≡N:), iso-cyanic acid HNCO (H-N:=C=:O:), acetylene C₂H₂ (H-C≡C-H) and hydroxy-cyanamide CH₂N₂O (H-:O:-:NH-C≡N:) from dihydrogen H₂, bicarbonate ions HCO₃^⊝ and dinitrogen N₂ (:N≡N:). Note that most of these reactions require the removal of one or more water molecules. For the same reasons as above, therefore, they cannot occur in water. But there's no problem here, as serpentine is a lamellar structure that can intercalate hydrophilic chemical species between two sheets, thus isolating them from the surrounding aqueous medium. Of course, it is also possible to manufacture fatty acids according to the balance sheet:

HCO₃^⊝ + n CO + (2n+1) H₂ = C H_n2n+1 CO₂^⊝ + (n+1) H₂O

So, let's start with the possibility of making membranes from fatty acids. Such molecules are, in fact, ideal for forming an enormous variety of nanostructures via self-assembly reactions (Figure 18). Here, the fatty acid is characterized by its volume V, the area A swept by its carboxylate polar head and the maximum length L of the fully stretched hydrocarbon chain [68]. Now let R be the radius of the cavity in which the fatty acid will be solubilized in water. For a spherical cavity we have a topological condition R = 3V/A ≤ L. It follows, then, that a criterion for having a spherical micelle is that the stacking parameter PP = V/(L·A) is such that PP ≤ ⅓. If PP > ⅓, the system will seek to reduce its curvature. So, for a cylinder, we'll have a new criterion R = 2V/A ≤ L, i.e. PP ≤ ½. And, if PP > ½, the idea is to make closed spherical bilayers with a radius equal to twice the hydrocarbon chain length L, R = 3V/2A ≤ L, i.e. PP ≤ ⅔. And, if PP > ⅔, a new topology can then be a planar bilayer such that R= V/A ≤ L i.e. PP ≤ 1. Finally, if PP > 1, the surface area of the polar head is too small to form bilayers and inverted micellar structures are then obtained. Among all these topologies, evolution has retained spherical vesicle- or liposome-type bilayers, which partition water into compartments. On the one hand, there's the water inside the compartment, which will later become intracellular water. This first type of water is capable of rejecting the sodium ions Na^⊕ or calcium Ca^⊕⊕ as well as the chloride ion Cl^⊝ and the oxygen molecule O₂ outside it [70]. On the other hand, all living organisms persist in accumulating certain elements, essentially C, N, H, P, S, K, Mg and Fe. The second type of water is water outside the compartment, which will later become extracellular water. The problem of the emergence of life, then, boils down to how metabolism, replicators and enzymatic systems could develop, all attached to the same membrane system. In other words, without membranes and water, no life is possible...

Prebiotic Soup (3900 Ma...3870 Ma)

The complexity of the problem of the origin of life stems from the fact that the useful markers of biological evolution cannot be the traditional organic chemicals, such as DNA, RNA, proteins or even complex metabolites. In fact, it's only the very small carbon molecules, CO₂ and CH₄, that could be called environmental markers. Alas, these molecules are not directly controllable by cells. Hence the impossibility of tracking their changes over the period of time stretching from 4.0 Gyr to the present day. One peculiarity is that CH₄, formed as a result of the reductive degradation of organic molecules, reacts very slowly with oxygen. This leaves only molecules such as N₂, NH₃, O₂ and the soluble ions SO₄²^⊝ and H₂PO₄^⊝ as long-term markers, via the modification of their isotopic composition linked to any cellular evolution. As far as metal cations are concerned, we can particularly track changes in environmental availability and use of the ions Mg²^⊕, Ca²^⊕, Zn²^⊕, Mn²^⊕, Fe²^⊕, Co^⊕, Ni^⊕ and Cu^⊕ (Cu²^⊕) which are incorporated, mainly, into proteins.

It is therefore time to recall the role of these species in a cell [67]. Figure 19 shows the structures of the main metalloproteins. First and foremost are the Na^⊕ and K^⊕ ions, which are systematically involved in the regulation of osmotic equilibrium. Indeed, all cells reject Na^⊕ (10⁻³ M), Cl^⊝ (10⁻³ M) and Ca²^⊕ (10⁻⁶ M) compared to seawater concentrations. Then comes magnesium Mg²^⊕ which is involved in the glycolytic pathway (enolase), in all kinases, in most synthesis, in all signaling (transcription factors), in DNA/RNA structures and for light capture (chlorophylls). In fact, it appears that adenosine triphosphate (ATP) is always close to 10⁻³ M, very close to the concentration of free Mg²^⊕. It follows that MgATP should be the active agent in most reactions. This homeostasis also applies to mobile coenzymes such as NADH, and certainly to the cytoplasmic pH of cells. The concentration of free cytoplasmic Ca²^⊕ ions is always below 10⁻⁶ M and there are no intracellular Ca²^⊕-binding proteins in early cells. Certain cellular gradients were therefore established early in life and included the use of proton gradients to drive many non-spontaneous activities. On the other hand, the Ca²^⊕ ion stabilizes the membrane and wall, and may be involved in certain signaling activities.

The ferrous ion Fe²^⊕, for its part, is involved in the reverse citric acid cycle, CO₂ incorporation, signaling transcription factors, control of protein synthesis (deformylation) and light capture (hemes and ferredoxins). Manganese Mn²^⊕ is involved in the photolysis of water to release dioxygen O₂. The Ni^⊕ ion is found in cofactor F430 of the enzyme methyl coenzyme M reductase (MCR), which is involved in the final stage of methanogenesis by archaea: CH₃-S-CoM + HS-CoB = CH₄ + CoM-S-S-CoB. The Co^⊕ ion, meanwhile, is found in cobalamin, an enzyme involved in methyl radical metabolism -CH₃. Finally, the elements molybdenum (Mo) and tungsten (W) enable oxygen atom transfer at low oxidation/reduction potential. Hence the possibility of incorporating oxygen to obtain carboxylates from aldehydes, without using oxygen itself. Two ions, Zn²^⊕ and Cu²^⊕ have virtually no internal role. However, they are both excellent evolutionary markers. For, in the most primitive single-cell anaerobes, the unavailable oxygen and copper cannot be used. Hence the absence of their protein partners. On the other hand, in unicellular aerobic prokaryotes, calcium and the proteins with which it associates are little or not utilized. However, calcium signaling is becoming increasingly important in unicellular eukaryotes, where new calcium-binding proteins are emerging. Finally, multicellular organisms use more Ca-, Zn-, Cu- and Fe-based proteins and many elements outside the cell in controlled fluids, where new regulated proteins are emerging.

Anaerobic organism types are generally considered to be the most primitive organisms. As for the "material" side, all these cells, have a free concentration of K^⊕ (10⁻¹ M), Mg²^⊕ (10⁻³ M) and Fe²^⊕ (10⁻⁷ M), and they use mainly, the ferrous ion Fe²^⊕ with some cobalt and nickel, but very little manganese and zinc. And, most probably, never any copper- or calcium-based ions in the intracellular environment. On the "software" side, it's the possibility of obtaining purine and pyrimidine bases. For example, we know that hydrocyanic acid polymerization can lead to adenine (A): 5 HCN = C₅H₅N₅. And, if one molecule of HCN is replaced by one molecule of isocyanic acid HNCO, guanine (G) can be made: 4 HCN + HNCO = C₅H₅N₅O. If acetylene is used in combination with isocyanic acid HNCO, uracyl (U) can be obtained: C₂H₂ + 2 HNCO = C₄H₄N₂O₂. And, with hydroxy-cyanamide CH₂N₂O or formaldehyde H₂CO, the following molecules can be obtained:

-: Cytosine C (DNA): C₂H₂ + CH₂N₂O + HCN = C₄H₅N₃O
-: Thymine T (DNA): C₂H₂ + HNCO + HCN + H₂CO = C₅H₆N₂O₂
-: Nicotinamide (NAD): 2 C₂H₂ + 2 HNCO + H₂ = C₆H₆N₂O + H₂O
-: Isoalloxazine (FAD, FMN): 3 C₂H₂ + 4 HNCO = C₁₀H₆N₄O₂ + 2 H₂O

On a practical level, adenine and guanine, the two nitrogenous bases involved in RNA formation, can also be easily produced using an ice/hydrogen cyanide eutectic (H₂O/HCN) and sunlight. The ice/urea eutectic (H₂O/NH₂CONH₂ ), for its part, could have produced pyrimidine, cytosine and uracil, other key constituents of the RNA molecule. Via the bases (U, A, G, C, T), it became possible to have the "software" function ensuring the replication of information, in addition to the "hardware" function of the metabolic type (NAD, FAD, FMN). All this, of course, in the morphogenic water that orchestrates all this ionic, molecular and self-assembly chemistry in the background. All these more or less reduced molecules must have been available in the vicinity of "hydrothermal" vents, due to the serpentinization reaction.

Replication and Phosphorylation (3870 Myr)

Thanks to serpentinization, planet Earth had an almost inexhaustible source of reduced hydrocarbon matter, unaffected by random lightning strikes or equally random meteorite bombardments. In order to develop, life was thus able to address the far more delicate issue of molecular replication. One of life's obsessions will of course be to develop its capacity to store information and, above all, to stabilize it. Evolution will require us not to rely on water/gas or water/oil interfaces, which are far too labile. Indeed, while these interfaces are ideal for emerging from molecular chaos and managing the movement necessary for life, they do not ensure stability over four eons. As species evolve, we need to recognize the different entities we're dealing with. Hence the imperative need to reproduce identically so that the information patiently acquired is not lost. And with modern biology, we know that the final solution consists of a DNA/(RNA)/protein triplet, using nucleic acids of the RNA (ribonucleic acid) or DNA (deoxyribonucleic acid) type for genetic information on the one hand, and proteins for regulation and structural function on the other. This is where we come up against the chicken-and-egg problem. Since nucleic acid replication is dependent on protein enzymes, these same enzymes depend on the existence of nucleic acids in order to exist. This clearly means that, at the origin of life, another system predominated. But which is capable of self-replication: nucleic acids or proteins? The answer here is quite clear: nucleic acids.

This leaves the problem of non-enzymatic nucleotide synthesis and non-enzymatic polymerization to form RNAs with random sequences. Another problem is the non-enzymatic copying and/or replication of RNA. And, finally, there's the problem of the emergence, via natural selection, of a set of functional catalysts made of RNA. A set that was able to maintain exponential growth in a prebiotic environment. This hypothesis of an "RNA world" is therefore very promising, even if all the details are still a long way from being elucidated [71,72,73]. What seems certain, however, is that life could not have arisen within oceanic water masses. For, here, the level of dilution is such that it is highly unlikely that long polymeric chains of RNA or proteins could have formed. A more serious hypothesis therefore seems to be a combination of clay and water or the formation of a eutectic with ice so that the organic matter has a chance of polymerizing [74].

Indeed, evaporation of acidic nucleotide solutions leads to complex mixtures containing very short oligonucleotides in which the 2'-5' and 3'-5' phosphodiester bonds are random. The presence of external activating agents such as montmorillonite therefore seems indispensable. Montmorillonite is a mineral composed of hydrated aluminum-magnesium silicate, with formula (Na,Ca)_0.3(Al,Mg)₂Si₄O₁₀(OH)₂·nH₂O, and belonging to the smectite group, of the phyllosilicate family. It is also known as terre de Sommières. This aluminosilicate lamellar clay swells easily, enabling it to accommodate large molecules between its sheets so that it can catalyze the formation of phosphodiester bonds from previously activated ribonucleotides in this way. Montmorillonite is also capable of accelerating the conversion of fatty acid micelles into vesicles, and RNA adsorbed on this clay can be encapsulated in these vesicles.

The other hypothesis is the development of life in the vicinity of oceanic hydrothermal vents that could provide favorable conditions to support abiotic synthesis and accumulation of reduced carbon compounds [75]. With regard to the prebiotic manufacture of RNA, one problem has long been that the condensation of sugar (ribose) and nucleobase (purines and pyrimidines) does not work [72]. However, a recent paper was able to show how to avoid this sugar and base condensation step [76]. And, therefore, spontaneously assemble pyrimidine ribonucleotide monomers from molecules that are plausible on a purely prebiotic level. On the other hand, as there is still no credible prebiotic synthesis pathway for purine ribonucleotides, there is currently no convincing evidence for total prebiotic RNA synthesis on primitive Earth. On the one hand, yields are still far too low and, on the other, we always obtain racemic mixtures and not the biologically dominant D-nucleotide. Nevertheless, research continues apace. And, no doubt, a solution will eventually be found and published.

It is therefore clear that nucleic acid synthesis, duplication and mutation are the driving forces of evolution. This is because, according to Watson and Crick [77], nucleic bases may be paired with the following schemes: A...T, A...U and C...G. Hence the property that a polynucleotide is capable of directing the synthesis of as complementary strand starting from mononucleotides or small oligonucleotides. Hence the hypothesis that RNA acted as a precursor to proteins and DNA. In the sense that it can act both as a catalyst (like protein enzymes) and as a vector for genetic information. In 1986, the idea was born of an autonomous organism made entirely of RNA and capable of carrying out all vital functions, such as catalysis, heredity, recombination and evolution, thanks to this single molecule. This followed the discovery of catalytic RNA molecules, ribozymes, capable of carrying out enzymatic reactions [78,79].

The ribozymes found in living organisms today play a vital role, even if they are rather limited in the range of reactions they can catalyze. The best-known ribozyme is the ribosome [80]. And it has now been demonstrated that peptide bond formation during protein synthesis is catalyzed by the RNA of the ribosome without the direct intervention of the protein itself [81]. These same ribozymes also catalyze RNA splicing. RNA is therefore both a transporter of genetic information and an enzyme. The existence of ribozymes consisting of RNA has thus made plausible the existence of a primitive RNA world in which all enzymes were RNAs with no proteins [82]. Because the catalytic site that synthesizes proteins must have preceded the proteins themselves, ribosomes and consequently ribozymes must predate protein enzymes.

The existence of an RNA world greatly simplifies the problem of the origin of life on Earth. For, it avoids asking the question of the origin of all the other molecular components found in a cell. Just because DNA or proteins, are only a consequence of a process of natural selection in a prebiotic soup full of ribozymes. However, this hypothesis casts an opaque veil between current biochemistry and prebiotic chemistry. In the context of the RNA world hypothesis, the problem of the origin of life on Earth begins with the question of non-enzymatic nucleotide synthesis. As far as sugars are concerned, we have the "Formose reaction", in which formaldehyde is polymerized [83]. Probably in the presence of inorganic catalysts based on lamellar magnesium and aluminum hydroxides according to the balance: n H₂CO = HOCH₂-[CH(OH)]_n-2-CHO. Hence sugars (Figure 20) such as ribose (n = 5) or glucose (n = 6). This Formose reaction is of great interest. For it is the only example of a cyclic autocatalytic process taking place in an aqueous medium capable of converting a very simple substance, formaldehyde, into a mixture of complex molecules, most of which are important biochemical molecules.

Another major concern for the emergence of life is that the phosphate ion is incorporated into all nucleotides and many lipids, as well as being a component of many metabolites. We're talking here about phosphorylation, a process that activates molecules and causes them to react with each other. Something they would be reluctant to do were it not for this crucial reaction:

∆ + R-OH + HO-P(O)X₂ ⇄ R-O-P(O)X₂ + H₂O

The interesting thing is that this type of reaction can occur in both directions, as indicated by the double arrow. However, esterification with water elimination is an endothermic process that absorbs heat (symbol ∆). What's more, such esterification generates one molecule of water, which requires an anhydrous medium for the reaction to take place. As, it's just impossible to eliminate water if you're already in water. On the other hand, the opposite reaction, hydrolysis, consumes water and spontaneously releases heat. As always, we find the water without which life would be impossible. Of course, it's impossible to carry out these reactions, which, nowadays, require proteins that didn't exist on primitive Earth. Hence the phosphorylating bottleneck, as phosphorylation is absolutely essential to the formation of any complex biomolecule. And, up to now, there is no known alternative. Moreover, in the sea, the phosphate ion cannot exceed around 10⁻⁶ M due to the presence of calcium ions. Cellular phosphate requirements can therefore only be met by excluding calcium from the intracellular medium and pumping phosphate into the cells, where the concentration of free calcium is greatly reduced.

One trick is therefore to use the hydrolysis of the pyrophosphate ion [P₂O₇]⁴^⊝ , which is a spontaneous process. For, as we know, the earth's crust contains around 5×10¹³ kg of phosphate minerals [84], most of which are in the form of apatite Ca₅(PO₄)₃(X)₂, where X is a hydroxide ion OH^⊝, or a fluoride ion F^⊝. And, upon heating, apatite generates pyrophosphate ions [P₂O₇]^4⊝ (PP) or more condensed polyphosphates (Poly-P). Hence the name litho-phosphorylation to describe this inorganic phosphorylation, as opposed to catalytic phosphorylation, which requires enzymes and cells. It's therefore almost certain that the world of nucleic acids couldn't have existed in the primitive ocean. As, here, the enormous amount of water would lead to strong dilution and inhibit any esterification reaction. Instead, it could very well have developed in terrestrial saline polar pools subject to hydrothermal activity. This is because, on Earth, periodic freezing can form eutectics capable of significantly concentrating any prebiotic soup. What's more, a relatively cold frozen environment is more favorable to the stability of condensed nucleic acids and self-assembling membranes than a warm one. It follows that the first proto-cellular vesicles (hereinafter referred to as PCVs) were more likely to be psychrophilic (cold-loving) or mesophilic (lukewarm-loving) than thermophilic (warm-loving). So, at the end of this prebiotic soup phase, we expect to find in these pools two types of molecules destined for a great future. On the one hand, replicases, which are nucleotidyl-transferases catalyzing the reaction: nucleoside triphosphate + RNA_n ⇌ PPi + RNA_n+1 , where PPi designates one of the acid-base forms of the pyrophosphate ion. The other molecule was a non-specific kinase capable of transferring a phosphate ion from a polyP or PyroP to activate nucleotides or other molecules such as amino acids.

An RNA World (3870-3850 Ma)

As we said earlier, before matter-based life, there was immaterial consciousness (information). Nowadays, artificial intelligence (AI) has infiltrated all areas of our daily lives. And here too, there's a clear distinction between hardware and software. Let's remember that hardware includes all the parts made of matter. Whereas software refers to the components that enable us to process that intangible thing we call "information". Figure 7 shows the main elements necessary for life, but also, thanks to the little icon of a cell phone, the elements that are mandatory for AI. The idea here is that, if such a dichotomy exists today with AI, it must also have been present at the very beginning with the first forms of life. Hence, a certain correspondence between computer science on the one hand, and biology on the other. Of course, if you have the hardware, but without the software, there's no life. All we have are physicochemical transformations subject to the laws of thermodynamics (abiotic metabolism). Conversely, if you have the software without the hardware, there's no life either. We just have "viruses" waiting for the hardware to arrive so they can replicate. This inability of viruses to be autonomous means that their metabolic function is more primitive than their replicative function.

RNA replication without the aid of an enzymatic protein is a major feature of the RNA world hypothesis. It seems likely, but not necessarily certain, that the synthesis of a complementary RNA from a preformed RNA template, without the intervention of an informational catalyst, played a role in bringing about an RNA world. Thus, if a polynucleotide is incubated at a sufficiently low temperature with an appropriate mixture of complementary mononucleotides or small oligonucleotides, double- or triple-helix complexes are obtained in most cases. The complexes are structurally similar to double- or triple-stranded nucleic acids, but with an interrupted chain. The problem is that both 3'-5' and 2'-5' linkages are usually obtained. Here too, sugar phosphorylation seems to favor the formation of 3'-5' links to the detriment of 2'-5' links. On the other hand, all prebiotic synthesis leads to ribonucleotides in the form of racemates. However, the L-enantiomers of activated nucleotides are highly effective inhibitors of any matrix synthesis involving the D-enantiomers. Unfortunately, this is a major obstacle to any self-replication of polynucleotides using plausible prebiotic monomeric substrates.

For life to start, there must therefore have been a natural selection of a set of functional catalysts made of RNA that, taken together, were able to maintain exponential growth in a prebiotic environment. In evolutionary terms, we know that the large ribosomal subunit had only 20 proteins instead of 31 at the time when the bacterial kingdom began to diverge from the archaeal and eukaryotic kingdoms. The first ribosome was therefore very probably made entirely of RNA. On the other hand, eubacteria share only 20 proteins of the large ribosomal subunit with eukaryotes and archaea. This suggests that ribosomal proteins were late evolutionary additions. For its part, the peptidyl transferase center, 3-4 nm in size, is conserved in all three kingdoms of the tree of life, and contains no globular proteins but only a large number of linear protein chains. This is very convincing evidence for the existence of a primitive RNA world.

Unfortunately, the invention of protein synthesis was the beginning of the decline of the RNA world. We now know that RNA is capable of catalyzing many reactions. We have even been able to develop a catalytic RNA which has most of the essential properties of RNA polymerase. When presented with a single-stranded RNA template as an RNA primer in a mixture of the four nucleotide triphosphates, the complementary strand of the template is obtained. At present, it is impossible to copy templates with more than 14 residues, although in vitro copying of much longer RNAs is conceivable. However, the intractable problem of separating the double-stranded product of the copying reaction remains to be resolved before a second round of copying can be initiated.

We saw earlier that life as we know it today required three prerequisites: membranes to differentiate between inside and outside, genes to transmit any information acquired through natural selection, and a metabolism based on catalysts for non-spontaneous reactions such as phosphorylation. On a strictly molecular level, ribonucleic acids (RNA) have the particularity of being able to combine two of the three prerequisites. By joining together in a double helix, they can perform the genetic function of replication. By remaining single-stranded and folding on itself, they become catalysts at the origin of metabolism (Figure 20). On the other hand, these RNAs cannot play the role of membranes, the preserve of lipids alone. Hence the idea that nucleic acids "invented" proteins by drawing on the intelligence and consciousness associated with lipid membranes. Consequently, some 3.9 billion years ago, a self-replicating RNA world may have emerged from a mixture of mud, ice and various organic molecules.

But this RNA-based world soon came up against the problem of the proliferation of selfish, self-replicating entities: viruses. Indeed, many viruses can reproduce without the intervention of lipids, whereas without lipids a cell cannot reproduce. What enabled the emergence of cellular life from a viral world was therefore a symbiosis between nucleic acids, lipids and proteins. Of course, once lipids had invented proteins, viruses were able to use them to their advantage to build capsids to protect their RNA or DNA genetic material, thus becoming virions. Later, when cell membranes were well developed, some virions also found it useful to surround themselves with a lipid membrane, borrowed from cells, in order to better infect their target host cells. Cells capable of autonomous reproduction and self-replicating viruses, genetic parasites of cells, thus live side by side, for better or for worse. The best comes from horizontal gene transfer, ensuring good genetic diversity. The worst is cell death through the hijacking and plundering of reproductive capacities.

If we liken the genetic reproduction system of a cell to a computer system, this is perfectly consistent with Gödel's theorem: "No program that does not alter the operating system of a computer can detect all the programs that are capable of doing so". In other words, viruses are inevitable, no matter what protection systems we devise against them. So, there's no point in fighting viruses, we'll just have to content ourselves with containing them to their role as genetic mixers.

As we know, it is the association of a long lipophilic tail covalently linked to a hydrophilic head that enables lipid membranes to form spontaneously by self-assembly, provided they are in water. Two particularly interesting topologies are planar bilayers (membranes) and bilayer or multilayer vesicles (liposomes). Depending on conditions of temperature, pressure, pH and electrolyte concentration, these two topologies can interconvert into one another. As far as the RNA/membrane association is concerned, it is imperative that the RNAs are placed on the outside of the vesicles and not on the inside. This is to ensure competition for the external nutrient medium with other non-encapsulated RNAs. The first step towards the formation of a proto-organism was therefore to be able to attach RNAs to the outside of a membrane. The next step was to encapsulate this primitive vesicle, decorated on its outer surface, in another vesicle to ensure its protection. And, as evolution has taken place in the meantime, we'll be thinking of equipping this outer envelope with pores to ensure and control the passage of food. At the same time, viral nucleic acids from the external environment will be prevented from using the patiently elaborated internal machinery for their own replication.

In those remote times, each sub-glacial saltwater pond could be the site of enormous genetic variability, which varied greatly from pond to pond. This biodiversity within sheets of clay was well protected from frost and, above all, from the intense ultraviolet radiation emitted by the sun. For there was no ozone layer to absorb this radiation, which could pass unhindered through the earth's atmosphere. What's more, thermally-generated polyphosphates, tri-metaphosphates and pyrophosphates could be periodically leached to colder areas, much to the delight of PCVs competing greedily for such a source of phosphorus.

In fact, we know that RNAs of at least 50 nucleotides can form spontaneously on contact with clay or phosphate mineral surfaces. In particular, phosphate minerals can activate monomers, while clay, such as montmorillonite, catalyzes their condensation. A genetic code is therefore not yet required. All that's required is for the first enzyme to be a non-specific phosphotransferase capable of activating amino acids (proto-amino-acyl-tRNA synthetase) and indifferently adding nucleotides (replicase) or amino acids in the 3' position. Under these conditions, a single, relatively short self-replicating polymer would suffice for life to begin. Indeed, in its double-stranded form, the self-replicating polymer can perform the function of a gene. In its single-stranded form, however, it or its complement becomes a "nucleozyme", i.e. an accumulator providing the functions of replicase, proto-peptidyl transferase, proto-amino-acyl-tRNA synthetase and also proto-tRNA due to self-complementarity. The replicase function, i.e. the addition of a nucleotide at the 3' position, would be a process requiring the presence of a template or boss, whereas the addition of an amino acid at this same 3' position would be totally free, requiring no template. The addition of the amino acid in the 3' position would thus have enabled the nucleozymes to cling to the negatively charged clay and phosphate mineral surfaces via the positively charged amine function below pH9, instead of being subjected to the chaotic Brownian motion prevailing in the aqueous solution. This would have greatly favored the replicase function, considerably increasing the probability of encounters. Finally, given the non-specificity of the putative phosphotransferase function, these nucleozymes could also transfer phosphate ions directly from mineral polyphosphates to amino acids, nucleosides or nucleotides in order to activate them, thus becoming polyphosphate kinases.

On a molecular level, it turns out that the central part of a ribonucleotide is formed by a D-aldopentose. In other words, a sugar containing 5 carbon atoms, 1 aldehyde function -CHO and 4 -OH groups. Hence the presence of 3 centers of chirality leading to 4 pairs of enantiomers: (D,L)-ribose, (D,L)-arabinose, (D,L)-xylose and (D,L)-lyxose (Figure 21). For each of the 4 diastereoisomers, the carbon atom bearing the aldehyde function is numbered 1', while the last carbon atom bearing the primary alcohol function is numbered 5'. During cyclization of the sugar to form the pyranose ring, the alcohol function on carbon 4' reacts with the aldehyde function on carbon 1' to form the hemiacetal function: RO-CH(OH)-R', leading to an α-isomer if the OH function of the hemiacetal group is on the opposite side of the pyranose ring to the alcohol function 5', or to a β-isomer if these two functions are on the same side of the pyranose ring. In the case of ribonucleotides, we have the D-β-ribopyranose isomer. The hemiacetal carbon atom 1' is used to attach a purine base (adenine or guanine with 9 carbon atoms, denoted 1-9) or a pyrimidine base (cytosine, thymine or uracil with 6 carbon atoms, denoted 1-6), while the alcohol functions 5' and 3' are used to attach phosphate groups. The OH function on carbon 2' remains unused in the ribonucleotides that form RNA, and is even replaced by a single hydrogen atom in the deoxyribonucleotides that form DNA. However, because their phosphate groups are attached to carbohydrates, nucleozymes are naturally excluded from the interior of lipid bilayers. This condemns them to eternal wandering on their polar surfaces, with no hope of binding.

It is precisely at this point that a decisive invention will take place, tipping the balance definitively in favor of protocells to the detriment of viruses. When a strand of DNA or RNA is synthesized, nucleotides are always condensed in the 5' → 3' direction for reading in the opposite 3' → 5' direction, because the template strand and the synthesized strand are always complementary and antiparallel. The great innovation of around 3.9 billion years ago was therefore to condense the 3' alcohol function of the sugar with a polyphosphate-activated amino acid. This transformed the nucleozyme into a proto-amino-acyl-transferase, putting a stop to its growth. This birth of "runt" nucleozymes didn't initially upset the ruthless world of nucleic acids. Until one day, when one of these runts learned to condense its terminal amine function with the acid function of another amino acid. In so doing, it became a proto-peptidyl transferase. In short, this new catalyst was capable of creating a peptide bond between two amino acids. Of course, this was a real revolution compared with the transfer of a single amino acid to an RNA in the 3' position via a proto-amino-acyl-transferase. Indeed, the cooperation between the two brothers, the elder activating an amino acid and the younger welding it to a terminal amine position, will give this new type of nucleozyme a new capacity for growth. But this time, instead of making an RNA, we'll have a hybrid molecule, with an RNA chain on one side (thesis) and a peptide chain on the other (antithesis) that can be lengthened at will (synthesis).

The Birth of a Genetic Code

The nucleozymes concerned by this revolution are those with an amino acid in the 3' terminal position authorizing the growth of a protein chain. They are therefore the direct ancestors of the large ribosomal subunits that possess the catalytic peptidyl transferase function. The basic idea is, once again, very simple. It has to do with the lipophilic nature of the interior of lipid bilayers, which spontaneously attract any sufficiently long hydrocarbon chain. Among the amino acids used by today's cells, five appear to have a very marked lipophilic character: alanine (Ala), valine (Val), proline (Pro), leucine (Leu) and isoleucine (Ile). This is because their saturated side chains lack hydrophilic functions. Logically, these are also the amino acids each encoded by at least 4 different codons (N = G, A, C or U) for alanine (GCN), valine (GUN), proline (CCN), 3 codons AUPy/A for isoleucine (Py = pyrimidine base C or U) and no less than 6 codons for the highly lipophilic amino acid leucine (CUN and UUPu, Pu = purine base G or A). We can therefore assume that the original function of the large ribosomal subunit was not to make proteins. Rather, it was to add as many lipophilic residues as possible to the 3' end of nucleozymes. This was to enable them to anchor themselves via this lipophilic tail in the lipid bilayers of abiotically synthesized vesicles. Such anchoring would enable these nucleozymes to still be itinerant, while at the same time providing them with a surface on which to continue increasing their genetic diversity in two-dimensional encounters, rather than the three-dimensional encounters seen in solution.

Anchoring on the same membrane surface will also make it possible to move from a single ancestor with all functions to an entity made up of 4 specialized nucleozymes. Nucleozymes encoded by 4 separate genes, paving the way for independent optimization of each of the 4 basic phosphotransferase activities: replicase, proto-amino-acyl-tRNA synthetase, proto-peptidyl transferase and proto-tRNA. The first proto-tRNAs were probably helical hairpins with a 3 or 4-nucleotide terminal unmatched loop. This loop would later become the anticodon loop, with a marked preference for G and C bases over A and U bases. This applies to the first two codon positions. The third position is generally considered, on a purely semantic level, to be redundant. The coding itself probably started after association of a new RNA acting as proto-mRNA to hold the proto-tRNA to the nucleozyme acting as peptidyl transferase. The specificity of the code could be minimal, simply selecting the most lipophilic amino acid possible from the pre-biotic soup. A precursor of the small ribosomal subunit rRNA was probably also selected at this time to stabilize the mRNA/tRNA assembly. The pairing between mRNA and small rRNA was most likely a very rudimentary initiation mechanism. It is likely that the first two amino acids to be encoded were valine and alanine, given their abundance in meteorites [72]. The strong conservation of the tRNA structure implies that, before becoming a true rRNA, the proto-tRNA already possessed 75 nucleotides folded into a cloverleaf shape, and that genes of similar length could have encoded signal peptides with up to 25 amino acids. The emergence of the mixed nucleic acid-protein world can therefore be summarized in the following five stages:

Appearance of a nucleozyme with replicase function (R)
Appearance of a nucleozyme with polyphosphate kinase function (K)
Appearance of a nucleozyme with peptidyl-transferase (P) function, acting as a proto-grand-RNA capable of adding amino acids to the 3' ends of R, K and itself.
Appearance of GC pair-rich duplicators acting as proto-tRNAs and preferentially binding to hydrophobic amino acids.
Appearance of proto-mRNAs and proto-small rRNAs to help proto-tRNAs bind to proto-peptidyl transferase.

It follows that a rudimentary peptide synthesis directly capable of evolving into the current coding system could start with just 4 different genes, two encoding proto-rRNA, one proto-tRNA and one proto-mRNA. If we add a gene encoding the replicase function and one the kinase function, we obtain a minimal PCV with 6 genes capable of evolving into a real cell later on.

At this stage of evolution, only the 5 most lipophilic amino acids were selected to form a hydrophobic tail capable of anchoring genes or nucleozymes to the outer surface of a lipid bilayer vesicle. This PCV would have used 11 of the 64 possible NYN codons to select these 5 lipophilic amino acids, using Y = U as the code for the most lipophilic amino acids (isoleucine, leucine and valine) and Y = C for the less lipophilic amino acids (alanine and proline). So, let's see how to obtain such amino acids under prebiotic conditions. Let's start with the ten simplest amino acids requiring just one molecule of carbon dioxide and having no sulfur atoms:

n CO + CO₂ + q HCN + m H₂ + γ = C_n+q+1H_2(m-n)+qN_qO₂ + n H₂O

The only amino acid requiring no carbon monoxide (n = 0) is glycine (Gly) with q = 1 and m = 2. Six amino acids require a single molecule of HCN (q = 1): Alanine (Ala, n = 1, m = 4), Proline (Pro, n = 3, m = 7), Valine (Val, n = 3, m = 8), Leucine and Isoleucine (Leu, Ile, n = 4, m = 10) and Phenylalanine (Phe, n = 7, m = 12). Two amino acids require two molecules of HCN (q = 2): Lysine (Lys, n = 3, m = 9) and Tryptophan (Trp, n = 8, m = 13). Finally, a single amino acid requires three molecules of HCN (q = 3): Histidine (His, n = 2, m = 5). We see that our five highly lipophilic amino acids are indeed there.

The advantage of a code based solely on highly lipophilic amino acids is that it can tolerate many translation errors. This, without altering the main aim, which was to have a chain long enough to anchor itself in the lipid bilayer of any vesicle. Once the genetic code for the lipophilic residues had been fine-tuned, hydrophilic domains had to be added to the membrane surface very quickly. This was to enable the attachment of critical hydrophilic molecules such as polyphosphates. This led to the development of 5 new proto-tRNAs to select hydrophilic amino acids such as serine (UCN/AGPy), threonine (ACN), glycine (GGN), aspartic acid (GAPy) and glutamic acid (GAPu). We've already seen how to obtain glycine. For the other four amino acids, an additional molecule of carbon dioxide is logically required to obtain a second group of eight "oxidized" amino acids:

n CO + 2 CO₂ + q HCN + m H₂ + γ = C_n+q+2H_2(m-n-k)+qN_qO_4-k + (n + k) H₂O

The two amino acids that do not require carbon monoxide (n = 0, m = 4 and k = 1) are serine (Ser) with q = 1 and asparagine (Asn) with q = 2. We can also add arginine with n = 0, m = 7, k = 2 and q = 4. Then come the three amino acids that require only a single molecule of CO (n = 1): Aspartate (Asp with q = 1, m = 4 , k = 0), Threonine (Thr, q = 1, m = 6, k = 1) and Glutamine (Gln, q = 2, m = 6, k = 1). And finally, the last two amino acids: Glutamate (Glu, n = 2, q = 1, m = 6, k = 0) and Tyrosine (Tyr, n = 6, q = 1, m = 12, k = 1). That leaves the two sulfur-containing amino acids, where synthesis involves carbon oxysulfide COS (:O:=C=:S:) formed by reacting carbon dioxide with hydrogen sulfide H₂S: CO₂ + H₂S = COS + H₂O. Hence the balance where COS replaces one molecule of CO:

(n-1) CO + CO₂ + COS + q HCN + m H₂ + γ = C _n+q+1H_2(m-n)+qN_qO₂S + n H₂O

And so, with one molecule of HCN (q = 1), we obtain cysteine (Cys, n = 1, m = 4) and methionine (Met, n = 3, m = 8).

Thus, a proto-mRNA rich in CG codes on the 5' side and rich in AU codes on the 3' side, could have encoded the synthesis of a lipophilic signal peptide possessing a hydrophilic tRNA-supporting surface domain. The fact that many glucokinases and several families of ATP-binding proteins have aspartic acid, glycine and threonine as key amino acids supports this scenario. It was at this stage that the first proto-amino-acyl-tRNA synthetases appeared, capable of binding a specific amino acid to a tRNA with the appropriate anticodon, whereas until now it was the tRNA itself that took on this task (self-loading). By means of a set of 10 proto-amino-acyl-tRNA synthetases using between 22 and 27 of the 64 codons available, a PCV would already be capable of encoding a wide variety of large enzymes or structural proteins capable of complex folding.

A PCV can therefore begin protein synthesis as soon as it has six replicative nucleic acids on the outer surface of its membrane. It is highly probable, however, that two additional genes encoding a ligase and an endonuclease had to be added relatively early in order to be able to manipulate the genes. Ligase enables a bond to be formed between the 5'-phosphate group of a nucleic acid segment and the 3'-OH group of the preceding segment on the same strand. Ligases are essential for linking the various replicating entities into a continuous chromosome, ensuring their unity in the event of any fragmentation of the lipid membrane. Ligases are also used to combat viruses attempting to parasitize the PCV.

Endonucleases, on the other hand, are indispensable for cutting nucleic acid into shorter fragments. Ribonuclease P (RNase P), for example, is an endonuclease present in all living cells, whose function is the maturation of transfer RNAs. Like the ribosome, it acts as a ribozyme capable of cleaving an RNA sequence on the 5' side of tRNA precursors, releasing the 5' extension and the monophosphate-matured 5' tRNA. RNase P plus a second nucleozyme cleaving its tRNA adjacent to the 3' end is indeed indispensable for cutting into functional genes a chromosome made up of mRNAs, rRNAs punctuated by tRNAs. However, replication of a relatively long chromosome would pose problems for a nucleozyme. As a result, multigenic chromosomes could not evolve without the appearance of an RNA- or DNA-polymerase-type protein. Since primases do little differentiation between ribo- and deoxy-ribonucleotides and require no complex machinery for initiation, there's a good chance that a primase was the first RNA- or DNA-polymerase protein. In fact, primase is capable of synthesizing an RNA primer de novo, from a double strand of nucleic acids, unlike DNA polymerases which are only capable of elongating an already partially double-stranded region, by adding a nucleotide to an already present 3' hydroxyl end. The primase thus enables the synthesis of short RNA segments, which are then used as primers by the replicative DNA polymerase. We can therefore remember that a chromosome can only evolve if a ligase, an RNase P, a second endonuclease and a protein polymerase are available. It was at this stage that a clear distinction was made between replication and transcription. The invention of polymerases, peptidyl transferases and amino-acyl-tRNA synthetases marked the end of the RNA world, which in the end was very brief [84].

It's worth noting that an exonuclease must also have been invented at this stage of evolution. This is an enzyme capable of cutting nucleic acids (DNA or RNA). The prefix “exo” specifies that this cut is made from one end, one nucleotide at a time, and in a 5' to 3' direction. This makes it possible to digest other replicators, in an extremely dynamic and unforgiving world. Thanks to this dozen or so amino acids, the first enzymes were able to appear. Hence a very primary metabolism, but sufficient to ensure the "material" part. Not forgetting that there is also a purely "inorganic" part to this same metabolism. These include sodium (Na), potassium (K), calcium (Ca), magnesium (Mg), iron (Fe), manganese (Mn), chlorine (Cl) and phosphorus (P). There are, of course, others, but as we are interested in origins, it is clear for these that their concentrations in intracellular water must have been closely maintained and regulated throughout evolution [85]. Here, it is rocks eroded by the water cycle that can provide these elements. Examples include dolomite (Ca_1-xMg_x)CO₃, hydroxyapatite Ca₅(PO₄)₃(OH), rhodochrosite (MnCO₃), pyrite (FeS₂ ), and rock salt (Na,K)Cl. Once dissolved in water, all these ions end up stored in the oceans.

Moreover, let’s also recall the unique chirality of amino acids (all L-) and sugars (all D-) as a signature of life. This empirical fact has fascinated scientists and laymen alike since Pasteur's first careful separation of enantiomorphs crystals of a tartrate salt in 1848 [86,87]. Recent studies investigating a plausible new prebiotic pathway to proteinogenic peptides have shown that the creation of a peptide bond favors the ligation of L-monomers with D-monomers. This finding seems problematic for the prebiotic emergence of homochiral L-peptides. However, it has nevertheless been shown that this heterochiral preference provides a mechanism for enantiomeric enrichment in homochiral chains [88,89]. Symmetry breaking, chiral amplification and chirality transfer occur for all reactants and products in competitive multi-component reactions. Indeed, solubility considerations justify further chemical purification and increased chiral amplification. Experimental data and kinetic modeling support this plausible biotic mechanism for the emergence of homochiral biological polymers. Dipeptide- and pyridoxal-mediated kinetic resolution of racemic amino acids provides a plausible prebiotic route to proteinogenic amino acids enriched in L-type enantiomers. The kinetic resolution of racemic precursors therefore appears to be a general route to enantiomeric enrichment under prebiotic conditions. And, if in the near future this explanation of kinetic resolution proves to be wrong, there would still remain the explanation based on the influence of a powerful supernova explosion [90,91].

Finally, there is also the problem of the aggregation of organic polymers in water above a certain critical concentration. Fortunately, adenosine triphosphate (ATP) has been shown to possess the properties of a biological hydrotrope [92]. In other words, this molecule can both prevent the formation of protein aggregates and dissolve aggregates already formed. This chemical property manifests itself at physiological concentrations of between 5 and 10 mM. So, as well as being a source of phosphate for biological reactions at micro-molar concentrations, ATP at milli-molar concentrations of could help keeping proteins in solution. This could explain, in part, why the ATP molecule is present at very high concentrations in living cells.

Photosynthesis and Expansion of the Genetic Code

We also know that there was originally no oxygen in the Earth's primitive atmosphere. There was, however, a lot of hydrogen sulfide H₂S, as a result of numerous volcanic eruptions. Hence the precipitation of certain metal cations with a strong affinity for sulfur, leading to the formation of highly water-insoluble sulfides. And, therefore very low concentrations of the following elements in order [84]:

Cu < Zn < Ni < Co < Fe < Mn and Mo < W

This is why strict anaerobes today are still very low in Cu, Zn and Mo compared to the elements Fe, Mn and Mg, which were available at 10⁻⁶ M or thereabouts and were abundant in primitive cells.

Three billion years ago, life on Earth depended on organic molecules produced by lightning or geothermal sources, with the risk of rapid depletion. Once photosynthesis was discovered, life on earth really took off. The idea was to combine carbon dioxide in the air with water to create carbohydrates. Today, photosynthesis is the foundation of life on Earth. Every living organism on Earth, with a few exotic exceptions, depends on this reaction.

Thanks to the combination of hardware metabolism and software replication, it has become possible to produce an enzyme called "photosystem-II" [93]. This enzyme is the first link in the photosynthesis chain. It is made up of a set of proteins (25-30 subunits) which absorb light energy via a set of membranes called the "thylakoid", from the Greek thylakos, meaning "sack". In the chloroplasts of green plants, this membrane network is organized into grana (granum in the singular). Light-absorbing proteins are located on the inner surface of the grana's thylakoid membrane. To do this, they use different molecules called "chlorophylls", from the Greek khlôrós ("green") and phúllon ("leaf"). The most common chromophore is chlorophyll-a, formed from a porphine molecule surrounding a magnesium ion, attached to a C₂₀ terpenoid alcohol, phytol (see Figure 22).

Porphine: 8 C₂H₂ + 3 HNCO + HCN = C₂₀H₁₄N₄ + 3 H₂O

Chlorophyll is a hydrophobic molecule that can be anchored to a lipid membrane. Five reactions are required to produce chlorophyll-a:

-: Proto-porphyrin-IX: 15 C₂H₂ + 4 HNCO = C₃₄H₃₄N₄O₄
-: Mg-Proto-porphyrin-IX: C₃₄H₃₄N₄O₄ + Mg^⊕⊕ = C₃₄H₃₂MgN₄O₄ + 2 H^⊕
-: Divinyl proto-chlorophillide "a": C₃₄H₃₂MgN₄O₄ + CH₃OH = C₃₅H₃₄MgN₄O₄ + H₂O
-: Monovinyl chlorophillide "a": C₃₅H₃₄MgN₄O₄ + H₂O₂ = C₃₅H₃₄MgN₄O₅ + H₂O
-: Phytol: 13 CH₄ + 7 CO = C₂₀H₄₀O + 6 H₂O
-: Chlorophyll -a: C₃₅H₃₄MgN₄O₅ + C₂₀H₄₀O = C₅₅H₇₂MgN₄O₅ + H₂O

I've used chlorophyll-a as an example, because it's a universal molecule found in all species capable of photolysis of water (plants, algae or cyanobacteria). This chlorophyll-a has the characteristic of strongly absorbing wavelengths of 460 nm and 664 nm. The advantage of decorating porphin with methyl groups -CH₃ (4 for chlorophyll-a) is that one can be oxidized to an aldehyde function (-CHO):

-: Chlorophyllide-b or -f: C₃₅H₃₄N₄O₅ + O₂ = C₃₅H₃₂N₄O₆ + H₂O
-: Chlorophyll-b or -f: C₃₅H₃₂N₄O₆ + C₂₀H₄₀O = C₅₅H₇₀MgN₄O₆ + H₂O
-: Chlorophyllide-d: C₃₅H₃₄MgN₄O₅ + O₂ = C₃₄H₃₂MgN₄O₆ + H₂CO
-: Chlorophyll-d: C₃₄H₃₂MgN₄O₆ + C₂₀H₄₀O = C₅₄H₇₀MgN₄O₆ + H₂O

As a result, for chlorophyll-b (plants and green algae), the molecule still absorbs at 460 nm, but the second absorption shifts from 664 nm to 647 nm. This gives it an olive-green color. It is also more soluble in aqueous media than chlorophyll-a, due to the presence of the carbonyl group. In terrestrial plants, chlorophyll-b is mainly found around photosystem II. In the case of chlorophyll-f, found in cyanobacteria, absorption at 460 nm disappears, while absorption at 664 nm doubles to 727 and 745 nm. For chlorophyll-d, also found in cyanobacteria, absorption at 460 nm splits at 401 and 405 nm, while absorption at 664 nm rises to 696 nm.

In addition to chlorophyll molecules, there are also carotenoids, which have a long chain of carbon-carbon double bonds, forming a set of highly colored molecules that also capture light:

-: Lycopene (red): 16 C₂H₂ + 2 C₂H₄ + 4 CH₄ = C₄₀H₅₆
-: Astaxanthin (pink): 14 C₂H₂ + 2 C₂H₄ + 4 CH₄ + 4 CO = C₄₀H₅₂O₄
-: Lutein, canthaxanthin, zeaxanthin (yellow): 16 C₂H₂ + 6 CH₄ + 2 CO = C₄₀H₅₆O₂

After capturing light photons, chlorophylls or carotenoids transmit their energy to an active center, called the OEC, to split the water molecule into hydrogen ions, electrons and oxygen:

2 H₂O + γ = 4 H⊕ + 4 e^⊖ + O₂↑

This gas then forms bubbles which, when they burst, release oxygen into the atmosphere. This reaction is the source of all the oxygen we breathe today. Hydrogen ions, meanwhile, are used to fuel the synthesis of a molecule of adenosine triphosphate or ATP (Mg₂P₃O₉) via the enzyme ATP-synthase:

MgHP₂O₆ (ADP) + MgHPO₄ (P_i) + 2 H^⊕(out) = Mg₂P₃O₉ (ATP) + H₂O + 2 H^⊕(in)

Electrons, in turn, are transmitted along a chain of electron-carrying proteins to reduce two molecules of plastoquinone (PQ) to plastoquinol (H₂PQ):

4 H^⊕ + 4 e^⊖ + 2 PQ = 2 H₂PQ

The core of photosystem-II, known as the OEC, is a cluster of four manganese ions Mn²^⊕ and one calcium ion Ca²^⊕ linked by a µ₂-oxo bridge, three µ₃-oxo bridges and a µ₄-oxo bridge [93]. This is cluster that seizes the two water molecules and removes four electrons from them. The binding site of the two water molecules is not known with certainty, but it is highly likely that the gateway is at the level of the calcium ion. This OEC is surrounded by histidines, aspartates and glutamates, which hold it in place. Right next to the cluster is a key chlorophyll molecule that establishes a tyrosine bridge with the water-binding site. When it absorbs light, one of the electrons in this chlorophyll is excited to a higher energy. This excited electron then jumps down, through several other pigmented molecules, to a first plastoquinone A, and finally to plastoquinone B. When it obtains enough electrons, this small quinone is released from the photosystem and delivers its electrons to the next link in the electron transfer chain. Following this electron loss, the upper half of the OEC is tasked with replacing it with a lower-energy electron from water. It therefore extracts an electron from the water and passes it on to the amino acid tyrosine, which then sends it to the chlorophyll, making it ready to absorb another photon.

Of course, the whole process wouldn't be very efficient if plants had to wait for photons to reach that special chlorophyll in the reaction center. Fortunately, the energy of an electron excited by light is easily transferred thanks to the phenomenon of resonance between two molecules, close enough together. This is why photosystems feature large antennae filled with light-absorbing molecules. This enables them to capture light and transfer the light energy thus captured to the interior of the OEC.

Let's now consider photosystem-I, the second reaction center used by cyanobacteria, algae and plants [95]. It is located on the outer surface of the thylakoid membrane of the grana. It is a trimeric complex which forms a large disc embedded in the membrane, with large flat faces exposed above and below the membrane. Each of the three subunits of photosystem-I is a complex of a dozen proteins which together support and position over a hundred cofactors. Some of these cofactors are shown in green (chlorophylls) and orange (carotenoids). They are exposed around the perimeter of the complex, while many others are buried within it. In contrast to photosystem-II, here there is a higher concentration of chlorophyll-a than chlorophyll-b. In cyclic photophosphorylation, photosystem-I synthesizes ATP, and in non-cyclic photophosphorylation, it synthesizes NADPH. The heart of photosystem-I is an electron transfer chain (ETC), composed of chlorophyll (green), phylloquinone (orange) and three iron-sulfur clusters (yellow and red at the top) called "ferredoxins" [96]. Ferredoxins are electron transfer proteins containing one or more active sites consisting of two or four iron atoms linked together by sulfide bridges and bound to organic matter by four cysteine sulfhydryl groups. There is therefore no photolysis of water here.

The two chlorophyll molecules at the bottom catch the light first. In doing so, an electron is excited into a higher-energy state. Normally, this electron would quickly de-excite, giving off heat or releasing a new photon of slightly lower energy. But before this can happen, the electron is transferred to the cofactor chain. At the top, the electron is transferred to a small ferredoxin protein, which then forwards it to the other stages of photosynthesis. At the bottom, the hole left by this stray electron is filled by an electron from another protein, plastocyanin. This plastocyanin is found in the cytochrome-b6f complex (Cyt-b6f), whose function is to accumulate protons in the thylakoid lumen during the transfer of high-potential electrons from photosystem-II to photosystem-I. The Cyt-b6f complex receives the plastoquinone produced by photosystem-II and sends it to copper-based plastocyanin (CuPC), which ensures electron transfer and proton accumulation:

H₂PQ + 2 CuPC²^⊕ + 2 H^⊕ = PQ + 2 CuPC^⊕ + 4 H^⊕

Photosystem-I receives electrons from plastocyanin or cytochrome-b6f on the lumenal side of the thylakoid membrane and uses light energy to transfer them across the membrane to a ferredoxin on the stromal side. Note that it is normally more difficult to add an electron to ferredoxin than to plastocyanin. This is where photosystem-I uses the energy of light to force the electron from plastocyanin to ferredoxin. Figure 22 shows the photosystem-I cofactor chain when the protein is made transparent. These "antenna" molecules each absorb light and transfer the energy to their neighbors. Before long, all the energy is routed to the three reaction centers, where it is captured to create activated electrons. The central electron-transfer pathway features chlorophyll, colored from green to yellow, associated with orange phylloquinone (vitamin K) molecules, and iron/sulfur clusters colored red and yellow. In the surrounding antenna, chlorophyll is colored green, magnesium turquoise and beta-carotene pink.

Thanks to these two major inventions, photosynthetic cells have unlimited access to two key metabolism molecules: ATP and NADPH. Indeed, if we forget the details, here's the balance of the Calvin cycle represented in Figure 22:

3 Mg₂[C₅H₈O₁₁P₂] + 3 H₂O + 3 CO₂ = 6 Mg[C₃H₄O₇P]^⊖ + 6 H^⊕

6 Mg[C₃H₄O₇P]^⊖ + 6 Mg₂P₃O₉ + 6 H⊕ = 6 Mg₂[C₃H₄O₁₀P₂] + 6 MgHP₂O₆

6 Mg₂[C₃H₄O₁₀P₂] + 6 Mg₂NADPH = 5 Mg[C₃H₅O₆P] + Mg[C₃H₅O₆P] + 6 Mg₂NADP⊕ + 6 MgPO₄^⊖

5 Mg[C₃H₅O₆P] + 2 H₂O = 3 Mg[C₅H₉O₈P] + 2 MgHPO₄^⊖

3 Mg[C₅H₉O₈P] + 3 Mg₂P₃O₉ = 3 Mg₂[C₅H₈O₁₁P₂] + 3 MgHP₂O₆

---------------------------------------------------------------------------------------------------------------------------

5 H₂O + 3 CO₂ + 9 Mg₂P₃O₉ + 6 Mg₂NADPH =

Mg[C₃H₅O₆P] + 9 MgHP₂O₆ + 6 Mg₂NADP⊕ + 2 MgHPO₄ + 6 MgPO₄^⊖

Or: 5 H₂O + 3 CO₂ + 9 ATP + 6 NADPH = GAP + 9 ADP + 6 NADP⊕ + 8 P_i

It's easy to see how ATP and NADPH molecules can be used to produce a molecule of glyceraldehyde-3-phosphate (GAP or G3P). GAP is an aldo-triose, an important metabolic intermediate in glycolysis and gluconeogenesis, as well as in tryptophan biosynthesis. For example, it enables the production of fructose diphosphate, which can then be used to manufacture glucose, sucrose, starch and other carbohydrates (anabolism). Remember that anabolism is the set of non-spontaneous chemical reactions involving reduction (supply of electrons) leading to the formation of the body's constituents from the simple elements of digestion. Catabolism, on the other hand, is the phase of metabolism during which relatively large, complex molecules are broken down, by oxidation, into smaller, simpler ones. On the catabolic side, GAP is also involved in a step of glycolysis to produce pyruvate.

The invention of photosynthesis explains the development of copper-hungry aerobic bacteria, which prefer molybdenum to tungsten. Indeed, the key enzymes that use copper as a cofactor in functional catalytic reactions are: cytochrome-c oxidase (mitochondrial respiratory chain); superoxide dismutase-1 (free radical eradication); lysyl oxidase (speed-limiting steps in the collagen and elastin cross-linking reaction) and tyrosinase (melanin formation). It took around 2 Gyr for the concentration of free oxygen in the atmosphere to increase significantly. Let's say up to 1% of current levels 500 million years ago [97]. The main species involved in this oxidation were, on the non-metal side, a powerfully reducing molecule such as H₂S and its derivative ion HS^⊝ which will find themselves reduced to sulfate ions SO₄²^⊝. In the case of metallic species, it is the free Fe²^⊕ ferrous ions that will be oxidized to ferric Fe³^⊕ ions with very low solubility (≈ 10⁻¹⁷ M). Hence the precipitation of banded iron formations (BIF) in surface geological minerals, or of baryte BaSO₄.

Other chemical species that will disappear include the very low-solubility cuprous ion Cu^⊕ , which will be replaced by the much better-solubility cupric ion Cu²^⊕ (≈ 10⁻¹⁰ M). The last two species are the two thiomolybdate and thiotungstate which will be replaced by oxo-anions MoO₄²^⊝ (≈ 10⁻⁷ M) and WO₄²^⊝ (≈ 10⁻⁹ M). The sea thus became very rich in molybdenum and vanadium at the start of ocean oxygenation, since in the order of sulfide oxidation vanadium comes before molybdenum. The other divalent species do not change in nature, but see their solubility increase: Zn²^⊕ (< 10⁻⁸ M); Ni²^⊕ (< 10⁻⁹ M); Co²^⊕ (≈ 10⁻¹¹ M); except for manganese Mn²^⊕ (≈ 10⁻⁹ M). The result of this oxidation is that seawater gains one pH unit from pH ≈ 7 ([H^⊕ ] ≈ 10⁻⁷ M) about 4 Gyr ago to pH ≈ 8 ([H^⊕ ] ≈ 10⁻⁸ M) 2 Gyr later.

Another problem was that life always needed hydrogen, which became very scarce in an oxidizing environment. Hence the discovery that water could be a source of hydrogen, producing oxygen as a waste product. It was this rejection of oxygen, along with that of Na^⊕, Ca²^⊕, Cl^⊝ (and perhaps Mn²^⊕) ions, that created a very strong environmental pressure pushing in, chemically speaking, an ever more oxidized direction. But, for nascent life, oxygen's first effect is that of a poison, through its partially reduced products such as superoxide O₂^•⊝ and peroxide in the form of hydrogen peroxide H₂O₂. Consequently, even before oxygen or these derivatives were used, a mechanism had to be developed to protect against these "reactive oxygen species" (ROS). Hence the very early appearance, in anaerobes, of enzymes eliminating not only dioxygen O₂ via reduction by NADH, but also the superoxide ion or via iron- and manganese-based superoxide dismutases. Later in evolution, these three products will find a use thanks to the universal ternary progression: Poison/Protective device/Use of the "poison". Some prokaryotes even developed new metabolic pathways to utilize poisons derived from the "poison" oxygen. Hence the exploitation of new non-metal states, such as SO₄²^⊝ or even NO₃^⊝, and, the systematic use of newly available metals such as zinc and copper. New sub-classes of aerobic chemotypes have thus emerged, including sulfate-, nitrogen- and nitrate-dependent bacteria. But there are also "siderophores" (from the Greek pherein and sideros meaning "to transport iron"). These are powerful Fe³^⊕ chelating agents, synthesized and secreted by micro-organisms in particular, to enable them to draw on the iron essential for their development. The result is increasingly complex organisms.

As a result, the first organisms were gradually confronted with an increasingly hostile environment. The Na^⊕, Cl^⊝ and Ca²^⊕ ions were still present in the sea, but became increasingly active as they lost access to C, N, S, Se and Fe²^⊕. There was also a growing presence of oxygen and its non-metallic products. As well as a number of increasingly available transition metal ions. In chemical terms, we would say that chemotype was changing, by analogy with genotype, which refers to individual species and the specific genes that define them. Animals with nerves found a whole new use for the Na^⊕ and Cl^⊝ in these fluids, requiring new proteins to pump these ions. All these characteristics could, of course, be attributed to new DNA sequences.

Nonmetals other than sulfur were also oxidized, in particular the original carbon monoxide CO, as well as nitric oxide NO or ammonia NH₃, which were replaced by carbon dioxide CO₂ and nitrate ions NO₃^⊝. From a genetic point of view, this phototrophic proto-cellular world having evolved between 3850 and3500 Myr, was based on a set of 20-30 genes [84]. It was during this phase that the genetic code was extended and completed, with the coding, firstly of Tyrosine (Tyr,) phenylalanine (Phe), cysteine (Cys), histidine (His) and aspargine (Asn). This is followed by glutamine (Gln), lysine (Lys), tryptophan (Trp), arginine (Arg), methionine (Met) and selenocysteine (Sec).

Bacteria, Eukaryotes and Archaea

All in all, it took around 400 Myr to go from an inanimate prebiotic soup to a replicative PCV-based on lipid membranes and capable of internal metabolism. The next step was the appearance of the first cell, equipped with a double membrane and capable of autonomous movement. Three major inventions were responsible for this PCV -> bacterial transition, which took place 3500 Myr ago. These were the invention of peptidoglycan, the synthesis of lipopolysaccharides or endotoxins and the development of flagella. It would seem that a total of 2,000 genes would be sufficient to encode such a bacterium [98]. For the sake of brevity, Figure 23 shows the chronology of diversification of this extraordinarily varied bacterial world.

A major innovation in the evolution of the bacterial world was the replacement, some two billion years ago, of peptidoglycan by glycerol. This gave rise to a new class of cells known as "eukaryotes". The increased flexibility of their outer membrane, due to the inclusion of cholesterol, enabled them to digest prokaryotes, obviating the need to synthesize the chemicals essential to both groups. This increasingly led to symbioses in which the higher organism was a source of certain basic foods needed by the lower organism. The latter very often supplied the higher organism with more complex molecules, coenzymes, for example flavin, or molecules such as ammonia, which were difficult to produce from dinitrogen N₂.

As seen previously, prokaryotes were forced to create an abrupt Ca²^⊕ ion gradient ranging from around 10⁻³ M on the outside to less than 10⁻⁶ M on the inside. In eukaryotes, Ca²^⊕ ion was allowed to reach 10⁻³ M in endoplasmic reticulum vesicles, but the same cytoplasm/environment gradient had to be maintained. These huge gradients are ideal for conversion and use in new signaling devices, particularly when coupled to internal cytoplasmic signaling, for example, by phosphates. This is how eukaryotic cells gain knowledge of changes in their external environment, advantageous or disadvantageous, through the opening of calcium entry channels in the cytoplasm.

A fascinating new chemical feature thus emerged with the eukaryotic revolution. Because of the rigidity of their cell wall, prokaryotes had a certain awareness of changes in their external environment, but this was very slow. Hence their main response, also very slow, which was the mutation and development of their genes. In contrast, with their highly flexible cell membrane, eukaryotes could react very quickly to external events. The result was more or less reversible changes in form and metabolism, and very little change in genes. Always the eternal duality between hardware (metabolism) and software (genes). When hardware evolves very quickly, software changes very little. But as soon as the hardware stagnates, it's the software that becomes more refined.

At the enzymatic level, the eukaryotic revolution saw the development of Zn²^⊕- dependent transcription factors (zinc fingers). While, in order to combat the highly toxic reactive oxygen species, a new protective enzyme, superoxide dismutase, based on copper and zinc appeared. Free zinc in cells is still slightly below 10⁻¹⁰ M and free copper, meanwhile, has remained at around 10⁻¹⁵ M by necessity. This is in sharp contrast to the superoxide dismutases of prokaryotes, which are still largely based on iron or manganese. Eukaryotes have also come to depend on bacteria for the other element as essential to life as carbon, namely nitrogen. Eukaryotes cannot obtain nitrogen from dinitrogen, and many are unable to denitrify nitrates. A large part of the new communication system for organic molecules is therefore linked to the increasing availability of two metal ions, zinc and copper. The lives of higher animals are totally dependent on plants for food and bacteria for digestion and coenzymes (vitamins), which means that animals lose several metabolic pathways.

At the same time, bacteria develop extra-vesicular compartments such as the thylakoid, which allows localized production of protons and thus a highly acidic environment with an internal pH locally below 5.0. This, while maintaining the pH of the cytoplasm slightly above 7.0. Similarly, the subsequent device for oxidative phosphorylation will replace the pH gradient with an external membrane potential. Another example of evolutionary adaptation is provided by the anammox bacterium, which oxidizes toxic ammonia with nitric oxide inside a separate vesicle. Then, another remarkable switch in the tree occurred 850 Ma ago.

Back in the 70s, Carl Woese was working on a seemingly innocuous subject: finding a way to classify this richly diverse bacterial world. But, while this seemed an obvious task, it turned out that bacteria had so far resisted all attempts at classification. The traditional method of looking for differences in appearance, structure or metabolism had failed miserably. All bacteria look and act very much alike. This makes it very difficult to establish a chronology for their appearance. Big names in microbiology have thrown in the towel on this problem. But Woese had an idea: to use the RNA of their ribosomes, because he knew that most ribosomal RNA mutations had catastrophic consequences for the offspring, who therefore sought to avoid these mutations at all costs. As a result, changes in ribosomal RNA occur very rarely. However, after several billion years of microbial life on Earth, such mutations do eventually occur, making this molecule of great interest for understanding relationships that extend far back in time. Hence a decade of painstaking work to sequence ribosomal RNA into small pieces and identify them. Then something unexpected happened. A colleague named Ralph Wolf suggested that Woese use his method to study an unusual group of methane-producing bacteria. Although these bacteria form pasty clumps with a wide variety of shapes, their biochemistry and metabolism seemed very similar. However, when Woese studied the RNA sequences of these "methanogens", they turned out not to be bacteria at all. In fact, they lacked complete oligonucleotide sequences normally found in bacteria. Thinking that the samples had been contaminated, he studied new ones. But the result was confirmed, and Woese found that the methanogens were not bacteria, although morphologically speaking they resembled bacteria. However, Woese was well aware that morphology meant nothing for bacteria, and that only their molecules could tell them apart. And the molecules said that methanogens resembled no other prokaryote or eukaryote. In short, they were a new kingdom, the "archaea", forming a third branch of life [99].

After all this hard work Woese had just discovered a new world of microbes which to our eyes looked like bacteria. But, in fact, they were so unique, biochemically speaking, that they turned out to be closer to eukaryotes than to bacteria. Woese's observations were, of course, greeted with great skepticism. In fact, archaea are ubiquitous in hydrothermal vents, salt lakes, ice, seawater, soil and, of course, the human body. In many ways, archaea are more like eukaryotes than bacteria. In fact, eukaryotes are life-forms that house their DNA packaged in nuclei. The eukaryote group includes just about every living thing except archaea and bacteria. Archaea possess RNA- and DNA-polymerases, enzymes that replicate DNA and RNA, but in a simpler version than that found in eukaryotes. Their single circular chromosome can have more than one origin for replication like eukaryotes, in marked contrast to bacteria.

In fact, bacteria condense their DNA inside the cell to protect it, thanks to a protein called "Gyrase", which winds up their DNA like a coil. Archaea do the same, but wind their DNA around proteins called histones. And, again, these appear to be simplified versions of the histones employed by eukaryotes to perform this crucial task. Bacteria, on the other hand, do not possess histones. This obvious similaritý between archaea and eukaryotes has led some to suggest the existence of a symbiosis between mitochondria and chloroplasts. But, in addition, other symbioses or an even more mysterious chimerism seems to have taken place between archaea and bacteria. This gave rise to the first proto-eukaryotic cell. This may thus mean that eukaryotes actually evolved́ from archaea, an idea that was to be hotly debated.

The outer membranes of archaea, on the other hand, are very different from anything else on Earth. Indeed, the membrane lipids of bacteria and eukaryotes have the same general structure. A phosphate group attached to a glycerol molecule forms the head of the lipid, while fatty chains form the tail. And, as in bacteria, the glycerol hydroxyl heads are linked to the fatty acid chains by ester bonds. Archaeal membrane lipids are very different from those of bacteria and eukaryotes (Figure 24). Archaea have tails made of branched isoprene-based units instead of fatty acids, and are 20-carbon phytanyl-type. These lipid tails can be branched in extremely complex ways or even incorporate cycles leading to very strange shapes that bacterial or eukaryotic membrane lipids can never adopt. Moreover, phytanyl tails are attached to glycerol using ether bonds, which are much more heat-resistant than ester bonds. Finally, their glycerol is of opposite chirality to the glycerol of bacterial or eukaryotic lipid membranes.

So, the fact that archaeal and bacterial enzymes use glycerol molecules with opposite chirality implies that bacteria and archaea split up a very long time ago indeed. Some archaeal lipids also have a property that is rarely, if ever, encountered in eukaryotes or bacteria. Bacteria and eukaryotes have membranes made of lipid bilayers where the upper lipids are independent of the lower ones. In contrast, archaeal phytanyl tails can be covalently linked to each other to form a lipid monolayer with two heads and a single body - a veritable membrane hydra. It's probably this feature that enables Archean lipid monolayers to withstand the scorching acidic infernos in which hyperthermophilic archaea manage to survive. Such is the case of Pyrolobus fumarii, the only known representative of the Pyrolobus genus belonging to the Crenarchaeota phylum, which can live and multiply at temperatures of up to 113°C. Growth is impossible at temperatures below 90°C. This facultative aerobic, chemolithoautotrophic species was first discovered in 1997 in the vicinity of a submarine hydrothermal vent on the Atlantic Ridge [100]. A microbe of the same family, Geogemma barosii, managed to survive and reproduce in an autoclave at 121°C for 10 hours, dying only when the temperature reached 130°C [101,102]. Between 121°C and 130°C, it cannot reproduce, but remains alive and resumes growth as soon as the temperature drops. Before its discovery, no cell could survive 15 minutes at such temperatures. And experiments suggest that there may be archaea species that can tolerate temperatures of 140-150°C. The ability to survive at 121°C is crucial for medicine, as this is the temperature chosen to sterilize medical equipment. Fortunately, Geogemma barosii cannot survive at 37°C, making it non-infectious. It uses dihydrogen H₂ as an electron donor and Fe(III) as an electron acceptor, reducing it to Fe(II) in the form of magnetite.

Contrary to our own genetic and protein machinery, our lipids resemble those of bacteria and not those of archaea, which could be an indication of very ancient chimerism. No archaea are known to be parasitic or pathogenic. This is not to say that they don't exist. Archaea existed long before we discovered them, and today we find that they really are everywhere. Bacteria and eukaryotes have developed myriads of pernicious parasites, and it seems very strange that an entire field of life should be devoid of them. Could the chemistry of archaea be so unique that they are ill-equipped to survive inside advanced organisms? This does not seem to be the case. So why haven't they gone over to the dark side? Is there something fundamental about their metabolism or chemistry? The Archean species most likely to act pathogenically as a parasite is Nanoarcheum equitans, the world's second-smallest unicellular being (400 nm in diameter for a genome of 490,885 nucleotides) after Mycoplasma genitalium (200-300 nm in diameter). It was discovered in 2002 in a hydrothermal vent and grows at a temperature of 80°C with a saline concentration of 2% [103]. It is found all over the world, in hydrothermal vents, in Yellowstone's colored lake, in Iceland and under the Arctic Ocean. Wherever it is found, it seems to live exclusively on the surface of larger archeans such as Ignicoccus, which can house up to ten N. equitans individuals on its lipid mantle. In fact, Nanoarcheum doesn't seem to be able to manufacture its own lipids, nucleotides or amino acids - everything seems to come from Ignicoccus. On the other hand, N. equitans can repair its own DNA and manufacture its own DNA, RNA and proteins.

This is not to say that archaea are free of parasites and pathogens. On the contrary, many archaea find themselves on the menu of other micro-organisms, or can be infested by a very broad spectrum of DNA viruses. When archaea were first discovered, they were considered strange and bizarre. They live in salt ponds, hydrothermal vents, burning acid lakes and methane-infested swamps. So, they're not normal microbes. Square, flat archaea have been discovered that divide into sheets like postage stamps and live in real brines. They use proteins called bacterio-rhodopsin, which are structurally and functionally similar to the rhodopsin protein of the vertebrate eye. The one that enables energy to be generated from light. Other species of salt-loving archaea have a variety of polyhedral shapes that can even change shape between generations. But like most microbes, archaea are difficult to cultivate in the laboratory. When the search for archaeal DNA began, these microbes were found just about everywhere. This includes normal places like seawater and ocean and ocean sediments, soil as well as the intestines or vaginas of mammals. Archaea can make up to 40% of the microbial biomass in the oceans, although bacteria are around three times more numerous and can make up to 20% of the total mass of terrestrial biomass. Despite their heat-loving reputation, archaea are also found in all the coldest spots on the planet, including Arctic seawater and ice. Much to our surprise, we found giant filamentous archaea so large they could be seen with the naked eye living on mangrove roots. We found methanogenic archaea that interact with protozoa in the intestines of cows and termites to help these organisms break down cellulose to recover energy. We've even found an archaeon living in symbiosis with a sponge...

At the molecular level, archaea differ quite markedly in their use of nickel, particularly at the level of cofactor F430. Of particular interest are the four coenzymes linked to the porphyrin skeleton and to metal ions: heme (Fe), coenzyme B12 (Co), chlorophyll (Mg) and factor F430 (Ni). Indeed, these four components involving invariable metal ions act as if they were four new elements. Porphyrin may well have appeared before cells even existed. Note that the F430 (Ni) factor only appears in archaea that do not produce chlorophyll (Mg), which makes it possible to distinguish between sub-chemotypes. Another example of coenzyme development is that of the tungsten (W) and molybdenum (Mo) dithiolate complexes, where the (W) complex is present in archaea. Early on, molybdenum was precipitated in the form of its sulfide MoS₂. Similarly, the chemistry of nickel, cobalt and tungsten hardly developed over the course of evolution to such an extent that these elements disappeared from many higher organisms. Around 2 Gyr ago, the first truly complex single cells with multiple compartments appeared simultaneously in all lineages, from the first aerobic bacteria and archaea to plants (using light), fungi and animals [98].

Frames of Thinking

In this section, before concluding, we'll take a step back. For our main proposition here is that we must not decorrelate the phenomenon of consciousness, which is essentially spiritual in nature, from that of biological evolution, which is materialistic in essence. This is particularly important, given that we have very recently been confronted with a major crisis in materialistic scientific medicine via the so-called COVID-19 crisis. This is not the place to discuss the sociological issues that led to such a crisis. What is clear, however, is that during this crisis, the immaterial side of our ideas, rooted in quantum field physics (also known as second quantization), and the spiritual side, linked to the notion of consciousness, were totally sidelined or even ignored. It is our conviction that this must not happen again. If we truly wish to evolve towards a more harmonious society that respects nature, whether this nature is expressed in bacterial, plant, animal or human form, it becomes crucial to constantly refer to the triptych (consciousness, information, water). Consequently, in parallel with this proposed overhaul of the origin of life, we might also consider the parallel evolution of human societies. And, by the same token, the evolution of so-called artistic practices. And among these artistic practices, there's one that deserves a closer look: medicine, or rather, the art of curing living beings from the moment they are declared "sick".

Here, too, we need to be realistic, and not blind ourselves to the facts. If medicine were truly scientific in nature, disease would not exist. Or, at least, it would be cured with a 100% success rate. In particular, we wouldn't have all these medical studies demanding complete anonymity and double- or triple-blind procedures. If such precautions are necessary, it's because medicine doesn't hold all the cards. Whatever it does, there's always that unanimously recognized thing called the "placebo effect". We're talking here, of course, about the therapeutic effect obtained through the administration of various substances and procedures that have no specific effect on the disease being treated [104,105,106]. If the placebo effect does exist, then medicine can only be an art, the art of healing, and not a science. The relevance of our formulation of the origin of life then becomes clear. If life is indeed produced by consciousness, then spontaneous healing becomes possible thanks to this universal consciousness, whether we call it "Tao" or "Ether". Chinese medicine, Ayurveda and other so-called "energetic" medicines can no longer be dismissed with a simple shrug of the shoulders.

If we look at the problem of life from this angle, we can identify seven modes of thought [107], giving rise to seven major types of medicine. The first question that arises is why exactly seven, and not ten or fourteen? One reason is that the number 7 appears in many remarkable natural phenomena. For example, during or after rain, a rainbow can appear, which is a breakdown of sunlight into seven main colors: red, orange, yellow, green, blue, indigo and violet. At first glance, such a division may seem rather arbitrary, except that we owe it to the great British physicist Sir Isaac Newton (1643-1727 E.C.). Indeed, in his second major book on the physical sciences, Newton deals with optics and the refraction of light. In this work, Newton analyzes the fundamental nature of light, its diffraction and the behavior of color mixtures. And, to clarify the subject, he proposes to link the fundamental rules of light to those of the musical scale, composed of seven notes [108]. For the color spectrum is then considered to be made up of just five colors: red, yellow, green, blue and violet. In an attempt to reconcile music and science, he decided to add orange between red and yellow, and to separate violet into two colors, indigo and mauve. Hence the seven colors of the rainbow, which are in perfect harmony with the seven notes of earthly music or the seven wandering stars in the sky: Sun, Moon, Mercury, Venus, Mars, Jupiter and Saturn, noted since ancient times. It also resonates with the seven alchemical metals: gold, silver, quicksilver, copper, iron, tin and lead, or the seven alchemical operations: Calcinatio, Solutio, Coagulatio, Sublimatio, Circulacio, Mortificatio and Putrefactio. Moreover, if we refer to the Bible, Elohim creates the heavens and the Earth in six days, then rests and sanctifies on the seventh (Genesis 1-2:4). But there's also the New Testament and its apocalypse. Here, the seventh trumpet announces the resurrection of the dead and the Last Judgment. Then come the seven plagues, which correspond to the seven vials of divine wrath poured out by the seven angels into the world. In the ancestral traditions of India, as we saw above, the Vedic scriptures and yogic practices have for millennia described seven chakras or seven wheels of life influencing our physical and spiritual existence. Finally, in Chinese culture, the number seven is synonymous with neutrality, with both positive and negative aspects. Thus, seven is written (七 - qī) and pronounced similarly to the words 起 (qǐ - to rise, to begin) and 气 (qì - vital energy). It is therefore considered a lucky number for relationships. But it's also sometimes seen as an ominous sign, because the 7th month is "the month of ghosts". And during this period, tradition dictates that spirits held in the underworld are released... Hence, ultimately, a neutral thing.

All this means that the number seven seems to be the link between the subtle spiritual world and the physical, material world. This is why, in 2020, I proposed to distinguish seven frames of thought [6,107]. The starting point is that what matter and spirit have in common is the use of whole numbers to express themselves. Matter, quantitatively, as a sum of units via quantum physics, mind, more qualitatively, as a division of a single unit (philosophy). On the philosophical side, we have the number 0, which, for our Ancients, symbolized the entire universe in its unmanifested, latent, potential and invisible state. The symbol of the ouroboros, the snake biting its own tail, is a perfect illustration of this. However, another number, 1, could also play this role. But it described a manifest, real and visible state of this same universe. Here, the snake has stopped biting its own tail, and can unfold as a ripple that has no beginning and no end. In short, we have a unit, the 1, and thus an essence for everything that follows. The number 2, on the other hand, was the number of discriminations. In other words, a manifestation of polarity, allowing us to differentiate between the head and tail of the cosmic serpent. This polarity is of course a source of instability, of perpetual oscillation between right and left? In short, as soon as two appears, nothing can ever be the same again. The virtual (0) and the real (1) interpenetrate deeply.

Hence the need to seek a compromise expressed by the number 3, which is the production number of all tangible and stable things. The Egyptians engraved it in stone in the form of a triangle (pyramids), while the Greeks founded philosophy on the notions of thesis, antithesis and synthesis. Isn't it said: "Never 2 without 3"? The triangle is in fact the first creator of regular three-dimensional solid shapes such as the tetrahedron, octahedron and icosahedron. And it's at this level that an eminently remarkable geometric construction based precisely on the number 3 comes into play. The idea is to consider its first three powers: 3⁰ = 1, 3¹ = 3 and 3² = 9, and to draw three concentric circles (A, B, C). Here, the second (B) should have a diameter three times that of the first (A). As for the third (C), its diameter will again be triple that of the second (B). Then, starting at any point on circle C, trace a tangent to the small inner circle A, extending it until you reach the middle circle B (Figure 25). At this point, we trace a new tangent to circle A, which takes us back to another point on circle C. We then repeat the same operation from this new point, seven times. And, remarkably, by the seventh time, we're right back where we started.

The result is a double seven-pointed star (Figure 25). All we need to do now is associate each outer branch of this star with a specific way of thinking, and a medical technique associated with it. For example, the most primitive way of thinking is shamanism, which can be summed up by the phrase "All is Spirit". Within this framework, the treatment method is similar to the various shamanic trance techniques.

The second frame of thought appeals to materialism, with its apothegm "All is Matter". The emphasis here is on everything that is concrete and visible. In other words, everything that can be seen, heard, touched, smelled or tasted. Herbal medicine (phytotherapy) fits in perfectly with this way of thinking about the world. And the various pharmacopoeias of China, Ayurveda, Africa, Europe, the Caribbean and Polynesia validate this way of healing.

The third frame of thought is determinism. This framework is linked to the idea that nothing happens by chance and can always be understood through logical, coherent reasoning. Here, natural events are subject to a set of mathematical equations that allow us to predict with certainty what will happen given a given set of initial conditions. We recognize here the framework of scientific thought developed from the 17th^e century onwards, mainly in Europe, with its apothegm: "Everything is equation". A framework that presupposes that, alongside matter, there can also be light. This is the framework of modern science, and its so-called "allopathic" medicine, in which disease is fought using drugs that have an effect opposite to the pathological phenomena. Here, the remedy can be natural or synthetic, i.e., manufactured through the ingenuity of the human mind, whatever the case may be. The only problem was that, at the beginning of the twentieth century, this deterministic framework of thought proved totally inadequate to describe phenomena on the scale of a billionth of a meter (nanometer).

Hence the birth of the fourth frame of thinking, probabilism, in which the deterministic equations of the macroscopic world are replaced by probabilistic equations of the microscopic world derived from quantum physics. Here, the apothegm "Everything is vibration" reigns, meaning that reality is described either in terms of "corpuscles" or "wave functions". In other words, there's a wave/corpuscle duality, and because of such duality, it's impossible to predict everything with certainty, as in frame #3. Hence, of course, new treatment techniques that take this wave aspect into account, and the name "quantum therapies". It's at this point that the scientific community splits into two distinct groups. The first group validates the idea that the quantum revolution of the 1930s should be taken into account in medicine. However, this should only apply to medical techniques for diagnosing disease, such as X-rays, positron emission tomography (PET-Scan) or magnetic resonance imaging (MRI). In surgery, this includes the use of coherent light lasers to cut tissue, vaporize thrombi in arteries or detect cancerous tumors, etc. On the other hand, this first group categorically refuses to admit that probability waves can be used for treatment [109]. A second group, on the other hand, admits this possibility and relies on machines that aim to harmonize or balance the energy flow of body and mind. Here, the line is relatively blurred between devices using waves of an electromagnetic nature and devices with no active electronic components. Hence the skepticism of the first group, who prefer to stick to the fact that quantum laws only apply to atoms and molecules, and certainly not to other bodies operating on a macroscopic scale.

But before we say anything more about this heated debate between conventional and quantum medicine, let's note that this fourth probabilistic framework is based entirely on a physics of first quantization, illustrated by the concept of wave/corpuscle duality. From the foregoing, we know that there is a fifth frame of thought in which matter is considered not to exist in its own right, being merely a very high-frequency vibration of a relativistic ether. Hence the name immaterialism, which is based on quantum field theory and the maxim "all is coherence". Here, there are no more waves or corpuscles, only "quantum fields" which, depending on experimental conditions, can create particles or waves at will in a four-dimensional space-time, from a quantum vacuum that is the ultimate source of all reality. In this paper, we propose to link homeopathic medicine, which uses more or less diluted aqueous solutions, to this fifth frame of thought. But also, all the so-called "energetic" medicines, where the physical body is subjected to energetic exercises such as Yoga or Qi Gong, Tui Na massage or acupuncture. It would be madness to deny that these often ancient "holistic" techniques are ineffective. On the other hand, allowing them to have their own framework of thought, with its clear apothegm rooted in modern physics, can only be beneficial to all.

It should be noted that a very large majority of physicists believe that this fifth framework is sufficient to describe all physical reality. However, a small minority, including myself, believe that this framework also has its limitations, as it does not take into account symmetry operations of the "dilation" type, which imply that the object under study remains invariant through change of scale (vide supra). It is at this sixth level that new so-called "scaling waves" come into play, enabling the same physical system to recognize itself at different scales of size and duration [110]. For this sixth frame of thought, we would have a new apothegm: "All is harmony". The associated treatment method would be the use of music (music therapy), hence the name "musicalism". For, here too, it is imperative to find a place for all agricultural techniques using music to minimize viral or bacterial attacks on plants. And, if these musical techniques do indeed work for plants [111,112], there's no reason why they shouldn't also apply to animals and human beings.

It is in this sixth frame of thought that we can consider water as capable of providing a sound reference or tuning fork. Indeed, in the fifth dimension of the universe, masses must synchronize on a musical scale, as energy can be expressed in two different and intrinsically equivalent ways. On the one hand, any mass m can be considered as energy according to the relation E = m·c², where c = 299,792,458 m·s⁻¹ is the propagation speed of light in a vacuum. On the other hand, according to quantum physics, any energy can be considered as a frequency f, according to the relation E = h·f, where h = 6.62607015×10⁻³⁴ J-s represents Planck's quantum of action. Assuming the same energy E is involved in both cases, it follows that m·c² = h·f. This means that any mass m can be associated with a characteristic frequency f, and vice versa. However, for molecules, mass is usually expressed in Daltons (Da = g-mo⁻¹), which means we need to go through Avogadro's constant, N_A = 6.02214076×10²³ mol⁻¹, to obtain a mass m expressed in kilograms (kg). Hence the fundamental relationship:

f/Hz = k_MF ×M(/Da), with k_MF = c²/(1000×N_A×h) = 2.25234272×10²⁴ (Hz·Da⁻¹).

So, for a water molecule of mass m = 18.01528 Da, we rigorously calculate a quantum frequency f = 4.0577×10²⁵ Hz. This is where the notion of scale invariance comes into play, coupling the world of the infinitely small to our macroscopic scale. In music, this invariance of scale is expressed by the principle of octave identity, recognized since Antiquity. At the frequency level, this principle corresponds to division or multiplication by a factor of 2. As the quantum frequencies of molecules are really very high, the most convenient way is to use the base-2 logarithm function, noted log₂, which allows us to write: f₀/2⁷⁶ (Hz) = 2.980951×(m/Da). Then, as m[H₂O] = 18.01528 Da, there comes f₀(H₂O) = 53.70267 Hz. Since this frequency is too low to correspond to an A4 tuning fork, we simply raise it by three octaves to obtain a value of 429.62 Hz known as the "water tuning fork". This gives a value close to the average, 430.5 Hz, between the lowest (404 Hz) and highest (457 Hz) pitches used in Western music [113]. Of course, this kind of calculation can be performed for any chemical molecule. Hence the possibility of transforming any substance whose chemical composition is known into a sequence of musical notes. Then, from these notes, it is possible to derive a mode to create a totally harmonized accompaniment according to musical laws. A collection of musical pieces, all tuned to the tuning fork of water, is now available for free download from the Internet [114].

Finally, the seventh and last framework of thought will be symbolism, to account for the capacity of consciousness to manipulate information and give it meaning [29]. This framework is of course the most general, since its apothegm is "Everything is information". As we have seen, this information can be stored both in the ether and in the coherence domains that can appear when water undergoes virtual excitations from this same ether. And this framework has everything it takes to support a final form of healing, which consists, when faced with an illness, in persuading oneself that it is possible to cure via any substance or technique, or even by the sheer force of thought. This is the placebo effect, which obliges adherents of the third frame of thought to carry out randomized, double-blind studies to validate the therapeutic effect of a medicinal substance. The placebo effect thus completes the panoply of medical techniques that can be used to overcome all kinds of illnesses.

The point of Figure 25 is to provide a sound, practical basis for any kind of medical practice. This is crucial insofar as, in the field of medicine, it is often difficult to distinguish between a genuine desire to heal and a desire to make substantial profits. After all, a person in poor health will have an innate and spontaneous tendency to do whatever it takes to get better. Hence the possible abuse of therapists to provide expensive treatments of dubious efficacy. In fact, this rather perverse aspect of medicine and pharmacy was long thought to be non-existent, or merely the ravings of publicity-hungry minds. However, since the COVID-19 crisis, it has become clear that science and medical research have not always been beyond reproach, as demonstrated by the "Lancetgate" affair [115,116].

Prior to this major crisis in medicine, it was of course the questioning of the efficacy of homeopathy, the medicine proposed by Samuel Hahnemann as early as 1796, that was attracting all the attention. Yet prestigious researchers such as Jacques Benvéniste and the 2008 Nobel Prize winner for Medicine, Luc Montagnier, have carried out highly advanced and sophisticated fundamental scientific research. On the basis of their duly published findings, homeopathic treatment consists of using only the information contained in any remedy, instead of the material itself. Of course, if such therapeutic information is stripped of its natural support, the molecule, it must be transferred to another medium. And that other medium is water or sugar. And, provided we place ourselves within the framework of so-called second quantization quantum field physics, where matter is perceived as a vibration of the ether, there's nothing extraordinary about this transfer between a dissolved molecule and the solvent that takes it in. The physics of coherence domains [37,38] provides a solid and indisputable scientific basis for this phenomenon. Paradoxically, equally "immaterial" practices such as acupuncture, Qi Gong and yoga have not come under the same attack as homeopathy. So, it's time to make medical debates less dogmatic and more dispassionate.

Conclusion

We've come to the end of this little journey from the Big Bang to the advent of the Internet:

Big Bang → Light → Hydrogen → Stars → Atoms → Water → Planets → Metabolism → Lipids → RNA → Viruses → Ribozyme → Proteins → Bacteria, Archaea → Eukaryotes → Sex → Plants → Animals → Humans → Computers → Internet.

What sets this paper apart from others on the same subject is that it gives pride of place to the notion of consciousness. This immaterial consciousness pre-exists matter and drives it via a substance with extraordinary properties: water. In the process, we encountered and discussed the philosophical foundations of all the great human civilizations. From this we have drawn a universal ternary recipe: thesis - antithesis - synthesis, for evolving while maintaining efficiency and stability. Water, by the way, with its formula H₂O is an excellent illustration of this highly creative trinity. For example, seeing O as the basic antithesis of the acidity provided by H. Or seeing O as the oxidizing antithesis of the reduction provided by H. Not to mention the electronegativity associated with O, the antithesis of the electropositivity associated with H. Hence the ability to solvate both anionic and cationic species, and to form micelles with non-polar solutes. The water molecule is thus a synthesis of the highest availability to bring about that priceless thing we call life.

But there's more to water, the substance that makes up the vast majority of living cells. For it is also an association between an oxygen atom and two non-atoms of hydrogen. And the fact that hydrogen is not an atom, but an association between three quarks (proton) and a lepton (electron), means that to understand water, we have to deal with the physics of second quantization. Physics where the wave or the corpuscle have no tangible reality, since here only the quantum vacuum or ether exists, generator or annihilator of all things. In short, throughout this article, I've tried to reframe biology in its most fundamental terms: consciousness and water. Hence the possible unification of age-old medical practices that have largely proved their worth, such as shamanic trance, phytotherapy, allopathy, classical or quantum electro-magnetotherapy, homeopathy, music therapy and even placebo therapy. In other words, no single medicine can claim to hold the secret to good health and longevity. This article calls for a reconciliation between all therapists. Whatever their country of origin or philosophical convictions.

Another original feature of this paper is the care taken to ensure that not only the "bonding" electrons (chemical bonds) are always shown alongside the atoms, but also the "non-bonding" doublets generally overlooked in most biology treatises. Similarly, for formulas involving phosphorus, the crucial element without which there can be no life, we have systematically used the strict octet rule with its formal charges. This is because quantum chemical methods have confirmed that single bonds between elements in the first row are weak, while multiple bonds are strong [117]. For elements in the second or higher row, however, the opposite is true. Here, single bonds are strong, while multiple bonds are weak. The "extended valence" (violation of the octet rule) observed in compounds of the elements of the top main group has little to do with the availability of d-orbitals, but is rather due to the size of these atoms and thus to the reduced steric hindrance between ligands and, to a lesser extent, to the lower electronegativity of heavy atoms. Here, a model based on the concept of electron-rich multicentric bonds is certainly closer to reality than one involving hybrid orbitals with the participation of d-orbitals. XO bonds in phosphane oxides, sulfoxides and related compounds are best formulated as semi-polar bonds rather than true double bonds. Hence the absence of any P=O double bonds in this article. And, by implication, the clear highlighting of the electron richness of the P-O bond which implies the possibility of a strong multicentric resonance on the tetrahedral PO₄ entity. After all, reasoning with false schemes that are unrepresentative of chemical reality is unhealthy and can only lead to errors in subsequent analysis.

This article also opens up the possibility of seeing the water molecule not only as an essential biological reference, but also as a fascinating musical one. Indeed, any conversion of musical notes into sound frequencies calls for a universal tuning fork of 440 Hz. But there's nothing in physics to justify such a value. On the other hand, it is relatively easy to transform the average isotopic mass of a water molecule into a sound frequency of 429.62 Hz, according to the laws of physics. This article therefore strongly urges all composers and musicians to adopt this new musical reference value in place of the purely commercial 440 Hz. Those who have already done so have all confirmed that this water pitch provides a much deeper musical experience than the standard 440 Hz pitch. Of course, this is only a suggestion, and is unlikely to be proven. For that, we'd need to have enough statistical data to see exactly what's going on. So, it's still too early to draw any definitive conclusions. But in the meantime, there's nothing to stop you trying.

Appendix

In this paper, we have chosen to be as rigorous as possible in writing biological chemical formulae. Indeed, modern biology is full of acronyms such as ATP, ADP, NADPH, NAD⊕ etc... The greatest laxity reigns in the matter, with totally fictitious charges that mean nothing and, worse, non-conservation of mass. For example, a biologist will write ATP + H₂O = ADP + Pi for the hydrolysis of the adenosine triphosphate molecule (ATP) giving rise to adenosine diphosphate (ADP) and a phosphate ion (Pi). Here, the oxygen atom and the two hydrogen atoms of the water molecule disappear completely. Worse still, there's only one P (phosphorus) symbol on the left, and two on the right. The consequence of these dubious practices is that one must constantly perform intellectual gymnastics to follow the fate of matter and electrical charges in any biological transformation. What's more, all these acronyms make the discipline highly hermetic. As a result, it becomes the preserve of specialists with enough years of scientific study behind them to follow the transformations. Surprisingly, it's not difficult to be rigorous in writing down chemical species, whether charged or electrically neutral.

Chemistry teaches us that when two atoms decide to chemically bond to each other, three categories of electrons appear. Electrons that are not affected by the bond, forming so-called "non-bonding" doublets. Let λ be the total number of these doublets. Then there are the electrons that are shared. Here, we can expect to find single bonds or multiple bonds, double bond (symbol "=") or triple bond (symbol "≡"). Let σ be the number of single bonds and π the number of double (one π-bond) or triple bonds (2 π-bonds). The deterministic laws of chemistry (way of thinking #3), then, dictate that if we know the total number of atoms n, the total number of hydrogen atoms h, the total number of rings c and N the total number of electrons, then, we must have (strict octet rule):

(n, h, N, c) \Rightarrow \{\begin{matrix} σ = n + c - 1 \\ π + c = 3 (n - h) - N / 2 + 1 - N % 2 \\ λ = N - 4 n + 3 h \end{matrix}

The symbol N%2 means "remainder of division by 2".) The remainder is 0 unless the species is a radical with half-integer spin (odd number of electrons), in which case the symbol is 1. When calculating the total number of electrons, only valence electrons are considered. If e designates the number to be considered for a given element, we proceed by column in the periodic table of elements:

H...Fr : e = 1

Be...Ra : e = 2

Sc...La, B...Tl, lanthanides: e = 3

C...Pb : e = 4

N...Bi : e = 5

O...Po : e = 6

F...At : e = 7

Transition metal complexes that do not obey the octet rule are excluded from this formalism. In this case, the octet rule is applied to obtain the ligand's electronic structure. Ligand field theory is then applied to the complex.

Let's take a few examples to see how this works in practice. For methane with the empirical formula CH₄, we have: (n, h, N, c) = (4+1, 4, 4×1 + 1×4, 0) = (5, 4, 8, 0), i.e. (σ, π, λ) = (5+0-1, 3×(5-4)-8/2+1-0-0, 8-4×5+3×4) = (4,0,0). Hence the familiar image of 4 single bonds emanating from a central carbon atom. For ethylene with the empirical formula C₂H₄, we predict: (n, h, N, c) = (4+2, 4, 4×2 + 1×4, 0) = (6, 4, 12, 0), i.e. (σ, π, λ) = (6+0-1, 3×(6-4)-12/2+1-0-0, 12-4×6+3×4) = (5,1,0). Hence the existence of a C=C double bond and 5 single bonds, one C-C and four C-H. Similarly, for acethylene with the empirical formula C₂H₂, we predict: (n, h, N, c) = (2+2, 2, 4×2 + 2×1, 0) = (4, 2, 10, 0), i.e. (σ, π, λ) = (4+0-1, 3×(4-2)-10/2+1-0-0, 10-4×4+3×2) = (3,2,0). Hence the existence of a C≡C triple bond and 3 single bonds, one C-C and two C-H. Finally, for benzene of formula C₆H₆, it comes: (n, h, N, c) = (6+6, 6, 4×6 + 6×1, 1) = (12, 6, 30, 1), i.e. (σ, π, λ) = (12+1-1, 3×(12-6)-30/2+1-0-1, 30-4×12+3×6) = (12,3,0). We recover the familiar image of 12 single bonds, 6 of the C-C type forming a ring (c = 1) and 6 of the C-H type associated with 3 C=C double bonds (Kékulé's non-aromatic formula).

Now let's see how this works for a radical species like nitric oxide with the empirical formula NO, i.e. (n, h, N, c) = (1+1, 0, 5+6, 0) = (2, 0, 11, 0), or (σ, π, λ) = (2+0-1, 3×(2-0)-11/2+1-1-0, 11-4×2+3×0) = (1,1,3). Again, the familiar picture of a single N-O bond, an N=O double bond and three non-bonding doublets (one on the nitrogen atom and two on the oxygen atom) with a single electron, i.e. :N=:O:-. If I remove this electron to form the cation NO⊕, we'll have (n, h, N, c) = (1+1, 0, 5+6-1, 0) = (2, 0, 10, 0), i.e. (σ, π, λ) = (2+0-1, 3×(2-0)-10/2+1-0-0, 10-4×2+3×0) = (1,2,2), i.e. the image :N≡O:^⊕. Note here the notion of formal charge. To calculate it, we take each atom one by one and subtract from its number of valence electrons e, one electron for each covalent bond, single or multiple, and two electrons for each non-bonding doublet. Thus, for the species :N≡O:^⊕, the formal charge on nitrogen is zero, since here e = 5 and q(N) = 5 - 2 - 3×1 = 0. On the other hand, for the oxygen atom (e = 6), q(O) = 6 - 2 - 3×1 = 1, i.e. q(O) = +1. The positive charge is therefore written on the oxygen atom's side. Figure 26 shows other examples in the field of biology and inorganic chemistry.

Figure 26. Application of the strict octet rule to a few molecules of biological interest and to reduced (HS^⊝, N₂) or oxidized (SO₄²^⊝, NO₃^⊝) molecular derivatives of Sulphur or Nitrogen.

References

M. Henry (2021), « Thermodynamics of life », Substantia, 5(1): 43-71.
M. Henry, L. Schwartz (2019), « Entropy export as a driving force of evolution », Substantia, 3(2) Suppl.: 29-56.
S. Ginzburg, A. A. Vinogradova, E. I. Fedorova, E. V. Nikitich, and A. V. Karpov, (2014), « Content of Oxygen in the Atmosphere over Large Cities and Respiratory Problems », Izvestiya Atmospheric and Oceanic Physics, 50(8), 782–792. [CrossRef]
https://www.calctool.org/atmospheric-thermodynamics/air-density#what-is-the-density-of-air-considering-humidity.
Tianyi Wu, Alexander D. Ost, Jean-Nicolas Audinot, Martin Wiesmeier, Tom Wirtz,Franz Buegger, Werner Häusler, Carmen Höschen, Carsten W. Mueller, (2022) « Association of fresh low-molecular-weight organic compounds with clay-sized mineral fraction in soils of different organic carbon loading », Geoderma, 409, 115657. [CrossRef]
Marc Henry (2020), « L’eau morphogénique : Santé, information et champs de conscience. Les 7 cadres de pensées pour comprendre », EAN : 978-2-7033-1269-7, Dangles, Escalquens (253 pages).
F.C. Neidhardt (1996), Escherichia coli and Salmonella: Cellular and Molecular Biology, Vol 1, ASM Press, Washington DC, pp. 14.
K. J. Ellis (1990), « Reference man and woman more fully characterized », Biological Trace Element Research, G. N. Schrauzer Ed., The Humana Press Inc., pp. 385-400.
Lao-Tzu, Tao Te Ching, Chap. 42, J. Legge, Translator (1891) in « Sacred Books of the East », Vol. 39.
Henri Poincaré (1914), La Science et l’Hypothèse, Flammarion, Chap. XIV, « La Fin de la Matière », p. 126.
P. Destouches-Février & J.-L. Destouches, (1946), « Sur l’interprétation physique de la mécanique ondulatoire », C. R. Acad. Sci. Paris, 222, 1087-1089.
K. Hornberger, S. Gerlich, P. Haslinger, S. Nimrichter, M. Arndt (2012), « Colloquium: Quantum interference of clusters and molecules », Rev. Mod. Phys., 84, 157-173.
Tonomura, F. Nori (2008), « Disturbance without the force », Nature, 452, 298-299. [CrossRef]
Einstein (1920), « Äther und Relativitätstheorie », Berlin, Julius Springer, p. 15.
J. P. Gerbaulet, M. Henry (2019) « The ‘Consciousness-Brain’ relationship», Substantia 3(1), 113-118.
Luc Brisson, Le même et l’autre dans la structure ontologique du Timée de Platon, Collection « International Plato Studies », Vol. 2, Saint Augustin, Academia Verlag, 1994, p. 222.
George Boole (1854), « An investigation of the laws of thought on which are founded the mathematical theories of logic and probabilities », Walton and Maberly, London, 1854.
Heyting (1930) « Die formalen Regeln der intuitionistischen Logik », 3 parts, In: Sitzungsberichte der preußischen Akademie der Wissenschaften. phys.-math. Klasse, 1930, 42–56, 57-71, 158-169.
Johansson (1937), « Der Minimalkalkül, ein reduzierter intuitionistischer Formalismus », Compositio Mathematica, 4, pp. 119–136.
P. Watzlawick, J. Beavin-Bavelas, D. A. Jackson (1967), « Pragmatics of Human Communication », W. W. Norton & Company, New York. [CrossRef]
G. Bateson (1972), « Steps to an Ecology of Mind », Jason Aronson Inc., London, pp. 276, 321,460. [CrossRef]
E. Shannon (1948), « A mathematical theory of communication », Bell Syst. Tech. J., 27: 379-423. [CrossRef]
S. Lloyd, H. Pagels (1988), « Complexity as Thermodynamic Depth », Ann. Phys., 188: 186-213.
T. Nørretranders (1991), « The User Illusion », Viking, New York.
N. Wiener (1948), « Cybernetics or control and communication in the animal and the machine », John Wiley & Sons, New York.
E. T. Jaynes (1965), « Gibbs vs Boltzmann Entropies », Am. J. Phys., 33: 391-398.
Prigogine (1977), « Time, structure and fluctuations », Nobel Lecture, 8 December.
J. A. Wheeler, K. Ford (1998), « Geons, Black Holes and Quantum Foam. A Life in Physics », W.W. Norton & Co., New York, pp. 63-64. [CrossRef]
M. Henry (2020), « Consciousness, Information, Electromagnetism and Water », Substantia, 4(1): 23-36.
L. Montagnier, J. Aïssa, C. Lavallee, M. Mbamy, MJ. Varon, H. Chenal (2009), « Electromagnetic detection of HIV DNA in the blood of AIDS patients treated by antiretroviral therapy », Interdiscip Sci. Comput. Life Sci., 1: 245-253.
L. Montagnier, J. Aissa, E. Del Giudice, C. Lavallee, A. Tedeschi, G. Vitiello (2011), « DNA waves and water », Journal of Physics: Conference Series, 306: 012007.
L. Montagnier, E. Del Giudice, J. Aïssa, C. Lavallee, S. Motschwiller, A. Capolupo, A. Polcari, P. Romano, A. Tedeschi, G. Vitiello (2015), « Transduction of DNA information through water and electromagnetic waves », Electromagnetic Biology and Medicine, 34: 1-10. [CrossRef]
L. Montagnier, J. Aïssa, A. Capolupo, T. J. A. Craddock, P. Kurian, C. Lavallée, A. Polcari, P. Romano, A. Tedeschi, G. Vitiello (2017) « Water bridging dynamics of polymerase chain reaction in the gauge theory paradigm of quantum fields », Water (MDPI), 9: 339-357. [CrossRef]
Qing Tang, Tongju Li, Xuemei Bai, Minyi Zhao, Bing Wang, Glen Rein, Yongdong Yang, Peng Gao, Xiaohuan Zhang, Yanpeng Zhao, Qian Feng, Zhongzhen Cai, Yu Chen (2018), « Rate limiting factors for DNA transduction induced by weak electromagnetic field », Electromagnetic Biology and Medicine 38:1, 55-65. [CrossRef]
Del Giudice, G. Preparata, G. Vitiello (1998), « Water as a free electric dipole laser », Phys. Rev. Lett., 619.: 1085-1088. [CrossRef]
R. Arani, I. Bono, E. Del Giudice, G. Preparata (1995), « QED coherence and the thermodynamics of water », Int. J. Mod. Phys. B, 9: 1813-1842. [CrossRef]
Bono, E. Del Giudice, L. Gamberale, M. Henry (2012), « Emergence of the Coherent Structure of Liquid Water », Water (MDPI), 4: 510-532. [CrossRef]
S. Sen, K. S. Gupta, M. J. D. Coey (2015), « Mesoscopic structure formation in condensed matter due to vacuum fluctuations », Phys. Rev. B, 92: 155115. [CrossRef]
H. B. G. Casimir (1948), « On the attraction between two perfectly conducting planes », Kon. Ned. Akad. Wetensch. Proc., 51: 793-795.
C. Wilson, G. Johansson, A., Pourkabirian, M. Simoen, J. R. Johansson, T. Duty, F. Nori, P. Delsing (2011), « Observation of the dynamical Casimir effect in a superconducting circuit », Nature 479: 376–379. [CrossRef]
M. Henry (2014), in « Aqua Incognita: Why Ice Floats on Water and Galileo 400 Years on », P. Lo Nostro, B. W. Ninham (eds), Connor Court Pub., Ballarat, chap. IX: 197-239.
P. Gürtler, V. Saile, E. E. Koch (1977), «Rydberg series in the absorption spectra of H₂O and D₂O in the vacuum ultraviolet », Chem. Phys. Lett., 51: 386-391.
S. Sen, K. S. Gupta, J. M. D. Coey (2015), « Mesoscopic structure formation in condensed matter due to vacuum fluctuations » Phys. Rev. B, 92, 155115. [CrossRef]
31. E. Bianconi, A. Piovesan, F. Facchin, A. Beraudi, R. Casadei, F. Frabetti, L. Vitale, M. C. Pelleri, S. Tassani, F. Piva, S. Perez-Amodio, P. Stripolli, S. Canaider (2013), « An estimation of the number of cells in the human body », Ann. Hum. Biol., 40(6): 463-471. [CrossRef]
G. H. Pollack (2013), « The Fourth Phase of Water: Beyond Solid, Liquid, and Vapor », Ebner and Sons Publishers, Seattle.
K. J. Ellis (2000), « Human body composition: in vivo methods », Physiol. Rev., 80(2): 649-680. [CrossRef]
P. C. Benias, R. G. Wells, B. Sackey-Aboagye, H. Klavan, J. Reidy, D. Buonocore, M. Miranda, S. Kornacki, M. Wayne, D. L. Carr-Locke, N. D. Theise (2018), « Structure and Distribution of an Unrecognized Interstitium in Human Tissues », Scientific Reports, 8(1):4947. [CrossRef]
R. Sender, S. Fuchs, R. Milo (2016), « Revised Estimates for the Number of Human and Bacteria Cells in the Body », PLOS Biology, 14: e1002533. [CrossRef]
W. B. Whitman, D. C. Coleman, W. J. Wiebe (1998), « Prokaryotes: The unseen majority », Proc. Natl. Acad. Sci. USA, 95: 6578-6583. [CrossRef]
Comptage instantané : https://www.worldometers.info/.
S. Sen (2018), « Measuring Consciousness », J. Consciousness Studies, 25: 228-251.
M. Burgin, R. Feistel (2017), « Structural and Symbolic Information in the Context of the General Theory of Information », Information, 8(4):139. [CrossRef]
J. B. Leiper, A. Carnie, R. J. Maughan (1996), « Water turnover rates in sedentary and exercising middle aged men », Br. J. Sports Med., 30(1): 24-26. [CrossRef]
https://explodingtopics.com/blog/data-generated-per-day.
L. Sherwood (1997) in « Human Physiology: From Cells to Systems », Wadsworth publishing company, 3rd edition, table 10.1, p. 311.
Hager, H. Kaemmerer, U. Rapp-Bernhardt, S. Blücher, K. Rapp, T. Bernhardt, M. Galanski, J. Hess (2002), « Diameters of the thoracic aorta throughout life as measured with helical computed tomography », J. Thoracic Cardiovasc. Surgery, 123(6):1060-1066. [CrossRef]
Haugen, S. Berg, M. B. Kjell, H. Torp, A. S. Stig, S. Terje, O. S. Stei (2002), « Blood flow velocity profiles in the aortic annulus: A 3-dimensional freehand color flow Doppler imaging study », J. Amer. Soc. Echocardiography, 15: 328-333. [CrossRef]
T. Nakagaki, H. Yamada, A. Toth (2000), « Maze-solving by an amoeboid organism », Nature, , 28:407(6803):470. [CrossRef]
T. Saigusa, A. Tero, T. Nakagaki, Y. Kuramoto (2008), « Amoebae Anticipate Periodic Events » Phys. Rev. Lett., 100: 018101. [CrossRef]
J. C. Mathai, S. Tristam-Nagle, J. F. Nagle, M. L. Zeidel (2008), « Structural determinants of water permeability through the lipid membrane », J. Gen. Physiol., 131: 69-76. [CrossRef]
S. Freud (1923), « Das Ich und das Es », Internationaler psychoanalytischer Verlag, Leipzig, « The Ego and the Id », English translation by Joan Riviere, The Hogarth Press, 1926.
C. G. Jung (1966), The Collected Works of C. G. Jung, Vol. 7 : « Two Essays on Analytical Psychology », Princeton University Press, Princeton, pp. 269-273.
J. Chalmers (2018), « The Meta-Problem of Consciousness », Journal of Consciousness Studies, 25(9-10): 6-61.
D. C. Dennett (2018), « Facing up to the hard question of consciousness », Phil. Trans. R. Soc. B, 373(1755): 20170342. [CrossRef]
S. Hameroff, R. Penrose (2003), « Conscious Events as Orchestrated Space-Time Selections », NeuroQuantology, 1: 10-35. [CrossRef]
Einstein (1946), « An Interview with Michael Amrine », The New York Times Magazine, 23 juin, pp. 7 et 42-44.
R. J. P. Williams (2007), « A system’s view of the evolution of life »; J. R. Soc. Interface, 4: 1049-1070.
J. Israelachvili (1994), « The science and applications of emulsions – an overview », Colloids and Surfaces, 91:1-8.
S. Guillot, K. Hattori (2013), « Serpentinites: Essential Roles in Geodynamics, Arc Volcanism, Sustainable Development, and the Origin of Life », Elements, 9: 95-98. [CrossRef]
T. Cavalier-Smith (2006), « Cell evolution and Earth history: stasis and revolution », Phil. Trans. R. Soc. B (2006), 361: 969-1006. [CrossRef]
F. Joyce (2002), « The antiquity of RNA-based evolution », Nature, 418: 214–221. [CrossRef]
L. E. Orgel (2004), « Prebiotic Chemistry and the Origin of the RNA World », Crit. Rev. Biochem. Mol. Biol., 39: 99-123. [CrossRef]
R. F. Gesteland, T. R. Czech, J. F. Atkins, Eds (2006), « The RNA World », Cold Spring Harbor Laboratory Press.
Dyson (1999), « Origins of Life », 2^nd Ed., Cambridge University Press, Cambridge.
P. Baaske, F. M. Weinert, S. Duhr, K. H. Lemke, M. J. Russell, D. Braun (2007), « Extreme accumulation of nucleotides in simulated hydrothermal pore systems », Proc. Natl. Acad. Sci. USA, 104: 9346-9351. [CrossRef]
M. W. Powner, B. Gerland, J. D. Sutherland (2009), « Synthesis of activated pyrimidine ribonucleotides in prebiotically plausible conditions », Nature, 459: 239-242. [CrossRef]
J. D. Watson, F. H. C. Crick (1953), « Molecular Structure of Nucleic Acids: A Structure for Deoxyribose Nucleic Acid », Nature, 171 (4356) : 737-738. [CrossRef]
K. Kruger, P. J. Grabowski, A. J. Zaug, J. Sands, D. E. Gottschling, T. R. Cech (1982), «Self-splicing RNA: autoexcision and autocyclization of the ribosomal RNA intervening sequence of Tetrahymena», Cell, 31: 147–157. [CrossRef]
T. R. Cech (1986), «A model for the RNA-catalyzed replication of RNA», Proc. Natl Acad. Sci. USA, 83: 4360–4363. [CrossRef]
C. Guerrier-Takada, K. Gardiner, T. Marsh, N. Pace, S. Altman (1983), «The RNA moiety of ribonuclease P is the catalytic subunit of the enzyme», Cell, 35: 849–857. [CrossRef]
T. A. Steitz, P. B. Moore (2003), «RNA, the first macromolecular catalyst: the ribosome is a ribozyme», Trends Biochem. Sci., 28: 411–418.
W. Gilbert (1986), « The RNA world », Nature, 319: 618.
Butlerov (1861), « Formation synthétique d’une substance sucrée », Compt. Rend. Acad. Sci., 53: 145–147.
T. Cavalier-Smith (2001), « Obcells as Proto-Organisms: Membrane Heredity, Lithophosphorylation, and the Origins of the Genetic Code, the First Cells, and Photosynthesis », J. Molec. Evol., 53:555-595. [CrossRef]
R. J. P. Williams (2007), « Systems biology of evolution, the involvement of metal ions », Biometals, 20: 107-112. [CrossRef]
L. Pasteur (1848), « Mémoire sur la relation qui peut exister entre la forme cristalline et la composition chimique, et sur la cause de la polarisation rotatoire », Comptes rendus Acad. Sci. (Paris), 26: 535–538.
L. Pasteur (1848), « Sur les relations qui peuvent exister entre la forme cristalline, la composition chimique et le sens de la polarisation rotatoire », Ann. Chim. Phys., 3rd series, 24(6): 442–459.
J. Yu, A. Darú, M. Deng, D. G. Blackmond (2024), « Prebiotic access to enantioenriched amino acids via peptide-mediated transamination reactions », Proc. Natl. Acad. Sci. USA, 121(7): e2315447121. [CrossRef]
M. Deng, J. Yu, D. G. Blackmond (2024), « Symmetry breaking and chiral amplification in prebiotic ligation reactions », Nature, 626(8001): 1019-1024. [CrossRef]
D. B. Cline (2005), « On the physical origin of the homochirality of life », Eur. Rev., 13, Supp. No. 2: 49–59.
R. N. Boyd, T. Kajino, T. Onaka (2011), « Supernova, Neutrinos and the chirality of amino acids », Int. J. Mol. Sci., 12: 3432-3444. [CrossRef]
Patel, L. Malinovska, S. Saha, J. Wang, S. Alberti, Y. Krishnan, A. A. Hyman (2017), « ATP as a biological hydrotrope” », Science, 356: 753-756. [CrossRef]
J. Barber (2003), « Photosystem II : the Engine of Life», Quart. Revs. Biophys., 36: 71-89.
K.N. Ferreira, T.M. Iverson, K. Maghlaoui, J. Barber et S. Iwata (2004), « Architecture of the Photosynthetic Oxygen-Evolving Center », Science, 303: 1831-1838. [CrossRef]
P. R. Chitnis (2001), « Photosystem I : function and physiology », Ann. Rev. Plant Phys. Plant Mol. Biol., 52: 593-626. [CrossRef]
P. Jordan, P. Fromme, H. T. Witt, O. Kuklas, W. Saenger, N. Krauss (2001), « Three-dimensional structure of cyanobacterial photosystem I at 2.5 A resolution », Nature, 411: 909-917. [CrossRef]
R. Frei, C. Gaucher, S. W. Poulton, D.E. Canfield (2009), «Fluctuations in Precambrian atmospheric oxygenation recorded by chromium isotopes», Nature, 461: 250-253. [CrossRef]
T. Cavalier-Smith (2006), « Rooting the tree of life by transition analyses », Biology Direct, 1:19. [CrossRef]
R. Woese, G. E. Fox (1977), « Phylogenetic structure of the prokaryotic domain: the primary kingdoms », Proc. Natl. Acad. Sci. USA, 74: 5088–5090. [CrossRef]
E. Blochl, R. Rachel, S. Burggraf, D. Hafenbradl, H. W. Jannasch, K. O. Stetter (1997), « Pyrolobus fumarii, gen. and sp. nov., represents a novel group of archaea, extending the upper temperature limit for life to 113 degrees C », Extremophiles, 1: 14-21.
K. Kashefi, D.R. Lovley (2003), « Extending the upper temperature limit for life», Science, 301: 934. [CrossRef]
L. Margarita (2006), « Recent developments in the thermophilic microbiology of deep-sea hydrothermal vents », Extremophiles, 10: 85-96. [CrossRef]
Huber, M. J. Huber, M. J. Hohn, R. Rachel, T. Fuchs, V. C. Wimmer, K. O. Stetter (2002), « A new phylum of Archaea represented by a nanosized hyper-thermophilic symbiont », Nature, 417: 63–67.
S. Wolf (1959), « The pharmacology of placebos »; Pharmacol. Rev., 11: 689-704.
K. Shapiro, E. Shapiro (1997), « The placebo: is it much ado about nothing », In: Harrington A, ed., The placebo effect: an interdisciplinary exploration, Harvard University Press (Cambridge): 2-36.
P. Lemoine (1996), « Le mystère du placebo »; Odile Jacob, Paris (238 pages).
M. Henry, S. Bridoux (2024), « Symmetry, Music and Water », J. Hum. Soc. Sci., 7(4): 1-25. [CrossRef]
Newton (1704), « Opticks: or, A Treatise of the Reflexions, Refractions, Inflexions and Colours of Light », Proposition VI, Problem II, London.
M. Henry (2020), « L’Eau morphogénique : santé, information et champs de conscience. Les sept cadres de pensée pour comprendre », Éditions Dangles, Escalquens, France. 978-2-7033-1269-7.
C. Aslangul (2016), « Théorie quantique et médecine : le point de vue d’un physicien », Hegel, 2: 130-139.
Sternheimer (1983), « Musique des particules élémentaires », C. R. Acad. Sci. Paris, Ser. II, 297: 829-834.
Y. Orhan, B. A. Gulbahar (2016), « Stimulation of Protein Expression through the Harmonic Resonance of Frequency-Specific Music. », Clinical Investigative Medicine, 39(6): S34-S38. [CrossRef]
V. Prévost, K. David, P. Ferrandiz, O. Gallet, M. Hindié (2020), « Diffusions of Sound Frequencies Designed to Target Dehydrins Induce Hydric Stress Tolerance in Pisum Sativum Seedings » Heliyon, 6(9): e04991. [CrossRef]
N. Scotto Di Carlo (1997), « Les divas et le diapason », Médecine des Arts, 21: 10-13.
D. Raoult (11/2020), « Lancet gate: a matter of fact or a matter of concern », New Microbes New Infect., 38: 100758. [CrossRef]
M. R. Mehra, F. Ruschitzka, A. N. Pate (June 2020), « Retraction—Hydroxychloroquine or chloroquine with or without a macrolide for treatment of COVID-19: a multinational registry analysis », The Lancet, 395: 1820. [CrossRef]
W. Kutzelnigg (1984), « Chemical Bonding in Higher Main Group Elements », Angew. Chem. Int. Ed. Eng., 23: 272-295. [CrossRef]

Figure 1. Summary of Greek philosophy from Thales to Lucretius.

Figure 2. Air seen as a collection of 14 gaseous molecules. The number associated with each molecule gives its molar proportion for a total of 10,000,000 molecules.

Figure 3. Comparison between the volume of the earth and the volume of terrestrial water with the molar proportions of the elements making up minerals, water, soil organic matter (CHONPS) and air for a total of 10,000 molecules.

Figure 4. Molar proportions of the molecular constituents of a living E. Coli bacterial cell. Expressed for a total of 1,000 molecules.

Figure 5. Molar proportions of molecular constituents in humans (male and female). Expressed for a total of 1,000 molecules.

Figure 6. Summary of Chinese philosophy with the five-pointed star of the Wu-Xing and the octagon of the Ba-Gua.

Figure 7. Dmitri Mendeleev's Periodic Table of the Elements, showing the relative abundances on earth via the size of the cells. This table also shows the elements that are absolutely essential for making a cell phone or a living cell.

Figure 8. Summary of first quantum physics according to Heisenberg and Schrödinger. (a) Instability of the atom according to Newton's and Maxwell's classical laws. (b) Necessity of using complex numbers with a real part and an imaginary part. (c) Equivalence between a complex number and a wave (left) and probability clouds for electrons around nuclei (right). (d) Wave/corpuscle duality and indeterminacy relations. (e) Quantifying energy in an infinite potential well. (f) Indeterminacy relations between position x and momentum p, explaining the existence of a "quantum blur". (g) Artistic representations of this first quantization.

Figure 9. Summary of Dirac's second quantization quantum physics. (a) Phase/number-of-objects uncertainty relation. (b) Ultimate constituents of matter and light: quarks, leptons and vector bosons. (c) Possibility of creating and annihilating any corpuscle of matter or light in relation to the existence of the quantum vacuum. (d) Static (left) and dynamic (right) Casimir effect.

Figure 10. Summary of Indian and Ayurvedic philosophy. The trimurti, the three physical constitutions (doshas), the five elements (mahabhutas), the seven chakras and the twenty functional principles (gunas).

Figure 11. Summary of alchemical philosophy with the elements and their correspondences with the five Platonic solids. The three principles of alchemy and the four humors of the human body.

Figure 12. Peano-Cantor's construction for a better understanding of the orientalist concept of vacuity and the various philosophical and/or artistic representations of this concept in relation to the Greek ouroboros, which has neither beginning nor end, the Moëbius ribbon, which has neither top nor bottom, the alchemical pelican or the Klein bottle, which has neither inside nor outside.

Figure 13. Demonstration of the fact that the water molecule H₂O is essentially made up of vacuum at over 99%.

Figure 14. The Sheffer bar (↑) as a generator of the sixteen logical operations of analytic consciousness. Equivalence with truth tables or Venn diagrams.

Figure 15. Concept of coherence domain (CD). (a) Energetic electronic excitation spectrum of the water molecule. (b) Gaseous state. Any absorption of a photon from the quantum vacuum leads to an increase in the size of the water molecule without any visible consequence (so-called "van der Waals" bonding). (c) Liquid state. Here, the same process of absorption of a virtual photon leads to its delocalization onto around 10 million water molecules, which then share the same quantum phase. (d) Graphical representation of the phenomenon within the framework of the second quantization. (e) The "true" quantum chemical formula of water. (f) Illustration of the phase coherence phenomenon with macroscopic objects: grains of sand, fish, starlings.

Figure 16. Chain of causality from pure consciousness (ouroboros) to water-based materialistic life. Vital role of information and context (exformation). Superiority of the concept of entropy over the concept of energy and the crucial role of the quantum phase in relation to the notion of coherence.

Figure 17. Micellar self-assembly according to a form factor ρ_F defined as the ratio between the volume V_L of a molecule and the product of the average area <A> swept by a "hydrophilic" head by a maximum length D_m of a "hydrophobic" tail.

Figure 18. The serpentinization reaction, in which olivine comes into contact with water to produce dihydrogen in a totally abiotic process. The waste product is magnetite. Also shown are the dozen or so small, more or less "reduced" molecules that can be obtained in the vicinity of the serpentinization site.

Figure 19. Some key molecules involving a metal cation chelated by small organic molecules. Evolution over time of a few key elements used extensively by all living cells.

Figure 20. Nucleic acids, key molecules for catalyzing chemical reactions and storing and transmitting genetic information (a) The formose reaction for the abiotic synthesis of sugars such as ribose (b) The five nucleotides for making RNA or DNA: adenosine, guanosine, uridine, cytidine and thymidine. (b) The five nucleotides to make RNA or DNA: adenosine, guanosine, uridine, cytidine and thymidine. (c) Single-stranded RNA to catalyze or transmit information and double-stranded DNA to store or transmit information from generation to generation. (d) Formation of phosphodiester bonds between two nucleotides. (e) Catalysis of the peptide bond formation reaction using an RNA-based ribozyme.

Figure 21. Stereochemistry of some sugars with five carbon atoms. Linear, cyclized pyranose form for D-Ribose.

Figure 22. Photosynthesis. (a) Chlorophyll structure and light absorption spectrum of some derivatives. (b) The type II photosystem, responsible for photolysis of the water molecule via its CaMn₅ cluster and producing oxygen. (c) The type I photosystem with its electron transfer chain based on iron-sulfur clusters of the ferredoxin type. (d) The Calvin cycle producing glyceraldehyde-3-phosphate. (f) Anoxygenic photosynthesis without oxygen release with these two types -I and -II reaction centers.

Figure 23. The three great inventions responsible, 3.5 billion years ago, for the transition from proto-cellular vesicles (PCVs) to the first Gram-negative bacterial unicellular: peptidoglycan, lipopolysaccharide and flagellum. Subsequent unicellular tree of life until the split between eukaryotes and archaea.

Figure 24. Bacteria, archaea and eukaryotes: (a) Archaeal phospholipid based on ether bonds and one molecule of L-glycerol versus bacterial phospholipid based on ester bonds and one molecule of D-glycerol. (b) Evolution of plants, animals and fungi from eukaryotic protists. (c) The three types of RNA polymerase found in bacteria, archaea and eukaryotes. (d) Time summary from the Big Bang to modern civilization.

Figure 25. The seven frameworks of human thought capable of reconciling therapists the world over, whatever their age-old practice.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Water and the Origin of Life

Abstract

Keywords:

Subject:

1. Introduction

Matter, Elements, Emptiness and Movement

Water, Water, Everywhere

Chinese Philosophy and Tao

And What About the Vacuum?

First Quantification

Second Quantization

Ether in Indian and Greek philosophy

The Ether in Greek Culture

In the Beginning Was Emptiness...

Consciousness and Mathematics

Information

Energy or Entropy?

Water and Information

The Origin of Life

End of Meteorite Bombardment (3900 Myr)

Replication and Phosphorylation (3870 Myr)

An RNA World (3870-3850 Ma)

The Birth of a Genetic Code

Photosynthesis and Expansion of the Genetic Code

Bacteria, Eukaryotes and Archaea

Frames of Thinking

Conclusion

Appendix

References

MDPI Initiatives

Important Links

Subscribe