Preprint
Article
Thermal Energy Storage and Recovery in Fractured Granite Reservoirs: Numerical Modeling and Efficiency Analysis
Altmetrics
Downloads
106
Views
95
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
05 August 2024
Posted:
06 August 2024
You are already at the latest version
Alerts
Abstract
Fractured media are seldom considered viable for storing excess thermal energy seasonally, compared to the more commonly used porous aquifers, due to their heterogeneity, lower storage capacity, and potential for unpredictable flow paths. This study employs COMSOL Multiphysics to create a numerical model of a fractured granite reservoir located below the Bedretto underground laboratory. The energy efficiency of both single-well and doublet systems was evaluated over 25 cycles, each comprising four 91-day phases: injection, storage, production, and resting. Results indicated that the single-well system was more efficient, with energy efficiency increasing with the flow rate. For an injection temperature of 60 °C, the system achieved energy efficiencies of up to 59.3% and 67.7%, after 10 and 25 cycles, respectively, aligning with porous Aquifer Thermal Energy Storage (ATES) system efficiencies at this temperature. Exploration of electricity production using water injected at 120 °C revealed it to be uneconomical and ineffective. However, the most promising use of the retrieved water was found to be direct ground heating for a greenhouse. This technology offers a potential alternative for thermal energy storage in regions lacking suitable porous aquifers, although identifying appropriate locations with the necessary geological characteristics may present significant challenges.
Keywords:
Subject: Environmental and Earth Sciences - Geophysics and Geology
1. Introduction
Reducing greenhouse gas emissions is a key objective for many governments, including the EU [1] and the UN [2]. In line with this goal, Switzerland aims to achieve net-zero emissions by 2050, as set by the Federal Council [3]. Achieving this target will require the introduction of new technologies to the energy market alongside existing renewable sources. Given that heating and cooling buildings account for 40% of global fossil fuel consumption, they are significant contributors to greenhouse gas emissions [4,5,6,7]. One promising solution to reduce energy consumption and greenhouse gas emissions is surplus thermal energy storage. This method addresses the seasonal imbalance in energy demand and supply, particularly in regions with moderate climates [4]. During the summer, buildings often experience a surplus of heat, while in winter, there is a significant heat shortage. Seasonal energy storage efficiently reduces energy consumption during periods of heat shortage, such as in winter. However, despite its potential, this energy storage method remains underutilized in Switzerland [8].
An appropriate method for heat storage must be selected based on factors such as storage capacity, storage duration, and supply and demand temperatures [8]. Underground Thermal Energy Storage (UTES) is an effective solution for long-term heat storage due to its high storage efficiency [9,10] and large storage capacity [8]. UTES can be divided into two categories: open-loop and closed-loop systems.
Open-loop systems are known as aquifer thermal energy storage (ATES) systems. These systems leverage natural groundwater flow within aquifers to store and retrieve thermal energy [8]. Closed-loop UTES, on the other hand, are referred to as borehole thermal energy storage (BTES) systems [8]. In these systems, a network of boreholes is drilled into the ground and filled with a heat transfer fluid that circulates to store and retrieve thermal energy [8]. Other types of thermal energy storage include Pit Thermal Energy Storage (PTES), Tank Thermal Energy Storage (TTES), and Cavern Thermal Energy Storage (CTES), where heat and cold are stored in dug pits filled with gravel and water, thermally stratified storage tanks, or naturally occurring cavities, respectively [8]. Among these methods, ATES stands out for its superior storage capacity, making it an ideal choice for large-scale applications where substantial amounts of thermal energy need to be stored and retrieved efficiently [11].
The concept of ATES originated in the mid-1960s in Shanghai, initially developed for industrial cooling in the textile industry [8,12]. The first of several experiments involving ATES for storing higher temperatures (>40 °C) took place in Neuchâtel in 1974 [8,13]. These early attempts faced numerous challenges, including scaling and clogging of wells and heat exchangers, well corrosion, buoyancy flow or thermal breakthrough, imbalance between stored heat and cold, and the swelling of clay minerals [8]. Since these problems were easier to resolve in low-temperature (LT) ATES systems (<40 °C) and after several failed test experiments in high-temperature (HT) ATES systems, the focus was shifted towards LT-ATES [8]. Today, the Netherlands leads in the deployment of LT-ATES systems with around 2,500 installations, followed by Sweden with approximately 220 systems [8]. Only about 1% of the ATES systems worldwide are HT-ATES [8].
In general, LT-ATES systems are commonly used in commercial and public buildings and operate in cyclic modes with injection, storage, and production phases, usually providing direct cooling and indirect heating [8]. The well layouts typically consist of doublets or multi-doublets, with storage temperatures ranging from 5 °C to 25 °C. These systems are usually implemented in shallow, porous aquifers, more frequently unconfined than confined, at depths ranging from 10 to 100 meters [8].
Despite the predominant use of shallow, low-temperature reservoirs, there is growing interest in exploring deeper storage options. Indeed, in Switzerland, the previous limitation of heating the subsurface by more than 3 °C was lifted in 2023, which now allows for a greater development of the technology throughout the country [14]. For instance, the Forsthaus project in Bern, Switzerland is a high-temperature heat storage project set to take place in sandstones at a depth of 500 meters [15].
Storing thermal energy at greater depths offers several advantages. The higher temperature of the rock at these depths allows for the injection of water at higher temperatures, which reduces heat loss and increases the amount of heat to be stored. This makes the storage system more efficient and capable of maintaining higher energy outputs. One of the most critical parameters in evaluating the performance of an ATES system is the energy efficiency. This is expressed as the ratio of the extracted thermal energy to the injected energy considering the undisturbed aquifer temperature [16]. Similarly, retrieval ratio is determined by the same principle, but uses the temperatures of the injected- and retrieved-water relative to the aquifer temperature [17].
Several factors control the efficiency of an ATES system, with the most critical process in high-temperature ATES projects being density-driven flow interacting with ambient groundwater [18]. Other general factors contributing to heat losses include heat conduction, dispersion due to mixing at the thermal front, and hydrogeological heterogeneities that affect heat distribution [19]. These processes are less significant and more predictable in porous aquifers compared to fractured rock reservoirs and to the authors’ knowledge, no Fractured Thermal Energy Storage (FTES) systems have been implemented. However, since a large part of Switzerland’s underground is composed of fractured crystalline rocks, it is crucial to consider this type of storage to achieve Switzerland’s net-zero emissions target by 2050.
Some theoretical studies have investigated heat transport and storage in fractures, revealing the complexity of such systems. De La Bernardie et al. [20] identified three main parameters controlling the transport and exchange of heat between water and rock in fractured media: the cumulative surface area of the fractures, the cumulative volume of the fractures, and the volume of rock effectively accessible during the thermal storage process. Furthermore, research by Klepikova et al. [21] demonstrated that effective hydraulic transmissivity plays a crucial role in thermal transport within a single fracture. Similarly, Zhou et al. [22] found that the fracture-rock matrix system is highly sensitive to factors such as fluid flow velocities, thermal dispersivity, and the matrix’s thermal conductivity. Therefore, for geothermal heat storage to be effective, the storage periods must closely align with the water transit time through the fracture network, depending on the fracture volume and fluid flow rates [20].
To address these challenges and harness the potential of FTES, the Bedretto underground laboratory in Switzerland has been established as a test site for conducting experiments on thermal energy storage in fractured crystalline rocks. This facility provides a unique opportunity to study and develop FTES systems in a controlled environment, contributing valuable insights into optimizing storage efficiency and overcoming the complexities associated with fractured media. The laboratory is equipped with multiple boreholes that cross several faults of interest for this project, allowing for comprehensive data collection and analysis.
Before conducting real-world experiments, a preliminary study using numerical modeling is being undertaken. This study leverages extensive data on faults and fractures acquired through previous experiments. The objective is to determine the energy efficiency of key faults using numerical modeling and to investigate the impact of different flow rates and temperatures on system efficiency. Additionally, the study will compare the efficiency of two well configurations: a single-well system and a doublet system. The efficiency will be analyzed using a base case where an energy storage cycle consists of four phases: injection, storage, production, and resting. Each phase of the cycle corresponds to a season: injection in summer, storage in autumn, production in winter, and resting in spring. This approach will be applied to the most transmissive fractures and faults to maximize efficiency. Moreover, the potential applications for the extracted energy will be explored, including district heating and greenhouse farm heating. These applications complement the study by Halter et al. [23], which proposed a district heating system for the village of Bedretto, utilizing tunnel water to supply heat pumps for residents. An economic analysis for electricity production will also be conducted to evaluate the feasibility and relevance of generating electricity using FTES.
2. Site Characterization
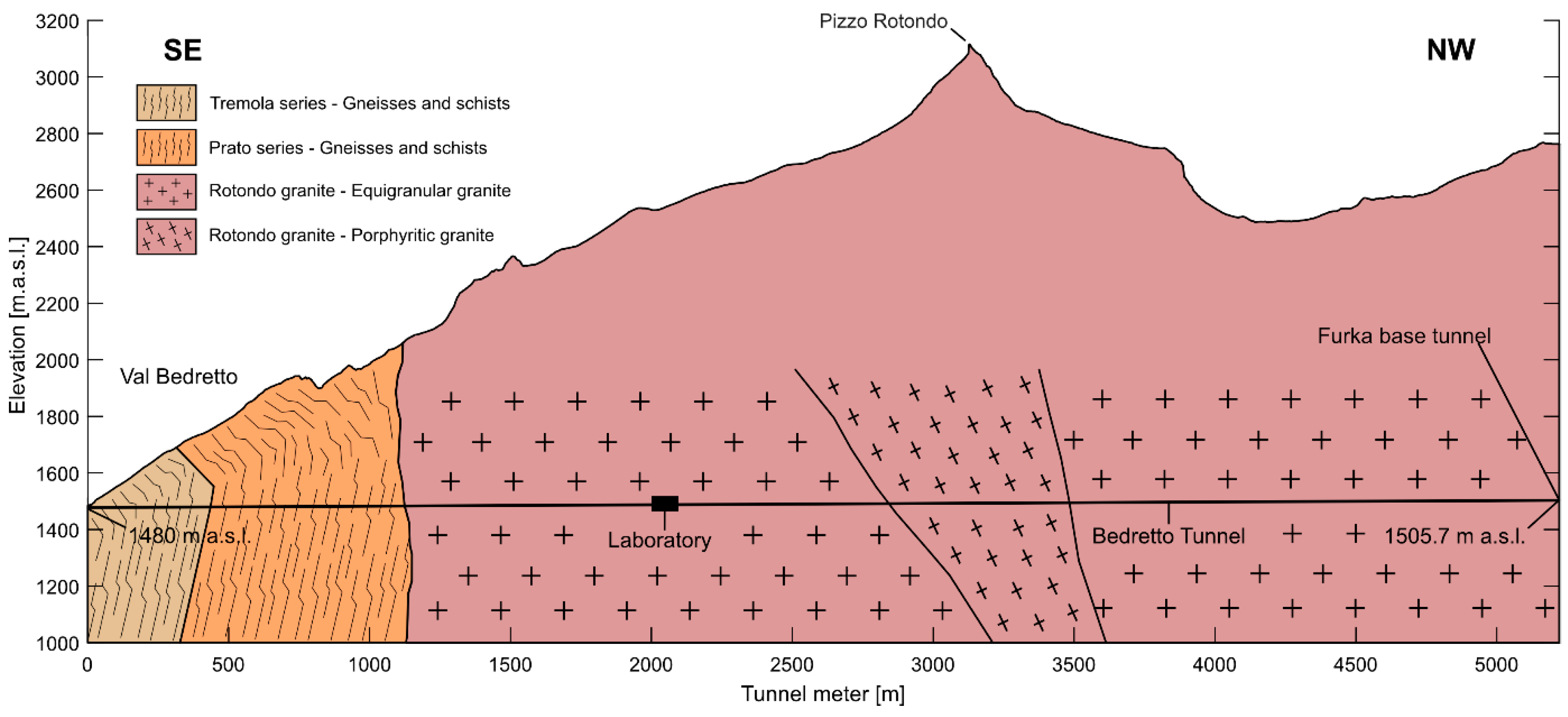
The Bedretto tunnel, constructed between 1971 and 1982, is a 5.2-km-long gallery which served to construct the Furka railway tunnel [24]. The tunnel has a northwest to southeast orientation and exits on the Furka tunnel on the north-west end and to the Bedretto valley on the south-east end (Figure 1). The Bedretto valley is in the Swiss Alps, in the canton of Ticino, close to the border with Italy. In this gallery, there is an underground research facility for deep geothermal energy, known as the Bedretto Underground Laboratory for Geosciences and Geoenergies (BULGG), belonging to the Swiss Federal Institute of Technology (ETH) in Zürich. The measurement system within the tunnel is denoted in tunnel meters (TM), beginning at the south portal with TM 0. The main part of the laboratory is located between TM 2000 and 2100, under about 1 km of overburden. In this section, several boreholes have been drilled — two for stimulation and seven for monitoring [25] — which are the central part of the study. A detailed description of the underground facility can be found in Ma et al. [26].
2.1. Geology at the Laboratory
The Bedretto tunnel crosses various geological formations of the Gotthard massif, including the Tremola series, the Val Nalps gneiss complex of the Prato series, and the Rotondo granite [29], as illustrated in Figure 2. In the laboratory, Rotondo granite is characterized as an equigranular granite composed of quartz, alkali feldspar, plagioclase, and biotite [29]. This granite exhibits a range of fracture patterns, with some areas remaining intact with isolated fractures and others being highly fractured [25].
Significant permeable zones have been identified within these formations, which will be detailed in Section 3.1. These zones are particularly suitable for heat storage due to their ability to facilitate the injection and extraction of thermal energy. The combination of intact and fractured granite, along with the identified permeable zones, enhances the potential for efficient thermal energy storage in this geological setting. For more detailed information on the geology of Bedretto, refer to Rast et al. [29].
2.2. Injection and Production Boreholes
In the laboratory, between TM 2000 and TM 2100, two stimulation boreholes (ST1 and ST2), and seven monitoring boreholes (MBs) were drilled on the southwestern tunnel wall at an angle of approximately 45° [25]. This study focuses on the stimulation boreholes, ST1 and ST2, which have lengths of 399 m and 349 m, respectively, and a diameter of 21.6 cm [25]. These boreholes are open holes equipped with packers and/or geophone strings [25]. Hydraulic testing in the different intervals of the packers in the MB and ST boreholes provided transmissivities ranging between 10–11 m2/s and 10–6 m2/s, with higher values in intervals containing a high density of fractures [25]. More detailed descriptions of the boreholes and the faults/fractures can be found in Hertrich et al. [25], Plenkers et al. [32], Bröker et al. [33], and Gholizadeh et al. [34].
3. Methodology
We employed COMSOL Multiphysics to simulate fluid flow and heat transfer in the faults and fractures intersected by the stimulation boreholes ST1 and ST2. COMSOL Multiphysics is a numerical solver that models coupled physical processes through finite element (FEM) analysis, solving partial differential equations across various physics domains [35].
A base case scenario was established to determine the energy efficiency of the storage system and for further analyses. The energy storage operation cycle comprises four phases: injection, storage, production, and resting, each lasting 91 days to correspond with the four seasons of the year. The injection phase takes place during the warmest months, from June to August, when hot water consumption is minimal. Conversely, the production phase occurs from December to February, aligning with peak heat demand. This cycle repeats over a 25-year period, reflecting the average operational lifetime of an ATES system [36].
Two well configurations were selected in the most transmissive structures crossed by the injection and production boreholes, ST1 and ST2: a doublet system and a single-well system. The doublet system involves injecting water into ST1 and producing it from ST2, with the wells connected by multiple fractures and faults. The single-well system operates within a fault in ST1. Injection temperatures were set at 60 °C, the maximum achievable by a heat pump, and 120 °C, to explore the potential for electricity production. To create a hydraulic gradient between the wells of the doublet, the injection and production of water take place simultaneously during the entire duration of the injection and production phases. During the production phase of the doublet system, water injected into ST1 is sourced from the tunnel water circulating at TM 2000, maintaining a temperature of 16.8 °C. It is assumed that the mass of water produced from the well is the same as the one injected.
To assess the influence of the injection rate on energy efficiency, three injection rates were selected for both the single-well and doublet systems: 3 kg/s, 4 kg/s, and 5 kg/s. These rates were chosen based on previous experiments and the estimated minimum principal stress magnitude in the reservoir, ensuring they are unlikely to induce hydraulic fracturing.
In addition to determining the energy efficiency of the storage system, other analyses using the produced water were conducted, including transportation to a usage site and a cost analysis for electricity production. These additional analyses were performed considering the greatest injection rate used, 5 kg/s, which we assume is equal to the production rate.
3.1. Reservoir and Fracture Setup
The reservoir model used in this study, along with the corresponding generated mesh, is shown in Figure 3. As shown in the figure, this model includes the two stimulation boreholes, ST1 in blue and ST2 in orange intersected by various faults and fractures represented as planar structures. The reservoir is represented by a 250 m × 220 m × 340 m granitic domain, the properties of which appear in Table 1. The structure of the tunnel, located at the top of the wells, was excluded from the mesh.
The well ST1 is equipped with a multipacker system and is divided into 14 intervals. The well ST2 is cased, cemented, and perforated at specific depths [37,38]. The two most transmissive fault zones intersected by ST1 are found in packed Intervals 8 and 13 and are used in this case study for injection as part of the numerical model. The measured depth of Interval 8 spans between 186.7 m and 216.8 m in ST1, crossing the major permeable fault zone at 208.2 m. Interval 13 in ST1 spans from 103.4 m to 121.7 m, crossing the major permeable fault zone at 107.5 m. Geophysical logs and previous injection experiments [34,39,40] indicate that fractures/faults within each interval exhibit comparable transmissivity, allowing us to assume uniform transmissivity across all fractures/faults within the same interval. Previous experiments have shown that water injected into Interval 8 of ST1 reaches ST2, likely at a depth of 211.8 m and 285.7 m [37,38,41]. On the other hand, the connection between the two wells does not occur in Interval 13 of ST1. Therefore, Interval 8 in ST1 is used for a doublet system with ST2 as production well, and the main fault of Interval 13 is modeled as a single-well system, serving for both injection and production of hot water from the same interval.
Given the dip and strike angles of the principal fault in Interval 8 in ST1, it is unlikely that injected water will exit through the same fault at Site ST2. Consequently, the model has incorporated separate faults, identified from geophysical data, which likely channel water toward ST2. As a result, three fractures connecting ST2 to the faults of Interval 8 in ST1 were included. These fractures, intersecting ST1 at depths between 170.8 meters and 185.2 meters in Interval 9, serve as crucial hydraulic conduits also linking Intervals 8 and 9. They were selected based on experimental data demonstrating their high transmissivity within these intervals [40]. While other fractures might also enhance transmissivity, quantifying their contributions precisely remains difficult. In essence, the model facilitates the injection of water into ST1’s most transmissive fault in Interval 8, which then migrates to ST2, reaching depths of 211.8 m and 285.7 m through the interconnected faults in Interval 9. Given the initially low transmissivity of the faults at ST2, it is assumed that stimulation will enhance the fractures’ transmissivity by an order of magnitude before operational cycles begin, thus optimizing the wells for water production without inducing excessively low pressures. The transmissivity of Intervals 8, 9, and 13 in ST1 are 1.1 × 10–6 m2/s, 8.4 × 10–7 m2/s, and 2.3 × 10–8 m2/s, respectively [40]. The transmissivity of the faults at ST2 are 1.6 × 10–7 m2/s at 211.8 m and 7.7 × 10–7 m2/s at 286.7 m, respectively [37].
The properties of the faults and fractures including the permeability values are presented in Table 1. The permeability of each fracture/fault was calculated based on the ratio of their aperture, estimated based on the geophysical logs, to the length of their respective intervals, and its transmissivity. The permeability is determined from the transmissivity using the relation in Equation 1 [42]:
where k is the permeability (m2), t is the transmissivity (m2/s), w is the width of the fracture (m), m is the dynamic viscosity (Pa×s), g is the gravitational acceleration (m/s2), and rw is the density of the water (kg/m3).
Table 1.
Properties of the fractures and faults used in the COMSOL Multiphysics numerical model [33,34,38,39,40].
| Borehole—Interval | Intersection Depth Fracture/Fault in Well (m) |
Purpose | Azimuth/Dip | Width (m) | Permeability (m2) |
|---|---|---|---|---|---|
| T1 – Interval 13 | 107.5 | Injection and Production |
334.7/69.7 | 1.3 | 1.50 × 10–13 |
| ST1 – Interval 9 | 180.8 | Flow path | 311.9/40.2 | 0.005 | 8.48 × 10–14 |
| ST1 – Interval 9 | 182.3 | Flow path | 332.6/59.4 | 0.022 | 8.48 × 10–14 |
| ST1 – Interval 9 | 183.2 | Flow path | 317.8/68.2 | 0.010 | 8.48 × 10–14 |
| ST1 – Interval 8 | 208.2 | Injection | 319.1/60.3 | 0.694 | 2.16 × 10–13 |
| ST2 | 211.8 | Production | 331.0/64.8 | 0.554 | 3.94 × 10–13 |
| ST2 | 285.7 | Production | 350.7/78.2 | 0.175 | 5.91 × 10–12 |
The parameters of the Rotondo granite, the fault material, and temperature dependent properties of the water are shown in Table 2.
The compressibility of the fractures (ct) was also included in the model, calculated from the specific storage, assumed as 10–6 m–1 for faults [46,47,48], with Equation 2 [49]:
Where ct is the compressibility of the fracture (Pa–1), Ss is the specific storage (m–1), r the density of the rock, g the gravitational acceleration (m/s2), and f the porosity of the fracture. The compressibility for the medium (ct) used in the numerical model is 7.98 × 10–10 (Pa–1). The rock matrix inside the fault is nevertheless assumed to be incompressible.
A temperature gradient was applied to the model using temperature values recorded by installed fiber optics in ST1 on April 15, 2024, ranging from 17.63 °C at the top of ST1 (wellhead) to 25.55 °C at the bottom of the borehole. A constant radius of 100 m is assumed for all fractures/faults included in the model. The granitic rock domain was extended vertically in the model to include the upper part of the fault in Interval 13, reaching above the wells. A constant temperature, matching the top temperature recorded in ST1, was applied from the top of the model to the wellhead. The temperature values were linearly extrapolated below ST1 wellhead. The natural heat flux from the bottom of the model was assumed negligible and thus not included, mainly due to the relatively short time scale of this case study. A pressure gradient was also applied using recorded pressure values, linearly extrapolated from the ST1 wellhead depth to the bottom of the model, ensuring 1 atm at the wellhead. The pressure from the top of the model to the depth of ST1 wellhead is assumed constant at 1 atm. The model boundaries were set to constant pressure according to the ST1 pressure profile versus depth.
3.2. Energy Efficiency
The energy efficiency of the storage system is calculated using Equation 3 below [16]:
Where F represents the energy efficiency, EExt and EInj are the extracted and injected energy respectively, calculated here in MWhth (“th” stands for thermal) per cycle and relative to the undisturbed temperature of the system.
3.3. Water Flow in Pipes
The water extracted from the wells should be conveyed to its end-user location through insulated pipes. Properties of pipes from companies like Jansen, exemplified by the JANSEN bianco model [50], were selected for the quantitative analysis of the system. These pipes are made of polyethylene and insulated with a layer of polyurethane (PU) foam, which has a thermal conductivity of 0.03 W/(m×K) [50]. The chosen pipe has a diameter of 11 cm and an insulation thickness of 3 cm, a standard configuration that balances effective insulation with manageable heat loss due to friction. The pipes are assumed to be buried, so advection of heat on the outside of the pipe is not considered in Equation 4 when calculating the temperature loss.
The temperature inside the tunnel, used in Equation 4, is determined based on measurements from the existing fiber optic system installed along the tunnel, which continuously records tunnel temperature. The external temperature of -4 °C represents the regional average between December and February, crucial for the same equation [51]. The temperature loss during the hot water flow will be calculated for the most efficient system, either the single-well or doublet, as identified in the following section. Two locations are considered for the usage of the water: Bedretto village, 1.6 km from the tunnel’s south portal, and a hypothetical greenhouse farm, 200 m from the tunnel portal.
The temperature loss can be calculated using Equation 4 [52]:
Where Te(L) is the temperature (K) of the fluid inside the pipe at a distance L (m), Tt is the outside temperature (K), Te0 is the initial temperature of the fluid (K), K is the heat transfer coefficient of the pipe (W/(m×K)), L is the length of the pipe (m), Qwater is the mass flow rate (kg/s), and Cp,w is the specific heat capacity of the water (J/(kg×K)).
Where lPU-Foam is the thermal conductivity of the polyurethane foam insulation (W/(m×K)), d is the pipe diameter (m), and s is the insulation thickness (m).
3.4. Calculation of the Thermal Energy in Water
The thermal energy contained in a certain amount of water can be calculated using Equation 6 [53]:
Where Cp,w is the specific heat capacity of water (J/kg/K), Qwater is the mass flow rate (kg/s), and DT is the temperature difference of the water before and after a heat exchange process (K), such as through a heat pump or with the surrounding fractures. The power P is expressed in Wth.
Equation 6 is used to determine the thermal energy that can be converted to electricity in case of injection of 120 °C water, as described in Section 3.5.
3.5. System Efficiency Analysis
To evaluate the effectiveness and economic viability of the heat storage system, we use the temperature of the water extracted from the production wells in cases of two injection temperatures: 60 °C and 120 °C.
3.5.1. Injection Temperature of 60 °C
For water injected at 60 °C, this scenario assumes using a solar panel installation outside the tunnel to power a heat pump and a plunger pump at TM 2000, both utilizing tunnel water. The temperature loss of the water retrieved from the production well after the transportation will be estimated using Equations 5 and 6, considering its end-use location, whether for greenhouse heating near the south portal of the tunnel or for district heating in the village of Bedretto, located 1.6 km from the south portal. The benefits of this investment, including solar panels, a heat pump, and water transport infrastructure, will be compared to using the tunnel water for district heating as described by Halter et al. [23] and to the potential for hypothetical greenhouse farm heating. This comparison is discussed qualitatively in Section 5.3 and Section 5.4
3.5.2. Injection Temperature of 120 °C
For the 120 °C injection scenario, an additional electrical boiler is necessary to heat the water from 60 °C to 120 °C. To ensure a continuous supply of hot water during both day and night in the summer, it is assumed that some of the electricity generated during the day is stored in batteries for use at night.
During the production phase, if the produced water temperature exceeds 80 °C—such as when water is injected at 120 °C—an Organic Rankine Cycle (ORC) engine will be used to generate electricity, with an anticipated net efficiency of 3-5% [54]. The temperature of the water after passing through the engine is assumed to be 30 °C. The cost of electricity generated by the ORC engine, considering the necessary investment, will be compared to the grid electricity price in Bedretto, which is CHF 0.28 (Swiss Francs) per kWhe as of 2024 [55]. The total investment and operating costs, including pumping power as presented in Equation 7, will be divided by the total electricity produced over a 25-year period—the average lifespan of an ATES system [36]—to estimate the price per kWhe generated.
The investment costs required for heating the water and for electricity production are estimated to range between kCHF 450 and kCHF 550 [56,57,58,59,60]. This investment comprises a solar panel installation capable of providing electricity for the heat pump, the plunger pump for the injection of the water, and the electrical boiler simultaneously. The investment also includes the heat pump, the electrical boiler, and the ORC engine. Given that the boreholes and equipment such as the pumps are already in place, their exclusion from the estimation of electricity costs highlights the existing infrastructure’s significant contribution and underscores Bedretto’s unique opportunity for this project.
During the rest of the year, energy consumption will be supplied by the grid. Therefore, the energy required by the pumps to produce water must also be considered for the calculation of the electricity production costs. This energy can be estimated using Equation 7 [61] as follows:
Where r is the pumping rate (m3/h), rw is the density of the water (kg/m3), g is the gravitational acceleration (m/s2), h is the well depth (m), and h is the overall pump efficiency, chosen to be of 60% [62]. The power P in this formula is expressed in kWe. The production is considered non-interrupted during the production phase of the cycles.
3.6. Numerical Modeling of Heat and Fluid Flow
The COMSOL Multiphysics numerical model employs governing equations for fluid flow and heat transfer in fractured porous media to simulate the reservoir behavior and the propagation of the thermal front within the faults and the intact rock. The coefficients used in these equations assume an isotropic medium, which simplifies the representation of the physical properties in the model. In the model, fracture flow is handled by treating fractures as having no thickness in the mesh, with the fracture aperture mathematically implemented in the numerical differential equations. The model simplifies fracture representation without considering rock deformation mechanics, justified by the model’s objectives, computational feasibility, and the primary goal of understanding thermal processes in such reservoirs rather than mechanical interactions within the rock mass. Jin et al. [63] found that the effect of rock mechanics on porosity due to temperature changes was negligible in their numerical model, supporting this approach. Therefore, rock deformation modeling is omitted in this study to maintain focus on fluid dynamics and thermal behavior in fractured porous media. Moreover, the model assumes no background groundwater flow, implying a negligible natural gradient that would otherwise influence the movement of injected water. Additionally, heat loss through the borehole walls during the injection and production phases was not considered, under the premise that it would have a minimal impact on the overall heat transfer within the system.
The fluid flow in fractures is governed by the time-dependent Darcy’s law, which is described by the Equation 8 as follows [35,64]:
Here, ϵp represents the porosity of the medium, rw is the density of water, u is the Darcy velocity representing the flow rate per unit area through the porous medium, and Qm is a source term representing mass sources or sinks, such as the injected water. The first term on the left side of Equation 8, ∂/∂t(ϵprw), accounts for the change in water mass per unit volume over time within the porous medium and the second part, ∇(ρwu), represents the divergence of the water flux, accounting for the spatial distribution and movement of water flow within the medium. The Darcy velocity u is calculated as follows using Equation 9 [35,64]:
where k is the permeability of the medium, m is the dynamic viscosity of the fluid, ∇p is the pressure gradient, and g is the acceleration due to gravity [35,64]. The Darcy velocity equation combines these parameters to describe how the fluid flows through the porous medium, considering both the pressure-driven flow and the gravitational effects [35,64].
Here, (rCp)eff represents the effective heat capacity of the medium, Cp,w is the specific heat capacity of water, ∇T is the temperature gradient, q is the heat flux vector, QV are the volumetric heat sources or sinks, Qp is the heat source due to phase changes, Qvd is the heat from viscous dissipation, and Qgeo is the geothermal heat source [35,65]. Equation 10 describes how heat is transferred within the porous medium, considering conduction, advection, and other heat sources or sinks [35,65]. The heat flux vector q is computed as follows with Equation 11 [35,65]:
with keff as the effective thermal conductivity of the medium. Equation 11 describes the rate of heat transfer through the porous medium due to conduction, where keff represents the effective ability of the medium to conduct heat [35,65].
3.7. Meshing and Sensitivity Analysis for Optimal Size Selection
We employed linear tetrahedral elements for simulating fluid flow and heat transfer within the rock matrix, and linear triangular elements to model fluid flow and heat transfer within fractures. The mesh size is a critical parameter that influences the number of degrees of freedom in the model, directly affecting the precision of the simulation results, such as the temperature distribution along fractures, faults, and at the production well. A finer mesh size increases the number of degrees of freedom, thereby enhancing accuracy/resolution but also significantly increasing computation time. Therefore, a sensitivity analysis was performed to find an optimal balance between the number of degrees of freedom, the computational efficiency, and result precision. In this sensitivity analysis, we varied the mesh size for the faults/fractures measuring the water temperature at the production well in ST2 at the measured depth of 288.7 m after 90 days of continuous injection at a rate of 5 kg/s and an injection temperature of 120 °C. Additionally, we examined the impact of relative tolerance, a parameter that specifies the acceptable level of relative error in the simulation results. A smaller relative tolerance yields higher resolution results but requires greater computational effort. Overall, the aim of this analysis is to ensure that the model parameters are optimized, avoiding unnecessary computational load, while maintaining the desired precision of the simulation.
4. Results
4.1. Mesh Sensitivity Analysis
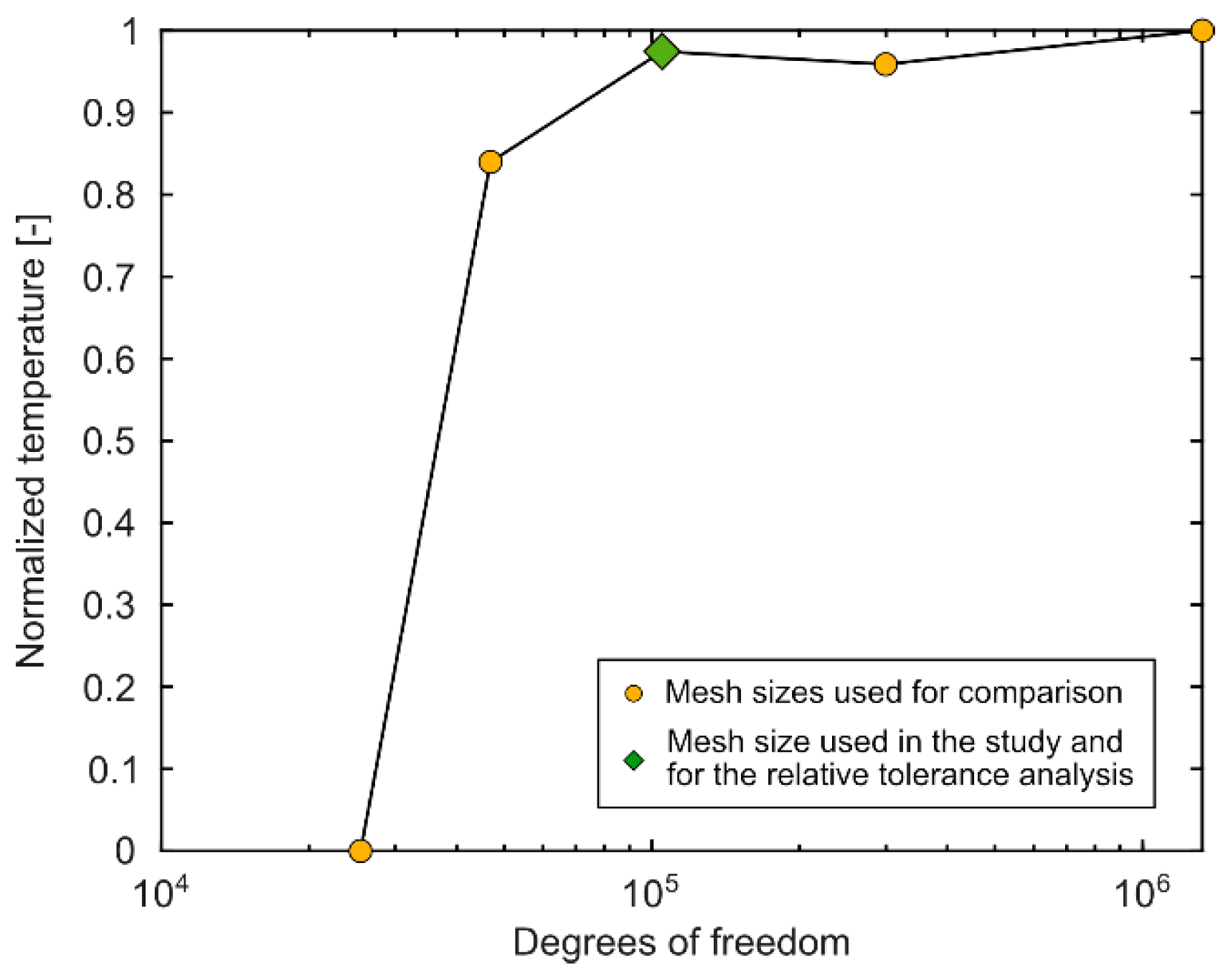
Figure 4 illustrates the impact of mesh size on the accuracy of the numerical model for heat storage. Mesh sizes for faults and fractures were varied using predefined settings in COMSOL Multiphysics, ranging from ‘coarser’ to ‘finer’. A relative tolerance of 10-2 was selected for the mesh size sensitivity analysis presented in Figure 4.
Our results demonstrate that mesh size significantly influences the accuracy of the temperature readings at the monitoring point. Additionally, the effect of relative tolerance on result accuracy was evaluated, varying it between 10-5 and 10-2, with no observed changes in the recorded temperature. Consequently, a relative tolerance of 10-2 was chosen for the remainder of the study.
The accuracy of the results, measured as the normalized temperature at the production well ST2 at a depth of 288.7 m (where 0 corresponds to the smallest temperature recorded and 1 to the maximum), improves rapidly with decreasing mesh size and eventually stabilizes (Figure 4). A reasonable balance between mesh size and computational time, indicated by the green diamond in Figure 4, was selected for our simulations. Smaller mesh sizes in the fault and fracture structures are concentrated around the edges, wells, and intersections of these structures.
Figure 4.
Mesh size sensitivity analysis. All the markers are parameters used for comparison, while the green diamond corresponds to the parameter used in the study. The temperature was measured in the production well ST2 at a depth of 285.7 m after 90 days.
Figure 4.
Mesh size sensitivity analysis. All the markers are parameters used for comparison, while the green diamond corresponds to the parameter used in the study. The temperature was measured in the production well ST2 at a depth of 285.7 m after 90 days.
4.2. Heat Storage Model
The numerical results of the heat storage are shown in Figure 5, illustrating two view angles of the temperature distribution in the faults at the end of the fifth production phase, corresponding to an injection rate of 5 kg/s at a temperature of 60 °C.
Figure 5a displays the injection well during the production phase, where tunnel water is injected at 16.8 °C during the colder seasons to create a pressure gradient between the two wells. The production well of the doublet system is in ST2 at the measured depth of 285.7 m. Figure 5b shows the second production well of the doublet system, located at a depth of 211.8 m, during the production phase. It also depicts the injection well of the single-well system, where the warm water appears to flow toward the left of the fault. Notably, heat storage was performed simultaneously in both wells.
Figure 5.
Temperature distribution in the system at the end of the production phase of the fifth cycle in two view angles (a) and (b).
Figure 5.
Temperature distribution in the system at the end of the production phase of the fifth cycle in two view angles (a) and (b).
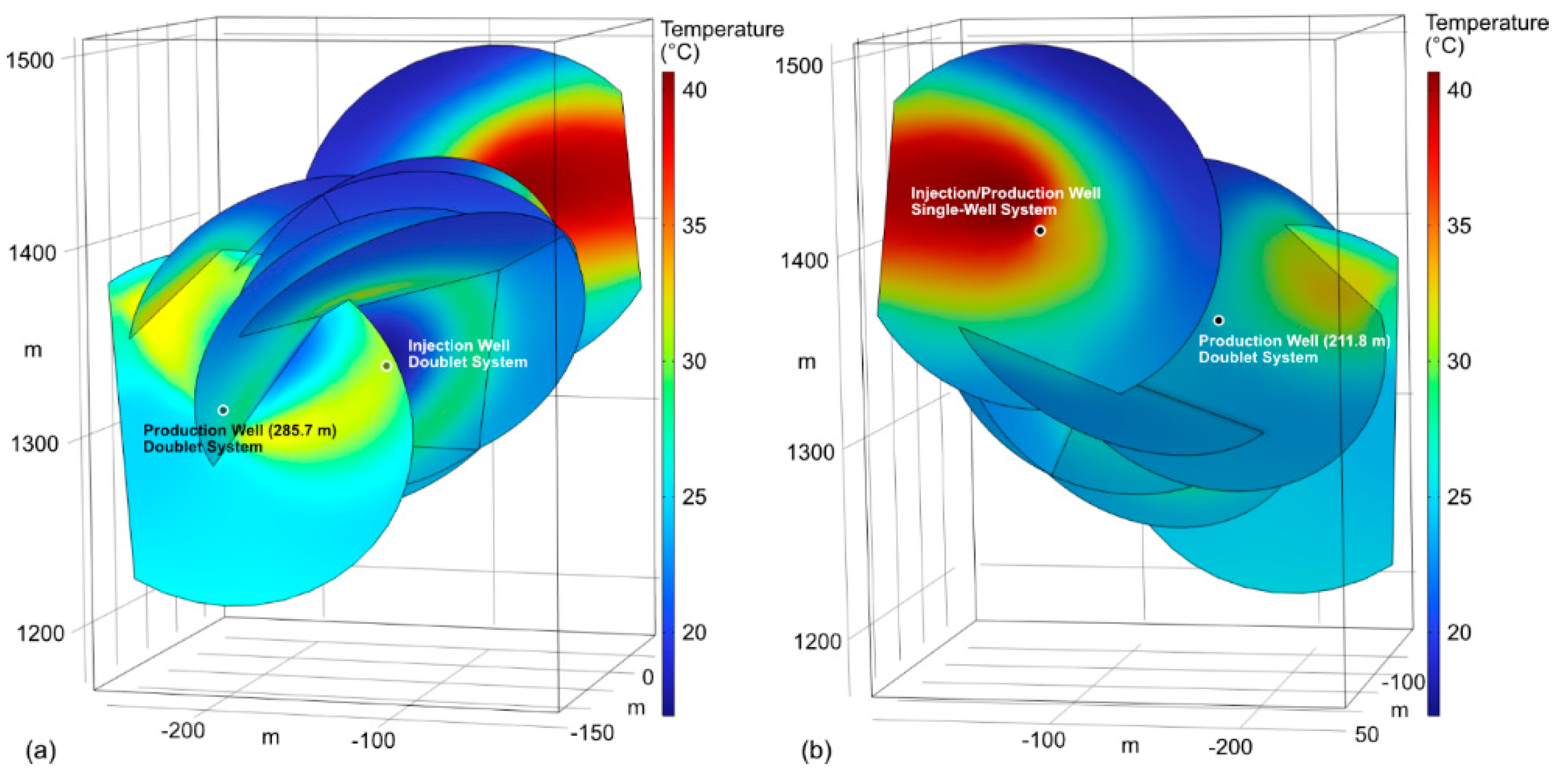
Figure 6 illustrates the temperature distribution in cross-sections of the granite domain and faults around the injection wells for both the single-well and doublet systems. Temperature diffusion into the surrounding rock is evident around the injection wells of both systems, extending several tens of meters radially, though without significantly impacting each other.
4.3. Breakthrough Time in the Doublet System
The breakthrough time, defined as the time required for the injected thermal front to reach the production well ST2 at depths of 211.8 m and 285.7 m (i.e. when the temperature starts to increase), was determined for three injection rates (3 kg/s, 4 kg/s, and 5 kg/s) and two injection temperatures (60 °C and 120 °C). Temperature evolutions at the production well were monitored over a period of 1000 days during continuous warm water injection. The results are depicted in Figure 7 for the production point at 211.8 m and in Figure 8 for the production point at 285.7 m:
A slight decrease in temperature was observed before the subsequent increase caused by the injected water. This phenomenon can be attributed to the downward flow of cooler water within the fracture towards the production well, originating from higher regions influenced by the geothermal gradient, and gravitational effects (buoyancy).
Figure 7.
Normalized temperature at the production point at 211.8 m in ST2 for the doublet system: (a) for water injected at 60 °C and (b) for water injected at 120 °C in Interval 8 of ST1.
Figure 7.
Normalized temperature at the production point at 211.8 m in ST2 for the doublet system: (a) for water injected at 60 °C and (b) for water injected at 120 °C in Interval 8 of ST1.
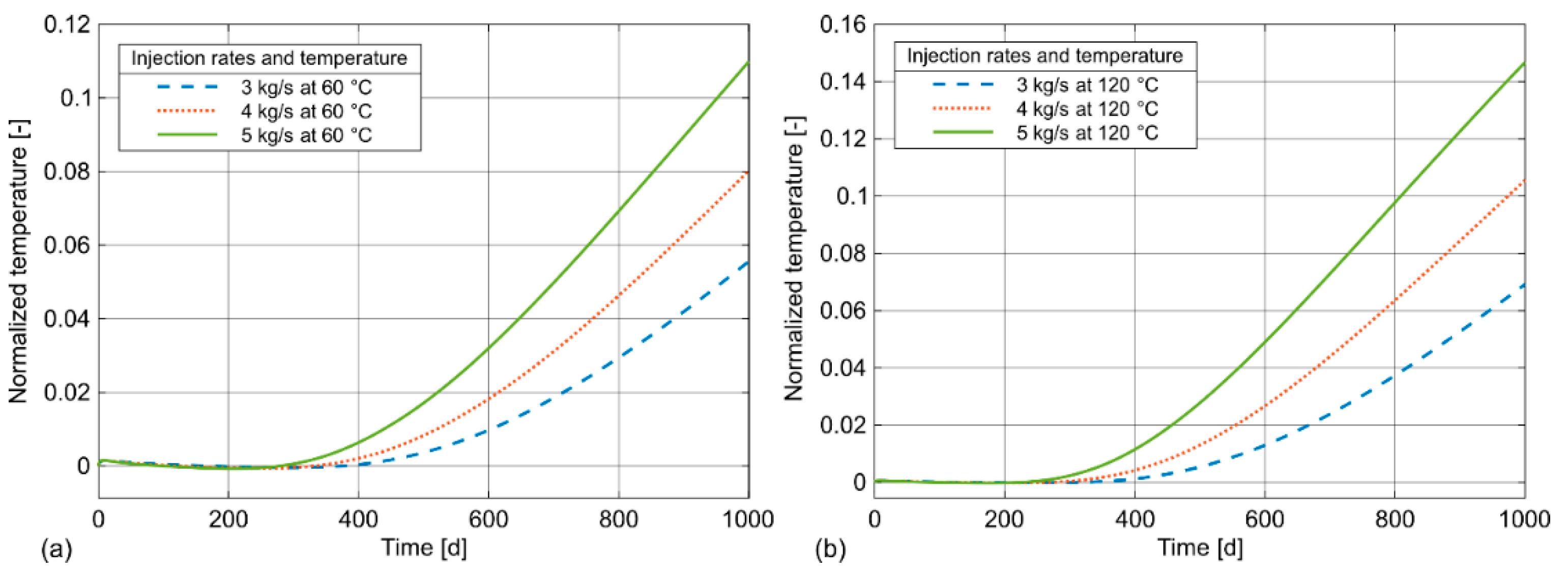
Figure 8 illustrates the breakthrough times at the production point at 285.7 m:
Thermal breakthrough occurs significantly sooner at the production point at 285.7 m compared to the production point at 211.8 m in the doublet system. After the 1000-day period, the temperatures reach up to 44.1 °C for an injection temperature of 60 °C and a flow rate of 5 kg/s, and 77.0 °C for an injection temperature of 120 °C and a flow rate of 5 kg/s. In contrast, for the production point at 211.8 m, the maximum temperatures reached are 25.7 °C for an injection temperature of 60 °C and a flow rate of 5 kg/s, and 35.9 °C for an injection temperature of 120 °C and a flow rate of 5 kg/s.
Figure 8.
Normalized temperature at the production point at 285.7 m in ST2 for the doublet system: (a) for water injected at 60 °C and (b) for water injected at 120 °C in Interval 8 of ST1.
Figure 8.
Normalized temperature at the production point at 285.7 m in ST2 for the doublet system: (a) for water injected at 60 °C and (b) for water injected at 120 °C in Interval 8 of ST1.

4.4. Energy Efficiency
The energy efficiency for each injection rate and temperature was calculated for both the single-well and doublet systems over 25 cycles according to Equations 3 and 6. The results for the single-well system are shown in Figure 9a,b. A rapid increase in efficiency can be observed over the first 10 cycles, with an increase of more than 20% during this period. In the last 15 cycles, the efficiency continues to improve but at a slower rate. It is also evident that higher flow rates result in greater efficiency. The efficiencies after 10 and 25 cycles are 51.3.0% and 59.2%, respectively, for an injection rate of 3 kg/s at 60 °C, 55.6% and 64.2% for 4 kg/s, and 59.4% and 67.7% for 5 kg/s. For an injection temperature of 120 °C, the efficiencies after 10 and 25 cycles are 51.0% and 57.7%, respectively, for 3 kg/s, 55.5% and 62.6% for 4 kg/s, and 59.3% and 66.7% for 5 kg/s.
Figure 10 presents the energy efficiency over 25 production cycles for the doublet system. Figure 10a shows the results for an injection temperature of 60 °C, and Figure 10b shows the results for an injection temperature of 120 °C. Compared to the single-well system shown in Figure 9, the doublet system shows a smaller rate of increase in efficiency over the first 10 cycles, followed by a decrease in efficiency towards the last cycles. The maximum efficiencies observed for an injection temperature of 60 °C are 17.4% for 3 kg/s, 18.7% for 4 kg/s, and 20.3% for 5 kg/s. For the injection temperature of 120 °C, the maximum efficiencies are 12.6% for 3 kg/s, 15.0% for 4 kg/s, and 16.5% for 5 kg/s.
4.5. Water Flow and Temperature Loss
Figure 11a illustrates the temperature of the water and the temperature loss during its flow from the production well at TM 2000 to the village of Bedretto (ca. 3600 m of piping distance), and Figure 11b shows the same for the hypothetical greenhouse farm (ca. 2200 m of piping distance). In both cases presented in Figure 11, the best output scenario was chosen, namely the single-well system with an injection rate of 5 kg/s, as mentioned in Section 4.4. The outside air temperature was set to -4 °C, reflecting the average temperature in Bedretto between December and February [51]. The temperature at the end destination and the temperature loss were calculated using Equations 5 and 6. The colored zones in Figure 11 correspond to the minimum and maximum values, whether temperature or temperature loss, for each full cycle.
The minimum temperature of the water arriving at the village of Bedretto is 24.2 °C during the first cycle, increasing to a minimum of 38.4 °C after 25 cycles (Figure 11a). The maximum temperature reaching the village ranges from 38.3 °C in the first cycle to 45.3 °C in the last cycle (Figure 11a). For the hypothetical greenhouse farm located 200 meters from the tunnel portal, the minimum temperature of the arriving water is 26.2 °C during the first cycle and 41.3 °C during the last cycle (Figure 11b). The maximum temperature reaching the greenhouse farm ranges from 41.2 °C to 48.7 °C over the same period (Figure 11b). The mean temperature loss is greater by 2.2 °C during the first cycle between both locations, increasing to 3.1 °C after 25 cycles (Figure 11b).
4.6. Cost of the Electricity Produced
Temperatures exceeding 80 °C were achieved during the production phases of the single-well system while injecting water at 120 °C. The amount of electrical energy produced was calculated using an Organic Rankine Cycle (ORC) engine with net efficiencies of 3% and 5%, as detailed in Section 3.5. The electrical power required for the pump, calculated using Equation 7, was subtracted, as this power is not supplied by the excess energy produced by the solar panels.
The cost for the electricity produced was calculated only for the injection rate of 5 kg/s, as it is the most effective. For an efficiency of the ORC engine of 3%, the energy produced is estimated to reach 22.60 kWe for a flow rate of 5 kg/s. For an efficiency of 5%, the energy produced is estimated to be 43.50 kWe.
The pumping costs for the injection/production rate were calculated for the single-well system over a period of 25 years. The electricity cost to pump the water from the well is estimated at kCHF 134.5 for the flow rate of 5 kg/s.
The range of prices is based on the assumed efficiencies of the ORC engine, which vary between 3% and 5%. The price ranges from 0.25 to 0.47 CHF/kWhe for an initial investment of kCHF 450, and from 0.29 to 0.55 CHF/kWhe for an initial investment of kCHF 550. A summary table of the prices appears in Table 3.
5. Discussion
In the field of thermal energy storage, porous aquifers are the standard reservoir type [8]. Notable examples of ATES systems include the Oslo airport in Norway [66], the Hospital of Zwammerdam in the Netherlands [67], and the Shinshu University in Japan [68]. To the author’s knowledge, there are no existing thermal energy storage systems in fractured media worldwide. Several factors motivate the preference for porous aquifers over fractured media. Porous aquifers can contain substantial volumes of water—often several hundreds to thousands cubic meters [69]— and have a more regular and predictable shape and permeability compared to fractured media. Additional advantages of porous aquifers include easier location selection due to their larger reservoir size, which facilitates installations close to consumers, and simpler methods for identifying suitable reservoirs. However, fractured media, with their abundance in the Earth’s crust, could still offer viable energy storage solutions in regions where porous aquifers are not available, as will be discussed below.
The following discussion will address the efficiency of thermal energy storage in a specific case, the fractured rock volume in the Bedretto Laboratory investigated by numerical modeling. We will compare the efficiencies of two different well configurations and explore potential applications for the heat extracted during the production phase. Finally, the viability of this alternative storage method will be evaluated for this specific user case.
The Bedretto user case has several advantages over a not yet developed field, which needs to be considered in general. The exclusion of borehole drilling costs and existing equipment from the cost estimations at Bedretto underscores the substantial contribution of the pre-existing infrastructure, emphasizing Bedretto’s unique opportunity for this project. Furthermore, water is readily available in the tunnel, flowing in a channel towards the south portal, and can be utilized for injection. All following discussions apply to this specific user case and can be different for any real-world scenario.
5.1. Limitations of the Numerical Model
The numerical model developed in this study has several inherent limitations due to the assumptions and simplifications made during its construction. These limitations, while necessary for maintaining computational feasibility and focusing on the primary goal of understanding thermal processes in fractured reservoirs, introduce certain constraints on the model’s applicability and accuracy in representing real-world scenarios.
Firstly, the model assumes an isotropic medium, while geological formations often exhibit anisotropic characteristics with properties that vary in different directions. Although our focus on flow in more permeable fractures may mitigate some impact of this assumption, it still presents a limitation. In the model, fracture flow is represented by mathematically implementing the fracture aperture in the numerical differential equations. This approach simplifies the complex geometry and connectivity of fractures, potentially oversimplifying the actual fluid pathways.
Additionally, the model does not account for rock deformation mechanics, concentrating instead on fluid dynamics and thermal behavior. Laboratory-scale experiments have demonstrated that circulating water in granite fractures with micrometer-range apertures for durations averaging 100 hours can result in a 20% to 75% decrease in aperture size due to thermal effects [70]. Although these apertures are smaller than those considered in this study, this suggests that thermal dilation should be examined further. However, it also implies that flow in high-temperature fractured systems may be restricted to the largest fractures, potentially limiting water loss from the system.
The assumption of no background groundwater flow implies a negligible natural gradient, which simplifies the model but may not accurately reflect the actual hydrogeological conditions. In real-world scenarios, natural groundwater flow can significantly influence the movement of injected water, affecting both the distribution of thermal energy and the efficiency of the storage system.
Moreover, the model does not consider heat loss through the borehole walls. While this assumption helps streamline the model, in practical applications, heat loss through borehole walls can contribute to thermal dissipation, potentially affecting the efficiency of heat storage and retrieval.
Overall, while the numerical model contains multiple assumptions, it still provides valuable insights into the thermal behavior and fluid dynamics of fractured porous media.
5.2. Well Disposition and Energy Efficiency
The results from Section 4.3 and Section 4.4 indicate that in the doublet system, it takes 8 to 18 days for the injected water temperature to reach the production well at 285.7 m and a minimum of 229 days at 211.8 m, creating an offset in the cycle phases. This offset may explain why the efficiency curve does not increase over time as it does for the single-well system. Additionally, during the production phase, colder water is injected to create a pressure gradient, which cools the previously heated reservoir and mixes with the warmer water. The doublet system also experiences significantly greater heat loss along the faults compared to the single-well system, as demonstrated by the energy efficiencies. This increased heat loss is due to the greater distance that water travels per cycle in the doublet system, allowing more heat transfer to the surrounding rock. Furthermore, using the single-well system appears to be more effective for reducing heat losses and achieving higher energy efficiencies in the Bedretto case. However, scenarios exist where a configuration with two or more wells might be advantageous. In highly transmissive faults, larger water volumes could be injected with proportionally less heat loss, leading to higher energy efficiencies. Further stimulation operations within the reservoir could enhance transmissivity and improve heat storage efficiency. Additionally, the results indicate that a shorter distance between the production points contributes to a smaller breakthrough time, which should be considered when planning the drilling of the wells.
It is important to note that the background hydraulic gradient was not considered in the numerical simulation. If significant, this gradient could substantially affect the results by causing hot water to flow away from the well during the storage period. In Bedretto, according to the numerical model, there is a possibility that the temperature breakthrough could reach the tunnel intersecting the fault in Interval 13, resulting in permanent heat loss. This effect would be even more pronounced in more transmissive fractures, leading to lower recovery factors.
Injection rates also play a significant role in energy efficiency, with higher flow rates leading to greater efficiencies. This finding suggests that creating such storage systems in larger reservoirs could maximize efficiency. The numerical model shows that in the best-case scenario—an injection rate of 5 kg/s at 60 °C in the single-well system—efficiency starts at 31.4% for the first cycle and reaches 59.4% and 67.7% after 10 and 25 cycles, respectively. Additionally, the energy efficiency is not significantly different for the two different injection temperatures, showcasing similar ranges of values. Additionally, the energy efficiency is not significantly different for the two different injection temperatures, showcasing similar ranges of values, and thus being promising for high temperature FTES. For comparison, energy efficiencies for a single-well system in a modeled porous aquifer in the Bucharest region, Romania, are 40% for the first cycle and increase to 70% over the first 10 years of operation for a similar injection rate of 60 °C [16]. Moreover, this aquifer has an at-rest temperature of 20 °C, close to that of the Rotondo granite reservoir, making it a good comparison. Therefore, the Rotondo granite reservoir shows promising potential, and further stimulation operations in the reservoir volume are expected to increase the efficiency of heat storage even further by enhancing transmissivity.
Typical recovery efficiencies for ATES systems between 30 °C and 60 °C range from 60% to 80%, while those with higher temperatures (>60 °C) typically range from 40% to 70% [18]. The energy efficiency in the fractured reservoir for initial injection temperatures of 60 °C and 120 °C therefore falls within these ranges, although on the lower end for the 60 °C injection temperature and only after 11 cycles. It is important to note that the trajectory and placement of boreholes within the Bedretto reservoir volume were initially designed for reservoir monitoring and stimulation purposes. Further modeling and characterization are anticipated to identify more optimal locations for the boreholes, thereby enhancing operational efficiency even further. Although the current results for heat storage in a typical fractured reservoir are already optimistic, improvements in well placement and reservoir stimulation indicate that heat storage in fractured media has great potential as an alternative to ATES.
5.3. District Heating
One of the suggested potential usages for the retrieved hot water from the reservoir is district heating in the village of Bedretto. However, certain limitations exist. Firstly, transporting the water 3.6 km from its source to the village results in significant temperature losses, as shown in Section 4.6, further decreasing the system’s energy efficiency. Moreover, there are considerable logistical challenges involved. Halter et al. [23] suggest that tunnel water could be sourced directly and transported to the village through buried pipes for use in individual heat pumps for house heating. This initial investment, estimated at around kCHF 800, would require substantial contributions from the state and connection fees from residents to be amortized [23].
Additionally, transporting water extracted from the reservoir after storage would necessitate additional insulated pipes to prevent mixing the warm extracted water with the tunnel water, if it was used as a complement to the district heating system using tunnel water. This would add further costs to the already high investment and require additional financial contributions to amortize over the system’s lifetime. The extracted water’s temperature and quality may not be sufficient for direct use, necessitating an additional heat exchange process. Overall, the benefits of such a system would only marginally improve the efficiency of some heat pumps in the district heating system due to the relatively small discharge. Furthermore, using high-temperature heat sources requires specialized heat pumps, complicating the system’s use and potentially necessitating mixing the extracted water with tunnel water to lower the temperature, thus counteracting the system’s efficiency.
The potential for utilizing the fracture thermal energy storage system for cooling should also be considered; however, given that summer temperatures in the area rarely exceed 24 °C [51], the need for district cooling is minimal. Nonetheless, this consideration remains relevant for similar future applications in such reservoirs.
5.4. Greenhouse Heating
An alternative usage for the warm water extracted from the storage system is greenhouse farm heating. One option is to directly heat the ground by circulating warm water through thermally conductive metallic pipes buried around the crops. This method can maintain stable temperatures around the crops, potentially eliminating the need for air heating for certain cool season crops such as lettuce or spinach [71].
At an altitude of 1470 meters and located in a remote area, Bedretto benefits from significantly less air pollution compared to urban environments, potentially reducing harvest losses by up to 15% [72]. While the cooler climate may pose challenges for some vegetables, Bedretto still supports the cultivation of a diverse range of crops including beetroot, carrots, cucurbits, cabbage, spinach, onions, and potatoes [73]. Furthermore, the greenhouse structure effectively addresses common altitude farming challenges such as wind and snow [74]. Unlike many high-altitude farming regions, Bedretto enjoys ample water availability directly at the tunnel’s exit [74], alleviating the typical constraint of water scarcity.
Constructing a greenhouse near the tunnel portal would significantly reduce heat loss to the outside air compared to transporting the water to the village of Bedretto, as shown in Figure 11. This setup guarantees a minimum temperature of 30-35 °C during the first cycles and 35 °C after the fifth cycle, reaching more than 45 °C. In this configuration, the heat extracted in winter could be used for direct heating, while a heat pump utilizing the tunnel water’s heat could provide warmth during other cooler parts of the year.
Although this alternative is more cost-effective than a district heating system, it still requires substantial initial investments to heat the water in summer before its injection. Directly using the tunnel water year-round would considerably reduce initial costs, limiting the investment to just a heat pump and piping system.
5.5. Electricity Production
Given that the water temperature in the production well of the single-well system exceeded 80 °C, electricity generation was considered as a potential application. However, the initial investment required for heating the water and converting the heat to electricity using an ORC engine was found to be higher compared to the amount of electricity produced. The estimated cost ranged from 0.23 to 0.51 CHF/kWhe. In the best-case scenario, the cost of producing a kWhe with the technology used in this study went below the current price in Bedretto of 0.28 CHF/kWhe, which is at an all-time high in 2024 [55]. However, the grid price for a kWhe includes various costs, such as network utilization and taxes, meaning the energy cost alone is 0.091 CHF/kWhe [55]. This disparity implies that energy companies may hesitate to invest in this technology due to production costs that exceed market prices. Therefore, private investors who can utilize the energy produced independently of the grid might find this investment more suitable. Nevertheless, the constraints of this storage technology could potentially prevent electricity costs from falling within the lower end of the estimated range, as detailed in Section 5.5.
While this alternative incurs fewer losses during the transport phase compared to transporting heat via water, there are additional significant losses inherent in the electricity generation process. The proposed plan involved using solar panels to generate electricity to heat the water before injection, with an efficiency of between 15% and 20% [75]. Once retrieved, the thermal energy would then be converted into electricity using an ORC engine with a net efficiency of 3-5%, typically used for waste heat. The results indicate that such a system not only produces electricity that is too expensive to be competitive but also is inefficient in terms of energy use. Therefore, exploring alternatives that minimize the number of energy conversions between thermal energy and electricity is advisable.
5.6. Viability of the Technology
The numerical model demonstrated promising results for the energy efficiency of the system, particularly for the single-well configuration. Efficiency increased rapidly, reaching 59.3% after ten years for the three injection rates at a temperature of 60 °C and reaching up to 67.7%, making it comparable with standard porous ATES systems. Typical recovery efficiencies for ATES systems between 30 °C and 60 °C range from 60% to 80%, while those with higher temperatures (> 60 °C) typically range from 40% to 70% [18].
While the utilization of the recovered thermal energy is currently limited by the geographic and demographic characteristics of the Bedretto region, this technology has the potential to be more viable when implemented closer to densely populated areas, where district heating could be the primary application. Indeed, ATES systems can achieve low payback periods of 8.7 years, and even shorter, down to 5.6 years, when also used for cold storage [61].
However, several challenges must be addressed to determine the overall viability of this technology. Firstly, the initial investment costs for a new system, including expenses for exploration, drilling boreholes, and purchasing equipment, are likely to be higher than for porous ATES systems due to the complexity of fractured reservoirs. Additionally, identifying suitable fractures/faults is inherently complicated. The fractures need to be sufficiently transmissive but not excessively so, to prevent the water from dissipating. Furthermore, the natural hydraulic gradient must be minimal to ensure water remains within the desired section of the reservoir. Geophysical studies alone may not be sufficient to locate optimal fractures, necessitating the drilling of exploratory boreholes.
A potential solution to overcome these challenges and increase both capacity and energy efficiency is to stimulate the fractures to enhance their transmissivity. Further stimulation operations within the reservoir could significantly improve heat storage efficiency by increasing the flow rate and reducing heat losses.
To design the system adequately, detailed characterization of faults is essential, including determining their geometry and aperture. There is, however, always the risk of undiscovered fractures that could impact the system’s performance. Moreover, there is a significant risk that water could be lost in overly conductive faults, reducing system efficiency and reliability.
While the storage capacity of fractured rock systems is relatively small, increasing the distance between wells to enhance capacity results in longer heat travel times to the production well, leading to more heat loss. The optimal scenario would involve boreholes intersecting multiple faults and fractures, creating efficient pathways for water between wells. Alternatively, deploying several single-well systems within the same borehole might be advantageous.
Furthermore, in an optimized system, the distance between injection and production wells can be defined based on operational parameters, particularly the duration of the different phases of heat storage and recovery. In such cases, there could be a possibility that the energy efficiency of a doublet system might be even higher than that of a single-well system. This suggests that with careful optimization and strategic planning, the potential benefits of using fractured rock for thermal energy storage could be significantly enhanced, offering a viable alternative to porous ATES systems.
6. Conclusions
This study investigated the potential of faults and fractures in crystalline rock for seasonal heat storage and proposed applications for the use of the retrieved water. Using COMSOL Multiphysics, we developed a numerical model of a granite reservoir, specifically the BULGG underground reservoir, incorporating several permeable fault/fracture planes to simulate fluid flow and heat transfer.
The results demonstrated relatively good energy efficiency, particularly in the single-well configuration, with efficiencies exceeding 59% after ten years and reaching up to 67.7%. These values suggest that fractured rock can be a viable medium for thermal energy storage. However, the efficiency in this site-specific case could be further optimized by stimulating the fractures to enhance their transmissivity and allowing for greater flow rates. While our chosen site provided promising results, other locations may also suit the purpose depending on their geological characteristics.
For future developments of fractured storage systems, the usage of the retrieved water should be as close as possible to the end-user to avoid thermal losses during transport. Moreover, electricity production from the stored thermal energy could be viable if a significant excess of energy was produced during the summer. However, the current efficiency levels suggest that this application is not ideal unless the system can be further optimized to improve economic feasibility.
Several challenges must be addressed to realize the full potential of this technology. High initial investment costs, including those for exploration, drilling boreholes, and purchasing equipment, pose a significant barrier. Identifying suitable fractures is also inherently challenging, requiring faults with high but not excessive transmissivity and minimal background hydraulic gradients to prevent the injected water from dissipating. These challenges are not unique to this technology and are common in any ATES system.
Despite these challenges, the potential benefits of using fractured rock for thermal energy storage, especially in regions lacking suitable aquifers, make it a promising area for further research and development. This site-specific case demonstrated the efficiency of such systems for one example setup. To further explore the possibility of this specific system, a more detailed model is needed, including the whole reservoir volume and different operational parameters with various storage scenarios.
Future studies should focus on refining exploration techniques and improving fault characterization to develop strategies that mitigate water loss and thermal dissipation. Additionally, investigating the assumptions made in this study, such as the effects of rock deformation, natural groundwater flow, and heat exchange between the fluid and borehole walls, is crucial. These factors become particularly significant due to the periodic changes in injection fluid temperature, which can influence the overall efficiency and feasibility of the thermal storage system.
Supplementary Materials
There is no supplementary material.
Author Contributions
Théo Halter wrote the main manuscript, created the figures, and did the numerical modeling. Nima Gholizadeh Doonechaly contributed to numerical modeling. Alexis Shakas provided the fault structures for the numerical modeling. Marian Hertrich lead the geophysical well logging operations. All authors provided significant inputs and feedback to the study and the text. Nima Gholizadeh Doonechaly, Marian Hertrich, and Domenico Giardini supervised the project.
Funding
There is no funding for this specific project.
Data Availability Statement
The datasets generated/analyzed during the current study are available from the corresponding author on reasonable request.
Acknowledgments
In the “Bedretto Underground Laboratory for Geosciences and Geoenergies”, ETH Zurich studies in close collaboration with national and international partners techniques and procedures for a safe, efficient, and sustainable use of geothermal heat and questions related to earthquake physics. The BedrettoLab is financed by the Werner Siemens Foundation, ETH Zürich and the Swiss National Science Foundation. The research in this publication was conducted within the project the Swiss Federal Office of Energy (SFOE) (project VALTER), the EU Horizon 2020 (project DESTRESS). We thank Emil Zylis for his IT support and Thomas Haag for the information he provided regarding pumping power requirements. Authors would also like to thank all members of the BedrettoLab team for their contribution and support. The authors would like to thank ETH Zurich for providing funding to make this article open access.
Conflicts of Interest
There is no conflict of interest for this project.
Nomenclature
| d | Diameter of the pipe (m) |
| Cp | Specific heat capacity at constant pressure (J/(kg×K)) |
| ct | Compressibility of the fracture (Pa-1) |
| CHF | Swiss franc |
| EInj | Energy injected (MWhth) |
| EExt | Energy extracted (MWhth) |
| g | Gravitational acceleration (m/s2) |
| h | Well depth (m) |
| k | Permeability of the porous medium (m2) |
| keff | Effective thermal conductivity of the porous medium (W/(m×K)) |
| K | Heat transfer coefficient of the pipe (W/(m×K)) |
| L | Distance from the point of reference (m) |
| ∇p | Pressure gradient (Pa/m) |
| q | Heat flux vector (W) |
| Qwater | Mass flow rate (kg/s) |
| QV | Volumetric heat sources or sinks (W/m3) |
| Qgeo | Heat sources or sinks due to geothermal effects (W/m3) |
| Qm | Source or sink of mass (kg/m2/s) |
| Qp | Heat sources or sinks due to fluid-porous matrix interactions (W/m3) |
| Qvd | Heat sources or sinks due to geothermal effects (W/m3) |
| r | Pumping rate (m3/h) |
| s | Thickness of the foam layer (m) |
| Ss | Specific storage (m-1) |
| Te | Temperature of the fluid in the pipe at a distance L (K) |
| Tt | Outside temperature (K) |
| Te0 | Temperature of the fluid in the pipe at the reference point (K) |
| T | Temperature (K) |
| u | Darcy velocity (m/s) |
| w | Width of the fracture (m) |
| ϵp | Porosity of the porous medium (-) |
| f | Porosity (-) |
| F | Energy efficiency (-) |
| h | Pump efficiency (-) |
| l | Thermal conductivity (W/(m×K) |
| m | Dynamic viscosity of the fluid (Pa×s) |
| r | Density (kg/m3) |
| t | Transmissivity (m2/s) |
References
- EU. Directive on the Energy Performance of Buildings; Union, OJotE, Ed.; EU-Parliament, European Union: Strasbourg, France, 2010; Volume 153, pp. 13–35. [Google Scholar]
- UN. Adoption of the Paris agreement. Paris: United Nations, Framework Convention on Climate Change. 2015.
- Swiss Federal Office of Energy. Energy Strategy 2050. 2024. Available online: https://www.bfe.admin.ch/bfe/en/home/policy/energy-strategy-2050.html/ (accessed on 6 June 2024).
- Bloemendal, M.; Jaxa-Rozen, M.; Olsthoorn, T. Methods for planning of ATES systems. Appl. Energy 2018, 216, 534–557. [Google Scholar] [CrossRef]
- EIA. Residential energy consumption survey. US Energy Information Administration 2009.
- Jong, K.d. Warmte in Nederland (heat in the Netherlands). Steenwijk. 2016.
- RHC. Strategic Research and Innovation Agenda for Renewable Heating & Cooling; Renewable Heating & Cooling, European Technology Platform: Brussels, 2013. [Google Scholar]
- Fleuchaus, P.; Godschalk, B.; Stober, I.; Blum, P. Worldwide application of aquifer thermal energy storage–A review. Renew. Sustain. Energy Rev. 2018, 94, 861–876. [Google Scholar] [CrossRef]
- Li, G. Sensible heat thermal storage energy and exergy performance evaluations. Renew. Sustain. Energy Rev. 2016, 53, 897–923. [Google Scholar] [CrossRef]
- Caliskan, H.; Dincer, I.; Hepbasli, A. Thermodynamic analyses and assessments of various thermal energy storage systems for buildings. Energy Convers. Manag. 2012, 62, 109–122. [Google Scholar] [CrossRef]
- Dincer, I.; Rosen, M.A. Energy storage systems. Thermal Energy Storage: Systems and Applications 2010, 51–82. [Google Scholar] [CrossRef]
- Shi, X.; Jiang, S.; Xu, H.; Jiang, F.; He, Z.; Wu, J. The effects of artificial recharge of groundwater on controlling land subsidence and its influence on groundwater quality and aquifer energy storage in Shanghai, China. Environ. Earth Sci. 2016, 75, 1–18. [Google Scholar] [CrossRef]
- Tsang, C.F.; Hopkins, D.; Hellstroem, G. Aquifer Thermal Energy Storage: A Survey (No. LBL-10441); Lawrence Berkeley National Lab.(LBNL): Berkeley, CA, USA, 1980. [Google Scholar] [CrossRef]
- The Swiss Parliament. Commission de l’environnement, de l’aménagement du territoire et de l’énergie du Conseil des États. 2023. Available online: https://www.parlament.ch/en/ratsbetrieb/suche-curia-vista/geschaeft?AffairId=20223702 (accessed on 8 July 2024).
- Link, K.; Lupi, N.; Siddiqi, G. Geothermal Energy in Switzerland Country Update 2015–2020. In Proceedings of the World Geothermal Congress; 2020. [Google Scholar]
- Zeghici, R.M.; Essink, G.H.O.; Hartog, N.; Sommer, W. Integrated assessment of variable density–viscosity groundwater flow for a high temperature mono-well aquifer thermal energy storage (HT-ATES) system in a geothermal reservoir. Geothermics 2015, 55, 58–68. [Google Scholar] [CrossRef]
- Welsch, B.; Rühaak, W.; Schulte, D.O.; Bär, K.; Homuth, S.; Sass, I. A comparative study of medium deep borehole thermal energy storage systems using numerical modelling. Proceedings of World Geothermal Congress; 2015. [Google Scholar]
- Drijver, B.; van Aarssen, M.; Zwart, B.D. High-temperature aquifer thermal energy storage (HT-ATES): sustainable and multi-usable. Proceedings of the Innostock 2012, 1–10. [Google Scholar]
- Doughty, C.; Hellström, G.; Tsang, C.F.; Claesson, J. A dimensionless parameter approach to the thermal behavior of an aquifer thermal energy storage system. Water Resour. Res. 1982, 18, 571–587. [Google Scholar] [CrossRef]
- de La Bernardie, J.; de Dreuzy, J.R.; Bour, O.; Lesueur, H. Synthetic investigation of thermal storage capacities in crystalline bedrock through a regular fracture network as heat exchanger. Geothermics 2019, 77, 130–138. [Google Scholar] [CrossRef]
- Klepikova, M.; Méheust, Y.; Roques, C.; Linde, N. Heat transport by flow through rough rock fractures: a numerical investigation. Adv. Water Resour. 2021, 156, 104042. [Google Scholar] [CrossRef]
- Zhou, D.; Tatomir, A.; Niemi, A.; Tsang, C.F.; Sauter, M. Study on the influence of randomly distributed fracture aperture in a fracture network on heat production from an enhanced geothermal system (EGS). Energy 2022, 250, 123781. [Google Scholar] [CrossRef]
- Halter, T.; Gholizadeh Doonechaly, N.; Notzon, A.; Rybach, L.; Hertrich, M.; Giardini, D. Exploring the Feasibility of Energy Extraction from the Bedretto Tunnel in Switzerland. Energies 2024. [CrossRef]
- BULGG. History—Bedretto Lab. 2024. Available online: http://www.bedrettolab.ethz.ch/en/home/ (accessed on 25 January 2024).
- Hertrich, M.; Brixel, B.; Broeker, K.; Driesner, T.; Gholizadeh, N.; Giardini, D.; Jordan, D.; Krietsch, H.; Loew, S.; Ma, X.; Maurer, H.; Valley, B. Characterization, hydraulic stimulation, and fluid circulation experiments in the Bedretto Underground Laboratory for Geosciences and Geoenergies. In ARMA US Rock Mechanics/Geomechanics Symposium (pp. ARMA-2021); ARMA, 2021. [Google Scholar]
- Ma, X.; Hertrich, M.; Amann, F.; Bröker, K.; Gholizadeh Doonechaly, N.; Gischig, V.; Hochreutener, R.; Kästli, P.; Krietsch, H.; Marti, M.; Nägeli, B.; Bethmann, F. Multi-disciplinary characterizations of the BedrettoLab–a new underground geoscience research facility. Solid Earth 2022, 13, 301–322. [Google Scholar] [CrossRef]
- Federal Office of Topography swisstopo. Topological map of Switzerland. 2024. Available online: https://map.geo.admin.ch/ (accessed on 7 January 2024).
- geocat. swissSURFACE3D Raster Estompage du Relief Monodirectionnel. 2020. Available online: https://www.geocat.ch/geonetwork/srv/fre/catalog.search#/metadata/ac330de2-572c-4602-acbc-ca4ba80e9d69 (accessed on 6 June 2024).
- Rast, M.; Galli, A.; Ruh, J.B.; Guillong, M.; Madonna, C. Geology along the Bedretto tunnel: kinematic and geochronological constraints on the evolution of the Gotthard Massif (Central Alps). Swiss J. Geosci. 2022, 115, 8. [Google Scholar] [CrossRef]
- Keller, F.; Schneider, T.R. Geologie und Geotechnik. Schweiz. Ing. Und Archit. 1982, 100, 512–520. [Google Scholar]
- Schneider, T. Basistunnel Furka—Geologische Aufnahme des Fensters Bedretto. Brig, Furka- Oberalp-Bahn AG. 1985. [Google Scholar]
- Plenkers, K.; Reinicke, A.; Obermann, A.; Gholizadeh Doonechaly, N.; Krietsch, H.; Fechner, T.; Hertrich, M.; Kontar, K.; Maurer, H.; Philipp, J.; Rinderknecht, B.; Wiemer, S. Multi-disciplinary monitoring networks for mesoscale underground experiments: advances in the bedretto reservoir project. Sensors 2023, 23, 3315. [Google Scholar] [CrossRef]
- Bröker, K.; Valley, B.; Gholizadeh Doonechaly, N.; Rosskopf, M.; Hertrich, M.; Giardini, D.; Rinaldi, A.P.; Clasen Repolles, V.; Obermann, A.; Ma, X. The influence of stress heterogeneity on hectometer scale hydraulic stimulation experiments; ARMA (American Rock Mechanics Association): Golden, USA, 2024. [Google Scholar]
- Gholizadeh Doonechaly, N.; Bröker, K.; Hertrich, M.; Rosskopf, M.; Obermann, A.; Durand, V.; Serbeto, F.; Shakas, A.; Ma, X.; Rinaldi, A.P.; et al. Insights from Subsurface Monitoring for Engineering of the Stimulation Pattern in Fractured Reservoirs. Rock Mechanics and Rock Engineering Submitted. 2024.
- COMSOL Multiphysics. Version 6.1. COMSOL Inc.: Stockholm, Sweden. 2023. Available online: https://www.comsol.com/ (accessed on 24 July 2024).
- Hartog, N.; Drijver, B.; Dinkla, I.; Bonte, M. Field assessment of the impacts of Aquifer Thermal Energy Storage (ATES) systems on chemical and microbial groundwater composition. In Proceedings of the European Geothermal Conference, Pisa, Italy; 2013; pp. 3–7. [Google Scholar]
- Castilla, R.; Meier, P.; Bethmann, F.; Christie, F.; Serbeto, F. A European endeavor for optimizing Zonal Isolation, Drilling and Exploitation of EGS projects—The ST2 Borehole in the Bedretto Underground Lab for Geosciences and Geoenergies (BULGG). Geo-Energie Suisse. 2011.
- Meier, P. ZoDrEx: Zonal Isolation, Drilling and Exploitation of EGS projects. Geothermica. 2022.
- Bröker, K.; Ma, X.; Gholizadeh Doonechaly, N.; Rinaldi, A.P.; Obermann, A.; Rosskopf, M.; Hertrich, M. and Giardini, D. Systematic multi-stage hydraulic stimulation experiments in a hectometer-scale fractured rock volume at the Bedretto Underground Laboratory, Switzerland, Copernicus Meetings. 2024. [CrossRef]
- Gholizadeh Doonechaly, N.; Bröker, K.; Ma, X.; Scarabello, L.; Villiger, L.; Wenning, Q.; Rinaldi, A.P.; Repollés, V.C.; Shakas, A.; Hertrich, M.; et al. Flow Path Alterations during Hydraulic Stimulation at Bedretto Underground Laboratory for Geosciences and Geoenergies. Geotherm. Resour. Counc. Trans. 2023, 47, 2746–2759. [Google Scholar]
- Geissler, N.; Garsche, F.; Samus, V.; Polat, B.; Di Mare, F.; Bracke, R. Proof of Concept in a Full-Scale Field Test for the Novel Micro-Turbine Drilling Technology from a Cased Borehole in Granite Rock. SPE J. 2024, 1–9. [Google Scholar] [CrossRef]
- Zwahlen, F.; Renard, P. Hydrogéologie générale. 2002. Available online: http://members.unine.ch/philippe.renard/hydrogen/hydrogen.html (accessed on 3 July 2024).
- David, C.; Nejati, M.; Geremia, D. On petrophysical and geomechanical properties of Bedretto Granite. ETH Zurich. 2020. [CrossRef]
- Cho, W.; Kwon, S.; Choi, J. The thermal conductivity for granite with various water contents. Eng. Geol. 2009, 107, 167–171. [Google Scholar] [CrossRef]
- gchem. General Chemistry, University of Texas—Database of Heat Capacities. 2024. Available online: https://gchem.cm.utexas.edu/data/section2.php?target=heat-capacities.php (accessed on 29 January 2024).
- Jacob, C.E. On the flow of water in an elastic artesian aquifer. Eos Trans. AGU 1940, 21, 574–586. [Google Scholar] [CrossRef]
- Illman, W.A.; Liu, X.; Takeuchi, S.; Yeh, T.C.; Ando, K.; Saegusa, H. Hydraulic tomography in fractured granite: Mizunami Underground Research site, Japan. Water Resour. Res. 2009, 45, W01406. [Google Scholar] [CrossRef]
- Illman, W.A.; Tartakovsky, D.M. Asymptotic Analysis of Cross-Hole Hydraulic Tests in Fractured Granite. Groundwater 2006, 44, 555–563. [Google Scholar] [CrossRef] [PubMed]
- Adams, J.; Wyss, E. Hyraulic packer testing in the Wellenberg boreholes SB1 and SB2: methods and field results. Nagra. 1994.
- Jansen. Système à Double paroi—Liste de Prix 2022. 2022. Available online: https://www.jansen.com/fileadmin/Downloadcenter/PlasticSolutions/Preislisten/Entwaesserung/preisliste_plastic-solutions_doppelwandsysteme_de_fr.pdf (accessed on 1 March 2024).
- Meteoblue. Archive météo Bedretto. 2024. Available online: https://www.meteoblue.com/fr/meteo/historyclimate/weatherarchive/bedretto_suisse_2661582 (accessed on 5 May 2024).
- Wilhelm, J. Concept de drainage des tunnels en vue d’une optimisation de l’utilisation géothermique. Technical report, Office fédéral de l’énergie. 2006.
- Wilhelm, J.; Rybach, L. The geothermal potential of Swiss Alpine tunnels. Geothermics 2003, 32, 557–568. [Google Scholar] [CrossRef]
- Kosmadakis, G.; Manolakos, D.; Papadakis, G. Experimental investigation of a low-temperature organic Rankine cycle (ORC) engine under variable heat input operating at both subcritical and supercritical conditions. Appl. Therm. Eng. 2016, 92, 1–7. [Google Scholar] [CrossRef]
- Swiss Federal Electricity Commission (ElCom). Electricity prices: Bedretto. 2024. Available online: https://www.prix-electricite.elcom.admin.ch/municipality/5063?priceComponent=total&view=collapsed&period=2024 (accessed on 8 February 2024).
- alpha Innotec. Liste de Prix et Assortiments. 2023. Available online: https://www.alpha-innotec.ch/fileadmin/content/marketing/Preislisten/Preisliste_alpha_2024_CH-FR.pdf (accessed on 29 May 2024).
- Solstis Energy, SA. Coûts et Amortissement de Votre Installation Solaire. 2024. Available online: https://www.home-energy.ch/fr/notre-offre/panneaux-solaires/installations-solaires-chiffres-et-faits (accessed on 3 June 2024).
- Turboden. ORC System. 2024. Available online: https://www.turboden.com/products/2463/orc-system (accessed on 18 June 2024).
- Cleaver-Brooks. Boilers. 2024. Available online: https://cleaverbrooks.com/Catalog/boilers (accessed on 18 June 2024).
- Kamat. High-Pressure Triplex Plunger Pump K25000-3G. 2024. Available online: https://www.kamat.de/en/high-pressure-solutions/high-pressure-pump/high-pressure-triplex-plunger-pump-k25000-3g/ (accessed on 9 July 2024).
- Schüppler, S.; Fleuchaus, P.; Blum, P. Techno-economic and environmental analysis of an Aquifer Thermal Energy Storage (ATES) in Germany. Geotherm Energy 2019, 7, 11. [Google Scholar] [CrossRef]
- Liang, X.; Fleming, E. Power consumption evaluation for electrical submersible pump systems. In Proceedings of the IEEE/IAS 48th Industrial & Commercial Power Systems Technical Conference (I&CPS), Louisville, KY, USA, 20–24 May 2012. [Google Scholar] [CrossRef]
- Jin, W.; Atkinson, T.; Neupane, G.; McLing, T.; Doughty, C.; Spycher, N.; Dobson, P.; Smith, R. Influence of mechanical deformation and mineral dissolution/precipitation on reservoir thermal energy storage. In ARMA US Rock Mechanics/Geomechanics Symposium (pp. ARMA-2022); ARMA, 2022. [Google Scholar] [CrossRef]
- Darcy, H. Les Fontaines Publiques de la Ville de Dijon; Victor Dalmont: Paris, France, 1856. [Google Scholar]
- Bergman, T.L. Fundamentals of Heat and Mass Transfer; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Midttømme, K.; Hauge, A.; Grini, R.S.; Stene, J.; Skarphagen, H. Underground thermal energy storage (UTES) with heat pumps in Norway. Proc. Effstock 2009, 15–17. [Google Scholar]
- Sanner, B. ECES Annex 12: High Temperature Underground Thermal Energy Storage: Fifth report to the Executive Committee. 2006.
- Tomigashi, A.; Fujinawa, K. Enhanced aquifer thermal energy storage for cooling and heating of Shinshu University building using a nested well system. In Sustainable Development and Planning 2011; Brebbia, C.A., Beriatos, E., Eds.; WIT Press: Southampton, UK, 2011; pp. 871–882. [Google Scholar] [CrossRef]
- Bakr, M.; van Oostrom, N.; Sommer, W. Efficiency of and interference among multiple Aquifer Thermal Energy Storage systems; A Dutch case study. Renew. Energy 2013, 60, 53–62. [Google Scholar] [CrossRef]
- Lima, M.G.; Vogler, D.; Querci, L.; Madonna, C.; Hattendorf, B.; Saar, M.O.; Kong, X.Z. Thermally driven fracture aperture variation in naturally fractured granites. Geotherm. Energy 2019, 7, 1–28. [Google Scholar] [CrossRef]
- Goldammer, T. Greenhouse Management: A Guide to Operations and Technology (Updated 1st ed.). Apex Publishers, 2019; ISBN 978-0-9675212-4-4. updated 2021. [Google Scholar]
- Federal Office for the Environment. Air: In brief. 2022. Available online: https://www.bafu.admin.ch/bafu/en/home/topics/air.html (accessed on 2 July 2024).
- Gerbeaud. Un Potager en Montagne. 2021. Available online: https://www.gerbeaud.com/jardin/fiches/potager-montagne,1738.html (accessed on 2 July 2024).
- Shankhwar, A.K.; Tamta, P.; Paliwal, R.; Srivastava, R.K. High Altitude Agro-ecosystems: Challenges and Opportunities. Microbiol. Adv. High. Alt. Agro-Ecosyst. Sustain. 2020, 1–13. [Google Scholar] [CrossRef]
- Sharp Electronics. Énergie Solaire. 2024. Available online: https://www.sharp.ch/fr/energie-solaire/en-savoir-plus-sur-les-panneaux-solaires (accessed on 21 June 2024).
Figure 1.
Topographic map of the Bedretto valley with the Furka railway tunnel and the Bedretto tunnel displayed in red [27,28]. Coordinates correspond to the Swiss Grid (CH1903+).
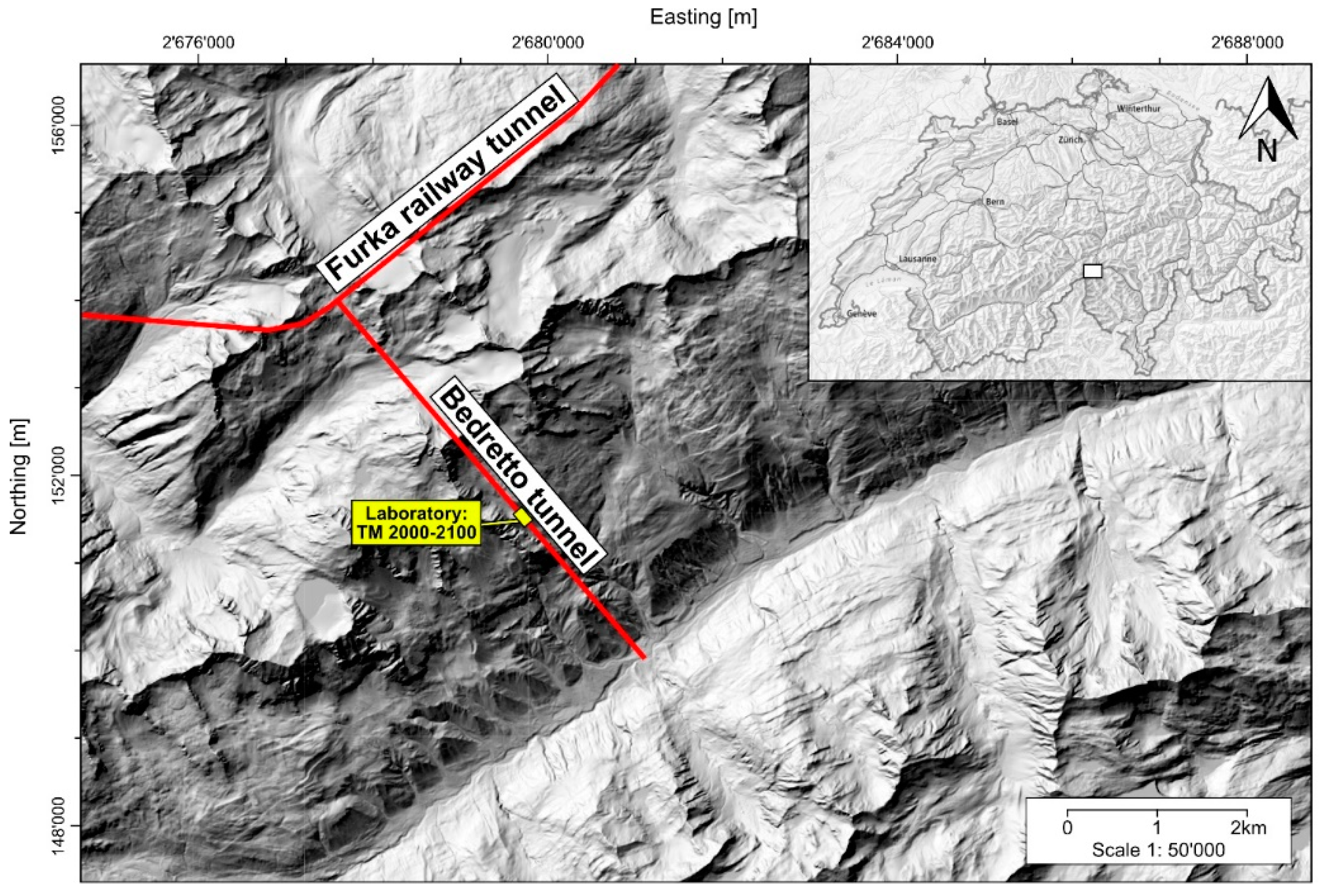
Figure 3.
Reservoir model, including the wells ST1 (injection, in blue) and ST2 (production, in orange) as well as seven main faults along with the generated mesh shown in two view angles.
Figure 3.
Reservoir model, including the wells ST1 (injection, in blue) and ST2 (production, in orange) as well as seven main faults along with the generated mesh shown in two view angles.
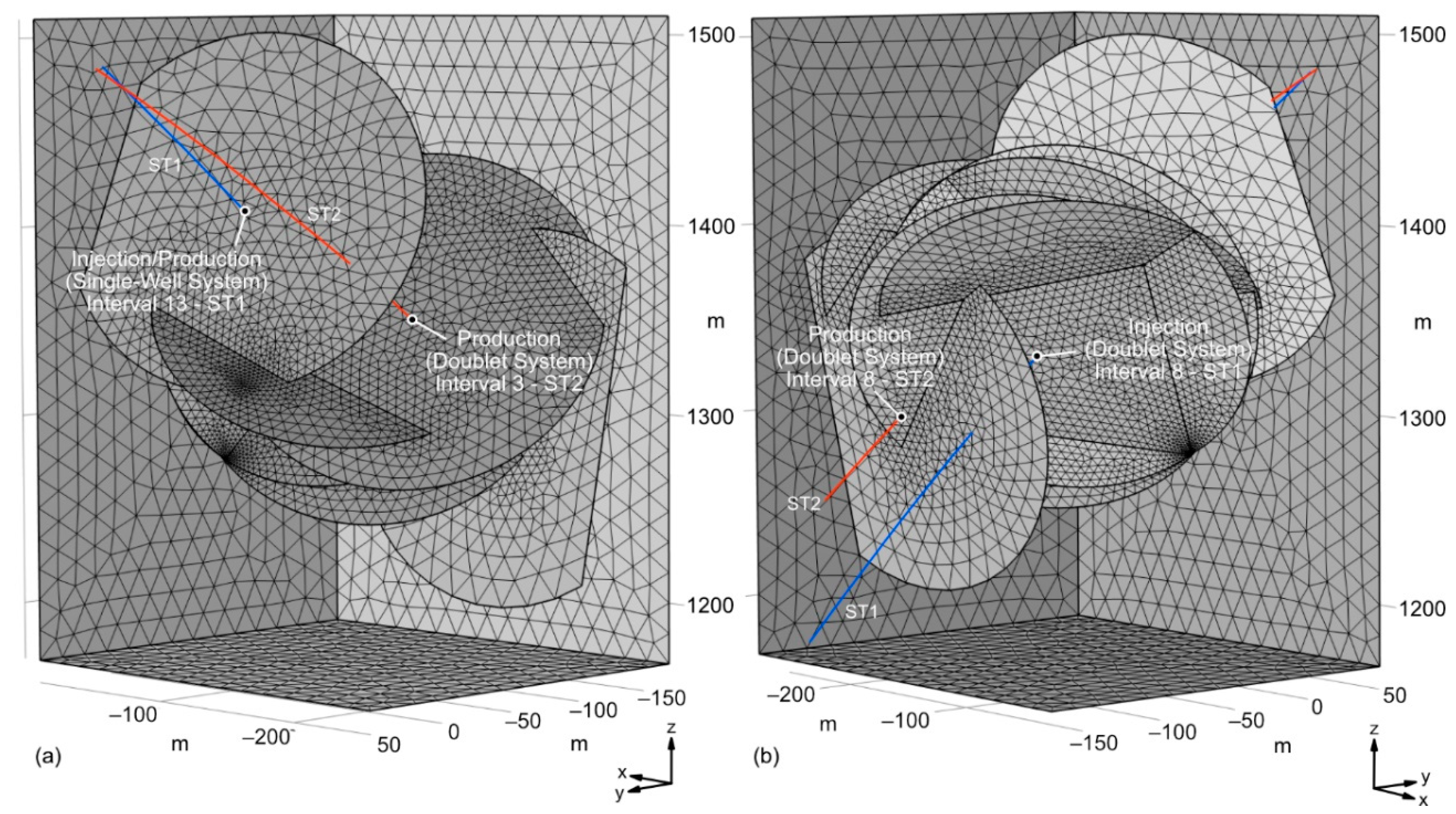
Figure 6.
Cross-sectional views of the model at the end of the fifth production phase, showing temperature diffusion in the surrounding rock, with a focus on (a) the injection point of the single-well system at y = –33 m and (b) the injection point of the doublet system at y = –79.5 m.
Figure 6.
Cross-sectional views of the model at the end of the fifth production phase, showing temperature diffusion in the surrounding rock, with a focus on (a) the injection point of the single-well system at y = –33 m and (b) the injection point of the doublet system at y = –79.5 m.
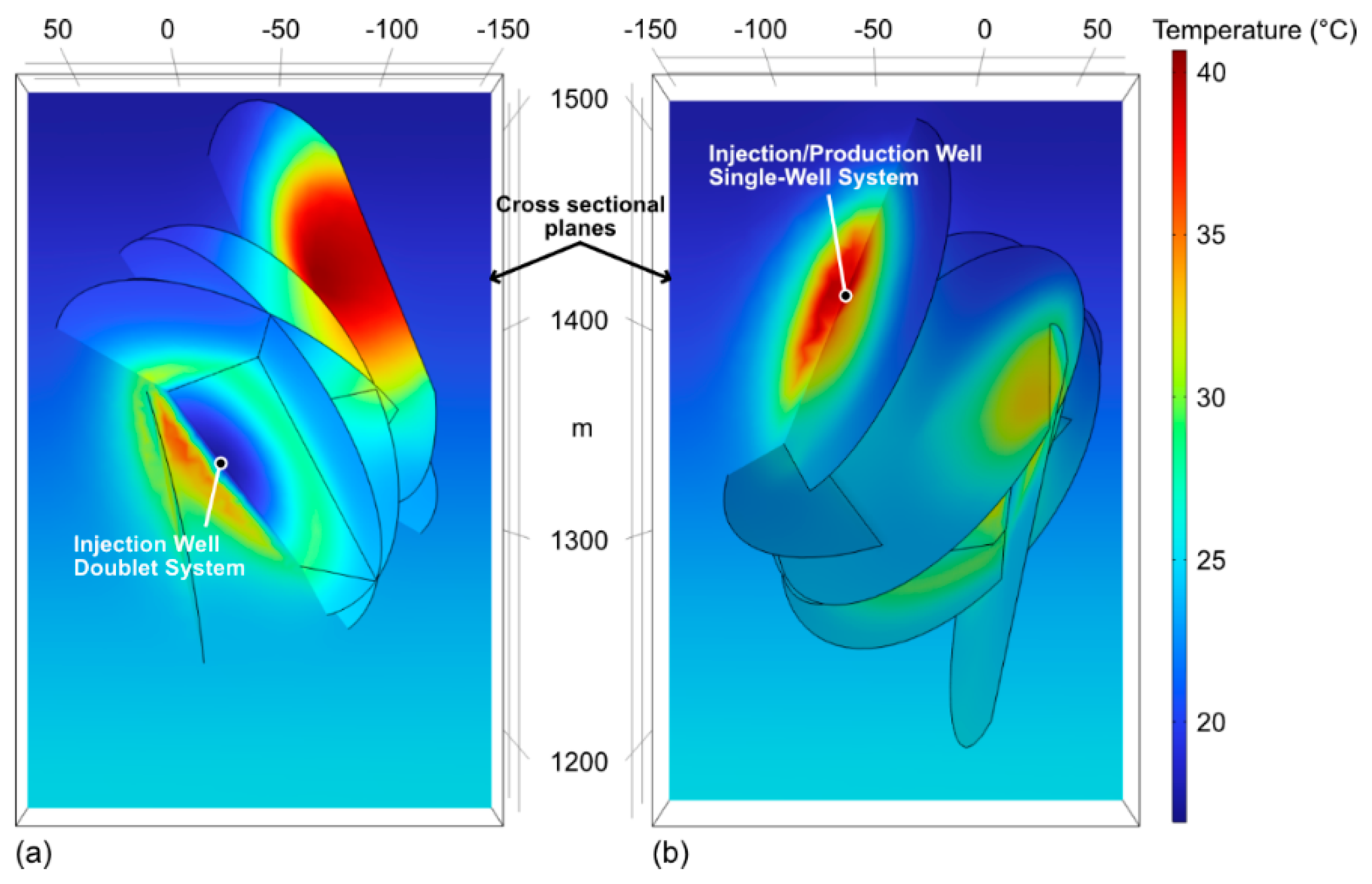
Figure 9.
Energy efficiency of the single-well system over 25 cycles at production rates of 3 kg/s, 4 kg/s, and 5 kg/s with injection temperatures of (a) 60 °C and (b) 120 °C.
Figure 9.
Energy efficiency of the single-well system over 25 cycles at production rates of 3 kg/s, 4 kg/s, and 5 kg/s with injection temperatures of (a) 60 °C and (b) 120 °C.
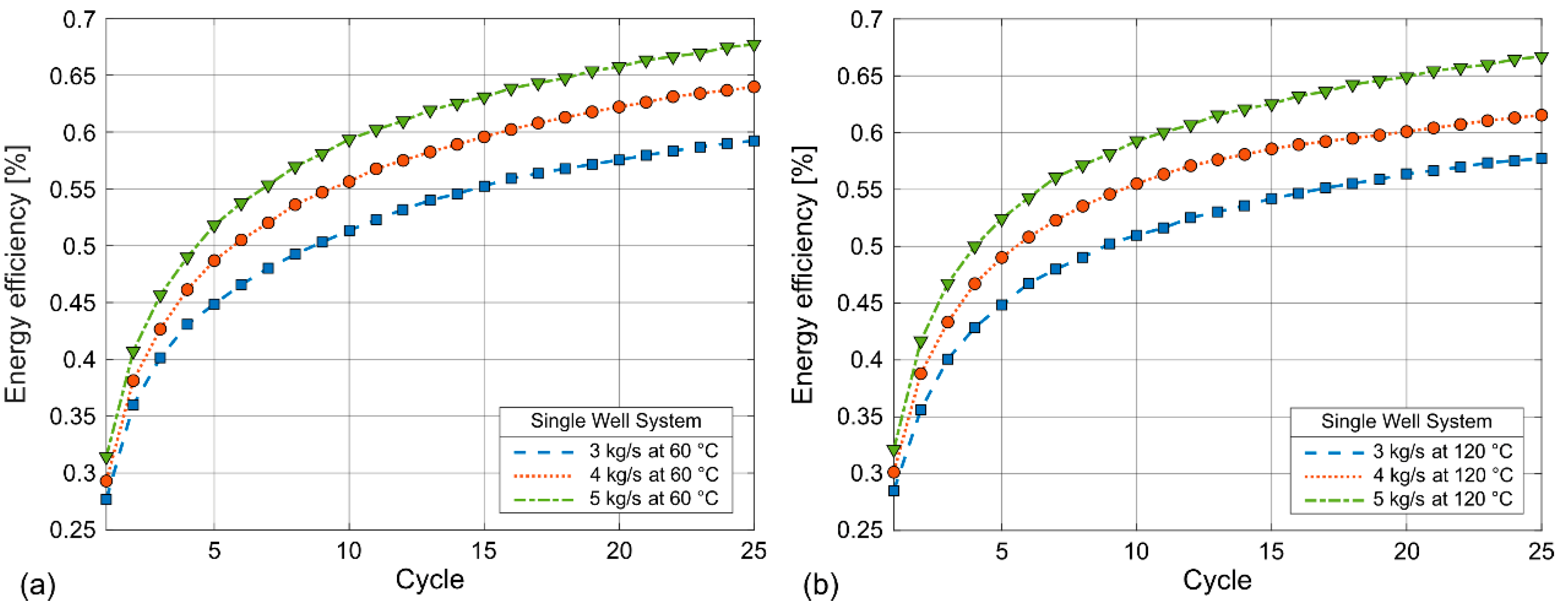
Figure 10.
Energy efficiency of the doublet system over 25 cycles at production rates of 3 kg/s, 4 kg/s, and 5 kg/s with an injection temperature of (a) 60 °C and (b) 120 °C.
Figure 10.
Energy efficiency of the doublet system over 25 cycles at production rates of 3 kg/s, 4 kg/s, and 5 kg/s with an injection temperature of (a) 60 °C and (b) 120 °C.
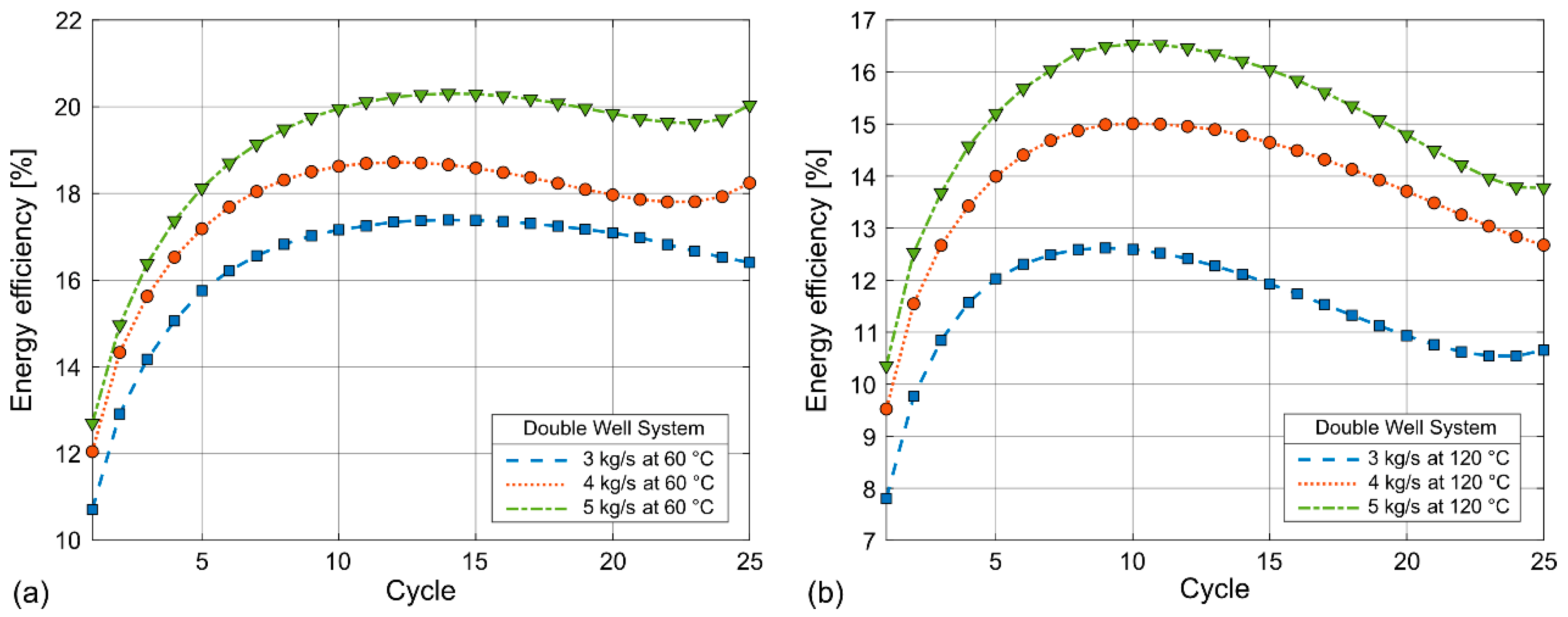
Figure 11.
Mean temperature loss of the water after its transport in insulated pipes (solid orange line) and mean delivered temperature (dashed blue line) after the transport of the water produced in buried insulated pipes to (a) the village of Bedretto (ca. 3600 m of pipe length) and (b) a hypothetical greenhouse (ca. 2200 m of pipe length) assuming a temperature of -4 °C for the outside air temperature [44].
Figure 11.
Mean temperature loss of the water after its transport in insulated pipes (solid orange line) and mean delivered temperature (dashed blue line) after the transport of the water produced in buried insulated pipes to (a) the village of Bedretto (ca. 3600 m of pipe length) and (b) a hypothetical greenhouse (ca. 2200 m of pipe length) assuming a temperature of -4 °C for the outside air temperature [44].
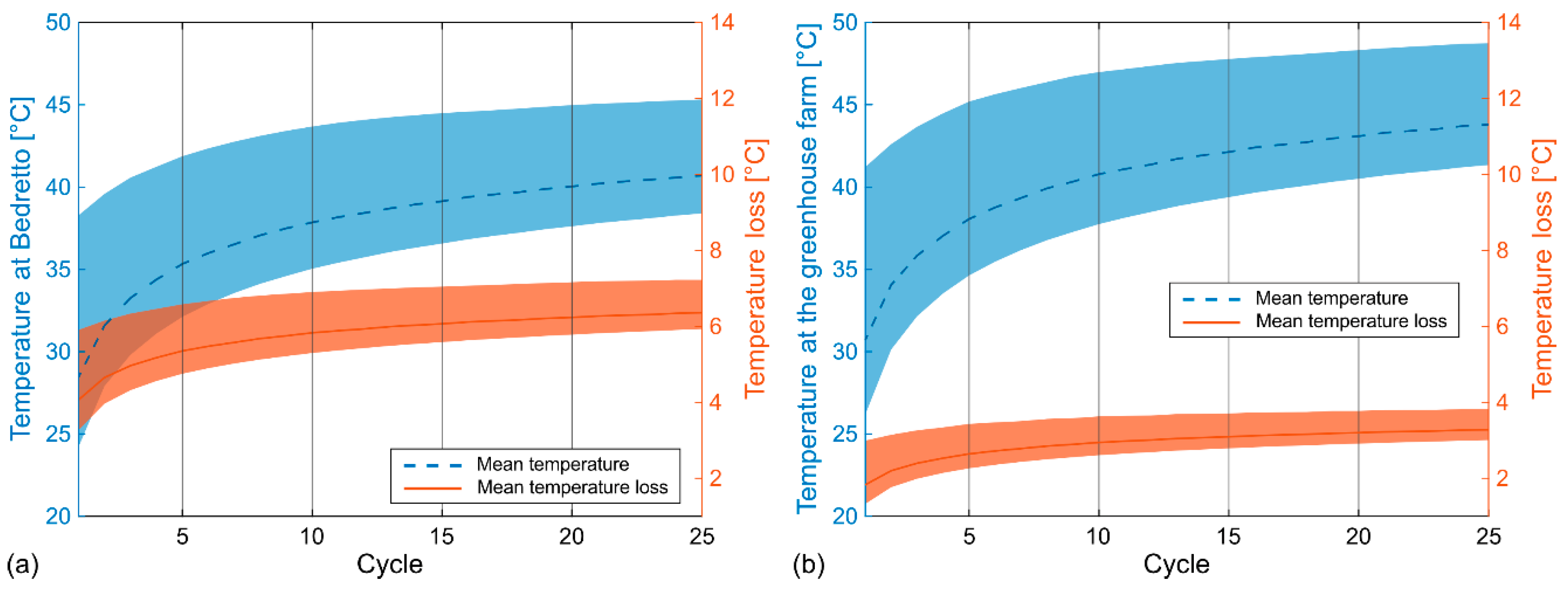
Table 2.
Parameters used for the COMSOL Multiphysics model of heat injection and storage [35,43,44,45]. The numbers in the formulas used to calculate the properties of the water were rounded to four digits for presentation purposes. For the complete numbers, refer to [35].
| Material Properties | |||
|---|---|---|---|
| Granite (Reservoir) | Faults | Water | |
| Density (kg/m3) | 2606 | 1200 | (1.0335 × 10–5 × T3) – (1.3395 × 10–2 × T2) + (4.9693 × T) + 432.2571 |
| Specific heat capacity (J/(kg×K)) | 790 | 790 | (12010.1471 – 80.4073 × T1) + (0.3099 × T2) – (5.3819 × 10–4 ×T3) + (3.6254 × 10–7 × T4) |
| Thermal conductivity (W/(m×K)) | 3 | 3 | – 0.8691 + (8.9488 × 10–3 × T1) – (1.5837 × 10–5 × T2) + (7.9754 × 10–9 × T3) |
| Dynamic viscosity (Pa×s) | - | - | 1.3780 - 0.0212 × T1 + 1.3605 × 10–4 × T2 - 4.6454 × 10–7 × T3 + 8.9043 × 10–10 × T4 - 9.0791 × 10–13 × T5 + 3.8457 × 10–16 × T6 |
| Connected porosity (%) | 1.36 | - | - |
| Total porosity (%) | 1.75 | - | - |
| Permeability (m2) | 3.64 × 10–18 | Table 1 | - |
Table 3.
Ranges of electricity prices for the single-well system and a production rate of 5 kg/s.
| Electricity costs in CHF/kWhe | |||
|---|---|---|---|
| Investment Costs | |||
| 450 kCHF | 550 kCHF | ||
| ORC engine efficiency | 3% | 0.47 | 0.55 |
| 5% | 0.25 | 0.29 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated