An Agent-Based Method for Feature Recognition and Path Optimization of CNC Machining Trajectories

In recent years, artificial intelligence technology has seen increasingly widespread application in the field of intelligent manufacturing, particularly with deep learning offering novel methods for recognizing geometric shapes with specific features. In traditional CNC machining, computer-aided manufacturing (CAM) typically generates G-code for specific machine tools based on existing models. However, the tool paths for most CNC machines consist of a series of collinear motion commands (G01), often resulting in discontinuities in the curvature of adjacent tool paths, leading to machining defects. To address these issues, this paper proposes a method for CNC system machining trajectory feature recognition and path optimization based on intelligent agents. This method employs intelligent agents to construct models, analyze the key geometric information in the G-code generated during CNC machining, and uses the MCRL deep learning model incorporating linear attention mechanisms and multiple neural networks for recognition and classification. Path optimization is then carried out using mean filtering, Bezier curve fitting, and an improved novel adaptive coati optimization algorithm (NACOA) according to the degree of unsmoothness of the path. Taking the optimization of a gear model’s process file as an example, the effectiveness of the proposed method is verified. The research results indicate that the CNC system machining trajectory feature recognition and path optimization method based on intelligent agents can significantly enhance the smoothness of CNC machining paths, reduce machining defects, and has substantial application value.

Keywords:

Subject: Engineering - Industrial and Manufacturing Engineering

1. Introduction

The rapid advancement of artificial intelligence and machine learning technologies has established CNC technology as a crucial foundation in the field of intelligent manufacturing [1]. These emerging technologies have begun to directly influence the machining process, enhancing the accuracy of CNC systems, optimizing efficiency, bolstering competitiveness and sustainability, and significantly improving the quality of the produced workpieces [2,3]. As a core technology in modern manufacturing, Numerical Control (NC) systems profoundly impact production capacity, precision, and efficiency in the industry.

In the manufacturing process of most mechanical parts, various machining features are typically involved. Traditionally, these features required manual extraction and designation through conventional CNC feature recognition methods, limiting their applicability to the analysis of simple or specific features. However, as the manufacturing industry continues to evolve and upgrade, traditional CNC systems face increasing challenges in feature recognition. The advent of deep learning technology, with its capabilities for automatic learning and feature extraction, significantly reduces the complexity and difficulty of these tasks [4]. Deep learning not only provides more precise feature recognition, benefiting from its robust data fitting and learning abilities, but it also adapts to more complex patterns and variations [5]. Its models can dynamically adjust parameters to accommodate new data or environments, a flexibility constrained in traditional CNC systems. Additionally, deep learning can process large-scale data, deriving insights from extensive datasets, enabling more accurate simulation and prediction of the manufacturing process, thereby facilitating intelligent decision-making and optimization.

Path optimization is paramount in modern manufacturing. It can substantially reduce waste, enhance efficiency and precision, thereby boosting competitiveness and sustainability. Effective path optimization minimizes ineffective reciprocation, ensures smooth and continuous machine tool movement, reduces wear and tear, extends equipment lifespan, and lowers energy consumption, achieving green manufacturing [6,7,8]. Path optimization not only enhances machining efficiency but also significantly improves product quality. By reducing excessive machine movements and conflicts, unnecessary errors are avoided, machining precision is increased, and product quality is ensured. Furthermore, path optimization can flexibly accommodate various complex machining demands, enhancing the adaptability and flexibility of the manufacturing process, making it a critical component of modern intelligent manufacturing [9].

Despite significant progress in the aforementioned research, there remains room for improvement in feature recognition accuracy and path optimization smoothness. The primary contributions of this paper are summarized as follows:

a.

Introduced an agent-based CNC system architecture, leveraging artificial intelligence technology to enhance the performance and efficiency of CNC systems.

b.

Proposed a deep neural network integrating multiple neural network models and linear attention mechanisms for improved feature recognition efficiency.

c.

Employed four mechanisms to improve the COA in order to enhance the smoothness:

Used the honey badger algorithm to initialize the coati population, enhancing the initial population quality and optimization efficiency.
Embedded information such as population size, iteration count, and fitness function into the improved path update rules, allowing the new rules to optimize the search process based on the current population status, improving convergence speed.
Introduced a dynamic multi-population strategy to comprehensively explore the search space and maintain population diversity.
Proposed a gradient descent fitness-guided strategy to dynamically adjust the learning rate, controlling the magnitude of each path point update for quicker convergence to the optimal solution.

In this study, we explore a novel method for CNC system process optimization, incorporating deep learning into CNC feature recognition and applying optimization algorithms for trajectory optimization. Our goal is to achieve automatic machining trajectory recognition and utilize artificial intelligence to make the trajectory optimization process more autonomous and intelligent, thereby enhancing the operational efficiency and precision of CNC systems to meet the rapid development needs of the manufacturing industry. This work will contribute to the advancement of CNC technology, providing new pathways for realizing more intelligent manufacturing.

The remainder of this paper is structured as follows: Section 2 provides a comprehensive review of related work on feature recognition and path optimization methods; Section 3 introduces the agent-based CNC system architecture; Section 4 presents the theory of machining feature recognition and the improved coati optimization algorithm; Section 5 showcases the experimental results of the deep learning network and path optimization; finally, Section 6 concludes the paper.

2. Related Work

In the realm of numerical control, feature recognition and path optimization are two critical technical aspects. These technologies not only play a pivotal role in enhancing machining accuracy but also significantly improve the efficiency and automation level of the machining process. Through feature recognition technology, CNC systems can automatically identify the geometric features of workpieces, thus formulating more precise machining strategies. Concurrently, path optimization technology ensures that the tool moves along the optimal path during machining, minimizing processing time and energy consumption while enhancing surface quality and machining precision. The integration of these technologies renders the CNC machining process more intelligent and efficient, effectively reducing human error and improving product quality and production stability.

2.1. Feature Recognition in CNC Machining Based on Deep Learning

In the digital age, CNC machining feature recognition technology has become increasingly important. Whether for machining parts or creating complex workpieces, it greatly enhances production efficiency and ensures product quality. This technology has profound implications in computer-aided design (CAD), computer-aided process planning (CAPP), and computer-aided manufacturing (CAM), which are critical components of modern engineering design and manufacturing. Feature recognition technology provides robust support for accomplishing these tasks. CAD systems enable users to perform complex engineering design work with the aid of computer technology. The complexity of design mainly lies in the numerous shapes and sizes of workpieces. To better accomplish the design, feature recognition technology becomes essential. By employing various advanced algorithms and artificial intelligence, it plays a crucial role in enhancing the efficiency and accuracy of the design process. Zhang et al. [10] proposed a deep learning network called BrepMFR for machining feature recognition of B-rep models, effectively handling complex geometric structures and intersecting features.

Once the design is completed, the production process must be considered, involving CAPP. This encompasses deciding material types, determining production steps, and setting machine parameters. Feature recognition technology plays a vital role in this process, enabling appropriate settings and optimization based on the features of the workpiece. Wang et al. [11] introduced a hybrid learning framework called DeepFeature, based on graph neural networks (GNN), to further enhance this aspect. After successfully recognizing all features of the workpiece, precise machining programs can be generated, optimizing the machining process, reducing costs, shortening machining time, and improving product quality. In the CAM domain, feature recognition technology can automatically transform design and process planning into actual products, truly realizing intelligent manufacturing and enabling efficient and precise production. Wu et al. [12] proposed a semi-supervised learning framework that utilizes both labeled and unlabeled data to learn meaningful visual representations, providing a powerful tool for workpiece feature recognition. These methods can enhance feature recognition efficiency, achieving automated processing, reducing production costs, and ensuring manufacturing quality.

2.2. CNC Machining Path Optimization

In contemporary manufacturing, the importance of optimizing CNC machining paths has become increasingly prominent. Tool path optimization technology can significantly enhance machining efficiency, reduce production costs, and improve product quality. The initial machining paths generated by CAD/CAM systems through automatic programming are based on design models and predetermined machining strategies, forming G-code. However, in practical application, this process may produce errors. The computational accuracy of CAD/CAM systems may be somewhat limited by current hardware and software conditions, resulting in initial tool paths that suffer from overfitting or lack smoothness. These factors may cause the machine to stop and restart abruptly during operation, increasing wear and tear and reducing its lifespan. Discontinuous tool paths can also affect machining precision, leading to unstable product quality. Fang et al. [13] proposed a real-time smooth trajectory algorithm, genera-smooth, ensuring higher-order continuity of tool trajectories in three-axis hybrid machining. This algorithm can address initial path discontinuities to some extent, enhancing machine stability.

Regarding the continuity of mixed G01 and G02/G03 codes, Shi et al. [14] introduced a comprehensive tool path smoothing method based on a motion overlap strategy, employing heuristic algorithms to seek optimal motion parameters, thereby meeting the requirements of mixed coding motion constraints and high efficiency. For particularly complex three-dimensional models, CAD/CAM systems may struggle to find an optimal solution when generating initial machining paths. In such cases, G-code generation might encounter issues like discontinuities or excessive spacing at corners, causing severe vibrations when the machine makes sharp turns, impacting machining precision and efficiency. Hua et al. [15] offered an effective solution by proposing a method that adjusts tool tip positions based on the discrete curvature of each tip point, reducing vibration at tool tip corners. Zhang et al. [16] presented an adaptive tool path generation method using a dual-head snake algorithm based on the least squares method to study the original part contours and generate smooth trajectories composed of lines and arcs. This method also demonstrated excellent performance in reducing machine vibration and improving precision and efficiency.

The aforementioned research effectively addresses the issue of path discontinuities, ensuring smoother tool movement during machining, reducing machine vibration during sharp turns, and thereby enhancing machining precision and efficiency.

3. Agent-Based CNC System Architecture

In recent years, with the continuous development of the manufacturing industry, CNC machining technology has played a crucial role in enhancing production efficiency and machining precision. However, traditional CNC path planning methods often rely on preset rules and algorithms, which struggle to adapt to complex and dynamic machining environments. To address this issue, an agent-based CNC system architecture has been proposed, encompassing the modeling and driving of intelligent CNC. This includes the digital twin of intelligent CNC and machine tool machining, considering the application of deep learning technology in feature recognition and path optimization within CNC machining, providing practical references for achieving intelligent CNC.

3.1. Intelligent Requirements

Intelligent manufacturing systems achieve optimal manufacturing outcomes by integrating the capabilities of machines, humans, and processes, optimizing the use of manufacturing resources, adding value to people’s lives and careers, and reducing waste. Thus, intelligent manufacturing systems hold significant importance in modern societal development [17]. CNC systems, as the core component of CNC technology, play a vital role in CNC machining. Intelligent CNC systems offer higher programmability and flexibility, significantly improving manufacturing quality and efficiency [18]. CNC machines control the movement and machining processes of machine tools through CNC systems, executing automated machining based on pre-written program instructions.

The servo system is a critical part of CNC machines, comprising servo motors, drivers, and feedback devices. It is crucial for coordinating the trajectory accuracy between multiple feed axes and ensuring contour precision [19]. Digital twin technology is a potential solution for enhancing automation and advancing towards intelligent manufacturing [20]. By utilizing data collected from sensors, digital twin technology can monitor the operational status of CNC machines and servo systems in real-time and generate their real-time digital models. Feature recognition is a key issue in intelligent manufacturing, enabling the extraction of valuable geometric information from solid models, thus achieving seamless digital connectivity from design to manufacturing [11]. For identified defective paths, optimization algorithms are employed to enhance the path quality.

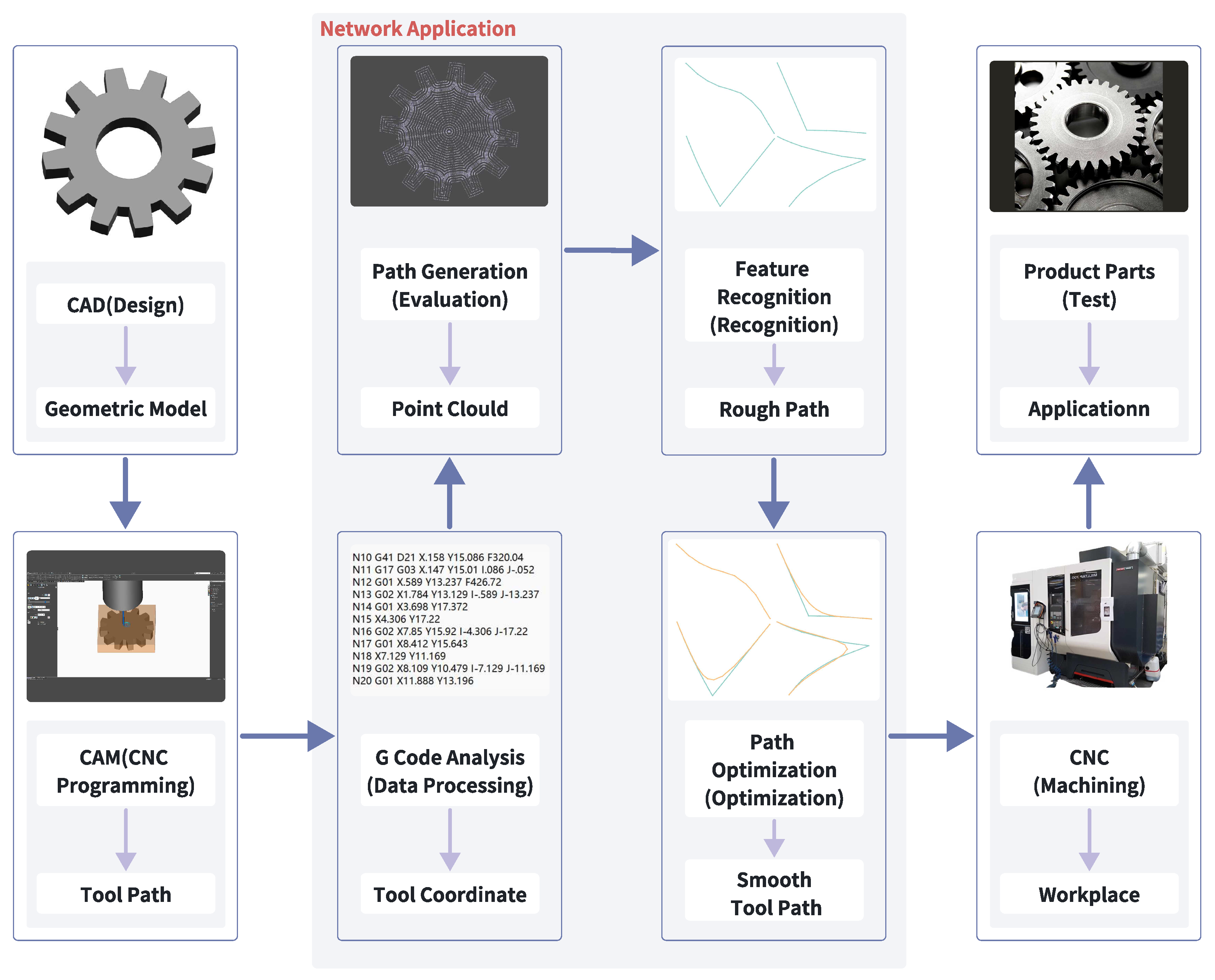
In traditional manufacturing modes, design and manufacturing are separate, with tool path defects only fed back after manufacturing flaws are detected, requiring extensive effort to adjust and redesign the model. This paper proposes a new workflow, as shown in Figure 1. The red dashed box indicates the newly added workflow. After the CAM system generates the initial tool trajectory, feature recognition and optimization are performed to generate high-quality, smooth paths for subsequent manufacturing.

3.2. System Model and Structure

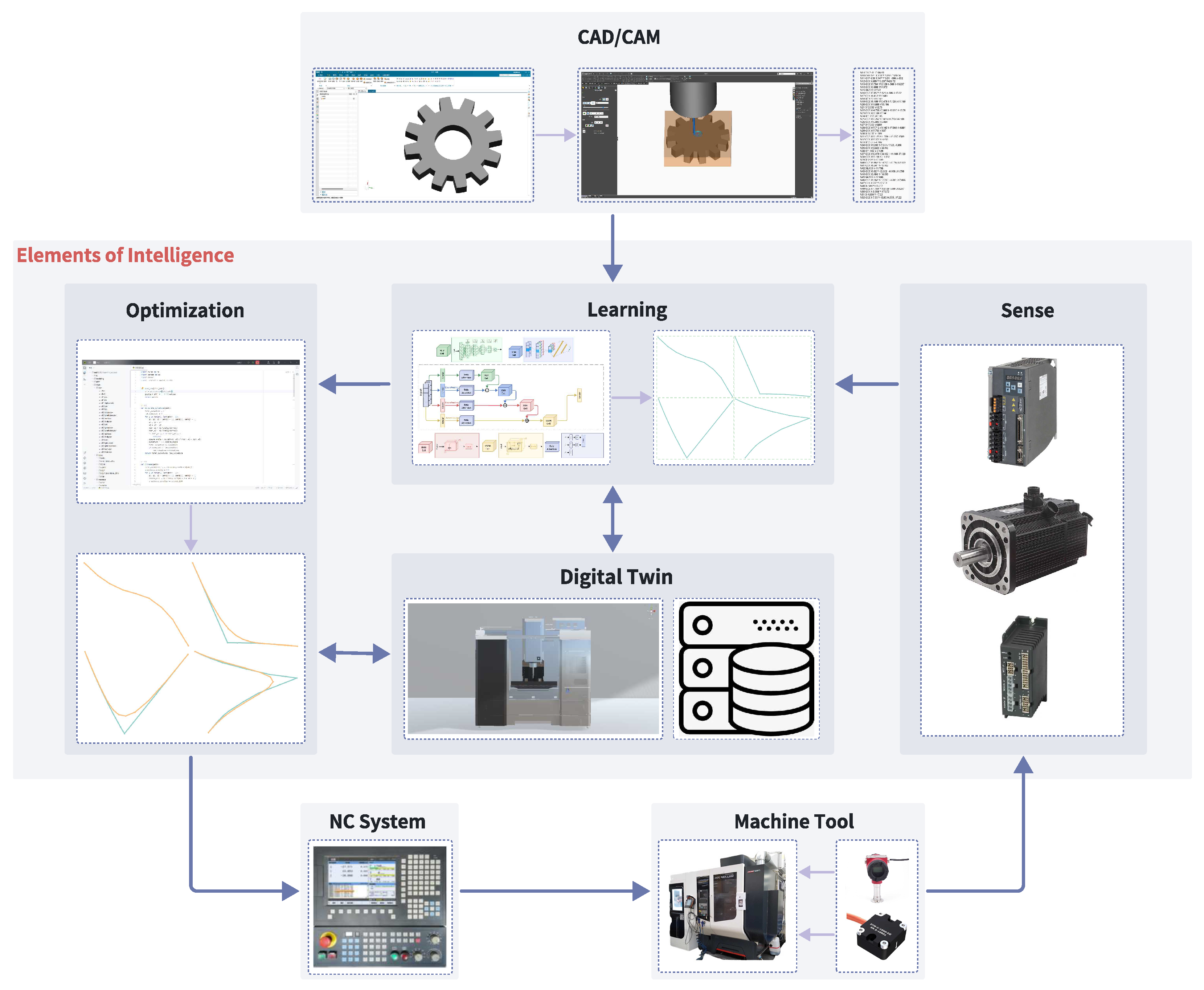
A modular structure plays a critical role in the design of CNC systems. The synergy between various intelligent components across modules fosters a dynamic environment for learning and self-optimization, as illustrated in Figure 2. The intelligent elements include:

CAD/CAM: The process of design and manufacturing using computer software. This is the input part of the intelligent system, providing design data and manufacturing instructions.
Learning: Extracting useful information from data to optimize models and manufacturing processes.
Digital Twin: Providing a virtual environment for testing and optimization, enhancing efficiency and precision.
Sense: Monitoring various parameters during the manufacturing process, providing real-time feedback to the digital twin and optimization modules.
Optimization: The process of optimizing system performance based on learning and sensing data, reducing resource consumption, and refining manufacturing processes.
NC System and Machine Tool: Receiving instructions from the optimization module and performing machining and manufacturing according to CNC system directives.

The intelligent CNC model encompasses the entire process from model design to final mechanical processing, including real-time feedback. This model begins with CAD/CAM software, which is crucial in both the design and manufacturing stages. Achieving the required precision and surface quality is mainly addressed by selecting tool path density and appropriate cutting conditions. However, these measures are not always sufficient, and even with optimal choices, surface quality and precision often decline [14]. By utilizing deep learning technology for feature extraction and pattern recognition, a seamless digital connection from design to manufacturing can be established based on the concept of features [21]. The optimization stage is a critical link in the entire process, focusing on optimizing the process flow based on data analyzed by the learning module. For identified rough paths, further calculations and adjustments through optimization algorithms are necessary to enhance path efficiency and precision. To achieve smooth and continuous machine motion, local corners must be smoothed to ensure the continuity and smoothness of the machining path [6]. Digital twins represent virtual replicas of the physical manufacturing environment, providing new opportunities for real-time monitoring of the machining process. They can simulate the actual production environment while considering changes in the machining process and operating conditions [22]. This enables testing and validation in a virtual environment, thereby reducing risks in actual production.

The sensing module involves sensors and other devices that collect real-time data from physical machines, monitoring various parameters in the production process and feeding data back to the system. The CNC system, as the brain of the machine tool [23], needs to control the machine based on inputs from the optimization and sensing modules to achieve precise control of the machine tool. The machine tool, being the physical apparatus that performs manufacturing tasks, plays a critical role in manufacturing as its performance significantly impacts product quality and production efficiency [24]. Hence, intelligent modules need to be added to facilitate communication. The information flow process begins with CAD/CAM design, inputting the design into the learning module, which processes the data and inputs it into the optimization module. The optimization module communicates with the digital twin for simulation and validation processes, and the digital twin returns data to the learning module for further optimization. The sensing module collects real-time data from physical machines and sends it to the digital twin and learning module. The optimized and validated process is sent to the NC system, which controls the machine tool to execute manufacturing tasks, and the data from the machine tool is collected and fed back by the sensing module, completing the feedback loop.

The proposed system model demonstrates the interaction and data flow among various components in an intelligent manufacturing system, emphasizing a continuous loop of learning, optimization, and real-time feedback to improve manufacturing processes. Through this closed-loop system, the manufacturing process becomes more intelligent, automated, and efficient, thereby enhancing production quality and efficiency while reducing costs and risks.

3.3. Assembly Line Work Mode

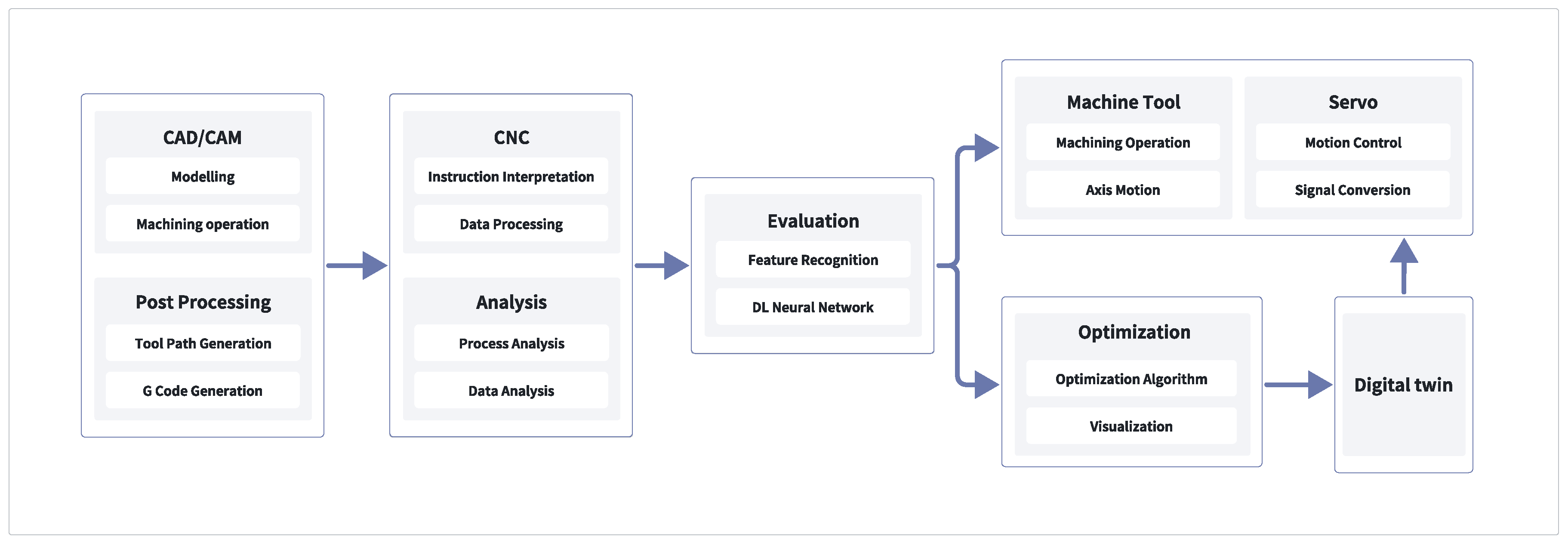
In this study, the design of the intelligent agent module revolves around the CNC system processing workflow, as illustrated in Figure 3. The intelligent agent module acts as a critical node in the integrated processing chain of the CNC system, facilitating information transmission and processing, thereby achieving more efficient and precise perception and control of the machining process. Manufacturing activities start from the CAD/CAM design stage, including modeling and CNC machining. Next is the post-processing stage, involving tool path generation and G-code generation. Subsequently, the CNC system receives these instructions and performs instruction interpretation and data processing. At this stage, process and data analysis are also conducted.

To evaluate the machining process, this study employs feature recognition technology based on deep learning neural networks to analyze and assess the results. The optimization stage utilizes optimization algorithms and visualization tools to improve the machining process, ensuring operational efficiency and precision. The process then moves into the servo control and machine tool machining stage, where actual machining operations and axis movements occur, along with motion control and signal conversion. Digital twin technology is used for feedback and improvement of the entire process, dynamically adapting to the actual machining requirements and conditions by combining virtual and real elements, thus achieving comprehensive monitoring and optimization of the machining process. This information flow is not unidirectional but aids in the dynamic adaptation of the system, better aligning with actual machining requirements and conditions.

4. Mathematical Model

In this section, the feature design of machining trajectories and the fundamental procedure of the improved COA are introduced.

4.1. Machining Path Feature Design

By analyzing the physical characteristics of the control system’s machining paths, feature extraction and recognition are performed for paths exhibiting uneven smoothness. The features of the machining paths are defined as follows:

A path consists of a series of coordinates

(x_{i}, y_{i})

. Given that the contribution of the z-axis coordinates is minimal, the path is identified using its two-dimensional coordinates. For each point i on the path, define the direction vector

v_{i}

as the vector from point i to point

i + 1

v_{i} = (x_{i + 1} - x_{i}, y_{i + 1} - y_{i})

The dot product of two vectors

v_{i}

and

v_{i - 1}

is defined by Eq. (1):

v_{i} \cdot v_{i - 1} = (x_{i + 1} - x_{i}) (x_{i} - x_{i - 1}) + (y_{i + 1} - y_{i}) (y_{i} - y_{i - 1})

(1)

The Euclidean length of vector

v_{i}

is defined by Eq. (2):

| v_{i} | = \sqrt{{(x_{i + 1} - x_{i})}^{2} + {(y_{i + 1} - y_{i})}^{2}}

(2)

The local curvature is defined as the sum of the curvatures for all vectors from the first point to the nth point, as given by Eq. (3):

LocalCurvature = \sum_{i = 1}^{n - 2} (1 - \frac{v_{i} \cdot v_{i - 1}}{| v_{i} | | v_{i - 1} |})

(3)

Where:

$v_{i} \cdot v_{i - 1}$ is the dot product of vectors $v_{i}$ and $v_{i - 1}$ .
$| v_{i} |$ and $| v_{i - 1} |$ are the Euclidean lengths of vectors $v_{i}$ and $v_{i - 1}$ respectively.

This calculation reflects the changes in curvature by computing the real angle between adjacent vectors. When the dot product

v_{i} \cdot v_{i - 1}

is normalized by the product of their Euclidean lengths, the curvature is reduced if the vectors are closely aligned. By summing the deviations between adjacent vectors, the overall path roughness can be quantified. Therefore, a higher LocalCurvature value indicates a rougher path composed of n points; conversely, a lower value indicates a smoother path.

In view of the degree of path fluctuation, when

n = 50

, the LocalCurvature values are classified, as shown in Table 1.

After completing feature classification, these feature points and their labels are used to train a hybrid network model incorporating parallel branches of MLP, CNN, RNN, and LSTM, to automatically identify features in new, unlabeled samples. This model learns to recognize the smoothness of paths from the input coordinates. The workflow for machining path feature recognition is detailed in Algorithm 1.

Algorithm 1

Require: A: A set of points {a₁, a₂,…, a_n}, where a_i = (x_i, y_i);

Ensure: LabelPath: A path with a feature label;

The point set A is grouped into groups of 50 points and stored in the Group list: [g₁, g₂, …, g_n], where g_i = [p₁, p₂, …, p₅₀], p_i = (x_i, y_i);

for each group g in Group do

for each point p in g do

Generate initial set of vectors V_i: {v₁, v₂, …, v₉}, where v_i = (x_i+1 − x_i, y_i+1 − y_i);

Compute the local curvature of V_i:

LocalCurvature = \sum_{i = 2}^{49} (1 - \frac{v_{i} \cdot v_{i - 1}}{| v_{i} | | v_{i - 1} |})

;

if LocalCurvature ≤ 1.9 then

Label V_i as "Category 1";

else if 1.9 < LocalCurvature < 3.5 then

Label V_i as "Category 2";

else if 3.5 < LocalCurvature < 7.6 then

Label V_i as "Category 3";

else

Label V_i as "Category 4";

end if

end for

LabelPath = {all labeled path from steps 17 and 18};

LabelPath was used to train the MCRL model;

return LabelPath

4.2. Path Optimization Design

The Coati Optimization Algorithm (COA) [25] is a biomimetic algorithm inspired by the foraging behavior of South American coatis. During their foraging, coatis mark their paths using visual and olfactory cues, and share location information. These markers fade over time, but their concentration remains higher on shorter paths. Thus, the coati group can detect these markers and select an optimal path, moving towards areas with stronger signals.

This section proposes four mechanisms to overcome the shortcomings of the traditional coati algorithm. Firstly, the Honey Badger Algorithm (HBA) is introduced to initialize the coati population, enhancing optimization efficiency by increasing population diversity. Secondly, an improved heuristic function is proposed to enhance the algorithm’s goal orientation, effectively reducing randomness in the search. Thirdly, a dynamic multi-population strategy is introduced to prevent the algorithm from falling into local optima, thereby enhancing global search capabilities. Finally, a gradient descent fitness-guided strategy is proposed to accelerate convergence. These four mechanisms are combined to form a new algorithm, referred to as the Novel Adaptive Coati Optimization Algorithm (NACOA).

4.2.1. Honey Badger Algorithm for Population Initialization

The initialization of the coati population may have several shortcomings: despite optimizing the selection process, the quality of the initial population may be influenced by the initial input data and parameter settings, leading to unstable results. If the individuals in the initial dataset exhibit limited genetic diversity, the algorithm may struggle to overcome this limitation, ultimately resulting in insufficient genetic diversity within the population. The algorithm’s effectiveness depends on high-quality, comprehensive initial data. If the data is inaccurate or incomplete, it may affect the algorithm’s performance and the effectiveness of population initialization.

To address these issues, the Honey Badger Algorithm (HBA) [26] is used to initialize the coati population. This algorithm mimics the search and hunting behavior of honey badgers, optimizing individual selection and distribution strategies to ensure that the population consists of highly adaptable and survivable individuals. The HBA has a dynamic adjustment capability, allowing it to continuously optimize initialization strategies based on the actual population situation, adapting to changes in different environments and conditions.

Moreover, the HBA has high computational efficiency, enabling it to find optimal solutions in a relatively short time, thereby reducing human intervention and decision-making time. By automating selection and optimization processes, the algorithm reduces human bias and errors, enhancing the scientific rigor and rationality of population initialization. The HBA can also simulate individual adaptability under different environmental conditions, helping to select individuals best suited to new environments, thus improving the overall adaptability of the population.

The basic process of generating the coati initialization population using the Honey Badger Algorithm is as follows:

a. Initialization phase

Generate an initial HBA population and optimize it to obtain a more optimal initial population.

i. Generate initial honey badger population

A two-dimensional point set path = ${P_{1}, P_{2}, \dots, P_{n}}$ represents a set of points on the path, where $P_{i} = (x_{i}, y_{i})$ .
Set the start and end points: $s t a r t_p o i n t = P_{1}$ , $e n d_p o i n t = P_{n}$ .
Randomly insert points: Randomly select the remaining points and randomly insert them into a certain position on the path until all points are inserted.

ii. Initialize each individual $p_{k}$ in the population

$p_{k} = {P_{1}, P_{k, 2}, P_{k, 3}, \dots, P_{k, n - 1}, P_{n}}$ , where ${P_{k, 2}, P_{k, 3}, \dots, P_{k, n - 1}}$ are random permutations of ${P_{2}, P_{3}, \dots, P_{n - 1}}$ , and the population size is $p o p_s i z e = N$ .

b. Defining intensity

Define the intensity

I_{i}

as in Eq. (4).

\{\begin{matrix} I_{i} = r_{1} \times \frac{S}{4 π d_{i}^{2}} \\ S = |p_{k} [i + 1] - p_{k} [i]| \\ d_{i} = |g_{b e s t} [i] - p_{k} [i]| \end{matrix}

(4)

where:

$r_{1}$ is a random number, uniformly distributed in (0,1).
S is the intensity.
$p_{k} [i]$ is the i-th point of individual k.
$g_{b e s t} [i]$ is the i-th point of the global best position.
$d_{i}$ represents the distance between the global best position and the current point.

c. Simulation of honey badger foraging behavior

The process of updating positions is divided into two parts: the "digging phase" and the "foraging phase," as shown in Eq. (5):

p_{k} {[i]}^{'} = \{\begin{matrix} g_{best} [i] + β \times I \times g_{best} [i] + r_{2} \times α_{1} \times d_{i} \times |cos (2 π r_{3}) \times [1 - cos (2 π r_{4})]| & if r_{6} \leq 0.5 \\ g_{best} [i] + r_{5} \times α_{1} \times d_{i} & else \end{matrix}

(5)

where:

$α_{1}$ is a constant.
$β$ is a constant indicating the honey badger’s ability to obtain food.
$p_{k} {[i]}^{'}$ represents the updated position.
$r_{2}, r_{3}, r_{4}, r_{5}, r_{6}$ are random numbers between 0 and 1.

d. Fitness function

i. Curvature calculation

Calculate the curvature of every three adjacent points as in Eq. (6).

c u r v a t u r e_{i} = 1 - \frac{v_{i} \cdot v_{i - 1}}{|v_{i}| |v_{i - 1}|}

(6)

where:

v_{i} = (x_{i + 1} - x_{i}, y_{i + 1} - y_{i})

The total curvature is given by Eq. (7).

L o c a l C u r v a t u r e = \sum_{i = 2}^{n - 1} c u r v a t u r e_{i}

(7)

ii. Smoothness penalty

The smoothness penalty is given by Eq. (8).

S m o o t h n e s s P e n a l t y = \sum_{i = 2}^{n - 1} s e c o n d_d i f f_{i}

(8)

where the second difference

s e c o n d_d i f f_{i}

is calculated by Eq. (9):

s e c o n d_d i f f_{i} = | | P_{i + 1} - 2 P_{i} + P_{i - 1} | | = \sqrt{{(x_{i + 1} - 2 x_{i} + x_{i - 1})}^{2} + {(y_{i + 1} - 2 y_{i} + y_{i - 1})}^{2}}

(9)

iii. Fitness function

The fitness function is given by Eq. (10).

F i t n e s s (p_{k}) = L o c a l C u r v a t u r e + S m o o t h n e s s P e n a l t y

(10)

e. Updating the honey badger population

Iteratively update each individual in the population, searching for better paths. In each iteration, update the paths and calculate their fitness to find the current best path. The update rule is given by Eq. (11).

g_{b e s t} = arg min_{p_{k} \in p o p u l a t i o n} F i t n e s s (p_{k}) over generations

(11)

f. Initialization of COA population

Use the population generated by HBA as the initial population for COA.

Through the above steps, the HBA can effectively enhance the quality and efficiency of the initial population.

4.2.2. Enhanced Path Update Rule

In the Bat Algorithm, the fixed parameter

α_{2}

cannot adapt dynamically during the search process, resulting in the inability to balance between global and local searches to find the optimal solution. This might lead to a decline in search efficiency. Therefore, we adopt

α_{2}

r_{7}

, and

r_{8}

to balance the global and local search, as illustrated in Eq (12):

p_{k} {[i]}^{'} = p_{k} [i] + α_{2} \cdot r_{7} \cdot (g_{best} [i] - p_{k} [i]) + α_{2} \cdot r_{8} \cdot (rand - 0.5)

(12)

where

α_{2}

is shown in Eq. (13):

α_{2} = α_{\max} - (α_{\max} - α_{\min}) \cdot \frac{g}{G}

(13)

where:

$α_{\max}$ is the initial maximum value of $α_{2}$ .
$α_{\min}$ is the minimum value of $α_{2}$ .
g is the current iteration number, incrementing from 1 to G.
G is the total number of iterations in the algorithm.

r_{7}, r_{8}

, population fitness standard deviation std_dev, and average population fitness

\bar{F}

are defined as shown in Eq. (14):

\{\begin{matrix} r_{7} = rand \cdot (1 + \frac{std_dev}{\bar{F}}) \\ r_{8} = rand \cdot (1 + \frac{std_dev}{\bar{F}}) \\ std_dev = \sqrt{\frac{1}{N} \sum_{k = 1}^{N} {(Fitness (p_{k}) - \bar{F})}^{2}} \\ \bar{F} = \frac{1}{N} \sum_{k = 1}^{N} Fitness (p_{k}) \end{matrix}

(14)

In the early stages of the algorithm, a higher adaptive

α_{2}

encourages extensive exploration, covering a broader search space and aiding in escaping local optima. As the algorithm progresses,

α_{2}

gradually decreases, promoting fine-tuned exploitation and assisting in converging to the optimal solution. The adaptive

α_{2}

enhances the flexibility and precision of the search, leading to higher solution quality, closer approximation to the global optimum, and faster convergence.

By employing standard deviation-based adjustments for

r_{7}

and

r_{8}

, the current population’s state can be leveraged to optimize the search process. In regions with higher fitness, the search efficiency increases, accelerating convergence and reducing the iterations needed to reach the optimal solution. In areas of lower diversity, random perturbations help avoid local optima, improving the likelihood of discovering the global optimum.

4.2.3. Dynamic Multi-Population Strategy

In the Bat Algorithm, as individuals converge prematurely near local optima, the population may lack diversity, making it difficult to find the global optimum. A single population strategy can lose balance between exploration (searching new solutions) and exploitation (using known good solutions), resulting in a limited search space. Hence, employing a dynamic multi-population strategy can enhance the optimization process by dividing the population into multiple sub-populations. Each sub-population searches in different areas, increasing the probability of finding the global optimum.

a. Multi-Population Initialization

Divide the population into

M_{0}

sub-populations, each containing

N_{g}

individuals:

population = {{sub_pop}_{1}, {sub_pop}_{2}, \dots, {sub_pop}_{M_{0}}}

where

{sub_pop}_{a}

represents the a-th sub-population, the total population size is N, and the size of each sub-population

{sub_pop}_{a}

is given by Eq. (15):

N_{g} = \frac{N}{M_{0}}

(15)

b. Updating Sub-Population Size

In generation g, dynamically adjust the current sub-population size

M_{g}

using the adjustment rule in Eq. (16):

M_{g} = max (M_{min}, min (M_{max}, M_{0} - ⌊\frac{g \cdot (M_{0} - M_{min})}{G}⌋))

(16)

where:

$M_{\min}$ : Minimum sub-population size
$M_{\max}$ : Maximum sub-population size

c. Selection of the Optimal Individual

Within each sub-population

{sub_pop}_{a}

, identify the individual with the minimum fitness value, as expressed in Eq. (17):

p_{{best}_{a}} = min_{p_{k} \in {sub_pop}_{a}} Fitness (p_{k})

(17)

The global optimal individual is denoted by Eq. (18):

g_{best} = min_{a \in {1, \dots, M_{0}}} p_{{best}_{a}}

(18)

d. Individual Exchange Strategy

Every T iterations, perform an exchange of individuals between sub-populations. Let

p_{k}

and

p_{t}

be individuals randomly chosen from sub-populations

{sub_pop}_{a}

and

{sub_pop}_{b}

, respectively. The exchange rule is illustrated in Eq. (19):

\{\begin{matrix} {sub_pop}_{a} = {sub_pop}_{a} \cup {p_{t}} ∖ {p_{k}} \\ {sub_pop}_{b} = {sub_pop}_{b} \cup {p_{k}} ∖ {p_{t}} \end{matrix}

(19)

In the early stages of the algorithm, the number of sub-populations is approximately

M_{0} = 10

, each with a size of

\frac{N}{M_{0}} = 100

individuals. This larger number of sub-populations maintains diversity and helps to explore a broader search space, thus preventing premature convergence to local optima. During the middle stages, the number of sub-populations gradually decreases to approximately

M_{g} = 6

, each with a size of

\frac{N}{6} \approx 167

individuals. As the number of sub-populations decreases, the search transitions to a more focused phase, balancing exploration and exploitation. Adjusting the sub-population size dynamically based on iterations ensures that the algorithm can efficiently search in appropriate regions, enhancing flexibility and reducing the risk of local optima entrapment through inter-sub-population exchanges every

T = 10

iterations. In the final stages, the number of sub-populations decreases to

M_{\min} = 2

, each with a size of

\frac{N}{2} = 500

, concentrating on fine-tuning the optimal solutions, thereby improving the final solution quality.

4.2.4. Gradient Descent-Based Adaptive Guidance Strategy

In the Bat Algorithm, the optimization process relies heavily on global search and random perturbations. This broad search in the solution space may slow down the convergence rate due to a lack of precise local tuning, ultimately leading to suboptimal solutions in complex solution spaces. To address this issue, a gradient descent-based adaptive guidance strategy can be employed. This approach utilizes gradient information for fine-tuning local adjustments, swiftly steering the search towards the optimal solution. The strategy provides directional information, guiding how to adjust points on the path, reducing both total curvature and gradient penalties, thus avoiding local optima and enhancing optimization precision. Compared to random perturbations, this directional adjustment reduces unnecessary searches, accelerating convergence. The gradient descent-based adaptive guidance strategy smooths out the optimization process through continuous small-scale adjustments, mitigating the disruptive effects of large random perturbations.

a. Fitness Function

For each point

P_{k, i}

on the path of

p_{k}

, we define the fitness function

Fitness (p_{k})

, which incorporates both curvature and smoothness penalties, as shown in Eq. (20):

Fitness (p_{k}) = \sum_{i = 2}^{n - 1} {curvature}_{i} + {second_diff}_{i}

(20)

b. Gradient Calculation

To minimize the cost function

Fitness (p_{k} [i])

, we need to compute its gradient. We can calculate the gradient of the curvature,

{curvature}_{i}

, and the gradient penalty,

{second_diff}_{i}

, for this purpose.

i. Gradient of the Curvature

First, we need to compute the gradients of

v_{i - 1}

and

v_{i}

, and then use the chain rule to determine the gradient of the curvature, as shown in Eq. (21):

\nabla {curvature}_{i} = \frac{\partial {curvature}_{i}}{\partial P_{k, i}} = \frac{\partial (1 - cos (θ_{i}))}{\partial P_{k, i}} = - \frac{\partial cos (θ_{i})}{\partial P_{k, i}}

(21)

where the partial derivative of

cos (θ_{i})

with respect to

P_{k, i}

is given by Eq. (22):

\frac{\partial cos (θ_{i})}{\partial P_{k, i}} = \frac{\partial (\frac{v_{i - 1} \cdot v_{i}}{∥ v_{i - 1} ∥ ∥ v_{i} ∥})}{\partial P_{k, i}}

(22)

Due to the complexity of the calculation, we approximate the gradient numerically using the central difference formula in Eq. (23):

\nabla {curvature}_{i} \approx \frac{curvature (P_{k, i} + ϵ) - curvature (P_{k, i} - ϵ)}{2 ϵ}

(23)

where

ϵ \in (10^{- 6}, 10^{- 4})

ii. Gradient of the Smoothness Penalty

The gradient of the smoothness penalty is given by Eq. (24):

\nabla {second_diff}_{i} = 4 P_{k, i} - 2 P_{k, i - 1} - 2 P_{k, i + 1}

(24)

c. Gradient Descent

By iteratively updating each point on the path to minimize the fitness function

Fitness (p_{k})

, the updated path

P_{k} {[i]}^{'}

is represented by Eq. (25):

P_{k} {[i]}^{'} = P_{k} [i] - η (g) \nabla Fitness (p_{k} [i])

(25)

where:

η (g)

is the exponentially decaying learning rate, defined by Eq. (26):

η (g) = η_{0} \cdot e^{- λ \cdot g}

(26)

with:

$η_{0}$ : Initial learning rate
$λ$ : Decay rate
g: Current iteration number

2. The gradient of the fitness function at each point is given by Eq. (27):

\nabla Fitness (p_{k} [i]) = \nabla {curvature}_{i} + \nabla {second_diff}_{i}

(27)

By dynamically adjusting the learning rate, the amplitude of each point’s update on the path can be controlled, allowing the path to converge quickly to an optimal solution. The gradient descent-based adaptive guidance strategy can find relatively optimal solutions in fewer generations, thereby reducing computation time.

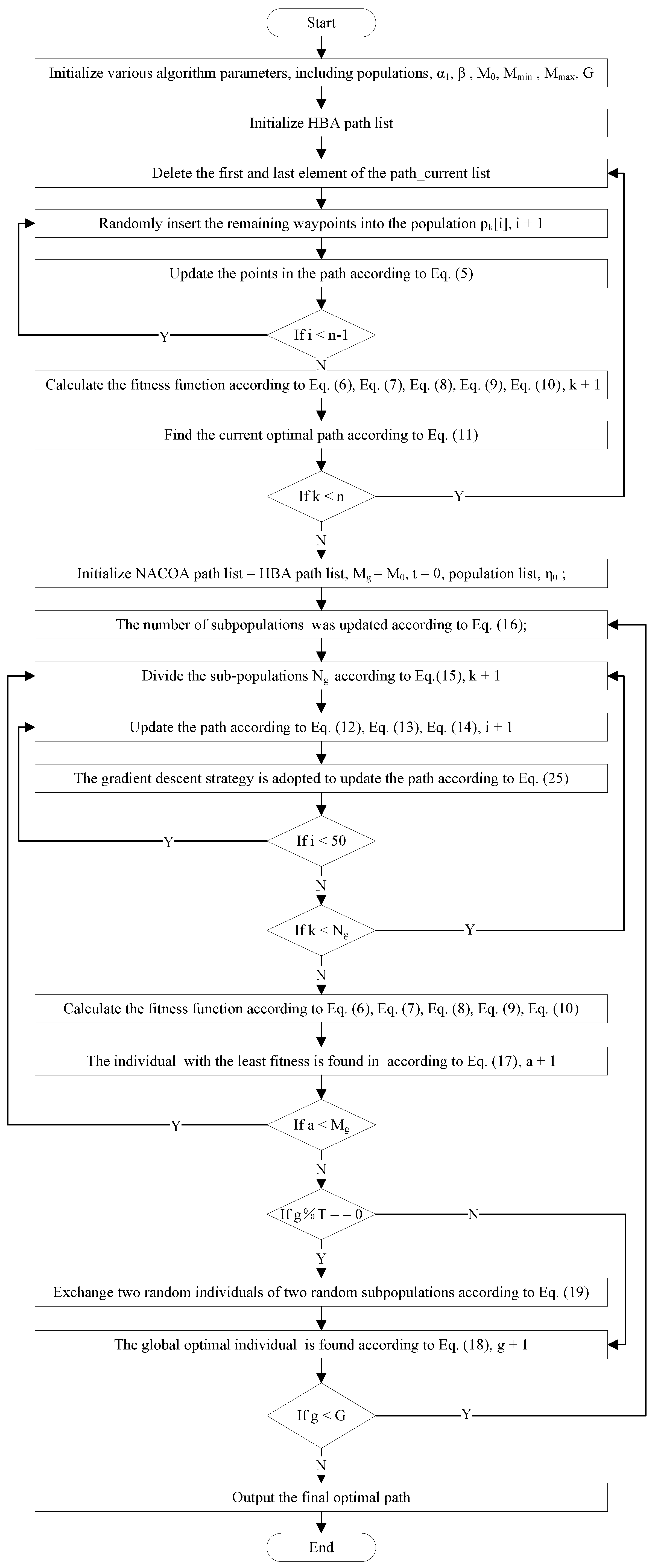
In this study, four major improvements are introduced to the traditional COA, including the initialization of the bat population with honey hunting strategy, the advanced dynamic multi-population strategy, and the gradient descent-based adaptive guidance strategy. Subsequently, a new COA variant, named NACO, is proposed. The pseudocode for NACO is presented in Algorithm 2, and the flowchart of NACO is illustrated in Figure 4.

Algorithm 2
1:	Initialize various algorithm parameters, including a₁, β, M₀, M_min, M_max, G;
2:	Initialize HBA path list;
3:	for k from 1 to n do increasing n by 1 each time do
4:	path_current = path;
5:	Delete the first and last element of the path_current list;
6:	for i from 2 to n − 1 do increasing t by 1 each time do
7:	t ← randomly generate, and the range of t is between [1, n − i];
8:	p_k[i] = path_current[t], and p_k is a member of populations;
9:	Delete path_current[t];
10:	Update the points in the path according to Eq. (5);
11:	end for
12:	Calculate the fitness function according to Eq. (6), Eq. (7), Eq. (8), Eq. (9), Eq. (10);
13:	Find the current optimal path according to Eq. (11);
14:	end for
15:	Initialize NACO path list = HBA path list, M_g = M₀, $N_{g} = \frac{N}{M_{0}}$ , t = 0, η₀;
16:	for g from 1 to G do increasing G by 1 each time do
17:	The number of subpopulations M_g was updated according to Eq. (16);
18:	population.clear();
19:	for a from 1 to M_g do increasing M_g by 1 each time do
20:	sub_pop_a.clear();
21:	for k from 1 to N_g do increasing N_g by 1 each time do
22:	t = t + 1;
23:	sub_pop_a[k] = p_t;
24:	p_k = sub_pop_a[k];
25:	for i from 1 to 50 do increasing 50 by 1 each time do
26:	Update the path according to Eq. (12), Eq. (13), Eq. (14);
27:	Gradient descent strategy is adopted to update the path according to Eq. (25);
28:	end for
29:	end for
30:	Calculate the fitness function according to Eq. (6), Eq. (7), Eq. (8), Eq. (9), Eq. (10);
31:	Individual p_{best_a} with the least fitness is found in sub_pop_a according to Eq. (17);
32:	population.append(sub_pop_a);
33:	end for
34:	if g%T == 0 then
35:	Exchange two random individuals of two random sub_pop according to Eq. (19);
36:	end if
37:	The global optimal individual g_best is found according to Eq. (18);
38:	end for
39:	Output the final optimal path.

5. Experiments

We evaluated our proposed hybrid network model and its four constituent base models using various performance metrics. For the unsmoothed paths identified by model features, we applied mean filtering, Bezier curve fitting, and NACOA according to the level of roughness. This chapter presents the network experiments, results, and optimization experiments and results.

5.1. Network Experiments and Results

5.1.1. Network Architecture

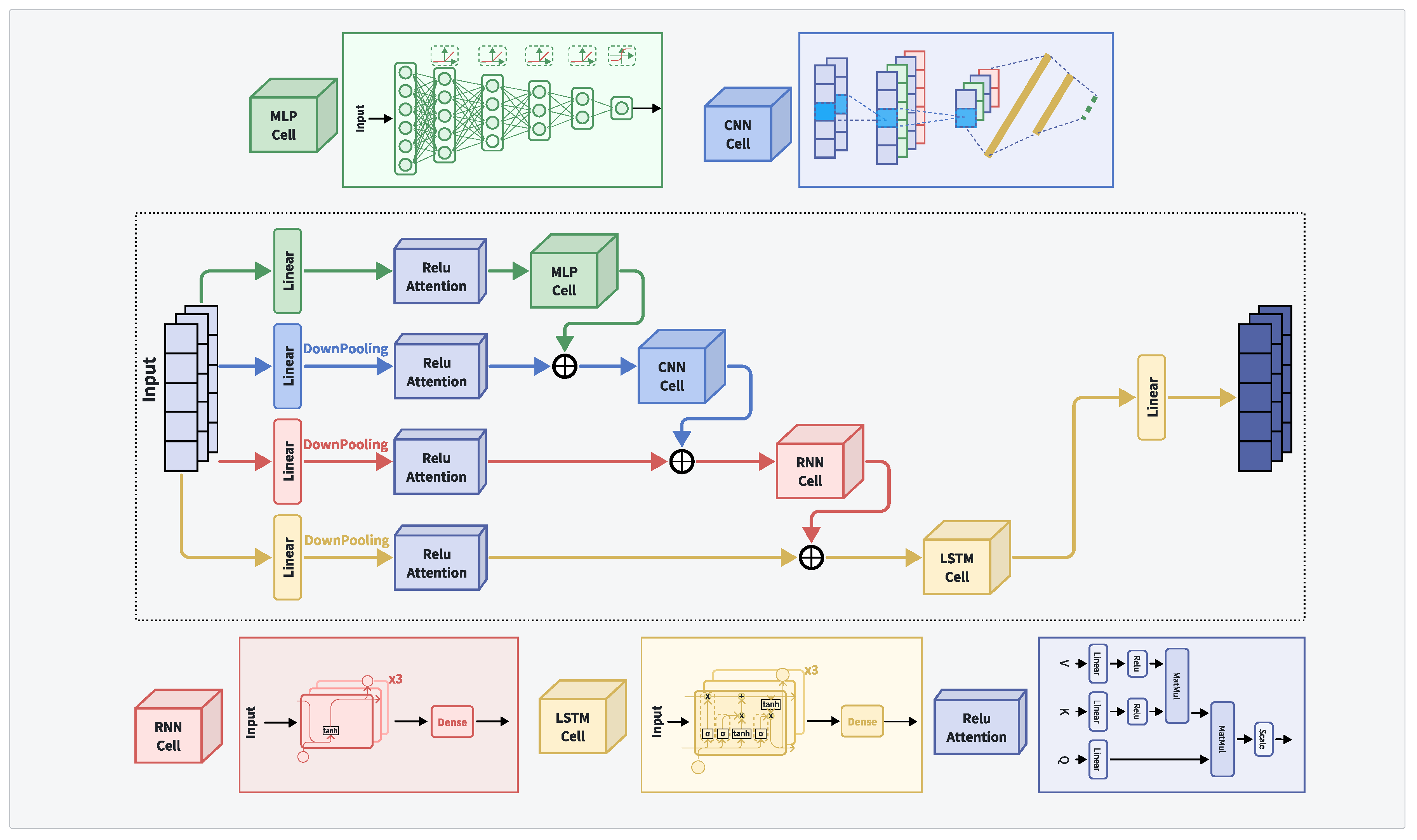
The structure of the hybrid network model MCRL, which combines the base neural network models MLP, CNN, RNN, and LSTM with a linear attention mechanism, is shown in Figure 5.

The model employs a decay function to initialize the optimizer with a learning rate, starting at 0.01, decaying by 10% every 1000 steps. The input vector size is

50 \times 2

, which is initially divided into four branches and processed through linear transformations.

The first branch utilizes the ReLU linear attention mechanism to process data, which is then fed into the MLP. Initially, the two-dimensional output vector is flattened using TensorFlow’s flatten module into a one-dimensional vector of size

100 \times 1

. This vector is then passed through four hidden layers with 128, 64, 32, and 16 nodes, each followed by a ReLU activation function, finally transforming the output vector to a size of

16 \times 1

. It then passes through a hidden layer with 4 nodes and a Softmax activation function to produce the output.

The second branch downsamples the data, converting the two-dimensional output vector to a size of

30 \times 2

. After processing with the ReLU linear attention mechanism, the data is fused with the MLP output and fed into the CNN unit. It first passes through a

3 \times 3

convolutional layer with 32 kernels, followed by a

2 \times 2

max-pooling layer, resulting in an output vector of size

15 \times 32

. This is followed by a dropout layer with a default probability of 0.2, then flattened to a

480 \times 1

vector. The vector is then passed to a hidden layer with 512 nodes using ReLU activation and finally through a hidden layer with 4 nodes using Softmax activation to produce the output.

The third branch downsamples the data, converting the two-dimensional output vector to a size of

20 \times 2

. After processing with the ReLU linear attention mechanism, the data is fused with the CNN output and fed into the RNN unit. It passes through three hidden layers with 128, 64, and 64 nodes, the third layer returning only the last timestep output, resulting in a

64 \times 1

vector, each followed by a Tanh activation function. Finally, it passes through a hidden layer with 4 nodes using Softmax activation to produce the output.

The fourth branch downsamples the data, converting the two-dimensional output vector to a size of

10 \times 2

. After processing with the ReLU linear attention mechanism, the data is fused with the RNN output and fed into the LSTM unit. It passes through three hidden layers with 64, 32, and 32 nodes, the third layer returning only the last timestep output, resulting in a

32 \times 1

vector, each followed by a Tanh activation function. Finally, it passes through a hidden layer with 4 nodes using Softmax activation to produce the output.

The outputs of the four branches are finally fused and output through linear transformation.

5.1.2. Experimental Results

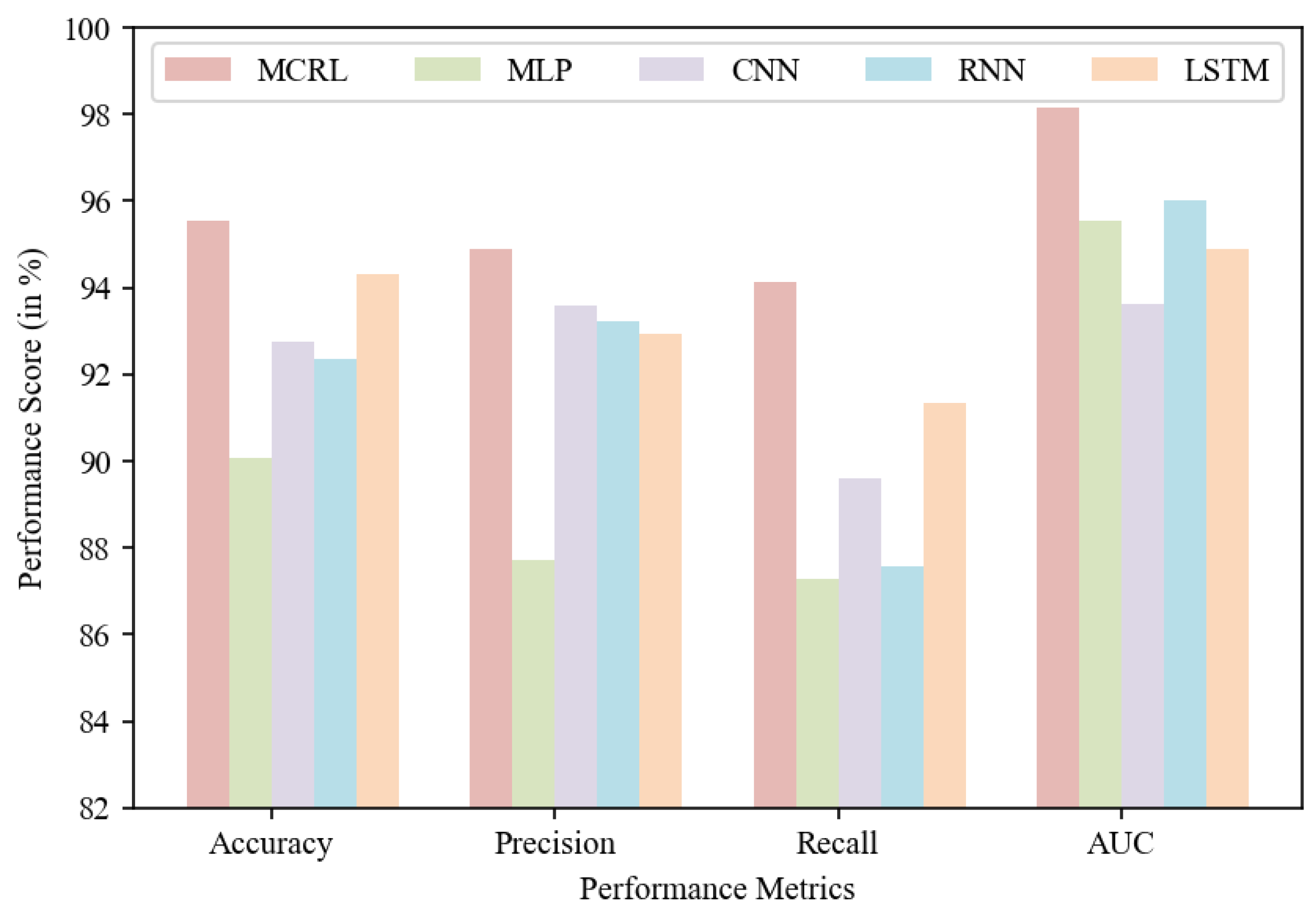
The dataset used consists of G-code for machining gears of aerospace transmission devices, with the model classifying the paths in the dataset. Table 2 and Figure 6 present the performance and error analysis of our hybrid network model. The accuracy rates for MCRL, MLP, CNN, RNN, and LSTM are 95.56%, 90.09%, 92.76%, 92.34%, and 94.32%, respectively; precision rates are 94.9%, 87.72%, 93.6%, 93.23%, and 92.94%; recall rates are 94.14%, 87.3%, 89.61%, 87.56%, and 91.34%; and AUCs are 98.17%, 95.55%, 93.61%, 96.02%, and 94.88%. Among all models, MCRL performs the best, with an accuracy of 95.56%, precision of 94.9%, recall of 94.14%, and AUC of 98.17%.

Similarly, the losses for MCRL, MLP, CNN, RNN, and LSTM are 12.44%, 28.92%, 14.86%, 22.67%, and 15.98%, respectively. Among all models, MCRL has the lowest loss at 12.44%.

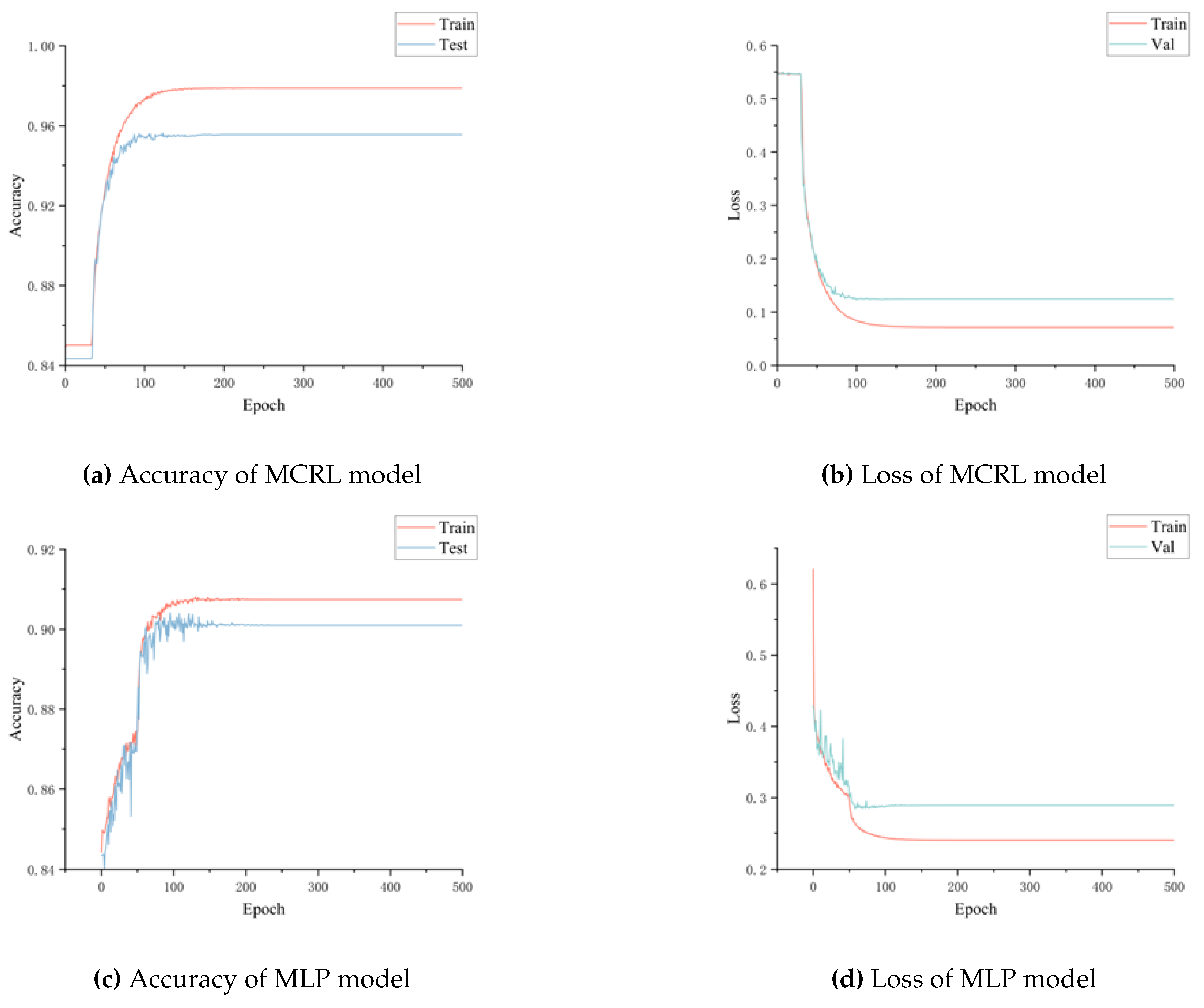
Figure 7 illustrates the accuracy and loss graphs for all models. As the number of epochs increases, accuracy rises while loss decreases. Below is a brief analysis of all accuracy and loss graphs:

MCRL: In Figure 7(a), the training and testing accuracies are smooth and close, with training accuracy nearing 97.89% and testing accuracy around 95.56%. Figure 7(b) shows that the training and validation error rates are also close, with training error near 7.16% and validation error around 12.44%.
MLP: Figure 7(c) shows that the training and testing accuracies are not smooth, with training accuracy around 90.74% and testing accuracy about 90.09%. Figure 7(d) indicates a considerable difference between training and validation error rates, with training error close to 24.01% and validation error about 28.92%.
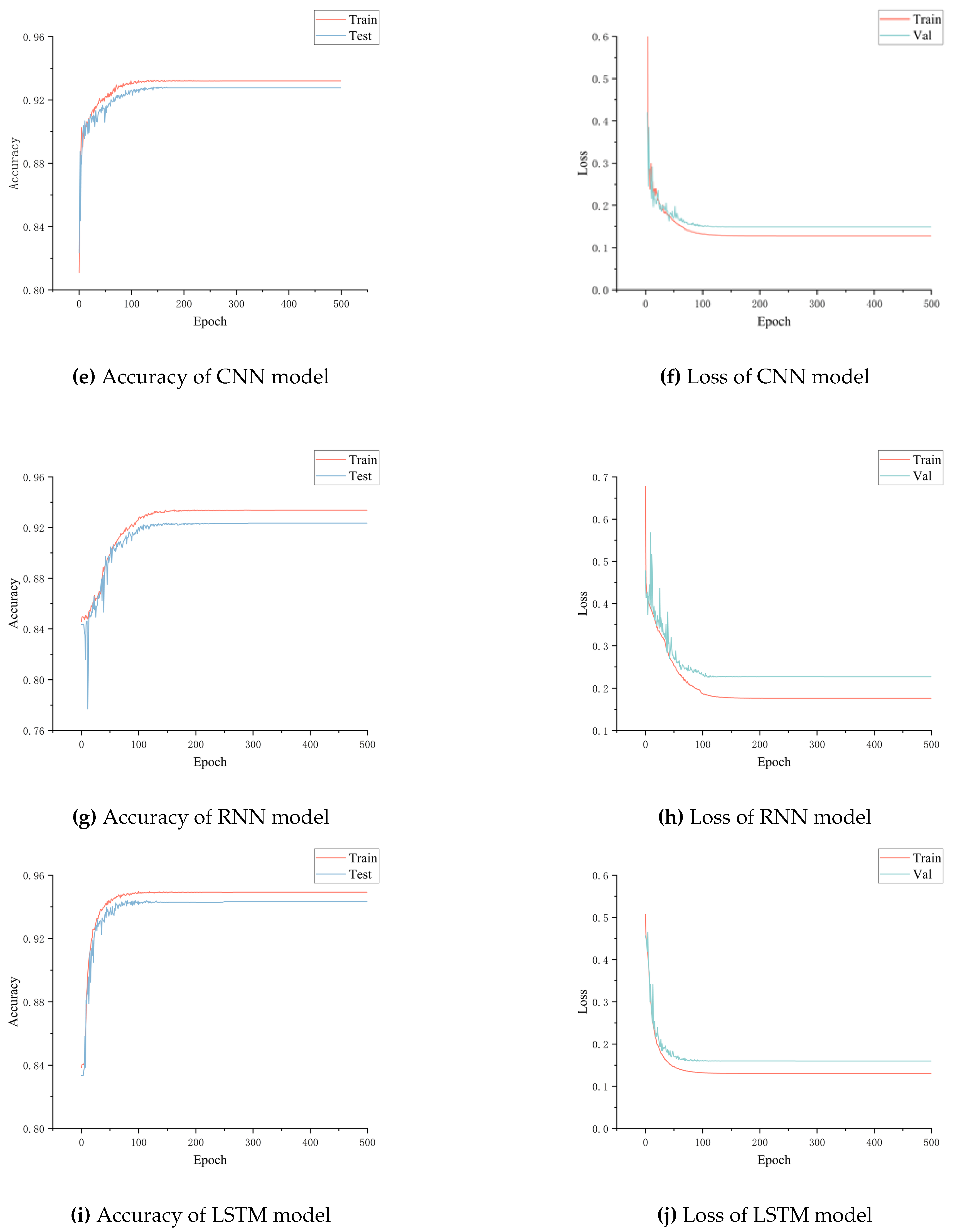
CNN: In Figure 7(e), the training and testing accuracies are somewhat close, with training accuracy around 93.21% and testing accuracy about 92.76%. Figure 7(f) demonstrates that the training and validation error rates are also somewhat close, with training error near 12.79% and validation error around 14.86%.
RNN: In Figure 7(g), the training and testing accuracies differ slightly, with training accuracy near 93.37% and testing accuracy around 92.34%. Figure 7(h) shows a considerable difference between training and validation error rates, with training error near 17.61% and validation error about 22.67%.
LSTM: In Figure 7(i), the training and testing accuracies are very close, with training accuracy around 94.92% and testing accuracy about 94.32%. Figure 7(j) reveals that the training and validation error rates are also close, with training error near 13.02% and validation error around 15.98%.

After a comprehensive analysis of all performance metrics, we conclude that among the provided deep learning network models, MCRL exhibits the best performance and the lowest error rate. The results indicate that MCRL has the highest overall performance, with an accuracy rate of 95.56%. Among the proposed models, MCRL also boasts the highest precision, recall, and AUC.

We randomly selected four curves from the dataset based on categories and examined the classification accuracy within the network. Green lines indicate correct classifications, while red lines denote incorrect classifications, as shown in Table 3.

The analysis reveals that the MCRL model has the best overall classification effect, achieving a perfect classification for all curves. In contrast, the MLP, CNN, RNN, and LSTM models each exhibited one misclassified curve within the given set.

In summary, MCRL combines the strengths of MLP, CNN, RNN, and LSTM, significantly enhancing the overall performance of the model, making it the most effective deep learning network model for the given task.

5.2. Optimization Experiments and Results

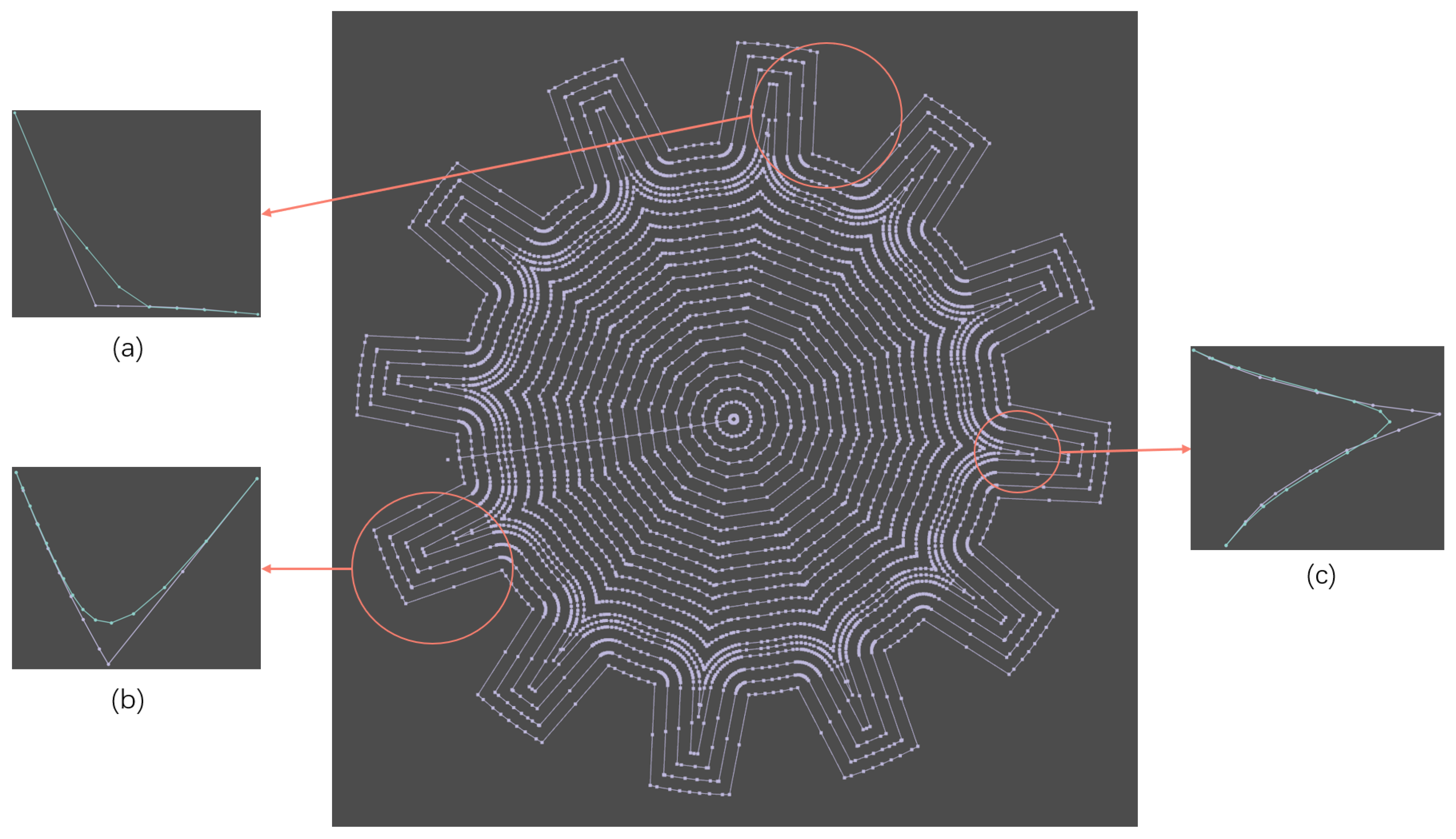
Figure 8 illustrates the optimization of randomly selected paths with different degrees of roughness using mean filtering, Bezier curve fitting, and NACOA. Figure 9(a) compares the curves before and after optimization using mean filtering, showing a curvature reduction of 54%. Figure 9(b) compares the curves before and after optimization using Bezier curve fitting, showing a curvature reduction of 67%. Figure 9(c) compares the curves before and after optimization using NACOA, showing a curvature reduction of 78%.

Overall, the optimized curves significantly improve the smoothness of the machining model, effectively reducing machine tool vibrations.

6. Conclusions

This paper introduces a deep learning method for feature recognition of unsmooth paths, employing filtering, fitting, and the proposed NACOA to address sharp corner issues based on the degree of roughness. The MCRL deep learning network model integrates MLP, CNN, RNN, and LSTM models along with a linear attention mechanism. We evaluated the model’s performance using various metrics to demonstrate its substantial advancements. Experimental validation on a gear machining G-code dataset proved the proposed model’s high efficacy in accurately identifying unsmooth paths, achieving a classification accuracy of 95.56%. In four randomly selected path curves, MCRL achieved perfect classification, while other models exhibited varying degrees of misclassification. Further research indicates that MCRL surpasses its constituent models in terms of precision.

We anticipate that the developed model and algorithm can be implemented in machining environments to more accurately identify and optimize unsmooth paths. Depending on the identified degree of path roughness, we utilized mean filtering, Bezier curve fitting, and NACOA for sharp corner recognition. Visual comparisons show that the optimized paths are smoother than the original paths, effectively reducing machine tool vibrations.

In the future, we plan to adopt more advanced deep learning network integration techniques and optimization algorithms, incorporating a broader range of workpiece machining G-code datasets to further refine our proposed MCRL model and NACOA optimization algorithm. Additionally, we aim to apply interpretable AI techniques to gain deeper insights into the decision-making processes of the MCRL model and NACOA optimization algorithm, thereby enhancing the accuracy of unsmooth path recognition and the smoothness of algorithm optimization.

Author Contributions

Conceptualization, P.L. and M.C.; methodology, P.L. and M.C.; software, P.L.; validation, P.L., M.C., and C.J.; investigation, P.L. and X.L.; resources, D.Y.; data curation, Z.Z., C.J. and X.L.; writing—original draft preparation, P.L.; writing—review and editing, P.L. and M.C.; visualization, P.L. and C.J.; supervision, M.C. and D.Y.; project administration, D.Y.; funding acquisition, D.Y. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Manufacturing Industry High-quality Development Special Program grant number 2023ZY01018-04.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available upon request from the corresponding author. They are restricted to the experimental results.

Acknowledgments

This work was supported by the Manufacturing Industry High-quality Development Special Program under Grant No. 2023ZY01018-04.

Conflicts of Interest

The authors declare no conflict of interest.

References

Du, S. Analysis of the application of intelligent CNC technology in machinery manufacturing. Journal of Physics: Conference Series. IOP Publishing, 2023, Vol. 2649, p. 012010.
Soori, M.; Arezoo, B.; Dastres, R. Machine learning and artificial intelligence in CNC machine tools, a review. Sustainable Manufacturing and Service Economics 2023, 2, 100009. [Google Scholar] [CrossRef]
Molina, L.M.; Teti, R.; Alvir, E.M.R. Quality, efficiency and sustainability improvement in machining processes using artificial intelligence. Procedia CIRP 2023, 118, 501–506. [Google Scholar] [CrossRef]
Ning, F.; Shi, Y.; Cai, M.; Xu, W. Part machining feature recognition based on a deep learning method. Journal of Intelligent Manufacturing 2023, 34, 809–821. [Google Scholar] [CrossRef]
Yao, X.; Wang, D.; Yu, T.; Luan, C.; Fu, J. A machining feature recognition approach based on hierarchical neural network for multi-feature point cloud models. Journal of Intelligent Manufacturing 2023, 34, 2599–2610. [Google Scholar] [CrossRef]
Guangwen, Y.; ZHANG, D.; Jinting, X.; Yuwen, S. Corner smoothing for CNC machining of linear tool path: A review. Journal of Advanced Manufacturing Science and Technology 2023, 3, 2023001–2023001. [Google Scholar]
Zhang, H.; Wu, Y.; Shen, Z.; Zhang, P.; Li, H.; Lou, F. Five-axis path smoothing based on sliding convolution windows for CNC machining. CIRP Journal of Manufacturing Science and Technology 2024, 49, 80–94. [Google Scholar] [CrossRef]
Shen, Z.; Wu, Y.; Guo, P.; Zhang, H.; Zhang, P.; Li, H.; Lou, F. Convolution synchronous smoothing for tool position and posture of continuous line-segment path in 5-axis machining. Journal of Manufacturing Processes 2024, 112, 136–149. [Google Scholar] [CrossRef]
Zhang, H.; Wu, Y.; Shen, Z.; Zhang, P.; Li, H.; Lou, F.; Guo, P. Mixed tiny path smoothing method based on sliding convolution windows for CNC machining. Journal of Manufacturing Processes 2023, 102, 685–699. [Google Scholar] [CrossRef]
Zhang, S.; Guan, Z.; Jiang, H.; Wang, X.; Tan, P. BrepMFR: Enhancing machining feature recognition in B-rep models through deep learning and domain adaptation. Computer Aided Geometric Design 2024, 111, 102318. [Google Scholar] [CrossRef]
Wang, P.; Yang, W.A.; You, Y. A hybrid learning framework for manufacturing feature recognition using graph neural networks. Journal of Manufacturing Processes 2023, 85, 387–404. [Google Scholar] [CrossRef]
Wu, H.; Lei, R.; Huang, P.; Peng, Y. A semi-supervised learning framework for machining feature recognition on small labeled sample. Applied Sciences 2023, 13, 3181. [Google Scholar] [CrossRef]
Fang, J.; Li, B.; Zhang, H.; Ye, P. Real-time smooth trajectory generation for 3-axis blending tool-paths based on FIR filtering. The International Journal of Advanced Manufacturing Technology 2023, 126, 3401–3416. [Google Scholar] [CrossRef]
Kučera, D.; Linkeová, I.; Stejskal, M. The influence of CAD model continuity on accuracy and productivity of CNC machining. The International Journal of Advanced Manufacturing Technology 2023, 124, 1115–1128. [Google Scholar] [CrossRef]
Hua, L.; Huang, N.; Yi, B.; Zhao, Y.; Zhu, L. Global toolpath smoothing for CNC machining based on B-spline approximation with tool tip position adjustment. The International Journal of Advanced Manufacturing Technology 2023, 125, 3651–3665. [Google Scholar] [CrossRef]
Zhang, L.; Lu, J.; Ou, C.; Ma, J.; Liao, X. Smoothing and compressing algorithm of toolpath with complex contour in NC machining. The International Journal of Advanced Manufacturing Technology 2023, 125, 4841–4854. [Google Scholar] [CrossRef]
Feng, K.; Ji, J.; Ni, Q. A novel gear fatigue monitoring indicator and its application to remaining useful life prediction for spur gear in intelligent manufacturing systems. International Journal of Fatigue 2023, 168, 107459. [Google Scholar] [CrossRef]
Yao, Y.; Liu, M.; Du, J.; Zhou, L. Design of a machine tool control system for function reconfiguration and reuse in network environment. Robotics and computer-integrated manufacturing 2019, 56, 117–126. [Google Scholar] [CrossRef]
Wu, S.F.; Lee, C.H.; Tseng, B.R. Intelligent Servo Tuning of High-Speed Machine Tools Using Circular Test. IEEE Sensors Journal 2023, 23, 12084–12092. [Google Scholar] [CrossRef]
Böttjer, T.; Tola, D.; Kakavandi, F.; Wewer, C.R.; Ramanujan, D.; Gomes, C.; Larsen, P.G.; Iosifidis, A. A review of unit level digital twin applications in the manufacturing industry. CIRP Journal of Manufacturing Science and Technology 2023, 45, 162–189. [Google Scholar] [CrossRef]
Wang, P.; Yang, W.A.; You, Y. A hybrid learning framework for manufacturing feature recognition using graph neural networks. Journal of Manufacturing Processes 2023, 85, 387–404. [Google Scholar] [CrossRef]
Liu, Z.; Lang, Z.Q.; Gui, Y.; Zhu, Y.P.; Laalej, H. Digital twin-based anomaly detection for real-time tool condition monitoring in machining. Journal of Manufacturing Systems 2024, 75, 163–173. [Google Scholar] [CrossRef]
Iliyas Ahmad, M.; Yusof, Y.; Mustapa, M.S.; Daud, M.E.; Latif, K.; Kadir, A.Z.A.; Saif, Y.; Adam, A.; Hatem, N. A novel integration between service-oriented IoT-based monitoring with open architecture of CNC system monitoring. The International Journal of Advanced Manufacturing Technology 2024, 131, 5625–5636. [Google Scholar] [CrossRef]
Liu, C.; Zheng, P.; Xu, X. Digitalisation and servitisation of machine tools in the era of Industry 4.0: a review. International journal of production research 2023, 61, 4069–4101. [Google Scholar] [CrossRef]
Dehghani, M.; Montazeri, Z.; Trojovská, E.; Trojovskỳ, P. Coati Optimization Algorithm: A new bio-inspired metaheuristic algorithm for solving optimization problems. Knowledge-Based Systems 2023, 259, 110011. [Google Scholar] [CrossRef]
Hashim, F.A.; Houssein, E.H.; Hussain, K.; Mabrouk, M.S.; Al-Atabany, W. Honey Badger Algorithm: New metaheuristic algorithm for solving optimization problems. Mathematics and Computers in Simulation 2022, 192, 84–110. [Google Scholar] [CrossRef]

Figure 1. Web application as communication between CAM and machine tools.

Figure 2. Modeling Scheme of Intelligent elements in CNC.

Figure 3. Intelligent-based CNC system machining process flow structure.

Figure 4. The flow chart of NACOA.

Figure 5. MCRL network model structure.

Figure 6. Performance comparison of different network models.

Figure 7. Training results of network model.

Figure 8. Path optimization results.

Table 1. Path roughness categories.

LocalCurvature	Description	Category	Evaluation
$L o c a l C u r v a t u r e \leq 1.9$	Smooth	Category 1	Good
$1.9 < L o c a l C u r v a t u r e < 3.5$	Slightly Rough	Category 2	Moderate
$3.5 < L o c a l C u r v a t u r e < 7.6$	Rugged	Category 3	Poor
$L o c a l C u r v a t u r e \geq 7.6$	Sharp Turning Corner	Category 4	Very Poor

Table 2. Performance comparison of different network models.

Network Models	Accuracy	Loss	Precision	Recall	AUC
MCRL	95.56	12.44	94.9	94.14	98.17
MLP	90.09	28.92	87.72	87.3	95.55
CNN	92.76	14.86	93.6	89.61	93.61
RNN	92.34	22.67	93.23	87.56	96.02
LSTM	94.32	15.98	92.94	91.34	94.88

Table 3. Classification results of random curves by different network models.

	Category 1	Category 1	Category 1	Category 1
MCRL
MLP
CNN
RNN
LSTM

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

An Agent-Based Method for Feature Recognition and Path Optimization of CNC Machining Trajectories

Abstract

1. Introduction

2. Related Work

2.1. Feature Recognition in CNC Machining Based on Deep Learning

2.2. CNC Machining Path Optimization

3. Agent-Based CNC System Architecture

3.1. Intelligent Requirements

3.2. System Model and Structure

3.3. Assembly Line Work Mode

4. Mathematical Model

4.1. Machining Path Feature Design

4.2. Path Optimization Design

4.2.1. Honey Badger Algorithm for Population Initialization

a. Initialization phase

i. Generate initial honey badger population

ii. Initialize each individual p k in the population

b. Defining intensity

c. Simulation of honey badger foraging behavior

d. Fitness function

i. Curvature calculation

ii. Smoothness penalty

iii. Fitness function

e. Updating the honey badger population

f. Initialization of COA population

4.2.2. Enhanced Path Update Rule

4.2.3. Dynamic Multi-Population Strategy

a. Multi-Population Initialization

b. Updating Sub-Population Size

c. Selection of the Optimal Individual

d. Individual Exchange Strategy

4.2.4. Gradient Descent-Based Adaptive Guidance Strategy

a. Fitness Function

b. Gradient Calculation

i. Gradient of the Curvature

ii. Gradient of the Smoothness Penalty

c. Gradient Descent

5. Experiments

5.1. Network Experiments and Results

5.1.1. Network Architecture

5.1.2. Experimental Results

5.2. Optimization Experiments and Results

6. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

ii. Initialize each individual $p_{k}$ in the population