1. Introduction
Time-of-Flight cameras have gained increasing attention in recent years for their ability to capture 3D scenes in real-time. By employing a low-cost sensor coupled with an active light source, ToF cameras measure the distance to objects based on the time it takes for light to travel. This technology offers distinct advantages for machine vision applications, as it requires minimal processing power while delivering reliable data.
The compact design of ToF cameras further expands their range of applications. Smartphones, for instance, can benefit from ToF cameras in face authentication and mobile 3D scanning. In the automotive industry, ToF cameras enable gesture control systems that remain unaffected by varying lighting conditions. Moreover, ToF cameras find utility in simultaneous localization and mapping (SLAM) for autonomous vehicles and reality-altering devices. Despite the numerous applications, ToF cameras are still susceptible to various artifacts that compromise the quality of the captured data. To address this issue, algorithms are used to correct the errors [
1,
2]. However, traditional approaches are limited in their effectiveness to detect and process features.
Consequently, deep learning has emerged as a powerful tool, enabling the extraction of patterns and features from complex data. As a result, many learning-based approaches that aim to remove errors from ToF data have been proposed recently [
3,
4,
5,
6]. They either rely on physically simulated synthetic ToF data or employ unsupervised learning methods. However, the quality and content of the training data play a crucial role in the effectiveness of these approaches. While physically simulated synthetic data has shown promising results, it may neglect certain critical real-world components [
7]. As the usage of neural networks for ToF error removal continues to increase, there is a growing demand for realistic training data. To address this, existing datasets that include high-quality point clouds can be extended to the ToF domain, as many available datasets [
8,
9,
10] contain high-quality laser scan data but lack corresponding ToF camera data.
This work presents a learning-based approach that uses high-quality laser scan data to generate amplitude modulated continuous-wave (AMCW) ToF camera artifacts. Throughout this paper, we will refer to these simply as ToF camera artifacts. The approach involves domain transfer in two steps. First, the laser scan data is transformed into the ToF camera domain using MCW-Net [
11]. The network is trained on RWU3D [
12], a real-world dataset consisting of a high-quality laser scan and multiple ToF images. In the second step, a noise model is added to the network’s output to account for the lack of noise in the first step. The noise model is determined experimentally and applied based on the scan data. The evaluation of the proposed method is based on the reference scenes presented by Bulczak et al. [
13].
2. Realted Work
Keller et al. [
14] described a simulation framework with all necessary parameters, which is a rough guideline for further work. Peters et al. [
15] focus on simulating bistatic effects that occur due to an illumination ring co-positioned to the sensor. Another simulator provided by Keller and Kolb [
16] focuses on computing in real time. Their approach includes local illumination with a Lambertian reflection model, to determine high-resolution phase images. Subsequently, to generate flying pixels, they simply downscale the phase images by averaging over small pixel areas. Finally, they add a Gaussian noise model containing a signal-to-noise ratio part and an intensity-related noise to the phase images. Lambers et al. [
17] describe a realistic sensor model covering light propagation and illumination as well as physically accurate charge behavior at the readout circuit level of sensor pixels in response to incident photons. Their simulation is limited to scene materials that are Lambertian reflectors and based on the assumption that the modulated light source and the focus point of the camera are located at the same position.
None of the previously mentioned simulators include the modeling of multipath effects, which are significant ToF artifacts. Furthermore, there has been a lack of evaluation regarding the simulated sensor data in comparison to real acquisition data from an actual ToF sensor.
Meister et al. [
18] introduced a simulator that tackles the multipath challenge through a global illumination approach. Their method uses bidirectional path tracing, where rays are emitted from both the light source and the camera. By using the local bidirectional reflectance distribution function (BRDF) of the scene surfaces, they compute the second-order ray. To capture multipath effects, the suggested maximum recursion depth is set to 8, which results in a high computational cost. Meister et al. also provide a visual comparison with real data on a range image basis for two test scenes “corner” and “box” as well as with a limited quantitative comparison.
In the work of Bulzack et al. [
13] a simulation of multipath errors at realistic framerates together with a quantified evaluation for simulated range images is presented. The reflection model, based on BRDF, makes use of measured data from real-world materials. However, the light propagation only accounts for single-bounce multipath, which leads to incorrect simulation for strongly reflecting surfaces. The proposed evaluation is based on three different scene geometries, which are all corners either without a cube, a cube, or a shifted cube in the center. Despite the single-bounce limitation, the mean absolute error for two selected materials across all three geometries is approximately 2.5 cm.
Guo et al. [
4] created the synthetic dataset FLAT with the help of transient rendering, where the received irradiance of each time frame is simulated. The simulated data is used to train a neural network to mitigate ToF artifacts. There is no evaluation of the simulated ToF data compared to a real sensor, only the training results are evaluated. Yan et al. [
19] concentrate on background irradiance in space and the BRDFs of satellite materials within their simulator. They introduce an improved path-tracing algorithm, which considers the cosine component of the modulated light signal. In the evaluation of one ground test scene, their method performed better than the simulator proposed by Bulzack et al. [
13]. Notably, no learning-based methods for simulating ToF data have been identified thus far.
3. Proposed Method
The proposed method aims to perform domain transfer from a highly precise laser scanner depth map to a low-resolution Time-of-Flight camera depth map using a network-based approach. The output of the network is then refined using a noise model to generate a realistic ToF depth map.
3.1. Deep Learning for Generating ToF Data
3.1.1. Network Architecture
The network architecture used in this work is a modified version of MCW-Net [
11] which is inspired by the encoder-decoder architecture of U-Net [
20]. The MCW-Net was originally designed for rain removal, which targets the identification and manipulation of specific image features. The encoder captures the essential features of the image, while the decoder reconstructs the image, applying learned modifications. This structure is equally useful for ToF artifact simulation.
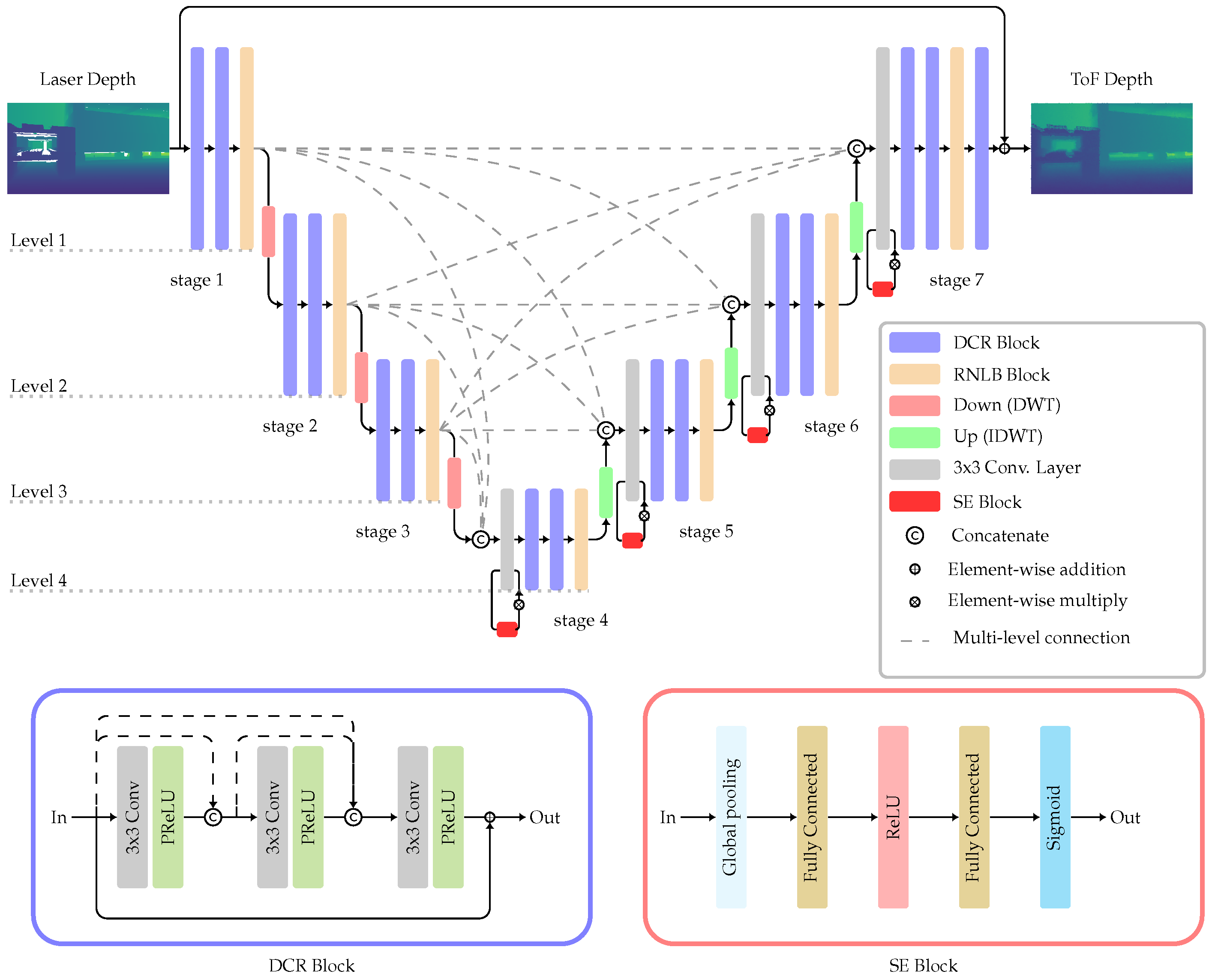
In the encoder phase, the network gradually downsamples the input image to capture lower-resolution representations of the features. These features are then utilized in the decoder phase to generate a new image through an upsampling process. Figure fig:mcw-net provides an overview of the MCW-Net architecture.
Figure 1.
MCW-Net Architecture. The levels represent the size of the feature map. The stages consist of multiple blocks on the same level.
Figure 1.
MCW-Net Architecture. The levels represent the size of the feature map. The stages consist of multiple blocks on the same level.
MCW-Net consists of four levels, each representing a specific feature map size. Within each level, a set of layers is defined as a stage. Inspired by U-Net, skip connections are integrated between stages of the same level to mitigate information loss in the second half of the network. MCW-Net additionally connects stages at different levels as seen in fig:mcw-net. The multi-level connections allow the decoder to access features of varying sizes and levels, which is particularly beneficial when dealing with region-based errors like MPI.
Within each stage of MCW-Net, feature extraction is achieved by combining two densely connected residual (DCR) blocks and a regional non-local block (RNLB). The DCR block consists of three sequential 3 × 3 convolutional layers, followed by a parametric rectified linear unit (PReLU) activation function [
21].
The following RNLB further enhances the spatial awareness of the network. It operates by dividing the feature map into patches and performing non-local convolutions. In each non-local operation, the response at a specific position is computed as a weighted sum of features from all spatial positions within the patch. While the original MCW-Net proposed wide rectangular grids for the RNLB [
11], a squared grid is implemented in this work. By employing a squared grid, the number of horizontal and vertical features becomes equal, achieving a balanced distribution of information across both dimensions.
MCW-Net uses direct wavelet transform (DWT) for downsampling and inverse DWT (IDWT) for upsampling processes. This avoids the information loss caused by conventional subsampling, like max-pooling where only strong features are considered. The DWR is simply implemented by the Haar transform which consists of four 2 × 2 filters. Therefore the feature map size is halved and the number of channels quadrupled in the downsampling steps and vice versa in the inverse operation.
The stages in the decoder are designed with a necessary squeeze-and-excitation (SE) block [
22] to rescale the feature maps obtained from the multi-level connections, see fig:mcw-net. The number of channels is adjusted by a 1 × 1 convolutional layer.
The scalability of the model is achieved by adjusting the number of channels, as demonstrated in the work of Park et al. [
11]. They presented two variants of the model: large and small. The large model contains eight times more channels compared to the small model, resulting in 129.5 million parameters for the large model and 2.2 million parameters for the small model. However, due to the limited amount of training data, experiments revealed that the large model tends to overfit quickly. As a result, subsequent discussions only consider the small version of the model. To properly adapt the network to the depth maps the input and output channels have been set to one, which is another modification from the original MCW-Net architecture.
3.1.2. Training
The RWU3D dataset is split into 40 train scenes and 17 validation scenes. Each scene consists of a single laser depth map which serves as the input image, and a set of n ToF depth maps with a size , referred to as labels . During training, a random patch of 256 × 256 is cropped from the input image, and a batch size of 4 is utilized. Not a Number (NaN) values in the input data are appropriately handled by setting them to zero, while NaNs in the labels do not contribute to the loss function. The Adam optimizer is employed, with an initial learning rate of 0.0005 and a learning rate decay of 1/2 every 100 epochs. The model is trained for a total of 400 epochs.
To harness the potential of the dataset, two distinct loss functions were investigated. The first loss function is characterized by the L1 Loss, computed between the mean of all available labels and the network’s prediction
, as depicted in Equation
1. This approach aims to constrain the network’s prediction to a singular solution instead of considering the 20 different possibilities.
On the other hand, the second loss function is determined by calculating the minimum L1 distance among all individual labels in the dataset, as shown in equation
2. This emphasizes precise predictions, favoring scenarios where multiple outcomes are appreciated.
Data augmentation is applied using horizontal and vertical flipping to increase the diversity of the training dataset. This augmentation is especially important due to the presence of floor areas at the bottom of each scene. Furthermore, the impact of noise on data augmentation is explored. Three distinct input types are employed:
No noise
Additive Gaussian noise, denoted as [Laser+Noise]
Gaussian noise introduced on a separate channel, referred to as [Laser, Noise]
In addition to the enhanced robustness achieved through data augmentation, the implementation also has the objective of ensuring that the network’s output predicts realistic noise characteristics. However, results show that all of the above-mentioned models suffer to produce realistic noise.
3.2. ToF Noise Model
The behavior of the utilized model made clear that a noise model is needed. Developing an accurate depth noise model for ToF sensors is still a topic of current calibration research. Thus, similar to [
16] a simple noise model is presented. This noise component will be combined with the model’s predictions to simulate realistic noise characteristics.
Various noise sources contribute to the overall noise in ToF cameras. The statistical distribution of ToF cameras can be approximated reasonably well by a Gaussian distribution, as shown in previous studies [
16,
23]. To quantify the spread of this distribution, three key parameters that affect the noise were examined: distance, angle of incidence, and the presence of edges. These parameters were selected based on the available input data, which is the depth map obtained from the laser scanner. The output functions of the three distinct noise sources are combined to generate a pixel-wise standard deviation.
The standard deviation as a function of distance is approximated by the linear model in equation
3. The coefficients
and
for the linear function are determined from values specified in the datasheet provided by the manufacturer [
24]. The standard deviation
does not require any pre-processing and only uses the distance
d in the laser depth map.
To compute the standard deviation on edges, the training data’s edge-containing areas undergo analysis. Utilizing the Canny edge detection algorithm on the depth map identifies these edges. The ensuing step involves calculating the mean standard deviation at the edges, resulting in a mean value of 0.03 m across all training images. This value is then applied to stddist if the pixel location is at an edge in the validation image.
The third parameter which contributes to the total standard deviation is the angle of incidence . To determine it from the depth map, first, the normal map is computed by using trigonometric functions. For each pixel, the angle between the normal vector and the incidence vector is calculated. Therefore two assumptions have been made. Since the ToF data is transformed to the RGB sensor this minor change in perspective as well as the co-positioning of the illumination element are not taken into account. Secondly, the light direction is set to a global constant vector which is equal to the normal of the sensor plane.
In order to determine the standard deviation based on the angle of incidence the characteristics of the sensor were investigated. For this purpose, a target plane positioned at a distance of 1 meter, is captured at various angles. To achieve this, a target plane is mounted on a 3D printed platform that allows the plane to be rotated in 5° increments from 0° to 85°. The utilized material of the target plane is the less reflective wood in one series, while in a separate series, the target plane made of rigid foam is captured. Therefore an effective comparison between the two materials with different reflectivity is made.
In line with the experimental setup described by Chiabrando et al. [
25], a sequence of 50 frames for each angle set is recorded. Notably, tests using a sequence of 500 frames showed no discernible difference in standard deviation as the number of frames increased.
As the angle increases, the area of the target visible to the sensor decreases while the edges of the target become more present, which can lead to inaccurate measurements. Therefore a thin region of interest (ROI) with 5 × 20 pixels is investigated to calculate the mean standard deviation at each angle. However, since it couldn’t be avoided that even this area is affected by higher values at the edges, the measurement at 85° is discarded.
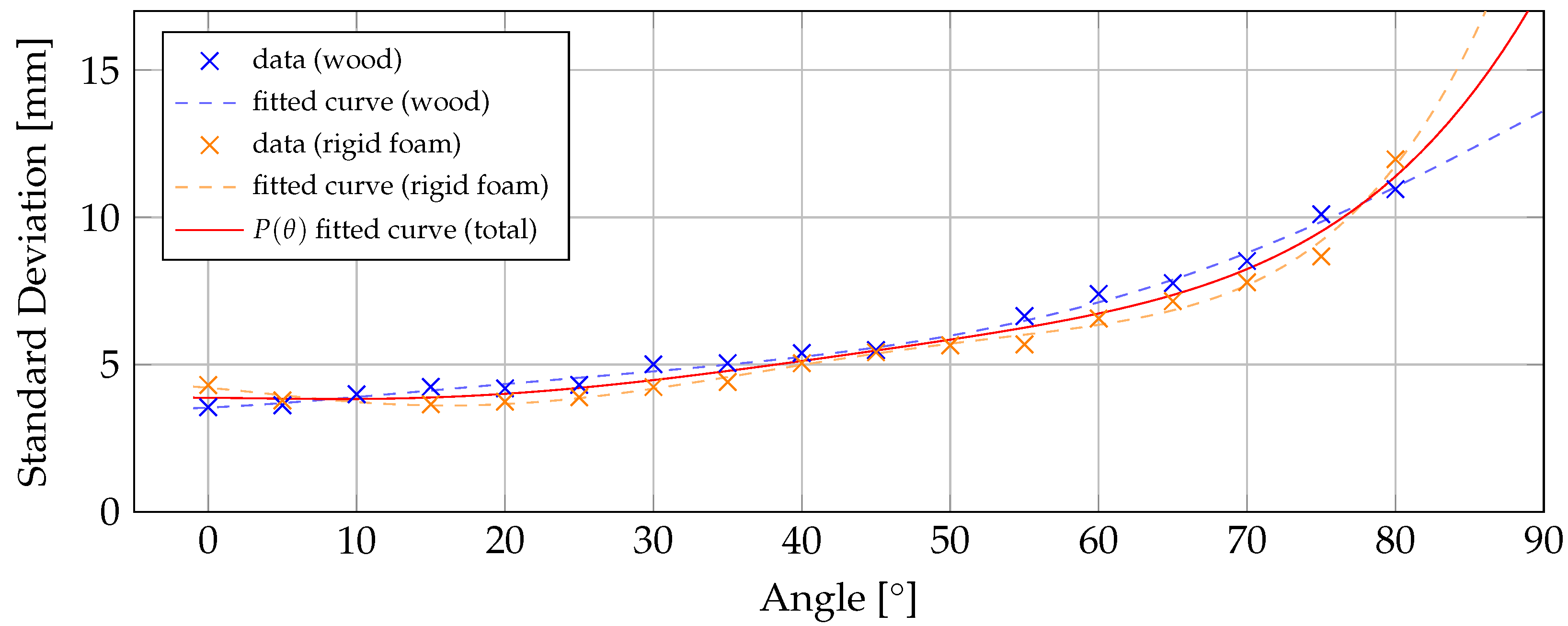
Inspired by the work of Keller et al. [
16] fitting of a polynomial is used to approximate the measured data points. For each sequence, a polynomial function of degree 5 is fitted to the measured values. The results are plotted in fig:angstddata. Considering that the variation among the utilized materials is relatively small in comparison to the overall range of the functions within the interval [0, 90], the final function
includes the data points from both materials.
To compensate the offset of
which
already incorporates a bias term
b is subtracted. Combining the results from all three parameters gives the total standard deviation
by
Furthermore, this leads to the resulting noise distribution:
where
is the total standard deviation matrix and
is the noise matrix around zero.
Figure 2.
Standard Deviation as a function of the Angle of Incidence for wood (blue) and rigid foam (orange). Fitted curves are polynomials of degree 5.
Figure 2.
Standard Deviation as a function of the Angle of Incidence for wood (blue) and rigid foam (orange). Fitted curves are polynomials of degree 5.
The resulting noise is finally added to the model’s predicted depth map, enabling a more realistic simulation of ToF camera behavior. It’s important to note that the noise model is not used during the training phase.
4. Evaluation
In this evaluation, the two outcomes of the proposed method are compared with the actual ToF depth images in the evaluation set. The first outcome is the model’s prediction, denoted as PredToF. The second outcome is the model’s prediction enhanced with the noise model referred to as SimToF.
Cross-section plots have been recognized as a suitable visual evaluation technique in previous studies [
6,
13,
18,
26], and therefore, they are employed for the evaluation in this study. To better understand the geometry of the cross-sections, the color images are also provided. A green line is superimposed to indicate the position of the cross-section. In addition, error maps are presented to provide a global visual evaluation of the scene. These maps visually represent the differences between the actual ToF depth images and the outcomes of the methods being compared. Furthermore, to quantify the evaluation, following the approach by [
13], the Mean Absolute Error (MAE), Mean Squared Error (MSE), and Root Mean Squared Error (RMSE) are utilized. Since multiple labels are available for one input always the minimum error is reported. It is worth noting that the proposed network architecture does not generate NaN values but instead outputs small values. Consequently, any values of PredTof that are less than 0.4 m are treated as NaNs.
4.1. Analysis of the Training Methods
The employed variations of training methods demonstrated successful outcomes throughout the training process. The training loss consistently decreased as expected, indicating a common and desirable behavior. Furthermore, there were no signs of overfitting observed during the training. Consequently, all methods used are considered valid for evaluation purposes.
Table 1 presents the error values of the PredToF variations in the evaluation set. In contrast to the assumption that the mean loss training requires less information due to the removal of noise, our results show that this assumption is not valid. In fact, reducing the training data by using the mean loss results in a less robust model instead of the expected improvement.
Both methods that include noise to the input data could not improve the error of PredToF. Furthermore, no noticeable effects of realistic ToF noise in the prediction are observed, by this approach. Adding noise to the input data worsens the result. This indicates that the model relies on minor variations in laser depth to accurately predict the ToF behavior. By adding noise to the laser data, this crucial information is blurred, making it less effective.
On the other hand, the noise introduced in a second channel does not modify the laser data. Instead, it utilizes filters to extract features. As a result, fewer filters are available for the depth data, leading to a worse prediction.
The most successful training case is achieved by using the original, unmodified laser depth data along with the minimum loss criterion. This combination leads to the best results, with an achieved mean absolute error of 0.0533 m. Consequently, all the following analyses and evaluations are based on this particular training method.
4.2. Results on the Corner Scenes
SimToF achieved promising results on all corner scenes, with a mean absolute error of 0.0372 m. In contrast, the input data’s mean absolute error relative to the actual ToF on the same set is 0.1011 m. This corresponds to an improvement of more than 60 %.
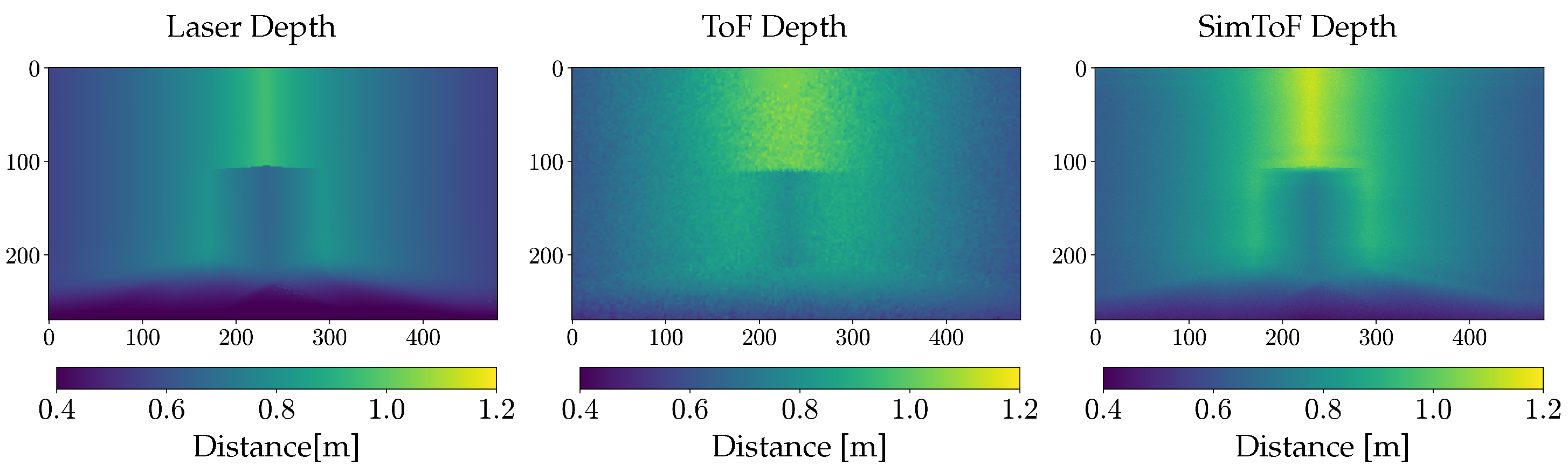
In
Figure 3 a comparison of the depth map of SimToF and the actual ToF depth map, next to the ground truth of the laser scan is shown. The visual comparison illustrates the less accurate edges and an overall higher depth of SimToF compared to the input. However, in the depth map of the ToF camera, these effects are more pronounced, and there is a notable presence of noise.
The error of SimToF with respect to the actual ToF data on the corner scenes is presented in
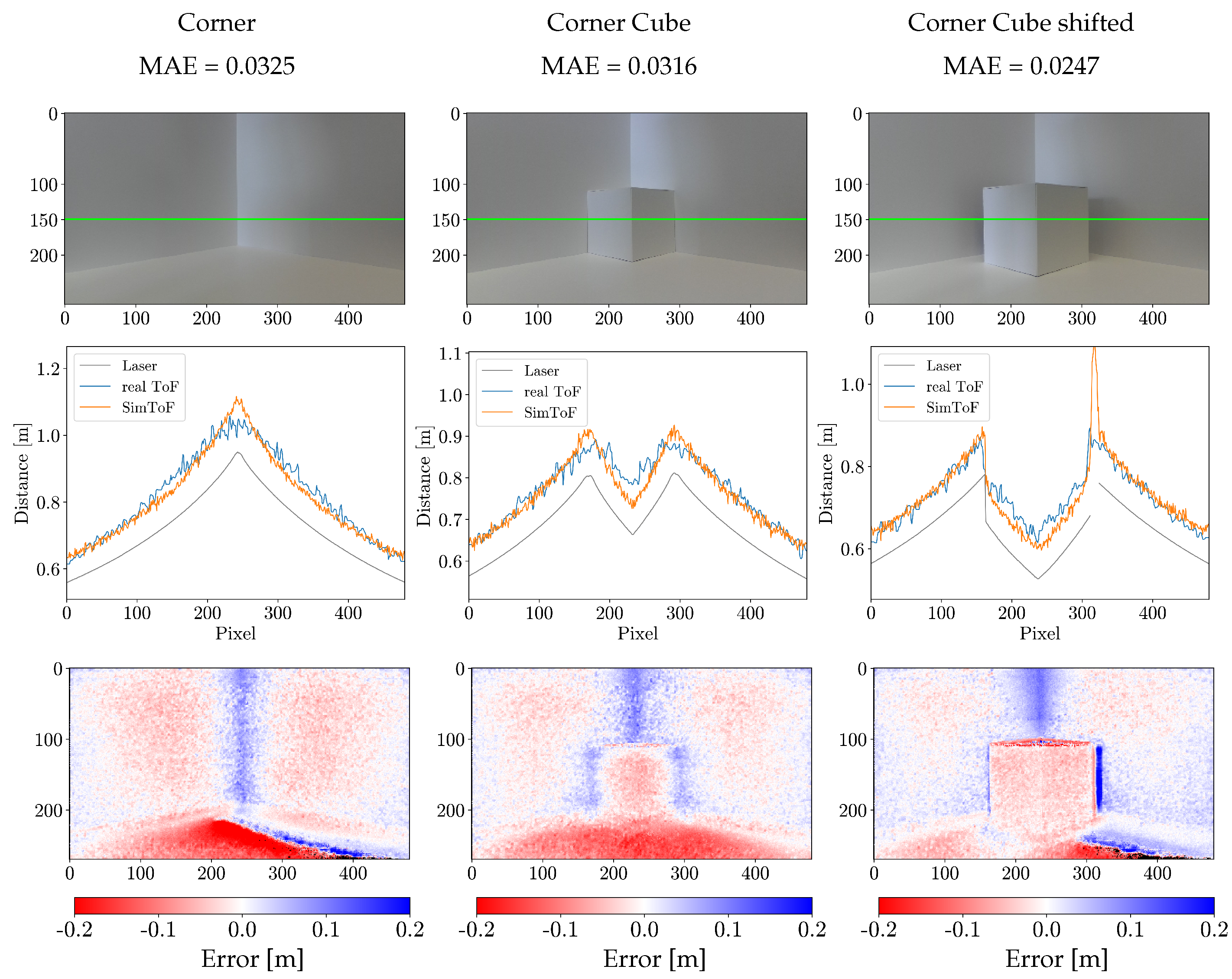
Table 2. The results show that SimToF performs best on the corner scenes with Material C. Compared to the results of the physical simulator presented by Bulzack et al. (SimSingle, [
13]) on a similar scene the proposed method could improve the error in the Corner Cube shifted scene by 1.11 cm. However, SimSingle achieved better results on the Corner (MAE = 0.0200 m) and the Corner Cube (MAE = 0.0138 m) scene.
Figure 4 displays the cross-section plots along with the error map showing the corner scenes. The cross-section effectively visualizes the multipath error of the actual ToF camera in the corner regions. A closer look at SimToF in this particular region shows that the MPI effects are not modeled accurately. In other parts of the scene, however, SimToF generates well-fitting ToF data.
The error maps reveal the main limitations of SimToF. These primarily include the vertical corner regions and areas with a flat incident angle. Both areas are prone to MPI correlated errors. Additionally, the dark blue areas indicate regions where no input data is available. To compensate for this lack of data, SimToF generates interpolation data. This characteristic can also be seen as a peak around pixel 310 in the cross-section of the Corner Cube shifted scene. In the example of the corner scenes set, the interpolation occurs on 0.5 % of the data and increases the overall error by 1.08 %.
4.3. Results on the Real Scenes
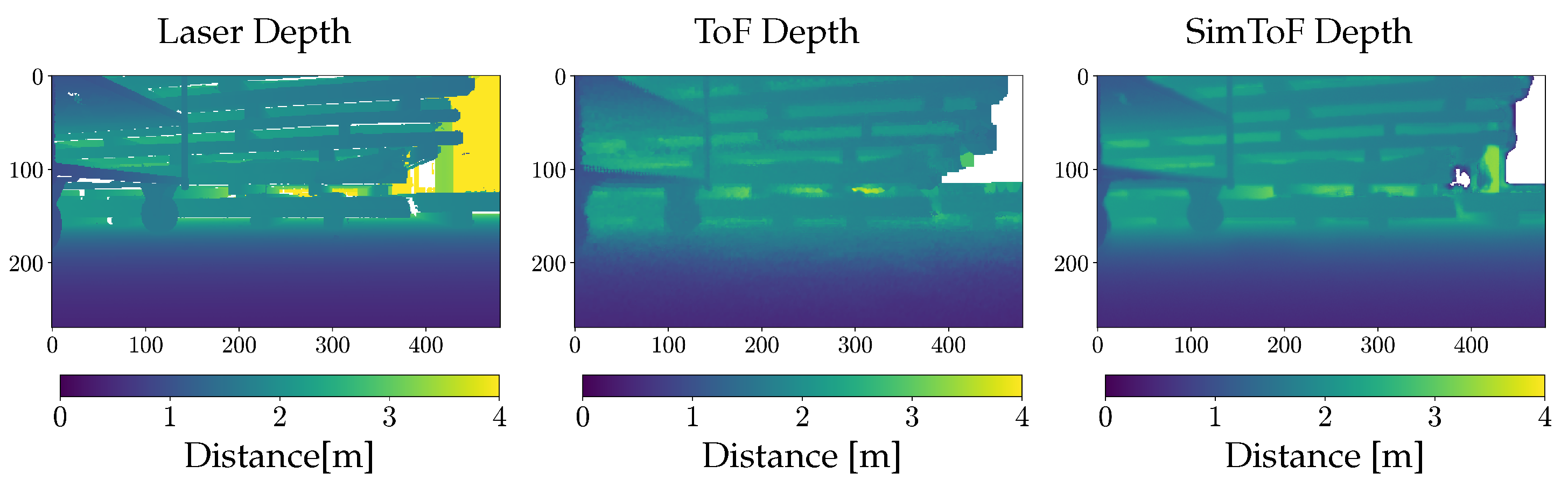
SimToF also achieved promising results on the evaluation set of real scenes, with a mean absolute error of 0.0660 m. In comparison, the mean absolute error of the input data relative to the actual ToF on the same set is 0.1694 m. This translates into an improvement of more than 60 %.
Figure 5 illustrates the result of SimToF as a depth image compared to input and the real ToF camera depth image. The visualization shows that SimToF fills in the missing values in the input data, primarily found between the shelves. Additionally, SimToF produces NaN values at greater depths, similar to what the real ToF camera captures. Based on the depth images, the visual analysis shows comparable blurring results. However, the noise level of the actual ToF is noticeably higher compared to SimToF.
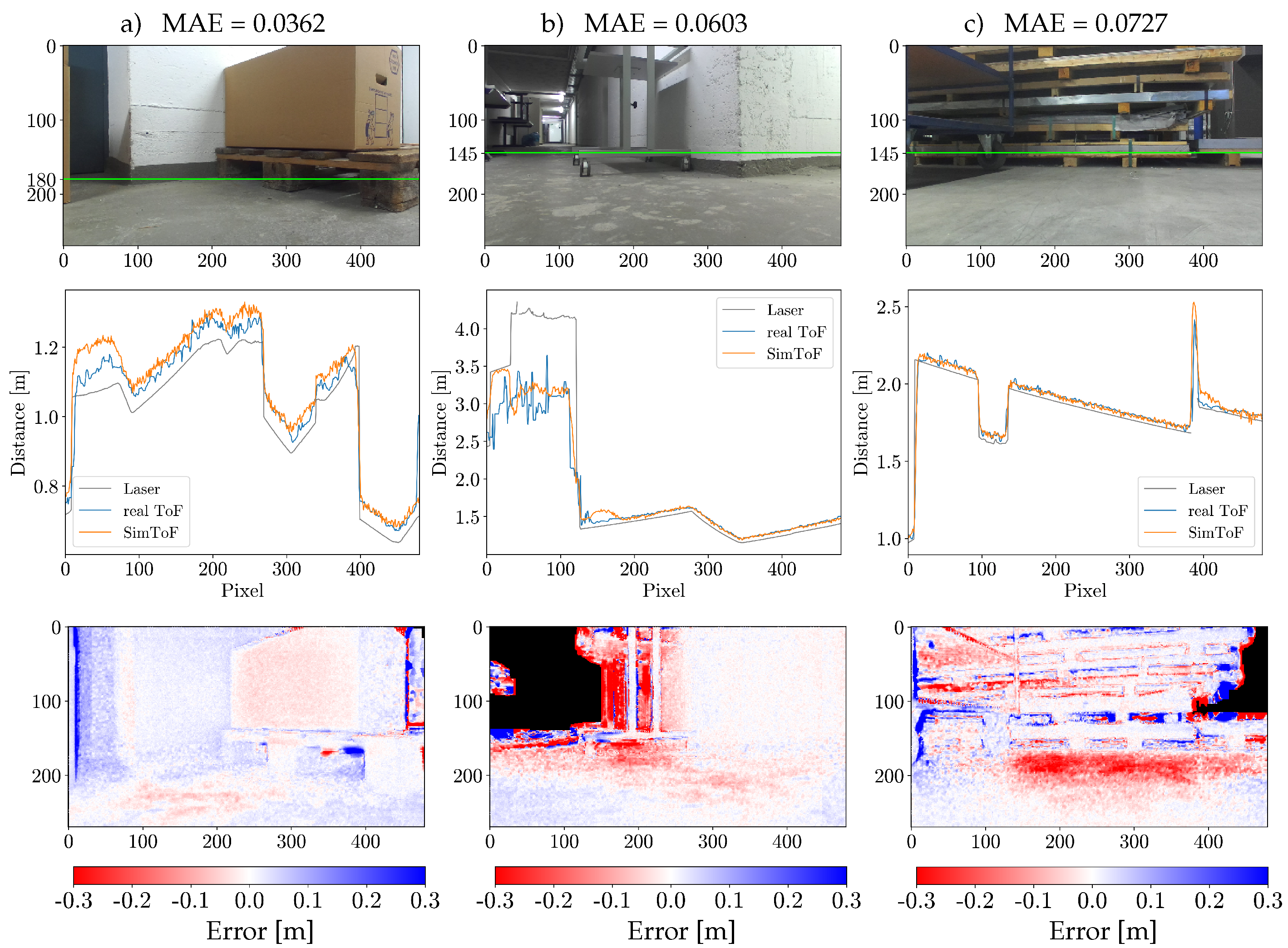
The cross-section plots in
Figure 6 provide insights into the behavior of SimToF when applied to more complex geometries. The comparison shown in
Figure 6 demonstrates the accurate interpretation of the ToF camera. Furthermore, SimToF generates realistic depth data for areas where the input depth exceeds 4 m (see
Figure 6b). Within this range, the actual ToF measurements fluctuate between no data and measurements which are too short. SimToF reproduces this behavior, although with higher errors compared to regions closer to the sensor.
However, there are anomalies in the prediction where higher deviations occur. In the cross-section plot of
Figure 6a, between pixels 10 and 90 a recognizable higher deviation can be seen. Additionally, anomalies can be observed in the cross-section plots of
Figure 6b around pixel 150 and in
Figure 6c around pixel 400. Furthermore, the error map in
Figure 6c reveals an error source in the floor area before the shelf. This confirms the lack of accurate MPI reproduction in SimToF, which was initially identified in the corner scenes.
In the sample scene shown in
Figure 6c, SimToF shows the ability to generate realistic values for missing input data, which can be seen in the cross-section plot around pixel 390. However, similar to the corner scenes the overall error increases due to the lack of input data. Among the real scenes 3.02 % of the input data are NaN values. The higher error rates in such areas contribute to a 4.62 % increase in the mean absolute error.
5. Conclusion
In summary, SimToF successfully simulates realistic ToF camera behavior and provides accurate predictions over a wide range of geometries. While there are some limitations, such as MPI correlated errors and objects in the far distance, the error maps highlight its strong performance across large image areas. Consequently, SimTof provides a reliable foundation for training neural networks. Quantitatively, this is evidenced by the fact that 84.34 % of the data achieved a mean absolute error of less than m.
One notable aspect is the ability of the network to predict the maximum measuring distance of the actual camera. Another notable feature is the generation of realistic ToF data in scenarios where no input data is available. This significantly improves the domain transfer to a ToF depth image and expands the potential applications of the model.
However, it is important to acknowledge the existing limitations at this stage. The prediction of SimToF is inaccurate, especially for objects with highly reflective materials. The evaluation revealed that none of the NaN values resulting from the filtering process of the ToF camera within its operating range are predicted. Furthermore, the noise model is restricted to one material, as it does not use material properties as input.
Author Contributions
Conceptualization, T.M., T.S., S.E and J.E.; methodology, T.M.; software, T.M.; validation, T.M., T.S., S.E and J.E.; investigation, T.M.; writing—original draft preparation, T.M.; writing—review and editing, T.S., S.E and J.E.; visualization, T.M.; supervision, S.E and J.E.; All authors have read and agreed to the published version of the manuscript.
Funding
This work is part of the 3D Robust project, which is funded by the Federal Ministry of Education and Research (BMBF).
Data Availability Statement
The data presented in this study are available on request from the corresponding author
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| ToF |
Time of Flight |
| MPI |
Multi-Path-Interference |
| SLAM |
Simultaneous Localization and Mapping |
| AMCW |
Amplitude Modulated Continuous-Wave |
| BRDF |
Bidirectional Reflectance Distribution Function |
| RNLB |
Regional Non-Local Blocks |
| DWT |
Direct Wavelet Transform |
| DCR |
Densely Connected Residual |
| SE |
Squeeze-and-Excitation |
| PReLU |
Parametric Rectified Linear Unit |
| MSE |
Mean Squared Error |
| NaN |
Not a Number |
References
- Freedman, D.; Smolin, Y.; Krupka, E.; Leichter, I.; Schmidt, M. SRA: Fast removal of general multipath for ToF sensors. Computer Vision–ECCV 2014: 13th European Conference, Zurich, Switzerland, September 6-12, 2014, Proceedings, Part I 13. Springer International Publishing, 2014, pp. 234–249.
- Godbaz, J.P.; Dorrington, A.A.; Cree, M.J. Understanding and ameliorating mixed pixels and multipath interference in amcw lidar. TOF Range-Imaging Cameras 2013, pp. 91–116.
- Mutny, M.; Nair, R.; Gottfried, J.M. Learning the correction for multi-path deviations in time-of-flight cameras. arXiv preprint arXiv:1512.04077 2015.
- Guo, Q.; Frosio, I.; Gallo, O.; Zickler, T.; Kautz, J. Tackling 3d tof artifacts through learning and the flat dataset. Proceedings of the European Conference on Computer Vision (ECCV), 2018, pp. 368–383.
- Buratto, E.; Simonetto, A.; Agresti, G.; Schäfer, H.; Zanuttigh, P. Deep learning for transient image reconstruction from ToF data. Sensors 2021, 21, 1962. [Google Scholar] [CrossRef] [PubMed]
- Su, S.; Heide, F.; Wetzstein, G.; Heidrich, W. Deep end-to-end time-of-flight imaging. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2018, pp. 6383–6392.
- Agresti, G.; Zanuttigh, P. Deep learning for multi-path error removal in ToF sensors. Proceedings of the European Conference on Computer Vision (ECCV) Workshops, 2018, pp. 0–0.
- Geiger, A.; Lenz, P.; Stiller, C.; Urtasun, R. Vision meets robotics: The kitti dataset. The International Journal of Robotics Research 2013, 32, 1231–1237. [Google Scholar] [CrossRef]
- Caesar, H.; Bankiti, V.; Lang, A.H.; Vora, S.; Liong, V.E.; Xu, Q.; Krishnan, A.; Pan, Y.; Baldan, G.; Beijbom, O. nuscenes: A multimodal dataset for autonomous driving. Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 2020, pp. 11621–11631.
- Hackel, T.; Savinov, N.; Ladicky, L.; Wegner, J.D.; Schindler, K.; Pollefeys, M. Semantic3d. net: A new large-scale point cloud classification benchmark. arXiv preprint arXiv:1704.03847 2017.
- Park, Y.; Jeon, M.; Lee, J.; Kang, M. MCW-Net: Single image deraining with multi-level connections and wide regional non-local blocks. Signal Processing: Image Communication 2022, 105, 116701. [Google Scholar] [CrossRef]
- Agrawal, A.; Müller, T.; Schmähling, T.; Elser, S.; Eberhardt, J. RWU3D: Real World ToF and Stereo Dataset with High Quality Ground Truth. 2023 Twelfth International Conference on Image Processing Theory, Tools and Applications (IPTA). IEEE, 2023, pp. 1–6.
- Bulczak, D.; Lambers, M.; Kolb, A. Quantified, interactive simulation of AMCW ToF camera including multipath effects. Sensors 2017, 18, 13. [Google Scholar] [CrossRef] [PubMed]
- Keller, M.; Orthmann, J.; Kolb, A.; Peters, V. A simulation framework for time-of-flight sensors. 2007 International Symposium on Signals, Circuits and Systems. IEEE, 2007, Vol. 1, pp. 1–4.
- Peters, V.; Loffeld, O.; Hartmann, K.; Knedlik, S. Modeling and bistatic simulation of a high resolution 3D PMD-camera. Proc. Congress on Modelling and Simulation (EUROSIM), 2007.
- Keller, M.; Kolb, A. Real-time simulation of time-of-flight sensors. Simulation Modelling Practice and Theory 2009, 17, 967–978. [Google Scholar] [CrossRef]
- Lambers, M.; Hoberg, S.; Kolb, A. Simulation of time-of-flight sensors for evaluation of chip layout variants. IEEE Sensors Journal 2015, 15, 4019–4026. [Google Scholar] [CrossRef]
- Meister, S.; Nair, R.; Kondermann, D. Simulation of Time-of-Flight Sensors using Global Illumination. VMV, 2013, pp. 33–40.
- Yan, Z.; Wang, H.; Liu, X.; Ning, Q.; Lu, Y. Physics-Based TOF Imaging Simulation for Space Targets Based on Improved Path Tracing. Remote Sensing 2022, 14, 2868. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, October 5-9, 2015, Proceedings, Part III 18. Springer, 2015, pp. 234–241.
- Trottier, L.; Giguere, P.; Chaib-Draa, B. Parametric exponential linear unit for deep convolutional neural networks. 2017 16th IEEE international conference on machine learning and applications (ICMLA). IEEE, 2017, pp. 207–214.
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. Proceedings of the IEEE conference on computer vision and pattern recognition, 2018, pp. 7132–7141.
- Mufti, F.; Mahony, R. Statistical analysis of signal measurement in time-of-flight cameras. ISPRS journal of photogrammetry and remote sensing 2011, 66, 720–731. [Google Scholar] [CrossRef]
- ifm electronic gmbh. https://www.ifm.com/, 2023. Last accessed in 2023.
- Chiabrando, F.; Chiabrando, R.; Piatti, D.; Rinaudo, F. Sensors for 3D imaging: Metric evaluation and calibration of a CCD/CMOS time-of-flight camera. Sensors 2009, 9, 10080–10096. [Google Scholar] [CrossRef] [PubMed]
- Agresti, G.; Schaefer, H.; Sartor, P.; Zanuttigh, P. Unsupervised domain adaptation for tof data denoising with adversarial learning. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2019, pp. 5584–5593.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).