Prerpints.org logo
Preprint
Article

Fractianal Calculus for Non-discrete Signed Measures

Altmetrics

Downloads

88

Views

27

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

06 August 2024

Posted:

07 August 2024

You are already at the latest version

Alerts
Abstract
In this paper we suggest a first ever construction of fractional integral and differential operators based on signed measures including a vector-valued case. The study focuses on constructing the fractional power of the Riemann-Stieltjes integral with a signed measure, using semigroup theory. The main result is a theorem that provides the exact form of a semigroup for the Riemann-Stieltjes integral with a measure having a countable number of extrema. The article provides examples of semigroups based on integral operators with signed measures and discusses the fractional powers of differential operators with partial derivatives.
Keywords: 
Subject: Physical Sciences  -   Mathematical Physics

1. Introduction

1.1. Short Historic and Bibliographic Overview

The basic goal of fractional calculus is to derive a formula that, for a given operator L and a range of parameters α , will produce a set of operators { L α } endowed with characteristics typical of powers. Specifically, L n should align with the conventional iterated power L n = L · L · . . . · L (n times) when α is a positive integer n, and the law of indices L α + β = L α L β should be applicable whenever L α , L β , and L α + β exist.
It is widely recognized that there are several methods available for defining fractional powers of L = d d x , which correspond to fractional derivatives and integrals (see, for example, [1,2,3]). Besides, there are multiple techniques available for the creation of operator families { L α } , with each technique being suitable for a distinct category of operators. For instance, several researchers such as Balakrishnan [7], Krasnoselski [8], Komatsu [9], Westphal [10], and Yosida [11] have explored the challenge of formulating an expression for ( − L ) α in scenarios where L represents a closed operator within a Banach space.
The Riemann-Stieltjes integral
∫ a t f ( y ) d F ( y ) , t ∈ [ a , b ]
extends the concept of the Riemann integral by allowing integration with respect to a more general class of functions called Stieltjes integrators F. The simplest existence theorem states that if f is continuous and F is of bounded variation on [ a , b ] , then the Riemann-Stieltjes integral exists. The corresponding to (1) differential operator is d d F ( t ) . The Riemann-Stieltjes integral has various applications in Probability Theory, Control Theory, Finance and Economics, Signal Processing, Function Approximation, etc.
Let us consider the approach to the conception of fractional integrals and derivatives of a function f with respect to another function F.
In [4,5,6] for the space X = C [ a , b ] of continuous functions on [ a , b ] with the topology of the uniform convergence and for a positive and continuous function p ( t ) in [ a , b ] , a < b the operator
( I a + , p α f ) ( t ) = 1 Γ ( α ) ∫ a t f ( τ ) ∫ τ t p ( s ) d s α − 1 p ( τ ) d τ ,
where α > 0 , t ∈ [ a , b ] , f ∈ C [ a , b ] was studied. This operator is realised as a negative fractional power of 1 p ( t ) d d t on [ a , b ] :
( I a + , p α f ) ( t ) = 1 p ( t ) d d t − α .
Let F be a strictly increasing function having a continuous derivative. Practically the same definition as (2) was given in [1], p. 326, formula 18.25 in the form
( I a + , F α f ) ( t ) = 1 Γ ( α ) ∫ a t f ( τ ) F ( t ) − F ( τ ) α − 1 d F ( τ ) , α > 0 .
The fractional derivative of a function f with respect to another function F is defined for α ∈ ( 0 , 1 ) as
( D a + , F α f ) ( t ) = 1 F ′ ( t ) d d t ( I a + , F 1 − α f ) ( t ) .
When F ( t ) > 0 we can also consider the Marchaud fractional derivative of order α ∈ ( 0 , 1 )
( D + , F α f ) ( t ) = 1 Γ ( − α ) ∫ 0 ∞ ( f ( t ) − f ( t − τ ) ) ( F ( τ ) ) − α − 1 d F ( τ ) .
Formulas (3)-(4) are valid only when F ( t ) is a strictly increasing function. But in applications function F can be not monotone and even discrete. Applications of a signed measure in differential equations were considered in [12]. Probabilistic interpretation of a signed measure can be found in [13]. Integrals of a function with respect to a signed measure are used in stochastics to model and analyze complex systems, such as financial markets where both positive and negative quantities exist (see [14]).
In this study, we will concentrate on constructing the fractional power of the Riemann–Stieltjes integral, expressed as (1), where function F ( t ) is continuous and has a bounded variation on [ a , b ] . We will use formulas of U. Westphal and semi-group theory.
It is worth mentioning that there exist different concepts of the general fractional calculus operators defined in a completely different form compared to those mentioned above. In particular, we refer to [2], where general fractional calculus considered with probabilistic applications and to [15,16,17,18,19,20].

1.2. Preliminaries: Powers Based on Semigroups

In this article we explore a convenient method for constructing the fractional power of an operator using semigroups. Such approach was carried out by U. Westphal in [10], see also [3].
Let T t , 0 ≤ t be a contraction semi-group in a real or complex Banach space X, and A be its infinitesimal generator.
In [10] the fractional power ( − A ) α , 0 < α < 1 was defined by the formula
( − A ) α f = 1 Γ ( − α ) ∫ 0 ∞ t − α − 1 ( T t − I ) f ( x ) d t , f ∈ D ( A ) .
In the case 1 < α < ℓ , ℓ = 2 , 3 , . . . this formula can be written with the usage of "finite differences" ( I − T t ) ℓ :
( − A ) α f = 1 C α ( ℓ ) ∫ 0 ∞ t − α − 1 ( I − T t ) ℓ f ( x ) d t ,
where C α ( ℓ ) = Γ ( − α ) A α ( ℓ ) , A α ( ℓ ) = ∑ k = 0 ℓ ( − 1 ) k − 1 ℓ k = ∑ k = 0 ℓ ( − 1 ) k − 1 ℓ ! k ! ( ℓ − k ) ! .
The negative power of the operator ( − A ) for 0 < α < 1 can be defined by the equation
( − A ) − α f = 1 Γ ( α ) ∫ 0 ∞ t α − 1 T t f ( x ) d t .
In order to get fractional integral of the order α greater than 1 one can just apply iterated integral to (8).
Example 1. If the operator A = − d d x , then A is the generating operator of the strongly continuous semigroup T t f ( x ) = f ( x − t ) on L 2 [ 0 , ∞ ) .
By (6) we get
d d x α f ( x ) = 1 Γ ( − α ) ∫ 0 ∞ t − α − 1 ( f ( x − t ) − f ( x ) ) d t , 0 < α < 1 .
Easy calculations confirm that
( I − T t ) ℓ f ( x ) = ∑ k = 0 ℓ ( − 1 ) k ℓ k f ( x − k t ) = ( Δ t ℓ f ) ( x )
is a finite difference. So for α > 1 , α not an integer, ℓ = [ α ] + 1 , we can write
d d x α f ( x ) = 1 C α ( ℓ ) ∫ 0 ∞ t − α − 1 ( I − T t ) ℓ f ( x ) d t = 1 C α ( ℓ ) ∫ 0 ∞ ( Δ t ℓ f ) ( x ) t α + 1 d t .
Therefore, d d x α represents the Marchaud fractional derivatives (see [1], p. 111).
For α > 0 , the negative power of the operator d d x can be defined by equality (8)
d d x − α f ( x ) = 1 Γ ( α ) ∫ 0 ∞ t α − 1 f ( x − t ) d t = 1 Γ ( α ) ∫ − ∞ x ( x − t ) α − 1 f ( t ) d t = ( I + α f ) ( x ) .
So we obtain fractional Riemann–Liouville integral on the whole real axis (see formula (5.2) from [1], p. 94).
If we want to get fractional Riemann–Liouville integral on half-axis (see formula (5.1) from [1], p. 94)
( I 0 + α f ) ( x ) = 1 Γ ( α ) ∫ 0 x ( x − t ) α − 1 f ( t ) d t , 0 < x ,
we should take
T t f ( x ) = f ( x − t ) , t ≤ x ; f ( 0 ) , t > x
for such functions that f ( 0 ) = 0 .

1.3. Detailed Content

The rest of the article is organised as follows. In the second section, the focus is on integral operators of the form I g f ( x ) = ∫ a x f ( y ) g ( y ) d y and their inverse operators (derivatives) D g f ( x ) = d g ( x ) d x f ( x ) . We provide examples of semigroups based on integral operators with power measure and with cosine measure.
The third section describes a mathematical result related to the construction of an operator semigroup based on I f ( t ) = ∫ a t f ( y ) d F ( y ) , where F ( y ) is continuous of locally finite variation and such that for a discrete set a k ∈ R , k ∈ Z , | k | < K with K ∈ N or K = ∞ , F is strictly increasing on [ a 2 k , a 2 k + 1 ] and strictly decreasing on [ a 2 k − 1 , a 2 k ] for all k. In this section we also present examples and corollaries related to fractional powers of operators, including their probabilistic representations.
The fourth section presents new fractional operators, focusing on examples of fractional powers of integral operators with signed measures. It presents calculations for fractional powers of specific integral operators, such as L = D k = − d ( k + 1 ) x k d x and L = D s = d sin x d x , and their corresponding Feller processes. The text also explores fractional powers of differential operators with partial derivatives and discusses applications in defining fractional Poisson and Heisenberg brackets in classical and quantum mechanics.

2. Simple Examples of Semigroups Based on Integral Operators with Signed Measures

Let us consider an integral operator
I g f ( x ) = ∫ a x f ( y ) g ( y ) d y
ans its inverse operator (derivative)
D g f ( x ) = d g ( x ) d x f ( x ) .
In order to define fractional powers of I g and D g using formulas (6)–(8) we need to build the semigroup T t generated by D g , and it must be a contraction semigroup.
If g is strictly positive, then G ( x ) = 1 / g ( x ) is as well. The group (even group, not just semigroup) T t generated by G has explicit representation (solution of first order linear pde via characteristics):
T t f ( x ) = f ( X x ( t ) ) ,
where X x ( t ) is the solution of the ode x ˙ = G ( x ) with initial condition x at a.
Now, interesting thing occurs when g changes sign and G gets infinite values. On the first sight one may think that everything breaks down, but remarkably it is not. The group may be still well defined. Assume that zeros of g are discrete and degenerate in the sense that g ′ does not vanish there. Then the dynamics x ˙ = G ( x ) moves from any x 0 monotonically to the nearest zero of g, where g ′ is negative (by assumed nondegeneracy it always takes finite time to reach this point) and then stays there for ever after. Well defined contraction semigroup and formulas (6)–(8) applies.
Consider some examples.
Example 2. Integral operator
I k f ( x ) = − ∫ 0 x ( k + 1 ) y k f ( y ) d y
with an odd integer k has an inverse operator (derivative)
D k f ( x ) = − d ( k + 1 ) x k d x f ( x ) .
To calculate the semigroup via characteristics one has to solve the ODE
( k + 1 ) x k x ˙ = − 1 , or x k + 1 = − t + x 0 k + 1 ,
where x 0 is an initial point. We obtain that the semigroup T t = exp ( t D k ) is given by
T t f ( x ) = f ( 0 ) , t ≥ x k + 1 , f ( sgn ( x ) ( x k + 1 − t ) 1 / ( k + 1 ) ) , t ≤ x k + 1 .
This semigroup is Feller (strongly continuous) in C ∞ ( R ) with the domain of the generator consisting of continuously differentiable functions from C ( R ) s.t. f ′ ( x ) = o ( x k ) for x → ∞ and a finite limit lim x → 0 f ′ ( x ) x k exists.
Example 3. Integral operator
I s f ( x ) = ∫ 0 x sin y f ( y ) d y .
has an inverse operator (derivative)
D s f ( x ) = d sin x d x f ( x ) .
In order to calculate the semigroup via characteristics one has to solve the ODE
sin x x ˙ = 1 , or d cos x = − d t .
Due to the periodicity of the sine, solutions preserve the intervals [ 2 π k , 2 π ( k + 1 ) ] , k ∈ Z . The solution starting at x ∈ [ 0 , 2 π ] is
X x ( t ) = π , t ≥ 1 + cos x , arccos ( cos x − t ) , t ≤ 1 + cos x , x ∈ ( 0 , π ] , 2 π − arccos ( cos x − t ) , t ≤ 1 + cos x , x ∈ [ π , 2 π ) .
The semigroup T t = exp ( t D s ) is Feller on each interval [ 2 π k , 2 π ( k + 1 ) ] given by
T t f ( x ) = f ( 2 π k + π ) , t ≥ 1 + cos x , f ( 2 π k + arccos ( cos x − t ) ) , t ≤ 1 + cos x , x ∈ [ 2 π k , 2 π k + π ] , f ( 2 π ( k + 1 ) − arccos ( cos x − t ) ) , t ≤ 1 + cos x , x ∈ [ 2 π k + π , 2 π ( k + 1 ) ] .

3. Main Result. General Semigroup Operator

Let us consider the integral I f ( t ) = ∫ a t f ( y ) d F ( y ) with some a ∈ R . Assume that F is continuous of locally finite variation and such that for a discrete set a k ∈ R , k ∈ Z , | k | < K with K ∈ N or K = ∞ , F is strictly increasing on [ a 2 k , a 2 k + 1 ] and strictly decreasing on [ a 2 k − 1 , a 2 k ] for all k. Let S is some appropriate function. Then the inverse differential operator solving equation I G = S is given by the formula
G ( x ) = ( L S ) ( x ) = d S ( x ) d F ( x ) = lim δ → 0 S ( x + δ ) − S ( x ) F ( x + δ ) − F ( x ) ,
which holds for any continuous G and all points x. By our assumptions on F, the derivative F ′ ( x ) exists and does not vanish for almost all points x. For these points,
G ( x ) = L S ( x ) = S ′ ( x ) F ′ ( x ) .
Theorem 1. 
Under the assumptions on F given above, the operator L generates a strongly continuous semigroup on the set of functions that are continuous away from the set { a 2 k } with left and right limits at these points. The semigroup has invariant spaces C ( [ a 2 k , a 2 k + 2 ] ) , where it acts by the formula
T t S ( x ) = S [ ( F − F ( a 2 k ) ) − 1 ( t + F ( x ) − F ( a 2 k ) ) ] , x ∈ [ a 2 k , a 2 k + 1 ] , t ≤ F ( a 2 k + 1 ) − F ( x ) , S [ ( F − F ( a 2 k + 2 ) ) − 1 ( t + F ( x ) − F ( a 2 k + 2 ) ) ] , x ∈ [ a 2 k + 1 , a 2 k + 2 ] , t ≤ F ( a 2 k + 1 ) − F ( x ) , S ( a 2 k + 1 ) , x ∈ [ a 2 k , a 2 k + 2 ] , t ≥ F ( a 2 k + 1 ) − F ( x ) .
Remark. Let us stress for clarity that ( F − F ( a 2 k ) ) − 1 denote the inverse functions to F ( x ) − F ( a 2 k ) , which are well defined and continuous on x ∈ [ a 2 k , a 2 k + 1 ] , due to the assumed continuity and strong monotonicity of F on these intervals.
Proof. 
In order to see, where formula (10) comes from, let us look at x ∈ [ a 2 k , a 2 k + 1 ] and assume that F ′ ( x ) is well defined and positive for all x ∈ ( a 2 k , a 2 k + 1 ) . To shorten formulas, let us assume F ( a 2 k ) = 0 . Observe then that the action of the semigroup S t ( x ) = T t S ( x ) , generated by L, on a function S ( x ) is given by the solution of the linear first order partial differential equation
∂ S t ∂ t ( x ) = L S t ( x ) = 1 F ′ ( x ) ∂ S t ( x ) ∂ x .
Solution to this Cauchy problem can be defined via characteristics, which solve the equation
X ˙ = 1 F ′ ( X ) .
Namely, denoting X x ( t ) the solution to this equation starting from a point x, we will have
S t ( x ) = S ( X x ( t ) ) .
Solving the equation X ˙ = 1 / F ′ ( X ) yields F ′ ( X ) X ˙ = 1 , or F ( X x ( t ) ) = t + F ( x ) . Thus X x ( t ) = F − 1 ( t + F ( x ) ) yielding for S t ( x ) the first line of (10). The specific feature of our problem is that this holds only for finite times t < F ( a 2 k + 1 ) − F ( x ) . For t = F ( a 2 k + 1 ) − F ( x ) and thus X x ( t ) = a 2 k + 1 , the equation X ˙ = 1 / F ′ ( X ) is not defined at all, since F ′ ( x ) either does not exist or equals to zero. It is then natural to define X x ( t ) = a 2 k for t ≥ F ( a 2 k + 1 ) − F ( x ) , because the point a 2 k is stable in the sense that the vector field 1 / F ′ ( x ) points towards this point both from the right and from the left. For x = a 2 k , where the equation is also not defined, the formula for X x ( t ) is obtained by continuity having in mind that this point is repulsive for characteristic equation. And (10) follows.
Now, once formula (10) is obtained (by whatever heuristical reasons and with whatever simplifying assumptions), it is straightforward to see that it does specify a strongly continuous semigroup under the assumptions of the theorem. One just has to show that whenever the generator is defined, it is given by (9). And this is mostly straightforward. In fact, from (9),
( L S ) ( x ) = lim δ → 0 S ( x + δ ) − S ( x ) F ( x + δ ) − F ( x ) .
Let us denote ϵ = F ( x + δ ) − F ( x ) . By the continuity of F, ϵ → 0 as δ → 0 . Moreover, x + δ = F − 1 ( F ( x ) + ϵ ) . Hence
L S ( x ) = lim ϵ → 0 S [ F − 1 ( ϵ + F ( x ) ) ] − S ( x ) ϵ = lim ϵ → 0 T t S ( x ) − S ( x ) ϵ ,
which is the defining formula for the generator of T t . The proof is complete. □
Example 4. Let
F ( x ) = x i f 0 ≤ x ≤ 1 ; 2 − x i f 1 < x ≤ 2
and f ∈ C [ 0 , 2 ] such that f ( 1 ) = 0 . Then a 0 = 0 , a 1 = 1 , a 2 = 2 and the semi-group constructed by (10) is
T t f ( x ) = f x + t , x ∈ [ 0 , 1 ) , t ≤ 1 − x , f x − t , x ∈ [ 1 , 2 ] , t ≤ x − 1 , 0 , x ∈ [ 0 , 2 ] , t > 1 − F ( x ) .
Corollary 1. Under the assumptions of the theorem
( − L ) α S ( x ) = 1 Γ ( − α ) ∫ 0 ∞ t − α − 1 ( T t f ( x ) − f ( x ) ) d t
is well defined with T t given by (10). The corresponding fractional integrals
( − L ) − α f ( x ) = 1 Γ ( α ) ∫ 0 ∞ t α − 1 T t f ( x ) d t
are well defined for functions f ( x ) that vanish at the points x = a 2 k + 1 for all k.
Corollary 2. The fractional powers ( − L ) α are seen to be given in the Lévy-Khintchine form, so that they generate Feller semigroups and Feller processes, say X x α ( t ) . Therefore the potential operators ( − L ) − α can be expressed in probabilistic representation as path integrals
− ( − L ) − α f ( x ) = E ∫ 0 τ x f ( X x α ( t ) ) d t ,
where τ x is the time the process X x α ( t ) reaches one of the points a 2 k .

4. New Fractional Operators

In this section we consider some examples of fractional powers.

4.1. Examples of Fractional Powers of Integral Operators with Signed Measures

Example 6. Using semi-group from Example 2 and formula (6) we get that the fractional power α ∈ ( 0 , 1 ) of L = D k = − d ( k + 1 ) x k d x with an odd integer k and with inverse sign is
− ( − L ) α f ( x ) = − d ( k + 1 ) x k d x α f ( x ) = = − 1 Γ ( − α ) ∫ 0 ∞ t − α − 1 ( T t − I ) f ( x ) d t = = − 1 Γ ( − α ) ∫ 0 x k + 1 t − α − 1 [ f ( sgn ( x ) ( x k + 1 − t ) 1 / ( k + 1 ) ) − f ( x ) ] d t + + x − α ( k + 1 ) Γ ( 1 − α ) ( f ( 0 ) − f ( x ) ) .
This is clearly the generator of a Feller process, say X x α ( t ) , whose potential operator − ( − L ) − α is calculated via the semigroup and represents the fractional integral. Namely, − ( − L ) − α , the analog of Riemann-Liouville fractional integral is defined for continuous functions vanishing at zero as
− ( − L ) − α f ( x ) = E ∫ 0 τ x f ( X x α ( t ) ) d t ,
where τ x is the time the process X x α ( t ) reaches zero.
Formula (8) we can use only if f ( 0 ) = 0 , then applying (8) we get for 0 < α < 1
( − L ) − α f = d d x k + 1 − α f ( x ) = = 1 Γ ( α ) ∫ 0 ∞ t α − 1 T t f ( x ) d t = = 1 Γ ( α ) ∫ 0 x k + 1 t α − 1 f sgn ( x ) ( x k + 1 − t ) 1 / ( k + 1 ) d t .
Remark. If x > 0 putting sgn ( x ) ( x k + 1 − t ) 1 / ( k + 1 ) = τ in (11) and (12) we get
( − L ) α f = d d x k + 1 α f ( x ) = = 1 Γ ( − α ) ∫ 0 x ( x k + 1 − τ k + 1 ) − α − 1 f ( τ ) − f ( x ) d τ + + x − α ( k + 1 ) Γ ( 1 − α ) ( f ( x ) − f ( 0 ) )
and
( − L ) − α f = d d x k + 1 − α f ( x ) = 1 Γ ( α ) ∫ 0 x ( x k + 1 − τ k + 1 ) α − 1 f ( τ ) d τ k + 1
that are the Erdélyi–Kober derivative in the Marchaud form and (3) for a = 0 , g ( x ) = x k + 1 , respectivy.
Example 7. Using semi-group from Example 3 and formula (6) the fractional power of L = D s = d sin x d x with inverse sign is given for f ∈ C ( [ 2 π k , 2 π ( k + 1 ) ] ) by
− ( − L ) α f ( x ) = = − − d sin x d x α f ( x ) = = − 1 Γ ( − α ) ∫ 0 1 + cos x t − α − 1 [ f ( 2 π k + arccos ( cos x − t ) ) − f ( x ) ] d t + + ( 1 + cos x ) − α Γ ( 1 − α ) ( f ( 0 ) − f ( x ) )
for x ∈ [ 2 π k , 2 π k + π ] and symmetrically for x ∈ [ 2 π k + π , 2 π ( k + 1 ) ] .
This is clearly the generator of a Feller process, say X x α ( t ) , whose potential operator − ( − L α ) − 1 is calculated via the semigroup and represents the fractional integral. Namely, − ( − L α ) − 1 , the analog of Riemann-Liouville fractional integral is defined for functions f ∈ C ( [ 2 π k , 2 π ( k + 1 ) ] ) vanishing at 2 π k + π as
− ( − L α ) − 1 f ( x ) = E ∫ 0 τ x f ( X x α ( t ) ) d t ,
where τ x is the time the process X x α ( t ) reaches 2 π k + π .
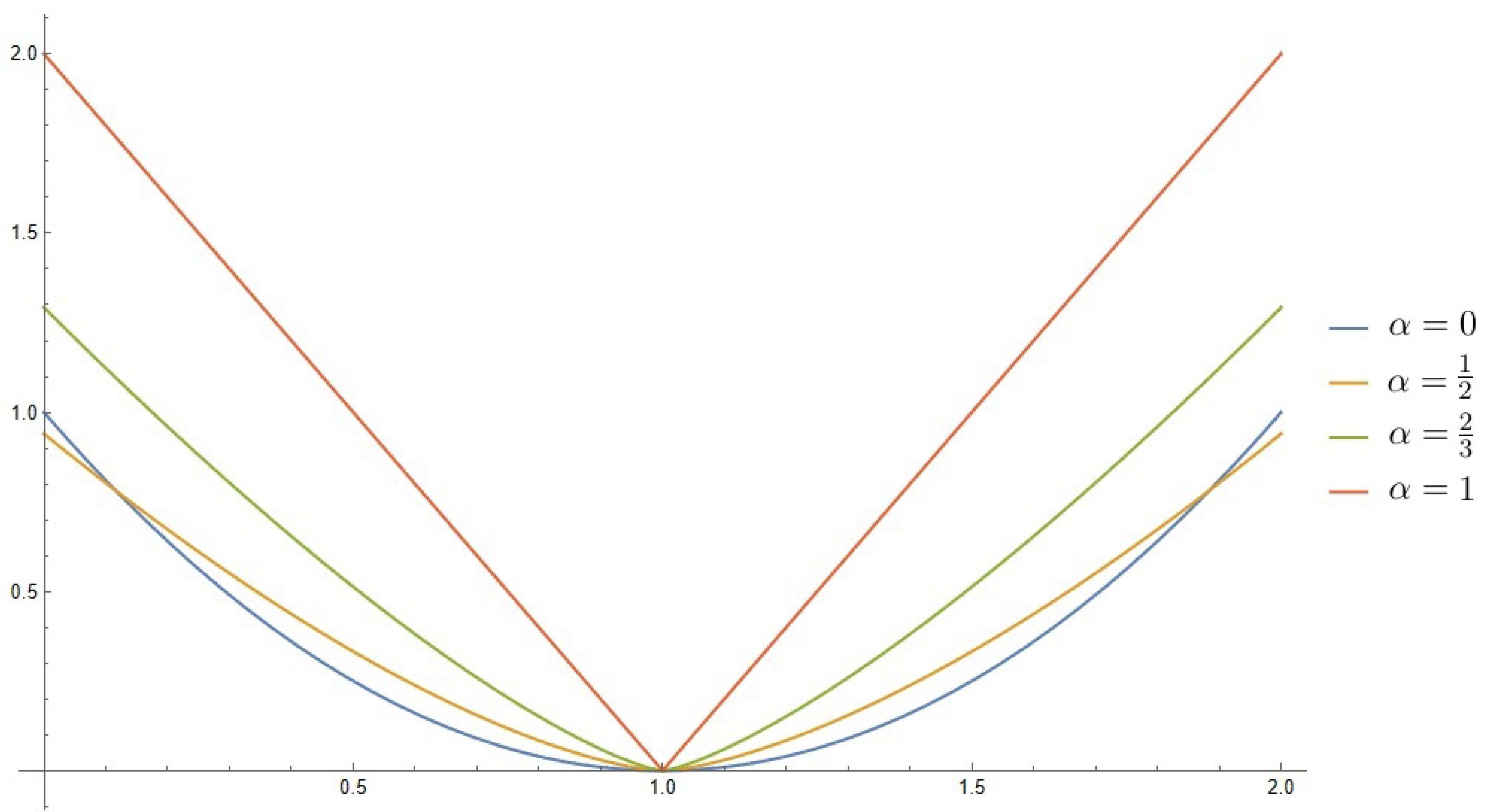
Example 8. Let us consider an integral operator I F f ( x ) = ∫ 0 x f ( y ) d F ( y ) and its inverse operator (derivative) D F f ( x ) = d d F ( x ) f ( x ) , where F ( x ) is from Example 4. Let f ( 1 ) = 0 , then by (6) we get
− d d F ( x ) α f ( x ) = 1 Γ ( − α ) [ I [ 0 , 1 ] ( x ) ∫ 0 1 − x t − α − 1 ( f ( x + t ) − f ( x ) ) d t + + I [ 1 , 2 ] ( x ) ∫ 0 x − 1 t − α − 1 ( f ( x − t ) ) − f ( x ) ) d t + ] = = 1 Γ ( − α ) [ I [ 0 , 1 ] ( x ) ∫ x 1 ( t − x ) − α − 1 ( f ( t ) − f ( x ) ) d t − − I [ 1 , 2 ] ( x ) ∫ 1 x ( x − t ) − α − 1 ( f ( t ) − f ( x ) ) d t ] .
For f ( x ) = ( x − 1 ) 2 , α = 0 ; 1 2 ; 2 3 ; 1 plots of − d d F ( x ) α f ( x ) are presented in Figure 1.

4.2. Fractional Powers of Differential Operators with Partial Derivatives

In the remaining brief comments of the paper we like to demonstrate that the semigroup method used above for integrals with signed can be effectively and easily applied in many other situations.
For instance, let us look at differential operators of first order with partial derivatives:
L S ( x ) = g ( x ) ∂ S ∂ x = ∑ j = 1 n g j ( x ) ∂ S ∂ x j ,
with g Lipschitz. Let X x ( t ) denote the solution of the equation x ˙ = g ( x ) starting from x at time zero. Then L generates a conservative Feller semigroup in C ∞ ( R n ) :
T t f ( x ) = f ( X x ( t ) ) .
The power of this operator can be written in the form
( − L ) α f ( x ) = 1 Γ ( − α ) ∫ 0 ∞ t − α − 1 ( T t − I ) f ( x ) d t = 1 Γ ( − α ) ∫ 0 ∞ t − α − 1 [ f ( X x ( t ) ) − f ( x ) ] d t
for Lipschitz (sufficiently Holder) f. This operator (with inverse sign) also generates a Feller semigroup in C ∞ ( R n ) . The corresponding fractional integral (potential operator of the semigroup) is
( − L ) − α f ( x ) = 1 Γ ( α ) ∫ 0 ∞ t α − 1 T t f ( x ) d t = 1 Γ ( α ) ∫ 0 ∞ t α − 1 f ( X x ( t ) ) d t .
Operator ( − L ) − α can be define for functions f supported on some domain Ω such that X x ( t ) exits Ω in finite time.

4.3. Fractional Poisson and Heisenberg Brackets

As an insightful example, we can use the construction of the previous section to define the fractional power of the Poisson bracket
L S ( x , p ) = { H , S } = ∂ H ∂ p ∂ S ∂ x − ∂ H ∂ x ∂ S ∂ p
for a Hamiltonian function H ( x , p ) as the operator
( − L ) α f ( x ) = 1 Γ ( − α ) ∫ 0 ∞ t − α − 1 [ f ( X , P ) x , p ( t ) ) − f ( x , p ) ] d t ,
where ( X , P ) x , p ( t ) solves the corresponding Hamiltonian system.
Similarly, one can define fractional Heisenberg operators of quantum mechanics. The standard Heisenberg equation has the form
A ˙ ( t ) = L H ( A ) = − i [ H , A ( t ) ] ,
where A ( t ) , H are self-adjoint operators in a Hilbert space, H called a Hamiltonian.
An operator A → i [ A , H ] is known to generate a semigroup T t acting on the space of operators as
T t A = exp { − i H t } A exp { i H t } .
Thus one obtains the fractional power
( − L H ) α A = 1 Γ ( − α ) ∫ 0 ∞ t − α − 1 ( exp { − i H t } A exp { i H t } − A ) d t .
This operator was constructed in a slightly different way (via resolvents) in paper [21]. Different approaches to classical and quantum fractional brackets ware developed in [22] and [23]. Fractional Heisenberg equations represent one approach to building fractional quantum mechanics. Another approach develops the theory of fractional Schrödinger equation, see e.g. [24] for closed quantum systems and [25] for open quantum systems.

5. Conclusion

In this article, for the first time, fractional integrals and derivatives were constructed with respect to a signed measure. An approach based on semigroup theory was used. The suggested fractional powers have stochastic and quantum mechanic applications.

Author Contributions

Conceptualization, V. N. Kolokoltsov; methodology, V. N. Kolokoltsov and E. L. Shishkiha; validation, V. N. Kolokoltsov and E. L. Shishkiha; formal analysis, V. N. Kolokoltsov and E. L. Shishkiha; investigation, V. N. Kolokoltsov; resources, V. N. Kolokoltsov and E. L. Shishkiha; data curation, E. L. Shishkiha; writing—original draft preparation, V. N. Kolokoltsov and E. L. Shishkiha; writing—review and editing, V. N. Kolokoltsov and E. L. Shishkiha; visualization, V. N. Kolokoltsov and E. L. Shishkiha; supervision, V. N. Kolokoltsov; project administration, V. N. Kolokoltsov and E. L. Shishkiha. All authors have read and agreed to the published version of the manuscript.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Acknowledgments

The authors would like to thank the Isaac Newton Institute for Mathematical Sciences, Cambridge, for support and hospitality during the programme "Fractional differential equations" where work on this paper was initiated.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Samko, S. G.; Kilbas, A. A.; Marichev, O. I. Fractional integrals and derivatives, Gordon and Breach Science Publishers: Amsterdam, Netherlands, 1993; 976 p.
  2. Kolokoltsov, V. N. The Probabilistic Point of View on the Generalized Fractional Partial Differential Equations. FCAA 2019, 22, 543–600. [Google Scholar] [CrossRef]
  3. Hilfer, R. Anomalous Transport: Foundations and Applications, Editors: R. Klages, G. Radons, I. M. Sokolov, Eds.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim an der Bergstrasse, Germany, 2008; pp. 17–73. [Google Scholar]
  4. Talenti, G. Sul Problema di Cauchy per le Equazioni a Derivate Parziali. Ann. Mat. Pura Appl. 1965, LXVII, 365–394. [Google Scholar] [CrossRef]
  5. Chrysovergis, A. Some Remarks on Talenti’s Semigroup. Canad. Math. Bull. 1971, 14, 147–150. [Google Scholar] [CrossRef]
  6. Seidman, T. I. A Remark on Talenti’s Semigroup. Canad. Math. Bull. 1975, 18(4), 591–592. [Google Scholar] [CrossRef]
  7. Balakrishnan, A. V. An operational calculus for infinitesimal generators of semigroups. Trans. Amer. Math. Soc. 1959, 91, 330–353. [Google Scholar]
  8. Krasnoselski, M. A.; Zabreyko, P. P.; Pustilnik, E. I.; Sobolevski, P.S. Integral Operators in the Spaces of Summable Functions, Nauka: Moscow, Russia, 1966; 500 p.
  9. Komatsu, H. Fractional powers of operators. Pacific J. Math. 1966, 19, 285–346. [Google Scholar] [CrossRef]
  10. Westphal, U. Ein Kalkül für gebrochene Potenzen infinitesimaler Erzeuger von Halbgruppen und Gruppen von Operatoren, Teil I: Halbgruppenerzeuger, Teil II : Gruppenerzeuger’. Gompositio Math. 1970, 22, 67–103. [Google Scholar]
  11. Yosida, K. Functional Analysis, 6 th ed., Springer-Verlag: Berlin, Germany, 1980; 504 p.
  12. Bonicatto, P.; Gusev, N. A. Non-uniqueness of signed measure-valued solutions to the continuity equation in presence of a unique flow. Atti Accad. Naz. Lincei Cl. Sci. Fis. Mat. Natur. 30 2019, 3, 511–531. [Google Scholar] [CrossRef]
  13. Hochberg, K. J. A Signed Measure on Path Space Related to Wiener Measure. Ann. Probab. 1978, 6(3), 433–458. [Google Scholar] [CrossRef]
  14. Cohen, S. N.; Elliott, R. J. Stochastic Calculus and Applications, Birkhäuser, New York (2015).
  15. Kiryakova, V. Generalized Fractional Calculus and Applications, Pitman Res. Notes Math., Longman Scientific & Technical, Harlow, Co-publ. John Wiley, New York, 301 (1994).
  16. Kochubei, A.; Luchko, Yu. Handbook of Fractional Calculus with Applications. Vol.1: Basic Theory, Vol.2: Fractional Differential Equations, Walter de Gruyter: Berlin/Boston, 2019.
  17. Podlubny, I. Fractional differential equations. An introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. Mathematics in Science and Engineering, 198, Academic Press, SanDiego, 1999.
  18. Luchko, Y. General fractional integrals and derivatives and their applications. Physica D: Nonlinear Phenomena 2023, 455, 133906. [Google Scholar] [CrossRef]
  19. Al-Refai, M.; Luchko, Y. The General Fractional Integrals and Derivatives on a Finite Interval. Mathematics 2023, 11, 1031. [Google Scholar] [CrossRef]
  20. Fernandez, A.; Fahad, H.M. Weighted fractional calculus: A general class of operators. Fractal Fract. 2022, 6. [Google Scholar] [CrossRef]
  21. Tarasov, V. E. Fractional Heisenberg Equation. Physics Letters A 2006, 372, 2984–2988. [Google Scholar] [CrossRef]
  22. Golmankhaneh, A. Kh. Fractional Poisson Bracket. Turk. J. Phys. 2008, 32, 241–250. [Google Scholar]
  23. Rabei, E.M.; Tarawneh, D.M.; Muslih, S.I.; Baleanu, D. Heisenberg’s Equations of Motion with Fractional Derivatives. Journal of Vibration and Control 2007, 13, 1239–1247. [Google Scholar] [CrossRef]
  24. Laskin, N. Fractional Schrödinger equation. Phys. Rev. 2002, E 66, Art. 056108. [Google Scholar] [CrossRef]
  25. Kolokoltsov, V. N. Continuous time random walks modeling of quantum measurement and fractional equations of quantum stochastic filtering and control. FCAA 2022, 25, 128–165. [Google Scholar] [CrossRef]
Preprints 114473 g001
Figure 1. − d d F ( x ) α ( x − 1 ) 2
Figure 1. − d d F ( x ) α ( x − 1 ) 2
Preprints 114473 g001
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated