Prerpints.org logo
Preprint
Article

Optimizing Schedules in Manufacturing: Unleashing the Power of Mathematical Optimization

Altmetrics

Downloads

129

Views

43

Comments

0

Submitted:

06 August 2024

Posted:

07 August 2024

You are already at the latest version

Alerts
Abstract
Mathematical optimization offers a valuable approach to tackle Industry scheduling problems. By formulating the scheduling challenge as a mathematical problem, mathematical optimization enables efficient and effective decision-making processes. Mathematical optimization is particularly beneficial in complex scheduling scenarios, such as in networked manufacturing environments, where multiple jobs and resources need to be coordinated. By leveraging optimization models and algorithms, it becomes possible to generate optimal process plans, considering factors like job dependencies, resource availability, and timing constraints. Through mathematical optimization, organizations can achieve improved efficiency, reduced lead times, and enhanced utilization of resources. Rigorous mathematical formulations and optimization techniques enables to surpass traditional manual planning methods and brings forth powerful computational capabilities. By optimizing various scheduling objectives, from minimizing makespan to maximizing resource utilization, mathematical optimization provides organizations with valuable insights and actionable plans. The purpose of this study is to discuss scheduling solutions for multiple jobs in a networked manufacturing setting based on mathematical optimization process. The study analyses a solver-based approach to generate the optimal process plans for multiple jobs and compare it with a more traditional game-theoretic approach. The objectives aim to develop two solver-based model using Z3 and Gurobi to generate optimal process plans; implement a game-theoretic model to solve for the same set of scheduling problems, and compare the computational time, solution quality, and efficiency of both approaches. To achieve this, the methodology will start with the problem definition. Multiple jobs are to be scheduled on a set of parallel machines. Each job has predefined processing times, deadlines, and priorities. The objective is to minimize the total completion time and maximize machine utilization while meeting all deadlines.
Keywords: 
Subject: Computer Science and Mathematics  -   Computational Mathematics

1. Introduction

Artificial intelligence (AI), recognized as an academic discipline since 1955, encompasses numerous subfields [1]. Machine learning notably stand out. Machine learning algorithms utilize statistical models and rely on sample data, or 'training data', to perform assigned tasks or make predictions. The defining feature of machine learning is the capacity of the computer to learn automatically, negating the need for human intervention or assistance. Despite its potential, the system's opacity and heavy reliance on extensive datasets for learning cast a shadow on its utility and efficiency. Critically, the lack of transparency in machine learning processes is a central concern. Often labeled as a "black box", machine learning models are challenging to understand and interpret. With inputs fed into a system and outputs produced, it's usually difficult for humans to comprehend what happens in between those stages. This black box nature can create distrust and confusion, making it challenging for users to accept and correctly use the AI system's outputs. As a result, decision-making based on machine learning can potentially involve unexplained errors or biases, leading to inaccurate and potentially unethical outcomes. They require also substantial amounts of data for training. This substantial requirement creates potential logistical and ethical issues, from data storage and processing capabilities to data privacy concerns [2, 3]. For businesses and organizations, feeding machine learning systems with the necessary sizable data sets may present financial, technical, and ethical challenges. Recently, a shift towards mathematical optimization has been observed [4]. This technology emphasizes transparency, consistency, and interpretability more than the previous approaches. In contrast to machine learning, mathematical optimization employs high-level, human-readable models to represent problems, thus making them more understandable and transparent [5]. This transparency is crucial for businesses needing to decipher how a system is making decisions for both ethical and operational reasons. For ethical considerations, a transparent decision-making process ensures accountability and reduces the risk of hidden biases. As companies become more aware and understanding of the implications of different sophisticated approaches, they can better weigh their options and choose the methods that best align with their ethical, operational, technological, and financial capabilities and needs. The rising popularity of mathematical optimization may be indicative of a broader trend towards more comprehensible, ethical, and transparent sophisticated technologies [6].

2. Mathematical Optimization vs Machine Learning

Mathematical optimization is a highly functional discipline that involves the pursuit of the best item, as per specific criteria, from an assortment of available choices [7]. This field is further segmented into two key areas: discrete optimization and continuous optimization. Discrete optimization revolves around problems involving discrete variables. It's a search in a countable set, and the objective is to find a specific object like an integer, permutation, or graph which aligns best with the established function. Essentially, the possible solutions for discrete optimization exist in a set of distinct points, which could range from deciding optimal routes for a delivery service to defining the best sequence of operations in manufacturing processes. On the other hand, continuous optimization deals with problems that have continuous variables. It involves the quest to discover the ideal value within a continuous function—think of it as trying to find the highest or lowest point on a curve, a task known as unimodal optimization. However, the quest becomes more complex in multimodal optimization, where the curve has multiple peaks and troughs. Continuous optimization can encompass both constrained problems, where certain conditions or limits envelop the variables, and multimodal problems with multiple correct solutions. The applications for continuous optimization are diverse, spanning from designing antenna in telecommunications to sculpting investment portfolios in finance. In situations where constraints exist – financial restrictions in a budget, for instance – and an optimal allocation of resources is sought, continuous optimization plays a crucial role. Fundamentally, both discrete and continuous optimization are integral elements of mathematical optimization that shed light on the best choice among a set of available alternatives based on predefined criteria. Each serves a unique purpose and caters to distinct types of problems, playing a crucial in crafting solutions within their respective realms [8]. Mathematical optimization and machine learning, both considered sophisticated advanced analytics software technologies, exhibit fundamental differences while sharing common applications within a wide range of fields. Mathematical optimization, focuses on identifying the best possible solution from a set of available choices, utilizing established criteria. It is a field deeply rooted in mathematical and computational techniques that leverage algorithms to systematically search for optimal solutions. Mathematical optimization is especially effective in scenarios where decision-making involves resource allocation, scheduling, and strategic planning. Its application spans diverse sectors, including logistics, finance, engineering, and operations research. On the other hand, machine learning is an AI-driven approach that enables systems to learn and improve from data without being explicitly programmed. It involves the development of algorithms and statistical models that learn patterns and relationships within given datasets to make predictions or decisions. With its ability to handle complex, unstructured data, machine learning finds applications in diverse fields such as healthcare, finance, marketing, and autonomous driving. While both mathematical optimization and machine learning are vital analytical tools, their approaches and objectives differ significantly. Mathematical optimization is primarily concerned with seeking optimal solutions based on predefined criteria, relying on mathematical programming techniques. In contrast, machine learning aims to extract patterns and insights from data, enabling decision-making based on learned patterns and statistical models. Although their primary purposes diverge, mathematical optimization and machine learning often intersect in practice [9]. Optimization algorithms can be used within machine learning to fine-tune models or optimize their performance. Similarly, machine learning techniques can be employed within mathematical optimization to enhance decision-making by leveraging data-driven insights [10]. Ultimately, the choice between mathematical optimization and machine learning will depend on the specific requirements and nature of the problem at hand. Both technologies bring immense value and contribute to advanced analytics capabilities, offering distinct approaches to tackle complex challenges across numerous domains.
Mathematical optimization and machine learning may have distinct objectives and approaches, but they share several similarities that contribute to their status as powerful AI problem-solving tools. Some key similarities between the two are:
  • Powerful AI Problem-Solving Tools: Both mathematical optimization and machine learning are advanced analytics technologies that enable the resolution of complex problems. They provide systematic frameworks for decision-making, enabling businesses to leverage data and mathematical models to optimize their processes and achieve desired outcomes.
  • Data-Driven Approaches: Both mathematical optimization and machine learning heavily rely on data as inputs. In mathematical optimization, data helps define constraints, objectives, and optimization variables. In machine learning, data serves as the training set to develop models and algorithms. In both cases, the quality, quantity, and relevance of the data play a crucial role in achieving accurate and effective results.
  • Extensive Computing Resources: Both mathematical optimization and machine learning demand significant computing capabilities, especially for complex and large-scale optimization problems or machine learning tasks. Access to sufficient computing resources is essential to process and analyze vast amounts of data, perform complex calculations, and derive valuable insights.
  • Advancements in Computing and Data Availability: Both fields have benefitted immensely from recent advancements in computing power and the availability of extensive datasets. Over the past few decades, improvements in hardware capabilities and data acquisition processes have paved the way for more sophisticated mathematical optimization and machine learning techniques. These advancements have increased the efficiency, accuracy, and scalability of both technologies.
  • Solving Complex Business Problems: Both mathematical optimization and machine learning find widespread application in solving complex problems across diverse areas of business. From supply chain optimization to financial risk modeling and from marketing campaign optimization to fraud detection, both technologies can tackle real-world challenges and provide valuable insights and solutions.
While mathematical optimization and machine learning have their unique characteristics and specific use cases, they share commonalities in their power, reliance on data and computing resources, advancements driven by technology, and applicability to complex business problems [11]. Recognizing these similarities can help organizations leverage the strengths of both technologies for more effective and comprehensive problem-solving. Mathematical optimization is highly effective in scenarios where the problem can be precisely defined, and the objective is to find the best solution based on given criteria while considering constraints. It leverages advanced mathematical techniques and algorithms to optimize processes and resource allocation within defined boundaries. Mathematical optimization is particularly useful when the problem can be formulated as a mathematical program with clear objectives and constraints. Machine learning, on the other hand, is designed to learn patterns and insights from data without explicit programming. It is well-suited for complex problems where the interactions between variables are not well-defined or too numerous to be explicitly programmed. Machine learning excels in cases where there is a need to make accurate predictions, classification, or pattern recognition based on large and complex datasets. It can adapt and improve as it is exposed to more data, enabling it to make informed decisions in uncertain or evolving environments.
The choice between mathematical optimization and machine learning depends on several factors, including the nature of the problem, data availability, interpretability requirements, constraints, and the desired outcomes. Often, a combination of both approaches may yield the best results. For example, mathematical optimization can be used to determine optimal parameters or configurations within a machine learning algorithm [12].
Ultimately, neither mathematical optimization nor machine learning is superior in all scenarios. They are distinct tools with their own advantages and applications. Choosing the appropriate technique involves carefully considering the specific problem at hand and evaluating which approach aligns better with the given circumstances. Machine learning and mathematical optimization, though both labeled as reaching the "peak of inflated expectations" by Gartner at different times, have distinct characteristics and widespread applications. While machine learning may be experiencing its peak in terms of hype and expectation today, mathematical optimization has proven its value as a widely adopted and dependable technology since the early 1970s. Machine learning, with its ability to extract patterns and insights from data, has generated significant enthusiasm and anticipation. It has been hailed as a transformative force across various industries, from healthcare and finance to marketing and transportation. However, as with any emerging technology, it is essential to manage expectations and recognize that achieving its full potential requires continued development and refinement. On the other hand, mathematical optimization has earned its place as a proven and reliable technology. Its wide-ranging applications and impact in optimizing processes, resource allocation, and decision-making have led to its extensive adoption by companies across industries. Mathematical optimization techniques have been refined over decades, leveraging advanced algorithms and mathematical models to drive operational efficiencies and improve outcomes.

3. Manufacturing Problem: Case Study

In many manufacturing environments, process planning, and scheduling are essential to ensuring efficient and smooth production. By carefully planning and scheduling production tasks, companies can minimize wasted time and resources, and ensure that products are delivered on time and to the correct specifications. In some cases, process planning, and scheduling can also be used to improve customer satisfaction by ensuring that products are delivered when customers need them. In a manufacturing setting, process planning, and scheduling are usually handled independently, with little concern for how they might affect each other. With increasingly flexible manufacturing operations, it is becoming more important to generate optimal process plans that consider dynamic constraints such as the status of resources [13, 14, 15].
The Flexible Job-Shop Scheduling Problem (FJSP) is an example of complex and difficult problem to solve. In a flexible Job-Shop, there are several machines, each with its own queue of jobs [16, 17]. The order in which the jobs are processed on each machine is not fixed in advance and can be changed to some extent depending on the order in which jobs arrive. The objective of the flexible Job-Shop problem is to find an order in which the jobs can be processed on the machines such that the makespan (the total time taken to process all the jobs) is minimized [18]. Many different formulations have been proposed, each with their own strengths and weaknesses [19, 20, 21, 22]. The flexible Job-Shop problem is a combinatorial optimization problem that seeks to find an optimal schedule for a set of jobs on a set of machines [23, 24].
The proposed approach is a solution for the problem of competition relationship between jobs of process planning and scheduling by adopting a solver. When it comes to deciding on a solving approach for a given problem, it is important to keep in mind the specific features of the problem at hand and the capabilities of the various solver types [25, 26, 27, 28, 29]. In general, solvers are equipped to handle problems with complex logical constraints and can be used for a wide range of problem types, like finding optimal solutions [30]. We make use of Z3 and Gurobi solvers [31, 32, 33, 34].
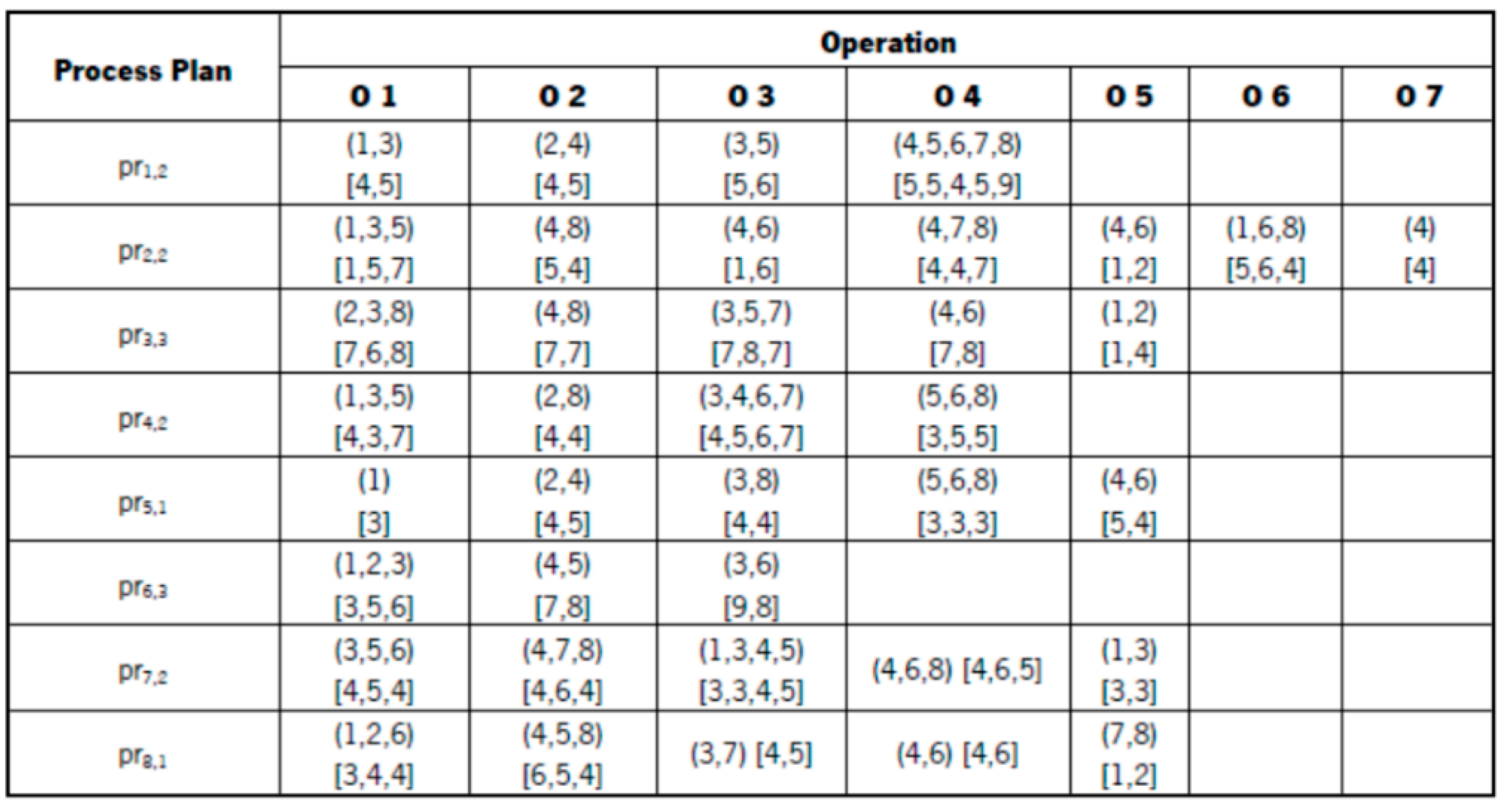
In this experimental study, we assume that there exist 8 jobs submitted by different customers and each job possesses until seven sequential operations. We also assume that there exist 8 machines related to these 8 jobs that are geographically distributive. Each operation has one or more alternative machines. The objective of the problem is to find an order in which the jobs can be processed on the machines such that the makespan (the total time taken to process all the jobs) is minimized. In a flexible job-shop, the makespan is the sum of the durations of the operations to be performed on each machine. This data was retrieved from Zhou et al. [35] and Cátia Alves [36]. Figure 1 lists the initial data of the jobs and their correspondent strategy profile (candidate machines). The cell contains two groups of data: one encircled by a pair of rounded parentheses represents candidate machines for operations and another encircled by a pair of quadrate parentheses that stands for process times on correspondent candidate machines. For example, the first operation related to process plan pr1,2 contains (1, 3) and [4, 5], which indicates that operation can be processed on machine 1 or 3 and the correspondent process time is 4 or 5 time units.
Multiple jobs are to be scheduled on a set of parallel machines. Each job has predefined processing times, deadlines, and priorities. The objective is to minimize the total completion time and maximize machine utilization while meeting all deadlines.
In this study framework, two solver are used, i.e. Z3 and Gurobi solvers. The authors formulate the scheduling problem as a set of logical constraints, define variables for job start times and end times, add constraints for non-overlapping jobs, enable sequential jobs, and finally use solver’s optimization capabilities to find a model that minimizes total completion time.
Figure 2 presents a Picat formulation1, formulated as an Integer Programming, to solves the FJSP problem. The Picat language is a rule-based programming language created with the intention of being straightforward to learn and use. As a functional programming language, it features a declarative syntax that simplifies the process of writing programs that are both readable and easy to understand. Solvers like Z3 or Gurobi can be employed using the same source code to solve combinatorial problems.
Preprints 114488 g002aPreprints 114488 g002b
Figure 3. FJSP problem formulation.
Figure 3. FJSP problem formulation.
Preprints 114488 g002aPreprints 114488 g002b
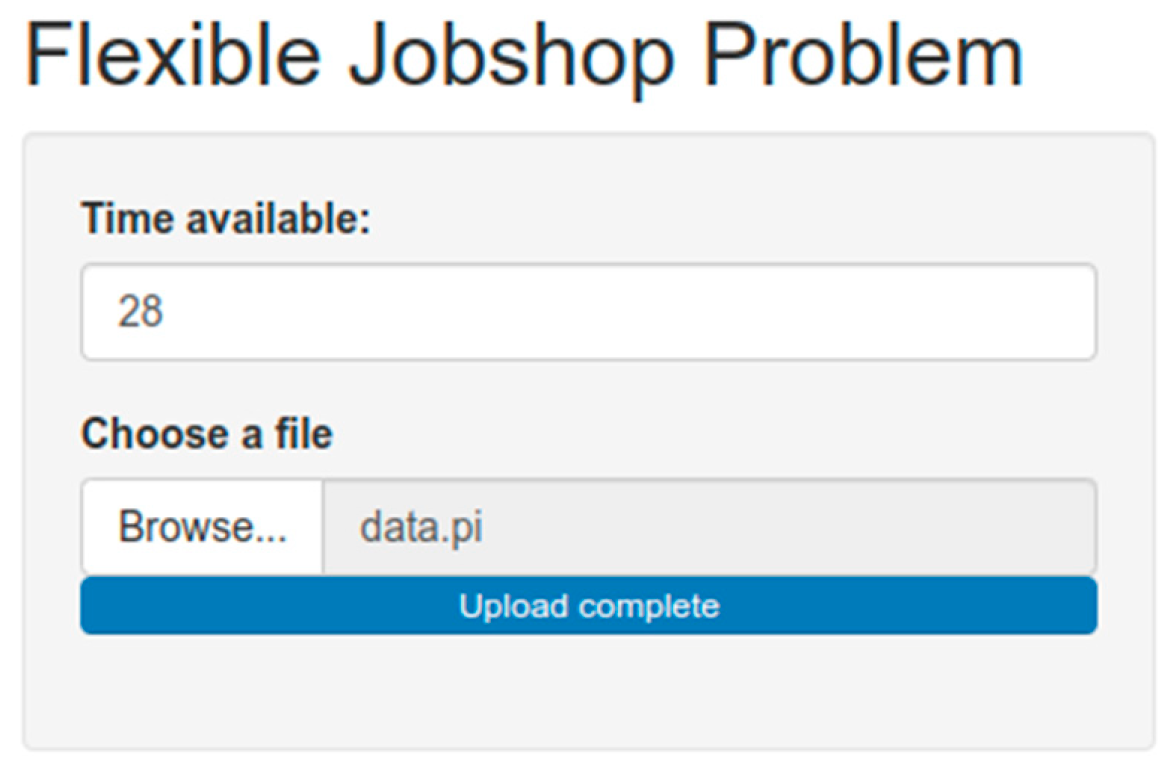
A web application was developed enabling users to interact with job data and optimization results (cf. Fig. 3). This application provides an intuitive interface where users can upload Job-Shop scheduling data, such as job sequences, processing times, and machine assignments. Once the data is entered, the web app displays the information in a clear and organized manner, allowing users to easily navigate and modify entries as needed. In addition to data management, the application offers tools for users to define and set constraints, such as available time windows for job completion and resource availability. The application integrates with an optimization algorithm to compute the most efficient job schedules based on these inputs.
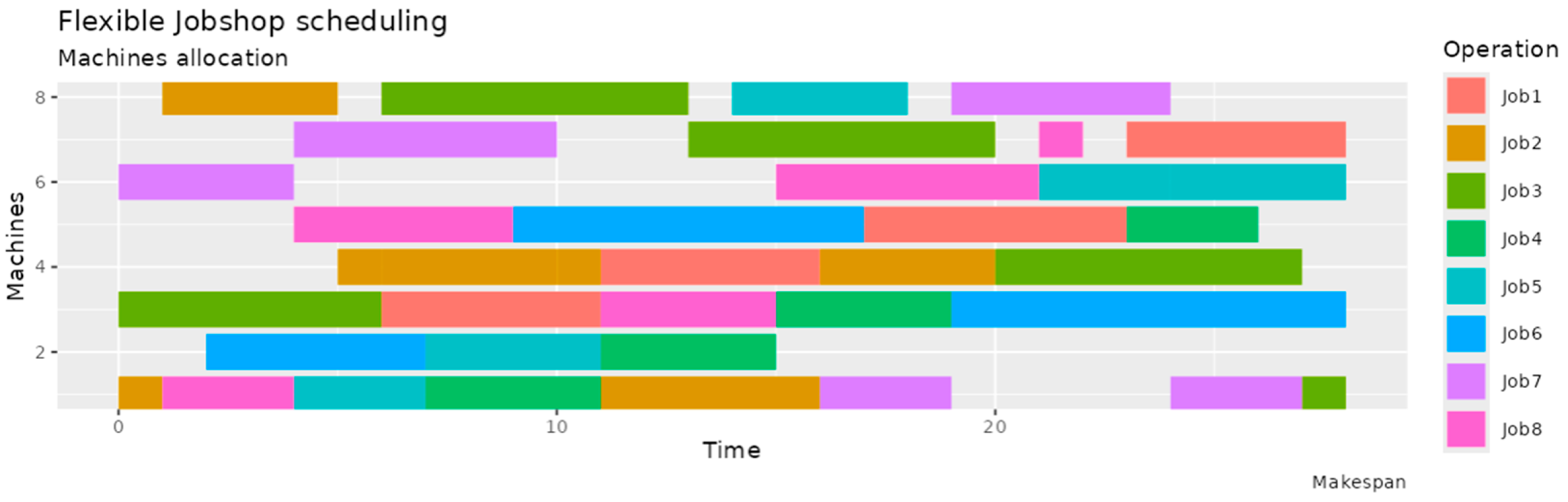
After running the optimization process, the web app presents the results through interactive visualizations, including Gantt charts, which help users understand the proposed schedules. Users can adjust parameters and rerun optimizations to explore different scenarios and their impacts on job completion times and overall efficiency.
Moreover, the application supports collaboration features, enabling multiple users to work together simultaneously, share data, and discuss optimization strategies within the platform. Overall, the web application serves as a comprehensive tool for managing Job-Shop scheduling tasks, enhancing decision-making, and improving operational efficiency through effective data interaction and optimization capabilities.
Preprints 114488 g003
Figure 3. Job-Shop web application.
Figure 3. Job-Shop web application.
Preprints 114488 g003
Figure 4 shows the web application output related to the optimal schedule for FJSP data described in fig. 1, obtained through Z3 or Gurobi solvers. This web application output shows that it’s possible to complete all jobs within 28-time units. The obtained optimizing schedule involves complex decision-making processes to enhance efficiency and minimize production time. This problem is particularly challenging due to the combinatorial nature of scheduling tasks across multiple machines with various constraints. Z3 and Gurobi solvers demonstrate to be powerful tools in tackling these optimization problems. The proposed solution based on solvers obtains better results and higher solving efficiency compared to the game theory solution approach. The obtained makespan is 28 units with Z3 and Gurobi solvers, much better than the Zhou et. al with 41 units through a game-theoretic approach [37].
Primarily designed for checking the satisfiability of logical formulas, Z3 has been effectively utilized in optimization problems, including job-shop scheduling. Z3’s strength lies in its ability to handle constraints efficiently. Alternatively, Gurobi is one of the most powerful and versatile commercial solvers available, known for its efficiency in solving large-scale linear, mixed-integer, and quadratic programming problems.
This case study demonstrates that optimizing job-shop schedules using solvers like Z3 and Gurobi can dramatically improve operational efficiency and reduce production times. By leveraging these advanced solvers, industries can achieve significant enhancements in productivity and resource utilization.
Solvers can help to reduce the competition relationship between jobs of process planning and scheduling. The solver can help optimize the manufacturing process by reducing the overall processing time and improving the utilization of resources. By using a solver, the process of manufacturing can be made more efficient and effective.
The discussed approach based on mathematical optimization obtains better results and higher solving efficiency compared to the game theory solution algorithm. This is because the mathematical optimization algorithm can find the global optimum solution, while the game theory algorithm can only find a local optimum solution. In addition, the mathematical optimization algorithm can find the optimum solution in a shorter amount of time than the game theory algorithm.

4. Discussion

Various studies have been conducted regarding optimizing Job-Shop scheduling. Some of them utilize a solver to improve the outcomes. In [38], a new mathematical model for the flow shop scheduling problem has been developed, taking into account not only cycle time, but also peak power load, energy consumption, and carbon footprint. The model has been applied to a simple case study involving a flow shop with two machines producing various parts. Apart from the sequence in which jobs are processed, the model also takes into consideration the speed of operation as an independent factor, with the ability to manipulate it to minimize peak load and energy consumption. However, due to the complexity of finding the optimal solution for a single objective, using commercial software directly for this multi-objective problem would require a significant amount of computation time. This paper suggests the need for specialized algorithms to be developed specifically for this new scheduling problem and explores alternative approaches that are more computationally feasible in finding a near-optimal schedule.
Another study [39], considers the integrated scheduling problem of production and delivery on parallel batch processing machines with non-identical capacities in different locations in cloud manufacturing. The study assumes that the jobs have varying release times, sizes, processing times, and customer information. The total service completion time is determined by the production completion time and delivery duration. The goal of the problem is to minimize this time. To solve this problem, a mixed-integer programming (MIP) model is provided. Due to its complexity, efficient heuristic and improved particle swarm optimization algorithms are used. The algorithms are then compared to the Gurobi optimization solver through extensive experiments, proving their effectiveness.
In [40], the authors introduce the multi-site additive manufacturing (AM) machine scheduling problem considering carbon emissions caused by production and transportation. A mathematical model using mixed-integer linear programming has been created with the goal of optimizing two objectives in a diverse environment of unrelated additive manufacturing machines. One objective focuses on economic sustainability, considering the cost of production, transportation, set-up, and tardiness penalties. The other objective evaluates environmental sustainability, considering the total carbon emissions from production and transportation. The model has been solved using Gurobi. This study introduces an approach of considering both economic and environmental sustainability in relation to production and transportation, and validates its performance through a comprehensive experimental study.
An auto mixed integer linear programming (Auto-MILP) model is proposed by Huang, L., & Su, R. ([41]) to tackle the flexible job shop scheduling problem. The Auto-MILP model allows the precedence between operations of a job to be given by an arbitrary directed acyclic graph rather than a linear order. The main objective is to reduce the total time needed to complete all operations. By including the allocation of tasks to resources, the Auto-MILP model enables the use of multiple production lines in the workshop. This means that more than one machine can perform the same operation, and the selection of machines is determined by the algorithm. Time separation is utilized to determine the capacity of each machine, making it flexible for different job scheduling situations. To measure the performance of the Auto-MILP model, simulated scheduling cases and real data from a job shop are used for evaluation.
Fan, H., & Su, R. investigates the optimization of the scheduling problem by the mathematical modelling and heuristic approaches [42]. The mathematical programming model of the problem is presented, and it is used as an exact solution approach for solving small instances optimally. To tackle larger problems, a solution has been incorporated to generate near-optimal solutions. The results of the approach reveal that the proposed algorithm outperforms the conventional ones. Additionally, a comparison is made between the mathematical programming approach and a heuristic approach to the problem. Moreover, a sensitivity analysis is carried out to examine the impact of buffer capacity on the performance of the manufacturing system.
The approach, based on solvers, described in this paper is an effective solution for the problem of competition relationship between jobs of process planning and scheduling in manufacturing. In our experiment, we utilize a dataset containing 8 jobs with up to 8 operations each, all running on 8 distinct machines. Each job has one or more operations, and each operation can be performed on one of multiple machines, although only one machine can be chosen. The main objective is to determine the optimal order in which the jobs can be completed on the machines, minimizing the makespan (total processing time for all jobs). To reach a solution, decision variables must be assigned values for each operation of each job, identifying which machine will perform it and when it will start. Previous work, using solvers, showed improved positives results in solving through solvers compared to the game-theoretic approach [43]. In this work, a web application has been developed and used to interact with jobs’ data and optimization results. In this project, we have developed a robust web application tailored to facilitate interaction with job scheduling data and optimization results. This web application serves multiple functions, encapsulating various features to streamline the workflow for users dealing with complex scheduling problems. The application boasts an intuitive interface where users can easily input job data, including job sequences, processing times, machine assignments, and more. Users have the option to upload data from CSV files or other formats, streamlining the data entry process. Similarly, optimized schedules and related data can be exported for offline analysis. Changes to input data or constraints are reflected in real-time, allowing users to see immediate updates without needing to refresh or restart the application. The web application allows users to set a variety of constraints, including due dates, machine availability, and job priorities. The application incorporates advanced solvers, such as the Z3 and Gurobi solvers, which can handle the Flexible Job-Shop Scheduling Problem efficiently. The optimization results are displayed using Gantt charts, providing a visual representation of job schedules across different machines over time. The web application supports multiple users, allowing collaboration across teams. Users can share schedules, discuss optimization strategies, and work together in real-time. By incorporating these features, the web application not only simplifies the tasks of data management and optimization but also enhances the user's capability to analyze, visualize, and improve job schedules effectively. The application stands as a comprehensive tool, catering to various industries that require sophisticated job scheduling solutions

5. Conclusions

Manufacturing environments are gaining increasing recognition within the manufacturing sector for their inherent benefits related to flexibility and scalability. These dynamic environments require the generation of optimal process plans to effectively handle multiple jobs, a challenge that we tackled in our study through the utilization of a mathematical optimization approach.
Our study specifically aimed to address the challenge of generating optimal schedules for the flexible Job-Shop problem. This type of scheduling allows for the adjustment of task order, facilitating a reduction in overall manufacturing time while maintaining the correctness of the final products. The flexible Job-Shop problem entails a complex mathematical puzzle, as it seeks to identify the most efficient schedule that adheres to these constraints within a manufacturing process.
In our study, we discussed an approach to address the problem and conducted a comparative analysis against a game theory-based method. The solution, rooted in mathematical optimization principles, surpassed the game theory-based approach by delivering superior results in terms of effectiveness and reliability for scheduling. Mathematical modeling and advanced algorithm allowed to optimize the use of available resources while efficiently managing production timelines, ensuring that every task was completed within the specified constraints. By harnessing the power of mathematical optimization and employing sophisticated algorithms, the methodology provides a comprehensive solution that enhances scheduling outcomes, generates optimal resource allocation plans, and maximizes productivity in multi-job environments. Our study holds significant importance as it offers manufacturers a reliable and efficient solution to address the challenges associated with complex problems. Through the utilization of mathematical optimization techniques, companies can effectively optimize their manufacturing processes, resulting in improved resource utilization, streamlined operations, and ultimately, higher levels of productivity and customer satisfaction. Flexible job-shop scheduling is a prominent research area in the field of operations management.
The Flexible Job-Shop problem's real-world environment can be effectively represented through mathematical relations. In our proposed model, we utilize Z3/Gurobi solvers to find an optimal scheduling solution that minimizes the overall job execution times. By leveraging these solvers, we aim to optimize the sequencing of tasks and improve the efficiency of the Job-Shop process.
Employing mathematical optimization for scheduling problems allows for data-informed decision-making and facilitates scenario analysis to evaluate different scheduling scenarios. Furthermore, this approach can be coupled with real-time data integration and advanced algorithms, enabling dynamic and adaptive scheduling in response to changing requirements or disruptions.
As industries continue to address complex scheduling challenges, from production lines to transportation networks, mathematical optimization proves to be a valuable tool for problem-solving. Its ability to generate optimal schedules and consider diverse constraints and objectives makes it a dependable and adaptable approach for scheduling optimization. By leveraging the power of mathematical optimization, organizations can enhance their operational efficiency, minimize costs, and ultimately achieve improved performance across a range of scheduling applications.

6. Limitations of This Work and Future Research

Although this work has achieved its objectives, i.e., seeking to emphasize the power of mathematical optimization applied to scheduling problems, it has limitations.
One of the major limitations is that mathematical optimization techniques rely heavily on the accuracy of the data and assumptions used in the model. If there are errors in the data or if the assumptions are flawed, the resulting schedule may not be as efficient as expected. This can be a problem in real-world scenarios where there are often uncertainties and unforeseen events that can impact the schedule. Another limitation is that mathematical optimization techniques are only as good as the model used. This means that the model must be able to accurately represent the problem at hand. In some cases, the complexity of a scheduling problem may make it difficult to develop an accurate model, which can affect the effectiveness of the optimization techniques. Additionally, there are certain scheduling problems that are inherently difficult to solve using mathematical optimization. For example, problems with many variables or constraints may be too complex for current optimization methods to handle. This can limit the applicability of these techniques in certain industries or situations.
It's also worth noting that mathematical optimization solutions may not always be feasible in terms of practical implementation. While the resulting schedule may be optimal in theory, it may not be feasible to implement in the real world due to various constraints such as resource availability or operational limitations.
In conclusion, while mathematical optimization techniques are powerful tools for solving scheduling problems, they do have limitations that should be considered. It's important to understand these limitations and use them in conjunction with other methods and approaches to ensure the best possible schedule is created. By recognizing the limitations, we can better use mathematical optimization to its full potential in creating efficient schedules.
More questions and a larger sample would certainly give more consistency to our work and could help to confirm that the use of mathematical optimization can contribute to more manufacturing efficient production.
Future research with more questions may reinforce the methodology based on the mathematical optimization presented in this study. It would also be important, in future work, to make use of real-world scenarios and to combine with other technologies such as Artificial Intelligence to enhance the quality of results.

Author Contributions

Conceptualization, J.C.S. and S.C; methodology, J.C.S., S.C. and G.S.; software, J.C.S. and S.C.; validation, J.C.S., S.C. and G.S; formal analysis, J.C.S., S.C. and G.S.; investigation, J.C.S. and S.C.; resources, J.C.S. and S.C.; data curation, J.C.S., S.C. and G.S.; writing—original draft preparation, J.C.S. and S.C.; writing—review and editing, J.C.S., S.C. and G.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research did not receive external funding.

Institutional Review Board Statement

The study, carried out in the field of mathematical optimization, it was conducted according to the guidelines of the Declaration of Helsinki. The authors declare that according to Portuguese legislation does not require pre-approval by an ethical committee.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data are available on request.

Conflicts of Interest

The authors declare no conflicts of interest.

Ethical statement

The study was conducted according to the guidelines of the Declaration of Helsinki, according to Portuguese legislation that does not require pre-approval by an ethical committee.

Note

1
Picat – a logic-based multi-paradigm programming language: http://picat-lang.org/

References

  1. Yang, Lu. Artificial intelligence: a survey on evolution, models, applications and future trends. Journal of Management Analytics 2019, 6, 1–29. [Google Scholar] [CrossRef]
  2. Zhang, B. , Zhu, J. & Su, H (2023). Toward the third-generation artificial intelligence. Sci. China Inf. Sci. 1211; 66. [Google Scholar] [CrossRef]
  3. Massimo Bertolini, Davide Mezzogori, Mattia Neroni, Francesco Zammori (2021) Machine Learning for industrial applications: A comprehensive literature review, Expert Systems with Applications, Volume 175, 2021, 114820, ISSN 0957-4174. [CrossRef]
  4. Pallaschke, D. E. , & Rolewicz, S. (2013). Foundations of mathematical optimization: convex analysis without linearity (Vol. 388). Springer Science & Business Media.
  5. Chong, E. K., Lu, W. S., & Żak, S. H. (2023). An introduction to optimization. John Wiley & Sons.
  6. Snyman, J. A., & Wilke, D. N. (2005). Practical mathematical optimization (pp. 97-148). Springer Science+ Business Media, Incorporated.
  7. Anjos, M. F. , & Vieira, M. V. Mathematical optimization approaches for facility layout problems: The state-of-the-art and future research directions. European Journal of Operational Research 2017, 261, 1–16. [Google Scholar]
  8. Kallrath, J. (Ed.). (2004). Modeling languages in mathematical optimization (Vol. 88). Springer Science & Business Media.
  9. Liu, A. , Luh, P. B., Sun, K., Bragin, M. A., & Yan, B. (2023). Integrating machine learning and mathematical optimization for job shop scheduling. IEEE Transactions on Automation Science and Engineering.
  10. Morinaga, E. , Tang, X., Iwamura, K., & Hirabayashi, N. An improved method of job shop scheduling using machine learning and mathematical optimization. Procedia Computer Science 2023, 217, 1479–1486. [Google Scholar]
  11. Bethge, J. , Findeisen, R., Duc Le, D., Merkert, M., Sager, S., Savchenko, A., & Rewald, H. (2022). Mathematical optimization and machine learning for efficient urban traffic. In German Success Stories in Industrial Mathematics (pp. 113-120). Cham: Springer International Publishing.
  12. Hijazi, A. (2023). Resource Allocation Using Mathematical Optimization and Machine Learning.
  13. Mellor, P. A review of job shop scheduling. Journal of the Operational Research Society 1966, 17, 161–171. [Google Scholar] [CrossRef]
  14. Yamada, T. , & Nakano, R. Job shop scheduling. IEE control Engineering series 1997, 134–134. [Google Scholar]
  15. McKay, K. N. , Safayeni, F. R., & Buzacott, J. A. Job-shop scheduling theory: What is relevant? Interfaces 1988, 18, 84–90. [Google Scholar]
  16. Hoitomt, D. J. , Luh, P. B., & Pattipati, K. R. A practical approach to job-shop scheduling problems. IEEE transactions on Robotics and Automation 1993, 9, 1–13. [Google Scholar]
  17. Zhong, R.Y. , Xu, C.: A Job-Shop Scheduling Model with Real-Time Feedback for Physical Internet-Based Manufacturing Shopfloor. In: 2015 IEEE 12th Intl Conf on Ubiquitous Intelligence and Computing and 2015 IEEE 12th Intl Conf on Autonomic and Trusted Computing and 2015 IEEE 15th Intl Conf on Scalable Computing and Communications and Its Associated Workshops (UIC-ATC-ScalCom). pp. 638–641. Freeman, San Francisco (2015). [CrossRef]
  18. Philipp Winklehner, Viktoria A. Hauder, Flexible job-shop scheduling with release dates, deadlines and sequence dependent setup times: a real-world case, Procedia Computer Science, Volume 200, 2022, Pages 1654-1663, ISSN 1877-0509. [CrossRef]
  19. Jones, A., Rabelo, L. C., & Sharawi, A. T. (1998). Survey of job shop scheduling techniques. NISTIR, National Institute of Standards and Technology, Gaithersburg, MD.
  20. Fattahi, P. , Saidi Mehrabad, M., & Jolai, F. Mathematical modeling and heuristic approaches to flexible job shop scheduling problems. Journal of intelligent manufacturing 2007, 18, 331–342. [Google Scholar]
  21. Roshanaei, V. , Azab, A., & ElMaraghy, H. Mathematical modelling and a meta-heuristic for flexible job shop scheduling. International Journal of Production Research 2013, 51, 6247–6274. [Google Scholar]
  22. Brandimarte, P. : Routing and scheduling in a flexible Job-Shop by tabu search. Annals of Operations Research. 41, 157–183 (1993). [CrossRef]
  23. Carlier, J. , & Pinson, É. An algorithm for solving the job-shop problem. Management science 1989, 35, 164–176. [Google Scholar]
  24. Applegate, D. , & Cook, W. A computational study of the job-shop scheduling problem. ORSA Journal on computing 1991, 3, 149–156. [Google Scholar]
  25. Gomes, C. P. , Kautz, H., Sabharwal, A., & Selman, B. Satisfiability solvers. Foundations of Artificial Intelligence 2008, 3, 89–134. [Google Scholar]
  26. Hanafi, S. , & Todosijević, R. Mathematical programming based heuristics for the 0–1 MIP: a survey. Journal of Heuristics 2017, 23, 165–206. [Google Scholar]
  27. Gong, W. , & Zhou, X. (2017, June). A survey of SAT solver. In AIP Conference Proceedings (Vol. 1836, No. 1, p. 020059). AIP Publishing LLC.
  28. Gu, J. , Purdom, P. W., Franco, J., & Wah, B. W. Algorithms for the satisfiability (SAT) problem: A survey. DIMACS series in discrete mathematics and theoretical computer science 1997, 35, 19–151. [Google Scholar]
  29. Oliveras, A. (2014, January). Survey of satisfiability modulo theories (SMT). In Banff International Research Station for Mathematical Innovation and Discovery (BIRS) Workshop Lecture Videos. Banff International Research Station for Mathematical Innovation and Discovery.
  30. Roselli, S. F. , Bengtsson, K., & Åkesson, K. (2018, August). SMT solvers for job-shop scheduling problems: Models comparison and performance evaluation. In 2018 IEEE 14th International Conference on Automation Science and Engineering (CASE) (pp. 547-552). IEEE.
  31. Moura, L. D. , & Bjørner, N. (2008, March). Z3: An efficient SMT solver. In International conference on Tools and Algorithms for the Construction and Analysis of Systems (pp. 337-340). Springer, Berlin, Heidelberg.
  32. De Moura, L. , & Bjørner, N. (2012). Z3-a Tutorial. Microsoft, Albuquerque, NM, USA, Tech. Rep.
  33. Gurobi Optimization, L. L. C. (2019). Gurobi—The Fastest Solver.
  34. Bixby, B. The gurobi optimizer. Transp. Re-search Part B 2007, 41, 159–178. [Google Scholar]
  35. Zhou, G. , Xiao, Z., Jiang, P., & Huang, G. Q. A game-theoretic approach to generating optimal process plans of multiple jobs in networked manufacturing. International Journal of Computer Integrated Manufacturing 2010, 23, 1118–1132. [Google Scholar]
  36. Alves, C. F. V. (2017). Modelling and evaluation of" Fixed Horizon"," Rolling Horizon" and" Real Time Management" production scheduling paradigms in ubiquitous production networks under conditions of dynamic environments for economic and environmental sustainability.
  37. Jiang, W. R., Lu, C., & Li, F. Z. (2011). A Game Theoretic Approach to Job Shop Scheduling. In Applied Mechanics and Materials (Vol. 66, pp. 960-965). Trans Tech Publications Ltd.
  38. Fang, K. , Uhan, N., Zhao, F., & Sutherland, J. W. A new approach to scheduling in manufacturing for power consumption and carbon footprint reduction. Journal of Manufacturing Systems 2011, 30, 234–240. [Google Scholar]
  39. Zhang, H. , Li, K., Chu, C., & Jia, Z. H. Parallel batch processing machines scheduling in cloud manufacturing for minimizing total service completion time. Computers & Operations Research 2022, 146, 105899. [Google Scholar]
  40. Kucukkoc, I. (2023). Scheduling of distributed additive manufacturing machines considering carbon emissions. An International Journal of Optimization and Control: Theories & Applications (IJOCTA).
  41. Huang, L. , & Su, R. An Auto-MILP Model for Flexible Job Shop Scheduling Problem. IFAC-PapersOnLine 2022, 55, 137–142. [Google Scholar]
  42. Fan, H. , & Su, R. Mathematical Modelling and Heuristic Approaches to Job-shop Scheduling Problem with Conveyor-based Continuous Flow Transporters. Computers & Operations Research 2022, 148, 105998. [Google Scholar]
  43. Silva, João & Lopes, Nuno & Alves, Cátia & Putnik, Goran & Varela, Leonilde & Ferreira, Luis & Cruz-Cunha, Manuela. Evaluation of Solvers’ Performance for Solving the Flexible Job-Shop Scheduling Problem. Procedia Computer Science 2023, 219, 1043–1048. [Google Scholar] [CrossRef]
Preprints 114488 g001
Figure 1. Initial data for experiment (retrieved from [35]).
Figure 1. Initial data for experiment (retrieved from [35]).
Preprints 114488 g001
Preprints 114488 g004
Figure 4. Web application output’s optimal schedule minimizing the total completion time and maximizing machine utilization (28 time units).
Figure 4. Web application output’s optimal schedule minimizing the total completion time and maximizing machine utilization (28 time units).
Preprints 114488 g004
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated