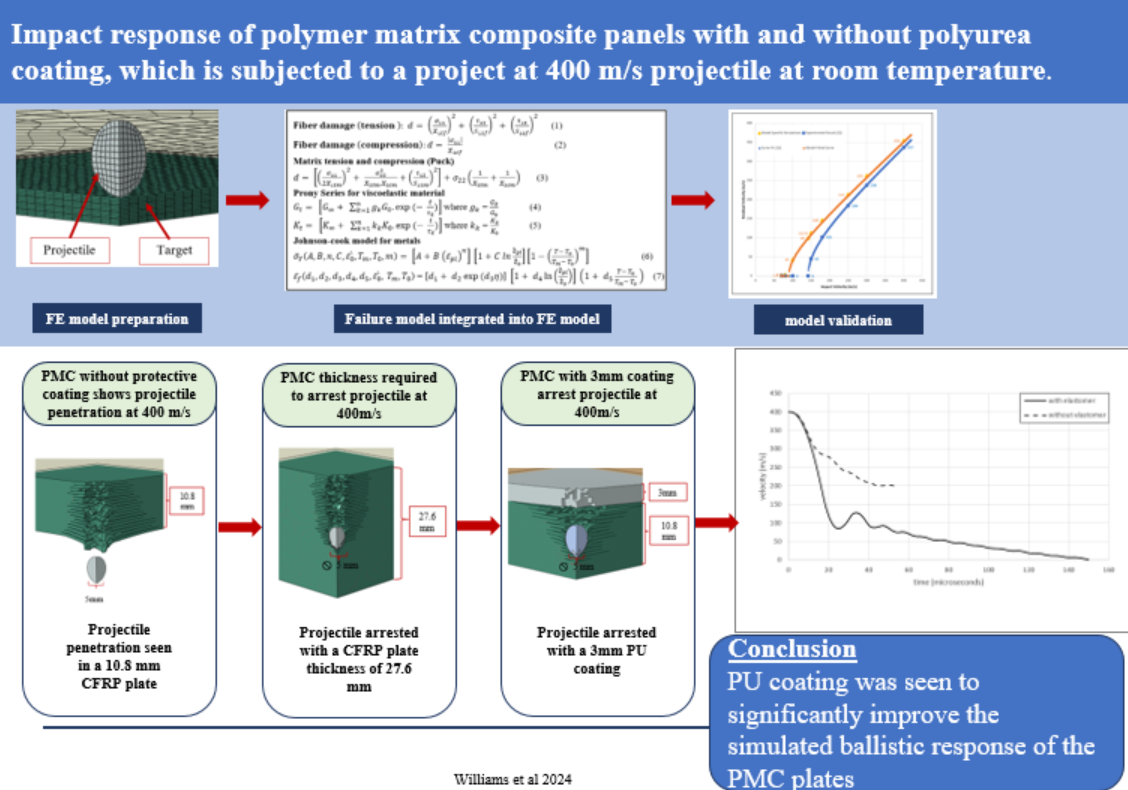
I. Introduction
1.1. Current LPT Tanks and Their Potential Issues
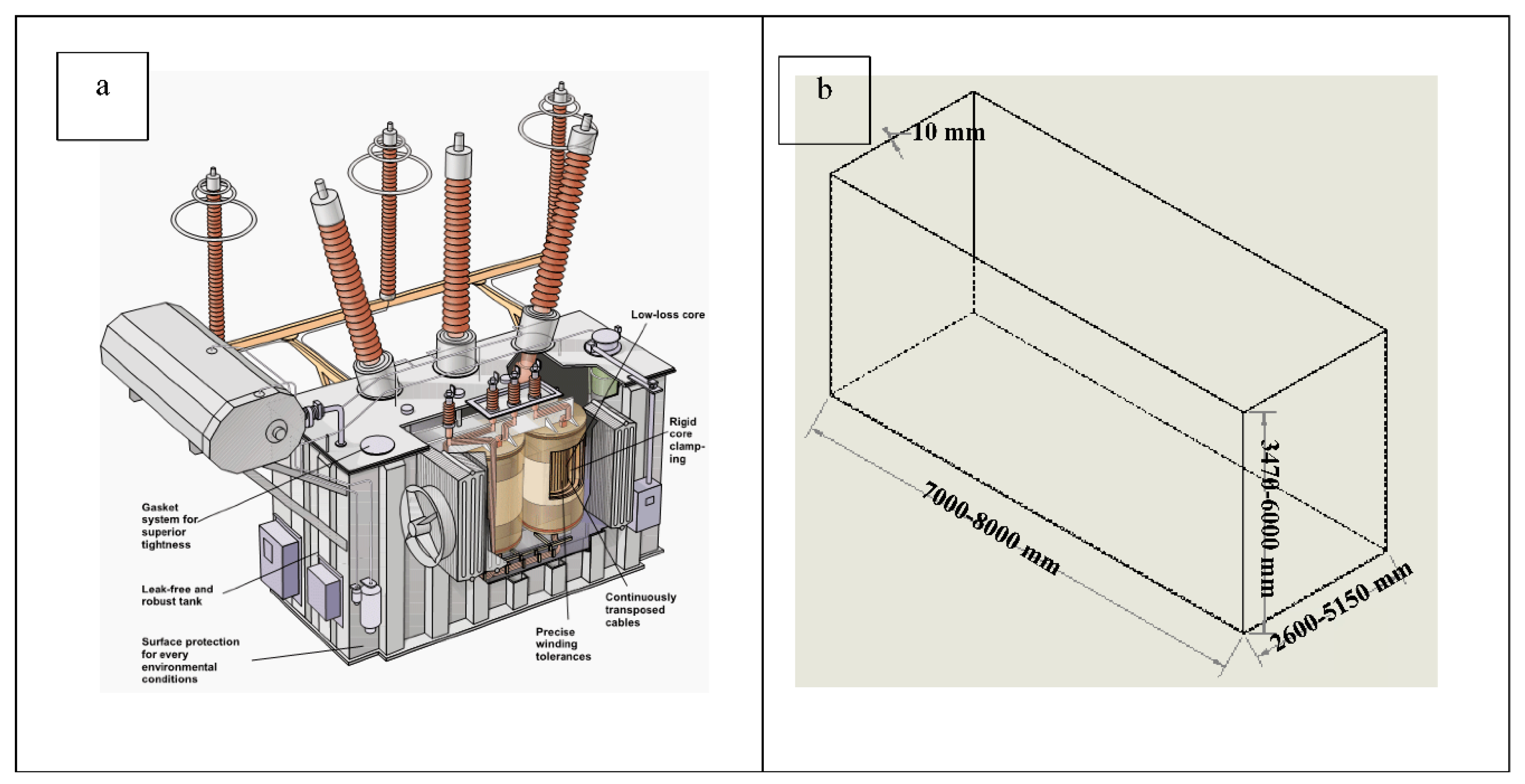
A large power transformer (LPT) is an oil-filled complex mechanical and electrical system that steps up or down the voltages for safe transmission from power generation to distribution for consumption downstream. A LPT consists of numerous parts for different purposes, as shown in the schematic in
Figure 1. A LPT’s operational performance is highly sensitive to external concerns like moisture, particles in air that could contaminate the oil, extreme weather, impact loads, and internal issues such as temperature and electrical charges. The tank of a LPT plays a critical role in ensuring optimal operational delivery and a long life cycle.
The current LPT tanks are structural encasements that prevent the external environment from reaching the transformer core and disrupting its operation. It also prevents the transformer oil from leaking. The tank is made of Low Carbon Steel (LCS) for many reasons, including durability, ductility, strength, and its ability to act as an electromagnetic cage. As described in [
1], LPT tanks made out of LCS can suffer from corrosion and weight issues, vibrational damping problems, hotspot formation, and extreme mechanical loads. LPTs can be damaged by vandalism through high-powered rifle fire causing the tank’s oil to leak. Aside from the attack on the Metcalf substation in California on April 16, 2013 [
2] which caused roughly
$16 million in damage, an analysis done by the Wall Street Journal reported that there were 274 cases of power grid vandalism in the United States between 2012 and 2014 [
3,
4] . Industry has swiftly responded by engineering retrofits that could mitigate the extent of the damage to the LPT by potential ballistic attacks [
2]. Authors of [
2] argued that steel is the preferred material for LPT tanks for safeguarding against ballistic attacks because of its high absolute strength, ductility, and durability, as well as its, being a cost-effective bullet-resistant solution. For these reasons an encasement (a retrofit) that could meet UL 752 level 10 bullet resistance standards was proposed by the authors of [
2].
Although the retrofit designed by [
2] could provide a solution to the penetration caused by a high-velocity projectile, a potential fix that could be more efficient without the retrofit costs, is to replace LCS with other materials. Similar to the movement to composite materials in aircraft and automobiles, recently the employment of these advanced materials has been proposed for LPT tanks [
1]. The authors suggested that polymer matrix composites (PMCs) can favorably mitigate impact damage and other challenges as the reliability of grid components becomes critical in the presence of increasing vandalism. The next-generation PMC LPT tanks could be designed to meet UL 752 level 10 bullet-resistance standards without incurring higher costs, additional mass, or bullet-resistant appendages. The armor industry has recently designed a fiberglass plate that can meet UL 752 level 8 bullet-resistance standards [
5]. PMCs could also provide the benefits of self-healing, smart sensing, and monitoring which could further improve the reliability of the LPT tanks [
1].
1.2. PMCs for Impact Protection
In experimental work done by [
6,
7], the authors proposed a PMC laminate sandwich architecture consisting of two different composite types that offered the best impact resistance over several other composite architectures with an improvement of over 40 times. The laminate consisted of face sheets of 5 unidirectional Carbon Fiber Reinforced Polymer (CFRP) plies (top and bottom) with a core made up of 10 plies of unidirectional Glass Fiber Reinforced Polymer (GFRP). The improved impact resistance of the sandwich structure was attributed to the process of delamination at the CFRP/GFRP interfaces which was shown to absorb much of the energy. However, the investigation was limited to quasi-static loads. The experimental work done by [
8] addressed the ballistic impact response of 2D woven fabric composite laminates which were impacted with a rigid cylindrical projectile at speeds between 168 and 173 m/s. The energy dissipated by the projectile was absorbed by various failure modes of the target, such as shear plugging, tensile failure of yarns/layers, compression of the surrounding material, delamination, matrix cracking, friction between projectile and target, and conical deformation at the target’s back face. The authors of [
9] showed that for a spherical projectile with impact velocities of 300 – 500 m/s, a 3D woven composite with z-yarns does not significantly improve the ballistic performance of the structure when compared with 2D woven composites. This was explained by the fact that the damage caused during impact was localized around the projectile in both cases. The same authors agreed that the impact behavior of PMCs can be enhanced by using two or more fiber types but their arrangements and stacking configurations were not specified. A major characteristic of high-velocity impact is that damage is localized essentially because of the speed of the projectile, as opposed to low-velocity impact where damage may spread a significant distance from the impact zone [
6,
7,
9,
10].
1.3. Polyurea for Impact Protection
Polyurea’s (PU) ballistic resistance capability is known to be due to its so-called ‘high-strain rate sensitivity’. Under high strain rates (10
5/s to 10
7/s ) [
11,
12], certain types of PU respond with high shear strength which can be higher than that of steel. The shear strength of PU in a ballistic event greatly depends on the thickness of the substrate [
12]. In a high pressure and strain rate situation, PU’s shear strength can exceed most engineering materials that are used in protection technology. When used as a coating on metals and composites an impact resistant polymer should have a significant glass transition temperature well below LPT operating temperatures which could be -20 to about 300 ͦ C. It has been shown in [
13] and discussed by [
11], that for PU the strain-rate-induced glass transition (the broad α-transition) leads to enhanced energy dissipation upon impact. This occurs when the deformation rate is comparable to the rate of motion of the soft segment in the PU chain, which for several PUs is of the order of 10
5 to 10
7/s at room temperature. At quasi-static strain rates (10
-2/s) this α-transition occurs around -50 to -60
oC, well below LPT operating temperatures. For the LPT tank, PU could offer significant additional advantages in terms of durability and resilience for protection against environmental elements. PU has an estimated 75-year life span [
14], with good resistance to ultraviolet (UV) light.
PU is not known to be used alone as an impact resistant material. However, PU has been used as a coating for several substrates such as steel, aluminum, ceramics, etc. [
12,
15,
16,
17,
18], but has only been recently studied as a coating for brittle composites such as CFRP to improve blast resistance [
19]. A very interesting observation made in [
19] was that placing the PU on the rear side of the CFRP textile structure provided significantly better impact protection than having the coating on the front side. This might not be feasible with the LPT tank since the elastomer would then interface directly with the transformer fluid. However, it is expected that the placement of PU on the exterior surface of the tank could still improve the impact resistance of the tank. In a related study on the impact behavior of porcelain bushings on LPTs, it was shown that the bushings can be protected against impact when coated with Polyurethane-Urea (LINEX) [
10,
20,
21].
1.4. Approach
In this work, Finite Element (FE) Analysis was used to compare the impact resistance of current (LCS) and potential replacement (PMC) materials for LPT tanks. To accomplish this, versatile FE models were built using Python scripts for use with the Abaqus Explicit solver, utilizing various material models. Published experimental impact data with complete material models were not always available to validate the numerical models developed in this research, and thus some allowances had to be made. For the verification of the metal models, a simulation was compared with published aluminum 2024- T3/T351 alloy (ALU2024) impact data [
22]. For the verification of the FE model applied in the ballistic simulations of PMCs, the work done by [
23,
24] was utilized where a carbon fiber cross-ply PMC plate served as the target.
Once the validations were completed, simulations were conducted using LCS, CFRP, and GFRP to determine minimum thicknesses required to prevent ballistic penetration of a 400 m/s 12.7 mm spherical steel projectile. Additionally, the result of replacing a steel projectile with lead was evaluated in the case of an LCS plate. Finally, the significant benefit of adding a thin PU coating to the underlying substrates was analyzed numerically.
[NEED PARAGRAPH ABOUT NOVELTY OF THIS WORK]
II. Materials and Failure Models
2.1. Materials
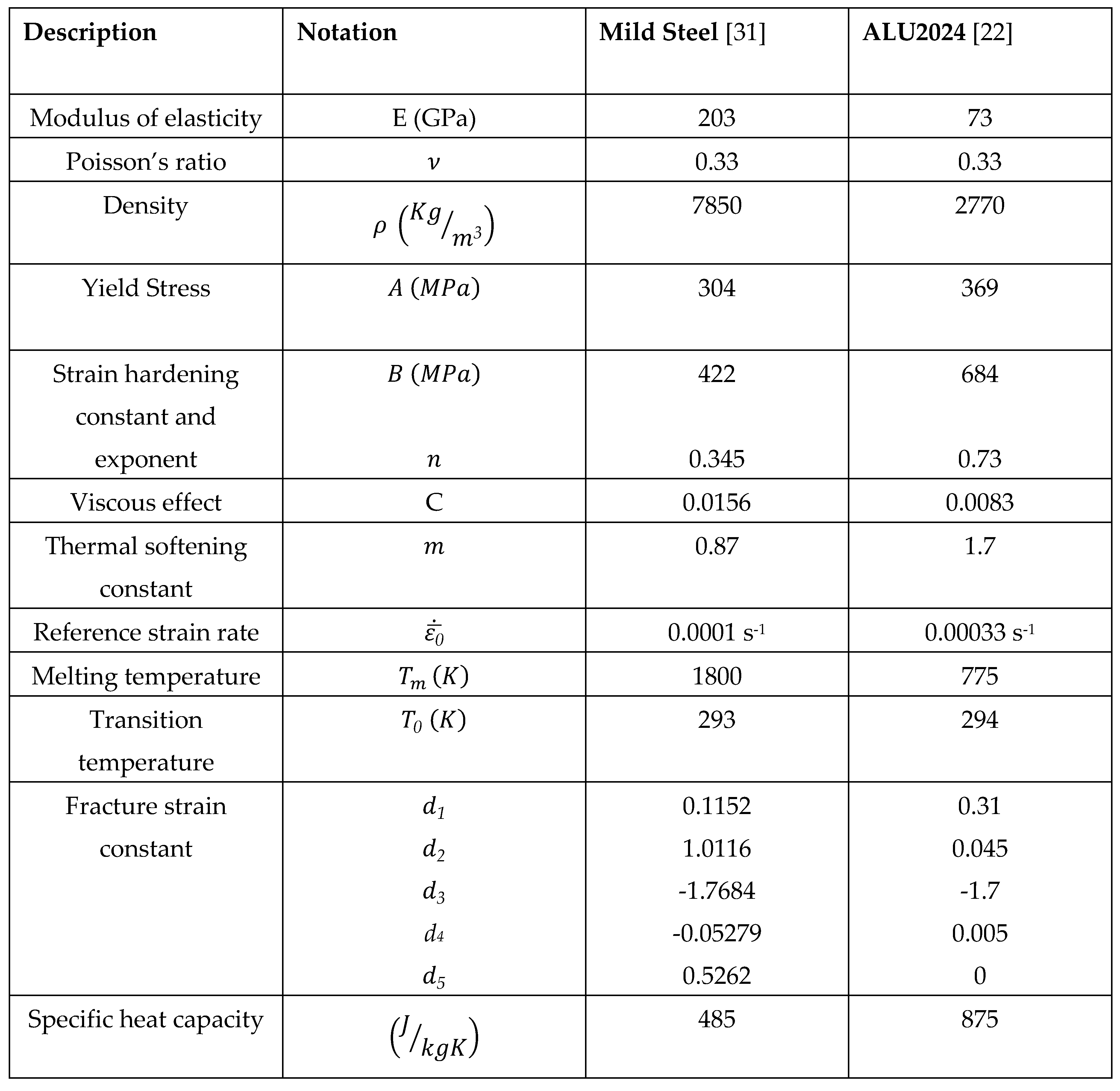
The primary materials considered in this study were LCS, CFRP, GFRP, and PU. The material properties of mild steel (assumed to be very similar to LCS) were obtained from the average values in GRANTA EDUPACK [
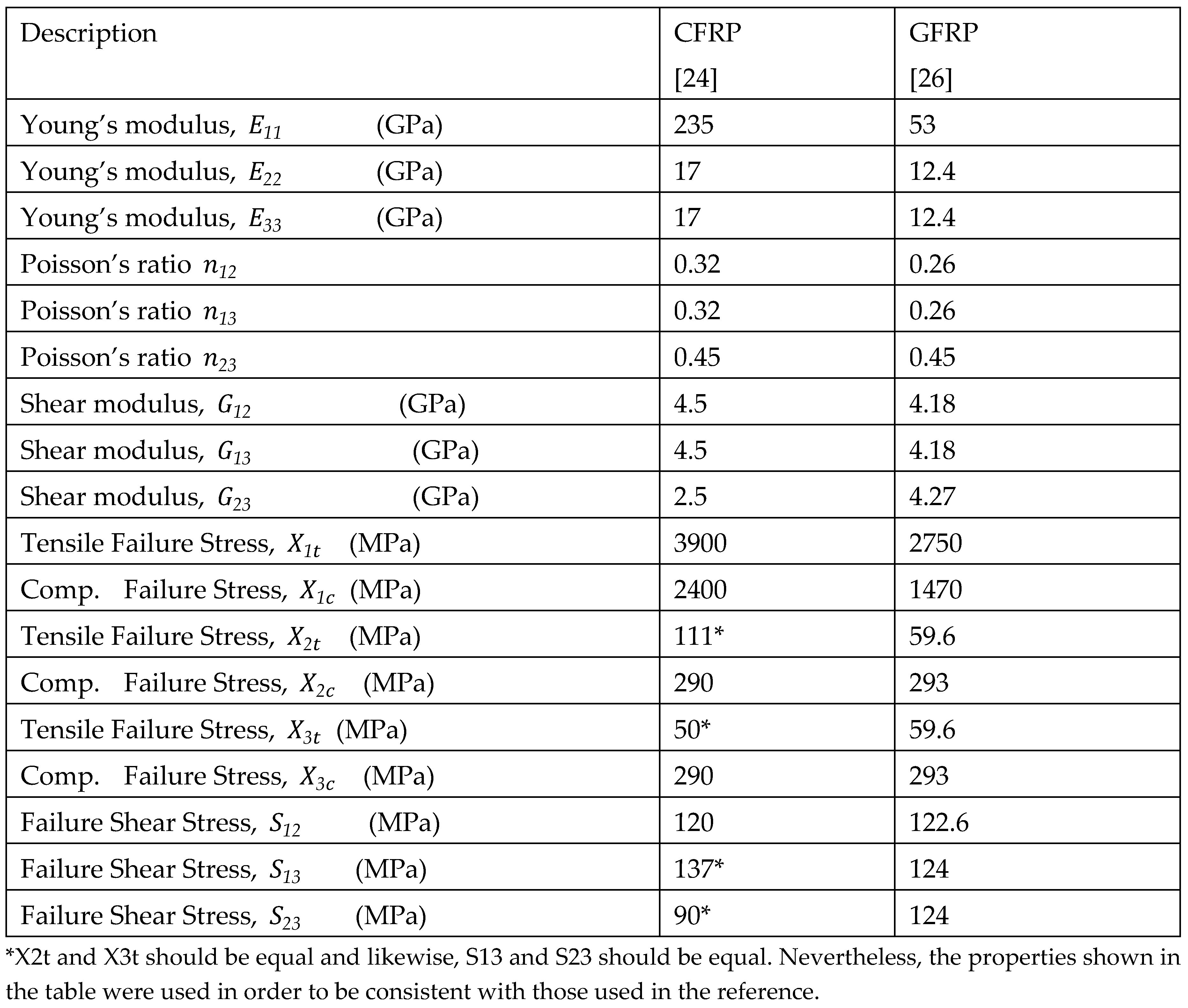
25]. In addition, a cross-ply CFRP laminate and a cross-ply GFRP laminate were analyzed individually, and in combination as a hybrid composite. The properties of the CFRP laminae came from [
24]. The properties of GFRP were computed using Helius Composite software and its references and knowledge network [
26].
Additional materials utilized in verifications and evaluations were ALU2024, chrome steel, lead, and cold-rolled steel. The projectile used in the ALU2024 aluminum alloy published experiment [
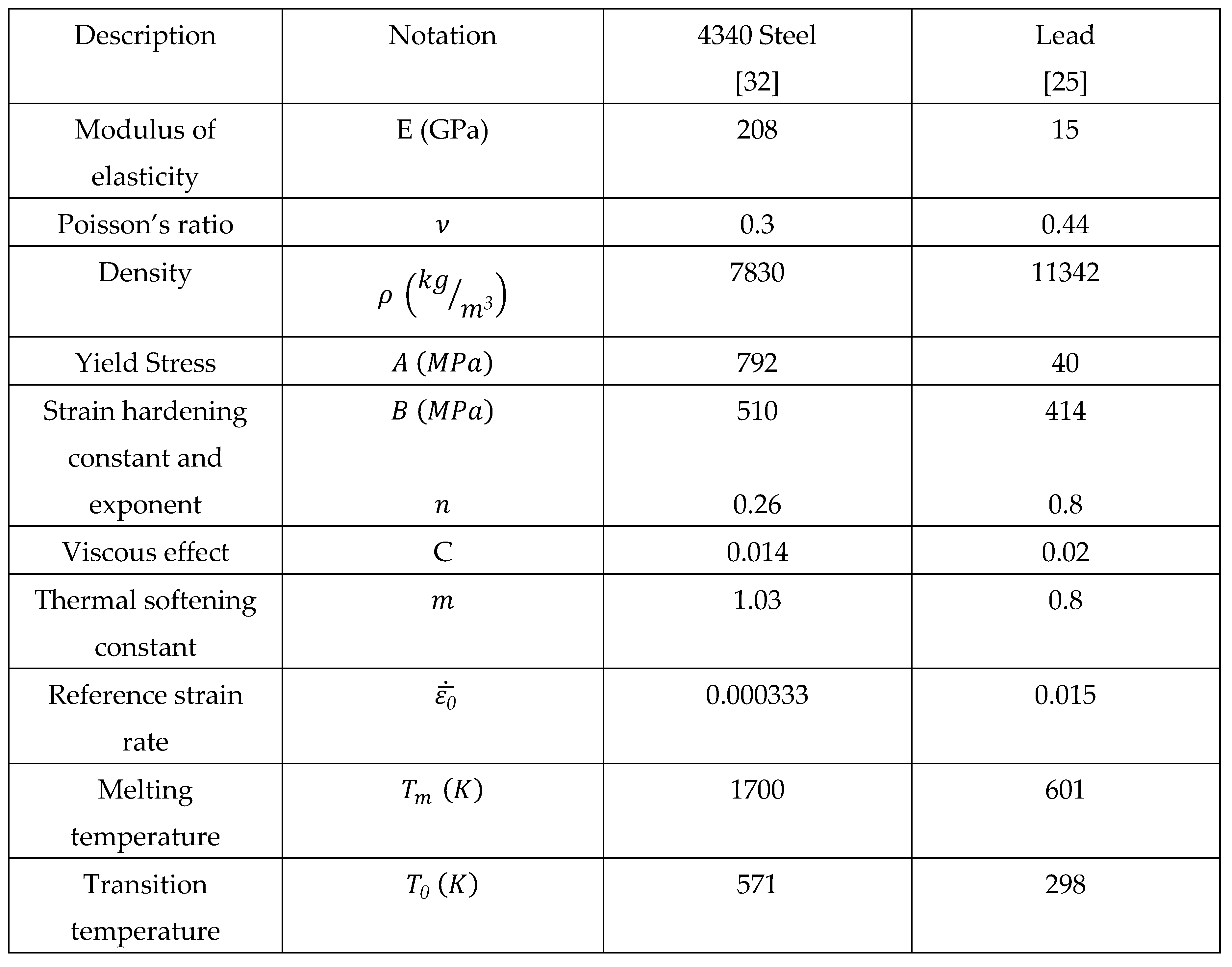
22] was a Chrome 52100 alloy steel whose critical properties for modeling were unavailable. To overcome this, the Chrome steel projectile was modeled as a rigid material. The properties of the lead projectile that was included for comparison and the cold-rolled 4340 steel projectile used in the PMC simulations was a, were both obtained from GRANTA [
25].
The material model properties of the metals simulated in this study (projectiles and targets) are listed in tables I and II, respectively. All these values are room temperature properties. The properties of the PMCs and PU are presented in tables III and IV.
2.2. Failure Models
Failure models describing the onset and evolution of failure used in our numerical simulations were the Johnson-Cook (JC) [
27] for the metals, Virtual User Material (VUMAT) [
28] developed by Dassault Systems for the PMCs, and the Prony series and Virtual User Defined Field (VUSDFLD) for PU [
27,
29]. The script developed allows for the joint application of diverse material models when analyzing several different impact conditions.
2.2.1. Johnson-Cook Model
The material model and the calibrated Johnson-Cook (J-C) failure parameters were used in the verification script for the ALU2024. The material response is linear elastic up to its yield strength, after which it deforms plastically until its failure strain [
27]. The yield stress (
) and the strain at failure (
[
30] are expressed by equations (1) and (2).
(1)
= (2)
In equations 1 and 2, η= -p⁄q represents the triaxiality, defined as the hydrostatic pressure divided by the deviatoric stress or (Von Mises stress), is the reference strain rate, T is the attained temperature of the material, Tm is the melting point, T0 is the ambient temperature or the reference temperature, is the plastic strain, and the plastic strain rate, C is the viscous effect constant, n is the strain hardening exponent, m is the thermal softening exponent, and are damage parameters.
2.2.2. Adiabatic Considerations
During impact, the high plastic strain rate causes the dissipation of energy as heat which raises the temperature (T) of each of the impacted elements in the model. The temperature rise is exclusive to each element and there is no heat conduction assumed between the elements. The inelastic heat fraction applied in the simulation was 0.9, that is, 90% of the energy dissipated by the plastic deformation was converted to heat.
Table 1.
Properties of aluminum and steel plates used for numerical verification.
Table 1.
Properties of aluminum and steel plates used for numerical verification.
Table 2.
Johnson-Cook properties for 4340 steel and lead projectiles.
Table 2.
Johnson-Cook properties for 4340 steel and lead projectiles.
2.2.2. Virtual User Material for Polymer Matrix Composites
The subroutine for composite progressive damage, Virtual User Material (VUMAT), was made available by Simulia [
24] in their documentation. The material properties of CFRP linked to the VUMAT subroutine that was applied in this study were also from [
24] and are summarized in Table III. The VUMAT subroutine was enhanced by utilizing Hashin’s damage model for composites [
33] for the initiation and evolution of the through-thickness damage to the fiber and matrix for PMCs. In the subroutine, the Hashin damage criterion was specified for the fiber failure mode while the Puck criterion [
24,
34] was applied to the matrix damage modes. The relationship between fiber and matrix damage utilized in the VUMAT subroutine is given by [
24]:
(3)
(4)
Matrix tension and compression (Puck)
(5)
where are the effective stress tensors, are the fiber tensile, compressive, and shear strengths. are the matrix tensile failure stress in the 1 and 2 directions (1 is the fiber direction), is the matrix compressive failure stress in the 2-direction, and , is the matrix failure shear stress.
Table 3.
CFRP and GFRP Unidirectional (UD) Laminae Properties.
Table 3.
CFRP and GFRP Unidirectional (UD) Laminae Properties.
Table 4.
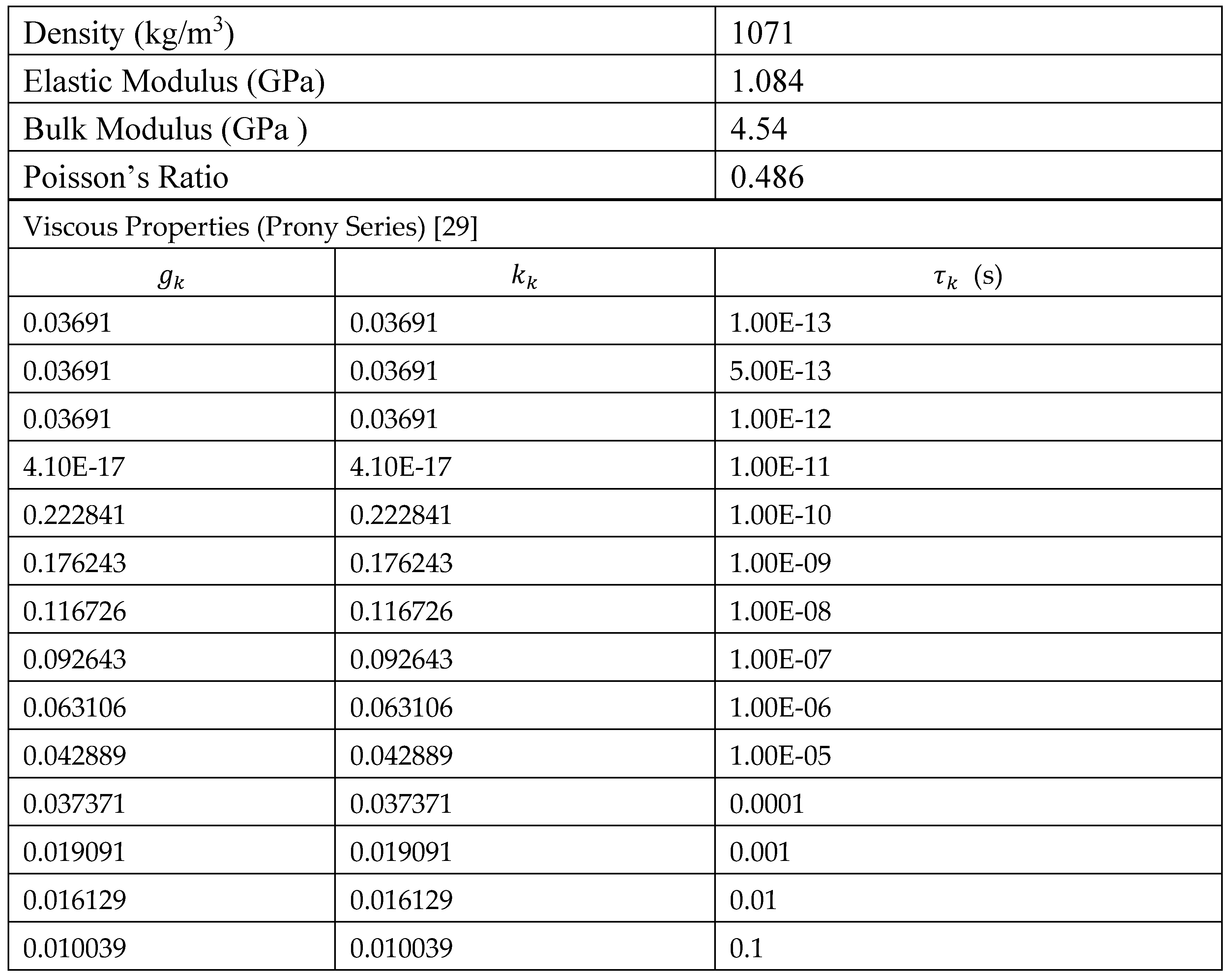
Material Properties for Polyurea [
29].
Table 4.
Material Properties for Polyurea [
29].
2.2.3. PU Material Model
The material properties of the particular PU (four parts of Versalink
®P1000 and one part of Isonate
®143L) investigated by [
29] are listed in Table IV. PU exhibits a linear and viscous response in its stress/strain characteristics. The time-dependent behavior of PU is attributed to the material’s hard and soft segments, i.e., the motion of the chain at different time scales. PU has been modeled as a linear viscoelastic isotropic solid material by [
29] using the material’s shear relaxation modulus G. The Prony series was used in [
21] and in this work to model the relaxation of a polymer consisting of
n decaying exponentials. Equations 6 and 7 describe the time dependent shear and bulk moduli of PU under high strain rates [
35].
where = (6)
where = (7)
The terms g
k and k
k in equations (6) and (7
) are the ratios of the shear and bulk moduli to the shear and bulk moduli of the kth element at the onset of deformation, and
τk is the relaxation time of the kth element, that is the time it takes to ‘relax’ the stress to about 38% (1/
e) of the initial applied stress.
, and
are the shear and bulk moduli at time t = 0,
are the shear and bulk moduli of the first element in the generalized Maxwell model. These are the viscous properties needed for input in a Prony series in the time domain in the Abaqus explicit simulation. In this work, 14 terms of the Prony series, provided by the experimental work of [
29] were used in the simulation. Finally, a Virtual User Defined Field (VUSDFLD) [
27] subroutine was used to assess the response of PU. VUSDFLD is a custom constitutive model used for modeling the high strain rate behavior of PU. The VUSDFLD subroutine computes the strain in the material at each time step using the Prony series and then compared it with a critical strain value at which the material fails. For our work, the critical strain at failure value for PU was set at 0.25, in the middle of the range of values for PU subjected to strain rates experienced in ballistic impacts at the prescribed velocity.
III. Independent Verification of FE Models
3.1. FE Model Verification on Aluminum
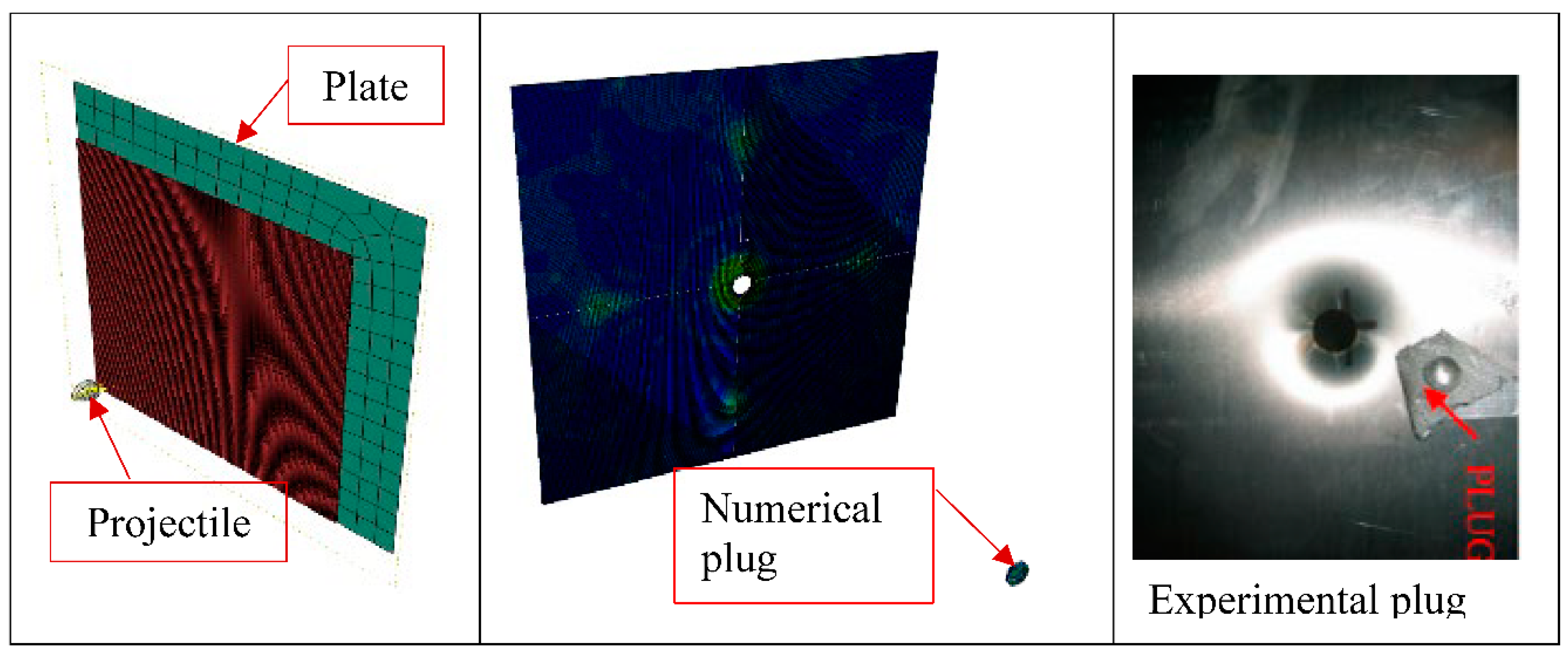
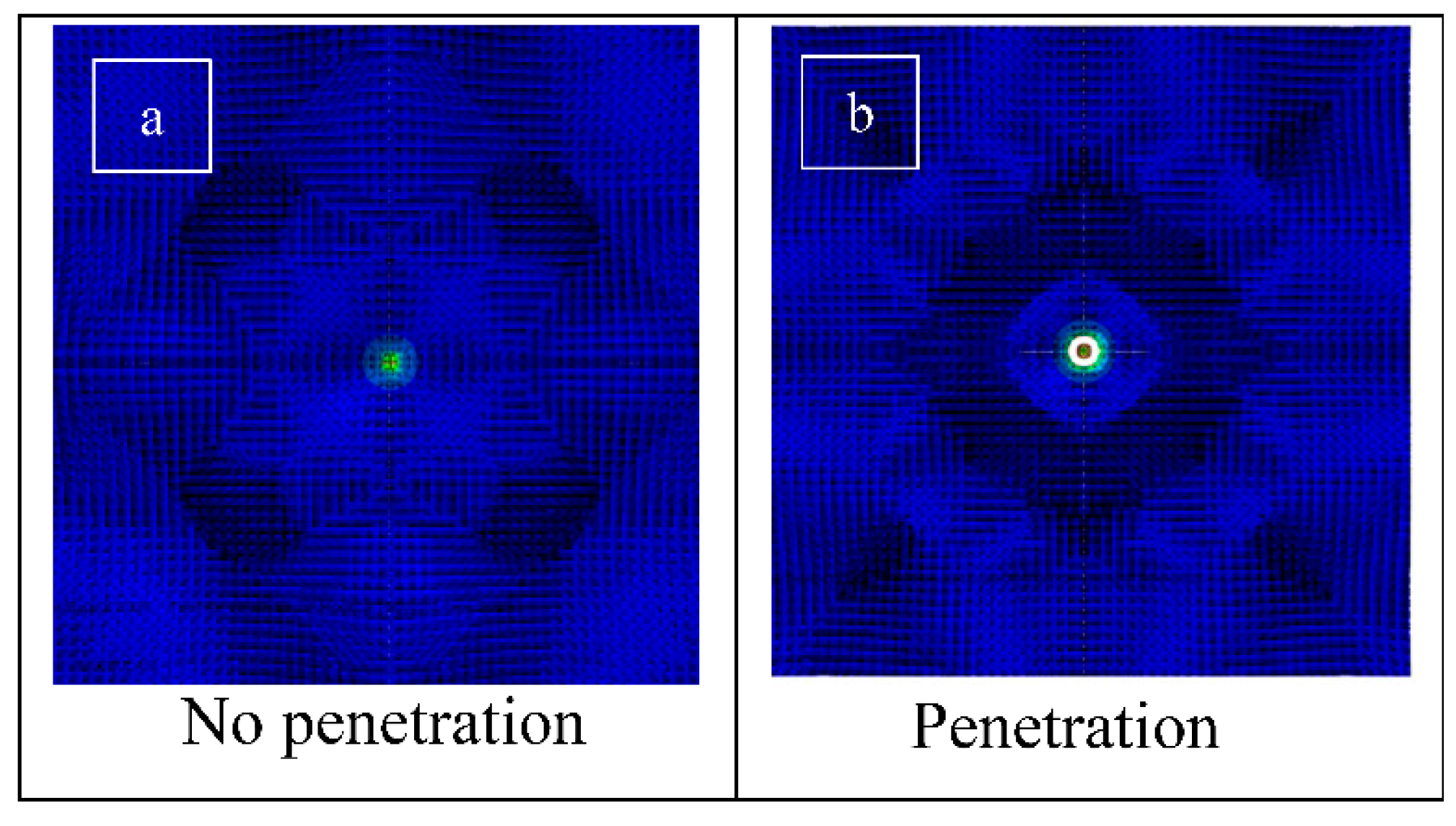
A 304.8 × 304.8 mm plate of ALU2024 with a thickness of 1.5875 mm was modeled in 2 regions. In the target area of 254 × 254 mm, solid elements (C3D8R) and a fine mesh were used to capture the damage, while for the other non-target part, shell elements (S4R) and a coarse mesh were employed. This was done to reduce computation time. These two regions were joined together using shell-to-solid coupling. The spherical Chrome steel projectile of 12.7 mm diameter was modeled as a rigid body because of the unavailability of the material properties for the J-C constitutive equation. To increase computer efficiency and decrease simulation time, a quarter model was used because of the presence of geometric symmetry of the target and the projectile. Edges of the plate were fixed in place. A plug was reported in the experimental work by [
22]. The numerical plug was adequately captured in this work and is presented in
Figure 2.
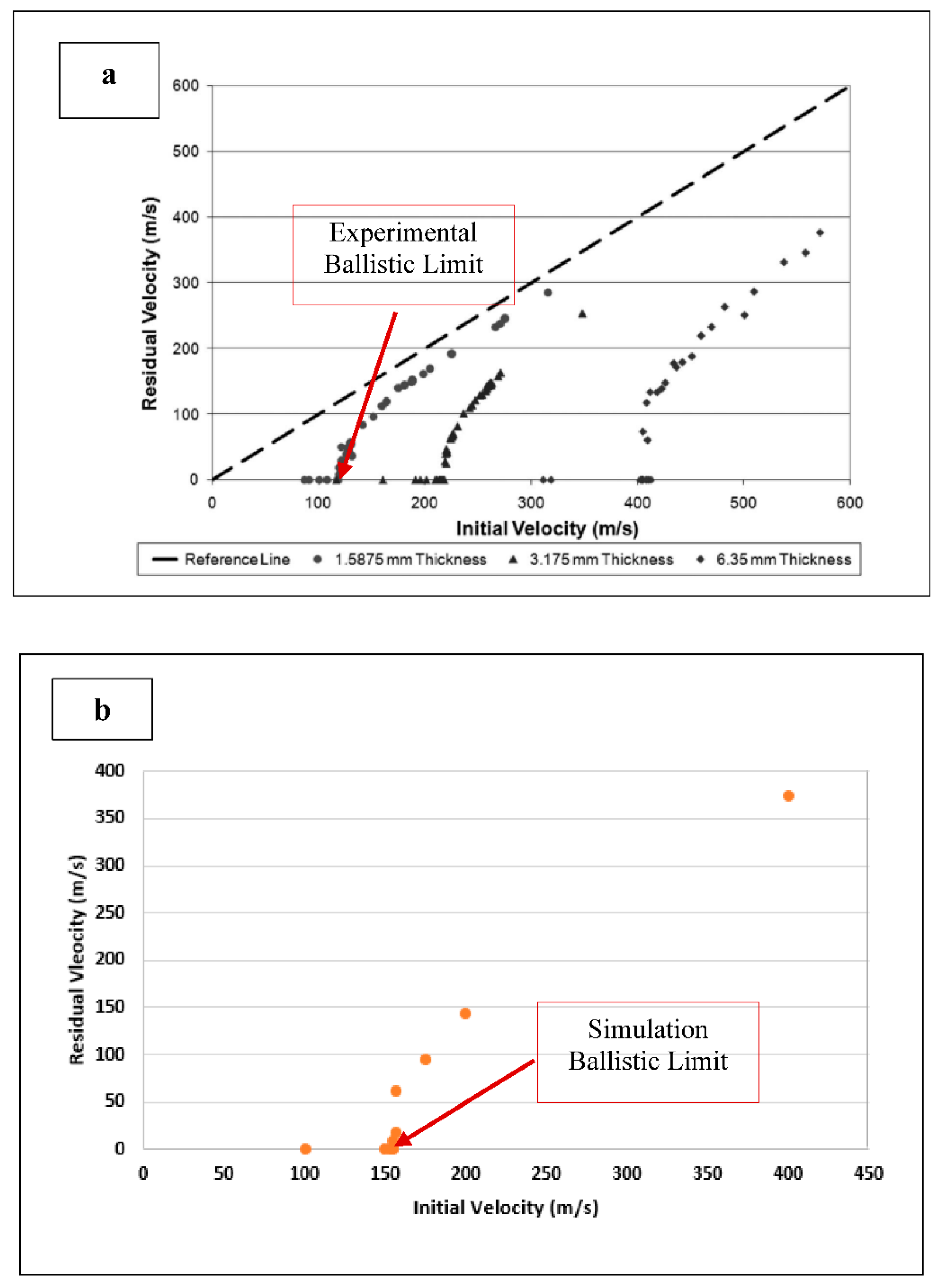
Subsequently, a mesh convergence study was performed by refining the target mesh until the residual velocity stabilized. Final element sizes averaged 0.5 x 0.5 mm in the planar direction and 0.53 in the thickness direction, giving 3 elements through the thickness. A fair agreement was obtained between the numerical and experimental residual velocities as illustrated in
Figure 3a,b. Notice that the ballistic limit for the actual test (circles) is about 121.9 m/s and that of the validation numerical simulation is about 154.3 m/s.
3.2. FE Model Verification on CFRP Panels
To confirm the validity of the PMC model, a comparison was made to an experiment conducted by [
23]. In that work, a 5 mm diameter spherical steel projectile of mass 0.51 g was fired at three different velocities at a multi-ply composite panel and the residual velocities were measured. The composite panel was a [0,90,0]
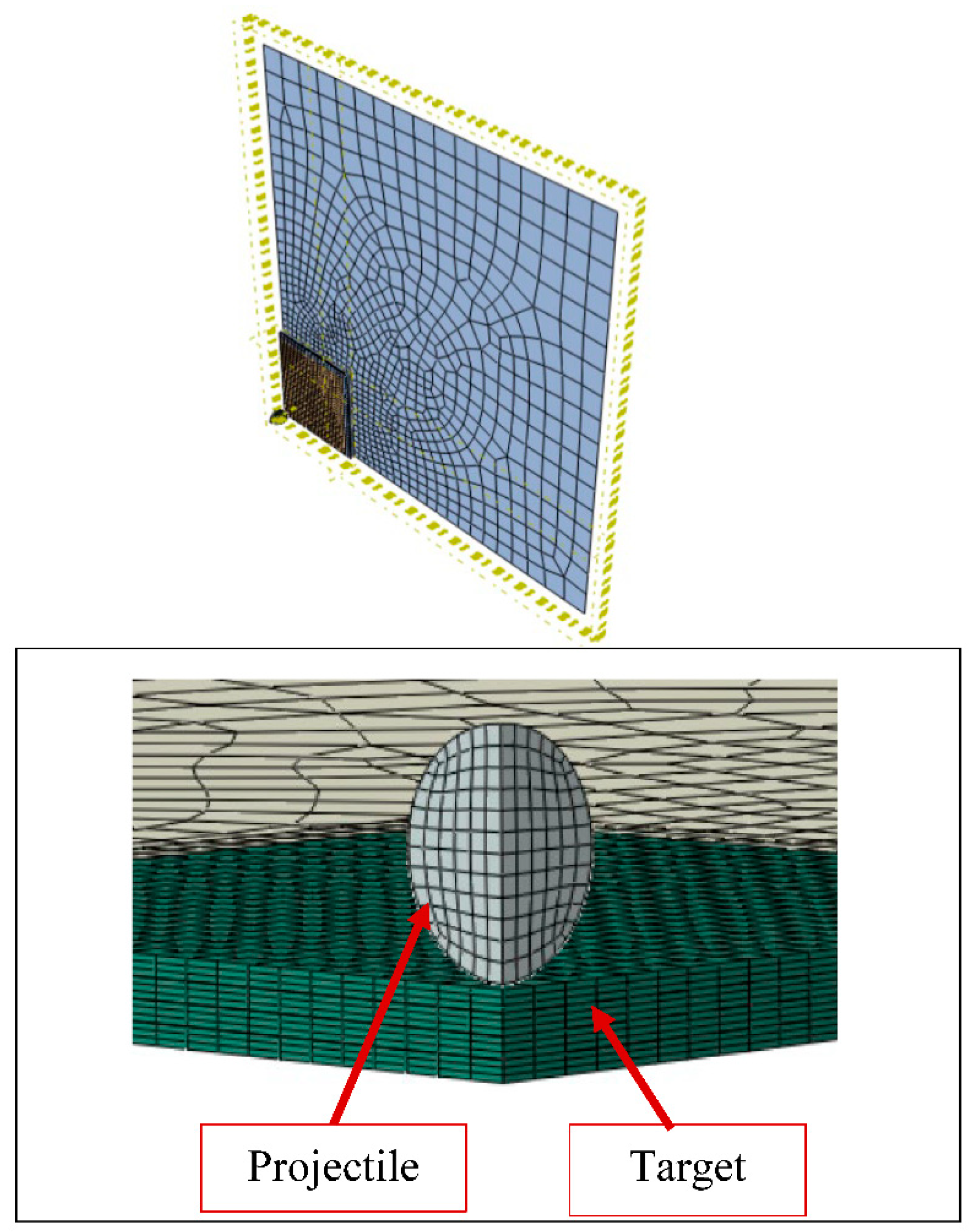
ns 12 or 18 layer CFRP, in which n=2 or 3 respectively, and the panel thickness ranged from 1.8 mm to 2.7 mm. For this validation, the 12-layer (n=2) experiment was used. A PMC 200 x 200 mm panel was simulated with a target area of 50 x 50 mm to reduce computation costs. Taking advantage of symmetry, a quarter model was developed as seen in
Figure 4a,b. The plies and thickness of the model followed those of the experiment [
23]. The target was divided into sub-laminates, where each [0,90,0] sub-laminate was separated by a cohesive zone. The cohesive zones were modeled with cohesive elements (COH3D8) with maximum degradation set to 1 kJ. The finite element model is shown in
Figure 4. The region of the plate outside the target area was modeled with shell elements (S4R) to reduce the computational cost. The target region was represented with first-order C3D8R continuum elements [
24] (layer-by-layer) to capture the damage in detail. Edges of the plate were fixed in place. To make the model more versatile, a python script was used to develop the model where geometry conditions, mesh parameters, contact parameters, speed of the projectile, and boundary conditions were defined as variables.
The exact properties of the steel projectile used in the experiment in [
23] were not stated. In our work cold- rolled steel was used to model the projectile as a deformable spherical solid following [
24]. We specifically selected cold-rolled 4340 steel for the projectile. The projectile yield followed the Johnson-Cook parameters listed in Table II. These complete parameters may be used to simulate both the initiation and propagation of the damage in the projectile under elastoplastic conditions. However, this study limits the projectile to a perfectly elastic material in order to simplify the model.
A mesh sensitivity study was conducted for the target with mesh sizes of between 0.3 and 1.0 mm, and for the projectile, with mesh sizes of between 0.35mm and 0.55mm. A good correlation was found with the experimental result at mesh sizes of 0.85 mm in the planar directions and at one element per ply in the thickness direction (0.15 mm) for the target and 0.4 mm for the projectile. We utilized the tools developed by [
24] but compared our simulation results directly with the experiment [
23] due to some concerns about the geometry assumptions used by [
24].
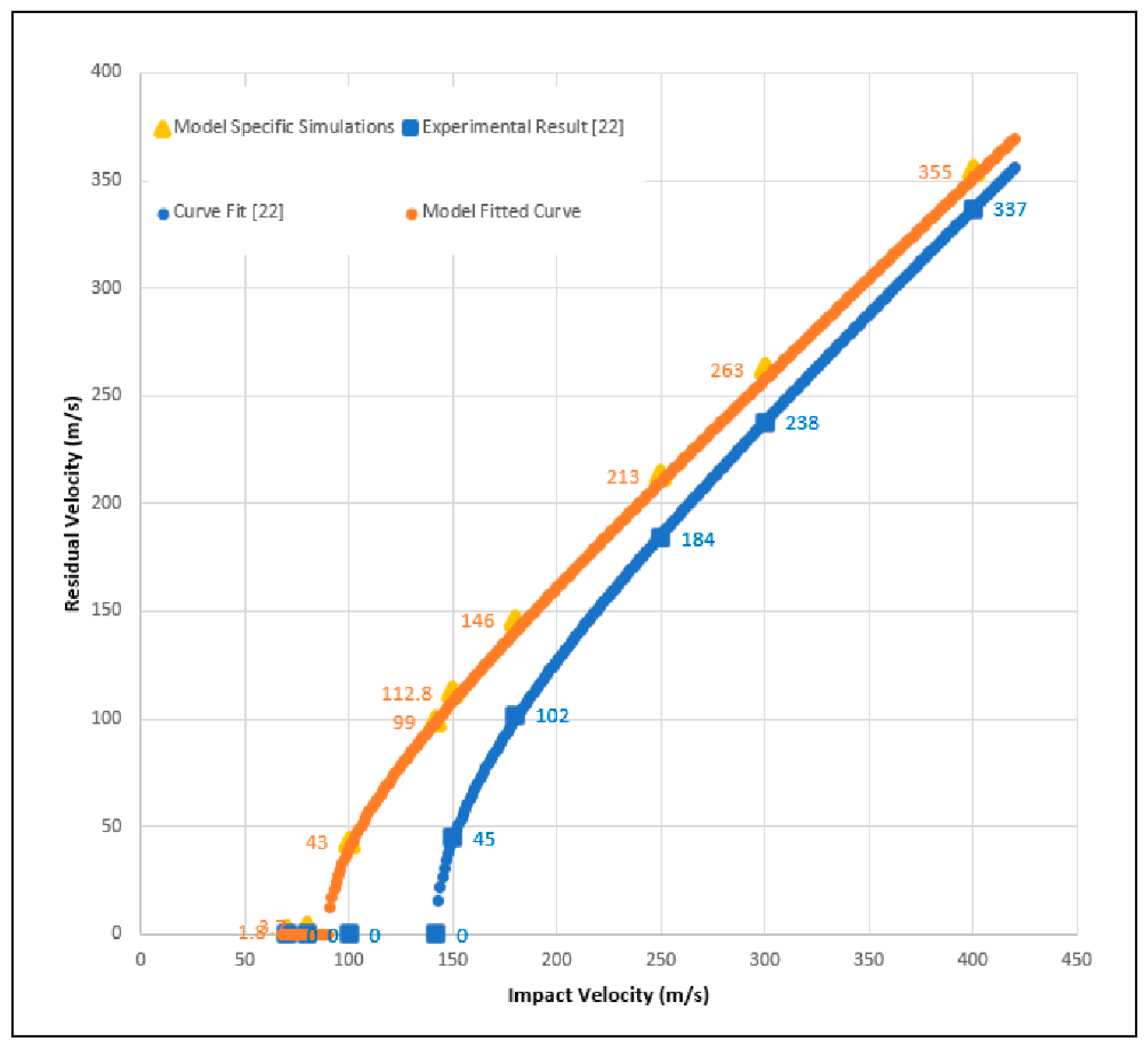
The bottom curve in
Figure 5 is the fitted curve from [
23] for the 12-layer panel. This fitted curve utilizes the function.
(8)
where V
i is the impact velocity, V
bl is the ballistic limit, and α is a function of the mass of the projectile and the masses of the fragments released from the plate upon impact (for more information see [
23]). Certain points along that curve are specified for comparison with the model where those same velocities were simulated. A curve using the same parameters as the experiment (i.e., with α = 0.9) is fitted to those points and displayed in the top curve of
Figure 5. It is to be noted that while the variation in the residual velocities decreases as impact velocity increases as shown in
Figure 5, the difference in the residual kinetic energies of the projectile between the experiment and the simulation stays roughly constant. Using either measure, the simulation produces a conservative estimate of the energy dissipated by the composite plates and thus the actual results should be better than those predicted by the modeling.
Figure 5.
Comparison of CFRP model with experimental results from [
23].
Figure 5.
Comparison of CFRP model with experimental results from [
23].
IV. Impact SIMULATION of Low Carbon Steel Including the Effect of PU Coating
After verifying our numerical impact models by comparing our predictions against available impact data for aluminum and composites, LCS was subjected to impact. In particular, it was investigated whether there would be penetration on a standard LCS LPT panel from a lead projectile with an impact velocity of 400 m/s. The same simulation was repeated using a 4340-steel projectile. The penetration depth in a thicker LCS by a 4340-steel projectile at 400 m/s was also simulated. Finally, the benefit of adding a 3 mm coating of PU was investigated. mm for PU (where applicable). Edges of the plate were fixed in place and S4R elements were used for the non-target areas.
4.1. LCS Plate Response to Ballistic Impact at 400m/s
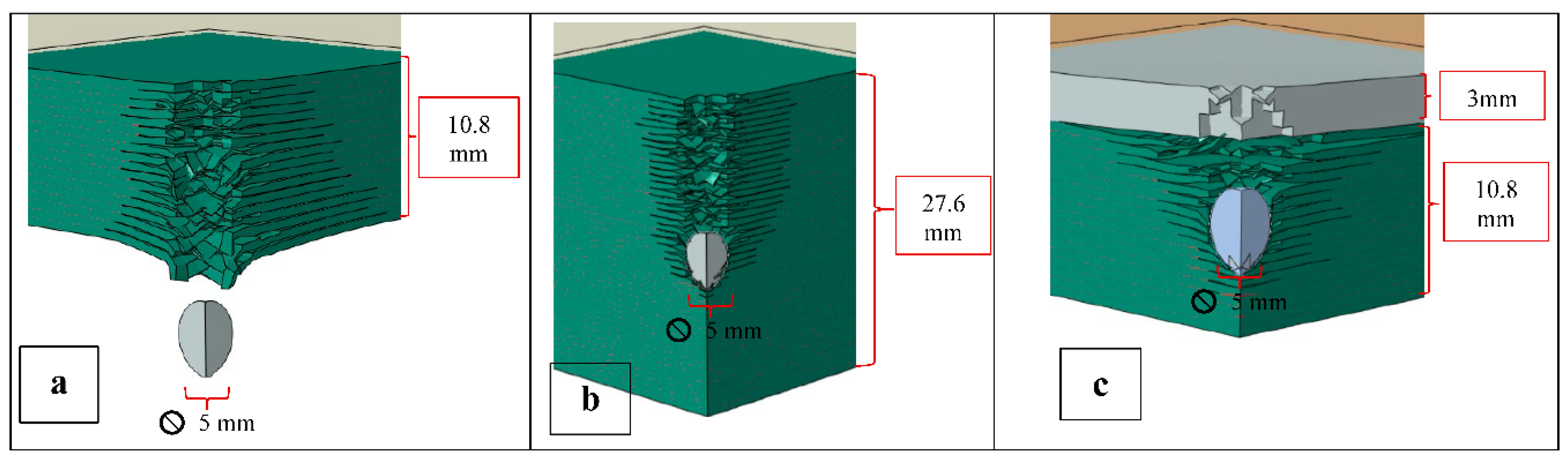
When a 10mm thick LCS plate, the standard material and thickness of modern LPT tanks, was impacted with a 5 mm diameter projectile made of lead at 400m/s, the projectile did not penetrate. Instead, a dent was created on the LCS plate as shown in
Figure 6a. Mild steel is roughly 14 times stiffer than lead, making steel almost impenetrable to lead. When the projectile material was replaced with 4340 steel, a penetration was observed as shown in
Figure 6b. Therefore, it is clear that penetration of 10 mm thick LCS could occur with high-velocity projectiles. Thus, there are two obvious solutions to this problem. One way is to increase the thickness of the steel. The other solution could be to add a ballistic protection coating. These two options are discussed in the sections below.
4.1.1. Option 1 – Thicker LCS Tank
With a thicker LCS tank, an arrest can be made. For a sufficiently thick tank, our simulation showed that a 5 mm diameter projectile made of 4340 steel impacting at 400 m/s would be arrested about 14 mm into the tank (please refer to the results in table VI and
Figure 7). However, any increase in the thickness of the tank would come with significant weight penalties as discussed in [
1].
4.1.2. Option 2 – Addition of PU Coating
An alternative solution to the penetration of LCS plates by 400 m/s projectiles (or higher) is to coat the plates with PU. Three thicknesses of coatings were investigated: 1, 2, and 3 mm. With a 1 or 2 mm coating, the plate was still fully penetrated. However, with a 3 mm coating, the projectile was arrested 6.2 mm into the mild steel tank portion (9.2 mm from the surface of the PU). Clearly, the coating effect on the LCS was significant. It is interesting to note that even if the critical strain on PU were set at the bottom of the 0.2-0.3 range, the required thickness of PU to prevent penetration in the simulation only increased to 4 mm. This demonstrates that PU could be effective even with conservative parameters.]
Figure 7.
Quarter cross-section through LCS showing: (a) perforation through 10mm without coating, (b) an arrest through a 27.6 mm without coating, and (c) an arrest of the projectile with a 3mm coating of PU on 10 mm of LCS. All three are impacted with 4340 steel projectiles at 400 m/s.
Figure 7.
Quarter cross-section through LCS showing: (a) perforation through 10mm without coating, (b) an arrest through a 27.6 mm without coating, and (c) an arrest of the projectile with a 3mm coating of PU on 10 mm of LCS. All three are impacted with 4340 steel projectiles at 400 m/s.
Table 6.
Thickness and coating effect on the penetration of and arrest by LCS plates.
Table 6.
Thickness and coating effect on the penetration of and arrest by LCS plates.
| Thickness and coating |
Structure
Thickness
(mm) |
Arrest
Depth I
(mm) |
| Mild Steel |
10 |
Penetration |
| 3mm PU + 10 mm Mild Steel |
13 |
9.2 |
| Mild Steel |
27.6 |
14.2 |
V. Impact Response of CFRP and GFRP Plates and the Effect of PU Coating
Next, the impact resistance of CFRP and GFRP composites was evaluated using the same model that was verified in
Section 3.2. All of the simulations utilized individual unidirectional 0.2 mm plies in a [0/90/0] architecture. Thus each [0/90/0] sub-laminate was 0.6 mm thick. The target and plate lateral dimension were the same as those used in the PMC verification and for the LCS modeling in the prior section. Again, C3D8R elements were used in the target area and S4R elements in the non-target area. The PMC target element mesh sizes were the same as those used in the LCS simulations and the edges of the plates were likewise fixed. The thickness dimension of the PMC mesh corresponded to one element per ply. When included, the same PU mesh dimensions as those used in the LCS-PU case were used.
At first 18 layers of sub-laminates for a total thickness of 10.8 mm for both CFRP and GFRP were found in the simulation to be penetrated by a 400 m/s 4340 steel spherical projectile with a 5 mm diameter. The thicknesses for both the CFRP and the GFRP plates were then increased by adding additional sub-laminates to find the minimum thickness that would prevent penetration. Subsequently, a consistent thickness of 27.6 mm was evaluated to allow for the comparison of penetration depths and to see whether penetration depths would significantly change if the thicknesses were increased beyond the minimum penetration prevention thickness. The results are presented in Table VII(a).
Following the proposal of [
6], two hybrid architectures of CFRP/GFRP and GFRP/CFRP (where the projectile impacts the first material listed before the second and both components were of equal thickness) were evaluated. In both cases, the initial 10.8 mm thick hybrid plates were unable to prevent full penetration from the 400 m/s steel projectile. The same process to estimate minimum thicknesses and penetration depths as discussed in the prior paragraph was then conducted for these hybrid structures. The results are presented in Table VII(b). Finally, based on the successful enhancement of the LCS steel as discussed in Section IV, a 3 mm coating of PU was added to the impact side of 10.8 mm plates for CFRP, GFRP, and a CFRP/GFRP hybrid composite. The results are presented in Table VII (c).
The results in table VII show that the projectiles were arrested with a 19.8 mm thick CFRP plate and a 21.2 mm GFRP plate. When the thicknesses for both of these structures were increased to 27.6 mm, the arrest distances were similar to those for the near minimum arrest thickness plates. With the addition of 3 mm of PU to the original 10.8 mm thick plates, the CFRP/PU plate successfully arrested the 400 m/s projectile as shown in Table VII(c). However, with the GFRP plate, the addition of the PU only allowed for the partial arrest of the projectile. A hybrid combination of PU/CFRP/GFRP with a total thickness of 13.8 mm also successfully arrested the projectile. Also see
Figure 8 a–c for simulation schematics.
Figure 8.
Penetrations of and arrests in CFRP plates using a 400 m/s projectile: (a) penetration in 10.8 mm plate, (b) arrest in a 27.6 mm thick plate, and (c) arrest in a 10.8 mm plate coated with 3 mm of PU.
Figure 8.
Penetrations of and arrests in CFRP plates using a 400 m/s projectile: (a) penetration in 10.8 mm plate, (b) arrest in a 27.6 mm thick plate, and (c) arrest in a 10.8 mm plate coated with 3 mm of PU.
Table 7.
Penetration results from 400 m/s test with 4340 steel projectile: a) CFRP and GFRP laminates, b) CFRP and GFRP hybrid composites, and c) CFRP, GFRP, and hybrid composites with PU coating.
Table 7.
Penetration results from 400 m/s test with 4340 steel projectile: a) CFRP and GFRP laminates, b) CFRP and GFRP hybrid composites, and c) CFRP, GFRP, and hybrid composites with PU coating.
Target
(Individual PMCs)
a
|
Structure
Thickness
(mm) |
Arrest
Depth I
(mm) |
Constant
Structure thickness (mm) |
Arrest Depth II
(mm) |
| CFRP |
19.8 |
17.1 |
27.6 |
17.3 |
| GFRP |
22.2 |
21.2 |
27.6 |
20.8 |
Target
(Hybrid PMCs)
b
|
Structure
Thickness
(mm) |
Arrest
Depth I
(mm) |
Constant
Structure thickness (mm) |
Arrest Depth II
(mm) |
| CFRP + GFRP |
19.8 |
17.6 |
27.6 |
17.5 |
| GFRP + CFRP |
21.6 |
18.7 |
27.6 |
18.8 |
Target
(individual PMCs with coating)
c
|
Structure
Thickness
(mm) |
Arrest Depth
Depth
(mm) |
| 3 mm PU + 10.8 mm CFRP |
13.8 |
12.05 |
| 3 mm PU + 10.8 mm GFRP |
13.8 |
13.77 (partial penetration) |
| 3 mm PU + 5.4 mm CFRP + 5.4 mm GFRP |
13.8 |
12 |
The results in table VIIa clearly show that there are critical arrest distances for the projectile at 400 m/s which are between 17.1 and 17.3 for CFRP and between 21.2 and 20.8 for GFRP. It can also be seen that when the thickness was increased by approximately 30-40%, the critical arrest distances did not change materially. This suggests that we can simulate the projectile arrest with plate thickness relatively close to the arrest distance. However, this might create a bulge at the backface of the plate containing delaminations which could affect the projectile arrest process. The projectile would be stopped but the backface would be severely damaged leading to a partial arrest. Consistent results were obtained using hybrid CFRP + GFRP plates, regardless of their order (Table VIIb).
Table VIIc reveals an interesting effect of the 3 mm PU coating on CFRP and GFRP plates having 10.8 mm thicknesses that were close to that of the 10 mm steel plate in table VI. There were comparable arrest depths for both CFRP and steel plates. However, the coated GFRP allowed partial penetration. In this case, the thickness of the coating or of the GFRP would have to be increased in order to achieve a full arrest. If we further compare the data in Table VII a and c, one important observation can be made. By applying a 3 mm coating of PU, the thickness of the CFRP composite plate to just prevent penetration could be significantly reduced. Of course, the same coating thickness could also reduce the required steel plate thickness substantially (Table VI).
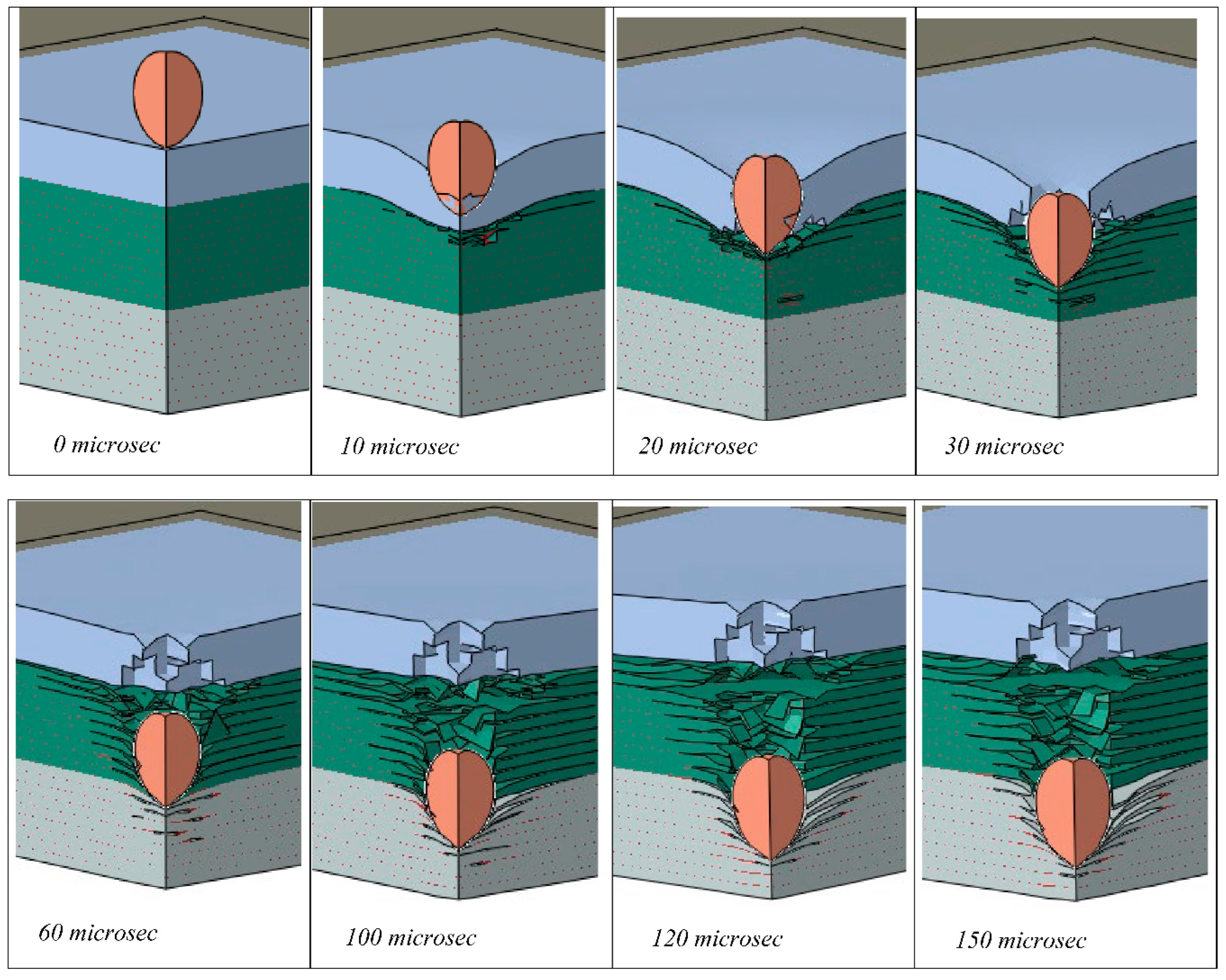
We have shown in this research that PU could play a major role in the impact protection of advanced PMCs, for example in the protection of LPT tanks. To further demonstrate this effect,
Figure 9 and
Figure 10 are presented. We analyzed the damage formation process in the PU/CFRP/GFRP laminate (
Figure 9), from the onset of the projectile impact until the projectile is fully arrested inside the laminate. Eight stages of the damage progression between 0 to 150 microseconds are shown.
Figure 10 shows the velocities of the projectile in the hybrid laminate with and without the PU coating.
Several important observations can be made when analyzing the data presented in
Figure 9 and
Figure 10. First, the projectile decelerations (change in velocities) are markedly different between the coated and uncoated composites in
Figure 10. The reduction in the velocity of the projectile in the coating is significantly larger than in the composite. For example, the time it takes for the projectile to decelerate from 400 to 200 m/s with PU is approximately 15 microseconds while for the same deceleration without PU it takes about 45 microseconds which is 3 times longer. Thus the PU has a significantly beneficial effect on the deceleration of the projectile. Note that while the coated plates fully arrested the projectile and brought its velocity to zero, the projectile retained an exit velocity of about 200 m/s after penetrating the uncoated hybrid laminate.
VII. Conclusions
This research analyzed LCS, CFRP, GFRP, and CFRP/GFRP plates either uncoated or coated with Polyurea under projectile impact at 400m/s. This was done by performing dynamic FE simulations using a steel projectile. The FE models built to simulate impact in the steel and PMC plates were first extensively verified by performing numerical simulations of published experimental impact tests. Using our independently verified FE models, we determined that the perforation of the plates and the arrest of the projectile all strongly depend on the type of materials simulated and their thicknesses.
For a 10 mm LCS plate, perforation was observed with a 4340 steel projectile at 400 m/s but not with a lead projectile at the same velocity even in spite of he fact that the lead projectile with a higher density had more kinetic energy. To arrest the steel projectile in LCS, the thickness of the plate had to be significantly increased. Consequently, the projectile was arrested at about 14 mm. It was also shown that by adding a 3 mm PU coating, the projectile was arrested at about 8 mm into the 10 mm LCS plate.
Typical CFRP, GFRP, and CFRP/GFRP composite plates behave in a very similar fashion under 4340 steel projectile impact. The damage evolution in the composites was essentially the same with the arrest depths ranging from 17 to 21 mm. When the thicknesses of the plates were increased by about 30-40 %, the depths of arrest did not significantly change.
PU was seen to significantly improve the ballistic response of the PMC plates. When a 3 mm PU coating was applied to a 10.8 mm CFRP plate, the steel projectile was arrested at about 12 mm depth. Meanwhile, there was a partial penetration for GFRP of the same thickness and coating. The CFRP/GFRP hybrid with coating showed a similar arrest depth as that of the CFRP with coating. We showed that the projectile decelerated from 400 to 200 m/s in 15 microseconds for the PU/CFRP/GFRP sample while it took three times longer to reach that same reduced velocity in the 10.8 mm uncoated hybrid sample.
For the 400 m/s impact simulations, the penetration depth for steel was about 14 mm while for the composites was about 17-21 mm, depending on the fiber types. For both types of materials, the addition of a 3 mm coating of PU had a dramatic effect on the penetration depths, reducing the steel penetration depth to 11 mm and the composite depth to 12 mm.
We have noticed that our models underestimate the energies absorbed by the composites and overestimate those absorbed by the metals. We believe this indicates that actual composite plates could perform even better in comparison with metals. Therefore, for projectile impacts up to at least 400 m/s, a CFRP/GFRP composite could be a good replacement for LCS in LPT tanks when PU coatings are applied. This seems to us a better alternative to LCS since, in addition to the comparable response to such impacts, PMCs could offer additional capabilities in self-healing, stress distribution monitoring, hot-spot avoidance, and corrosion resistance as has already been presented to the electric power transmission community [
1].
VIII. Acknowledgments
This work was supported by the US Department of Energy and other members of the National Science Foundation (NSF) Industry/University Cooperative Research Center for Novel High Voltage/Temperature Materials and Structures (HVT Center) under Grant IIP 1362135.
References
- J. Williams, J. Hoffman, P. Predecki, and M. S. Kumosa, “Application of Polymer Matrix Composites in Large Power Transformer Tanks,” IEEE Transactions on Power Delivery, pp. 1–1, 2022. [CrossRef]
- Siemens, “Bullet resistant power transformer retrofit.” Siemens Industry, Inc, 2018.
- R. Smith, “Assault on California Power Station Raises Alarm on Potential for Terrorism,” WSJ. http://online.wsj.com/article/SB10001424052702304851104579359141941621778.html (accessed Dec. 05, 2022).
- Mike Sheppard, Saqib Saeed, “Bullet and weather concerns driver of retrofits in US market,” Bullet and weather concerns driver of retrofits in US market, Oct. 26, 2017. https://powertechresearch.com/bullet-and-weather-concerns-driver-of-retrofits-in-us-market/.
- Armorcore, “Armorcore Bullet Resistance Fiberglass Panels.” Armorcore. [Online]. Available: https://www.armorcore.com/assets/files/Test-Results-UL-Levels-5-8.pdf.
- P. Beaumont, P. Riewald, and C. Zweben, “Methods for Improving the Impact Resistance of Composite Materials,” in Foreign Object Impact Damage to Composites, L. Greszczuk, Ed. 100 Barr Harbor Drive, PO Box C700, West Conshohocken, PA 19428-2959: ASTM International, 1975, pp. 134-134–25. [CrossRef]
- B. Lusk, “Blast Protection for Power Transformer - Blast and Ballistic Final Report,” National Institute for Hometown Security (NIHS)-University of Kentucky, 2012.
- K. Pandya, C. V. S. Kumar, N. Nair, P. Patil, and N. Naik, “Analytical and experimental studies on ballistic impact behavior of 2D woven fabric composites,” International Journal of Damage Mechanics, vol. 24, no. 4, pp. 471–511, May 2015. [CrossRef]
- R. Muñoz, F. Martínez-Hergueta, F. Gálvez, C. González, and J. LLorca, “Ballistic performance of hybrid 3D woven composites: Experiments and simulations,” Composite Structures, vol. 127, pp. 141–151, Sep. 2015. [CrossRef]
- C. N. Henderson, C. S. DeFrance, P. Predecki, and M. Kumosa, “Damage prevention in transformer bushings subjected to high-velocity impact,” International Journal of Impact Engineering, vol. 130, pp. 1–10, Aug. 2019. [CrossRef]
- Y. Sun, S. E. Kooi, K. A. Nelson, A. J. Hsieh, and D. Veysset, “Impact-induced glass-to-rubber transition of polyurea under high-velocity temperature-controlled microparticle impact,” Appl. Phys. Lett., vol. 117, no. 2, p. 021905, Jul. 2020. [CrossRef]
- R. G. S. Barsoum, Elastomeric Polymers with High Rate Sensitivity: Applications in Blast, Shockwave, and Penetration Mechanics. William Andrew, 2015.
- R. B. Bogoslovov, C. M. Roland, and R. M. Gamache, “Impact-induced glass transition in elastomeric coatings,” Appl. Phys. Lett., vol. 90, no. 22, p. 221910, May 2007. [CrossRef]
- Primeaux Associates LLC, “Polyurea Technology Life Expectancy Discussion”.
- D. Mohotti, T. Ngo, P. Mendis, and S. N. Raman, “Polyurea coated composite aluminium plates subjected to high velocity projectile impact,” Materials & Design (1980-2015), vol. 52, pp. 1–16, Dec. 2013. [CrossRef]
- Y. Jiang, B. Zhang, J. Wei, and W. Wang, “Study on the impact resistance of polyurea-steel composite plates to low velocity impact,” International Journal of Impact Engineering, vol. 133, p. 103357, Nov. 2019. [CrossRef]
- D. T., A. Gobiraman, P. Venkatachalam, M. Anish, J. Jayaprabakar, and J. Sajin, “Effect of Plural Spray Coating Process Parameters on Bonding Strength of Polyurea with Steel and Aluminum for Liquid Storage Applications,” Jun. 2020. [CrossRef]
- Y. Xiao, Z. Tang, and X. Hong, “Low velocity impact resistance of ceramic/polyurea composite plates: experimental study,” J Mech Sci Technol, vol. 35, no. 12, pp. 5425–5434, Dec. 2021. [CrossRef]
- Q. Liu et al., “Investigating ballistic resistance of CFRP/polyurea composite plates subjected to ballistic impact,” Thin-Walled Structures, vol. 166, p. 108111, Sep. 2021. [CrossRef]
- C. N. Henderson, J. Monteith, E. Solis-Ramos, R. Godard, P. Predecki, and M. Kumosa, “Impact protection of borosilicate glass plates with elastomeric coatings in drop tower tests,” International Journal of Impact Engineering, vol. 137, p. 103460, Mar. 2020. [CrossRef]
- C. N. Henderson et al., “Ballistic fragmentation confinement of coated brittle transformer bushing models,” International Journal of Impact Engineering, vol. 122, pp. 363–373, Dec. 2018. [CrossRef]
- M. Buyuk, S. Kan, and M. J. Loikkanen, “Explicit Finite-Element Analysis of 2024-T3/T351 Aluminum Material under Impact Loading for Airplane Engine Containment and Fragment Shielding,” Journal of Aerospace Engineering, vol. 22, no. 3, pp. 287–295, Jul. 2009. [CrossRef]
- H. Kasano, “Impact perforation of orthotropic and quasi-isotropic CFRP laminates by a steel ball projectile,” Advanced Composite Materials, vol. 10, no. 4, pp. 309–318, Jan. 2001. [CrossRef]
- Simulia, “Projectile Impact on a Carbon Fiber Reinforced Plate,” Apr. 2007.
- “M. Ashby, Cambridge. GRANTA CES EDUPACK (2007) Accessed: Feb. 12, 2019. [Online]. Available.”.
- “References | Helius Composite | Autodesk Knowledge Network.” https://knowledge.autodesk.com/support/helius-composite/learn-explore/caas/CloudHelp/cloudhelp/2017/ENU/ACMPDS/files/GUID-062281EC-35AD-4201-AB7B-D43282175B22-htm.html (accessed Oct. 20, 2022).
- Abaqus v 6.6 Documentaion, “ABAQUS User Reference Manual.” https://classes.engineering.wustl.edu/2009/spring/mase5513/abaqus/docs/v6.6/books/sub/default.htm?startat=ch01s02asb04.html.
- Smith, Michael, ABAQUS/Standard User’s Manual, Version 6.9. Dassault Systèmes Simulia Corp.
- C. A. Gamez, “Failure mechanisms of polyurea under high strain-rate,” UCLA, 2017. Accessed: Feb. 06, 2022. [Online]. Available: https://escholarship.org/uc/item/10c9c1qq.
- “Abaqus Analysis User’s Guide (2016).” http://130.149.89.49:2080/v2016/books/usb/default.htm?startat=pt05ch23s02abm23.html#d0e265842 (accessed Nov. 01, 2022).
- K. Senthil, M. A. Iqbal, P. Bhargava, and N. K. Gupta, “Experimental and Numerical Studies on Mild Steel Plates against 7.62 API Projectiles,” Procedia Engineering, vol. 173, pp. 369–374, Jan. 2017. [CrossRef]
- B. Banerjee, “Material point method simulations of fragmenting cylinders,” Jan. 2012.
- “Failure Criteria for Unidirectional Fiber Composites | J. Appl. Mech. | ASME Digital Collection.” https://asmedigitalcollection.asme.org/appliedmechanics/article-abstract/47/2/329/390775/Failure-Criteria-for-Unidirectional-Fiber?redirectedFrom=PDF (accessed Jan. 27, 2022).
- “References | Helius PFA 2016 | Autodesk Knowledge Network.” https://knowledge.autodesk.com/support/helius-pfa/learn-explore/caas/CloudHelp/cloudhelp/2016/ENU/ACMPAN/files/GUID-2F40E192-7868-4AA7-8820-DE7CCE7C2B6C-htm.html (accessed Jan. 27, 2022).
- Ever J. Barbero, Finite Element Analysis of Composite Materials Using Abaqus. Boca Raton, FL 33487-2742: CRC Press, 2013.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).