Preprint
Review
Self-Organizing Systems: What, How, and Why?
Altmetrics
Downloads
626
Views
1444
Comments
0
This version is not peer-reviewed
Submitted:
06 August 2024
Posted:
08 August 2024
Read the latest preprint version here
Alerts
Abstract
I present a personal account of self-organizing systems. As such, it is necessarily biased and partial. Nevertheless, it should be useful to motivate useful discussions. The relevant contribution is not my attempts at answering questions (maybe all my answers are wrong), but the steps towards framing relevant questions to better understand self-organization, information, complexity, and emergence. With this aim, I start with a notion and examples of self-organizing systems (what?), continue with their properties and related concepts (how?), and close with applications (why?).
Keywords:
Subject: Physical Sciences - Other
1. What Are Self-Organizing Systems?
“Being ill defined is a feature common to all important concepts.”
—Benoit Mandelbrot
I will not attempt to define a “self-organizing system”, as it involves the cybernetic problem of defining “system” [3,40,82], the informational problem of defining “organization” [4,68], and the ontological problem of defining “self” [31]. Still, there are plenty of examples of systems that we can usefully call self-organizing: flocks of birds, schools of fish, swarms of insects, herds of cattle, and some crowds of people [10,22]. In these animal examples, the collective behavior is a product of the interactions of individuals, not determined by a leader or an external signal. There are also several examples from non-living systems, such as vortexes, crystallization, self-assembly, and pattern formation in general [7,14]. In these cases, elements of a system also interact to achieve a global pattern.
Self-organization or similar concepts have been present since antiquity [32,42,44,75]. The term “self-organizing system” was proposed by Ashby [2] in the early days of cybernetics [3,40,66,69,83,86]. Ashby’s purpose was to describe deterministic machines that could change their own organization. And since, it has been used in a broad range of disciplines [73], including statistical mechanics [15,88], supramolecular chemistry [48], computer science [45,51], and artificial life [36].
There is an unavoidable subjectivity when speaking about self-organizing systems, as the same system can be described as self-organizing or not [35]. So, the question should not be whether a system is self-organizing, but rather when is it useful to describe a system as self-organizing? The answer will slowly unfold along this paper, but in short it can be said that self-organization is a useful description when we are interested on describing systems at multiple scales, and understanding how these affect each other. For example, collective motion [81] and cyber-physical systems [30] can benefit from such a description, compared to a single-scale narrative/model. This is common with complexity [16], as interactions can generate novel information that is not present in initial nor boundary conditions, limiting predictability [28].
So rather than a definition, we can do with a notion: a system can be described as self-organizing when its elements interact to produce a global function or behavior [26]. This is in contrast with centralized systems, where a single or few elements “control” the rest, or in simply distributed systems, where a global problem can be divided and each element does its part, but there is no need to interact nor integrate elementary solutions. And the “self” implies that the “control” comes from within the system, rather than from an external signal/controller that would explicitly indicate elements what to do.
For example, we can decide to call a society “self-organizing” if we are interested on how individual interactions lead to the formation of fashion, ideologies, opinions, norms, and laws; but at the same time, how the emerging global properties affect the behavior of the individuals. If we were interested in an aggregate property of a population, e.g. its average height, then calling the group of individuals “self-organizing” would not give any extra information, and thus would not be useful.
2. How do Self-Organizing Systems Function?
“It is the function of science to discover the existence of a general reign of order in nature and to find the causes governing this order. And this refers in equal measure to the relations of man — social and political — and to the entire universe as a whole."
—Dmitri Mendeleev
Even when self-organization had been described intuitively since antiquity, the proper tools for studying it became available only recently: computers [55]. Since self-organizing systems require the description of elements and interactions, our brains, blackboards, and notebooks are too limited to consider the number of required variables to study the properties of self-organizing systems. It was only through the relatively recent development of information technology that we were able to study the richness of self-organization, just like we were unable to study the microcosmos before microscopes and the macrocosmos before telescopes.
2.1. Information
Computation can be generally described as the transformation of information, although Alan Turing [78] formally defined computable numbers with the purpose of proving limits of formal systems (in particular, Hilbert’s decision problem). In the same environment where the first digital computers were built in the mid XX century, Claude Shannon [72] defined information to quantify its transmission, showing that information could be reliably transmitted through unreliable communication channels. As it turned out, Shannon’s information H is mathematically equivalent to Boltzmann-Gibbs entropy:
where K is a positive constant and p is the probability of receiving symbol i from a finite alphabet of size n. This dimensionless measure will be maximal for a homogeneous probability distribution, and minimal when only one symbol has a probability . In binary, we have only two symbols (), and information would be minimal with a string of only ones or zeroes. This implies that having more bits will not tell us anything new, because we already know (assuming the probability distribution will not change) what the next bits will be. With a random string, information is maximal, because no matter how much previous information we have (full knowledge of the probability distribution), we will not be able to predict what the next bit might be better than chance.
In parallel, Norbert Wiener — one of the founders of cybernetics [66,86] — proposed an alternative measure of information, which was basically the same as Shannon’s, but without the minus sign [87]. Wiener’s information measured what one knows already, so it is minimal when we have a random string (homogeneous probability distribution) because all the information we already have is “useless” (to predict the next symbol), and maximal when we have a single symbol repeating (maximally biased probability distribution), because the information we have allows us to predict exactly the next symbol. Nevertheless, Shannon’s information is the one that everyone has used, and we will do the same.
Shannon’s information is also known as Shannon’s entropy, which can be also used as a measure of “disorder”. We already saw that it is maximal for random strings, and thus minimal for particularly ordered strings. Then, we can use the negative of Shannon’s information (which would be Wiener’s information) as a measure of organization [23,35,87]. If the organization is a result of internal dynamics, then we can also use this measure for self-organization.
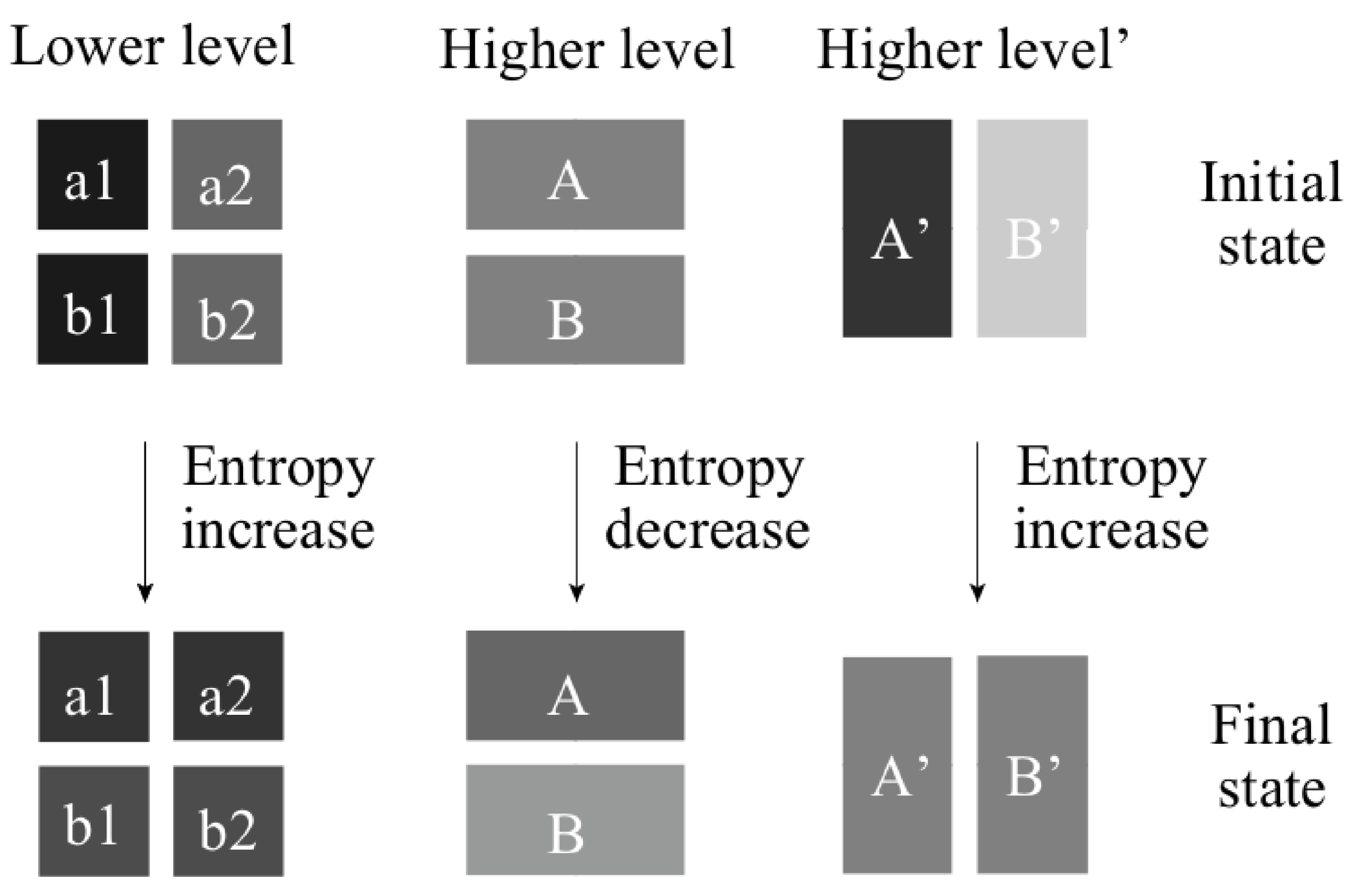
Nevertheless, just like with many measures, the interpretation depends on how the observer performs the measurement. Figure 1 shows how the same system, divided into four microstates or two macrostates (with probabilities represented as shades of gray) can increase its entropy/information (become more homogeneous) or decrease it.
Still, the fact that self-organization is partially subjective does not mean that it cannot be useful. We just have to be aware that a shared description and interpretation should be agreed upon.
2.2. Complexity
Self-organizing systems are intimately related to complex systems [8,53]. Again, the question is not so much whether a system is self-organizing or complex, but when is it useful to describe it as such.
Etymologically, complexity comes from the Latin plexus, which could be translated as entwined [16]. We can say that complex systems are those where interactions make it difficult to separate the components and study them in isolation, because of their interdependence [28,39]. These interactions can generate novel information that limit predictability in an inherent way, as it is not present in initial nor boundary conditions. In other words, there is no shortcut to the future, but we have to go through all intermediate steps, as interactions partially determine the future states of the system.
For example, markets tend to be unpredictable because different agents make decisions depending on what they think other agents will decide [21]. But since it is not possible to know what everyone will decide in advance, the predictability of markets is rather limited.
Given the above notion of self-organizing systems, then all of them would also be complex systems, but not necessarily vice versa. Thus, understanding complexity should be essential for the study of self-organization.
2.3. Emergence
One of the most relevant and controversial properties of complex systems is emergence [1,9,52,62]. It could be seen as problematic because last century some people described emergent properties as “surprising”. So then emergence would be a measure of our ignorance, and then it would be reduced once we understood the mechanisms behind emergent properties. Also, there are different flavors of emergence, some easier to study and accept than others. But in general, emergence can be described as information that is present at one scale and not at another scale [33].
For example, we can have full knowledge of the properties of carbon atoms. But if we focus only on the atoms, i.e. without interactions, we will not be able to know whether they are part of a molecule of graphite, diamond, graphene, buckyballs, etc. (all composed only of carbon atoms) which have drastically different macroscopic properties. Thus, we cannot derive the conductivity, transparency, or density of these materials by looking only at the atomic properties of carbon. The difference lies precisely in how the atoms are organized, i.e. how they interact.
If emergence can be described in terms of information, we can use Shannon’s measure also for emergence (understanding that we are measuring only the information that is absent from another scale). Thus, emergence would be the opposite of self-organization. This might seem contradictory, as usually emergence and self-organization are both present in complex systems [22]. But if we take each to its extreme, we can see that maximum emergence (information) occurs when there is (quasi)randomness, so no organization. And maximum (self-)organization occurs when entropy is minimal (no new information, and thus, no emergence). Because of this, complexity can be seen as a balance between emergence and self-organization [23].
3. Why Should We Use Self-Organizing Systems?
“It is as though a puzzle could be put together simply by shaking its pieces."
—Christian De Duve
Self-organization can be used to build adaptive systems [25]. This is useful for non-stationary problems, i.e., those that change in time. Since interactions can generate novel information, complexity often leads to non-stationarity. Thus, when a problem changes, the elements of a self-organizing system can adapt through their interactions. Then, designers do not need to specify precisely the problem beforehand, or how it will change, but just to define/regulate interactions to achieve a desired goal [5,26,71].
For example, if we want to improve passenger flow in public transportations systems, we cannot really change the elements of the system (passengers). Still, we can change how they interact. In 2016, we successfully implemented such a change to regulate the boarding and alighting in Mexico City metro [11]. In a similar way, we cannot change teachers in an education system. But we can change their interactions to improve learning. We cannot change politicians, but we can regulate their interactions to reduce corruption and improve efficiency. We cannot change businesspeople, but we can control their interactions to promote sustainable economic growth.
There have been many other examples of applications of self-organization [77], in physics [6,37,54], chemistry [24,47,79,85], artificial intelligence [45], animal movements [13], ecology [49], communication networks [59], robotics [18,41,56,63,67,70,80,84], linguistics [64,74], social science [12,20], urbanism [29,58], philosophy [42], and many other fieds.
In particular, self-organization has been applied successfully in several branches of engineering [17], such as power grids [65], computing [51], sensor networks [19], traffic light coordination [46,89], supply networks and production systems [38], bureaucracies [27], and more.
In general, self-organization has been a promising approach to build adaptive systems, as mentioned above. It might seem counterintuitive to speak about controlling self-organization, since we might think that self-organizing systems are difficult to regulate because of a certain autonomy of their components. Still, we can speak about a balance between control and independence, in what has been called “guided self-organization" [60,61].
4. Conclusions
“We can never be right, we can only be sure when we are wrong"
—Richard Feynman
There are many open questions related to the scientific study of self-organizing systems. Even when their potential has been promising, they are far from being commonly used to address non-stationary problems. Could it be because of a lack of literacy in concepts related to complex systems? Might there be any conceptual or technical obstacle? Do we need further theories? Independently of the answers, these questions are worth exploring.
For example, we have yet to explore the relationship between self-organization and antifragility [76]: the property of systems that benefit from perturbaitons. Self-organization seems to be correlated with antifragility [43,50,57], but why or how still has to be investigated. In a similar vein, a systematic exploration of the “slower is faster” effect [34] might be useful to better understand self-organizing systems and vice versa.
Many problems and challenges we are facing — climate change, migration, urban growth, social polarization, etc. — are clearly non-stationary. It is not certain that with self-organization we will be able to improve the situation in all of them. But it is almost certain that with the current tools we have, we will not be able to make much more progress (otherwise we would have made it already). It would be imprudent not to make efforts to use self-organization, even if for slightly improving situations related to only one of these challenges.
References
- Anderson, P. W. (1972). More is different. Science 177: 393–396.
- Ashby, W. R. (1947). Principles of the self-organizing dynamic system. Journal of General Psychology 37: 125–128.
- Ashby, W. R. (1956). An Introduction to Cybernetics. Chapman & Hall, London. URL http://pcp.vub.ac.be/ASHBBOOK.html.
- Ashby, W. R. (1962). Principles of the self-organizing system. In Principles of Self-Organization, H. V. Foerster and G. W. Zopf, Jr., (Eds.). Pergamon, Oxford, 255–278.
- Babaoglu, O., Jelasity, M., Montresor, A., Fetzer, C., Leonardi, S., van Moorsel, A., andvan Steen, M. (2005). Self-star properties in complex information systems: conceptual and practical foundations. Vol. 3460. Springer.
- Bak, P., Tang, C., andWiesenfeld, K. (1987). Self-organized criticality: An explanation of the 1/f noise. Phys. Rev. Lett. 59 (4) (July): 381–384. URL . [CrossRef]
- Ball, P. (1999). The self-made tapestry: pattern formation in nature.
- Bar-Yam, Y. (1997). Dynamics of Complex Systems. Studies in Nonlinearity. Westview Press, Boulder, CO, USA. URL http://www.necsi.org/publications/dcs/.
- Bedau, M. A.andHumphreys, P., Eds. (2008). Emergence: Contemporary readings in philosophy and science. MIT Press, Cambridge, MA, USA.
- Camazine, S., Deneubourg, J.-L., Franks, N. R., Sneyd, J., Theraulaz, G., andBonabeau, E. (2003). Self-Organization in Biological Systems. Princeton University Press, Princeton, NJ, USA. URL http://www.pupress.princeton.edu/titles/7104.html.
- Carreón, G., Gershenson, C., andPineda, L. A. (2017). Improving public transportation systems with self-organization: A headway-based model and regulation of passenger alighting and boarding. PLOS ONE 12 (12) (12): 1–20. URL . [CrossRef]
- Conte, R., Gilbert, N., Bonelli, G., Cioffi-Revilla, C., Deffuant, G., Kertesz, J., Loreto, V., Moat, S., Nadal, J. P., Sanchez, A., Nowak, A., Flache, A., San Miguel, M., andHelbing, D. (2012). Manifesto of computational social science. The European Physical Journal Special Topics 214 (1): 325–346. URL . [CrossRef]
- Couzin, I. D., Krause, J., Franks, N. R., andLevin, S. A. (2004). Effective leadership and decision-making in animal groups on the move. Nature 433: 513–516.
- Cross, M.andGreenside, H. (2009). Pattern formation and dynamics in nonequilibrium systems. Cambridge University Press.
- Crutchfield, J. P. (2011). Between order and chaos. Nature Physics 8: 17 EP –. URL . [CrossRef]
- De Domenico, M., Camargo, C., Gershenson, C., Goldsmith, D., Jeschonnek, S., Kay, L., Nichele, S., Nicolás, J., Schmickl, T., Stella, M., Brandoff, J., Salinas, Á. J. M., andSayama, H. (2019). Complexity explained: A grassroot collaborative initiative to create a set of essential concepts of complex systems. URL https://complexityexplained.github.io.
- De Wolf, T., Samaey, G., andHolvoet, T. (2005). Engineering self-organising emergent systems with simulation-based scientific analysis. In Proceedings of the International Workshop on Engineering Self-Organising Applications. Utrecht, The Netherlands,, pp. 46–160. URL http://tinyurl.com/y2vmau.
- Dorigo, M., Trianni, V., Şahin, E., Groß, R., Labella, T. H., Baldassarre, G., Nolfi, S., Deneubourg, J.-L., Mondada, F., Floreano, D., andGambardella, L. (2004). Evolving self-organizing behaviors for a swarm-bot. Autonomous Robots 17 (2-3): 223–245. URL http://www.swarm-bots.org.
- Dressler, F. (2007). Self-Organization in Sensor and Actor Networks. John Wiley & Sons.
- Epstein, J. M.andAxtell, R. L. (1996). Growing Artificial Societies: Social Science from the Bottom Up. Brookings Institution Press MIT Press, Cambridge, MA, USA. URL http://www.brookings.org/press/books/artifsoc.htm.
- Farmer, J. D. (2024). Making Sense of Chaos: A Better Economics for a Better World. Penguin Random House, London, UK.
- Feltz, B., Crommelinck, M., andGoujon, P., Eds. (2006). Self-organization and Emergence in Life Sciences. Synthese Library, vol. 331. Springer.
- Fernández, N., Maldonado, C., andGershenson, C. (2014). Information measures of complexity, emergence, self-organization, homeostasis, and autopoiesis. In Guided Self-Organization: Inception, M. Prokopenko, (Ed.). Emergence, Complexity and Computation, vol. 9. Springer, Berlin Heidelberg, 19–51. URL http://arxiv.org/abs/1304.1842.
- Fontana, W. (1991). Algorithmic chemistry: A model for functional self-organization. In Artificial Life II, C. G. Langton, C. Taylor, J. D. Farmer, and S. Rasmussen, (Eds.). Addison-Wesley, Boston, MA, 159–202.
- Frei, R.andDi Marzo Serugendo, G. (2011). Advances in complexity engineering. International Journal of Bio-Inspired Computation 3 (4): 199–212. URL http://www.reginafrei.ch/pdf/IJBIC030401%20FREI%20published.pdf.
- Gershenson, C. (2007). Design and Control of Self-organizing Systems. CopIt Arxives, Mexico. TS0002EN. URL https://copitarxives.fisica.unam.mx/TS0002EN/TS0002EN.html.
- Gershenson, C. (2008). Towards self-organizing bureaucracies. International Journal of Public Information Systems 2008 (1): 1–24. URL http://www.ijpis.net/ojs/index.php/IJPIS/article/view/51.
- Gershenson, C. (2013a). The implications of interactions for science and philosophy. Foundations of Science 18 (4): 781–790. URL http://arxiv.org/abs/1105.2827.
- Gershenson, C. (2013b). Living in living cities. Artificial Life 19 (3 & 4) (Summer/Fall): 401–420. URL . [CrossRef]
- Gershenson, C. (2020). Guiding the self-organization of cyber-physical systems. Frontiers in Robotics and AI 7: 41. URL https://www.frontiersin.org/article/10.3389/frobt.2020.00041.
- Gershenson, C. (2021). On the Scales of Selves: Information, Life, and Buddhist Philosophy. In ALIFE 2021: The 2021 Conference on Artificial Life, J. Čejková, S. Holler, L. Soros, and O. Witkowski, (Eds.). MIT Press, Prague, Czech Republic, p. 2. URL . [CrossRef]
- Gershenson, C. (2023a). Complexity and Buddhism: Understanding interactions. Buddhism Today 52: 44–48.
- Gershenson, C. (2023b). Emergence in Artificial Life. Artificial Life 29 (2) (05): 153–167. URL . [CrossRef]
- Gershenson, C.andHelbing, D. (2015). When slower is faster. Complexity 21 (2): 9–15. URL . [CrossRef]
- Gershenson, C.andHeylighen, F. (2003). When can we call a system self-organizing? In Advances in Artificial Life, 7th European Conference, ECAL 2003 LNAI 2801, W. Banzhaf, T. Christaller, P. Dittrich, J. T. Kim, and J. Ziegler, (Eds.). Springer, Berlin, 606–614. URL http://arxiv.org/abs/nlin.AO/0303020.
- Gershenson, C., Trianni, V., Werfel, J., andSayama, H. (2020). Self-organization and artificial life. Artificial Life 26 (3) (09): 391–408. URL . [CrossRef]
- Haken, H. (1988). Information and Self-organization: A Macroscopic Approach to Complex Systems. Springer-Verlag, Berlin.
- Helbing, D., Seidel, T., Lämmer, S., andPeters, K. (2006). Self-organization principles in supply networks and production systems. In Econophysics and Sociophysics, B. K. Chakrabarti, A. Chakraborti, and A. Chatterjee, (Eds.). Wiley, Weinheim, 535–559. URL . [CrossRef]
- Heylighen, F., Cilliers, P., andGershenson, C. (2007). Complexity and philosophy. In Complexity, Science and Society, J. Bogg and R. Geyer, (Eds.). Radcliffe Publishing, Oxford, 117–134. URL http://arxiv.org/abs/cs.CC/0604072.
- Heylighen, F.andJoslyn, C. (2001). Cybernetics and second order cybernetics. In Encyclopedia of Physical Science and Technology, 3rd ed., R. A. Meyers, (Ed.). Vol. 4. Academic Press, New York, 155–170.
- Holland, O.andMelhuish, C. (1999). Stigmergy, self-organization, and sorting in collective robotics. Artificial Life 5 (2): 173–202. URL . [CrossRef]
- Juarrero-Roqué, A. (1985). Self-organization: Kant’s concept of teleology and modern chemistry. The Review of Metaphysics 39 (1): 107–135. URL http://www.jstor.org/stable/20128282.
- Kim, H., Pineda, O. K., andGershenson, C. (2019). A multilayer structure facilitates the production of antifragile systems in Boolean network models. Complexity 2019: 11. URL . [CrossRef]
- Kirk, G. S. (1951). Natural change in Heraclitus. Mind 60 (237): 35–42.
- Kohonen, T. (2000). Self-Organizing Maps, 3rd ed. Springer.
- Lämmer, S.andHelbing, D. (2008). Self-control of traffic lights and vehicle flows in urban road networks. J. Stat. Mech. 2008: P04019. URL . [CrossRef]
- Lehn, J.-M. (1990). Perspectives in supramolecular chemistry—from molecular recognition towards molecular information processing and self-organization. Angewandte Chemie International Edition in English 29 (11): 1304–1319. URL . [CrossRef]
- Lehn, J.-M. (2017). Supramolecular chemistry: Where from? where to? Chem. Soc. Rev. 46: 2378–2379. URL . [CrossRef]
- Levin, S. A. (2005). Self-organization and the emergence of complexity in ecological systems. AIBS Bulletin 55 (12): 1075–1079.
- López-Díaz, A. J., Sánchez-Puig, F., andGershenson, C. (2023). Temporal, structural, and functional heterogeneities extend criticality and antifragility in random Boolean networks. Entropy 25 (2). URL https://www.mdpi.com/1099-4300/25/2/254.
- Mamei, M., Menezes, R., Tolksdorf, R., andZambonelli, F. (2006). Case studies for self-organization in computer science. Journal of Systems Architecture 52 (8-9): 443–460.
- McLaughlin, B. P. (1992). The rise and fall of British emergentism. In Emergence or reduction? Essays on the prospects of nonreductive physicalism, Beckerman, Flohr, and Kim, (Eds.). Walter de Gruyter, Berlin, 49–93.
- Mitchell, M. (2009). Complexity: A Guided Tour. Oxford University Press, Oxford, UK.
- Nicolis, G.andPrigogine, I. (1977). Self-Organization in Non-Equilibrium Systems: From Dissipative Structures to Order Through Fluctuations. Wiley, Chichester.
- Pagels, H. R. (1989). The Dreams of Reason: The Computer and the Rise of the Sciences of Complexity. Bantam Books, New York City, NY, USA.
- Pfeifer, R., Lungarella, M., andIida, F. (2007). Self-organization, embodiment, and biologically inspired robotics. Science 318: 1088–1093.
- Pineda, O. K., Kim, H., andGershenson, C. (2019). A novel antifragility measure based on satisfaction and its application to random and biological Boolean networks. Complexity 2019: 10. URL . [CrossRef]
- Portugali, J. (2000). Self-organization and the City. Springer Verlag. URL http://tinyurl.com/2v9kb9z.
- Prehofer, C.andBettstetter, C. (2005). Self-organization in communication networks: principles and design paradigms. Communications Magazine, IEEE 43 (7): 78–85. URL . [CrossRef]
- Prokopenko, M. (2009). Guided self-organization. HFSP Journal 3 (5): 287–289. URL http://www.ncbi.nlm.nih.gov/pmc/articles/PMC2801529/.
- Prokopenko, M., Ed. (2014). Guided Self-Organization: Inception. Emergence, Complexity and Computation, vol. 9. Springer, Berlin Heidelberg. URL . [CrossRef]
- Prokopenko, M., Boschetti, F., andRyan, A. J. (2009). An information-theoretic primer on complexity, self-organisation and emergence. Complexity 15 (1): 11–28. URL . [CrossRef]
- Reina, A., Valentini, G., Fernández-Oto, C., Dorigo, M., andTrianni, V. (2015). A design pattern for decentralised decision making. PLOS ONE 10 (10) (10): 1–18. URL . [CrossRef]
- Rocha, L. (1998). Selected self-organization and the semiotics of evolutionary systems. In Evolutionary Systems, G. van de Vijver, S. Salthe, and M. Delpos, (Eds.). Springer Netherlands, 341–358. URL http://link.springer.com/chapter/10.1007/978-94-017-1510-2_25.
- Rohden, M., Sorge, A., Timme, M., andWitthaut, D. (2012). Self-organized synchronization in decentralized power grids. Phys. Rev. Lett. 109: 064101. URL https://link.aps.org/doi/10.1103/PhysRevLett.109.064101.
- Rosenblueth, A., Wiener, N., andBigelow, J. (1943). Behavior, purpose and teleology. Philosophy of Science 10 (1): 18–24.
- Rubenstein, M., Cornejo, A., andNagpal, R. (2014). Programmable self-assembly in a thousand-robot swarm. Science 345 (6198): 795–799.
- Rupe, A.andCrutchfield, J. P. (2024). On principles of emergent organization. Physics Reports 1071: 1–47. URL https://www.sciencedirect.com/science/article/pii/S0370157324001327.
- Saratxaga Arregi, A. (2024). Heinz von Foerster’s operational epistemology: orientation for insight into complexity. Kybernetes ahead-of-print (ahead-of-print) (2024/06/28). URL . [CrossRef]
- Schranz, M., Umlauft, M., Sende, M., andElmenreich, W. (2020). Swarm robotic behaviors and current applications. Frontiers in Robotics and AI 7. URL https://www.frontiersin.org/journals/robotics-and-ai/articles/10.3389/frobt.2020.00036.
- Schweitzer, F., Ed. (1997). Self-Organization of Complex Structures: From Individual to Collective Dynamics. Gordon and Breach, London.
- Shannon, C. E. (1948). A mathematical theory of communication. Bell System Technical Journal 27 (3 and 4) (July and October): 379–423 and 623–656. URL . [CrossRef]
- Skår, J.andCoveney, P. V., Eds. (2003). Self-Organization: The Quest for the Origin and Evolution of Structure. Phil. Trans. R. Soc. Lond. A 361(1807). Proceedings of the 2002 Nobel Symposium on self-organization.
- Steels, L. (1995). A self-organizing spatial vocabulary. Artificial Life 2 (3): 319–332.
- Stengers, I. (1985). Généalogies de l’auto-organisation. Cahiers du C.R.E.A., vol. 8. Centre de recherche sur l’épistémologie et l’autonomie, France. URL https://books.google.com.mx/books?id=WmXCnAEACAAJ.
- Taleb, N. N. (2012). Antifragile: Things That Gain From Disorder. Random House, London, UK.
- Turcotte, D. L.andRundle, J. B. (2002). Self-organized complexity in the physical, biological, and social sciences. Proceedings of the National Academy of Sciences of the United States of America 99 (Suppl 1): 2463–2465. URL . [CrossRef]
- Turing, A. M. (1936). On computable numbers, with an application to the Entscheidungsproblem. Proc. London Math. Soc. 2 (42): 230–265.
- Vanag, V. K.andEpstein, I. R. (2001). Pattern formation in a tunable medium: The Belousov-Zhabotinsky reaction in an aerosol ot microemulsion. Physical review letters 87 (22): 228301.
- Vásárhelyi, G., Virágh, C., Somorjai, G., Nepusz, T., Eiben, A. E., andVicsek, T. (2018). Optimized flocking of autonomous drones in confined environments. Science Robotics 3 (20). URL http://robotics.sciencemag.org/content/robotics/3/20/eaat3536.full.pdf.
- Vicsek, T.andZafeiris, A. (2012). Collective motion. Physics Reports 517: 71–140. URL . [CrossRef]
- von Bertalanffy, L. (1968). General System Theory: Foundations, Development, Applications. George Braziller, New York.
- von Foerster, H. (1960). On self-organizing systems and their environments. In Self-Organizing Systems, M. C. Yovitts and S. Cameron, (Eds.). Pergamon, New York, pp. 31–50.
- Werfel, J., Petersen, K., andNagpal, R. (2014). Designing collective behavior in a termite-inspired robot construction team. Science 343 (6172): 754–758. URL http://www.sciencemag.org/content/343/6172/754.abstract.
- Whitesides, G. M.andGrzybowski, B. (2002). Self-assembly at all scales. Science 295 (5564): 2418–2421. URL http://www.sciencemag.org/content/295/5564/2418.short.
- Wiener, N. (1948). Cybernetics; or, Control and Communication in the Animal and the Machine. Wiley and Sons, New York.
- Wiener, N. (1950). Cybernetics. Bulletin of the American Academy of Arts and Sciences 3 (7): 2–4. URL http://www.jstor.org/stable/3822945.
- Wolfram, S. (1983). Statistical mechanics of cellular automata. Reviews of Modern Physics 55 (3) (July): 601–644.
- Zubillaga, D., Cruz, G., Aguilar, L. D., Zapotecatl, J., Fernández, N., Aguilar, J., Rosenblueth, D. A., andGershenson, C. (2014). Measuring the complexity of self-organizing traffic lights. Entropy 16 (5): 2384–2407. URL . [CrossRef]
Figure 1.
The same system, observed at different levels or with different coarse grainings can be said to be disorganizing (entropy increasing) or organizing (entropy decreasing) [35]. Probabilities are represented as shades of gray, so it is easy to observe which configurations are more homogeneous (i.e. with higher entropy).
Figure 1.
The same system, observed at different levels or with different coarse grainings can be said to be disorganizing (entropy increasing) or organizing (entropy decreasing) [35]. Probabilities are represented as shades of gray, so it is easy to observe which configurations are more homogeneous (i.e. with higher entropy).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





