Prerpints.org logo
Preprint
Article

Enhanced Microgrid Control through Genetic Predictive Control: Integrating Genetic Algorithms with Model Predictive Control for Improved Non-Linearity and Non-Convexity Handling

Altmetrics

Downloads

81

Views

31

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

07 August 2024

Posted:

09 August 2024

You are already at the latest version

Alerts
Abstract
Microgrid (MG) control is essential for efficient, reliable, and sustainable energy management in distributed energy systems. Genetic Algorithm-based energy management systems (GA-EMS) can optimally control a MG by finding global optima and handling complex, non-linear, and non-convex problems, but they can be computationally intensive, making real-time control challenging. Model Predictive Control (MPC)-based EMS predicts future behaviour over a defined horizon, ensuring optimal performance and constraint satisfaction but typically relies on linear models. This paper proposes a novel Genetic Predictive Control (GPC) method, combining GA and MPC to enhance resource allocation, balance multiple objectives, and adapt dynamically to changing conditions. Integrating GA with MPC significantly improves the handling of non-linearities and non-convexity in the system model, leading to more accurate and effective control. Comparative analysis shows that GPC significantly reduces excess power production—surplus power generated beyond load demand—improving resource allocation efficiency. For instance, in the Mutation–Random Selection scenario, GPC reduced excess power to 76.0W compared to 87.0W with GA. Additionally, GPC balances cost, emissions, and power efficiency. In the Crossover-Elitism scenario, GPC achieved a daily cost of $113.94 compared to GA's $127.80, and carbon emissions of 52.83 kg CO2e compared to GA's 69.71 kg CO2e, demonstrating GPC's cost efficiency and environmental benefits. While MPC optimizes a weighted sum of objectives, designing appropriate weights can be challenging and may result in non-convex problems. GA handles multiple, conflicting objectives through multi-objective optimization, providing Pareto-optimal solutions. GPC's dynamic adaptability maintains optimal performance by forecasting future load demands and adjusting control actions. GPC consistently achieves lower emissions than GA across various scenarios and, although it sometimes incurs higher costs, such as $113.94 compared to $131.90 in the Crossover–Random Selection scenario, its holistic approach balances these costs with other metrics, making it cost-effective in the long run. By reducing excess power production and emissions, GPC contributes to economic savings and promotes sustainable practices. These findings underscore GPC's potential as a versatile, efficient, and environmentally beneficial optimization tool for power generation systems.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

Microgrids (MGs) play a crucial role in contemporary energy systems as they consist of distributed energy resources and loads, guaranteeing efficient, dependable, and sustainable distribution of energy [1,2]. This is particularly significant in situations where traditional power systems encounter obstacles, such as in remote or isolated regions [3]. Efficient control and energy management in MG is essential for effectively distributing resources between supply and demand, resulting in reduced operational expenses and environmental effects [4,5]. Conventional control approaches encounter challenges because of the intrinsic nonlinearity and nonconvexity of MG systems [6,7].
Genetic algorithms (GAs) have been utilized to swiftly discover optimal solutions and tackle very intricate issues that may be unsolvable using conventional mathematical approaches. GAs excel at finding global optimal solutions and are capable of handling complex, non-linear, and non-convex problems [8,9]. Although conventional genetic algorithms have strong optimization capabilities, they can be computationally demanding and may encounter difficulties in real-time control applications [10]. On the other hand, Model Predictive Control (MPC) is often favoured due to its inherent capacity to forecast future actions within a specified timeframe, while simultaneously ensuring optimal performance and compliance with restrictions [11]. However, MPC typically operates with linear models, which limits its effectiveness in controlling the nonlinear dynamics of MGs [12].
This work introduces a novel approach to controlling MGs, known as GPC. The integration of GA with MPC improves the allocation of resources, the balance of numerous objectives, and the responsiveness to dynamic changes. By combining the strong optimization capabilities of GA with the predictive capability of MPC, it becomes possible to develop a control approach that is significantly more precise and effective. The suggested use of GA into MPC enhances the ability to manage nonlinearities and non-convexities in the system being analyzed.
The subsequent sections of the paper are structured in the following manner: The paper begins with a comprehensive examination of the literature to identify the most efficient GAs and the challenges associated with MPC. This is followed by a detailed explanation of the methodology used to implement genetic predictive control (GPC). The subsequent section presents the results of a comparative analysis, demonstrating the enhanced performance achieved through the use of GPC-based energy management systems (EMSs). Finally, the paper concludes with a discussion of the findings and potential avenues for future research.

1.1. Literature Review

Energy management of MG has been a highly researched field, with a growing focus on developing an EMS that is efficient, independent, and environmentally friendly. Several EMSs have been suggested and put into practice, each having its advantages and disadvantages in terms of their performance and the problem formulation.
GAs are a type of evolutionary algorithm that imitates the process of natural selection. Due to the implementation of natural selection in GAs, it is anticipated that they possess the potential to effectively solve highly nonlinear, nonconvex, and difficult optimization problems [13,14]. GA has been effectively utilized for optimizing MG control in several settings, such as:
1. Energy Dispatch Optimization: GA is utilized to optimize the distribution of energy for DERs to decrease operational costs and carbon emission, while ensuring the satisfaction of energy demand [15,16]. This research has demonstrated the efficacy of GAs in achieving or approaching near-global optimal solutions in cases where traditional methods are unable to owing to the complexity of the problem space, as observed in multiple investigations [17,18].
2. Multi-Objective Optimization: Multi-objective optimization is a problem-solving technique that uses GAs to find solutions that are Pareto-optimal. These solutions can balance numerous conflicting objectives. This capability is significant for managing MGs; cost, carbon emission, and power efficiency trade-offs must be addressed [19,20]. Existing literature has confirmed that achieving a balance among these three objectives leads to effective solutions and a wide range of alternatives that are valuable for decision-makers [21,22].
Nevertheless, the computational demand of GA can be quite high, particularly in real-time applications [23]. The iterative nature of GAs, which includes selection, crossover, and mutation processes, can be computationally demanding and significantly restricts its use in settings requiring fast responses [24].
Recent research has been focused on finding ways to improve the effectiveness of GA in MG applications. For example, advanced algorithms like the NSGA-II have been used to optimize EMS for an MG by considering many objectives related to cost and emission functions [25,26,27]. Another development involves the integration of GAs with other optimization approaches to achieve enhanced performance [28].
MPC is a control approach that uses a system model to forecast future states and aims to find the best control actions within a defined prediction horizon. MPC is widely applied in MG control, as it not only incorporates standard prediction and optimization capabilities, but also effectively addresses constraints and continuously optimizes performance [29]. Recent advancements in MG optimization include the development of hybrid intelligent control systems that integrate rule-based control and deep learning techniques. For instance, a hybrid intelligent control system for adaptive MG optimization that integrates rule-based control and deep learning techniques has been proposed, demonstrating significant improvements in adaptive control of microgrids [30]. Another approach involves a hybrid method based on a logic predictive controller for flexible hybrid microgrids with plug-and-play capabilities, enhancing the adaptability and efficiency of microgrid management [31]. Furthermore, the Switched Auto-Regressive Neural Control (S-ANC) method has been developed for energy management of hybrid microgrids, showcasing effective energy optimization and management [32]. In addition, a comprehensive review of MG energy management strategies from the energy trilemma perspective highlights the importance of balancing energy security, environmental sustainability, and economic viability in MG operations [33]. These strategies emphasize the need for flexible and adaptive control methods to meet the dynamic demands of MG systems [34].
The primary uses of MPC in MG control are:
1. Predictive Energy Management: MPC anticipates future energy demands and adjusts control actions to minimize operational costs, reduce emissions, and ensure dependable operation [35]. Several researchers have conducted studies and provided evidence of the efficacy of MPC in preserving optimal performance in dynamic contexts [36].
2. Managing Uncertainties: Incorporating forecasting and constraints into the optimization process allows MPC to effectively handle uncertain fluctuations in renewable generation and demand load changes [37]. This capability is particularly crucial in MGs with high penetration levels of renewable generation [38].
Nevertheless, a significant limitation of MPC is its reliance on linear models. The majority of MG systems demonstrate nonlinear behaviour, which linear models are unable to accurately define [39]. This scenario can result in a decline in performance and a decrease in the accuracy of control activities [27]. Many advances have been implemented to address this disadvantage and advanced optimization techniques incorporated into the MPC framework. For instance, several adaptive MPC strategies have been developed to modify the control model using real-time data to enhance the accuracy and efficacy of MG control [40]. However, this new variation of MPC does not address the issue of dealing with non-linear models. For these reasons, the objective of this work is to integrate GAs with MPC to leverage the advantages of both approaches while mitigating their limitations. The GPC approach enhances the control of MG by combining the robust optimization characteristics of GA with the predictive capabilities of MPC.
1. Enhanced Management of Nonlinearities and Non-convexity: GPC incorporates GAs to optimize control actions derived from MPC. This allows for effective consideration of system characteristics that are either nonlinear or non-convex in nature [41].
2. Dynamic Adaptability: The GPC maintains optimal performance by dynamically adjusting control actions based on future load demands and system conditions. These adjustments are based on the forecasted future load needs and system circumstances provided by the MPC system [20].
3. Enhanced multi-objective optimization: GPC achieves a balance between several objectives, including cost, carbon emission, and power efficiency, by utilizing multi-objective optimization capability using a GA [26].
Unlike purely GA-based methods, our GPC approach leverages the predictive capabilities of MPC to anticipate future system states and adjust control actions accordingly. This integration enhances the robustness and efficiency of MG operations by dynamically balancing multiple objectives, including cost, emissions, and power generation alignment. The following sections provide a detailed description of the GPC implementation process and evaluate its performance across various scenarios, highlighting the significant improvements over traditional GA and MPC methods.

2. Methodology of Building and Implementing GPC

This study proposes a solution utilizing GPC, which integrates the advantageous characteristics of GAs and MPC through the implementation of clearly defined methodologies for MG control and optimization. The technique will consist of establishing the control objective, constructing a model of the MG system, developing the GA and MPC subsystems, integrating the GA with MPC, and simulating the GPC implementation. The next subsections provide a comprehensive discussion of each phase and the corresponding equations that need to be implemented inside the GPC framework.
The primary control objectives of GPC for the MG are:
  • Minimizing excess power production: Optimize power generation to closely match load demand with the aim of minimizing overgeneration and consequently minimizing the power injection in the upstream network.
  • Balancing cost and emissions: Achieve a balance between cost and carbon emissions to maximize the economic and environmental viability of the MG.

2.1. MG System Model

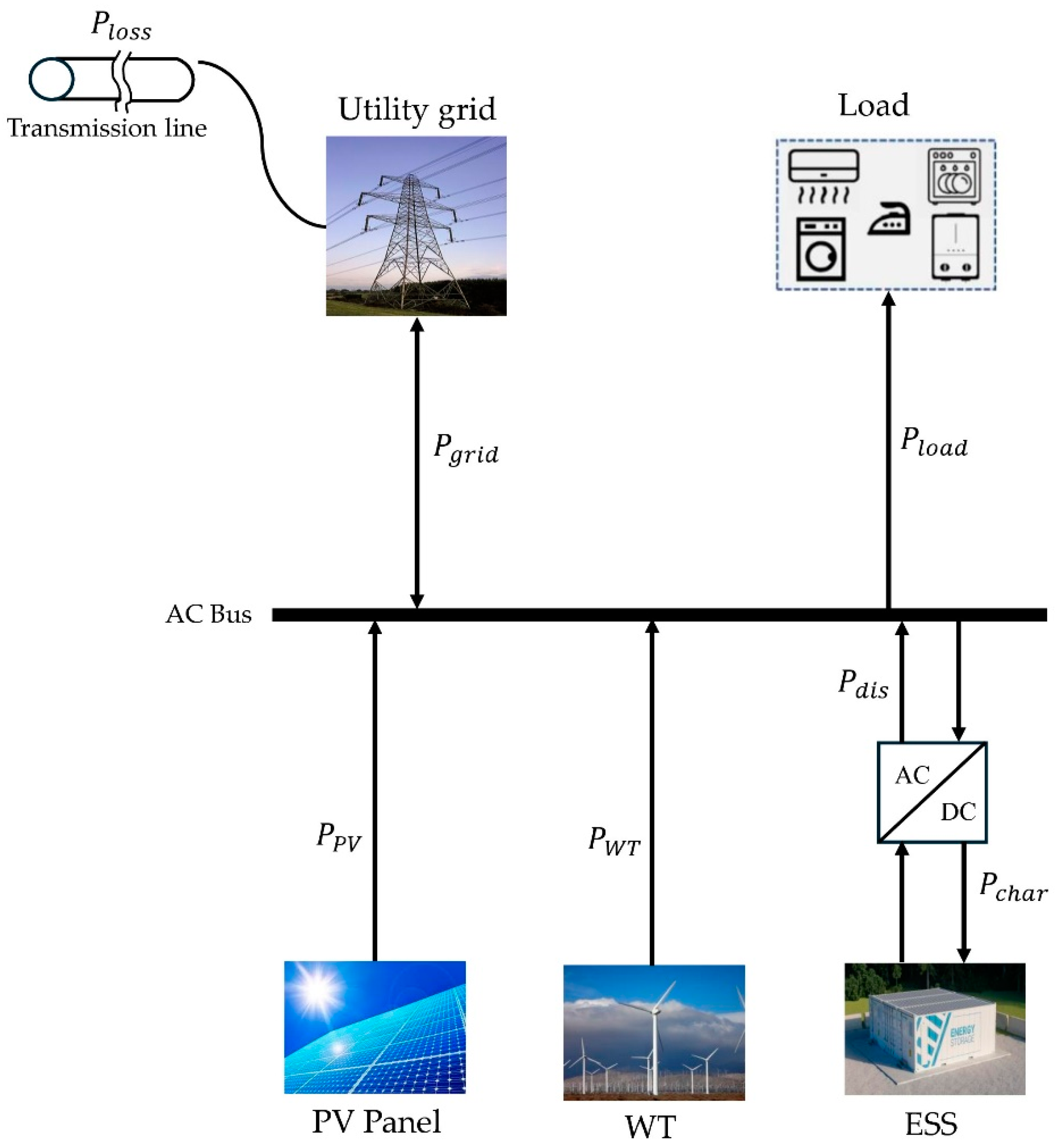
Figure 1 shows a schematic diagram of the overall power balancing in an MG system and describes the main power flows between major components. The total generated power is composed of multiple DERs, renewable generators like photovoltaic (PV) panels and wind turbines (WTs), and conventional ones. It is shown that the power generated by DERs is fed into the system to supply the load demand, representing the power needed by consumers inside the MG. Utility grid power is the general surplus power produced in excess of load demand and can therefore be stored in energy storage systems (ESSs) or curtailed. Additionally, it considers the loss of power through transmission, distribution, and inefficiencies in conversion within a MG. The need for effective EMS and advanced control systems is highlighted by this comprehensive depiction to ensure the reliable and sustainable operation of MGs.
This diagram illustrates in Figure 1 the role that the EMS will play in coordinating and optimizing the multiple operations occurring within this MG. The EMS integrates all sources of information to manage power flows and assure efficient distribution of energy. This complete diagram shows the need for an effective EMS and sophisticated control systems for the reliable and sustainable operation of MGs.
The power balancing equation for the MG is expressed as follows:
P g e n k = P P V k + P W T k
P g e n k + P d i s k = P l o a d k + P c h a r k + P l o s s k + P g r i d ( k )
where P P V ( k ) and P W T ( k ) are the power outputs from PV, and WT respectively. P c h a r and P d i s are charging and discharging power of ESS, respectively. P g e n k represents the total power generated by DERs, P l o a d k is the load demand, P g r i d k is the power from/to the utility grid. The inclusion of ESS impacts the equation by allowing excess power to be stored when available and discharged to meet load demand or balance supply during periods of low generation. P l o s s k represents the power losses in the system at the instant time k .

2.2. The Implementation of MPC

To design the MPC system for the MG described, we need to define the control vector, state vector, and output vector. These vectors are crucial for formulating the MPC problem, which optimizes the MG operation over a prediction horizon.
  • The control vector u k consists of the variables that the MPC can manipulate to achieve the desired performance.
u k = [ P g e n k ; P c h a r k ; P d i s k ]
  • The state vector x k includes variables that represent the current status of the system.
x k = [ S O C k ]
  • The output vector y k consists of the variables that the MPC aims to regulate or track.
y k = [ P l o s s k ; P g r i d k ]
To define the state-space representation of the system for MPC, we need to establish the matrices A , B and C at describe the dynamics and relationships within the MG. These matrices relate the state vector, control vector, and output vector.
x k + 1 = A x k + B u ( k ) y k = C x k + D u ( k )
The A matrix represents the relationship between the current state and the next state. For the MG system, it includes how the state of charge (SOC) of the ESS evolves over time. Given that the SOC depends on the charging and discharging activities can be considered as an input or part of the state:
A = 1
The B matrix represents the influence of the control inputs on the state vector. For our microgrid, the control inputs are the charging and discharging powers of the ESS, and the power exchange with the utility grid.
B = η c h a r − η d i s 0
The C matrix maps the state vector to the output vector. It includes how the states contribute to the outputs, which in our case are the power losses, and power exchanged with the grid.
C = 0 0 0
The D matrix directly relates the control inputs to the outputs. Given the definitions of the output vector components, this matrix includes the direct contributions of the control inputs:
D = 0 0 1 0 0 1 1 0 1
The main task of MPC is to cope with the non-linearity in this paper. To clearly explain it:
  • For the PV panel and wind turbine, the power output P P V and P W T can be modelled as:
P P V k = f i r r a d i a n c e , t e m p e r a t u r e = η P V . A P V . i r r a d i a n c e . ( 1 − β P V . t e m p e r a t u r e − T r e f ) f x = 0 ,     i f   w i n d   s p e e d ≤   v c u t i n o r w i n d   s p e e d > v c u t _ o u t 1 2 ρ A W T C P ( w i n d   s p e e d ) 3 ,     i f   v c u t i n ≤ w i n d   s p e e d ≤ v r a t e d P r a t e d ,     i f   v c u t r a t e d ≤ w i n d   s p e e d ≤ v c u t _ o u t
where g w i n d s p e e d is a non-linear function. η P V is the efficiency of the PV system. A P V is the area of the PV panels. β P V   is the temperature coefficient of power (°C⁻¹). T r e f is the reference temperature, typically 25°C. ρ is the air density (1.225 kg/m³). A W T is the swept area of the wind turbine blades (in m²). C P is the power coefficient of the wind turbine (a dimensionless value, typically around 0.4 to 0.5). v c u t _ i n is the cut-in wind speed (the minimum wind speed at which the turbine generates power). v c u t _ o u t is the cut-out wind speed (the wind speed at which the turbine stops to prevent damage). v r a t e d is the rated wind speed (the wind speed at which the turbine generates its rated power). P r a t e d is the rated power output of the wind turbine.
  • Power losses in transmission and distribution lines can be expressed as:
P l o s s k = I 2 R
where I is the current and R is the resistance of the line. I 2 is the non-linear value in the Equation (12).
  • The SOC of the ESS and its charging/discharging efficiency can be modelled as:
S O C k + 1 = S O C k + η c h a r P c h a r − η d i s P d i s
where η c h a r and η d i s are non-linear functions of the charging and discharging power.
Charging and discharging for the ESS, cannot happen simultaneously, as is implied by the following:
P c h a r k P d i s k ≤ 0
For the charging, the constraint can be written by:
P d i s k ≤ 0 P d i s k ≥ 0
For the discharging, the constraint can be written by:
P c h a r k ≤ 0 P c h a r k ≥ 0
MPC optimizes control inputs by solving a constrained optimization problem over a finite prediction horizon, N P . The general form of the MPC optimization problem can be expressed as:
min u k ⁡ ∑ m = 0 N P J x k + m , u k + m
s u b j e c t   t o : x k + m + 1 = f x k + m , u k + m ,
x k + m ∈ X ,
u k + m ∈ U ,
where J is a given cost function, N P is a given number of prediction steps, f is the system dynamics, and X and U are the sets of admissible states and control inputs, respectively.
The cost function J typically has terms that trade off against tracking performance, control effort, and constraint violations. For the specific MG control problem, the cost function J can be defined as:
J = ∑ m = 0 N P J w 1 P g e n k + m − P l o a d k + m 2 + w 2 C k + m + w 3 E k + m
where w 1 , w 2 , and w 3 are weighting factors, C ( k ) represents the cost of power generation, and E ( k ) represents the emissions. From Equation (2), P g r i d is minus P g e n and ( P l o a d + P l o s s + P E S S ) . This can be negative or positive.
The constraints for the MPC problem include:
  • 1.Power Balance Constraint:
P b a l a n c e k = ∑ i = 1 N D E R P i ( k ) = P l o a d ( k ) + P c h a r ( k ) + P l o s s ( k ) + P g r i d ( k ) − P d i s ( k )
where P i ( k ) is the power generated by the i -th DER and N D E R is the number of DERs.
2.
Generation Capacity Constraints:
P i , m i n ≤ P i ( k ) ≤ P i , m a x
where P i , m i n and P i , m a x are the minimum and maximum power generation limits of the i -th DER.
3.
Ramp Rate Constraints:
− R i ≤ P i k − P i k − 1 ≤ R i
where R i is the ramp rate limit of the i -th DER.
4.
Emissions Constraint:
E k = ∑ i = 1 N D E R E i ( k ) ≤ E m a x
where E i ( k ) is the emission produced by the i -th DER and E m a x is the maximum allowable emission.

2.3. The Implementation of GA Algorithm

GA finds an optimal solution u ( k ) to control inputs in MG by evolving a population of candidate solutions. Selection, crossover, and mutation are automated optimization processes in GA for MG control. The fitness function of GA in MG control is expressed as the inverse of the cost function J :
F i t n e s s u = 1 J x , u
The GA process is summarized by:
  • Initialization: An initial population of candidate solutions, chromosomes in the form of control inputs.
  • Selection: Parent chromosomes are selected and survive according to computed fitness values for each chromosome.
  • Crossover: Parents chromosomes are combined to produce the offspring.
  • Mutation: It introduces small random changes in chromosomes of offspring to provide an element of randomness and to retain diversity.
  • Evaluation: Compute the fitness of offspring chromosomes.
  • Replacement: Create a new population considering the best chromosomes of the current population and offsprings.
The key operations in GA are defined as:
  • Crossover: A single-point crossover operation can be defined as:
O f f s p r i n g 1 = P a r e n t 1 :   m ,   P a r e n t 2 m   : O f f s p r i n g 2 = P a r e n t 2 :   m ,   P a r e n t 1 m   :
where m is the crossover point.
  • Mutation: A mutation operation can be defined as:
O f f s p r i n g i = O f f s p r i n g i + ∆
where ∆ is a random perturbation.

2.4. The Implementation of GPC

The GPC method integrates GA with MPC by using GA to optimize the control inputs over the MPC prediction horizon. The integrated GPC formulation is developed as follows:
  • Prediction: Use system model to predict future states over the prediction horizon.
  • Optimization: Apply GA to optimize the control inputs u ( k ) over the prediction horizon.
  • Implementation: Implement the optimized control inputs in the MG system.
  • Repetition: Execute repetition of the process at each of the control steps to adapt to the changing conditions.
GA solves the MPC problem formulated by Equations (10)–(14).
The GPC method was developed using Python. Basically, the simulation model is with the DER model at higher level of details along with the models of the load profiles and the distribution power components. Its actual working has been compared with the conventional methods of MPC and GA and further assessed under several scenarios to evaluate its real-time efficacy to achieve the set control objectives.
The key metrics used for evaluation include:
  • Excess Power Production: Measured as the total surplus power generated beyond the load demand, and the power to be stored in the ESS. This power will be injected into upstream grid.
  • Power Generation Costs: Calculated as an estimate of the operational costs for DERs.
  • Emissions: Quantified in terms of the total emissions produced by the MG.
The simulation results showed that the GPC-based method considerably decreases excess power production, increasing the efficiency of resource allocation and balancing multiple objectives much better than the conventional methods based on MPC and GA.

2.5. Practical Implementation Steps of GPC

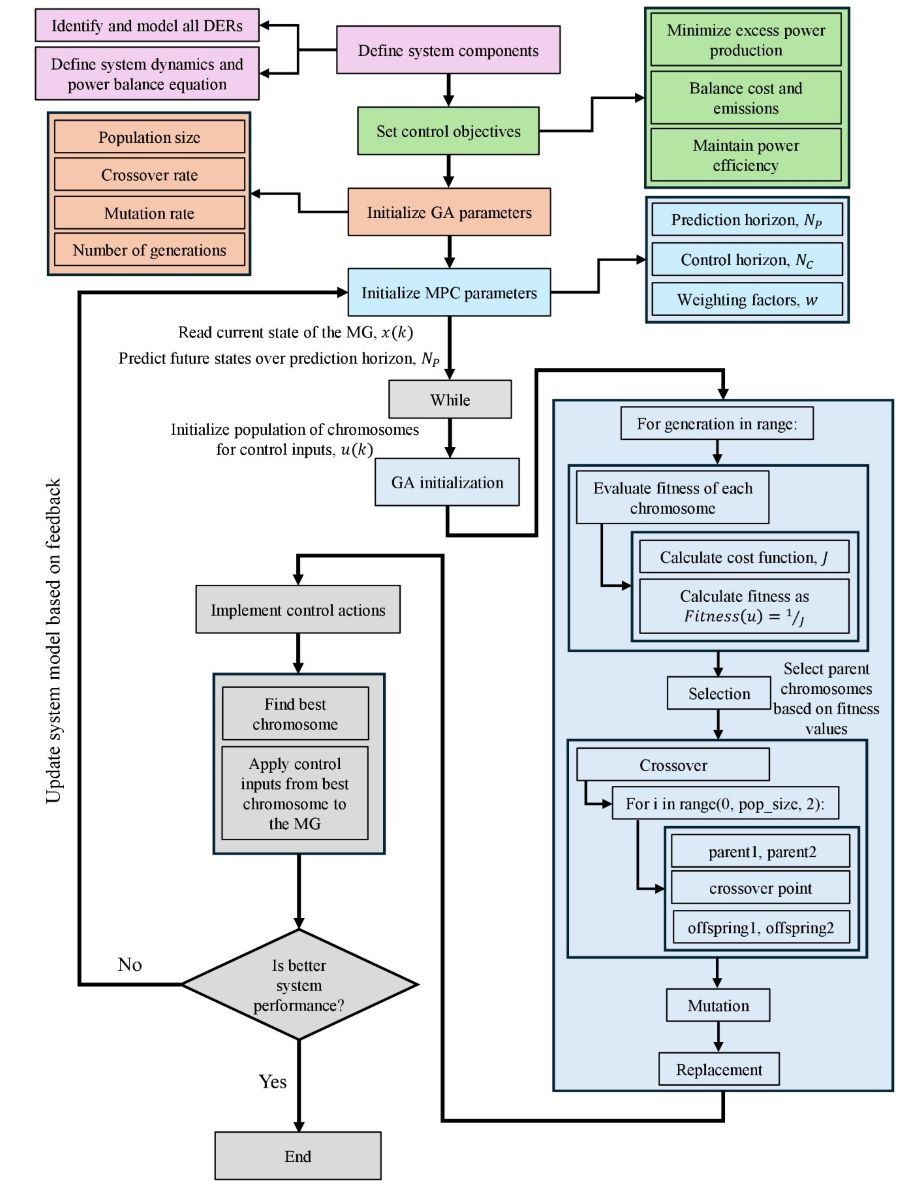
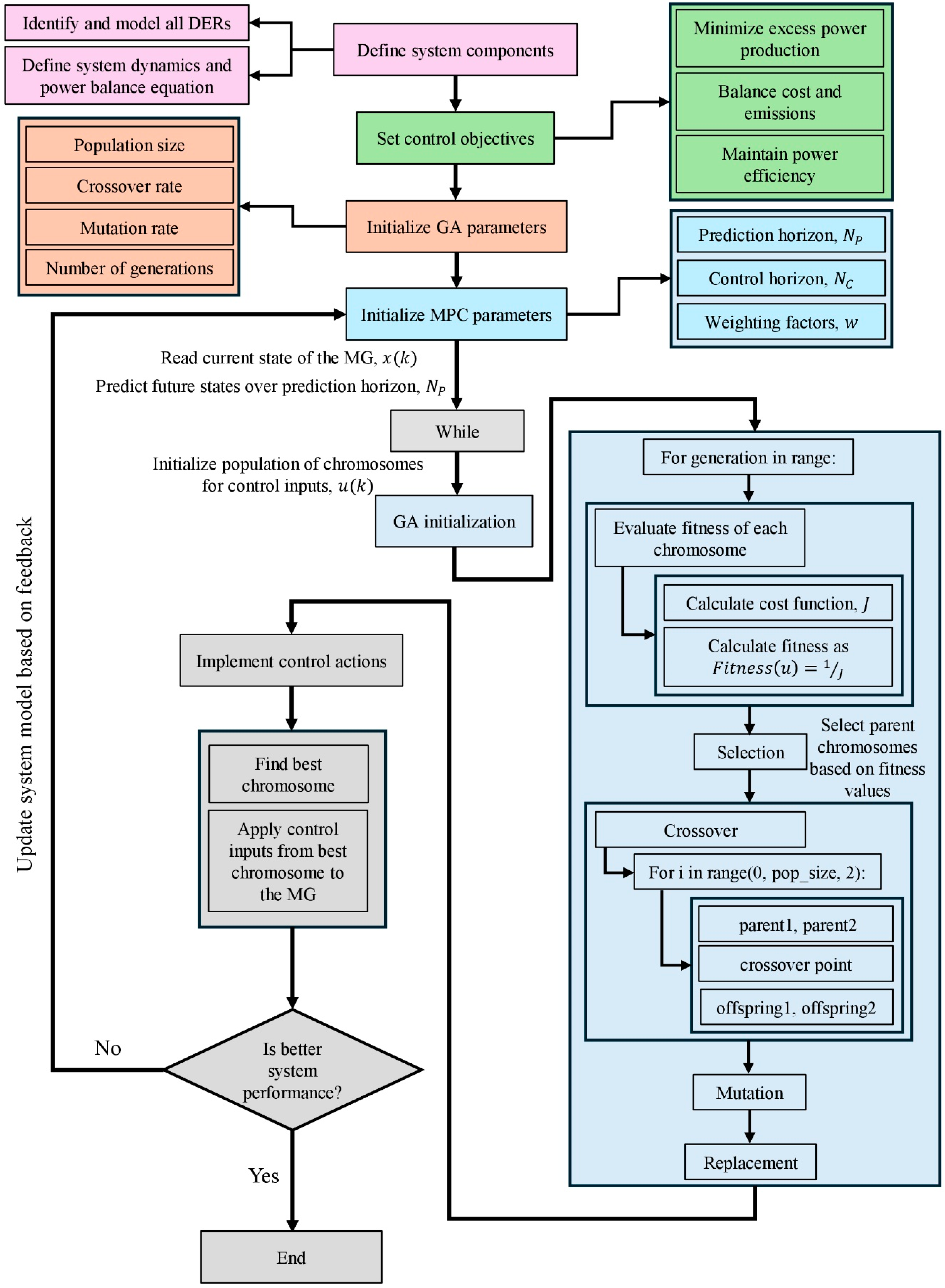
The implementation of GPC in a MG follows a well-defined process so that the developed control presents efficiency and accuracy. As shown in Figure 2, the process begins by defining all system components, including DERs, loads, and storage systems. Control objectives are then outlined-some of the common objectives are minimisation of excess power production, cost versus emissions trade-off, and maximization of overall power efficiency.
In this, the next step is the initialization of parameters for both GA and MPC: population size, crossover rate, mutation rate, and also the number of generations for the GA; prediction horizon, control horizon, and weighting factors for the cost function for the MPC.
As soon as these parameters are set, an initial work in GA begins, where it first reads the current state of MG to get its operational status and power levels. An MPC predicts future states over the prediction horizon, followed by the initialization of the population of chromosomes, each representing potential control actions in Figure 2.
The core of the GPC process lies in the iterative loop of the GA. For a specified number of generations, parent chromosomes are selected based on their fitness values. The fitness of each chromosome is evaluated through the calculation of the cost function, and fitness is inversely related to this cost. During crossover, pairs of parent chromosomes exchange genetic information at a specified crossover point, producing offspring. Mutation makes some genes change randomly so genetic diversity can be retained. Then the offspring replace part of the adult population with new generation.
The control actions are considered for only implementing the chromosome that contains the best value, in other words, the one with the highest fitness. Its control inputs are then applied to the MG. The system performance is tracked to determine whether that new control action has provided improvement. If not, the system model is updated based on feedback, and the process is repeated. If performance has improved, the process concludes. This structured design of GPC is very effective in steering the non-linearity and non-convexity of the MG system, by virtue of the optimization features of GAs, within the MPC framework optimization strategy; effective in ensuring proficient, accurate, and effective control.

3. Results

3.1. The Case Study Description

To provide a comprehensive understanding of the MG system and the context in which the GPC method is applied, this section presents the parameters and data used in the case study, including solar irradiation and wind speed curves, capacities of DERs, load profiles, efficiencies, ESS capacity, and price signals. These parameters as shown in Table 1 and Table 2 are crucial for understanding the simulation results and the effectiveness of the proposed GPC method in optimizing the MG's performance.
MPC, a core component of the GPC method, is particularly adept at handling non-linearities and dynamic changes in the system. MPC's predictive capabilities allow it to anticipate future states and adjust control actions, accordingly, ensuring optimal performance. This is especially beneficial in managing the complexities of microgrids, where demand and generation can be highly variable. MPC’s ability to incorporate constraints directly into the optimization process ensures that the system operates within safe and efficient limits, enhancing both reliability and sustainability. It is worthy to note that in GPC, the combination of different genetic operators (mutation and crossover) with selection strategies (random selection and elitism) is critical for optimizing the performance of the algorithm. This study considers four distinct scenarios by combining these operators and strategies to comprehensively evaluate their impact on the optimization process.

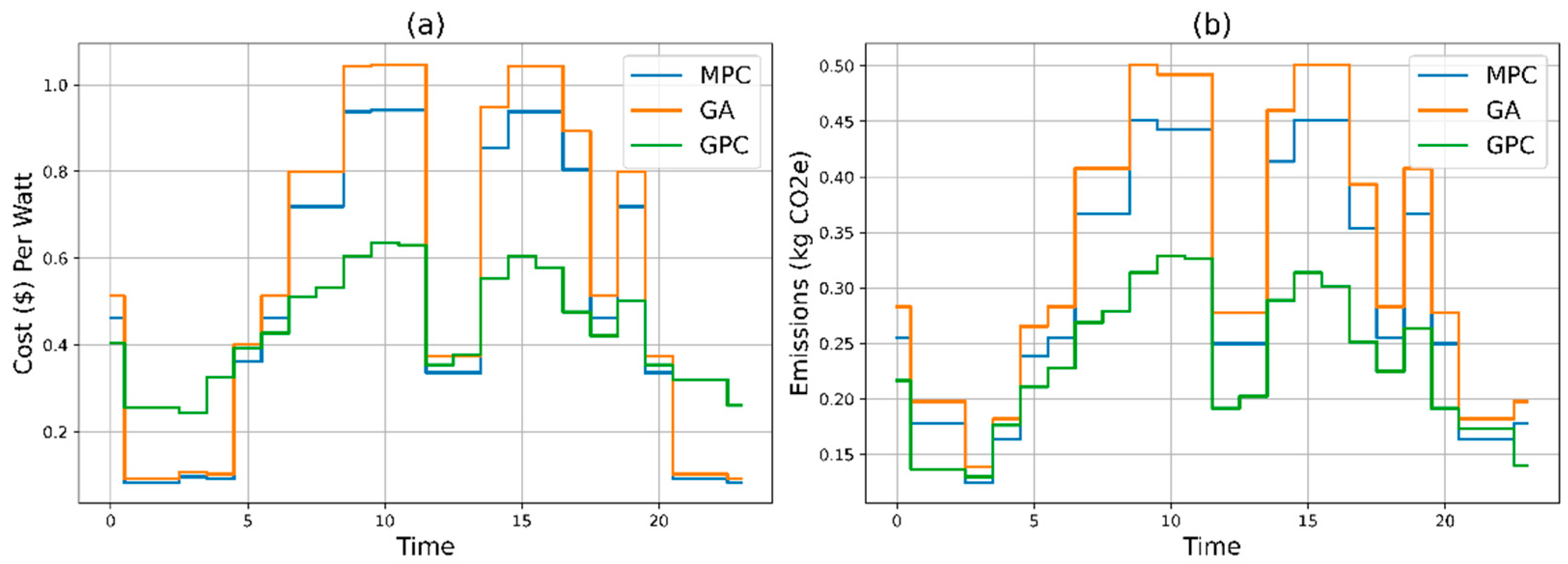
3.2. Mutation–Random Selection

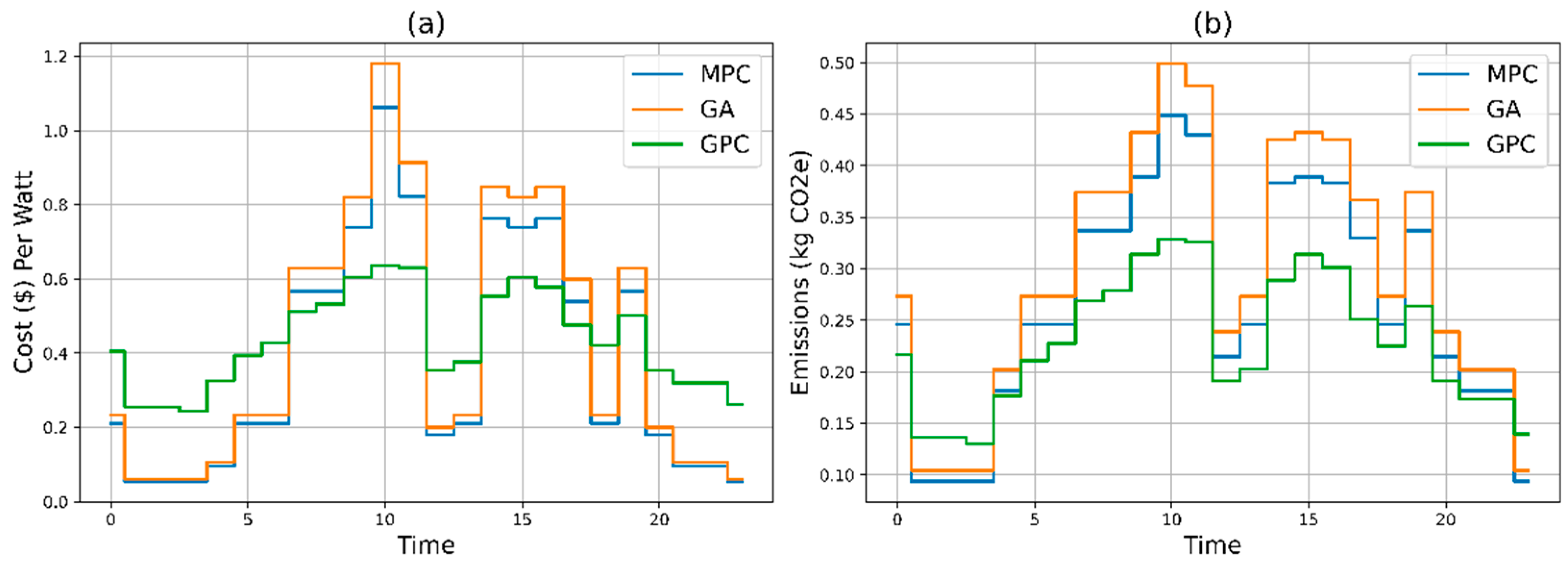
The integration of MPC within GA offers several benefits, particularly in handling non-linearity and improving overall performance. MPC enhances GPC by predicting future system behaviors and optimizing control actions accordingly. The comparison of three methods—MPC, GA, and the proposed GPC, which combines the strengths of MPC and GA—highlights the superior performance of GPC in both cost efficiency and environmental impact. Over the course of a day, GPC achieved the lowest total cost of $110.83 (in Figure 3a) and the lowest total emissions of 52.83 kg CO2e (Figure 3b), significantly outperforming MPC and GA. The key advantage of MPC lies in its capability to handle system non-linearity and make real-time adjustments, ensuring robust performance under varying conditions. However, while MPC is effective in managing non-linearities, it often results in higher costs and emissions compared to GPC. By integrating the optimization strengths of GA with MPC's real-time adaptability, GPC not only maintains lower costs and emissions consistently throughout the day but also leverages MPC’s robustness in handling complex system dynamics. This combination makes GPC a more effective and sustainable approach for optimizing energy usage, providing significant cost savings and reducing environmental impact.

3.3. Mutation–Elitism

In Figure 4, the comparison of MPC, GA, and the GPC method, which synergizes MPC's capability to handle system non-linearity with GA's optimization strengths, clearly demonstrates the superior performance of GPC. The GPC method achieves the lowest total cost of $113.94 (Figure 4a) and the lowest total emissions of 52.83 kg CO2e over a day (Figure 4b), outperforming MPC's cost of $127.23 and emissions of 71.46 kg CO2e, as well as GA's cost of $144.64 and emissions of 73.73 kg CO2e. While MPC effectively manages non-linearities, its cost and emissions are higher compared to GPC. GA, despite its optimization capabilities, shows the highest cost and emissions. Therefore, GPC stands out as the most effective and sustainable approach, offering significant cost savings and reduced environmental impact by integrating the best aspects of both MPC and GA.

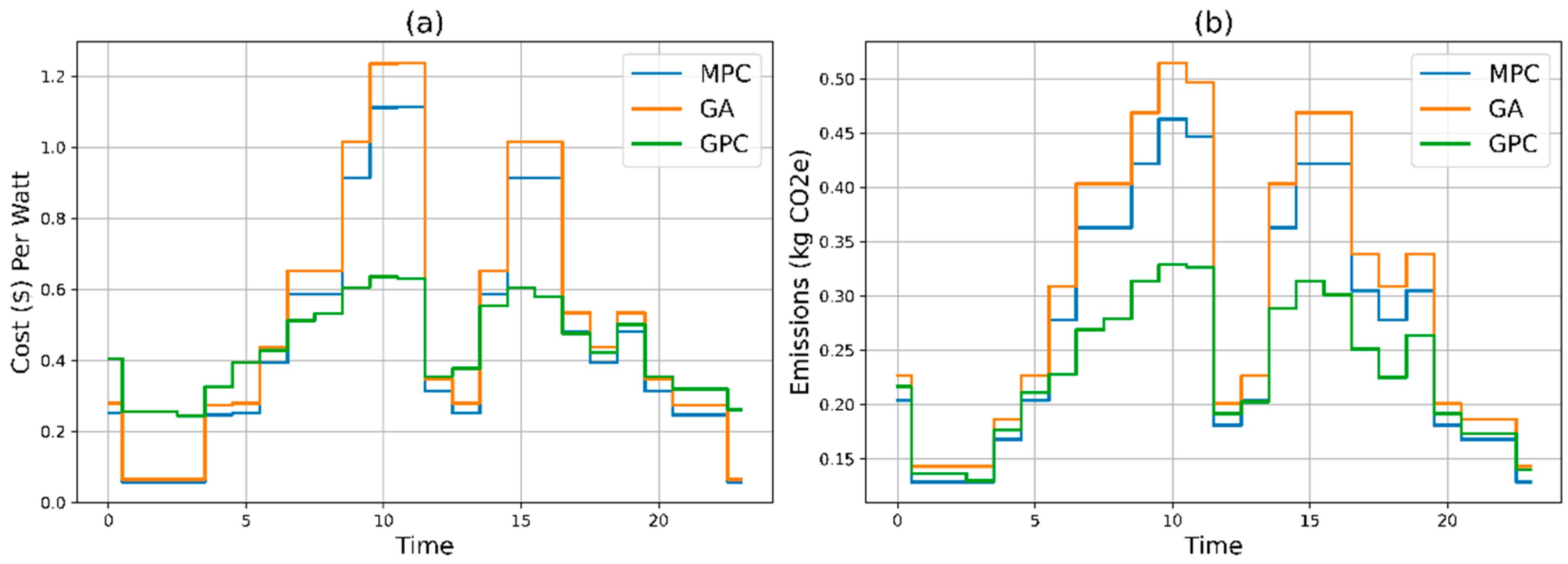
3.4. Crossover-Random Selection

In Figure 5, The GPC method achieves the lowest total cost of $113.94 and the lowest total emissions of 52.83 kg CO2e over a day, outperforming MPC's cost of $136.06 and emissions of 67.85 kg CO2e, as well as GA's cost of $131.90 and emissions of 69.10 kg CO2e. While MPC effectively manages non-linearities, its cost and emissions are higher compared to GPC. GA, despite its optimization capabilities, shows higher costs and emissions than GPC. Therefore, GPC stands out as the most effective and sustainable approach, offering significant cost savings and reduced environmental impact by integrating the best aspects of both MPC and GA.

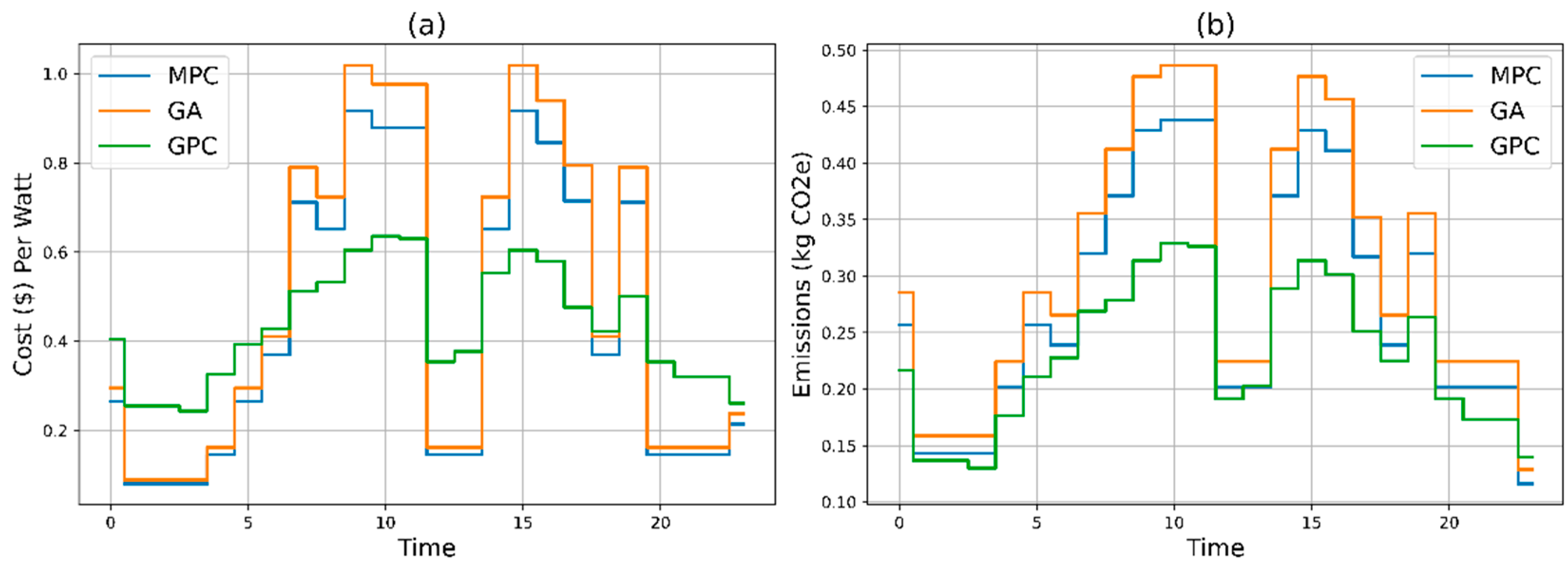
3.5. Crossover-Elitism

In Figure 6a, in the Crossover-Elitism approach, GPC achieves the lowest total cost of $113.94 and the lowest total emissions of 52.83 kg CO2e over a day. This performance is significantly better compared to MPC, which has a cost of $122.76 and emissions of 69.53 kg CO2e, and GA, which incurs a cost of $127.80 and emissions of 69.71 kg CO2e in Figure 6b. While MPC effectively manages system non-linearity, it results in higher costs and emissions relative to GPC. GA, despite its strong optimization abilities, performs worse than GPC in both cost and emissions. Thus, GPC stands out as the most effective and sustainable approach, combining the robustness of MPC with the optimization efficiency of GA, leading to significant cost savings and reduced environmental impact.

4. Discussion

The integration of MPC within GPC showcases significant advantages over the traditional GA across different scenarios. The analysis of the four sets of results highlights these benefits in terms of cost efficiency, emissions reduction, power generation, and overall optimization performance. The results of the comparison between MPC, GA, and the proposed GPC highlight the distinct advantages and performance metrics of each method in the context of optimizing energy usage and reducing environmental impact.

4.1. Performance Analysis

Cost Efficiency: The GPC method consistently demonstrates the lowest total cost for the day across various scenarios, including Mutation-Elitism and Crossover-Elitism. Specifically, GPC achieves a total cost of $113.94, which is significantly lower than both MPC and GA. In the Crossover-Elitism scenario, GPC’s cost is $113.94 compared to MPC's $122.76 and GA's $127.80. This cost efficiency can be attributed to GPC’s ability to effectively combine the real-time adaptability and non-linearity handling of MPC with the robust optimization capabilities of GA. This synergy allows GPC to minimize costs by making more informed and precise adjustments throughout the day.
Environmental Impact: In terms of emissions, GPC again outperforms both MPC and GA. The GPC method achieves the lowest total emissions of 52.83 kg CO2e, significantly lower than MPC’s 69.53 kg CO2e and GA’s 69.71 kg CO2e in the Crossover-Elitism scenario. The reduction in emissions is a crucial advantage, as it underscores the potential of GPC to contribute to sustainability goals and reduce the carbon footprint of energy systems. The lower emissions are a direct result of the GPC’s optimized control strategy, which ensures efficient energy usage and reduces wasteful emissions.

4.2. Methodological Insights

MPC: MPC’s strength lies in its ability to handle non-linearities and make real-time adjustments based on system dynamics. This capability ensures robust performance under varying conditions. However, MPC’s approach, while effective in managing non-linearities, often results in higher operational costs and emissions compared to GPC. The peaks in cost and emissions observed in the MPC results suggest that while it adapts well to changes, it may not always find the most cost-effective or environmentally friendly solution.
GA: The GA is known for its powerful optimization capabilities, which enable it to explore a wide solution space and identify optimal strategies. However, GA’s higher variability in cost and emissions indicates that it may lack the real-time adaptability required to handle dynamic changes as effectively as MPC. The results show that GA, although efficient in optimization, tends to incur higher costs and emissions compared to GPC, particularly when not combined with a robust real-time control mechanism.
GPC: The GPC method, which integrates the strengths of both MPC and GA, emerges as the superior approach. GPC leverages MPC’s ability to handle non-linearities and make real-time adjustments while utilizing GA’s optimization strength to continuously refine control strategies. This combination allows GPC to maintain lower costs and emissions consistently. The fitness graphs further support this, showing that GPC achieves higher and more stable fitness levels throughout the iterations, indicating a more effective and sustained optimization process.

4.3. Limitations and Challenges

Although the GPC method offers a number of advantages, important improvements over traditional approaches, there are a number of limitations and challenges that need to be addressed for practical implementation and wide diffusion.
Computational Complexity: While effective in optimizing MG operations, the integration of GA and MPC in the GPC method results in high computational complexity. In that respect, the intrinsic interactivity of GA adds to predictive capabilities brought about by MPC, which requires high computational effort. This might be more problematic in real-time applications; specifically, where fast decision-making is necessary. This computational burden may limit applicability in smaller MGs or scenarios where advanced computation infrastructures are unavailable. While the GPC method offers substantial benefits in terms of efficiency, sustainability, and cost-effectiveness, addressing the aforementioned limitations and challenges is crucial for its successful implementation. Future research should focus on developing solutions to mitigate these challenges, enhancing the practicality and robustness of the GPC method in diverse MG settings.

5. Conclusions

The comparative analysis of MPC, GA, and the proposed GPC method underscores the superior performance and advantages of GPC in optimizing energy usage. GPC, which synergizes MPC’s adept handling of non-linearity with GA’s powerful optimization capabilities, consistently achieves the lowest total cost and emissions across different scenarios, including Mutation-Elitism and Crossover-Elitism. GPC demonstrated the lowest total cost of $113.94 and the lowest total emissions of 52.83 kg CO2e, outperforming both MPC and GA significantly. This performance highlights GPC’s ability to maintain economic efficiency and environmental sustainability, making it a more attractive option for energy management. While MPC effectively manages system non-linearities and adapts to real-time changes, it incurs higher costs and emissions compared to GPC. MPC’s robust performance under dynamic conditions is valuable, but it does not achieve the same level of cost-effectiveness or environmental efficiency as GPC. GA excels in exploring a wide solution space and identifying optimal strategies, but its higher cost and emission levels indicate that it lacks the real-time adaptability necessary for dynamic energy management. When used alone, GA does not perform as efficiently as GPC. The GPC leverages the best features of both MPC and GA, resulting in superior performance in terms of cost and emissions. By integrating MPC’s real-time control with GA’s optimization, GPC provides a balanced and highly effective approach to energy management. Implementing GPC in real-world energy systems can lead to substantial cost savings and significant reductions in emissions, supporting both economic and environmental goals. Its robust performance across various scenarios suggests that GPC is well-suited for diverse applications, including renewable energy integration and industrial energy management. The GPC method stands out as the most effective and sustainable approach for optimizing energy usage, combining the strengths of MPC and GA to achieve significant cost savings and reduced environmental impact. Its adoption can play a crucial role in addressing modern energy management challenges and contributing to global sustainability efforts.

Author Contributions

Conceptualization, M.C. and A.A.; methodology, M.C. and A.A.; software, M.C.; validation, M.C. and A.A.; formal analysis, M.C.; investigation, M.C. and A.A.; resources, M.C.; data curation, M.C.; writing—original draft preparation, M.C. and A.A.; writing—review and editing, M.C. and A.A.; visualization, M.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

https://github.com/cavusmuhammed68/Energies---MDPI.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. X. He, S. X. He, S. Cui, Y.-W. Wang, and J.-W. Xiao, “A Data-Driven MPC-Based Energy Optimization and Management Framework of an Energy Building,” in 2021 33rd Chinese Control and Decision Conference (CCDC), IEEE, 21, pp. 5139–5144. 20 May. [CrossRef]
  2. K. Qian, D. K. Qian, D. Liu, Y. Yan, Y. Xu, H. Wei, and J. Zhang, “Research on configuration optimization of integrated energy system considering equipment nonlinearity,” in 2023 IEEE 6th International Electrical and Energy Conference (CIEEC), IEEE, 23, pp. 3722–3726. 20 May. [CrossRef]
  3. S. Chapaloglou, E. F. S. Chapaloglou, E. F. Alves, V. Trovato, and E. Tedeschi, “Optimal Energy Management in Autonomous Power Systems With Probabilistic Security Constraints and Adaptive Frequency Control,” IEEE Transactions on Power Systems, vol. 39, no. 1, pp. 1543–1554, Jan. 2024. [CrossRef]
  4. I. Dincer, M. A. I. Dincer, M. A. Rosen, and P. Ahmadi, Optimization of Energy Systems. Wiley, 2017. [CrossRef]
  5. K. Ma, G. K. Ma, G. Hu, and C. J. Spanos, “Energy Management Considering Load Operations and Forecast Errors With Application to HVAC Systems,” IEEE Trans Smart Grid, vol. 9, no. 2, pp. 605–614, Mar. 2018. [CrossRef]
  6. F. Carreras and H. Kirchsteiger, “An Empirical Approach to Optimize non-linear Problems of Domestic Energy Management Systems,” CONECT. International Scientific Conference of Environmental and Climate Technologies, p. 54, 23. 20 May. [CrossRef]
  7. J. Müller, “Evolutionary optimization under uncertainty in energy management systems,” it - Information Technology, vol. 59, no. 1, pp. 23–29, Feb. 2017. [CrossRef]
  8. M. Sadees, A. M. Sadees, A. Raju, U. Mukherjee, and K. Vijayakumar, “Genetic Algorithm Based Energy Management in Microgrid,” 2022, pp. 445–455. [CrossRef]
  9. A.A. El-Fergany and M. A. El-Hameed, “Efficient frequency controllers for autonomous two-area hybrid microgrid system using social-spider optimiser,” IET Generation, Transmission & Distribution, vol. 11, no. 3, pp. 637–648, Feb. 2017. [CrossRef]
  10. S. V Sah, V. S. V Sah, V. Prakash, P. K. Pathak, and A. K. Yadav, “Fractional Order AGC Design for Power Systems via Artificial Gorilla Troops Optimizer,” in 2022 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), IEEE, Dec. 2022, pp. 1–6. [CrossRef]
  11. K. S. Joshal and N. Gupta, “Microgrids with Model Predictive Control: A Critical Review,” Energies (Basel), vol. 16, no. 13, p. 4851, Jun. 2023. [CrossRef]
  12. H. Li, C. H. Li, C. Zang, P. Zeng, H. Yu, and Z. Li, “A genetic algorithm-based hybrid optimization approach for microgrid energy management,” in 2015 IEEE International Conference on Cyber Technology in Automation, Control, and Intelligent Systems (CYBER), IEEE, Jun. 2015, pp. 1474–1478. [CrossRef]
  13. M. Ramesh, A. K. M. Ramesh, A. K. Yadav, and P. K. Pathak, “Artificial Gorilla Troops Optimizer for Frequency Regulation of Wind Contributed Microgrid System,” J Comput Nonlinear Dyn, vol. 18, no. 1, Jan. 2023. [CrossRef]
  14. W. Li, R. W. Li, R. Wang, T. Zhang, M. Ming, and H. Lei, “Multi-scenario microgrid optimization using an evolutionary multi-objective algorithm,” Swarm Evol Comput, vol. 50, p. 100570, Nov. 2019. [CrossRef]
  15. S. J. Nanda and G. Panda, “A survey on nature inspired metaheuristic algorithms for partitional clustering,” Swarm Evol Comput, vol. 16, pp. 1–18, Jun. 2014. [CrossRef]
  16. B.-Y. Qu and P. N. Suganthan, “Novel multimodal problems and differential evolution with ensemble of restricted tournament selection,” in IEEE Congress on Evolutionary Computation, IEEE, Jul. 2010, pp. 1–7. [CrossRef]
  17. E. F. Camacho and C. Bordons, Model Predictive control. London: Springer London, 2007. [CrossRef]
  18. L. Wang, Model Predictive Control System Design and Implementation Using MATLAB®. London: Springer London, 2009. [CrossRef]
  19. J. B. Rawlings and D. Q. Mayne, Model Predictive Control Theory and Design. Nob Hill Pub, Llc, 2009.
  20. S. J. Qin and T. A. Badgwell, “A survey of industrial model predictive control technology,” Control Eng Pract, vol. 11, no. 7, pp. 733–764, Jul. 2003. [CrossRef]
  21. M. H. Moradi, “Predictive control with constraints,” Int J Adapt Control Signal Process, vol. 17, no. 3, pp. 261–262, Apr. 2003. [CrossRef]
  22. A.Panday and H. O. Bansal, “Energy management strategy for hybrid electric vehicles using genetic algorithm,” Journal of Renewable and Sustainable Energy, vol. 8, no. 1, Jan. 2016. [CrossRef]
  23. G. Pannocchia, “Handbook of Model Predictive Control [Bookshelf],” IEEE Control Syst, vol. 40, no. 5, pp. 96–99, Oct. 2020. [CrossRef]
  24. R. Maouedj, A. R. Maouedj, A. Mammeri, M. D. Draou, and B. Benyoucef, “Performance Evaluation of Hybrid Photovoltaic-wind Power Systems,” Energy Procedia, vol. 50, pp. 797–807, 2014. [CrossRef]
  25. N. Ding, K. N. Ding, K. Prasad, and T. T. Lie, “Design of a hybrid energy management system using designed rule-based control strategy and genetic algorithm for the series-parallel plug-in hybrid electric vehicle,” Int J Energy Res, vol. 45, no. 2, pp. 1627–1644, Feb. 2021. [CrossRef]
  26. A. Alzahrani et al., “Multi-Objective Energy Optimization with Load and Distributed Energy Source Scheduling in the Smart Power Grid,” Sustainability, vol. 15, no. 13, p. 9970, Jun. 2023. [CrossRef]
  27. Z. Ren, X. Z. Ren, X. Qu, M. Wang, and C. Zou, “Multi-Objective Optimization for DC Microgrid Using Combination of NSGA-II Algorithm and Linear Search Method,” IEEE J Emerg Sel Top Circuits Syst, vol. 13, no. 3, pp. 789–796, Sep. 2023. [CrossRef]
  28. R. Elazab, A. T. R. Elazab, A. T. Abdelnaby, and A. A. Ali, “A comparative study of advanced evolutionary algorithms for optimizing microgrid performance under dynamic pricing conditions,” Sci Rep, vol. 14, no. 1, p. 4548, Feb. 2024. [CrossRef]
  29. C. Bordons, F. C. Bordons, F. Garcia-Torres, and M. A. Ridao, Model Predictive Control of Microgrids. Cham: Springer International Publishing, 2020. [CrossRef]
  30. O. Akbulut, M. O. Akbulut, M. Cavus, M. Cengiz, A. Allahham, D. Giaouris, and M. Forshaw, “Hybrid Intelligent Control System for Adaptive Microgrid Optimization: Integration of Rule-Based Control and Deep Learning Techniques,” Energies (Basel), vol. 17, no. 10, p. 2260, 24. 20 May. [CrossRef]
  31. M. Cavus, A. M. Cavus, A. Allahham, K. Adhikari, and D. Giaouris, “A hybrid method based on logic predictive controller for flexible hybrid microgrid with plug-and-play capabilities,” Appl Energy, vol. 359, p. 122752, Apr. 2024. [CrossRef]
  32. M. Cavus, Y. F. M. Cavus, Y. F. Ugurluoglu, H. Ayan, A. Allahham, K. Adhikari, and D. Giaouris, “Switched Auto-Regressive Neural Control (S-ANC) for Energy Management of Hybrid Microgrids,” Applied Sciences, vol. 13, no. 21, p. 11744, Oct. 2023. [CrossRef]
  33. T. Pamulapati, M. T. Pamulapati, M. Cavus, I. Odigwe, A. Allahham, S. Walker, and D. Giaouris, “A Review of Microgrid Energy Management Strategies from the Energy Trilemma Perspective,” Energies (Basel), vol. 16, no. 1, p. 289, Dec. 2022. [CrossRef]
  34. M. Cavus, A. M. Cavus, A. Allahham, K. Adhikari, M. Zangiabadia, and D. Giaouris, “Control of microgrids using an enhanced Model Predictive Controller,” in 11th International Conference on Power Electronics, Machines and Drives (PEMD 2022), Institution of Engineering and Technology, 2022, pp. 660–665. [CrossRef]
  35. G. Shankar and V. Mukherjee, “Load frequency control of an autonomous hybrid power system by quasi-oppositional harmony search algorithm,” International Journal of Electrical Power & Energy Systems, vol. 78, pp. 715–734, Jun. 2016. [CrossRef]
  36. A. Villalón, M. A. Villalón, M. Rivera, Y. Salgueiro, J. Muñoz, T. Dragičević, and F. Blaabjerg, “Predictive Control for Microgrid Applications: A Review Study,” Energies (Basel), vol. 13, no. 10, p. 2454, 20. 20 May. [CrossRef]
  37. P. P. Vergara, R. P. P. Vergara, R. Torquato, and L. C. P. da Silva, “Towards a real-time Energy Management System for a Microgrid using a multi-objective genetic algorithm,” in 2015 IEEE Power & Energy Society General Meeting, IEEE, Jul. 2015, pp. 1–5. [CrossRef]
  38. D. Q. Mayne, J. B. D. Q. Mayne, J. B. Rawlings, C. V. Rao, and P. O. M. Scokaert, “Constrained model predictive control: Stability and optimality,” Automatica, vol. 36, no. 6, pp. 789–814, Jun. 2000. [CrossRef]
  39. F. Garcia-Torres, A. F. Garcia-Torres, A. Zafra-Cabeza, C. Silva, S. Grieu, T. Darure, and A. Estanqueiro, “Model Predictive Control for Microgrid Functionalities: Review and Future Challenges,” Energies (Basel), vol. 14, no. 5, p. 1296, Feb. 2021. [CrossRef]
  40. P. Zhang, MPC for microgrids: Theory and practice (IEEE Press Series on Power and Energy Systems), 1st edition. Wiley-IEEE Press, 2024.
  41. L. S. N. D. and M. R., “Review on advanced control techniques for microgrids,” Energy Reports, vol. 10, pp. 3054–3072, Nov. 2023. [CrossRef]
Preprints 114646 g001
Figure 1. Power flow representation in the MG.
Figure 1. Power flow representation in the MG.
Preprints 114646 g001
Preprints 114646 g002
Figure 2. Flowchart of practical implementation steps for GPC.
Figure 2. Flowchart of practical implementation steps for GPC.
Preprints 114646 g002
Preprints 114646 g003
Figure 3. Mutation – Random Selection: (a) cost and (b) emissions comparisons MPC, GA and GPC methods.
Figure 3. Mutation – Random Selection: (a) cost and (b) emissions comparisons MPC, GA and GPC methods.
Preprints 114646 g003
Preprints 114646 g004
Figure 4. Mutation – Elitism: (a) cost and (b) emissions comparisons MPC, GA and GPC methods.
Figure 4. Mutation – Elitism: (a) cost and (b) emissions comparisons MPC, GA and GPC methods.
Preprints 114646 g004
Preprints 114646 g005
Figure 5. Crossover-Random Selection: (a) cost and (b) emissions comparisons MPC, GA and GPC methods.
Figure 5. Crossover-Random Selection: (a) cost and (b) emissions comparisons MPC, GA and GPC methods.
Preprints 114646 g005
Preprints 114646 g006
Figure 6. Crossover-Elitism: (a) cost and (b) emissions comparisons MPC, GA and GPC methods.
Figure 6. Crossover-Elitism: (a) cost and (b) emissions comparisons MPC, GA and GPC methods.
Preprints 114646 g006
Table 1. Solar irradiation, wind speed and load demand profile for the building.
Table 1. Solar irradiation, wind speed and load demand profile for the building.
Time (Hours) Solar Irradiation (W/m2) Wind Speed (m/s) Load Demand (kW)
01:00 0 12 50
02:00 0 11 45
03:00 0 10 43
04:00 0 9 35
05:00 50 8 30
06:00 100 6 40
07:00 200 5 54
08:00 400 14 60
09:00 600 12 74
10:00 800 10 80
11:00 1000 10 90
12:00 1100 7 105
13:00 1000 7 97
14:00 800 8 98
15:00 600 9 99
16:00 400 7 87
17:00 200 11 102
18:00 100 13 101
19:00 50 15 105
20:00 0 14 98
21:00 0 13 99
22:00 0 7 96
23:00 0 6 94
24:00 0 7 90
Table 2. Some parameters for the study.
Table 2. Some parameters for the study.
Parameters Values Parameters Values
ESS capacity 150 kWh Daytime price (7 AM - 7 PM) $0.20 per kWh
PV panels 100 kW Nighttime price (7 PM - 7 AM) $0.10 per kWh
WTs 90 kW S O C m a x 0.9 (90%)
n c h a r 0.95 S O C m i n 0.15 (15%)
n d i s 0.90 S O C ( 1 ) 0.5 (50%)
P i , m i n 0 kW R 0.5 ohms
P i , m a x 110 kW N P 24 h
w 1 1.0 N C 5 h
w 2 0.6 mutation rate 0.1
w 3 0.4 emission factor 0.22499 kg CO2e per kWh
A P V 200 m² β P V -0.0045 (°C⁻¹)
η P V 0.18 (18%) A W T 90 m²
P r a t e d 50 kW v c u t _ i n 3 m/s
v c u t _ o u t 25 m/s v r a t e d 12 m/s
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated