Prerpints.org logo
Preprint
Brief Report

Noise as an Optimization Tool for Spiking Neural Networks

Altmetrics

Downloads

88

Views

30

Comments

0

This version is not peer-reviewed

Submitted:

09 August 2024

Posted:

09 August 2024

You are already at the latest version

Alerts
Abstract
Standard ANNs lack flexibility when handling corrupted input due to their fixed structure. Spiking Neural Networks (SNNs) can utilize biological temporal coding features, such as noise-induced stochastic resonance and dynamical synapses to increase a model’s performance when its parameters are not optimized for a given input. Using the analog XOR task as a simplified Convolutional Neural Network analog, this paper demonstrates two key results: (1) SNNs solve the problem linearly inseparable in ANN with over 10% improvement in the optimal setting, and (2) in SNNs, the synaptic noise and dynamical synapses compensate for non-optimal parameters, achieving near-optimal results.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

Spiking Neural Networks (SNNs) have been shown to outperform conventional static Artificial Neural Networks (ANNs) [13] in energy efficiency when running models on Neuromorphic chips [3,17], ability to self-optimize to changing probability distributions, such as the likelihood of a reward [11], and adaptability of a dynamical motor control system to a changing environment [5]. This paper shows that noise sensitivity in SNNs drives changes in neural synchronization, leading to surprisingly better performance than ANNs when parameters are not fully optimized.
Unlike ANNs, training the synaptic weights of SNNs is challenging due to the instantaneous spiking activity and dynamic synaptic characteristics that hinder gradient computation. Several methods exist to achieve trained SNNs: (1) obtain synaptic weights by ANN-backpropagation and apply them to SNN [16], (2) SNN-backpropagation [10], (3) hybrid learning of STDP-based pre-training and fine-tuning [9], and (4) gradient-free training method for SNN [14].
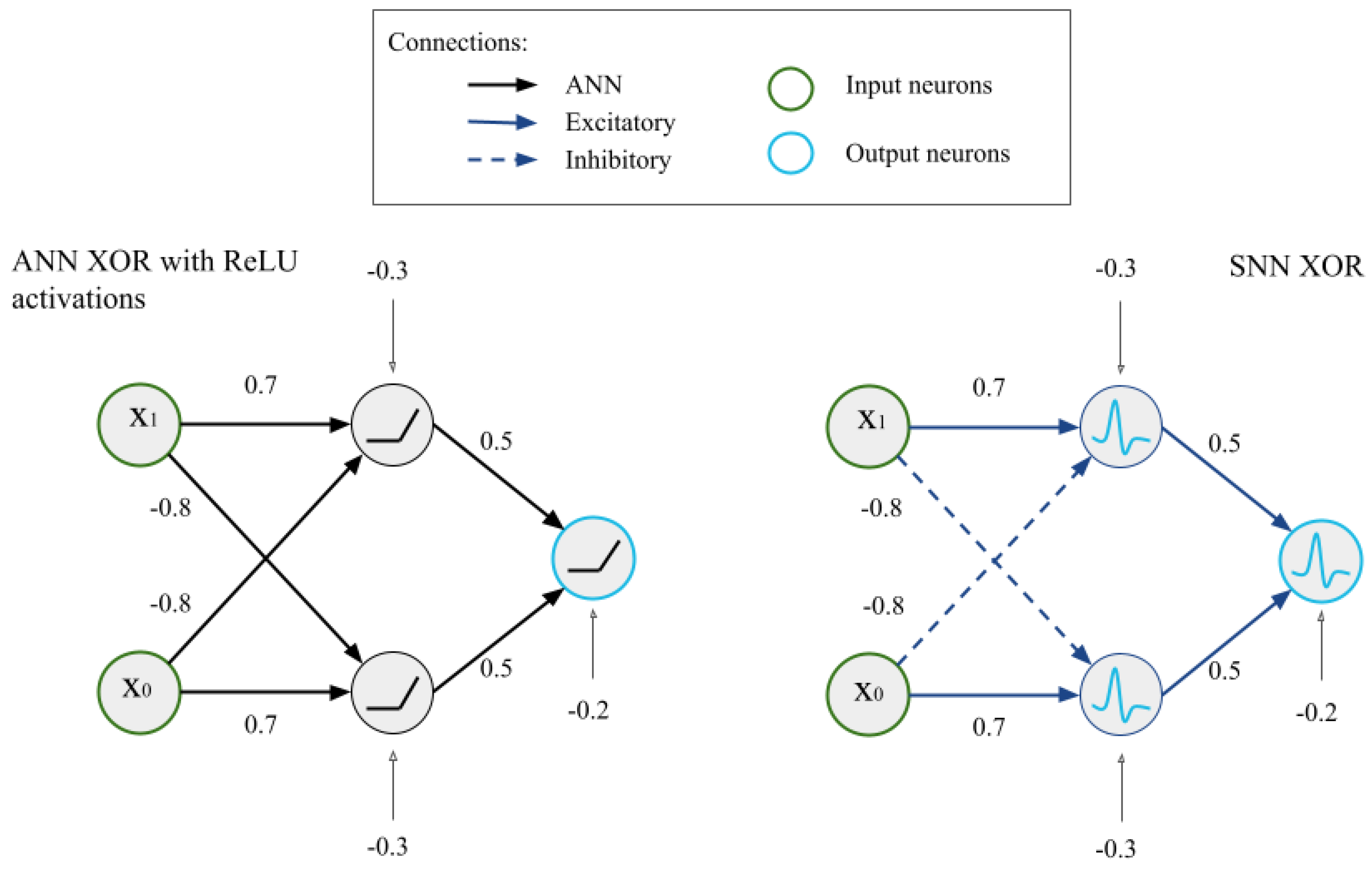
Aiming to compare the adaptability of ANN and SNN models, this paper is based on method (1): we create two similarly structured networks designed to run the analog XOR function. The network structure diagrams are shown in (Figure 1) of the materials and methods section. The goal of the analog XOR task is to check whether the inputs are within a certain range of each other; if they are, then the output is low; otherwise, it is high. The analog XOR task is a simple way to analyze networks’ internal processes that can be generalized to Convolutional Neural Networks, audio processing, and sensor systems.
Differently from the pioneering network comparison/translation research [3,16], our networks have a multiplicative noise component to leverage temporal coding features of spiking neurons. The interest in creating noisy spiking models originates from the conclusions that noise influences the synchronization of inputs and inhibition, and synchronous input is more strongly propagated [6,7].
Another difference from the weight translation method (1) [16], is the use of dynamical synapses (another temporal coding feature) in our SNN. Dynamical synapses maintain the output frequency and defined thresholds comparable while applying noise. While this setup gives us an opportunity to study noise sensitivity in ANN and SNNs, it disrupts the ANN activations-to-SNN firing rates alignment and requires additional input and weight gain parameters to compensate for the synaptic time constant, τ s y n (a dynamical synapse parameter). While parameter tuning in dynamical synapse models poses challenges for scalability, the inherent robustness of our spiking network mitigates the need for extensive optimization. The intrinsic adaptability of our spiking network allows it to maintain functionality even with suboptimal parameter configurations.

2. Materials and Methods

Consider the analog XOR task. Given two inputs ( x 0 , x 1 ) ∈ [ 0.00 , 1.00 ] , the output neuron will exceed the firing threshold h, when exactly one of the input neurons is greater or equal to a boundary value b. The output is normalized with h ∈ ( 0.00 , 1.00 ) . The accuracy of a circuit is determined post-normalization assuming a decision boundary pair (b, h).
For example, assume we have a boundary value of b = 0.42. If both inputs are smaller (or larger) than 0.42, then the output should be low. If only one input is less than 0.42, then the output should be high. The value that is considered "high" enough is called h and is decided upon normalized output. With (b, h) selected we observe how the circuit performs against it with noise added and parameters skewed.
The spiking circuit is simulated with NEST 2.20.1 [8], consisting of Leaky Integrate-and-Fire iaf_psc_exp neurons with dynamical synapses [19] and parameters listed in Table 1.
The neurons’ membrane potential is defined by:
τ m d V m d t = − V m ( t ) + I b i a s + I ( t ) + I n o i s e ( t ) ,
where:
  • I b i a s is the base current (18 pA) plus the biases set by the network architecture
  • I ( t ) is the postsynaptic input current
  • The synaptic noise current I n o i s e ( t ) is given by the normal distribution with 0 mean and standard deviation D:
    I n o i s e ( t ) = 1 D 2 π * e − 1 2 ( x D ) 2 * I ( t ) .
In this experiment, noise is applied to the input neurons only and is scaled by the input values to mimic synaptic multiplicative noise, i.e. accumulated voltages that do not generate a spike [7]. The noise component can be common (equal) between both inputs or independent (different noise components of the same distribution).
In the non-spiking circuit of Figure 3, each input is tested with 20000 different noise components drawn from the same distribution, and then all 20000 trials are averaged for a single output. The same operation repeats 20 times for each noise level D to have more samples for the average accuracy result. The spiking circuit is simulated for 20 seconds per input, with a new noise component added every 0.1 ms (NEST resolution setting), with a total of 200,000 noise components per input. This repeats 20 times for each noise level D. Since accuracy is measured on normalized data, the standard deviation of the average accuracy is low.
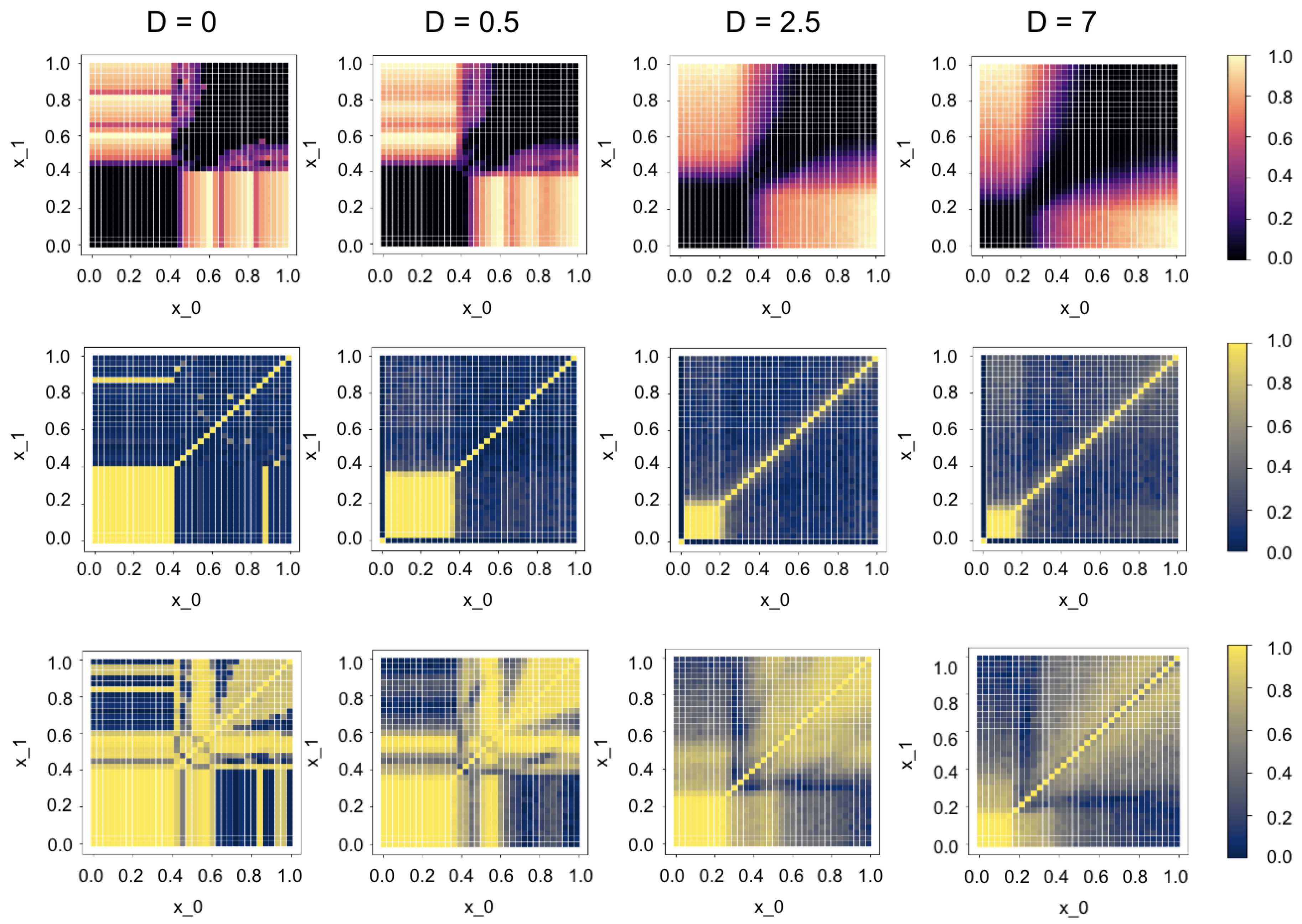
There are fundamental differences in noise application in both networks. In SNN, noise is continuously interacting with the circuit before the final answer is given, affecting synchronization and inhibition (Figure 4). In ANN, on the other hand, negative activations are ReLU-ignored, and the contribution of noise is smoothed over by averaging the output.
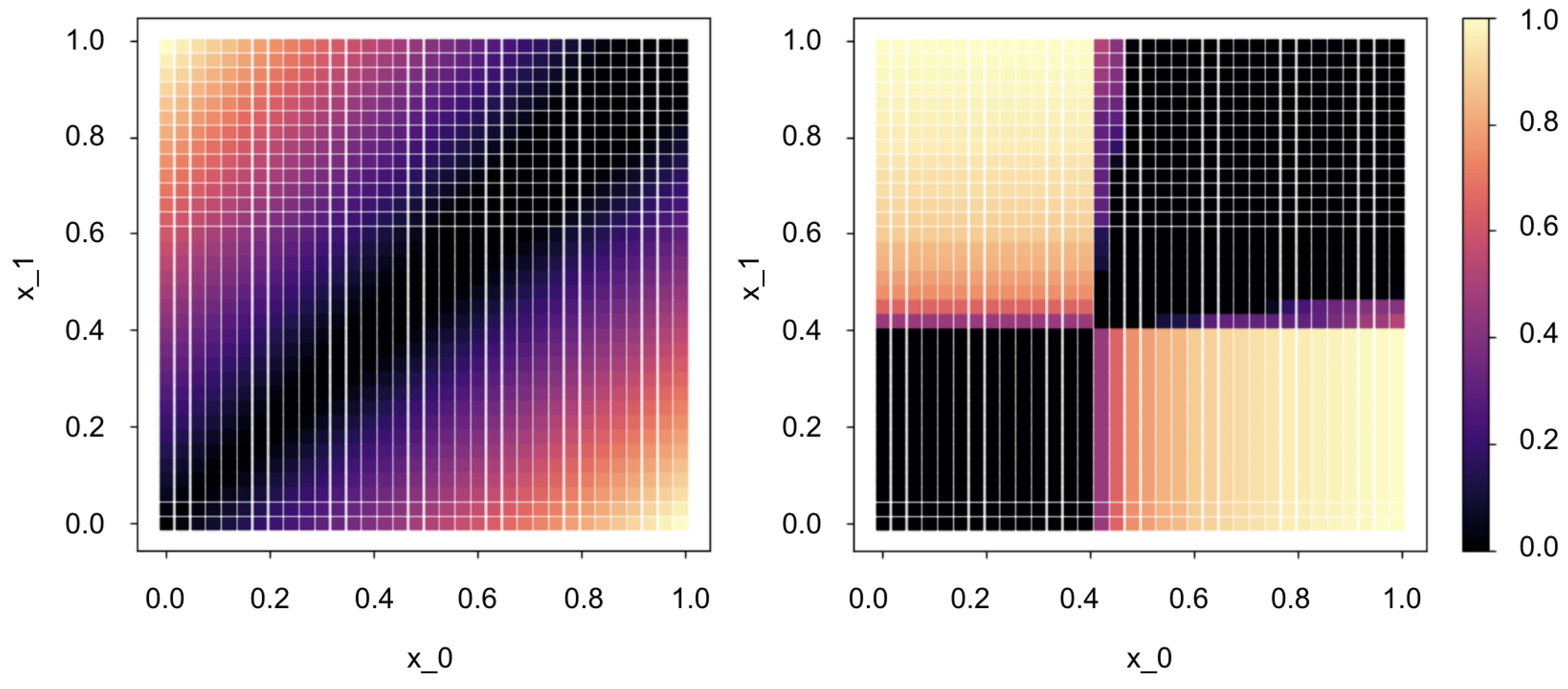
Preprints 114778 g002
Figure 2. a (left): Output activation of the ANN XOR and b (right): output frequency of SNN XOR with τ s y n = 20ms, input gain=5, weight gain=17.
Figure 2. a (left): Output activation of the ANN XOR and b (right): output frequency of SNN XOR with τ s y n = 20ms, input gain=5, weight gain=17.
Preprints 114778 g002
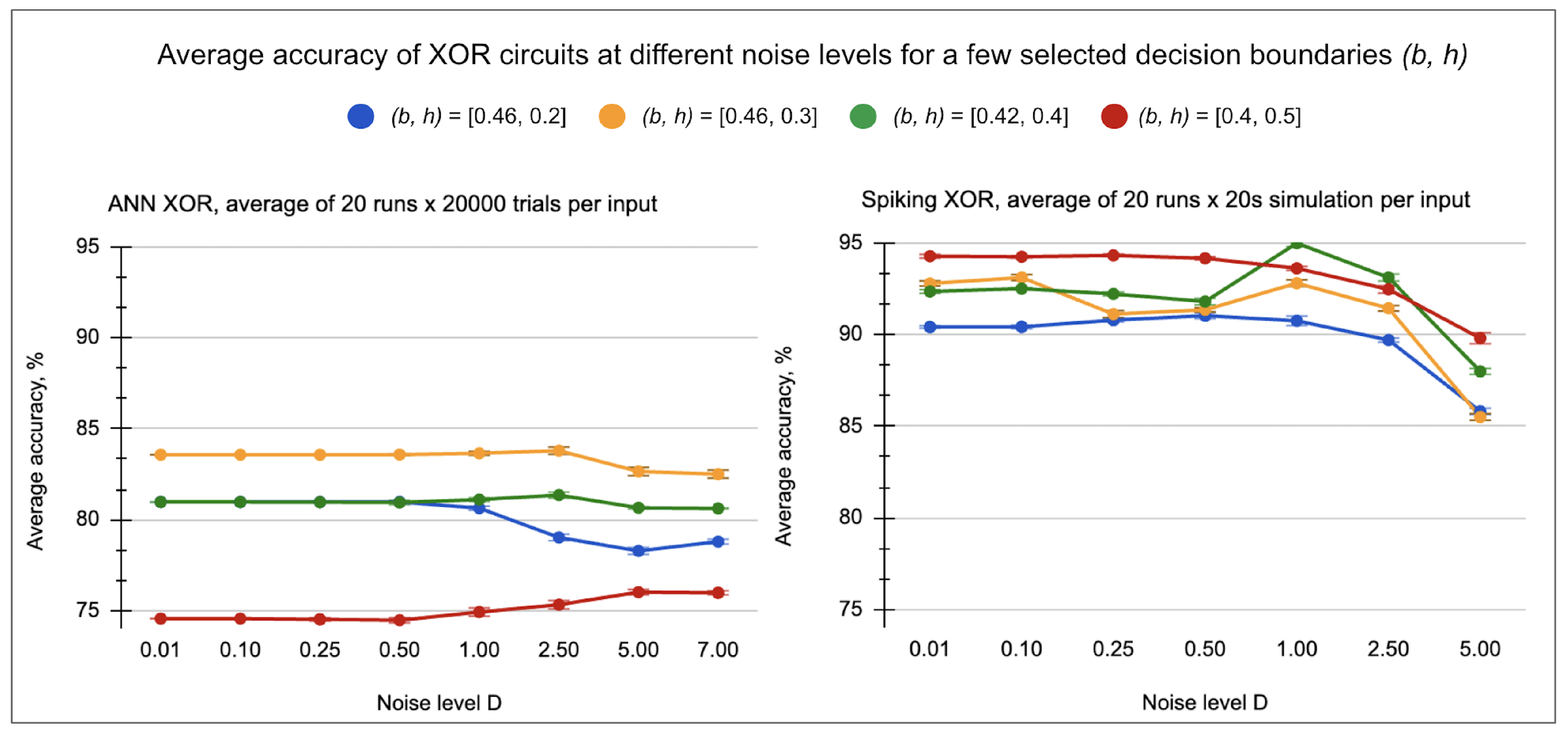
Preprints 114778 g003
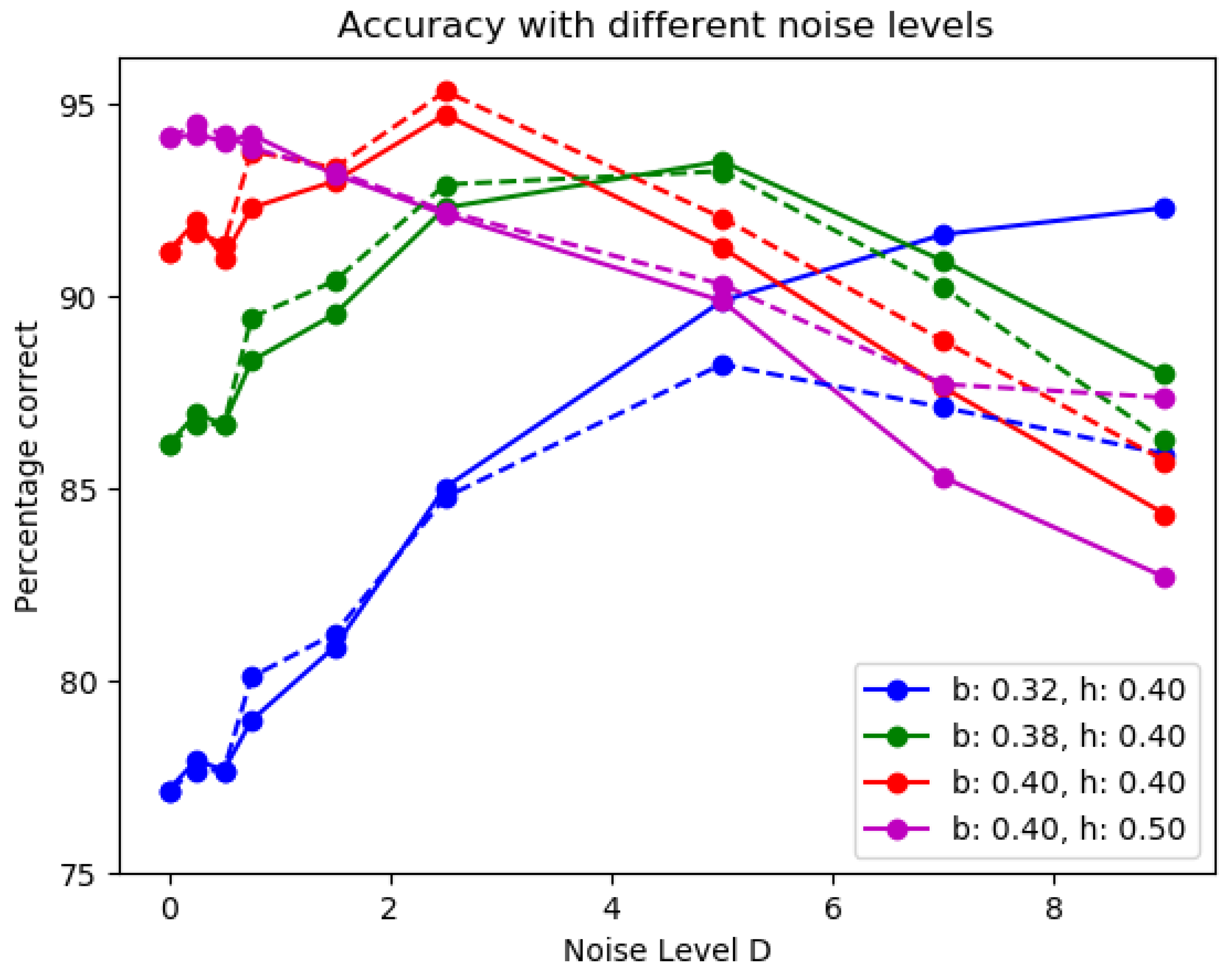
Figure 3. Accuracy percentage for selected "good" boundaries across different levels of common multiplicative noise. a (left): ANN XOR performance at different noise levels. b (right): The spiking circuit performance with "well-selected" gain parameters for τ s y n =1ms: input gain=5, weight gain=110. ANN circuit is tested with the same gain parameters.
Figure 3. Accuracy percentage for selected "good" boundaries across different levels of common multiplicative noise. a (left): ANN XOR performance at different noise levels. b (right): The spiking circuit performance with "well-selected" gain parameters for τ s y n =1ms: input gain=5, weight gain=110. ANN circuit is tested with the same gain parameters.
Preprints 114778 g003
Preprints 114778 g004
Figure 4. The spiking circuit behavior with "well-selected" parameters for τ s y n =1ms: input gain=5, weight gain=110. a (top row): normalized firing frequencies output with different noise intensity D; b (middle row): Phase Locking Value (PLV) between the two input neurons; c (bottom row): PLV between the two hidden layer neurons.
Figure 4. The spiking circuit behavior with "well-selected" parameters for τ s y n =1ms: input gain=5, weight gain=110. a (top row): normalized firing frequencies output with different noise intensity D; b (middle row): Phase Locking Value (PLV) between the two input neurons; c (bottom row): PLV between the two hidden layer neurons.
Preprints 114778 g004

3. Results

3.1. Firing Rates Output Example - Linear Separation with SNN

Note, that while the analog XOR problem is linearly inseparable for the ANN circuit, there is a set of parameters and a decision boundary (b, h) for which the spiking network produces a clear separation.

3.2. Comparing Models’ Performance at Different Noise Levels

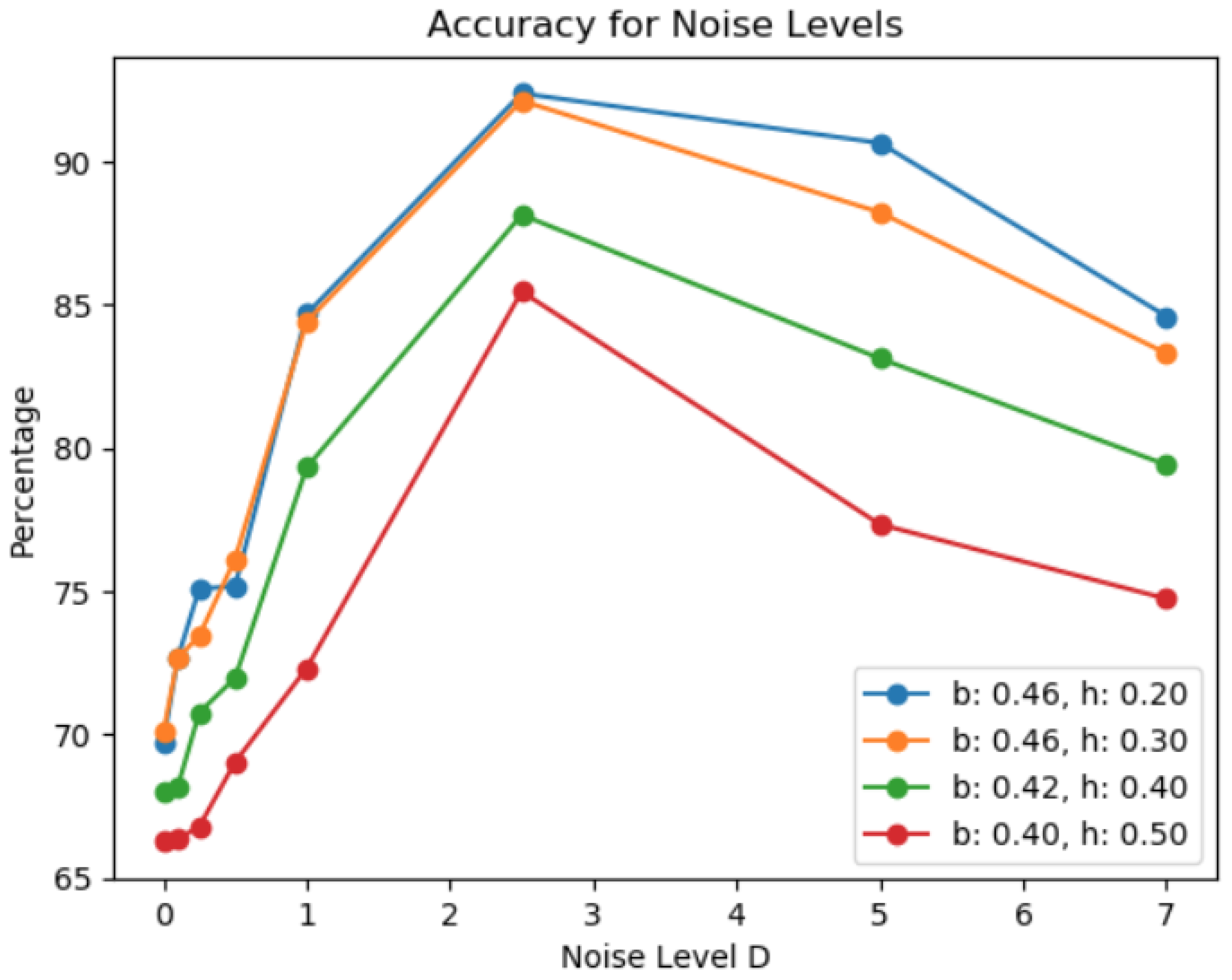
The non-spiking network in Figure 3 has the highest accuracy of 83.56% due to the linear inseparability; the highest accuracy for our current network parameters is achieved with the boundary input value of b=0.46, and firing frequency/activation threshold h=0.3. The spiking version of the circuit yields the following results (the first two are not relevant to noise): (1) 10% improvement for the same decision boundary due to an effect similar to Figure 2, (2) up to 20% improvement for the other non-optimal boundaries indicating non-equivalence gap, and (3) minor noise improvement up to 1-3% for some non-optimal boundaries in both networks.

3.3. Synchronization in Spiking Neurons at Different Noise Levels

3.4. the Independent Vs Common Noise in Spiking Circuit

Figure 5 shows other decision boundaries in the same "well-selected" setting ( τ s y n =1ms, input gain=5, weight gain=110). The independent noise gives slightly more improvement than the common noise at first, but the trend reverses for less optimal boundaries with high noise intensity. Overall, the noise boosts the performance to comparable levels for lower boundaries, making the network more sensitive to input as a consequence of stochastic resonance. A similar effect is observed in Figure 6 with a set of non-optimal gain parameters.

3.5. Example of Improved Performance under Non-Optimal Gain Parameters

4. Discussion

The ability to adapt to changing or missing input is embedded in the brain’s regime of stable propagation of synchronous neural activity among asynchronous global activity [2,6], a combination of rate and temporal coding [15]. The contributing physical properties to temporal coding are the inhibitory connections (feedback) [12], the presence of noise [18], and the short-term plasticity of dynamical synapses [19,20]. These properties are usually omitted in the standard ANN-to-SNN rate-coding-based conversion method [3,4,16].
This work implements temporal features in the XOR network by using synaptic noise and dynamical synapses. The synaptic noise has been shown to have amplifying power due to stochastic resonance, having a stronger effect when the network is not optimally tuned. The short-term plasticity of dynamical synapses has a role of temporal filtering of the firing rates [20], thus allowing the decision boundaries comparable between different noise levels. However, it requires adjusting the gain parameters depending on a selected synaptic time constant and corrupts the equivalency of the ANN and SNN models. Other ways to implement temporal features could be the addition of inhibitory neuron pools [1] or taking the synchronization index into account similar to [15].
While ANNs are fixed to the data they are trained on, SNNs can use noise and other perturbations to improve their performance. The XOR circuit example shows that SNNs can solve problems that ANNs cannot, and they can do so even when their parameters are not optimally tuned.

Author Contributions

Conceptualization, Y.G., S.Y. and Y.K.; methodology, Y.G.; software, Y.G. and S.Y.; validation, S.Y. and Y.K.; resources, Y.G. and S.Y.; writing—original draft preparation, Y.G.; writing—review and editing, Y.G. and S.Y.; supervision, S.Y. and Y.K. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Informed Consent Statement

Not applicable

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors on request.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Abeles, M.; Hayon, G.; Lehmann, D. Modeling compositionality by dynamic binding of synfire chains. J. Comput. Neurosci. 2004, 17, 179–201. [Google Scholar] [CrossRef] [PubMed]
  2. Aviel, Y.; Horn, D.; Abeles, M. Synfire waves in small balanced networks. Neurocomputing 2004, 58–60, 123–127. [Google Scholar] [CrossRef]
  3. Cao, Y.; Chen, Y.; Khosla, D. Spiking deep convolutional neural networks for energy-efficient object recognition. Int. J. Comput. Vis. 2015, 113, 54–66. [Google Scholar] [CrossRef]
  4. Diehl, P.U.; Neil, D.; Binas, J.; Cook, M.; Liu, S.C.; Pfeiffer, M. Fast-classifying, high-accuracy spiking deep networks through weight and threshold balancing. In Proceedings of the IJCNN; 2015; pp. 1–8. [Google Scholar] [CrossRef]
  5. Favier, K.; Yonekura, S.; Kuniyoshi, Y. Spiking neurons ensemble for movement generation in dynamically changing environments. In Proceedings of the IEEE/RSJ; 2020; pp. 3789–3794. [Google Scholar] [CrossRef]
  6. Fries, P. A mechanism for cognitive dynamics: Neuronal communication through neuronal coherence. TiCS 2005, 9, 474–480. [Google Scholar] [CrossRef] [PubMed]
  7. Gerstner, W.; Kistler, W.M. Spiking neuron models: Single neurons, populations, plasticity, 2002.
  8. Gewaltig, M.O.; Diesmann, M. Nest (neural simulation tool). Scholarpedia 2007, 2, 1430. [Google Scholar] [CrossRef]
  9. Lee, C.; Panda, P.; Srinivasan, G.; Roy, K. Training deep spiking convolutional neural networks with stdp-based unsupervised pre-training followed by supervised fine-tuning. Front. Neurosci. 2018, 12. [Google Scholar] [CrossRef] [PubMed]
  10. Lee, J.H.; Delbruck, T.; Pfeiffer, M. Training deep spiking neural networks using backpropagation. Front. Neurosci. 2016, 10, 508. [Google Scholar] [CrossRef] [PubMed]
  11. Legenstein, R.; Maass, W. Ensembles of spiking neurons with noise support optimal probabilistic inference in a dynamically changing environment. PLoS Comput Biol 2014, 10, e1003859. [Google Scholar] [CrossRef] [PubMed]
  12. Liang, H.; Gong, X.; Chen, M.; Yan, Y.; Li, W.; Gilbert, C.D. Interactions between feedback and lateral connections in the primary visual cortex. Proc Natl. Acad. Sci. 2017, 114, 8637–8642. [Google Scholar] [CrossRef] [PubMed]
  13. McGonagle, J. Feedforward neural networks. Brilliant.org, 2024.
  14. Nakajima, M.; Inoue, K.; Tanaka, K.; Kuniyoshi, Y.; Hashimoto, T.; Nakajima, K. Physical deep learning with biologically inspired training method: Gradient-free approach for physical hardware. Nat Commun 2022, 13, 7847. [Google Scholar] [CrossRef] [PubMed]
  15. Reichert, D.P.; Serre, T. Neuronal synchrony in complex-valued deep networks. arXiv 2013, arXiv:1312.6115. [Google Scholar] [CrossRef]
  16. Rueckauer, B.; Lungu, I.A.; Hu, Y.; Pfeiffer, M.; Liu, S.C. Conversion of continuous-valued deep networks to efficient event-driven networks for image classification. Front. Neurosci. 2017, 11, 682. [Google Scholar] [CrossRef] [PubMed]
  17. Stöckl, C.; Maass, W. Optimized spiking neurons classify images with high accuracy through temporal coding with two spikes. Nature Machine Intelligence 2021, 3, 230–238. [Google Scholar] [CrossRef]
  18. Sutherland, C.; Doiron, B.; Longtin, A. Feedback-induced gain control in stochastic spiking networks. Biol. Cybern. 2009, 100, 475–489. [Google Scholar] [CrossRef] [PubMed]
  19. Tsodyks, M.; Uziel, A.; Markram, H. Synchrony generation in recurrent networks with frequency-dependent synapses. J. Neurosci. 2000, 20, RC50. [Google Scholar] [CrossRef] [PubMed]
  20. Tsodyks, M.; Wu, S. Short-term synaptic plasticity. Scholarpedia 2013, 8, 3153. [Google Scholar] [CrossRef]
Preprints 114778 g001
Figure 1. a (left): ANN XOR circuit and b (right): SNN XOR diagrams. Each circuit has two input neurons, two hidden layer neurons, and one output neuron. The circuits` input and weights are scaled.
Figure 1. a (left): ANN XOR circuit and b (right): SNN XOR diagrams. Each circuit has two input neurons, two hidden layer neurons, and one output neuron. The circuits` input and weights are scaled.
Preprints 114778 g001
Preprints 114778 g005
Figure 5. Accuracy percentage for some boundaries across different noise levels in spiking circuit with well-selected parameters for τ s y n =1ms: input gain=5, weight gain=110. Solid line is common noise, dashed line is independent noise.
Figure 5. Accuracy percentage for some boundaries across different noise levels in spiking circuit with well-selected parameters for τ s y n =1ms: input gain=5, weight gain=110. Solid line is common noise, dashed line is independent noise.
Preprints 114778 g005
Preprints 114778 g006
Figure 6. Accuracy for some boundaries across different common noise levels in SNN XOR with non-optimized gain parameters for τ s y n =1ms: input gain=4, weight gain=105.
Figure 6. Accuracy for some boundaries across different common noise levels in SNN XOR with non-optimized gain parameters for τ s y n =1ms: input gain=4, weight gain=105.
Preprints 114778 g006
Table 1. Neuron and simulation parameters for iaf_psc_exp used in the experiment.
Table 1. Neuron and simulation parameters for iaf_psc_exp used in the experiment.
Variable Description, Units Value
C_m Membrane capacitance, pF 10.0
tau_m Membrane time constant, ms 10.0
E_L Resting membrane potential, mV 0.0
V_m Initial membrane potential, mV 0.0
V_reset Reset potential of the membrane, mV 16.0
V_min Lowest value for the membrane potential -1.798e+308
refractory_input Discard input during refractory period False
I_e Constant input current, pA 18. + bias
V_th Spike threshold, mV 20.
tau_fac Synapse facilitation time constant, ms 1
tau_rec Synapse recovery time constant, ms 10
tau_syn Synaptic time constant ( τ s y n ), ms 1
- Simulation resolution, ms 0.1
- Simulation time, s 20.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated