Prerpints.org logo
Preprint
Article

Compressible Diagnosis of the Membrane Fouling Based on the Transfer Entropy

Altmetrics

Downloads

51

Views

24

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

08 August 2024

Posted:

09 August 2024

You are already at the latest version

Alerts
Abstract
Membrane fouling caused by many direct and indirect triggering factors has become an obstacle to the application of membrane bioreactor (MBR). The nonlinear relationship between those factors is subject to complex causality or affiliation, which is difficult to clarify for the diagnosis of membrane fouling. To solve this problem, this paper proposes a compressible diagnosis model (CDM) based on transfer entropy to facilitate the fault diagnosis of the root cause for membrane fouling. Firstly, a framework of CDM between membrane fouling and causal variables is built based on a feature extraction algorithm and mechanism analysis. The framework can identify fault transfer scenarios following the changes in operating conditions. Secondly, the fault transfer topology of CDM based on transfer entropy is constructed to describe the causal relationship between variables dynamically. Thirdly, an information compressible strategy is designed to simplify the fault transfer topology. This strategy can eliminate the repetitious affiliation relationship, which contributes to the root causal variables speedily and accurately. Finally, the effectiveness of the proposed CDM is verified by the measured data from an actual MBR.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

Membrane fouling is an important factor affecting wastewater treatment processes with membrane bioreactor (MBR), which can lead to the loss of membrane flux, deterioration of effluent quality, etc. [1,2,3]. To prevent this phenomenon, it is necessary to accurately diagnose the future case of membrane fouling before implementing efficient strategies [4,5]. However, in MBR, the biochemical process that triggers membrane fouling is complicated and involves amounts of causal variables, such as aeration, reflux, and dosing. The relationship between these variables is time-varying and nonlinear [6,7]. Therefore, it is challenging to establish an accurate diagnosis model for membrane fouling.
To establish the causal relationship between the variables and membrane fouling, some scholars have studied the mechanism of membrane fouling to diagnose its occurrence directly [8,9,10,11]. Lewis et al. analyzed the growth of filter cake in the process of low-pressure cross-flow microfiltration in MBR with fluid dynamics gauging [12]. Then, the diagnosis of membrane fouling was realized by quantifying the significance of membrane pore-level fouling phenomena at the early stage of filtration. In [13], a mechanism model was built for diagnosing membrane fouling by combining adenosine triphosphate and total cell count. The results displayed that this model was suitable for biological fouling diagnosis. In addition, MBR is affected by the flow distribution and hydraulic conditions in the reactor. A residence time distribution technique was developed to determine the impact of membrane geometry, orientation, and mixing efficiency on MBR performance [14]. Azizighannad et al. employed the Raman chemical image to identify the morphology of the membrane fouling [15]. This strategy could diagnose different types of membrane fouling with its observed appearance under specific static conditions. However, the above mechanism methods are difficult to adapt to different working conditions. Since the correction of a large number of parameters is complicated, they are time-consuming for maintaining model accuracy. To dissolve this problem, some data-driven diagnosis models, based on support vector regression (SVR), kernel function (KF) and artificial neural network (ANN) with strong adaptability, were established for membrane fouling [16,17,18,19]. For example, Liu et al. designed an SVR model with a LibSVM package to diagnose the case of membrane fouling in MBR by mapping the relationship between extracellular polymer substances, organic loading rate, transmembrane pressure difference and total membrane resistance [17]. The results showed that the relevant influencing factors of membrane fouling could be uncovered effectively. Han et al. proposed a multi-category diagnosis method based on KF for the detection and early warning of membrane fouling [18]. This method combined multiple binary classifiers to identify the causal variables of membrane fouling. Mittal et al. employed ANN to identify membrane fouling to minimize the risk of its occurrence [19]. The parameters of this model were updated based on the genetic algorithm, which was able to adapt to different operating conditions. The data-driven diagnosis models have the capability of sharpening the nonlinear relationship between input variables and output variables so that causal variables of membrane fouling can be distinguished. However, the existing models lack interpretability and struggle to straighten up interaction among different variables. Then, abundant variables with overlap and collinearity will increase the complexity and confusion of diagnosis.
To achieve a diagnosis process with interpretability, Chen et al. simplified the causality diagram through Granger causality and maximum spanning tree to diagnose the root causal variables of process abnormalities [20]. However, Granger causality analysis is only applicable to the causality analysis of linear processes, which cannot explain the nonlinearity in the membrane fouling. To conquer this challenge, Waghen et al. proposed a multi-level interpretable logic tree to clarify the nonlinear relationship between root causes, intermediate causes, and faults [21]. In addition, several intelligent tools are also introduced to explain the nonlinear process of membrane fouling. For example, Duan et al. developed an accident-relevance tree based on the analysis of the formation mechanism of quality accidents [22]. The method located the root causes of quality accidents utilizing the fuzzy mechanism and the vague nature of datasets. Velásquez et al. combined the decision tree learner and ANN to diagnose power transformer faults of membrane fouling, which reduced the calculation cost and improved the accuracy of fault classification simultaneously [23]. Other similar nonlinear methods can be observed in [24,25]. However, the methods mentioned in [21,22,23,24,25] only focus on the causality between local variables by constructing a tree causality diagram, rather than the interaction between all relevant variables. To provide the causal variables of faults comprehensively, Amin et al. synthesized principal component analysis (PCA) and Bayesian network to capture the nonlinear dependence of high-dimensional process data [26]. Then, the root causal variables of faults were diagnosed with the discretization of continuous data. In [27], a Bayesian network was developed to describe the relationship between alarm variables and root causal variables in thermal power plants. The parameters of the network were updated in a recursive way, which promoted to accurate detection of the root causal variables. Furthermore, Han et al. proposed recursive kernel PCA and Bayesian network to diagnose sludge bulking in the wastewater treatment process [28]. This method effectively captured the nonlinear and time-varying characteristics of sludge bulking to diagnose the root causal variables with high accuracy. However, once the diagnosis models in [26,27,28] are constructed with given datasets, they always hold the invariant information transfer path due to their complexity. When the operating conditions of MBR are changed frequently or drastically, it may be difficult to maintain acceptable accuracy for those models. Additionally, the relationship between those variables of membrane fouling exhibits both time-varying and nonlinear characteristics primarily because membrane fouling is a dynamic and complex process that is influenced by multiple, interacting factors. These characteristics can make it challenging to diagnose membrane fouling effectively.
Based on the above analysis, this paper proposes a compressible diagnosis model (CDM) based on transfer entropy. This model is used to depict the fault transfer topology (FTT) of membrane fouling and further explore the root cause following the operating conditions. The novelties of this work are as follows.
1) Based on the mechanism analysis associated with membrane fouling, the relationship between causal variables and membrane fouling is clarified with the feature extraction algorithm. Then, the related variables of membrane fouling are obtained under different operating conditions. Different from the data-driven diagnosis models in [15,16,17,18,19] with given causal variables, the feature extraction algorithm will enable the proposed CDM to transform raw data into informative representations that can be utilized for diagnosis.
2) Instead of using a mapping relationship with simple input-output representation such as the decision tree [21,22] and the Bayesian network [24,25], a topology based on transfer entropy is constructed. This approach not only provides a qualitative evaluation of the causal relationships between variables by observing the dynamic transfer path, but it also offers a quantitative description of those variables. It helps uncover the path of fault occurrence and further obtain the fault cause priority that may change over time as the operating conditions change.
3) The information compressible strategy (ICS) is designed to delete the redundant or repetitious affiliation relationship between the causal variables. With this strategy, the simplified FTT is obtained with low complexity during the update of fault transfer topology, which can maintain the diagnosis of membrane fouling speedily and accurately.
The rest of this paper is organized as follows. Section II introduces the background of membrane fouling. Section III introduces the diagnosis methods of membrane fouling in detail. Then, the experimental results of diagnosing membrane fouling are introduced in Section IV. Finally, Section V concludes this paper.

2. Background of Membrane Fouling

A. Membrane Fouling

Membrane fouling refers to the increase of water resistance and the decrease of permeation flux caused by the deposition of pollutants on the membrane surface or in its pores. The mechanisms of membrane fouling mainly include: (1) plugging of membrane pores by colloidal and SMP, fouling adhesion and gel layer formation; (2) formation and consolidation of the cake layer; (3) variation in pollutants due to long-term functioning of the reactor; (4) osmotic pressure effect. The membrane fouling has different characteristics, which can be divided into three types: (1) removable fouling, which usually generates in the filter cake layer and can be removed by physical means; (2) irremovable fouling, which usually requires chemical cleaning to remove the pore blockage; (3) irreversible fouling, which cannot be removed by any cleaning operation. In addition, there are various methods for studying membrane fouling, with the Hermia model being the most widely used. This semiempirical parametric model assigns physical significance to its parameters, which is effectively described by this model. The generalized Hermia model is a form of a nonlinear differential equation. It displays the dynamic of membrane fouling and its complex relationships between factors of membrane fouling. According to these characteristics, it is difficult to design a diagnosis method to diagnose the root cause of membrane fouling accurately.

B. Membrane Fouling Diagnosis System

The membrane fouling diagnosis system used for online locating root causal variables in the actual MBR wastewater treatment process is shown in Figure 1. The system consists of four modules: data acquisition module, feature extraction module, online prediction module, and online diagnosis module. The data acquisition module retrieves the value of process variables from sensors and transfers the acquired variables to the database via a programmable logic controller. The feature extraction module is designed to filter the collected process data. In this module, multiple related variables are selected as the preselected variables. Then, the partial least squares (PLS) method is used to reduce the dimension of the preselected variables to obtain the feature variables with a high correlation with the predicted variables. The online prediction module predicts the indicators for identifying membrane states. Finally, the online diagnosis module constructs an FTT to locate root causal variables. It is crucial to take corresponding measures to control membrane fouling.

3. Diagnostic Method of Membrane Fouling

In this section, the CDM based on transfer entropy is proposed to diagnose membrane fouling. First, this method extracts relevant features, which preliminary simplifies the complexity of the system and focuses on key factors influencing membrane fouling. Second, the transfer entropy qualitative is calculated to quantify the causal transfer between different variables, and dynamically analyze the transfer path to form FFT. Finally, the root causal variable is found through the topology. With the design of the information compressible strategy, the causal relationship is further simplified between variables by deleting redundant or repetitive dependencies between causal variables.

A. Feature Variable Selection

In this part, the advantages of the linear regression algorithm and the typical PLS are integrated. Hence, the characteristic variables that have a great impact on membrane fouling detection can be selected. To be specific, the PLS algorithm is adopted in this study and the steps are as follows:
the data of the independent variable is given as P=[p1,p2,…,pj], pj= (p1j, p2j,…, pij)T, i = 1,2,…,m, j = 1,2,…,n, and the dependent variable Q=[q1, q2,…, qi]T. The standard treatment is as follows:
{ p ′ i j = p i j − p ¯ j s j q ′ i = q i − q ¯ s ,
where the standardized P and Q are recorded as E0 and F0. pʹij and qʹi represent the elements in E0 and F0, respectively. p̅j and sj represent the average value and standard deviation of the elements in column j of P, respectively. q̅ and s represent the average value and standard deviation of all elements in Q, respectively. p̅j and q̅ can be expressed by
{ p ¯ j = 1 m ∑ i = 1 m p i j , s j = 1 m − 1 ∑ i = 1 m ( p i j − p ¯ j ) 2 q ¯ = 1 m ∑ i = 1 m q i , s = 1 m − 1 ∑ i = 1 m ( q i − q ¯ ) 2 .
The principal component of the variable is found via the following formula:
{ a h = E h - 1 T F 0 / ‖ E h - 1 T F 0 ‖ 2 v h = E h − 1 a h b h = E h - 1 T v h / ‖ v h ‖ 2 r h = F h - 1 T v h / ‖ v h ‖ 2 E h = E h − 1 − v h b h ,
where h is the number of extracted principal components. Ehis the standardized independent variable matrix when h components are extracted. Fh is the standardized dependent variable matrix when h components are extracted. vh is the component extracted from Eh-1. ah, bhand rh represent the intermediate vectors.
The cross-validity Q h 2 is used to determine the number of final extracted components with
Q h 2 = 1 - L ( h ) / L L ( h − 1 ) ,
where L(h) and LL(h) can be expressed by
L ( h ) = ∑ d = 1 m ( q ′ d − q ′ ^ h ( - d ) ) 2 ， L L ( h ) = ∑ d = 1 m ( q ′ d − q ′ ^ h ( d ) ) 2 ,
where q’d is the dth (0<d≤h+1) element in F0, q̂’ represents the fitting quantity. Sample point d is deleted when modeling with the linear regression model, and h components are taken for regression modeling to obtain the coefficients αi. Then, the fitting value of the dth sample point is calculated and recorded as q̂‘h(-d). Besides, all sample points are used, and h components are taken for regression modeling to obtain coefficients ςi. Finally, the fitting value of the dth sample point is calculated and recorded as q̂‘h(d).
In the process of extracting components, when Q k + 1 2 <0.0975 and the model accuracy reaches the expected requirements, the process of extracting components stops. The number of extracted principal components is m. And the feature variables are represented as X=[x1,x2,…,xm].

B. Membrane Fouling Detection Model

Autoencoder (AE) is a multi-layer neural network of unsupervised learning in deep learning technique, which includes an encoder and a decoder (as shown in Figure 2). The encoder compresses the input data X=[x1,x2,…,xm] to obtain the outputs of the hidden layer H=[h1, h2,…, hs]. And the decoder takes the outputs of the hidden layer as the input and gets the output X̂= [x̂1, x̂2,…, x̂m]. H can be expressed as
H = f ( W x X ) ,
where f(x)=1/(1+e-x) is the activation function. Wx represents the weight between the input layer and the hidden layer, and s<m. The output value X̂ can be expressed as
X ∧ = f ( W h H ) ,
where Wh is the weight between the hidden layer and the output layer.
The back-propagation algorithm is used to adjust the parameters of AE in the training process. For the input variable X=[x1, x2,…, xm], the objective function is defined as
J = 1 2 m ∑ i = 1 m ‖ x i − x i ^ ‖ 2 .
To judge the existence of membrane fouling, the collected data samples for the autoencoder are tested after training. If the reconstruction error is greater than the threshold, it means the membrane fouling exists in the wastewater treatment process.

C. Construction of Fault Transfer Topology

Since transfer entropy can represent the direction of information transfer between variables, it can represent the relationship between fault variables. The transfer entropy is given as follows:
T ( X i + 1 | X , Y ) = ∑ x i + 1 , x i , y j p ( x i + 1 , x i ( k ) , y j ( l ) ) log 2 p ( x i + 1 | x i ( k ) , y j ( l ) ) p ( x i + 1 | x i ( k ) ) ,
where p(·|·) is the conditional probability. xi and yj represent the measured values of X and Y at time i and time j, respectively. Xi+1 represents the measured value of X at the next time. k and l are the implantation dimensions of X and Y, respectively. The transfer entropy represents the influence of the existence of yj on the state of xi+1.
By calculating the transfer entropy between preselected variables, the information transfer relationship between all variables can be obtained. The transfer entropy of Y to X is different from X to Y, which shows that there are differences in the amount of information transferred in two directions. It reflects the difference in the degree of interaction between variables. The direction of causality between variables can be determined by the difference of two transfer entropy:
T Y → X = T ( X i + 1 | X , Y ) − T ( Y i + 1 | Y , X ) .
If TY→X is positive, it means that Y has a greater impact on the information entropy of X than the impact X has on the information entropy of Y. At this time, Y is the causal variable of X. On the contrary, if TY→X is negative, it means that X is the causal variable of Y.
The transfer entropy between all selected variables is calculated to determine the causality, which can build an adjacency matrix A∊Rk×k. Then, the position in the adjacency matrix A is determined according to the direction of causality between variables. If TY→X is positive, it means Y is the causal variable of X. The value of TY→X is placed in row Y and column X of A:
A = ( 0 … 0 … T 1 → a ⋮ ⋱ ⋮ ⋱ ⋮ T a → 1 ⋯ 0 ⋯ 0 ⋮ ⋱ ⋮ ⋱ ⋮ 0 … T a → b … 0 ) ,
where the diagonal value of A is 0. Ta→1 means that the ath variable is the causal variable of the first variable. In turn, the value of T1→a is 0.
Thus, the adjacency matrix between variables can be obtained, and the related variables can be connected by lines according to the values in the matrix to obtain the fault transfer topology. After determining the causal relationship between all variables, FTT can be obtained as shown in Figure 3.

D. Simplification of Fault Propagation Topology

FTT expresses the complex relationship between the variables, which will affect the search for the root causal variables of membrane fouling. Therefore, it is necessary to simplify this topology to identify the main impact relationships.
When X and Y are disrupted, a new sequence is constructed as follows:
{ X s = [ X i , X i + 1 , ... , X i + M − 1 ] Y s = [ Y j , Y j + 1 , ... , Y j + M − 1 ] ,
where M is the number of samples of the new sequence, and N is the total number of samples of the original sequence. The value range of i and j is [1, N-M+1].
The new sequence is a subset of the original sequence. The statistical characteristics in the stationary sequence are the same as those in the original sequence. To ensure no correlation between the two sequences, i and j need to meet ||i-j||≥e, where e is a sufficiently large integer. Then the new sequence formula has two variables with a large time interval. It can be considered that the correlation between the two variables is eliminated by a large time interval. Thus, two variable sequences without causality are obtained. The transfer entropy tes of the multiple sets of such new sequences are calculated and stored in NET with NET = [te1, te2 ,…, tes]. Then, the significance threshold is calculated by
S Y → X = μ N E T + 3 σ N E T ,
where µNET is the mean value of NET and σNET is the standard deviation of NET. The greater difference in transfer entropy than the threshold value represents that there is a causal relationship between variables.
To further simplify the fault transfer topology, an ICS based on a BIC score function is proposed. The designed ICS mainly includes two parts. First, the fitting degree is considered. Then, the complexity of the structure is reduced to avoid the decline in diagnosis accuracy caused by complex models and many other parameters.
For the dataset D = {D1, D2, D3,…, Dm}, m represents the size of the sample dataset. The logarithmic likelihood function of the parameter θ can be expressed as:
I ( θ | D ) = ∑ l = 1 m log P ( D l | θ ) = ∑ i = 1 n ∑ j = 1 q i ∑ k = 1 r i m i j k log θ i j k ,
where θ ={θijk|i=1,2,…,n, j=1,2,…,qi, k=1,2,…,ri}. θijk represents the probability that the value of node Xi is k when the parent node value of node Xi is j. qi represents the total number of parent node set values of node Xi, and qi = 1 when node Xi has no parent node. ri represents the number of possible value types of node Xi, and mijk represents the number of samples that meet Xi = k and the parent node is j in D.
The ICS based on the BIC score function can be expressed as
B I C ( G | D ) = I ( θ | D ) − ∑ i = 1 n q i ( r i − 1 ) 2 log m ,
where BIC(G|D) represents the score for structure G. Through ICS, the indirect connection of variables is scored to determine whether to delete. The presentation of the indirect connection is shown in Figure 4. Then, the simplified FTT is obtained after using ICS.
The information relevance strategy is proposed to find the root causal variables. The main idea of information relevance is to select a node as the starting node arbitrarily, and calculate the sum of transfer entropy of the remaining paths. When the sum of transfer entropy has the maximum value, the variable represented by this node is the root causal variable. The sum of transfer entropy can be expressed as
K i = ∑ v = 1 N T v ( X i + 1 | X , Y ) ,
where Ki represents the sum of the transfer entropy of all paths when the ith node is the starting node. N is the number of paths of the current structure, and Tv represents the transfer entropy corresponding to the vth path. Therefore, the corresponding node variable is selected as the root causal variable when Ki takes the maximum value. The specific steps of membrane fouling diagnosis are shown in Table 1. Additionally, the change in operating conditions will lead to changes in the input distribution of CDM. This means that the potential relationship between process variables will change, the insignificant variables that previously led to membrane fouling may become the root cause and effect variables of the fault. The proposed CDM has two mechanisms to perceive this kind of scenario: 1) The least square method in the process of feature extraction will produce new principal components, which may lead to changes in the composition and number of filtered variables. 2) After recalculating the transfer entropy of the fault variable, FFT will obtain a completely different causal relationship. When these scenarios happen, the steps of membrane fouling diagnosis will be refreshed.

4. Experimental Studies

The effectiveness of CDM is verified in an actual WWTP. The performance of this method is evaluated by diagnosis accuracy (DA). All the simulation experiments were programmed with MATLAB version 2018 and run on a PC with one clock speed of 3.0 GHz and 8 GB of RAM under a Microsoft Windows 10 environment. All data were acquired in real WWTPs from January 1, 2016, to February 27, 2016. 2000 groups of data were selected as samples.

A. Feature Variable Selection

In this experiment, 5000 normal data samples, collected in the actual WWTP, are used to select the feature variables. Chemical oxygen demand (COD), influent NH3-N, influent flow volume, NO3-N in the anoxic zone, influent total phosphorus (TP), oxidation-reduction potential (ORP) in the anaerobic zone, mixed dissolved oxygen (DO) in the aerobic zone, sludge concentration in the aerobic zone, effluent flow volume, liquor suspended solid of the aerobic zone, aeration, effluent turbidity, water temperature, pH, F/M of aerobic zone, transmembrane pressure (TMP) are replaced by numbers 1 to 16, which are selected as pre-selected fault variables in this experiment. The regression coefficient in the obtained regression equation was expressed as the correlation between independent and dependent variables. The coefficients corresponding to all independent variables are shown in Figure 5.
By sorting the coefficients, 12 variables with large regression coefficients are selected as the inputs of the membrane fouling detection model and membrane fouling diagnosis model, which are COD, influent NH3-N, influent TP, ORP in the anaerobic zone, DO in the aerobic zone, sludge concentration in the aerobic zone, effluent flow, aeration, effluent turbidity, water temperature, pH and TMP.

B. Membrane Fouling Detection Model

In this part, 2000 samples of selected variables are used in the training dataset. 800 samples of selected variables are used in the test dataset. The number of nodes in the input layer and output layer of the Autoencoder is 12, and the number of nodes in the hidden layer is 5. The threshold can be determined by the maximum root mean square error in the training process of normal data samples.
The experimental results are shown in Figure 6 and Figure 7. The maximum RMSE of the normal training samples in Figure 6 is used as the threshold, which is shown as the red line in Figure 7. It can be found from Figure 7 that the data samples from 0 to 650 are under normal conditions, while membrane fouling happens in the data samples from 650 to 800. Therefore, it can prove the effectiveness of this method.
A 1 = ( 0 0 0 0.810403 0.464642 0.057451 0.942594 1.247714 0.192291 0.11872 0.094991 1.058295 0.010245 0 0 0.730733 0.43716 0.05863 1.000398 1.228595 0.20512 0.134615 0.122252 1.100775 0.016909 0.001415 0 0.403387 0.28396 0.031732 0.611236 0.579717 0.133133 0.047092 0.073589 0.639023 0 0 0 0 0 0 0.255535 0.470007 0 0 0 0.394362 0 0 0 0.476931 0 0 0.822288 1.030058 0.010018 0 0 0.958113 0 0 0 0.756785 0.276084 0 0.90815 1.065932 0.121703 0.003572 0 1.030733 0 0 0 0 0 0 0 0.244137 0 0 0 0.155584 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.22354 0 0 0.306308 0.342152 0 0 0 0.311331 0 0 0 0.852613 0.355963 0 1.032178 1.267596 0.1403 0 0 1.146267 0 0 0 0.846681 0.325523 0.009613 1.018529 1.201856 0.212144 0.01461 0 1.119884 0 0 0 0 0 0 0 0.140916 0 0 0 0 )
A 2 = ( 0 0 0 0.810403 0 0 0.942594 1.247714 0 0 0 1.058295 0 0 0 0.730733 0 0 1.000398 1.228595 0 0 0 1.100775 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.822288 1.030058 0 0 0 0.958113 0 0 0 0.756785 0 0 0.90815 1.065932 0 0 0 1.030733 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.852613 0 0 1.032178 1.267596 0 0 0 1.146267 0 0 0 0.846681 0 0 1.018529 1.201856 0 0 0 1.119884 0 0 0 0 0 0 0 0 0 0 0 0 )
C. Membrane Fouling Diagnosis Model
According to the experimental results in Figure 5, for simplicity, COD, influent NH3-N, influent TP, ORP in the anaerobic zone, DO in the aerobic zone, sludge concentration in the aerobic zone, effluent flow, aeration, effluent turbidity, water temperature, pH and TMP are replaced by numbers 1 to 12, respectively. The above 12 variables are used as the input of the diagnostic model. 2000 groups of data are selected as samples to construct the initial FTTas shown in Figure 8. The adjacency matrix between variables is shown in A1. It can be found from Figure 8 that the FTT has high complexity, so it is necessary to extract stronger causality. The FTT can be simplified by setting a threshold value. The adjacency matrix between variables is shown in A2. As shown in Figure 9, the simplified FTT is obtained, which can represent the relationship between fault variables.
As shown in Figure 10, the information compressible strategy is used to further simplify the fault transfer topology. The adjacency matrix between the variables is shown in A3. In this experiment, the root causal variables of membrane fouling are diagnosed according to the simplified fault transfer topology, and the effectiveness of CDM is compared with other diagnosis methods.
A 3 = ( 0 0 0 0.810403 0 0 0.942594 1.247714 0 0 0 1.058295 0 0 0 0.730733 0 0 1.000398 1.228595 0 0 0 1.100775 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.822288 0 0 0 0 0.958113 0 0 0 0.756785 0 0 0 1.065932 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1.267596 0 0 0 1.146267 0 0 0 0.846681 0 0 1.018529 1.201856 0 0 0 1.119884 0 0 0 0 0 0 0 0 0 0 0 0 )
To evaluate the diagnostic efficiency of fault transfer topology (FTT) with an information compressible strategy (ICS) and a threshold, the results were compared with some other methods: FTT with threshold, initial FTT, Bayesian network (BN), ANN, and fuzzy logic (FL). The comparison results of FTT with ICS and a threshold to other methods are involved with diagnosis time, number of connections, and accuracy. In Table 2, it can be seen that the proposed FTT with ICS and a threshold achieves the least number of connections compared to FTT without ICS or a threshold. It means that the designed ICS and threshold can simplify the failover topology which also contributes to speeding the diagnosis of membrane fouling. In addition, the accuracy of FTT with ICS and a threshold is also best compared to other methods, which indicates that the proposed FFT in CDM is in favor of exploring the root causal variables of membrane fouling.

D. Analysis of Experimental Results

Based on the above experimental results and analysis, the performance of CDM is significantly superior to other existing methods. The main merits of CDM are summarized as follows.
1) Good detection. It is essential for CDM to identify incidents of membrane fouling with specific causal variables. The proposed autoencoder can summarize thresholds by RMSE for any membrane fouling, assuming it covers the entire normal conditions of MBR. These thresholds can serve as a reference for operators to monitor the occurrence of membrane fouling without the need of a physical or mathematical model. The results in Figs 6-7 also illustrate the efficacy of this method.
2) Intuitive diagnosis. By constructing fault transfer topology with CDM in Figure 8, the dynamic observation of causal relationships between variables facilitates the determination of causal factors leading to membrane fouling. Additionally, to eliminate repetitive affiliation relationships, the fault transfer topology is simplified using an information compressible strategy, as shown in Figs. 9-10. Table 2 also demonstrates that the proposed CDM significantly enhances the speed and accuracy of diagnosis.

5. Conclusions

Membrane fouling is a bottleneck problem to the wide application of MBR. A CDM is proposed, which can diagnose the root causal variables of membrane fouling and improve the diagnosis accuracy. Firstly, the causal relationship between variables is judged based on the transfer entropy to obtain the initial fault transfer topology. Then, the typical causal relationship of variables is extracted based on the significance threshold to obtain the simplified fault transfer topology. For each feasible structure, the fitting degree between data structures and the complexity of the structure are comprehensively considered through the information compressible strategy. The fault transfer topology can be simplified to improve the diagnosis accuracy. The experimental results show that this compressible diagnosis model can accurately diagnose membrane fouling, which is significant for decision-making of membrane fouling. Future research will focus on investigating its generalizability to different MBR systems and other membrane-based processes.

Author Contributions

All authors contributed to the study conception and design. Material preparation, data collection and analysis were performed by Wu Xiaolong, Hou Dongyang, Yang Hongyan and Han Honggui. The first draft of the manuscript was written by Wu Xiaolong and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.

Funding

This work was supported by the National Key Research and Development Project under Grants 2018YFC1900800-5, National Natural Science Foundation of China under Grants 61890930-5 and 61622301, Beijing Natural Science Foundation under Grant 4172005.

Ethical approval

This article does not contain any studies with human participants performed by any of the authors.

Data Availability Statement

The datasets generated during and/or analysed during the current study are not publicly available due to the corporate privacybut are available from the corresponding author on reasonable request.

Conflicts of Interest

The authors have no relevant financial or non-financial interests to disclose.

References

  1. X. Eng. J. 434 (2022) 134666. [CrossRef]
  2. M. B. Tanis-Kanbur, N. R. M. B. Tanis-Kanbur, N. R. Tamilselvam, J.W. Chew, Membrane fouling mechanisms by BSA in aqueous-organic solvent mixtures, J. Ind. Eng. Chem. 108 (2022) 389–399. [CrossRef]
  3. Z. Technol. 347 (2022) 126684. [CrossRef]
  4. S. Membr. Sci. 643 (2022) 120080. [CrossRef]
  5. I. Ruigómez, E. I. Ruigómez, E. González, L. Rodríguez-Gómez, L. Vera, Fouling control strategies for direct membrane ultrafiltration: Physical cleanings assisted by membrane rotational movement, Chem. Eng. J. 436 (2022) 135161. [CrossRef]
  6. P. D. Sutrisna, K. A. P. D. Sutrisna, K. A. Kurnia, U. W. R. Siagian, S. Ismadji, I. G. Wenten, Membrane fouling and fouling mitigation in oil–water separation: A review, J. Environ. Chem. Eng. 10 (2022) 107532. [CrossRef]
  7. J. Environ. Manage. 307 (2022) 114585. [CrossRef]
  8. X. 137 (2023) 108476. [CrossRef]
  9. Y. Environ. Chem. Eng. 9 (2021) 106676. [CrossRef]
  10. S. Environ. Chem. Eng. 10 (2022) 107465. [CrossRef]
  11. C. 296 (2022) 134056. [CrossRef]
  12. W. J. T. Lewis, T. W. J. T. Lewis, T. Mattsson, Y. M. J. Chew, M. R. Bird, Investigation of cake fouling and pore blocking phenomena using fluid dynamic gauging and critical flux models, J. Membr. Sci. 533 (2017) 38–47. [CrossRef]
  13. J.S. Vrouwenvelder, S.A. J.S. Vrouwenvelder, S.A. Manolarakis, J.P. van der Hoek, J.A.M. van Paassen, W.G.J. van der Meer, J.M.C. van Agtmaal, H.D.M. Prummel, J.C. Kruithof, M.C.M. van Loosdrecht, Quantitative biofouling diagnosis in full scale nanofiltration and reverse osmosis installations, Water Res. 42 (2008) 4856–4868. [CrossRef]
  14. Y. Wang, Sanly, M. Brannock, G. Leslie, Diagnosis of membrane bioreactor performance through residence time distribution measurements-a preliminary study, Desalination. 236 (2009) 120–126. [CrossRef]
  15. S. Azizighannad, Raman imaging of membrane fouling, Sep. Purif. Technol. (2020) 6.
  16. K. Membr. Sci. 626 (2021) 119208. [CrossRef]
  17. J. Technol. Innov. 19 (2020) 100844. [CrossRef]
  18. H. Pract. 96 (2020) 104305. [CrossRef]
  19. S. Mittal, A. S. Mittal, A. Gupta, S. Srivastava, M. Jain, Artificial neural network based modeling of the vacuum membrane distillation process: Effects of operating parameters on membrane fouling, Chem. Eng. Process. - Process Intensif. 164 (2021) 108403. [CrossRef]
  20. H. S. Chen, Z. H. S. Chen, Z. Yan, X. Zhang, Y. Liu, Y. Yao, Root cause diagnosis of process faults using conditional granger causality analysis and maximum spanning tree, IFAC-Pap. 51 (2018) 381–386. [CrossRef]
  21. K. Appl. 178 (2021) 115035. [CrossRef]
  22. Y. 171(2023) 113497. [CrossRef]
  23. X. 128(2022) 107858. [CrossRef]
  24. P. Ind. Eng. 147 (2020) 106643. [CrossRef]
  25. R. M. Arias Velásquez, J. V. R. M. Arias Velásquez, J. V. Mejía Lara, Root cause analysis improved with machine learning for failure analysis in power transformers, Eng. Fail. Anal. 115 (2020) 104684. [CrossRef]
  26. Md. T. Amin, F. Md. T. Amin, F. Khan, S. Ahmed, S. Imtiaz, A data-driven Bayesian network learning method for process fault diagnosis, Process Saf. Environ. Prot. 150 (2021) 110–122. [CrossRef]
  27. J. Wang, Z. J. Wang, Z. Yang, J. Su, Y. Zhao, S. Gao, X. Pang, D. Zhou, Root-cause analysis of occurring alarms in thermal power plants based on Bayesian networks, Int. J. Electr. Power Energy Syst. 103 (2018) 67–74. [CrossRef]
  28. H. G. Han, L. X. H. G. Han, L. X. Dong, J. F. Qiao, Data-knowledge-driven diagnosis method for sludge bulking of wastewater treatment process, J. Process Control. 98 (2021) 106–115. [CrossRef]
Preprints 114687 g001
Figure 1. Membrane fouling diagnosis system.
Figure 1. Membrane fouling diagnosis system.
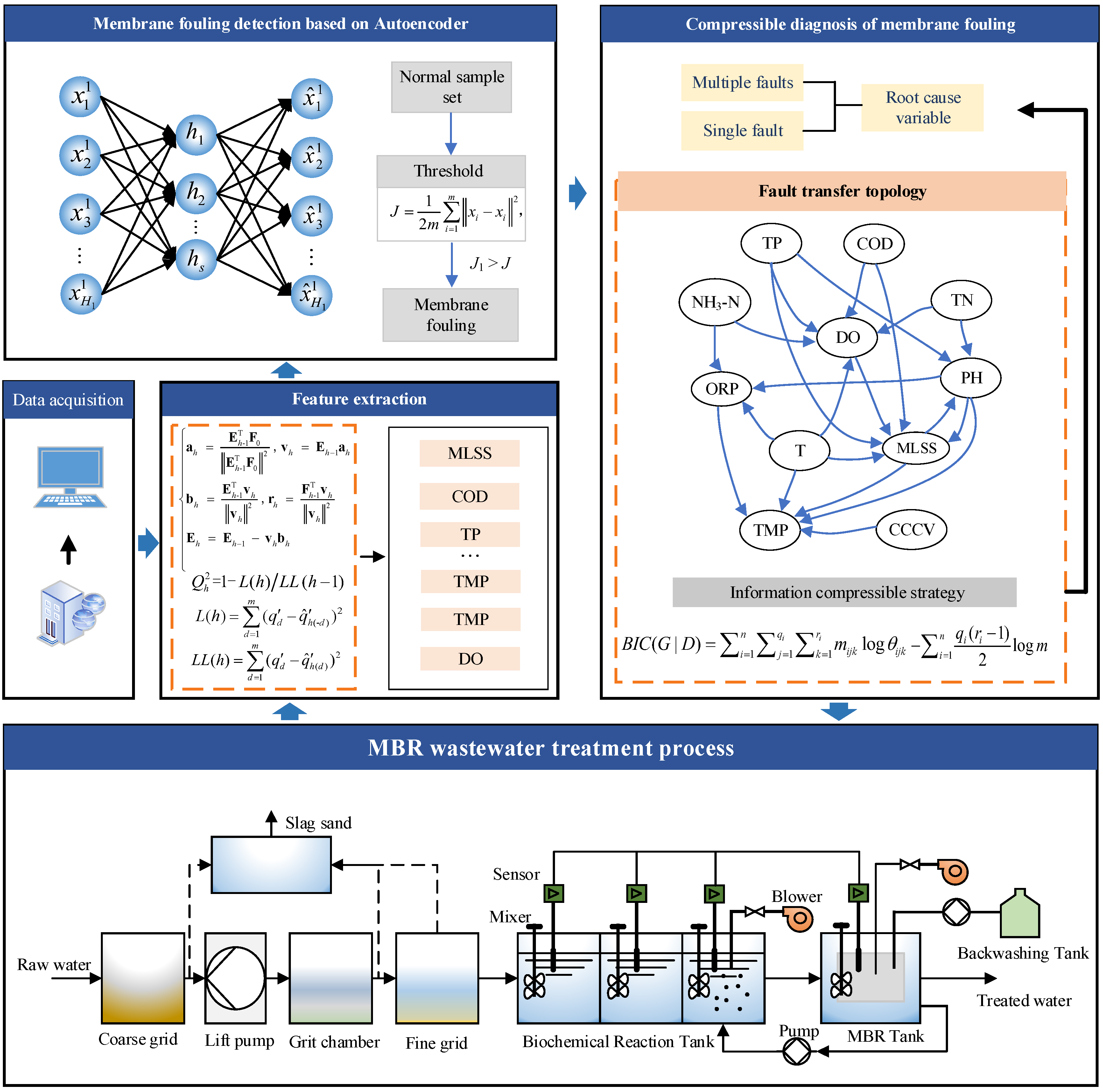
Preprints 114687 g001
Preprints 114687 g002
Figure 2. Autoencoder structure.
Figure 2. Autoencoder structure.
Preprints 114687 g002
Preprints 114687 g003
Figure 3. Fault transfer topology.
Figure 3. Fault transfer topology.
Preprints 114687 g003
Preprints 114687 g004
Figure 4. Indirect connection.
Figure 4. Indirect connection.
Preprints 114687 g004
Preprints 114687 g005
Figure 5. Characteristic variable selection.
Figure 5. Characteristic variable selection.
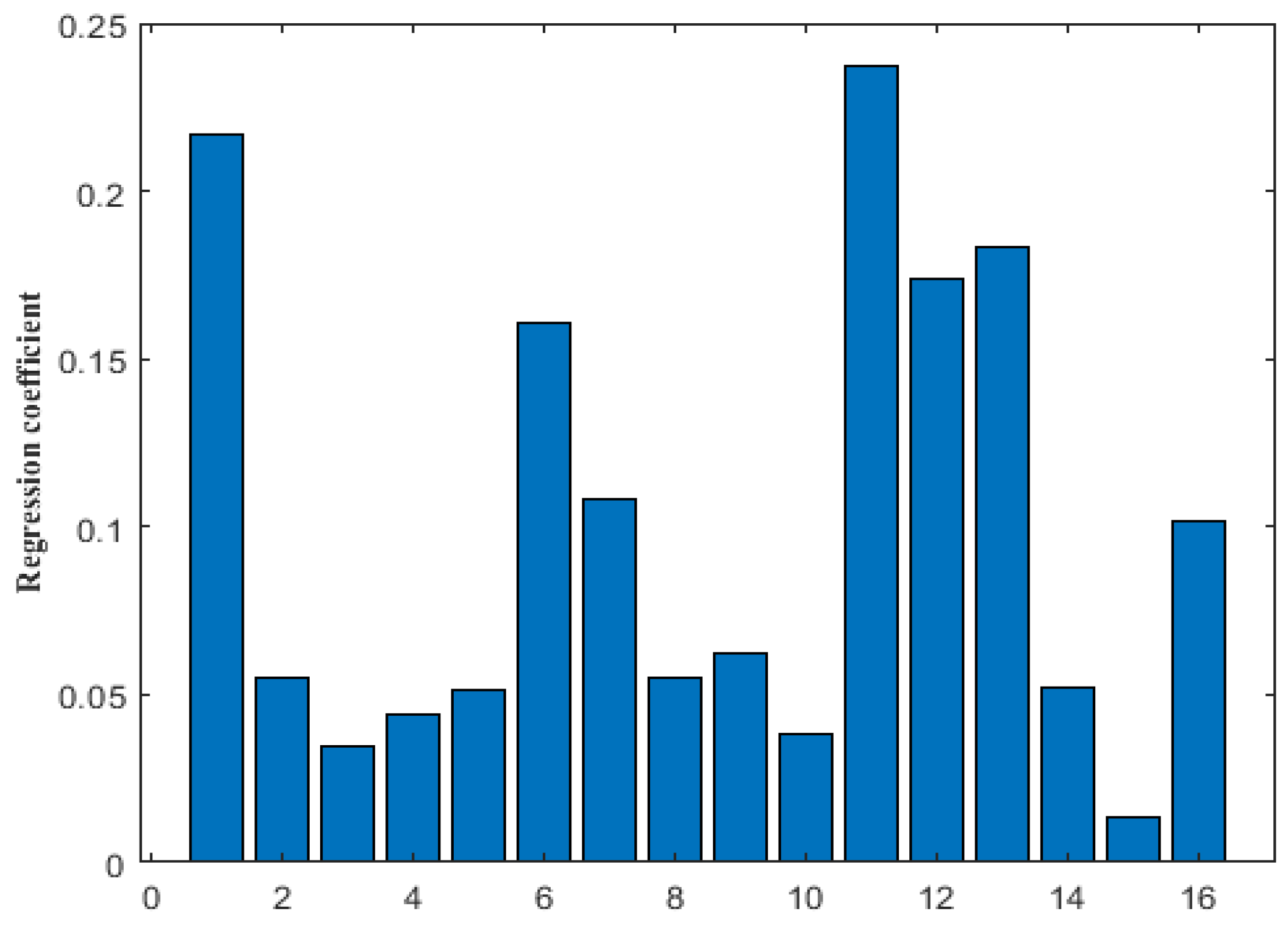
Preprints 114687 g005
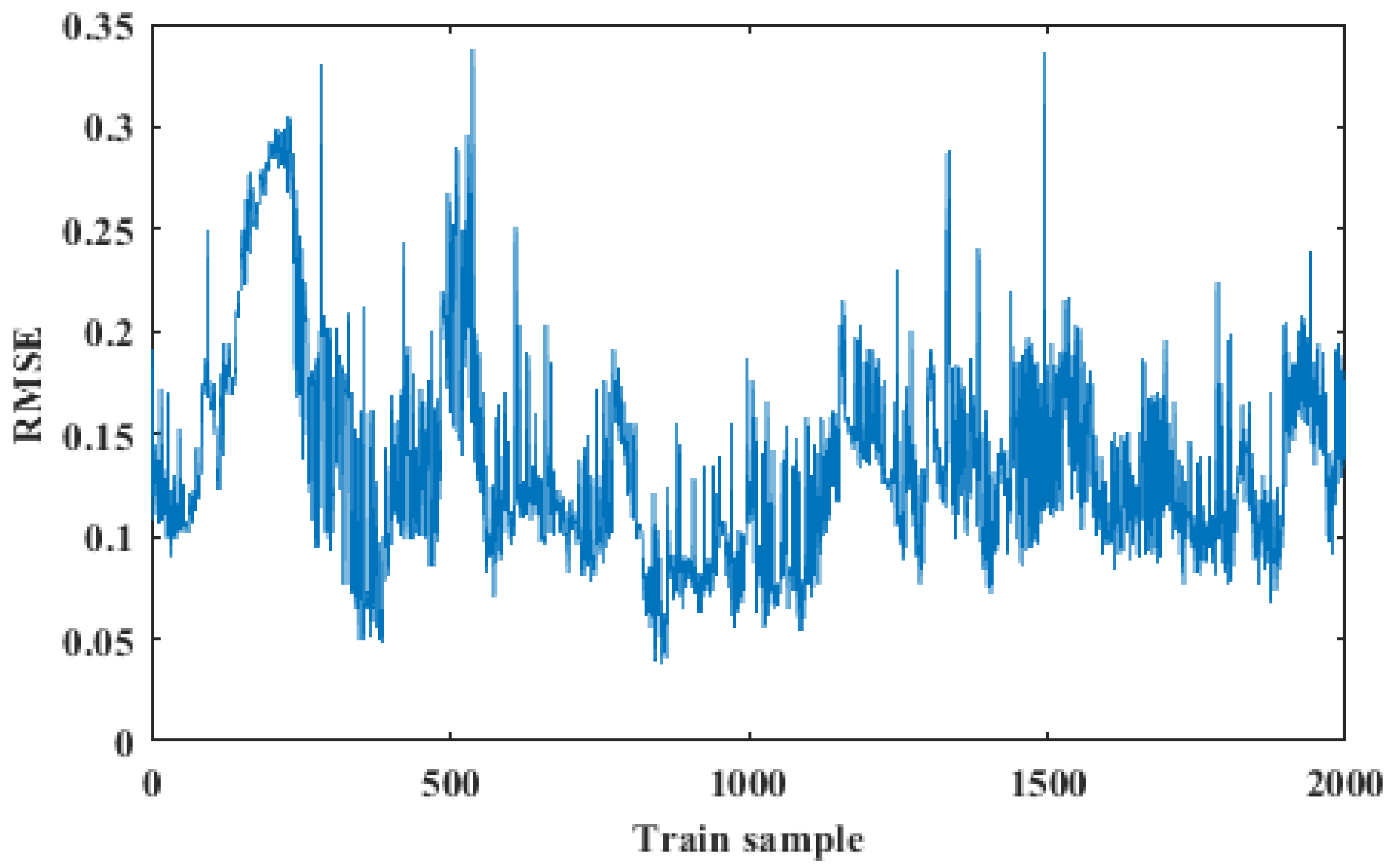
Preprints 114687 g006
Figure 6. The RMSE during the training process.
Figure 6. The RMSE during the training process.
Preprints 114687 g006
Preprints 114687 g007
Figure 7. The RMSE during the detection process.
Figure 7. The RMSE during the detection process.
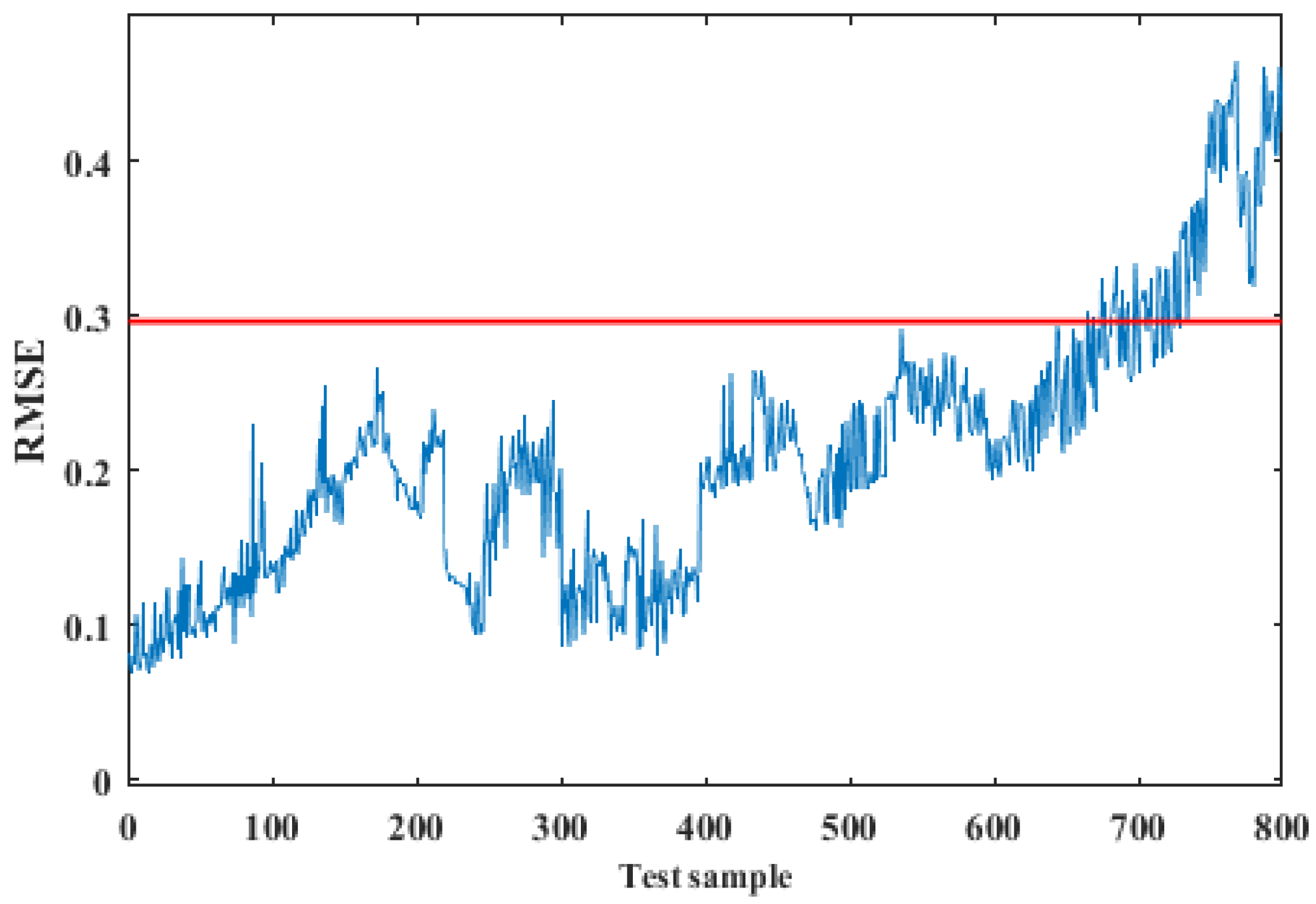
Preprints 114687 g007
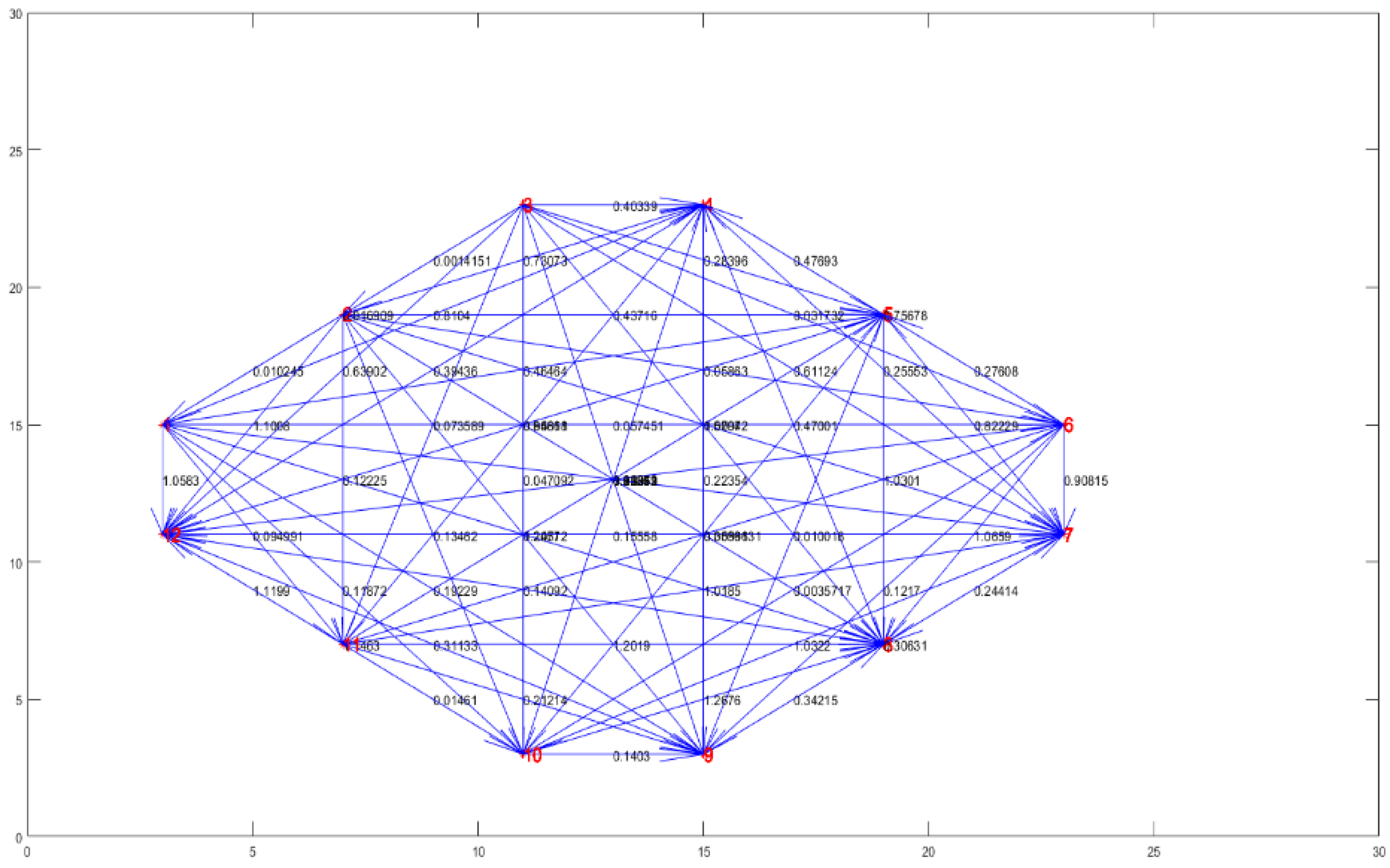
Preprints 114687 g008
Figure 8. Initial fault transfer topology.
Figure 8. Initial fault transfer topology.
Preprints 114687 g008
Preprints 114687 g009
Figure 9. Fault transfer topology after setting the threshold.
Figure 9. Fault transfer topology after setting the threshold.
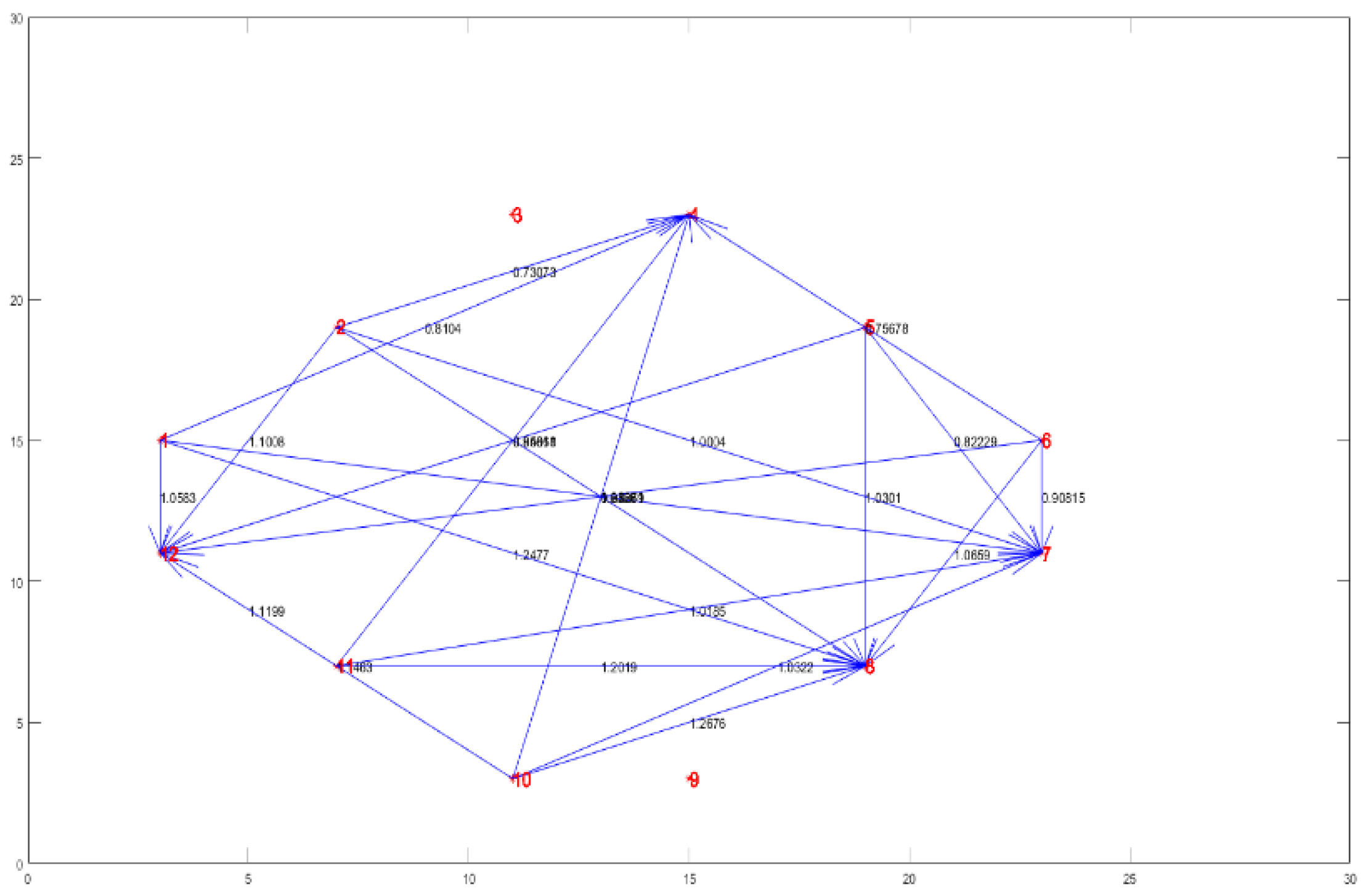
Preprints 114687 g009
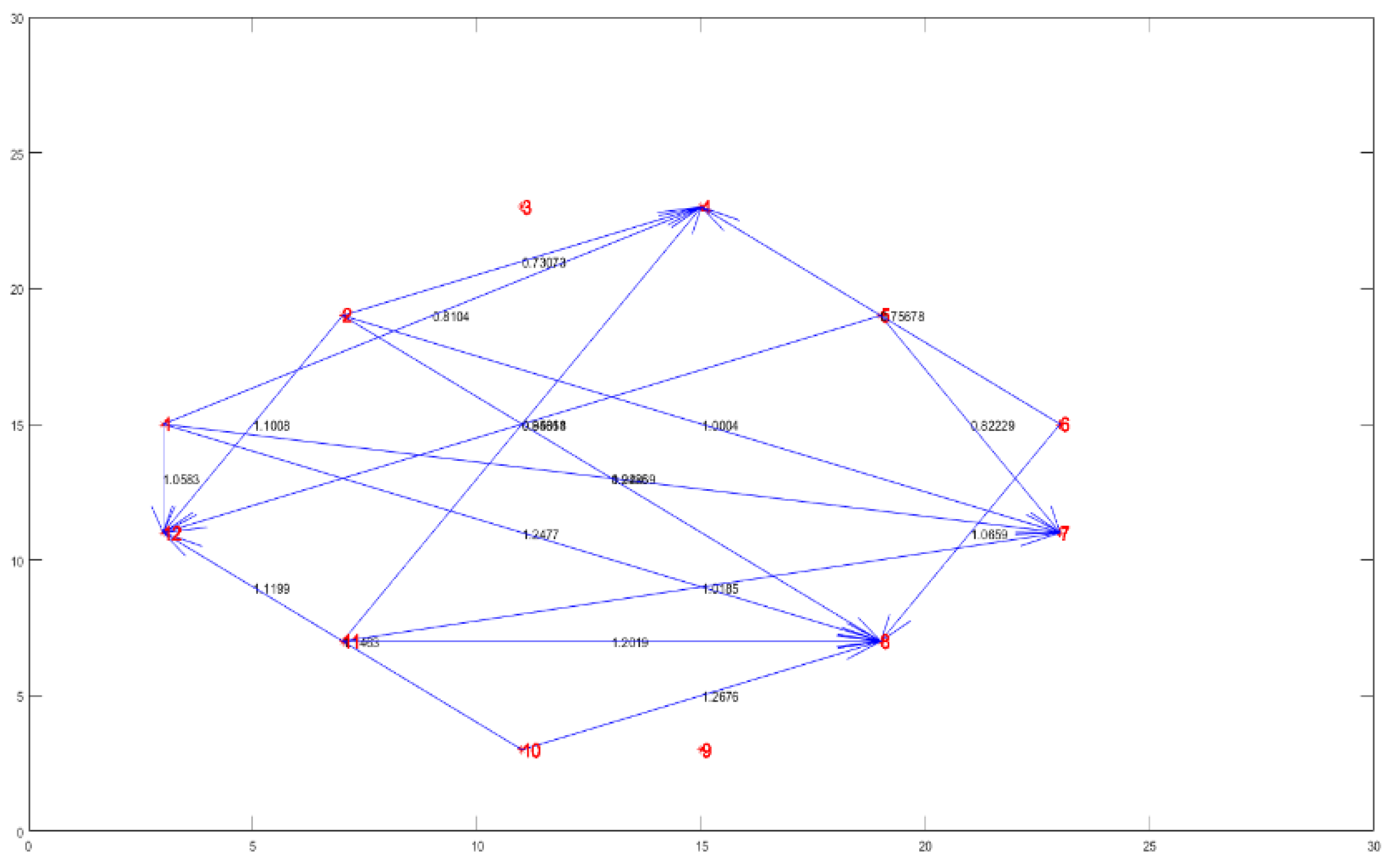
Preprints 114687 g010
Figure 10. Fault transfer topology based on information compressible strategy.
Figure 10. Fault transfer topology based on information compressible strategy.
Preprints 114687 g010
Table 1. Specific steps of membrane fouling diagnosis.
Table 1. Specific steps of membrane fouling diagnosis.
%Characteristic variable selection刘1 Standardize the data to obtain E0 and F0 % Equations (1) and (2)刘2 Get the principal component of the variable % Equation (3)刘3 Determine the number of final extracted components % Equations (4) and (5)刘Obtain K variables that have a great influence on membrane fouling 刘%Membrane fouling detection model刘1 Acquire normal data and train an autoencoder刘2 Obtain the threshold of reconstruction error J0 of normal samples刘3 Use the autoencoder to detect the data collected in real time, and the reconstruction error J is obtained刘4 If J > J0, the membrane fouling exists刘% Calculate the transfer entropy between variables刘Get the influence relationship between variables TY→X % Equations (9) and (10)刘% Generate adjacency matrix Akk刘for j=1: k do刘for i=j+1: k do刘if Tj→i>0 刘Aji= Tj→i刘else刘Aij= Tj→i刘end for刘end for刘FTT is obtained because the relationship between variables is connected by lines according to the adjacency matrix Akk.刘% Simplify fault transfer topology刘Set threshold刘1 Select two data segments with a long time distance from historical data of the two variables刘2 Calculate of entropy transfer tei between the above two data segments % Equation (10)刘3 Repeat steps 1 and 2, calculate multiple sets of such transfer entropy NET = [te1, te2 ,…, tes]刘4 Calculate the average value and standard deviation of NET to get the threshold % Equation (13)刘Information compressible strategy 刘1 Filter all direct and indirect transfer relationships between variables刘2 Calculate the score of the structure for each transfer relationship % Equations (14) and (15)刘3 Choose the transfer relationship corresponding to the highest score刘The root causal variables are determined according to the simplified fault transfer topology
Table 2. Performance of different methods.
Table 2. Performance of different methods.
Methods Time(s) Number of connections Accuracy(%)
FTT with ICS and threshold 8.3 18 93.4%
FTT with threshold 9.5 23 91.0%
Initial FTT 14.9 66 86.7%
BN 12.1 -- 85.1%
ANN 13.3 -- 82.3%
FL 19.8 -- 82.1%
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated