Anion and Cation Dynamics in Mixed-Anion Hydroborate Na3(BH4)(B12H12): 1H, 11B, and 23Na NMR Studies

Sodium borohydride-closo-hydroborate Na3(BH4)(B12H12) exhibits the high room-temperature ionic conductivity and high electrochemical stability. To study the dynamical properties of this mixed-anion compound at the microscopic level, we have measured the 1H, 11B, and 23Na nuclear magnetic resonance spectra and nuclear spin-lattice relaxation rates over the temperature range of 8 – 573 K. Our 1H and 11B spin-lattice relaxation measurements have revealed two types of reorientational jump motion. The faster motional process attributed to reorientations of the [BH4]− anions is characterized by the activation energy of 159 meV, and the corresponding reorientational jump rate reaches ~10^8 s^-1 near 130 K. The slower process ascribed to reorientations of the larger [B12H12]− anions is characterized by the activation energy of 319 meV, and the corresponding reorientational jump rate reaches ~10^8 s^-1 near 240 K. The results of the 23Na nuclear magnetic resonance measurements are consistent with the fast long-range diffusion of Na+ ions in Na3(BH4)(B12H12). The diffusive jump rate of Na+ is found to reach ~10^4 s^-1 at 300 K and ~8 × 10^8 s^-1 at 530 K. Comparison of these jump rates with the ionic conductivity data suggests the importance of correlations between diffusing ions.

Keywords:

Subject: Chemistry and Materials Science - Physical Chemistry

1. Introduction

Metal hydroborates are a fascinating class of materials that exhibit remarkably diverse structural chemistries and properties [1,2]. The discovery of superionic conductivity in alkali-metal borohydrides [3] and closo-borates [4,5] has attracted additional interest to these materials as prospective solid electrolytes for batteries [6,7,8]. It should be noted that high ionic conductivities are usually observed above the order-disorder phase transition points, while the ordered (low-temperature) phases of both borohydrides and closo-borates exhibit poor ionic conductivities. Since the order-disorder phase transitions in these compounds typically occur above room temperature, for practical applications, it would be desirable to reduce the phase transition point and to retain the disordered phase down to lower temperatures. One of the possible strategies for stabilizing the disordered phase is based on anion mixing. This strategy has proved to be effective both for borohydrides (where [BH₄]⁻ anions are partially replaced by halide anions [9,10]) and for closo-borates (where nearly spherical [B₁₂H₁₂]²⁻ or [CB₁₁H₁₂]⁻ anions are partially substituted by ellipsoid-shaped [B₁₀H₁₀]²⁻ or [CB₉H₁₀]⁻ [11,12,13,14]). Recently, the mixed-anion borohydride – closo-hydroborate compounds Na₃(BH₄)(B₁₂H₁₂), (Li_0.7Na_0.3)₃(BH₄)(B₁₂H₁₂), and K₃(BH₄)(B₁₂H₁₂) have been synthesized using mechanochemistry methods [15,16]. Na₃(BH₄)(B₁₂H₁₂) is found to retain the same structure in a wide temperature range of 100 – 653 K showing rather high ionic conductivity of 0.5×10^-3 S/cm at room temperature [15]. In contrast, K₃(BH₄)(B₁₂H₁₂) exhibits two structural phase transitions at high temperatures (at ~565 K and ~680 K) and the low ionic conductivity of 2×10^-6 S/cm at 380 K [16].

The important dynamical feature of metal hydroborates is that the complex anions can participate in the fast reorientational (rotational) motion [17]. This motion strongly contributes to the balance of energies determining the thermodynamic stability of hydroborates. Furthermore, the reorientational motion of complex anions may play a significant role in the ionic conductivity mechanisms, facilitating fast cation diffusion [18,19,20,21]. In the present work, we use ¹H, ¹¹B, and ²³Na nuclear magnetic resonance (NMR) measurements of the spectra and nuclear spin-lattice relaxation rates to obtain microscopic information on both the reorientational motion of complex anions ([BH₄]⁻ and [B₁₂H₁₂]²⁻) and the diffusive motion of Na⁺ cations in the mixed-anion hydroborate Na₃(BH₄)(B₁₂H₁₂). The results will be compared to those for the previously investigated mixed-anion compound K₃(BH₄)(B₁₂H₁₂) [16].

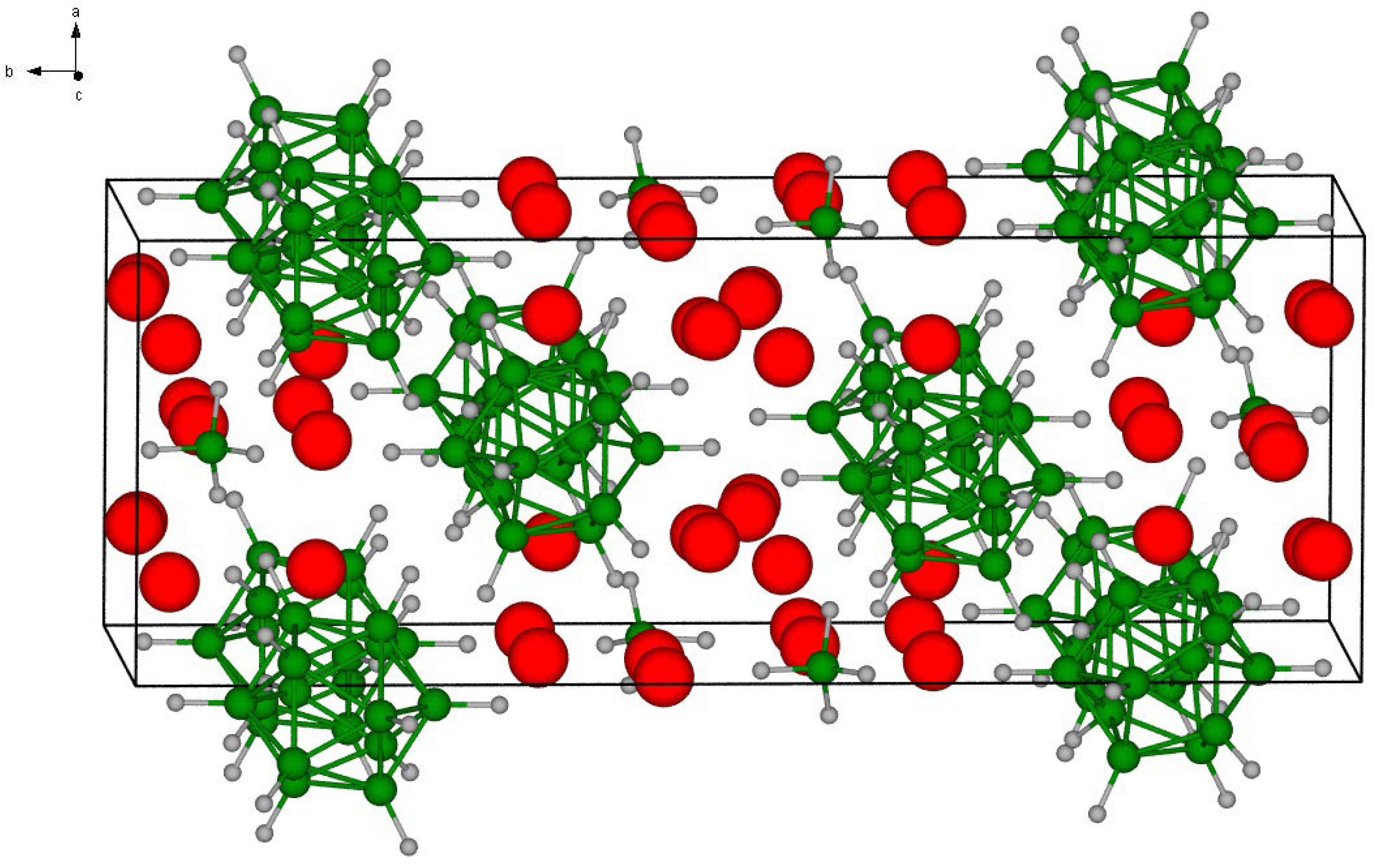
2. Materials and Methods

The synthesis of Na₃(BH₄)(B₁₂H₁₂) was analogous to that described in Ref. [15]. The mixed-anion compound was prepared by ball-milling the 1:1 mixture of NaBH₄ (from Sigma-Aldrich) and Na₂B₁₂H₁₂ (from Katchem) and consecutive heat treatment to 673 K in aluminum crucible in a closed system at the rate of 5 K/min. All sample handling was done in a glovebox under argon atmosphere. According to X-ray powder diffraction analysis [15], Na₃(BH₄)(B₁₂H₁₂) retains the orthorhombic crystal structure (space group Cmc2₁) in the temperature range of 100 – 653 K with the lattice parameters a = 8.0083(4) Å, b = 21.881(1) Å, and c = 7.7672(4) Å at 523 K. The schematic view of this structure is shown in Figure 1.

For NMR experiments, the sample was flame-sealed in a quartz tube under vacuum. Low-field NMR measurements of the spectra and spin-lattice relaxation rates were performed on a pulse spectrometer with quadrature phase detection at the frequencies ω/2π = 14 and 28 MHz (¹H), 28 MHz (¹¹B) and 23 MHz (²³Na). The magnetic field was provided by a 2.1 T iron-core Bruker magnet. A home-built multinuclear continuous-wave NMR magnetometer working in the range 0.32 – 2.15 T was used for field stabilization. For rf pulse generation, we used a SpinCore PB24-100-4K computer-controlled pulse programmer, the PTS frequency synthesizer (Programmed Test Sources, Inc.), and a 1 kW Kalmus wideband pulse amplifier. Typical values of the π/2 pulse length were 2 – 3 μs for ¹H and 3 – 4 μs for ¹¹B and ²³Na. A probe head with the sample was placed into an Oxford Instruments CF1200 continuous-flow cryostat using nitrogen or helium as a cooling agent. The sample temperature, monitored by a chromel-(Au-Fe) thermocouple, was stable to ±0.1 K. Measurements at T > 450 K were performed using a furnace probe head; for this setup, the sample temperature, monitored by a copper – constantan thermocouple, was stable to ±0.5 K. High-field measurements of the ²³Na spin-lattice lattice relaxation rate were performed on a Bruker AVANCE III 500 spectrometer at the frequency ω/2π = 132 MHz. The nuclear spin-lattice relaxation rates were measured using the saturation–recovery method. NMR spectra were recorded by Fourier transforming the solid echo signals (pulse sequence π/2_x – t – π/2_y).

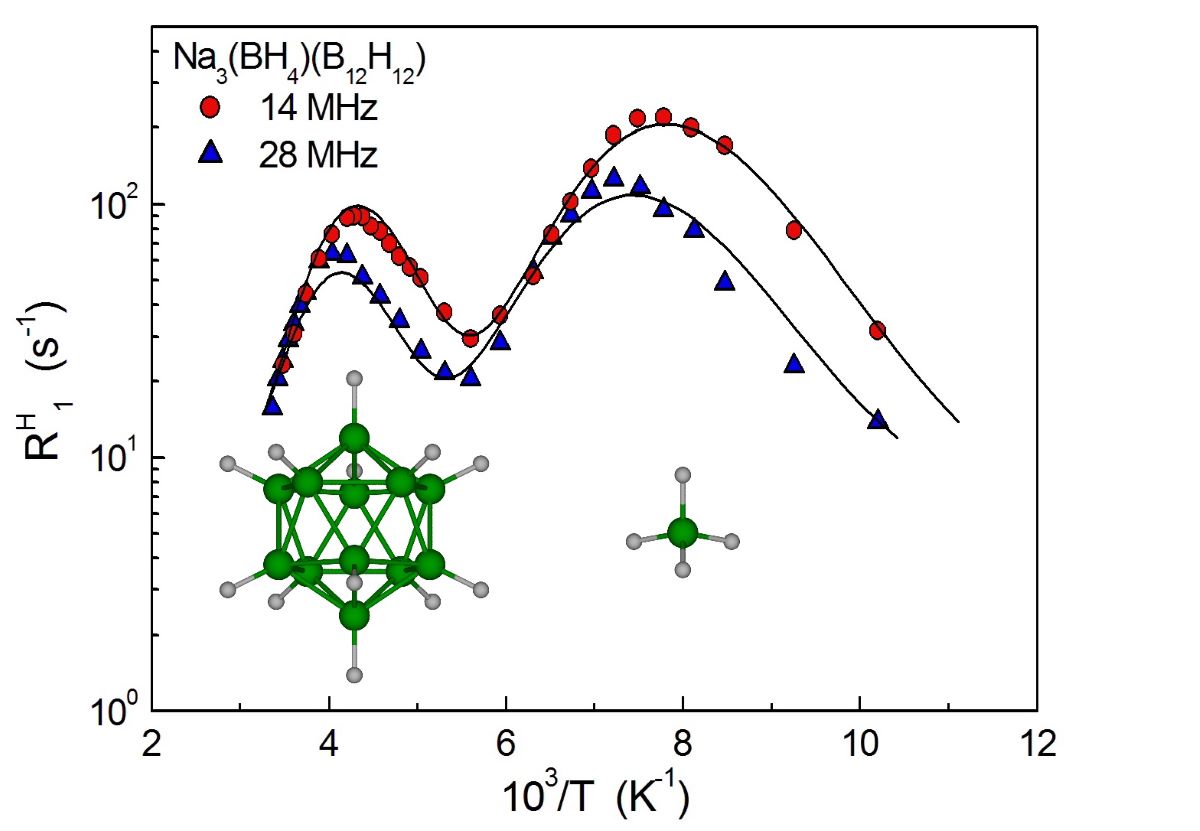
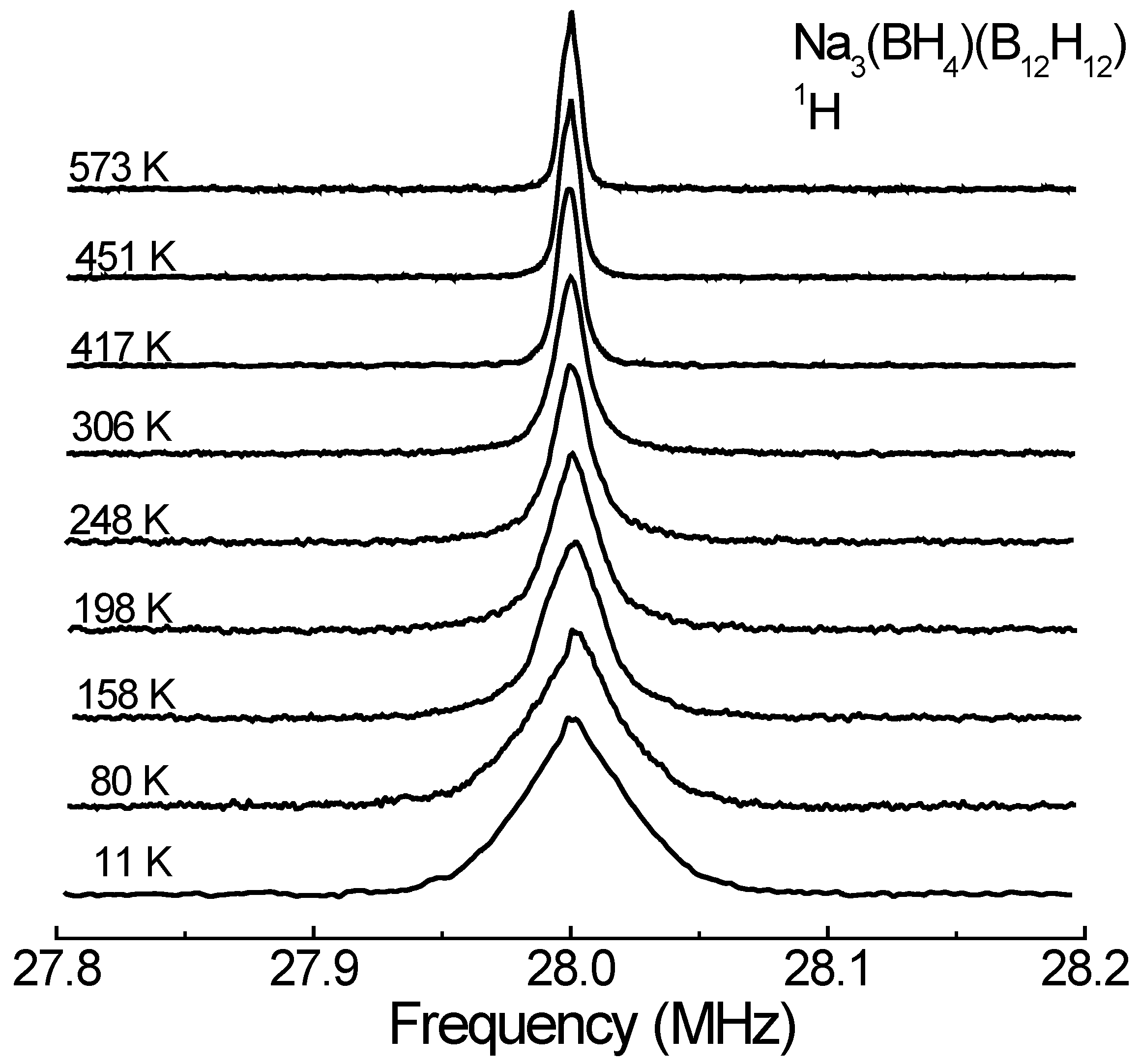
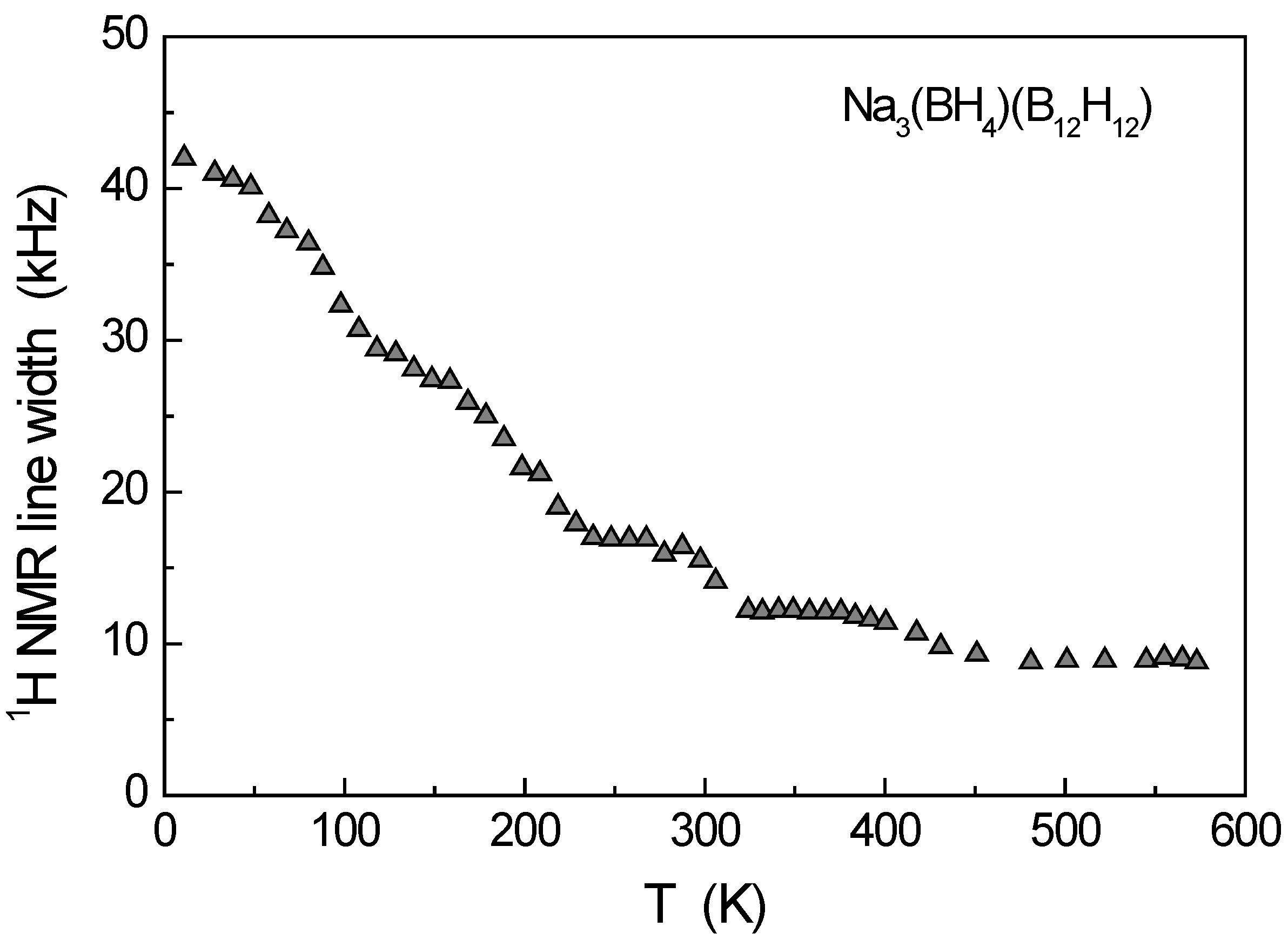
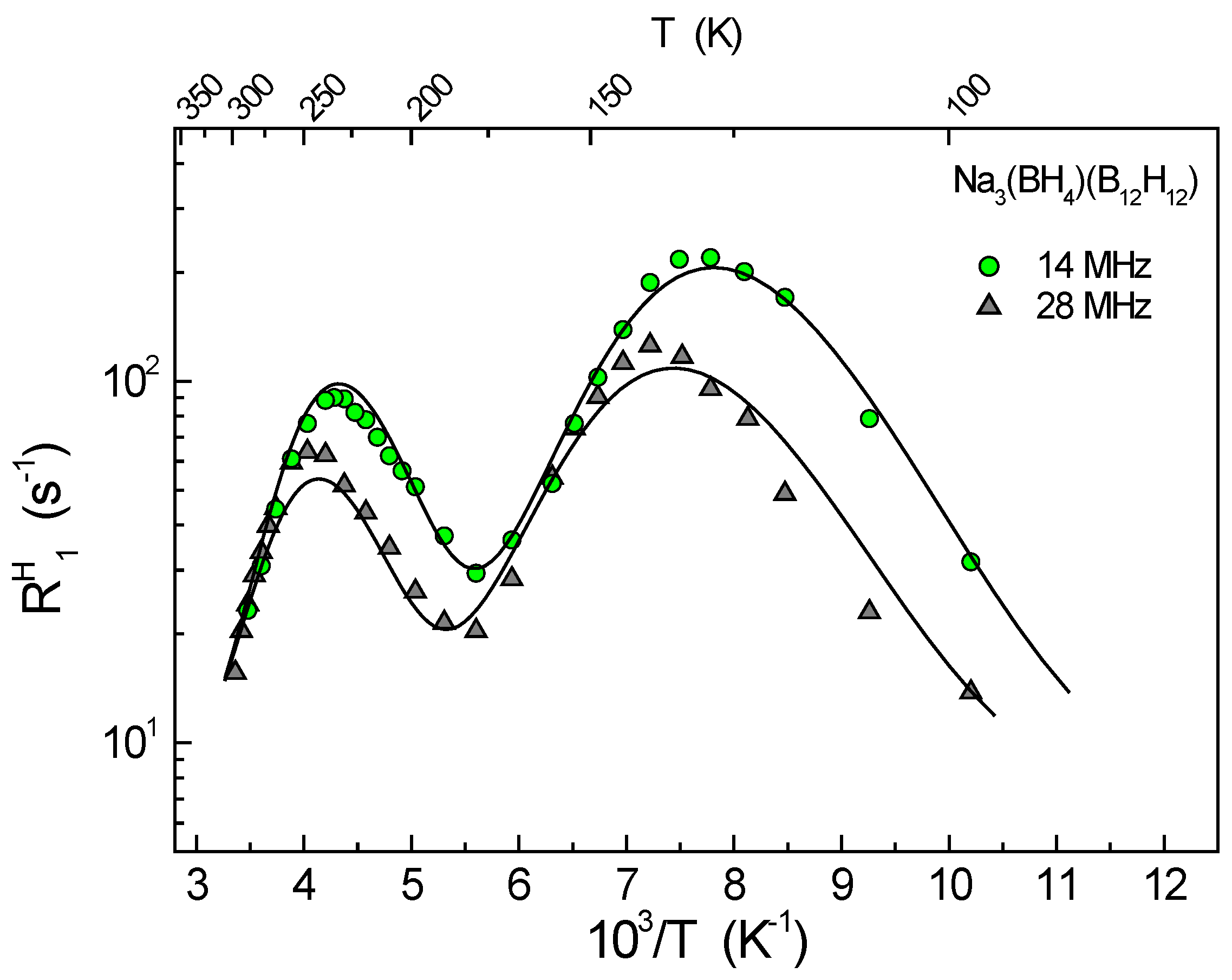
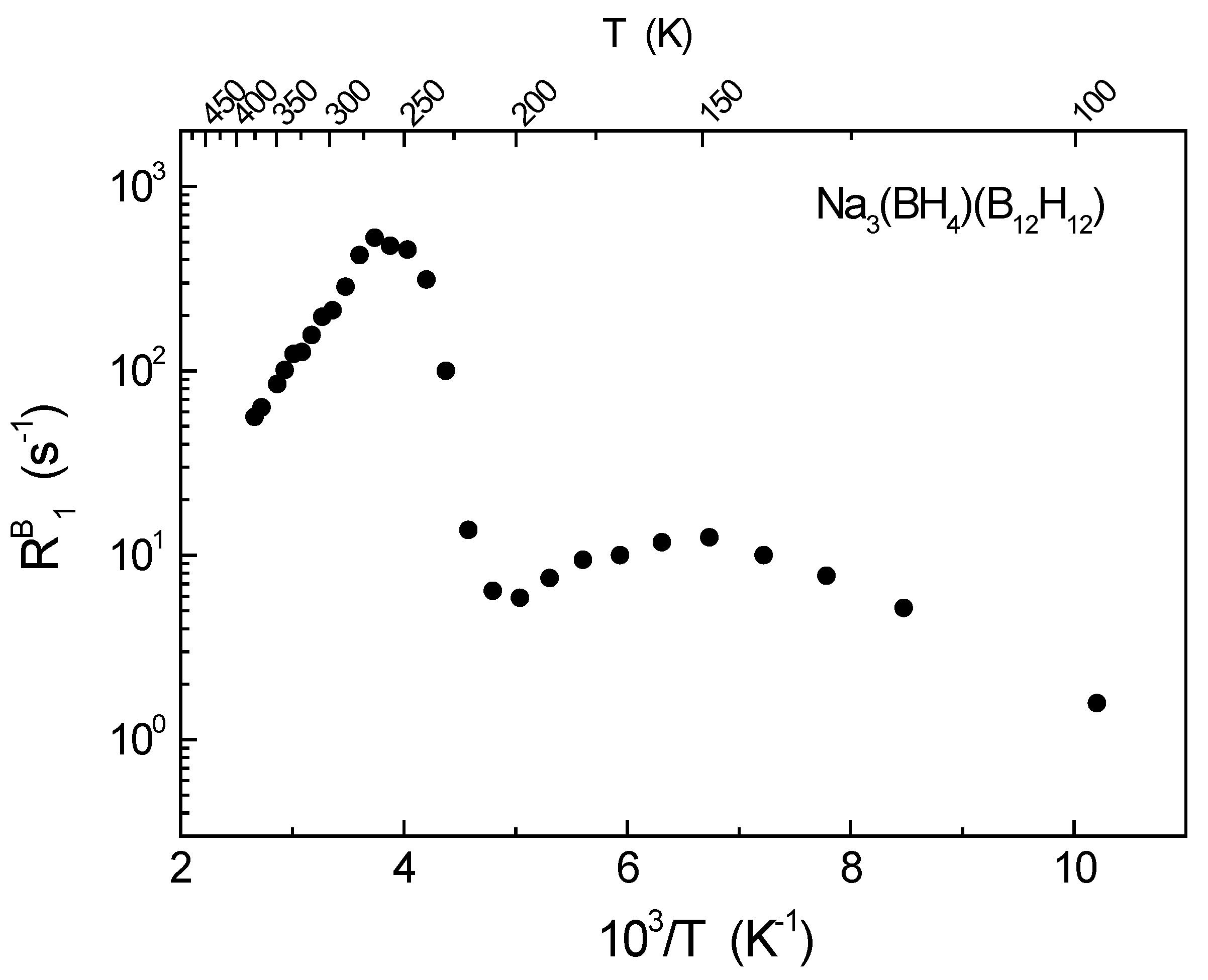
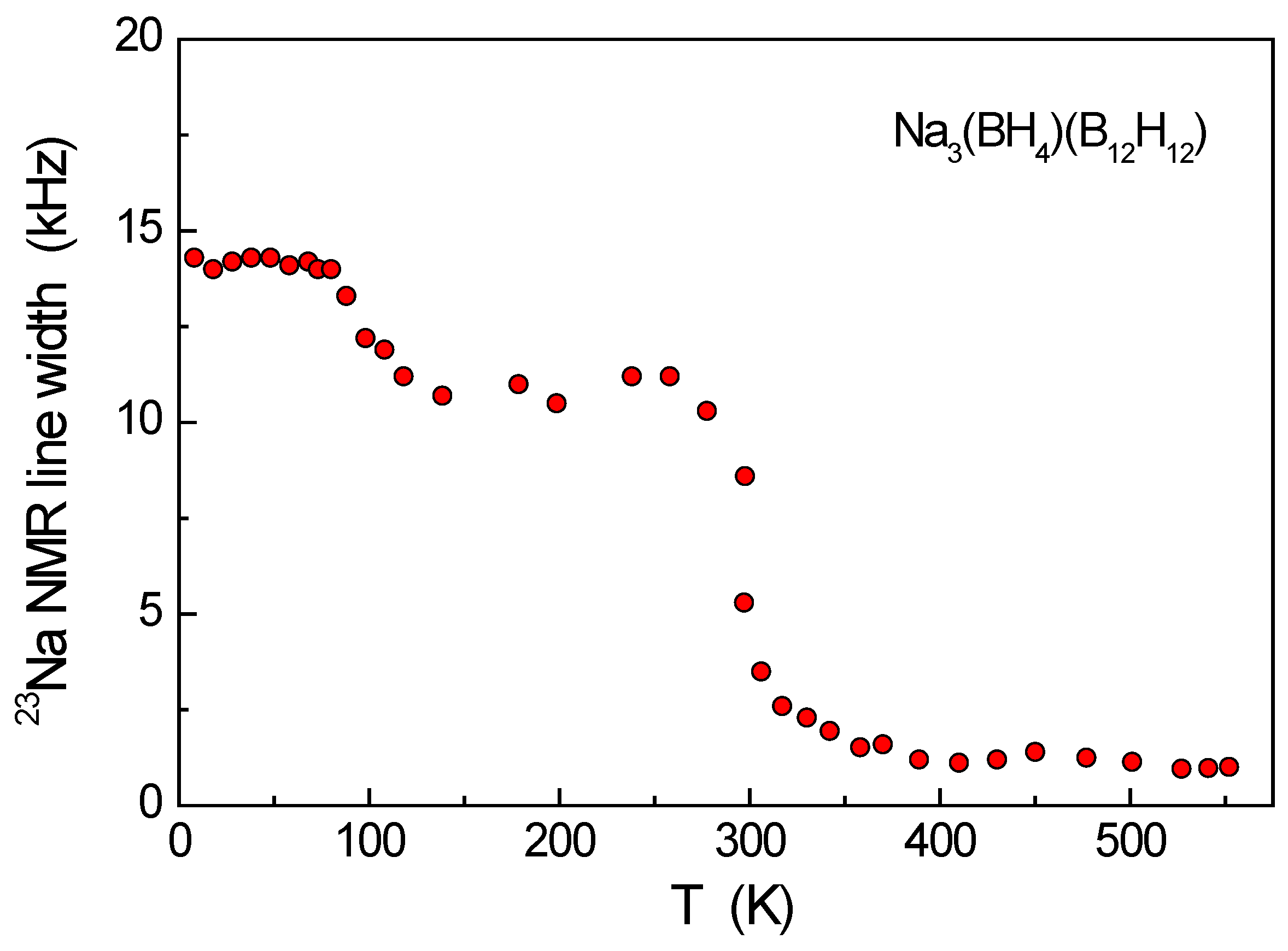
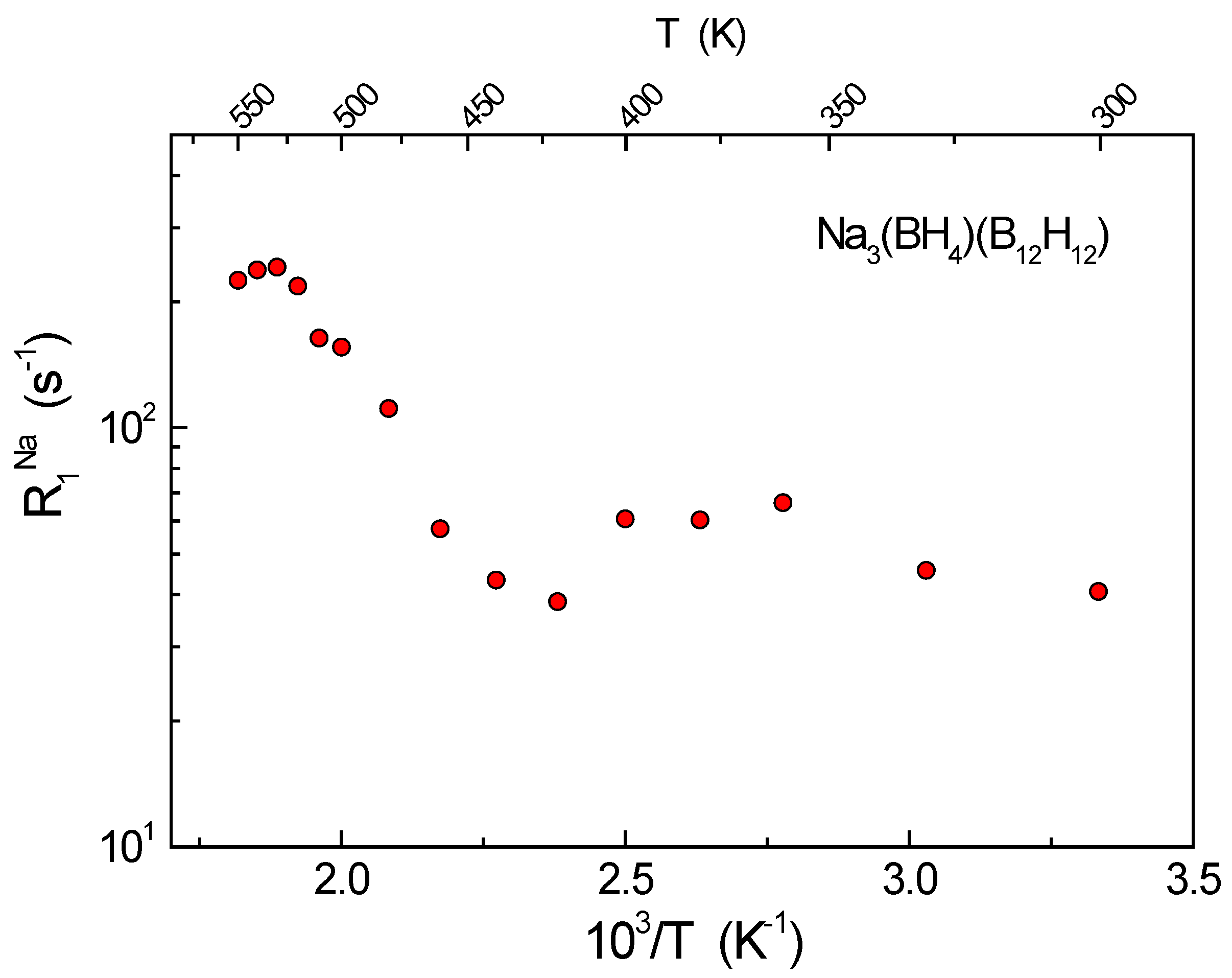
3. Results and Discussion

¹H and ¹¹B nuclear magnetic resonance results. The evolution of the ¹H NMR spectra for Na₃(BH₄)(B₁₂H₁₂) with temperature is shown in Figure 2. The spectra exhibit a considerable narrowing with increasing temperature, which can be attributed to a partial averaging of dipole-dipole interactions of ¹H spins due to jump motion of H atoms. Figure 3 shows the temperature dependence of the ¹H line width Δ_H (full width at half-maximum). It should be noted that at high temperatures, Δ_H does not drop to very small values, remaining on a plateau of approximately 10 kHz. This feature (typical of all the studied hydroborates [17,19,22]) indicates the localized nature of the motion of H atoms, as can be expected for anion reorientations. In contrast to the long-range translational diffusion, the localized motion leads to only partial averaging of the dipole-dipole interactions between moving nuclear spins.

Quantitative information on the H jump rates

τ^{- 1}

can be obtained from measurements of the ¹H spin-lattice relaxation rate

R_{1}^{H}

. Figure 4 shows the measured ¹H spin-lattice relaxation rates at two resonance frequencies ω/2π as functions of the inverse temperature. As can be seen from this figure,

R_{1}^{H} (T)

exhibits two frequency-dependent peaks near 240 K and 130 K. Such

R_{1}^{H} (T)

peaks are typical of many hydroborate systems [17,19,22]; they occur at the temperatures, at which the jump rates

τ^{- 1}

of anion reorientations become approximately equal to the resonance frequency ω (~10⁸ s^-1). The observation of two

R_{1}^{H} (T)

maxima indicates a coexistence of two types of reorientational motion with different characteristic rates, as can be expected in the case of two types of the anions.

To distinguish between reorientations of the [BH₄]⁻ and [B₁₂H₁₂]²⁻ anions, we have used the behavior of the ¹¹B spin-lattice relaxation rate

R_{1}^{B}

. For

R_{1}^{B} (T)

, we may also expect the peaks related to the reorientational motion; however, the amplitudes of these peaks should differ significantly. The amplitude of the

R_{1}^{B} (T)

peak due to B₁₂H₁₂ reorientations is determined by strong fluctuations of the electric quadrupole interaction of ¹¹B nuclei [22]. This amplitude should be considerably higher than the amplitude of the

R_{1}^{B} (T)

peak due to BH₄ reorientations, since for the latter the quadrupole interaction is relatively unimportant, because of the special position of B atom in the center of the nearly regular tetrahedron. Indeed, a reorientational jump of BH₄ tetrahedron does not change a configuration of H atoms surrounding B atom, and the electric field gradient at B site remains nearly the same. The difference between the amplitudes of the

R_{1}^{B} (T)

peaks due to B₁₂H₁₂ and BH₄ reorientations is consistent with the experimental results for closo-borates and borohydrides [17,22,23].

The results of the ¹¹B spin-lattice relaxation measurements for Na₃(BH₄)(B₁₂H₁₂) are shown in Figure 5. It should be noted that at T < 200 K the recovery of the ¹¹B nuclear magnetization deviates from a single-exponential behavior. As in the case of K₃(BH₄)(B₁₂H₁₂) [16], such deviations may be related to nonzero electric quadrupole moment of ¹¹B nuclei [24] and to the presence of several well-separated inequivalent ¹¹B nuclei relaxing with different rates. The relaxation curves at T < 200 K can be satisfactorily approximated by sums of two exponential components. The ¹¹B spin-lattice relaxation rates shown in Figure 5 correspond to the single exponent at T > 200 K and to the faster (dominant) exponential component at T < 200 K.

As can be seen from Figure 5,

R_{1}^{B} (T)

exhibits two peaks in the same temperature ranges as the corresponding

R_{1}^{H} (T)

peaks. On the basis of the observed amplitudes of the

R_{1}^{B} (T)

peaks, we can conclude that the low-temperature peak originates from BH₄ reorientations, and the high-temperature one is due to B₁₂H₁₂ reorientations. Note that the ¹H and ¹¹B relaxation results resemble those found for K₃(BH₄)(B₁₂H₁₂) [16]; however, the relaxation-rate peaks for the Na-based system (near 240 K and near 130 K) are shifted to considerably lower temperatures with respect to those for the K-based system (near 390 K and near 200 K, respectively [16]). These results indicate higher reorientational mobility of both [BH₄]⁻ and [B₁₂H₁₂]²⁻ anions in the Na-based compound. Such a difference may be related to the smaller size of Na⁺ cations.

For parametrization of the proton spin-lattice relaxation data, we have used the model based on two independent reorientational processes with the H jump rates

τ_{i}^{- 1}

(i = 1, 2). Similar model have been previously employed for K₃(BH₄)(B₁₂H₁₂) [16]. We assume that i = 1 corresponds to the faster process. According to the standard theory of nuclear spin-lattice relaxation due to the motionally-modulated dipole-dipole interaction [25], in the limit of slow motion (ωτ_i » 1),

R_{1 i}^{H}

is proportional to ω^-2τ_i^-1, and in the limit of fast motion (ωτ_i « 1),

R_{1 i}^{H}

is proportional to τ_i, being frequency-independent. If the temperature dependence of both H jump rates follows the Arrhenius law,

τ_{i}^{- 1} = τ_{0 i}^{- 1} \exp (- E_{a i} / k_{B} T)

(1)

with the activation energy E_ai for the ith type of motion, for each of the peaks, the plot of ln

R_{1 i}^{H}

vs. T ^-1 is expected to be linear in the limits of both slow and fast motion with the slopes of −E_ai/k_B and E_ai/k_B, respectively. The behavior of the proton spin-lattice relaxation rate shown in Figure 4 exhibits some deviations from the predictions of the standard theory. First, for both relaxation rate peaks, the high-T slope appears to be steeper than the low-T one. Second, at the low-T slope of each of the peaks, the frequency dependence of

R_{1 i}^{H}

is weaker than the predicted ω^-2 dependence. These features suggest the presence of a certain distribution of the H jump rates [26]. The simplest approach to introducing such a distribution is based on using a Gaussian distribution of the activation energies [26]. The details of the two-peak model [27] used for analysis of the proton spin-lattice relaxation data for Na₃(BH₄)(B₁₂H₁₂) are presented in the Supplementary Information. The model parameters are the average activation energies

{\bar{E}}_{a i}

, the distribution widths (dispersions) ΔE_ai, the pre-exponential factors τ_0i, and the amplitude factors ΔM_i determined by the strength of the fluctuating part of dipole-dipole interaction between nuclear spins for the ith type of motion. These parameters have been varied to find the best fit of the model to the experimental

R_{1}^{H} (T)

data at two resonance frequencies simultaneously. The results of this simultaneous fit over the temperature range of 98 – 298 K are shown by black solid curves in Figure 4; the corresponding parameters are

{\bar{E}}_{a 1}

= 159(5) meV, ΔE_a₁ = 14(2) meV, τ₀₁ = 5.9(3) × 10^-15 s, ΔM₁ = 8.2(2) × 10⁹ s^-2 (for the faster process of BH₄ reorientations), and

{\bar{E}}_{a 2}

= 319(4) meV, ΔE_a₂ = 26(3) meV, τ₀₂ = 1.2(2) × 10^-15 s, ΔM₂ = 3.8(2) × 10⁹ s^-2 (for the slower process of B₁₂H₁₂ reorientations). Comparison of these results with those obtained for K₃(BH₄)(B₁₂H₁₂) [16] indicates that the average activation energies for both reorientational processes in Na₃(BH₄)(B₁₂H₁₂) are considerably lower than the corresponding activation energies in K₃(BH₄)(B₁₂H₁₂) (236 meV for BH₄ reorientations and 594 meV for B₁₂H₁₂ reorientations [16]). This is consistent with the higher reorientational mobility of both anions in Na₃(BH₄)(B₁₂H₁₂).

²³Na nuclear magnetic resonance results. Information on the cation (Na⁺) dynamics can be obtained from ²³Na NMR measurements. The ²³Na NMR spectra have been studied in the low magnetic field (at the resonance frequency of 23 MHz) over a wide temperature range (8 – 552 K). The ²³Na spin-lattice relaxation rate measurements (which require better signal-to-noise ratios) have been performed in the high field (at the resonance frequency of 132 MHz) above room temperature. Representative shapes of the ²³Na NMR spectra at three temperatures are shown in Figure S1 of the Supplementary Information. Figure 6 shows the temperature dependence of the ²³Na NMR line width Δ_Na (full width at half-maximum).

As the temperature increases, the line width becomes smaller due to motional averaging of the local magnetic and electric fields at Na sites. As can be seen from Figure 6, the temperature dependence of Δ_Na exhibits two characteristic “steps”. The minor “step” near 100 K can be ascribed to the excitation of the reorientational motion of BH₄ groups inducing fluctuations of the ¹H – ²³Na dipole-dipole interaction. The major “step” near 300 K can be attributed to diffusive motion of Na⁺ cations themselves, since this motion averages out all dipole-dipole and quadrupole interactions of ²³Na nuclei. Indeed, in contrast to the case of Δ_H, the ²³Na line width at high temperatures is very small (~ 1 kHz), which indicates that Na⁺ cations participate in the long-range diffusion. At the temperature of the main “step”, the diffusive jump rate

τ_{d}^{- 1}

is expected [25] to become nearly equal to the “rigid lattice” line width (~ 10⁴ s^-1).

To probe the diffusive motion in the range of higher jump rates, we can use the ²³Na spin-lattice relaxation measurements, since for these measurements, the characteristic frequency scale is determined by the resonance frequency ω (~ 10⁸ – 10⁹ s^-1). Figure 7 shows the measured ²³Na spin-lattice relaxation rate

R_{1}^{N a}

as a function of the inverse temperature.

As can be seen from this figure, above 420 K,

R_{1}^{N a} (T)

exhibits a significant increase, reaching a maximum near 530 K. The measured

R_{1}^{N a}

values in the region of the maximum are much higher than those expected for the ²³Na – ¹H dipole-dipole interaction; therefore, the ²³Na spin-lattice relaxation is dominated by fluctuations of the quadrupole interaction resulting from Na⁺ jumps. This is a typical feature of all the studied sodium hydroborates [5,17,22]. At the temperature of the

R_{1}^{N a} (T)

maximum, the Na⁺ jump rate is expected to be nearly equal to the resonance frequency, i. e.,

τ_{d}^{- 1}

(530 K) ≈ 8 × 10⁸ s^-1. The activation energy for Na⁺ diffusion estimated from the slope of the

R_{1}^{N a} (T)

peak is 390 meV. For comparison, the activation energy derived from the ionic conductivity data in the range of 273 – 468 K is 340 meV [15].

Possible diffusion pathways were analyzed on the basis of the structure of Na₃(BH₄)(B₁₂H₁₂) [15]. According to this analysis, Na⁺ cations jump between the tetrahedral interstitial sites forming layers perpendicular to the b axis, i. e., the diffusion is expected to be quasi-two-dimensional [15]. The distance between the nearest-neighbor Na sites is approximately 2.30 Å. Neglecting any correlations in diffusive jump motion, the tracer diffusion coefficient of Na⁺ ions for the case of two-dimensional diffusion can be estimated as D = L²/4τ_d, where L is the elementary jump length. Taking the distance between the nearest-neighbor Na sites as an estimate of L, and using τ_d at the temperature of the

R_{1}^{N a} (T)

maximum, we obtain D(530 K) ≈ 1.1 × 10^-7 cm²/s. This value is close to that found from the direct pulsed-field-gradient (PFG) NMR measurements of Li⁺ diffusivity in LiLa(BH₄)₃Cl (D(403 K) = 1.13 × 10^-7 cm²/s [28]). However, the estimated diffusivity in Na₃(BH₄)(B₁₂H₁₂) at 530 K is much lower than the record Na⁺ diffusivity found from the PFG-NMR measurements for the mixed-anion Na₂(CB₉H₁₀)(CB₁₁H₁₂) (D(403 K) = 8.7 × 10^-6 cm²/s [29]).

Following Matsuo et al. [3], for comparison of the NMR diffusivity data with the ionic conductivity σ, we can use the Nernst-Einstein equation,

σ = nD(Ze)²/k_BT

(2)

where n is the number of charge carriers per unit volume, and Ze is the electrical charge of the carrier. It should be noted that this equation assumes uncorrelated diffusion. Using the above estimate of D(530 K) and the value of n = 8.8 × 10²¹ cm^-3 found on the basis of the structural data [15], we obtain from Eq. (2) that σ(530 K) = 4.3 × 10^-3 S/cm. Experimentally, the ionic conductivity was measured up to 473 K, and its value at this temperature was 1.5 × 10^-2 S/cm [15]. Taking into account the Arrhenius-type behavior of the measured σ [15], its extrapolation to 530 K gives σ_ext(530 K) = 5.0 × 10^-2 S/cm. Thus, the ionic conductivity estimated from the NMR diffusivity data appears to be nearly an order of magnitude lower than the corresponding experimental (extrapolated) value. Similar situation has been well documented in the case of the mixed-anion Li(CB₉H₁₀)_0.7(CB₁₁H₁₂)_0.3 system [7] and the disordered LiCB₉H₁₀ phase [28], where the measured conductivities are considerably higher than those derived from the PFG-NMR diffusivity data on the basis of the Nernst-Einstein equation. Such effects have been attributed to strong correlations between the diffusing ions (concerted diffusion) [30,31,32].

4. Conclusions

The results of our ¹H and ¹¹B spin-lattice relaxation measurements have revealed two types of reorientational jump motion in the mixed-anion hydroborate Na₃(BH₄)(B₁₂H₁₂). The faster motional process is assigned to reorientations of the [BH₄]⁻ anions. This process is characterized by the activation energy of 159(5) meV, and the corresponding reorientational jump rate reaches ~10⁸ s^-1 near 130 K. The slower process attributed to reorientations of the larger [B₁₂H₁₂]⁻ anions is characterized by the activation energy of 319(4) meV, and the corresponding reorientational jump rate reaches ~10⁸ s^-1 near 240 K. Comparison of these results with those obtained for the related mixed-anion hydroborate K₃(BH₄)(B₁₂H₁₂) with rather low ionic conductivity [16] shows that the reorientational mobilities of both anions in the Na-based compound are considerably higher than the corresponding mobilities in the K-based counterpart. Such a comparison supports the idea that anion reorientations may facilitate the cation diffusion.

The results of the ²³Na NMR measurements are consistent with the fast long-range diffusion of Na⁺ ions in Na₃(BH₄)(B₁₂H₁₂). The diffusive jump rate is found to reach ~10⁴ s^-1 at 300 K and ~8 × 10⁸ s^-1 at 530 K. The tracer diffusion coefficient of Na-ions estimated at 530 K is 1.1 × 10^-7 cm²/s. However, this diffusivity appears to be nearly an order of magnitude lower than that estimated from the measured ionic conductivity [16] on the basis of the Nernst-Einstein relation; this may be attributed to strong correlations between diffusing ions.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org. Expressions used for analysis of the proton spin-lattice relaxation rates, Figure S1: Representative shapes of the ²³Na NMR spectra at 8 K, 198 K, and 552 K.

Author Contributions

O. A. B.: Investigation, Software, Formal Analysis, Writing – original draft; Y. S.: Synthesis and Characterization; R. V. S.: Investigation, Visualization; A. V. S. (Alexei V. Soloninin): Investigation, Methodology, Validation; A. V. S. (Alexander V. Skripov): Supervision, Writing – review and editing. All the authors have read and agreed to the final version of the manuscript.

Funding

This work was performed within the assignment of the scientific program “Function” (No. 122021000035-6) of the Ural Branch of the Russian Academy of Sciences.

Acknowledgments

The authors are grateful to R. Černý for useful discussions.

Data Availability: Data are available on request from the authors.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Paskevicius, M.; Jepsen, L.; Schouwink, P.; Černý, R.; Ravnsbæk, D.B.; Filinchuk, Y.; Dornheim, M.; Besenbacher, F.; Jensen, T.R. Metal Borohydrides and Derivatives – Synthesis, Structure and Properties. Chem.Soc. Rev. 2017, 46, 1565–1634. [Google Scholar] [CrossRef] [PubMed]
Černý, R.; Brighi, M.; Murgia, F. The Crystal Chemistry of Inorganic Hydroborates. Chemistry 2020, 2, 805–826. [Google Scholar] [CrossRef]
Matsuo, M.; Nakamori, Y.; Orimo, S.; Maekawa, H.; Takamura, H. Lithium Superionic Conduction in Lithium Borohydride Accompanied by Structural Transition. Appl. Phys. Lett. 2007, 91, 224103. [Google Scholar] [CrossRef]
Udovic, T.J.; Matsuo, M.; Unemoto, A.; Verdal, N.; Stavila, V.; Skripov, A.V.; Rush, J.J.; Takamura, H.; Orimo, S. Sodium Superionic Conduction in Na₂B₁₂H₁₂. Chem. Commun. 2014, 50, 3750–3752. [Google Scholar] [CrossRef] [PubMed]
Tang, W.S.; Matsuo, M.; Wu, H.; Stavila, V.; Zhou, W.; Talin, A.A.; Soloninin, A.V.; Skoryunov, R.V.; Babanova, O.A.; Skripov, A.V.; Unemoto, A.; Orimo, S.; Udovic, T.J. Liquid-like Ionic Conduction in Solid Lithium and Sodium Monocarba-Closo-Decaborates Near or at Room Temperature. Adv. Energy Mater. 2016, 6, 1502237. [Google Scholar] [CrossRef]
Yoshida, K.; Sato, T.; Unemoto, A.; Matsuo, M.; Ikeshoji, T.; Udovic, T.J.; Orimo, S. Fast Sodium Ionic Conduction in Na₂B₁₀H₁₀-Na₂B₁₂H₁₂ Complex Hydride and Application to a Bulk-Type All-Solid-State Battery. Appl. Phys. Lett. 2017, 110, 103901. [Google Scholar] [CrossRef]
Kim, S.; Oguchi, H.; Toyama, N.; Sato, T.; Takagi, S.; Otomo, T.; Arunkumar, D.; Kuwata, N.; Kawamura, J.; Orimo, S. A Complex Hydride Lithium Superionic Conductor for High-Energy-Density All-Solid-State Lithium Metal Batteries. Nat. Commun. 2019, 10, 1081. [Google Scholar] [CrossRef] [PubMed]
Duchêne, L.; Remhof, A.; Hagemann, H.; Battaglia, C. Status and Prospects of Hydroborate Electrolytes for All-Solid-State Batteries. Energy Storage Mater. 2020, 25, 782–794. [Google Scholar] [CrossRef]
Maekawa, H.; Matsuo, M.; Takamura, H.; Ando, M.; Noda, Y.; Karahashi, T.; Orimo, S. Halide-Stabilized LiBH₄, A Room-Temperature Lithium Fast-Ion Conductor. J. Am. Chem. Soc. 2009, 131, 894–895. [Google Scholar] [CrossRef]
Rude, L.H.; Groppo, E.; Ambjerg, L.M.; Ravnsbæk, D.B.; Malmkjær, M.A.; Filinchuk, Y.; Baricco, M.; Besenbacher, F.; Jensen, T.R. Iodide Substitution in Lithium Borohydride, LiBH₄ – LiI. J. Alloys Compd. 2011, 509, 8299–8305. [Google Scholar] [CrossRef]
Tang, W.S.; Yoshida, K.; Soloninin, A.V.; Skoryunov, R.V.; Babanova, O.A.; Skripov, A.V.; Dimitrievska, M.; Stavila, V.; Orimo, S.; Udovic, T.J. Stabilizing Superionic-Conducting Structures via Mixed-Anion Solid Solutions of Monocarba-Closo-Borate Salts. ACS Energy Lett. 2016, 1, 659–664. [Google Scholar] [CrossRef]
Duchêne, L.; Kühnel, R.-S.; Rentsch, D.; Remhof, A.; Hagemann, H.; Battaglia, C. A Highly Stable Sodium Solid-State Electrolyte Based on a Dodeca/Deca-Borate Equimolar Mixture. Chem. Commun. 2017, 53, 4195–4198. [Google Scholar] [CrossRef] [PubMed]
Brighi, M.; Murgia, F.; Łodziana, Z.; Schouwink, P.; Wołczyk, A.; Černý, R. A Mixed Anion Hydroborate/Carba-Hydroborate as a Room Temperature Na-Ion Solid Electrolyte. J. Power Sources, 2018, 404, 7–12. [Google Scholar] [CrossRef]
Brighi, M.; Murgia, F.; Černý, R. Closo-Hydroborate Sodium Salts as an Emerging Class of Room-Temperature Solid Electrolytes. Cell Rep. Phys. Sci. 2020, 1, 100217. [Google Scholar] [CrossRef]
Sadikin, Y.; Brighi, M.; Schouwink, P.; Černý, R. Superionic Conduction of Sodium and Lithium in Anion-Mixed Hydroborates Na₃BH₄B₁₂H₁₂ and (Li_0.7Na_0.3)₃BH₄B₁₂H₁₂. Adv. Energy Mater. 2015; 1501016. [Google Scholar]
Sadikin, Y.; Skoryunov, R.V.; Babanova, O.A.; Soloninin, A.V.; Łodziana, Z.; Brighi, M.; Skripov, A.V.; Černý, R. Anion Disorder in K₃BH₄B₁₂H₁₂ and Its Effect on Cation Mobility. J. Phys. Chem. C 2017, 121, 5503–5514. [Google Scholar] [CrossRef]
Skripov, A.V.; Soloninin, A.V.; Babanova, O.A.; Skoryunov, R.V. Anion and Cation Dynamics in Polyhydroborate Salts: NMR Studies. Molecules 2020, 25, 2940. [Google Scholar] [CrossRef] [PubMed]
Skripov, A.V.; Soloninin, A.V.; Ley, M.B.; Jensen, T.R.; Filinchuk, Y. Nuclear Magnetic Resonance Study of BH₄ Reorientations and Li Diffusion in LiLa(BH₄)₃Cl. J. Phys. Chem. C 2013, 117, 14965–14972. [Google Scholar] [CrossRef]
Skripov, A.V.; Soloninin, A.V.; Babanova, O.A.; Skoryunov, R.V. Nuclear Magnetic Resonance Studies of Atomic Motion in Borohydride-Based Materials: Fast Anion Reorientations and Cation Diffusion. J. Alloys Compd. 2015, 645, S428–S433. [Google Scholar] [CrossRef]
Kweon, K.; Varley, J.B.; Shea, P.; Adelstein, N.; Mehta, P.; Heo, T.W.; Udovic, T.J.; Stavila, V.; Wood, B.C. Structural, Chemical, and Dynamical Frustration: Origins of Superionic Conductivity in Closo-Borate Solid Electrolytes. Chem. Mater. 2017, 29, 9142–9153. [Google Scholar] [CrossRef]
Dimitrievska, M.; Shea, P.; Kweon, K.E.; Bercx, M.; Varley, J.B.; Tang, W.S.; Skripov, A.V.; Stavila, V.; Udovic, T.J.; Wood, B.C. Carbon Incorporation and Anion Dynamics as Synergistic Drivers for Ultrafast Diffusion in Superionic LiCB₁₁H₁₂ and NaCB₁₁H₁₂. Adv. Energy Mater. 2018, 8, 1703422. [Google Scholar] [CrossRef]
Skripov, A.V.; Babanova, O.A.; Soloninin, A.V.; Stavila, V.; Verdal, N.; Udovic, T.J.; Rush, J.J. Nuclear Magnetic Resonance Study of Atomic Motion in A₂B₁₂H₁₂ (A = Na, K, Rb, Cs): Anion Reorientations and Na⁺ Mobility. J. Phys. Chem. C 2013, 117, 25961–25968. [Google Scholar] [CrossRef]
Babanova, O.A.; Soloninin, A.V.; Stepanov, A.P.; Skripov, A.V.; Filinchuk, Y. Structural and Dynamical Properties of NaBH₄ and KBH₄: NMR and Synchrotron X-Ray Diffraction Studies. J. Phys. Chem. C 2010, 114, 3712–3718. [Google Scholar] [CrossRef]
Kim, C.; Ku, J.; Hwang, S.J.; Bowman, R.C.; Reiter, J.W. Nuclear Magnetic Relaxation Studies of BH₄ in Metal Borohydrides. Bull. Corean Chem. Soc. 2021, 1–12. [Google Scholar] [CrossRef]
Abragam, A. The Principles of Nuclear Magnetism; Clarendon Press: Oxford, 1961. [Google Scholar]
Markert, J.T.; Cotts, E.J.; Cotts, R.M. Hydrogen Diffusion in the Metallic Glass a-Zr₃RhH_3.5. Phys. Rev. B 1988, 37, 6446–6452. [Google Scholar] [CrossRef] [PubMed]
Skripov, A.V.; Soloninin, A.V.; Babanova, O.A.; Hagemann, H.; Filinchuk, Y. Nuclear Magnetic Resonance Study of Reorientational Motion in α-Mg(BH₄)₂. J. Phys. Chem. C 2010, 114, 12370–12374. [Google Scholar] [CrossRef]
Skripov, A.V.; Majer, G.; Babanova, O.A.; Skoryunov, R.V.; Soloninin, A.V.; Ley, M.B.; Jensen, T.R.; Orimo, S.; Udovic, T.J. Lithium-Ion Diffusivity in Complex Hydrides: Pulsed-Field-Gradient NMR Studies of LiLa(BH₄)₃Cl, Li₃(NH₂)₂I and Li-1-CB₉H₁₀. Solid State Ionics 2021, 362, 115585. [Google Scholar] [CrossRef]
Skripov, A.V.; Majer, G.; Babanova, O.A.; Skoryunov, R.V.; Soloninin, A.V.; Dimitrievska, M.; Udovic, T.J. Na⁺ Diffusivity in Carbon-Substituted Nido- and Closo-Hydroborate Salts: Pulsed-Field-Gradient NMR Studies of Na-7-CB₁₀H₁₃ and Na₂(CB₉H₁₀)(CB₁₁H₁₂). J. Alloys Compd. 2021, 850, 156781. [Google Scholar] [CrossRef]
Okazaki, H. Deviation from the Einstein Relation in Average Crystals Self-Diffusion of Ag⁺ Ions in α-Ag₂S and α-Ag₂Se. J. Phys. Soc. Jpn. 1967, 23, 355–360. [Google Scholar] [CrossRef]
He, X.; Zhu, Y.; Mo, Y. Origin of Fast Ion Diffusion in Super-Ionic Conductors. Nat. Commun. 2017, 8, 15893. [Google Scholar] [CrossRef] [PubMed]
Sau, K.; Takagi, S.; Ikeshoji, T.; Kisu, K.; Sato, R.; dos Santos, E.C.; Li, H.; Mohtadi, R.; Orimo, S. Unlocking the Secrets of Ideal Fast Ion Conductors for All-Solid-State Batteries. Commun. Mater. 2024, 5, 122. [Google Scholar] [CrossRef]

Figure 1. Schematic view of the crystal structure of Na₃(BH₄)(B₁₂H₁₂) on the basis of X-ray powder diffraction data at 523 K [15]. Red spheres: partially occupied Na sites; green spheres: B atoms; gray spheres: H atoms.

Figure 2. Evolution of the ¹H NMR spectra for Na₃(BH₄)(B₁₂H₁₂) with temperature.

Figure 3. Temperature dependence of the width (full width at half-maximum) of the ¹H NMR spectra measured at 28 MHz for Na₃(BH₄)(B₁₂H₁₂).

Figure 4. Proton spin-lattice relaxation rates measured at 14 and 28 MHz for Na₃(BH₄)(B₁₂H₁₂) as functions of the inverse temperature. The solid curves show the simultaneous fit of the two-peak model with Gaussian distributions of the activation energies in the temperature range of 98 – 298 K.

Figure 5. ¹¹B spin-lattice relaxation rates measured at 28 MHz as functions of the inverse temperature. At T > 200 K, the data points represent the results of a single-exponential approximation of the ¹¹B longitudinal relaxation, and at T < 200 K, they represent the faster component of the two-exponential relaxation.

Figure 6. Temperature dependence of the ²³Na NMR line width (full width at half-maximum) measured at 23 MHz.

Figure 7. ²³Na spin-lattice relaxation rate measured at 132 MHz as a function of the inverse temperature.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer